Letzte Änderung am 23. March 2024 um 18:28:54

“Die Vergangenheit ist geschrieben, aber die Zukunft ist noch nicht in Stein gemeißelt.” — Jean-Luc Picard, Star Trek: The Next Generation

Bitte bei der Analyse von Zeitreihen gleich von Anfang an beachten!

Die Analyse von Zeitreihen kann sehr quälend sein, wenn dein Datumsformat nicht richtig ist. Bitte achte darauf, dass du in der Spalte mit dem Datum immer das gleiche Format vorliegen hast. Dann können wir das Format später richtig transformieren. Danach geht dann alles einfacher…

In diesem Kapitel wollen wir uns mit Zeitreihen (eng. time series) beschäftigen. Was ja auch irgendwie zu erwarten war, denn so heißt ja auch das Kapitel hier. Im Gegensatz zu dem vorherigen Kapitel, wollen wir uns hier aber mit den “echten” Zeitreihen beschäftigen. Mit echten Zeitreihen meine ich Zeitreihen, die im statistischen Sinne eine Reihe von Zeiten sind. Wir haben somit auf der \(x\)-Achse einer potenziellen Visualisierung die Zeit dargestellt. Wir können aber auch nur eine Reihe von zeitlichen Abständen vorliegen haben. Wir wollen dann auswerten, ob es über den zeitlichen Verlauf einen Trend gibt oder wir ein gutes Modell für den Verlauf der Beobachtungen anpassen können. Ziel ist es dabei den zukünftigen Verlauf vorherzusagen. Es geht hier also weniger um statistisches Testen als um eine Modell für eine Vorhersage. Also wir suchen ein Modell für den zukünftigen Verlauf eines Messwertes oder aber zeitlichen Abständen.

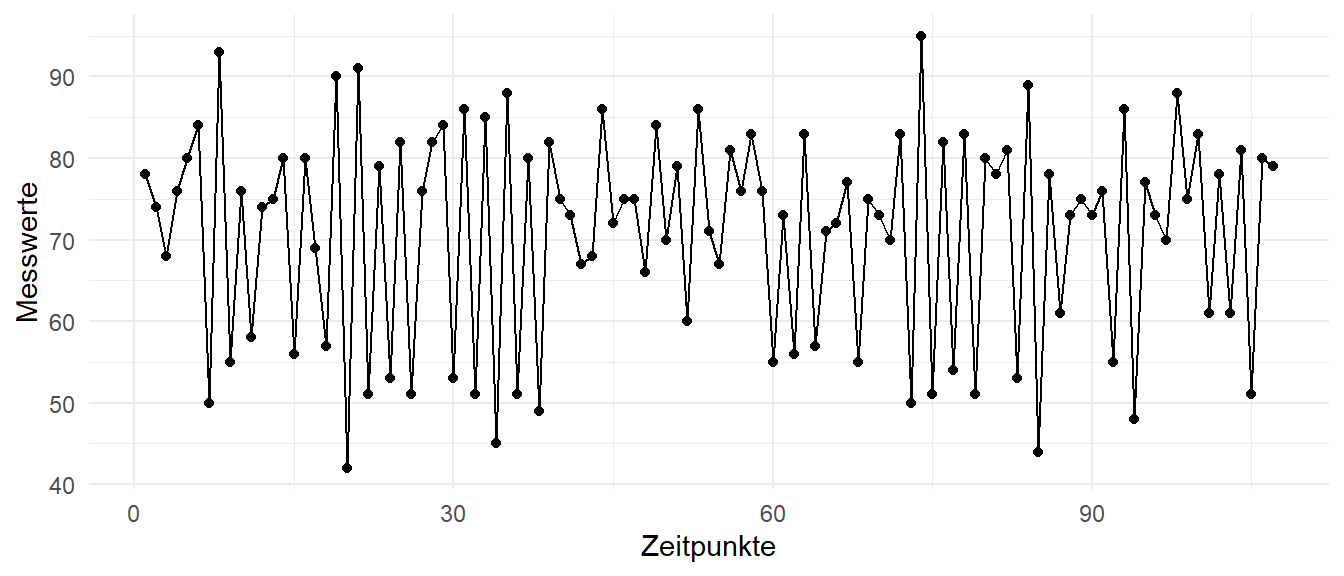
In der Abbildung 67.1 sehen wir eine typische Zeitreihe, die in der klassischen Analyse von Zeitreihen erwartet wird. Mit erwartet wird meine ich, dass wir hier einen Messwert über eine längere Zeit beobachten und wir dabei eine zyklische Abfolge der Messwerte über die Zeit sehen. Die Idee der Zeitreihenanalyse ist unn den weiteren Verlauf der Zeitreihe in der Zukunft vorherzusagen. Wie würden die Messwerte für die zukünftigen Zeitpunkte aussehen? Was können wir erwarten? Diese Fragen wollen wir in diesem Kapitel einmal näher betrachten.

Abbildung 67.1— Eine Zeitreihe, wie sie in der klassischen Analyse von Zeitreihen erwartet wird. Wir haben über einen längeren Zeitraum ein zyklisches Verhalten von Messwerten vorliegen. Nicht immer liegt so eine Form der Zeitreihe vor. Häufig ist der Zeitraum zu kurz gewählt.

Was bei anderen Themen gilt, gilt natürlich auch für Zeitreihen. Für die Analyse von Zeitreihen wurden und werden ganze Bücher geschrieben. Damit kann ich in diesem Übersichtskapitel nicht dienen. Aber das ist ja auch hier nicht das Ziel. So tiefgreifend kann ich hier nicht die Zusammenhänge darstellen. Aber vermutlich so ausreichend dargestellt, dass du dann in anderen Büchern weiterlesen kannst. Was sollst du also lesen, wenn du mehr wissen willst als hier in dem Kapitel steht? Ich würde dir Forecasting: Principles and Practice als erstes Buch empfehlen. Du hast hier sogar YouTube Videos für die wichtigsten Inhalte. Dann würde ich den Kurs STAT 510: Applied Time Series Analysis als umfangreichen, theoretischen Hintergrund empfehlen. Du findest dort auch teilweise R Code etwas in den Skript vergraben. Wenn du noch mehr lesen willst, dann kann ich dir folgende Literatur empfehlen. Robert u. a. (2006) liefert eine gute Übersicht über die Anwendung in R, ist aber schon etwas älter. Das Gleiche gilt dann auch für das Buch von Chan und Cryer (2008) und Cowpertwait und Metcalfe (2009). Dennoch bilden alle drei Bücher die Grundlagen der Analysen von Zeitreihen super ab. Für eine Abschlussarbeit sollten die Quellen also allemal reichen.

Es gibt reichlich R Pakete, die ich teilweise tiefer vorstellen werden. Mit den R Paketen {tktime}, {fable} und {modeltime} gibt es neben den built-in Paketen einiges zur Auswahl. Ich werde hier aber auch alle drei Pakete einmal vorstellen und diskutieren. Mehr geht natürlich immer deshalb kann ich dir da noch die Übersicht auf dem Big Book of R – Time Series Analysis and Forecasting empfehlen. Dort findest du dann noch mehr frei verfügbare Literatur und auch das ein oder andere R Paket, was genau in der entsprechenden Literatur genutzt und besprochen wird.

Wenn es um Zeitreihen geht, dann ist die Formatierung der Spalte mit dem Datum eigentlich so ziemlich das aufwendigste. Achte bitte darauf, dass du eine einheitlich formatierte Datumsspalte hast, die sich nicht im Laufe der Zeilen ändert. Wenn das der Fall ist, dann musst du meist händisch nochmal die Daten anpassen und das ist meistens sehr aufwendig. Das R Paket {timetk} liefert dankenswerterweise Funktionen für die Konvertierung von verschiedenen Zeitformaten in R. Deshalb schaue einmal in die Hilfeseite Time Series Class Conversion – Between ts, xts, zoo, and tbl und dann dort speziell der Abschnitt Conversion Methods. Leider ist Zeit in R wirklich relativ.

Weitere Tutorien für die Analyse von Zeitreihen

Wir oben schon erwähnt, kann dieses Kapitel nicht die umfangreiche Analyse von Zeitreihen abarbeiten. Daher präsentiere ich hier eine Liste von Literatur und Links, die mich für dieses Kapitel hier inspiriert haben. Nicht alles habe ich genutzt, aber vielleicht ist für dich was dabei.

  • Forecasting: Principles and Practice – Wenn ich keine Zeit hätte mich durch sehr viele Tutorien zu arbeiten, dann würde ich vermutlich mit diesem Online-Buch starten. Es ist alles drin was man braucht um die Zeitreihenanalyse tiefer zu verstehen, als dass ich es hier aufarbeiten kann. Wenn du dann noch das R Paket {tktime} oder {modeltime} nutzt, passt dann wieder alles.
  • STAT 510: Applied Time Series Analysis – Ein umfangreicher Kurs der Penn State - Eberly College of Science. Hier ist dann der R Anteil sehr eingeschränkt bzw. schon etwas älter aber dafür sind die Erklärungen umfangreicher als in diesem Kapitel. Es lohnt sich also nochmal dort für weitere Beispiele einmal reinzuschauen.
  • Was geht alles um eine Zeitreihe zu analysieren? Eine Menge wie Michael Clark in seinem Artikel Exploring Time - Multiple avenues to time-series analysis zeigt. Hier kannst du noch mehr Modelle und Methoden anschauen, als es dann teilweise bei den anderen Tutorien vorkommen.
  • Welcome to a Little Book of R for Time Series! – Du findest hier eine sehr gute Übersicht über die Möglichkeiten einer Zeitreihenanalyse mit der Möglichkeit Vorhersagen durchzuführen. Teilweise sind die Funktionen etwas veraltet, ich würde da eher das R Paket {timetk} empfehlen. Der Text um die Funktionen herum ist immer noch lesenswert.
  • timetk for R – Hier hast du das aktuelle R Paket, welches ich auch in diesem Kapitel teilweise vorstelle. Leider gibt es hier aber nicht sehr viel Erklärtext, daher musst du dich dann auf andere Quellen verlassen. Die Funktionen und die Anwendbarkeit ist aber sehr schön.
  • 14 Time Series Analysis – Du findest hier neben der klassischen Analyse von Zeitreihen noch Informationen zu anderen Möglichkeiten der Analyse von Zeitreihen. Eingebettet ist das Kapitel zu Zeitreihen in ein umfangreiches Buch über die Analyse von Daten und der Programmierung.
  • Analysing Time Series Data – Modelling, Forecasting and Data Formatting in R – Du findest hier nochmal ein gutes und in sich kompaktes Tutorium zu der Zeitreihenanalyse. Hier findest du dann auch mehr erklärenden Text. Auch werden die Datumsformate nochmal genauer auseinander genommen und erklärt. Für den Einstieg sicherlich eine gute Quelle.

67.1 Genutzte R Pakete

Wir wollen folgende R Pakete in diesem Kapitel nutzen.

R Code [zeigen / verbergen] 
pacman::p_load(tidyverse, magrittr, janitor, see, readxl,
               xgboost, tidymodels, modeltime, forecast,
               lubridate, plotly, zoo, timetk, xts,
               corrplot, GGally, conflicted)
conflicts_prefer(dplyr::filter)
conflicts_prefer(magrittr::set_names)
conflicts_prefer(plyr::mutate)
conflicts_prefer(dplyr::slice)

An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.

67.2 Daten & Visualisierung

In diesem Abschnitt wollen wir uns einmal ein paar “echte” Zeitreihen anschauen, die den Anforderungen der klassischen Zeitreihenanalyse an eine Zeitreihe genügen. Du kennst ja schon aus dem vorherigen Kapitel die Möglichkeiten der Visualisierung, deshalb packe ich hier auch gleich zu den Daten die entsprechenden Abbildungen. Dann wird dir der Zusammenhang auch schneller bewusst. Wenn die Daten nochmal wegen dem Datum formatiert werden mussten, dann habe ich das auch gleich hier in einem Abwasch erledigt. Wenn da noch Fragen sind, dann schaue gerne nochmal in das vorherige Kapitel, da findest du dann noch mehr Beispiele. Hier soll es mehr um die Verläufe und die Vorhersage gehen.

Inspirationen von The R Graph Gallery

Wenn du noch Inspirationen suchst, wie du deine Zeitreihe noch schöner darstellen könntest, dann besuche doch The R Graph Gallery - Time Series. Dort findest du verschiedene Darstellungen einer Zeitreihe mit {ggplot}. Ich finde den Lollipop-Chart im Kontext einer Zeitreihe sehr spannend. Aber lass dich einfach mal inspirieren.

Fangen wir also mit dem ersten Datensatz an. Im Sommer 1987 maßen die Ranger des Yellowstone-Nationalparks die Zeit zwischen den Ausbrüchen des Old Faithful Geysirs. Dieser Geysir ist für seine relativ regelmäßigen Ausbrüche bekannt, aber wie du dir vorstellen kannst, ist der Geysir keine Uhr. Ein Ziel bei der Erfassung der Zeiten war es, eine Möglichkeit zu finden, den Zeitpunkt des nächsten Ausbruchs vorherzusagen, um den Touristen, die auf einen Ausbruch warten, die Wartezeit zu erleichtern. Wir haben also eine Zeitreihe in Minuten aus dem Yellowstone-Nationalpark vorliegen. Die Daten in Minuten für \(n=107\) fast aufeinanderfolgende Wartezeiten lauten dann wie folgt.

R Code [zeigen / verbergen] 
erupt <- c(78, 74, 68, 76, 80, 84, 50, 93, 55, 76, 58, 74, 75, 80, 56, 80, 69, 57,
           90, 42, 91, 51, 79, 53, 82, 51, 76, 82, 84, 53, 86, 51, 85, 45, 88, 51,
           80, 49, 82, 75, 73, 67, 68, 86, 72, 75, 75, 66, 84, 70, 79, 60, 86, 71,
           67, 81, 76, 83, 76, 55, 73, 56, 83, 57, 71, 72, 77, 55, 75, 73, 70, 83,
           50, 95, 51, 82, 54, 83, 51, 80, 78, 81, 53, 89, 44, 78, 61, 73, 75, 73,
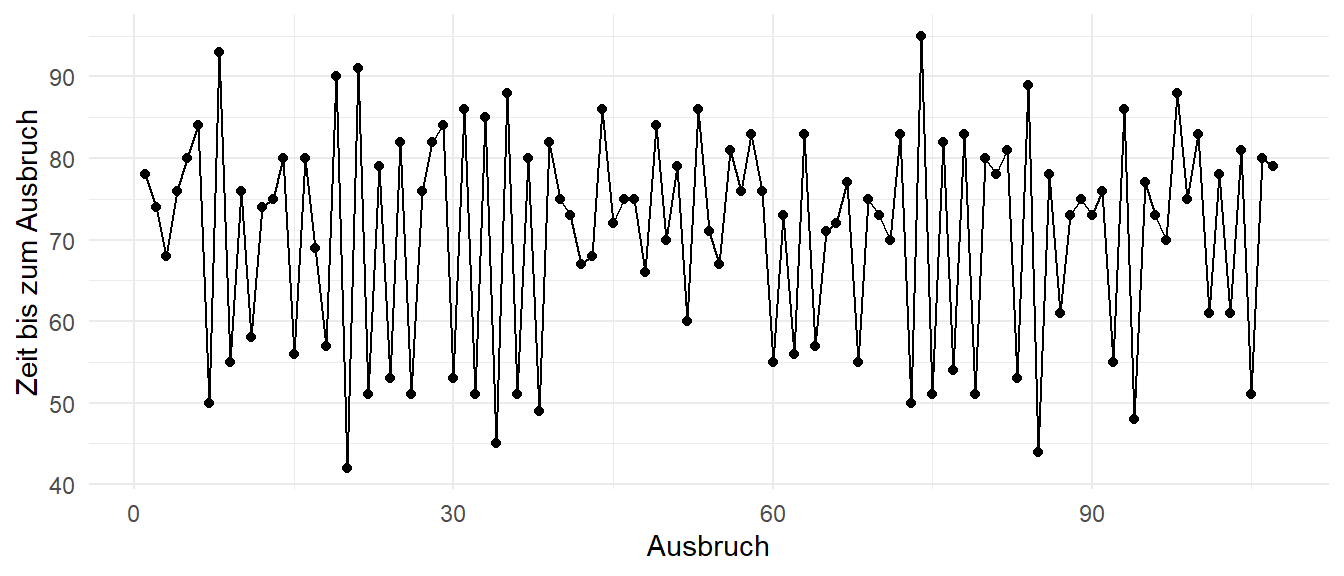
           76, 55, 86, 48, 77, 73, 70, 88, 75, 83, 61, 78, 61, 81, 51, 80, 79)

Wir haben hier also eine echte Zeitreihe vorliegen. Wir haben die zeitlichen Abstände zwischen zwei Ausbrüchen. Das ist dann auch die einfachste mögliche Zeitreihe. Dennoch können wir dann an diesem Beispiel sehr viel erklären und uns die gängigen Konzepte der klassischen Zeitreihenanalyse veranschaulichen. In der Abbildung 67.2 siehst du dann nochmal den Verlauf der Eruptionen über die Zeit. Dir kommt die Abbildung sicherlich aus der Einleitung des Kapitels bekannt vor. Dort habe ich die Abbildung einmal für ein generelles Beispiel genutzt, hier ist dann der richtige Kontext.

Abbildung 67.2— Dauer zwischen zwei Eruptionen des Old Faithful Geysirs. Eine klare zyklische Zeitreihe lässt sich aus der Abbildung ableiten.

Als nächstes Datenbeispiel möchte ich den schon fast ikonischen Anstieg an \(CO_2\) in der Atmosphäre einmal betrachten. Ich habe die Daten von dem Global Monitoring Laboratory heruntergeladen. Du kannst dir auch gern einmal die Daten für \(CH_4\) \(N_2O\) und \(SF_6\) anschauen. Auch hier liegen Verläufe vor, die du dann einmal visualisieren und vorhersagen kannst. Wenn du noch mehr Beispiele von echten Daten haben möchtest, dann besuch doch die Webseite Our World in Data.

Ich muss mich hier etwas strecken um die Daten richtig sauber einzulesen. Zum einen nutze ich die \(CO_2\) Daten für die Monate und dann einmal für die Tage. Als erste habe ich das Problem, dass ich erstmal einiges an zeilen überspringen muss, bis die echten Daten kommen. Leider hat das Datumsformat auch eine echt schlimme Kodierung in den Daten. Daher nutze ich die Funktion parse_date_time() um mir ein Datum wiedergeben zu lassen. Vorher muss ich die Monate noch so umbauen, dass die Monate immer zwei Zeichen lang sind. Leider braucht as.Date() immer einen Tag, was bei den monatlichen Daten nicht gegeben ist. In den folgenden Analysen nutze ich dann beide Datensätz um mal zu schauen, wie deatiliert die Informationen vorliegen müssen. Reicht ein Wert pro Monat oder aber macht es ein Wert pro Tag besser?

R Code [zeigen / verbergen] 
co2_monthly_tbl <- read_csv("data/co2_mm_mlo.csv", skip = 40) |> 
  mutate(month = str_pad(month, 2, pad = "0", side = "left"),
         date = parse_date_time(str_c(year, month), "ym"))

co2_daily_tbl <- read_csv("data/co2_daily_mlo.csv", skip = 32, col_names = FALSE) |> 
  set_names(c("year", "month", "day", "decimal date", "average")) |> 
  mutate(month = str_pad(month, 2, pad = "0", side = "left"),
         date = parse_date_time(str_c(year, month, day), "ymd"))

In der Abbildung 67.3 siehst du einmal die Verläufe des \(CO_2\) Anstiegs in der Atmosphäre. Beachte hier, dass die beiden Zeitreihen unterschiedlich lang sind. Die monatlichen Daten beginnen in den 1960ziger Jahren wobei wir die Daten für die täglichen Messungen erst ab den späten 70zigern vorliegen haben. Ich habe hier jetzt einmal die Funktion plot_time_series() aus dem R Paket {timetk} genutzt. Es gibt natürlich auch noch andere Möglichkeiten, aber ich mag die interaktive Funktion, die du sonst über den Umweg über {plotly} nutzen müsstest. Aber da gibt es dann in dem vorherigen Kapitel genug Beispiele für. Mehr findest du auch auf der Seite von R Coder - Evolution charts.

R Code [zeigen / verbergen] 
co2_monthly_tbl |> 
    plot_time_series(date, average, .interactive = TRUE) 
co2_daily_tbl |> 
    plot_time_series(date, average, .interactive = TRUE)
(a) Gemittelt über den Monat.
(b) Gemittelt über den Tag.
Abbildung 67.3— Verlauf des \(CO_2\) Anstiegs in der Atmosphäre. Hier einmal die Darstellung mit der Funktion plot_time_series() aus dem R Paket {timetk}. Die beiden Datensätze haben aber nicht die gleiche Zeitspanne beobachtet.

Einen weiteren Datensatz, den wir uns anschauen wollen, ist ein Datensatz zu der Milchleistung von Kühen stammt aus dem Tutorium Analysing Time Series Data – Modelling, Forecasting and Data Formatting in R. Wir haben hier ein idealisierten Datensatz vorliegen, so dass wir uns nicht mit dem Datumsformat quälen müssen. Der Datensatz wurde auch für die Analysen künstlich erstellt. Daher ist die Milchleistung auch nicht als echt anzusehen. Wir haben es hier im Prinzip mit simulierten Daten zu tun.

R Code [zeigen / verbergen] 
milk_tbl <- read_csv("data/monthly_milk.csv")

In der Tabelle 67.1 siehst du nochmal einen Auszug aus den Milchdaten. An jedem Tag haben wir die Milchleistung für eine Kuh aufgetragen. Ich würde hier davon ausgehen, dass es sich um die mittlere Leistung handelt. In Wirklichkeit sind die Daten vermutlich etwas komplizierter und wir haben nicht nur eine Leistungsbewertung pro Tag für eine Kuh. Aber für diese Übersicht soll es reichen.

Tabelle 67.1— Auszug aus den Daten zu der Milchleistung von Kühen.
month milk_prod_per_cow_kg
1962-01-01 265.05
1962-02-01 252.45
1962-03-01 288
1962-04-01 295.2
… …
1975-09-01 367.65
1975-10-01 372.15
1975-11-01 358.65
1975-12-01 379.35

Um die Milchdaten in der Abbildung 67.4 darzustellen nutzen wir die Funktion plot_time_series() aus dem R Paket {timetk}. Eigentlich ist es ein Zusammenschluss von {ggplot} und {plotly}. Wenn du die Option .interactive = TRUE wie ich setzt, dann bekommst du einen semi-interaktiven Plot durch {plotly} wiedergegeben. Mehr Informationen erhälst du dann auf der Hilfeseite von timetk zu Visualizing Time Series. Wie immer wenn du so generische Funktionen nutzt, musst du schauen, ob dir die Abbildung so gefällt. Du verlierst hier etwas Flexibilität und erhälst dafür aber schneller deine Abbildungen.

Wir erkennen ganz gut, dass wir hier einen Effekt der Saison oder aber der Jahreszeit haben. Wir haben zyklische Peaks der Milchleistung über das Jahr verteilt. Gegen Ende unserer Zeitreihe sehen wir aber eine Art Plateau der Milchleistung. In der folgenden Analyse wollen wir einmal schauen, ob wir die zukünftige Milchleistung anhand der bisherigen Daten vorhersagen können.

R Code [zeigen / verbergen] 
milk_tbl |>
  plot_time_series(month, milk_prod_per_cow_kg, .interactive = TRUE)
Abbildung 67.4— Die Darstellung der Milchdaten durch das R Paket {timetk} und der Funktion plot_time_series(), die durch die Option .interactive = TRUE intern dann {plotly} aufruft.

67.3 Analysen von Zeitreihen

Bis jetzt haben wir uns in dem vorherigen Kapitel die Visualisierung von Zeitreihen angeschaut. Häufig reicht die Visualisierung auch aus, wenn es um die Darstellung von Temperaturverläufen in einer Abschlussarbeit geht. Wir gehen jetzt aber einen Schritt weiter und wollen unsere Zeitreihe einmal statistisch Analysieren. Die Zeitreihenanalyse oder auch Zeitreihenprognose ist die Verwendung eines Modells zur Vorhersage künftiger Werte auf der Grundlage zuvor beobachteter Werte. Für dich bedeutet dies, dass Prognosen darüber erstellt werden, wie sich solche Zeitreihen in der Zukunft entwickeln werden. Wie in vielen anderen Tutorien auch, werde ich mir hier mal das häufigste Modell mit dem ARIMA Modell anschauen. Das ARIMA Modell ist eine Kombination aus der Auto-Regression (AR) und gleitendem Durchschnitt (MA). Neben dem ARIMA Modell gibt es noch weitere Möglichkeiten eine Zeitreihe zu analysieren. Ich gehe zwar auf einige Aspekte ein, aber eine bessere Übersicht als Michael Clark in seinem Artikel Exploring Time - Multiple avenues to time-series analysis schaffe ich hier nicht. Es gibt dann auch zu viele R Pakete aus denen du wählen könntest.

67.3.1 Definitionen und Überblick

In dem folgenden Abschnitt möchte ich gerne einmal einen Überblick über die wichtigsten Begriffe in der Analyse von Zeitreihen geben. Jetzt geht es also los mit der “richtigen” Zeitreihenanalyse. Teilweise sind es etwas speziellere Begriffe, so dass ich hier erstmal etwas zu den Begriffen schreibe und dann die einzelnen Begriffe nochmal tiefer erkläre. Als vertiefenden Einstieg kann ich hier auch das Buch Forecasting: principles and practice von Hyndman und Athanasopoulos (2018) empfehlen. Das Buch ist dann gleichzeitig als eine Webseite hinterlegt. Darüber hinaus gibt es dann noch passende erklärende Videos dazu.

Stationarität (eng. stationarity)

Eine gängige Annahme bei vielen Zeitreihenverfahren ist, dass die Daten stationär sind. Das klingt etwas seltsam, denn eigentlich soll sich doch was über die Zeit verändern. Wie kann dann eine Vorbedingung an Zeitreihen sein, dass Zeitreihen stationär sind? Ein stationärer Prozess hat die Eigenschaft, dass sich der Mittelwert, die Varianz und die Autokorrelationsstruktur im Laufe der Zeit nicht ändern. Wir sprechen hier also von statistischen Eigenschaften über den Zeitverlauf. Solange die Zeitreihe nicht stationär ist, können wir kein Zeitreihenmodell erstellen. Insbesondere sind AR oder MA nicht auf nicht-stationäre Reihen anwendbar. Es gibt drei grundlegende Kriterien, damit eine Reihe als stationäre Reihe eingestuft wird:

  1. Der Mittelwert der Reihe darf keine Funktion der Zeit sein, sondern muss konstant sein. Zeitpunkte in der Zukunft haben keine größeren mittleren Werte.
  2. Die Varianz der Reihe sollte keine Funktion der Zeit sein. Diese Eigenschaft wird als Homoskedastizität bezeichnet. Die Varianz steigt nicht mit der Zeit an und damit ist die Varianz homogen über die Zeitpunkte.
  3. Die Kovarianz des \(i\)-ten Messwerts und des (\(i + m\))-ten Messwert sollte keine Funktion der Zeit sein. Die Zeitpunkte untereinander zeigen nur eine eingeschränkte Korrelation. Das heißt, dass unsere Zeitpunkte zwar korreliert sein dürfen, aber der Effekt darf nicht zu stark sein.

Es gibt verschiedene Methoden um aus Daten, die keine stationären Daten sind, einen stationären Datensatz zu erschaffen. Wir transformieren also unsere Daten so, dass es dann stationäre Daten werden. Für die spätere Darstellung können wir dann die Daten wieder zurücktransformieren.

Lag (deu. Zeitverzögerung)

Mit Lag (deu. Zeitverzögerung, abk. p) ist im Wesentlichen eine Verzögerung gemeint. Das Konzept des Lag ist zentral für das Verständnis der Zeitreihenanalyse. Betrachte dafür eine Folge von Zeitpunkten. Bei einem Lag von 1 vergleichst du die Zeitreihe \(t\) mit einer verzögerten Zeitreihe \(t-1\). Du verschiebst die Zeitreihe um einen Zeitpunkt, bevor du die Zeitreihe mit sich selbst vergleichst. So gehst du dann für gesamte Länge der Zeitreihe vor. Machen wir einmal ein Beispiel. Wir haben eine Autokorrelationsfunktion für das Lag 1 vorliegen. Wenn wir also eine Zeitreihe \(t\) haben und das Lag 1 berechnen wollen, dann entfernen wir den letzten Zeitpunkt und haben eine \(t-1\) gelaggte Zeitreihe. Wenn du das Lag 2 berechnest, dann entfernst du die letzten beiden Zeitpunkte aus den Daten. Wir schreiben anstatt des Lag 1 auch gerne \(p(1)\). Das Lag 2 wäre dann durch \(p(2)\) dargestellt. Mehr zu Lags mit Beispielen kannst du unter Time Series as Features finden.

Differenz

Die Differenz (abk. d) zwischen zwei Zeitpunkten in einer Zeitreihe wird auch häufig benötigt um einen stationäre Zeitreihe zu erreichen. Dabei wird häufig auch von der Ordnung (eng. order) der Differenz gesprochen. Die Ordnung gibt aber nur an, die wievielte Differenz wir berechnet haben. Klingt wild, ist aber nichts anders als immer wieder die Differenz zwischen zwei Zahlen zu berechnen. Die Differenz 1. Ordnung \(d(1)\) zwischen den Zahlen \(y = {2, 6, 7, 5}\) ist \(d(1) = {4, 1, 2}\). Die Differenz 2. Ordnung \(d(2)\) ist dann nur noch die Differenz in der 1. Ordnung und damit \(d(2) = {3, 1}\).

Autokorrelation

Wenn wir die Zeitreihen \(t_1\) und \(t_2\) vorliegen haben, so zeigt die normale Korrelation \(\rho(t_1, t_2)\), wie sehr sich die zwei Zeitreihen ähneln. Die Autokorrelation hingegen beschreibt, wie ähnlich die Zeitreihe \(t_1\) oder \(t_2\) sich selbst ist. Damit beschreibt die Autokorrelation die inhärente Ähnlichkeit einer Zeitreihe \(t\). Anhand der Werte der Autokorrelationsfunktion können wir erkennen, wie stark sie mit sich selbst korreliert. Dafür nutzen wir ein sogenanntes Lag (deu. Verzögerung) um aus einer Zeitreihe \(t\) eine zweite Zeitreihe zu bauen. Bei jeder Zeitreihe ist die Korrelation bei einem Lag von 0 perfekt, da man dieselben Werte miteinander vergleicht. Wenn du nun eine Zeitreihe verschiebst, wirst du feststellen, dass die Korrelationswerte zwischen den Lags abnehmen. Wenn die Zeitreihe aus völlig zufälligen Werten besteht, gibt es nur eine Korrelation bei Lag gleich 0, aber keine Korrelation überall sonst. Bei den meisten Zeitreihen ist dies nicht der Fall, da die Werte im Laufe der Zeit abnehmen und somit eine gewisse Korrelation bei niedrigen Lag-Werten besteht. Damit kann die Autokorrelationsfunktion die Frequenzkomponenten einer Zeitreihe aufzeigen.

AR Modell

Das AR-Modell (autoregressive model) setzt den aktuellen Wert der Reihe in Beziehung zu ihren vergangenen Werten. Es geht davon aus, dass die Vergangenheitswerte in einem linearen Verhältnis zum aktuellen Wert stehen. Deshalb brauchen wir auch eine Art stationären Zeitverlauf.

MA Modell

Das MA-Modell (moving average model) setzt den aktuellen Wert der Reihe mit dem weißen Rauschen oder den Fehlertermen der Vergangenheit in Beziehung. Es erfasst die Schocks oder unerwarteten Ereignisse der Vergangenheit, die sich noch immer auf die Reihe auswirken. Wir betrachten hier also hier den Fehler aus einer Regression und nicht die tatsächlichen Werte.

ARIMA Modell

Wenn wir die beiden Modelle AR und MA kombinieren erhalten wir das ARIMA Modell (abk. autoregressive integrated moving average, deu. autoregressiver gleitender Durchschnitt). Das ARIMA Modell ist dabei eine Erweiterung schon existierender Modelle und wird sehr häufig für die Analyse von Zeitreihen genutzt. Als wichtigste Anwendung gilt die kurzfristige Vorhersage. Das ARIMA Modell besitzt einen autoregressiven Teil (AR-Modell) und einen gleitenden Mittelwertbeitrag (MA-Modell). Das ARIMA Modell erfordern eigentlich stationäre Zeitreihen. Eine stationäre Zeitreihe bedeutet, dass sich die Randbedingungen einer Zeitreihe nicht verändern. Die zugrunde liegende Verteilungsfunktion der gemessenen Werte über die Zeitreihe muss zeitlich konstant sein. Das heißt konkret, dass die Mittelwerte und die Varianz zu jeder Zeit gleich sind. Gewisse Trends lassen sich durch ein ARIMA Modell herausfiltern.

Exponential smoothing

Alternative zu ARIMA Modell gibt es noch das Exponential smoothing (abk. ets) was wir uns hier aber nicht mehr tiefer anschauen. Später nehmen wir das Exponential smoothing nochmal mit in den Modellvergleich gehen aber nicht auf die Theorie dahin ein.

Cross Correlation Functions and Lagged Regressions

Cross Correlation Functions and Lagged Regressions beschreibt die Korrelation zwischen verschiedenen Zeitreihen. Dabei vergleichen wir aber nicht die Zeitreihen an einem Zeitpunkt, sondern wollen wissen ob die eine Zeitreihe eine verschobene Zeitreihe der anderen ist. Auch hier gehe ich vorerst nicht auf die Analyse ein.

67.3.2 Grundlagen der Modellierung von Zeitreihen

Im Folgenden wollen wir einmal die Grundlagen der Zeitreihenanalyse verstehen. Wir brauchen nämlich als erstes stationäre Daten, wenn wir mit einem ARIMA-Modell unsere Daten analysieren wollen. Dann arbeiten wir uns zu der Autokorrelation bzw. dem autoregressiven Prozess (abk. AR-Prozess) vor. Wir brauchen die Idee des Lag und der Differenz um eine Autokorrelation und daraus dann auch einen AR-Prozess ableiten zu können. Zum Verständnis des Lag nutzen wir einmal unsere Daten für die Ausbrüchen des Old Faithful Geysirs im Yellowstone-Nationalpark.

Fangen wir also mit dem Beispiel für ein Lag an. Was ist nun also ein Lag? Ein Lag ist einfach nur eine Verschiebung der Daten um einen Wert. Wir schauen uns also für das Lag 1 die Werte ohne den letzten Wert an. Bei dem Lag 2 löschen wir die ersten letzten beiden Werte. Und dann ist schon fast klar was wir bei dem Lag 3 machen, wir löschen die letzten drei Werte. Wenn wir dann dennoch die paarweise Korrelation berechnen, dann berechnen wir nicht die Korrelation mit sich selber, das wäre bei Lag 0, sondern eben die Korrelation mit sich selbst verschoben um den Lag. Deshalb nennt sich das dann auch Autokorrelation der Zeitreihe.

Dann berechnen wir einmal mit der Funktion lag aus dem R Paket {dplyr} die Lags 1, 2, und 3. Alle Lags packen wir dann mit den originalen Daten zusammen in einen Datensatz und haben somit auch gleich einen Vergleich.

R Code [zeigen / verbergen] 
erupt_tbl <- tibble(erupt, 
                    erupt_p1 = dplyr::lag(erupt, 1),
                    erupt_p2 = dplyr::lag(erupt, 2),
                    erupt_p3 = dplyr::lag(erupt, 3))
erupt_tbl
# A tibble: 107 × 4
   erupt erupt_p1 erupt_p2 erupt_p3
   <dbl>    <dbl>    <dbl>    <dbl>
 1    78       NA       NA       NA
 2    74       78       NA       NA
 3    68       74       78       NA
 4    76       68       74       78
 5    80       76       68       74
 6    84       80       76       68
 7    50       84       80       76
 8    93       50       84       80
 9    55       93       50       84
10    76       55       93       50
# ℹ 97 more rows

Wie du siehst, haben wir immer eine Verschiebung um einen Wert dadurch, dass wir die letzten Werte entfernen. Daher können wir jetzt trotzdem eine lineare Regression auf die verschiedenen Lags und den originalen Daten rechnen. Dabei fliegen natürlich alle Zeilen aus den Datensatz wo wir einen fehlenden Wert haben, aber das ist ja dann auch gewünscht. In den folgenden Tabs kannst du einmal sehen, wie ich für verschiedene Lags die lineare Regression gerechnet habe. Nichts anderes ist dann auch ein AR-Modell. Wir berechnen über die lineare Regression die Korrelation für jedes Lag zu den originalen Daten.

R Code [zeigen / verbergen] 
lm(erupt_p1 ~ erupt, erupt_tbl) |> 
  coef()
(Intercept)       erupt 
119.4877108  -0.6846253
R Code [zeigen / verbergen] 
lm(erupt_p2 ~ erupt, erupt_tbl) |> 
  coef()
(Intercept)       erupt 
 31.8097211   0.5504338
R Code [zeigen / verbergen] 
lm(erupt_p3 ~ erupt, erupt_tbl) |> 
  coef()
(Intercept)       erupt 
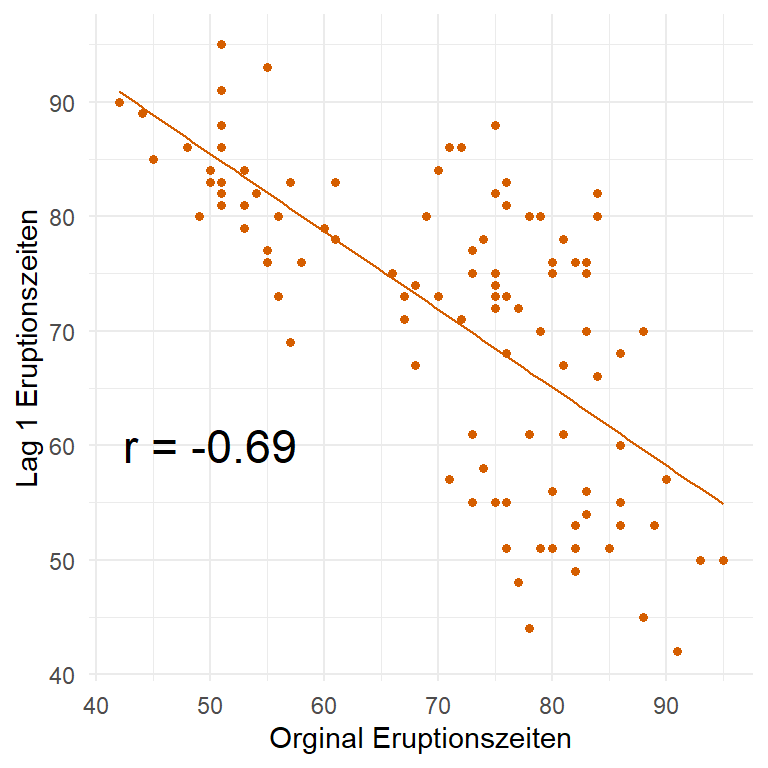
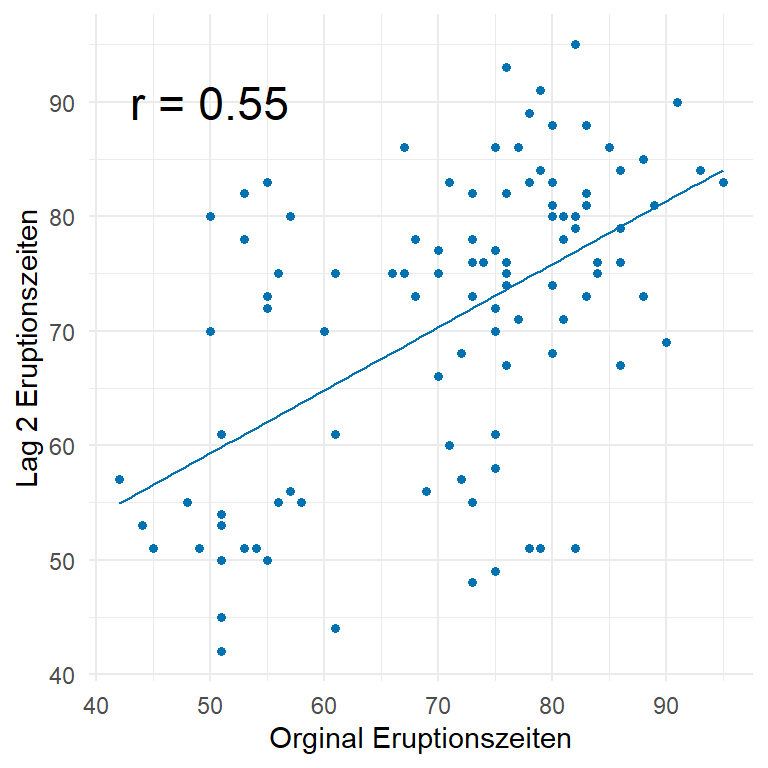
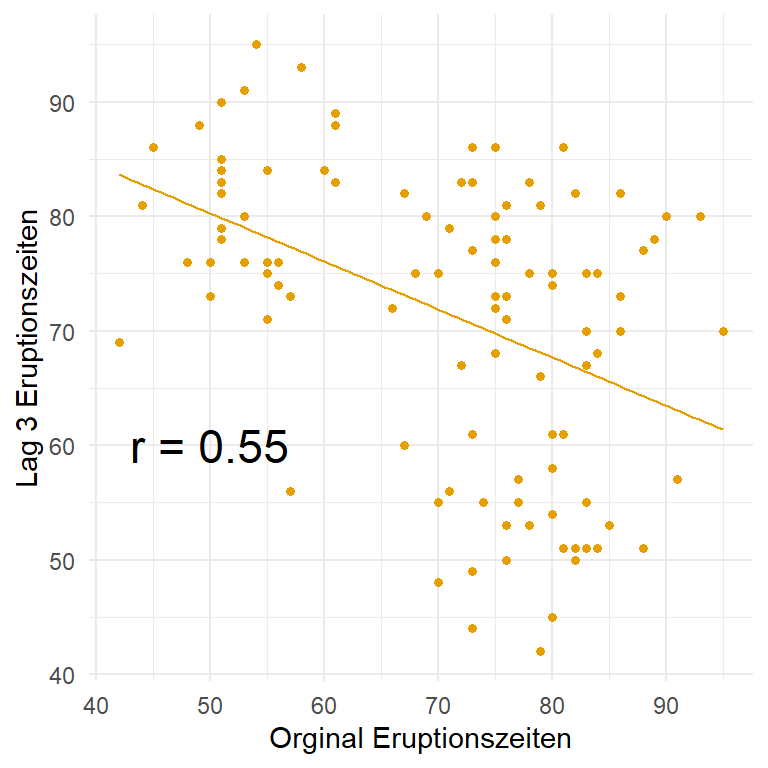
101.2796080  -0.4264714

In der Abbildung 67.5 siehst du nochmal die verschobenen Daten auf der \(y\)-Achse und die originalen Daten auf der \(x\)-Achse. Durch die Verschiebung ändert sich immer die Punktewolke und damit dann auch die Regression sowie die berechnete Korrelation als Vorzeichen der Steigung der Geraden. Die Idee ist eben, einen Zyklus in den Eruptionen zu finden. Wenn wir also immer kurz/lang Wartezeiten hätten, dann würde sich auch immer die Korrelation ändern, wenn wir um einen Wert verschieben. Das trifft natürlich nur zu, wenn es eben der Rhythmus um einen Zeitpunkt verschoben ist. Häufig ist aber nicht ein Zeitpunkt sondern eben zwei oder mehr. Das müssen wir dann durch eine Modellierung herausfinden.

(a) p(1) vs. Orginal Eruptionszeiten.
(b) p(2) vs. Orginal Eruptionszeiten.
(c) p(3) vs. Orginal Eruptionszeiten.
Abbildung 67.5— Dastellung der orginalen Eruptionszeiten des Old Faithful Geysirs sowie die entsprechenden Daten für die Lag 1 bis 3. Die Regressiongleichung wurde für alle Zusammenhänge ergänzt.

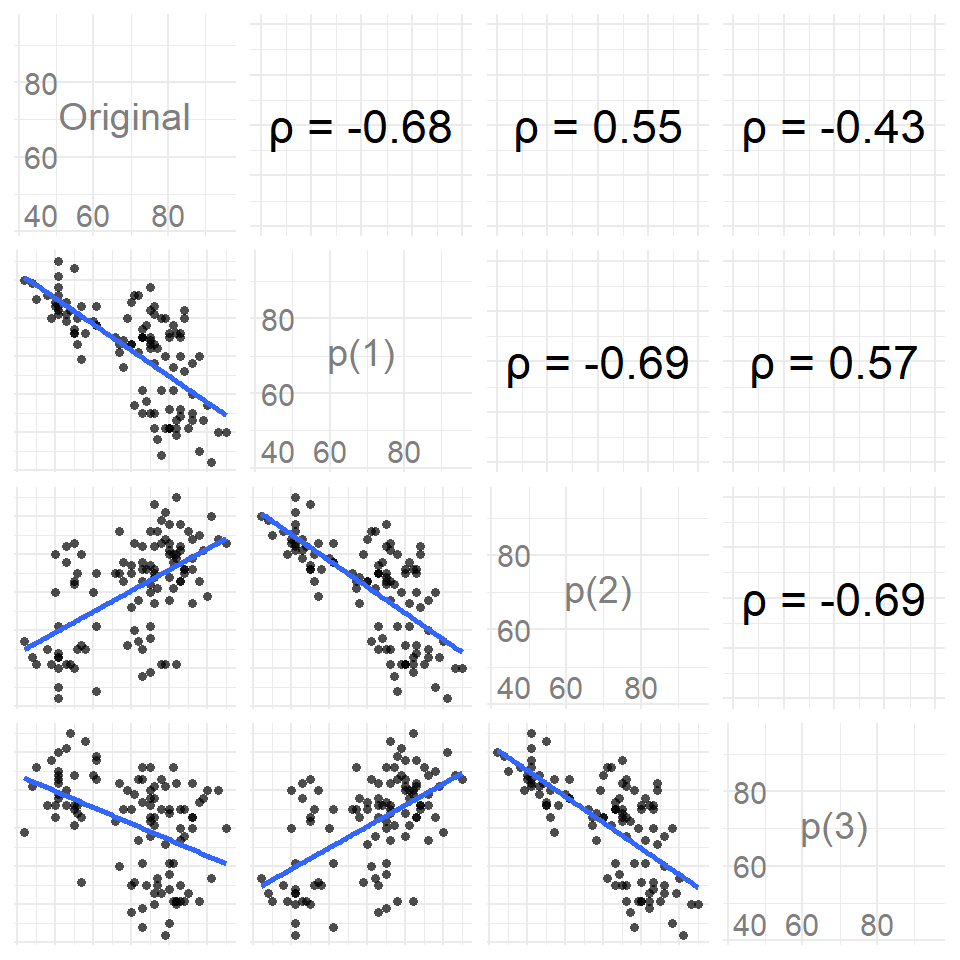
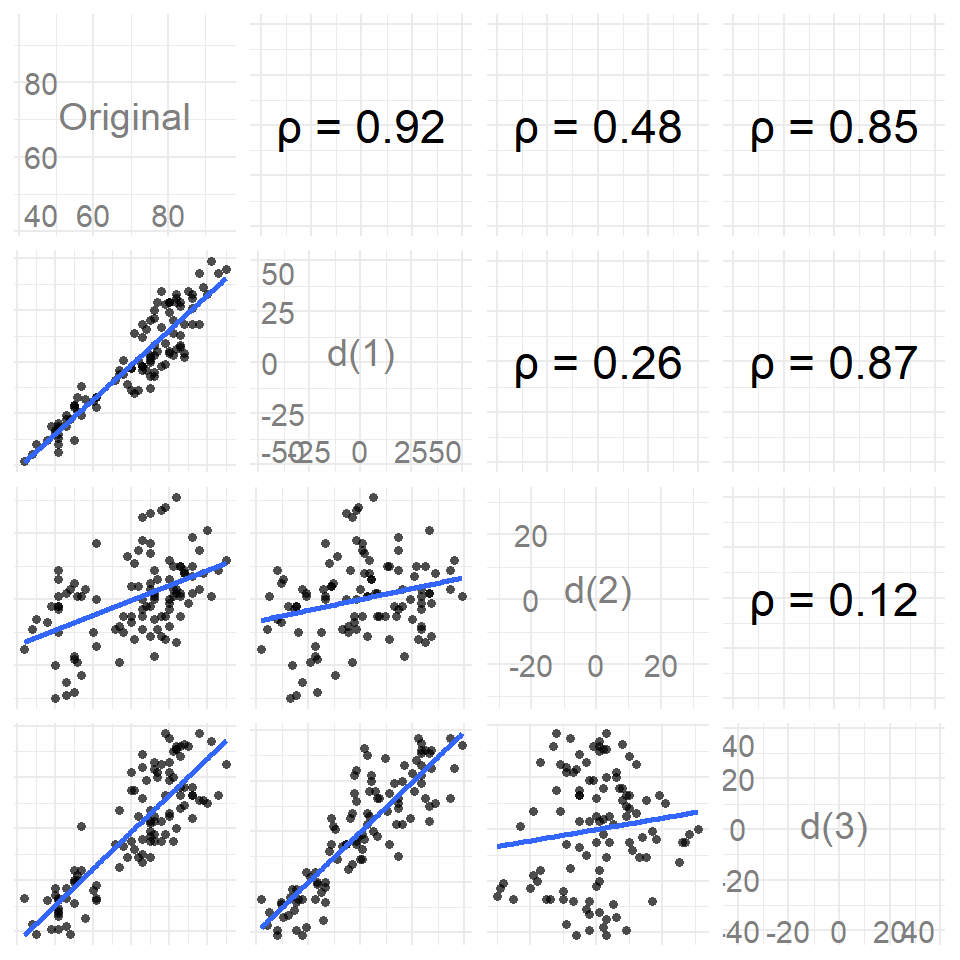
Bevor wir aber mit der Modellierung von Zeitreihen beginnen, hier nochmal die vollständige Korrelationsmatrix für alle Lags \(p\) und den originalen Daten. Ich habe den Zusammenhang einmal in der Abbildung 67.6 dargestellt. Wenn du mehr über die Visualisierung der Korrelation erfahren möchtest, dann besuche das Kapitel zur Korrelation. Hier sehen wir dann gut, wie mit jedem Schritt im Lag die Korrelation im Vorzeichen flippt. Ein Zeichen, dass wir es hier mit einer zyklischen Zeitreihe zu tun haben und wir etwas in den Daten entdecken könnten.

Abbildung 67.6— Korrelation zwischen den originalen Daten und den Lags, auch als \(p\) bezeichnet. Im unteren Bereich des Korrelationsplot sind die Scatterplost mit der Regressionsgraden eingezeichnet. Im oberen Bereich finden sich die berechneten Korrelationskoeffizienten \(\rho\) für die paarweisen Vergleiche.

Das war jetzt die händische Darstellung. Wir können uns die Autokorrelation auch über eine Zeitreihe anschauen. Wir nutzen hier die etwas primitive Funktion acf(), da nur die “alten” Funktionen nur mit einem Vektor von Zeiten klar kommen. Eigentlich brauchen wir ja zu jedem Wert ein Datum. Das haben wir hier aber nicht, deshalb müssen wir hier zu der alten Implementierung greifen.

R Code [zeigen / verbergen] 
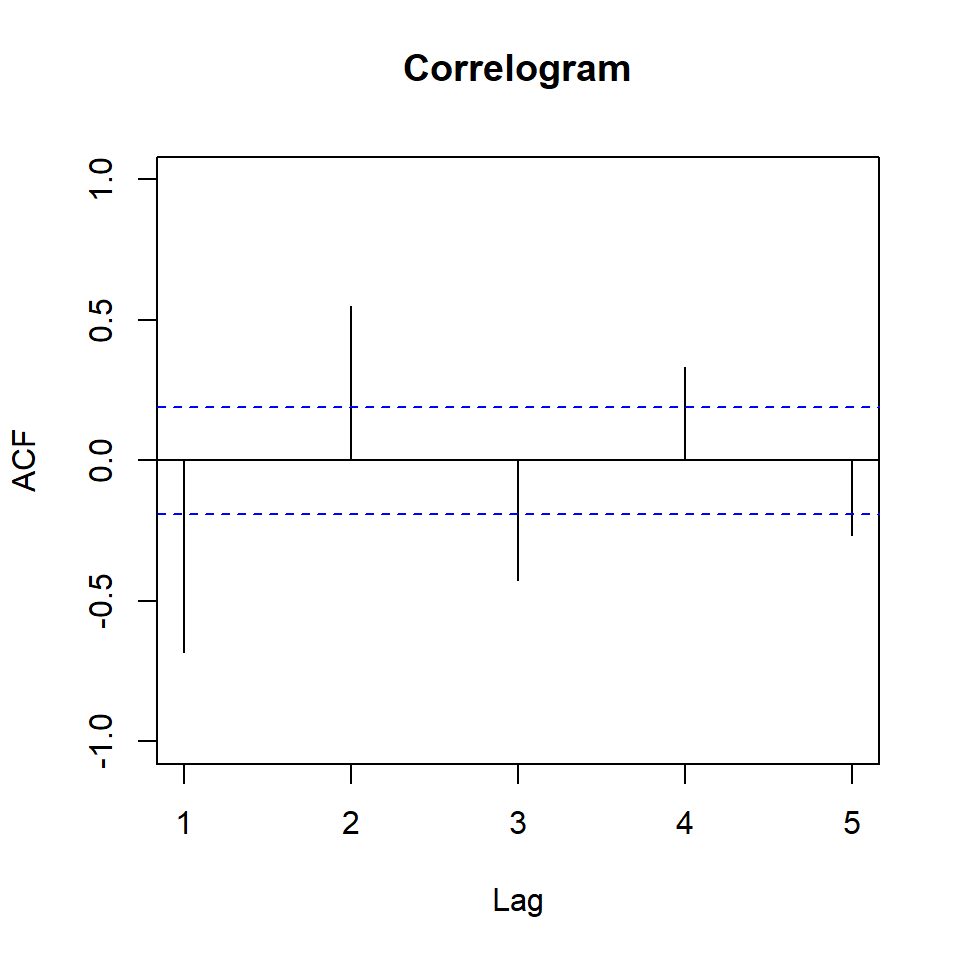
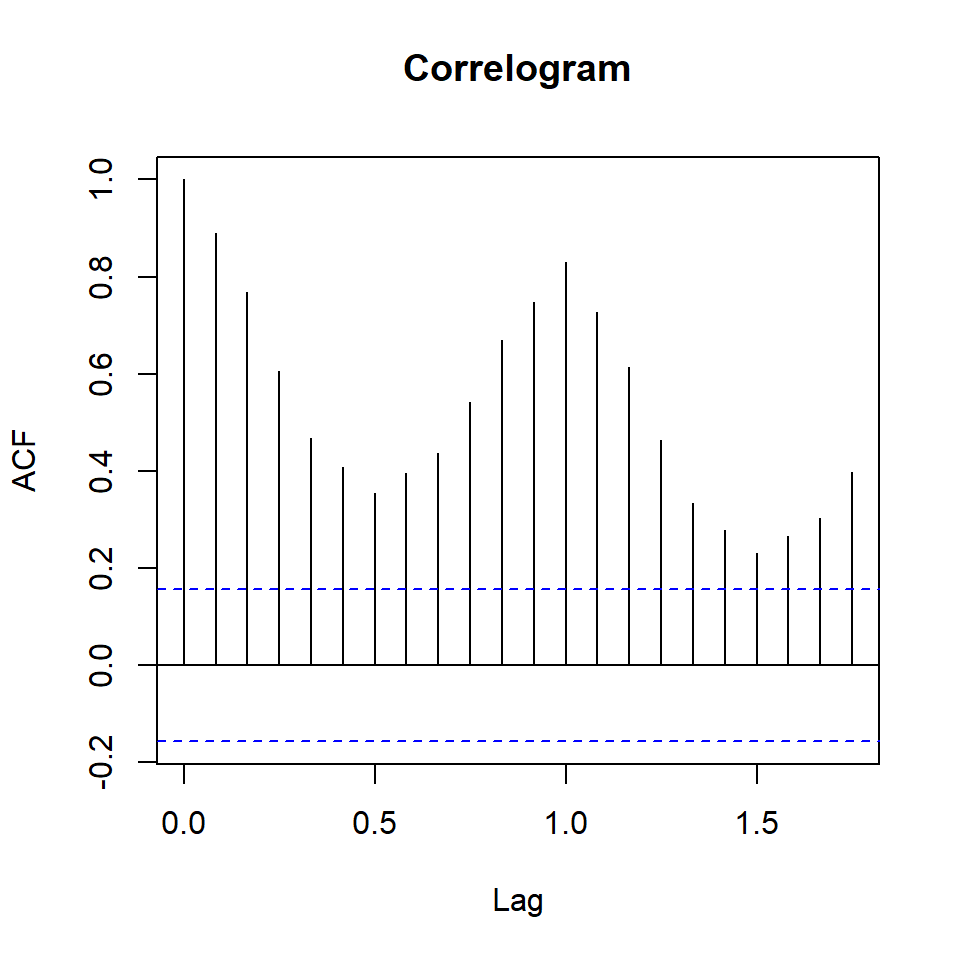
erupt_ts <- tk_ts(erupt)

In der Abbildung Abbildung 67.7 (a) sehen wir die Autokorrelation zwischen den Orginaldaten des Geysirs und den entsprechenden Korrelationen zu den Lags 1 bis 5. Wenn du nochmal weiter oben schaust, dann haben wir für die Korrelationen von den Orginaldaten zu den entsprechenden Lags folgende Korrelationen berechnet. Wir hatten eine Korrelation von \(\rho = -0.68\) zu Lag 1, eine Korrelation von \(\rho = 0.55\) zu Lag 2 und ein \(\rho = -0.43\) zum Lag 3 beobachtet. Die Korrelationen findest du dann als Striche auch in der Abbildung wieder.

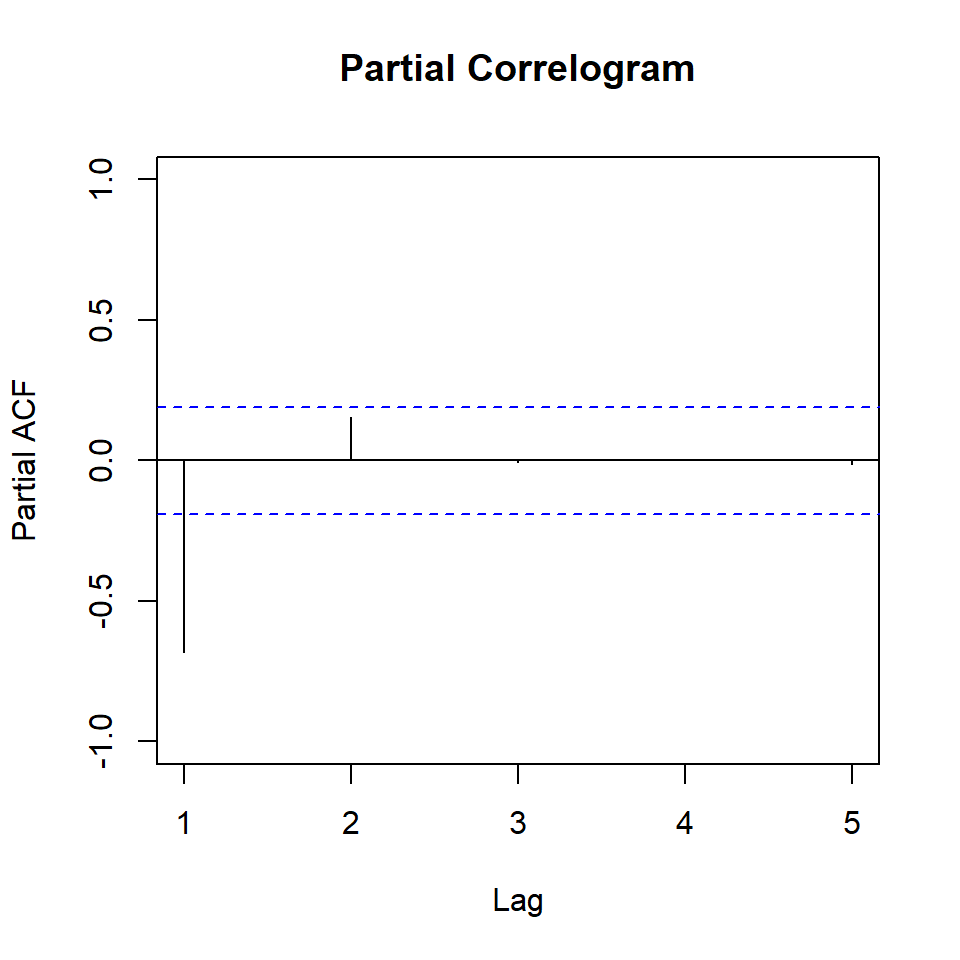
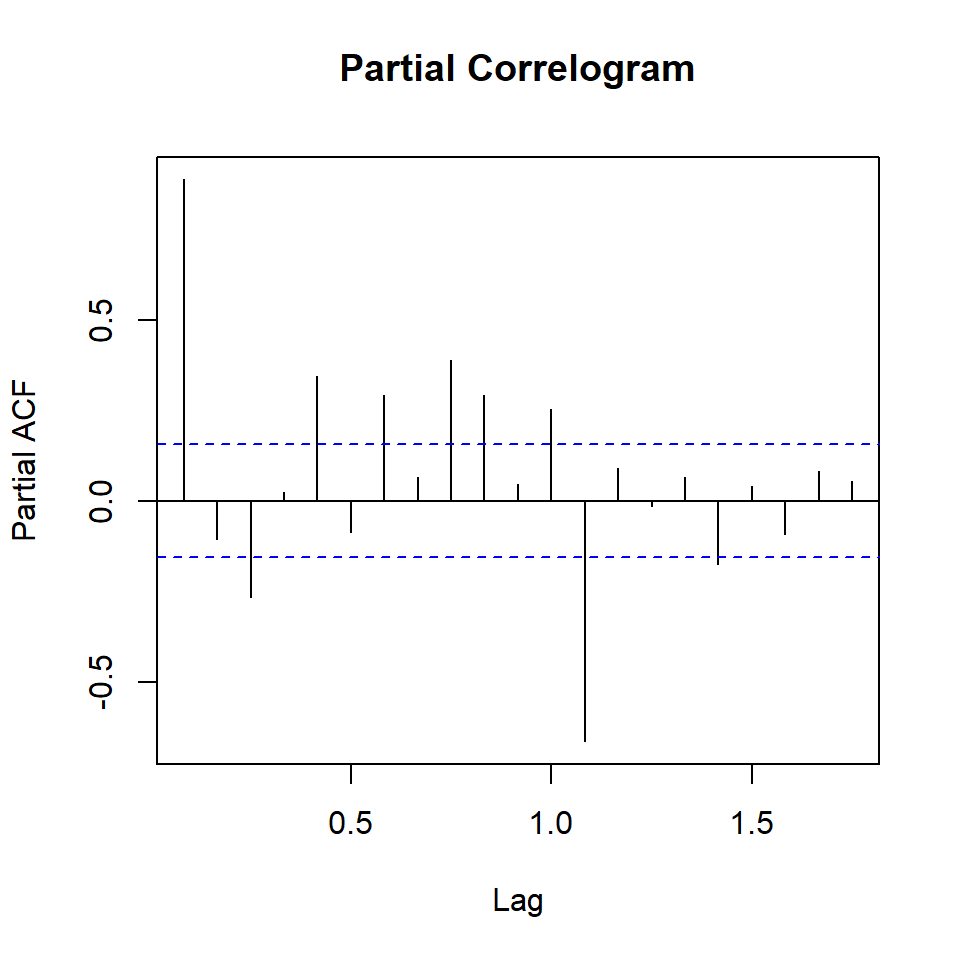
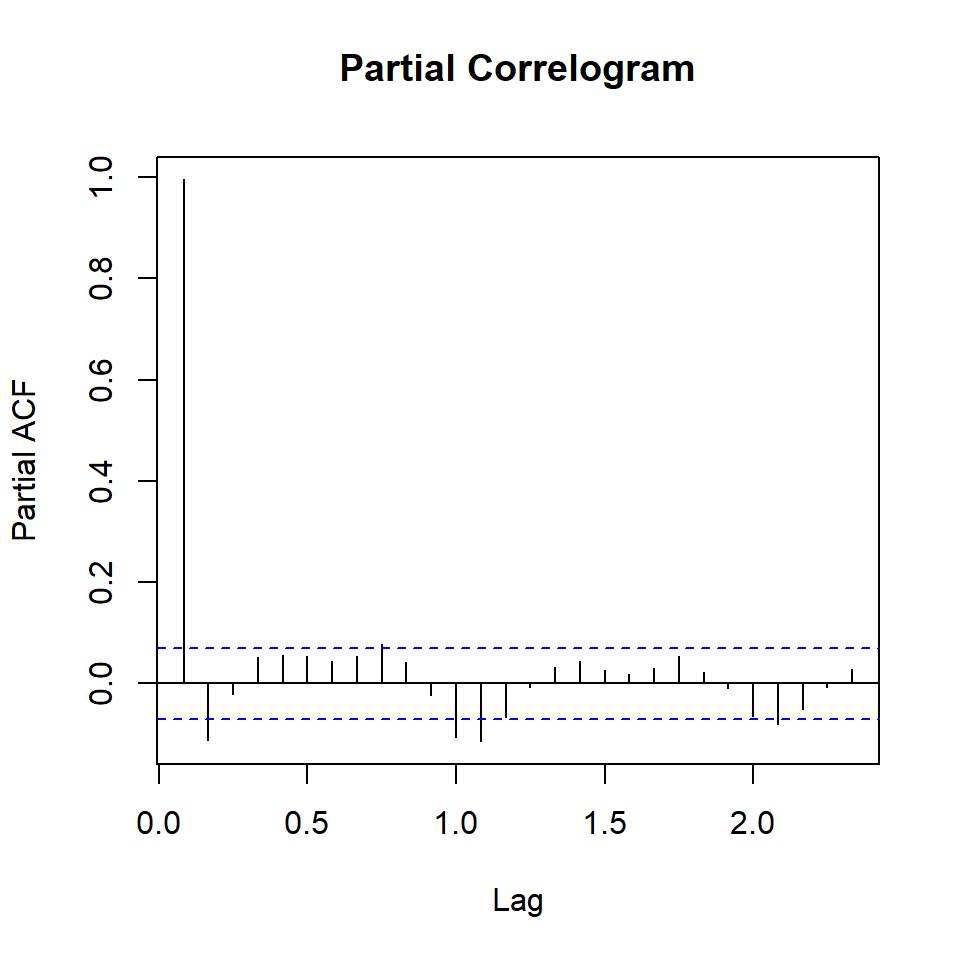
Nun ist es aber so, dass natürlich die Lags untereinander auch korreliert sind. Diese Korrelation untereinander wollen wir dann einmal raus rechnen, so dass wir nur die partielle Korrelation haben, die zu den jeweiligen Lags gehört. Dabei entsteht natürlich eine Ordnung. Das Lag 1 wird vermutlich die meiste Korrelation erklären und dann folgen die anderen Lags. Deshalb nennen wir diese Art der Korrelation auch partial Autokorrelation (deu. partielle). Du siehst die Anteile der partiellen Korrelation zu den jeweiligen Lags dann in der Abbildung 67.7 (b). Wir werden dann später bei {tktime} eine bessere Art und Weise sehen die Abbildungen zu erstellen. Zum Verstehen sind die Abbildungen gut, aber schön sind die Abbildungen nicht.

R Code [zeigen / verbergen] 
erupt_ts |> 
  acf(main = "Correlogram", lag.max = 5, 
      ylim = c(-1, 1), xlim = c(1, 5))

erupt_ts |> 
  pacf(main = "Partial Correlogram", lag.max = 5, 
       ylim = c(-1, 1))
(a) Correlogram.
(b) Partial Correlogram.
Abbildung 67.7— Korrelationsabbildungen mit der Option lag.max = 5. Daher werden nur die ersten fünf Lags betrachtet. Die Abbildungen dienen der Veranschaulichung vom Lag. Für eine Veröffentlichung bitte die Funktionen aus {tktime} verwenden. Beim Correlogram ist das Lag 0 entfernt, da die Korrelation mit sich selbst immer 1 ist.

Als zweites schauen wir uns die Differenz einer Zeitreihe an um einen stationäre Zeitreihe zu erhalten. Wir berechnen hierbei die Differenz der Zeitpunkte untereinander. Das klingt jetzt wieder komplizierter als es eigentlich ist. Wir können die Berechnung der Differenzen einmal in den folgenden Tabs durchführen. Die Differenz höher Ordnung ist dann einfach die Differenz der vorherigen Differenz.

R Code [zeigen / verbergen] 
erupt[1:10]
 [1] 78 74 68 76 80 84 50 93 55 76
R Code [zeigen / verbergen] 
diff(erupt[1:10], differences = 1)
[1]  -4  -6   8   4   4 -34  43 -38  21
R Code [zeigen / verbergen] 
diff(erupt[1:10], differences = 2)
[1]  -2  14  -4   0 -38  77 -81  59
R Code [zeigen / verbergen] 
diff(erupt[1:10], differences = 3)
[1]   16  -18    4  -38  115 -158  140

Dann können wir einmal die Differenzen für die Ausbrüche des Old Faithful Geysirs im Yellowstone-Nationalpark berechnen. Ich beschränke mich hier einmal auf die ersten drei Differenzen. Auch dafür können wir dann die Funktion diff() nutzen und müssen immer nur noch ein NA am Anfang hinzufügen damit die Vektoren die gleiche Länge behalten. Bei jeder Differenzenbildung verlieren wir ja einen Wert aus dem Vektor.

R Code [zeigen / verbergen] 
diff_tbl <- tibble(erupt,
                   erupt_d1 = c(NA, diff(erupt, 1)),
                   erupt_d2 = c(NA, NA, diff(erupt, 2)),
                   erupt_d3 = c(NA, NA, NA, diff(erupt, 3)))

In der Abbildung 67.8 siehst du einmal die verschiedenen Differenzen und deren Korrelationen abgebildet. Wir erreichen dann mit einer Differenz \(d(3)\) schon eine fast stationäre Zeitreihe.

Abbildung 67.8— Korrelation zwischen den originalen Daten und den Lags. Im unteren Bereich des Korrelationsplot sind die Scatterplost mit der Regressionsgraden eingezeichnet. Im oberen Bereich finden sich die berechneten Korrelationskoeffizienten \(\rho\) für die paarweisen Vergleiche. Wir erreichen immer stationärere Daten.

Dann wenden wir die Differenzen auch einmal auf unsere Klimadaten sowie unserer Milchleistung einmal an. Wir nutzen dann hier die Funktion plot_time_series() aus dem R Paket {timetk}. Die Funktion ist super einfach zu nutzen uns liefert auch die Ergebnisse, die wir wollen. Darüber hinaus können wir dann auch direkt {plotly} aktivieren. Wie wir dann in der Abbildung 67.9 sehen, kommen wir mir der Differenz \(d(1)\) schon sehr nah an einen stationären verlauf der Zeitreihe ran. Später müssen wir das dann nicht händisch machen, es gibt Funktionen, die für uns das beste Lag und die optimale Differenz bestimmen. Dafür nutzen wir zum Beispiel dann die Funktion auto.arima(), die uns dann die optimale Ordung für das Lag und die Differenz wiedergibt.

R Code [zeigen / verbergen] 
co2_monthly_tbl |> 
  mutate(diff = c(NA, diff(average, 1))) |> 
  plot_time_series(date, diff, .interactive = TRUE) 
milk_tbl |> 
  mutate(diff = c(NA, diff(milk_prod_per_cow_kg, 1))) |> 
  plot_time_series(month, diff, .interactive = TRUE)
(a) CO\(_2\) Daten.
(b) Milch Daten.
Abbildung 67.9— Stationäre Abbildungen der CO\(_2\)-Daten sowie der Milchdaten nach der Differenzbildung mit \(d(1)\). Wir sehen, dass wir einen stationären Verlauf erreichen.

67.4 Vorhersagen von Zeitreihen

Immer wenn ich mit Zeitreihen anfange, muss ich mich erinnern, dass die Algorithmen immer einer Vorhersage treffen wollen. Das heißt, wir wollen wissen wie sich eine Zeitreihe gegeben der vorherigen Ereignisse in der Zukunft verändern wird. Wir haben eine weitreichende Auswahl an R Paketen und jedes löst das Problem der Vorhersage von Zeitreihen etwas anders. Damit ich hier nicht endlos immer das Gleiche darstelle, konzentriere ich mich einmal auf die Standardimplementierung mit auto.arima() sowie dem R Paket {modeltime}. Am Ende sei hier nochmal auf die Übersicht von Michael Clark in seinem Artikel Exploring Time - Multiple avenues to time-series analysis verwiesen. Wir halten uns aber an seine folgende Empfehlung.

“I would also recommend {modeltime} as starting point for implementing a variety of model approaches for time series data with R. It was still pretty new when this was first written, but has many new features and capabilities, and could do some version of the models shown here.”

Ich verweise aber gerne nochmal in dem folgenden Kasten auf die anderen Möglichkeiten in R eine Zeitreihe auszuwerten. Eventuell ist etwas dabei, was für sich besser passt. Man kann sich hier sehr schnell in den Möglichkeiten verlieren.

Weitere R Paket zur Vorhersage von Zeitreihen

Folgende R Pakete lösen ebenfalls das Problem einer Vorhersage über die Zeit. Wir immer, ist es meistens eine andere Implementierung. Ob die Implementierung besser ist, hängt dann von vielen Faktoren ab.

  • Das R Paket {timetk} ist von den gleichen Machern wie das hier vorgestellte R Paket {modeltime}. Ich kann das Pakt empfehlen und es gibt auch keinen Grund es nicht zu nutzen. Ich halte aber {modeltime} für das aktuellere Paket.
  • Das R Paket {fable} und das R Paket {feasts} ist die Implementierung des Onlinebuches Forecasting: Principles and Practice. Dementsprechend empfiehlt sich auch diese Pakete zu nutzen, wenn du dich tiefer mit den dortigen Quellen beschäftigst.
  • R Paket {tstibble} ist nochmal eine andere Art Zeit in R darzustellen. Ich habe mich ehrlich gesagt nicht weiter mit dem R Paket beschäftigt. Das R Paket {feasts} baut aber auf {tstibble}, so dass ich das Paket hier noch erwähnen wollte.

67.4.1 mit {ts}

Eigentlich ist {ts} kein eigens Paket sondern die built-in Lösung von R, aber ich möchte hier dann doch {ts} als Paket schreiben, damit hier mehr Ordnung drin ist. Wenn wir eine Vorhersage auf einem zeitlichen Verlauf rechnen wollen, dann brauchen wir als aller erstes einen Datensatz, der auch eine echte Zeitreihe über mehrere zeitliche Zyklen enthält. Das ist dann meistens die Herausforderung so eine Zeitreihe in einer Abschlussarbeit zu erzeugen. In ein paar Monaten einen zyklischen Verlauf zu finden ist schon eine echte Leistung. Deshalb nehmen wir hier als Beispiel einmal unsere künstlichen Daten zur Milchleistung von Kühen. Wie du in der obigen Abbildung 67.4 klar erkennen kannst, haben wir hier Zyklen über die einzelnen Jahre hinweg. Es liegt ein stetiger, zyklischer Anstieg der Milchleistung über die beobachteten Jahre vor. Wir wollen jetzt den Verlauf modellieren und einen zukünftigen Verlauf vorhersagen. Oder andersherum, wie die zukünftigen Zyklen aussehen könnten.

In diesem Beispiel nutzen wir das R Paket {zoo} und die Funktion ts() für die Standardimplemetierung von Zeitreihen in R. Das hat immer ein paar Nachteile, da wir hier die veralteten Speicherformen für eine Zeitreihe nutzen. Auf der anderen Seite sind viele Tutorien im Internet noch genau auf diese Funktionen ausgerichtet. Hier seien dann die beiden Tutorien Time Series - ARMA Models in R und Time Series Analysis with auto.arima() in R als Anlaufpunkt empfohlen. Deshalb auch hier einmal die Erklärung der etwas älteren Funktionen. Später schauen wir dann auch die neuere Implementierung in dem R Paket {modeltime} einmal an.

Wir wandeln also erstmal unsere Milchdaten mit der Funktion tk_ts() in ein ts-Zeitobjekt um. Dafür müssen wir angeben von wann bis wann die Jahre laufen und wie viele Beobachtungen jedes Jahr hat. Glücklicherweise müssen nicht alle Jahre gefüllt werden und die Funktion erlaubt auch einen anderen Startmonat als Jan. Wir haben nämlich bei den CO\(_2\)-Daten den März als Startdatum, deshalb müssen wir den Start etwas anpassen. Wie du gleich siehst, dann haben wir eine Art Matrix als Ausgabe.

Im Folgenden also einmal die Milchdaten als ein ts-Objekt. Wichtig ist hier zu wissen, wie oft den nun ein Wert gemessen wurde. Problematisch wird es, wenn wir Nesswiederholungen vorliegen haben, dann können wir hier nicht weiterarbeiten.

R Code [zeigen / verbergen] 
milk_ts <- milk_tbl %$%
  tk_ts(milk_prod_per_cow_kg, start = 1962, end = 1975, frequency = 12)
milk_ts
        Jan    Feb    Mar    Apr    May    Jun    Jul    Aug    Sep    Oct
1962 265.05 252.45 288.00 295.20 327.15 313.65 288.00 269.55 255.60 259.65
1963 270.00 254.70 293.85 302.85 333.90 322.20 297.00 277.65 262.35 264.15
1964 282.60 278.10 309.60 317.25 346.50 331.20 305.10 287.55 271.80 274.95
1965 296.10 279.90 319.05 324.90 351.90 340.20 315.90 293.85 276.75 279.45
1966 304.65 285.75 331.20 339.75 364.95 359.10 330.75 313.65 297.45 300.15
1967 320.85 300.15 342.90 352.80 376.65 367.65 345.15 324.90 306.45 309.15
1968 322.65 313.20 348.75 358.20 386.10 371.70 352.35 333.00 315.45 317.70
1969 330.30 310.50 353.25 362.25 391.95 380.25 360.45 343.80 326.25 325.35
1970 337.50 318.15 363.15 370.80 398.70 386.55 368.55 352.35 333.00 336.15
1971 361.80 340.20 387.00 395.10 423.90 410.85 391.05 375.30 355.50 360.00
1972 371.70 359.55 400.50 405.00 432.45 420.75 402.30 384.75 364.05 364.50
1973 369.45 347.85 397.35 404.10 430.65 415.80 396.45 376.65 352.80 355.95
1974 372.60 350.10 400.05 405.90 436.05 426.15 408.60 390.15 366.75 365.40
1975 375.30                                                               
        Nov    Dec
1962 248.85 261.90
1963 254.25 269.10
1964 267.30 285.30
1965 270.90 285.75
1966 290.25 309.60
1967 297.00 314.10
1968 304.65 319.95
1969 310.50 330.30
1970 319.95 337.95
1971 343.35 360.00
1972 344.70 362.25
1973 342.00 360.90
1974 347.85 365.85
1975

Wir erhalten eine Matrix mit den 12 Monaten als Spalten und in den Zeilen die jeweiligen Jahr. Wenn du nicht im Januar startest, wie bei den CO\(_2\)-Daten, dann musst du das explizit angeben.

Die CO\(_2\)-Daten starten nicht im Januar sondern im März, so dass wir hier nochmal den Startpunkt ändern müssen. Ich zeige dir hier nicht die Ausgabe, weil die Matrix entschieden zu groß ist. Immerhin sind es ja fünfundsechzig Zeilen für die gesamte Zeitspanne.

R Code [zeigen / verbergen] 
co2_monthly_ts <- co2_monthly_tbl  %$%
  tk_ts(average, start = c(1958, 3), end = 2023, frequency = 12)

Ein ARIMA Modell setzt sich aus, wie oben schon vorgestellt, aus drei Komponenten wie folgt zusammen. Du kennst die Modelle und Konzepte schon aus der Einleitung dieses Abschnitts.

  1. Dem verwendeten Lag \(p\) der Zeitreihe (eng. autoregressiv model oder AR-Modell), die wir für die Berechnung der Autokorrelation der Zeitreihe nutzen.
  2. Der verwendeten Differenz \(d\), mit der wir unsere Zeitreihe anpassen.
  3. Der laufenden Durchschnitt \(q\) (eng. moving average model oder MA-Modell). Dies ist im Wesentlichen die Größe der “Fenster”-Funktion über die Zeitreihendaten. Ein MA-Prozess ist eine lineare Kombination von Fehlern aus der Vergangenheit oder eben das Modellieren des Rauschens.

Neben diesen Komponenten gibt es auch noch die saisonalen Komponenten, aber das überstiegt hier das Kapitel bei weitem. Insbesondere sei dir hier nochmal die Hilfe unter Tips to using auto_arima() empfohlen. Auf alle Details gehe ich dann hier nicht ein.

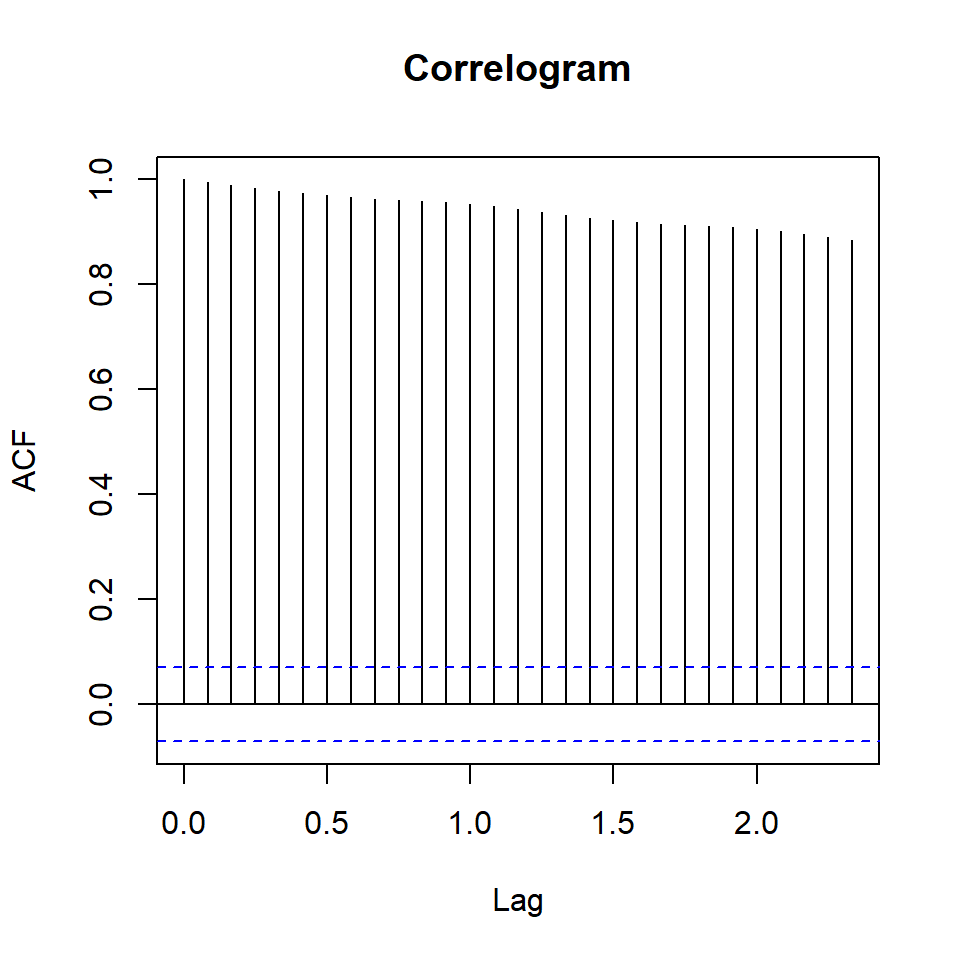
In den folgenden beiden Tabs findest du einmal die Korrelationsabbildungen für die Milchdaten wir auch die CO\(_2\)-Daten. Beachte bitte, dass die \(x\)-Achse etwas ungünstig formatiert ist. Die Lags werden nicht als ganzzahlig angezeigt sondern als seltsame Kommazahlen. Bitte schau dir auch die Funktion plot_acf_diagnostics() in der Abbildung 67.16 an, die Funktion ist um Welten besser. Auch hilft hier die Hilfeseite von {timetk} mit Plotting Seasonality and Correlation. Ja, die neueren Pakete können dann wirklich mehr. Insbesondere da wir hort dann auch das Paket {ploty} nutzen.

R Code [zeigen / verbergen] 
milk_ts |> 
  acf(main = 'Correlogram')

milk_ts |> 
  pacf(main = 'Partial Correlogram' )
(a) Correlogram.
(b) Partial Correlogram.
Abbildung 67.10— Korrelationsabbildungen der Lags über die Zeit für die Milchdaten. Wir sehen eine klaren zyklischen Verlauf, die sich über die Zeit ausdehnt. Das macht ja auch Sinn, den die Milchleistung wird auch von den Jahreszeiten abhängen. Bitte bachte, dass Lag 1.0 nicht das erste Lag beschreibt. Bei der partiziellen Korrelation beobachten wir, dass wir ebenfalls einen kurvigen Verlauf vorliegen haben.
R Code [zeigen / verbergen] 
co2_monthly_ts |> 
  acf(main = 'Correlogram')

co2_monthly_ts |> 
  pacf(main = 'Partial Correlogram' )
(a) Correlogram.
(b) Partial Correlogram.
Abbildung 67.11— Korrelationsabbildungen der Lags über die Zeit für die CO\(_2\)-Daten. Wir sehen, dass die Korrelation der Werte über die Zeit langsam abnimmt. Bitte bachte, dass Lag 1.0 nicht das erste Lag beschreibt. Dabei ist der erste Wert des Lag immer am stärksten mit seinem Nachbarn korreliert.

Mit der Funktion decompose() können wir uns anschauen, wie die Zeitreihe aufgebaut ist. Gibt es einen Trend? Haben wir einen saisonalen Effekt über die Zeit? Und wie sieht dann unser Rauschen aus, wenn wir den Trend und den saisonalen Effekt rausgerechnet haben?

R Code [zeigen / verbergen] 
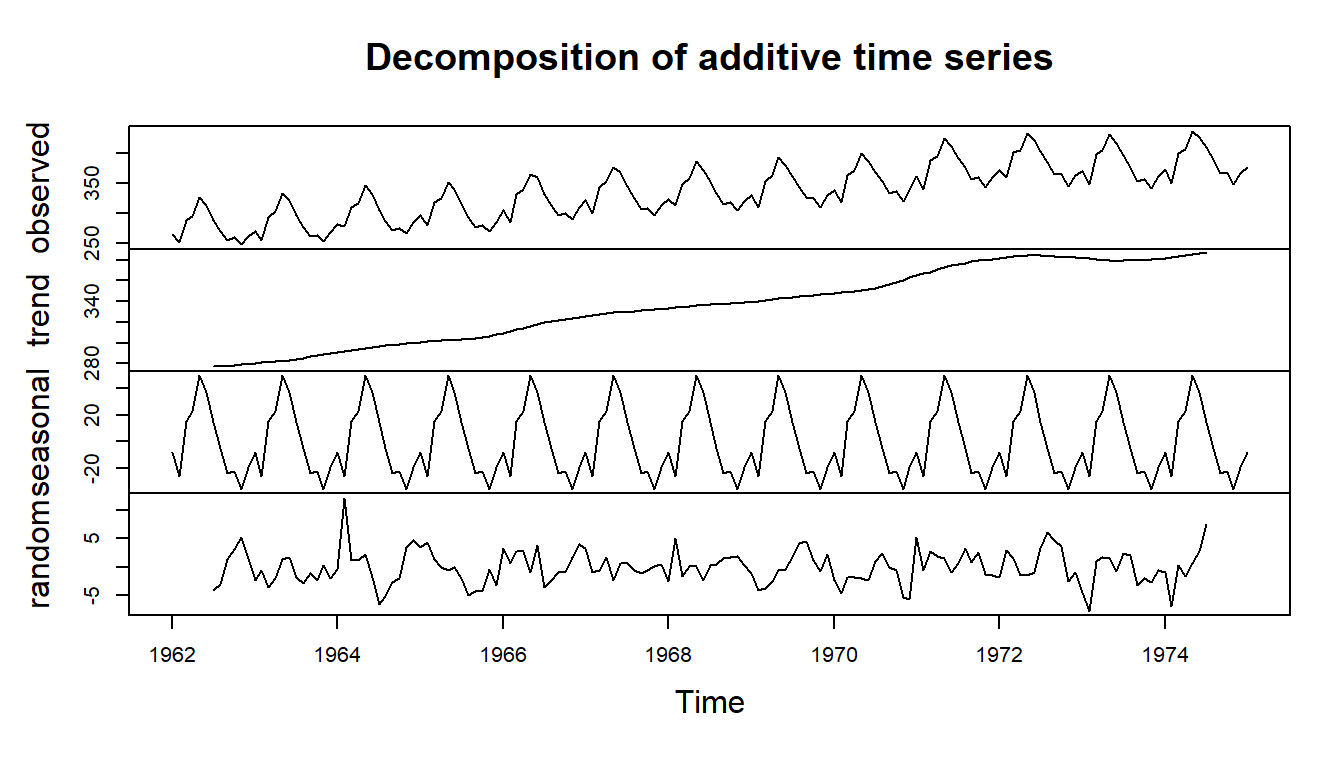
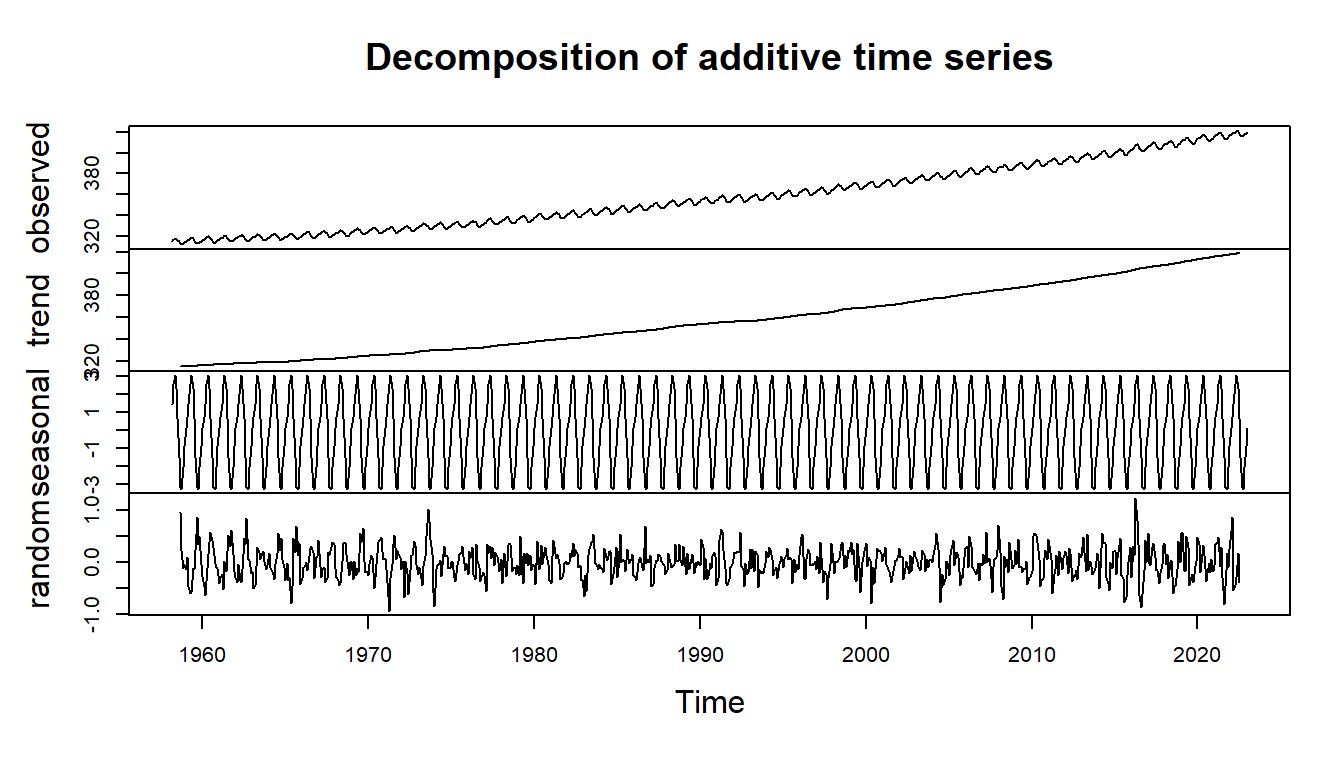
decomp_milk_obj <- decompose(milk_ts)
decomp_co2_obj <- decompose(co2_monthly_ts)

Wir wollen uns dann in den beiden Tabs dann einmal die Dekomposition der Zeitreihen anschauen. Wir werden die Ergebnisse jetzt nicht tiefer nutzen. Wir könnten an der Dekomposition unser armia()-Modell optimieren, aber wir sind hier gleich faul und nutzen einen automatischen Algorithmus.

R Code [zeigen / verbergen] 
plot(decomp_milk_obj)
Abbildung 67.12— Dekomposition der Zeitreihen der Milchdaten in dn Trend, den saisonalen Effekt sowie das Rauschen was übrig bleibt. Wir sehen einen klaren Trend in der Milchleitsung mit einem zyklischen Effekt über die Jahre.
R Code [zeigen / verbergen] 
plot(decomp_co2_obj)
Abbildung 67.13— Dekomposition der Zeitreihen der CO\(_2\)-Daten in dn Trend, den saisonalen Effekt sowie das Rauschen was übrig bleibt. Wir sehen einen klaren Trend in des CO\(_2\) Gehaltes mit einem zyklischen Effekt über die Jahre.

Dann können wir auch schon mit der Funktion auto.arima() unser Modell für die Vorhersage der Zeitreihen rechnen. Ich verweise hier nochmal auf das Tutorium Tips to using auto_arima(), wenn du tiefer in die Modellinterpretation einsteigen willst. Wir nutzen gleich einmal das Modell um dann unsere Prognose zu rechnen.

R Code [zeigen / verbergen] 
milk_arima_obj <- auto.arima(milk_ts)
milk_arima_obj
Series: milk_ts 
ARIMA(2,0,1)(2,1,1)[12] with drift 

Coefficients:
         ar1     ar2      ma1     sar1     sar2     sma1   drift
      0.7957  0.1309  -0.0896  -0.1313  -0.1141  -0.4901  0.7465
s.e.  0.3089  0.2774   0.3015   0.1681   0.1197   0.1563  0.1173

sigma^2 = 11:  log likelihood = -379.43
AIC=774.86   AICc=775.92   BIC=798.67
R Code [zeigen / verbergen] 
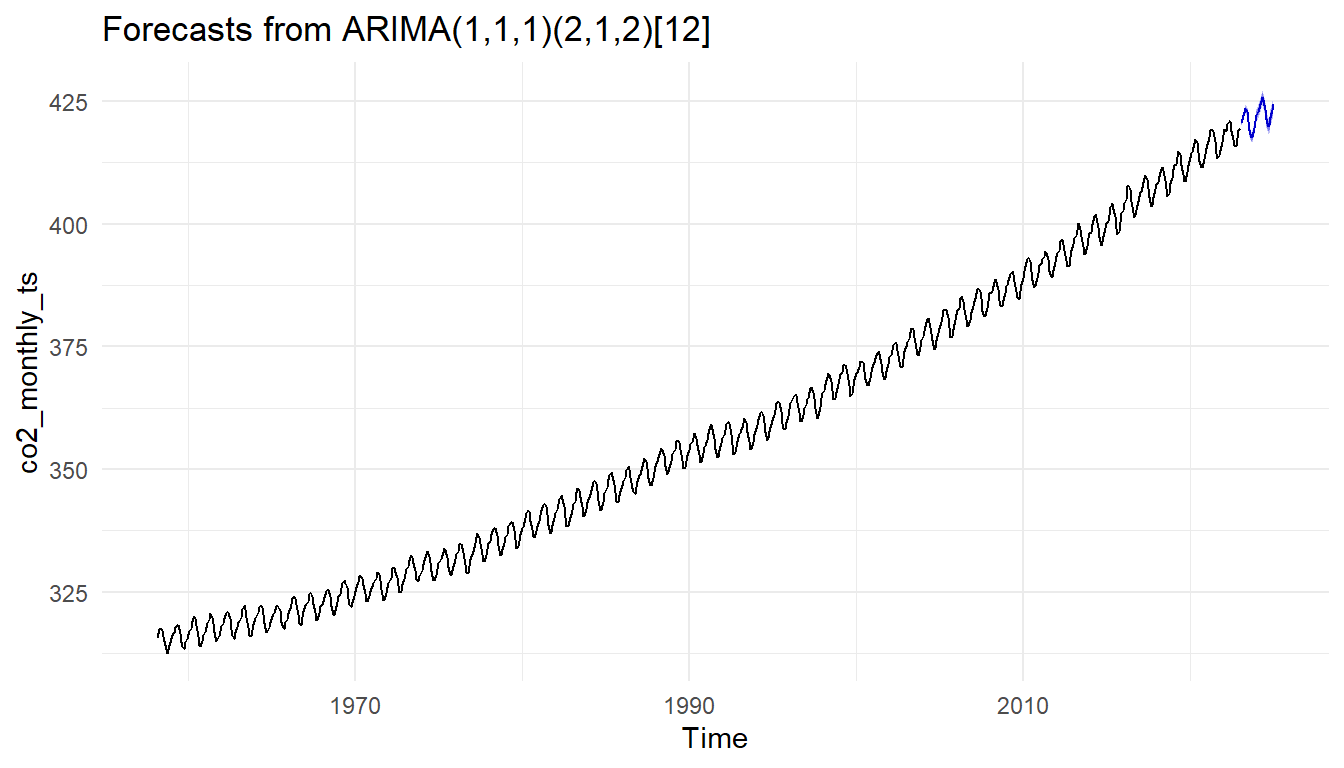
co2_arima_obj <- auto.arima(co2_monthly_ts)
co2_arima_obj
Series: co2_monthly_ts 
ARIMA(1,1,1)(2,1,2)[12] 

Coefficients:
         ar1      ma1     sar1     sar2     sma1     sma2
      0.2177  -0.5819  -0.3161  -0.0161  -0.5462  -0.2731
s.e.  0.0883   0.0740   1.6095   0.0421   1.6094   1.3910

sigma^2 = 0.1001:  log likelihood = -204.22
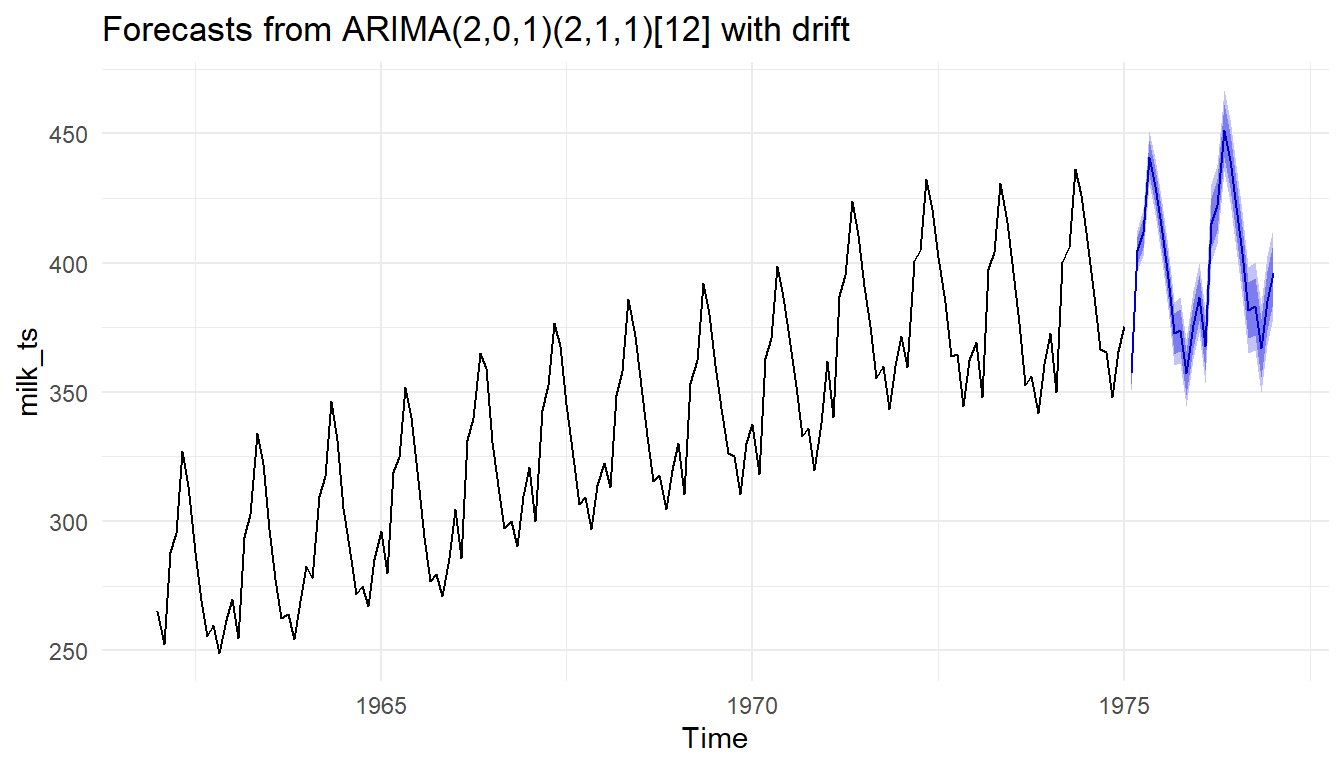
AIC=422.43   AICc=422.58   BIC=454.92

Die Funktion forecast() erlaubt uns über einen Zeitraum die folgenden Verläufe einer Zeitreihe aus einem ARIMA-Modell vorherzusagen. Ich habe mich hier einmal für zwei Jahre also 24 Monate entschieden. Tendenziell ist natürlich anzuraten nicht so weit in die Zukunft vorherzusagen, aber prinzipiell ist es technisch möglich. Aber Achtung, manchmal macht das Ergebnis biologisch keinen Sinn mehr. Irgendwann ist die Milchleistung von Kühen auch mal gedeckelt und mehr geht dann einfach nicht mehr.

R Code [zeigen / verbergen] 
milk_mdl <- forecast(milk_arima_obj, 24)
co2_mdl <- forecast(co2_arima_obj, 24)

In den Folgenden beiden Tabs siehst du dann einmal die Vorhersagen der weiteren zeitlichen Verläufen für die Milchleistung und den CO\(_2\) Gehalt in der Luft. Wir nutzen hier die Funktion auto_plot() die es uns direkt erlaubt eine Abbildung zu erstellen. Wir immer kannst du das Objekt natürlich auch mit str() zerlegen und dann deine eigene ggplot()-Abbildung bauen.

R Code [zeigen / verbergen] 
autoplot(milk_mdl) +
  theme_minimal()
Abbildung 67.14— Vorhersage der Milchleistung der Kühe für die nächsten zwei Jahre zusammen mit einem Fehlerbereich.
R Code [zeigen / verbergen] 
autoplot(co2_mdl) +
  theme_minimal()
Abbildung 67.15— Vorhersage der CO\(_2\)-Daten für die nächsten zwei Jahre zusammen mit einem Fehlerbereich.

67.4.2 mit {modeltime}

Am Ende hier nochmal eine Möglichkeit sehr effizient Zeitreihen mit dem R Paket {modeltime} zu modellieren und eine Vorhersage für zukünftige Verläufe zu machen. Ich empfehle hier die Hilfeseite Getting Started with {modeltime}. Auf der Seite erfährst du dann die Grundlagen für die Anwendung von dem R Paket {modeltime}. Hier kannst du dann tief in den Kaninchenbau reingehen. Wir machen hier nur die einfache Vorhersage ohne viel Schnickschnack. Neben dem R Paket {modeltime} findest du im Ökosystem {modeltime} noch andere spannende R Pakete, die dir weitere und vertiefende Modellierungen zur Vorhersage erlauben. Wenn dir die Begriffe zu der Vorhersage und der Klassifikation etwas komisch vorkommen, dann kannst du in dem Kapitel Grundlagen der Klassifikation reinschauen und nachlesen wo du dann noch Lücken hast. Ich gehe hier dann nicht mehr so tief auf die einzelnen Punkte ein, sondern führe hier eher grob durch den Code.

Wir konzentrieren uns hier jetzt nur auf die Milchdaten. Wenn du willst, kannst du den folgenden Code auch einfach für die CO\(_2\)-Daten anpassen und durchführen. Da wir auch eine lineare Regression auf den Daten durchführen wollen, muss ich nochmal das Datum in eine numerische Variable sowie einen Faktor für den Monat aufteilen. Aber ja, du kannst den ganzen Kram auch hier nur mit einer linearen Regression lösen, was auch irgendwie spannend ist, denn so ein lineares Modell ist auch wirklich ein einfaches Modell.

R Code [zeigen / verbergen] 
milk_tbl <- milk_tbl |> 
  mutate(month_fac = factor(month(month, label = TRUE), ordered = FALSE),
         month_num = as.numeric(month)) 
milk_tbl |> print(n = 7)
# A tibble: 168 × 4
  month      milk_prod_per_cow_kg month_fac month_num
  <date>                    <dbl> <fct>         <dbl>
1 1962-01-01                 265. Jan           -2922
2 1962-02-01                 252. Feb           -2891
3 1962-03-01                 288  Mar           -2863
4 1962-04-01                 295. Apr           -2832
5 1962-05-01                 327. May           -2802
6 1962-06-01                 314. Jun           -2771
7 1962-07-01                 288  Jul           -2741
# ℹ 161 more rows

In der Abbildung 67.16 siehst du die so viel besseren Korrelationsabbildungen der Lags für die Milchdaten. Wir sehen hier erstmal die richtige Bezeichnung auf der \(x\)-Achse und habe auch einen sehr weiten Verlauf. Dank {plotly} können wir dann auch die Werte in der Abbildung ablesen und einen Schluss daraus ziehen. Dementsprechend ist diese Art der Abbildung auf jeden Fall den anderen vorzuziehen. Hier ist das Paket {timetk} wirklich super gemacht.

R Code [zeigen / verbergen] 
milk_tbl |> 
  plot_acf_diagnostics(month, milk_prod_per_cow_kg)
Abbildung 67.16— Korrelationsabbildungen der Lags über die Zeit für die Milchdaten in {plotly}. Wir sehen eine klaren zyklischen Verlauf, die sich über die Zeit ausdehnt. Das macht ja auch Sinn, den die Milchleistung wird auch von den Jahreszeiten abhängen. Bei der partiziellen Korrelation beobachten wir, dass wir ebenfalls einen kurvigen Verlauf vorliegen haben, aber der Effekt sich auf die ersten Lags beschränkt.

Wenn wir jetzt eine Vorhersage rechnen wollen, dann müssen wir eigentlich unsere Daten in einen Trainings- und Testdatensatz aufteilen. Das machen wir hier mit der Funktion initial_time_split() die uns einen Trainings- und Testdatensatz baut. Wir wollen dann hier 90% der Daten in den Trainingsdaten haben und 10% in den Testdaten.

R Code [zeigen / verbergen] 
splits <- initial_time_split(milk_tbl, prop = 0.9)

Im Folgenden bauen wir uns dann einmal drei Modelle. Zum einen das auto.arima() Modell und lassen darauf unsere Trainsgdaten modellieren.

R Code [zeigen / verbergen] 
model_fit_arima_no_boost <- arima_reg() |>
    set_engine(engine = "auto_arima") |>
    fit(milk_prod_per_cow_kg ~ month, data = training(splits))

Damm nutzen wir noch ein anderes Modell mit exponential smoothing auf das wir hier nicht tiefer eingehen wollen.

R Code [zeigen / verbergen] 
model_fit_ets <- exp_smoothing() |>
    set_engine(engine = "ets") |>
    fit(milk_prod_per_cow_kg ~ month, data = training(splits))

Abschließen nutze ich noch ein lineares Modell und modelliere den Trend mit month_num und den Effekt der Saison mit month_fac. Schauen wir mal wie gut das Modell so ist.

R Code [zeigen / verbergen] 
model_fit_lm <- linear_reg() |>
    set_engine("lm") |>
    fit(milk_prod_per_cow_kg ~ month_num + month_fac,
        data = training(splits))

Dann packe ich alle Modelle einmal in einen Datensatz zusammen.

R Code [zeigen / verbergen] 
models_tbl <- modeltime_table(
    model_fit_arima_no_boost,
    model_fit_ets,
    model_fit_lm
)

Ich nutze nun die Funktion modeltime_calibrate() um auf die Modelle aus den Trainingsdaten einmal die Testdaten anzuwenden.

R Code [zeigen / verbergen] 
calibration_tbl <- models_tbl |>
    modeltime_calibrate(new_data = testing(splits))

Abschließend können wir uns in der Abbildung 67.17 einmal die Vorhersage aus den drei Modellen anschauen. Wir stellen mit erstaune fest, dass die lineare Regression gar nicht so schlecht abschneidet. Hier hilft dann vor allem einmal das Reinzoomen mit {plotly} sehr um sich die Unterschiede nochmal genauer anzuschauen. Am Ende packe ich noch meine Legende unter die Abbildung, damit die Abbildung nicht so gestaucht wird.

R Code [zeigen / verbergen] 
calibration_tbl |>
    modeltime_forecast(
        new_data = testing(splits),
        actual_data = milk_tbl
    ) |>
    plot_modeltime_forecast(
      .legend_max_width = 25, 
      .interactive = TRUE) |>
  plotly::layout(legend = list(orientation = "h",   
                               xanchor = "center",  
                               x = 0.5))
Abbildung 67.17— Vorhersageplot der drei Modelle für die Milchdaten dargestellt mit {plotly}.

Dann können wir uns in der Tabelle 67.2 nochmal die Gütezahlen ausgeben lassen, die wir aus der Klassifikation schon kennen. Ich habe dir dann gleich nochmal die Übersetzungen der Maßzahlen unter die Tabelle gepackt. Am Ende können wir uns hier verschiedene Maßzahlen anschauen und entscheiden welches Modell das beste Modell ist. Ich finde hier am spannendsten, dass unsere einfache lineare Regression gar nicht mal so schlecht abgeschnitten hat und ähnlich gute Fehlerwerte und ein Bestimmtheitsmaß hat, wie die anderen beiden Modelle, die um einiges komplizierter sind.

R Code [zeigen / verbergen] 
calibration_tbl |>
    modeltime_accuracy() |>
    table_modeltime_accuracy(
      .interactive = FALSE
    )
Tabelle 67.2— Gütezahlen für die Vorhersage der Testdaten auf den Modellen der Trainiungsdaten. Verschiedene Maßzahlen wie Fehler und das Bestimmtheitsmaß erlauben eine Bewertung der Modelle.
Accuracy Table
.model_id .model_desc .type mae mape mase smape rmse rsq
1 ARIMA(2,0,1)(2,1,1)[12] WITH DRIFT Test 12.03 3.13 0.68 3.08 13.02 0.97
2 ETS(A,A,A) Test 11.72 3.06 0.67 3.01 12.59 0.96
3 LM Test 15.51 4.06 0.88 3.97 16.30 0.96

Hier nochmal die Übersetzung der Maßzahlen und die Links zu den Hilfeseiten der entsprechenden Funktionen. Fehler sollten immer klein sein und somit ist ein kleiner Fehler bei einem Modell ein gutes Zeichen. Deshalb ist zum Beispiel das ETS Modell in unserem Fall zu bevorzugen, denn das Modell hat den geringsten Fehler über alle Fehlerarten.

  • MAE - Mean absolute error, mae()
  • MAPE - Mean absolute percentage error, mape()
  • MASE - Mean absolute scaled error, mase()
  • SMAPE - Symmetric mean absolute percentage error, smape()
  • RMSE - Root mean squared error, rmse()
  • RSQ - R-squared, rsq()

War es das schon? Nein, natürlich nicht. Das R Paket {modeltime} liefert noch mehr Modelle um deine Zeitreihe zu modellieren. Ebenso haben wir kein Refit durchgeführt, also die neuen Daten nochmal genutzt um das Modell noch besser zu machen. Darüber hinaus gibt es noch mehr Diagnosemöglichkeiten und Darstellungsformen. Aber das sprengt hier den Rahmen und ich entscheide mal, dass dieses Kapitel jetzt gut genug ist.

Referenzen

Chan K-S, Cryer JD. 2008. Time series analysis with applications in R. Springer.
Cowpertwait PS, Metcalfe AV. 2009. Introductory time series with R. Springer Science & Business Media.
Hyndman RJ, Athanasopoulos G. 2018. Forecasting: principles and practice. OTexts.
Robert H, others. 2006. Time Series Analysis and Its Applications With R Examples Second Edition.