Testen von Hypothesen

Letzte Änderung am 23. April 2024 um 10:31:50

“Das ist die Logik der Forschung, die nie verifizieren, sondern immer nur jene Erklärungen beibehalten kann, die beim derzeitigen Erkenntnisstand am wenigsten falsifiziert sind.” — Wößmann, L.

Das statistische Hypothesentesten - eine Geschichte voller Missverständnisse. Wir wollen uns in den folgenden Kapiteln mit den Grundlagen des frequentistischen Hypothesentestens beschäftigen. Wenn ich hier einen Unterschied mache, dann muss es ja auch noch ein anderes Hypothesentesten geben. Ja, das nennt man dann bayesianische Statistik und kommt eventuell mal später. Wir konzentrieren uns aber zuerst auf frequentistische Hypothesentesten was seit gut hundert Jahren genutzt wird. Beginnen wir mit der Logik der Forschung oder allgemeiner formuliert, als die Grundlage der Wissenschaft. Wir basieren all unsere Entscheidungen in der Wissenschaft auf dem Falsifikationsprinzip. Also bitte merken, wir können nur ablehnen (eng. reject). Wir ersetzen schlechte Modelle (der Wirklichkeit) durch weniger schlechte Modelle (der Wirklichkeit) – das ist die Logik der Forschung. Forschung basiert auf dem Falsifikationsprinzip. Wir können nur ablehnen und behalten das weniger schlechte Modell bei.

Wir wollen hier auf keinen Fall die Leistungen von Altvorderen schmälern. Dennoch hatten Ronald Fischer (1890 - 1962), als der Begründer der Statistik, andere Vorraussetzungen als wir heutzutage. Als wichtigster Unterschied sei natürlich das Gerät genannt, an dem du gerade diese Zeilen liest: dem Computer. Selbst die Erstellung einfachster Abbildungen war sehr, sehr zeitaufwendig. Die Berechnung von Zahlen lohnte sich mehr, als die Zahlen zu visualisieren. Insbesondere wenn wir die Explorative Datenanalyse nach John Tukey (1915 - 2000) durchführen. Undenkbar zu den Zeiten von Ronald Fischer mehrere Abbildungen unterschiedlich nach Faktoren einzufärben und sich die Daten anzugucken.

Neben dieser Begrenzung von moderner Rechenkapazität um 1900 gab es noch eine andere ungünstige Entwicklung. Stark vereinfacht formuliert entwickelte Ronald Fischer statistische Werkzeuge um abzuschätzen wir wahrscheinlich die Nullhypothese unter dem Auftreten der beobachteten Daten ist. Nun ist es aber so, dass wir ja auch eine Entscheidung treffen wollen. Nach der Logik der Forschung wollen wir ja eine Hypothese falsifizieren, in unserem Fall die Nullhypothese. Die Entscheidungsregeln, also die statistische Testtheorie, kommen nun von Jerzy Neyman (1894 - 1981) und Egon Pearson (1895 - 1980), beide als die Begründer der frequentistischen Hypothesentests.

Schlussendlich gibt es noch eine andere Strömung in der Statistik, die auf den mathematischen Formeln von Thomas Bayes (1701 - 1761) basieren. In sich eine geschlossene Theorie, die auf der inversen Wahrscheinlichkeit basiert. Das klingt jetzt etwas schräg, aber eigentlich ist die bayesianische Statistik die Statistik, die die Fragen um die Alternativehypothese beantwortet. Der Grund warum die bayesianische Statistik nicht angewendet wurde, war der Bedarf an Rechenleistung. Die bayesiansiche Statistik lässt sich nicht händisch in endlicher Zeit lösen. Dieses technische Problem haben wir aber nicht mehr. Eigentlich könnten wir also die bayesiansiche Statistik verwenden. Wir wollen hier aber (noch) nicht auf die bayesianische Statistik eingehen, das werden wir später tun. Wenn du allgemein Interesse hast an der Geschichte der Statistik dann sei auf Salsburg (2001) verwiesen. Ein sehr schönes Buch, was die geschichtlichen Zusammenhänge nochmal aufzeigt.

Wenn du mehr über die aktuellen Entwicklungen erfahren willst, dann ist Gigerenzer u. a. (2004) ein guter Einstieg. Zum Teil kommt Gigerenzer u. a. (2004) auch in meinen Vorlesungen vor, aber nicht explizit sondern eher als Hintergrundrauschen. Das wir ein Problem mit dem statistischen Testen und im Besonderen mit dem \(p\)-Wert haben, diskutiert Wasserstein u. a. (2019) als Eröffnungsartikel in der Artikelserie Statistical Inference in the 21st Century: A World Beyond p < 0.05. Aber das ist nun wirklich nur was für Interessierte.

Beispiel: Bin ich im Urlaub?

Hier nochmal zusammengefasst die Idee der frequentistischen Testtheorie anhand der Frage, ob ich im Urlaub bin. Du versteht die Idee vielleicht besser, wenn du dich einmal durch die folgenden Kapitel gearbeitet hast. Ja gearbeitet, nur lesen ist dann einfach zu wenig.

  • Bin ich im Urlaub?
  • Wie wahrscheinlich bin ich im Urlaub? \(Pr(U)\)
  • Wie wahrscheinlich bin ich nicht im Urlaub? \(Pr(\bar{U})\)
  • Wie wahrscheinlich sind wir nicht im Urlaub? \(Pr(\bar{U})\)
  • Wie wahrscheinlich ist es, die Daten \(D\) zu beobachten, wenn wir nicht im Urlaub sind? \(Pr(D|\bar{U})\)

Wir würden meinen, dass wir die Frage “Bin ich im Urlaub?” beantworten können. Das stimmt aber nicht. Durch das Falsifikationsprinzip können wir nur eine Aussage über “nicht-im-Urlaub-sein” treffen. Darüber hinaus können wir keine Entscheidungen per se treffen sondern erhalten eine Wahrscheinlichkeitsaussage. Um die Sachlage noch komplizierter zu machen, treffen wir Aussagen über eine Population. Also sind wir im nicht im Urlaub. Abschließend treffen wir eine Aussage über die beobachteten Daten und können dann eine Wahrscheinlichkeit berechnen diese Daten beobachtet zu haben, wenn wir nicht im Urlaub sind.

  1. Wir machen Aussagen über Wahrscheinlichkeiten!
  2. Wir machen Aussagen über Populationen!
  3. Wir machen Aussagen über den Nicht-Zustand/Keinen Effekt!

Die frequentistische Statistik basiert - wie der Name andeutet - auf Wiederholungen in einem Versuch. Daher der Name frequentistisch. Also eine Frequenz von Beobachtungen. Ist ein wenig gewollt, aber daran gewöhnen wir uns schon mal. Konkret, ein Experiment welches wir frequentistisch Auswerten wollen besteht immer aus biologischen Wiederholungen. Wir müssen also ein Experiment planen in dem wir wiederholt ein Outcome an vielen Tieren, Pflanzen oder Menschen messen. Auf das Outcome gehen wir noch später ein. Im Weiteren konzentrieren wir uns hier auf die parametrische Statistik. Die parametrische Statistik beschäftigt sich mit Parametern von Verteilungen.

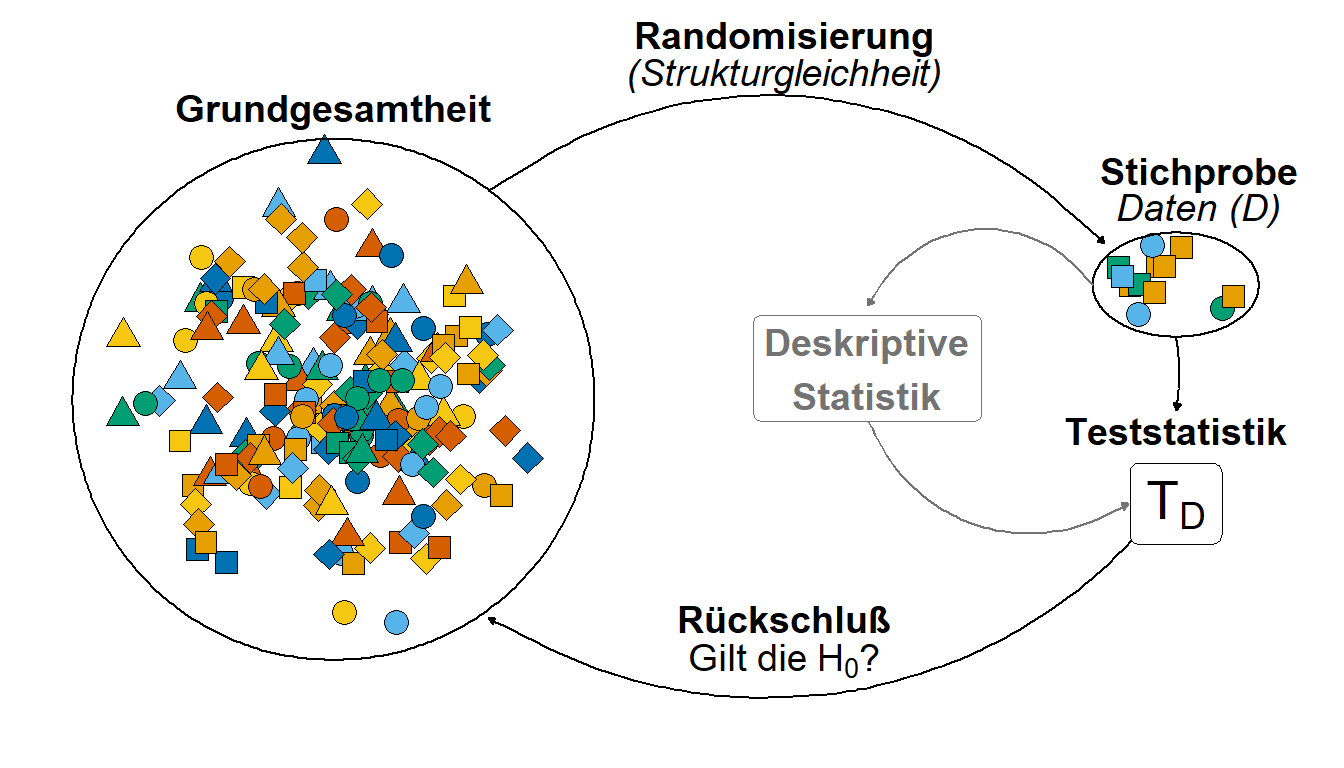
Nehmen wir das Beispiel, dass wir die Sprungweite von Hunde- und Katzenflöhen vergleichen wollen. Wir können nicht alle Hunde- und Katzenflöhe messen. Wir können nur eine Stichprobe an Daten \(D\) erheben. Über diese Daten \(D\) können wir dann später durch statistische Algorithmen eine Aussage treffen. Wichtig ist hier sich zu merken, dass wir eine Grundgesamtheit haben aus der wir eine Stichprobe ziehen. Wir müssen darauf achten, dass die Stichprobe repräsentativ ist und damit strukturgleich zur Grundgesamtheit ist. Die Strukturgleichkeit erreichen wir durch Randomisierung. Wir veranschaulichen diesen Zusammenhang in Abbildung 1. Ein Rückschluss von der Stichprobe ist nur möglich, wenn die Stichprobe die Grundgesamtheit repräsentiert. Auch eine Randomisierung mag dieses Ziel nicht immer erreichen. Im Beispiel der Hundeflöhe könnte wir eine Art an Flöhen übersehen und diese Flohart nicht mit in die Stichprobe aufnehmen. Ein Rückschluß auf diese Flohart wäre dann mit unserem Experiment nicht möglich.

Abbildung 1— Abbildung über die Grundgesamtheit und der Stichprobe \(D\). Durch Randomisierung wird Sturkturgleichheit erreicht, die dann einen Rückschluß von der Stichprobe auf die Grundgesamtheit erlaubt. Jede Stichprobe ist anders und nicht jede Randomisierung ist erfolgreich was die Strukturgleicheit betrifft. Die Berechnung der Teststatistik \(T_D\) aus den Daten \(D\) erfolgt nicht direkt sondern über statistische Maßzahlen aus der deskriptiven Statistik. [Zum Vergrößern anklicken]

Tabelle 1 zeigt nochmal die Zusammenfassung von der Grundgesamtheit un der Stichprobe im Vergleich. Wichtig ist zu merken, dass wir mit unserem kleinen Experiment Daten \(D\) generieren mit denen wir einen Rückschluß und somit eine Verallgemeinerung erreichen wollen.

Tabelle 1— Vergleich von Grundgesamtheit und Stichprobe.
Grundgesamtheit Stichprobe
… \(n\) ist riesig bis unfassbar. … \(n_1\) von \(D_1\) ist klein.
… der Mittelwert wird mit \(\mu_y\) beschrieben. … der Mittelwert wird mit \(\bar{y}\) beschrieben.
… die Varianz wird mit \(\sigma^2\) beschrieben. … die Varianz wird mit \(s^2\) beschrieben.
… die Standardabweichung wird mit \(\sigma\) beschrieben. … die Standardabweichung wird mit \(s\) beschrieben.

Referenzen

Gigerenzer G, Krauss S, Vitouch O. 2004. The null ritual. The Sage handbook of quantitative methodology for the social sciences 391–408.
Salsburg D. 2001. The lady tasting tea: How statistics revolutionized science in the twentieth century. Macmillan.
Wasserstein RL, Schirm AL, Lazar NA. 2019. Moving to a world beyond „p< 0.05“. The American Statistician 73: 1–19.