21 Die Testtheorie
Letzte Änderung am 03. September 2024 um 11:29:22
“My god, it’s full of stars” — Stanley Kubrick, 2001: A Space Odyssey
In diesem Kapitel wollen wir uns nochmal tiefer mit der Testtherorie und dem \(\alpha\)-Fehler und der \(\beta\)-Fehler beschäftigen. Was heißt eigentlich einseitig oder zweiseitig Testen? Auch müssen wir nochmal einen Blick auf das mutliple Testen und die \(\alpha\)-Adjustierung werfen.
Wir können auf allen Daten einen statistischen Test rechnen und erhalten statistische Maßzahlen wie eine Teststatistik, einen p-Wert oder ein 95% Konfidenzintervall. Wie wir aus dem vorherigen Kapitel wissen testet jeder statistische Test eine Nullhypothese. Ob diese zu testende Nullhypothese dem Anwender nun bekannt ist oder nicht, ein statistischer Test testet eine Nullhypothese. Daher müssen wir uns immer klar sein, was die entsprechende Nullhypothese zu unserer Fragestellung ist. Manchmal ist das gar nicht so klar und die Nullhypothese zu einer Fragestellung zu finden ist auch nicht einfach. Hier musst du vermutlich etwas überlegen oder dir Hilfe suchen.
Wiederholen wir nochmal was eine statistische Hypothese ist. Eine statistische Hypothese ist eine Aussage über einen Parameter einer Population. Die Nullhypothese \(H_0\) nennen wir auch die Null oder Gleichheitshypothese. Die Nullhypothese sagt aus, dass zwei Gruppen gleich sind oder aber kein Effekt zu beobachten ist. In diesem Beispiel sind die beiden Mittelwerte gleich.
\[ H_0: \bar{y}_{1} = \bar{y}_{2} \]
Die Alternativehypothese \(H_A\) oder \(H_1\) auch Alternative genannt nennen wir auch Unterschiedshypothese. Die Alternativehypothese besagt, dass ein Unterschied vorliegt oder aber ein Effekt vorhanden ist. In diesem Beispiel unterscheiden sich die beiden Mittelwerte.
\[ H_A: \bar{y}_{1} \neq \bar{y}_{2} \]
Das Falisifkationsprinzip - wir können nur Ablehnen - kommt hier zusammen mit der frequentistischen Statistik in der wir nur eine Wahrscheinlichkeitsaussage über das Auftreten der Daten \(D\) - unter der Annahme \(H_0\) gilt - treffen können. Es ist wichtig sich in Erinnerung zu rufen, dass wir nur und ausschließlich Aussagen über die Nullhypothese treffen können. Das frequentistische Hypothesentesten kann nichts anders. Wir kriegen keine Aussage über die Alternativhypothese sondern nur eine Abschätzung der Wahrscheinlichkeit des Auftretens der Daten im durchgeführten Experiment, wenn die Nullhypothese wahr wäre.
21.1 Der \(\alpha\)-Fehler und der \(\beta\)-Fehler
Vielleicht ist die Idee der Testtheorie und der Testentscheidung besser mit der Analogie des Rauchmelders zu verstehen. Wir nehmen an, dass der Rauchmelder der statistische Test ist. Der Rauchmelder hängt an der Decke und soll entscheiden, ob es brennt oder nicht. Daher muss der Rauchmelder entscheiden, die Nullhypothese “kein Feuer” abzulehnen oder die Hypothese “kein Feuer” beizubehalten.
\[ \begin{aligned} H_0&: \mbox{kein Feuer im Haus} \\ H_A&: \mbox{Feuer im Haus} \\ \end{aligned} \]
Wir können jetzt den Rauchmelder so genau einstellen, dass der Rauchmelder bei einer Kerze losgeht. Oder aber wir stellen den Rauchmelder so ein, dass er erst bei einem Stubenbrand ein Piepen von sich gibt. Wie sensibel auf Rauch wollen wir den Rauchmelder einstellen? Soll der Rauchmelder sofort die Nullhypothese ablehnen? Wenn also nur eine Kerze brennt. Soll also der \(\alpha\)-Fehler groß sein? Erinnere dich, mit einem großen \(\alpha\)-Fehler würden wir mehr Nullhypothesen ablehnen oder anders gesprochen leichter die Nullhypothese ablehnen. Wir würden ja den \(\alpha\)-Fehler zum Beispiel von 5% auf 20% setzen können. Das wäre nicht sehr sinnvoll. Die Feuerwehr würde schon bei einer Kerze kommen oder wenn wir mal was anbrennen. Wir dürfen also den \(\alpha\)-Fehler nicht zu groß einstellen.
Intuitiv würde man meinen, ein sehr kleiner \(\alpha\)-Fehler nun sinnvoll sei. Wenn wir aber den Rauchmelder sehr unsensibel einstellen, also der Rauchmelder erst bei sehr viel Rauch die Nullhypothese ablehnt, könnte das Haus schon unrettbar in Flammen stehen. Dieser Fehler, Haus steht in Flammen und der Rauchmelder geht nicht, wird als \(\beta\)-Fehler bezeichnet. Wie du siehst hängen die beiden Fehler miteinander zusammen. Wichtig hierbei ist immer, dass wir uns einen Zustand vorstellen, das Haus brennt nicht (\(H_0\) ist wahr) oder das Haus brennt nicht (\(H_A\) ist wahr). An diesem Zustand entscheiden wir dann, wie hoch der Fehler jeweils sein soll diesen Zustand zu übersehen.
Der \(\alpha\)-Fehler und \(\beta\)-Fehler als Rauchmelderanalogie
Häufig verwirrt die etwas theoretische Herangehensweise an den \(\alpha\)-Fehler und \(\beta\)-Fehler. Wir versuchen hier nochmal die Analogie eines Rauchmelders und dem Feuer im Haus.
- \(\boldsymbol{\alpha}\)-Fehler
-
Alarm without fire. Der statistische Test schlägt Alarm und wir sollen die \(H_0\) ablehnen, obwohl die \(H_0\) in Wahrheit gilt und kein Effekt vorhanden ist.
- \(\boldsymbol{\beta}\)-Fehler
-
Fire without alarm. Der statistische Test schlägt nicht an und wir sollen die \(H_0\) beibehalten, obwohl die \(H_0\) in Wahrheit nicht gilt und ein Effekt vorhanden ist.
Wie sieht nun die Lösung, erstmal für unseren Rauchmelder, aus? Wir müssen Grenzen für den \(\alpha\) und \(\beta\)-Fehler festlegen bei denen der Rauchmelder angeht und wir die Feuerwehr rufen.
- Wir setzen den \(\alpha\)-Fehler auf 5%. Somit haben wir in 1 von 20 Fällen das Problem, dass uns der Rauchmelder angeht obwohl gar kein Feuer da ist. Wir lehnen die Nullhypothese ab, obwohl die Nullhypothese gilt.
- Auf der anderen Seite setzen wir den \(\beta\)-Fehler auf 20%. Damit brennt uns die Bude in 1 von 5 Fällen ab ohne das der Rauchmelder einen Pieps von sich gibt. Wir behalten die Nullhypothese bei, obwohl die Nullhypothese nicht gilt.
Nachdem wir uns die Testentscheidung mit der Analogie des Rauchmelders angesehen haben, wollen wir uns wieder der Statistik zuwenden. Betrachten wir das Problem nochmal von der theoretischen Seite mit den statistischen Fachbegriffen.
Soweit haben wir es als gegeben angesehen, dass wir eine Testentscheidung durchführen. Entweder mit der Teststatistik, dem \(p\)-Wert oder dem 95% Konfidenzintervall. Immer wenn wir eine Entscheidung treffen, können wir auch immer eine falsche Entscheidung treffen. Wie wir wissen hängt die berechnete Teststatistik \(T_{D}\) nicht nur vom Effekt \(\Delta\) ab sondern auch von der Streuung \(s\) und der Fallzahl \(n\). Auch können wir den falschen Test wählen oder Fehler im Design des Experiments gemacht haben. Schlussendlich gibt es viele Dinge, die unsere simple mathematischen Formeln beeinflussen können, die wir nicht kennen. Ein frequentistischer Hypothesentest gibt immer nur eine Aussage über die Nullhypothese wieder. Also ob wir die Nullhypothese ablehnen können oder nicht.
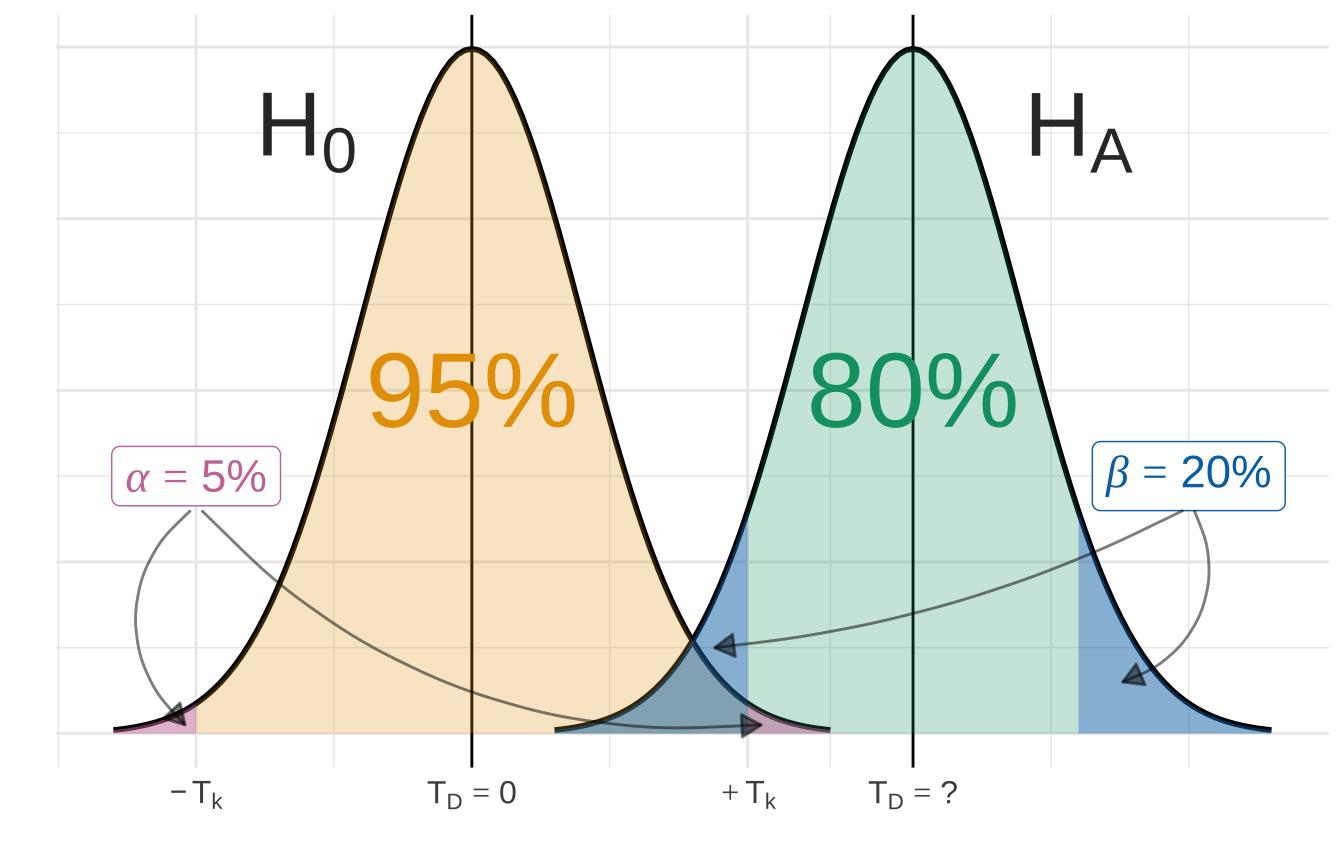
Abbildung 21.2 zeigt die theoretische Verteilung der Nullyhypothese und der Alternativehypothese. Wenn die beiden Verteilungen sehr nahe beieinander sind, wird es schwer für den statistischen Test die Hypothesen klar voneinander zu trennen. Die Verteilungen überlappen. Es gibt einen sehr kleinen Unterschied in den Sprungweiten zwischen Hunde- und Katzenflöhen. In dem Beispiel wurde der gesamte \(\alpha\)-Fehler auf die rechte Seite gelegt. Das macht die Darstellung etwas einfacher.
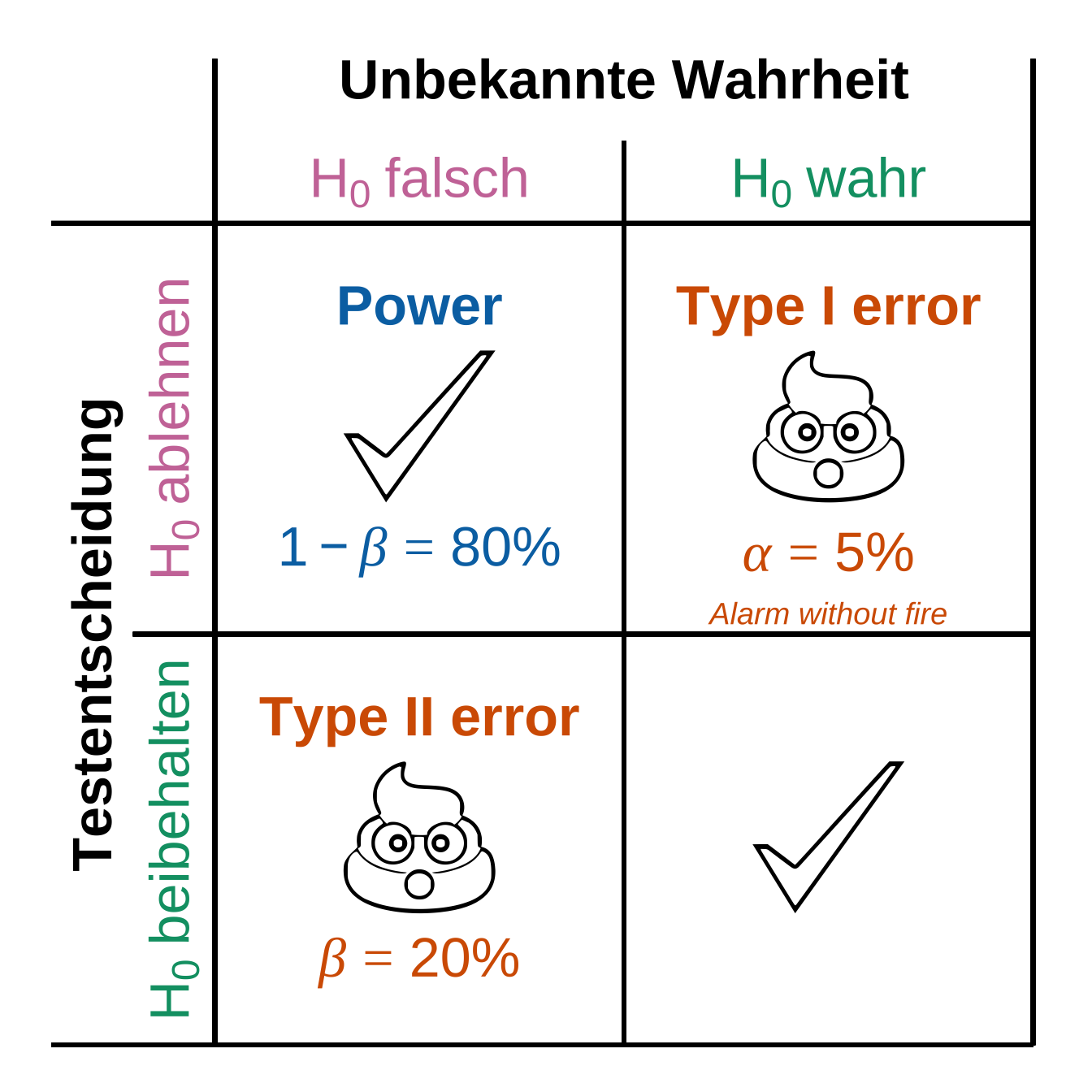
Wir können daher bei statistischen Testen zwei Arten von Fehlern machen. Zum einen den \(\alpha\) Fehler oder auch Type I Fehler (eng. type I error) genannt. Zum anderen den \(\beta\) Fehler oder auch Type II Fehler (eng. type II error) genannt. Die Grundidee basiert darauf, dass wir eine Testentscheidung gegen die Nullhypothese machen. Diese Entscheidung kann richtig sein, da in Wirklichkeit die Nullhypothese gilt oder aber falsch sein, da in Wirklichkeit die Nullhypothese nicht gilt. In der Regression wird uns auch wieder das \(\beta\) als Symbol begegnen. In der statistischen Testtheorie ist das \(\beta\) ein Fehler; in der Regression ist das \(\beta\) ein Koeffizient der Regression. Hier ist der Kontext wichtig. In Abbildung 21.3 wird der Zusammenhang in einer 2x2 Tafel veranschaulicht.
Beide Fehler sind Kulturkonstanten. Das heißt, dass sich diese Zahlen von 5% und 20% so ergeben haben. Es gibt keinen rationalen Grund diese Zahlen so zu nehmen. Prinzipiell schon, aber die Gründe leigen eher in der Anwendbarkeit von feststehenden Tabellen vor der Entwicklung des Computers. Man kann eigentlich sagen, dass die 5% und die 20% eher einem Zufall entsprungen sind, als einer tieferen Rationalen. Wir behalten diese beiden Zahlen bei aus den beiden schlechtesten Gründe überhaupt: i) es wurde schon immer so gemacht und ii) viele machen es so. Die Diskussion über den \(p\)-Wert und dem Vergleich mit dem \(\alpha\)-Fehler wird in der Statistik seit 2019 verstärkt diskutiert (Wasserstein u. a. 2019). Das Nullritual wird schon lamge kritisiert (Gigerenzer u. a. 2004). Siehe dazu auch The American Statistician, Volume 73, Issue sup1 (2019).
Eine weitere wichtige statistische Maßzahl im Kontext der Testtheorie ist die \(Power\) oder auch \(1-\beta\). Die \(Power\) ist die Gegenwahrscheinlichkeit von dem \(\beta\)-Fehler. In der Analogie des Rauchmelders wäre die \(Power\) daher Alarm with fire. Das heißt, wie wahrscheinlich ist es einen wahren Effekt - also einen Unterschied - mit dem statistischen Test auch zu finden. Oder anders herum, wenn wir wüssten, dass die Hunde- und Katzenflöhe unterschiedliche weit springen, mit welcher Wahrscheinlichkeit würde diesen Unterschied ein statistischer Test auch finden? Mit eben der \(Power\), also gut 80%. Tabelle 21.1 zeigt die Abhängigkeit der \(Power\) vom Effekt \(\Delta\), der Streuung \(s\) und der Fallzahl \(n\). Die \(Power\) ist eine Wahrscheinlichkeit und sagt nichts über die Relevanz des Effektes aus.
| \(\boldsymbol{Power (1-\beta)}\) | \(\boldsymbol{Power (1-\beta)}\) | ||
|---|---|---|---|
| \(\Delta \uparrow\) | steigt | \(\Delta \downarrow\) | sinkt |
| \(s \uparrow\) | sinkt | \(s \downarrow\) | steigt |
| \(n \uparrow\) | steigt | \(n \downarrow\) | sinkt |
21.2 Einseitig oder zweiseitig?
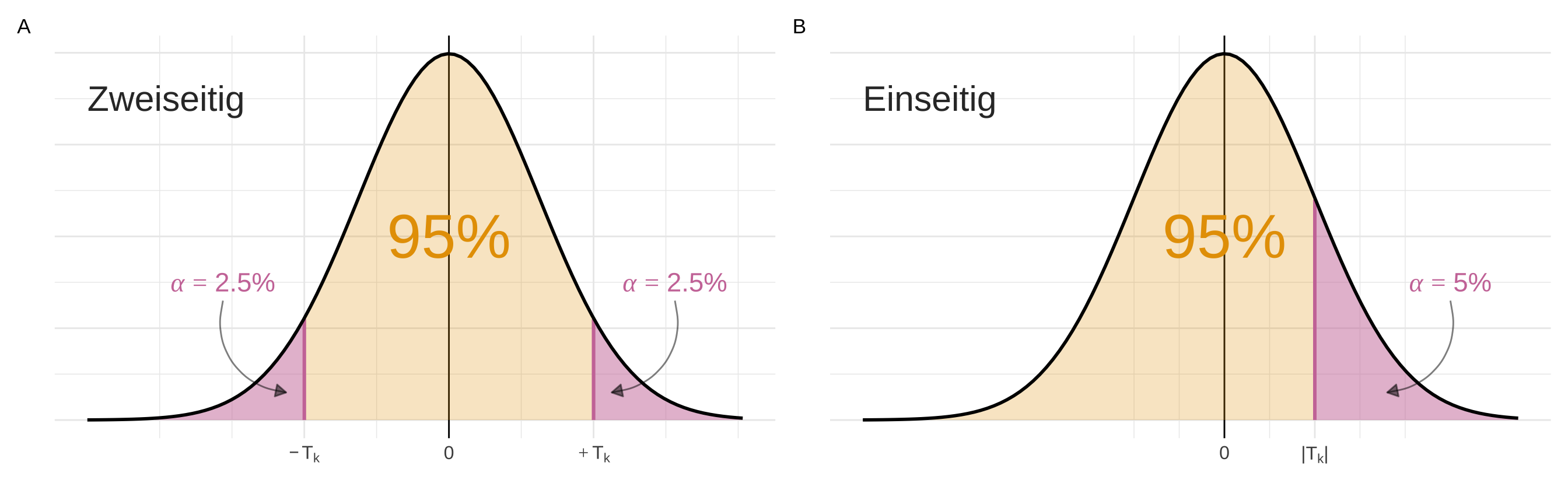
Manchmal kommt die Frage auf, ob wir einseitig oder zweiseitig einen statistischen Test durchführen wollen. Beim Fall des zweiseitigen Testens verteilen wir den \(\alpha\)-Fehler auf beide Seiten der Testverteilung mit jeweils \(\alpha/2\). In dem Fall des einseitigen Tests liegt der gesamte \(\alpha\)-Fehler auf der rechten oder linken Seite der Testverteilung. In Abbildung 21.4 wird der Zusammenhang beispielhaft an der t-Verteilung gezeigt.
In der Anwendung testen wir immer zweiseitig. Der Grund ist, dass das Vorzeichen von der Teststatik davon abhängt, welche der beiden Gruppen den größeren Mittelwert hat. Da wir die Mittelwerte vor der Auswertung nicht kennen, können wir auch nicht sagen in welche Richtung der Effekt und damit die Teststatistik laufen wird.
Es gibt theoretisch Gründe, die für ein einseitiges Testen unter bestimmten Bedingungen sprechen, aber wir nutzen in der Anwendung nur das zweiseite Testen. Wir müssen dazu in R auch nichts weiter angeben. Ein durchgeführter statistischer Test in R testet automatisch immer zweiseitig.
Einseitig oder zweiseitig im Spiegel der Regulierungsbehörden
In den allgemeinen Methoden des IQWiG, einer Regulierungsbehörde für klinische Studien, wird grundsätzlich das zweiseitige Testen empfohlen. Wenn einseitig getestet werden sollte, so soll das \(\alpha\)-Niveau halbiert werden. Was wiederum das gleiche wäre wie zweiseitiges Testen - nur mit mehr Arbeit.
Zur besseren Vergleichbarkeit mit 2-seitigen statistischen Verfahren wird in einigen Guidelines für klinische Studien eine Halbierung des üblichen Signifikanzniveaus von 5 % auf 2,5 % gefordert. – Allgemeine Methoden Version 6.1 vom 24.01.2022, p. 180
21.3 Adjustierung für multiple Vergleiche
Im Kapitel 40 werden wir mehrere multiple Gruppenvergleiche durchführen. Das heißt, wir wollen nicht nur die Sprungweite von Hunde- und Katzenflöhen miteinander vergleichen, sondern auch die Sprungweite von Hunde- und Fuchsflöhen sowie Katzen- und Fuchsflöhen. Wir würden also \(k = 3\) t-Tests für die Mittelwertsvergleiche rechnen.
Dieses mehrfache Testen führt aber zu einer Inflation des \(\alpha\)-Fehlers oder auch Alphafehler-Kumulierung genannt. Daher ist die Wahrscheinlichkeit, dass mindestens eine Nullhypothese fälschlicherweise abgelehnt wird, nicht mehr durch das Signifikanzniveau \(\alpha\) kontrolliert, sondern kann sehr groß werden.
Gehen wir von einer Situation mit \(k\) Null- und Alternativhypothesen aus. Wir rechnen also \(k\) statistische Tests und alle Nullhypothesen werden zum lokalen Niveau \(\alpha_{local} = 0.05\) getestet. Im Weiteren nehmen wir an, dass tatsächlich alle Nullhypothesen gültig sind. Wir rechnen also \(k\) mal einen t-Test und machen jedes mal einen 5% Fehler Alarm zu geben, obwohl kein Effekt vorhanden ist.
Die Wahrscheinlichkeit für einen einzelnen Test korrekterweise \(H_0\) abzulehnen ist \((1 − \alpha)\). Da die \(k\) Tests unabhängig sind, ist die Wahrscheinlichkeit alle \(k\) Tests korrekterweise abzulehnen \((1 − \alpha)^k\). Somit ist die Wahrscheinlichkeit, dass mindestens eine Nullhypothese fälschlicherweise abgelehnt wird \(1-(1-\alpha)^k\). In der Tabelle 21.2 wird dieser Zusammenhang nochmal mit Zahlen für verschiedene \(k\) deutlich.
| Anzahl Test \(\boldsymbol{k}\) | \(\boldsymbol{1-(1-\alpha)^k}\) |
|---|---|
| 1 | 0.05 |
| 2 | 0.10 |
| 10 | 0.40 |
| 50 | 0.92 |
Aus Tabelle 21.3 können wir entnehmen, dass wenn 100 Hypothesen getestet werden, werden 5 Hypothesen im Schnitt fälschlicherweise abgelehnt. Die Tabelle 21.3 ist nochmal die Umkehrung der vorherigen Tabelle 21.2.
| Anzahl Test \(\boldsymbol{k}\) | \(\boldsymbol{\alpha \cdot k}\) |
|---|---|
| 1 | 0.05 |
| 20 | 1 |
| 100 | 5 |
| 200 | 10 |
Nachdem wir verstanden haben, dass wiederholtes statistisches Testen irgendwann immer ein signifikantes Ergebnis produziert, müssen wir für diese \(\alpha\) Inflation unsere Ergebnisse adjustieren. Ich folgenden stelle ich verschiedene Adjustierungsverfahren vor.
Wie können wir nun die p-Werte in R adjustieren? Zum einen passiert dies teilweise automatisch zum anderen müssen wir aber wissen, wo wir Informationen zu den Adjustierungsmethoden finden. Die Funktion p.adjust() ist hier die zentrale Anlaufstelle. Hier finden sich alle implementierten Adjustierungsmethoden in R.
Im folgenden Code erschaffen wir uns 50 \(z\)-Werte von denen 25 aus einer Normalverteilung \(\mathcal{N}(0, 1)\) und 25 aus einer Normalverteilung mit \(\mathcal{N}(3, 1)\) kommen. Die Fläche unter allen Normalverteilungen ist Eins, da die Standatdabweichung Eins ist. Wir berechnen die \(p-Wert\) anhand der Fläche rechts von dem \(z\)-Wert. Wir testen zweiseitig, deshalb multiplizieren wir die \(p\)-Werte mit Zwei. Diese \(p\)-Werte können wir nun im Folgenden für die Adjustierung nutzen.
R Code [zeigen / verbergen]
z <- rnorm(50, mean = c(rep(0, 25), rep(3, 25)))
p <- 2*pnorm(sort(-abs(z)))Über die eckigen Klammern [] und das : können wir uns die ersten zehn p-Werte wiedergeben lassen.
R Code [zeigen / verbergen]
p[1:10] |> round(5) [1] 0.00000 0.00001 0.00007 0.00009 0.00027 0.00050 0.00124 0.00251 0.00324
[10] 0.00442Wir sehen, dass die ersten fünf p-Werte hoch signifikant sind. Das würden wir auch erwarten, immerhin haben wir ja auch 25 \(z\)-Werte mit einem Mittelwert von Drei. Du kannst dir den \(z\)-Wert wie den \(t\)-Wert der Teststatistik vorstellen.
21.3.1 Bonferroni Korrektur
Die Bonferroni Korrektur ist die am weitesten verbreitete Methode zur \(\alpha\) Adjustierung, da die Bonferroni Korrektur einfach durchzuführen ist. Damit die Wahrscheinlichkeit, dass mindestens eine Nullhypothese fälschlicherweise abgelehnt wird beim simultanen Testen von \(k\) Hypothesen durch das globale (und multiple) Signifikanzniveau \(\alpha = 5\%\) kontrolliert ist, werden die Einzelhypothesen zum lokalen Signifikanzniveau \(\alpha_{local} = \tfrac{\alpha_{5\%}}{k}\) getestet.
Dabei ist das Problem der Bonferroni Korrektur, dass die Korrektur sehr konservativ ist. Wir meinen damit, dass das tatsächliche globale (und multiple) \(\sum\alpha_{local}\) Niveau liegt deutlich unter \(\alpha_{5\%}\) und somit werden die Nullhypothesen zu oft beibehalten.
Adjustierung des \(\boldsymbol{\alpha}\)-Fehlers
- Das globale \(\alpha\)-Level wird durch die Anzahl \(k\) an durchgeführten statistischen Tests geteilt.
- \(\alpha_{local} = \tfrac{\alpha}{k}\) für die Entscheidung \(p < \alpha_{local}\)
Adjustierung des \(\boldsymbol{p}\)-Wertes
- Die p-Werte werden mit der Anzahl an durchgeführten statistischen Tests \(k\) multipliziert.
- \(p_{adjust} = p_{raw} \cdot k\) mit \(k\) gleich Anzahl der Vergleiche.
- wenn \(p_{adjust} > 1\), wird \(p_{adjust}\) gleich 1 gesetzt, da \(p_{adjust}\) eine Wahrscheinlichkeit ist.
Wir schauen uns die ersten zehn nach Bonferroni adjustierten p-Wert nach der Anwendung der Funktion p.adjust() einmal an.
R Code [zeigen / verbergen]
p.adjust(p, "bonferroni")[1:10] |> round(3) [1] 0.000 0.000 0.004 0.005 0.014 0.025 0.062 0.126 0.162 0.221Nach der Adjustierung erhalten wir weniger signifikante \(p\)-Werte als vor der Adjustierung. Wir sehen aber, dass wir weit weniger signifikante Ergebnisse haben, als wir eventuell erwarten würden. Wir haben immerhin 25 \(z\)-Werte mit einem Mittelwert von Drei. Nach der Bonferroni-Adjustierung hgaben wir nur noch sechs signifikante \(p\)-Werte.
21.3.2 Benjamini-Hochberg
Die Benjamini-Hochberg Adjustierung für den \(\alpha\)-Fehler wird auch Adjustierung nach der false discovery rate (abk. FDR) bezeichnet. Meistens werden beide Namen synoym verwendet, der Trend geht jedoch hin zur Benennung mit der Abkürzung FDR. In der Tabelle 21.4 sehen wir einmal ein Beispiel für die FDR Adjustierung. Die Idee ist, dass wir uns für jeden der \(m\) Vergleiche eine eigene lokale Signifikanzschwelle \(\alpha_{local}\) berechnen. Dafür rangieren wir zuerst unsere Vergleiche nach dem \(p\)-Wert. Der kleinste \(p\)-Wert kommt zuerst und dann der Rest der anderen \(p\)-Werte. Wir berechnen jedes lokale Signifkanzniveau mit \(\alpha_{local} =(i/m)\cdot Q\). Dabei steht das \(i\) für den jeweiligen Rang und das \(m\) für unsere Anzahl an Vergleichen. In unserem Beispiel haben wir \(m = 25\) Vergleiche. Jetzt kommt der eugentlich spannende Teil. Wir können jetzt \(Q\) als unsere false discovery rate selber wählen! In unserem Beispiel setzen wir die FDR auf 25%. Es geht aber auch 20% oder 10%. Wie du möchtest.
In der letzten Spalte der Tavbelle siehst du die Entscheidung, ob eine Variable noch signifkant ist oder nicht. Wir entscheiden nach folgender Regel. Der fettgedruckte p-Wert für den fertilizer ist der höchste p-Wert, der auch kleiner mit \(0.042 < 0.050\) als der kritische Wert ist. Alle darüber liegenden Werte und damit diejenigen mit niedrigeren p-Werten werden hervorgehoben und als signifikant betrachtet, auch wenn diese p-Werte unter den kritischen Werten liegen. Beispielsweise sind N und sun einzeln nicht signifikant, wenn Sie das Ergebnis mit der letzten Spalte vergleichen. Mit der FDR-Korrektur werden sie jedoch als signifikant angesehen.
| Variable | \(\boldsymbol{Pr(D|H_0)}\) | Rang (\(\boldsymbol{i}\)) | \(\boldsymbol{(i/m)\cdot Q}\) | |
|---|---|---|---|---|
| fe | 0.001 | 1 | \(1/25 \cdot 0.25 = 0.01\) | s. |
| water | 0.008 | 2 | \(2/25 \cdot 0.25 = 0.02\) | s. |
| N | 0.039 | 3 | \(3/25 \cdot 0.25 = 0.03\) | s. |
| sun | 0.041 | 4 | \(4/25 \cdot 0.25 = 0.04\) | s. |
| fertilizer | 0.042 | 5 | \(5/25 \cdot 0.25 = 0.05\) | s. |
| infected | 0.060 | 6 | \(6/25 \cdot 0.25 = 0.06\) | n.s. |
| wind | 0.074 | 7 | \(7/25 \cdot 0.25 = 0.07\) | n.s. |
| S | 0.205 | 8 | \(8/25 \cdot 0.25 = 0.08\) | n.s. |
| … | … | … | … | … |
| block | 0.915 | 25 | \(25/25 \cdot 0.25 = 0.25\) | n.s. |
Die adjustierten \(p\)-Werte nach der Benjamini-Hochberg-Prozedur ist etwas umständlicher, deshalb benutzen wir hier die Funktion p.adjust() in R und erhalten damit die adjustierten \(p\)-Werte wieder.
R Code [zeigen / verbergen]
p.adjust(p, "BH")[1:10] |> round(3) [1] 0.000 0.000 0.001 0.001 0.003 0.004 0.009 0.016 0.018 0.022Mit der Bonferroni Adjustierung und der FDR Adjustierung haben wir zwei sehr gute Möglichkeiten für das multiple Testen zu korrigieren. Die FDR Korrektur wird häufiger in der Genetik bzw. Bioinformatik eingesetzt. In dem Kontext kommt auch die recht ähnliche Benjamini & Yekutieli (abk. BY) Adjustierung vor. Die Benjamini & Yekutieli unterscheidet sich aber nur in Nuancen unter bestimmten Rahmenbedingungen von der FDR Adjustierung. Wir lassen den statistischen Engel hier mal am Straßenrand stehen und wenden uns der letzten Adjustierung zu.
21.3.3 Dunn-Sidak
Die Sidak Korrektur berechnet das lokale Signifikanzniveau \(\alpha_{local}\) auf folgende Art und Weise. Wir haben ein globales \(\alpha\) von 5%. Das \(\alpha_{local}\) berechnen wir indem wir die Anzahl der Vergleiche \(m\) wie folgt miteinander verbinden.
\[ \alpha_{local} = 1 - (1 - \alpha)^{\tfrac{1}{m}} \]
Die Sidak Korrektur ist weniger streng als die Bonferroni-Korrektur, aber das auch nur sehr geringfügig. Zum Beispiel beträgt für \(\alpha = 0.05\) und \(m = 10\) das Bonferroni-bereinigte lokale Signifikanzniveau \(\alpha_{local} = 0.005\) und das nach Sidak Korrektur ungefähr \(0.005116\). Das ist jetzt auch kein so großer Unterschied. Wir finden die Sidak Korrektur dann im R Paket {emmeans} für die Adjustierung bei den multiplen Vergleichen wieder.
Referenzen
Gigerenzer G, Krauss S, Vitouch O. 2004. The null ritual. The Sage handbook of quantitative methodology for the social sciences 391–408.
Wasserstein RL, Schirm AL, Lazar NA. 2019. Moving to a world beyond „p< 0.05“. The American Statistician 73: 1–19.