30  Die ANOVA

Letzte Änderung am 15. April 2025 um 14:10:10

“Yeah, I might seem so strong; Yeah, I might speak so long; I’ve never been so wrong.” — London Grammar, Strong

Die ANOVA (eng. analysis of variance) ist wichtig. Was für ein schöner Satz um anzufangen. Historisch betrachtet ist die ANOVA, das statistische Verfahren was gut per Hand ohne Computer berechnet werden kann. Daher war die ANOVA von den 20zigern bis in die frühen 90ziger des letzten Jahrhunderts das statistische Verfahren der Wahl. Wir brauchen daher die ANOVA aus mehreren Gründen. Die Hochzeiten der ANOVA sind eigentlich vorbei, wir haben in der Statistik für viele Fälle mittlerweile besser Werkzeuge, aber als Allrounder ist die ANOVA immer noch nutzbar. Insbesondere wenn wir uns mit einem faktoriellen Design beschäftigen, dann komt die Stärke der ANOVA voll zu tragen. Da wir in den agrarwissenschaften eben dann doch sehr viele Feldexperimente in einem faktoriellen Design vorliegen haben, hat auch die ANOVA ihren Platz in der praktischen Auswertung. Wir werden immer wieder in diesem Buch auf die ANOVA inhaltlich zurück kommen und in vielen Abschlussarbeiten wird die ANOVA immer noch als integraler Bestandteil genutzt.

Der ANOVA Pfad

“Patience, my children; one hour of suffering will bring more true happiness than a whole life of pleasure.” — The Pathfinder

Ich nenne es immer liebevoll den ANOVA Pfad, was wir hier mit der ANOVA machen. Wir wollen eigentlich einen multiplen Gruppenvergleich rechnen. Dafür führen wir folgende Schritte durch.

1. Wir erstellen uns ein Modell mit einem Messwert \(y\) und mindestens einem Faktor \(f\).
2. Wir rechnen auf dem Modell eine ANOVA um herauszufinden ob wir einen signfikanten Unterschied in den Gruppen vorliegen haben.
3. Wir rechnen einen Post-hoc Test um die signifikanten paarweisen Vergleiche in den Gruppen zu finden.

Das ganze machen wir dann für jeden unserer Messwerte.

Was findest du in diesem Übersichtskapitel zur ANOVA? Wir werden uns in diesem Kapitel auf die einfaktorielle ANOVA (eng. one-way ANOVA) sowie die zweifaktorielle ANOVA (eng. two-way ANOVA) konzentrieren. Ich gehe dann auch noch auf ein mehrfaktorielles Modell ein. In dem Kapitel zur ANCOVA findest du dann alle Informationen, wenn du zusärtzlich zu deinen Faktoren noch eine numerische Kovariate mit in dein Modell nehmen willst. Häufig wird die ANOVA auch verwendet, wenn du Messwiederholungen in deinen Daten vorliegen hast. Hierfür habe ich dann das Kapitel zur repeated & mixed ANOVA geschrieben, wo du dann einmal schauen musst. Am Ende kommt dann noch das Kapitel zur multivariate ANOVA, wenn du simultan mehr als einen Messwert \(y\) in dein Modell nehmen willst. Wie immer, du musst dann schauen, was zu deiner wissenschaftlichen Fragetstellung passt.

30.1 Allgemeiner Hintergrund

Fangen wir also mit der zentralen Idee der ANOVA an und arbeiten uns dann vor. Du kannst gerne den allgemeinen wie auch den theoretischen Teil überspringen und dir gleich das passende Datenbeispiel für deine Fragestellung raussuchen. Der Teil hier vorab dient nur dem tieferen Verständnis und du brauchst es eigentlich nicht um einfach nur eine ANOVA anzuwenden und ein Ergebnis zu erhalten. Da ist die ANOVA ziemlich gut zu interpretieren und anzuwenden. Wir fangen hier jetzt aber einmal an uns eine grundsätzliche Frage über unser experimentellen Versuch zu stellen.

Ist eine hohe Varianz in dem Messwert \(\boldsymbol{y}\) zu vermeiden?

Es gibt eigentlich zwei Fehlannahmen (eng. misconception) an die ANOVA. Zum einen, dass die ANOVA die Varianzen vergleichen würde. Das stimmt nur bedingt. Die Nullhypothese der ANOVA ist die Gleichheit der Mittelwerte in den Gruppen. Zum anderen, dass wenig Varianz in den Messwerten \(y\) per se gut wäre und ein angestrebtes Ziel in einem geplanten Feldexperiment.

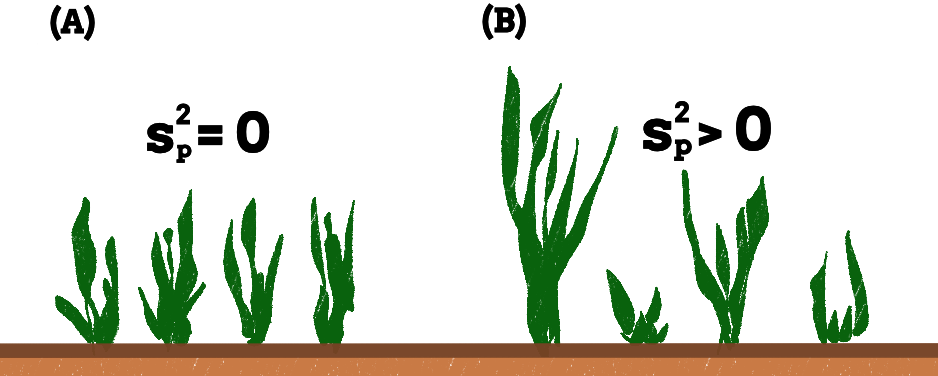
In der folgenden Abbildung siehst du einmal vier Maisspflanzen mit jeweils einer Behandlung für ein gesteigertes Wachstum. In der linken Abbildung haben wir eine geringe Varianz und damit auch gleiche Mittelwerte. Die Behandlungen haben überhaupt keinen Einfluß auf den Wuchs. In der rechten Abbildung siehst du eine hohe Varianz, weil eben die Behandlungen einen Effekt auf das Wachstum haben. Wenn du also ein geplantes Experiment mit Kontrolle und Behandlungen durchführst, dann erwartest du eine hohe Varianz in dem Messwert \(y\). Ansonsten würde deine Behandlung überhaupt nicht wirken.

Abbildung 30.1— Feldexperiment mit vier Behandlungen zur Steigerung der Wuchshöhe von Maispflanzen. Jede Pflanze stellt vereinfacht eine Behandlung dar. (A) Die gepoolte Varianz \(s^2_p\) über die Gruppen ist klein (\(s^2_p=0\)), die Behandlungen haben keinen Effekt auf das Wachstum. (B) Die gepoolte Varianz \(s^2_p\) über die Gruppen ist groß (\(s^2_p>0\)), die Behandlungen haben einen Effekt auf das Wachstum der Maisspflanzen.

Arbeiten wir uns nun einmal durch die Themen der Hypothesen sowie der Idee des faktoriellen Modells. Wir brauchen eine Idee des faktoriellen Modells um die verschiednen Typen der ANOVA unterscheiden zu können. Teilweise sind es eben dann nur Erweiterungen des immer gleichen Grundgerüst. Dann schauen wir nochmal auf die Voraussetzungen der ANOVA an deine Daten. Zum einen mit dem Fokus auf die Normalverteilung deines Messwert \(y\) und zum anderen die Varianzhomogenität in deinen Faktoren. Bevor wir dann nochmal als Einschub die Theorie behandlen, stelle ich dir R Pakete vor, die dir die ANOVA rechnen können.

Das Modell

Beginnen wir also mit der Festlegung welche Art der Analyse wir rechnen wollen. Wichtig ist hier, dass du einen normmalverteiten Messwert \(y\) vorliegen hast und ein oder mehrere Faktoren \(f\). Was sind im Kontext von R Faktoren? Ein Faktor ist eine Behandlung oder eben eine Spalte in deinem Datensatz, der verschiedene Gruppen oder Kategorien beinhaltet. Wir nennen diese Kategorien Level. In den folgenden Datenbeispielen ist die Spalte animal ein Faktor mit drei Leveln. Wir haben dort nämlich die Sprungweiten von drei Floharten gemessen. Jetzt kann es aber auch sein, dass du neben einem Faktor noch eine numeriche Kovariate \(c\) gemessen hast. Oder aber du hast zwei Messwerte, die du dann gemeinsam mit einem Faktor vergleichen willst. Diese drei Analysetypen wollen wir uns in den folgenden Tabs mal näher anschauen.

ANOVA (faktoriell)

Das faktorielle Modell der klassischen ANOVA beinhaltet einen Messwert \(y\), der normalverteilt ist. Darüber hinaus haben wir noch ein bis mehrere Faktoren \(f\). Wir bezeichnen hier die Faktoren mit den Indizes \(A\), \(B\) und \(C\) und die jeweiligen Level des Faktors \(A\) als \(A.1, A.2,..., A.k\). Häufig haben wir aber zwei Faktoren in einem Modell mit zwei bis fünf Leveln. Aber hier gibt es sicherlich auch noch Fragestellungen mit mehr Gruppen und damit Leveln in einem Faktor. Wir schreiben ein faktorielles Modell wie folgt.

\[ y \sim f_A + f_B + ... + f_P + f_A \times f_B + ... + f_A \times f_B \times f_C \]

mit

• \(y\) gleich dem Messwert oder Outcome
• \(f_A + f_B + ... + f_P\) gleich experimenteller Faktoren
• \(f_A \times f_B\) gleich einem beispielhaften Interaktionsterm erster Ordnung
• \(f_A \times f_B \times f_C\) gleich einem beispielhaften Interaktionsterm zweiter Ordnung

Zusätzlich können noch Interaktionsterme höherer Ordnungen entstehen, aber hier wird es extrem schwierig diese Interaktionsterme dann auch zu interpretieren. Ich würde grundsätzlich vermeiden Interaktionen zweiter und höherer Ordnungen mit ins Modell zu nehmen. Was genau eine Interaktion ist, besprechen wir in einem folgenden Abschnit. Um eine Interaktion beobachten zu können, brauchst du aber mindestens zwei Faktoren in deiner Analyse.

ANCOVA (faktoriell und numerisch)

Wenn wir neben einem bis mehreren Faktoren \(f\) noch eine numerische Kovariate \(c\) mit modellieren wollen, dann nutzen wir die ANCOVA (eng. Analysis of Covariance). Hier kommt dann immer als erstes die Frage, was heißt den Kovariate \(c\)? Hier kannst du dir eine numerische Variable vorstellen, die ebenfalls im Experiment gemessen wird. Es kann das Startgewicht oder aber die kummulierte Wassergabe sein. Wir haben eben hier keinen Faktor als Kategorie vorliegen, sondern eben etwas numerisch gemessen. Daher ist unsere Modellierung etwas anders.

\[ y \sim f_A + f_B + ... + f_P + f_A \times f_B + c_1 + ... + c_p \]

mit

• \(y\) gleich dem Messwert oder Outcome
• \(f_A + f_B + ... + f_P\) gleich experimenteller Faktoren
• \(f_A \times f_B\) gleich einem beispielhaften Interaktionsterm erster Ordnung
• \(c_1 + ... + c_p\) gleich einer oder mehrer numerischer Kovariaten

Hier muss ich gleich die Einschränkung machen, dass wir normalerweise maximal ein zweifaktorielles Modell mit einem Faktor \(A\) und einem Faktor \(B\) sowie einer Kovariate \(c\) betrachten. Sehr selten haben wir mehr Faktoren oder gar Kovariaten in dem Modell. Wenn das der Fall sein sollte, dann könnte eine andere Modellierung wie eine multiple Regression eine bessere Lösung sein. Mehr Informationen zur der Berechnung findest du in dem Kapitel zur ANCOVA

MANOVA (multivariat)

Am Ende des Kapitels schauen wir uns noch einen weiteren Spezialfall an. Nämlich den Fall, dass wir nicht nur einen Messwert \(y\) vorliegen haben sondern eben mehrere die wir simultan auswerten wollen. Das klingt jetzt erstmal etwas schräg, aber es wird dann klarer, wenn wir uns die Sachlage einmal an einem Beispiel anschauen.

\[ (y_1, y_2, ..., y_j) \sim f_A + f_B + ... + f_P + f_A \times f_B \]

mit

• \((y_1, y_2)\) gleich der Messwerte oder Outcomes
• \(f_A + f_B + ... + f_P\) gleich experimenteller Faktoren
• \(f_A \times f_B\) gleich einem beispielhaften Interaktionsterm erster Ordnung

Die ganze multivariate Analyse ist dann etwas seltener, da wir hier dann doch schon einiges an Fallzahl brauchen, damit es dann auch einen Sinn macht. Einiges an Fallzahl heißt dann hier, dass wir dann schon mehr als sechs Beobachtungen in einer Gruppe haben sollten. Wenn du weniger hast, kann es sein, dass du keine signifikanten Unterschiede findest. Mehr Informationen zur der Berechnung findest du in dem Kapitel zur MANOVA

Daneben gibt es natürlich noch Spezialfälle wie die gemischte ANOVA (eng. mixed ANOVA), wenn wir Beobachtungen wiederholt messen. Dieses Modell schauen wir uns dann auch nochmal an. Der Unterschied in der Modellierung ist ein Fehlerterm (eng. Error), den wir dann nochmal mit angeben müssen. Dazu dann aber mehr in dem Kapitel zur repeated & mixed ANOVA.

Hypothesen

Wenn wir von der ANOVA sprechen, dann kommen wir natürlich nicht an den Hypothesen vorbei. Die ANOVA ist ja auch ein klassischer statistischer Test. Hier müssen wir unterscheiden, ob wir eine Behandlung mit zwei Gruppen, also einem Faktor \(A\) mit \(2\) Leveln vorliegen haben. Oder aber eine Behandlung mit drei oder mehr Gruppen vorliegen haben, also einem Faktor \(A\) mit \(\geq 3\) Leveln in den Daten haben. Da wir schnell in einer ANOVA mehrere Faktoren haben, haben wir auch schnell viele Hypothesen zu beachten. Jeweils ein Hypothesenpaar pro Faktor muss dann betrachtet werden. Das ist immer ganz wichtig, die Hypothesenpaare sind unter den Faktoren mehr oder minder unabhängig.

Faktor mit \(2\) Leveln

Bei einem Faktor \(A\) mit nur zwei Leveln \(A.1\) und \(A.2\) haben wir eine Nullhypothese, die du schon aus den Gruppenvergleichen wie dem t-Test kennst. Wir wollen zwei Mittelwerte vergleichen und in unserer Nullhypothese steht somit die Gleichheit. Da wir nur zwei Gruppen haben, sieht die Nullhypothese einfach aus.

\[ H_0: \; \bar{y}_{A.1} = \bar{y}_{A.2} \]

In der Alternativehypothese haben wir dann den Unterschied zwischen den beiden Mittelwerten. Wenn wir die Nullhypothese ablehnen können, dann wissen wir auch welche Mittelwertsunterschied signifikant ist. Wir haben ja auch nur einen Unterschied getestet.

\[ H_A: \; \bar{y}_{A.1} \neq \bar{y}_{A.2} \] Das Ganze wird dann etwas komplexer im Bezug auf die Alternativehypothese wenn wir mehr als zwei Gruppen haben. Hier kommt dann natürlich auch die Stärke der ANOVA zu tragen. Eben mehr als zwei Mittelwerte vergleichen zu können.

Faktor mit \(\geq 3\) Leveln

Die klassische Nullhypothese der ANOVA hat natürlich mehr als zwei Level. Hier einmal beispielhaft die Nullhypothese für den Vergleich von drei Gruppen des Faktors \(A\). Wir wollen als Nullhypothese testen, ob alle Mittelwerte der drei Gruppen gleich sind.

\[ H_0: \; \bar{y}_{A.1} = \bar{y}_{A.2} = \bar{y}_{A.3} \]

Wenn wir die Nullhypothese betrachten dann sehen wir auch gleich das Problem der Alternativehypothese. Wir haben eine Menge an paarweisen Vergleichen. Wenn wir jetzt die Nullhypothese ablehnen, dann wissen wir nicht welcher der drei paarweisen Mittelwertsvergleiche denn nun unterschiedlich ist. Praktisch können es auch alle drei oder eben zwei Vergleiche sein.

\[ \begin{aligned} H_A: &\; \bar{y}_{A.1} \ne \bar{y}_{A.2}\\ \phantom{H_A:} &\; \bar{y}_{A.1} \ne \bar{y}_{A.3}\\ \phantom{H_A:} &\; \bar{y}_{A.2} \ne \bar{y}_{A.3}\\ \phantom{H_A:} &\; \mbox{für mindestens einen Vergleich} \end{aligned} \]

Wenn wir die Nullhypothese abgelhent haben, dann müssen wir noch einen sogenannten Post-hoc Test anschließen um die paarweisen Unterschiede zu finden, die dann signifikant sind. Das ganze machen wir dann aber in einem eigenen Kapitel zum Post-hoc Test.

Normalverteilung und Varianzhomogenität

“Soll ich’s wirklich machen oder lass ich’s lieber sein? Jein…” — Fettes Brot, Jein

Wenn wir die ANOVA nutzen wollen, dann kommen wir um die Voraussetzungen der Normalverteilung an den Messwert \(y\) sowie die Varianzhomogenität in den Faktorleveln oder Behandlungsgruppen \(f\) nicht herum. In dem Kapitel zum Pre-Test oder Vortest gehe ich nochmal detailierter auf mögliche Tests auf die Normalverteilung und die Varianzhomogenität ein. In diesem Kapitel findest du in dem Abschnitt Test auf Normalverteilung und Varianzhomogenität einmal ein Vorgehen für das Testen der Annahmen. Ich würde davon allgemein abraten, aber es wird immer wieder verlangt, also stelle ich es hier auch vor. Kurzfassung, die ANOVA ist realtiv robust gegen eine Abweichung von der Normalverteilung der Messwerte. Ebenso kann die ANOVA mit leichter Varianzheterogenität umgehen.

Häufig kommt jetzt die Frage, ob mein Messwert \(y\) wirklich normalverteilt ist und ich nicht den Messwert auf Normalverteilung testen sollte. Die kurze Antwort lautet nein, da du meistens zu wenig Beobachtungen pro Gruppe vorliegen hast. Die etwas längere liefert Kozak und Piepho (2018) mit dem Artikel What’s normal anyway? Residual plots are more telling than significance tests when checking ANOVA assumptions.

Kommen wir nun zur Varianzhomogenität oder Varianzhterogenität in den Gruppen des Behandlunsgfaktors. Wir betrachten also meistens nur den wichtigen Faktor \(f_A\) und ignorieren ein wenig den zwieten Faktor. Prinzipiell kannst du natürlich auch den zweiten Fakto anschauen, aber dann werden es immer mehr Gruppen und Fakotrkombinationen. Am Ende kommt dann sowieso heraus, dass über alle Gruppen hinweg keine homogenen Varianzen vorliegen. Wenn du mehr lesen willst so gibt es auf der Seite DSFAIR noch einen Artikel zu {emmeans} und der Frage Why are the StdErr all the same?

Wann liegt vermutlich Varianzheterogenität in deinen experimentellen Faktoren \(f\) vor?

Es gibt so ein paar Daumenregeln, die dir helfen abzuschätzen, ob in deinen Gruppen Varianzheterogenität vorliegt. Um es kurz zu machen, vermutlich hast du mindestens leichte Varianzhterogenität in den Daten vorliegen.

1. Du hat viele Behandlungsgruppen. Je mehr Gruppen du hast oder eben dann auch Faktorkombinationen, die du testen möchtest, desto wahrscheinlicher wird es, dass mindestens eine Gruppe eine unterschiedliche Varianz hat. Du hast Varianzheterogenität vorliegen.
2. Du misst deine Gruppen über die Zeit. Je größer, schwerer oder allgemein höher ein Messwert wird, desto größer wird auch die Varianz. Schaust du dir deine Messwerte über die Zeit an hast du meistens Varianzheterogenität vorliegen.
3. Deine Kontrolle ohne Behandlung verhält sich meistens nicht so, wie die Gruppen, die eine Behandlung erhalten haben. Wenn du nichts machst in deiner negativen Kontrolle, dann hast du meistens eine andere Streuung der Messwerte als unter einer Behandlung.
4. Diene Behandlungen sind stark unterschiedlich. Wenn deine Behandlungen sich biologisch oder chemisch in der Wirkung unterscheiden, denn werden vermutlich deine Messwerte auch anders streuen. Hier spielt auch die Anwendung der Behandlung und deren Bereitstellung eine Rolle. Wenn was nicht gleich ist, dann wird es vermutlich nicht gleiche Messwerte erzeugen.
5. Du hast wenig Fallzahl pro Gruppe oder Faktorkombination. Wenn du wenig Fallzahl in einer Gruppe hast, dann reicht schon eine (zufällige) Messabweichung und schon sind deine Varianzen heterogen.

Gut, jetzt wissen wir, dass du vermutlich Varianzheterogenität in deinen Daten vorliegen hast. Erstmal ist das kein so großes Problem.

Tut Varianzhterogenität anstatt Varianzhomogenität weh?

Nein. Meistens ist die Varianzheterogenität nicht so ausgeprägt, dass du nicht auch eine ANOVA rechnen kannst. Über alle Gruppen hinweg wird dann zwar in einer ANOVA die Varianz gemmittelt und es kann dann zu weniger signifkanten Ergebnissen führen, aber so schlimm ist es nicht. Im Post-hoc Test solltest du aber die Varianzhterogenität berücksichtigen, da du ja immer nur zwei Gruppen gleichzeitig betrachtest.

Welche Pakete gibt es eigentlich?

Wenn um die Anwendung der ANOVA in R geht, dann haben wir eine Menge Pakete zur Auswahl. Wie immer macht die Fragestellung und das gewählte Modell den Großteil der Entscheidungsindung aus. Ich zeige dir später in der Anwendung dann auch alle Pakete einmal, gebe dir dann aber auch immer eine Empfehlung mit. In der folgenden Tabelle gebe ich dir einmal eine kurze Übersicht über die beiden Annahmen an die ANOVA. Normalerweise brauchen wir einen normalverteilten Messwert \(y\) und Varianzhomogenität in den Faktoren. In den letzten Jahren wurden aber noch weitere Implementierungen der ANOVA entwickelt, so dass hier auch Alternativen vorliegen.

Tabelle 30.1— Übersicht über Funktion der ANOVA in ausgewählten Paketen und Excel. Die Aussagen sind nicht als absolut zu verstehen sondern eher als Empfehlung und Leitplanken zur Orientierung.

	{base}	{car}	{afex}	{WRS2}	Excel
Normalverteilt \(y\)	ja	ja	ja	nein	ja
Varianzhomogenität \(f\)	ja	optional	ja	nein	ja
Messwiederholungen	nein	nein	ja	ja	nein

Gehen wir jetzt mal die Pakete durch. Wir immer gibt es einiges an Möglichkeiten und ich zeige dir hier eben die Auswahl. Es gibt hier das ein oder andere noch zu beachten, aber da gehe ich dann bei den jeweiligen Methoden drauf ein. Es macht eben dann doch einen Unterschied ob ich eine einfaktorielle oder komplexere ANOVA rechnen will. Nicht alles geht in allen R Pakten oder gar Excel.

Der Standard mit der Funktion aov() aus {base}

Die Standardfunktion aov() erlaubt es eine einfaktorielle oder zweifaktorielle ANOVA direkt auf einem Datensatz zu rechnen. Hier brauchen wir nur ein Modell in der in R üblichen Formelschreibweise y ~ f. Du kannst diesen Ansatz als schnelle ANOVA begreifen. Dein Messwert \(y\) muss hier normalverteilt sein.

Der erweiterte Standard mit der Funktion anova() aus {base}

Die Funktion anova() erlaubt es auch auf anderen Modellen eine ANOVA zu rechnen. Wi nutzen hier die Funktion lm(), die einen normalverteilten Messwert \(y\) annimmt. Es ginge aber auch mit anderen Modellierungen und der Funktion glm() für Zähldaten einer Possionverteilung oder noch anderen Verteilungen. Die anova() Funktion ist sehr reudziert, tut aber im Sinne einer ANOVA was die Funktion machen soll.

Mit der Funktion Anova() aus {car}

Das R Paket {car} bietet eine Verbesserung der Standardfunktionen der ANOVA an. Insbesondere die Berücksichtigung und die Modellierung eines Interaktionseffektes in einer zweifaktoriellen ANOVA sticht heraus. Daher ist die Funktion hier etwas flexibeler als der Standard. In einer einfaktoriellen ANOVA bemerkst du keinen Unterschied.

Mit den ANOVA Funktionen aus {afex}

Wir können die ANOVA auch anwenden, wenn wir Messwiederholungen vorliegen haben. Daher bietet sich hier das R Paket {afex} an. Du musst bei den Funktionen von {afex} immer eine ID mitlaufen lassen, die angibt welche Individuen wiederholt gemessen wurden. Also hat jede Zeile eine Nummer, die beschreibt welche Beobachtung hier vorliegt. Besonders wichtig bei Messungen über die Zeit. Darüber hinaus kann das Paket sehr gut Interaktionen schätzen und Bedarf dort keiner zusätzlichen Optionen.

“ANOVAs are generally robust to ‘light’ heteroscedasticity, but there are various other methods (not available in {afex}) for getting robust error estimates.” — Testing the Assumptions of ANOVAs

Das Paket {afex} kann nicht mit Varianzheterogenität umgehen, aber dafür mit Messwiederholungen. Ich würde das Paket {afex} nehmen, wenn ich Messwiederholungen vorliegen habe oder mich die Interaktion in einem zweifaktoriellen Modell interessiert.

Mit den ANOVA Funktionen aus {WRS2}

Eine Annahme an die ANOVA ist, dass wir es mit normalverteilten Messwerten \(y\) sowie Varianzhomogenität in den Faktoren \(f\) vorliegen haben. Das R Paket {WRS2} mit der hervorragenden Vingette Robust Statistical Methods Using WRS2 erlaubt nun aber diese beiden Annahmen zu umgehen und bietet eine robuste ANOVA an. Robust meint hier, dass wir uns nicht um die Normalverteilung und Varianzhomogenität kümmern müssen.

Mit Excel

Hier muss ich sagen, dass es schon etwas weh tut die einfaktorielle und zweifaktorielle ANOVA in Excel zu rechnen. Ich habe dir bei der einfaktoriellen sowie der zweifaktoriellen ANOVA ein Video für die ANOVA in Excel ergänzt. Eigentlich ist es nur der letzte Strohhalm, wenn du keine Zeit mehr hast dich in R nochmal einzuarbeiten.

Weitere Tutorien für die ANOVA

Wir oben schon erwähnt, kann dieses Kapitel nicht alle Themen der ANOVA abarbeiten. Daher präsentiere ich hier eine Liste von Literatur und Links, die mich für dieses Kapitel hier inspiriert haben. Nicht alles habe ich genutzt, aber vielleicht ist für dich was dabei.

• ANOVA in R
• One-Way ANOVA Test in R
• Two-Way ANOVA Test in R
• MANOVA Test in R: Multivariate Analysis of Variance
• ANOVA in R | A Complete Step-by-Step Guide with Examples

30.2 Theoretischer Hintergrund

Im folgenden Abschnitt schauen wir uns einmal den theoretischen Hintergrund zu der ANOVA an. Ich fokusiiere mich hier einmal für die Theorie auf die einfaktorielle ANOVA. Die Prinzipien lassen sich dann auch auf die zweifaktorielle und mehrfaktoriellen Algorithmen der ANOVA anwenden. Was dann später noch dazukommt sind dann die Interaktionen. Dabei ist zu bachten, dass wir natürlich eine Interaktion nur in einem zweifaktoriellen Modell beobachten können. Daher hier der Start mit der einfaktoriellen ANOVA und dann die Vertiefung zur Interaktion mit der zweifaktoriellen ANOVA.

In der ersten Version dieses Kapitels habe ich noch sehr viel beispielhaft für eine einfaktorielle ANOVA durchgerechnet. Wie sich dann in den Jahren herausstellte, hat es dir wenig geholfen, die ANOVA zu verstehen oder anzuwenden. Wer rechnet schon die ANOVA per Hand? Daher hier eben das klassische lying-to-children und ich erkläre dir die ANOVA mehr konzeptionell als rein mathematisch korrekt.

Wir müssen jetzt einmal für dei Haupteffekte eines Faktors \(A\) oder \(B\) unterschieden sowie deren Interaktion untereinander. Deshalb besprechen wir jetzt erstmal einen Haupteffekt eines Faktors \(A\) mit drei Levels \(A.1\), \(A.2\) sowie \(A.3\) und arbeiten uns dann vor. Ich habe auf großartige Mathematik und Formeln verzichtet. Du findest die entsprechenden händischen Rechenoperation auf Wikipedia oder in einem entsprechenden statistischen Lehrbuch zur ANOVA und Statistik wie das verlinkte Buch von Van Emden (2019).

30.2.1 Haupteffekte \(f_A\)

Für die Theorie konzentrieren wir uns nur auf die einfaktoriele ANOVA. Das heißt wir haben einen Faktor \(A\) mit drei Levels \(A.1\), \(A.2\) sowie \(A.3\) vorliegen. Du kannst dir die drei Level als drei Gruppen vorstellen. Entweder sind es verschiedene Düngestufen oder aber eben drei Floharten, die unterschiedlich weit springen. Erinnere dich nochmal an die Abbildung 30.1 zu Beginn des Kapitels. Wir wollen in unseren Daten Varianz haben, denn nur dann haben wir auch wirklich einen Unterschied zwischen den Gruppen in unserer Behandlung. Fangen wir also mit der wichtigste Frage einmal an.

Wann sind drei oder mehr Mittelwerte gleich?

Für unseren Gedankengang nehmen wir mal drei Mittelwerte für die drei Gruppen \(A.1\), \(A.2\) sowie \(A.3\) an. Wir brauchen ja in der Nullhypothese Gleichheit. Das heißt, dass alle drei Mittelwerte \(\bar{y}_{A.1}\), \(\bar{y}_{A.2}\) und \(\bar{y}_{A.3}\) gleich sein müssen. Wir nennen diese Mittelwerte der Gruppen daher auch lokale Mittelwerte. Wir können also wie folgt schreiben.

\[ \bar{y}_{A.1} = \bar{y}_{A.2} = \bar{y}_{A.3} \]

Jetzt kommt der eigentlich Hauptgedanke. Wir können auch einen globalen Mittelwert \(\beta_0\) berechnen in dem wir die drei Mittelwerte mitteln oder aber den Faktor vergessen und über alle Beobachtungen den Mittelwert berechnen. Wenn wir mehr Mittelwerte oder eben Gruppen haben, dann ändert sich natürlich der Nenner.

\[ \beta_0 = \cfrac{\bar{y}_{A.1} + \bar{y}_{A.2} + \bar{y}_{A.3}}{3} \]

Wenn die drei Mittelwerte gleich sind, dann ist auch das globale Mittel \(\beta_0\) gleich der drei Mittelwerte. Das klingt jetzt erstmal etwas schräg, aber wir hätten dann folgenden Zusammenhang. Aber das ist eigentlich was wir brauchen. Eine statistische Maßzahl, die Null ist, wenn Gleichheit in den Gruppen vorherrscht.

\[ \mbox{Wenn}\; \beta_0 = 0\; \mbox{dann}\; \bar{y}_{A.1} = \bar{y}_{A.2} = \bar{y}_{A.3} \]

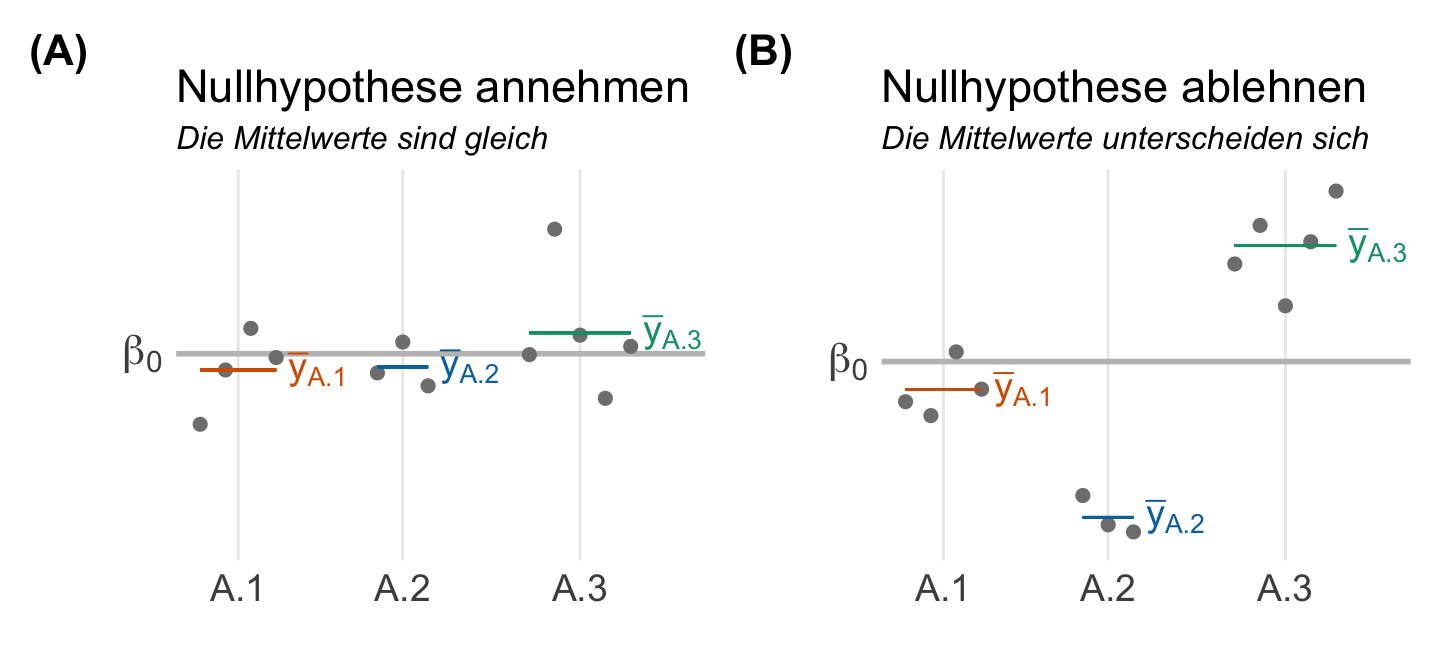
In der folgenden Abbildung 30.2 wird dir es vielleicht nochmal klarer. Wir haben hier einmal den globalen Mittelwert \(\beta_0\) sowie von lokalen Mittelwerten \(\bar{y}_{A.1}\), \(\bar{y}_{A.2}\) und \(\bar{y}_{A.3}\) der einzelen Gruppen des Faktors \(A\) dargsstellt. In der linken Abbildung siehst du, dass die lokalen Mittelwerte der Gruppen alle auf einer Höhe liegen. Die Mittelwerte der Gruppen sind gleich. Es gibt keinen Uterschied. Darüber hinaus sind die Abstände der lokalen Mittelwerte zum gloabeln Mittelwert Null. Die Nullhypothese gilt.

Wenn sich jetzt die lokalen Mittelwerte untereinander unterscheiden, dann liegen die lokalen Mittelwerte nicht mehr auf einer Ebene. Damit entstehen auch positive und negative Abstände von den lokalen Mittelwerten zu dem globalen Mittelwert. Diese Abstände sind nämlich jetzt nicht mehr Null. Daher haben wir auch nicht mehr Gleichkeit vorliegen. Wir können daher die Nullhypothese ablehnen. Je größer die Abstände der lokalen Mittelwerte zum globalen Mittelwert werden, desto mehr würden wir die Nullhypothese ablehnen und an einen Gruppenunterschied glauben.

Abbildung 30.2— Zusammenhang zwischen dem globalen Mittelwert \(\beta_0\) und den drei Mittelwerten \(\bar{y}_{A.1}\), \(\bar{y}_{A.2}\) und \(\bar{y}_{A.3}\) der Gruppen \(A.1\), \(A.2\) sowie \(A.3\). (A) Wenn die drei Mittelwerte gleich sidn und damit die Nullhypothese gilt, dann liegen die drei Mittelwerte auf dem globalen Mittelwert. (B) Wenn die drei Mittelwerte sich unterschieden, dann kann die Nullhypothese abgelehnt werden und die drei Mittelwerte liegen nicht auf dem globalen Mittel. [Zum Vergrößern anklicken]

Damit haben wir jetzt das zentrale Prinzip der ANOVA verstanden. Es geht um die Abstände von lokalen Gruppenmittelwerten zu einem globalen Mittelwert über alle Gruppen.

Wie werden die Abstände von den lokalen Mittelwert zum globalen Mittelwert berechnet?

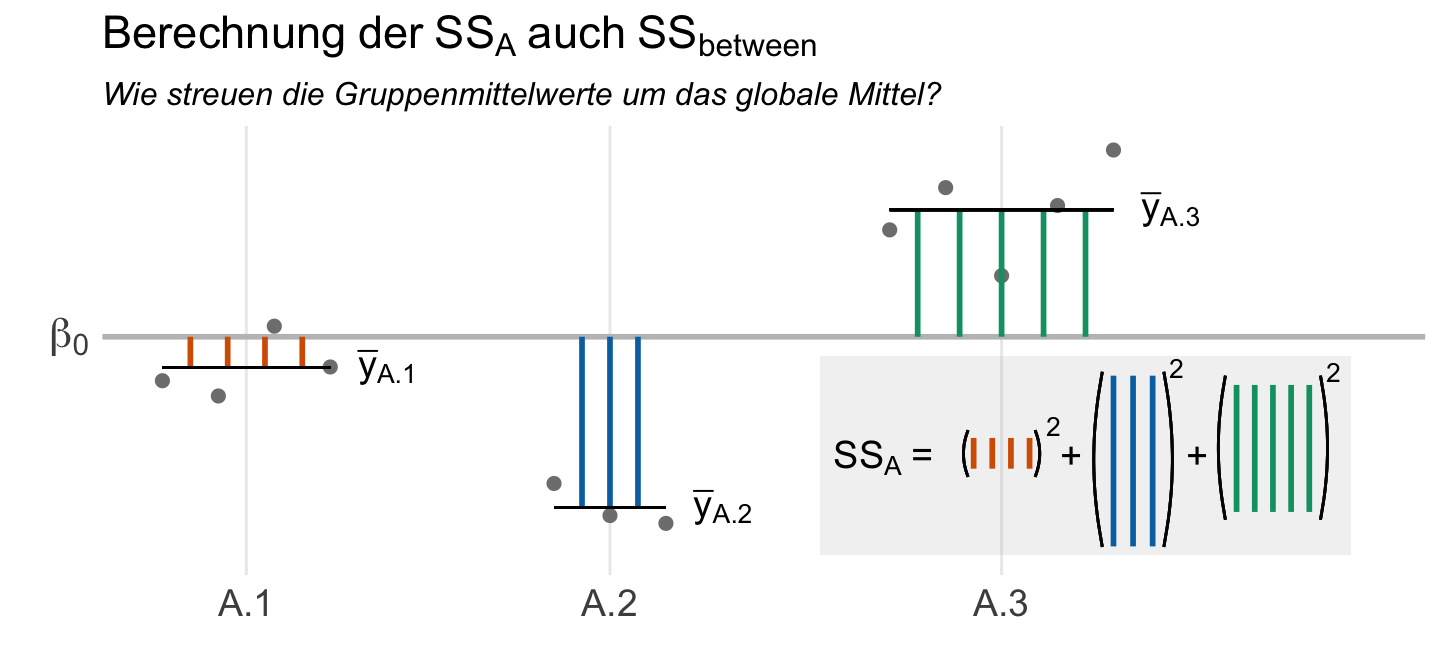
Nun könnten wir einfach sagen, dass wenn die aufsummierten Abstände nicht Null sind, wir einen Effekt in den Gruppen vorliegen haben. Hier tritt wieder das Problem auf, dass wir positive Abweichung und negative Abweichungen von den lokalen Mittelwerten zu dem gloablen mittelwert haben. Daher berechnen wir nicht die Abstände sondern die quadratischen Abstände und summieren diese dann auf. Wir berechnen die Abweichungsquadrate (eng. sum of squares, abk. SS). Daher sagen wir auch, dass die Abstände der lokalen Mittelwerte zum globalen Mittel als Abweichungsquadrate berechnet werden. In der folgenden Abbildung siehst du einmal die Visualsierung der Berechnung der Abweichungsquadrate des Faktors \(A\) oder eben \(SS_A\).

Abbildung 30.3— Visualsierung der Berechnung der Abweichungsquadrate des Faktors \(A\) als \(SS_A\) bezeichnet. Für jede Beobachtung wird einmal der Abstand des lokalen Mittelwerts der Gruppe zum globalen Mittelwert berechnet und quadriert. Die Abstände werden dann aufsummiert.

Jetzt tritt aber wiederum ein anderes Problem auf. Je mehr Gruppen wir haben, desto größer werden unsere Abweichungsquadrate. Deshalb mitteln wir auch die Abweichungsquadrate um die mittleren Abweichungsquadrate (eng. mean of squares, abk. MS) zu erhalten. Jetzt könnten wir natürlich sagen, wenn \(MS_A\) gleich Null ist, dann können wir die Nullhypothese nicht ablehnen. Aber hier nochmal ein kurzer Einwurf zur Teststatistik.

Wie sieht eine Teststatistik aus?

Eine Teststatistik teilt immer den Effekt (signal) durch die Streuung des Effekts (noise). Dabei muss eine Teststatistik Null sein, wenn die Nullhypothese gilt. Daher haben wir dann folgenden Zusammenhang.

\[ T_D = \cfrac{\mbox{signal}}{\mbox{noise}} = \cfrac{\mbox{Effekt}}{\mbox{Streuung}} \]

In unserem Fall wäre dann der Effekt die mittleren Abweichungsquadrate des Faktors A also \(MS_A\). Das passt auch in soweit, dass wenn die mittlere Abweichung der lokalen Mittelwerte zum globalen Mittelwert Null ist, dann können wir die Nullhypothese nicht ablehnen. Es fehlt also noch ein statistisches Maß für die Streuung.

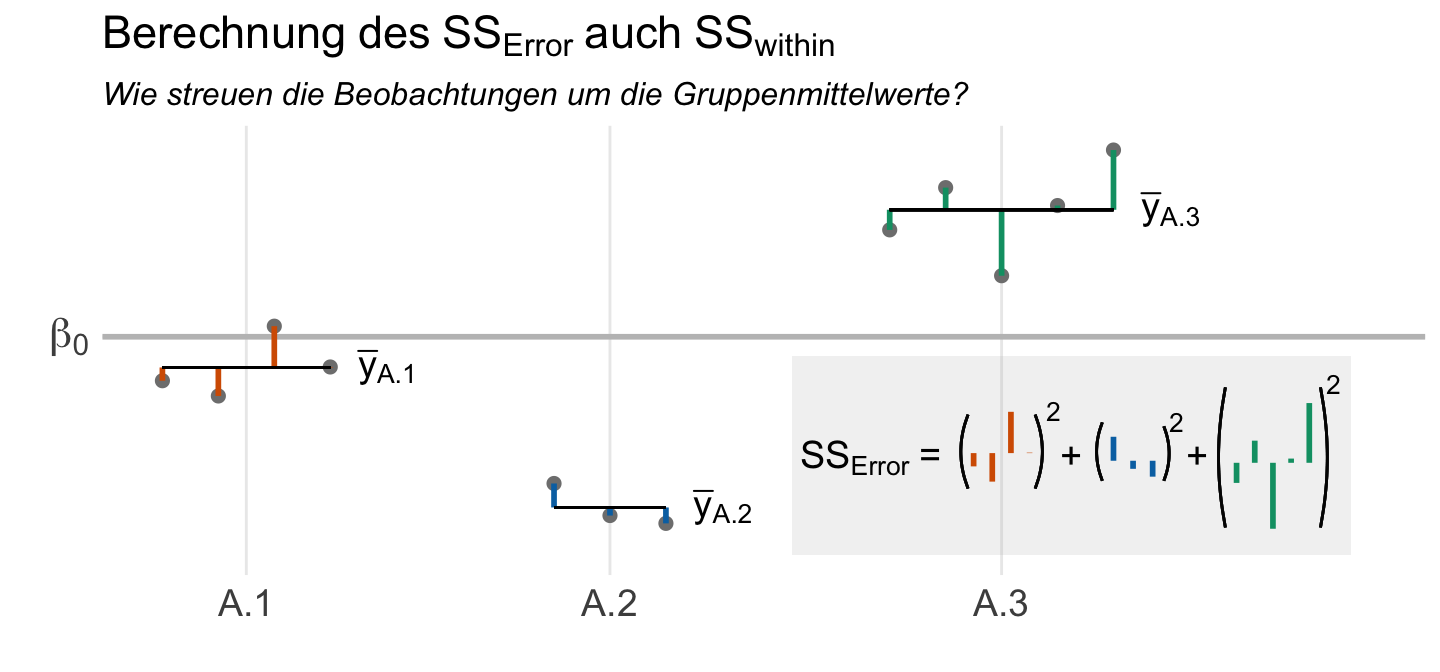
Wir haben aber noch die Streuung innerhalb der einzelnen Gruppen. Diese Streuung innerhalb der Gruppen nennen wir gerne Reststreuung, da diese nicht von den Gruppen erklärt wird. Oder aber ganz kurz, den Fehler (eng. error). Wir berechnen also nochmal die quadrierten Abstände der einzelnen Beobachtungen um die jeweiligen Gruppenmittelwerte und nennen diese dann \(SS_{Error}\). Dann summieren wir die quadrierten Abstände einmal auf, wie du in der folgenden Abbildung einmal sehen kannst. Am Ende mitteln wir auch die quadratische Abweichung der Fehler zu \(MS_{Error}\) umd die mittlere Abweichung der einzelnen Beobachtungen zu den lokalen Mittelwerten darzustellen.

Abbildung 30.4— Visualsierung der Berechnung der Abweichungsquadrate des Fehlers \(Error\) als \(SS_{Error}\) bezeichnet. Für jede Beobachtung wird einmal der Abstand zum lokalen Mittelwert der Gruppe berechnet und quadriert. Die Abstände werden dann aufsummiert.

In der folgenden Tabelle siehst du nochmal die wichtigen Begrifflichkeiten der Varianz in einer ANOVA als mittleren quadratischen Abweichung \(MS\) zusammengefasst. Die gesamte Varianz wird auch als \(MS_{Total}\) bezeichnet und du kennst diese schon als gepoolte Varianz \(s^2_p\) aus dem Student t-Test.

Tabelle 30.2— Zusammenfassung der Begrifflichkeit der mittleren quadratischen Abweichung \(MS\) in einer ANOVA.

Varianz zwischen den Gruppen	\(MS_A\)	\(MS_{between}\)
Varianz innerhalb der Gruppen	\(MS_{Error}\)	\(MS_{within}\)
Varianz aller Gruppen	\(MS_{Total}\)	\(MS_{Total}\)	\(s^2_p\)

Da wir jetzt alle statistischen Maßzahlen zusammen haben können wir jetzt auch einen statistischen Test rechnen. Wir haben damit dann einmal als Effekt die mittleren Abweichungsquadrate der lokalen Mittelwerte zum globalen Mittelwert des Faktors \(A\) als \(MS_A\) vorliegen. Das ist jetzt unser statistisches Maß für den Mittelwertsunterschied oder eben allgemeiner dem Effekt. Auch wenn wir diesen Effekt nicht biologisch interpretieren können. Dann haben wir noch als Streuung den Fehler, als mittlere Abweichungsquadrate der Beobachtungen zu den jeweiligen Gruppenmittewerten. Daraus können wir uns jetzt die Testststatistik \(F_D\) der ANOVA bauen.

\[ F_D = \cfrac{MS_A}{MS_{Error}} \] mit

• \(MS_A\) gleich der mittleren Abweichungsquadrate der lokalen Mittelwerte zum globalen Mittelwert des Faktors \(A\).
• \(MS_{Error}\) mittlere Abweichungsquadrate der Beobachtungen zu den jeweiligen Gruppenmittewerten.

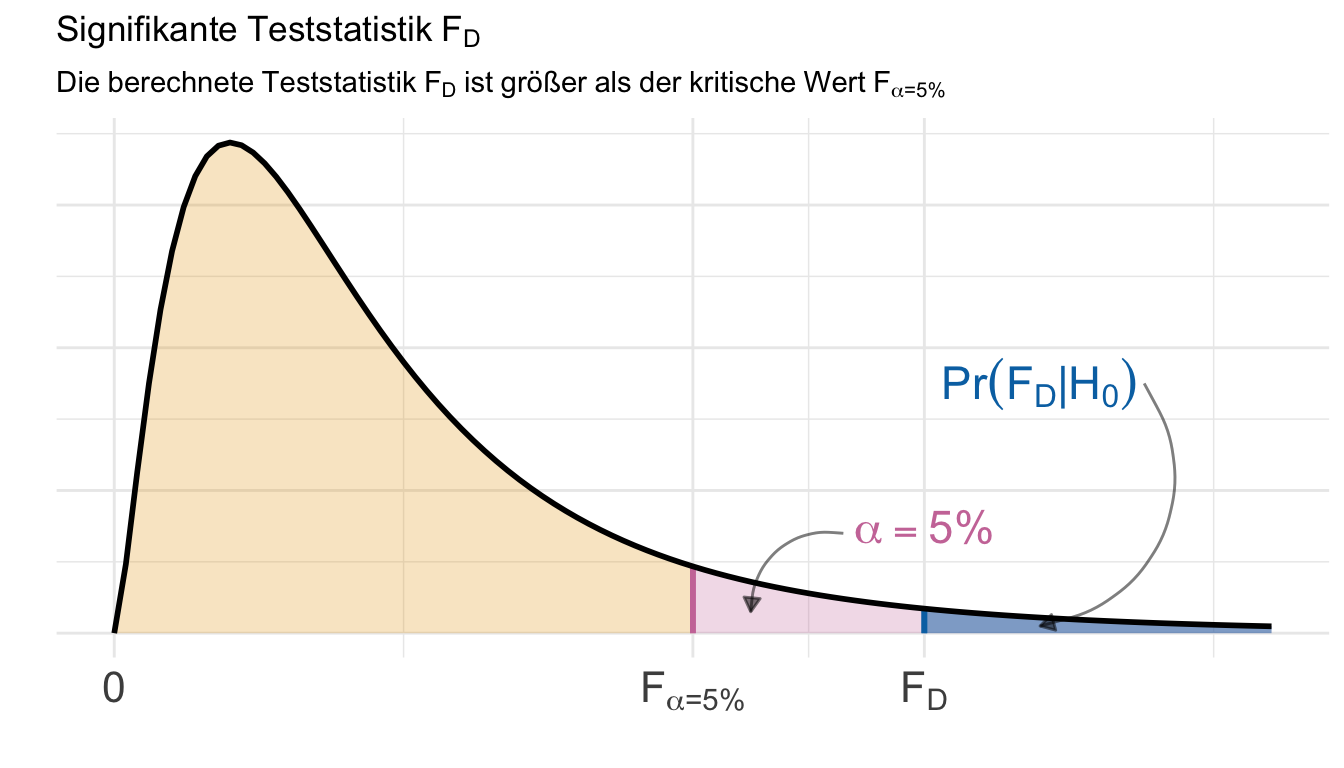
Wenn die Nullhypothese gilt, dann sind die mittleren Abweichungsquadrate der lokalen Mittelwerte zum globalen Mittelwert \(MS_A\) gleich Null und die Teststatistik \(F_D\) ist ebenfalls Null. Es kann aber keine negativen Werte für die F Statistik geben, da es keien ngeativen Werte für \(MS_A\) geben kann. In der folgenden Abbildung siehst du nochmal die F Statistik visualisert.

Abbildung 30.5— Visualiserung der F Statistik einer ANOVA mit dem kritischen Wert \(F_{\alpha = 5\%}\) und der berechneten Teststatistik \(F_D\) aus den Daten. Eingezeichnet sind als Flächen das Signifkanzniveau \(\alpha\) gleich 5% und der p-Wert mit \(Pr(F_D|H_0)\).

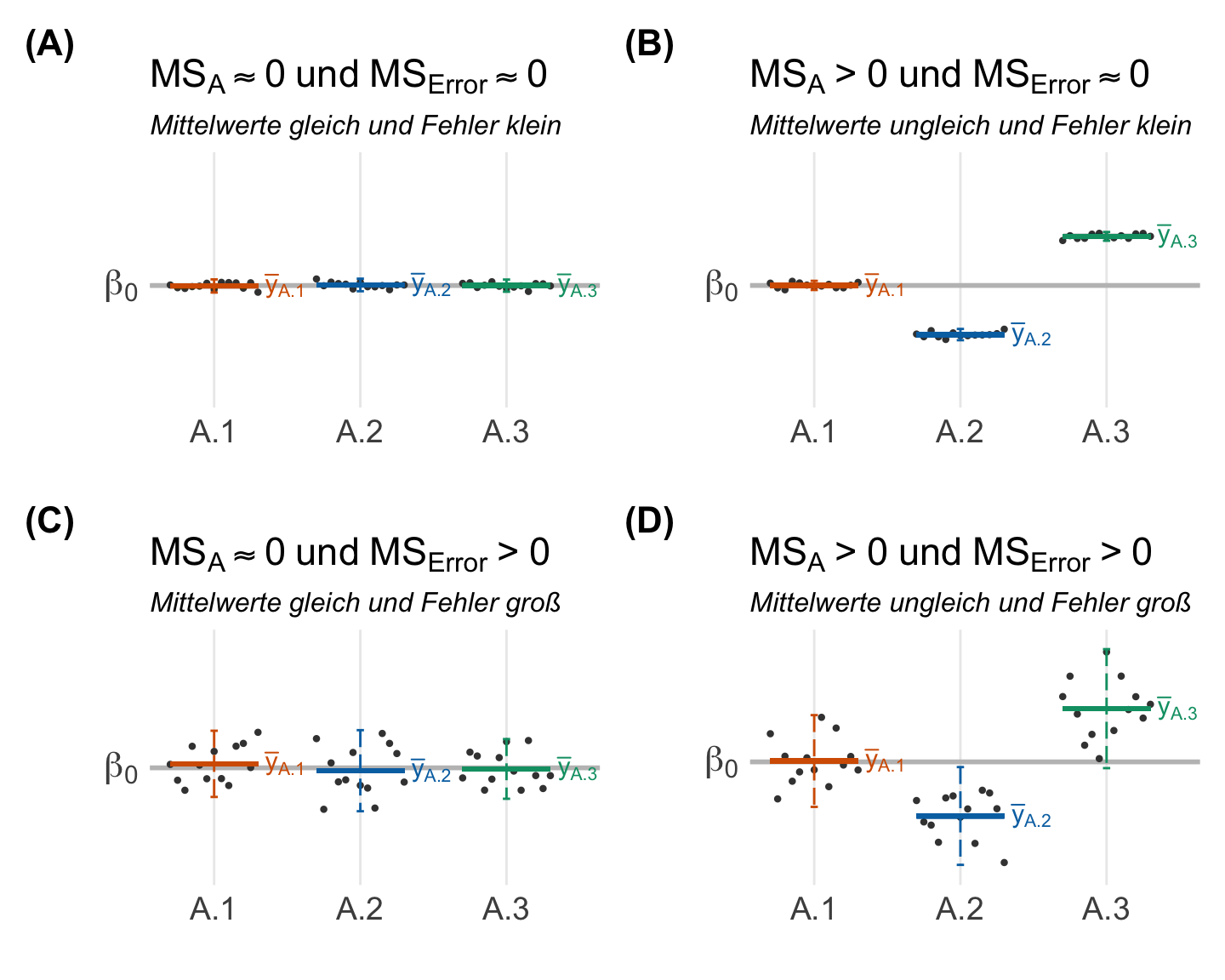
Jetzt bietet es sich an nochmal den Zusammenhang von \(MS_A\) und \(MS_{Error}\) in der folgenden Abbildung 31.1 näher zu betrachten. Wir können ja kleine Werte oder große Werte für die mittleren Abweichungsquadrate der lokalen Mittelwerte zum globalen Mittelwert \(MS_A\) vorliegen haben. Ebenso können die mittlere Abweichungsquadrate der Beobachtungen zu den jeweiligen Gruppenmittewerten \(MS_{Error}\) klein oder groß sein. Wir sehen sofort, dass ein großer Effekt \(MS_A > 0\) und ein kleiner Fehler \(MS_{Error} \approx 0\) es erleichtern einen signifikanten Unterschied nachzuweisen. Steigt der Fehler oder wird der Effekt klein, wird es schwerer einen signifikanten Unterschied zwischen den Gruppen zu zeigen. Die Gruppenmittelwerte liegen dann meistens auf einer Ebene oder die Fehlerbalken überlappen sich.

Abbildung 30.6— Visualisierung des Zusammenhangs zwischen den mittleren Abweichungsquadrate der lokalen Mittelwerte zum globalen Mittelwert \(MS_A\) sowie der mittleren Abweichungsquadrate der Beobachtungen zu den jeweiligen Gruppenmittewerten \(MS_{Error}\). [Zum Vergrößern anklicken]

Am Ende können wir dann die Abweichungsquadrate \(SS\) und die mittleren Abweichungsquadrate \(MS\) in einer Übersichtstabelle darstellen. Wir nennen diese Übersichtstabelle auch gerne die Ergebnistabelle der ANOVA. Wir können dann auch die \(F_D\) Teststatistik ergänzen. Jeder Faktor hat eine eigene Zeile. Dabei addieren sich dann die \(SS_A\) und \(SS_{Error}\) zu den gesammten \(SS_{Total}\) auf. Die Ergebnistabelle wird dir dann später in R berechnet. Insbesondere die Berechnung der Freiheitsgrade \(df\) ist eine eigene Wissenschaft für sich und du würdest diese Berechnung dann in einem statistsichen Buch nachschlagen. Hier dient die Ergebnistabelle dann nur zur Übersicht.

Tabelle 30.3— Ergebnistabelle der einfaktoriellen ANOVA in der theoretischen Darstellung. Die Abweichungsquadrate \(SS\) müssen noch zu den mittleren Abweichungsquadraten \(MS\) gemittelt werden. Abschließend wird die \(F_D\) Teststatistik als Prüfgröße berechnet.

Quelle	df	Sum of squares (SS)	Mean squares (MS)	Teststatistik F\(_{\boldsymbol{D}}\)
\(A\)	\(df_A\)	\(SS_A\)	\(MS_A = \cfrac{SS_A}{df_A}\)	\(F_{D} = \cfrac{MS_A}{MS_{Error}}\)
\(Error\)	\(df_{Error}\)	\(SS_{Error}\)	\(MS_{Error} = \cfrac{SS_{Error}}{df_{Error}}\)
\(Total\)	\(df_{total}\)	\(SS_{Total}\)

Wenn es dann die Ergebnistabelle für die einfaktorielle ANOVA gibt, dann gibt es natürlich auch eine Ergebnistabelle für eine zweifaktorielle ANOVA. Im Folgenden einmal die Ergebnistabelle gezeigt. Wenn du mehr Faktoren in deine ANOVA aufnimmst, dann erhälst du mehr Zeilen. Insbesondere der Interaktionsterm \(A \times B\) kann erst auftreten, wenn du zwei oder mhr Faktoren in dein Modell nimmst. Am Ende berechnest du aber immer die F Statistik indem du die mittleren Abweichungsquadrate des entsprechenden Fakotr in der Zeile durch den mittleren Fehler teilst. Es wird eben immer komplexer und hier nimmt uns R die Arbeit dann ab.

Tabelle 30.4— Ergebnistabelle der zweifaktoriellen ANOVA in der theoretischen Darstellung mit Interaktionsterm für die beiden Faktoren. Die Abweichungsquadrate \(SS\) müssen noch zu den mittleren Abweichungsquadraten \(MS\) gemittelt werden. Abschließend wird die \(F_D\) Teststatistik als Prüfgröße für jeden Faktor separat berechnet.

Quelle	df	Sum of squares (SS)	Mean squares (MS)	Teststatistik F\(_{\boldsymbol{D}}\)
\(A\)	\(df_A\)	\(SS_{A}\)	\(MS_{A} = \cfrac{SS_A}{df_A}\)	\(F_{D} = \cfrac{MS_{A}}{MS_{Error}}\)
\(B\)	\(df_B\)	\(SS_{B}\)	\(MS_{B} = \cfrac{SS_B}{df_B}\)	\(F_{D} = \cfrac{MS_{B}}{MS_{Error}}\)
\(A \times B\)	\(df_{A \times B}\)	\(SS_{A \times B}\)	\(MS_{A \times B} = \cfrac{SS_{A \times B}}{df_{A \times B}}\)	\(F_{D} = \cfrac{MS_{A \times B}}{MS_{Error}}\)
\(Error\)	\(df_{Error}\)	\(SS_{error}\)	\(MS_{Error} = \cfrac{SS_{Error}}{df_{Error}}\)
\(Total\)	\(df_{total}\)	\(SS_{total}\)

Damit wären wir fast schon am Ende der theoretischen Betrachtung des Haupteffekts eines Fakots in der einfaktoriellen ANOVA. Was mir jetzt noch bleibt, ist auf die Varianzhomogenität einzugehen. Wie du sicherlich schon gelesen hast, müssen alle Gruppen die gleiche Varianz haben. Wir berechnen ja auch nur einen Fehlerterm durch den wir dann teilen. Der ist ja für jeden Faktor der gleiche Wert. Daher hier nochmal ein Satz zur Varianzhomogenität.

Die Annahme der Varianzhomogenität theoretisch betrachtet

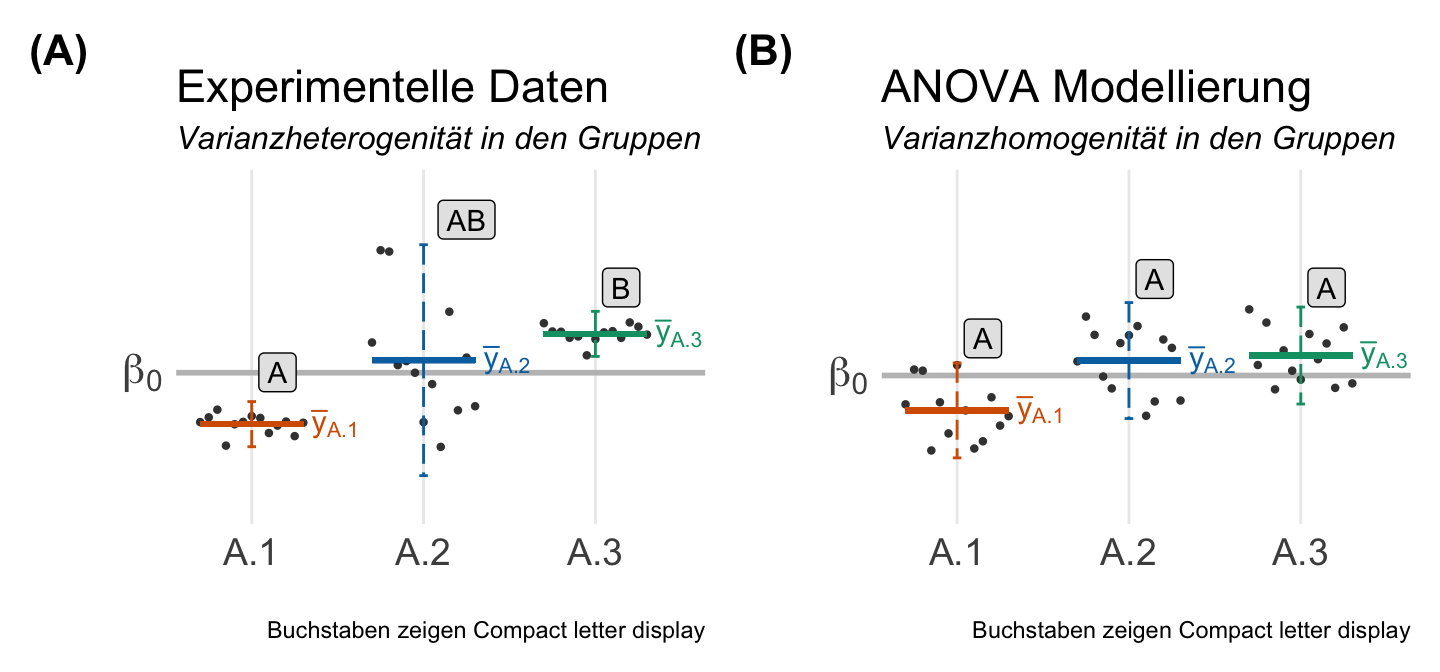
Wir wollen nochmal die Annahme an die Varianuhomogenität theoretisch betrachten und herausfinden, warum wir homogene Varianzen über die Gruppen brauchen. Wir du in der folgenden Abbildung 30.7 einmal siehst, modelliert die ANOVA unter der Annahme der Varianzhomogenität in den Gruppen die Daten. Wir haben in den linken Plot unsere experimentellen Datan mit starker Varianzheterogenität. Die Varianz in der Gruppe \(A.2\) ist viel größer als in den anderen beiden Gruppen. Dabei unterscheiden sich die Gruppen \(A.1\) und \(A.3\) signifikant. Die beiden Gruppen teilen sich nicht den gleichen Buchstaben des Compact letter displays. Wenn wir jetzt die ANOVA rechnen, dann teilen sich alle Gruppen die gemittlete Varianz über alle Gruppen. Das sehen wir dann in der rechten Abbilung. Die beiden Gruppen \(A.1\) und \(A.3\) erhalten viel mehr Streuung und die Gruppe \(A.2\) weniger. Am Ende haben alle Gruppen faktisch gleich viel Streuung. So sehen dann die Daten aus, die die ANOVA modelliert. Wir können am Ende keinen signifikanten Unterschied mehr nachweisen. Daher kann es passieren, dasss eine ANOVA keinen Unterschied nachweisen kann, aber {emmeans} mit der Adjustierung für Varianzheterogenität dennoch einen Unterschied findet.

Abbildung 30.7— Visualisierung der Annahme der Varianzhomogenität in den Gruppen. (A) Die experimentellen Daten zeigen eine Varianzheterogenität in den Gruppen. Die Gruppe \(A.1\) unterscheidet sich signifikant von der Gruppe \(A.3\) dargestellt durch das Compact letter display. (B) Die ANOVA modelliert gleiche Varianzen in allen Gruppen. Dadurch verschwindet der signifikante Unterschied, da der Fehler über alle Gruppen gemittelt wird [Zum Vergrößern anklicken]

Somit wären wir mit den theoretischen Teil durch. In dem folgenden Kasten sprechen wir nochmal über die Idee der Varianzzerlegung und wie das ganze mit der ANOVA funktioniert. Dann berechnen wir einmal den Effektschätzer der ANOVA. Bis jetzt haben wir ja nur eine Aussage über die Signifikanz, aber noch keinen Effekt berechnet.

Danach verlassen wir dann die einfaktorielle ANOVA und schauen auch schon weiter. Wir betrachten dann die Interaktion in einer zweifaktoriellen ANOVA. Der zweite Faktor in einer zweifaktoriellen ANOVA wird nämlich ähnlich behandelt wie der erste Faktor. Da tut sich dann konzeptionell nicht mehr so viel. Und den statistischen Engel nehme ich dann mit für die Aussage.

Exkurs: Die Idee der Varianzzerlegung

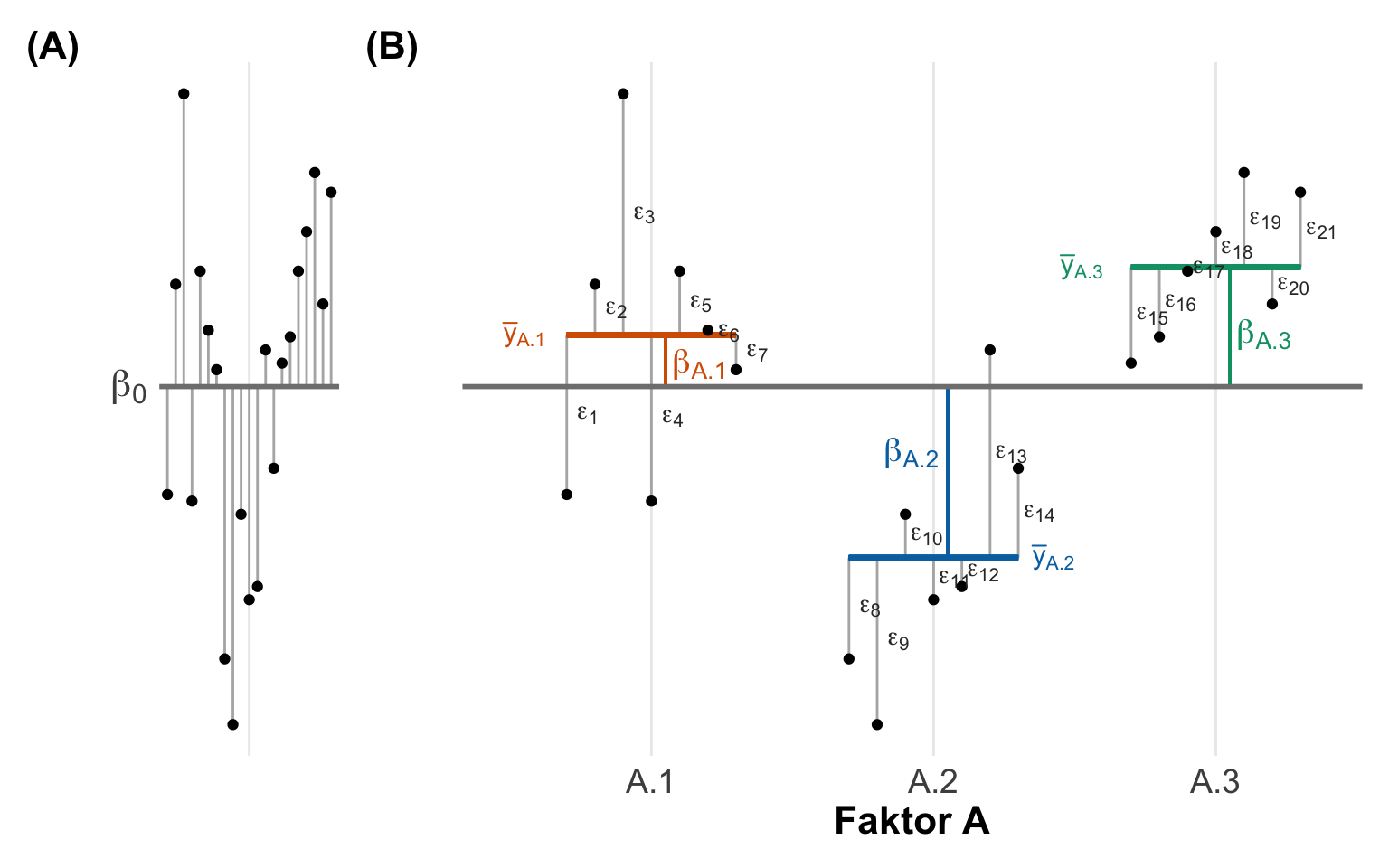
Häufig spricht man bei der ANOVA auch von einer Varianzzerlegung. Das ist richtig, verwirrt aber, wenn du damit gedanklich anfängst. Die ANOVA vergleicht primär Mittelwerte und die Nullhypothese ist auch entsprechend gebaut. Was die ANOVA dennoch tut, ist die gloable Streuung oder Varianz als \(SS_{Total}\) auf die unterschiedlichen Quellen zu verteilen. Wenn der Faktor \(A\) keinen Einfluss hätte dann würde alle Streuung nur durch den Fehler \(MS_{Error}\) dargestellt und nichts von der Streuung durch die Verschiebung der lokalen Mittelwerte \(MS_A\). In der folgenden Abbildung siehst du den Zusammenhang einmal dargestellt. In der linken Abbdilung vergessen wir einmal, dass wir einen Faktor A haben. Unsere Beobachtungen streuen um den globalen Mittelwert. Wie du dann aber rechts siehst, kommt ein Teil der Streuung durch die lokalen Mittelwerte des Faktors A. Wir können also die Streuung durch die unterschiedlichen Gruppenmittelwerte teilweise erklären. Diese Verschiebungen nennen wir dann auch \(\beta_{A.1}\), \(\beta_{A.2}\) und \(\beta_{A.3}\). Wäre nur der Faktor A ursächlich für die Streuung, dann würden alle Beobachtungen auf den entsprechenden lokalen Mittelwerten liegen. Die Fehlerterme \(\epsilon\) wären dann alle Null. Somit kannst du dann am Ende jeden Messwert y einer Beobachtung aus den Informationen des gloabeln Mittelwerts, dem Gruppenmittel und dem entspechenden Restfehler der Beobachtung zurückrechnen.

Abbildung 30.8— Visualisierung der Varianzzerlegung anhand eines Faktors A mit unterschiedlichen Gruppenmittelwerten. Die Verschiebung der einzelnen Gruppenmittelwerte wird mit \(\beta_{A.1}\), \(\beta_{A.2}\) und \(\beta_{A.3}\) bezeichnet. Die restliche Streuung dann als Fehler \(\epsilon\) der einzelnen Beobachtung zu dem zugehörigen Gruppenmittel. Somit kann jeder Messwert y einer Beobachtung aus den Informationen des gloabeln Mittelwerts, dem Gruppenmittel und dem entspechenden Restfehler der Beobachtung zurückrechnen werden [Zum Vergrößern anklicken]

30.2.2 Effektschätzer

Nachdem wir uns mit der Theorie der ANOVA beschäftigt haben und verstehen, wie der Haupteffekt des Faktors A bestimmt wird, müssen wir uns noch Fragen, wie stark ist denn der Effekt nun? Wir rechnen zwar die Abqweichungsquadrate der einzlenen lokalen Mittelwerte zum globalen Mittel mit \(SS_A\) aus, aber was sagt uns nun der Wert? Hierzu müssen wir nochmal einen Schritt zurücktreten und über die Abweichungsquadrate im Allgmeinen sprechen. Die gesamten Abweichungquadrate jeder Beobachtung zum globalen Mittelwert \(SS_{Total}\) setzen sich aus den Abweichungsquadraten vom Faktor \(SS_{Faktor}\), der Interaktion \(SS_{Interaktion}\) sowie dem Fehler \(SS_{Error}\) zusammen. Wir haben dann folgenden Zusammenhang.

\[ SS_{Total} = SS_{Faktor} + SS_{Interaktion} + SS_{Error} \]

mit

• \(SS_{Total}\) den gesamten Abweichungsquadraten jeder Beobachtung zum gloablen Mittel
• \(SS_{Faktor}\) den Abweichungsquadraten der Faktoren im Modell
• \(SS_{Interaktion}\) den Abweichungsquadraten möglicher Interaktionen der Faktoren
• \(SS_{Error}\) dem nicht erkläreten Rest der Abweichungsquadrate

Aus diesem Zusammenhang können wir dann verschiedene Effektschätzer berechnen, je nachdem wie wir dann die einzelnen Abweichungsquadrate ins Verhältnis setzen. Die Hilfeseite des R Pakets {effectsize} unter Effect Sizes for ANOVAs stellt eine Reihe von Effektschätzern für die ANOVA vor. Wir konzentrieren uns hier einmal auf die häufigsten angewendeten Effektschätzer. Es gibt immer mehr, aber da musst du dann nochmal selber in die Hilfeseite schauen. Dazu dann auch mehr in der Arbeit von Olejnik und Algina (2003) mit dem Titel Generalized eta and omega squared statistics: measures of effect size for some common research designs.

Eta\(^2\)

Der häufigste angewendete Effektschätzer ist Eta squared oder auch \(\eta^2\) geschrieben. Wir können \(\eta^2\) relativ einfach aus den Abweichungsquadraten des Faktors \(SS_A\) geteilt durch die gesamten Abweichungsquadrate \(SS_{Total}\) berechnen. Das \(\eta^2\) funktioniert besonders gut in der Anwenbdung einer einfaktoriellen ANOVA. Wir haben dann folgenden Zusammenhang.

\[ \eta^2 = \cfrac{SS_A}{SS_{Total}} \]

mit

• \(SS_A\) den Abweichungsquadraten der lokalen Mittel des Faktor A zum globalen Mittel
• \(SS_{Total}\) den gesamten Abweichungsquadraten jeder Beobachtung zum gloablen Mittel

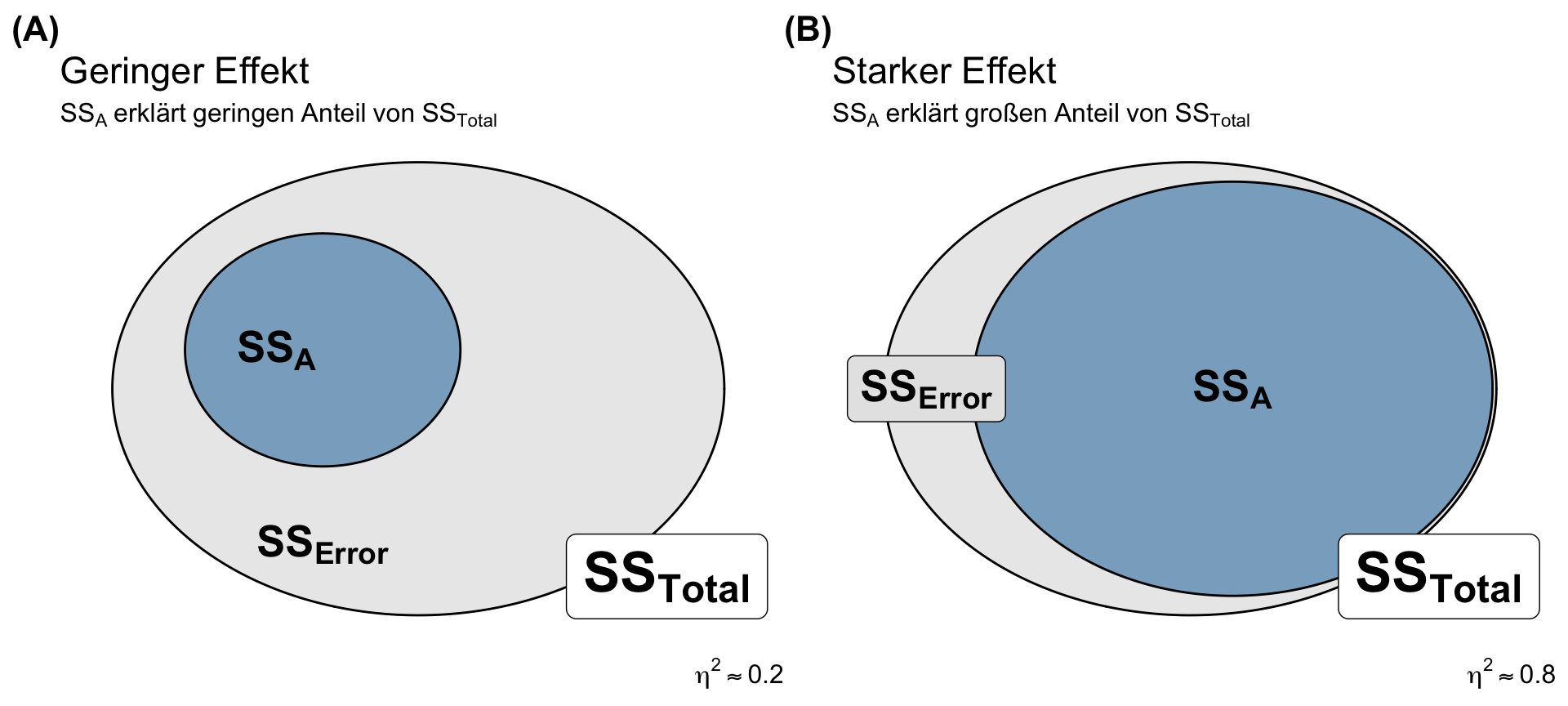
Wir rechnen hier also im Prinzip einmal einen Anteil aus. Da es sich bei den Abweichungsquadraten faktisch um eine Varianz handelt, können wir sagen, dass wir mit \(\eta^2\) den Anteil der Varianz berechnen, der durch den Faktor A erklärt wird. Ich habe den Zusammenhang nochmal in der folgenden Abbildung 30.9 dargestellt. Auf der linken Seite finden wir ein \(\eta^2\) von \(0.2\) und damit machen die \(SS_A\) nur einen geringen Anteil der \(SS_{Total}\) aus. Wir sagen, dass 20% der Varianz in den Daten durch den Faktor A erklärt wird. Der meiste Anteil der Abweichungsquadrate macht der Fehler \(SS_{Error}\) aus. In der rechten Abbildung sehen wir dann ein \(\eta^2\) von \(0.8\) und damit ist der Anteil von \(SS_A\) an \(SS_{Total}\) groß. Wir sagen, dass 80% der Varianz in den Daten durch den Faktor A erklärt wird.

Abbildung 30.9— Visualisierung von \(\eta^2\) für eine einfaktorielle ANOVA mit dem Faktor A. Gezeigt wird der Anteil der Abweichungsquadrate \(SS_A\) an den gesamten Abweichungsquadraten \(SS_{Total}\). (A) Geringer Effekt mit einem \(\eta^2\) von \(0.2\). Der Faktor A erklärt nur einen kleinen Teil der Varianz. (B) Starker Effekt mit einem \(\eta^2\) von \(0.8\). Der Fakotor A erklärt fast die gesamte Varianz. [Zum Vergrößern anklicken]

Das R Paket {effectsize} hat auch die Funktion interpret_eta_squared() implementiert, die ich persönlich nicht so sinnvoll halte, da wir das \(\eta^2\) relativ gut biologisch und statistisch erklären können. Das \(\eta^2\) sagt dann eben aus, ob wir große oder kleine Messwerte durch unsere Behandlung durch den Faktor A vorliegen haben.

Tabelle 30.5— Interpretation einiger \(\eta^2\) Werte für den Faktor A mit einer Behandlung.

\(\eta^2 = 0.1\)	Faktor A erklärt 10% Varianz vom Messwert \(y\)
\(\eta^2 = 0.5\)	Faktor A erklärt 50% Varianz vom Messwert \(y\)
\(\eta^2 = 0.8\)	Faktor A erklärt 80% Varianz vom Messwert \(y\)

Wenn du ein geplantes Experiment durchführst bei dem du durch Randomisierung und andere Maßnahmen fast alle Einflussgrößen kontrollierst, dann sollest du als Varianzquelle nur onch deinen Behandlungsfaktor A übrigbehalten. So ist dann die Daumenregel, dass wir in einem geplanten Feldexperiment ein \(\eta^2\) von mindestens \(0.7\) erwarten sollten. Die Streuung deines Messwerts \(y\) sollte dann eignentlich nur von deiner Behandlung abhängen.

Omega\(^2\) und Epsilon\(^2\)

Neben dem \(\eta^2\) gibt es auch noch zwei weitere Effektschätzer mit dem Omega Squared als \(\omega^2\) geschrieben sowie dem Epsilon Squared als \(\epsilon^2\) dargestellt. Du findest dazu auf der Hilfeseite des R Pakets {effectsize} unter Other Measures of Effect Size noch weitere Informationen. Oder wie das R Paket {effectsize} wie folgt schreibt.

“Though Omega is the more popular choice (Albers and Lakens, 2018), Epsilon is analogous to adjusted R2 (Allen, 2017, p. 382), and has been found to be less biased (Carroll & Nordholm, 1975).” — Other Measures of Effect Size

Beide Effektschätzer haben ihre Verwendung eher in der zweifaktoriellen ANOVA, wenn wir dann auch einen Interaktionsterm vorliegen haben. Die Interpretation ist dann nicht mehr so einfach wie bei dem \(\eta^2\). Im Allgemeinen kannst du das \(\epsilon^2\) wie das Bestimmtheitsmaß \(R^2\) in der linearen Regression interpretieren. Ein \(\epsilon^2\) gleich 0 ist als kein Effekt und ein \(\epsilon^2\) gleich 1 als ein starker Effekt anzusehen. Hier verliert sich das Ganze aber ins ungefähre und ich würde empfehlen dann die Mittelwertsdifferenzen in einem Post-hoc Test zu berechnen. Diese Differenzen der Mittelwerte sind dann direkt interpretierbar und damit vorzuziehen.

Für beide Effektschätzer gibt es dann die Funktionen interpret_omega_squared() und interpret_epsilon_squared() aus dem R Paket {effectsize}, die dir dann bei der Interpretation des Effekts helfen. Hier ist dann nicht mehr eine so einfache biologische Interpretation wie bei dem \(\eta^2\) möglich. Insbesondere bei noch komplexeren mehrfaktoriellen Modellen wird die Interpretation schwerer. Ich zeige dir dann die Anwendung einmal in den unteren Beispielen in R. Da einfach mal reingucken.

30.2.3 Interaktion \(f_A \times f_B\)

Wenn du mehr als einen Faktor \(f_A\) in deinem Modell vorliegen hast, dann kannst du eine Interaktion zwischen den Faktoren vorliegen haben. In diesem Abschnitt schauen wir uns eine Interaktion zwischen einem Faktor \(f_A\) und einem Faktor \(f_B\) einmal theoretisch näher an. Wir schreiben in R einen Interaktionsterm mit dem Doppelpunkt : zwischen den Variablennamen der beiden Faktoren. Wenn wir also die Interaktion zwischen dem Faktor \(f_1\) und \(f_2\) in R modellieren wollen, dann schreiben wir fa:fb. In der mathematischen Schreibweise haben wir dann häufig die Form \(f_A \times f_B\) vorliegen. Ich schreibe hier häufig dann die mathematische Notation im Fließtext und natürlich im R Code dann die entsprechende Notation in R.

Tabelle 30.6— Vergleich der Schreibweise einer Interaktion zwischen den Faktoren \(f_A\) und \(f_B\) einmal mathematisch und einmal in R.

	Mathematisch	R
Interaktion zwischen Faktor \(A\) und \(B\)	\(f_A \times f_B\)	fa:fb

Der folgende Abschnitt teilt sich grob in zwei Teile. Einmal der theoretische Hintergrund zur Interaktion und was dort eigentlich die Herausforderungen in der Modellierung sind sowie einen Abschnitt zur visuellen Überprüfung der Interaktion in einer zweifaktoriellen Analyse.

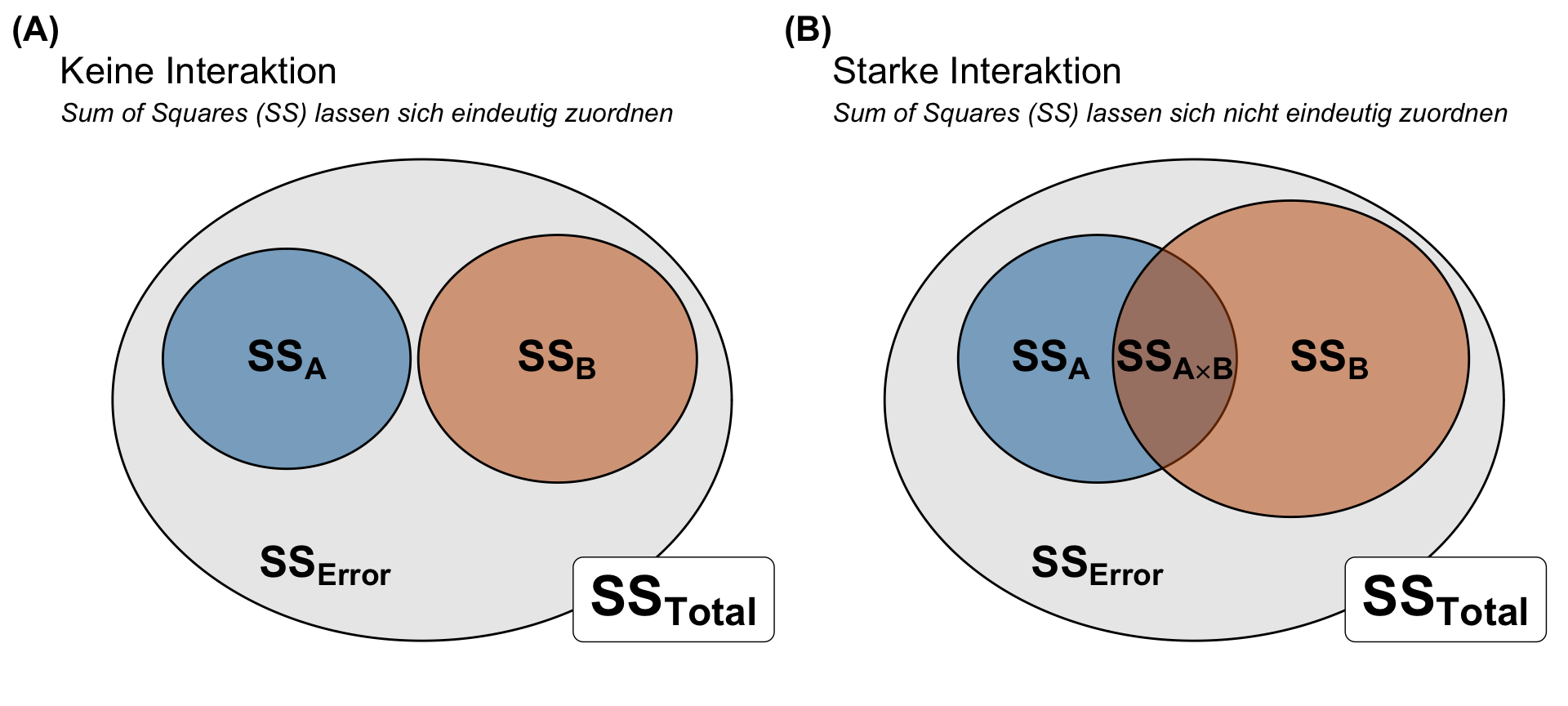
Beginnen wir mit der eigentlichen Problemstellung in einer zweifaktoriellen ANOVA. Wenn wir zwei Faktoren haben, dann müssen wir ja die Abweichungsquadrate den jeweiligen Faktoren zuordnen. Wenn wir keien Interaktion vorliegen haben, dann haben wir den linken Fall in der unteren Abbildung 30.10 vorliegen. Der Faktor A hat seine Abweichungsquadrate mit \(SS_A\) und der Faktor B auch einen Anteil der Abweichungsquadrate mit \(SS_B\) vorliegen. Der Rest von den gesamten Abweichungsquadraten \(SS_{Total}\) geht dann in den Fehler mit \(SS_{Error}\). Wenn wir aber eine Interaktion, wie in der rechten Abbildung vorliegen haben, dann können wir einen Teil der Abweichungsquadrate \(SS_{A \times B}\) unterschiedlich zuordnen. Den die Interaktionsabweichungsquadrate \(SS_{A \times B}\) könnten wir vollständig \(SS_A\) oder \(SS_B\) zurechnen oder aber irgendwie aufteilen. Daher gibt es jetzt verschiedene Typen von einer ANOVA, die sich eben darum drehen, wie wir die Interaktionsabweichungsquadrate \(SS_{A \times B}\) verteilen.

Abbildung 30.10— Visualisierung der Interaktion für eine zweifaktorielle ANOVA mit dem Faktor A und B. Gezeigt wird der Anteil der Abweichungsquadrate \(SS_A\) und \(SS_B\)an den gesamten Abweichungsquadraten \(SS_{Total}\). (A) Keine Interaktion. Alle Abweichungsquadrate können eindeutig einer Quelle zugeordnet werden. (B) Starke Interaktion. Ein Teil der Abweichungsquadrate \(SS_{A \times B}\) kann nicht eindeutig einem Faktor zugeordnet werden. [Zum Vergrößern anklicken]

Das zentrale Problem bleibt also, wie will ich die Abweichungsquadrate berechnen? Will ich die gesamten Interaktionsabweichungsquadrate \(SS_{A \times B}\) auf den Faktor A geben? Oder wie will ich die Verteilung darstellen. Hier gibt es jetzt bei der ANOVA drei verschiedene Typen. In dem Tutorium Anova – Type I/II/III SS explained findest du noch mehr Informationen und etwas Geschichte dazu. Ich fasse hier einmal die drei Typen zusammen und evrsuche mich mal an einer Empfehlung.

Type I

Die Type I ANOVA berechnet die Abweichungsquadrate in der sequenziellen Ordnung der Faktoren in dem Modell. Es werden also erst die Abweichungsquadrate für den Faktor A berechnet, dann für den Faktor B was noch von Faktor A an Abweichungsquadraten übrig ist. Am Ende wird dann die Interaktion betrachtet, wo wir dann den Anteil der Abweichungsquadrate finden, die nicht zu dem Faktor A oder Faktor B eindeutig zugeordnet werden konnten. Es macht also einen Unterschied wie du dein Modell baust. Insbesondere wenn du unterschiedliche Anzahlen an Beobachtungen in den Gruppen vorliegen hast.

\[ \begin{aligned} &SS(A) \; \mbox{für den Faktor A} \\ &SS(B \mid A) \; \mbox{für den Faktor B gegeben Faktor A}\\ &SS(A \times B \mid B, A) \; \mbox{für die Interaktion gegeben Faktor B und A} \end{aligned} \]

Die Funktionen aov() und anova() in R rechnen immer eine Type I ANOVA. Es gibt hier nichts umzustellen, du musst hier auf die Ordnung der Faktoren in deinem Modell achten. Der wichtigere Faktor nach deiner wissenschaftlichen Fragestellung muss immer als erstes ins Modell.

Type II

Die Type II ANOVA berechnet die Abweichungsquadrate eines Faktors unter der Berücksichtigung des anderen Faktors. Die Type II ANOVA ist damit der Type I ANOVA überlegen, was das finden eines signifkanten Unterschieds ausmacht. Darüber hinaus ist es auch egal welche Reihenfolge wir für unser Modell nehmen. Wenn deine beiden Faktoren im Modell also gleichwertig sind, dann ist die Type II ANOVA auf jeden Fall besser geeignet. Wichtig ist nur, dass die Type II ANOVA nur sinnvoll ist, wenn keine Interaktion zwischen den Faktoren vorliegt.

\[ \begin{aligned} &SS(A \mid B) \; \mbox{für den Faktor A gegeben Faktor B} \\ &SS(B \mid A) \; \mbox{für den Faktor B gegeben Faktor A}\\ \end{aligned} \]

Die Type II ANOVA kannst du im R Paket {car} mit der Funktion Anova(..., type = "II") anwenden. Hier empfiehlt es sich erst eine Type I Anova in aov() zu rechnen um zu schauen, ob eine signifikante Interaktion vorliegt. Wenn keine signifikante Interaktion zwischen den Faktoren in der Type I ANOVA vorliegt, dann ist die Type II ANOVA die bessere Wahl.

Type III

Die Type III ANOVA verwenden wir, wenn wir eine Interaktion in unseren Daten vorliegen haben. Die Type III ANOVA berücksichtigt die jeweilige Interaktion und die Abweichungsquadrate des anderen Faktors B bei der Berechnung der Abweichungsquadrate des Faktors A. Insbesondere bei der Anwesenheit von einer signifkanten Interaktion liefert die Type III ANOVA passende Ergebnisse. Leider lassen sich dadurch die Haupteffekte der Faktoren A und B nicht ohne die Interaktion interpretieren. Da ist dann wieder die Frage im Raum, was will ich eigentlich in der ANOVA nachweisen und wie passt die ANOVA zu meiner wissenschaftlichen Fragestellung?

\[ \begin{aligned} &SS(A \mid B,\, A \times B) \; \mbox{für den Faktor A gegeben Interaktion und Faktor B} \\ &SS(B \mid A,\, A \times B) \; \mbox{für den Faktor B gegeben Interaktion und Faktor A}\\ \end{aligned} \]

Wir können die TYPE III Anova in dem R Paket {car} mit der Funktion Anova(..., type = "III") rechnen. Hier musst du aber aufpassen, wie du das Modell baust, welches du in die Funktion Anova() steckst. Dazu dann mehr gleich weiter unten zur Treamtent und Effect Kodierung. Als bessere Alternative bietet sich dann die Funktion aov_car() aus dem R Paket {afex} an. Heir wird das Modell passend zur Type III Anova kodiert.

Jetzt haben wir da einiges an Zeug gelesen und fragen uns nun, was soll ich denn verwenden? Ich versuche jetzt mich aml an zwei etwas gewagten Empfehlungen für die Modellierung der ANOVA.

Keine Interaktion zwischen den Faktoren A und B

Wir verwenden die Type II ANOVA aus dem R Paket {car} mit der Funktion Anova(..., type = "II"). Hier haben wir die besten Chancen einen Unterschied zu finden und wir müssen nicht entscheiden, welcher Faktor uns wichtiger ist. Die Reihenfolge spielt keine Rolle im Modell.

Interaktion zwischen den Faktoren A und B

Wir verwenden die Type III Anova aus dem R Paket {afex} mit der Funktion aov_car(). Dann wird die Interaktion in den Haupteffekten der Faktoren A und B berücksichtigt. Wie wir dann weitermachen ist dann noch eine andere Sache, aber {emmeans} kann auch mit Interaktionen umgehen.

Welcher ANOVA Typ nun konkret in deiner Modellierung der richtige Typ ist kann ich dir leider Allgemein nicht sagen. Fühl dich aber nicht verunsichert. Auch eine aov() liefert gut Ergebnisse im Zusammenspiel mit {emmeans} im Post-hoc Test. Das Aua hält der statistische Engel aus.

Jetzt haben wir uns mit den Typen der ANOVA beschäftigt. Wie erkenne ich denn nun das wir eine vermutliche Interaktion in den Daten vorliegen haben? Hierfür kann ich dann die visuelle Überprüfung empfehlen. Eine explorative Datenanalyse ist immer der erste Schritt und auch eine vermeidliche Interaktion lässts ich gut erkennen. Dann kannst du auch schauen, ob deine ANOVA Modellierung zu den visualisierten Daten passt.

Visuelle Überprüfung

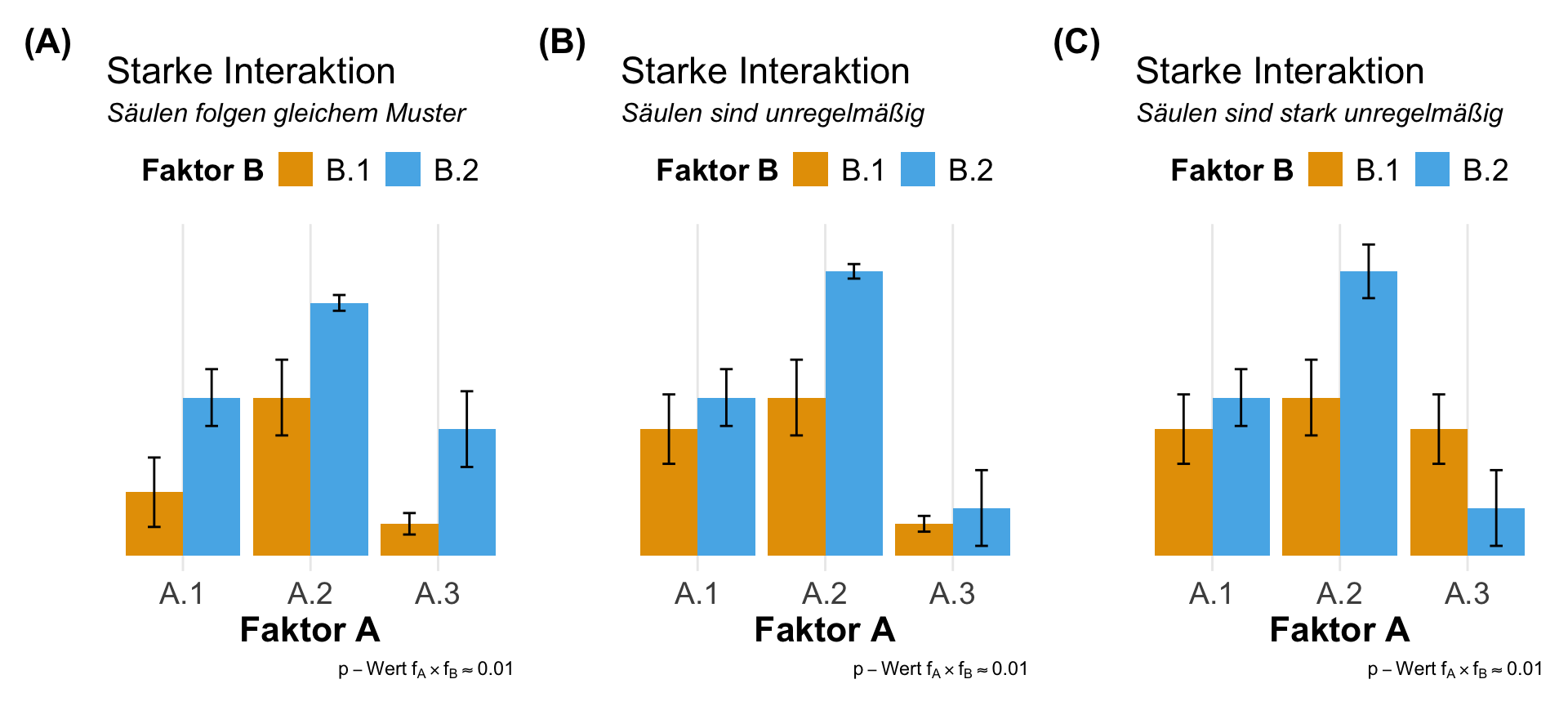
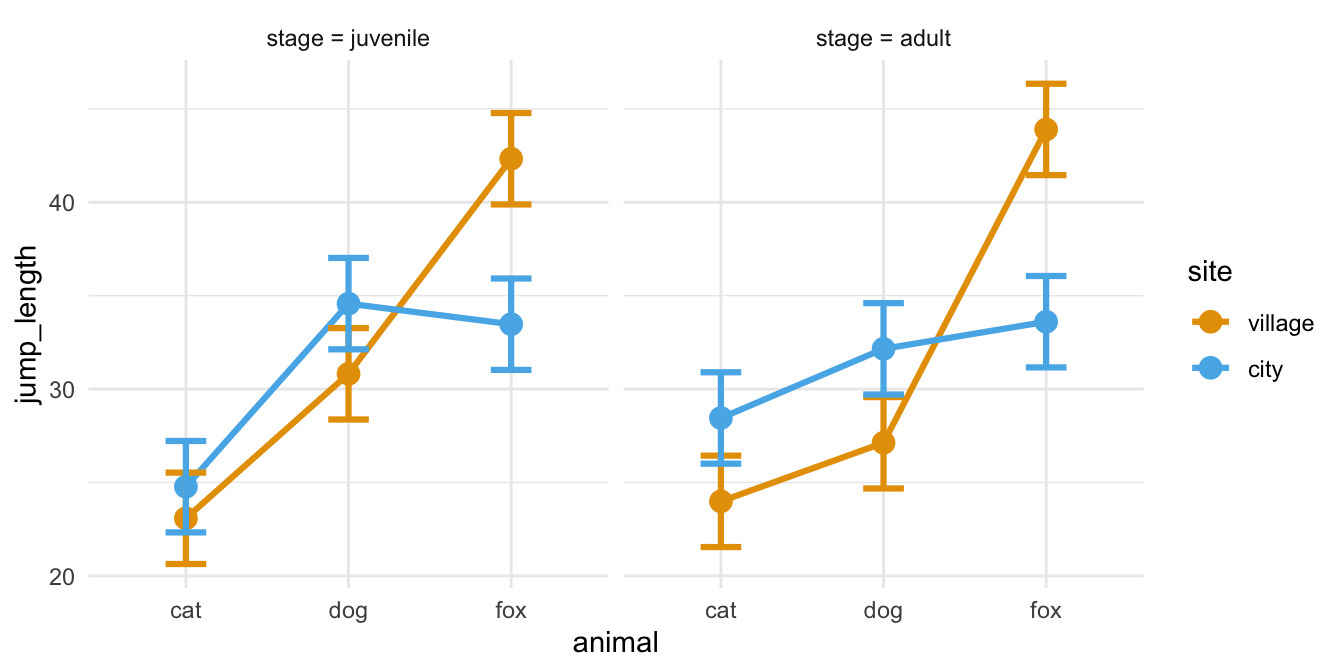
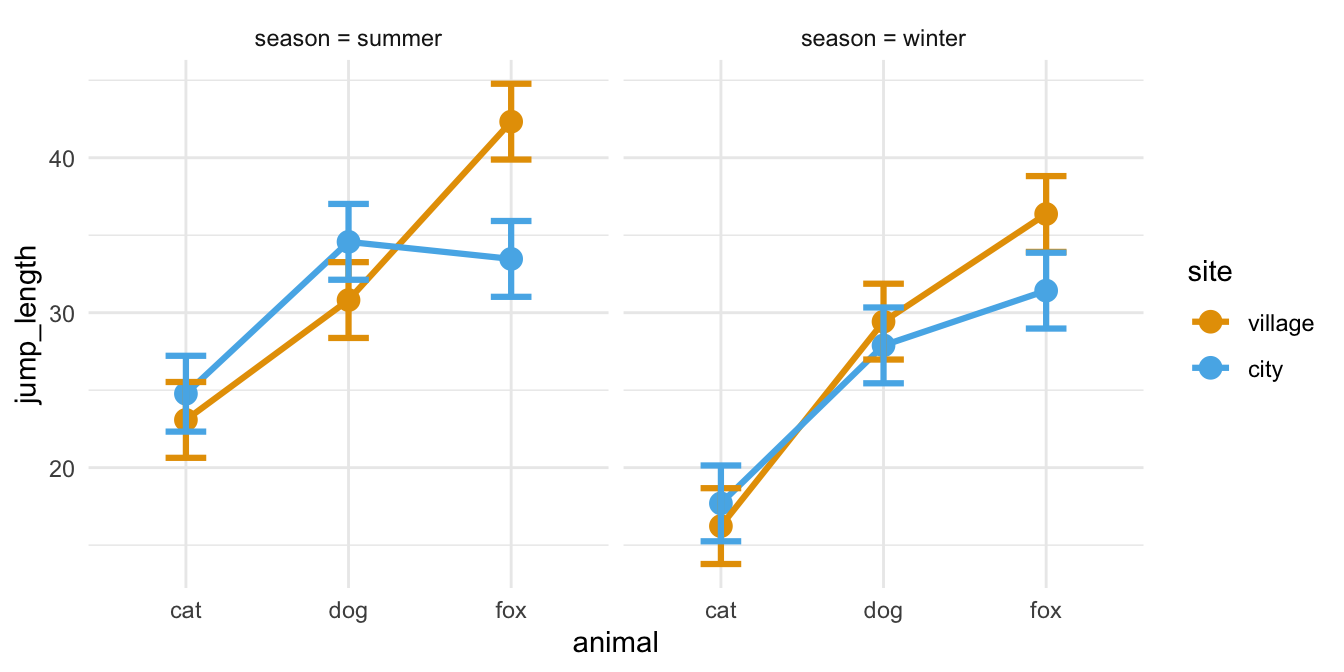
Die visuelle Überprüfung der Interaktion zwischen zwei Faktoren A und B ist eigentlich die beste Möglichkeit einmal zu schauen, ob wir überhaupt eine Wechselwirkung zwischen den Leveln des Faktors A und den Leveln des Faktors B vorliegen haben. Wenn es mehr Faktoren sind, dann wird die Sache sehr viel unübersichtlicher. Aber wir schauen uns meistens nur die Interaktion zwischen zwei Faktoren an. Für diesen Fall ist die visuelle Überprüfung auf jeden Fall geeignet. Wir haben die Wahl zwischen einem Liniendiagramm, den Boxplots oder aber den meist schon vorhandenen Barplots.

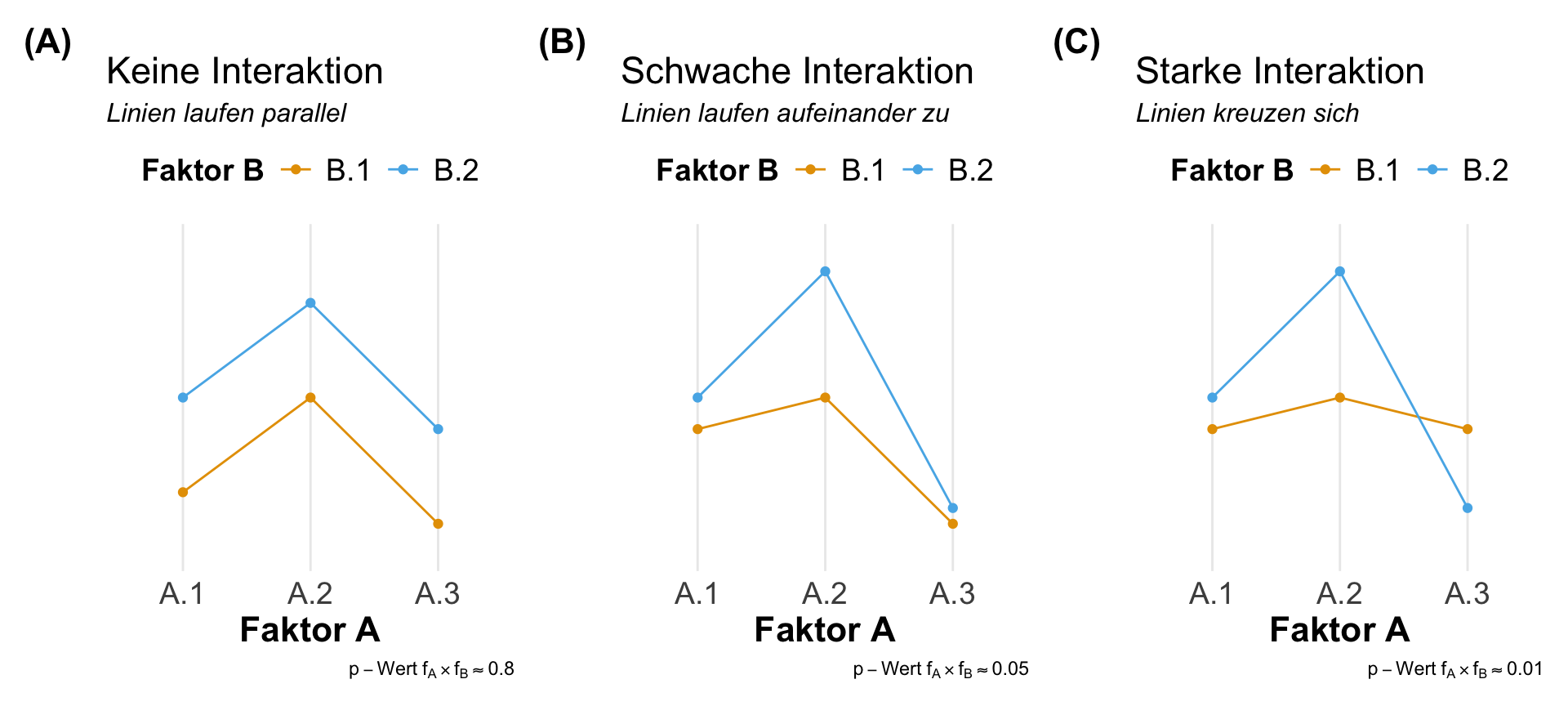
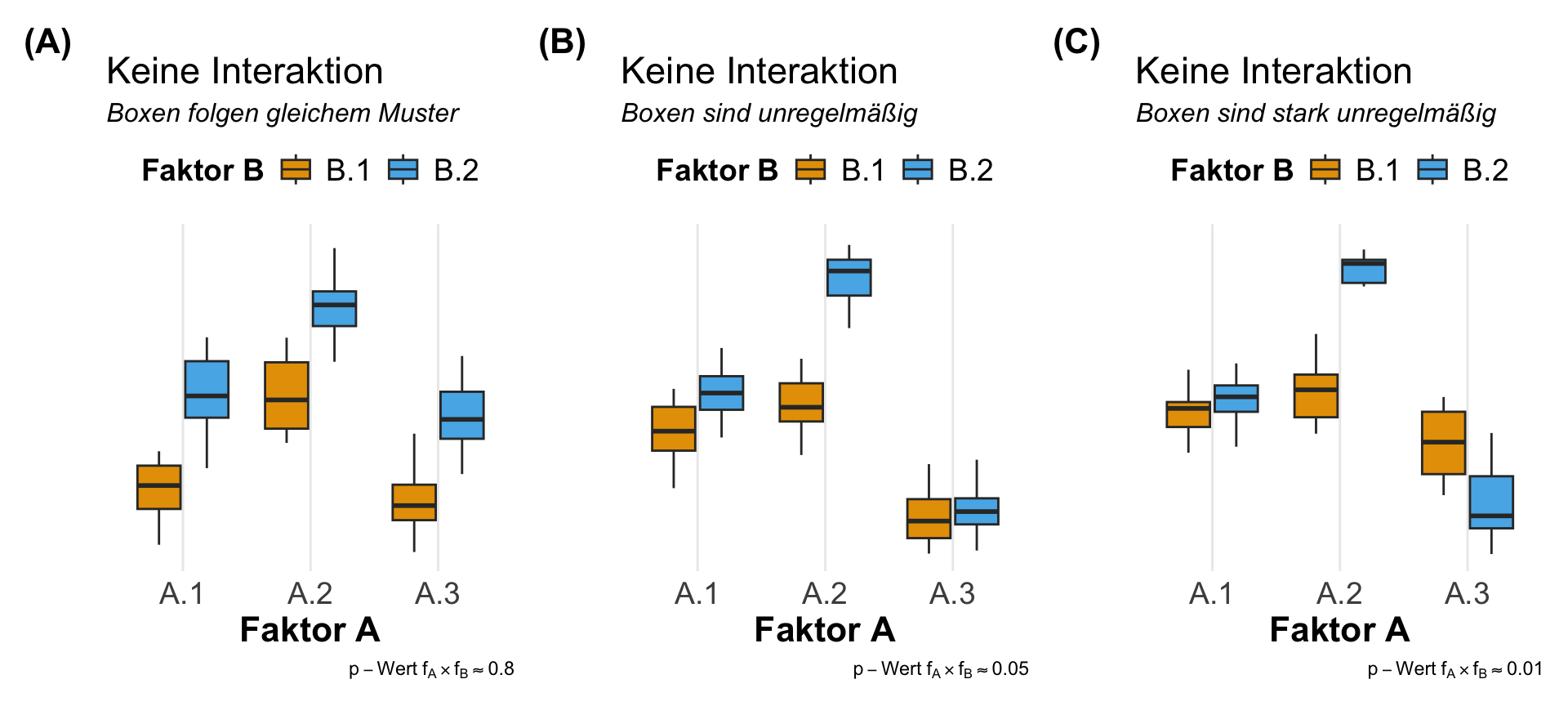
Wir betrachten hier alle drei Möglichkeiten der visuellen Überprüfung, wobei ich die Liniendiagramme mit den Mittelwerten der Faktorlevel auf jeden Fall bevorzuge. Die Boxplots gehen auch, sind aber schon etwas schwerer zu interpretieren. Von den Barplots würde ich abraten, man sieht dort wirklich schlecht eine Interaktion. In allen folgenden Abbildungen sind die Daten mehr oder minder gleich. Du musst selber entscheiden, wo du dann am besten was erkennst. Du findest den R Code für das Liniendiagramm weiter unten bei der Auswertung der zwei- und mehrfaktoriellen ANOVA.

Liniendiagramm

Abbildung 30.11— Visualisierung der Interaktion zwischen dem Faktor A mit drei Leveln und dem Faktor B mit zwei Leveln. Dargestellt sind die mit Linien verbundenen Mittelwerte aller Faktorkombinationen. Es empfiehlt sich den Faktor mit den meisten Leveln auf die x-Achse zu legen. (A) Keine Interaktion. Die Linien der Mittelwerte der Level des Faktors B laufen parallel über die drei Level des Faktors A. (B) Schwache Interaktion. Die Linien der Mittelwerte des Faktors B laufen aufeinander zu. (C) Starke Interaktion. Die Linien der Mittelwerte des Faktors B kreuzen sich. [Zum Vergrößern anklicken]

Boxplot

Abbildung 30.12— Visualisierung der Interaktion zwischen dem Faktor A mit drei Leveln und dem Faktor B mit zwei Leveln. Dargestellt sind die Boxplots aller Faktorkombinationen. Es empfiehlt sich den Faktor mit den meisten Leveln auf die x-Achse zu legen. (A) Keine Interaktion. Die Boxen folgen dem gleichem Muster mit B.2 ist immer über B.1 mit etwa gleichem Abstand. (B) Schwache Interaktion. Die Boxen sind unregelmäßig mit B.2 nur teilweise über B.1 und die Abstände sind unregelmäßig. (C) Starke Interaktion. Die Boxen sind unregelmäßig und folgen keinem wiederholenden Muster. [Zum Vergrößern anklicken]

Barplot

Abbildung 30.13— Visualisierung der Interaktion zwischen dem Faktor A mit drei Leveln und dem Faktor B mit zwei Leveln. Dargestellt sind die Barplots der Mittelwerte aller Faktorkombinationen. Es empfiehlt sich den Faktor mit den meisten Leveln auf die x-Achse zu legen. (A) Keine Interaktion. Die Säulen folgen dem gleichem Muster mit B.2 ist immer über B.1 mit etwa gleichem Abstand. (B) Schwache Interaktion. Die Säulen sind unregelmäßig mit B.2 nur teilweise über B.1 und die Abstände sind unregelmäßig. (C) Starke Interaktion. Die Säulen sind unregelmäßig und folgen keinem wiederholenden Muster. [Zum Vergrößern anklicken]

Interaktion in R

Wenn wir uns Interaktionen in einer mehrfaktoriellen ANOVA anschauen wollen dann gibt es einige Möglichkeiten. Ich zeige jetzt nicht alle R Pakete in den folgenden Beispielen. Deshalb hier nochmal eine kleine Liste, wo du nochmal schauen kannst, wenn du mehr Informationen zu der Bereücksichtigung von Interaktionen in R benötigst.

• Das R Paket {effectsize} gibt nochmal ein Übersichtskapitel zu Interakionen in verschiedenen Modellen. Darüber hinaus diskutiert die Hilfeseite auch nochmal die verschiedenen Typen und Möglichkeiten eine ANOVA zu rechnen.
• Das R Paket {interactions} enhält eine Reihe von Funktione, die eine Analyse der Interaktion in einem mehrfaktoriellen Modell erleichtern. Hier wird nicht nur auf auf Faktoren sondern auch auf kontinuierliche Werte als Einflussvariablen eingegangen. Ein sehr rundes Paket für die Analyse von Interaktionen.
• Das R Paket {emmeans} kann hier nicht fehlen, da wir ja meistens bis immer nach einer ANOVA einen Post-hoc Test rechnen wollen. Hier empfehle ich ja immer {emmeans}. Daher hat natürlich auch {emmeans} eine entsprechende Hilfeseite für die Berücksichtigung von Interaktionen in einem Modell.

Damit wären wir dann auch schon durch. Den Rest an R Paketen zeige ich dann einmal weiter unten bei den Beispieln. So hat das R Paket {afex} auch noch Möglichkeiten sich Interaktionen anzeigen zu lassen, aber das zeige ich dann teilweise in der Anwendung des Paketes weiter unten. Damit wären wir fast schon mit der Theorie durch. Als nächstes schauen wir uns dann die passenden Datensätze für die verschiedenen ANOVAs einmal an.

Exkurs: Treatment coding vs. effect coding

Worum geht es in diesem Exkurs? Zum einen geht es darum zu verstehen, wie die verschiedenen Modelle – je nachdem wie die Modelle gebaut werden – die Mittelwerte schätzen. Es gibt da nämlich verschiedene Arten dies zu tun. Eine dieser Arten nennt sich treatment coding und eine andere effect coding. Die erstere Codierung nutzen wir als Standard in der Modellierung in R. Das effect coding ist aber für die Berechnung und Interpretation einer Interaktion bei Faktoren viel besser geeignet. Also bevor wir jetzt lange rumreden, zeige ich dir den Unterschied an einem Beispiel. Wir haben folgende Datentabelle vorliegen.

Tabelle 30.7— Datentabelle von einem Faktor A mit drei Gruppen \(A.1\), \(A.2\) und \(A.3\) je drei Beobachtungen.

A.1	A.2	A.3
1	7	10
2	8	11
3	9	12

Dabei habe ich die Daten so gebaut, dass wir folgende Mittelwerte für die einzelnen Gruppen wiederfinden. Damit können wir jetzt ein Modell anpassen und schauen, wie das Modell unsere Mittelwerte abbildet.

Tabelle 30.8— Mittelwerte der drei Gruppen \(A.1\), \(A.2\) und \(A.3\) des Faktors A.

Faktor A	Mittelwert
A.1	2
A.2	8
A.3	11

Wir haben jetzt hier zwei Möglichkeiten uns die Koeffizienten des Modells wiedergeben zu lassen. Wichtig ist, dass beide Kodierungen gleichwertig sind, was am Ende die Effekte angeht. Nur die Interpretation der numerischen Werte der Ausgabe der Modelle ist eben eine Andere. Es gibt noch mehr Contrast codings, je nachdem wie dein Messwert \(y\) oder deine Faktoren \(f\) beschaffen sind. Aber das geht hier entschieden zu weit.

Treatment coding

Im Falle des treatment codings ist der (Intercept) der Mittelwert der Gruppe \(A.1\) und die Koeffizienten von \(A.2\) und \(A.3\) mit faA.2 und faA.3 zeigen die Differenz zum Mittelwert der Gruppe \(A.1\). Klingt wirr, ist aber mathematisch eine Lösung des Problems. Wir rechnen eben in einer Regression eine Steigung aus und die Differenzen sind eben Steigungen.

lm(rsp ~ fa, f1_contr_sum_tbl, contrasts = list(fa = "contr.treatment")) |> 
  coef() |> round(2)

(Intercept)       faA.2       faA.3 
          2           6           9 

Effect coding

Im Falle des effect codings ist der (Intercept) der gloable Mittelwert \(\beta_0\) aller Beobachtungen. Damit sind dann die Koeffizienten fa1 die Differenz des lokalen Mittelwerts von \(A.1\) zu dem globalen Mittelwert. Ebenso ist dies der Fall für den Koeffizienten fa2, der die Differenz des lokalen Mittelwerts von \(A.2\) zum globalen Mittel beschreibt. Wo ist jetzt der Koeffizient für \(A.3\)? Der fehlt, lässt sich aber leicht berechnen, da die Summe der lokalen Mittelwerte Null sein muss. Damit wäre \(\bar{y}_{A.3}\) gleich 4.

lm(rsp ~ fa, f1_contr_sum_tbl, contrasts = list(fa = "contr.sum")) |> 
  coef() |> round(2)

(Intercept)         fa1         fa2 
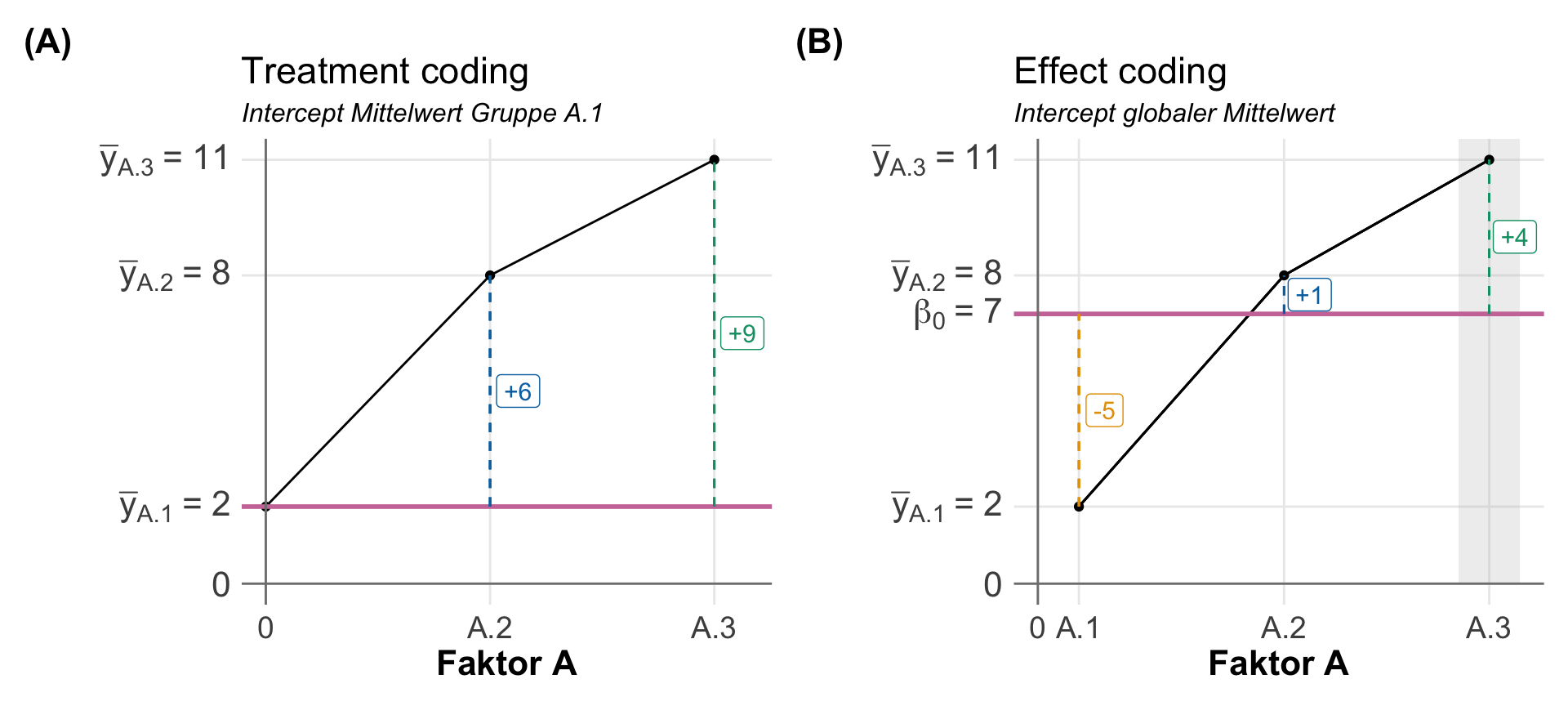
          7          -5           1 

Wir können uns die Sachlage auch einmal in der folgenden Abbildung einmal visualisieren. Auf der linken Seite siehst du das treatment coding mit den jeweiligen lokalen Mittelwerten und als rote Linie den y-Achsenabschnitt der jeweiligen Kodierung. Hier sieht man dann auch sehr schon auf der rechten Seite, dass das effect coding die Theorie der ANOVA viel besser abbildet.

Abbildung 30.14— Visualisierung der Mittelwerte des Datensatzes. (A) Treatment Coding mit dem (Intercept) auf dem Mittelwert der Gruppe \(A.1\). Die Koeffizienten des Modells beschreiben die Differenz der anderen Gruppen zum Mittel der Gruppe \(A.1\). (B) Effect coding mit dem (Intercept) auf dem globalen Mittelwert \(\beta_0\). Die Koeffizienten des Modells beschreiben die Abweichungen der Gruppenmittel zum globalen Mittel. Der Koeffizient für \(A.3\) ist nicht im Modell enthalten, dargestellt als graue Fläche [Zum Vergrößern anklicken]

Jetzt wo wir den Unterschied zwischen dem treatment coding und dem effect coding verstanden haben, können wir uns einmal den Interaktionsterm in einer zweifaktoriellen ANOVA mit effect coding anschauen. Wie wir gleich sehen werden ist die Interpretation etwas einfacher, wenn wir uns eine Interaktion im Sinne des effect codings bauen. Wir setzen dann eben alle Koeffizienten in den Bezug zum globalen Mittel. Das macht die Interpretation dann in einer zweifaktoriellen ANOVA einfacher.

Effect coding ohne Interaktion

Beginnen wir einmal mit dem effect coding ohne Interaktion. In diesem Fall haben wir einen einfacheren zweifaktoriellen Datensatz in folgender Tabelle mit dem Faktor A und drei Leveln sowie den Faktor B mit zwei Leveln vorliegen. Es sieht jetzt etwas größer aus, aber ich habe die Daten so gebaut, dass faktisch keine Streuung in den Daten ist.

Tabelle 30.9— Datentabelle ohne Interaktion zwischen einem Faktor A mit drei Gruppen \(A.1\), \(A.2\) und \(A.3\) je drei Beobachtungen sowie einem Faktor B mit zwei Gruppen \(B.1\) und \(B.2\). Insgesamt liegen sechs Faktorkombinationen vor.

	B.1	B.2
A.1	79	39
A.1	80	40
A.1	81	41
A.2	149	99
A.2	150	100
A.2	151	101
A.3	199	149
A.3	200	150
A.3	201	151

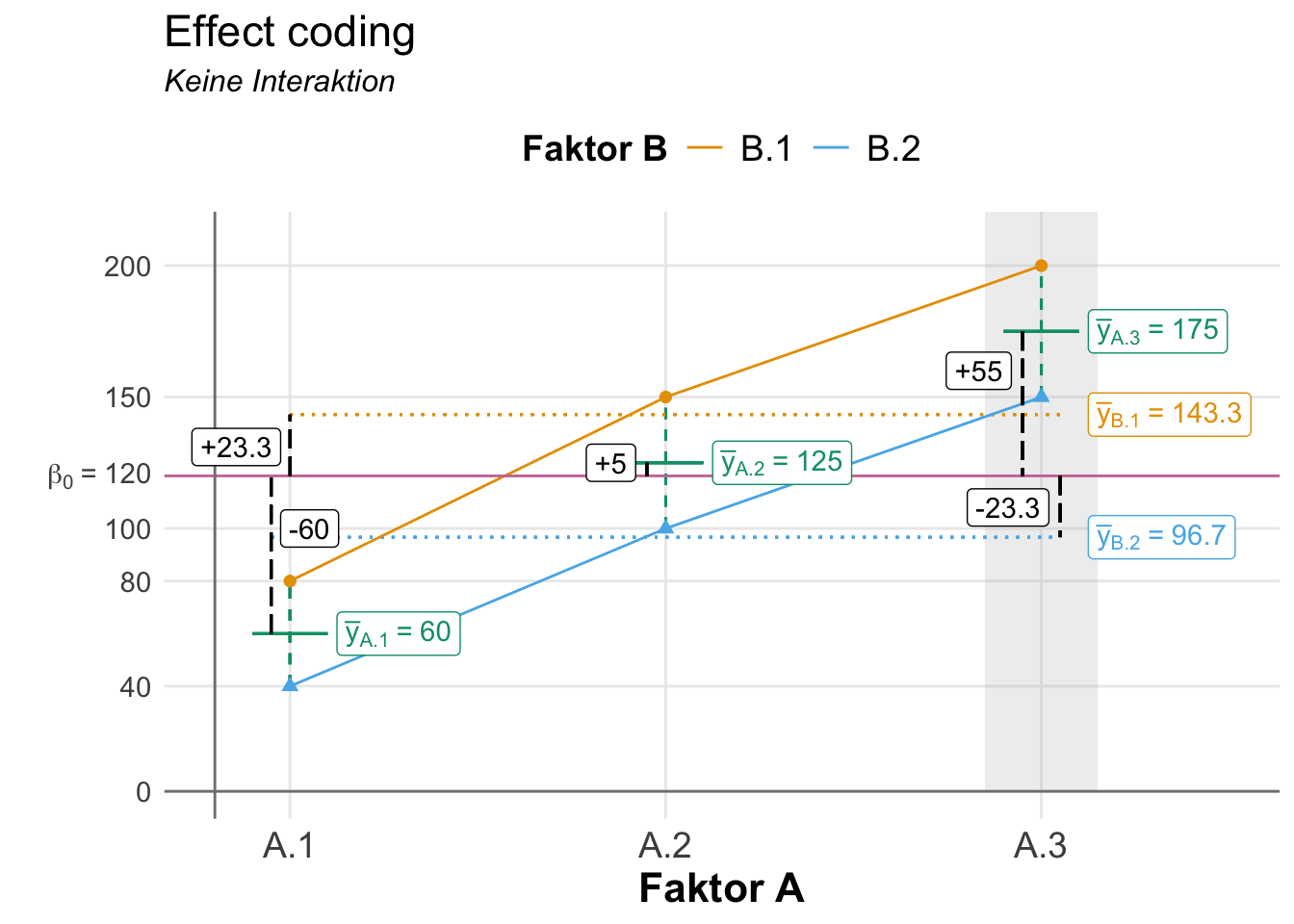
Jetzt können wir uns die Mittelwerte für jede der sechs Faktorkombinationen berechnen. Ich habe das einmal in der folgenden Tabelle gemacht. Ich finde es immer sehr schwer, hier was zu sehen, aber mit einer Visualisierung wird es gleich einfacher. Wenn keine Interaktion vorliegt, dann müssen die Level des Faktors B über die Level des Faktors A parallel wie in der folgenden Abbildung 30.15 laufen.

Tabelle 30.10— Mittelwerte der sechs Faktorkombination von Faktor A und Faktor B. Es liegt keine Interaktion in den Daten vor. Der Faktor B verhält sich über alle Level des Faktors A gleich.

Faktor A	Faktor B	Mittelwert
A.1	B.1	80
A.1	B.2	40
A.2	B.1	150
A.2	B.2	100
A.3	B.1	200
A.3	B.2	150

Jetzt wollen wir einmal eine lineare Regression mit dem vollen Modell der beiden Faktoren und dem Interaktionsterm rechnen um die Koeffizienten als Effekte zu erhalten. Wenn wir ein effect coding in R nutzen wollen, dann müssen wir das der Funktion lm() mit der Option contrast = ... mitteilen. In R heißt dann efffect coding eben contr.sum und damit leben wir dann. Wir ziehen uns die Koeffizienten und runden noch kurz.

lm(rsp ~ fa + fb + fa:fb, f2_contr_sum_nointer_tbl, 
   contrasts = list(fa = "contr.sum", fb = "contr.sum")) |> 
  coef() |> round(2)

(Intercept)         fa1         fa2         fb1     fa1:fb1     fa2:fb1 
     120.00      -60.00        5.00       23.33       -3.33        1.67 

In unseren Daten ist keine Interaktion. Deshalb ist der Effekt der Interaktion mit \(-3.33\) und \(1.64\) für die beiden Interaktionsterme sehr klein. Den Hauptteil der Effekte machen die beiden Faktoren A und B aus. In der folgenden Tabelle siehst du einmal für den y-Wert \(80\) wie sich die Effekte durch die Faktoren aufaddieren.

Tabelle 30.11— Beispielhafte Berechnung des Messwertes \(y\) für die Faktorkombination von \(A.1\) und \(B.1\) aus den Koeffizienten des effect codings.

\(y\)		\(\beta_0\)	\(\beta_{A.1}\)	\(\beta_{B.1}\)	\(\beta_{A.1 \times B.1}\)
\(80\)	\(=\)	\(120\)	\(-60\)	\(+23.3\)	\(-3.3\)

Du kannst die obige Berechnung auch in der folgenden Abbildung mit den Effekten einmal nachvollziehen. Wir wollen ja den y-Wert \(80\) vom y-Achsenabschnitt \(120\) kommend erreichen. Der Wert \(80\) kommt durch die Faktorkombination A.1 und B.1 zustande. Deshalb ziehen wir \(-60\) vom y-Achsenabschnitt für den Effekt von A.1 ab und addieren \(+23.33\) für den Effekt von B.1. Der Rest, der mit \(-3.33\) dann noch übrig ist, geht auf das Konto der Interaktion von A.1 und B.1.

Abbildung 30.15— Visualisierung des effect coding mit keiner Interaktion zwischen den Faktoren A und B. Die berechneten Effekte als Differenzen in Mittelwerten beziehen sich jeweils auf den globalen Mittelwert. Die Effekte für A.3 werden nicht vom Modell wiedergegeben sondern müssen aus dem Modell berechnet werden [Zum Vergrößern anklicken]

Jetzt fehlen natürlich noch die Effekte für das Level A.3 aus dem Faktor A sowie die Effekte des Levels B.2 aus dem Faktor B. Auch müssen wir noch die letzte Interaktion von A.3 mit B.1 berechnen. Wichtig ist, dass alle Effekte als Mittelwertsdifferenzen zum globalen Mittel aufsummiert Null ergeben müssen. Das mache ich jetzt einmal für die fehlenden Effekte händisch.

Tabelle 30.12— Effekte von dem Faktor A. Den Effekt des Levels A.3 berechnen wir händisch.

	\(\beta_{A.1}\) oder fa1	\(\beta_{A.2}\) oder fa2	\(\beta_{A.3}\) oder fa3
\(\sum = 0\)	\(-60\)	\(+5\)	\(+55\)

Tabelle 30.13— Effekte von dem Faktor B. Den Effekt des Levels B.2 berechnen wir händisch.

	\(\beta_{B.1}\) oder fb1	\(\beta_{B.2}\) oder fb2
\(\sum = 0\)	\(+23.33\)	\(-23.33\)

Tabelle 30.14— Effekte der Interaktion zwischen dem Faktor A und dem Faktor B. Den Effekt der Interaktion von A.3 und B.1 berechnen wir händisch.

	\(\beta_{A.1 \times B.1}\) oder fa1:fb1	\(\beta_{A.2 \times B.1}\) oder fa2:fb1	\(\beta_{A.3 \times B.1}\) oder fa3:fb1
\(\sum = 0\)	\(-3.33\)	\(+1.67\)	\(+1.67\)

Effect coding mit Interaktion

Nachdem du einmal das effect cosing ohne Interaktion zwischen den Faktoren A und B verstanden hast, schauen wir usn das gleiche Setting nochmal mit Interaktion an. Wir haben wieder den Faktor A mit drei Leveln und den Faktor B mit zwei Leveln vorliegen. Jetzt haben wir aber in der folgenden Datentabelle eine Interaktion zwischen den beiden Faktoren vorliegen. Die Messwerte für die Faktorkombination A.1 und B.1 sind nicht in der Richtung und Werten gleich wie in der Faktorkombination A.3 und B.1. Das ist hier schwer in den Zahlen zu sehen, aber faktisch drehen sich die Werte einmal. In dem Level A.1 ist B.1 großer als B.2 aber in dem Level A.3 ist es genau umgekehrt. Eine klassische Interaktion finden wir hier.

Tabelle 30.15— Datentabelle mit Interaktion zwischen einem Faktor A mit drei Gruppen \(A.1\), \(A.2\) und \(A.3\) je drei Beobachtungen sowie einem Faktor B mit zwei Gruppen \(B.1\) und \(B.2\). Insgesamt liegen sechs Faktorkombinationen vor. Die Interaktion in den Daten von \(B.1\) ist orange hervorgehoben.

	B.1	B.2
A.1	209	39
A.1	210	40
A.1	211	41
A.2	159	99
A.2	160	100
A.2	161	101
A.3	59	149
A.3	60	150
A.3	61	151

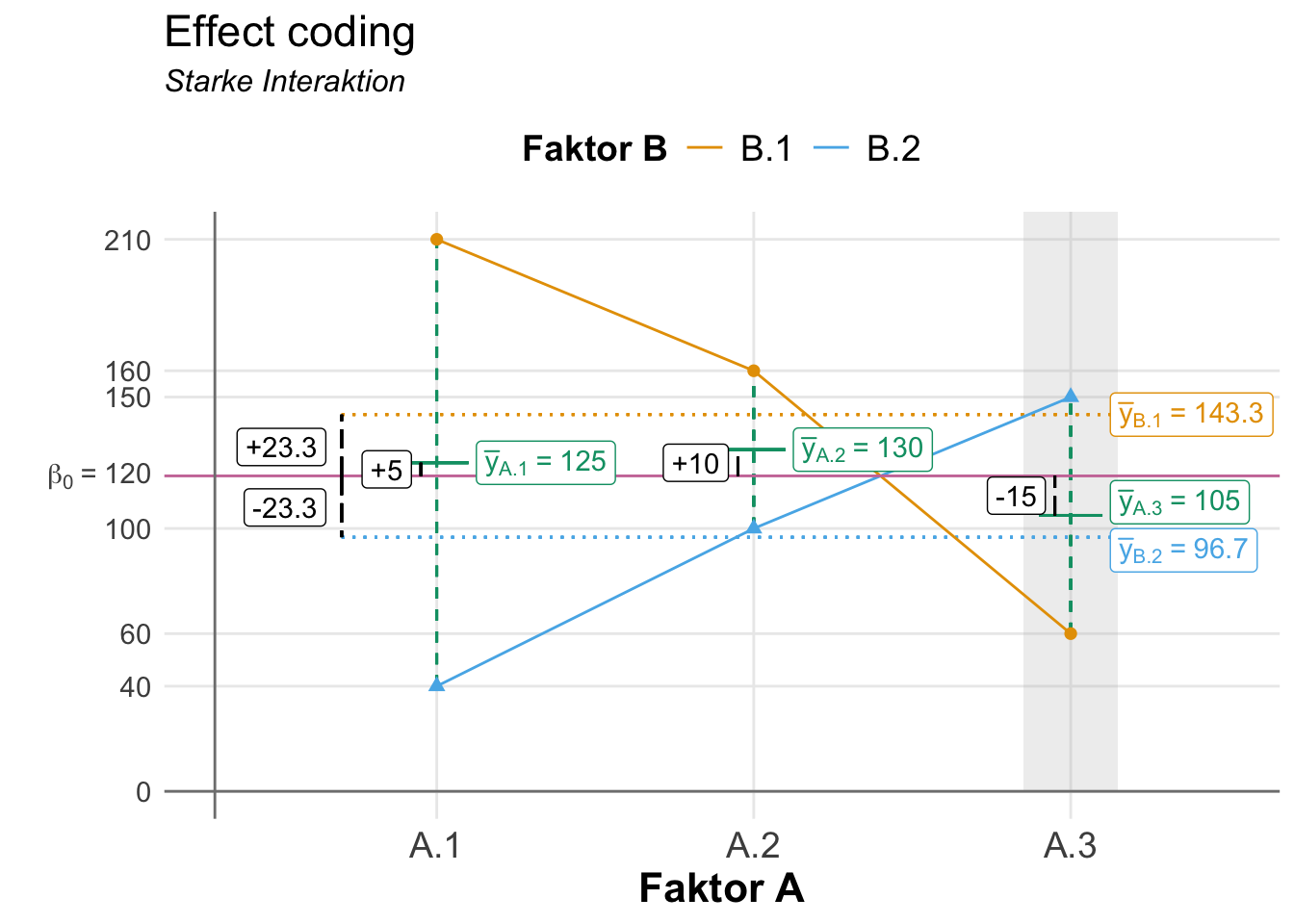
Dann nochmal für alle sechs Faktorkombinationen den Mittlwert berechnet. Ich habe dir auch hier einmal die Interaktion farblich hervorgehoben. Du siehst den Zusammenhang aber sehr viel besser in der folgenden Abbildung 30.16. Die Linien der Mittelwerte kreuzen sich, es liegt eine Interaktion zwischen den Faktoren vor.

Tabelle 30.16— Mittelwerte der sechs Faktorkombination von Faktor A und Faktor B. Die Interaktion in den Mittelwerten von \(B.1\) ist orange hervorgehoben.

Faktor A	Faktor B	Mittelwert
A.1	B.1	210
A.1	B.2	40
A.2	B.1	160
A.2	B.2	100
A.3	B.1	60
A.3	B.2	150

Auch hier wollen wir einmal eine lineare Regression mit dem vollen Modell der beiden Faktoren und dem Interaktionsterm rechnen um die Koeffizienten als Effekte zu erhalten. Wenn wir ein effect coding in R nutzen wollen, dann müssen wir das der Funktion lm() mit der Option contrast = ... mitteilen. In R heißt dann efffect coding eben contr.sum und damit leben wir dann. Wir ziehen uns die Koeffizienten und runden noch kurz. Hier sehen wir dann die Effekte in der Interaktion auch numerisch klar. Die Koeffizienten der Interaktion sind sehr viel größer als die Haupteffekte der Faktoren.

lm(rsp ~ fa + fb + fa:fb, f2_contr_sum_inter_tbl, 
   contrasts = list(fa = "contr.sum", fb = "contr.sum")) |> 
  coef() |> round(2)

(Intercept)         fa1         fa2         fb1     fa1:fb1     fa2:fb1 
     120.00        5.00       10.00       23.33       61.67        6.67 

Auch hier können wir einmal beispielhaft ausrechnen wie wir auf den y-Wert von \(120\) kommen würden. Nur ein kleiner Teil des Wertes machen die Haupteffekte der Faktoren aus. Ein Großteil des Wertes wird von der Interaktion erkärt. Um auf den Wert von \(210\) zu kommen reichen die Effekte von A.1 und B.1 nicht aus. Ein Großteil des Wertes muss durch eine Interaktion der beiden Level beschrieben werden.

Tabelle 30.17— Beispielhafte Berechnung des Messwertes \(y\) für die Faktorkombination von \(A.1\) und \(B.1\) aus den Koeffizienten des effect codings.

\(y\)		\(\beta_0\)	\(\beta_{A1}\)	\(\beta_{B1}\)	\(\beta_{A1:B1}\)
\(210\)	\(=\)	\(120\)	\(+5\)	\(+23.3\)	\(+61.67\)

Abbildung 30.16— Visualisierung des effect coding mit einer Interaktion zwischen den Faktoren A und B. Die Linien der Mittelwerte kreuzen sich. Die berechneten Effekte als Differenzen in Mittelwerten beziehen sich jeweils auf den globalen Mittelwert. Die Effekte für A.3 werden nicht vom Modell wiedergegeben sondern müssen aus dem Modell berechnet werden [Zum Vergrößern anklicken]

Jetzt fehlen natürlich noch die Effekte für das Level A.3 aus dem Faktor A sowie die Effekte des Levels B.2 aus dem Faktor B. Auch müssen wir noch die letzte Interaktion von A.3 mit B.1 berechnen. Das ist ja hier mit Interaktion der interessante Teil! Wichtig ist, dass alle Effekte als Mittelwertsdifferenzen zum globalen Mittel aufsummiert Null ergeben müssen. Das mache ich jetzt einmal für die fehlenden Effekte händisch.

Tabelle 30.18— Effekte von dem Faktor A. Den Effekt des Levels A.3 berechnen wir händisch.

	\(\beta_{A.1}\) oder fa1	\(\beta_{A.2}\) oder fa2	\(\beta_{A.3}\) oder fa3
\(\sum = 0\)	\(+5\)	\(+10\)	\(-15\)

Tabelle 30.19— Effekte von dem Faktor B. Den Effekt des Levels B.2 berechnen wir händisch.

	\(\beta_{B.1}\) oder fb1	\(\beta_{B.2}\) oder fb2
\(\sum = 0\)	\(+23.33\)	\(-23.33\)

Tabelle 30.20— Effekte der Interaktion zwischen dem Faktor A und dem Faktor B. Den Effekt der Interaktion von A.3 und B.1 berechnen wir händisch.

	\(\beta_{A.1 \times B.1}\) oder fa1:fb1	\(\beta_{A.2 \times B.1}\) oder fa2:fb1	\(\beta_{A.3 \times B.1}\) oder fa3:fb1
\(\sum = 0\)	\(+61.67\)	\(6.67\)	\(-68.33\)

30.3 Genutzte R Pakete

Wir wollen folgende R Pakete in diesem Kapitel nutzen.

pacman::p_load(tidyverse, magrittr, broom, WRS2, scales,
               readxl, see, car, patchwork, emmeans,
               interactions, effectsize, afex, report,
               performance, conflicted)
conflicts_prefer(dplyr::mutate)
conflicts_prefer(dplyr::summarize)
conflicts_prefer(dplyr::filter)
conflicts_prefer(dplyr::arrange)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73", 
                "#F0E442", "#0072B2", "#D55E00", "#CC79A7")

An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.

30.4 Daten

Wir immer bringe ich hier ein paar Datensätze mit damit wir dann verstehen, was eigentlich in den folgenden Analysen in R und den entsprechenden R Paketen passiert. Ich zeige hier an den Daten nur die Anwendung in R und nicht eine händische Berechnung der ANOVA. Deshalb fehlen dann hier auch die Mittelwerte und andere deskritptive Maßzahlen. Schauen wir jetzt also mal in unsere Beispieldaten für die einfaktorielle, zweifaktorielle und mehrfaktorielle ANOVA rein. Wie immer nehme ich hier als normalverteilten Messwert die Sprungweite von Floharten.

Einfaktorieller Datensatz

Beginnen wir mit einem einfaktoriellen Datensatz. Wir haben hier als Messwert die Sprungweite von Flöhen in [cm] vorliegen. Wissen wollen wir, ob sich die Sprungweite für drei verschiedene Floharten unterscheidet. Damit ist dann in unserem Modell der Faktor animal und die Sprungweite jump_length als Messwert. Ich lade einmal die Daten in das Objekt fac1_tbl und ergänze noch eine ID Spalte für das R Paket {afex}. Wir haben jeden Floh nur einmal gemessen, also kriegt jeder Floh eine eigene ID.

fac1_tbl <- read_xlsx("data/flea_dog_cat_fox.xlsx") |>
  select(animal, jump_length) |> 
  mutate(animal = as_factor(animal))|> 
  rowid_to_column(".id")

Dann schauen wir uns die Daten einmal in der folgenden Tabelle als Auszug einmal an. Wichtig ist hier nochmal, dass du eben einen Faktor animal mit drei Leveln also Gruppen vorliegen hast. Wir wollen jetzt die drei Tierarten hinsichtlich ihrer Sprungweite in [cm] miteinander vergleichen.

Tabelle 30.21— Tabelle der Sprungweiten in [cm] als Messwert \(y\) von Hunde-, Katzen- und Fuchsflöhen. Der Datensatz ist einfaktoriell, da wir nur einen Faktor vorliegen haben.

.id	animal	jump_length
1	dog	5.7
2	dog	8.9
3	dog	11.8
...	...	...
19	fox	10.6
20	fox	8.6
21	fox	10.3

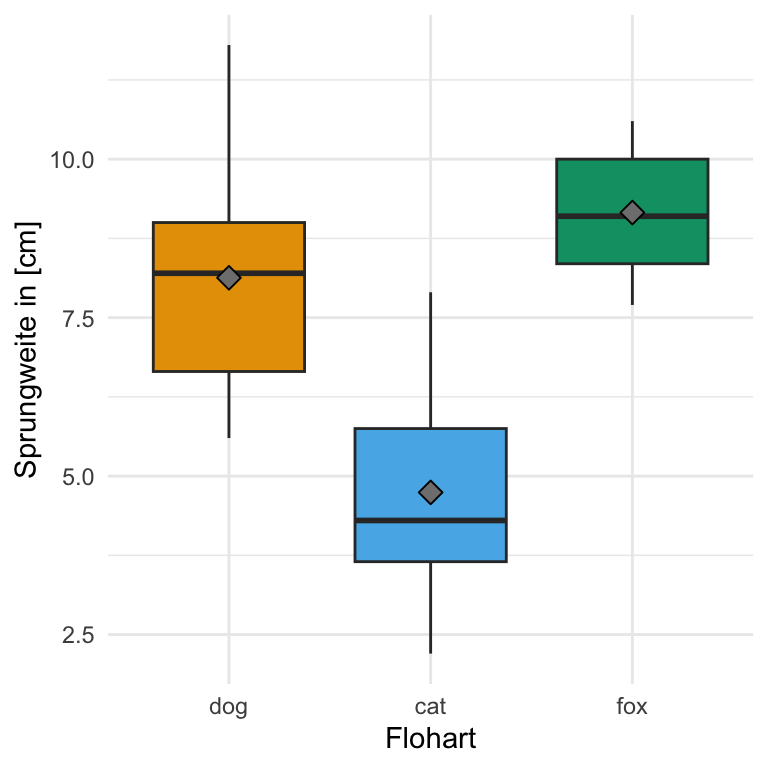
Und dann wollen wir uns noch einmal die Daten als einen einfachen Boxplot anschauen. Wir sehen, dass die Daten so gebaut sind, dass wir einen signifikanten Unterschied zwischend den Sprungweiten der Floharten erwarten. Die Boxen der Boxplots überlappen sich nicht und die Boxplots liegen auch nicht auf einer Ebene.

Abbildung 30.17— Beispielhafter einfaktorieller Boxplot für die Sprungweiten in [cm] gruppiert nach den Floharten.

Zweifaktorieller Datensatz

Neben dem einfaktoriellen Datensatz wollen wir uns noch den häufigeren Fall mit zwei Faktoren anschauen. Wir haben also nicht nur die drei Floharten vorliegen und wollen wissen ob diese unterschiedlich weit springen. Darüber hinaus haben wir noch einen zweiten Faktor gewählt. Wir haben die Sprungweiten der Hunde-, Katzen- und Fuchsflöhe nämlich an zwei Messorten, der Stadt und dem Dorf, gemessen. Dadurch haben wir jetzt den Faktor animal und den Faktor site vorliegen. Wiederum fragen wir usn, ob sich die Sprungweite in [cm] der drei Floharten in den beiden Messorten unterscheidet. Im Folgenden lade ich einmal den Datensatz in das Objekt fac2_tbl und ergänze noch eine ID Spalte für das R Paket {afex}. Wir haben jeden Floh nur einmal gemessen, also kriegt jeder Floh eine eigene ID.

fac2_tbl <- read_xlsx("data/flea_dog_cat_fox_site.xlsx") |> 
  select(animal, site, jump_length) |> 
  filter(site %in% c("city", "village")) |> 
  mutate(animal = as_factor(animal),
         site = as_factor(site))|> 
  rowid_to_column(".id")

Betrachten wir als erstes einen Auszug aus der Datentabelle. Wir haben hier als Messwert oder Outcome \(y\) die Sprungweite jump_length vorliegen. Als ersten Faktor die Variable animal und als zweiten Faktor die Variable site festgelegt.

Tabelle 30.22— Tabelle der Sprungweiten in [cm] als Messwert \(y\) von Hunde-, Katzen- und Fuchsflöhen an zwei verschiedenen Messorten Stadt und Dorf. Der Datensatz ist zweifaktoriell, da wir einen Behandlungsfaktor mit animal und einen zweiten Faktor mit site vorliegen haben.

.id	animal	site	jump_length
1	cat	city	12.04
2	cat	city	11.98
3	cat	city	16.1
...	...	...	...
58	fox	village	16.96
59	fox	village	13.38
60	fox	village	18.38

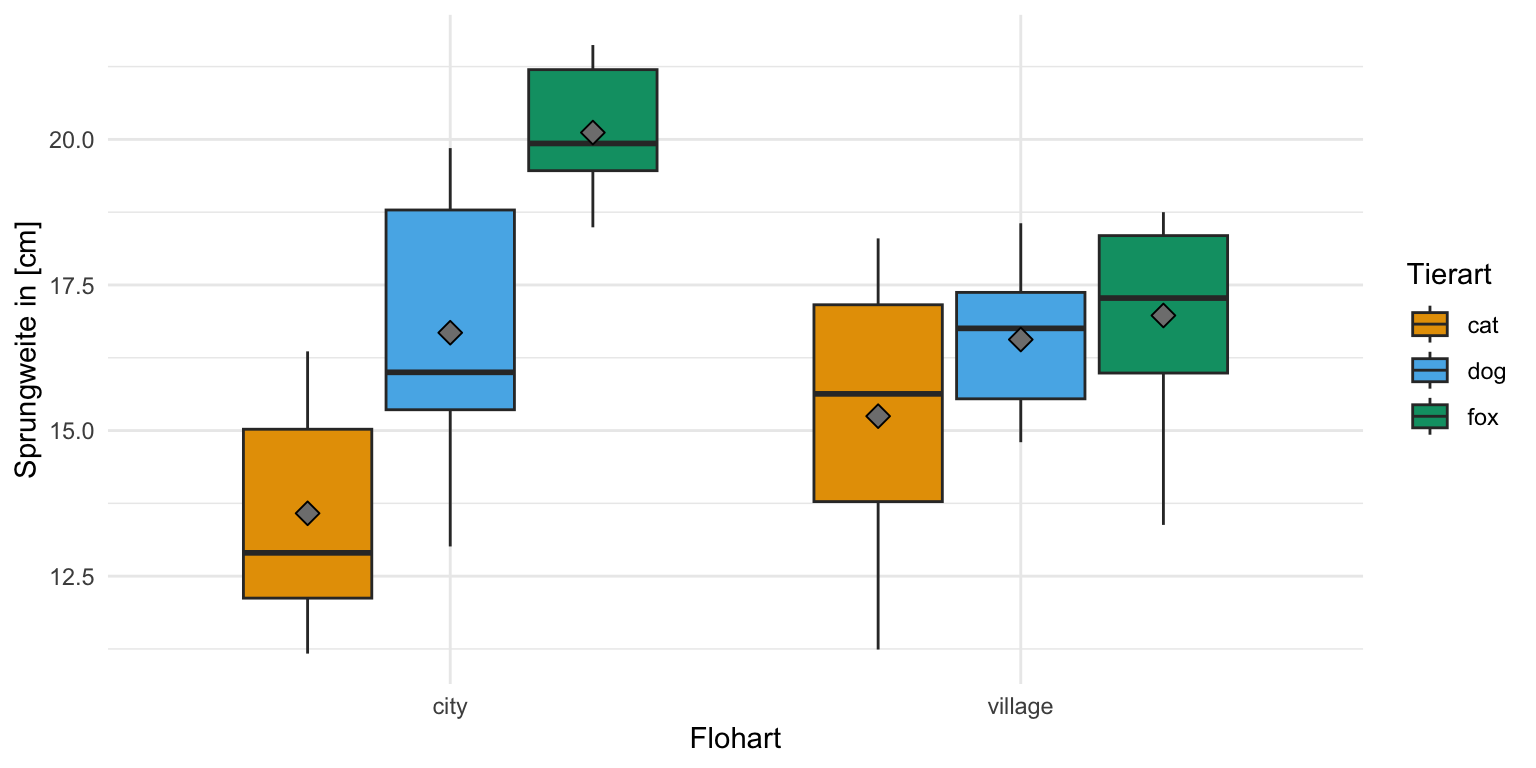
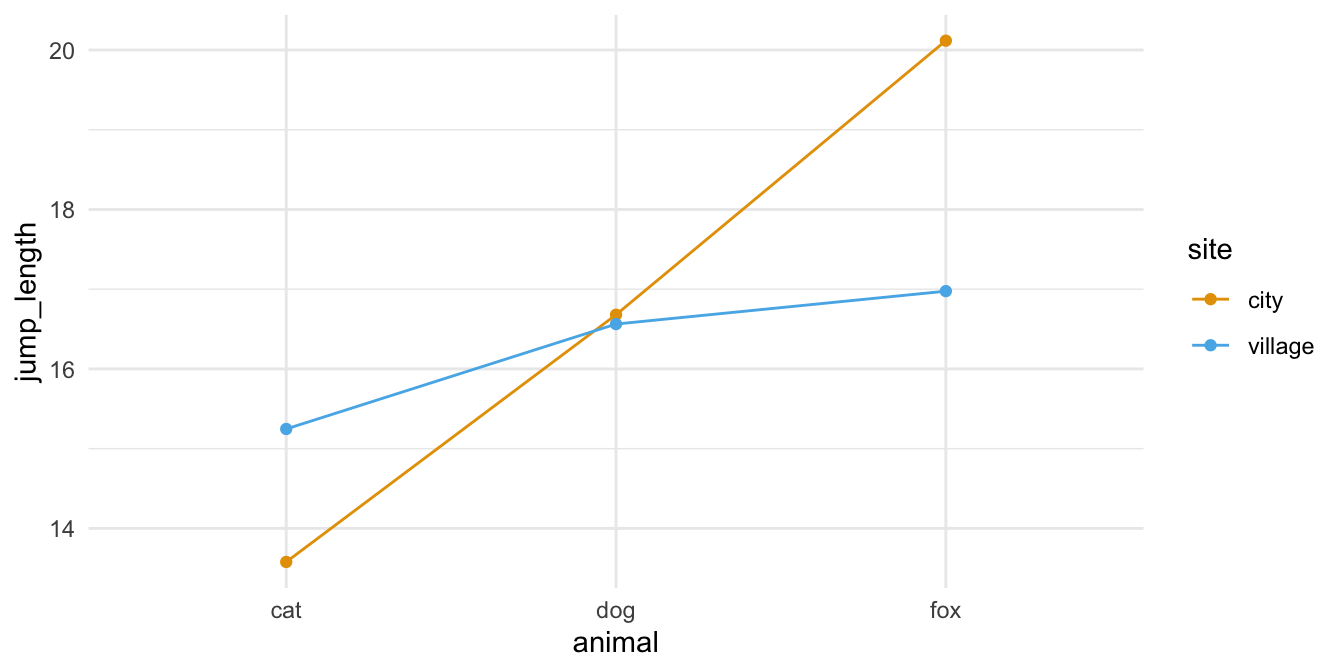
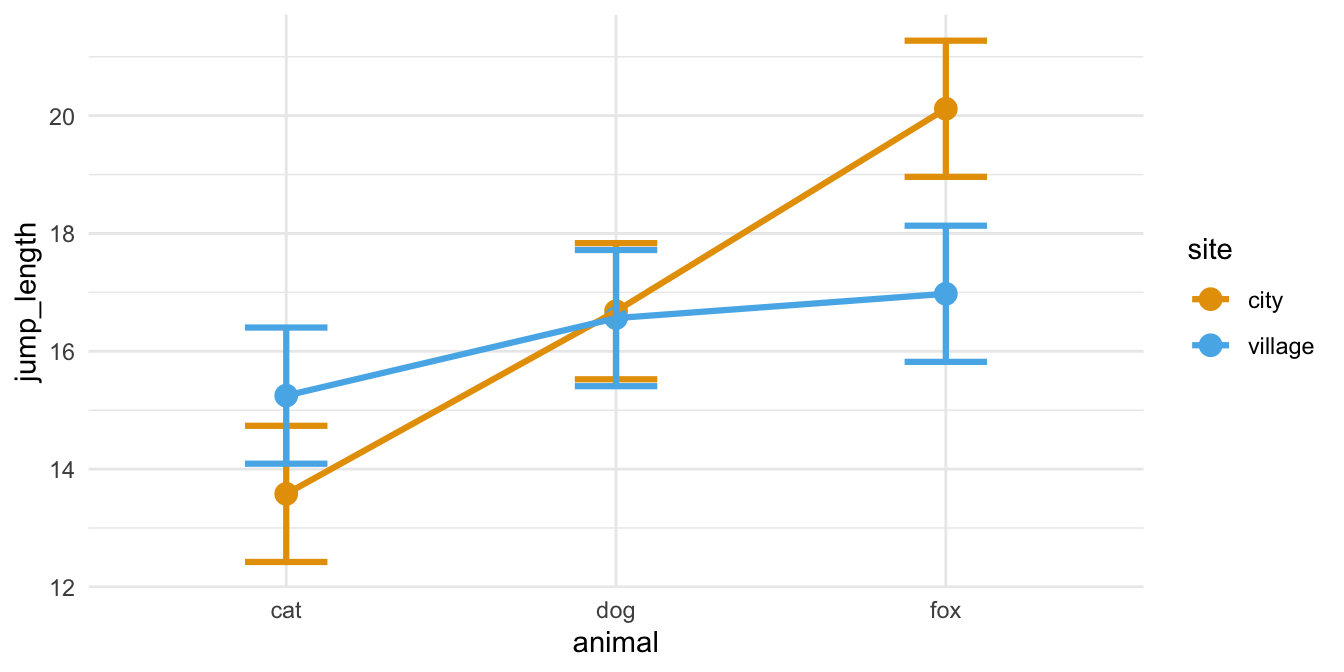
Auch hier schauen wir uns einmal die Daten in einem Boxplot an. Wir sehen zum einen den Effekt der Floharten. Hier sehen wir aber auch eine klare Interaktion in den Daten. Die Flöhe springen in der Stadt unterschiedlich weit als in dem Dorf. So ist der Effekt und damit der Unterschied zwischen den Floharten in der Stadt ein anderer als auf dem Dorf. Wir haben eine vermutliche Interaktion zwichen den beiden Faktoren animal und site vorliegen.

Abbildung 30.18— Beispielhafter zweifaktorieller Boxplot für die Sprungweiten in [cm] gruppiert nach den Floharten und den beiden Messorten.

Multifaktorieller Datensatz

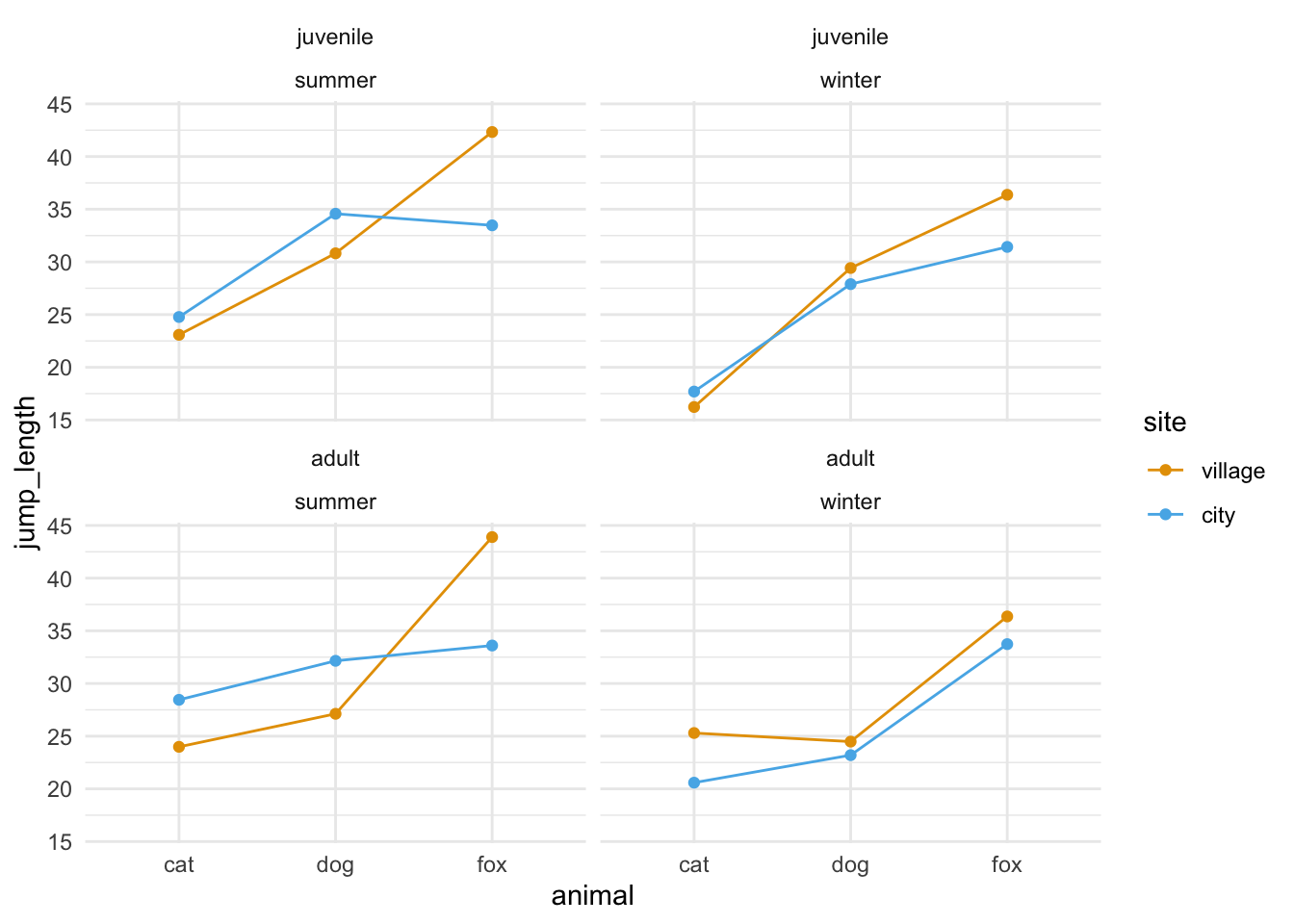
Als letzten Datensatz lade ich noch einen multifaktoriellen Datensatz. Wir haben hier mehrere Faktoren vorliegen. Neben den Floharten animal haben wir auch den Entwicklungsstand stage sowie die Messorte site bestimmt. Dazu kommt dann noch der Faktor season als Jahreszeit. Damit haben wir dann einen vierfaktoriellen oder kurz multifaktoriellen Datensatz vorliegen. Hier wird die Sachlage dann schnell unübersichtlich und solche mehrfaktoriellen Datensätze kommen in der Praxis eher selten vor. Im Folgenden lade ich einmal den Datensatz in das Objekt fac4_tbl und ergänze noch eine ID Spalte für das R Paket {afex}. Wir haben jeden Floh nur einmal gemessen, also kriegt jeder Floh eine eigene ID.

fac4_tbl <- read_excel("data/fleas_complex_data.xlsx", sheet = "fac4") |> 
  select(animal, stage, site, season, jump_length) |> 
  mutate(animal = as_factor(animal),
         stage = factor(stage, level = c("juvenile", "adult")),
         site = as_factor(site),
         season = as_factor(season),
         jump_length = round(jump_length, 2))|> 
  rowid_to_column(".id")

Betrachten wir als erstes einen Auszug aus der Datentabelle. Wir haben hier als Messwert oder Outcome \(y\) die Sprungweite jump_length vorliegen. Als ersten Faktor die Variable animal und als zweiten Faktor die Variable site festgelegt sowie als dritten Faktor den Entwicklungsstand stage der Flöhe.

Tabelle 30.23— Tabelle der Sprungweiten in [cm] als Messwert \(y\) von Hunde-, Katzen- und Fuchsflöhen an zwei verschiedenen Messorten Stadt und Dorf. Dazu wurde noch der Entwicklungsstand mit erwachsen und jugendlich erhoben. Der Datensatz ist dreifaktoriell, da wir einen Behandlungsfaktor mit animal und einen zweiten Faktor mit site vorliegen haben sowie den Entwicklungsstand stage.

.id	animal	stage	site	season	jump_length
1	cat	adult	village	summer	21.42
2	cat	adult	village	summer	23.42
3	cat	adult	village	summer	22.3
...	...	...	...	...	...
190	fox	juvenile	city	winter	34.05
191	fox	juvenile	city	winter	34.9
192	fox	juvenile	city	winter	29.28

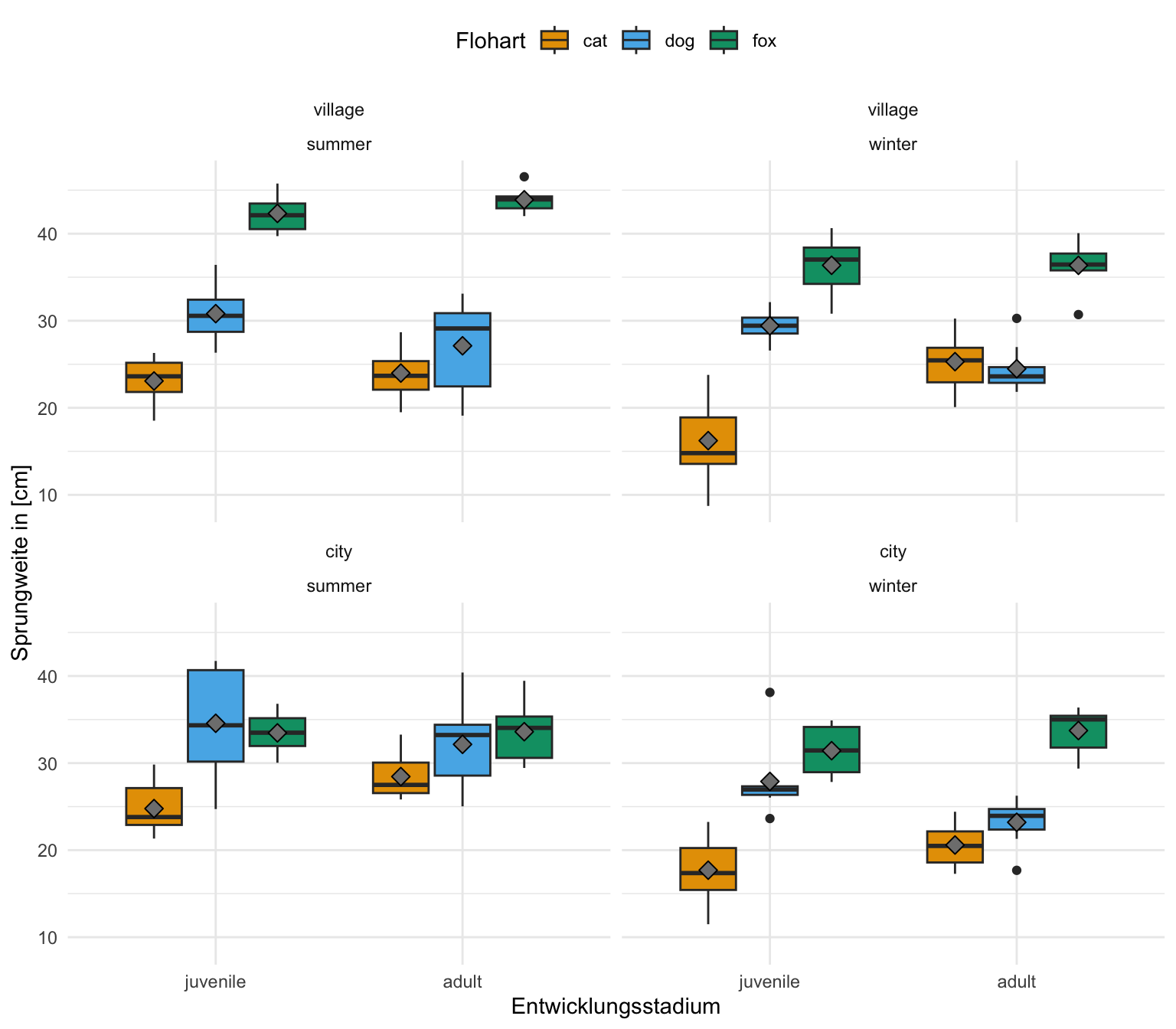
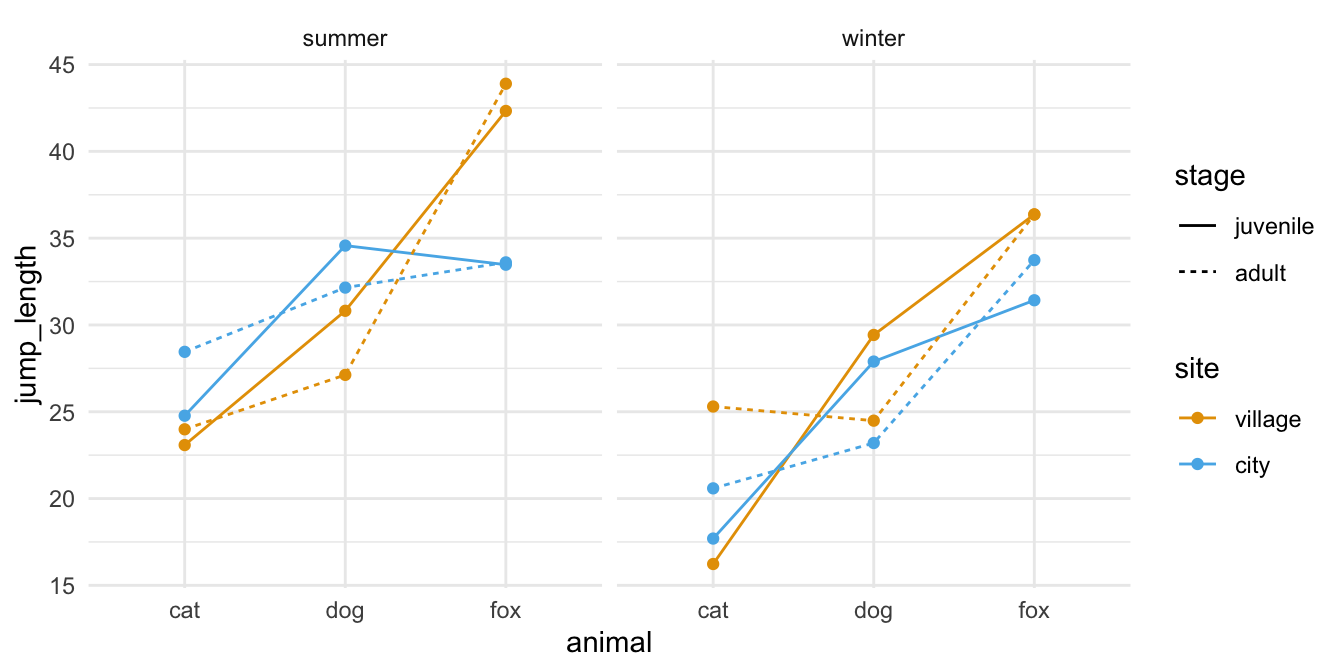
Wenn wir im Folgenden einmal die Boxplots betrachten, dann sehen wir auch einen Effekt der Floharten. Die Boxplots der Sprungweiten für die einzelnen Floharten sind unterschiedlich und liegen nicht auf einer Ebene. Die juvenilen und erwachsen Flöhe scheinen recht ähnlich zu springen. Wir sehen hier eventuell nur eine leichte Verschiedung. Darüber hinaus springen aber Dorfflöhe anders als Stadtflöhe. Hier wird es jetzt aber schwierig mit der visuellen Abschätzung, da müssen wir jetzt wirklich mal mit einer ANOVA ran und schauen was signifikant unterschiedlich ist.

Abbildung 30.19— Beispielhafter vierfaktorieller Boxplot für die Sprungweiten in [cm] gruppiert nach den Floharten und den beiden Messorten sowie dem Entwicklungstand der Flöhe an verschiedenen Jahreszeiten.

30.5 Test auf Normalverteilung und Varianzhomogenität

Die ANOVA hat als Annahme an deinen Messwert, dass dier Messwert normalverteilt ist. Ebenso müssen die Varianzen in den Leveln des Faktors gleich sein. Wir sprechen dann von varianzhomogenität. In dem folgenden Abschnitt testen wir einmal auf Normalverteilung in dem Messwert \(y\) und Varianzmomogenität in den Faktoren \(f_A\) und \(f_B\). Die hier vorhandenen Ergebnisse schreibst du meistens nicht in deine Abschlussarbeit oder zeigst dort die hier vorgestellten Abbildungen. Das dient hier nur zur Überprüfung in deinem statistischen Arbeitsprozess. Du findest noch im Tutorium Testing the Assumptions of ANOVAs ein paar mehr Informationen, wenn es um die ANOVA und die Annahmen geht.

Achtung, bitte beachten!

Wenn du keine normalverteilten Daten hast, dann wird häufig empfholen, dass du deinen Messwert \(y\) transformieren sollst. Das ist eine Lösung, wenn du dann nur bei deiner ANOVA bleiben würdest oder dich die Effekte auf der Einheit des Messwert \(y\) nicht interessieren. Durch eine Transformation von \(y\) verlierst du immer die direkte biologische Interpretation der Effekte aus einem statistischen Test.

Ich zeige dir hier einmal die Funktionen check_normality() und check_homogeneity() aus dem R PAket {performance}. Beide Funktionen funktionieren super und man muss nicht so viel programmieren um die Funktionen zum laufen zu kriegen. Dammit du was testen kannst, musst du auch ein Modell haben was du testen kannst. Ich nutze hier einmal das einfaktorielle, zweifaktorielle sowie mehrfaktorielle Modell aus einer linearen Regression. Da sind die Annhamen die gleichen wie bei einer ANOVA.

Normalverteilung des Messwerts \(y\)

Wenn du überprüfen willst, ob dein Messwert \(y\) einer Normalverteilung folgt, dann kannst du die Funktion check_normality() nutzt. Die Funktion rechnet dann den Shapiro-Wilk-Test um auf eine Abweichung von der Normalverteilung zu testen. Hierzu ist anzumerken, dass der Test relativ empfindlich bei Abweichungen in den Verteilungsschwänzen ist. Darüber hinaus braucht der Shapiro-Wilk-Test auch etwas Fallzahl, damit er auf die Normalverteilung testen kann. Im Folgenden schauen wir uns den Code für ein einfaktorielles, zweifaktorielles und dreifaktorielles Modell einmal an. Am Ende des Abschnitts gehe ich nochmal darauf ein, was du machen kannst, wenn du keine Normalverteilung in deinem Messwert \(y\) vorliegen hast.

Einfaktoriell

Beginnen wir wieder mit einem einfaktoriellen Modell. Wir wollen wissen, ob unsere Sprungweite in [cm] über unsere verschiedenen Floharten normalverteilt ist. Wir bauen also erstmal das Modell und schicken es dann in die Funktion check_normality() aus dem R Paket {performance}.

lm(jump_length ~ animal, data = fac1_tbl) |> 
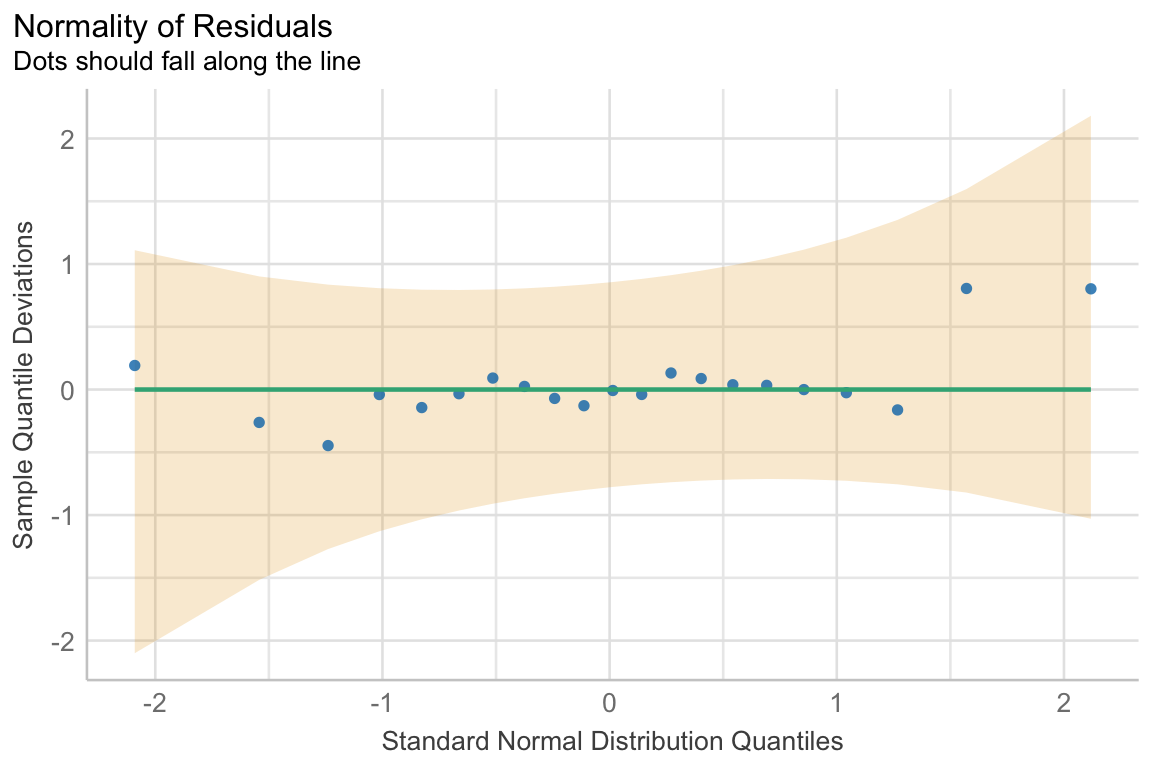
  check_normality()

OK: residuals appear as normally distributed (p = 0.514).

Die Funktion sagt, dass wir eine Normalverteilung in unseren Daten vorliegen haben. Wir können uns auch einen Diagnoseplot wiedergeben lassen. Dafür müssen wir die Funktion nur an die Funktion plot() weiterleiten. Das Schöne ist, dass die Abbildung uns auch gleich sagt, was wir zu erwarten haben um eine Normalverteilung anzunehmen.

lm(jump_length ~ animal, data = fac1_tbl) |> 
  check_normality() |> 
  plot() +
  scale_fill_okabeito()

Abbildung 30.20— Schnelle Abbildung der Residuen aus check_normality() zur Überprüfung der Normalverteilung des Messwerts in einem einfaktoriellen Modell.

Zweifaktoriell

Im zweifaktoriellen Fall ändert sich jetzt nur das Model. Wir haben eben zwei Faktoren vorliegen und diese müssen wir dann mit ins Modell nehmen. Ich habe hier auch gleich den Interaktionsterm mit ergänzt, ich teste gerne das Modell, was ich dann später auch auswerten möchte.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
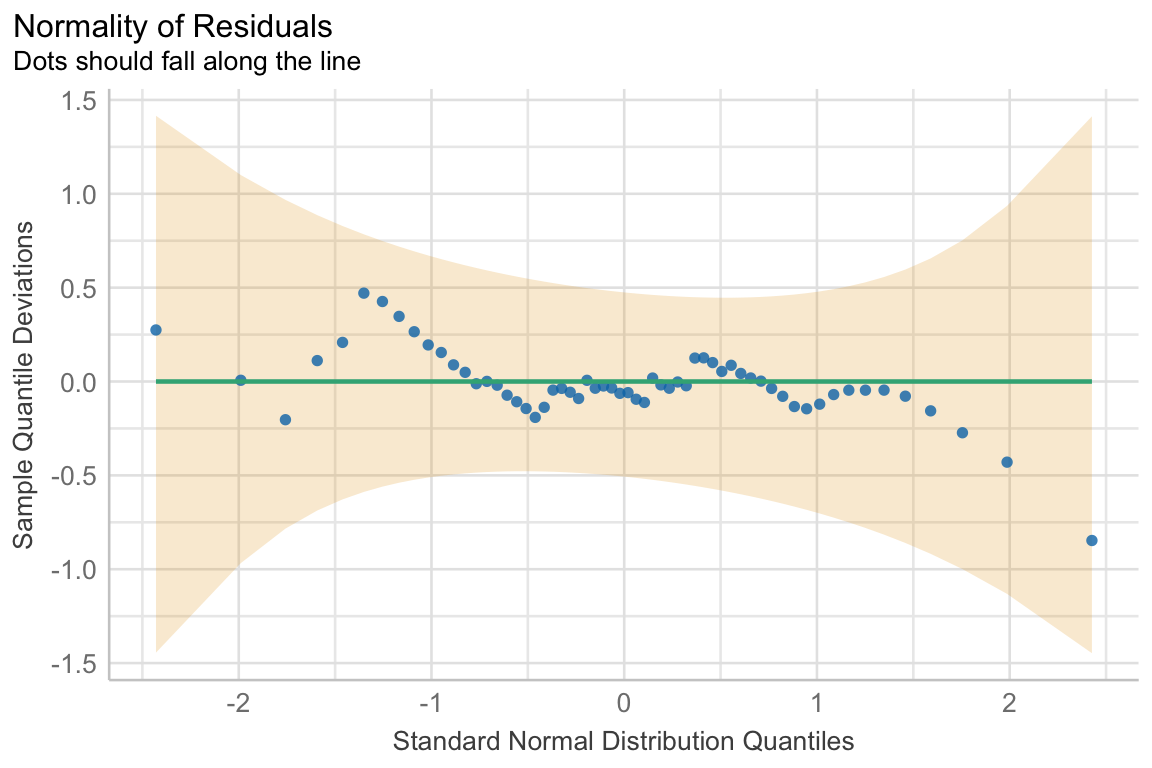
  check_normality()

OK: residuals appear as normally distributed (p = 0.239).

Auch hier haben wir eine Normalverteilung in den Daten vorliegen. Gerne schaue ich mir auch die Abbildung der Residuen einmal an und das geht dann flott über die Funktion plot(). Da musst du nur die Ausgabe der Funktion check_normality() weiterleiten. Die leichten Bögen in den Punkten kommen von den unterschiedlichen Faktoren und deren Effekten auf die Sprungweite.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  check_normality() |> 
  plot() +
  scale_fill_okabeito()

Abbildung 30.21— Schnelle Abbildung der Residuen aus check_normality() zur Überprüfung der Normalverteilung des Messwerts in einem zweifaktoriellen Modell.

Mehrfaktoriell

Am Ende dann nochmal ein mehrfaktorielles Modell. Hier möchte ich dann auch alle Faktorkombinationen einmal testen und nutze dafür die Kurzschreibweise in R mit dem Malzeichen. Ich kann mir sonst nicht alle Kombinationen der drei Faktoren mit den entsprechenden Interaktionstermen merken. Deshalb lasse ich hier mal die beiden Jahreszeiten aus dem Modell raus.

lm(jump_length ~ animal*site*stage, data = fac4_tbl) |> 
  check_normality()

OK: residuals appear as normally distributed (p = 0.460).

Auch hier sehen wir, dass die Funktion normalverteilte Sprungweiten findet. Auch hier können wir uns die Residuen des Modells einmal in einer Abbildung anschauen. Hier haben wir auch wieder leichte Bögen in den Punkten aber das kommt durch die vielen Faktoren und deren Effekten. Solange alles in den gelben Bändern bleibt, ist alles in Ordnung.

lm(jump_length ~ animal*site*stage, data = fac4_tbl) |> 
  check_normality() |> 
  plot() +
  scale_fill_okabeito()

Abbildung 30.22— Schnelle Abbildung der Residuen aus check_normality() zur Überprüfung der Normalverteilung des Messwerts in einem mehrfaktoriellen Modell.

Varianzhomogenität der Faktoren \(f\)

Nachdem wir die Normalverteilung des Messwertes \(y\) getestet haben, wollen wir jetzt noch schauen, ob unsere Faktoren einer Varianzhomogenität über die Gruppen genügt. Die Funktion check_homogeneity() nutzt den Bartlett-Test um auf eine Abweichung von der Varianzhomogenität zu testen. Es gibt noch verschiedene andere Tests, aber ich würde hier empfehlen bei eiem Test zu bleiben und dann mit dem Ergebnis zu leben. Wild verschiedene Tests auf Varianzhomogenität durchzuführen führt dann auch nur zu einem wilden Fruchtsalat an Ergebnissen mit denen keiner was anfangen kann. Im Folgenden schauen wir uns den Code für ein einfaktorielles, zweifaktorielles und dreifaktorielles Modell einmal an. Am Ende des Abschnitts gehe ich nochmal darauf ein, was du machen kannst, wenn du keine Varianzhomogenität in deinen Faktoren vorliegen hast.

Einfaktoriell

Beginnen wir wieder mit dem einfaktoriellen Modell. Wir stecken das Modell dann einfach in die Funktion check_homogeneity() und erhalten die Information über die Varianzhomogenität wiedergegeben.

lm(jump_length ~ animal, data = fac1_tbl) |> 
  check_homogeneity()

OK: There is not clear evidence for different variances across groups (Bartlett Test, p = 0.297).

Wunderbar, wir haben keine Abweichung von der Varianzhomongenität. Wir können uns auch die Daten nochmal anschauen. Hier sehen wir aber schon, dass die Daten etwas heterogen aussehen der Test aber die Homogenität nicht ablehnt. Das ist immer schwierig bei kleinen Fallzahlen. Aber an irgendwas muss man eben glauben.

lm(jump_length ~ animal, data = fac1_tbl) |> 
  check_homogeneity() |> 
  plot() +
  scale_fill_okabeito()

Abbildung 30.23— Schnelle Abbildung der Residuen aus check_homogeneity() zur Überprüfung der Varianzhomogenität der Faktoren in einem einfaktoriellen Modell.

Zweifaktoriell

Jetzt können wir mal schauen, was passiert wenn wir die Anzahl an möglichen Faktorkombinationen erhöhen indem wir ein zweifaktorielles Modell nutzen. Hier haben wir dann ja sechs Faktorkombinationen oder Gruppen die dann alle homogen in den Varianzen sein müssen.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  check_homogeneity()

OK: There is not clear evidence for different variances across groups (Bartlett Test, p = 0.205).

Wir haben auch hier Varianzhomogenität über alle Gruppen der Faktoren vorliegen. Wenn du dir jetzt die Abbildung zu dem Test anschaust, dann siehst du auch hier, dass die Violinplots eben dann doch alle etas anders aussehen. Wir haben aber hier auch das gleiche Problem wie bei dem einfaktoriellen Fall, wir haben eben dann doch recht wenig Fallzahl in unseren Daten.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  check_homogeneity() |> 
  plot() +
  scale_fill_okabeito()

Abbildung 30.24— Schnelle Abbildung der Residuen aus check_homogeneity() zur Überprüfung der Varianzhomogenität der Faktoren in einem zweifaktoriellen Modell.

Mehrfaktoriell

Am Ende dann nochmal ein mehrfaktorielles Modell. Hier möchte ich dann auch alle Faktorkombinationen einmal testen und nutze dafür die Kurzschreibweise in R mit dem Malzeichen. Ich kann mir sonst nicht alle Kombinationen der drei Faktoren mit den entsprechenden Interaktionstermen merken. In diesem Fall sind es dann ganze zwölf Kombinationen. Deshalb lasse ich hier mal die beiden Jahreszeiten aus dem Modell raus.

lm(jump_length ~ animal*site*stage, data = fac4_tbl) |> 
  check_homogeneity()

Warning: Variances differ between groups (Bartlett Test, p = 0.007).

Hier haben wir dann eine Abweichung von der Varianzhomogenität. Zum einen, weil ich die Daten so gebaut habe und zum anderen da wir jetzt echt viele Gruppen haben, wie du in der folgenden Abbidlugn sehen kannst. Es wird dann eben schwieriger in biologischen Echtdaten über viele Gruppen immer die gleiche Varianz zu haben. Irgendwann ist dann alles heterogen. Hier passt dann die Abbildung aber besser zu der Ausgabe des statistischen Tests.

lm(jump_length ~ animal*site*stage, data = fac4_tbl) |> 
  check_homogeneity() |> 
  plot() 

Abbildung 30.25— Schnelle Abbildung der Residuen aus check_homogeneity() zur Überprüfung der Varianzhomogenität der Faktoren in einem dreifaktoriellen Modell.

Weder Normalverteilung noch Varianzhomogenität?

In dem Fall kannst du das R Paket {WRS2} nutzen, was ich dir in den folgenden Tabs auch immer wieder vorstelle. Das Paket {WRS2} kann mit getrimmten Mittelwerten mit nicht normalverteilten Daten sowie Vamrianzhterogenität umgehen. Das ist eine bessere Lösung als die nicht-parametrischen Verfahren, wenn du auf dem ANOVA Pfad bleiben willst.

Das R Paket {car} erlaubt unter der Annahme der Normalverteilung des Messwertes \(y\) auch eine Varianzhterogenität zu modellieren. Hier musst du dann die entsprechende Option wählen. Alles dazu findest du dann weiter unten in den entsprechenden Tabs zu der ANOVA in {car}.

Eine weitere Möglichkeit ist es deine Daten zu transformieren, wie ich es oben schon erwähnt habe. Hier findest du dann im Kaptitel zur Transformation von Daten mehrere Optionen. Was da die beste Transformation ist, hängt dann stark von deiner wissenschaftlichen Fragestellung ab. Hier kann ich dann leider keine allgemeine Empfehlung abgeben.

30.6 Einfaktorielle ANOVA

Was für eine Menge an Text und Abbildungen bevor wir hier dann endlich mit der einfaktoriellen ANOVA anfangen. Wenn du dir nichts zu dem allgemeinen Hintergrund oder theoretischen Hintergrund durchgelesen hast, ist das überhaupt kein Problem. Wir nutzen jetzt hier die ANOVA auf unserem einfaktoriellen Datensatz zu der Sprungweite in [cm] von verschiedenen Floharten. Wir wollen wissen, ob sich die Sprungweite signifikant für die Hunde-, Katzen- oder Fuchsflöhe unterscheidet.

Was sagt mir eine signifikante einfaktorielle ANOVA?

Wenn wir ein signifikantes Ergebnis in einer einfaktoriellen ANOVA vorliegen haben, dann wissen wir nur, dass die Floharten alle nicht gleich weit springen. Eine signifikante ANOVA haben wir vorliegen, wenn der p-Werte kleiner ist das Signifikanzniveau \(\alpha\) gleich 5% oder eben 0.05 als Kommazahl. Welche Floharten sich konkret unterscheiden müssen wir dann noch in einem Post-hoc Test herausfinden.

Wir haben jetzt die Wahl zwischen vier Implementierungen in R und einer holprigen Lösung in Excel. Bitte rechne die einfaktorielle ANOVA in R. Welches Paket du jetzt in R nimmst, hängt dann wiederum zum Teil von deiner Fragestellung und deinen Daten ab. Meistens ist die Standardimplementierung in {base} mit der Funktion aov() ausreichend. Da ich dann aber auch immer mal wieder was anderes brauche, zeige ich hier einmal alles.

{base}

Beginnen wir mit der Standardfunktion aov() für die einfaktorielle ANOVA. Wir nehmen einfach ein Modell und spezifizieren noch die Datenquelle. Wichtig ist, dass die Reihenfolge der Faktoren in deinem Modell eine Rolle spielt. Ja, das ist bei einem Faktor egal, aber ich schreibe es hier schonmal. Dann nutze ich noch die Funktion tidy() aus dem R Paket {broom} für eine schönere Ausgabe. Dann habe ich alles zusammen.

aov(jump_length ~ animal, data = fac1_tbl) |> 
  tidy()

# A tibble: 2 × 6
  term         df sumsq meansq statistic   p.value
  <chr>     <dbl> <dbl>  <dbl>     <dbl>     <dbl>
1 animal        2  74.7  37.3       11.9  0.000511
2 Residuals    18  56.5   3.14      NA   NA       

Wir können die Ausgabe der Funktion aov() direkt weiter bei {emmeans} verwenden. Die etwas allgemeinere Form eine einfaktorielle ANOVA zu rechnen, ist erst das lineare Modell zu schätzen. Hier nutze ich einmal eine lineare Regression mit der Funktion lm(). Dann nutzen wir aber die Funktion anova() um die ANOVA zu rechnen.

lm(jump_length ~ animal, data = fac1_tbl) |> 
  anova() |> 
  tidy()

# A tibble: 2 × 6
  term         df sumsq meansq statistic   p.value
  <chr>     <int> <dbl>  <dbl>     <dbl>     <dbl>
1 animal        2  74.7  37.3       11.9  0.000511
2 Residuals    18  56.5   3.14      NA   NA       

Wir sind am Ende aber nur am p-Wert interessiert und auch der ist hier signifikant, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt. Wie du siehst sind die Ergebnisse numerisch gleich. Warum dann überhaupt zwei Funktionen? Mit lm() und anova() bist du etwas flexibler was das genutzte Modell angeht.

{car}

Jetzt könnte man meinen, warum noch eine weitere Implementierung der ANOVA, wenn wir schon die Funktion aov() haben? Die Funktion aov() rechnet grundsätzlich Type I ANOVAs. Das macht jetzt bei einer einfaktoriellen ANOVA nichts aus, aber wir können eben in {car} auch Type II und Type III ANOVAs rechnen. Darüber hinaus erlaubt das Paket auch für Varianzheterogenität in der ANOVA zu adjustieren.

Varianzhomogenität

In dem klassischen Aufruf der Funktion Anova() nutzen wir wieder ein Modell und dann gebe ich dir wieder die aufgeräumte Ausgabe mit tidy() wieder. Wenn du nichts extra angibst, dann rechnest du natürlich eine ANOVA unter der Annahme der Varianzhomogenität.

lm(jump_length ~ animal, data = fac1_tbl) |> 
  Anova() |> 
  tidy()

# A tibble: 2 × 5
  term      sumsq    df statistic   p.value
  <chr>     <dbl> <dbl>     <dbl>     <dbl>
1 animal     74.7     2      11.9  0.000511
2 Residuals  56.5    18      NA   NA       

Wenn du die Zahlen mit der Funktion aov() vergleichst, siehst du das da die gleichen Werte rauskommen. Das sollte natürlich auch in einer einfaktoriellen ANOVA mit den gleichen Annahmen so sein.

Varianzheterogenität

Der Vorteil des Pakets {car} ist, dass wir in der Funktion Anova() auch für Varianzheterogenität adjustieren können. Wir nutzen dazu die Option white.adjust = TRUE. Ja, ich weiß, das ist überhaupt nicht naheliegend. Wenn wir das machen, dann werden die Abweichungsquadrate anders berechnet und unsere Ausgabe ändert sich entsprechend.

lm(jump_length ~ animal, data = fac1_tbl) |> 
  Anova(white.adjust = TRUE)  |> 
  tidy()

Coefficient covariances computed by hccm()

# A tibble: 2 × 4
  term         df statistic   p.value
  <chr>     <dbl>     <dbl>     <dbl>
1 animal        2      12.1  0.000462
2 Residuals    18      NA   NA       

Wir sind am Ende aber nur am p-Wert interessiert und auch der ist hier signifikant, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt.

{afex}

Das R Paket {afex} ist eigentlich für Messwiederholungen am besten geeignet, aber ich zeige es auch hier im einfaktoriellen Fall, dann hier geht es eben auch. Das einzige was etwas anders ist, ist das wir eine ID für die Funktion brauchen. Das Paket {afex} möchte nämlich explizit wissen, welcher Wert zu welcher Beobachtung gehört.

aov_car(jump_length ~ animal + Error(.id), data = fac1_tbl) 

Contrasts set to contr.sum for the following variables: animal

Anova Table (Type 3 tests)

Response: jump_length
  Effect    df  MSE         F  ges p.value
1 animal 2, 18 3.14 11.89 *** .569   <.001
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

Da die Berechnung dann auch noch etwas anders verläuft haben wir dann leicht andere Werte raus. Wir sind am Ende aber nur am p-Wert interessiert und auch der ist hier signifikant, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt.

{WRS2}

Jetzt wird es eigentlich erst spannend. Das R Paket {WRS2} von Mair und Wilcox (2020) erlaubt es auch bei nicht normalverteilten Daten sowie Varianzheterogenität eine ANOVA zu rechnen. Ja, du könntest dir auch die ganzen Vortests sparen und gleich eien ANOVA mit dem R Paket {WRS2} rechnen. Da wir es aber mit einer robusten Methode zu tun haben, werden deine Daten etwas getrimmt oder beschnitten. Wenn du also zu wenige Beobachtungen in den Gruppen hast, dann ist das R Paket {WRS2} nicht die beste Idee.

t1way(jump_length ~ animal, data = fac1_tbl)

Call:
t1way(formula = jump_length ~ animal, data = fac1_tbl)

Test statistic: F = 12.8677 
Degrees of freedom 1: 2 
Degrees of freedom 2: 7.72 
p-value: 0.00348 

Explanatory measure of effect size: 0.95 
Bootstrap CI: [0.62; 1.09]

Wir kriegen neben dem p-Wert noch ein Explanatory measure of effect size wiedergegeben. Du kannst den Wert wie folgt interpretieren. Ein Wert von 0.1 deutet auf einen kleinen, ein Wert von 0.3 auf einen mittleren und ab 0.5 auf einen Starken Effekt hin. Wir sind am Ende aber nur am p-Wert interessiert und auch der ist hier signifikant, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt.

Geht es dann im Post-hoc Test dann einfach weiter? Ja, du kannst dann auch Funkionen aus dem {WRS2} Paket nutzen oder aber du machst mit {emmeans} weiter.

Excel

Ja, du kannst auch eine einfakorielle ANOVA in Excel rechnen. Das ist dann mit etwas mehr Aufwand verbunden was die Daten angeht, aber am Ende kommt da auch was raus. Mehr dazu in dem folgenden Video. Empfehlen kann ich dir Excel nicht, aber manchmal muss das Schwein durchs Nadelöhr und dann ist das auch okay so.

Nachdem wir einmal die p-Werte aus unserer einfaktoriellen ANOVA erhalten und dann noch geschaut haben, ob wir ein signifikantes Ergebnis haben, können wir jetzt weiter machen. Was fehlt noch? Wir müssen noch schauen, ob wir einen Effekt zwischen den Gruppen in unserem Faktor vorliegen haben. Eine Signifikanz bedeutet ja nicht gleich Relevanz und deshalb berechnen wir auch gerne einmal einen Effektschätzer. Ein Effektschätzer sagt dir, wie stark sich die Gruppen voneinander unterscheiden. Oder anders herum formuliert, wie stark ist der Einfluss des Faktors auf den Messwert?

Dann müssen wir natürlich auch noch die Ergebnisse der einfaktoriellen ANOVA berichten. Dafür gibt es aber das R Paket {report} welches dir dann bei der Interpretation der Ausgabe deiner ANOVA hilft. Nicht alle Varianten der ANOVA in R funktionieren mit dem Paket {report}, deshalb hier nur ein Beispiel. Aber du kannst dich dann an der Ausgabe einmal orientieren.

Effektschätzer

Beginnen wir mit den drei Effektschätzern der ANOVA. Ich empfehle ja bei einer einfaktoriellen ANOVA immer das \(\eta^2\) (eng. eta squared) als Effektmaß. Wir haben ja mit dem \(\eta^2\) einen Wert für den Anteil der Varianz des Messwertes der durch den Behandlungsfaktor erklärt wird. Je mehr Vairanz durch die Behandlung erklärt wird, desto besser in unserem geplanten Experiment.

aov(jump_length ~ animal, data = fac1_tbl) |> 
  eta_squared() |> 
  interpret_eta_squared(rules = "field2013")

# Effect Size for ANOVA

Parameter | Eta2 |       95% CI | Interpretation
------------------------------------------------
animal    | 0.57 | [0.27, 1.00] |          large

- One-sided CIs: upper bound fixed at [1.00].
- Interpretation rule: field2013

Wir nehmen hier die Regeln nach Field (2013) um zu entscheiden, wie bedeutend der Wert von \(\eta^2\) ist. Hier kommt es dann aber auch auf das Experiment an. In einem geplanten Feldexperiment, wo nur die Gruppen variieren, sollte \(\eta^2\) größer als 70% sein.

Neben dem \(\eta^2\) gibt es noch das \(\epsilon^2\) (eng. epsilon squared) sowie das \(\omega^2\) (eng. omega squared). Ich habe beide Maßzahlen weiter oben nochmal vorgestellt. Beide Effektschätzer sind eine Möglichkeit, aber ich würde bei einer einfaktoriellen ANOVA immer das \(\eta^2\) vorziehen. Beide Effektschätzer haben dann eben nicht so die klare Interpretation. Kurz gesagt, ist \(\epsilon^2\) wie das \(\eta^2\) bei kleinen Fallzahlen.

aov(jump_length ~ animal, data = fac1_tbl) |> 
  epsilon_squared() |> 
  interpret_epsilon_squared(rules = "field2013")

# Effect Size for ANOVA

Parameter | Epsilon2 |       95% CI | Interpretation
----------------------------------------------------
animal    |     0.52 | [0.21, 1.00] |          large

- One-sided CIs: upper bound fixed at [1.00].
- Interpretation rule: field2013

Dann hier nochmal das \(\omega^2\), was seine Stärke bei mehreren Faktoren hat. Das \(\omega^2\) ist das adjustierte \(\eta^2\) für mehrere Faktoren. Daher ist es hier auch nur so mäßig von Interesse.

aov(jump_length ~ animal, data = fac1_tbl) |> 
  omega_squared() |> 
  interpret_omega_squared(rules = "field2013")

# Effect Size for ANOVA

Parameter | Omega2 |       95% CI | Interpretation
--------------------------------------------------
animal    |   0.51 | [0.19, 1.00] |          large

- One-sided CIs: upper bound fixed at [1.00].
- Interpretation rule: field2013

R Paket {report}

Das R Paket {report} liefert nochmal die Möglichkeit sich die Ausgabe einer einfaktoriellen ANOVA in Textform wiedergeben zu lassen. Wie immer, wenn man alleine vor dem Rechner sitzt, ist das doch eine super Hilfestellung. Hier dann einmal mit der Anova() Funktion aus dem R Paket {car}.

lm(jump_length ~ animal, data = fac1_tbl) |> 
  Anova() |> 
  report()

The ANOVA suggests that:

  - The main effect of animal is statistically significant and large (F(2, 18) =
11.89, p < .001; Eta2 = 0.57, 95% CI [0.27, 1.00])

Effect sizes were labelled following Field's (2013) recommendations.

Wir haben dann auch die Möglichkeit etwas schönere Tabellen uns wiedergeben zu lassen. Das funktioniert aber nicht bei jeder ANOVA Implementierung.

lm(jump_length ~ animal, data = fac1_tbl) |> 
  Anova() |> 
  report_table()

Parameter | Sum_Squares | df | Mean_Square |     F |      p | Eta2 |  Eta2 95% CI
---------------------------------------------------------------------------------
animal    |       74.68 |  2 |       37.34 | 11.89 | < .001 | 0.57 | [0.27, 1.00]
Residuals |       56.53 | 18 |        3.14 |       |        |      |             

Das war dann auch die einfaktorielle ANOVA. Wenn du die ANOVA in deiner Abschlussarbeit anwendest, musst du jetzt noch schauen, welche paarweisen Gruppenvergleiche in deinem Faktor signifikant sind. Jetzt könnte man sagen, dafür brauchst du eine signifikante ANOVA, aber meistens machen wir dann doch den ANOVA Pfad zu Ende.

30.7 Zweifaktorielle ANOVA

Die zweifaktorielle ANOVA. Punkt. Gibt es eine häufigere genutzte Methode in den Agrarwissenschaften im Kontext eines geplanten Feldexperiments? Ich glaube eher nicht. Viele Versuche sind so gebaut, dass du die Versuche mit einer zweifaktoriellen ANOVA auswerten kannst oder aber die Versuche so über einen Faktor mittelst, dass dann auch dein mehrfaktorielles Experiment zu einem zweifaktoriellen wird.

Auch hier überspringe ich dann den Teil mit dem allgemeinen und theoretischen Hintergrund und gehe dann auf die Implementierungen in R ein. Wir schauen uns hier das Beispiel der normalverteilten Sprungweiten in [cm] von Hunde-, Katzen-, und Fuchsflöhen an. Die Sprungweite wurde dann aber noch an zwei verschiedenen Orten gemessen, so dass wir ein zweifaktoriellens Design vorliegen haben.

Was sagt mir eine signifikante zweifaktorielle ANOVA?

Wenn wir ein signifikantes Ergebnis in einer zweifaktoriellen ANOVA vorliegen haben, dann wissen wir nur, dass die Floharten alle nicht gleich weit springen. Oder aber das sich die Messworte unterscheiden. Eine signifikante ANOVA haben wir vorliegen, wenn der p-Werte kleiner ist das Signifikanzniveau \(\alpha\) gleich 5% oder eben 0.05 als Kommazahl. Welche Floharten oder Messorte sich konkret unterscheiden müssen wir dann noch in einem Post-hoc Test herausfinden.

In der folgenden Abbildung 30.26 siehst die nochmal die möglichen Effekte zweier Faktoren A und B. Das ist nochmal wichtig, da mit du eine Idee davon kriegst, wann ein Faktor vermutliche signifikant ist und wie die beiden Faktoren zusammenspielen. Ich empfehle immer den Faktor mit den meisten Leveln auf die x-Achse zu legen. Wenn es deine Fragestellung verlangt, macht auch einen andere Sortierung natürlich auch Sinn. Die p-Werte sind in der Abbildung abgeschätzt und dienen der Orientierung. Wir haben keine Interaktion zwischen den Faktoren A und B vorliegen.

Abbildung 30.26— Visualisierung möglicher Kombinationen von Effekten der Faktoren A mit den Leveln \(A.1\), \(A.2\) und \(A.3\) sowie dem Faktor B mit den Leveln \(B.1\) und \(B.2\) anhand von Boxplots. Eine Interaktion \(A \times B\) wird nicht dargestellt. Die p-Werte sind abgeschätzt. (A) Kein Effekt in A und B. Die Boxplots aller Gruppen liegen auf dem gloablen Mittelwert. (B) Effekt von B. Die Boxplots sind um den Effekt von B verschoben. Der Faktor A liegt auf einer Ebene in B. (C) Effekt von A. Die Boxplots sind um den Effekt von A verschoben. Der Faktor B zeigt keinen Unterschied im Faktor A. (D) Effekt von A und B. Die Faktoren A und B sind zum globalen Mittel verschoben. Der Faktor B ist in A in gleicher Richtung und Wert verschoben, dargestellt durch den grünen Pfeil [Zum Vergrößern anklicken]

Wenn wir uns eine zweifaktorielle ANOVA anschauen, dann haben wir immer die Haupteffekte der Faktoren A und B sowie eine potenzielle Interaktion zwischen den beiden Faktoren vorliegen. Daher betrachte ich zuerst die Haupteffekte und schauen dabei aber auch, ob wir eine Interaktion vorliegen haben. Beachte auch hier, dein Ziel ist es dann den ANOVA Pfad mit einem Post-hoc Test abzuschließen. Die zweifaktorielle ANOVA alleine reicht alleine meist nicht aus. Du musst auch wissen, welche paarweisen Vergleiche dann signifikant sind.

30.7.1 Haupteffekte

Im ersten Schritt wollen wir wissen, ob wir einen signifkanten Unterschied der Mittelwerte in den Gruppen des Faktors animal und dem Faktor site finden. Dann schauen wir noch, ob wir eine Interaktion vorliegen haben. Die Interaktion betrachten wir dann im Anschluss nochmal separat. Daher nennen wir jezt die Analyse der Faktoren auch Haupteffekte.

{base}

Beginnen wir mit der Standardfunktion aov() für die zweifaktorielle ANOVA. Wir nehmen einfach ein Modell und spezifizieren noch die Datenquelle. Wichtig ist, dass die Reihenfolge der Faktoren in deinem Modell eine Rolle spielt. Daher nehme immer deine wichtigere Behandlung als erstes in das Modell oder nutze eine Type II ANOVA im R Paket {car}. Dann nutze ich noch die Funktion tidy() aus dem R Paket {broom} für eine schönere Ausgabe. Dann habe ich alles zusammen.

aov(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  tidy() |> 
  mutate(p.value = pvalue(p.value))

# A tibble: 4 × 6
  term           df  sumsq meansq statistic p.value
  <chr>       <dbl>  <dbl>  <dbl>     <dbl> <chr>  
1 animal          2 171.    85.6      25.7  <0.001 
2 site            1   4.21   4.21      1.27 0.265  
3 animal:site     2  59.1   29.5       8.89 <0.001 
4 Residuals      54 179.     3.32     NA    <NA>   

Wir können die Ausgabe der Funktion aov() direkt weiter bei {emmeans} verwenden. Die etwas allgemeinere Form eine zweifaktorielle ANOVA zu rechnen, ist erst das lineare Modell zu schätzen. Auch hier ist die Reihenfolge von Wichtigkeit. Hier nutze ich einmal eine lineare Regression mit der Funktion lm(). Dann nutzen wir aber die Funktion anova() um die ANOVA zu rechnen.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  anova() |> 
  tidy() |> 
  mutate(p.value = pvalue(p.value))

# A tibble: 4 × 6
  term           df  sumsq meansq statistic p.value
  <chr>       <int>  <dbl>  <dbl>     <dbl> <chr>  
1 animal          2 171.    85.6      25.7  <0.001 
2 site            1   4.21   4.21      1.27 0.265  
3 animal:site     2  59.1   29.5       8.89 <0.001 
4 Residuals      54 179.     3.32     NA    <NA>   

Wir sind am Ende aber nur am p-Wert der beiden Faktoren interessiert und auch der ist hier für die Floharten animal signifikant, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt. Der p-Wert für den Messort site ist dagegen nicht signifkant. Wir haben eine signifikante Interaktion animal:site vorliegen. Wie du siehst sind die Ergebnisse numerisch gleich.

{car}

Jetzt könnte man meinen, warum noch eine weitere Implementierung der ANOVA, wenn wir schon die Funktion aov() haben? Die Funktion aov() rechnet grundsätzlich Type I ANOVAs. Das macht jetzt bei einer zweifaktoriellen ANOVA schon einen Unterschied welchen Typ ANOVA wir rechnen. Wir können eben in {car} auch Type II und Type III ANOVAs rechnen. Darüber hinaus erlaubt das Paket auch für Varianzheterogenität in der ANOVA zu adjustieren.

Varianzhomogenität

In dem klassischen Aufruf der Funktion Anova() nutzen wir wieder ein Modell und dann gebe ich dir wieder die aufgeräumte Ausgabe mit tidy() wieder. Wenn du nichts extra angibst, dann rechnest du natürlich eine ANOVA unter der Annahme der Varianzhomogenität.

Keine Interaktion zwischen den Faktoren A und B

Wir rechnen dann eine Type II ANOVA, wenn wir keine Interaktion zwischen den Faktoren vorliegen haben. Ja, dass müssen wir dann natürlich vorab einmal Testen, dazu kannst du einfach die Funktion aov() nutzen. Wenn wir keine Interaktion vorliegen haben, dann nehmen wir auch die Interaktion aus dem Modell und testen nur die Haupteffekte mit einer Type II ANOVA. Damit ist dann auch soweit alles in Ordnung.

lm(jump_length ~ animal + site, data = fac2_tbl) |> 
  Anova(type = "II") |> 
  tidy()  |> 
  mutate(p.value = pvalue(p.value))

# A tibble: 3 × 5
  term       sumsq    df statistic p.value
  <chr>      <dbl> <dbl>     <dbl> <chr>  
1 animal    171.       2    20.1   <0.001 
2 site        4.21     1     0.989 0.324  
3 Residuals 239.      56    NA     <NA>   

Wir sehen, dass der Faktor animal signifkant ist, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt. Die Messorte site sind nicht signifikant.

Interaktion zwischen den Faktoren A und B

Wir rechnen dann eine Type III ANOVA, wenn wir eine Interaktion zwischen den beiden Faktoren vorliegen haben. Dann werden die Haupteffekte unter der Berücksichtigung der Interaktion berechnet. Aber Achtung, du musst leider in {car} die Kontraste anders definieren sonst testet die Funktion Anova() nicht das was sie soll. Da ist dann die Funktion aov_car() aus dem Paket {afex} anwenderfreundlicher.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl,
    contrasts = list(
    animal = "contr.sum",
    site = "contr.sum"
  )) |> 
  Anova(type = "III") |> 
  tidy()  |> 
  mutate(p.value = pvalue(p.value))

# A tibble: 5 × 5
  term           sumsq    df statistic p.value
  <chr>          <dbl> <dbl>     <dbl> <chr>  
1 (Intercept) 16389.       1   4931.   <0.001 
2 animal        171.       2     25.7  <0.001 
3 site            4.21     1      1.27 0.265  
4 animal:site    59.1      2      8.89 <0.001 
5 Residuals     179.      54     NA    <NA>   

Hier ändert sich jetzt nicht soviel. Die Entscheidungen anhand des p-Wertes sind hier gleich zu der Type II ANOVA. Wir sehen aber eine deutliche Interaktion, daher müssen wir uns die Interaktion zwischen den Haupteffekten nochmal anschauen.

Varianzheterogenität

Der Vorteil des Pakets {car} ist, dass wir in der Funktion Anova() auch für Varianzheterogenität adjustieren können. Wir nutzen dazu die Option white.adjust = TRUE. Ja, ich weiß, das ist überhaupt nicht naheliegend. Wenn wir das machen, dann werden die Abweichungsquadrate anders berechnet und unsere Ausgabe ändert sich entsprechend. Auch hier nutze ich dann mal die Type II ANOVA und betrachte nur die Haupteffekte.

lm(jump_length ~ animal + site, data = fac2_tbl) |> 
  Anova(white.adjust = TRUE, type = "II")  |> 
  tidy() |> 
  mutate(p.value = pvalue(p.value))

Coefficient covariances computed by hccm()

# A tibble: 3 × 4
  term         df statistic p.value
  <chr>     <dbl>     <dbl> <chr>  
1 animal        2    16.8   <0.001 
2 site          1     0.923 0.341  
3 Residuals    56    NA     <NA>   

Wir sind am Ende aber nur am p-Wert interessiert und auch der ist hier signifikant für den Faktor animal, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt. Wir finden hier keinen signifikanten Unterschied für den Messort site.

{afex}

Der Vorteil von dem R Paket {afex} ist, dass wir hier mit der Funktion aov_car() eine Type III ANOVA rechnen, die korrekt angepasst ist. Wir müssen also nicht noch extra ein Modell mit Kontrasten anpassen. Wir können auch die ANOVA Type II rechnen. Eine Besonderheit ist, dass wir einen Fehlerterm mit Error() der Funktion übergeben müssen, damit {afex} rechnen kann. Die Stärke von {afex} liegt eigentlich in der repeated und mixed ANOVA. Dort brauchen wir dann die Information zwingend, welche Zeile zu welcher Beobachtung gehört.

Interaktion zwischen den Faktoren A und B

Wir rechnen dann eine Type III ANOVA, wenn wir eine Interaktion zwischen den Faktoren vorliegen haben. Die Funktion aov_car() rechnet automatisch eine Type III ANOVA, wenn wir nichts anderes angeben. Das macht uns das Leben sehr viel einfacher. Wir müssen also nicht extra schauen, ob die Kontraste stimmen.

aov_car(jump_length ~ animal + site + animal:site + Error(.id), data = fac2_tbl) 

Contrasts set to contr.sum for the following variables: animal, site

Anova Table (Type 3 tests)

Response: jump_length
       Effect    df  MSE         F  ges p.value
1      animal 2, 54 3.32 25.74 *** .488   <.001
2        site 1, 54 3.32      1.27 .023    .265
3 animal:site 2, 54 3.32  8.89 *** .248   <.001
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

An den Ergebnissen ändert sich nicht so viel. Wir haben eine signifikanten Unterschied für den Faktor animal sowie für die Interaktion animal:site vorliegen, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt.

Keine Interaktion zwischen den Faktoren A und B

Wir rechnen in {afex} eine Type II ANOVA, wenn wir keine Interaktion zwischen den Faktoren vorliegen hätten. Hier müssen wir dann den Type extra angeben, damit nicht automatisch eine Type III ANOVA gerechnet wird.

aov_car(jump_length ~ animal + site + Error(.id), data = fac2_tbl, type = "II") 

Contrasts set to contr.sum for the following variables: animal, site

Anova Table (Type II tests)

Response: jump_length
  Effect    df  MSE         F  ges p.value
1 animal 2, 56 4.26 20.08 *** .418   <.001
2   site 1, 56 4.26      0.99 .017    .324
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

Die Ergebnisse entsprechen aber hier auch der Type III ANOVA. Wir haben einen signifikanten Unterschied für den Faktor animal und damit den Floharten vorliegen, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt. Die Messorte sind nicht signifikant.

{WRS2}

Jetzt wird es eigentlich wieder erst spannend. Das R Paket {WRS2} von Mair und Wilcox (2020) erlaubt es auch bei nicht normalverteilten Daten sowie Varianzheterogenität eine ANOVA zu rechnen. Ja, du könntest dir auch die ganzen Vortests sparen und gleich eien ANOVA mit dem R Paket {WRS2} rechnen. Da wir es aber mit einer robusten Methode zu tun haben, werden deine Daten etwas getrimmt oder beschnitten. Wenn du also zu wenige Beobachtungen in den Gruppen hast, dann ist das R Paket {WRS2} nicht die beste Idee.

t2way(jump_length ~ animal + site + animal:site, data = fac2_tbl)

Call:
t2way(formula = jump_length ~ animal + site + animal:site, data = fac2_tbl)

              value p.value
animal      37.1763   0.001
site         0.1375   0.715
animal:site 13.0813   0.008

Wir sind am Ende aber nur am p-Wert interessiert und auch der ist hier für die Floharten animal sowie der Interaktion animal:site signifikant, da der p-Wert unter dem Signifikanzniveau \(\alpha\) gleich 5% liegt. Wir erhalten hier keinen Effektschätzer wie bei der einfaktoriellen ANOVA. Dafür müssen wir uns nicht um die Annahmen kümmern.

Excel

Ja, du kannst auch eine zweifakorielle ANOVA in Excel rechnen. Das ist dann mit etwas mehr Aufwand verbunden was die Daten angeht, aber am Ende kommt da auch was raus. Auch hier dann mehr dazu in dem folgenden Video. Ich würde es dir aber wirklich nicht empfehlen eine zweifaktorielle ANOVA in Excel zu rechen. Wirklich nicht.

Nachdem wir einmal die p-Werte aus unserer zweifaktoriellen ANOVA erhalten und dann noch geschaut haben, ob wir ein signifikantes Ergebnis haben, können wir jetzt weiter machen. Was fehlt noch? Wir müssen noch schauen, ob wir einen Effekt zwischen den Gruppen in unserem Faktoren vorliegen haben. Eine Signifikanz bedeutet ja nicht gleich Relevanz und deshalb berechnen wir auch gerne einmal einen Effektschätzer. Ein Effektschätzer sagt dir, wie stark sich die Gruppen voneinander unterscheiden. Oder anders herum formuliert, wie stark ist der Einfluss des Faktors auf den Messwert? Dann schauen wir uns noch die Möglichkeit einmal an mit dem R Paket {report} eine bessere Ausgabe zu erhalten. Das funktioniert aber nicht bei allen Implementierungen.

Effektschätzer

Auch hier betrachten wir dann alle drei Effektschätzer \(\eta^2\) (eng. eta squared) sowie das \(\epsilon^2\) (eng. epsilon squared) und das \(\omega^2\) (eng. omega squared). Hier ist dann zu beachten, dass das \(\eta^2\) für mehrere Faktoren nicht mehr so gut den Anteil der Varianz, die duch die Behandlung erklärt wird, wiedergibt. Hier ist dann das \(\epsilon^2\) sowie das \(\omega^2\) besser geeignet. Die Interpretation ist gleich, aber wir haben eine bessere Schätzung der Werte unter Berücksichtigung der zwei Faktoren und der Interaktion. Die 95% Konfidenzintervalle sind meiner Meinung nach schwer zu interpretieren, wenn die Fallzahl klein ist.

aov(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  eta_squared() |> 
  interpret_eta_squared(rules = "field2013")

# Effect Size for ANOVA (Type I)

Parameter   | Eta2 (partial) |       95% CI | Interpretation
------------------------------------------------------------
animal      |           0.49 | [0.32, 1.00] |          large
site        |           0.02 | [0.00, 1.00] |          small
animal:site |           0.25 | [0.09, 1.00] |          large

- One-sided CIs: upper bound fixed at [1.00].
- Interpretation rule: field2013

Wir nehmen hier die Regeln nach Field (2013) um zu entscheiden, wie bedeutend der Wert von \(\eta^2\) ist. Hier kommt es dann aber auch auf das Experiment an. In einem geplanten Feldexperiment, wo nur die Gruppen variieren, sollte \(\eta^2\) größer als 70% sein.

Dann schauen wir uns noch das \(\epsilon^2\) einmal an. Auch hier haben wir ähnliche Werte. Der größte Teil der Varianz in unseren Sprungweiten, nähmlich fast 50%, wird von den Floharten erklärt. Der Rest fällt dann auf die Interaktion.

aov(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  epsilon_squared() |> 
  interpret_epsilon_squared(rules = "field2013")

# Effect Size for ANOVA (Type I)

Parameter   | Epsilon2 (partial) |       95% CI | Interpretation
----------------------------------------------------------------
animal      |               0.47 | [0.30, 1.00] |          large
site        |           4.85e-03 | [0.00, 1.00] |     very small
animal:site |               0.22 | [0.07, 1.00] |          large

- One-sided CIs: upper bound fixed at [1.00].
- Interpretation rule: field2013

Das \(\omega^2\) berücksichtigt die Faktoren besser und adjustiert für die drei Berechnungen des \(\omega^2\)-Wertes für den Faktor animal sowie site und der Interaktion. Bei mehr als einem Faktor ist dann das \(\omega^2\) vorzuziehen. Hier ist dann der erklärte Anteil der Varianz der Floharten auch etwas niedriger und nur noch bei 45%.

aov(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  omega_squared() |> 
  interpret_omega_squared(rules = "field2013")

# Effect Size for ANOVA (Type I)

Parameter   | Omega2 (partial) |       95% CI | Interpretation
--------------------------------------------------------------
animal      |             0.45 | [0.28, 1.00] |          large
site        |         4.44e-03 | [0.00, 1.00] |     very small
animal:site |             0.21 | [0.06, 1.00] |          large

- One-sided CIs: upper bound fixed at [1.00].
- Interpretation rule: field2013

R Paket {report}

Das R Paket {report} liefert nochmal die Möglichkeit sich die Ausgabe einer zweifaktoriellen ANOVA in Textform wiedergeben zu lassen. Wie immer, wenn man alleine vor dem Rechner sitzt, ist das doch eine super Hilfestellung. Hier dann einmal mit der Anova() Funktion aus dem R Paket {car}. Ich mag hier besonders die Hilfe bei einer zweifaktoriellen ANOVA. Hier wird es dann sehr schnell sehr unübersichtlich und da ist doch die report() Funktion hilfreich.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  Anova() |> 
  report()

The ANOVA suggests that:

  - The main effect of animal is statistically significant and large (F(2, 54) =
25.74, p < .001; Eta2 (partial) = 0.49, 95% CI [0.32, 1.00])
  - The main effect of site is statistically not significant and small (F(1, 54)
= 1.27, p = 0.265; Eta2 (partial) = 0.02, 95% CI [0.00, 1.00])
  - The interaction between animal and site is statistically significant and
large (F(2, 54) = 8.89, p < .001; Eta2 (partial) = 0.25, 95% CI [0.09, 1.00])

Effect sizes were labelled following Field's (2013) recommendations.

Dann können wir uns die Ergebnistabelle der ANOVA nochmal schöner mit der Funktion report_table() wiedergeben lassen. Wie immer funktioniert das Paket {report} nicht mit jeder Implementierung der ANOVA.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  Anova() |> 
  report_table()

Parameter   | Sum_Squares | df | Mean_Square |     F |      p | Eta2 (partial) | Eta2_partial 95% CI
----------------------------------------------------------------------------------------------------
animal      |      171.13 |  2 |       85.56 | 25.74 | < .001 |           0.49 |        [0.32, 1.00]
site        |        4.21 |  1 |        4.21 |  1.27 | 0.265  |           0.02 |        [0.00, 1.00]
animal:site |       59.10 |  2 |       29.55 |  8.89 | < .001 |           0.25 |        [0.09, 1.00]
Residuals   |      179.47 | 54 |        3.32 |       |        |                |                    

Wenn du die ANOVA in deiner Abschlussarbeit anwendest, musst du jetzt noch schauen, welche paarweisen Gruppenvergleiche in deinem Faktor signifikant sind. Das würden wir dann in einem Post-hoc Test am Ende machen. Das war dann auch schon fast mit der zweifaktoriellen ANOVA, wenn es nicht noch die Interaktion zwischen den beiden Faktoren geben würde. Hier werfen wir dann nochmal einen Blick drauf.

30.7.2 Interaktion

In dem theoretischen Hintergrund habe ich dir verschiedene Arten gezeigt sich die Interaktion zu visualiseren. Ich nutze jetzt hier nur das Liniendiagramm in {ggplot} und dann noch die Darstellung aus dem R Paket {interactions}. Ebenso habe ich die Beschreibung der Abbildungen auf das wesentliche reduziert. Selten zeigst du diese Abbildungen prominent sondern eher im Anhang oder du nutzt diese Abbidlungen nur in deiner statistischen Analyse. Ich jedenfalls schaue mir gerne die Interaktion einmal an und vergleiche so die Abbildung mit den Ergebnissen einer ANOVA. Beides muss immer zusammenpassen.

Was ist das Problem einer Interaktion?

Wenn du eine Interaktion zwischen deinen beiden Faktoren vorliegen hast, dann kannst du keine allgemeine Aussage über die Gruppen der beiden Faktoren treffen. Die Effekte und Unterschiede, die du nachweist, hängen davon ab welche Faktorkombination du betrachtest. Manchmal willst du eien solche Interaktion zeigen, aber häufig wird eine Interaktion als störend in einem Experiment wahrgenommen.

{ggplot}

Betrachten wir also einmal die Interaktion zwischen den beiden Faktoren animal und site anhand eines Liniendiagramms welches uns die Mittelwerte aller sechs Faktorkombinationen zeigt. Wenn wir keine Interaktion vorliegen haben, dann laufen die Linien parallel zueinander. Wenn wir eine Interaktion vorliegen haben, dann beginnen sich die Linien anzunähern oder bewegen sich voneinander weg. Bei einer starken Interaktion kreuzen sich die Geraden. Wir du in der folgenden Abbildung sehen kannst, haben wir eine starke Interaktion zwischen unseren beiden Faktoren vorliegen. Die Floharten verhalten sich nicht gleich über die beiden Messorte. Es macht eben einen Unterschied wo du die Floharten misst.

fac2_tbl |> 
  ggplot(aes(x = animal, y = jump_length,
             color = site, group = site)) +
  theme_minimal() +
  stat_summary(fun = "mean", geom = "point") +
  stat_summary(fun = "mean", geom = "line") +
  scale_color_okabeito()

Abbildung 30.27— Liniendigramm mit den Mittelwerten aller sechs Faktorkombinationen der beiden Faktoren animal und site. Die Linien kreuzen sich, es liegt eine starke Interaktion vor. Eine allgmeine Aussage über die Sprungweite und die Flohart lässt sich nicht unabhängig vom Messort treffen.

{interactions}

Neben der händsich gebauten Variante in {ggplot} gibt es auch das R Paket {interactions} mit der Funktion car_plot(). Hier übergeben wir ein Modell und erhalten dann aus dem Modell ein Liniendiagramm zur Bewertung der Interaktion. Wie immer kann das Paket mehr als diese eine Funktion. Aber hier soll es dann erstmal so reichen. Die Funktion erstellt dann noch Fehlerbalken, die meiner Meinung nach nicht sein müssten, aber ich lasse diese mal hier mit drin. Die Aussage ist aber die gleiche wie bei {ggplot}, die Linien kreuzen sich, es ist von einer starken Interaktion auszugehen. Eine allgemeine Aussage über die Sprungweite und die Floharten ist nicht möglich ohne die Betrachtung des jeweiligen Messortes.

lm(jump_length ~ animal + site + animal:site, data = fac2_tbl) |> 
  cat_plot(modx = site, pred = animal, geom = "line") +
  theme_minimal() +
  scale_color_okabeito()

Abbildung 30.28— Liniendigramm mit den Mittelwerten aller sechs Faktorkombinationen der beiden Faktoren animal und site. Die Linien kreuzen sich, es liegt eine starke Interaktion vor. Eine allgmeine Aussage über die Sprungweite und die Flohart lässt sich nicht aunabhängig vom Messort treffen.

Das war dann auch die zweifaktorielle ANOVA. Wenn du die ANOVA in deiner Abschlussarbeit anwendest, musst du jetzt noch schauen, welche paarweisen Gruppenvergleiche in deinen Faktoren signifikant sind. Jetzt könnte man sagen, dafür brauchst du eine signifikante ANOVA, aber meistens machen wir dann doch den ANOVA Pfad zu Ende und testen nochmal alles mit einem Post-hoc Test durch.

30.8 Mehrfaktorielle ANOVA

Achtung, bitte beachten!

Die Erfahrung aus meiner statistischen Beratung zeigt oft, dass du gar keine mehrfaktorielle ANOVA im eigentlichen Sinne vorliegen hast, sondern manchmal in den Daten und den Faktoren verloren bist. Deshalb empfiehlt es sich hier nochmal innezuhalten und zu überlegen, was deine Fragestellung ist und du wirklich alle Faktoren und deren Wechselwirkungen mit ins Modell nehmen willst.

Wenn es die zweifaktorielle ANOVA gibt dann gibt es natürlich auch noch mehr als nur zwei Faktoren in einer ANOVA. Wir können auch eine mherfaktorielle ANOVA rechnen. Ich habe hier einen vierfaktoriellen Datensatz, den wir uns aber als einen dreifaktoriellen Datensatz in {WRS2} anschauen werden. Nicht jedes Paket kann mit mehr als drei Faktoren umgehen. Das hat den Grund, dass eigentlich in der Anwendung kaum Designs mit mehr als drei Behandlungsfaktoren auftreten. Die zusätzlichen Faktoren sind dann meistens Randomisierungseinheiten wie Block oder Spalte sowie Zeile.

Habe ich wirklich mehr als drei Behandlungsfaktoren?

Das ist eine sehr wichtige Frage. Häufig kann es sein, dass du eben wirklich eine zeitliche Komponente als Fakotr mit in deeinen Daten hast. Dann willst du vielleicht eine repeated ANOVA oder eine mixed ANOVA rechnen. Manchmal haben wir auch eine lokale Komponente mit drin, dann ist die Frage, ob du hier nicht über den Ort mittlen willst. Deshalb muss man hier immer sehr genau schauen, was ist eigentlich die wissenschaftliche Fragestellung und was habe ich in den Daten.

Wir schauen usn als mehrfaktoriellen Datensatz jetzt einmal eine große Studie zu der Sprungweite von Floharten animal in verschiedenen Orten site sowie verschiedenen Entwicklungsstadien stage an. Dann messen wir alles nochmal im Sommer und im Winter und haben so noch den Faktor season mit in unserem Modell. Teilweise wird es jetzt in den verschiedenen Implementierungen recht wild, aber das liegt eben daran, dass so eine vierfaktorielle ANOVA eben dann doch schon ein echtes Extrem ist. Insbesondere bei der mehrfaktroiellen ANOVA bietet es sich an die Ergebnisse mit der Funktion filter() nach den signifikanten p-Werten zu filtern, so dass alles übersichtlicher bleibt.

30.8.1 Haupteffekte

In unserem Fall haben wir jetzt vier Haupteffekte. Das ist eher selten der Fall und man könnte auch meinen, dass die Modellierung der Jahreszeiten oder aber der Messorte so nicht unbedingt nötig ist, aber da wir auch nur zwei Jahreszeiten sowie zwei Messorte haben, machen wir das jetzt mal so. In der Praxis haben wir dann bei so vielen Faktoren dann nicht noch sehr viele Level pro Faktor. Denke an die Regel, dass du eben nur weißt, dass wir einen Gruppenunterschied irgendwo im Faktor haben, wenn der p-Wert kleiner als das Signifikanzniveau \(\alpha\) gleich 5% ist.

{base}

Dann wollen wir mal anfangen. Ich zeige jetzt hier nur die aov() Variante. Du findest dann bei der zweifaktoriellen ANOVA auch den Code für die lm() Variante mit der Funktion anova(). Hier wird das dann aber viel zu viel Output, der dann einfach gleich ist. Darüber hinaus findest du die Modellierung dann auch im Tab zum R Paket {car}. Ich schreibe hier einmal die Modellschreibweise mit dem Malzeichen * da ich selber nie und nimmer alle Faktorkombinationen hinkriege noch tippen will. Bedenke hier, es kommt bei der aov() auf die Reihenfolge der Faktoren an. Wir haben ja hier eine Type I ANOVA vorliegen.

aov(jump_length ~ animal*stage*site*season, data = fac4_tbl) |> 
  tidy() |> 
  mutate(p.value = pvalue(p.value))

# A tibble: 16 × 6
   term                        df    sumsq   meansq statistic p.value
   <chr>                    <dbl>    <dbl>    <dbl>     <dbl> <chr>  
 1 animal                       2 6194.    3097.     252.     <0.001 
 2 stage                        1    7.73     7.73     0.629  0.429  
 3 site                         1  106.     106.       8.64   0.004  
 4 season                       1 1029.    1029.      83.7    <0.001 
 5 animal:stage                 2  530.     265.      21.6    <0.001 
 6 animal:site                  2  652.     326.      26.5    <0.001 
 7 stage:site                   1    0.337    0.337    0.0274 0.869  
 8 animal:season                2   14.8      7.42     0.604  0.548  
 9 stage:season                 1    6.65     6.65     0.541  0.463  
10 site:season                  1   29.6     29.6      2.41   0.122  
11 animal:stage:site            2   14.4      7.19     0.585  0.558  
12 animal:stage:season          2   60.5     30.3      2.46   0.088  
13 animal:site:season           2  327.     164.      13.3    <0.001 
14 stage:site:season            1   12.9     12.9      1.05   0.307  
15 animal:stage:site:season     2   82.4     41.2      3.35   0.037  
16 Residuals                  168 2064.      12.3     NA      <NA>   

Wir treten einen Schritt zurück und erschaudern bei dem Output. Hier hilft es dann wirklich nochmal die Funktion filter() und select() zu nutzen um sich einen kleineren Datensatz mit den wichtigen Informationen zu bauen. Ich sehe da sonst nichts mehr und wir übersehen dann mal schnell einen signifikanten p-Wert und das wäre ja nicht so gut.

aov(jump_length ~ animal*stage*site*season, data = fac4_tbl) |> 
  tidy() |> 
  filter(p.value <= 0.05) |> 
  select(term, p.value) |> 
  mutate(p.value = pvalue(p.value)) 

# A tibble: 7 × 2
  term                     p.value
  <chr>                    <chr>  
1 animal                   <0.001 
2 site                     0.004  
3 season                   <0.001 
4 animal:stage             <0.001 
5 animal:site              <0.001 
6 animal:site:season       <0.001 
7 animal:stage:site:season 0.037  

Was sehen wir jetzt? Zum einen, dass wir signifikante Haupteffekte vorliegen haben. Der Entwicklungsstatus ist als einiziges nicht signifikant. Darüber hinaus haben wir noch eine Menge signifikante Interaktionen. Das schauen wir uns dann nochmal separat in dem Abschnitt zu den Interaktionen weiter unten an.

{car}

Jetzt könnte man meinen, warum noch eine weitere Implementierung der ANOVA, wenn wir schon die Funktion aov() haben? Die Funktion aov() rechnet grundsätzlich Type I ANOVAs. Das macht jetzt bei einer mehrfaktoriellen ANOVA schon einen gewaltigen Unterschied ausmachen welchen Typ ANOVA wir rechnen. Wir können eben in {car} auch Type II und Type III ANOVAs rechnen. Darüber hinaus erlaubt das Paket auch für Varianzheterogenität in der ANOVA zu adjustieren.

Varianzhomogenität

In dem klassischen Aufruf der Funktion Anova() nutzen wir ein Modell und dann gebe ich dir wieder die aufgeräumte Ausgabe mit tidy() wieder. Wenn du nichts extra angibst, dann rechnest du natürlich eine ANOVA unter der Annahme der Varianzhomogenität.

Keine Interaktion zwischen den Faktoren A und B

Wir rechnen dann eine Type II ANOVA, wenn wir keine Interaktion zwischen den Faktoren vorliegen haben. Ja, dass müssen wir dann natürlich vorab einmal Testen, dazu kannst du einfach die Funktion aov() nutzen. Wenn wir keine Interaktion vorliegen haben, dann nehmen wir auch die Interaktion aus dem Modell und testen nur die Haupteffekte mit einer Type II ANOVA. Manchmal ist das ganz gut, damit wir überhaupt mal eine Übersicht kriegen.

lm(jump_length ~ animal + stage + site + season, data = fac4_tbl) |> 
  Anova(type = "II") |> 
  tidy()  |> 
  mutate(p.value = pvalue(p.value))

# A tibble: 5 × 5
  term        sumsq    df statistic p.value
  <chr>       <dbl> <dbl>     <dbl> <chr>  
1 animal    6194.       2   152.    <0.001 
2 stage        7.73     1     0.379 0.539  
3 site       106.       1     5.21  0.024  
4 season    1029.       1    50.4   <0.001 
5 Residuals 3795.     186    NA     <NA>   

Interaktion zwischen den Faktoren A und B

Wir rechnen dann eine Type III ANOVA, wenn wir eine Interaktion zwischen den beiden Faktoren vorliegen haben. Dann werden die Haupteffekte unter der Berücksichtigung der Interaktion berechnet. Aber Achtung, du musst leider in {car} die Kontraste anders definieren sonst testet die Funktion Anova() nicht das was sie soll. Da ist dann die Funktion aov_car() aus dem Paket {afex} anwenderfreundlicher.

lm(jump_length ~ animal*stage*site*season, data = fac4_tbl,
    contrasts = list(
    animal = "contr.sum",
    stage = "contr.sum",
    site = "contr.sum",
    season = "contr.sum"
  )) |> 
  Anova(type = "III") |> 
  tidy()  |> 
  mutate(p.value = pvalue(p.value))

# A tibble: 17 × 5
   term                          sumsq    df  statistic p.value
   <chr>                         <dbl> <dbl>      <dbl> <chr>  
 1 (Intercept)              163784.        1 13329.     <0.001 
 2 animal                     6194.        2   252.     <0.001 
 3 stage                         7.73      1     0.629  0.429  
 4 site                        106.        1     8.64   0.004  
 5 season                     1029.        1    83.7    <0.001 
 6 animal:stage                530.        2    21.6    <0.001 
 7 animal:site                 652.        2    26.5    <0.001 
 8 stage:site                    0.337     1     0.0274 0.869  
 9 animal:season                14.8       2     0.604  0.548  
10 stage:season                  6.65      1     0.541  0.463  
11 site:season                  29.6       1     2.41   0.122  
12 animal:stage:site            14.4       2     0.585  0.558  
13 animal:stage:season          60.5       2     2.46   0.088  
14 animal:site:season          327.        2    13.3    <0.001 
15 stage:site:season            12.9       1     1.05   0.307  
16 animal:stage:site:season     82.4       2     3.35   0.037  
17 Residuals                  2064.      168    NA      <NA>   

Auch hier hilft ein Filtern weiter. Ansonsten sieht man echt überhaupt nichts und wir kommen nur durcheinander. Was du auf jeden Fall schon mal siehst, wenn es mehr Faktoren werden, dann macht der Typ der ANOVA schon was aus. Wir haben hier am Ende aber die gleichen signifikanten Ergebnisse wie bei der aov() vorliegen.

lm(jump_length ~ animal*stage*site*season, data = fac4_tbl,
    contrasts = list(
    animal = "contr.sum",
    stage = "contr.sum",
    site = "contr.sum",
    season = "contr.sum"
  )) |> 
  Anova(type = "III") |> 
  tidy() |> 
  filter(p.value <= 0.05) |> 
  select(term, p.value) |> 
  mutate(p.value = pvalue(p.value)) 

# A tibble: 8 × 2
  term                     p.value
  <chr>                    <chr>  
1 (Intercept)              <0.001 
2 animal                   <0.001 
3 site                     0.004  
4 season                   <0.001 
5 animal:stage             <0.001 
6 animal:site              <0.001 
7 animal:site:season       <0.001 
8 animal:stage:site:season 0.037  

Varianzheterogenität

Der Vorteil des Pakets {car} ist, dass wir in der Funktion Anova() auch für Varianzheterogenität adjustieren können. Wir nutzen dazu die Option white.adjust = TRUE. Ich gehe hier jetzt nicht näher auf die Ausgabe ein. Die Ausgabe ist analog zu den anderen Ergebnissen zu interpretieren. Ich habe hier jetzt gleich gefiltert damit die Ausgabe etwas aufgeräumter ist.

lm(jump_length ~ animal*stage*site*season, data = fac4_tbl,
    contrasts = list(
    animal = "contr.sum",
    stage = "contr.sum",
    site = "contr.sum",
    season = "contr.sum"
  )) |> 
  Anova(white.adjust = TRUE, type = "III")  |> 
  tidy() |> 
  filter(p.value <= 0.05) |> 
  select(term, p.value) |> 
  mutate(p.value = pvalue(p.value)) 

Coefficient covariances computed by hccm()

# A tibble: 8 × 2
  term                     p.value
  <chr>                    <chr>  
1 (Intercept)              <0.001 
2 animal                   <0.001 
3 site                     0.007  
4 season                   <0.001 
5 animal:stage             <0.001 
6 animal:site              <0.001 
7 animal:site:season       <0.001 
8 animal:stage:site:season 0.026  

{afex}

Der Vorteil von dem R Paket {afex} ist, dass wir hier mit der Funktion aov_car() eine Type III ANOVA rechnen, die korrekt angepasst ist. Wir müssen also nicht noch extra ein Modell mit Kontrasten anpassen. Wir können auch die ANOVA Type II rechnen indem wir di Option type = "II" wählen. Dazu dann einfach einmal bei der zweifaktoriellen ANOVA reinschauen, da zeige ich den Code dazu. Eine Besonderheit ist, dass wir einen Fehlerterm mit Error() der Funktion übergeben müssen, damit {afex} rechnen kann. Die Stärke von {afex} liegt eigentlich in der repeated und mixed ANOVA. Dort brauchen wir dann die Information zwingend, welche Zeile zu welcher Beobachtung gehört. Ich verzichte hier auf die Aufteilung mit und ohne Interaktion.

aov_car(jump_length ~ animal*stage*site*season + Error(.id), 
        data = fac4_tbl) 

Contrasts set to contr.sum for the following variables: animal, stage, site, season

Anova Table (Type 3 tests)

Response: jump_length
                     Effect     df   MSE          F   ges p.value
1                    animal 2, 168 12.29 252.05 ***  .750   <.001
2                     stage 1, 168 12.29       0.63  .004    .429
3                      site 1, 168 12.29    8.64 **  .049    .004
4                    season 1, 168 12.29  83.73 ***  .333   <.001
5              animal:stage 2, 168 12.29  21.57 ***  .204   <.001
6               animal:site 2, 168 12.29  26.52 ***  .240   <.001
7                stage:site 1, 168 12.29       0.03 <.001    .869
8             animal:season 2, 168 12.29       0.60  .007    .548
9              stage:season 1, 168 12.29       0.54  .003    .463
10              site:season 1, 168 12.29       2.41  .014    .122
11        animal:stage:site 2, 168 12.29       0.58  .007    .558
12      animal:stage:season 2, 168 12.29     2.46 +  .028    .088
13       animal:site:season 2, 168 12.29  13.32 ***  .137   <.001
14        stage:site:season 1, 168 12.29       1.05  .006    .307
15 animal:stage:site:season 2, 168 12.29     3.35 *  .038    .037
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

Ja, dann ist das Filtern der {afex} Ausgabe dann doch etwas nerviger als gedacht. Dennoch solltest du das tun, denn dann sehen wir besser, was hier eigentlich signifikant ist. Die Ausgabe von aov_car() kürzt so seltsam die p-Werte, so dass es noch unübersichtlicher wird für mich. Die Ausgabe ist dann wie immer zu interpretieren nur das wir eben schon alle signifkanten p-Werte gefiltert haben.

aov_car(jump_length ~ animal*stage*site*season + Error(.id), 
        data = fac4_tbl) |>  
  pluck("anova_table") |> 
  as_tibble(rownames = "term") |> 
  janitor::clean_names() |> 
  filter(pr_f <= 0.05) |> 
  select(term, pr_f) |> 
  mutate(pr_f = pvalue(pr_f)) 

Contrasts set to contr.sum for the following variables: animal, stage, site, season

# A tibble: 7 × 2
  term                     pr_f  
  <chr>                    <chr> 
1 animal                   <0.001
2 site                     0.004 
3 season                   <0.001
4 animal:stage             <0.001
5 animal:site              <0.001
6 animal:site:season       <0.001
7 animal:stage:site:season 0.037 

{WRS2}

Das R Paket {WRS2} von Mair und Wilcox (2020) erlaubt es auch bei nicht normalverteilten Daten sowie Varianzheterogenität eine ANOVA zu rechnen. Dabei ist die maximale Anzahl an Faktoren auf drei Faktoren begrenzt. Daher können wir auch nur eine dreifaktorielle ANOVA (eng. three-way ANOVA) rechnen. Ich habe mich dazu entschieden dann die Entwicklungsstatdien aus dem Modell zu nehmen, da diese ja in den anderen Implementierungen nicht signifikant waren. Daher kann es sich lohnen mal mit den Implementierungen zu spielen und zu schauen, was da so rauskommt.

t3way(jump_length ~ animal*site*season, data = fac4_tbl)

Call:
t3way(formula = jump_length ~ animal * site * season, data = fac4_tbl)

                        value p.value
animal             396.190830  0.0001
site                 7.032921  0.0110
season              53.603295  0.0010
animal:site         43.075907  0.0010
animal:season        1.897799  0.4010
site:season          1.218229  0.2750
animal:site:season  21.974268  0.0010

In dem dreifaktoriellen Fall bleibt ja die Ergebnistabelle relativ übersichtlich. Wir sehen hier ähnliche Ergebnisse wie bei den anderen Implementierungen und die Entscheidungen nach dem p-Wert bleiben auch hier gleich. Einzig die Interaktionen zwischen den Jahreszeiten und Floharten sowie dem Messort sind nicht signifikant.

Nachdem wir einmal die p-Werte aus unserer mehrfaktoriellen ANOVA erhalten und dann noch geschaut haben, ob wir ein signifikantes Ergebnis haben, können wir jetzt weiter machen. Was fehlt noch? Wir müssen noch schauen, ob wir einen Effekt zwischen den Gruppen in unserem Faktoren vorliegen haben. Eine Signifikanz bedeutet ja nicht gleich Relevanz und deshalb berechnen wir auch gerne einmal einen Effektschätzer. Ein Effektschätzer sagt dir, wie stark sich die Gruppen voneinander unterscheiden. Oder anders herum formuliert, wie stark ist der Einfluss des Faktors auf den Messwert? Dann schauen wir uns noch die Möglichkeit einmal an mit dem R Paket {report} eine bessere Ausgabe zu erhalten. Das funktioniert aber nicht bei allen Implementierungen. Insbesondere in einer mehrfaktoriellen ANOVA ist es jetzt wichtig zu schauen, ob die Interaktionen überhaupt eine Bedeutung haben oder wir die Interaktionen dann doch vom Effekt her als irrelevant betrachten können.

Effektschätzer

In einer mehrfaktoriellen ANOVA lassen wir den Effektschätzer für \(\eta^2\) (eng. eta squared) weg und konzentrieren uns auf das \(\epsilon^2\) (eng. epsilon squared) und das \(\omega^2\) (eng. omega squared). Das \(\eta^2\) ist nicht geeigent für mehrere Faktoren und da sind dann die anderen beiden Effektschätzer besser und auch für ausgelegt. Ich nutze dann noch die Filterfunktion um mir nur die Werte anzeigen zu lassen, die über \(0.01\) liegen. Hier kannst du auch noch strenger filtern, aber filtern solltest du. Dann sortiere ich mir noch die Werte absteigend desc() mit der Funktion arrange(). Auch hier kannst du die Werte für die 95% Konfidenzintervalle bei unserer kleinen Fallzahl ignorieren.

aov(jump_length ~ animal*stage*site*season, data = fac4_tbl) |> 
  epsilon_squared() |> 
  filter(Epsilon2_partial >= 0.01) |> 
  arrange(desc(Epsilon2_partial)) |> 
  interpret_epsilon_squared()

# Effect Size for ANOVA (Type I)

Parameter                | Epsilon2 (partial) |       95% CI | Interpretation
-----------------------------------------------------------------------------
animal                   |               0.75 | [0.70, 1.00] |          large
season                   |               0.33 | [0.24, 1.00] |          large
animal:site              |               0.23 | [0.14, 1.00] |          large
animal:stage             |               0.19 | [0.11, 1.00] |          large
animal:site:season       |               0.13 | [0.05, 1.00] |         medium
site                     |               0.04 | [0.01, 1.00] |          small
animal:stage:site:season |               0.03 | [0.00, 1.00] |          small
animal:stage:season      |               0.02 | [0.00, 1.00] |          small

- One-sided CIs: upper bound fixed at [1.00].
- Interpretation rule: field2013

Wir sehen, dass die Interaktionen dann doch einen Teil der Varianz ausmachen. Die Werte addieren sich ja nicht mehr auf Eins auf, aber dennoch können wir die Werte realtiv zueinander vergleichen. Wir haben hier eben dann doch einen starken Einfluss auf die Sprungweite durch die Faktorombinationen und damit wo, wann und was wir messen. Wir sehen den gleichen Trend dann auch im Folgenden für die \(\omega^2\) Werte.

aov(jump_length ~ animal*stage*site*season, data = fac4_tbl) |> 
  omega_squared() |> 
  filter(Omega2_partial >= 0.01) |> 
  arrange(desc(Omega2_partial)) |> 
  interpret_omega_squared()

# Effect Size for ANOVA (Type I)

Parameter                | Omega2 (partial) |       95% CI | Interpretation
---------------------------------------------------------------------------
animal                   |             0.72 | [0.67, 1.00] |          large
season                   |             0.30 | [0.21, 1.00] |          large
animal:site              |             0.21 | [0.12, 1.00] |          large
animal:stage             |             0.18 | [0.09, 1.00] |          large
animal:site:season       |             0.11 | [0.04, 1.00] |         medium
site                     |             0.04 | [0.00, 1.00] |          small
animal:stage:site:season |             0.02 | [0.00, 1.00] |          small
animal:stage:season      |             0.02 | [0.00, 1.00] |          small

- One-sided CIs: upper bound fixed at [1.00].
- Interpretation rule: field2013

Welche der beiden Maßzahlen der Effektschätzer sollest du nun berichten? Nach der Hilfeseite von dem R Paket {effectsize} ist “Omega is the more popular choice”. Daher würde ich dann zu den \(\omega^2\) Werten in einer mehrfaktoriellen ANOVA tendieren. Mehr dazu dann aber weiter oben im Abschnitt zu der theoretischen Betrachtung der Effektschätzer in der ANOVA. Mehr dazu dann auch unter Other Measures of Effect Size auf der Hilfeseite des R Pakets {effectsize}.

R Paket {report}

Das R Paket {report} liefert nochmal die Möglichkeit sich die Ausgabe einer zweifaktoriellen ANOVA in Textform wiedergeben zu lassen. Wie immer, wenn man alleine vor dem Rechner sitzt, ist das doch eine super Hilfestellung. Hier dann einmal mit der Anova() Funktion aus dem R Paket {car}. Ich mag hier besonders die Hilfe bei einer mehrfaktoriellen ANOVA. Hier wird es dann sehr schnell sehr unübersichtlich und da ist doch die report() Funktion hilfreich.

lm(jump_length ~ animal*stage*site*season, data = fac4_tbl) |> 
  Anova() |>
  report()

The ANOVA suggests that:

  - The main effect of animal is statistically significant and large (F(2, 168) =
252.05, p < .001; Eta2 (partial) = 0.75, 95% CI [0.70, 1.00])
  - The main effect of stage is statistically not significant and very small
(F(1, 168) = 0.63, p = 0.429; Eta2 (partial) = 3.73e-03, 95% CI [0.00, 1.00])
  - The main effect of site is statistically significant and small (F(1, 168) =
8.64, p = 0.004; Eta2 (partial) = 0.05, 95% CI [9.50e-03, 1.00])
  - The main effect of season is statistically significant and large (F(1, 168) =
83.73, p < .001; Eta2 (partial) = 0.33, 95% CI [0.24, 1.00])
  - The interaction between animal and stage is statistically significant and
large (F(2, 168) = 21.57, p < .001; Eta2 (partial) = 0.20, 95% CI [0.12, 1.00])
  - The interaction between animal and site is statistically significant and
large (F(2, 168) = 26.52, p < .001; Eta2 (partial) = 0.24, 95% CI [0.15, 1.00])
  - The interaction between stage and site is statistically not significant and
very small (F(1, 168) = 0.03, p = 0.869; Eta2 (partial) = 1.63e-04, 95% CI
[0.00, 1.00])
  - The interaction between animal and season is statistically not significant
and very small (F(2, 168) = 0.60, p = 0.548; Eta2 (partial) = 7.14e-03, 95% CI
[0.00, 1.00])
  - The interaction between stage and season is statistically not significant and
very small (F(1, 168) = 0.54, p = 0.463; Eta2 (partial) = 3.21e-03, 95% CI
[0.00, 1.00])
  - The interaction between site and season is statistically not significant and
small (F(1, 168) = 2.41, p = 0.122; Eta2 (partial) = 0.01, 95% CI [0.00, 1.00])
  - The interaction between animal, stage and site is statistically not
significant and very small (F(2, 168) = 0.58, p = 0.558; Eta2 (partial) =
6.91e-03, 95% CI [0.00, 1.00])
  - The interaction between animal, stage and season is statistically not
significant and small (F(2, 168) = 2.46, p = 0.088; Eta2 (partial) = 0.03, 95%
CI [0.00, 1.00])
  - The interaction between animal, site and season is statistically significant
and medium (F(2, 168) = 13.32, p < .001; Eta2 (partial) = 0.14, 95% CI [0.06,
1.00])
  - The interaction between stage, site and season is statistically not
significant and very small (F(1, 168) = 1.05, p = 0.307; Eta2 (partial) =
6.22e-03, 95% CI [0.00, 1.00])
  - The interaction between animal, stage, site and season is statistically
significant and small (F(2, 168) = 3.35, p = 0.037; Eta2 (partial) = 0.04, 95%
CI [1.21e-03, 1.00])

Effect sizes were labelled following Field's (2013) recommendations.

Wenn du die ANOVA in deiner Abschlussarbeit anwendest, musst du jetzt noch schauen, welche paarweisen Gruppenvergleiche in deinem Faktor signifikant sind. Das würden wir dann in einem Post-hoc Test am Ende machen. Das war dann auch schon fast mit der mehrfaktoriellen ANOVA, wenn es nicht noch die Interaktion zwischen den Faktoren geben würde. Hier werfen wir dann nochmal einen Blick drauf, denn das ist jetzt schon noch ein bedeutender Teil.

30.8.2 Interaktion

“Auch Holzwege müssen zu Ende gegangen werden.” — Angela Merkel

Die Interaktion in einem mehrfaktoriellen Modell kann einen ganz schön ins schwitzen bringen, wenn man sich nicht sehr gut mit dem Experiment und dem dahinterliegenden biologischen Zusammenhängen auskennt. Schnell kann man da auf dem Holzweg gelangen und irrt durch die Daten. Hier möchte ich mir dann auch die Interaktionen einmal visualiseren, so dass ich eine Idee bekomme was in den Daten los ist. Wir wissen ja schon durch die ANOVA, wo wir hinschauen müssen und welche Interaktionen wir zu erwarten haben.

Was sagt mir die signifikante Interaktion in einem mehrfaktoriellen Modell?

Wir haben ja in unserer ANOVA zwei signifikante Interaktionen höherer Ordnung. Das heißt, wir haben nicht nur eine Interaktion zwischen zwei Faktoren sondern drei oder mehr Faktoren. Das ist immer schwer zu interpretieren, wenn man nicht die Abbildungen dazu sieht. In der Anwendung heißen signifikante Interaktionen höherer Ordnung, dass wir unsere Ergebnisse nicht über alle Faktorkombinationen verallgemeinern können.

Da es bei den Interaktionen der höheren Ordnung schnell mal unübersichtlich wird habe ich nochmal eine Tabelle zur Erklärung erstellt. Dabei ist es wichtig zu wissen, dass die gesamte Interaktionen als ganzes zu sehen ist. Das macht es dann recht schwierig alles im Kopf zu behalten, welche Faktoren sich wie ändern sollen, damit wir eine Interaktion sehen. Oder andersherum, ich finde Interaktionen höhrer Ordnung auch immer schwer zu verstehen.

Tabelle 30.24— Bedeutung der höhren Ordnungen der Interaktionsterme in der multifaktoriellen ANOVA.

Interaktionsterm	Bedeutung
animal:site:season	Die Interaktion zwischen dem Faktor animal und site und dem Faktor season. Verhalten sich die Floharten an den Messorten und den Jahreszeiten gleich?
animal:stage:site:season	Die Interaktion zwischen dem Faktor animal und site sowie stage und dem Faktor season. Verhalten sich die Floharten an den Messorten und den Jahreszeiten für beide Entwicklungsstadien gleich?

Schauen wir uns einmal die Interaktionen in dem mehrfaktoriellen Datensatz einmal an. Ich zeige dir hier auch die Implementierung in dem R Paket {interactions} für den dreifaktoriellen Fall. Wenn wir den vierfaktoriellen Fall vorliegen haben, dann müssen wir uns die Abbdilungen selber in {ggplot} bauen.

{ggplot}

Wenn wir mehr asl zwei Faktoren in einem Liniendiagramm abilden wollen, dann müssen wir uns entscheiden, welche zusätzliche Darstellung eines Faktors wir wollen. Ich zeige hier einmal die Lösung mit einem zusätzlichen Typ an Linien mit linetype = stage sowie einer Aufteilung der Abbildung in zwei Unterabbildungen nach der Jahreszeit durch die Funktion facet_wrap(~ season). Dadurch erhalten wir verschiedene Linientypen für den Entwicklungszustand und spalten die Abbildung einmal nach der Jahreszeit der Messung auf.

fac4_tbl |> 
  ggplot(aes(x = animal, y = jump_length,
             color = site, linetype = stage, 
             group = interaction(site, stage))) +
  theme_minimal() +
  stat_summary(fun = "mean", geom = "point") +
  stat_summary(fun = "mean", geom = "line") +
  scale_color_okabeito() +
  facet_wrap(~ season)

Abbildung 30.29— Liniendiagramm zur Überprüfung der Interaktion in einem vierfaktoriellen Versuchsdesign. Wenn sich die Linien kreuzen so ist von einer Interaktion auszugehen.

Wir sehen in der Abbildung mehrere Interaktionen. Ich versuche die Interaktionen einmal mit dem p-Wert und der Abbildung überein zu bringen. Eine Interaktion sollte man eigentlich immer sehen. Häufig muss man nur sehr genau schauen und mal die Faktoren durchpermutieren. Je nachdem was auf der x-Achse liegt siehst du was anderes leichter.

1. Interaktion animal:stage mit dem p-Wert von \(<0.001\): Hier haben wir ein Überkreuzen der Linien von dem Faktor animal und stage. Adulte Katzenflöhe springen im Mittel weiter als adulte Flöhe. Dieser Zusammenhang dreht sich bei den Hunden um.
2. Interaktion animal:site mit dem p-Wert von \(<0.001\): Hier haben wir ein Überkreuzen der Linien von dem Faktor animal und site. Katzenflöhe springen in der Stadt weiter als auf dem Dorf. Dieser Zusammenhang dreht sich dann bei den Fuchsflöhen um. Dort springen die Dorffuchsflöhe weiter als die Stadtfuchsflöhe.
3. Interaktion animal:site:season mit dem p-Wert von \(<0.001\): Die Sprungweiten der Floharten der drei Tiere über die Messorte im Sommer und Winter sind mehr als nur verschoben. Die Mittelwerte der Sprungweiten der Füchse sind in der Stadt im Sommer niedriger als im Winter im Bezug zum Messort im Dorf.
4. Interaktion animal:stage:site:season mit dem p-Wert von \(0.037\): Diese Interaktion ist jetzt die schwerste zu sehende Interaktion. Wir haben eben noch den Dreher der Sprungweiten bei den Hunden von Sommer zu Winter mit drin. Bei den Hunden verändert sich die Reihenfolge der Mittelwerte für stage und juvenile von Sommer zu Winter. Das Ganze kann man auch leicht bei den Katzenflöhen sehen.

Jetzt können wir uns die Abbildung auch über die Funktion facet_wrap(~ stage * season) für die Kombinationen an Entwicklungsstand und Jahreszeit einmal aufteilen. Dann haben wir nur die Farben für den Messort und die Floharten auf der x-Achse. Das ist manchmal dann auch etwas übersichtlicher, wenn du nicht so viele Gruppen in den Faktoren hast.

fac4_tbl |> 
  ggplot(aes(x = animal, y = jump_length,
             color = site, group = site)) +
  theme_minimal() +
  stat_summary(fun = "mean", geom = "point") +
  stat_summary(fun = "mean", geom = "line") +
  scale_color_okabeito() +
  facet_wrap(~ stage * season) 

Abbildung 30.30— Liniendiagramm zur Überprüfung der Interaktion in einem vierfaktoriellen Versuchsdesign. Die Aufteilung erfolgt hier über die Faktorkombinationen von stage * season. Wenn sich die Linien kreuzen so ist von einer Interaktion auszugehen.

{interactions}

In dem R Paket {interactions} können wir nur maximal eine dreifaktorielle ANOVA mit Interaktion darstellen. Wir legen dafür den ersten Faktor mit der Option modx = fest. Der zweite Faktor kommt dann in die Option mod2 =. Der Faktor auf der x-Achse wird dann in der Option pred = festgelegt. Dann können wir uns auch schon den Interaktionsplot einmal ansehen. Ich blende in der ersten Abbildung dann einmal den Faktor season aus.

lm(jump_length ~ animal*stage*site*season, data = fac4_tbl) |> 
  cat_plot(modx = site, mod2 = stage, pred = animal,  geom = "line") +
  theme_minimal() +
  scale_color_okabeito()

Abbildung 30.31— Liniendiagramm mit Fehlerbalken zur Überprüfung der Interaktion in einem dreifaktoriellen Versuchsdesign. Wenn sich die Linien kreuzen so ist von einer Interaktion auszugehen. Der Faktor season wird ignoriert und ausgeblendet.

Dann können wir uns die Abbildung auch nochmal mit dem ausgeblendeten Faktor stage anschauen. Am Ende muss man festhalten, dass wir in einer vierfaktoriellen ANOVA natürlich nur bedingt uns die Interaktion in zerlegten dreifaktoriellen Abbildungen anschauen können. Auf der anderen Seite betrifft es dann natürlich nur die Interaktion animal:stage:site:season, die wir nicht anschauen können. Das ist dann auch meistens verschmerzbar, da diese selten signifikant ist.

lm(jump_length ~ animal*stage*site*season, data = fac4_tbl) |> 
  cat_plot(modx = site, mod2 = season, pred = animal,  geom = "line") +
  theme_minimal() +
  scale_color_okabeito()

Abbildung 30.32— Liniendiagramm mit Fehlerbalken zur Überprüfung der Interaktion in einem dreifaktoriellen Versuchsdesign. Wenn sich die Linien kreuzen so ist von einer Interaktion auszugehen. Der Faktor stage wird ignoriert und ausgeblendet.

30.9 Am Ende

“Auf dem Weg der Tugend wird dir viel Leid widerfahren, doch dein Lohn wird Achtung, Verehrung und Liebe der Menschen sein.” — Herakles am Scheideweg

Wie kommen wir jetzt zum Ende? Wenn du eine signifikante ANOVA vorliegen hast, dann musst du noch einen Post-hoc Test rechnen um herauszufinden, welche paarweisen Vergleiche signifkant sind. Diese paarweisen signifkanten Unterschiede sind es ja, die die ANOVA erst signifikant gemacht haben. Ehrlicherweise ist es meist so, dass du immer einen Post-hoc Test rechnest, da man sich nie sicher sein kann, ob die ANOVA nicht fälschlicherweise die Nullhypothese beibehalten hat. Oder einfach weil wir eben immer einen Post-hoc Test in einer Abschlussarbeit rechnen. Also, dann auf ins Kapitel zum Post-hoc Testen.

Referenzen

Field A. 2013. Discovering statistics using IBM SPSS statistics.

Kozak M, Piepho H-P. 2018. What’s normal anyway? Residual plots are more telling than significance tests when checking ANOVA assumptions. Journal of agronomy and crop science 204: 86–98.

Mair P, Wilcox R. 2020. Robust statistical methods in R using the WRS2 package. Behavior research methods 52: 464–488.

Olejnik S, Algina J. 2003. Generalized eta and omega squared statistics: measures of effect size for some common research designs. Psychological methods 8: 434.

Van Emden HF. 2019. Statistics for terrified biologists. John Wiley & Sons.