| Anzahl Gruppen | Anzahl Vergleiche | Signifikanzniveau \(\alpha\) | Maximal signifikanter p-Wert | \(H_0\) fälschlich abgelehnt |
|---|---|---|---|---|
| 2 | 1 | 5% | 0.0500 | 0 |
| 3 | 3 | 14% | 0.0167 | 0 |
| 4 | 6 | 26% | 0.0083 | 0 |
| 5 | 10 | 40% | 0.0050 | 0 |
| 6 | 15 | 54% | 0.0033 | 0 |
| 7 | 21 | 66% | 0.0024 | 1 |
| 8 | 28 | 76% | 0.0018 | 1 |
| 9 | 36 | 84% | 0.0014 | 1 |
| 10 | 45 | 90% | 0.0011 | 2 |
| 11 | 55 | 94% | 0.0009 | 2 |
| 12 | 66 | 97% | 0.0008 | 3 |
44 Der Post-hoc Test
Letzte Änderung am 06. June 2025 um 20:54:30
“Comparison is the thief of joy.” — Theodore Roosevelt
In diesem Kapitel wollen wir uns mit den multiplen Vergleichen (eng. post hoc analysis) oder auch paarweise Gruppenvergleiche genannt beschäftigen. Wir kennen diese multiplen Tests auch unter dem Namen Post-hoc Tests, da wir historisch diese Tests nach einer ANOVA durchgeführt haben. Das heißt, wir wollen statistisch Testen, ob sich verschiedene Gruppen einer Behandlung voneinander unterschieden. Technisch Testen wir dabei, ob sich die Level eines Faktors voneinander unterscheiden. Wir können dabei mehrere Faktoren bzw. Behandlungen berücksichtigen und gleichzeitig Testen. Wenn wir nur einen Faktor betrachten, dann sprechen wir von einem einfaktoriellen Vergleich. Wenn wir zwei Behandlungen betrachten, dann entsprechend von einem zweifaktoriellen Vergleich. Sehr selten haben wir dann noch den Fall vorliegen, dass wir drei Faktoren betrachten wollen. In einer Abschlussarbeit haben wir faktisch keine Versuche wo wir mehr als drei Faktoren in einem Gruppenvergleich berücksichtigen.
{emmeans}!
Dieses Kapitel ist lang und vieles habe ich hier gerechnet, damit du es nicht musst. Wenn du keine Zeit hast, dann springe gleich in den Abschnitt mit dem effektiven Pfad mit {emmeans} und lasse den Rest links und rechts liegen. Wir freuen uns das es den Rest gibt, aber du willst ja fertig werden und nicht staunen, was andere so alles entwickelt haben. Und das ist vollkommen okay!
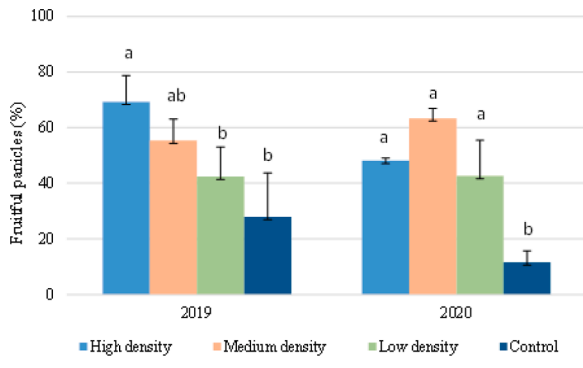
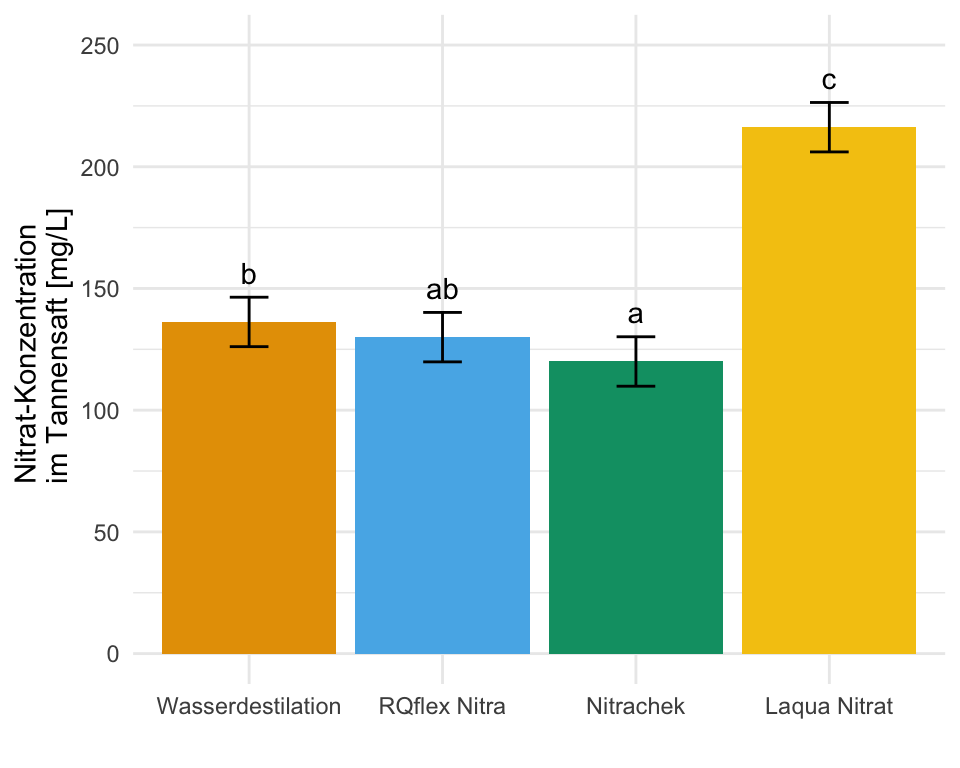
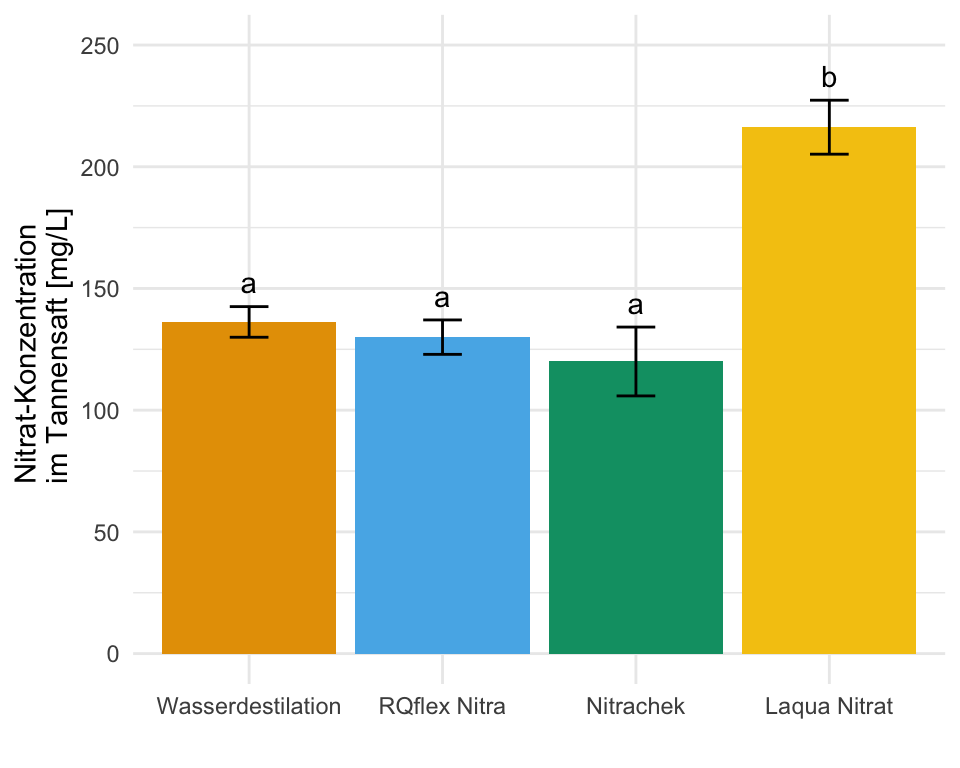
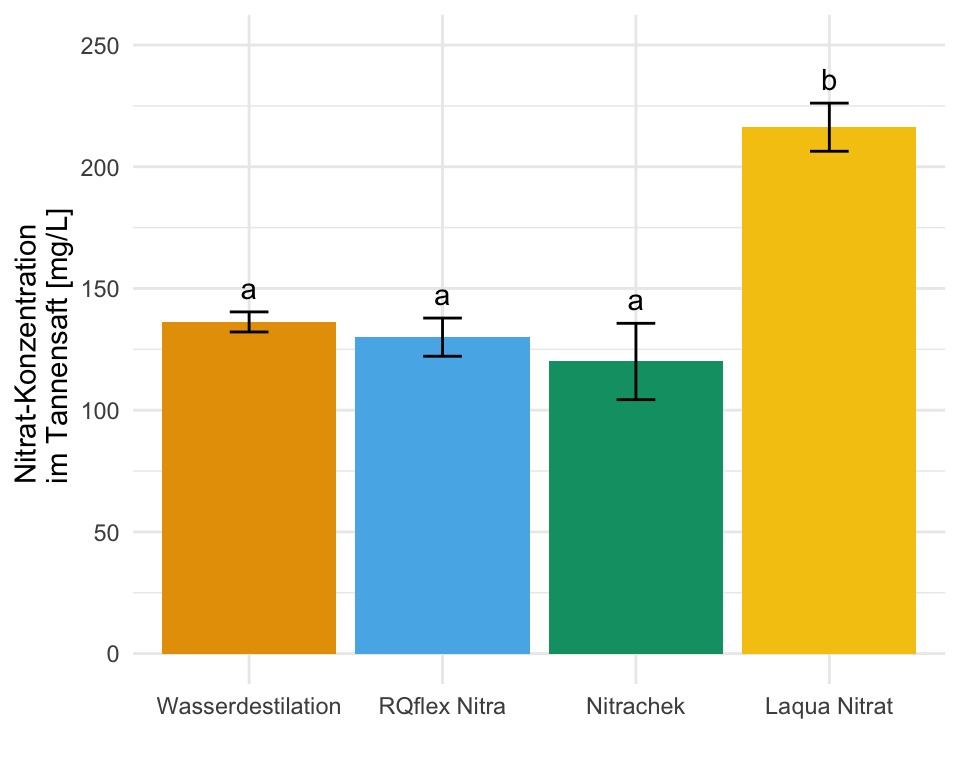
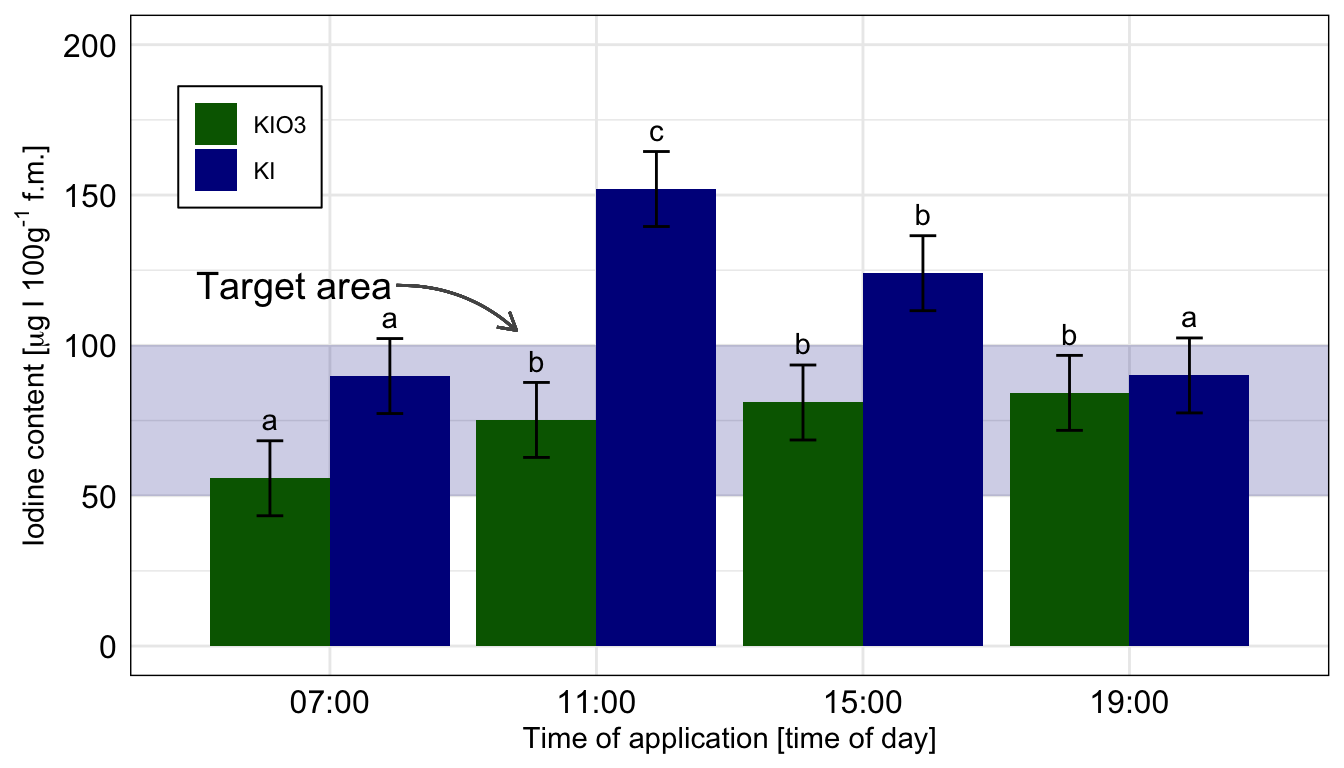
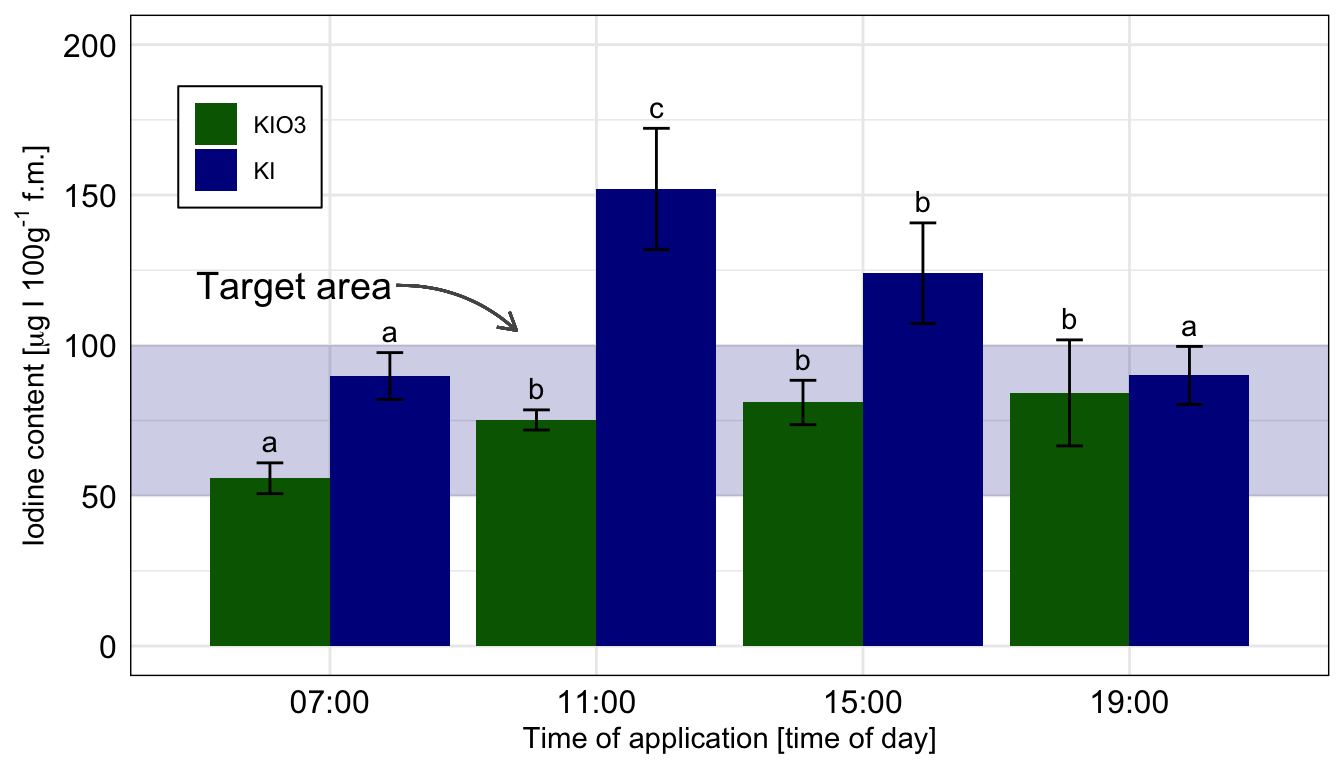
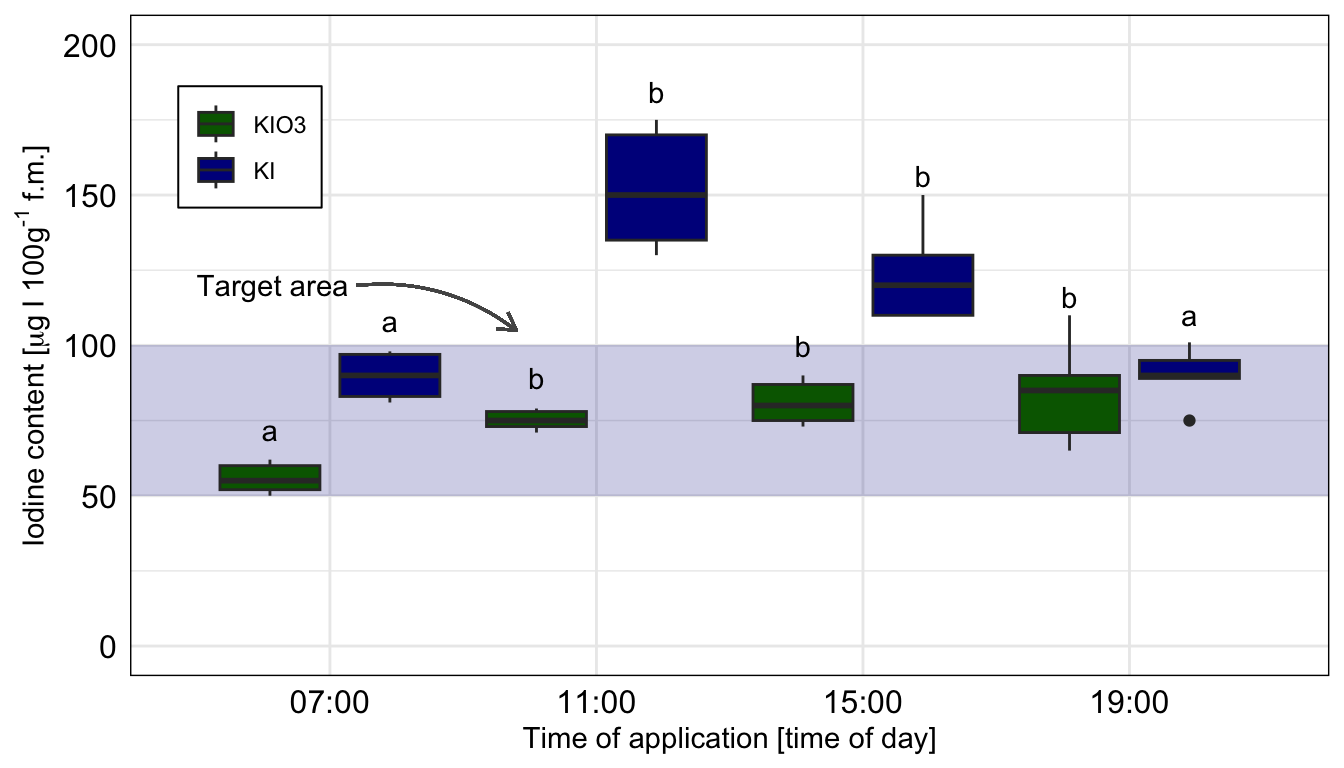
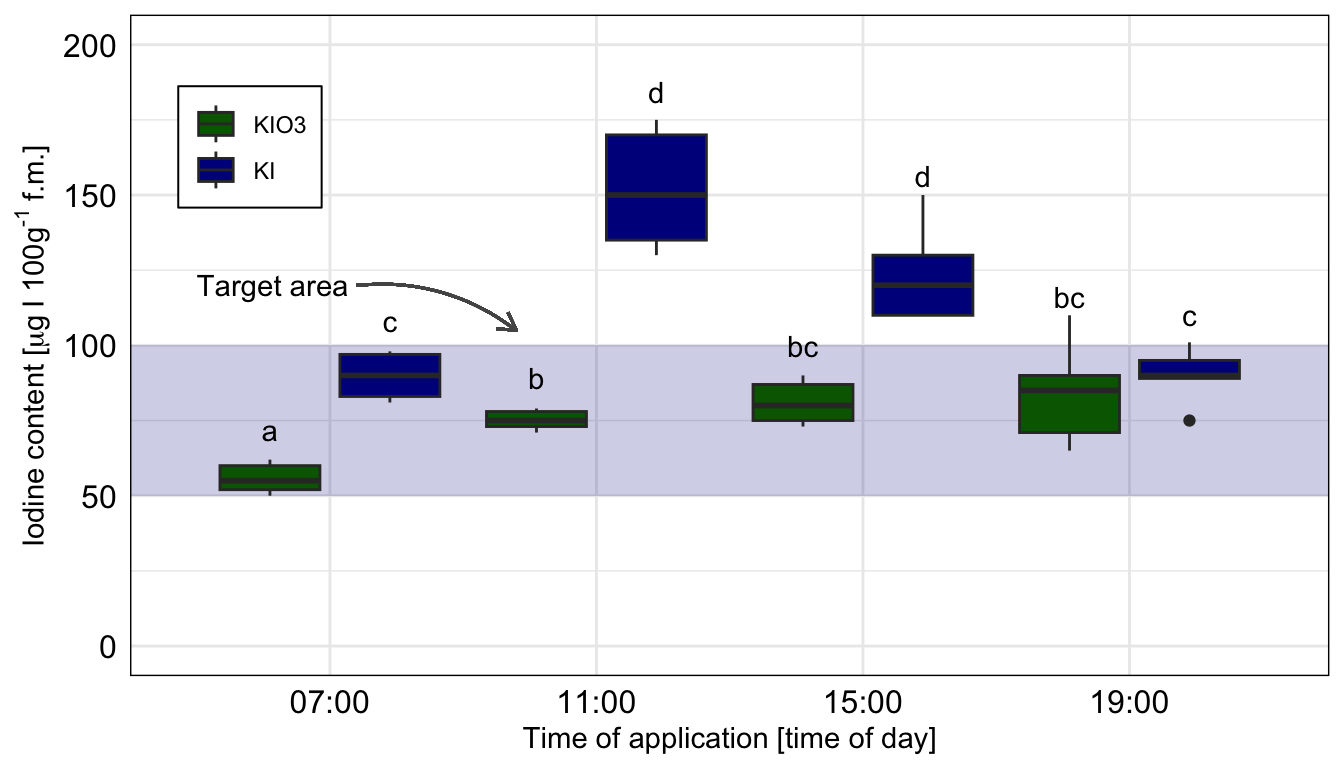
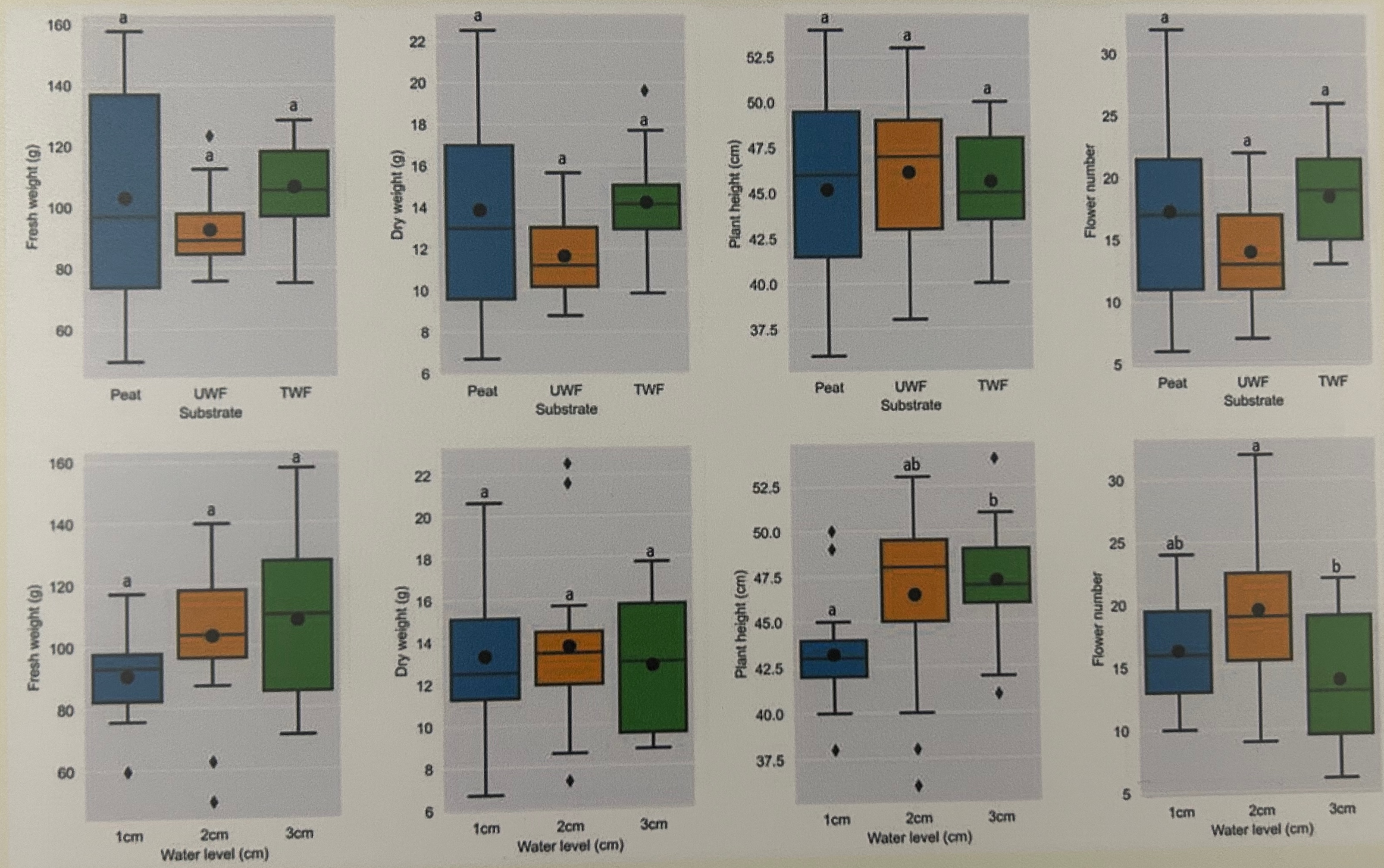
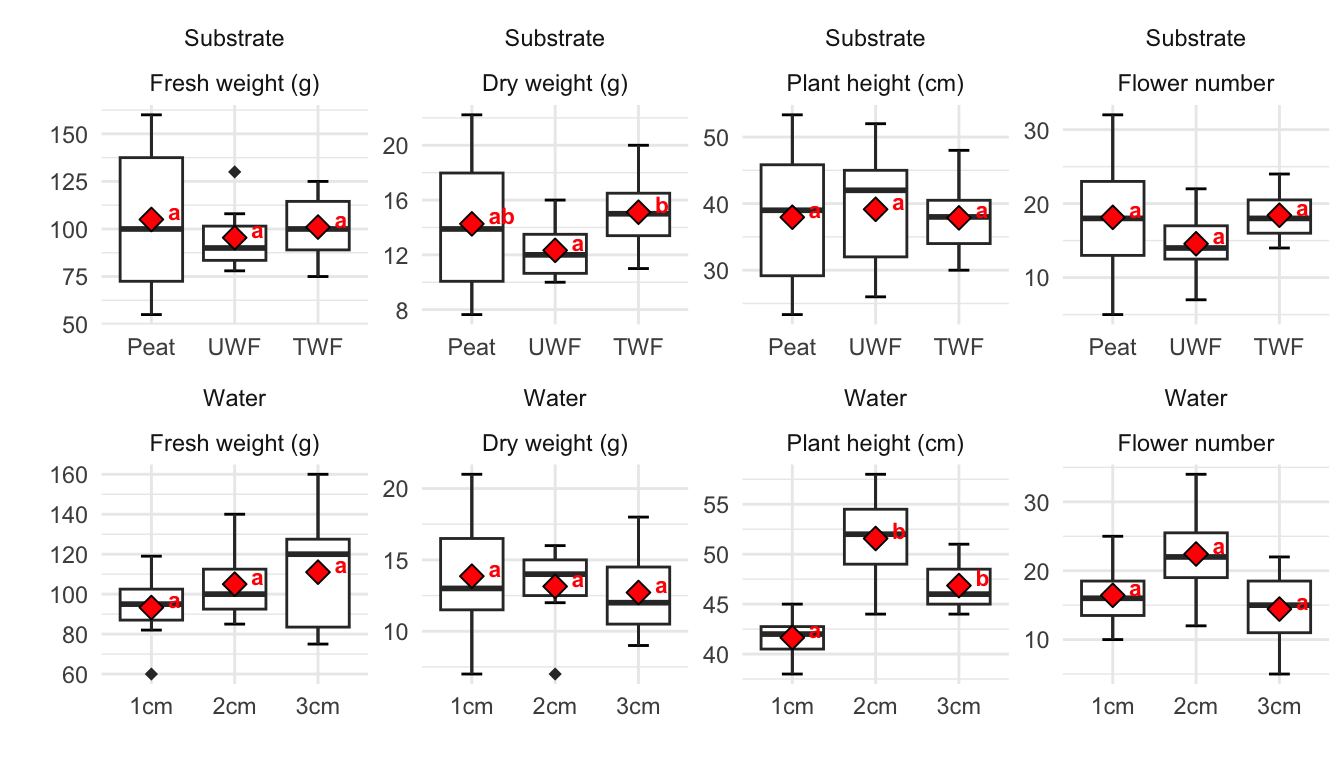
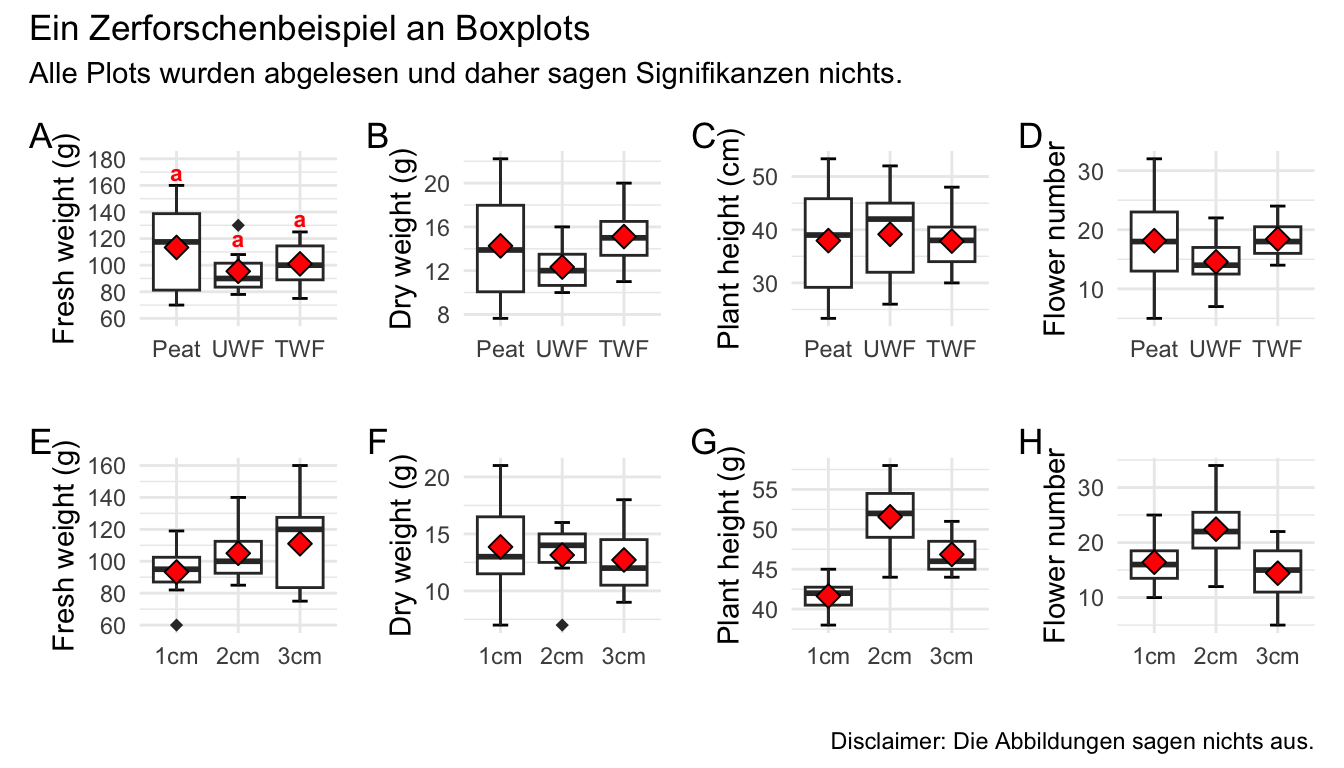
Wo wollen wir also mit unserem Post-hoc Test hin? Betrachten wir dazu einmal eine wissenschaftliche Veröffentlichungen als Beispiele. In der folgenden Abbildung sehen wir ein Säulendigramm aus der wissenschaftlichen Veröffentlichung von Sánchez et al. (2022) mit dem Titel “Hoverfly pollination enhances yield and fruit quality in mango under protected cultivation”. Dargestellt ist der mittlere Anteil an tragenden Rispen (eng. panicles) von Mango unter verschiedenen Ausbringungsdichten von Schwebfliegen (eng. hoverfly).
Wir haben hier ein typisches zweifaktorielles Design vorliegen. Zum einen den Faktor treatment mit den Gruppen High density, medium density, Low density und Control. Der zweite Faktor ist dann das Jahr der Messung mit zwei Jahren. Wir sehen hier die Buchstaben des Compact letter displays über den Mittelwerten als Säulen dargestellt. Das Compact letter display wollen wir dann hier in diesem Kapitel erstellen. Ein weiteres Beispiel findest du in der wissenschaftlichen Veröffentlichung von Salinas et al. (2023) mit dem Titel “Plant Growth, Yield, and Fruit Size Improvements in ‘Alicia’ Papaya Multiplied by Grafting”.
44.1 Theoretischer Hintergrund
In diesem Kapitel werde ich ein paar Engel der Statistik niedergeschlagen oder überfahren. Ich lasse aus Gründen der Didaktik ein paar Sachen weg und dadurch wird einiges leider dann mathematisch unkorrekt. Oder eben das klassische lying-to-children. Ich kann damit leben und nehme es auf mich damit du deine Abschlussarbeit fertig bekommst.
Fangen wir nochmal mit etwas theoretischen Hintergrund an. Das heißt wir schauen uns nochmal die wichtigsten Konzepte vom multiplen Testen einmal an. Wichtig ist hier, dass du eben mehr als zwei Gruppen miteinander vergleichen willst. Teilweise hast du mehr als sieben Gruppen und dann wird es schon eine Menge an Vergleichen. Wenn du alle möglichen vergleiche zwischen allen Gruppen rechnen willst, dann nennt man dies den all-pair Vergleich. Es werden eben alle möglichen Paare an Gruppen verglichen. Beginnen wir also mit der Frage nach der Anzahl an möglichen Vergleichen und was dies für unsere statistische Auswertung bedeutet.
- Wie viel ist den all-pair? Also alle möglichen Vergleiche?
-
Wenn du alle möglichen Mittelwertkombinationen testen willst, dann ist die Formel für die Berechnung der durchzuführenden Vergleiche \(r = m(m-1)/2\). Oder um es einmal in der folgenden Tabelle etwas konkreter darzustellen, werden es sehr schnell sehr viele Vergleiche. Dabei drückst du mit jeder zusätzlichen Behandlungsgruppe das Signifikanzniveau \(\alpha\) weiter runter, da die Anzahl an potenziellen Vergleichen sehr schnell ansteigt. So fällt dann auch der maximal noch signifikante p-Wert schnell ab. Damit brauchst du dann immer stärkere Effekt, wie einen Mittelwertsunterschied, um überhaupt noch was signifikantes aus einem statistischen Test wiedergeben zu bekommen. In der folgenden Tabelle siehst du dann nochmal den Zusammenhang. Ohne Adjustierung des Signifikanzniveaus erhalten wir schon ab sechs Gruppen mindestens einen signifikanten Unterschied auch wenn es gar keinen Unterschied in den Daten gibt. Denke immer daran, das Signifikanzniveau \(\alpha\) gibt an wie groß unsere Fehlerrate an falsch positiven Ergebnissen ist. Also die Nullhypothese mit dem statistischen Test abzulehnen, obwohl wir eigenlich keinen Unterschied vorliegen haben.
Jetzt kommt natürlich die Frage auf, ob ich immer adjustieren muss oder nicht. Wir immer gibt es da keine so richtig klare Antwort drauf. Rubin (2024) diskutiert in der wissenschaftlichen Veröffentlichung Inconsistent multiple testing corrections: The fallacy of using family-based error rates to make inferences about individual hypotheses das wir es auch lassen können mit der Adjustierung. Es gibt Gründe, die p-Werte zu adjustieren und es gibt auch gute Gründe die p-Werte ohne Adjustierung für multiple Vergleiche anzugeben. Hier hilft dann aber die statistische Betrachtung nicht weiter sondern du musst dir den Sachverhalt im Kontext deiner wissenschaftlichen Fragestelllung nochmal genauer anschauen.
- Was bedeutet konservativ und was liberal?
-
Häufiger schreibe ich mal das ein statistischer Test konservativ wird oder aber eher liberal testet. Das klingt jetzt etwas schräg sind aber bekannte Begriffe in der Fachsprache der Statistik. Es geht hierbei um die Bewertung des globalen Signifikanzniveau über alle Vergleiche hinweg. Wichtig ist, dass wir häufig nicht exakt wissen, wie groß das Signifikanzniveau in deinem speziellen Datenfall ist. Deshalb ist konservativ und liberal eher als Tendenz zu verstehen.
Wenn wir von einem konservativen Test sprechen, dann meinen wir, dass wir weniger signifikante Ergebnisse erwarten werden, als es bei einem Signifikanzniveau von \(\alpha\) gleich 5% zu erwarten wäre. Der Post-hoc Test nutzt nicht die vollen 5% Fehlerrate sondern testet global zu einem niedrigeren Signifikanzniveau. Wenn wir von einem liberalen Test sprechen, dann testen wir zu einem höheren Signifikanzniveau als \(\alpha\) gleich 5%. Wir werden also mehr signifikante Unterschiede finden als wir mit einer globalen Fehlerrate von 5% erwarten würden.
| Globales Signifikanzniveau \(\alpha\) | Bemerkung | |
|---|---|---|
| konservativ | \(\leq 5\%\) | Weniger signifikante Unterschiede |
| liberal | \(\geq 5\%\) | Mehr signifikante Unterschiede |
- Wie viele multiple Tests gibt es eigentlich?
-
Es gibt eine Menge an multiplen Tests oder auch Post-hoc Tests. Ich habe dir hier mal eine kleine Tabelle mitgebracht, die dir vier Post-hoc Tests im Vergleich zeigt. Ich habe die Auswahl etwas willkürlich getroffen, es gibt noch viel mehr Post-hoc Tests als ich in diesem Kapitel vorstelle. Wichtig für dich ist aber, dass es eigentlich auf die Entscheidung zwischen dem Tukey HSD Test oder eben dem R Paket
{emmeans}herausläuft. Ja, es gibt eben noch die anderen Tests, aber diese haben eine eher Nischenanwendung. Darüber hinaus kannst du{emmeans}so konfigurieren, dass du im Prinzip einen besseren Tukey HSD Test für Varianzhomogenität oder aber einen Games Howell Test für Vanrianzheterogenität rechnest ohne die Nachteil der orginalen Implemntierung. Das ist doch toll!
In einer normalen agarwissenschaftlichen Abschlussarbeit mit einem Feldexperiment und zwei Faktoren \(f_1\) und \(f_2\) läuft es eben dann doch auf den Tukey HSD Test oder Games Howell Test heraus. So ist eben die Normalverteilung des Messwertes \(y\) eben ein sehr starkes Kriterium zur Wahl des Tests. Da dann häufig noch die ANOVA vorgeschaltet wird sind wir dann im ANOVA Pfad mit dem Tukey HSD Test. Wichtig ist noch, dass du schauen musst, ob die Varianz in deinen Gruppen \(x\) eher homogen oder heterogen ist. Davon hängt dann die Entschiedung für oder gegen den Tukey HSD Test ab. Wenn dein Messwert \(y\) nicht normalverteilt ist, dann musst du eine anderes Modell rechnen, diese Modelle stelle ich später noch vor. Auch ist die Frage, ob du adjustierte p-Werte möchtest oder nicht. Hier hängt es auch von der Anwendung ab, ob du die Adjustierung für multiple Vergleiche ausstellen kannst.
{emmeans} mit seiner Flexibilität und einfachen Handbarkeit heraus. Die Mindestfallzahl per Gruppe \(n_g\) ist eher als Empfehlung zu verstehen und als untere Grenze. Achtung, teilweise müssen die Optionen aktiv von dir aktiviert werden. Sie dazu auch den Friedhof der Post-ho Tests in diesem Kapitel.
| Tukey HSD | Games Howell | {emmeans} |
{multcomp} |
|
|---|---|---|---|---|
| Verteilung von \(y\) | normalverteilt | normalverteilt | beliebig | beliebig |
| Varianzen der Gruppen \(x\) | homogen | heterogen | beliebig | beliebig |
| Fallzahl per Gruppe \(n_g\) | balanciert; \(n_g \geq 4\) | beliebig; \(n_g \geq 6\) | beliebig; \(n_g \geq 4\) | beliebig; \(n_g \geq 4\) |
| Adjustierte p-Werte | immer | immer | beliebig | beliebig |
| Mögliche Vergleiche | all-pair | all-pair | beliebig | beliebig |
44.2 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
pacman::p_load(tidyverse, readxl, knitr, kableExtra, see, nparcomp,
multcomp, emmeans, multcompView, nlme, janitor,
parameters, patchwork, agricolae, broom, rstatix,
DescTools, rcompanion, magrittr, quantreg, effectsize,
conflicted)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)
conflicts_prefer(magrittr::set_names)
conflicts_prefer(effectsize::eta_squared)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
"#F0E442", "#0072B2", "#D55E00", "#CC79A7")An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
44.3 Daten
Auch brauchen wir hier in diesem Kapitel einfache Datensätze an denen wir eine einfaktorielle und eine zweifaktorielle Analyse nachvollziehen können. Ich habe dir in einem Abschnitt noch ein paar Fallbeispiele in {emmeans} mitgebracht, die dann einen stärkeren agrarwissenschaftlichen Bezug haben. Für den Anfang reichen aber die beiden Beispiele für das Verständnis dieses Kapitels vollkommen aus. Die Visualisierung der Datensätze schauen wir uns dann in dem Abschnitt zur Abschätzung der Varianzhonogenität und Varianzheterogenität nochmal näher an.
Der erste Datenstaz besteht aus der Sprungweite in [cm] von verschiedenen Tierarten. Dabei ist dann die Sprungllänge unser Messwert \(y\) oder Outcome. Unsere Behandlung sind dann die drei Tierarten Hund, Katze und Fuchs. Wir fragen uns also, die verschiedenen Floharten unterschiedlich weit springen. Ich habe dir einmal die Daten in das Objekt fac1_tbl geladen.
R Code [zeigen / verbergen]
fac1_tbl <- read_xlsx("data/flea_dog_cat_fox.xlsx") |>
select(animal, jump_length) |>
mutate(animal = as_factor(animal))Dann schauen wir uns die Daten einmal in der folgenden Tabelle als Auszug einmal an. Wichtig ist hier nochmal, dass du eben einen Faktor animal mit drei Leveln also Gruppen vorliegen hast. Wir wolen jetzt die drei Tierarten hinsichtlich ihrer Sprungweite in [cm] miteinander vergleichen. Weil wir jetzt mehr als zwei Gruppen vorliegen haben, sprechen wir von einem multiplen Vergleich.
animal vorliegen haben.
| animal | jump_length |
|---|---|
| dog | 5.7 |
| dog | 8.9 |
| dog | 11.8 |
| … | … |
| fox | 10.6 |
| fox | 8.6 |
| fox | 10.3 |
Wir vergleichen natürlich nicht die Sprungweiten in [cm] direkt mitteinandern sondern rechnen natürlich vorher die deskriptive Statistiken wie Mittelwert und Standardabweichung aus. Für die Berechnung des Standardfehlers nutzen wir die Funktion standard_error() aus dem R Paket {parameters}. Am Ende vergleichen wir die mittleren Sprungweiten der Hunde-, Katzen-, und Fuchsflöhe miteinander. Wir können anhand der Mittelwerte schon Tendenzen in den Gruppen sehen.
| animal | Mittelwert | Standardabweichung | SE |
|---|---|---|---|
| dog | 8.13 | 2.14 | 0.81 |
| cat | 4.74 | 1.90 | 0.72 |
| fox | 9.16 | 1.10 | 0.42 |
Neben dem einfaktoriellen Datensatz wollen wir uns noch den häufigeren Fall mit zwei Faktoren anschauen. Wir haben also nicht nur die drei Floharten vorliegen und wollen wissen ob diese unterschiedlich weit springen. Darüber hinaus haben wir noch einen zweiten Faktor gewählt. Wir haben die Sprungweiten der Hunde-, Katzen- und Fuchsflöhe nämlich an zwei Messorten, der Stadt und dem Dorf, gemessen. Dadurch haben wir jetzt den Faktor animal und den Faktor site vorliegen. Wiederum fragen wir usn, ob sich die Sprungweite in [cm] der drei Floharten in den beiden Messorten unterscheidet. Im Folgenden lade ich einmal den Datensatz in das Objekt fac2_tbl.
R Code [zeigen / verbergen]
fac2_tbl <- read_xlsx("data/flea_dog_cat_fox_site.xlsx") |>
select(animal, site, jump_length) |>
filter(site %in% c("city", "village")) |>
mutate(animal = as_factor(animal),
site = as_factor(site))Betrachten wir als erstes einen Auszug aus der Datentabelle. Wir haben hier als Messwert oder Outcome \(y\) die Sprungweite jump_length vorliegen. Als ersten Faktor die Variable animal und als zweiten Faktor die Variable site festgelegt.
animal und einen zweiten Faktor mit site vorliegen haben.
| animal | site | jump_length |
|---|---|---|
| cat | city | 12.04 |
| cat | city | 11.98 |
| cat | city | 16.1 |
| … | … | … |
| fox | village | 16.96 |
| fox | village | 13.38 |
| fox | village | 18.38 |
Auch hier schauen wir uns einmal die deskritive Zusammenfassung der Daten an. Hier musst du natürlich beachten welchen Faktor du in welchem verschaltest hast. Klingt jetzt erstmal sperrig, aber es wird vermutlich am Beispiel klarer. Wir haben ja an jedem Messort alle drei Tierarten gemessen. Daher wollen wir natürlich für jeden Messort die Zusammenfassung der drei Tierarten haben. Du kannst das auch andersherum gruppieren, aber für mich macht es sorum mehr Sinn. Für die Berechnung des Standardfehlers nutzen wir die Funktion standard_error() aus dem R Paket {parameters}. Wie du siehst, sind die Mittelwerte unterschiedlich, was auf einen Unterschied zwischen den Floharten im Bezug auf die Sprungweite hindeutet.
| animal | site | Mittelwert | Standardabweichung | SE |
|---|---|---|---|---|
| cat | city | 13.58 | 1.88 | 0.59 |
| cat | village | 15.25 | 2.35 | 0.74 |
| dog | city | 16.68 | 2.26 | 0.71 |
| dog | village | 16.56 | 1.21 | 0.38 |
| fox | city | 20.12 | 1.15 | 0.37 |
| fox | village | 16.98 | 1.73 | 0.55 |
44.4 Modell
Beginnen wir mit der Frage, was ein Modell ist. Ein Modell beschreibt, wie du deine Daten auswerten willst. Zuerst einmal beschreibt es in der formula-Schreibweise, welche Spalten du aus deinem Datensatz auswerten willst. Du musst den Funktionen in R ja mitteilen welche Variablen du analysieren möchtest. In dem nachfolgenden Abschnitt schauen wir uns einmal den Messwert \(y\) näher an und entscheiden dann noch, ob wir in den Gruppen \(x\) eine Varianzhomogenität vorliegen haben oder eher eine Varianzheterogenität finden.
44.4.1 Faktorielle Analyse
Beginnen wir also mit der Festlegung welche Art der Analyse wir rechnen wollen. Wir schauen uns jetzt einmal das einfaktorielle sowie das zweifaktorielle Modell näher an. Du könntest auch mehr als zwei Faktoren auswerten wollen, aber dann musst du einmal in ein anderes Kapitel wechseln. Wir beginnen hier mit dem einfacheren Fall oder auch den häufigsten. Zurst einmal haben wir ein faktorielles Modell vorliegen. Hier einmal die generelle Form mit belieb vielen Faktoren \(f\).
\[ y \sim f_1 + f_2 + ... + f_p + f_1 \times f_2 + ... + f_1 \times f_2 \times f_3 \]
mit
- \(y\) gleich dem Messwert oder Outcome
- \(f_1 + f_2 + ... + f_p\) gleich experimenteller Faktoren
- \(f_1 \times f_2\) gleich einem beispielhaften Interaktionsterm erster Ordnung
- \(f_1 \times f_2 \times f_3\) gleich einem beispielhaften Interaktionsterm zweiter Ordnung
Zusätzlich können noch Interaktionsterme höherer Ordnungen entstehen, aber hier wird es extrem schwierig diese Interaktionsterme dann auch zu interpretieren. Wir werden uns aber in diesem Kapitel auf ein einfaktorielles sowie zweifaktorielles Modell beschränken. Wenn du theoretisch das zweifaktorielle Modell anwenden kannst, dann kannst auch mit mehr Faktoren einen Post-hoc Test rechnen.
Einfaktorielles Modell
Beginnen wir mit dem einfaktoriellen Modell (eng. one-way design). In einem einfaktoriellen Modell haben wir einen Messwert \(y\) sowie einen Faktor mit beliebig vielen Leveln vorliegen. Dabei beschreiben die Level dann die einzelnen Gruppen. In unserem Fall hier haben wir es mit multiplen Vergleichen zu tun, so dass der Faktor natürlich mehr als zwei Level hat.
\[ y \sim f_1 \]
mit
- \(y\) gleich dem Messwert oder Outcome, wie die Sprungweite in [cm] als
jump_length. - \(f_1\) gleich der Behandlung als Faktor mit mehr als zwei Gruppen, wie die Tierart als
animal.
Wir würden dann folgende Schreibweise in R in einem Modell nutzen.
R Code [zeigen / verbergen]
as.formula(jump_length ~ animal)jump_length ~ animalZweifaktorielles Modell
Weit aus häufiger kommt das zweifaktorielle Modell (eng. two-way design) in den Agarwissenschaften vor. Wir haben hier nicht nur den Behandlungsfaktor \(f_1\) sondern eben noch einen zweiten Faktor \(f_2\) vorliegen. Was der zweite Faktor beschreibt, kann von Fragestellung zu Fragestellung sehr unterschiedlich sein. Wenn wir zwei Faktoren vorliegen haben, dann können wir auch die Interaktion zwischen den beiden Faktoren modelliere. Damit wollen wir die Frage beantworten, ob sich jede Faktorkombination gleich verhält oder ob es Unterschiede bei gewissen Faktorkombination gibt. Vielleicht verhalten sich ja Fuchsflöhe in der Stadt ganz anders als im Dorf im Vergleich zu Hunde-, und Katzenflöhen.
\[ y \sim f_1 + f_2 + f_1 \times f_2 \]
mit
- \(y\) gleich dem Messwert oder Outcome, wie die Sprungweite in [cm] als
jump_length. - \(f_1\) gleich der Behandlung als ersten Faktor mit mehr als zwei Gruppen, wie die Tierart als
animal. - \(f_2\) gleich dem zweiten Faktor, wie der Messort als
site. - \(f_1 \times f_2\) gleich dem Interaktionsterm zwischen den beiden Faktoren Tierart und Messort.
Wir würden dann folgende Schreibweise in R in einem Modell nutzen.
R Code [zeigen / verbergen]
as.formula(jump_length ~ animal + site + animal:site)jump_length ~ animal + site + animal:siteMehrfaktorielles Modell
Am Ende können wir dann noch den Fall haben, dass wir noch mehr Faktoren \(z\) in unserem Modell berücksichtigen wollen. Hier wird es dann komplizierter. Wichtig ist hier, dass du meistens auch zwei Faktoren hast, die dich am meisten interessieren und deren Interaktion du berücksichtigen willst. Ich mehr Interaktionen du rechnen willst desto mehr Fallzahl brauchst du, so dass hier meisten nur eine oder zwei Interaktionen funktionieren.
\[ y \sim f_1 + f_2 + f_1 \times f_2 + z_1 + \cdots + z_p \]
mit
- \(y\) gleich dem Messwert oder Outcome, wie die Sprungweite in [cm] als
jump_length. - \(f_1\) gleich der Behandlung als ersten Faktor mit mehr als zwei Gruppen, wie die Tierart als
animal. - \(f_2\) gleich dem zweiten Faktor, wie der Messort als
site. - \(f_1 \times f_2\) gleich dem Interaktionsterm zwischen den beiden Faktoren Tierart und Messort.
- \(z_1 + \cdots + z_p\) als weitere experimentelle Faktoren der Umwelt, Zeit oder anderer Einwirkung auf den Messwert sowie einzelene Messungen von Beobachtungen.
Wir würden dann folgende Schreibweise in R in einem Modell nutzen. Hier habe ich noch beispielhaft die beiden Faktoren Jahreszeit season und Fütterungszustand feeding ergänzt.
R Code [zeigen / verbergen]
as.formula(jump_length ~ animal + site + animal:site + season + feeding)jump_length ~ animal + site + animal:site + season + feedingWenn du ein komplexes, mehrfaktorielles Modell auswerten willst, dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für gemischte Modelle in dem entsprechenden Kapitel zu linearen gemischten Modellen an.
Ein weitere Möglichkeit ist, dass du einfach über den Faktoren \(z_1 + \cdots + z_p\) mittelst. Du schaust dir also weiterhin nur die beiden Hauptfaktoren \(f_1\) und \(f_2\) an und mittelst für jede Faktorkombination von \(f_1\) und \(f_2\) die Werte für die anderen Faktoren \(z_1 + \cdots + z_p\). Hier verlierst du dann zwar einiges an Informationen, aber dies wird häufig für die einzelnen Pflanzenmessungen je Parzelle gemacht. Du mittelst alle Pflanzen in einer Parzelle und schaust dir die einzelnen Pflanzen als Faktor gar nicht an.
44.4.2 Der Messwert \(y\)
In diesem Kapitel rechne ich alles einmal mit einem normalverteilten Messwert \(y\) durch. Daher ist die Sprungweite jump_length normalverteilt und ich kann daher als Modell die Funktion aov() nutzen. Das Kapitel würde zu groß, wenn ich alle möglichen Verteilungen und deren Funktionen in R hier zeigen würde.
Bevor wir mit dem multiplen Vergleich anfangen können, müssen wir uns Fragen welcher Verteilungsfamilie eigentlich unser Messwert \(y\) folgt. Je nachdem was du misst, musst du eine andere Verteilung modellieren und dann auch eine andere Funktion in R dafür nutzen. Welche statistische Modellierung für das \(y\) soll ich für meinen Gruppenvergleich wählen? Ich habe in den jeweiligen Kapiteln zu den statistischen Modellen die jeweiligen Schritte für die Gruppenvergleiche hinterlegt und beschrieben. Daher kannst du in den Kapiteln einmal schauen, wie dein Messwert dort ausgewertet wird. Du findest dort auch immer ein Beispiel mit entsprechenden Daten. Ich konzentriere mich hier in diesem Kapitel auf einen normalverteilten Messwert \(y\) mit der Sprungweite in [cm].
Normalverteilte Messwerte \(\boldsymbol{y}\)
Beispiel: Frischgewicht, Trockengewicht, Chlorophyllgehalt, Pflanzenhöhe
| freshmatter | drymatter | chlorophyll | height |
|---|---|---|---|
| 8.23 | 1.21 | 45.88 | 24.19 |
| 2.61 | 0.87 | 43.91 | 18.51 |
| 4.81 | 0.34 | 37.44 | 21.74 |
Ich rechne in diesem Kapitel alles einmal auf einem normalverteilten Messwert \(y\) mit der Sprungweite der Floharten durch. Wenn du mehr Informationen zum modellieren brauchst, dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für normalverteilte Daten gerne einmal an. Das ist eigentlich der Standardfall und vieles in diesem Kapitel dreht sich um normalverteilte Daten.
Die Modellierung in R führen wir im Allgemeinen mit der Funktion lm() durch. Da wir hier meistens erst eine ANOVA gerechnet haben um dann des Post-hoc Test zu rechnen nutze ich direkt die Modellierung mit der Funktion aov().
R Code [zeigen / verbergen]
lm(freshmatter ~ ...)
aov(freshmatter ~ ...)Die genaue Anwendung der Funktionen auf Beispielen findest du dann in den unteren Abschnitten oder aber in dem Kapitel zur Gaussian linearen Regression. Dort gehe ich dann auch näher auf das Modell und der Güte der Modellanpassung ein.
“Soll ich’s wirklich machen oder lass ich’s lieber sein? Jein…” — Fettes Brot, Jein
Häufig kommt jetzt die Frage, ob mein Messwert \(y\) wirklich normalverteilt ist und ich nicht den Messwert auf Normalverteilung testen sollte. Die kurze Antwort lautet nein, da du meistens zu wenig Beobachtungen pro Gruppe vorliegen hast. Die etwas längere liefert Kozak & Piepho (2018) mit dem Artikel What’s normal anyway? Residual plots are more telling than significance tests when checking ANOVA assumptions.
Poissonverteilte Messwerte \(\boldsymbol{y}\) bzw. Zähldaten
Beispiel: Anzahl Insekten, gekeimte Pflanzen, Schädlinge
| Anzahl Blätter | Gekeimte Samen | Anzahl Schädlinge | Verzweigungen |
|---|---|---|---|
| 8 | 18 | 45 | 4 |
| 2 | 10 | 43 | 5 |
| 4 | 22 | 37 | 4 |
Wenn du mehr über die Modellierung von Zähldaten und deren Auswertung wissen willst, dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für Zähldaten an. Die Modellierung führen wir mit der Funktion glm() durch.
R Code [zeigen / verbergen]
glm(freshmatter ~ ..., family = poission)Die genaue Anwendung der Funktionen auf Beispielen findest du dann in dem Kapitel zur Poisson Regression. Dort gehe ich dann auch näher auf das Modell und der Güte der Modellanpassung ein. Bei Zähldaten gibt es die eine oder andere Besonderheit beim Modellieren.
Ordinalverteilte Messwerte \(\boldsymbol{y}\) bzw. Noten
Beispiel: Bonitur von Rasen, Holstrunk, Bonitur von Wurzelwachstum, Zufriedenheit
| Bonitur von Rasen | Holstrunk | Bonitur von Wurzelwachstum | Zufriedenheit |
|---|---|---|---|
| 8 | 1 | 5 | 6 |
| 8 | 2 | 4 | 6 |
| 1 | 7 | 7 | 9 |
Wenn du Noten vorliegen hast, dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für Boniturdaten an. Es sei den du bist an der mittleren Note pro Gruppe interessiert und willst die mittleren Noten miteinander vergleichen. Dann kannst du auch ein Modell unter der Annahme einer Normalverteilung mit heterogenen Varianzen rechnen. Die Modellierung führen wir mit der Funktion clm() durch.
R Code [zeigen / verbergen]
clm(freshmatter ~ ...)Die genaue Anwendung der Funktionen auf Beispielen findest du in dem Kapitel zur Multinomiale / Ordinale Regression. Dort gehe ich dann auch näher auf das Modell und der Güte der Modellanpassung ein.
Binomialverteilte Messwerte \(\boldsymbol{y}\) bzw. Anteile
Beispiel: Infektionsstatus, Verstorben, Zielgewicht erreicht, Gekeimt
| Infektionsstatus | Verstorben | Zielgewicht erreicht | Gekeimt |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
Wenn du nur einen Messwert mit der Ausprägung \(0/1\) oder \(ja/nein\) vorliegen hast, dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für Anteile an. Die Modellierung führen wir mit der Funktion glm() durch.
R Code [zeigen / verbergen]
glm(freshmatter ~ ..., family = binomial)Die genaue Anwendung der Funktionen auf Beispielen findest du dann in den unteren Abschnitten oder aber in dem Kapitel zur Logistische Regression. Dort gehe ich dann auch näher auf das Modell und der Güte der Modellanpassung ein.
Betaverteilte Messwerte \(\boldsymbol{y}\) bzw. Wahrscheinlichkeiten
Beispiel: Anteil infizierte Pflanzen, Jagderfolg, Auftreten Spezies, Erfolg/Misserfolg einer Anwendung
| Anteil infizierte Pflanzen | Jagderfolg | Auftreten Spezies | Erfolg/Misserfolg einer Anwendung |
|---|---|---|---|
| 0.34 | 0.22 | 0.19 | 0.67 |
| 0.29 | 0.78 | 0.11 | 0.71 |
| 0.31 | 0.77 | 0.27 | 0.82 |
Wenn du Prozente oder die Wahrscheinlichkeit für das Eintreten eines Ereignisses oder aber die Rate eines Erfolges an Misserfolgen gemessen hast, dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für Wahrscheinlichkeiten an. Die Modellierung führen wir mit der Funktion betareg() durch.
R Code [zeigen / verbergen]
betareg(freshmatter ~ ...)Die genaue Anwendung der Funktionen auf Beispielen findest du in dem Kapitel zur Beta Regression. Dort gehe ich dann auch näher auf das Modell und der Güte der Modellanpassung ein. Insbesondere hier gibt es dann einige unschöne Limitierungen wenn du zu nah an der Grenze von \([0,1]\) bist.
44.4.3 Die Faktoren \(f\)
Neben dem Messwert \(y\) müssen wir natürlich auch die Faktoren \(f\) mit dem ersten Faktor \(f_1\) und dem zweiten Faktor \(f_2\) berücksichtigen. Meistens haben wir hier aber einen Hauptfaktor mit den Behandlungsgruppen und dann noch einen zweiten Faktor der uns nicht so ganz interessiert. Das hängt aber von der Fragestellung ab, es kann auch zwei Hauptfaktoren geben. Im Folgenden betrachten wir jedenfalls jeden Faktor getrennt. Wir schauen jetzt einmal, ob sich die Fallzahlen in den Gruppen unterscheiden, wie wir mit der Varianz in den Gruppen umgehen und was schlussendlich als Fehlerbalken dargestellt werden soll.
Balanciert oder unbalanciert
Eine der ersten Fragen an die Gruppen ist, ob wir ein balanciertes Desgin vorliegen haben oder ein unbalanciertes Design. Im Falle eines balancierten Design sind die Fallzahlen in jeder Behandlungsgruppe gleich groß. Du solltest dein Experiment immer so planen, dass die Gruppen immer gleich groß sind. Das macht vieles einfacher. Manachmal kann es passieren, dass du eine Beobachtung verlierst oder aber eine Messung nicht klappt. Dann hast du ein unbalanciertes Design vorliegen. In einem unbalancierten Design ist die Fallzahl in allen Gruppe nicht gleich groß.
- Balanciertes Design
-
Alle Behandlungsgruppen \(1, 2, ..., p\) haben die gleiche Fallzahl \(n_g\) in den Behandlungsgruppen.
- Unbalanciertes Design
-
Die Behandlungsgruppen \(1, 2, ..., p\) haben unterschiedliche Fallzahlen \(n_1, n_2, ..., n_p\) in den Behandlungsgruppen.
Um es gleich vorwegzunehmen das R Paket {emmeans} wurde extra dafür gebaut mit balancierten und im Besonderen mit unbalancierten Daten umzugehen. Eine ANOVA kann prinzipiell auch mit unbalancierten Daten umgehen. Beim Tukey HSD Test und anderen älteren Implementierungen eines Post-hoc Test wird es dann schwieriger.
Wenn du unbedingt balancierte Daten ohne fehlende Werte brauchst, dann kannst du die fehlenden Werte in einer Gruppe durch den Mittelwert der jeweiligen Gruppe ersetzen. Das hat dann nicht so starke Auswirkungen, aber überfährt auch einen statistischen Engel.
Varianzhomogenität und Varianzheterogenität
Kommen wir nun zur Varianzhomogenität oder Varianzhterogenität in den Gruppen des Behandlunsgfaktors. Wir betrachten also meistens nur den wichtigen Faktor \(f_1\) und ignorieren ein wenig den zweiten Faktor. Prinzipiell kannst du natürlich auch den zweiten Faktor anschauen, aber dann werden es immer mehr Gruppen und Faktorkombinationen. Am Ende kommt dann sowieso heraus, dass über alle Gruppen hinweg keine homogenen Varianzen vorliegen. Wenn du mehr lesen willst so gibt es auf der Seite DSFAIR noch einen Artikel zu {emmeans} und der Frage Why are the StdErr all the same?
- Wann liegt vermutlich Varianzheterogenität in deinen experimentellen Faktoren \(f\) vor?
-
Es gibt so ein paar Daumenregeln, die dir helfen abzuschätzen, ob in deinen Gruppen Varianzheterogenität vorliegt. Um es kurz zu machen, vermutlich hast du mindestens leichte Varianzhterogenität in den Daten vorliegen.
- Du hat viele Behandlungsgruppen. Je mehr Gruppen du hast oder eben dann auch Faktorkombinationen, die du testen möchtest, desto wahrscheinlicher wird es, dass mindestens eine Gruppe eine unterschiedliche Varianz hat. Du hast Varianzheterogenität vorliegen.
- Du misst deine Gruppen über die Zeit. Je größer, schwerer oder allgemein höher ein Messwert wird, desto größer wird auch die Varianz. Schaust du dir deine Messwerte über die Zeit an hast du meistens Varianzheterogenität vorliegen.
- Deine Kontrolle ohne Behandlung verhält sich meistens nicht so, wie die Gruppen, die eine Behandlung erhalten haben. Wenn du nichts machst in deiner negativen Kontrolle, dann hast du meistens eine andere Streuung der Messwerte als unter einer Behandlung.
- Diene Behandlungen sind stark unterschiedlich. Wenn deine Behandlungen sich biologisch oder chemisch in der Wirkung unterscheiden, denn werden vermutlich deine Messwerte auch anders streuen. Hier spielt auch die Anwendung der Behandlung und deren Bereitstellung eine Rolle. Wenn was nicht gleich ist, dann wird es vermutlich nicht gleiche Messwerte erzeugen.
- Du hast wenig Fallzahl pro Gruppe oder Faktorkombination. Wenn du wenig Fallzahl in einer Gruppe hast, dann reicht schon eine (zufällige) Messabweichung und schon sind deine Varianzen heterogen.
Gut, jetzt wissen wir, dass du vermutlich Varianzheterogenität in deinen Daten vorliegen hast. Erstmal ist das kein so großes Problem.
- Tut Varianzheterogenität anstatt Varianzhomogenität weh?
-
Nein. Meistens ist die Varianzheterogenität nicht so ausgeprägt, dass du nicht auch eine ANOVA rechnen kannst. Über alle Gruppen hinweg wird dann zwar in einer ANOVA die Varianz gemittelt und es kann dann zu weniger signifikanten Ergebnissen führen, aber so schlimm ist es nicht. Im Post-hoc Test solltest du aber die Varianzheterogenität berücksichtigen, da du ja immer nur zwei Gruppen gleichzeitig betrachtest.
Wie immer kannst du alles natürlich auch statistisch Testen. Das ist dann bei der Varianzhomogenität nicht anders. Mehr dazu dann im Kapitel zum Pre-Test oder Vortest. Hier konzentriere ich mich auf die visuelle Überprüfung, die meistens in einem Setting mit niedriger Fallzahl in den Gruppen vollkommen ausreicht. Die Tests liefern meist eine falsche numerische Sicherheit, die so nicht stimmt.
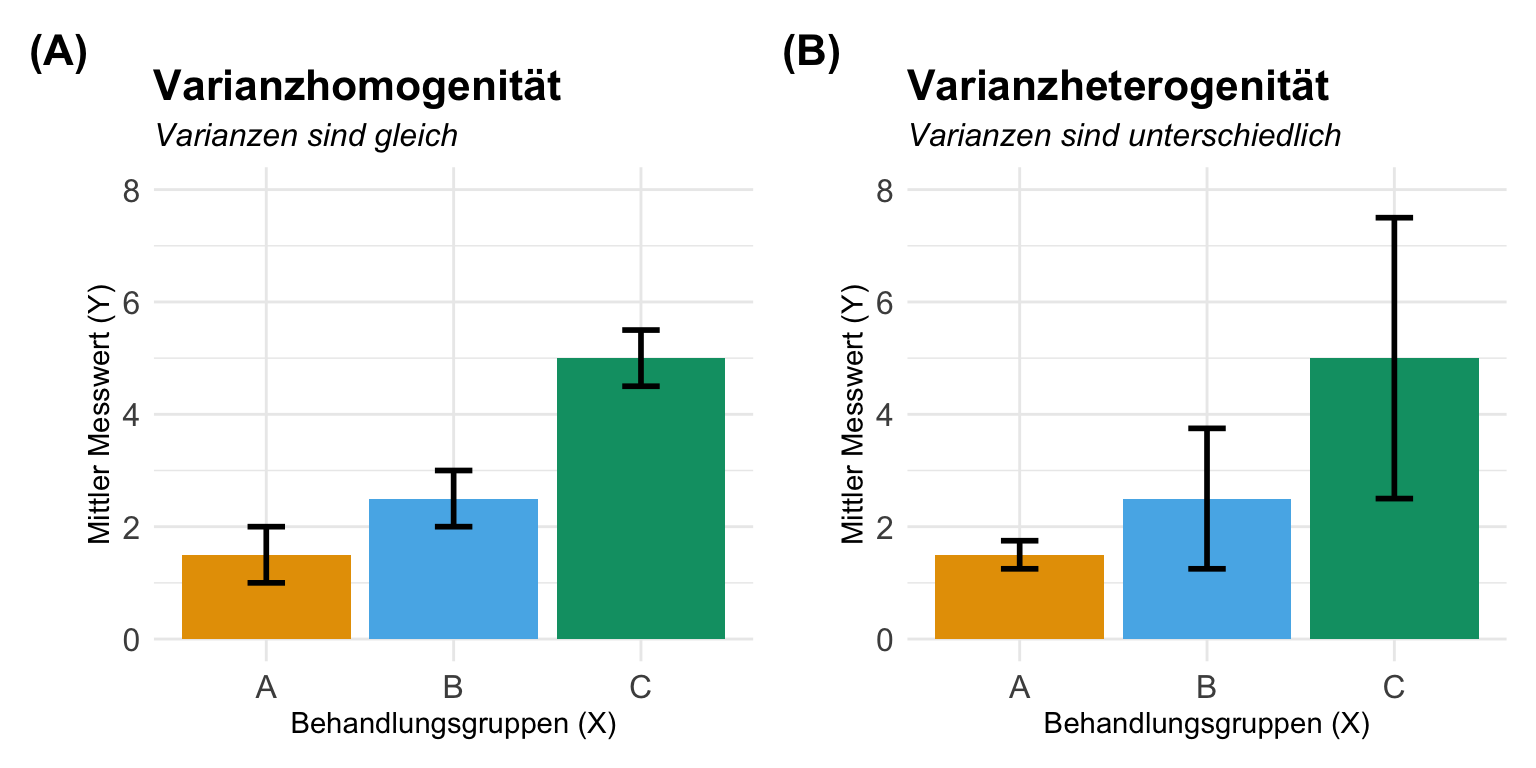
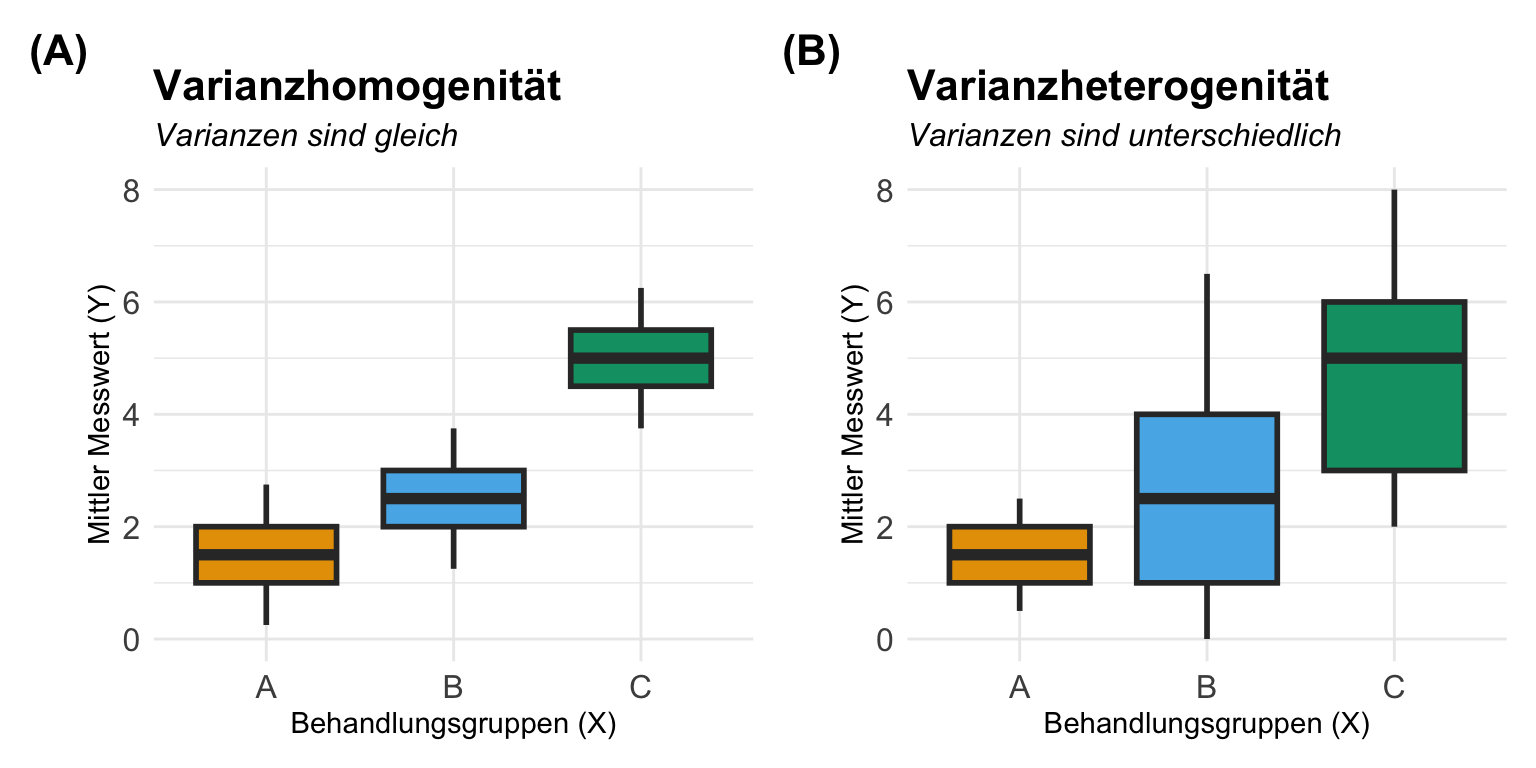
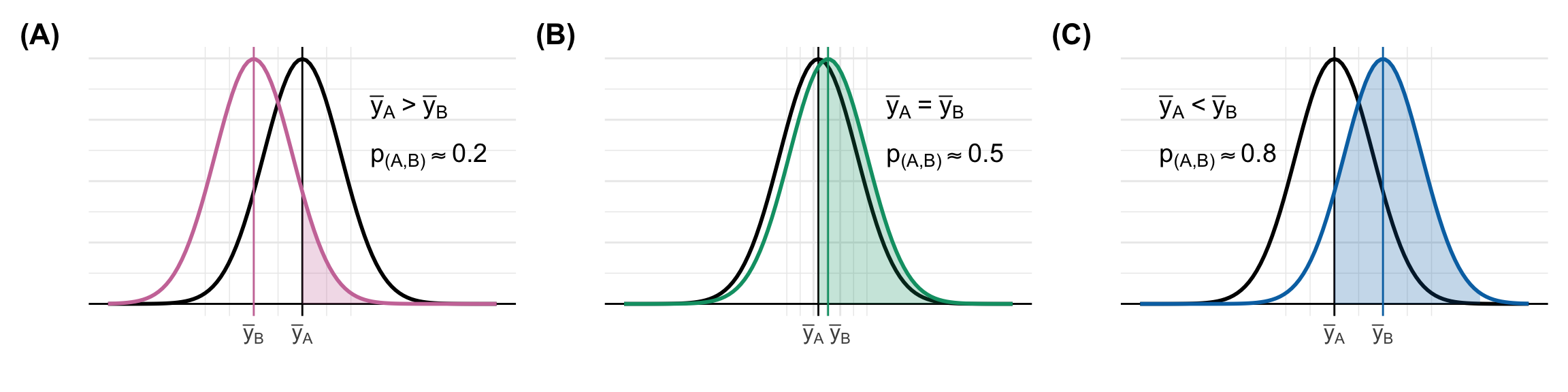
Hier einmal die theoretischen Abbilungen von drei Gruppen mit Varianzhomogenität und Varianzheterogenität. Hier wird schnell klar, dass du mit mehr Behandlungsgruppen kaum die Annahme für Varianzhomogenität aufrecht erhalten kannst. Insbesondere Kontrollen oder Standardbehandlungen haben große oder kleinere Varianzen als der Rest der Behandlungen. Manchaml hat man aber Glück und die Varianzen sind eher homogen.
Wir bauen wir usn jetzt die Barplots oder Säulendiagramme? Entweder direkt aus {ememans}, wie ich dir das weiter unten zum Compact letter display zeige oder eben als Wiederholung des Kapitels zur Visualisierung von Daten. Wir bauen uns also einmal den einfaktoriellen Barplot wie auch den zweifaktoriellen Barplot.
44.4.4 Einfaktorieller Barplot
Für den einfaktoriellen Barplot brauchen wir einmal den Mittelwert und die Standardabweichung der einzelne Floharten.
R Code [zeigen / verbergen]
stat_fac1_tbl <- fac1_tbl |>
group_by(animal) |>
summarise(mean = mean(jump_length),
sd = sd(jump_length))
stat_fac1_tbl# A tibble: 3 × 3
animal mean sd
<fct> <dbl> <dbl>
1 dog 8.13 2.14
2 cat 4.74 1.90
3 fox 9.16 1.10Dann können wir uns auch schon den Barplot mit {ggplot} erstellen. Später willst du dann noch das Compact letter display über den Balken als Mittelwerte ergänzen.
R Code [zeigen / verbergen]
ggplot(data = stat_fac1_tbl,
aes(x = animal, y = mean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2) +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() 44.4.5 Zweifaktorieller Barplot
Für den zweifaktoriellen Barplot brauchen wir einmal den Mittelwert und die Standardabweichung der einzelne Floharten getrennt für die beiden Messorte. Das geht natürlich auch umgedreht, also die Messorte für die Floharten. Das kommt dann auf deine Fragestellung an.
R Code [zeigen / verbergen]
stat_fac2_tbl <- fac2_tbl |>
group_by(animal, site) |>
summarise(mean = mean(jump_length),
sd = sd(jump_length))
stat_fac2_tbl# A tibble: 6 × 4
# Groups: animal [3]
animal site mean sd
<fct> <fct> <dbl> <dbl>
1 cat city 13.6 1.88
2 cat village 15.2 2.35
3 dog city 16.7 2.26
4 dog village 16.6 1.21
5 fox city 20.1 1.15
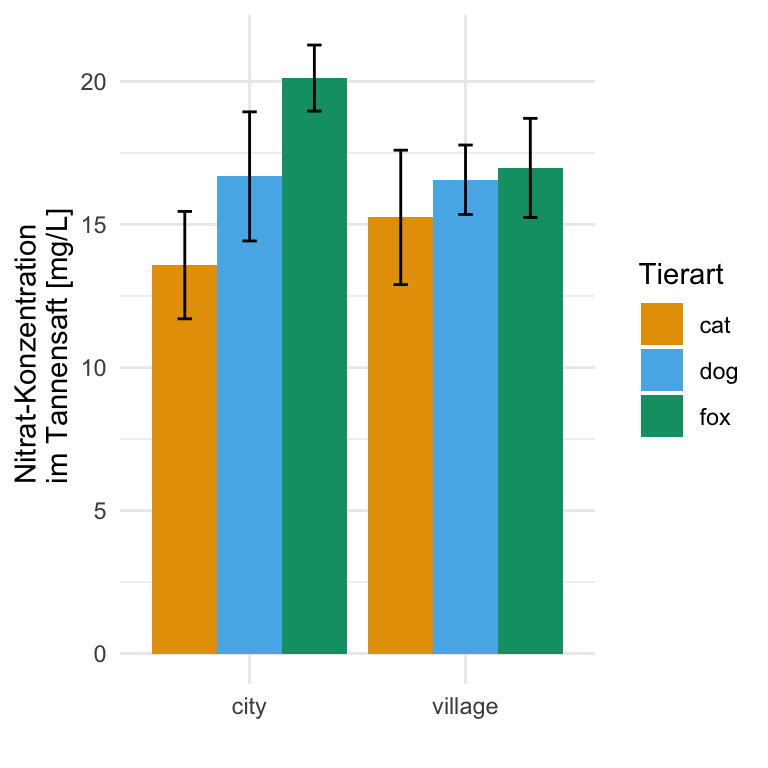
6 fox village 17.0 1.73Und dann können wir auch schon den zweifaktoriellen Barplot in {ggplot} erstellen. Du musst schauen, was du auf die x-Achse legst und was du dann auf die Legende und daher mit fill gruppierst. Damit die Positionen passen, spiele ich hier noch mit der Funktion position_dodge() rum.
R Code [zeigen / verbergen]
ggplot(data = stat_fac2_tbl,
aes(x = site, y = mean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity", width = 0.9,
position = position_dodge(0.9)) +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2,
position = position_dodge(0.9)) +
labs(x = "Flohart", y = "Sprungweite in [cm]", fill = "Tierart") +
scale_fill_okabeito() 44.4.6 Einfaktorieller Boxplot
Das praktische bei den Boxplots ist, dass wir hier nichts mehr vorrechnen müssen, sondern direkt die Boxplots in {ggplot} erstellen können. Ich finde man sieht immer in einem Boxplot besser, ob die Streuung um den Median eher homogen oder eher heterogen ist. Gerne ergänze ich noch den Mittelwert mit der Funktion stat_summary().
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = animal, y = jump_length, fill = animal)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point",
shape=23, size = 5, fill = "gray50") +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() 44.4.7 Zweifaktorieller Boxplot
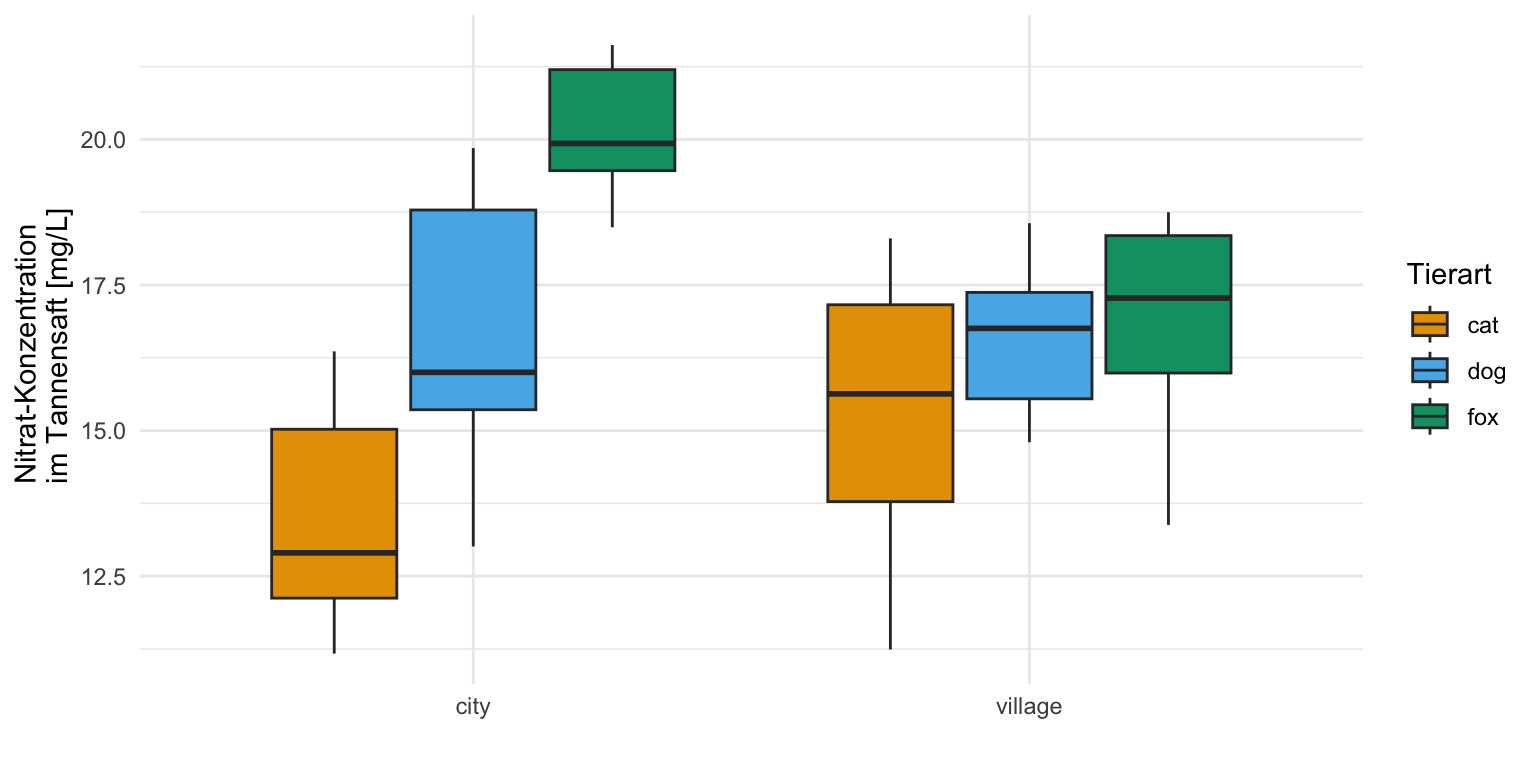
Den zweifaktoriellen Boxplot erstellen wir für die einzelnen Floharten getrennt für die beiden Messorte. Du musst schauen, was du auf die x-Achse legst und was du dann auf die Legende und daher mit fill gruppierst. Gerne ergänze ich noch den Mittelwert mit der Funktion stat_summary(), muss hier aber schauen, dass ich nach dem Faktor animal gruppiere und dann noch mit der Funktion position_dodge() die richtige Position finde.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = site, y = jump_length, fill = animal)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point", aes(group = animal),
shape=23, size = 5, fill = "gray50",
position = position_dodge(0.75)) +
labs(x = "Flohart", y = "Sprungweite in [cm]", fill = "Tierart") +
scale_fill_okabeito() Dann habe ich mich doch noch hingesetzt und einmal für dich die Videos gemacht, wie du dann einen Barplot oder eben ein Säulendigramm in Excel erstellst. Daran kannst du natürlich auch überprüfen, ob die Varianzen homogen sind oder nicht. Das ganze macht dann nur als Video Sinn, denn sonst kannst du ja nicht nachvollziehen, was ich geklickt habe.
Hier also erstmal die einfachere Variante mit dem einfaktoriellen Barplot. Beginnen wollen wir wie immer mit der Berechnung der Mittelwerte und der Standardabweichung. Bitte nutze für die Standardabweichung die Funktion STABW.S() in Excel.
Und im Anschluss nochmal das Video für den zweifaktoriellen Barplot. Du hast jetzt eben nicht nur eine Behandlungsgruppe vorliegen sondern zwei Behandlungsgruppen. Dann musst du etwas mehr Arbeit reinstecken um alle Mittelwerte und Standardabweichungen zu berechnen. Bitte nutze auch hier für die Standardabweichung die Funktion STABW.S() in Excel.
Standardfehler oder Standardabweichung
Wenn wir uns jetzt entschieden haben, wie wir die Varianz modellieren wollen, stellt sich häufig die Frage, was wollen wir denn eigentlich in den Säulendiagrammen darstellen. Wie du in dem vorherigen Abschnitt ja schon gesehen hast, zeige ich nicht die Mittelwerte und die Varianz sondern eben die Mittelwerte und die Standardabweichung als Fehlerbalken. Dies ist auch die übliche Darstellung, wenn wir uns einen Barplot anschauen. Ein Barplot stellt den Mittelwert und die Standardabweichung als Fehlerbalken dar. Neben dem der Standardabweichung könntest du auch den Standardfehler als Fehlerbalken wählen. Hier nochmal die Formel für den Standardfehler und die Umstellung nach der Standardabweichung.
\[ SE = \cfrac{s}{\sqrt{n_g}};\; s = SE \cdot \sqrt{n_g} \]
mit
- \(SE\), dem Standardfehler der jeweiligen Gruppe.
- \(s\), der Standardabweichung der jeweiligen Gruppe.
- \(n_g\), der jeweiligen Gruppengröße.
Zu den Fehlerbalken liefert die Publikation Error bars in experimental biology von Cumming et al. (2007) nochmal einen Überblick über Fehlerbalken und welche Fehlerbalken man den nun nutzen sollte. Ich gebe hier nochmal eine kurze Übersicht.
- Der Standardfehler
-
Statistische Tests nutzen den Standardfehler um eine Aussage über die Signifikanz zu treffen. Der Standardfehler bleibt immer im Wertebereich des Messwertes.
- Die Standardabweichung
-
Barplots oder Säulendiagramme nutzen die Standardabweichung als Fehlerbalken um eine Aussage über die Streuung um den Mittelwert zu treffen. In bestimmten Fällen macht es Sinn dennoch den Standardfehler als Fehlerbalken zu nutzen, wenn dein Messwert im Wertebereich, wie eine Boniturnote, begrenzt ist.
Am Ende gibt dazu dann auch eine passend die Publikation von Kozak & Piepho (2020) mit dem Titel Analyzing designed experiments: Should we report standard deviations or standard errors of the mean or standard errors of the difference or what?
44.5 Der effektive Pfad mit {emmeans}
Das tolle an {emmeans} ist die Flexibilität. Du kannst sehr einfach viele Methoden in {emmeans} abdecken. Wenn du die Option für die Adjustierung auf tukey stellst, dann rechnest du faktisch einen besseren Tukey HSD Test. Wenn du dann noch in {emmeans} die Option mit der Varianzheterogenität wählst, rechnest du einen besseren Games Howell Test. Mehr dazu dann am Ende des Abschnitts, wie du die Ergebnisse präsentierst, da musst du dann gar nicht so viel schreiben.
Wenn du ein zweifaktorielles Design mit etwas wenig Fallzahl pro Gruppe vorliegen hast, dann ist {emmeans} die Antwort auf deine Herausforderungen. Darüber hinaus können wir auch sehr einfach Varianzheterogenität modellieren, die Adjustierung für multiple Vergleiche an und ausschalten sowie direkt das Compact letter display erhalten. Das Paket {emmeans} ist damit die effiktive Lösung für einen Gruppenvergleich in den Agarwissenschaften und darüber hinaus. Schauen wir uns also im Folgenden einmal das Paket näher an. Ich verzichte hier auf eine tiefere händische Berechnung sondern konzentriere mich auf die Anwendung der häufigsten Analysefälle.
Ich kann in diesem Abschnitt hier nicht alles erklären und im Detail durchgehen was {emmeans} alles kann. Hier gibt es noch ein Tutorium zu {emmeans} mit dem Titel Getting started with emmeans. Daneben gibt es auch noch die Einführung mit Theorie auf der Seite des R Paktes oder aber auch der Starter unter Quick start guide for emmeans. Wenn du eine allgemeine Übersicht der Themen in {emmeans} brauchst dann hilft dir der Index of vignette topics – emmeans package, Version 1.10.6. Beginnen wir aber wie immer mit den drängensten Fragen. Wie sieht es mit der Varianz, der Adjustierung und der möglichen Vergleiche sowie der Fallzahl in den einzelnen Behandlungsgruppen aus?
- Varianzhomogenität oder Varianzheterogenität
-
Wir können in
{emmeans}eine mögliche Varianzheterogenität modellieren, wenn wir das nicht tun, dann rechnet{emmeans}immer unter der Annahme von Varianzhomogenität. Wenn du nicht für die Varianzheterogenität adjustieren möchtest, dann rechnest du faktisch einen Tukey HSD Test, wenn die Fallzahl in den Gruppen gleich ist. Der Tukey HSD Test rechnet immer mit Varianzhomogenität. In allen Beispielen hier, werde ich aber für Varianzheterogenität adjustieren. Dazu nutze ich dann die Optionvcov. = sandwich::vcovHACimemmeans()Funktionsaufruf. In dem R Paket{sandwich}gibt es eine riesige Anzahl an möglichen Funktionen um für Varianzheterogenität zu adjustieren. Wir nutzen hier die AdjustierungvcovHAC, die in vielen Fällen vollkommen ausreichend ist. - Adjustierung für multiple Vergleiche
-
Das Paket
{emmeans}kann sehr einfach für die Adjustierung von multiplen Vergleichen angepasst werden um adjustierte p-Werte zu erhalten. In der Standardeinstellung nutzt{emmeans}die Quartile aus einem Tukey HSD Test und somit ist{emmeans}gar nicht so weit weg von dem Tukey HSD Test. Ich stelle aber meistens die Adjustierung auf Bonferroni mit der Optionadjust = "bonferroni", da diese Adjustierung etwas eingängiger ist. Das bleibt aber dir überlassen, ob du überhaupt eine Adustierung wählen willst. Mit der Optionadjust = "none"stellst du die Adjustierung für multiple Vergleiche aus. Du erhälst die rohen p-Werte, die manchmal auch nützlich sind. - Mögliche multiple Vergleiche
-
In den folgenden Beispielen rechne ich immer einen
all-pairVergleich. Ich werde also alle Gruppen mit allen anderen Gruppen vergleichen. Ob das jetzt wirklich immer Sinn macht sei dahingestellt. Du kannst abr auch alle Gruppen nur zu eienr Kontrolle vergleichen. Dann müssen wir die Funktioncontrast()anders aufbauen. Wir nutzen dann die Optionmethodsowierefum mitzuteilen welche Behandlungsgruppe die Kontrolle ist. Wir erhalten dann folgenden Funktionsaufrufcontrast(method = "trt.vs.ctrl", ref = "fox"). Die Hilfeseite contrast-methods gibt dir nochmal eine Übersicht was alles in{emmeans}möglich ist. Welche Kontrast dann neben demall-pairnoch passend ist hängt dann sehr von deiner Fragestellung ab. Hier kann ich dann keine allgemeine Aussage zu treffen. - Fallzahl in den einzelnen Behandlungsgruppen
-
Die Stärke von
{emmeans}ist, dass du dir keine Gedanken machen musst, wie die Fallzahlen in deinen einzelnen Behandlungsgruppen sind. Im Idealfall sind die Fallzahlen balanciert, also die hast in jeder Gruppe die gleiche Anzahl an Beobachtungen. Machmal klappt das aber nicht in einem Experiment und dir fehlen irgendow Beobachtungen, dann rechnet dir{emmeans}aber dennoch richtige statistische Maßzahlen aus. Das ist eine wunderbare Eigenschaft von{emmeans}. Wenn alles balanciert ist, dann ist alles super. Wenn du aber unbalancierte Daten hast, musst du dich nicht drum kümmern.
Die Stärke der Berücksichtigung von unbalancierten Gruppengrößen kommt von der Berechngn der marginal effects. Deshalb heißt das Paket ja auch {emmeans} für Estimated Marginal Means. Wenn du dich jetzt fragst, was sind denn diese marginal means dann gibt es darauf hier und jetzt keine kurze Antwort. Dafür verweise ich auf Heiss (2022) und das Onlinetutorium Marginalia: A guide to figuring out what the heck marginal effects, marginal slopes, average marginal effects, marginal effects at the mean, and all these other marginal things are. Heiss erklärt dort sehr schön die Zusammenhänge. Dazu dann noch der Verweis auf die Webseite Model to Meaning von Arel-Bundock et al. (2024) um nochmal tiefer in das Modellieren von Daten einzusteigen.
Wichtig ist aber, du musst marginal effects oder das Konzept dahinter nicht verstanden haben um das R Paket {emmeans} sinnvoll nutzen zu können. Ja, damit überfahren wir wieder einen statistischen Engel, aber so ist es manchmal, wenn wir hier Sachen auf die Straße bringen wollen. Also fangen wir hier jetzt einmal an die einfaktorielle und zweifaktorielle Analyse in {emmeans} zu rechnen und zu interpretieren.
Einfaktorielle Analyse
Beginnen wir mit der einfaktorielle Analyse in dem wir erstmal ein ANOVA Modell rechnen. Wir nehmen hier die Sprungweite in [cm] als unseren Messwert \(y\) und dann die Tierrasse \(f_1\) als Faktor in das Modell. Hier brauchen wir das ANOVA Modell nur zur Berechnung unserer statistischen Maßzahlen. Wir könnten die Interpreation also auch weglassen.
R Code [zeigen / verbergen]
fac1_aov <- aov(jump_length ~ animal, data = fac1_tbl)Ich nutze jetzt das ANOVA Modell gleich für den Aufruf der emmeans() Funktion, die uns die Mittelwerte und die Varianzen in den Gruppen berechnet. Ich wähle hier die Adjustierung für die Varianzheterogenität mit der Option vcov. als Standard. Eiegntlich rechne ich immer unter der Annahme der Varianzheterogenität, da ich nicht viel verliere aber viel falsch machen kann, wenn ich die Heterogenität nicht berücksichtige.
R Code [zeigen / verbergen]
emm_fac1_obj <- fac1_aov |>
emmeans(~ animal, vcov. = sandwich::vcovHAC)
emm_fac1_obj animal emmean SE df lower.CL upper.CL
dog 8.13 0.427 18 7.23 9.03
cat 4.74 0.810 18 3.04 6.44
fox 9.16 0.468 18 8.17 10.14
Confidence level used: 0.95 Wir erhalten also unser {emmeans} Objekt für unsere einfaktorielle Analyse. Darin ist eigentlich alles enthalten was wir jetzt brauchen. Die Mittelwerte der Gruppen sind da und auch die entsprechende Standardfehler der Gruppen. Wenn du die Standardabweichung zurückrechnen willst, dann musst du \(SE \cdot \sqrt{n_g}\) rechnen mit der Gruppengröße \(n_g =7\) in unserem Fall. Denn nun ist ja die Frage, was willst du haben? Ich zeige dir in den folgenden Tabs einmal wie du die p-Werte, das Comapct letter display und die 95% Konfidenzintervalle berechnest.
Beginnen wir mit den p-Werten, die jeder braucht. Wir können das emm_fac1_obj Objekt von oben jetzt einfach in die Funktion {contrast} stecken und dann definieren welche Vergleiche gerechnet werden sollen. In den agrarwissenschaftlichen Fächern ist des dann meist ein all-pair Vergleich. Wir vergleichen alles mit allem. Am Ende wähle ich onch die Adjustierung für multiple Vergleiche nach Bonferroni.
R Code [zeigen / verbergen]
emm_contrast_fac1_obj <- emm_fac1_obj |>
contrast(method = "pairwise", adjust = "bonferroni")
emm_contrast_fac1_obj contrast estimate SE df t.ratio p.value
dog - cat 3.39 0.904 18 3.744 0.0045
dog - fox -1.03 0.635 18 -1.620 0.3678
cat - fox -4.41 0.997 18 -4.425 0.0010
P value adjustment: bonferroni method for 3 tests Wir sehen, dass wir die Vergleiche für die einzelnen Floharten für die Sprunglänge erhalten. Der estimate ist der Effekt und damit die Differenz der Mittelwerte für die Sprungweite in [cm] für den jeweiligen Verleiche. Dann sehen wir in der Spalte SE noch, dass wir richtig für Varianzhterogenität adjustiert haben, da der Vergleich dog - cat nur \(2/3\) der Varianz der beiden anderen Vergleiche zeigt. Wir sehen dann am Ende, dass die Vergleiche dog - cat und cat - fox signifikant unterschiedlich sind. Die p-Werte liegen unter dem Signifikanzniveau von 5%.
Jetzt ist es manchmal so, dass du die Mittelwerte, die Differenz der Mittelwerte und die p-Werte haben möchtest. Das kannst du ganz einfach durch die Funktion pwpm() erreichen. Hier gibt es dann natürlich nur die paarweisen Vergleiche.
R Code [zeigen / verbergen]
emm_contrast_fac1_obj |>
pwpm(adjust = "bonferroni") dog - cat dog - fox cat - fox
dog - cat [ 3.39] 0.0010 0.0012
dog - fox 4.41 [-1.03] 0.0045
cat - fox 7.80 3.39 [-4.41]
Row and column labels: contrast
Upper triangle: P values adjust = "bonferroni"
Diagonal: [Estimates] (estimate)
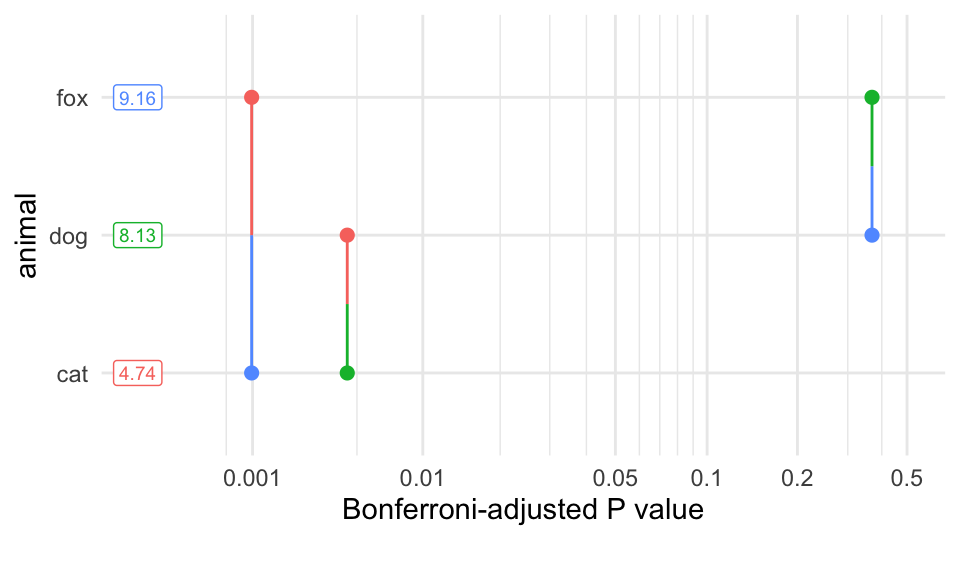
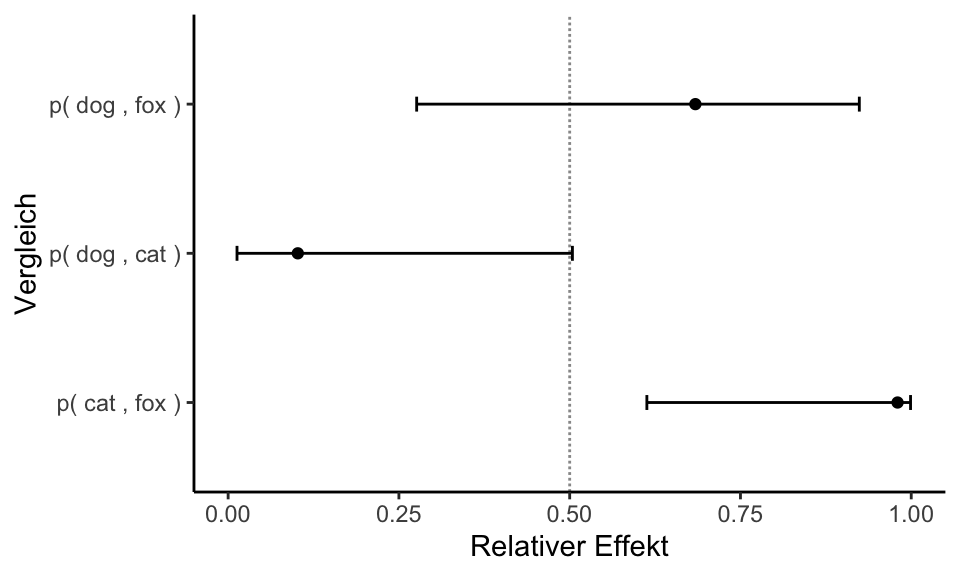
Lower triangle: Comparisons (estimate) earlier vs. laterAm Ende gibt es in {emmeans} noch den paarweisen p-Wert Plot, der die p-Werte einmal auf der x-Achse visualisiert. Da siehst du dann nochmal die Ordnung der Signifikanz über die gesamten Vergleiche. Die Abbildung finde ich persönlich manchmal interessant und manchmal wenig aussagekräftig. Kommt immer auf den Fall an.
Nachdem wir in dem vorherigen Tab die p-Werte berechnet haben, könen wir jetzt einmal das Compact letter display erstellen. Hier hat das R Paket {emmeans} eine eigene Funktion mit cld(). Die Funktion nimmt das Objekt emm_fac1_obj und berechnet darauf das nach Bonferroni adjustierte Compact letter display.
R Code [zeigen / verbergen]
emm_cld_fac1_obj <- emm_fac1_obj |>
cld(Letters = letters, adjust = "bonferroni")
emm_cld_fac1_obj animal emmean SE df lower.CL upper.CL .group
cat 4.74 0.810 18 2.61 6.88 a
dog 8.13 0.427 18 7.00 9.25 b
fox 9.16 0.468 18 7.92 10.39 b
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 3 estimates
P value adjustment: bonferroni method for 3 tests
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
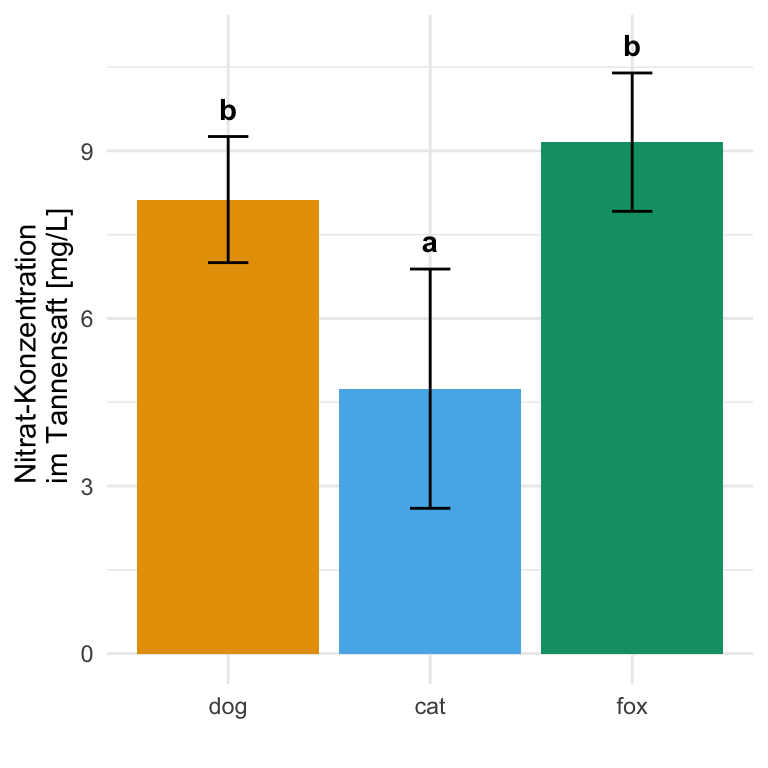
But we also did not show them to be the same. Der größte Vorteil von {emmeans} ist jetzt, dass wir die Ausgabe des Compact letter displays direkt nutzen können um unseren Barplot zu zeichnen. Wir müssen nur einmal die Werte der Standardfehler mit der Wurzel der Gruppenfallzahl multiplizieren um auf die Standardabweichung zu kommen. Wenn du möchtest, kannst du auch den Standardfehler als Fehlerbalken nutzen, musst es nur Angeben. Da wir hier sieben Flöhe je Tierart gemessen haben, multiplizieren wir den Standardfehler mit der Wurzel von 7 um auf die Standardabweichung zu kommen. Dann entferne ich noch die Leerzeichen in der Spalte .group mit der Funktion str_trim() und ich kann den Barplot erstellen.
R Code [zeigen / verbergen]
emm_cld_fac1_obj |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(7)) |>
ggplot(aes(x = animal, y = emmean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2) +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 0.5),
fontface = 2)Am Ende können wir dann auch aus den paarweisen Vergleichen die 95% Konfidenzintervalle berechnen. Hier nutzen wir dann die Funktion tidy() aus dem Paket {broom} um uns die 95% Konfidenzintervalle sauber wiedergeben zu lassen. Du kannst noch die Kontraste auf revpairwise stellen, wenn die Vergleiche umdrehen willst.
R Code [zeigen / verbergen]
emm_ci_fac1_obj <- emm_fac1_obj |>
contrast(method = "pairwise", adjust = "bonferroni") |>
tidy(conf.int = TRUE) |>
select(contrast, estimate, adj.p.value, conf.low, conf.high)
emm_ci_fac1_obj# A tibble: 3 × 5
contrast estimate adj.p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl>
1 dog - cat 3.39 0.00446 0.999 5.77
2 dog - fox -1.03 0.368 -2.70 0.647
3 cat - fox -4.41 0.000980 -7.05 -1.78 Die Stärke eines 95% Konfidenzintervalls ist ja die Signifikanz mit der Relevanz zu verbinden. Daher setze ich jetzt mal die Relevanzschwelle relevance_lvl auf \(>0.75cm\). Wenn also Floharten im Mittel sich mindestens um \(0.75cm\) unterscheiden, dann ist der Vergleich relevant. Das habe ich jetzt einfach so entschieden. Wir schauen hier dann auf größer/gleich, was auch mehr Sinn macht. Theoretisch kannst du auch in beide Richtungen die Relevanz definieren, aber in der Anwendung ist es eher selten, dass uns beide Richtungen interessieren.
R Code [zeigen / verbergen]
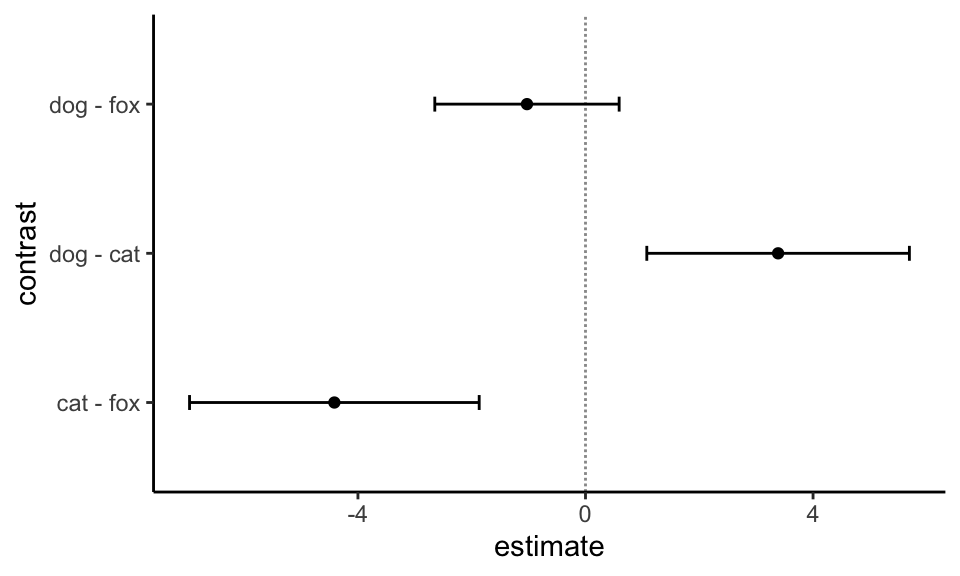
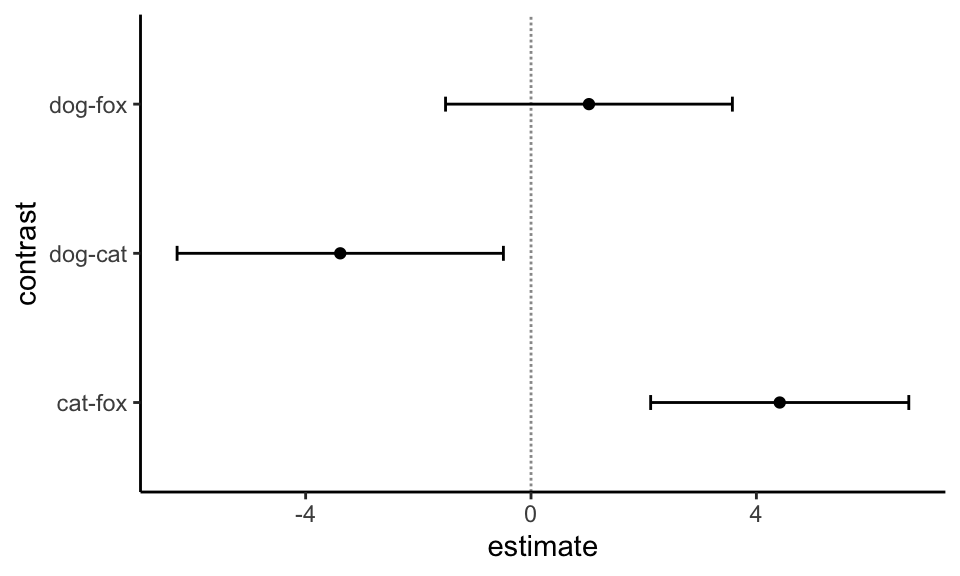
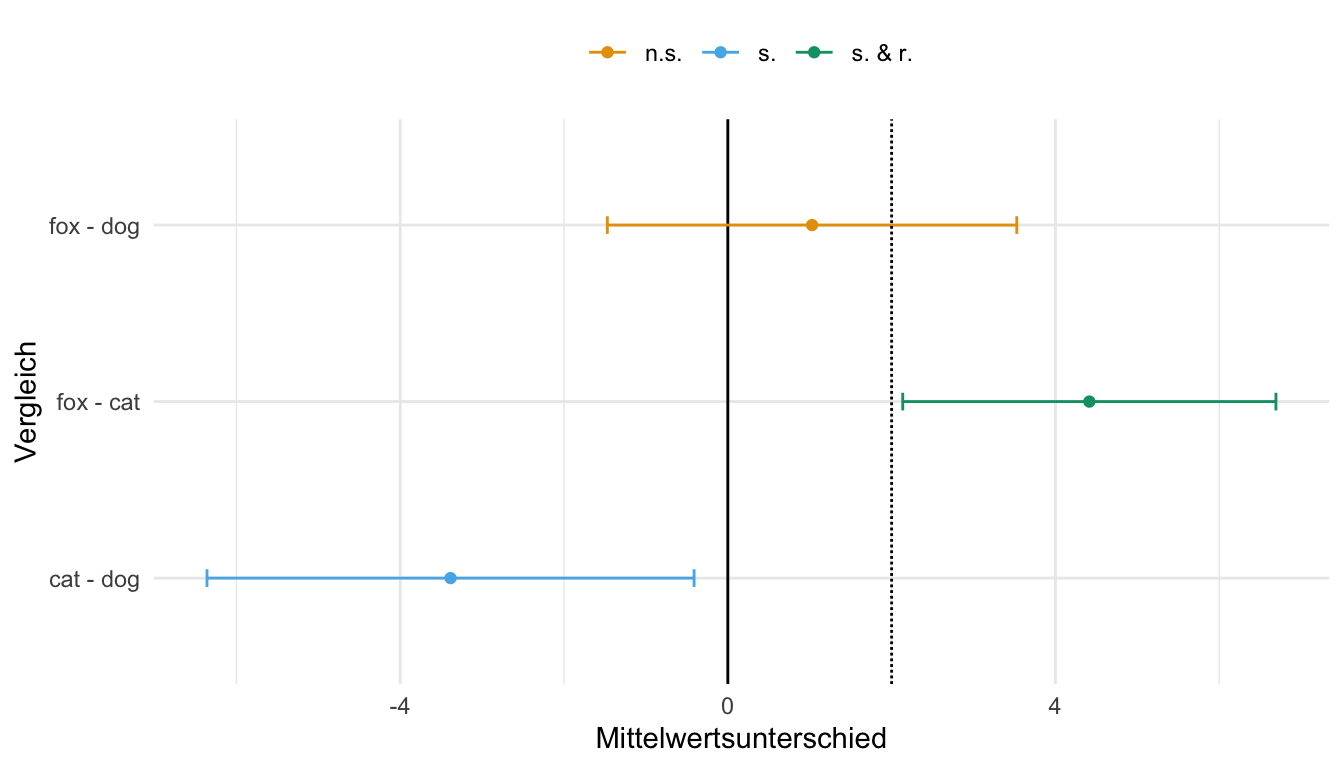
relevance_lvl <- 0.75In der folgenden Abbildung siehst du einmal die 95% Konfidenzintervalle für alle paarweisen Vergleiche. Ich habe am Anfang nochmal eine Regel mit case_when() erstellt, nachder ich dann die 95% Konfidenzintervall nach der Signifikanz und Relevanz einfärbe. Das ist ja die Stärke der 95% Konfidenzintervalle und dann sollte man die auch Nutzen. Wo du die Relevanzschwelle legst, ist dann dir selber überlassen. Das hängt von deiner wissenschaftlichen Fragestellung ab.
R Code [zeigen / verbergen]
emm_ci_fac1_obj |>
mutate(sig_lgl = case_when(between(rep(0, n()), conf.low, conf.high) ~ "n.s.",
relevance_lvl < conf.low ~ "s. & r.",
.default = "s.")) |>
ggplot(aes(contrast, y = estimate,
ymin = conf.low, ymax = conf.high, color = sig_lgl)) +
theme_minimal() +
geom_hline(yintercept = 0) +
geom_errorbar(width = 0.1) +
geom_hline(yintercept = relevance_lvl, linetype = "11",
color = "#009E73") +
geom_point() +
coord_flip() +
scale_color_okabeito() +
labs(x = "Vergleich", y = "Mittelwertsunterschied", color = "") +
theme(legend.position = "top")Zweifaktorielle Analyse
Nachdem wir uns die einfaktorielle Analyse angeschaut haben, kommen wir jetzt du der eigentlich interessanten Analyse. Wir wollen nämlich jetzt mal zwei Faktoren in einer zweifaktoriellen Analyse auswerten. Meistens haben wir nicht nur einen Faktor vorliegen sondern minestens zwei. Daher hier einmal das MOdell für unsere Sprungweite in [cm] für den Faktor animal mit den drei Floharten sowie dem Faktor site und den zwei Messorten Stadt und Dorf. Ich ahbe hier absichtlich den zweiten Faktor nur auf zwei Level begrenz, sonst werden die Ausgaben der Funktionen so groß. Später können deine Faktoren natürlich mehr Level oder Gruppen haben. Wir rechnen also einmal eine ANOVA um uns die statistsichen Maßzahlen als ein Modell wiedergeben zu lassen.
R Code [zeigen / verbergen]
fac2_aov <- aov(jump_length ~ animal + site + animal:site, data = fac2_tbl)Wenn wir zwei Faktoren vorliegen haben, dann müssen wir entscheiden, wie wir die zwei Faktoren auswerten wollen. Hierbei kommen wir um den Begriff nested (deu. verschachtelt, nicht gebräuchlich) herum. In der folgenden Abbildung habe ich das Konzept einmal dargestellt. In unserem Fall ist der Faktor animal in dem zweiten Faktor site genested. Alle Floharten wurden an allen Messorten gemessen.
flowchart LR
A(animal):::factor --- B(((nested))) --> C(site):::factor
classDef factor fill:#56B4E9,stroke:#333,stroke-width:0.75px
animal nested im Faktor site.
Damit gilt dann auch, dass jeder Messort alle Floharten enthält und die Floharten damit innerhalb eines Messortes randomsiert wurden. Ich habe dir das nochmal etwas anders dargestellt. Es ist wichtig sich den Zusammenhang klar zu machen, damit du später die Auswertung für deine wissenschaftliche Fragestellung richtig machst. Ich zeige dir hier jetzt einen Weg und du musst dann entscheiden, ob der bei dir auch so passt.
\[ \underbrace{\mbox{Messorte}}_{f_2} \xrightarrow[]{beinhaltet\; alle} \overbrace{\mbox{Floharten}}^{f_1} \]
Wir müssen uns jetzt entscheiden wie wir die beiden Faktoren \(f_1\) mit animal und \(f_2\) mit site auswerten wollen. Wir können den Faktor animal getrennt (eng. separate) für jedes Level des Faktors site vergleichen oder wir vergleichen alle Faktorkombinationen gemeinsam (eng. combined). Welcher Fakotr das bei dir dann in deiner Auswertung ist, kann ich natürlich nicht sagen. Aber meistens ist es dann klarer wenn du mit der Auswertung beginnst und dir die Ergebnisse versuchst zu interpretieren. Im Folgenden zeige ich dir einmal wie du die separierte und kombinierte Analyse in {emmeans} rechnest.
Wenn du den ersten Faktor animal separiert also getrennt für den zweiten Faktor site rechnen willst, dann nutzt du den Separator | um die getrennte Analyse zu rechnen. Du siehst, dass die Mittelwerte für die Floharten getrennt für die Messorte berechnet werden. Wiederum entscheide ich mich hier für die Adjustierung für die Varianzheterogenität.
R Code [zeigen / verbergen]
emm_fac2_separate_obj <- fac2_aov |>
emmeans(~ animal | site, vcov. = sandwich::vcovHAC)
emm_fac2_separate_objsite = city:
animal emmean SE df lower.CL upper.CL
cat 13.6 0.603 54 12.4 14.8
dog 16.7 0.693 54 15.3 18.1
fox 20.1 0.395 54 19.3 20.9
site = village:
animal emmean SE df lower.CL upper.CL
cat 15.2 0.834 54 13.6 16.9
dog 16.6 0.246 54 16.1 17.1
fox 17.0 0.489 54 16.0 18.0
Confidence level used: 0.95 Wenn du den ersten Faktor animal mit allen Kombinationen des zweiten Faktors site berechnen willst, dann nutzt du den Kombinator * um die kombinierte Analyse zu rechnen. Du siehst, dass die Mittelwerte für die Floharten für jeden Messort berechnet wird und die Ausgabe am Ende zusammengefasst wird. Wiederum entscheide ich mich hier für die Adjustierung für die Varianzheterogenität.
R Code [zeigen / verbergen]
emm_fac2_combinded_obj <- fac2_aov |>
emmeans(~ animal * site, vcov. = sandwich::vcovHAC)
emm_fac2_combinded_obj animal site emmean SE df lower.CL upper.CL
cat city 13.6 0.603 54 12.4 14.8
dog city 16.7 0.693 54 15.3 18.1
fox city 20.1 0.395 54 19.3 20.9
cat village 15.2 0.834 54 13.6 16.9
dog village 16.6 0.246 54 16.1 17.1
fox village 17.0 0.489 54 16.0 18.0
Confidence level used: 0.95 Wir erhalten also unser {emmeans} Objekt für unsere zweifaktorielle Analyse. Darin ist eigentlich alles enthalten was wir jetzt brauchen. Denn nun ist ja die Frage, was willst du haben? Ich zeige dir in den folgenden Tabs einmal wie du die p-Werte, das Comapct letter display und die 95% Konfidenzintervalle für die getrennte Analyse nach den zweiten Faktor berechnest. Deshalb erst überlegen, wie du die beiden Faktoren \(f_1\) und \(f_2\) auswerten willst. Je nachdem du dich dann entscheidest, kommen natürlich andere Egebnisse heraus.
Beginnen wir wieder die p-Werte für unseren Vergleich der Floharten für die mittleren Sprungweiten zu berechnen. Wir nutzen hierzu wieder die Funktion contrast() wie auch schon im einfaktoriellen Fall. Das ist jetzt auch so eine Stärke von {emmeans}, wenn wir das Modell hinkriegen, dann können wir auch mehr Faktoren beliebig ergänzen. Mir gefällt hier nicht die Reihenfolge in den Vergleichen. Statt cat - dog möchte ich lieber den Kontrast dog - cat. Daher wähle ich als Methode revpairwise und drehe damit einmal meine Vergleiche.
R Code [zeigen / verbergen]
emm_contrast_fac2_separate_obj <- emm_fac2_separate_obj |>
contrast(method = "revpairwise", adjust = "bonferroni")
emm_contrast_fac2_separate_objsite = city:
contrast estimate SE df t.ratio p.value
dog - cat 3.101 0.919 54 3.376 0.0041
fox - cat 6.538 0.721 54 9.070 <.0001
fox - dog 3.437 0.798 54 4.310 0.0002
site = village:
contrast estimate SE df t.ratio p.value
dog - cat 1.316 0.869 54 1.514 0.4076
fox - cat 1.729 0.967 54 1.789 0.2377
fox - dog 0.413 0.547 54 0.755 1.0000
P value adjustment: bonferroni method for 3 tests Jetzt erhalten wir für den zweiten Faktor site die Vergleiche der Sprungweiten der Hunde- und Katzenflöhe einmal wiedergegeben. Dabei sehen wir, dass sich die mittleren Sprungweiten signifikant in der Stadt unterscheiden, jedoch nicht auf dem Dorf. Die p-Werte in den Vergleichen in der Stadt sind alle unter dem Signifikanzniveau \(\alpha\) gleich 5%. Wir können hier also die Nullhypothese ablehnen, dass die Mitelwerte für den jeweiligen Vergleich gleich sind.
Jetzt können wir uns auch die Vergleiche als eine Matrix getrennt für den Faktor site anzeigen lassen. Hier ist es natürlich praktisch, dass wir gleich die Mittelwerte sowie die mittleren Differenzen als auch die p-Werte in einer Ausgabe vorliegen haben.
R Code [zeigen / verbergen]
emm_contrast_fac2_separate_obj |>
pwpm(adjust = "bonferroni")
site = city
dog - cat fox - cat fox - dog
dog - cat [3.10] 0.0002 1.0000
fox - cat -3.437 [6.54] 0.0041
fox - dog -0.336 3.101 [3.44]
site = village
dog - cat fox - cat fox - dog
dog - cat [1.316] 1.0000 1.0000
fox - cat -0.413 [1.729] 0.4076
fox - dog 0.903 1.316 [0.413]
Row and column labels: contrast
Upper triangle: P values adjust = "bonferroni"
Diagonal: [Estimates] (estimate)
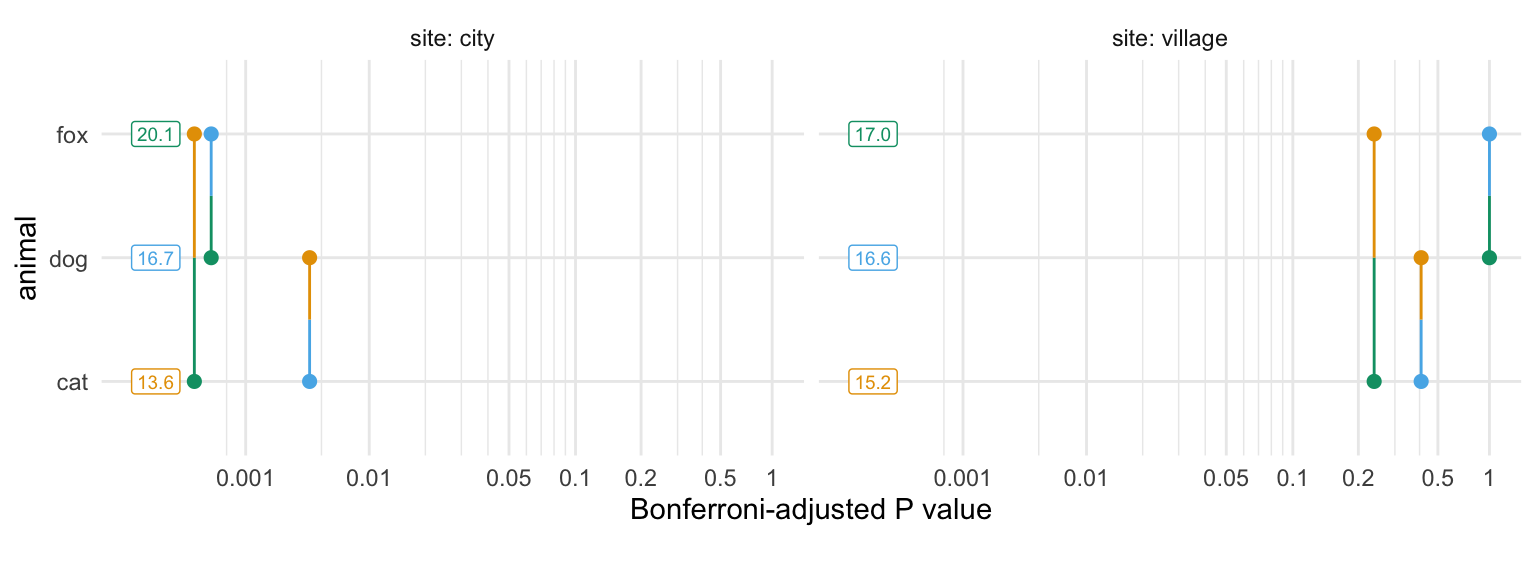
Lower triangle: Comparisons (estimate) earlier vs. laterIm einfaktoriellen Fall fand ich den paarweisen p-Wert Plot nicht so richtig informativ. Wenn du dir aber zwei Faktoren anschaust, dann kann man da schon mehr erkennen. Bilden die p-Werte in dem einen Level des zweiten Faktors ein anderes Muster als in einem anderen Level des Faktors? Hier sehen wir sehr schön, dass wir in der Stadt sehr kleine p-Werte erhalten aber auf dem Land im Dorf sehr große p-Werte. Das zeigt nochmal sehr deutlich, wie sich der erste Faktor animal in den Leveln des zweiten Faktor site unterscheidet.
Nachdem wir in dem vorherigen Tab die p-Werte berechnet haben, könen wir jetzt einmal das Compact letter display erstellen. Hier hat das R Paket {emmeans} eine eigene Funktion mit cld(). Die Funktion nimmt das Objekt emm_fac2_separate_obj und berechnet darauf das nach Bonferroni adjustierte Compact letter display.
R Code [zeigen / verbergen]
emm_cld_fac2_separate_obj <- emm_fac2_separate_obj |>
cld(Letters = letters, adjust = "bonferroni")
emm_cld_fac2_separate_objsite = city:
animal emmean SE df lower.CL upper.CL .group
cat 13.6 0.603 54 12.1 15.1 a
dog 16.7 0.693 54 15.0 18.4 b
fox 20.1 0.395 54 19.1 21.1 c
site = village:
animal emmean SE df lower.CL upper.CL .group
cat 15.2 0.834 54 13.2 17.3 a
dog 16.6 0.246 54 16.0 17.2 a
fox 17.0 0.489 54 15.8 18.2 a
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 3 estimates
P value adjustment: bonferroni method for 3 tests
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
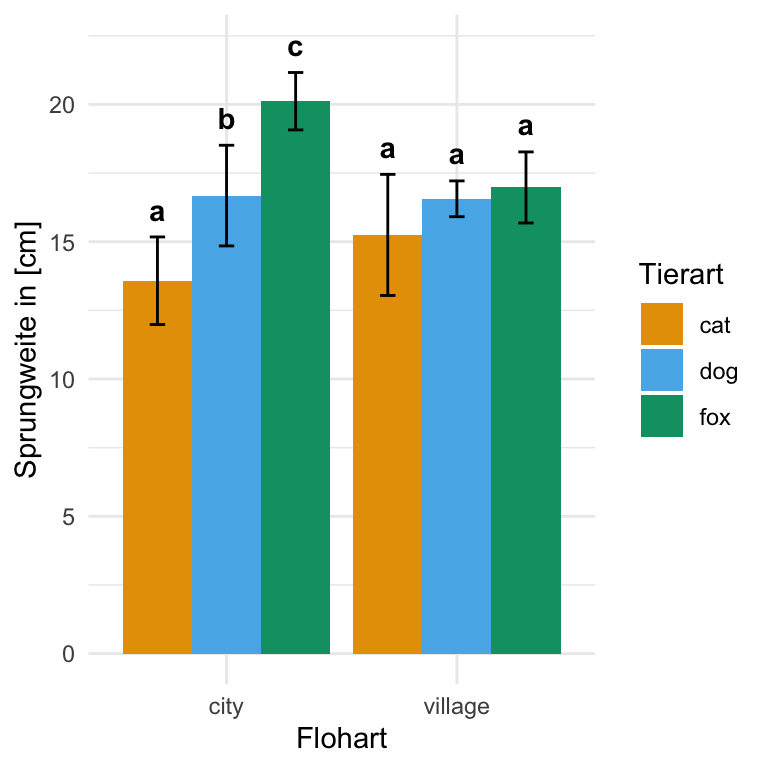
But we also did not show them to be the same. Auch hier ist der große Vorteil von {emmeans}, dass wir die Ausgabe des Compact letter displays direkt nutzen können um unseren Barplot zu zeichnen. Wir müssen nur einmal die Werte der Standardfehler mit der Wurzel der Gruppenfallzahl multiplizieren um auf die Standardabweichung zu kommen. Da wir hier sieben Flöhe je Tierart gemessen haben, multiplizieren wir den Standardfehler mit der Wurzel von 7 um auf die Standardabweichung zu kommen. Dann entferne ich noch die Leerzeichen in der Spalte .group mit der Funktion str_trim() und ich kann den Barplot erstellen. Wichtig ist hier, dass wir uns die beiden Messorte city und village voneinander getrennt betrachten. Daher haben wir im Dorf auch den Buchstaben a wie auch in der Stadt, obwohl es klare Unterschiede gibt. Wenn du alle Barplots kombiniert ein Compact letter displays haben willst, dann schaue in der Analyse weiter unten nach.
R Code [zeigen / verbergen]
emm_cld_fac2_separate_obj |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(7)) |>
ggplot(aes(x = site, y = emmean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity", width = 0.9,
position = position_dodge(0.9)) +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2,
position = position_dodge(0.9)) +
labs(x = "Flohart",
y = "Sprungweite in [cm]",
fill = "Tierart") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 1),
fontface = 2, position = position_dodge(0.9))Am Ende können wir dann auch aus den paarweisen Vergleichen die 95% Konfidenzintervalle berechnen. Hier nutzen wir dann die Funktion tidy() aus dem Paket {broom} um uns die 95% Konfidenzintervalle sauber wiedergeben zu lassen. Ich habe hier einmal die Kontraste auf revpairwise gestellt um die Vergleiche wie bei den p-Werten zu drehen.
R Code [zeigen / verbergen]
emm_ci_fac2_separate_obj <- emm_fac2_separate_obj |>
contrast(method = "pairwise", adjust = "bonferroni") |>
tidy(conf.int = TRUE) |>
select(contrast, site, estimate, conf.low, conf.high) Die Stärke eines 95% Konfidenzintervalls ist ja die Signifikanz mit der Relevanz zu verbinden. Daher setze ich jetzt mal die Relevanzschwelle relevance_lvl auf \(>2cm\). Wenn also Floharten im Mittel sich mindestens um \(2cm\) unterscheiden, dann ist der Vergleich relevant. Das habe ich jetzt einfach so entschieden. Wir schauen hier dann auf größer/gleich, was auch mehr Sinn macht. Theoretisch kannst du auch in beide Richtungen die Relevanz definieren, aber in der Anwendung ist es eher selten, dass uns beide Richtungen interessieren.
R Code [zeigen / verbergen]
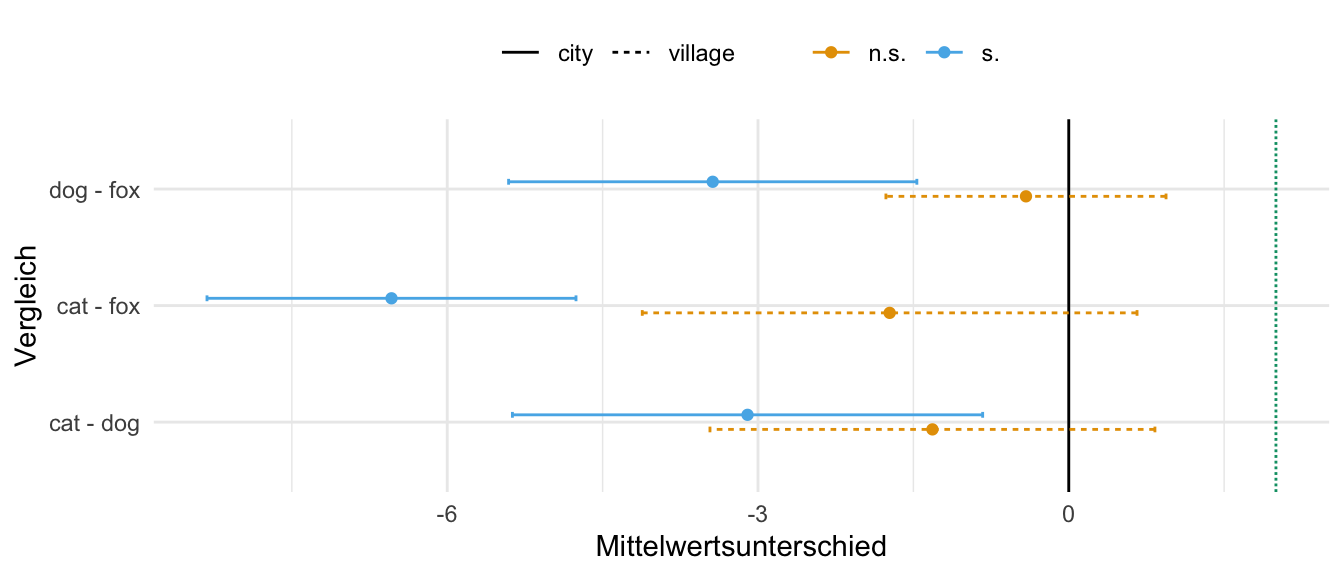
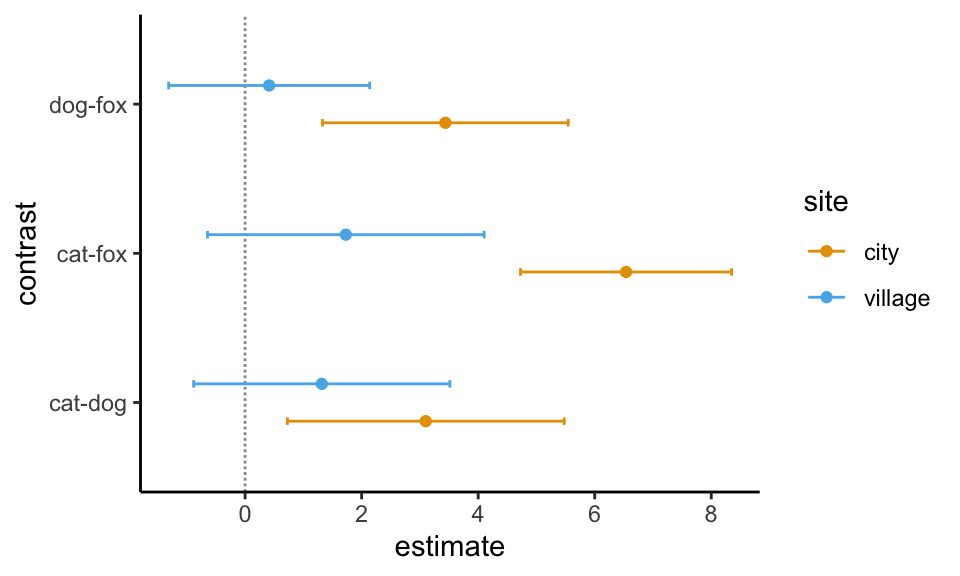
relevance_lvl <- 2In der folgenden Abbildung siehst du einmal die 95% Konfidenzintervalle für alle paarweisen Vergleiche. Ich habe am Anfang nochmal eine Regel mit case_when() erstellt, nachder ich dann die 95% Konfidenzintervall nach der Signifikanz und Relevanz einfärbe. Das ist ja die Stärke der 95% Konfidenzintervalle und dann sollte man die auch Nutzen. Wo du die Relevanzschwelle legst, ist dann dir selber überlassen. Das hängt von deiner wissenschaftlichen Fragestellung ab. Beachte, dass ich hier noch die Linienart ändern musste um die Messorte mit einzeichnen zu können. Wir haben am Ende nur einen relevanten und signifikanten Vergleich. Nämlich den Vergleich der Fuchsflöhe zu den Katzenflöhen in der Stadt.
R Code [zeigen / verbergen]
emm_ci_fac2_separate_obj |>
mutate(sig_lgl = case_when(between(rep(0, n()), conf.low, conf.high) ~ "n.s.",
relevance_lvl < conf.low ~ "s. & r.",
.default = "s.")) |>
ggplot(aes(contrast, y = estimate,
ymin = conf.low, ymax = conf.high,
color = sig_lgl, linetype = site)) +
theme_minimal() +
geom_hline(yintercept = 0) +
geom_errorbar(width = 0.1, position = position_dodge(0.25)) +
geom_hline(yintercept = relevance_lvl, linetype = "11",
color = "#009E73") +
geom_point(position = position_dodge(0.25)) +
coord_flip() +
scale_color_okabeito() +
labs(x = "Vergleich", y = "Mittelwertsunterschied",
color = "", linetype = "") +
theme(legend.position = "top")Eben gerade haben wir das {emmeans} Objekt für unsere zweifaktorielle Analyse für die getrennte Analyse über den zweiten Faktor genutzt. Jetzt zeige ich dir in den folgenden Tabs einmal wie du die p-Werte, das Comapct letter display und die 95% Konfidenzintervalle für die kombinierte Analyse über die beiden Faktoren \(f_1\) und \(f_2\) berechnest. Das heißt, wir wollen jetzt nicht mehr getrennt die Floharten über die Messorte anschauen, sondern die Interaktionen zwischen den Floharten und Messorten analysieren. Daher werden wir jetzt ein paar mehr Vergleiche rechnen als eben gerade im obigen Fall der getrennten Analyse.
Beginnen wir wieder die p-Werte für unseren Vergleich der Floharten für die mittleren Sprungweiten zu berechnen. Wir nutzen hierzu wieder die Funktion contrast() wie auch schon im einfaktoriellen Fall. Das ist jetzt auch so eine Stärke von {emmeans}, wenn wir das Modell hinkriegen, dann können wir auch mehr Faktoren beliebig ergänzen.
R Code [zeigen / verbergen]
emm_contrast_fac2_combined_obj <- emm_fac2_combinded_obj |>
contrast(method = "pairwise", adjust = "bonferroni")
emm_contrast_fac2_combined_obj contrast estimate SE df t.ratio p.value
cat city - dog city -3.101 0.919 54 -3.376 0.0206
cat city - fox city -6.538 0.721 54 -9.070 <.0001
cat city - cat village -1.668 1.010 54 -1.655 1.0000
cat city - dog village -2.984 0.651 54 -4.581 0.0004
cat city - fox village -3.397 0.776 54 -4.375 0.0008
dog city - fox city -3.437 0.798 54 -4.310 0.0010
dog city - cat village 1.433 1.100 54 1.305 1.0000
dog city - dog village 0.117 0.743 54 0.157 1.0000
dog city - fox village -0.296 0.848 54 -0.349 1.0000
fox city - cat village 4.870 0.922 54 5.279 <.0001
fox city - dog village 3.554 0.465 54 7.639 <.0001
fox city - fox village 3.141 0.633 54 4.964 0.0001
cat village - dog village -1.316 0.869 54 -1.514 1.0000
cat village - fox village -1.729 0.967 54 -1.789 1.0000
dog village - fox village -0.413 0.547 54 -0.755 1.0000
P value adjustment: bonferroni method for 15 tests Das sind eine Menge an Vergleichen. Daher ist es jetzt erstmal die Frage was hier eigentlich wie signifkant ist. Wiederum sieht man dann doch hier, das das Compact letter display gar nicht so schlecht ist um eine Übersicht zu kriegen. Hier ist es dann doch sehr unübersichtlich, welcher Vergleich nun wie signifikant ist. Vorallem lässt sich schwer ein übergeordnetes Muster erkennen.
Jetzt können wir uns auch die Vergleiche als eine Matrix anzeigen lassen. Hier ist es natürlich praktisch, dass wir gleich die Mittelwerte sowie die mittleren Differenzen als auch die p-Werte in einer Ausgabe vorliegen haben. Darüber hinaus sortiert die Matrix auch die vergleiche einmal sinnvoll und wir können viel besser sehen, welche Vergleiche signifikant sind. So lässt sich auch einfacher die Frage beantworten, ob wir Floharten oder Orte haben, wo alles signifikant ist oder die Signifikanz eher zufällig über die Vergleiche verteilt ist.
R Code [zeigen / verbergen]
emm_fac2_combinded_obj |>
pwpm(adjust = "bonferroni") cat city dog city fox city cat village dog village fox village
cat city [13.6] 0.0206 <.0001 1.0000 0.0004 0.0008
dog city -3.101 [16.7] 0.0010 1.0000 1.0000 1.0000
fox city -6.538 -3.437 [20.1] <.0001 <.0001 0.0001
cat village -1.668 1.433 4.870 [15.2] 1.0000 1.0000
dog village -2.984 0.117 3.554 -1.316 [16.6] 1.0000
fox village -3.397 -0.296 3.141 -1.729 -0.413 [17.0]
Row and column labels: animal:site
Upper triangle: P values adjust = "bonferroni"
Diagonal: [Estimates] (emmean)
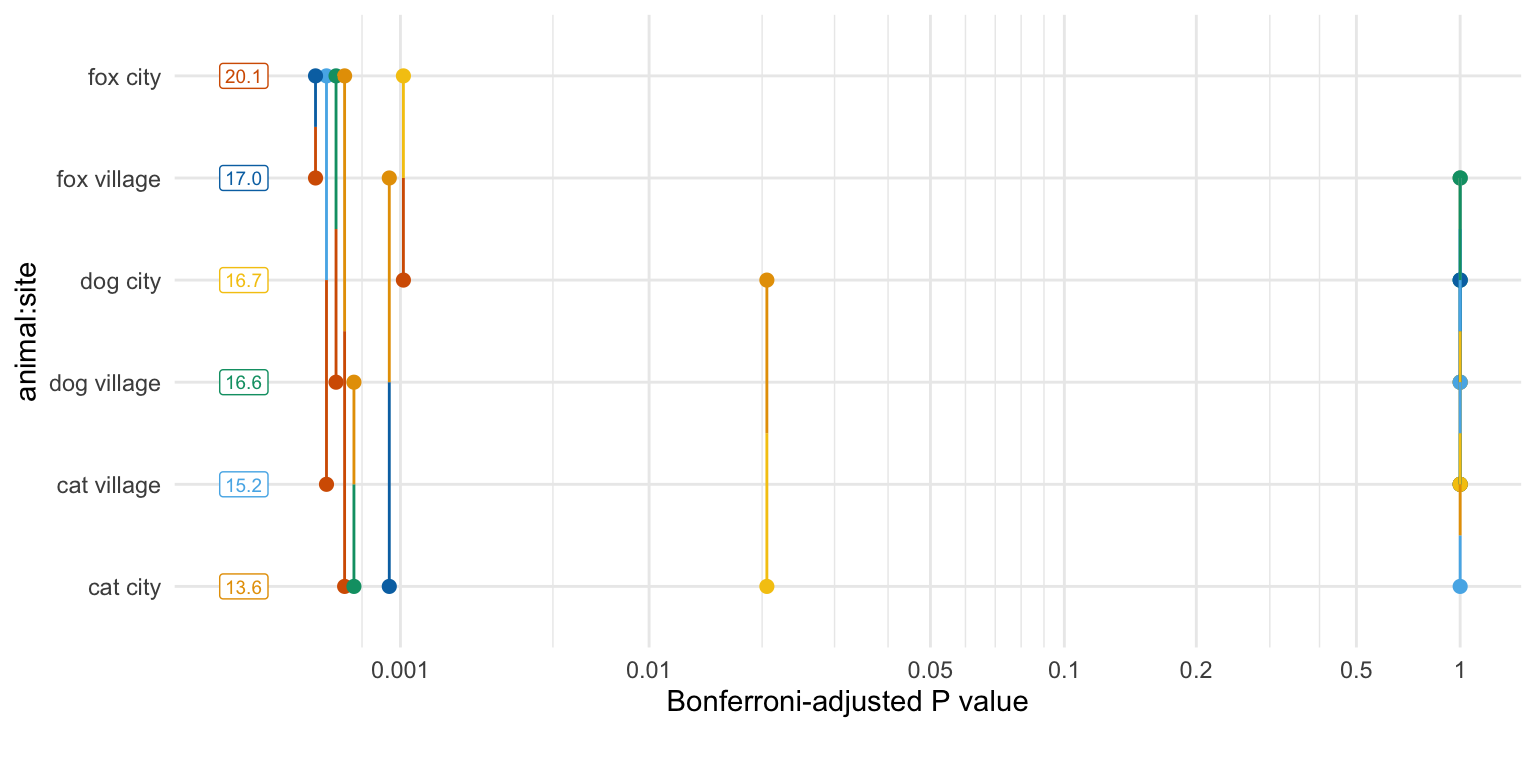
Lower triangle: Comparisons (estimate) earlier vs. laterDen paarweisen p-Wert Plot finde ich dann mit so vielen vergleichen dann schon wieder nicht so informativ. Wir haben eben sehr viele signifikante Unterschiede. Dann liegen auchs ehr viele Linien an der linken Seite und es ist schwer zu lesen, was wir hier vorliegen haben. Eventuell müsste man nochmal animal * site in dem emmeans() Aufruf auf site * animal drehen und schauen, ob dann die Ordnung der Vergleiche auf der y-Achse etwas besser ist. Aber das ändert auch nichts and er Anzahl an Vergleichen. Jede Abbildung hat dann so seine Grenzen.
Nachdem wir in dem vorherigen Tab die p-Werte berechnet haben, könen wir jetzt einmal das Compact letter display erstellen. Hier hat das R Paket {emmeans} eine eigene Funktion mit cld(). Die Funktion nimmt das Objekt emm_fac2_combindedobj und berechnet darauf das nach Bonferroni adjustierte Compact letter display.
R Code [zeigen / verbergen]
emm_cld_fac2_combined_obj <- emm_fac2_combinded_obj |>
cld(Letters = letters, adjust = "bonferroni")
emm_cld_fac2_combined_obj animal site emmean SE df lower.CL upper.CL .group
cat city 13.6 0.603 54 11.9 15.2 a
cat village 15.2 0.834 54 13.0 17.5 ab
dog village 16.6 0.246 54 15.9 17.2 b
dog city 16.7 0.693 54 14.8 18.6 b
fox village 17.0 0.489 54 15.6 18.3 b
fox city 20.1 0.395 54 19.0 21.2 c
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 6 estimates
P value adjustment: bonferroni method for 15 tests
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
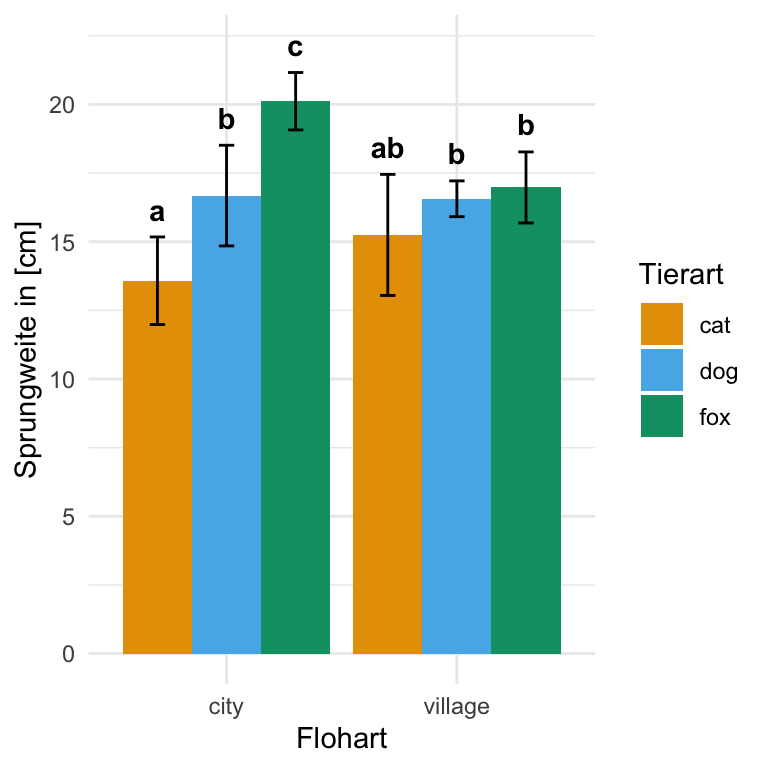
But we also did not show them to be the same. Der große Vorteil von {emmeans} ist, dass wir die Ausgabe des Compact letter displays direkt nutzen können um unseren Barplot zu zeichnen. Wir müssen nur einmal die Werte der Standardfehler mit der Wurzel der Gruppenfallzahl multiplizieren um auf die Standardabweichung zu kommen. Da wir hier sieben Flöhe je Tierart gemessen haben, multiplizieren wir den Standardfehler mit der Wurzel von 7 um auf die Standardabweichung zu kommen. Dann entferne ich noch die Leerzeichen in der Spalte .group mit der Funktion str_trim() und ich kann den Barplot erstellen.
R Code [zeigen / verbergen]
emm_cld_fac2_combined_obj |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(7)) |>
ggplot(aes(x = site, y = emmean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity", width = 0.9,
position = position_dodge(0.9)) +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2,
position = position_dodge(0.9)) +
labs(x = "Flohart",
y = "Sprungweite in [cm]",
fill = "Tierart") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 1),
fontface = 2, position = position_dodge(0.9))Am Ende können wir dann auch aus den paarweisen Vergleichen die 95% Konfidenzintervalle berechnen. Hier nutzen wir dann die Funktion tidy() aus dem Paket {broom} um uns die 95% Konfidenzintervalle sauber wiedergeben zu lassen. Ich habe hier einmal die Kontraste auf revpairwise gestellt um die Vergleiche wie bei den p-Werten zu drehen.
R Code [zeigen / verbergen]
emm_ci_fac2_combined_obj <- emm_fac2_combinded_obj |>
contrast(method = "pairwise", adjust = "bonferroni") |>
tidy(conf.int = TRUE) |>
select(contrast, estimate, conf.low, conf.high) Die Stärke eines 95% Konfidenzintervalls ist ja die Signifikanz mit der Relevanz zu verbinden. Weil wir jetzt hier so viele paarweise Vergleiche haben, macht es dann doch Sinn die Relevanzschwelle in beide Richtungen zu definieren. Daher setze ich jetzt mal die Relevanzschwelle relevance_lvl auf \(<2cm\) und \(>2cm\). Wenn also Floharten im Mittel sich mindestens um \(\pm 2cm\) unterscheiden, dann ist der Vergleich relevant. Das habe ich jetzt einfach so entschieden.
R Code [zeigen / verbergen]
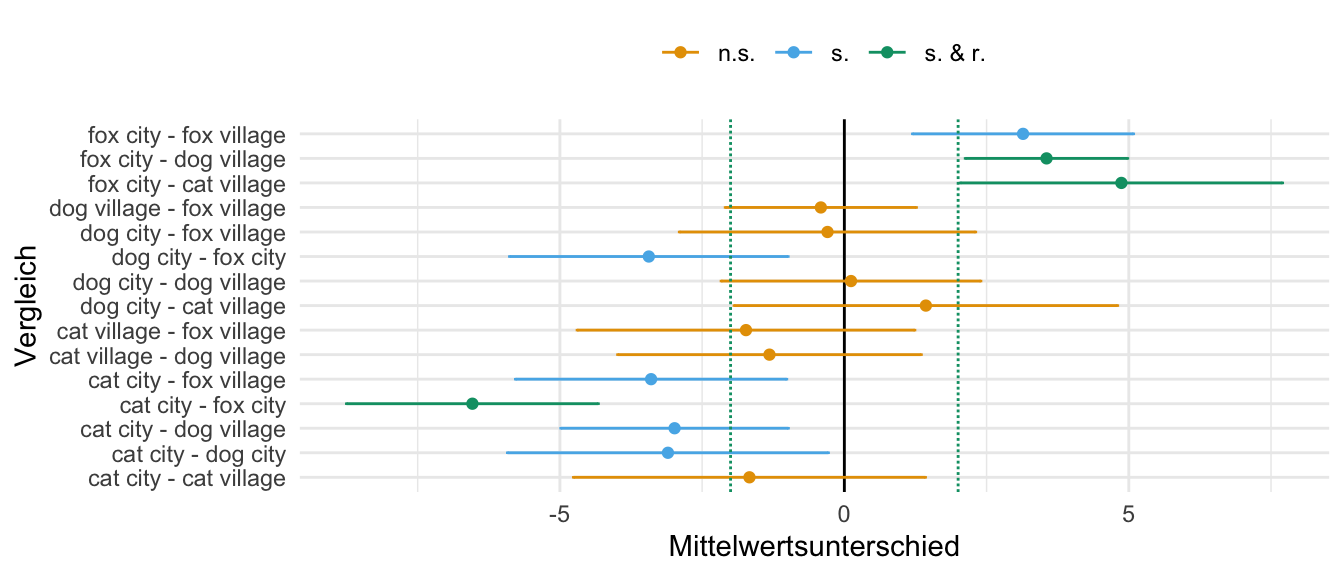
relevance_lvl <- c(-2, 2)In der folgenden Abbildung siehst du einmal die 95% Konfidenzintervalle für alle paarweisen Vergleiche. Ich habe am Anfang nochmal eine Regel mit case_when() erstellt, nachder ich dann die 95% Konfidenzintervall nach der Signifikanz und Relevanz einfärbe. Hier ist es dann etwas komplexer, weil ich eben beide Richtungen berücksichtigen will. Wo du die Relevanzschwelle legst, ist dann dir selber überlassen. Das hängt von deiner wissenschaftlichen Fragestellung ab. Wir haben dann drei signifikante und relevante Vergleiche am Ende. In allen drei Fällen ist jeweils der Fuchs in der Stadt enthalten. Wobei in zwei Vergleichen der Unterschied zum Dorf signifikant sowie relevant ist und in einem Vergleich zum Stadtkatzenfloh. Spannendes Ergebnis in diesem Fall.
R Code [zeigen / verbergen]
emm_ci_fac2_combined_obj |>
mutate(sig_lgl = case_when(between(rep(0, n()), conf.low, conf.high) ~ "n.s.",
relevance_lvl[2] < conf.low |
relevance_lvl[1] > conf.high ~ "s. & r.",
.default = "s.")) |>
ggplot(aes(contrast, y = estimate,
ymin = conf.low, ymax = conf.high, color = sig_lgl)) +
theme_minimal() +
geom_hline(yintercept = 0) +
geom_errorbar(width = 0.1) +
geom_hline(yintercept = c(relevance_lvl), linetype = "11",
color = "#009E73") +
geom_point() +
coord_flip() +
scale_color_okabeito() +
labs(x = "Vergleich", y = "Mittelwertsunterschied", color = "") +
theme(legend.position = "top")Weitere möglichen Analysen
Ich möchte hier nur kurz noch auf weitere mögliche Analysen mit {emmeans} eingehen. Zum einen gibt es die Hilfeseite von {emmeans} zur Interaction analysis in emmeans. Dort findet sich auch die Funktion joint_test(), die dir nochmal erlaubt auf einem Modell die Interaktionen in der richtigen Reihenfolge zu testen. Mehr dazu im Kapitel zur ANOVA.
“[…] tests the interaction contrasts for all effects in the model and compiles them in one Type-III-ANOVA-like table”
R Code [zeigen / verbergen]
fac2_aov |> joint_tests() model term df1 df2 F.ratio p.value
animal 2 54 25.745 <.0001
site 1 54 1.268 0.2652
animal:site 2 54 8.891 0.0005Ebenso gibt es noch die Möglichkeit dir die Effektstärken mit effsize() zu berechnen. Hier nutzen wir die Informationen aus dem Objekt fac1_aov um mit der Varianz und der Freiheitsgerade Cohen`s d zu berechnen. Mehr dazu dann auch im Kapitel zu dem Effektschätzer.
R Code [zeigen / verbergen]
eff_size(emm_fac1_obj, sigma = sigma(fac1_aov), edf = fac1_aov$df.residual) contrast effect.size SE df lower.CL upper.CL
dog - cat 1.91 0.601 18 0.647 3.174
dog - fox -0.58 0.371 18 -1.360 0.199
cat - fox -2.49 0.699 18 -3.960 -1.022
sigma used for effect sizes: 1.772
Confidence level used: 0.95 Mehz zu den weiteren Vergleichen von {emmeans} dann auch unter Comparisons and contrasts in emmeans. Das ist hier eher so der offene Abschnitt. Vielleicht kommt noch was dazu.
Hier nochmal ein kurzer Textvorschlag für deinen Material und Methodenteil, wenn du deine Abschlussarbeit schreibst. Ich halte den Text bewusst knapp, dann kannst du den Text noch ausschmücken. Gerne kannst du den Teil noch ausführlicher schreiben.
Die Analyse wurde in RStudio (Version 2024.12.0.467) und R (Version 4.2.3) durchgeführt. Die Gruppenvergleiche wurden mit einem Tukey HSD Test in dem R Paket emmeans (Version 1.10.0) berechnet und entsprechend für multiple Vergleiche adjustiert.
Die Analyse wurde in RStudio (Version 2024.12.0.467) und R (Version 4.2.3) durchgeführt. Die Gruppenvergleiche wurden mit einem Games Howell Test unter Berücksichtigung der Varianzheterogenität in den Versuchsgruppen in dem R Paket emmeans (Version 1.10.0) berechnet und entsprechend für multiple Vergleiche adjustiert.
Du findest die Informationen zu den genutzen Paketen wie {emmeans} und deiner R Version mit den folgenden Funktionen. Damit hast du dann alles zusammen um im Methodenteil einmal zu schreiben was du gemacht hast.
R Code [zeigen / verbergen]
packageVersion("emmeans")
version$version.string
RStudio.Version()$version44.6 Fallbeispiele mit {emmeans}
In den folgenden Zerforschenkästen findest du dann noch einige Fallbeispiele zu {emmeans}. Ich bin über den Campus Haste der Hochschule Osnabrück gelaufen und habe mal ein paar Fotos von Posterabbildungen gemacht. Dann habe ich die Abbildungen zerforscht und mit ausgedachten Daten versehen. Vielleicht findest du hier nochmal eine Inspiration für deine eingenen Auswertungen.
{emmeans}
In diesem Zerforschenbeispiel wollen wir uns einen einfaktoriellen Barplot oder Säulendiagramm anschauen. Daher fangen wir mit der folgenden Abbildung einmal an. Wir haben hier ein Säulendiagramm mit compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Behandlungen jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung. Die Standardabweichung addieren und subtrahieren wir dann jeweils von dem Mittelwert und schon haben wir die Fehlerbalken. Für eine detaillierte Betrachtung der Erstellung der Abbildung schauen einmal in das Kapitel zum Barplot oder Balkendiagramm oder Säulendiagramm.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_simple.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die vier Werte alle um den Mittelwert streuen lassen. Dabei habe ich darauf geachtet, dass die Streuung dann in der letzten Behandlung am größten ist.
R Code [zeigen / verbergen]
barplot_tbl <- read_excel("data/zerforschen_barplot_simple.xlsx") |>
mutate(trt = factor(trt,
levels = c("water", "rqflex", "nitra", "laqua"),
labels = c("Wasserdestilation",
"RQflex Nitra",
"Nitrachek",
"Laqua Nitrat")))
barplot_tbl # A tibble: 16 × 2
trt nitrat
<fct> <dbl>
1 Wasserdestilation 135
2 Wasserdestilation 130
3 Wasserdestilation 145
4 Wasserdestilation 135
5 RQflex Nitra 120
6 RQflex Nitra 130
7 RQflex Nitra 135
8 RQflex Nitra 135
9 Nitrachek 100
10 Nitrachek 120
11 Nitrachek 130
12 Nitrachek 130
13 Laqua Nitrat 230
14 Laqua Nitrat 210
15 Laqua Nitrat 205
16 Laqua Nitrat 220Im Folgenden sparen wir uns den Aufruf mit group_by() den du aus dem Kapitel zum Barplot schon kennst. Wir machen das alles zusammen in der Funktion emmeans() aus dem gleichnamigen R Paket. Der Vorteil ist, dass wir dann auch gleich die Gruppenvergleiche und auch das compact letter display erhalten. Einzig die Standardabweichung \(s\) wird uns nicht wiedergegeben sondern der Standardfehler \(SE\). Da aber folgernder Zusammenhang vorliegt, können wir gleich den Standardfehler in die Standardabweichung umrechnen.
\[ SE = \cfrac{s}{\sqrt{n}} \]
Wir rechnen also gleich einfach den Standardfehler \(SE\) mal der \(\sqrt{n}\) um dann die Standardabweichung zu erhalten. In unserem Fall ist \(n=4\) nämlich die Anzahl Beobachtungen je Gruppe. Wenn du mal etwas unterschiedliche Anzahlen hast, dann kannst du auch einfach den Mittelwert der Fallzahl der Gruppen nehmen. Da überfahren wir zwar einen statistischen Engel, aber der Genauigkeit ist genüge getan.
In den beiden Tabs siehst du jetzt einmal die Modellierung unter der Annahme der Varianzhomogenität mit der Funktion lm() und einmal die Modellierung unter der Annahme der Varianzheterogenität mit der Funktion gls() aus dem R Paket nlme. Wie immer lässt sich an Boxplots visuell überprüfen, ob wir Homogenität oder Heterogenität vorliegen haben. Oder aber du schaust nochmal in das Kapitel Der Pre-Test oder Vortest, wo du mehr erfährst.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim().
R Code [zeigen / verbergen]
emmeans_homogen_tbl <- lm(nitrat ~ trt, data = barplot_tbl) |>
emmeans(~ trt) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(4))
emmeans_homogen_tbl# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 5.08 12 109. 131. a 10.2
2 RQflex Nitra 130 5.08 12 119. 141. ab 10.2
3 Wasserdestilation 136. 5.08 12 125. 147. b 10.2
4 Laqua Nitrat 216. 5.08 12 205. 227. c 10.2In dem Objekt emmeans_homogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. Wie dir vielleicht auffällt sind alle Standardfehler und damit alle Standardabweichungen für alle Gruppen gleich, das war ja auch unsere Annahme mit der Varianzhomogenität.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket und natürlich in den Abschnitt zu dem Gruppenvergleich unter Varianzheterogenität. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim().
R Code [zeigen / verbergen]
emmeans_hetrogen_gls_tbl <- gls(nitrat ~ trt, data = barplot_tbl,
weights = varIdent(form = ~ 1 | trt)) |>
emmeans(~ trt) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(4))
emmeans_hetrogen_gls_tbl# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 7.07 3.00 97.5 143. a 14.1
2 RQflex Nitra 130 3.54 3.00 119. 141. a 7.07
3 Wasserdestilation 136. 3.15 3.00 126. 146. a 6.29
4 Laqua Nitrat 216. 5.54 3.00 199. 234. b 11.1 In dem Objekt emmeans_hetrogen_gls_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket und natürlich in den Abschnitt zu dem Gruppenvergleich unter Varianzheterogenität. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim().
R Code [zeigen / verbergen]
emmeans_hetrogen_vcov_tbl <- lm(nitrat ~ trt, data = barplot_tbl) |>
emmeans(~ trt, vcov. = sandwich::vcovHAC) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(4))
emmeans_hetrogen_vcov_tbl# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 7.84 12 103. 137. a 15.7
2 RQflex Nitra 130 3.92 12 121. 139. a 7.84
3 Wasserdestilation 136. 2.06 12 132. 141. a 4.12
4 Laqua Nitrat 216. 4.94 12 205. 227. b 9.88In dem Objekt emmeans_hetrogen_vcov_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
Und dann haben wir auch schon die Abbildungen hier erstellt. Ja vielleicht passen die Standardabweichungen nicht so richtig, da könnte man nochmal an den Daten spielen und die Werte solange ändern, bis es besser passt. Du hast aber jetzt eine Idee, wie der Aufbau funktioniert. Die beiden Tabs zeigen dir dann die Abbildungen für die beiden Annahmen der Varianzhomogenität oder Varianzheterogenität. Der Code ist der gleiche für die drei Abbildungen, die Daten emmeans_homogen_tbl oder emmeans_hetrogen_gls_tbl ober emmeans_hetrogen_vcov_tbl sind das Ausschlaggebende.
R Code [zeigen / verbergen]
ggplot(data = emmeans_homogen_tbl, aes(x = trt, y = emmean, fill = trt)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2) +
labs(x = "",
y = "Nitrat-Konzentration \n im Tannensaft [mg/L]") +
ylim(0, 250) +
theme(legend.position = "none") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 10))R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_gls_tbl, aes(x = trt, y = emmean, fill = trt)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2) +
labs(x = "",
y = "Nitrat-Konzentration \n im Tannensaft [mg/L]") +
ylim(0, 250) +
theme(legend.position = "none") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 10))R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_vcov_tbl, aes(x = trt, y = emmean, fill = trt)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2) +
labs(x = "",
y = "Nitrat-Konzentration \n im Tannensaft [mg/L]") +
ylim(0, 250) +
theme(legend.position = "none") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 10))Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
ggsave("my_ggplot_barplot.png", width = 5, height = 3){emmeans}
In diesem Zerforschenbeispiel wollen wir uns einen zweifaktoriellen Barplot anschauen. Wir haben hier ein Säulendiagramm mit compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Zeitpunkte und der Kontrolle jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung. Da wir hier aber noch mit emmeans() eine Gruppenvergleich rechnen wollen, brauchen wir mehr Beobachtungen. Wir erschaffen uns also fünf Beobachtungen je Zeit/Jod-Kombination. Für eine detaillierte Betrachtung der Erstellung der Abbildung schauen einmal in das Kapitel zum Barplot oder Balkendiagramm oder Säulendiagramm.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_2fac_target_emmeans.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die fünf Werte alle um den Mittelwert streuen lassen. Ich brauche hier eigentlich mehr als fünf Werte, sonst kriegen wir bei emmeans() und der Interaktion im gls()-Modell Probleme, aber da gibt es dann bei kleinen Fallzahlen noch ein Workaround. Bitte nicht mit weniger als fünf Beobachtungen versuchen, dann wird es schwierig mit der Konsistenz der Schätzer aus dem Modell.
Ach, und ganz wichtig. Wir entfernen die Kontrolle, da wir die Kontrolle nur mit einer Iodid-Stufe gemessen haben. Dann können wir weder die Interaktion rechnen, noch anständig eine Interpretation durchführen.
R Code [zeigen / verbergen]
barplot_tbl <- read_excel("data/zerforschen_barplot_2fac_target_emmeans.xlsx") |>
mutate(time = factor(time,
levels = c("ctrl", "7", "11", "15", "19"),
labels = c("Contr.", "07:00", "11:00", "15:00", "19:00")),
type = as_factor(type)) |>
filter(time != "Contr.")
barplot_tbl # A tibble: 40 × 3
time type iodine
<fct> <fct> <dbl>
1 07:00 KIO3 50
2 07:00 KIO3 55
3 07:00 KIO3 60
4 07:00 KIO3 52
5 07:00 KIO3 62
6 07:00 KI 97
7 07:00 KI 90
8 07:00 KI 83
9 07:00 KI 81
10 07:00 KI 98
# ℹ 30 more rowsIm Folgenden sparen wir uns den Aufruf mit group_by() den du aus dem Kapitel zum Barplot schon kennst. Wir machen das alles zusammen in der Funktion emmeans() aus dem gleichnamigen R Paket. Der Vorteil ist, dass wir dann auch gleich die Gruppenvergleiche und auch das compact letter display erhalten. Einzig die Standardabweichung \(s\) wird uns nicht wiedergegeben sondern der Standardfehler \(SE\). Da aber folgernder Zusammenhang vorliegt, können wir gleich den Standardfehler in die Standardabweichung umrechnen.
\[ SE = \cfrac{s}{\sqrt{n}} \]
Wir rechnen also gleich einfach den Standardfehler \(SE\) mal der \(\sqrt{n}\) um dann die Standardabweichung zu erhalten. In unserem Fall ist \(n=5\) nämlich die Anzahl Beobachtungen je Gruppe. Wenn du mal etwas unterschiedliche Anzahlen hast, dann kannst du auch einfach den Mittelwert der Fallzahl der Gruppen nehmen. Da überfahren wir zwar einen statistischen Engel, aber der Genauigkeit ist genüge getan.
In den beiden Tabs siehst du jetzt einmal die Modellierung unter der Annahme der Varianzhomogenität mit der Funktion lm() und einmal die Modellierung unter der Annahme der Varianzheterogenität mit der Funktion gls() aus dem R Paket nlme. Wie immer lässt sich an Boxplots visuell überprüfen, ob wir Homogenität oder Heterogenität vorliegen haben. Oder aber du schaust nochmal in das Kapitel Der Pre-Test oder Vortest, wo du mehr erfährst.
Wenn du jeden Boxplot miteinander vergleichen willst, dann musst du in dem Code emmeans(~ time * type) setzen. Dann berechnet dir emmeans für jede Faktorkombination einen paarweisen Vergleich.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim(). Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen. Wenn du alles mit allem Vergleichen willst, dann setze bitte emmeans(~ time * type).
R Code [zeigen / verbergen]
emmeans_homogen_tbl <- lm(iodine ~ time + type + time:type, data = barplot_tbl) |>
emmeans(~ time | type) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(5))
emmeans_homogen_tbl# A tibble: 8 × 9
time type emmean SE df lower.CL upper.CL .group sd
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 07:00 KIO3 55.8 5.58 32 44.4 67.2 a 12.5
2 11:00 KIO3 75.2 5.58 32 63.8 86.6 b 12.5
3 15:00 KIO3 81 5.58 32 69.6 92.4 b 12.5
4 19:00 KIO3 84.2 5.58 32 72.8 95.6 b 12.5
5 07:00 KI 89.8 5.58 32 78.4 101. a 12.5
6 19:00 KI 90 5.58 32 78.6 101. a 12.5
7 15:00 KI 124 5.58 32 113. 135. b 12.5
8 11:00 KI 152 5.58 32 141. 163. c 12.5In dem Objekt emmeans_homogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. Wie dir vielleicht auffällt sind alle Standardfehler und damit alle Standardabweichungen für alle Gruppen gleich, das war ja auch unsere Annahme mit der Varianzhomogenität.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim(). Da wir hier etwas Probleme mit der Fallzahl haben, nutzen wir die Option mode = "appx-satterthwaite" um dennoch ein vollwertiges, angepasstes Modell zu erhalten. Du kannst die Option auch erstmal entfernen und schauen, ob es mit deinen Daten auch so klappt. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen. Wenn du alles mit allem Vergleichen willst, dann setze bitte emmeans(~ time * type).
R Code [zeigen / verbergen]
emmeans_hetrogen_tbl <- gls(iodine ~ time + type + time:type, data = barplot_tbl,
weights = varIdent(form = ~ 1 | time*type)) |>
emmeans(~ time | type, mode = "appx-satterthwaite") |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(5))
emmeans_hetrogen_tbl# A tibble: 8 × 9
time type emmean SE df lower.CL upper.CL .group sd
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 07:00 KIO3 55.8 2.29 3.98 49.4 62.2 a 5.12
2 11:00 KIO3 75.2 1.50 3.96 71.0 79.4 b 3.35
3 15:00 KIO3 81.0 3.30 4.02 71.8 90.2 b 7.38
4 19:00 KIO3 84.2 7.88 4.01 62.3 106. b 17.6
5 07:00 KI 89.8 3.48 4.03 80.2 99.4 a 7.79
6 19:00 KI 90.0 4.31 4.00 78.0 102. a 9.64
7 15:00 KI 124 7.48 3.98 103. 145. b 16.7
8 11:00 KI 152 9.03 3.99 127. 177. c 20.2 In dem Objekt emmeans_hetrogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
Dann bauen wir usn auch schon die Abbildung. Wir müssen am Anfang einmal scale_x_discrete() setzen, damit wir gleich den Zielbereich ganz hinten zeichnen können. Sonst ist der blaue Bereich im Vordergrund. Dann färben wir auch mal die Balken anders ein. Muss ja auch mal sein. Auch nutzen wir die Funktion geom_text() um das compact letter display gut zu setzten. Die \(y\)-Position berechnet sich aus dem Mittelwert emmean plus Standardabweichung sd innerhalb des geom_text(). Da wir hier die Kontrollgruppe entfernen mussten, habe ich dann nochmal den Zielbereich verschoben und mit einem Pfeil ergänzt. Die beiden Tabs zeigen dir dann die Abbildungen für die beiden Annahmen der Varianzhomogenität oder Varianzheterogenität. Der Code ist der gleiche für beide Abbildungen, die Daten emmeans_homogen_tbl oder emmeans_hetrogen_tbl sind das Ausschlaggebende. Wie du sehen wirst, haben wir hier mal keinen Unterschied vorliegen.
R Code [zeigen / verbergen]
ggplot(data = emmeans_homogen_tbl, aes(x = time, y = emmean, fill = type)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0.25, xmax = 4.75, ymin = 50, ymax = 100,
alpha = 0.2, fill = "darkblue") +
annotate("text", x = 0.5, y = 120, hjust = "left", label = "Target area",
size = 5) +
geom_curve(aes(x = 1.25, y = 120, xend = 1.7, yend = 105),
colour = "#555555",
size = 0.5,
curvature = -0.2,
arrow = arrow(length = unit(0.03, "npc"))) +
geom_bar(stat = "identity",
position = position_dodge(width = 0.9, preserve = "single")) +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2,
position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_manual(name = "Type", values = c("darkgreen", "darkblue")) +
theme(legend.position = c(0.1, 0.8),
legend.title = element_blank(),
legend.spacing.y = unit(0, "mm"),
panel.border = element_rect(colour = "black", fill=NA),
axis.text = element_text(colour = 1, size = 12),
legend.background = element_blank(),
legend.box.background = element_rect(colour = "black")) +
labs(x = "Time of application [time of day]",
y = expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +
scale_y_continuous(breaks = c(0, 50, 100, 150, 200),
limits = c(0, 200)) +
geom_text(aes(label = .group, y = emmean + sd + 2),
position = position_dodge(width = 0.9), vjust = -0.25) ggplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen. Die Kontrolle wurde entfernt, sonst hätten wir hier nicht emmeans in der einfachen Form nutzen können. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen.
R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_tbl, aes(x = time, y = emmean, fill = type)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0.25, xmax = 4.75, ymin = 50, ymax = 100,
alpha = 0.2, fill = "darkblue") +
annotate("text", x = 0.5, y = 120, hjust = "left", label = "Target area",
size = 5) +
geom_curve(aes(x = 1.25, y = 120, xend = 1.7, yend = 105),
colour = "#555555",
size = 0.5,
curvature = -0.2,
arrow = arrow(length = unit(0.03, "npc"))) +
geom_bar(stat = "identity",
position = position_dodge(width = 0.9, preserve = "single")) +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2,
position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_manual(name = "Type", values = c("darkgreen", "darkblue")) +
theme(legend.position = c(0.1, 0.8),
legend.title = element_blank(),
legend.spacing.y = unit(0, "mm"),
panel.border = element_rect(colour = "black", fill=NA),
axis.text = element_text(colour = 1, size = 12),
legend.background = element_blank(),
legend.box.background = element_rect(colour = "black")) +
labs(x = "Time of application [time of day]",
y = expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +
scale_y_continuous(breaks = c(0, 50, 100, 150, 200),
limits = c(0, 200)) +
geom_text(aes(label = .group, y = emmean + sd + 2),
position = position_dodge(width = 0.9), vjust = -0.25) ggplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen. Die Kontrolle wurde entfernt, sonst hätten wir hier nicht emmeans in der einfachen Form nutzen können. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
ggsave("my_ggplot_barplot.png", width = 5, height = 3){emmeans}
In diesem Zerforschenbeispiel wollen wir uns einen zweifaktoriellen Boxplot unter der Annahme nicht normalverteilter Daten anschauen. Dabei ist Iodanteil in den Pflanzen nicht normalverteilt, so dass wir hier eine Quantilesregression rechnen wollen. Die Daten siehst du wieder in der unteren Abbildung. Ich nehme für jede der vier Zeitpunkte jeweils fünf Beobachtungen an. Für die Kontrolle haben wir dann nur drei Beobachtungen in der Gruppe \(KIO_3\) vorliegen. Das ist wichtig, denn sonst können wir nicht mit emmeans rechnen. Wir haben einfach zu wenige Beobachtungen vorliegen.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_2fac_target_emmeans.xlsx selber ausgedacht. Ich nehme hier die gleichen Daten wie für den Barplot. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die fünf Werte alle um den Mittelwert streuen lassen. Ich brauche hier eigentlich mehr als fünf Werte, sonst kriegen wir bei emmeans() und der Interaktion im gls()-Modell Probleme, aber da gibt es dann bei kleinen Fallzahlen noch ein Workaround. Bitte nicht mit weniger als fünf Beobachtungen versuchen, dann wird es schwierig mit der Konsistenz der Schätzer aus dem Modell.
Ach, und ganz wichtig. Wir entfernen die Kontrolle, da wir die Kontrolle nur mit einer Iodid-Stufe gemessen haben. Dann können wir weder die Interaktion rechnen, noch anständig eine Interpretation durchführen.
R Code [zeigen / verbergen]
boxplot_tbl <- read_excel("data/zerforschen_barplot_2fac_target_emmeans.xlsx") |>
mutate(time = factor(time,
levels = c("ctrl", "7", "11", "15", "19"),
labels = c("Contr.", "07:00", "11:00", "15:00", "19:00")),
type = as_factor(type)) |>
filter(time != "Contr.")
boxplot_tbl # A tibble: 40 × 3
time type iodine
<fct> <fct> <dbl>
1 07:00 KIO3 50
2 07:00 KIO3 55
3 07:00 KIO3 60
4 07:00 KIO3 52
5 07:00 KIO3 62
6 07:00 KI 97
7 07:00 KI 90
8 07:00 KI 83
9 07:00 KI 81
10 07:00 KI 98
# ℹ 30 more rowsHier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim(). Wichtig ist hier, dass wir zur Modellierung die Funktion rq() aus dem R Paket quantreg nutzen. Wenn du den Aufbau mit den anderen Zerforschenbeispielen vergleichst, siehst du, dass hier viel ähnlich ist. Achtung, ganz wichtig! Du musst am Ende wieder die Ausgabe aus der cld()-Funktion nach der Zeit time und der Form type sortieren, sonst passt es gleich nicht mit den Beschriftungen der Boxplots.
Du musst dich nur noch entscheiden, ob du das compact letter display getrennt für die beiden Jodformen type berechnen willst oder aber zusammen. Wenn du das compact letter display für die beiden Jodformen zusammen berechnest, dann berechnest du für jede Faktorkombination einen paarweisen Vergleich.
Hier rechnen wir den Vergleich nur innerhalb der jeweiligen Jodform type. Daher vergleichen wir die Boxplots nicht untereinander sondern eben nur in den jeweiligen Leveln \(KIO_3\) und \(KI\).
R Code [zeigen / verbergen]
emmeans_quant_sep_tbl <- rq(iodine ~ time + type + time:type, data = boxplot_tbl, tau = 0.5) |>
emmeans(~ time | type) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group)) |>
arrange(time, type)
emmeans_quant_sep_tbl# A tibble: 8 × 8
time type emmean SE df lower.CL upper.CL .group
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
1 07:00 KIO3 55 3.15 32 48.6 61.4 a
2 07:00 KI 90 5.51 32 78.8 101. a
3 11:00 KIO3 75 1.97 32 71.0 79.0 b
4 11:00 KI 150 13.8 32 122. 178. b
5 15:00 KIO3 80 4.72 32 70.4 89.6 b
6 15:00 KI 120 7.87 32 104. 136. b
7 19:00 KIO3 85 7.48 32 69.8 100. b
8 19:00 KI 90 2.36 32 85.2 94.8 a Dann einmal die Berechnung über alle Boxplots und damit allen Faktorkombinationen aus Zeit und Jodform. Wir können dann damit jeden Boxplot mit jedem anderen Boxplot vergleichen.
R Code [zeigen / verbergen]
emmeans_quant_comb_tbl <- rq(iodine ~ time + type + time:type, data = boxplot_tbl, tau = 0.5) |>
emmeans(~ time*type) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group)) |>
arrange(time, type)
emmeans_quant_comb_tbl# A tibble: 8 × 8
time type emmean SE df lower.CL upper.CL .group
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
1 07:00 KIO3 55 3.15 32 48.6 61.4 a
2 07:00 KI 90 5.51 32 78.8 101. c
3 11:00 KIO3 75 1.97 32 71.0 79.0 b
4 11:00 KI 150 13.8 32 122. 178. d
5 15:00 KIO3 80 4.72 32 70.4 89.6 bc
6 15:00 KI 120 7.87 32 104. 136. d
7 19:00 KIO3 85 7.48 32 69.8 100. bc
8 19:00 KI 90 2.36 32 85.2 94.8 c Für die Boxplots brauchen wir dann noch ein Objekt mehr. Um das nach den Faktorkombinationen sortierte compacte letter dislay an die richtige Position zu setzen brauchen wir noch eine \(y\)-Position. Ich nehme hier dann das 95% Quantile. Das 95% Quantile sollte dann auf jeden Fall über die Schnurrhaare raus reichen. Wir nutzen dann den Datensatz letter_pos_tbl in dem geom_text() um die Buchstaben richtig zu setzen.
R Code [zeigen / verbergen]
letter_pos_tbl <- boxplot_tbl |>
group_by(time, type) |>
summarise(quant_90 = quantile(iodine, probs = c(0.95)))
letter_pos_tbl# A tibble: 8 × 3
# Groups: time [4]
time type quant_90
<fct> <fct> <dbl>
1 07:00 KIO3 61.6
2 07:00 KI 97.8
3 11:00 KIO3 78.8
4 11:00 KI 174
5 15:00 KIO3 89.4
6 15:00 KI 146
7 19:00 KIO3 106
8 19:00 KI 99.8Das Problem sind natürlich die wenigen Beobachtungen, deshalb sehen die Boxplots teilweise etwas wild aus. Aber wir wollen hier eben die Mediane darstellen, die wir dann auch in der Quantilesregression berechnet haben. Wenn du mehr Beobachtungen erstellst, dann werden die Boxplots auch besser dargestellt.
Hier nehmen wir das compact letter display aus dem Objekt emmeans_quant_sep_tbl. Wichtig ist, dass die Sortierung gleich der Beschriftung der \(x\)-Achse ist. Deshalb nutzen wir weiter oben auch die Funktion arrange() zur Sortierung der Buchstaben. Beachte, dass wir hier jeweils die beiden Jodformen getrennt voneinander betrachten.
R Code [zeigen / verbergen]
ggplot(data = boxplot_tbl, aes(x = time, y = iodine,
fill = type)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0.25, xmax = 4.75, ymin = 50, ymax = 100,
alpha = 0.2, fill = "darkblue") +
annotate("text", x = 0.5, y = 120, hjust = "left", label = "Target area") +
geom_curve(aes(x = 1.1, y = 120, xend = 1.7, yend = 105),
colour = "#555555",
size = 0.5,
curvature = -0.2,
arrow = arrow(length = unit(0.03, "npc"))) +
geom_boxplot(position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_manual(name = "Type", values = c("darkgreen", "darkblue")) +
theme(legend.position = c(0.1, 0.8),
legend.title = element_blank(),
legend.spacing.y = unit(0, "mm"),
panel.border = element_rect(colour = "black", fill=NA),
axis.text = element_text(colour = 1, size = 12),
legend.background = element_blank(),
legend.box.background = element_rect(colour = "black")) +
labs(x = "Time of application [time of day]",
y = expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +
scale_y_continuous(breaks = c(0, 50, 100, 150, 200),
limits = c(0, 200)) +
geom_text(data = letter_pos_tbl,
aes(label = emmeans_quant_sep_tbl$.group,
y = quant_90 + 5),
position = position_dodge(width = 0.9), vjust = -0.25) ggplot als Boxplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen, dafür müssen wir uns aber nochmal ein Positionsdatensatz bauen. Hier ist das compact letter display getrennt für die beiden Jodformen berechnet.
Und hier nutzen wir das compact letter display aus dem Objekt emmeans_quant_comb_tbl. Wichtig ist, dass die Sortierung gleich der Beschriftung der \(x\)-Achse ist. Deshalb nutzen wir weiter oben auch die Funktion arrange() zur Sortierung der Buchstaben. Hier betrachten wir jeden Boxplot einzelne und du kannst auch jeden Boxplot mit jedem Boxplot vergleichen.
R Code [zeigen / verbergen]
ggplot(data = boxplot_tbl, aes(x = time, y = iodine,
fill = type)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0.25, xmax = 4.75, ymin = 50, ymax = 100,
alpha = 0.2, fill = "darkblue") +
annotate("text", x = 0.5, y = 120, hjust = "left", label = "Target area") +
geom_curve(aes(x = 1.1, y = 120, xend = 1.7, yend = 105),
colour = "#555555",
size = 0.5,
curvature = -0.2,
arrow = arrow(length = unit(0.03, "npc"))) +
geom_boxplot(position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_manual(name = "Type", values = c("darkgreen", "darkblue")) +
theme(legend.position = c(0.1, 0.8),
legend.title = element_blank(),
legend.spacing.y = unit(0, "mm"),
panel.border = element_rect(colour = "black", fill=NA),
axis.text = element_text(colour = 1, size = 12),
legend.background = element_blank(),
legend.box.background = element_rect(colour = "black")) +
labs(x = "Time of application [time of day]",
y = expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +
scale_y_continuous(breaks = c(0, 50, 100, 150, 200),
limits = c(0, 200)) +
geom_text(data = letter_pos_tbl,
aes(label = emmeans_quant_comb_tbl$.group,
y = quant_90 + 5),
position = position_dodge(width = 0.9), vjust = -0.25) ggplot als Boxplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen, dafür müssen wir uns aber nochmal ein Positionsdatensatz bauen. Hier ist das compact letter display für jede einzelne Faktorkombination berechnet.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
ggsave("my_ggplot_boxplot.png", width = 5, height = 3){emmeans}
Hier wollen wir einmal eine etwas größere Abbildung 44.28 mit einer Menge Boxplots zerforschen. Da ich den Datensatz dann nicht zu groß machen wollte und Boxplots zu zerforschen manchmal nicht so einfach ist, passen die Ausreißer dann manchmal dann doch nicht. Auch liefern die statistischen Tests dann nicht super genau die gleichen Ergebnisse. Aber das macht vermutlich nicht so viel, hier geht es ja dann eher um den Bau der Boxplots und dem rechnen des statistischen Tests in {emmeans}. Die Reihenfolge des compact letter displays habe ich dann auch nicht angepasst sondern die Buchstaben genommen, die ich dann erhalten habe. Die Sortierung kann man ja selber einfach ändern. Wir haben hier ein einfaktorielles Design mit einem Behandlungsfaktor mit drei Leveln vorliegen. Insgesamt schauen wir uns vier Endpunkte in veränderten Substrat- und Wasserbedingungen an.
Im Folgenden lade ich einmal den Datensatz, den ich dann per Auge zusammengesetzt habe. Das war jetzt etwas anstrengender als gedacht, da ich nicht weiß wie viele Beobachtungen einen Boxplot bilden. Je mehr Beobachtungen, desto feiner kann man den Boxplot abstimmen. Da ich hier nur mit sieben Beobachtungen ja Gruppe gearbeitet habe, habe ich es nicht geschafft die Ausreißer darzustellen. Das wäre mir dann zu viel Arbeit geworden. Nachdem ich jetzt die Daten geladen habe, muss ich noch über die Funktion pivot_longer() einen Datensatz passenden im Longformat bauen. Abschließend mutiere ich dann noch alle Faktoren richtig und vergebe bessere Namen als labels sonst versteht man ja nicht was die Spalten bedeuten.
R Code [zeigen / verbergen]
boxplot_mult_tbl <- read_excel("data/zerforschen_boxplot_mult.xlsx") |>
pivot_longer(cols = fresh_weight:flower_number,
values_to = "rsp",
names_to = "plant_measure") |>
mutate(trt = as_factor(trt),
plant_measure = factor(plant_measure,
levels = c("fresh_weight", "dry_weight",
"plant_height", "flower_number"),
labels = c("Fresh weight (g)", "Dry weight (g)",
"Plant height (cm)", "Flower number")),
type = factor(type, labels = c("Substrate", "Water"))) Ich habe mir dann die beiden Behandlungen substrate und water in die neue Spalte type geschrieben. Die Spaltennamen der Outcomes wandern in die Spalte plant_measure und die entsprechenden Werte in die Spalte rsp. Dann werde ich hier mal alle Outcomes auf einmal auswerten und nutze dafür das R Paket {purrr} mit der Funktion nest() und map(). Ich packe mir als die Daten nach type und plant_measure einmal zusammen. Dann habe ich einen neuen genesteten Datensatz mit nur noch acht Zeilen. Auf jeder Zeile rechne ich dann jeweils mein Modell. Wie du dann siehst ist in der Spalte data dann jeweils ein Datensatz mit der Spalte trt und rsp für die entsprechenden 21 Beobachtungen.
R Code [zeigen / verbergen]
boxplot_mult_nest_tbl <- boxplot_mult_tbl |>
group_by(type, plant_measure) |>
nest()
boxplot_mult_nest_tbl# A tibble: 8 × 3
# Groups: type, plant_measure [8]
type plant_measure data
<fct> <fct> <list>
1 Substrate Fresh weight (g) <tibble [21 × 2]>
2 Substrate Dry weight (g) <tibble [21 × 2]>
3 Substrate Plant height (cm) <tibble [21 × 2]>
4 Substrate Flower number <tibble [21 × 2]>
5 Water Fresh weight (g) <tibble [21 × 2]>
6 Water Dry weight (g) <tibble [21 × 2]>
7 Water Plant height (cm) <tibble [21 × 2]>
8 Water Flower number <tibble [21 × 2]>Zur Veranschaulichung rechne ich jetzt einmal mit mutate() und map() für jeden der Datensätze in der Spalte data einmal ein lineares Modell mit der Funktion lm(). Ich muss nur darauf achten, dass ich die Daten mit .x einmal an die richtige Stelle in der Funktion lm() übergebe. Dann habe ich alle Modell komprimiert in der Spalte model. Das geht natürlcih auch alles super in einem Rutsch.
R Code [zeigen / verbergen]
boxplot_mult_nest_model_tbl <- boxplot_mult_nest_tbl |>
mutate(model = map(data, ~lm(rsp ~ trt, data = .x)))
boxplot_mult_nest_model_tbl # A tibble: 8 × 4
# Groups: type, plant_measure [8]
type plant_measure data model
<fct> <fct> <list> <list>
1 Substrate Fresh weight (g) <tibble [21 × 2]> <lm>
2 Substrate Dry weight (g) <tibble [21 × 2]> <lm>
3 Substrate Plant height (cm) <tibble [21 × 2]> <lm>
4 Substrate Flower number <tibble [21 × 2]> <lm>
5 Water Fresh weight (g) <tibble [21 × 2]> <lm>
6 Water Dry weight (g) <tibble [21 × 2]> <lm>
7 Water Plant height (cm) <tibble [21 × 2]> <lm>
8 Water Flower number <tibble [21 × 2]> <lm> Jetzt können wir einmal eskalieren und insgesamt acht mal die ANOVA rechnen. Das sieht jetzt nach viel Code aus, aber am Ende ist es nur eine lange Pipe. Am Ende erhalten wir dann den \(p\)-Wert für die einfaktorielle ANOVA für die Behandlung trt wiedergegeben. Wir sehen, dass wir eigentlich nur einen signifikanten Unterschied in der Wassergruppe und der Pflanzenhöhe erwarten sollten. Da der \(p\)-Wert für die Wassergruppe und der Blütenanzahl auch sehr nah an dem Signifikanzniveau ist, könnte hier auch etwas sein, wenn wir die Gruppen nochmal getrennt testen.
R Code [zeigen / verbergen]
boxplot_mult_nest_model_tbl |>
mutate(anova = map(model, anova)) |>
mutate(parameter = map(anova, model_parameters)) |>
select(type, plant_measure, parameter) |>
unnest(parameter) |>
clean_names() |>
filter(parameter != "Residuals") |>
select(type, plant_measure, parameter, p)# A tibble: 8 × 4
# Groups: type, plant_measure [8]
type plant_measure parameter p
<fct> <fct> <chr> <dbl>
1 Substrate Fresh weight (g) trt 0.813
2 Substrate Dry weight (g) trt 0.381
3 Substrate Plant height (cm) trt 0.959
4 Substrate Flower number trt 0.444
5 Water Fresh weight (g) trt 0.384
6 Water Dry weight (g) trt 0.843
7 Water Plant height (cm) trt 0.000138
8 Water Flower number trt 0.0600 Dann schauen wir uns nochmal das \(\eta^2\) an um zu sehen, wie viel Varianz unsere Behandlung in den Daten erklärt. Leider sieht es in unseren Daten sehr schlecht aus. Nur bei der Wassergruppe und der Pflanzenhöhe scheinen wir durch die Behandlung Varianz zu erklären.
R Code [zeigen / verbergen]
boxplot_mult_nest_model_tbl %>%
mutate(eta = map(model, eta_squared)) %>%
unnest(eta) %>%
clean_names() %>%
select(type, plant_measure, eta2) # A tibble: 8 × 3
# Groups: type, plant_measure [8]
type plant_measure eta2
<fct> <fct> <dbl>
1 Substrate Fresh weight (g) 0.0228
2 Substrate Dry weight (g) 0.102
3 Substrate Plant height (cm) 0.00466
4 Substrate Flower number 0.0863
5 Water Fresh weight (g) 0.101
6 Water Dry weight (g) 0.0188
7 Water Plant height (cm) 0.628
8 Water Flower number 0.268 Dann können wir auch schon den Gruppenvergleich mit dem R Paket {emmeans} rechnen. Wir nutzen hier die Option vcov. = sandwich::vcovHAC um heterogene Varianzen zuzulassen. Im Weiteren adjustieren wir nicht für die Anzahl der Vergleiche und lassen uns am Ende das compact letter display wiedergeben.
R Code [zeigen / verbergen]
emm_tbl <- boxplot_mult_nest_model_tbl |>
mutate(emm = map(model, emmeans, ~trt, vcov. = sandwich::vcovHAC)) |>
mutate(cld = map(emm, cld, Letters = letters, adjust = "none")) |>
unnest(cld) |>
select(type, plant_measure, trt, rsp = emmean, group = .group) |>
mutate(group = str_trim(group))
emm_tbl# A tibble: 24 × 5
# Groups: type, plant_measure [8]
type plant_measure trt rsp group
<fct> <fct> <fct> <dbl> <chr>
1 Substrate Fresh weight (g) UWF 95.4 a
2 Substrate Fresh weight (g) TWF 101 a
3 Substrate Fresh weight (g) Peat 105 a
4 Substrate Dry weight (g) UWF 12.3 a
5 Substrate Dry weight (g) Peat 14.3 ab
6 Substrate Dry weight (g) TWF 15.1 b
7 Substrate Plant height (cm) TWF 37.9 a
8 Substrate Plant height (cm) Peat 38.0 a
9 Substrate Plant height (cm) UWF 39.1 a
10 Substrate Flower number UWF 14.6 a
# ℹ 14 more rowsDa die Ausgabe viel zu lang ist, wollen wir ja jetzt einmal unsere Abbildungen in {ggplot} nachbauen. Dazu nutze ich dann einmal zwei Wege. Einmal den etwas schnelleren mit facet_wrap() bei dem wir eigentlich alles automatisch machen lassen. Zum anderen zeige ich dir mit etwas Mehraufwand alle acht Abbildungen einzeln baust und dann über das R Paket {patchwork} wieder zusammenklebst. Der zweite Weg ist der Weg, wenn du mehr Kontrolle über die einzelnen Abbildungen haben willst.
Die Funktion facet_wrap() erlaubt es dir automatisch Subplots nach einem oder mehreren Faktoren zu erstellen. Dabei muss auch ich immer wieder probieren, wie ich die Faktoren anordne. In unserem Fall wollen wir zwei Zeilen und auch den Subplots erlauben eigene \(x\)-Achsen und \(y\)-Achsen zu haben. Wenn du die Option scale = "free" nicht wählst, dann haben alle Plots alle Einteilungen der \(x\)_Achse und die \(y\)-Achse läuft von dem kleinsten zu größten Wert in den gesamten Daten.
R Code [zeigen / verbergen]
boxplot_mult_tbl |>
ggplot(aes(trt, rsp)) +
theme_minimal() +
stat_boxplot(geom = "errorbar", width = 0.25) +
geom_boxplot(outlier.shape = 18, outlier.size = 2) +
stat_summary(fun.y = mean, geom = "point", shape = 23, size = 3, fill = "red") +
facet_wrap(~ type * plant_measure, nrow = 2, scales = "free") +
labs(x = "", y = "") +
geom_text(data = emm_tbl, aes(y = rsp, label = group), size = 3, fontface = "bold",
position = position_nudge(0.2), hjust = 0, vjust = 0, color = "red")Jetzt wird es etwas wilder. Wir bauen uns jetzt alle acht Plots einzeln und kleben diese dann mit dem R Paket {patchwork} zusammen. Das hat ein paar Vorteile. Wir können jetzt jeden einzelnen Plot bearbeiten und anpassen wie wir es wollen. Damit wir aber nicht zu viel Redundanz haben bauen wir uns erstmal ein Template für ggplot(). Dann können wir immer noch die Werte für scale_y_continuous() in den einzelnen Plots ändern. Hier also einmal das Template, was beinhaltet was für alle Abbildungen gelten soll.
R Code [zeigen / verbergen]
gg_template <- ggplot() +
aes(trt, rsp) +
theme_minimal() +
stat_boxplot(geom = "errorbar", width = 0.25) +
geom_boxplot(outlier.shape = 18, outlier.size = 2) +
stat_summary(fun.y = mean, geom = "point", shape = 23, size = 3, fill = "red") +
labs(x = "")Ja, jetzt geht es los. Wir bauen also jeden Plot einmal nach. Dafür müssen wir dann jeweils den Datensatz filtern, den wir auch brauchen. Dann ergänzen wir noch die korrekte \(y\)-Achsenbeschriftung. So können wir dann auch händisch das compact letter display über die Whisker einfach setzen. Im Weiteren habe ich dann auch einmal als Beispiel noch die \(y\)-Achseneinteilung mit scale_y_continuous() geändert. Ich habe das einmal für den Plot p1 gemacht, der Rest würde analog dazu funktionieren.
R Code [zeigen / verbergen]
p1 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Substrate" & plant_measure == "Fresh weight (g)") +
labs(y = "Fresh weight (g)") +
annotate("text", x = c(1, 2, 3), y = c(170, 120, 135), label = c("a", "a", "a"),
color = "red", size = 3, fontface = "bold") +
scale_y_continuous(breaks = seq(40, 180, 20), limits = c(60, 180))
p2 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Substrate" & plant_measure == "Dry weight (g)") +
labs(y = "Dry weight (g)")
p3 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Substrate" & plant_measure == "Plant height (cm)") +
labs(y = "Plant height (cm)")
p4 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Substrate" & plant_measure == "Flower number") +
labs(y = "Flower number")
p5 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Water" & plant_measure == "Fresh weight (g)") +
labs(y = "Fresh weight (g)")
p6 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Water" & plant_measure == "Dry weight (g)") +
labs(y = "Dry weight (g)")
p7 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Water" & plant_measure == "Plant height (cm)") +
labs(y = "Plant height (g)")
p8 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Water" & plant_measure == "Flower number") +
labs(y = "Flower number")Dann kleben wir die Abbildungen einfach mit einem + zusammen und dann wählen wir noch aus, dass wir vier Spalten wollen. Dann können wir noch Buchstaben zu den Subplots hinzufügen und noch Titel und anderes wenn wir wollen würden. Dann haben wir auch den Plot schon nachgebaut. Ich verzichte hier händisch überall das compact letter display zu ergänzen. Das macht super viel Arbeit und endlos viel Code und hilft dir dann aber in deiner Abbildung auch nicht weiter. Du musst dann ja bei dir selber die Positionen für die Buchstaben finden.
R Code [zeigen / verbergen]
patch <- p1 + p2 + p3 + p4 + p5 + p6 + p7 + p8 +
plot_layout(ncol = 4)
patch + plot_annotation(tag_levels = 'A',
title = 'Ein Zerforschenbeispiel an Boxplots',
subtitle = 'Alle Plots wurden abgelesen und daher sagen Signifikanzen nichts.',
caption = 'Disclaimer: Die Abbildungen sagen nichts aus.')Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
ggsave("my_ggplot_boxplot.png", width = 12, height = 6)44.7 Der ANOVA Pfad mit Tukey HSD
Der Tukey HSD Test (abk. HSD Test) hat viele Namen. Im Englischen kennen wir den Tukey HSD Test auch als Tukey’s range test oder aber als Tukey’s test, Tukey method, Tukey’s honest significance test oder eben Tukey’s HSD (honestly significant difference) Test. Dabei steht die Abkürzung HDS für honestly significant difference (deu. ehrlich signifikanter Unterschied). Für mich etwas weit aus dem Fenster gelehnt, aber der Name sagt hier mal was auch wirklich gemacht wird. Im Prinzip stellen wir nur die Formel von den Student t-Test einmal um und benennen alles neu. Dann sieht man auch nicht gleich, was Sache ist und jeder denkt, es wäre was Neues. Wir werden hier aber mal den Tukey HSD Test zerforschen. Wir nutzen aber die ANOVA um einmal die Streuung und die Effekte zu berechnen. Daher nenne ich das ganze hier auch den ANOVA Pfad. Der Tukey HSD Test basiert eben mehr oder minder auf der Ausgabe einer ANOVA. Mehr Informationen gibt es auch im Tutorium Post-Hoc Analysis with Tukey’s Test. Ach, der Tukey HSD Test ist schon etwas älter und kann nicht so viel wie neuere Implementierungen wie das R Paket {emmeans} und {multcomp}.
- Varianzhomogenität
-
Es ist wichtig zu wissen, dass der Tukey HSD Test auf der ANOVA basiert und die ANOVA nimmt Varianzhomogenität an. Damit meine ich, dass alle Gruppen in der Behandlung die gleiche Varianz haben. Du kannst leider den Tukey HSD Test nur unter der Annahme von Varianzhomogenität nutzen. Wenn das dir eine zu starke Annahme ist, dann nutze einfach das R Paket
{emmeans}, wie ich es dir weiter unten im Kapitel vorstelle. - Adjustierung für multiple Vergleiche
-
Der Tukey HSD Test adjustiert für die \(\alpha\)-Inflation bei multiplen Vergleichen. Wir müssen da auch nichts weiter machen um die Adjustierung durchzuführen. Das macht die Funktion
TukeyHSD()für uns automatisch. Auf der anderen Seite können wir die Adjustierung für multiple Vergleiche aber auch nicht ausschalten. Du erhälst immer adjustierte p-Werte aus einem Tukey HSD Test. Wenn du das nicht möchtest, dann nutze einfach das R Paket{emmeans}, welches du weiter unten findest. - Mögliche multiple Vergleiche
-
Wir können immer nur alle Gruppen mit allen anderen Gruppen vergleichen. Wir rechnen also einen all pair Vergleich. Wenn du zum Beispiel nur die Behandlungsgruppen zur Kontrolle vergleichen willst, aber nciht untereinander, dann ist das nicht mit dem Tukey HDS Test möglich. Dafür musst du dann das R Paket
{ememans}oder für noch komplexere Gruppenvergleiche das R Paket{multcomp}nutzen. - Fallzahl in den einzelnen Behandlungsgruppen
-
Der Tukey HSD Test geht von einem balancierten Design aus. Daher brauchen wir in allen Behandlungsgruppen die gleiche Anzahl an Beobachtungen. Wenn wir kein balanciertes Design vorliegen haben, dann wird die Fallzahl mehr oder minder über die Gruppen gemittelt. Teilweise funktioniert dann auch der Tukey HSD Test nicht mehr richtig. Daher ist von der Nutzung es Tukey HSD Tests bei ungleich großen Gruppen abzuraten. Auch hier ist dann der Ausweg das R Paket
{emmeans}, welches genau für den unblancierten Fall ursprünglich entworfen wurde.
Schauen wir uns nun einmal an, wie der Tukey HSD Test theoretisch funktioniert und wie die Implmentierugn in R dargestellt ist. Wir haben die Wahl zwischen der Funktion TukeyHSD() und der Funktion HSD.test() aus dem R Paket {agricolae}. Die Funktion HSD.test() liefert auch gleich das Compact letter display in der Ausgabe mit. Sonst sind die beiden Funktionen sehr ähnlich. Oft wird eben der Tukey HSD Test noch verwendet, weil er eben sehr alt ist und somit schon sehr lange verwendet wurde.
Zuerst einmal die Formel des Tukey HSD Test. Wir berechnen dabei als statistische Maßzahl den HSD-Wert, der nichts anderes aussagt als der minimal Mittelwertsunterschied, den wir gegeben der Streuung und der Fallzahl in den Daten als signifikant nachweisen können. Sozusagen der minimalste mögliche signifikante Mittelwertsunterschied.
\[ HSD = q_{\alpha=5\%, k, n-k} \cdot \sqrt{\tfrac{MSE}{n}} \]
mit
- \(HSD\), den zu berechnenden minimalsten möglichen signifikanten Mittelwertsunterschied.
- \(q_{\alpha=5\%, k, n-k}\), den kritischen Wert gegeben aus dem Signifikanzniveau \(\alpha\) gleich 5% der Anzahl an zu vergleichenden Gruppen \(k\) und einem Freiheitsgrad \(n-k\).
- \(\sqrt{\tfrac{MSE}{n}}\), der Streuung in den Daten gewichtet für die Fallzahl \(n\). Hier wird die Streuung über alle Gruppen hinweg berechnet.
Wir können uns das Ganze auch nochmal in der folgenden Tabelle als Vergleich zu dem Student t-Test anschauen. Hier dann erstmal noch die beiden Formeln.
\[ \begin{array}{c|c} HSD = q_{\alpha=5\%, k, n-k} \cdot \sqrt{\tfrac{MSE}{n}} & \bar{y}_1 - \bar{y}_2 = T_{\alpha=5\%} \cdot s_p\sqrt{\tfrac{2}{n_g}} \end{array} \]
Ich habe dort einmal die statistischen Maßzahlen aus einem Tukey HDS Test den statistischen Maßzahlen eines Student t-Test in der folgenden Tabelle gegenüber gestellt. Du siehst, dass wir hier eigentlich nur eine Umstellung der t-Test Formel haben.
| Tukey HSD Test | Student t-Test | |
|---|---|---|
| Effekt | \(HSD\) | \(\bar{y}_1 - \bar{y}_2\) |
| Streuung | \(\tfrac{MSE}{n}\) | \(s_p\sqrt{\tfrac{2}{n_g}}\) |
| Kritischer Wert | \(q_{\alpha=5\%, k, n-k}\) | \(T_{\alpha=5\%}\) |
Um die Idee des Tukey HDS Test zusammenzufassen, setzen wir für \(q_{\alpha=5\%, k, n-k}\) den Wert ein, den wir mindestens erreichen müssen um einen signifikanten Unterschied nachweisen zu können. Bei dem Student t-Test war es meist \(T_{\alpha=5\%}\) gleich \(1.96\), hier ist der Wert für \(q_{\alpha=5\%, k, n-k}\) natürlich anders. Dann können wir den minimalen Mittelwertsunterschied mit \(\bar{y}_1 - \bar{y}_2\) oder eben \(HSD\) berechnen, denn wir mindestens erreichen müssen um einen signifikanten Unterschied nachweisen zu können. Alle Mittelwertsdifferenzen größer als der \(HDS\) Wert werden dann signifikant sein und alle Mittelwertsdifferenzen kleiner als der \(HDS\) Wert nicht signifikant sein.
Wenn eine Mittelwertsdifferenz \(\bar{y}_i - \bar{y}_j\) eines Gruppenvergleiches größer ist als der HDS Wert dann wird die Nullhypothese (H\(_0\)) abgelehnt. Ist die Mittelwertsdifferenz \(\bar{y}_i - \bar{y}_j\) eines Gruppenvergleiches ist als der HDS Wert dann wird die Nullhypothese (H\(_0\)) beibehalten.
Im Folgenden wollen wir einmal den Tukey HSD Test nachvollziehen. Dafür hier nochmal die Formel, die wir dann mit den entsprechenden Werten ausfüllen müssen. Wir beginnen mit dem q-Wert und erhalten den MSE Wert aus einer ANOVA.
\[ HSD = q_{\alpha=5\%, k, n-k} \cdot \sqrt{\tfrac{MSE}{n}} \]
Für die semihändische Berechnung des Tukey HSD Test brauchen wir erstmal die Werte für die gesamte Fallzahl in dem Datensatz \(N\), dann noch die Anzahl an Behandlungsgruppen \(k\) und abschließend die Fallzahl pro Gruppe \(n\). Ich nutze hier dann den Datensatz fac1_tbl mit der Sprungweite von 21 Flöhen von drei Tierrassen mit jeweils sieben Beobachtungen pro Gruppe. Dann geben wir das Ganze einmal bei R ein.
R Code [zeigen / verbergen]
N <- 21
k <- 3
n <- 21 / 3Die Funktion qtukey() gibt uns den q-Wert anhand des Signifikanzniveaus \(1 - \alpha\) sowie der Anzahl an Gruppen \(k\) und der dem Freiheitsgrad \(N-k\) wieder.
R Code [zeigen / verbergen]
qtukey(p = 0.95, nmeans = k, df = N - k)[1] 3.609304Dann brauchen wir noch den Wert für die Streuung \(MSE\). Den MSE Wert könnten wir auch händisch berechnen, aber normalerweise nutzen wir auch die ANOVA um an den Wert zu gelangen. Daher hier einmal die ANOVA und wir lesen den Wert für MSE in der Ergebnistabelle ab.
R Code [zeigen / verbergen]
fac1_av <- aov(jump_length ~ animal, data = fac1_tbl)
summary(fac1_av) Df Sum Sq Mean Sq F value Pr(>F)
animal 2 74.68 37.34 11.89 0.000511 ***
Residuals 18 56.53 3.14
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Nun wissen wir den Wert für \(MSE\) mit \(3.14\) aus der Tabelle der einfaktoriellen ANOVA. Dann können wir auch schon den HSD Wert anhand der Formel berechnen in dem wir die Werte einsetzen.
R Code [zeigen / verbergen]
hsd <- 3.61 * sqrt(3.14 / 7)
hsd[1] 2.417815Am Ende müssen wir dann die Mittelwertsdifferenzen unserer Tierarten mit dem HDS Wert vergleichen. Dafür ahbe ich einmal die folgende Tabelle aufgebaut. Wichtig ist hier, dass wir mit den Beträgen der Mittelwertsdifferenz rechnen, sonst macht der Vergleich zum HDS Wert keinen Sinn. Wir erhalten also zwei signifikante Vergleiche. Die Sprungweiten der Katzenflöhe unterscheiden sich von den Sprungweiten der Fuchs- und Hundeflöhe.
| Vergleich | Mittelwertsdifferenz | HDS Testentscheidung |
|---|---|---|
| cat-dog | \(4.74 - 8.13 = -3.39\) | \(\mid-3.39\mid\; \geq 2.42 \rightarrow \mbox{signifikant}\) |
| fox-dog | \(9.16 - 8.13 = \phantom{-}1.03\) | \(\mid1.03\mid\; \geq 2.42 \rightarrow \mbox{nicht signifikant}\) |
| fox-cat | \(9.16 - 4.74 = \phantom{-}4.42\) | \(\mid4.42\mid\; \geq 2.42 \rightarrow \mbox{signifikant}\) |
Am Ende willst du das natürlich nicht händische machen sondern wir nutzen die Funktionen in R um uns die Testentscheidung auch mit einem p-Wert berechnen zu lassen. Ganz wichtig hier nochmal, wir glauben daran, dass die Varianz in allen drei Tierarten gleich ist. Wir haben Varianzhomogenität vorliegen.
Die Standardfunktion für den Tukey HDS Test ist TukeyHSD(). Wir können den Tukey HSD Test mit nur einem Faktor oder zwei Faktoren rechnen. Ich stelle hier die einfaktorielle sowie zweifaktorielle Analyse einmal vor. Am Ende zeige ich dann nochmal, wie du das Compact letter display erhälst. Hier müssen wir noch ein zusätzliches Paket nutzen. Die Funktion HSD.test() aus dem Paket {agricolae}, die du im nächsten Tab findest, gibt dir sofort das Compact letter display wieder. Der Ablauf ist aber in beiden Fällen der gleiche. Wir rechnen erst eine ANOVA mit der Funktion aov() um dann den Tukey HSD Test zu rechnen.
Einfaktorielle Analyse
Am Anfang rechnen wir erst eine einfaktorielle ANOVA mit der Funktion aov(). Wir erhalten dann alle notwendigen Informationen in dem Ausgabeobjekt für die Berechnung des Tukey HSD Test. Darüber hinaus können wir auch auch gleich schauen, ob unsere Behandlung überhaupt einen signifikanten Einfluss auf unser Outcome der Sprunglänge hat.
R Code [zeigen / verbergen]
fac1_av <- aov(jump_length ~ animal, data = fac1_tbl)
summary(fac1_av) Df Sum Sq Mean Sq F value Pr(>F)
animal 2 74.68 37.34 11.89 0.000511 ***
Residuals 18 56.53 3.14
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1An dem p-Wert sehen wir, dass wir einen signifikanten Effekt der Tierart animal auf die Sprunglänge der Flöhe vorliegen haben. Wir können jetzt einen Tukey HSD Test rechnen um rauszufinden welche der drei Tierarten sich unterscheiden. Wir erhalten dann als Ausgabe die Mittlwertsdifferenzen zusammen mit den 95% Konfidenzintervallen und den adjustierten p-Werten.
R Code [zeigen / verbergen]
tukey_fac1_obj <- TukeyHSD(fac1_av)
tukey_fac1_obj Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = jump_length ~ animal, data = fac1_tbl)
$animal
diff lwr upr p adj
cat-dog -3.385714 -5.803246 -0.9681827 0.0058404
fox-dog 1.028571 -1.388960 3.4461031 0.5346652
fox-cat 4.414286 1.996754 6.8318173 0.0005441Du erhälst immer adjustierte p-Werte aus einem Tukey HSD Test. Das muss dir klar sein. Die p-Werte kannst du dann mit dem Signifikanzniveau \(\alpha\) von 5% vergleichen. Wir sehen dass sich die Sprungweiten der Katzenflöhe von den Sprungweiten der Fuchs- und Hundeflöhe signifikant unterscheiden.
Dann kannst du noch die Funktion mulcompLetters() aus dem R Paket {mulcompView} nutzen um dir das Compact letter display wiedergeben zu lassen. Das Compact letter display kannst du dann entsprechend zu deinen Barplots ergänzen.
R Code [zeigen / verbergen]
multcompLetters(extract_p(tukey_fac1_obj$animal))cat fox dog
"a" "b" "b" Auch hier sei angemerkt, dass du dan schauen muss, ob das Compact letter display zu deinen Daten passt. Sind die Mittelwerte wirklich unterschiedlich? Kannst du die Unterschiede in den Barplots erkennen? Wenn das der Fall ist, dann spricht nichts gegen die Verwendung des Tukey HSD Test.
Zweifaktorielle Analyse
Jetzt können wir die Sache etwas kürzer machen, da wir auch in einem zweifaktoriellen Fall den gleichen Weg wie im einfaktoriellen Fall durchgehen. Wir rechnen erst eine ANOVA mit den beiden Faktoren und dem Interaktionsterm, dargestellt durch den Doppelpunkt zwischen den beiden Faktoren.
R Code [zeigen / verbergen]
fac2_av <- aov(jump_length ~ animal + site + animal:site, data = fac2_tbl)
summary(fac2_av) Df Sum Sq Mean Sq F value Pr(>F)
animal 2 171.13 85.56 25.745 1.41e-08 ***
site 1 4.21 4.21 1.268 0.26516
animal:site 2 59.10 29.55 8.891 0.00046 ***
Residuals 54 179.47 3.32
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1In diesem Fall finden wir eine signifikante Interaktion. Daher verhalten sich die Tierarten animal in den beiden Messorten in dem Faktor site nicht gleich. Die Interaktion kannst du auch in der Visualisierung der Daten in der weiter oben sehen. Für die Füchse ändert sich die Sprungweite von city zu village. Bei Hunden- und Katzenflöhen springen in der Tendenz Dorfflöhe weiter als Stadtflöhe. Wir nutzen jetzt das Modell einmal in der Funktion TukeyHSD() um uns einmal einen Tukey HSD Test berechnen zu lassen.
R Code [zeigen / verbergen]
tukey_fac2_obj <- TukeyHSD(fac2_av)
tukey_fac2_obj Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = jump_length ~ animal + site + animal:site, data = fac2_tbl)
$animal
diff lwr upr p adj
dog-cat 2.2085 0.8191476 3.597852 0.0009626
fox-cat 4.1335 2.7441476 5.522852 0.0000000
fox-dog 1.9250 0.5356476 3.314352 0.0042936
$site
diff lwr upr p adj
village-city -0.53 -1.473715 0.413715 0.2651614
$`animal:site`
diff lwr upr p adj
dog:city-cat:city 3.101 0.6922358 5.5097642 0.0046806
fox:city-cat:city 6.538 4.1292358 8.9467642 0.0000000
cat:village-cat:city 1.668 -0.7407642 4.0767642 0.3308895
dog:village-cat:city 2.984 0.5752358 5.3927642 0.0072069
fox:village-cat:city 3.397 0.9882358 5.8057642 0.0015002
fox:city-dog:city 3.437 1.0282358 5.8457642 0.0012805
cat:village-dog:city -1.433 -3.8417642 0.9757642 0.5010180
dog:village-dog:city -0.117 -2.5257642 2.2917642 0.9999910
fox:village-dog:city 0.296 -2.1127642 2.7047642 0.9991270
cat:village-fox:city -4.870 -7.2787642 -2.4612358 0.0000027
dog:village-fox:city -3.554 -5.9627642 -1.1452358 0.0008014
fox:village-fox:city -3.141 -5.5497642 -0.7322358 0.0040284
dog:village-cat:village 1.316 -1.0927642 3.7247642 0.5930304
fox:village-cat:village 1.729 -0.6797642 4.1377642 0.2923986
fox:village-dog:village 0.413 -1.9957642 2.8217642 0.9957142Wie du an der sehr langen Ausgabe sehen kannst, erhalten wir erstmal die Informationen zu der Tierart, dort sehen wir dann, dass sich alle drei Sprungweiten der Tierarten voneinander unterscheiden. Dann erhalten wir die Information über den Ort oder eben den zweiten Faktor. Am Ende nochmal sehr detailliert alle Interaktionen aufgeschlüsselt. Leider ist die Tabelle dann sehr schlecht zu lesen, aber hier siehst du dann welche Faktorkombination dann signifikant ist. Wenn du eine signifikante Interaktion vorliegen hast, dann kannst du keine pauschale Aussage über die Sprungweiten der Tierarten machen. Es kommt eben immer drauf an, welches Level du im zweiten Faktor betrachtest.
Am Ende wollen wir dann doch noch das Compact letter display haben. Ich wähle hier einmal die Gruppe der Tierarten aus. Du kannst das auch für die anderen Faktoren machen, aber hier einmal zur Demonstration. Wir sehen, dass sich alle Tierarten in der Sprungweite unterscheiden, keine Tierart hat den gleichen Buchstaben. Wenn du willst, kannst du dir natürlich auch andere Buchstaben rausziehen.
R Code [zeigen / verbergen]
multcompLetters(extract_p(tukey_fac2_obj$animal))dog fox cat
"a" "b" "c" Hier nochmal Achtung, die Interaktion wird natürlich nicht berücksichtigt. Im Zweifel dann doch lieber {emmeans} nutzen. Du findest die Anwendung im folgenden Tab. Allgemeine Aussagen zur Interaktion kann ich immer schwer treffen, es hängt sehr von der wissenschaftlichen Fragestellung und den Daten ab.
Wir können auch den Tukey HSD Test mit {emmeans} rechnen, wenn wir nichts an der Standardeingabe ändern. Dann nutzen wir nämlich die Adjustierung nach Tukey und somit rechnen wir faktisch einen Tukey HSD Test. Im einfaktoriellen Fall sind die p-Werte dann auch identisch zu der Funktion TukeyHSD(). Das ist aber nur der Fall wenn wir wirklich gleiche Fallzahlen in den Gruppen haben und der Algorithmus von {emmeans} ist natürlich nicht identisch mit der Berechnung eines Tukey HSD Tests.
Einfaktorielle Analyse
Auch hier brauchen wir erstmal das Modell für unseren Tukey HSD Test mit {emmeans}. Dafür nutze ich auch hier wieder die Funktion aov().
R Code [zeigen / verbergen]
fac1_av <- aov(jump_length ~ animal, data = fac1_tbl)
summary(fac1_av) Df Sum Sq Mean Sq F value Pr(>F)
animal 2 74.68 37.34 11.89 0.000511 ***
Residuals 18 56.53 3.14
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wenn du alle paarweisen Vergleiche rechnen willst, dann nutzt du die Funktion emmeans() und anschließend die Funktion contrast(), die dir dann alle paarweisen Vergleiche wiedergibt. In einem balancierten Design unter der Annahme von Varianzhomogenität kommt hier dann auch das gleiche wie bei dem Tukey HSD Test raus. Hier sind nur die Vorzeichen im Vergleich zum TukeyHSD() gedreht, da wir hier nicht cat - dog rechnen sondern alles einmal gedreht.
R Code [zeigen / verbergen]
fac1_av |>
emmeans(~ animal) |>
contrast(method = "pairwise") contrast estimate SE df t.ratio p.value
dog - cat 3.39 0.947 18 3.574 0.0058
dog - fox -1.03 0.947 18 -1.086 0.5347
cat - fox -4.41 0.947 18 -4.660 0.0005
P value adjustment: tukey method for comparing a family of 3 estimates Abschließend können wir uns dann auch noch das Compact letter display wiedergeben lassen. Auch hier haben wir dann das gleiche Ergebnis vorliegen.
R Code [zeigen / verbergen]
fac1_av |>
emmeans(~ animal) |>
cld(Letters = letters) animal emmean SE df lower.CL upper.CL .group
cat 4.74 0.67 18 3.34 6.15 a
dog 8.13 0.67 18 6.72 9.54 b
fox 9.16 0.67 18 7.75 10.56 b
Confidence level used: 0.95
P value adjustment: tukey method for comparing a family of 3 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Zweifaktorielle Analyse
Im zweifaktoriellen Fall müssen wir wiederum erstmal die ANOVA rechnen um ein Modell vorliegen zu haben. Auf diesem Modell können wir dann die Funktionen von {emmeans} rechnen. Der Vorteil liegt es jetzt der flexibeln Auswertung der Interaktion animal:site. Mehr dazu dann im obigen Abschnitt zu {emmeans}.
R Code [zeigen / verbergen]
fac2_av <- aov(jump_length ~ animal + site + animal:site, data = fac2_tbl)
summary(fac2_av) Df Sum Sq Mean Sq F value Pr(>F)
animal 2 171.13 85.56 25.745 1.41e-08 ***
site 1 4.21 4.21 1.268 0.26516
animal:site 2 59.10 29.55 8.891 0.00046 ***
Residuals 54 179.47 3.32
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Hier rechne ich jetzt eine kombinierte Analyse für die beiden Faktoren animal und site. Wenn du die Analysen getrennt rechnen möchtest dann ersetze den Stern * durch einen Strich |. Mehr dazu ebenfalls weiter oben im Abschnitt zu {emmeans}. Im Weiteren rechne ich dann alle paarweisen Vergleiche und zwar zwischen allen Faktorkombinationen. Dann möchte ich mir das Ergebnis noch kompakt wiedergeben lassen.
R Code [zeigen / verbergen]
fac2_av |>
emmeans(~ animal * site) |>
contrast(method = "pairwise", simple = "each", combine = TRUE) site animal contrast estimate SE df t.ratio p.value
city . cat - dog -3.101 0.815 54 -3.804 0.0033
city . cat - fox -6.538 0.815 54 -8.019 <.0001
city . dog - fox -3.437 0.815 54 -4.216 0.0009
village . cat - dog -1.316 0.815 54 -1.614 1.0000
village . cat - fox -1.729 0.815 54 -2.121 0.3470
village . dog - fox -0.413 0.815 54 -0.507 1.0000
. cat city - village -1.668 0.815 54 -2.046 0.4109
. dog city - village 0.117 0.815 54 0.144 1.0000
. fox city - village 3.141 0.815 54 3.853 0.0028
P value adjustment: bonferroni method for 9 tests Ich kann mir dann auch über alle Faktorkombinationen das Compact letter display wiedergeben lassen. Hier ist jetzt der Vorteil, dass ich wirklich die Buchstaben für jeden Messort site und die jeweilige Tierrasse animal habe.
R Code [zeigen / verbergen]
fac2_av |>
emmeans(~ animal * site) |>
cld(Letters = letters) animal site emmean SE df lower.CL upper.CL .group
cat city 13.6 0.576 54 12.4 14.7 a
cat village 15.2 0.576 54 14.1 16.4 ab
dog village 16.6 0.576 54 15.4 17.7 b
dog city 16.7 0.576 54 15.5 17.8 b
fox village 17.0 0.576 54 15.8 18.1 b
fox city 20.1 0.576 54 19.0 21.3 c
Confidence level used: 0.95
P value adjustment: tukey method for comparing a family of 6 estimates
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Beachte, dass über die gleiche Varianz angenommen wird. das kann sein, dass es nicht passt und daher schaue dir dann einmal oben {emmeans} mit Varianzheterogenität an.
Die Funktion HSD.test() kann nur ein einfaktorielles Modell rechnen und ignoriert weitere Faktoren oder Interaktionsterme im aov() Modell. Du erhälst zwar immer eine Ausgabe, aber nur als einfaktorielle Analyse. Unabhängig von dem Modell was du in die Funktion HSD.test() reinsteckst! Und ohne weitere Warnung.
Eine zweite Variante den Tukey HSD Test in R durchzuführen ist die Funktion HSD.test() aus dem R Paket {agricolae}. Persönlich entwickle ich so langsam eine Aversion gegen das Paket, da ich selten eine so rundimentäre und lustlose Hilfe für die Funktion gesehen habe wie in {agricolae}. Prinzipiell haben wir die gleichen Möglichkeiten wie auch mit dem Tukey HSD Test für ein einfaktorielles Versuchsdesign. Wir nutzen auch erste eine ANOVA um uns alle wichtigen statistischen Maßzahlen berechnen zu lassen und dann können wir mit denen den Tukey HSD Test durchführen. Leider erhalten wir keine p-Werte. Was auch irgendwie irre ist. Dafür dann aber das Compact letter display ohne einen weiteren Schritt.
Einfaktorielle Analyse
Am Anfang rechnen wir auch hier eine einfaktorielle ANOVA mit der Funktion aov(). Wir erhalten dann alle notwendigen Informationen in dem Ausgabeobjekt für die Berechnung des Tukey HSD Test. Darüber hinaus können wir auch auch gleich schauen, ob unsere Behandlung überhaupt einen signifikanten Einfluss auf unser Outcome der Sprunglänge hat.
R Code [zeigen / verbergen]
fac1_av <- aov(jump_length ~ animal, data = fac1_tbl)
summary(fac1_av) Df Sum Sq Mean Sq F value Pr(>F)
animal 2 74.68 37.34 11.89 0.000511 ***
Residuals 18 56.53 3.14
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1An dem p-Wert sehen wir, dass wir einen signifikanten Effekt der Tierart animal auf die Sprunglänge der Flöhe vorliegen haben. Wir können jetzt einen Tukey HSD Test rechnen um rauszufinden welche der drei Tierarten sich unterscheiden. Wir erhalten dann als Ausgabe die Mittelwerte ohne p-Werte und müssten uns sogar die Mittelwertsdifferenzen selber berechnen. Keine Ahnung was das soll. Dafür dann aber das Compact letter display, was ja auch irgendwie reicht.
R Code [zeigen / verbergen]
tukey_fac1_obj <- HSD.test(fac1_av, trt = 'animal')
tukey_fac1_obj$statistics
MSerror Df Mean CV MSD
3.140476 18 7.342857 24.13419 2.417532
$parameters
test name.t ntr StudentizedRange alpha
Tukey animal 3 3.609304 0.05
$means
jump_length std r se Min Max Q25 Q50 Q75
cat 4.742857 1.901628 7 0.6698055 2.2 7.9 3.65 4.3 5.75
dog 8.128571 2.144539 7 0.6698055 5.6 11.8 6.65 8.2 9.00
fox 9.157143 1.098267 7 0.6698055 7.7 10.6 8.35 9.1 10.00
$comparison
NULL
$groups
jump_length groups
fox 9.157143 a
dog 8.128571 a
cat 4.742857 b
attr(,"class")
[1] "group"Wenn du keinen p-Werte haben möchtest sondern nur das Compact letter display, dann macht es dir die Funktion HSD.test() etwas leichter. Dann brauchst du dir nicht nochmal eine Funktion zusätzlich laden. Wenn du p-Werte brauchst, dann stehst du hier im Regen. Dann nutze bitte die Funktion TukesHSD() im vorherigen Tab.
Zweifaktorielle Analyse
Eine zweifaktorielle Analyse ist in der Funktion HSD.test() nicht möglich. Ein zweifaktorielles Modell wird wie ein einfaktorielles Modell behandelt und damit der zweite Faktor sowie der Interaktionsterm von der Funktion HSD.test() ignoriert. Du erhälst keine Warnung sondern eben das Ergebnis einer einfaktoriellen Analyse wiedergeben. Ich bin immer noch sprachlos was das soll.
44.8 Weitere Pfade
44.8.1 Paarweise Tests
Wenn du nur eine einfaktorielle Analyse rechnen willst, dann kann man natürlich auch die einfachste aller Arten als Post-hoc Test rechnen. Du rechnest nämlich alle paarweisen Vergleiche mit einem t-Test oder aber mit einem Wilxonon Test. Da du dann natürlich sehr viele Tests rechnen müsstest, gibt es auch eine Funktion in R, die das für dich übernimmt. Die Funktion pairwise.*.test() kann nämlich verschiedene Gruppentests einmal automatisieren über alle möglichen Vergleiche.
Die Funktionen pairwise.*.test() sind etwas älter und deshalb etwas sperrig zu nutzen. Du gibt hier kein Modell an sondern musst erst das \(y\) als einen Vektor und dann die Gruppenvariable \(x\) als einen Vektor der Funktion übergeben. Dann entscheidest du dich noch für die Methode der Adjustierung der p-Werte und ob du Vrainzheterogenität vorliegen hast. Ich habe mich mit der Option pool.sd = FALSE für Varianzheterogenität und damit gegen Varianzhomogenität entschieden. Die Annahme ist hier, dass unser Outcome \(y\) näherungsweise normalverteilt ist.
R Code [zeigen / verbergen]
pairwise.t.test(fac1_tbl$jump_length, fac1_tbl$animal,
p.adjust.method = "bonferroni",
pool.sd = FALSE)
Pairwise comparisons using t tests with non-pooled SD
data: fac1_tbl$jump_length and fac1_tbl$animal
dog cat
cat 0.0267 -
fox 0.8642 0.0012
P value adjustment method: bonferroni Wenn du dir bei deinem \(y\) nicht so sicher bist, was die Normalverteilung angeht, dann kannst du auch einen paarweisen Wilcoxon Test rechnen. Dafür bietet sich die folgende Funktion an.
R Code [zeigen / verbergen]
pairwise.wilcox.test(fac1_tbl$jump_length, fac1_tbl$animal,
p.adjust.method = "bonferroni")
Pairwise comparisons using Wilcoxon rank sum exact test
data: fac1_tbl$jump_length and fac1_tbl$animal
dog cat
cat 0.0332 -
fox 0.8307 0.0035
P value adjustment method: bonferroni Am Ende kannst du dir dann auch mit folgendem Code das Compact letter display wiedergeben lassen. Wegen der etwas sperrigen Struktur der Ausgabe der Funktion pairwise.*.test() müssen wir hier etwas mehr arbeiten um an das Compact letter display zu kommen.
R Code [zeigen / verbergen]
pairwise.t.test(fac1_tbl$jump_length, fac1_tbl$animal,
p.adjust.method = "bonferroni") |>
extract2("p.value") |>
fullPTable() |>
multcompLetters()dog cat fox
"a" "b" "a" Am Ende bieten beide Funktionen einen schnellen Weg ein einfaktorielles Design auszuwerten. Ja, es ist etwas ruppig und am Ende vermutlich auch nicht so schön, aber für eine Abschlussarbeit mit Fokus jenseits der statistischen Auswertung mag es Sinn machen.
44.8.2 Games Howell Test
Der Games Howell Test ist eine Alternative zu dem Paket {multcomp} und dem Paket {emmeans} für ein einfaktorielles Design. Wir können auch ein zweifakorielles Design rechnen, dann würden wir aber die Analyse getrennt für den zweiten Faktor durchführen. Gemeinsam geht dann nur in {emmeans}. Wir nutzen den Games Howell Test, wenn die Annahme der Homogenität der Varianzen, der zum Vergleich aller möglichen Kombinationen von Gruppenunterschieden verwendet wird, verletzt ist. Dieser Post-Hoc-Test liefert Konfidenzintervalle für die Unterschiede zwischen den Gruppenmitteln und zeigt, ob die Unterschiede statistisch signifikant sind. Der Test basiert auf der Welch’schen Freiheitsgradkorrektur und adjustiert die \(p\)-Werte. Der Test vergleicht also die Differenz zwischen den einzelnen Mittelwertpaaren mit einer Adjustierung für den Mehrfachtest. Es besteht also keine Notwendigkeit, zusätzliche p-Wert-Korrekturen vorzunehmen.
- Varianzheterogenität
-
Es ist wichtig zu wissen, dass der Games Howell Test faktisch das Äquivalent zum Welch t-Test ist und daher Varianzheterogenität annimmt. Du kannst den Games Howell Test nicht unter der Annahme von Varianzhomogenität rechnen. Das wäre dann der Tukey HSD Test, der ja auf der ANOVA basiert und die ANOVA Varianzhomogenität annimmt. Prinzipiell kann es dir dann passieren, das die Ergebnisse eines Games Howell Test nicht mehr mit denen einer vorgeschalteten ANOVA zusammenpassen.
- Adjustierung für multiple Vergleiche
-
Der Games Howell Test adjustiert für die \(\alpha\)-Inflation bei multiplen Vergleichen. Wir müssen da auch nichts weiter machen um die Adjustierung durchzuführen. Auf der anderen Seite können wir die Adjustierung für multiple Vergleiche aber auch nicht ausschalten. Du erhälst immer adjustierte p-Werte aus einem Games Howell Test. Wenn du das nicht möchtest, dann nutze einfach das R Paket
{emmeans}. - Mögliche multiple Vergleiche
-
Wir können immer nur alle Gruppen mit allen anderen Gruppen vergleichen. Wir rechnen also einen all pair Vergleich. Wenn du zum Beispiel nur die Behandlungsgruppen zur Kontrolle vergleichen willst, aber nicht untereinander, dann ist das nicht mit dem Games Howell Test möglich. Dafür musst du dann das R Paket
{ememans}oder für noch komplexere Gruppenvergleiche das R Paket{multcomp}nutzen.
Für den Games Howell Test aus dem Paket {rstatix} müssen wir kein lineares Modell fitten. Wir schreiben einfach die wie in einem t-Test das Outcome und den Faktor mit den Gruppenleveln in die Funktion games_howell_test(). Es gibt sehr wenige Implemtierungen des Games Howell Test, da er nicht so weit genutzt wird. Häufig will man dann doch eine ANOVA rechnen und dann den Tukey HSD Test anschließen. Wenn der Games Howell Test passt, dann passt ja meist eine ANOVA mit der Annahme von Varianzhomogenität nicht. Ein Problem mit der Fallzahl bleibt aber, so dass wir mindestens sechs Beobachtungen haben.
“However, the smaller the number of samples in each group, the [Games Howell Post-hoc Tests] is more tolerant to the type I error control. Thus, this method can be applied when the number of samples is six or more.” — Games Howell Post-hoc Tests in
{rstatix}
Ich zeige jetzt einmal wie wir die einfaktorielle und dann die zweifaktorielle Analyse eines Games Howell Test in R rechnen. Ich habe mich hier gegen die händisch Berechnung entschieden, da wir hier dann sehr viel rechnen müssen, was eigentlich dann der Welch t-Test ist. Wenn dich die Formeln nochmal gesondert interessieren dann findest du die im Tutorium Games-Howell Post-Hoc Test. Hier lasse ich dann gleich ganz bewusst eine ANOVA weg und starte gleich mit dem paarweisen Vergleich.
Einfaktorielle Analyse
Wenn wir den Games Howell Test rechnen wollen dann nutzen wir die Funktion games_howell_test() aus dem R Paket {rstatix}. Die Funktion benötigt kein ANOVA Modell, was ja wenig Sinn machen würde. Wir bräuchten für die ANOVA homogene Varianzen und der Games Howell Test ist ja direkt für heterogene Varianzen entwickelt worden. Daher verzichten wir auch grundsätzlich auf eine vorgestellte ANOVA, wenn wir einen Games Howell Test rechnen.
R Code [zeigen / verbergen]
ght_fac1_obj <- games_howell_test(jump_length ~ animal, data = fac1_tbl) Mit dem Objekt des Games Howell Test können wir uns dann die statistischen Maßzahlen wiedergeben lassen.
Die p-Werte finden sich dann direkt in dem Objekt der Ausgabe der Funktion games_howell_test(). Da müssen wir nicht viel machen. Ich habe hier nochmal die p-Werte mit der Funktion pvalue() einmal etwas angepasst. Das musst du natürlich nicht machen. Du erhälst immer adjustierte p-Werte. Die Adjustierung für multiple Vergleiche lässt sich nicht ausschalten.
R Code [zeigen / verbergen]
ght_fac1_obj |>
mutate(p.adj = pvalue(p.adj))# A tibble: 3 × 8
.y. group1 group2 estimate conf.low conf.high p.adj p.adj.signif
<chr> <chr> <chr> <dbl> <dbl> <dbl> <chr> <chr>
1 jump_length dog cat -3.39 -6.28 -0.490 0.022 *
2 jump_length dog fox 1.03 -1.52 3.57 0.521 ns
3 jump_length cat fox 4.41 2.12 6.71 0.001 *** Das Ergebnis ähnelt dem Tukey HSD Test. Nur wenn wir wirklich starke heterogene Varianzen vorliegen haben, werden wir wirklich einen Unterschied zwischen den Tests sehen. Häufig sind sich der Tukey HSD Test und der Games Howell Test ähnlich in den Ergebnissen.
Für das Compact letter display aus dem Games Howell Test müssen wir uns einmal etwas strecken, da wir erst die Kontraste bauen müssen, die die Funktion multcompLetters() braucht. Sonst ist der Rest dann relativ einfach.
R Code [zeigen / verbergen]
ght_fac1_obj |>
mutate(contrast = str_c(group1, "-", group2)) |>
pull(p.adj, contrast) |>
multcompLetters() dog cat fox
"a" "b" "a" Auch hier sehen wir ähnliche Ergebnisse. Was uns aber auch nicht so überrascht. Wenn die Varianzen eher homogen sind, dann macht der Games Howell Test keinen großen Unterschied zum Tukey HSD Test.
In der folgenden Abbildung sind die simultanen 95% Konfidenzintervalle nochmal in einem ggplot visualisiert. Die Kontraste und die Position hängen von dem Faktorlevel ab. Auch hier müssen wir uns erst die Vergleiche zusammenkleben, damit die Konfidenzintervalle richtig darstellbar sind.
R Code [zeigen / verbergen]
ght_fac1_ci_obj <- ght_fac1_obj |>
mutate(contrast = str_c(group1, "-", group2))Dann können wir aber auch schon die 95% Konfidenzintervalle einmal darstellen. Da wir hier Mittelwerte vergleichen, ist die die Signifikanzschwelle die Null. Wenn die Null mit im Konfidenzintervall enthalten ist können wir die Nullhypothese nicht ablehnen.
R Code [zeigen / verbergen]
ggplot(ght_fac1_ci_obj, aes(contrast, y=estimate, ymin=conf.low, ymax=conf.high)) +
geom_hline(yintercept=0, linetype="11", colour="grey60") +
geom_errorbar(width=0.1, position = position_dodge(0.5)) +
geom_point(position = position_dodge(0.5)) +
coord_flip() +
theme_classic()Die Entscheidungen nach den 95% Konfidenzintervallen sind die gleichen wie nach dem \(p\)-Wert. Ob du die Konfidenzintervalle brauchst, hängt dann von deiner Fragestellung in deiner Abschlussarbeit ab.
Zweifaktorielle Analyse
Die Funktion games_howell_test() aus dem R Paket {rstatix} kann keinen zweifaktoriellen Vergleich über die Faktoren des zweiten Faktors rechnen. Wenn du das möchtest, dann nutze bitte das R Paket {emmeans}. Wir rechnen hier eine einfaktorielle Analyse getrennt für jedes Level des zweiten Faktors. In unserem konkreten Fall rechnen wir also eine einfaktorielle Analyse für den Vergleich der Tierrassen einmal für das Level city und einmal für das Level village für den Faktor site. Wir erhalten dann jeweils die getrennten p-Werte sowie Compact letter display und Konfidenzintervalle. Dazu nutzen wir die Funktion group_by().
R Code [zeigen / verbergen]
ght_fac2_obj <- fac2_tbl |>
group_by(site) |>
games_howell_test(jump_length ~ animal) Dan können wir uns auch schon wie in dem einfaktorielle Fall die statistischen Maßzahlen wiedergeben lassen. Die p-Werte sind hier nicht so das Problem, etwas frickeliger wird es dann bei dem Compact letter display. Hier kann ich dann nur raten gleich {emmeans} zu nutzen.
Die adjustierten p-Werte lassen sich dann direkt aus dem Objekt der Funktion wiedergeben. Hier mache ich mir noch die Freude einmal die p-Werte etwas anders darzustellen, dass musst du aber nicht unbedingt machen. Wie immer erhalten wir nur adjustierte p-Werte, wir können die Adjustierung nicht ausstellen.
R Code [zeigen / verbergen]
ght_fac2_obj |>
mutate(p.adj = pvalue(p.adj))# A tibble: 6 × 9
site .y. group1 group2 estimate conf.low conf.high p.adj p.adj.signif
<fct> <chr> <chr> <chr> <dbl> <dbl> <dbl> <chr> <chr>
1 city jump_len… cat dog 3.10 0.725 5.48 0.010 **
2 city jump_len… cat fox 6.54 4.73 8.35 <0.0… ****
3 city jump_len… dog fox 3.44 1.33 5.55 0.002 **
4 village jump_len… cat dog 1.32 -0.882 3.51 0.290 ns
5 village jump_len… cat fox 1.73 -0.645 4.10 0.178 ns
6 village jump_len… dog fox 0.413 -1.31 2.14 0.813 ns Das etwas nervige ist jetzt, dass wir die p-Werte eben getrennt vorliegen haben. Wir können also nicht Tierrassen aus der Stadt mit den Ergebnissen der Tierrassen aus dem Dorf vergleichen. Dafür wurde übriegens auch nicht adjustiert. Die Adjustierung ist auch nur getrennt für die Level des zweiten Faktors. Am Ende doch etwas unbefriedigend.
Für das Compact letter display müssen wir uns ganz schön strecken. Das hat damit zu tun, dass wir eben die Analyse getrennt für den zweiten Faktor durchführen und daher auch das Comapct letter display getrennt für den zweiten Faktor bauen müssen. Daher nutze ich hier die Funktion map() um hier etwas fortgeschrittener zu programmieren.
R Code [zeigen / verbergen]
ght_fac2_obj |>
mutate(contrast = str_c(group1, "-", group2)) |>
split(~ site) |>
map(pull, p.adj, contrast) |>
map(~multcompLetters(.x)$Letters) |>
bind_rows(.id = "site") # A tibble: 2 × 4
site cat dog fox
<chr> <chr> <chr> <chr>
1 city a b c
2 village a a a Wir immer, dass muss nicht so kompliziert mit allen Nachteilen der getrennten Auswertung sein. Das R Paket {emmeans} kann es schneller, einfacher und noch besser. Daher ist das hier eher eine Demonstration als eine Empfehlung.
In der folgenden Abbildung sind die simultanen 95% Konfidenzintervalle nochmal in einem ggplot visualisiert. Die Kontraste und die Position hängen von dem Faktorlevel ab. Auch hier müssen wir uns erst die Vergleiche zusammenkleben, damit die Konfidenzintervalle richtig darstellbar sind.
R Code [zeigen / verbergen]
ght_fac2_ci_obj <- ght_fac2_obj |>
mutate(contrast = str_c(group1, "-", group2))Eigentlich ist es für die Konfidenzintervalle etwas einfacher, nur haben wir hier auch das Problem, dass eigentlich nur das Signifikanzniveau \(\alpha\) für jedes Level des zweiten Faktors eingehalten wird. Deshalb eine in sich schwer zu interpretierende Abbildung.
R Code [zeigen / verbergen]
ggplot(ght_fac2_ci_obj, aes(contrast, y=estimate, ymin=conf.low, ymax=conf.high,
color = site, group = site)) +
geom_hline(yintercept=0, linetype="11", colour="grey60") +
geom_errorbar(width=0.1, position = position_dodge(0.5)) +
geom_point(position = position_dodge(0.5)) +
scale_color_okabeito() +
coord_flip() +
theme_classic()Die Entscheidungen nach den 95% Konfidenzintervallen sind die gleichen wie nach dem \(p\)-Wert. Da wir hier es mit einem Mittelwertsvergleich zu tun haben, ist die Entscheidung gegen die Nullhypothese zu treffen wenn die 0 im Konfidenzintervall ist. Abgesehen von der etwas wirren Adjustierung durch die getrennte Analyse.
44.8.3 R Paket {multcomp}
Das Paket {multcomp} kann beliebige faktorielle Modelle berechnen. Das einfaktorielle Modell ist hierbei relativ einfach durchzuführen und die Stärke liegt hier auch in der Flexibiltät der möglichen Vergleiche oder auch Kontrast genannt. Wenn du ein zweifaktorielles Modell vorliegen hast, geht es auch mit {multcomp}, aber hier musst du dann mehr selber machen damit es gut wird. Das Paket {emmeans} ist hier besser in der Bedienung.
Der große Vorteil von {multcomp} liegt in der möglichen Auswahl an komplexen Mittelwertsvergleichen oder auch Mittelwertskontrasten. Das Wort Kontrast steht hier für die Art und Weise wie wir verschiedene Mittelwerte miteinander vergleichen wollen. Daher ist der Fokus auch eher auf der einfaktoriellen als auf der mehrfaktoriellen Analyse. Die Fokus des Paketes liegt daher auch auf der Erstellung der 95% Konfidenzintervalle und deren Darstellung. Wenn dich die 95% Konfidenzintervalle nicht primär interessieren und du auch eigentlich nur einen all-pair Vergleich rechnen willst, dann ist das R Paket {emmeans} auch wieder die einfachere Variante für dich.
Ein Kontrast teilt uns mit, welche Mittelwert von welchem anderem Mittelwert abgezogen werden soll. Oder eben, welche Gruppen miteinander vergleichen werden sollen. Nehmen wir einmal an, wir wollen die Sprungweite der Hundeflöhe mit der Sprungweite der Katzenflöhe vergleichen. Dazu berechnen wir dann die beiden Mittelwerte der jeweiligen Sprungweiten. Wenn wir uns nun einen Kontrast bauen, sagen wir nichts anders aus, welcher Mittelwert von welchen Mittelwert abgezogen werden soll. Im Folgenden mal ein beispielhafter Kontrast \(cat-dog\) für den Mittelwertsvergleich \(\bar{y}_{cat} - \bar{y}_{dog}\).
\[ \matrix{ ~ & cat & dog \\ cat - dog & 1 & -1 } \] Wir setzen den Hund auf \(-1\) und die Katze auf \(1\), da wir den Mittelwert der Hunde vom Mittelwert der Katzen abziehen wollen. Jetzt sieht das erstmal von kompliziert aus wird aber praktisch, wenn wir noch den Fuchs mit dazunehmen.
\[ \matrix{ ~ & cat & dog & fox \\ cat - dog & 1 & -1 & 0 \\ fox - dog & 0 & -1 & 1 \\ fox - cat & -1 & 0 & 1 } \]
Jetzt können wir nämlich den all-pair Vergleich durch eine Matrix abbilden. Wenn ein Mittelwert nicht in den Vergleich soll, dann erhält die Gruppe eine \(0\). Die zu vergleichenden Gruppen erhalten vereinfacht erstmal eine \(1\) oder \(-1\). Diesen all-pair Vergleich nennen wir auch gerne Tukey Kontrast genannt. Leider hat Tukey hier nichts mit dem Tukey HSD Test zu tun.
Ein weiterer oft genutzter Kontrast ist der many-to-one Kontrast oder auch Dunnett Kontrast genannt. Hier vergleichen wir alle Gruppen zu einer Gruppe. Meistens alle Gruppen zu einer Kontrolle.
\[ \matrix{ ~ & cat & dog & fox \\ cat - dog & -1 & 1 & 0 \\ cat - fox & -1 & 0 & 1 } \]
Der eigentliche Witz des Kontrasttest ist jetzt, dass wir nicht nur \(-1\) oder \(1\) eintragen können. Zwar muss die Summe der Werte für einen Kontrast Null sein, wir können aber auch andere Zahlen eintragen. So zum Beispiel \(0.5\) und \(0.5\) für zwei Gruppen. Dann vergleichen wir die gemittelten Mittelwerte zweier Gruppen mit einer anderen Gruppe.
Der Dunnett Kontrast vergleicht einen Mittwelwert gegen die Mittelwerte der anderen Gruppen. Dabei muss dann eine Gruppe als Kontrolle mit der Option base gewählt werden. Ich habe mich hier für die zweite Gruppe entschieden.
R Code [zeigen / verbergen]
contrMat(n = c(cat = 5, dog = 5, fox = 5, cow = 5, ape = 5, bee = 5),
type = c("Changepoint"), base = 2)
Multiple Comparisons of Means: Changepoint Contrasts
cat dog fox cow ape bee
C 1 -1.0000 0.2000 0.2000 0.2000 0.2000 0.2000
C 2 -0.5000 -0.5000 0.2500 0.2500 0.2500 0.2500
C 3 -0.3333 -0.3333 -0.3333 0.3333 0.3333 0.3333
C 4 -0.2500 -0.2500 -0.2500 -0.2500 0.5000 0.5000
C 5 -0.2000 -0.2000 -0.2000 -0.2000 -0.2000 1.0000Der Changepoint Kontrast vergleicht ein laufendes Mittel. So wird erst der erste Mittelwert der ersten Gruppe gegen die gemittelten Mittelwerte der restlichen Gruppen verglichen. Dann werden die ersten beiden Gruppen gegen den Rest vergleichen. Das machen wir dann so lange, bis wir den letzten Mittelwert gegen das Mittel der vorherigen Gruppen vergleichen.
R Code [zeigen / verbergen]
contrMat(n = c(cat = 5, dog = 5, fox = 5, cow = 5, ape = 5, bee = 5),
type = c("Changepoint"))
Multiple Comparisons of Means: Changepoint Contrasts
cat dog fox cow ape bee
C 1 -1.0000 0.2000 0.2000 0.2000 0.2000 0.2000
C 2 -0.5000 -0.5000 0.2500 0.2500 0.2500 0.2500
C 3 -0.3333 -0.3333 -0.3333 0.3333 0.3333 0.3333
C 4 -0.2500 -0.2500 -0.2500 -0.2500 0.5000 0.5000
C 5 -0.2000 -0.2000 -0.2000 -0.2000 -0.2000 1.0000Als letztes Beispiel noch den AVE Kontrast oder auch Average Kontrast. Hier wird dann jeder Mittelwert gegen das Mittel der anderen Gruppen verglichen. Das ist jetzt nicht der Anwendungsfall, den du immer mal brauchen wirst, aber manchmal gut zu wissen, dass es geht.
R Code [zeigen / verbergen]
contrMat(n = c(cat = 5, dog = 5, fox = 5, cow = 5, ape = 5, bee = 5),
type = c("AVE"))
Multiple Comparisons of Means: AVE Contrasts
cat dog fox cow ape bee
C 1 1.0 -0.2 -0.2 -0.2 -0.2 -0.2
C 2 -0.2 1.0 -0.2 -0.2 -0.2 -0.2
C 3 -0.2 -0.2 1.0 -0.2 -0.2 -0.2
C 4 -0.2 -0.2 -0.2 1.0 -0.2 -0.2
C 5 -0.2 -0.2 -0.2 -0.2 1.0 -0.2
C 6 -0.2 -0.2 -0.2 -0.2 -0.2 1.0Einfaktorielle Analyse
Im Zentrum von {multcomp} steht die einfaktorielle Analyse. Das muss dir zuerst bewusst sein. Ja, es gehen auch mehrere Faktoren oder ein komplexeres Modell, aber dann wird es mit den Kontrasten schwieriger, was ja wiederum die Stärke von {multcomp} ist. Du kannst ein belibiges Modell berechnen und dieses dann als Grundlage für die zentrale Funktion glht() in {multcomp} nutzen. Ich rechne hier einmal ein lineares Modell um die Sprunglängen der Hunde- und Katzenflöhe miteinander zu vergleichen.
R Code [zeigen / verbergen]
fac1_fit <- lm(jump_length ~ animal, data = fac1_tbl)Jetzt kommt der etwas sperrige Aufruf der Funktion glht() um den multiplen Vergleich zu rechnen. Warum ist der Aufruf so sperrig? Zum einen müssen wir erst das Modell angeben, was wir nutzen wollen. Dann brauchen wir aber noch die Variable, die wir dann mit einem Kontrast vergleichen wollen. Das Ganze spezifizieren wir dann in der Option linfct. Du musst dann bei dir im Prinzip nur animal gegen deinen Variablennamen austauschen.
Wir können auch hier für eine mögliche Varianzheterogenität anpassen und entsprechend eine Varianzschätzer mit der Option vcov. wählen. Ich habe hier den Standard gewählt. Am Ende dieses Kapitels kannst du dann nochmal über andere Varianzschätzer lesen.
R Code [zeigen / verbergen]
multcomp_fac1_obj <- glht(fac1_fit, linfct = mcp(animal = "Tukey"),
vcov. = sandwich::vcovHC) Leider sehen wir die Anpassung für die Varianzheterogenität nicht in der Ausgabe von glht, was immer etwas nervig ist. Deshalb musst du nochmal gucken, was die Funktion vcov() dir zurückgibt. Wir brauchen nur die Diagonale der Varianz/Covarianzmatrix um zu schauen ob wir heterogene Varianzen geschätzt bekommen haben. Sieht auf jeden Fall gut aus, die Varianzen sind nicht alle gleich.
R Code [zeigen / verbergen]
vcov(multcomp_fac1_obj) |> diag()cat - dog fox - dog fox - cat
1.3692063 0.9675397 0.8037302 Wenn wir die Funktion durchgeführt haben können wir uns mit der Wiedergabe die statistischen Maßzahlen berechnen lassen. Du kannst natürlich auch die Adjustierung für die heterogenen Varianzen weglassen, aber so viel aus machen tut die Adjustierung nicht.
Per Standardeinstellung erhalten wir die adjustierten p-Werte wieder. Ich nutze noch die Helferfunktion tidy() um mir eine bessere Ausgabe zu erschaffen. Dann wähle ich noch den Kontrast, den Mittelwertsunterschied sowie die adjustierten p-Werte aus.
R Code [zeigen / verbergen]
multcomp_fac1_obj |>
tidy() |>
select(contrast, estimate, adj.p.value)# A tibble: 3 × 3
contrast estimate adj.p.value
<chr> <dbl> <dbl>
1 cat - dog -3.39 0.0243
2 fox - dog 1.03 0.554
3 fox - cat 4.41 0.000268Wir können auch die Adjustierung der p-Werte ausschalten indem wir nochmal die Funktion summary() mit der entsprechenden Option dazwischenschalten. Das ist dann auf jeden Fall nochmal eine gute Option, wenn man beides haben möchte.
R Code [zeigen / verbergen]
multcomp_fac1_obj |>
summary(test = adjusted("none")) |>
tidy() # A tibble: 3 × 7
term contrast null.value estimate std.error statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 animal cat - dog 0 -3.39 1.17 -2.89 0.00968
2 animal fox - dog 0 1.03 0.984 1.05 0.310
3 animal fox - cat 0 4.41 0.897 4.92 0.000110Die p-Werte sind ähnlich wie schon in den anderen Analysen, was auch zu erwarten war. Die einfaktorielle Analyse für einen all-pair Vergleich ist recht ähnlich.
Bei dem Compact letter display müssen wir einmal die Leerzeichen aus den Kontrastnamen entfernen damit die Funktion multcompLetters die entsprechenden Buchstaben erstellen kann.
R Code [zeigen / verbergen]
multcomp_fac1_obj |>
tidy() |>
mutate(contrast = str_replace_all(contrast, "\\s", "")) |>
pull(adj.p.value, contrast) |>
multcompLetters() cat fox dog
"a" "b" "b" Wir erhalten dann ein ähnliches Ergebnis wie schon bei den anderen Analysen. Du musst dann immer schauen, was besser zu deiner Fragestellung passt.
Die Stärke von {multcomp} sind die simultanen 95% Konfidenzintervalle die auch alle damit die Fehlerrate des Signifikanzniveaus von 5% über alle Vergleiche einhalten. Das funktioniert besonders git in dem Fall, dass wir eine einfaktorielle Analyse vorliegen haben. Wir müssen aber die Funktion tidy() aufrufen, damit uns die 95% Konfidenzintervalle wiedergegeben werden.
R Code [zeigen / verbergen]
relevance_lvl <- 2
multcomp_fac1_obj |>
tidy(conf.int = TRUE) |>
mutate(sig_lgl = case_when(between(rep(0, n()), conf.low, conf.high) ~ "n.s.",
relevance_lvl < conf.low ~ "s. & r.",
.default = "s.")) |>
ggplot(aes(contrast, y = estimate,
ymin = conf.low, ymax = conf.high,
color = sig_lgl)) +
theme_minimal() +
geom_hline(yintercept = 0) +
geom_errorbar(width = 0.1) +
geom_hline(yintercept = c(2), linetype = "11") +
geom_point() +
coord_flip() +
scale_color_okabeito() +
labs(x = "Vergleich", y = "Mittelwertsunterschied", color = "") +
theme(legend.position = "top")Zweifaktorielle Analyse
Es ist acuh möglich in {multcomp} eine mehrfaktorielle Analyse druchzuführen. Hierbei können wir wieder jedes Modell nehmen was wir zu Verfügung haben. Damit es hier einfach bleibt, bleibe ich bei einem linearen Modell für einen normalverteilten Messwert. Wir haben wieder unsere Tierrassen und dann noch den Messort vorliegen. Mehr zu dem Thema findest du auch in der Arbeit von Hothorn et al. (2008) in dem Dokument multcomp: Simultaneous Inference in General Parametric Models.
R Code [zeigen / verbergen]
fac2_fit <- lm(jump_length ~ animal + site + animal:site, data = fac2_tbl)Jetzt müssen wir aber einiges an Option auswählen, damit wir die zweifaktorielle Analyse auch gut durchrechnen können. Wichtig ist hier, dass wir über den zweiten Faktor mitteln. Daher verlieren wir den zweiten Faktor in der Betrachung der folgenden Ergebnisse. Manchmal wollen wir das, häufig wollen wir das nicht. Deshalb nutzen wir die Option covariate_average = TRUE und interaction_average = TRUE um eben über den zweiten Faktor site und die Interaktion animal:site zu mitteln (eng. average). Optimal ist es dann trotzdem nicht.
R Code [zeigen / verbergen]
multcomp_fac2_obj <- glht(fac2_fit, linfct = mcp(animal = "Tukey",
covariate_average = TRUE, interaction_average = TRUE),
vcov. = sandwich::vcovHC) Auch hier schauen wir dann einmal, ob die Anpassung der Varianzen geklappt hat und wir sehen, dass wir unterschiedliche Varianzen rausbekommen.
R Code [zeigen / verbergen]
vcov(multcomp_fac2_obj) |> diag()dog - cat fox - cat fox - dog
0.4335275 0.3715813 0.3027267 Jetzt haben wir alles toll über den zweiten Faktor und die Interaktion gemittelt. Das ist aber nicht so super, wenn wir eine signifikante Interaktion vorliegen haben. Da sollten wir uns den ersten Faktor getrennt für den zweiten Faktor anschauen. Und das wird dann in {multcomp} etwas sperrig um es mal freundlich auszudrücken. Wir müssen uns erstmal eine neue Variable bauen, die alle Faktorkombinationen enthält. Das macht die Funktion interaction() für uns.
R Code [zeigen / verbergen]
fac2_inter_tbl <- fac2_tbl |>
mutate(inter_animal_site = interaction(animal, site))Dann können wir das Modell einfaktoriell nur mit der Variable der Interaktion rechnen. Das ist natürlich auch so halb eine Lösung.
R Code [zeigen / verbergen]
fac2_inter_fit <- lm(jump_length ~ inter_animal_site, data = fac2_inter_tbl)Mit dem künstlichen einfaktoriellen Modell können wir dann wieder unsere Funktion glht() aufrufen. Hier dann einmal simple ohne Adjustierung für Varianzheterogenität. Hier macht es dann sehr Sinn alle Vergleiche zu rechnen. Obwohl du dann natürlich echt viele Vergleiche rechnest und du damit das Signifikanzniveau sehr drückst. Je mehr ich darüber nachdenke, desto weniger würde ich es so machen. Dann lieber doch alles in {emmeans}.
R Code [zeigen / verbergen]
multcomp_fac2_inter_obj <- glht(fac2_inter_fit,
linfct = mcp(inter_animal_site = "Tukey")) Im Folgenden lassen wir uns einmal die p-Werte für das Interaktionmodell wiedergeben. Sonst wäre es mehr oder minder die Wiederholung des einfaktoriellen Modells nur mit gemittelten Werten für den zweiten Faktor und der Interaktion.
Jetzt erhalten wir einiges an Vergleichen, da wir ja auch eine Menge an Tests rechnen. Für jede Faktorkombination kriegst du jetzt einen adjustierten p-Wert wiedergegeben und damit wird es wirklich etwas unübersichtlich. Leider fällt mir auch keine bessere Ordnung ein. Hier hilft dann wirklich mal die Funktion pvalue() umd die p-Werte einheitlich zu formatieren.
R Code [zeigen / verbergen]
multcomp_fac2_inter_obj |>
tidy() |>
mutate(adj.p.value = scales::pvalue(adj.p.value)) |>
select(contrast, estimate, adj.p.value)# A tibble: 15 × 3
contrast estimate adj.p.value
<chr> <dbl> <chr>
1 dog.city - cat.city 3.10 0.005
2 fox.city - cat.city 6.54 <0.001
3 cat.village - cat.city 1.67 0.331
4 dog.village - cat.city 2.98 0.007
5 fox.village - cat.city 3.40 0.002
6 fox.city - dog.city 3.44 0.001
7 cat.village - dog.city -1.43 0.501
8 dog.village - dog.city -0.117 >0.999
9 fox.village - dog.city 0.296 >0.999
10 cat.village - fox.city -4.87 <0.001
11 dog.village - fox.city -3.55 <0.001
12 fox.village - fox.city -3.14 0.004
13 dog.village - cat.village 1.32 0.593
14 fox.village - cat.village 1.73 0.292
15 fox.village - dog.village 0.413 0.996 Besonders bei so vielen Vergleichen macht es eventuell Sinn einmal die p-Wert Adjustierung für multiple Vergleiche auszuschalten und sich die rohen p-Werte in Ruhe zu betrachten.
R Code [zeigen / verbergen]
multcomp_fac2_inter_obj |>
summary(test = adjusted("none")) |>
tidy() # A tibble: 15 × 7
term contrast null.value estimate std.error statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 inter_animal_site dog.city … 0 3.10 0.815 3.80 3.65e- 4
2 inter_animal_site fox.city … 0 6.54 0.815 8.02 9.19e-11
3 inter_animal_site cat.villa… 0 1.67 0.815 2.05 4.57e- 2
4 inter_animal_site dog.villa… 0 2.98 0.815 3.66 5.74e- 4
5 inter_animal_site fox.villa… 0 3.40 0.815 4.17 1.12e- 4
6 inter_animal_site fox.city … 0 3.44 0.815 4.22 9.54e- 5
7 inter_animal_site cat.villa… 0 -1.43 0.815 -1.76 8.45e- 2
8 inter_animal_site dog.villa… 0 -0.117 0.815 -0.144 8.86e- 1
9 inter_animal_site fox.villa… 0 0.296 0.815 0.363 7.18e- 1
10 inter_animal_site cat.villa… 0 -4.87 0.815 -5.97 1.88e- 7
11 inter_animal_site dog.villa… 0 -3.55 0.815 -4.36 5.90e- 5
12 inter_animal_site fox.villa… 0 -3.14 0.815 -3.85 3.12e- 4
13 inter_animal_site dog.villa… 0 1.32 0.815 1.61 1.12e- 1
14 inter_animal_site fox.villa… 0 1.73 0.815 2.12 3.86e- 2
15 inter_animal_site fox.villa… 0 0.413 0.815 0.507 6.15e- 1Am Ende bleibt eine sehr lange Liste, die schon bei drei Tierrassen und zwei Messorten sehr lang ist. Wenn du dann mehr Level in jedem Faktor hast, dann wird die Sachlage noch unübersichtlicher. Hier würde ich dann die Reißleine ziehen und dann nicht mehr {multcomp} nutzen.
Das Compact letter display leidet auch etwas unter der großen Anzahl an Vergleichen. Dadurch kann es dir passieren, dass dir die Buchstaben ausgehen! Das ist jetzt hier noch nicht der Fall, aber das müsstest du mit in Betracht ziehen.
R Code [zeigen / verbergen]
multcomp_fac2_inter_obj |>
tidy() |>
mutate(contrast = str_replace_all(contrast, "\\s", "")) |>
pull(adj.p.value, contrast) |>
multcompLetters() dog.city fox.city cat.village dog.village fox.village cat.city
"a" "b" "ac" "a" "a" "c" Auch hier erhälst du dann eine Menge Vergleiche, die dich vielleicht alle gar nicht interesieren. Dadurch wird dann aber alles noch unübersichtlicher, obwohl die Übersichtlichkeit ja gerade eine Stärke des Compact letter displays ist.
Dann schauen wir uns noch die 95% Konfidenzintervalle an, die hier dann doch etwas übersichtlicher daherkommen. Wir haben zwar eine riesige Menge an Kondfidenzintervallen aber immerhin sieht man hier ganz gut, wie relevant die einzelnen Vergleiche sind. Also wie weit ist denn jetzt das Konfidenzintervall von der Null weg für den jeweiligen Vergleich? Hier lässt sich dann auch eine Relevanzschwelle gut einzeichnen. Ich habe hier mal einen Mittelwertsunterschied von 2cm als relevant eingezeichnet.
R Code [zeigen / verbergen]
relevance_lvl <- 2
multcomp_fac2_inter_obj |>
tidy(conf.int = TRUE) |>
mutate(sig_lgl = case_when(between(rep(0, n()), conf.low, conf.high) ~ "n.s.",
relevance_lvl < conf.low ~ "s. & r.",
.default = "s.")) |>
ggplot(aes(contrast, y = estimate,
ymin = conf.low, ymax = conf.high,
color = sig_lgl)) +
theme_minimal() +
geom_hline(yintercept = 0) +
geom_errorbar(width = 0.1) +
geom_hline(yintercept = c(2), linetype = "11") +
geom_point() +
coord_flip() +
scale_color_okabeito() +
labs(x = "Vergleich", y = "Mittelwertsunterschied", color = "") +
theme(legend.position = "top")Am Ende kannst du dann anhand der Signifikanzschwelle und der Relevanzschwelle deine Ergebnisse entsprechend sortieren und eine Entscheidung treffen. Am Ende steht und fällt es dann natürlich mit der Definition der Relevanzschwelle und der Anzahl an Faktorkombinationen. Wenn es dann zu viele sind, dann siehst du gar nichts mehr.
44.8.4 R Paket {nparcomp}
Das Paket {nparcomp} kann nur ein einfaktorielles Modell rechnen. Dafür brauchst du kein normalverteiltes \(y\) in deinen Daten. Darüber hinaus ist die Interpretation des Effekts biologisch nicht möglich. Jedenfalls nicht im klassischen Sinne einer Relevanzbetrachtung auf der Einheit der Messwerte deines \(y\). Das Compact letter display kannst du aber problemlos nutzen.
Das R Paket {nparcomp} wird gerne genutzt, wenn du ein nicht normalverteiltes Outcome \(y\) vorliegen hast und nur eine Behandlung \(x\). Dieser Fall kommt sehr oft in der Zellbiologie vor oder aber allgemein in den Humanwissenschaften. Teilweise dann auch in Mausmodellen, wo wir dann nur drei bis vier Behandlungen vorliegen haben und diese dann zu einer Kontrolle vergleichen. Dafür ist das R Paket {nparcomp} nützlich. Aber auch nur, wenn du an p-Werten und vielleicht noch dem Compact letter display interessiert bist. Alles andere ist dann nicht sinnvoll abbildbar.
Hier einmal kurz der niedergeschlagende Engel. In diesem Abschnitt zu
{nparcomp}werde ich ein paar Engel der Statistik niedergeschlagen und dann noch überfahren. Ich lasse aus Gründen der Didaktik ein paar Sachen weg und dadurch wird einiges leider dann mathematisch unkorrekt. Ich kann damit leben und nehme es auf mich damit du deine Abschlussarbeit fertig bekommst. Somit sind alle Abbildungen eher Näherungen als mathematisch korrekt.
Das R Paket {nparcomp} hat viele Stärken. In den meisten praktischen Situationen ist die Verteilung der gemessenen Daten \(Y\) unbekannt. Dann kann es auch sein, dass du eine Reihe von atypischen Messungen und Ausreißern vorliegen hast. Mit dem R Paket {nparcomp} hast fast keine Annahmen an die Daten, so dass du hier sehr flexibel bist. Einzig die Verteilungen der Gruppen müssen ähnlich sein. Das ist aber in einem in sich geschlossenen Experiment eigentlich immer der Fall.
Betrachten wir also einmal die Funktionsweise von {nparcomp} an einem simplen Beispiel. Ich gehe hier nicht auf die tiefen der Berechnung ein, sondern wir wollen einmal verstehen, was die Ausgabe von {naparcomp} uns sagen will. Da das Verfahren nicht auf den klassischen statistischen Maßzahlen wie Mittelwert und Standardabweichung beruht ist die Ausgabe nicht ganz so einfach zu verstehen. In der folgenden Tabelle siehst du einmal die Ausgabe der Funktion npar.t.test() in der ich nur die Sprungweiten der Hunde- und Katzenflöhe miteinander vergleichen habe.
npar.t.test() für den paarweisen Vergleichs von der Sprunglänge in [cm] von Hunde- und Kartzenflöhen. Die Fuchsflöhe wurden einmal entfernt um nur einen paarweisen Vergleich zu rechnen.
| Effect | Estimator | Lower | Upper | T | p.Value |
|---|---|---|---|---|---|
| p(dog,cat) | 0.102 | -0.085 | 0.289 | -4.684 | 0.001 |
Wir wissen anhand der Ausgabe von npar.t.test(), dass wir einen signifikanten Unterschied zwischen den Sprungweiten der Hunde- und Katzenflöhe vorliegen haben. Der p-Wert \(0.001\) ist kleiner als das Signifikanzniveau \(\alpha\) gleich 5%. Aber wie groß ist jetzt der Unterschied oder anders gefragt, was ist der berechnete Effekt? Das R Paket {nparcomp} berechnet hierbei den relativen Effekt \(p(a,b)\). Das heißt wiederum, dass wir die Einheit der Sprungweite verlieren und nur eine Wahrscheinlichkeit wiedergeben bekommen.
- Was sagt der relative Effekt \(\boldsymbol{p(a,b)}\) aus?
-
Wenn der relative Effekt \(p(a,b)\) größer ist als \(1/2\), dann tendiert die Gruppe \(b\) dazu größer zu sein als die Gruppe \(a\). Oder etwas anders formuliert. Wenn wir einen relativen Effekt größer als \(1/2\) vorliegen haben, dann spricht der relative Effekt für größere Mittelwerte in der Gruppe \(b\) im Vergleich zur Gruppe \(a\). Wir können dann sagen, dass \(\bar{y}_b > \bar{y}_a\) ist. Oder dur schreibst statt \(p(a,b)\) eben \(p(b > a)\). Ja, ist etwas schief…aber wir leben damit. Mehr zu der Betrachtung des relativen Effekts auch im Kapitel zum U-Test und der Einführung in die Nichtparametrik.
Betrachten wir einmal die Darstellung der beiden Verteilungen der Sprungweiten für die Hunde- und Katzenflöhe. Die Katzenflöhe haben einen niedrigeren Mittelwert mit \(\\bar{y}_{cat} = 4.74\) und springen nicht so weit wie die Hundeflöhe mit einem hören Mittelwert von \(\\bar{y}_{dog} = 8.13\). Wir erhalten einen relativen Effekt \(p_{(dog, cat)}\) von \(0.102\). Was sagt uns nun der Wert aus? In der folgenden Abbidlung habe ich dir einmal den Zusammenhang visualisert. Die eingefärbte Fläche ist die Wahrscheinlichkeit \(p_{(dog, cat)}\) von \(0.102\) zufällig größere Sprungweiten von Katzenflöhen als von Hundeflöhen zu beobachten. Da die Katzenflöhe ja nicht weiter als die Hundeflöhe springen, ist die Wahrscheinlichkeit \(p_{(dog, cat)}\) klein.
Wir können uns nun die Sachlage auch einmal für alle drei Fälle visualisieren. Daher wir schauen uns an, wie sehen die unterscheidlichen relativen Effektschätzer aus? Zum einen kann ja der Wert des relativen Effekts \(p(a,b)\) klein sein und daher eher nahe Null. Damit spricht der relative Effekt dafür das \(a\) kleiner ist als \(b\). Oder der Wert von \(p(a,b)\) ist 0.5, dann ist \(a\) vermutlich gleich \(b\). Im letzte Fall kann \(p(a,b)\) nahe Eins sein, dann spricht es für größere Werte in \(b\) als in \(a\). Ich kann mit den Zusammenhang besser als eingefärbte Flächen merken, daher habe ich dir nochmal den relativen Effektschätzer etwas anders dargestellt. Mehr zu der Betrachtung des relativen Effekts auch im Kapitel zum U-Test.
44.8.4.1 Einfaktorielle Analyse
In dem Paket {naprcomp} können wir nur eine einfaktorielle Analyse rechnen. Da ist hier nochmal wichtig zu wissen. Sonst musst du dir die Arbeit nicht machen. Wir müssen einiges Einstellen bei der gleichnamigen Hauptfunktion nparcomp() aber dann funktioniert alles relativ reibungslos. Das Paket ist schon älter und hat damit nicht die Funktionalität des {tidyverse} oder anderen Paketen. Hier sieht man dann auch, dass {naprcomp} nicht so oft genutzt wird, denn ansonsten wäre ja auch der Bedarf einer besseren Integration dar. Aber das lassen wir mal so im Raum stehen.
Leider hat die Funktion nparcomp() einem sehr viele Informationen auf der R Konsole auszugeben auch wenn man das nicht will und es einen eigentlich mehr verwirrt als gutes tut. Deshalb stelle ich immer die Option info = FALSE ein. Wir wollen eigentlich immer alle Gruppen miteinander vergleichen, so dass wir als Option type = "Tukey" nehmen. Achtung, das hat jetzt nichts mit dem Tukey HSD Test zu tun. Wir müssen uns dann auch noch aus der Ausgabe den Teil rausziehen, denn wir dann brauchen.
R Code [zeigen / verbergen]
nparcomp_fac1_res <- nparcomp(jump_length ~ animal, data = fac1_tbl, type = "Tukey",
alternative = "two.sided", info = FALSE)
nparcomp_fac1_res |> pluck("Analysis") Comparison Estimator Lower Upper Statistic p.Value
1 p( dog , cat ) 0.102 0.013 0.503 -2.345283 0.05277451
2 p( dog , fox ) 0.684 0.277 0.924 1.050004 0.60508449
3 p( cat , fox ) 0.980 0.614 0.999 2.681488 0.02105876Was wir eigentlich brauchen ist der p-Wert in der letzten Spalte. Spannend ist hier, dass nparcomp() den Vergleich von Hunde- und Katzenflöhen nicht als signifikant findet. Das ist eine Folge davon, dass nparcomp() etwas konservativer ist als die anderen hier vorgestellten Verfahren. Wenn du nochmal nachvollziehen willst, wie der relative Effekt Estimator zu interpretieren ist, habe ich dir nochmal im folgenden eine zusammenfassende Tabelle mit den Mittelwerten der einzelnen Gruppen gebaut. Für mich ist der Wert immer noch von hinten durch die Brust. Leider hat der relative Effekt keinen Bezug zur biologischen Einheit der Messwerte. Deshalb ist die Interpretation im günstigsten Fall schwierig.
| Vergleich | Relativer Effekt |
|---|---|
| \(\bar{y}_{cat} \stackrel{?}{>} \bar{y}_{dog}\) | \(4.74 \stackrel{?}{>} 8.13 \rightarrow p(dog, cat) = 0.102\) |
| \(\bar{y}_{fox} \stackrel{?}{>} \bar{y}_{dog}\) | \(9.16 \stackrel{?}{>} 8.13 \rightarrow p(dog, fox) = 0.684\) |
| \(\bar{y}_{fox} \stackrel{?}{>} \bar{y}_{cat}\) | \(4.74 \stackrel{?}{>} 9.16 \rightarrow p(cat, fox) = 0.980\) |
Für das Compact letter display brauchen wir wieder einmal das Objekt einer nparcomp() Analyse. Wir nutzen hier den gleichen Aufruf wie schon bei den p-Werten. Die Optionen sind damit die gleichen wie im Tab zu den p-Werten. Wir sind jetzt aber nur an den reinen p-Werten interessiert und nicht an den relativen Effekten.
R Code [zeigen / verbergen]
nparcomp_fac1_res <- nparcomp(jump_length ~ animal, data = fac1_tbl, type = "Tukey",
alternative = "two.sided", info = FALSE)Leider ist es so, dass {nparcomp} nicht für die Erstellung des Compact letter displays optimiert ist. Daher müssen wir uns erst einen Vektor für die Vergleiche mit einem Minuszeichen ohne Leerzeichen bauen.
R Code [zeigen / verbergen]
contrast_vec <- nparcomp_fac1_res |>
pluck("Contrast") |>
row.names() |>
str_replace_all("\\s", "")Wenn wir die Namen der Vergleiche haben, können wir uns die p-Werte aus dem nparcomp() Objekt ziehen und entsprechend dem Vergleich benennen.
R Code [zeigen / verbergen]
adj_p_values_vec <- nparcomp_fac1_res |>
pluck("Analysis", "p.Value") |>
set_names(contrast_vec)Abschließend können wir uns dann mit der Funktion multcompLetters() das Compact letter display wiedergeben lassen.
R Code [zeigen / verbergen]
adj_p_values_vec |> multcompLetters() cat fox dog
"a" "b" "ab" Hier ist der Weg etwas länger aber wenn wir uns nur auf das Compact letter displays konzentrieren liefert {nparcomp} in einem einfaktoriellen Fall eigentlich alles was wir brauchen. Hier unterscheidet sich das Compact letter display von den anderen Analysen, da wir hier auch etwas andere p-Werte erhalten.
Ja, die 95% Konfidenzintervalle und
{nparcomp}, eine für mich schwierige Sache. Eigentlich liefern die 95% Konfidenzintervalle in{nparcomp}nicht so richtig was wir eigentlich wollen. Nämlich eine biologisch zu interpretierende Relevanz und Signifikanz. Die relativen Effekte \(p(a,b)\) aus der Funktionnparcomp()sind eben dann doch wieder nur Wahrscheinlichkeiten.
Wenn du die 95% Konfidenzintervalle brauchst, dann kannst du die Funktion nparcomp() wie in den Tab zu den p-Werten nutzen. Hier ändert sich nichts bei dem Funktionsaufruf. Praktischerweise liefert dir die Ausgabe von nparcomp() auch gleich die 95% Konfidenzintervalle mit.
R Code [zeigen / verbergen]
nparcomp_fac1_res <- nparcomp(jump_length ~ animal, data = fac1_tbl, type = "Tukey",
alternative = "two.sided", info = FALSE)In der folgenden Abbildung siehst du dann einmal die 95% Konfidenzintervalle visualisiert. Durch die Eigenschaft des relativen Effekt eine Wahrscheinlichkeit zu sein, hast du die Begrenzungen von \([0, 1]\) und damit dann auch keine symmetrischen 95% Konfidenzintervalle mehr. Die Entscheidung gegen die Nullhypothese liegt bei \(p(a,b) = 0.5\).
R Code [zeigen / verbergen]
ggplot(nparcomp_fac1_res$Analysis,
aes(Comparison, y = Estimator, ymin = Lower, ymax = Upper)) +
theme_classic() +
geom_hline(yintercept=0.5, linetype="11", colour="grey60") +
geom_errorbar(width=0.1) +
geom_point() +
coord_flip() +
ylim(0, 1) +
labs(x = "Vergleich", y = "Relativer Effekt"){nparcomp} Der relative Effekt ist eine Wahrscheinlichkeit, daher die Begrenzungen bei \([0, 1]\). Die Entscheidung gegen die Nullhypothese liegt bei \(p(a,b) = 0.5\).
44.8.4.2 Zweifaktorielle Analyse
Eine zweifaktorielle Analyse ist in dem Paket {nparcomp} nicht möglich. Damit war das hier viel Arbeit für mich für vermutlich nicht viel für dich. Dafür habe ich aber eine Menge über {nparcomp} gelernt und du musst dich dafür nicht durch das sehr mathematische Paper von Konietschke et al. (2015) quälen. Denn in den Agrarwissenschaften haben wir eigentlich immer ein zweifaktorielles Modell und selten nur ein Modell mit einem Faktor vorliegen. Daher ist dieses Paket auch hier unten im Kapitel eingeordnet und würde ich nicht empfehlen.
44.9 Weitere Dinge von Interesse
Es gibt immer wieder Dinge von Interesse, die ich im Rahmen der multiplen Vergleiche oder Post-hoc Tests so finde. Meistens ist es dann nicht so wichtig, dass ich es in den obigen Abschnitten noch einbauen möchte. Auf der anderen Seite will ich es dann aber auch nicht vergessen, so dass es eben hier steht. SO kannst du über die Suchfunktion noch Sachen finden, die ich dann eben hier parke. Du kannst es nutzen und manchmal ist es dann auch nützlich.
44.9.1 Friedhof der Post-hoc Tests
Hier gebe ich eine – nicht vollständige – Liste an Post-hoc Tests, die es einmal gab und auch noch erwähnt werden, aber dann eigentlich alle irgendwie veraltet sind. Wie immer sind diese Tests nicht per se schlecht. Aber es gibt dann eben besseres. Die Daumenregel lautet dabei, dass es {emmeans} oder {multcomp} besser können. Zwei Übersichtsarbeiten helfen hier nochmal Ordnung in das Dickicht der multiplen Vergleiche zu bringen. Einmal die Arbeit On the use of post-hoc tests in environmental and biological sciences: A critical review von Agbangba et al. (2024) sowie die Veröffentlichung A discussion and evaluation of statistical procedures used by JIMB authors when comparing means von Klasson (2024). Im Folgenden bieten sich zwei Pakete an die etwas älteren Post-hoc Tests zu rechnen. Zum einen das Paket {descTools}, welches einfacher zu bedienen ist und auch mal zweifaktoriell rechnen kann oder das R Paket {agricolae}, was den Fokus auf ein einfaktorielles Design hat aber dafür direkt das Compact letter display ohne p-Werte wiedergibt. Ich verzichte hier auch auf die händische Herleitung, auch wenn es gerade bei den älteren Anwendungen auch möglich ist, aber wir wollen diese Tests eigentlich nicht mehr nutzen.
- LSD Test oder auch Fisher`s least Significant Difference (LSD)
-
Der LSD Test ist veraltet. Was überhaupt gegen die Nutzung des LSD Test spricht ist, das der LSD Test das Signifikanzniveau \(\alpha\) von 5% über alle Vergleiche nicht einhälst. Sie dazu auch Agbangba et al. (2024) mit der klaren Aussage: “LSD does not control for family-wise type I error”. Die einzige Ausnahme ist der seltene Fall, dass du dir nur drei Behandlungsgruppen anschaust, wie von Klasson (2024) diskutiert. Aber am Ende ich kann den LSD Test nicht empfehlen.
In dem R Paket {descTools} kannst du den LSD Test einmal einfaktoriell rechnen, wie in dem folgenden Modell. Bitte beachte immer, das wir nicht für das multiple Testen adjustieren. Daher kann es dann zu Abweichungen zu anderen Post-hoc Tests kommen. Hier aber erstmal die einfaktorielle ANOVA.
R Code [zeigen / verbergen]
fac1_av <- aov(jump_length ~ animal, data = fac1_tbl)Ebenso kannst du eine zweifaktorielle ANOVA nutzen. Hier ist die Herausforderung dann die p-Werte zu extrahieren und das Compact letter display zu berechnen. Wir können dann das Modell in die Funktion PostHocTest() stecken und dann einmal mit der Option method = "lsd" den entsprechenden Test auswählen.
R Code [zeigen / verbergen]
lsd_obj <- PostHocTest(fac1_av, method = "lsd")
lsd_obj
Posthoc multiple comparisons of means : Fisher LSD
95% family-wise confidence level
$animal
diff lwr.ci upr.ci pval
cat-dog -3.385714 -5.3758086 -1.395620 0.00217 **
fox-dog 1.028571 -0.9615229 3.018666 0.29187
fox-cat 4.414286 2.4241914 6.404380 0.00019 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Und dann können wir uns auch mit einer leichten Umgehung auch das Compact letter display erstellen lassen. Leider ist das immer etwas schwieriger, wenn die Ausgabe der Funktion nicht so richtig zu den der Compact letter display passt. Wir nutzen hier explizit die Funktion extract() aus dem R Paket {magrittr}. Bei dir heißt aber die Variable "animal" der Behandlung natürlich anders.
R Code [zeigen / verbergen]
lsd_obj |>
pluck("animal") |>
magrittr::extract(, 4) |>
multcompLetters() cat fox dog
"a" "b" "b" Im zweifaktoriellen Fall würde ich dir aber eher {emmeans} empfehlen, da du dort besser und leichter an das Compact letter display kommst.
Das R Paket {agricolae} erlaubt auch einen LSD Test zu rechnen. Wir brauchen nur das Modell einer einfaktoriellen ANOVA und können dann damit weiterrechnen. Ein zweiter Faktor ist in {agricolae} nicht möglich und wird ohne Fehlermeldung einfach von der Funktion ignoriert.
R Code [zeigen / verbergen]
fac1_av <- aov(jump_length ~ animal, data = fac1_tbl)Witzigerweise gibt die Funktion von alleine keine Ausgabe wieder. Wie wild dieses Verhalten einer Funktion ist, kann ich gar nicht ausdrücken. Wichtig ist hier, dass wir nur das Compact letter display wiedergegeben bekommen aber keine p-Werte für die paarweisen Vergleiche.
R Code [zeigen / verbergen]
LSD.test(fac1_av, trt = "animal", p.adj = "bonferroni") |>
pluck("groups") jump_length groups
fox 9.157143 a
dog 8.128571 a
cat 4.742857 bWenn du p-Werte brauchst oder ein zweifaktorielles Design vorliegen hast, dann nutze bitte die Funktionen aus dem R Paket descTools oder eben gleich {emmeans}, was einfach das bessere Paket ist.
- Scheffé Test
-
Der Scheffé Test ist im Prinzipn eng mit dem Tukey HSD Test verwandt. Was aber Agbangba et al. (2024) anmerkt ist, dass “the test is too conservative compared to methods like Tukey’s HSD”. Aus dem Grund würde ich den Test nicht empfehlen. Auch testet der Scheffé Test mehr Vergleiche als du meistens möchtest. Es ist eben nicht ein reiner all-pair Vergleich sondern testet auch noch alle anderen möglichen Kombinationen der Mittelwerte.
Wir können den Scheffé Test im R Paket {DescTools} mit der Funktion ScheffeTest() finden. Wir könnten auch die Funktion PostHocTest() nutzen und die Option method = "scheffe" wählen. Wir nutzen wieder das Modell aus der ANOVA, ob nun einfaktoriell oder zweifaktoriell, um dann den Scheffé Test zu rechnen. Ich zeige hier einmal die einfaktorielle Variante.
R Code [zeigen / verbergen]
fac1_av <- aov(jump_length ~ animal, data = fac1_tbl)Dann brauchen wir nur noch die Funktion ScheffeTest aufrufen. Ich ziehe mir hier gleich mit der Funktion pluck() die notwendigen Informationen direkt raus. Deine Gruppenspalte in deinen Daten heißt ja anders, deshalb musst du dann "animal" entsprechend durch deinen Variablennamen ersetzen. Beachte, dass du hier adjustierte p-Werte wiedergegeben bekommst.
R Code [zeigen / verbergen]
scheffe_obj <- ScheffeTest(fac1_av) |> pluck("animal")
scheffe_obj diff lwr.ci upr.ci pval
cat-dog -3.385714 -5.911354 -0.8600741 0.0080098476
fox-dog 1.028571 -1.497069 3.5542116 0.5649416800
fox-cat 4.414286 1.888646 6.9399259 0.0008066705Und dann können wir uns auch mit einer leichten Umgehung auch das Compact letter display erstellen lassen. Leider ist das immer etwas schwieriger, wenn die Ausgabe der Funktion nicht so richtig zu den der Compact letter display passt. Wir nutzen hier explizit die Funktion extract() aus dem R Paket {magrittr}.
R Code [zeigen / verbergen]
scheffe_obj |>
magrittr::extract(, 4) |>
multcompLetters() cat fox dog
"a" "b" "b" Wir können auch den Scheffé Test in dem R Paket {agricolae} rechnen. Dafür brauchen wir wieder ein einfaktorielles Modell. Wir können kein zweifaktorielles rechnen, sondern eben nur für einen Behandlungsfaktor. Deshalb hier einmal das ANOVA Modell.
R Code [zeigen / verbergen]
fac1_av <- aov(jump_length ~ animal, data = fac1_tbl)Dann können wir de Funktion scheffe.test() nutzen. Auch hier erhalten wir keine Ausgabe sondern müssen die Ausgabe selber anfordern. Wir schauen hier direkt das Compact letter display an. Wir erhlaten keine p-Werte aus der Funktion.
R Code [zeigen / verbergen]
scheffe.test(fac1_av, trt = "animal") |>
pluck("groups") jump_length groups
fox 9.157143 a
dog 8.128571 a
cat 4.742857 bWenn du p-Werte brauchst oder ein zweifaktorielles Design vorliegen hast, dann nutze bitte die Funktionen aus dem R Paket descTools oder eben gleich {emmeans}, was einfach das bessere Paket ist.
44.9.2 Re-engineering des Compact letter displays
In dem kurzen Kapitel zu Re-engineering CLDs in der Vingette des R Pakets {emmeans} geht es darum, wie das Compact letter display auch anders gebaut werden könnte. Nämlich einmal als wirkliches Anzeigen von Gleichheit über die Option delta oder aber über das Anzeigen von Signifikanz über die Option signif. Damit haben dann auch wirklich die Information, die wir dann wollen. Also eigentlich was Schönes. Wie machen wir das nun?
Wenn wir das Cact letter display in dem Sinne der Gleichheit der Behandlungen interpretieren wollen, also das der gleiche Buchstabe bedeutet, dass sich die Behandlungen nicht unterscheiden, dann müssen wir ein delta setzen in deren Bandbreite oder Intervall die Behandlungen gleich sind. Ich habe hier mal ein delta von 4cm gewählt und wir adjustieren bei einem Test auf Gleichheit nicht.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
emmeans(~ animal) |>
cld(Letters = letters, adjust = "none", delta = 4) animal emmean SE df lower.CL upper.CL .equiv.set
cat 4.74 0.67 18 3.34 6.15 a
dog 8.13 0.67 18 6.72 9.54 b
fox 9.16 0.67 18 7.75 10.56 b
Confidence level used: 0.95
Statistics are tests of equivalence with a threshold of 4
P values are left-tailed
significance level used: alpha = 0.05
Estimates sharing the same symbol test as equivalent Wie wir jetzt sehen, bedeuten gleiche Buchstaben, dass die Behandlungen gleich sind. In dem Sinne gleich sind, dass die Behandlungen im Mittel nicht weiter als der Wert in delta auseinanderliegen. Wie du jetzt das delta bestimmst ist eine biologische und keine statistische Frage.
Können wir uns auch signifikante Unterschiede anzeigen lassen? Ja, können wir auch, aber das ist meiner Meinung nach die schlechtere der beiden Anpassungen. Wir haben ja im Kopf, dass das Compact letter display eben mit gleichen Buchstaben das Gleiche anzeigt. Jetzt würden wir diese Eigenschaften zu Unterschied ändern. Schauen wir uns das einmal an einem kleineren Datensatz einmal an.
Dann können wir uns hier einmal das Problem mit den Buchstaben anschauen. Wir kriegen jetzt mit der Option signif = TRUE wiedergeben Estimates sharing the same symbol are significantly different und das ist irgendwie auch wirr, dass gleiche Buchstaben einen Unterschied darstellen. Das Compact letter display wird eben als Gleichheit gelesen, so dass wir hier mehr verwirrt werden als es hilft.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
emmeans(~ animal) |>
cld(Letters = letters, adjust = "bonferroni", signif = TRUE) animal emmean SE df lower.CL upper.CL .signif.set
cat 4.74 0.67 18 2.98 6.51 ab
dog 8.13 0.67 18 6.36 9.90 a
fox 9.16 0.67 18 7.39 10.92 b
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 3 estimates
P value adjustment: bonferroni method for 3 tests
significance level used: alpha = 0.05
Estimates sharing the same symbol are significantly different Deshalb würde ich auf die Buchstaben verzichten und die Zahlen angeben, damit hier nicht noch mehr Verwirrung aufkommt. Wir nehmen also die Option für die Buchstaben einmal aus dem cld() Aufruf raus. Dann haben wir Zahlen als Gruppenzuweisung, was schon mal was anderes ist als die Buchstaben aus dem Compact letter display.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
emmeans(~ animal) |>
cld(adjust = "bonferroni", signif = TRUE) animal emmean SE df lower.CL upper.CL .signif.set
cat 4.74 0.67 18 2.98 6.51 12
dog 8.13 0.67 18 6.36 9.90 1
fox 9.16 0.67 18 7.39 10.92 2
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 3 estimates
P value adjustment: bonferroni method for 3 tests
significance level used: alpha = 0.05
Estimates sharing the same symbol are significantly different Innerhalb des selben Konzepts dann zwei Arten von Interpretation des Compact letter display zu haben, ist dann auch nicht zielführend. Den auch die gleichen Zahlen bedeuten jetzt einen Unterschied. Irgendwie mag ich persönlich nicht diese sehr verdrehte Interpretation nicht. Deshalb lieber ein delta einführen und auf echte Gleichheit testen.
44.9.3 Modellierung von Varianzheterogenität
In diesem Kapitel modelliere ich ja immer die Varianzheterogenität, wenn ich das kann. Es gibt aber eine Reihe von Möglichkeiten die Adjustierung durchzuführen. In den folgenden Tabs findest du dann noch andere Ideen und Anregungen. Ich muss hier nochmal aufräumen, aber wie immer, wenn es nicht dringlich ist, dann lagere ich es hier lieber. Es es bestimmt nochmal nützlich.
Wenn du noch etwas weiter gehen möchtest, dann kannst du dir noch die Hilfeseite von dem R Paket {performance} Robust Estimation of Standard Errors, Confidence Intervals, and p-values anschauen. Die Idee ist hier, dass wir die Varianz/Kovarianz robuster daher mit der Berücksichtigung von Varianzheterogenität (eng. heteroskedasticity) schätzen.
Hier also jetzt einmal eine Übersicht über die Möglichkeiten mit der Varianzheterogenität in Behandlungsgruppen umzugehen.
Neben dem Games Howell Test gibt es auch die Möglichkeit Generalized Least Squares zu nutzen. Hier haben wir dann auch die Möglichkeit mehrfaktorielle Modelle zu schätzen und dann auch wieder emmeans zu nutzen. Das ist natürlich super, weil wir dann wieder in dem emmeans Framework sind und alle Funktionen von oben nutzen können. Deshalb hier auch nur die Modellanpassung, den Rest kopierst du dir dann von oben dazu.
Die Funktion gls() aus dem R Paket {nlme} passt ein lineares Modell unter Verwendung der verallgemeinerten kleinsten Quadrate an. Die Fehler dürfen dabei aber korreliert oder aber ungleiche Varianzen haben. Damit haben wir ein Modell, was wir nutzen können, wenn wir Varianzheterogenität vorliegen haben. Hier einmal das simple Beispiel für die Tierarten. Wir nehmen wieder die ganz normale Formelschreiweise. Wir können jetzt aber über die Option weights = angeben, wie wir die Varianz modellieren wollen. Die Schreibweise mag etwas ungewohnt sein, aber es gibt wirklich viele Arten die Varianz zu modellieren. Hier machen wir uns es einfach und nutzen die Helferfunktion varIdent und modellieren dann für jedes Tier eine eigene Gruppenvarianz.
R Code [zeigen / verbergen]
gls_fac1_fit <- gls(jump_length ~ animal,
weights = varIdent(form = ~ 1 | animal),
data = fac1_tbl)Dann können wir die Modellanpasssung auch schon in emmeans() weiterleiten und schauen uns mal das Ergebnis gleich an. Wir achten jetzt auf die Spalte SE, die uns ja den Fehler der Mittelwerte für jede Gruppe wiedergibt.
R Code [zeigen / verbergen]
gls_fac1_fit |>
emmeans(~ animal) animal emmean SE df lower.CL upper.CL
dog 8.13 0.811 6.00 6.15 10.1
cat 4.74 0.719 6.01 2.98 6.5
fox 9.16 0.415 6.00 8.14 10.2
Degrees-of-freedom method: satterthwaite
Confidence level used: 0.95 Wir sehen, dass wir für jedes Tier eine eigene Varianz über den Standardfehler SE geschätzt haben. Das war es ja auch was wir wollten. Bis hierhin wäre es auch mit dem Games Howell Test gegangen. Was ist aber, wenn wir ein zweifaktorielles Design mit Interaktion schätzen wollen? Das können wir analog wie eben machen. Wir erweitern einfach das Modell um die Terme site für den zweiten Faktor und den Interaktionsterm animal:site.
R Code [zeigen / verbergen]
gls_fac2_fit <- gls(jump_length ~ animal + site + animal:site,
weights = varIdent(form = ~ 1 | animal),
data = fac2_tbl)Dann können wir uns wieder die multiplen Vergleiche getrennt für die Interaktionsterme wiedergeben lassen. Blöderweise haben jetzt alle Messorte site die gleiche Varianz für jede Tierart, aber auch da können wir noch ran.
R Code [zeigen / verbergen]
gls_fac2_fit |>
emmeans(~ animal | site)site = city:
animal emmean SE df lower.CL upper.CL
cat 13.6 0.672 18 12.2 15.0
dog 16.7 0.573 18 15.5 17.9
fox 20.1 0.466 18 19.1 21.1
site = village:
animal emmean SE df lower.CL upper.CL
cat 15.2 0.672 18 13.8 16.7
dog 16.6 0.573 18 15.4 17.8
fox 17.0 0.466 18 16.0 18.0
Degrees-of-freedom method: satterthwaite
Confidence level used: 0.95 Die eigentliche Stärke von gls() kommt eigentlich erst zu tragen, wenn wir auch noch erlauben, dass wir die Varianz über alle Tierarten, Messsorte und Interaktionen variieren kann. Das machen wir, in dem wir einfach animal*site zu der varIdent() Funktion ergänzen.
R Code [zeigen / verbergen]
gls_fac2_fit <- gls(jump_length ~ animal + site + animal:site,
weights = varIdent(form = ~ 1 | animal*site),
data = fac2_tbl)Dann noch schnell in emmeans() gesteckt und sich das Ergebnis angeschaut.
R Code [zeigen / verbergen]
gls_fac2_fit |>
emmeans(~ animal | site)site = city:
animal emmean SE df lower.CL upper.CL
cat 13.6 0.594 8.93 12.2 14.9
dog 16.7 0.713 9.03 15.1 18.3
fox 20.1 0.365 9.01 19.3 20.9
site = village:
animal emmean SE df lower.CL upper.CL
cat 15.2 0.743 9.00 13.6 16.9
dog 16.6 0.384 9.00 15.7 17.4
fox 17.0 0.548 9.22 15.7 18.2
Degrees-of-freedom method: satterthwaite
Confidence level used: 0.95 Wie du jetzt siehst schätzen wir die Varianz für jede Tierart und jeden Messort separat. Wir haben also wirklich jede Varianz einzeln zugeordnet. Die Frage ist immer, ob das notwendig ist, denn wir brauchen auch eine gewisse Fallzahl, damit die Modelle funktionieren. Aber das kommt jetzt sehr auf deine Fragestellung an und müssten wir nochmal konkret besprechen.
Hier noch {sandwich} und {clubSandwich} ergänzen.
Wir immer gibt es noch eine weitere Möglichkeit die Varianzheterogenität zu behandeln. Wir nutzen jetzt hier einmal die Funktionen aus dem R Paket {sandwich}, die es uns ermöglichen Varianzheterogenität (eng. heteroskedasticity) zu modellieren. Es ist eigentlich super einfach, wir müssen als erstes wieder unser Modell anpassen. Hier einmal mit einer simplen linearen Regression.
R Code [zeigen / verbergen]
lm_fac1_fit <- lm(jump_length ~ animal, data = fac1_tbl)Dann können wir auch schon für einen Gruppenvergleich direkt in der Funktion emmeans() für die Varianzheterogenität adjustieren. Es gibt verschiedene mögliche Sandwich-Schätzer, aber wir nehmen jetzt mal einen der häufigsten mit vcovHC. Der Schätzer für die Varianzstruktur ist realtiv stabil und in den häufigsten Fällen vollkomen ausreichend
Wir laden jetzt nicht das ganze Paket {sandwich}, sondern nur die Funktion mit sandwich::vcovHAC. Achtung, hinter der Option vcov. ist ein Punkt. Ohne den Aufruf vcov. = funktioniert die Funktion dann nicht. Das hat mich mal sehr viele Nerven gekostet.
R Code [zeigen / verbergen]
em_obj <- lm_fac1_fit |>
emmeans(~ animal, method = "pairwise", vcov. = sandwich::vcovHAC)
em_obj animal emmean SE df lower.CL upper.CL
dog 8.13 0.427 18 7.23 9.03
cat 4.74 0.810 18 3.04 6.44
fox 9.16 0.468 18 8.17 10.14
Confidence level used: 0.95 Wir du siehst, die Standardfehler sind jetzt nicht mehr über alle Gruppen gleich. Wir haben also erfolgreich füe die Varianzheterogenität adjustiert.
Es gibt eine ganze Reihe von anderen Schätzern in dem R Paket {sandwich} und {clubSandwich}. HIer einmal die Referenzen der beiden Pakete zum nachschlagen, was es da noch so gibt.