Letzte Änderung am 14. June 2025 um 15:30:29
“It’s easy to lie with statistics. It’s hard to tell the truth without statistics.” — Andrejs Dunkels
Willkommen in der Gruft. Der Friedman Test ist schlecht und sollte nicht angewendet werden. Das Kapitel existiert eigentlich nur, damit du es finden kannst und gleich lesen kannst, dass du den Friedman Test sein lassen sollst. Weder tut der Friedman Test, dass was du von ihm verlangst, noch macht er das was er tut besonders im statistischen Sinne gut. Am besten rechnest du nach Zimmerman & Zumbo (1993) auf den rangtransformierten Messwerten eine repeated ANOVA, wie ich dir weiter unten zeige.
“Sollte man statistische Test schlecht machen? Vermutlich ja. Einige Tests haben einfach Ihren Zenit erreicht und sind einfach nicht mehr der Stand der Wissenschaft im 21. Jahrhundert. Deshalb bitte einfach zurücklassen und sich nicht mehr drum kümmern.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
Der Friedman Test ist der Kruskal Wallis Test für abhängige Daten. Oder doch nicht? Wenn man sich mit den Friedman Test beschäftigt, dann wird einem nach einer etwas längeren Internetscuhe dann doch klar, dass hier irgendwas nicht so richtig stimmt. Es gibt nämlich zwei Arten des Friedman Tests. Also eigentlich auch nein, es gibt nur einen Friedman Test aber zwei Arten den Test anzuwenden. Wir können den Friedman Test einmal in den Agrarwissenschaften nutzen um ein randomisiertes vollständiges Blockdesign (eng. Randomized Complete Block Design) auszuwerten. In den Geisteswissenschaften wird der Friedman Test gerne für ein einfaches Design mit wiederholten Messungen (eng. Simple Repeated Measures Design) genutzt. Damit fängt es schon an, denn die beiden Designs haben was gemeinsam aber dann auch wieder nicht. Also wir merken uns, je nachdem aus welcher Fachrichtung du kommst, mag der Firedman Test für dich was anderes bedeuten. In beiden Fällen heißt es aber “Beware the Friedman test!”
Hilft ja alles nichts, fangen wir also einmal an uns anzuschauen, was der Friedman Test macht. Du findest noch ein gutes Tutorium zum Friedman Test sowie die Alternative einer repeated ANOVA auf den rangtransformierten Messwerten nach Zimmerman & Zumbo (1993). Wir schauen uns diese Lösung dann auch einmal an. Wichtig ist noch zu wissen, dass die asymptotische Effizienz des Friedman-Tests bei \(0.955 \cdot J/(J+1)\), also bei \(0.64\) für \(J=2\) und \(0.87\) für \(J=10\) liegt. Wir beschrieben mit \(J\) die Anzahl der Gruppen oder Versuchsbedingungen also den Spalten ist. Bei einer Effizienz von \(0.64\) braucht der Friedman Test somit eine um \((100-64)/64\) gleich \(0.56\) also eine ca. 50% größere Stichprobe um die selbe Signifikanz zu erreichen. Oder etwas anders, dass der Friedman Test \(50\%\) mehr Fallzahl benötigt um die gleiche Effizienz zu haben wie eine einfaktorielle ANOVA, deren Annahmen an die Normalverteilung und Varianzhomogenität erfüllt werden. Der Begriff der Effizienz ist hier natürlich etwas wage, aber du kannst den Begriff für dich auch vereinfacht als gleiche statistische Eigenschaften was die Signifikanz angeht lesen. Der Friedman Test braucht also sehr viele Gruppen in den Spalten.
Sprechen wir nochmal über das Datenformat. In der Datentabelle für den Friedman Test haben wir keine Wiederholungen für die Faktorkombinationen vorliegen, wie du in der folgenden Tabelle siehst. Solltest du wiederholt Faktorkombinationen gemessen haben, dann müsstest du die Daten erst Aggregieren. Was wiederum wirr ist, denn damit verlierst du Informationen. Heutzutage kannst du auch auf den vollen Datensätzen rechnen. Wir haben also in den Spalten den Faktor \(A\) mit den Leveln \(A.1\) bis \(A.4\) vorliegen. Der Faktor \(A\) beschreibt die Versuchsbedingungen, wie Behandlung oder Sorte. Du kannst natürlich auch mehr als vier Behandlungen vorliegen haben. In den Zeilen findest du dann den Faktor \(B\) für die Messwiederholungen oder Blöcke. Wir haben hier fünf Level im Faktor \(B\) vorliegen. Damit sieht die Tabelle eher wie eine Kreuztabelle einer deskriptiven Statistik aus als ein Datensatz.
| Faktor B | A.1 | A.2 | A.3 | A.4 |
|---|---|---|---|---|
| B.1 | 9.1 | 10.2 | 12.2 | 14.1 |
| B.2 | 4.2 | 5.2 | 6.2 | 7.3 |
| B.3 | 12.1 | 14.5 | 12.5 | 13.7 |
| B.4 | 1.2 | 3.6 | 3.5 | 7.1 |
| B.5 | 4.1 | 4.5 | 4.7 | 8.1 |
Dann wollen wir gleich einmal den Friedman Test anwenden. Dafür habe ich dann auch wieder die passenden R Paket sowie zwei Datensätze mitgebracht. Am Ende musst du schauen, ob du deine Daten mit dem Friedman Test auswerten möchtest. Der Friedman Test hat Probleme bei wenigen Behandlungen und Blöcken einen Effekt signifikant zu finden. Solltest du nur eine aggregierte Datentabelle haben, dann mag der Friedman Test eine Lösung für dein Problem sein.
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
pacman::p_load(tidyverse, magrittr, broom, pgirmess,
readxl, rstatix, coin, nparcomp,
effectsize, PMCMRplus, rcompanion,
afex, conflicted)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
Eigentlich sind die Datensätze hier zweimal das Gleiche, aber es gibt eben diese zwei Arten des Friedman Tests, die im Orbit rumgeistern. Deshalb hier im Folgenden einmal der agrawissenschaftliche Datensatz mit einem, Block in den Zeilen sowie einen Datensatz zu Messwiederholungen an Individuen mit unseren Flöhen. Damit haben wir beide Fälle abgefrühstückt und können uns dann die Auswertung einmal näher anschauen.
Beginnen wir einmal mit dem randomisierten vollständigen Blockdesign (eng. Randomized Complete Block Design). Wir haben die Daten in der folgenden Datei in dem Reiter block abliegen. Die Besonderheit ist hier, dass wir dennoch Messwiederholungen in den Blöcken vorliegen haben. Sehe einfahc die Blöcke als verschiedene Käfige. Ich habe die Daten mal etwas realistischer gebaut. Wir haben hier pro Block jeweils die Sprungweite von drei Hundeflöhen gemessen. Dabei sind die Flöhe dann unter verschiedenen Ernährungsformen gesprungen. Wir haben aber nicht den gleichen Floh in jeder Behandlung gemessen. Jeder Zahlenwert entspricht der Sprungweite eines individuellen Hundeflohs. Der Weg hier vom Wide-Format zum Long-Format über die Aggregation ist etwas lang, aber geht so nicht anders.
block_raw_tbl <- read_excel("data/friedman_data.xlsx",
sheet = "block") In der folgenden Datentabelle siehst du einmal den Datensatz mit den Sprungweiten unter den verschiedenen Ernährungsformen. Wir haben eine Wiederholung in den Blöcken vorliegen, diese Wiederholung müssen wir dann noch aggregieren, so dass wir dann nur eine Zeile pro Block haben.
| rep | block | ctrl | blood | ketchup |
|---|---|---|---|---|
| 1 | 1 | 6.3 | 5.3 | 1.5 |
| 2 | 1 | 7.8 | 5.6 | 1.3 |
| 3 | 1 | 7.1 | 5.8 | 1.5 |
| 1 | 2 | 7.3 | 8.1 | 2.4 |
| ... | ... | ... | ... | ... |
| 3 | 4 | 6.5 | 5.8 | 7.3 |
| 1 | 5 | 2.3 | 8.2 | 3.2 |
| 2 | 5 | 2.8 | 8.6 | 3.5 |
| 3 | 5 | 2.9 | 8.5 | 3.8 |
Dann bilden wir einmal den Mittelwert über jede Zeile für jeden Block. Somit haben wir dann die Blockmittel für jede Ernährungsform und nur noch einen Wert für die Sprungweite für jede Faktorkombination. In jeden Zahlenwert gehen jetzt die individuellen Sprungweiten der drei Hundeflöhe auf.
block_tbl <- block_raw_tbl |>
group_by(block) |>
summarise(across(ctrl:ketchup, mean)) In der folgenden Tabelle siehst du dann das Ergebnis der Aggregation. Wir haben dann nur noch eine Sprungweite der Hundeflöhe für jede Faktorkombination der Ernährungsform und des Blocks vorliegen.
| block | ctrl | blood | ketchup |
|---|---|---|---|
| 1 | 7.07 | 5.57 | 1.43 |
| 2 | 7.33 | 8.17 | 2.50 |
| 3 | 9.43 | 4.50 | 4.30 |
| 4 | 6.33 | 5.43 | 7.20 |
| 5 | 2.67 | 8.43 | 3.50 |
Das reicht dann aber natürlich wieder nicht, den wir haben damit die Daten im Wide-Format in der vorherigen Tabelle vorliegen. Die Analysen in R verlangen aber da Long-Format, so dass ich hier nochmal mit der Funktion pivot_longer() einen entsprechenden Datensatz baue. Dann kann ich auch gleich die entsprechenden Faktoren umwandeln.
block_long_tbl <- block_tbl |>
pivot_longer(cols = ctrl:ketchup,
names_to = "feeding",
values_to = "jump_length") |>
mutate(block = as_factor(block),
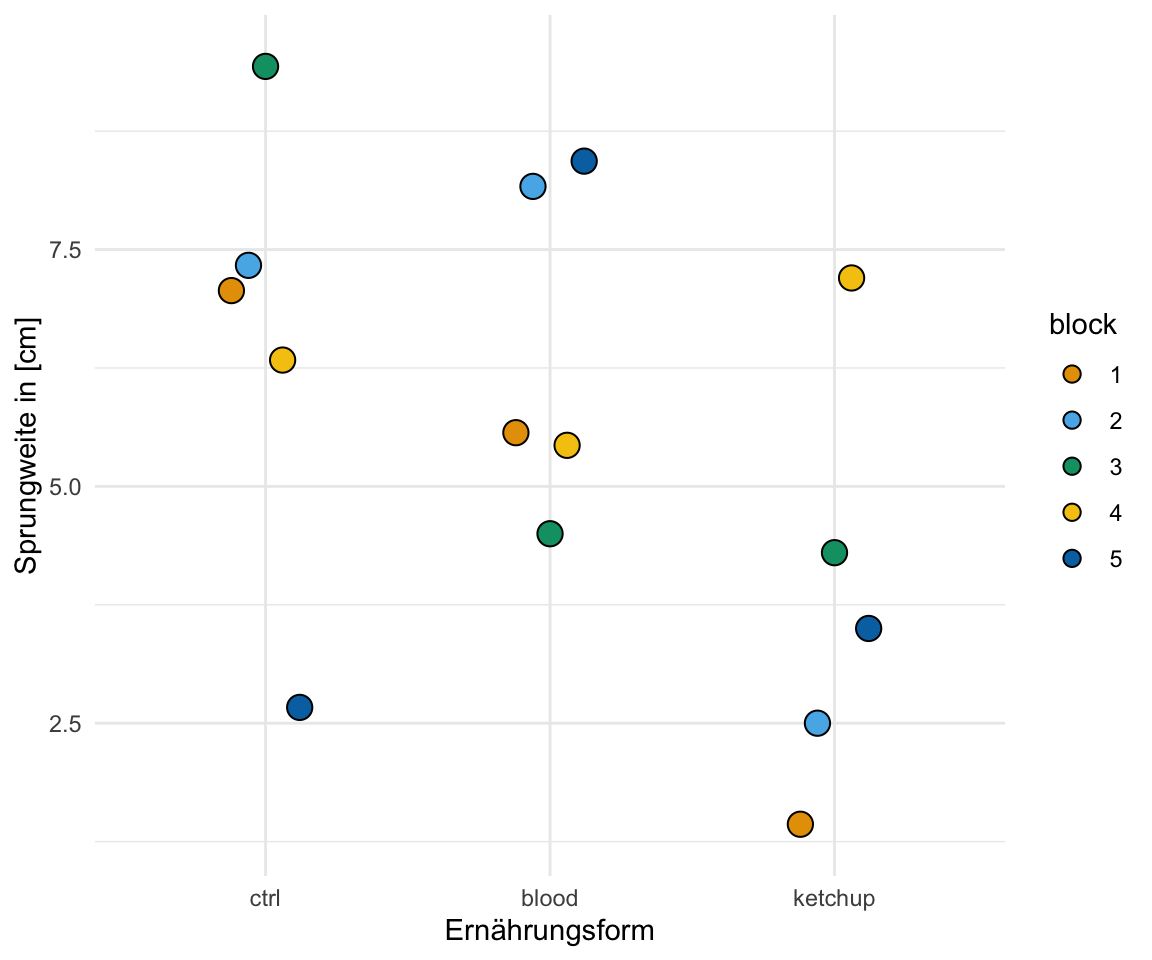
feeding = as_factor(feeding))Der Weg war jetzt etwas länger, aber so ist es manchmal, wenn wir mit etwas veralteten Algorithmen rechnen wollen. In der folgenden Abbildung siehst du dann nochmal die Daten in einem Dotplot dargestellt. Wir sehen, dass die Kontrolle eine etwas weitere Sprungweite hat als das Blut und auch die Ernährung mit Ketchup.
ggplot(block_long_tbl, aes(feeding, jump_length, fill = block)) +
theme_minimal() +
geom_dotplot(binaxis = "y", stackdir='center',
position=position_dodge(0.3)) +
labs(x = "Ernährungsform", y = "Sprungweite in [cm]", color = "Block") +
scale_fill_okabeito() 
Den zweiten Datensatz, den wir uns anschauen wollen, zeigt ein einfaches Design mit wiederholten Messungen (eng. Simple Repeated Measures Design). Wir haben hier also fünf Hundeflöhe vorliegen, die wir dann viermal springen lassen. Wir messen dann nach jedem Sprung einmal die Sprungweite. Damit haben wir dann über die Zeilen eine Messwiederholung in unseren Daten vorliegen.
repeated_tbl <- read_excel("data/friedman_data.xlsx",
sheet = "repeated") Wir haben damit folgenden Datensatz vorliegen. In den Zeilen sind die fünf Hundeflöhe, die jeweils zu vier Zeitpunkten einmal gesprungen sind. Wir haben dann zu jedem Zeitpunkt einmal die Sprungweite erfasst und aufgeschrieben. Die Messwerte sind damit abhängig. Damit ist der Datensatz sehr klassisch für einen Friedman Test.
| flea_id | t1 | t2 | t3 | t4 |
|---|---|---|---|---|
| 1 | 10.2 | 12.4 | 11.1 | 13.4 |
| 2 | 8.3 | 9.1 | 6.8 | 7.1 |
| 3 | 12.1 | 15.1 | 11.3 | 12.5 |
| 4 | 7.8 | 8.1 | 5.6 | 8.2 |
| 5 | 8.6 | 10.3 | 8.1 | 11.3 |
Das reicht dann aber natürlich noch nicht, den wir haben die Daten noch im Wide-Format in der vorherigen Tabelle vorliegen. Die Analysen in R verlangen aber da Long-Format, so dass ich hier nochmal mit der Funktion pivot_longer() einen entsprechenden Datensatz baue. Dann kann ich auch gleich die entsprechenden Faktoren umwandeln.
repeated_long_tbl <- repeated_tbl |>
pivot_longer(cols = t1:t4,
names_to = "time",
values_to = "jump_length") |>
mutate(flea_id = as_factor(flea_id),
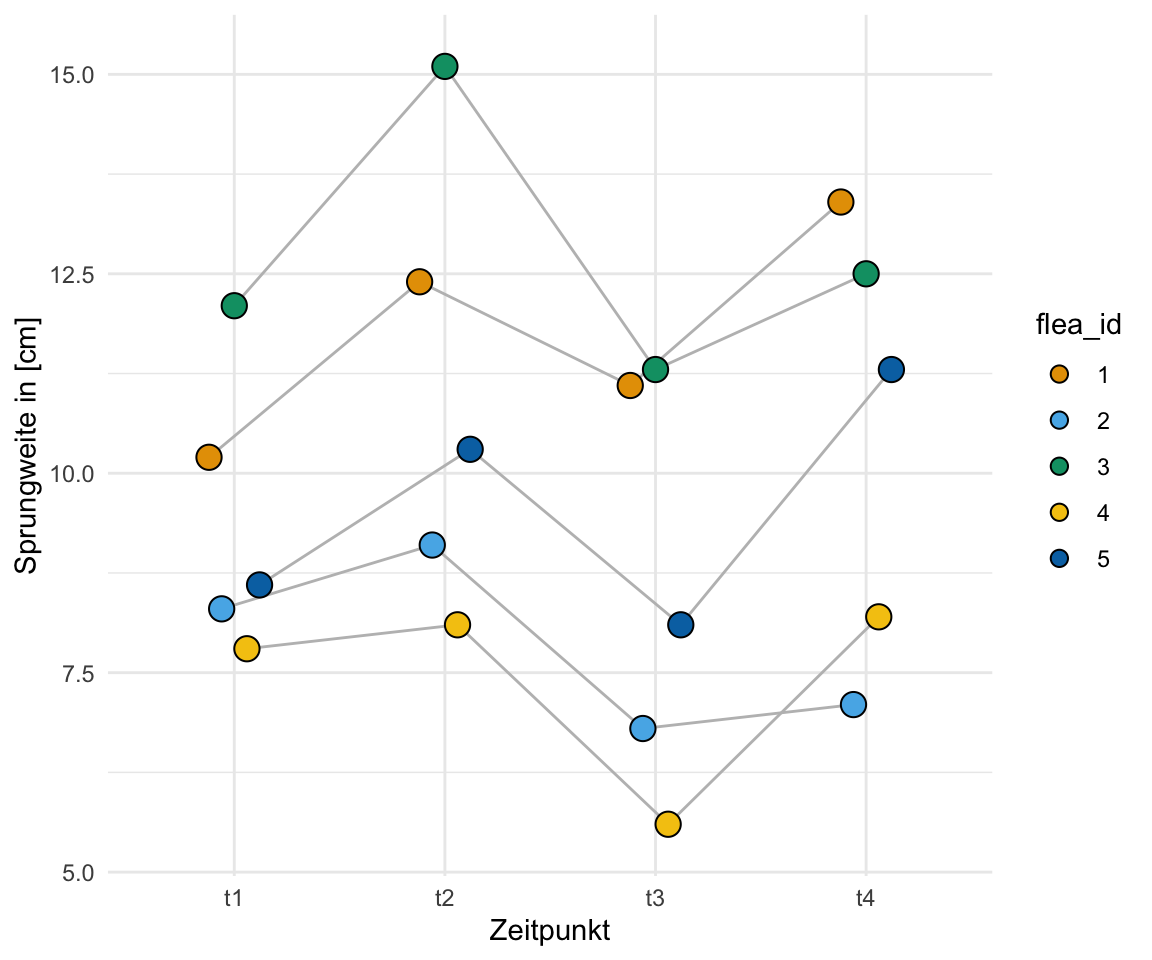
time_fct = as_factor(time))In der folgenden Abbildung siehst du dann nochmal die Daten in einem Dotplot dargestellt. Die Linien verbinden die einzelnen Flöhe und die Sprungweiten über die Zeiten miteinander. Wie wir sehen, haben wir die höchsten Sprungweiten zu dem Zeitpunkt t2 und weniger zu dem Zeitpunkt t3. Hier scheint es einen Effekt der Zeit zu geben.
ggplot(repeated_long_tbl, aes(time_fct, jump_length, fill = flea_id)) +
theme_minimal() +
geom_line(aes(group = flea_id), color = "gray",
position=position_dodge(0.3)) +
geom_dotplot(binaxis = "y", stackdir='center',
position=position_dodge(0.3)) +
labs(x = "Zeitpunkt", y = "Sprungweite in [cm]", color = "Floh ID") +
scale_fill_okabeito() 
Ich habe hier nochmal beide Datenformate dargestellt. Wir können in den Agrarwissenschaften nicht in den verschiedenen Blöcken wiederholt messen. Was wir in den einen Block Pflanzen wächst in dem einen Block und kann nicht nochmal woanders gemessen werden. Zwar ist ein Block eine Versuchseinheit, aber die Pflanzen oder Tiere, die in dem ersten Block stehen, stehen dann eben nicht in dem zweiten Block. Das ist technisch ja gar nicht möglich. Das hier zwei so unterschiedliche Fragestellungen angeblich mit dem gleichen Test beantwortet werden können, sollte einen schon stutzig machen.
Der Friedman Test betrachtet die Gruppen und Ränge um einen Unterschied nachzuweisen. Daher haben wir in der Nullhypothese als Gleichheitshypothese folgende Prosahypothese. Mehr zu den Hintergründen der Hypothesen in einem nichtparametrischen Test findest du im Kapitel zum U-Test.
\(H_0:\) Die Gruppen werden aus Populationen mit identischen Verteilungen entnommen. Typisch ist, dass die Stichprobenpopulationen stochastische Gleichheit aufweisen. Daher sind häufig die Mediane gleich.
Die Alternative lautet, dass sich mindestens ein paarweiser Vergleich unterschiedet. Hierbei ist das mindestens ein Vergleich wichtig. Es können sich alle Gruppen unterschieden oder eben nur ein Paar. Wenn ein Friedman Test die \(H_0\) ablehnt, also ein signifikantes Ergebnis liefert, dann wissen wir nicht, welche Gruppen sich unterscheiden und einen entsprechenden Post-hoc Test rechnen.
\(H_A:\) Die Gruppen werden aus Populationen mit unterschiedlichen Verteilungen entnommen. Typischerweise weist eine der untersuchten Populationen eine stochastische Dominanz auf. Die Mediane sind häufig verschieden.
Wir schauen uns jetzt einmal den Friedman Test theoretisch an bevor wir uns mit der Anwendung des Friedman Test in R beschäftigen.
Beginnen wir nun mit der Umsetzung des Friedman Tests. Ich zeige dir hier beide Anwendungsfelder. Nur der erste Fall für ein randomisiertes vollständiges Blockdesign macht überhaupt Sinn. Andere Fall für ein einfaches Design mit Messwiederholungen ist nur hier um dich zu warnen. Der Friedman Test leidet unter Mängeln und sollte nicht verwendet werden.
Der Friedman Test ist in R in verschiedenen Paketen implementiert. Alle Funktionen liefern mehr oder minder das gleiche Ergebnis. Wichtig ist wie wir in der Funktion das Modell definieren. Wir nutzen das Symbol | um die Behandlung von dem Block zu trennen. Vor dem | Symbol steht die Behandlung, hinter dem | steht der Block. Damit sieht das Modell etwas anders aus, aber im Prinzip ist die Definition des Modells einfach. Diese Schreibweise ist in allen drei vorgestellten Paketen und Funktionen gleich. Ich würde keine der drei Funktionen benutzen, da ich den Friedman Test nicht rechnen würde. Betrachten wir aber zuerst einmal den theoretischen Teil.
Die Frage bei den nichtparametrischen Tests ist ja immer, wie wir die Ränge bilden. In dem Fall des Friedman Tests bilden wir die Ränge über die Zeilen. Das heißt, wir schauen uns den ersten Block an und sortieren die beobachteten Sprungweiten und vergeben dann absteigend Ränge. Der größte Wert kriegt den ersten Rang und der kleinste Werte den letzten Rang. Das machen wir dann für jede weitere Zeile. Am Ende bilden wir dann die Rangsummen für jede Ernährungsform. Dafür addieren wir die Ränge einfach auf.
| Block | Kontrolle | Blut | Ketchup |
|---|---|---|---|
| 1 | \(7.07 \rightarrow 1\) | \(5.57 \rightarrow 2\) | \(1.43 \rightarrow 3\) |
| 2 | \(7.33 \rightarrow 2\) | \(8.17 \rightarrow 1\) | \(2.50 \rightarrow 3\) |
| 3 | \(9.43 \rightarrow 1\) | \(4.50 \rightarrow 2\) | \(4.30 \rightarrow 3\) |
| 4 | \(6.33 \rightarrow 2\) | \(5.43 \rightarrow 3\) | \(7.20 \rightarrow 1\) |
| 5 | \(2.67 \rightarrow 3\) | \(8.43 \rightarrow 1\) | \(3.50 \rightarrow 2\) |
| \(\sum\) | \(9\) | \(9\) | \(12\) |
Wenn wir keinen Effekt der Ernährungsformen erwarten würden, dann würde immer mal wieder jede Ernährungsform große oder kleine Ränge erhalten. Bei einer zufälligen Anordnung würden wir daher eine Rangsumme von \(E(R)\) gleich 10 erwarten.
\[ E(R) = \cfrac{N(k+1)}{2} = \cfrac{5(3+1)}{2} = 10 \]
mit
Wir sehen, dass wir nahe dran sind und fragen uns jetzt, ob die leichte Abweichung schon signifikant sein kann. Dafür können wir hier ein \(\mathcal{X_D}^2\) Statistik berechnen, die uns bei der Beantwortung hilft. Ja, wir können auch in anderen Tests wieder auf andere bekannte Teststatistiken zurückgreifen.
\[ \mathcal{X_D}^2 = \cfrac{12}{N \cdot k \cdot (k+1)} \cdot \sum R^2 - 3 \cdot N \cdot (k+1) \]
mit
Dann setzen wir mal alle Zahlen in die Formel ein und rechnen einmal aus, was wir für eine \(\mathcal{X_D}^2\) Statistik erhalten. Je größer die Teststatistik ist, desto eher lehnen wir die Nullhypothese ab.
\[ \begin{aligned} \mathcal{X_D}^2 &= \cfrac{12}{5 \cdot 3 \cdot (3+1)} \cdot (9^2 + 9^2 + 12^2) - 3 \cdot 5 \cdot (3+1) \\ &= 0.2 \cdot 306 - 60 \\ &= 1.6 \end{aligned} \]
Wir haben den kritischen Wert \(\mathcal{X}^2_{\alpha = 5\%}\) in unserem Fall mit \(5.99\) gegeben. Wenn die \(\mathcal{X_D}^2\) Statistik größer ist als der kritische Wert, können wir die Nullhypothese ablehnen. Das ist hier nicht der Fall. Wir sehen also keinen signifikanten Unterschied zwischen den Ernährungsformen.
Dann kommen wir auch schon zu dem statistischen Test in {stats}. Wir müssen hier nur schauen, dass die Zeilen als Faktor hinter dem Strich | stehen. Dann rechnet sich alles sehr schnell.
friedman.test(jump_length ~ feeding | block, data = block_long_tbl)
Friedman rank sum test
data: jump_length and feeding and block
Friedman chi-squared = 1.2, df = 2, p-value = 0.5488Nachdem wir die Funktion aufgerufen haben, erhalten wir auch gleich den \(p\)-Wert von \(0.5488\) wieder. Da der \(p\)-Wert größer ist als das Signifikanzniveau \(\alpha\) von 5% können wir die Nullhypothese nicht ablehnen. Das war auch anhand des Doplots zu erwarten.
Dann kommen wir auch schon zu dem statistischen Test in {coin} mit der Funktion friedman_test(). Da die Funktion gleich heißt wie im R Paket {rstatix} muss ich die Funktion nochmal explizit aufrufen. Wir müssen hier nur schauen, dass die Zeilen als Faktor hinter dem Strich | stehen. Dann rechnet sich alles sehr schnell.
coin::friedman_test(jump_length ~ feeding | block, data = block_long_tbl)
Asymptotic Friedman Test
data: jump_length by
feeding (ctrl, blood, ketchup)
stratified by block
chi-squared = 1.2, df = 2, p-value = 0.5488Nachdem wir die Funktion aufgerufen haben, erhalten wir auch gleich den \(p\)-Wert von \(0.5488\) wieder. Das gleiche Eregbnis wie schon vorher. Da der \(p\)-Wert größer ist als das Signifikanzniveau \(\alpha\) von 5% können wir die Nullhypothese nicht ablehnen. Das war auch anhand des Doplots zu erwarten.
Dann kommen wir auch schon zu dem statistischen Test in {rstatix} mit der Funktion friedman_test(). Da die Funktion gleich heißt wie im R Paket {coin} muss ich die Funktion nochmal explizit aufrufen. Wir müssen hier nur schauen, dass die Zeilen als Faktor hinter dem Strich | stehen. Dann rechnet sich alles sehr schnell. Mehr zu der Funktion erfährst du auch im Tutorium Friedman Test in R.
rstatix::friedman_test(jump_length ~ feeding | block, data = block_long_tbl)# A tibble: 1 × 6
.y. n statistic df p method
* <chr> <int> <dbl> <dbl> <dbl> <chr>
1 jump_length 5 1.2 2 0.549 Friedman testNachdem wir die Funktion aufgerufen haben, erhalten wir auch gleich den \(p\)-Wert von \(0.5488\) wieder. Das gleiche Eregbnis wie schon vorher. Da der \(p\)-Wert größer ist als das Signifikanzniveau \(\alpha\) von 5% können wir die Nullhypothese nicht ablehnen. Das war auch anhand des Doplots zu erwarten.
Wie wir sehen erhalten wir aus allen drei Funktionen den gleichen p-Wert. Hier kommt es dann eher darauf an mit welchem Paket du sonst so rechnest. Vermutlich würde ich dir das R Paket {rstatix} empfehlen, weil wir hier dann auch gleich den Effektschätzer mit berechnen können. Sonst nehmen sich die Pakete bei einem so simplen Algorithmus wie dem Friedman Test nichts.
Wir können den Effektschätzer Kendall’s \(W\) im R Paket {rstatix} mit der Funktion friedman_effsize() berechnen. Dann erhalten wir auch gleich noch die Interpretation mitgeliefert, was es dann auch sehr viel einfacher macht. Kendall’s \(W\) hat nämlich keine direkte biologische Interpretation und so brauchen wir hier eine entsprechende Einordnung.
friedman_effsize(jump_length ~ feeding | block, data = block_long_tbl)# A tibble: 1 × 5
.y. n effsize method magnitude
* <chr> <int> <dbl> <chr> <ord>
1 jump_length 5 0.12 Kendall W small Wir haben also herausgefunden, dass wir einen schwachen Effekt haben und sich die Mediane der Gruppen nicht unterscheiden. Damit sind wir dann auch soweit schon mit dem Friedman test durch, wir können hier dann auch nicht mehr berechnen. Auch erhalten wir keine 95% Konfidenzintervalle für die Effekte.
Dann hier auch die parametrische Lösung des Problems mit der zweifaktoriellen ANOVA. Wir wollen jetzt einfach nur unsere Messwerte einmal Rangtransformieren. Dafür nutze ich entweder die Funktion rank() oder aber die folgende Funktion signed_rank(), wenn ich negative Werte in meinen Messungen erwarte.
signed_rank <- function(x) sign(x) * rank(abs(x))Konkret habe ich meine Sprungweiten der Flöhe. Jetzt mutiere ich die Sprungweite über die Funktion signed_rank() in Ränge und nutze diese Spalte dann für die ANOVA.
block_long_ranked_tbl <- block_long_tbl |>
mutate(ranked_jump_length = signed_rank(jump_length))Ich nutze hier die Funktion anova_test() aus dem R Paket {rstatix}, da ich dann einfacher pipen kann. Dann wähle ich noch die passenden Spalten und sehe, dass die Entscheidung die gleiche wäre wie bei den obigen Implementierungen des Friedman Tests. Wir können die Nullhypothese nicht ablehnen, wir haben einen signifikanten Unterschied in den Sprungweiten.
block_long_ranked_tbl |>
anova_test(ranked_jump_length ~ feeding + block) ANOVA Table (type II tests)
Effect DFn DFd F p p<.05 ges
1 feeding 2 8 1.989 0.199 0.332
2 block 4 8 0.214 0.923 0.097Dann können wir die Daten auch in der Form als Messwiederholungen innerhalb des Blocks modellieren, was dann die jeweiligen Blockeffekte miteinschließt. Dann haben wir ein einfaktorielles repeated Design für die ANOVA. Hier nutze ich die Funktion aov_car() aus dem R Paket {afex}. Aber auch hier sehen wir, dass wir dann doch keinen signifikanten Unterschied finden unser p-Wert ist mit \(0.202\) immer noch größer als das Signifikanzniveau \(\alpha\).
aov_car(ranked_jump_length ~ feeding + Error(block/feeding),
data = block_long_ranked_tbl)Anova Table (Type 3 tests)
Response: ranked_jump_length
Effect df MSE F ges p.value
1 feeding 1.91, 7.66 22.79 1.99 .310 .202
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1
Sphericity correction method: GG Beware the Friedman test! Das ist der wichtigste Punkt. Wenn du den Friedman Test rechnen willst, weil in deinen Zeilen Messwiederholungen sind, dann bitte lassen. Du also bei jedem Floh wiederholt die Sprungweite gemessen und möchtest jetzt wissen, ob es einen Unterschied in den Zeitpunkten gibt. Die Alternativen hat Zimmerman & Zumbo (1993) einmal diskutiert und ich zeige dir dann auch die besseren Lösungen.
Die Frage ist, warum sollte man auf Messwiederholungen einen Friedman Test rechnen? Weil die Normalverteilung für den Messwert in einer ANOVA nicht gegeben ist. Dafür brauchen wir aber nicht den Friedman Test wir können da auch einen anderen Weg gehen. Nach dem folgenden Zitat können wir auch eine repeated ANOVA rechnen. Das machen wir dann auch gleich im Anschluss. Wenn du dich dafür entscheidest, die Alternative zu nutzen, dann kannst du gerne einmal die Arbeit von Zimmerman & Zumbo (1993) zitieren.
“[In cases] where one-way repeated measures ANOVA is not appropriate, rank transformation followed by ANOVA will provide a more robust test with greater statistical power than the Friedman test.” — Beware the Friedman test! und Zimmerman & Zumbo (1993)
Aber wie immer zeige ich natürlich auch die Anwendung des Friedman Test auf unser Design mit wiederholten Messungen. Hier haben wir dann unsere einzelnen Hundeflöhe wiederholt zu unterschiedlichen Zeitpunkten gemessen. Daher sind die einzelnen Zeitpunkte für jeden Floh nicht unabhängig voneinander. Leider ignoriert der Friedman Test jegliche Beziehungen zwischen den Flöhen, so dass hier der Test mit Vorsicht zu genießen ist.
Die Frage bei den nichtparametrischen Tests ist ja immer, wie wir die Ränge bilden. In dem Fall des Friedman Tests bilden wir die Ränge über die Zeilen. Das heißt, wir schauen uns den ersten Block an und sortieren die beobachteten Sprungweiten und vergeben dann absteigend Ränge. Der größte Wert kriegt den ersten Rang und der kleinste Werte den letzten Rang. Das machen wir dann für jede weitere Zeile. Am Ende bilden wir dann die Rangsummen für jeden Zeitpunkt. Dafür addieren wir die Ränge einfach auf.
| Floh | Zeitpunkt 1 | Zeitpunkt 2 | Zeitpunkt 3 | Zeitpunkt 4 |
|---|---|---|---|---|
| 1 | \(10.2 \rightarrow 4\) | \(12.4 \rightarrow 2\) | \(11.1 \rightarrow 3\) | \(13.4 \rightarrow 1\) |
| 2 | \(8.3 \rightarrow 2\) | \(9.1 \rightarrow 1\) | \(6.8 \rightarrow 4\) | \(7.1 \rightarrow 3\) |
| 3 | \(12.1 \rightarrow 3\) | \(15.1 \rightarrow 1\) | \(11.3 \rightarrow 4\) | \(12.5 \rightarrow 2\) |
| 4 | \(7.8 \rightarrow 3\) | \(8.1 \rightarrow 2\) | \(5.6 \rightarrow 4\) | \(8.2 \rightarrow 1\) |
| 5 | \(8.6 \rightarrow 3\) | \(10.3 \rightarrow 2\) | \(8.1 \rightarrow 4\) | \(11.3 \rightarrow 1\) |
| \(\sum\) | \(15\) | \(8\) | \(19\) | \(8\) |
Wenn wir keinen Effekt der Ernährungsformen erwarten würden, dann würde immer mal wieder jede Ernährungsform große oder kleine Ränge erhalten. Bei einer zufälligen Anordnung würden wir daher eine Rangsumme von \(E(R)\) gleich 12.5 erwarten.
\[ E(R) = \cfrac{N(k+1)}{2} = \cfrac{5(4+1)}{2} = 12.5 \]
mit
Wir sehen, dass wir nahe dran sind und fragen uns jetzt, ob die Abweichung schon signifikant sein kann. Dafür können wir hier ein \(\mathcal{X_D}^2\) Statistik berechnen, die uns bei der Beantwortung hilft. Ja, wir können auch in anderen Tests wieder auf andere bekannte Teststatistiken zurückgreifen.
\[ \mathcal{X_D}^2 = \cfrac{12}{N \cdot k \cdot (k+1)} \cdot \sum R^2 - 3 \cdot N \cdot (k+1) \]
Dann setzen wir mal alle Zahlen in die Formel ein und rechnen einmal aus, was wir für eine \(\mathcal{X_D}^2\) Statistik erhalten. Je größer die Teststatistik ist, desto eher lehnen wir die Nullhypothese ab.
\[ \begin{aligned} \mathcal{X_D}^2 &= \cfrac{12}{5 \cdot 4 \cdot (4+1)} \cdot (15^2 + 8^2 + 19^2 + 8^2) - 3 \cdot 5 \cdot (4+1) \\ &= 0.12 \cdot 714 - 75 \\ &= 10.68 \end{aligned} \]
Wir haben den kritischen Wert \(\mathcal{X}^2_{\alpha = 5\%}\) in unserem Fall mit \(7.82\) gegeben. Wenn die \(\mathcal{X_D}^2\) Statistik größer ist als der kritische Wert, können wir die Nullhypothese ablehnen. Das ist hier tatsächlich der Fall. Wir sehen also einen signifikanten Unterschied zwischen den Zeitpunkten.
Dann kommen wir auch schon zu dem statistischen Test in {stats}. Wir müssen hier nur schauen, dass die Zeilen als Faktor hinter dem Strich | stehen. Dann rechnet sich alles sehr schnell.
friedman.test(jump_length ~ time_fct | flea_id, data = repeated_long_tbl)
Friedman rank sum test
data: jump_length and time_fct and flea_id
Friedman chi-squared = 10.68, df = 3, p-value = 0.01359Nachdem wir die Funktion aufgerufen haben, erhalten wir auch gleich den \(p\)-Wert von \(0.014\) wieder. Da der \(p\)-Wert kleiner ist als das Signifikanzniveau \(\alpha\) von 5% können wir die Nullhypothese ablehnen. Das war auch anhand des Doplots zu erwarten.
Dann kommen wir auch schon zu dem statistischen Test in {rstatix} mit der Funktion friedman_test(). Da die Funktion gleich heißt wie im R Paket {coin} muss ich die Funktion nochmal explizit aufrufen. Wir müssen hier nur schauen, dass die Zeilen als Faktor hinter dem Strich | stehen. Dann rechnet sich alles sehr schnell. Mehr zu der Funktion erfährst du auch im Tutorium Friedman Test in R.
rstatix::friedman_test(jump_length ~ time_fct | flea_id, data = repeated_long_tbl)# A tibble: 1 × 6
.y. n statistic df p method
* <chr> <int> <dbl> <dbl> <dbl> <chr>
1 jump_length 5 10.7 3 0.0136 Friedman testNachdem wir die Funktion aufgerufen haben, erhalten wir auch gleich den \(p\)-Wert von \(0.012\) wieder. Damit fast das gleiche Eregbnis wie schon vorher. Da der \(p\)-Wert kleiner ist als das Signifikanzniveau \(\alpha\) von 5% können wir die Nullhypothese ablehnen. Das war auch anhand des Doplots zu erwarten.
Abschöießend gibt es noch in dem R Paket {nparcomp} die Funktion mctp.rm() die es uns ermöglicht eine repeated ANOVA mit einem nichtparametrischen Verfahren zu rechnen. Daher ist diese Variante natürlich den anderen beiden vorzuziehen. Wir erhalten hier aber keine globale Aussage sondern gleich die paarweisen Vergleiche. Sozusagen der Post-hoc Test in einem Test. Wir müssen uns hier leider merken welche Faktorlevel wir vorliegen haben, den die Ausgabe gibt uns leider nur die Zahlen und nicht die Gruppennamen. Das ist natürlich unschön und fehleranfällig. Wir haben eine automatische Adjustierung für multiple Vergleiche.
mctp.rm_obj <- mctp.rm(jump_length ~ time_fct, data = repeated_long_tbl,
info = FALSE)
mctp.rm_obj$Analysis Estimator Lower Upper Statistic p.Value
2 - 1 0.394 -0.265 1.052 2.208 0.20248654
3 - 1 -0.297 -1.397 0.803 -0.997 0.66981250
4 - 1 0.320 -1.121 1.761 0.820 0.76811647
3 - 2 -0.690 -1.241 -0.140 -4.632 0.02409675
4 - 2 -0.074 -1.028 0.881 -0.286 0.98255427
4 - 3 0.617 -0.004 1.238 3.668 0.05057679Wir sehen, dass nur der Zeitpunkt t3 mit dem Zeitpunkt t2 signifikant unterschiedlich ist. Alle anderen Zeitpunkte sind zeigen keinen p-Wert unter dem Signifikanzniveau \(\alpha\) vo 5%.
Dann hier auch die parametrische Lösung des Problems mit der repeated ANOVA. Wir wollen jetzt einfach nur unsere Messwerte einmal Rangtransformieren. Dafür nutze ich entweder die Funktion rank() oder aber die folgende Funktion signed_rank(), wenn ich negative Werte in meinen Messungen erwarte.
signed_rank <- function(x) sign(x) * rank(abs(x))Konkret habe ich meine Sprungweiten der Flöhe. Jetzt mutiere ich die Sprungweite über die Funktion signed_rank() in Ränge und nutze diese Spalte dann für die ANOVA.
repeated_long_ranked_tbl <- repeated_long_tbl |>
mutate(ranked_jump_length = signed_rank(jump_length))Wir können die Daten in der Form als Messwiederholungen innerhalb des Flöhe modellieren. Dann haben wir ein einfaktorielles repeated Design für die ANOVA. Hier nutze ich die Funktion aov_car() aus dem R Paket {afex}. Hier sehen wir, dass wir dann einen signifikanten Unterschied finden unser p-Wert ist mit \(0.041\) immer noch kleiner als das Signifikanzniveau \(\alpha\). Der p-Wert ist nicht ganz so klein wie bei dem Friedman Test.
aov_car(ranked_jump_length ~ time_fct + Error(flea_id/time_fct),
data = repeated_long_ranked_tbl)Anova Table (Type 3 tests)
Response: ranked_jump_length
Effect df MSE F ges p.value
1 time_fct 1.38, 5.53 11.46 6.53 * .156 .041
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1
Sphericity correction method: GG Wenn wir dann einen signifikanten Unterschied gefunden haben, dann müssen wir ja noch einen Post-hoc Test rechnen. Für das einfache Design mit den Messwiederholungen würde ich dann gleich {nparcomp} empfehlen, wenn es ein nichtparametrischer Test sein soll. Dort haben wir dann auch gleich die paarweisen Vergleiche mit drin. Wenn es dann doch klassischer mit Friedman als Vortest sein soll, dann hier die zwei Alternativen für den Post-hoc Test. Beide Pakete sind schon etwas älter, was die Bedienung der Funktionen angeht.
Das R Paket {pgirmess} erlaubt es mit dem friedmanmc() einen paarweisen Friedman Test zu rechnen. Wir haben hier eine veraltete Nutzung ohne die Formelschreibweise, so dass wir hier die einzelnen Variablen händisch den Optionen zuordnen müssen. Wir müssten händisch das Signifikanzniveau adjustieren oder aber händisch die p-Werte anpassen, wenn wir für multiple Vergleiche adjustieren wollen würden.
friedmanmc_res <- friedmanmc(y = block_long_tbl$jump_length,
groups = block_long_tbl$feeding,
blocks = block_long_tbl$block)
friedmanmc_resMultiple comparisons between groups after Friedman test
alpha: 0.05
Comparisons
obs.dif critical.dif stat.signif p.value
ctrl-blood 0 7.570429 FALSE 1
ctrl-ketchup 3 7.570429 FALSE 1
blood-ketchup 3 7.570429 FALSE 1Dann sehen wir auch schon, dass wir keinen signifkanten Unterschied in den paarweisen Vergleichen vorliegen haben. Alle p-Werte sind größer als das Signifikanzniveau \(\alpha\) von 5%. Wir können keine Nullhypothese der Vergleiche ablehnen.
friedmanmc_tbl <- friedmanmc_res$dif.com |>
rownames_to_column("comparison") |>
as_tibble()Am Ende wollen wir dann noch das Compact letter display haben und nutzen dann dafür die Funktion cldList(). Wir sehen dann aber natürlich hier auch keinen Unterschied. Leider gibt es keine Möglichkeit die 95% Konfidenzintervalle zu erhalten. Wir auch beim Kruskal-Wallis-Test erhalten wir bei dem Friedman Test keine 95% Konfidenzintervalle und müssen im Zweifel mit dieser Einschränkung leben.
cldList(p.value ~ comparison, data = friedmanmc_tbl) Group Letter MonoLetter
1 ctrl a a
2 blood a a
3 ketchup a aWenn du willst kannst du den paarweisen Vergleich auch für das einfache Design für die Messweiderholungen einmal selber rechnen. Die Funktionen sind die gleichen aber du musst natürlich den Datensatz und die Variablen anpassen.
Nachdem wir jetzt festgestellt haben, dass sich mindestens ein Gruppenunterschied zwischen den Weizensorten finden lassen muss, wollen wir noch feststellen wo dieser Unterschied liegt. Wir nutzen dafür den Siegel- und Castellan-Vergleichstests für alle Paare durch. Der Test ist mit der Funktion frdAllPairsSiegelTest() in dem R Paket {PMCMRplus} implementiert und einfach nutzbar. In dem Paket sind noch eine weitere Reihe an statistischen Test für paarweise nicht-parametrische Test enthalten. Leider sind das Paket und die Funktion schon älter, so dass wir nicht einmal die Formelschreibweise zu Verfügung haben. Wir müssen alle Spalten aus unserem Datensatz mit dem $ einzeln selektieren und den Optionen zuordnen.
siegel_test_res <- frdAllPairsSiegelTest(y = block_long_tbl$jump_length,
groups = block_long_tbl$feeding,
blocks = block_long_tbl$block,
p.adjust.method = "none")
siegel_test_res ctrl blood
blood 1.00 -
ketchup 0.34 0.34 Ich empfehle ja immer eine Adjustierung für multiple Vergleiche, aber du kannst das selber entscheiden. Wenn du für die multiplen Vergleiche adjustieren willst, dann nutze gerne die Option p.adjust.method = "bonferroni" oder eben statt bonferroni die Adjustierungsmethode fdr.
Damit wir auch das compact letter display aus unseren \(p\)-Werte berechnen können, müssen wir unser Ergebnisobjekt nochmal in eine Tabelle umwandeln. Dafür gibt es dann auch eine passende Funktion mit PMCMRTable. Wir sehen, es ist alles etwas altbacken.
siegel_test_tab <- PMCMRTable(siegel_test_res)
siegel_test_tab Comparison p.value
1 blood - ctrl = 0 1
2 ketchup - ctrl = 0 0.343
3 ketchup - blood = 0 0.343Nachdem wir die Tabellenschreibweise der \(p\)-Werte vorliegen haben, können wir dann das compact letter display uns über die Funktion cldList() anzeigen lassen. Leider gibt es keine Möglichkeit die 95% Konfidenzintervalle zu erhalten. Wir auch beim Kruskal-Wallis-Test erhalten wir bei dem Friedman Test keine 95% Konfidenzintervalle und müssen im Zweifel mit dieser Einschränkung leben.
cldList(p.value ~ Comparison, data = siegel_test_tab) Group Letter MonoLetter
1 blood a a
2 ketchup a a
3 ctrl a aAm compact letter display sehen wir im Prinzip das gleiche Muster wie in den \(p\)-Werten. Nur nochmal etwas anders dargestellt und mit dem Fokus auf die nicht Unterschiede.