53 Gaussian Regression
Letzte Änderung am 08. June 2025 um 12:26:14
“Regression analysis is the hydrogen bomb of the statistics arsenal.” — Charles Wheelan, Naked Statistics: Stripping the Dread from the Data
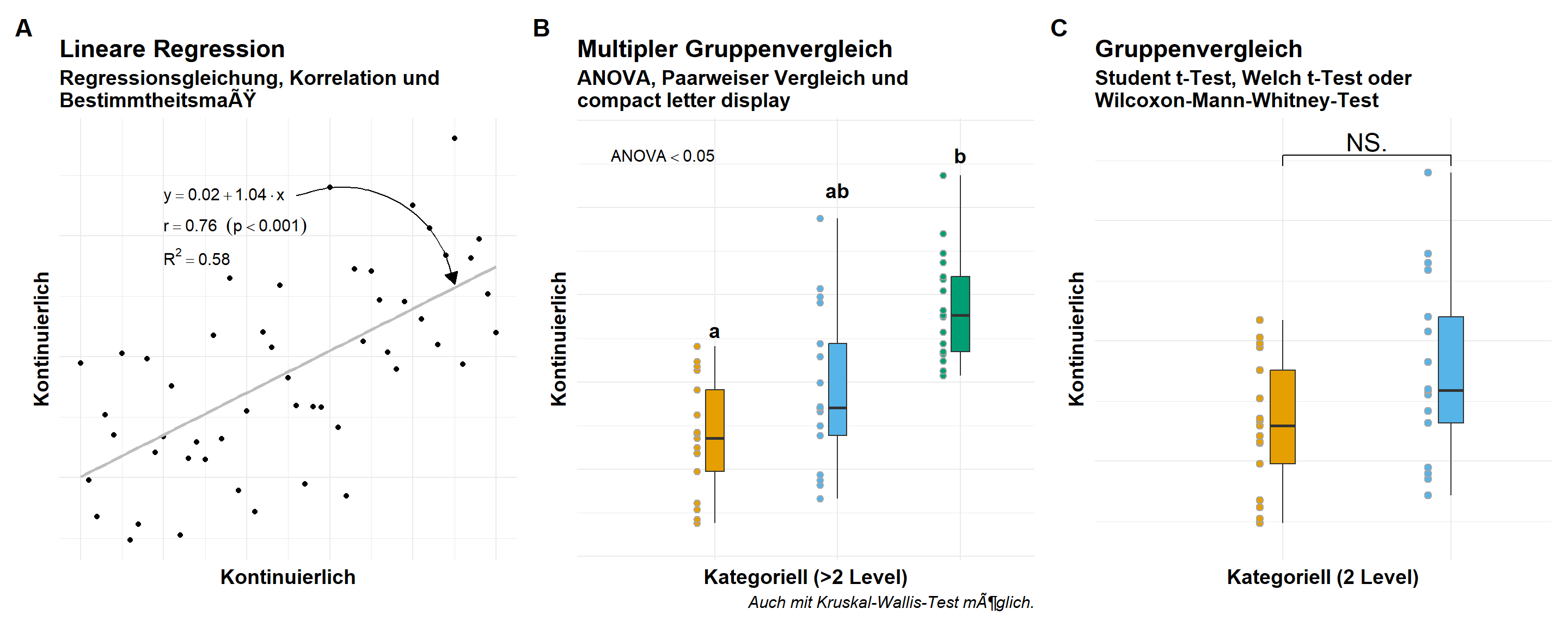
Selten nutzen wir eine multiple gaussian lineare Regression alleine. Häufig haben wir dann ein normalverteiltes Outcome, weshalb wir die Gaussian Regression überhaupt rechnen, und dann noch mehrere Faktoren über die wir eine Aussagen treffen wollen. In der folgenden Abbildung 53.1 siehst du nochmal den Zusammenhang zwischen einem normalverteilten Outcome, wie Gewicht oder Größe, im Bezug zu einem kontinuierlichen oder kategoriellen \(x\) als Einflussgröße. Wir sind dann eher im Bereich der Posthoc-Tests mit kategoriellen \(x\) als in wirklich einer Interpretation einer Gaussian Regression mit einem kontinuierlichen \(x\). Dennoch müssen wir wissen, ob die Gaussian Regression gut funktioniert hat. Die Überprüfung der Modellierung können wir dann in diesem Kapitel einmal durchgehen.
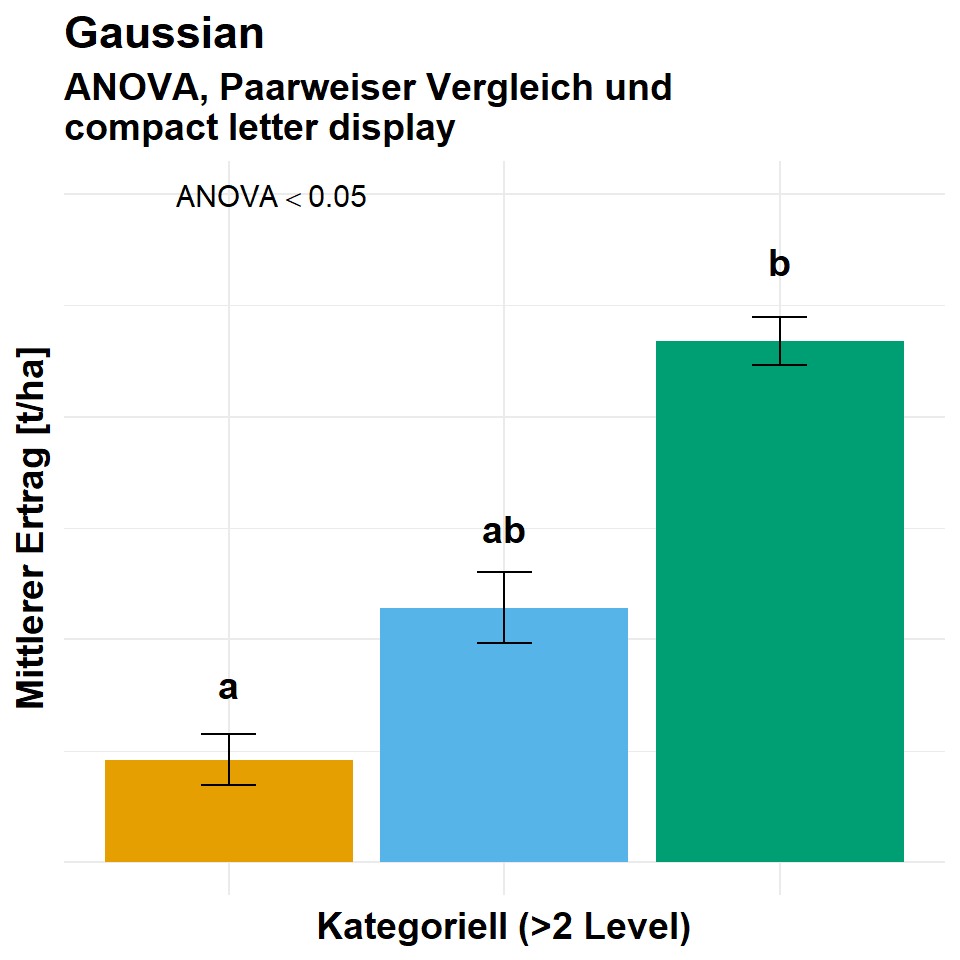
Häufig wollen wir dann die Ergebnisse aus einer Gaussian Regression dann im Falle eines kategoriellen \(x\) dann als Barplots wie in der Abbildung 53.2 darstellen. Hier musst du dann einmal weiter unten in den Abschnitt zu den Gruppenvergleichen springen.
Im diesem Kapitel zu der multiplen Gaussian linearen Regression gehen wir davon aus, dass die Daten in der vorliegenden Form ideal sind. Das heißt wir haben weder fehlende Werte vorliegen, noch haben wir mögliche Ausreißer in den Daten. Auch wollen wir keine Variablen selektieren. Wir nehmen alles was wir haben mit ins Modell. Sollte eine oder mehre Bedingungen nicht zutreffen, dann schaue dir einfach die folgenden Kapitel an.
- Wenn du fehlende Werte in deinen Daten vorliegen hast, dann schaue bitte nochmal in das Kapitel 50 zu Imputation von fehlenden Werten.
- Wenn du denkst, dass du Ausreißer oder auffällige Werte in deinen Daten hast, dann schaue doch bitte nochmal in das Kapitel 48 zu Ausreißer in den Daten.
- Wenn du denkst, dass du zu viele Variablen in deinem Modell hast, dann hilft dir das Kapitel 49 bei der Variablenselektion.
Wir gehen jetzt einmal die lineare Regression mit einem normalverteilten Outcome \(y\) einmal durch. Wie schon oben erwähnt, meistens nutzten wir die Gaussian Regression als vorangestelltes Modell für eine ANOVA oder dann eben einen Posthoc-Test in {emmeans}.
Zerforschen: Einfaktorieller Barplot mit
lm(), gls() oder sandwich
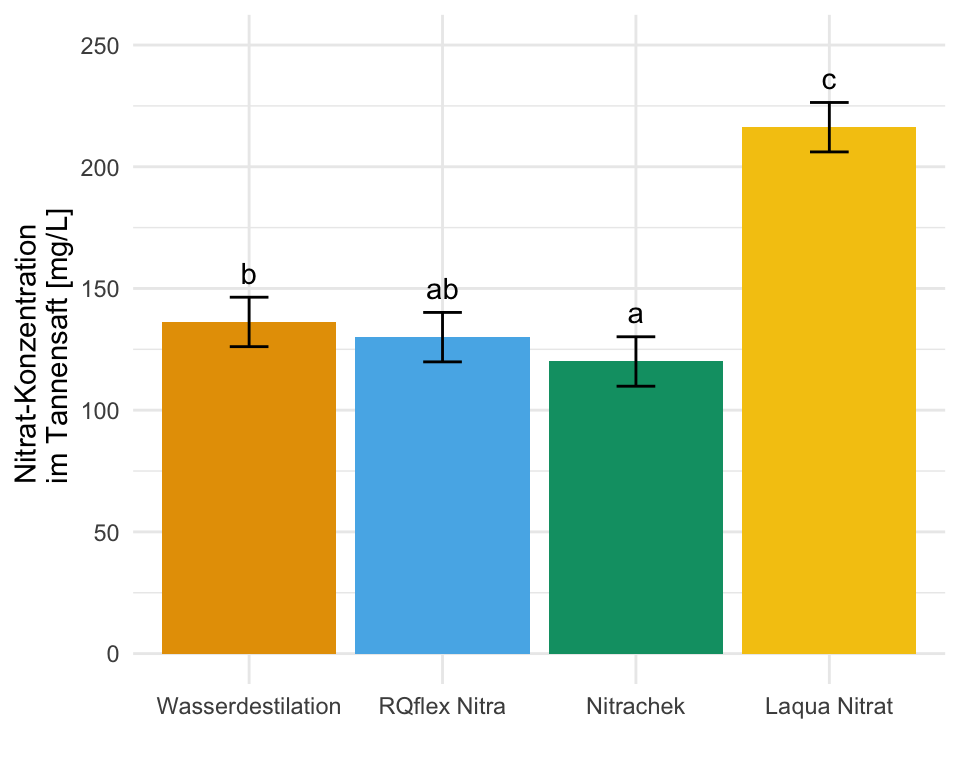
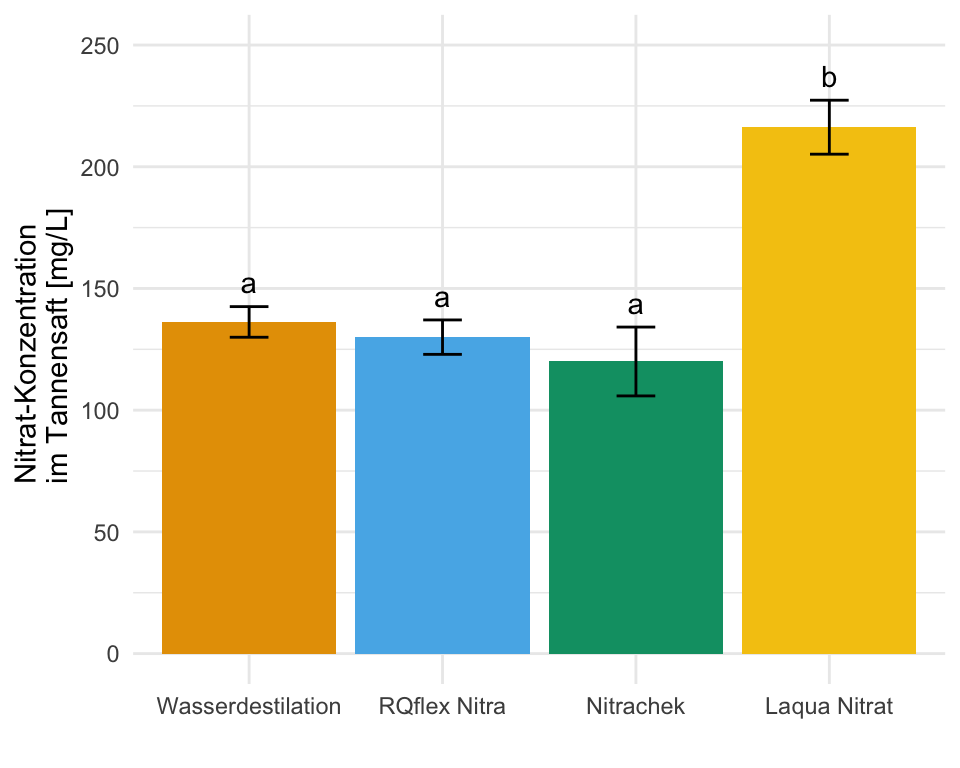
In diesem Zerforschenbeispiel wollen wir uns einen einfaktoriellen Barplot oder Säulendiagramm anschauen. Daher fangen wir mit der folgenden Abbildung einmal an. Wir haben hier ein Säulendiagramm mit compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Behandlungen jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung. Die Standardabweichung addieren und subtrahieren wir dann jeweils von dem Mittelwert und schon haben wir die Fehlerbalken. Für eine detaillierte Betrachtung der Erstellung der Abbildung schauen einmal in das Kapitel zum Barplot oder Balkendiagramm oder Säulendiagramm.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_simple.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die vier Werte alle um den Mittelwert streuen lassen. Dabei habe ich darauf geachtet, dass die Streuung dann in der letzten Behandlung am größten ist.
R Code [zeigen / verbergen]
barplot_tbl <- read_excel("data/zerforschen_barplot_simple.xlsx") |>
mutate(trt = factor(trt,
levels = c("water", "rqflex", "nitra", "laqua"),
labels = c("Wasserdestilation",
"RQflex Nitra",
"Nitrachek",
"Laqua Nitrat")))
barplot_tbl # A tibble: 16 × 2
trt nitrat
<fct> <dbl>
1 Wasserdestilation 135
2 Wasserdestilation 130
3 Wasserdestilation 145
4 Wasserdestilation 135
5 RQflex Nitra 120
6 RQflex Nitra 130
7 RQflex Nitra 135
8 RQflex Nitra 135
9 Nitrachek 100
10 Nitrachek 120
11 Nitrachek 130
12 Nitrachek 130
13 Laqua Nitrat 230
14 Laqua Nitrat 210
15 Laqua Nitrat 205
16 Laqua Nitrat 220Im Folgenden sparen wir uns den Aufruf mit group_by() den du aus dem Kapitel zum Barplot schon kennst. Wir machen das alles zusammen in der Funktion emmeans() aus dem gleichnamigen R Paket. Der Vorteil ist, dass wir dann auch gleich die Gruppenvergleiche und auch das compact letter display erhalten. Einzig die Standardabweichung \(s\) wird uns nicht wiedergegeben sondern der Standardfehler \(SE\). Da aber folgernder Zusammenhang vorliegt, können wir gleich den Standardfehler in die Standardabweichung umrechnen.
\[ SE = \cfrac{s}{\sqrt{n}} \]
Wir rechnen also gleich einfach den Standardfehler \(SE\) mal der \(\sqrt{n}\) um dann die Standardabweichung zu erhalten. In unserem Fall ist \(n=4\) nämlich die Anzahl Beobachtungen je Gruppe. Wenn du mal etwas unterschiedliche Anzahlen hast, dann kannst du auch einfach den Mittelwert der Fallzahl der Gruppen nehmen. Da überfahren wir zwar einen statistischen Engel, aber der Genauigkeit ist genüge getan.
In den beiden Tabs siehst du jetzt einmal die Modellierung unter der Annahme der Varianzhomogenität mit der Funktion lm() und einmal die Modellierung unter der Annahme der Varianzheterogenität mit der Funktion gls() aus dem R Paket nlme. Wie immer lässt sich an Boxplots visuell überprüfen, ob wir Homogenität oder Heterogenität vorliegen haben. Oder aber du schaust nochmal in das Kapitel Der Pre-Test oder Vortest, wo du mehr erfährst.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim().
R Code [zeigen / verbergen]
emmeans_homogen_tbl <- lm(nitrat ~ trt, data = barplot_tbl) |>
emmeans(~ trt) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(4))
emmeans_homogen_tbl# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 5.08 12 109. 131. a 10.2
2 RQflex Nitra 130 5.08 12 119. 141. ab 10.2
3 Wasserdestilation 136. 5.08 12 125. 147. b 10.2
4 Laqua Nitrat 216. 5.08 12 205. 227. c 10.2In dem Objekt emmeans_homogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. Wie dir vielleicht auffällt sind alle Standardfehler und damit alle Standardabweichungen für alle Gruppen gleich, das war ja auch unsere Annahme mit der Varianzhomogenität.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket und natürlich in den Abschnitt zu dem Gruppenvergleich unter Varianzheterogenität. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim().
R Code [zeigen / verbergen]
emmeans_hetrogen_gls_tbl <- gls(nitrat ~ trt, data = barplot_tbl,
weights = varIdent(form = ~ 1 | trt)) |>
emmeans(~ trt) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(4))
emmeans_hetrogen_gls_tbl# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 7.07 3.00 97.5 143. a 14.1
2 RQflex Nitra 130 3.54 3.00 119. 141. a 7.07
3 Wasserdestilation 136. 3.15 3.00 126. 146. a 6.29
4 Laqua Nitrat 216. 5.54 3.00 199. 234. b 11.1 In dem Objekt emmeans_hetrogen_gls_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket und natürlich in den Abschnitt zu dem Gruppenvergleich unter Varianzheterogenität. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim().
R Code [zeigen / verbergen]
emmeans_hetrogen_vcov_tbl <- lm(nitrat ~ trt, data = barplot_tbl) |>
emmeans(~ trt, vcov. = sandwich::vcovHAC) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(4))
emmeans_hetrogen_vcov_tbl# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 7.84 12 103. 137. a 15.7
2 RQflex Nitra 130 3.92 12 121. 139. a 7.84
3 Wasserdestilation 136. 2.06 12 132. 141. a 4.12
4 Laqua Nitrat 216. 4.94 12 205. 227. b 9.88In dem Objekt emmeans_hetrogen_vcov_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
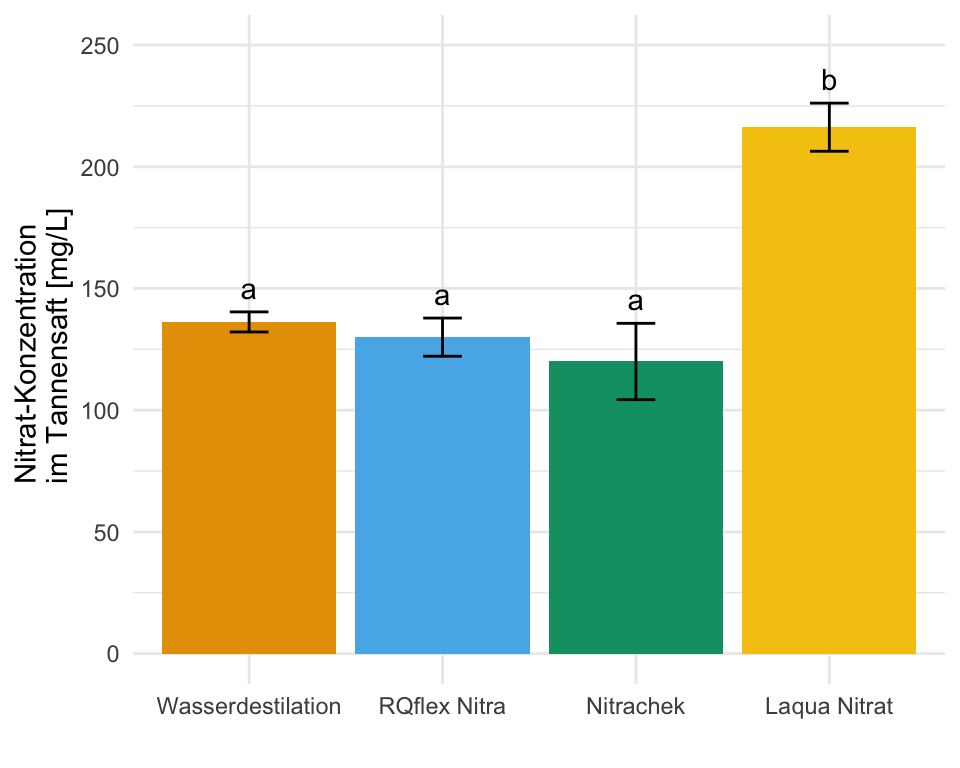
Und dann haben wir auch schon die Abbildungen hier erstellt. Ja vielleicht passen die Standardabweichungen nicht so richtig, da könnte man nochmal an den Daten spielen und die Werte solange ändern, bis es besser passt. Du hast aber jetzt eine Idee, wie der Aufbau funktioniert. Die beiden Tabs zeigen dir dann die Abbildungen für die beiden Annahmen der Varianzhomogenität oder Varianzheterogenität. Der Code ist der gleiche für die drei Abbildungen, die Daten emmeans_homogen_tbl oder emmeans_hetrogen_gls_tbl ober emmeans_hetrogen_vcov_tbl sind das Ausschlaggebende.
R Code [zeigen / verbergen]
ggplot(data = emmeans_homogen_tbl, aes(x = trt, y = emmean, fill = trt)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2) +
labs(x = "",
y = "Nitrat-Konzentration \n im Tannensaft [mg/L]") +
ylim(0, 250) +
theme(legend.position = "none") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 10))
ggplot nachgebaut mit den Informationen aus der Funktion emmeans(). Das compact letter display wird dann über das geom_text() gesetzt.
R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_gls_tbl, aes(x = trt, y = emmean, fill = trt)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2) +
labs(x = "",
y = "Nitrat-Konzentration \n im Tannensaft [mg/L]") +
ylim(0, 250) +
theme(legend.position = "none") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 10))
ggplot nachgebaut mit den Informationen aus der Funktion emmeans(). Das compact letter display wird dann über das geom_text() gesetzt. Die Varianzheterogenität nach der Funktion gls() im obigen Modell berücksichtigt.
R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_vcov_tbl, aes(x = trt, y = emmean, fill = trt)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2) +
labs(x = "",
y = "Nitrat-Konzentration \n im Tannensaft [mg/L]") +
ylim(0, 250) +
theme(legend.position = "none") +
scale_fill_okabeito() +
geom_text(aes(label = .group, y = emmean + sd + 10))
ggplot nachgebaut mit den Informationen aus der Funktion emmeans(). Das compact letter display wird dann über das geom_text() gesetzt. Die Varianzheterogenität nach der Funktion sandwich::vcovHAC im obigen Modell berücksichtigt.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
ggsave("my_ggplot_barplot.png", width = 5, height = 3)
Zerforschen: Zweifaktorieller Barplot mit
lm() oder gls()
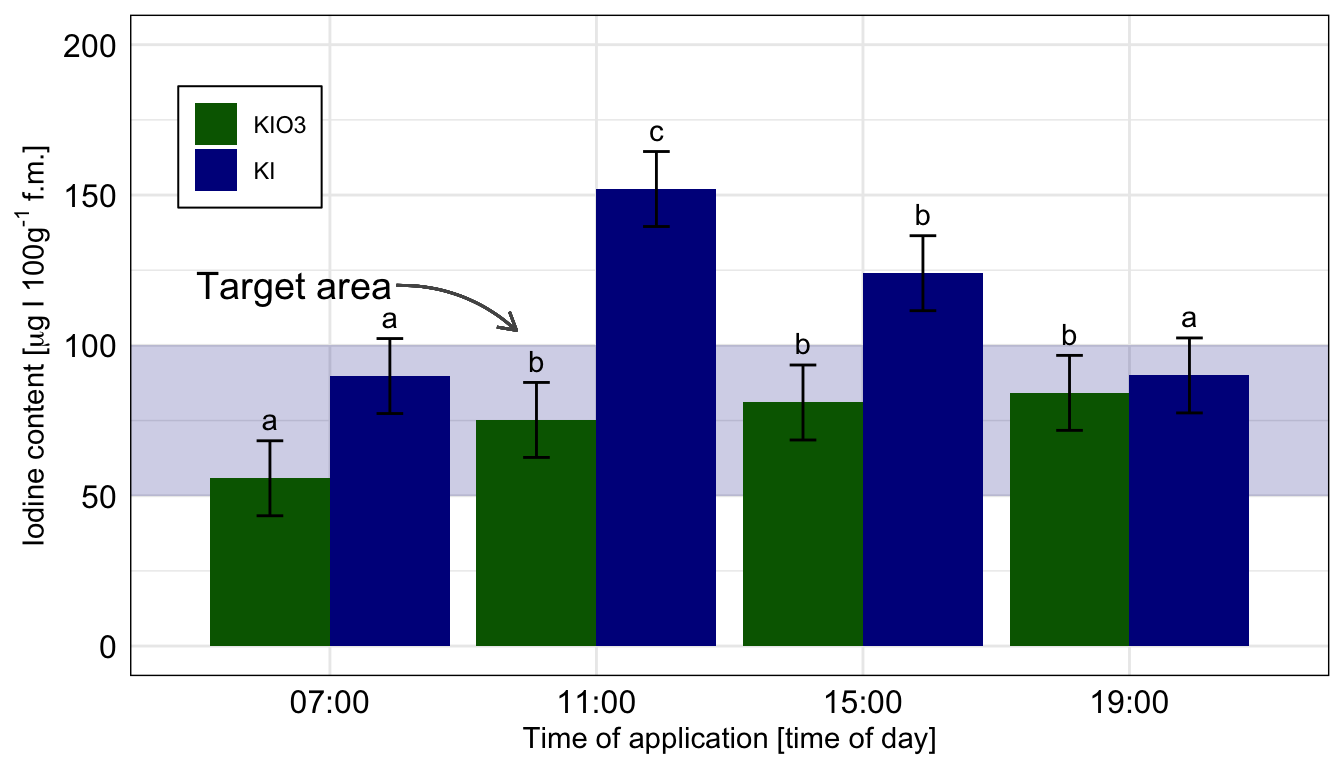
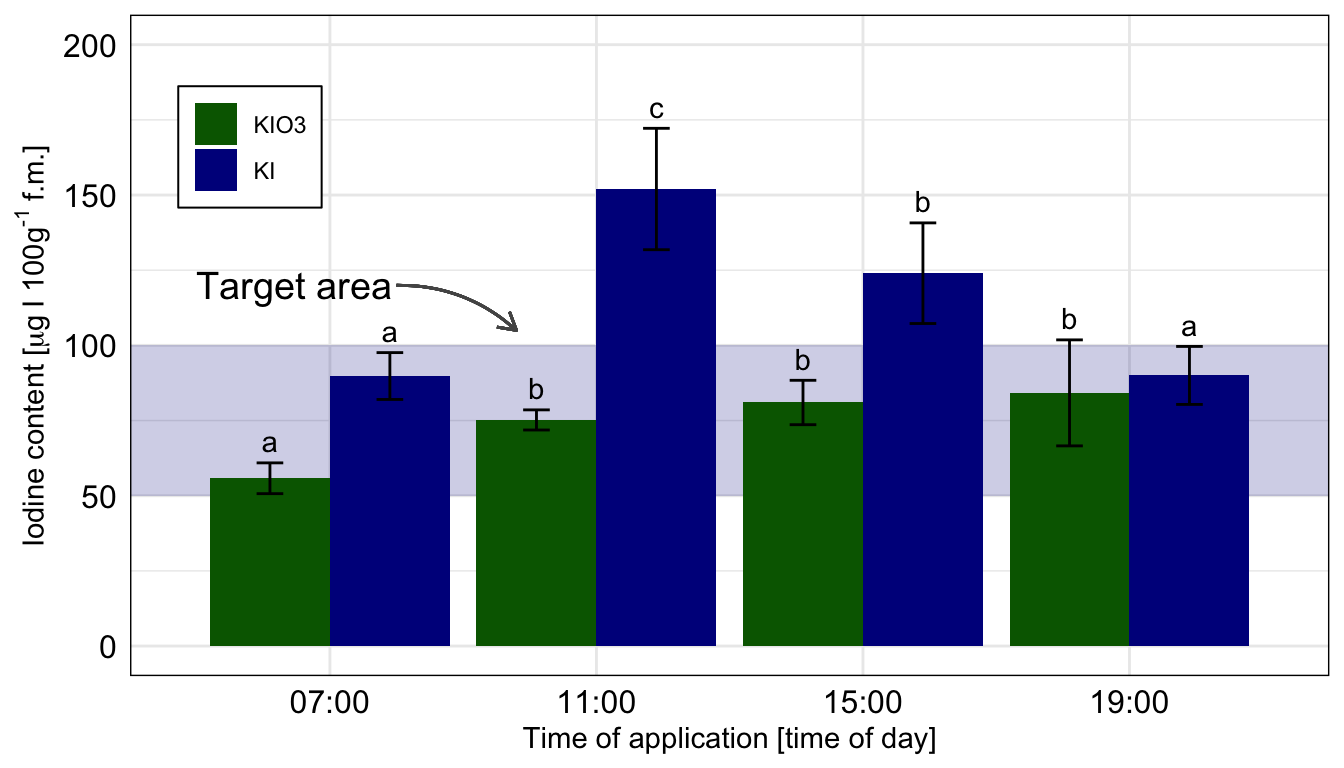
In diesem Zerforschenbeispiel wollen wir uns einen zweifaktoriellen Barplot anschauen. Wir haben hier ein Säulendiagramm mit compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Zeitpunkte und der Kontrolle jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung. Da wir hier aber noch mit emmeans() eine Gruppenvergleich rechnen wollen, brauchen wir mehr Beobachtungen. Wir erschaffen uns also fünf Beobachtungen je Zeit/Jod-Kombination. Für eine detaillierte Betrachtung der Erstellung der Abbildung schauen einmal in das Kapitel zum Barplot oder Balkendiagramm oder Säulendiagramm.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_2fac_target_emmeans.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die fünf Werte alle um den Mittelwert streuen lassen. Ich brauche hier eigentlich mehr als fünf Werte, sonst kriegen wir bei emmeans() und der Interaktion im gls()-Modell Probleme, aber da gibt es dann bei kleinen Fallzahlen noch ein Workaround. Bitte nicht mit weniger als fünf Beobachtungen versuchen, dann wird es schwierig mit der Konsistenz der Schätzer aus dem Modell.
Ach, und ganz wichtig. Wir entfernen die Kontrolle, da wir die Kontrolle nur mit einer Iodid-Stufe gemessen haben. Dann können wir weder die Interaktion rechnen, noch anständig eine Interpretation durchführen.
R Code [zeigen / verbergen]
barplot_tbl <- read_excel("data/zerforschen_barplot_2fac_target_emmeans.xlsx") |>
mutate(time = factor(time,
levels = c("ctrl", "7", "11", "15", "19"),
labels = c("Contr.", "07:00", "11:00", "15:00", "19:00")),
type = as_factor(type)) |>
filter(time != "Contr.")
barplot_tbl # A tibble: 40 × 3
time type iodine
<fct> <fct> <dbl>
1 07:00 KIO3 50
2 07:00 KIO3 55
3 07:00 KIO3 60
4 07:00 KIO3 52
5 07:00 KIO3 62
6 07:00 KI 97
7 07:00 KI 90
8 07:00 KI 83
9 07:00 KI 81
10 07:00 KI 98
# ℹ 30 more rowsIm Folgenden sparen wir uns den Aufruf mit group_by() den du aus dem Kapitel zum Barplot schon kennst. Wir machen das alles zusammen in der Funktion emmeans() aus dem gleichnamigen R Paket. Der Vorteil ist, dass wir dann auch gleich die Gruppenvergleiche und auch das compact letter display erhalten. Einzig die Standardabweichung \(s\) wird uns nicht wiedergegeben sondern der Standardfehler \(SE\). Da aber folgernder Zusammenhang vorliegt, können wir gleich den Standardfehler in die Standardabweichung umrechnen.
\[ SE = \cfrac{s}{\sqrt{n}} \]
Wir rechnen also gleich einfach den Standardfehler \(SE\) mal der \(\sqrt{n}\) um dann die Standardabweichung zu erhalten. In unserem Fall ist \(n=5\) nämlich die Anzahl Beobachtungen je Gruppe. Wenn du mal etwas unterschiedliche Anzahlen hast, dann kannst du auch einfach den Mittelwert der Fallzahl der Gruppen nehmen. Da überfahren wir zwar einen statistischen Engel, aber der Genauigkeit ist genüge getan.
In den beiden Tabs siehst du jetzt einmal die Modellierung unter der Annahme der Varianzhomogenität mit der Funktion lm() und einmal die Modellierung unter der Annahme der Varianzheterogenität mit der Funktion gls() aus dem R Paket nlme. Wie immer lässt sich an Boxplots visuell überprüfen, ob wir Homogenität oder Heterogenität vorliegen haben. Oder aber du schaust nochmal in das Kapitel Der Pre-Test oder Vortest, wo du mehr erfährst.
Wenn du jeden Boxplot miteinander vergleichen willst, dann musst du in dem Code emmeans(~ time * type) setzen. Dann berechnet dir emmeans für jede Faktorkombination einen paarweisen Vergleich.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim(). Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen. Wenn du alles mit allem Vergleichen willst, dann setze bitte emmeans(~ time * type).
R Code [zeigen / verbergen]
emmeans_homogen_tbl <- lm(iodine ~ time + type + time:type, data = barplot_tbl) |>
emmeans(~ time | type) |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(5))
emmeans_homogen_tbl# A tibble: 8 × 9
time type emmean SE df lower.CL upper.CL .group sd
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 07:00 KIO3 55.8 5.58 32 44.4 67.2 a 12.5
2 11:00 KIO3 75.2 5.58 32 63.8 86.6 b 12.5
3 15:00 KIO3 81 5.58 32 69.6 92.4 b 12.5
4 19:00 KIO3 84.2 5.58 32 72.8 95.6 b 12.5
5 07:00 KI 89.8 5.58 32 78.4 101. a 12.5
6 19:00 KI 90 5.58 32 78.6 101. a 12.5
7 15:00 KI 124 5.58 32 113. 135. b 12.5
8 11:00 KI 152 5.58 32 141. 163. c 12.5In dem Objekt emmeans_homogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. Wie dir vielleicht auffällt sind alle Standardfehler und damit alle Standardabweichungen für alle Gruppen gleich, das war ja auch unsere Annahme mit der Varianzhomogenität.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim(). Da wir hier etwas Probleme mit der Fallzahl haben, nutzen wir die Option mode = "appx-satterthwaite" um dennoch ein vollwertiges, angepasstes Modell zu erhalten. Du kannst die Option auch erstmal entfernen und schauen, ob es mit deinen Daten auch so klappt. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen. Wenn du alles mit allem Vergleichen willst, dann setze bitte emmeans(~ time * type).
R Code [zeigen / verbergen]
emmeans_hetrogen_tbl <- gls(iodine ~ time + type + time:type, data = barplot_tbl,
weights = varIdent(form = ~ 1 | time*type)) |>
emmeans(~ time | type, mode = "appx-satterthwaite") |>
cld(Letters = letters, adjust = "none") |>
as_tibble() |>
mutate(.group = str_trim(.group),
sd = SE * sqrt(5))
emmeans_hetrogen_tbl# A tibble: 8 × 9
time type emmean SE df lower.CL upper.CL .group sd
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 07:00 KIO3 55.8 2.29 3.88 49.4 62.2 a 5.12
2 11:00 KIO3 75.2 1.50 3.99 71.0 79.4 b 3.35
3 15:00 KIO3 81.0 3.30 3.96 71.8 90.2 b 7.38
4 19:00 KIO3 84.2 7.88 4.04 62.4 106. b 17.6
5 07:00 KI 89.8 3.48 3.97 80.1 99.5 a 7.79
6 19:00 KI 90.0 4.31 3.96 78.0 102. a 9.64
7 15:00 KI 124 7.48 3.99 103. 145. b 16.7
8 11:00 KI 152 9.03 4.01 127. 177. c 20.2 In dem Objekt emmeans_hetrogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
Dann bauen wir usn auch schon die Abbildung. Wir müssen am Anfang einmal scale_x_discrete() setzen, damit wir gleich den Zielbereich ganz hinten zeichnen können. Sonst ist der blaue Bereich im Vordergrund. Dann färben wir auch mal die Balken anders ein. Muss ja auch mal sein. Auch nutzen wir die Funktion geom_text() um das compact letter display gut zu setzten. Die \(y\)-Position berechnet sich aus dem Mittelwert emmean plus Standardabweichung sd innerhalb des geom_text(). Da wir hier die Kontrollgruppe entfernen mussten, habe ich dann nochmal den Zielbereich verschoben und mit einem Pfeil ergänzt. Die beiden Tabs zeigen dir dann die Abbildungen für die beiden Annahmen der Varianzhomogenität oder Varianzheterogenität. Der Code ist der gleiche für beide Abbildungen, die Daten emmeans_homogen_tbl oder emmeans_hetrogen_tbl sind das Ausschlaggebende. Wie du sehen wirst, haben wir hier mal keinen Unterschied vorliegen.
R Code [zeigen / verbergen]
ggplot(data = emmeans_homogen_tbl, aes(x = time, y = emmean, fill = type)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0.25, xmax = 4.75, ymin = 50, ymax = 100,
alpha = 0.2, fill = "darkblue") +
annotate("text", x = 0.5, y = 120, hjust = "left", label = "Target area",
size = 5) +
geom_curve(aes(x = 1.25, y = 120, xend = 1.7, yend = 105),
colour = "#555555",
size = 0.5,
curvature = -0.2,
arrow = arrow(length = unit(0.03, "npc"))) +
geom_bar(stat = "identity",
position = position_dodge(width = 0.9, preserve = "single")) +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2,
position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_manual(name = "Type", values = c("darkgreen", "darkblue")) +
theme(legend.position = c(0.1, 0.8),
legend.title = element_blank(),
legend.spacing.y = unit(0, "mm"),
panel.border = element_rect(colour = "black", fill=NA),
axis.text = element_text(colour = 1, size = 12),
legend.background = element_blank(),
legend.box.background = element_rect(colour = "black")) +
labs(x = "Time of application [time of day]",
y = expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +
scale_y_continuous(breaks = c(0, 50, 100, 150, 200),
limits = c(0, 200)) +
geom_text(aes(label = .group, y = emmean + sd + 2),
position = position_dodge(width = 0.9), vjust = -0.25) 
ggplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen. Die Kontrolle wurde entfernt, sonst hätten wir hier nicht emmeans in der einfachen Form nutzen können. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen.
R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_tbl, aes(x = time, y = emmean, fill = type)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0.25, xmax = 4.75, ymin = 50, ymax = 100,
alpha = 0.2, fill = "darkblue") +
annotate("text", x = 0.5, y = 120, hjust = "left", label = "Target area",
size = 5) +
geom_curve(aes(x = 1.25, y = 120, xend = 1.7, yend = 105),
colour = "#555555",
size = 0.5,
curvature = -0.2,
arrow = arrow(length = unit(0.03, "npc"))) +
geom_bar(stat = "identity",
position = position_dodge(width = 0.9, preserve = "single")) +
geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),
width = 0.2,
position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_manual(name = "Type", values = c("darkgreen", "darkblue")) +
theme(legend.position = c(0.1, 0.8),
legend.title = element_blank(),
legend.spacing.y = unit(0, "mm"),
panel.border = element_rect(colour = "black", fill=NA),
axis.text = element_text(colour = 1, size = 12),
legend.background = element_blank(),
legend.box.background = element_rect(colour = "black")) +
labs(x = "Time of application [time of day]",
y = expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +
scale_y_continuous(breaks = c(0, 50, 100, 150, 200),
limits = c(0, 200)) +
geom_text(aes(label = .group, y = emmean + sd + 2),
position = position_dodge(width = 0.9), vjust = -0.25) 
ggplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen. Die Kontrolle wurde entfernt, sonst hätten wir hier nicht emmeans in der einfachen Form nutzen können. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
ggsave("my_ggplot_barplot.png", width = 5, height = 3)53.1 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
pacman::p_load(tidyverse, magrittr, broom,
see, performance, scales, parameters,
olsrr, readxl, car, gtsummary, emmeans,
multcomp, conflicted)
conflicts_prefer(dplyr::select)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
"#F0E442", "#0072B2", "#D55E00", "#CC79A7")An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
53.2 Daten
Im Folgenden schauen wir uns die Daten eines Pilotprojektes zum Anbau von Kichererbsen in Brandenburg an. Wir haben an verschiedenen anonymisierten Bauernhöfen Kichererbsen angebaut und das Trockengewicht als Endpunkt bestimmt. Darüber hinaus haben wir noch andere Umweltparameter erhoben und wollen schauen, welche dieser Parameter einen Einfluss auf das Trockengewicht hat. In Kapitel 7.3 findest du nochmal mehr Informationen zu den Daten.
R Code [zeigen / verbergen]
chickpea_tbl <- read_excel("data/chickpeas.xlsx") In der Tabelle 53.1 ist der Datensatz chickenpea_tbl nochmal als Ausschnitt dargestellt. Insgesamt haben wir \(n = 95\) Messungen durchgeführt. Wir sehen, dass wir verschiedene Variablen gemessen haben. Unter anderem, ob es geregent hat oder an welcher Stelle in Brandenburg die Messungen stattgefunden haben. Ebenso haben wir geschaut, ob ein Wald in der Nähe der Messung war oder nicht. Wir nehmen als Outcome \(y\) das normalverteilte Trockengewicht dryweight.
| temp | rained | location | no3 | fe | sand | forest | dryweight |
|---|---|---|---|---|---|---|---|
| 25.26 | high | north | 5.56 | 4.43 | 63 | >1000m | 253.42 |
| 21.4 | high | northeast | 9.15 | 2.58 | 51.17 | <1000m | 213.88 |
| 27.84 | high | northeast | 5.57 | 2.19 | 55.57 | >1000m | 230.71 |
| 24.59 | low | north | 7.97 | 1.47 | 62.49 | >1000m | 257.74 |
| … | … | … | … | … | … | … | … |
| 25.47 | low | north | 6.92 | 3.18 | 64.55 | <1000m | 268.58 |
| 29.04 | low | north | 5.64 | 2.87 | 53.27 | >1000m | 236.07 |
| 24.11 | high | northeast | 4.31 | 3.66 | 63 | <1000m | 259.82 |
| 28.88 | low | northeast | 7.92 | 2 | 65.75 | >1000m | 274.75 |
Im Folgenden werden wir die Daten nur für das Fitten eines Modells verwenden. In den anderen oben genannten Kapiteln nutzen wir die Daten dann anders.
53.3 Fit des Modells
Wir rechnen jetzt den Fit für das vollständige Modell mit allen Variablen in dem Datensatz. Wir sortieren dafür einmal das \(y\) mit dryweight auf die linke Seite und dann die anderen Variablen auf die rechte Seite des ~. Wir haben damit unser Modell chickenpea_fit wie folgt vorliegen.
R Code [zeigen / verbergen]
chickenpea_fit <- lm(dryweight ~ temp + rained + location + no3 + fe + sand + forest,
data = chickpea_tbl)Soweit so gut. Wir können uns zwar das Modell mit der Funktion summary() anschauen, aber es gibt schönere Funktionen, die uns erlauben einmal die Performance des Modells abzuschätzen. Also zu klären, ob soweit alles geklappt hat und wir mit dem Modell weitermachen können.
53.4 Performance des Modells
Da ich die Daten selber gebaut habe, ist mir bekannt, dass das Outcome dryweight normalverteilt ist. Immerhin habe ich die Daten aus einer Normalverteilung gezogen. Manchmal will man dann doch Testen, ob das Outcome \(y\) einer Normalverteilung folgt. Das R Paket {oslrr} bietet hier eine Funktion ols_test_normality(), die es erlaubt mit allen bekannten statistischen Tests auf Normalverteilung zu testen. Wenn der \(p\)-Wert kleiner ist als das Signifikanzniveau \(\alpha\), dann können wir die Nullhypothese, dass unsere Daten gleich einer Normalverteilung wären, ablehnen. Darüber hinaus bietet das R Paket {olsrr} eine weitreichende Diagnostik auf einem normalverteilten Outcome \(y\).
R Code [zeigen / verbergen]
ols_test_normality(chickenpea_fit) -----------------------------------------------
Test Statistic pvalue
-----------------------------------------------
Shapiro-Wilk 0.9809 0.1806
Kolmogorov-Smirnov 0.088 0.4287
Cramer-von Mises 8.2878 0.0000
Anderson-Darling 0.5182 0.1837
-----------------------------------------------Wir sehen, testen wir viel, dann kommt immer was signifikantes raus. Um jetzt kurz einen statistischen Engel anzufahren, wir nutzen wenn überhaupt den Shapiro-Wilk-Test oder den Kolmogorov-Smirnov-Test. Für die anderen beiden steigen wir jetzt hier nicht in die Theorie ab.
Nachdem wir die Normalverteilung nochmal überprüft haben wenden wir uns nun dem Wichtigen zu. Wir schauen jetzt auf die Varianz des Modells. Um zu überprüfen, ob das Modell funktioniert können wir uns den Anteil der erklärten Varianz anschauen. Wie viel erklären unsere \(x\) von der Varianz des Outcomes \(y\)? Wir betrachten dafür das Bestimmtheitsmaß \(R^2\). Da wir mehr als ein \(x\) vorliegen haben, nutzen wir das adjustierte \(R^2\). Das \(R^2\) hat die Eigenschaft immer größer und damit besser zu werden je mehr Variablen in das Modell genommen werden. Wir können dagegen Adjustieren und daher das \(R^2_{adj}\) nehmen.
R Code [zeigen / verbergen]
r2(chickenpea_fit)# R2 for Linear Regression
R2: 0.903
adj. R2: 0.894Wir erhalten ein \(R^2_{adj}\) von \(0.87\) und damit erklärt unser Modell ca 87% der Varianz von \(y\) also unserem Trockengewicht. Das ist ein sehr gutes Modell. Je nach Anwendung sind 60% bis 70% erklärte Varianz schon sehr viel.
Im nächsten Schritt wollen wir nochmal überprüfen, ob die Varianzen der Residuen auch homogen sind. Das ist eine weitere Annahme an ein gutes Modell. Im Prinzip überprüfen wir hier, ob unser Ourtcome auch wirklcih normalveteilt ist bzw. der Annahme der Normalverteilung genügt. Wir nutzen dafür die Funktion check_heteroscedasticity() aus dem R Paket {performance}.
R Code [zeigen / verbergen]
check_heteroscedasticity(chickenpea_fit)OK: Error variance appears to be homoscedastic (p = 0.512).Auch können wir uns einmal numerisch die VIF-Werte anschauen um zu sehen, ob Variablen mit anderen Variablen ungünstig stark korrelieren. Wir wollen ja nur die Korrelation des Modells, also die \(x\), mit dem Outcome \(y\) modellieren. Untereinander sollen die Variablen \(x\) alle unabhängig sein. Für können uns die VIF-Werte für alle kontinuierlichen Variablen berechnen lassen.
R Code [zeigen / verbergen]
vif(chickenpea_fit) GVIF Df GVIF^(1/(2*Df))
temp 1.067042 1 1.032977
rained 1.067845 1 1.033366
location 1.119450 2 1.028611
no3 1.062076 1 1.030571
fe 1.135119 1 1.065420
sand 1.072182 1 1.035462
forest 1.070645 1 1.034720Alle VIF-Werte sind unter dem Threshold von 5 und damit haben wir hier keine Auffälligkeiten vorliegen.
Damit haben wir auch überprüft, ob unsere Varianzen homogen sind. Also unsere Residuen annähend normalverteilt sind. Da unsere Daten groß genug sind, können wir das auch ohne weiteres Anwenden. Wenn wir einen kleineren Datensatz hätten, dann wäre die Überprüfung schon fraglicher. bei kleinen Fallzahlen funktioniert der Test auf Varianzheterogenität nicht mehr so zuverlässig.
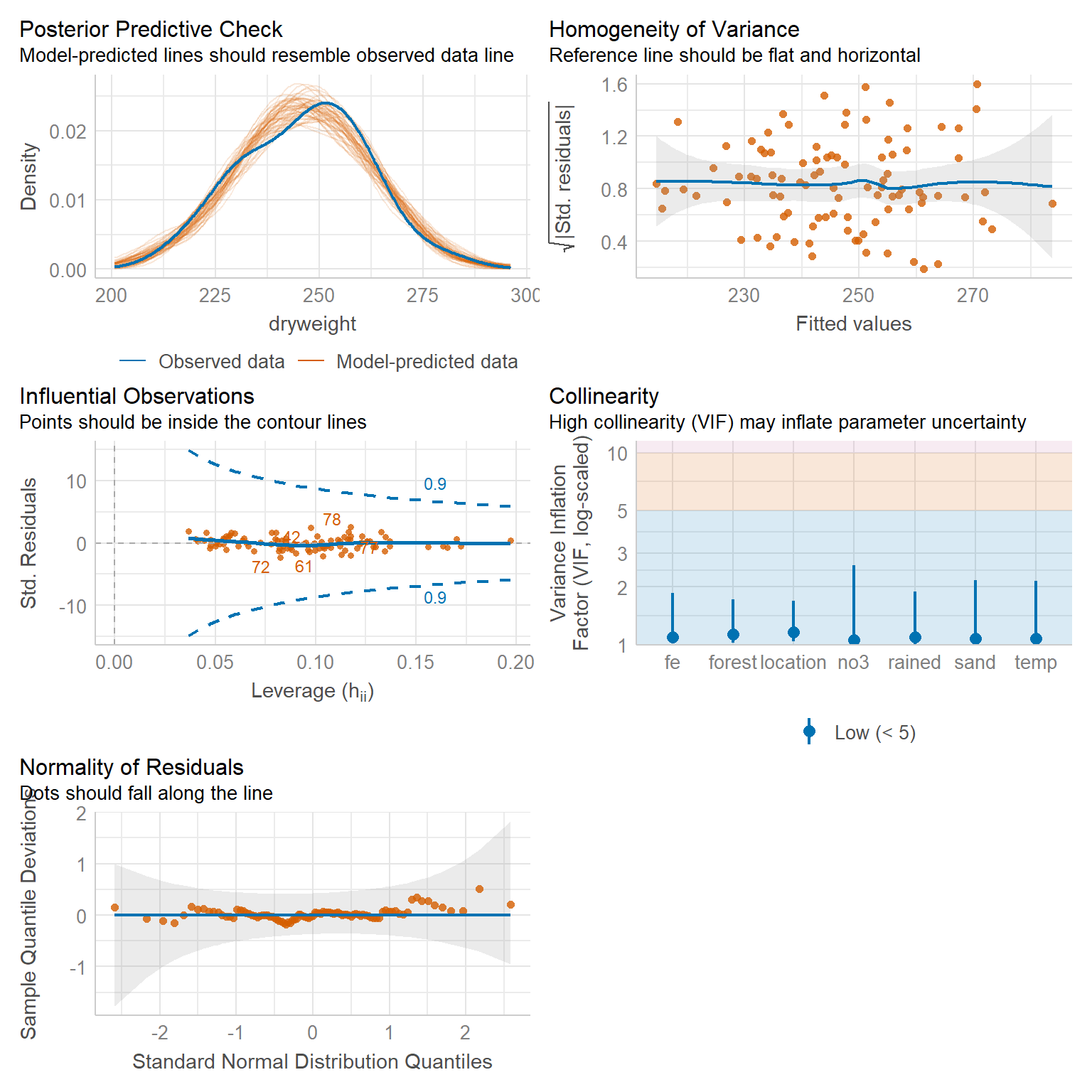
In Abbildung 53.10 sehen wir nochmal die Visualisierung verschiedener Modellgütekriterien. Wir sehen, dass unsere beobachte Verteilung des Trockengewichts mit der vorhergesagten übereinstimmt. Ebenso ist der Residualplot gleichmäßig und ohne Struktur. Wir haben auch keine Ausreißer, da alle unsere Beobachtungen in dem gestrichelten, blauen Trichter bleiben. Ebenso zeigt der QQ-Plot auch eine approximative Normalverteilung der Residuen. Wir haben zwar leichte Abweichungen, aber die sind nicht so schlimm. Der Großteil der Punkte liegt auf der Diagonalen. Ebenso gibt es auch keine Variable, die einen hohen VIF-Wert hat und somit ungünstig mit anderen Variablen korreliert.
R Code [zeigen / verbergen]
check_model(chickenpea_fit, colors = cbbPalette[6:8],
check = c("qq", "outliers", "pp_check", "homogeneity", "vif")) 
check_model().
53.5 Interpretation des Modells
Nachdem wir nun sicher sind, dass das Modell unseren statistischen Ansprüchen genügt, können wir jetzt die Ergebnisse des Fits des Modells einmal interpretieren. Wir erhalten die Modellparameter über die Funktion model_parameters() aus dem R Paket {parameters}.
R Code [zeigen / verbergen]
chickenpea_fit |>
model_parameters()Parameter | Coefficient | SE | 95% CI | t(86) | p
----------------------------------------------------------------------------
(Intercept) | -5.11 | 9.74 | [-24.48, 14.26] | -0.52 | 0.601
temp | 2.37 | 0.22 | [ 1.93, 2.80] | 10.80 | < .001
rained [low] | 1.78 | 1.19 | [ -0.60, 4.15] | 1.49 | 0.140
location [northeast] | -0.10 | 1.20 | [ -2.50, 2.29] | -0.09 | 0.931
location [west] | 1.96 | 1.63 | [ -1.29, 5.20] | 1.20 | 0.234
no3 | 1.49 | 0.41 | [ 0.68, 2.29] | 3.67 | < .001
fe | 0.66 | 0.53 | [ -0.40, 1.72] | 1.24 | 0.220
sand | 3.04 | 0.12 | [ 2.80, 3.27] | 25.63 | < .001
forest [>1000m] | -3.02 | 1.14 | [ -5.29, -0.75] | -2.64 | 0.010 Schauen wir uns die einzelnen Zeilen aus der Ausgabe einmal in Ruhe an. Wir sind eigentlich nur an den Spalten Coefficient für das \(\beta\) als Effekt der Variablen sowie der Spalte p als \(p\)-Wert für die Variablen interessiert. Wir testen immer als Nullhypothese, ob sich der Parameter von 0 unterscheidet.
(Intercept)beschreibt den den \(y\)-Achsenabschnitt. Wir brauen den Intercept selten in der Interpretation. Wir nehmen hier erstmal hin, dass wir einen von 0 signifikant unterschiedlichen Intercept haben. Meist löschen wir den Intrcept auch aus der finalen Tabelle raus.tempbeschreibt den Effekt der Temperatur. Wenn die Temperatur um ein Grad ansteigt, dann erhalten wir \(1.75\) mehr Trockengewicht als Ertrag. Darüber hinaus ist der Effekt der Temperatur signifikant.rained [low]beschreibt den Effekt des Levelslowdes Faktorsrainedim Vergleich zum Levelhigh. Daher haben wir bei wenig Regen einen um \(1.33\) höheren Ertrag als bei viel Regen.location [northeast]beschreibt den Effekt des Levelsnortheastzu dem Levelnorthdes Faktorslocation. Wir haben also einen \(-1.38\) kleineren Ertrag an Kichererbsen als im Norden von Brandenburg. Wenn du hier eine andere Sortierung willst, dann musst du mit der Funktionfactor()die Level anders sortieren.location [west]beschreibt den Effekt des Levelswestzu dem Levelnorthdes Faktorslocation. Wir haben also einen \(-2.40\) kleineren Ertrag an Kichererbsen als im Norden von Brandenburg. Wenn du hier eine andere Sortierung willst, dann musst du mit der Funktionfactor()die Level anders sortieren.no3beschreibt den Effekt von Nitrat im Boden. Wenn wir die Nitratkonzentration um eine Einheit erhöhen dann steigt der Ertrag um \(1.11\) an. Wir haben hier einen \(p\)-Wert von \(0.012\) vorliegen und können hier von einem signifkianten Effekt sprechen.febeschreibt den Effekt des Eisens im Boden auf den Ertrag an Kichererbsen. Wenn die Konzentration von Eisen um eine Einheit ansteigt, so sinkt der Ertrag von Kichererbsen um \(-0.72\) ab.sandbeschreibt den Anteil an Sand in der Bodenprobe. Wenn der Anteil an Sand um eine Einheit ansteigt, so steigt der Ertrag an Kichererbsen um \(3.03\) an. Dieser Effekt ist auch hoch signifikant. Kichererbsen scheinen sandigen Boden zu bevorzugen.forest [>1000m]beschreibt die Nähe des nächsten Waldstückes als Faktor mit zwei Leveln. Daher haben wir hier einen höheren Ertrag von \(0.67\) an Kichererbsen, wenn wir weiter weg vom Wald messen>1000als Nahe an dem Wald<1000.
Das war eine Wand an Text für die Interpretation des Modells. Was können wir zusammenfassend mitnehmen? Wir haben drei signifikante Einflussfaktoren auf den Ertrag an Kichererbsen gefunden. Zum einen ist weniger Regen signifikant besser als viel Regen. Wir brauchen mehr Nitrat im Boden. Im Weiteren ist ein sandiger Boden besser als ein fetter Boden. Am Ende müssen wir noch schauen, was die nicht signifikanten Ergebnisse uns für Hinweise geben. Der Ort der Messung ist relativ unbedeutend. Es scheint aber so zu sein, dass im Norden mehr Ertrag zu erhalten ist. Hier müsste man einmal schauen, welche Betriebe hier vorliegen und wie die Bodenbeschaffenheit dort war. Im Weiteren sehen wir, dass anscheinend ein Abstand zum Wald vorteilhaft für den Ertrag ist. Hier könnte Wildfraß ein Problem gewesen sein oder aber zu viel Schatten. Auch hier muss man nochmal auf das Feld und schauen, was das konkrete Problem sein könnte. Hier endet die Statistik dann.
53.6 Gruppenvergleich
Häufig ist es ja so, dass wir das Modell für die Gaussian Regression nur schätzen um dann einen Gruppenvergleich zu rechnen. Das heißt, dass es uns interessiert, ob es einen Unterschied zwischen den Leveln eines Faktors gegeben dem Outcome \(y\) gibt. Wir nehmen hier einen ausgedachten Datensatz zu Katzen-, Hunde- und Fuchsflöhen. Dabei erstellen wir uns einen Datensatz mit mittleren Gewicht an Flöhen pro Tierart. Ich habe jetzt ein mittleres Gewicht von \(20mg\) bei den Katzenflöhen, eine mittleres Gewicht von \(30mg\) bei den Hundeflöhen und ein mittleres Gewicht von \(10mg\) bei den Fuchsflöhen gewählt. Wir generieren uns jeweils \(20\) Beobachtungen je Tierart. Damit haben wir dann einen Datensatz zusammen, den wir nutzen können um einmal die Ergebnisse eines Gruppenvergleiches zu verstehen zu können.
R Code [zeigen / verbergen]
set.seed(20231202)
n_rep <- 20
flea_weight_tbl <- tibble(animal = gl(3, n_rep, labels = c("cat", "dog", "fox")),
weight = c(rnorm(n_rep, 20, 1),
rnorm(n_rep, 30, 1),
rnorm(n_rep, 10, 1)))Wenn du gerade hierher gesprungen bist, nochmal das simple Modell für unseren Gruppenvergleich unter einer Gaussian Regression. Wir haben hier nur einen Faktor animal mit in dem Modell. Am Ende des Abschnitts findest du dann noch ein Beispiel mit drei Faktoren zu Gewicht von Brokkoli.
R Code [zeigen / verbergen]
lm_fit <- lm(weight ~ animal, data = flea_weight_tbl) Eigentlich ist es recht einfach, wie wir anfangen. Wir rechnen jetzt als erstes die ANOVA. Hier müssen wir dann einmal den Test angeben, der gerechnet werden soll um die p-Werte zu erhalten. Dann nutze ich noch die Funktion model_parameters() um eine schönere Ausgabe zu erhalten.
R Code [zeigen / verbergen]
lm_fit |>
anova() |>
model_parameters()Parameter | Sum_Squares | df | Mean_Square | F | p
-------------------------------------------------------------
animal | 3960.78 | 2 | 1980.39 | 2525.37 | < .001
Residuals | 44.70 | 57 | 0.78 | |
Anova Table (Type 1 tests)Im Folgenden nutzen wir das R Paket {emmeans} um die mittleren Gewichte der Flöhe zu berechnen.
R Code [zeigen / verbergen]
emm_obj <- lm_fit |>
emmeans(~ animal)
emm_obj animal emmean SE df lower.CL upper.CL
cat 20.2 0.198 57 19.77 20.6
dog 30.1 0.198 57 29.66 30.5
fox 10.2 0.198 57 9.76 10.6
Confidence level used: 0.95 Wir rechnen jetzt den paarweisen Vergleich für alle Tierarten und schauen uns dann an, was wir erhalten haben. Wie du gleich siehst, erhalten wir die Differenzen der Mittelwerte der Flohgewichte für die verschiedenen Tierarten. Hier also einmal die paarweisen Vergleiche, darunter dann gleich das compact letter display.
R Code [zeigen / verbergen]
emm_obj |>
pairs(adjust = "bonferroni") contrast estimate SE df t.ratio p.value
cat - dog -9.9 0.28 57 -35.336 <.0001
cat - fox 10.0 0.28 57 35.732 <.0001
dog - fox 19.9 0.28 57 71.068 <.0001
P value adjustment: bonferroni method for 3 tests Und fast am Ende können wir uns auch das compact letter display erstellen. Auch hier nutzen wir wieder die Funktion cld() aus dem R Paket {multcomp}. Hier erhälst du dann die Information über die mittleren Flohgewichte der jeweiligen Tierarten und ob sich die mittleren Flohgewichte unterscheidet. Ich nutze dann die Ausgabe von emmeans() um mir dann direkt das Säulendiagramm mit den Fehlerbalken und dem compact letter display zu erstellen. Mehr dazu dann im Kasten weiter unten zu dem Beispiel zu den Gewichten des Brokkoli.
R Code [zeigen / verbergen]
emm_obj |>
cld(Letters = letters, adjust = "none") animal emmean SE df lower.CL upper.CL .group
fox 10.2 0.198 57 9.76 10.6 a
cat 20.2 0.198 57 19.77 20.6 b
dog 30.1 0.198 57 29.66 30.5 c
Confidence level used: 0.95
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Auch hier sehen wir, dass sich alle drei Gruppen signifikant unterschieden, keine der Tierarten teilt sich einen Buchstaben, so dass wir hier von einem Unterschied zwischen den mittleren Flohgewichten der drei Tierarten ausgehen können.
Damit sind wir einmal mit unserem Gruppenvergleich für die Gaussian Regression auf normalverteilte Daten durch. In dem Kapitel zu den Multiple Vergleichen oder Post-hoc Tests findest du dann noch mehr Inspirationen für die Nutzung von {emmeans}. Hier war es dann die Anwendung auf normalverteilte Dateb zusammen mit einem Faktor. Wenn du dir das Ganze nochmal an einem Beispiel für zwei Faktoren anschauen möchtest, dann findest du im folgenden Kasten ein Beispiel für die Auswertung von Brokkoli nach Gabe verschiedener Dosen eines Düngers und Zeitpunkten.
Anwendungsbeispiel: Dreifaktorieller Vergleich für das Erntegewicht
Im folgenden Beispiel schauen wir uns nochmal ein praktische Auswertung von einem agrarwissenschaftlichen Beispiel mit Brokkoli an. Wir haben uns in diesem Experiment verschiedene Dosen fert_amount von einem Dünger aufgebracht sowie verschiedene Zeitpunkte der Düngung fert_time berücksichtigt. Auch hier haben wir einige Besonderheiten in den Daten, da nicht jede Faktorkombination vorliegt. Wir ignorieren aber diese Probleme und rechnen einfach stumpf unseren Gruppenvergleich.
R Code [zeigen / verbergen]
broc_tbl <- read_excel("data/broccoli_weight.xlsx") |>
mutate(fert_time = factor(fert_time, levels = c("none", "early", "late")),
fert_amount = as_factor(fert_amount),
block = as_factor(block)) |>
select(-stem_hollowness) Dann können wir auch schon die Gaussian Regression mit lm() rechnen.
R Code [zeigen / verbergen]
lm_fit <- lm(weight ~ fert_time + fert_amount + fert_time:fert_amount + block,
data = broc_tbl) Jetzt rechnen wir in den beiden folgenden Tabs einmal die ANOVA und dann auch den multiplen Gruppenvergleich mit {emmeans}. Da wir hier normalveteilte Daten haben, können wir dann einfach die Standardverfahren nehmen. Eventuell müssten wir bei dem Gruppenvergleich mit emmeans() nochmal für Varianzheterogenität adjustieren, aber da erfährst du dann mehr in dem Kapitel zu den Multiple Vergleichen oder Post-hoc Tests.
Wir rechnen hier einmal die ANOVA und nutzen den \(\mathcal{X}^2\)-Test für die Ermittelung der p-Werte. Wir müssen hier einen Test auswählen, da per Standardeinstellung kein Test gerechnet wird. Wir machen dann die Ausgabe nochmal schöner und fertig sind wir.
R Code [zeigen / verbergen]
lm_fit |>
anova() |>
model_parameters()Parameter | Sum_Squares | df | Mean_Square | F | p
-------------------------------------------------------------------------
fert_time | 2.44e+06 | 2 | 1.22e+06 | 44.12 | < .001
fert_amount | 2.11e+06 | 2 | 1.05e+06 | 38.06 | < .001
block | 7.21e+06 | 3 | 2.40e+06 | 86.73 | < .001
fert_time:fert_amount | 26973.84 | 2 | 13486.92 | 0.49 | 0.615
Residuals | 4.28e+07 | 1544 | 27692.44 | |
Anova Table (Type 1 tests)Wir sehen, dass der Effekt der Düngerzeit und die Menge des Düngers signifikant ist, jedoch wir keinen signifikanten Einfluss durch die Interaktion haben. Wir haben aber also keine Interaktion vorliegen. Leider ist auch der Block signifikant, so dass wir eigentlich nicht über den Block mitteln sollten. Wir rechnen trotzdem die Analyse gemittelt über die Blöcke. Wenn du hier mehr erfahren möchtest, dann schaue dir das Beispiel hier nochmal im Kapitel zu dem linearen gemischten Modellen an.
Im Folgenden rechnen wir einmal über alle Faktorkombinationen von fert_time und fert_amount einen Gruppenvergleich. Dafür nutzen wir die Option fert_time * fert_amount. Wenn du die Analyse getrennt für die Menge und den Zeitpunkt durchführen willst, dann nutze die Option fert_time | fert_amount. Dann adjustieren wir noch nach Bonferroni und sind fertig.
R Code [zeigen / verbergen]
emm_obj <- lm_fit |>
emmeans(~ fert_time * fert_amount) |>
cld(Letters = letters, adjust = "bonferroni")
emm_obj fert_time fert_amount emmean SE df lower.CL upper.CL .group
none 0 169 33.97 1544 77.1 260 a
late 150 400 11.25 1544 369.8 430 b
early 150 432 11.05 1544 401.8 461 bc
late 225 467 11.20 1544 436.9 497 cd
early 225 497 7.97 1544 475.2 518 de
late 300 506 11.40 1544 475.1 537 de
early 300 517 11.38 1544 486.8 548 e
early 0 nonEst NA NA NA NA
late 0 nonEst NA NA NA NA
none 150 nonEst NA NA NA NA
none 225 nonEst NA NA NA NA
none 300 nonEst NA NA NA NA
Results are averaged over the levels of: block
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 7 estimates
P value adjustment: bonferroni method for 21 tests
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
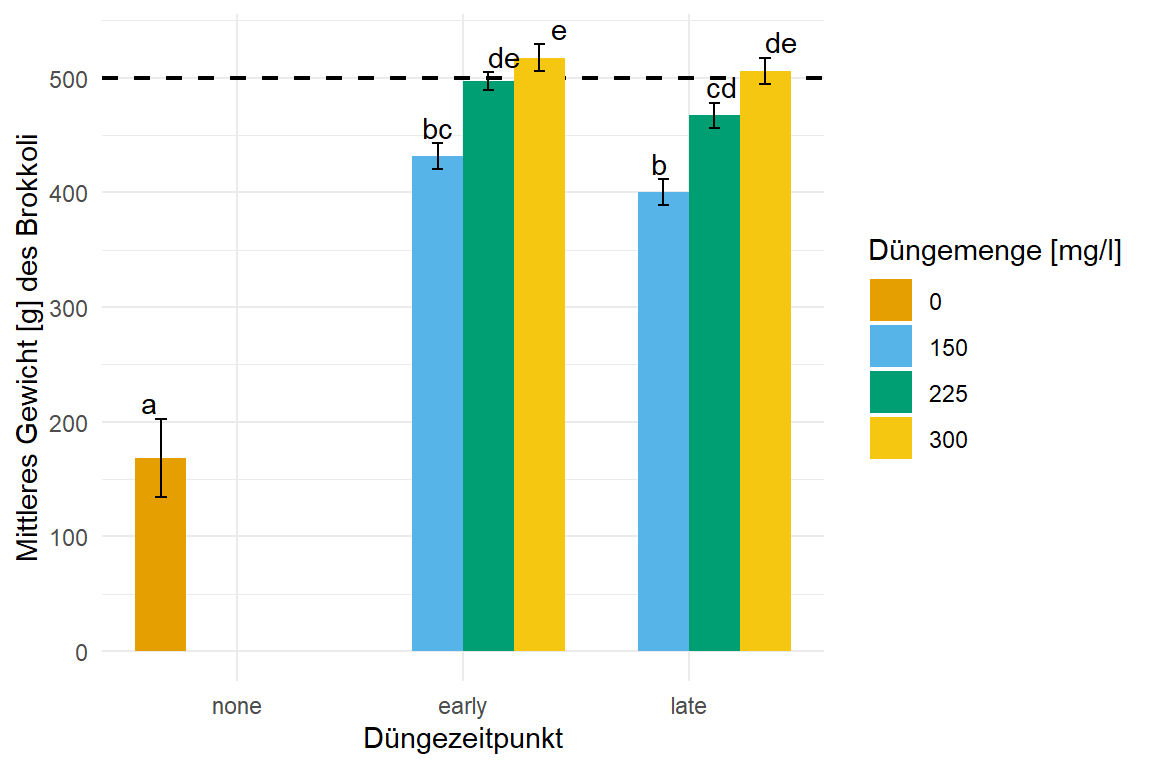
But we also did not show them to be the same. Das emm_obj Objekt werden wir dann gleich einmal in {ggplot} visualisieren. Die emmean stellt den mittleren Gewicht des Brokkoli je Faktorkombination dar gemittelt über alle Blöcke. Das Mitteln über die Blöcke ist eher fragwürdig, da wir ja einen Effekt der Blöcke in der ANOVA gefunden hatten. Hier schauen wir dann nochmal auf das Beispiel im Kapitel zu den linearen gemischten Modellen. Dann können wir zum Abschluss auch das compact letter display anhand der Abbildung interpretieren.
In der Abbildung 59.18 siehst du das Ergebnis der Auswertung in einem Säulendiagramm. Wir sehen einen klaren Effekt der Düngezeitpunkte sowie der Düngermenge auf das Gewicht von Brokkoli. Wenn wir ein mittleres Gewicht von \(500g\) für den Handel erreichen wollen, dann erhalten wir das Zielgewicht nur bei einer Düngemenge von \(300mg/l\). Hier stellt sich dann die Frage, ob wir bei \(225mg/l\) und einem frühen Zeitpunkt der Düngung nicht auch genug Brokkoli erhalten. Das Ziel ist es ja eigentlich in einen Zielbereich zu kommen. Die Köpfe sollen ja nicht zu schwer und auch nicht zu leicht sein. Aber diese Frage und andere Fragen der biologischen Anwendung lassen wir dann hier einmal offen, denn das Beispiel soll ja nur ein Beispiel sein.
R Code [zeigen / verbergen]
emm_obj |>
as_tibble() |>
ggplot(aes(x = fert_time, y = emmean, fill = fert_amount)) +
theme_minimal() +
labs(y = "Mittleres Gewicht [g] des Brokkoli", x = "Düngezeitpunkt",
fill = "Düngemenge [mg/l]") +
scale_y_continuous(breaks = seq(0, 500, by = 100)) +
geom_hline(yintercept = 500, size = 0.75, linetype = 2) +
geom_bar(stat = "identity",
position = position_dodge(width = 0.9, preserve = "single")) +
geom_text(aes(label = .group, y = emmean + SE + 0.01),
position = position_dodge(width = 0.9), vjust = -0.25) +
geom_errorbar(aes(ymin = emmean-SE, ymax = emmean+SE),
width = 0.2,
position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_okabeito()
lm()-Modell berechnet das mittler Gewicht des Brokkoli in jeder Faktorkombination. Das compact letter display wird dann in {emmeans} generiert. Wir nutzen hier den Standardfehler, da die Standardabweichung mit der großen Fallzahl rießig wäre. Wir haben noch ein Mindestgewicht von 500g ergänzt.