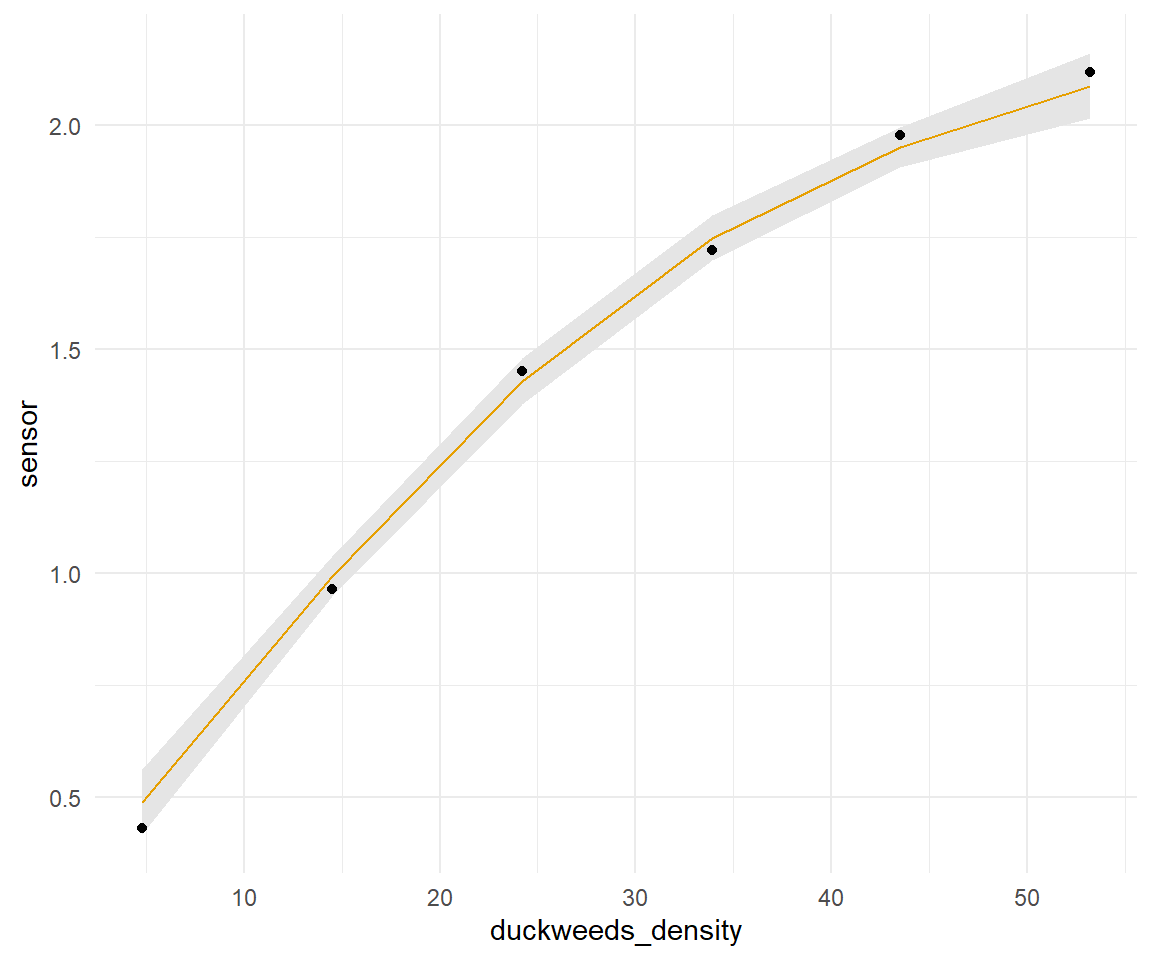# Nicht lineare Regression {#sec-non-linear}
```{r}
#| echo: false
pacman::p_load(tidyverse, readxl, knitr, kableExtra, see, latex2exp, mfp)
cb_pal <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
"#F0E442", "#0072B2", "#D55E00", "#CC79A7")
```
*Letzte Änderung am `r format(fs::file_info("stat-modeling-non-linear.qmd")$modification_time, '%d. %B %Y um %H:%M:%S')`*
> *"And you may ask yourself; Well... How did I get here?; And you may ask yourself; 'How do I work this?'" --- Talking Heads - Once in a Lifetime*
Was wollen wir mit der nicht-linearen Regression erreichen? Zum einen erhalten wir durch die nicht-lineare Regression die Möglichkeit auch Abhängigkeiten zu modellieren, die nicht linear sind. Zum anderen wollen wir auch nicht nur Gruppen miteinander vergleichen, sondern auch Verläufe modellieren. Häufig sind diese Verläufe über die Zeit nicht linear. Es gibt Sättigungskurven oder aber auch einen exponentiellen Verfall oder ein exponentielles Wachstum. All dies können wir mit nicht-linearen Modellen abbilden und modellieren. Für Zeitreihen habe ich dann noch ein eigenes Kapitel geschrieben, hier wollen wir uns dann mal mit den Verläufen beschäftigen und schauen, dass wir die Koeffizienten einer Geradengleichung erhalten.
Wichtig hierbei ist, dass wir oft nicht statistisch Testen, sondern ein Modell haben wollen, dass die Punkte gut beschreibt. Mit Modell meinen wir hier die Gerade, die durch die Punkte läuft. Für diese Grade wollen wir die Koeffizienten schätzen also rausfinden, wie wir später die Gerade zeichnen könnten, wenn wir die Punkte nicht vorliegen hätten. Also die Frage beantworten, wie $y$ nicht-linear von $x$ abhängt. Wir immer gibt es eine Reihe von Möglichkeiten das Problem zu lösen einer Geradengleichung zu erhalten, die nicht linear ist. Normalerweise haben wir ja eine Regressionsgleichung für eine simple lineare Regression in der folgenden Form vorliegen.
$$
y \sim \beta_0 + \beta_1 \cdot x
$$
Wenn wir jetzt aber eine nicht-lineare Regression rechnen wollen, dann müssen wir hier zum Beispiel ein Polynom einfügen. Damit schreiben wir nicht mehr $x$ sondern $x^b$ und erhalten folgende, beispielhafte Formel. Warum beispielhaft? Je nach Fragestellung brauchen wir verschiedene Parameter die wir dann für den Kurvenverlauf bestimmen müssen.
$$
y \sim \beta_0 + \beta_1 \cdot x^b
$$
Dieses $b$ (eng. *power*) und die anderen Koeffizienten müssen wir jetzt irgendwie berechnen. Manchmal fällt das $\beta_1$ dann auch weg oder aber wir haben eben eine noch komplexere Art der mathematischen Darstellung. Wir gehen daher hier dann mal verschiedene Lösungen für das Problem durch. Nicht alle Lösungen liefern auch eine Geradengleichung, die du dann auch aufschreiben kannst.
Und damit kommen wir auch zu dem zentralen Problem. Woher weiß ich, welche Gerade oder Kurve ich berechnen will? Eine super Hilfestellung liefert die Seite [A collection of self-starters for nonlinear regression in R](https://www.statforbiology.com/2020/stat_nls_usefulfunctions/). Dort kannst du einmal schauen, welche Funktionen es gibt, die du dann zum Beispiel in `nls()` aus dem R Paket `{stats}` modellieren kannst. Das R Paket `{stats}` kommt gleich mit R mit und muss nicht installiert werden. Mit Modellieren meine ich dann, die Gradenfunktion bestimmen kannst. Die richtige Startfunktion zu finden ist aber wirklich nicht trivial. Dafür gibt es dann aber mit dem R Paket `{mfp}` eine Lösung, dafür kann das Paket dann andere Sachen nicht. Schau dich also einmal um und entscheide, was du brauchst um deine Fragestellung zu beantworten.
::: callout-tip
## Weitere Tutorien für die Analyse von nicht-linearen Daten
Wie immer gibt es auch für die Frage nach dem Tutorium für die nicht-lineare Regression verschiedene Quellen. Ich kann noch folgende Informationen und Hilfen empfehlen.
- Das R Paket `{nlraa}` ist direkt für die Nutzung in den Agrarwissenschaften ausgelegt. Es finden sich auf der Hilfseite [nlraa: An R package for Nonlinear Regression Applications in Agricultural Research](https://cran.r-project.org/web/packages/nlraa/vignettes/nlraa.html) auch komplexere Beispiele für die Modellierung von Daten.
- Die Autoren @archontoulis2015nonlinear mit der wissenschaftlichen Veröffentlichung [Nonlinear Regression Models and Applications in Agricultural Research](https://acsess.onlinelibrary.wiley.com/doi/pdf/10.2134/agronj2012.0506) liefern nochmal einen wunderbaren Überblick über die Möglichkeiten der nicht-linearen Regression in den Agrarwissenschaften.
- Wenn es einfach nur eine Kurve durch die Punkte sein soll ohne eine mathematische Gleichung, dann kann das Tutorium zu [GAM and LOESS smoothing](https://andrewirwin.github.io/data-visualization/smoothing.html) helfen. Denn weder GAM noch LOESS liefern eine Gleichung die du aufschreiben kannst, dafür sehr gute Anpassungen an Punkte.
- Wie schon erwähnt, konzentrieren wir uns hier auf ein paar zentrale Pakete in R. Wir immer gibt es aber auch hier noch mehr wie bei dem Tutorium [Nonlinear Modelling using nls, nlme and brms](https://www.granvillematheson.com/post/nonlinear-modelling-using-nls-nlme-and-brms/). Du musst dann mal rechts und links schauen, auch für mich ist das ja eine Linksammlung zu der ich dann mal zurückkehre.
- Der Blogeintrag [On curve fitting using R](https://davetang.org/muse/2013/05/09/on-curve-fitting/) liefert nochmal die Lösung Daten mit der Funktion `poly()` in der Funktion `lm()` zu modellieren. Ich habe jetzt darauf verzichtet, da das Kapitel schon sehr voll war. Es spricht aber nichts dagegen, ein Problem der nicht linearen Regression mit einem Polinom zu lösen.
- Das Buch von M. Clark zu [Generalized Additive Models](https://m-clark.github.io/generalized-additive-models/) liefert auch nochmal eine gute Übersicht über die Nutzung von GAMs in R.
- Weitere R Pakete sind noch das [R Paket `{polypoly}`](https://cran.r-project.org/web/packages/polypoly/vignettes/overview.html), welches sich nochmal mit der polynomialen Regression beschäftigt.
- Das Tutorium [Polynomial Regression - An example](https://www.geo.fu-berlin.de/en/v/soga-r/Basics-of-statistics/Linear-Regression/Polynomial-Regression/Polynomial-Regression---An-example/index.html) und das Tutorium [Fitting Polynomial Regression in R](https://datascienceplus.com/fitting-polynomial-regression-r/) gehen dann nochmal auf die polynomiale Regression ein, die es dann erlaubt effizient quadratische Gleichungen zu rechnen.
- Manchmal wollen wir auch um die Grade Konfdenzbänder oder aber einen Bereich der Unsicherheit zeichnen. Dann können wir einmal im Tutorium [Confidence and Prediction Bands Methods for Nonlinear Models](https://cran.r-project.org/web/packages/nlraa/vignettes/Confidence-Bands.html) und dem R Paket `{nlraa}` nachschauen.
:::
Schaue dir auch die folgenden Zerforschenbeispiele einmal an, wenn dich mehr zu dem Thema der Abbildung von nicht-linearen Regressionen interessiert. Du findest in den Kästen Beispiele für Posterabbildungen zur nicht-linearen Regression, die ich dann zerforscht habe. Dann habe ich auch noch gleich die nicht-lineare Regression gerechnet um die Geradengleichungen sauber darzustellen.
::: {.callout-note collapse="true"}
## Zerforschen: Nicht-lineare Regression
{{< include zerforschen/zerforschen-non-linear-simple.qmd >}}
:::
::: {.callout-note collapse="true"}
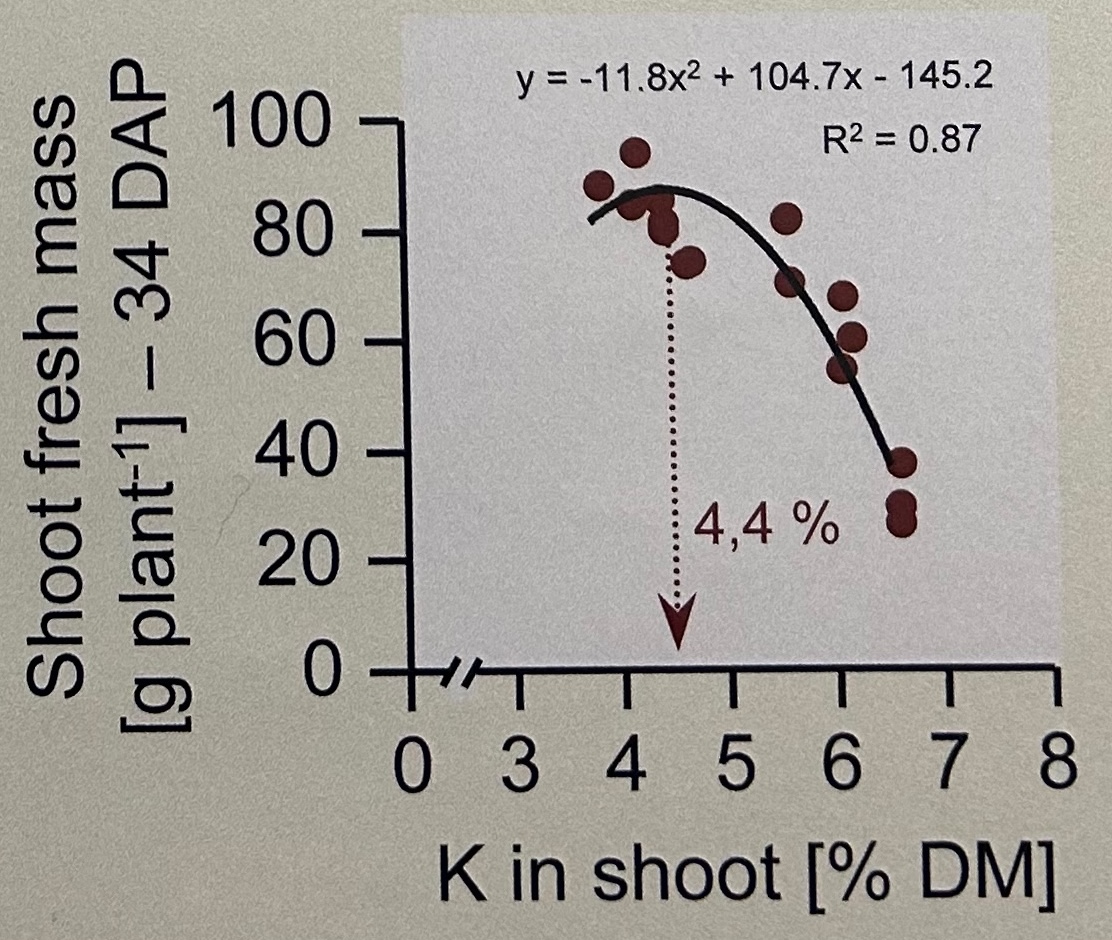
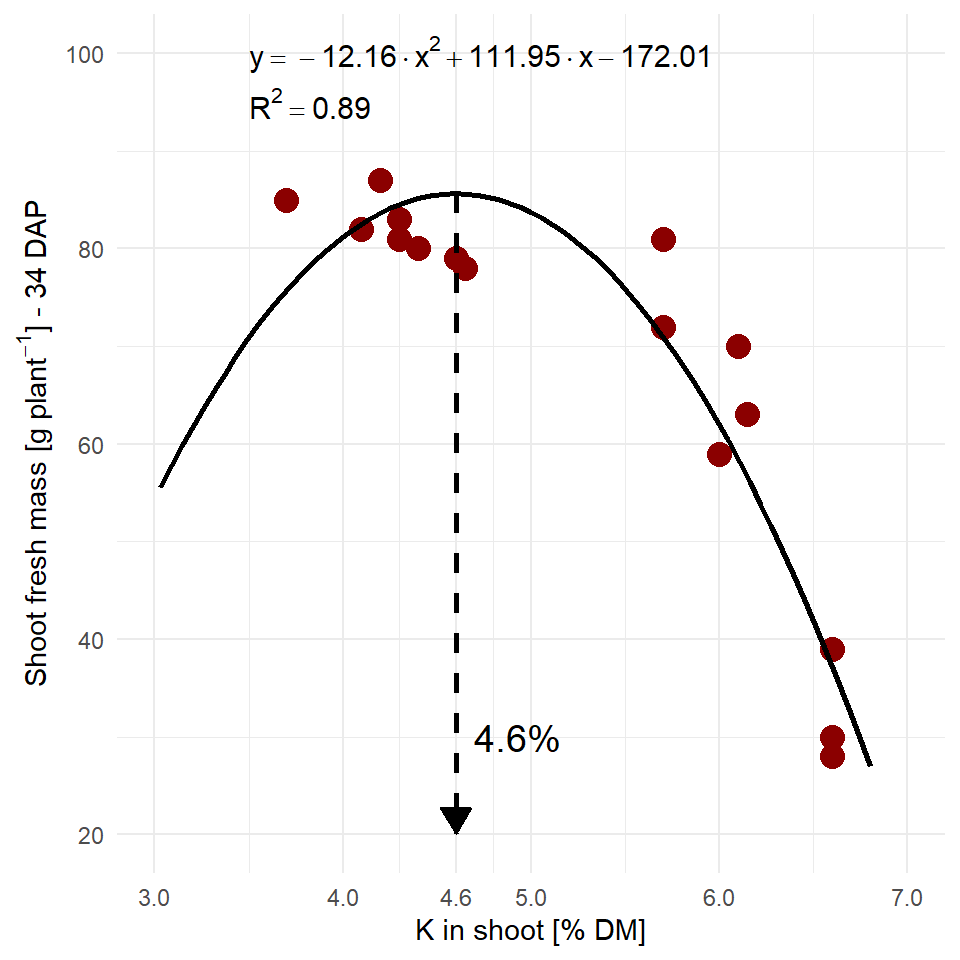
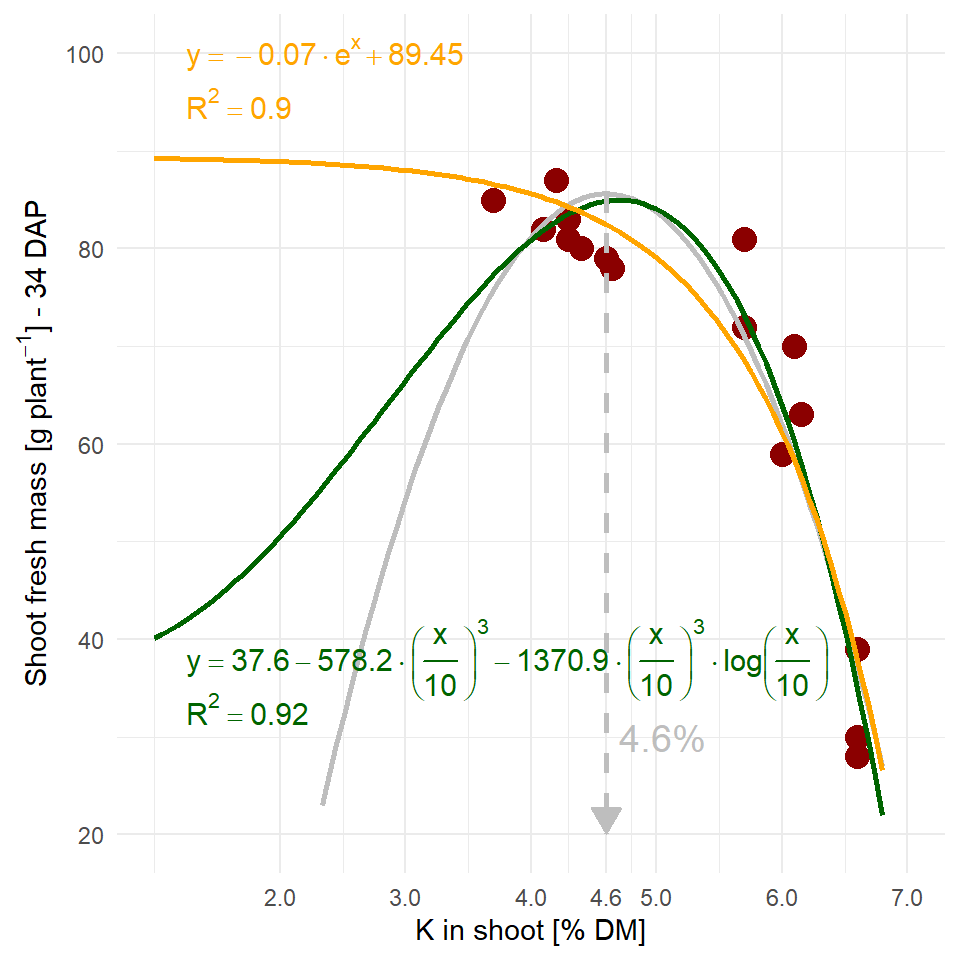
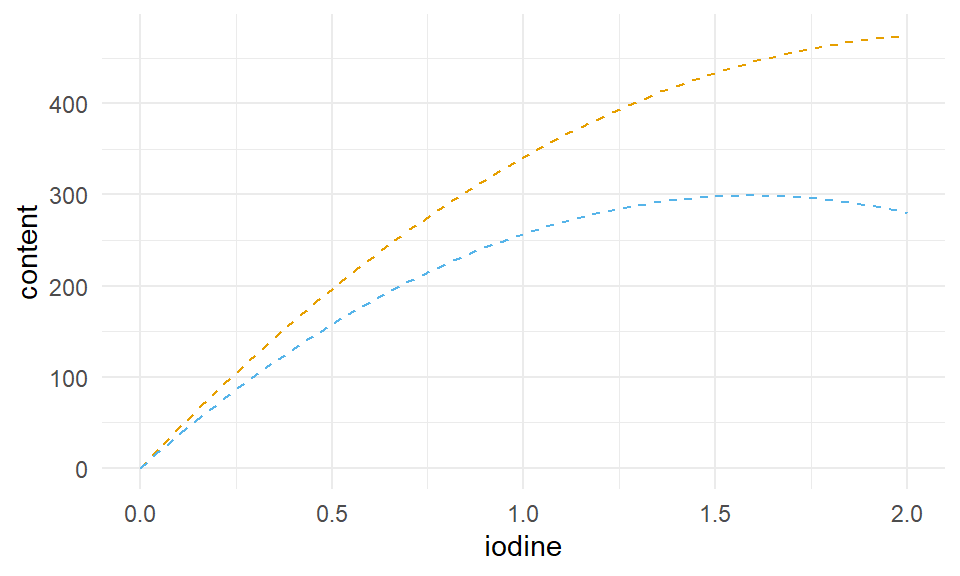
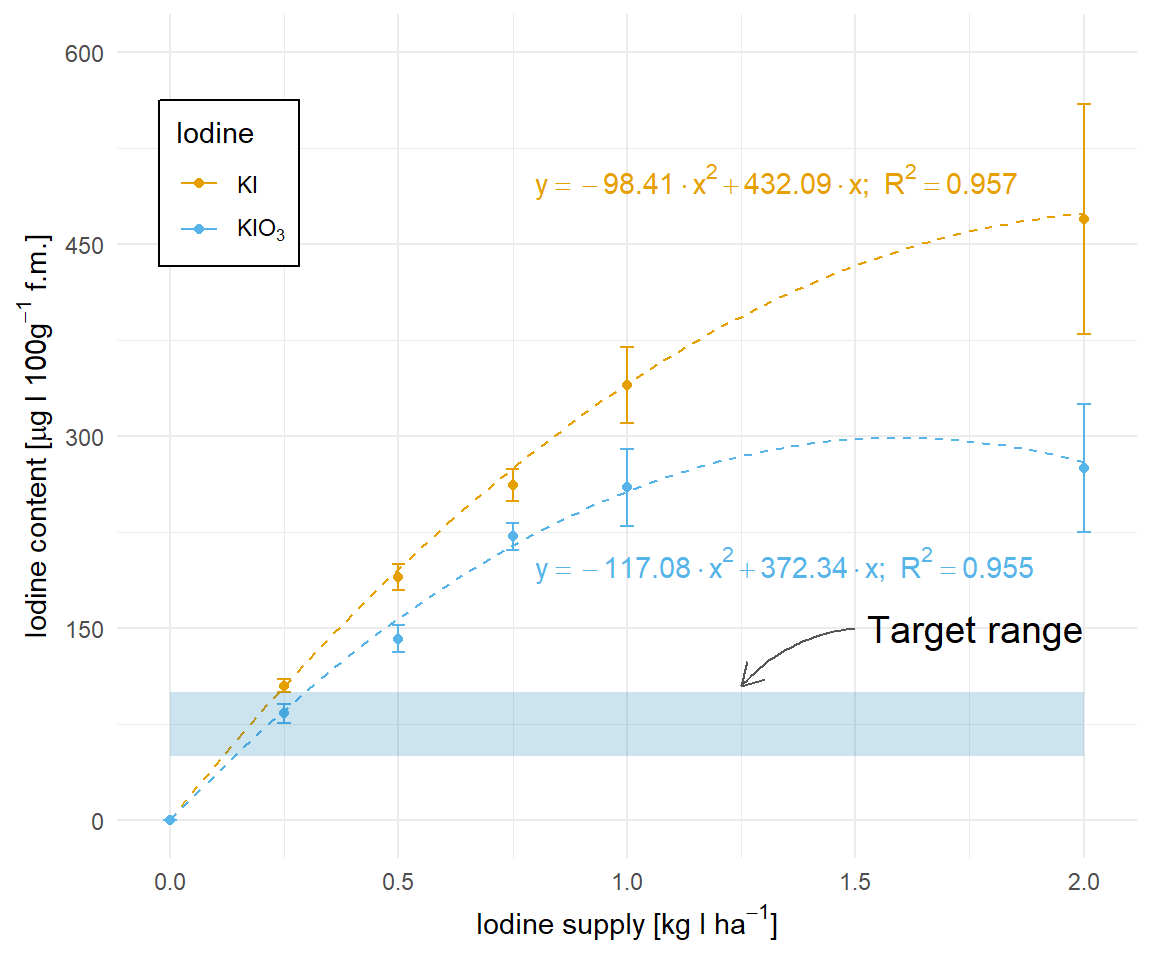
## Zerforschen: Nicht-lineare Regression mit Zielbereich
{{< include zerforschen/zerforschen-non-linear-target.qmd >}}
:::
::: {.callout-note collapse="true"}
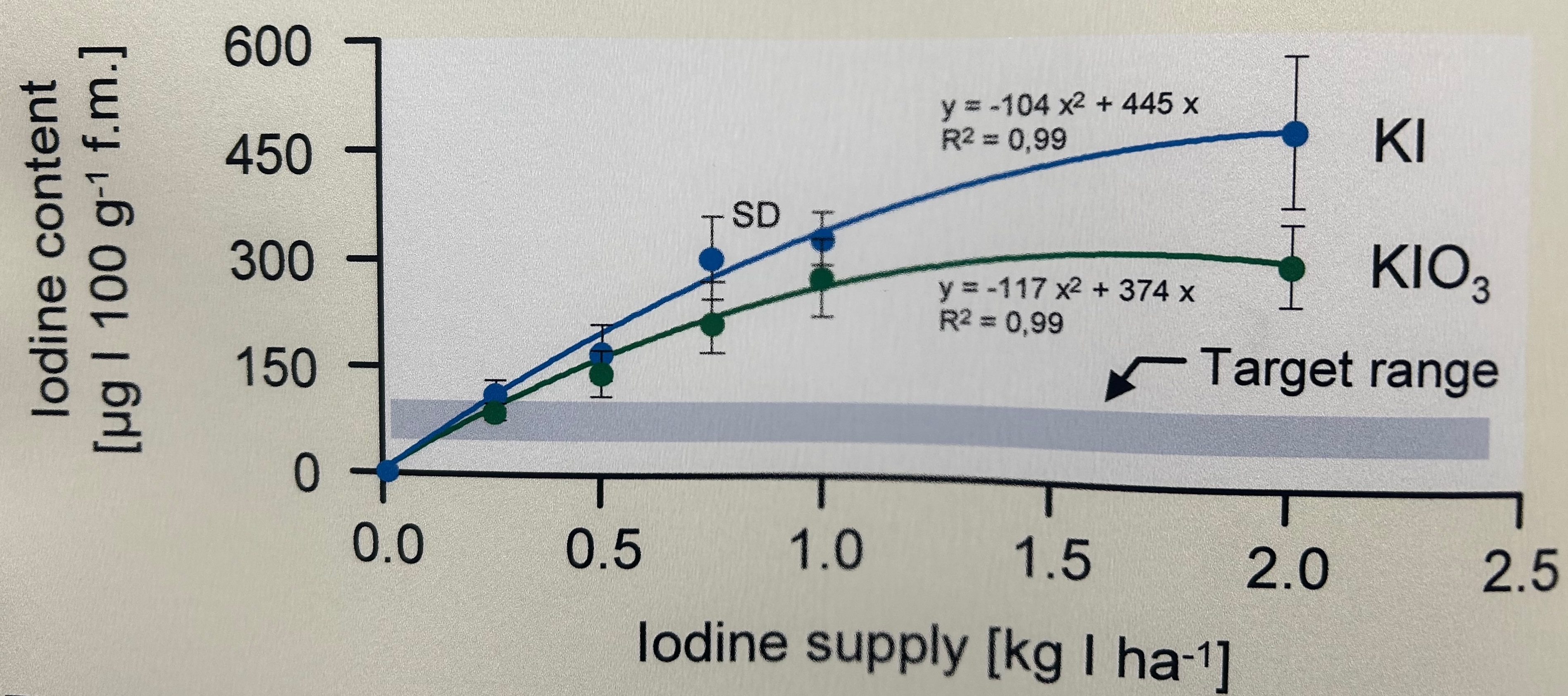
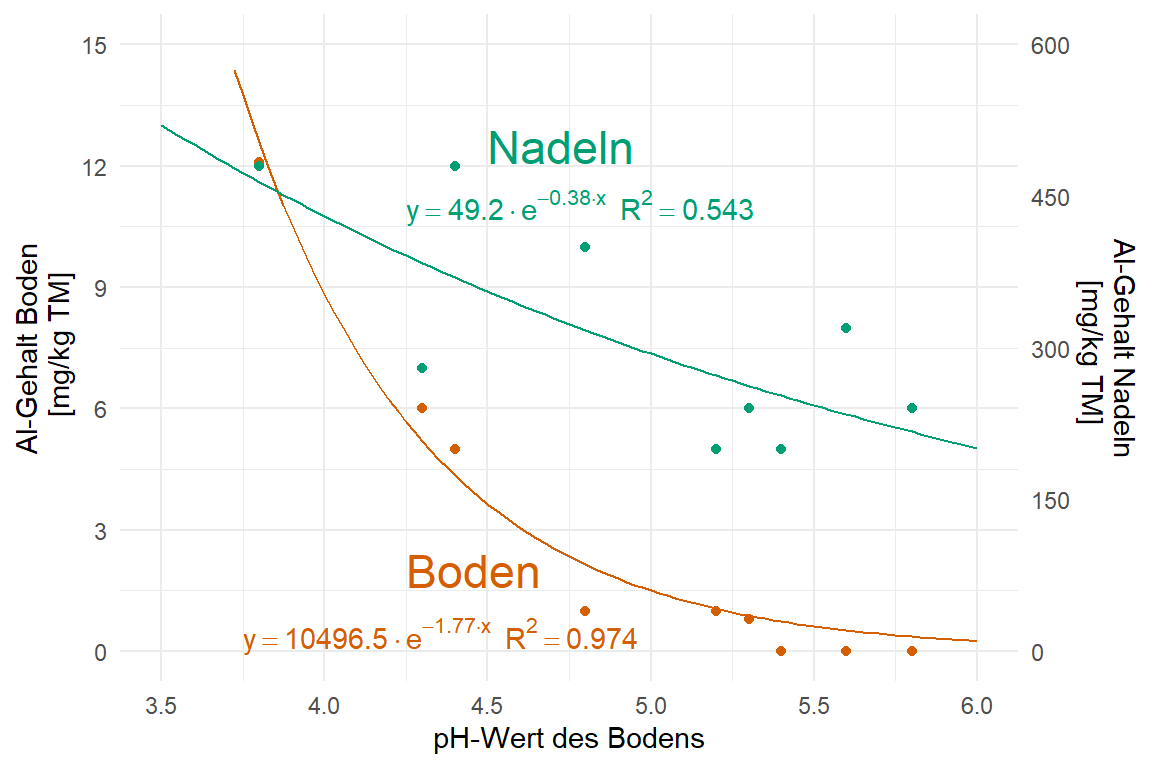
## Zerforschen: Nicht-lineare Regression und zwei $\boldsymbol{y}$-Achsen
{{< include zerforschen/zerforschen-non-linear-2axis.qmd >}}
:::
## Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
```{r}
#| message: false
#| echo: true
pacman::p_load(tidyverse, magrittr, broom, nlraa, modelsummary,
parameters, performance, see, mgcv, mfp, marginaleffects,
gratia, readxl, nlstools, janitor, ggeffects, nls.multstart,
conflicted)
cb_pal <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
"#F0E442", "#0072B2", "#D55E00", "#CC79A7")
```
An der Seite des Kapitels findest du den Link *Quellcode anzeigen*, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
## Daten
In unserem Datenbeispiel schauen wir uns die Wachstumskurve von Hühnchen an. Wir verfolgen das Gewicht über 36 Tage. Dabei messen wir an jedem Tag eine unterschiedliche Anzahl an Kücken bzw. Hünchen. Wir wissen auch nicht, ob wir immer die gleichen Hühnchen jedes Mal messen. Dafür war die Hühnchenmastanlage zu groß. Wir wissen aber wie alt jedes Hühnchen bei der Messung war.
```{r}
#| message: false
chicken_tbl <- read_csv2("data/chicken_growth.csv")
```
In @tbl-chicken sehen wir nochmal die Daten für die ersten drei und die letzten drei Zeilen. Alleine überschlagsmäßig sehen wir schon, dass wir es nicht mit einem linearen Anstieg des Gewichtes zu tun haben. Wenn wir einen linearen Anstieg hätten, dann würde ein Hühnchen, dass am Tag 1 ca. 48g wiegt, nach 36 Tagen ca. 1728g wiegen. Das ist hier eindeutig nicht der Fall. Wir haben vermutlich einen nicht-linearen Zusammenhang.
```{r}
#| echo: false
#| message: false
#| warning: false
#| label: tbl-chicken
#| tbl-cap: "Auszug aus Hühnchendatensatz."
rbind(head(chicken_tbl, n = 3),
rep("...", times = ncol(chicken_tbl)),
tail(chicken_tbl, n = 3)) |>
kable(align = "c", "pipe")
```
Schauen wir uns die Daten dann gleich einmal in einer Visualisierung mit `ggplot()` an um besser zu verstehen wie die Zusammenhänge in dem Datensatz sind.
Neben dem Hünchendatensatz haben wir noch einen Datenstatz zu dem Wachstum von Wasserlinsen. Wir haben einmal händisch die Dichte bestimmt `duckweeds_density` und einmal mit einem Sensor gemessen. Dabei sind die Einheiten der Sensorwerte erstmal egal, wir wollen aber später eben nur mit einem Sensor messen und dann auf den Wasserlinsengehalt zurückschließen. Wir haben hier eher eine Sätigungskurve vorliegen, denn die Dichte der Wasserlinsen ist ja von der Oberfläche begrenzt. Auch können sich die Wasserlinsen nicht beliebig teilen, es gibt ja nur eine begrenzte Anzahl an Ressourcen.
```{r}
duckweeds_tbl <- read_excel("data/duckweeds_density.xlsx")
```
In der @tbl-duckweeds siehst du dann einmal einen Auszug aus den Daten zu den Wasserlinsen. Es ist ein sehr einfacher Datensatz mit nur zwei Spalten. Wie du siehst, scheint sich das bei der nicht linearen Regression durchzuziehen. Es gehen auch komplexere Modelle, aber dann kann ich die Ergebnisse schlechter visualisieren.
```{r}
#| echo: false
#| message: false
#| warning: false
#| label: tbl-duckweeds
#| tbl-cap: "Auszug aus Wasserlinsendatensatz."
rbind(head(duckweeds_tbl, n = 3),
rep("...", times = ncol(duckweeds_tbl)),
tail(duckweeds_tbl, n = 3)) |>
kable(align = "c", "pipe")
```
Auch die Wasserlinsendaten wollen wir uns erstmal in einer Abbildung anschauen und dann sehen, ob wir eine Kurve durch die Punkte gelegt kriegen.
## Visualisierung
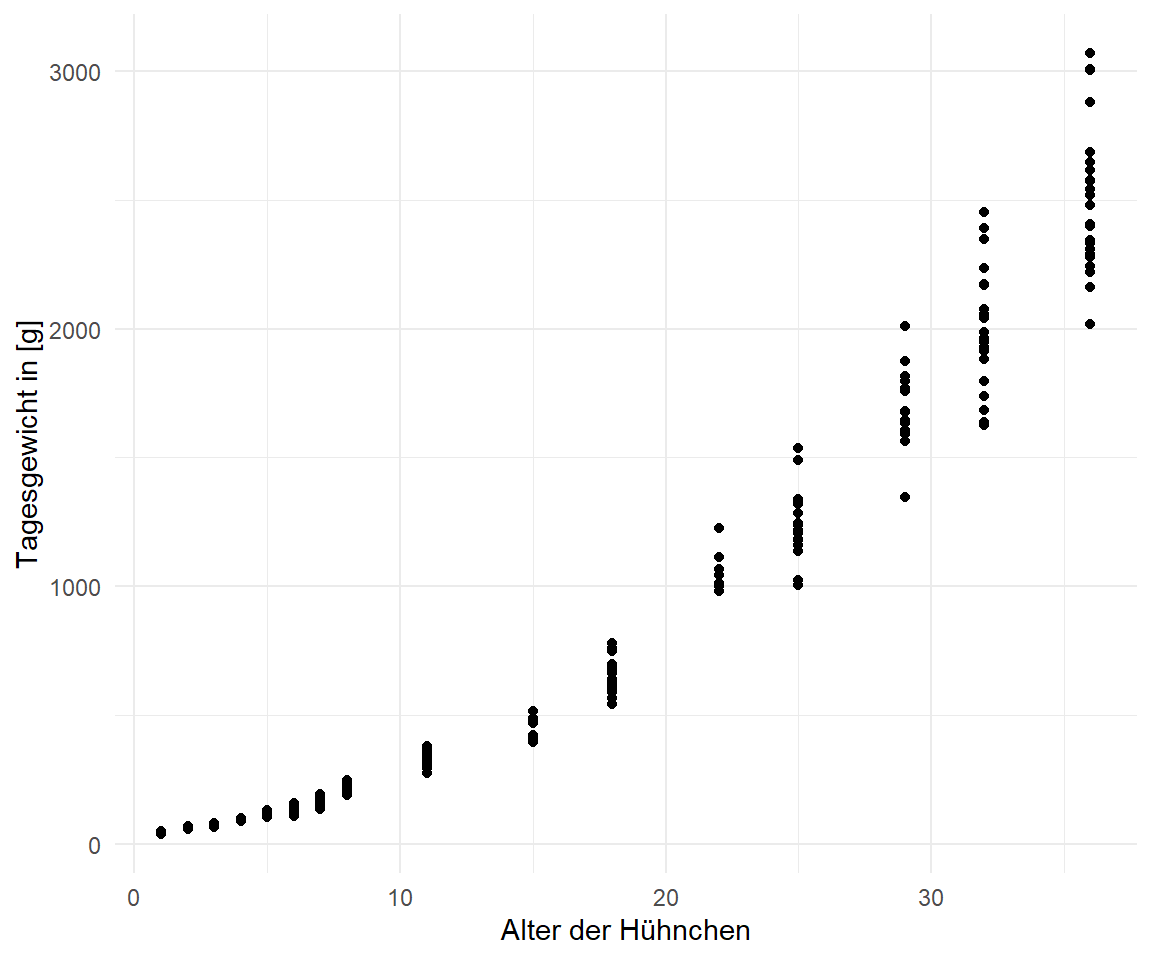
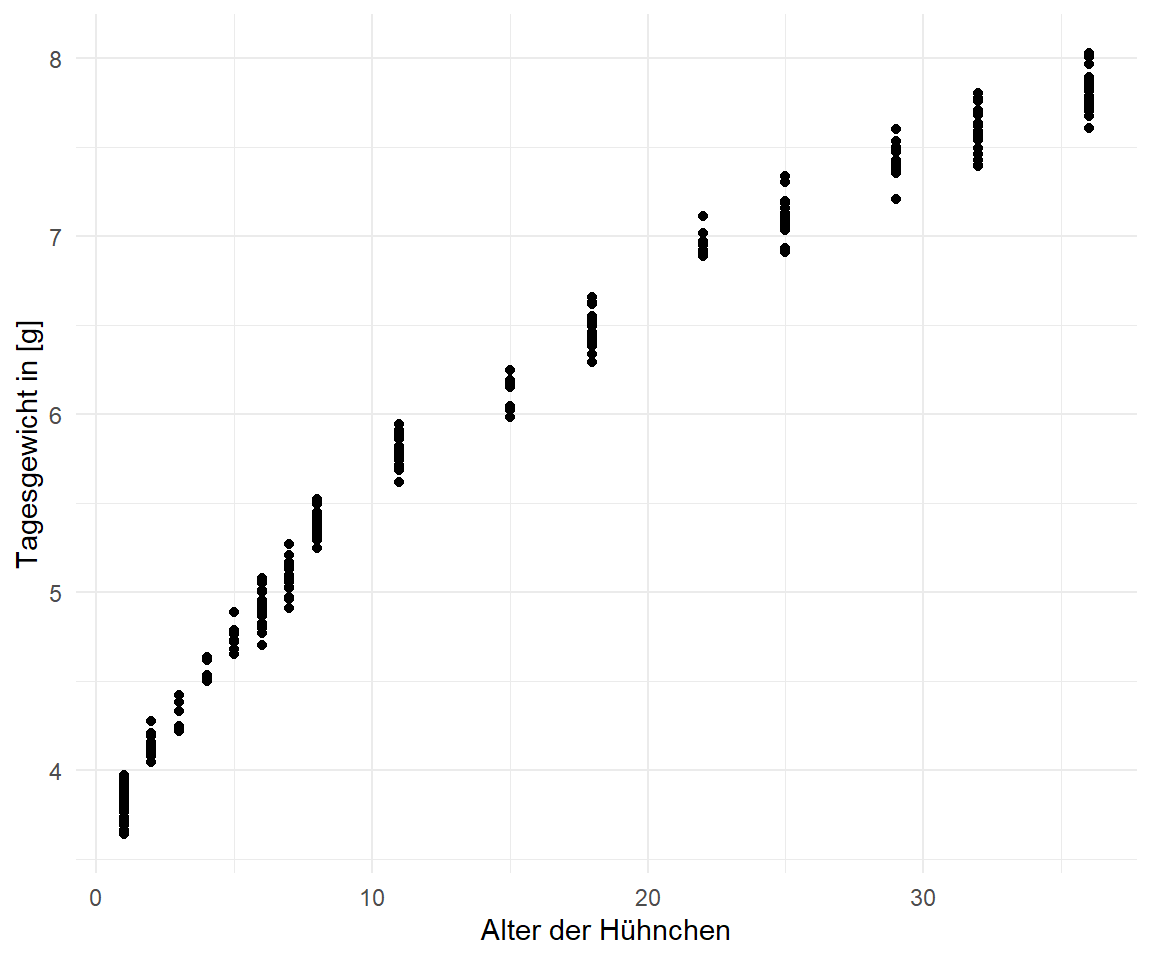
In @fig-nls-00-1 sehen wir die Visualisierung der Hühnchengewichte nach Alter in Tagen. Zum einen sehen wir wie das Körpergewicht exponentiell ansteigt. Zum anderen sehen wir in @fig-nls-00-2, dass auch eine $log$-transformiertes $y$ nicht zu einem linearen Zusammenhang führt. Der Zusammenhang zwischen dem Körpergewicht und der Lebensalter bleibt nicht-linear.
```{r}
#| echo: false
#| message: false
#| eval: true
#| label: fig-nls-00
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Hühnchengewichte nach Alter in Tagen. Auch mit $log$-transformierten Körpergewicht liegt immer noch kein linearer Zusammenhang zwischen dem Lebensalter und dem Körpergewicht vor. "
#| fig-subcap:
#| - "Ohne transformierten $y$."
#| - "Mit $log$-transformierten $y$."
#| layout-nrow: 1
ggplot(chicken_tbl, aes(age, weight)) +
theme_minimal() +
geom_point() +
labs(x = "Alter der Hühnchen", y = "Tagesgewicht in [g]")
ggplot(chicken_tbl, aes(age, log(weight))) +
theme_minimal() +
geom_point() +
labs(x = "Alter der Hühnchen", y = "Tagesgewicht in [g]")
```
Deshalb wollen wir den Zusammenhang zwischen dem Körpergewicht der Hühnchen und dem Lebensalter einmal mit einer nicht-linearen Regression modellieren. Wir sind also nicht so sehr an $p$-Werten interessiert, wir sehen ja, dass die gerade ansteigt, sondern wollen wissen wie die Koeffizienten einer möglichen exponentiellen Gleichung aussehen.
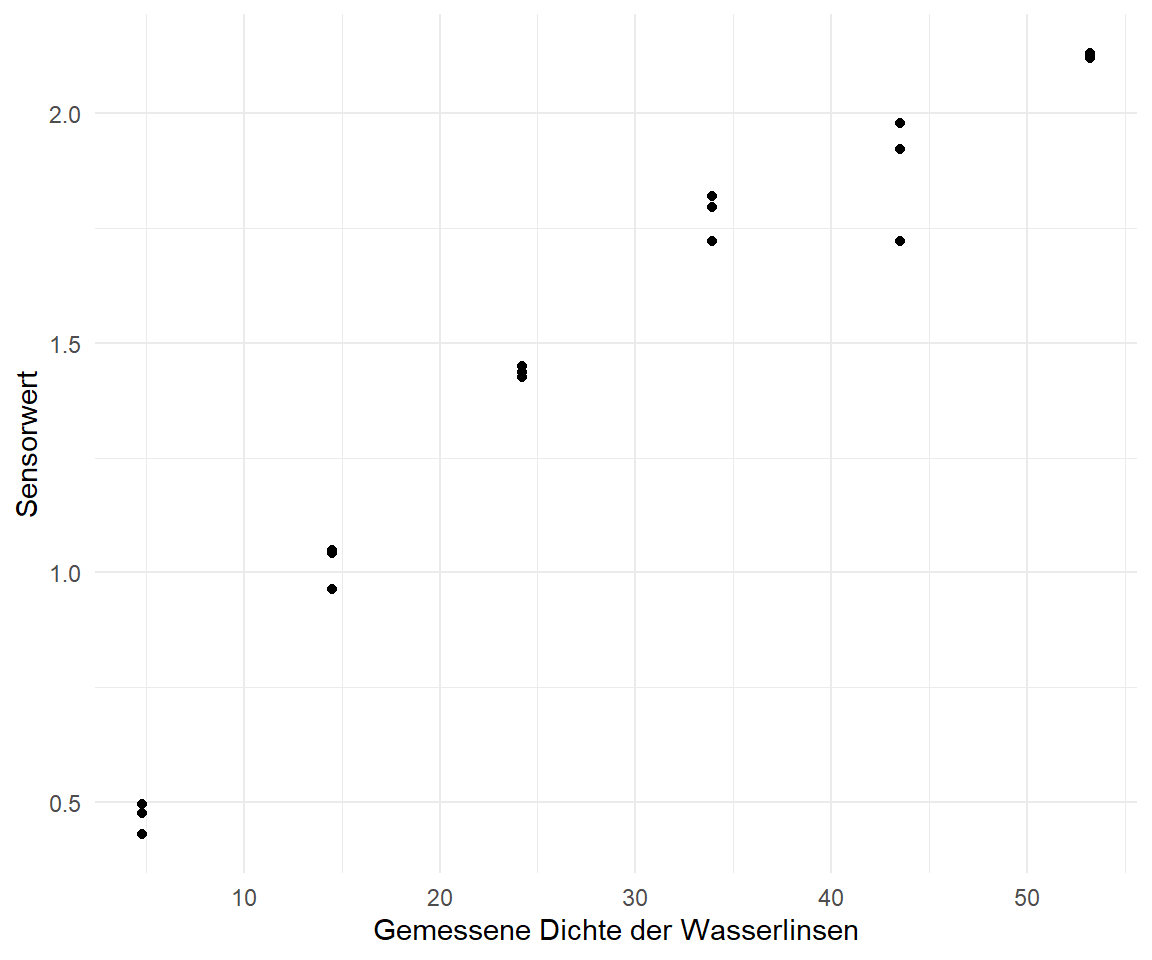
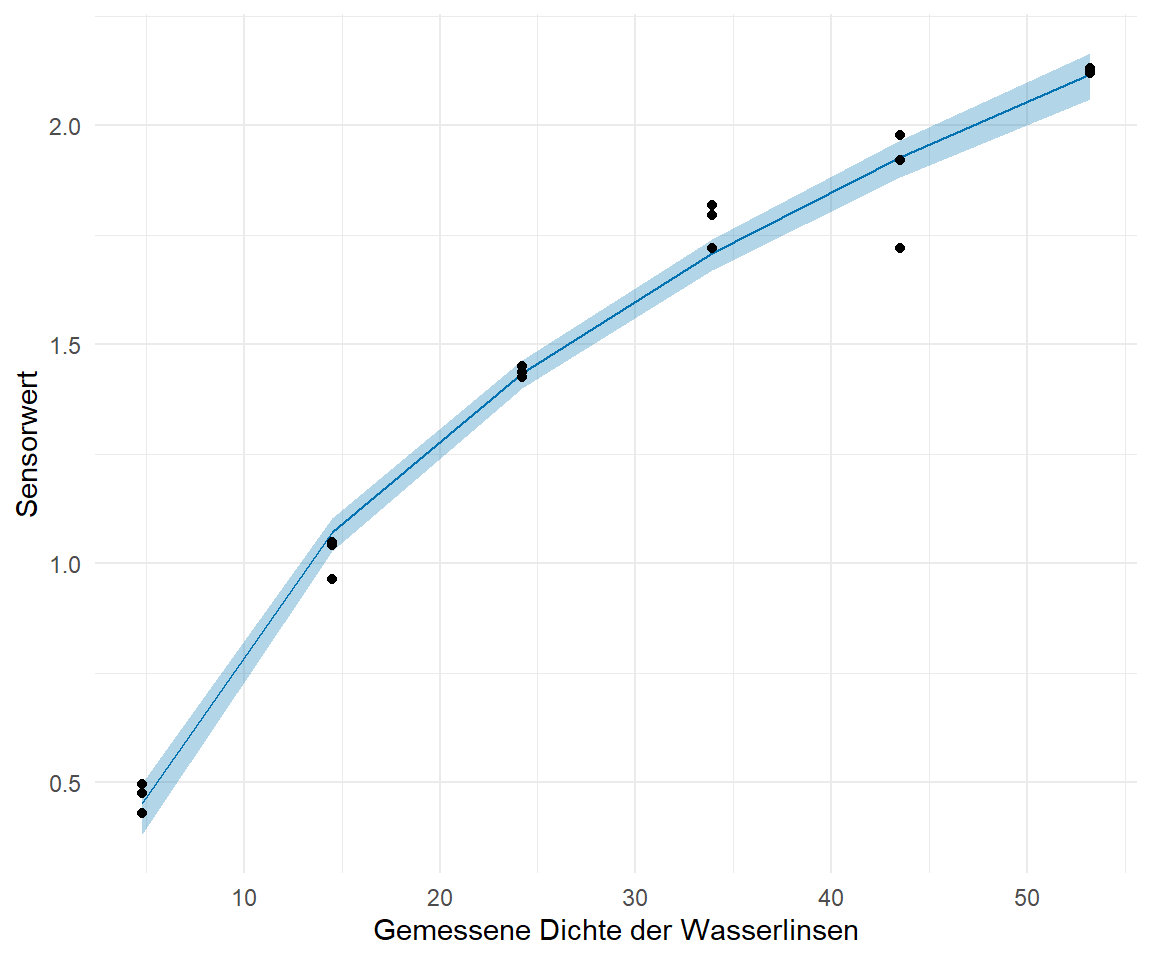
Für die Visualisierung der Wasserlinsendaten in der @fig-gam-duckweeds-01 verzichte ich einmal auf die logarithmische Darstellung. Wir wollen hier dann eine Kurve durch die Punkte legen so wie die Daten sind. Auffällig ist erstmal, dass wir sehr viel weniger Beobachtungen und auch Dichtemesspunkte auf der $x$-Achse haben. Wir haben dann zu den jeweiligen Wasserlinsendichten dann drei Sensormessungen. Das könnte noch etwas herausfordernd bei der Modellierung werden.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-gam-duckweeds-01
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Sensorwerte nach Wasserlinsendichte. Pro Dichtewert liegen drei Sensormessungen vor."
ggplot(duckweeds_tbl, aes(duckweeds_density, sensor)) +
geom_point() +
theme_minimal() +
labs(x = "Gemessene Dichte der Wasserlinsen", y = "Sensorwert")
```
## Nonlinear least-squares mit `nls()`
Zum nicht-linearen Modellieren nutzen wir die Funktion `nls()` (eng. *nonlinear least-squares*). Die Funktion `nls()` ist das nicht-lineare Äquivalent zu der linearen Funktion `lm()`. Nur müssen wir mit der `nls()` Funktion etwas anders umgehen. Zum einen müssen wir die `formula()` anders definieren. Der große Vorteil von `nls()` ist, dass wir hier auch die Koeffizienten unser Geradengleichung wiederkriegen. In den anderen Möglichkeiten kriegen wir dann teilweise nicht die Informationen zu einer Kurve wieder. Wir haben dann zwar ein wunderbares Modell, können das Modell aber nicht einfach als eine mathematische Gleichung aufschreiben. Daher hier `nls()` etwas ausführlicher, da wir dann mit `nls()` schon die Sachen auch erhalten, die wir meist wollen.
### ... von Wachstum
In unserem Hühnchenbeispiel nehmen ein exponentielles Wachstum an. Daher brauchen wir einen geschätzten Koeffizienten für den Exponenten des Alters sowie einen Intercept. Wir gehen nicht davon aus, dass die Hühnchen mit einem Gewicht von 0g auf die Welt bzw. in die Mastanlage kommen. Unsere Formel sehe dann wie folgt aus.
$$
weight \sim \beta_0 + age^{\beta_1}
$$
Da wir in R keine $\beta$'s schreiben können nutzen wir die Buchstaben `b0` für $\beta_0$ und `b1` für $\beta_1$. Im Prinzip könnten wir auch andere Buchstaben nehmen, aber so bleiben wir etwas konsistenter zu der linearen Regression. Somit sieht die Gleichung dann in R wie folgt aus.
$$
weight \sim b_0 + age^{b_1}
$$
Wichtig hier, wir müssen R noch mitteilen, dass wir `age` hoch `b1` rechnen wollen. Um das auch wirklich so zu erhalten, zwingen wir R mit der Funktion `I()` auch wirklich einen Exponenten zu berechnen. Wenn wir nicht das `I()` nutzen, dann kann es sein, dass wir aus versehen eine Schreibweise für eine Abkürzung in der `formula` Umgebung nutzen.
Im Weiteren sucht die Funktion iterativ die besten Werte für `b0` und `b1`. Deshalb müssen wir der Funktion `nls()` Startwerte mitgeben, die in etwa passen könnten. Hier tippe ich mal auf ein `b0 = 1` und ein `b1 = 1`. Wenn wir einen Fehler wiedergegeben bekommen, dann können wir auch noch an den Werten drehen.
```{r}
#| results: hide
fit <- nls(weight ~ b0 + I(age^b1), data = chicken_tbl,
start = c(b0 = 1, b1 = 1))
```
::: callout-note
## Bessere Startwerte für `nls()`
Leider müssen wir in `nls()` die Startwerte selber raten. Das kannst du natürlich aus der Abbildung der Daten abschätzen, aber ich muss sagen, dass mir das immer sehr schwer fällt. Deshalb gibt es da einen Trick. Wir rechnen ein lineares Modell und zwar logarithmieren wir beide Seiten der Gleichung. Dann können wir die Koeffizienten aus dem Modell als Startwerte nehmen.
```{r}
lm(log(weight) ~ log(age), chicken_tbl)
```
Manchmal musst du auch nur die linke Seite logarithmieren.
```{r}
#| eval: false
lm(log(weight) ~ age, chicken_tbl)
```
Es hängt dann immer etwas vom Modell ab und wie die Werte dann anschließend in `nls()` konvergieren. Ich habe eigentlich immer mit einem der beiden Methoden Startwerte gefunden. Wir nehmen hier mal die Startwerte aus dem ersten Ansatz mit der doppelten Logarithmierung.
Wir erhalten hier für den `Intercept` den Wert 3.475 und für die Steigung den Wert 1.085. Da in meiner obigen Gleichung die Steigung `b1` ist und der `Intercept` dann `b0` setzen wir die Zahlen entsprechend ein. Für den `Intercept` müssen wir dann noch den Exponenten wählen.
```{r}
nls(weight ~ b0 + I(age^b1), data = chicken_tbl,
start = c(b0 = exp(3.475), b1 = 1.085))
```
Jetzt sollten wir keine Fehlermeldung erhalten haben, dass unser Modell nicht konvergiert ist oder anderweitig kein Optimum gefunden hat.
Das [R Paket `{nls.multstart}`](https://github.com/padpadpadpad/nls.multstart) versucht das Problem der Startwerte nochmal algorithmisch zu lösen. Wenn du also keine guten Startwerte mit den Trick über `lm()` findest, dann ist das R Paket hier nochmal ein guter Startpunkt. Es geht auch komplexer wie das Tutorium unter [Nonlinear Modelling using nls, nlme and brms](https://www.granvillematheson.com/post/nonlinear-modelling-using-nls-nlme-and-brms/) nochmal zeigt.
```{r}
nls_multstart(weight ~ b0 + I(age^b1), data = chicken_tbl,
lower = c(b0 = 0, b1 = 0),
upper = c(b0 = Inf, b1 = Inf),
start_lower = c(b0 = 0, b1 = 0),
start_upper = c(b0 = 500, b1 = 5),
iter = 500)
```
Natürlich kommt hier das Gleiche raus, aber manchmal findet man dann wirklich nicht die passenden Startwerte. Die Funktion macht ja nichts anderes als der ursprünglichen `nls()` Funktion etwas unter die Arme zugreifen.
:::
Wir nutzen wieder die Funktion `model_parameters()` aus dem R Paket `{parameters}` um uns eine aufgeräumte Ausgabe wiedergeben zu lassen.
```{r}
#| message: false
fit |>
model_parameters() |>
select(Parameter, Coefficient)
```
Die $p$-Werte interessieren uns nicht weiter. Wir sehen ja, dass wir einen Effekt von dem Alter auf das Körpergewicht haben. Das überrascht auch nicht weiter. Wir wollen ja die Koeffizienten $\beta_0$ und $\beta_1$ um die Gleichung zu vervollständigen. Mit dem Ergebnis aus der Funktion `nls()` können wir jetzt wie folgt schreiben.
$$
weight \sim 92.20 + age^{2.18}
$$
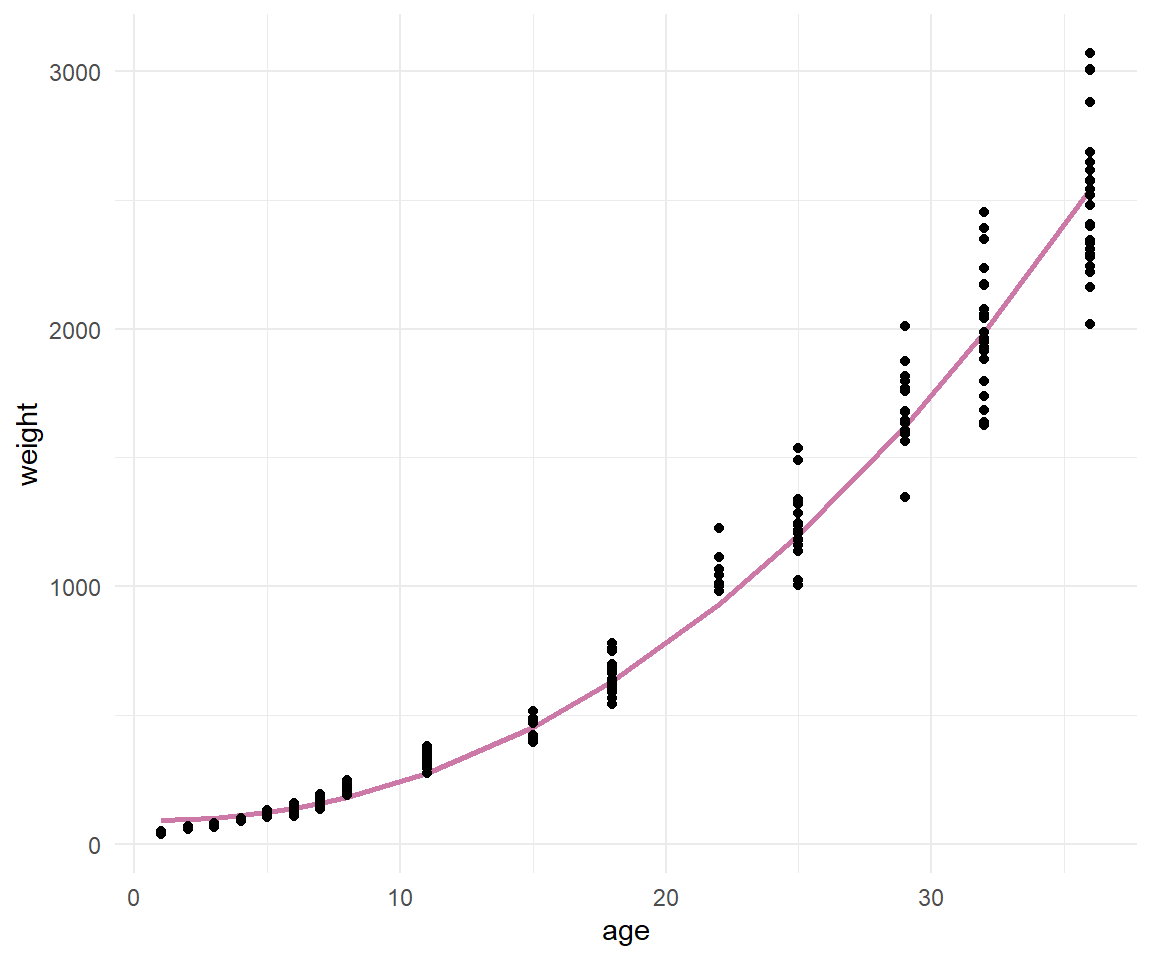
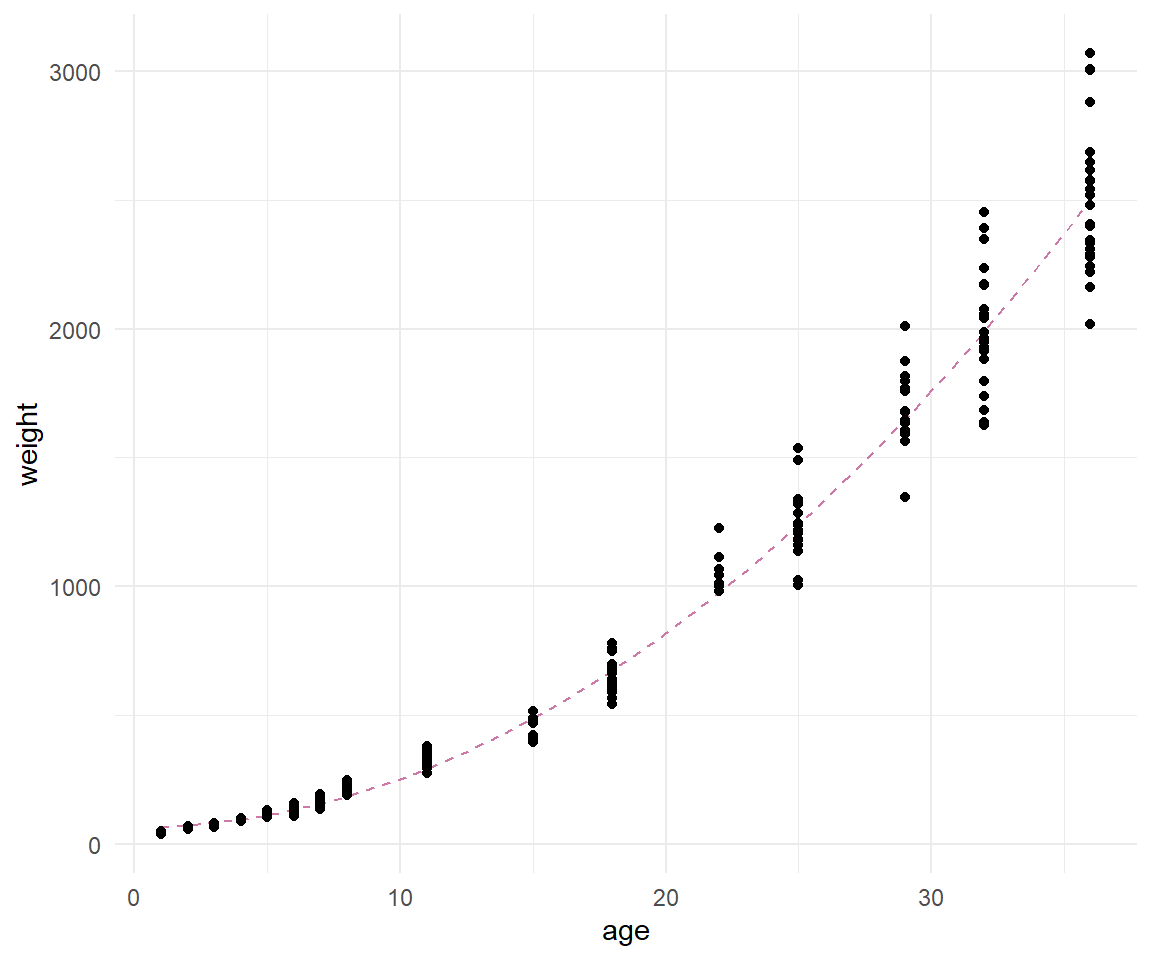
Damit haben wir dann auch unsere nicht-lineare Regressionsgleichung erhalten. Passt den die Gleichung auch zu unseren Daten? Das können wir einfach überprüfen. Dafür müssen wir nur in die Funktion `predict()` unser Objekt des Fits unseres nicht-linearen Modells `fit` stecken und erhalten die vorhergesagten Werte für jedes $x$ in unserem Datensatz. Oder etwas kürzer, wir erhalten die "Gerade" der Funktion mit den Koeffizienten aus dem `nls()` Modell wieder. In @fig-nls-01 sehen wir die gefittete Gerade.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-01
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Hühnchengewichte nach Alter in Tagen mit der geschätzen nicht-linearen Regressionsgleichung."
ggplot(chicken_tbl, aes(age, weight)) +
geom_line(aes(y = predict(fit)), size = 1, color = "#CC79A7") +
geom_point() +
theme_minimal()
```
Wie wir erkennen können sieht die Modellierung einigermaßen gut aus. Wir haben zwar einige leichte Abweichungen von den Beobachtungen zu der geschätzten Geraden, aber im Prinzip könnten wir mit der Modellierung leben. Wir hätten jetzt also eine nicht-lineare Gleichung die den Zusammenhang zwischen Körpergewicht und Lebensalter von Hühnchen beschreibt. Die Verwendung von `nest()` und `map()` ist schon erweiterte Programmierung in R. Du findest hier mehr über [broom and dplyr](https://cran.r-project.org/web/packages/broom/vignettes/broom_and_dplyr.html) und die Anwendung auf mehrere Datensätze.
Nun könnte man argumentieren, dass wir vielleicht unterschiedliche Abschnitte des Wachstums vorliegen haben. Also werden wir einmal das Alter in Tagen in vier gleich große Teile mit der Funktion `cut_number()` schneiden. Beachte bitte, dass in jeder Gruppe gleich viele Beobachtungen sind. Du kannst sonst händisch über `case_when()` innerhalb von `mutate()` dir eigene Gruppen bauen. Wir nutzen auch die Funktion `map()` um über alle Subgruppen des Datensatzes dann ein `nls()` laufen zu lassen.
```{r}
#| results: hide
nls_tbl <- chicken_tbl |>
mutate(grp = as_factor(cut_number(age, 4))) |>
group_by(grp) |>
nest() |>
mutate(nls_fit = map(data, ~nls(weight ~ b0 + I(age^b1), data = .x,
start = c(b0 = 1, b1 = 2))),
pred = map(nls_fit, ~predict(.x)))
```
Um den Codeblock oben kurz zu erklären. Wir rechnen vier nicht-lineare Regressionen auf den vier Altersgruppen. Dann müssen wir uns noch die vorhergesagten Werte wiedergeben lassen damit wir die gefittete Gerade zeichnen können. Wir nutzen dazu die Funktion `unnest()` um die Daten zusammen mit den vorhergesagten Werten zu erhalten.
```{r}
nls_pred_tbl <- nls_tbl |>
unnest(c(data, pred))
```
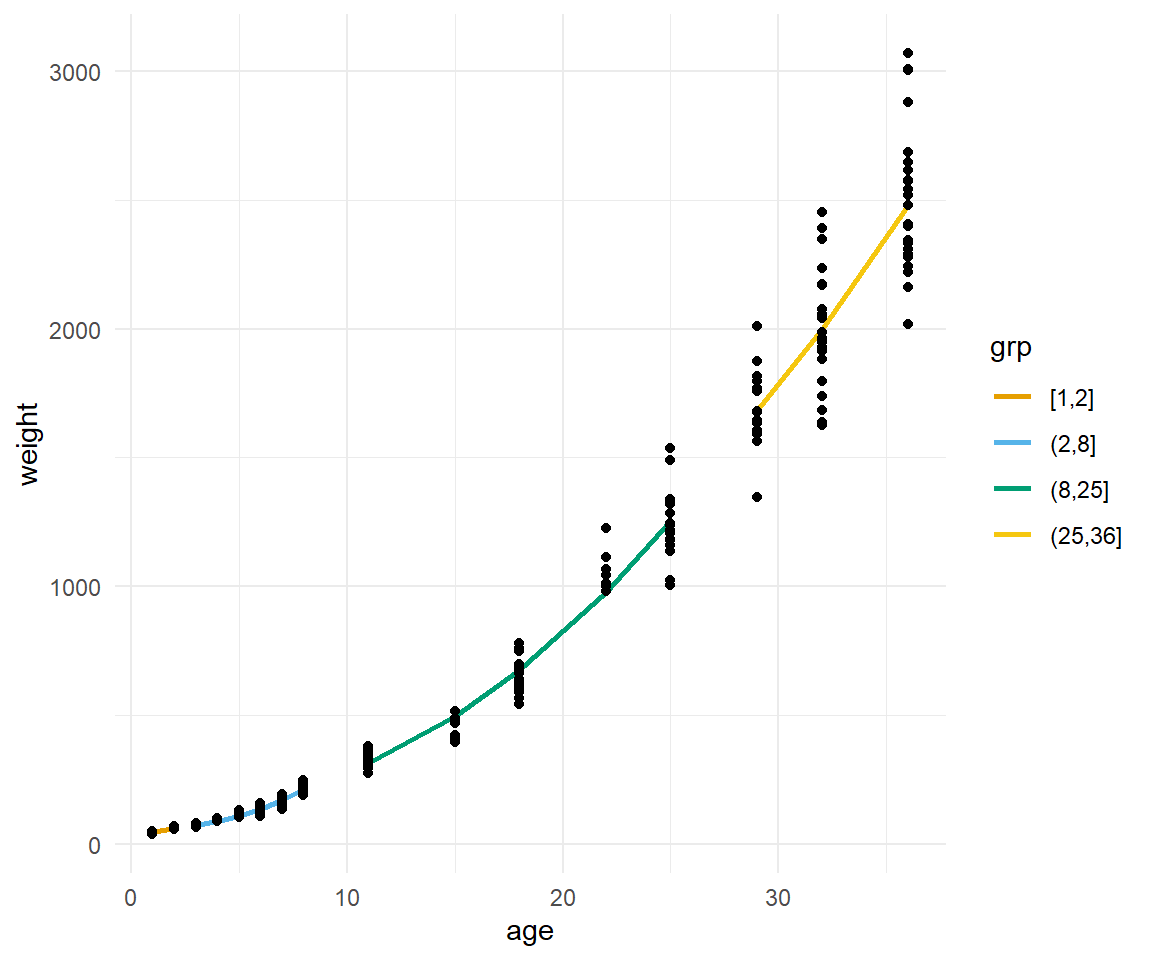
In @fig-nls-02 sehen wir die vier einzelnen Geraden für die vier Altersgruppen. Wir sind visuell besser als über alle Altersgruppen hinweg. Das ist doch mal ein schönes Ergebnis.
```{r}
#| echo: false
#| message: false
#| label: fig-nls-02
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Hühnchengewichte nach Alter in Tagen mit der geschätzen nicht-linearen Regressionsgleichung aufgeteilt nach vier Altersgruppen."
ggplot(chicken_tbl, aes(age, weight)) +
geom_line(data = nls_pred_tbl, aes(age, pred, color = grp), size = 1) +
geom_point() +
theme_minimal() +
scale_color_okabeito()
```
Wir können uns jetzt noch die `b0` und `b1` für jede der vier Altergruppen wiedergeben lassen. Wir räumen etwas auf und geben über `select()` nur die Spalten wieder, die wir auch brauchen und uns interessieren.
```{r}
nls_tbl |>
mutate(tidied = map(nls_fit, tidy)) |>
unnest(tidied) |>
select(grp, term, estimate)
```
Was sehen wir? Wir erhalten insgesamt acht Koeffizienten und können darüber dann unsere vier exponentiellen Gleichungen für unsere Altergruppen erstellen. Wir sehen, dass besonders in der ersten Gruppe des Alters von 1 bis 2 Tagen wir den Intercept überschätzen und den Exponenten unterschätzen. In den anderen Altersgruppen passt dann der Exponent wieder zu unserem ursprünglichen Modell über alle Altersgruppen.
$$
weight_{[1-2]} \sim 44.4 + age^{4.21}
$$
$$
weight_{(2-8]} \sim 60.1 + age^{2.42}
$$
$$
weight_{(8-25]} \sim 128.0 + age^{2.18}
$$
$$
weight_{(25-36]} \sim 330.0 + age^{2.14}
$$
Je nachdem wie zufrieden wir jetzt mit den Ergebnissen der Modellierung sind, könnten wir auch andere Altersgruppen noch mit einfügen. Wir belassen es bei dieser Modellierung und schauen uns nochmal die andere Richtung an.
### ... von Sättigung
Schauen wir uns jetzt einmal ein Beispiel der Sättigung an. Hier nehmen wir dann eine *Power*-Funktion in der Form $y = a + x^b$. Wir könnten noch eine Konstante $c$ als Multiplikator einfügen, wir schauen jetzt aber mal, ob unsere einfache Parametrisierung jetzt funktioniert. Prinzipiell sehen ja unsere Punkte wie eine *Power*-Funktion aus. Daher bauen wir uns einmal die Fomel in `nls()` und lassen uns die Koeffizienten $a$ und $b$ wiedergeben. Dann schauen wir, ob die Koeffizienten Sinn machen und die Punkte auch gut beschreiben.
```{r}
duckweeds_nls_fit <- nls(sensor ~ a + I(duckweeds_density^b), data = duckweeds_tbl,
start = c(a = 0, b = 0))
duckweeds_nls_fit
```
Schauen wir uns einmal das Bestimmtheitsmaß $R^2$ für die Anpassung an. Das ist ja immer unser erstes abstraktes Maß für die Modellgüte und wie gut die Kurve durch die Punkte gelaufen ist. Das sieht doch schon sehr gut aus. Wir wollen den Wert aber dann noch gleich einmal visuell überprüfen.
```{r}
#| warning: false
#| message: false
duckweeds_nls_fit |> r2()
```
Dann können wir auch schon die mathematische Gleichung aufschreiben. Wir haben einen negativen $y$-Achsenabschnitt $a$ sowie eine *Power* kleiner als 1. Damit sollte unsere Kurve mit steigenden $x$-Werten abflachen. Ich kann mir immer nicht vorstellen, wie so eine Funktion aussehen würde, dafür fehlt mir die mathematische Phantasie.
$$
sensor = -1.1468 + duckweeds\_density^{0.2975}
$$
Dann wollen wir einmal die Funktion visualisieren. Wir haben zwei Möglichkeiten. Entweder bauen wir uns die mathematische Funktion in R nach und plotten dann die mathematische Funktion mit `geom_function()` oder wir nutzen nur den Fit `duckweeds_nls_fit` direkt in `ggplot()`. Erstes erlaubt nochmal sicherzugehen, dass wir auch die mathematische Funktion richtig aufgeschrieben haben. Wenn du die nicht brauchst, dann ist die zweite Variante natürlich weit effizienter.
::: panel-tabset
## Mit `geom_function()`
Jetzt nehmen wir einmal unsere Koeffizienten aus dem `nls()`-Modell und bauen uns eine Funktion nach. Das ist im Prinzip die mathematische Formel nur in der Schreibweise in R.
```{r}
duckweed_func <- \(x){-1.1468 + x^{0.2975}}
```
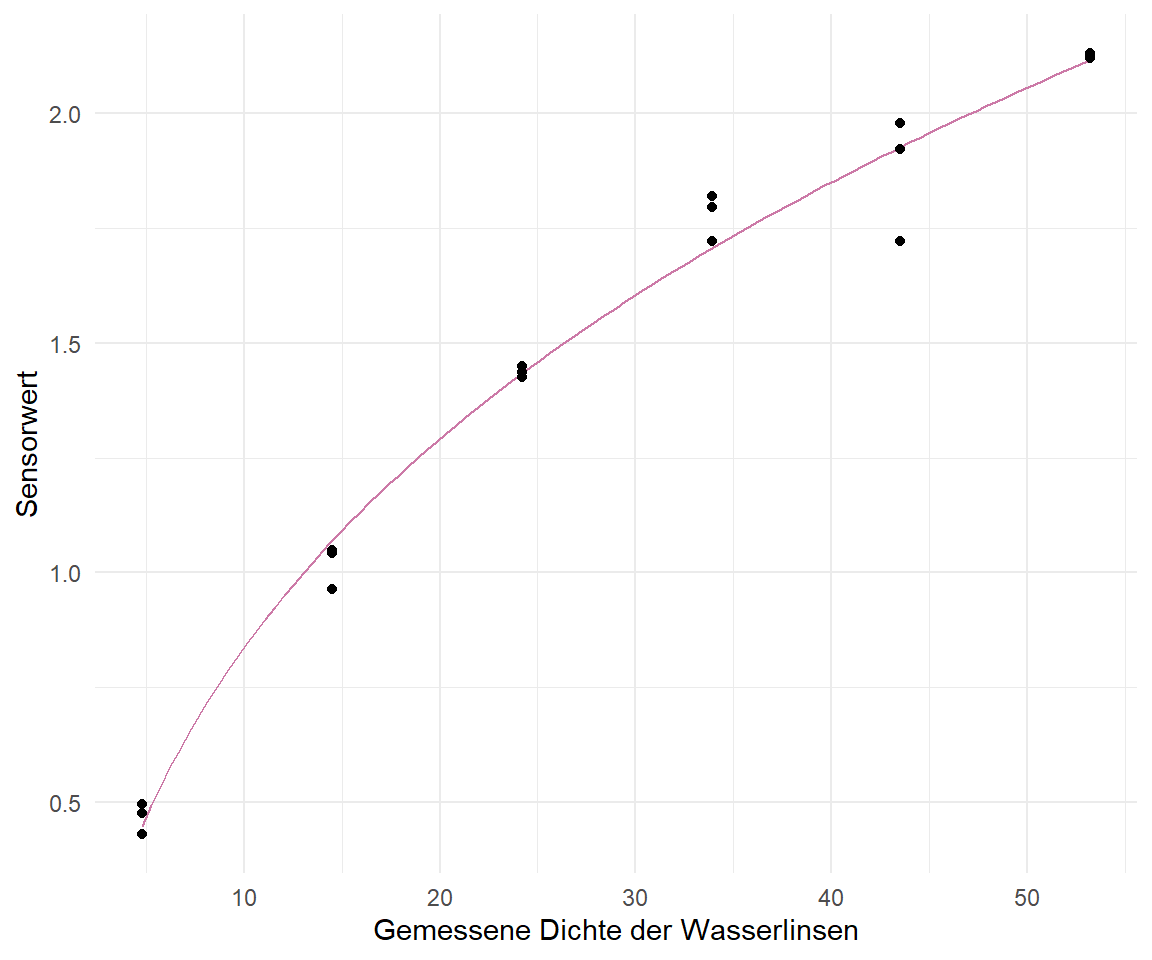
Dann können wir auch schon die Kurve durch die Punkte in der folgenden Abbildung legen. Da wir hier eine Funktion vorliegen haben, ist der Verlauf auch sehr schön glatt. Wir sehen aber auch, dass die Funktion sehr schön passt. Die Kurve läuft gut durch die Punkte. Etwas was wir auch schon von dem $R^2$ erwartet hatten.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-duckweed-01a
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Angepasste Kurve aus der Funktion `nls()` dargestellt mit der Funktion `geom_function()`."
ggplot(duckweeds_tbl, aes(duckweeds_density, sensor)) +
geom_function(fun = duckweed_func, color = "#CC79A7") +
geom_point() +
theme_minimal() +
labs(x = "Gemessene Dichte der Wasserlinsen", y = "Sensorwert")
```
## Mit `geom_line()` und `predict()`
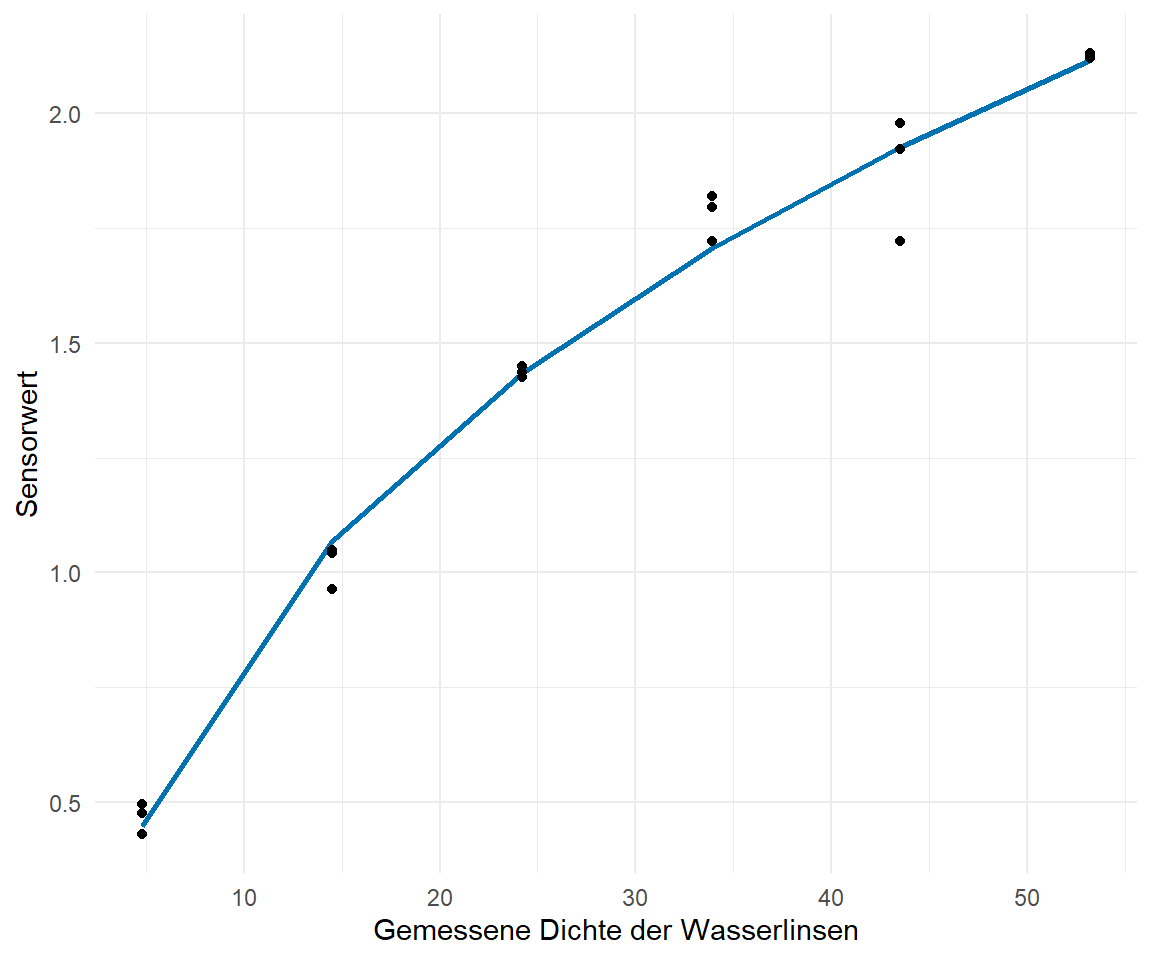
Schneller geht es in der Funktion `geom_line()` und `predict()`, wo wir dann die Anpassung unseres Modells direkt als $y$-Werte übergeben. Da wir hier jetzt nur die $x$-Werte nutzen, die wir auch in den Daten vorliegen haben, wirkt die Kurve bei so wenigen Messpunkten auf der $x$-Achse etwas stufig. Aber auch hier sehen wir, dass die Kurve gut durch unsere Punkte läuft. Diese Variante ist die etwas schnellere, wenn du nicht an der mathematischen Formulierung interessiert bist.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-duckweed-01b
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Angepasste Kurve aus der Funktion `nls()` dargestellt mit der Funktion `geom_line()` und `predict()`."
ggplot(duckweeds_tbl, aes(duckweeds_density, sensor)) +
geom_line(aes(y = predict(duckweeds_nls_fit)), size = 1, color = "#0072B2") +
geom_point() +
theme_minimal() +
labs(x = "Gemessene Dichte der Wasserlinsen", y = "Sensorwert")
```
:::
Jetzt bietet es sich nochmal an die Vorhersageintervalle oder Prädiktionsintervalle (eng. *prediction interval*) der Abbildung hinzuzufügen. Neben den Vorhersageintervallen könntne wir auch die 95% Konfidenzintervalle (eng. *confidence interval*) hinzufügen. Hier müssen wir gleich entscheiden, was wir eigentlich zeigen wollen. Wir müssen also zwischen den beiden Intervallen unterscheiden. Vorhersageintervalle machen eine Aussage zu der Genauigkeit von zukünftigen Beobachtungen wohingegen die die Konfidenzintervalle eine Aussage über die Koeffizienten des Modells treffen. Mehr dazu gibt es auch hier Stack Exchange unter [Prediction interval vs. confidence interval in linear regression analysis](https://stats.stackexchange.com/questions/225652/prediction-interval-vs-confidence-interval-in-linear-regression-analysis). Konfidenzintervalle geben dir also die Bandbreite wieder in der die Gerade verläuft. Dafür nutzen die Konfidenzintervalle die Daten und geben dir ein Intervall an, in dem die Gerade durch die Koeffizienten des Modells mit 95% Sicherheit verläuft. Das Vorhersageintervall gibt dir an mit welchen Bereich zukünftige Beobachtung mit 95% Sicherheit fallen werden. Das Vorhersageintervall ist breiter als das Konfidenzintervall und nicht jede Methode liefert auch beide Intervalle.
Es ist uns möglich über Bootstrap, also einer Simulation aus unseren Daten, ein Vorhersageintervall sowie ein Konfidenzintervall zu generieren. Zu dem Bootstrapverfahren kannst du in den Klassifikationskapiteln mehr lesen. Ich nutze hier 500 Simulationen um mir die Intervalle ausgeben zu lassen. Bei einer echten Analyse würde ich die Anzahl auf 1000 bis 2000 setzen. Wir brauchen also als erstes unser Bootstrapobjekt mit dem wir dann in den Tabs weitermachen.
```{r}
nls_boot_obj <- nlsBoot(duckweeds_nls_fit, niter = 500)
```
Ich habe jetzt das Prädiktionsintervall und das Konfidenzintervall jeweils in einem der Tabs berechnet. Wenn du deine Daten auswertest musst du dich dann für ein Intervall entscheiden. Meistens nutzen wir das Konfidenzintervall, da die Interpretation und die Darstellung im Allgemeinen bekannter ist.
::: panel-tabset
## Vorhersageintervall (eng. *prediction interval*)
Um das Vorhersageintervall zu erstellen nutzen wir die Funktion `nlsBootPredict()` und übergeben als neue Daten unseren Datensatz. Dann müssen wir natürlich noch als Option `interval = "prediction"` wählen um das Vorhersageintervall wiedergegeben zu bekommen. Ich muss dann noch etwas aufräumen und auch die $x$-Werte wieder ergänzen damit wir gleich alles in `ggplot()` darstellen können. Auch nerven mich die doppelten Werte, die brauche ich nicht für die Darstellung und entferne sie über `distinct()`.
```{r}
pred_plim_tbl <- nlsBootPredict(nls_boot_obj, newdata = duckweeds_tbl, interval = "prediction") |>
as_tibble() |>
clean_names() |>
mutate(duckweeds_density = duckweeds_tbl$duckweeds_density) |>
distinct(duckweeds_density, .keep_all = TRUE)
pred_plim_tbl
```
Aus der mittleren Abweichung des Medians zu der unteren 2.5% Grenze `x2_5_percent` sowie zu der oberen 97.5% Grenze `x97_5_percent` lässt sich leicht noch eine Konstante $\phi$ errechnen, die wir dann zu unserer mathematischen Formel ergänzen können. Dann hätten wir auch die mathematische Formel für die obere und untere Kurve des Vorhersageintervalls. Im Prinzip ist das Vorhersageintervall ja nur eine verschobene Kurve der ursprünglichen Geradengleichung. Wir subtrahieren und addieren also unser $\phi$ jeweils zu dem $y$-Achsenabschnitt von $-1.1468$ aus dem `nls()`-Modell.
```{r}
with(pred_plim_tbl, x2_5_percent - median) |> mean()
with(pred_plim_tbl, x97_5_percent - median) |> mean()
```
Damit hätten wir dann für die 2.5% und 97.% Grenzen des Vorhersageintervalls folgende mathematische Formel. Ich ersetze hier einmal $duckweeds\_density$ durch $x$ um die Formel etwas aufzuräumen und zu kürzen.
$$
[-1.358 + x^{0.298}; \; -1.031 + x^{0.298}]
$$
Wir machen es uns etwas einfacher und nutzen hier dann die Funktion `geom_ribbon()` um die Fläche des Vorhersageintervalls. Wir nutzen hier also nicht die Informationen aus unserem `nls()`-Modell direkt sondern erschaffen uns die Informationen nochmal über eine Bootstrapsimulation. Es ist einfach noch ein Extraschritt, wenn du eben noch ein Intervall haben willst. Nicht immer ist es notwendig und die Breite des Vorhersageintervalls hängt auch maßgeblich von der Anzahl an Beobachtungen ab.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-duckweed-02
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Angepasste Kurve aus der Funktion `nls()` zusammen mit dem Vorhersageintervall."
ggplot(duckweeds_tbl, aes(duckweeds_density, sensor)) +
geom_line(data = pred_plim_tbl, aes(y = median), color = "#CC79A7") +
geom_ribbon(data = pred_plim_tbl, fill = "#CC79A7", alpha = 0.3,
aes(x = duckweeds_density, ymin = x2_5_percent, ymax = x97_5_percent), inherit.aes = FALSE) +
geom_point() +
theme_minimal() +
labs(x = "Gemessene Dichte der Wasserlinsen", y = "Sensorwert")
```
## Konfidenzintervall (eng. *confidence interval*)
Um das Konfidenzintervall zu erstellen nutzen wir ebenfalls die Funktion `nlsBootPredict()` und übergeben als neue Daten unseren Datensatz. Dann müssen wir natürlich noch als Option `interval = "confidence"` auswählen um das Konfidenzintervall wiedergegeben zu bekommen. Ich muss dann auch hier aufräumen und die $x$-Werte wieder ergänzen damit wir gleich alles in `ggplot()` darstellen können. Auch nerven mich die doppelten Werte, die brauche ich nicht für die Darstellung und entferne sie über `distinct()`.
```{r}
pred_clim_tbl <- nlsBootPredict(nls_boot_obj, newdata = duckweeds_tbl, interval = "confidence") |>
as_tibble() |>
clean_names() |>
mutate(duckweeds_density = duckweeds_tbl$duckweeds_density) |>
distinct(duckweeds_density, .keep_all = TRUE)
pred_clim_tbl
```
Aus der mittleren Abweichung des Medians zu der unteren 2.5% Grenze `x2_5_percent` sowie zu der oberen 97.5% Grenze `x97_5_percent` lässt sich leicht noch eine Konstante $\phi$ errechnen, die wir dann zu unserer mathematischen Formel ergänzen können. Dann hätten wir auch die mathematische Formel für die obere und untere Kurve des Konfidenzintervalls. Im Prinzip ist das Konfidenzintervall ja nur eine verschobene Kurve der ursprünglichen Geradengleichung. Wir subtrahieren und addieren also unser $\phi$ jeweils zu dem $y$-Achsenabschnitt von $-1.1468$ aus dem `nls()`-Modell.
```{r}
with(pred_clim_tbl, x2_5_percent - median) |> mean()
with(pred_clim_tbl, x97_5_percent - median) |> mean()
```
Damit hätten wir dann für die 2.5% und 97.% Grenzen des Konfidenzintervalls folgende mathematische Formel. Ich ersetze hier einmal $duckweeds\_density$ durch $x$ um die Formel etwas aufzuräumen und zu kürzen.
$$
[-1.1978 + x^{0.298}; \; -1.1098 + x^{0.298}]
$$
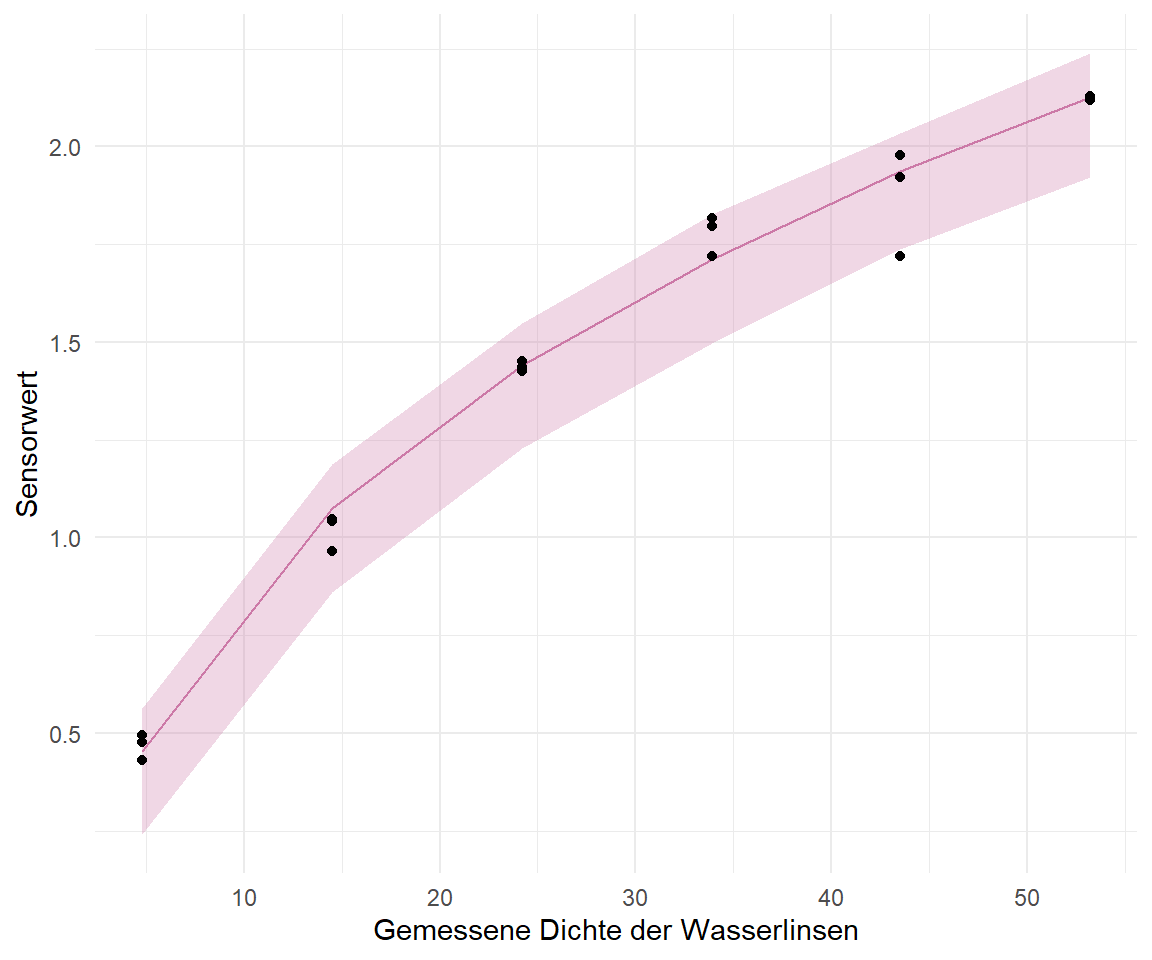
Wir machen es uns einfacher und nutzen hier dann die Funktion `geom_ribbon()` um die Fläche des Konfidenzintervalls. Wir nutzen hier also nicht die Informationen aus unserem `nls()`-Modell direkt sondern erschaffen uns die Informationen nochmal über eine Bootstrapsimulation. Es ist einfach noch ein Extraschritt, wenn du eben noch ein Intervall haben willst. Nicht immer ist es notwendig und die Breite des Konfidenzintervalls hängt auch maßgeblich von der Anzahl an Beobachtungen ab.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-duckweed-03
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Angepasste Kurve aus der Funktion `nls()` zusammen mit dem Konfidenzintervall."
ggplot(duckweeds_tbl, aes(duckweeds_density, sensor)) +
geom_line(data = pred_clim_tbl, aes(y = median), color = "#0072B2") +
geom_ribbon(data = pred_clim_tbl, fill = "#0072B2", alpha = 0.3,
aes(x = duckweeds_density, ymin = x2_5_percent, ymax = x97_5_percent), inherit.aes = FALSE) +
geom_point() +
theme_minimal() +
labs(x = "Gemessene Dichte der Wasserlinsen", y = "Sensorwert")
```
:::
### ... von Zerfall
Nachdem wir uns einem exponentiellen Anstieg und die Sättigung angeschaut haben, wollen weit uns nun einmal mit einem exponentiellen Zerfall beschäftigen. Wir betrachten einen exponentziellen Zerfall einer Blattläuse Population. Wir wollen die folgende Gleichung lösen und die Werte für die Konstante $a$ und den Exponenten $\beta_1$ schätzen. Nun haben wir diesmal keinen Intercept vorliegen.
$$
count \sim a \cdot week^{\beta_1}
$$
Die Daten sind angelegt an ein Experiment zu Blattlauskontrolle. Wir haben ein neues Biopestizid welchen wir auf die Blattläuse auf Rosen sprühen. Wir zählen dann automatisiert über eine Kamera und Bilderkennung wie viele Blattläuse sich nach den Wochen des wiederholten Sprühens noch auf den Rosen befinden. Wir erhalten damit folgende Daten im Objekt `exp_tbl`.
```{r}
set.seed(20221018)
exp_tbl <- tibble(count = c(rnorm(10, mean = 17906, sd = 17906/4),
rnorm(10, mean = 5303, sd = 5303/4),
rnorm(10, mean = 2700, sd = 2700/4),
rnorm(10, mean = 1696, sd = 1696/4),
rnorm(10, mean = 947, sd = 947/4),
rnorm(10, mean = 362, sd = 362/4)),
weeks = rep(1:6, each = 10))
```
Wir müssen ja wieder die Startwerte in der Funktion `nls()` angeben. Meistens raten wir diese oder schauen auf die Daten um zu sehen wo diese Werte in etwa liegen könnten. Dann kann die Funktion `nls()` diese Startwerte dann optimieren. Es gibt aber noch einen anderen Trick. Wir rechnen eine *lineare* Regression über die $log$-transformierten Daten und nehmen dann die Koeffizienten aus dem linearen Modell als Startwerte für unsere nicht-lineare Regression.
```{r}
lm(log(count) ~ log(weeks), exp_tbl)
```
Aus der linearen Regression erhalten wir einen Intercept von $9.961$ und eine Steigung von $-2.025$. Wir exponieren den Intercept und erhalten den Wert für $a$ mit $\exp(9.961)$. Für den Exponenten $b1$ tragen wir den Wert $-2.025$ als Startwert ein. Mit diesem Trick erhalten wir etwas bessere Startwerte und müssen nicht so viel rumprobieren.
```{r}
#| results: hide
fit <- nls(count ~ a * I(weeks^b1), data = exp_tbl,
start = c(a = exp(9.961), b1 = -2.025))
```
Wir können uns noch die Koeffizienten wiedergeben lassen und die Geradengleichung vervollständigen. Wie du siehst sind die Werte natürlich anders als die Startwerte. Wir hätten aber ziemlich lange rumprobieren müssen bis wir nahe genug an die Startwerte gekommen wären damit die Funktion `nls()` iterativ eine Lösung für die Gleichung findet.
```{r}
#| message: false
fit |>
model_parameters() |>
select(Parameter, Coefficient)
```
Abschließend können wir dann die Koeffizienten in die Geradengleichung eintragen.
$$
count \sim 17812.11 \cdot week^{-1.69}
$$
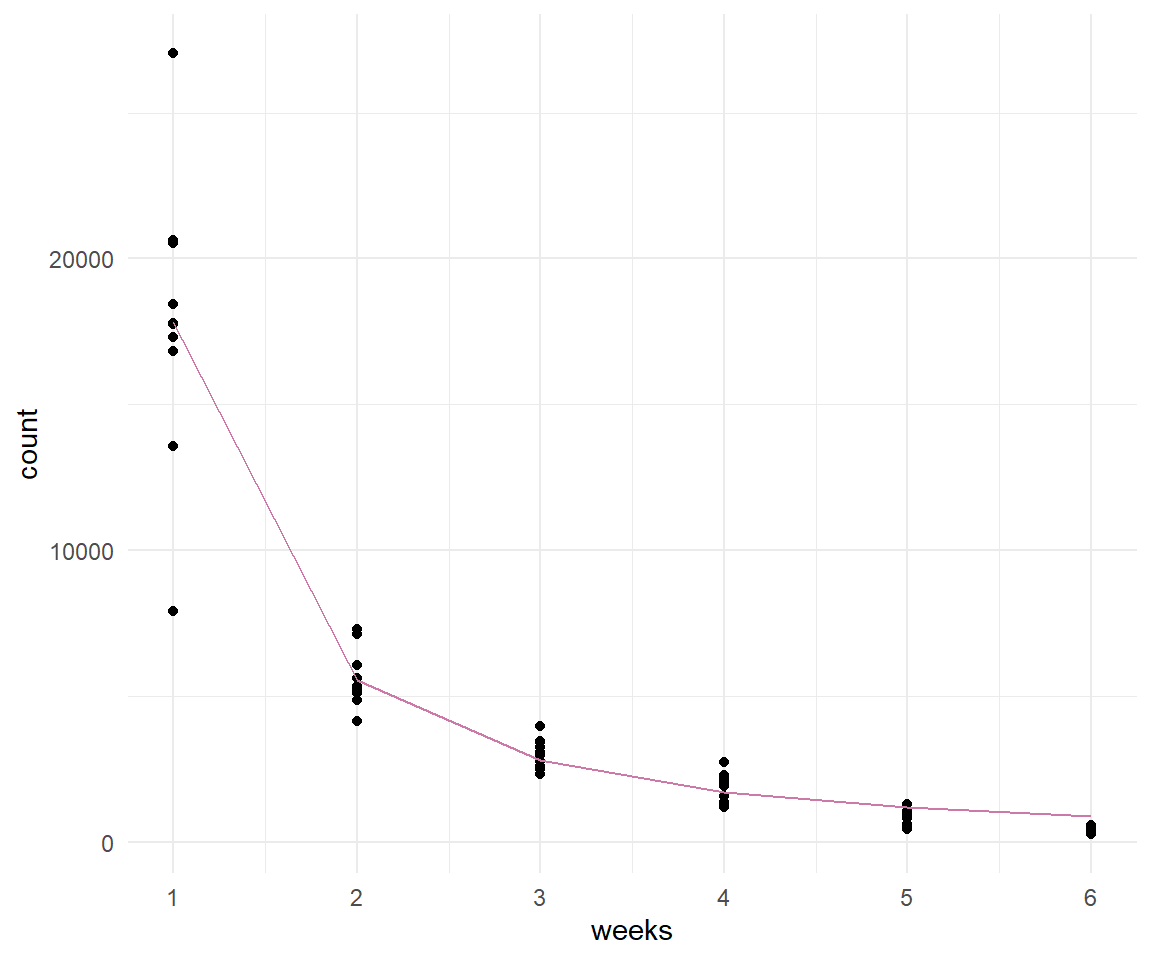
In @fig-nls-03 sehen wir die Daten zusammen mit der gefitteten Gerade aus der nicht-linearen Regression. Wir sehen, dass die Gerade ziemlich gut durch die Mitte der jeweiligen Punkte läuft.
```{r}
#| echo: true
#| message: false
#| warning: false
#| label: fig-nls-03
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Sterberate von Blattläusen nach Aufbringen eines Bio-Pestizides mit der nicht-linearen Regressionsgleichung."
ggplot(exp_tbl, aes(weeks, count)) +
theme_minimal() +
geom_point() +
geom_line(aes(y = predict(fit)), color = "#CC79A7") +
scale_x_continuous(breaks = 1:6)
```
### ... der Michaelis-Menten Gleichung
In diesem Abschnitt wollen wir uns mit dem Modellieren einer Sättigungskurve beschäftigen. Daher bietet sich natürlich die Michaelis-Menten-Gleichung an. Die Daten in `enzyme.csv` geben die Geschwindigkeit $v$ des Enzyms saure Phosphatase ($\mu mol/min$) bei verschiedenen Konzentrationen des Substrats Nitrophenolphosphat, \[S\] (mM), an. Die Daten können mit der Michaelis-Menten-Gleichung modelliert werden und somit kann eine nichtlineare Regression kann verwendet werden, um $K_M$ und $v_{max}$ zu schätzen.
```{r}
#| message: false
enzyme_tbl <- read_csv2(file.path("data/enzyme.csv")) |>
rename(S = concentration, v = rate)
```
In @tbl-enzyme sehen wir einen Auszug aus den Enzymedaten. Eigentlich relativ klar. Wir haben eine Konzentration $S$ vorliegen und eine Geschwindigkeit $v$.
```{r}
#| echo: false
#| message: false
#| warning: false
#| label: tbl-enzyme
#| tbl-cap: Auszug aus Enzymedatensatz.
rbind(head(enzyme_tbl, n = 3),
rep("...", times = ncol(enzyme_tbl)),
tail(enzyme_tbl, n = 3)) |>
kable(align = "c", "pipe")
```
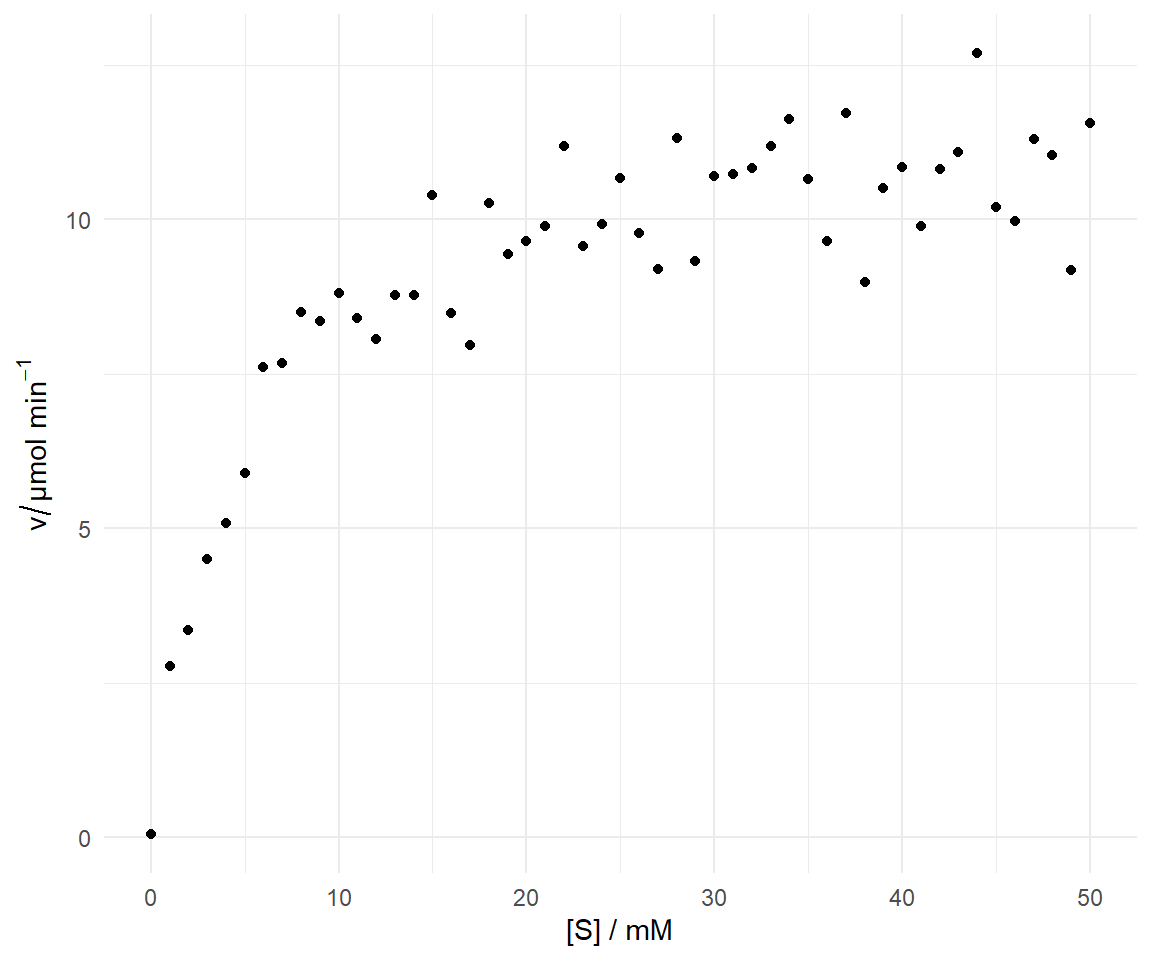
Schauen wir uns die Daten einmal in der @fig-nls-04 an. Wir legen die Konzentration $S$ auf die $x$-Achse und Geschwindigkeit $v$ auf die $y$-Achse.
```{r}
#| echo: true
#| message: false
#| warning: false
#| label: fig-nls-04
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Geschwindigkeit $v$ des Enzyms saure Phosphatase bei verschiedenen Konzentrationen des Substrats Nitrophenolphosphat."
ggplot(enzyme_tbl, aes(x = S, y = v)) +
theme_minimal() +
geom_point() +
labs(x = "[S] / mM", y = expression(v/"µmol " * min^-1))
```
Die Reaktionsgleichung abgeleitet aus der Michaelis-Menten-Kinetik lässt sich allgemein wie folgt darstellen. Wir haben die Konzentration $S$ und die Geschwindigkeit $v$ gegeben und wollen nun über eine nicht-lineare Regression die Werte für $v_{max}$ und $K_M$ schätzen.
$$
v = \cfrac{v_{max} \cdot S}{K_M + S}
$$
Dabei gibt $v$ die initiale Reaktionsgeschwindigkeit bei einer bestimmten Substratkonzentration \[S\] an. Mit $v_{max}$ beschreiben wir die maximale Reaktionsgeschwindigkeit. Eine Kenngröße für eine enzymatische Reaktion ist die Michaeliskonstante $K_M$. Sie hängt von der jeweiligen enzymatischen Reaktion ab. $K_M$ gibt die Substratkonzentration an, bei der die Umsatzgeschwindigkeit halbmaximal ist und somit $v = 1/2 \cdot v_{max}$ ist. Wir haben dann die Halbsättigung vorliegen.
Bauen wir also die GLeichung in R nach und geben die Startwerte für $v_{max}$ und $K_M$ für die Funktion `nls()` vor. Die Funktion `nls()` versucht jetzt die beste Lösung für die beiden Koeffizienten zu finden.
```{r}
enzyme_fit <- nls(v ~ vmax * S /( KM + S ), data = enzyme_tbl,
start = c(vmax = 9, KM = 2))
```
Wir können uns dann die Koeffizienten ausgeben lassen.
```{r}
#| message: false
enzyme_fit |>
model_parameters() |>
select(Parameter, Coefficient)
```
Jetzt müssen wir die Michaelis-Menten-Gleichung nur noch um die Koeffizienten ergänzen.
$$
v = \cfrac{11.85 \cdot S}{4.28 + S}
$$
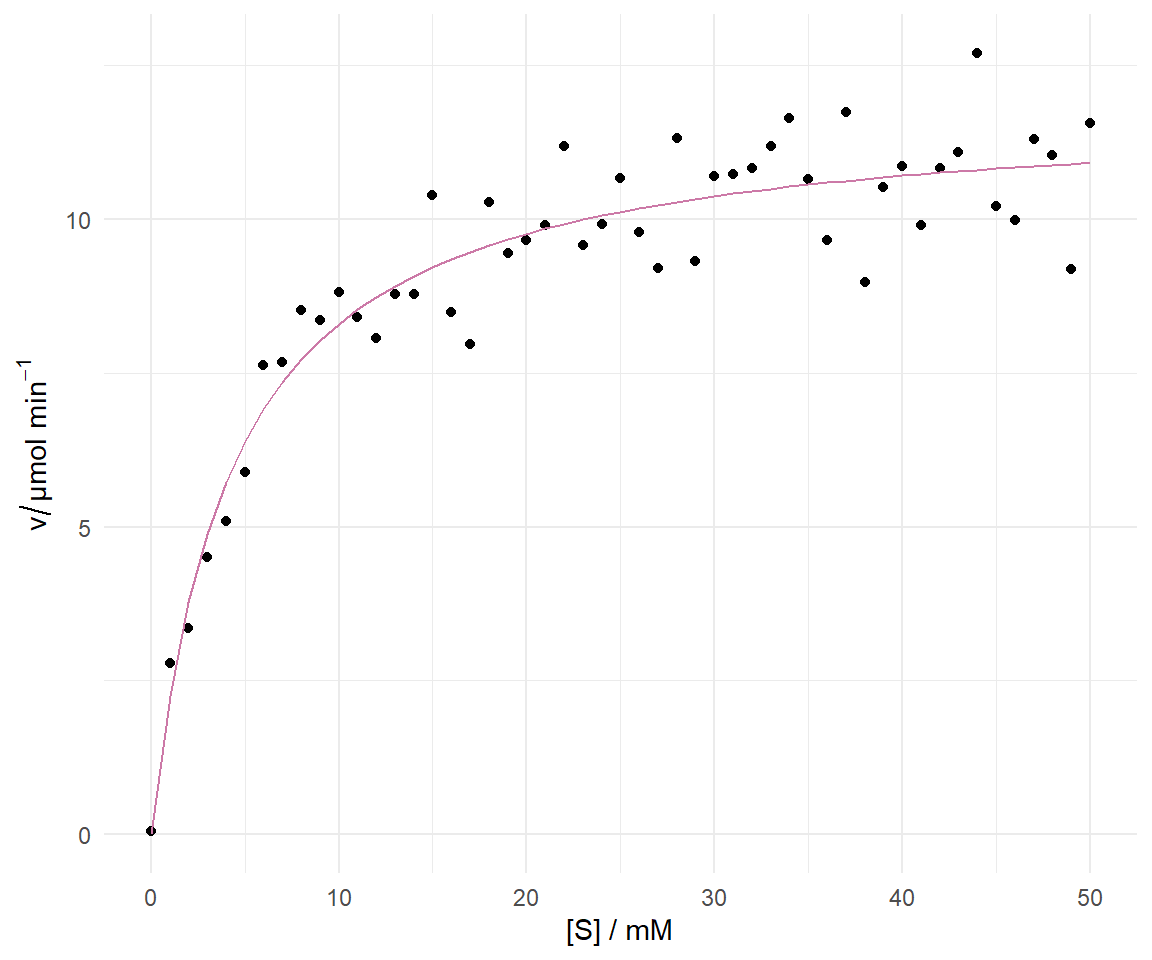
In der @fig-nls-05 können wir die gefittete Gerade nochmal überprüfen und schauen ob das Modellieren geklappt hat. Ja, hat es die Gerade läuft direkt mittig durch die Punkte.
```{r}
#| echo: true
#| message: false
#| warning: false
#| label: fig-nls-05
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Michaelis-Menten-Kinetik zusammen mit der gefitteten Gerade aus einer nicht-linearen Regression."
ggplot(enzyme_tbl, aes(x = S, y = v)) +
theme_minimal() +
geom_point() +
geom_line(aes(y = predict(enzyme_fit)), color = "#CC79A7") +
labs(x = "[S] / mM", y = expression(v/"µmol " * min^-1))
```
## Multivariate Fractional Polynomials mit `{mfp}`
Manchmal haben wir keine Ahnung, welche mathematische Formel denn überhaupt passen könnte. Ohne eine mathematische Formel können wir dann auch schlecht in `nls()` Startwerte angeben. Ohne die Angabe von Startwerten für die Formel können wir dann auch nichts rechnen. Die wenigsten Menschen haben eine exponentielle Idee im Kopf, wenn sie eine Kurve sehen. Aus dem Grund wurden die *Multivariate Fractional Polynomials* (abk. *mfp*) entwickelt, die dir dann eine Formel wiedergeben. Das Schöne daran ist, dass du einfach nur sagen musst, welche Variable als Polynom in die Formel soll und den Rest macht die Funktion `mfp` aus dem gleichnamigen R Paket `{mfp}` dann für sich. Hier sei auch einmal auf das Tutorial [Multivariate Fractional Polynomials: Why Isn’t This Used More?](https://towardsdatascience.com/multivariate-fractional-polynomials-why-isnt-this-used-more-1a1fa9ead12c) verwiesen. Die Entwickler des R Paketes `{mfp}` haben auch eine eigene Hilfeseite unter [Multivariable Fractional Polynomials (MFP)](https://mfp.imbi.uni-freiburg.de/) eingerichtet. Wir immer ist das Thema zu groß, daher hier nur die simple Anwendung.
Der wichtigste Schritt ist einmal die Variable zu bezeichnen, die als Polynom behandelt werden soll. Wir machen das hier mit der Funktion `fp()`. Wir sagen damit der Funktion `mfp()`, dass wir bitte die Koeffizienten und eine "Hochzahl" $a$ für das Alter haben wollen. Wir erhalten also die Koeffizienten für die folgende mathematische Formel mit Zahlen wieder.
$$
weight \sim \beta_0 + \beta_1 \cdot age^{a}
$$
Dann rechnen wir also einfach schnelle einmal das Modell.
```{r}
mfp_fit <- mfp(weight ~ fp(age), data = chicken_tbl)
```
Wir können dann auch gleich einmal in die Zusammenfassung reinschauen und sehen, was dort für eine Formel für das Alter `age` geschätzt wurde.
```{r}
summary(mfp_fit)
```
Es ist auch möglich sich die Formel direkt wiedergeben zu lassen. Hier ist dann wichtig zu verstehen, was wir dort sehen. Die Funktion `mfp()` testet immer verschiedene ganzzahlige `a`-Werte für die Potenz. Dann versucht die Funktion `mfp()` die restlichen Koeffizienten optimal den Daten anzupassen.
```{r}
mfp_fit$formula
```
Nun haben wir erstmal die Informationen über das Alter und die Potenz $a$ und wie diese beiden miteinander zusammengehören. Jetzt fehlen aber noch die Koeffizienten für die Steigung und den y-Achsenabschnitt. Die haben wir auch oben in der `summary()` gesehen, aber wir können uns die Werte auch separat anzeigen lassen.
```{r}
mfp_fit$coefficients
```
Dann können wir auch einmal die etwas kompliziertere mathematische Gleichung aufschreiben. Da wir an ganzzahlige Potenzen gebunden sind, muss der Rest etwas anderes aussehen. Aber die Formel geht eigentlich noch. Da wir eben auch eine ganzzahlige Potenz haben, können wir auch selber mit einem Taschenrechner rechnen. Das wird ja bei Kommazahlen schon etwas mühseliger.
$$
weight \sim 66.3 + 188 \cdot \left(\cfrac{age}{10}\right)^{2}
$$
Dann können wir die Funktion auch schon in R übersetzen. Wir machen eigentlich nichts anderes als das wir das $age$ durch durch $x$ ersetzen, was generischer ist. Und wir brauchen diese Art der Darstellung dann auch in `ggplot()`.
```{r}
age_func <- \(x) {66.3 + 188 * (x/10)^2}
```
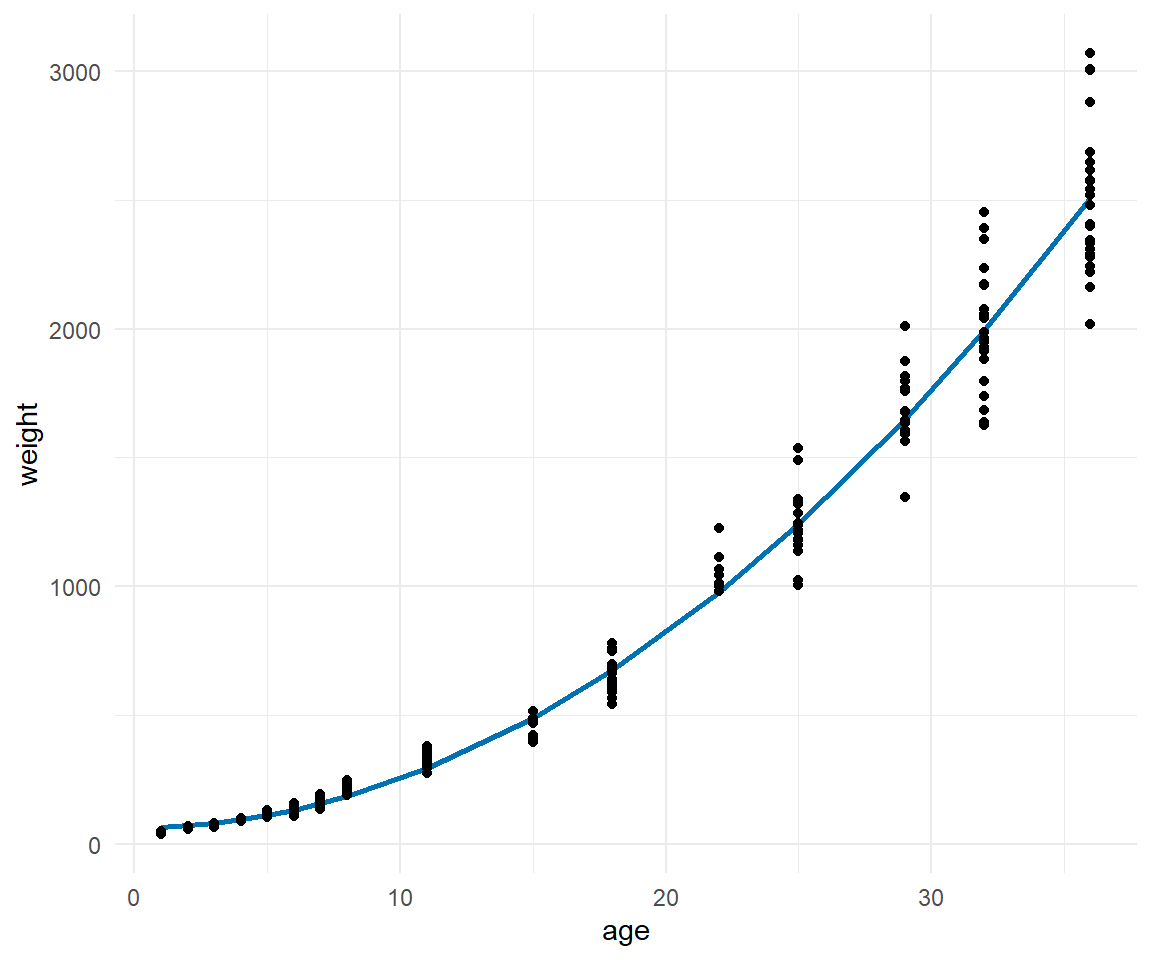
In der @fig-nls-mfp-1 sehen wir einmal das Ergebnis der Anpassung. Ich habe hier einmal beides gemacht, einmal mit der Funktion `geom_function()` und einmal mit `geom_line()` und `predict()`. So kannst du mal sehen, dass wir hier das gleiche rauskriegen. Die erste Variante ist eben die bessere, wenn du auch die mathematische Gleichung angeben wilst. Dann bist du dir sicher, dass auch die Gleichung zu der angepassten Kurve passt.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-mfp-1
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Hühnchengewichte nach Alter in Tagen mit der geschätzen nicht-linearen Regressionsgleichung nach der Funktion `mfp()`. Die geschätzten Kurven sind natürlich in beiden Fälle die gleichen Kurven. Es geht hier um die Form der Umsetzung in `{ggplot}`."
#| fig-subcap:
#| - "... mit `geom_function()`"
#| - "... mit `geom_line()` und `predict()`"
#| layout-nrow: 1
ggplot(chicken_tbl, aes(age, weight)) +
geom_function(fun = age_func, color = "#CC79A7", linetype = 'dashed') +
geom_point() +
theme_minimal()
ggplot(chicken_tbl, aes(age, weight)) +
geom_line(aes(y = predict(mfp_fit)), size = 1, color = "#0072B2") +
geom_point() +
theme_minimal()
```
Und welche der beiden mathematischen Gleichungen ist denn nun besser? Dafür fitten wir nochmal das `nls()` Modell von oben und vergleichen das Modell einmal zu dem `mfp()`-Modell von eben.
```{r}
#| results: hide
nls_fit <- nls(weight ~ b0 + I(age^b1), data = chicken_tbl,
start = c(b0 = 1, b1 = 1))
```
In der @tbl-model-comp-nls-mfp sehen wir die Funktion `modelsummary()` und den entsprechenden Modellvergleich der beiden Modelle zu Anpassung einer nicht-linearen Regression. Welche der beiden Modelle und damit mathematischen Gleichungen beschreibt unsere Daten besser? Leider ist es so, dass wir aus dem `nls()`-Modell nicht so viele Informationen erhalten wie es zu wünschen wäre. Wir könnten das AIC als Kriterium nehmen und da gilt, dass ein kleineres AIC besser ist, nehmen wir das `mfp()`-Modell.
```{r}
#| message: false
#| echo: true
#| warning: false
#| tbl-cap: "Modellvergleich für das `nls()` Modell mit dem `mfp()` Modell. Wir vergleichen hier nur die beiden Modelle, da beide Modelle eine mathematische Gleichung wiedergeben, die wir dann berichten können."
#| label: tbl-model-comp-nls-mfp
modelsummary(lst("nls Modell" = nls_fit,
"mfp Modell" = mfp_fit))
```
Und am Ende nochmal, wie gut war die Anpassung des Modells an die Daten*punkte* eigentlich? Hier können wir dann wieder das Bestimmtheitsmaß $R^2$ nutzen. Wie immer siehst du Bestimmtheitsmaß $R^2$ auch in der `summary()` aber hier dann einmal als direkter Aufruf.
```{r}
mfp_fit |> r2()
```
```{r}
#| message: false
#| warning: false
nls_fit |> r2()
```
Da sich jetzt die beiden Bestimmtheitsmaße $R^2$ wirklich nicht unterscheiden, ist es wohl eher eine Frage des Geschmacks, welche mathematische Formel besser passt. In unserem Beispiel sind ja auch die eher jüngeren Hühner das Problem und nicht so die etwas älteren Hühner. Aber diese Frage lasse ich dann mal offen, du kannst oben die `map()` Funktion auch mit `mfp()` laufen lassen.
## Generalized Additive Models (GAM) mit `{mgcv}`
Neben den Modellen, die uns eine mathematische Funktion wiedergeben, gibt es natürlich noch Modelle, die effizienter und besser sind. Diese Effizienz und bessere Modellanpassung bezahlen wir dann aber mit der schwierigeren Darstellbarkeit als Formel. Wenn du also ein Modell anpassen willst, was sehr gut durch Punkte läuft und dann dieses Modell nutzen willst um zukünftige Werte vorherzusagen, dann kannst du [Generalized Additive Models](https://m-clark.github.io/generalized-additive-models/) (abk. *GAM*) nutzen. Du erhälst aber keine Formel wieder sondern das Modell liegt dann als Objekt in R vor. Damit kannst du dann arbeiten und Prognosen rechnen aber keine Formel in deine Abbildung schreiben. Es gibt zu GAM einmal das gute Tutorium [Advanced Data Analysis from an Elementary Point of View](https://www.stat.cmu.edu/~cshalizi/ADAfaEPoV/) sowie das [R Paket {gratia}](https://gavinsimpson.github.io/gratia/), welches bei der Darstellung von einem GAM-Modell hilft. Aber nochmal, wenn du eine Formel in deine Abbildung schreiben willst, dann ist das *Generalized Additive Model* nicht die Antwort auf deine Frage. Selbst wenn ein GAM das beste Modell sein sollte, was du findest. Die Hilfeseite [How to solve common problems with GAMs](https://www.r-bloggers.com/2021/03/how-to-solve-common-problems-with-gams/) ist auch ein guter Anlaufpunkt, wenn mal eine GAM_modellierung nicht funktionieren will.
Wenn wir jetzt ein GAM rechnen wollen, dann müssen wir einmal über die Funktion `s()` dem GAM mitteilen, welcher der variablen als Polynom in das Modell rein soll. Das ist sehr ähnlich dem `mfp`-Modell und der Funktion `fp()`. Wie immer kannst du der Funktion `s()` noch zusätzliche Informationen mitgeben aber das übersteigt diese Einführung hier.
```{r}
gam_fit <- gam(weight ~ s(age), data = chicken_tbl)
```
Und dann können wir uns auch schon die Modellgüte des GAM einmal anschauen. Das ist eigentlich das Schöne der Implementierung in dem R Paket `{mgvc}`, dass wir hier auch alle Helferfunktionen der anderen Pakete nutzen können.
```{r}
gam_fit |>
model_performance()
```
Wir sehen auch hier, dass wir ein sehr gutes Modell mit einem Bestimmtheitsmaße $R^2$ von $98\%$. Wir könnten uns auch die Modellkoeffizienten anschauen, aber leider kriegen wir hier nur die Information, ob der Intercept signifikant unterschiedliche von der Null ist und ob wir einen signifikanten Anstieg haben. Beides ist zwar nett, aber interessiert uns eher nicht in unsere Fragestellungen.
```{r}
gam_fit |>
model_parameters()
```
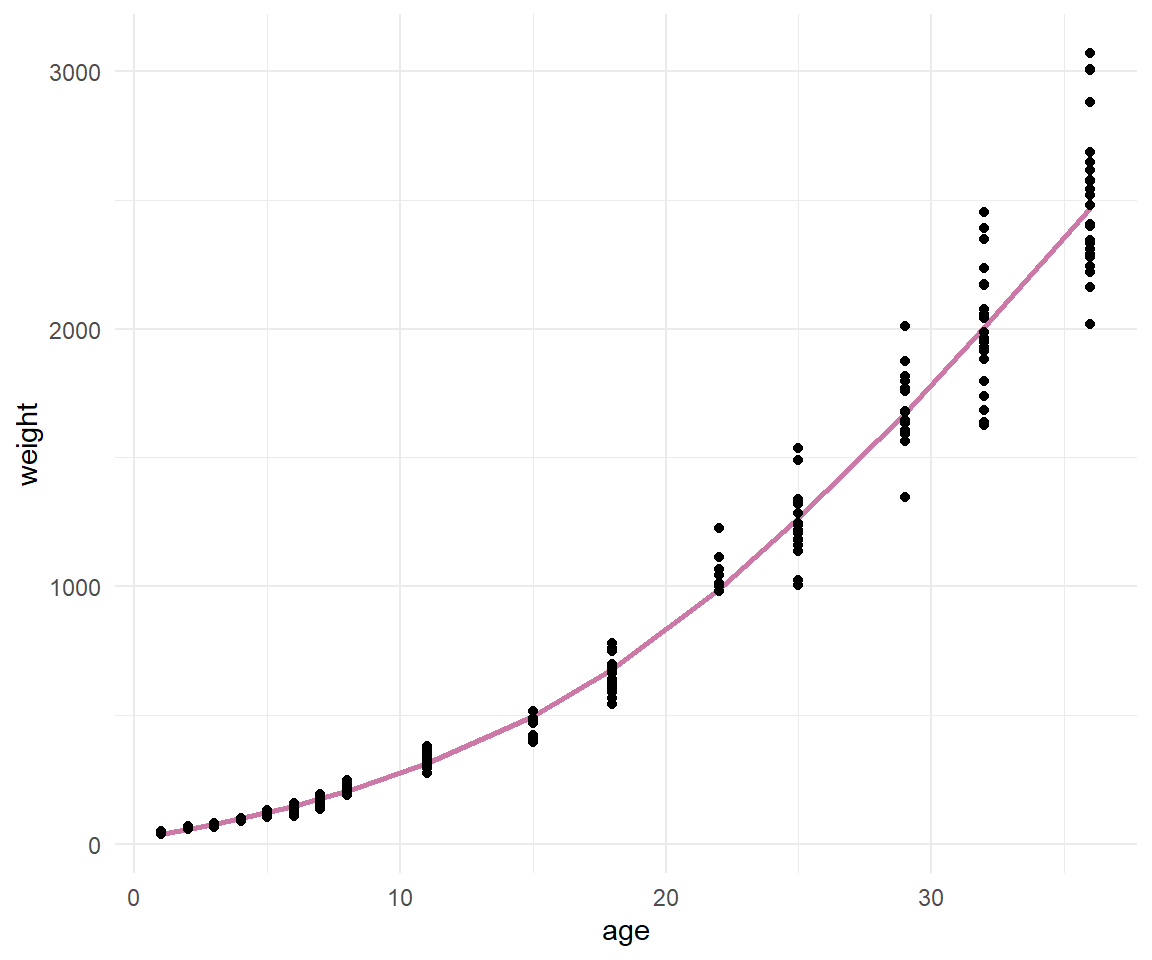
Dann können wir auch in der @fig-nls-gam-1 einmal das Modell sehen. Wir sehen, dass wir eine sehr gute Modellanpassung haben. Wir können also das Modell gut nutzen um das Gewicht von zukünftigen Hünchen zu schätzen. Eine mathematische Formel erhalten wir aber nicht.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-gam-1
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Visualisierung der Hühnchengewichte nach Alter in Tagen mit der geschätzen nicht-linearen Regressionsgleichung."
ggplot(chicken_tbl, aes(age, weight)) +
geom_line(aes(y = predict(gam_fit)), size = 1, color = "#CC79A7") +
geom_point() +
theme_minimal()
```
Dann machen wir das auch gleich mal in dem wir uns drei Hühnchen mit einem Alter von 10, 20 und 30 Tagen vorgeben. Wir wollen jetzt das Gewicht der drei Hühnchen vorhersagen.
```{r}
test_tbl <- tibble(age = c(10, 20, 30))
```
Dafür können wir dann die Funktion `predict()` nutzen in der wir dann zum einen unser Modell `gam_fit` eingeben sowie die Testdaten `test_tbl` mit den drei Altersangaben für die drei neuen Hühnchen. Wir erhalten dann das vorhergesagt Gewicht an den drei Zeitpunkten. Ob das jetzt sinnvoll ist oder nicht, hängt wie immer von der Fragestellung ab. Hier sei es einfach einmal präsentiert.
```{r}
predict(gam_fit, newdata = test_tbl)
```
Damit sind wir schon fast durch mit dem ersten Beispiel und GAM. In `{ggplot}` musst du aber gar nicht den langen Weg gehen, wenn du nur mit GAM eine Kurve in deine Punkte zeichnen willst. Das geht sehr einfach mit der Funktion `stat_smooth()`. Du hast dann auch dort die Möglichkeit neben GAM auch andere Arten der Anpassung einer Funktion an deine Daten zu wählen.
Als zweites Beispiel wollen wir uns nochmal die Wasserlinsen anschauen und sehen, was passiert, wenn wir weniger Messpunkte auf der $x$-Achse haben als bei unseren Hühnchendaten. Wenn du zu wenige Beobachtungen auf der $x$-Achse hast, dann kann das GAM-Modell Probleme bekommen eine Anpassung zu rechnen. Hier hat mir dann die Seite [How to solve common problems with GAMs](https://www.r-bloggers.com/2021/03/how-to-solve-common-problems-with-gams/) sehr geholfen. Ich musste einfach die Anzahl an Dimensionen $k$ für den Glättungsterm auf eine niedrigere Zahl setzen. Wenn du also zu wenige Messwerte hast, dann ist das Setzen von $k<5$ eine guter Startpunkt.
```{r}
duckweeds_gam_fit <- gam(sensor ~ s(duckweeds_density, k = 3), data = duckweeds_tbl)
```
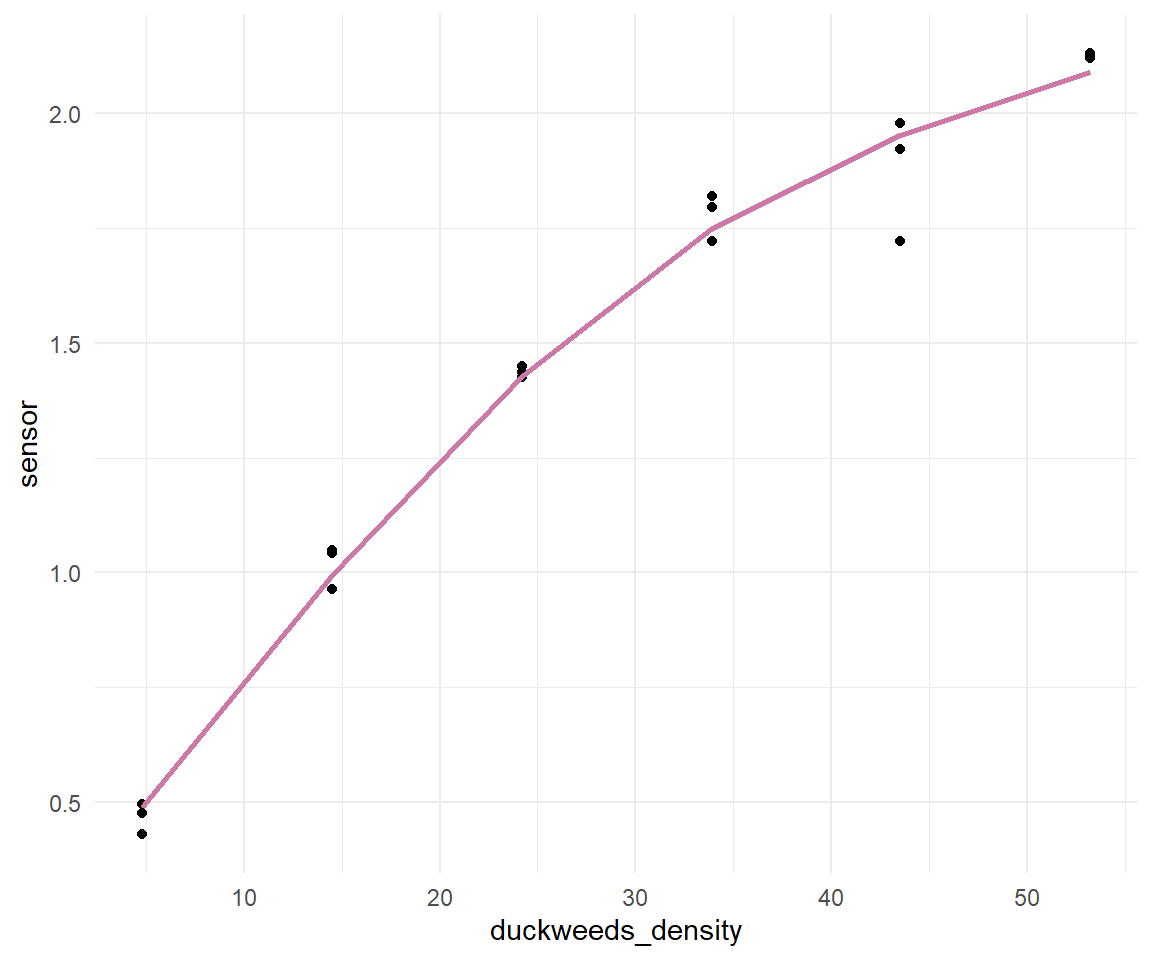
Dann können wir uns auch schon in der @fig-nls-ggplot-gam-fit die Anpassung der Kurve aus GAM an die Beobachtungen anschauen. Da die Methode keine mathematische Formel oder entaprechende Koeffizienten wiedergibt, müssen wir hier mit der `predict()` Funktion arbeiten. Das Ergebnis sieht aber sehr gut aus, wir laufen mit der Kurve sehr gut durch die Beobachtungen.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-ggplot-gam-fit
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Angepasste Kurve aus der Funktion `gam()`."
ggplot(duckweeds_tbl, aes(duckweeds_density, sensor)) +
geom_point() +
geom_line(aes(y = predict(duckweeds_gam_fit)), size = 1, color = "#CC79A7") +
theme_minimal()
```
Wenn wir GAM nutzen dann können wir uns auf verschiedenen Wegen ein Konfidenzintervall wiedergeben lassen. Ein Vorhersageintervall ist nur mit sehr viel Arbeit und eigenem Programmieren möglich. Mir was das in dem Tutorium [Prediction intervals for Generalized Additive Models (GAMs)](https://mikl.dk/post/2019-prediction-intervals-for-gam/) einfach zu krass. Für mich lohnt es sich nicht auf die Art und Weise ein Vorhersageintervall zu berechnen, da bleibe ich lieber bei den Implementierungen, die es schon gibt. Daher jetzt einmal das Konfidenzintervall aus dem [R Paket `{ggeffects}`](https://strengejacke.github.io/ggeffects/index.html), dem [R Paket `{marginaleffects}`](https://marginaleffects.com/) sowie dem [R Paket `{gratia}`](https://gavinsimpson.github.io/gratia/reference/confint.gam.html). Wie immer ist es auch eien Sammlung an Möglichkeiten. Wenn ich entscheiden müsste, dann würde ich das R Paket `{marginaleffects}` bevorzugen, die Funktionalität ist einfach. Das R Paket `{gratia}` hat den Vorteil für GAM-Modelle entwickelt zus ein.
::: panel-tabset
## Mit `{marginaleffects}`
Das R Paket `{marginaleffects}` erlaubt es ziemlich direkt die vorhergesagten Werte über die Funktion `predictions()` aus den Daten zu erhalten. Es gibt auch eine Hilfeseite unter [GAM -- Estimate a Generalized Additive Model](https://marginaleffects.com/vignettes/gam.html). Wir müssen hier noch etwas aufräumen und die doppelten Werte für die Wasserlinsendichte über die Funktion `distinct()` entfernen. Wir erhalten hier auch etwas mehr Informationen also wir in den anderen Paekten wiedergegeben kriegen.
```{r}
marg_pred_tbl <- predictions(duckweeds_gam_fit, newdata = duckweeds_tbl) |>
as_tibble() |>
select(duckweeds_density, sensor, estimate, std.error, conf.low, conf.high) |>
distinct(duckweeds_density, .keep_all = TRUE)
marg_pred_tbl
```
Im Folgenden werde ich gleich die Ausgabe `marg_pred_tbl` nutzen um in dem `ggplot` die Konfidenzintervalle einmal zu visualisieren. Da wir alle Informationen haben, geht das sehr direkt aus der Funktion heraus.
## Mit `{gratia}`
Das R Paket `{gratia}` erlaubt mit der Funktion `confint()` die Konfidenzintervalle des GAM-Modells zu schätzen. Hier müssen wir dann einiges angeben. Wenn du die Option `shift = TRUE` vergisst, dann wird nicht der Intercept auf die Konfidenzintervalle addiert und dein Konfidenzintervall liegt dann sauber auf dem Ursprung. Das war super nervig rauszufinden warum das am Anfang so war. Auch heißt es hier mal `data` statt `newdata`, aber das war dann schon nicht das Problem mehr. Auch hier schmeiße ich am Ende alle doppelten Wasserlinsendichten aus den Daten mit der Funktion `distinct()` raus.
```{r}
gratia_pred_tbl <- confint(duckweeds_gam_fit, parm = "s(duckweeds_density)",
shift = TRUE, type = "confidence", data = duckweeds_tbl) |>
select(duckweeds_density, .estimate, .se, .lower_ci, .upper_ci) |>
distinct(duckweeds_density, .keep_all = TRUE)
gratia_pred_tbl
```
Neben der Funktion `confint()` hat das R Paket noch eine weitreichende Fülle an zusätzlichen Funktionen für die Darstellung von komplexeren GAM-Modellen. Es lohnt sich also auf jeden Fall einmal die [Hilfeseite von `{gratia}`](https://gavinsimpson.github.io/gratia/) zu besuchen und mehr über das R Paket zu erfahren, wenn du tiefergreifend mit der Modellierung von GAM's beginnen willst.
## Mit `{ggeffects}`
R Paket `{ggeffects}` liefert mit der Funktion `ggpredict()` eine super aufgeräumte Funktion um die vorhergesagten Werte von dem Sensor für die Wasserlinsendichte zu erhalten. Dann kriegen wir auch noch ein Konfidenzintervall dazu. Der einzige Manko ist, dass wir die Ausgabe für die weitere Verwertung dann etwas mehr bearbeiten müssen.
```{r}
gg_pred_obj <- ggpredict(duckweeds_gam_fit, terms = "duckweeds_density")
gg_pred_obj
```
Wenn du die Ausgabe dann weiter verwenden willst, dann musst du hier noch etwas mehr Arbeit rein stecken und die Ausgabe dann über die Umwandlung in einen `tibble` weiterverarbeiten.
:::
In der @fig-gam-duckweed-02 siehst du dann einmal die angepasste Kurve aus der Funktion `gam()` zusammen mit dem Konfidenzintervall aus `{marginaleffects}`. Wenn du oben in den Tabs einmal die Ausgaben aus den Funktionen vergleichst, wirst du feststellen, dass die numerischen Werte alle sehr ähnlich sind. Daher ist es eher eine Geschmacks- und Anwendungsfrage, welches Paket du verwendest. Wenn du viel mit GAM-Modellen rechnest, dann kannst du auch alles sehr gut in der Umgebung des R Paketes `{gratia}` machen. Die Kurve läuft jedenfalls super durch unser Konfidenzintervall, daher können wir uns ziemlich sicher sein, gute Koeffizienten für das GAM-Modell gefunden zu haben. Wie schon oben geschrieben, an ein mathematisches Modell mit Funktion kommst du in GAM nicht ran. Dafür musst du dann eine andere Implementierung wie `nls()` oder `mfp()` nutzen.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-gam-duckweed-02
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Angepasste Kurve aus der Funktion `gam()` zusammen mit dem Konfidenzintervall aus `{marginaleffects}`."
#|
ggplot(marg_pred_tbl, aes(duckweeds_density, sensor)) +
geom_ribbon(aes(ymin = conf.low, ymax = conf.high), fill = "grey90") +
geom_point() +
geom_line(aes(y = estimate), color = cb_pal[2]) +
theme_minimal()
```
::: callout-note
## Gam und Loess in `{ggplot}`
In `{ggplot}` können wir direkt über die Funktion `stat_smooth()` eine Kurve durch unsere Punkte legen. Wenn du mehr Lesen willst, dann empfehle ich einmal das Tutorium zu [GAM and LOESS smoothing](https://andrewirwin.github.io/data-visualization/smoothing.html). Ich gehe hier nicht weiter auf die [Local Regression (LOESS)](https://thomasleeper.com/Rcourse/Tutorials/localregression.html) ein, da wir weder ein Bestimmtheitsmaße $R^2$ noch eine mathematische Geradengleichung. Daher lohnt sich aus meiner Sicht die Anwendung der Funktion `loess()` einfach in der Praxis nicht. für die Visualisierung mag es aber dann doch sinnvoll sein. Damit können wir auch einfach eine GAM oder Loess-Funktion in `ggplot()` direkt anwenden ohne über zusätzliche Pakete oder Funktionen zu gehen.
```{r}
#| echo: true
#| warning: false
#| message: false
#| label: fig-nls-ggplot-gam
#| fig-align: center
#| fig-height: 5
#| fig-width: 6
#| fig-cap: "Direkte Anwednung von GAM und Loess in `ggplot()` ohne eine zusätzliche Funktion."
#| fig-subcap:
#| - "GAM"
#| - "Loess"
#| layout-nrow: 1
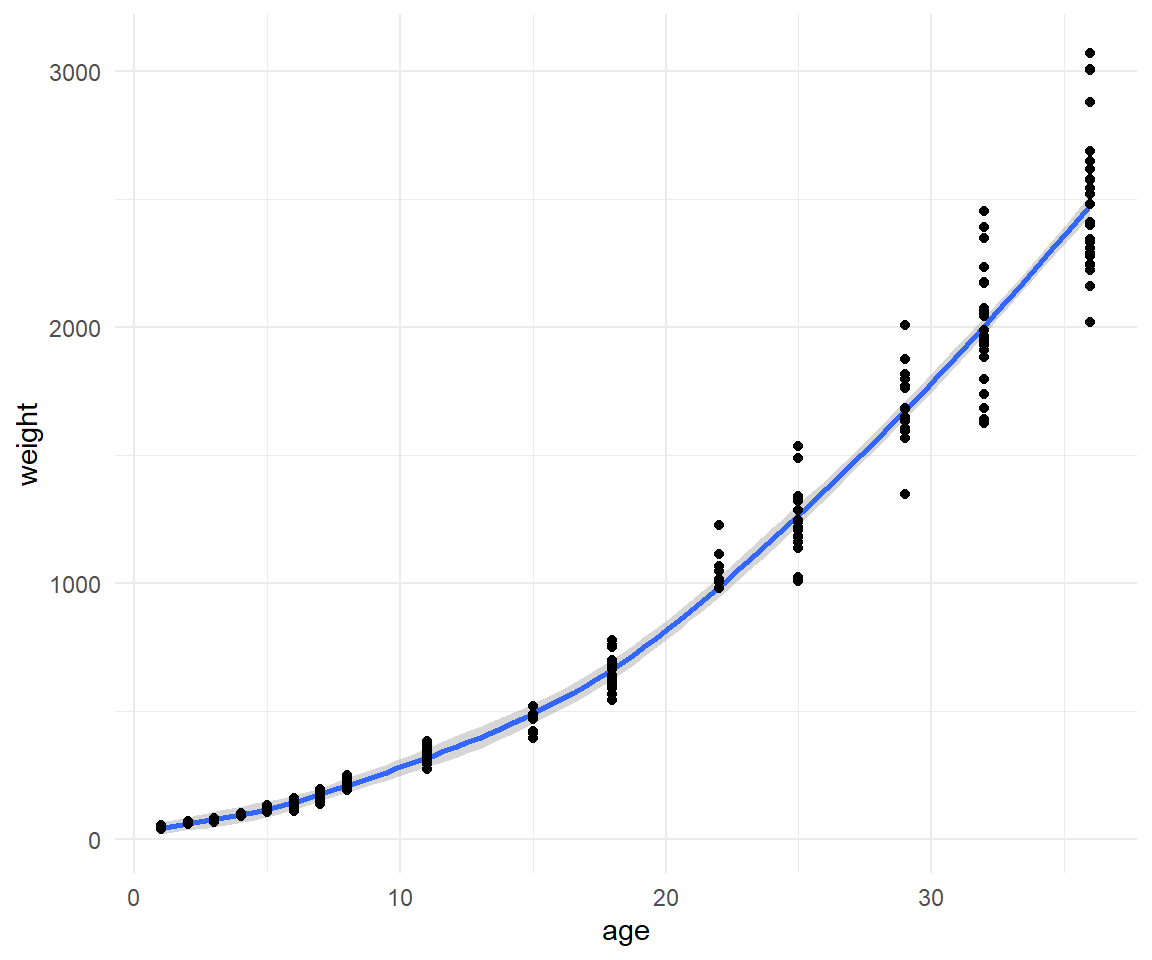
ggplot(chicken_tbl, aes(age, weight)) +
stat_smooth(method = "gam") +
geom_point() +
theme_minimal()
```
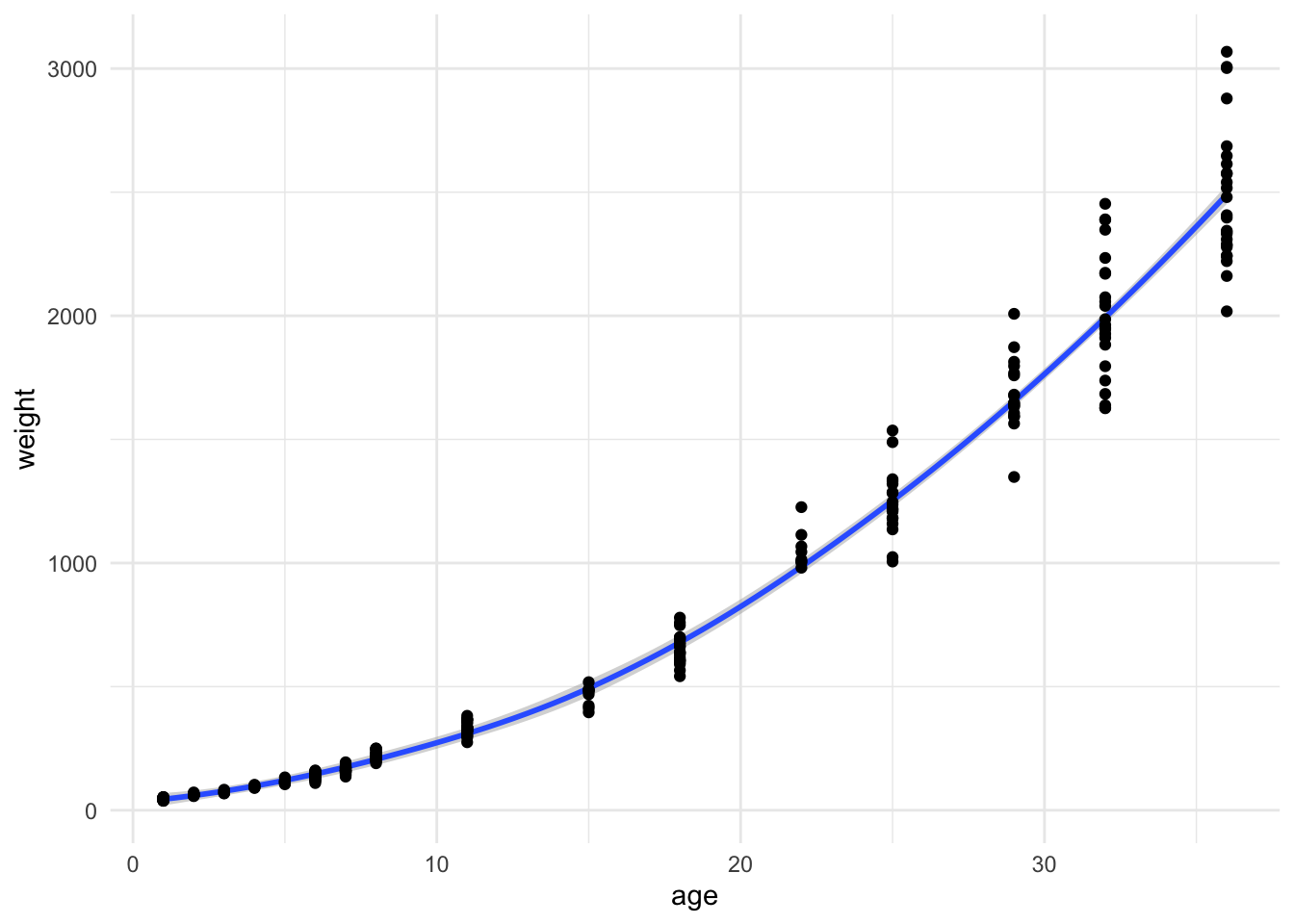
```{r}
ggplot(chicken_tbl, aes(age, weight)) +
stat_smooth(method = "loess") +
geom_point() +
theme_minimal()
```
:::
## Referenzen {.unnumbered}