Grundlagen des Modellierens

Letzte Änderung am 15. February 2024 um 14:48:38

“Curiosity is the beginning of knowledge. Action is the beginning of change.” — James Clear

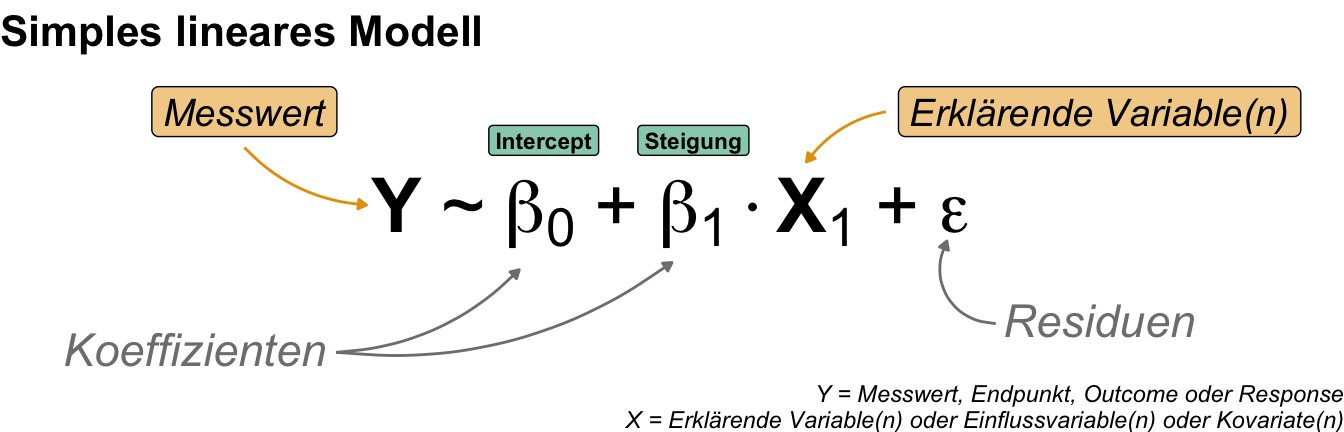
In diesem Teil des Buches und den folgenden Kapiteln wollen wir uns mit der Modellierung von Daten beschäftigen. Wir fangen erstmal mit einem simplen linearen Modell an und erweitern dann dieses Modell zu einem multiplen Modell. Das heißt, wir haben ein Outcome \(y\), was normalverteilt ist, sowie eine Einflussvariable \(x_1\), die eine kontinuierliche Variable ist. Wir wollen jetzt herausfinden, welchen Einfluss oder Effekt das \(x_1\) auf das \(y\) hat. Sehr simple Gesprochen legen wir eine Gerade durch eine Punktewolke. Im Weiteren konzentrieren wir uns hierbei aber erst einmal auf ein normalverteiltes Outcome mit einer Gaussian linearen Regression.

Dabei hat ein simples lineares Modell nur eine Einflussvariable \(x_1\).

\[ y \sim x_1 \]

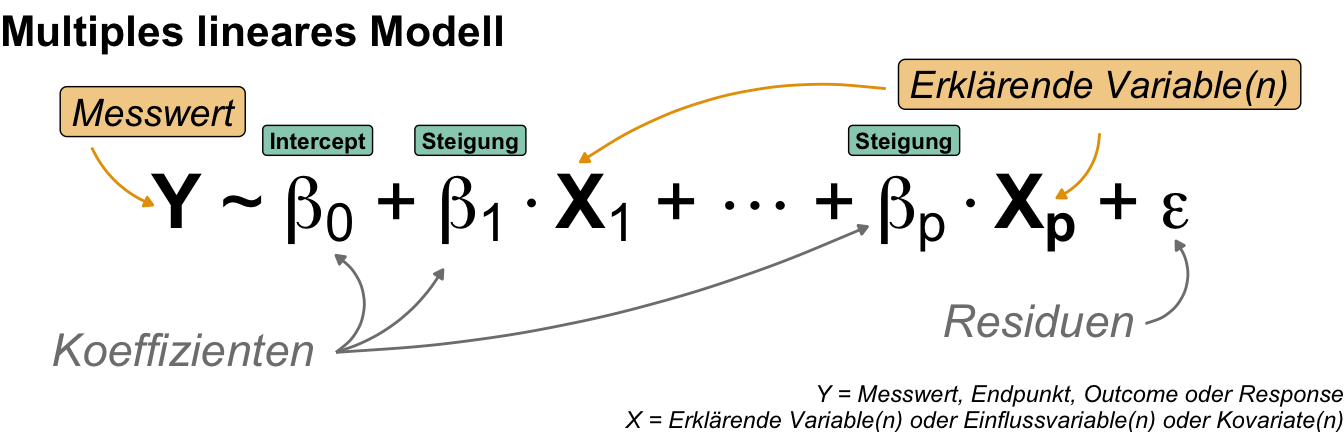
Ein multiples lineares Modell hat mehrere Einflussvariablen \(x_1, ..., x_p\).

\[ y \sim x_1 + x_2 + ... + x_p \]

Viele der Konzepte in diesem Teil des Buches brauchen wir in den folgenden Kapiteln des Teils zum statistischen Modellieren. Wir lernen hier also eher die Aufwärmübungen und Konzepte um dann multiple lineare Regressionen mit anderen Verteilungsfamilien als der Normalverteilung rechnen zu können. In den seltensten Fällen reichen simple lineare Modell aus, um die Realität abzubilden. Fangen wir also mit den Grundlagen an und bauen dann systematisch die Konzepte der simplen linearen Regression auf.