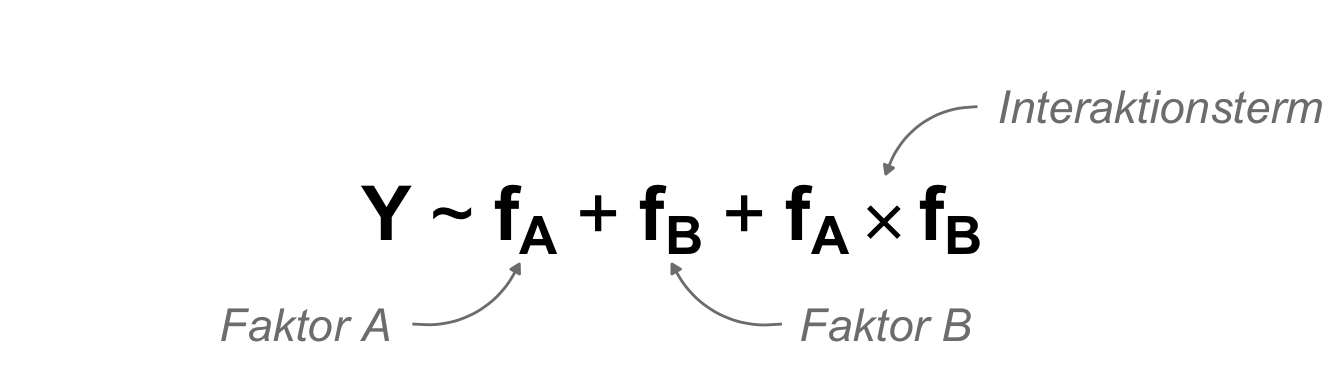46 Multiple lineare Regression
Letzte Änderung am 15. October 2025 um 20:18:58
“All models are approximations. Essentially, all models are wrong, but some are useful. However, the approximate nature of the model must always be borne in mind.” — George E. P. Box
In diesem Kapitel geht es um die multiple lineare Regression. Der große Unterschied zu der simplen linearen Regression ist, dass wir in der multiplen Regression mehr als eine Einflussvariable vorliegen haben. Damit wird unser Modell um einiges komplexer. Hier gibt es jetzt gewisse Überschneidungen mit den Marginal effect models, die im Prinzip die Erweiterung der multiplen Regression sind. Wir können mit den Marginal effect models eben dann doch etwas anders lineare und nicht linare Regressionen interpretieren. Damit kannst du in dem Kapitel dann mehr über eine alternative Art der Interpretation von multiplen Modellen lernen. Ebenso gehe nicht hier so stark auf das Modellieren in R ein. Hier kannst du dann in dem entsprechenden Kapitel auch nochmal mehr lesen. Hier zeige ich dann die Basisanwendungen. Am Ende habe ich mich auch entschieden hier nur einen normalverteilten Messwert zu betrachten. Sonst wird es einfach viel zu komplex, wenn wir hier noch andere Verteilungen berücksichtigen. Dazu dann mehr in den entsprechenden Kapiteln zur statistischen Modellierung.
“In den folgenden Kapiteln gibt es immer mal wieder Redundanzen. Teilweise sind diese Redundanzen gewollt, denn eine gute Wiederholung hilft ja immer. Meistens habe ich aber den Überblick verloren und fand, dass das Thema dann an der Stelle doch nochmal gut reinpasste. Ist so passiert.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
46.1 Allgemeiner Hintergrund
“This idea of ‘holding everything constant’ though can be tricky to wrap your head around.” — Andrew Heiss
Wenn wir über die multiple lineare Regression sprechen, dann sprechen wir immer über mehr als eine Einflussvariable. Dadurch können wir den Fall haben, dass wir nicht nur eine Kovariate sondern mehrere Kovariaten in einem Modell vorliegen haben. Zum Beispiel wollen wir wissen, ob die Sprungweite von dem Gewicht der Flöhe oder der Anzahl an Beinhaaren abhängt. Wir haben hier also mehrere kontinuierliche Einflussvariablen vorliegen. Ebenso können wir den Fall haben, dass uns nur kategoriale Einflussvariablen interessieren. Hat die Ernährungsform oder aber der Entwicklungsstand einen Einfluss auf die Sprungweite der Flöhe. Klassischerweise wären wir hier zwar auf dem ANOVA Pfad eines faktoriellen Experiments, aber wir können natürlich die Koeffzienten eines mehfaktoriellen Modells in der Form einer multiplen Regression interpretieren. Wenn wir dann keinen normalverteilten Messwert haben, dann bietet sich natürlich dennoch die multiple Regression als eine Analyseform an. Abschließend können wir natürlich auch kombinierte Modelle vorliegen haben. Wir haben also in unseren multiple Modell nicht nur Kovariaten oder Faktoren sondern eben eine Mischung aus beiden Formen. Das führt dann zu einer noch komplexeren Interpretation. Alle Fälle wollen wir uns hier in diesem Kapitel einmal an einem normalverteilten Messwert anschauen.
Sprachlicher Hintergrund
“In statistics courses taught by statisticians we don’t use independent variable because we use independent on to mean stochastic independence. Instead we say predictor or covariate (either). And, similarly, we don’t say”dependent variable” either. We say response.” — User berf auf r/AskStatistics
Wenn wir uns mit dem statistischen Modellieren beschäftigen wollen, dann brauchen wir auch Worte um über das Thema reden zu können. Statistik wird in vielen Bereichen der Wissenschaft verwendet und in jedem Bereich nennen wir dann auch Dinge anders, die eigentlich gleich sind. Daher werde ich mir es hier herausnehmen und auch die Dinge so benennen, wie ich sie für didaktisch sinnvoll finde. Wir wollen hier was verstehen und lernen, somit brauchen wir auch eine klare Sprache.
“Jeder nennt in der Statistik sein Y und X wie er möchte. Da ich hier nicht nur von Y und X schreiben will, führe ich eben die Worte ein, die ich nutzen will. Damit sind die Worte dann auch richtig, da der Kontext definiert ist. Andere mögen es dann anders machen. Ich mache es eben dann so. Danke.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
In dem folgenden Kasten erkläre ich nochmal den Gebrauch meiner Begriffe im statistischen Testen. Es ist wichtig, dass wir hier uns klar verstehen. Zum einen ist es angenehmer auch mal ein Wort für ein Symbol zu schreiben. Auf der anderen Seite möchte ich aber auch, dass du dann das Wort richtig einem Konzept im statistischen Modellieren zuordnen kannst. Deshalb einmal hier meine persönliche und didaktische Zusammenstellung meiner Wort im statistischen Modellieren. Du kannst dann immer zu dem Kasten zurückgehen, wenn wir mal ein Wort nicht mehr ganz klar ist. Die fetten Begriffe sind die üblichen in den folgenden Kapiteln. Die anderen Worte werden immer mal wieder in der Literatur genutzt.
“Die Grenzen meiner Sprache bedeuten die Grenzen meiner Welt.” — Ludwig Wittgenstein
Hier kommt einmal die Tabelle mit den wichtigsten Begriffen im statistischen Modellieren und wie ich die Worte benutzen werde. Damit wir uns verstehen und du was lernen kannst. In anderen Büchern und Quellen findest du teilweise die Worte in einem anderen Sinnzusammenhang. Das ist gut so dort. Bei mir ist es anders.
| Symbol | Deutsch | Englisch | |
|---|---|---|---|
| LHS | \(Y\) / \(y\) | Messwert / Endpunkt / Outcome / Abhängige Variable | response / outcome / endpoint / dependent variable |
| RHS | \(X\) / \(x\) | Einflussvariable / Erklärende Variable / Fester Effekt / Unabhängige Variable | risk factor / explanatory / fixed effect / independent variable |
| RHS | \(Z\) / \(z\) | Zufälliger Effekt | random effect |
| \(X\) ist kontinuierlich | \(c_1\) | Kovariate 1 | covariate 1 |
| \(X\) ist kategorial | \(f_A\) | Faktor \(A\) mit Level \(A.1\) bis \(A.j\) | factor \(A\) with levels \(A.1\) to \(A.j\) |
Am Ende möchte ich nochmal darauf hinweisen, dass wirklich häufig von der abhängigen Variable (eng. dependent variable) als Messwert und unabhängigen Variablen (eng. independent variable) für die Einflussvariablen gesprochen wird. Aus meiner Erfahrung bringt die Begriffe jeder ununterbrochen durcheinander. Deshalb einfach nicht diese Worte nutzen.
Wie multiple Einflussvariablen interpretieren?
Wie schon im Zitat am Anfang erwähnt, heißt die Regel, dass wir jeden Koeffizienten unseres Modell nur in soweit interpretieren können, wenn sich die anderen Einflussvariablen nicht ändern. Das klingt jetzt kryptisch und macht eigentlich nur Sinn, wenn man schon alles verstanden hat. Deshalb hier einmal die Analogie mit Schaltern und Schieberegelern. Wir können eine kategoriale Variable oder Faktor durch die Level durchschalten. Daher können wir uns den Effekt von weiblichen oder männlichen Flöhen anschauen. Es gibt aber nur diese beiden Möglichkeiten. Entweder steht der Schalter auf männlichen Floh oder aber auf weiblichen Floh. Etwas anderes ist es wenn wir uns eine Kovariate vorliegen haben. Eine kontinuierliche Einflussvariable können wir beliebig einstellen. Wir können das Gewicht eines Flohs eben hin und herschieben um einen Wert zu haben.
In einer multiplen Regression kombinieren wir nun alles miteinander. Wir haben eben eine Art Mischpult vorliegen. Auf unserem Mischpult finden wir eben Schalter und Schieberegler. Wir haben dann auch in unserem Modell Faktoren und Kovariaten vorliegen. Dann können wir auch Schalter auf verschiedene Positionen setzen und die Regler verschieden einstellen.
Worher kommt nun die Interpretation, dass wir eine Einflussvaribale nur interpretieren können, wenn wir den Rest der Einflussvariablen konstant halten? Wenn wir an dem Schieberegler des Gewichts der Flöhe drehen, dann müssen die anderen Schalter und Regler still stehen. Wir interpretieren dann eben das sich änderende Gewicht, für weibliche Flöhe unter der Ernährung mit Ketchup. Wir können nicht global das gesmate Modell interpretieren. Einen Ausweg bieten die Marginal effect models, aber diese werden wir in diesem Kapitel nur am Rande behandeln. Dafür ist das Thema zu komplex. Daher behalte ich Kopf, wenn wir später einzelne Einflussvariablen betrachten, dann tuen wir das immer im Kontext fixierter anderer Einflussvariablen.
Eine Frage der Einheit!
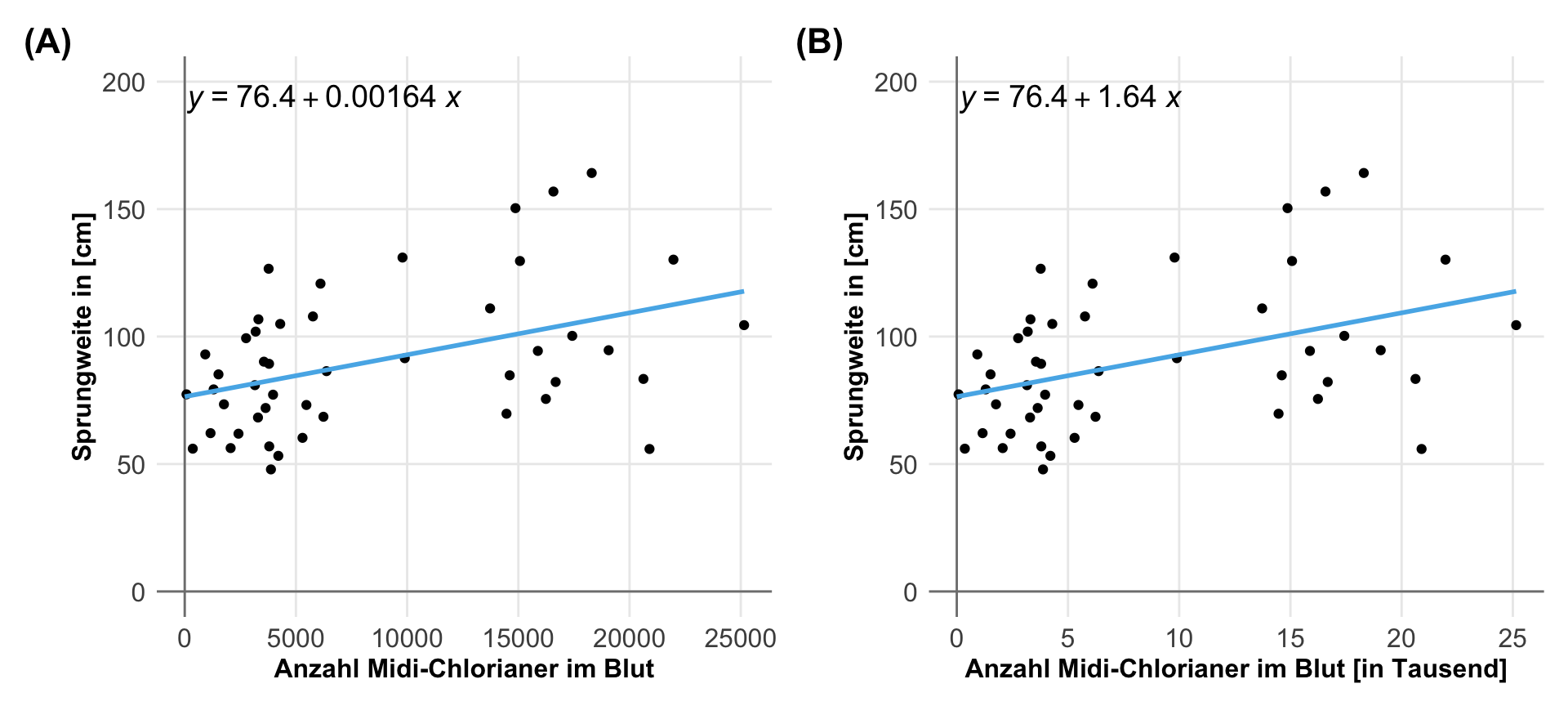
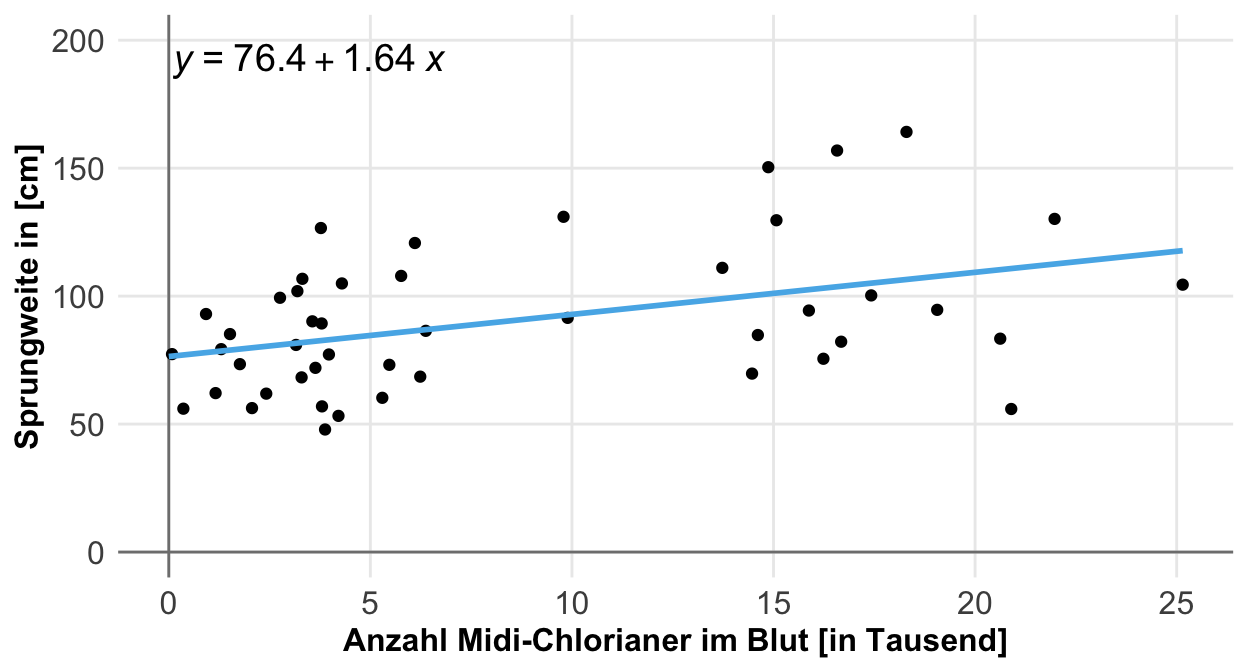
Die Einheit von den Messwerten oder auch Kovariaten hat einen nicht zu unterschätzenden Einfluss auf die Interpretation der Koeffizienten oder eben der Effekt einer multiplen linearen Modellierung. Da wir ja mehrere Einflussvariablen vorliegen haben bist du schnell dabei die Koeffizienten der Steigung untereinander zu vergleichen. Dann kommt man schnell zu einem Schluss der eventuell nicht wahr ist. Ich zeige dir hier einmal in der folgenden Abbildung den Fall, wo wir visuell die gleiche Steigung in den Daten vorliegen haben. Was sich aber in den beiden Abbildungen fundamental unterscheidet ist die Einheit der Kovariate.
In der linken Abbildung ist der Koeffizient der Steigung des Kopfgewichts \(0.021\) mehr mittlere Boniturnote pro Gramm Kopfgewicht. Das wirkt sehr klein. Im Gegensatz ist der Koeffizient der Steigung des Strunkdurchmessers \(5.15\) mehr mittlere Boniturnoten pro Zentimeter Strunkdurchmesser. Es wirkt als hätte der Strunkdurchmesser einen viel größeren Effekt als das Gewicht auf die Boniturnoten. Das ist aber ein Trugschluss, wie wir dann gleich nochmal sehen werden. Ich zeige dir den Zusammenhang hier nochmal in der Tabelle.
| Kopfgewicht [g] | Strunkdurchmesser [cm] | |
|---|---|---|
| Gradengleichung | \(y = 0.021 \cdot x - 8.42\) | \(y = 5.15 \cdot x - 16.65\) |
| Bestimmtheitsmaß | \(R^2 = 0.74\) | \(R^2 = 0.93\) |
| Faktor Steigung | \(\times1\) | \(\times 245.24\) |
Wir würden jetzt meinen, dass der Effekt des Strunkdurchmessers 245mal größer ist als der des Kopfgewichts. Das ist aber ein Trugschluss! Wir haben die Einheiten nicht beachtet. Die Spannweite bei dem Kopfgewicht geht von etwas über 450 Gramm bis fast 750 Gramm. Daher ist die Steigerung um eine Einheit nur eine kleine Menge mehr an Boniturnote. Bei dem Strunkdurchmesser haben wir als kleinsten Wert 3.5cm und als höchsten Wert 5cm für die Grade. Erhöhen wir den Strunkdurchmesser um 1 Zentimeter durchlaufen wir fast die gesamte Spannweite. Wenn du für den Vergleich eine einheitslose Steigung brauchst, dann schaue nochmal in dem Kapitel zur Korrelation vorbei oder weiter unten in dem entsprechenden Abschnitt zur Einheit.
Wie verschiedene Modelle darstellen?
Häufig stellt sich dann die Frage, wie so multiple Regressionsmodelle dargestellt werden können. Daher hier gleich einmal vorweg ein Beispiel für eine Darstellung einer multiplen linearen Regression in einer wissenschaftlichen Arbeit. In der Arbeit Energy expenditure and obesity across the economic spectrum von McGrosky et al. (2025) wird die multiple lineare Regression genutzt um den Zusammenhang von Energieaufnahme und dem Energieverbauch in veschiedenen Entwicklungsstufen von Ländern zu modellieren. Dabei kommt eigentlich ein recht spannendes Ergebnis heraus, wenn ich das einmal sehr kanpp zitieren darf. Es kommt eben mehr auf die Energieaufnahme als auf den Verbrauch an. Oder anders herum, wenn du abnehmen willst achte auf dein Essen und nicht so sehr auf deine Bewegung.
“Our analyses suggest that increased energy intake has been roughly 10 times more important than declining total energy expenditure (TEE) in driving the modern obesity crisis.” — McGrosky et al. (2025)
In der folgenden Tabelle siehst du dann eimal das multiple lineare Modell mit dem prozentualen Körperfettanteil als Messwert. Es wurden dann acht verschiedene multiple Modelle gerechnet und in jedem Modell wurden andere Einflussvariablen aufgenommen. In der vorletzten Zeile findest du dann noch das Bestimmtheitsmaß \(R^2\), was dir angibt wie gut das Modell funktioniert hat. Hier wollen wir eigentlich einen Wert gegen Eins sehen, aber in Beobachtungsdaten wie hier, ist eine höhere Zahl erstmal eine bessere Zahl.
Was sagt uns jetzt die Tabelle aus? Zuerst einmal rechnen wir hier acht Modelle in den Spalten der Tabelle, die wir dann untereinander vergleichen. Wir nehmen verschiedene Einflussvariablen mit in das Modell, die alle in den Zeilen stehen. Teilweise ist das bei kategorialen Variablen wie dem Geschlecht die Gruppe angegeben. Wie interpretieren wir nun diese Tabelle? Hier einmal ein Auszug zu dem Einfluss des Fleischkonsum (eng. per capita meat consumption) in den letzten drei Spalten auf den Messwert Körperfetrprozent.
“[…], per capita meat consumption, another dietary change associated with development, was not significantly associated with fat percentage when added to models including percent ultraprocessed foods (UPF) [i.e., industrial formulations of five or more ingredients (29)]” — McGrosky et al. (2025)
Was lesen wir hier? Wenn wir den Fleischkonsum zusammen mit den hochverarbeiteten Lebensmittel mit ins Modell nehmen, dann wird der Fleichkonsum nicht signifikant. Dies ist eine Art eine multiple lineare Regression zu rechnen und die Einflussvariablen untereinander zu vergleichen. Mehr dazu dann in den folgenden Abschnitten und den entsprechenden Kapiteln zur statistischen Modellierung.
Wir können in der Abrbeit von Gibney (2019) nocheinmal nachlesen, was die aktuelle Definition eines hochverarbeiteten Lebensmittel (eng. ultraprocessed foods) ist. Das ist ja immer wieder ein Streitpunkt, der aktuell ja auch noch offen ist. Wir halten uns einmal an die folgende Definition.
“Industrial formulations typically with 5 or more and usually many ingredients. Besides salt, sugar, oils, and fats, ingredients of ultra-processed foods include food substances not commonly used in culinary preparations, such as hydrolyzed protein, modified starches, and hydrogenated or interesterified oils, and additives whose purpose is to imitate sensorial qualities of unprocessed or minimally processed foods and their culinary preparations or to disguise undesirable qualities of the final product, such as colorants, flavorings, nonsugar sweeteners, emulsifiers, humectants, sequestrants, and firming, bulking, de-foaming, anticaking, and glazing agents.” — Gibney (2019)
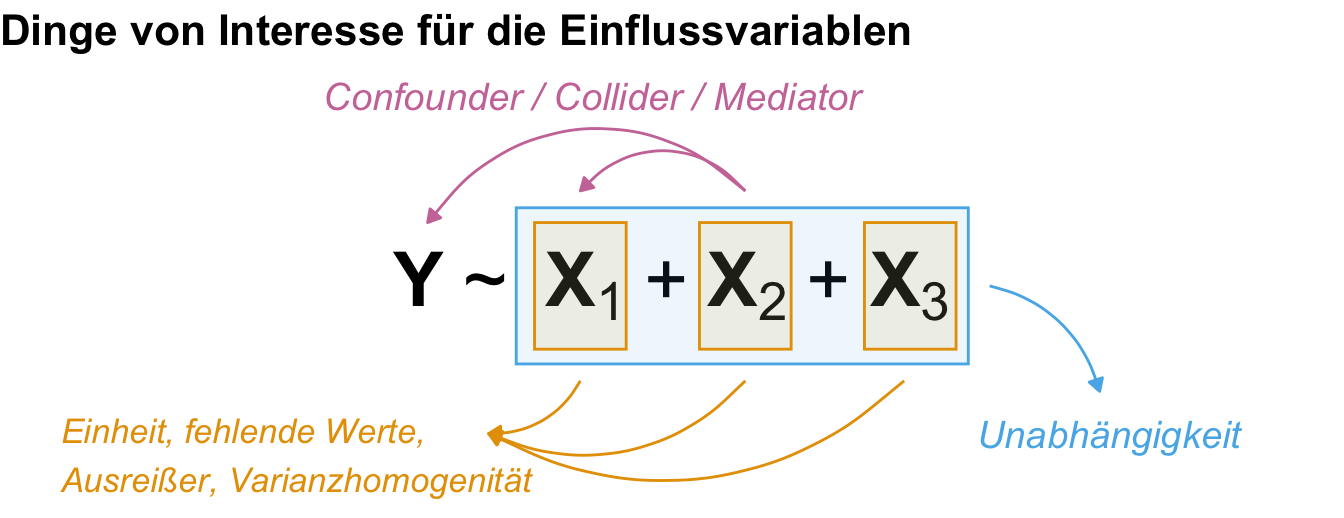
In diesem Kapitel findest du dann noch am Ende einige Abschnitte zu Dingen von Interesse. Wenn wir nämlich über den Effekt sprechen, dann müssen wir auch nochmal über die Einheiten von den Einflussvariablen sprechen. Wenn diese sehr unterschiedliche sind, dann kann das zu Problemen führen. Auch können Einflussvariablen mit sehr großen numerischen Werten ein Problem in der Interpretation sein. Dann schauen wir nochmal auf die Korrelation der Einflussvariablen. Eigentlich sollten ja alle Einflussvariablen untereinander unabhängig sein. Dann wollen wir nochmal schauen, wie wir den verschiedene multiple Modelle untereinander vergleichen können um das beste multiple Modell zu finden.
Jetzt kommen wir aber nochmal zu dem theoretischen Hintergrund. Wir wollen hier nochmal gleich verstehen, wie die multiplen Modelle aufgebaut sind und wie die Modelle in R dargestellt werden. Wenn du dich mit dem allgemeinen Hintergrund zufrieden gibst, dann kannst du auch gerne direkt in die Beispiele und deren Auswertung springen. Oder eben dann nochmal später zurückkommen, wenn der Bedarf besteht.
46.2 Theoretischer Hintergrund
In dem theoretischen Hintergrund der multiplen Modelle bleibe ich etwas oberflächlich und gehe nicht auf die mathematischen Hintergründe tiefer ein. Das lohnt hier auch nicht weiter. In den Anwendungen habe ich dann immer noch die theoretische Berechnung in R ergänzt, die dir dann nochmal zeigt, wie in R intern die Modelle gerechnet werden. Ganz allgemein kann ich das Buch von Kéry (2010) wärmstens empfehlen. Dort habe ich viel über die Modelle und die Berechnungen gelernt. In dem Zusammenhang kann ich auch noch Dormann (2013) empfehlen, wenn es um die Maximum Likelihood Methode geht, die dort gut beschrieben ist. Ich gebe hier dann die Zusammenfassung wieder.
Beginnen wir nochmal mit dem klassischen statistischen Modell in der folgenden Abbildung. Wir haben Daten vorliegen, die wir in ein Modell und einen Fehler zerlegen wollen. Das liest sich sehr allgemein, in der Praxis haben wir auf der linken Seite den beobachteten Messwert Y stehen und auf der linken Seite das Modell aus dem der erklärte Anteil am Y rauskommt. Die Differenz zu den beobachteten Messwerten ist dann der Fehler. Somit ist unser Modell die Kombination aus dem Messwert und unseren Einflussvariablen. Was die Einflussvariablen an dem Messwert nicht erklären können wandert in den Fehler. Somit wollen wir einen geringen Fehler in unserer Modellierung.
Erinnern wir uns nochmal an das simple und multiple lineares Modell. Die beiden Modelle entscheiden sich durch die Anzahl an Einflussvariablen. In der folgenden Abbildung siehst du nochmal das simple lineare Modell. Wir haben hier eine Einflussvariable X. Dann kommen noch die Koeffizienten \(\beta_0\) für den Intercept und der Koeffizient \(\beta_1\) für die Steigung der eine Einflussvariable hinzu. Alles was wir nicht durch die Grae erklären können, wandert dann in die Residuen oder Fehler \(\epsilon\). Eine klassische Gradengleichung mit einer Einflussvariable.
In diesem Kapitel erweitern wir das simple lineare Modell um mehr Einflussvariablen. Dann erhalten wir ein multiples lineares Modell wie in der folgenden Abbildung. Meistens haben wir dann mehr als zwei Einflussvariablen sondern eben \(p\) Stück. Jede dieser Einflussvariablen hat dann eine eigene Stigung. Wir haben dann aber immer noch nur einen Intercept vorliegen. Auch haben wir dann am Ende nur einen Wert für die Residuen oder Fehler. Die Einflussvariablen können eine beliebige Kombination an Kovariten und Faktoren sein.
Jetzt können wir uns nochmal die Formelschreibweise in R anschauen. Wir brauchen hier natürlich nicht die Koeffizienten zu benennen, denn wir wollen die Werte für die Steigung und den Intercept ja durch die multiple Regression bestimmen. Wir schreiben dann auf die linke Seite der Tilde ~ unseren Messwert und auf die rechte Seite dann die Einflussvariablen durch ein Plus + miteinander verbunden. Wir lernen dann im Kapitel zum Modellieren in R noch andere Möglichkeiten in der Formelschreibweise in R. Häufig reichen die Grundlagen aber aus.
Jetzt könnte man meinen, so kompliziert ist es ja dann doch nicht. Dafür musst du aber noch wissen, dass wir nicht nur eine Art von Messwert vorliegen haben. Jeder Messwert auf der linken Seite der Tilde folgt einer Verteilung. Zwar sind die Arten der Verteilungen in etwa begrenz, aber wir haben doch einige vorliegen. Daher müssen wir abhängig von der Verteilunsgfamilie noch die Regression ändern. In der folgenden Abbildung habe ich dir einmal den Zusammenhang der schrecklich netten Verteilunsgfamilie zusammengefasst. Wir müssen eben entscheiden, welcher Verteilungsfamilie unser Messwert angehört und dann eben schauen, wie unsere Einflussvariablen beschaffen sind. Daraus ergibt sich dann die Interpretation des statistischen Modells. Mehr dazu dann in den folgenden Abschnitten und den entsprechenden Kapiteln zur statistischen Modellierung.
Damit sind wir hier für das erste auch durch mit der theoretischen Betrachtung. Ich habe dann bei dem kausalen Modellen immer noch einen Tab ergänzt in dem ich mehr auf die Hinetrgründe eingehe. Wir wollen hier aber nichts händsich rechnen, so dass ich mich auf die praktsiche Umsetzung in R konzentriere. Teilweise gibt es dann wieder Überschneidungen mit der ANOVA oder anderen Kapiteln, aber das ist dann eben auch so gewollt.
Wenn du jetzt denkst ‘Hä? Was soll denn mehrdimensional bedeuten?’, dann besuche doch einmal die fantastische Seite Explained Visually | Ordinary Least Squares Regression um selber zu erfahren, was eine multiple lineare Regression macht. Auf der Seite findest du interaktive Abbildungen, die dir das Konzept der linearen Regression sehr anschaulich nachvollziehen lassen.
Wir immer geht natürlich mehr als ich hier Vorstellen kann. Du findest im Folgenden Tutorien, die mich hier in dem Kapitel inspiriert haben. Ich habe mich ja in diesem Kapitel auf die Durchführbarkeit in R und die allgemeine Verständlichkeit konzentriert.
- Wir funktioniert nun so eine lineare Regression und was sind den jetzt eigentlich die Koeffizienten \(\beta_0\) und \(\beta_1\) eigentlich? Hier gibt es die fantastische Seite Explained Visually | Ordinary Least Squares Regression, die dir nochmal erlaubt selbe mit Punkten in einem Scatterplot zu spielen und zu sehen wie sich dann die Regressionsgleichung ändert.
- Das Buch Tidy Modeling with R gibt nochmal einen tieferen Einblick in das Modellieren in R. Wir immer, es ist ein Vorschlag aber kein Muss.
- Das R Paket
{jtools}gibt nochmal Möglichkeiten sich schnöneresummary()Ausgaben erstellen zu lassen. - Das R Paket
{modelsummary}ist perfekt dafür geeignet nochmal verschiedene Modelle miteinander zu vergleichen.
46.3 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
pacman::p_load(tidyverse, magrittr, broom, correlation, jtools,
see, performance, car, parameters, modelsummary,
ggpmisc, tinytable, ggdag, conflicted)
conflicts_prefer(magrittr::set_names)
conflicts_prefer(ggplot2::annotate)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
"#F0E442", "#0072B2", "#D55E00", "#CC79A7")An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
46.4 Daten
In diesem Kapitel schauen wir uns zwei Datensätze an. Zum einen den Datensatz zu den Sprungweiten von Flöhen und anderen Messwerten. Eigentlich ein faktorielles Experiment mit zwei Faktoren und einiges an spannenden Kovariaten. An diesem Datensatz können wir dann die verschiedenen multiplen Regressionen einmal nachvollziehen. Als zweiten Datensatz habe ich Schlangen mitgebracht. Der Datensatz ist super klein und auch sehr künstlich, da wir uns hier nur die theoretischen Berechnungen in R anschauen wollen. Da brauche ich nicht viel und da habe ich diesen Datensatz dann genutzt.
Modellierung von Flöhen
Der folgende Datensatz zu den Sprungweiten und anderen Messwerten von juvenilen und adulten Flöhen ist von mir so gebaut, dass wir hier usn einige Aspekte der multiplen Regression gut anschauen können. Als Hauptfaktor haben wir hier drei verschiedene Ernährungsformen vorliegen und betrachten als zweiten Faktor eben den Entwicklungsstand der Flöhe. Dazu kommen dann noch eine ganze Reihe von Einflussvariablen wie das Gewicht und Laborwerte. Insgesamt also ein sehr großer Datensatz. Wir schauen uns dann aber immer nur einzelene Kombinationen von Einflussvariablen an. Als meinen Messwert nehme ich dann immer die Sprungweite als einen normalverteilten Messwert.
R Code [zeigen / verbergen]
flea_model_tbl <- read_excel("data/fleas_model_data.xlsx") |>
mutate(feeding = as_factor(feeding),
stage = as_factor(stage),
bonitur = as.numeric(bonitur),
infected = as_factor(infected))Da der Datensatz so groß ist, schaue ich mir hier nicht alle möglichen Abbildungen an sondern gebe dir hier einmal einen Auszug aus der Tabelle wieder. Wie du siehst haben wir einiges an Möglichkeiten mit den Daten. Wir haben hier verschiedene Einflussvariablen sowie verschiedene Messwerte vorliegen.
| .id | feeding | stage | weight | hatched | K | Mg | CRP | Hb | BSG | jump_length | count_leg | count_leg_left | count_leg_right | bonitur | infected | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | sugar_water | adult | 16.42 | 516.41 | 33.67 | 17.8 | 9.74 | 108.18 | 50.31 | 77.2 | 63 | 64 | 62 | 4 | 1 | 3971.61 |
| 2 | sugar_water | adult | 12.62 | 363.5 | 41.93 | 17.54 | 8.22 | 112.81 | 47.63 | 56.25 | 55 | 56 | 54 | 1 | 0 | 2064.13 |
| 3 | sugar_water | adult | 15.57 | 303.01 | 39.41 | 17.11 | 7.55 | 96.17 | 47.42 | 73.42 | 112 | 112 | 111 | 2 | 0 | 1763.43 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 46 | ketchup | juvenile | 7.18 | 429.18 | 32.45 | 19.53 | 15.67 | 81.7 | 15.6 | 83.38 | 423 | 420 | 425 | 4 | 1 | 20623.49 |
| 47 | ketchup | juvenile | 6.6 | 629.58 | 28.84 | 21.37 | 15.27 | 80.79 | 19.44 | 104.48 | 548 | 548 | 547 | 5 | 1 | 25149.36 |
| 48 | ketchup | juvenile | 4.19 | 192.66 | 26.61 | 20.06 | 13.95 | 80.32 | 16.07 | 130.18 | 869 | 872 | 866 | 5 | 0 | 21972.23 |
In den folgenden Abschnitten nehem ich dann immer wieder einzelne Einflussvariablen und kombiniere diese miteinander in ein statistsiches Modell. Dabei nehme ich als Messwert immer die Sprungweite der Flöhe. Mehr Informationen findest du dann im Kapitel zu von der Modellierung der Flöhe. Dort sind dann auch die Einheiten und übersichtliche Abbildungen zu finden.
Theoretischer Datensatz
Abschließend kommen wir noch zu einem theoretischen Datensatz dem ich Kéry (2010) entlehnt habe. Ich möchte nochmal zeigen, wie R intern mit der Modellmatrix die Berechnungen durchführt. Das hat mich interessiert und deshalb habe ich es einmal für mein Verständnis aufgeschrieben. Wenn es dich auch interessiert, dann kannst du in den entsprechenden Tabs weiter unten einmal nachschauen. Hier also erstmal ein sehr simpler theoretischer Datensatz zu Körperlängen von Schlangen. Wir müssen hier dann noch die Faktoren einmal umwandeln, damit wir auch später die Modellmatrix sauber vorliegen haben. Deshalb hier die explizite Benennung der Level der Faktoren in dem Datensatz.
R Code [zeigen / verbergen]
snake_tbl <- read_xlsx("data/regression_data.xlsx", sheet = "theory_mult") |>
mutate(region = factor(region, levels = c("west", "nord")),
color = factor(color, levels = c("schwarz", "rot", "blau")))In der folgenden Tabelle ist der Datensatz snake_tbl nochmal dargestellt. Wir haben die Schlangenlänge svl als Messwert sowie das Gewicht der Schlangen mass sowie den Durchmesser der Schlange \(diameter\) als kontinuierliche Einflussvariable, die Sammelregion region und die Farbe der Schlangen color und als kategoriale Einflussvariablen mit unterschiedlichen Anzahlen an Gruppen. Die Region region ist also ein Faktor mit zwei Leveln und die Schlangenfarbe color ein Faktor mit drei Leveln. Ich nutze den Datensatz also einmal als einen Spieldatensatz um die Modellierung theoretisch besser nachvollziehen zu können.
| svl | mass | diameter | region | color |
|---|---|---|---|---|
| 40 | 6 | 9 | west | schwarz |
| 45 | 8 | 3 | west | schwarz |
| 39 | 5 | 6 | west | rot |
| 51 | 7 | 7 | nord | rot |
| 52 | 9 | 5 | nord | rot |
| 57 | 11 | 4 | nord | blau |
| 58 | 12 | 10 | nord | blau |
| 49 | 10 | 11 | nord | blau |
Damit haben wir dann auch die beiden Datensätze zusammen. Im Folgenden gehe ich dann einmal auf das kausale Modell sowie das prädktive Modell ein. Hier nimmt das kausale Modell mehr Platz ein, da wir eigentlich in der multiplen Regression mehr an dem Zusammenhang interessiert sind. Die Prädiktion ist aber immer mehr im Vormarsch und es kommt hier wirklich auf deine Fragestellung an. Es kann sogar sein, dass du mit vorgesagten Werten mehr Informationen aus deinen Daten ziehen kannst, als mit einem kausalen Modell.
46.5 Kausales Modell
Was ist das kausale Modell? Wir wollen wissen, welchen Einfluss die Einflussvariablen auf den Messwert haben. Das ist jetzt erstmal einleuchtend. Wir bauen uns ein Modell und wollen wissen, ob es einen kausalen Zusammenhang zwischen einzelnen Kovariaten oder Faktoren und einem Messwert gibt. Dabei müssen nicht alle Kovariaten und alle Faktoren einen signifikanten Einfluss haben. Es geht hier eher um eine Art vor und zurück. Wir probieren verschiedene Modell aus und wollen das beste Modell finden. Dafür müssen wir abr verstehen, was die Interpretation der einzelnen Modell ist. Daher schauen wir uns jetzt einmal rein kovariate Modelle, reine faktorielle Modelle und Kombinationen davon an.
46.5.1 Mehrkovariates Modell
Beginnen wir mit einem mehrkovariaten Modell. Im Gegensatz zu einem einkovaraten Modell in der simplen linearen Regression haben wir jetzt nicht mehr nur eine Kovariate sondern mindestens zwei Kovariaten im Modell. Für die Interpretation nutzen wir hier nur ein zweikovariates Modell inhaltlich lässt sich das Modell aber auch auf mehr als zwei Kovariaten erweitern. In der folgenden Abbildung siehst du einmal das Modell dargestellt. Wir haben einen Messwert auf der linken Seite und zwei Kovariaten auf der rechten Seite. Wir wollen jetzt wissen, wie die beiden Kovariaten den Messwert erklären.
Die Grundidee ist in der folgenen Abbildung einmal dargestellt. Du kennst dich ja schon mit der simplen linearen Regression aus. In dem mehrkovariaten Fall haben wir nun im zweikovariaten Fall einen Scatterplit in drei Dimensionen vorliegen. Je mehr Kovariaten desto hoöher wird die Dimension. Ich kann aber nicht einen vier dimensionalen Scatterplot darstellen, daher hier die Einschränkung auf zwei Kovariaten. Wie du siehst zeichnen wir jetzt nicht eine Grade im eigentlichen Sinne sondern eine Ebene durch die Punkte hindurch. Dennoch wird der quadratische Abstand zu den Punkten eben über diese Ebene minimiert. Wir erhalten somit auch nur für jede einzelne Beobachtung einen Wert für die Residuen wieder.
Die Darstellung einer multiplen linearen Regression ist vollkommen unüblich. Wir zeigen eigentlich nicht die Daten als Visualisierung sondern müssen uns dann mit statistischen Maßzahlen helfen, wenn wir wissen wollen, ob unsere Regression gelungen ist. Deshalb auch im Folgenden einmal die praktische Anwendung in R und wie wir die zweikovariate Regression interpretieren.
Dann rechnen wir einmal eine zweikovariate Analyse in R. Dafür brauchen wir einmal einen normalverteilten Messwert. Das ist nicht notwendig, aber für die Interpretation gleich viel einfacher. Dann nehmen wir noch die zwei Kovariten des Flohgewichts und der mitleren Anzahl an Beinhaaren mit ins Modell. Damit haben wir also ein klassisches kovariates Modell.
R Code [zeigen / verbergen]
cov2_fit <- lm(jump_length ~ weight + count_leg, data = flea_model_tbl) Dann können wir uns auch schon die drei Koeffizienten für den Intercept und die Steigungen für die beiden Kovariaten wiedergeben lassen. Da wir das Modell so rechnen, dass wir beide Kovariaten mit ins Modell nehmen, haben wir hier natürlich auch jeweils für die anderen Kovariate den Effekt adjustiert. Will heißen, wir schauen uns den Effekt des Gewichts bereinigt um den Effekt der Beinhaare auf die Sprungweiten an. Und eben umgekehrt dann auch.
R Code [zeigen / verbergen]
cov2_fit |>
coef() |> round(2)(Intercept) weight count_leg
52.71 1.58 0.10 Jetzt müssen wir bei den Koeffizienten aufpassen. Ohne die Einheit, würde man denken, dass der Effekt der mittleren Beinzahl auf die Sprungweite klein wäre. Aber wir haben hier die Steigung pro Änderung der Einheit um Eins in den Einflussvariablen. Die Beinhaare haben aber eine Spannweite von 9 bis 1351! Das ist eine ganz andere Änderung als beim Gewicht mit einer Spannweite von 2.71mg bis 25.73mg. Deshalb brauchen wir auch hier dann die zusammenfassende Ausgabe um einmal die Signifikanz bewerten zu können.
R Code [zeigen / verbergen]
cov2_fit |> summary()
Call:
lm(formula = jump_length ~ weight + count_leg, data = flea_model_tbl)
Residuals:
Min 1Q Median 3Q Max
-24.985 -12.823 -3.065 8.259 49.525
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 52.708201 6.389140 8.250 1.50e-10 ***
weight 1.584911 0.490155 3.233 0.00229 **
count_leg 0.098382 0.008789 11.193 1.35e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 17.78 on 45 degrees of freedom
Multiple R-squared: 0.7359, Adjusted R-squared: 0.7242
F-statistic: 62.71 on 2 and 45 DF, p-value: 9.728e-14Die Zusammenfassugn ist manchmal etwas schwer zu lesen, deshalb habe ich dir einmal die Ausgabe im Folgenden annotiert. Hier siehst du dann auch sehr schön, dass die mittlere Anzahl an Haaren auf den Beinen auch signifikant ist. Ansonsten sieht unser Modell recht gut aus. die Resdiuen sind einigermaßen normalverteilt und auch das Bestimmtheitsmaß ist relativ hoch. Der Fehler der Residuen könnte mit 17.78 etwas kleiner sein. Am Ende passt das Modell.
summary() aus einer linearen Modellanpassung mit der Funktion lm(). Die Ausgabe der Funktion teilt sich grob in drei informative Bereiche: Informationen zu den Residuen, Informationen zu den Koeffizienten und Informationen zu der Modelgüte. [Zum Vergrößern anklicken]
Was sagt jetzt noch diese seltsame ANOVA aus? Wir scheinen hier ja noch eine ANOVA am Ende zu rechnen. Das ist hier jetzt nicht die einfaktorielle ANOVA, die wir aus den simplen linearen Regressionen kennen, sondern beinhaltet einen Modellvergleich. Welche Modelle vergleichen wir aber nun? In diesem Fall einmal das Nullmodell und das volle Modell, welches wir gerechnet haben. Was soll der Name Nullmodell bedeuten? Wir haben in diesem Modell nichts weiter außer dem Intercept. Hier einmal das Nullmodel gerechnet.
R Code [zeigen / verbergen]
lm(jump_length ~ 1, data = flea_model_tbl)
Call:
lm(formula = jump_length ~ 1, data = flea_model_tbl)
Coefficients:
(Intercept)
93.19 Wir erhalten also einmal den globalen Mittelwert über alle Sprungweiten wiedergeben. Jetzt können wir mit der ANOVA auch einen MOdellvergleich rechnen. Wir wollen wissen, ob sich unser volles zweifaktorielles Modell von dem Modell nur mit dem Intercept unterscheidet. Da sehen wir wieder den p-Wert wie wir ihn auch oben in der Ausgabe haben.
R Code [zeigen / verbergen]
anova(lm(jump_length ~ 1, data = flea_model_tbl),
lm(jump_length ~ weight + count_leg, data = flea_model_tbl))Analysis of Variance Table
Model 1: jump_length ~ 1
Model 2: jump_length ~ weight + count_leg
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 53886
2 45 14229 2 39657 62.71 9.728e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Brauchen wir den Vergleich? Meistens nicht. Denn wir können ja direkt schauen, ob sich die Koeffizienten sigifkant von Nhull unterscheiden. Dann brauchen wir auch nur sehr selten den Vergleich zu dem Nullmodell. Das Nullmodell beinhaltet eigentlich nie eine Information, die wir wirklich brauchen. Daher ist es eher ein Artefakt der Programmierung aus den Anfangstagen. Wir können es, also packen wir es mit in die Ausgabe rein.
Die folgende Abbildung dient hier nur der Anschauung. Wir publizieren eigentlich nicht eine Visualisierung in drei Dimensionen. Wie du hier schon siehst, ist die Darstellung durch die unterschiedlich Minima- und Maximawerte des Gewichts und der Anzahl an Beinhaaren sehr verdreht. Häufig sieht dann die Abbildung in drei Dimensionen nur gut aus, wenn alle drei Achsen die gleichen Spannweiten an Werten haben. Daher dient die Abbildung eher nochmal zum Verständnis der Berechnungen der Residuen aus der Ebene der Regression.
Die folgenden Abschnitte wiederholen sich für jedes Modell, da am Ende alles sehr gleich ist. Ich empfehle einmal es selber nachzuvollziehen. Ich habe beim Schreiben am meisten gelernt.
Intern rechnet R eine Modellmatrix. Was ist eine Modellmatrix? Eine Modellmatrix beinhaltet die Informationen welche Koeffizienten für welche Beobachtungen genutzt werden sollen um am Ende auf den Messwert für jede Beobachtung zu kommen. Faktisch also eine Zuordnung der Koeffizienten und Residuen zu den einzelnen Beobachtungen. Daher hat auch eine Modellmatrix immer so viele Zeilen wie Beobachtungen.
Damit wir hier nicht verrückter werden als wir schon sind, nutze ich den Schlangendatensatz. Wir haben also die Körperlänge vorliegen und wollen dann anhand von zwei Kovariaten den Zusammenhang darstellen. Daher ergibt sich folgende Modellmatrix.
R Code [zeigen / verbergen]
model.matrix(svl ~ mass + diameter, data = snake_tbl) |> as_tibble() # A tibble: 8 × 3
`(Intercept)` mass diameter
<dbl> <dbl> <dbl>
1 1 6 9
2 1 8 3
3 1 5 6
4 1 7 7
5 1 9 5
6 1 11 4
7 1 12 10
8 1 10 11Wir können die Modellmatrix auch einmal im Ganzen aufschreiben, dann macht es auch mehr Sinn. Hier musst du dann wissen, dass wir in der Matrixmultiplikation, die erste Spalte mit dem ersten Koeffizienten malnehmen. Die zweite Spalte dann mit dem zweiten Koeffizienten malnehmen und so weiter.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 50 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 1 & 6 & 9 \\ 1 & 8 & 3 \\ 1 & 5 & 6 \\ 1 & 7 & 7 \\ 1 & 9 & 5 \\ 1 & 11& 4 \\ 1 & 12& 10 \\ 1 & 10& 11 \\ \end{pmatrix} \times \begin{pmatrix} \beta_0 \\ \beta_{mass} \\ \beta_{diameter} \\ \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \epsilon_6 \\ \epsilon_7 \\ \epsilon_8 \\ \end{pmatrix} \]
Dann rechnen wir einmal das zweikovariate Modell und schauen welche Koeffizienten wir erhalten.
R Code [zeigen / verbergen]
cov2_fit <- lm(svl ~ mass + diameter, data = snake_tbl)Wir runden jetzt einmal, damit wir nicht so viel in die Modellmatrix schreiben müssen.
R Code [zeigen / verbergen]
cov2_fit |> coef() |> round(2)(Intercept) mass diameter
28.27 2.67 -0.30 Dann brauchen wir noch die Residuen.
R Code [zeigen / verbergen]
cov2_fit |> residuals() |> round(2) 1 2 3 4 5 6 7 8
-1.56 -3.71 -0.80 6.17 1.22 0.58 0.73 -2.63 Am Ende baue ich dann einmal das volle Modell mit der Modellmatrix auf. Auf der linken Seite siehst du die Körperlängen. Dann kommt der Intercept gefolgt von den Koeffizienten multipliziert mit den Kovariaten. Am Ende addieren wir dann noch die Residuen.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 28.27 & 6 \cdot 2.67 & 9 \cdot -0.30 \\ 28.27 & 8 \cdot 2.67 & 3 \cdot -0.30 \\ 28.27 & 5 \cdot 2.67 & 6 \cdot -0.30 \\ 28.27 & 7 \cdot 2.67 & 7 \cdot -0.30 \\ 28.27 & 9 \cdot 2.67 & 5 \cdot -0.30 \\ 28.27 & 11 \cdot 2.67 & 4 \cdot -0.30 \\ 28.27 & 12 \cdot 2.67 & 10 \cdot -0.30 \\ 28.27 & 10 \cdot 2.67 & 11 \cdot -0.30 \\ \end{pmatrix} + \begin{pmatrix} -1.56 \\ -3.71 \\ -0.80 \\ +6.17 \\ +1.22 \\ +0.58 \\ +0.73 \\ -2.63 \\ \end{pmatrix} \]
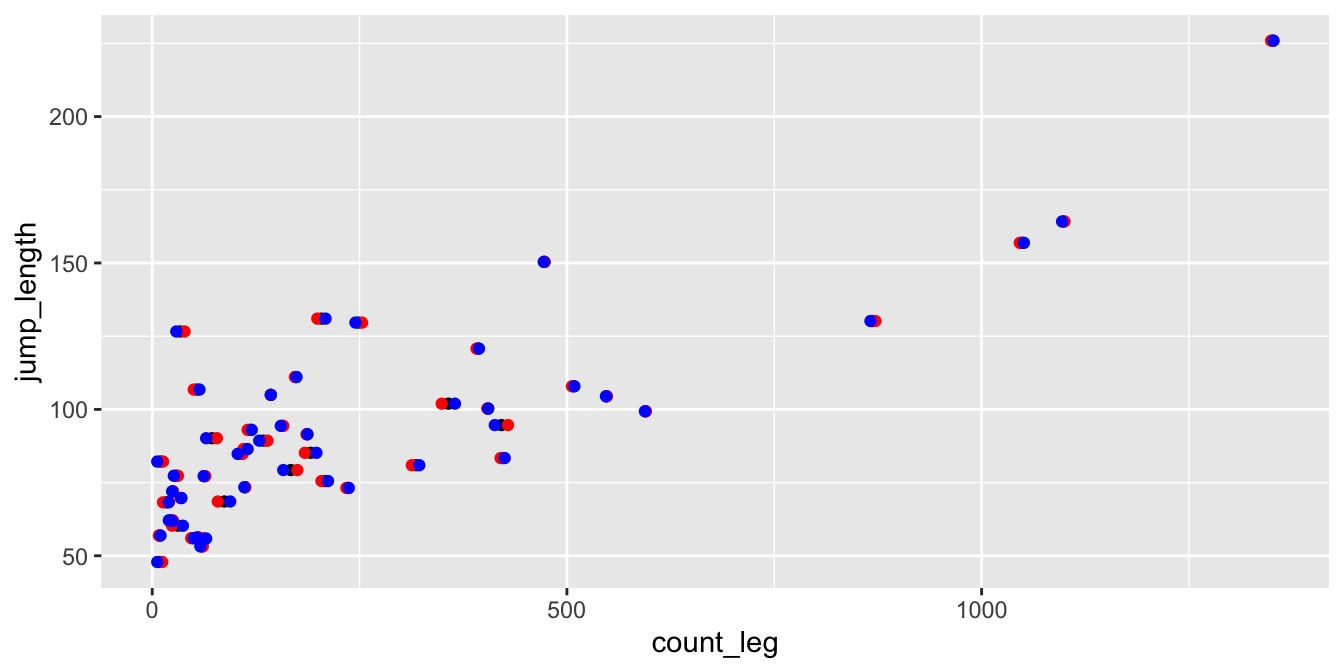
Jetzt kannst du dich fragen, kommt das denn auch hin? Dafür alles nochmal in R getippt und geschaut welche Zahlen am Ende für die Körperlänge rauskommen.
R Code [zeigen / verbergen]
c(28.27 + 6*2.67 + 9*(-0.30) - 1.56,
28.27 + 8*2.67 + 3*(-0.30) - 3.71,
28.27 + 5*2.67 + 6*(-0.30) - 0.80,
28.27 + 7*2.67 + 7*(-0.30) + 6.17,
28.27 + 9*2.67 + 5*(-0.30) + 1.22,
28.27 + 11*2.67 + 4*(-0.30) + 0.58,
28.27 + 12*2.67 + 10*(-0.30) + 0.73,
28.27 + 10*2.67 + 11*(-0.30) - 2.63) |> round()[1] 40 45 39 51 52 57 58 49Und dann hier nochmal der Vergleich zu den ursprünglichen Werten der Körperlänge der Schlangen. Das passt ja hervorragend.
R Code [zeigen / verbergen]
snake_tbl |> pull(svl)[1] 40 45 39 51 52 57 58 49Musst du das hier im Detail verstehen? Kommt drauf an. Hier wird eben dargestellt wie sich in R intern die Koeffizienten ergeben. Das macht dann eben auch was aus für die Interpretation. Je nachdem wie sich dein Modell zusammensetzt ist dann auch die Modellmatrix komplizierter.
Dieser Abschnitt beinhaltet eine kurze Simulation in R mit einem Tibble und der Erstellung eines normalverteilten Messwerts. Mehr zu der Generierung von Daten dann im entsprechenden Kapitel. Ich habe alles ausgelagert, da es dann hier zu voll wurde. Daher ist es hier eher so eine kleine Spielweise.
R Code [zeigen / verbergen]
cov2_tbl <- tibble(c_1 = rnorm(10, 0, 1),
c_2 = rnorm(10, 0, 1),
y = 2 +
1 * c_1 +
2 * c_2 +
rnorm(10, 0, 0.001))Dann schauen wir uns einmal an, ob wir dann den Intercept und die Koeffizienten wiederfinden. Wenn du den Fehler in rnorm() von \(0.001\) hochsetzt, dann werden auch die Koeffizienten in dem folgenden Modell ungenauer. Hat aber gut geklappt, wir erhalten die gerundeten Koeffizienten, die wir eingestellt hatten einigermaßen wiedergegeben.
R Code [zeigen / verbergen]
lm(y ~ c_1 + c_2, cov2_tbl) |>
coef() |> round(2)(Intercept) c_1 c_2
2 1 2 46.5.2 Mehrfaktorielles Modell
Betrachten wir nun ein mehrfaktorielles Modell. Hier sei aber gleich gesagt, dass wir eigentlich in einem mherfaktoriellen Modell an den Vergleichen der Level in den Faktoren interessiert sind. Wir wollen also eigentlich einen paarweisen Vergleich über die Gruppen rechnen. Damit sind wir dann auf dem ANOVA Pfad mit der ANOVA und den Post-hoc Tests. Wir schauen uns hier also erstmal die Koeffizienten des Modells an, sehr häufig nutzen wir diese Koeffizienten dann aber nicht. Das hat den Grund, dass der Referenzwert ja der Interecept im Modell ist und wir wenig an dem Vergleich zu dem Intercept interessiert sind. Dazu dann aber gleich mehr. Hier dann erstmal das zweifaktorielle Modell mit dem Interaktionsterm. Zu der Interaktion kannst du im Kapitel zur ANOVA mehr erfahren.
Im Folgenden wollen wir also einmal ein multiples Modell rechnen und die Koeffizienten für die einzelnen Faktoren ermitteln. Dabei hat es dann eine Auswirkung wie viele Level ein Faktor hat und wie wir das Modell bauen. Wir machen hier gleich das volle Modell mit Interaktion. Ohne die Interaktion lassen sich dann die Koeffizienten etwas leichter zu interpretieren. Am Ende ist es dann doch die ANOVA, die wir eigentlich wollen. Hier also bitte nicht verwirren lassen, es kommt immer auf die wissenschaftliche Fragestellung an.
Beginnen wir wieder mit dem zweifaktoriellen Modell. Wir nehmen hier beide Faktoren mit ins Modell und wollen auch den Interaktionsterm mit modellieren. Wenn wir den Interaktionsterm weglassen, dann können wir die Koeffizienten des Modells etwas leichter interpretieren. Wenn also unsere Interaktion nicht signifikant ist, dann kannst du die Interaktion auch aus dem Modell entfernen und so es etwas einfacher machen.
R Code [zeigen / verbergen]
fac2_fit <- lm(jump_length ~ feeding + stage + stage:feeding, data = flea_model_tbl) Jetzt erhalten wir die Koeffizienten des Modells mit einem Intercept und der Steigung zu den einzelnen Gruppenmittelwerten. Oder anders ausgedrückt, die Differenz der Gruppenmittelwerte zum Intercept. Dazu dann noch die Koeffizienten der Interaktion. Hier sehen wir noch nicht, ob die Koeffizienten der Interaktion signifikant sind.
R Code [zeigen / verbergen]
fac2_fit |>
coef() |> round(2) (Intercept) feedingblood
78.98 20.73
feedingketchup stagejuvenile
13.17 -17.94
feedingblood:stagejuvenile feedingketchup:stagejuvenile
34.26 37.03 Jetzt müssen wir uns einmal die Zusammenfassung des Modells wiedergeben lassen, damit wir abschätzen können, ob unsere Koeffizienten signifikant sind. Auch erhalten wir die statistischen Maßzahlen für die Modelgüte wiedergegeben. Unser Interaktion ist für beide Koeffizienten nicht signifikant, daher könnten wir die Interaktion auch aus dem Modell nehmen.
R Code [zeigen / verbergen]
fac2_fit |> summary()
Call:
lm(formula = jump_length ~ feeding + stage + stage:feeding, data = flea_model_tbl)
Residuals:
Min 1Q Median 3Q Max
-55.340 -16.617 -3.921 11.003 109.901
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 78.98 10.48 7.539 2.48e-09 ***
feedingblood 20.73 14.81 1.400 0.1690
feedingketchup 13.17 14.81 0.889 0.3790
stagejuvenile -17.94 14.81 -1.211 0.2326
feedingblood:stagejuvenile 34.26 20.95 1.635 0.1095
feedingketchup:stagejuvenile 37.03 20.95 1.768 0.0844 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 29.63 on 42 degrees of freedom
Multiple R-squared: 0.3158, Adjusted R-squared: 0.2343
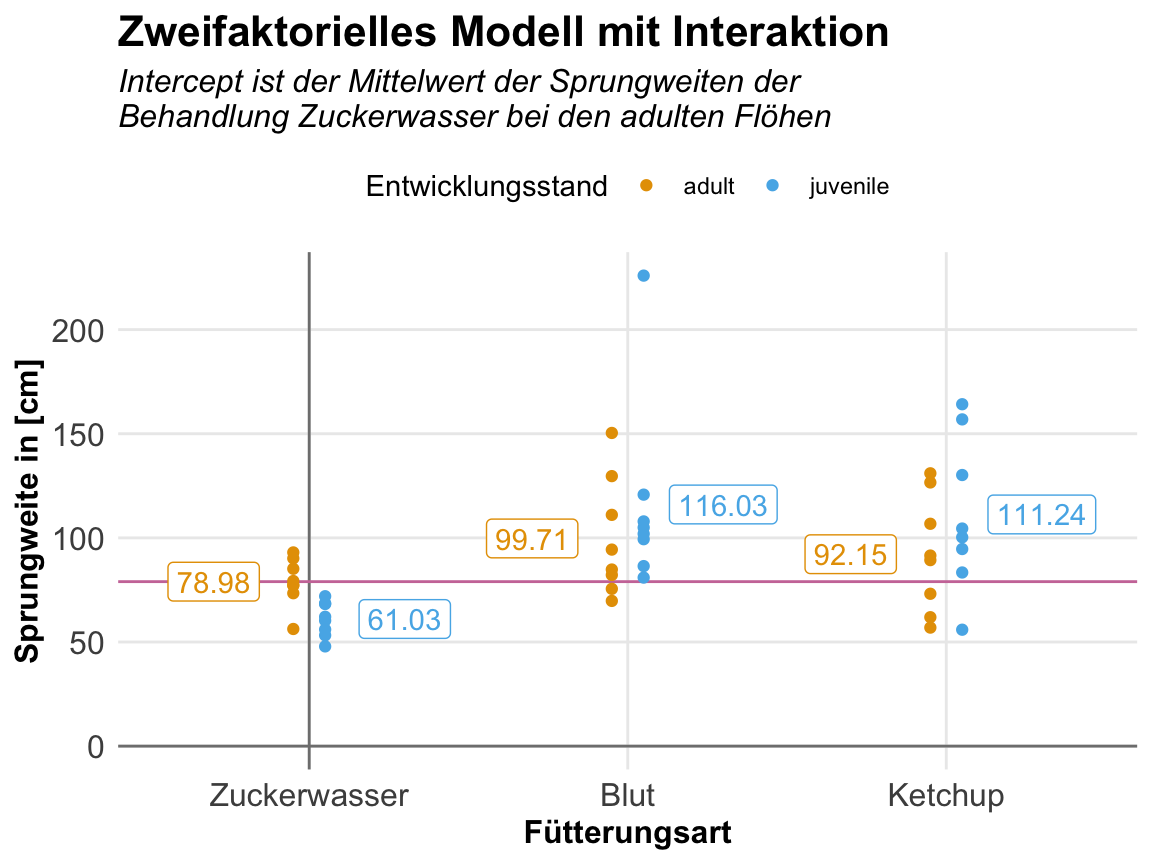
F-statistic: 3.877 on 5 and 42 DF, p-value: 0.005594Dann habe ich dir in der folgenden Abbildung nochmal die Ausgabe der Zusammenfassung annotiert. Der spannendeste Teil ist eigentlich, was der Intercept repräsentiert. Der Intercept ist nämlich das lokale Gruppenmittel der Behandlung Zuckerwasser für die adulten Flöhe. Dann haben wir die einzlenen statistischen Tests, ob sich die Koeffizienten von Null unterscheiden. Somit eigentlich die Frage, ob die lokalen Mittelwerte der Gruppen sich vom Intercept unterscheiden.
summary() aus einer linearen Modellanpassung mit der Funktion lm(). Die Ausgabe der Funktion teilt sich grob in drei informative Bereiche: Informationen zu den Residuen, Informationen zu den Koeffizienten und Informationen zu der Modelgüte. Die Erklärung der Schätzer (eng. estimate) kann in der folgenden Tabelle nachvollzogen werden. [Zum Vergrößern anklicken]
Das Ganze mag etwas kryptisch sein, aber das Ziel ist es eigentlich die Mittelwerte der Faktorkombinationen abzubilden. Wir haben hier etwas Glück, dass die Residuen faktisch Null sind und somit keien Rolle spielen, wie du im Folgenden siehst. Sonst müssten wir die Werte der Residuen natürlich immer nochmal berücksichtigen. Das kannst du dann in den kombinierten Modellen teilweise beobachten.
R Code [zeigen / verbergen]
fac2_fit |>
augment() |>
group_by(feeding, stage) |>
summarise(mean_resid = round(mean(.resid), 2))# A tibble: 6 × 3
# Groups: feeding [3]
feeding stage mean_resid
<fct> <fct> <dbl>
1 sugar_water adult 0
2 sugar_water juvenile 0
3 blood adult 0
4 blood juvenile 0
5 ketchup adult 0
6 ketchup juvenile 0In der folgenden Tabelle habe ich dir einmal gezeigt, wie wir von den Koeffizienten auf die Mittelwerte der Sprungweiten in den einzelnen Gruppen der Faktorkombinationen kommen. Jetzt siehst du auch, dass die Koeffizienten nur einen sehr kleinen Teil der Unterschiede in den Sprungweiten beschreiben. Daher nutzen wir dann lieber Post-hoc Tests um alle paarweisen Mittelwertsvergleiche rechnen zu können.
| \(f_{feeding}\) | \(f_{stage}\) | \(\bar{Y}\) | \(\boldsymbol{\beta_{0}}\) | \(\boldsymbol{\beta_{blood}}\) | \(\boldsymbol{\beta_{ketchup}}\) | \(\boldsymbol{\beta_{juvenile}}\) | \(\boldsymbol{\beta_{blood \times juvenile}}\) | \(\boldsymbol{\beta_{ketchup \times juvenile}}\) | \(\boldsymbol{\epsilon}\) |
|---|---|---|---|---|---|---|---|---|---|
| sugar | adult | 78.90 | 78.98 | 0 | |||||
| sugar | juvenile | 61.03 | 78.98 | -17.94 | 0 | ||||
| blood | adult | 99.71 | 78.98 | 20.73 | 0 | ||||
| blood | juvenile | 116.03 | 78.98 | 20.73 | -17.94 | 34.26 | 0 | ||
| ketchup | adult | 92.15 | 78.98 | 13.17 | 0 | ||||
| ketchup | juvenile | 111.24 | 78.98 | 13.17 | -17.94 | 37.03 | 0 |
Dann wird dir alles wahrscheinlich klarer, wenn wir uns nochmal die Abbildung zu dem zweifaktoriellen Versuch anschauen. Wir haben hier unsere y-Achse mit dem Intercept direkt durch den lokalen Gruppenmittelwert der adulten Flöhe, die Zuckerwasser trinken. Dann kannst du die jeweiligen Abweichungen aus der obigen Tabelle der Mittelwerte in der Abbildung nachvollziehen.
Die folgenden Abschnitte wiederholen sich für jedes Modell, da am Ende alles sehr gleich ist. Ich empfehle einmal es selber nachzuvollziehen. Ich habe beim Schreiben am meisten gelernt.
Intern rechnet R eine Modellmatrix. Was ist eine Modellmatrix? Eine Modellmatrix beinhaltet die Informationen welche Koeffizienten für welche Beobachtungen genutzt werden sollen um am Ende auf den Messwert für jede Beobachtung zu kommen. Faktisch also eine Zuordnung der Koeffizienten und Residuen zu den einzelnen Beobachtungen. Daher hat auch eine Modellmatrix immer so viele Zeilen wie Beobachtungen.
Damit wir hier nicht verrückter werden als wir schon sind, nutze ich den Schlangendatensatz. Wir haben also die Körperlänge vorliegen und wollen dann anhand von zwei Faktoren den Zusammenhang darstellen. Ich lassen hier aus Gründen der Einfachheit die Interaktion weg. Der Datensatz ist auch zu klein für eine saubere Darstellung einer Interaktion. Daher ergibt sich folgende Modellmatrix.
R Code [zeigen / verbergen]
model.matrix(svl ~ color + region, data = snake_tbl) |> as_tibble() # A tibble: 8 × 4
`(Intercept)` colorrot colorblau regionnord
<dbl> <dbl> <dbl> <dbl>
1 1 0 0 0
2 1 0 0 0
3 1 1 0 0
4 1 1 0 1
5 1 1 0 1
6 1 0 1 1
7 1 0 1 1
8 1 0 1 1Wir können die Modellmatrix auch einmal im Ganzen aufschreiben, dann macht es auch mehr Sinn. Hier musst du dann wissen, dass wir in der Matrixmultiplikation, die erste Spalte mit dem ersten Koeffizienten malnehmen. Die zweite Spalte dann mit dem zweiten Koeffizienten malnehmen und so weiter. Hier siehst du dann auch, dass nicht jede Beobachtung für jeden Koeffizienten berücksichtigt wird. Die Faktoren werden anhand ihrer Level aufgespalten und das erste Level wandert immer in den Intercept. Wir sprechen auch von einer Dummykodierung.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 50 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ \end{pmatrix} \times \begin{pmatrix} \beta_0 \\ \beta^{color}_{rot} \\ \beta^{color}_{blau} \\ \beta^{region}_{nord} \\ \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \epsilon_6 \\ \epsilon_7 \\ \epsilon_8 \\ \end{pmatrix} \]
Dann rechnen wir einmal das zweifaktorielle Modell und schauen welche Koeffizienten wir erhalten.
R Code [zeigen / verbergen]
fac2_fit <- lm(svl ~ color + region, data = snake_tbl)Wir runden jetzt einmal, damit wir nicht so viel in die Modellmatrix schreiben müssen.
R Code [zeigen / verbergen]
fac2_fit |> coef() |> round(2)(Intercept) colorrot colorblau regionnord
42.50 -3.50 -0.33 12.50 Dann brauchen wir noch die Residuen.
R Code [zeigen / verbergen]
fac2_fit |> residuals() |> round(2) 1 2 3 4 5 6 7 8
-2.50 2.50 0.00 -0.50 0.50 2.33 3.33 -5.67 Am Ende baue ich dann einmal das volle Modell mit der Modellmatrix auf. Auf der linken Seite siehst du die Körperlängen. Dann kommt der Intercept gefolgt von den Koeffizienten multipliziert mit den Dummykodierungen. Am Ende addieren wir dann noch die Residuen.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 42.50 & 0 \cdot -3.50 & 0 \cdot -0.33 & 0 \cdot 12.50 \\ 42.50 & 0 \cdot -3.50 & 0 \cdot -0.33 & 0 \cdot 12.50 \\ 42.50 & 1 \cdot -3.50 & 0 \cdot -0.33 & 0 \cdot 12.50 \\ 42.50 & 1 \cdot -3.50 & 0 \cdot -0.33 & 1 \cdot 12.50 \\ 42.50 & 1 \cdot -3.50 & 0 \cdot -0.33 & 1 \cdot 12.50 \\ 42.50 & 0 \cdot -3.50 & 1 \cdot -0.33 & 1 \cdot 12.50 \\ 42.50 & 0 \cdot -3.50 & 1 \cdot -0.33 & 1 \cdot 12.50 \\ 42.50 & 0 \cdot -3.50 & 1 \cdot -0.33 & 1 \cdot 12.50 \\ \end{pmatrix} + \begin{pmatrix} -2.50 \\ +2.50 \\ 0.00 \\ -0.50 \\ +0.50 \\ +2.33 \\ +3.33 \\ -5.67 \\ \end{pmatrix} \]
Jetzt kannst du dich fragen, kommt das denn auch hin? Dafür alles nochmal in R getippt und geschaut welche Zahlen am Ende für die Körperlänge rauskommen.
R Code [zeigen / verbergen]
c(42.50 + 0*(-3.50) + 0*(-0.33) + 0*12.50 - 2.50,
42.50 + 0*(-3.50) + 0*(-0.33) + 0*12.50 + 2.50,
42.50 + 1*(-3.50) + 0*(-0.33) + 0*12.50 + 0.00,
42.50 + 1*(-3.50) + 0*(-0.33) + 1*12.50 - 0.50,
42.50 + 1*(-3.50) + 0*(-0.33) + 1*12.50 + 0.50,
42.50 + 0*(-3.50) + 1*(-0.33) + 1*12.50 + 2.33,
42.50 + 0*(-3.50) + 1*(-0.33) + 1*12.50 + 3.33,
42.50 + 0*(-3.50) + 1*(-0.33) + 1*12.50 - 5.67) |> round()[1] 40 45 39 51 52 57 58 49Und dann hier nochmal der Vergleich zu den ursprünglichen Werten der Körperlänge der Schlangen. Das passt ja hervorragend.
R Code [zeigen / verbergen]
snake_tbl |> pull(svl)[1] 40 45 39 51 52 57 58 49Musst du das hier im Detail verstehen? Kommt drauf an. Hier wird eben dargestellt wie sich in R intern die Koeffizienten ergeben. Das macht dann eben auch was aus für die Interpretation. Hier lernen wir dann nochmal, was eigentlich die Dummykodierung bedeutet. Je nachdem wie sich dein Modell zusammensetzt ist dann auch die Modellmatrix komplizierter.
Dieser Abschnitt beinhaltet eine kurze Simulation in R mit einem Tibble und der Erstellung eines normalverteilten Messwerts. Mehr zu der Generierung von Daten dann im entsprechenden Kapitel. Ich habe alles ausgelagert, da es dann hier zu voll wurde. Daher ist es hier eher so eine kleine Spielweise. Beachte auch hier die Interaktion, die als Multiplikation der beiden Faktoren in der Generierung entsteht. Das ist aber dann nur eine Möglichkeit eine Interaktion zu bauen.
R Code [zeigen / verbergen]
fac2_tbl <- tibble(f_a = rep(gl(3, 5), 2),
f_b = gl(2, 15),
y = 2 +
2 * as.numeric(f_a) +
3 * as.numeric(f_b) +
2 * as.numeric(f_a) * as.numeric(f_b) +
rnorm(15, 0, 0.001))Dann schauen wir uns einmal an, ob wir dann den Intercept und die Koeffizienten wiederfinden. Wenn du den Fehler in rnorm() von \(0.001\) hochsetzt, dann werden auch die Koeffizienten in dem folgenden Modell ungenauer. Hat aber gut geklappt, wir erhalten die gerundeten Koeffizienten, die wir eingestellt hatten einigermaßen wiedergegeben.
R Code [zeigen / verbergen]
lm(y ~ f_a + f_b + f_a:f_b, fac2_tbl) |>
coef() |> round(2)(Intercept) f_a2 f_a3 f_b2 f_a2:f_b2 f_a3:f_b2
9 4 8 5 2 4 46.5.3 Kombinierte Modelle
Kommen wir jetzt zu dem wirklich spannenden Teil. Wir kombinieren Kovariaten zusammen mit Faktoren in einem Modell. Zum einen haben wir hier jetzt eine klassische ANCOVA vorliegen, wenn wir an den Faktoren als Haupteffekt interessiert sind. Wenn es eher um die Kovariaten geht, dann ist eben eine klassische Regression. Hier kommt es dann auf die wissenschaftliche Fragestellung an. Wollen wir wissen wie sich die Kovariate in den Faktoren ändert oder wollen wir die Faktoren für eine Kovariate adjustieren? Das kannst nur du beantworten.
- Was passiert wenn wir eine Kovariate und einen Faktor kombinieren?
-
Wenn wir eine Kovariate mit einem Faktor kombinieren, dann kippen wir den Intercept der Graden um die Steigung der Kovariate. Die Level der Faktoren liegen dann auf den Mittelwerten der Kovariaten für das entsprechende Level des Faktors. Wenn wir dann noch eine Interaktion hinzunehmen, dann erlauben wir jedem Level des Faktors eine eigene Steigung der Kovariaten.
Das erstmal die sehr allgemeine Beschreibung. mehr dazu dann gleich in der Durchführung in R. Ich hoffe, dass dann das ein oder andere nochmal klarer wird. Wir wollen uns insgesamt drei Typen von multiplen Regressionen anschauen. Einmal das kombinierte Modell mit einem Faktor und einer Kovariate. Dann das gleiche Modell nur mit einm Faktor mehr. Am Ende dann noch das zweikovariate und zweifaktorielle Modell. Weiter unten diskutiere ich dann noch die Modellauswahl, wenn du dich fragst, wie viel der Einflussvariablen sollen denn jetzt in ein Modell mit rein.
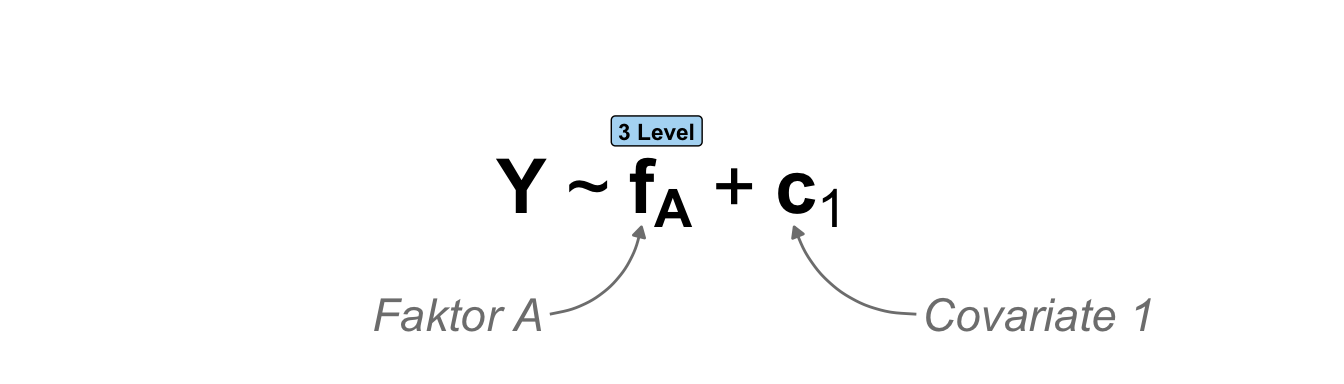
\(f_A + c_1\)
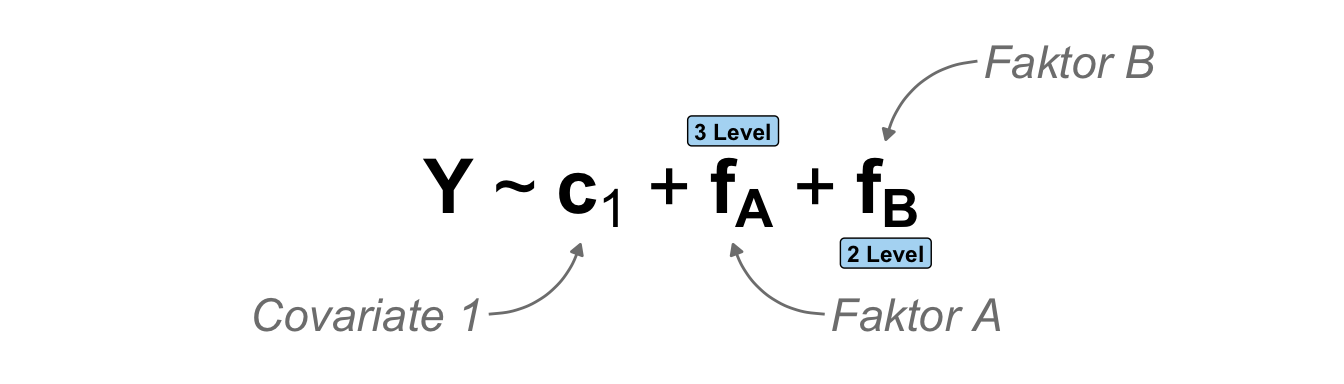
Beginnen wir ein kombiniertes Modell mit einem Faktor und einer Kovariate. Wenn es hier mit einem faktoriellen Experiment zu tun haben in dem wir noch eine Kovariate gemessen haben, dann rechnen wir hier eigentlich eine klassische einfaktorielle ANCOVA (eng. analysis of covariance). Daher kommt es immer etwas auf die Perspektive an. Wenn wir einfach nur Daten beobachtet haben und eine Kovariate sowie einen Faktor erhoben haben, dann mag die multiple Regression eine bessere Möglichkeit zur Interpretation der Daten sein. In der folgenden Abbildung zeige ich dir nochmal das schematische Modell mit einem Faktor mit drei Leveln sowie einer Kovariate.
Dann wollen wir einmal das kombinierte Modell mit einer Kovariate und einem Faktor in R rechnen. Dann kannst du dir nochmal die Berechnung theoretisch anschauen sowie eine kleine Simulation. Hier zeige ich dir auch nochmal die Auswirkungen der Interaktion zwischen der Kovariate und dem Faktor. Das lässt sich in dem einfachen Fall hier am besten zeigen.
Wir haben jetzt die Wahl einmal das kombinierte Modell mit einem Interaktionsterm oder ohne einen Interaktionsterm für die Kovariate und den Faktor anzuschauen. Ich mache in diesem einfachen Beispiel dann nochmal beides. Wenn du jetzt denkst, dass wir eigentlich ja keine Interaktion mit Kovariaten als kontinuierlichen Einflussvariablen rechnen können stimmt es nur bedingt. Wir ja einen Faktor und wir haben die mittleren Werte der Kovariaten für die jeweiligen Faktorlevel. Damit können wir dann auch eine Interaktion mit bestimmen. Aber das wird vermutlich gleich im Beispiel klarer.
Dann wollen wir einmal im Folgenden uns den Einfluss der Ernährung auf die Sprungweite der Flöhe anschauen. Wir mitteln hier über die beiden Entwicklungsstadien, da wir das Alter der Flöhe in dem Modell hier ignorieren. Wir nutzen ja nur einen Faktor. Dann nehmen wir noch den Kaliumgehalt im Blut der Flöhe als eine Kovariate mit in das Modell hinein. Damit würden wir dann auch sagen, dass wir die Ernährungsbedingungen um den Kaliumgehalt im Blut adjustieren. Wir nutzen ununterbrochen das Wort Adjustieren in jeglichen Kontexten in der Statistik. Es ist manchmal dann nicht so einfach.
Ohne Interaktion
Wenn wir das kombinierte Modell mit einem Faktor und einer Kovariate ohne Interaktion bauen, dann nehmen wir einfahc die beiden Einflussvariablen in das Modell und schauen uns an, was die Koeffizienten ergeben. Hier nehmen wir dann die Ernährung und den Kaliumgehalt im Blut der Flöhe.
R Code [zeigen / verbergen]
cov1_fac1_fit <- lm(jump_length ~ feeding + K, data = flea_model_tbl) Dann können wir uns auch schon gleich die Koeffizienten einmal anschauen. Wir sehen hier vier Werte. Wiederrum als erstes den Intercept und dann die Steigungen zu der Ernährung Blut und Ketchup. Am Ende dann noch ein kleiner Wert für die Steigung des Kaliumgehalts. Aber Achtung, die Zahlen sind immer auf die Änderung der Einheit bezogen. Faktoren haben sehr häufig größere Werte als Kovariaten.
R Code [zeigen / verbergen]
cov1_fac1_fit |>
coef() |> round(2) (Intercept) feedingblood feedingketchup K
58.48 39.31 34.64 0.34 Als nächstes lassen wir uns die zusammenfassende Tabelle des Modells wiedergeben. Hier erhalten wir dann auch die p-Werte und die weiteren Informationen zu der Modelgüte. Ich annotiere dir hier nicht nochmal die zusammenfassende Tabelle, das wird sehr redundant. Dazu dann einfach nochmal oben bei den mehrkovariaten oder mehrfaktoriellen Modellen reinschauen.
R Code [zeigen / verbergen]
cov1_fac1_fit |> summary()
Call:
lm(formula = jump_length ~ feeding + K, data = flea_model_tbl)
Residuals:
Min 1Q Median 3Q Max
-49.952 -17.163 -5.820 8.661 115.648
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 58.4806 17.3429 3.372 0.001564 **
feedingblood 39.3101 10.8621 3.619 0.000759 ***
feedingketchup 34.6434 11.4092 3.036 0.004014 **
K 0.3420 0.4633 0.738 0.464270
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 30.22 on 44 degrees of freedom
Multiple R-squared: 0.2543, Adjusted R-squared: 0.2035
F-statistic: 5.002 on 3 and 44 DF, p-value: 0.004523Wir wollen uns hier nochmal auf die Koeffizienten konzentrieren und was uns jetzt die Koeffizienten aussagen. Dafür habe ich nochmal die lokalen Mittelwerte der Sprungweite und der Kovariate für jedes Level der Ernährungsform bestimmt. Sie mittlere Sprungweite der Zuckerflöhe ist damit 70cm und der mittlere Kaliumgehalt im Blut der Zuckerflöhe liegt bei 33.7mmol/l.
R Code [zeigen / verbergen]
flea_model_tbl |>
group_by(feeding) |>
summarise(mean(jump_length),
mean(K))# A tibble: 3 × 3
feeding `mean(jump_length)` `mean(K)`
<fct> <dbl> <dbl>
1 sugar_water 70.0 33.7
2 blood 108. 29.5
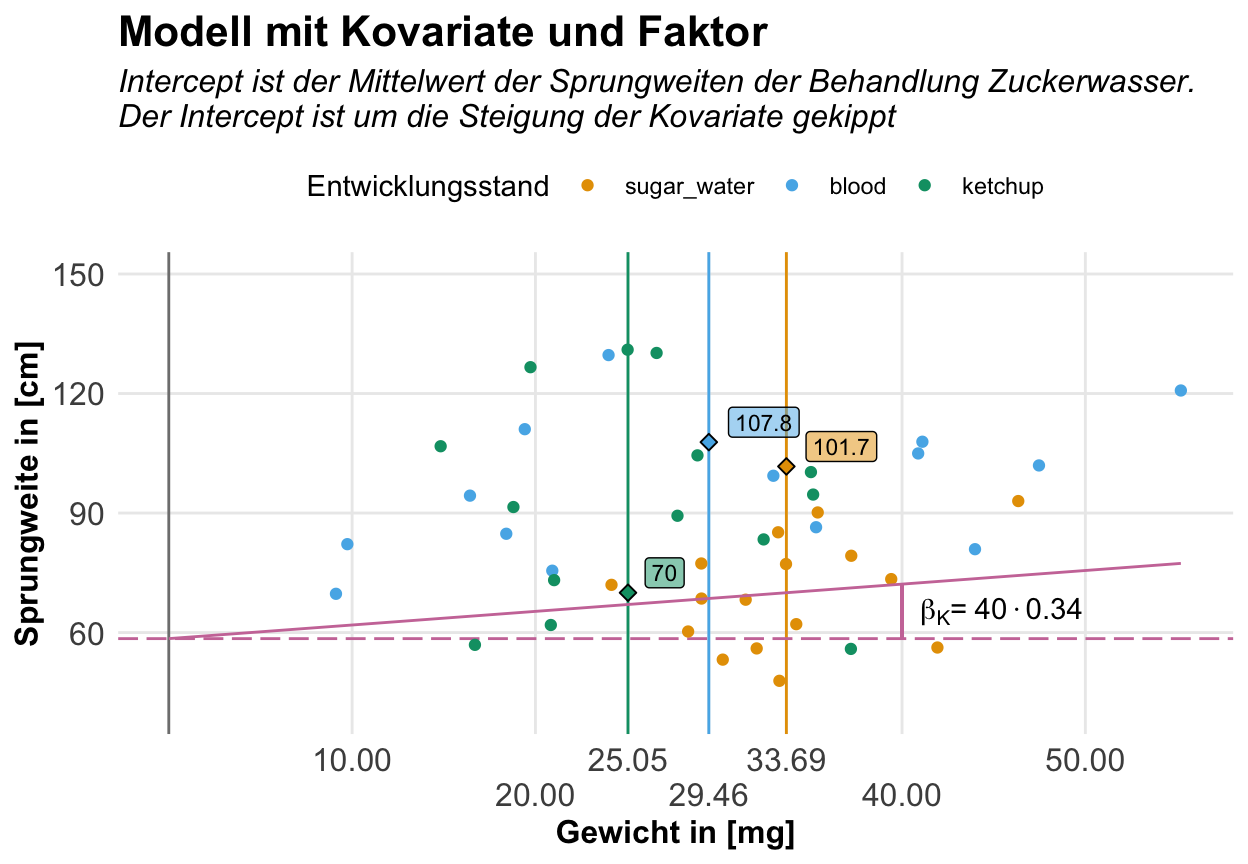
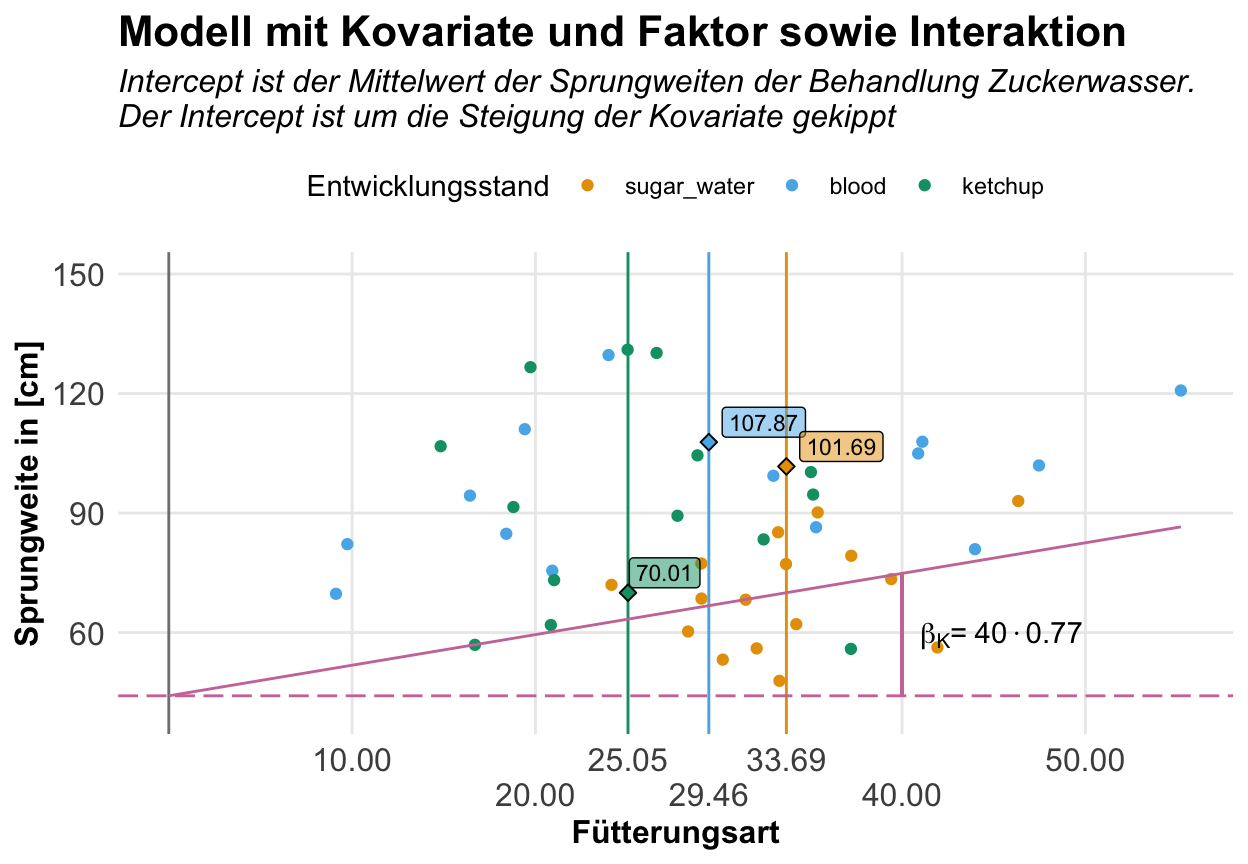
3 ketchup 102. 25.1Damit können wir jetzt besser verstehen, was die Koeffizienten der Einflussvariablen uns sagen wollen. In der folgenden Tabelle habe ich dir einmal für die Faktorlevel die Mittelwerte der Kovariaten sowie des Messswerts der Sprungweite dargestellt. Wie setzt sich jetzt der Mittelwert der Sprungweiten aus den Koeffizienten zusammen? Der Intercept liegt auf dem lokalen Mittel der Zuckerflöhe. Jedenfalls fast. Denn wir müssen noch die Steigung des Kaliumsgehalt mit dem mittleren Kaliumgehalt in den Zuckerflöhen multiplizieren. Dieser Betrag fehlt noch zum lokalen Mittel der Zuckerflöhe. Faktisch kippen wir die Grade durch den Intercept um die Steigung der Kovariaten. Die mittleren Residuen sind in diesem Beispiel gerade Null und speilen somit keine Rolle.
| \(f_{feeding}\) | \(\bar{c}_{K}\) | \(\bar{Y}\) | \(\boldsymbol{\beta_{0}}\) | \(\boldsymbol{\beta_{blood}}\) | \(\boldsymbol{\beta_{ketchup}}\) | \(\boldsymbol{\bar{c}_{K}\cdot\beta_{K}}\) | \(\boldsymbol{\epsilon}\) |
|---|---|---|---|---|---|---|---|
| sugar | 33.69 | 70.01 | 58.48 | \(11.45 = 33.69 \cdot 0.34\) | 0 | ||
| blood | 29.47 | 107.87 | 58.48 | 39.31 | \(10.02 = 29.47 \cdot 0.34\) | 0 | |
| ketchup | 25.06 | 101.69 | 58.48 | 34.64 | \(8.52 = 25.06 \cdot 0.34\) | 0 |
Wir können uns dann den Zusammenhang auch nochmal visualisieren. Wir legen auf die x-Achse die Kaliumwerte. Die Mittelwerte der Sprungweite für die Ernärhungstypen der Flöhe liegen jetzt exakt auf den Mittwelwerten der Kaliumwerte in den entsprechenden Gruppen. Im Endeffekt kippen wir die Grade durch den Intercept um die Steigung der Kovariaten. Hier haben wir dann eine Steigung für alle Gruppen der Ernährung für den Kaliumgehalt. Wenn wir eine Interaktion zulassen, dann erhält jede Gruppe der Ernährung nochmal ‘eine Art eigene Steigung’. Das ist nicht super korekt, aber so kann man sich das vorstellen.
Mit Interaktion
Jetzt schauen wir uns das gleiche Modell nochmal mit der Interaktion zwischen den Ernährungsformen und dem Kaliumgehalt im Blut der Flöhe an. Im Prinzip erlauben wir jetzt jeder Ernährungsform eine eigene Steigung für den Kaliumghalt. Das heißt aber auch im Umkehrschluss, dass wir die Steigung nicht richtig ohne die Interaktionsterme bewerten können. Irgendwas ist ja immer.
R Code [zeigen / verbergen]
cov1_fac1_fit <- lm(jump_length ~ feeding + K + feeding:K, data = flea_model_tbl) Schauen wir uns einmal die zusammenfassende Ausgabe des Modells an. Wir sehen hier, dass wir noch zwei Koeffizienten für die Interaktion zwischen der Bluternährung und dem Kaliumgehalt sowie der Ketchupernährung und dem Kaliumgehalt zusätzlich erhalten haben. Du kannst die Interaktion als Steigung für Kalium in den Gruppen interpretieren zusammen mit der Steigung für die Zuckerflöhe. In der Steigung für das Kalium ist jetzt die Gruppe der Zuckerernährung direkt mit drin. Das führt jetzt gleich zu einer etwas umständlicheren Interpretation. Mehr dazu in der Tabelle weiter unten.
R Code [zeigen / verbergen]
cov1_fac1_fit |> summary()
Call:
lm(formula = jump_length ~ feeding + K + feeding:K, data = flea_model_tbl)
Residuals:
Min 1Q Median 3Q Max
-52.799 -15.960 -4.885 10.009 113.476
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 44.1255 48.1386 0.917 0.365
feedingblood 44.5900 51.4164 0.867 0.391
feedingketchup 81.6294 55.2411 1.478 0.147
K 0.7681 1.4110 0.544 0.589
feedingblood:K -0.1181 1.5168 -0.078 0.938
feedingketchup:K -1.7283 1.7520 -0.987 0.330
Residual standard error: 30.23 on 42 degrees of freedom
Multiple R-squared: 0.2877, Adjusted R-squared: 0.2029
F-statistic: 3.393 on 5 and 42 DF, p-value: 0.01155In der folgenden Tabelle zeige ich dir einmal wie sich die lokalen Mittelwerte für die Sprungweiten und den Ernährungsformen zusammensetzen. Die mittleren Residuen sind in diesem Beispiel gerade Null und speilen somit keine Rolle. Wir erhalten eine höhere Steigung für den Kaliumgehall als ohne die Interaktion. Die Steigung beschreibt ja jetzt Grade für die Zuckerflöhe. Damit wir jetzt mit den aufaddierten Effekten der Ernährung wieder bei den lokalen Mitteln landen, müssen wir noch die mittleren Werte der Kovariaten gewichtet um die Steigung abziehen. Das klingt jetzt komplizierter als es ist. Schaue dir einfach mal die Tabelle an.
| \(f_{feeding}\) | \(\bar{c}_{K}\) | \(\bar{Y}\) | \(\boldsymbol{\beta_{0}}\) | \(\boldsymbol{\beta_{blood}}\) | \(\boldsymbol{\beta_{ketchup}}\) | \(\boldsymbol{\bar{c}_{K}\cdot\beta_{K}}\) | \(\boldsymbol{\bar{c}_{K}\cdot\beta_{blood\times K}}\) | \(\boldsymbol{\bar{c}_{K}\cdot\beta_{ketchup\times K}}\) | \(\boldsymbol{\epsilon}\) |
|---|---|---|---|---|---|---|---|---|---|
| sugar | 33.69 | 70.01 | 44.13 | \(25.94 = 33.69 \cdot 0.77\) | 0 | ||||
| blood | 29.47 | 107.87 | 44.13 | 44.59 | \(22.69 = 29.47 \cdot 0.77\) | \(-3.54 = 29.47 \cdot -0.12\) | 0 | ||
| ketchup | 25.06 | 101.69 | 44.13 | 81.63 | \(19.29 = 25.06 \cdot 0.77\) | \(-43.35 = 25.06 \cdot -1.73\) | 0 |
In der folgenden Abbildung können wir uns dann den Zusammenhang nochmal visualisieren. Wir sehen hier, dass die Steigung größer ist. Wir haben auf der anderen Seite aber auch einen geringeren Intercept als in dem Modell ohne Interaktion. Das liegt daran, das sich die Steigung des Kaliumsgehalt jetzt auf die Zuckerflöhe bezieht und nicht mher auf alle drei Ernährungsformen. Die Steigung der anderen Ernährungsformen wird dann durch die Werte der Koeffizenten der Interaktion abgebildet. Daher ist die Interpretation nicht mehr ganz so eingängig und einfach zu interpretieren. Wichtig ist aber, dass du verstehst, dass wir es hier in der Interaktion mit einer Steigung zu tun haben.
Die folgenden Abschnitte wiederholen sich für jedes Modell, da am Ende alles sehr gleich ist. Ich empfehle einmal es selber nachzuvollziehen. Ich habe beim Schreiben am meisten gelernt.
Intern rechnet R eine Modellmatrix. Was ist eine Modellmatrix? Eine Modellmatrix beinhaltet die Informationen welche Koeffizienten für welche Beobachtungen genutzt werden sollen um am Ende auf den Messwert für jede Beobachtung zu kommen. Faktisch also eine Zuordnung der Koeffizienten und Residuen zu den einzelnen Beobachtungen. Daher hat auch eine Modellmatrix immer so viele Zeilen wie Beobachtungen.
Damit wir hier nicht verrückter werden als wir schon sind, nutze ich den Schlangendatensatz. Wir haben also die Körperlänge vorliegen und wollen dann anhand von einer Kovariate und einem Faktor den Zusammenhang darstellen. Ich lassen hier aus Gründen der Einfachheit die Interaktion weg. Der Datensatz ist auch zu klein für eine saubere Darstellung einer Interaktion. Daher ergibt sich folgende Modellmatrix.
R Code [zeigen / verbergen]
model.matrix(svl ~ mass + color, data = snake_tbl) |> as_tibble() # A tibble: 8 × 4
`(Intercept)` mass colorrot colorblau
<dbl> <dbl> <dbl> <dbl>
1 1 6 0 0
2 1 8 0 0
3 1 5 1 0
4 1 7 1 0
5 1 9 1 0
6 1 11 0 1
7 1 12 0 1
8 1 10 0 1Wir können die Modellmatrix auch einmal im Ganzen aufschreiben, dann macht es auch mehr Sinn. Hier musst du dann wissen, dass wir in der Matrixmultiplikation, die erste Spalte mit dem ersten Koeffizienten malnehmen. Die zweite Spalte dann mit dem zweiten Koeffizienten malnehmen und so weiter. Hier siehst du dann auch, dass nicht jede Beobachtung für jeden Koeffizienten berücksichtigt wird. Der Faktor wird anhand seiner Level aufgespalten und das erste Level wandert immer in den Intercept. Wir sprechen auch von einer Dummykodierung.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 50 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 1 & 6 & 0 & 0 \\ 1 & 8 & 0 & 0 \\ 1 & 5 & 1 & 0 \\ 1 & 7 & 1 & 0 \\ 1 & 9 & 1 & 0 \\ 1 & 11 & 0 & 1 \\ 1 & 12 & 0 & 1 \\ 1 & 10 & 0 & 1 \\ \end{pmatrix} \times \begin{pmatrix} \beta_0 \\ \beta_{mass}\\ \beta^{color}_{rot} \\ \beta^{color}_{blau} \\ \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \epsilon_6 \\ \epsilon_7 \\ \epsilon_8 \\ \end{pmatrix} \]
Dann rechnen wir einmal das kombinierte Modell und schauen welche Koeffizienten wir erhalten.
R Code [zeigen / verbergen]
cov1_fac1_fit <- lm(svl ~ mass + color, data = snake_tbl)Wir runden jetzt einmal, damit wir nicht so viel in die Modellmatrix schreiben müssen.
R Code [zeigen / verbergen]
cov1_fac1_fit |> coef() |> round(2)(Intercept) mass colorrot colorblau
19.17 3.33 4.83 -1.17 Dann brauchen wir noch die Residuen.
R Code [zeigen / verbergen]
cov1_fac1_fit |> residuals() |> round(2) 1 2 3 4 5 6 7 8
0.83 -0.83 -1.67 3.67 -2.00 2.33 0.00 -2.33 Am Ende baue ich dann einmal das volle Modell mit der Modellmatrix auf. Auf der linken Seite siehst du die Körperlängen. Dann kommt der Intercept gefolgt von den Koeffizienten multipliziert mit der Masse und den Dummykodierungen. Am Ende addieren wir dann noch die Residuen.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 19.17 & 6 \cdot 3.33 & 0 \cdot 4.83 & 0 \cdot -1.17 \\ 19.17 & 8 \cdot 3.33 & 0 \cdot 4.83 & 0 \cdot -1.17 \\ 19.17 & 5 \cdot 3.33 & 1 \cdot 4.83 & 0 \cdot -1.17 \\ 19.17 & 7 \cdot 3.33 & 1 \cdot 4.83 & 0 \cdot -1.17 \\ 19.17 & 9 \cdot 3.33 & 1 \cdot 4.83 & 0 \cdot -1.17 \\ 19.17 & 11 \cdot 3.33 & 0 \cdot 4.83 & 1 \cdot -1.17 \\ 19.17 & 12 \cdot 3.33 & 0 \cdot 4.83 & 1 \cdot -1.17 \\ 19.17 & 10 \cdot 3.33 & 0 \cdot 4.83 & 1 \cdot -1.17 \\ \end{pmatrix} + \begin{pmatrix} +0.83 \\ -0.83 \\ -1.67 \\ +3.67 \\ -2.00 \\ +2.33 \\ 0.00 \\ -2.33 \\ \end{pmatrix} \]
Jetzt kannst du dich fragen, kommt das denn auch hin? Dafür alles nochmal in R getippt und geschaut welche Zahlen am Ende für die Körperlänge rauskommen.
R Code [zeigen / verbergen]
c(19.17 + 6*(3.33) + 0*(4.83) + 0*(-1.17) + 0.83,
19.17 + 8*(3.33) + 0*(4.83) + 0*(-1.17) - 0.83,
19.17 + 5*(3.33) + 1*(4.83) + 0*(-1.17) - 1.67,
19.17 + 7*(3.33) + 1*(4.83) + 0*(-1.17) + 3.67,
19.17 + 9*(3.33) + 1*(4.83) + 0*(-1.17) - 2.00,
19.17 + 11*(3.33) + 0*(4.83) + 1*(-1.17) + 2.33,
19.17 + 12*(3.33) + 0*(4.83) + 1*(-1.17) + 0.00,
19.17 + 10*(3.33) + 0*(4.83) + 1*(-1.17) - 2.33) |> round()[1] 40 45 39 51 52 57 58 49Und dann hier nochmal der Vergleich zu den ursprünglichen Werten der Körperlänge der Schlangen. Das passt ja hervorragend.
R Code [zeigen / verbergen]
snake_tbl |> pull(svl)[1] 40 45 39 51 52 57 58 49Musst du das hier im Detail verstehen? Kommt drauf an. Hier wird eben dargestellt wie sich in R intern die Koeffizienten ergeben. Das macht dann eben auch was aus für die Interpretation. Hier lernen wir dann nochmal, was eigentlich die Dummykodierung bedeutet. Je nachdem wie sich dein Modell zusammensetzt ist dann auch die Modellmatrix komplizierter.
Dieser Abschnitt beinhaltet eine kurze Simulation in R mit einem Tibble und der Erstellung eines normalverteilten Messwerts. Mehr zu der Generierung von Daten dann im entsprechenden Kapitel. Ich habe alles ausgelagert, da es dann hier zu voll wurde. Daher ist es hier eher so eine kleine Spielweise.
R Code [zeigen / verbergen]
cov1_fac1_tbl <- tibble(c_1 = rnorm(15, 0, 1),
f_a = gl(3, 5),
y = 2 +
1 * c_1 +
2 * as.numeric(f_a) +
rnorm(15, 0, 0.001))Dann schauen wir uns einmal an, ob wir dann den Intercept und die Koeffizienten wiederfinden. Wenn du den Fehler in rnorm() von \(0.001\) hochsetzt, dann werden auch die Koeffizienten in dem folgenden Modell ungenauer. Hat aber gut geklappt, wir erhalten die gerundeten Koeffizienten, die wir eingestellt hatten einigermaßen wiedergegeben.
R Code [zeigen / verbergen]
lm(y ~ f_a + c_1, cov1_fac1_tbl) |>
coef() |> round(2)(Intercept) f_a2 f_a3 c_1
4 2 4 1 \(c_1 + f_A + f_B\)
Dann kommen wir jetzt zu einem Modell mit drei Einflussvariablen. Wir haben jetzt eine Kovariate sowie zwei Faktoren mit in dem Modell. Wenn wir hier von der Seite der Faktoren schauen und ein faktorielles Experiment mit einem Hauptfaktor vorliegen haben, dann rechnen wir eigentlich eine klassische zweifaktorielle ANCOVA (eng. analysis of covariance). Es kommt dann aber immer auf die Perspektive der wissenschaftlichen Fragestellung an. Wenn wir wirklich alles gleichwertig ansehen und unsere Faktoren eher beobachtete kategoriale Einflussvariablen sind, dann müssen wir das Modell eher im Sinne einer multiplen Regression betrachten. Das wollen wir dann hier auch einmal machen.
Jetzt wird es komplizierter. Je mehr Einflussvariablen wir in ein Modell nehmen, desto komplexer werden die Modelle. Besonders Faktoren verursachen dann immer mehr Level, die sich dann im Intercept konzentrieren. So kann es sehr schnell sein, dass der Intercept aus dem Mittel einer Faktorkombination von vielen ist. Dann wird die Interpretation herausfordernd, da der Bezug zum Intercept herausfordernd ist.
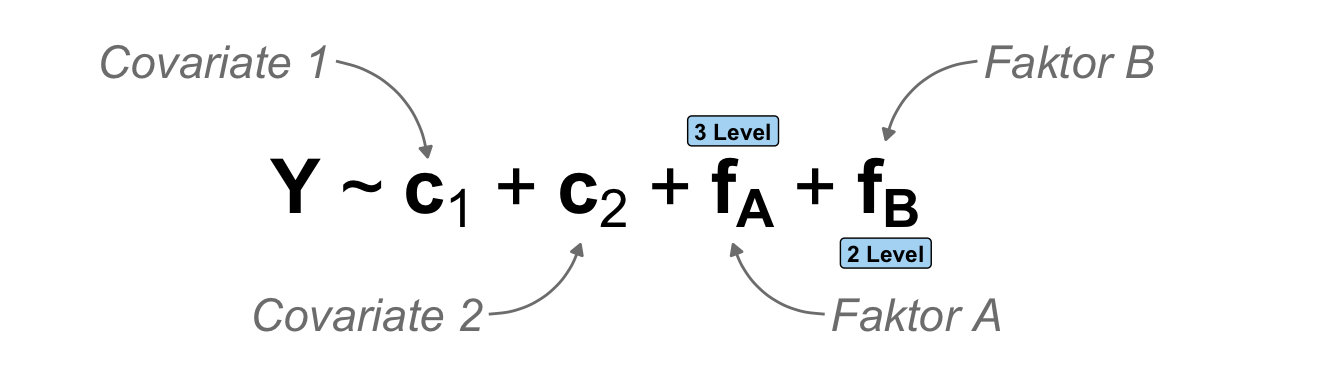
In der folgenden schematischen Darstellung siehst du dann einmal unser multiples Modell. Wir haben einen Messwert sowie eine Kovariate und zwei Faktoren. Ein Faktor hat drei Level und der andere Faktor dann nur zwei Level. Im Prinizip können wir auch noch Faktoren mit mehr Leveln vorliegen haben, aber dann wird das Modell immer größer. Die grundsätzlichen Ideen bleiben aber gleich.
Jetzt können wir das Modell einmal in R rechnen. Dazu nehmen wir dann in das Modell einmal den Kaliumgehalt im Blut der Flöhe sowie die Fütterungsart und das Alter der Flöhe in den beiden Gruppen juvenile und adult. Ich nehme hier mal keine Interaktion mit ins Modell, das wird dann sehr groß. Wir können ja hier verschiedene Interaktionen berechnen, die dann sehr stark von der Fragestellung abhängn. Die Interpretation ist dann aber ähnlich wie in dem Modell mit einer Kovariate und einem Faktor weiter oben.
Im Folgenden siehst du einmal das multiple Modell mit drei Einflussvariablen. Wir schauen uns die Kovariate Kalium an sowie die beiden Faktoren Enrährung und Entwicklungsstand. Dabei hat die Ernährung dann drei Gruppen und der Entwicklungsstand betrachtet die juvenilen und adulten Flöhe. Ich habe hier dann mal keine Interaktion mit ins Modell genommen.
R Code [zeigen / verbergen]
cov1_fac2_fit <- lm(jump_length ~ K + feeding + stage, data = flea_model_tbl) Dann können wir uns schon die Koeffizienten des Modells anschauen. Die Level der Faktoren, die jetzt fehlen kummulieren dann in dem Intercept. Das heißt jetzt für uns, dass der Intercept die adulten Zuckerflöhe repräsentiert. Die Änderung zu dem Intercept erklären jetzt die Koeffizienten. Darüber hinaus haben wir dann noch die Steigung der Kovariate, die eben dann den Effekt des Kaliumgehalt im Blut auf die Sprungleistung entspricht.
R Code [zeigen / verbergen]
cov1_fac2_fit |>
coef() |> round(2) (Intercept) K feedingblood feedingketchup stagejuvenile
59.72 0.25 38.93 33.87 3.58 Wir erhlaten dann in der Zusammenfassung nochmal mehr Informationen. Ich habe auch hier auf die Annotierung verzichtet, da sich hier viel wiederholt und ich die Koeffizienten dann gleich nochmal gesondert erkläre. Wir sehen hier aber, dass unser Modell nicht so gut funktioniert hat, da wir eine Abweichung von der Normalverteilung in den Residuen vorliegen haben. Der Median sollte eigentlich Null sein. Die restlichen Gütezahlen sind dann auch nur okay.
R Code [zeigen / verbergen]
cov1_fac2_fit |> summary()
Call:
lm(formula = jump_length ~ K + feeding + stage, data = flea_model_tbl)
Residuals:
Min 1Q Median 3Q Max
-50.649 -17.904 -6.268 10.202 114.492
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 59.7160 17.8543 3.345 0.001717 **
K 0.2523 0.5309 0.475 0.637056
feedingblood 38.9310 11.0224 3.532 0.000999 ***
feedingketchup 33.8682 11.7259 2.888 0.006042 **
stagejuvenile 3.5770 9.9973 0.358 0.722244
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 30.52 on 43 degrees of freedom
Multiple R-squared: 0.2565, Adjusted R-squared: 0.1874
F-statistic: 3.709 on 4 and 43 DF, p-value: 0.01112Für die Interpretation der Koeffizienten helfen dann auch immer die lokalen Mittlwerte der SPrungweiten und der Kaliumgehalte für die Faktorkombinationen. Ich habe die die Mittelwerte dann einmal in der folgenden Tabelle dargestellt.
R Code [zeigen / verbergen]
flea_model_tbl |>
group_by(feeding, stage) |>
summarise(mean(jump_length),
mean(K))# A tibble: 6 × 4
# Groups: feeding [3]
feeding stage `mean(jump_length)` `mean(K)`
<fct> <fct> <dbl> <dbl>
1 sugar_water adult 79.0 37.0
2 sugar_water juvenile 61.0 30.4
3 blood adult 99.7 17.3
4 blood juvenile 116. 41.7
5 ketchup adult 92.1 20.6
6 ketchup juvenile 111. 29.5Das eigentlich spannende sind jetzt die Koeffizienten. Hier müssen wir nochmal aufpassen, dass sich in dem Intercept die adulten Zuckerflöhe verstecken. Die Änderung zu dieser Faktorkombination stellen dann die Koeffizienten dar. Um dann auf die entgültigen lokalen Mittelwerte der Sprungweiten in den Faktorkombinationen zu kommen, müssen wir die lokalen Mittelwerte des Kaliumgehalts mit der Steigung der Kovariate multiplizieren. Dazu benötigen wir auch die mittleren Residuen für die Faktorkombinationen. Ja, das ist echt eine Menge. Ich berechne also einmal die mittleren Residuen als Fehler.
R Code [zeigen / verbergen]
cov1_fac2_fit |>
augment() |>
group_by(feeding, stage) |>
summarise(mean_resid = round(mean(.resid), 2))# A tibble: 6 × 3
# Groups: feeding [3]
feeding stage mean_resid
<fct> <fct> <dbl>
1 sugar_water adult 9.92
2 sugar_water juvenile -9.92
3 blood adult -3.29
4 blood juvenile 3.29
5 ketchup adult -6.63
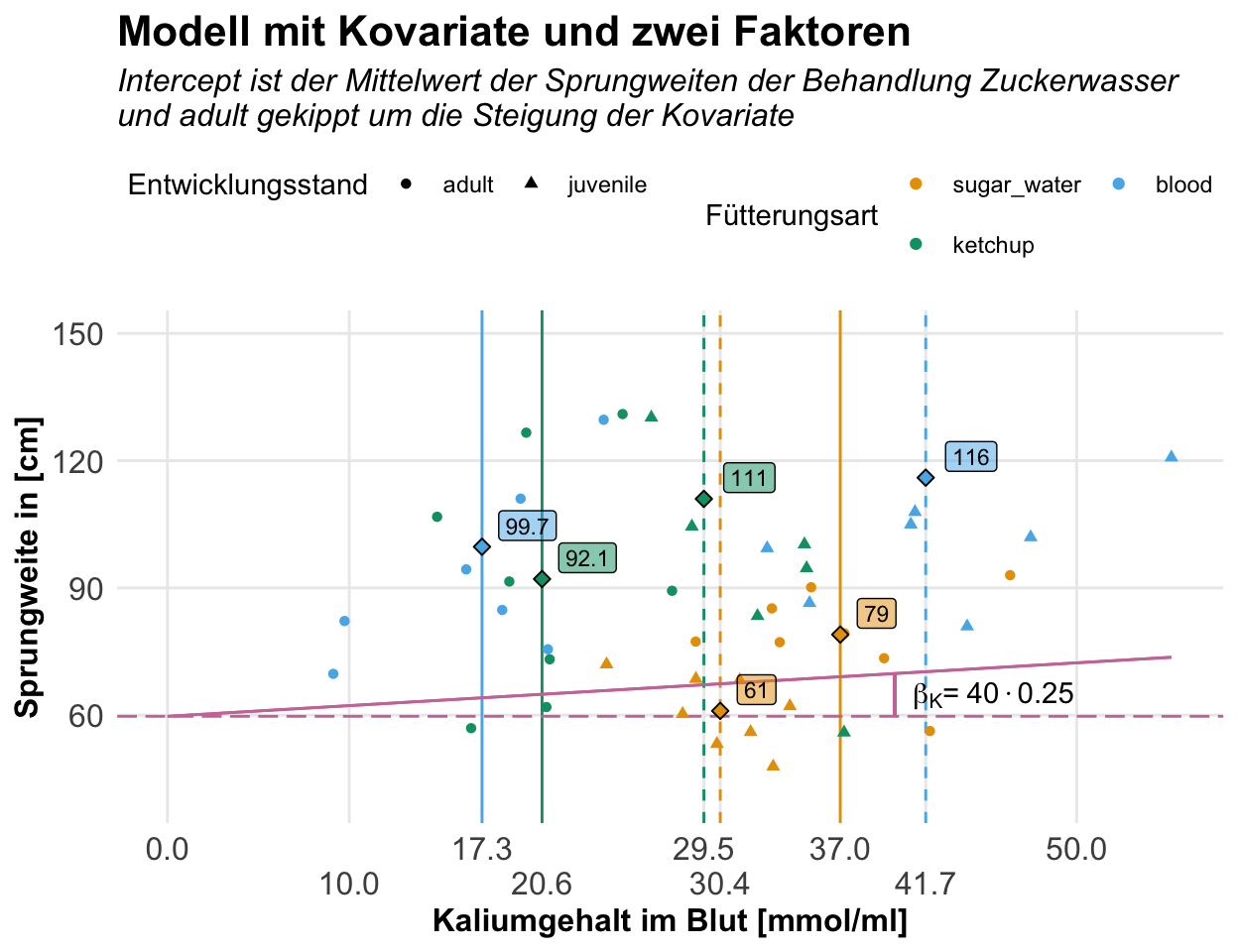
6 ketchup juvenile 6.63Dann können wir alles zusammenbringen. Ziel ist es für jede Faktorkombination aus der Ernährung und dem Entwicklungsstand einmal die lokalen Mittelwerte der Sprungweiten aus den Koeffizienten und den Residuen zusammenzubauen. So haben wir dann den Intercept als lokalen Mittelwert der adulten Zuckerflöhe auf dem Mittel der Kovariaten. Je nach Faktorkombination müssen wir dann andere Koeffizienten zusammen mit den Residuen aufaddieren um auf die lokalen Mittel der Sprungweiten zu kommen. Du musst dir das eine Zeit anschauen, auch für mich war die Berechnung nicht gleich klar.
| \(f_{feeding}\) | \(f_{stage}\) | \(\bar{c}_{K}\) | \(\bar{Y}\) | \(\boldsymbol{\beta_{0}}\) | \(\boldsymbol{\bar{c}_{K}\cdot\beta_{K}}\) | \(\boldsymbol{\beta_{blood}}\) | \(\boldsymbol{\beta_{ketchup}}\) | \(\boldsymbol{\beta_{juvenile}}\) | \(\boldsymbol{\epsilon}\) |
|---|---|---|---|---|---|---|---|---|---|
| sugar | adult | 37.0 | 79.0 | 59.71 | \(9.25 = 37.0 \cdot 0.25\) | 9.9 | |||
| sugar | juvenile | 30.4 | 61.0 | 59.71 | \(7.6 = 30.4 \cdot 0.25\) | 3.58 | -9.9 | ||
| blood | adult | 17.3 | 99.7 | 59.71 | \(4.3 = 17.3 \cdot 0.25\) | 38.93 | -3.3 | ||
| blood | juvenile | 41.7 | 116.0 | 59.71 | \(10.4 = 41.7 \cdot 0.25\) | 38.93 | 3.58 | 3.3 | |
| ketchup | adult | 20.6 | 92.1 | 59.71 | \(5.2 = 20.6 \cdot 0.25\) | 33.89 | -6.6 | ||
| ketchup | juvenile | 29.5 | 111.0 | 59.71 | \(7.4 = 29.5 \cdot 0.25\) | 33.89 | 3.58 | 6.6 |
In der folgenden Abbildung habe ich versucht dir den Zusammenhang nochmal darzustellen. Die lokalen Mittelwerte der Sprungweiten für die Faktorkombinationen liegen dann auf den Mittelwerten der Kovariaten. Wir kippen dann den Intercept um die Steigung der Kovariaten um dann die Abweichungen an den lokalen Mitteln zu bestimmen. Ja, es klingt wild, aber so wird es eben gerechnet. Daher wird die Darstellung auch immer schwerer, da wir hier jetzt sechs Punktewolken haben, die natürlich nicht aufsteigend sortiert nach den Kovariaten sind. Die gestrichelte Linie dient dir nochmal als Orientierung für einen konstanten Intercept.
Die folgenden Abschnitte wiederholen sich für jedes Modell, da am Ende alles sehr gleich ist. Ich empfehle einmal es selber nachzuvollziehen. Ich habe beim Schreiben am meisten gelernt.
Intern rechnet R eine Modellmatrix. Was ist eine Modellmatrix? Eine Modellmatrix beinhaltet die Informationen welche Koeffizienten für welche Beobachtungen genutzt werden sollen um am Ende auf den Messwert für jede Beobachtung zu kommen. Faktisch also eine Zuordnung der Koeffizienten und Residuen zu den einzelnen Beobachtungen. Daher hat auch eine Modellmatrix immer so viele Zeilen wie Beobachtungen.
Damit wir hier nicht verrückter werden als wir schon sind, nutze ich den Schlangendatensatz. Wir haben also die Körperlänge vorliegen und wollen dann anhand von einer Kovariate und zwei Faktoren den Zusammenhang darstellen. Ich lassen hier aus Gründen der Einfachheit die Interaktion weg. Der Datensatz ist auch zu klein für eine saubere Darstellung einer Interaktion. Daher ergibt sich folgende Modellmatrix.
R Code [zeigen / verbergen]
model.matrix(svl ~ mass + region + color, data = snake_tbl) |> as_tibble() # A tibble: 8 × 5
`(Intercept)` mass regionnord colorrot colorblau
<dbl> <dbl> <dbl> <dbl> <dbl>
1 1 6 0 0 0
2 1 8 0 0 0
3 1 5 0 1 0
4 1 7 1 1 0
5 1 9 1 1 0
6 1 11 1 0 1
7 1 12 1 0 1
8 1 10 1 0 1Wir können die Modellmatrix auch einmal im Ganzen aufschreiben, dann macht es auch mehr Sinn. Hier musst du dann wissen, dass wir in der Matrixmultiplikation, die erste Spalte mit dem ersten Koeffizienten malnehmen. Die zweite Spalte dann mit dem zweiten Koeffizienten malnehmen und so weiter. Hier siehst du dann auch, dass nicht jede Beobachtung für jeden Koeffizienten berücksichtigt wird. Die Faktoren werden anhand ihrer Level aufgespalten und das erste Level wandert immer in den Intercept. Wir sprechen auch von einer Dummykodierung.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 1 & 6 & 0 & 0 & 0 \\ 1 & 8 & 0 & 0 & 0\\ 1 & 5 & 0 & 1 & 0\\ 1 & 7 & 1 & 1 & 0\\ 1 & 9 & 1 & 1 & 0\\ 1 & 11& 1 & 0 & 1\\ 1 & 12& 1 & 0 & 1\\ 1 & 10& 1 & 0 & 1\\ \end{pmatrix} \times \begin{pmatrix} \beta_0 \\ \beta_{mass} \\ \beta^{region}_{nord} \\ \beta^{color}_{rot} \\ \beta^{color}_{blau} \\ \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \epsilon_6 \\ \epsilon_7 \\ \epsilon_8 \\ \end{pmatrix} \]
Dann rechnen wir einmal das kombinierte Modell und schauen welche Koeffizienten wir erhalten.
R Code [zeigen / verbergen]
cov1_fac2_fit <- lm(svl ~ mass + region + color, data = snake_tbl)Wir runden jetzt einmal, damit wir nicht so viel in die Modellmatrix schreiben müssen.
R Code [zeigen / verbergen]
cov1_fac2_fit |> coef() |> round(2)(Intercept) mass regionnord colorrot colorblau
25.00 2.50 5.00 1.50 -2.83 Dann brauchen wir noch die Residuen.
R Code [zeigen / verbergen]
cov1_fac2_fit |> residuals() |> round(2) 1 2 3 4 5 6 7 8
0.00 0.00 0.00 2.00 -2.00 2.33 0.83 -3.17 Am Ende baue ich dann einmal das volle Modell mit der Modellmatrix auf. Auf der linken Seite siehst du die Körperlängen. Dann kommt der Intercept gefolgt von den Koeffizienten multipliziert mit der Kovariaten und den Dummykodierungen. Am Ende addieren wir dann noch die Residuen.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 50 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 25 & \phantom{0}6 \cdot 2.5 & 0 \cdot 5 & 0 \cdot 1.5& 0 \cdot -2.83 \\ 25 & \phantom{0}8 \cdot 2.5 & 0 \cdot 5 & 0 \cdot 1.5& 0 \cdot -2.83\\ 25 & \phantom{0}5 \cdot 2.5 & 0 \cdot 5 & 1 \cdot 1.5& 0 \cdot -2.83\\ 25 & \phantom{0}7 \cdot 2.5 & 1 \cdot 5 & 1 \cdot 1.5& 0 \cdot -2.83\\ 25 & \phantom{0}9 \cdot 2.5 & 1 \cdot 5 & 1 \cdot 1.5& 0 \cdot -2.83\\ 25 & 11\cdot 2.5 & 1 \cdot 5 & 0 \cdot 1.5& 1 \cdot -2.83\\ 25 & 12\cdot 2.5 & 1 \cdot 5 & 0 \cdot 1.5& 1 \cdot -2.83\\ 25 & 10\cdot 2.5 & 1 \cdot 5 & 0 \cdot 1.5& 1 \cdot -2.83\\ \end{pmatrix} + \begin{pmatrix} \phantom{+}0.00 \\ \phantom{+}0.00 \\ \phantom{+}0.00 \\ +2.00 \\ -2.00 \\ +2.33 \\ +0.83 \\ -3.17 \\ \end{pmatrix} \]
Jetzt kannst du dich fragen, kommt das denn auch hin? Dafür alles nochmal in R getippt und geschaut welche Zahlen am Ende für die Körperlänge rauskommen.
R Code [zeigen / verbergen]
c(25 + 6*2.5 + 0*5 + 0*1.5 + 0*-2.83 + 0.00,
25 + 8*2.5 + 0*5 + 0*1.5 + 0*-2.83 + 0.00,
25 + 5*2.5 + 0*5 + 1*1.5 + 0*-2.83 + 0.00,
25 + 7*2.5 + 1*5 + 1*1.5 + 0*-2.83 + 2.00,
25 + 9*2.5 + 1*5 + 1*1.5 + 0*-2.83 - 2.00,
25 + 11*2.5 + 1*5 + 0*1.5 + 1*-2.83 + 2.33,
25 + 12*2.5 + 1*5 + 0*1.5 + 1*-2.83 + 0.83,
25 + 10*2.5 + 1*5 + 0*1.5 + 1*-2.83 - 3.17) [1] 40 45 39 51 52 57 58 49Und dann hier nochmal der Vergleich zu den ursprünglichen Werten der Körperlänge der Schlangen. Das passt ja hervorragend.
R Code [zeigen / verbergen]
snake_tbl |> pull(svl)[1] 40 45 39 51 52 57 58 49Musst du das hier im Detail verstehen? Kommt drauf an. Hier wird eben dargestellt wie sich in R intern die Koeffizienten ergeben. Das macht dann eben auch was aus für die Interpretation. Hier lernen wir dann nochmal, was eigentlich die Dummykodierung bedeutet. Je nachdem wie sich dein Modell zusammensetzt ist dann auch die Modellmatrix komplizierter.
Dieser Abschnitt beinhaltet eine kurze Simulation in R mit einem Tibble und der Erstellung eines normalverteilten Messwerts. Mehr zu der Generierung von Daten dann im entsprechenden Kapitel. Ich habe alles ausgelagert, da es dann hier zu voll wurde. Daher ist es hier eher so eine kleine Spielweise.
R Code [zeigen / verbergen]
cov1_fac2_tbl <- tibble(c_1 = rnorm(30, 0, 1),
f_a = rep(gl(3, 5), 2),
f_b = gl(2, 15),
y = 2 +
1 * c_1 +
2 * as.numeric(f_a) +
3 * as.numeric(f_b) +
rnorm(15, 0, 0.001))Dann schauen wir uns einmal an, ob wir dann den Intercept und die Koeffizienten wiederfinden. Wenn du den Fehler in rnorm() von \(0.001\) hochsetzt, dann werden auch die Koeffizienten in dem folgenden Modell ungenauer. Hat aber gut geklappt, wir erhalten die gerundeten Koeffizienten, die wir eingestellt hatten einigermaßen wiedergegeben.
R Code [zeigen / verbergen]
lm(y ~ c_1 + f_a + f_b, cov1_fac2_tbl) |>
coef() |> round(2)(Intercept) c_1 f_a2 f_a3 f_b2
7 1 2 4 3 \(c_1 + c_2 + f_A + f_B\)
Am Ende kommen wir dann nochmal zu einem Modell mit zwei Kovariaten und zwei Faktoren. Auch wenn wir dann die Interaktionen weglassen, wird das Modell immer komplexer. Hier können wir uns dann das Modell auch nicht mehr visualiseren. Prinzipiell ginge es schon mit einem dreidimensionalen Scatterplot, aber es wird dadurch eigentlich nicht übersichtlicher. Wir hätten dann die Faktorkombinationen auf den kombinierten Mittelwerten der Kovariaten. Das wird dann eigentlich immer nur noch ein Durcheinander, da wir ja auch noch alle Beobachtungen als Scatterplot vorliegen haben. Deshalb hier dann ohne Visualisierung. Das ist dann eigentlich aucb üblich, dass wir dann ab einer Kovariaten und Faktor dann keine Visualisierung mehr nutzen.
Jetzt wird es komplizierter. Je mehr Einflussvariablen wir in ein Modell nehmen, desto komplexer werden die Modelle. Besonders Faktoren verursachen dann immer mehr Level, die sich dann im Intercept konzentrieren. So kann es sehr schnell sein, dass der Intercept aus dem Mittel einer Faktorkombination von vielen ist. Dann wird die Interpretation herausfordernd, da der Bezug zum Intercept herausfordernd ist.
Damit haben wir dann folgendes Modell vorliegen. Im Prinzip kannst du noch mehr Kovariaten oder Faktoren mit ins Modell nehmen. Wir enden dann aber einmal bei diesem Modell mit zwei Kovariaten und zwei Faktoren. Hier ist dann wichtig, dass der Intercept die beiden ersten Level der beiden Faktoren einschließt. Das klingt erstmal kompliziert, wird dann aber im Folgenden hoffentlich klarer. Je mehr Faktoren du hast, desto wichtiger wird dann die Ordnung der Level in den Faktoren, da das niedrigste Level ja über alle Faktoren im Intercept zusammengefasst wird.
Dann wollen wir uns einmal das multiple Modell in R anschauen. In den weiteren Tabs findest du dann nochmal die theoretische Betrachtung in R sowie eine kleine Simulation zum nachvollziehen, wie so die Effekte zusammenkommen. Am Ende kommt es bei komplexeren Modellen sehr auf die wissenschaftliche Fragestellung an. Ein gutes Modellieren dauert dann eben seine Zeit. Insbesondere da wir hier ja noch nicht mal quadratische oder komplexere Zusammenhänge wir in dem Kapitel zu nicht linearen Regression betrachten.
Bauen wir also zuerst einmal unser multiples Modell in R. Dafür nutze ich hier die beiden Kovariaten Kaliumgehalt und Magnesiumgehalt im Blut der Flöhe sowie die beiden Faktoren der Ernährung und dem Entwicklungsstand. Wir wollen wissen, ob es einen kausalen Zusammenhang zwischen den Einflussvariablen und der Sprungweite gibt. Dabei könnte ich noch Interaktionen mit in das Modell nehme, entscheide mich aber aus Gründen der Komplexität dagegen. Wir bauen dann einmal das Modell.
R Code [zeigen / verbergen]
cov2_fac2_fit <- lm(jump_length ~ K + Mg + feeding + stage, data = flea_model_tbl) Wenn wir uns jetzt die Koeffizienten ansehen, dann sehen wir recht wenig. In einem multiplen Modell musst du immer aufpassen, dass du die Effekte der Faktoren nicht überinterpretierst und die Effekte der Kovariaten unterschätzt. Die Effekte hängen von den Einheiten und der Anzahl an Leveln ab. Daher haben Faktoren mesit sehr große Effekte im Vergleich zu den Kovariaten im Modell.
R Code [zeigen / verbergen]
cov2_fac2_fit |>
coef() |> round(2) (Intercept) K Mg feedingblood feedingketchup
52.26 0.26 0.42 38.92 31.82
stagejuvenile
6.22 Wir brauchen also einmal die Ausgabe der Zusammenfassung des Modells. Hier sehen wir schon etwas mehr. Das Modelll ist mit einem adjustierten Bestimmtheitsmaß \(R^2\) von 0.1695 nicht gerade gut. Auch sind die Residuen eher weniger normalverteilt. Wir können aber soweit einmal mit dem Modell leben. Wir sehen auch, dass nur die Fütterungen signifikant sind. Achtung, in dem Intercept sind hier die adulten Zuckerflöhe zu denen dann die Steigung der adulten Blutflöhe und Ketchupflöhe verglichen wird. Meistens ist es dann nicht mehr die Frage, die du an die Daten hast. Deshalb sind eventuell die Marginal effect models hilfreicher bei der Beantwortung deiner Fragen.
R Code [zeigen / verbergen]
cov2_fac2_fit |> summary()
Call:
lm(formula = jump_length ~ K + Mg + feeding + stage, data = flea_model_tbl)
Residuals:
Min 1Q Median 3Q Max
-51.184 -17.259 -6.157 9.851 116.101
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 52.2631 32.9993 1.584 0.12075
K 0.2579 0.5372 0.480 0.63368
Mg 0.4198 1.5561 0.270 0.78865
feedingblood 38.9151 11.1434 3.492 0.00114 **
feedingketchup 31.8151 14.0868 2.259 0.02917 *
stagejuvenile 6.2236 14.0847 0.442 0.66085
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 30.86 on 42 degrees of freedom
Multiple R-squared: 0.2578, Adjusted R-squared: 0.1695
F-statistic: 2.918 on 5 and 42 DF, p-value: 0.02383Um die Effekte der einzelnen Faktorkombinationen dann zu verstehen, brauchen wir wie immer einmal die lokalen Mittelwerte aller Faktorkombinationen der Sprungweiten und dann eben auch die Mittelwerte der Kovariaten. Daher hier ein großes Set an an Mittelwerten für die jeweiligen sechs Faktorkombinationen.
R Code [zeigen / verbergen]
flea_model_tbl |>
group_by(feeding, stage) |>
summarise(mean(jump_length),
mean(K),
mean(Mg))# A tibble: 6 × 5
# Groups: feeding [3]
feeding stage `mean(jump_length)` `mean(K)` `mean(Mg)`
<fct> <fct> <dbl> <dbl> <dbl>
1 sugar_water adult 79.0 37.0 18.6
2 sugar_water juvenile 61.0 30.4 9.70
3 blood adult 99.7 17.3 19.2
4 blood juvenile 116. 41.7 9.29
5 ketchup adult 92.1 20.6 19.4
6 ketchup juvenile 111. 29.5 18.9 Dann brauchen wir noch die gemittelten Residuen für die Faktorkombinationen damit dann auch am Ende die Zaheln wieder aufgehen. Wir wollen dann ja am Ende die Sprungweiten aus den Koeffizienten und den Residuen wieder zusammensetzen können.
R Code [zeigen / verbergen]
cov2_fac2_fit |>
augment() |>
group_by(feeding, stage) |>
summarise(mean_resid = round(mean(.resid), 2))# A tibble: 6 × 3
# Groups: feeding [3]
feeding stage mean_resid
<fct> <fct> <dbl>
1 sugar_water adult 9.35
2 sugar_water juvenile -9.35
3 blood adult -3.98
4 blood juvenile 3.98
5 ketchup adult -5.37
6 ketchup juvenile 5.37Am Ende haben wir dann diese riesige Tabelle mit Koeffizienten und Mittelwerten der Kovariaten für die Faktorkombinationen. Das sieht wild aus und du musst dich da vermutlich einmal reinknien damit du die Zuammenhänge einmal siehst. Em Ende wollen wir den Mittelwert der Sprungweiten \(\bar{Y}\) aus den Koeffizienten für die Faktorkombinatioen wieder haben. Dafür müssen sich die Koeffzienten und die Residuen eben zu den lokalen Mitteln der Sprungweiten aufaddieren lassen. Hier siehst du dann auch gut, wie dann eben der Intercept aus den Zuckerflöhen gebildet wird und die Koeffizienten dann die Abweichungen zu den Zuckerflöhen beschreiben. Meistens ist es dann doch nicht so ganz was man möchte. Das ist eben das generelle Problem von großen multiplen Modellen mit vielen Faktoren. Am Ende ist der Intercept eine sehr spezifische Subgruppe.
| \(f_{feeding}\) | \(f_{stage}\) | \(\bar{c}_{K}\) | \(\bar{c}_{Mg}\) | \(\bar{Y}\) | \(\boldsymbol{\beta_{0}}\) | \(\boldsymbol{\bar{c}_{K}\cdot\beta_{K}}\) | \(\boldsymbol{\bar{c}_{Mg}\cdot\beta_{Mg}}\) | \(\boldsymbol{\beta_{blood}}\) | \(\boldsymbol{\beta_{ketchup}}\) | \(\boldsymbol{\beta_{juvenile}}\) | \(\boldsymbol{\epsilon}\) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| sugar | adult | 37.0 | 18.6 | 79.0 | 52.3 | \(9.62 = 37.0 \cdot 0.26\) | \(7.8 = 18.6 \cdot 0.42\) | 9.35 | |||
| sugar | juvenile | 30.4 | 9.7 | 61.0 | 52.3 | \(7.9 = 30.4 \cdot 0.26\) | \(4.1 = 9.7 \cdot 0.42\) | 6.22 | -9.35 | ||
| blood | adult | 17.3 | 19.2 | 99.7 | 52.3 | \(4.5 = 17.3 \cdot 0.26\) | \(8.1 = 19.2 \cdot 0.42\) | 38.92 | -3.98 | ||
| blood | juvenile | 41.7 | 9.3 | 116.0 | 52.3 | \(10.8 = 41.7 \cdot 0.26\) | \(3.9 = 9.3 \cdot 0.42\) | 38.92 | 6.22 | 3.98 | |
| ketchup | adult | 20.6 | 19.4 | 92.1 | 52.3 | \(5.4 = 20.6 \cdot 0.26\) | \(2.2 = 19.4 \cdot 0.42\) | 31.82 | -5.37 | ||
| ketchup | juvenile | 29.5 | 18.9 | 111.0 | 52.3 | \(7.7 = 29.5 \cdot 0.26\) | \(7.9 = 18.9 \cdot 0.42\) | 31.82 | 6.22 | 5.37 |
Hier bietet es sich dann nochnmal an zu Testen, ob unser Modell überhaupt besser ist als das reine Nullmodell nur mit dem Intercept. Wir können hier die ANOVA dafür nutzen. Wir erhalten dann als p-Wert den gleichen p-Werte wie schon in der letzten Zeile in der Widergabe der Zusammenfassung unseres Modells. Mit einem p-Wert von gerade einmal 0.02 sehen wir dann auch, dass unser Modell nicht sehr viel erklärt.
R Code [zeigen / verbergen]
anova(lm(jump_length ~ 1, data = flea_model_tbl),
lm(jump_length ~ K + Mg + feeding + stage, data = flea_model_tbl))Analysis of Variance Table
Model 1: jump_length ~ 1
Model 2: jump_length ~ K + Mg + feeding + stage
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 53886
2 42 39993 5 13892 2.9178 0.02383 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Bitte schaue dann für die Entscheidung welches Modell besser ist dann weiter unten in de Abschnitt zur Vergleich von Modellen nochmal rein. Du kannst beliebig viele Modelle bauen und schauen, welches Modell am besten abschneidet. Du darfst dabei natürlich nicht deine Fragestellung aus den Augen verlieren, aber das ist ja sowieso immer die Herausforderung. Am Ende ist man so im Kaninchenbau, dass man vergisst was das Ziel eigentlich war.
Die folgenden Abschnitte wiederholen sich für jedes Modell, da am Ende alles sehr gleich ist. Ich empfehle einmal es selber nachzuvollziehen. Ich habe beim Schreiben am meisten gelernt.
Intern rechnet R eine Modellmatrix. Was ist eine Modellmatrix? Eine Modellmatrix beinhaltet die Informationen welche Koeffizienten für welche Beobachtungen genutzt werden sollen um am Ende auf den Messwert für jede Beobachtung zu kommen. Faktisch also eine Zuordnung der Koeffizienten und Residuen zu den einzelnen Beobachtungen. Daher hat auch eine Modellmatrix immer so viele Zeilen wie Beobachtungen.
Damit wir hier nicht verrückter werden als wir schon sind, nutze ich den Schlangendatensatz. Wir haben also die Körperlänge vorliegen und wollen dann anhand von zwei Kovariaten und zwei Faktoren den Zusammenhang darstellen. Ich lassen hier aus Gründen der Einfachheit die Interaktion weg. Der Datensatz ist auch zu klein für eine saubere Darstellung einer Interaktion. Daher ergibt sich folgende Modellmatrix.
R Code [zeigen / verbergen]
model.matrix(svl ~ mass + diameter + region + color, data = snake_tbl) |> as_tibble() # A tibble: 8 × 6
`(Intercept)` mass diameter regionnord colorrot colorblau
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 6 9 0 0 0
2 1 8 3 0 0 0
3 1 5 6 0 1 0
4 1 7 7 1 1 0
5 1 9 5 1 1 0
6 1 11 4 1 0 1
7 1 12 10 1 0 1
8 1 10 11 1 0 1Wir können die Modellmatrix auch einmal im Ganzen aufschreiben, dann macht es auch mehr Sinn. Hier musst du dann wissen, dass wir in der Matrixmultiplikation, die erste Spalte mit dem ersten Koeffizienten malnehmen. Die zweite Spalte dann mit dem zweiten Koeffizienten malnehmen und so weiter. Hier siehst du dann auch, dass nicht jede Beobachtung für jeden Koeffizienten berücksichtigt wird. Die Faktoren werden anhand ihrer Level aufgespalten und das erste Level wandert immer in den Intercept. Wir sprechen auch von einer Dummykodierung.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 1 & 6 & 9 & 0 & 0 & 0 \\ 1 & 8 & 3 & 0 & 0 & 0\\ 1 & 5 & 6 & 0 & 1 & 0\\ 1 & 7 & 7 & 1 & 1 & 0\\ 1 & 9 & 5 & 1 & 1 & 0\\ 1 & 11 & 4 & 1 & 0 & 1\\ 1 & 12 & 10 & 1 & 0 & 1\\ 1 & 10 & 11 & 1 & 0 & 1\\ \end{pmatrix} \times \begin{pmatrix} \beta_0 \\ \beta_{mass} \\ \beta_{diameter} \\ \beta^{region}_{nord} \\ \beta^{color}_{rot} \\ \beta^{color}_{blau} \\ \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \epsilon_6 \\ \epsilon_7 \\ \epsilon_8 \\ \end{pmatrix} \]
Dann rechnen wir einmal das kombinierte Modell und schauen welche Koeffizienten wir erhalten.
R Code [zeigen / verbergen]
cov2_fac2_fit <- lm(svl ~ mass + diameter + region + color, data = snake_tbl)Wir runden jetzt einmal, damit wir nicht so viel in die Modellmatrix schreiben müssen.
R Code [zeigen / verbergen]
cov2_fac2_fit |> coef() |> round(2)(Intercept) mass diameter regionnord colorrot colorblau
31.18 1.94 -0.37 6.68 0.38 -1.40 Dann brauchen wir noch die Residuen.
R Code [zeigen / verbergen]
cov2_fac2_fit |> residuals() |> round(2) 1 2 3 4 5 6 7 8
0.56 -0.56 0.00 1.81 -1.81 0.71 2.02 -2.73 Am Ende baue ich dann einmal das volle Modell mit der Modellmatrix auf. Auf der linken Seite siehst du die Körperlängen. Dann kommt der Intercept gefolgt von den Koeffizienten multipliziert mit den Kovariaten und den Dummykodierungen. Am Ende addieren wir dann noch die Residuen.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 50 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 31.18 & 6 \cdot 1.94 & 9 \cdot -0.37 & 0 \cdot 6.68 & 0 \cdot 0.38 & 0 \cdot -1.40 \\ 31.18 & 8 \cdot 1.94 & 3 \cdot -0.37 & 0 \cdot 6.68 & 0 \cdot 0.38 & 0 \cdot -1.40\\ 31.18 & 5 \cdot 1.94 & 6 \cdot -0.37 & 0 \cdot 6.68 & 1 \cdot 0.38 & 0 \cdot -1.40\\ 31.18 & 7 \cdot 1.94 & 7 \cdot -0.37 & 1 \cdot 6.68 & 1 \cdot 0.38 & 0 \cdot -1.40\\ 31.18 & 9 \cdot 1.94 & 5 \cdot -0.37 & 1 \cdot 6.68 & 1 \cdot 0.38 & 0 \cdot -1.40\\ 31.18 & 11\cdot 1.94 & 4 \cdot -0.37 & 1 \cdot 6.68 & 0 \cdot 0.38 & 1 \cdot -1.40\\ 31.18 & 12\cdot 1.94 & 10 \cdot -0.37 & 1 \cdot 6.68 & 0 \cdot 0.38 & 1 \cdot -1.40\\ 31.18 & 10\cdot 1.94 & 11 \cdot -0.37 & 1 \cdot 6.68 & 0 \cdot 0.38 & 1 \cdot -1.40\\ \end{pmatrix} + \begin{pmatrix} 0.56 \\ -0.56 \\ 0.00 \\ +1.81 \\ -1.81 \\ +0.71 \\ +2.02 \\ -2.73 \\ \end{pmatrix} \]
Jetzt kannst du dich fragen, kommt das denn auch hin? Dafür alles nochmal in R getippt und geschaut welche Zahlen am Ende für die Körperlänge rauskommen.
R Code [zeigen / verbergen]
c(31.18 + 6*1.94 + 9*-0.37 + 0*6.68 + 0*0.38 + 0*-1.40 + 0.56,
31.18 + 8*1.94 + 3*-0.37 + 0*6.68 + 0*0.38 + 0*-1.40 - 0.56,
31.18 + 5*1.94 + 6*-0.37 + 0*6.68 + 1*0.38 + 0*-1.40 + 0.00,
31.18 + 7*1.94 + 7*-0.37 + 1*6.68 + 1*0.38 + 0*-1.40 + 1.81,
31.18 + 9*1.94 + 5*-0.37 + 1*6.68 + 1*0.38 + 0*-1.40 - 1.81,
31.18 + 11*1.94 + 4*-0.37 + 1*6.68 + 0*0.38 + 1*-1.40 + 0.71,
31.18 + 12*1.94 + 10*-0.37 + 1*6.68 + 0*0.38 + 1*-1.40 + 2.02,
31.18 + 10*1.94 + 11*-0.37 + 1*6.68 + 0*0.38 + 1*-1.40 - 2.73) |> round()[1] 40 45 39 51 52 57 58 49Und dann hier nochmal der Vergleich zu den ursprünglichen Werten der Körperlänge der Schlangen. Das passt ja hervorragend.
R Code [zeigen / verbergen]
snake_tbl |> pull(svl)[1] 40 45 39 51 52 57 58 49Musst du das hier im Detail verstehen? Kommt drauf an. Hier wird eben dargestellt wie sich in R intern die Koeffizienten ergeben. Das macht dann eben auch was aus für die Interpretation. Hier lernen wir dann nochmal, was eigentlich die Dummykodierung bedeutet. Je nachdem wie sich dein Modell zusammensetzt ist dann auch die Modellmatrix komplizierter.
Dieser Abschnitt beinhaltet eine kurze Simulation in R mit einem Tibble und der Erstellung eines normalverteilten Messwerts. Mehr zu der Generierung von Daten dann im entsprechenden Kapitel. Ich habe alles ausgelagert, da es dann hier zu voll wurde. Daher ist es hier eher so eine kleine Spielweise.
R Code [zeigen / verbergen]
cov2_fac2_tbl <- tibble(c_1 = rnorm(30, 0, 1),
c_2 = rnorm(30, 0, 1),
f_a = rep(gl(3, 5), 2),
f_b = gl(2, 15),
y = 2 +
1 * c_1 +
-1 * c_2 +
2 * as.numeric(f_a) +
3 * as.numeric(f_b) +
rnorm(15, 0, 0.001))Dann schauen wir uns einmal an, ob wir dann den Intercept und die Koeffizienten wiederfinden. Wenn du den Fehler in rnorm() von \(0.001\) hochsetzt, dann werden auch die Koeffizienten in dem folgenden Modell ungenauer. Hat aber gut geklappt, wir erhalten die gerundeten Koeffizienten, die wir eingestellt hatten einigermaßen wiedergegeben.
R Code [zeigen / verbergen]
lm(y ~ c_1 + c_2 + f_a + f_b, cov2_fac2_tbl) |>
coef() |> round(2)(Intercept) c_1 c_2 f_a2 f_a3 f_b2
7 1 -1 2 4 3 46.6 Prädiktives Modell
Neben dem klassischen kausalen Modell können wir auch ein prädiktives Modell rechnen. In einem prädiktiven Modell wollen wir wissen, welche Werte unser Messwert für neue Werte der Einflussvariable annehmen würde. Auch in einem prädiktiven Modell rechnen wir erstmal ganz normal eine multiple lineare Regression. Dann nutzen wir das Modell der Regression um neue Werte für unseren Messwert anhand neuer oder alter Werte der Einflussvariable vorherzusagen. Daher können wir auch beides miteinander verbinden. Du schaust erst was das kausale Modell ergibt und lässt dir dann neue Messwerte vorhersagen. Dabei musst du immer beachten, dass die vorhergesagten Messwerte auf der angepassten Ebene der Regression liegen. Daher nennen wir die vorhergesagten Messwerte auch angepasste Messwerte (eng. fitted). Wir werden später in der Klassifikation, der Vorhersage von \(0/1\)-Werten, noch andere Prädktionen und deren Maßzahlen kennen lernen. Die vorgehensweise ist aber so identisch mit der im Kapitel zur simplen linearen Regression, so dass ich hier nicht nochmal alles wiederhole. Einfach nochmal dort schauen und die Modelle von oben verwenden. Weitere allgemeine Beispiel finden sich auch in den Kapitel zu den Marginal effect models und dem Modellieren in R.
46.7 Weiteres von Interesse
In den folgenden Abschnitten schauen wir nochmal in weitere Dinge von Interesse, die hier direkt mit der multiplen Regression verbunden sind. Deshalb hier nochmal eine Übersicht von statistischen Dingen, die du bei deinen Einflussvariablen beachten musst. Teilweise gehen wir in den folgenden Abschnitten darauf ein oder aber in den folgenden Kapiteln. Wenn das Problem zu groß wurde habe ich das Thema eben ausgelagert.
In den folgenden Abschnitten schauen wir uns noch andere Dinge von Interesse in einer multiplen Regression einmal an. Zum einen haben wir ein Problem, wenn unsere Einflussvariablen untereinander zu stark korreliert sind. Das zeige ich dann einmal an den Beinhaaren bei den Flöhen. Auch ist es problematisch, wenn wir eine Einheit gewählt hat, die sehr große Werte beinhaltet. Das kann ich dir gleich einmal an den Yediflöhen aufzeigen. Dann schauen wir nochmal in die Unabhängigkeitsannahme der Einflussvariablen. Neben der Korrelation sollten die Einflussvariablen auch wirklich unabhängig voneinander sein und sich nicht als Modell selbst erklären. Dann am Ende wollen wir natürlich auch noch wissen, was das beste Modell für unsere Daten wäre. Welche Einflussvariablen kann ich den reinnehmen und was ist dann das beste Modell? Darauf gehe ich dann hier auch nochmal ein.
46.7.1 Einheit der Kovariaten
Kommen wir nun nochmal zu einem Problem der Einheit. Wir können einen sehr kleinen Effekt vorliegen haben, der dann signifikant ist. Schnell denken wir dann, dass dieser Effekt sehr klein ust und damit nicht relevant. Wir sprechen aber bei einer Regression immer von der Steigung als Effekt. Wenn sich also die Einheit der Einflussvariable um Eins erhöht, dann steigt der Messwert um den Wert des Koeffizienten der Steigung. Wenn wir also sehr große Werte messen, dann ist die Änderung in einer Einheit sehr klein. Schauen wir uns mal das Beispiel der Jediflöhe an.
Manche Flöhe haben hohe Werte der Midi-Chlorianer oder einfach M-Werte. Damit sind diese Flöhe insbesondere sensitiv für die Macht und somit Jediflöhe. Jediflöhe könnten damit auch höhere Sprungweiten vorliegen haben, da die Jediflöhe ja einen teil ihrer MAcht dazu nutzen könnten weiter zu springen. Daher wollen wir mal in einer einfachen simplen Regression mit nur den M-Werten schauen, ob die M-Werte einen Einfluss auf die Sprungweiten haben. Ich lasse mir jetzt nur die Tabelle der Koeffizienten wiedergeben.
R Code [zeigen / verbergen]
lm(jump_length ~ M, data = flea_model_tbl) |>
summary() |> coef() |> round(3) Estimate Std. Error t value Pr(>|t|)
(Intercept) 80.412 7.356 10.932 0.000
M 0.002 0.001 2.254 0.029Wie wir jetzt sehen ist der Effekt mit 0.002cm extrem gering aber dennoch signifkant. Der p-Wert ist kleiner als das Signifikanzniveau \(\alpha\) gleich 5%. Ist also der Wert der Midi-Chlorianer nicht relevant? Hier kommt es auf die Einheit und damit die Spannweite der M-Wert an. Die M-Werte laufen von 80.19 bis 25149.36 Anzahl Midi-Chlorianer im Blut. Damit ist eine kleine Änderung in den M-Werten auch nur mit einer kleinen Änderung in den Sprungweiten verbunden. Also Achtung bei Kovariaten mit großer Spannweite und kleinen Einheiten.
Eine Lösung ist es dann die Einheiten zu vergrößern. In unserem Beispiel können wir die M-Werte auf einer Skale in Tausend angeben, dann haben wir gleich viel kleinere Werte und die Spannweite ist nicht so groß. Daher ist es immer eine Überlegung wert zu prüfen, ob du Gramm nicht in Kilo darstellen willst oder aber Zentimeter in Meter. Ich habe dir den Zusammenhang in der folgenden Abbildung nochmal veranschaulicht. Die Punkte auf der Abbildung sehen gleich aus, der Koeffizient der Steigung ist es aber nicht mehr. Damit lassen sich die Ergebnisse auch besser interpretieren.
46.7.2 Confounderanalyse
Ich gebe hier nur einen kurzen Einblick in die Confounderanalyse, da mir dann aufgefallen ist, dass das Thema dann doch größer wird. Daher bitte dann nochmal ins Kapitel zur Mediatoranalyse schauen, wenn du nach dem Lesen meinst, dass du mehr brauchst. Hier also eine kurze Übersicht über die Idee der Confounderanalyse.
In diesem Abschnitt erkläre ich nur einen konzeptionellen Ausschnitt aus der Confounderanalyse. Wir konzentrieren uns hier auf ein Beispiel mit den M-Werten der Flöhe und den Zusammenhang mit den Sprungweiten. Mehr zu Confoundern, Collidern und Mediatoeren gibt es in dem Kapitel zur Mediatoranalyse nochmal aufgearbeitet. Ich habe hier beim Schreiben des Kapitels gemerkt, dass das Thema zu groß ist um mal eben in einem Abschnitt abgearbeitet zu werden. Für unsere Betrachtung möglicher Confounder in der Analyse der M-Werte nehme ich hier nicht die M-Werte auf der Originalenskala sondern auf in Tausend, damit mir die Koeffizienten nicht so klein werden.
R Code [zeigen / verbergen]
flea_model_tbl <- flea_model_tbl |>
mutate(M = M/1000)Betrachten wir nochmal die simple lineare Regression der Anzahl Midi-Chlorianer im Blut in Tausend auf die Sprungweite in [cm]. Wir sehen, dass wir einen signifikanten Koeffizienten mit einem positiven Koeffizienten vorliegen haben. Jetzt ist die Frage, ist das jetzt ein wahrer Zusammenhang oder haben wir eventuell Störgrößen (eng. confounder) in den Daten vorliegen?
Was ist also die Idee einer Confounderanalyse? In der folgenden schematischen Darstellung habe ich dir mal einen Fall eines Disturbers (deu. Störenfrieds) als Störgröße darsgetellt. Wir wollen den Effekt von X auf Y modellieren. Wir haben aber noch eine andere Einflussvariable als Störer vorliegen. Dieser Störer hat einen Effekt auf X sowie auf Y. Die Interpretation des Zusammenhangs von X auf Y ist so nicht möglich, da der Zusammenhang verzerrt ist. Wir müssen also erstmal den Störer finden. Was in der Theorie irgendwie einleuchtend klingt, ist in der Praxis extrem mühselig.
Betrachten wir also einmal als Beispiel für eine etwas naheliegende Analyse nochmal die Anzahl Midi-Chlorianer im Blut und die Sprungweite. Wir können jetzt einmal schauen, ob es noch andere Einflussvariablen gibt, die die Sprungweite beeinflussen. Damit natürlich dann auch indirekt die Anzahl der Midi-Chlorianer im Blut. Wir schauen uns einmal an, wie es mit der Ernärung und dem Flohschnupfen so aussieht. In der folgenden Abbildung siehts du dann mal den Effekt der Midi-Chlorianer im Blut auf die Sprungweite, wenn wir uns noch die Ernährung mit anschauen. Wir erhalten auf einmal in den Ernärhungsgruppen kaum noch einen Effekt oder gar einen klar negativen Effekt auf die Sprungweiten. Bei der Infektion ist die Lage nicht so eindeutig. Was aber auffällt ist, dass Flöhe mit hoher Anzahl an Midi-Chlorianer im Blut alle Flohschnupfen haben. Ist hier etwa der Flohschnupfen ein Confounder, der auf die Sprungweite und die Midi-Chlorianer im Blut eine Auswirkung hat?
Wir können uns hier einmal die drei Modell zusammenbauen um diese dann einmal von den Koeffizienten und den p-Werten miteinander vergleichen zu können. Dann können wir einmal die Modelle untereinander vergleichen. Wir nehmen einmal das Modell nur mit den M-Werten und dann einmal das Modell mit den M-Werten und jeweils der Ernährung und dem Infektionstatus.
R Code [zeigen / verbergen]
fit_1 <- lm(jump_length ~ M, data = flea_model_tbl)
fit_2 <- lm(jump_length ~ M + feeding, data = flea_model_tbl)
fit_3 <- lm(jump_length ~ M + infected, data = flea_model_tbl)Wir nutzen hier die tollen Funktionen aus dem R Paket {modelsummary} und dann dem R Paket {tinytable} um uns einmal die Modelle im Vergleich anzuschauen. Wir sehen sofort, dass der Effekt der Midi-Chlorianer nicht mehr signifikant wird, wenn wir noch die Ernährung oder aber die Infektion mit ins Modell nehmen. Zwar ist der Flohschnupfen nicht signifikant, aber haben wir hier auch eine verringerte Sprungweite bei den gesunden Flöhen zu den kranken Flöhen. Wir können hier von einem Confoundereffekt ausgehen.
| Model | |||
|---|---|---|---|
| I | II | III | |
| + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001 | |||
| Midi-Chlorianer | 1.515* | 0.323 | 1.331+ |
| p = 0.029 | p = 0.683 | p = 0.090 | |
| Ernährung (Blut) | 35.519** | ||
| p = 0.005 | |||
| Ernährung (Ketchup) | 28.478* | ||
| p = 0.037 | |||
| Flohschnupfen (nein) | -5.455 | ||
| p = 0.617 | |||
| Num.Obs. | 48 | 48 | 48 |
| R2 | 0.099 | 0.248 | 0.105 |
| R2 Adj. | 0.080 | 0.197 | 0.065 |
Die Confounderanalyse verlangt sehr viel vor und zurück bei der Modellierung und damit auch Modellbildung. Wir müssen uns verschiedene Modelle anschauen und entscheiden, welche Einflussvariable vermutlich einen Einfluss auf unseren Messwert hat oder nicht. Was in der Theorie dann irgendwie immer plausibel scheint, scheitert in der Praxis meistens an zu wenigen Daten. Wenn der potenzielle Confounder nicht als Einflussvariable in den Daten vorhanden ist, dann kann das beste Modell nichts finden. Der Confounder ist ja nicht erhoben worden.
46.7.3 Korrelation der Kovariaten
Die Einlfussvariablen haben neben der Einheit noch andere Probleme. Teilweise sind diese Probleme nicht ganz so offensichtlich, wie gleich in meinem Beispiel gewählt. Probleme treten auf, wenn die Einflussvariablen untereinander zu stark miteinander korreliert sind. Mehr zur Korrelation erfährst du im Kapitel zur Korrelation. Hier wiederhole ich jetzt nicht die Grundlagen. Wenn also Einflussvariablen sehr stark miteinander korrelaiert sind, dann erklären die Variablen mehr oder minder das Gleiche. In der folgenden Abbildung siehst du den Zusammenhang zwischen der Sprungweite und der Anzahl an Haaren auf den Flohbeinen. Wie es so ist, können wir hier natürlich verschiedene Beine oder die mittlere Anzahl betrachten. Vermeintlich glücklicherweise haben aber alle den gleichen Koeffizienten.
Dann können wir uns auch einmal die Korrelation zwischen den drein Kovariaten anschauen. Wie zu erwarten ist die Korrelation maximal mit Eins. Die Sterne zeigen die Signifikanz an. Das Beispiel ist hier konstruiert, aber in biologischen Systemen oder Laborwerten können wir schnell sehr hohe Korrelationen erreichen. Das Gewicht und der BMI ist sehr hoch korreliert. Blutwerte wie Hämoglobin, Eisengehalt und Sauerstoffsättigung können das Gleiche anzeigen.
R Code [zeigen / verbergen]
flea_model_tbl |>
select(count_leg, count_leg_left, count_leg_right) |>
correlation() |>
summary(redundant = TRUE)# Correlation Matrix (pearson-method)
Parameter | count_leg | count_leg_left | count_leg_right
--------------------------------------------------------------
count_leg | | 1.00*** | 1.00***
count_leg_left | 1.00*** | | 1.00***
count_leg_right | 1.00*** | 1.00*** |
p-value adjustment method: Holm (1979)Naheliegend wäre es jetzt ein Modell zu bauen in dem alle drei Kovariaten enthalten sind. Dann müssen wir uns nicht entscheiden welche wir nehmen und erhalten für jede Kovariate eine Information. Wenn du nochmal auf die Abbildung schaust, wir erwarten hier eigentlich eine signifikante Steigung.
R Code [zeigen / verbergen]
cov2_fit <- lm(jump_length ~ count_leg + count_leg_left + count_leg_right, data = flea_model_tbl) Wenn wir nun die Koeffizienten betrachten, dann werden wir schon stutzig. Wir erhalten eine negative Steigung für die mittlere Anzahl und dann für die beiden Beine dann eine positive Steigung, die auch grob nur halb so groß ist. Das ist schon mal nicht so gut.
R Code [zeigen / verbergen]
cov2_fit |>
coef() |> round(2) (Intercept) count_leg count_leg_left count_leg_right
75.11 -15.07 7.79 7.37 Betrachten wir also einmal das Modell in der Zusammenfassung um zu sehen, wie die Koeffizienten und die Residuen aussehen. Die Modelgüte ist akzeptabel. Was aber auffällt ist, dass keine der Kovariaten signifikant ist. Das ist sehr seltsam, wenn wir die Abbildung betrachten. Wir sehen hier die direkte Folge von hoch korrelierter Kovariaten. Wenn diese hoch korreliert sind, dann werden alle nicht signfikant.
R Code [zeigen / verbergen]
cov2_fit |> summary()
Call:
lm(formula = jump_length ~ count_leg + count_leg_left + count_leg_right,
data = flea_model_tbl)
Residuals:
Min 1Q Median 3Q Max
-29.307 -14.465 -4.338 11.832 46.265
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 75.111 5.243 14.327 <2e-16 ***
count_leg -15.069 12.130 -1.242 0.221
count_leg_left 7.790 6.028 1.292 0.203
count_leg_right 7.372 6.128 1.203 0.235
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 19.51 on 44 degrees of freedom
Multiple R-squared: 0.6892, Adjusted R-squared: 0.668
F-statistic: 32.52 on 3 and 44 DF, p-value: 3.082e-11Dann vergleichen wir einmal alle drei Modelle mit den tollen Funktionen aus dem R Paket {modelsummary} und dann dem R Paket {tinytable}. Wir bauen also erstmal das simple Modell mit nur der mittleren Beinanzahl und dann ergänzen wir schrittweise die Anzahl der Haare der linken und rechten Beine. Dadurch sehen wir dann einmal den Effekt der Kovariaten, wenn wir diese zu einem Modell hinzunehmen.
R Code [zeigen / verbergen]
fit_4 <- lm(jump_length ~ count_leg, data = flea_model_tbl)
fit_5 <- lm(jump_length ~ count_leg + count_leg_left, data = flea_model_tbl)
fit_6 <- lm(jump_length ~ count_leg + count_leg_left + count_leg_right, data = flea_model_tbl) Jetzt können wir alle drei Modell nebeneinander direkt miteinander vergleichen. Wir sehen hier sehr schön, wie der p-Wert der mitttleren Beinanzahl immer weiter anstiegt je mehr korrelierte Kovariaten in das Modell kommen. Spannenderweise bleibt die Modellgüte immer gleich. Wir sehen also das Problem nicht, wenn wir uns zum Beispiel das Bestimmtheitsmaß nur anschauen. Du musst also immer vorab auf die Korrelation schauen.
| Model | |||
|---|---|---|---|
| IV | V | VI | |
| + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001 | |||
| Mittlere Beinhaare | 0.091*** | -0.504 | -15.069 |
| p = <0.001 | p = 0.510 | p = 0.221 | |
| Linke Beinhaare | 0.595 | 7.790 | |
| p = 0.437 | p = 0.203 | ||
| Rechte Beinhaare | 7.372 | ||
| p = 0.235 | |||
| Num.Obs. | 48 | 48 | 48 |
| R2 | 0.675 | 0.679 | 0.689 |
| R2 Adj. | 0.668 | 0.665 | 0.668 |
46.7.4 Variance inflation factor (VIF)
Wenn wir uns die Korrelation der Einflussvariablen ansschauen, dann schauen wir ja mehr oder minder immer auf paarweise Vergleiche. Wenn wir aber wissen wollen, ob eine Einflussvariable von den anderen Einflussvariablen teilweise oder ganz erklärt wird, dann nutzen wir den Variance inflation factor (abk. VIF). Hierzu gibt es dann kein deutsches Wort. Wir wird der Variance inflation factor definiert? Im Prinzip haben wir es hier mit einem Verwandten des Bestimmtheitsmaß \(R^2\) zu tun. Hier erstmal die Formel für die Berechnung des Variance inflation factors.
\[ VIF = \cfrac{1}{1- R^2} \]
mit
- \(VIF\), dem Variance inflation factor für die untersuchte Einflussvariable.
- \(R^2\), dem Bestimmtheitsmaß für die Einflussvariable, wenn die Einflussvariable als Messwert \(Y\) im Modell verwendet wird.
Bevor wir dann gleich nochmal zu der Berechnung kommen, hier erstmal die Interpretation der VIF-Werte. Die VIF-Werte helfen dir, den Grad der Multikollinearität in deinem Modell zu bewerten. Den die Multikollinearität beschreibt nichts anderes, als das deine Einflussvariablen sich untereinander selber erklären.
- VIF = 1: Es gibt keine Multikollinearität. Alles ist okay und du kannst dein Modell so verwenden wie gedacht.
- VIF zwischen 1 und 5: Es liegt moderate Multikollinearität vor, die in der Regel unproblematisch ist. Dami ignorieren wir solche VIF-Werte und machen ganz normal weiter.
- IF > 5: Es gibt eine hohe Multikollinearität, die die Koeffizienten unzuverlässig machen kann. Hier sollten Maßnahmen ergriffen werden. Das heißt wir überlegen, ob wir nicht Einflussvariablen aus unserem Modell entfernen um die VIF-Werte zu senken.
- VIF > 10: Dies deutet auf eine sehr hohe Multikollinearität hin, die dringend korrigiert werden muss. Auch hier müssen wir dann schauen, welche Einflussvariablen wir entfernen wollen.
Wichtig hier nochmal zu wissen, dass du nicht unbedingt die Variable mit dem hohen VIF-Wert rausschmeißen musst. Manachmal hilft es auch andere Variablen zu entfernen und dann gehen die VIF-Werte global runter. Hier kommt es darauf an, welche Einflussvariablen du wirklich im Modell haben willst und welche eher nicht. Das hängt stark von deiner wissenschaftlichen Fragestellung ab.
Wir bauen uns jetzt einmal ein Modell und wollen dann schauen, in wie weit die Vairablen untereinander unabhängig sind. Dafür nehme ich jetzt einmal einen kleineren Datensatz und zwar nur die jugendlichen Flöhe. Das hat den Grunf, dass wir in den Daten mehr Abhänigkeiten haben. Ich habe die Daten so gebaut, dass es eben auch hohe VIF-Werte gibt.
R Code [zeigen / verbergen]
juvenile_flea_tbl <- filter(flea_model_tbl, stage == "juvenile")Dann bauen wir unser Modell. Wir nehmen hier mal nur Kovariate mit ins Modell. Faktisch geht der VIF auch mit faktoriellen Einflussvariablen, dann berechnen wir die sogenannten GVIF-Werte. Hier zeige ich dir die Kovariaten, da es üblicher ist sich die Kovariaten eher anzuschauen.
R Code [zeigen / verbergen]
juvenile_fit <- lm(jump_length ~ K + Mg + CRP + Hb + BSG + M,
data = juvenile_flea_tbl)Nachdem wir das Modell angepasst haben können wir auf verschiedene Arten den Variance inflation factor berechnen. Wenn dich nicht so richtig interessiert woher der Variance inflation factor kommt, dann ist das R Paket {car} und das R Paket {performance} die richtige Wahl. Ich zeige dir dann im letzten Tab nochmal die händische Durchführung in R. Da wird nochmal klarer wie der VIF-Wert aus dem Bestimmtheitsmaß berechnet wird.
Wenn wir einfach nur die VIF-Werte brauchen, dann können wir die Funktion vif() aus dem R Paket {car} nutzen. Wir erhalten hier die VIF-Werte ohne Interpretation wiedergegeben. Wir müssen dann selber schauen, welche Werte groß sind.
R Code [zeigen / verbergen]
vif(juvenile_fit) K Mg CRP Hb BSG M
1.972761 18.659889 13.733641 8.787982 3.921379 13.132223 Hier hilft dann nochmal selber eine Überprüfung, damit wir nichts übersehen. Insbesondere wenn du viele Einflussvariablen vorliegen hast, dann ist die folgende Abfrage schon hilfreich. Hier kannst du dann gleich ablesen, welche Variablen einen zu hohen VIF-Wert haben.
R Code [zeigen / verbergen]
vif(juvenile_fit) > 5 K Mg CRP Hb BSG M
FALSE TRUE TRUE TRUE FALSE TRUE Wir würden jetzt einmal schauen, ob wir nicht Magnesium oder den CRP-Wert aus dem Modell nehmen würden. Du kannst das auch mit dem Hb-Wert oder M-Werten machen. Dann gucken wir wie sich die VIF-Werte ändern und arbeiten uns so vor. Die Variable an der wir am meisten interessiert sind, versuchen wir so lange wie möglich im Modell zu belassen.
Wenn wir den Variance inflation factor berechnen wollen, dann nutzen wir die Funktion check_model(). Wir können uns mit der Funcktion check_model() aus dem R Paket {performance} auch die Unsicherheit mit angeben lassen. In unserem Beispiel hieft dies gerade nicht sehr viel weiter. Wir bleiben bei den geschätzen Werten und ignorieren das Intervall. Das schöne ist eben, dass wir hier auch gleich eine Abbildung mit der Interpretation erhalten. Das macht die Anwendung dann angenehm einfach.
Und wie machen wir die VIF Berechnung nun händisch? Wir brauchen erstmal die Variance inflation factor Formel in R. Die Funktion baue ich dir einmal nach. Diese können wir dann nutzen um aus einem Bestimmtheitsmaß \(R^2\) den entsprechenden Variance inflation factor für die Einflussvariable zu berechnen.
R Code [zeigen / verbergen]
vif_fct <- function(x) 1/(1-x)Der Witz ist jetzt, dass wir die Einflussvariable für den Variance inflation factor nun als Messwert in das Modell setzen und die anderen Einflussvariablen so belassen. Der ursprüngliche Messwert kommt dann in der Berechnung des Variance inflation factor nicht mehr vor. Wie du in den folgenden Berechnungen siehst, ist immer die Einflussvariable für den VIF-Wert auf der linken Seite der Tilde und fehlt auf der rechnten Seite dann entsprechend. Die berechneten VIF-Werte entsprechen dann den Werten aus der Funktion vif() im R Paket {car} aus dem ersten Tab.
R Code [zeigen / verbergen]
lm(K ~ Mg + CRP + Hb + BSG + M, data = juvenile_flea_tbl) |>
r2() |>
pluck("R2") |> vif_fct() |> set_names("K") K
1.972761 R Code [zeigen / verbergen]
lm(Mg ~ K + CRP + Hb + BSG + M, data = juvenile_flea_tbl) |>
r2() |>
pluck("R2") |> vif_fct() |> set_names("Mg") Mg
18.65989 R Code [zeigen / verbergen]
lm(CRP ~ K + Mg + Hb + BSG + M, data = juvenile_flea_tbl) |>
r2() |>
pluck("R2") |> vif_fct() |> set_names("CRP") CRP
13.73364 R Code [zeigen / verbergen]
lm(Hb ~ K + Mg + CRP + BSG + M, data = juvenile_flea_tbl) |>
r2() |>
pluck("R2") |> vif_fct() |> set_names("Hb") Hb
8.787982 R Code [zeigen / verbergen]
lm(BSG ~ K + Mg + CRP + Hb + M, data = juvenile_flea_tbl) |>
r2() |>
pluck("R2") |> vif_fct() |> set_names("BSG") BSG
3.921379 R Code [zeigen / verbergen]
lm(M ~ K + Mg + CRP + Hb + BSG, data = juvenile_flea_tbl) |>
r2() |>
pluck("R2") |> vif_fct() |> set_names("M") M
13.13222 46.7.5 Vergleich von Modellen
Im Folgenden wollen wir einmal verschiedene Modelle miteinander Vergleichen und uns statistisch wiedergeben lassen, was das beste Modell ist. Und hier holen wir auch einmal kurz Luft, denn wir entschieden nur was das statistisch beste Modell ist. Es kann sein, dass ein Modell biologisch mehr Sinn macht und nicht auf Platz 1 der statistischen Maßzahlen steht. Das ist vollkommen in Ordnung. Du musst abwägen, was für sich das beste Modell ist.
Wir bauen uns jetzt fünf Modelle von fit_7 bis fit_11. Jedes dieser Modelle hat andere Einflussvariablen aber den gleichen Messwert. Im Weiteren sortieren wir die Modelle von einfach nach komplex. Ich versuche immmer das einfachste Modell mit der niedrigsten Nummer zu benennen. Im Idealfall benennst du die Modellobjekte nach den Modellen, die in en Objekten gespeichert sind. Oft sind die Modelle aber sehr groß und die Objekte der Fits haben dann sehr lange Namen.
R Code [zeigen / verbergen]
fit_7 <- lm(jump_length ~ feeding, data = flea_model_tbl)
fit_8 <- lm(jump_length ~ feeding + stage, data = flea_model_tbl)
fit_9 <- lm(jump_length ~ feeding + stage + weight, data = flea_model_tbl)
fit_10 <- lm(jump_length ~ feeding + stage + count_leg, data = flea_model_tbl)
fit_11 <- lm(jump_length ~ stage + weight, data = flea_model_tbl)Als Ergänzung zum Bestimmtheitsmaß \(R^2\) wollen wir uns noch das Akaike information criterion (abk. \(AIC\)) anschauen. Du kannst auch das \(R^2\) bzw. das \(R^2_{adj}\) für die Modellauswahl nehmen. Das \(AIC\) ist neuer und auch für komplexere Modelle geeignet. Es gilt hierbei, je kleiner das \(AIC\) ist, desto besser ist das \(AIC\). Wir wollen also Modelle haben, die ein kleines \(AIC\) haben. Wir gehen jetzt nicht auf die Berechnung der \(AIC\)’s für jedes Modell ein. Wir erhalten nur ein \(AIC\) für jedes Modell. Die einzelnen Werte des \(AIC\)’s sagen nichts aus. Ein \(AIC\) ist ein mathematisches Konstrukt. Wir können aber verwandte Modelle mit dem \(AIC\) untereinander vergleichen. Daher berechnen wir ein \(\Delta\) über die \(AIC\). Dafür nehmen wir das Modell mit dem niedrigsten \(AIC\) und berechnen die jeweiligen Differenzen zu den anderen \(i\) Modellen. In unserem Beispiel ist \(i\) dann gleich fünf, da wir fünf Modelle haben.
\[ \Delta_i = AIC_i - AIC_{min} \]
- wenn \(\Delta_i < 2\), gibt es keinen Unterschied zwischen den Modellen. Das \(i\)-te Modell ist genauso gut wie das Modell mit dem \(AIC_{min}\).
- wenn \(2 < \Delta_i < 4\), dann gibt es eine starke Unterstützung für das \(i\)-te Modell. Das \(i\)-te Modell ist immer noch ähnlich gut wie das \(AIC_{min}\).
- wenn \(4 < \Delta_i < 7\), dann gibt es deutlich weniger Unterstützung für das \(i\)-te Modell;
- Modelle mit \(\Delta_i > 10\) sind im Vergleich zu dem besten \(AIC\) Modell nicht zu verwenden.
Nehmen wir ein \(AIC_1 = AIC_{min} = 100\) und \(AIC_2\) ist \(100,7\) an. Dann ist \(\Delta_2=0,7<2\), so dass es keinen wesentlichen Unterschied zwischen den Modellen gibt. Wir können uns entscheiden, welches der beiden Modelle wir nehmen. Hier ist dann wichtig, was auch die Biologie sagt oder eben andere Kriterien, wie Kosten und Nutzen. Wenn wir ein \(AIC_1 = AIC_{min} = 100000\) und \(AIC_2\) ist \(100700\) vorliegen haben, dann ist \(\Delta_2 = 700 \gg 10\), also gibt es keinen Grund für das \(2\)-te Modell. Das \(2\)-te Modell ist substantiell schlechter als das erste Modell. Mehr dazu kannst du unter Multimodel Inference: Understanding AIC and BIC in Model Selection nachlesen.
Wir können das \(\Delta_i\) auch in eine Wahrscheinlichkeit umrechnen. Wir können \(p_i\) berechnen und damit die relative im Vergleich zu \(AIC_{min}\) Wahrscheinlichkeit, dass das \(i\)-te Modell den AIC minimiert.
\[ p_i = \exp\left(\cfrac{-\Delta_i}{2}\right) \]
Zum Beispiel entspricht \(\Delta_i = 1.5\) einem \(p_i\) von \(0.47\) (ziemlich hoch) und ein \(\Delta_i = 15\) entspricht einem \(p_i =0.0005\) (ziemlich niedrig). Im ersten Fall besteht eine Wahrscheinlichkeit von 47%, dass das \(i\)-te Modell tatsächlich eine bessere Beschreibung ist als das Modell, das \(AIC_{min}\) ergibt, und im zweiten Fall beträgt diese Wahrscheinlichkeit nur 0.05%. Wir können so einmal nachrechnen, ob sich eine Entscheidung für ein anderes Modell lohnen würde. Neben dem \(AIC\) gibt es auch das Bayesian information criterion (\(BIC\)). Auch beim \(BIC\) gilt, je kleiner das BIC ist, desto besser ist das BIC.
Du siehst schon, es gibt eine Reihe von Möglichkeiten sich mit der Güte oder Qualität eines Modells zu beschäftigen. Wir nutzen die Funktion model_performance() um uns die Informationen über die Güte eines Modells wiedergeben zu lassen. Im folgenden Codeblock habe ich mich nur auf das \(AIC\) und das \(BIC\) konzentriert.
R Code [zeigen / verbergen]
model_performance(fit_7) |>
as_tibble() |>
select(AIC, BIC)# A tibble: 1 × 2
AIC BIC
<dbl> <dbl>
1 468. 475.Gut soweit. Du kannst jetzt für jedes der Modelle das \(AIC\) berechnen und dann dir die Modelle entsprechend ordnen. Wir müssen das aber nicht tun. Wir können uns auch die Funktion compare_performance() zu nutze machen. Die Funktion gibt uns die \(R^2\)-Werte wieder wie auch die \(AIC\) sowie die \(s^2_{\epsilon}\) als sigma wieder. Wir haben also alles zusammen was wir brauchen. Darüber hinaus kann die Funktion auch die Modelle rangieren. Das nutzen wir natürlich gerne.
R Code [zeigen / verbergen]
comp_res <- compare_performance(fit_7, fit_8, fit_9, fit_10, fit_11, rank = TRUE)
comp_res# Comparison of Model Performance Indices
Name | Model | R2 | R2 (adj.) | RMSE | Sigma | AIC weights
------------------------------------------------------------------
fit_10 | lm | 0.770 | 0.749 | 16.061 | 16.970 | 1.000
fit_9 | lm | 0.308 | 0.244 | 27.867 | 29.443 | 3.26e-12
fit_7 | lm | 0.245 | 0.212 | 29.112 | 30.067 | 2.96e-12
fit_8 | lm | 0.253 | 0.202 | 28.966 | 30.254 | 1.38e-12
fit_11 | lm | 0.028 | -0.015 | 33.037 | 34.120 | 6.83e-15
Name | AICc weights | BIC weights | Performance-Score
-------------------------------------------------------
fit_10 | 1.000 | 1.000 | 100.00%
fit_9 | 3.26e-12 | 3.26e-12 | 18.49%
fit_7 | 5.17e-12 | 1.92e-11 | 15.10%
fit_8 | 1.89e-12 | 3.53e-12 | 15.03%
fit_11 | 1.19e-14 | 4.44e-14 | 0.00%Anhand der Ausgabe der Funktion compare_performance() sehen wir, dass unser Modell fit_10 das beste Modell ist. In der folgenden Abbildung sehen wir die Ausgabe der Funktion compare_performance() nochmal visualisiert. Wir können dann die einzelnen Modelle nochmal besser vergleichen. Auch siehst du hier, ob ein Modell in einem Bereich sehr schlecht ist oder aber nur in einem Bereich sehr gut.
Zum Ende stellt sich die Frage nach dem statistischen Test. Können wir auch statistisch Testen, ob das Modell fit_10 signifikant unterschiedlich ist? Ja wir können die Funktion test_vuong() nutzen um das erste Modell in der Funktion zu den anderen Modellen zu vergleichen. Wenn du mehrere Modelle miteinander vergleichen möchtest, dann muss du die Funktion mehrfach ausführen.
R Code [zeigen / verbergen]
test_vuong(fit_10, fit_7, fit_8, fit_9, fit_11)Name | Model | Omega2 | p (Omega2) | LR | p (LR)
----------------------------------------------------
fit_10 | lm | | | |
fit_7 | lm | 1.81 | < .001 | 3.06 | 0.001
fit_8 | lm | 1.68 | < .001 | 3.15 | < .001
fit_9 | lm | 1.81 | < .001 | 2.84 | 0.002
fit_11 | lm | 1.63 | < .001 | 3.91 | < .001
Each model is compared to fit_10.Zum Abschluss dann auch hier nochmal die Zusammenstellung aller fünf Modell in einer Tabelle durch das R Paket {modelsummary}. Wir haben dann alles in einer Tabelle und können die Einflussvariablen alle miteinander vergleichen. Wir sehen dann auch wie sich die Koeffizienten ändern, wenn wir eine Einflussvariable mit ins Modell nehmen oder weglassen. Wir sehen auch hier hier, dass das Modell X das beste Modell ist. Für eine bessere Übersicht habe ich einmal den Intercept entfernt.
| Model | |||||
|---|---|---|---|---|---|
| VII | VIII | IX | X | XI | |
| + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001 | |||||
| Ernährung (Blut) | 37.865*** | 37.865*** | 41.033*** | 12.707+ | |
| (10.630) | (10.696) | (10.548) | (6.522) | ||
| Ernährung (Ketchup) | 31.689** | 31.689** | 34.735** | 3.029 | |
| (10.630) | (10.696) | (10.538) | (6.669) | ||
| Entwicklung (juvenile) | 5.821 | 24.406+ | -18.246** | 16.842 | |
| (8.734) | (13.121) | (5.475) | (15.058) | ||
| Gewicht [mg] | 2.267+ | 1.344 | |||
| (1.219) | (1.389) | ||||
| Anzahl Beinhaare | 0.099*** | ||||
| (0.010) | |||||
| Num.Obs. | 48 | 48 | 48 | 48 | 48 |
| R2 | 0.245 | 0.253 | 0.308 | 0.770 | 0.028 |
| R2 Adj. | 0.212 | 0.202 | 0.244 | 0.749 | -0.015 |
| AIC | 467.8 | 469.4 | 467.7 | 414.8 | 480.0 |
| BIC | 475.3 | 478.7 | 478.9 | 426.0 | 487.5 |
| RMSE | 29.11 | 28.97 | 27.87 | 16.06 | 33.04 |




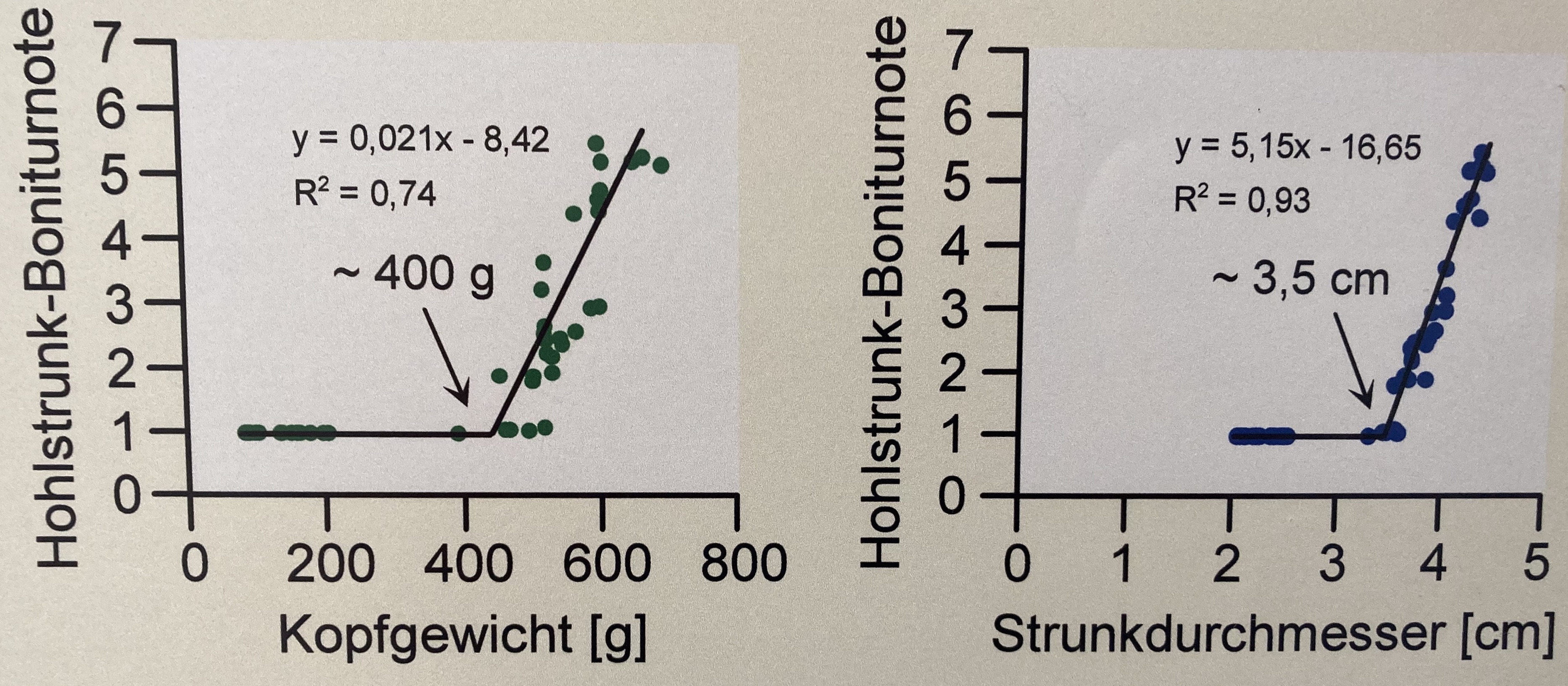
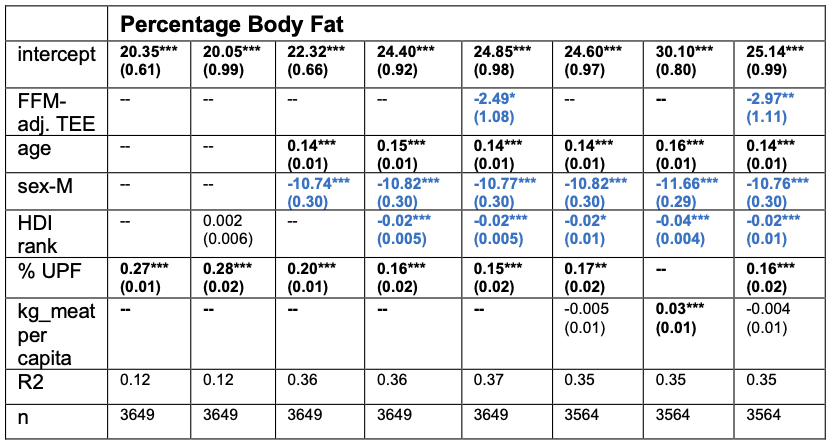

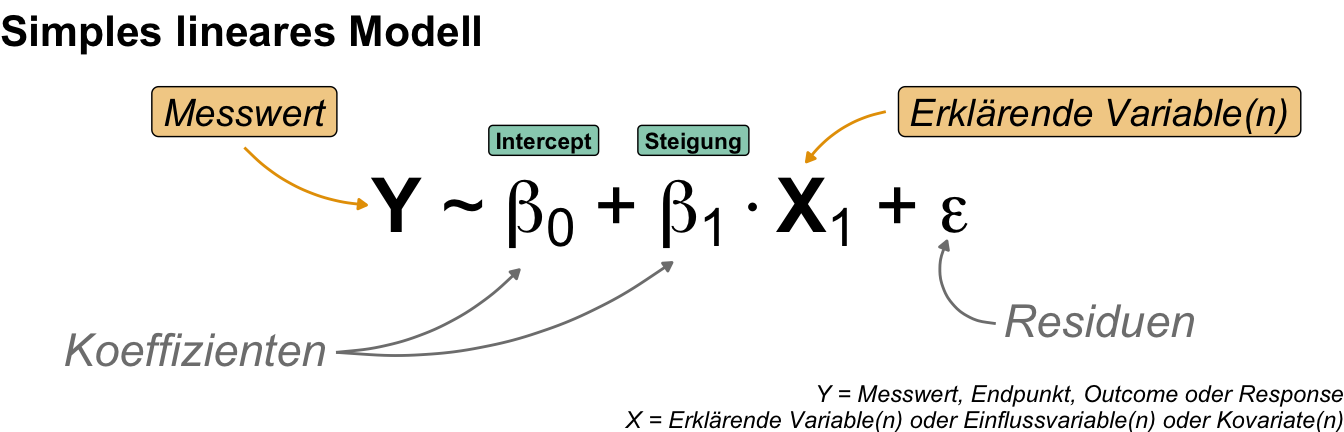
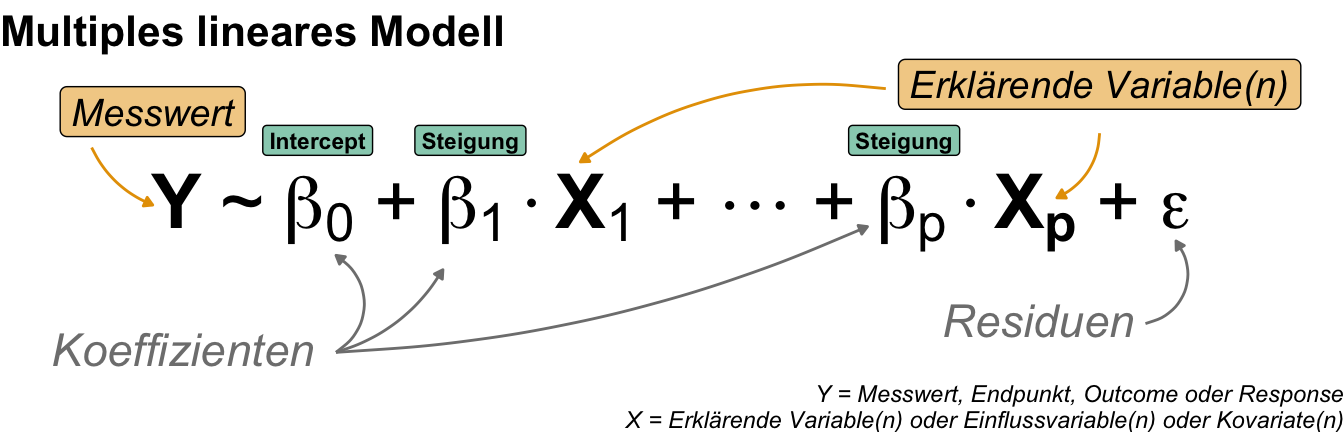

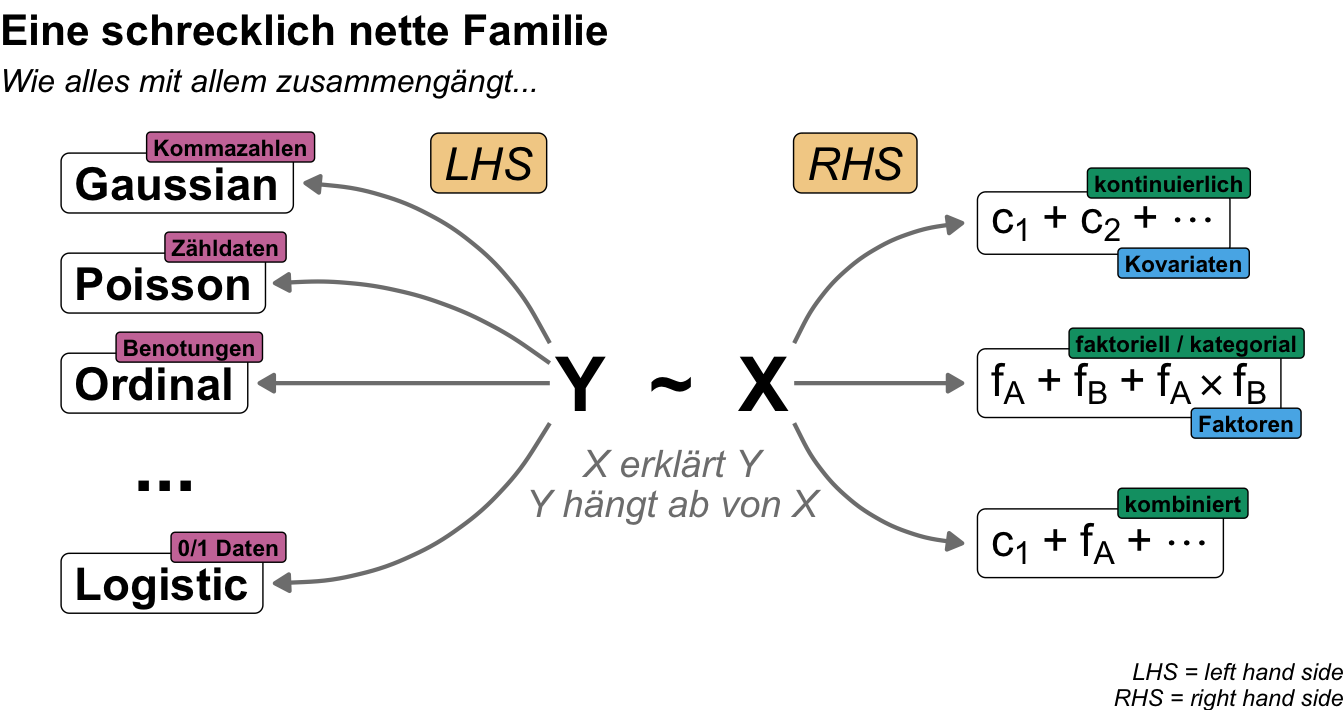



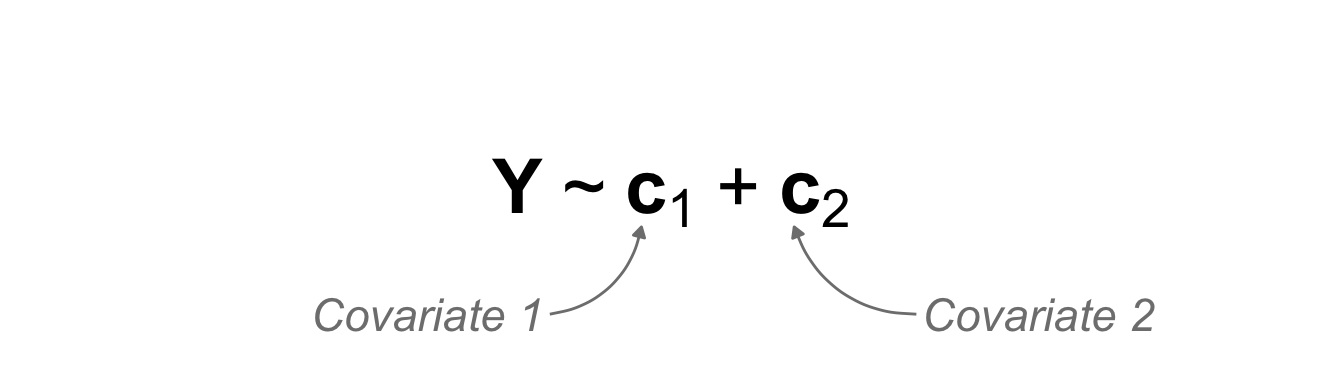
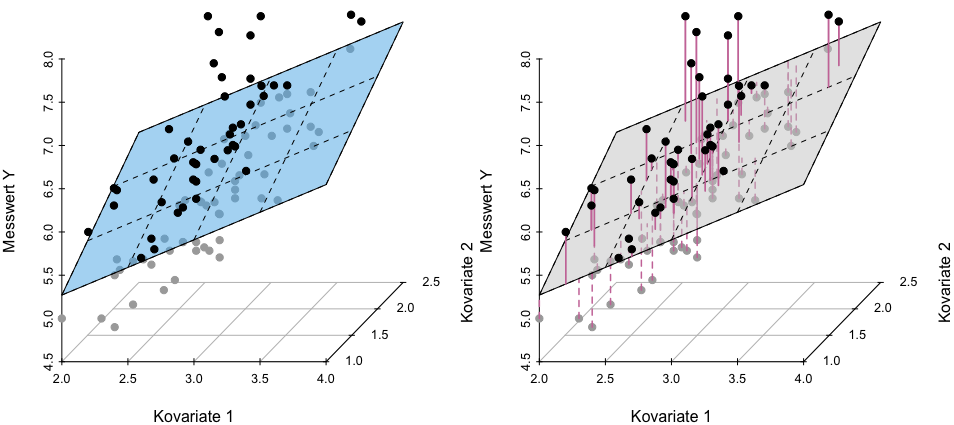

![Ein 3D Scatterplot von den zwei Kovariaten Gewicht der Flöhe in [mg] sowie der mittleren Anzahl an Beinhaaren und der Sprungweite in drei Dimensionen. Statt eine Grade wird ein Ebene (eng. regression plane) durch die Punkte im dreidimensionalen Raum gelegt. Die Residuen sind die Abweichungen der Beobachtungen zu den Werten auf der Ebene.](images/mult-reg-scatter3d-01.png)