flowchart LR
C(Behandlungen):::factor --- D(((nested))) --> E(Tische):::factor --- F(((nested))) --> G(Gewächshäuser):::factor
classDef factor fill:#56B4E9,stroke:#333,stroke-width:0.75px
24 Versuchsplanung in R
Letzte Änderung am 23. March 2024 um 19:02:54
“Today’s scientists have substituted mathematics for experiments, and they wander off through equation after equation, and eventually build a structure which has no relation to reality.” — Nikola Tesla
In diesem Kapitel wollen wir uns die Versuchsplanung in R einmal genauer anschauen. Das heißt, dass wir hier den Fokus auf die Funktionen und Pakete legen. In den dann folgenden Kapiteln schauen wir uns die Anwendung auf die gängigen experimentellen Designs in den Agrarwissenschaften an. Wie immer schauen wir erst auf die Anwendung und gehen dann auf die Theorie. Das ist in diesem Kapitel im Besonderen der Fall. Mir geht es hier mehr um die technische Umsetzung als um den eigentlichen Hintergrund.
Wenn wir über die Versuchsplanung und R sprechen, dann kommen wir an folgender Sammlung Design of Experiments (DoE) & Analysis of Experimental Data nicht vorbei. Du findest hier nochmal alle Informationen sehr kompakt. Ich nutze die Sammlung gerne einmal als Nachschlagewerk. Nirgendwo sonst findest du so einen Überblick über mögliche Pakete und Anwendungen in R. Wir schauen uns hier dann nur eine Auswahl an Möglichkeiten an. Ich selber habe mir noch nicht alles angeschaut, dass ist einfach zu viel. Je nach Fragestellung bietet sich ja auch ein anderes Paket an. Wir belassen es wie immer bei den Grundlagen. Die Grundlagen sind ja meistens dann ausreichend und manchmal auch schon kompliziert genug.
Ein Weiteres umfangreiches Tutorium zum Planen von einem experimentellen Design liefert DSFAIR von P. Schmidt. Hier finden sich auch weiterführende Literatur und weitere Beispiele. Allgemein ist die Webseite sehr zu empfehlen, da du einiges an Beispielanalysen findest.
Wenn es um die Planung geht, dann schaue gerne einmal in Principles, planning and Implementation of Agricultural Field Trials. Ich finde die Zusammenstellung immer noch sehr aktuell und hilfreich. Besonders wenn du noch gar nicht mit der Planung in Verbindung gekommen bist, dann ist dieser Text sehr nützlich. Es geht wirklich um das Feld und was du dort auf dem Feld beachten musst. Also gar keien trockene Mathematik sondern eben praktisches experimentelles Design. Auch kann ich in diesem Zusammenhang die Arbeit von Onofri u. a. (2010) mit der wissenschaftlichen Publikation Current statistical issues in Weed Research empfehlen. Es geht zwar um Getreide, aber eigentlich ist es egal, das Thema ist sehr allgemein beschrieben, so dass du auch für deine Experimente was finden solltest.
Jetzt müssen wir doch noch auf den Begriff nested (deu. verschachtelt) kommen. Wenn wir über nested sprechen, dann meinen wir, dass Faktoren \(f\) ineinander verschachtelt sind. Mit Faktoren \(f\) meine ich experimentelle Bedingungen. Das klingt jetzt etwas wirr, aber wir machen das mal an einem Beispiel fest. Wir haben den Faktor table und auf dem Tisch stehen die Behandlungen des Faktors trt mit den jeweiligen Pflanzen. Also ist die Behandlung in den Tischen genested. Die Tische mögen in verschiedenen Gewächshäusern mit dem Faktor location stehen, also sind die Tische in den Gewächshäusern genested. Wir haben folgendes Schema vorliegen.
\[ \overbrace{\mbox{Behandlungen}}^{f_1} \xrightarrow[]{nested} \underbrace{\mbox{Tische}}_{f_2} \xrightarrow[]{nested} \overbrace{\mbox{Gewächshauser}}^{f_3} \]
Damit haben wir dann aber auch meistens folgende Abhängigkeit von den jeweiligen Beobachtungen untereinander nach der wir dann unser Experiment planen müssen.
\[ \overbrace{\mbox{Gewächshauser}}^{f_3} \xrightarrow[alle]{beinhaltet} \underbrace{\mbox{Tische}}_{f_2} \xrightarrow[alle]{beinhaltet} \overbrace{\mbox{Behandlungen}}^{f_1} \]
Wir werden uns dann aber die Zusammenhänge etwas anders visualisieren, da wir teilweise später auch zwei Faktoren haben, die in den Blöcken genested sind. Daher nutzen wir dann ein Schema wie in Abbildung 24.1 dargestellt. Wir haben die Faktoren in den blauen Knoten. Die Abhänigigkeitsstruktur der Faktoren untereinander werden wir über den Knoten nested abbilden.
Okay, das ist jetzt bis hierher sehr abstrakt. Machen wir das mal konkret mit einem Beispiel mit drei Behandlungen gegen Blattläuse auf jeweils vier Tischen in drei Gewächshäusern. Pro Behandlung nehmen wir fünf Pflanzen. Damit ergibt sich folgendes Schema mit den jeweiligen Anzahlen darübergeschrieben.
\[ \overbrace{\mbox{Gewächshauser}}^{n_g = 3} \xrightarrow[alle]{beinhaltet} \underbrace{\mbox{Tische}}_{n_t = 4} \xrightarrow[alle]{beinhaltet} \overbrace{\mbox{Behandlungen}}^{n_b = 3} \xrightarrow[alle]{beinhaltet} \underbrace{\mbox{Beobachtungen}}_{n_w = 5} \]
Jetzt können wir auch ausrechnen, wie viele Pflanzentöpfe wir brauchen. Wir multiplizieren alle \(n\)-Angaben miteinander und erhalten \(n_{gesamt} = n_g \cdot n_t \cdot n_b \cdot n_w = 3 \cdot 4 \cdot 3 \cdot 5 = 180\) Pflanzen. Jetzt ist immer die Frage, sind das zu viele oder zu wenig? Das wollen wir uns dann am Ende in dem Kapitel zur Fallzahlplanung anschauen. Hier geht es erstmal um die technische Umsetzung.
Wichtig ist auch sich zu erinnern, dass wir zwei Komponenten haben. Zum einen haben wir das Design oder auch das Feld, wo wir eine Positionsangabe haben. Häufig haben wir deshalb auch in den Ausgaben der Funktionen eine Information zur den Zeilen rows und Spalten cols. Damit wird dann verdeutlicht, wo die Pflanze stehen soll. Zum Anderen müssen wir ja auch noch eine Randomisierung ergänzen. Wir werden hier immer eine Randomisierung ergänzen, da es ohne eine Randomisierung keinen Sinn macht hier ein Experiment zu planen.
24.1 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
set.seed(20230812)
pacman::p_load(tidyverse, magrittr, writexl, agricolae,
desplot, dae, FielDHub,
conflicted)
conflicts_prefer(magrittr::set_names)An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
24.2 Selbermachen mit expand_grid()
Wenn wir uns das experimentelle Design selber zusammen programmieren können wir auf das tidyverse Paket zurückgreifen und haben dann ein schöneres Leben. Wir müssen zwar etwas mehr beachten, aber dafür sind wir auch sehr viel mehr flexibel. Deshalb stelle ich für die einfacheren Designs in den folgenden Kapiteln auch immer den Code zum Selbermachen vor. Hier gibt es jetzt einmal die Grundidee am Complete randomized design (CRD). Wir gehen immer von einem balancierten Design aus, dass heißt in jeder Behandlungsgruppe sind gleich viele Beobachtungen.
Nehmen wir folgendes simples Modell. Wir wollen untersuchen, ob das Trockengewicht drymatter von einer Behandlung trt abhängt. Wir werden uns dann gleich noch entscheiden, wie viele Behandlungsgruppen wir wollen und wie viele Wiederholungen wir pro Behandlungsgruppe nehmen.
\[ drymatter \sim \overbrace{trt}^{f_1} \]
Zentral für unsere Überlegungen ist die Funktion expand_grid(), die es uns einfach erlaubt alle Faktorkombinationen aus zwei oder mehr Vektoren zu erstellen. Wir haben im Folgenden im Vektor a die Zahlen 1 bis 3 und in dem Vektor b die Zahlen 1 und 2. Jetzt wollen wir alle Kombinationen von a und b haben und nutzen dafür expand_grid().
R Code [zeigen / verbergen]
expand_grid(a = 1:3, b = 1:2)# A tibble: 6 × 2
a b
<int> <int>
1 1 1
2 1 2
3 2 1
4 2 2
5 3 1
6 3 2Jetzt einmal konkreter auf unser Beispiel angewandt. Wir wollen vier Behandlungsgruppen und in jeder Behandlungsgruppe fünf Wiederholungen rep. Dann benennen wir noch die Behandlungen mit ctrl, A, B und C. Unsere Wiederholungen kriegen die Zahlen von 1 bis 5. Dann ergänzen wir noch eine Pflanzenidentifizierungsnummer pid über die wir dann später randomisieren können. Wenn du willst, kannst du dir dann über select() noch die Spalten sauber sortieren.
R Code [zeigen / verbergen]
crd_long_tbl <- expand_grid(trt = 1:4, rep = 1:5) |>
mutate(trt = factor(trt, labels = c("ctrl", "A", "B", "C")),
rep = factor(rep, labels = 1:5),
pid = 1:n()) |>
select(pid, everything())
crd_long_tbl# A tibble: 20 × 3
pid trt rep
<int> <fct> <fct>
1 1 ctrl 1
2 2 ctrl 2
3 3 ctrl 3
4 4 ctrl 4
5 5 ctrl 5
6 6 A 1
7 7 A 2
8 8 A 3
9 9 A 4
10 10 A 5
11 11 B 1
12 12 B 2
13 13 B 3
14 14 B 4
15 15 B 5
16 16 C 1
17 17 C 2
18 18 C 3
19 19 C 4
20 20 C 5 Dann kannst du dir die Datei mit der Funktion write_xlsx() aus dem R Paket writexl raus schreiben und dann entsprechend mit deinen Messwerten für das Trockengewicht ergänzen.
R Code [zeigen / verbergen]
crd_long_tbl |>
write_xlsx("template_sheet.xlsx")Wenn du für deine zwanzig Pflanzen noch ein Randomisierungmuster brauchst, dann empfehle ich dir die Folgende schnelle Art und Weise. Du nimmst die Pflanzen ID’s von 1 bis 20 und mischt die Zahlen einmal mit der Funktion sample() durch. Dann erstellst du dir als dein Grid für deine Pflanzen mit einer \(4 \times 5\)-Matrix und pflanzt nach diesem Grid die Pflanzen ein.
R Code [zeigen / verbergen]
crd_long_tbl$pid |>
sample() |>
matrix(nrow = 4, ncol = 5,
dimnames = list(str_c("Reihe", 1:4, sep = "-"),
str_c("Spalte", 1:5, sep = "-"))) Spalte-1 Spalte-2 Spalte-3 Spalte-4 Spalte-5
Reihe-1 5 16 2 19 12
Reihe-2 3 1 20 13 11
Reihe-3 18 9 6 10 4
Reihe-4 14 8 15 7 17Es gibt natürlich noch andere Möglichkeiten, aber das ist jetzt die schnellste Variante ein gutes Randomisierungsmuster hinzukriegen.
Spielecke mit
expand_grid()
Hier nochmal für mich ein paar Punkte zum expand_grid(), die ich immer mal wieder brauche, aber gerne mal vergesse.
R Code [zeigen / verbergen]
## Erstellung eines zweifaktoriellen Grids
tbl <- expand_grid(block = 1:2, trt = 1:4)
## Vollständige Randomisierung
tbl |>
slice_sample(prop = 1)
## Randomisierung im Faktor trt
tbl |>
group_by(trt) |>
slice_sample(prop = 1)
## Randomisierung im Faktor trt und Subgruppe id ergänzt
tbl |>
group_by(trt) |>
slice_sample(prop = 1) |>
expand_grid(id = 1:3)24.3 Das R Paket {FielDHub}
Bevor du alles selber machst, schaue dir unbedingt das tolle R Paket {FielDHub} einmal an. Bei dem Paket handelt es sich um eine Shiny App, so dass du eine super Oberfläche in einem Browser hast. In der Shiny App kannst du dann selber die Designs auswählen und die verschiedenen Parameter ändern. Die Darstellung erfolgt dann teilweise auch in den hier vorgestellten R Paketen wie {desplot}, aber eben schon sehr gut aufgearbeitet. Du erhältst dann auch gleich ein Feldbuch, welches du dir als Exceltabelle exportieren lassen kannst. Das Feldbuch kannst du dann gleich zum randomisieren nutzen und auch deine gemessenen Werte eintragen. Dann wollen wir einmal loslegen, der Code ist nur zwei Zeilen lang und dann startet die Shiny App in deinem Browser.
R Code [zeigen / verbergen]
library(FielDHub)
run_app()Hier kannst du dann auch erstmal stoppen, wenn es dir nur um die Anwendung geht. Das R Paket {FielDHub} ist allen anderen Paketen hier was die Anwendbarkeit angeht überlegen. Ich nutze in den folgenden Kapiteln immer die R Implementierung von {FielDHub} und nicht die Shiny App. Es gibt dafür auf der Hilfeseite von {FielDHub} eine Übersicht über alle Funktionen und implementierten experimentellen Designs.
Hier kommt das Video
24.4 Das R Paket {agricolae}
Für die Erstellung von komplexeren experimentellen Designs führt kein Weg an dem R Paket agricolae vorbei. Bei den einfacheren Designs ist es dann so eine Sache, ob du dir mit agricolae einen Gefallen tust oder eher die Sache sehr stark verkomplizierst. Ich würde dir bei den einfacheren Designs empfehlen einfach exoand_grid() wie oben beschrieben zu nutzen. Das ist einfacher und funktioniert auch gut, wenn nicht gar besser. Darüber hinaus ist die Hilfe der Funktionen teilweise etwas sehr mager und die Weiterentwicklung eher fraglich. Für das Paket agricolae gibt es zwe i ziemlich identische Tutorien einmal das Tutorium agricolae als PDF und einmal mit Beispielen von der Webseite Experimental Designs with agricolae. Beide Tutorien sind identisch, dass eine ist ein PDF und das andere eine Webseite.
So dann schauen wir uns mal die gängigen Parameter bei der Erstellung des Designs mit den Funktionen von agricolae an:
series: legt fest wie viele Zeichen plus 1 die Nummerierung der Zeile haben soll. Wenn wirseries = 2setzen, dann zählen wir mit 101, 102, 203 usw. die Zeilen hoch. Im Falle eines vollständig randomisierten Designs ist die Nummerierung fortlaufend.seed: der Seed für die Zufallsgenerierung und sein Wert ist eine beliebige Zahl.kinds: die Methode der Zufallsgenerierung, standardmäßig “Super-Duper” und interessiert uns hier nicht besonders.randomization: Soll das Design randomisiert werden?
Und Folgendes kommt dann bei agricolae als Ausgabe raus. Zwar nicht immer, aber das ist der grobe Überblick.
parameters: die Eingabe zur Generierung des Designs. Wir erhalten also nochmal unsere Werte wieder, die wir eingegeben haben. Meistens nicht von Interesse.book: Das Feldbuch indem das wichtige drin steht, nämlich unsere generiertes Faktordesign.statistics: die Informationsstatistiken das Design, die wir noch zusätzlich kriegen. Diese nutzen wir nur für komplexere Designs.sketch: Verteilung der Behandlungen im Feld. Wird uns nicht immer wiedergeben und ist als Hilfe für die direkte Anwendung gedacht.
Wenn wir Parzellen anlegen, dann erhalten wir auch noch folgende Informationen wieder. Dfür muss dann aber auch das experimentelle Design entsprechende Parzellen haben.
zigzag: ist eine Funktion, die es erlaubt die Verteilung der Beobachtungen entlang der Parzellen zu kontrollieren. Meistens ist es etwas zu viel des Guten, aber gut das du hier noch Änderungen vornehmen kannst.fieldbook: Ausgabe des Zickzacks aus der obigen Funktion und das entsprechende Feldbuch mit dem Design.
Es gibt eine weitreichende Anzahl an design.*-Funktionen für sehr viele Designs. Wir schauen uns also jetzt einmal als Beispiel die Funktion design.crd() an um ein complete randomized design zu erstellen. Der Vorteil der Funktion ist hier, dass wir verschiedene Anzahlen von Individuen in die Generierung des Designs nehmen können. Also zum Beispiel drei Pflanzen in der Kontrolle und dann jeweils fünf Pflanzen in der Behandlung. Weil es aber dann meistens nicht auf die zwei Kontrollpflanzen weniger ankommt, machen wir immer ein balanciertes Design. Wenn es aber unbalanciert sein soll, dann ist es natürlich hier einfacher umzusetzen als mit expand_grid().
In den Designfunktionen haben wir meistens einmal die Option für die Behandlung trt sowie für die Wiederholungen r. Leider ist es so, dass je nach Design die Option r mal die Wiederholungen oder aber die Blöcke beschreibt. Schau dir da bitte die Beispiele an. Im Weiteren haben wir dann noch die serie Option, die einfach die Nummerierung auf Hunderter setzt.
R Code [zeigen / verbergen]
crd_obj <- design.crd(trt = c("ctrl", "A", "B", "C"),
r = c(3, 5, 5, 5), serie = 2)Nun ist es so, dass die Funktion den Spaltennamen der Behandlung auf c("ctrl", "A", "B", "C") setzt anstatt auf einen Namen. Dafür müssten wir dann einen Vektor trt übergeben, aber das wird mir dann irgendwann zu wirr. Deshalb nenne ich dann alle Spalten nochmal mit der Funktion set_names() entsprechend um und erschaffe mir einen tibble.
R Code [zeigen / verbergen]
crd_book <- crd_obj |>
pluck("book") |>
as_tibble() |>
set_names(c("plots", "r", "trt"))
crd_book# A tibble: 18 × 3
plots r trt
<dbl> <int> <chr>
1 101 1 C
2 102 2 C
3 103 1 B
4 104 2 B
5 105 1 A
6 106 1 ctrl
7 107 2 A
8 108 3 C
9 109 4 C
10 110 3 B
11 111 2 ctrl
12 112 3 A
13 113 5 C
14 114 4 B
15 115 4 A
16 116 3 ctrl
17 117 5 B
18 118 5 A Wir haben kein sketch aus der Funktion. Daher müssen wir uns selber überlegen, wie wir dann die Pflanzen anordnen würden. Darüber hinaus ist die Ordnung wild, ich sehe da eher weniger Struktur in der Ausgabe, als das mir es hilft. Aber dazu dann mehr in den folgenden Kapiteln. Hier ist es erstmal die stumpfe Durchführung am Beispiel des complete randomized design.
Das Paket agricolae hat keine interne Möglichkeit sich die Designs zu visualisieren.
Fehlende Einbindung von
{agricolae} in andere R Pakete
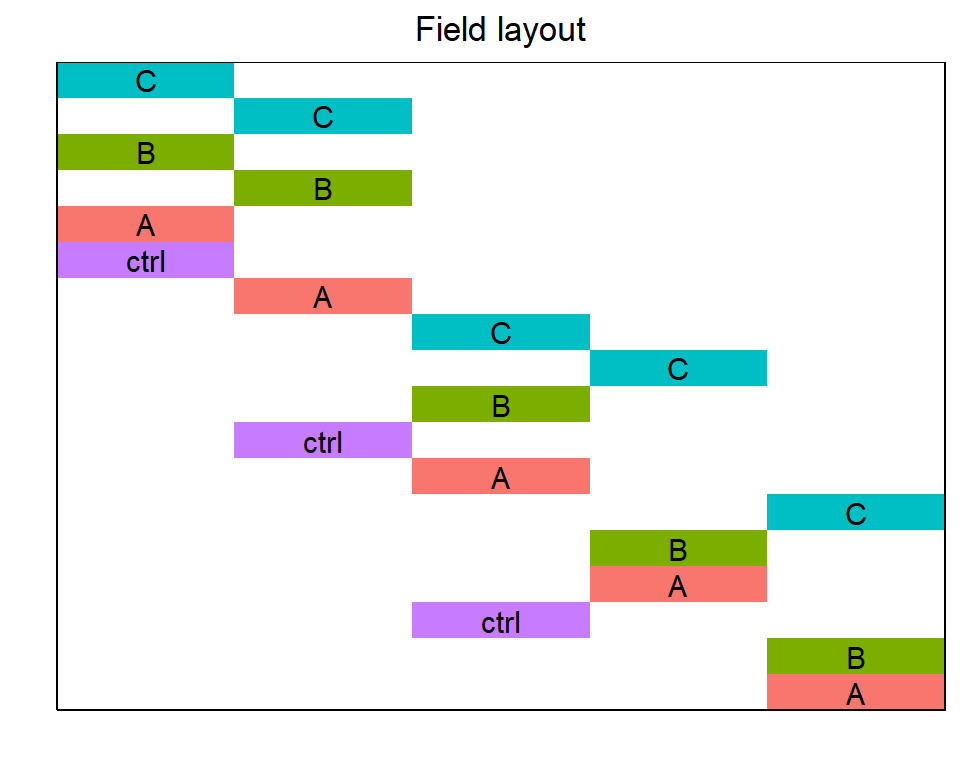
In der Abbildung 24.3 sehen wir die Problematik mit der fehlenden Einbindung von agricolae in das Paket desplot. Die Abbildung ist einfach suboptimal. Da wir in dem Feldbuch von agricolae keine Zeilen und Spalten der Position wiederbekommen, können wir das Design nicht sauber darstellen. Leider liefert uns die Funktion design.crd() auch keine Verteilung der Behandlungen im Feld, so dass wir hier alles selber bauen müssten. Dann geht es mit expand_grid() schneller.
R Code [zeigen / verbergen]
ggdesplot(data = crd_book, flip = TRUE,
form = trt ~ r + plots,
text = trt, cex = 1, shorten = "no",
main = "Field layout", show.key = F) 
agricolae durch desplot. Da agricolae für durch die Funktion design.crd() keine Positionen in Zeile und Spalte liefert kann nur ein suboptimaler Plot erstellt werden.
24.5 Das R Paket {desplot}
Wenn wir uns das Design eines Esperiments abbilden wollen, dann können wir das R Paket desplot nutzen. Die Hilfeseite Plotting field maps with the desplot package liefert nochmal mehr Informationen. Auch finde ich die Beispiele für die Anwendung von desplot von DSFAIR - Designing experiments sehr schön. Wir besprechen aber die einzelnen Abbildungen dann in den separaten Abschnitten in den folgenden Kapiteln.
Wir nehmen wieder unseren eigenes Design für das complete randomized design aus dem Objekt crd_long_tbl. Wir können aber das Design nicht einfach so abbilden, wir brauchen noch die Position der einzelne Behandlungen auf dem Feld. Die Positionen bestimmen wir durch Reihen rows und Spalten cols. Jetzt müssen wir also unser Grid ergänzen auf dem wir unsere Pflanzen stellen wollen. In unserem Fall wollen wir unsere Pflanzen auf vier Zeilen rows und fünf Spalten cols stellen. Das bietet sich bei zwanzig Pflanzen dann ja auch an.
R Code [zeigen / verbergen]
crd_grid <- expand_grid(rows= 1:4, cols = 1:5)
crd_grid # A tibble: 20 × 2
rows cols
<int> <int>
1 1 1
2 1 2
3 1 3
4 1 4
5 1 5
6 2 1
7 2 2
8 2 3
9 2 4
10 2 5
11 3 1
12 3 2
13 3 3
14 3 4
15 3 5
16 4 1
17 4 2
18 4 3
19 4 4
20 4 5Unser Grid der Positionen können wir jetzt mit unserem Design durch die Funktion bind_cols() verbinden. Würden wir das nur so machen, dann hätten wir keine Randomsierung drin. Deshalb durchmischen wir die Daten einmal vollständig mit der Funktion slice_sample(). Dann haben wir unser Objekt crd_plot_tbl ferti und können damit weitermachen.
R Code [zeigen / verbergen]
crd_plot_tbl <- crd_long_tbl |>
slice_sample(prop = 1) |>
bind_cols(crd_grid)
crd_plot_tbl # A tibble: 20 × 5
pid trt rep rows cols
<int> <fct> <fct> <int> <int>
1 1 ctrl 1 1 1
2 4 ctrl 4 1 2
3 17 C 2 1 3
4 10 A 5 1 4
5 2 ctrl 2 1 5
6 6 A 1 2 1
7 12 B 2 2 2
8 13 B 3 2 3
9 11 B 1 2 4
10 15 B 5 2 5
11 3 ctrl 3 3 1
12 8 A 3 3 2
13 19 C 4 3 3
14 7 A 2 3 4
15 20 C 5 3 5
16 16 C 1 4 1
17 9 A 4 4 2
18 14 B 4 4 3
19 5 ctrl 5 4 4
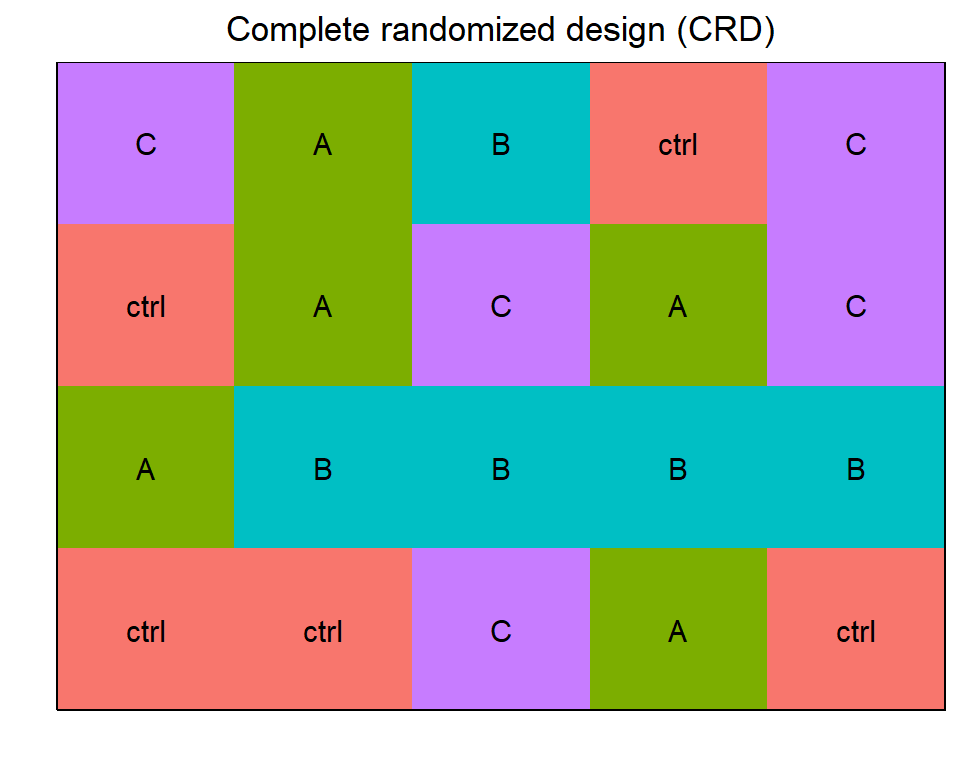
20 18 C 3 4 5In der Abbildung 24.2 sehen wir einmal unser complete randomized design Design aus dem Objekt crd_plot_tbl dargestellt. Wir sehen, dass wir die vier Behandlungen mit den fünf Wiederholungen zufällig über den ganzen Tisch verteilt haben. Wichtig ist, dass du einmal die Form form angibst, wie sich der Plot aufbaut. Links von der Tilde ~ steht die Behandlung und rechts von der Tilde ~ die Positionsangaben. Je nach Design ändert sich das noch etwas und wir ergänzen noch andere visuelle Parameter. Dann wollen wir alles mit den Labels von der Behandlung trt beschriften. Dafür nutzen wir dann die Option text. Der Rest der Optionen sind dann noch quality of life Funktionen, die du an- oder abstellen kannst.
R Code [zeigen / verbergen]
ggdesplot(data = crd_plot_tbl,
form = trt ~ cols + rows,
text = trt, cex = 1, show.key = FALSE,
shorten = "no",
main = "Complete randomized design (CRD)")
desplot dargestellt.
24.6 Das R Paket {dae}
Ein weiteres R Paket, was es ermöglicht komplexere Experimente zu planen ist das R Paket dae. Über die Hilfeseite dae: Functions Useful in the Design and ANOVA of Experiments kannst du dir das Tutorium anschauen, was ich dir auch empfehlen würde. Wir machen wie immer hier nur einen kleinen Teil, den Rest musst du dann selber nach schauen. Wenn es aber um komplexere experimentelle Designs geht, dann ist das Paket dae auf jeden Fall geeignet.
Das R Paket dae hat für die Faktorerstellung in Gruppen eine eigne Funktion fac.gen(). Mit der Funktion können wir besonders gut Faktoren generieren. Bei einfachen Beispielen wie dem randomized complete block design (RCBD) bräuchten wir die Funktion eigentlich nicht, aber hier einmal zur Demonstration. Bei komplexeren Beispielen ist die Funktion nicht wegzudenken. Deshalb einmal hier unser Modell mit einem zusätzlichen Block zu unserer Behandlung.
\[ drymatter \sim \overbrace{trt}^{f_1} + \underbrace{block}_{f_2} \]
Jetzt können wir die Funktion fac.gen() wiederholt nutzen und uns daraus dann einen Datensatz zusammenbauen. Wir sehen auch gleich nochmal eine Alternative für dieses relativ einfache Beispiel. Wir brauchen ja nur ein Positionsgrid und dann die Zuordnung der Behandlungen mit den entsprechenden Gruppenleveln.
R Code [zeigen / verbergen]
rcbd_sys <- cbind(fac.gen(generate = list(rows = 5, cols = 4)),
fac.gen(generate = list(trt = LETTERS[1:4]), times = 5))Wir können auch mit der Funktion expand_grid() von weiter oben relativ einfach das Pflanzengrid nachbauen. Da brauchen wir eigentlich nicht die Funktion fac.gen(). Wie immer, bei einfachen Beispielen reicht auch viel was in R finden, bei komplexeren Designs würde ich immer zu fac.gen() wechseln.
R Code [zeigen / verbergen]
rcbd_sys <- expand_grid(rows = 1:5,
cols = 1:4) |>
mutate(trt = factor(cols, labels = LETTERS[1:4]),
rows = as_factor(rows),
cols = as_factor(cols))Die Ergebnisse sind in beiden Fällen gleich. Wir erhalten einen Datensatz, der uns die Positionen und die Behandlungen mit den Gruppen wiedergibt. Dann können wir schon die Funktion designRandomize() mit den Informationen füttern. Wir haben hier wieder den Fall, dass wir erst die Positionen in einem Griddatensatz bauen und dann die Randomisierung ergänzen. Folgende Optionen müssen wir dabei in unserem etwas einfacheren Fall nur berücksichtigen.
allocated: Ist meistens der Faktor unserer Behandlung und damit der zugeordnete Faktor. Das heißt, wir wollen diesen Faktor auf das Grid aus Zeilen und Spalten verteilen bzw. zuordnen. In unserem Fall die vier Behandlungen mittrt.recipient: Sind die Faktoren, die den Behandlungsgruppen zugeordnet werden. Damit auch das Grid, was den Behandlungsfaktor empfängt. Wir haben hier also Zeilenrowsund Spaltencolumnsin denen unsere Behandlung zufällig verteilt werden soll.nested.recipients: Hier wird angegeben, in welcher Abhängigkeitsstruktur das Grid vorliegt. Unsere Blöcke sind in diesem Fall über die Zeilenrowsorientiert.
Dann rufen wir einmal die Funktion auf und erhalten unseren randomisierten Datensatz wieder. So einfach ist die Funktion leider dann nicht zu verstehen - intuitiv ist was anders. Dennoch liefert dae sehr viele Möglichkeiten. Du musst dich da im Zweifel etwas länger durch die Hilfeseiten arbeiten. Ich werde in den folgenden Kapiteln und Abschnitten versuchen die gängigsten experimentellen Designs in dae abzubilden.
R Code [zeigen / verbergen]
rcbd_lay <- designRandomize(allocated = rcbd_sys["trt"],
recipient = rcbd_sys[c("rows", "cols")],
nested.recipients = list(cols = "rows"),
seed = 1134)
rcbd_lay rows cols trt
1 1 1 C
2 1 2 D
3 1 3 B
4 1 4 A
5 2 1 C
6 2 2 A
7 2 3 D
8 2 4 B
9 3 1 B
10 3 2 A
11 3 3 C
12 3 4 D
13 4 1 B
14 4 2 C
15 4 3 A
16 4 4 D
17 5 1 A
18 5 2 C
19 5 3 D
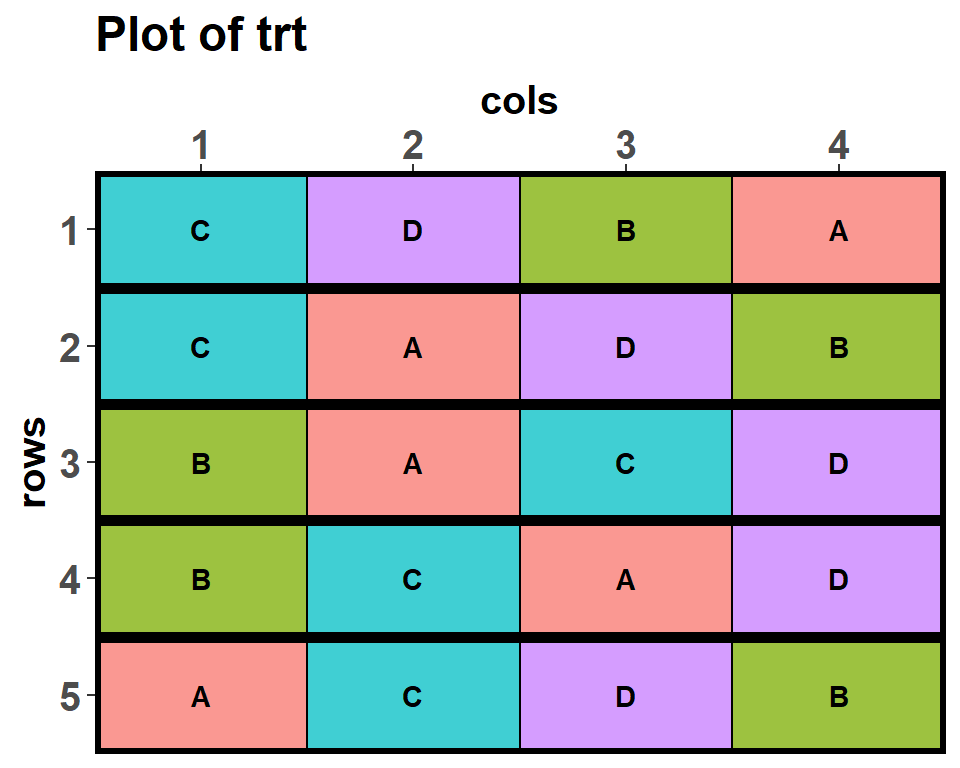
20 5 4 BIn der Abbildung 24.4 sehen wir das Ergebnis unseres Designs einmal visualisiert. Hier müssen wir wieder den Datensatz übergeben und einmal angeben, wie wir über labels die Fläche beschriften wollen. Dann müssen wir die Spalten in unserem Designdatensatz über row.factors = "rows" und column.factors = "cols" benennen, in dem die Zeilen und Spalten enthalten sind. Am Ende definieren wir noch die Blöcke von der Spalte 1 bis 4 und dann haben wir das soweit einmal fertig.
R Code [zeigen / verbergen]
designGGPlot(rcbd_lay, labels = "trt",
row.factors = "rows", column.factors = "cols",
cellalpha = 0.75,
blockdefinition = cbind(1, 4),
blocklinecolour = "black")
designGGPlot() dargestellt.
Damit haben wir dann auch eine Möglichkeit das experimentelle Design innerhalb von dem Paket dae zu visualisieren. Leider ist es aber so, dass die Hilfe für die Funktion designGGPlot() wirklich zu wünschen übrig lässt. Ich würde annehmen, dass wenn ich ein Objekt an eine Funktion in einem Paket übergebe, dass diese Funktionen dann miteinander gut kommunizieren. Später sehen wir, dass die Erstellung einer Visualisierung eines Split plot Designs sehr viel Recherche bedarf. Ja, es ist vieles möglich in dae, aber es verlangt auch eine tief ergreifende Lektüre der Design Notes von dae und der dortigen Beispiele. Wie immer habe ich mein Bestes versucht in den folgenden Abschnitten und Kapiteln die Visualisierung der experimentellen Designs in dae zu zeigen. Manchmal war es dann noch einfacher das Paket desplot zu nutzen. Aber das ist ja wie immer eigentliche eine Frage des Geschmacks.
Am Ende ermöglicht das Paket dae super flexibel experimentelle Design zu erstellen. Ich werde das Paket vermutich auch für Designs im Rahmen der Analyse von linearen gemischten Modellen nutzen. Dafür ist das Paket super. Du musst aber wissen, dass das Paket einiges an Einarbeitung benötigt und du auch die Philosophie hinter den Funktionen verstehen musst. Mal eben schnell, geht leider nicht. Dafür kann das Paket dae mehr als als andere Pakete im Bereich der Erstellung von experimentellen Designs. Wenn du also mal im Bereich der Versuchsplanung arbeiten willst, dann schaue dir auf jeden Fall das Paket nochmal genauer an.
24.7 Das R Paket {agridat}
Eine wunderbare Sammlung von Datensätzen aus dem Bereich der Agarwissenschaften liefert das R Paket agridat. Über die Hilfeseite agridat: Agricultural Datasets findest du dann einmal einen gesamten Überblick und auch die Informationen über einige ausgewählte Datensätze aus Dutzenden von Datensätzen. Alle Datensätze der wichtigen Bücher zu dem experimentellen Designs sind dort eigentlich enthalten und einmal kuratiert. Hier noch der Link zu agridat - Datensätze mit Abbildungen in desplot. Du musst dann auf die jeweiligen Datensätze in der Liste klicken und dann komsmt du zu dem Datensatz mit mehr Details sowie meistens auch einer Abbildung in desplot.
Referenzen
Onofri A, Carbonell E, Piepho H-P, Mortimer A, Cousens R. 2010. Current statistical issues in Weed Research. Weed Research 50: 5–24.