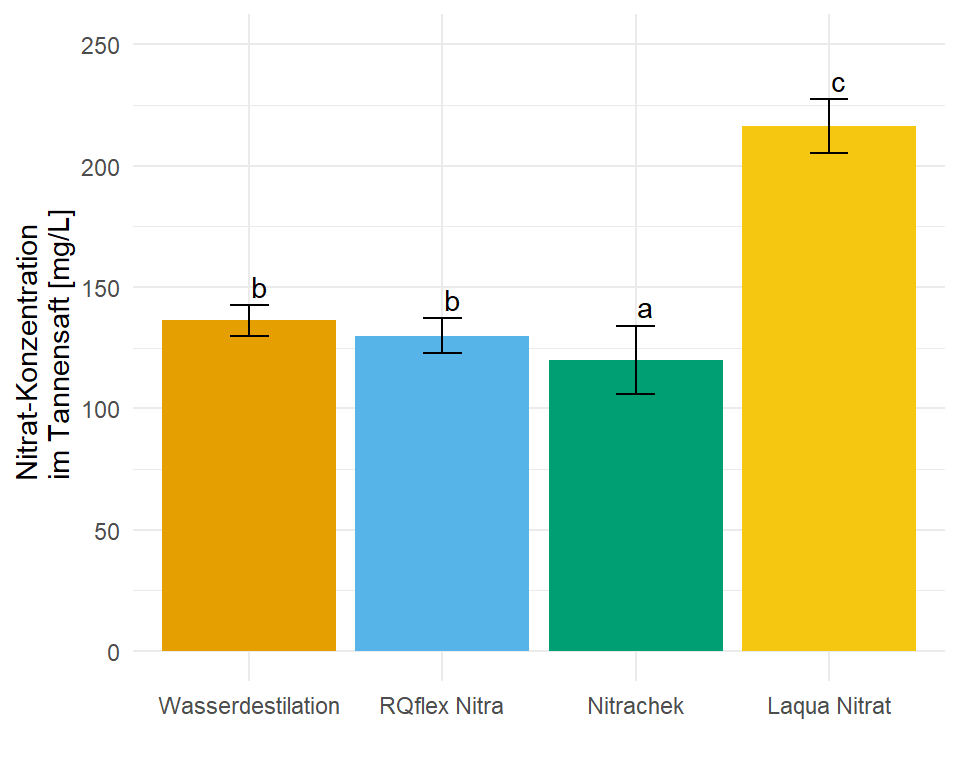18 Visualisierung von Daten
Letzte Änderung am 25. November 2025 um 14:52:12
“The greatest value of a picture is when it forces us to notice what we never expected to see.” — John Tukey
Worum geht es in der explorativen Datenanalyse? Die explorative Datenanalyse wurde von John Tukey (1915–2000) begründet. Er war ein Pionier im Bereich der frühen Informatik und Computerwissenschaften. Warum explorativ, was wollen wir den erforschen? Denn nichts anderes bedeutet ja explorativ (deu. erforschend, erkundend, untersuchend) – wir wollen etwas entdecken. Die Idee war ziemlich innovativ und neu als Tukey et al. (1977) in seinem Buch die explorative Datenanalyse erstmal als Begriff vorstellte. Schon vorher beschrieb Tukey (1962) in seinem Artikel “The Future of Data Analysis” die zukünftige Datenanalyse, wie Tukey sie sich vorstellte, was auch sein folgendes Zitat belegt.
“I know of no person or group that is taking nearly adequate advantage of the graphical potentialities of the computer.” — John Tukey
Nun musst du wissen, dass in den 60’ziger Jahren der Computer in den Kinderschuhen steckte. Mal eben eine Berechnung durchführen, dass war dann schon so eine Sache der damaligen Zeit. Vieles bis fast alles wurde als Tabellen veröffentlicht und selten wurde eine Abbildung händisch dazu erstellt. An dieser Stelle sei einmal auf die Microsoft Excel Werbung aus dem Jahr 1990 verwiesen. Daher war die Idee, sich Daten zu visualisieren entsprechend neu und wirklich ein wissenschaftlicher Fortschritt. Erstaunlicherweise glauben wir heute manchmal dann Zahlen in einer Tabelle mehr als einer Abbildung. Wir schreiben dann den Zahlen eine größere Genauigkeit und Aussagekraft zu, als einer explorativen Abbildung. Dabei können wir in einer Abbildung viel mehr sehen, als in einer Tabelle.
“There is no data that can be displayed in a pie chart, that cannot be displayed BETTER in some other type of chart.” — John Tukey
Daher ist ein wichtiger Teil in der Analyse von Daten die Visualisierung und damit die Darstellung in einer Abbildung. Wir haben aber eine großem Auswahl an möglichen Abbildungen, deshalb auch das lange Kapitel hier. Siehe dazu auch die Arbeit von Riedel et al. (2022) mit dem Titel Replacing bar graphs of continuous data with more informative graphics: are we making progress? um mehr über die Nutzung der Abbildungen im Laufe der Zeit zu erfahren. Nicht alles was schon immer genutzt wurde, macht auch Sinn weiter genutzt zu werden. Wir haben mit R und {ggplot} eine Möglichkeit Abbildungen von Daten sehr viel besser zu erstellen als noch vor ein paar Jahrzehnten möglich war.
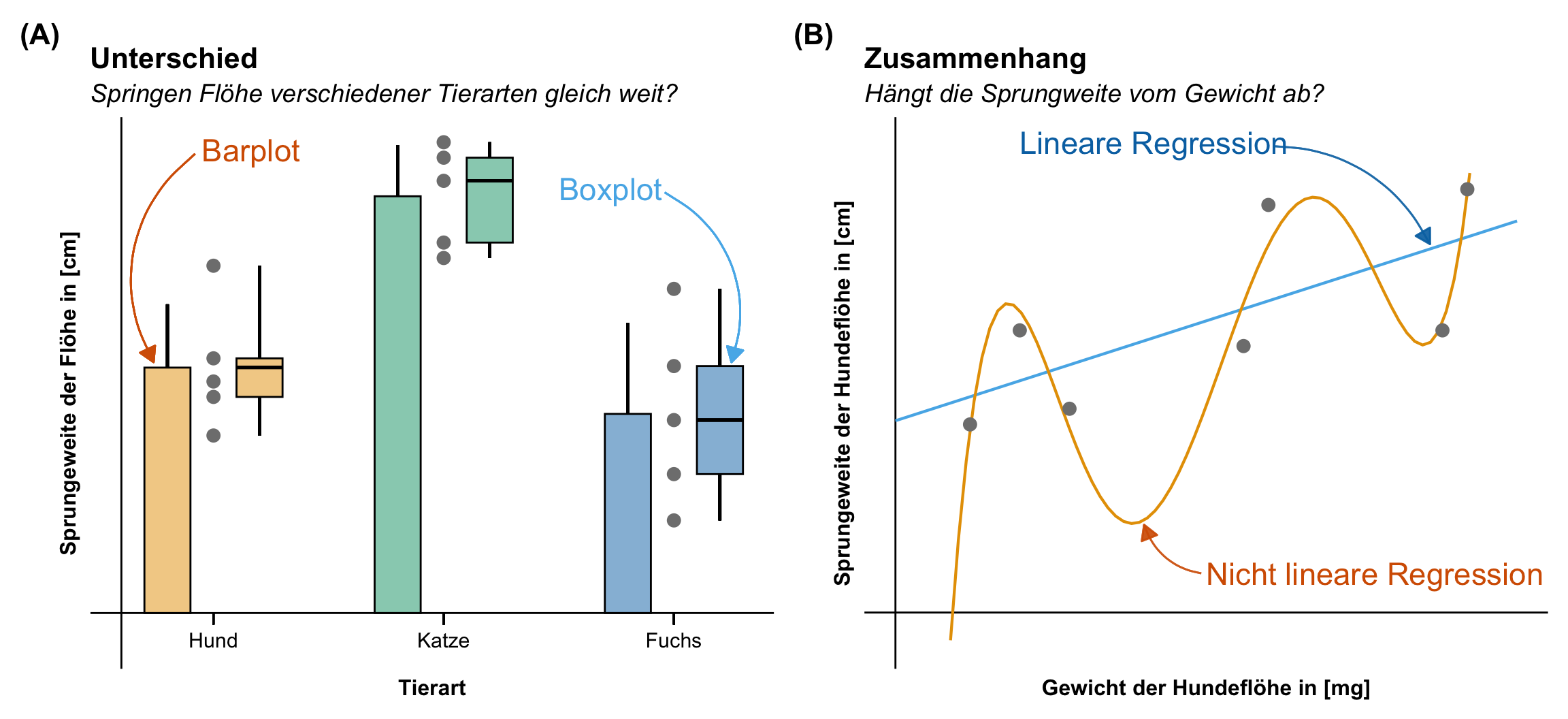
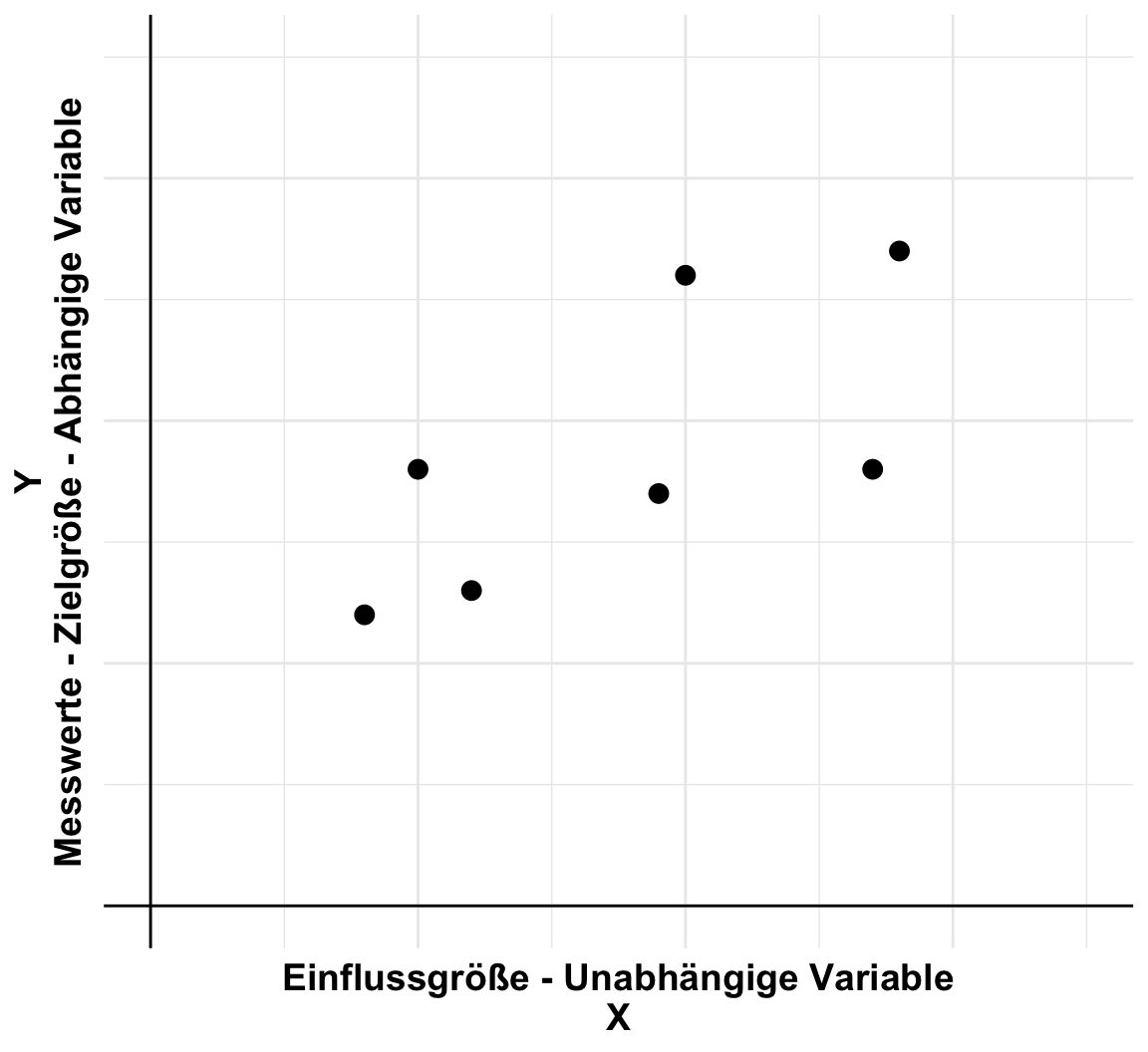
Grundsätzlich glauben wir dabei keiner Auswertung eines mathematischen Algorithmus, wenn wir nicht die Bestätigung in einer Abbildung sehen. Wenn wir also einen signifikanten Unterschied aus einem Algorithmus wiedergegeben bekommen, dann müssen wir auch den Unterschied in einer Abbildung sehen können. Eine statistische Analyse und deren Visualisierung gehen Hand in Hand. Daher ist die Visualisierung die Grundlage für ein fundiertes, wissenschaftliches Arbeiten. In diesem Kapitel stelle ich dir verschiedene Abbildungen vor, die uns helfen werden zu Verstehen ob es einen Zusammenhang zwischen \(y\) und \(x\) gibt. Wir haben ein \(y\) vorliegen, was wir auf die y-Achse eines Graphen legen und daneben dann mehrere Variablen bzw. Spalten die wir \(x\) nennen. Eine der Variablen legen wir auf die x-Achse des Graphen. Nach den anderen \(x\) färben wir die Abbildung ein. Wir nennen dabei eine Abbildung auch häufig Plot. Das ist der englische Begriff und hat nichts in unserem Kontext mit einer Fläche oder einer Handlung in einem Film zu zu tun. Im den beiden folgenden Abbildungen siehst du einmal die beiden häufigsten wissenschaftlichen Fragestellungen in der explorativen Datenanalyse.
In diesem Kapitel wollen wir durch die bedeutendsten Abbildungen in der explorativen Datenanalyse durchgehen. Ich habe die Abbildungen etwas nach Kontext sortiert und geschaut, dass die Abbildungen zum Gruppennterschied oder Zusammenhang zweier Variablen als erstes besprochen werden.
- Barplot für 5 und mehr Beobachtungen (pro Gruppe). Der Barplot oder das Balkendiagramm bzw. Säulendiagramm stellt den Mittelwert und die Standardabweichung da.
- Boxplot für 5 bis 20 Beobachtungen (pro Gruppe). Ebenso wie bei einem Histogramm, geht es bei einem Boxplot auch um die Verteilung der einer Variable. Wir können in einem Boxplot auch erkennen, ob sogenannte auffällige Werte oder Ausreißer vorliegen.
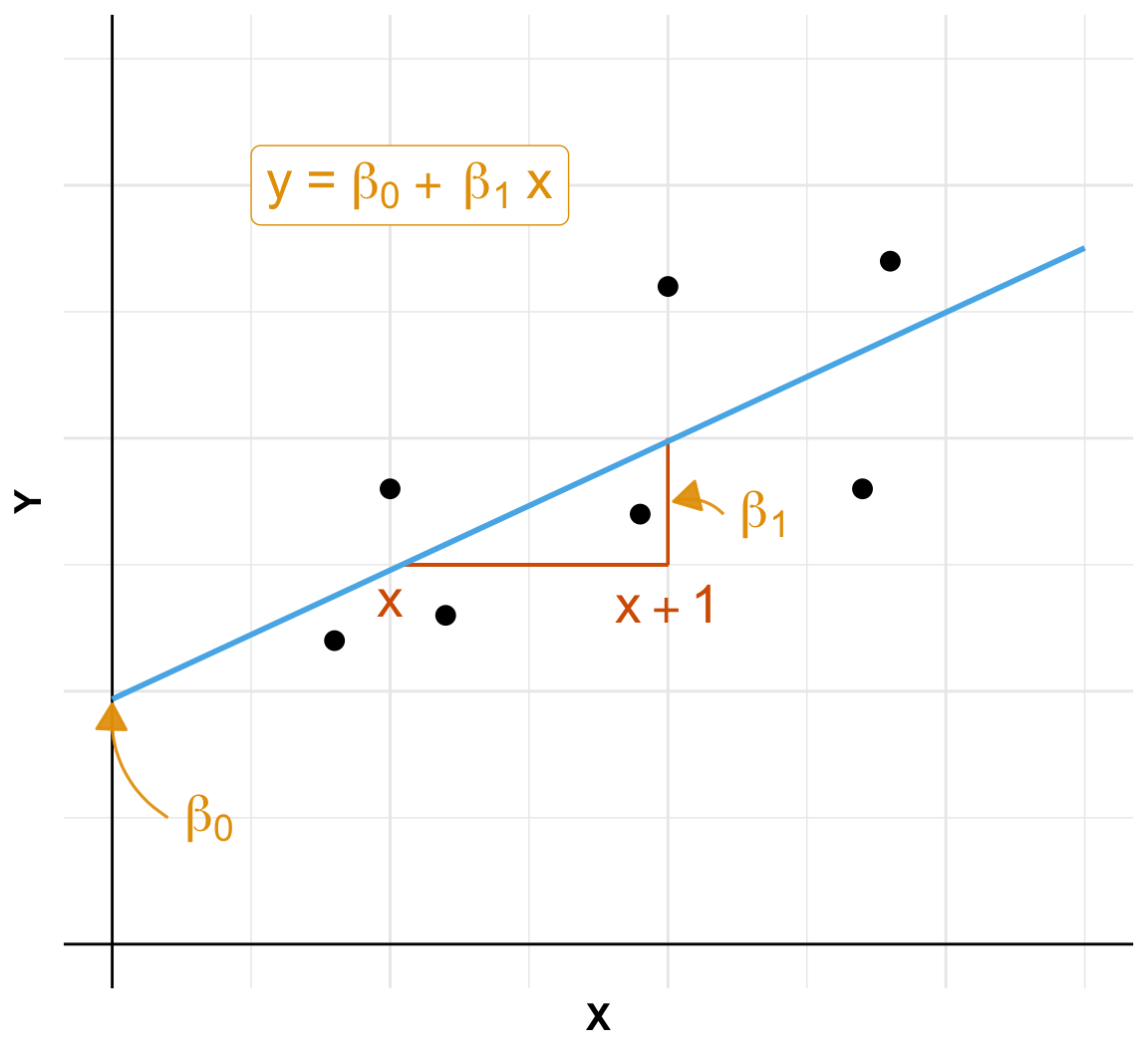
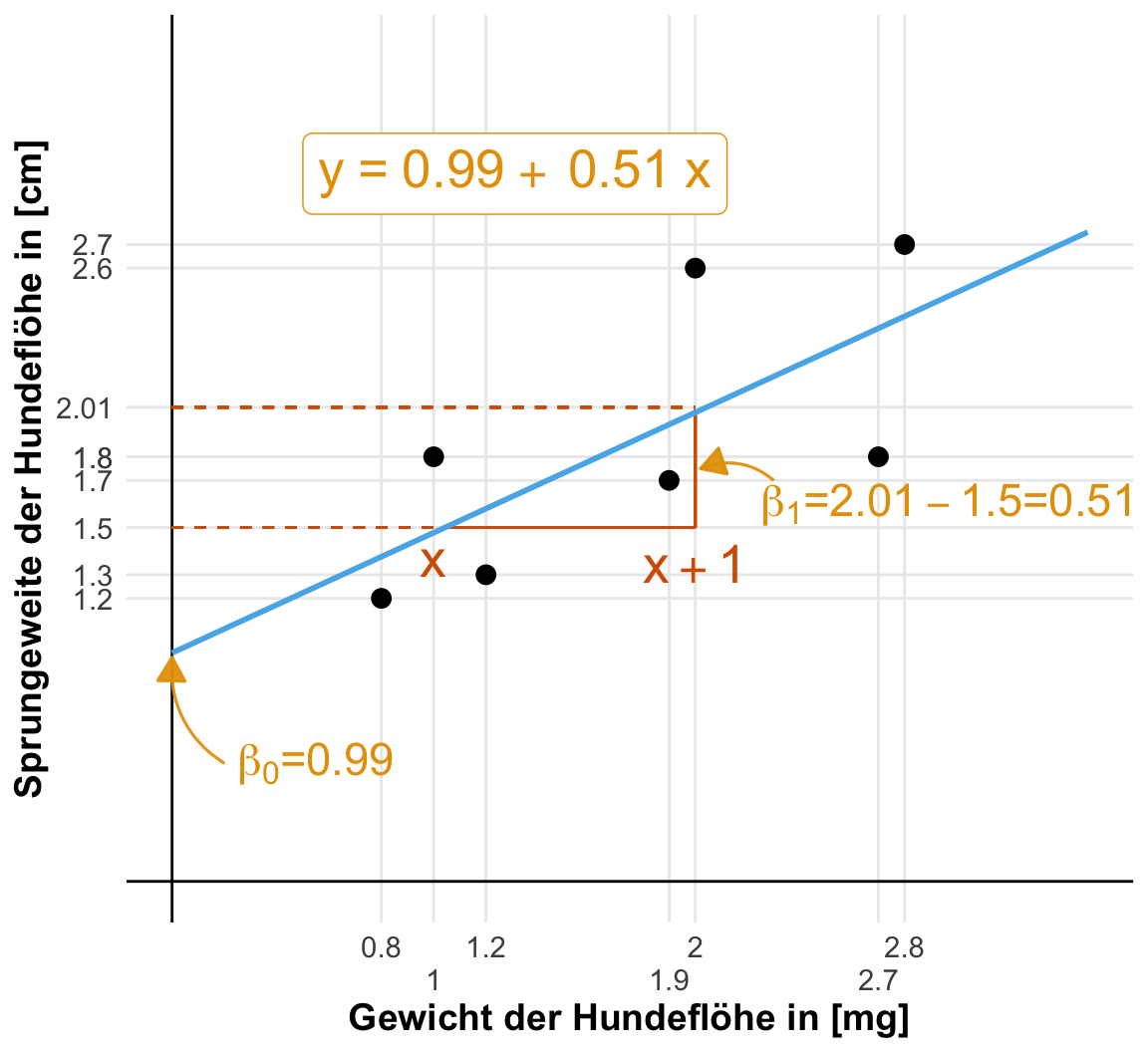
- Scatterplot für zwei kontinuierliche Variablen. Auch xy-Plot genannt. Die Abbildung, die dir bekannt sein müsste. Wir zeichnen hier eine Grade durch eine Punktewolke.
- Mosaicplot für zwei diskrete Variablen. Eine etwas seltene Abbildung, wenn wir Variablen abbilden wollen, die diskret sind bzw. aus Kategorien bestehen.
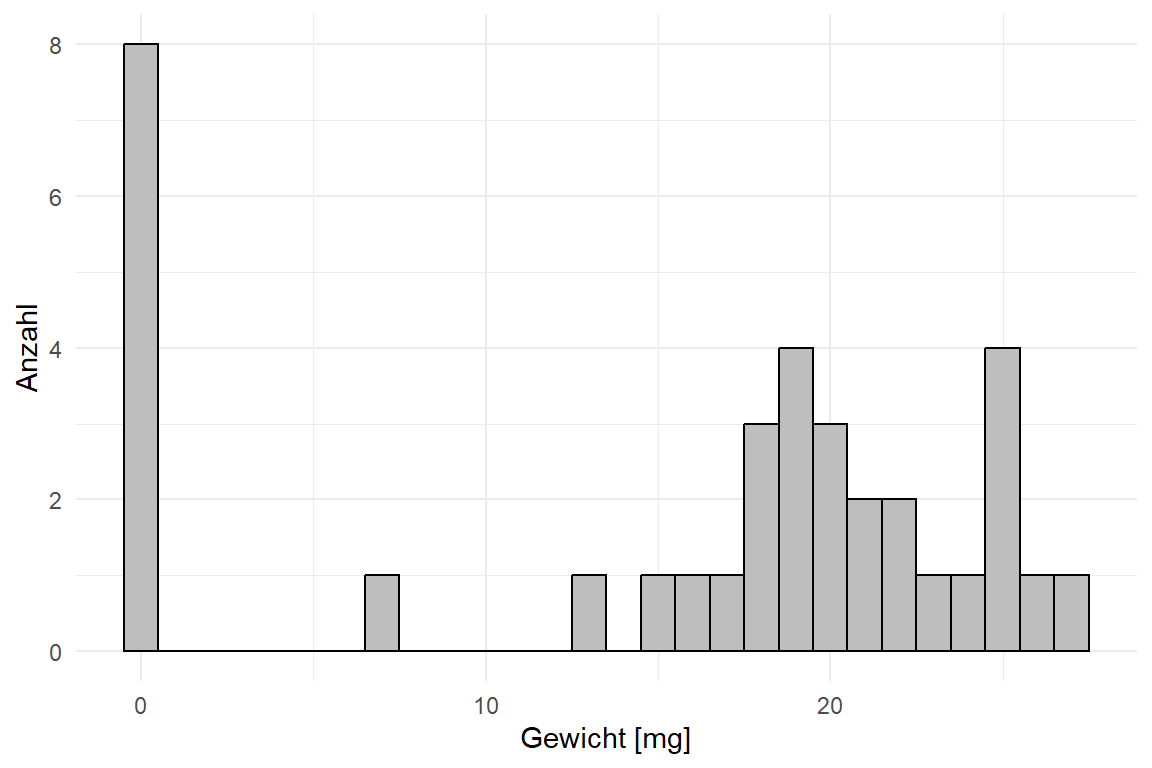
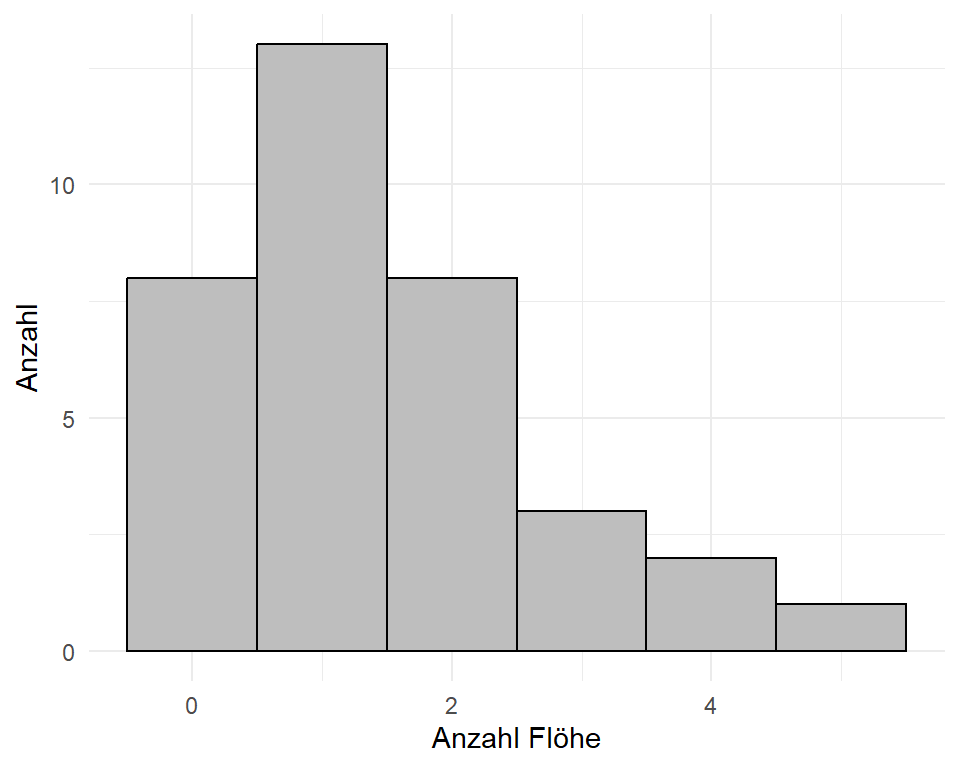
- Histogramm für mehr als 20 Beobachtungen (pro Gruppe). Wir nutzen ein Histogramm um die Verteilung einer Variable zu visualisieren.
- Dotplot für 3 bis 5 Beobachtungen (pro Gruppe). Hier geht es weniger um die Verteilung der Variable, sondern darum die wenigen Beobachtungen zu visualisieren.
- Violinplot für die Kombination von einem Densityplot und einem Boxplot. Dann können wir hier noch den Dotplot ergänzen und haben eine sehr informative Übersichtsabbildung.
Beginnen wir also mit dem Teil, der in der Statistik der mir immer am meisten Spaß macht. Oder aber um es in den Worten von John Tukey, den Begründer der explorativen Datenanalyse zu sagen:
“This is my favorite part about analytics: Taking boring flat data and bringing it to life through visualization.” — John Tukey
Wir immer geht natürlich hier auch noch viel mehr am Abbildungen. Du musst nicht alles in ggplot machen und darüber hinaus gibt es dann auch noch einiges an anderen R Paketen. In dem folgenden Kasten habe ich dir mal ein paar Quellen rausgesucht, wo du einmal gucken kannst, wenn du noch mehr Inspiration benötigst. Ich nutze die Seiten auch als Inspiration, den meisten weiß man gar nicht was alles geht, bis man die Visualisierung gesehen hat.
Im Folgenden einmal eine Auswahl an weiteren Möglichkeiten sich Abbildungen in R zu visualisieren. Teilweise ist es dann auch eine Sammlung an Informationen für mich, damit ich eine Idee habe, was noch so alles geht. Manchmal braucht man ja auch noch eine zusätzlich Inspiration.
- Data visualization with ggplot2 :: Cheat Sheet – als Überblick über alles was eigentlich in
ggplotmöglich ist. Du kriegst dann nochmal ein Überblick über diegeome, die es gibt und wie die einzelnen Funktionen und Möglichkeiten miteinander interagieren. Du kannst dir das Cheat Sheet auch auf Deutsch runterladen.
- R Charts by R Coder – ein großer Überblick über alle möglichen Abbildungen sortiert nach verschiedenen Kategorien. Hier würde ich auf jeden Fall mal drüber schauen, dann kriegst du nochmal eine Idee was neben
ggplotnoch so alles geht. Ich finde die Seite immer sehr inspirierend. - ALL YOUR FIGURE ARE BELONG TO US ist eine weitere tolle Übersicht an möglichen Abbildungen in
{ggplot}Universum. Die Übersicht zeigt nochmal verschiedene R Pakte mit den entsprechenden möglichen Abbildungen. - sjPlot - Data Visualization for Statistics in Social Science – auch hier geitbes dann die Möglichkeit nochmal etwas anders auf die Visualisierung zu schauen. Denn hier haben wir dann die Möglichkeiten der Sozialwissenschaften mehr abgedeckt. Das mag insbesondere im Bereich von Fragebögen und Marketing von Interesse sein.
- Als spannende zusätzlichen Ressourcen seinen das R Paket
{cowplot}sowie das R Paket{ggpubr}genannt. Besonders das Paketcowplotliefert noch schöne Formatierungsmöglichkeiten wobei dannggpubrstatistische Test mit der Visualisierung verbindet. - {plotly} R Open Source Graphing Library sowie im besonderen dann die Seite Getting Started with {plotly} in {ggplot2} liefert dann interaktive Abbildungen, wo du dann direkt hereinzoomen kannst. Das ist bei sehr großen Abbildungen immer sehr praktisch. Auch kannst du die Werte einer einzelnen Beobachtung gleich im Plot ablesen.
- How to create BBC style graphics – einmal als ein Beispiel für die Anwendung von
ggplotin der Wirtschaft und Data Science. Auch hier sieht man schön die Ideen die möglich sind. - Visualizing Distributions with Raincloud Plots (and How to Create Them with ggplot2) – manchmal ist dann der Barplot oder Dynamiteplot dann doch irgendwie nicht das richtige Werkzeug um die Daten zu zeigen. Daher hier nochmal der Blogpost mit einer Diskussion was neben dem Säulendiagramm noch so alles gehen könnte.
- ggplot Wizardry Hands-On zeigt nochmal sher schön was alles in
{ggplot}geht, wenn die entsprechenden zusätzlichen Pakete geladen werden. Ich schaue auch hier immer mal wieder rein, wenn ich eine Abbildung besonders schön machen möchte. Hier liegt dann der Fokus auf dem R Paket{gghalves}sowie dem R Paket{ggdist}. - Die Publikation Error bars in experimental biology von Cumming et al. (2007) liefert nochmal einen Überblick über Fehlerbalken und welche Fehlerbalken man den nun nutzen sollte.
18.1 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
pacman::p_load(tidyverse, magrittr, readxl, ggmosaic,
janitor, see, patchwork, latex2exp, ggbeeswarm,
ggdist, gghalves, ggbreak, duke, wesanderson,
tidyplots, conflicted)
conflicts_prefer(dplyr::summarise)
conflicts_prefer(dplyr::filter)
conflicts_prefer(latex2exp::TeX)An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
18.2 Daten
Wir immer bringe ich hier ein paar Datensätze mit damit wir dann verstehen, was eigentlich in den folgenden Visualisierungen in {ggplot} und den entsprechenden zusätzlichen R Paketen passiert. Ich zeige hier an den Daten nur die Anwendung in R. Deshalb fehlen dann hier auch die Mittelwerte und andere deskriptive Maßzahlen. Schauen wir jetzt also mal in unsere Beispieldaten für die einfaktorielle und zweifaktorielle Datenanalyse rein. Was heißt das nochmal? Wenn wir einen einfaktoriellen Datensatz vorliegen haben, dann haben wir nur einen Behandlunsgfaktor. Bei einem zweifaktorielle Datenanalyse betrachten wir eben dann zwei Behandlungen. Es wird dann aber gleich in den Beispielen klarer.
Einfaktorieller Datensatz
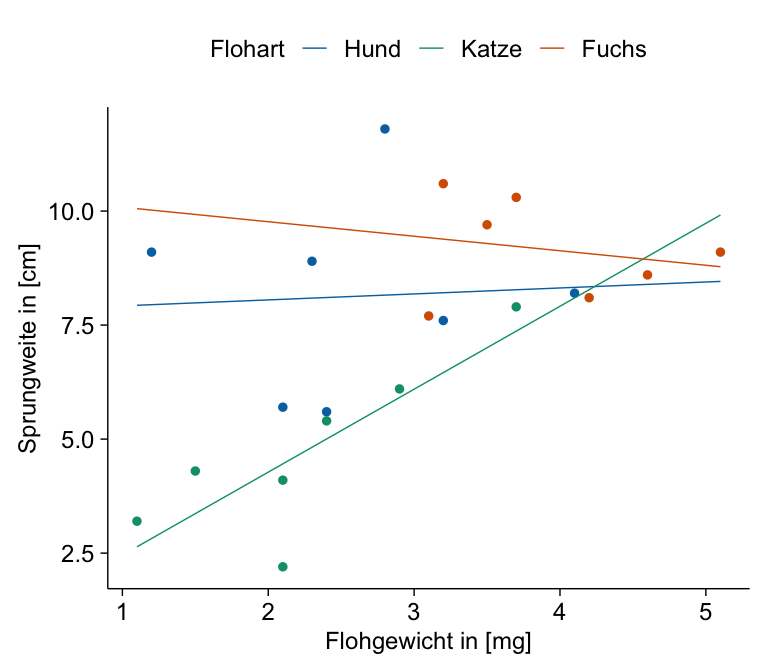
Beginnen wir mit einem einfaktoriellen Datensatz. Wir haben hier als Messwert die Sprungweite von Flöhen in [cm] vorliegen. Wissen wollen wir, ob sich die Sprungweite für drei verschiedene Floharten unterscheidet. Damit ist dann in unserem Modell der Faktor animal und die Sprungweite jump_length als Messwert. Ich lade einmal die Daten in das Objekt fac1_tbl.
R Code [zeigen / verbergen]
fac1_tbl <- read_xlsx("data/flea_dog_cat_fox.xlsx") |>
mutate(animal = as_factor(animal))Dann schauen wir uns die Daten einmal in der folgenden Tabelle als Auszug einmal an. Wichtig ist hier nochmal, dass du eben einen Faktor animal mit drei Leveln also Gruppen vorliegen hast. Wir wollen jetzt die drei Tierarten hinsichtlich ihrer Sprungweite in [cm] miteinander vergleichen.
| animal | jump_length |
|---|---|
| dog | 5.7 |
| dog | 8.9 |
| dog | 11.8 |
| … | … |
| fox | 10.6 |
| fox | 8.6 |
| fox | 10.3 |
Zweifaktorieller Datensatz
Neben dem einfaktoriellen Datensatz wollen wir uns noch den häufigeren Fall mit zwei Faktoren anschauen. Wir haben also nicht nur die drei Floharten vorliegen und wollen wissen ob diese unterschiedlich weit springen. Darüber hinaus haben wir noch einen zweiten Faktor gewählt. Wir haben die Sprungweiten der Hunde-, Katzen- und Fuchsflöhe nämlich an zwei Messorten, der Stadt und dem Dorf, gemessen. Dadurch haben wir jetzt den Faktor animal und den Faktor site vorliegen. Wiederum fragen wir uns, ob sich die Sprungweite in [cm] der drei Floharten in den beiden Messorten unterscheidet. Im Folgenden lade ich einmal den Datensatz in das Objekt fac2_tbl.
R Code [zeigen / verbergen]
fac2_tbl <- read_xlsx("data/flea_dog_cat_length_weight.xlsx") |>
select(animal, sex, weight, jump_length) |>
mutate(animal = as_factor(animal),
sex = as_factor(sex))Betrachten wir als erstes einen Auszug aus der Datentabelle. Wir haben hier als Messwert oder Outcome \(y\) die Sprungweite jump_length vorliegen. Als ersten Faktor die Variable animal und als zweiten Faktor die Variable sex festgelegt.
animal und einen zweiten Faktor mit site vorliegen haben.
| animal | sex | weight | jump_length |
|---|---|---|---|
| cat | male | 6.02 | 15.79 |
| cat | male | 5.99 | 18.33 |
| cat | male | 8.05 | 17.58 |
| … | … | … | … |
| fox | female | 9.26 | 24.35 |
| fox | female | 8.85 | 24.36 |
| fox | female | 7.89 | 22.13 |
Der Gummibärchendatensatz
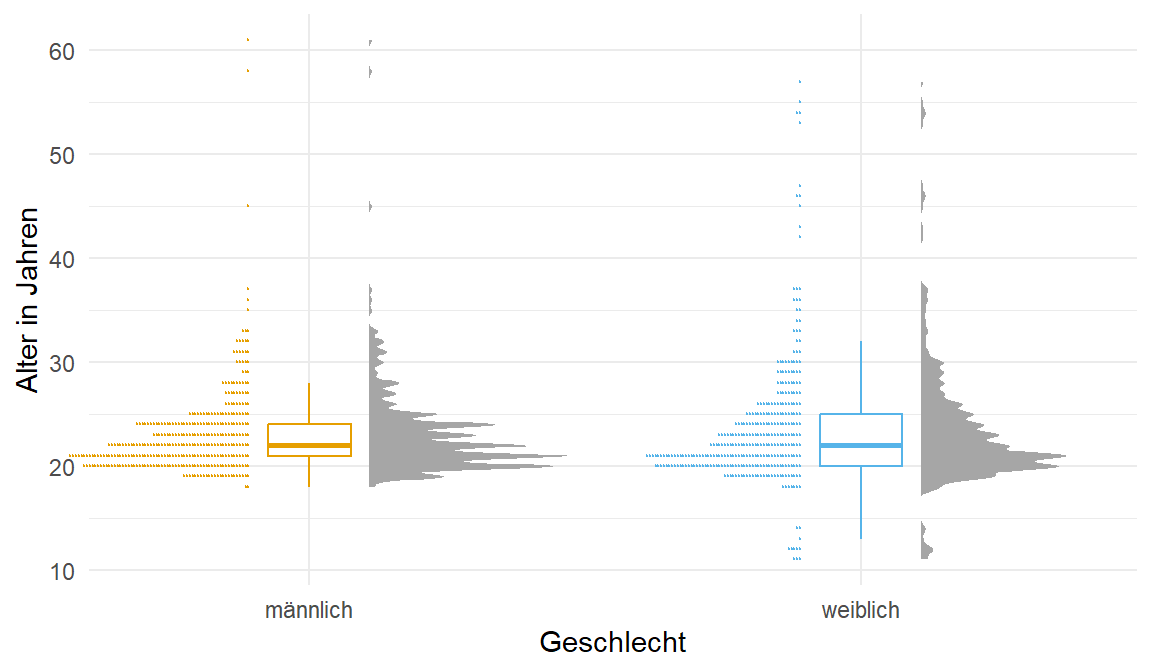
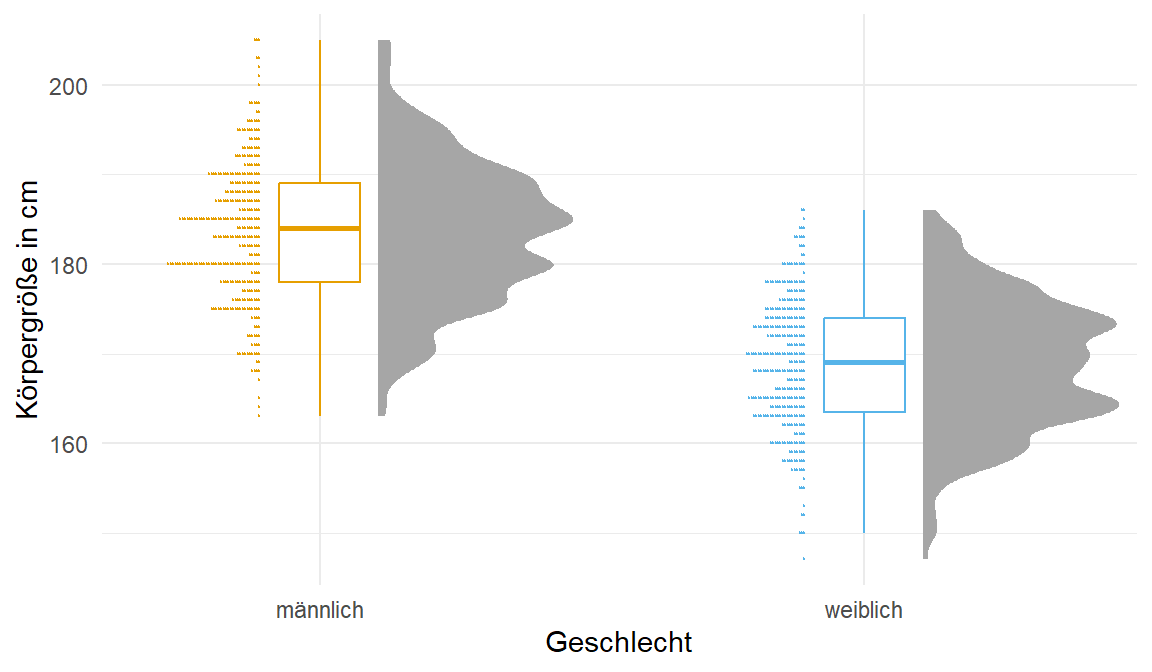
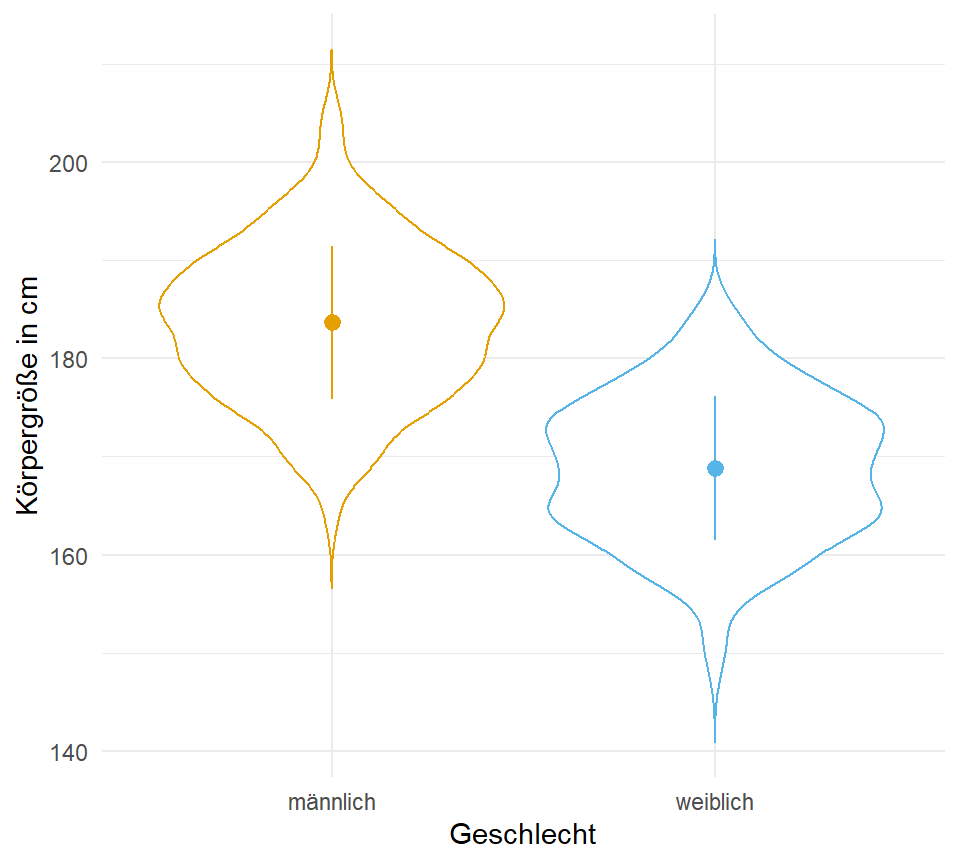
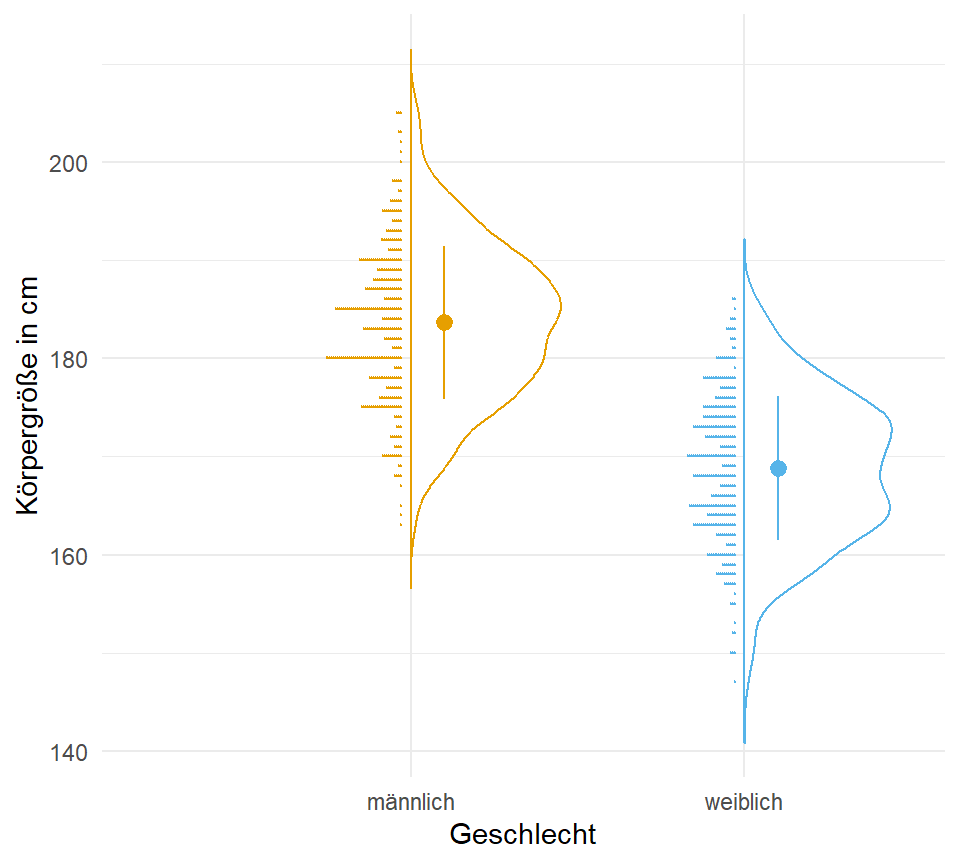
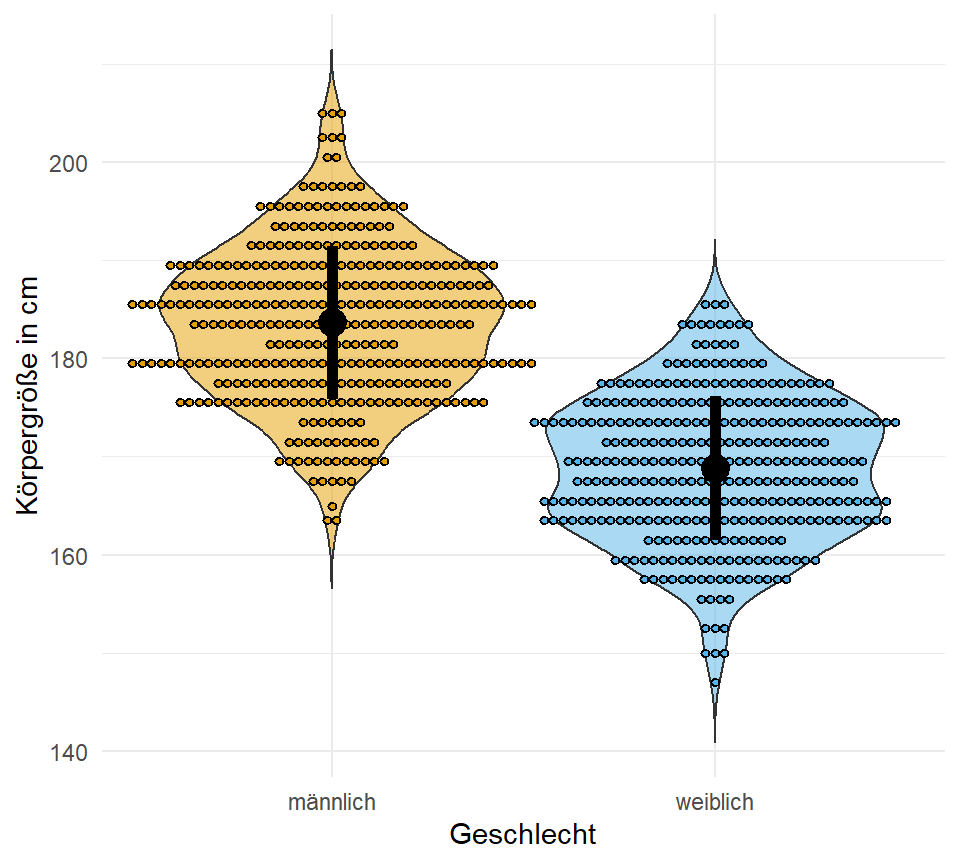
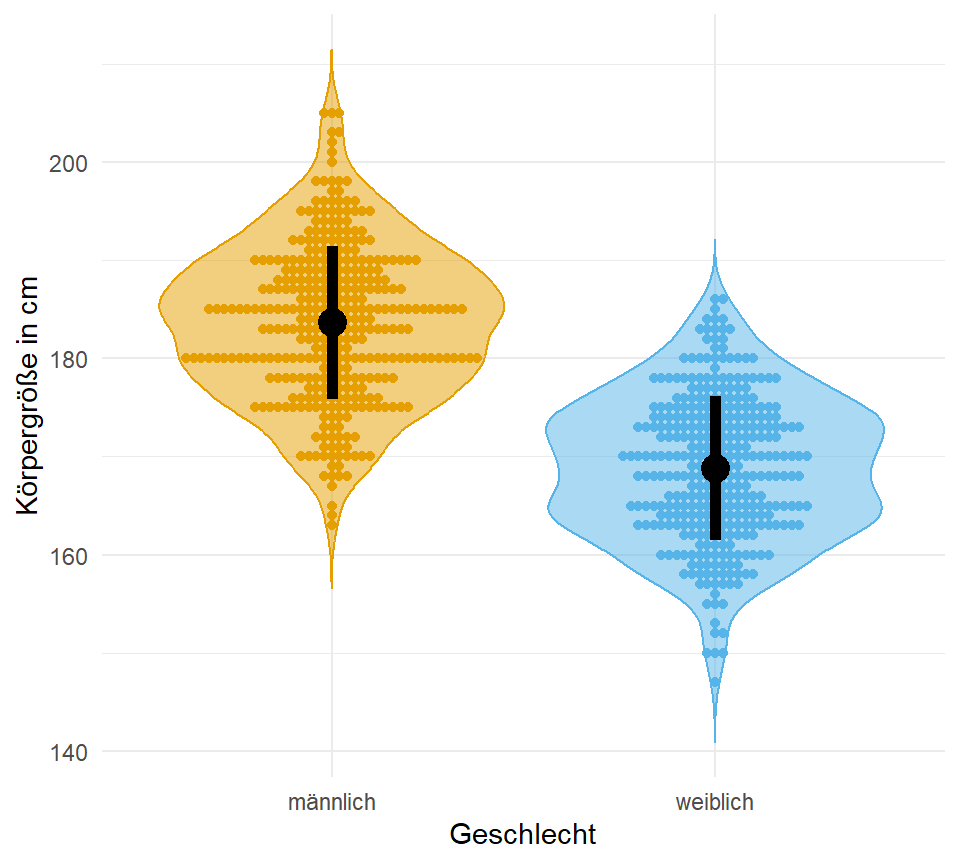
Wir brauchen dann ab und an auch nochmal mehr Datenpunkte, daher nehmen wir auch einmal den Gummibärchendatensatz und schauen uns dort die Variablen gender, height und age einmal genauer an. Wie immer nutzen wir die Funktion select() um die Spalten zu selektieren. Abschließend verwandeln wir das Geschlecht gender noch in einen Faktor und entfernen alle fehlenden Werte mit na.omit().
R Code [zeigen / verbergen]
gummi_tbl <- read_excel("data/gummibears.xlsx") |>
select(gender, height, age, most_liked) |>
mutate(gender = factor(gender, labels = c("männlich", "weiblich"))) |>
na.omit()Und hier dann einmal der ausgewählte Datensatz der Gummibärchendaten. Ich zeige hier nur die ersten sieben Zeilen als Ausschnitt, die eigentlichen Daten sind mit \(n = 931\) Beobachtungen viel größer.
| gender | height | age |
|---|---|---|
| m | 193 | 35 |
| w | 159 | 21 |
| w | 159 | 21 |
| … | … | … |
| w | 178 | 21 |
| m | 176 | 22 |
| w | 170 | 24 |
18.3 Grundlagen im…
18.3.1 R Paket {ggplot}
Wir nutzen in R das R Paket {ggplot2} um unsere Daten zu visualisieren. Die zentrale Idee von {ggplot2} ist, dass wir uns eine Abbildung wie ein Sandwich bauen. Zuerst legen wir eine Scheibe Brot hin und legen uns dann Scheibe für Scheibe weitere Schichten übereinander. Oder die Idee eines Bildes, wo wir erst die Leinwand definieren und dann Farbschicht über Farbschicht auftragen. Im Gegensatz zu dem Pipe-Operator |> nutzt {ggplot2} den Operator + um die verschiedenen Funktionen (geom_) miteinander zu verbinden. Das Konzept von {ggplot2}ist schlecht zu beschreiben deshalb habe ich auch noch zwei Videos hierfür gemacht. Um den Prozess von {ggplot2} zu visualisieren - aber wie immer, nutze was du brauchst.
Erstellen wir also erstmal unseren erste Visualisierung in dem R Paket {ggplot2}. Im Folgenden spreche ich dann aber immer von {ggplot}. Die Funktion ggplot() ist die zentrale Funktion, die die Leinwand erschafft auf der wir dann verschiedene Schichten aufbringen werden. Diese Schichten heißen geom. Es gibt nicht nur ein geom sondern mehrere. Zum Beispiel das geom_boxplot() für die Erstellung von Boxplots, das geom_histogram() für die Erstellung von Histogrammen. Die Auswahl ist riesig. Die einzelnen Schichten werden dann über den Operator + miteinander verbunden. Soviel erstmal zur Trockenübung. Schauen wir uns das ganze einmal an einem Beispiel an. Dafür müssen wir dann erstmal einen Datensatz laden, damit wir auch etwas zum abbilden haben.
Wie immer empfehle ich dir dann auch das entsprechende Video auf YouTube anzuschauen. In Textform ist eine echte Herausforderung zu erklären wie man Plots baut. Der folgende R Code erstellt die Leinwand in der Abbildung 18.3 für die folgende, zusätzliches Schichten (geom). Wir haben also immer erst eine leere Leinwand auf der wir dann zusätzlich geome plotten. Wir bauen uns sozusagen ein Sandwich.
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = animal , y = jump_length)) +
theme_minimal()Wir schauen uns einmal den Code im Detail an.
ggplotruft die Funktion auf. Die Funktion ist dafür da den Plot zu zeichnen.data = fac1_tblbenennt den Datensatz aus dem der Plot gebaut werden soll.aes()ist die Abkürzung für aesthetics und beschreibt, was auf die \(x\)-Achse soll, was auf die \(y\)-Achse soll sowie ob es noch andere Faktoren in den Daten gibt. Wir können nämlich noch nach anderen Spalten die Abbildung einfärben oder anderweitig ändern.xbraucht den Spaltennamen für die Variable auf der \(x\)-Achse.ybraucht den Spaltennamen für die Variable auf der \(y\)-Achse.
+ theme_minimal()setzt das Canvas oder die Leinwand auf schwarz/weiß. Sonst wäre die Leinwand flächig grau.
Mit Faktoren meine ich hier andere Gruppenvariablen. Variablen sind ein anderes Wort für Spalten. Also Variablen die wir mit as_factor erschaffen haben und die uns noch mehr über unsere Daten dann verraten können. Hier ist es dann etwas abstrakt, aber es wird dann später in der Anwendung klarer.
Am Ende sehen wir, dass wir nichts sehen. In der Abbildung 18.3 ist nichts dargestellt. Der Grund ist, dass wir noch kein geom hinzugefügt haben. Das geom beschreibt nun wie die Zahlen in der Datentabelle fac1_tbl visualisiert werden sollen. Wir habe eine sehr große Auswahl an geomen, deshalb gibt es gleich einmal eine Auswahl an Abbildungen. Du findest dann auch weitere Optionen in {ggplot} im Kapitel zum {ggplot} Cookbook.
18.3.2 R Paket {tidyplots}
Fortschritt lässt sich ja nicht aufhalten und was am Ende dann fortschrittlich ist, ist dann ja wieder die Frage. Manchmal brauchen wir einfach nicht die ganzen Funktionen und Möglichkeiten, die uns {ggplot} liefert. Wir wollen dann irgendwie alles etwas einfacher haben. In diese Lücke stößt die Arbeit von Engler (2025) mit dem R Paket {tidyplots}. Was macht also da R Paket {tidyplots} anders? Zum einen vereinfacht es die Benutzung von {ggplot}. Du hast nur noch eine große Auswahl, aber keien erschlagende Auswahl mehr. Dennoch basiert {tidyplots} auf {ggplot} und somit sind die Abbildungen auch echt schön und gut anzusehen. Am Ende ist es dann eine Geschmacksfrage was dir besser gefällt. Mich haben die {tidyplots} so sehr überzeugt, dass ich die {tidyplots} auf jeden Fall hier einmal vorstellen möchte. Vielleicht brauchst du auch nur diese Art der Darstellung und nicht die volle Batterie der Funktionen von {ggplot}. Deshalb vielleicht auch hier der Disclaimer, vieles geht dann schon, aber ich nutze weiterhin für viele Anwendunsgfälle dann doch {ggplot}.
Auch hier kann ich nicht alles erklären und auch die beispielhaften Abbildungen in den folgenden Abschnitten können das nicht. Daher schaue dir doch nochmal die Hilfes von {tidyplots} an.
- Die Hilfeseite Get started liefert dir einen ersten Überblick über die Funktionen und Möglichkeiten.
- Es gibt auch eine Reihe von tollen Use cases, die dir ermöglichen einmal zu schauen was alles so geht.
- Das
{tidyplots}Cheatsheet hilft am Ende dann nur, wenn du dich schon mit den Funktionen auseinandergestezt hast. Sonst finde ich es etwas unübersichtlich.
Fangen wir einmal mit dem Standardaufruf in {tidyplots} an. Wir nutzen die Funktion tidyplot(), ohne das s wie im Namen des Pakets, um einen tidyplot zu erstellen. Wichtig ist hier nocoh, dass wir nicht das Pluszeichen + nutzen sondern alles mit dem Pipe-Operator |> erledigen. Hier siehst du die Verwendung einmal mit der Funktion adjust_size(), die es uns erlaubt die Größe der Abbildung zu steuern.
R Code [zeigen / verbergen]
tidyplot(data = fac1_tbl,
x = animal , y = jump_length) |>
adjust_size(width = NA, height = NA)Wir schauen uns einmal den Code im Detail an.
tidyplotruft die Funktion auf. Die Funktion ist dafür da den Plot zu zeichnen.data = fac1_tblbenennt den Datensatz aus dem der Plot gebaut werden soll.xbraucht den Spaltennamen für die Variable auf der \(x\)-Achse.ybraucht den Spaltennamen für die Variable auf der \(y\)-Achse.adjust_size(width = NA, height = NA)ist hier nochmal wichtig, da wir hiermit die Größe der Abbildung kontrollieren können. Ich möchte hier maximale Größe, deshalb sind die Breitewidthund Höheheightauf den WertNAgesetzt.
Wenn wir jetzt den Code ausführen, erhalten wir folgende leere Abbildung. Wir können dann einfach noch weitere Layer, wie auch bei {ggplot} ergänzen. Mehr dazu dann in den jeweiligen Tabs in den folgenden beispielhaften Abbildungen, die wir dann häufig nutzen.
Du findest dann auch weitere Optionen in {tidyplot} im Kapitel zum {ggplot} Cookbook. Oder aber eben auf den Hilfeseiten des R Paket {tidyplots}. Dann fangen wir einmal an uns die häufigsten Abbildungen in der explorativen Datenanalyse anzuschauen.
18.4 Die häufigsten Abbildungen
Im Folgenden gehen wir dann einmal die wichtigsten Abbildungen einmal durch. Viele der Abbildungen kennst du vielleicht schon und dann musst du hier nur noch schauen, wie die Abbildungen in ggplot zu realisieren sind. Ansonsten gilt wie immer, es ist nur ein kleiner Ausschnitt, du findest auf der Hilfeseite von ggplot eine sehr viel größere Übersicht.
18.4.1 Barplot
Der Barplot oder das Balkendiagramm auch Säulendiagramm ist eigentlich veraltet. Wir haben mit dem Boxplot eine viel bessere Methode um eine Verteilung und gleichzeitig auch die Gruppenunterschiede zu visualisieren. Warum nutzen wir jetzt so viel den Barplot? Das hat damit zu tun, dass früher - oder besser bis vor kurzem - in Excel kein Boxplot möglich war. Daher nutzte jeder der mit Excel seine Daten auswertet den Barplot.
- Muss die 0 mit auf die y-Achse?
-
Der einzige Grund, warum wir einen Barplot nutzen wollen würden, wäre wenn wir unbedingt die 0 mit auf der y-Achse haben wollten.
Weil aber eben noch viel der Barplot genutzt wird, stelle ich natürlich den Barplot auch hier vor. Der Barplot beinhaltet aber weniger Informationen als der Boxplot. Wir haben nur die Standardabweichung als Maßzahl für die Streuung. Beim Boxplot haben wir den Interquartilesabstand (abk . IQR), der uns mehr über die Streuung aussagt. Aber gut, häufig musst du den Barplot in deiner Abschlussarbeit machen. Zuerst betrachten wir die theoretische Darstellung. Dann zeige ich dir die Werte für unsere Sprungweiten der Hundeflöhe. Im letzten Tab findest du dann die Implementierung in {ggplot}.
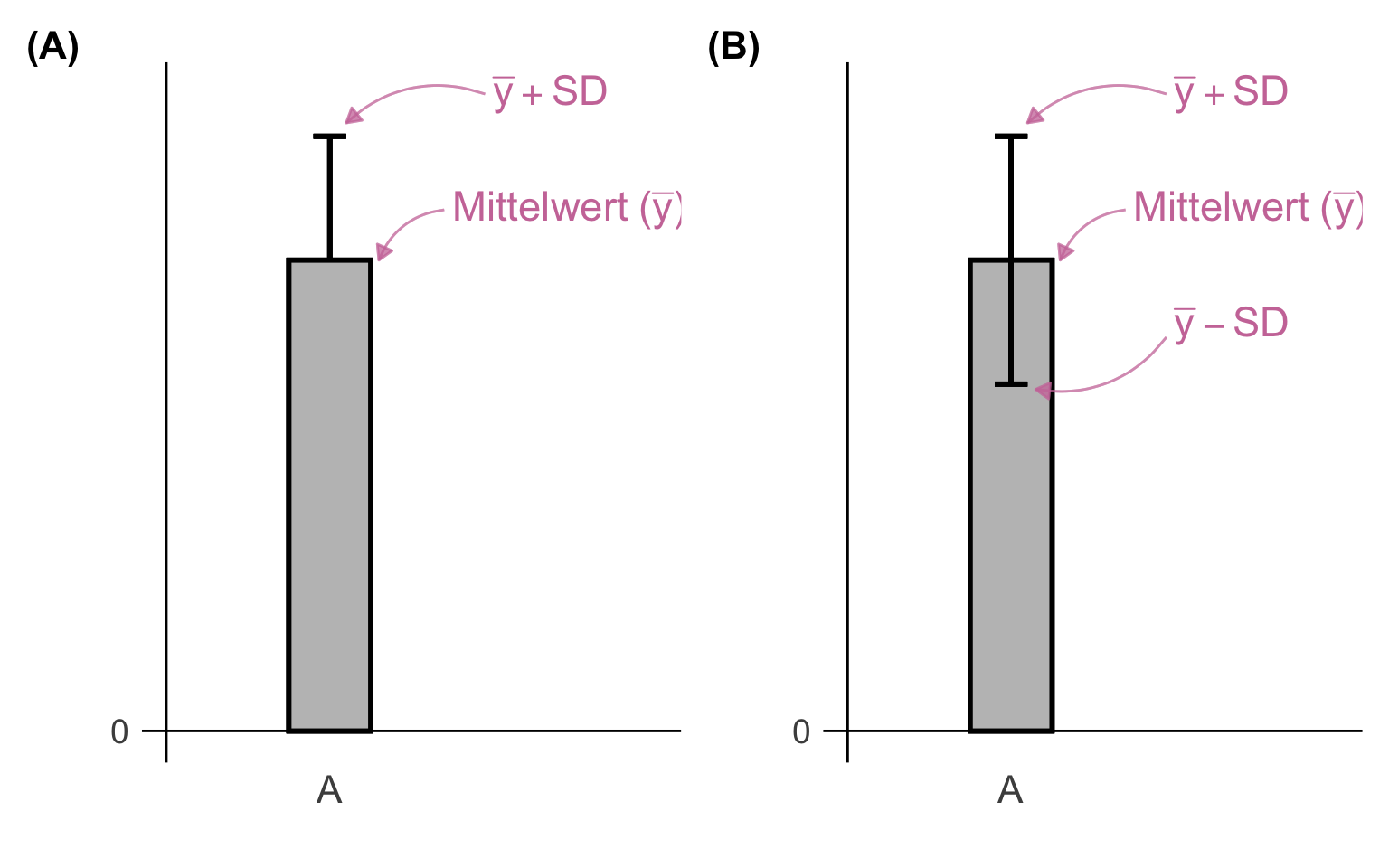
In den folgenden beiden Abbildungen siehst du einmal zwei Säulendigramme. Die Säulen gehen exakt so hoch wie der Mittelwert \(\bar{y}\) der entsprechenden Gruppe \(A\). Dann berechnen wir noch für die Fehlerbalken die Standardabweichung (abk. SD). Je nachdem wie wir die Säulendigramme darstellen wollen, zeigen wir nur \(\bar{y} + SD\) oder aber \(\bar{y} \pm SD\). Hier gibt es keine richtige Regel, das hängt sehr vom Geschmack ab und unterscheidet sich auch von Publikation zu Publikation. Je nachdem was wir als Outcome gemessen haben, können wir auch Überlegen anstatt der Standardabweichung den Standardfehler (abk. SE) zu nutzen.
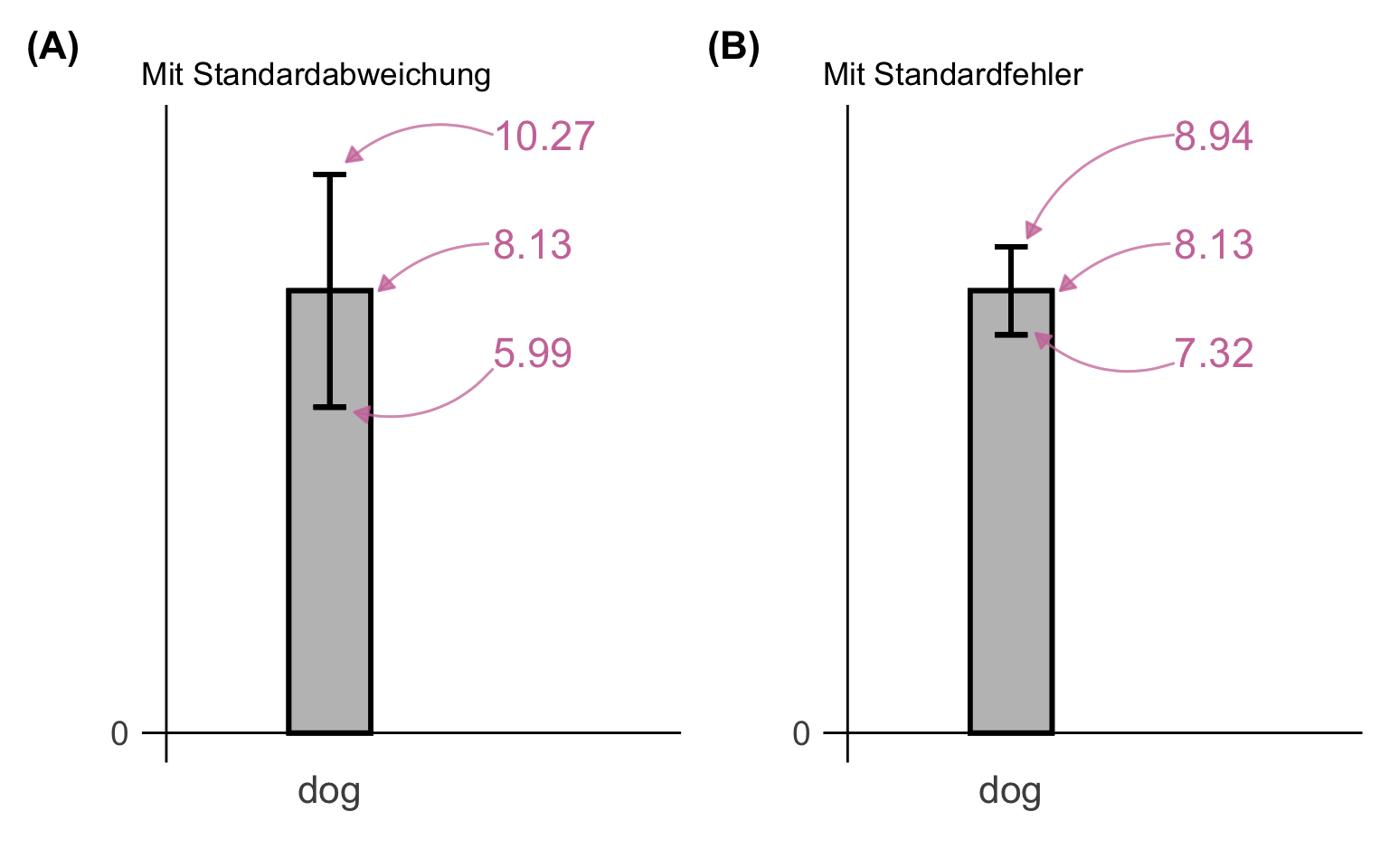
In den beiden folgenden Abbildungen siehst du einmal die Sprungweite der Hundeflöhe als ein Säulendigramm dargestellt. Wir haben den Mittelwert mit 8.13 sowie die Standardabweichung mit 2.14 berechnet. Daraus ergeben sich dann die Grenzen der Fehlerbalken. Ich habe dann in der rechten Abbildung die Fehlerbalken dann noch mit dem Standardfehler von 0.81 dargestellt. Wie du siehst, werden dann die Fehlerbalken kleiner, der Mittelwert bleibt natürlich in beiden Fällen gleich. Mehr dazu dann in dem Kapitel zur deskriptiven Statistik und unter diesem Kasten.
Wir schauen uns hier einmal in {ggplot} den einfaktoriellen sowie zweifaktoriellen Barplot an. Wenn wir von einem einfaktoriellen Barplot sprechen, dann haben wir nur eine Gruppe auf der x-Achse vorliegen. Wenn wir einen zweifaktoriellen Barplot bauen wollen, dann brauchen wir noch einen zweiten Gruppenfaktor für die Legende. Das klingt jetzt etwas wirr, wird aber gleich im Beispiel klarer.
Einfaktorieller Barplot
Wenn wir ein Säulendigramm in ggplot() erstellen wollen, dann müssen wir jetzt den Mittelwert und die Streuung für die Gruppen in unseren Daten der Hunde- und Katzenflöhe berechnen. Du kannst als Streuung die Standardabweichung sd oder den Standardfehler se nehmen. Wir nehmen wir einmal die Standardabweichung für die Abbildung.
R Code [zeigen / verbergen]
stat_fac1_tbl <- fac1_tbl |>
group_by(animal) |>
summarise(mean = mean(jump_length),
sd = sd(jump_length),
se = sd/sqrt(n()))Wir nutzen nun das Objekt stat_tbl um den Barplot mit der Funktion ggplot() zu erstellen. Dabei müssen wir zum einen schauen, dass die Balken nicht übereinander angeordnet sind. Nebeneinander angeordnete Balken kriegen wir mit der Option stat = "identity" in dem geom_bar(). Dann müssen wir noch die Fehlerbalken ergänzen mit dem geom_errorbar(). Hier kann nochmal mit der Option width = an der Länge der Fehlerenden gedreht werden.
R Code [zeigen / verbergen]
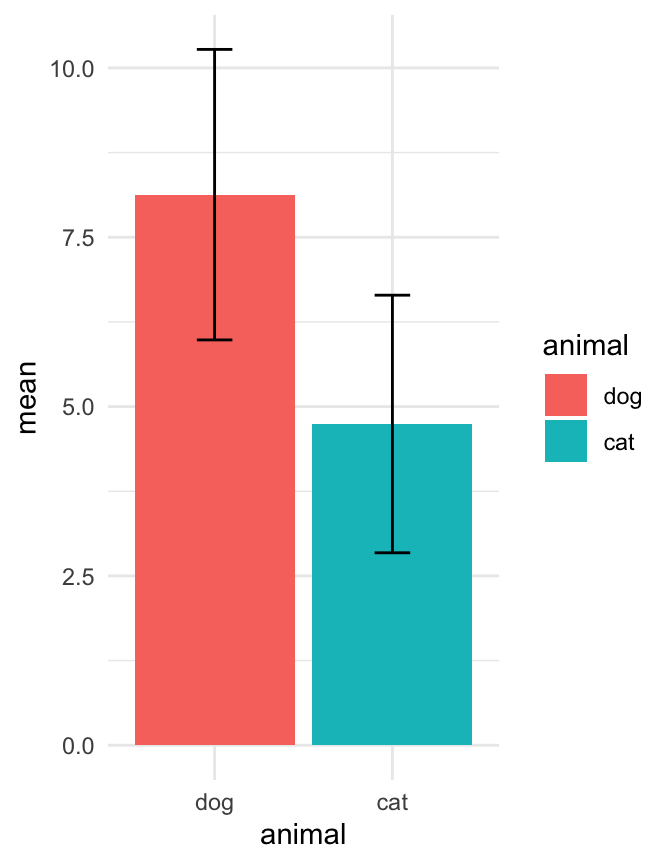
ggplot(stat_fac1_tbl, aes(x = animal, y = mean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2)Dank der Funktion coord_flip() können wir auch schnell aus dem Säulendiagramm ein Balkendiagramm bauen. Du musst dann immer schauen, was besser in deine Visualisierung passt.
R Code [zeigen / verbergen]
ggplot(stat_fac1_tbl, aes(x = animal, y = mean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2) +
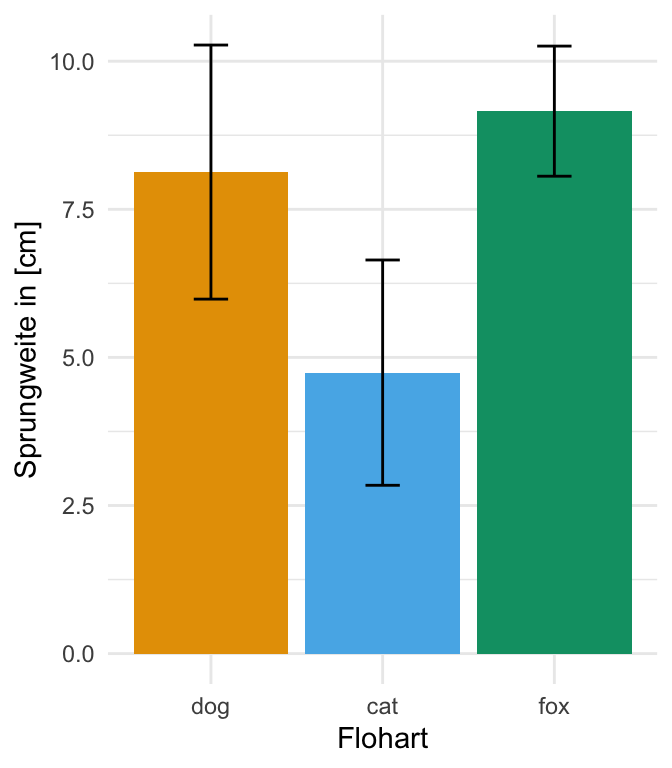
coord_flip()In der folgenden Abbildung siehst du dann nochmal den Barplot mit mehr Optionen und Informationen dargestellt. Auch habe ich die Farbpalette scale_fill_okabeito() aus dem R Paket {see} genutzt.
R Code [zeigen / verbergen]
ggplot(data = stat_fac1_tbl,
aes(x = animal, y = mean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2) +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() Zweifaktorieller Barplot
Für den zweifaktoriellen Barplot brauchen wir einmal den Mittelwert und die Standardabweichung der einzelne Floharten getrennt für die beiden Messorte. Das geht natürlich auch umgedreht, also die Messorte für die Floharten. Das kommt dann auf deine Fragestellung an.
R Code [zeigen / verbergen]
stat_fac2_tbl <- fac2_tbl |>
group_by(animal, sex) |>
summarise(mean = mean(jump_length),
sd = sd(jump_length))
stat_fac2_tbl# A tibble: 6 × 4
# Groups: animal [3]
animal sex mean sd
<fct> <fct> <dbl> <dbl>
1 cat male 15.4 1.85
2 cat female 20.5 1.78
3 dog male 18.1 1.90
4 dog female 22.9 2.06
5 fox male 20.7 1.95
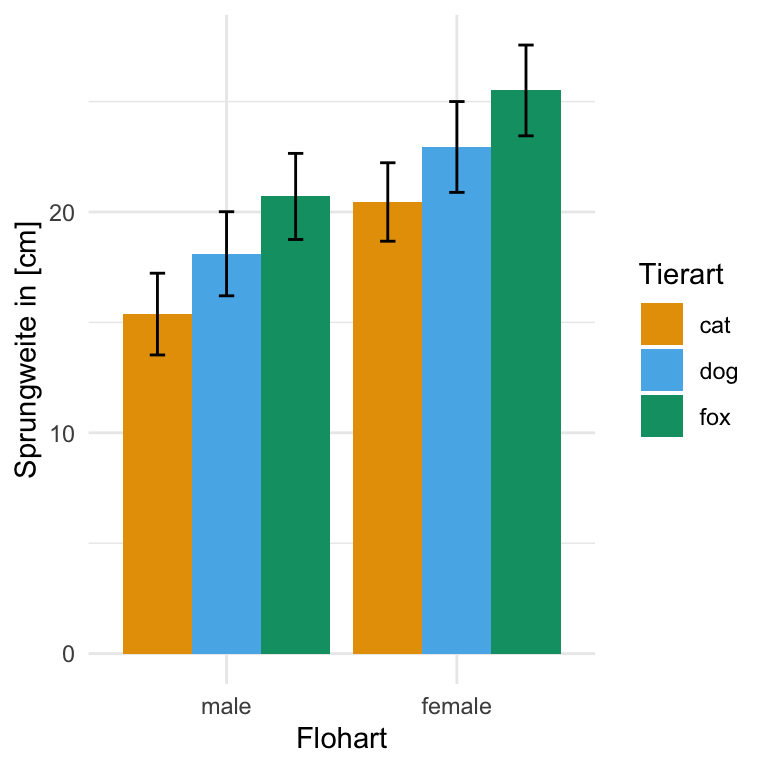
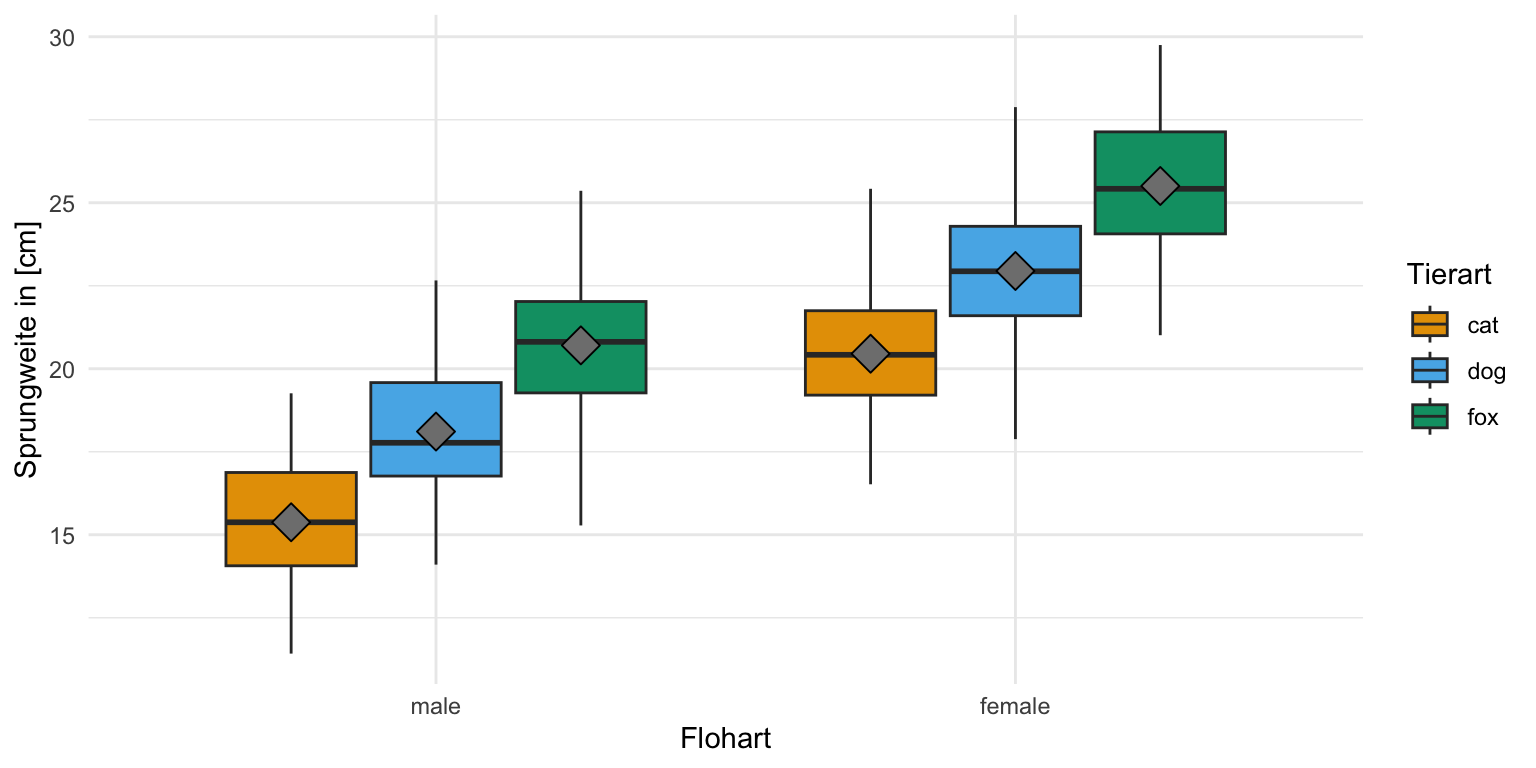
6 fox female 25.5 2.06Und dann können wir auch schon den zweifaktoriellen Barplot in {ggplot} erstellen. Du musst schauen, was du auf die x-Achse legst und was du dann auf die Legende und daher auch so gruppierst. Damit die Positionen passen, spiele ich hier noch mit der Funktion position_dodge() rum.
R Code [zeigen / verbergen]
ggplot(data = stat_fac2_tbl,
aes(x = sex, y = mean, fill = animal)) +
theme_minimal() +
geom_bar(stat = "identity", width = 0.9,
position = position_dodge(0.9)) +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2,
position = position_dodge(0.9)) +
labs(x = "Flohart", y = "Sprungweite in [cm]", fill = "Tierart") +
scale_fill_okabeito() Gestapelter Barplot
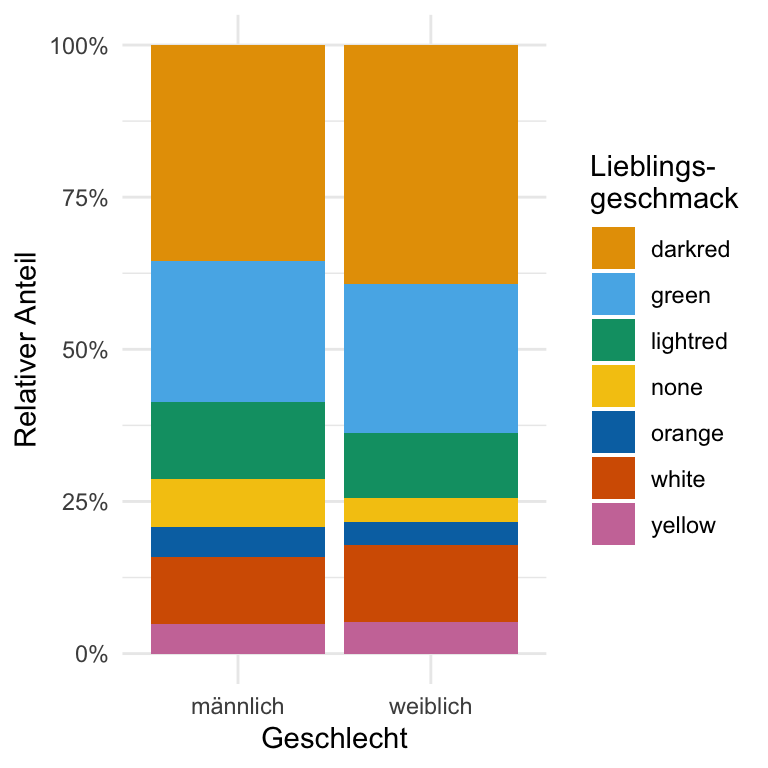
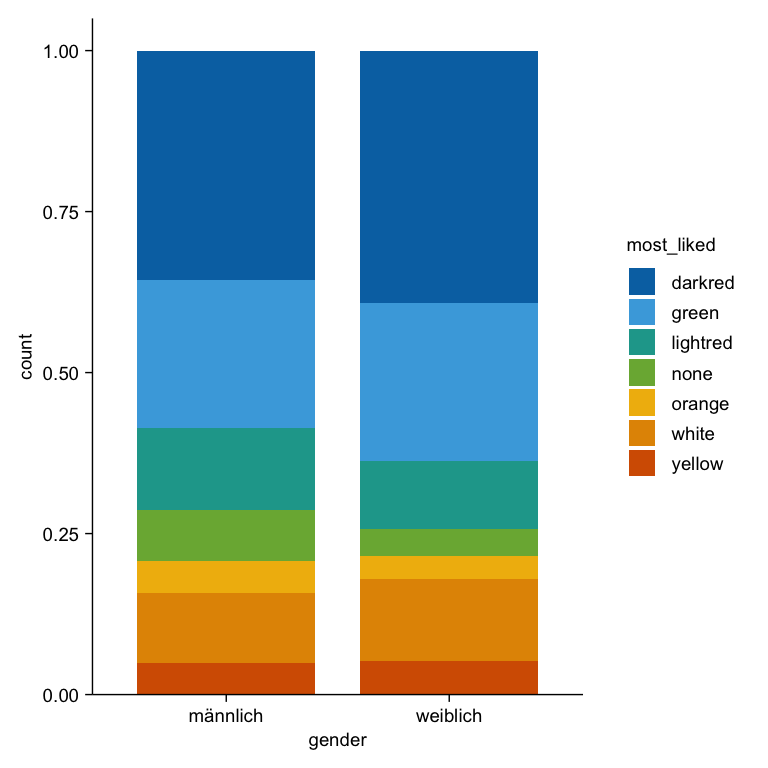
Dann auch nochmal hier ganz kurz der gestaüelte Barplot für die Auswertung von Kategorien wie eben den Lieblingsgeschmack. Ich habe dann noch die Prozente auf der y-Achse ergänzt und nochmal die Beschriftungen angepasst.
R Code [zeigen / verbergen]
gummi_tbl |>
ggplot(aes(x = gender, fill = most_liked)) +
geom_bar(position = "fill") +
theme_minimal() +
scale_y_continuous(labels = scales::percent) +
labs(x = "Geschlecht", y = "Relativer Anteil",
fill = "Lieblings-\ngeschmack") +
scale_fill_okabeito()Was mich überzeugt hat einmal das R Paket {tidyplots} vorzustellen, war dann die Verwendung für die Erstellung von Barplots. Ich finde den Weg in {ggplot} über die summarise() Funktion dann immer etwas umständlich. Ja, die Idee ist nicht schlecht, aber in {tidyplots} gibt es die Funktion add_mean_bar() was einfach das macht, was ich will. Und dann können wir auch einfach über die Funktion add_sd_errorbar() einen Fehlerbalken ergänzen. Mehr wollen wir ja auch nicht. Ich zeige jetzt gleich noch emhr, aber das hat den Grund, das wir ja auch die Abbildungen dann schöner haben wollen.
Einfaktorieller Barplot
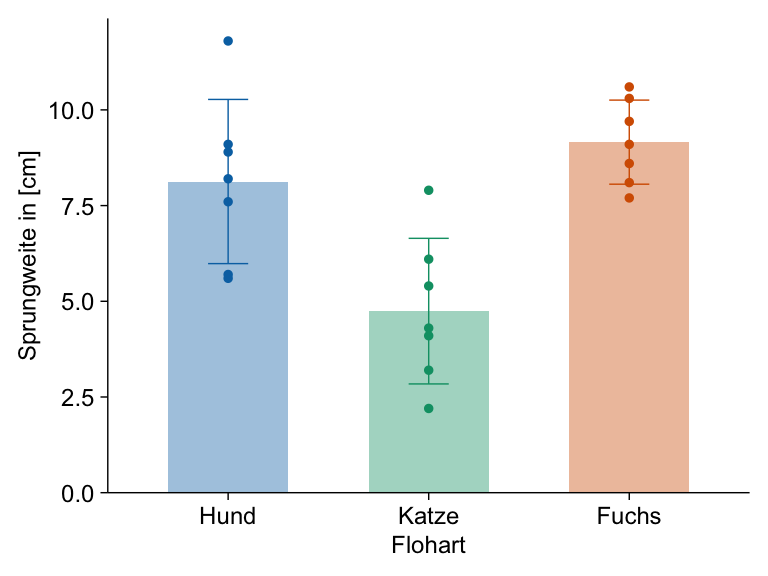
Der Code für die Erstellung wirkt etwas länger, das hat aber den Grund, dass ich noch einiges an Optionen ergänze. Ich möchte noch die Legende entfernen und dann noch die Variablen umbenennen. Dann kommt da immer was zusammen. Gerne lösche mal die ein oder andere Zeile um mehr zu verstehen was die Funktion macht. Viele Funktionen erklären sich ja vom Namen her von alleine. Die letzte Zeile mit adjust_size(width = NA, height = NA) brauche ich hier noch aktuell im meinem Skript und du kannst die weglassen oder eine andere Größe des Plots wählen.
R Code [zeigen / verbergen]
tidyplot(data = fac1_tbl,
x = animal, y = jump_length, color = animal) |>
add_data_points() |>
add_mean_bar(alpha = 0.4) |>
add_sd_errorbar(width = 0.2) |>
remove_legend() |>
adjust_font(fontsize = 9) |>
adjust_x_axis_title("Flohart") |>
adjust_y_axis_title("Sprungweite in [cm]") |>
rename_x_axis_labels(new_names = c("dog" = "Hund", "cat" = "Katze", "fox" = "Fuchs")) |>
adjust_size(width = NA, height = NA) |>
add_annotation_text(c("A", "B", "A"), fontsize = 12,
x = c(1.1, 2.1, 3.1), y = c(8.5, 5.1, 9.5))Zweifaktorieller Barplot
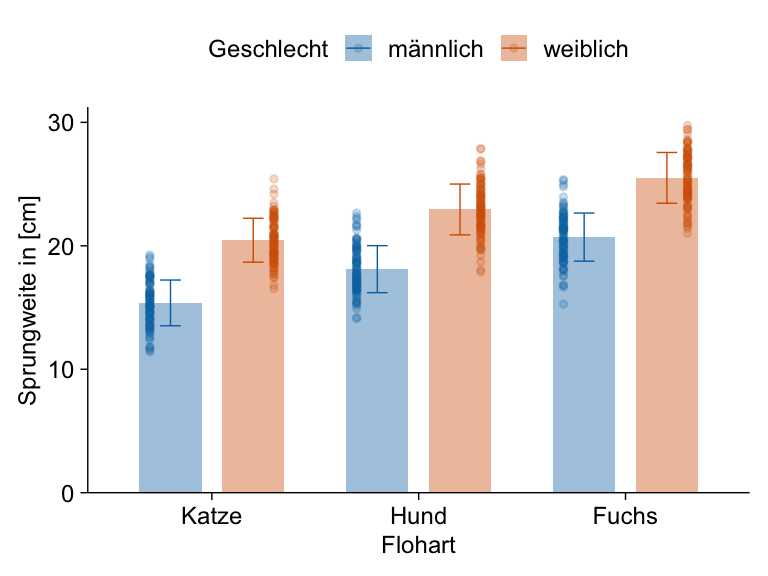
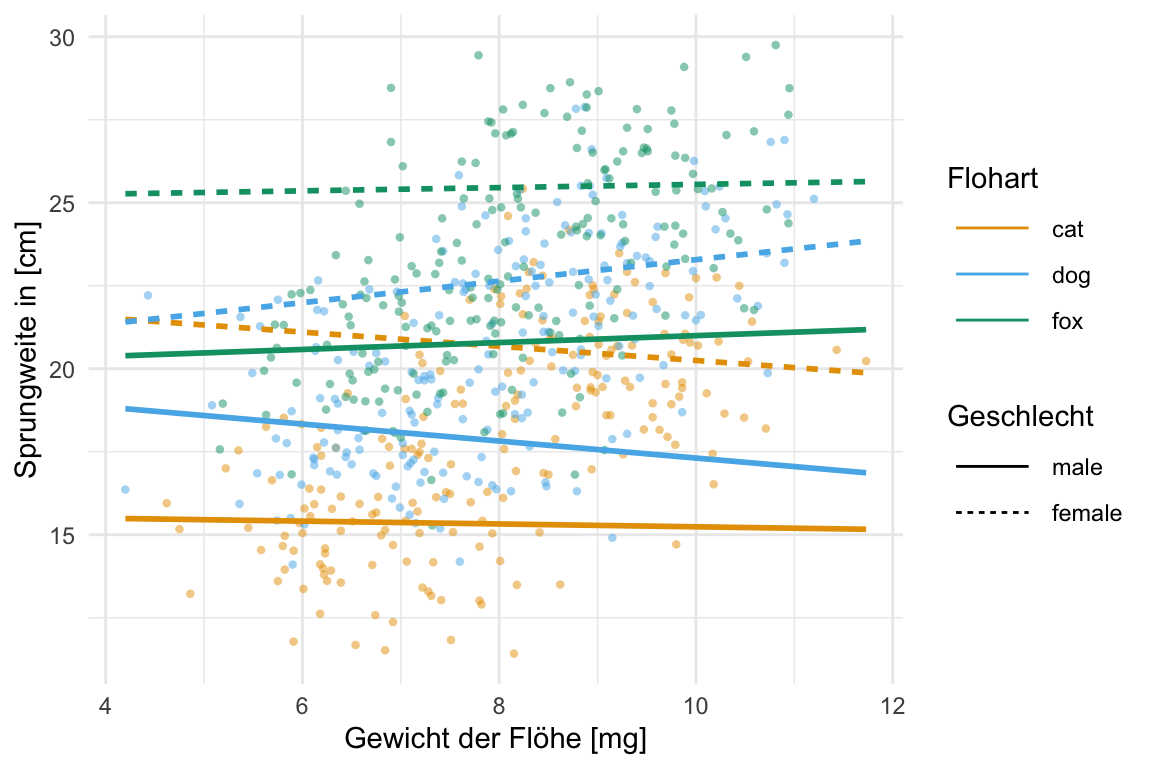
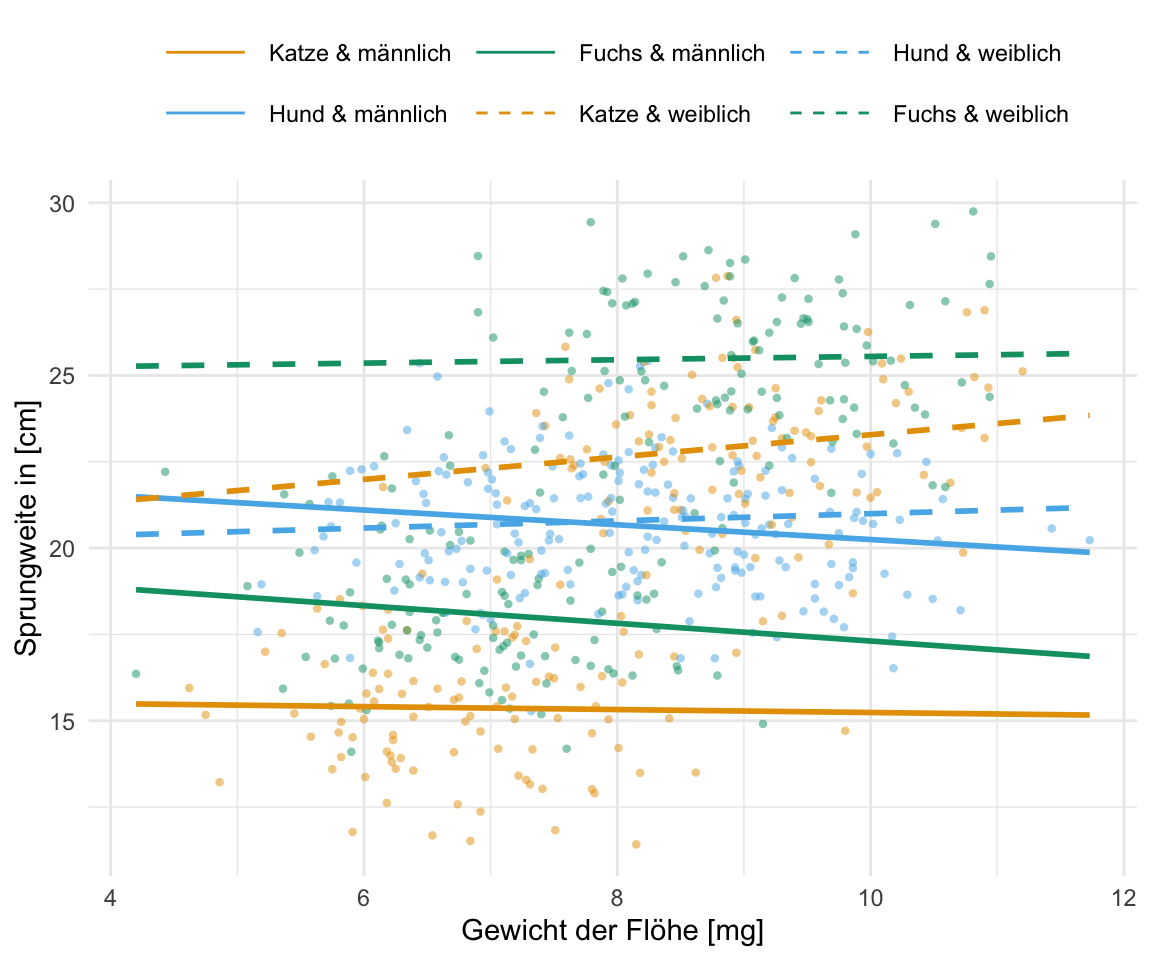
Bei dem zweifaktoriellen Barplot habe ich noch die Beobachtungen etwas aus der Mitte geschoben und dann noch etwas ausgeblendet. Dann habe ich noch die Legende nach oben verlegt und auch hier die Variablen einmal in dem Plot umbenannt. Die letzte Zeile mit adjust_size(width = NA, height = NA) brauche ich hier noch aktuell im meinem Skript und du kannst die weglassen oder eine andere Größe des Plots wählen.
R Code [zeigen / verbergen]
tidyplot(data = fac2_tbl,
x = animal, y = jump_length, color = sex) |>
add_data_points(alpha = 0.2, dodge_width = 1.2) |>
add_mean_bar(alpha = 0.4) |>
add_sd_errorbar(width = 0.2) |>
adjust_font(fontsize = 9) |>
adjust_x_axis_title("Flohart") |>
adjust_y_axis_title("Sprungweite in [cm]") |>
adjust_legend_title("Geschlecht") |>
adjust_legend_position("top") |>
rename_x_axis_labels(new_names = c("dog" = "Hund", "cat" = "Katze", "fox" = "Fuchs")) |>
rename_color_labels(new_names = c("male" = "männlich", "female" = "weiblich")) |>
adjust_size(width = NA, height = NA) |>
add_annotation_text(c("A", "B", "A", "A", "B", "A"), fontsize = 12,
x = c(0.8, 1.2, 1.8, 2.2, 2.8, 3.2),
y = c(19, 24, 22, 27, 24, 29))Gestapelter Barplot
Dann auch nochmal hier ganz kurz der gestaüelte Barplot für die Auswertung von Kategorien wie eben den Lieblingsgeschmack. Ich habe dann noch die Prozente auf der y-Achse ergänzt und nochmal die Beschriftungen angepasst.
R Code [zeigen / verbergen]
gummi_tbl |>
tidyplot(x = gender, color = most_liked) |>
add_barstack_relative() |>
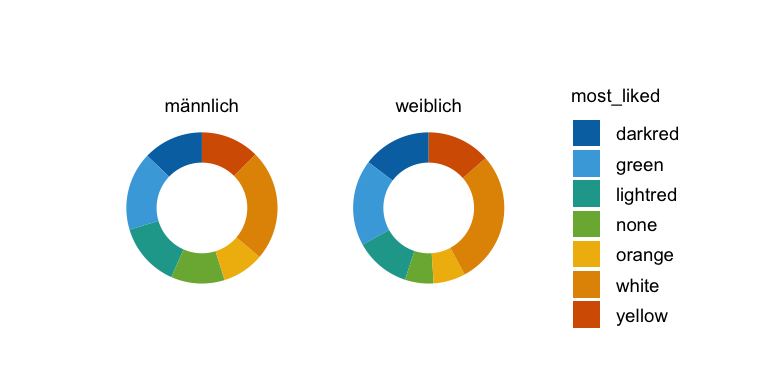
adjust_size(width = NA, height = NA)Dann auch hier einmal zur Vollständigkeit der Donutplot aufgeteilt nach dem Geschlecht.
R Code [zeigen / verbergen]
gummi_tbl |>
tidyplot(y = most_liked, color = most_liked) |>
add_donut() |>
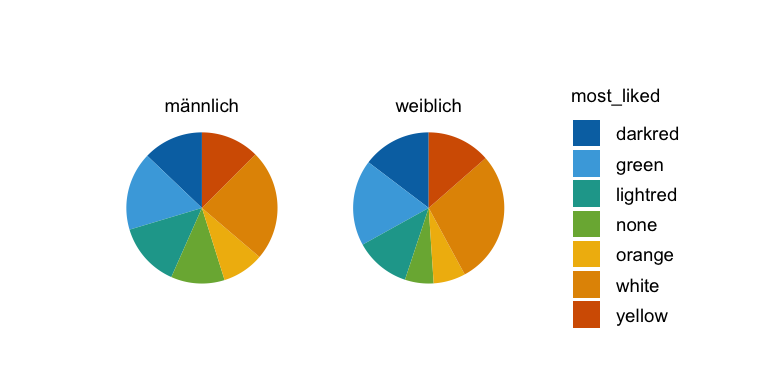
split_plot(by = gender)Weil dann danach gefragt wurde, auch hier einmal das schnelle Kuchendiagramm für die Lieblingsgeschmäcker.
Dann habe ich mich doch noch hingesetzt und einmal für dich die Videos gemacht, wie du dann einen Barplot oder eben ein Säulendigramm in Excel erstellst. Das ganze macht dann nur als Video Sinn, denn sonst kannst du ja nicht nachvollziehen, was ich geklickt habe.
Hier also erstmal die einfachere Variante mit dem 1-faktoriellen Barplot. Beginnen wollen wir wie immer mit der Berechnung der Mittelwerte und der Standardabweichung. Bitte nutze für die Standardabweichung die Funktion STABW.S() in Excel.
Und im Anschluss nochmal das Video für den 2-faktoriellen Barplot. Du hast jetzt eben nicht nur eine Behandlungsgruppe vorliegen sondern zwei Behandlungsgruppen. Dann musst du etwas mehr Arbeit reinstecken um alle Mittelwerte und Standardabweichungen zu berechnen. Bitte nutze auch hier für die Standardabweichung die Funktion STABW.S() in Excel.
Bei der Darstellung des Barplots haben wir die Wahl wie wir den Fehlerbalken darstellen. Dazu haben wir dann verschiedene Maßzahlen zu Auswahl. Theoretisch haben wir die freie Wahl zwischen der Standardabweichung und dem Standardfehler, aber es gibt Ausnahmen.
- Standardabweichung (abk. SD) oder Standardfehler (abk. SE) als Fehlerbalken?
-
Wenn du etwas misst, was natürliche numerische Grenzen hat, wie zum Beispiel relative Anteile \([0,1]\) oder aber etwas zählst \([0, \infty]\), dann empfiehlt sich der Standardfehler, da dieser nicht über die numerischen Grenzen geht. Die Standardabweichung kann hier negative Werte oder aber prozentuale Werte größer 1 oder kleiner 0 liefern. Das wollen wir nicht.
Schau dir auch hier mal in den Kästen zum Zerforschen rein, da findest du dann noch mehr Inspiration aus anderen Abbildungen, die ich nachgebaut habe. Ich bin einmal über den Campus gelaufen und habe geschaut, welche Abbildungen auf den Postern verwendet werden und habe diese nachgebaut.
In diesem Zerforschenbeispiel wollen wir uns einen einfaktoriellen Barplot oder Säulendiagramm anschauen. Daher fangen wir mit der folgenden Abbildung einmal an. Wir haben hier ein Säulendiagramm mit Compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Behandlungen jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung. Die Standardabweichung addieren und subtrahieren wir dann jeweils von dem Mittelwert und schon haben wir die Fehlerbalken.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_simple.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die vier Werte alle um den Mittelwert streuen lassen. Dabei habe ich darauf geachtet, dass die Streuung dann in der letzten Behandlung am größten ist. Da wir beim Einlesen keine Umlaute oder sonstige Leerzeichen wollen, habe ich alles sehr simple aufgeschrieben und dann in R in der Funktion factor() richtig über die Option levels sortiert und über die Option labels sauber beschrieben. Dann passt auch die Sortierung der \(x\)-Achse.
R Code [zeigen / verbergen]
barplot_tbl <- read_excel("data/zerforschen_barplot_simple.xlsx") |>
mutate(trt = factor(trt,
levels = c("water", "rqflex",
"nitra", "laqua"),
labels = c("Wasserdestilation",
"RQflex Nitra",
"Nitrachek",
"Laqua Nitrat")))
barplot_tbl # A tibble: 16 × 2
trt nitrat
<fct> <dbl>
1 Wasserdestilation 135
2 Wasserdestilation 130
3 Wasserdestilation 145
4 Wasserdestilation 135
5 RQflex Nitra 120
6 RQflex Nitra 130
7 RQflex Nitra 135
8 RQflex Nitra 135
9 Nitrachek 100
10 Nitrachek 120
11 Nitrachek 130
12 Nitrachek 130
13 Laqua Nitrat 230
14 Laqua Nitrat 210
15 Laqua Nitrat 205
16 Laqua Nitrat 220Jetzt brauchen wir noch die Mittelwerte und die Standardabweichung für jede der vier Behandlungen. Den Code kennst du schon von oben wo wir die Barplots für die Sprungweiten der Hunde- und Katzenflöhe gebaut haben. Hier habe ich dann den Code entsprechen der Daten barplot_tbl angepasst. Wir haben ja als Gruppierungsvariabel trt vorliegen und wollen die Mittelwerte und die Standardabweichung für die Variable nitrat berechnen.
R Code [zeigen / verbergen]
stat_tbl <- barplot_tbl |>
group_by(trt) |>
summarise(mean = mean(nitrat),
sd = sd(nitrat))
stat_tbl# A tibble: 4 × 3
trt mean sd
<fct> <dbl> <dbl>
1 Wasserdestilation 136. 6.29
2 RQflex Nitra 130 7.07
3 Nitrachek 120 14.1
4 Laqua Nitrat 216. 11.1 Und dann haben wir auch schon die Abbildung 18.18 erstellt. Ja vielleicht passen die Standardabweichungen nicht so richtig, da könnte man nochmal an den Daten spielen und die Werte solange ändern, bis es besser passt. Du hast aber jetzt eine Idee, wie der Aufbau funktioniert.
R Code [zeigen / verbergen]
ggplot(data = stat_tbl, aes(x = trt, y = mean,
fill = trt)) +
theme_minimal() +
geom_bar(stat = "identity") +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2) +
labs(x = "",
y = "Nitrat-Konzentration \n im Tannensaft [mg/L]") +
ylim(0, 250) +
theme(legend.position = "none") +
scale_fill_okabeito() +
annotate("text",
x = c(1.05, 2.05, 3.05, 4.05),
y = stat_tbl$mean + stat_tbl$sd + 8,
label = c("b", "b", "a", "c"))- 1
- Hier werden die Säulen des Säulendiagramms erstellt.
- 2
-
Hier werden die Fehlerbalken erstellt. Die Option
widthsteuert wie breit die Fehlerbalken sind. - 3
- Hier wird eine Farbpalette für farbblinde Personen geladen.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
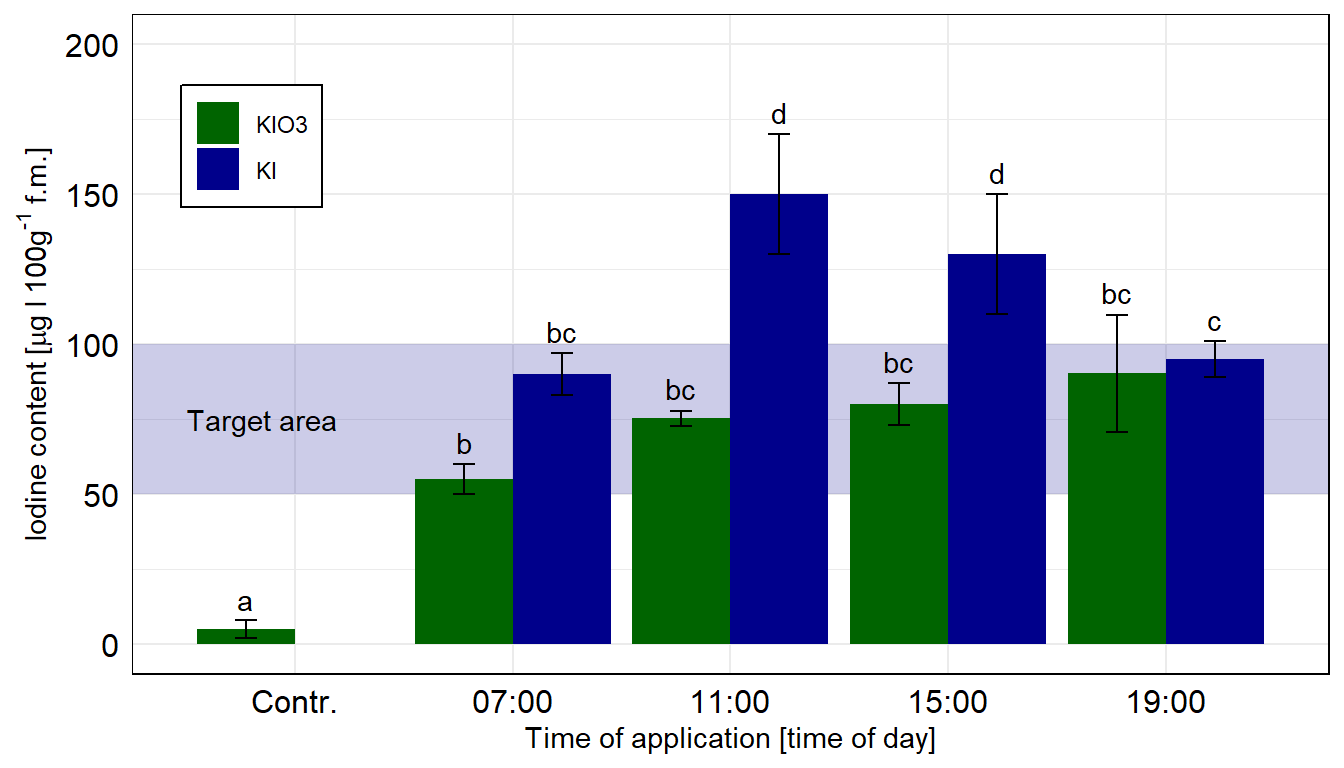
ggsave("my_ggplot_barplot.png", width = 5, height = 3)In diesem Zerforschenbeispiel wollen wir uns einen zweifaktoriellen Barplot oder Säulendiagramm anschauen. Wir haben hier ein Säulendiagramm mit compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Zeitpunkte und der Kontrolle jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung. Die Standardabweichung addieren und subtrahieren wir dann jeweils von dem Mittelwert und schon haben wir die Fehlerbalken.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_2fac_target.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die drei Werte alle um den Mittelwert streuen lassen. Da wir beim Einlesen keine Umlaute oder sonstige Leerzeichen wollen, habe ich alles sehr simple aufgeschrieben und dann in R in der Funktion factor() richtig über die Option levels sortiert und über die Option labels sauber beschrieben. Dann passt auch die Sortierung der \(x\)-Achse.
R Code [zeigen / verbergen]
barplot_tbl <- read_excel("data/zerforschen_barplot_2fac_target.xlsx") |>
mutate(time = factor(time,
levels = c("ctrl", "7", "11", "15", "19"),
labels = c("Contr.", "07:00", "11:00", "15:00", "19:00")),
type = as_factor(type))
barplot_tbl # A tibble: 27 × 3
time type iodine
<fct> <fct> <dbl>
1 07:00 KIO3 50
2 07:00 KIO3 55
3 07:00 KIO3 60
4 07:00 KI 97
5 07:00 KI 90
6 07:00 KI 83
7 11:00 KIO3 73
8 11:00 KIO3 75
9 11:00 KIO3 78
10 11:00 KI 130
# ℹ 17 more rowsJetzt brauchen wir noch die Mittelwerte und die Standardabweichung für jede der vier Behandlungen. Hier nur kurz, den Code kennst du schon aus anderen Zerforschenbeispielen zu den Barplots.
R Code [zeigen / verbergen]
stat_tbl <- barplot_tbl |>
group_by(time, type) |>
summarise(mean = mean(iodine),
sd = sd(iodine))
stat_tbl# A tibble: 9 × 4
# Groups: time [5]
time type mean sd
<fct> <fct> <dbl> <dbl>
1 Contr. KIO3 5 3
2 07:00 KIO3 55 5
3 07:00 KI 90 7
4 11:00 KIO3 75.3 2.52
5 11:00 KI 150 20
6 15:00 KIO3 80 7
7 15:00 KI 130 20
8 19:00 KIO3 90.3 19.5
9 19:00 KI 95 6 Und dann geht es auch schon los. Wir müssen am Anfang einmal scale_x_discrete() setzen, damit wir gleich den Zielbereich ganz hinten zeichnen können. Sonst ist der blaue Bereich im Vordergrund. Dann färben wir auch mal die Balken anders ein. Muss ja auch mal sein. Auch nutzen wir die Funktion geom_text() um das compact letter display gut zu setzten. Die \(y\)-Position berechnet sich aus dem Mittelwert plus Standardabweichung innerhalb des geom_text(). Leider haben wir nur einen Balken bei der Kontrolle, deshalb hier nachträglich der Buchstabe mit annotate(). Ich habe mich dann noch entschieden neben dem Barplot noch den Boxplot als Alternative zu erstellen.
Einmal der Barplot wie beschrieben. Am besten löscht du immer mal wieder eine Zeile Code damit du nachvollziehen kannst, was die Zeile Code in der Abbildung macht. Vergleiche auch einmal diese Abbildung der Barplots mit der Abbildung der Boxplots und überlege, welche der beiden Abbildungen dir mehr Informationen liefert.
R Code [zeigen / verbergen]
ggplot(data = stat_tbl, aes(x = time, y = mean,
fill = type)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0.25, xmax = 5.75, ymin = 50, ymax = 100,
alpha = 0.2, fill = "darkblue") +
annotate("text", x = 0.5, y = 75, hjust = "left", label = "Target area") +
geom_bar(stat = "identity",
position = position_dodge(width = 0.9, preserve = "single")) +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2,
position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_manual(name = "Type", values = c("darkgreen", "darkblue")) +
theme(legend.position = c(0.1, 0.8),
legend.title = element_blank(),
legend.spacing.y = unit(0, "mm"),
panel.border = element_rect(colour = "black", fill=NA),
axis.text = element_text(colour = 1, size = 12),
legend.background = element_blank(),
legend.box.background = element_rect(colour = "black")) +
labs(x = "Time of application [time of day]",
y = expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +
scale_y_continuous(breaks = c(0, 50, 100, 150, 200),
limits = c(0, 200)) +
geom_text(aes(label = c("", "b", "bc", "bc", "d", "bc", "d", "bc", "c"),
y = mean + sd + 2),
position = position_dodge(width = 0.9), vjust = -0.25) +
annotate("text", x = 0.77, y = 15, label = "a") Für die Boxplost brauchen wir dann noch ein Objekt mehr. Um das compacte letter dislay an die richtige Position zu setzen brauchen wir noch eine \(y\)-Position. Ich nehme hier dann das 90% Quantile. Das 90% Quantile sollte dann auf jeden Fall über die Schnurrhaare raus reichen. Wir nutzen dann den Datensatz letter_pos_tbl in dem geom_text() um die Buchstaben richtig zu setzen.
R Code [zeigen / verbergen]
letter_pos_tbl <- barplot_tbl |>
group_by(time, type) |>
summarise(quant_90 = quantile(iodine, probs = c(0.90)))
letter_pos_tbl# A tibble: 9 × 3
# Groups: time [5]
time type quant_90
<fct> <fct> <dbl>
1 Contr. KIO3 7.4
2 07:00 KIO3 59
3 07:00 KI 95.6
4 11:00 KIO3 77.4
5 11:00 KI 166
6 15:00 KIO3 85.6
7 15:00 KI 146
8 19:00 KIO3 106
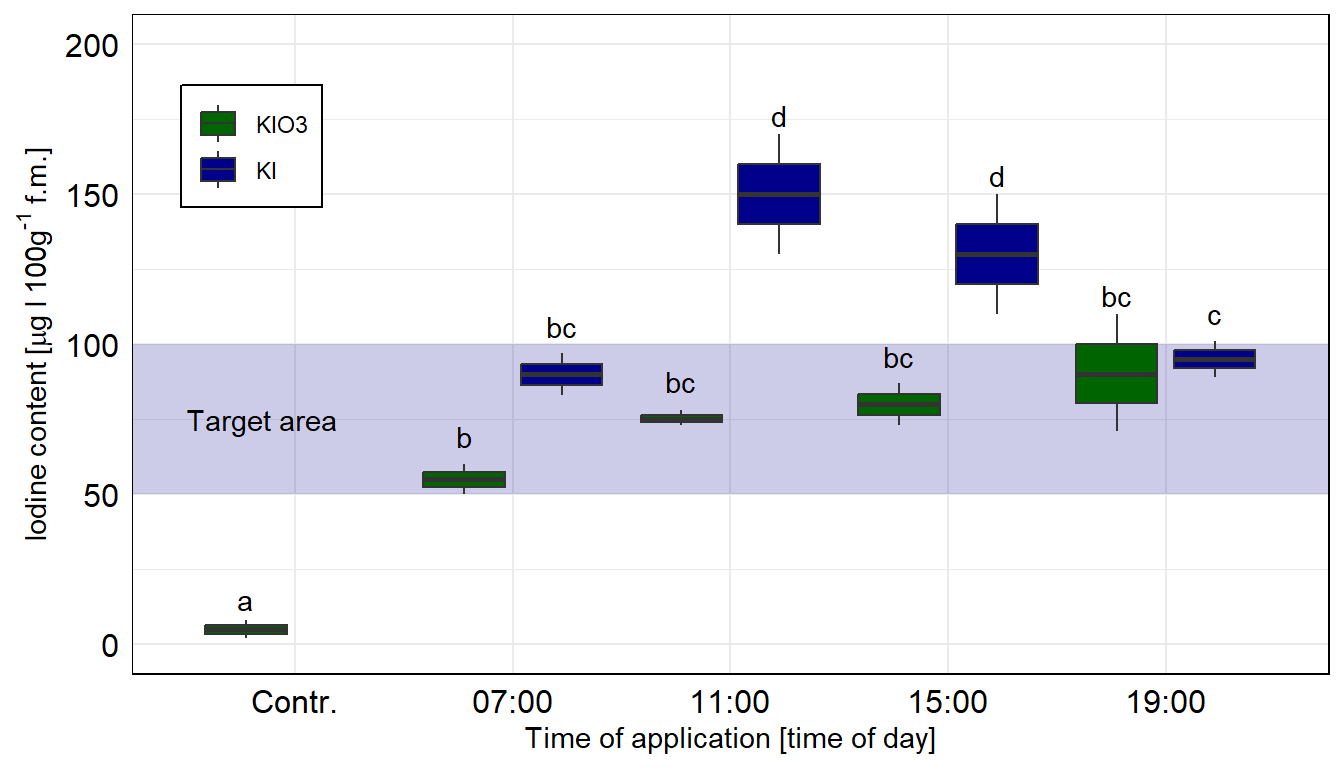
9 19:00 KI 99.8Und dann müssen wir nur noch das geom_bar() und geom_errorbar() entfernen und durch das geom_boxplot() ersetzen. Dann haben wir auch schon unsere wunderbaren Boxplots. Das Problem sind natürlich die wenigen Beobachtungen, deshalb sehen die Boxplots teilweise etwas wild aus. Beachte auch das wir die Orginaldaten nutzen und nicht die zusammengefassten Daten.
R Code [zeigen / verbergen]
ggplot(data = barplot_tbl, aes(x = time, y = iodine,
fill = type)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0.25, xmax = 5.75, ymin = 50, ymax = 100,
alpha = 0.2, fill = "darkblue") +
annotate("text", x = 0.5, y = 75, hjust = "left", label = "Target area") +
geom_boxplot(position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_manual(name = "Type", values = c("darkgreen", "darkblue")) +
theme(legend.position = c(0.1, 0.8),
legend.title = element_blank(),
legend.spacing.y = unit(0, "mm"),
panel.border = element_rect(colour = "black", fill=NA),
axis.text = element_text(colour = 1, size = 12),
legend.background = element_blank(),
legend.box.background = element_rect(colour = "black")) +
labs(x = "Time of application [time of day]",
y = expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +
scale_y_continuous(breaks = c(0, 50, 100, 150, 200),
limits = c(0, 200)) +
geom_text(data = letter_pos_tbl,
aes(label = c("", "b", "bc", "bc", "d", "bc", "d", "bc", "c"),
y = quant_90 + 5),
position = position_dodge(width = 0.9), vjust = -0.25) +
annotate("text", x = 0.77, y = 15, label = "a") Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
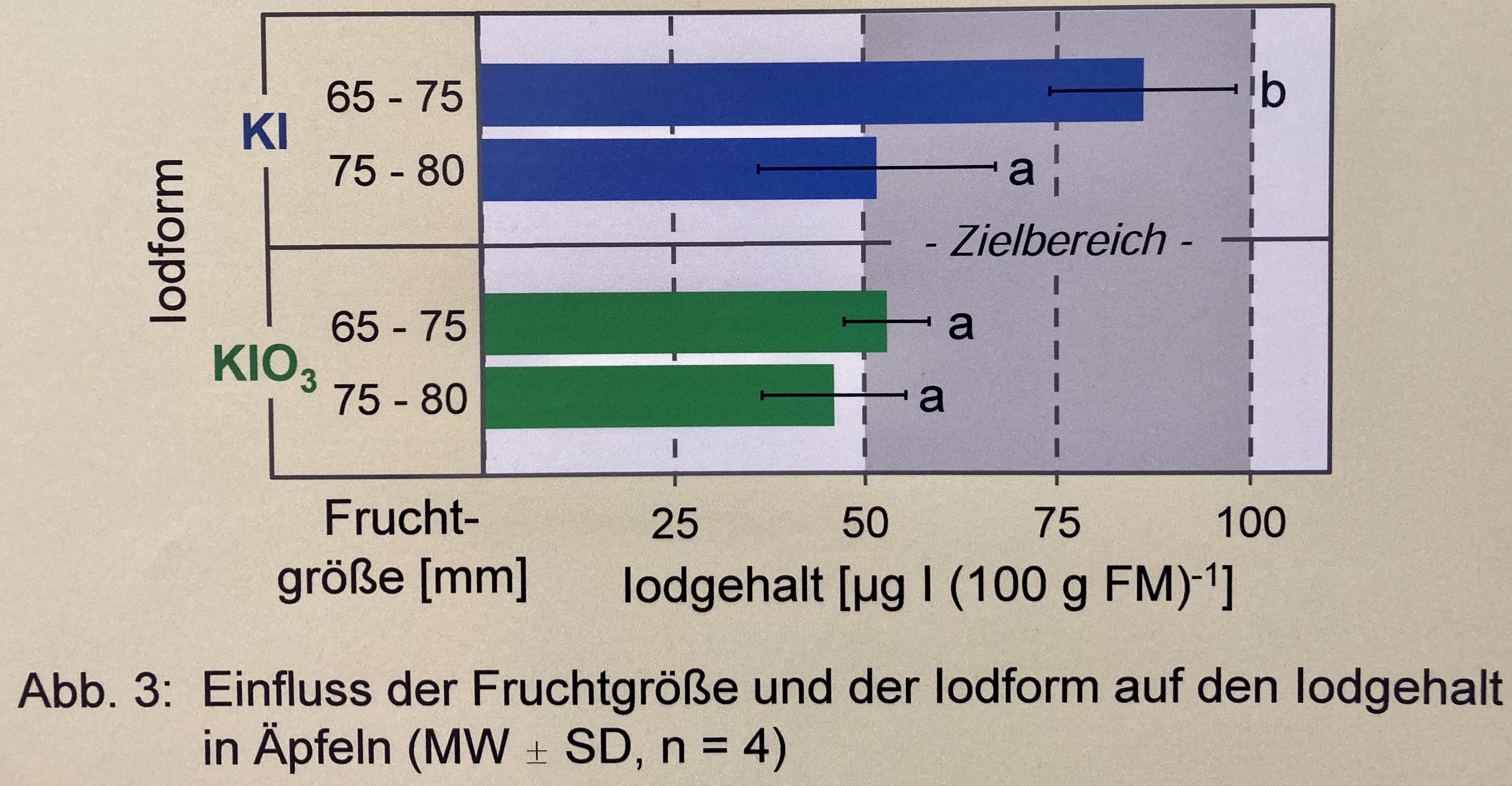
ggsave("my_ggplot_barplot.png", width = 5, height = 3)In diesem Zerforschenbeispiel wollen wir uns einen zweifaktoriellen Barplot oder Balkendiagramm anschauen. Wir haben hier ein echtes Balkendiagramm mit compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Zeitpunkte und der Kontrolle jeweils einmal einen Mittelwert für die Länge des Balkens sowie einmal die Standardabweichung. Die Standardabweichung addieren und subtrahieren wir dann jeweils von dem Mittelwert und schon haben wir die Fehlerbalken. Ich habe hier dann jeweils drei Werte für jede Faktorkombination. Die brauche ich dann auch, weil ich später nochmal vergleichend den Boxplot erstellen möchte. Der macht meiner Ansicht nach hier mehr Sinn.
Als erstes brauchen wir wieder die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_2fac.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die drei Werte alle um den Mittelwert streuen lassen. Das war es dann auch schon.
R Code [zeigen / verbergen]
barplot_tbl <- read_excel("data/zerforschen_barplot_2fac_flipped.xlsx") |>
mutate(iod = fct_rev(iod),
fruit = fct_rev(fruit))
barplot_tbl# A tibble: 12 × 3
iod fruit iod_yield
<fct> <fct> <dbl>
1 KI 65-75 85
2 KI 65-75 100
3 KI 65-75 75
4 KI 75-80 52
5 KI 75-80 70
6 KI 75-80 30
7 KIO3 65-75 55
8 KIO3 65-75 48
9 KIO3 65-75 60
10 KIO3 75-80 45
11 KIO3 75-80 53
12 KIO3 75-80 38Jetzt brauchen wir noch die Mittelwerte und die Standardabweichung für jede der vier Behandlungen. Hier nur kurz, den Code kennst du schon aus anderen Zerforschenbeispielen zu den Barplots.
R Code [zeigen / verbergen]
stat_tbl <- barplot_tbl |>
group_by(iod, fruit) |>
summarise(mean = mean(iod_yield),
sd = sd(iod_yield))
stat_tbl# A tibble: 4 × 4
# Groups: iod [2]
iod fruit mean sd
<fct> <fct> <dbl> <dbl>
1 KIO3 75-80 45.3 7.51
2 KIO3 65-75 54.3 6.03
3 KI 75-80 50.7 20.0
4 KI 65-75 86.7 12.6 Im Folgenden stelle ich die zusammengefassten Daten stat_tbl als Balkendiagramm dar. Die ursprünglichen Daten barplot_tbl kann ich nutzen um die Boxplots zu erstellen. Hier ist wichtig nochmal zu erinnern, das wir Barplots auf dem Mittelwert und der Standardabweichung darstellen und die Boxplots auf den Originaldaten. Mit der unteren Grenze machen Boxplots mehr Sinn, wenn du wissen willst, ob du einen Zielbereich vollkommen erreicht hast.
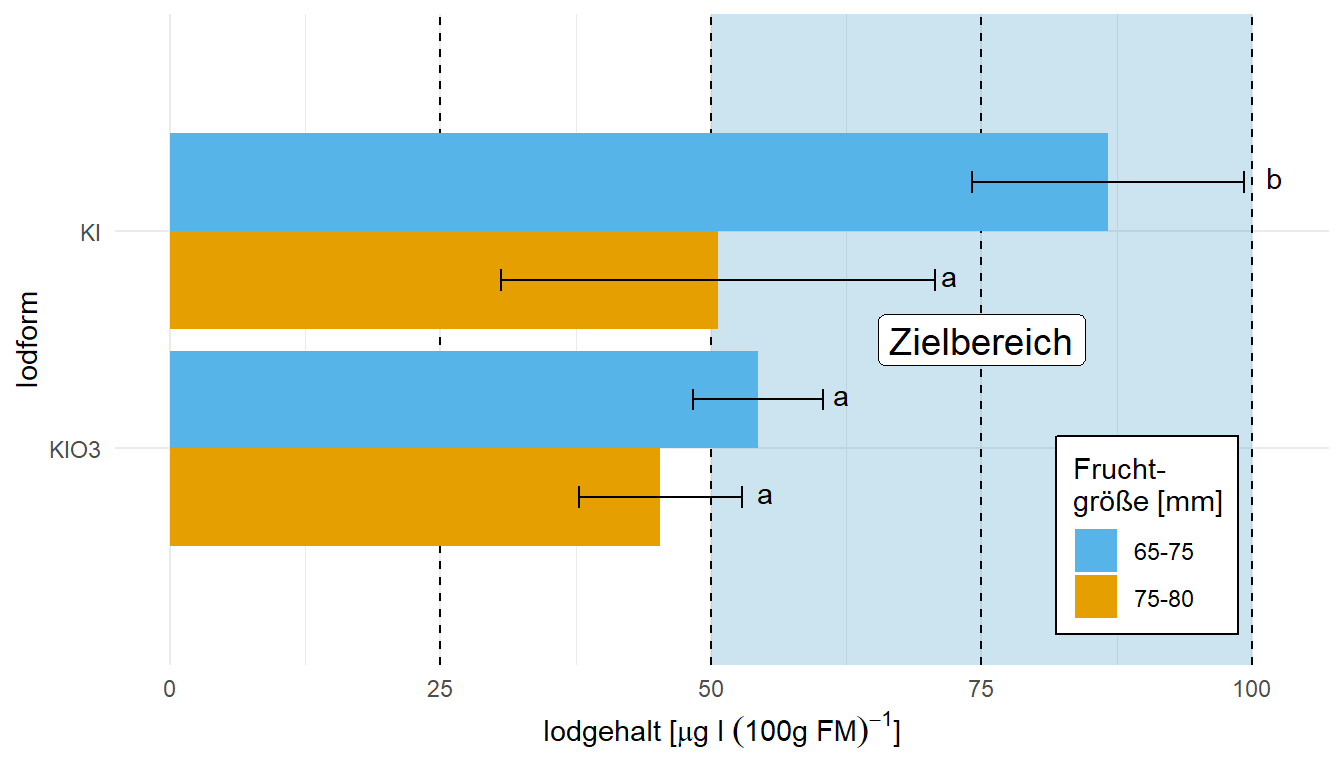
Zuerst einmal der Barplot, wie wir ihn auch schon oben in der Abbildung sehen. Wir nutzen hier zum einen die Funktion coord_flip() um ganz zum Schluss die Abbildung zu drehen. Deshalb musst du aufpassen, denn vor dem Flippen ist ja alles auf der \(y\)-Achse die \(y\)-Achse und umgekehrt. Deshalb müssen wir dann auch teilweise die Ordnung der Level in den einzelnen Faktoren drehen, damit wir wieder die richtige Reihenfolge nach dem Flip haben. Wir müssen ganz am Anfang einmal scale_x_discrete() setzen, damit wir den Zielbereich als erstes einzeichnen können. Sonst ist der Zielbereich nicht ganz hinten in der Abbildung und überdeckt die Balken. Deshalb ist das Wort “Zielbereich” auch recht weit hinten im Code, damit es eben im Vordergrund ist. Sonst ist eigentlich vieles gleich. Wir nutzen hier einmal das R Paket latex2exp für die Erstellung der mathematischen Formeln.
R Code [zeigen / verbergen]
ggplot(data = stat_tbl, aes(x = iod, y = mean,
fill = fruit)) +
theme_minimal() +
scale_x_discrete() +
annotate("rect", xmin = 0, xmax = 3, ymin = 50, ymax = 100,
alpha = 0.2, fill = cbbPalette[6]) +
geom_hline(yintercept = c(25, 50, 75, 100), linetype = "dashed") +
geom_bar(stat = "identity", position = position_dodge(0.9)) +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2, position = position_dodge(0.9)) +
labs(x = "Iodform",
y =TeX(r"(Iodgehalt $[\mu g\, l\, (100g\, FM)^{-1}]$)")) +
scale_fill_okabeito(name = "Frucht-\ngröße [mm]", breaks=c('65-75', '75-80')) +
theme(legend.position = c(0.85, 0.2),
legend.box.background = element_rect(color = "black"),
legend.box.margin = margin(t = 1, l = 1),
legend.text.align = 0) +
annotate("label", x = 1.5, y = 75, label = "Zielbereich", size = 5) +
annotate("text", x = c(0.8, 1.25, 1.8, 2.25), y = c(55, 62, 72, 102),
label = c("a", "a", "a", "b")) +
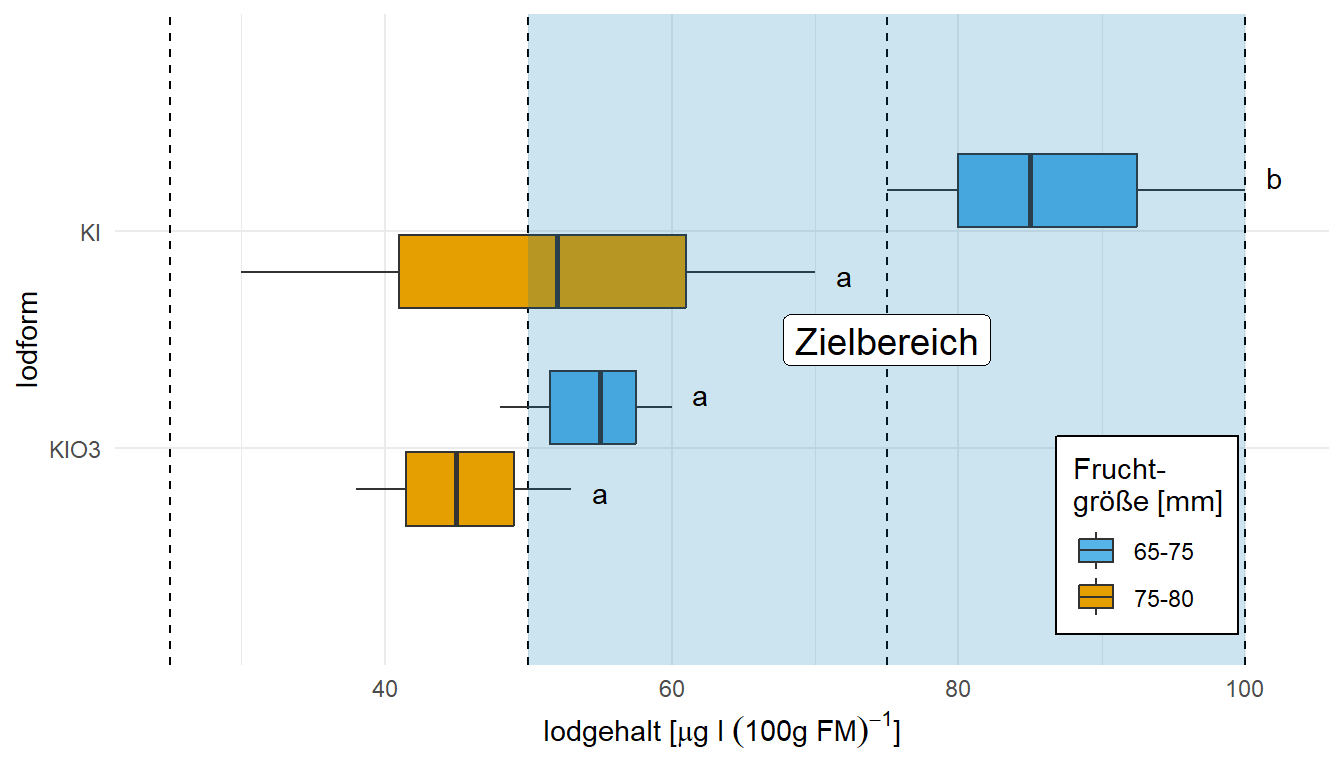
coord_flip() Für die Boxplots müssen wir gar nicht viel tun. Wir müssen nur noch das geom_bar() und geom_errorbar() entfernen und durch das geom_boxplot() ersetzen. Dann haben wir auch schon unsere wunderbaren Boxplots. Das Problem sind natürlich die wenigen Beobachtungen, deshalb sehen die Boxplots teilweise etwas wild aus. Beachte auch das wir die Orginaldaten nutzen und nicht die zusammengefassten Daten. Am Ende machen Boxplots mit einer unteren Grenze mehr Sinn, wenn wir uns Fragen, ob wir einen Zielbereich erreicht haben. Da sind dann doch Balkendiagramme etwas ungeeignet.
R Code [zeigen / verbergen]
ggplot(data = barplot_tbl, aes(x = iod, y = iod_yield,
fill = fruit)) +
theme_minimal() +
geom_hline(yintercept = c(25, 50, 75, 100), linetype = "dashed") +
geom_boxplot() +
labs(x = "Iodform",
y =TeX(r"(Iodgehalt $[\mu g\, l\, (100g\, FM)^{-1}]$)")) +
scale_fill_okabeito(name = "Frucht-\ngröße [mm]", breaks=c('65-75', '75-80')) +
theme(legend.position = c(0.85, 0.2),
legend.box.background = element_rect(color = "black"),
legend.box.margin = margin(t = 1, l = 1),
legend.text.align = 0) +
annotate("rect", xmin = 0, xmax = 3, ymin = 50, ymax = 100,
alpha = 0.2, fill = cbbPalette[6]) +
annotate("label", x = 1.5, y = 75, label = "Zielbereich", size = 5) +
annotate("text", x = c(0.8, 1.25, 1.8, 2.25), y = c(55, 62, 72, 102),
label = c("a", "a", "a", "b")) +
coord_flip() 18.4.2 Boxplot
Mit dem Boxplot können wir den Median und die Quartile visualisieren. Im Folgenden unterscheide ich dann einmal die theoretische Betrachtung des Boxplots sowie die händische Darstellung für unsere Flohdaten als Beispiel. Dann implementieren wir den Boxplot für die Sprungweiten der Hunde- und Katzenflöhe noch einmal abschließend in {ggplot}. Im Folgenden siehst du im ersten Tab einen Boxplot, der den Median und die Quartile eines beliebigen Datensatzes visualisiert.
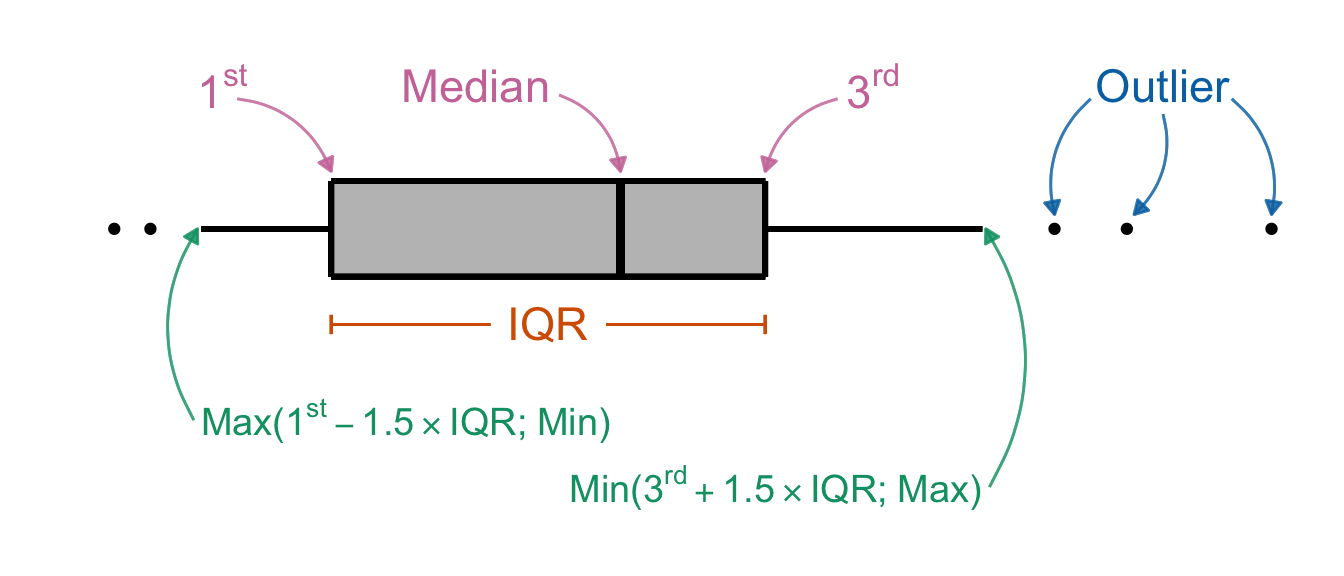
Die Box wird aus dem Interquartilesabstand (abk . IQR) gebildet. Der Median wird als Strich in der Box gezeigt. Die Schnurrhaare (eng. Whiskers) sind das 1.5-fache des IQR, wenn nicht das Minimum der Beobachtungen oder das Maximum jeweils größer oder kleiner ist. Punkte die außerhalb der Whiskers liegen werden als einzelne Punkte dargestellt. Diese einzelnen Punkte werden auch als Ausreißer (eng. Outlier) bezeichnet. Ob es sich nun wirklich um Ausreißer handelt, muss biologisch geklärt werden.
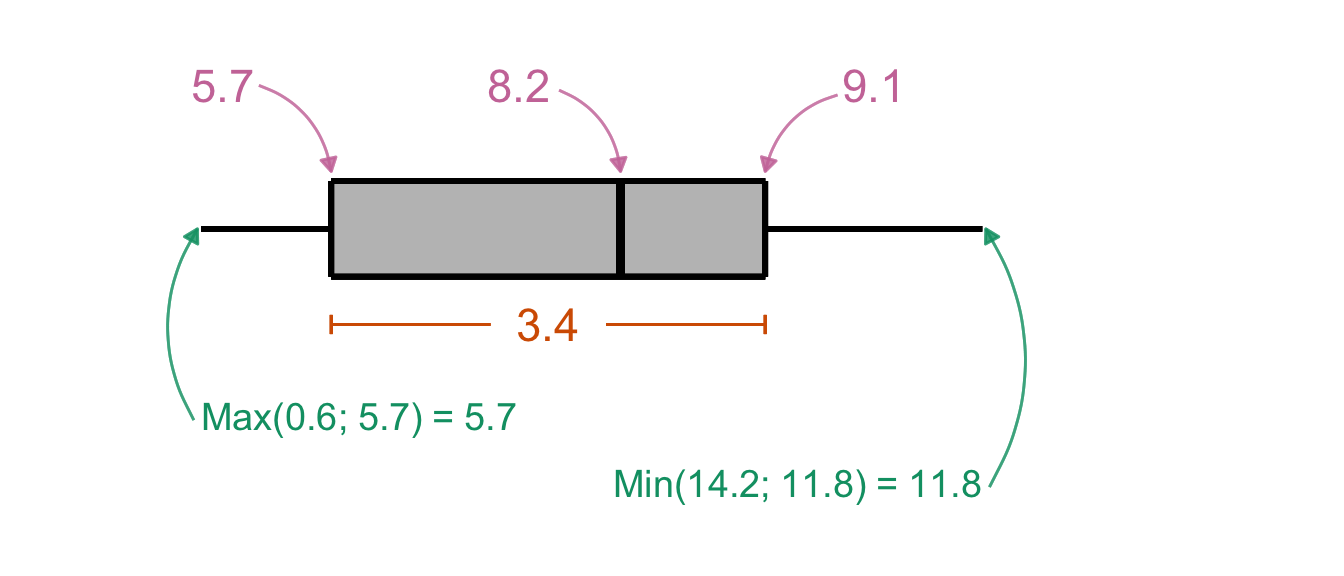
Jetzt können wir einmal händisch den Boxplot für die Hundeflöhe und der Sprungweite zeichnen. Ich habe dafür dann einmal die Werte für das \(1^{st}\) und \(3^{rd}\) Quartile mit jeweils 5.7 und 9.1 bestimmt. Der Median der Sprungweite der Hundeflöhe liegt bei 8.2 und der Interquartilesabstand (abk . IQR) ist 3.4, wie du in der nicht maßstabsgetreuen Abbildung sehen kannst. Die Länge der Whisker berechne ich einmal mit \(1^{st} - 1.5 \times IQR = 0.6\) sowie \(3^{rd} + 1.5 \times IQR = 14.2\) und vergleiche die beiden Werte mit dem Minimum von 5.7 und 11.8 der Sprungweite. In beiden Fällen entscheide ich mich dann für die Minimum und Maximum-Werte.
Auch wenn die Abbildung nicht maßstabsgetreu ist, können wir abschätzen, dass unsere Sprungweiten der Hundeflöhe in etwa normalverteilt sind, da der Median in etwa in der Mitte der Box liegt. Darüber hinaus sind auch die Whiskers in etwa gleich lang. Ja, in der Statistik ist vieles eine Abschätzung.
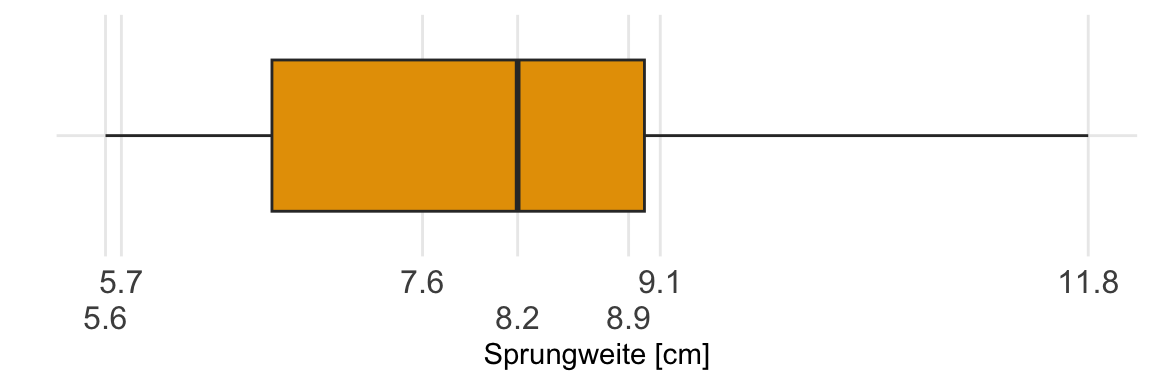
Jetzt kommt die Kür, wie erstellen wir einen Boxplot in R mit dem R Paket {ggplot}? Dafür schauen wir uns erstmal an, wie ein Boxplot aussehen würde. Im Folgenden siehst du einmal die Abbildung eines liegenden Boxplot der Hundeflöhe und deren Sprungweiten erstellt in {ggplot}. Wir du erkennen kannst, gibt es da kaum einen Unterschied zu der händischen Darstellung.
Nun ist ein liegender Boxplot eher ungewöhnlich in der Darstellung. Zum zeichnen und verstehen macht das schon Sinn, aber wenn wir später dann mit dem Boxplot arbeiten, dann nutzen wir die stehende Varaiante.
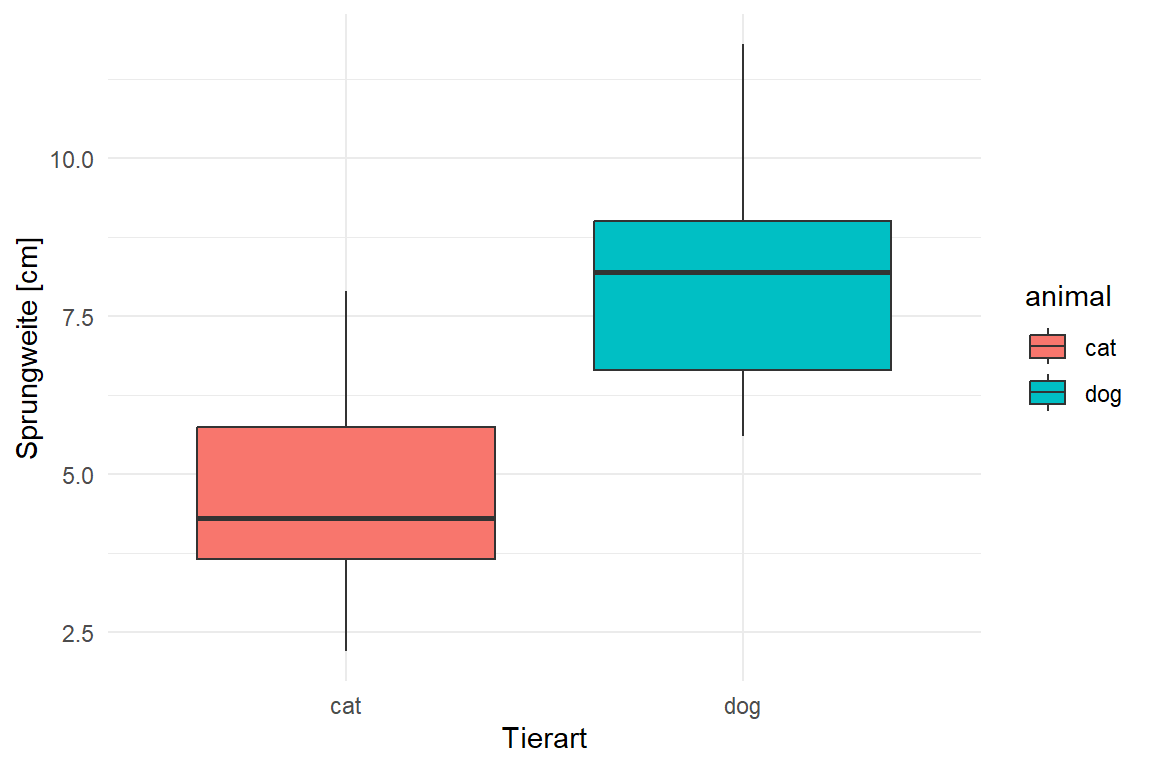
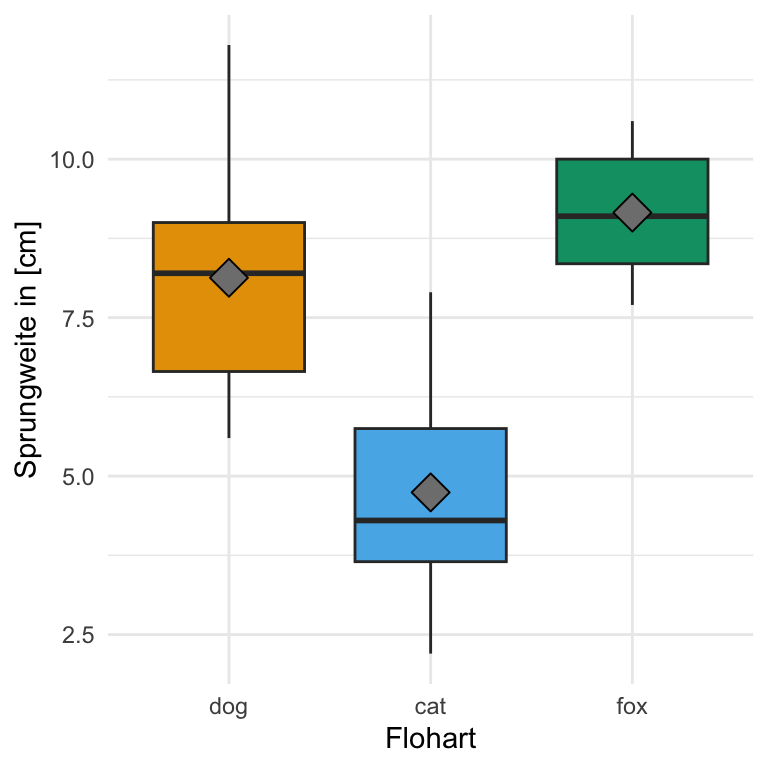
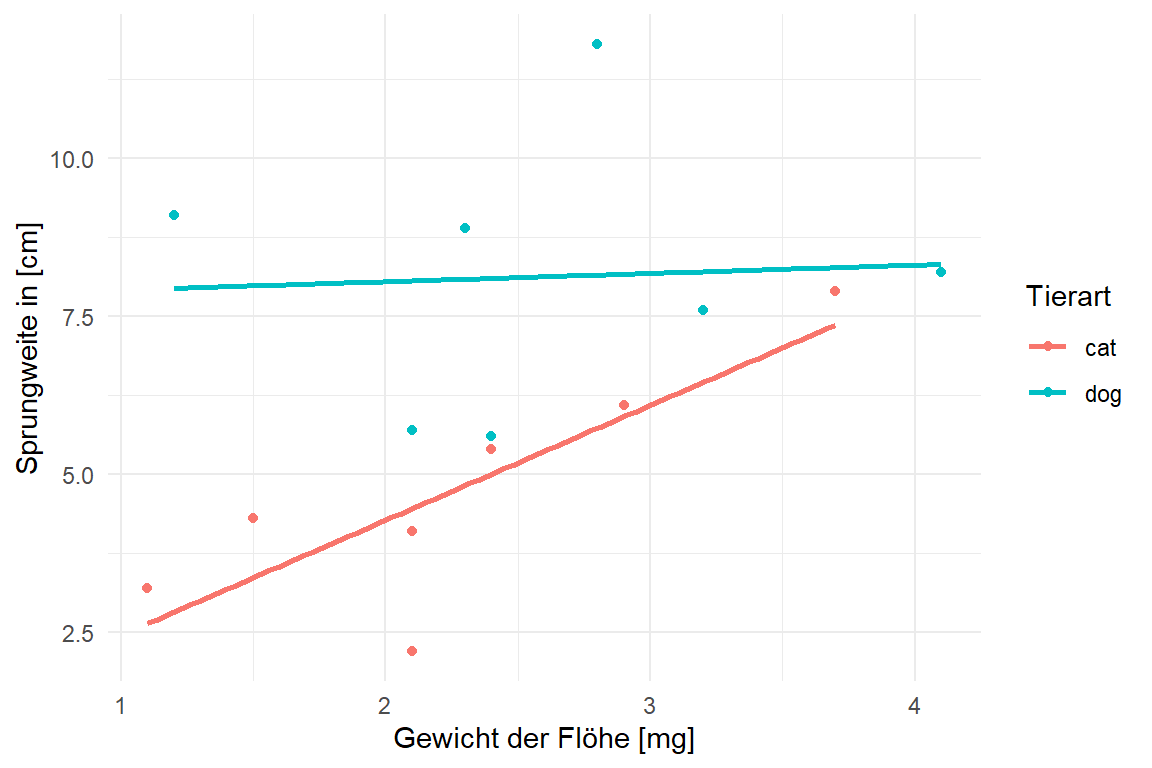
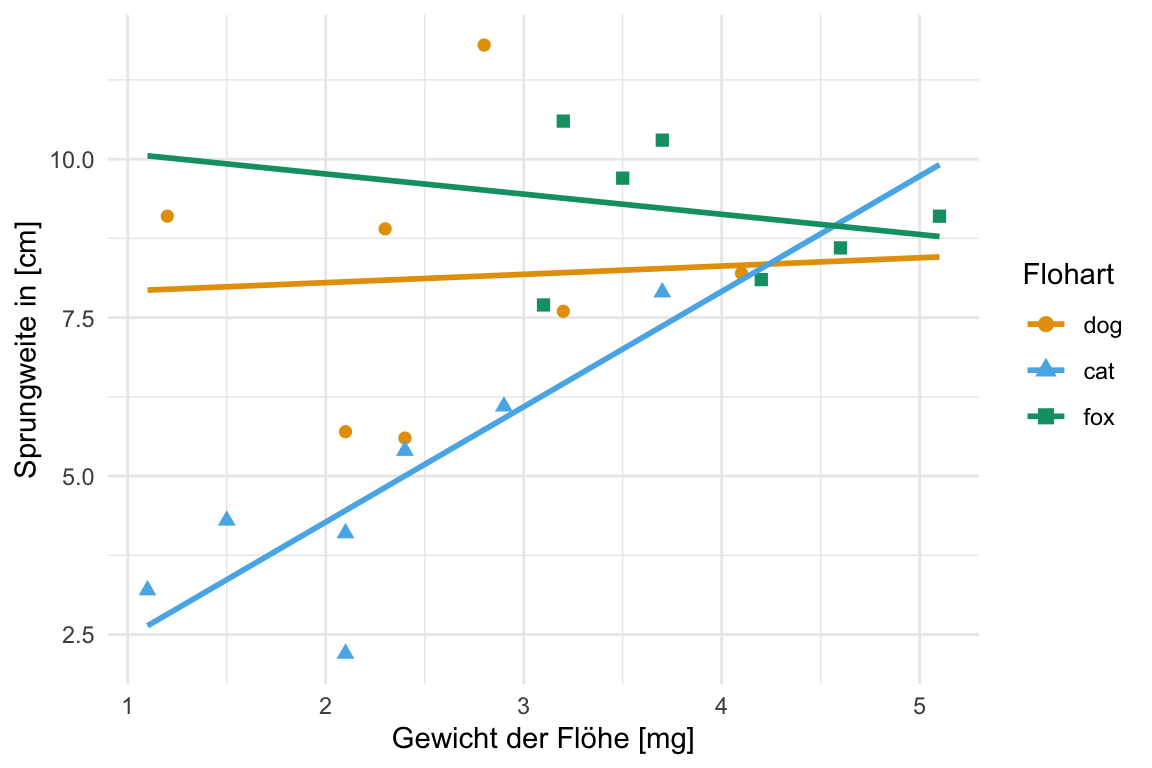
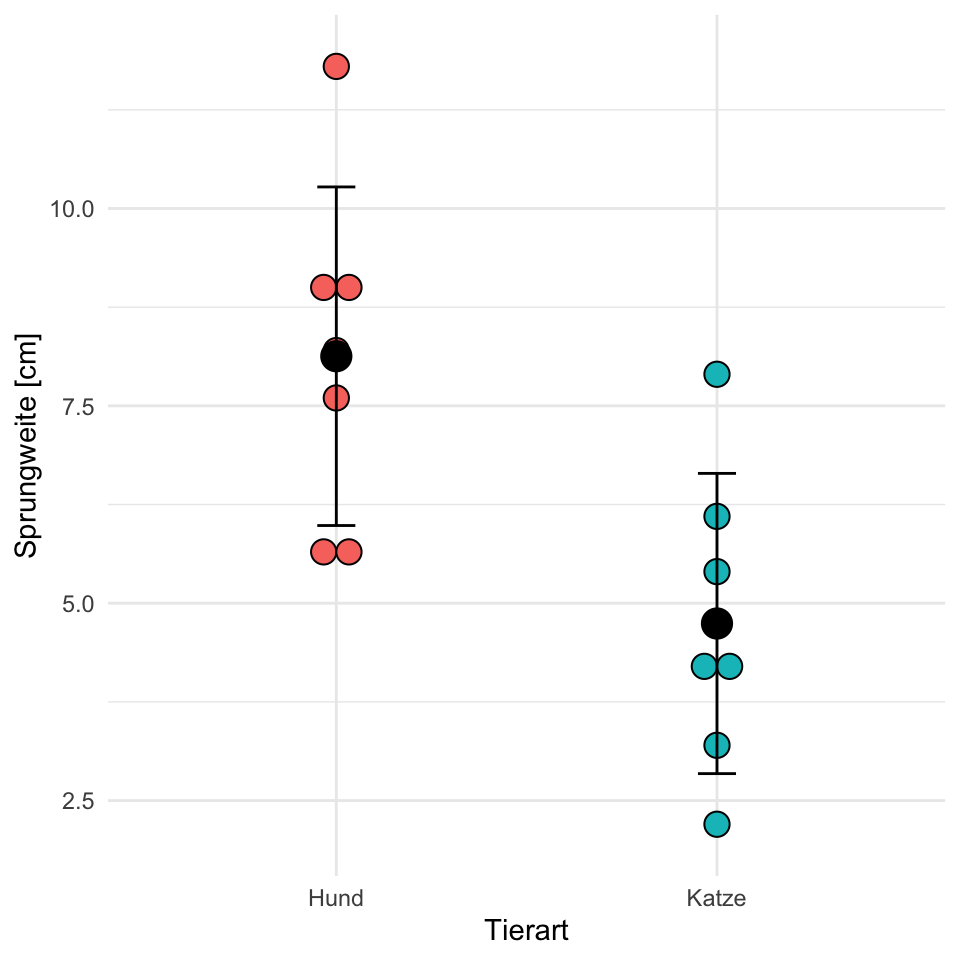
Wir schauen uns hier einmal in {ggplot} den einfaktoriellen sowie zweifaktoriellen Boxplot an. Wenn wir von einem einfaktoriellen Boxplot sprechen, dann haben wir nur eine Gruppe auf der x-Achse vorliegen. Wenn wir einen zweifaktoriellen Boxplot bauen wollen, dann brauchen wir noch einen zweiten Gruppenfaktor für die Legende. Häufig nutze wir Boxplots um Gruppen, wie hier die Tierarten, miteinander zu vergleichen. In den folgenden Abbildungen sind daher die Boxplots für die Sprungweite in [cm] der Hunde- und Katzen- und Fuchsflöhe dargestellt.
Wir erkennen auf einen Blick, dass die Sprungweite von den Hundeflöhen weiter ist als die Sprungweite der Katzenflöhe und die Fuchsflöhe am weitesten springen. Im Weiteren können wir abschätzen, dass die Streuung etwa gleich groß ist, bei den Füchsen eventuell etwas weniger. Die Boxen sind in etwa gleich groß und die Whiskers in etwa gleich lang. Dann können wir auch die Boxplots komplexer darstellen indem wir eben noch einen zweiten Faktor mit in die Darstellung aufnehmen. Hier schauen wir uns dann zwei Messorte mit an.
Einfaktorieller Boxplot
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = animal, y = jump_length, fill = animal)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point",
shape=23, size = 5, fill = "gray50") +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() Zweifaktorieller Boxplot
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = sex, y = jump_length, fill = animal)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point", aes(group = animal),
shape = 23, size = 5, fill = "gray50",
position = position_dodge(0.75)) +
labs(x = "Flohart", y = "Sprungweite in [cm]", fill = "Tierart") +
scale_fill_okabeito() Wie auch schon bei den Barplots überzeigt {tidyplots} eben dann durch die relativ einfach Zuweisung von Layern mit wichtigen Informationen. Hier haben wir dann zwar bei den Boxplots nicht so viele Vorteile, die Verwendung in {ggplot} ist nicht so kompliziert. In den {tidyplots} ist es dann aber einfacher den Mittelwert der Gruppen als Punkt zuzufügen. Den Rest fand ich dann nicht so unterschiedlich zu {ggplot}. Schön sehen die Abbildungen dann aber doch aus.
Einfaktorieller Boxplot
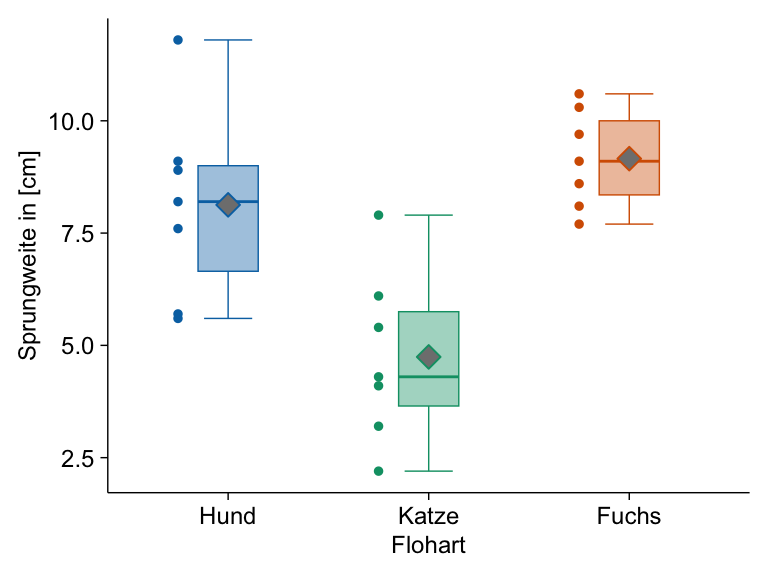
Hier haben wir dann einmal die einfaktoriellen Boxplots zusammen mit dem Mittelwert der Grupen als Raute dargestellt. Simpel und einfach erstellt. Der Rest des Codes dient eben dazu die Abbildung dann noch schöner zu machen. Die letzte Zeile mit adjust_size(width = NA, height = NA) brauche ich hier noch aktuell im meinem Skript und du kannst die weglassen oder eine andere Größe des Plost wählen.
R Code [zeigen / verbergen]
tidyplot(data = fac1_tbl,
x = animal, y = jump_length, color = animal) |>
add_data_points(dodge_width = 0.5, preserve = "single") |>
add_boxplot(alpha = 0.4, box_width = 0.3) |>
add_mean_dot(fill = "gray50", shape = 23, size = 3) |>
remove_legend() |>
adjust_font(fontsize = 9) |>
adjust_x_axis_title("Flohart") |>
adjust_y_axis_title("Sprungweite in [cm]") |>
rename_x_axis_labels(new_names = c("dog" = "Hund", "cat" = "Katze", "fox" = "Fuchs")) |>
adjust_size(width = NA, height = NA) Zweifaktorieller Boxplot
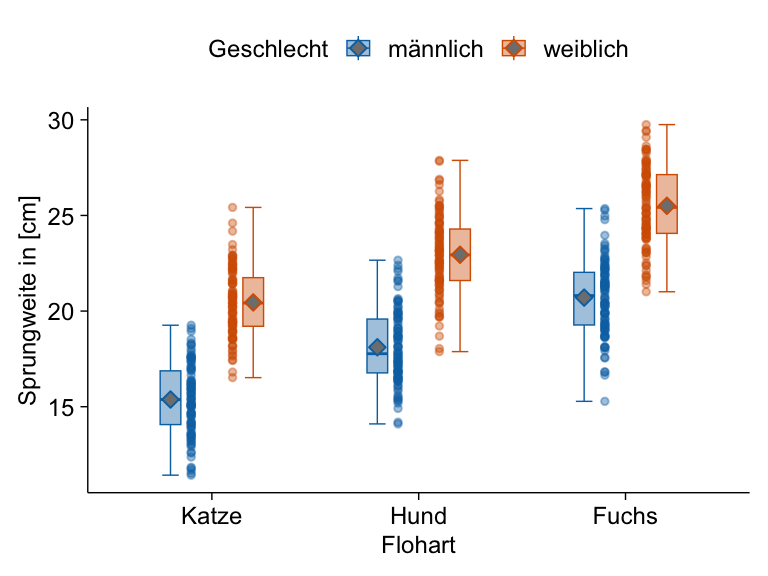
Auch der zweifaktorielle Fall lässt sich sehr gut abbilden und auch schnell erstellen. Wir haben hier kaum einen Unterschied zu dem Code des einfaktoriellen Boxplots. Wir müssen hier nur die Option color ergänzen und dann schauen, dass wir die Punkte etwas schieben, da wir hier doch sehr viele Beobachtungen vorliegen haben. Die letzte Zeile mit adjust_size(width = NA, height = NA) brauche ich hier noch aktuell im meinem Skript und du kannst die weglassen oder eine andere Größe des Plost wählen.
R Code [zeigen / verbergen]
tidyplot(data = fac2_tbl,
x = animal, y = jump_length, color = sex) |>
add_data_points(dodge_width = 0.4, alpha = 0.4) |>
add_boxplot(alpha = 0.4, box_width = 0.2) |>
add_mean_dot(fill = "gray50", shape = 23, size = 2) |>
adjust_font(fontsize = 9) |>
adjust_x_axis_title("Flohart") |>
adjust_y_axis_title("Sprungweite in [cm]") |>
adjust_legend_title("Geschlecht") |>
adjust_legend_position("top") |>
rename_x_axis_labels(new_names = c("dog" = "Hund", "cat" = "Katze", "fox" = "Fuchs")) |>
rename_color_labels(new_names = c("male" = "männlich", "female" = "weiblich")) |>
adjust_size(width = NA, height = NA) Der Boxplot erlaubt uns auch abzuschätzen, ob wir eine Normalverteilung vorliegen haben oder aber ob die Varianz in zwei oder. mehr Gruppen annähernd ist. Wir sprechen dann von Varianzhomogenität.
- Abschätzung der Normalverteilung
-
Der Median liegt in der Mitte der Box und die Whiskers sind ungefähr gleich lang. Wir können von einer approximativen Normalverteilung ausgehen.
- Abschätzung der Varianzhomogenität
-
Die Boxen sind über alle Gruppen ungefähr gleich groß und auch die Whiskers haben in etwa die gleiche Länge. Wir können dann von einer Varianzhomogenität über die Gruppen ausgehen.
Schau dir auch hier mal in den Kästen zum Zerforschen rein, da findest du dann noch mehr Inspiration aus anderen Abbildungen, die ich nachgebaut habe. Ich bin einmal über den Campus gelaufen und habe geschaut, welche Abbildungen auf den Postern verwendet werden und habe diese nachgebaut.
In diesem Zerforschenbeispiel wollen wir uns einen zweifaktoriellen Barplot oder Säulendiagramm anschauen. Wir haben hier ein Säulendiagramm mit den Mittelwerten über den Faktor auf der \(x\)-Achse vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der drei Fruchtgrößen jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung für die vier Stickstoffangebote. Das addiert sich dann auf, aber es geht noch. Die Standardabweichung addieren und subtrahieren wir dann später jeweils von dem Mittelwert und schon haben wir die Fehlerbalken. Da ich auch hier einmal als Alternative die Boxplots erstellen will, brauche ich hier mehr Werte aus denen ich dann die Mittelwerte und die Standardabweichung berechne.
Als erstes brauchen wir wieder die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_2fac.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die drei Werte alle um den Mittelwert streuen lassen. Das war es dann auch schon.
R Code [zeigen / verbergen]
barplot_tbl <- read_excel("data/zerforschen_barplot_2fac.xlsx") |>
mutate(frucht = factor(frucht,
levels = c("klein", "mittel", "groß"),
labels = c("Klein", "Mittel", "Groß")),
nmin = as_factor(nmin))
barplot_tbl # A tibble: 36 × 3
frucht nmin yield
<fct> <fct> <dbl>
1 Klein 150 1.5
2 Klein 150 2.2
3 Klein 150 2.8
4 Klein 200 2.4
5 Klein 200 1.9
6 Klein 200 2.9
7 Klein 250 3.7
8 Klein 250 3.9
9 Klein 250 3.5
10 Klein 300 2.5
# ℹ 26 more rowsJetzt brauchen wir noch die Mittelwerte und die Standardabweichung für jede der drei Fruchtgrößen und Stickstoffangebote. Hier nur kurz, den Code kennst du schon aus anderen Zerforschenbeispielen zu den Barplots. Das ist soweit erstmal nichts besonderes und ähnelt auch der Erstellung der anderen Barplots.
R Code [zeigen / verbergen]
stat_all_tbl <- barplot_tbl |>
group_by(frucht, nmin) |>
summarise(mean = mean(yield),
sd = sd(yield))
stat_all_tbl# A tibble: 12 × 4
# Groups: frucht [3]
frucht nmin mean sd
<fct> <fct> <dbl> <dbl>
1 Klein 150 2.17 0.651
2 Klein 200 2.4 0.5
3 Klein 250 3.7 0.2
4 Klein 300 2.5 0.4
5 Mittel 150 5.03 1.05
6 Mittel 200 7.03 0.252
7 Mittel 250 8 0.200
8 Mittel 300 7.7 0.200
9 Groß 150 6.1 1.95
10 Groß 200 8.27 0.702
11 Groß 250 9.07 1.00
12 Groß 300 8.97 1.00 Weil wir dann noch die globalen Mittelwerte der Früchte über alle Stickstofflevel wollen, müssen wir nochmal die Mittelwerte und die Standardabweichung nur für die drei Fruchtgrößen berechnen. Daher haben wir dann zwei Datensätze, die uns eine Zusammenfassung der Daten liefern.
R Code [zeigen / verbergen]
stat_fruit_tbl <- barplot_tbl |>
group_by(frucht) |>
summarise(mean = mean(yield))
stat_fruit_tbl# A tibble: 3 × 2
frucht mean
<fct> <dbl>
1 Klein 2.69
2 Mittel 6.94
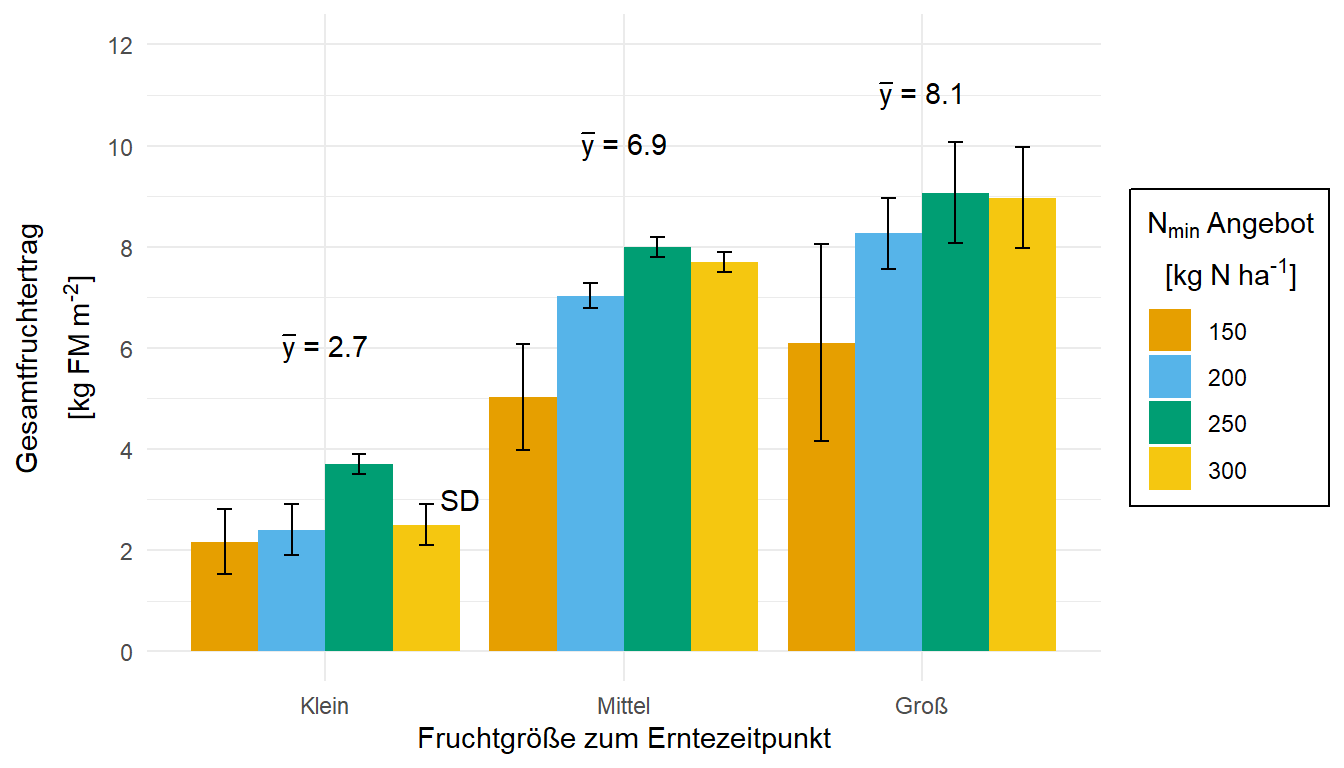
3 Groß 8.1 Auch hier möchte ich einmal den Barplot nachbauen und dann als Alternative noch den Barplot anbieten. Am nervigsten war der Zeilenumbruch in der Legendenbeschriftung mit N\(_min\). Es hat echt gedauert, bis ich die Funktion atop() gefunden hatte, die in einer expression() einen Zeilenumbruch erzwingt. Meine Güte war das langwierig. Der Rest ist eigentlich wie schon in den anderen Beispielen. Da schaue dann doch nochmal da mit rein.
Einmal der Barplot wie beschrieben. Vergleiche auch einmal diese Abbildung der Barplots mit der Abbildung der Boxplots in dem anderem Tab und überlege, welche der beiden Abbildungen dir mehr Informationen liefert.
R Code [zeigen / verbergen]
ggplot(data = stat_all_tbl, aes(x = frucht, y = mean,
fill = nmin)) +
theme_minimal() +
geom_bar(stat = "identity", position = position_dodge(0.9)) +
geom_errorbar(aes(ymin = mean-sd, ymax = mean+sd),
width = 0.2, position = position_dodge(0.9)) +
labs(x = "Fruchtgröße zum Erntezeitpunkt",
y = expression(atop("Gesamtfruchtertrag", "["*kg~FM~m^"-2"*"]")),
fill = expression(atop(N[min]~"Angebot", "["*kg~N~ha^"-1"*"]"))) +
scale_y_continuous(breaks = c(0, 2, 4, 6, 8, 10, 12),
limits = c(0, 12)) +
scale_fill_okabeito() +
theme(legend.position = "right",
legend.box.background = element_rect(color = "black"),
legend.box.margin = margin(t = 1, l = 1),
legend.text.align = 0) +
annotate("text", x = c(1, 2, 3, 1.45), y = c(6, 10, 11, 3),
label = c(expression(bar(y)*" = "*2.7),
expression(bar(y)*" = "*6.9),
expression(bar(y)*" = "*8.1),
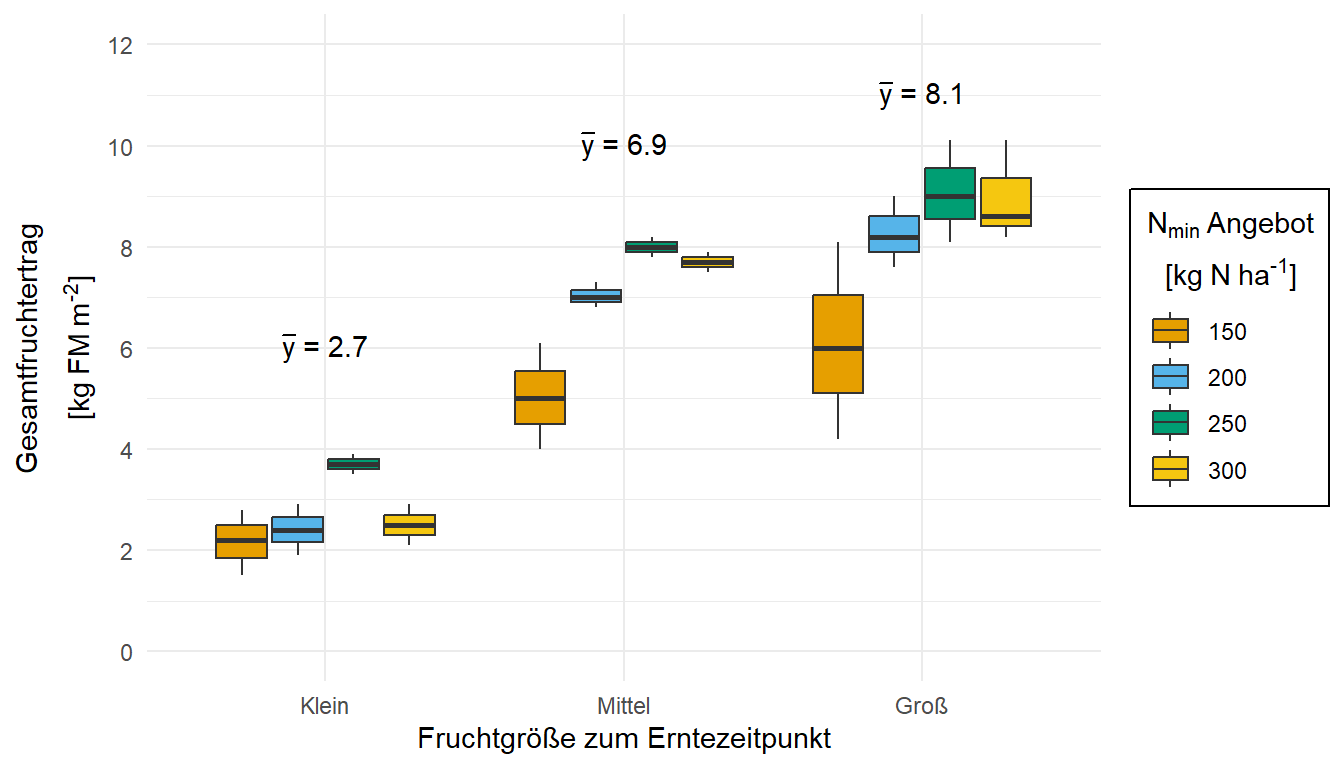
"SD"))Für die Boxplots müssen wir gar nicht viel tun. Wir müssen nur noch das geom_bar() und geom_errorbar() entfernen und durch das geom_boxplot() ersetzen. Dann haben wir auch schon unsere wunderbaren Boxplots. Das Problem sind natürlich die wenigen Beobachtungen, deshalb sehen die Boxplots teilweise etwas wild aus. Beachte auch das wir die Orginaldaten nutzen und nicht die zusammengefassten Daten.
R Code [zeigen / verbergen]
ggplot(data = barplot_tbl, aes(x = frucht, y = yield,
fill = nmin)) +
theme_minimal() +
geom_boxplot() +
labs(x = "Fruchtgröße zum Erntezeitpunkt",
y = expression(atop("Gesamtfruchtertrag", "["*kg~FM~m^"-2"*"]")),
fill = expression(atop(N[min]~"Angebot", "["*kg~N~ha^"-1"*"]"))) +
scale_y_continuous(breaks = c(0, 2, 4, 6, 8, 10, 12),
limits = c(0, 12)) +
scale_fill_okabeito() +
theme(legend.position = "right",
legend.box.background = element_rect(color = "black"),
legend.box.margin = margin(t = 1, l = 1),
legend.text.align = 0) +
annotate("text", x = c(1, 2, 3), y = c(6, 10, 11),
label = c(expression(bar(y)*" = "*2.7),
expression(bar(y)*" = "*6.9),
expression(bar(y)*" = "*8.1)))Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
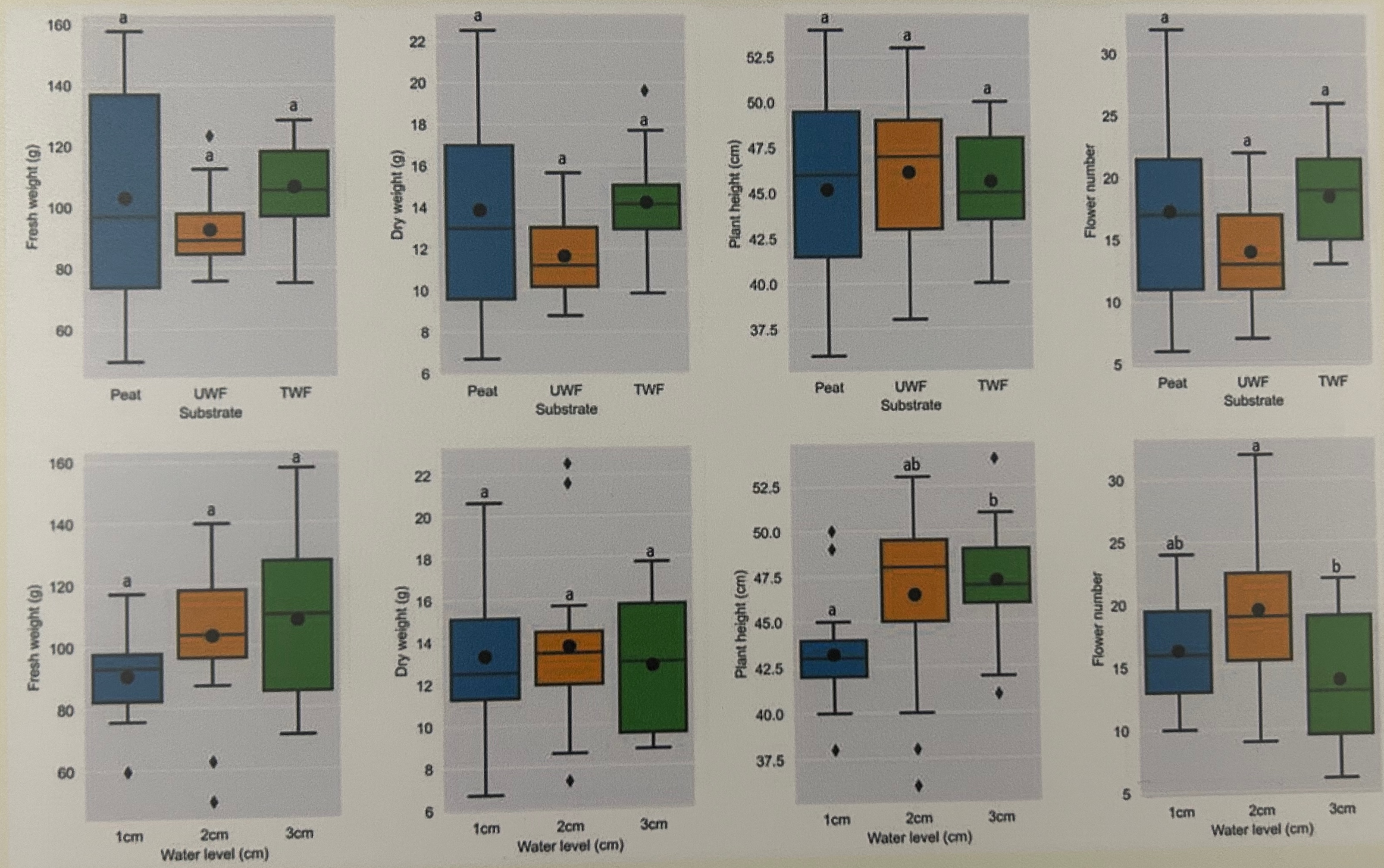
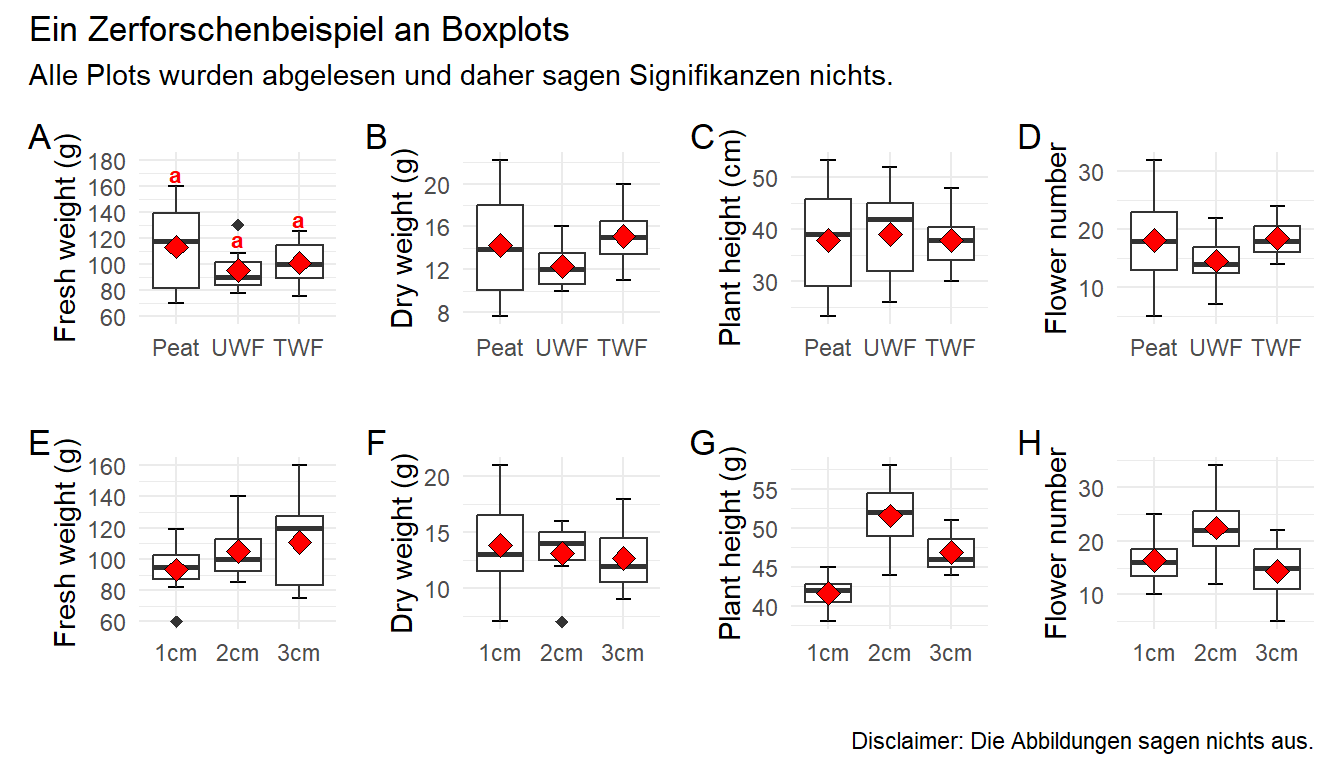
ggsave("my_ggplot_barplot.png", width = 5, height = 3)Hier wollen wir einmal eine etwas größere Abbildung 44.28 mit einer Menge Boxplots zerforschen. Da ich den Datensatz dann nicht zu groß machen wollte und Boxplots zu zerforschen manchmal nicht so einfach ist, passen die Ausreißer dann manchmal dann doch nicht. Auch liefern die statistischen Tests dann nicht super genau die gleichen Ergebnisse. Aber das macht vermutlich nicht so viel, hier geht es ja dann eher um den Bau der Boxplots und dem rechnen des statistischen Tests in {emmeans}. Die Reihenfolge des compact letter displays habe ich dann auch nicht angepasst sondern die Buchstaben genommen, die ich dann erhalten habe. Die Sortierung kann man ja selber einfach ändern. Wir haben hier ein einfaktorielles Design mit einem Behandlungsfaktor mit drei Leveln vorliegen. Insgesamt schauen wir uns vier Endpunkte in veränderten Substrat- und Wasserbedingungen an.
Im Folgenden lade ich einmal den Datensatz, den ich dann per Auge zusammengesetzt habe. Das war jetzt etwas anstrengender als gedacht, da ich nicht weiß wie viele Beobachtungen einen Boxplot bilden. Je mehr Beobachtungen, desto feiner kann man den Boxplot abstimmen. Da ich hier nur mit sieben Beobachtungen ja Gruppe gearbeitet habe, habe ich es nicht geschafft die Ausreißer darzustellen. Das wäre mir dann zu viel Arbeit geworden. Nachdem ich jetzt die Daten geladen habe, muss ich noch über die Funktion pivot_longer() einen Datensatz passenden im Longformat bauen. Abschließend mutiere ich dann noch alle Faktoren richtig und vergebe bessere Namen als labels sonst versteht man ja nicht was die Spalten bedeuten.
R Code [zeigen / verbergen]
boxplot_mult_tbl <- read_excel("data/zerforschen_boxplot_mult.xlsx") |>
pivot_longer(cols = fresh_weight:flower_number,
values_to = "rsp",
names_to = "plant_measure") |>
mutate(trt = as_factor(trt),
plant_measure = factor(plant_measure,
levels = c("fresh_weight", "dry_weight",
"plant_height", "flower_number"),
labels = c("Fresh weight (g)", "Dry weight (g)",
"Plant height (cm)", "Flower number")),
type = factor(type, labels = c("Substrate", "Water"))) Ich habe mir dann die beiden Behandlungen substrate und water in die neue Spalte type geschrieben. Die Spaltennamen der Outcomes wandern in die Spalte plant_measure und die entsprechenden Werte in die Spalte rsp. Dann werde ich hier mal alle Outcomes auf einmal auswerten und nutze dafür das R Paket {purrr} mit der Funktion nest() und map(). Ich packe mir als die Daten nach type und plant_measure einmal zusammen. Dann habe ich einen neuen genesteten Datensatz mit nur noch acht Zeilen. Auf jeder Zeile rechne ich dann jeweils mein Modell. Wie du dann siehst ist in der Spalte data dann jeweils ein Datensatz mit der Spalte trt und rsp für die entsprechenden 21 Beobachtungen.
R Code [zeigen / verbergen]
boxplot_mult_nest_tbl <- boxplot_mult_tbl |>
group_by(type, plant_measure) |>
nest()
boxplot_mult_nest_tbl# A tibble: 8 × 3
# Groups: type, plant_measure [8]
type plant_measure data
<fct> <fct> <list>
1 Substrate Fresh weight (g) <tibble [21 × 2]>
2 Substrate Dry weight (g) <tibble [21 × 2]>
3 Substrate Plant height (cm) <tibble [21 × 2]>
4 Substrate Flower number <tibble [21 × 2]>
5 Water Fresh weight (g) <tibble [21 × 2]>
6 Water Dry weight (g) <tibble [21 × 2]>
7 Water Plant height (cm) <tibble [21 × 2]>
8 Water Flower number <tibble [21 × 2]>Zur Veranschaulichung rechne ich jetzt einmal mit mutate() und map() für jeden der Datensätze in der Spalte data einmal ein lineares Modell mit der Funktion lm(). Ich muss nur darauf achten, dass ich die Daten mit .x einmal an die richtige Stelle in der Funktion lm() übergebe. Dann habe ich alle Modell komprimiert in der Spalte model. Das geht natürlcih auch alles super in einem Rutsch.
R Code [zeigen / verbergen]
boxplot_mult_nest_model_tbl <- boxplot_mult_nest_tbl |>
mutate(model = map(data, ~lm(rsp ~ trt, data = .x)))
boxplot_mult_nest_model_tbl # A tibble: 8 × 4
# Groups: type, plant_measure [8]
type plant_measure data model
<fct> <fct> <list> <list>
1 Substrate Fresh weight (g) <tibble [21 × 2]> <lm>
2 Substrate Dry weight (g) <tibble [21 × 2]> <lm>
3 Substrate Plant height (cm) <tibble [21 × 2]> <lm>
4 Substrate Flower number <tibble [21 × 2]> <lm>
5 Water Fresh weight (g) <tibble [21 × 2]> <lm>
6 Water Dry weight (g) <tibble [21 × 2]> <lm>
7 Water Plant height (cm) <tibble [21 × 2]> <lm>
8 Water Flower number <tibble [21 × 2]> <lm> Jetzt können wir einmal eskalieren und insgesamt acht mal die ANOVA rechnen. Das sieht jetzt nach viel Code aus, aber am Ende ist es nur eine lange Pipe. Am Ende erhalten wir dann den \(p\)-Wert für die einfaktorielle ANOVA für die Behandlung trt wiedergegeben. Wir sehen, dass wir eigentlich nur einen signifikanten Unterschied in der Wassergruppe und der Pflanzenhöhe erwarten sollten. Da der \(p\)-Wert für die Wassergruppe und der Blütenanzahl auch sehr nah an dem Signifikanzniveau ist, könnte hier auch etwas sein, wenn wir die Gruppen nochmal getrennt testen.
R Code [zeigen / verbergen]
boxplot_mult_nest_model_tbl |>
mutate(anova = map(model, anova)) |>
mutate(parameter = map(anova, model_parameters)) |>
select(type, plant_measure, parameter) |>
unnest(parameter) |>
clean_names() |>
filter(parameter != "Residuals") |>
select(type, plant_measure, parameter, p)# A tibble: 8 × 4
# Groups: type, plant_measure [8]
type plant_measure parameter p
<fct> <fct> <chr> <dbl>
1 Substrate Fresh weight (g) trt 0.813
2 Substrate Dry weight (g) trt 0.381
3 Substrate Plant height (cm) trt 0.959
4 Substrate Flower number trt 0.444
5 Water Fresh weight (g) trt 0.384
6 Water Dry weight (g) trt 0.843
7 Water Plant height (cm) trt 0.000138
8 Water Flower number trt 0.0600 Dann schauen wir uns nochmal das \(\eta^2\) an um zu sehen, wie viel Varianz unsere Behandlung in den Daten erklärt. Leider sieht es in unseren Daten sehr schlecht aus. Nur bei der Wassergruppe und der Pflanzenhöhe scheinen wir durch die Behandlung Varianz zu erklären.
R Code [zeigen / verbergen]
boxplot_mult_nest_model_tbl %>%
mutate(eta = map(model, eta_squared)) %>%
unnest(eta) %>%
clean_names() %>%
select(type, plant_measure, eta2) # A tibble: 8 × 3
# Groups: type, plant_measure [8]
type plant_measure eta2
<fct> <fct> <dbl>
1 Substrate Fresh weight (g) 0.0228
2 Substrate Dry weight (g) 0.102
3 Substrate Plant height (cm) 0.00466
4 Substrate Flower number 0.0863
5 Water Fresh weight (g) 0.101
6 Water Dry weight (g) 0.0188
7 Water Plant height (cm) 0.628
8 Water Flower number 0.268 Dann können wir auch schon den Gruppenvergleich mit dem R Paket {emmeans} rechnen. Wir nutzen hier die Option vcov. = sandwich::vcovHAC um heterogene Varianzen zuzulassen. Im Weiteren adjustieren wir nicht für die Anzahl der Vergleiche und lassen uns am Ende das compact letter display wiedergeben.
R Code [zeigen / verbergen]
emm_tbl <- boxplot_mult_nest_model_tbl |>
mutate(emm = map(model, emmeans, ~trt, vcov. = sandwich::vcovHAC)) |>
mutate(cld = map(emm, cld, Letters = letters, adjust = "none")) |>
unnest(cld) |>
select(type, plant_measure, trt, rsp = emmean, group = .group) |>
mutate(group = str_trim(group))
emm_tbl# A tibble: 24 × 5
# Groups: type, plant_measure [8]
type plant_measure trt rsp group
<fct> <fct> <fct> <dbl> <chr>
1 Substrate Fresh weight (g) UWF 95.4 a
2 Substrate Fresh weight (g) TWF 101 a
3 Substrate Fresh weight (g) Peat 105 a
4 Substrate Dry weight (g) UWF 12.3 a
5 Substrate Dry weight (g) Peat 14.3 ab
6 Substrate Dry weight (g) TWF 15.1 b
7 Substrate Plant height (cm) TWF 37.9 a
8 Substrate Plant height (cm) Peat 38.0 a
9 Substrate Plant height (cm) UWF 39.1 a
10 Substrate Flower number UWF 14.6 a
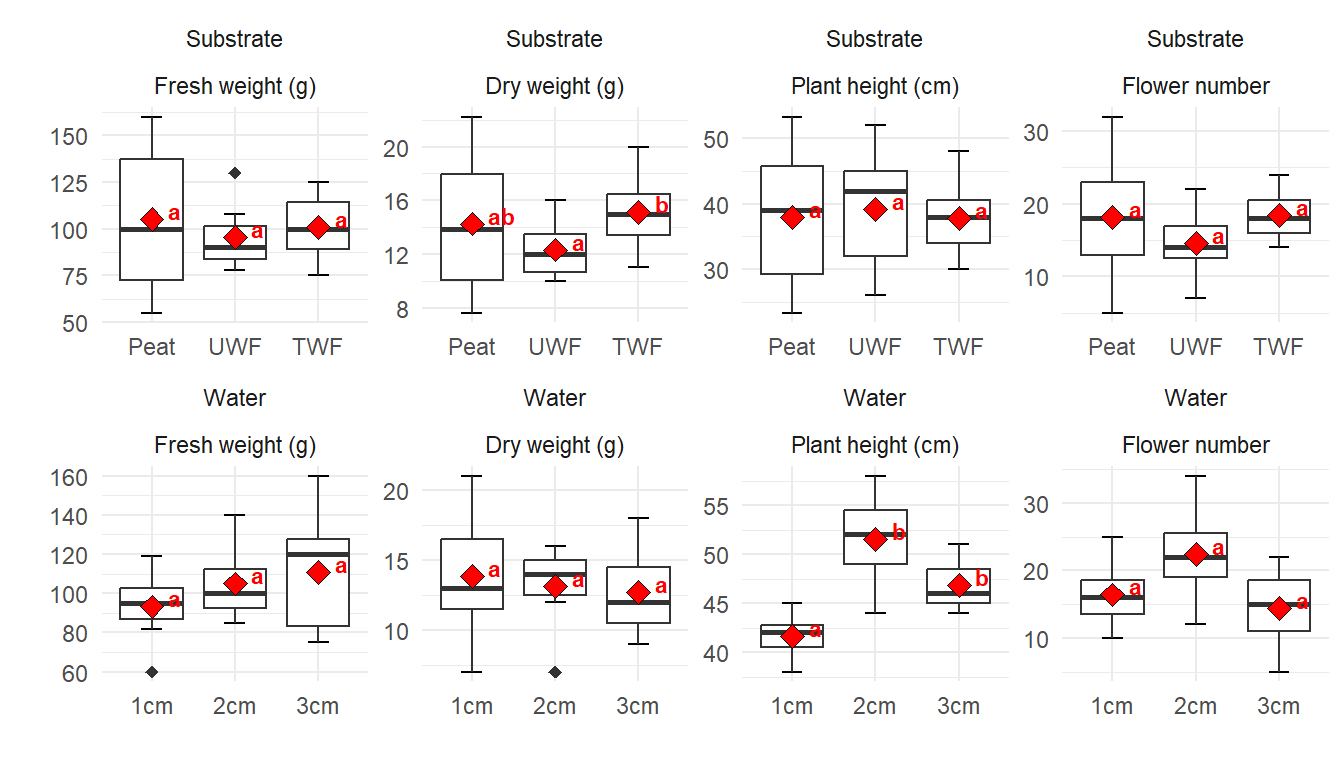
# ℹ 14 more rowsDa die Ausgabe viel zu lang ist, wollen wir ja jetzt einmal unsere Abbildungen in {ggplot} nachbauen. Dazu nutze ich dann einmal zwei Wege. Einmal den etwas schnelleren mit facet_wrap() bei dem wir eigentlich alles automatisch machen lassen. Zum anderen zeige ich dir mit etwas Mehraufwand alle acht Abbildungen einzeln baust und dann über das R Paket {patchwork} wieder zusammenklebst. Der zweite Weg ist der Weg, wenn du mehr Kontrolle über die einzelnen Abbildungen haben willst.
Die Funktion facet_wrap() erlaubt es dir automatisch Subplots nach einem oder mehreren Faktoren zu erstellen. Dabei muss auch ich immer wieder probieren, wie ich die Faktoren anordne. In unserem Fall wollen wir zwei Zeilen und auch den Subplots erlauben eigene \(x\)-Achsen und \(y\)-Achsen zu haben. Wenn du die Option scale = "free" nicht wählst, dann haben alle Plots alle Einteilungen der \(x\)_Achse und die \(y\)-Achse läuft von dem kleinsten zu größten Wert in den gesamten Daten.
R Code [zeigen / verbergen]
boxplot_mult_tbl |>
ggplot(aes(trt, rsp)) +
theme_minimal() +
stat_boxplot(geom = "errorbar", width = 0.25) +
geom_boxplot(outlier.shape = 18, outlier.size = 2) +
stat_summary(fun.y = mean, geom = "point", shape = 23, size = 3, fill = "red") +
facet_wrap(~ type * plant_measure, nrow = 2, scales = "free") +
labs(x = "", y = "") +
geom_text(data = emm_tbl, aes(y = rsp, label = group), size = 3, fontface = "bold",
position = position_nudge(0.2), hjust = 0, vjust = 0, color = "red")Jetzt wird es etwas wilder. Wir bauen uns jetzt alle acht Plots einzeln und kleben diese dann mit dem R Paket {patchwork} zusammen. Das hat ein paar Vorteile. Wir können jetzt jeden einzelnen Plot bearbeiten und anpassen wie wir es wollen. Damit wir aber nicht zu viel Redundanz haben bauen wir uns erstmal ein Template für ggplot(). Dann können wir immer noch die Werte für scale_y_continuous() in den einzelnen Plots ändern. Hier also einmal das Template, was beinhaltet was für alle Abbildungen gelten soll.
R Code [zeigen / verbergen]
gg_template <- ggplot() +
aes(trt, rsp) +
theme_minimal() +
stat_boxplot(geom = "errorbar", width = 0.25) +
geom_boxplot(outlier.shape = 18, outlier.size = 2) +
stat_summary(fun.y = mean, geom = "point", shape = 23, size = 3, fill = "red") +
labs(x = "")Ja, jetzt geht es los. Wir bauen also jeden Plot einmal nach. Dafür müssen wir dann jeweils den Datensatz filtern, den wir auch brauchen. Dann ergänzen wir noch die korrekte \(y\)-Achsenbeschriftung. So können wir dann auch händisch das compact letter display über die Whisker einfach setzen. Im Weiteren habe ich dann auch einmal als Beispiel noch die \(y\)-Achseneinteilung mit scale_y_continuous() geändert. Ich habe das einmal für den Plot p1 gemacht, der Rest würde analog dazu funktionieren.
R Code [zeigen / verbergen]
p1 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Substrate" & plant_measure == "Fresh weight (g)") +
labs(y = "Fresh weight (g)") +
annotate("text", x = c(1, 2, 3), y = c(170, 120, 135), label = c("a", "a", "a"),
color = "red", size = 3, fontface = "bold") +
scale_y_continuous(breaks = seq(40, 180, 20), limits = c(60, 180))
p2 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Substrate" & plant_measure == "Dry weight (g)") +
labs(y = "Dry weight (g)")
p3 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Substrate" & plant_measure == "Plant height (cm)") +
labs(y = "Plant height (cm)")
p4 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Substrate" & plant_measure == "Flower number") +
labs(y = "Flower number")
p5 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Water" & plant_measure == "Fresh weight (g)") +
labs(y = "Fresh weight (g)")
p6 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Water" & plant_measure == "Dry weight (g)") +
labs(y = "Dry weight (g)")
p7 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Water" & plant_measure == "Plant height (cm)") +
labs(y = "Plant height (g)")
p8 <- gg_template %+%
filter(boxplot_mult_tbl, type == "Water" & plant_measure == "Flower number") +
labs(y = "Flower number")Dann kleben wir die Abbildungen einfach mit einem + zusammen und dann wählen wir noch aus, dass wir vier Spalten wollen. Dann können wir noch Buchstaben zu den Subplots hinzufügen und noch Titel und anderes wenn wir wollen würden. Dann haben wir auch den Plot schon nachgebaut. Ich verzichte hier händisch überall das compact letter display zu ergänzen. Das macht super viel Arbeit und endlos viel Code und hilft dir dann aber in deiner Abbildung auch nicht weiter. Du musst dann ja bei dir selber die Positionen für die Buchstaben finden.
R Code [zeigen / verbergen]
patch <- p1 + p2 + p3 + p4 + p5 + p6 + p7 + p8 +
plot_layout(ncol = 4)
patch + plot_annotation(tag_levels = 'A',
title = 'Ein Zerforschenbeispiel an Boxplots',
subtitle = 'Alle Plots wurden abgelesen und daher sagen Signifikanzen nichts.',
caption = 'Disclaimer: Die Abbildungen sagen nichts aus.')Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
ggsave("my_ggplot_boxplot.png", width = 12, height = 6)18.4.3 Scatterplot
Der Scatterplot wird auch \(xy\)-Plot genannt. Wir stellen in einem Scatterplot zwei kontinuierliche Variablen dar. Wir haben also auf der \(x\)-Achse Kommazahlen genauso wie auf der \(y\)-Achse. Aber dazu dann gleich mehr in den folgenden Tabs zur theoretischen Betrachtung, einem Beispiel und der Umsetzung in {ggplot}. Ein Scatterplot nutzen wir relativ häufig, wenn wir den Zusammenhang zwischen kontinuierlichen Zahlen zeigen wollen.
Das Ziel eines Scatterplots ist es eine Abhängigkeit zwischen den Werten auf der \(y\)-Achse und der \(x\)-Achse darzustellen. Wenn sich die Werte auf der \(x\)-Achse ändern, wie ändern sich dann die Werte auf der \(y\)-Achse? Im einfachsten Fall zeichnen wir für die Wertepaare von \(x\) und \(y\) jeweils ein Punkt in unserer Koordinatensystem.
Um den Zusammenhang zwischen \(y\) und \(x\) zu visualisieren legen wir eine Linie durch die Punkte. Diese Gerade folgt dann einer Geradengleichung der Form \(y = \beta_0 + \beta_1 x\). Wobei der Wert für \(\beta_0\) den y-Achsenabschnitt beschreibt und der Wert für \(\beta_1\) die Steigung der Geraden. Wir wir methodisch zu den Zahlen einer Geradengleichung kommen und damit den Werten für \(\beta_0\) und \(\beta_1\), kannst du dann später in dem Kapitel zur linearen Regression nachlesen. Im Prinzip fragen wir uns also, wie hänge die Werte auf der \(y\)-Achse von den Werten auf der \(x\)-Achse ab? Wenn sich also die Werte auf der \(x\)-Achse erhöhen oder kleiner werden, wie verhalten sich dann die Werte auf der \(y\)-Achse?
Wenn wir ein Scatterplot zeichnen wollen, dann brauchen wir erstmal paarweise Werte für \(x\) und \(y\). In der folgenden Tabelle findest du die Informationen von sieben HUndeflöhen zu der Sprungweite in [cm] und dem Gewicht der Flöhe in [mg]. Gibt es nun einen Zusammenhang zwischen der Sprungweite und dem Gewicht der Flöhe? Springen kräftigere Flöhe weiter? Oder eher nicht so weit, weil schwere Flöhe eben nicht so hoch springen können? Diesen Zusammenhang können wir dann mit einem Scatterplot visualisieren.
| Index | jump_length | weight |
|---|---|---|
| 1 | 1.2 | 0.8 |
| 2 | 1.8 | 1.0 |
| 3 | 1.3 | 1.2 |
| 4 | 1.7 | 1.9 |
| 5 | 2.6 | 2.0 |
| 6 | 1.8 | 2.7 |
| 7 | 2.7 | 2.8 |
In der folgenden Abbildung siehst du einmal den Zusammenhang zwischen der Sprungweite und dem Gewicht von von unseren sieben Hundeflöhen. Für das dritte und fünfte Tier habe ich dir einmal das Wertepaar mit \((x_3, y_3)\) und \((x_5, y_5)\) beschriftet.
Nun können wir auch hier einmal die Geradengleichung ergänzen. Wenn wir das ganze händisch machen, dann würden wir die Werte für \(\\beta_0\) als y-Achsenabschnitt und \(\\beta_1\) als Steigung der Gerade visuell abschätzen. Das machen wir natürlich nicht in der Anwendung. Dafür habe ich dann das Kapitel zur linearen Regression geschrieben. Aus einer linearen Regression erhalten wir dann auch die Werte \(\beta_0 = 0.99\) und \(\beta_1 = 0.51\), die wir dann in die Regressiongleichung einsetzen. In der folgenden Abbildung siehst du den Zusammenhang nochmal dargestellt.
Als erstes brauchen wir wieder einen kleineren Datensatz und ich nehme hier mal die Sprungweiten und das Körpergewicht von sieben Katzenflöhen. Dafür nutze ich die Funktionen filter() und select() um mir einen kleineren Datensatz zu bauen.
R Code [zeigen / verbergen]
flea_cat_jump_weight_tbl <- fac1_tbl |>
filter(animal == "cat") |>
select(jump_length, weight)Die Abbildung 18.43 zeigt den Scatterplot für die Spalte weight auf der \(x\)-Achse und jump_length auf der \(y\)-Achse für unsere sieben Katzenflöhe. Mit der Funktion geom_point() können wir die Punktepaare für jede Beobachtung zeichnen. Wie du erkennen kannst, hat das Gewicht der Katzenflöhe einen Einfluss auf die Sprungweite.
R Code [zeigen / verbergen]
ggplot(data = flea_cat_jump_weight_tbl, aes(x = weight, y = jump_length)) +
theme_minimal() +
geom_point() +
labs(x = "Gewicht der Katzenflöhe [mg]", y = "Sprungweite in [cm]") +
ylim(0, NA) + xlim(0, NA)Jetzt wollen wir noch die Geradengleichung aus einer simplen linearen Regression zu der Abbildung ergänzen. Die Gleichung ist dabei wie folgt.
\[ jump\_length = 0.6377 + 1.8188 \cdot weight \]
Wir bauen uns hier eine Funktion in R, die die Geradengleichung repräsentiert.
R Code [zeigen / verbergen]
jump_func <- \(x){0.6377 + 1.8188 * x}Wir können jetzt die Geradengleichung einmal über die Funktion geom_function() zu der Abbildung ergänzen. Es gebe auch die Möglichkeit die Funktion geom_smooth() zu nutzen, aber dann haben wir nicht die Werte für die Gerade sondern nur die Gerade in der Abbildung. Das macht besonders bei mehreren Gruppen Sinn, wenn wir mal schauen wollen, ob es einen Zusammenhang gibt.
R Code [zeigen / verbergen]
ggplot(data = flea_cat_jump_weight_tbl, aes(x = weight, y = jump_length)) +
theme_minimal() +
geom_point() +
geom_function(fun = jump_func, color = "blue") +
labs(x = "Gewicht der Katzenflöhe [mg]", y = "Sprungweite in [cm]") +
ylim(0, NA) + xlim(0, NA)Einfaktorieller Scatterplot
Hier dann einmal der einfaktorieller Scatterplot mit einen Faktor. Wie du siehst, können wir die Graden getrennt nach der Tierart durch die Punkte laufen lassen. Je nach Steigung der Graden haben wir dann einen Effekt des Gewichts auf die Sprungweite oder nicht.
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = weight, y = jump_length, color = animal,
shape = animal)) +
theme_minimal() +
geom_point(size = 2, show.legend = TRUE) +
stat_smooth(method = "lm", se = FALSE, fullrange = TRUE) +
labs(x = "Gewicht der Flöhe [mg]", y = "Sprungweite in [cm]",
color = "Flohart", shape = "Flohart") +
scale_color_okabeito() +
guides(shape = guide_legend(override.aes = list(size = 2.5)))Neben der klassischen Form eine Grade durch die Punkte zu zeichnen haben wir auch die Möglichkeit das R Paket {ggpmisc} zu nutzen. Hier nehmen wir wieder unsere Daten und wollen dann wissen, ob sich die Sprungweite über das Gewicht der Flöhe unterscheidet.
R Code [zeigen / verbergen]
flea_cat_jump_weight_tbl <- fac1_tbl |>
filter(animal == "cat") |>
select(jump_length, weight)Der große Vorteil im Paket {ggpmisc} ist die einfache Anwendung. Wir können auch hier eine Grade anpassen aber dann recht einfach mit der Funktion stat_poly_eq() die Gradengleichung und das Bestimmtheitsmaß \(R^2\) ergänzen. Es geht auf jeden Fall noch mehr, aber das hier nur als ein Beispiel für eine optimierte Art die Gleichung zu bestimmen, wenn es nur die Gleichung sein soll. Wenn du mehr über die Koeffizienten aussagen willst, dann musst du klassisch über lm() die Koeffizienten bestimmen.
R Code [zeigen / verbergen]
ggplot(data = flea_cat_jump_weight_tbl, aes(x = weight, y = jump_length)) +
theme_minimal() +
geom_point() +
stat_poly_line(formula = y ~ x, se = FALSE) +
stat_poly_eq(formula = y ~ x, mapping = use_label(c("eq", "r2"))) +
labs(x = "Gewicht der Katzenflöhe [mg]", y = "Sprungweite in [cm]") +
ylim(0, NA) + xlim(0, NA)Zweifaktorieller Scatterplot
Wenn wir uns einen zweifaktoriellen Scatterplot anschauen wollen, dann wird die Sachlage schon spannender. hier müssen wir dann mehr programmieren. Ich muss selbe gestehen, dass die gemeinsame Legende immer so eine Sache ist und ich dann und ich dann auch immer länger brauche, bis ich alles zusammen habe. Aber das ist bei komplexeren Abbildungen eigentlich immer der Fall. Hier wollen wir dann ja auch vier Spalten mit den Sprungweiten, dem Gewicht sowie der Flohart und dem Geschlecht in einer Abbildung darstellen und das ist dann auch komplexer.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = weight, y = jump_length, color = animal,
linetype = sex)) +
theme_minimal() +
geom_point2(show.legend = FALSE, alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, fullrange = TRUE) +
scale_color_okabeito() +
labs(x = "Gewicht der Flöhe [mg]", y = "Sprungweite in [cm]",
linetype = "Geschlecht", color = "Flohart") +
theme(legend.key.width = unit(1.2, "cm")) +
guides(linetype = guide_legend(override.aes = list(color = "black", linewidth = 0.5)),
color = guide_legend(override.aes = list(linewidth = 0.5)))stat_smooth() für jede Faktorkombination ergänzt. Hier wird die Legende getrennt für das Geschlecht und die Floharten dargestellt. Die einzelnen Beobachtungen wurden ausgegraut.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = weight, y = jump_length, color = interaction(sex, animal),
linetype = interaction(sex, animal))) +
theme_minimal() +
geom_point2(show.legend = FALSE, alpha = 0.5) +
stat_smooth(method = "lm", se = FALSE, fullrange = TRUE) +
scale_color_manual(name = "Geschlecht & Flohart",
labels = c("Katze & männlich", "Hund & männlich", "Fuchs & männlich",
"Katze & weiblich", "Hund & weiblich", "Fuchs & weiblich"),
values = rep(c("#E69F00", "#56B4E9", "#009E73"), 2)) +
scale_linetype_manual(name = "Geschlecht & Flohart",
labels = c("Katze & männlich", "Hund & männlich", "Fuchs & männlich",
"Katze & weiblich", "Hund & weiblich", "Fuchs & weiblich"),
values = rep(c(1, 2), each = 3)) +
labs(x = "Gewicht der Flöhe [mg]", y = "Sprungweite in [cm]") +
theme(legend.position = "top",
legend.key.width = unit(1.3,"cm"),
legend.title = element_blank()) +
guides(linetype = guide_legend(override.aes = list(linewidth = 0.5)))stat_smooth() für jede Faktorkombination ergänzt. Hier wird die Legende zusammen für das Geschlecht und die Floharten dargestellt. Die Legende wurde dann auch über die Abbildung gesetzt. Die einzelnen Beobachtungen wurden ausgegraut.
Der Scaterplot lässt sich nict so gut in {tidyplots} darstellen, wenn wir dann noch eine Gleichung oder ein Modell ergänzen wollen. Da ist dann {ggplot} einfach besser. Hier also dann einmal den simplen Plot für den Zusammenhang von der Sprungweite und den Floharten. Oder andersherum, für die Darstellung von Scatterplots mit Regressionen würde ich dann nicht {tidyplots} nutzen.
Einfaktorieller Scatterplot
Wir brauchen für den Scatterplot nur die Funktion add_data_points() für die Darstellung der Punkte und dann noch die Funktion add_curve_fit() für die Geraden durch die Punkte. Der Rest dient dann dazu die Abbildung zu formatieren und hübscher zu machen.
R Code [zeigen / verbergen]
tidyplot(data = fac1_tbl,
x = weight, y = jump_length, color = animal) |>
add_data_points(show.legend = FALSE) |>
add_curve_fit(method = "lm", se = FALSE, fullrange = TRUE) |>
adjust_font(fontsize = 9) |>
adjust_x_axis_title("Flohgewicht in [mg]") |>
adjust_y_axis_title("Sprungweite in [cm]") |>
adjust_legend_title("Flohart") |>
adjust_legend_position("top") |>
rename_color_labels(new_names = c("dog" = "Hund", "cat" = "Katze", "fox" = "Fuchs")) |>
adjust_size(width = NA, height = NA) Zweifaktorieller Scatterplot
Der zweifaktorielle Scatterplot ist hier in {tidyplots} noch nicht möglich. Ich schaue aber immer mal wieder in {tidyplots} rein udn vielleicht ist es dann doch noch möglich. Es ist ja aber auch etwas gegen die Philosophie so komplexe Abbildungen zu bauen und die dann auch noch generisch einfach zu halten. Dann machen wir das dann einfach in {ggplot}.
Dann habe ich mich doch noch hingesetzt und einmal für dich ein Video gemacht, wie du dann einen Scatterplot mit Trendlinie und Formel in Excel erstellst. Das ganze macht dann nur als Video Sinn, denn sonst kannst du ja nicht nachvollziehen, was ich geklickt habe.
Wenn du mehr über die Regression lernen willst schau dir auch hier mal in den Kästen zum Zerforschen rein, da findest du dann noch mehr Inspiration aus anderen Abbildungen, die ich nachgebaut habe. Ich bin einmal über den Campus gelaufen und habe geschaut, welche Abbildungen auf den Postern verwendet werden und habe diese nachgebaut.
In diesem Zerforschenbeispiel wollen wir uns eine simple lineare Regression in einem Scatterplot anschauen. Das schöne an dem Beispiel ist, dass wir hier zum einen noch einen Pfeil einfügen wollen und dass wir nur einen Bereich darstellen wollen. Die Gerade fürht also nicht durch den gesamten Plot. Sonst haben wir dann noch die Herausforderung, dass wir einmal die Geradengleichung zusammen mit dem Bestimmtheitsmaß \(R^2\) ergänzen müssen.
Auch hier mache ich es mir etwas einfacher und erschaffe mir die Daten dann direkt in R. Ich baue mir also einen tibble() mit den ungefähren Werten aus der Abbildung. Das war ein wenig aufwendig, aber nach einigem Hin und Her passte dann auch die Werte zu der Abbildung.
R Code [zeigen / verbergen]
shoot_n_tbl <- tibble(n_in_shoot = c(2.5, 3.5, 3.9, 4.1, 4.2, 4.3 ,4.5, 4.7, 5.1, 5.1, 5.8),
freshmass = c(7.5, 9, 12.5, 11, 18, 16, 12, 17, 16, 20, 21))Dann rechnen wir auch schon die lineare Regression mit der Funktion lm() die uns dann die Koeffizienten der Geraden wiedergibt.
R Code [zeigen / verbergen]
shoot_n_fit <- lm(freshmass ~ n_in_shoot, data = shoot_n_tbl)Dann einmal die Koeffizienten mit der Funktion coef() ausgelesen. Den Rest brauchen wir hier nicht für die Abbildung.
R Code [zeigen / verbergen]
shoot_n_fit |> coef()(Intercept) n_in_shoot
-4.333333 4.353599 Aus den Koeffizienten baue ich mir dann auch die Geradengleichung einmal in R. Ich kann dann die Gleichung mit der Funktion geom_function() gleich in meine nachgebaute Abbildung ergänzen.
R Code [zeigen / verbergen]
shoot_n_func <- \(x){4.35 * x - 4.33}Ich berechne dann einmal das Bestimmtheitsmaß \(R^2\) mit der Funktion r2() aus dem R Paket {performance}. Wir sehen, ich habe die Werte recht gut abgelesen, dass passt ganz gut mit dem Bestimmtheitsmaß \(R^2\).
R Code [zeigen / verbergen]
shoot_n_fit |> r2()# R2 for Linear Regression
R2: 0.750
adj. R2: 0.722Und dann bauen wir uns schon die Abbildung 18.51 einmal nach. Der etwas aufwendigere Teil sind die Achsenbeschriftungen sowie die Ergänzung des Pfeils und der Beschriftung. Das verbraucht dann immer etwas mehr Code und Platz. Ich habe dann etwas die Achseneinteilung geändert und stelle nicht den ganzen Bereich dar. Es reicht auch vollkommen nur den Bereich zu visualisieren, der von Interesse ist. Daher beginnt dann meine \(x\)-Achse auch bei Zwei und nicht bei Null.
R Code [zeigen / verbergen]
shoot_n_tbl |>
ggplot(aes(n_in_shoot, freshmass)) +
theme_minimal() +
geom_point(size = 4, color = "red4") +
geom_function(fun = shoot_n_func, color = "black", size = 1, xlim = c(2.5, 6)) +
labs(x = "N in shoot [% DM]", y = TeX(r"(Shoot fresh mass \[g plant$^{-1}$\] - 17 DAP)")) +
scale_x_continuous(breaks = c(2, 3, 4, 5, 6), limits = c(2, 6)) +
scale_y_continuous(breaks = c(0, 5, 10, 15, 20, 25), limits = c(0, 25)) +
annotate("text", x = 2.5, y = 22, hjust = "left", color = "black", size = 4,
label = TeX(r"($y = 4.35 \cdot x - 4.33$)")) +
annotate("text", x = 2.5, y = 20, hjust = "left", color = "black", size = 4,
label = TeX(r"($R^2 = 0.75$)")) +
geom_curve(x = 3.5, y = 5.1, xend = 2.55, yend = 7,
arrow = arrow(length = unit(0.03, "npc"), type = "closed"),
curvature = -0.5) +
annotate("text", x = 3.6, y = 4.5, label = "Trt. with\n50% cattail",
hjust = "left", size = 4)In diesem Zerforschenbeispiel wollen wir uns eine simple lineare Regression in einem Scatterplot anschauen. Das stimmt nicht so ganz, den die Schwierigkeit liegt darin, dass es sich um zwei Scatterplots handelt. Klar, du kannst die beiden Abbildungen einfach getrennt erstellen und dann wäre gut. Ich zeige dir dann aber noch zwei weitere Möglichkeiten. Daher fangen wir mit der folgenden Abbildung einmal an. Wir haben hier zwei Scatterplots mit jeweils einer linearen Regression, dargestellt durch eine Gerade mit Regressionsgleichung, vorliegen. Hier brauchen wir dann mal ein paar mehr Zahlen, die ich mir dann aber so grob aus der Abbildung abgeleitet habe.
Wir laden als erstes wieder den Datensatz, den ich mir aus der obigen Abbildung erstellt habe. Wie immer beim Zerforschen habe ich nicht so genau drauf geachtet nur das die Zahlen so grob stimmen. Die Erstellung der Daten kann hier recht langwierig sein, aber hier geht es ja mehr um die Nutzung von ggplot. Also mach dir keinen Gedanken, wenn die Punkte nicht so perfekt passen.
R Code [zeigen / verbergen]
regression_tbl <- read_excel("data/zerforschen_regression_linear.xlsx") |>
mutate(type = factor(type, labels = c("Basil", "Oregano")))
regression_tbl # A tibble: 40 × 3
type washed unwashed
<fct> <dbl> <dbl>
1 Basil 0 0
2 Basil 10 15
3 Basil 20 18
4 Basil 30 32
5 Basil 40 36
6 Basil 50 52
7 Basil 60 59
8 Basil 70 72
9 Basil 80 85
10 Basil 100 105
# ℹ 30 more rowsDen folgenden Teil kannst du überspringen, wenn es dir um die Abbildung geht. Ich möchte in den zwei folgenden Tabs einmal die simple lineare Regression für die Abbildung mit dem Basilikum und einmal für das Oregano rechnen.
Wir erstellen uns einmal eine simple lineare Regression mit der Funktion lm(). Mehr zu dem Thema und die Maßzahlen der Güte einer linearen Regression wie das Bestimmtheitsmaß \(R^2\) findest du im Kapitel zur simplen linearen Regression. Deshalb hier nur die Durchführung und nicht mehr.
R Code [zeigen / verbergen]
fit <- lm(unwashed ~ washed, data = filter(regression_tbl, type == "Basil"))
fit |>
parameters::model_parameters() |>
select(Parameter, Coefficient)# Fixed Effects
Parameter | Coefficient
-------------------------
(Intercept) | 2.10
washed | 1.00R Code [zeigen / verbergen]
performance::r2(fit)# R2 for Linear Regression
R2: 0.994
adj. R2: 0.994Wir nutzen jetzt gleich die Koeffizienten aus der linearen Regression für die Erstellung der Geradengleichung.
Auch hier gilt wie im anderen Tab, dass wir uns einmal eine simple lineare Regression mit der Funktion lm() erstellen. Mehr zu dem Thema und die Maßzahlen der Güte einer linearen Regression wie das Bestimmtheitsmaß \(R^2\) findest du im Kapitel zur simplen linearen Regression. Deshalb hier nur die Durchführung und nicht mehr.
R Code [zeigen / verbergen]
fit <- lm(unwashed ~ washed, data = filter(regression_tbl, type == "Oregano"))
fit |>
parameters::model_parameters() |>
select(Parameter, Coefficient)# Fixed Effects
Parameter | Coefficient
-------------------------
(Intercept) | 8.17
washed | 0.99R Code [zeigen / verbergen]
performance::r2(fit)# R2 for Linear Regression
R2: 0.997
adj. R2: 0.996Wir nutzen jetzt gleich die Koeffizienten aus der linearen Regression für die Erstellung der Geradengleichung.
Soweit so gut. In den beiden obigen Tabs haben wir jetzt die Koeffizienten der Regressionsgleichung berechnet. Wir kriegen also aus der Funktion lm() die Steigung und den y-Achsenabschnitt (eng. Intercept). Damit können wir uns dann die beiden Funktionen für die Gerade der Basilikumdaten und der Oreganodaten bauen. Wir werden dann in ggplot mit der Funktion geom_function() die entsprechenden Gerade zeichnen.
R Code [zeigen / verbergen]
basil_func <- \(x){2.10 + 1.00 * x}
oregano_func <- \(x){8.17 + 0.99 * x}Du hast jetzt im Folgenden die Wahl zwischen drei Lösungen des Problems. Jede dieser Lösungen ist vollkommen in Ordnung und ich zeige dir hier nur die Möglichkeiten. Nimm einfach die Lösung, die dir am besten gefällt und passt. Was machen wir nun? Wir stellen einmal die beiden Abbildungen getrennt voneinander dar. Im Weiteren nutzen wir einmal die Funktion facet_wrap() um nach einem Faktor die Abbildungen aufzutrennen. Am Ende nutzen wir noch das R Paket patchwork um aus zwei Abbildungen dann eine schön annotierte Abbildung zu machen.
Der Kern der Abbildung 66.2 und Abbildung 66.3 ist die Funktion filter(). Wir bauen uns sozusagen zweimal einen Datensatz und leiten dann den Datensatz in die Funktion ggplot() weiter. Der Trick ist eigentlich, dass wir große Teile des Codes kopieren und dann für das Oregano wieder verwenden. Wenn du dir beide Chunks mal näher anschaust, wirst du große Änlichkeiten sehen. Im Prinzip musst du nur aufpassen, dass du jeweils die richtigen Geradenfunktionen einsetzt.
R Code [zeigen / verbergen]
filter(regression_tbl, type == "Basil") |>
ggplot(aes(x = washed, y = unwashed, color = type)) +
theme_minimal() +
geom_function(fun = basil_func, color = cbbPalette[2], linetype = 'dashed') +
geom_point(color = cbbPalette[2]) +
scale_x_continuous(name = TeX(r"(Iodine content in \textbf{unwashed} herbs $[\mu g\, l \, (100 g\, FM)^{-1}]$)"),
breaks = seq(0, 600, 150)) +
scale_y_continuous(name = TeX(r"(Iodine content in \textbf{washed} herbs $[\mu g\, l \, (100 g\, FM)^{-1}]$)"),
breaks = seq(0, 600, 150)) +
theme(legend.position = "none") +
annotate("text", x = 150, y = 100, hjust = "left", color = cbbPalette[2],
label = TeX(r"($y = 2.10 + 1.00 \cdot x;\; R^2 = 0.99$)")) Und nochmal die simple Regression in dem Scatterplot für das Oregano. Bitte beachte einmal die Beschreibungen im Code und du wirst sehen, dass hier sehr viel gleich zum obigen Codeblock ist. In dem Tab zum R Paket patchwork zeige ich dir dann noch die Möglichkeit ein Template zu erstellen und dann einiges an Zeilen an Code zu sparen. Aber es geht auch so.
R Code [zeigen / verbergen]
filter(regression_tbl, type == "Oregano") |>
ggplot(aes(x = washed, y = unwashed, color = type)) +
theme_minimal() +
geom_function(fun = oregano_func, color = cbbPalette[3], linetype = 'dashed') +
geom_point(color = cbbPalette[3]) +
scale_x_continuous(name = TeX(r"(Iodine content in \textbf{unwashed} herbs $[\mu g\, l \, (100 g\, FM)^{-1}]$)"),
breaks = seq(0, 900, 150)) +
scale_y_continuous(name = TeX(r"(Iodine content in \textbf{washed} herbs $[\mu g\, l \, (100 g\, FM)^{-1}]$)"),
breaks = seq(0, 900, 150)) +
theme(legend.position = "none") +
annotate("text", x = 150, y = 100, hjust = "left", color = cbbPalette[3],
label = TeX(r"($y = 8.17 + 0.99 \cdot x;\; R^2 = 0.99$)")) Hier brauchen wir jetzt das R Paket grid damit wir am Anschluss noch unsere Abbildungen mit den Gleichungen beschriften können. Die Idee ist eigentlich recht simple. Wir haben den Faktor type und nutzen die Funktion facet_wrap() um nach diesem Faktor zwei Abbildungen zu bauen. Unser Faktor hat zwei Level Basilikum und Oregano und deshalb erhalten wir auch zwei Subbplots. Wir können dann auch entscheiden, wie die Abbildungen angeordnet werden sollen, aber da bitte einmal bei Hilfeseite von facet_wrap(). Sonst sit alles gleich wie im ersten Tab. Also bitte nochmal da schauen.
R Code [zeigen / verbergen]
ggplot(data = regression_tbl, aes(x = washed, y = unwashed,
color = type)) +
theme_minimal() +
scale_color_okabeito() +
geom_function(data = filter(regression_tbl, type == "Basil"),
fun = basil_func, color = cbbPalette[2], linetype = 'dashed') +
geom_function(data = filter(regression_tbl, type == "Oregano"),
fun = oregano_func, color = cbbPalette[3], linetype = 'dashed') +
geom_point() +
facet_wrap(~ type) +
scale_x_continuous(name = TeX(r"(Iodine content in \textbf{unwashed} herbs $[\mu g\, l \, (100 g\, FM)^{-1}]$)"),
breaks = seq(0, 900, 150)) +
scale_y_continuous(name = TeX(r"(Iodine content in \textbf{washed} herbs $[\mu g\, l \, (100 g\, FM)^{-1}]$)"),
breaks = seq(0, 900, 150)) +
theme(legend.position = "none")
grid::grid.text(TeX(r"($y = 2.10 + 1.00 \cdot x;\; R^2 = 0.99$)"),
x = 0.2, y = 0.2, just = "left", gp = grid::gpar(col = cbbPalette[2]))
grid::grid.text(TeX(r"($y = 8.17 + 0.99 \cdot x;\; R^2 = 0.99$)"),
x = 0.65, y = 0.2, just = "left", gp = grid::gpar(col = cbbPalette[3]))Und dann sind wir auch schon fertig. Gut, das ist jetzt mit der Regressionsgleichung etwas fricklig, aber das ist es meistens, wenn du viel auf einmal darstellen willst. Vielleicht ist dann noch die Idee mit dem R Paket patchwork im nächsten Tab hilfreich.
Jetzt drehen wir nochmal frei und holen alles raus was geht. Wir nutzen zum einen das R Paket patchwork um zwei Abbildungen miteinander zu verbinden. Prinzipiell geht das auch mit dem R Paket grid und der Funktion grid.arrange(), aber dann wird das hier sehr voll. Wir nutzen am Ende nur eine Funktion aus dem Paket grid um wiederum die \(x\)-Achse schön hinzukriegen. Als erstes wollen wir uns aber ein Template in ggplot bauen, dass wir dann mit einem neuen Datensatz durch den Operator %+% mit einem neuen Datensatz versehen können.
Im Folgenden stecken wir den ganzen Datensatz in eine ggplot()-Funktion. Später wählen wir dann mit filter() die beiden Kräuterdatensätze aus. Wir definieren in dem Template alles, was wir auch für die beiden Abbildungen brauchen würden. Das spart dann etwas an Zeilen Code. Manchmal dann aber auch nicht ganz so viel, denn wir müssen für die einzelnen Datensätze dann doch noch einiges anpassen.
R Code [zeigen / verbergen]
p_template <- ggplot(regression_tbl, aes(x = washed, y = unwashed,
color = type)) +
theme_minimal() +
geom_point() +
scale_x_continuous(name = "",
breaks = seq(0, 900, 150), limits = c(0, 900)) +
scale_y_continuous(name = TeX(r"(\textbf{Washed} herbs $[\mu g\, l \, (100 g\, FM)^{-1}]$)"),
breaks = seq(0, 900, 150), limits = c(0, 900)) +
theme(legend.position = "none")Wir nutzen jetzt das p_template und ergänzen den gefilterten Datensatz für das Basilikum mit dem Operator %+%. Dann wählen wir noch die passende Farbe über die Option order = 1 aus und ergänzen die Geradengleichung sowie den Titel für die Abbildung.
R Code [zeigen / verbergen]
p_basil <- p_template %+%
filter(regression_tbl, type == "Basil") +
scale_color_okabeito(order = 1) +
geom_function(fun = basil_func, color = cbbPalette[2],
linetype = 'dashed') +
annotate("text", x = 150, y = 100, hjust = "left", color = cbbPalette[2],
label = TeX(r"($y = 2.10 + 1.00 \cdot x;\; R^2 = 0.99$)")) +
ggtitle("Basil")Das Ganze dann nochmal für das Oregano, aber hier entfernen wir die \(y\)-Achse. Wir brauchen nur eine auf der linken Seite. Das ist auch der Grund warum wir keine \(x\)-Achse benannte haben, dass machen wir dann über die beiden Plots zusammen ganz am Ende. Auch hier ergänzen wir dann die Gweradengleichung sowie den Titel der Abbildung.
R Code [zeigen / verbergen]
p_oregano <- p_template %+%
filter(regression_tbl, type == "Oregano") +
scale_color_okabeito(order = 2) +
geom_function(fun = oregano_func, color = cbbPalette[3],
linetype = 'dashed') +
theme(axis.title.y = element_blank()) +
annotate("text", x = 150, y = 100, hjust = "left", color = cbbPalette[3],
label = TeX(r"($y = 8.17 + 0.99 \cdot x;\; R^2 = 0.99$)")) +
ggtitle("Oregano")Jetzt geht es los mit dem Zusammenbauen. Wir können dazu einfach das + nutzen. Wenn du mehr wissen willst, was du noch ändern kannst, dann schaue einmal das Tutorium Adding Annotation and Style für das R Paket patchworkan. Da kannst du dann auch die Schriftgröße und weiteres ändern. Wir müssen dann ganz am Ende nochmal mit der Funktion grid.draw() die gemeinsame \(x\)-Achse ergänzen. Am Ende habe ich noch die Achsenbeschriftungen gekürzt und die Informationen in den Titel mit der Funktion plot_annotation geschoben. Dann habe ich noch die Subplots mit einem Buchstaben versehen. Und dann sind wir auch schon fertig.
R Code [zeigen / verbergen]
p_basil + p_oregano +
plot_annotation(title = 'Iodine content in herbs',
subtitle = 'The iodine content is measured in washed and unwashed herbs',
caption = 'Disclaimer: The measurement has been done in freshmatter',
tag_levels = 'A')
grid::grid.draw(grid::textGrob(TeX(r"(\textbf{Unwashed} herbs $[\mu g\, l \, (100 g\, FM)^{-1}]$)"),
y = 0.07))ggplot nachgebaut. Die Abbildung A zeigt die Punkte und die Geradengleichung für das Basilikum. Die Abbildung B die entsprechenden Informationen für das Oregano. Die beiden Achsenbeschriftungen wurden gekürzt und die Informationen in den Titel übernommen.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
R Code [zeigen / verbergen]
ggsave("my_ggplot_simple_regression.png", width = 5, height = 3)18.4.4 Histogramm
Wozu nutzen wir das Histogramm? Wir brauchen das Histogramm um die Verteilung der Messwerte \(y\) abzuschätzen. Daher wie sind unsere Sprungweiten, Anzahlen oder Gewichte unserer Hunde- und Katzenflöhe verteilt. Zuerst brauchen wir aber viele Beobachtungen. Wir brauchen für ein anständiges Histogramm, wo du auch was erkennen kannst, mindestens 20 Beobachtung pro Gruppe. Hier ist das pro Gruppe sehr wichtig. Zwar haben wir auch in unseren Hunde- und Katzenflohdaten vierzehn Beobachtungen, aber nur sieben pro Gruppe! Da können wir dann mit einem Histogramm nicht viel erkennen und dann nutzen wir den Boxplot für die Abschätzung der Verteilung. Häufig irritiert bei einem Histogramm auch, dass wir auf der x-Achse die Werte der y-Achse darstellen und dann auf der y-Achse des Histogramms die Anzahlen zählen. Aber dazu dann gleich mehr in den folgenden Tabs zur theoretischen Betrachtung, einem Beispiel und der Umsetzung in {ggplot}. Ein Histogramm nutzen wir eigentlich in einer laufenden Analyse als ein statistisches Tool und berichten es eher selten.
Für die Erstellung eines Histogramm müssen wir unterscheiden, ob wir als Outcome etwas zählbares vorliegen haben. Also ob unser Outcome Kategorien hat. Wir zählen die Anzahl an Haaren eines Flohbeins oder aber die Noten von Schülern. Wir können aber auch andere Kategorien vorliegen haben, aber es müssen schon ein paar sein. Mit ein paar meine ich dann mehr als fünf Kategorien. Ein Notenspiegel macht ja auch nur Sinn, da wir da gut zehn Notenschritte drin haben. Im Folgenden siehst du einmal eine Abbildung mit den Kategorien A bis I. Jetzt zählen wir wie oft kommt A vor, wie oft kommt B vor und so weiter. Die Anzahlen tragen wir dann als Balken ein. Dann haben wir die absoluten Anzahlen gezählt. Wenn wir aber Histogramme mit unterschiedlichen Beobachtungen vergleichen wollen, dann macht es mehr Sinn sich die relativen Häufigkeiten anzuschauen. In unserem Fall haben wir achtzehn Beobachtungen vorliegen, also bedeutet eine Beobachtung \(1/18 = 0.055\) relativen Anteil.
Wenn wir keine Kategorien vorliegen haben, dann müssen wir uns für unser Outcome welche Überlegen. Das heißt wir nutzen das so genannte bining (deu. eindosen, ungebräuchlich). Wenn du das Gewicht von Flöhen misst, dann hast du Kommazahlen und damit kontinuierliche Daten vorliegen. Damit unterscheiden sich alle deine Messwerte vermutlich. Deshalb fasst du “gleiche” Werte zusammen. Meistens machen wir das, indem wir Beobachtungen in zwischen zwei Zahlen als eine Kategorie zählen. Wie da die Grenzen liegen, ist immer unterschiedlich und hängt von der Fragestellung ab.
Betrachten wir einmal die Erstellung eine Histogramms für einen Endpunkt mit Kategorien. Dafür habe ich mir einmal die Boniturnoten für achtzehn Hundeflöhe in der folgenden Tabelle ausgedacht. Wir brauchen eben mehr Daten als wir in den ursprünglichen Hunde- und Katzenflohdaten vorliegen haben. Jetzt wollen wir uns einmal die Verteilung der Boniturnoten anschauen.
| 3 | 7 | 2 | 4 | 6 | 4 | 4 | 5 | 2 | 3 | 5 | 3 | 3 | 6 | 4 | 3 | 1 | 2 |
In der folgenden Abbildung siehst du einmal die Verteilung der achtzehn Boniturnoten der Hundeflöhe dargestellt. Wir sehen sofort, dass wir am meisten die Note 3 vergeben haben. Wir haben nämlich fünfmal die Note 3 an unseren Flöhen festgestellt. Die Boniturnote 5 haben wir dann an zwei Flöhen erhoben. Da wir achtzehn Flöhe haben, entspricht jede Anzahl dann \(5.5%\) auf der relativen Skala.
Schauen wir uns im zweiten Beispiel einmal das Gewicht von achtzehn Hundeflöhen an. Hier siehst du, dass wir Kommazahlen also kontinuierliche Daten vorliegen haben. Keine der Zahlen ist doppelt, so dass wir hier dann keine Balken hochzählen können. Damit wir das aber können, bilden wir Zahlenräume in denen wir die Gewichte zusammenfassen.
| 2 | 3 | 3.8 | 2.8 | 2.7 | 7.4 | 4.1 | 4.9 | 2.1 | 1.7 | 5.9 | 6.1 | 3.3 | 4 | 0.7 | 5.2 | 3.1 | 4.3 |
In der folgenden Abbildung siehst du einmal die Zusammenfassung unserer Flohgewichte in die Zahlenräume der Größe \(1mg\). Gewichte, die in den Bereich \(x \pm 0.5\) fallen, werden dann in einem Balken zusammengefasst. Wir haben zum Beispiel in dem Bereich mit \(x = 2\) und somit \(2 \pm 0.5\) dann die drei Werte 1.7, 2.0 und 2.1 vorliegen. Wir zeichnen einen Balken der Höhe drei. Ebenso haben wir in dem Bereich \(5.5 < x \leq 6.5\) zwei Beobachtungen vorliegen. Wir zeichnen hier einen Balken der Höhe zwei. Die Entscheidung wie weit der Zahlenraum zum zusammenfassen reichen soll, ist meist ein Ausprobieren. Das ist natürlich bei der händischen Erstellung problematisch.
Für die Erstellung eines Histogramms mit {ggplot} nutzen wir unsere Spieldaten aus dem Tab zur händischen Erstellung eines Histogramms. Nun schauen wir uns jetzt einmal achtzehn Hundflöhe an und bestimmen die Boniturnote, dargestellt in der Spalte grade. Darüber hinaus bestimmen wir auch noch das mittlere Gewicht der Flöhe auf dem jeweiligen Hund, dargestellt in der Spalte weight.
R Code [zeigen / verbergen]
flea_hist_tbl <- tibble(grade = c(1, 2, 2, 2, 3, 3, 3, 3, 3,
4, 4, 4, 4, 5, 5, 6, 6, 7),
weight = c(0.7, 1.7, 2.0, 2.1, 2.7,
2.8, 3.0, 3.1, 3.3, 3.8,
4.0, 4.1, 4.3, 4.9, 5.2,
5.9, 6.1, 7.4))In {ggplot} können wir ein Histogramm mit der Funktion geom_histogram() erstellen. Dabei ist es dann immer etwas verwirrend, dass wir unser Outcome als \(y\) dann auf der x-Achse darstellen. Wir können die Option binwidth nutzen, um zu entscheiden, wie viele Noten in einem Balken zusammengefasst werden sollen. Sinnvoll ist natürlich hier eine binwidth von 1, da wir pro Balken eine Boniturnote zählen wollen.
R Code [zeigen / verbergen]
ggplot(data = flea_hist_tbl, aes(x = grade)) +
geom_histogram(binwidth = 1, fill = "gray", color = "black") +
theme_minimal() +
labs(x = "Boniturnote", y = "Anzahl") Anders sieht es für kontinuierliche Variablen mit Kommazahlen aus. Schauen wir uns das Gewicht der Flöhe an, so sehen wir, dass es sehr viele Zahlen gibt, die nur einmal vorkommen. Hier können wir dann mit binwidth den Bereich einstellen, in denen die Zahlen fallen sollen. Auch hier ist es immer ein Gefummel, wenn wir zu wenige Beobachtungen vorliegen haben. Die beste Bandbreite für die Balken zu finden, ist immer ein Ausprobieren.
Wir können auch auf den folgenden Daten ein Histogramm in {tidyplots} erstellen. Dafür nutzen wir wieder folgenden kleinen Datensatz. Hier haben wir dann wieder einmal die Boniturdaten, die wir dann einfach in einem Histogramm darestellen können.
R Code [zeigen / verbergen]
flea_hist_tbl <- tibble(grade = c(1, 2, 2, 2, 3, 3, 3, 3, 3,
4, 4, 4, 4, 5, 5, 6, 6, 7))Dann erhalten wir auch schon ein schnelles Histogramm. Eigentlich brauchen wir hier nur zwei Zeilen Code. Der Rest dient nur der Anpassung hier in dem Skript. Wenn du mehr willst, dann musst du nochmal bei {ggplot} schauen. MIr persönlich ist das zu wenig, aber für den alltäglichen schnellen Gebrauch reicht es.
18.4.5 Density Plot
Eine weitere Möglichkeit sich eine Verteilung anzuschauen, ist die Daten nicht als Balkendiagramm sondern als Densityplot - also Dichteverteilung - anzusehen. Im Prinzip verwandeln wir die Balken in eine Kurve. Damit würden wir im Prinzip unterschiedliche Balkenhöhen ausgleichen und eine “glattere” Darstellung erreichen. Wir wir aber gleich sehen werden, benötigen wir dazu eine Menge an Beobachtungen und auch dann ist das Ergebnis eventuell nicht gut zu interpretieren. Eine händische Darstellung ist nicht möglich, wir machen Dichteverteilungen nur in R aber nicht selber auf einem Blattpapier.
Anbei einmal die Darstellung des Densityplots mit einem Histogramm im Hintergrund. Auf der \(y\)-Achse ist die Dichte als schwer zu interpretieren angeben. Im Prinzip interpretieren wir die Dichte nicht direkt sondern schätzen an der Kurve die Verteilung der Daten ab. Wie die Dichtekurve entsteht, ist hier nicht von Belang. Wir nutzen die Dichtekurve auch häufig zusammen mit anderen Abbildungen.
Schauen wir uns einmal die Densityplots in {ggplot} an. Wir nutzen dazu die Funktion geom_density(). Die Werte der Dichte interpretieren wir nicht direkt sondern betrachten nur die Form der Dichtekurve. In unserem Fall sieht die Kurve sehr nach einer Normalverteilung aus. Um die ganze Kurve zu sehen muss ich nochmal an xlim() drehen und den x-Achsenbereich erhöhen.
R Code [zeigen / verbergen]
ggplot(data = flea_hist_tbl, aes(x = grade)) +
geom_density(fill = "#CC79A7", color = "#CC79A7", alpha = 0.3) +
theme_minimal() +
xlim(-1, 10) +
labs(x = "Boniturnote", y = "Dichte")18.4.6 Mosaicplot
Der Mosaicplot ist ein eher seltener Plot. Wir nutzen ihn aber häufig in der Fragebogenanalyse oder aber in den Gesundheitswissenschaften. Da wir dann aber immer wieder Überschneidungen haben, wollen wir hier auch den Mosaicplot lernen. Was macht der Mosaicplot? Wir können mit dem Mosaicplot zwei Variablen, die nur aus Kategorien bestehen visualisieren. Ein Mosaicplot macht dabei für nur eine Gruppe keinen Sinn. Wir brauchen immer ein \(X\) mit mindestens zwei Gruppen sowie ein \(Y\) mit mindestens zwei Gruppen. Betrachten wir also einmal den Mosaicplot theoretisch, dann einmal händisch am Beispiel der mit Flohschnupfen infizierten Hunde- und Katzenflöhe sowie die Umsetzung in {ggplot}.
{tidyplots}
Das R Paket {tidyplots} bietet auch noch andere Alternativen für die Darstellung von Anteilen in deinen Daten unter Visualisierung von Anteilen. Vielleicht findest du da auch noch eine bessere Abbildung als hier mit dem Mosaicplot.
Ein Mosaicplot ist nichts anderes als die Visualisierung einer 2x2 Kreuztabelle. Daher im Folgenden einmal eine typische 2x2 Kreuztabelle als Abbildung. Wir schreiben in die Kästen die jeweiligen Anzahlen des Auftretens und berechnen dann die Anteile in der Spalte. Hier ist schon die erste Entscheidung zu treffen. Wie wollen wir die Anteile berechnen? Auf der ganzen Tabelle und daher durch \(n\) teilen? Oder aber über die Zeilen und damit über die Kategorien von \(Y\)? Häufig wollen wir wissen, wie sich die Gruppen in \(X\) im Bezug auf \(Y\) unterscheiden. Daher werden die Gruppen in die Spalten geschrieben und wir berechnen die Anteile spaltenweise. In der folgenden 2x2 Tafl siehst du einmal die Erstellung für den spaltenweisen Anteilsvergleich.
Der Mosaicplot ist jetzt nichts anderes als die Visualisierung der obigen theoretischen 2x2 Kreuztabelle. Dabei kippen wir einmal die Beschriftung der Spalten von oben nach unten, da wir es ja jetzt mit einer Abbildung zu tun haben und nicht mit einer Abbildung. Der eigentliche Witz eines Mosaicplot ist jetzt die Flächen spaltenweise den berechneten Anteilen anzupassen. Auf diese Weise können wir die Anteile der Gruppen sofort visuell erfassen.
Für unsere händische Erstellung des Mosaicplots brauchen wir erstmal eine 2x2 Kreuztabelle. Hierz nutzen wir den Anteil der Flöhe mit Flohschnupfen in unseren Hunde- und Katzenflohdaten. Dabei wollen wir wissen, ob sich die beiden Tierarten als Gruppen voneinander unterscheiden. Damit ist unser \(Y\) der Infektionsstatus (ja/nein) und unser \(X\) die beiden Tierarten (dog/cat). Es ergibt sich dann die folgende 2x2 Kreuztabelle. Beachte auch die entsprechenden Randsummen, die auch noch eine Information über die Daten beinhalten. So finden wir nämlich mehr gesunde Tiere in unseren Daten als kranke Tiere über die beiden Tierart hinweg.
Leider sind die Prozentzahlen in der 2x2 Kreuztabelle schwer visuell zu unterscheiden. Deshalb zeichnen wir den Mosaicplot so, dass die Flächen die Anteile in den Spalten widerspiegeln. So ist die Fläche von 43% kranken Hundeflöhen fast doppelt so groß wie die Fläche der 29% kranken Katzen. Daher lassen sich so schnell die Gruppen miteinander vergleichen. Wir sehen hier sehr schön, dass weit weniger Katzenflöhe mit Flohschnupfen infiziert sind als Hundeflöhe.
Für unseren Mosaicplot in R nutzen wir das R Paket {ggmosaic} welches uns dann ermöglicht einen Mosaicplot in {ggplot} zu erstellen. Zuerst müssen wir uns aber noch die Daten zusammenbauen. Dafür brauchen wir die Spalten infected und animal einmal als Faktoren und nicht als Zahlen oder Wörter. Um die 2x2 Tabelle in R in der richtigen Orientierung vorliegen zu haben, müssen wir nochmal einen kleinen Klimmzug über mutate() nehmen. Wir wandeln die Variable infected in einen Faktor um und sortieren die Level entsprechend, so dass wir die richtige Ordnung wie später im Mosaicplot haben.
R Code [zeigen / verbergen]
flea_dog_cat_mosaic_tbl <- fac1_tbl |>
mutate(animal = factor(animal, levels = c("dog", "cat")),
infected = factor(infected, levels = c(0, 1))) |>
na.omit()Betrachten wir jetzt einmal die 2x2 Kreuztabelle der beiden Spalten animal und infected mit der Funktion tabyl() aus dem R Paket {janitor} um einen Überblick zu erhalten.
R Code [zeigen / verbergen]
flea_dog_cat_mosaic_tbl %>%
tabyl(infected, animal) infected dog cat
0 4 5
1 3 2Dannn können wir uns einmal den Mosaicplot in {ggplot} anschauen. Wir nutzen dafür das R Paket {ggmosaic} mit der Funktion geom_mosaic(). Abbildung 18.70 zeigt den Mosaic Plot für die Variable animal und infected. Die unterschiedlich großen Flächen bilden die Verhältnisse der 2x2 Tabelle ab. So sehen wir, dass es mehr uninfizierte Flöhe als infizierte Tiere Flöhe. Am meisten gibt es uninfizierte Katzenflöhe.
R Code [zeigen / verbergen]
ggplot(data = flea_dog_cat_mosaic_tbl) +
theme_minimal() +
geom_mosaic(aes(x = product(infected, animal), fill = animal)) +
theme(legend.position = "none")18.4.7 Dotplot, Beeswarm und Raincloud Plot
Wenn wir weniger als fünf Beobachtungen haben, dann ist meist ein Boxplot verzerrend. Wir sehen eine Box und glauben, dass wir viele Datenpunkte vorliegen haben. Bei 3 bis 7 Beobachtungen je Gruppe bietet sich der Dotplot als eine Lösung an. Wir stellen hier alle Beobachtungen als einzelne Punkte dar. Wie erstellen wir nun einen Dotplot in R? Wir nutzen dazu die Funktion geom_dotplot() wie folgt.
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = animal, y = grade, fill = animal)) +
geom_dotplot(binaxis = "y", stackdir = "center") +
theme_minimal() +
labs(x = "Tierart", y = "Boniturnote [1-9]") Wir können uns mit dem Dotplot auch kontinuierliche Daten, wie die Sprungweite anschauen. Dann hilft es immer, sich auch den Mittelwert und die Standardabweichung mit einzuzeichnen. Ich nutze hierzu die Funktion stat_summary() für die Mittelwerte und die Standardabweichung. Da die Fehlerbalken genau eine Standardabweichung lang sein sollen, wähle ich noch die Option fun.args = list(mult=1) aus.
R Code [zeigen / verbergen]
ggplot(fac1_tbl, aes(x = animal, y = jump_length, fill = animal)) +
theme_minimal() +
geom_dotplot(binaxis = 'y', stackdir = 'center') +
stat_summary(fun.data = mean_sdl, fun.args = list(mult=1),
geom = "errorbar", color = "black", width = 0.1) +
stat_summary(fun = "mean", geom="point", color="black", size = 5) +
labs(x = "Tierart", y = "Sprungweite [cm]") +
theme(legend.position = "none") +
scale_x_discrete(labels = c("Hund", "Katze")) In Abbildung 18.71 sehen wir den Dotplot aus der Datei flea_dog_cat.xlsx. Auf der x-Achse sind die Level des Faktors animal dargestellt und auf der y-Achse die Notenbewertung grade der einzelnen Hunde und Katzen. Die Funktion geom_dotplot() erschafft das Layer für die Dots bzw. Punkte. Wir müssen in der Funktion noch zwei Dinge angeben, damit der Plot so aussieht, dass wir den Dotplot gut interpretieren können. Zum einen müssen wir die Option binaxis = y wählen, damit die Punkte horizontal geordnet werden. Zum anderen wollen wir auch, dass die Punkte zentriert sind und nutzen dafür die Option stackdir = center.
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl, aes(x = animal, y = grade, fill = animal)) +
geom_dotplot(binaxis = "y", stackdir = "center") +
stat_summary(fun = median, fun.min = median, fun.max = median,
geom = "crossbar", width = 0.5) +
theme_minimal() +
labs(x = "Tierart", y = "Boniturnote [1-9]") Nun macht es wenig Sinn bei sehr wenigen Beobachtungen noch statistische Maßzahlen mit in den Plot zu zeichnen. Sonst hätten wir auch gleich einen Boxplot als Visualisierung der Daten wählen können. In Abbildung 18.73 sehen wir die Ergänzung des Medians. Hier müssen wir etwas mehr angeben, aber immerhin haben wir so eine Idee, wo die “meisten” Beobachtungen wären. Aber auch hier ist Vorsicht geboten. Wir haben sehr wenige Beobachtungen, so dass eine Beobachtung mehr oder weniger große Auswirkungen auf den Median und die Interpretation hat.
Dann möchte ich hier den Beeswarm als eine Alternative zu dem Dotplot vorstellen. Insbesondere wenn du sehr viele Beobachtungen hast, dann hat der Beeswarm bessere Eigenschaften als der Dotplot. Es gibt hier auch die tolle Hilfeseite zu Beeswarm plot in ggplot2 with geom_beeswarm() und natürlich noch die Möglichkeit ein Violin Plot zu ergänzen. Auch hier dann mal bei der Hilfeseite Violin plot with data points in ggplot2 schauen. In Abbildung 18.74 siehst du dann einmal das Alter und die Körpergröße für die beiden Geschlechter in den Gummibärchendaten aufgeteilt.
R Code [zeigen / verbergen]
ggplot(data = gummi_tbl, aes(x = gender, y = age,
color = gender)) +
geom_beeswarm() +
theme_minimal() +
labs(x = "Geschlecht", y = "Alter in Jahren") +
theme(legend.position = "none")
ggplot(data = gummi_tbl, aes(x = gender, y = height,
color = gender)) +
geom_beeswarm() +
theme_minimal() +
labs(x = "Geschlecht", y = "Körpergröße in cm") +
theme(legend.position = "none")Und dann bringen wir in der Abbildung 18.75 mal verschiedene Abbildungen zusammen mit dem R Paket{gghalves}. Wir können mit {gghalves} halbe Plots erstellen und diese dann miteinander kombinieren. Damit packen wir dann in die Mitte Boxplots. Links von den Boxplots zeichnen wir die einzelnen Beobachtungen als Punkte mit stat_dots() und die Verteilung der einzelnen Beobachtungen zeichnen wir mit dem R Paket {ggdist}. Das Tutorium Visualizing Distributions with Raincloud Plots liefert dann noch mehr Anleitungen für noch mehr Varianten. Wie du aber schon am R Code siehst, ist das eine etwas komplexere Abbildung geworden.
R Code [zeigen / verbergen]
ggplot(gummi_tbl, aes(x = gender, y = age, color = gender)) +
theme_minimal() +
stat_halfeye(adjust = 0.5, width = 0.4, .width = 0,
justification = -0.3, point_colour = NA) +
geom_boxplot(width = 0.15, outlier.shape = NA) +
stat_dots(side = "left", justification = 1.12, binwidth = .25) +
coord_cartesian(xlim = c(1.2, 1.9), clip = "off") +
labs(x = "Geschlecht", y = "Alter in Jahren") +
scale_color_okabeito() +
theme(legend.position = "none")
ggplot(gummi_tbl, aes(x = gender, y = height, color = gender)) +
theme_minimal() +
stat_halfeye(adjust = 0.5, width = 0.4, .width = 0,
justification = -0.3, point_colour = NA) +
geom_boxplot(width = 0.15, outlier.shape = NA) +
stat_dots(side = "left", justification = 1.12, binwidth = .25) +
coord_cartesian(xlim = c(1.2, 1.9), clip = "off") +
labs(x = "Geschlecht", y = "Körpergröße in cm") +
scale_color_okabeito() +
theme(legend.position = "none"){gghalves}-Plot als Kombination vom Dotplot, Boxplot sowie Densityplot. Mit der Art der Abbildung spart man sich dann drei Abbildungen. Hier haben wir dann alle Informationen über die Körpergröße sowie dem Alter in Abhängigkeit vom Geschlecht in einer Abbildung.
18.4.8 Violinplot
Eine etwas neuere Abbildung, die eigentlich gar so neu ist, ist der Violinplot. Der Violinplot verbindet im Prinzip den Boxplot zusammen mit dem Densityplot. Wir haben am Ende eben eine Verteilung der Daten visualisiert. Wir schauen uns aber nicht wie in einem Histogramm die Werte als Balken an, sondern glätten die Balken zu einer Kurve. Wie immer gibt es auch ein Tutorium mit noch mehr Hilfe unter ggplot2 violin plot : Quick start guide - R software and data visualization. Wir schauen uns jetzt mal die Erstellung von Violinplots in verschiedenen Kombinationen mit anderen Abbildungen an.
Da ein Violinplot keinen Median oder sonst eine deskriptive Zahl beinhaltet, müssen wir uns eine Funktion erstellen, die den Mittelwert plusminus Standardabweichung wiedergibt. Die Funktion rufen wir dann innerhalb von ggplot() auf und erhalten dann den Mittelwert und Standardabweichung als einen Punkt mit zwei Linien dargestellt.
R Code [zeigen / verbergen]
data_summary <- function(y) {
m <- mean(y)
ymin <- m - sd(y)
ymax <- m + sd(y)
return(c(y = m, ymin = ymin, ymax = ymax))
}In der Abbildung 18.76 siehst du einmal einen Violinplot mit der Funktion geom_violin(). Ich nutze eigentlich immer die Option trim = FALSE damit die Violinplots nicht so abgeschnitten sind. Der Nachteil ist dann, dass eventuell Werte angezeigt werden, die in den Daten nicht vorkommen, aber das ist auch sonst der Fall bei anderen Densityplots. Hier sieht es dann einfach besser aus und deshalb nutze ich es gerne. Durch die Funktion stat_summary() ergänze ich dann noch den Mittelwert und die Standardabweichung.
R Code [zeigen / verbergen]
ggplot(data = gummi_tbl, aes(x = gender, y = height,
color = gender)) +
theme_minimal() +
geom_violin(trim = FALSE) +
theme(legend.position = "none") +
stat_summary(fun.data = data_summary) +
labs(x = "Geschlecht", y = "Körpergröße in cm") +
scale_color_okabeito()In der nächsten Abbildung 18.77 siehst du dann die Implementierung des Violinplot aus dem R Paket {see} mit der Funktion geom_violindot(). Auch hier trimme ich nicht die Spitzen der Violinplots und vergrößere die Punkte in dem Dotplot. Die Stärke von der Funktion ist der halbe Violinplot zusammen mit einem Dotplot, wir haben dann beides. Zum einen können wir die Werte sehen, wie sie sich in einem Histogramm anordnen würden. Zum anderen haben wir dann auch den Densityplot als geglättete Kurve daneben. Ich habe auch hier den Mittelwert und die Standardabweichung ergänzt, musste aber die Position in der \(x\)-Richtung etwas verschieben.
R Code [zeigen / verbergen]
ggplot(data = gummi_tbl, aes(x = gender, y = height,
color = gender)) +
theme_minimal() +
geom_violindot(dots_size = 4, trim = FALSE) +
theme(legend.position = "none") +
stat_summary(fun.data = data_summary,
position = position_nudge(x = 0.1)) +
labs(x = "Geschlecht", y = "Körpergröße in cm") +
scale_color_okabeito()Du musst natürlich keine Funktion aus einem anderen Paket nehmen. Der Violinplot lässt sich als ganzer Plot auch mit dem Dotplot kombinieren. Wir plotten als erstes in den Hintergrund den Violinplot, ergänzen dann darüber den Dotplot und zeichnen ganz zum Schluss noch die Mittelwerte und die Standardabweichung ein. So erhalten wir dann die Abbildung 18.78.
R Code [zeigen / verbergen]
ggplot(data = gummi_tbl, aes(x = gender, y = height,
fill = gender)) +
theme_minimal() +
geom_violin(alpha = 0.5, trim = FALSE) +
geom_dotplot(binaxis = "y", stackdir = "center",
dotsize = 0.5) +
stat_summary(fun.data = data_summary, size = 1, linewidth = 2) +
theme(legend.position = "none") +
labs(x = "Geschlecht", y = "Körpergröße in cm") +
scale_fill_okabeito()In der Abbildung 18.79 sehen wir dann anstatt von einem Dotplot einen Beeswarm. Wie immer ist es Geschmackssache welcher Plot einem mehr zusagt. Der Beeswarm wirkt immer etwas kompakter und so lässt sich hier auch mehr erkennen. Das Problem ist eher, dass die Punkte sich nicht füllen lassen, so dass wir dann doch ein recht einheitliches Bild kriegen. Hier muss ich dann immer überlegen, was ich dann wie einfärben will.
R Code [zeigen / verbergen]
ggplot(data = gummi_tbl, aes(x = gender, y = height,
fill = gender, color = gender)) +
theme_minimal() +
geom_violin(alpha = 0.5, trim = FALSE) +
geom_beeswarm() +
theme(legend.position = "none") +
stat_summary(fun.data = data_summary, size = 1, linewidth = 2,
color = "black") +
labs(x = "Geschlecht", y = "Körpergröße in cm") +
scale_fill_okabeito() +
scale_color_okabeito()18.5 Weitere Optionen in {ggplot}
Du findest dann auch weitere Optionen in {ggplot} im Kapitel zum {ggplot} Cookbook. Ich habe einen Teil der Optionen dann in das Programmieren ausgelagert, da wir dann dort mehr machen können und dieses Kapitel nicht zu voll wird. Es ist auch so, dass du in allen anderen Kapiteln zur Anwendung und statistischen Analyse dann entsprechende Visualisierungen in {ggplot} findest. Du musst dann immer schauen, was zu deiner wissenschaftlichen Fragestellung passt. Ich habe hier nicht alles aufgenommen, da es dann immer dieses Kapitel gesprengt hat. Hier geht es dann eben um die explorative Datenanalyse und nicht um das statistische Modellieren.