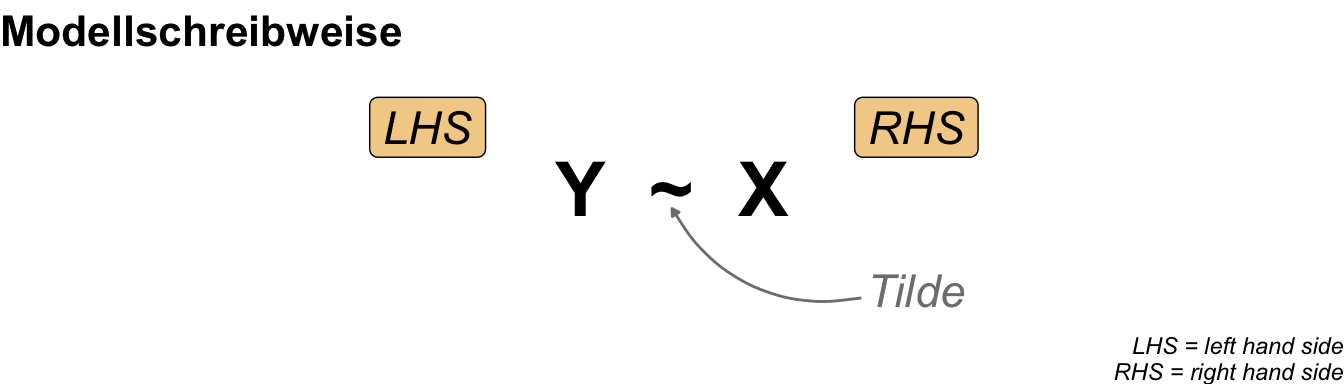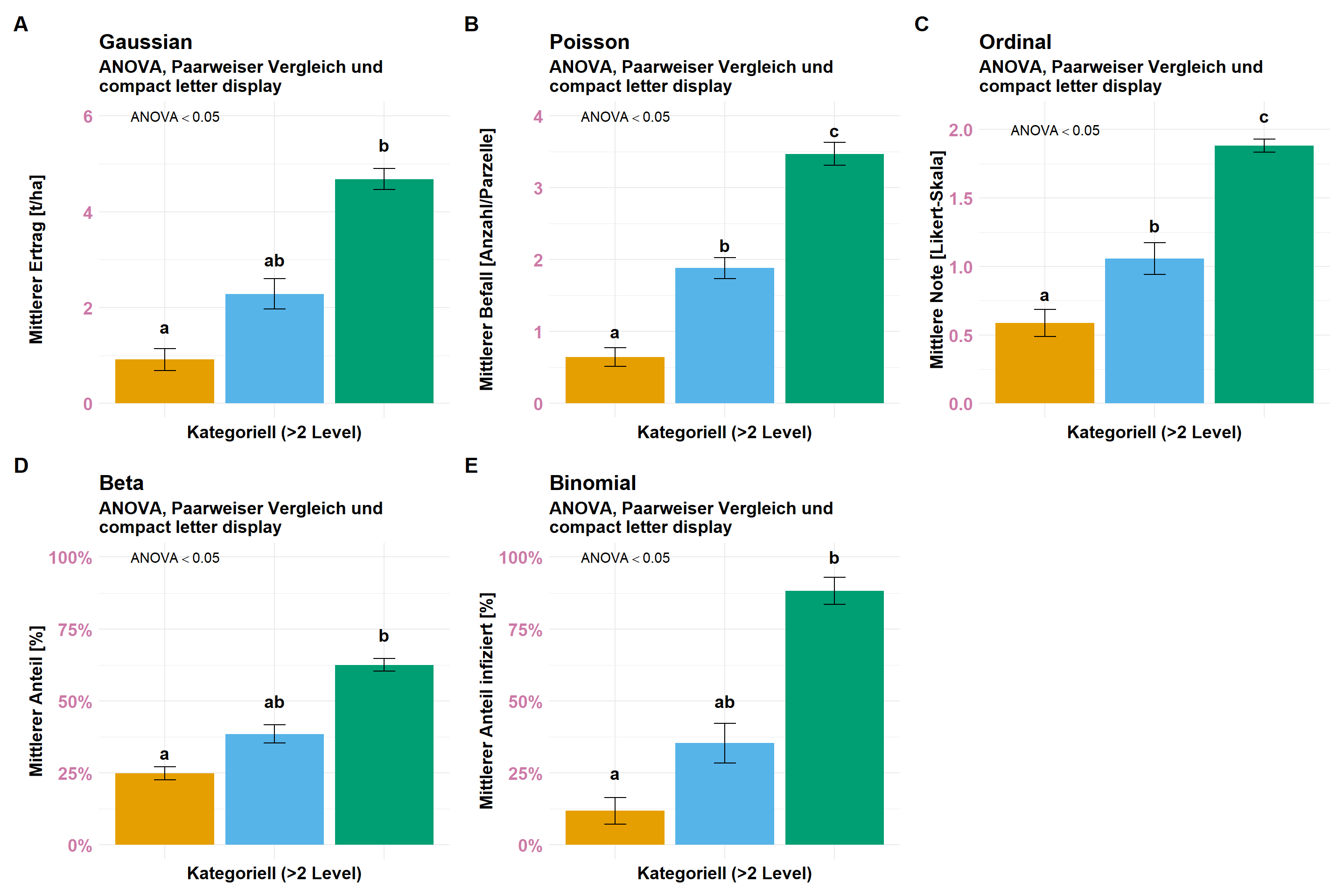Statistisches Modellieren
Letzte Änderung am 05. April 2024 um 19:31:05
“Sei bereit, sei bereit, sonst kommst du nicht sehr weit; Dann tut’s dir später leid, drum sei bereit; sei bereit sei bereit, sei clever und gescheit; so bist du gegen jeden Test gefeit” — Jan Delay Ziegen Song (sei Bereit)
Zum Einstieg in diesen großen Abschnitt zum statistischen Modellieren betrachten wir nochmal folgendes simples Modell mit einem Outcome \(y\) und einer Einflussvariable \(x\). Du kennst dieses einfache Modell schon aus dem Kapitel zur simplen linearen Regression. Später haben wir eine Vielzahl an möglichen \(x\) vorliegen, aber immer nur ein Outcome \(y\) im Modell. Dann rechnen wir eine multiple lineare Regression. 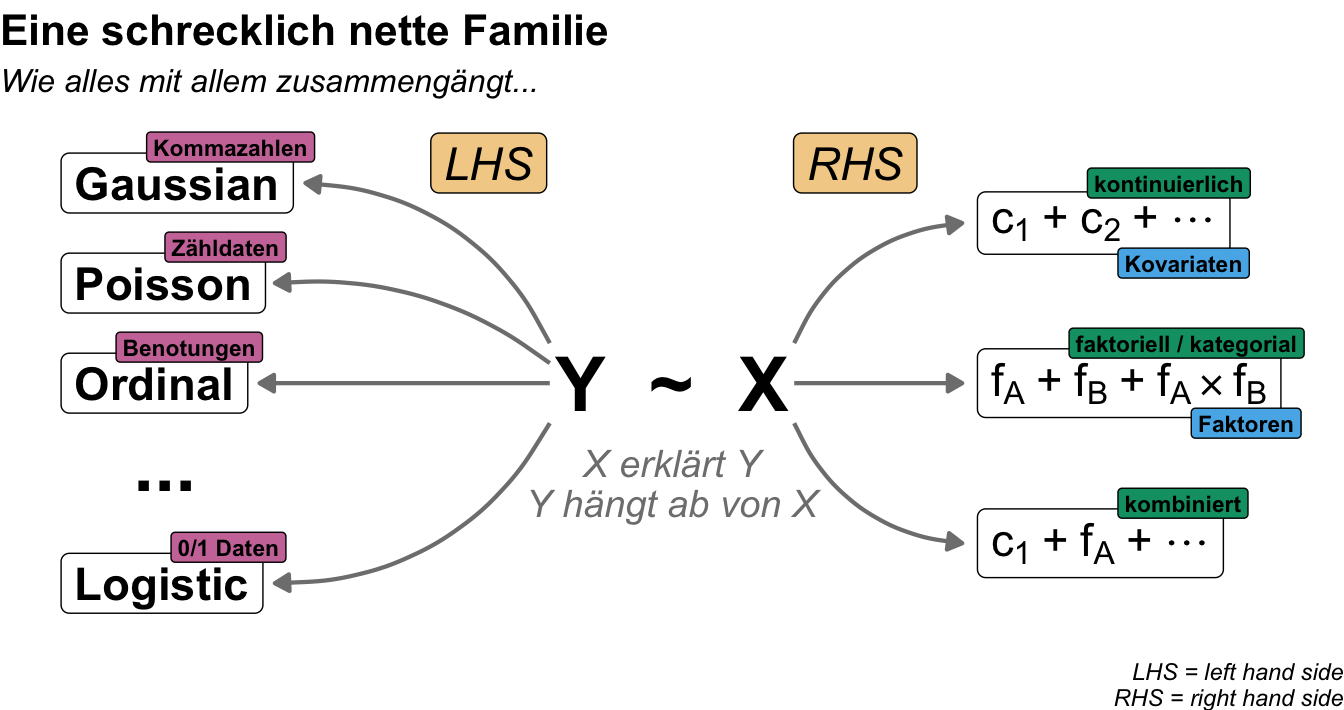Das Modell ist hier nochmal simple und beinhaltet jetzt erstmal nur ein Outcome und eine Einflussvariable.
\[ y \sim x \]
mit
- \(y\) als Outcome oder Messwert, welches einer Verteilungsfamilie zugehörig ist.
- \(x\) als Einflussvariable, welche kontinuierlich oder kategoriell ist.
Das \(x\) ist so eine spezielle Sache. Wenn du ein klassisches Feldexperiment hast, dann ist \(x\) meistens ein oder mehr Faktoren \(f\) mit unterschiedlichen vielen Leveln als Gruppen. Selten hast du dann noch ein kontinuierliches \(x\) mit in deinen Daten, welches du mit in dein Modell nehmen willst. Was dafür dann meistens noch mehr in deinen Daten vorkommt sind einiges an Spalten mit Messwerten \(y\) oder auch Outcome genannt. Das ist immer etwas schwerer zu realisieren, dass du für jedes Outcome \(y\) ein eigenes Modell und damit auch eigene statistische Tests rechnen musst. Deshalb kann es bei vielen Messwerten \(y\) zu einer ganzen Reihe von statistischen Analysen kommen. Wenn jetzt nicht alle Outcomes der gleichen Veteilungsfamilie angehören, dann musst du auch verschiedene Regressionen als statistische Analysen rechnen.
Jetzt können wir also verschiedene Outcomes \(y\) in einem Experiment vorliegen haben. Den jedes Outcome \(y\) repräsentiert ja auch eine Spalte mit Zahlen. Und je nachdem was wir gemessen haben, haben wir andere Werte in den Spalten stehen. Im Folgenden also einmal eine Auflistung an Verteilung und welchen Messwerte diese Verteilungen repräsentieren. Nach der Verteilung müssen wir uns dann einmal die Regression mit der passenden Verteilungsfamilie in den folgenden Kapiteln raussuchen. In der folgenden Tabelle habe ich einmal die gängigen Verteilungen in diesem Buch aufgelistet und dann einmal noch ein paar Beispiele dazu gegeben.
| Verteilung | Outcome \(\boldsymbol{y}\) | Beispiel |
|---|---|---|
| Gaussian / Normal | Kontinuierliche Kommazahlen | Größe; Gewicht; Höhe; Durchmesser |
| Poisson | Kontinuierliche Zähldaten | Anzahl Insekten; Anzahl Läsionen; Anzahl Früchte |
| Beta | Wahrscheinlichkeitswerte zwischen \([0,1]\) | Keimungsfähigkeit [%]; Jagderfolg [%]; Grünbedeckung [%] |
| Ordinal | Kategorielle Messwerte | Noten auf der Likert-Skala |
| Binomial | Kategorielle Messwerte \(0/1\) | Infiziert [ja/nein]; Beschädigt [ja/nein] |
Das heißt, je nachdem welchen Messwert du in deinem Experiment erhoben hast, musst du dich für eine andere Regression mit einer entsprechenden Verteilungsfamilie entscheiden.
Verteilungsfamilien
Wenn wir gleich in den folgenden Kapiteln dieses großen Abschnitts in R unsere Regressionsmodelle rechnen, dann müssen wir uns für die Funktion lm() oder glm() oder eine noch spezialisiertere Funktion entscheiden. Mehr dazu dann aber mehr in den einzelnen separaten Kapiteln zu den Regressionsanalysen oder aber in dem etwas umfangreicheren Kapitel zum Modellieren in R. Wir nutzen die Funktion lm(), wenn unser Outcome \(y\) einer Normalverteilung genügt und die Funktion glm() mit der Option family, wenn wir eine andere Verteilungsfamilie für unser Outcome benötigen. So werden zum Beispiel Zähldaten mit der Funktion glm() und der Option family = poisson für die Poissonverteilung ausgewertet. Aber wie schon gesagt, mehr erfährst du dann in den folgenden Kapiteln zu den einzelnen Regressionen. Dort stelle ich dann auch die Funktionen und die entsprechenden R Pakete vor, die du für die Analyse deiner Daten brauchst.
Gaussian / Normal
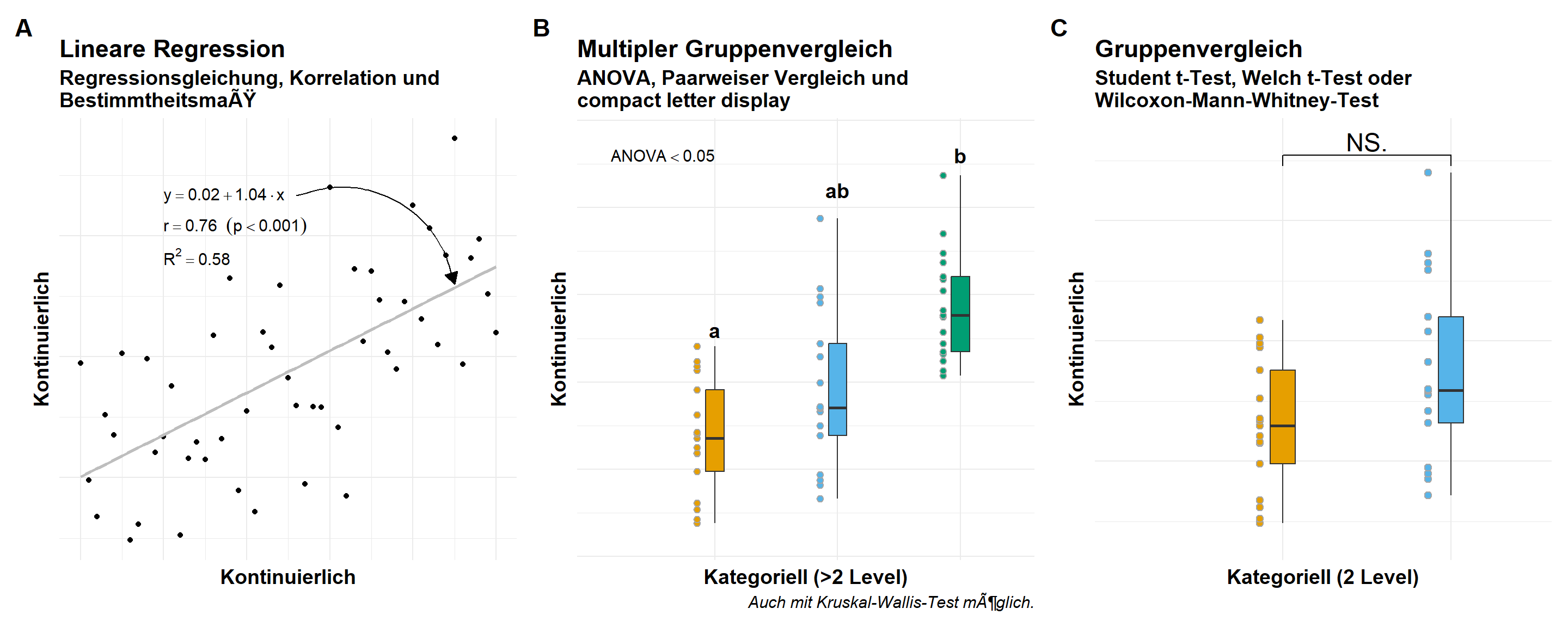
Die Gaussianverteilung ist die Normalverteilung. Da wir meistens von einer Normalverteilung sprechen, müssen wir hier auch wissen, dass wir in Statistik und R die Verteilung Gaussian benennen. Häufige Messwerte oder Outcomes, die einer Normalverteilung folgen, sind das Gewicht, die Größe, die Höhe oder der Umfang einer Beobachtung. Dementsprechend geht es dann in dem Kapitel zu der Gaussian Regression weiter. In der folgenden Abbildung 49.1 siehst du einmal den visuellen Zusammenhang zwischen den kontinuierlichen Outcome \(y\), welches einer Normalverteilung folgt und den möglichen Darstellungsformen je nachdem welches \(x\) du in deinen Daten vorliegen hast. Dazu habe ich dann noch die jeweiligen möglichen statistischen Analysen ergänzt.
Wir mitteln uns die Welt, wie sie uns gefällt…
“2 x 3 macht 4; Widdewiddewitt; und Drei macht Neune!; Wir machen uns die Welt; Widdewidde wie sie uns gefällt…” — Hey Pippi Langstrumpf
Wenn wir über die Normalverteilung sprechen, dann berechnen wir ja immer der Mittelwert und die Standardabweichung aus den Daten. Diese beiden statistischen Maßzahlen stellen wir dann in einem Barplot dar. Das können wir dann natürlich auch für alle anderen möglichen Messwerte machen. Denn einen Mittelwert kannst du natürlich über alles rechnen. Also, wo sind die Barplots hin? Ich habe dir mal die Barplots für alle Verteilungen in der Abbildung 2 dargestellt. Ja, die sehen alle sehr ähnlich aus, deshalb achte einmal auf die Skalierung der \(y\)-Achse. Hier unterscheiden sich die Barplots. Ich habe dir mal für alle folgenden Verteilungsfamilien die Barplots erstellt. Am Ende ist eben dann doch so, dass du jede andere Verteilung durch die Berechnung der Mittelwerte und der Standardabweichung in eine Normalverteilung zwingst. Du siehst eben nicht mehr wie die Daten ursprünglich mal verteilt sind. Ausreißer oder andere Strukturen in den Daten sind dann kaum zu erkennen.
Poisson
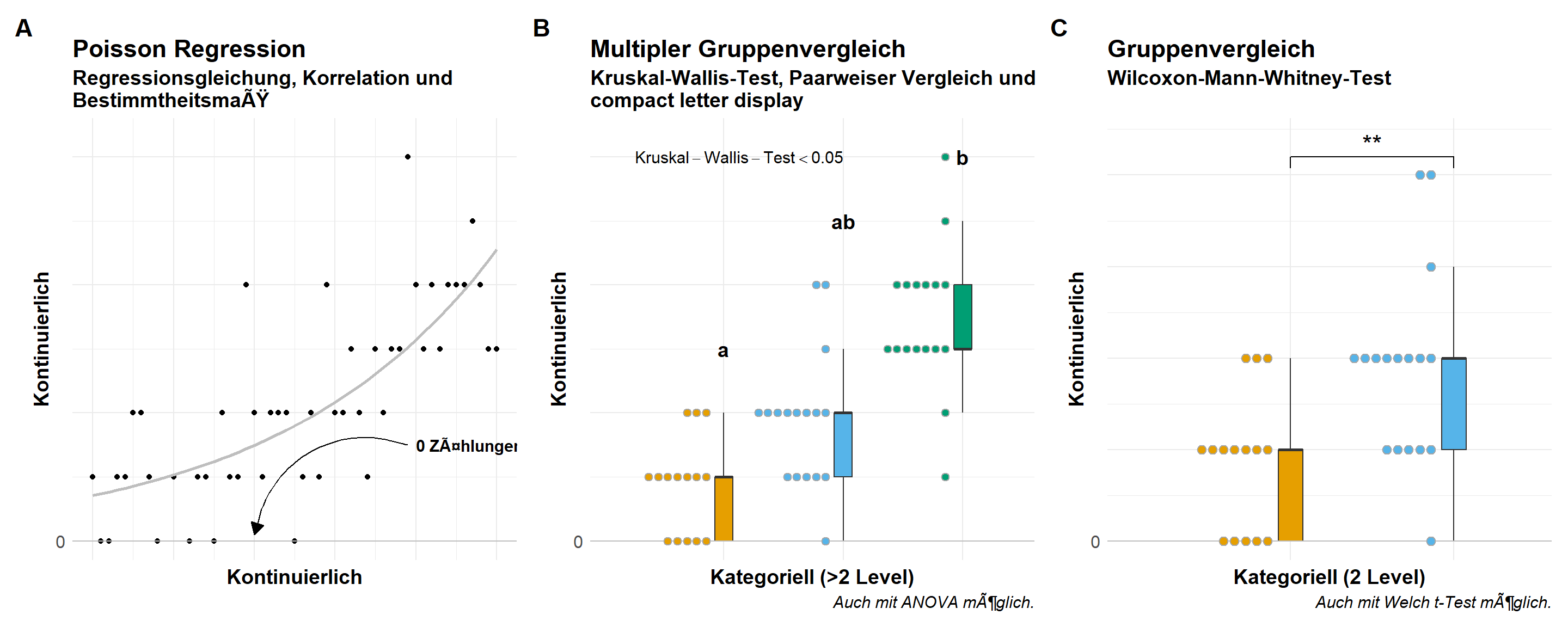
Wenn wir Zähldaten gemessen haben und diese Zähldaten dann als ein Outcome \(y\) auswerten wollen, dann nutzen wir eine Poissonverteilung. Was machen Zähldaten aus? Zum einen haben wir eine Grenze von Null. Wir können nicht weniger als Null zählen. Daher sollten wir also nur positive, ganzzahlige Messwerte vorliegen haben. Teilweise können wir ein Problem kriegen, wenn wir zu viele Nullen vorliegen haben, aber dazu dann mehr in dem Kapitel zur Poisson Regression. Wir haben also auf der \(y\)-Achse kontinuierliche Zähldaten ohne Kommawerte vorliegen. Wenn du deine Zähldaten eventuell gemittelt hast, dann musst du die Messwerte dann wieder auf ganzzahlige Zähldaten runden, wenn du eine Poisson Regression rechnen willst. In der folgenden Abbildung 3 siehst du einmal den visuellen Zusammenhang zwischen den kontinuierlichen Outcome \(y\), welches einer Poissonverteilung folgt und den möglichen Darstellungsformen je nachdem welches \(x\) du in deinen Daten vorliegen hast. Du siehst hier sehr deutlich die Ebenen, die sich durch die ganzzahligen Zähldaten ergeben. Dazu habe ich dann noch die jeweiligen möglichen statistischen Analysen ergänzt.
Beta
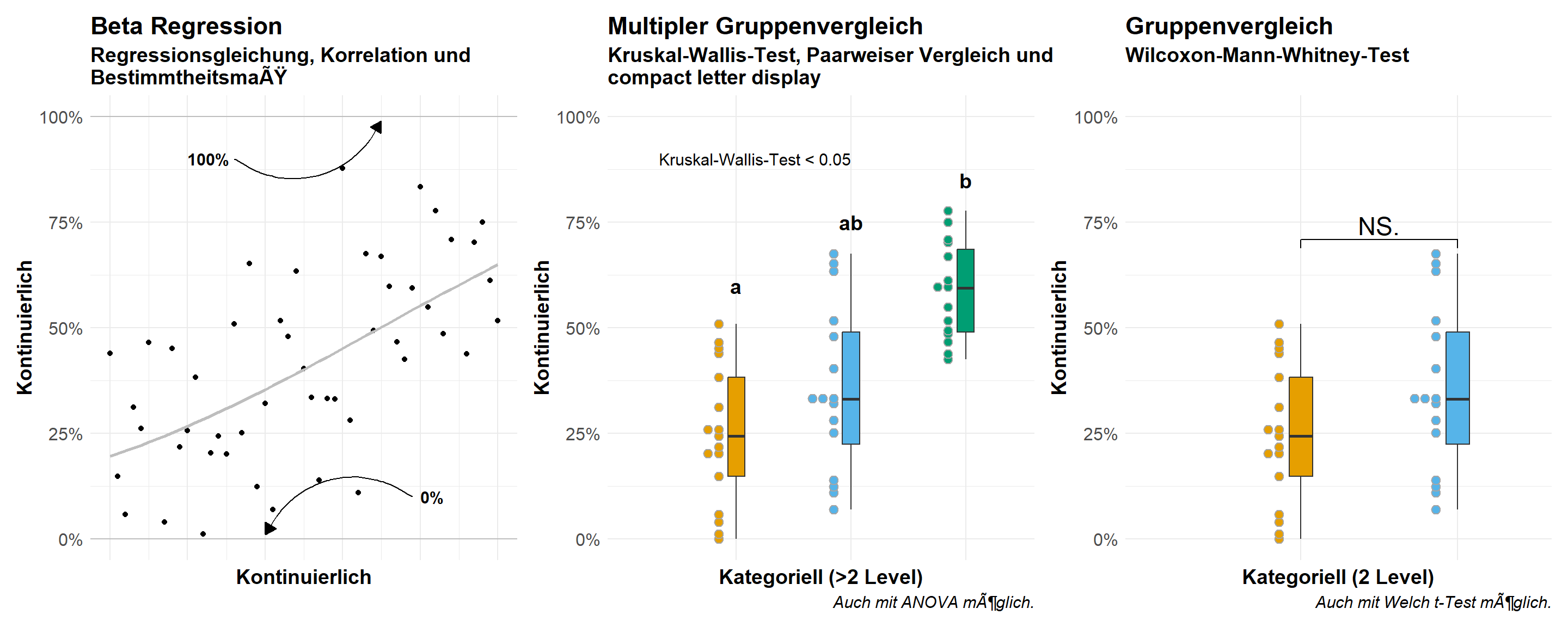
Wo wir bei der Possionverteilung mit Zähldaten keine Werte unter Null zählen können, so haben wir es bei einer Betaverteilung mit Prozenten zwischen Null und Eins zu tun. Wir können also hier keine Messwerte unter Null oder über Eins erhalten. Meistens handelt es sich bei einer Betaverteilung auch um Zähldaten, die skaliert wurden. So wurden die gekeimten Samen von einer Aussaat gezählt und wir erhalten dann einen Wert für die Keimfähigkeit in Prozent. Oder aber wir wollen den Jagderfolg ermitteln in dem wir den Anteil an erfolgreichen Versuchen durch die Gesamtzahl an Versuchen teilen. In der folgenden Abbildung 4 siehst du einmal den visuellen Zusammenhang zwischen den kontinuierlichen Outcome \(y\), welches einer Betaverteilung folgt und den möglichen Darstellungsformen je nachdem welches \(x\) du in deinen Daten vorliegen hast. Dazu habe ich dann noch die jeweiligen möglichen statistischen Analysen ergänzt.
Ordinal
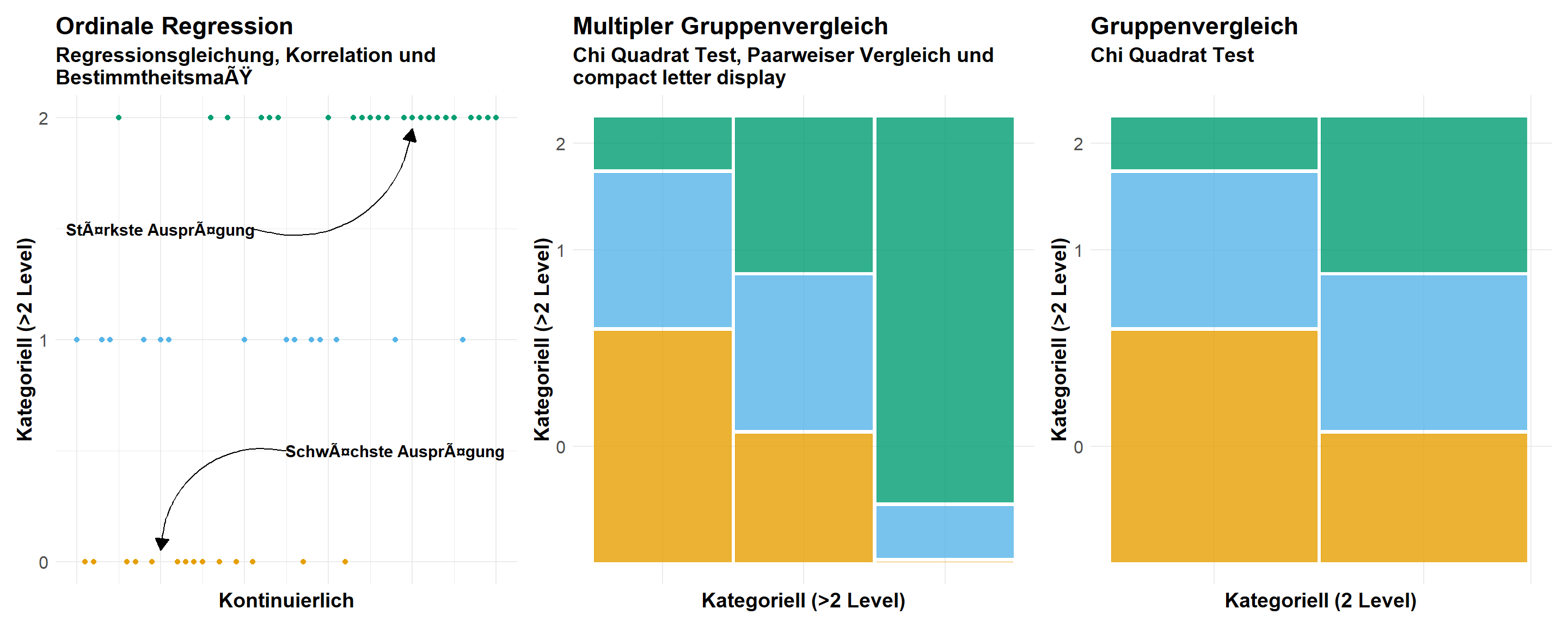
Mit der Ordinalverteilung begeben wir uns jetzt in die kategoriellen Verteilungen. Wir haben als unser Outcome \(y\) jetzt nichts mehr Kontinuierliches vorliegen sondern eben Kategorien auf der \(y\)-Achse. Was sind so typische Kategorien, die wir messen können? Eine der häufigsten, geordneten Kategorie sind die Noten auf einer Likert-Skala. Allgemein gesprochen sind alle Noten als Kategorien ordnialverteilt, aber häufig nehmen wir eben dann keine Schulnoten in der wissenschaftlichen Forschung sondern eben Noten nach der Likert-Skala. Die Besonderheiten fallen in der Abbildung 5 mit dem visuellen Zusammenhang sofort auf. Das kategoriellen Outcome \(y\), welches einer Ordinalverteilung folgt, bildet klare Ebenen. Das hat dann direkte Folgen für die möglichen Darstellungsformen je nachdem welches \(x\) du in deinen Daten vorliegen hast. Dazu habe ich dann noch die jeweiligen möglichen statistischen Analysen ergänzt. Wir haben dann eben nicht mehr die Möglichkeit Punkte darzustellen, wenn die \(x\)-Achse ebenfalls Kategorien als Faktor aufweist. Wir nehmen dann den Mosaicplot zur Hilfe. Du könntest zwar auch die mittleren Noten als Barplot wie in der Abbildung 2(C) darstellen. Hier musst du schauen, was du zeigen willst. Hast du viele Notenschritte, dann mag es sinnvoll sein eine mittlere Note zu bilden. Wenn du nur wenige Noten hast, dann macht der Mosaicplot mehr Sinn.
Binomial
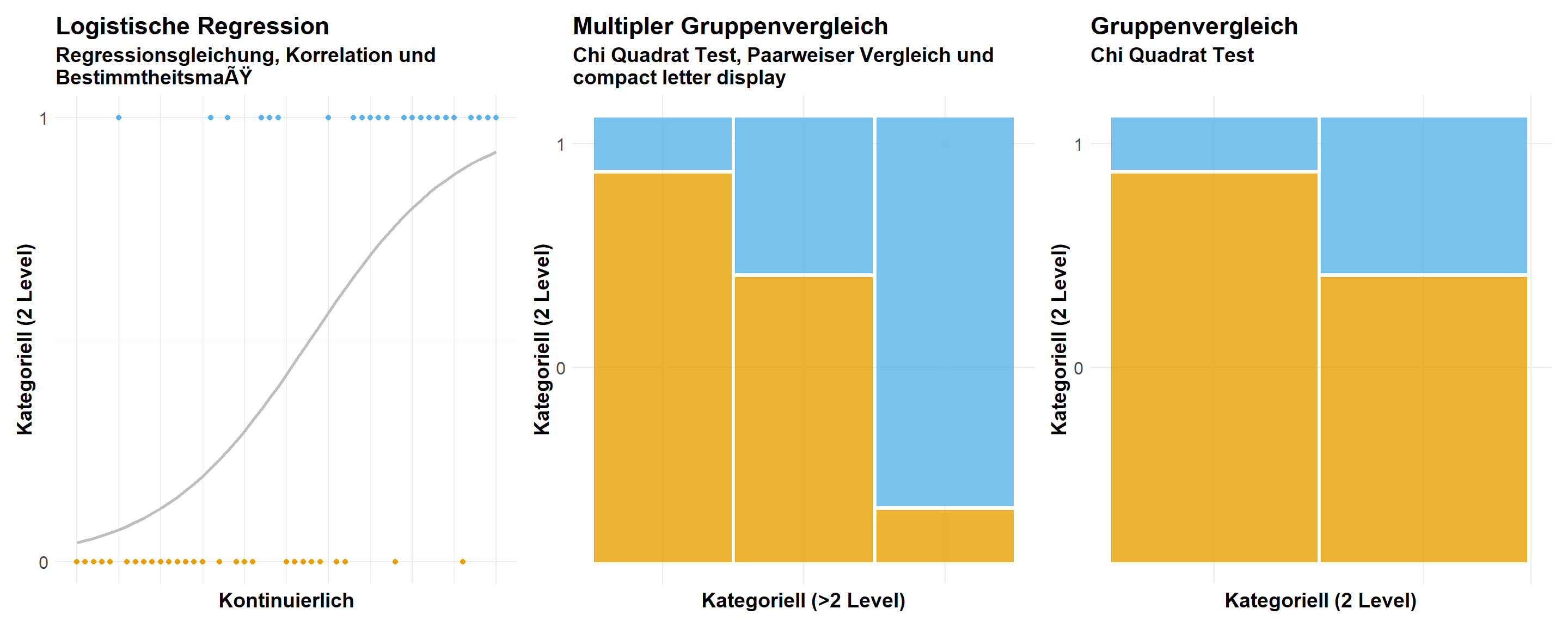
Abschließend wollen wir uns noch den extremsten Fall für ein Outcome \(y\) anschauen. Wir haben jetzt nämlich nur noch zwei Kategorien übrig. Also entweder hat eine Beobachtung ein Merkmal, dann erhält die Beobachtung eine Eins oder die Beobachtung hat das Merkmal nicht, dann erhält die Beobachtung eine Null. Wir sprechen dann von einer Binomialverteilung. Die Binomialverteilung tritt sehr häufig in den Humanwissenschaften auf, wenn es darum geht, ob ein Patient krank \((1)\) oder gesund \((0)\) ist. Auch nutzen wir die Binomialverteilung sehr häufig, wenn wir eine Vorhersage treffen wollen, denn auch hier wollen wir meist nur zwei Klassen \((0/1)\) vorhersagen. In der Abbildung 6 siehst du dann nochmal den visuellen Zusammenhang. Wie auch schon bei der Ordinalverteilung haben wir jetzt zwei Ebenen. Einmal die Beobachtungen mit einer Eins und einmal die Beobachtungen mit einer Null. Auch hier könnten wir dann bei eine kategoriellen \(x\) die mittlere Rate der Einsen berechnen, aber normalerweise nutzen wir hier dann auch Mosaicplots, da wir an den jeweiligen Raten für die Einsen und Nullen interessiert sind.
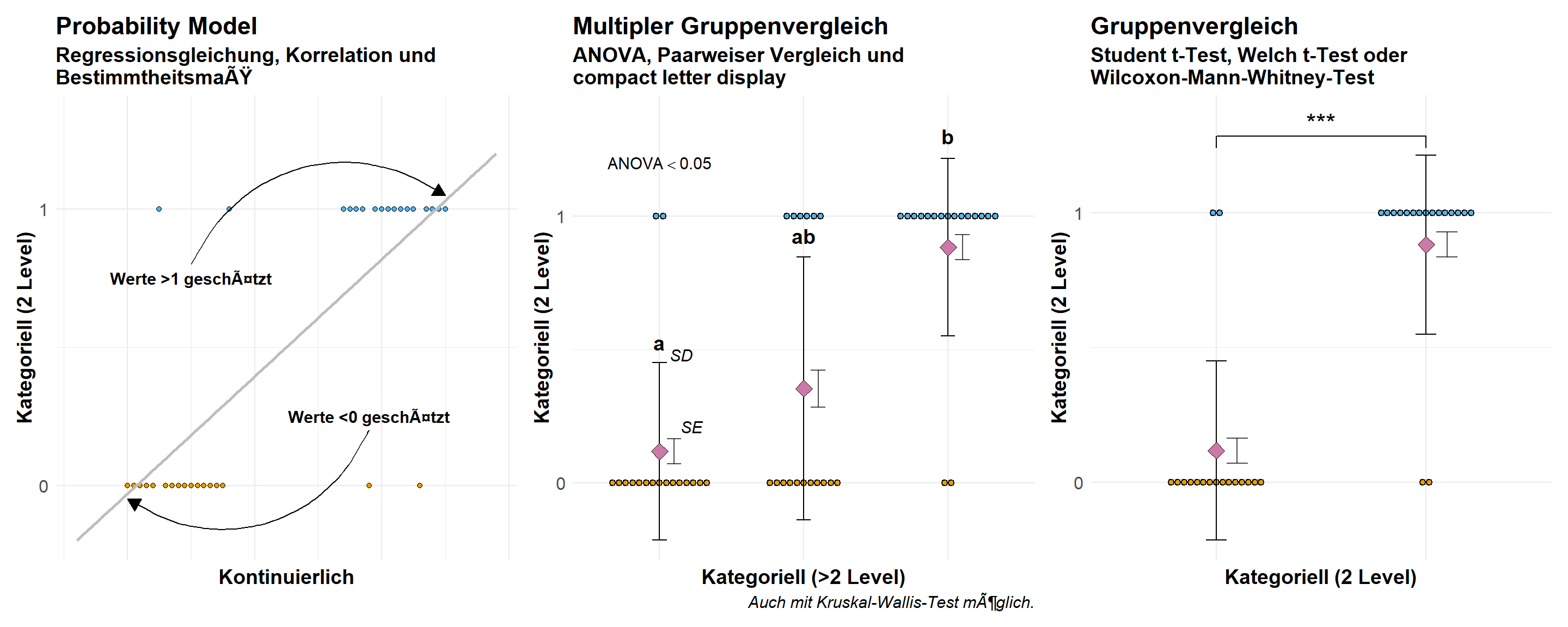
In der Abbildung 7 möchte ich dir nochmal die Möglichkeit des Probability models vorstellen, welches die kategoriellen Daten der Binomialverteilung wie eine Gaussianverteilung modelliert. Dadurch können an den Extremen von \(x\) dann auch Werte für \(y\) größer Eins und kleiner Null herauskommen. Schlussendlich ist es natürlich eine Verletzung der Modellannahmen. Den binomiale Daten folgen eben keiner Normalverteilung und sollten daher auch nicht mit einer Gaussian Regression ausgewertet werden. Dennoch sieht man das Probability model immer wieder in der Anwendung der Wirtschaftswissenschaften, so dass ich das Modell hier auch einmal präsentieren will. Wenn du das Modell für Gruppenvergleiche mit einem kategoriellen \(x\) verwendest, dann nutze bitte den Standardfehler \(SE\) und nicht die Standardabweichung \(SD\) sonst erhälst du Werte außerhalb des sinnvollen Rahmens. Allgemein wird von dem Student t-Test abgeraten, da Probability model zu heterogenen Varianzen neigen.
