pacman::p_load(tidyverse, magrittr, sandwich, lmtest,
emmeans, multcomp, see,
performance, broom, conflicted)
conflicts_prefer(dplyr::select)
conflicts_prefer(magrittr::extract)
conflicts_prefer(magrittr::set_names)52 Linear Probability Model
Letzte Änderung am 02. April 2024 um 09:52:43
Das Wahrscheinlichkeitsmodell (eng. probability model oder linear probability model) ist ein seltsames Konstrukt aus der Ökonomie und den Sozialwissenschaften. Wir nutzen hier auch den englischen Begriff, da der deutsche Begriff eigentlich nicht benutzt wird. Es handelt sich hier also um probability models. Was macht also das probability model? Eigentlich alles falsch, was man so im Allgemeinen meinen würde. Das probability model nimmt als Outcome \(y\) eine \(0/1\) Variable. Wir modellieren also wie bei der logistischen Regression ein Outcome \(y\) was sich nur durch zwei Ausprägungen darstellen lässt. Und damit wären wir dann auch beim Punkt angekommen. Anstatt das \(0/1\) Outcome jetzt richtig mit der logistischen Regression auszuwerten, nutzen wir die klassische Gaussian Regression mit der Annahme eines normalverteilten Outcomes. Wir nutzen hier also das falsche Modell für das gemessene Outcome. Warum machen wir das? Weil sich die Effektschätzer aus einer Gaussian Regression auf einem \(0/1\) Outcome besser interpretieren lassen. Wie immer gibt es viel Disput, ob du so was überhaupt machen darfst. Können tust es auf jeden Fall. Wir können auf alle Daten alle Modelle anwenden. Nun ist es aber so, dass die Auswertung von einem \(0/1\) Outcome mit einem probability model teilweise in der Ökonomie oder den Sozialwissenschaften sehr verbreitet ist. Deshalb findest du auch hier dieses etwas kurzes Kapitel.
Wir immer gibt es auch wieder zwei gute Tutorien auf die sich hier alles reimt. Einmal bitte das Tutorium Linear Probability Model sowie Binary Dependent Variables and the Linear Probability Model besuchen. Wenn du noch mehr über lm() und glm() lesen möchtest, dann kannst du das auch nochmal in der Frage zu Linear probability model: lm() und glm() machen.
52.1 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
52.2 Daten
In diesem Kapitel nutzen wir die infizierten Ferkel als Beispieldatensatz. Wir haben in dem Datensatz über vierhundert Ferkel untersucht und festgehalten, ob die Ferkel infiziert sind (\(1\), ja) oder nicht infiziert (\(0\), nein). Wir haben daneben noch eine ganze Reihe von Risikofaktoren erhoben. Hier sieht man mal wieder wie wirr die Sprache der Statistik ist. Weil wir rausfinden wollen welche Variable das Risiko für die Infektion erhöht, nennen wir diese Variablen Risikofaktoren. Wir nehmen hier jetzt aber nicht alle Variablen mit, sondern nur die Variablen für den Entzündungswert crp, das Geschlecht sex, dem Alter age und der Gebrechlichkeitskategorie frailty.
pig_tbl <- read_excel("data/infected_pigs.xlsx") |>
select(infected, crp, sex, age, frailty) Schauen wir uns nochmal einen Ausschnitt der Daten in der Tabelle 52.1 an.
| infected | crp | sex | age | frailty |
|---|---|---|---|---|
| 1 | 22.38 | male | 61 | robust |
| 0 | 18.64 | male | 53 | robust |
| 0 | 18.76 | female | 66 | robust |
| 0 | 19.37 | female | 59 | robust |
| … | … | … | … | … |
| 1 | 21.95 | male | 57 | robust |
| 1 | 23.1 | male | 61 | robust |
| 1 | 20.23 | female | 59 | pre-frail |
| 1 | 19.89 | female | 63 | robust |
Im Folgenden wollen wir einmal modellieren, ob es einen Zusammenhang von den Variablen crp, sex, age und frailty auf das \(0/1\)-Outcome infected gibt. Welche der Variablen erniedrigen oder erhöhen also das Risiko einer Ferkelinfektion?
52.3 Theoretischer Hintergrund
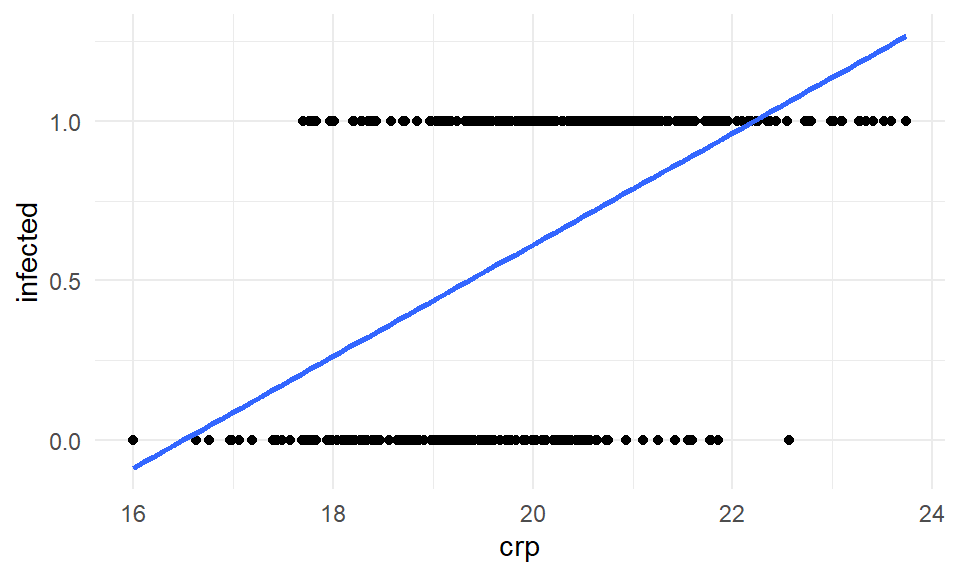
Den theoretischen Hintergrund belassen wir hier nur kurz. Die Idee sehen wir dann einmal in der Abbildung 52.1. Wir haben hier dann nur die Variable crp und das Outcome infected dargestellt. Wir sehe die klaren zwei Ebenen. Wir haben ja bei dem Infektionsstatus auch nur zwei mögliche Ausprägungen. Entweder ist unser Ferkel infiziert oder eben nicht. Da wir aber die Entzündungswerte kontinuierlich messen ergeben sich die beiden Ebenen.
ggplot(pig_tbl, aes(x = crp, y = infected)) +
theme_minimal() +
geom_point() 
Tja und dann rechnen wir einfach eine Gaussian linear Regression mit der Funktion lm(). Es ergibt sich dann eine gerade Linie, wie wir sie in der Abbildung 52.2 sehen. Da wir aber mit unserem Infektionsstatus auf \(0/1\) begrenzt sind, aber eine Gerade nicht, haben wir das Problem, dass wir in diesem Fall den Infektionsstatus für CRP-Werte größer als 22 überschätzen. Ich meine mit überschätzen dann auch wirklich Werte zu erhalten, die es dann gar nicht geben kann. Es kann keinen Infektionsstatus über ja geben.
ggplot(pig_tbl, aes(x = crp, y = infected)) +
theme_minimal() +
geom_point() +
stat_smooth(method = "lm", se = FALSE)
52.4 Modellierung
Dann können wir schon das probability model anpassen. Dazu nehmen wir die Funktion lm(), die wir auch für unsere Gaussian linearen Regression unter der Annahme eines normalverteilten Outcomes \(y\) nutzen. Wichtig ist hier, dass wir auf keinen Fall unseren Infektionsstatus infected als einen Faktor übergeben. Der Infektionsstatus infected muss numerisch sein.
lm_fit <- lm(infected ~ crp + age + sex + frailty, data = pig_tbl)Schauen wir uns aber gleich mal die Modellausgabe an. Wie immer, du kannst alle Zahlen und Spalten in eine Funktion stecken und am Ende kommt dann was raus. Woher soll auch die Funktion wissen, dass es sich um einen Faktor handelt oder eine numerische Variable?
lm_fit |>
summary()
Call:
lm(formula = infected ~ crp + age + sex + frailty, data = pig_tbl)
Residuals:
Min 1Q Median 3Q Max
-1.03273 -0.35437 0.09685 0.32293 0.82383
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.417891 0.410274 -8.331 1.25e-15 ***
crp 0.178221 0.014368 12.404 < 2e-16 ***
age 0.007962 0.004554 1.748 0.0811 .
sexmale 0.070018 0.041945 1.669 0.0958 .
frailtypre-frail -0.073455 0.067724 -1.085 0.2787
frailtyrobust -0.056849 0.063655 -0.893 0.3723
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4142 on 406 degrees of freedom
Multiple R-squared: 0.2797, Adjusted R-squared: 0.2709
F-statistic: 31.53 on 5 and 406 DF, p-value: < 2.2e-16Neben der sehr schlechten Modellgüte, die wir am Bestimmtheitsmaß \(R^2\) mit 0.24 erkennen, sind aber die Residuen nach den deskriptiven Maßzahlen einigermaßen okay. Wir werden aber gleich noch sehen, dass die Maßzahlen hier auch trügen können. Was ist den nun das Tolle am probability model? Wir können die Effektschätzer Estimate direkt als prozentuale Veränderung interpretieren. Das heißt, wir können sagen, dass pro Einheit crp die Wahrscheinlichkeit infiziert zu sein um 16.2087% ansteigt. Das ist natürlich eine sehr schöne Eigenschaft. Nur leider gibt es da meistens dann doch ein Problem. Dafür schauen wir uns einmal die Spannweite der vorhergesagten Werte an.
lm_fit |>
predict() |>
range() |>
round(2)[1] -0.16 1.27Wie du siehst, kriegen wir Werte größer als Eins und kleiner als Null aus dem Modell raus. Das macht jetzt aber recht wenig Sinn. Wir können die Werte aus predict() als Wahrscheinlichkeit infiziert zu sein interpretieren. Da unsere Ferkel aber nur gesund oder krank sein können, machen negative Werte der Wahrscheinlichkeit infiziert zu sein keinen Sinn. Auch Werte größer als Eins können wir nur sehr schwer interpretieren.
52.5 Varianzheterogenität
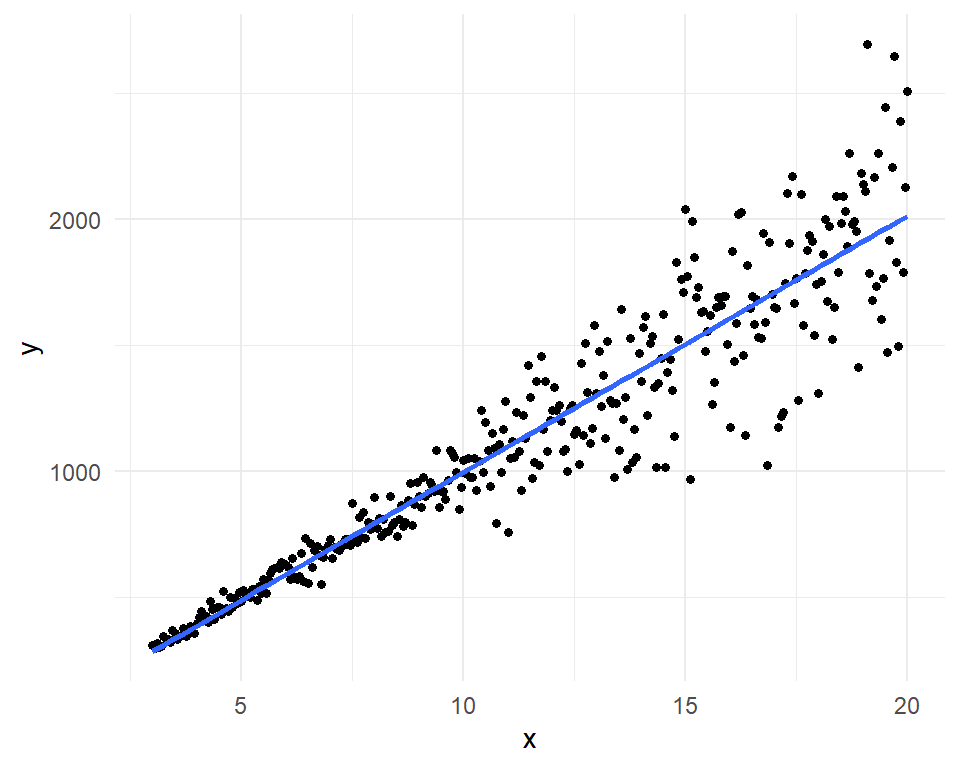
Wenn du das probability model durchführst, dann hast du in den meisten Fällen das Problem der Heteroskedastizität, auch Varianzheterogenität genannt. Oder in anderen Worten, die Residuen als Fehler unseres Modell sind nicht gleichmäßig mit gleich großen Werten verteilt um die Gerade. Gut, dass klingt jetzt etwas sperrig, hier einmal die Abbildung 52.3 um es besser zu verstehen.
Für unser Modell lm_fit von oben können wir auch gleich die Funktion check_heteroscedasticity() aus dem R Paket {performance} nutzen um zu Überprüfen ob wir Varianzheterogenität vorliegen haben. Aber Achtung, ich wäre hier sehr vorsichtig, wenn die Funktion sagt, dass wir keine Varianzheterogenität vorliegen haben.
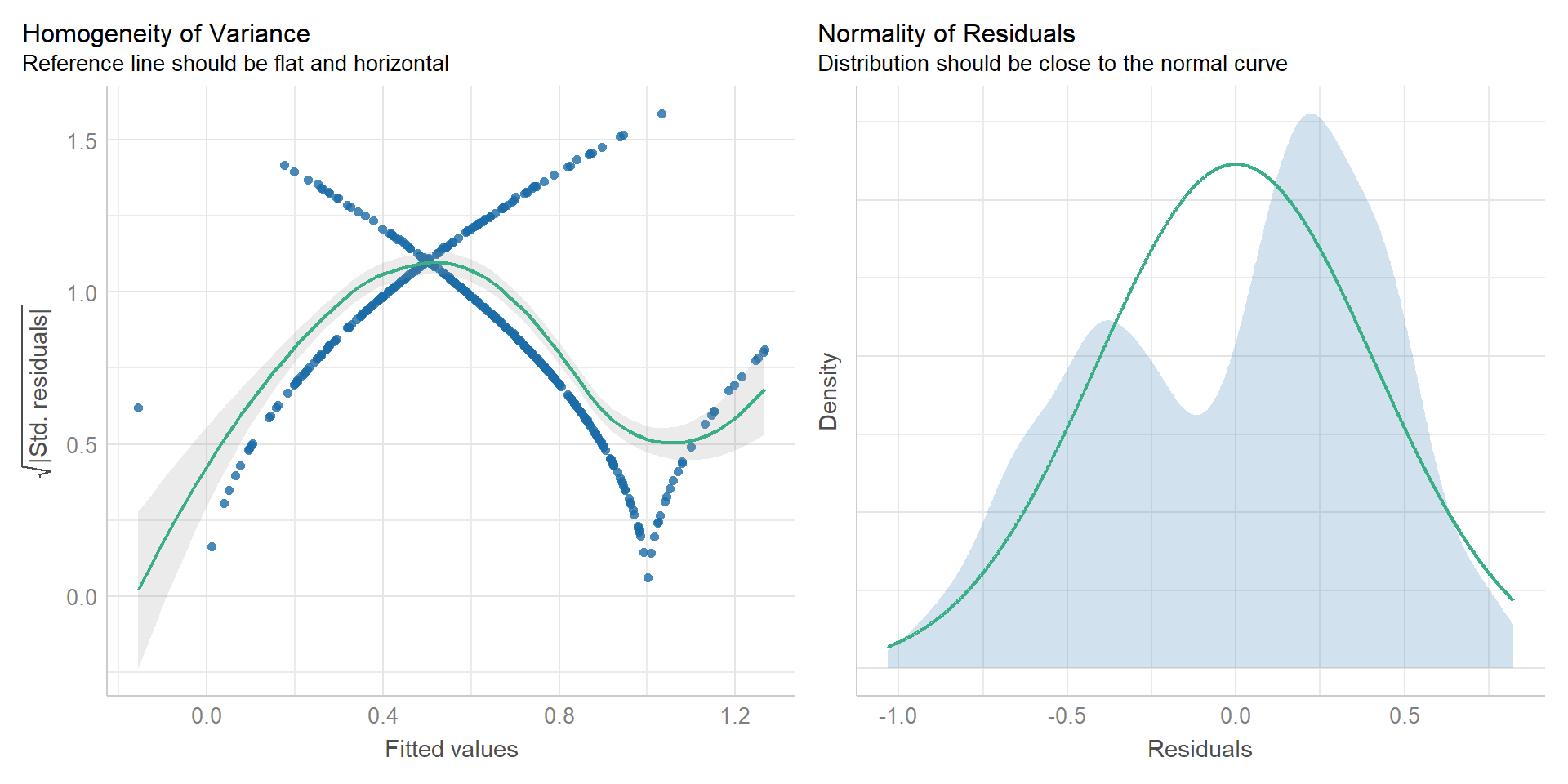
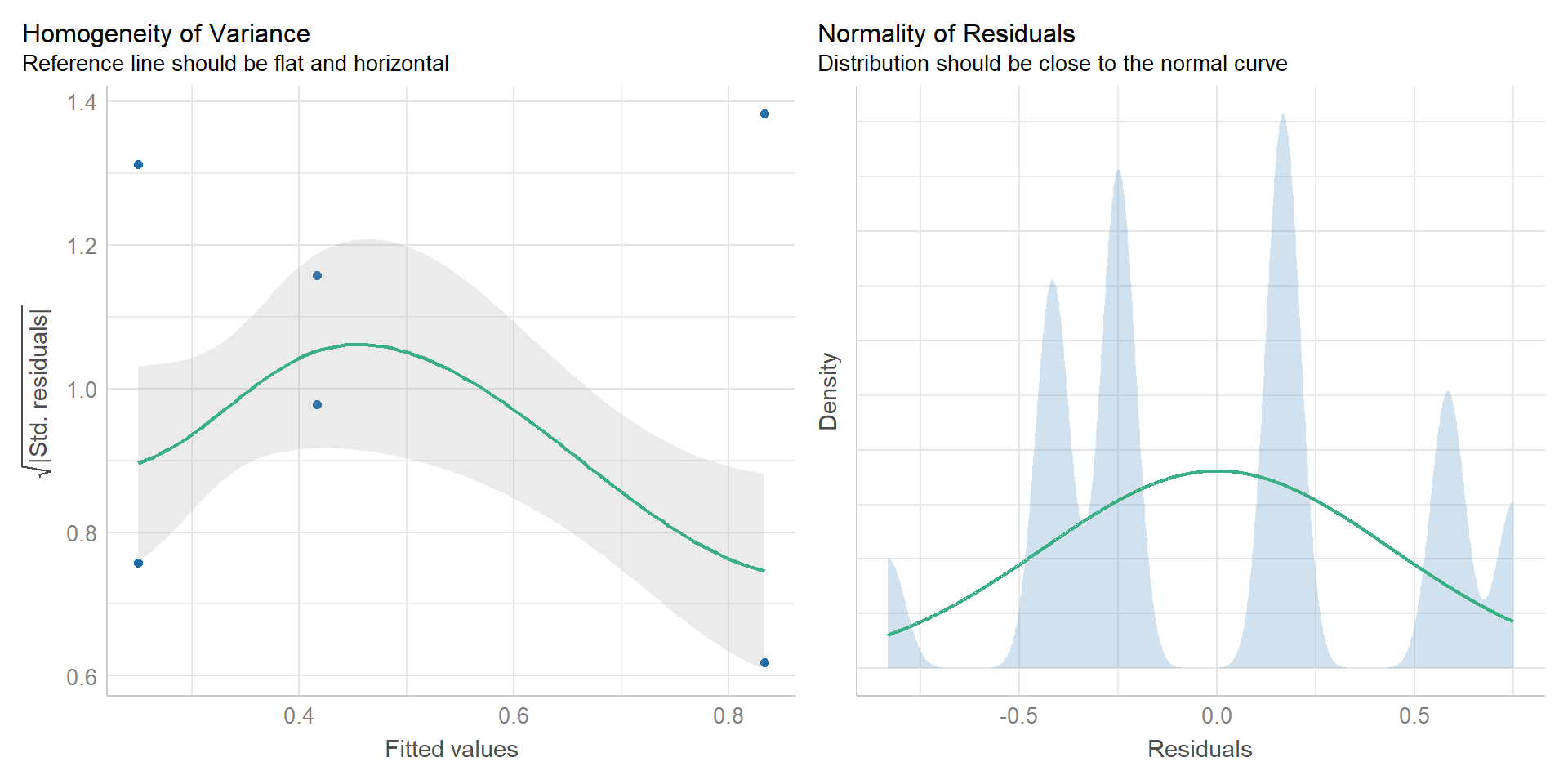
check_heteroscedasticity(lm_fit)Warning: Heteroscedasticity (non-constant error variance) detected (p = 0.008).Neben der Funktion check_heteroscedasticity() gibt es auch die Möglichkeit über check_model() sich die Varianzen und damit die Residuen einmal anzuschauen. Die visuelle Überprüfung ist auf jeden Fall Pflicht. Und wie du in der Abbildung 52.4 siehst, sind die Varianzen weder homogen noch irgendwie normalverteilt. Wir gehen also von Varianzheterogenität aus. Damit liegen wir in Linie mit der Funktion check_heteroscedasticity(), aber das muss nicht immer unbedingt sein. Besonders bei kleiner Fallzahl, kann es vorkommen, dass check_heteroscedasticity() eine Varianzheterogenität übersieht.
check_model(lm_fit, check = c("homogeneity", "normality"))
lm_fit mit der Funktion check_model(). Wir sehen hier eine klare Varianzheterogenität in dem Modell.
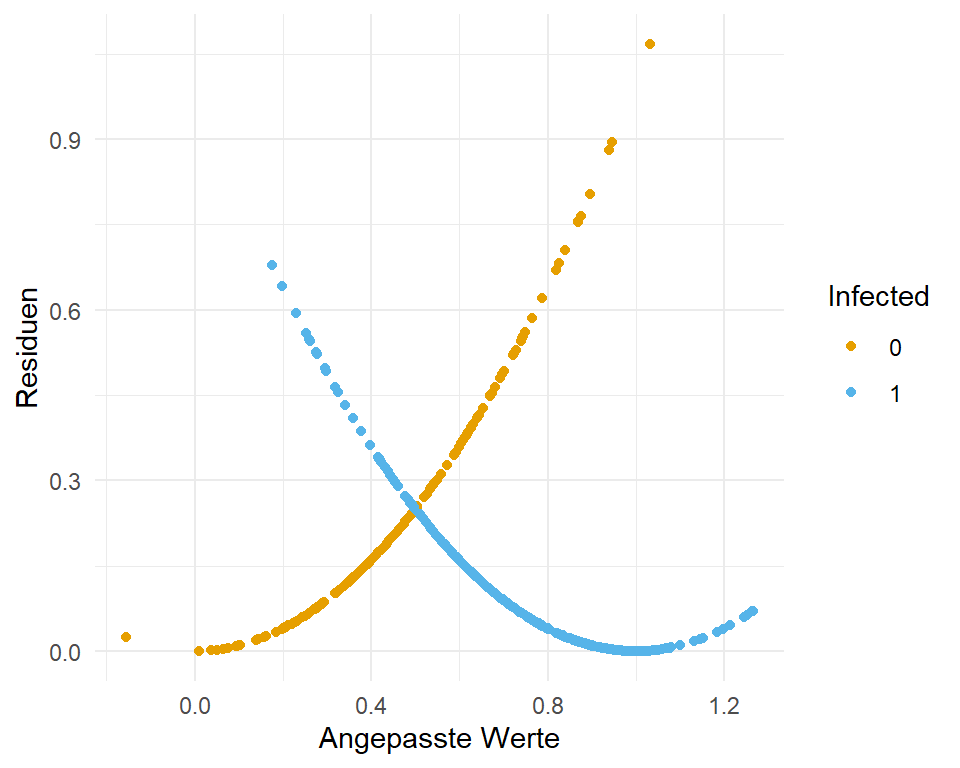
Jetzt kann man sich fragen, warum sind denn da so Bögen drin? Das kommt von den Abständen der Punkte auf den beiden Ebenen. Die Gerade läuft ja durch einen Bereich in dem keine Beobachtungen sind. Daher ist am Anfang der Abstand zu einer der beiden Ebenen, entweder der Null oder der Eins, minimal und erhöht sich dann langsam. Weil ja nicht alle Beobachtungen alle bei Null sind springen die Abstände von klein zu groß. In Abbildung 52.5 siehst du nochmal den Zusammenhang. Unsere angepasste Gerade steigt ja an, wie du in Abbildung 52.2 siehst. Daher sind die Abstände zu den Null Werten am Anfang sehr klein und stiegen dann an. Sobald die erste Beobachtung mit einem Infektionsstatus von Eins auftaucht, springt der Abstand natürlich sofort nach oben. Werte größer als Eins dürfte es auf der x-Achse gar nicht geben, den dort werden dann Werte größer als Eins geschätzt.
lm_fit |>
augment() |>
ggplot(aes(x = .fitted, y = .resid^2, color = as_factor(infected))) +
theme_minimal() +
geom_point() +
labs(x = "Angepasste Werte", y = "Residuen", color = "Infected") +
scale_color_okabeito()
.fitted und der Residuen .resid aus dem Modell lm_fit. Die Punkte sind nach dem Infektionsstatus eingefärbt.
52.6 Interpretation des Modells
Wir haben ja schon einmal weiter oben in das Modell geschaut und eine Interpretation vorgenommen. Wir erinnern uns, wir können die Effektschätzer Estimate aus einem probability model direkt als prozentuale Veränderung interpretieren. Das heißt, wir können sagen, dass pro Einheit crp die Wahrscheinlichkeit infiziert zu sein um 16.2087% ansteigt. Das ist natürlich eine sehr schöne Eigenschaft. Dann haben wir auch noch gleich die Richtung mit drin, wenn wir also negative Effekte haben, dann senkt die Variable das Risiko pro Einheit um den prozentualen Wert. Bei kategorialen Variablen haben wir dann den Unterschied zu der nicht vorhandenen Gruppe. Daher sind männliche Ferkel um 5% weniger infiziert als weibliche Ferkel. Leider geht der t-Test, der die \(p\)-Werte produziert, von homogenen Varianzen aus. Die haben wir aber nicht vorliegen.
lm_fit |>
summary() |>
pluck("coefficients") |>
round(4) Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.4179 0.4103 -8.3308 0.0000
crp 0.1782 0.0144 12.4039 0.0000
age 0.0080 0.0046 1.7484 0.0811
sexmale 0.0700 0.0419 1.6693 0.0958
frailtypre-frail -0.0735 0.0677 -1.0846 0.2787
frailtyrobust -0.0568 0.0637 -0.8931 0.3723Deshalb müssen wir nochmal ran. Wir können die Funktion coeftest() aus dem R Paket {lmtest} zusammen mit den R Paket {sandwich} nutzen um unsere Modellanpassung für die Varianzheterogenität zu adjustieren. Wir ändern also die Spalte Strd. Error. Es gibt aber sehr viele Möglichkeiten type die Varianz anzupassen. Das ist ein eigenes Kapitel worum wir uns hier nicht scheren. Wir nehmen mehr oder minder den Standard mit HC1.
lm_fit |>
coeftest(vcov. = vcovHC, type = "HC1") |>
round(4) |>
tidy()# A tibble: 6 x 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -3.42 0.366 -9.33 0
2 crp 0.178 0.0117 15.2 0
3 age 0.008 0.0045 1.76 0.0789
4 sexmale 0.07 0.0421 1.66 0.0974
5 frailtypre-frail -0.0735 0.0683 -1.08 0.282
6 frailtyrobust -0.0568 0.0628 -0.905 0.366 Wir schauen also als erstes auf den Standardfehler und sehen, dass unsere Gaussian lineare Regression (OLS) den Standardfehler als zu hoch geschätzt hat. Größer Standardfehler bedeutet kleinere Teststatistik und damit dann auch weniger signifikante \(p\)-Werte. In der Tabelle 52.2 siehst du nochmal die beiden Spalten der Standardfehler nebeneinander. Unser Sandwich-Schätzer (HC1) liefert da die besseren Fehlerterme, die eher der Realität der Varianzheterogenität entsprechen. Wir brauchen die adjustierten Standardfehler aber nur, wenn wir eine statistischen Test rechnen wollen und den \(p\)-Wert für die Bewertung der Signifikanz brauchen.
| OLS | HC1 | |
|---|---|---|
| (Intercept) | 0.4103 | 0.3663 |
| crp | 0.0144 | 0.0117 |
| age | 0.0046 | 0.0045 |
| sexmale | 0.0419 | 0.0421 |
| frailtypre-frail | 0.0677 | 0.0683 |
| frailtyrobust | 0.0637 | 0.0628 |
52.7 Gruppenvergleich
Häufig ist es ja so, dass wir das Modell nur schätzen um dann einen Gruppenvergleich zu rechnen. Das heißt, dass es uns interessiert, ob es einen Unterschied zwischen den Leveln eines Faktors gegeben dem Outcome \(y\) gibt. Wir machen den Gruppenvergleich jetzt einmal an der Gebrechlichkeit frailty einmal durch. Wir habe die drei Gruppen frail, pre-frail und robust vorliegen. Danach schauen wir uns nochmal die prinzipielle Idee des Gruppenvergleichs auf mittleren Wahrscheinlichkeiten infiziert zu sein an.
Eigentlich ist es recht einfach. Wir nehmen wieder unser lineares Modell, was wir oben schon angepasst haben. Wir schicken dann das Modell in die Funktion emmeans() um die Gruppenvergleiche zu rechnen. Jetzt müssen wir nur zwei Dinge noch machen. Zum einen wollen wir alle paarweisen Vergleiche zwischen den drei Leveln von dem Faktor frailty rechnen, deshalb setzen wir method = "pairwise". Dann müssen wir noch dafür sorgen, dass wir nicht homogene Varianzen schätzen. Deshalb setzen wir die Option vcov. = sandwich::vcovHAC. Damit wählen wir aus dem Paket {sandwich} den Sandwichschätzer vcovHAC und berücksichtigen damit die Varianzheterogenität in den Daten. Wenn du das Paket {sandwich} schon geladen hast, dann musst du das Paket nicht mit Doppelpunkt vor die Funktion des Sandwich-Schätzers setzen.
em_obj <- lm_fit |>
emmeans(~ frailty, method = "pairwise", vcov. = sandwich::vcovHAC)
em_obj frailty emmean SE df lower.CL upper.CL
frail 0.671 0.0568 406 0.559 0.783
pre-frail 0.598 0.0384 406 0.522 0.673
robust 0.614 0.0259 406 0.563 0.665
Results are averaged over the levels of: sex
Confidence level used: 0.95 Dann können wir auch schon uns die Kontraste und damit die Mittelwertsvergleiche wiedergeben lassen. Was heißt hier Mittelwertsvergleiche? Die Mittelwerte sind hier natürlich die mittlere Wahrscheinlichkeit infiziert zu sein. Wir adjustieren hier einmal die \(p\)-Werte für multiple Vergleiche nach Bonferroni, damit du auch mal die Optionen siehst.
em_obj |>
contrast(method = "pairwise", adjust = "bonferroni") contrast estimate SE df t.ratio p.value
frail - (pre-frail) 0.0735 0.0655 406 1.122 0.7880
frail - robust 0.0568 0.0620 406 0.917 1.0000
(pre-frail) - robust -0.0166 0.0441 406 -0.376 1.0000
Results are averaged over the levels of: sex
P value adjustment: bonferroni method for 3 tests Wir sehen also, dass es einen prozentualen Unterschied zwischen frail - (pre-frail) von -3% gibt. Daher ist die mittlere Wahrscheinlichkeit von pre-frail größer als die von frail. Den Zusammenhang sehen wir auch weiter oben in der Ausgabe von emmeans. Dort haben wir eine mittlere Infektionswahrscheinlichkeit von 66.8% für frail und eine mittlere Infektionswahrscheinlichkeit von 70.6% für pre-frail. Keiner der Vergleiche ist signifikant. Beachte, dass jeder Vergleich immer einen unterschiedlichen Standardfehler zugewiesen bekommt um die Varianzheterogenität zu berücksichtigen.
Jetzt lassen wir uns nochmal das unadjustierte compact letter display wiedergeben. Aber auch in dem unadjustierten Fall finden wir keine signifikanten Unterschiede.
em_obj |>
cld(Letters = letters, adjust = "none") frailty emmean SE df lower.CL upper.CL .group
pre-frail 0.598 0.0384 406 0.522 0.673 a
robust 0.614 0.0259 406 0.563 0.665 a
frail 0.671 0.0568 406 0.559 0.783 a
Results are averaged over the levels of: sex
Confidence level used: 0.95
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Am Ende möchte ich hier nochmal einen Spieldatensatz toy_tbl erstellen indem ich wiederum drei Gruppen miteinander vergleiche. Ich tue mal so als würden wir uns hier zwei Pestizide und eine Kontrolle anschauen. Unser Outcome ist dann, ob wir eine Infektion vorliegen haben oder das Pestizid alles umgebracht hat. Damit haben wir dann unser Outcome infected definiert. Wir bauen uns die Daten so, dass 80% der Beobachtungen in der Kontrolle infiziert sind. In den beiden Behandlungsgruppen sind jeweils 50% und 30% der Beobachtungen nach der Behandlung noch infiziert. Wir haben jeweils zwölf Pflanzen n_grp beobachtet. Das sind wirklich wenige Beobachtungen für einen \(0/1\) Endpunkt.
n_grp <- 12
toy_tbl <- tibble(trt = gl(3, n_grp, labels = c("ctrl", "roundUp", "killAll")),
infected = c(rbinom(n_grp, 1, 0.8), rbinom(n_grp, 1, 0.5), rbinom(n_grp, 1, 0.2)))Jetzt bauen wir uns wieder unser Modell zusammen.
toy_fit <- lm(infected ~ trt, data = toy_tbl)
toy_fit
Call:
lm(formula = infected ~ trt, data = toy_tbl)
Coefficients:
(Intercept) trtroundUp trtkillAll
0.8333 -0.4167 -0.5833 Wie du sehen kannst, treffen wir die voreingestellten Infektionswahrscheinlichkeiten nur einigermaßen. Wir wollen für die Kontrolle 80% und erhalten 83.3%. Für roundUp haben wir 50% gewählt und erhalten \(83.3 - 41.67 = 41.63\). Auch bei killAll sieht es ähnlich aus, wir wollen 20% und erhalten $83.3 - 58.33 = 24.97$. Wir haben aber auch echt wenige Beobachtungen. Auf der anderen Seite ist es dann für ein agrarwissenschaftliches Experiment gra nicht mal so wenig.
Und hier sehen wir dann auch gleich das Problem mit der Funktion check_heteroscedasticity(). Wegen der geringen Fallzahl sagt die Funktion, dass alles okay ist mit den Varianzen und wir keine Varianzheterogenität vorliegen haben.
check_heteroscedasticity(toy_fit)OK: Error variance appears to be homoscedastic (p = 0.527).Wenn wir uns aber mal die Abbildung 52.6 anschauen sehen wir, dass wir auf keinen Fall Varianzhomogenität vorliegen haben. Die geringe Fallzahl von zwölf Beobachtungen je Gruppe ist zu klein, damit die Funktion check_heteroscedasticity() eine signifikanten Abweichung finden kann. Deshalb schaue ich mir immer die Abbildungen an.
check_model(toy_fit, check = c("homogeneity", "normality"))
toy_fit mit der Funktion check_model(). Wir sehen hier eine klare Varianzheterogenität in dem Modell.
Wir können hier auch den coeftest() für Varianzheterogenität rechnen, aber wir sind ja hier an den Gruppenvergleichen interessiert, so dass wir dann gleich zu emmeans weitergehen.
coeftest(toy_fit, vcov. = vcovHC, type = "HC1")
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.83333 0.11237 7.4162 1.606e-08 ***
trtroundUp -0.41667 0.18634 -2.2361 0.032226 *
trtkillAll -0.58333 0.17225 -3.3865 0.001844 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wie schon oben gezeigt, können wir dann einfach emmeans() nutzen um die Gruppenvergleiche zu rechnen. Auch hier müssen wir einmal angeben, dass wir einen paarweisen Vergleich rechnen wollen. Wir wollen alle Gruppen miteinander vergleichen. Dann noch die Option vcov. = sandwich::vcovHAC gewählt um für heterogene Varianzen zu adjustieren.
em_obj <- toy_fit |>
emmeans(~ trt, method = "pairwise", vcov. = sandwich::vcovHAC)
em_obj trt emmean SE df lower.CL upper.CL
ctrl 0.833 0.106 33 0.6181 1.049
roundUp 0.417 0.173 33 0.0641 0.769
killAll 0.250 0.133 33 -0.0203 0.520
Confidence level used: 0.95 Auch hier sehen wir die mittlere Wahrscheinlichkeit infiziert zu sein in der Spalte emmean. Die Standardfehler SE sind für jede Gruppe unterschiedlich, die Adjustierung für die Varianzheterogenität hat geklappt. Dann kannst du noch die paarweisen Gruppenvergleiche über einen Kontrasttest dir wiedergeben lassen.
em_obj |>
contrast(method = "pairwise", adjust = "none") contrast estimate SE df t.ratio p.value
ctrl - roundUp 0.417 0.200 33 2.084 0.0449
ctrl - killAll 0.583 0.170 33 3.435 0.0016
roundUp - killAll 0.167 0.225 33 0.740 0.4645Oder aber du nutzt das compact letter display.
em_obj |>
cld(Letters = letters, adjust = "none") trt emmean SE df lower.CL upper.CL .group
killAll 0.250 0.133 33 -0.0203 0.520 a
roundUp 0.417 0.173 33 0.0641 0.769 a
ctrl 0.833 0.106 33 0.6181 1.049 b
Confidence level used: 0.95
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Da die Fallzahl sehr gering ist, können wir am Ende nur zeigen, dass sich die Kontrolle von der Behandlung killAll unterscheidet. Hätten wir mehr Fallzahl, dann könnten wir sicherlich auch zeigen, dass der Unterschied zwischen der Kontrolle zu der Behandlung roundUp in eine signifikante Richtung geht. So klein ist der Unterschied zwischen Kontrolle und roundUp mit 41.7% ja nicht.
Anwendungsbeispiel: Beschädigter Mais nach der Ernte
Im folgenden Beispiel schauen wir uns nochmal ein praktische Auswertung von einem agrarwissenschaftlichen Beispiel mit Mais an. Wir haben uns in diesem Experiment verschiedene Arten trt von Ernteverfahren von Mais angeschaut. Dann haben wir nach vier Zeitpunkten bestimmt, ob der Mais durch das Ernetverfahren nachträglich beschädigt war. Die Beschädigung selber wurde dann etwas komplizierter mit einem Labortest festgestellt, aber wir schauen uns nur die Ausprägung ja/nein also \(1/0\) als Outcome an. Durch einen Fehler im Labor müssen wir eine Kombination für den letzten Tag und der dritten Behandlung entfernen.
maize_tbl <- read_excel("data/maize_rate.xlsx") |>
mutate(damaged = ifelse(time == "5d" & trt == 3, NA, damaged),
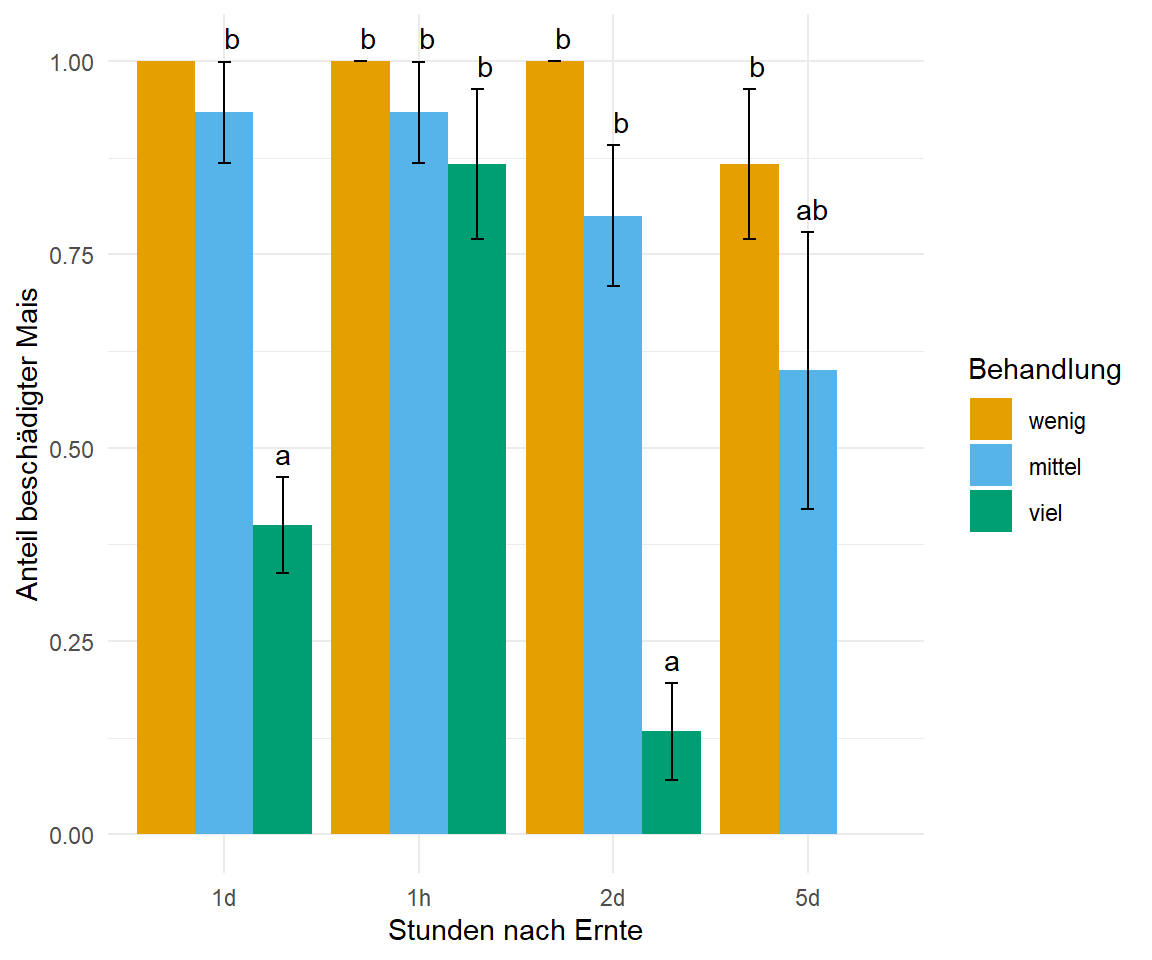
trt = factor(trt, labels = c("wenig", "mittel", "viel")))Dann rechnen wir auch schon das lm() Modell und nutzen {emmeans} für den Gruppenvergleich. Hier unbedingt SE als den Standardfehler für die Fehlerbalken nutzen, da wir sonst Fehlerbalken größer und kleiner als \(0/1\) erhalten, wenn wir die Standardabweichung nutzen würden. Du solltest auch immer von Varianzheterogenität ausgehen, deshalb nutze ich hier auch die Option vcov. = sandwich::vcovHAC in emmeans(). In der Abbildung 52.7 siehst du das Ergebnis der Auswertung in einem Säulendiagramm. Wir sehen einen klaren Effekt der Behandlung viel. Schade, dass wir dann nach 5 Tagen leider keine Auswertung für die dritte Behandlung vorliegen haben. Aber sowas passiert dann unter echten Bedingungen mal schnell.
lm(damaged ~ trt + time + trt:time, data = maize_tbl) |>
emmeans(~ trt * time, vcov. = sandwich::vcovHAC) |>
cld(Letters = letters, adjust = "bonferroni") |>
as_tibble() |>
ggplot(aes(x = time, y = emmean, fill = trt)) +
theme_minimal() +
labs(y = "Anteil beschädigter Mais", x = "Stunden nach Ernte",
fill = "Behandlung") +
geom_bar(stat = "identity",
position = position_dodge(width = 0.9, preserve = "single")) +
geom_text(aes(label = .group, y = emmean + SE + 0.01),
position = position_dodge(width = 0.9), vjust = -0.25) +
geom_errorbar(aes(ymin = emmean-SE, ymax = emmean+SE),
width = 0.2,
position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_okabeito()
lm()-Modell berechnet die Mittelwerte in jeder Faktorkombination, was dann die Anteile des beschädigten Mais entspricht. Das compact letter display wird dann in {emmeans} generiert.