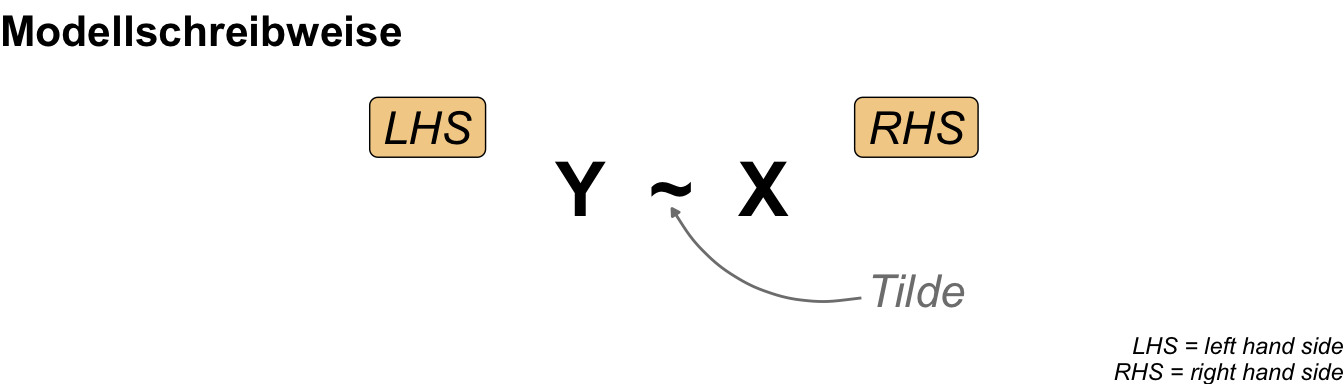45 Simple lineare Regression
Letzte Änderung am 15. October 2025 um 20:18:36
“Farewell to the Fairground; These rides aren’t working anymore.” — White Lies, Farewell to the Fairground
In diesem Kapitel wollen wir mit den Grundlagen des statistischen Modellierens beginnen. Wir nutzen dazu die simple lineare Regression als eine Methode um zu Verstehen, was eigentlich das statistische Modellieren macht. Dabei konzentrieren wir uns auf die lineare Regression, da wir hier ein lineares Modell vorliegen haben. Wir wollen also eine Grade Linie durch Punkte ziehen. Die Punkte sind in einem Scatterplot mit einer x-Achse und einer y-Achse dargestellt. Das ist für den Anfang schwierig genug. Später können wir auch nicht lineare Zusammenhänge modellieren. Dann nutzen wir auch nur eine Einflussvariable und nennen deshalb auch die Regression eine simple lineare Regression. Später in den folgenden Kapiteln erweitern wir dann die Regression und schauen uns auch an, wie gut die Regression geklappt hat. Mit gut meine ich, in wie weit die Grade durch die Punkte auch den Zusammenhang zwischen den x-Werten und den y-Werte erklärt. Dazu dann mehr mehr in dem Kapitel zu der Modelgüte einer Regression.
45.1 Allgemeiner Hintergrund
Was macht also eine simple lineare Regression? Die Regression ist eine Methode um eine lineare Grade durch eine Punktewolke in einem Scatterplot zu zeichnen. Dabei haben wir nur eine Einflussvariable \(x\) vorliegen, da unser Modell zuallerst simple sein soll. Der Messwert \(y\) ist in diesem Kapitel noch normalverteilt und damit auch kontinuierlich. Wir wollen also den Zusammenhang zwischen zwei kontinuierlichen Variablen durch eine Regression bestimmen. Wir sprechen in diesem Zusammenhang mit einer kontinuierlichen Einflussvariable von einer Kovariate. In einem nächsten Schritt ändern wir dann die Einflussvariable auf eine kategoriale Einflussvariable. Wir haben dann einen Faktor mit unterschiedlichen Gruppen vorliegen. Beide Fälle wollen wir uns dann einmal anschauen. Beginnen wollen wir aber mit einer allgemeinern Betrachtung. Welche Modelltypen oder Fragestellungen gibt es eigentlich? Bevor wir damit anfangen, einmal etwas sprachlicher Hintergrund.
Sprachlicher Hintergrund
“In statistics courses taught by statisticians we don’t use independent variable because we use independent on to mean stochastic independence. Instead we say predictor or covariate (either). And, similarly, we don’t say”dependent variable” either. We say response.” — User berf auf r/AskStatistics
Wenn wir uns mit dem statistischen Modellieren beschäftigen wollen, dann brauchen wir auch Worte um über das Thema reden zu können. Statistik wird in vielen Bereichen der Wissenschaft verwendet und in jedem Bereich nennen wir dann auch Dinge anders, die eigentlich gleich sind. Daher werde ich mir es hier herausnehmen und auch die Dinge so benennen, wie ich sie für didaktisch sinnvoll finde. Wir wollen hier was verstehen und lernen, somit brauchen wir auch eine klare Sprache.
“Jeder nennt in der Statistik sein Y und X wie er möchte. Da ich hier nicht nur von Y und X schreiben will, führe ich eben die Worte ein, die ich nutzen will. Damit sind die Worte dann auch richtig, da der Kontext definiert ist. Andere mögen es dann anders machen. Ich mache es eben dann so. Danke.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
In dem folgenden Kasten erkläre ich nochmal den Gebrauch meiner Begriffe im statistischen Testen. Es ist wichtig, dass wir hier uns klar verstehen. Zum einen ist es angenehmer auch mal ein Wort für ein Symbol zu schreiben. Auf der anderen Seite möchte ich aber auch, dass du dann das Wort richtig einem Konzept im statistischen Modellieren zuordnen kannst. Deshalb einmal hier meine persönliche und didaktische Zusammenstellung meiner Wort im statistischen Modellieren. Du kannst dann immer zu dem Kasten zurückgehen, wenn wir mal ein Wort nicht mehr ganz klar ist. Die fetten Begriffe sind die üblichen in den folgenden Kapiteln. Die anderen Worte werden immer mal wieder in der Literatur genutzt.
“Die Grenzen meiner Sprache bedeuten die Grenzen meiner Welt.” — Ludwig Wittgenstein
Hier kommt einmal die Tabelle mit den wichtigsten Begriffen im statistischen Modellieren und wie ich die Worte benutzen werde. Damit wir uns verstehen und du was lernen kannst. In anderen Büchern und Quellen findest du teilweise die Worte in einem anderen Sinnzusammenhang. Das ist gut so dort. Bei mir ist es anders.
| Symbol | Deutsch | Englisch | |
|---|---|---|---|
| LHS | \(Y\) / \(y\) | Messwert / Endpunkt / Outcome / Abhängige Variable | response / outcome / endpoint / dependent variable |
| RHS | \(X\) / \(x\) | Einflussvariable / Erklärende Variable / Fester Effekt / Unabhängige Variable | risk factor / explanatory / fixed effect / independent variable |
| RHS | \(Z\) / \(z\) | Zufälliger Effekt | random effect |
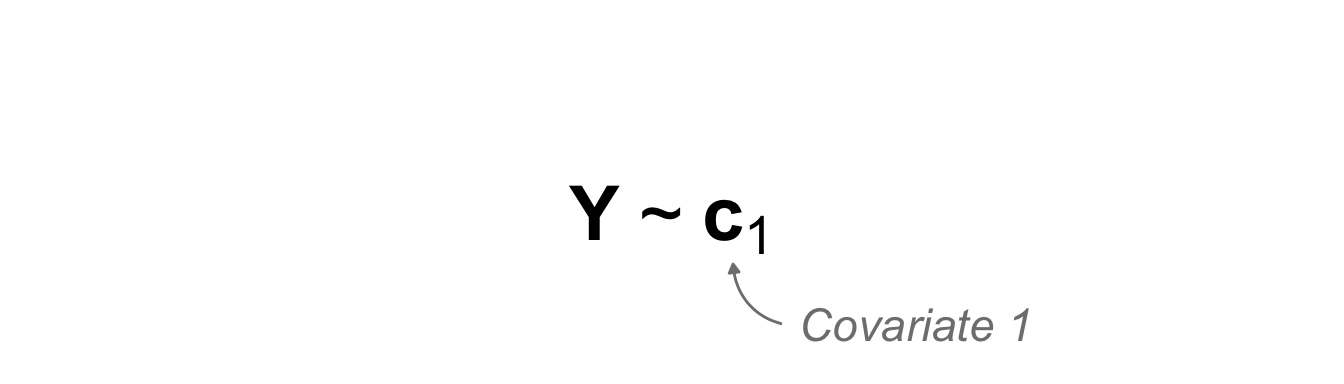
| \(X\) ist kontinuierlich | \(c_1\) | Kovariate 1 | covariate 1 |
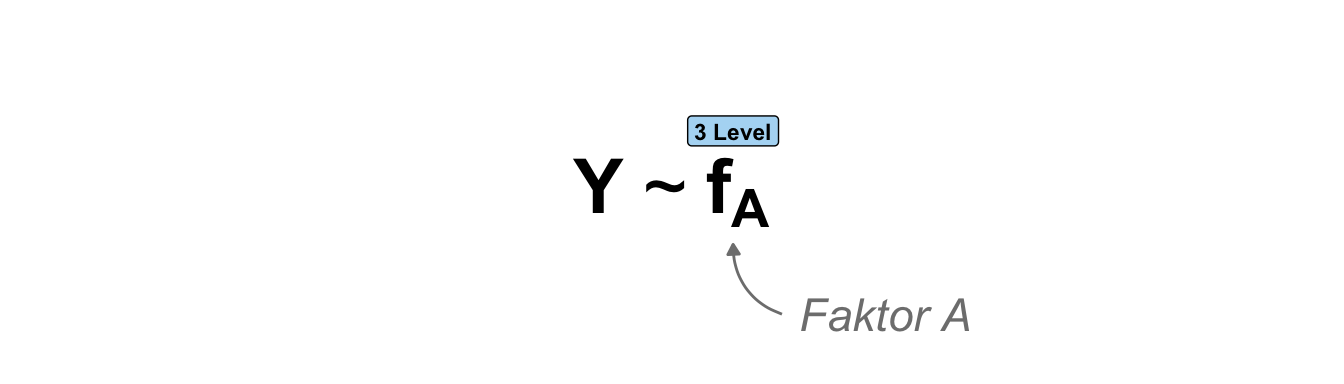
| \(X\) ist kategorial | \(f_A\) | Faktor \(A\) mit Level \(A.1\) bis \(A.j\) | factor \(A\) with levels \(A.1\) to \(A.j\) |
Am Ende möchte ich nochmal darauf hinweisen, dass wirklich häufig von der abhängigen Variable (eng. dependent variable) als Messwert und unabhängigen Variablen (eng. independent variable) für die Einflussvariablen gesprochen wird. Aus meiner Erfahrung bringt die Begriffe jeder ununterbrochen durcheinander. Deshalb einfach nicht diese Worte nutzen.
Das Modell
“Models are about what changes, and what doesn’t. Some are useful.” — Markus Gesmann
Fangen wir also erstmal allgemeiner an ein Modell und deren schreibweise zu verstehen. Was ist ein Modell im statistischen Sinne? Wenn du an ein Modell denkst und ein Modellauto oder aber ein Modell eines Hauses oder Landschaft vor dir siehst, dann ist das gar nicht so weit weg vonm einem statistischen Modell. Ein Modell eines Autos hat die Essenz eines Autos in sich. Wir erkennen das Auto wieder, haben aber natürlich nicht die gleichen Funktionalitäten wie bei einem echten Auto. So ist es auch bei dem statistischen Modellieren von Daten. Unser Auto sind also die erhobenen Daten und wir wollen ein Modell finden, was die Zusammenhänge und die Struktur in den Daten vereinfacht wiedergibt. Damit ist per se jedes Modell falsch, da es nur einen Teil der Wirklichkeit abbilden kann. Modelle sind aber manchmal nützlich. Wir können also erstmal wie folgt ein Modell zusammenfassen.
- Was ist ein Modell?
-
Ein Modell vereinfacht. Dabei behält es die Essenz der modellierten Sache bei. Ein statistisches Modell versucht eine Struktur in Daten zu finden. Dabei modelliert es den Zusammenhang zwischen dem Messwert und Einflussvariablen. Wir sprechen hier auch gerne von einer Modellanpassung (eng. fit).
Allgemeiner gesprochen versucht ein statistisches Modell deine Daten in ein erklärbaren Teil und einen unerklärbaren Teil zu zerlegen. Dafür nutzen wir dann den Zusammenhang von den Messwerten und den Einflussvariablen. Wir sprechen hier auch gerne von einer Modellanpassung (eng. fit). Wir passen ein Modell den Daten an. Je mehr die Einflussvariablen unseren Messwert erklären können, desto weniger bleibt unerklärt und somit kleiner ist auch der Fehler. Hierbei müssen wir etwas mit dem Wort Fehler aufpassen. Wir haben fast immer einen unerklärten Anteil von unserem Messwert nach dem Modellieren. Wir nennen diesen Anteil Fehler, meinen damit aber nicht, dass das Modell per se fehlerhaft ist.
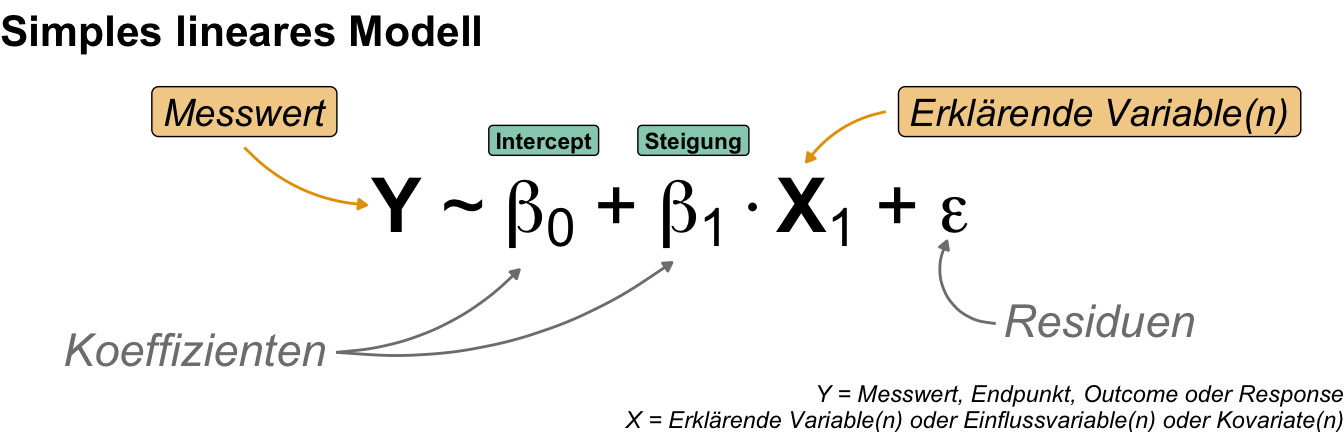
Da wir uns natürlich für die parktische Anwendung in R bewegen, nutzen wir auch die Modellschreibweise, die in R üblich ist. In R wird diese Schreibweise auch mit der Funktion formula() genutzt. Im Folgenden siehst du einmal ein Modell in einer abstrakten Form. Wir haben den Messwert \(Y\) auf der linken Seite (eng. left hand side, abk. LHS) der Tilde und die Einflussvariablen \(X\) auf der rechten Seite (eng. right hand side, abk. RHS). Dabei steht dann das \(X\) hier einmal als Platzhalter und Sammelbegriff für verschiedene Arten von möglichen Variablen.
Wenn wir jetzt zu R wechseln, sieht es dann etwas anders aus, da wir die Platzhalter \(Y\) für den Messwert und \(X\) für die Einflussvariable durch die Namen der Spalten in unserem Datensatz ersetzen. Der Datendatz liegt dann als tibble() in R vor. Mehr dann dazu in den folgenden Beispielen in den jeweiligen Kapiteln zum Modellieren. Dann sieht das Modell in R wie in der folgenden Abbildung aus.
Jetzt haben wir verstanden über was wir sprechen wollen, was ein Modell ist und wie wir das Modell in R aufbauen. Dann können wir schon einen Schritt weitergehen und uns fragen, was wir wigentlich mit dem Modell machen wollen. Welche Forschungsfragen können wir denn mit einem statistischen Modell beantworten? Prinzipiell haben wir da zwei große Felder, die wir bearbeiten können.
Kausales vs. prädiktives Modell
“Vor 2001 bestand Statistik gefühlt zu 10% aus der Prädiktion – heutzutage macht die Prädiktion die Mehrheit der Modellierungen aus.” — Gefühle einer anonymen Biometrikerin
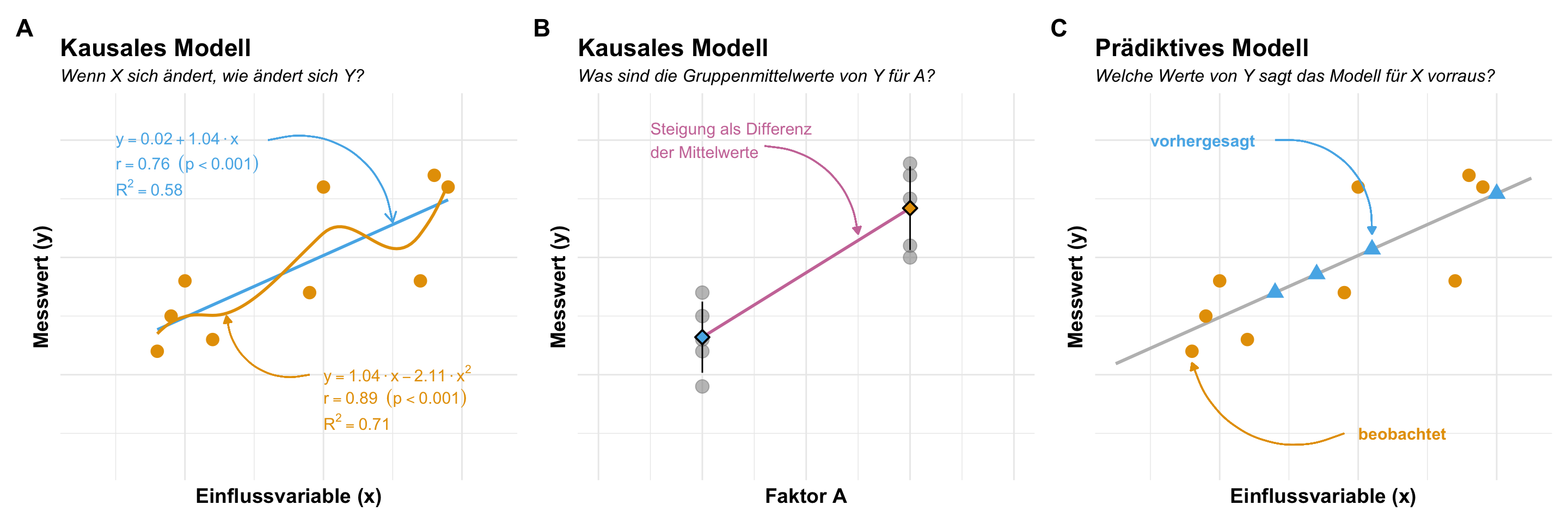
Wir können ein kausuales oder ein prädiktives Modell rechnen. Wenn wir ein kausales Modell rechnen, dann haben wir die Frage im Kopf, wie ändert sich der Messwert \(y\), wenn sich die Einflussvariable \(x\) um eine Einheit ändert. Wir können die Einheit auch weglassen und allgmeiner nach der Änderung in \(y\) durch die Änderung in \(x\) sprechen. Es geht hier also um Steigung (eng. slopes) oder eben die Ableitung (eng. derivative) von \(dy/dx\). In einem hier besprochenen linearen Modell ist die Frage nach der Steigung einfach zu beantworten. Schwieriger wird es im nicht linearen Modell. Hier nutzen wir dann Marginal effect models um die Steigungen entlang der Kurve zu bestimmen. Hier gilt im Besonderen, dass du ohne die Einheiten der Einflussvariable und des Messwertes kein statistisches Modell interpretieren kannst.
Eine andere Frage können wir durch ein prädiktives Modell oder eine Vorhersagen (eng. predictions) herausfinden. Hier wollen wir wissen, welche Messwerte ergeben sich durch unser Modell für neue Werte der Einflussvariablen. Das können wir durch eine Vorhersage erreichen. Auch hier ist das lineare Modell einfacher zu verstehen ale eine nicht lineare Kurve. Wir können einfach neue \(x\)-Werte in die Formel der Gradengleichung einsetzen und erhalten die entsprechenden vorhergesagten \(y\)-Werte wiedergegeben. Wenn wir kein normalverteilten Messwert haben, müssen wir hier nochmal etwas mehr aufpassen. Dazu dann aber auch mehr in den entsprechenden Kapiteln zu den verschiedenen Modellierungen.
- Was sind Steigungen?
-
Die Traktion der Graden über die Werte auf der x-Achse hinweg. Wenn \(x\) sich ändert, wir ändert sich dann der Messwert \(y\)? In einem linearen Modell haben wir nur einen Wert als Koeffizienten für die Steigung. Ohne die Einheiten der Einflussvariable sowie des Messwerts kann keine Steigung interpretiert werden.
- Was ist die Vorhersage?
-
Die y-Werte auf der Graden für jeden beliebigen Wert auf der x-Achse. Welche Werte vom Messwert \(y\) sagt das Modell für \(x\)-Werte vorraus? Wenn wir eine neue Beobachtung machen, welchen Messwert würde sich gegeben der Einflussvariable einstellen?
Damit ergibt sich grob die folgende Abbildung als Möglichkeiten in dem statistischen Modellieren. Wir haben hier nur ein simples Modell vorliegen und betrachten hier nur eine Einflussvariable. Die Einflussvariable kann kontinuierliche oder eben kategorial sein. Im kausalen Modell wollen wir wissen, wie sich eine Änderung in der Einflussvariablen auf den Messwert auswirkt. In dem prädiktiven Modell wollen wir eine Vorhersage des Messwertes für neue Beobachtungen machen.
Soviel zu dem allgemeinen Hintergrund. Nachdem wir jetzt auch die Fragestellungen erörtert haben, wollen wir jetzt einmal verstehen, wie die simple lineare Regression als ein statistisches Modell funktioniert und wie wir dort die Gradengleichung schätzen können. Die Berechungen kommen dann nochmal extra nach der Besprechung der Daten für die Beispiele.
45.2 Theoretischer Hintergrund
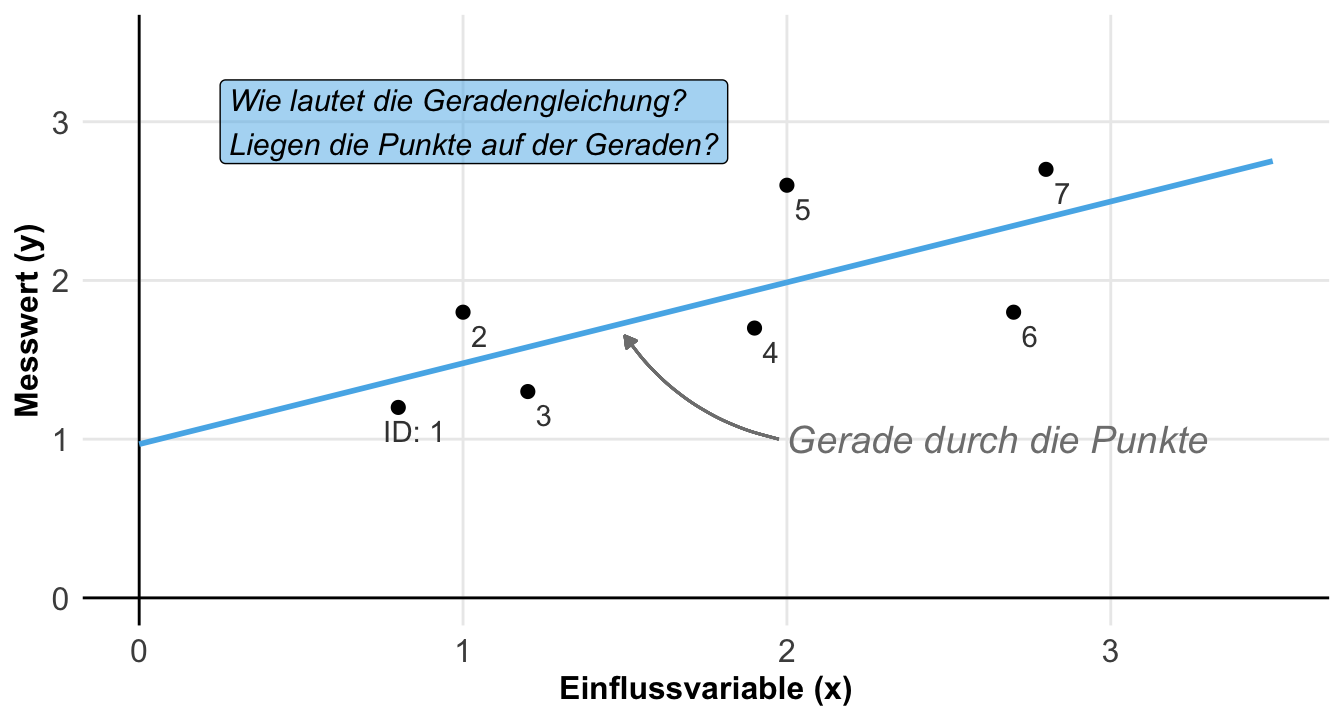
Beginnen wir damit was wir eigentlich erreichen wollen. In der folgenden Abbildung siehst du einmal die kontinuierliche Einflussvariable \(x\) und den kontinuierlichen Messwert \(y\) für sieben Beobachtungen. Jede der Beobachtungen hat einen Wert für \(x\) und einen Wert für \(y\). Wir können dann einen Scatterplot zeichnen. Jetzt wollen wir die optimale lineare Grade durch die Punkte finden. Wir erhalten dann die Gradengleichung. Darüber hinaus wollen wir auch noch wissen, wie gut die Grade durch die Punkte läuft.
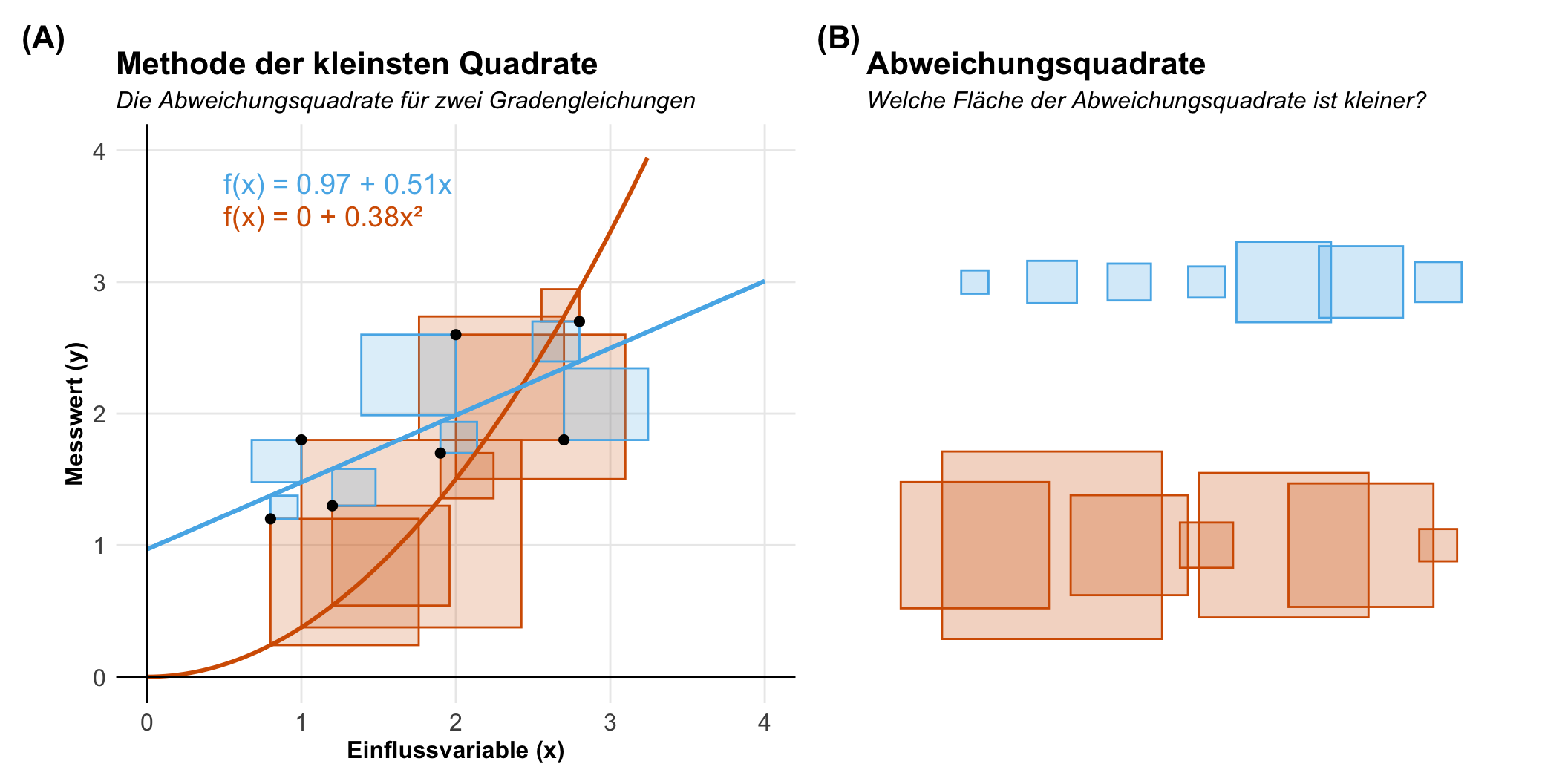
Wie finden wir die optimlare Grade? Hier kommt die Methode der kleinsten Quadrate (eng. least square method) zum Einsatz. Die Methode ist alt und wird dem Mathematiker Carl Gauß zugeschrieben. Im Jahr 1801 nutze Gaus die Methode um die Bahn des Zwergplaneten Ceres für eien kurze Zeitspanne korrekt vorherzusagen. Wir wollen hier die Methode der kleinsten Quadrate anwenden, um eben die beste Grade durch die Punkte zu finden. Wie wir in den folgenden Abbildung sehen, hat die lineare Grade eine kleinere Summe an Abweichungsquadraten als die quadratische Funktion. Wir würden hier also die blaue Grade der orangenen Graden vorziehen. Prinzipiell müssten wir also eine belibige Anzahl an Graden testen, in der Praxis gibt es aber eine geschlossende Formel für die optimale lineare Grade. Bei nicht linearen Zusammenhängen sieht es dann etwas anders aus. Dazu aber später mehr in dem entsprechenden Kapitel zu nicht lineare Regression.
Wenn du jetzt denkst ‘Hä?’, dann besuche doch einmal die fantastische Seite Explained Visually | Ordinary Least Squares Regression um selber zu erfahren, was eine lineare Regression macht. Auf der Seite findest du interaktive Abbildungen, die dir das Konzept der linearen Regression sehr anschaulich nachvollziehen lassen.
Am Ende modellieren oder minimieren wir die Varianz. Den nichts anders sind ja die Abweichungsquadrate. Je kleiner die Beobachtungen um die Grade streuen, desto besser passt auch die Grade zu den Punkten. Und eine quadratische Streuung in der Statistik ist nichts anderes als die Varianz, die wir schon aus der deskriptiven Statistik kennen.
Nachdem wir die Methode der kleinsten Quadrate durchgeführt haben, kriegen wir folgende Gradengleichung wieder. Die Grade wird durch die Koeffizienten des y-Achsenabschnitts (eng. intercept) und der Steigung (eng. slope) beschrieben. Der nicht durch die Gradengleichung erklärte Rest wird auch Fehler (eng. error) oder im Kontext der linearen Regression dann Residuen genannt.
Die Grade wird somit durch eine Gradengleichung wie oben beschreiben. Du kennst vermutlich noch die Form \(y = mx + b\). In der folgenden Tabelle siehst du nochmal den Vergleich von der Schreibweise der linearen Regression in der Schule und in der Statistik. Darüber hinaus sind die deutschen Begriffe den englischen Begriffen gegenüber gestellt. Warum schreiben wir die Gleichung in der Form? Damit wir später noch weitere \(\beta_px_p\)-Paare ergänzen könen und so multiple lineare Modelle bauen können.
| Schule | Statistik | Deutsch | Englisch |
|---|---|---|---|
| \(m\) | \(\beta_1\) | Steigung | Slope |
| \(x\) | \(x_1\) | Einflussvariable | Risk factor |
| \(b\) | \(\beta_0\) | y-Achsenabschnitt | Intercept |
| \(\epsilon\) | Residuen | Residual |
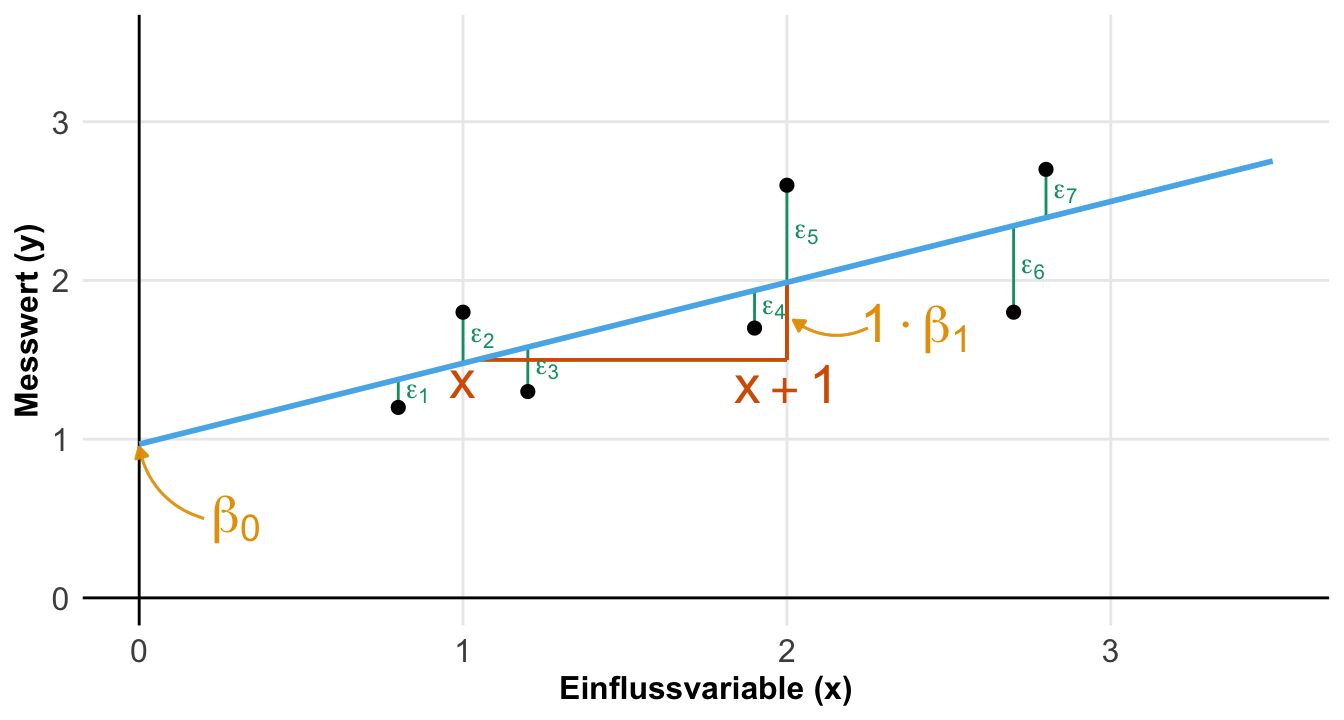
Wir können jetzt die Gradengleichung auch gleich nochmal in der Visualisierung beschriften. In der folgenden Abbildung sehen wir die Visualisierung des kovariaten Beispieldatensatzes. Die Grade läuft durch die Punktewolke und wird durch die statistischen Maßzahlen bzw. Parameter \(\beta_0\), \(\beta_1\) sowie den \(\epsilon\) beschrieben. Wir sehen, dass das \(\beta_0\) den Intercept darstellt und das \(\beta_1\) die Steigung der Graden. Wenn wir \(x\) um 1 Einheit erhöhen \(x+1\), dann steigt der \(y\) Wert um den Wert von \(\beta_1\). Die einzelnen Abweichungen der beobachteten \(y\)-Wert zu den \(y\)-Werten auf der Grade - auch \(\hat{y}\) bezeichnet - werden als Residuen oder auch \(\epsilon\) abgebildet.
Hier wird dann auch nochmal schneller klar, was der y-Achsenabschnitt ist und wie wir die Steigung zu interpretieren haben. Die Steigung sagt aus um welchen Wert sich der Messwert \(Y\) ändert, wenn sich die Einflussvariable um eine Einheit erhöht. Die Residuen sind hier auch nochmal dargestellt und beschreiben eben den Rest oder Abstand, den die lineare Gradengleichung nicht an den Messwert beschreiben kann. Wir hätten nur keine Residuen, wenn die Graden sich durch alle Punkte schlängeln würde. Das geht jedoch mit einer linearen Funktion nicht. Außer die Punkte liegen alle auf einer Linie, was in einem biologischen System sehr selten vorkommt.
Schauen wir uns einmal den Zusammenhang von \(y\), den beobachteten Werten, und \(\hat{y}\), den geschätzen Werten auf der Grade in unserem Beispiel an. In der folgenden Tabelle sehen wir die Berechnung der einzelnen Residuen für die Grade aus der obigen Abbildung. Die Daten kannst du dir dann nochmal im Datenabschnitt anschauen. Wir nehmen jedes beobachtete \(y\) und ziehen den Wert von \(y\) auf der Grade, bezeichnet als \(\hat{y}\), ab. Diesen Schritt machen wir für jedes Wertepaar \((y_i; \hat{y}_i)\). In R werden die \(\hat{y}\) auch angepasste Werte (eng fitted values) genannt. Die \(\epsilon\) Werte werden dann Residuen (eng. residuals) bezeichnet.
| x | y | \(\boldsymbol{\hat{y}}\) | Residuen (\(\boldsymbol{\epsilon}\)) | Wert |
|---|---|---|---|---|
| 0.8 | 1.2 | 1.38 | \(\epsilon_1 = y_1 - \hat{y}_1\) | \(\epsilon_1 = 1.2 - 1.38 = -0.18\) |
| 1.0 | 1.8 | 1.48 | \(\epsilon_2 = y_2 - \hat{y}_2\) | \(\epsilon_2 = 1.8 - 1.48 = +0.32\) |
| 1.2 | 1.3 | 1.58 | \(\epsilon_3 = y_3 - \hat{y}_3\) | \(\epsilon_3 = 1.3 - 1.58 = -0.28\) |
| 1.9 | 1.7 | 1.94 | \(\epsilon_4 = y_4 - \hat{y}_4\) | \(\epsilon_4 = 1.7 - 1.94 = -0.24\) |
| 2.0 | 2.6 | 1.99 | \(\epsilon_5 = y_5 - \hat{y}_5\) | \(\epsilon_5 = 2.6 - 1.99 = +0.61\) |
| 2.7 | 1.8 | 2.34 | \(\epsilon_6 = y_6 - \hat{y}_6\) | \(\epsilon_6 = 1.8 - 2.34 = -0.54\) |
| 2.8 | 2.7 | 2.40 | \(\epsilon_7 = y_7 - \hat{y}_7\) | \(\epsilon_7 = 2.7 - 2.40 = +0.30\) |
Die Residuen haben einen Mittelwert von \(\bar{\epsilon} = 0\) und eine Varianz von \(s^2_{\epsilon} = 0.17\). Wir schreiben, dass die Residuen normalverteilt sind mit \(\epsilon \sim \mathcal{N}(0, s^2_{\epsilon})\). Wir zeichnen die Grade also so durch die Punktewolke, dass die Abstände zu den Punkten, die Residuen, im Mittel null sind. Die Optimierung erreichen wir in dem wir die Varianz der Residuuen minimieren. Folglich modellieren wir die Varianz.
Wir immer geht natürlich mehr als ich hier Vorstellen kann. Du findest im Folgenden Tutorien, die mich hier in dem Kapitel inspiriert haben. Ich habe mich ja in diesem Kapitel auf die Durchführbarkeit in R und die allgemeine Verständlichkeit konzentriert. Es geht aber natürlich wie immer auch mathematischer…
- Wir funktioniert nun so eine lineare Regression und was sind den jetzt eigentlich die Koeffizienten \(\beta_0\) und \(\beta_1\) eigentlich? Hier gibt es die fantastische Seite Explained Visually | Ordinary Least Squares Regression, die dir nochmal erlaubt selbe mit Punkten in einem Scatterplot zu spielen und zu sehen wie sich dann die Regressionsgleichung ändert.
- Du kannst auf der Seite Manual linear regression analysis using R nochmal weiter über die lineare Regression lesen. Der Blogpost ist sehr umfangreich und erklärt nochmal schrittweise, wie die lineare Regression in R per hand funktioniert.
- Simple Regression auf Wikipedia mit weit mehr Informationen zu den Formeln und den Zusammenhängen. Ein toller zusammenfassender Artikel.
- Mehr zum Modellieren findest du im Openbook “Statistical Thinking for the 21st Century” in den beiden Kapiteln Statistical Thinking for the 21st Century — What is a model? und Statistical Thinking for the 21st Century — Practical statistical modeling?
45.3 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
pacman::p_load(tidyverse, magrittr, broom,
readxl, ggpmisc, conflicted)
conflicts_prefer(magrittr::set_names)
conflicts_prefer(ggplot2::annotate)
conflicts_prefer(dplyr::filter)An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
45.4 Daten
Für unsere Anwendung schauen wir uns jetzt einmal drei Datensätze an. Zuerst einen Datensatz mit der Sprungweite als kontinuierlichen Messwert und dem GEwicht als kontinuierliche Einflussvariable. Wir haben hier also einen einkovariaten Datensatz vorliegen. Dann möchte ich noch den Fall mit einer kategorialen Einflussvariable betrachten. Hier nehmen wir dann die verschiedenen Floharten als Faktor mit in den Datensatz. Wir haben dann einen einfaktoriellen Datensatz. Am Ende möchte ich dir immer nochmal zeigen, wie in R theoretisch die Berechnungen läufen. Dafür nutze ich dann einen theoretischen Datensatz mit Schlangenlängen aus Kéry (2010). Ich habe den Datensatz leicht angepasst.
Einkovariater Datensatz
Wir wollen uns erstmal mit einem einfachen Datenbeispiel beschäftigen. Wir können die lineare Regression auf sehr großen Datensätzen anwenden, wie auch auf sehr kleinen Datensätzen. Prinzipiell ist das Vorgehen gleich. Wir nutzen jetzt aber erstmal einen kleinen Datensatz mit \(n=7\) Hundeflöhen als Beobachtungen. In der folgenden Tabelle ist der Datensatz cov1_tbl dargestellt. Wir wollen den Zusammenhang zwischen der Sprungweite in [cm] und dem Gewicht in [mg] für sieben Hundeflöhe modellieren.
R Code [zeigen / verbergen]
cov1_tbl <- read_xlsx("data/regression_data.xlsx", sheet = "covariate")Dann schauen wir uns die Daten einmal in der folgenden Tabelle einmal an. Wir haben die Sprungweite und das Gewicht von sieben Hundeflöhen gemessen. Die Daten sind nach dem gewicht der Flöhe sortiert. Die Einflussvariable ist das Gewicht und der Messwert die Sprungweite.
| jump_length | weight |
|---|---|
| 1.2 | 0.8 |
| 1.8 | 1.0 |
| 1.3 | 1.2 |
| 1.7 | 1.9 |
| 2.6 | 2.0 |
| 1.8 | 2.7 |
| 2.7 | 2.8 |
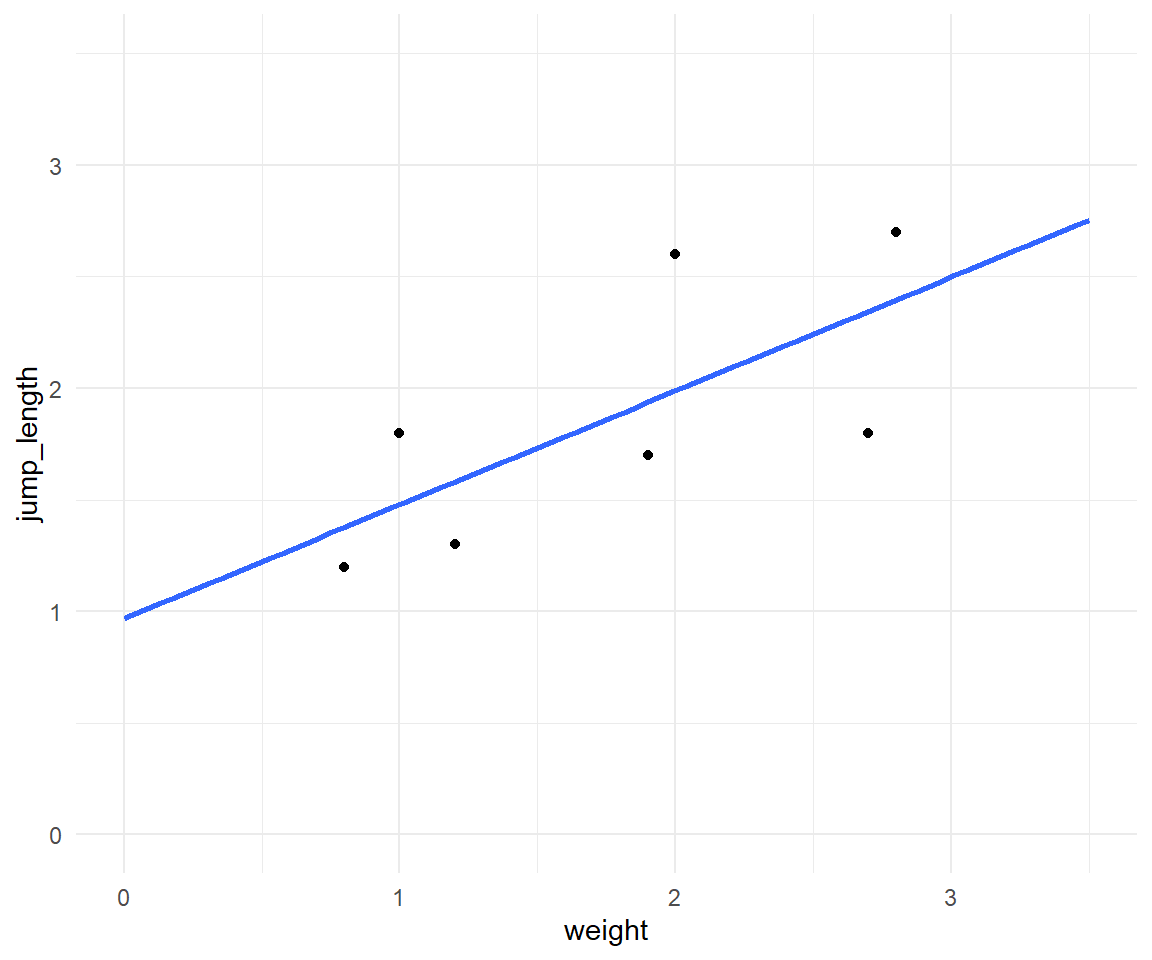
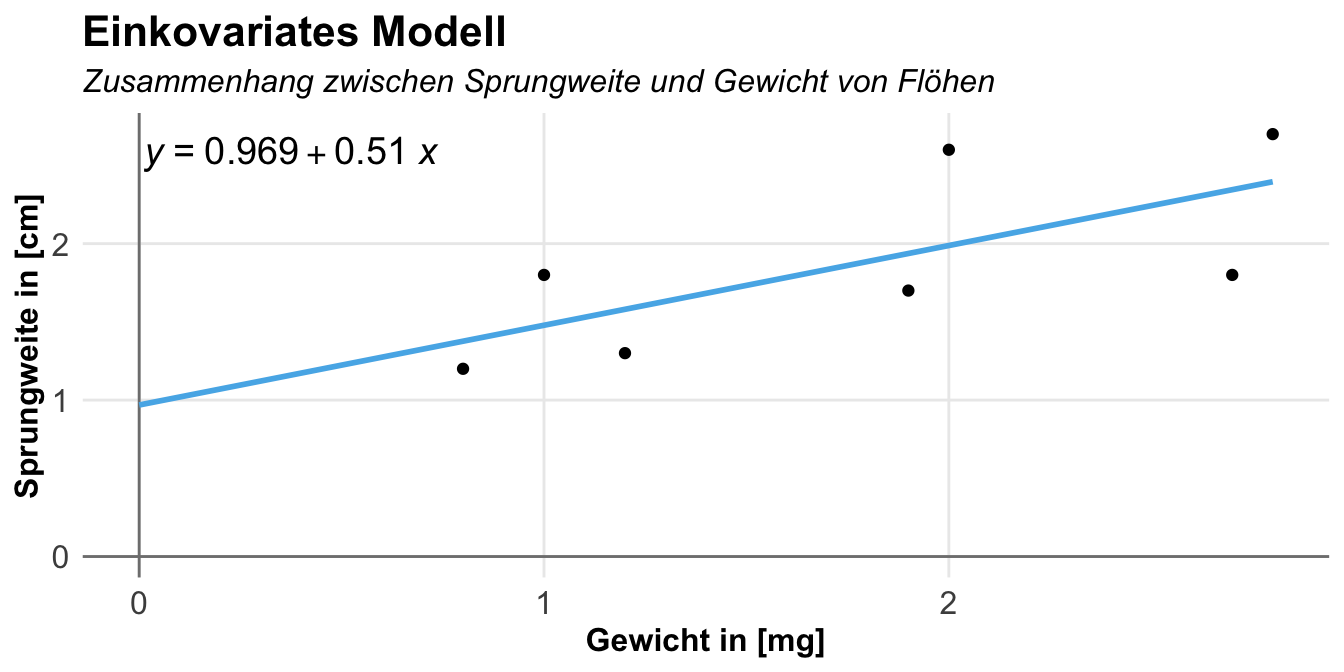
In der folgenden Abbildung sehen wir die Visualisierung der Daten cov1_tbl in einem Scatterplot mit einer geschätzen Grade durch die Punktewolke. Wir fragen uns, ob das Gewicht der Hundeflöhe einen Einfluss auf die Sprungweite der Flöhe hat. Da wir hier eine positive Steigung haben, können wir schließen, dass wir vermutlich einen positiven Zusammenhang vorliegen haben.
Einfaktorieller Datensatz
Etwas seltener in der reinen linearen Regression nutzen wir nur eine kategoriale Einflussvariable. Häufig sind wir dann hier schon in der einfaktoriellen ANOVA oder aber dem statistischen Gruppenvergleich. Hier wollen wir uns jetzt aber mal einen Datensatz mit der Sprungweite in [cm] als Messwert und der Tierart als kategoriale Einflussvariable anschauen. Wir haben die Sprungweite von Hunde-, Katzen- und Fuchsflöhen gemessen. Die Tierart ist unsere Gruppe und damit unserer Faktor.
R Code [zeigen / verbergen]
fac1_tbl <- read_xlsx("data/regression_data.xlsx", sheet = "factorial") |>
select(animal, jump_length) |>
mutate(animal = as_factor(animal))Dann schauen wir uns die Daten einmal in der folgenden Tabelle als Auszug einmal an. Wichtig ist hier nochmal, dass du eben die Einflussvariable Tierart einen Faktor animal mit drei Leveln also Gruppen vorliegen hast. Wir wollen jetzt die drei Tierarten hinsichtlich ihrer Sprungweite in [cm] miteinander vergleichen.
| animal | jump_length |
|---|---|
| dog | 5.7 |
| dog | 8.9 |
| dog | 11.8 |
| … | … |
| fox | 10.6 |
| fox | 8.6 |
| fox | 10.3 |
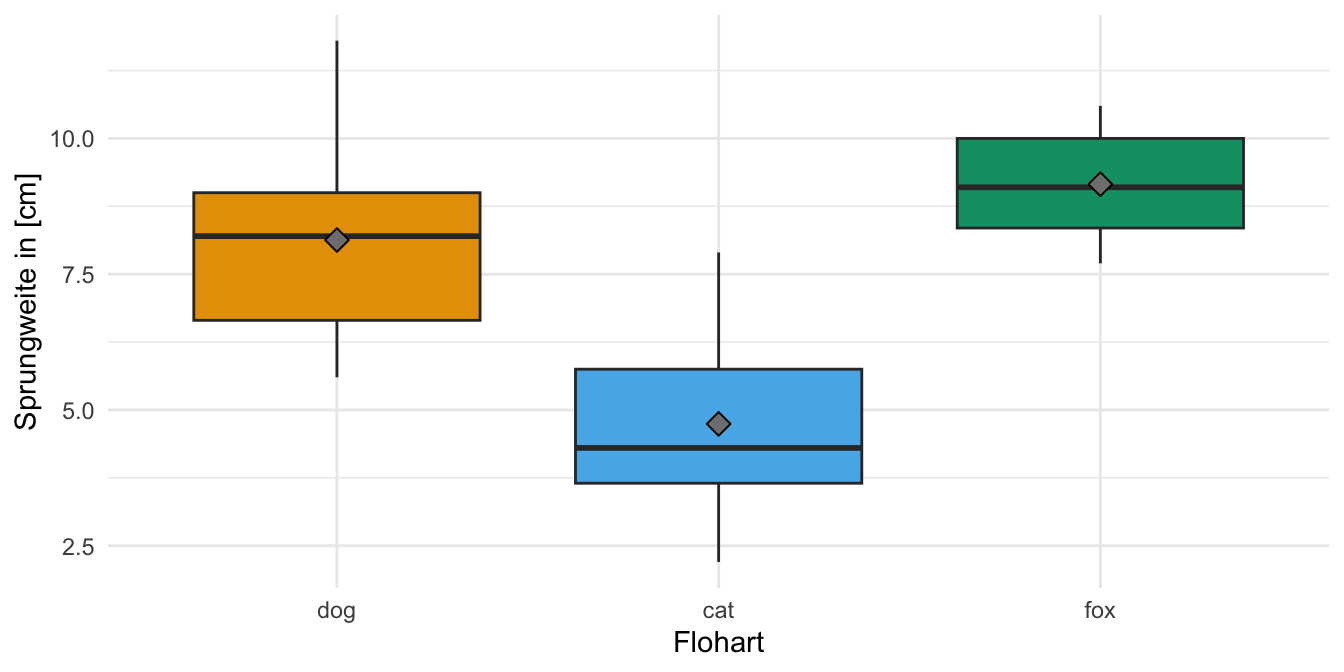
Und dann wollen wir uns noch einmal die Daten als einen einfachen Boxplot anschauen. Wir sehen, dass die Daten so gebaut sind, dass wir einen signifikanten Unterschied zwischend den Sprungweiten der Floharten erwarten. Die Boxen der Boxplots überlappen sich nicht und die Boxplots liegen auch nicht auf einer Ebene.
Theoretischer Datensatz
Abschließend kommen wir noch zu einem theoretischen Datensatz dem ich Kéry (2010) entlehnt habe. Ich möchte nochmal zeigen, wie R intern mit der Modellmatrix die Berechnungen durchführt. Das hat mich interessiert und deshalb habe ich es einmal für mein Verständnis aufgeschrieben. Wenn es dich auch interessiert, dann kannst du in den entsprechenden Tabs weiter unten einmal nachschauen. Hier also erstmal ein sehr simpler theoretischer Datensatz zu Körperlängen von Schlangen. Wir müssen hier dann noch die Faktoren einmal umwandeln, damit wir auch später die Modellmatrix sauber vorliegen haben. Deshalb hier die explizite Benennung der Level in der Funktion factor().
R Code [zeigen / verbergen]
snake_tbl <- read_xlsx("data/regression_data.xlsx", sheet = "theory") |>
mutate(region = factor(region, levels = c("west", "nord")),
color = factor(color, levels = c("schwarz", "rot", "blau")))In der folgenden Tabelle ist der Datensatz snake_tbl nochmal dargestellt. Wir haben die Schlangenlänge svl als Messwert \(y\) sowie das Gewicht der Schlangen mass als kontinuierliche Einflussvariable, die Sammelregion region und die Farbe der Schlangen color und als kategoriale Einflussvariablen mit unterschiedlichen Anzahlen an Gruppen. Die Region region ist also ein Faktor mit zwei Leveln und die Schlangenfarbe color ein Faktor mit drei Leveln. Ich nutze den Datensatz also einmal als einen Spieldatensatz um die Modellierung theoretisch besser nachvollziehen zu können.
| svl | mass | region | color |
|---|---|---|---|
| 40 | 6 | west | schwarz |
| 45 | 8 | west | schwarz |
| 39 | 5 | west | rot |
| 51 | 7 | nord | rot |
| 52 | 9 | nord | rot |
| 57 | 11 | nord | blau |
| 58 | 12 | nord | blau |
| 49 | 10 | nord | blau |
45.5 Kausales Modell
Beginnen wir einmal mit dem kausalen Modell. Wir wollen also wissen, wie sich der Messwert \(y\) ändert, wenn sich die Einflussvariable erhöht. Wir fragen hier also nach der Steigung. Da wir eine lineare Grade vorliegen haben, ist es eben einfach, wir müssen den Koeffizienten für die Steigung bestimmen und dann noch Testen. Wir wollen ja wissen, ob der Effekt auch signifikant ist. Mit dem Effekt meinen wir im Kontext der linearen Regression eben den Koeffizienten der Steigung. Wir betrachten jetzt also einmal das einkovariate Modell, mit einer kontinuierlichen Einflussvariable sowie einem faktoriellen Modell, mit einer kategorialen Variable. Der Messwert hier ist dann immer die kontinuierliche Sprungweite.
45.5.1 Einkovariates Modell
Die simple lineare Regression ist ein einkovariates Modell. Häufig wird das einkovariate Modell dann einfach nur die lineare Regression genannt. Wir haben einen kontinuierlichen Messwert sowie eine kontinuierliche Einflussvariable. Wir nennen die kontinuierliche Einflussvariable eine Kovariate. Es ergibt sich dann das folgende abstrakte simple Modell. Auf der linken Seite ist der MEsswert und auf der rechten Seite der Tilde ist unsere eine Kovariate.
Jetzt können wir dieses theoretische Modell einmal auf unser Beispiel zu den Sprungweiten als kontinuierlichen Messwert sowie dem Körpergewicht als Kovariate anwenden. Du findest in den folgenden Tabs einmal die Auswertung in R durch die Funktionen sowie die theoretische Betrachtung, wie R das kovariate Modell intern verrechnet. Aus praktischer Sicht brauchts du nur den ersten Tab.
Für die lineare Regression nutzen wir die Funktion lm() (eng. linear model) mit der Formelschreibweise. Wir schreiben auf der linken Seite den Messwert und auf die rechte Seite der Tilde dann die Kovariate. Dann müssen wir noch angeben in welchem Datensatz die beiden Variablen als Spalten zu finden sind. Dann schieben wir noch die Modellanpassung (eng. fit) in ein Objekt um uns verschiedene Informationen später ausgeben zu lassen. Mit Modelanpassung meinen wir, dass wir schauen, ob wir ein Modell finden, was zu den Daten passt.
R Code [zeigen / verbergen]
cov1_fit <- lm(jump_length ~ weight, data = cov1_tbl) Mit der Funktion coef() können wir dann die Koeffizienten der linearen Regression extrahieren. Wir erhalten einmal den Intercept als den y-Achsenabschnitt und die Steigung wieder. Die Steigung wird hier unter dem Namen der Spalte geschrieben.
R Code [zeigen / verbergen]
cov1_fit |>
coef()(Intercept) weight
0.9686434 0.5096368 Wir erhalten also einen y-Achsenabschnitt \(\beta_0\) von \(0.969\) sowie eine Steigung \(\beta_1\) von \(0.51\) wiedergegeben. In der folgenden Abbildung sehen wir dann einmal die Gerade durch die Punkte zusammen mit der Gradengleichung. Ich nutze hier die Funktion stat_poly_line() und die Funktion stat_poly_eq() um mir die Grade sowie die Gradengleichung einzeichnen zu lassen. Beide Funktionen findest du in dem R Paket {ggpmisc}.
Eigentlich wollen wir ja ein kausales Modell rechnen, da wir an dem Effekt der Kovariate Gewicht in [mg] der Hundeflöhe interessiert sind. Wenn also die Kovariate \(c_1\) um eine Einheit ansteigt, um wie viel verändert sich dann der Messwert \(y\)?
Der Koeffizient \(\beta_1\) als Steigung der Graden gibt uns also den Einfluss oder den kausalen Zusammenhang zwischen dem Messwert \(y\) und der Kovariate \(c_1\) wieder. Im einem ersten Schritt schauen wir uns die Ausgabe der Funktion summary() unseres Modells an.
R Code [zeigen / verbergen]
cov1_fit |> summary()Wir erhalten dann folgende Ausgabe mit den entsprechenden Kurzerkläruungen von mir. Keine Angst, die gehen wir dann alle in den nächsten Paragraphen einmal durch.
summary() aus einer linearen Modellanpassung mit der Funktion lm(). Die Ausgabe der Funktion teilt sich grob in drei informative Bereiche: Informationen zu den Residuen, Informationen zu den Koeffizienten und Informationen zu der Modelgüte. [Zum Vergrößern anklicken]
Zuerst sehen wir nochmal welche Funktion wir aufgerufen haben und welches Modell gerechnet wurde. Dann kommen die Informationen zu den Residuen. Wenn alle Beobachtungen auf der Graden liegen würden, dann wären alle Residuen gleich Null. Bei zu wenigen Beobachtungen erhalten wir dann leider keine zusammenfassende Information zu den Residuen. Die Information zum Median und den Quartilen müssen wir uns dann selber einmal bauen.
R Code [zeigen / verbergen]
cov1_fit |> residuals() |> summary() Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.5447 -0.2586 -0.1764 0.0000 0.3130 0.6121 Die negativen Abweichungen und die positiven Abweichungen sollten sich auf Null aufaddieren. Der Median sollte ebenfalls dabei Null sein. Das 1st Quartile und das 3rd Quartile sollten ebenfalls im Betrag gleich sein. Deshalb sind auch die Residuen bei einer guten Modellanpassung normalverteilt mit einem Mittelwert von Null. Hier haben wir aber einigermaßen normalverteilte Residuen vorliegen. Die Residuen schauen wir uns aber nochmal im Kapitel zur Modelgüte genauer an.
Der Reststandardfehler (R Residual standard error, abk. RSE) hat mehrere Vorteile. Er sagt dir direkt, wie genau die Vorhersagen des Modells unter Verwendung der Einheiten des Messwertes sind. Der Reststandardfehler gibt an, wie weit die Datenpunkte im Durchschnitt von der Graden entfernt sind.
Du erhälst immer eine Grade und du erhälst faktisch immer eine Modellanpassung. Du musst dann selber entscheiden, ob dein Modell zu den Daten passt. Deshalb schauen wir uns auch die Residuen an und schauen, ob die Annahme der Normalverteilung an die Residuen erfüllt ist. Wenn dies nicht der Fall ist, dann passt unser Modell nicht zu den Daten und wir müssen ein anderes Modell ausprobieren.
Als nächstes erhalten wir die Informationen zu den Koeffizienten. Die Koeffizienten sind in einem simplen Modell der Intercept und die Steigung. Die Steigung hat immer den Namen der betrachteten Kovariate. Hier nochmal die Wiedergabe der Koeffizienten als Auszug von der obigen Tabelle.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.9686434 0.4447001 2.178195 0.08129789
weight 0.5096368 0.2315464 2.201013 0.07899303Das heißt, wir kriegen dort \(\beta_0\) als y-Achsenabschnitt sowie die Steigung \(\beta_1\) für das Gewicht. Dabei ist wichtig zu wissen, dass immer als erstes der y-Achsenabschnitt (Intercept) auftaucht. Dann die Steigung der Kovariate in dem Modell. Wir können die Gradengleichung wie folgt formulieren.
\[ jump\_length \sim 0.97 + 0.51 \cdot weight \]
Was heißt die Gleichung nun? Wenn wir das Gewicht um eine Einheit erhöhen dann verändert sich die Sprungweite um den Wert von \(\beta_1\). Wir haben hier eine Steigung von \(0.51\) vorliegen. Ohne Einheit keine Interpretation! Wir wissen, dass das Gewicht in [mg] gemessen wurde und die Sprungweite in [cm]. Damit können wir aussagen, dass wenn ein Floh 1 mg mehr wiegt der Floh 0.51 cm weiter springen würde. Schauen wir nochmal in die saubere Ausgabe der tidy() Funktion aus dem R Paket {broom}. Wir sehen nämlich noch einen \(p\)-Wert für den Intercept und die Steigung vom Gewicht.
R Code [zeigen / verbergen]
cov1_fit |> tidy()# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.969 0.445 2.18 0.0813
2 weight 0.510 0.232 2.20 0.0790Da wir hier einen p-Wert für jeden Koeffizienten haben, müssen wir auch einen Test rechnen. Wenn wir einen \(p\)-Wert sehen, dann brauchen wir eine Nullhypothese, die wir dann eventuell mit der Entscheidung am Signifikanzniveau \(\alpha\) von 5% ablehnen können. Die Nullhypothese ist die Gleichheitshypothese. Wenn es also keinen Effekt von dem Gewicht auf die Sprungweite gebe, wie groß wäre dann \(\beta_1\)? Wir hätten dann keine Steigung und die Grade würde parallel zur x-Achse laufen. Das \(\beta_1\) wäre dann gleich Null. Die Nullhypothesen lauten dabei also jedesmal, dass die Koeffizienten gleich Null sind. Wir testen also, ob wir einen Intercept von Null und eine Steigung von Null als Nullhypothese ablehnen können. Wenn wir \(i\) Koeffizienten haben, dann haben wir alle alle \(i\) Koeffizienten die folgenden Hypothesenpaare.
\[ \begin{align*} H_0: \beta_i &= 0\\ H_A: \beta_i &\neq 0 \\ \end{align*} \]
Wir haben für jedes \(\beta_i\) ein eigenes Hypothesenpaar. Meistens interessiert uns der Intercept nicht. Ob der Intercept nun durch die Null geht oder nicht ist eher von geringem Interesse. Spannender ist aber wie sich der \(p\)-Wert berechnet. Der \(p\)-Wert basiert auf einer t-Statistik, also auf dem t-Test. Wir rechnen für jeden Koeffizienten \(\beta_i\) einen t-Test. Das machen wir in dem wir den Koeffizienten estimate durch den Fehler des Koeffizienten std.error teilen.
\[ \begin{align*} T_{(Intercept)} &= \cfrac{\mbox{estimate}}{\mbox{std.error}} = \cfrac{0.969}{0.445} = 2.18\\ T_{weight} &= \cfrac{\mbox{estimate}}{\mbox{std.error}} = \cfrac{0.510}{0.232} = 2.20\\ \end{align*} \]
Wir sehen in diesem Fall, dass weder der Intercept noch die Steigung vom Gewicht signifikant sind, da die p-Werte mit \(0.081\) und \(0.079\) leicht über dem Signifikanzniveau von \(\alpha\) gleich 5% liegen. Wir haben aber einen starkes Indiz gegen die Nullhypothese, da die Wahrscheinlichkeit die Daten zu beobachten sehr gering ist unter der Annahme das die Nullhypothese gilt.
Zun Abschluß noch die Funktion glance() ebenfalls aus dem R Paket {broom}, die uns erlaubt noch die Qualitätsmaße der linearen Regression zu erhalten. Klar sehen wir die Werte auch alle in dem dritten Abschnitt der Ausgabe, aber hier haben wir nochmal alles zusammen. Wir müssen nämlich noch schauen, ob die Regression auch funktioniert hat. Die Überprüfung geht mit einer Kovariate sehr einfach. Wir können uns die Grade ja anschauen. Das geht dann mit einem Model mit mehreren Einflussvariablen nicht mehr und wir brauchen andere statistische Maßzahlen. Im Kapitel zur Modelgüte diskutieren wir die statistischen Maßzahlen nochmal genauer. Hier reicht es zu wissen, dass wir ein hohes Bestimmtheitsmaß \(R^2\) (eng. r squared) nahe Eins haben wollen. Unser Bestimmtheitsmaß liegt hier bei \(0.492\) und ist somit gerade in Ordnung.
R Code [zeigen / verbergen]
cov1_fit |> glance() # A tibble: 1 × 12
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.492 0.391 0.455 4.84 0.0790 1 -3.24 12.5 12.3
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>Der p-Wert in der Ausgabe soll dich nicht irrtieren sondern dieser stammt aus einer ANOVA, die in diesem simplen Fall das gleiche testet wie der t-Test in der Zeile zum Gewicht. Wir erghhalten ja auch den gleichen p-Wert. Wir testen hier, ob unsere Kovariate einen Einfluss auf die Sprungweite im Allgemeinen hat. Hier nochmal die ANOVA ausgeschrieben mit der Funktion aov().
R Code [zeigen / verbergen]
aov(jump_length ~ weight, data = cov1_tbl) |> summary() Df Sum Sq Mean Sq F value Pr(>F)
weight 1 1.001 1.0011 4.844 0.079 .
Residuals 5 1.033 0.2066
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Ganz am Ende möchte ich dir noch die Funktion augment() aus dem Paket {broom} zeigen die dir kompakt alle Informationen zu den einzelnen Beobachtungen gibt. Die .fitted-Werte sind dabei die vorhergesagten Messwerte auf der Graden. Den Rest schauen wir uns dann noch in dem Kapitel zur Modelgüte oder dem Kapitel zu den Ausreißern teilweise an.
R Code [zeigen / verbergen]
cov1_fit |> augment()# A tibble: 7 × 8
jump_length weight .fitted .resid .hat .sigma .cooksd .std.resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1.2 0.8 1.38 -0.176 0.388 0.496 0.0778 -0.496
2 1.8 1 1.48 0.322 0.297 0.471 0.151 0.844
3 1.3 1.2 1.58 -0.280 0.228 0.483 0.0725 -0.701
4 1.7 1.9 1.94 -0.237 0.147 0.492 0.0275 -0.564
5 2.6 2 1.99 0.612 0.156 0.384 0.199 1.47
6 1.8 2.7 2.34 -0.545 0.367 0.376 0.656 -1.51
7 2.7 2.8 2.40 0.304 0.417 0.467 0.276 0.877“Warum das kovariate Modell nochmal so zerforschen? Weil es mich interessiert hat, wie die Modelle intern gerechnet werden. Vor allem liest man schnell von einer Modellmatrix im Zusammenhang der Modellierung. Hier also mal alles sehr zerforscht. Braucht man nicht um es anzuwenden, ist aber hilfreich zu wissen. Denke ich.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
Fangen wir also einmal an das kovariate Modell zu zerforschen. In einem ersten Schritt wollen wir uns einmal das lineare Modell mit einer kontinuierlichen Einflussvariable anschauen. Daher bauen wir uns ein lineares Modell mit der Kovariate mass aus unseren Schlangendaten und der Körperlänge der Schlangen svl als Messwert. Die Schlangendaten habe ich extra so gebaut, dass wir uns hier leicht was anschauen können. Wir erinnern uns, dass die Einslussvariable mass eine kontinuierliche Variable ist, da wir hier nur Zahlen in der Spalte finden. Die Funktion model.matrix() gibt uns die Modellmatrix wieder.
R Code [zeigen / verbergen]
model.matrix(svl ~ mass, data = snake_tbl) |> as_tibble()# A tibble: 8 × 2
`(Intercept)` mass
<dbl> <dbl>
1 1 6
2 1 8
3 1 5
4 1 7
5 1 9
6 1 11
7 1 12
8 1 10In der ersten Spalte ist der Intercept angegeben, danach folgt dann die Spalte mass als Kovariate. Wir können jetzt die Modellmatrix auch mathematisch schreiben und die \(y\) Spalte für den Messwert svl ergänzen. Eben so ergänzen wir die Koeffizienten \(\beta_0\) als Intercept und \(beta_{mass}\) als Steigung aus der linearen Regression sowie die Residuen als Abweichung von der angepassten Grade.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 1 & 6 \\ 1 & 8 \\ 1 & 5 \\ 1 & 7 \\ 1 & 9 \\ 1 & 11\\ 1 & 12\\ 1 & 10\\ \end{pmatrix} \times \begin{pmatrix} \beta_0 \\ \beta_{mass} \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \epsilon_6 \\ \epsilon_7 \\ \epsilon_8 \\ \end{pmatrix} \]
Jetzt brauche wir natürlich die Koeffizienten aus dem linearen Modell, welches wir wie folgt mit der Funktion lm() fitten. Wir nutzen dann die Funktion coef() um uns die Koeffizienten aus dem Objekt fit_1 wiedergeben zu lassen.
R Code [zeigen / verbergen]
snake_cov_fit <- lm(svl ~ mass, data = snake_tbl)
snake_cov_fit |> coef() |> round(2)(Intercept) mass
26.71 2.61 Die Funktion residuals() gibt uns die Residuen der Graden aus dem Objekt snake_cov_fit wieder.
R Code [zeigen / verbergen]
snake_cov_fit |> residuals() |> round(2) 1 2 3 4 5 6 7 8
-2.36 -2.57 -0.75 6.04 1.82 1.61 0.00 -3.79 Wir können jetzt die Koeffizienten in die Modellmatrix ergänzen. Wir haben den Intercept mit \(\beta_0 = 26.71\) geschätzt. Weiter ergänzen wir die Steigung aus dem linearen Modell für mass mit \(\beta_{mass}=2.61\). Ebenfalls setzen wir Werte für die Residuen für jede der Beobachtungen in die Gleichung ein. Wir erhalten dann folgende ausgefüllte Gleichung.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 26.71 & \phantom{0}6 \cdot 2.61\\ 26.71 & \phantom{0}8 \cdot 2.61\\ 26.71 & \phantom{0}5 \cdot 2.61\\ 26.71 & \phantom{0}7 \cdot 2.61\\ 26.71 & \phantom{0}9 \cdot 2.61\\ 26.71 & 11\cdot 2.61\\ 26.71 & 12\cdot 2.61\\ 26.71 & 10\cdot 2.61\\ \end{pmatrix} + \begin{pmatrix} -2.36\\ -2.57\\ -0.75 \\ +6.04\\ +1.82\\ +1.61\\ \phantom{+}0.00\\ -3.79\\ \end{pmatrix} \]
Wir können jetzt diese gewaltige Sammlung an Matrixen einmal auflösen. Steht denn nun wirklich rechts das Gleiche wie links von der Gleichung? Wir bauen uns die Zahlen von der rechten Seite der Gleichung einmal in R nach und schauen auf das Ergebnis. Wie du siehst ergänzen wir hier noch eine Reihe von Additionen um den Intercept mit der Steigung zu verbinden. Steht ja auch so in der Gleichung des linearen Modells drin, alles wird mit einem Plus miteinander verbunden.
R Code [zeigen / verbergen]
c(26.71 + 6*2.61 - 2.36,
26.71 + 8*2.61 - 2.57,
26.71 + 5*2.61 - 0.75,
26.71 + 7*2.61 + 6.04,
26.71 + 9*2.61 + 1.82,
26.71 + 11*2.61 + 1.61,
26.71 + 12*2.61 + 0.00,
26.71 + 10*2.61 - 3.79) |> round() [1] 40 45 39 51 52 57 58 49Oh ha! Die Zahlen, die wir rauskriegen, sind die gleichen Werte die unser Messwert der Schlangenlänge hat. Das heißt, die ganze Sache hat funktioniert. Wir können die Schlangenlänge durch die Kovariate der Körpermasse mit zwei Koeffizienten aus einem linearen Modell erklären.
Dann kommt hier noch ein kleiner Einschub. So wie Gauß kannst du auch die lineare Regression händisch ausrechnen. Das macht sicherlich auch dem einen oder anderen Spaß, aber nicht jedem. Ich zeige dir in dem folgenden Kasten einmal wie sich das einkovariate Modell händisch auflösen lässt. Und ja, ich nutze dann auch hier R um die Funktionen durchzuführen. Am Ende ist es dann aber auch eher ein großer Taschenrechner, den ich mit R nutze. Viel Spaß beim nachmachen.
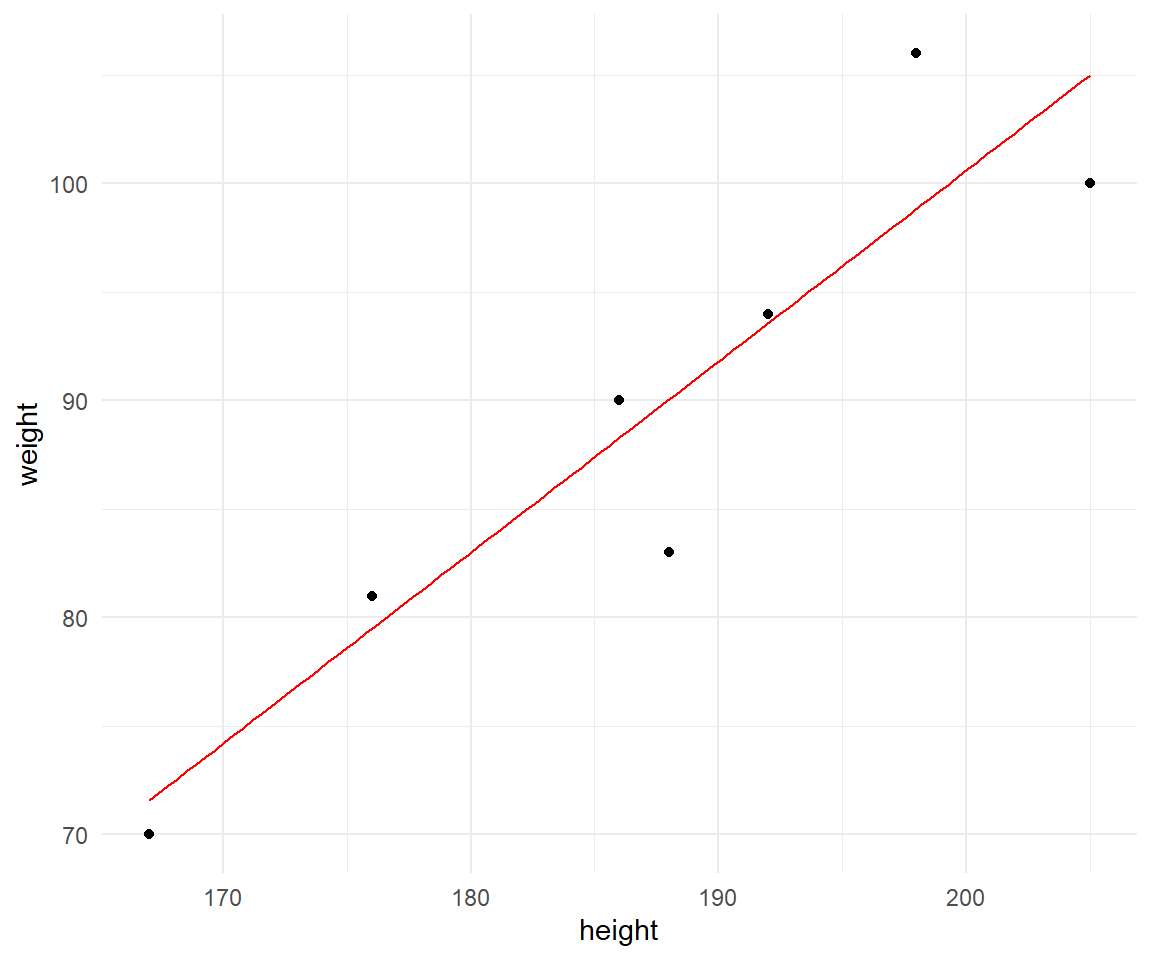
Gut, das war jetzt die theoretische Abhandlung der linearen Regression ohne eine mathematische Formel. Es geht natürlich auch mit den nackten Zahlen. In der folgenden Tabelle siehst du einmal sieben Beobachtungen mit dem Körpergewicht als \(y\) sowie der Körpergröße als \(x\). Wir wollen jetzt einmal die Regressionsgleichung bestimmen. Wir sehen also unsere Werte für \(\beta_0\) und \(\beta_1\) aus?
| height | weight |
|---|---|
| 167 | 70 |
| 188 | 83 |
| 176 | 81 |
| 186 | 90 |
| 192 | 94 |
| 205 | 100 |
| 198 | 106 |
Damit wir einmal wissen, was wir als Lösung erhalten würden, hier einmal die lineare Regression mit der Funktion \(lm()\) und die entsprechenden Werte für den (Intercept) und der Steigung.
R Code [zeigen / verbergen]
lm(weight ~ height, data = by_hand_tbl) |>
coef()(Intercept) height
-75.390377 0.877845 Wir suchen dann damit die folgende Regressionsgleichung mit der Körpergröße als \(x\) und dem zugehörigen Körpergewicht als \(y\).
\[ weight = \beta_0 + \beta_1 \cdot height \]
Da es dann immer etwas schwer ist, sich den Zusammenhang zwischen Körpergewicht und Körpergröße vorzustellen, habe ich nochmal in der folgenden Abbildung den Scatterplot der Daten erstellt. Die rote Grade stellt die Regressiongleichung dar. Wir erhalten ein y-Achsenabschnitt mit \(\beta_0\) von \(-75.39\) sowie eine Steigung mit \(\beta_1\) von \(0.88\) aus unseren Daten.
R Code [zeigen / verbergen]
ggplot(by_hand_tbl, aes(height, weight)) +
theme_minimal() +
geom_point() +
geom_function(fun = \(x) -75.39 + 0.88 * x, color = "#CC79A7")Jetzt stellt sich die Frage, wie wir händisch die Werte für den y-Achsenabschnitt mit \(\beta_0\) sowie der Steigung mit \(\beta_1\) berechnen. Dafür gibt es jeweils eine Formel. Hier müssen wir dann sehr viele Summen berechnen, was ich dann gleich einmal in einer Tabelle zusammenfasse.
- Formel für y-Achsenabschnitt mit \(\beta_0\)
-
\[ \beta_0 = \cfrac{(\Sigma Y)(\Sigma X^2) - (\Sigma X)(\Sigma XY)}{n(\Sigma X^2) - (\Sigma X)^2} \]
- Formel für Steigung mit \(\beta_1\)
-
\[ \beta_1 = \cfrac{n(\Sigma XY) - (\Sigma X)(\Sigma Y)}{n(\Sigma X^2) - (\Sigma X)^2} \]
In der folgenden Tabelle siehst du nochmal die originalen Datenpunkte und dann die entsprechenden Werte für das Produkt von weight und height mit \(XY\) und dann die jeweiligen Quadrate der beiden mit \(X^2\) und \(Y^2\). Wir brauchen dann aber nicht diese Werte sondern die Summen der Werte. Das Summieren lagere ich dann nochmal in eine weitere Tabelle aus.
| height | weight | \(XY\) | \(X^2\) | \(Y^2\) |
|---|---|---|---|---|
| 167 | 70 | 11690 | 27889 | 4900 |
| 188 | 83 | 15604 | 35344 | 6889 |
| 176 | 81 | 14256 | 30976 | 6561 |
| 186 | 90 | 16740 | 34596 | 8100 |
| 192 | 94 | 18048 | 36864 | 8836 |
| 205 | 100 | 20500 | 42025 | 10000 |
| 198 | 106 | 20988 | 39204 | 11236 |
In der abschließenden Tabelle findest du dann einmal die Summen der beobachteten Werte \(X\) und \(Y\) sowie des Produkts von \(X\) und \(Y\) sowie deren Quadrate mit \(X^2\) und \(Y^2\). Damit haben wir dann alles zusammen um die Formel oben zu füllen.
| height \((\Sigma X)\) | weight \((\Sigma Y)\) | \(\Sigma XY\) | \(\Sigma X^2\) | \(\Sigma Y^2\) |
|---|---|---|---|---|
| 1312 | 624 | 117826 | 246898 | 56522 |
Ich habe dann die ganzen Summen einmal händisch berechnet und dann in den Formeln von oben eingesetzt. Wir erhalten dann für den y-Achsenabschnitt \(\beta_0\) folgenden Wert.
\[ \beta_0 = \cfrac{624 \cdot 246898 - 1312 \cdot 117826}{7\cdot 246898 - 1312^2} = -75.39038 \]
Die ganze Berechnung habe ich dann auch einmal für die Steigung \(\beta_1\) ebenfalls einmal durchgeführt.
\[ b_1 = \cfrac{7\cdot 117826 - 1312\cdot624}{7\cdot246898 - 1312^2} = 0.877845 \]
Wir sehen, es kommen die gleichen Werte für den y-Achsenabschnitt \(\beta_0\) und die Steigung \(\beta_1\) raus. Das hat ja schonmal sehr gut geklappt. Eine andere Art die gleiche Werte effizienter zu berechnen ist die Matrixberechnung der Koeffizienten der linearen Regression. Wir könnten dann auch komplexere Modelle mit mehr als nur einem \(x\) und einem \(\beta_1\) berechnen. Die grundlegende Formel siehst du einmal im Folgenden dargestellt.
\[ \begin{pmatrix} \beta_0 \\ \beta_1 \end{pmatrix} = \mathbf{(X^T X)^{−1}(X^T Y)} \]
Wir brauchen jetzt einiges an Matrixrechnung um die jeweiligen Formelteile zu berechnen. Ich habe dir in den folgenden Tabs einmal Schritt für Schritt die einzelnen Teile berechnet. Wir immer machen wir das eigentlich nicht so richtig per Hand, sondern nutzen einen Computer. Prinzipiell wäre eine händische Lösung natürlich möglich.
R Code [zeigen / verbergen]
X <- as.matrix(c(167, 188, 176, 186, 192, 205, 198))
X <- cbind(rep(1, 7), X)
X [,1] [,2]
[1,] 1 167
[2,] 1 188
[3,] 1 176
[4,] 1 186
[5,] 1 192
[6,] 1 205
[7,] 1 198R Code [zeigen / verbergen]
Y <- as.matrix(c(70, 83, 81, 90, 94, 100, 106))
Y [,1]
[1,] 70
[2,] 83
[3,] 81
[4,] 90
[5,] 94
[6,] 100
[7,] 106R Code [zeigen / verbergen]
Xt <- t(X)
Xt [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 1 1 1 1 1 1 1
[2,] 167 188 176 186 192 205 198R Code [zeigen / verbergen]
XtX <- Xt %*% X
XtX [,1] [,2]
[1,] 7 1312
[2,] 1312 246898R Code [zeigen / verbergen]
XtY <- Xt %*% Y
XtY [,1]
[1,] 624
[2,] 117826R Code [zeigen / verbergen]
XtXinv <- solve(XtX)
XtXinv [,1] [,2]
[1,] 35.5658312 -0.188994526
[2,] -0.1889945 0.001008355Am Ende müssen wir dann alle Teile in der Form \(\mathbf{(X^T X)^{−1}(X^T Y)}\) einmal zusammenbringen. Das siehst dann in R wie folgt aus. Wir erhalten dann eine Matrix wieder wobei die erste Zeile der y-Achsenabschnitt \(\beta_0\) und die zweite Zeile die Steigung \(\beta_1\) ist. Wir erhalten fast die gleichen Werte wie auch schon oben.
R Code [zeigen / verbergen]
XtXinv %*% Xt %*% Y [,1]
[1,] -75.390377
[2,] 0.877845Wenn du dich tiefer in die Thematik einlesen willst, dann sind hier weitere Quellen zu der Thematik unter den folgenden Links und Tutorien.
Damit haben wir das einkovariate Modell abgeschlossen. Hier ist dann auch meistens Ende, wenn wir von der klassischen linearen Regression reden. Wir haben unseren kontinuierlichen Messwert und dann noch unsere kontinuierliche Einflussvariable. Dann legen wir eine Grade durch die Punkte und erhalten die Gradengleichung. Damit sind wir dann zufrieden. Eventuell wollen wir dann noch die Modellgüte betrachten oder aber noch die Korrelation berechnen. Das können wir dann noch machen. Hier wollen wir dann nochmal den Fall der kategorialen Einflussvariable anschauen.
45.5.2 Einfaktorielles Modell
Hier stoplerst du vielleicht einmal, denn was wir uns hier anschauen ist sehr nah an der einfaktoriellen ANOVA dran. Dort haben wir ja auch einen kontinuierlichen Messwert und einen Faktor. Wir wollen wissen, ob sich die Level des Faktors als Gruppen untereinander in dem mittleren Messwerten unterscheiden oder ob alle Gruppenmittel gleich sind. Ja, da gibt es jetzt gewisse Überschneidungen und vieles ist dann auch gleich. Insbesondere der Fall mit einem Faktor und zwei Leveln ist dann von einem Student t-Test algorithmisch nicht zu unterscheiden. Hier steigen wir also dann einmal in die einfaktoriellen Modelle aus der sich des statistischen Modellierens ein.
Heir unterscheiden wir dann zwei einfaktorielle Modelle. Zuerst schauen wir uns einmal ein einfaktorielles Modell mit einem Faktor und zwei Leveln an. Wir haben eben die Sprungweite der HUnde- und Katzenflöhe vorliegen. Dann betrachten wir noch ein Modell mit mehr als zwei Gruppen. Wir brschränken uns gleich mal auf drei Gruppen indem wir einfach noch die Fuchsflöhe mit in unsere Betrachtung nehmen. Es gehen auch mehr als Gruppen, aber dann wird die Ausgabe nur länger, die Interpretation bleibt gleich.
\(f_A\) mit 2 Leveln
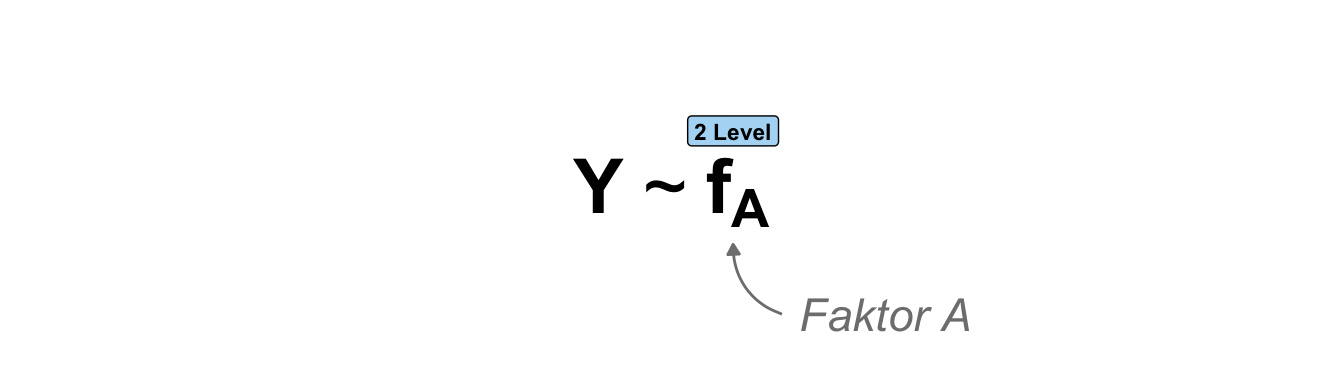
Unser einfaktorielles Modell mit einem Faktor und zwei Leveln sieht dann wie folgt aus. Wir haben auf der linken Seite unseren kontinuierlichen Messwert \(Y\) vorliegen und auf der rechten Seite dann unseren Faktor \(f_A\). Der Faktor hat nur zwei Gruppen und deshalb auch nur zwei Level.
\(f_A\) mit >2 Leveln
Unser einfaktorielles Modell mit einem Faktor und drei Leveln sieht dann fast gleich aus. Wir haben auf der linken Seite unseren kontinuierlichen Messwert \(Y\) vorliegen und auf der rechten Seite dann unseren Faktor \(f_A\). Der Faktor hat jetzt aber drei Gruppen und deshalb auch nur drei Level.
Jetzt können wir uns die Auswertung einmal praktisch in R anschauen. Dafür nutze ich dann einmal den einfaktoriellen Datensatz nur mit den Hunde- und Katzenflöhen für den Fall eines Faktors mit zwei Leveln. Dann erweitere ich noch die Tierart um die Fuchsflöhe um dann drei Level vorliegen zu haben. Dann habe ich noch in dem anderen Tab mir die Sachlage theoretisch in R angeschaut, da es mich nochmal interessiert hat, wie die Berechnung intern laufen.
Dann wollen wir einmal das einfaktorielle Modell auf unseren Daten zu den Sprungweiten der Floharten rechnen. Wir bauen uns dann einmal einen Datensatz nur mit den Hunde- und Katzenflöhen. Dann haben wir zwei Gruppen oder zwei Level vorliegen. Im Prinzip ist das der Student t-Test Fall und so ist dann auch das Ergebnis. Danach betrachten wir dann noch den Fall, dass wir mit den Füchsen drei Tierarten vorliegen haben. Das ist dann der einfaktoriellen ANOVA sehr viel näher. Wir sehen dann auch gleich, dass wir in der Ausgabe der lm() Funktion auch schon gleich eine ANOVA gerechnet kriegen.
\(f_A\) mit 2 Leveln
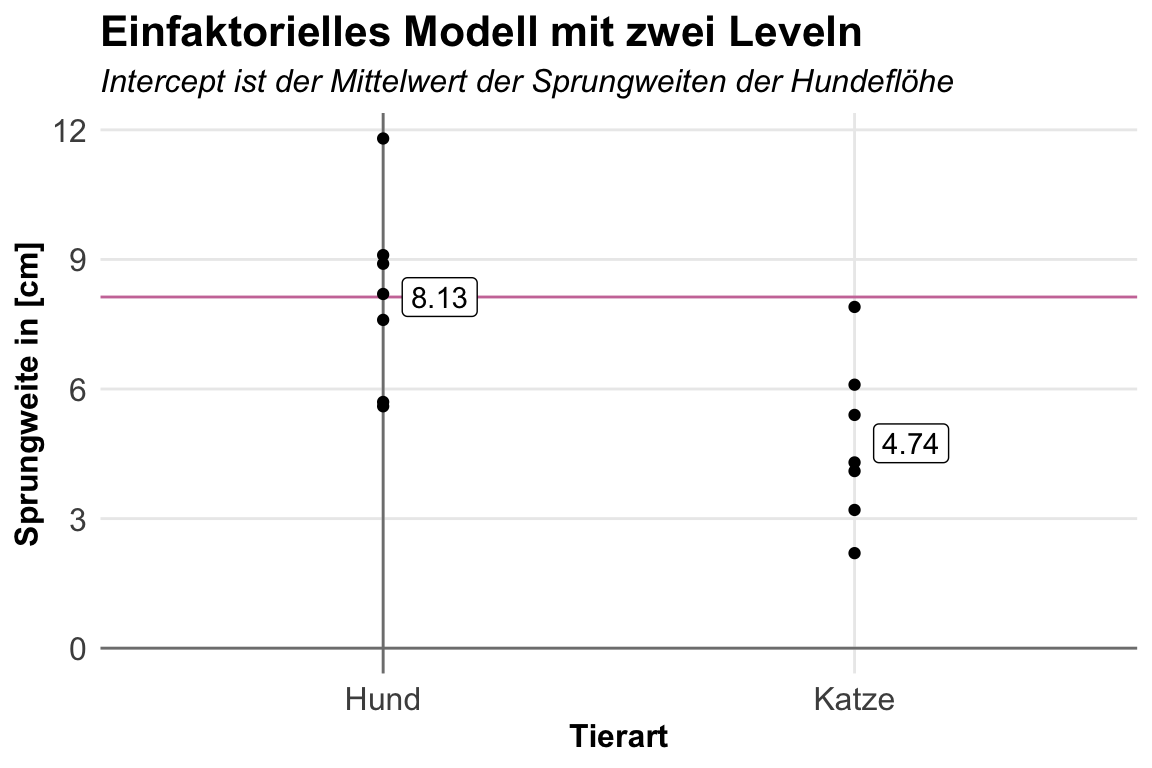
In dem folgenden Schritt entferne ich einmal die Fuchsflöhe aus den Daten. Wir haben dann nur zwei Gruppen, die Hunde- und Katzenflöhe, vorliegen. Die Sprungweite ist dann unser kontinuierlicher Messwert und die Tierart dann der Faktor.
R Code [zeigen / verbergen]
fac1_2lvl_tbl <- fac1_tbl |>
filter(animal != "fox")Dann können wir uns schon unser einfaktorielles Modell mit einem Faktor mit zwei Leveln bauen. Wir müssen hier auch nichts angeben. Ich mache das hier nur um dann gleich nochmal zu unterscheiden, wenn wir mehre Level im Faktor haben.
R Code [zeigen / verbergen]
fac1_2lvl_fit <- lm(jump_length ~ animal, data = fac1_2lvl_tbl) Jetzt kommt eigentlich der spannende Teil. Was sind die Koeffizienten unseres einfaktoriellen Modells? Wir erhalten einen Intercept wiedergeben sowie die Steigung von der Tierart der Katzenflöhe. Das ist auf den ersten Blick seltsam. Aber denk daran, dass in R die Level intern als Nummern codiert sind. Die Hunde haben daher das Level 1 und die Katzen das Level 2. Sehr vereinfacht ausgedrückt, können wir sagen, wenn wir also von Hunden zu Katzen wechseln ist das nichts anderes als die Einheit der Einflussvariable um Eins zu erhöhen. Soweit als simple Erklärung. Mehr dazu udn auch richtiger in dem nächste Tab zur Theorie in R.
R Code [zeigen / verbergen]
fac1_2lvl_fit |>
coef() |> round(2)(Intercept) animalcat
8.13 -3.39 Und was sind jetzt die beiden Zahlen genau? Die \(8.13cm\) sind der Mittelwert der Sprungweiten der Hundeflöhe. Du siehst hier den Zusammenhang nochmal in der folgenden Abbildung visualsiert. Wie du siehst liegen die Hundeflöhe auf der y-Achse und der Mittelwert der Sprungweiten der Hundeflöhe entspricht dem Intercept. Der Koeffizient animalcat ist nichts anders als die Mittelwertsdifferenz der Hunde- und Katzenflöhe. Rechne gerne einmal nach oder schaue genau in den Abbildung.
Dann schauen wir einmal genauer in die Ausgabe der Funktion summary() unseres einfaktoriellen Modells. Auch hier erhalten wir wieder eine Menge Informationen sowie statistischen Tests, dir wir hier dann so wie einen Student t-Test interpretieren können.
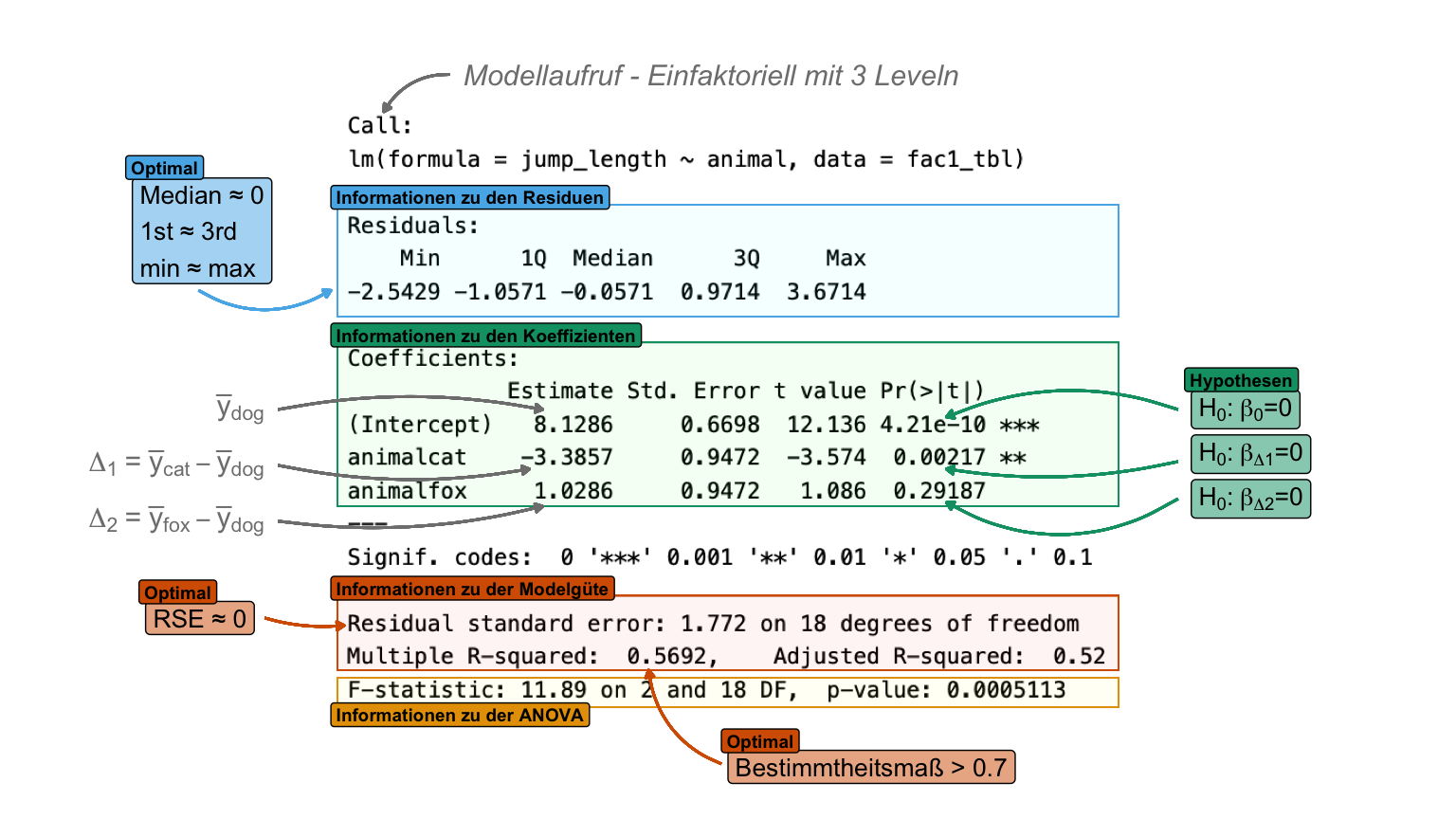
R Code [zeigen / verbergen]
fac1_2lvl_fit |> summary()Wir erhalten dann folgende Ausgabe mit den entsprechenden Kurzerkläruungen von mir. Keine Angst, die gehen wir dann alle in den nächsten Paragraphen einmal durch.
summary() aus einer linearen Modellanpassung mit der Funktion lm(). Die Ausgabe der Funktion teilt sich grob in drei informative Bereiche: Informationen zu den Residuen, Informationen zu den Koeffizienten undS Informationen zu der Modelgüte. [Zum Vergrößern anklicken]
Wir erhalten auch hier die Informationen zu den Residuen. Wir wollen hier einen Median von Null und gleiche absolute Werte für das 1st und 3rd Quartile haben. Ebenso sollte der minimale und maximale Wert vom Betrag her ähnlich sein. Wenn das vorliegt, dann können wir von normalverteilten Residuen ausgehen und das Modell sollte von der Seite aus stimmen.
Wenn wir die Koeffizienten betrachten, dann können wir zum einen die Frage beantworten, ob der Mittelwert der Sprungweiten der Hundeflöhe sich signifikant von Null unterscheidet. Meistens interessiert und das nicht so sehr. Dann kommt die Steigung, also die Differenz des Mittelwerts der Hundeflöhe zu dem Mittelwert der Katzenflöhe. Hier springen also die Katzenflöhe \(-3.386cm\) weniger weit als die Hundeflöhe. Hier testen wir dann, ob sich die Differenz signifikant von Null unterscheidet. Das ist dann aber nichts anderes als der Student t-Test, der uns auch die gleichen Zahlen liefert.
R Code [zeigen / verbergen]
t.test(jump_length ~ animal, data = fac1_2lvl_tbl, var.equal = TRUE)
Two Sample t-test
data: jump_length by animal
t = 3.1253, df = 12, p-value = 0.008768
alternative hypothesis: true difference in means between group dog and group cat is not equal to 0
95 percent confidence interval:
1.025339 5.746089
sample estimates:
mean in group dog mean in group cat
8.128571 4.742857 Dann betrachten wir nochmal den Standardfehler der Residuen (abk. RSE, eng. residual standard error) sowie das Bestimmtheitsmaß \(R^2\). Standardfehler der Residuen sollte klein sein und kann hier mit \(\pm2cm\) als gering angesehen werden. Wir können den Fehler ja direkt auf der Einheit der Sprungweiten interpretieren. Das Bestimmtheitsmaß ist nicht so super, wir sind hier weit von der Eins entfernt, dass heißt das die einzelnen Beobachtungen dann doch um die lokalen Mittelwerte entprechend streuen. Die Tierart ist dann doch nicht die einzige Ursache für die Sprungweitenunterschiede. Hier mag dann das Geschlecht oder das Gewicht als weitere Einflussvariablen noch eine Rolle spielen.
Am Ende dann noch die einfaktorielle ANOVA, die wir ja auch in der Ausgabe dann noch berechnet kriegen. Da hat man dann schon mehr als man eigentlich braucht zusammen.
R Code [zeigen / verbergen]
aov(jump_length ~ animal, data = fac1_2lvl_tbl) |> summary() Df Sum Sq Mean Sq F value Pr(>F)
animal 1 40.12 40.12 9.767 0.00877 **
Residuals 12 49.29 4.11
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die Nutzung eines linearen Modells mit einem Fakotr mit nur zwei Leveln mag jetzt ertsmal übertrieben scheinen, aber wir können hier einmal nachvollziehen, wie die Koeffizienten zu interpretieren sind.
\(f_A\) mit >2 Leveln
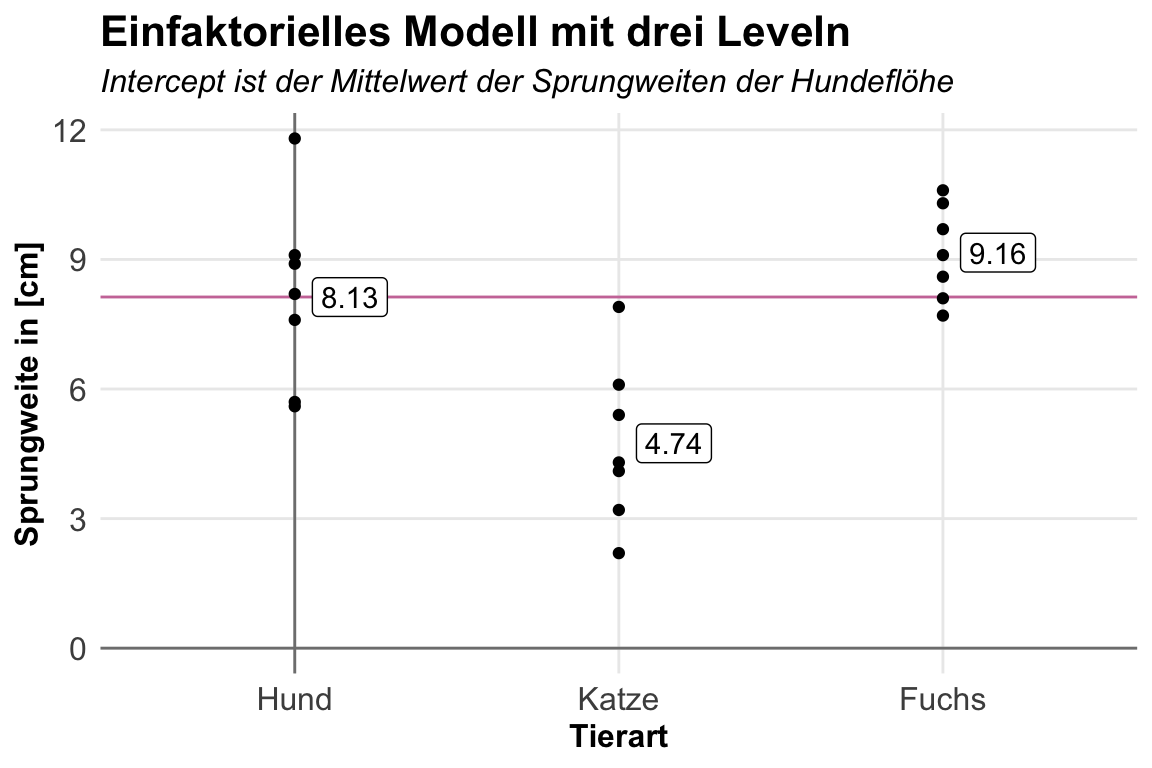
So und jetzt wird es eigentlich erst interessant. Wir wollen das faktorielle Modell einmal mit drei Leveln rechnen. Damit haben wir dann ja nicht mehr zwei Gruppen vorliegen sondern mit den zusätzlichen Fuchsflöhen drei Gruppen. Jetzt ändert sich erstmal nichts an dem Modell, wir haben hier den gleichen Aufruf. Wir nutzen jetzt eben den vollen Datensatz mit allen drei Tierarten.
R Code [zeigen / verbergen]
fac1_3lvl_fit <- lm(jump_length ~ animal, data = fac1_tbl) Die Koeffizienten können wir uns dann auch gleich wiedergeben lassen. Hier sehen wir dann auch das gleiche Bild wie eben schon. Wir haben anscheinend den Intercept auf dem Mittelwert der Sprungweiten der Hundeflöhe liegen.
R Code [zeigen / verbergen]
fac1_3lvl_fit |>
coef() |> round(2)(Intercept) animalcat animalfox
8.13 -3.39 1.03 Auch hier hilft dann einmal die folgende Visualisierung. Wir haben den Intercept auf dem Mittelwert der Sprungweiten der Hundeflöhe liegen. Die Hundeflöhe springen im Mittel eben \(8.13cm\) weit. Die anderen Koeffizienten sind die Änderung im Mittelwert in Bezug zu den Hundeflöhen. Wir haben hier also dann eben wieder eine Steigung aber immer in Referenz zu dem Intercept. Du kannst di Differenzen auch gut in der Abbildung nachvollziehen.
Dann schauen wir einmal genauer in die Ausgabe der Funktion summary() unseres einfaktoriellen Modells. Auch hier erhalten wir wieder eine Menge Informationen sowie statistischen Tests, dir wir hier dann zeilenweise so wie einen Student t-Test interpretieren können. Das heißt, dass eben die Differenz der Mittelwerte im Bezug zu den Hundeflöhen gegen die Null testen.
R Code [zeigen / verbergen]
fac1_3lvl_fit |> summary()Wir erhalten dann folgende Ausgabe mit den entsprechenden Kurzerkläruungen von mir. Keine Angst, die gehen wir dann alle in den nächsten Paragraphen einmal durch.
summary() aus einer linearen Modellanpassung mit der Funktion lm(). Die Ausgabe der Funktion teilt sich grob in drei informative Bereiche: Informationen zu den Residuen, Informationen zu den Koeffizienten und Informationen zu der Modelgüte. [Zum Vergrößern anklicken]
Wir erhalten auch hier die Informationen zu den Residuen. Wir wollen hier einen Median von Null und gleiche absolute Werte für das 1st und 3rd Quartile haben. Ebenso sollte der minimale und maximale Wert vom Betrag her ähnlich sein. Wenn das vorliegt, dann können wir von normalverteilten Residuen ausgehen und das Modell sollte von der Seite aus stimmen.
Wenn wir die Koeffizienten betrachten, dann können wir zum einen die Frage beantworten, ob der Mittelwert der Sprungweiten der Hundeflöhe sich signifikant von Null unterscheidet. Das war das Gleiche wie schon in dem obigen Modell mit zwei Leveln so. Meistens interessiert und das nicht so sehr. Dann kommt die Steigung, also die Differenz des Mittelwerts der Hundeflöhe zu dem Mittelwert der Katzenflöhe. Hier springen also die Katzenflöhe \(-3.386cm\) weniger weit als die Hundeflöhe. Hier testen wir dann, ob sich die Differenz signifikant von Null unterscheidet. Danach kommt dann der Test, ob sich die Differenz des Mittelwerts der Hundeflöhe zu dem Mittelwert der Fuchsflöhe signifikant unetrscheidet. Hier springen also die Fuchsflöhe \(1.029cm\) weiter als die Hundeflöhe. Wir erhalten keinen Test für die Differenz zwischen den Katzen- und Fuchsflöhen. Hier musst du dann auf die Posthoc-Tests ausweichen.
Am Ende dann noch die einfaktorielle ANOVA, die wir ja auch in der Ausgabe dann noch berechnet kriegen. Hier kann die ANOVA signifkant sein und die Steigungen dennoch nicht. Das liegt eben daran, dass du nicht alle paarweisen Vergleiche hier im Modell durch die Steigungen testen kannst. Deshalb ist die ANOVA in der Modellausgabe aus dieser Sicht dann doch sinnvoll.
R Code [zeigen / verbergen]
aov(jump_length ~ animal, data = fac1_tbl) |> summary() Df Sum Sq Mean Sq F value Pr(>F)
animal 2 74.68 37.34 11.89 0.000511 ***
Residuals 18 56.53 3.14
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Damit sind wir hier mit dieser Orchidee durch. Spannender wird es dann, wenn wir im multiplen linearen Modell verschiedene Kovariaten und Faktoren in einem Modell miteinander verbinden und dann gemeinsam zu interpretieren versuchen. Dazu dann aber mehr in den entsprechenden Kapiteln zur multiplen linearen Regression und dem Modellieren in R.
Schön das wir eine etwas wirre Wiedergabe der Koeffizienten in einem faktoriellen Modell haben. Warum das so ist, wird dir klarer, wenn wir uns die Modellierung einmal etwas genauer anschauen. Wir modellieren nämlich nicht direkt die Steigung. Sonst würden wir ja bei den Koeffizienten immer ein vielfaches der Differenz zum Intercept erhalten. Das ist nicht der Fall und warum das so ist, wollen wir mal zerforschen.
\(f_A\) mit 2 Leveln
In einem ersten Schritt wollen wir uns einmal das Modell mit einem Faktor mit 2 Leveln anschauen. Wir bauen uns hier ein Modell mit dem Datensatz der Körperlängen der Schlangen. Daher können wir dann die Variable region verwenden. Wir haben ja nur zwei Regionen in denen wir die Schlangen gesammelt haben. Die Funktion model.matrix() gibt uns die Modelmatrix wieder.
R Code [zeigen / verbergen]
model.matrix(svl ~ region, data = snake_tbl) |> as_tibble()# A tibble: 8 × 2
`(Intercept)` regionnord
<dbl> <dbl>
1 1 0
2 1 0
3 1 0
4 1 1
5 1 1
6 1 1
7 1 1
8 1 1In der ersten Spalte ist der Intercept angegeben, danach folgt dann die Spalte regionwest. In dieser Spalte steht die Dummykodierung für die Variable region. Die ersten drei Schlangen kommen nicht aus der Region nord und werden deshalb mit einen Wert von 0 versehen. Die nächsten fünf Schlangen kommen aus der Region nord und erhalten daher eine 1 in der Spalte. Die Spalte gibt im Prinzip eine ja/nein Antwort auf die Frage in dem Spaltennamen. Also in unserem Fall ist es die Frage: “Kommt die Schlange aus der Region nord?”.
Das sieht hier sehr seltsam aus, ist aber am Ende eine andere Art der Kodierung. Wir sprechen hier auch von der Dummykodierung damit wir dann die kategorialen Variablen in einem stattstischen Modell abbilden können. In der multiplen linearen Modellierung ist es dann noch wichtiger.
Wir können die Modellmatrix auch mathematisch schreiben und die \(y\) Spalte für das Outcome svl ergänzen. Eben so ergänzen wir die \(\beta\)-Werte als mögliche Koeffizienten aus der linearen Regression sowie die Residuen als Abweichung von der gefitteten Grade. Wir sehen dann hier einmal die Dummykodierung für zwei Level eines Faktors.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 1 & 0 \\ 1 & 0\\ 1 & 1\\ 1 & 1 \\ 1 & 1 \\ 1 & 1 \\ 1 & 1 \\ \end{pmatrix} \times \begin{pmatrix} \beta_0 \\ \beta^{region}_{nord} \\ \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \epsilon_6 \\ \epsilon_7 \\ \epsilon_8 \\ \end{pmatrix} \]
Jetzt brauche wir die Koeffizienten aus dem linearen Modell, welches wir wie folgt fitten. Wir nutzen dann die Funktion coef() um uns die Koeffizienten wiedergeben zu lassen.
R Code [zeigen / verbergen]
fit_1fac_2lvl <- lm(svl ~ region, data = snake_tbl)
fit_1fac_2lvl |> coef() |> round(2)(Intercept) regionnord
41.33 12.07 Die Funktion residuals() gibt uns die Residuen der Graden wieder.
R Code [zeigen / verbergen]
fit_1fac_2lvl |> residuals() |> round(2) 1 2 3 4 5 6 7 8
-1.33 3.67 -2.33 -2.40 -1.40 3.60 4.60 -4.40 Wir können jetzt die Koeffizienten ergänzen mit \(\beta_0 = 41.33\) für den Intercept. Weiter ergänzen wir die Koeffizienten für die Region und das Level nord mit \(\beta^{region}_{nord} = 12.07\). Ebenfalls setzen wir Werte für die Residuen für jede der Beobachtungen in die Gleichung ein. Hier sehen wir dann wunderbar, warum der Intercept der Mittelwert der Schlangen in der Region west sind. Der Unterschied zu den Schlangen in der Region nord ist ja der Koeffizient \(\beta^{region}_{nord}\). Den Rechnen wir nur ein, wenn wir auch eine Schlange aus der Region nord haben.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 41.33 & 0 \cdot 12.07 \\ 41.33 & 0 \cdot 12.07 \\ 41.33 & 0 \cdot 12.07 \\ 41.33 & 1 \cdot 12.07 \\ 41.33 & 1 \cdot 12.07 \\ 41.33 & 1 \cdot 12.07 \\ 41.33 & 1 \cdot 12.07 \\ 41.33 & 1 \cdot 12.07 \\ \end{pmatrix} + \begin{pmatrix} -1.33\\ +3.67 \\ -2.33 \\ -2.40 \\ -1.40 \\ +3.60 \\ +4.60 \\ -4.40 \\ \end{pmatrix} \]
Wir können jetzt diese gewaltige Sammlung an Matrixen einmal auflösen. Steht denn nun wirklich rechts das Gleiche wie links von der Gleichung? Wir bauen uns die Zahlen von der rechten Seite der Gleichung einmal in R nach und schauen auf das Ergebnis.
R Code [zeigen / verbergen]
c(41.33 + 0*12.07 - 1.33,
41.33 + 0*12.07 + 3.67,
41.33 + 0*12.07 - 2.33,
41.33 + 1*12.07 - 2.40,
41.33 + 1*12.07 - 1.40,
41.33 + 1*12.07 + 3.60,
41.33 + 1*12.07 + 4.60,
41.33 + 1*12.07 - 4.40) |> round() [1] 40 45 39 51 52 57 58 49Wir kriegen am Ende die gleichen Körperlängen der Schlangen wiedergegeben. Das hat also alles so funktioniert wie es sollte. Auch hier sehen wir, dass der Wert des Koeffzienten \(\beta^{region}_{nord} = 12.07\) nur im Fall von Schlangen aus der Region nord zu tragen kommt. Das sind dann eben auch die letzten fünf Schlangen. Wenn du das Prinzip verstanden hast, dann wird dir die Dummykodierung im folgenden Fall mit mehr Leveln noch klarer.
\(f_A\) mit >2 Leveln
Im nächsten Schritt wollen wir uns einmal das Modell mit einem Faktor mit drei Leveln anschauen. Prinzipiell geht es auch mit noch mehr Leveln, dann erweitern wir aber die Modellmatrix immer nur um eine weitere Spalte. Wir bauen uns hier nun ein Modell mit der Variable color, die ja drei Level hat. Die Funktion model.matrix() gibt uns die Modelmatrix wieder. Wir haben ja drei Farben der Schlangenhaut mit schwarz, rot und blauer Haut vorliegen.
R Code [zeigen / verbergen]
model.matrix(svl ~ color, data = snake_tbl) |> as_tibble()# A tibble: 8 × 3
`(Intercept)` colorrot colorblau
<dbl> <dbl> <dbl>
1 1 0 0
2 1 0 0
3 1 1 0
4 1 1 0
5 1 1 0
6 1 0 1
7 1 0 1
8 1 0 1In der ersten Spalte ist der Intercept angegeben, danach folgt dann die Spalten für color. Die Spalten colorrot und colorblau geben jeweils an, ob die Schlange das Level rot hat oder blau oder keins von beiden. Wenn die Schlange weder rot noch blau ist, dann sind beide Spalten mit einer 0 versehen. Dann ist die Schlange schwarz.
Wir können die Modellmatrix auch mathematisch schreiben und die \(y\) Spalte für das Outcome svl ergänzen. Eben so ergänzen wir die \(\beta\)-Werte als mögliche Koeefizienten aus der linearen Regression sowie die Residuen als Abweichung von der gefitteten Grade.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 1 & 0 & 0\\ 1 & 1 & 0\\ 1 & 1 & 0\\ 1 & 1 & 0\\ 1 & 0 & 1\\ 1 & 0 & 1\\ 1 & 0 & 1\\ \end{pmatrix} \times \begin{pmatrix} \beta_0 \\ \beta^{color}_{rot} \\ \beta^{color}_{blau} \\ \end{pmatrix} + \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \epsilon_6 \\ \epsilon_7 \\ \epsilon_8 \\ \end{pmatrix} \]
Jetzt brauche wir die Koeffizienten aus dem linearen Modell, welches wir wie folgt fitten. Wir nutzen dann die Funktion coef() um uns die Koeffizienten wiedergeben zu lassen.
R Code [zeigen / verbergen]
fit_1fac_2lvl <- lm(svl ~ color, data = snake_tbl)
fit_1fac_2lvl |> coef() |> round(2)(Intercept) colorrot colorblau
42.50 4.83 12.17 Die Funktion residuals() gibt uns die Residuen der Graden wieder.
R Code [zeigen / verbergen]
fit_1fac_2lvl |> residuals() |> round(2) 1 2 3 4 5 6 7 8
-2.50 2.50 -8.33 3.67 4.67 2.33 3.33 -5.67 Wir können jetzt die Koeffizienten ergänzen mit \(\beta_0 = 25\) für den Intercept. Weiter ergänzen wir die Koeffizienten für die Farbe und das Level rot mit \(\beta^{color}_{rot} = 4.83\) und für die Farbe und das Level blau mit \(\beta^{color}_{blau} = 12.17\). Ebenfalls setzen wir Werte für die Residuen für jede der Beobachtungen in die Gleichung ein. Auch hier sehen wir dann sehr gut, dass der Intercept der Mittelwert der schwarzen Schlangen sein muss. Die Änderung der Körperlängen der roten und blauen Schlangen zu den schwarzen Schlangen geben dann die Koeffizienten wieder.
\[ \begin{pmatrix} 40 \\ 45 \\ 39 \\ 51 \\ 52 \\ 57 \\ 58 \\ 49 \\ \end{pmatrix} = \begin{pmatrix} 42.50 & 0 \cdot 4.83& 0 \cdot 12.17 \\ 42.50 & 0 \cdot 4.83& 0 \cdot 12.17\\ 42.50 & 1 \cdot 4.83& 0 \cdot 12.17\\ 42.50 & 1 \cdot 4.83& 0 \cdot 12.17\\ 42.50 & 1 \cdot 4.83& 0 \cdot 12.17\\ 42.50 & 0 \cdot 4.83& 1 \cdot 12.17\\ 42.50 & 0 \cdot 4.83& 1 \cdot 12.17\\ 42.50 & 0 \cdot 4.83& 1 \cdot 12.17\\ \end{pmatrix} + \begin{pmatrix} -2.50 \\ +2.50 \\ -8.33 \\ +3.67 \\ +4.67 \\ +2.33 \\ +3.33 \\ -5.67 \\ \end{pmatrix} \]
Wir können jetzt diese gewaltige Sammlung an Matrixen einmal auflösen. Steht denn nun wirklich rechts das Gleiche wie links von der Gleichung? Wir bauen uns die Zahlen von der rechten Seite der Gleichung einmal in R nach und schauen auf das Ergebnis.
R Code [zeigen / verbergen]
c(42.50 + 0*4.83 + 0*-12.17 - 2.50,
42.50 + 0*4.83 + 0*-12.17 + 2.50,
42.50 + 1*4.83 + 0*-12.17 - 8.33,
42.50 + 1*4.83 + 0*-12.17 + 3.67,
42.50 + 1*4.83 + 0*-12.17 + 4.67,
42.50 + 0*4.83 + 1*-12.17 + 2.33,
42.50 + 0*4.83 + 1*-12.17 + 3.33,
42.50 + 0*4.83 + 1*-12.17 - 5.67) |> round()[1] 40 45 39 51 52 33 34 25Wir kriegen auch hier am Ende die gleichen Körperlängen der Schlangen wiedergegeben. Das hat also alles so funktioniert wie es sollte. Je nachdem welche Farbe unsere Schlange hat, nutzen wir eben einen anderen Koeffizienten. Die Koeffizienten, die wir nicht brauchen, multiplizieren wir mit Null und daher kommen diese Koeffizienten auch nicht mit in die Berechnung der Schlangenkörperlänge.
Damit sind wir mit dem einkovariaten und einfaktoriellen Modell durch. Wir haben jetzt verstanden, wie wir die Koeffizienten der beiden verschiedenen Modelle kausal erklären und verwenden können. In den einfaktoriellen Modell wollen wir dann meistens nicht nur die Änderung zu der Gruppe im Intercept berechnen. Daher ist das einfaktorielle Modell eher der Vorschritt für die ANOVA oder aber den Post-hoc Test. Wir wollen jetzt nochmal in die Prädiktion schauen und verstehen, wie wir dann neue Werte für unseren Messwert für bekannte oder unbekannte Werte der Einflussvariable berechnen können.
45.6 Prädiktives Modell
Neben dem klassischen kausalen Modell können wir auch ein prädiktives Modell rechnen. In einem prädiktiven Modell wollen wir wissen, welche Werte unser Messwert für neue Werte der Einflussvariable annehmen würde. Auch in einem prädiktiven Modell rechnen wir erstmal ganz normal eine lineare Regression. Dann nutzen wir das Modell der Regression um neue Werte für unseren Messwert anhand neuer oder alter Werte der Einflussvariable vorherzusagen. Daher können wir auch beides miteinander verbinden. Du schaust erst was das kausale Modell ergibt und lässt dir dann neue Messwerte vorhersagen. Dabei musst du immer beachten, dass die vorhergesagten Messwerte auf der angepassten Graden liegen. Dahe nennen wir die vorhergesagten Messwerte auch angepasste Messwerte (eng. fitted). Wir werden später in der Klassifikation, der Vorhersage von \(0/1\)-Werten, sowie in den Marginal effect models und dem Modellieren in R noch andere Prädktionen und deren Maßzahlen kennen lernen. Fangen wir also hier einmal an mit dem einkovariaten und einfaktoriellen Modell an. Die Vorgehensweise ist auch bei den multiplen linearen Modellen ähnlich, so dass ich mich dort auch auf dies hier beziehe.
45.6.1 Einkovariates Modell
Für unsere Vorhersage brauchen wir auch hier ein Modell. Wir nutzen hier das einkovariate Modell wie auch schon weiter oben in dem kausalen Modell zu einkovariaten Analyse. Wir nehmen als Messwert die Sprungweite der Flöhe und als Einflussvariable dann das Gewicht der Flöhe. Soweit sieht alles aus wie auch in einem kausalen Modell.
R Code [zeigen / verbergen]
cov1_fit <- lm(jump_length ~ weight, data = cov1_tbl)Jetzt können wir die Funktion predict() nutzen um uns neue Sprungweiten für neue Flohgewichte vorhersagen zu lassen. Oder aber wir lassen uns die Werte auf der Graden für die Sprungweiten wiedergeben. Jedes Gewicht hat ja einen Wert für die Sprungweite auf der Graden. Wir nennen diese Messwerte auf der Graden dann angepasste (eng. fitted) Werte.
Wir bauen uns hier einmal einen Datensatz nur mit dem Gewicht von vier neuen Flöhen. Wir wollen jetzt vorhersagen wie weit unsere vier neuen Flöhe gegeben ihres Gewichts springen würden.
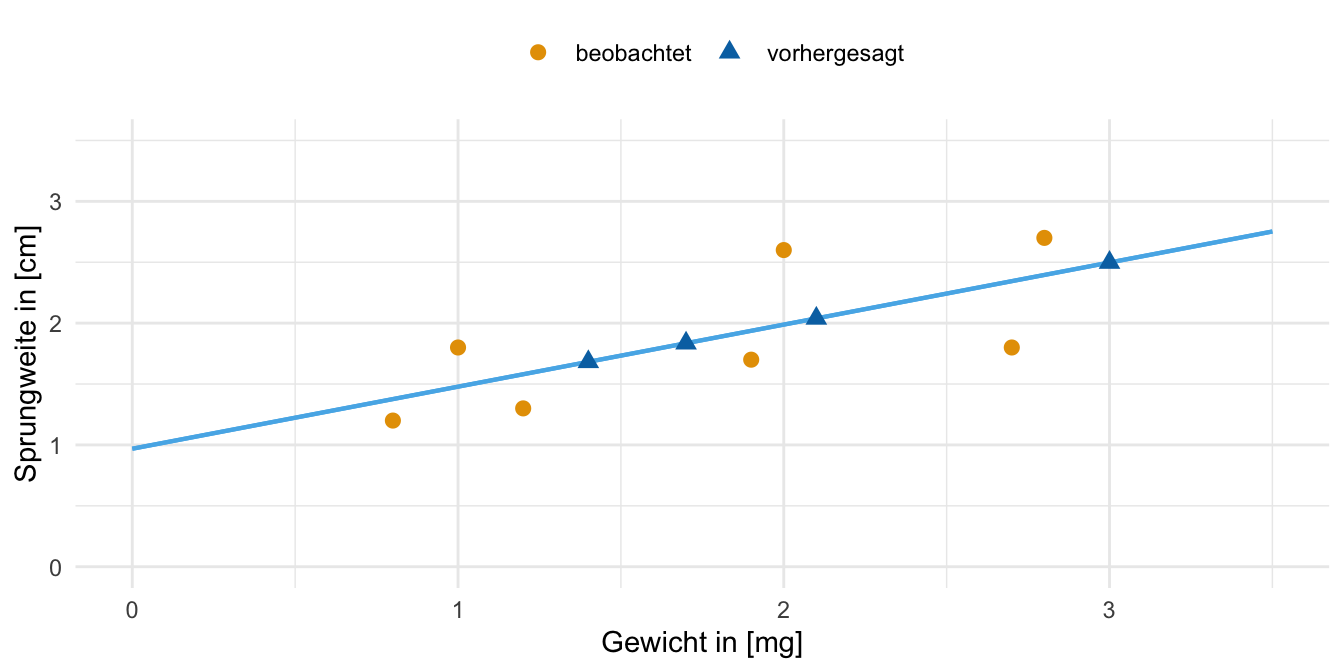
R Code [zeigen / verbergen]
cov1_new_tbl <- tibble(weight = c(1.7, 1.4, 2.1, 3.0))Jetzt verbinden wir mit der Funktion predict() das einkovariate Modell und den Datensatz mit den neuen Körpergewichten der Flöhe. Dann erhalten wir die vorhergesagten Sprungweiten der vier Flöhe wieder.
R Code [zeigen / verbergen]
predict(cov1_fit, newdata = cov1_new_tbl) |> round(2) 1 2 3 4
1.84 1.68 2.04 2.50 Das klingt jetzt erstmal etwas kryptisch, aber ich habe dir in der Abbildung weiter unten einmal die vier vorhergesagten Sprungweiten für die neuen Körpergewichte der Flöhe einmal dargestellt. Die vier neuen Sprungweiten liegen natürlich auf der Graden.
Du kannst dir natürlich auch für die schon beobachteten Werte des Gewichts der Flöhe die angepassten Werte auf der Graden für die Sprungweite wiedergeben lassen. Dafür nutze ich die Funktion augment() aus dem R Paket {broom}.
R Code [zeigen / verbergen]
cov1_fit |> augment() |>
select(jump_length, weight, .fitted, .resid)# A tibble: 7 × 4
jump_length weight .fitted .resid
<dbl> <dbl> <dbl> <dbl>
1 1.2 0.8 1.38 -0.176
2 1.8 1 1.48 0.322
3 1.3 1.2 1.58 -0.280
4 1.7 1.9 1.94 -0.237
5 2.6 2 1.99 0.612
6 1.8 2.7 2.34 -0.545
7 2.7 2.8 2.40 0.304Ich habe dann noch die Residuen mit rausgezogen. Die ursprünglichen Messwerte der Sprungweite sind dann die angepassten Werte plus die Werte der Residuen. Muss ja auch sein, den die Residuen sind ja die Abstände von unserer Graden zu den einzelnen Messwerten der Beobachtungen.
Dann habe ich hier nochmal die Abbildung der beobachteten Sprungweiten sowie der angepassten Grade durch die Punkte in einem Scatterplot dargestellt. Die vier neuen Flöhe haben vorhergesagte Sprungweiten auf der Graden erhalten. Die beobachteten Flöhe streuen natürlich um die Grade. Hier musst du natürlich aufpassen, dass du nicht Flohgewichte weit weg von den eigentlichen beobachteten Flöhen vorhersagst, aber das ist eigentlich selbsterklärend.
45.6.2 Einfaktorielles Modell
Abschließend möchte ich nochmal kurz auf die Vorhersage des einfaktoriellen Modells eingehen. Das macht jetzt eher so halb Sinn. Wir kriegen ja die Gruppenmittelwerte für die einzelnen Level im Faktor aus einem einfaktoriellen Modell wiedergeben. Das können wir hier auch einmal machen, der Code ist der gleiche wie auch schon in einem kausalen einfaktoriellen Modell.
R Code [zeigen / verbergen]
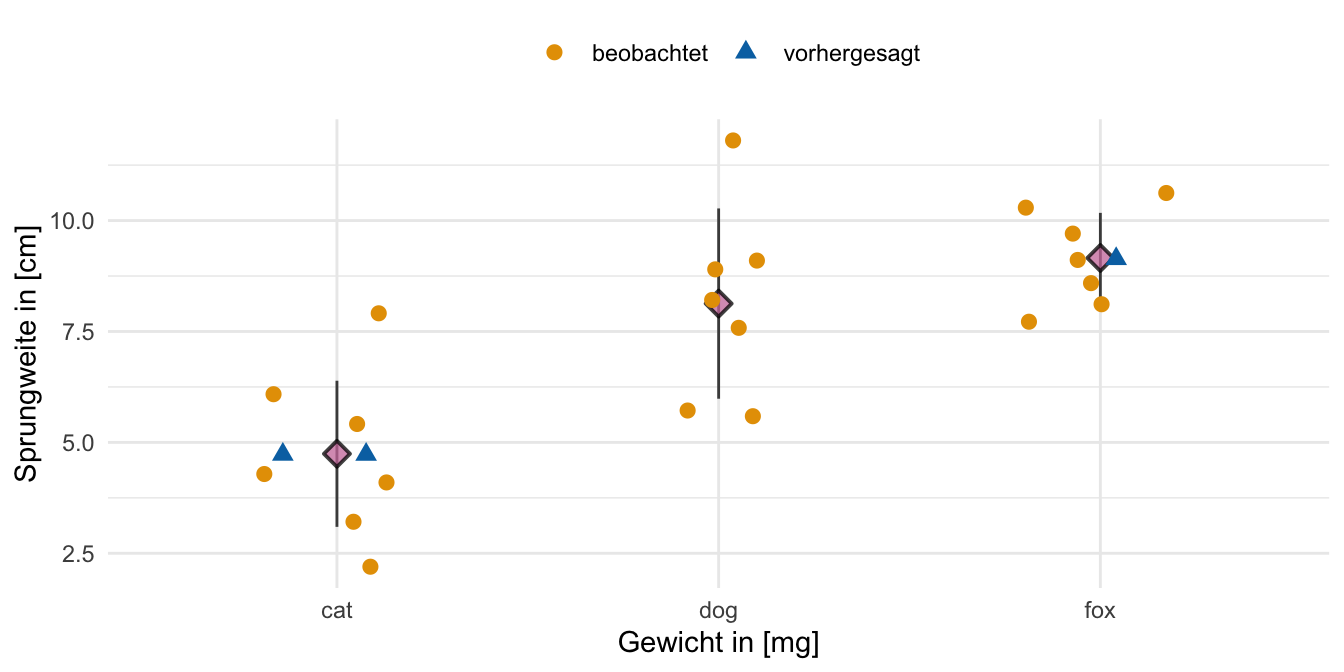
fac1_fit <- lm(jump_length ~ animal, data = fac1_tbl)Jetzt haben wir die Wahl neue mittlere Sprungweiten für die Tierarten vorherzusagen oder aber die vorhergesagten mittleren Sprungweiten für die beobachteten Flöhe zu erhalten. Beides zeige ich jetzt einmal.
Wenn wir jetzt also neue Katzenflöhe und einen Fuchsfloh messen, dann können wir uns die mittlere Sprungweite der beiden Tierarten vorhersagen lassen. Wir bauen uns dafür einen neuen Datensatz. Das ist in einem einfaktoriellen Modell etwas simple, aber so funktioniert eben das Modellieren.
R Code [zeigen / verbergen]
fac1_new_tbl <- tibble(animal = c("cat", "cat", "fox"))Jetzt nutzen wir die Funktion predict() zusammen mit dem einfaktoriellen Modell sowie den neuen Datensatz. Wir erhalten also die mittleren Sprungweiten der Katzen- und Fuchsflöhe wiedergeben.
R Code [zeigen / verbergen]
predict(fac1_fit, newdata = fac1_new_tbl) |> round(2) 1 2 3
4.74 4.74 9.16 Warum jetzt zweimal der gleiche Wert und dann ein anderer Wert für die Sprungweite? Du erhälst eben zweimal die mittlere Sprungweite für die Katzenflöhe und einmal die mittlere Sprungweite für den Fuchsfloh wiedergegeben. Mehr kann das einfaktorielle Modell erstmal nicht in der Vorhersage liefern. Ich habe dir unten nochmal den Zusammenhang in einer Abbildung dargestellt.
Dann kommen hier einmal die vorhergesagten Sprungweiten für die einzelnen Flöhe aus den jeweiligen Tierarten. Wie du hier sehr gut siehst, dann liegen alle vorhergesagten Sprungweiten auf dem Mittelwert der jeweiligen Gruppe. Nichts anderes macht ja auch eine einfaktorielle Modellierung. Wir bestimmen die lokalen Mittelwerte.
R Code [zeigen / verbergen]
fac1_fit |> augment() |>
select(jump_length, animal, .fitted, .resid) # A tibble: 21 × 4
jump_length animal .fitted .resid
<dbl> <fct> <dbl> <dbl>
1 5.7 dog 8.13 -2.43
2 8.9 dog 8.13 0.771
3 11.8 dog 8.13 3.67
4 5.6 dog 8.13 -2.53
5 9.1 dog 8.13 0.971
6 8.2 dog 8.13 0.0714
7 7.6 dog 8.13 -0.529
8 3.2 cat 4.74 -1.54
9 2.2 cat 4.74 -2.54
10 5.4 cat 4.74 0.657
# ℹ 11 more rowsIn einem einfaktoriellen Modell sind meistens dann die Residuen etwas größer, da wir hier ja immer die Differenz zu den lokalen Mittelwerten berechnen. Ja, das ist wirklich sehr ähnlich zu der ANOVA. Deshalb können wir auch ein lineares Modell in einer ANOVA weiter nutzen.
Manchmal ist es schwer zu verstehen warum wir bei einer Vorhersage in einem einfaktoriellen Modell immer den gleichen Wert für eine neue Beobachtung innnerhalb einer lokalen Gruppe erhalten. Ich habe dir in der folgenden Abbildung einmal die lokalen Mittelwerte sowie die drei neuen Beobachtungen ergänzt. Wie du siehst liegen die zwei Katzenflöhe auf dem lokalen Mittelwert der Sprungweiten der Katzenflöhe sowie der Fuchsfloh auf dem lokalen Mittel der Sprungweiten der Fuchsflöhe.
Das war dann auch schon unser Kapitel zu der simplen linearen Regression. Wir können natürlich auch noch mehr Einflussvariablen in ein Modell nehmen. Dann rechnen wir aber ein multiples lineares Modell. Dazu dann in dem folgenden Kapitel mehr zu den Grundlagen der multiplen linearen Regression. Je nach betrachteten Messwert müssen wir dann aber auch noch unsere Regression anpassen. Dazu findest du dann in dem großen Teil zum statistischen Modellieren mehr Informationen.
45.7 Glossar
Manchmal fragst du dich sicher, was soll den das Wort hier wieder heißen. Häufig hilft ja da auch die Suchfunktion, aber ich habe hier mal alle Fachbegriffe in einer Tabelle zusammengefasst. Dadurch sollte es dir einfacher sein mal den einen oder anderen Fachbegriff aus dem statistischen Modellieren nachzuschlagen.
| Symbol | Deutsch |
|---|---|
| \(RHS \sim LHS\) | Modellschreibweise mit der rechten Seite (eng. right hand site) und der linken Seite (eng. left hand side). |
| \(RHS\) | Rechte Seite der Tilde in der Modellschreibweise (eng. right hand site). |
| \(LHS\) | Linke Seite der Tilde in der Modellschreibweise (eng. left hand site). |
| \(Y \sim X\) | Modelschreibweise mit Platzhaltervariable X und Y für beliebige Einflussvariablen X sowie einem Messwert Y. |
| \(Y / y\) | Der Messwert über den du zum Beispiel den Mittelwert bilden möchtest. Der Messwert steht auf der y-Achse in unseren Abbildungen. |
| \(X / x\) | Die Einflussvariable die zum Beispiel deinen Messwert gruppiert. Die Einflussvariablen stehen auf der x-Achse in unseren Abbildungen. |
| \(\epsilon\) | Residuen oder Fehler aus einer Regressionsanalyse. Die Differenz der beobachteten Messwerte zu den Messwerten auf der Graden. |
| Fehler | Abweichung der vorhergesagten y-Werte durch das Modell auf der Graden zu den beobachteten y-Werten in den Daten. Auch Residuen gennannt. |
| \(\beta_0\) | Intercept oder y-Achsenabschnitt. Wo die Grade die y-Achse schneidet. |
| \(\beta_1\) | Steigung der ersten Einflussvariable. Wenn wir die Einflussvariable um eine Einheit erhöhen, dann steigt der MEsswert um den Wert des Koeffizienten der Steigung an. |
| Intercept | Der y-Achsenabschnitt wo die Grade die y-Achse schneidet. |
| \(\hat{y}\) | Vorhergesagte y-Werte durch das Modell auf der Graden. |
| Kovariate | Kontinuierliche Einflussvariable. |
| \(c_1\) | Kovariate. |
| Faktor | Kategoriale Einflussvariable. |
| Level | Gruppen eines Faktors. |
| \(f_A\) | Faktor. |
| \(A.1, ..., A.3\) | Level eines Faktors als Gruppen. |
| \(\mathcal{N}(0, 1)\) | Standardnormalverteilung mit einem Mittelwert von 0 und einer Varianz von 1. |
| Zufälliger Effekt | Faktor in einem gemischten Modell, der aus einer zufälligen Population stammt. |
| \(Z / z\) | Zufälliger Effekt. |
| Fester Effekt | Faktor in einem gemischten Modell, der aus einer experimentellen Population stammt. |
| schätzen | Berechnung der Koeffizienten in einem statistischen Modell. |
| Koeffizienten | Steigung und Intercept in einem statistischen Modell. Allgemeiner die Parameter die ein statistsiches Modell wiedergibt und die Grade beschreibt. |
| Residuen | Unerklärter Rest durch die Modellierung. Konkret der Abstand zwischen den y-Messwerten und den y-Werten auf der Geraden. |
| fitted | Die angepassten y-Werte auf der Graden. |