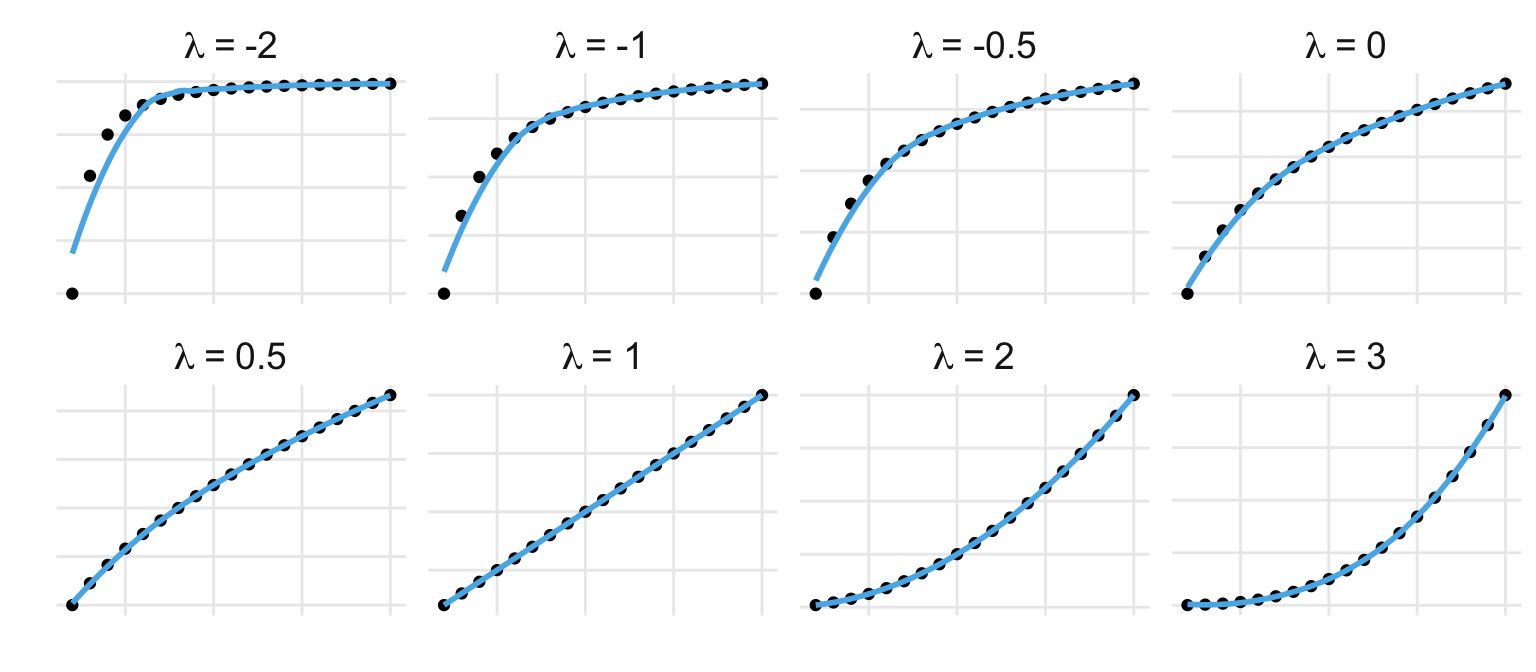20  Transformieren von Daten

Letzte Änderung am 26. June 2025 um 18:10:44

“It’s morphin’ time! I never get tired of that! Now, go, go Power Rangers!” — Power Rangers morphing phrase

In diesem Kapitel wollen wir uns nochmal mit der Transformation von Daten beschäftigen. Hier geht es aber jetzt nicht nur um vollständige Transformationen ganzer Exceldateien, sondern eher um die Transformation einzelner Messwerte. Wir haben also etwas gemessen, was uns auf der Skala der Einheiten wie wir es gemessen haben nicht gefällt. Deshalb nutzen wir eine mathematische Funktione, die uns aus unseren originalen Messwerten neue einheitslose Werte erschafft. Hier ist mal wieder wichtig, dass wir am Ende einheitslose Messwerte haben, die sich dann der biologischen Interpretation entziehen. Aber wie immer gilt, je nach Fragestellung ist die Transformation von Daten wichtig bis notwendig. Deshalb einmal hier alle gesammelt zu der Transformation.

20.1 Allgemeiner Hintergrund

Wenn wir von der Transformation sprechen, dann sprechen wir von einer überschaubaren Anzahl von sinnhaften mathematischen Operationen, die wir anwenden können. Es gibt natürlich unendliche viele mathematische Funktion und daher auch eine unendliche Anzahl an möglichen Transformationen. Dennoch haben sich in den Jahrzehnten der Anwendung mehrere Algorithmen durchgestetzt. Diese Hauptalgorithmen wollen wir hier einmal anaschauen. Teilweise sind es eben dann sehr simple Funktionen wie der Kehrwert oder aber die quadratische Wurzel. Alles im allen also kein Hexenwerk. Beginnen wir also einmal mit einigen Beispielen aus wissenschaftlichen Kontexten um uns die Transformation etwas klarer werden zu lassen.

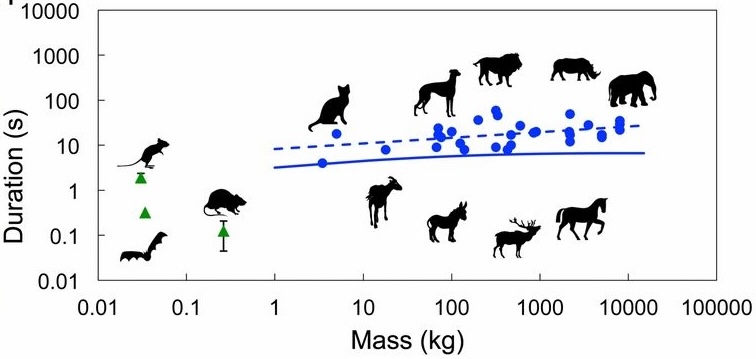
In der folgenden Abbildung aus Yang et al. (2014) siehst du einmal den Zusammenhang des Körpergewichts und der Dauer des Urinierens. Wir haben hier eine Darstellung auf der logarithmischen Skala der Zeit und des Gewichts. Daher können wir auch deas Gewicht der Maus und das Gewicht des Elefanten einigermaßen sinnvoll auf der Abbildung darstellen ohne das wir die Abbuildung sehr stark stauchen würden. Wir sehen das es keinen Unterschied gibt, die Gerade läuft parallel zu der Masse. Egal wie schwer ein Säugetier ist, es pinkelt immer die gleiche Zeit. Daher ist eine Anwendung der Transformation zusammenhänge zu zeigen, die auf sehr großen Skalen von Einheiten laufen. Die Maus ist leicht in Gramm und der Elefant ist schwer in Tonnen. Schnell haben wir hier Unetrschiede in der Einheit von \(10^6\) Gramm.

Abbildung 20.1— Zusammenhang zwischen dem Körpergewicht und der Dauer des Urinierens von verschiedneen Säugetieren auf der logarithmischen Skala. Einige der Punkte sind als Pictogramme der entprechenden Tiere dargestellt. Quelle: Yang et al. (2014)

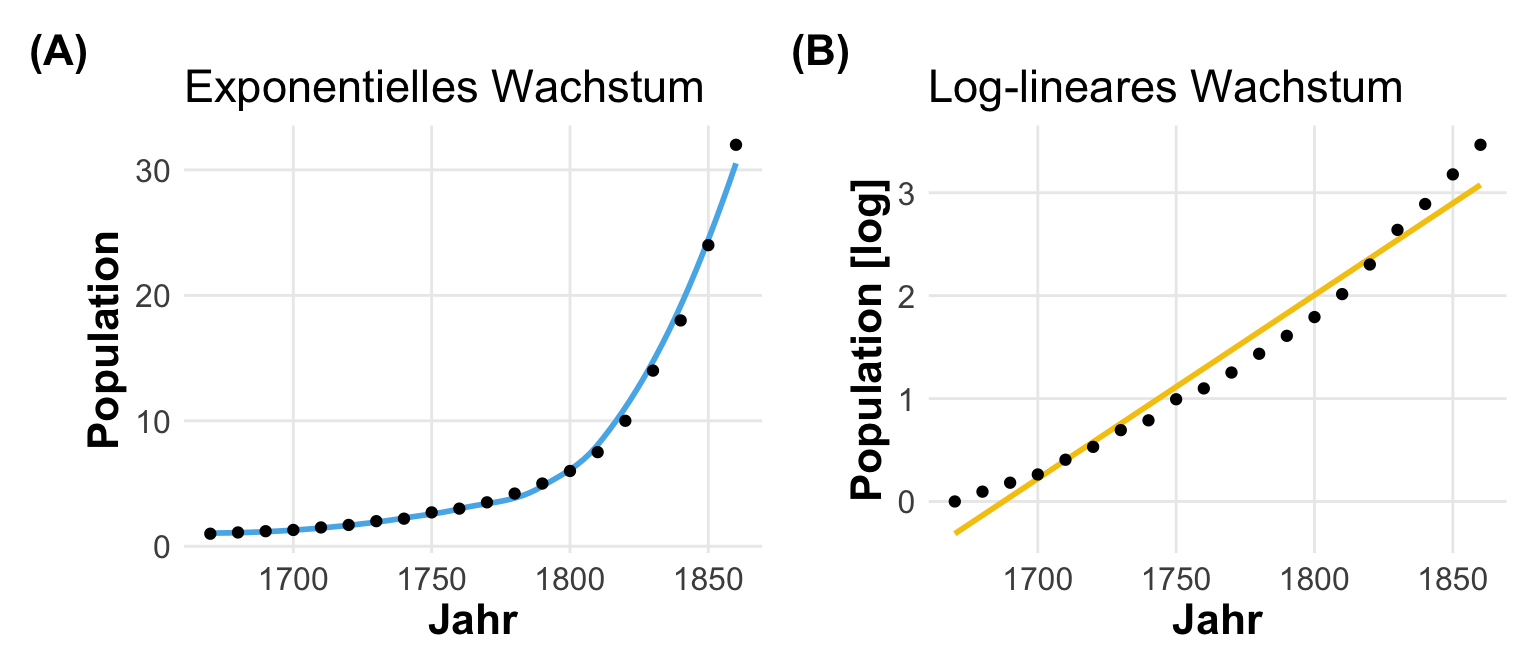
Nun stellt sich schnell die Frage, was ist eigentlich die beste Transformation für unsere Messwerte? Häufig hängt die Entscheidung auch von dem Modell ab was wir rechnen wollen. Viele Modelle verlangen einen linearen Zusammenhang. In der folgenden Abbildung siehst du einmal das exponentielle Wachstum der Bevölkerung in den Vereinigten Staaten. Wie du sehen kannst, haben wir einen sehr schnellen Anstieg. Um diesen Zusammenhang gut mit einem linearen Modell modellieren zu können, müssen wir einen einigermaßen linaren Zusammenhang erzeugen. Hier können wir die Anzahl der Menschen als Messwert \(y\) einmal mit dem Logarithmus transformieren. Wir sehen dann, dass wir hier einen fast linearen Zusammenhang vorliegen haben. Die Log-Transformation hat hier also gut funktioniert.

Abbildung 20.2— Wachstum der Bevölkerung in den Vereinigten Staaten. Viele Modelle verlangen einen linearen Zusammenhang. (A) Exponentzielles Wachstum auf der originalen Skala. (B) Log-Transformation der Population um einen linearen Zusammenhang zu erreichen. [Zum Vergrößern anklicken]

Nun könnte man annehmen, dass es recht mühselig ist sich verschiedene Transformationen auszudenken und dann jedes Mal zu gucken, ob wir einen linearen Zusammenhang vorliegen haben. Daher gab es den Vorschlag von Tukey eine Ladder of Powers zu nutzen. Wir modellieren folgende simple lineare Regression. Dabei wählen wir verschiedene Potenzen \(\lambda\) und schauen jedes Mal, ob wir einen linearen Zusammenhang vorliegen haben.

\[ y^{\lambda} = \beta_0 + \beta_1 \cdot x_1 \]

mit

• \(y\), dem Messwert wie Frischmasse oder Population.
• \(\lambda\), einer beliebigen Potenz.
• \(\beta_0, \beta_1\), den Koeffizienten der linearen Regression.
• \(x_1\), der Einflussvariabel, wie Wassergabe oder das Jahr.

Jetzt fragst du dich sicherlich, welche \(\lambda\)-Werte soll ich nehmen? Folgende Tabelle zeigt dir einmal die Zusammenhänge zwischen ausgewählten Lambda-Werten \(\lambda\) und der entsprechenden Transformation in dem Messwert \(y\). Du kannst auch jeden belieben Kommawert für \(\lambda\) einsetzen, aber die ganzahligen Werte können wir dann einfach darstellen. So ist ein \(\lambda\)-Wert von 1/2 nichts anderes als die Transformation mit der Quadratwurzel.

Tabelle 20.1— Tukey’s Ladder of Powers oder wie kann können Messwerte \(y\) transformiert werden? Das \(\lambda\) gibt die Potenz von dem Messwert \(y\) an.

\(\boldsymbol{\lambda}\)	\(\boldsymbol{y^\lambda}\)
\(-2\)	\(\cfrac{1}{y^2}\)
\(-1\)	\(\cfrac{1}{y}\)
\(-1/2\)	\(\cfrac{1}{\sqrt{y}}\)
\(0\)	\(\log{y}\)
\(1/2\)	\(\sqrt{y}\)
\(1\)	\(y\)
\(2\)	\(y^2\)

In der folgenden Abbildung habe ich dir dann mal verschiedene \(\lambda\)-Werte visualisiert. Das Ziel ist immer einen linearen Zusammenhang zu finden. Wie können wir die Potenz von \(y\) wählen, so dass wir dann einen linearen Zusammenhang finden? In der Abbildung hier haben wir dann einen linearen Zusammenhang gegeben und ich zeige einmal wie die verschiedene \(\lambda\)-Werte den Zusammenhang ändern. Wir müssen später wirklich nicht alle händisch durchprobieren, wir haben dann dafür automatisierte Transformationen in R vorliegen. Diese Algorithmen finden dann das beste \(\lambda\) für uns.

Abbildung 20.3— Verschiedene \(\lambda\) Transformationen für einen linearen Zusammenhang zwischen \(x\) und \(y\). Der \(\lambda\)-Wert ist als \(y^{\lambda}\) zu verstehen. Somit beschreibt der \(\lambda\)-Wert die Potenz vom Messwert. Gesucht ist der \(\lambda\)-Wert bei dem ein linearer Zusammenhang zwischen \(x\) und \(y\) vorliegt. [Zum Vergrößern anklicken]

Warum müssen wir Daten transformieren? Meistens hat dies drei Hauptgründe. Ich habe hier nochmal die Gründe zusammengefasst und sortiert. Sicherlich gibt es neben diesen drei Gründen auch noch weitere Gründe, aber ich denke, dass es die häufigsten sind. In einem faktoriellen Design wollen wir häufig für die Gruppenvergleiche eine ANOVA rechnen, so dass es sicherlich eine der häufigsten Ziele einer Transformation ist. Gehen wir mal die Gründe durch.

Wir brauchen eine Normalverteilung

Warum brauchen wir eine Normalverteilung in unseren Messwerten? Wir wollen eine ANOVA oder eine Gaussian lineare Regression rechen und benötigen ein normalverteiltes Outcome \(y\). Wir wollen also meist unsere Daten \(log\)-Transformieren um aus einem nicht-normalverteilten Messwert \(y\) ein \(log\)-normalverteilten Messwert \(y\) zu erschaffen. Dann können wir relativ entspannt einen Mittelwertsvergleich über den ANOVA Pfad rechnen.

Wir wollen eine Vorhersage machen

Immer häufiger wollen wir auch Modelle rechnen, wo wir verschiedene Einflussvariablen und Messwerte vorliegen haben. Wir wollen jetzt einen einen Algorithmus zur Prädiktion (deu. Vorhersage) nutzen und haben sehr viele Einflussvariablen \(x\) in sehr unterschiedlichen Einheiten. Wir wollen dann unsere Einflussvariablen Standardisieren oder Normalisieren. Wir brauchen normalisierte Daten später beim Klassifizieren im Rahmen von maschinellen Lernverfahren. Bitte beachte auch, dass die Transformationen hier in diesem Kapitel eher für kleine Datensätze geeignet sind. Im Kapitel zur Klassifikation gehe ich nochmal auf die Automatisierung über das R Paket {recipes} ein. Wenn du also einen großen Datensatz hast, den du vielleicht oft bearbeiten musst, dann mag dir dort mehr geholfen sein.

Wir wollen Gruppen / Cluster erkennen

Eine andere Anwendung ist auch das Gruppieren von Dtaen. Wir wollen eine komplexere Analyse wie die Hauptkomponentenanalyse oder Clusteranalyse rechnen und brauchen Variablen, die alle eine ähnliche Spannweite haben. Hier haben wir dann auch das Problem der Einheiten. Wenn wir zu unterschiedliche Einheiten vorliegen haben, funktionieren die Modelle nicht mehr. Wir wollen dann unsere Einflussvariablen Standardisieren oder Normalisieren. Auch hier können viele Funktionen in R das schon automatisch, deshalb einmal schauen, ob du überhaupt Transformieren musst. Es spricht aber nichts dagegen vorher zu Transformieren, da du dich dann schonmal mit den Ergebnissen der Transformation auseinander gesetzt hast. Dann hast du auch nicht eine algorithmische Blackbox vorliegen.

Wir wollen uns nun die Verfahren zur Transformation von Daten in den folgenden Abschnitten einmal näher anschauen. Zuerst gehe auf die Standardverfahren mit mutate() und den entsprechenden Funktionen ein. Danach zeige ich dir dann noch die automatisierten Varianten. Bei den automatisierten Varianten habe ich schon angefangen einmal aufzuräumen und die veralteten Funktionen in den Friedhof zur Referenzierung geschoben.

Weitere Tutorien für das Transformieren von Daten.

Wir oben schon erwähnt, kann dieses Kapitel nicht die umfangreiche Literatur der Transformation von Daten abarbeiten. Daher präsentiere ich hier eine Liste von Literatur und Links, die mich für dieses Kapitel hier inspiriert haben. Nicht alles habe ich genutzt, aber vielleicht ist für dich was dabei.

• Ich verweise hier auch nochmal auf das tolle Tutorium von Matus Seci auf dem Coding Club - Transforming and scaling data: Understand the fundamental concepts of manipulating data distributions for modelling and visualization. Du findest auch dort mehr Informationen zu der Rücktransformation und der Anwendung von Transformationen auf einen komplexeren Datensatz.
• Das Kapitel Transformations liefert auch nochmal einen schönen Überblick über verschiedene Transformtionen.
• Das Kapitel Transforming Data geht nochmal auf speziellere Funktionen ein und hilft hier nochmal bei der automatisierten Verwendung.

20.2 Genutzte R Pakete

Wir wollen folgende R Pakete in diesem Kapitel nutzen.

pacman::p_load(tidyverse, magrittr, scales, see, MASS, bestNormalize,
               rcompanion, LambertW, trafo, conflicted)
conflicts_prefer(MASS::boxcox)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)
conflicts_prefer(parameters::skewness)
conflicts_prefer(parameters::kurtosis)
conflicts_prefer(bestNormalize::boxcox)
conflicts_prefer(magrittr::set_names)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", 
                "#009E73", "#F0E442", "#F5C710", 
                "#0072B2", "#D55E00", "#CC79A7")

An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.

20.3 Daten

Wie immer brauchen wir Daten, wenn wir uns einmal mit den Transformationen von Daten beschäfltigen wollen. Ich habe hier wieder zwei Datensätze mitgebracht. Der erste Datensatz beschreibt die Sprungweite von Hunde-, Katzen und Fuchsflöhen sowie deren jeweiligen Schlupfzeiten. Der zweite Datensatz kommt von der Datenbank AnAge Database of Animal Ageing and Longevity und beschreibt das Alter von verschiedenen Tierarten und weiteren Eigenschaften, die mit dem Alter verbunden sein könnten.

Schlupfzeiten von Flöhen

In unserem ersten Datensatz betrachten wir die Schlupfzeiten sowie wie die Sprungweiten über alle Tiere hinweg. Wir werden dann später nochmal die Messwerte für die Hunde-, Katzen- und Fuchsflöhe aufteilen. Dann schauen wir, wie sich die jeweiligen Messwerte verteilen oder besser welcher Verteilung die Messwerte folgen.

fac1_tbl <- read_excel("data/flea_dog_cat_length_weight.xlsx") |>
  select(animal, jump_length, weight, hatch_time) |> 
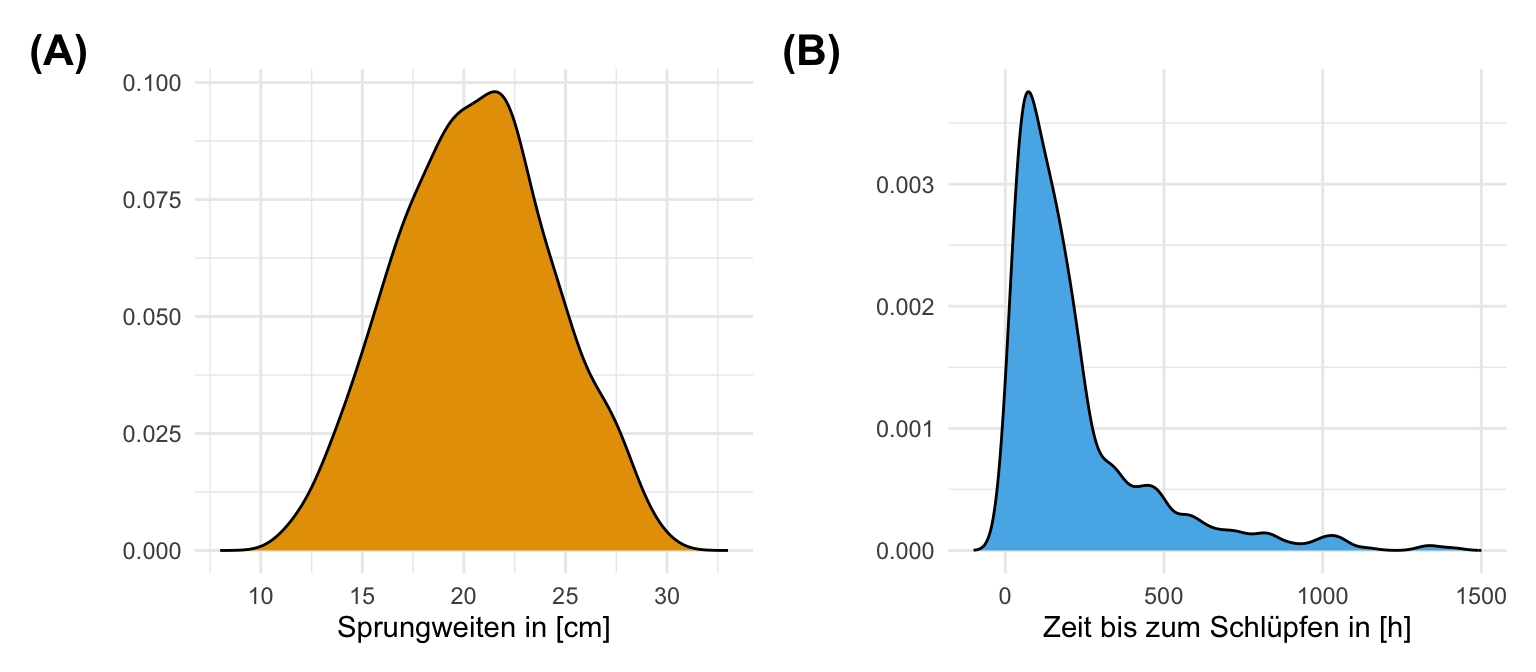
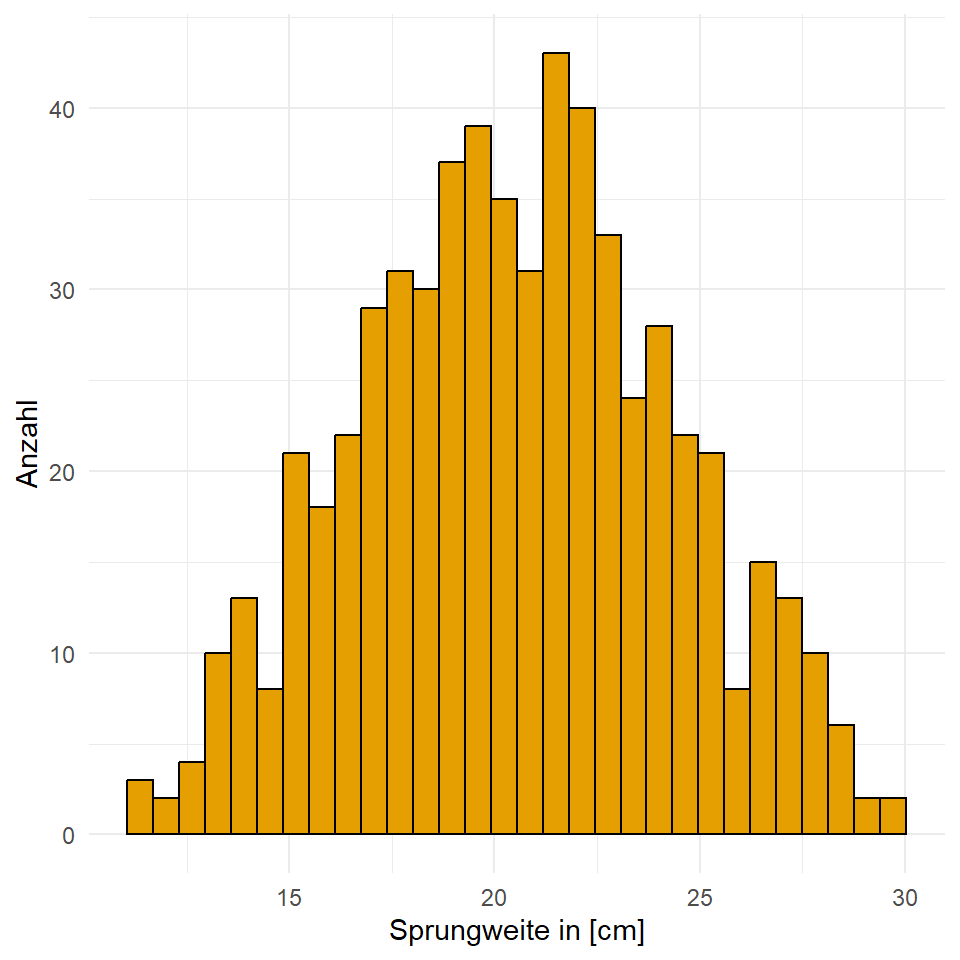
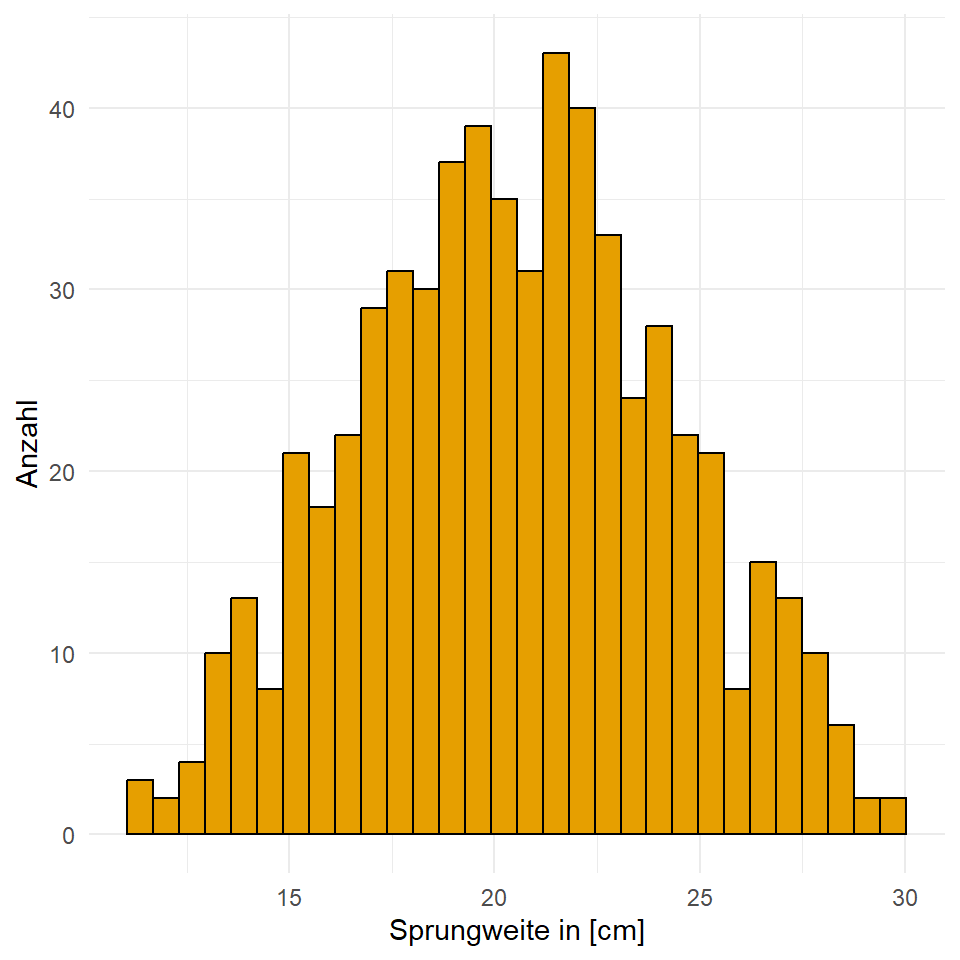
  filter(hatch_time <= 1500)

In der folgenden Tabelle siehst du dann nochmal die Werte für die Sprungweite und die Schlupfweiten. Wir nehmen mal an, dass die Sprungweiten eher normalverteilt sind und die Schlupfzeiten eher nicht.

Tabelle 20.2— Selektierter Datensatz mit einer normalverteilten Variable jump_length und der nicht-normalverteilten Variable hatch_time. Wir betrachten die ersten sieben Zeilen des Datensatzes.

animal	jump_length	hatch_time
cat	15.79	483.6
cat	18.33	82.56
cat	17.58	296.73
...	...	...
fox	24.35	182.68
fox	24.36	104.89
fox	22.13	62.99

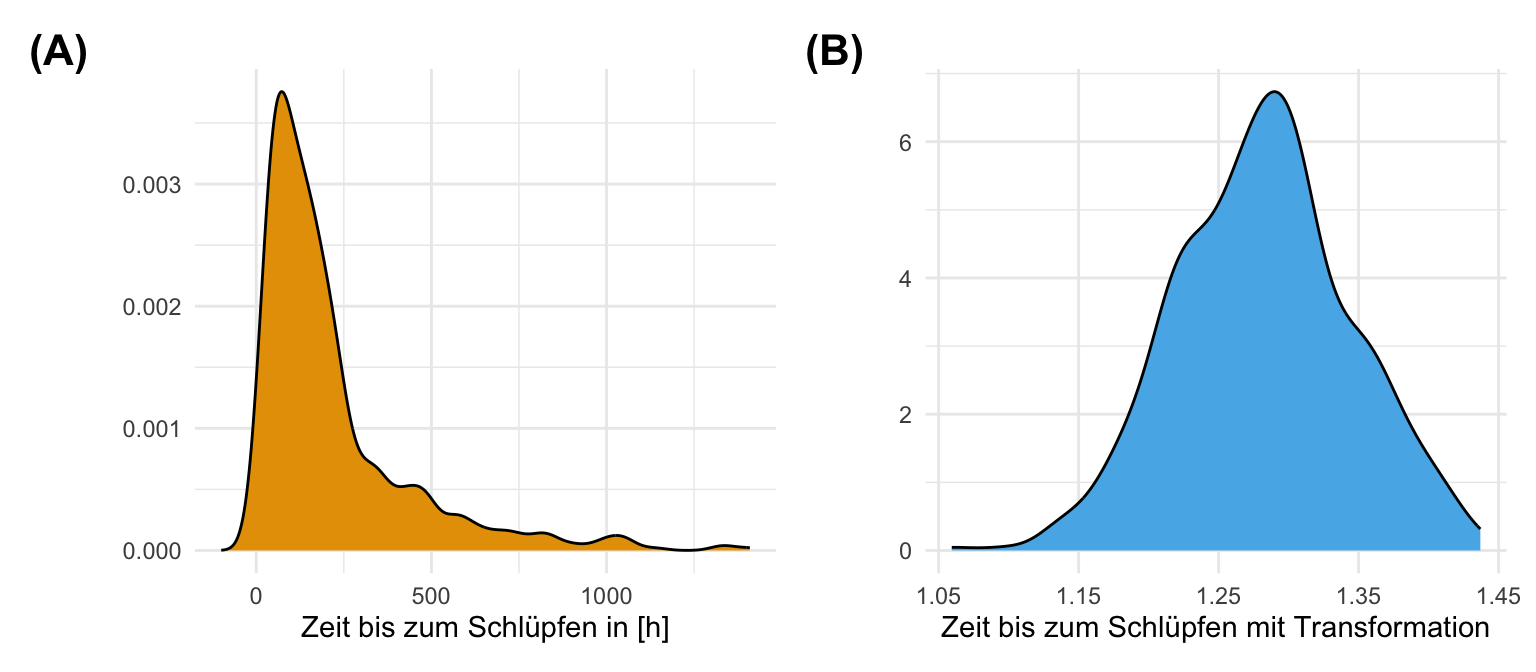
Dann wollen wir den Zusammenhang auch nochmal visualiseren. Wir sehen in der Abbildung sehr gut, dass die Sprungweiten eher einer Normalverteilung über alle Floharten folgt. Auch die Schlupfzeiten sind eher nicht normalverteilt. Wir sehen eine sehr rechtsschiefe Verteilung. Wir haben einige Flöhe mit sehr langen Schlupfzeiten. Daher könnten wir überlegen, die Schlupfzeiten zu transformieren und in eine Normalverteilung zu überführen. Dabei wirden wir natürlich die Einheit in Stunden verlieren.

Abbildung 20.4— Densityplot zur Abschätzung der Verteilung unserer Messwerte in dem Flohdatensatz. (A) Sprungweiten in [cm]. (B) Schlupfzeiten in [h]. [Zum Vergrößern anklicken]

Das Alter von Tieren

In dem zweiten Datensatz schauen wir uns das Alter von verschiedenen Tierarten an. Wir wollen wissen, ob es einen Zusammenhang zwischen dem Alter der Tiere und dem Gewicht der Tiere gibt. Leben also Elefanten länger als Mäuse, weil die Elefanten einfach schwerer sind? Es ist ein schöner Datensatz um nochmal die Skalierung von Daten zu zeigen oder aber die Log-Transformation aus der Einleitung zu zeigen. Wir wollen dann doch das Gewicht einmal in Kilogramm haben und nicht in Gramm. Dafür passe ich die Daten einmal an.

anage_tbl <- read_delim("data/anage_data.txt", delim = "\t") |> 
  select(name = "Common name", weight = "Adult weight (g)", 
         age = "Maximum longevity (yrs)") |> 
  mutate(weight = weight/1000) |> 
  na.omit() 

Dann schauen wir uns nochmal die Daten im Original an. Wie du sehen kannst, haben wir verschiedenste Tierarten und die entsprechende maximale Lebensspanne. Das Problem bei solchen Daten wird dann meistens nicht sofort klar, daher schauen wir uns gleich einmal die Visualisierung an.

Tabelle 20.3— foo

Common name	Adult weight (kg)	Maximum longevity (yrs)
American toad	21.7667	36
Southern toad	19.267	10
Cane toad	106.25	24.8
...	...	...
Spiky oreo	1100	100
Smooth oreo	2750	100
European john dory	4400	12

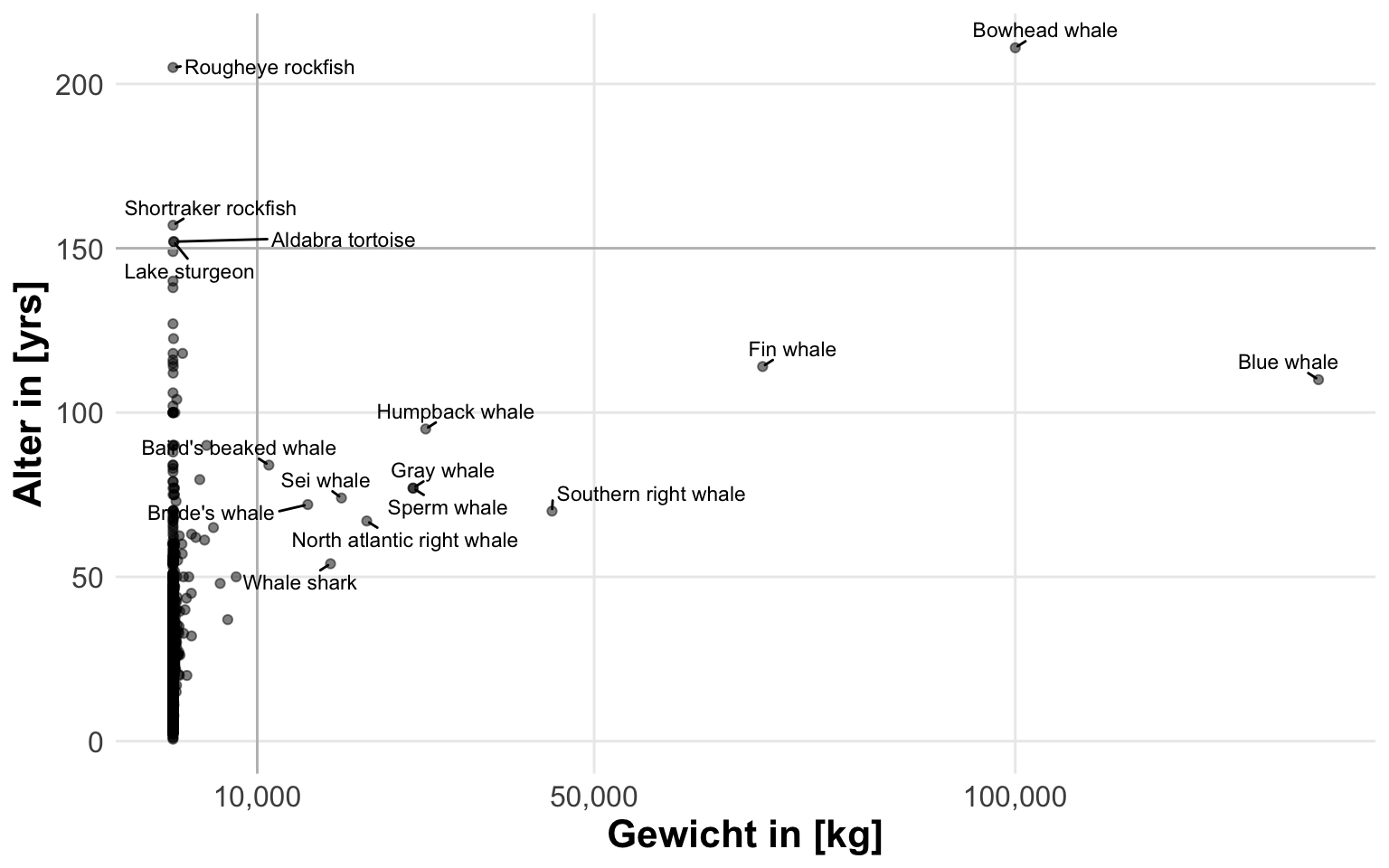
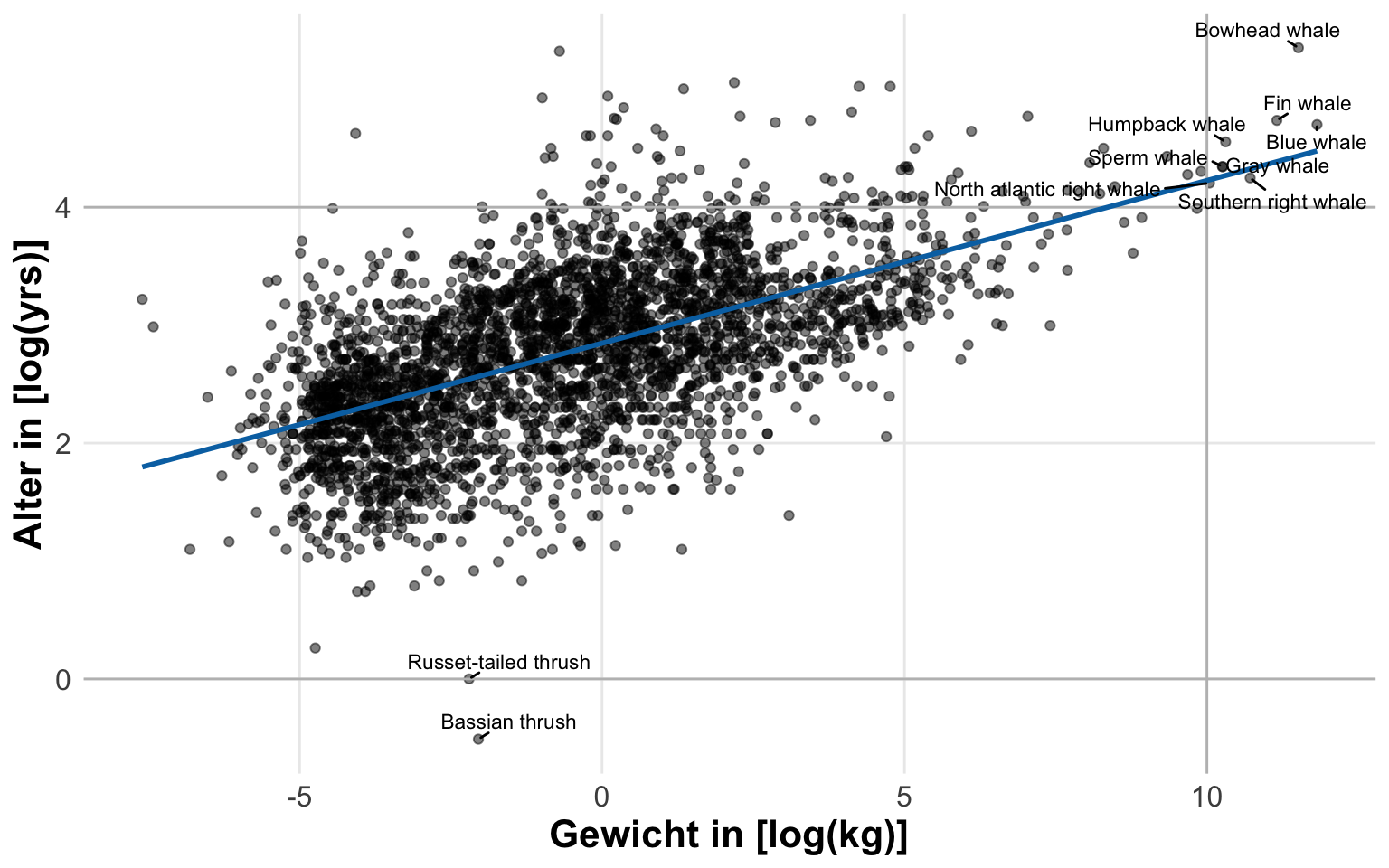
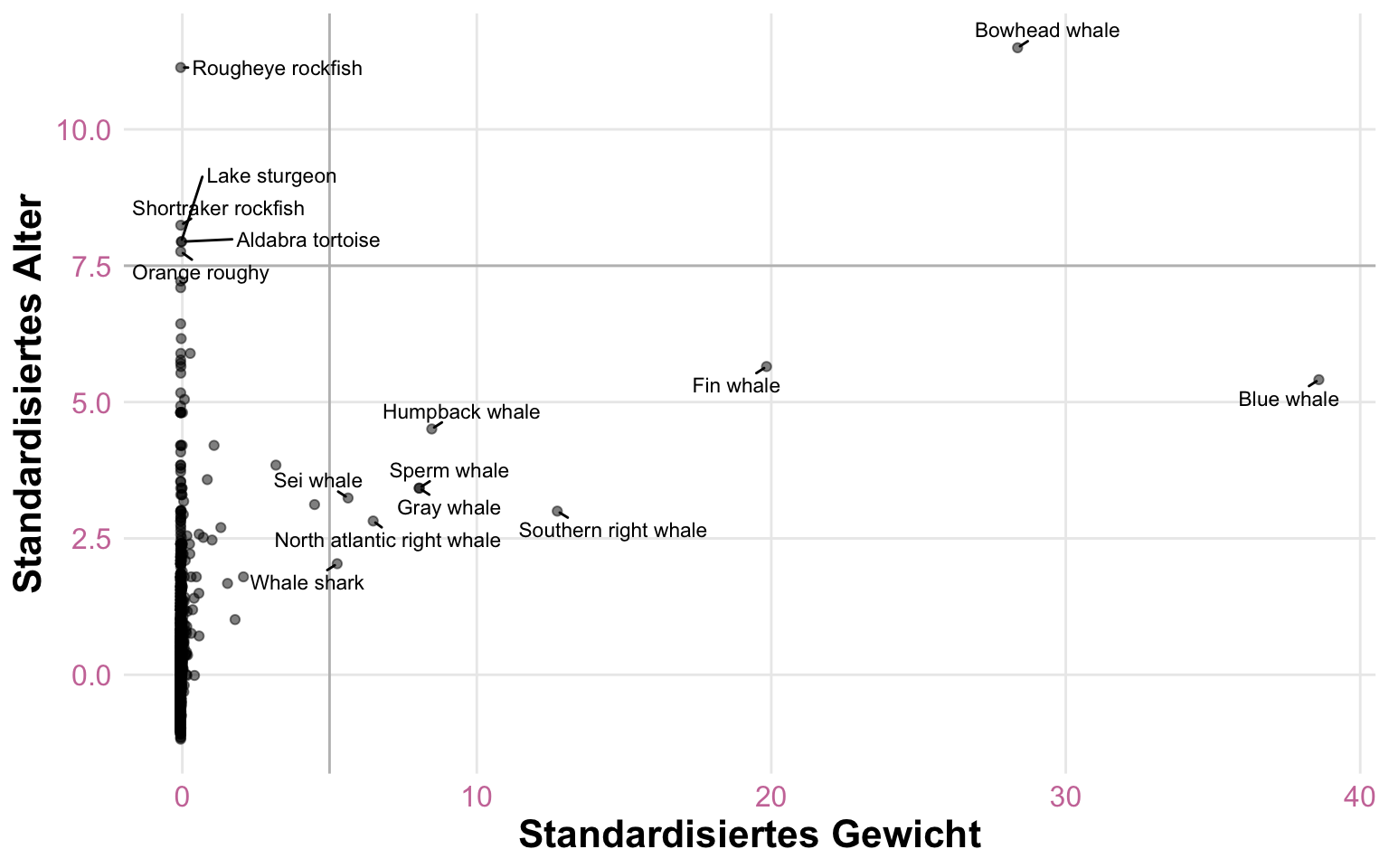
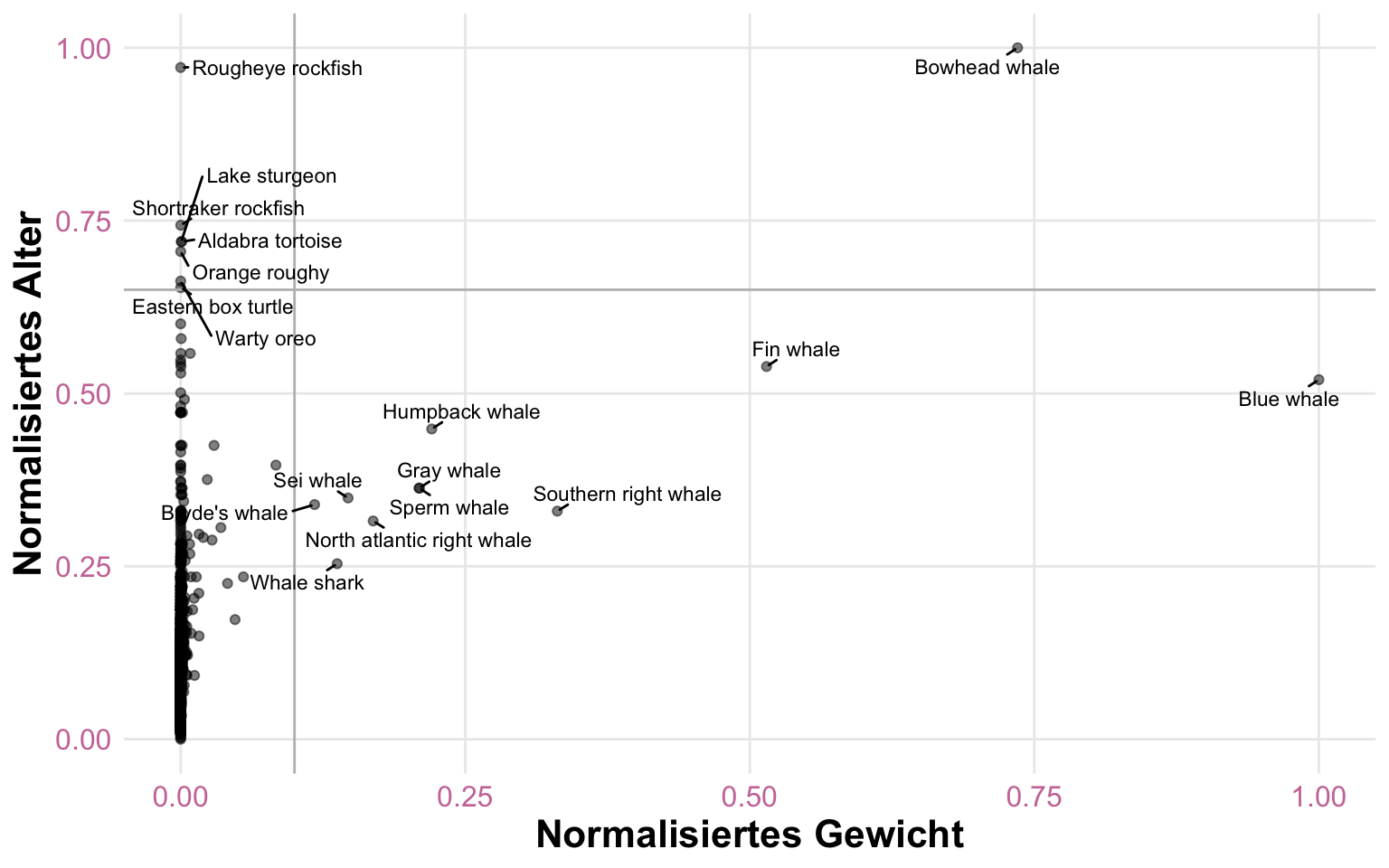
In der folgenden Abbildung siehst du dann einmal den Zusammenhang zwischen dem Körpergewicht und dem Alter in Jahren der ganzen Tierarten in dem Datensatz. Ich habe dir einmal die Arten mit einem hohen Gewicht und einem langem Lebensalter hervorgehoben. Einen Großteil der Arten siehst du aber gar nicht, da die Wale die Skala so weit nach rechts schieben, dass alles links zusammengepresst wird. Hier bieten sich Transformationen und Skalierungen an um mehr aus den Daten visuelle herauszuholen. Wir sehen hier gar nicht den Zusammenhang oder einen irgendwie gearteten Trend in den Daten.

Abbildung 20.5— Zusammenhang zwischen dem Gewicht in [kg] und dem Alter in [yrs] von Tierarten. Durch die große Bandbreite der Körpergewichte sind der überwiegende Teil der Tierarten nicht zu erkennen. Ein Trend lässt sich ebenfalls nicht ablesen. [Zum Vergrößern anklicken]

20.4 Transformationen

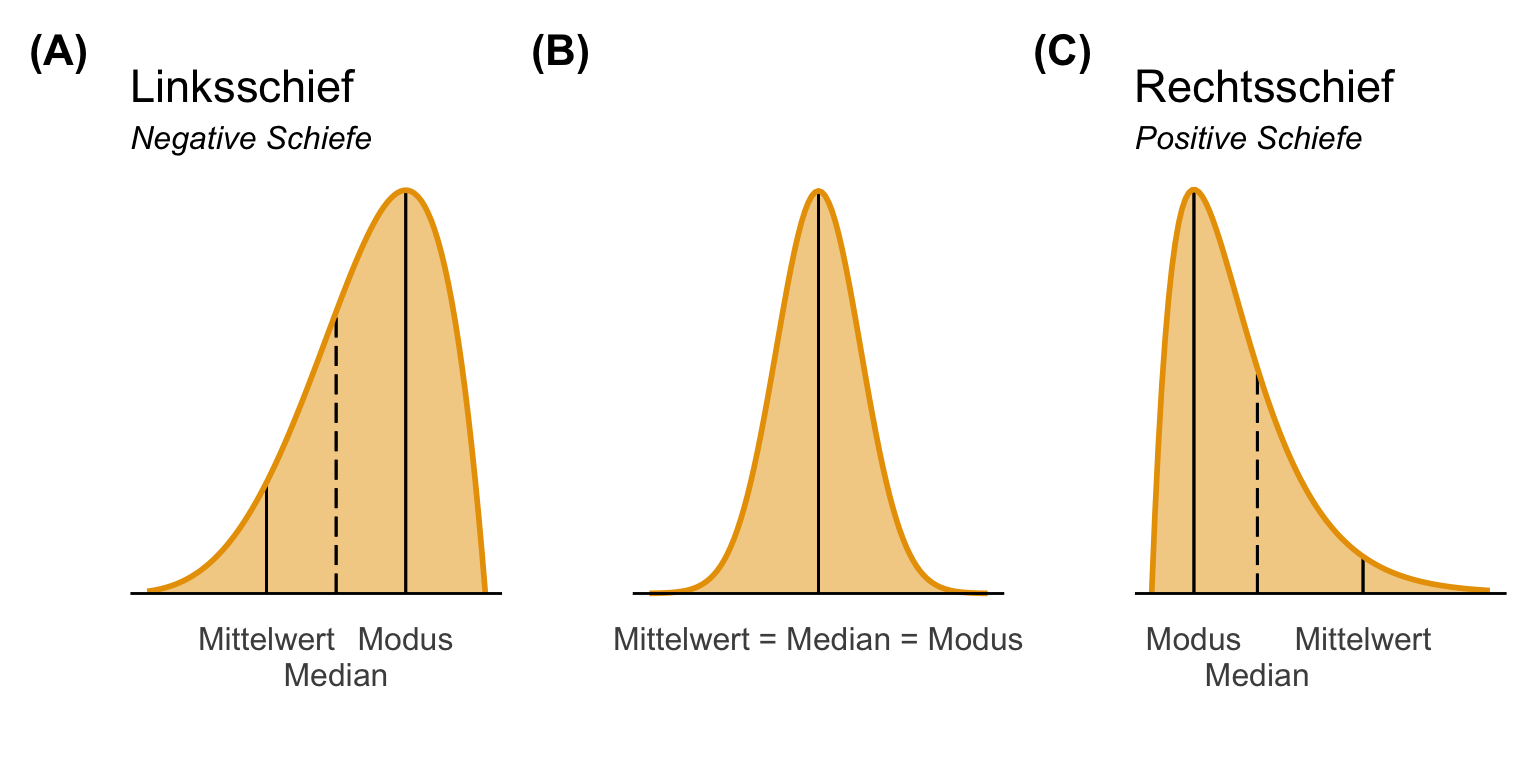
Beginnen wir also einmal mit der Transformation. Hier wollen wir durch eine mathematische Funktion die Messwerte so verändern, dass wir am Ende eine Normalverteilung oder eine approximative Normalverteilung erhalten. Hierbei ist nochmal wichtig zu wissen, dass wir eigentlich nur das Ziel einer Normalverteilung durch die Transformation kennen. Wir nutzen eigentlich keine andere Form der Transformation um nicht Linearität durch einen normalverteilten Messpunkt annährend zu erreichen. Daher schauen wir uns einmal in der folgenden Abbildung verschiedene Arten einer Verteilung an. Neben wilden Wabbeln gibt es eher linksschiefe Verteilungen und rechtsschiefe Verteilungen. Die Schiefe definiert sich durch einen längeren Verteilungsschwanz. Wir können auch durch die Ordnung des Modus, Median und dem Mittelwert abschätzen, ob wir eine schiefe Verteilung vorliegen haben oder nicht.

Abbildung 20.6— Zusammenhang vom Mittelwert, Median und dem Modus zur Feststellung einer Normalverteilung. Der Modus ist hierbei der häufigste Wert. (A) Linksschiefe Verteilung. Der Modus ist größer als der Median ist größer als der Mittelwert. (B) Symmetrische Normalverteilung. Der Mittelwert und Median sowie Modus sind gleich. (C) Rechtsschiefe Verteilung der Mittelwert ist größer als der Median ist größer als der Modus. [Zum Vergrößern anklicken]

Wir haben jetzt also erkannt, dass wir eine schiefe Verteilung in unseren Daten vorliegen haben. Wir nutzen dafür immer eine visuelle Überprüfung. Zwar gibt es statistsiche Tests auf die Abweichung von der Normalverteilung, aber diese Tests geben nicht wieder wie die Schiefe der Verteilung ist. Dann müssen wir auch bei einem signifikanten Vortest und der Ablehnung der Normalverteilung nochmal schauen in welche Richtung die Schiefe geht. Da sind wir dann wieder bei der visuellen Betrachtung. Jetzt gibt es verschiedene gängige mathematische Funktionen, die dir erlauben aus einer schiefen Verteilung eine Normalverteilung zu bauen.

Die Quadratwurzel für moderat schiefe Messwerte:

• sqrt(y) für positiv, schiefe Messwerte
• sqrt(max(y+1) - y) für negative, schiefe Messwerte

Der Logarithmus für starke schiefe Messwerte:

• log10(y) oder log() für positiv, schiefe Messwerte
• log10(max(y+1) - y) oder log(max(y+1) - y) für negative, schiefe Messwerte

Die Inverse für extrem, schiefe Messwerte:

• 1/y für positiv, schiefe Messwerte
• 1/(max(y+1) - y) für negative, schiefe Messwerte

Neben diesen sehr häufig vorkommenden Transformationen können wir auch eine inverse Normaltransformation nutzen oder aber die Transformation mit Rängen. Die inverse Normaltransformation ist teilweise sehr effizient aber auch umstritten, weil sie im Prinzip alle Daten in eine Normalverteilung presst, egal wie gut die Messwerte passen würden. Die Rangtransformation führt dann zu den Tests der Parametrik, wie dem U-Test und dem Kruskal-Wallis-Test. Hierzu erfährst du dann mehr in dem Abschnit weiter unten.

Wenn dir gleich das ganze Ausprobieren etwas zu anstrengend ist, dann zeige hier dir auch noch weiter unten die automatisierte Transformation. Es gibt mittlerweile Algorithmen, die eben dann eine ganze Reihe an Transformationen durchprobieren und dir die Transformation zurückgeben, die am Besten eine Normalverteilung in deinen Messwert erschafft. Das ist natürlich auch sehr praktisch und ist schneller als alles händisch durchzuprobieren.

Achtung, bitte beachten!

Wir müssen immer nach einer Transformation schauen, ob unser Messwert jetzt mehr einer Normalverteilung folgt oder nicht. Es kann auch sein, dass du durch eine Transformation einen Messwert erschaffst, der weniger normalverteilt ist als ohne Transformation. Bitte also immer die Transformation anschauen.

20.4.1 Quadratwurzel

Die Quadratwurzel-Transformationen ist eine etwas seltenere Transformation. Damit meine ich, dass wir die Transformation gerne einmal ausprobieren, uns aber dann meistens doch für eine andere Transformation entscheiden. Da die Transformation so einfach ist, probiere ich die Quadratwurzel-Transformationen immer aus. Auch hier müssen wir dann schauen, ob wir eine linksschiefe oder rechtsschiefe Verteilung vorliegen haben und dann entsprechend die Transformation wie weiter oben beschreiben anpassen. Meist wird die Quadratwurzel-Transformationen als die schwächere \(log\)-Transformation bezeichnet. Wir sehen in der folgenden Abbildung den Grund dafür. Aber zuerst müssen wir aber über die Funktion sqrt() unsere Daten transformieren.

sqrt_tbl <- fac1_tbl |> 
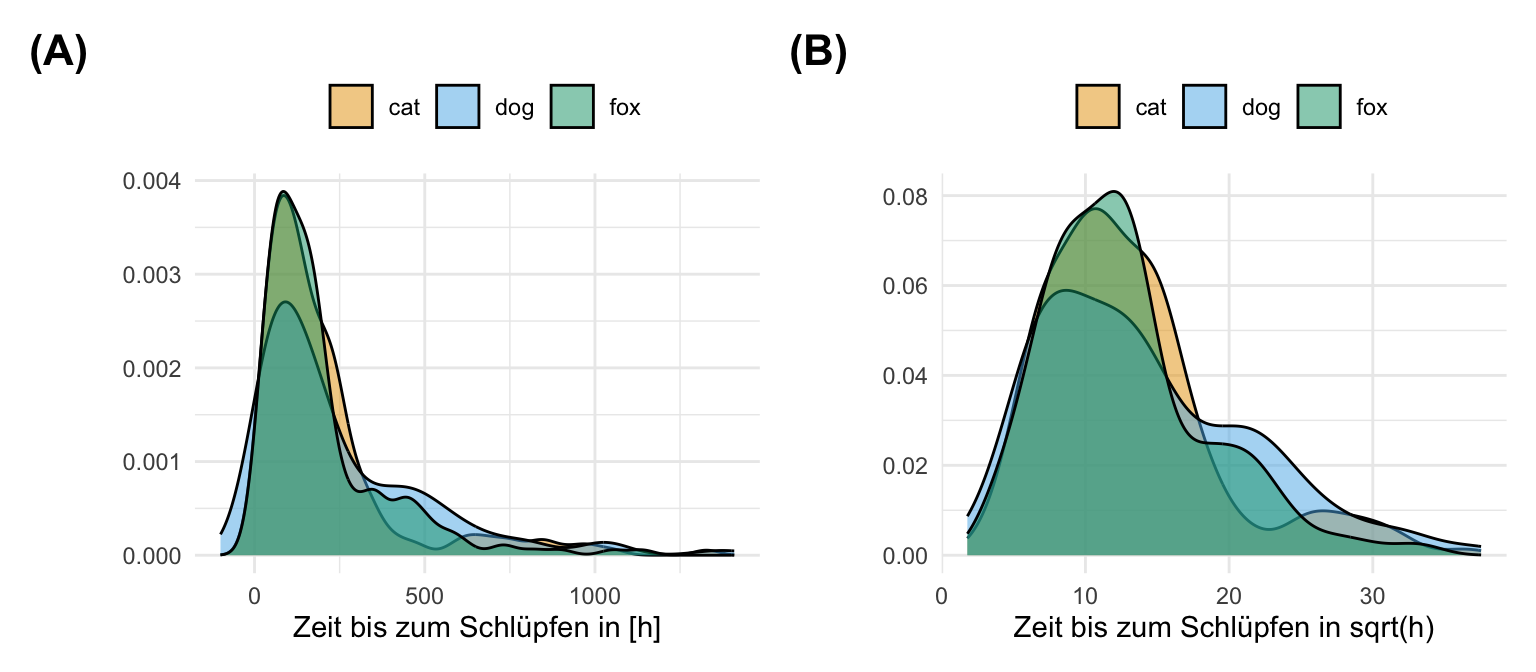
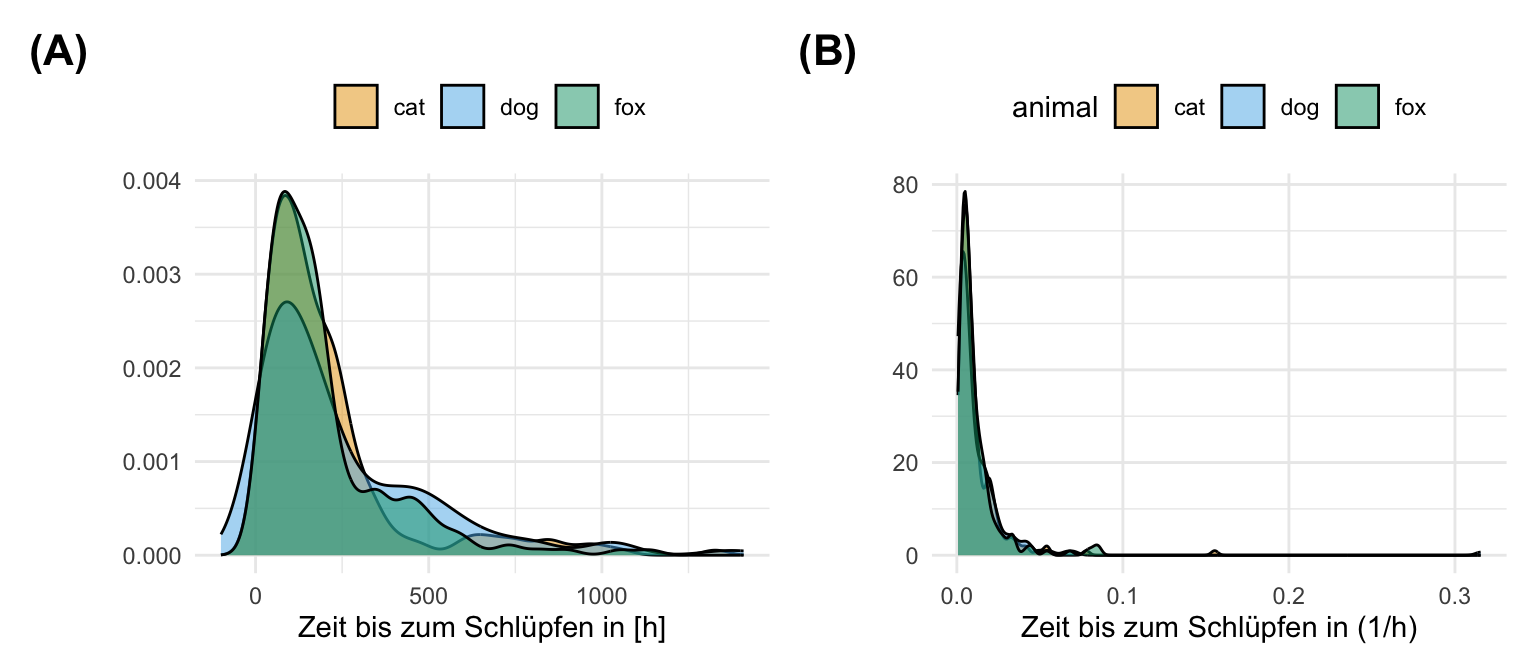
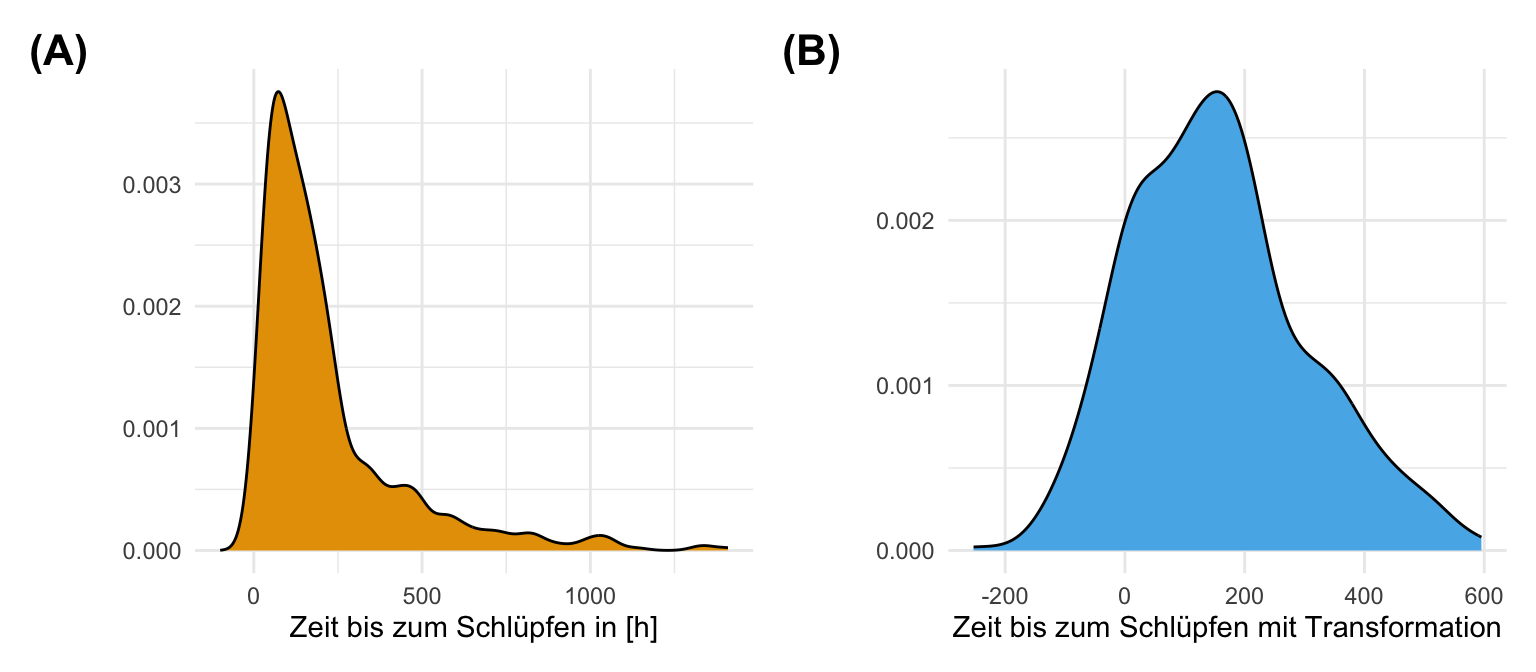
  mutate(sqrt_hatch_time = sqrt(hatch_time))

In der folgenden Abbildung sehen wir die nicht transformierte, rohe Daten sowie die transformierten Daten mit der Quadratwurzel. Es gibt einen klaren Peak Schlüpfzeiten am Anfang. Dann läuft die Verteilung langsam nach rechts aus. Wir können nicht annehmen, dass die Schlüpfzeiten normalverteilt sind. Unser Ziel besser normalverteilte Daten vorliegen zu haben, haben wir aber mit der Quadratwurzel-Transformationen nicht erreicht. Die Daten sind immer noch rechtsschief. Alle drei Floharten verhalten sich dabei gleich.

Abbildung 20.7— Histogramm der nicht transfomierten und transformierten Daten. (A) Nicht transformierte, rohe Daten. (B) Quadratwurzel-transformierte Daten. [Zum Vergrößern anklicken]

20.4.2 Logarithmus

Wir nutzen die \(log\)-Transformation, wenn wir aus einem nicht-normalverteiltem Outcome \(y\) ein approxomativ normalverteiltes Outcome \(y\) machen wollen. Diese Transformation wird so häufig verwendet, dass wir dann sogar sagen, dass unere Messwerte jetzt lognormalverteilt sind. Auch hier müssen wir dann schauen, ob wir eine linksschiefe oder rechtsschiefe Verteilung vorliegen haben und dann entsprechend die Transformation wie weiter oben beschreiben anpassen. Dabei ist wichtig, dass wir natürlich auch die Einheit mit \(log\)-transformieren. Im Folgenden sehen wir die \(log\)-Transformation der Variable hatch_time mit der Funktion log(). Wir erschaffen eine neue Spalte im tibble damit wir die beiden Variable vor und nach der \(log\)-Transformation miteinander vergleichen können.

log_tbl <- fac1_tbl |> 
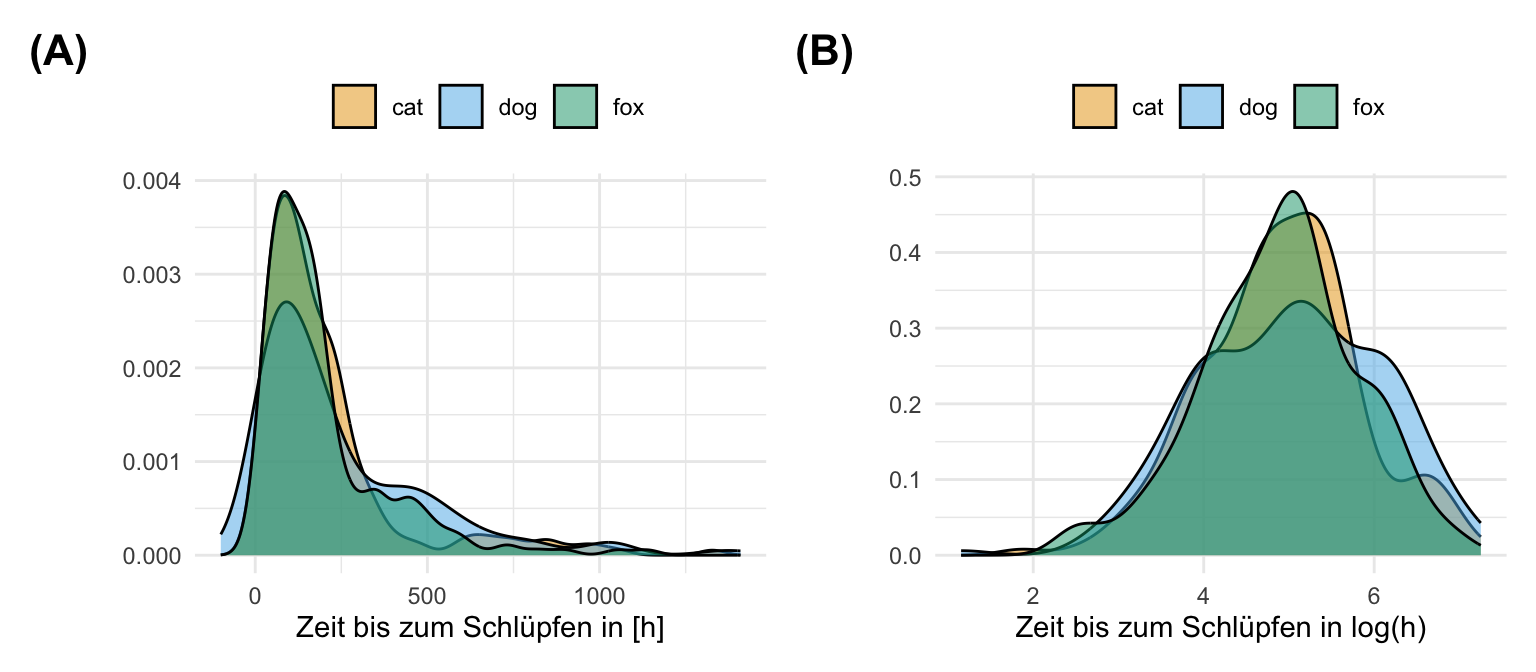
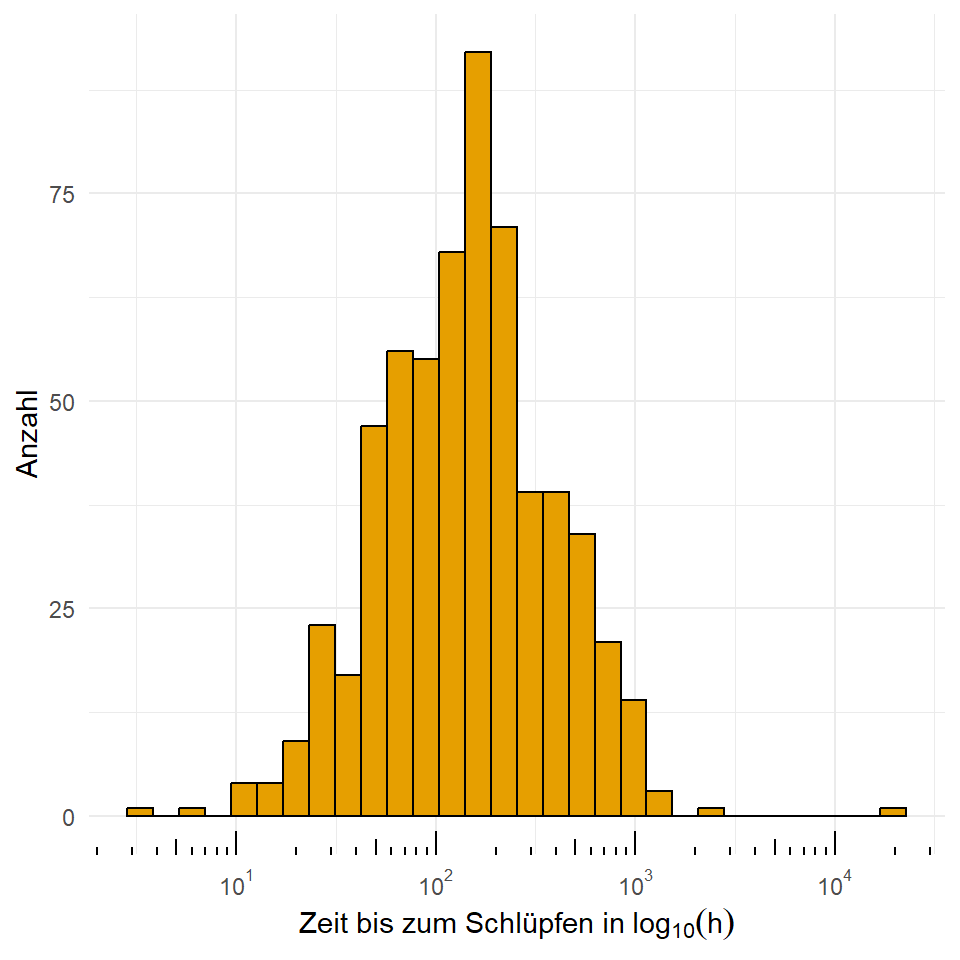
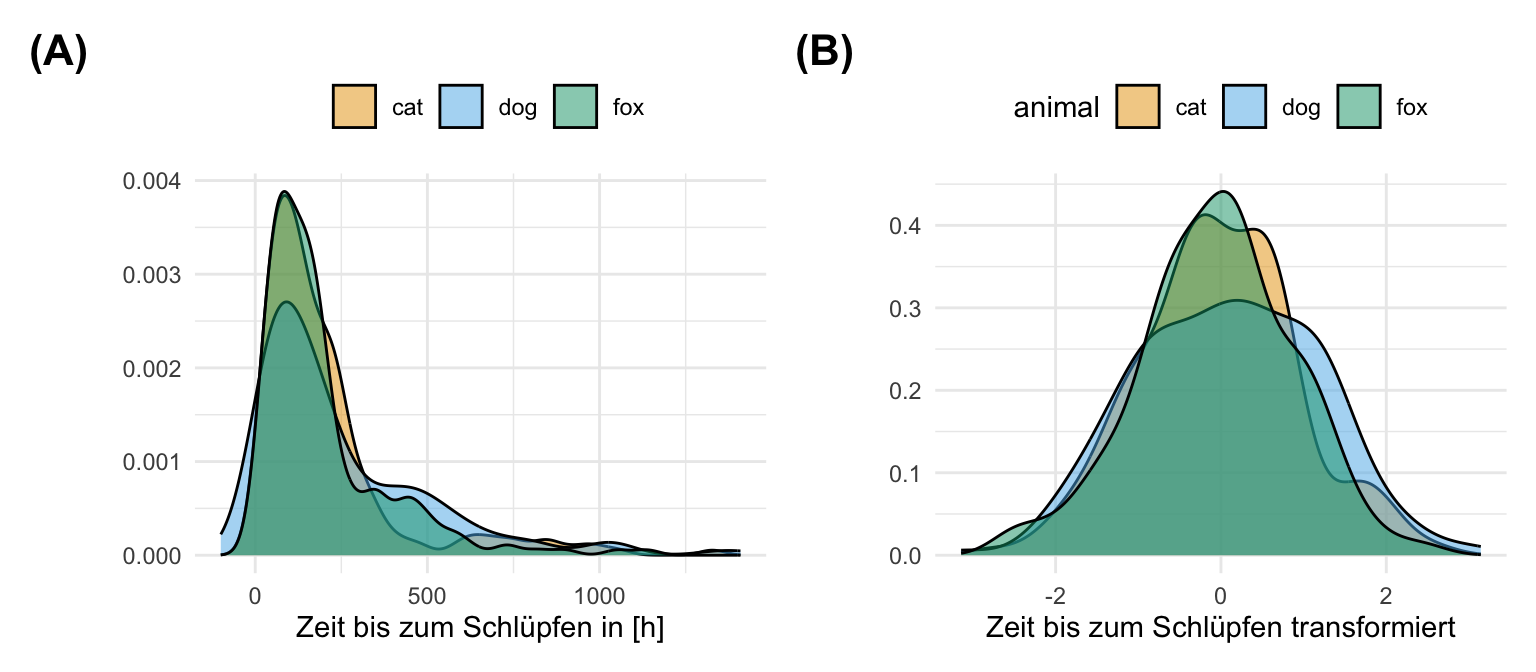
  mutate(log_hatch_time = log(hatch_time))

Wir können dann über ein Histogramm die beiden Verteilungen anschauen. In der folgenden Abbildung sehen wir die nicht transformierte, rohe Daten sowie die Log-transformierten Daten. Es gibt einen klaren Peak Schlüpfzeiten am Anfang. Dann läuft die Verteilung langsam aus. Wir können nicht annehmen, dass die Schlüpfzeiten normalverteilt sind. Die Log-Transformation hat einigermaßen funktioniert. Wir sehen in diesem Fall approximativ normalverteilte Daten. Wir haben also ein lognormalverteiltes Outcome \(y\) mit dem wir jetzt weiterechnen können. Die drei Floharten verhalten sich dabei gleich.

Abbildung 20.8— Histogramm der nicht transfomierten und transformierten Daten. (A) Nicht transformierte, rohe Daten. (B) log-transformierte Daten. [Zum Vergrößern anklicken]

In der folgenden Abbildung siehst du nochmal die Anwendung der \(\log\)-Skala in {ggplot} auf die Daten und Messwerte. Aber Achtung, die ursprünglichen Daten sind nicht transformiert. Du schaust dir hier nur an, wie die Daten transformiert aussehen würden. Es gibt auch hierzu ein kleines Tutorium zu ggplot log scale transformation. Da kannst du dann auch einmal nachschauen, wie die \(\log_2\)-Skala in {ggplot} funktioniert. Es ist immer so die Frage, ob du die Messwerte dann nicht doch lieber transformierst und darstellst. Hier kommt es dann auf den Geschmack drauf an.

ggplot(log_tbl, aes(hatch_time, fill = animal)) +
  geom_histogram(color = "black", position="dodge") +
  theme_minimal() +
  labs(x = expression("Zeit bis zum Schlüpfen in" ~ log[10](h)), y = "Anzahl",
       fill = "Flohart") +
  scale_fill_okabeito() +
  theme(legend.position = "top") +
  scale_x_log10(breaks = trans_breaks("log10", function(x) 10^x), 
                labels = trans_format("log10", math_format(10^.x))) + 
  annotation_logticks(sides = "b")  

Abbildung 20.9— Histogramm der nicht transfomierten Daten einmal auf der \(log_{10}\)-Skala in ggplot dargestellt. Achtung, hier ist nur die Darstellung transformiert. Die ursprünglichen Daten bleiben von der Transformation in {ggplot} unberührt.

In der Einleitung haben wir ja die Abbildung zu der Dauer des Urinierens und verschiedener Säugetiere gesehen. In der Abbildung wurde die x-Achse wie auch die y-Achse logtransformiert um einmal dazustellen, ob es einen Zusammenhang zwischen dem Gewicht und der Pinkeldauer gibt. Wir sehen dort eine Paralelle zu der x-Achse, so dass wir daraus schließen können, dass die Körpergröße nichts mit der Dauer des Urinierens zu tun hat. Hier habe ich dann nochmal die Beispieldaten zu dem Alter und dem Gewicht von Säugetieren mitgebracht. Wenn wir beide Messwerte logtransformieren, dann sehen wir auf einmal einen klaren Zusammenhang. Mit stiegendem Gewicht steigt auch die Lebensdauer an. Hier sehen wir dann einmal den Vorteil der Logtransformation, da wir jetzt einen besseren Zusammenhang erahnen können. Da beides auf der Logskala läuft ist es natürlich etwas schwerer die möglichen Koeffizienten einer linearen Regression zu interpretieren. Aber das ist dann noch ein anderes Thema.

Abbildung 20.10— Logaritmierter Zusammenhang zwischen dem Gewicht in [log(kg)] und dem Alter in [log(yrs)] von Tierarten. Durch die Logtransformation wird die große Bandbreite der Körpergewichte aufgebrochen. Ein linearer Trend lässt sich so ablesen. [Zum Vergrößern anklicken]

20.4.3 Inverse

Die inverse Transformation ist recht simple. Wir rechnen einfach \(1/y\) und haben dann schon unsere Transformation. Auch hier müssen wir dann schauen, ob wir eine linksschiefe oder rechtsschiefe Verteilung vorliegen haben und dann entsprechend die Transformation wie weiter oben beschreiben anpassen. Die Transformation ist dabei natürlich sehr einfach in R selber zu implementieren.

inverse_tbl <- fac1_tbl |> 
  mutate(inverse_hatch_time = 1/hatch_time)

In der folgenden Abbildung sehen wir, dass die Inverseransformation nicht funktioniert hat und unseren Messwert noch schiefer gemaht hat als vorher. Ein schönes Beispiel dafür, dass wir immer die Transformation nochmal anschauen müssen. Eine Transformation kann auch zu einem noch schlechter normalverteiltem Messwert führen. Daher immer schauen, ob die Transformation einen annährend normalverteilten Messwert hervorgebracht hat.

Abbildung 20.11— Histogramm der nicht transfomierten und transformierten Daten. (A) Nicht transformierte, rohe Daten. (B) inverse-transformierte Daten. [Zum Vergrößern anklicken]

20.4.4 Inverse Normaltransformation

Kommen wir fast zum Schluß noch zur inversen Normaltransformation. Die inverse Normaltransformation sieht ein wenig wild in der Formel aus. Ich zeige hier die Implementierung in R einmal und gehe nicht weiter mathematisch auf die Transformation ein. In den letzten Jahren wird die Transformation immer beliebter, so dass ich hier auch gerne auf die Arbeit von Beasley et al. (2009) und Rank-Based Inverse Normal Transformations are Increasingly Used, But are They Merited? verweise. Dann habe ich noch die Diskussion auf StackExchange mit What is the inverse normal transformation (INT) and what are the reasons behind using it? gelesen. Am Ende presst du deine Messwerte in eine Normalverteilung, denn du wirst durch die inversen Normaltransformation immer eine Normalverteilung erhalten. Die Idee ist eben, dass deine Messwerte in Wirklichkeit normalverteilt sind und du hier nur eine ungünstige Repräsentation in deiner Stichprobe hast. In R würden wir dann folgende Funktion nutzen.

invers_norm <- function(y) qnorm((rank(y, na.last="keep") - 0.5)/sum(!is.na(y)))

Dann können wir schon die Funktion auf unseren Messwert der Schlupfzeiten anwenden.

invers_norm_tbl <- fac1_tbl |> 
  mutate(inverse_hatch_time = invers_norm(hatch_time))

Wie zu erwarten presst die inverse Normaltransformation die Messwerte der Schlupfzeiten in einer Normalverteilung. Jetzt kann man argumentieren, dass es vielleicht nicht die beste Idee ist, da die Schlupfzeiten vermutich nicht normalverteilt sind und wir hier die Daten künstlich in eine Normalverteilung schieben. Auf der anderen Seite ist es eben dann auch das Ziel der Transformation eine Normalverteilung auf Teufel komm raus zu erhalten. Für mich eine mühsige Diskussion. Die inverse Normaltransformation funktioniert manchmal ganz gut, wie wir hier sehen und dann können wir auch diese Transformation verwenden.

Abbildung 20.12— Histogramm der nicht transfomierten und transformierten Daten. (A) Nicht transformierte, rohe Daten. (B) inversenormal-transformierte Daten. [Zum Vergrößern anklicken]

20.4.5 Rangtransformation

Der Ausweg schlechthin bis in die 90ziger Jahre war vermutlich die nichtparametrische Statistik, wenn es um nicht normalverteilte Messwerte ging. Es wird dann eben ein nichtparametrischer Test, wie der Wilcoxon oder eben Mann-Whitney gerechnet. Und hier kommt dann die Rangtransformations ins Spiel. Eigentlich ist die gesamte Nichtparametrik nur eine Rangtransformation auf der wir dann auch genauso gut dann einen t-Test oder eine ANOVA rechnen könnten. Dazu dann aber mehr in den jeweiligen Kapiteln zu den einzelnen nichtparametrischen Tests.

• Der Wilcoxon-Mann-Whitney-Test oder auch U-Test ist der t-Test auf den Rängen eines Messwertes. Wir vergleichen hier zwei Gruppen miteinander. Wenn wir mehr Gruppen haben, die wir vergleichen wollen, dann brauchen wir mehrere paarweise Wilcoxon Tests um die signifikanten Unterschiede zu bestimmen.
• Der Kruskal-Wallis-Test ist die einfaktorielle ANOVA auf den Rängen eines Messwertes. Wir vergleichen hier drei oder mehr Gruppen simultan miteinander. Wenn wir dann wissen wollen, welcher paarweise Vergleich signifikant ist, brauchen wir dann einen Posthoc-Test.

Was ist also die Rangtransformation? Wir geben einfach den sortierten Rang des Messwertes über alle Gruppen. Dann können wir auf dem rangierten Messwert weiterrechnen. Ich habe dir hier einmal die Funktion mitgebracht, die auch negative Messwerte korrekt mit berücksichtigt. Ansonsten geht natürlich auch ganz einfach die Funktion rank().

signed_rank <- function(x) sign(x) * rank(abs(x))

Ich gehe hier jetzt nicht weiter auf die Rangtransformation ein, denn du findest dann alle Informationen zu dieser Transformation in den Kapiteln zu dem nichtparametrischen Testen. Schaue einfach einmal dahin, wenn dich die Algorithmen um die Ränge von Messwerten interessieren. Dann verlässt du auch den ANOVA Pfad und nutzt andere Algorithmen.

20.5 Skalierung

Kommen wir jetzt noch zur Skalierung. Hier wird es manchmal dann etwas wild was das Verständnis angeht. Wir skalieren oder normalisieren Daten, um die Daten in einen fixen Werteraum zu kriegen. Die Normalisierung hat also nichts mit der Erschaffung von einer Normalverteilung zu tun. Wir nutzen beide Verfahren um Einheiten loszuwerden und Messwerte näher zueinander zu bringen. Ja, im Prinzip tut das auch die Logtransformation aber die Skalierung ist dann nochmal ein Extrafeld. Wir wenden die Skalierung gerne in der Klassifikation und dem maschinellen Lernen an. Oder allgemeiner Formuliert brauchen wir die Skalierung häufig für das statistische Modellieren und der Vorhersage von Messwerten. Dort brauchen wir sehr gleichförmige Variablen und da bietet sich die Skalierung für an. Hier gleich vorweg, häufig ändert sich die Verteilung nicht, sondern nur die Werte.

Je nach Fachbereich sind natürlich noch andere Skalierungen denkbar. Du findest in dem Tutorial Normalisierung vs. Standardisierung: Wie man den Unterschied erkennt nochmal weiterreichende Informationen und Ideen zur Skalierung von Daten. Es gibt dort auch nochmal ein paar Beispiele mit entsprechender Interpretation. Der Fokus liegt aber auch dort auf der Vorhersage von Messwerten aus einem statistischen Modell.

Achtung, bitte beachten!

Bitte bachte, dass die Standardisierung versucht die Symmetrie mit dem Mittelwert 0 und der Standardabweichung 1 zu erzwingen. Bei der Normalisierung ist die Wahrscheinlichkeit einer Schiefe größer, da Ihre Skalierungsfaktoren die beiden extremsten Datenpunkte sind.

20.5.1 Standardisierung

Die Standardisierung wird auch gerne \(z\)-Transformation genannt. In dem Fall der Standardisierung schieben wir die Daten auf den Nullursprung, in dem wir von jedem Datenpunkt \(y_i\) den Mittelwert \(\bar{y}\) abziehen. Dann setzen wir noch die Standardabweichung auf Eins in dem wir durch die Standardabweichung \(s\) teilen. Unser standardisiertes \(y\) ist nun standardnormalverteilt mit \(\mathcal{N(0,1)}\). Wir nutzen für die Standardisierung folgende Formel.

\[ y_z = \cfrac{y_i - \bar{y}}{s_y} \]

In R können wir für die Standardisierung die Funktion scale() verwenden. Wir müssen auch nichts weiter in den Optionen von scale() angeben. Die Standardwerte der Funktion sind so eingestellt, dass eine Standardnormalverteilung berechnet wird.

scale_tbl <- fac1_tbl |> 
  mutate(scale_jump_length = scale(jump_length))

In der folgenden Abbildung sehen wir nochmal die nicht transformierten, rohen Daten. Wir haben in diesem Beispiel die normalverteilte Variable jump_length gewählt. Der Mittelwert von jump_length ist 20.53 und die Standardabweichung ist 3.77. Ziehen wir nun von jedem Wert von jump_length den Mittelwert mit 19.3 ab, so haben wir einen neuen Schwerpunkt bei Null. Teilen wir dann jede Zahl durch 3.36 so haben wir eine reduzierte Spannweite der Verteilung. Es ergibt sich die folgende Abbildung als Standardnormalverteilung. Die Zahlen der auf der x-Achse haben jetzt aber keine Bedeutung mehr. Wie können die Sprungweite auf der \(z\)-Skala nicht mehr biologisch interpretieren.

Abbildung 20.13— Histogramm der nicht skalierten und skalierten Daten. Achtung, die Einheiten auf der x-Achse ändern sich. Die Form der Verteilung bleibt davon häufig unberührt. (A) Nicht skalierte, rohe Daten. (B) Standardisierte Daten. [Zum Vergrößern anklicken]

Wir können uns den Effekt der Standardisierung nochmal auf unseren Lebensdauerdaten verschiedener Tiere anschauen. Auf den ersten Blick hat sich eigentlich nichts geändert. Ich habe dir extra einmal die Werte auf der x-Achse und y-Achse rot hervorgehoben. Wir du siehst, rücken jetzt die Werte weiter zusammen. Wir haben also nicht mehr einen Abstand von tausenden Kilos auf der x-Achse sondern eben nur noch das zehnfache bis dreißigfache. Das Gleiche gilt dann auch für das Lebensalter. Ob das jetzt gut für einen Lernalgorithmus funktioniert, hängt dann vom Algorithmus und der Fragestellung ab.

Abbildung 20.14— Standardisierter Zusammenhang zwischen dem Gewicht und dem Alter von Tierarten. Durch die Standardisierung wird die große Bandbreite der Körpergewichte nicht aufgebrochen sondern die Werte näher aneinander geschoben. [Zum Vergrößern anklicken]

20.5.2 Normalisierung

Abschließend wollen wir uns nochmal die Normalisierung anschauen. In diesem Fall wollen wir die Daten so transformieren, dass die Daten nur noch in der Spannweite 0 bis 1 vorkommen. Egal wie die Einheiten vorher waren, alle Variablen haben jetzt nur noch eine Ausprägung von 0 bis 1. Das ist besonders wichtig wenn wir viele Variablen haben und anhand der Variablen eine Vorhersage machen wollen. Uns interessieren die Werte in den Variablen an sich nicht, sondern wir wollen ein Outcome [0/1] meist vorhersagen. Wir brauchen die Normalisierung später für das maschinelle Lernen und die Klassifikation. Die Formel für die Normalisierung lautet wie folgt.

\[ y_n = \cfrac{y_i - \min(y)}{\max(y) - \min(y)} \]

In R gibt es die Normalisierungsfunktion nicht direkt. Wir könnten hier ein extra Paket laden, aber bei so einer simplen Formel können wir auch gleich die Berechnung in R machen. Wir müssen nur etwas mit den Klammern aufpassen. Und dann nochmal die Implementierung in R als Funktion.

normalize <- function(y) {(y - min(y))/(max(y) - min(y))}

Hier dann die Anwendung mit mutate() für die Normalisierung. Später können wir dann hier auch Automatisierungen nutzen, wie du im Kapitel zur Klassifikation nachlesen kannst.

norm_tbl <- fac1_tbl |> 
  mutate(norm_jump_length = normalize(jump_length))

In der folgenden Abbildung auf der linken Seite sehen wir nochmal die nicht transformierten, rohen Daten. Auf der rechten Seiten sehen wir die normalisierten Daten. Hier fällt dann auf, dass die normalisierten Sprungweiten nur noch Werte zwischen Null und Eins annehmen. Die Zahlen der auf der x-Achse haben jetzt aber keine Bedeutung mehr. Wie können die normalisierten Sprungweiten nicht mehr biologisch interpretieren.

Abbildung 20.15— Histogramm der nicht skalierten und skalierten Daten. Achtung, die Einheiten auf der x-Achse ändern sich. Die Form der Verteilung bleibt davon häufig unberührt. (A) Nicht skalierte, rohe Daten. (B) Normalisierte Daten. [Zum Vergrößern anklicken]

Wir können uns den Effekt der Normalisierung nochmal auf unseren Lebensdauerdaten verschiedener Tiere anschauen. Auf den ersten Blick hat sich eigentlich nichts geändert. Ich habe dir extra einmal die Werte auf der x-Achse und y-Achse rot hervorgehoben. Wir du siehst, rücken jetzt die Werte auf einen Bereich zwischen Null und Eins zusammen. Wir haben also nicht mehr einen Abstand von tausenden Kilos auf der x-Achse sondern das leichteste Tier erhält die Null und das schwerste Tier die Eins. Alle anderen ordnen sich dazwischen ein. Das Gleiche gilt dann auch für das Lebensalter. Ob das jetzt gut für einen Lernalgorithmus funktioniert, hängt dann vom Algorithmus und der Fragestellung ab.

Abbildung 20.16— Normalisierter Zusammenhang zwischen dem Gewicht und dem Alter von Tierarten. Durch die Normalisierung wird die große Bandbreite der Körpergewichte nicht aufgebrochen sondern die Werte auf den Wertebereich [0/1] geschoben. [Zum Vergrößern anklicken]

20.6 Automatische Transformationen…

Es gibt eine Reihe von Pakten, die sich mit der automatischen Transformation von Messwerten in eine Normalverteilung beschäftigen. Ich zeige jetzt hier vier Pakete, wobei ich den Fokus auf das R Paket {bestNormalize} und {rcompanion} lege. Die beiden anderen Pakete erwähne ich nur. Das hat eher mit meinem Geschmack zu tun. Das R Paket {LambertW} doppelt sich etwas und das R Paket {trafo} hat eher den klaren Fokus in der linearen Regression. Wenn du also eher allgemeiner Transformieren willst, dann sind die ersten beiden Pakete deine Wahl. Wenn der Fokus eher auf einer Regression liegt, dann schaue auch einmal in {trafo} rein.

“Wie du gleich sehen wirst, produzieren die Pakete ziemlich die gleiche Verteilung der transformierten Werte. Also gehen wir hier verschiedene Wege und kommen am Ende dann doch in Rom raus. Dann kannst du auch schauen, welches Paket dir am besten gefällt.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

20.6.1 … mit {bestNormalize}

Dann sind wir bis hierher gekommen und fragen uns nun welche ist den jetzt die beste Transformation für unsere Daten um einigermaßen eine Normalverteilung hinzubekommen? Da hilft uns jetzt das R Paket {bestNormalize}. Die Kurzanleitung zum Paket erlaubt es automatisiert auf einem Datenvektor die beste Transformation zu finden um die Daten in eine Normalverteilung zu verwandeln. Das ist eigentlich auch nur der einzige Nachteil, wir müssen die Funktion mit einem Vektor füttern und können daher schlecht pipen. Kein echter Grund das Paket nicht zu verwenden.

Jetzt können wir die Funktion bestNormalize() nutzen um uns die beste Transformationsmethode wiedergeben zu lassen. Das ist super praktisch in der Anwendung. Wir können uns theoretisch noch verschiedene Gütekriterien aussuchen aber für hier reicht die Standardimplementierung. Wichtig ist noch, dass wir hier eine Kreuzvalidierung durchführen, so dass die Ergebnisse und die Auswahl des Algorithmus robust sein sollte. Oder andersherum, das Paket produziert valide Transformationen um einen normalverteilten Messwert zu erhalten.

bn_obj <- bestNormalize(fac1_tbl$hatch_time)
bn_obj

Best Normalizing transformation with 598 Observations
 Estimated Normality Statistics (Pearson P / df, lower => more normal):
 - arcsinh(x): 0.9141
 - Box-Cox: 0.994
 - Center+scale: 6.2647
 - Double Reversed Log_b(x+a): 9.466
 - Log_b(x+a): 0.9095
 - orderNorm (ORQ): 1.0397
 - sqrt(x + a): 2.1066
 - Yeo-Johnson: 1.0005
Estimation method: Out-of-sample via CV with 10 folds and 5 repeats
 
Based off these, bestNormalize chose:
Standardized Log_b(x + a) Transformation with 598 nonmissing obs.:
 Relevant statistics:
 - a = 0 
 - b = 10 
 - mean (before standardization) = 2.146128 
 - sd (before standardization) = 0.4215633 

Laut dem Algorithmus sollen wir eine Standardized Yeo-Johnson Transformation durchführen. Wie du siehst testet der Algorithmus noch eine Reihe von weiteren Transformationen. Was immer das jetzt auch konkret für eine Transformation ist wir leben damit. Okay, wie machen wir das jetzt? Wir hätten zwar die Parameter in der Ausgabe angegeben und die könnten wir dann auch in einer Veröffentlichung angeben, aber wenn es schneller gehen soll, dann können wir die Funktion predict() nutzen, die uns die transformierten Messwerte wiedergibt.

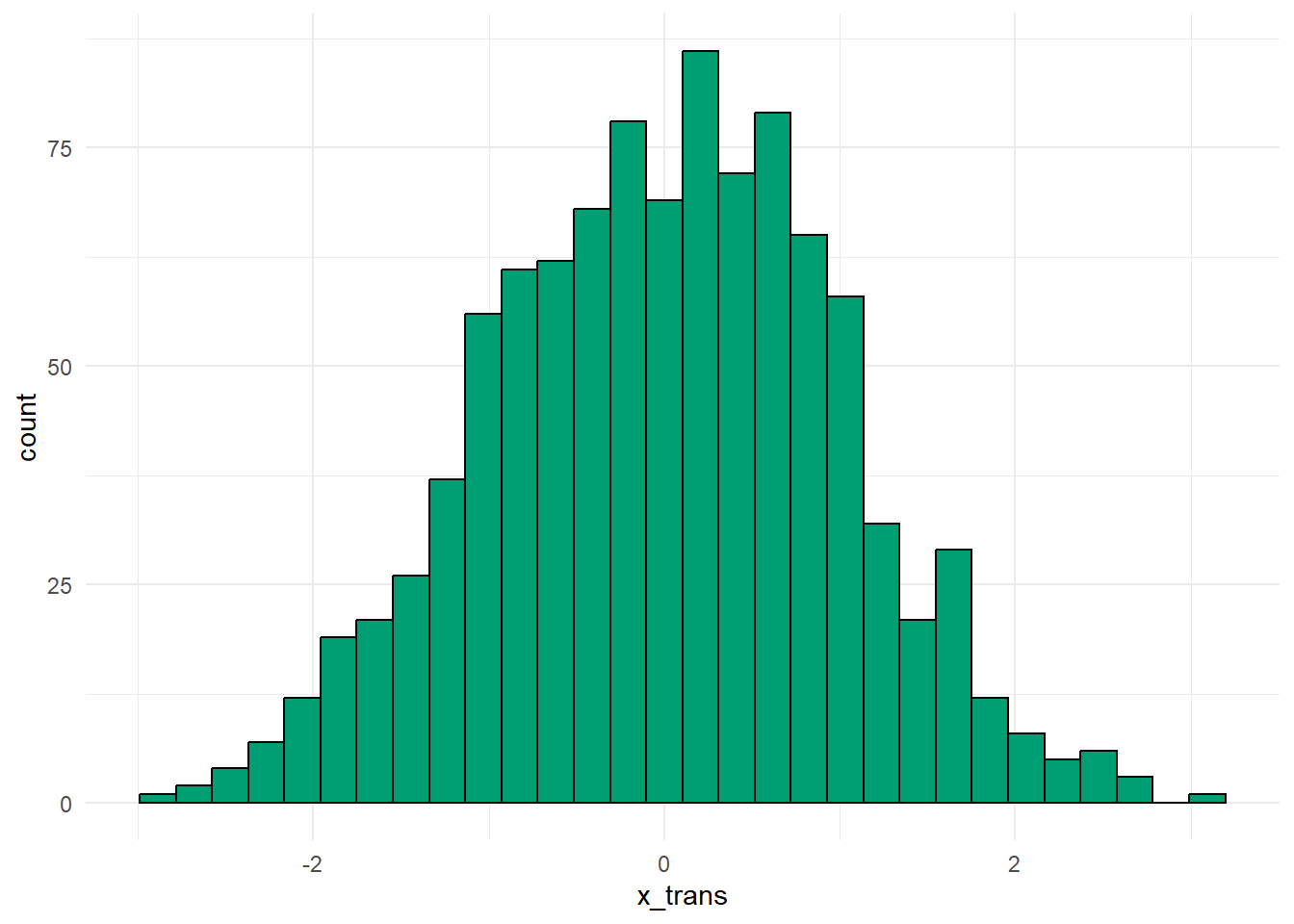
y_trans <- predict(bn_obj)

Und zum Abschluss schauen wir uns dann in der folgenden Abbildung einmal die transformierten Messwerte der Schlupfzeiten an. In der folgenden Abbildung siehst du dann einmal das entsprechende Histogramm. Das sieht doch sehr gut aus und wir mussten nicht zig verschiedene Algorithmen selber testen, sondern haben mi zwei Zeilen Code dann unsere annährend normalverteilten Daten.

Abbildung 20.17— Histogramm der transformierten Werte mit der Standardized Yeo-Johnson Transformation aus dem R Paket {bestNormalize} für die Schlupfzeiten. (A) Nicht skalierte, rohe Daten. (B) Transformierte Daten. [Zum Vergrößern anklicken]

20.6.2 … mit {rcompanion}

Zu Begin des Kapitels haben wir ja die Ladder of Powers von Tukey kennengelernt. Faktisch können wir aber jede beliebige Potenz für \(\lambda\) einsetzen. Das maht dann für uns die Funktion transformTukey() aus dem R Paket {rcompanion}. Der Algorithmus durchläuft im Prinzip einmal viele \(\lambda\)-Werte und schaut dann, welcher Wert die beste Normalverteilung in den Messwert verursacht. Diesen Wert erhalten wir zusammen mit den transformierten Messwerten ausgegeben. Die Funktion hat noch eine angenehme Visualisierung und du kannst dir dann eine Menge auch anschauen. Ich stelle das hier mal ab, du kannst aber den Code durchführen und die Wiedergabe der Abbildungen einfach auf TRUE setzen.

tt_obj <- transformTukey(fac1_tbl$hatch_time,
                         plotit = FALSE)

    lambda      W Shapiro.p.value
403   0.05 0.9966           0.243

if (lambda >  0){TRANS = x ^ lambda} 
if (lambda == 0){TRANS = log(x)} 
if (lambda <  0){TRANS = -1 * x ^ lambda} 

Dann können wir uns auch schon die Transformation einmal anschauen. Hier haben wir ein \(\lambda\)-Wert von \(0.05\) erhalten und nutzen diesen Wert für die Transformation. Spannenderweise sieht jetzt die Verteilung unser transformierten Werte gar nicht so unterschiedlich zu dem R Paket {bestNormalize} aus. Nur die Werte der Transformation unterschieden sich. Vermutlich weil es dann doch sehr simple Transformationen sind und es eben immer eine gewisse Ähnlichkeit zwischen den mathematischen Funktionen gibt.

Abbildung 20.18— Histogramm der transformierten Werte mit der \(\lambda = 0.05\) Transformation aus dem R Paket {rcompanion} für die Schlupfzeiten. (A) Nicht skalierte, rohe Daten. (B) Transformierte Daten. [Zum Vergrößern anklicken]

20.6.3 … mit {LambertW}

Dann gibt es noch die Funktion Gaussianize() aus dem R Paket {LambertW}, die eben wie der Name schon sagt uns dann normalverteilte Daten erschaffen will. Wir müssen bei dieser Funktion aber sagen, was für einen Typus wir an schiefen Messwerten vorliegen haben. Ein klarer Nachteil zu den beiden obigen Funktionen, da schmeißen wir die Messwerte rein und gut ist. Wir müssen also entscheiden welche Art der Schiefe wir vorliegen haben. Wir können uns zwischen symmetric heavy-tails “h” (default) oder skewed heavy-tails “hh” sowie skewed “s” entschieden. Ich habe hier alle drei durchprobiert und mich dann für s entschieden, da wir hier das beste Ergebnis gleich sehen. Du kannst dann auch alle drei einmal durchprobieren

gaus_obj <- Gaussianize(fac1_tbl$hatch_time, type = "s")

In der folgenden Abbildung siehst du dann einmal das Ergebnis der Transformation. Erstaunlicherweise sind dei Messwerte sehr ähnlich transformiert wie auch schon in den Paketen zuvor. Nur die Werte der Transformation unterschieden sich. Ich würde daher das Paket eher nicht verwenden. Du musst hier selber dreimal rumprobieren und dann am Ende entscheiden. Im besten Fall kriegst du das gleiche Ergebnis wie bei den anderen Paketen.

Abbildung 20.19— Histogramm der transformierten Werte mit der s Transformation aus dem R Paket {rcompanion} für die Schlupfzeiten. (A) Nicht skalierte, rohe Daten. (B) Transformierte Daten. [Zum Vergrößern anklicken]

20.6.4 … mit {trafo}

Kommen wir dann noch zum R Paket {trafo}. Das Paket ist groß und du kannst in der Vingette The R Package {trafo} for Transforming Linear Regression Models noch sehr viel mehr nachlesen. Die Idee ist eigentlich simple. Wir nehmen ein lineares Modell, was nicht funktioniert hat, da wir keine Normalverteilung in den Residuen und damit dem Messwert vorliegen haben. Dann können wir das Modell so transformieren, dass wir eine Normalverteilung vorliegen haben. Hier liegt der Reiz vorallem darin, dass wir hier auch komplexere Modelle transformieren können. Da wir dann aber die Einheiten verlieren handelt es sich hier mehr oder minder um statistische Modelle für die Vorhersage. Dazu dann aber mehr in dem Kapitel zu den Regressionen.

Hier also einmal eine lineare Regression für die Schlupzeit und dem Gewicht. Hat das Gewicht einen Einfluss auf die Schlupfzeit? Wir können erstmal wieder eine Regression mit lm() rechnen. Es gibt auch andere Modelle die prinzipiell in {trafo} gerechnet werden können, aber ich fokusiere mich hier einmal auf die klassische Regression mit der Annahme der Normalverteilung an die Residuen.

lm_fit <- lm(hatch_time ~ weight, data = fac1_tbl)

Dann können wir uns einmal das Ergebnis in der Funktion trafo_lm() anschauen. In dem ersten Tab zeige ich nur die Koeffizienten der Regression. Die Funktion trafo_lm() gibt dir erstmal das untransformierte Modell und einmal das transformierte Modell wieder. Du kannst dann direkt die Koeffizienten und andere statistische Maßzahlen miteinander vergleichen.

trafo_lm()

Im Folgenden also einmal das lineare Modell mit den Koeffizienten. Die Koeffizienten sind im untransformierten Modell noch zu interpretieren. Mit jedem Gramm mehr Gewicht sinkt die Schlupfzeit um 6.6 Stunden. Das Modell mag aber falsch sein, da wir hier nicht normalverteilte Daten vorliegen haben. Das transformierte Modell lässt sich nicht biologisch interpretieren.

trafo_lm(lm_fit) 

Untransformed model 

Call:
lm(formula = hatch_time ~ weight, data = fac1_tbl)

Coefficients:
(Intercept)       weight  
    270.558       -6.665  

Transformed model:  boxcox transformation 

Call:  lm(formula = formula, data = data) 
formula =  hatch_timet ~ weight 

Coefficients: 
(Intercept)       weight  
    6.08768     -0.02955  

summary()

Wenn wir die zusammenfassende Ausgabe der Funktion trafo_lm() betrachten, dann sehen wir schnell, dass wir im untransformierten Modell keien normalverteilten Residuen haben. Die Residuen sind nicht im Mittel bei Null und haben auch ungleiche Quartile. Das sieht sehr viel besser aus für das transformierte Modell. Daher können wir von einem annährend normalverteilten Modell durch die TRansformation ausgehen.

trafo_lm(lm_fit) |> summary()

Summary of untransformed model 

Call:
lm(formula = hatch_time ~ weight, data = fac1_tbl)

Residuals:
    Min      1Q  Median      3Q     Max 
-216.27 -145.26  -70.26   41.14 1189.45 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  270.558     52.422   5.161 3.35e-07 ***
weight        -6.665      6.468  -1.030    0.303    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 222.7 on 596 degrees of freedom
Multiple R-squared:  0.001778,  Adjusted R-squared:  0.0001034 
F-statistic: 1.062 on 1 and 596 DF,  p-value: 0.3032


Summary of transformed model:  boxcox transformation 

Formula in call:  hatch_timet ~ weight 

Call:
lm(formula = formula, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.6637 -0.9517  0.0019  0.8153  3.3606 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.08768    0.31263  19.472   <2e-16 ***
weight      -0.02955    0.03857  -0.766    0.444    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.328 on 596 degrees of freedom
Multiple R-squared:  0.0009835, Adjusted R-squared:  -0.0006927 
F-statistic: 0.5868 on 1 and 596 DF,  p-value: 0.444

20.7 Friedhof der R Pakete

Warum gibt es hier den Friedhof? Nun, es gibt nur eine begrenzte Anzahl an möglichen Transformationen. Diese Transformationen sind dann aber in vielen R Paketen eingebaut. Mit der Zeit habe ich dann neuere und bessere R Pakete gefunden, die ich hier weiter oben vorstelle. Die alten Pakete, die ich auch mal genutzt habe, schiebe ich dann hier in den Friedhof. Meistens können die neuren Pakete das was die alten können plus die neuen Pakete sind einfacher zu bedienen oder aber aber haben andere Vorteile. Als Referenz bleibt der Friedhof aber offen.

20.7.1 … mit {MASS}

Die Box-Cox-Transformation ist ein statistisches Verfahren zur Umwandlung von nicht normalverteilten Daten in eine Normalverteilung. Die Transformation ist nicht so einfach wie die logarithmische Transformation oder die Quadratwurzeltransformation und erfordert etwas mehr Erklärung. Beginnen wir zunächst die Gleichung zu verstehen, die die Transformation beschreibt. Die grundsätzliche Idee ist, dass wir unser \(y\) als Outcome mit einem \(\lambda\)-Exponenten transformieren. Die Frage ist jetzt, welches \(\lambda\) produziert die besten normalverteilten Daten? Wenn wir ein \(\lambda\) von Null finden sollten, dann rechnen wir einfach eine \(\log\)-Transformation. Die Idee ist also recht simpel.

\[ y(\lambda)=\left\{\begin{matrix} \dfrac{y^{\lambda}-1} {\lambda} & \quad \mathrm{f\ddot ur\;\;}\lambda \ne 0 \\[10pt] \log(y) &\quad \mathrm{f\ddot ur\;\;}\lambda = 0\end{matrix}\right. \]

Wir werden natürlich jetzt nicht händisch alle möglichen \(\lambda\) durchprobieren bis wir das beste \(\lambda\) gefunden haben. Dafür gibt es die Funktion boxcox aus dem R Paket {MASS}, die ein lineares Modell benötigt. Daher bauen wir usn erst unser lineares Modell und dann stecken wir das Modell in die Funktion boxcox().

jump_mod <- lm(jump_length ~ 1, data = fac1_tbl)

Jetzt einmal die Funktion boxcox() ausführen und danach das \(\lambda\) extrahieren. Hier ist es etwas umständlicher, da das \(\lambda\) in der Ausgabe der Funktion etwas vergraben ist. Dafür ist das R Paket {MASS} einfach nicht mehr das jüngste Paket und hat keine so guten Funktionen zum Erhalten von wichtigen Parametern. Ich möchte die Abbildung nicht haben, daher die Option plotit = FALSE.

bc_obj <- MASS::boxcox(jump_mod, plotit = FALSE)
lambda <- bc_obj$x[which.max(bc_obj$y)]
lambda

[1] 0.9

Wir erhalten also ein \(\lambda\) von 0.9 wieder. Dieses \(\lambda\) können wir dann nutzen um unsere Daten nach Box-Cox zu transformieren. Dafür übersetzen wir dann die obige Matheformel einmal in R Code.

fac1_tbl <- fac1_tbl |>
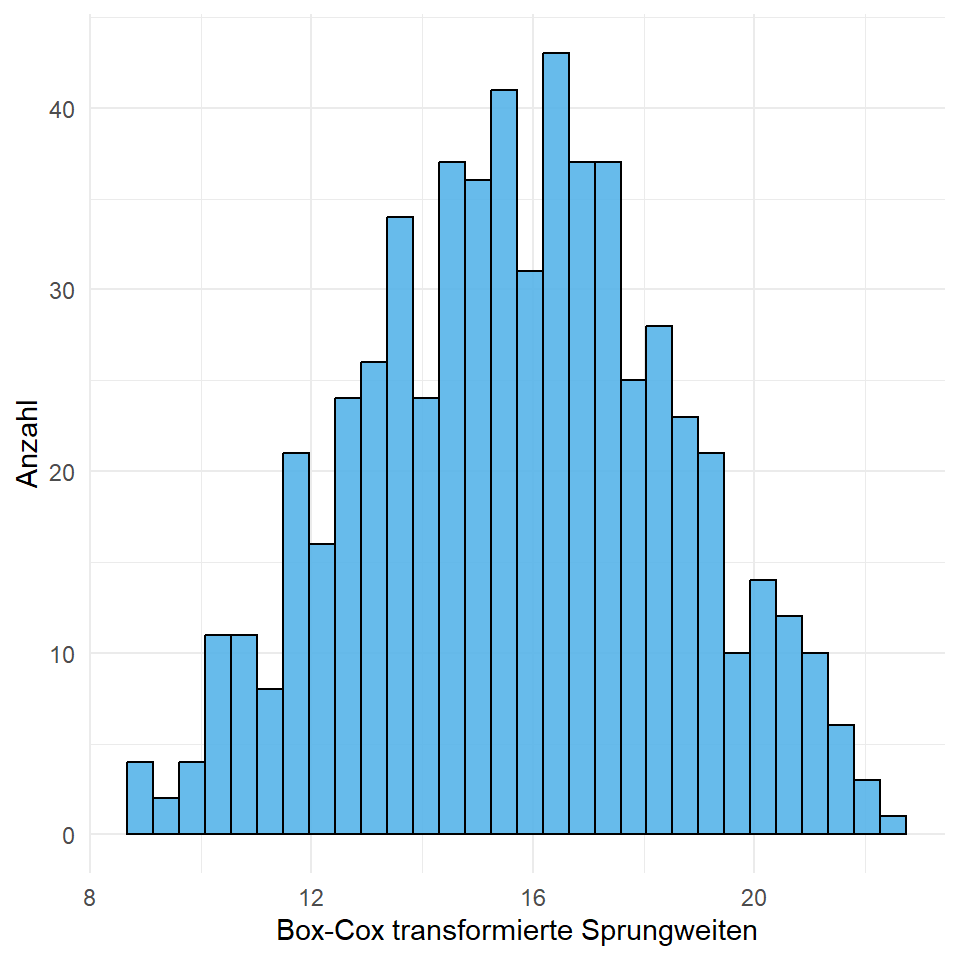
  mutate(jump_boxcox = ((jump_length ^ lambda - 1)/lambda))

In der Abbildung 20.20 sehen wir dann einmal das Ergebnis der Transformation. Sieht gar nicht mal so schlecht aus und noch besser als die reine \(\log\)-Transformation. Wie immer musst du aber auch hier rumprobieren, was dann am besten einer Normalverteilung folgt.

ggplot(data = fac1_tbl) +
  theme_minimal() +
  geom_histogram(aes(x = jump_boxcox), alpha = 0.9,
                 fill = cbbPalette[3], color = "black") +
  labs(x = 'Box-Cox transformierte Sprungweiten', y = 'Anzahl')

Abbildung 20.20— Histogramm der Box-Cox transfomierten Daten in ggplot dargestellt.

20.7.2 … mit {dlookr}

Achtung, bitte beachten!

Das R Paket {dlookr} lies sich eine Zeit nicht über CRAN installieren. Das Paket benötigt auch sehr lange um geladen zu werden. Daher habe ich mich dagegen entschieden, das Paket hier nochmal tiefer vorzustellen.

Zwischenzeitlich musste ich das R Paket {dlookr} aus dem Code entfernt, da ich das Paket über GitHub installieren musste. Das R Paket war zwischenzeitlich nicht mehr bei CRAN gelistet. Das führt bei mir zu Schluckauf im Code, so dass ich die Funktionen jetzthier benenne. Sollte das Paket sich mal nicht installieren lassen, dann gibt es hier noch einen alternativen Weg.

Alternative Installation von {dlookr}

Ist das R Paket {dlookr} mal nicht per Standard aus RStudio zu installieren kannst du das R Paket auch über GitHub installieren. Dafür einmal das R Paket {devtools} installieren und dann folgenden Code ausführen.

devtools::install_github("choonghyunryu/dlookr")

Du findest auf der Hilfeseite Data Transformation mit {dlookr} die Unterstützung, die du brauchst um mit der Funktion transform() deine einzelnen Messwerte einmal zu transformieren. Du kannst dann die Funktion einfach im Kontext von mutate() nutzen. Wie immer, dass Paket ist gut und hat auch seinen Nutzen. Viele Funktionen habe ich aus dem Paket auch selber schon genutzt. Es ist aber super ärgerlich, wenn das Paket auf einmal nicht mehr gewartet wird. Das ist zwar immer in R so, dass mal Pakete rausgehen können, aber hier war mir das dann doch zu wild.

Referenzen

Beasley, T. M., Erickson, S., & Allison, D. B. (2009). Rank-based inverse normal transformations are increasingly used, but are they merited? Behavior genetics, 39, 580–595.

Yang, P. J., Pham, J., Choo, J., & Hu, D. L. (2014). Duration of urination does not change with body size. Proceedings of the National Academy of Sciences, 111(33), 11932–11937.