Letzte Änderung am 25. June 2025 um 12:33:59
“Numerical quantities focus on expected values, graphical summaries on unexpected values.” — John Tukey
Vielleicht gibt es zwei statistische Tests an denen man in den Humanwissenschaften und Sozialwissenschaften nicht vorbeikommt. Zum einen ist es die logistische Regression und dann auch der eng damit verwandte Chi-Quadrat-Test oder auch hier \(\mathcal{X}^2\)-Test geschrieben. Ausgeschrieben würden wir Chi-Quadrat-Test lesen. Der Test ist häufig auch als Unabhängigkeitstest bekannt. Aber das ist eher nicht so die Schreibweise, die wir in der Literatur finden. In den Agrawissenschaften kommt der \(\mathcal{X}^2\)-Test eher seltener vor und dort auch eher in den Bereichen der Fragebogenanalyse. Dennoch hat er auch seinen Platz, wenn auch eher in einer Nische im Vergleich zu dem t-Test oder U-Test. Einzig in der Genetik zum Testen der Vererbung und den mendelschen Gesetzen nutzen wir den \(\mathcal{X}^2\)-Test als Anpassungstest gerne. Wir wollen hier einmal das Prinzip verstehen und schauen wir wir den \(\mathcal{X}^2\)-Test anwenden.
Im Bereich der Agrarwissenschaften kommt der \(\mathcal{X}^2\)-Test also eher selten vor. Im Bereich der Humanwissenschaften und vor allem der Epidemiologie ist der \(\mathcal{X}^2\)-Test weit verbreitet. Das eigentlich besondere an dem \(\mathcal{X}^2\)-Test ist gar nicht mal der Test selber sondern die Datenstruktur die der \(\mathcal{X}^2\)-Test zugrunde liegt: der Vierfeldertafel oder 2x2 Kreuztabelle. Wir werden diese Form von Tabelle noch später im maschinellen Lernen und in der Testdiagnostik als Kontingenztafel (eng. contingency table) wiederfinden.
Der \(\mathcal{X}^2\)-Test wird häufig verwendet, wenn wir nur zwei Gruppen in unserem Messwert \(y\) sowie in unserer Einflussgröße \(x\) vorliegen haben. Wir haben also eigentlich zwei Faktoren mit jeweils zwei Leveln vorliegen, die wir miteinander vergleichen wollen. Das heißt wir haben zum Beispiel unseren Faktor Einwicklungsstand der Flöhe stage mit den beiden Leveln juvenile und adult. Wir schauen uns jetzt noch den Infektionsstatus mit Flohschnupfen der Flöhe an. Wir haben also einen Faktor infected mit zwei Leveln yes und no vorliegen. Wir sprechen hier dann häufig auch von einem dichotomen oder binären Messwert. Der Messwert hat dann eben nur zwei Ausprägungen. Wir sind bei dem \(\mathcal{X}^2\)-Test nicht auf nur Faktoren mit zwei Leveln eingeschränkt. Traditionell wird aber versucht ein 2x2 Design zu erreichen. Das hat auch gute Gründe wie wir bei Sharpe (2015) in der Veröffentlichung Your Chi-Square Test is Statistically Significant: Now What? lesen können.
“If you can avoid chi-square contingency tables with greater than one degree of freedom, you should do so.” — Sharpe (2015)
Dabei haben die 2x2 Kreuztabellen als einziges einen Freiheitsgrad (eng. degree of freedom) von Eins. Sobald du deine Kreuztabelle um weitere Spalten oder Zeilen erweiterst gehen auch die Freiheitsgrade mit nach oben. Wenn es also irgendwie geht, versuche beim \(\mathcal{X}^2\)-Test bei einer 2x2 Kreuztabelle zu bleiben. Warum das so ist, lässt sich dann an der Fallzahl erklären. Wir haben ja in einer 2x2 Kreuztabelle dann vier Felder vorliegen. In jedem dieser Felder müssen genug Beobachtungen fallen. Wenn wir also junge und adulte Flöhe haben und diese dann krank oder gesund sein können, brauchen wir dann auch alle vier Kombinationen in ausreichender Menge in unseren Daten. Haben wir noch mehr Level in den Faktoren, wie ein zusätzliches Stadium oder einem zusätzlichen Krankheitsbild, dann brauchen wir immer mehr Beobachtungen insgesamt um die Kreuztabelle zu füllen. McHugh (2013) schreibt in der Veröffentlichung The chi-square test of independence unter Anderem zu der Fallzahl Folgendes.
“The value of the cell expecteds should be 5 or more in at least 80% of the cells, and no cell should have an expected of less than one. This assumption is most likely to be met if the sample size equals at least the number of cells multiplied by 5. Essentially, this assumption specifies the number of cases (sample size) needed to use the \(\mathcal{X}^2\) for any number of cells in that \(\mathcal{X}^2\).” — McHugh (2013)
Kurz zusammengefasst, du brauchst eine Menge an Beobachtungen, damit der \(\mathcal{X}^2\)-Test funktioniert. Wir sprechen hier schnell von 30 und mehr Beobachtungen. Das kommt eher selten in den Agrarwissenschaften vor. Wenn du sehr wenige Beobachtungen hast, dann wird auch häufig die Yates Korrektur automatisch in den Paketen durchgeführt. Ich stelle hier mit dem Stabardpaket {stats} und dem R Paket {janitor} zwei Pakete vor, wobei es natürlich noch andere Implementierungen für den Chi-Quadrat-Test gibt. Hier seinen dann noch die Pakete {coin} und {rstatix} genannt. Beide Pakete haben die gleichnamige Funktion chisq_test() implementiert. Wir werden auch hier nur auf den Anpassungstest sowie den Unabhängigkeitstest eingehen. Es gibt noch weitere Nutzungsfelder, wie den Modellvergleich, den wir hier aber nicht abarbeiten.
Wenn du direkt aus dem statistischen Testen hierher kommst, dann ist die Berechnung des Student t-Tests für dich kein Problem. Das machen wir im statistischen Testen ja schon als Beispiel für die Teststatistik und den p-Wert. Hier kommen dann gleich fertige Funktionen für die Berechnung des \(\mathcal{X}^2\)-Test in R, die dir alles in einem berechnen. Da ist es dann immer etwas schwerer nachzuvollziehen, was die einzelnen Schritte im statistischen Testen eigentlich sind.
Hier hilft dann das R Paket {infer} mit einer Schritt für Schritt Prozedur bei Durchführung des statistischen Testen. Dann machen wir es also einmal genau so, wie wir es schon kennen. Erst die Teststatistik \(\mathcal{X}^2_D\) der Daten berechen. Dann die Verteilung der Nullhypothese der Grundgesamtheit bestimmen und dann beides zusammenbringen. Ein weiterer Vorteil von {infer} ist, dass wir die Funktionen sehr gut mit dem |> Operator nutzen können.
Als erstes berechnen wir die Teststatistik für den \(\mathcal{X}^2\)-Test \(\mathcal{X}^2_D\) aus den beobachteten Daten. Dafür nutzen wir den Infektionsstatus der beiden Entwicklungsphasen der Flöhe. Mehr zu den Daten auch gleich weiter unten im Abschnitt zu den genutzen Daten im Kapitel.
chi_d <- fac1_tbl |>
specify(infected ~ stage, succes = "1") |>
calculate(stat = "Chisq", order = c("juvenile", "adult"))
chi_dResponse: infected (factor)
Explanatory: stage (factor)
# A tibble: 1 × 1
stat
<dbl>
1 3.05Mit der Teststatistik der Daten \(\mathcal{X}^2_D\) können wir so erstmal nichts anfangen. Wir brauchen noch einen vergleich zu der Verteilung der Nullhypothese. Daher bestimmen wir im Folgenden die Verteilung der Nullhypothese zu der wir unsere berechnete Teststatistik \(\mathcal{X}^2_D\) aus den Daten vergleichen wollen.
set.seed(202506)
null_dist_data <- fac1_tbl |>
specify(infected ~ stage, succes = "1") |>
hypothesize(null = "independence") |>
generate(reps = 10000, type = "bootstrap") |>
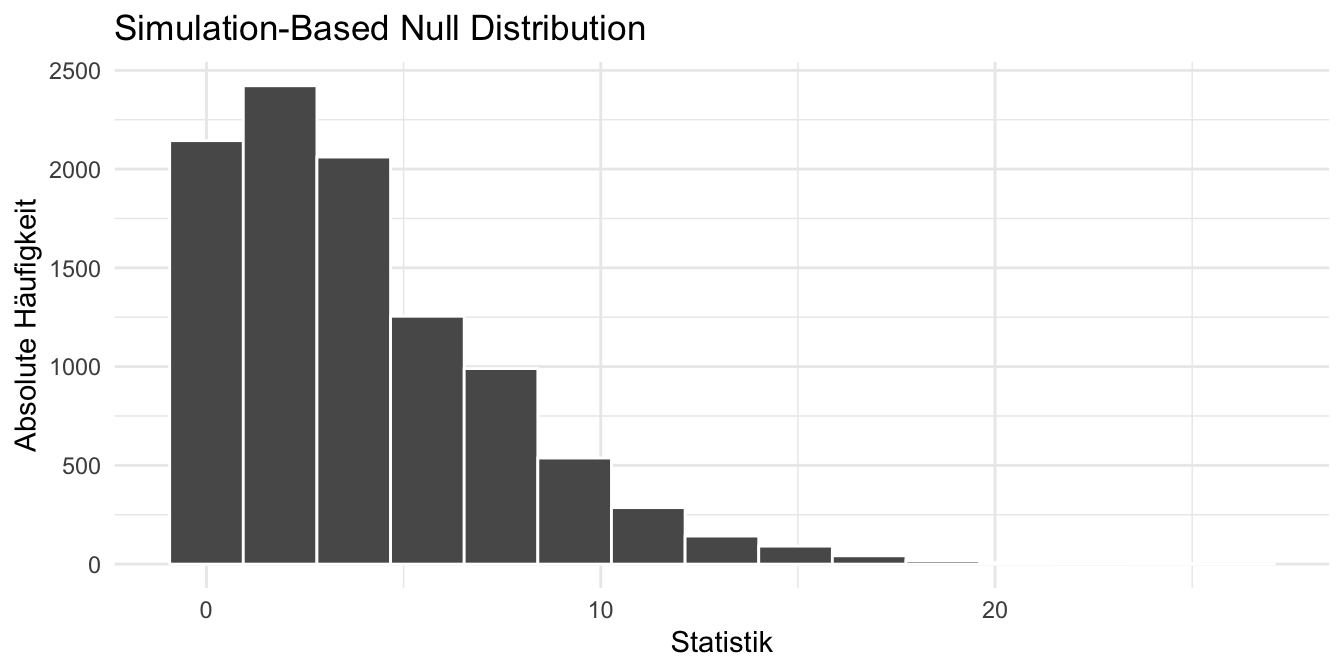
calculate(stat = "Chisq", order = c("juvenile", "adult"))Dann schauen wir uns einmal die Verteilung der Nullhypothese an. Wie wir sehen können, liegen die meisten Teststatistiken bei der Null. Macht ja auch Sinn, in der Nullhypothese haben wir ja auch Gleichheit zwischen den Entwicklungsphasen angenommen.
Dann wollen wir noch die Fläche neben unsere berechnete Teststatistik \(\mathcal{X}^2_D\) um damit den \(p\)-Wert zu bestimmen.
null_dist_data %>%
get_p_value(obs_stat = chi_d, direction = "greater")# A tibble: 1 × 1
p_value
<dbl>
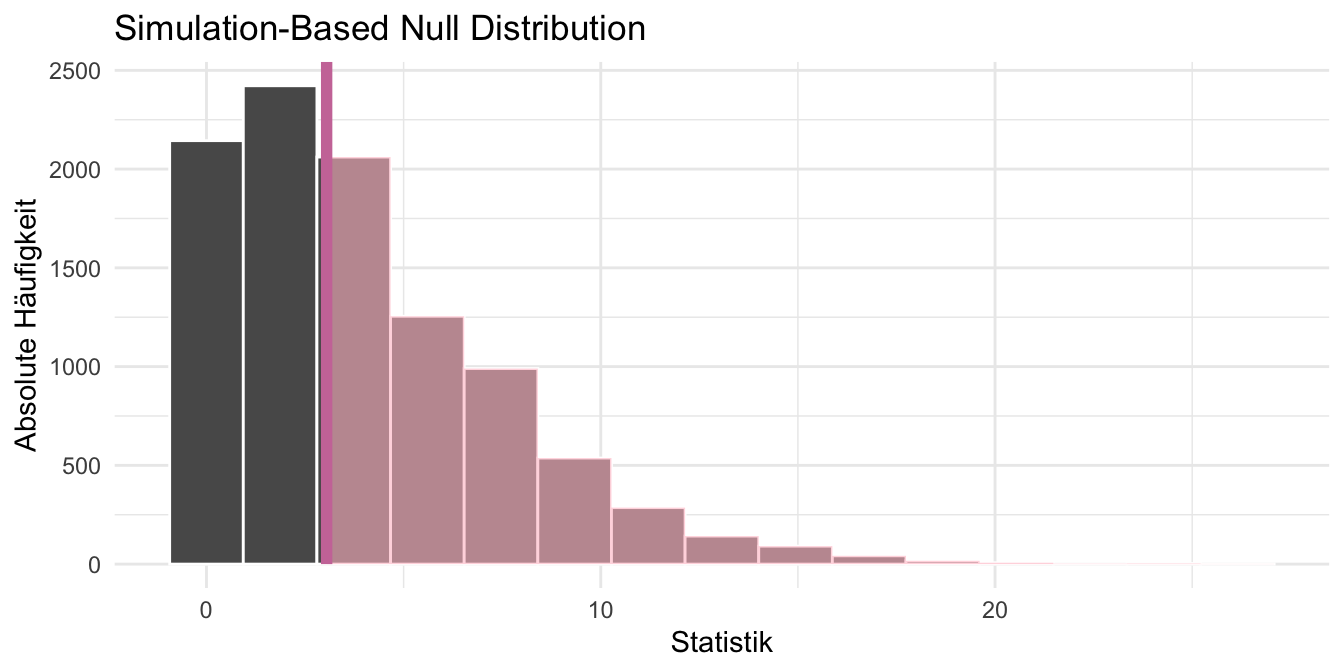
1 0.502Wie du dich noch erinnerst, ist der p-Wert die Fläche neben der berechneten Teststatistik \(\mathcal{X}^2_D\) zu den Verteilungsenden hin. Das wollen wir uns dann in der folgenden Abbildung nochmal anschauen, damit wir den Zusammenhang nochmal besser verstehen.
Die Abfolge der Schritte erfolgt so nicht in der generischen Funktion chisq.test(), die wir dann in der Anwendung viel nutzen. Daher ist das R Paket {infer} nochmal gut um die Schritte der Berechnung sich klar werden zu lassen. Später nutzen wir dann nur eine Funktion, aber der Prozess ist im Hintergrund immer sehr ähnlich.
Eine detailliertere Einführung mit mehr Beispielen für die Nutzung vom R Paket {infer} findest du im Kapitel Testen in R. Hier soll es dann bei der kurzen Gegenüberstellung bleiben.
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
pacman::p_load(tidyverse, magrittr, effectsize, rstatix,
scales, parameters, rcompanion, janitor,
ggmosaic, conflicted)
conflicts_prefer(stats::chisq.test)
conflicts_prefer(stats::fisher.test)Am Ende des Kapitels findest du nochmal den gesamten R Code in einem Rutsch zum selber durchführen oder aber kopieren.
Auch hier brauchen wir wieder ein Datenbeispiel an dem wir den \(\mathcal{X}^2\)-Test nachvollziehen können. Wir haben hier die Untersuchung des Flohschnupfens in Hundeflöhen vorliegen. Wir wollen also schauen, ob sich die Entwicklungsphasen juvenile und adult hinsichtlich des Befalls mit Flohschnupfen ja/nein unterscheiden. Daher haben wir hier zwei Faktoren stage mit zwei Leveln sowie den Infektionsstatus infected mit zwei Leveln vorliegen. Ich lese jetzt einmal die Daten ein und wähle nur die Spalten stage und infected. Eventuelle andere Untergruppen ignoriere ich hier bewusst. Wir bauen auf diesem Datensatz dann unsere 2x2 Krueztabelle.
fac1_tbl <- read_excel("data/fleas_model_data.xlsx") |>
select(stage, infected) |>
mutate(infected_num = as.numeric(infected),
stage = as_factor(stage),
infected = as_factor(infected))Wir haben eine Menge Mögglichkeiten in R eine Kreuztabelle zu bauen. Wir können die Standardfunktion table() nutzen oder aber die Funktion tabyl() aus dem R Paket {janitor}. Ich bevorzuge hier die zweite Funktion, da die Funktion etwas einfacher zu bedienen ist und gut zu pipen ist. Dann schauen wir uns mal die 2x2 Kreuztabelle an.
fac1_tbl |>
tabyl(infected, stage) infected adult juvenile
1 10 17
0 14 7Auf dieser Kreuztabelle werden wir dann später auch den \(\mathcal{X}^2\)-Test rechnen. Du musst immer erst deine Daten zusammenfassen und dann kannst du einen \(\mathcal{X}^2\)-Test rechnen. Wenn man mit dem \(\mathcal{X}^2\)-Test anfängt, ist das manchmal etwas verwirrend.
Hier dann nochmal die Prozente in den jeweiligen Kombinationen berechnet. Manchmal brauchen wir ja auch einen allgmeinen Überblick und da helfen dann auch die relativen Anteile recht gut weiter. Wir meinen hier einen gewissen Unterschied zu sehen. Die Anteile sind nicht in alle Zellen 50% oder aber gleich bei den jeweiligen Entwicklungsphasen.
fac1_tbl |>
tabyl(infected, stage) |>
adorn_percentages() |>
adorn_pct_formatting() infected adult juvenile
1 37.0% 63.0%
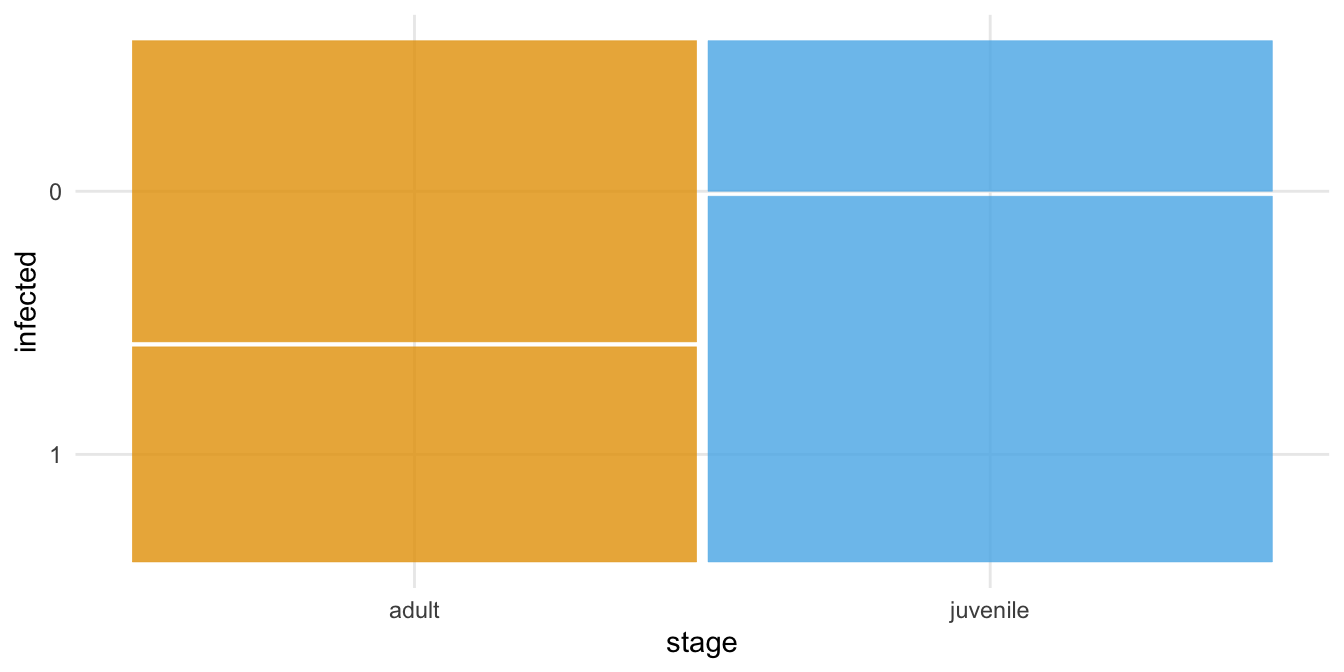
0 66.7% 33.3%Wenn wir eine 2x2 Kreuztabelle visualisieren wollen, dann nutzen wir gerne den Mosaicplot mit dem R Paket {ggmosaic}. Hier haben wir dann auch eine schnelle Visualisierung der Zusammenhänge und können abschätzen, ob sich die beiden Entwicklungsphase hinsichtlich des Infektionsstatus unterscheiden.
Der \(\mathcal{X}^2\)-Test betrachtet die Zellbelegung gegeben den Randsummen um einen Unterschied nachzuweisen. Daher haben wir die Nullhypothese als Gleichheitshypothese. In unserem Beispiel lautet die Nullhypothese, dass die Zahlen in den Zellen gegeben der Randsummen gleich sind. Wir betrachten hier nur die Hypothesen in Prosa und die mathematischen Hypothesen. Es ist vollkommen ausreichend, wenn du die Nullhypothese des \(\mathcal{X}^2\)-Test nur in Prosa kennst.
\[ H_0: \; \mbox{Zellbelegung sind gleichverteilt gegeben der Randsummen} \]
Die Alternative lautet, dass sich die Zahlen in den Zellen gegeben der Randsummen unterscheiden.
\[ H_A: \; \mbox{Zellbelegung sind nicht gleichverteilt gegeben der Randsummen} \]
Wir schauen uns jetzt einmal den \(\mathcal{X}^2\)-Test theoretisch an bevor wir uns mit der Anwendung des \(\mathcal{X}^2\)-Test in R beschäftigen. Dabei unterscheiden wir dann einmal zwischend dem Unabhängigkeitstest und dem Anpassungstest.
Der Unabhängigkeitstest ist der Chi-Quadrat-Test, den du eigentlich rechnen willst, wenn du zwei Gruppen miteinander hinsichtlich eines dichotomen Messwerts vergleichen willst. Der Messwert hat hierbei dann nur zwei Ausprägungen. In unserem Fall kann der Infektionsstatus nur krank oder gesund sein. Auch haben wir nur zwei Gruppen in den Entwicklungsphasen vorliegen. Unterscheiden sich als die beiden Entwicklungsphasen hinsichtlich des Infektionsstatus mit Flohschnupfen? Dafür wollen wir dann einmal einen \(\mathcal{X}^2\)-Test rechnen. Ich gehe hier einmal auf den theoretischen Weg ein und zeige dann die Anwendung in zwei R Paketen.
Wie eben schon benannt schauen wir uns für den \(\mathcal{X}^2\)-Test eine Vierfeldertafel oder aber 2x2 Kreuztabelle an. In der folgenden Tabelle sehen wir eine solche 2x2 Kreuztabelle einmal für unsere Daten dargestellt. Als Faustregel haben wir eine Mindestanzahl an Zellbelegung um überhaupt mit dem \(\mathcal{X}^2\)-Test rechnen zu können. Wir brauchen mindestens fünf Beobachtungen je Zelle, dass heißt mindestens 20 Tiere. Da wir dann aber immer noch sehr wenig haben, ist die Daumenregel, dass wir etwa 30 bis 40 Beobachtungen brauchen. In unserem Beispiel schauen wir uns 48 Tiere an, was nicht so viel ist.
| Stage | ||||
| adult | juvenile | |||
| Infected | yes (1) | \(10_{\;\Large a}\) | \(17_{\;\Large b}\) | \(\mathbf{a+b = 27}\) |
| no (0) | \(14_{\;\Large c}\) | \(7_{\;\Large d}\) | \(\mathbf{c+d = 21}\) | |
| \(\mathbf{a+c = 24}\) | \(\mathbf{b+d = 24}\) | \(n = 48\) |
In der Tabelle sehen wir, dass in den Zeilen die Level des Faktors infected angegeben sind und in den Spalten die Level des Faktors stage. Insgesamt haben wir 48 Tiere und die entsprechenden Randsummen aus den einzelnen Zellen gebildet. Im Prinzip schauen wir uns nur an, wie oft eine Faktorkombination vorkommt. Diese Zahlen sind die Messwerte, die wir in unserem Experiment erhoben und gemessen haben. Der \(\mathcal{X}^2\)-Test vergleicht nun die beobachteten Werte mit den anhand der Randsummen zu erwartenden Werte.
Wir betrachten gleich zwei Arten der Berechnung des \(\mathcal{X}^2\)-Test. Einmal berechnen wir den Test ohne Korrektur und einmal rechnen wir mit der Yates Korrektur für kleine Fallzahlen. In beiden Fällen benötigen wir aber die erwarteten Zellbelegungen, die wir uns in der folgenden Tabelle einmal berechnen. In der folgenden Tabelle kannst du sehen wie wir anhand der Randsummen die erwartenden Zellbelegungen berechnen. Hierbei können auch krumme Zahlen rauskommen. Wir würden keinen Unterschied zwischen den Entwicklunsgphasen gegeben deren Infektionsstatus erwarten, wenn die Abweichungen zwischen den beobachteten Werten und den zu erwartenden Werten klein wären. Wir berechnen nun die zu erwartenden Werte indem wir die Randsummen der entsprechenden Zelle multiplizieren und durch die Gesamtanzahl teilen.
| Stage | ||||
| adult | juvenile | |||
| Infected | yes (1) | \(\cfrac{24 \cdot 27}{48} = 13.5\) | \(\cfrac{24 \cdot 27}{48} = 13.5\) | \(\mathbf{27}\) |
| no (0) | \(\cfrac{24 \cdot 21}{48} = 10.5\) | \(\cfrac{24 \cdot 21}{48} = 10.5\) | \(\mathbf{21}\) | |
| \(\mathbf{24}\) | \(\mathbf{24}\) | \(n = 48\) |
Kommen wir jetzt also zu der Berechnung des \(\mathcal{X}^2\)-Test in dem wir die Werte aus der Tabelle mit den beobachteten Werte mit den Werten aus der Tabelle mit den erwarteten Werten vergleichen. Ohne Korrektur heißt hier, dass wir die Standardformel nutzen, die nicht für eine geringe Fallzahl adjustiert wurde.
Im Folgenden siehst du einmal die Formel für den \(\mathcal{X}^2\)-Test. Die Formel ist sehr kompakt und das eigentlich schwere ist Berechnung der erwarteten Werte. Das ist immer etwas komplizierter und nicht so sofort eingängig. Daher schaue doch nochmal in die obige Tabelle, wenn dir nicht klar geworden ist, wo die erwarteten Werte herkommen.
\[ \chi^2_{D} = \sum\cfrac{(O - E)^2}{E} \]
mit
Wir können dann die Formel für den \(\mathcal{X}^2\)-Test entsprechend ausfüllen. Dabei ist wichtig, dass die Abstände quadriert werden. Das ist ein Kernkonzept der Statistik, Abweichungen werden fast immer quadriert.
\[ \begin{aligned} \mathcal{X}^2_{D} &= \cfrac{(10 - 13.5)^2}{13.5} + \cfrac{(17 - 13.5)^2}{13.5} + \\ &\phantom{=}\;\; \cfrac{(14 - 10.5)^2}{10.5} + \cfrac{(7 - 10.5)^2}{10.5} = 4.14 \end{aligned} \]
Es ergibt sich ein \(\mathcal{X}^2_{D}\) von \(4.14\) mit der Regel, dass wenn \(\mathcal{X}^2_{D} \geq \mathcal{X}^2_{\alpha=5\%}\) die Nullhypothese abgelehnt werden kann. Mit einem \(\mathcal{X}^2_{\alpha=5\%} = 3.84\) können wir die Nullhypothese ablehnen. Es besteht Zusammenhang zwischen den Infektionsstatus mit Flohschnupfen und dem Entwicklungstand der Flöhe. Wir haben aber nur eine kleine Fallzahl vorliegen. Ja, auch mit fast 50 Flöhen gilt bei \(\mathcal{X}^2\)-Test noch als eine kleine Fallzahl.
Wen wir geringe Erwartungswerte in der 2x2 Kreuztabelle berechnen, dann werden wir vermutlich einen zu niedrigen p-Wert erhalten. Mit vermutlich meine ich, dass über mehrere Versuche hinweg, wir sehen würden, dass der p-Wert zu klein ist. Ob das jetzt konkret in deinem Experiment der Fall ist, ist dann wieder eine andere Frage. Statistik ist immer über Populationen. Auch wenn wir von Testeigenschaften reden. Dennoch gibt es die automatische Yates’s correction for continuity, die ich jetzt auch nicht aktiv ausschalten würde. Was macht jetzt die Korrektur? Wir ziehen einfach von dem Betrag der Differenz der beobachteten und der erwarteten Werte einmal 0.5 ab. Das war es dann schon, wie du in der folgenden Formel siehst.
\[ \chi^2_{D,\, Yates} = \sum\cfrac{(|O - E| - 0.5)^2}{E} \]
mit
Jetzt können wir wieder die \(\mathcal{X}^2_D\)-Teststatistik berechnen. Eigentlich ist es das Gleiche wie schon oben nur das wir eben nochmal die Differenzen kleiner machen als die Differenzen so wären. Damit machen wir auch den \(\mathcal{X}^2\)-Test weniger signifikant. Die Größe der Abstände macht ja die Siginifkanz dann am Ende aus.
\[ \begin{aligned} \mathcal{X}^2_{D} &= \cfrac{(|10 - 13.5| -0.5)^2}{13.5} + \cfrac{(|17 - 13.5| -0.5)^2}{13.5} + \\ &\phantom{=}\;\; \cfrac{(|14 - 10.5|-0.5)^2}{10.5} + \cfrac{(|7 - 10.5| -0.5)^2}{10.5} = 3.0476 \end{aligned} \]
Es ergibt sich ein \(\mathcal{X}^2_{D}\) von \(3.05\) mit der Regel, dass wenn \(\mathcal{X}^2_{D} \geq \mathcal{X}^2_{\alpha=5\%}\) die Nullhypothese abgelehnt werden kann. Mit einem \(\mathcal{X}^2_{\alpha=5\%} = 3.84\) können wir die Nullhypothese dann aufeinmal doch nicht mehr ablehnen. Ja, es ist auch immer wieder eine Krux mit den statistischen Tests. Je nachdem welchen Test du nimmst, kommt immer wieder numerisch was anderes raus.
“Wie immer gilt, liegt der p-Wert nahe an der Signifikanzschwelle von \(\alpha\) gleich 5%, dann ist die Aussage gewagt hier von einem oder keinen Unterschied zu sprechen. Wir sind eben numerisch an der Grenze und wenn du dann nochmal in die 2x2 Tafel schaust, dann würde ich sagen, dass wir höchstens einen Trend, aber nicht wirklich was bedeutendes vorliegen haben.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
Wenn wir den \(\mathcal{X}^2\)-Test in R rechnen wollen nutzen wir die Funktion chisq.test(), die eine Matrix oder Tabelle von Zahlen verlangt. Dies ist etwas umständlich. Ich nutze hier die Funktion table() um mir die 2x2 Tabelle zu bauen. Der Weg ist etwas umständlicher, da ich der Funktion direkt die Spalten übergeben muss.
Dann rechnen wir einmal den \(\mathcal{X}^2\)-Test ohne Korrektur und müssen das auch explizit einmal sagen. Wenn wir also die Korrektur ausstellen wollen, dann musst du die Option auf FALSE setzen.
table(fac1_tbl$infected, fac1_tbl$stage) |>
stats::chisq.test(mat, correct = FALSE)
Pearson's Chi-squared test
data: table(fac1_tbl$infected, fac1_tbl$stage)
X-squared = 4.1481, df = 1, p-value = 0.04168Wir erhalten hier den gleichen \(\mathcal{X}^2_D\)-Wert wie wir schon händisch berechnet haben. Damit haben wir dann auch einen p-Wert der kleiner ist als das Signifikanzniveau \(\alpha\) gleich 5%. Wir können die Nullhypothese ablehnen und haben einen signifikanten Unterschied. Der Infektionsstatus unterscheidet sich in den Entwicklungsphasen.
Wenn wir die Korrektur für kleine Fallzahlen anlassen wollen, dann brauchen wir keine Option setzen. Die Funktion schaut selber, ob die Korrektur angemessen ist oder nicht. Dann erhalten wir die gleiche Ausgabe nur eben mit anderen Werten.
table(fac1_tbl$infected, fac1_tbl$stage) |>
stats::chisq.test(mat)
Pearson's Chi-squared test with Yates' continuity correction
data: table(fac1_tbl$infected, fac1_tbl$stage)
X-squared = 3.0476, df = 1, p-value = 0.08086Auch hier erhalten wir den gleichen \(\mathcal{X}^2_D\)-Wert wie wir schon händisch berechnet haben. Somit erhalten wir hier auch eine andere Entscheidung. Damit haben wir dann auch einen p-Wert der größer ist als das Signifikanzniveau \(\alpha\) gleich 5%. Wir können die Nullhypothese nicht ablehnen und haben keinen signifikanten Unterschied. Der Infektionsstatus unterscheidet sich nicht in den Entwicklungsphasen.
Wenn wir schöner eine 2x2 Tabelle bauen wollen, die wir dann auch einfacher in den \(\mathcal{X}^2\)-Test pipen können, dann nutze ich die Funktion chisq.test() aus dem R Paket {janitor}. Hier haben wir dann zwar auch die Möglichkeit die Korrektur mit correct = FALSE abzustellen. Es kommt dann aber das Gleiche an Werten raus, also lasse ich hier einmal den Standard.
fac1_tbl |>
tabyl(infected, stage) |>
janitor::chisq.test()
Pearson's Chi-squared test with Yates' continuity correction
data: tabyl(fac1_tbl, infected, stage)
X-squared = 3.0476, df = 1, p-value = 0.08086Auch hier erhalten wir den gleichen \(\mathcal{X}^2_D\)-Wert wie wir schon händisch mit der Korrektur berechnet haben. Damit haben wir dann auch einen p-Wert der größer ist als das Signifikanzniveau \(\alpha\) gleich 5%. Wir können die Nullhypothese nicht ablehnen und haben keinen signifikanten Unterschied. Der Infektionsstatus unterscheidet sich nicht in den Entwicklungsphasen.
Als ein mögliches Effektmaß können wir Cramers \(V\) berechnen. Wir nutzen hierzu die Funktion cramers_v(). Auf einer reinen 2x2 Kreuztabelle wäre aber Pearsons \(\phi\) durch die Funktion phi() vorzuziehen. Siehe dazu auch \(\phi\) and Other Contingency Tables Correlations auf der Hilfeseite des R Paketes {effectsize}. Wir bleiben hier dann aber bei Cramers \(V\).
Wie stark ist nun der beobachtete Effekt? Wir konnten zwar die Nullhypothese für den korrigierten Fall nicht ablehnen, aber es wäre auch von Interesse für die zukünftige Versuchsplanung, wie stark sich die beiden Entwicklungsstadien im Flohschnupfen unterscheiden. Wir haben nun die Wahl zwischen zwei statistischen Maßzahlen für die Beschreibung eines Effektes bei einem \(\mathcal{X}^2\)-Test.
Zum einen Cramers \(V\), das wir in etwa interpretieren wie eine Korrelation und somit auch einheitslos ist. Wenn Cramers \(V\) gleich 0 ist, dann haben wir keinen Unterschied zwischen den Hunden und Katzen gegeben dem Flohbefall. Bei einem Cramers \(V\) von 0.5 haben wir einen sehr starken Unterschied zwischen dem Flohbefall zwischen den beiden Tierarten. Der Vorteil von Cramers V ist, dass wir Cramers \(V\) auch auf einer beliebig großen Kreuztabelle berechnen können. Die Formel ist nicht sehr komplex.
\[ V = \sqrt{\cfrac{\mathcal{X}^2/n}{\min(c-1, r-1)}} \]
mit
\[ V = \sqrt{\cfrac{3.0476/48}{1}} = 0.25 \]
Wir setzen also den Wert \(\chi^2_{D}\) direkt in die Formel ein. Wir wissen ja auch, dass wir \(n = 48\) Tiere untersucht haben. Da wir eine 2x2 Kreuztabelle vorliegen haben, haben wir \(r = 2\) und \(c = 2\) und somit ist das Minimum von \(r-1\) und \(c-1\) gleich \(1\). Wir erhalten ein Cramers \(V\) von \(0.25\) was für einen schwachen bis mittelstarken Effekt spricht. Wir können uns auch grob an der folgenden Tabelle der Effektstärken für Carmers \(V\) orientieren.
| schwach | mittel | stark | |
|---|---|---|---|
| Cramers \(V\) | 0.1 | 0.3 | 0.5 |
Wenn wir dann Cramers V in {effectsize} berechnen wollen, müssen wir wieder über die Standardfunktion table() gehen um uns einmal die 2x2 Tabelle zu bauen. Dann können wir auch die Werte direkt in die Funktion cramers_v() pipen. Wir erhalten auch hier den gleichen Wert, den wir schon händisch berechnet haben. Abweichungen können sich ergeben, wenn du in dem R Paket {effectsize} ein anderes Maß nutzt. Wir rechnen aber keine Effektmaße händisch, deshalb leben wir mit der Ausgabe der Funktionen in R.
table(fac1_tbl$infected, fac1_tbl$stage) |>
cramers_v() Cramer's V (adj.) | 95% CI
--------------------------------
0.26 | [0.00, 1.00]
- One-sided CIs: upper bound fixed at [1.00].
“Effektschätzer wie Cramers V habe ich selten berichtet gesehen. Wenn, dann wollen wir eher Odss Ratios haben, aber in dem Fall würde ich eher zu einer logistischen Regression raten, als hier einen \(\mathcal{X}^2\)-Test zu rechnen. In der logistischen Regression auf einem binären Endpunkt kommst du dann weiter.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
Der Anpassungstest (eng. goodness-of-fit) wird häufig in der Genetik verwendet, wenn wir testen wollen, ob wir ein erwartetes Spaltungsverhältnis beobachtet haben oder eben eine Abweichung vom Hardy-Weinberg Gesetz vorliegt. Noch allgemeiner gesprochen Testen wir hier, ob unsere beobachteten Werte von erwarteten Anteilen unterscheiden. Daher beobachten wir eben das Auftreten von drei genetischen Markern \(AA\), \(AB\) und \(BB\) und wollen jetzt wissen, ob diese auch in einem Verhältnis von 1:2:1 auftreten.
obs <- c(AA = 12, AB = 24, BB = 15)Bei einem Verhältnis von 1:2:1 sollten wir dann folgende Aufteilung erwarten.
exp <- c(AA = 1/4, AB = 2/4, BB = 1/4)Dann können wir die beobachteten Werte und die zu erwartenden Verhältnisse einmal in die Funktion chisq.test() stecken. Wir erhalten dann einen p-Wert, der uns aussagt, ob wir eine Abweichung vorliegen haben. Mit einem p-Wert von \(0.81\) können wir die Nullhypothese der Gleicheit nicht ablehnen. Die beobachteten Werte weichen nicht von einem Verhältnis von 1:2:1 ab.
chisq.test(x = obs, p = exp, simulate.p.value = TRUE)
Chi-squared test for given probabilities with simulated p-value (based
on 2000 replicates)
data: obs
X-squared = 0.52941, df = NA, p-value = 0.7946In den sehr seltenen Fällen wo du noch einen Effektschätzer brauchst, kannst du im R Paket {rcompanion} die Funktion cohenW() verwenden. Die Interpretation ist ähnlich wie bei Cramers V. Ein Wert nahe Null ist kein Effekt und je größer desto stärker.
cohenW(x = obs, p = exp)Cohen w
0.1019 Für vielleicht viele, auch für die sich schon länger mit der Statistik beschäftigen, ist es immer wieder eine Überraschung, dass sich die gängigen statistischen Tests auch als Modelle abbilden lassen. Die Übersicht Common statistical tests are linear models liefert hier nochmal eine wunderbare Tabelle. Ich zeige hier die Modellierungen in glm() sowie loglm(), die ja eigentlich als Regression gilt und nicht als Test. Hier siehst du, wie sich dann auch über die Jahre Zusammenhänge herausgestellt haben, die dann methodisch vereinheitlicht wurden. Ich habe dir den direkten Vergleich dann immer in den zweiten Tab gelegt.
Wir brauchen hier aber die Daten einmal als Long_Format, so dass ich hier einmal etwas die Daten bearbeiten muss, damit wir dann auch mit denen Rechnen können.
loglm_tbl <- fac1_tbl |>
tabyl(infected, stage) |>
as_tibble() |>
pivot_longer(cols = adult:juvenile,
names_to = "stage",
values_to = "freq")
loglm_tbl# A tibble: 4 × 3
infected stage freq
<fct> <chr> <dbl>
1 1 adult 10
2 1 juvenile 17
3 0 adult 14
4 0 juvenile 7Dann beginnen wir mit dem linearen Modell mit glm(), die dann auf einer kategoriellen Einflussvariable einen Chi-Quadrat-Test rechnet. Auch nutzen wir hier einmal nicht die klassische ANOVA sondern nochmal eine andere Implementierung. Die Ergebnisse sind gleich, wenn wir auf eine Korrektur nach Yates verzichten.
glm(freq ~ infected * stage, data = loglm_tbl, family = poisson()) |>
anova(test = 'Rao') Analysis of Deviance Table
Model: poisson, link: log
Response: freq
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Rao Pr(>Chi)
NULL 3 4.9663
infected 1 0.7520 2 4.2143 0.7500 0.38648
stage 1 0.0000 1 4.2143 0.0000 1.00000
infected:stage 1 4.2143 0 0.0000 4.1482 0.04168 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1fac1_tbl |>
tabyl(infected, stage) |>
janitor::chisq.test(correct = FALSE)
Pearson's Chi-squared test
data: tabyl(fac1_tbl, infected, stage)
X-squared = 4.1481, df = 1, p-value = 0.04168Die Nutzung des Funktion loglm() ist etwas einfacher und wir brauchen auch keine ANOVA um auf das Ergebnis zu kommen. Auch hier haben wir die gleiche Entscheidung wie bei einem unkorrigierten Chi-Quadrat-Test
MASS::loglm(freq ~ stage + infected, loglm_tbl)Call:
MASS::loglm(formula = freq ~ stage + infected, data = loglm_tbl)
Statistics:
X^2 df P(> X^2)
Likelihood Ratio 4.214299 1 0.04008462
Pearson 4.148148 1 0.04168008fac1_tbl |>
tabyl(infected, stage) |>
janitor::chisq.test(correct = FALSE)
Pearson's Chi-squared test
data: tabyl(fac1_tbl, infected, stage)
X-squared = 4.1481, df = 1, p-value = 0.04168Es gibt immer mal wieder statistische Tests nach denen ich gefragt werde, die eigentlich veraltet sind oder aber nicht mehr genutzt werden sollten. Dennoch wird danach gefragt und wenn ich die Tests hier nicht beschreibe, dann findest du die Tests auch nicht. Also hier einmal der Friedhof der Chi-Qudrat-Tests, die ich nicht mehr anwenden würde.
Im allgemeinen Sprachgebrauch der Statistik wird der Fisher Exakt Testa bei kleiner Zellbelegung verwendet. Wie du in dem Beitrag When and how to avoid inappropriate use of Fisher’s exact test nachlesen kannst, ist der Fisher Exakt Test nicht zu empfehlen. Darpber hinaus musst du die 2x2 Kreuztabelle richtig bauen. Sonst kommt bei den Odds Ratios als Effektschätzer nur Unsinn raus oder ist eben nicht interpretierbar.
Wenn wir gleich den Fisher Exakt Test rechnen, dann wollen wir Odds Ratios (OR) als Effektschätzer haben. Dabei berechnen sich die Odds Ratios als Chancenverhältnis aus den Zellwerten. Hier einmal die Formel für die Odds Ratios. Wir dividieren eigentlich die Produkte der Zelldiagonalen.
\[ OR = \cfrac{a \cdot d}{c \cdot b} = \cfrac{17 \cdot 14}{10 \cdot 7} = 3.4 \]
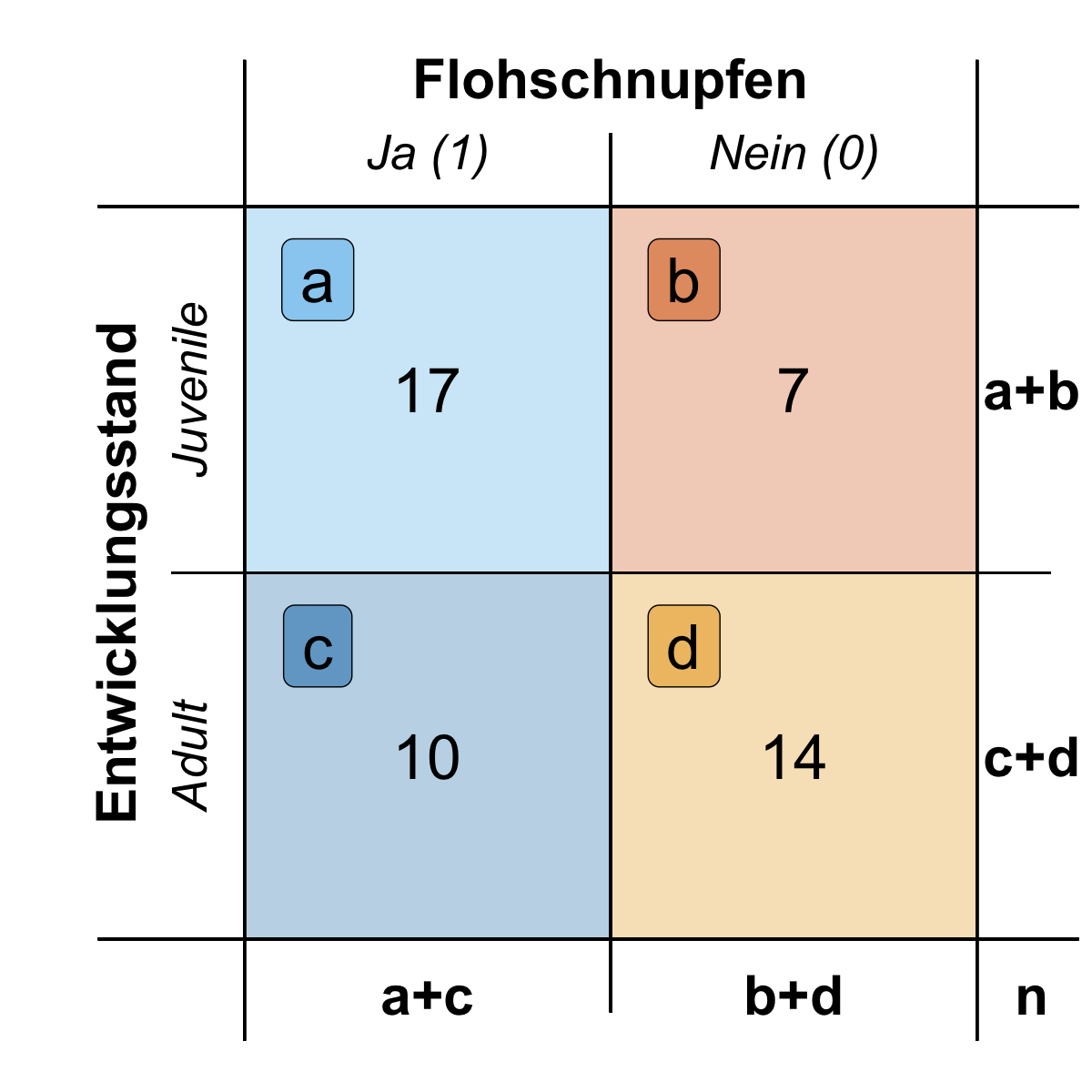
Wir interpretieren wir jetzt in unserem Fall die Odds Ratios? Wichtig ist, dass wir in der Spalten die Messwerte oder das Outcome vorliegen haben und in der linken Spalte die Werte für das schlechte Outcome, wie eben krank. Dann können wir die Odds Ratios im Bezug zu der ersten Zeile interpretieren.
In der folgenden Tabelle siehst du nochmal den Zusammenhang. Wir können jetzt sagen, dass die Chance an Flohschnupfen zu erkranken für juvenile Flöhe 3.4-fach erhöht ist. Die juvenilen Flöhe stehen in der ersten Zeile, also machen wir eine Aussage über diesen Entwicklungsstand. Da du die 2x2 Tabelle beliebig bauen kannst musst du sehr darauf achten, dass du die 2x2 Tabelle für die Odds Ratios richtig baust.
Haben wir also eine geringe Zellbelegung von unter 5 in einer der Zellen der 2x2 Kreuztabelle, dann verwenden wir den Fisher Exakt Test. Der Fisher Exakt Test hat auch den Vorteil, dass wir direkt die Odds Ratios wiedergegeben bekommen, wenn wir die 2x2 Kreuztabelle richtig formatieren. Wir können auch den Fisher Exakt Test rechnen, wenn wir viele Beobachtungen pro Zelle haben und einfach an die Odds Ratios rankommen wollen. Der Unterschied zwischen dem klassischen \(\mathcal{X}^2\)-Test und dem Fisher Exakt Test ist in der praktischen Anwendung nicht so groß. Wie schon bemerkt, heutzutage wird der Fisher Exakt Test nicht mehr empfohlen.
Hier müssen wir dann einmal die Tabelle richtig bauen. Zuerst muss der Flohschnupfen in die Spalten und wir brauchen die Eins in der linken Spalte. Dann wollen wir noch die Zeilen nach juvenile und adult sortieren. Dann haben wir das und können den Fisher Exakt Test rechnen und die Odds Ratios interpretieren.
OR_tab <- fac1_tbl |>
mutate(infected = ordered(infected, levels = c(1, 0)),
stage = ordered(stage, levels = c("juvenile", "adult"))) |>
tabyl(stage, infected)
OR_tab stage 1 0
juvenile 17 7
adult 10 14Ich nutze hier wieder die Implementierung in {janitor}, da ich dann einfacher pipen kann.
janitor::fisher.test(OR_tab)
Fisher's Exact Test for Count Data
data: OR_tab
p-value = 0.07977
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.8882825 13.4465108
sample estimates:
odds ratio
3.309326 Wir sehen auch hier den nicht signifikanten \(p\)-Wert sowie eine Odds Ratio von 3.3 berechnet. Juvenile Flöhe haben also eine um 3.3 höhere Chance sich mit Flohschnupfen zu infizieren.