34  Die MANOVA

Letzte Änderung am 29. June 2025 um 12:24:44

“The ‘C’ students run the world” — Harry Truman

In diesem Kapitel soll es um die MANOVA gehen. Die MANOVA ist ein altes statistisches Verfahren und wird immer mal wieder in den Agrarwissenschaften zitiert und auch genutzt. In den letzten Jahren ist aber die Nutzung zurückgegangen, da wir mit neueren statistischen Modellierungen einen globalen Test wie die MANOVA immer weniger brauchen. Dennoch hat fast jedes statistische Verfahren sein Nische und so zeige ich dir hier auch einmal die Anwendung. Ich gehe nicht so sehr in die Tiefe sondern fokussiere mich hier wieder auf die zügige Umsetzung. Wenn dich noch vertiefende Literatur interessiert, dann kann ich noch O’Brien & Kaiser (1985) mit der Veröffentlichung MANOVA method for analyzing repeated measures designs: an extensive primer sowie Warne (2014) mit der Arbeit A primer on multivariate analysis of variance (MANOVA) for behavioral scientists empfehlen. In den angegebenen Tutorien findest du dann nochmal mehr und weitergehende Hilfen.

34.1 Allgemeiner Hintergrund

Die MANOVA wird genutzt wenn wir nicht nur einen Messwert \(y\) in unser Modell stecken wollen sondern gleich mehrere. Daher haben wir nicht einen Messwert über den wir eine Aussage treffen wollen sondern eben zwei oder mehr. Wir nennen solche Modelle dan multivariat, da wir mehrere Messwerte im Modell haben. Daher erhalten wir dann auch nur die Information ob sich ein Faktor in den Messwerten simultan unterscheidet. Das mag von Interesse sein oder aber auch nicht. Da wir hier wieder sehr allgemein von außen drauf schauen und wie bei der klassichen ANOVA üblich keine Informationen über paarweise Vergleiche erhalten, ist die MANOVA manchmal etwas unbefriedigend. Die Nutzung geht auch immer weiter zurück, da wir mit neueren Verfahren dann eben doch univariate Modelle, mit nur einem Messwert haben, die uns mehr Aussagen liefern als die MANOVA. Darüber hinaus hat die MANOVA sehr viele Annahmen an die Daten, was zu weiteren Einschränkungen führt.

Die MANOVA hat einiges an Annahmen an die Daten. Es muss also ein ganz spezielles Set an Beobachtungen vorliegen, damit die MANOVA wirklich zuverlässig funktioniert. Dazu kommt dann noch, dass wir eigentlich noch recht hohe Fallzahlen brauchen, weit jenseits der vier bis fünf Beobachtungen pro Gruppe, um wirklich einen verlässliche Analyse zu erhalten. Dennoch kann es Sinn machen unabhängige Messwerte simultan für einen Faktor einmal miteinander zu vergleichen um mehr über die Wechselwirkungen zu erfahren. Dabei würde ich weder einer nicht signifikanten MANOVA noch einer signifikanten MANOVA sehr viel Gewicht beimessen. Der wichtige Teil ist dann die anschließende Analyse der einzelnen Zusammenhänge in möglichen Post-hoc Tests. Dort müssen wir dann aber alles wieder auseinandernehmen, denn in den Post-hoc Tests rechnen wir wieder mit nur einem Messwert.

Das Modell

Beginnen wir also mit der Festlegung welche Art der Analyse wir rechnen wollen. Wichtig ist hier, dass du mehrere normalverteiten Messwert \(y\) vorliegen hast und ein oder mehrere Faktoren \(f\). Was sind im Kontext von R Faktoren? Ein Faktor ist eine Behandlung oder eben eine Spalte in deinem Datensatz, der verschiedene Gruppen oder Kategorien beinhaltet. Wir nennen diese Kategorien Level. Die MANOVA ist in dem Sinne ein Spezialfall, dass wir nämlich nicht nur einen Messwert \(y\) vorliegen haben sondern eben mehrere die wir simultan auswerten wollen. Das klingt jetzt erstmal etwas schräg, aber es wird dann klarer, wenn wir uns die Sachlage einmal an einem Beispiel anschauen. Hier aber erstmal das Modell.

\[ (y_1, y_2, ..., y_j) \sim f_A + f_B + ... + f_P + f_A \times f_B \]

mit

• \((y_1, y_2)\) gleich der Messwerte oder Outcomes
• \(f_A + f_B + ... + f_P\) gleich experimenteller Faktoren
• \(f_A \times f_B\) gleich einem beispielhaften Interaktionsterm erster Ordnung

Die ganze multivariate Analyse ist dann etwas seltener, da wir hier dann doch schon einiges an Fallzahl brauchen, damit es dann auch einen Sinn macht. Einiges an Fallzahl heißt dann hier, dass wir dann schon mehr als sechs Beobachtungen in einer Gruppe haben sollten. Wenn du weniger hast, kann es sein, dass du keine signifikanten Unterschiede findest.

Häufig schauen wir uns auch gar nicht den zweifkatoriellen oder gar mehrfaktoriellen Fall in einer MANOVA an. Sehr viel üblicher ist die Betrachtung einer einfaktoriellen ANOVA zusammen mit zwei Messwerten, die simultan ausgewertet werden sollen. Hier gibt es dann auch meistens Überschneidungen mit der Hauptkomponentenanalyse. Die Fragestellungen sind nicht gleich, aber eventuell findest du in der Hauptkomponentenanalyse eine bessere Antwort auf deine Frage.

Annahmen an die MANOVA

Neben den klassischen Problemen wie Ausreißer und Varianzhomogenität gibt es noch einiges weiteres an Annahmen an die MANOVA. Das R Paket {rstatix} leifert hier eine Reihe an Funktionen, die es ermöglichen die Annahmen zu testen. Ich fokusiere mich hier auf zwei Kernannahmen, die ich dann gerne einmal vorab testen möchte.

1. Multivariate Normalverteilung können wir durch die Funktion mshapiro_test() überprüfen. Wir wollen das alle Messwerte zusammen einer Normalverteilung folgen. Das ist nicht ganz so schlimm, wenn es nicht der Fall ist, aber wir sollten eine mögliche Abweichung im Kinterkopf behalten.
2. Abwesenheit von Multikollinearität können wir mit der Funktion cor_test() oder cor_mat() überprüfen. Die Messwerte \(y\) sollten nicht über einem Korrelationkoeffizienten von 0.9 liegen. Ich persönlich finde das schon arg hoch und würde eher von 0.6 ausgehen. Aber auch hier gibt es sehr viele Grnezen und Interpretationen davon.

Das Tutorium One-Way MANOVA in R listet noch mehr Vortests auf, aber ich bin nicht so der Fan davon sich in die Ecke zu testen, wo nichts mehr geht. Wenn deine Daten in den Messwerten einigemaßen normalverteilt sind und nicht zu stark miteinander korreliert sind, dann kannst du MANOVA einmal ausprobieren und schauen was sich al Ergebnis ergibt.

Welche Pakete gibt es eigentlich?

Neben der Standardimplementierung in dem R Paket {stats} und der Funktion manova() gibt es noch zwei weitere Implementierungen, die ich hier einmal vorstellen will. Beide Implementierungen unterscheiden sich dabei im Ansatz. Die Implementierung mit {car} ist nochmal näher an dem Standard dran, die Implementierung in {MANOVA.RM} nutzt einen nichtparametrischen Algorithmus und hat daher andere Annahmen an die Daten.

• Das R Paket {car} rechnet mehr oder minder die Standardimplementierung nach. Wir haben hier aber noch ein paar mehr Optionen, die du dir dann nochmal genauer anschauen kannst. Wir haben hier die Auswahl an vier Algorithmen mit Pillai, Wilks, Hotelling-Lawley und Roy. Aktuell diskutiere ich hier nicht die Unterschiede aber du findest hier eine Interaktive Auswahl für die Tests. Ateş et al. (2019) liefert in der Arbeit Comparison of Test Statistics of Nonnormal and Unbalanced Samples for Multivariate Analysis of Variance in terms of Type-I Error Rates auch eine umfangreiche Diskussion der Sachlage.
• Das R Paket {MANOVA.RM} von Friedrich et al. (2019) stellt nochmal eine parameterfreie MANOVA vor, wo wir theoretisch nicht so strenge Annahmen an die Daten haben. Dennoch ist auch hier mit Bedacht zu rechnen, die Probleme der klassischen MANOVA hat auch diese Implementierung.

In der Anwendung zeige ich dir dann gleich einmal alle drei Pakete und diskutiere was bei den Analyse rausgekommen ist. Wie immer gibt es dabei natürlich leichte Unterschiede, dass hat dann aber natürlich mit den Algorithmen und teilweise mit den Fallzahlen zu tun. Ich habe nicht sehr große Datensätze gebaut.

Weitere Tutorien für die MANOVA

Wir oben schon erwähnt, kann dieses Kapitel nicht alle Themen der MANOVA abarbeiten. Daher präsentiere ich hier eine Liste von Literatur und Links, die mich für dieses Kapitel hier inspiriert haben. Nicht alles habe ich genutzt, aber vielleicht ist für dich was dabei.

• One-Way MANOVA in R liefert nochmal eine super Übersicht über die Anwendung der MANOVA in R und geht auch nochmal auf die Post-hoc Tests ein. Hier wird dann wirklcih jede Annahme überprüft.
• Master MANOVA in R: One-Way, Two-Way, & Interpretation gibt nochmal einen etwas kürzen Überblick und nimmt sich mehr Zeit für die Interpretation und der Visualisierung mit Boxplots. Ich fand das Tutorium gut zu lesen und informativ.

34.2 Genutzte R Pakete

Wir wollen folgende R Pakete in diesem Kapitel nutzen.

pacman::p_load(tidyverse, magrittr, broom, scales, MANOVA.RM,
               readxl, see, car, patchwork, rstatix, effectsize, 
               conflicted)
conflicts_prefer(dplyr::mutate)
conflicts_prefer(dplyr::summarize)
conflicts_prefer(dplyr::filter)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73", 
                "#F0E442", "#0072B2", "#D55E00", "#CC79A7")

An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.

34.3 Daten

Wir nutzen hier den Datensatz aus der ANCOVA einfach nochmal. Nur das wir hier dann eben nicht nur die Sprungweite als Messwert nehmen sondern auch gleich noch das Gewicht der Flöhe mit dazu. Als Gruppenfaktor haben wir dann wieder die Flohart in dem einfaktoriellen Fall. Für den zweifaktoriellen Datensatz nehmen wir dann noch den Faktor des Enticklungsstandes mit in das Modell. Wichtig ist hier, dass die beiden Messwerte einer Normalverteilung folgen sollten und nicht zu stark untereinander korreliert sind.

Einfaktorieller Datensatz

Beginnen wir also mit dem einfaktoriellen Datensatz. Wir haben hier die Sprungweiten und die Gewichte von verschiedenen Flöhen gemessen. Bisher war ja immer die Frage, ob sich die Sprugweiten der Hunde, Katzen- und Fuchsflöhe voneinander unterscheiden. Hier wollen wir jetzt noch das Gewicht der Flöhe mit in die Betrachtung nehmen. Damit die Daten etwas übersichtlicher sind Runde ich noch die Messwerte.

fac1_cov_tbl <- read_excel("data/fleas_complex_data.xlsx", sheet = "covariate-fac1") |> 
  select(animal, weight, jump_length) |> 
  mutate(animal = as_factor(animal),
         weight = round(weight, 2),
         jump_length = round(jump_length, 2))

Dann können wir uns schon die Daten einmal in der folgenden Tabelle einmal anschauen. Die Sprungweiten wurden in [cm] gemessen und das Gewicht der Flöhe in [mg] pro Floh. Wir haben hier als Faktor einmal die Flohart vorliegen.

Tabelle 34.1— Daten für die einfaktorielle MANOVA mit der Sprungweite in [cm] und dem Gewicht der Flöhe in [mg] für drei Floharten.

animal	weight	jump_length
cat	14	24.75
cat	12.9	30.59
cat	15.8	41.64
...	...	...
fox	23.7	55.81
fox	13	32.04
fox	25.5	46.92

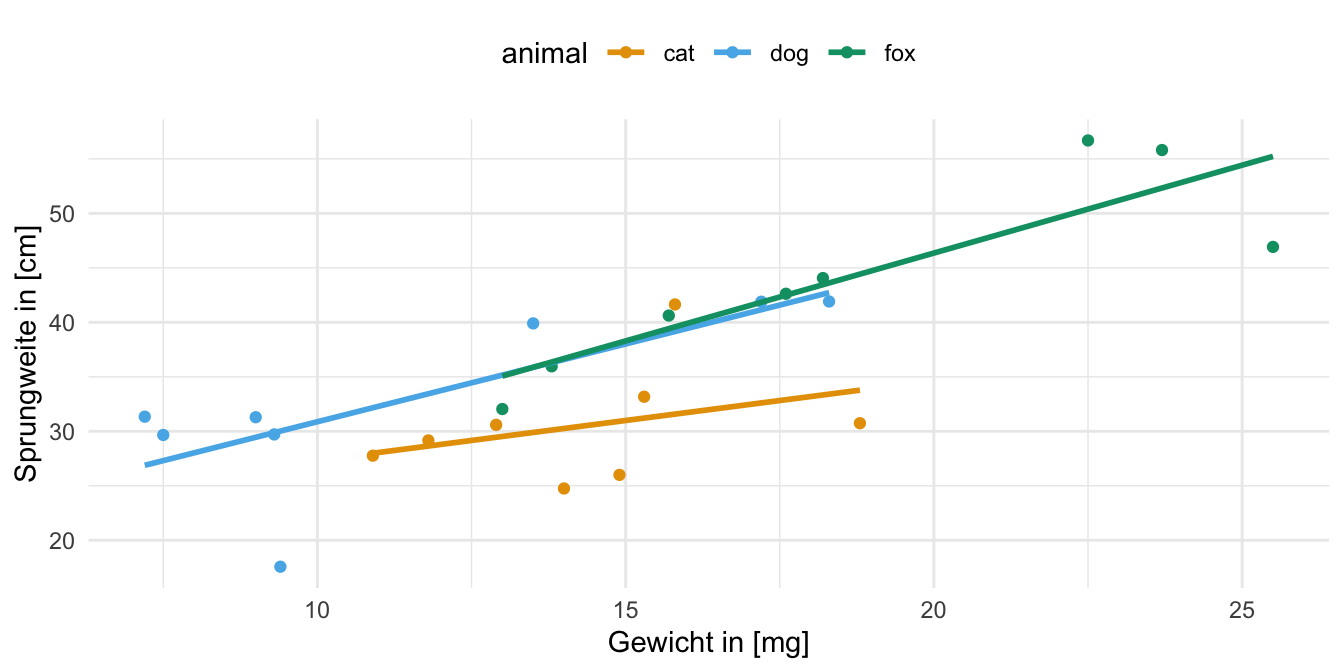
In der folgenden Abbildung zeige ich dann einmal den Zusammenhang zwischen dem Gewicht der Flöhe und der Sprungweite in einem Scatterplot. Wir sehen, dass mit steigendem Gewicht der Flöhe die Sprungweiten zunehmen. Diesen Trend können wir dann in allen drei Floharten sehen. Dabei ist der Effekt bei den Katzen nicht gnz so ausgeprägt, die Steigung ist nicht so große wie bei den Hunde- und Fuchsflöhen.

Abbildung 34.1— Zusammenhang zwischen dem Gewicht der Flöhe und der Sprungweite aufgeteilt nach der Flohart.

Zweifaktorieller Datensatz

Für den zweiten Datensatz erweitern wir einmal die Sprungweiten und Gewichte unserer Hunde-, Katzen- und Fuchsflöhe nochmal um einen weiteren Faktor. Wir wollen jetzt auch anschauen, ob der Entwicklungsstand der Flöhe einen Einfluss auf die kombinierten Sprungweiten und Körpergewichte der Flöhe hat. Dann habe ich mich noch entschieden einmal die Level im Faktor für die Entwicklungsstände zu drehen. Ich finde es logischer, dass erst juvenile und dann adult in den Abbildungen dargestellt wird. Auch hier Runde ich ein wenig die Zahlen, damit es etwas übersichtlicher ist.

fac2_cov_tbl <- read_excel("data/fleas_complex_data.xlsx", sheet = "covariate-fac2") |> 
  select(animal, stage, weight, jump_length) |> 
  mutate(animal = as_factor(animal),
         stage = factor(stage, level = c("juvenile", "adult")),
         weight = round(weight, 2),
         jump_length = round(jump_length, 2)) 

Dann können wir uns schon die Daten einmal in der folgenden Tabelle einmal anschauen. Die Sprungweiten wurden in [cm] gemessen und das Gewicht der Flöhe in [mg] pro Floh. Wir haben hier als Faktor einmal die Flohart und einmal den Entwicklungsstand vorliegen.

Tabelle 34.2— Daten für die zweifaktorielle MANOVA mit der Sprungweite in [cm] und dem Gewicht der Flöhe in [mg] für drei Floharten und zwei Entwicklungsstadien.

animal	stage	weight	jump_length
cat	adult	16.74	39.84
cat	adult	16.79	34.42
cat	adult	19.3	42.32
…	…	…	…
fox	juvenile	7.3	39.72
fox	juvenile	8.66	35.68
fox	juvenile	8.13	38.33

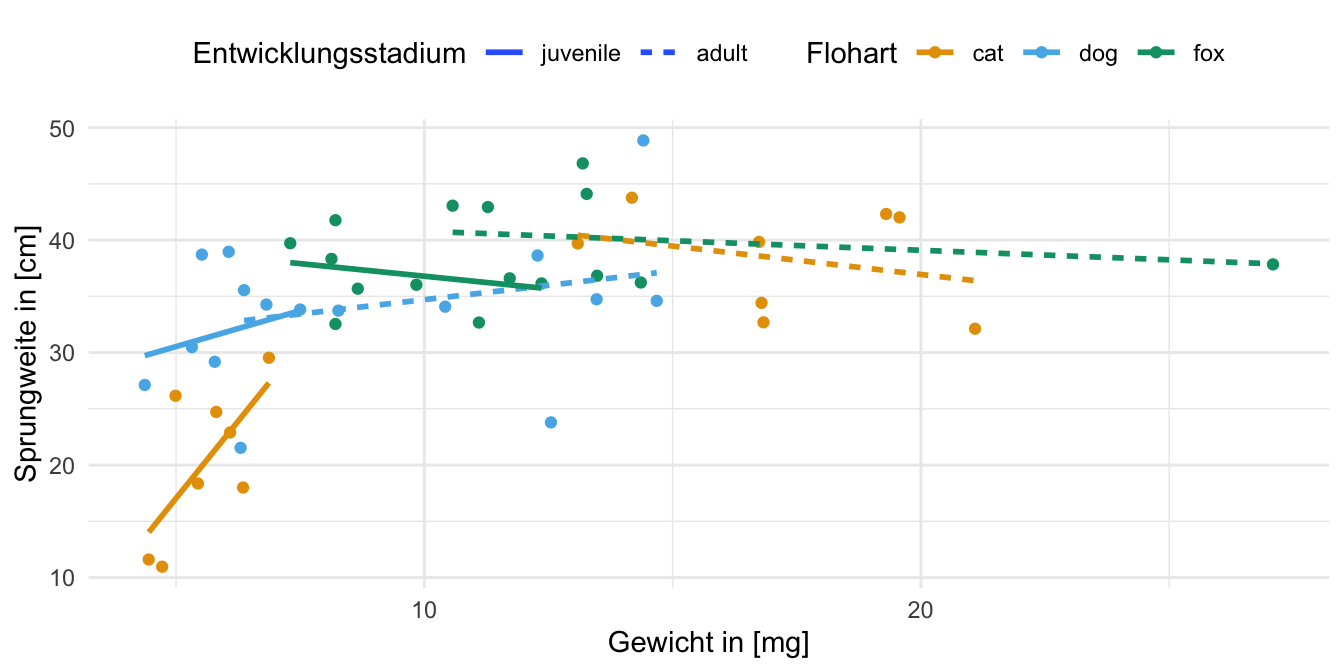
In der folgenden Abbildung sehen wir dann einmal den Zusammenhang zwischen dem Flohgewicht und den Sprungweiten. In der obigen Abbildung habe ich einmal die beiden Entwicklungsstadien zusammen in die Abbildung gelegt. In der unteren Abbildung einmal die Entwicklungsstadien aufgetrennt. Wir sehen hier sehr schön, dass bei den adulten Flöhen kein Effekt mehr zwischen dem Gewicht und den Sprungweiten vorliegt. Alle Linien der Floharten laufen parallel zur x-Achse. Bei den juvenilen Flöhen haben wir auf jeden Fall Unterschiede in den Floharten. Die Katzenflöhe scheinen mit steigendem Gewicht weiter zu springen wohingegen die Fuchsflöhe immer gleich weit mit steigendem Gewicht springen.

Abbildung 34.2— Zusammenhang zwischen dem Gewicht der Flöhe und der Sprungweite aufgeteilt nach der Flohart und dem Entwicklunsgstand der Flöhe. (A) Kombinierte Darstellung in einem Scatterplot (B) Aufgeteilte Darstellung für beide Entwicklungsstadien. [Zum Vergrößern anklicken]

34.4 Einfaktoriell

Nachdem wir uns nun einmal die Daten angeschaut haben, können wir jetzt einmal die einfaktorielle MANOVA rechnen. Auch hier nochmal wichtig, wir haben einen Faktor dafür aber zwei oder mehr Messwerte, die wir simultan auf einen Unterschied in dem Faktor testen. Der häufigste Fall ist sicherlich die einfaktorielle MANOVA. Zum einen da es immer schwerer wird mehr als zwei Messwerte sinnvoll simultan zu interpretieren, insbesondere wenn die Einheiten unterschiedlich sind. Zum anderen wird es auch bei mehr als einem Behandlungsfaktor sehr schnell schwierig die MANOVA zu interpretieren. Es sind eben dann schnell viele Faktorombinationen, die in einem kompelxen Modell interpretiert werden müssen.

Testen ausgewählter Annahmen

Wir können für die MANOVA einiges an Vorraussetzungen testen. Im Tutorium One-Way MANOVA in R wird nochmal die ganze Phalanx der Vortests gezeigt. Ich konzentriere mich hier einmal auf die beiden aus meiner Sicht wichtigsten Vortests. Zum einen ob wir wirklich eine multivariate Normalverteilung zwischen den beiden Messwerten vorliegen haben. Dazu können wir die Funktion mshapiro_test() nutzen. Der Shapiro-Test testet auf die Normalverteilung. Wenn wir die Nullhypothese ablehnen können, dann haben wir keine Normalverteilung vorliegen.

fac1_cov_tbl |> 
  select(jump_length, weight) |> 
  mshapiro_test()

# A tibble: 1 × 2
  statistic p.value
      <dbl>   <dbl>
1     0.981   0.910

Der Test kann die Nullhypothese nicht ablehnen. Wir haben keine Abweichung von der Normalverteilung vorliegen. Wir können also von einer multivariaten Normalverteilung in den beiden Messwerten der Sprungweite und Flohgewicht ausgehen.

Die MANOVA tut sich sehr schwer, wenn die beiden Messwerte sehr stark miteinander korrelieren. Damit meine ich, dass wir dann keine verlässlichen Ergebnisse aus einer MANOVA erwarten können. Daher schauen wir uns hier einmal die Korrelation zwischen den beiden Messwerten an. Wir nutzen die Funktion cor_test(). Wenn du mehr als zwei Variablen hast, dann nutze cor_mat(). Die Grenze liegt je nach Literatur zwischen 0.7 und 0.9, die dann die Korrelation nicht übersteigen darf.

fac1_cov_tbl |> 
  cor_test(jump_length, weight) |> 
  select(var1, var2, cor)

# A tibble: 1 × 3
  var1        var2     cor
  <chr>       <chr>  <dbl>
1 jump_length weight  0.79

Wir haben hier Glück und können unsere beiden Messwerte dann zusammen mit der MANOVA auswerten. Wenn du eien zu hohe Korrelation hast, dann solltest du von der Verwendung der MANOVA absehen. Deine Messwerte sind zu ähnlich, es macht keinen Sinn diese simultan auszuwerten. Immerhin sind die Messwerte bei einer hohen Korrelation untereinander austauschbar.

Einfakorielle MANOVA

In den folgenden Tabs findest du dann einmal die einfaktorielle MANOVA. Dabei ist die Implementierung in {stats} simple. Wir haben hier keine weiteren Optionen. Das R Paket {car} erlaubt mit der Funktion Manova() dann schon mehr Optionen. Hier musst du dann aber ein Modell aus der Funktion lm() weiterleiten. Als nichtparametrische Alternative für nichtnormalverteilte Messwerte zeige ich dann noch das R Paket {MANOVA.RM}.

{stats}

Das einzige Besondere in der Formelschreibweise ist, dass wir die Messwerte über dir Funktion cbind() miteinander verschmelzen müssen. Der Rest ist die bekannte Schreibweise in R. Dann können wir uns auch gleich die Ergebnisse anschauen.

manova(cbind(jump_length, weight) ~ animal, data = fac1_cov_tbl) |> 
  summary()

          Df  Pillai approx F num Df den Df   Pr(>F)    
animal     2 0.72364    5.953      4     42 0.000689 ***
Residuals 21                                            
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Wir haben einen signifikanten Effekt der Floharten auf die kombinierten Sprungweiten und Flohgewichte. Daher müssen wir jetzt im Anschluss nochmal schauen, wo die Signifikanz liegt. Sind die univariaten Modelle nnur mit der Sprungweite und dem Gewicht jeweils auch signifikant? Oder ist es wirklich das Wechselspiel der beiden Messwerte? Das sagt uns jetzt die MANOVA leider nicht.

{car}

Das R Paket {car} rechnet die gleiche MANOVA wie im vorherigen Tab. Der einzige Unterschied ist hier, dass wir auch eine andere Methode zum Testen nutzen könnten. Wir haben hier die Auswahl an vier Algorithmen mit Pillai, Wilks, Hotelling-Lawley und Roy. Der Standard ist hierbei Pillai und würde ich auch so lassen. Die Statistik nach Pillai hat gute Eigenschaften und sollte auch für die meisten Fälle genügen. Aktuell diskutiere ich hier nicht die Unterschiede aber du findest hier eine Interaktive Auswahl für die Tests. Ateş et al. (2019) liefert in der Arbeit Comparison of Test Statistics of Nonnormal and Unbalanced Samples for Multivariate Analysis of Variance in terms of Type-I Error Rates auch eine umfangreiche Diskussion der Sachlage.

lm(cbind(jump_length, weight) ~ animal, data = fac1_cov_tbl) |> 
  Manova()

Type II MANOVA Tests: Pillai test statistic
       Df test stat approx F num Df den Df   Pr(>F)    
animal  2   0.72364    5.953      4     42 0.000689 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Das Ergebnis ist identisch zum vorherigen Tab und dem R Paket {stats}. Wir haben einen signifikanten Effekt der Floharten auf die kombinierten Sprungweiten und Flohgewichte.

{MANOVA.RM}

Das Das R Paket {MANOVA.RM} von Friedrich et al. (2019) liefert nochmal die nichtparametrische MANOVA, wenn die Normalverteilung der Messwerte nicht gegeben ist. Dabei handelt es sich um einen Permutationstest, der genauer wird je mehr wir ihm erlauben Permutationen durch die Option iter zu rechnen. Sonst ist die Formelschreibweise gleich wie schon in den vorherigen Tabs.

MANOVA.wide(cbind(jump_length, weight) ~ animal, data = fac1_cov_tbl,
            iter = 1000) |> 
  summary()

Call: 
cbind(jump_length, weight) ~ animal

Descriptive:
  animal n jump_length  weight
1    cat 8      30.476  14.300
2    dog 8      32.909  11.425
3    fox 8      44.340  18.750

Wald-Type Statistic (WTS):
       Test statistic df  p-value 
animal "20.313"       "4" "<0.001"

modified ANOVA-Type Statistic (MATS):
       Test statistic
animal         25.707

p-values resampling:
       paramBS (WTS) paramBS (MATS)
animal "0.024"       "0.014"       

Das R Paket hat die Eigenschaften mehr Informationen zu liefern als man eigentlich will. Auf der einen Seite ja ganz nett, aber auf der anderen Seite immer wieder verwirrend was ich denn jetzt nehmen soll. Wir nutzen den p-Wert unter Wald-Type Statistic (WTS), der uns ebenfalls einen signifikanten Unterschied zeigt. Wir haben einen signifikanten Effekt der Floharten auf die kombinierten Sprungweiten und Flohgewichte.

34.5 Zweifaktoriell

Die zweifaktorielle MANOVA ist ziemlich selten. Jedenfalls ist mir die zweifaktorielle MANOVA noch nicht so oft in meinem Bereichen begegenet. In den Sozialwissenschaften mag das dann wieder anders sein. Warum ist die zweifaktorielle MANOVA nicht ganz so einfach? Zum einen verbinden wir hier wieder mehrere Messwerte miteinander. Darüber hinaus kommt jetzt aber nicht ein Faktor hinzu sondern eben zwei. Mit den zwei Faktoren haben wir dann auch noch eine mögliche Interaktion vorliegen, was die Modelle nochmal zusätzlich erschwert. Am Ende kann es dann in der Interpretation herausforderend sein. Die MANOVA gleibt ein globaler Test und woarum jetzt was signifikant ist, kann dann manachmal schwer zu ergründen sein.

Testen ausgewählter Annahmen

Wir können für die MANOVA einiges an Vorraussetzungen testen. Im Tutorium One-Way MANOVA in R wird nochmal die ganze Phalanx der Vortests gezeigt. Das Beispiel konzentriert sich zwar auf die einfaktorielle MANOVA in der Analyse, aber die Vortests gehen dann auch für die zweifaktorielle MANOVA. Ich konzentriere mich hier einmal auf die beiden aus meiner Sicht wichtigsten Vortests. Zum einen ob wir wirklich eine multivariate Normalverteilung zwischen den beiden Messwerten vorliegen haben. Dazu können wir die Funktion mshapiro_test() nutzen. Der Shapiro-Test testet auf die Normalverteilung. Wenn wir die Nullhypothese ablehnen können, dann haben wir keine Normalverteilung vorliegen.

fac2_cov_tbl |> 
  select(jump_length, weight) |> 
  mshapiro_test()

# A tibble: 1 × 2
  statistic  p.value
      <dbl>    <dbl>
1     0.905 0.000900

Der Test kann die Nullhypothese leider ablehnen. Wir haben damit dann eine Abweichung von der Normalverteilung vorliegen. Wir können also nicht von einer multivariaten Normalverteilung in den beiden Messwerten der Sprungweite und Flohgewicht ausgehen. Das ist jetzt etwas problematischer. Hier würde ich dann den Ergebnissen der nichtparametrischen MANOVA aus dem R Paket {MANOVA.RM} mehr vertrauen.

Die MANOVA tut sich sehr schwer, wenn die beiden Messwerte sehr stark miteinander korrelieren. Damit meine ich, dass wir dann keine verlässlichen Ergebnisse aus einer MANOVA erwarten können. Daher schauen wir uns hier einmal die Korrelation zwischen den beiden Messwerten an. Wir nutzen die Funktion cor_test(). Wenn du mehr als zwei Variablen hast, dann nutze cor_mat(). Die Grenze liegt je nach Literatur zwischen 0.7 und 0.9, die dann die Korrelation nicht übersteigen darf.

fac2_cov_tbl |> 
  cor_test(jump_length, weight) |> 
  select(var1, var2, cor)

# A tibble: 1 × 3
  var1        var2     cor
  <chr>       <chr>  <dbl>
1 jump_length weight  0.51

Wir haben hier dann ebenfalls Glück und können unsere beiden Messwerte dann zusammen mit der MANOVA auswerten. Wenn du eien zu hohe Korrelation hast, dann solltest du von der Verwendung der MANOVA absehen. Deine Messwerte sind zu ähnlich, es macht keinen Sinn diese simultan auszuwerten. Immerhin sind die Messwerte bei einer hohen Korrelation untereinander austauschbar.

Zweifakorielle MANOVA

In den folgenden Tabs findest du dann einmal die zweifaktorielle MANOVA. Dabei ist die Implementierung in {stats} simple. Wir haben hier keine weiteren Optionen. Das R Paket {car} erlaubt mit der Funktion Manova() dann schon mehr Optionen. Hier musst du dann aber ein Modell aus der Funktion lm() weiterleiten. Als nichtparametrische Alternative für nichtnormalverteilte Messwerte zeige ich dann noch das R Paket {MANOVA.RM}.

{stats}

Das einzige Besondere in der Formelschreibweise ist, dass wir die Messwerte über dir Funktion cbind() miteinander verschmelzen müssen. Der Rest ist die bekannte Schreibweise in R. Wir schreibe hier nur kürzer das Modell, da ich die beiden Haupteffekte und Interaktion mit betrachten möchte. Dann können wir uns auch gleich die Ergebnisse anschauen.

manova(cbind(jump_length, weight) ~ animal*stage, data = fac2_cov_tbl) |> 
  summary()

             Df  Pillai approx F num Df den Df    Pr(>F)    
animal        2 0.55007    7.967      4     84 1.706e-05 ***
stage         1 0.71783   52.151      2     41 5.439e-12 ***
animal:stage  2 0.43531    5.842      4     84 0.0003379 ***
Residuals    42                                             
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Wir haben einen signifikanten Effekt der Floharten sowie dem Entwicklungsstand auf die kombinierten Sprungweiten und Flohgewichte. Daher müssen wir jetzt im Anschluss nochmal schauen, wo die Signifikanz liegt. Sind die univariaten Modelle nnur mit der Sprungweite und dem Gewicht jeweils auch signifikant? Oder ist es wirklich das Wechselspiel der beiden Messwerte? Das sagt uns jetzt die MANOVA leider nicht. Auch haben wir eine signfikante Interaktion vorliegen. Das macht Sinn, da sich die juvenilen Katzenflöhe anders verhalten als die adulten Katzenflöhe. Wir sehen, dass Modell ist komplexer.

{car}

Das R Paket {car} rechnet die gleiche MANOVA wie im vorherigen Tab. Der einzige Unterschied ist hier, dass wir auch eine andere Methode zum Testen nutzen könnten. Wir haben hier die Auswahl an vier Algorithmen mit Pillai, Wilks, Hotelling-Lawley und Roy. Der Standard ist hierbei Pillai und würde ich auch so lassen. Die Statistik nach Pillai hat gute Eigenschaften und sollte auch für die meisten Fälle genügen. Aktuell diskutiere ich hier nicht die Unterschiede aber du findest hier eine Interaktive Auswahl für die Tests. Ateş et al. (2019) liefert in der Arbeit Comparison of Test Statistics of Nonnormal and Unbalanced Samples for Multivariate Analysis of Variance in terms of Type-I Error Rates auch eine umfangreiche Diskussion der Sachlage.

lm(cbind(jump_length, weight) ~ animal*stage, data = fac2_cov_tbl) |> 
  Manova()

Type II MANOVA Tests: Pillai test statistic
             Df test stat approx F num Df den Df    Pr(>F)    
animal        2   0.55007    7.967      4     84 1.706e-05 ***
stage         1   0.71783   52.151      2     41 5.439e-12 ***
animal:stage  2   0.43531    5.842      4     84 0.0003379 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Das Ergebnis ist identisch zum vorherigen Tab und dem R Paket {stats}. Wir haben einen signifikanten Effekt der Floharten sowie der Entwicklungsstadien plus einer signifikanten Interaktion auf die kombinierten Sprungweiten und Flohgewichte.

{MANOVA.RM}

Das Das R Paket {MANOVA.RM} von Friedrich et al. (2019) liefert nochmal die nichtparametrische MANOVA, wenn die Normalverteilung der Messwerte nicht gegeben ist. Dabei handelt es sich um einen Permutationstest, der genauer wird je mehr wir ihm erlauben Permutationen durch die Option iter zu rechnen. Sonst ist die Formelschreibweise gleich wie schon in den vorherigen Tabs.

MANOVA.wide(cbind(jump_length, weight) ~ animal*stage, data = fac2_cov_tbl,
            iter = 1000) |> 
  summary()

Call: 
cbind(jump_length, weight) ~ animal * stage

Descriptive:
  animal    stage n jump_length  weight
1    cat juvenile 8      20.280   5.590
2    cat    adult 8      38.360  17.199
3    dog juvenile 8      31.761   5.959
4    dog    adult 8      35.498  11.556
5    fox juvenile 8      37.102   9.304
6    fox    adult 8      40.062  14.293

Wald-Type Statistic (WTS):
             Test statistic df  p-value 
animal       "45.355"       "4" "<0.001"
stage        "106.846"      "2" "<0.001"
animal:stage "40.245"       "4" "<0.001"

modified ANOVA-Type Statistic (MATS):
             Test statistic
animal               43.924
stage               106.346
animal:stage         39.443

p-values resampling:
             paramBS (WTS) paramBS (MATS)
animal       "<0.001"      "<0.001"      
stage        "<0.001"      "<0.001"      
animal:stage "0.001"       "0.001"       

Das R Paket hat die Eigenschaften mehr Informationen zu liefern als man eigentlich will. Auf der einen Seite ja ganz nett, aber auf der anderen Seite immer wieder verwirrend was ich denn jetzt nehmen soll. Wir nutzen die p-Werte unter Wald-Type Statistic (WTS), die uns ebenfalls signifikante Unterschiede zeigen. Wir haben einen signifikanten Effekt der Floharten sowie der Entwicklungsstadien plus einer signifikanten Interaktion auf die kombinierten Sprungweiten und Flohgewichte.

34.6 Post-hoc Test

Am Ende können wir dann noch den Post-hoc Test rechnen. Ich beschränke mich dann einmal auf die zweifaktorielle Analyse. Den einfaktoriellen Fall kannst du dann gleichwertig selber einmal durchrechnen. Wir hätten hier auch die Wahl die beiden Messwerte aufzubrechen und dann jeweils für die Sprungweite und das Gewicht eine separate Post-hoc Analyse rechnen können. Hier kommt es dann auch deine Fragestellung an. Wir müsseh hier natürlich auch noch ein paar Einschränkungen machen. Wir nutzen die Funktion {MANOVA.wide} aus dem R Paket {MANOVA.RM} womit wir dann einen nichtparametrischen Ansatz wählen. Wir haben dadurch dann auch nicht die Notwendigkeit für einen normalverteilten Messwert. Dann rechnen wir einmal den Post-hoc Test an den Anschluss einer MANOVA. Ein Nachteil der Funktion ist natürlich, dass wir hier mehr Informationen kriegen als wir dann am Ende vermutlich wollen.

Zuerst müssen wir einmal mit der Funktion cbind() auf der linken Seite die beiden Messwerte in der Formelschreibweise zusammenbringen. Dann können wir auch auf der rechten Seite einmal die Faktoren difinieren. Ich möchte hier die Tierarten zusammen mit dem Entwicklungsstand und deren Interaktion modellieren. Am Ende noch die Option, wie genau das Modell sein soll. Am Ende ist es ein Permutationstest und der wird genauer je öfter er läuft. Ich setze den Test mal auf iter = 1000 Wiederholungen. Dann möchte ich noch alle paarweisen Vergleiche rechnen und nutze dafür die Funktion simCI(), die dann auch gleich die 95% Konfidenzintervalle produziert.

MANOVA.wide(cbind(jump_length, weight) ~ animal*stage, data = fac2_cov_tbl,
            iter = 1000) |> 
  simCI(contrast = "pairwise", type = "Tukey")

 #------ Call -----# 
 
 - Contrast:  Tukey 
 - Confidence level: 95 % 

 #------Multivariate post-hoc comparisons: p-values -----# 
 
                      contrast p.value
1     cat adult - cat juvenile   0.001
2  dog juvenile - cat juvenile   0.506
3     dog adult - cat juvenile   0.077
4  fox juvenile - cat juvenile   0.016
5     fox adult - cat juvenile   0.011
6     dog juvenile - cat adult   0.055
7        dog adult - cat adult   0.811
8     fox juvenile - cat adult   0.401
9        fox adult - cat adult   1.000
10    dog adult - dog juvenile   0.774
11 fox juvenile - dog juvenile   0.540
12    fox adult - dog juvenile   0.196
13    fox juvenile - dog adult   1.000
14       fox adult - dog adult   0.930
15    fox adult - fox juvenile   0.751

 #-----------Confidence intervals for summary effects-------------# 
 
                            Estimate      Lower      Upper
cat adult - cat juvenile      29.689  10.372469 49.0055312
dog juvenile - cat juvenile   11.850  -8.384588 32.0845876
dog adult - cat juvenile      21.184  -1.420090 43.7880899
fox juvenile - cat juvenile   20.536   3.612070 37.4599298
fox adult - cat juvenile      28.485   6.361304 50.6086958
dog juvenile - cat adult     -17.839 -35.790902  0.1129016
dog adult - cat adult         -8.505 -29.090847 12.0808475
fox juvenile - cat adult      -9.153 -23.268652  4.9626521
fox adult - cat adult         -1.204 -21.261172 18.8531721
dog adult - dog juvenile       9.334 -12.115645 30.7836450
fox juvenile - dog juvenile    8.686  -6.662022 24.0340224
fox adult - dog juvenile      16.635  -4.307786 37.5777865
fox juvenile - dog adult      -0.648 -19.007415 17.7114154
fox adult - dog adult          7.301 -15.939195 30.5411947
fox adult - fox juvenile       7.949  -9.815604 25.7136044

Zum einen erhalten wir dann alle paarweisen p-Werte für die kombinierte Analyse der Sprungweiten und des Gewichts der Flöhe. Hier können wir dann gewohnt mit dem p-Wert entscheiden. Dabei ist zu beachten, dass alle p-Werte für multiple Vergleiche adjustiert wurden. Dann kämen als nächstes die 95% Konfidenzintervalle, die hier auch einen direkten Effekt mitliefern. Wir können dann einmal in der Vingette nachlesen und erfahren dann Folgendes über den Effekt.

“Confidence intervals are calculated based on summary effects, i.e., averaging over all dimensions” — Friedrich et al. (2019)

Oder andersherum, dass ist ziemlich schwierig zu interpretieren, wenn unsere Sprungweite und unser Gewicht unterschiedliche Einheiten hat. Wir mitteln ja über Sprungweite in [cm] und das Gewicht in [mg]. Das hilft nur, wenn wir die gleiche Einheit in unseren Messwerten haben, ansonsten ist der Effekt wild und nicht biologisch zu interpretieren. Hier müsstest du dann eventuell vorher deine Messwerte skalieren, so dass du dann einheitslose Messwerte hast. Ob das dann sinnvoller ist, hängt von deiner Fragestellung ab.

“Persönlich finde ich die Interpretation einer eines Post-hoc Test über einen simultanen Messwert sehr schwer zu interpretieren. Gut, wir erhalten hier ja auch einen direkten Effekt wiedergegeben, aber trotzdem würde ich hier dann die Messwerte aufteilen und getrennte univariate Post-hoc Analysen einmal für die Sprungweite und einmal für das Gewicht der Flöhe rechnen.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

Referenzen

Ateş, C., Kaymaz, Ö., Kale, H. E., & Tekindal, M. A. (2019). Comparison of test statistics of nonnormal and unbalanced samples for multivariate analysis of variance in terms of type-I error rates. Computational and mathematical methods in medicine, 2019(1), 2173638.

Friedrich, S., Konietschke, F., & Pauly, M. (2019). Resampling-based analysis of multivariate data and repeated measures designs with the R package MANOVA. RM.

O’Brien, R. G., & Kaiser, M. K. (1985). MANOVA method for analyzing repeated measures designs: an extensive primer. Psychological bulletin, 97(2), 316.

Warne, R. (2014). A primer on multivariate analysis of variance (MANOVA) for behavioral scientists. Practical Assessment, Research, and Evaluation, 19(1).