25 Der Pre-Test oder Vortest
Letzte Änderung am 02. June 2025 um 09:43:40
“I struggle with some demons; They were middle class and tame.” — Leonard Cohen, You Want It Darker
In diesem Kapitel soll es um den Pre-Test oder auch Vortest gehen. Wir sind hier in einem experimentellen Design, welches verschiedene Gruppen beinhaltet oder aber wir wollen wissen, ob wir in einer linearen Regression die Normalverteilung unseres Messwertes \(y\) vorliegen haben. Grundsätzlich geht es erstmal darum herauszufinden, ob die Annahmen an einen statistischen Test in deinen Daten erfüllt sind. Häufig wollen wir eine ANOVA für einen Gruppenvergleich rechnen und dann anschließend einen multiplen Test oder Post-hoc Test durchführen. In beiden Fällen wird es einfacher wenn wir eine Normalverteilung in unseren Messwert \(y\) sowie eine Varianzhomogenität in unseren Behandlungsgruppen oder Faktoren \(f\) vorliegen haben. Mit einfacher meine ich, dass du auch mit einer Abweichung von der Normalvertielung und auch Varianzhterogenität heutzutage umgehen kannst. Der Standard im statistischen Testen war aber immer die Normalverteilung und die Varianzhomogenität. Wenn beides nicht vorlag, dann wurde es manchmal etwas dunkel. Wir aber aber im 21. Jahrhundert ein paat mehr Pfeile im Köcher und können mit unterschiedlichsten Daten und deren Eigenschaften umgehen. Mehr dazu findest du im Teil zum statistsichen Modellieren und den nachfolgenden Kapiteln.
“Eigentlich ist dieses Kapitel ein einziger Unfall. Auf der einen Seite mag ich diese Vortests überhaupt nicht, da den Vortests viel zu viel Glauben geschenkt wird, als sie wirklich beweisen können. Auf der anderen Seite sehe ich das Verlangen nach einen Beweis, welcher Art auch immer, durch einen Test zu erhalten. Ich beuge mich also dem Wunsch und schreibe diesen Leviatan runter.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
25.1 Allgemeiner Hintergrund
Wir werden uns in diesem Kapitel auf das faktorielle Experiment konzentrieren. Natürlich kannst du auch alle Funktionen in einem anderen Design anwenden. Wenn du wissen willst, ob eine Variable normalverteilt ist oder aber ein Gruppenfaktor homogen in den Varianzen, dann helfen dir hier auch die Funktionen weiter. Häufig werden aber die beiden Eigenschaften Normalverteilung und Varianzhomogenität in Gruppenvergleichen verwendet.
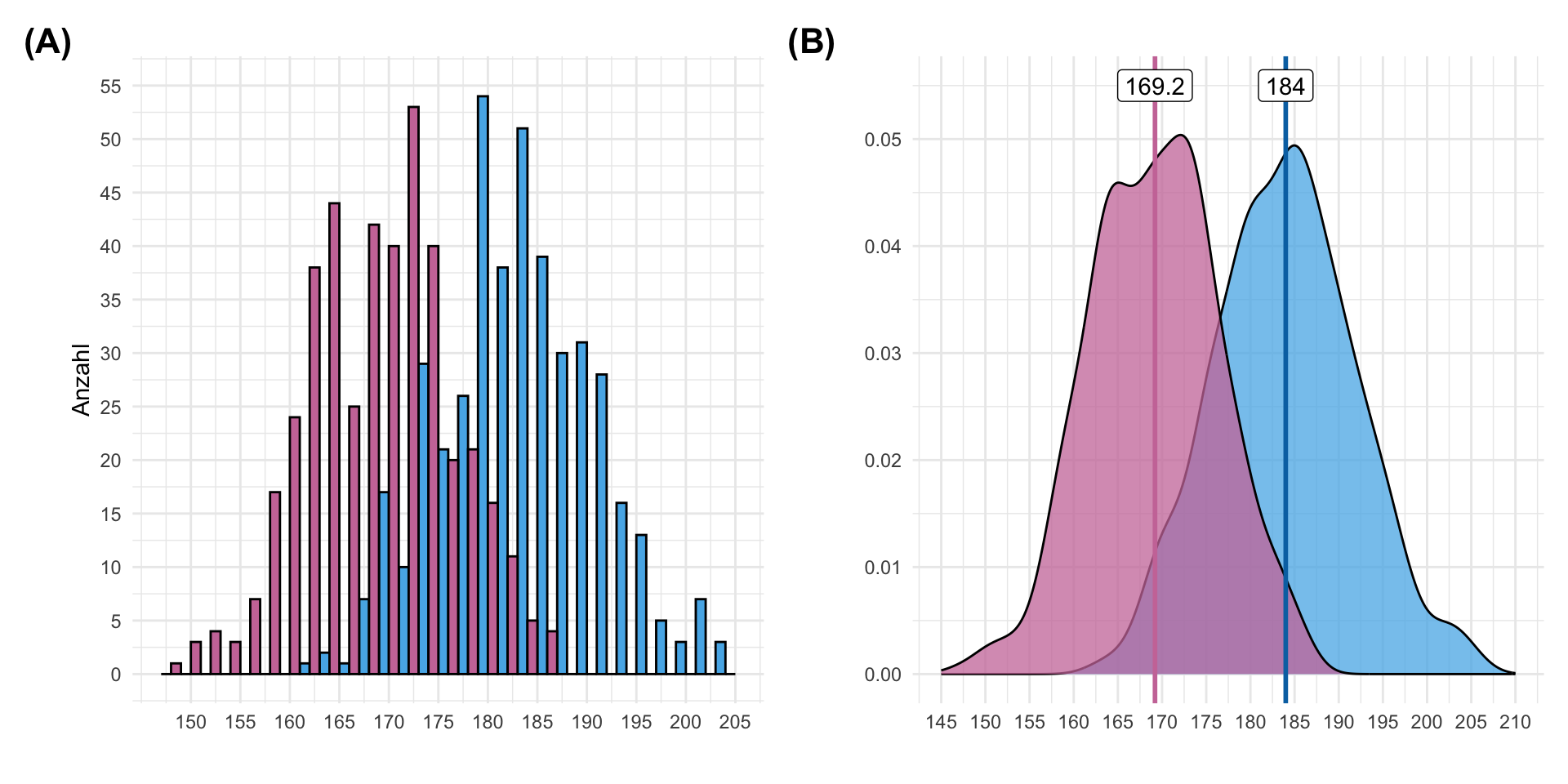
Eine Sache ist aber wichtig zu wissen. Wir untersuchen in unseren Experimenten ja immer nur eine Stichprobe der Grundgesamtheit und wollen dann von der Stichprobe einen Rückschluß auf die Grundgesamt machen. Wenn dich mehr dazu interessiert, dann schaue einmal in dem Kapitel zum Testen von Hypothesen rein. Es kann also sein, dass wir definitiv in der Grundgesamtheit einen normalverteilten Messwert vorliegen haben, wir aber noch zu wenige Beobachtungen in unsere Stichprobe vorliegen haben um diese Normalverteilung in einem Histogramm oder Densityplot zu sehen. Nehmen wir einmal die Körpergröße als ein normalverteilten Messwert \(y\) an. Wir wissen, dass die Körpergröße einer Normalverteilung folgt. In der folgenden Abbildung Abbildung 25.1 siehst du einmal die Körpergrößen von unseren Gummibärchendaten. Insgesamt haben \(444\) Männer und \(430\) Frauen bei der Gummibärchenumfrage mitgemacht. Dennoch beobachten wir keine saubere Normalverteilung, wie wir sie erwarten würden. Wir haben noch zu wenige Beobachtungen gemacht.
Wir sehen also, nur weil etwas wie die Körpergröße wirklich normalverteilt ist, ist es noch etwas ganz anders diese Normalverteilung dann auch in den Messwert \(y\) zu beobachten. Die Fallzahlen in der Grundgesamt und in der Stichprobe unterscheiden sich dann doch gewaltig und wir sind dann eben auch auf Annahmen angewiesen. Meistens passt es auch mit den Annahmen und wenn wir mal daneben liegen, kann es sein, dass es dann doch nicht so viel ausmacht, wenn der Effekt in unserer statistischen Auswertung groß genug ist.
Das Modell
Auch hier möchte ich einmal das statistische Modell besprechen was wir in dem Gruppenvergleich oder dem statistischen Modellieren benötigen. Im Folgenden findest du einmal ein faktorielles Modell mit einem Messwert \(y\) und zwei Gruppenfaktoren \(f_A\) und \(f_B\). Die beiden Faktoren entsprechen zwei unterschiedlichen kategoriellen Variablen mit verschiedenen Gruppen. Wir wollen uns ja in diesem Kapitel auf die Normalverteilung und die Varianzhomogenität konzentrieren. Die beiden Gütekriterien können aber ganz klar dem Messwert \(y\) und den experimentellen Faktoren zugeordnet werden.
\[ \underbrace{\;\mbox{Messwert}\; y\;}_{normalverteilt} \sim \overbrace{\;\mbox{Faktor}\; f_A + \mbox{Faktor}\; f_B\;}^{homogene\; Varianzen} \]
mit
- \(\mbox{Messwert}\; y\), gleich dem Messwert oder Outcome, wie die Sprungweite in [cm] als
jump_lengthin unseren Beispieldaten. - \(\mbox{Faktor}\; f_A\), gleich dem ersten Faktor \(f_A\), wie die Tierart als
animalmit unterschiedlichen Gruppen oder Leveln. - \(\mbox{Faktor}\; f_B\), gleich dem zweiten Faktor \(f_B\), wie der Messort als
sitemit unterschiedlichen Gruppen oder Leveln.
Damit haben wir uns erstmal für die Vortest für die Normalverteilung und die Varianzhomogenität geordnet. Wir wollen dann in den folgenden Abschnitten noch andere Gütekriterien eines Modells kurz anreißen, aber den Hauptteil findest du im Kapitel zur Modelgüte von linearen Modellen.
Gibt es noch mehr Vortests?
Jetzt könnte man meinen, dass mit der Normalverteilung und der Varianzhomogenität eigentlich die wichtigsten Gütekriterien vorgetestet werden. Es gibt aber für lineare Modelle, was ein Gruppenvergleich dann am Ende auch nur ist, noch andere Gütekriterien. Neben diesen beiden Eigenschaften können wir usn auch noch folgende weitere Gütekriterien anschauen. Ich verweise hier einmal auf die Hilfeseite des R Packetes {performance} für mehr Informationen und deren Referenzseite der Familie der check_*() Funktionen. Wie immer kommt es dann auf die Fragestellung und dann auf das enstprechende Modell sowie den verwendeten Algorithmus an. Je nachdem was du gemessen hast, also welche Werte dein \(y\) annimmt, musst du einen anderes Modell wählen. Je nach Modell hast du dann auch andere Annahmen. Das würde hier aber das Kapitel sprengen. Gerne kannst du als Startpunkt einmal in das Teil zum statistsichen Modellieren reinschauen.
Betrachten wir also einmal im Folgenden die beiden wichtigsten Annahmen an ein faktorielles Design oder aber Gruppenvergleich. Wir fragen uns, haben wir eine Normalverteilung in den Messwerten \(y\) und homogene Varianzen in den Faktoren oder Gruppen \(f\) vorliegen? Dann können wir ganz normal eine ANOVA oder einen Tukey HSD Test rechnen.
25.1.1 Normalverteilung
Fangen wir also mit der Annahme der Normalverteilung an die Daten an. Hierbei ist wichtig, dass wir nicht die Daten insgesamt betrachten sondern uns fragen, ob der betrachtete Messwert \(y\) im Modell oder statistischen Test normalverteilt ist. Wir haben uns den Zusammenhang ja schon oben einmal in dem statistischen Modell angeschaut. Häufig führt dies zu Verwirrungen, da verallgemeinert von den Daten gesprochen wird, die normalverteilt sein soll. Hier geht es dann wirklich nur um deinen Messwert \(y\). Das nochmal als Erinnerung für die weiteren Betrachtungen. Was wären also beispielhaft normalverteilte Messwerte?
Beispiel: Frischgewicht, Trockengewicht, Chlorophyllgehalt, Pflanzenhöhe
| freshmatter | drymatter | chlorophyll | height |
|---|---|---|---|
| 8.23 | 1.21 | 45.88 | 24.19 |
| 2.61 | 0.87 | 43.91 | 18.51 |
| 4.81 | 0.34 | 37.44 | 21.74 |
Nach dem zentralen Grenzwertsatz können wir bei Merkmalen, die sich aus verschiedenen Einflussfaktoren zusammensetzen, allgemein von einer Normalverteilung ausgehen. Die Körpergröße oder das Körpergewicht ist normalverteilt, da wir hier es mit vielen Einflussgrößen zu tun haben, die das tatsächliche Körpergewicht einer Beobachtung ausmachen. Das Körpergewicht hängt eben von der täglichen Kalorienmenge, verschiedensten Genen, dem Muskelanteil, dem Aktivitätsgrad, der sozialen Stellung und vielen weiteren Einflusfaktoren ab. Alles zusammen addiert sich dann zum Körpergewicht wobei jeder Einflussfaktor nur einen kleinen Teil ausmacht.
- Was heißt approximativ normalverteilt?
-
Wir sprechen von approximativ normalverteilt, wenn wir meinen, dass ein Messwert \(y\) in unserer Stichprobe annähernd normalverteilt ist. Wir sind uns also nicht zu hundertprozent sicher, glauben aber das die Normalverteilungsannahme an unseren Messwert passen wird. Häufig sagen wir auch, dass gewisse Tranformationen approximativ normalverteilt sind. So haben wir nach einer log-Transformation log-normalverteilte Messwerte vorliegen. Wir sagen dann meistens, dass ein log-transformierter Messwert approximativ normalverteilt ist.
25.1.2 Varianzhomogenität
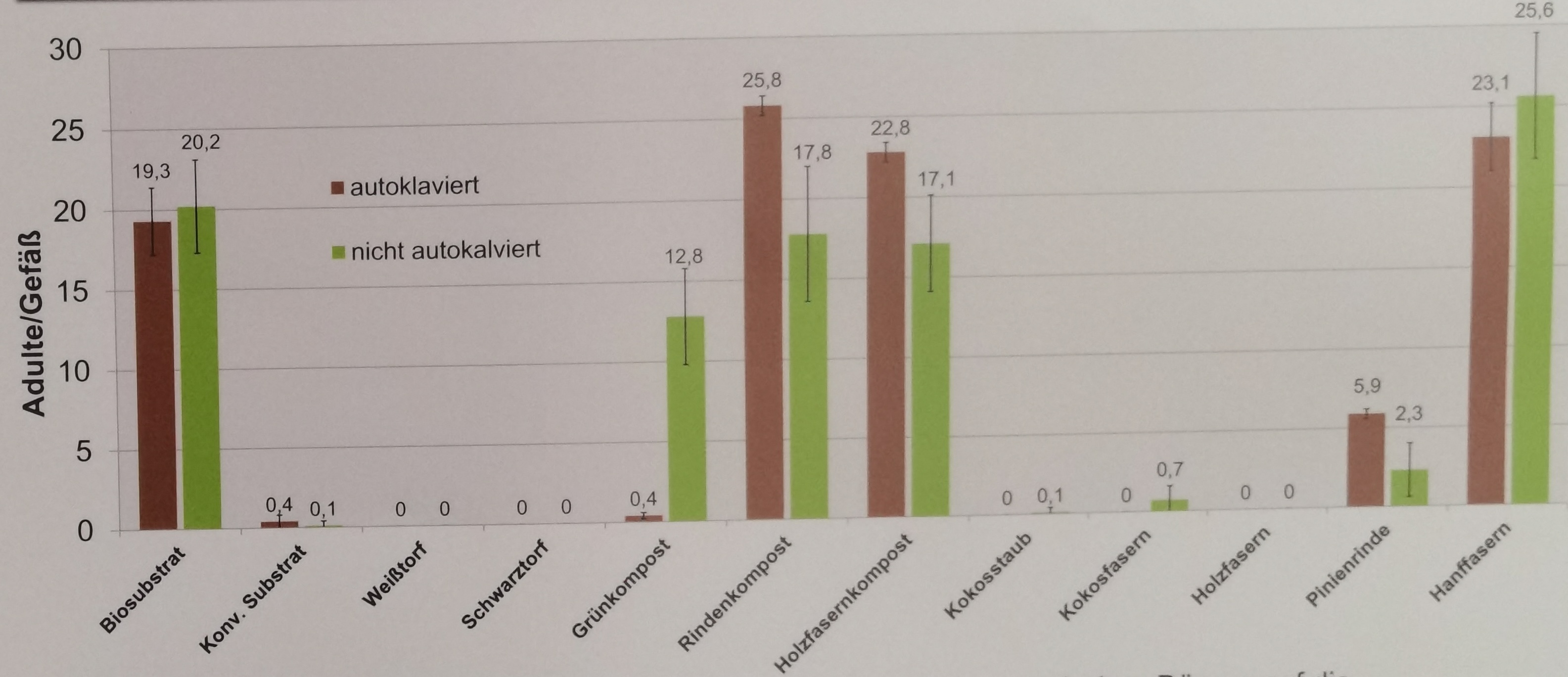
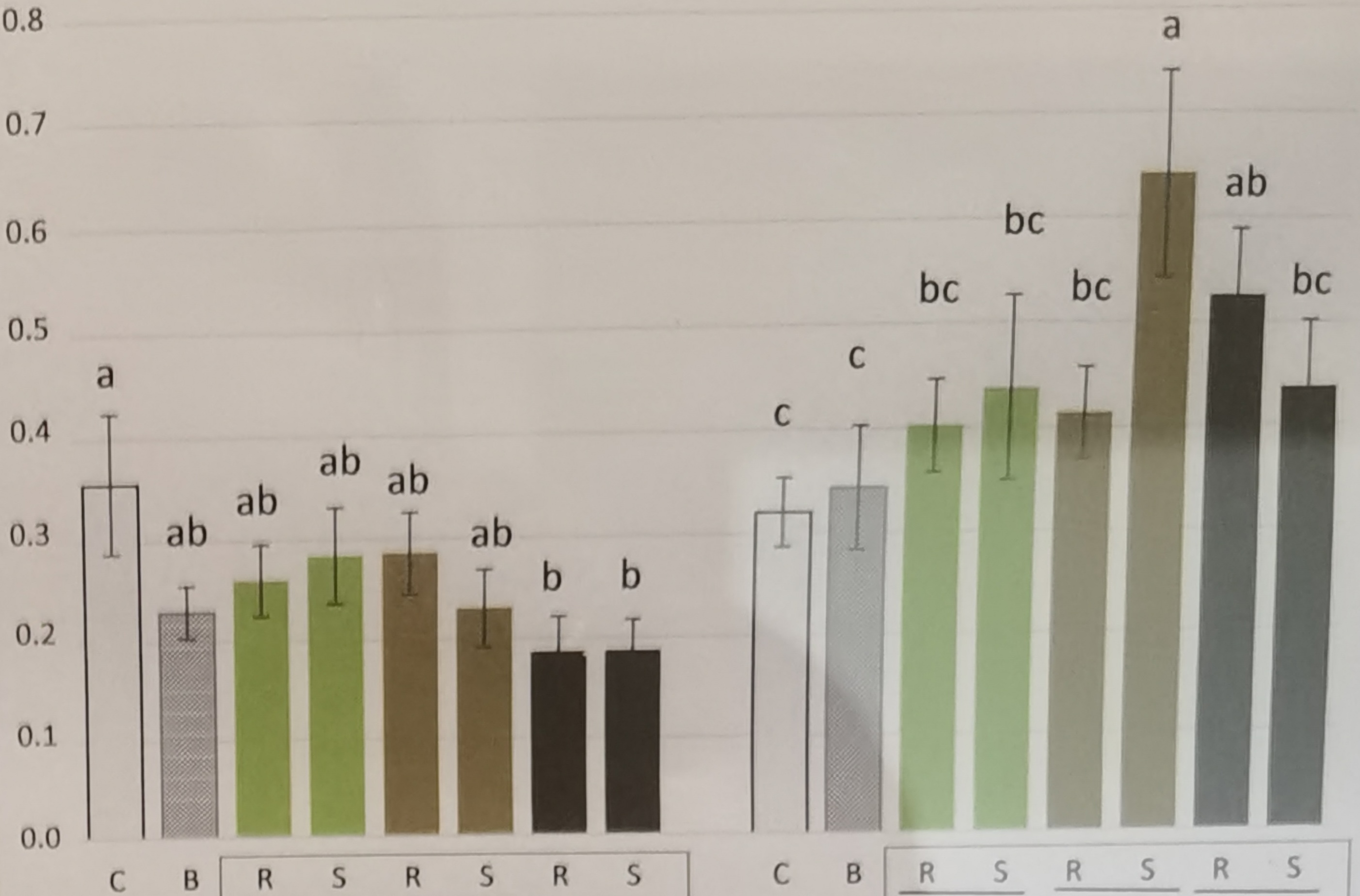
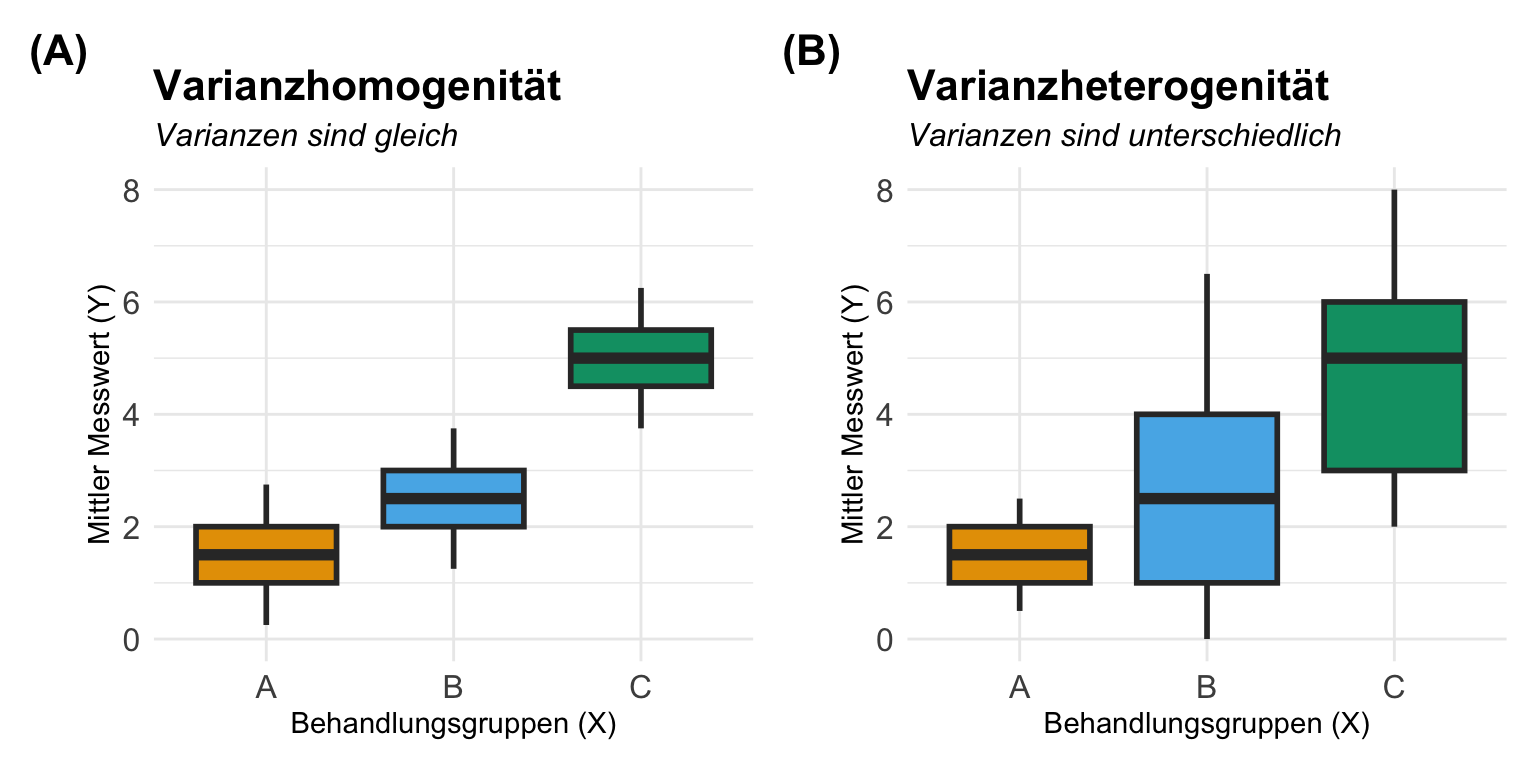
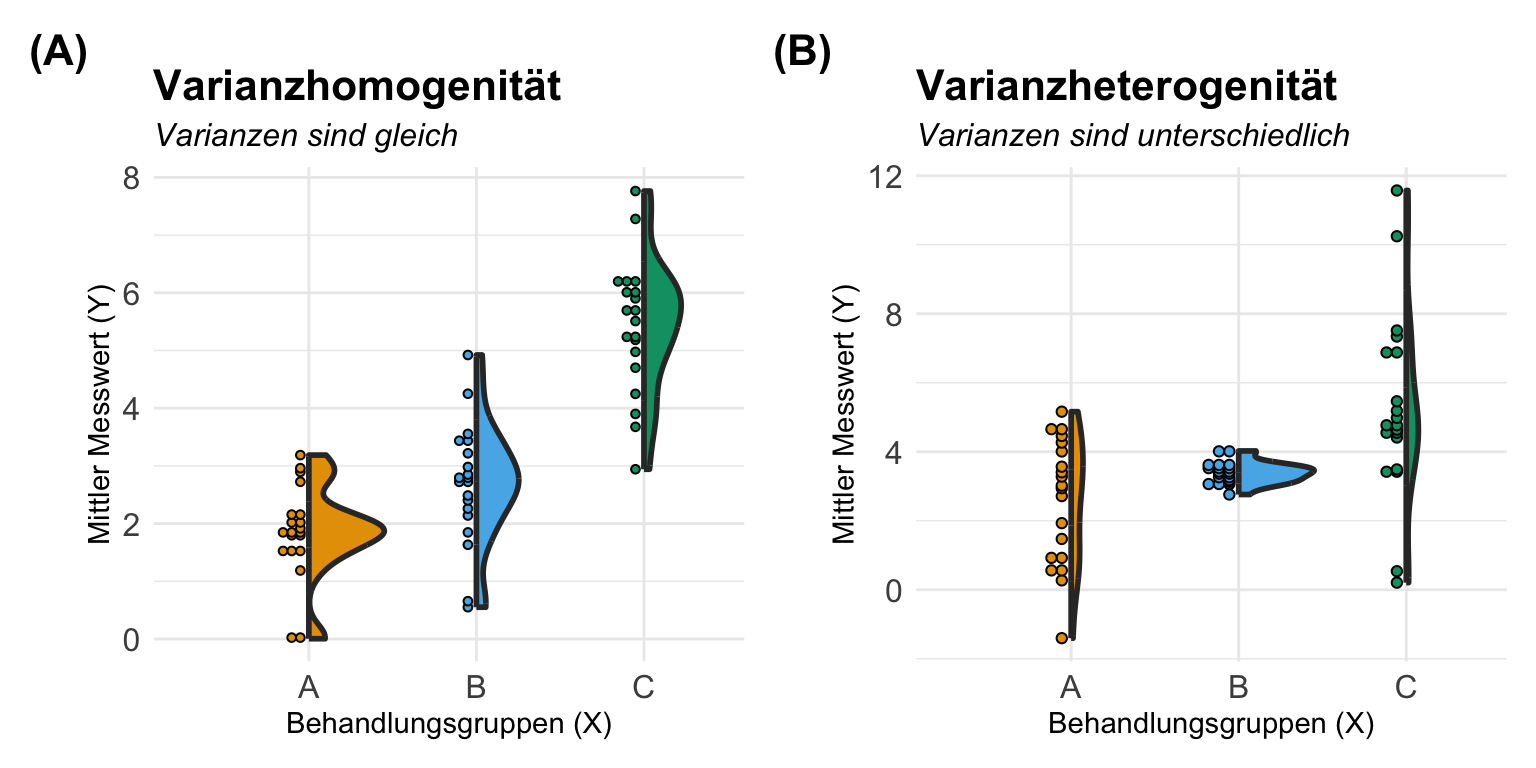
Kommen wir nun zur Varianzhomogenität oder Varianzheterogenität in den Gruppen des Behandlunsgfaktors. Je nachdem was du betrachtest, nennen wir es eben Varianzhomogenität oder Varianzheterogenität. Entweder sind die Varianzen gleich, dann haben wir Varianzhomogenität vorliegen oder die Varianzen in den Gruppen sind nicht gleich, dann hast du Varianzheterogenität in den Daten. Es gibt so ein paar Daumenregeln, die dir helfen abzuschätzen, ob in deinen Gruppen Varianzheterogenität vorliegt. Um es kurz zu machen, vermutlich hast du mindestens leichte Varianzheterogenität in den Daten vorliegen. Es ist bei kleinen Gruppengrößen nicht zu vermeiden, dass sich die Varianzen eben dann doch unterscheiden. Ich habe dir in der folgenden Abbildung vier theoretische Fälle mit Varianzheterogenität mitgebracht. Die Ursache der Heterogenität ist hierbei immer das experimentelle Design und muss dann in der entsprechenden Modellierung später berücksichtigt werden.
In den folgenden Beispielen habe ich dir einige Experimente mit einem faktoriellen Design mitgebracht. Die Fotos stammen aus wissenschaftlichen Publikationen wie einer wissenschaftlichen Veröffentlichung oder aber wissenschaftlichen Postern hier auf dem Gelände der Hochschule Osnabrück. Wie du siehst, sind dann die Foros doch immer mal anders als die theoretische Betrachtung der Varianzquellen.
Jetzt haben wir uns einmal die wichtigsten Abbildungen angeschaut und haben so eine erste Idee was Varianzhomogenität sein könnte. Wir schauen uns dann in den folgenden Abschnitten noch mehr zu der Bestimmung an. Dann bleibt eigentlich noch eine abschließende Frage für den einführende Abschnitt.
- Tut Varianzheterogenität anstatt Varianzhomogenität weh?
-
Nein. Meistens ist die Varianzheterogenität nicht so ausgeprägt, dass du nicht auch eine ANOVA oder anderen statistischen Test rechnen kannst. Über alle Gruppen hinweg wird dann zwar zum Beispiel in einer ANOVA die Varianz gemittelt und es kann dann zu weniger signifikanten Ergebnissen führen, aber so schlimm ist es nicht. Im Post-hoc Test solltest du aber die Varianzheterogenität berücksichtigen, da du ja immer nur zwei Gruppen gleichzeitig betrachtest. Aber auch hier gibt es dann die passenden Adjustierungen. Mehr dazu am Ende des Kapitels im Abschnitt zu den Auswegen.
25.2 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
pacman::p_load(tidyverse, magrittr, olsrr,
broom, car, performance,
see, scales, readxl, nlme,
moments, report, skedastic,
parameters, lmtest, conflicted)
conflicts_prefer(dplyr::filter)
conflicts_prefer(dplyr::select)
conflicts_prefer(moments::skewness)
conflicts_prefer(moments::kurtosis)An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
25.3 Daten
Wir immer bringe ich hier ein paar Datensätze mit damit wir dann verstehen, was eigentlich in den folgenden Analysen in R und den entsprechenden R Paketen passiert. Ich zeige hier an den Daten nur die Anwendung in R. Deshalb fehlen dann hier auch die Mittelwerte und andere deskriptive Maßzahlen. Schauen wir jetzt also mal in unsere Beispieldaten für die einfaktorielle und zweifaktorielle Datenanalyse rein.
Einfaktorieller Datensatz
Beginnen wir mit einem einfaktoriellen Datensatz. Wir haben hier als Messwert die Sprungweite von Flöhen in [cm] vorliegen. Wissen wollen wir, ob sich die Sprungweite für drei verschiedene Floharten unterscheidet. Damit ist dann in unserem Modell der Faktor animal und die Sprungweite jump_length als Messwert. Ich lade einmal die Daten in das Objekt fac1_tbl. Hier haben wir dann ein simples Design vorliegen.
R Code [zeigen / verbergen]
fac1_tbl <- read_xlsx("data/flea_dog_cat_fox.xlsx") |>
select(animal, jump_length) |>
mutate(animal = as_factor(animal))Dann schauen wir uns die Daten einmal in der folgenden Tabelle als Auszug einmal an. Wichtig ist hier nochmal, dass du eben einen Faktor animal mit drei Leveln also Gruppen vorliegen hast. Wir wollen jetzt die drei Tierarten hinsichtlich ihrer Sprungweite in [cm] miteinander vergleichen.
| animal | jump_length |
|---|---|
| dog | 5.7 |
| dog | 8.9 |
| dog | 11.8 |
| ... | ... |
| fox | 10.6 |
| fox | 8.6 |
| fox | 10.3 |
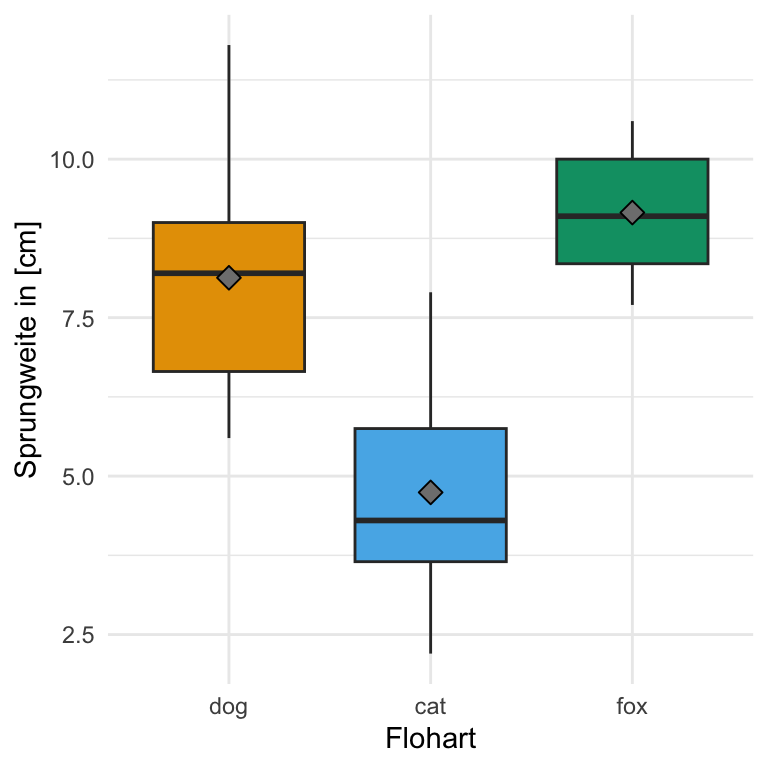
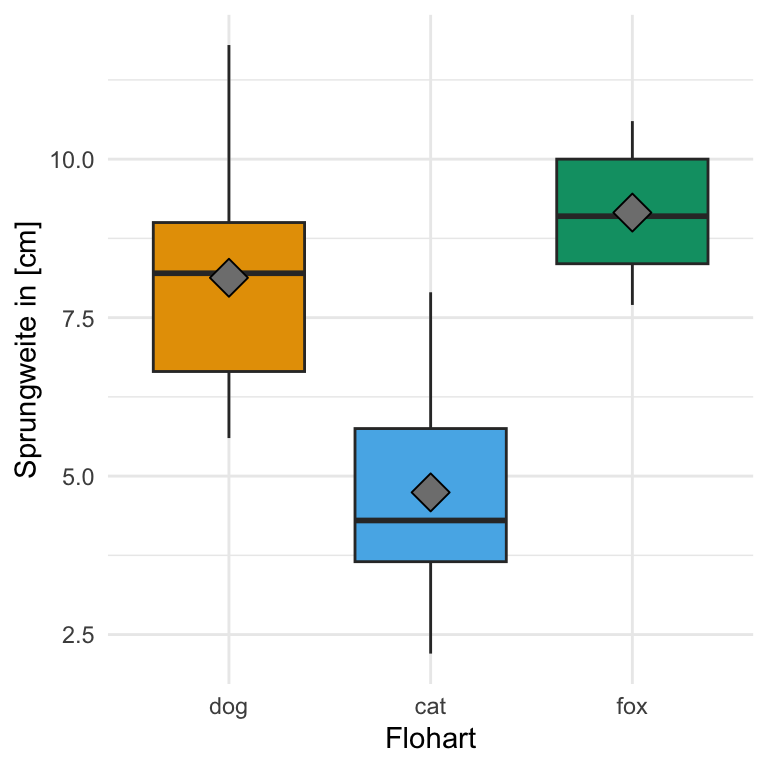
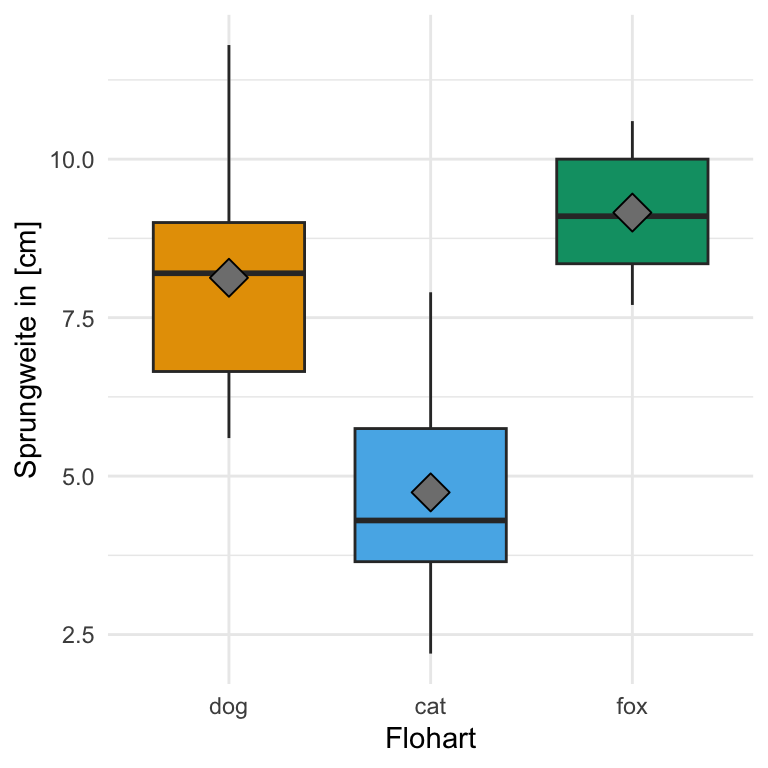
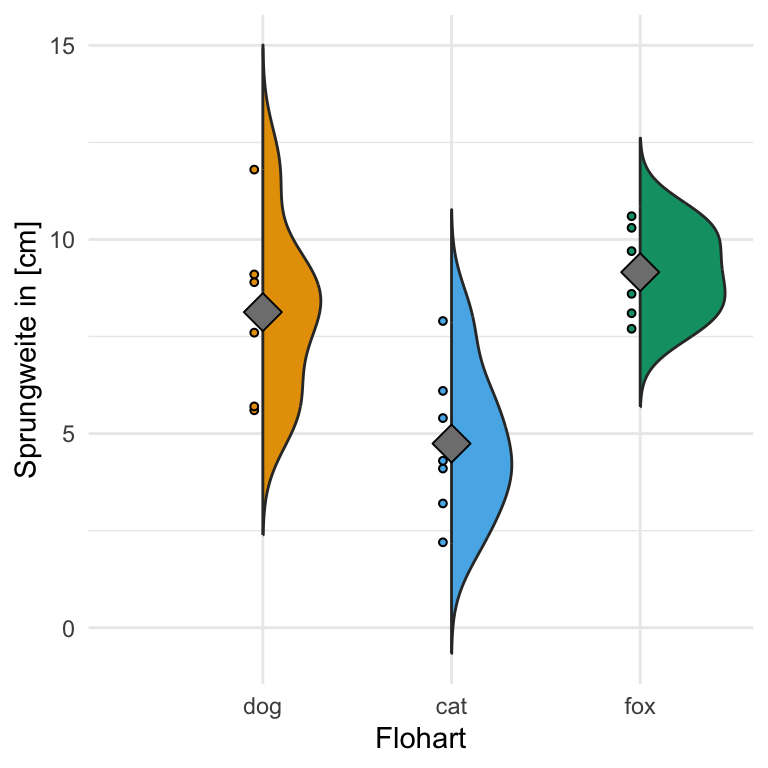
Und dann wollen wir uns noch einmal die Daten als einen einfachen Boxplot anschauen. Wir sehen, dass die Daten so gebaut sind, dass wir einen signifikanten Unterschied zwischend den Sprungweiten der Floharten erwarten. Die Boxen der Boxplots überlappen sich nicht und die Boxplots liegen auch nicht auf einer Ebene. Wir könnten hier von normalverteilten Daten und Varianzhomogenität ausgehen. Die Mediane liegen in der Mitte der Boxen und die Boxen sind ungefähr gleich groß.
Zweifaktorieller Datensatz
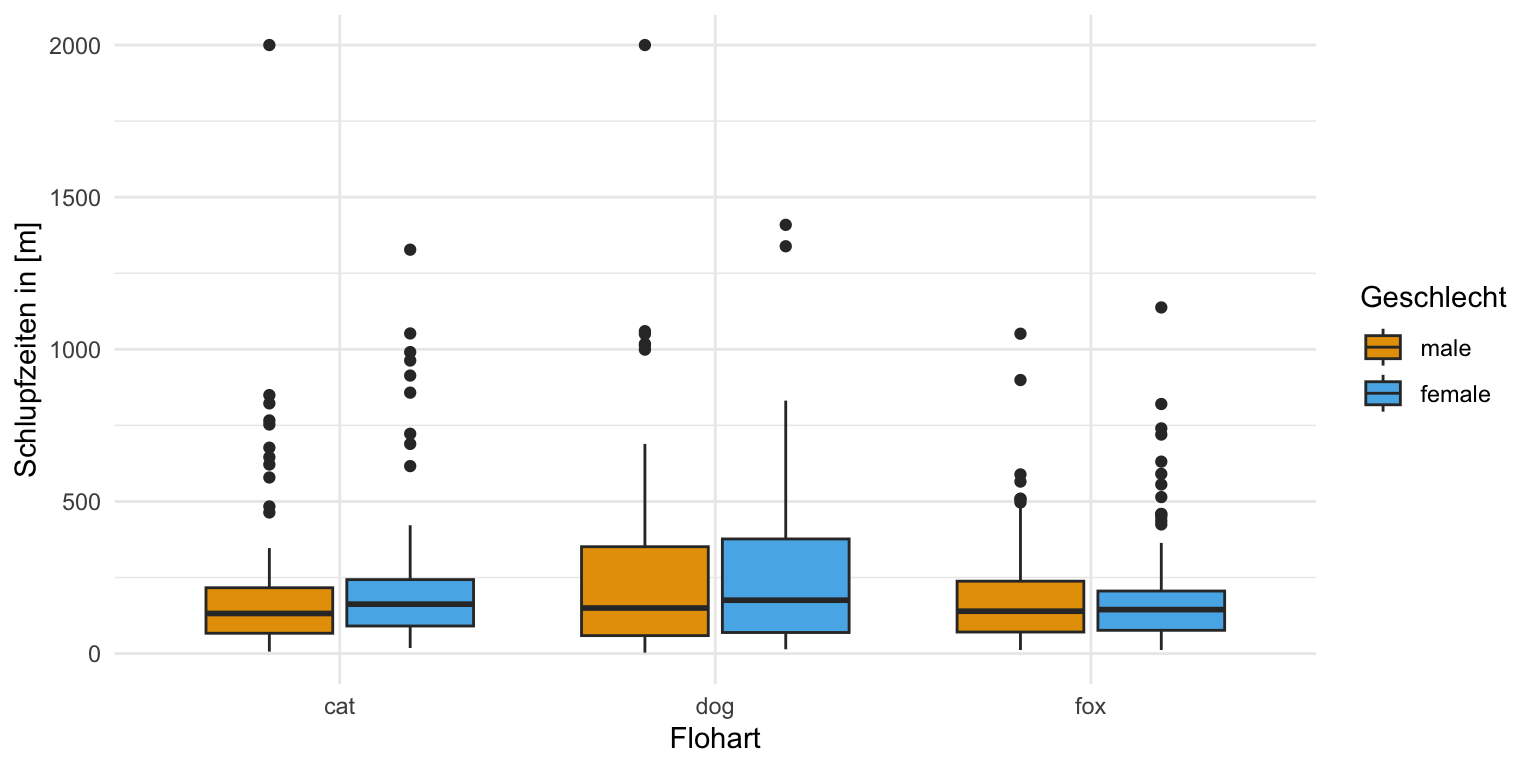
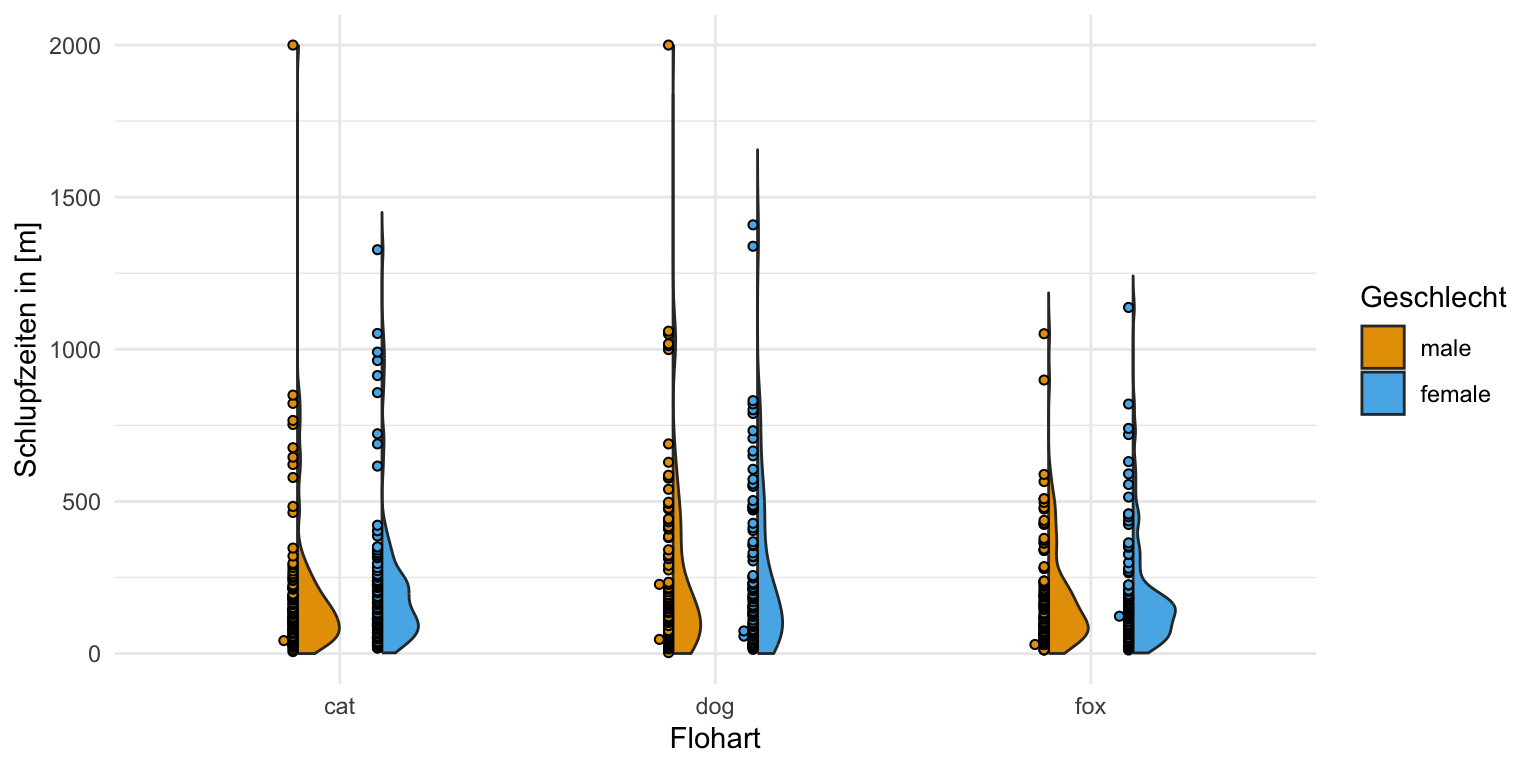
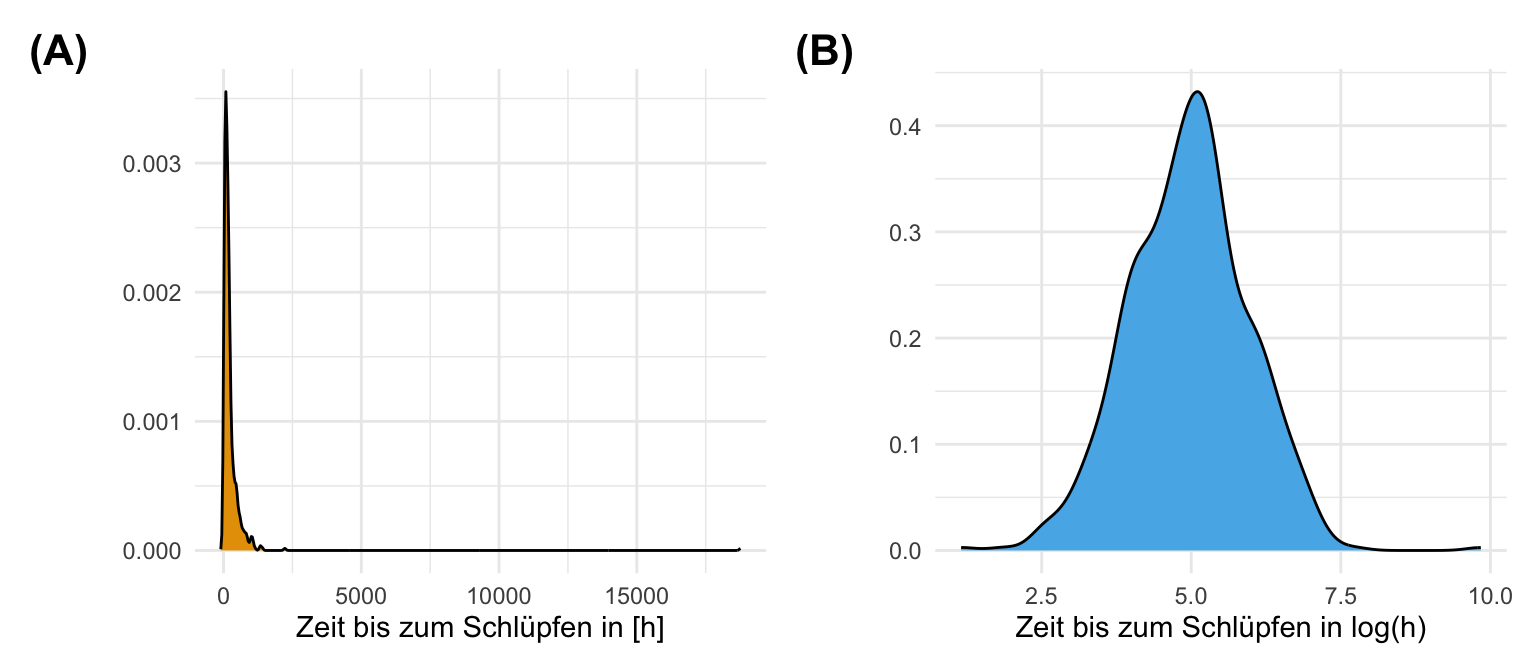
Neben dem einfaktoriellen Datensatz wollen wir uns noch den häufigeren Fall mit zwei Faktoren anschauen. Wir haben also nicht nur die drei Floharten vorliegen und wollen wissen ob diese unterschiedlich weit springen. Darüber hinaus haben wir noch einen zweiten Faktor gewählt. Wir haben die Sprungweiten der Hunde-, Katzen- und Fuchsflöhe nämlich für die beiden Geschlechter getrennt gemessen. Dadurch haben wir jetzt den Faktor animal und den Faktor sex vorliegen. Wiederum fragen wir uns, ob sich die Sprungweite in [cm] der drei Floharten in den beiden Geschlechtern unterscheidet. Darüber hinaus haben wir neben der Sprungweite noch die Schlupfzeiten in [m] gemessen. Im Folgenden lade ich einmal den Datensatz in das Objekt fac2_tbl und setze einmal zu lange Schlupfzeiten über 2000 Minuten auf fix 2000 Minuten mit der Funktion if_else().
R Code [zeigen / verbergen]
fac2_tbl <- read_xlsx("data/flea_dog_cat_length_weight.xlsx") |>
select(animal, sex, jump_length, hatch_time) |>
mutate(animal = as_factor(animal),
sex = as_factor(sex),
hatch_time = if_else(hatch_time > 2000, 2000, hatch_time)) Betrachten wir als erstes einen Auszug aus der Datentabelle. Wir haben hier als Messwert oder Outcome \(y\) die Sprungweite jump_length sowie die Schlupfzeiten hatch_time vorliegen. Als ersten Faktor die Variable animal und als zweiten Faktor die Variable sex festgelegt.
animal und einen zweiten Faktor mit sex vorliegen haben.
| animal | sex | jump_length | hatch_time |
|---|---|---|---|
| cat | male | 15.79 | 483.6 |
| cat | male | 18.33 | 82.56 |
| cat | male | 17.58 | 296.73 |
| ... | ... | ... | ... |
| fox | female | 24.35 | 182.68 |
| fox | female | 24.36 | 104.89 |
| fox | female | 22.13 | 62.99 |
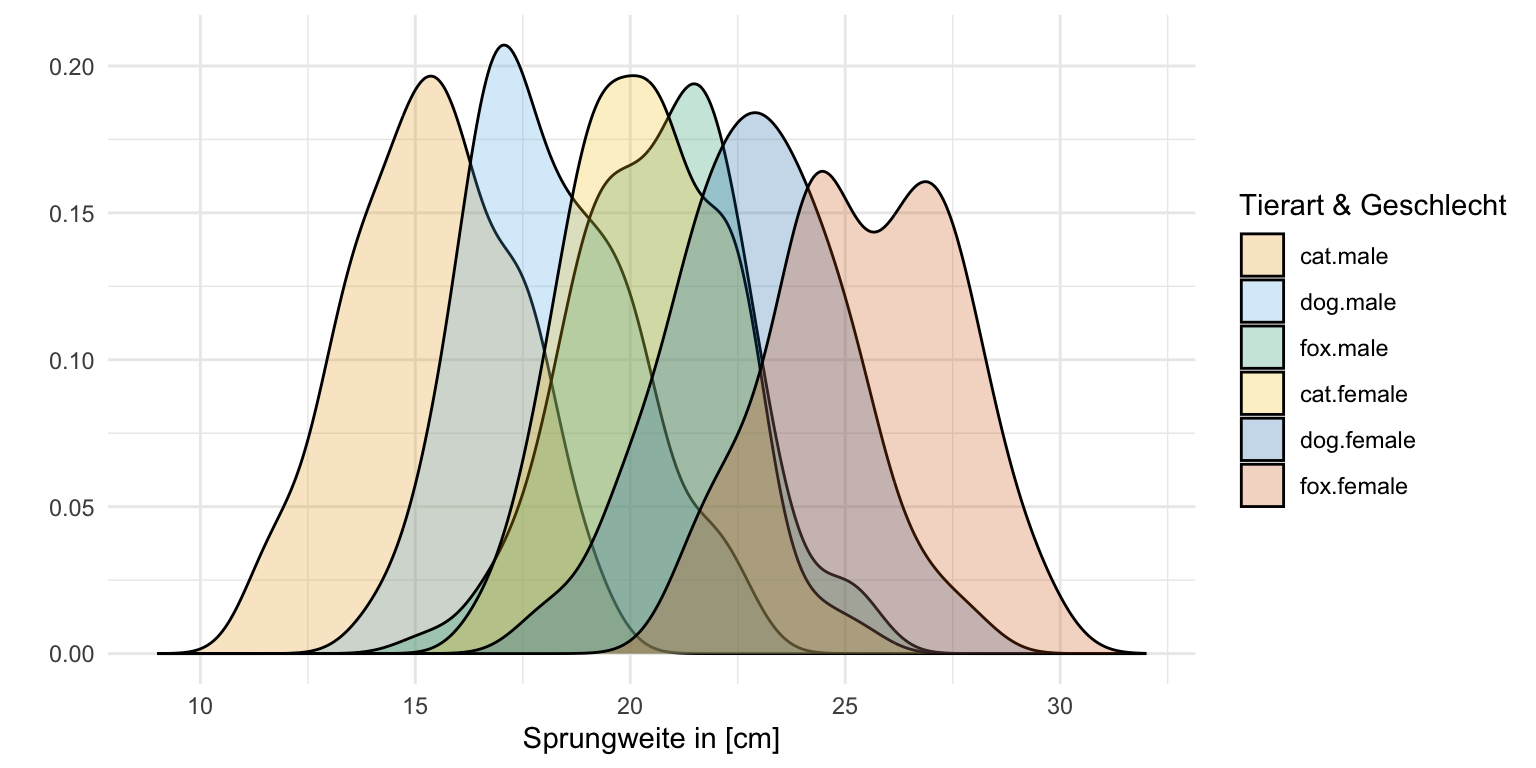
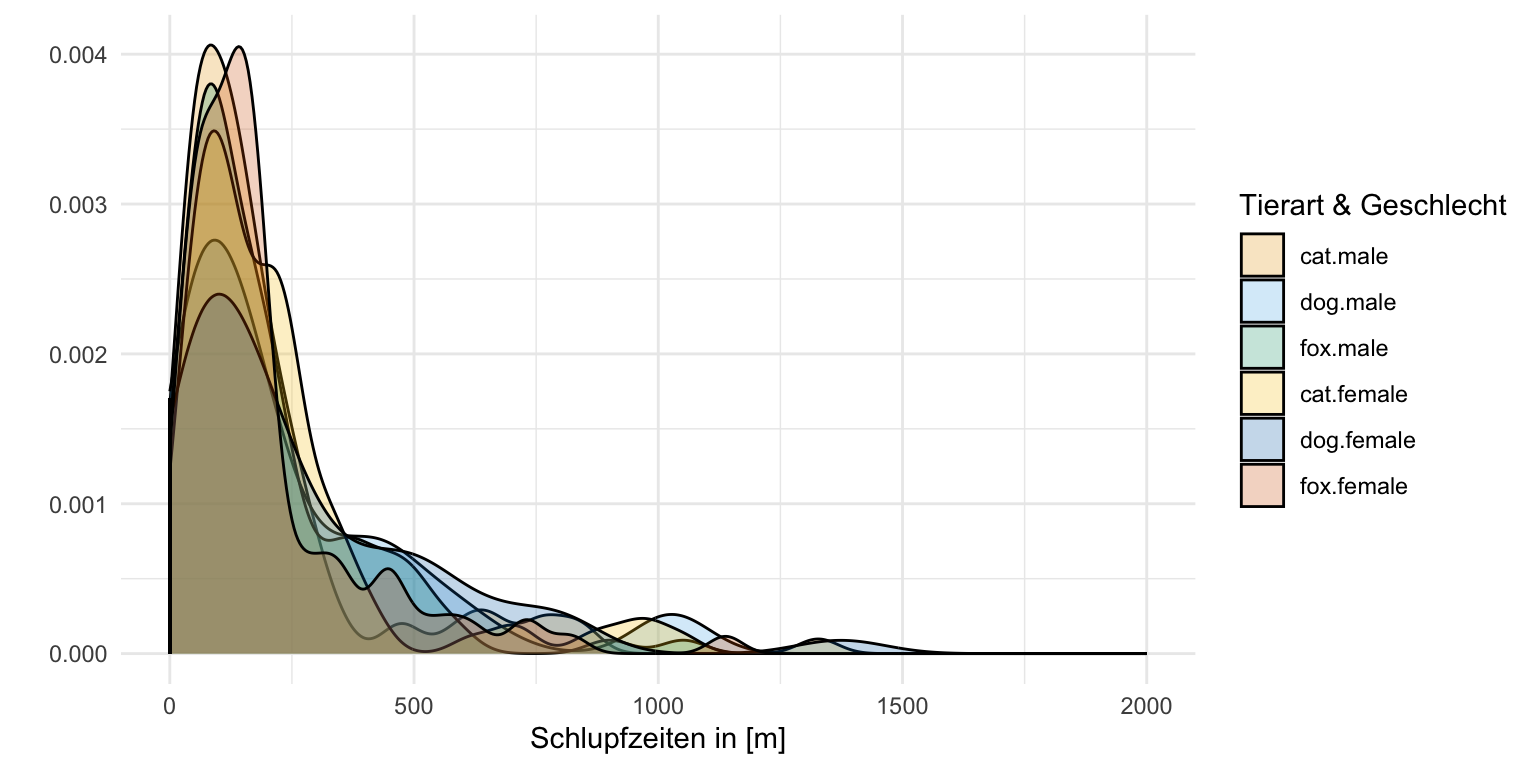
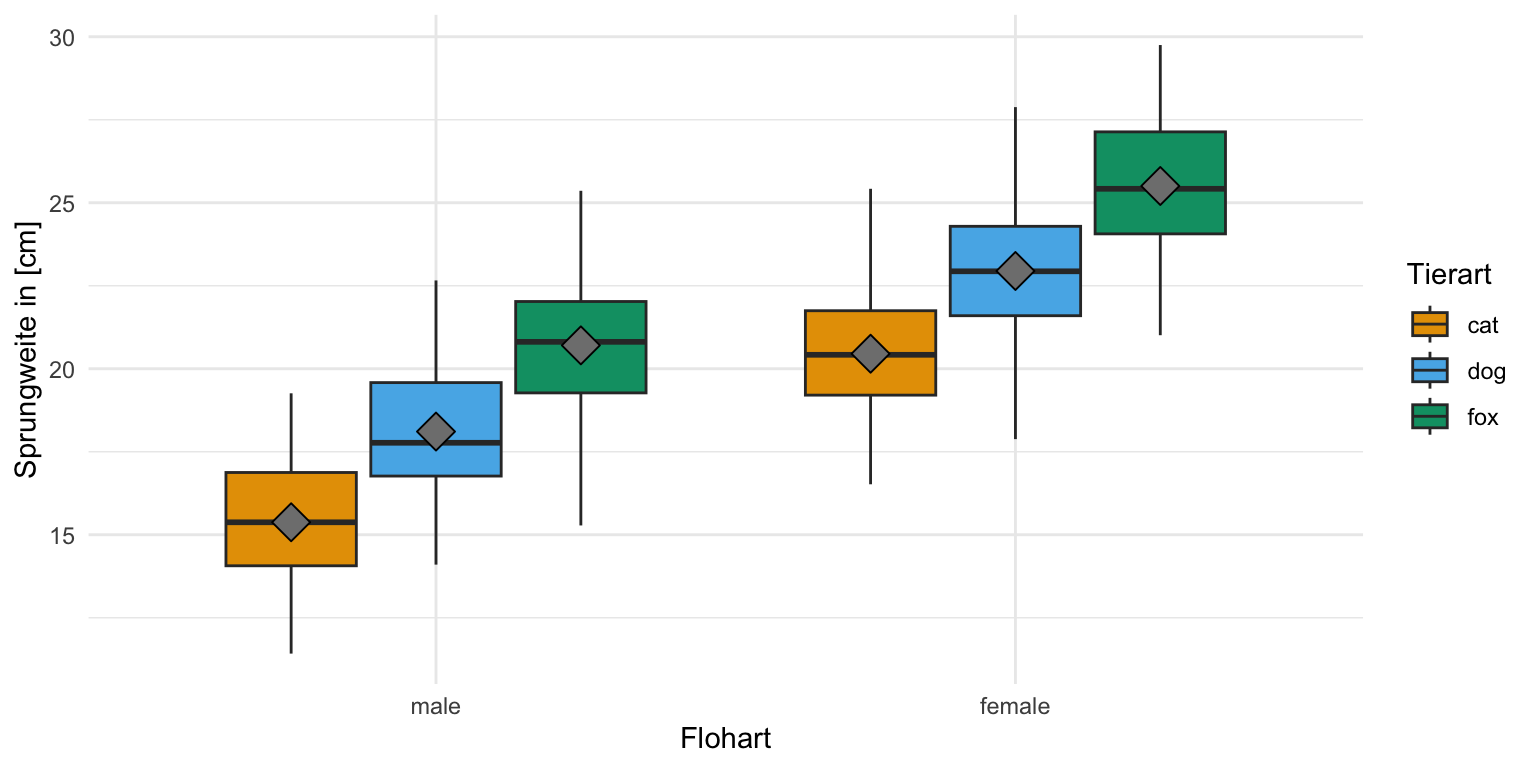
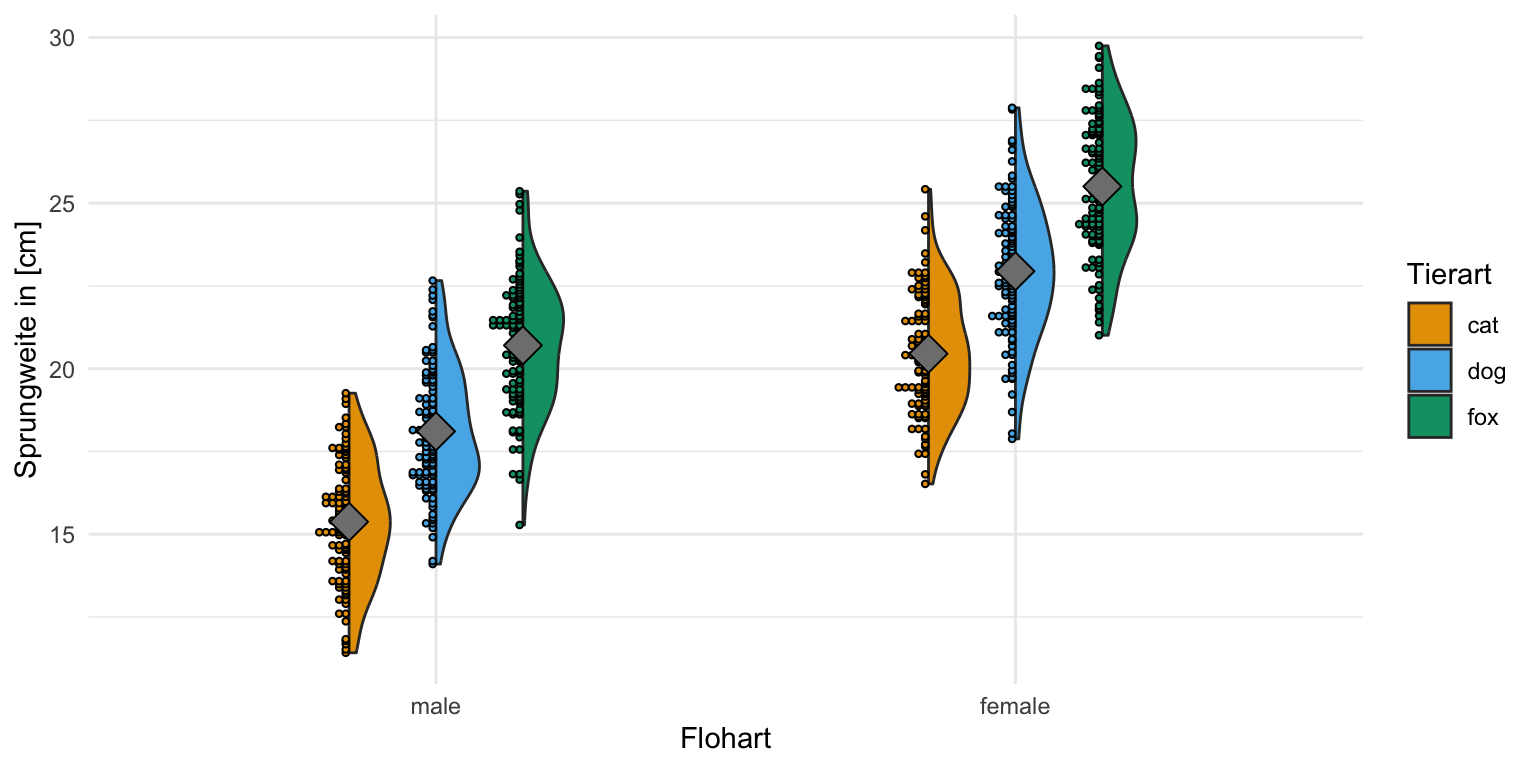
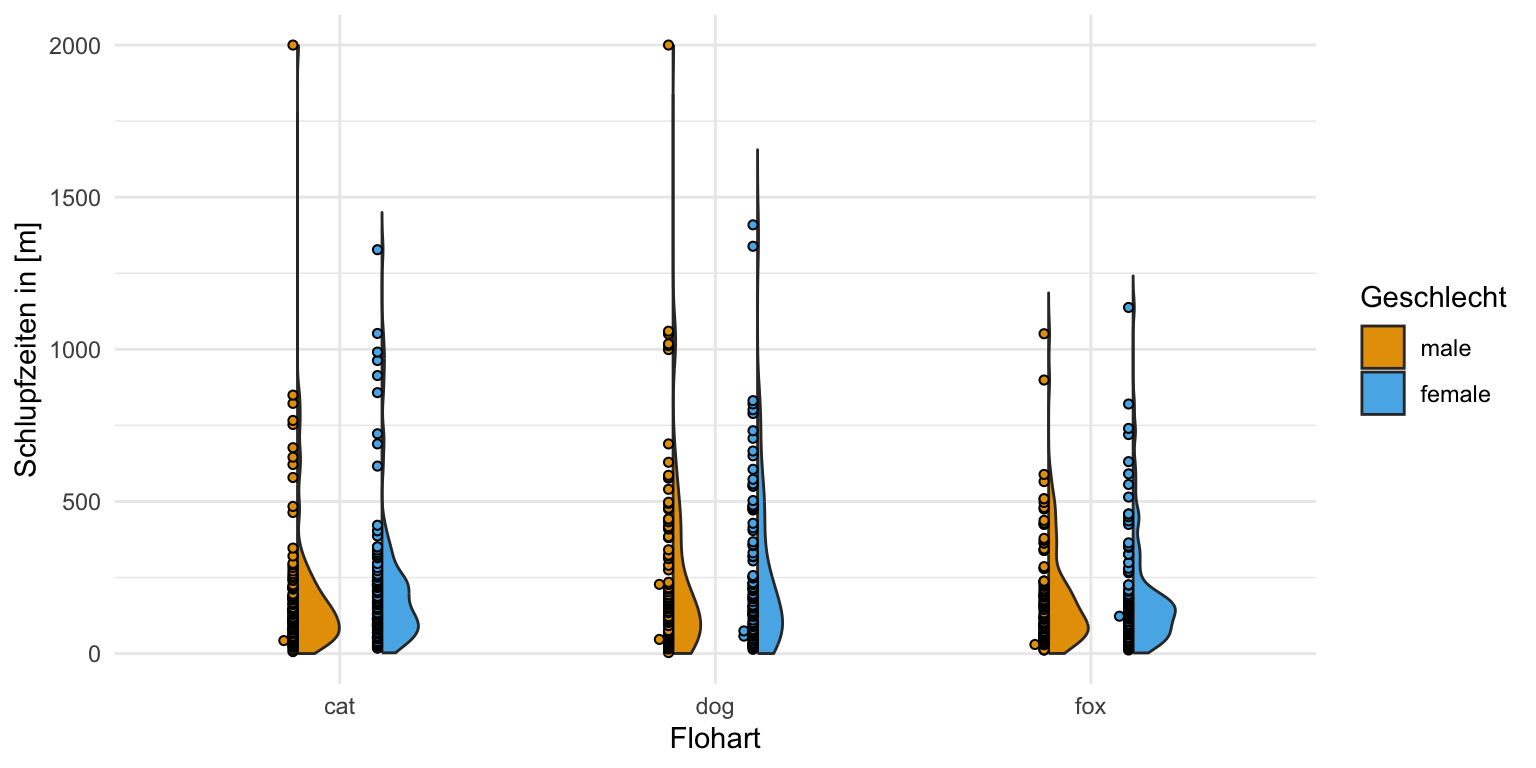
Auch hier schauen wir uns einmal die Daten in einem Boxplot und einem Densityplot an. Wir wollen ja sehen, ob sich zum einen die Gruppen unterscheiden und zum anderen wie unsere Messwerte der Sprungweiten und der Schlupfzeiten verteilt sind. Wir erkennen in den Boxplots und auch in den Densityplots, dass wir vermutlich eine approximative Normalverteilung in den Sprungweiten vorliegen haben, aber auf keinen Fall eine Normalverteilung in den Schlupfzeiten. Du siehst hier nochmal in den beiden Abbildungen die Schiefe in der Verteilung der Schlupfzeiten. Wir könnten dann bei den Schlupfzeiten über eine log-Transformation nachdenken um eine approximative lognormal Verteilung zu erhalten.
25.4 Visuelle Überprüfung
“Soll ich’s wirklich machen oder lass ich’s lieber sein? Jein…” — Fettes Brot, Jein
Häufig kommt jetzt die Frage, ob mein Messwert \(y\) wirklich normalverteilt ist und ich nicht den Messwert auf Normalverteilung testen sollte. Die kurze Antwort lautet nein, da du meistens zu wenig Beobachtungen pro Gruppe vorliegen hast. Wir werden uns gleich nochmal den Sachverhalt bei der visuellen Überprüfung der Normalverteilung näher anschauen, dann weißt du vielleicht was ich meine. Du kannst natürlich auch weiter Lesen wie die etwas längere Antwort von Kozak & Piepho (2018) mit dem Artikel What’s normal anyway? Residual plots are more telling than significance tests when checking ANOVA assumptions. Wenn du dazu dann noch Literatur für deine Abschlussarbeit brauchst, dann nutze doch die Arbeit von Zuur et al. (2010) mit dem Artikel A protocol for data exploration to avoid common statistical problems oder aber die Arbeit von Kozak & Piepho (2018) mit dem Artikel What’s normal anyway? Residual plots are more telling than significance tests when checking ANOVA assumptions.
Neben den klassischen Abbildungen in {ggplot} und deren Interpretation gibt es natürlich auch noch R Pakete, die dir bei der Bewertung helfen. Das R Paket {olsrr} erlaubt eine weitreichende Diagnostik auf einem normalverteilten Outcome \(y\). Es ist besser sich die Diagnostikplots anzuschauen, als die statistischen Pre-Tests zu rechnen. Besonders bei kleiner Fallzahl. Ich persönlich bevorzuge das R Paket {performance}, da wir hier dann einfach bessere Abbildungen vorliegen haben. Darüber hinaus funktioniert das R Paket {performance} auf mehr Modellen und ist auch einfacher zu bedienen. Wie immer hat natürlich jedes Paket seine Funktionen und ich stelle hier mal alles vor. Es ist ja ein Kochbuch, also suche dir dann raus was du brauchst für deine Analysen.
Im Folgenden erkläre ich dir dann einmal, wie du die Normalverteilung oder aber auch die Varianzhomogenität in einer visuellen Überprüfung erkennen kannst. Dabei nutzen wir verschiedene Abbildungen und vergleichen einmal die Ergebnisse untereinander. Wie du sehen wirst, funktioniert nicht jede Abbildung für jeden Datensatz oder Fragestellung.
25.4.1 Normalverteilung
Jetzt wollen wir uns fragen, ob unsere Messwerte in unseren Daten normalverteilt sind oder nicht. Dafür werden wir im ersten Schritt die Messwerte einmal visuelle überprüfen. Dafür haben wir verschiedene Möglichkeiten aus unserem Werkzeugkasten der explorativen Datenanalyse. Wir nutzen hier die gängigen Visualisierungen wie den Boxplot, das Histogramm oder den Densityplot. Hier lohnt sich dann aber auch ein Blick auf den Violinplot, der uns hier nochmal mehr Informationen liefert. Hier sei auch die Arbeit von Lord et al. (2020) erwähnt, der in seiner Arbeit SuperPlots: Communicating reproducibility and variability in cell biology noch eine Kombination aus verschiedenen Visualisierungen zeigt.
R Paket {ggplot}
Wir können alles per Hand machen und das wäre dann die Lösung mit {ggplot}. Das hat dann den Vorteil, dass wir uns die Abbildungen selber bauen können und besser verstehen was hier passiert. Dafür müssen wir dann auch schauen, was wir machen wollen. Ich habe die Abbildungen dann teilweise nicht stark aufgehübscht, da diese Abbildungen natürlich nur für dich sind. Selten packen wir die Abbildungen dann auch in die eigentlichen Arbeiten sondern in den Anhang.
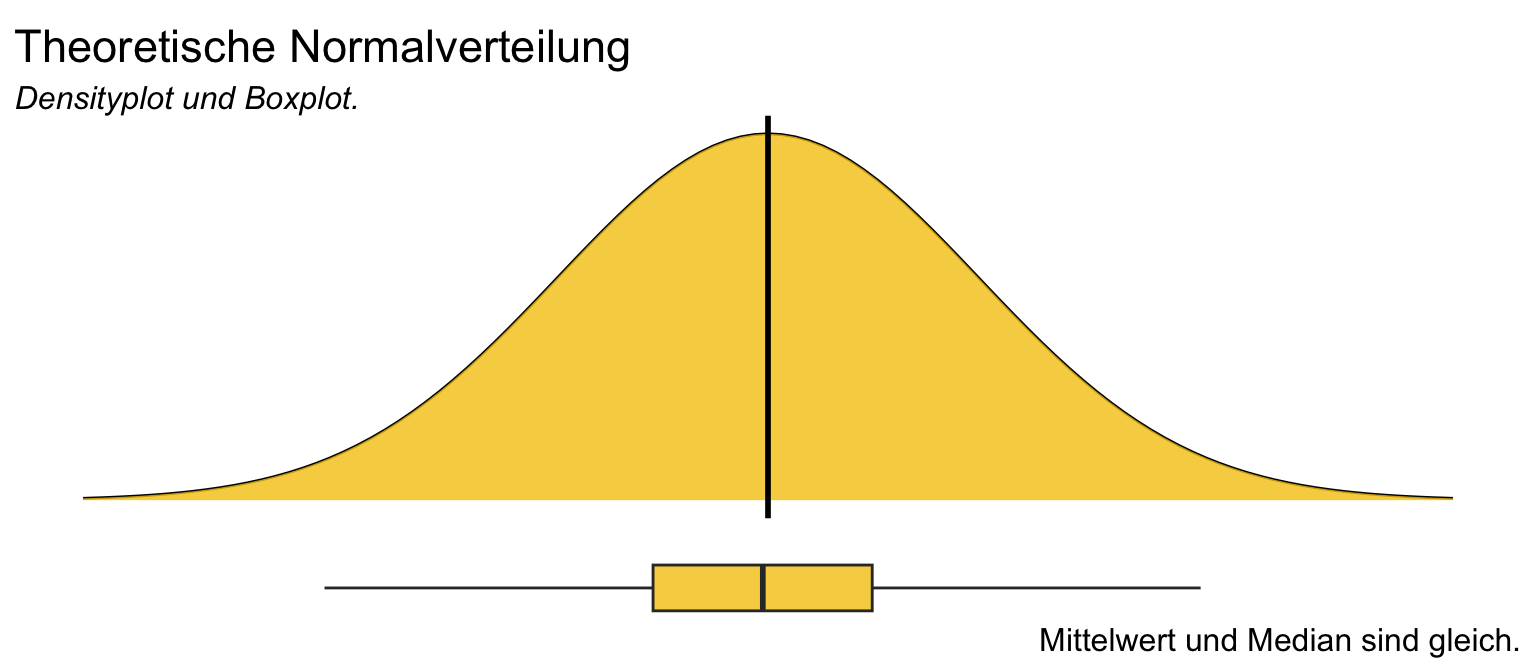
Beginnen wir einmal mit der theoretischen Betrachtung einer Normalverteilung. In der folgenden Abbildung siehst du einmal eine perfekte Normalverteilung in einem Densityplot als Glockenkurve. Schön perfekt sieht die Kurve aus. So eine Kurve wirst du niemals in der Realität beobachten, wenn du mit Fallzahlen unter tausenden von Beobachtungen arbeitest. Darunter dann der entsprechende perfekte Boxplot. Diesen Boxplot kannst du dann mit Glück schon mit geringen Fallzahlen sehen, was wiederum auch ein Teil der folgenden Problematik der visuellen Überprüfung ist. Aber dazu gleich dann mehr.
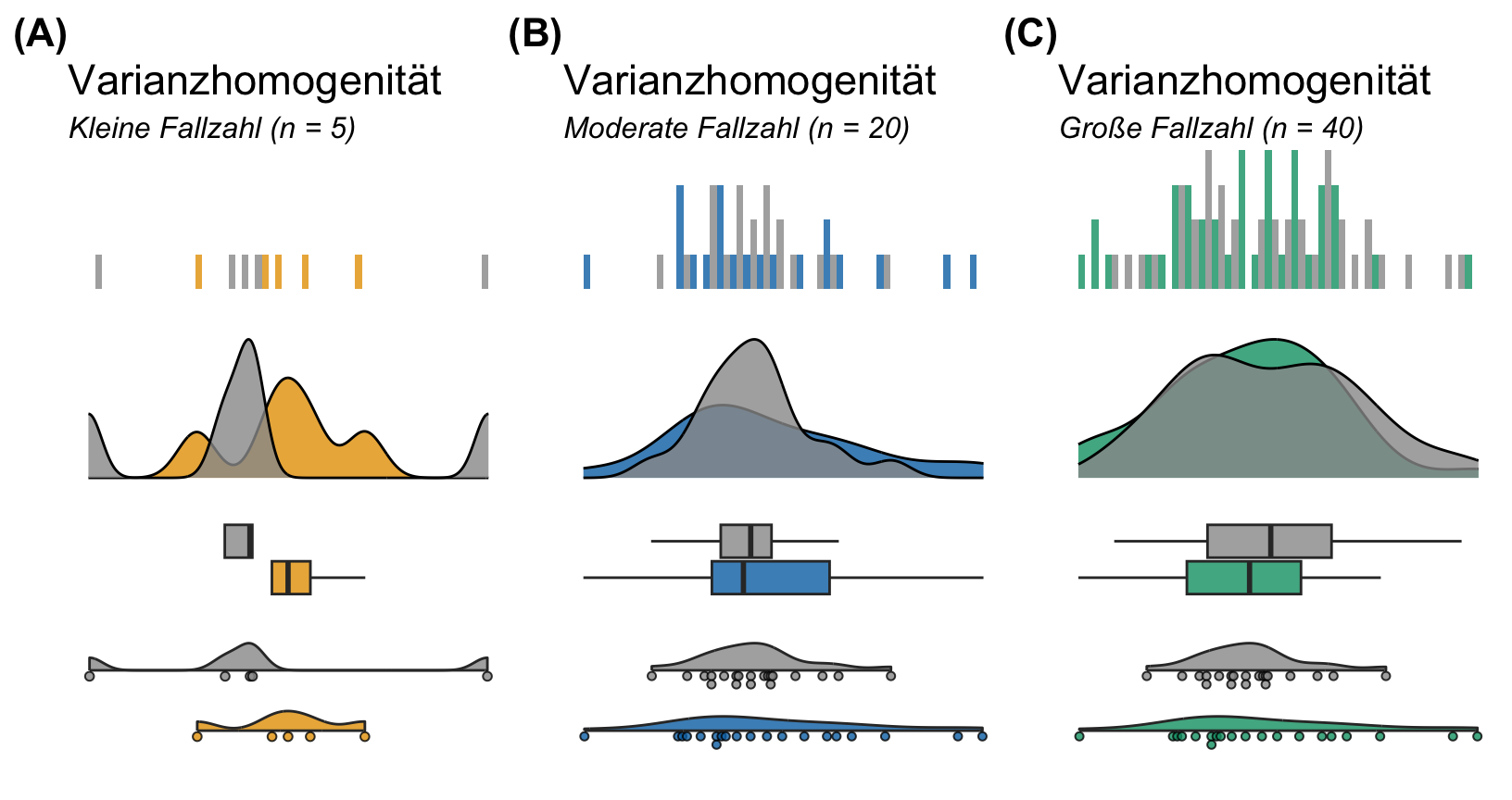
Wenn wir über die visuelle Überprüfung reden, dann müssen wir auch über die Fallzahl in deinem Experiment oder aber den Fallzahlen in deinen Behandlungsgruppen sprechen. In der folgenden Abbildung habe ich dir einmal normalverteilte Daten mitgebracht und in einem Histogramm, Densityplot, Boxplot sowie Violinplot visualisiert. Dabei habe ich dann zwischen einer kleinen Fallzahl mit 5 Beobachtungen, einer moderaten Fallzahl mit 20 Beobachtungen und einer großen Fallzahl von 40 Beobachtungen unterschieden. Wie du hier sehr gut sehen kannst, siehst man eine Normalverteilung mit sehr wenigen Beobachtungen kaum. Die visuelle Überprüfung kommt hier an die Grenze. Aber auch hier Achtung, ein statistischer Test mag hier auch nicht besser sein, als was du selber sehen kannst.
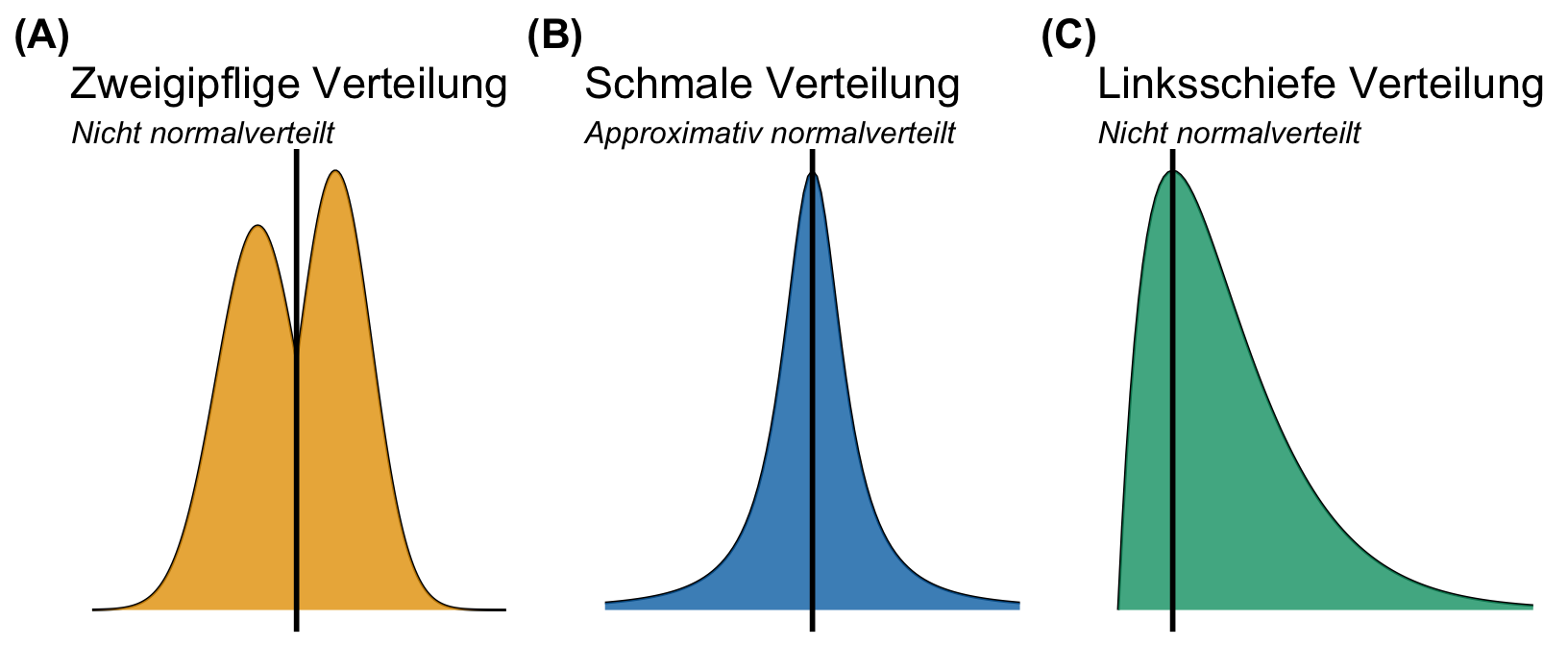
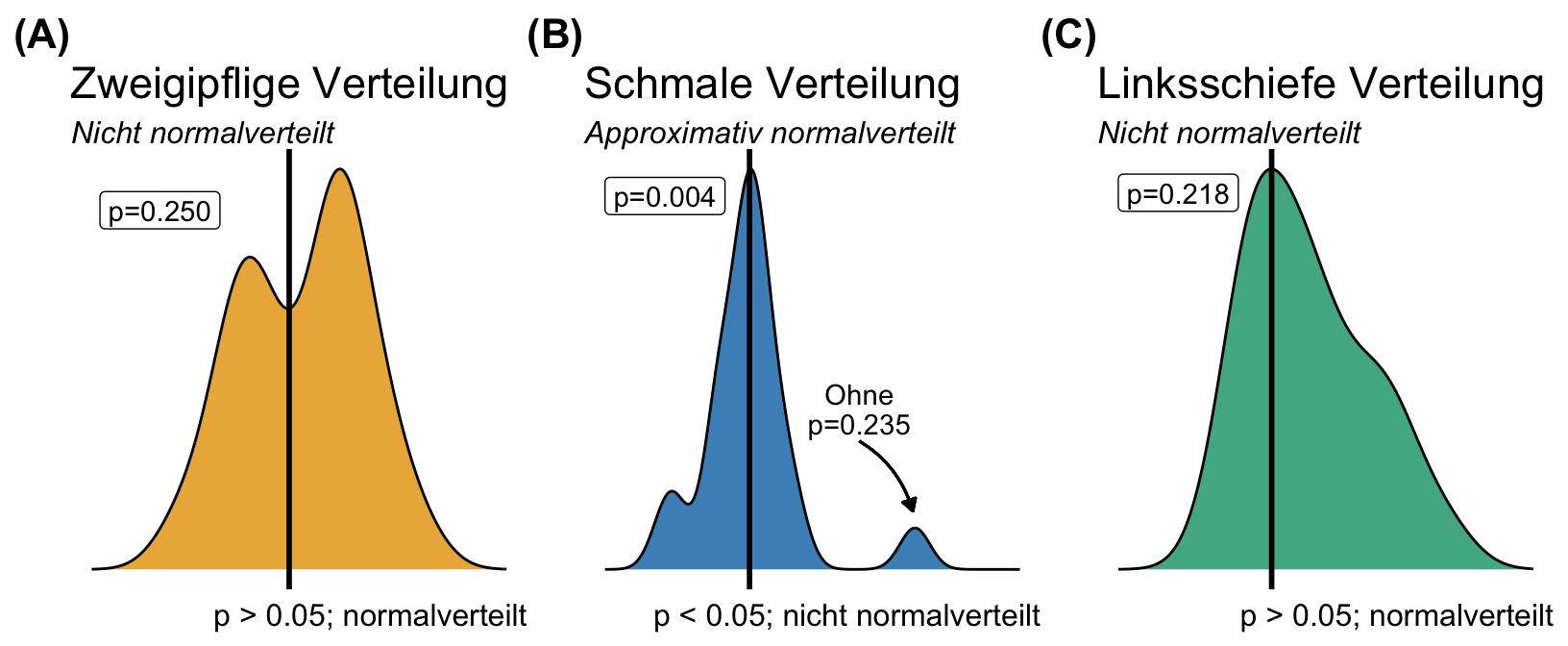
Im Weiteren betrachten wir nochmal andere Verteilungen, die einer Normalverteilung sehr nahe kommen, aber dann eventuell nicht als solche erkannt werden. Wie immer ist es wichtig zu Wissen, was du beobachten könntest um dann in deinen Daten abschätzen zu können, welche Verteilung eventuell vorliegt. Wir können nämliche auch zweigipflige Normalverteilungen vorfinden, dann haben wir es meistens mit zwei oder mehr Unterverteilungen zu tun, die sich zu einer Verteilung zusammensetzen. Oder aber deine Verteilung ist zu schmall, was jetzt ertsmal nicht so das große Problem ist. Im Weiteren können wir auch Schultern bei einer Verteilung beobachten. Dann sprechen wir auch gerne von schiefen Verteilungen. Eine schiefe Verteilung ist im geringsten Sinne noch normalverteilt.
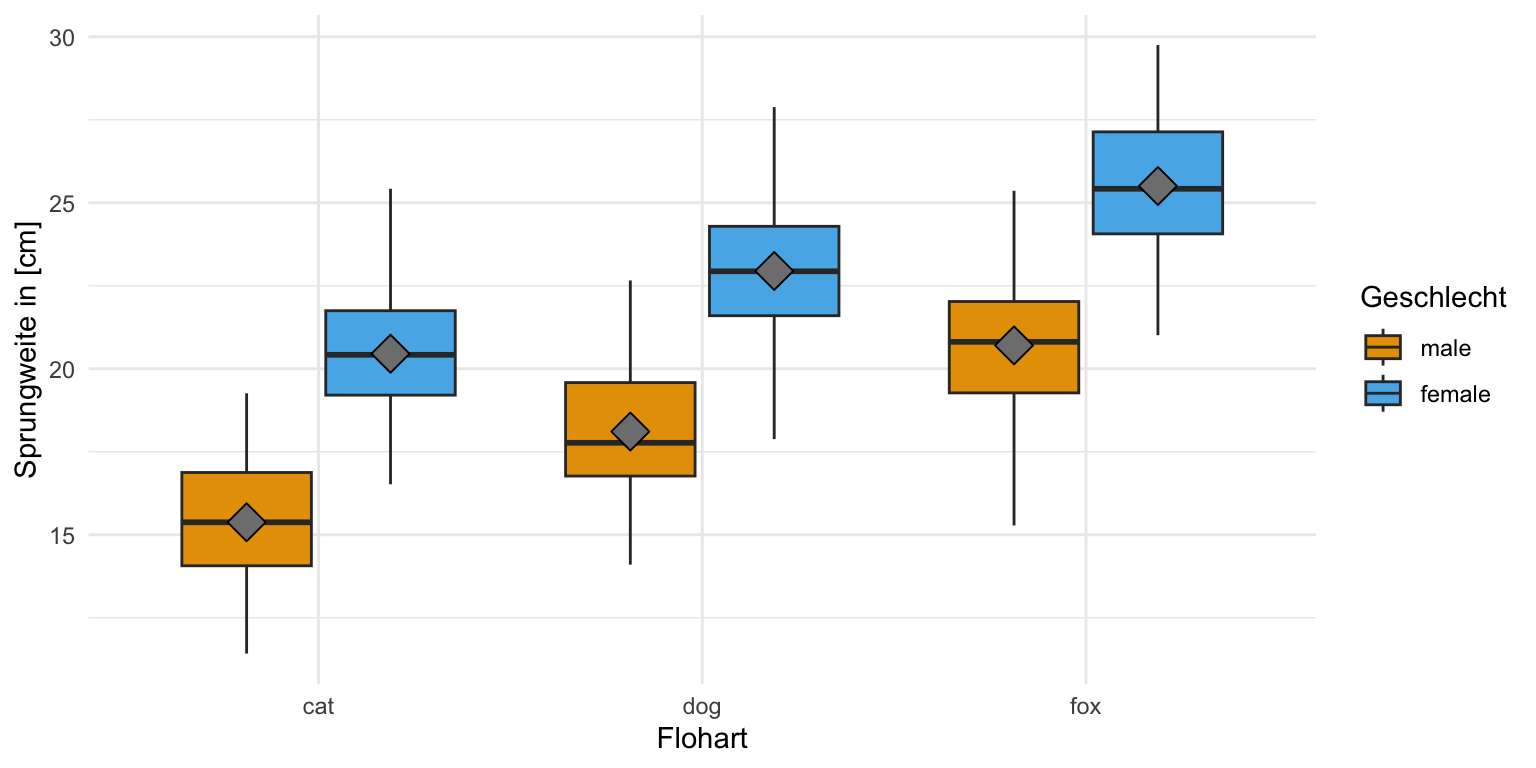
Im Folgenden betrachten wir einmal die visuelle Überprüfung in einem einfaktoriellen sowie einen zweifaktoriellen Boxplot. Ich habe auch immer den Mittelwert mit ergänzt damit wir sehen können, ob der Median und der Mittelwert in etwa gleich sind. Das ist immer ein Indiz, dass wir eine Normalverteilung in unseren Messwert vorliegen haben.
Einfaktorieller Boxplot
Das praktische bei den Boxplots ist, dass wir hier nichts mehr vorrechnen müssen, sondern direkt die Boxplots in {ggplot} erstellen können. Ich finde man sieht immer in einem Boxplot besser, ob die Streuung um den Median eher homogen oder eher heterogen ist. Gerne ergänze ich noch den Mittelwert mit der Funktion stat_summary(). Wir haben hier eher eine Normalverteilung vorliegen. Die Mittelwerte liegen in etwa auf den Medianen. Die Mediane liegen in der Mitte der Boxen. Das passt so im groben, daher haben wir hier zumindestens eine approximative Normalverteilung vorliegen.
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = animal, y = jump_length, fill = animal)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point",
shape=23, size = 5, fill = "gray50") +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() Zweifaktorieller Boxplot
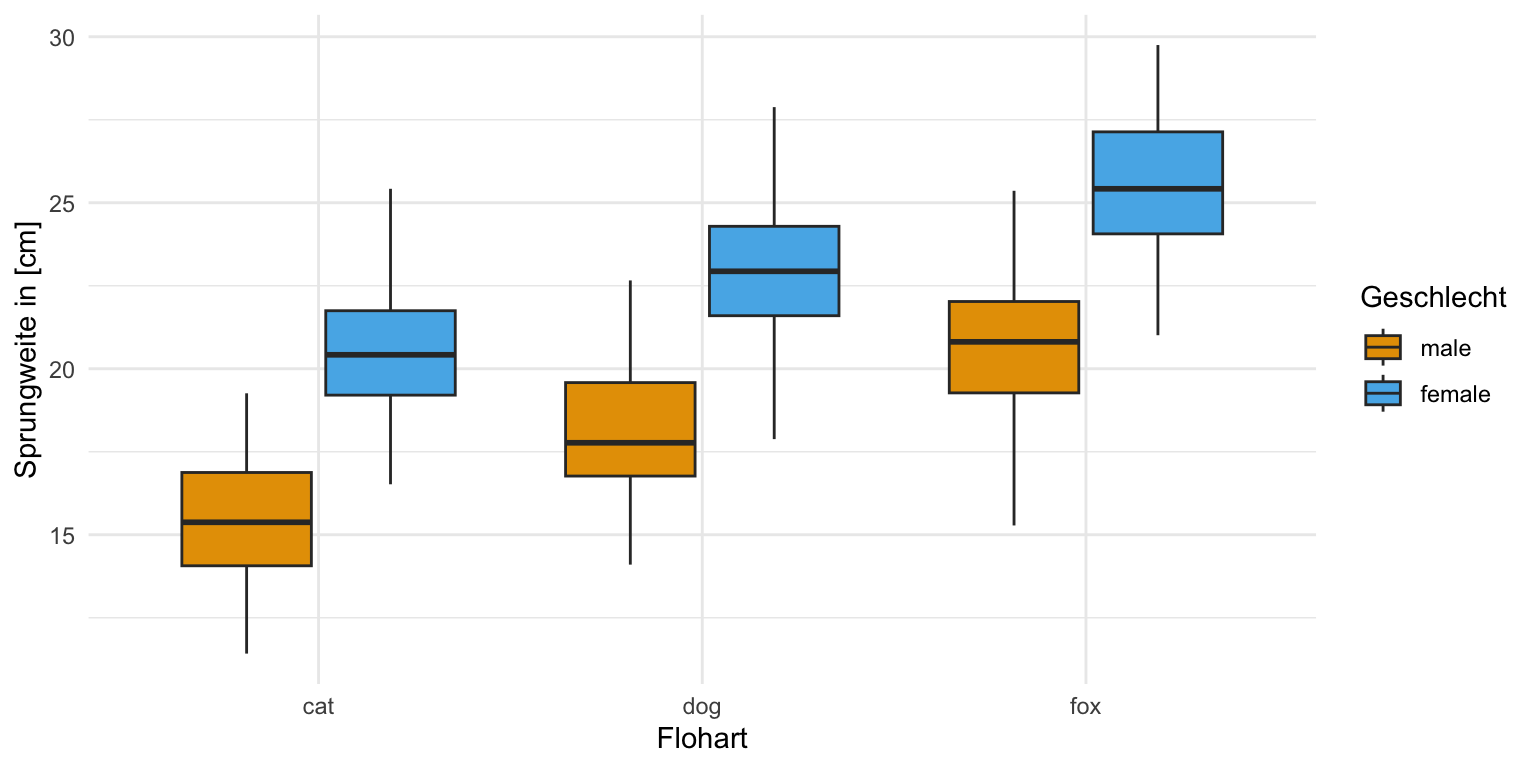
Dann können wir uns auch die zweifakoriellen Boxplots einmal anschauen. Hier haben wir dann im Fall der Sprungweite zu mindestens eine approximative Normalverteilung vorliegen. Die Mittelwerte liegen auf den Medianen und diese liegen dann auch alle in der Mitte der Box. Wir würden hier also mit einer Normalverteilung weiterrechnen und eine ANOVA anwenden.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = animal, y = jump_length, fill = sex)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point", aes(group = sex),
shape=23, size = 5, fill = "gray50",
position = position_dodge(0.75)) +
labs(x = "Flohart", y = "Sprungweite in [cm]", fill = "Geschlecht") +
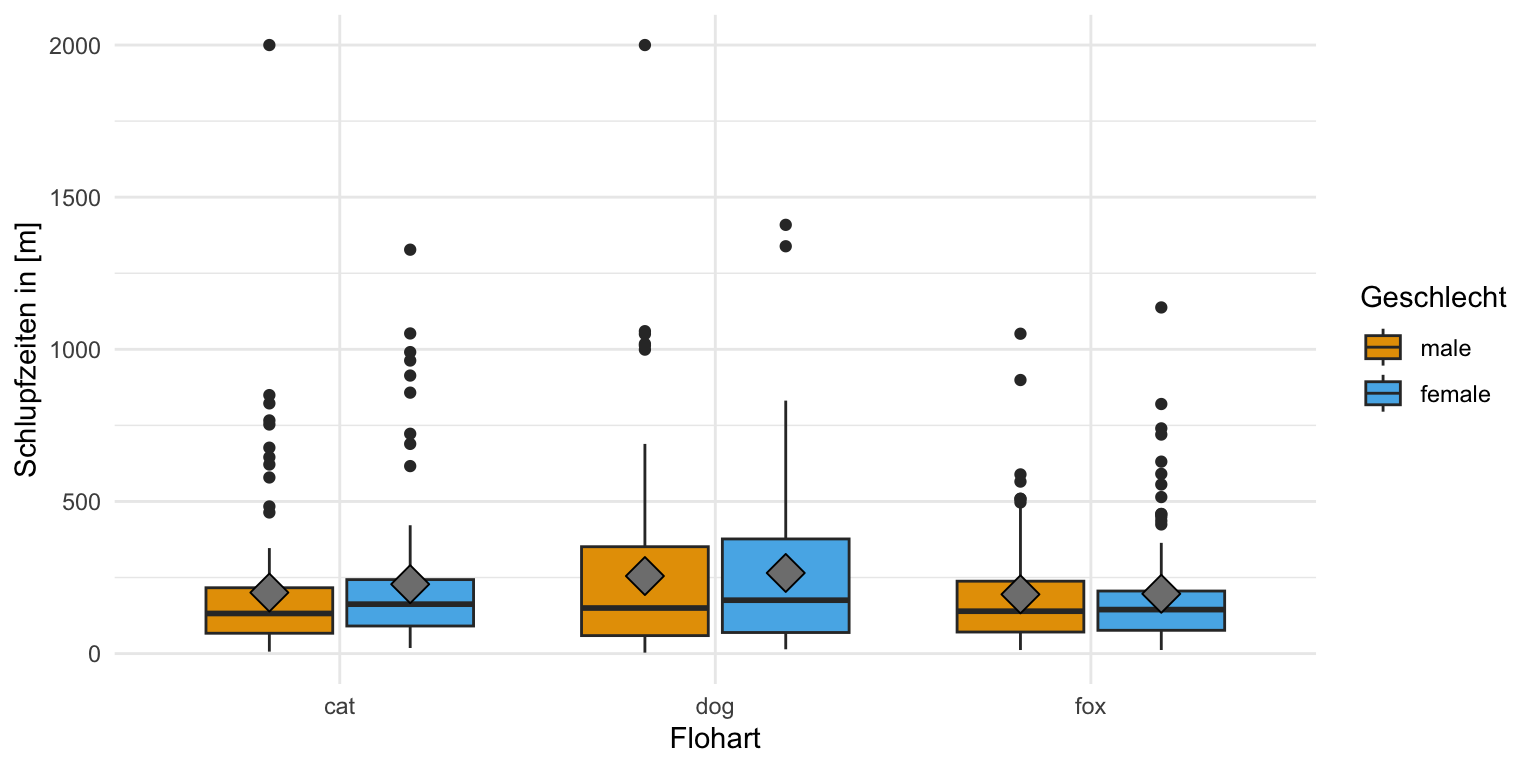
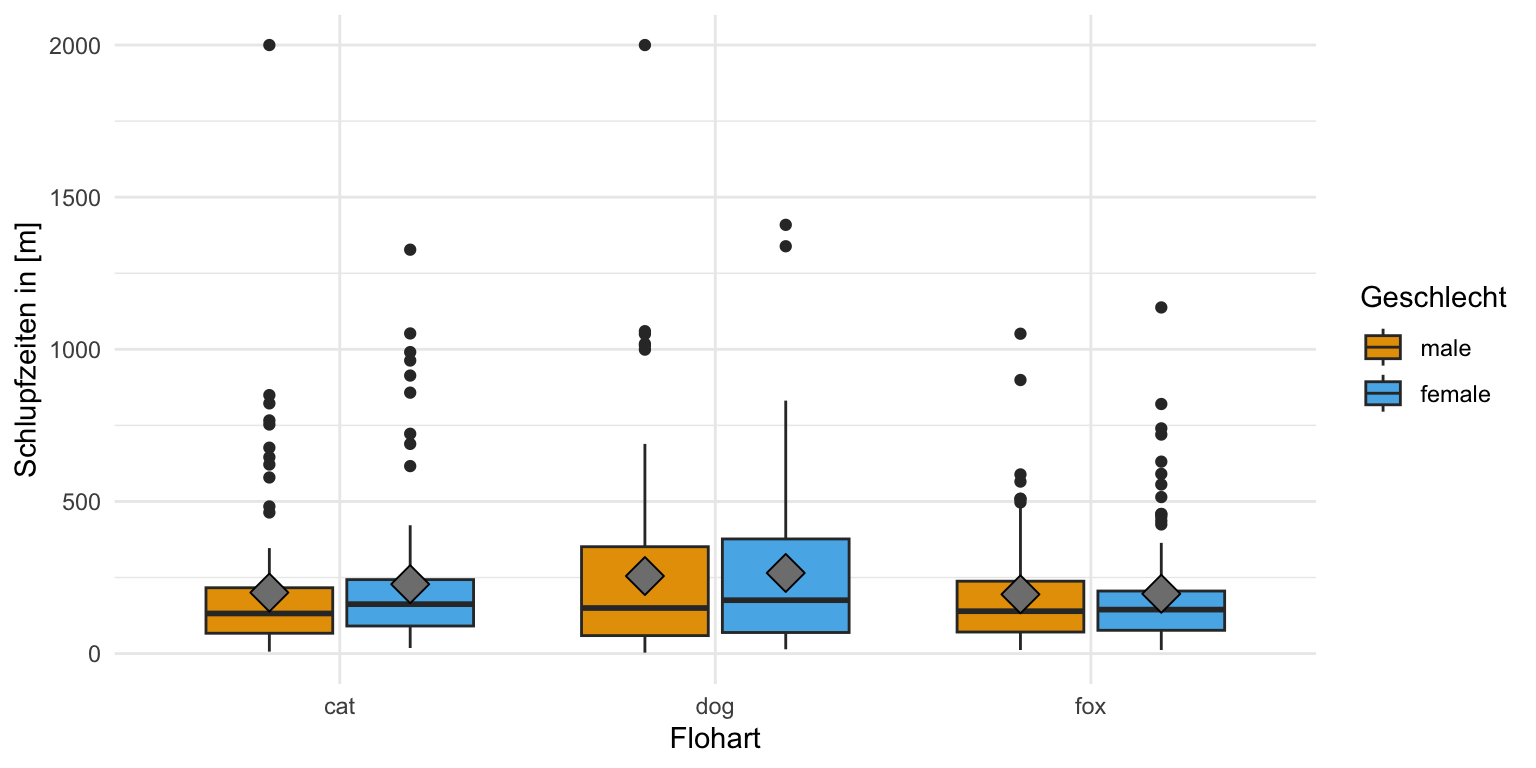
scale_fill_okabeito() Wenn wir dann die Schlupfzeiten betrachten haben wir ein anderes Bild vorliegen. Hier haben wir dann ganz klar keine Normalverteilung in den Schlupfzeiten vorliegen. Es sind einiges an Ausreißern in den Daten und die Mittelwerte liegen nicht auf den Medianen. Die Boxen sind auch nach oben gezogen und die Whiyskers sehr lang. Wir haben hier eine schiefe Verteilung vorliegen. Wir müssen hier also etwas tun und können nciht einfach eine ANOVA auf den Daten rechnen.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = animal, y = hatch_time, fill = sex)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point", aes(group = sex),
shape=23, size = 5, fill = "gray50",
position = position_dodge(0.75)) +
labs(x = "Flohart", y = "Schlupfzeiten in [m]", fill = "Geschlecht") +
scale_fill_okabeito() +
ylim(0, 2000)Neben den klassischen Boxplots können wir uns auch Violinplots anschauen. Hier haben wir dann die Kombination aus einem Dotplot und einem Densityplot aus dem R Paket {see} und der Funktion geom_violindot(). Ich persönlich mag reine Violinplots nicht so gerne, da wir dann eine Information doppelt haben und auch den Violinplot in der Mitte zerschneiden könnten. Das ist eben die Idee der Funktion geom_violindot(). Wir haben dann auch die einzelnen Punkte mit abgebildet und können uns ein besseres Bild machen. Hier dann einmal die Violinplots für das einfaktorielle und das zweifaktorielle Datenbeispiel.
Einfaktorieller Violinplot
Wir sehen hier sehr schön bei unseren Sprungweiten, dass der Mittelwert in der Mitte der Verteilung liegt und wir dann auch ungefähr gleiche Verteilungen vorliegen haben. Wir können hier also von einer Normaverteilung ausgehen. Auch haben wir hier genug Bobachtungen und diese Beobachtungen verteilen sich auch sinnvoll.
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = animal, y = jump_length, fill = animal)) +
theme_minimal() +
geom_violindot(dots_size = 4, trim = FALSE) +
stat_summary(fun.y = mean, geom = "point",
shape=23, size = 5, fill = "gray50") +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() Zweifaktorieller Violinplot
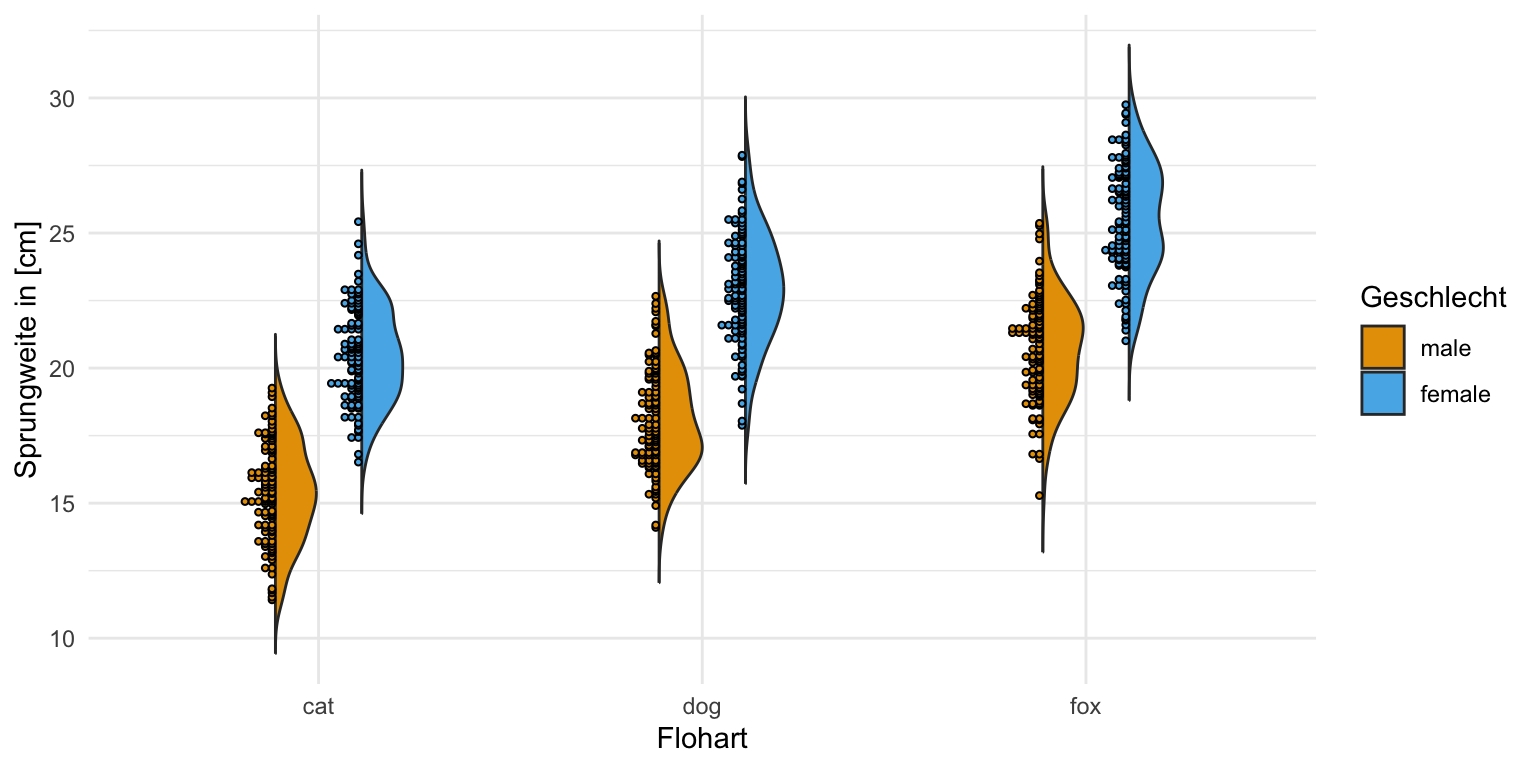
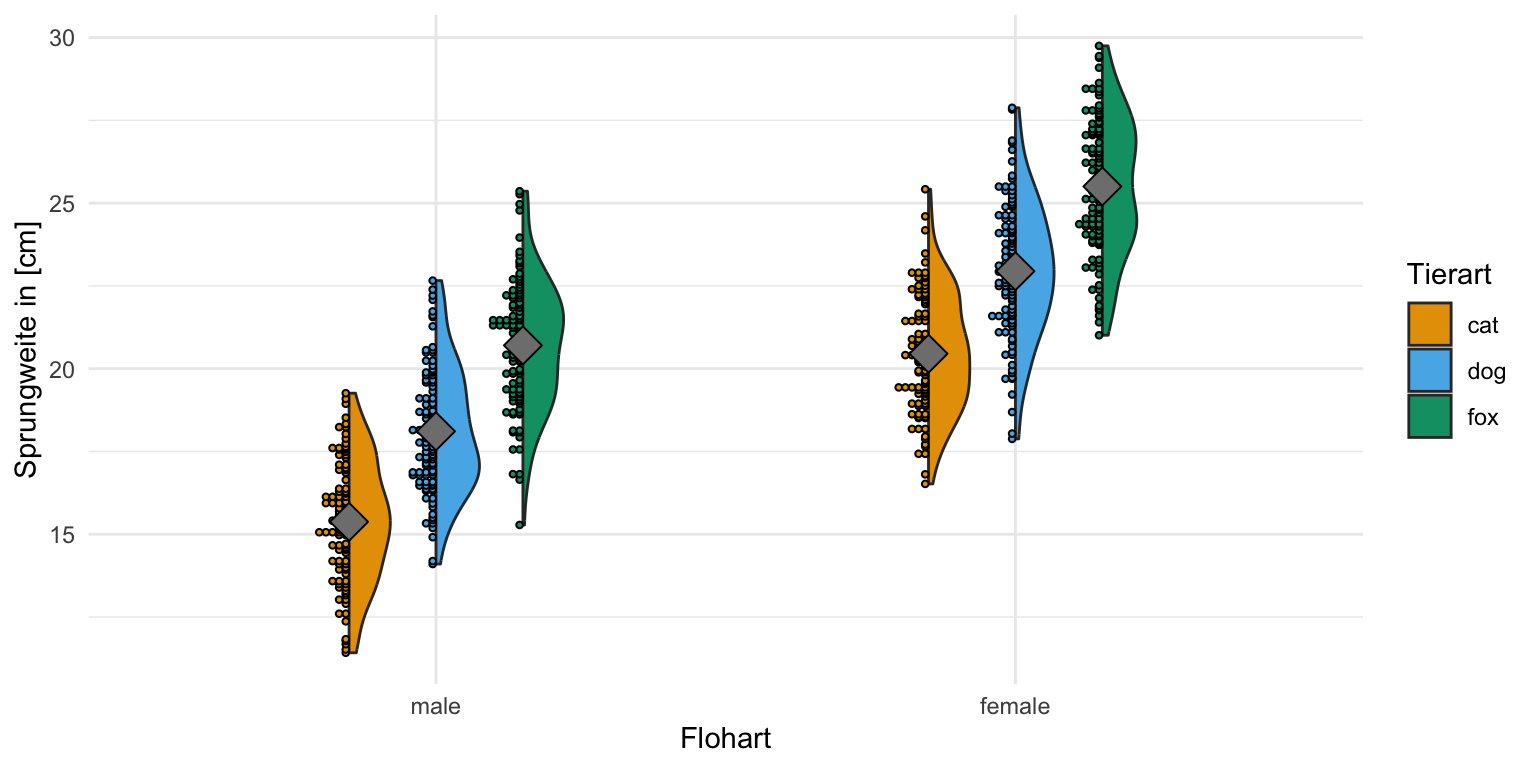
Für den zweifaktoriellen Violinplot habe ich dann mehr Beobachtungen mitgebracht und auch hier siehst du gut, dass die Sprungweite normalverteilt ist. Der Mittelwert liegt in der Mitte der Verteilung und die Beobachtungen der Sprungweite liegen gleichmäßig um den Mittelwert. Wir bleiben hier also bei der Annahme einer Normalverteilung an die Sprungweite und analysieren dann die Daten auch entsprechend.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = sex, y = jump_length, fill = animal)) +
theme_minimal() +
geom_violindot(dots_size = 4, position_dots = position_dodge(0.45)) +
stat_summary(fun.y = mean, geom = "point", aes(group = animal),
shape=23, size = 5, fill = "gray50",
position = position_dodge(0.45)) +
labs(x = "Flohart", y = "Sprungweite in [cm]", fill = "Tierart") +
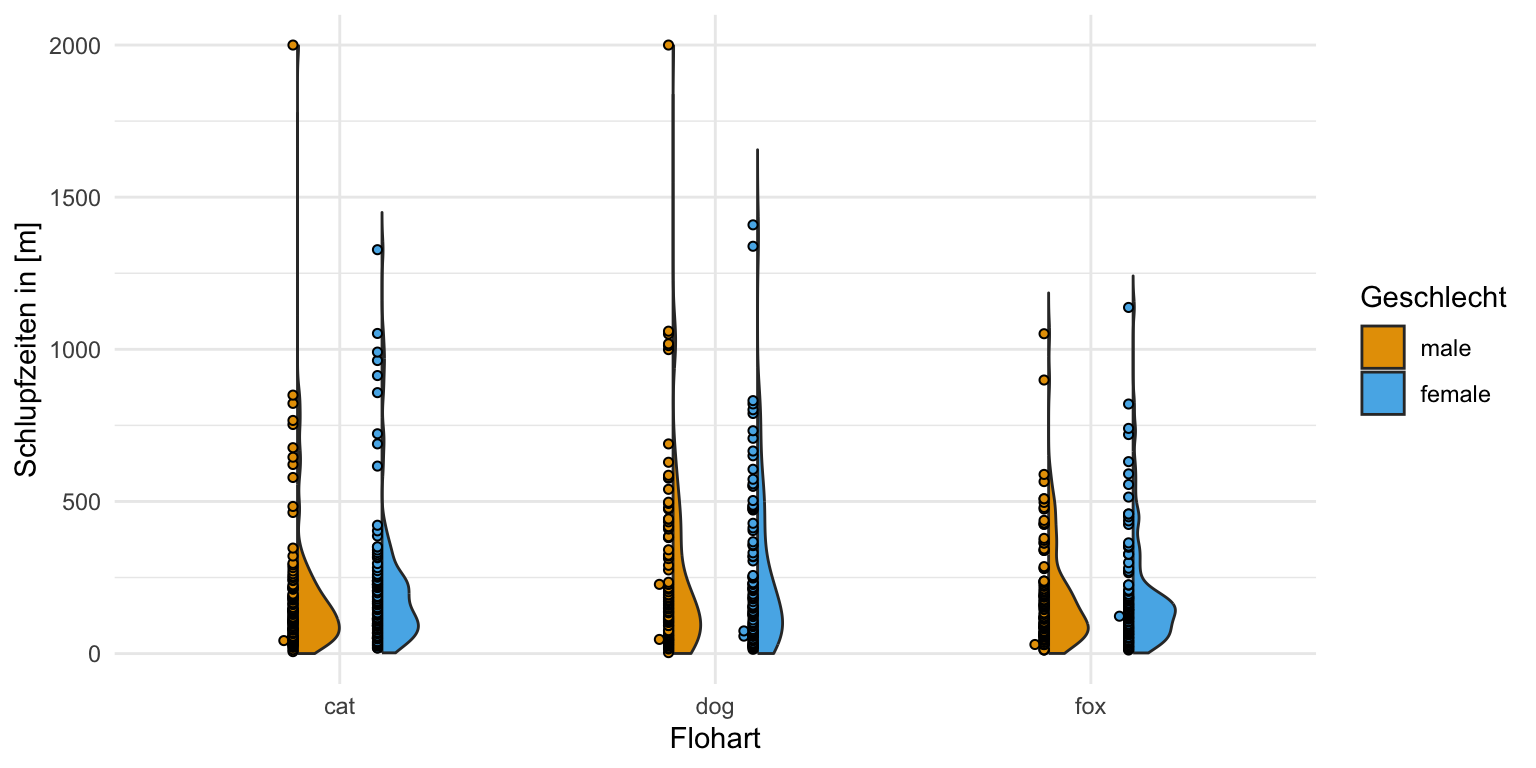
scale_fill_okabeito() Jetzt kommen wir aber zum spannenden Messwert mit der Schlupfzeit. Hier sehen wir klar, dass die Schlupfzeit nicht normalverteilt ist. Die meisten Beobachtungen sind am unteren Ende und es gibt einige längere Schlupfzeiten. Die Violinplots sind in die Länge gezogen. Wir würden hier auf jeden Fall von keiner Normalverteilung ausgehen. Die Messwerte der Schlupfzeiten sind vielleicht logarithmisch oder exponentiell verteilt. Die Daten sind auf jeden Fall schief. Wir müssen hier also etwas tun und können nicht einfach eine ANOVA auf den Daten rechnen.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = animal, y = hatch_time, fill = sex)) +
theme_minimal() +
geom_violindot(dots_size = 600, trim = FALSE,
position_dots = position_dodge(0.45)) +
labs(x = "Flohart", y = "Schlupfzeiten in [m]", fill = "Geschlecht") +
scale_fill_okabeito() +
ylim(0, 2000)Neben der klassischen Überprüfung mit {ggplot} gibt es natürlich auch noch R Pakete, die eine Visualisierung durchführen. Deshalb schauen wir uns im Anschluss nochmal zwei Pakete an, die dir dann auch gleich noch mehr Informationen liefern. Für mich würde auch eine Betrachtung in {ggplot} und deren Interpretation reichen, aber manchmal möchte man doch mehr in der eigenen Abschlussarbeit darstellen. Für mich gehört das hier zwar alles in den Anhang, aber das hängt vom persönlichen Geschmack ab.
R Paket {performance}
Das R Paket {performance} liefert die Möglichkeit auf einem statistischen Modell die Überprüfung der Normalverteilung zu rechnen. Das ist natürlich super praktisch, da du ja für die ANOVA ein Modell brauchst sowie auch für den multiplen Vergleich in {emmeans}. Auch hier habe ich mich dazu entschieden nicht nochmal mit die Abbildungen schöner zu machen. Teilweise ist es dann auch nicht so einfach möglich in den Funktionen von {performance} Änderungen vorzunehmen. Insbesondere die Funktion check_model() ist dann teilweise sehr resistent gegen Veränderungen, obwohl hier {ggplot} im Hintergrund läuft. Das tolle an der Funktion check_model() ist, dass du hier verschiedene Annahmen in einem Aufruf überprüfen kannst. Im Prinzip kannst du hier auch die Überprüfung der Normalverteilung und der Varianzhomogenität in eins machen.
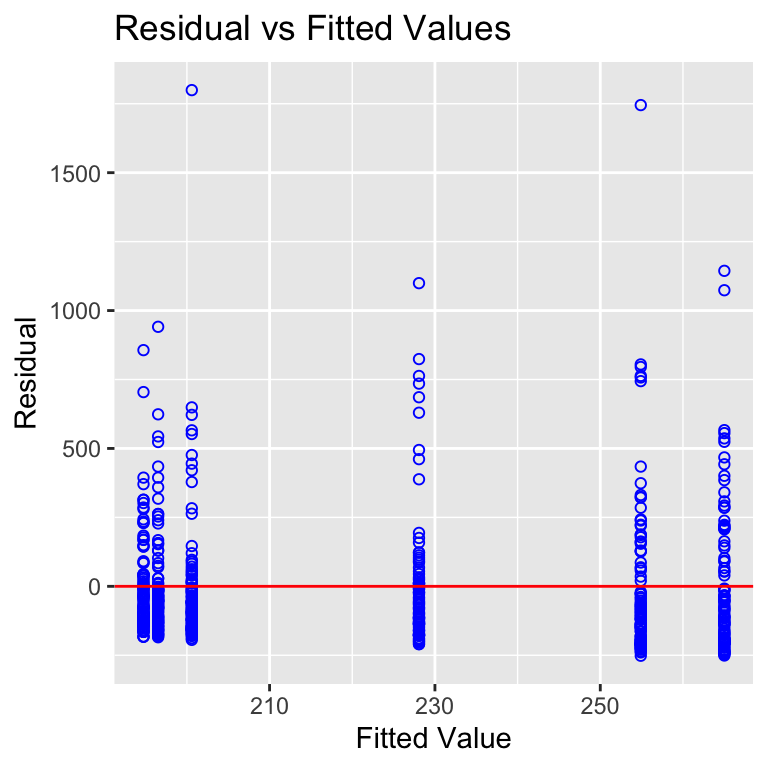
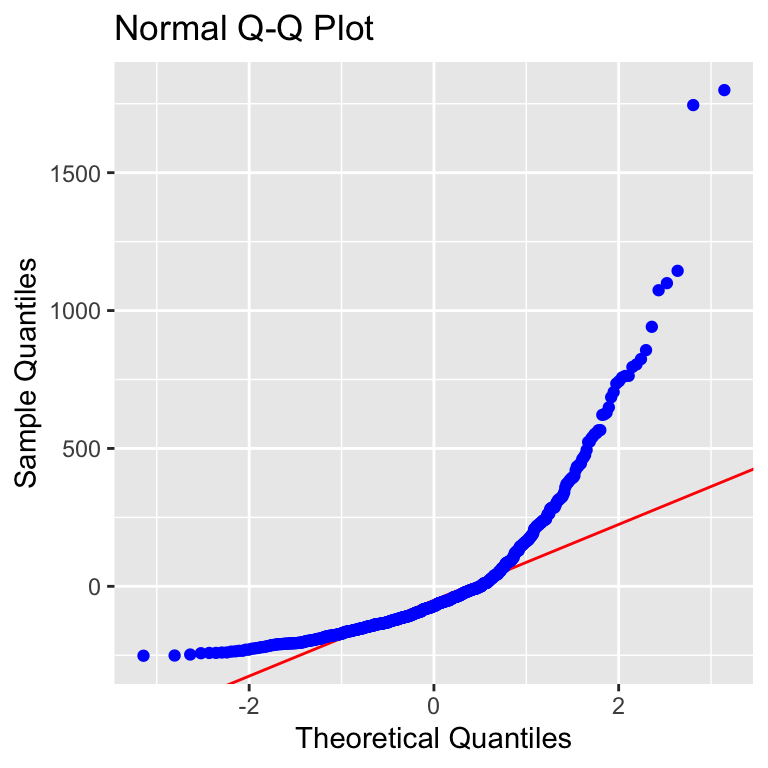
Die Funktion check_model() gibt dir eine Abbildung wieder in der du dann siehst, was du Überprüfen möchtest zusammen mit der Erwartung an die Abbildung. Das ist natürlich super praktisch, da du dann selber schnelle entscheiden kannst, ob eine Normalverteilung vorliegt oder nicht. In der Abbildung steht ja dann, wie die Abbildung aussehen sollte. Ich rechne hier jetzt einmal die Überprüfung getrennt für die Sprungweite und die Schlupfzeit für das zweifaktorielle Modell.
Wir bauen uns erstmal schnell das statistische Modell für unsere Sprungweite in unserem zweifaktoriellen Datensatz. Jetzt ist die Frage, ob unser Modell einer Normalverteilung in den Sprungweiten genügt.
R Code [zeigen / verbergen]
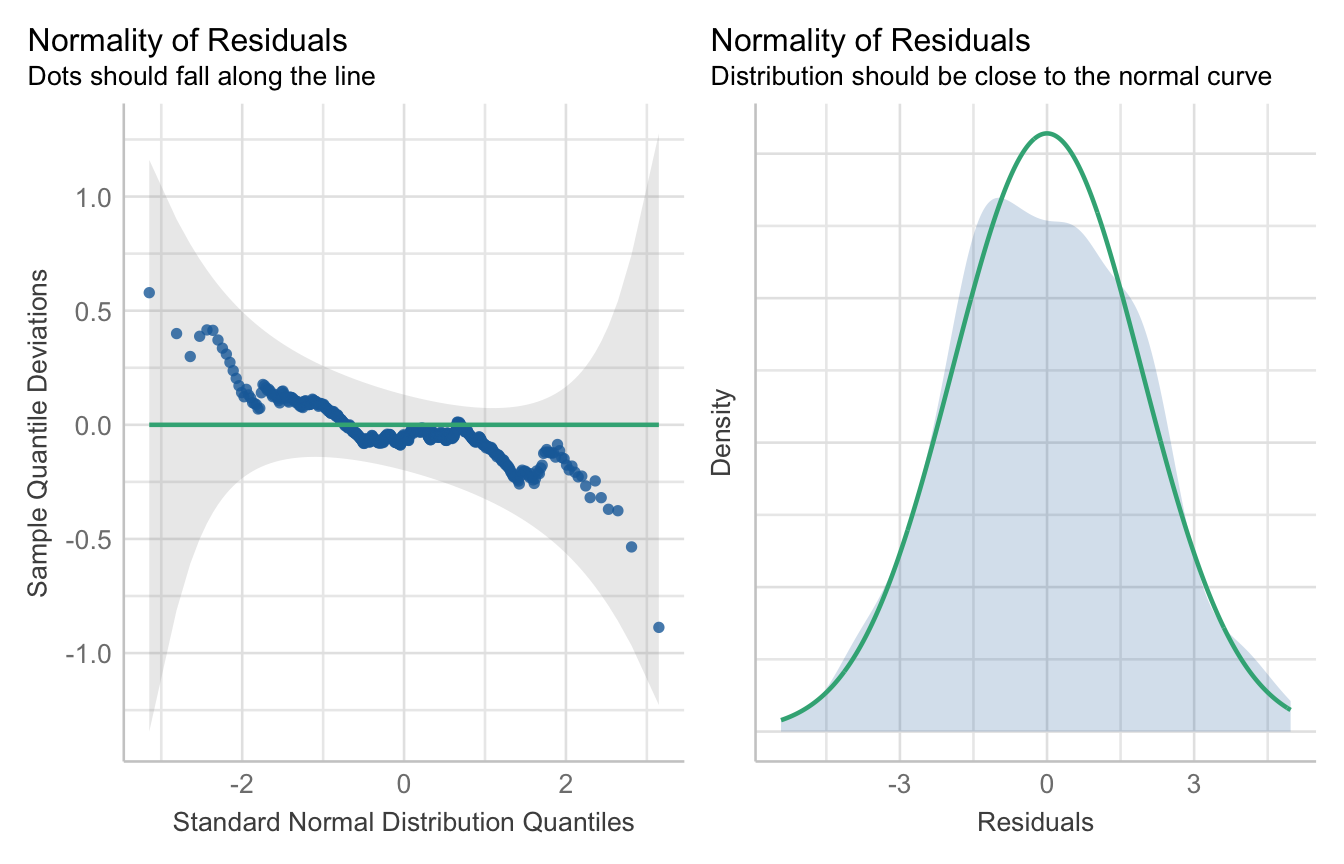
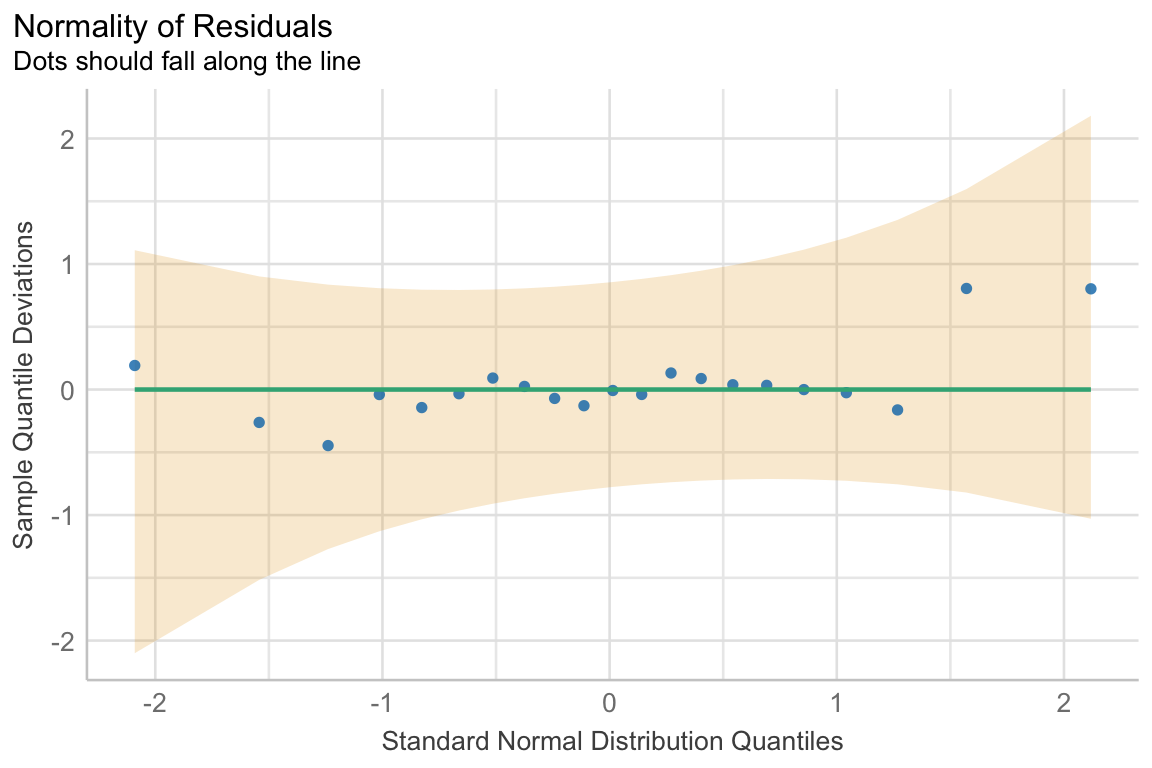
fac2_jump_fit <- lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) Die Funktion check_model() liefert uns jetzt zwei Abbildungen für die Überprüfung der Normalverteilung. Wie wir sehen, passt das ziemlich gut. Im ersten Fall sollen die Punkte entlang der Linie in den grauen Bereich fallen und im zweiten Fall sollte auch der graue Bereich nahe an der Linie sein. Das passt beides. Wir nehmen auch hier eine Normalverteilung der Sprungweite an.
R Code [zeigen / verbergen]
fac2_jump_fit |>
check_model(check = c("normality", "qq")) Kommen wir jetzt zu den Schlupfzeiten. Auch hier bauen wir uns erstmal schnell das statistische Modell für unsere Schlupfzeiten in unserem zweifaktoriellen Datensatz. Jetzt ist die Frage, ob unser Modell einer Normalverteilung in den Schlupfzeiten genügt.
R Code [zeigen / verbergen]
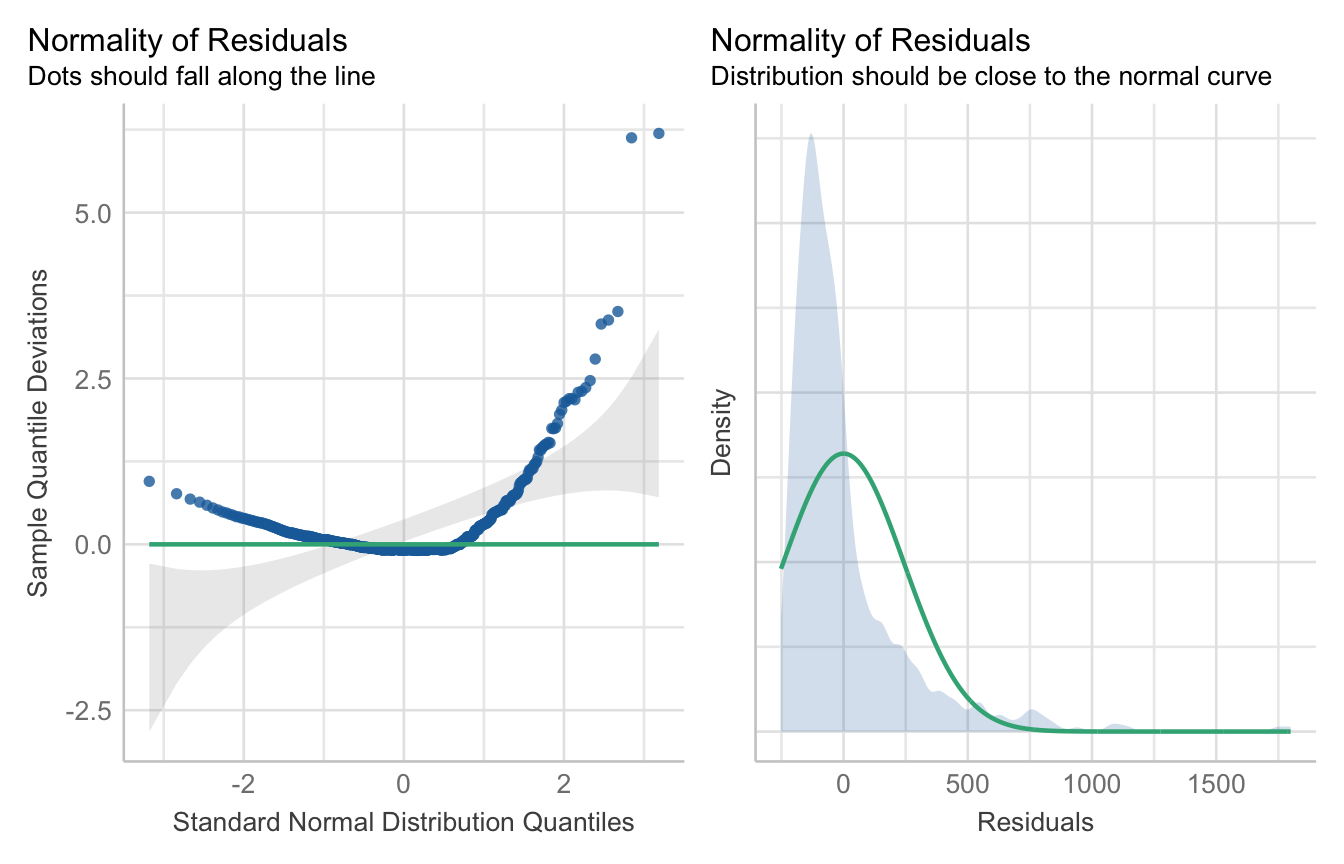
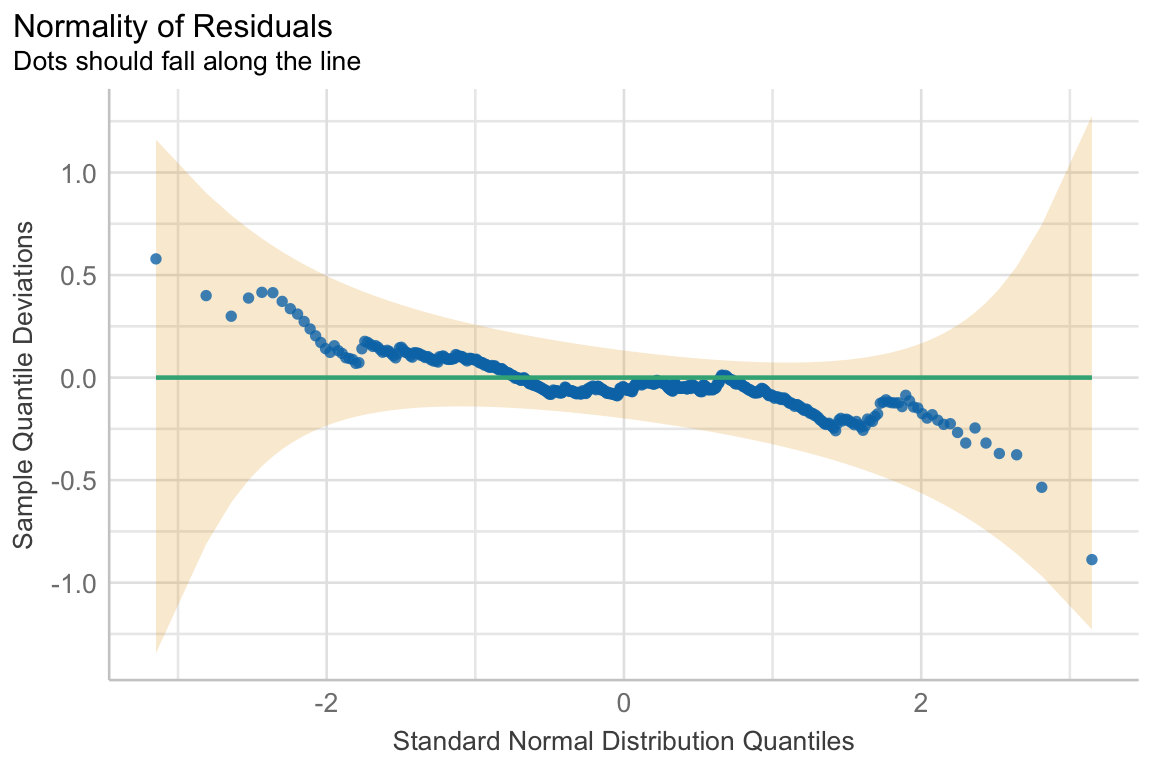
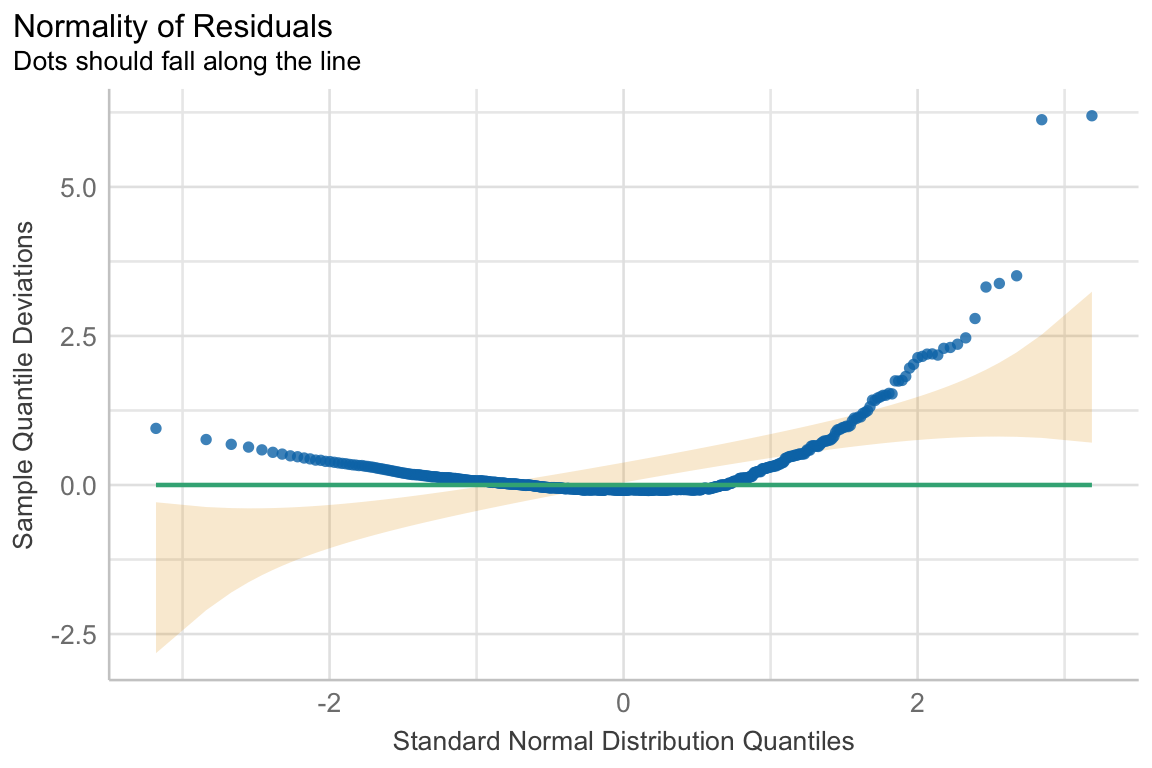
fac2_hatch_fit <- lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) Wie es zu erwarten war, sind die Schupfzeiten eben nicht normalverteilt. Wir sehen klar, dass die Punkte in der ersten Abbildung nicht auf der Linie oder dem grauen Bereich liegen. Auch haben wir keinen normalverteilten grauen Bereich in der zweiten Abbildung. Wir würden klar hier die Normalverteilung ablehnen. Die Schlupfzeiten können wir nicht mit dem obigen statistischen Modell auswerten und müssen uns eine andere Lösung als Ausweg suchen.
R Code [zeigen / verbergen]
fac2_hatch_fit |>
check_model(check = c("normality", "qq"))R Paket {oslrr}
Das R Paket {oslrr} produziert dann leider aus meiner Sicht etwas hässliche Abbildungen. Auch wenn im Hintergrund {ggplot} läuft können wir hier nicht einfach eine Änderungen in den Abbildungen vornehmen. Aber auch hier wollen wir nur schauen, ob wir die Normalverteilung in den Daten vorliegt oder nicht. Deshalb lasse ich es hier so stehen und wir würden dann die Abbildung nur in den Anhang machen. Mehr zu den Möglichkeiten anderer Abbildungen findest du dann auch auf der Hilfeseite vom R Paket unter Residual Diagnostics. Ich nutze eher das R Paket {performance} und nur für die Gaussian linearen Regression das R Paket {oslrr}. Hier liegt dann eben auch die Stärke von {oslrr}, die Bewertung einer Gaussian linearen Regression. Wie immer hast du die Wahl und es gibt gute Gründe sich für das eine oder andere Paket zu entscheiden.
Wir bauen uns erstmal schnell das statistische Modell für unsere Sprungweite in unserem zweifaktoriellen Datensatz. Jetzt ist die Frage, ob unser Modell einer Normalverteilung in den Sprungweiten genügt.
R Code [zeigen / verbergen]
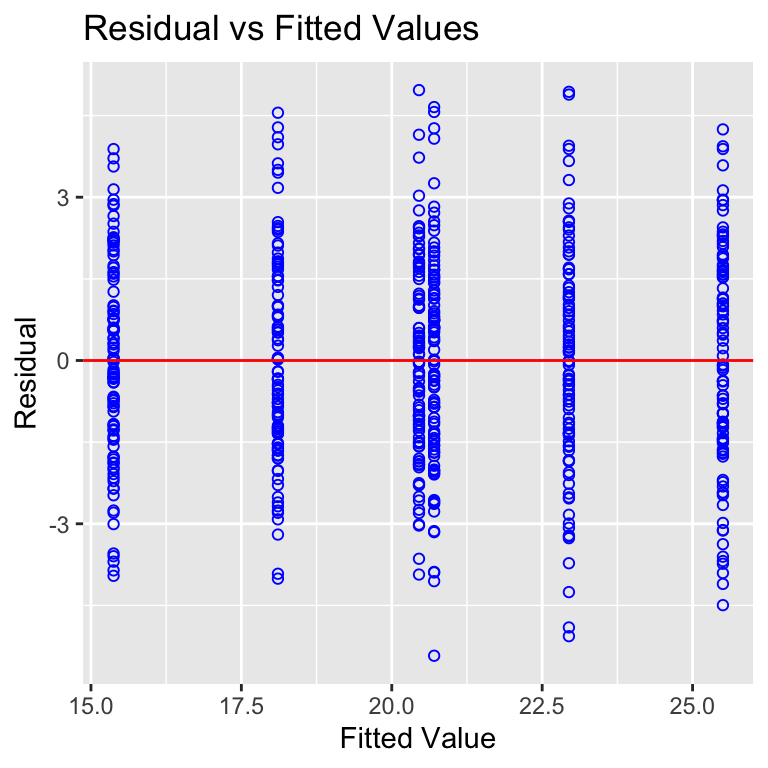
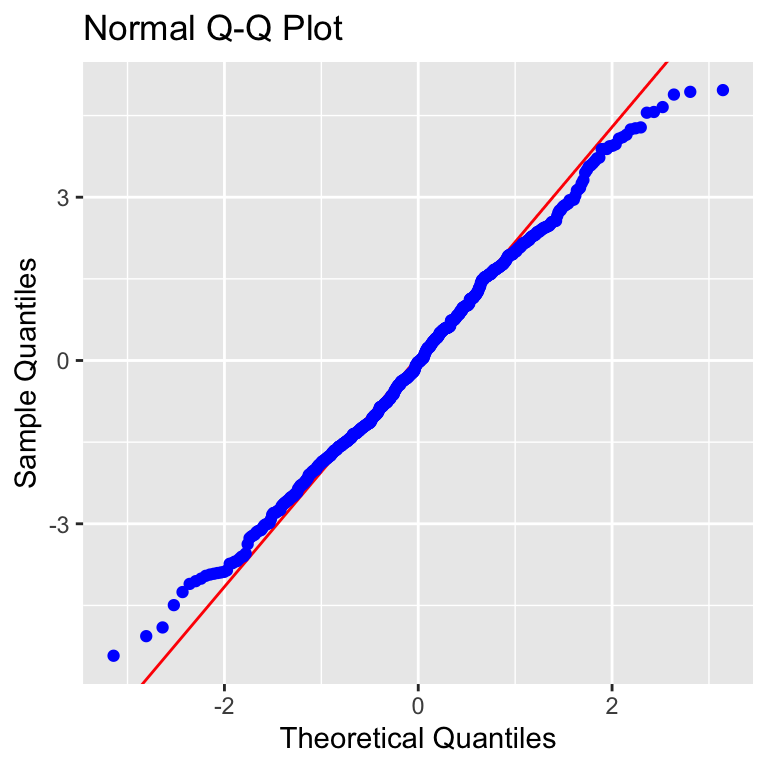
fac2_jump_fit <- lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) Die Funktion ols_plot_resid_fit() und ols_plot_resid_qq() liefert uns jetzt die beiden Abbildungen für die Überprüfung der Normalverteilung. Hier musst du jetzt wissen, was du erwarten sollst. Die Punkte sollten in der ersten Abbildung gleichmäßig um die Linie streuen. In der zweiten Abbildung sollten die Punkte auf der Linie liegen. Wie wir sehen, passt das ziemlich gut. Im ersten Fall sollen die Punkte entlang der Linie in den grauen Bereich fallen und im zweiten Fall sollte auch der graue Bereich nahe an der Linie sein. Das passt beides. Wir nehmen auch hier eine Normalverteilung der Sprungweite an.
R Code [zeigen / verbergen]
fac2_jump_fit |>
ols_plot_resid_fit()
fac2_jump_fit |>
ols_plot_resid_qq()Kommen wir jetzt zu den Schlupfzeiten. Auch hier bauen wir uns erstmal schnell das statistische Modell für unsere Schlupfzeiten in unserem zweifaktoriellen Datensatz. Jetzt ist die Frage, ob unser Modell einer Normalverteilung in den Schlupfzeiten genügt.
R Code [zeigen / verbergen]
fac2_hatch_fit <- lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) Wie es zu erwarten war, sind die Schupfzeiten eben nicht normalverteilt. Die beiden Funktionen ols_plot_resid_fit() und ols_plot_resid_qq() zeigen hier Abweichungen von den Erwartungen unter der Annahme einer Normalverteilung. Wir sehen klar, dass die Punkte in der ersten Abbildung nicht gleichmäßig um die Linie streuen. Auch liegen die Punkte nicht auf der Linie in der zweiten Abbildung. Wir würden klar hier die Normalverteilung ablehnen. Die Schlupfzeiten können wir nicht mit dem obigen statistischen Modell auswerten und müssen uns eine andere Lösung als Ausweg suchen.
R Code [zeigen / verbergen]
fac2_hatch_fit |>
ols_plot_resid_fit()
fac2_hatch_fit |>
ols_plot_resid_qq()Damit hätten wir die visuelle Überprüfung der Normalverteilung in unserem Messwert einmal abgeschlossen. Wir betrachten jetzt als nächstes die visuelle Überprüfung der Varianzhomogenität in den Gruppen oder aber Faktoren. Der Weg und die Funktionen sind ähnlich, aber auch hier gibt es dann ein paar Ausnahmen.
25.4.2 Varianzhomogenität
Jetzt schauen wir uns die Varianzhomogenität in den Gruppen an. Daher wollen wir jetzt eine Aussage über die Gleichheit der Varianzen in deinen Behandlunsggruppen treffen. Wir brauchen eben dann die Varianzhomogenität für die normale ANOVA oder aber den TukeyHSD Test. Es gibt auch andere Möglichkeiten, wenn wir keine Varianzhomogenität vorliegen haben, aber hier schauen wir jetzt erstmal, wie wir Varianzheterogenität als Abweichung von der Varianzhomogenität erkennen. Später schauen wir uns dann noch die Möglichkeit an die Varianzen in den Gruppen zu testen.
R Paket {ggplot}
Für die visuelle Überprüfung nutzen wir wieder das R Paket {ggplot} mit den beiden Funktionen geom_boxplot() und geom_violin(). Wir haben damit dann auch hier den besten Überblick über die Streuung in den einzelnen Gruppen oder eben Faktorkombinationen. Ich verzichte hier auf den Densityplot und auch auf das Hiytogramm, da wir meistens viel zu wenig Fallzahlen vorliegen haben. Dazu aber gleich mehr in der theoretischen Betrachtung.
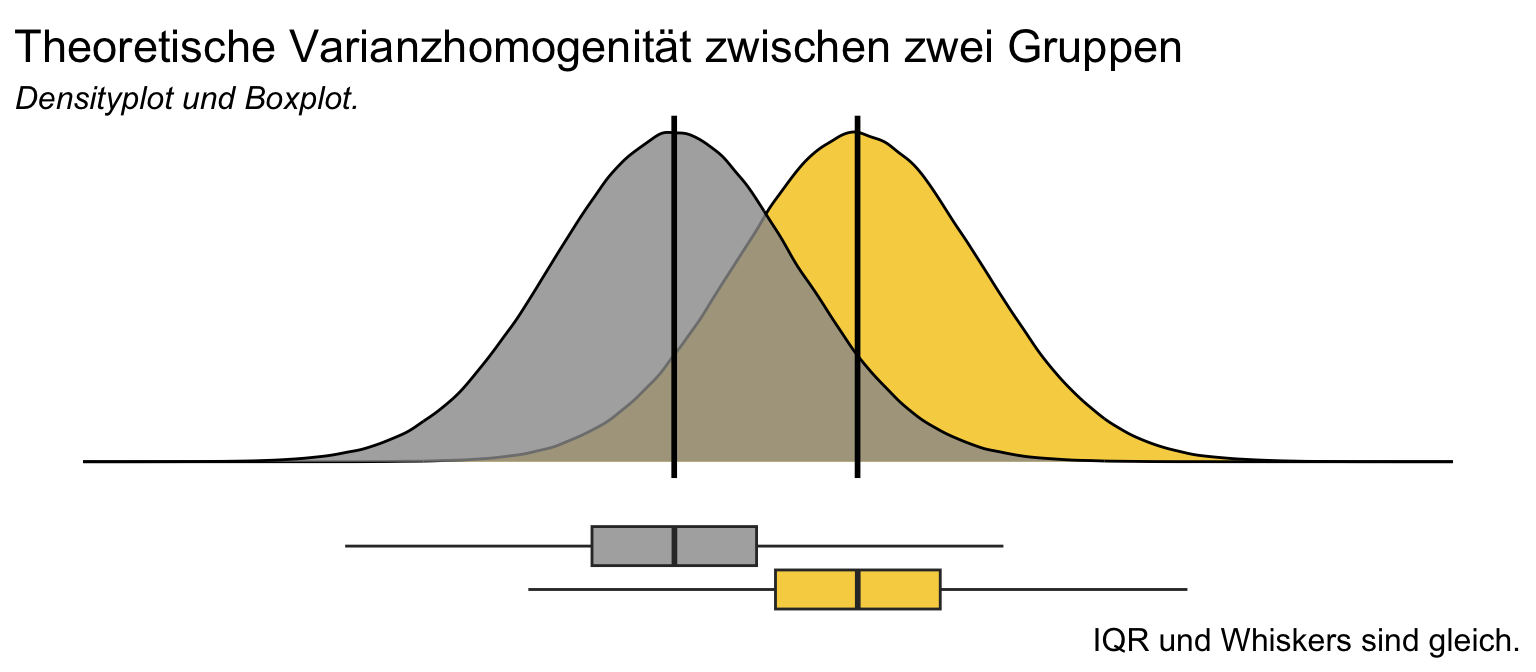
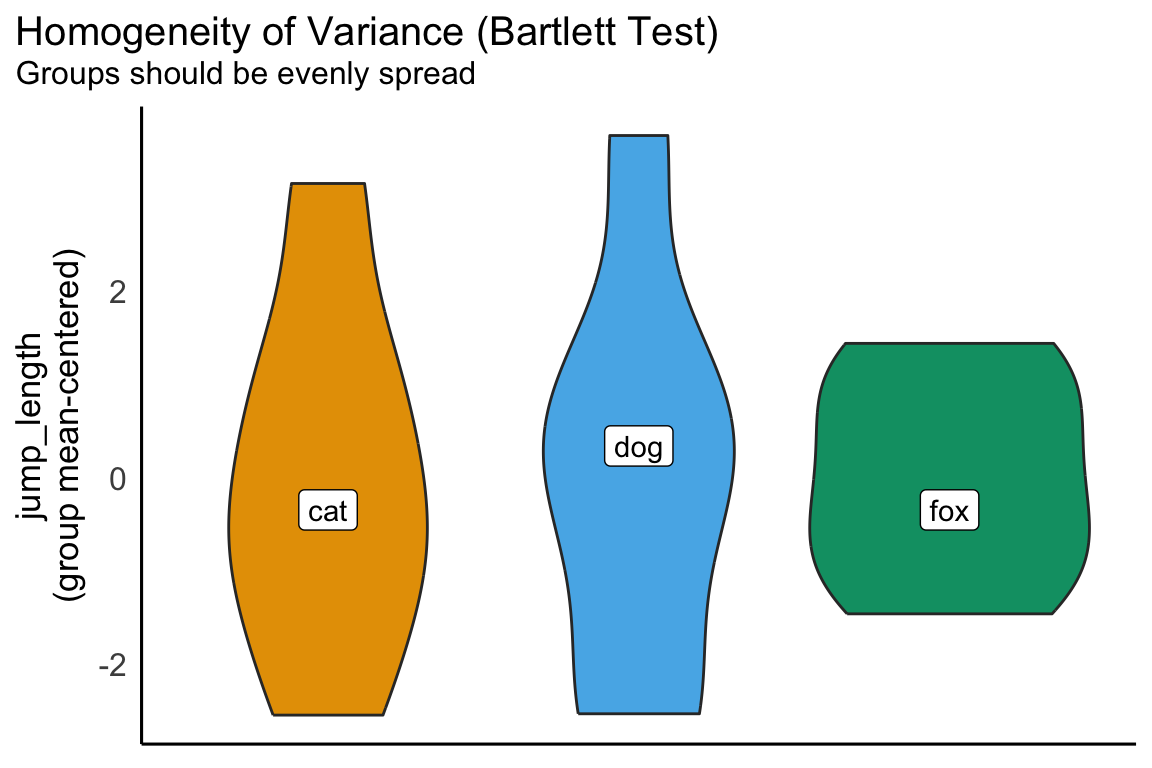
Hier einmal die theoretischen Abbildungen von zwei Gruppen mit Varianzhomogenität. Wir sehen, dass die Mittelwerte in der Mitte der beiden verteilungen liegen udn auch die Verteilungsenden alle gleich lang sind. Wenn wir dann die Boxplots betrachten, dann sehen diese auch identisch aus. Die Mediane liegen in der Mitte der Box und auch sind die Boxen gleich groß. Die Whiskers sind auch gleich lang. Am Ende haben wir natürlich immer nur Stichproben der Grundgesamtheit vorliegen, so dass wir nie wissen, ob wir eine echte Vrainzhomogenität vorliegen haben oder diese nur beobachten. Für die folgenden Analysen ist es dann aber gleich.
Was wir dann theoretsich erwarten sehen wir dann bei kleinen Fallzahlen eigentlich nie. ich habe in der folgenden Abbildung immer zwei Gruppen aus einer Grundgesamtheit mit gleichen varianzne gezogen. In der Grundgesamtheit haben also beide Gruppen dann die gleiche Varianz. Das Problem ist nur, dass wir mit kleinen Fallzahlen diesen Zusammenhang oder die Gleichheit der Varianzen nicht sehen können. Erst ab einer Gruppengröße von vierzig Beobachtungen erahnen wir die gegebene Gleichheit der Varianzen. Ich finde hier imm allgemeinen den Violinplot mit den Punkten zusätzlich schon fast besser als die reinen Boxplots. Ja, Varianzhomogenität ist ein scheues Reh und schwer zu beobachten bei kleinen Fallzahlen.
Fangen wir einmal an uns in einem Boxplot die Varianzhomogenität und die Varianzheterogenität anzuschauen. In der folgenden Abbildung habe ich dir einmal ein Beispiel für die Vairanzhomogenität zwischen den Behandlungsgruppen in der linken Abbilsung mitgebracht. Wie du sehen kannst, liegt der Median in der Mitte der Boxen. Viel wichtiger ist aber, dass die Boxen in allen Gruppen gleich groß sind und die Whisker gleich lang. Das ist hier in der linken Abbildung gegeben. In der rechten Abbidlung siehst du dann sehr gut die Abweichung von der Regel und damit auch die Varianzheterogenität in den Gruppen. Die Gruppen haben alle unterschiedlich große Boxen und die Whisker sind unterschiedlich lang. Wir haben also Varianzheterogenität vorliegen.
Schauen wir uns jetzt einmal die beispielhaften Daten in einem einfaktoriellen und einem zweifaktoriellen Boxplot einmal an. Die Sprungweite sollte hierbei eher einer Varianzhomogenität folgen als die Schlupfzeiten.
Einfaktorieller Boxplot
Das praktische bei den Boxplots ist, dass wir hier nichts mehr vorrechnen müssen, sondern direkt die Boxplots in {ggplot} erstellen können. Ich finde man sieht immer in einem Boxplot besser, ob die Streuung um den Median eher homogen oder eher heterogen ist. Gerne ergänze ich noch den Mittelwert mit der Funktion stat_summary(). Wir sehen hier schön, dass die Varianzhomogenität hier eher gegeben ist. Der einzige Punkt ist eben die etwas geringere Streuung in den Fuchsflöhen. Hier haben wir dann kürzere Whiskers und die Box ist kleiner.
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = animal, y = jump_length, fill = animal)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point",
shape=23, size = 5, fill = "gray50") +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() Zweifaktorieller Boxplot
Den zweifaktoriellen Boxplot erstellen wir für die einzelnen Floharten getrennt für die beiden Geschlechter. Du musst schauen, was du auf die x-Achse legst und was du dann auf die Legende und daher mit fill gruppierst. Gerne ergänze ich noch den Mittelwert mit der Funktion stat_summary(), muss hier aber schauen, dass ich nach dem Faktor animal gruppiere und dann noch mit der Funktion position_dodge() die richtige Position finde. Auch hier haben wir für die Sprungweite in allen Faktorkombinationen die gleiche Varianz vorliegen. Wir gehen also von Varianzhomogenität aus.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = sex, y = jump_length, fill = animal)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point", aes(group = animal),
shape=23, size = 5, fill = "gray50",
position = position_dodge(0.75)) +
labs(x = "Flohart", y = "Sprungweite in [cm]", fill = "Tierart") +
scale_fill_okabeito() In unserem zweiten Messwert der Schlupfzeiten sehen wir dann aber eine klare Abweichung in den Boxen untereinander. Die Boxen sind unterschiedlich groß und die Whisker nicht gleich lang. Wir haben es hier also bei den Schlupfzeiten eher mit einer Varianzheterogenität zu tun. Wir müssen dann also in den Modellen, die wir dann rechnen, die Varianzheterogenität berücksichtigen.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = animal, y = hatch_time, fill = sex)) +
theme_minimal() +
geom_boxplot() +
stat_summary(fun.y = mean, geom = "point", aes(group = sex),
shape=23, size = 5, fill = "gray50",
position = position_dodge(0.75)) +
labs(x = "Flohart", y = "Schlupfzeiten in [m]", fill = "Geschlecht") +
scale_fill_okabeito() +
ylim(0, 2000)Ich persönlich finde mittlerweile die Violinplots besser um die Verteilung eines Messwerts in den Gruppen abzuschätzen. Der Boxplot ist dann manchmal doch etwas verwirrend und nicht ganz so klar. Hier nutze ich dann noch die Verdindung des Dotplots mit dem Violinplot, was dann nochmal mehr Informationen liefert. Das R Paket {see} nutzt die Funktion geom_violindot() um dies abzubilden. In der folgenden Abbildung habe ich dir einmal Varianzhomogenität und einmal Varianzheterogenität dargestellt. Eins muss ich dazu gleich sagen, ich habe für die Darstellung dann eine Fallzahl von zwanzig Beobachtungen pro Gruppe gewählt. Diese Fallzahl siehst du dann in deinen Gruppen dann eher weniger. Aber das ist ja immer das Problem mit der Darstellung, wenn die Fallzahl zu klein ist, dann wird es schwer.
Einfaktorieller Violinplot
Hatt ich gerade geschrieben, dass es bei kleiner Fallzahl schwer wird? Hier haben wir dann mal einen einfaktoriellen Violinplot mit nur fünf Beobachtungen pro Gruppe. Hier sieht man dann sehr gut woraus dann die Densityhälfte entsteht und welche Beobachtungen abgebildet werden. Auf der anderen Seite sehen wir auch sehr schön, dass die Hunde- und Katzenflöhe sichtlich mehr streuen als die Fuchsflöhe. Nach dieser Abbildung in einem Violinplot mit Dotplot würde ich von Varianzheterogenität in den Gruppen ausgehen.
R Code [zeigen / verbergen]
ggplot(data = fac1_tbl,
aes(x = animal, y = jump_length, fill = animal)) +
theme_minimal() +
geom_violindot(dots_size = 4, trim = FALSE) +
stat_summary(fun.y = mean, geom = "point",
shape=23, size = 5, fill = "gray50") +
labs(x = "Flohart", y = "Sprungweite in [cm]") +
theme(legend.position = "none") +
scale_fill_okabeito() Zweifaktorieller Violinplot
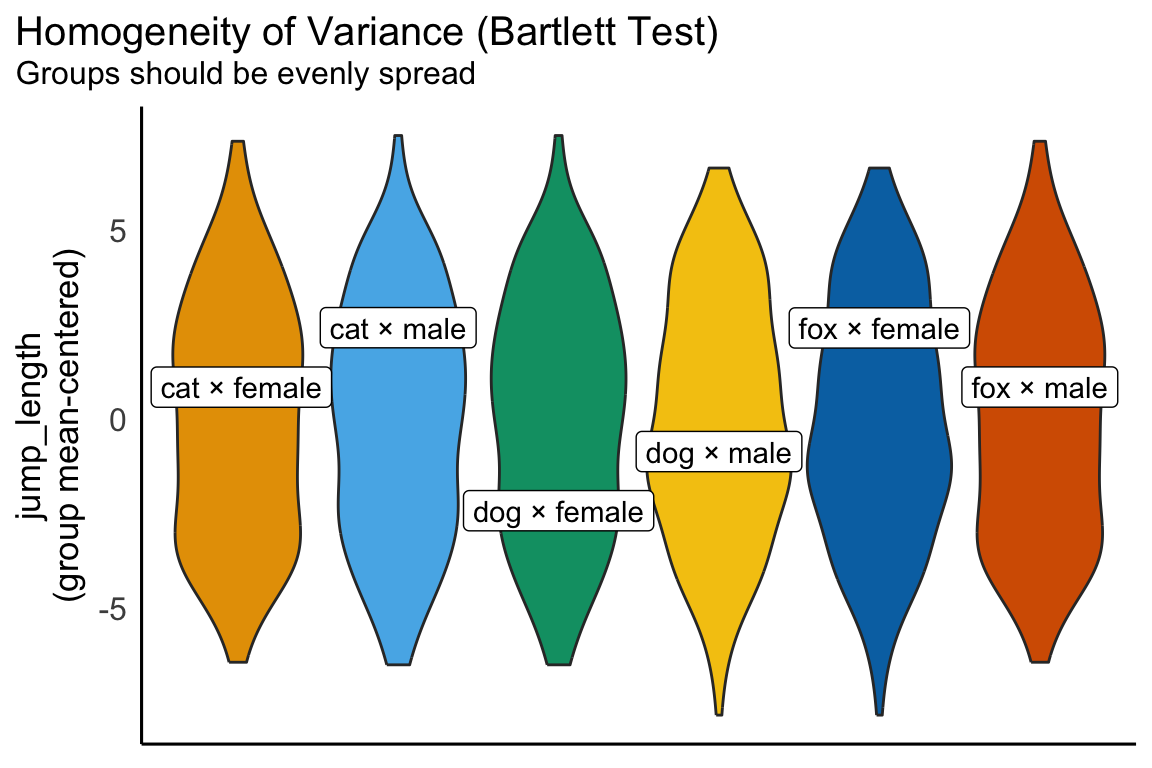
Ich fand denn zweifaktoriellen Violinplot etwas schwerer zu bauen, da wir hier dann noch die Dots als Repräsentation der Beobachtungen gesondert über die Option position_dots schieben mussten. Wenn wir das hier haben, dann sieht der Violinplot sehr gut aus. Hier sehen wir dann auch mit genügend Beobachtungen pro Gruppe, dass wir Varianzhomogenität zwischen den Gruppen aller Faktorkombinationen haben. Die Streuung in allen Gruppen ist gleich. Daher haben wir hier für die Sprungweiten Varianzhomgenität vorliegen.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = sex, y = jump_length, fill = animal)) +
theme_minimal() +
geom_violindot(dots_size = 4, position_dots = position_dodge(0.45)) +
stat_summary(fun.y = mean, geom = "point", aes(group = animal),
shape=23, size = 5, fill = "gray50",
position = position_dodge(0.45)) +
labs(x = "Flohart", y = "Sprungweite in [cm]", fill = "Tierart") +
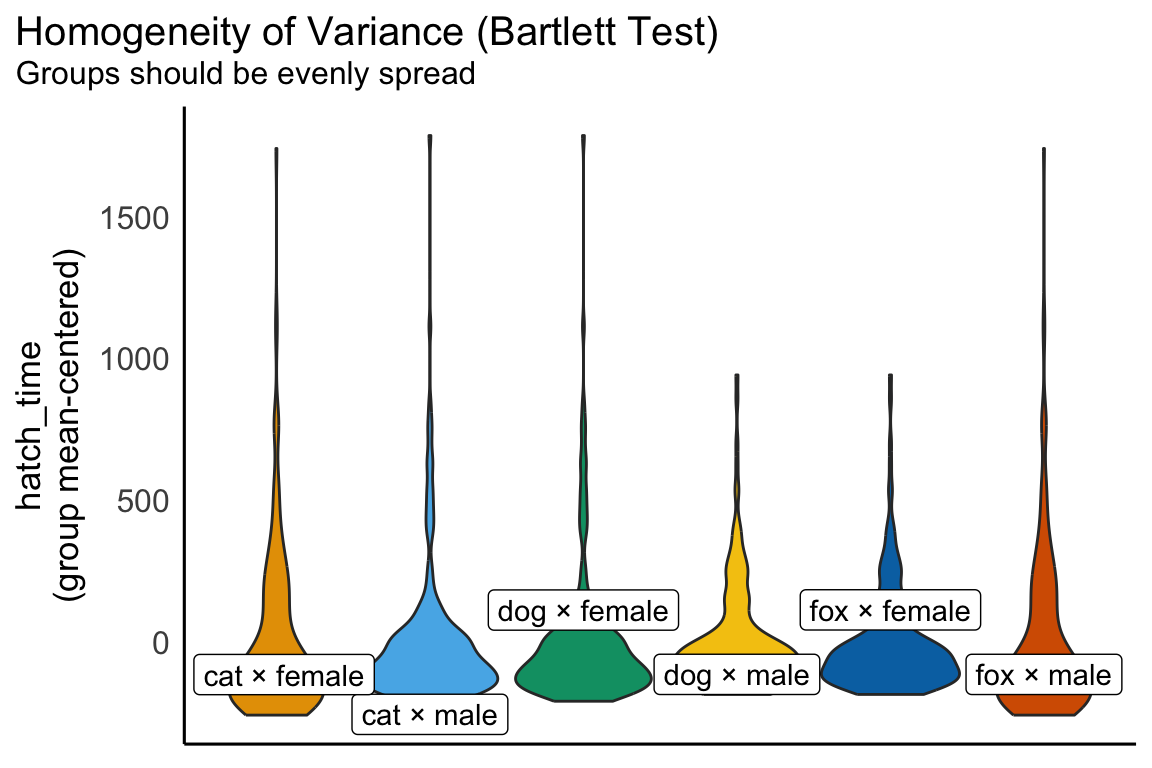
scale_fill_okabeito() Was in den Boxplots nicht so super zu sehen war wird jetzt in den Violinplots klarer. Wir schauen uns in der folgenden Abbildung einmal die Schlupfzeiten an. Hier sehen wir dann sehr schön die Varianzheterogenität zwischen den Gruppen. Teilweise sind die Violinplots sehr in die Länge gezogen und teilweise sehr kurz. Auf jeden Fall sind die Violinen nicht alle gleich über alle Faktorkombinationen. Wir würden hier visuell von einer Varianzheterogenität ausgehen. Die Schwierigkeit liegt hier eher darin, dass wir dann ja eigentlich auch eine Normalverteilung haben wollen, wenn wir eine ANOVA rechnen wollen. Das wird hier sehr schwierig und ich liefere dann später noch Auswege weiter unten.
R Code [zeigen / verbergen]
ggplot(data = fac2_tbl,
aes(x = animal, y = hatch_time, fill = sex)) +
theme_minimal() +
geom_violindot(dots_size = 600, trim = FALSE,
position_dots = position_dodge(0.45)) +
labs(x = "Flohart", y = "Schlupfzeiten in [m]", fill = "Geschlecht") +
scale_fill_okabeito() +
ylim(0, 2000)R Paket {performance}
Das R Paket {performance} liefert die Möglichkeit auf einem statistischen Modell die Überprüfung der Varianzhomogenität zu rechnen. Das Schöne hier ist, dass es dann auch nur eine Abbildung gibt. Das ist natürlich super praktisch, da du ja für die ANOVA ein Modell brauchst sowie auch für den multiplen Vergleich in {emmeans}. Auch hier habe ich mich dazu entschieden nicht nochmal mit die Abbildungen schöner zu machen. Teilweise ist es dann auch nicht so einfach möglich in den Funktionen von {performance} Änderungen vorzunehmen. Insbesondere die Funktion check_model() ist dann teilweise sehr resistent gegen Veränderungen, obwohl hier {ggplot} im Hintergrund läuft. Das tolle an der Funktion check_model() ist, dass du hier verschiedene Annahmen in einem Aufruf überprüfen kannst. Im Prinzip kannst du hier auch die Überprüfung der Varianzhomogenität und der Normalverteilung in eins machen.
Wir bauen uns erstmal schnell das statistische Modell für unsere Sprungweite in unserem zweifaktoriellen Datensatz. Jetzt ist die Frage, ob unser Modell einer Varianzhomogenität in den Gruppen der Sprungweiten genügt.
R Code [zeigen / verbergen]
fac2_jump_fit <- lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) Die Funktion check_model() liefert uns jetzt eine Abbildung für die Überprüfung der Varianzhomogenität. Wie wir sehen, passt das ziemlich gut. Im ersten Fall sollen die Punkte entlang der Linie sein. Das passt soweit. Wir nehmen auch hier eine Varianzhomogenität der Gruppen über die Sprungweite an.
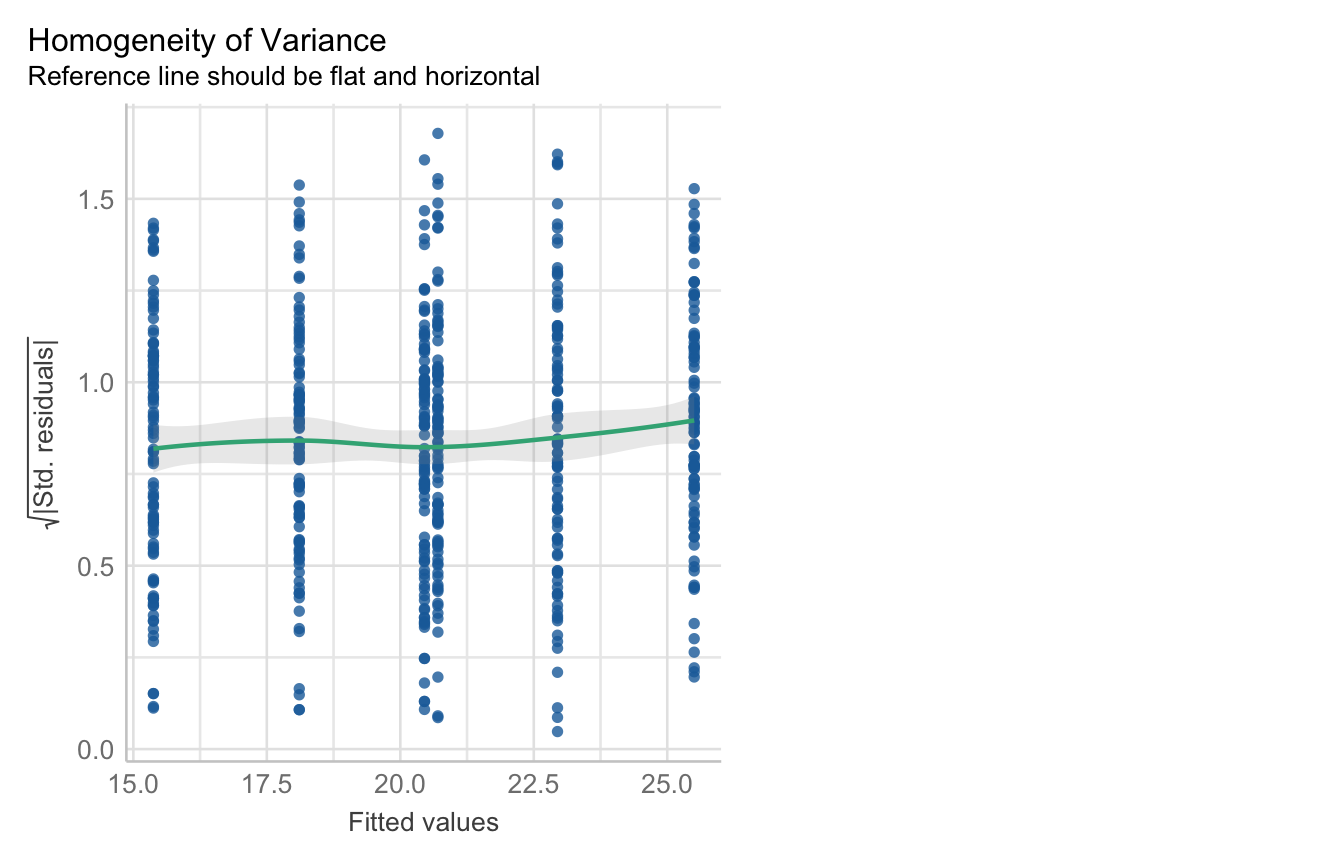
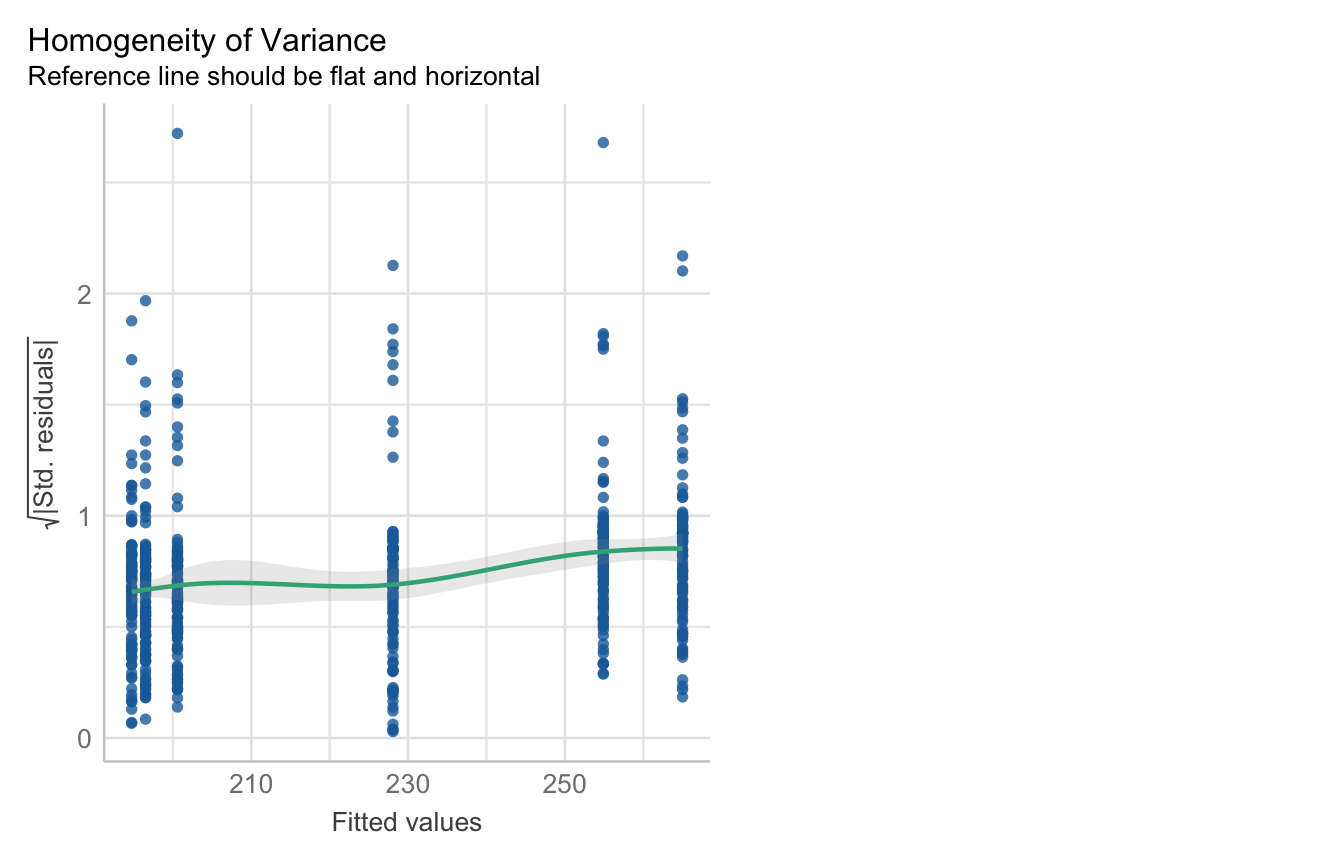
Kommen wir jetzt zu den Schlupfzeiten. Auch hier bauen wir uns erstmal schnell das statistische Modell für unsere Schlupfzeiten in unserem zweifaktoriellen Datensatz. Jetzt ist die Frage, ob unser Modell einer Varianzhomogenität in den Gruppen der Schlupfzeiten genügt.
R Code [zeigen / verbergen]
fac2_hatch_fit <- lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) Hier wird es schon schwieriger. Wir haben zwar in den Violinplots gesehen, dass sich die Violinen doch unterschieden haben, wenn wir uns aber die Modellierung anschauen, dann sehen wir, dass der Effekt der unterschiedlichen Streuung über alle Gruppen dann doch nicht so stark im Modell ist. Die Gerade ist zwar nicht perfekt horizontal aber auch nicht super schief. Es ist immer spannend, was ein Modell so ausgleichen kann und wo es dann Probleme gibt. Hier lohnt sich dann ja auch nochmal ein statistischer Test auf die Varianzhomogenität im folgenden Abschnitt.
25.5 Statistische Überprüfung
Kommen wir nun zum etwas kontroversen Teil. Der statistischen Überprüfung der Varianzhomogenität oder aber auch der Normalverteilung. Die folgenden Überlegungen stimmen aber im Prinzip auch für andere Vortest auf andere statistische Eigenschaften von Daten. Wir nutzen hier als Werkzeug eine statistische Simulation um mehr über die Eigenschaften eines Vortest oder allgemeiner eines statistischen Tests zu erfahren. Im Prinzip kannst du auch diesen Teil überspringen, wenn du einfach nur den Vortest rechnen willst und einen p-Wert brauchst. Ansonsten ist dieser Teil daneben dafür da für mich nochmal zu ordnen, was die Probleme eines Vortests sind. Jedenfalls aus statistischer Sicht und darum geht es mir dann ja.
Die folgenden Betrachtungen sind statistisch etwas schief und semantisch fragwürdig bis falsch. Aber ich nutze jetzt mal die Umgangssprache um die Sachlage besser verständlich zu machen. Ja, wir können nur Nullhypothesen ablehnen und nichts “erkennen”, aber darum geht es hier nicht. Klassisches lying-to-children was ich hier betreibe. Das ist dann eben so und auch gewollt.
Wir kommen dann hier nicht um das Kapitel zur Testtheorie herum. Du musst also schon wissen, dass es ein Signifikanzniveau sowie eine Power gibt. Ich wiederhole hier gleich nochmal alles, aber gehe nicht so tief auf alles ein. Daher schaue nochmal in das Kapitel, wenn dir etwas unklar ist. Du musst nämlich wissen, dass ein statistischer Test so gebaut ist, dass er im Idealfall eine 5% \(\alpha\)-Fehlerrate sowie eine 20% \(\beta\)-Fehlerate hat. Damit hat dann auch ein statistischer Test eine Power von 80%.
- Was heißt 5% \(\alpha\)-Fehlerrate?
-
Ein statistischer Test hat eine 5% \(\alpha\)-Fehlerrate und damit lehnt ein statistischer Test in 5% der Fälle eine Nullhypothese ab, obwohl die Nullhypothese wahr ist. In unserem Fall hieße das, dass ein Vortest in 5% der Fälle behauptet, es gebe keine Normalverteilung oder Varianzhomogenität.
- Was heißt 80% Power?
-
Jeder statistische Test ist so gebaut, dass er unter idealen Bedingungen in etwa in 80% der Fälle die Alternativhypothese nachweisen kann. Das heißt in unserem Fall, dass unsere Vortest nur in 80% der Fälle auch eine Varianzheterogenität oder Nichtnormalverteilung nachweisen können.
- Zu welcher globalen Fehlerrate testen wir dann eigentlich am Ende?
-
Dann gibt es natürlich noch die Frage der \(\alpha\)-Infaltion. Wenn wir zu viel Testen, dann wissen wir am Ende gar nicht mehr mit welchem globalen \(\alpha\)-Niveau wir unsere Auswertung gemacht haben. Das Problem ist nicht so schlimm und ich würde es auch erstmal hinten anstellen. Nimm nur soviel mit, es ist nicht gut alles mögliche zu Testen, wenn wir nicht die Fehlerraten kontrollieren.
Wie du siehst, gibt es schon ein paar Fragen, die man sich stellen kann, wenn wir so Vortests rechnen. Am Ende kannst du darüber nachdenken oder auch nicht. Manchmal hast du keine Wahl und musst einen Vortest rechnen. Die Abschlussarbeit will es und dann rechnen wir eben auch den Vortest. Manchmal hast du das Glück, dass du einfach weist, das deine Daten normalverteilt sind oder nicht. Aber gut, genug des Vorgerede beginnen wir mit den Vortest als statistischen Test.
25.5.1 Normalverteilung
Beginnen wir wie immer mit den Hypothesen, die der statistische Test im Fall der Überprüfung der Normalverteilung rechnen will. Wir haben folgendes Hypothesenpaar vorliegen. In der Nullhypothese steht die Gleichheit. Damit sagen wir, dass unser Messwert \(y\) gleich einer unbekannten Normalverteilung mit einem Mittelwert \(\mu\) und einer Streuung \(\sigma^2\) verteilt ist. Unsere Alternativehypothese besagt, dass unser Messwert \(y\) nicht aus einer Normalverteilung stammt.
\[ \begin{aligned} H_0: &\; y = \mathcal{N}(\mu, \sigma^2)\\ H_A: &\; y \ne \mathcal{N}(\mu, \sigma^2)\\ \end{aligned} \]
Jetzt wollen wir nochmal aufschreiben, was das jetzt für unseren statistischen Test auf die Annahme der Normalverteilung bedeutet. Das ist ja immer die Frage, die uns im folgenden Analysen umtreiben wird.
Bei der Entscheidung zur Normalverteilung gilt folgende Regel. Ist der \(p\)-Wert des Pre-Tests auf Varianzhomogenität kleiner als das Signifikanzniveau \(\alpha\) von 5% lehnen wir die Nullhypothese ab. Wir nehmen Varianzheterogenität an.
- Ist \(p \leq \alpha = 5\%\) so nehmen wir keine Normalverteilung im Messwert an. Der Messwert ist nicht normalverteilt.
- Ist \(p > \alpha = 5\%\) so nehmen wir eine Normalverteilung im Messwert an.
Auf jeden Fall sollten wir das Ergebnis unseres Pre-Tests auf Normalverteilung nochmal visuell bestätigen.
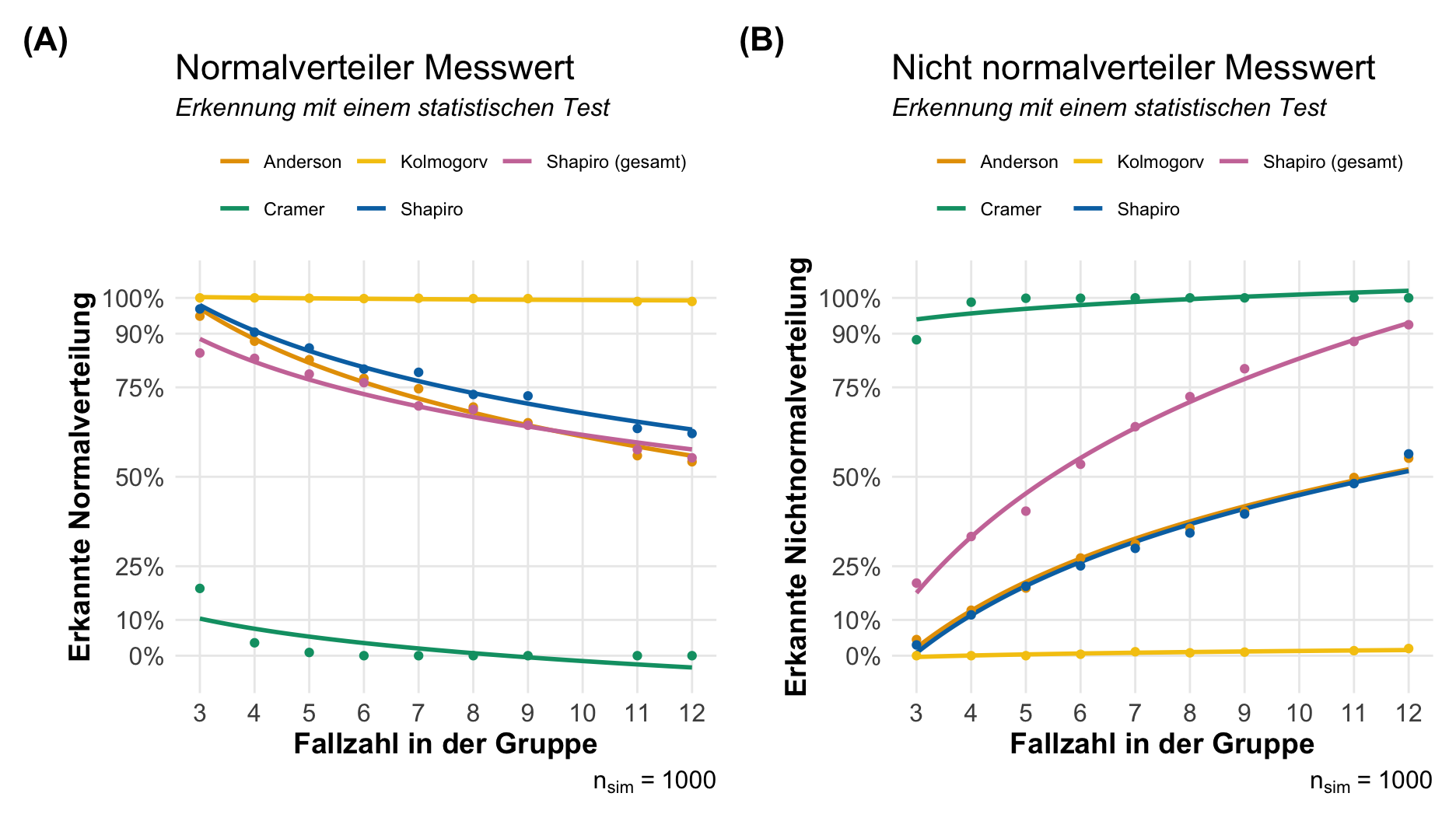
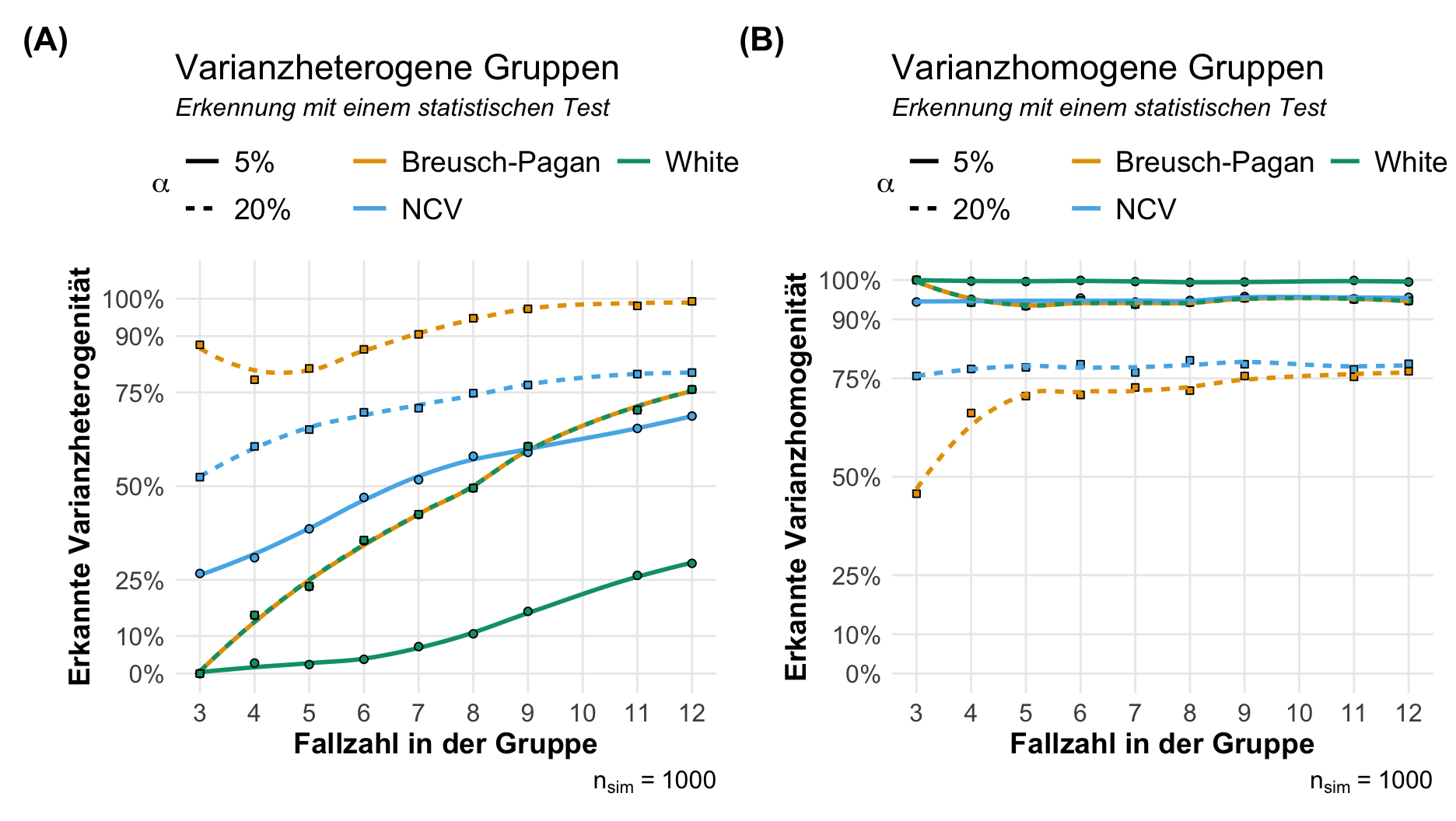
Wenn wir eine statistischen Test für die Überprüfung der Annahme der Normalverteilung rechnen wollen, dann nutzen wir meistens den Shapiro-Wilk Test. Neben diesem Test haben wir dann aber noch eine mindestens drei weitere Tests zur Auswahl. Auch ist die Frage, ob wir den Test auf dem Modell rechnen oder aber auf den reinen Messwert. Häufig macht das dann auch nochmal einen Unterschied in dem Testergebnis aus. Am Ende wissen wir dann meistens nicht so viel Neues. Für die Entscheidungsfindung habe ich einmal eine kleine Simulationsstudie gerechnet. Ich habe dafür einmal 1000 normalverteilte Datensätze sowie 1000 nichtnormalverteilte Datensätze mit jeweils drei Gruppen und einer variierenden Fallzahl in den Gruppen generiert. Dann habe ich geschaut, mit welchem Anteil die statistischen Tests die Normalverteilung oder die Nichtnormalverteilung erkannt haben. In der folgenden Abbildung siehst du einmal die Ergebnisse.
Was nehmen wir aus den wilden Linien denn nun mit in unsere praktische Auswertung? Ich habe hier die Implementierung aus dem R Paket {oslrr} genutzt und ein wirklich simples Design gebaut mit drei Gruppen gebaut. Also eigentlich der Klassiker, der keine Probleme machen sollte.
- Der Kolmogorow-Smirnow-Test (abk. Kolmogorv) erkennt immer eine Normalverteilung. Das sehen wir in der linken Abbildung. Das Problem ist eher, dass der Kolmogorow-Smirnow-Test aber dafür auch gar keine Nichtnormalverteilung erkennt. Für den Test ist alles normalvertielt und gut ist. Keine Empfehlung für den einfachen Anwender und einfach meiden.
- Der Cramér-von-Mises-Test (abk. Cramer) ist die Umkehrung des Kolmogorow-Smirnow-Test. Hier haben wir den Fall, dass wir keine Normalverteilung erkennen, dafür dann aber alles als eine Nichtnormalverteilung bewerten. Auch hier kann ich den Test nicht empfehlen. Die Eigenschaften sind nicht sinnführend für den einfachen Anwender.
- Der Anderson-Darling-Test (abk. Anderson) funktioniert ähnlich wie der Shapiro-Wilk-Test. Hier haben wir eher das Problem, dass wir mit steigender Fallzahl eben immer im statistischen leichter die Nullhypothese ablehnen können. Daher lehnen wir mit steigender Fallzahl auch eher die Nullhypothese ab. Auf der anderen Seite benötigen wir ca. 10 Beobachtungen per Gruppe um eine Nichtnormalverteilung mit 80% zu erkennen.
- Den Shapiro-Wilk-Test (abk. Shapiro) habe ich einmal modelbasiert gerechnet und einmal auf den vollen Messwertdaten. Wie du siehst kann der Shapiro-Wilk-Test auf den gesamten Daten die Nichtnormalverteilung leichter erkennen. Er hat dann ja auch mehr Fallzahl zu Verfügung. Sonst hat der Shapiro-Wilk-Test die gleichen Probleme mit der steigenden Fallzahl. Der Shapiro-Wilk-Test fängt dann an schneller die Nullhypothese abzulehnen.
Was lernen wir daraus? Das nicht jeder Vortest wirklich geeignet ist um die Frage nach der Normalverteilung zu beantworten. Auch ist es nicht sinnführend eine Funktion wie ols_test_normality() zu schreiben, die einfach alle vier Tests rechnet und einen dann im Regen stehen lässt. Welchen der p-Werte soll man denn nehmen? Zum Anderen ist es natürlich so, dass wir mit kleiner Fallzahl keine Varianzheterogeität finden und mit zu großer Fallzahl zu schnell die Nullhypothese ablehnen. Dann schauen wir uns mal an, was wir so machen können. In den folgenden Tabs findest du verschiedene Probleme. Lösungen muss ich schauen, ob welche dabei sind.
Die eigentlich Idee hinter den ganzen Vortests für die Normalverteilung ist eigentlich, dass die Normalvertielung eine symmetrische Verteilung um einen Mittelwert ist. Das heißt, die beiden Seiten der Verteilung sind gespiegelt am Mittelwert. Wenn das nicht der Fall ist, dann ist die Verteilung schief. Die Schiefe (eng. skewness) ist ein Maß für die Asymmetrie einer Verteilung. Dieser Wert kann positiv oder negativ sein.
- Wie interpretiert man den Wert der Schiefe?
-
Eine negative Schiefe deutet darauf hin, dass sich der Schwanz auf der linken Seite der Verteilung befindet, die sich in Richtung negativer Werte erstreckt. Eine positive Schiefe zeigt an, dass sich der Schwanz auf der rechten Seite der Verteilung befindet, die sich in Richtung positiver Werte erstreckt. Ein Wert von Null bedeutet, dass die Verteilung überhaupt nicht schief ist, d. h. die Verteilung ist vollkommen symmetrisch.
Neben der Schiefe messen wir auch die Kurtosis. Die Kurtosis (eng. kurtosis) ist ein Maß dafür, ob eine Verteilung im Vergleich zu einer Normalverteilung ein starkes oder schwaches Schwanzende aufweist.
- Wie interpretiert man den Wert der Kurtosis?
-
Die Kurtosis einer Normalverteilung beträgt 3. Wenn eine gegebene Verteilung eine Kurtosis von weniger als 3 aufweist, wird sie als playkurtisch bezeichnet, was bedeutet, dass sie dazu neigt, weniger und weniger extreme Ausreißer zu produzieren als die Normalverteilung. Wenn eine gegebene Verteilung eine Kurtosis größer als 3 hat, wird sie als leptokurtisch bezeichnet, was bedeutet, dass sie dazu neigt, mehr Ausreißer als die Normalverteilung zu produzieren. In einigen Formeln wird dann noch von der Kurtosis 3 abgezogen, um den Vergleich mit der Normalverteilung zu erleichtern. Nach dieser Definition hätte eine Verteilung eine größere Kurtosis als eine Normalverteilung, wenn der Kurtosis-Wert größer als 0 wäre.
Dann ist natürlich die Frage welche Grenzen es so gibt. Wir können in Curran et al. (1996) lesen, dass die Grenzen für Schiefe und Kurtosis bei 2 bis 7 liegen. Je anch Literatur sind es dann nochmal andere Grenzen, wie du in der Übersichtsichtsseite Testing normality including skewness and kurtosis mit Quellen nochmal nachlesen kannst. Am Ende sucht man sich eine Grenze aus und referenziert dann die Quelle dazu.
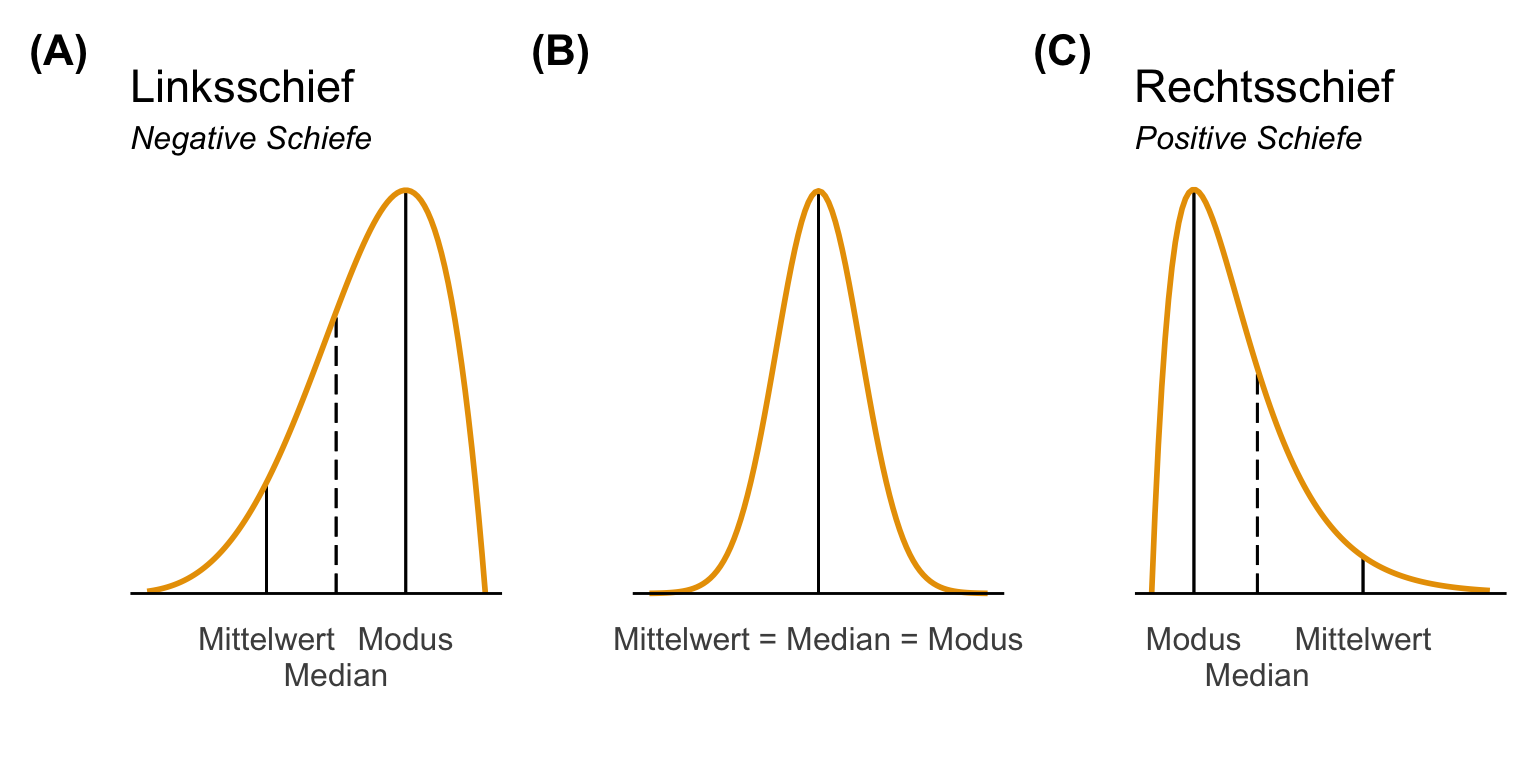
Ich habe dir den Zusammenhang hier nochmal in der folgenden Abbildung dargestellt. Wir betrachten dabei den Mittelwert, den Median sowie den Modus. Dabei ist der Modus der häufigste Wert in dem Messwert. Wenn wir eine symmetrische Normalverteilung vorliegen haben, dann sind alle statistischen Maßzahlen gleich.
Neben der visuellen Darstellung können wir uns auch in dem R Paket {moments} die Schiefe und Kurtosis wie folgt berechnen lassen. Wir nutzen die Funktion skewness() für die Schiefe.
R Code [zeigen / verbergen]
skewness(fac2_tbl$hatch_time)[1] 2.859213Dann gibt es noch die Funktion kurtosis() für die Berechnung der Kurtosis. Ist irgendwie dann auch einleuchtend.
R Code [zeigen / verbergen]
kurtosis(fac2_tbl$hatch_time)[1] 14.95786Manchmal wollen wir die Schiefe und Kurtosis nicht auf den gesamten Messwert sondern gruppiert nach den Faktorkombinationen berechnen. Das habe ich dann einmal im Folgenden gemacht.
R Code [zeigen / verbergen]
fac2_tbl |>
group_by(animal, sex) |>
summarise(kurtosis = kurtosis(hatch_time),
skewness = skewness(hatch_time))# A tibble: 6 × 4
# Groups: animal [3]
animal sex kurtosis skewness
<fct> <fct> <dbl> <dbl>
1 cat male 25.7 4.09
2 cat female 9.23 2.46
3 dog male 13.7 2.79
4 dog female 7.22 1.87
5 fox male 8.74 2.09
6 fox female 9.13 2.27Das R Paket {moments} bietet auch die Funktion jarque.test(), die einen Anpassungsgütetest durchführt, der feststellt, ob die Stichprobendaten eine Schiefe und eine Wölbung aufweisen, die einer Normalverteilung entsprechen oder nicht. Die Null- und Alternativhypothesen dieses Tests lauten wie folgt.
\(H_0\): Der Messwert \(y\) weist eine Schiefe und Wölbung auf, die einer Normalverteilung entspricht.
\(H_A\): Der Messwert \(y\) weist eine Schiefe und eine Kurtosis auf, die nicht mit einer Normalverteilung übereinstimmen.
Dann rechnen wir einmal den Test auf den gesamten Messwert und schauen einmal, ob die Schlupfzeiten dann normalverteilt sind. Wir wir sehen können, können wir die Normalverteilung ablehen. Wir gehen dann von nicht normalverteilten Schlupfzeiten aus.
R Code [zeigen / verbergen]
fac2_tbl |>
pull(hatch_time) |>
jarque.test()
Jarque-Bera Normality Test
data: pull(fac2_tbl, hatch_time)
JB = 4392.3, p-value < 2.2e-16
alternative hypothesis: greaterVielleicht möchtest du den ganzen Test dann auch über jede Faktorkombination rechnen, dafür müssen wir uns dann aber etwas strecken und ins {purrr} Kochbuch schauen. Aber am Ende haben wir dann für jede Flohart- und Geschlechtskombination einen Test auf die Schiefe und Kurtosis gerechnet. Ich habe dann noch die Entscheidungsregel mit dem p-Wert ergänzt und wir finden heraus, dass alle Faktorkombinationen nicht normalverteilt sind.
R Code [zeigen / verbergen]
fac2_tbl |>
split(~ animal + sex) |>
map(~jarque.test(.x$hatch_time)) |>
map(tidy) |>
bind_rows(.id = "test") |>
select(test, p.value) |>
mutate(decision = ifelse(p.value <= 0.05, "reject normal", "normal"),
p.value = pvalue(p.value, accuracy = 0.001))# A tibble: 6 × 3
test p.value decision
<chr> <chr> <chr>
1 cat.male <0.001 reject normal
2 dog.male <0.001 reject normal
3 fox.male <0.001 reject normal
4 cat.female <0.001 reject normal
5 dog.female <0.001 reject normal
6 fox.female <0.001 reject normalWenn du überprüfen willst, ob dein Messwert \(y\) einer Normalverteilung folgt, dann kannst du auch die Funktion check_normality() aus dem R Paket {performance} nutzen. Die Funktion rechnet dann den Shapiro-Wilk-Test um auf eine Abweichung von der Normalverteilung zu testen. Hierzu ist anzumerken, dass der Test relativ empfindlich bei Abweichungen in den Verteilungsschwänzen ist. Dazu mehr in dem Tab {stats} zum Shapiro-Wilk-Test. Darüber hinaus braucht der Shapiro-Wilk-Test auch etwas Fallzahl, damit er auf die Normalverteilung testen kann. Im Folgenden schauen wir uns den Code für ein einfaktorielles und zweifaktorielleseinmal an. Am Ende des Kapitels gehe ich nochmal darauf ein, was du machen kannst, wenn du keine Normalverteilung in deinem Messwert \(y\) vorliegen hast.
Einfaktoriell
Beginnen wir wieder mit einem einfaktoriellen Modell. Wir wollen wissen, ob unsere Sprungweite in [cm] über unsere verschiedenen Floharten normalverteilt ist. Wir bauen also erstmal das Modell und schicken es dann in die Funktion check_normality() aus dem R Paket {performance}.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
check_normality()OK: residuals appear as normally distributed (p = 0.514).Die Funktion sagt, dass wir eine Normalverteilung in unseren Daten vorliegen haben. Wir können uns auch einen Diagnoseplot wiedergeben lassen. Dafür müssen wir die Funktion nur an die Funktion plot() weiterleiten. Das Schöne ist, dass die Abbildung uns auch gleich sagt, was wir zu erwarten haben um eine Normalverteilung anzunehmen.
Zweifaktoriell
Im zweifaktoriellen Fall ändert sich jetzt nur das Modell. Wir haben eben zwei Faktoren vorliegen und diese müssen wir dann mit ins Modell nehmen. Ich habe hier auch gleich den Interaktionsterm mit ergänzt, ich teste gerne das Modell, was ich dann später auch auswerten möchte. Wir wir gleich in den Tabs sehen, sind die Sprungweiten normalverteilt und wie zu erwarten war die Schlupfzeiten nicht.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_normality()OK: residuals appear as normally distributed (p = 0.135).R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_normality()Warning: Non-normality of residuals detected (p < .001).Auch hier haben wir eine Normalverteilung oder eben keine Normalvertwilung in den Messwerten vorliegen. Gerne schaue ich mir auch die Abbildung der Residuen einmal an und das geht dann flott über die Funktion plot(). Da musst du nur die Ausgabe der Funktion check_normality() weiterleiten. Die leichten Bögen in den Punkten kommen von den unterschiedlichen Faktoren und deren Effekten auf die Sprungweiten oder eben auf die Schlupfzeiten. Für die weitere Betrachtung der visuellen Überprüfung schauen auch einmal weiter oben in den Abschnitten nach.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_normality() |>
plot() +
scale_fill_okabeito()R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_normality() |>
plot() +
scale_fill_okabeito()Dann kommen wir nochmal zu dem Klassiker für den Test auf Normalverteilung. Wir nutzen dazu die Funktion shapiro.test() aus dem Standardpaket {stats} um den Shapiro-Wilk-Test durchzuführen. Leider hat auch der Shapiro-Wilk-Test ein paar ungünstige Eigenschaften. Wir testen mehr oder minder die Verteilungsschwänze unserer Verteilung der Messwerte. Daher werden wir auch eher die Nullhypothese ablehnen, wenn wir Ausreißer oder eine schiefe Verteilung vorliegen haben. Wenn wir die Nullhypothese ablehnen, dann lehnen wir auch die Normalverteilung ab. Wenn die Schwänze symmetrisch sind, dann ist egal was in der Mitte der Verteilung passiert, dann ist alles normalverteilt. Ich habe dir den Zusammenhang einmal in der folgenden Abbildung dargestellt. Eine zweigipfelige Verteilung ist für den Shapiro-Wilk-Test normalverteilt, wenn eben die Schwänze symmetrisch sind. Eine Verteilung, die einen Ausreißer hat, wird als normalverteilt abgelehnt. Wenn die Verteilung schief ist, dann kommt es eben auf die Schiefe an. Visuell meinen wir schon was zu sehen, aber der Shapiro-Wilk-Test schafft es eben noch nicht die Normalverteilung abzulehnen.
Wir können wie immer einmal den Shapiro-Wilk-Test auf den gesamten Messwerten rechnen. Dafür müssen wir uns nur die Messwerte einmal raus ziehen und dann dann in die Funktion shapiro.test() weiterleiten. Hier wird es dann etwas wild. Wenn wir uns den gesamten Messwert über alle Gruppen zusammen anschauen, dann ist weder die Sprungweite noch die Schlupfzeit normalverteilt. In beiden Fällen ist der p-Wert kleiner als das Signifikanzniveau \(\alpha\) gleich 5%. Das würde ich bei der Sprungweite anzweifeln.
R Code [zeigen / verbergen]
fac2_tbl |>
pull(jump_length) |>
shapiro.test()
Shapiro-Wilk normality test
data: pull(fac2_tbl, jump_length)
W = 0.99407, p-value = 0.01916R Code [zeigen / verbergen]
fac2_tbl |>
pull(hatch_time) |>
shapiro.test()
Shapiro-Wilk normality test
data: pull(fac2_tbl, hatch_time)
W = 0.71273, p-value < 2.2e-16Auch ist es möglich die einzelnen Faktorkombinationen für die Abweichung von der Normalverteilung zu testen. Aber Achtung, hier geht dann natürlich die Fallzahl sehr in den Keller. Ich nutze hier das {purrr} Kochbuch um einmal alle Shapiro-Wilk-Tests zu rechnen. Spannenderweise sind jetzt alle Sprungweiten für alle Faktorkombinationen wieder normalverteilt. Bei den Schlupfzeiten sind dann alle Gruppen wiederum nicht normalverteilt. Du kannst dich echt in die Ecke testen. Hier würde ich echt das gruppenweise Testen und nicht auf dem gesamten Messwert bevorzugen.
R Code [zeigen / verbergen]
fac2_tbl |>
split(~ animal + sex) |>
map(~shapiro.test(.x$jump_length)) |>
map(tidy) |>
bind_rows(.id = "test") |>
select(test, p.value) |>
mutate(decision = ifelse(p.value <= 0.05, "reject normal", "normal"),
p.value = pvalue(p.value, accuracy = 0.001))# A tibble: 6 × 3
test p.value decision
<chr> <chr> <chr>
1 cat.male 0.442 normal
2 dog.male 0.131 normal
3 fox.male 0.835 normal
4 cat.female 0.657 normal
5 dog.female 0.991 normal
6 fox.female 0.210 normal R Code [zeigen / verbergen]
fac2_tbl |>
split(~ animal + sex) |>
map(~shapiro.test(.x$hatch_time)) |>
map(tidy) |>
bind_rows(.id = "test") |>
select(test, p.value) |>
mutate(decision = ifelse(p.value <= 0.05, "reject normal", "normal"),
p.value = pvalue(p.value, accuracy = 0.001))# A tibble: 6 × 3
test p.value decision
<chr> <chr> <chr>
1 cat.male <0.001 reject normal
2 dog.male <0.001 reject normal
3 fox.male <0.001 reject normal
4 cat.female <0.001 reject normal
5 dog.female <0.001 reject normal
6 fox.female <0.001 reject normalAm Ende dann noch die Variante aus dem R Paket {oslrr} wo wir einfach alle vier statistsichen Tests zur Normalverteilung auf unser Modell loslassen. Wir brauchen also auch hier erstmal unser lineares Modell und schauen dann im Nachgang, ob wir einen normalverteilten Messwert vorliegen haben. Etwas korrekter schauen wir, ob die Residuen nach dem Modellieren einer Normalverteilung folgen. Das ist aber in etwa das Gleiche. Daher einmal das zweifaktorielle Modell für die Sprungweite udn einmal das zweifaktorielle Modell für die Schlupfzeiten. Die beiden Modell stecken wir dann in die Funktion ols_test_normality(). Die Funktion liefert uns einfach vier Tests ohne weitere Kommentare oder Hilfestellungen. Das Paket {oslrr} ist schon älter.
Hier kommt dann einmal das zweifaktorielle Modell für die Sprungweiten mit den Floharten sowie dem Geschlecht und der entsprechenden Interaktion. Wir nutzen einmal das lineare Modell um dann im Anschluss zu überprüfen, ob das Modell so funktioniert hat.
R Code [zeigen / verbergen]
fac2_jump_fit <- lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) Dann lassen wir uns einmal alle vier statistsichen Tests auf die Normalverteilung wiedergeben und wundern uns, dass nicht alle Tests das gleiche Ergebnis haben. Welcher Test ist den nun der richtige Test? Das R Paket {oslrr} lässt uns hier alleine. Ich würde den Shapiro-Wilk Test nehmen und den Rest ignoieren.
R Code [zeigen / verbergen]
fac2_jump_fit |>
ols_test_normality()-----------------------------------------------
Test Statistic pvalue
-----------------------------------------------
Shapiro-Wilk 0.996 0.1354
Kolmogorov-Smirnov 0.0342 0.4834
Cramer-von Mises 38.654 0.0000
Anderson-Darling 0.6734 0.0783
-----------------------------------------------Auch hier kommt dann einmal das zweifaktorielle Modell für die Schlupfzeiten mit den Floharten sowie dem Geschlecht und der entsprechenden Interaktion. Wir nutzen einmal das lineare Modell um dann im Anschluss zu überprüfen, ob das Modell so funktioniert hat.
R Code [zeigen / verbergen]
fac2_hatch_fit <- lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) Ich lasse mir dann einmal alle vier statistsichen Tests auf die Normalverteilung wiedergeben und freue mich, dass alle Tests das gleiche Ergebnis haben. Damit können wir sicher die Normalverteilung ablehnen. Wir haben also nciht normalverteilte Schlupfzeiten vorliegen.
R Code [zeigen / verbergen]
fac2_hatch_fit |>
ols_test_normality()-----------------------------------------------
Test Statistic pvalue
-----------------------------------------------
Shapiro-Wilk 0.7335 0.0000
Kolmogorov-Smirnov 0.1978 0.0000
Cramer-von Mises 72.8651 0.0000
Anderson-Darling 41.8667 0.0000
-----------------------------------------------Damit haben wir uns einmal durch das Testen der Normalverteilung durchgearbeitet. Dabei siehst du recht schön, warum es manchmal schwierig ist mit den Vortest. Wenn die Fallzahl zu hoch ist, lehnen wir gerne mal vorschnell die Normalverteilung ab. Das ist schlecht, weil wir mit der Normalverteilung tolle Methoden haben, die auch relativ robust gegen eine leichte Abweichung von der Normalverteilung funktionieren. Auf der anderen Seite finden wir seltener eine Abweichung von der Normalverteilung wenn unsere Fallzahl zu klein ist. Daher ist es echt so eien Sache mit dem Test auf die Normalverteilung. Gucken wir also jetzt mal wie ein Schwein ins Uhrwerk zum Testen der Varianzhomogenität.
25.5.2 Varianzhomogenität
Beginnen wir wie immer mit den Hypothesen, die der statistische Test im Fall der Überprüfung der Varianzhomogenität rechnen will. Wir haben folgendes Hypothesenpaar vorliegen. In der Nullhypothese steht die Gleichheit. Damit sagen wir, dass unsere Gruppen alle die gleiche Varianz haben. Wir haben Varianzhomogenität vorliegen. Unsere Alternativehypothese besagt, dass unser Gruppen nicht die gleiche Varianz haben. Wir haben Varianzheterogenität vorliegen. Es ergeben sich folgende Hypothesen für den Pre-Test auf Varianzhomogenität. Ich schaue mir hier jetzt nur den Fall von zwei Gruppen an, wenn du mehr Gruppen hast, dann erweitert sich entsprechend die Nullhypothese und Alternativehypothese.
\[ \begin{aligned} H_0: &\; \sigma^2_A = \sigma^2_B\\ H_A: &\; \sigma^2_A \ne \sigma^2_B\\ \end{aligned} \]
Wir sehen, dass in der Nullhypothese die Gleichheit der Varianzen steht und in der Alternativehypothese der Unterschied, also die Varianzheterogenität. Ab wann sollten wir denn die Varianzhomogenität ablehnen? Wenn wir standardmäßig auf 5% testen, dann werden wir zu selten die Varianzhomogenität ablehnen. Wir drehen ja hier eigentlich etwas verqer die Hypothesen. Wir können ja nur den Test rechnen und schauen, ob wir die Nullhypothese ablehnen können. Ein statistischer Test beweist ja nicht die Nullhypothese. Daher wird häufiger vorgeschlagen in diesem Fall auf ein Signifikanzniveau von \(\alpha\) gleich 20% zu testen.
Jetzt wollen wir nochmal aufschreiben, was das jetzt für unseren statistischen Test auf die Annahme der Normalverteilung bedeutet. Das ist ja immer die Frage, die uns im folgenden Analysen umtreiben wird.
Bei der Entscheidung zur Varianzhomogenität gilt folgende Regel. Ist der \(p\)-Wert des Pre-Tests auf Varianzhomogenität kleiner als das Signifikanzniveau \(\alpha\) von 20% lehnen wir die Nullhypothese ab. Wir nehmen Varianzheterogenität an.
- Ist \(p \leq \alpha = 20\%\) so nehmen wir Varianzheterogenität an.
- Ist \(p > \alpha = 20\%\) so nehmen wir Varianzhomogenität an.
Auf jeden Fall sollten wir das Ergebnis unseres Pre-Tests auf Varianzhomogenität nochmal visuell bestätigen.
Bitte beachte, dass die meisten Implementierungen eigentlich immer zur einem \(\alpha\) von 5% testen, wenn die Tests eine schriftliche Bewertung von sich aus wiedergeben.
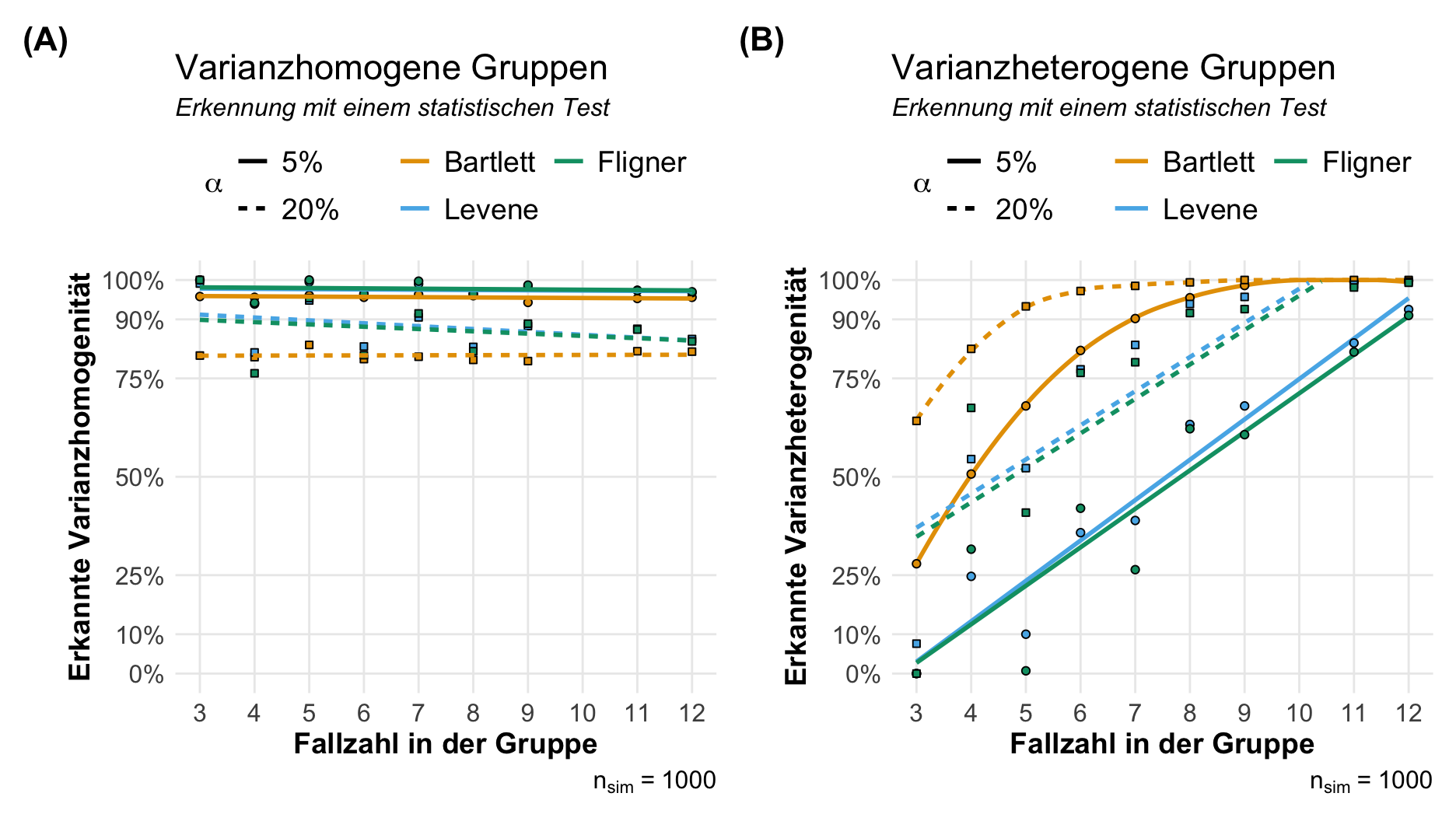
Aber auch in diesem Fall können wir natürlich eine Varianzhomogenität übersehen oder aber eine Varianzheterogenität fälschlicherweise annehmen. Daher habe ich dir einmal folgende Abbildung erstellt. Wie du siehst ist der Bartlett und der Levene Test gut in der Lage eine vorhandene Varianzhomogenität auch zu erkennen. Auch bei kleinen Fallzahlen klappt das gut. Anders sieht es bei der Varianzheterogenität aus. Hier ist der Bartlett Test auf jeden Fall besser, da wir hier mit Daten aus einer Normalverteilung arbeiten. Da hat es der Bartlett Test etwas einfacher ale der Levene Test. Dazu mehr dann gleich weiter unten. Wenn wir dann noch das Signifikanzniveau \(\alpha\) auf 20% anheben, dann finden wir noch eher eine Varianzheterogenität. Wenn wir aber zu einem Signifikanzniveau von \(\alpha\) gleich 20% testen, finden aber auch schwerer eine Varianzhomogenität.
Was nehmen wir aus den wilden Linien denn nun mit in unsere praktische Auswertung?
- Der Levene-Test (abk. Levene) ist einer der häufigsten genutzen Tests um auf Vairanzhomogenität zu testen. Wir können hier auch als Referenz den Median wählen und dann ist der Levene Test noch etwas robuster gegen Ausreißer in den Daten.
- Der Bartlett-Test (abk. Bartlett) basiert auf der Annahme, dass wir normalverteilte Messwerte vorliegen haben. Ist das nicht der Fall, dann hat der Bartlett Test Probleme eine Varianzheterogenität sicher zu finden.
- Der Fligner-Killeen (abk. Flinger) ist die nicht parametrische Variante und basiert auf Rängen. Wenn wir also sehr schiefe Messwerte vorliegen haben, dann ist der Fligner-Killeen eine Alternative. Wie wir aber sehen, ist der Test bei kleinen Fallzahlen nicht sehr gut um Finden von Varianzheterogenität.
Wir nutzen zum statistischen Testen den Levene-Test über die Funktion leveneTest() oder den Bartlett-Test über die Funktion bartlett.test(). Beide Tests sind in R implementiert und können unter anderem über das Paket {car} genutzt werden. Einfach ausgedrückt, überprüft der Bartlett-Test die Homogenität der Varianzen auf der Grundlage des Mittelwerts. Dementsprechend ist der Bartlett-Test empfindlicher gegen eine Abweichung von der Normalverteilung der Daten, die er überprüfen soll. Der Levene-Test überprüft die Homogenität der Varianzen auch auf der Grundlage des Mittelwerts ist daher ebenso anfällig gegen die Abweichung von der Normalverteilung. Wir haben aber auch die Wahl, den Median für den Levene-Test zu nutzen dann ist der Levene-Test robuster gegenüber Ausreißern.
Für den Levene Test werde ich mir nochmal die Formeln gleich anschauen, da der Levene und der Bartlett test eng miteinander verwandt sind. Im Weiteren nutzen wir auch noch die R Pakete {performance} und {oslrr} um etwas automatisierter zu testen ob wir Varianzhomogenität vorliegen haben. Ich empfehle ja immer das R Paket {performance} zu nutzen, da wir hier alles in einem Rustsch gut implementiert haben.
Im Folgenden wollen wir uns einmal in der Theorie den Levene-Test anschauen. Der Levene-Test ist eigentlich nichts anderes als eine etwas versteckte einfaktorielle ANOVA, aber dazu dann in den folgenden Tabs mehr. Dafür nutzen wir als erstes die folgende Formel um die Teststatistik zu berechnen. Dabei ist \(W\) die Teststatistik, die wir zu einer \(F\)-Verteilung, die wir schon aus der ANOVA kennen, vergleichen können.
Zur Veranschaulichung bauen wir uns einen simplen Datensatz mit \(N = 14\) Beobachtungen für \(k = 2\) Tierarten mit Hunden und Katzen. Damit hat jede Tierart \(7\) Beobachtungen der Sprunglängen der jeweiligen Hunde- und Katzenflöhe. Wir fragen uns nun, ob die Varianzen in den beiden Tierarten gleich sind. Dafür wollen wir dann einmal den Levene Test nutzen und verstehen.
| dog | cat |
|---|---|
| 5.7 | 3.2 |
| 8.9 | 2.2 |
| 11.8 | 5.4 |
| 8.2 | 4.1 |
| 5.6 | 1.1 |
| 9.1 | 7.9 |
| 7.6 | 8.6 |
Wir haben jetzt die Möglichkeit den Levene-Test einmal händisch zu rechnen oder aber in R in Schritten durchzugehen. Am Ende zeige ich nochmal die Gleichheit zwischen dem Levene Test und der einfaktoriellen ANOVA. Das passt natürlich nur hier für die eine Gruppe und wenn das Beispiel einfach ist.
Hier einmal die Formel des Levene Tests. Wir berechnen wie immer eine Teststatistik \(W\) und fragen uns, ob diese Teststatsitik extrem ist. Wir wollen uns hier aber nur mit der Berechnugn beschäftigen. Die Entscheidung anhand eines kritischen Werts überlassen wir dann R oder aber einer anderen Software.
\[ W = \frac{(N-k)}{(k-1)} \cdot \frac{\sum_{i=1}^k N_i (\bar{Z}_{i\cdot}-\bar{Z}_{\cdot\cdot})^2} {\sum_{i=1}^k \sum_{j=1}^{N_i} (Z_{ij}-\bar{Z}_{i\cdot})^2} \]
mit
- \(W\), der Teststatistik des Levene Tests.
- \(N\) und \(k\), der gesamten Fallzahl \(N\) und der Anzahl der Gruppen \(k\). Hier ist \(N\) gleich 14 und die Anzahl der Gruppen gleich 3.
- \(N_i\), der Fallzahl der Gruppe \(i\) mit jeweils 7 Flöhen pro Gruppe.
- \(\bar{Z}_{i\cdot}\), der lokalen Gruppenmittel der absoluten Differenzen \(Z\).
- \(\bar{Z}_{\cdot\cdot}\), dem globalen Mittelwert der absoluten Differenzen \(Z\).
- \(Z_{ij}\), der einzelnen absoluten Differenzen \(Z\).
Dann wollen wir mal die einzelnen Variablen durchgehen. Fangen wir mit den absoluten Differenzen \(Z\), die wir wie folgt bestimmen. Wie haben hier die Wahl den Mittelwert oder aber den Median als Referenz zu nehmen. Ich nehme hier den Mittelwert.
\[ Z_{ij} = \begin{cases} |Y_{ij} - \bar{Y}_{i\cdot}|\; \text{oder} \\ |Y_{ij} - \tilde{Y}_{i\cdot}| \end{cases} \]
mit
- \(Y_{ij}\), den Werten der einzelnen Beobachtungen, hier die Sprungweiten.
- \(\bar{Y}_{i\cdot}\) oder \(\tilde{Y}_{i\cdot}\), die lokalen Mittelwert oder lokalen Mediane der Gruppen.
Der Rest der Variablen ist dann wildes Gerechne. Wir haben dann oben zwei Terme stehen, weil wir einmal die Katzen und einmal die Hunde Sprungweiten haben. Im Nenner summieren wir die Abstände einmal auf. Dazu dann mehr in dem Tab zu R. Ich rechne hier die Summen und die Abweichungen der einzelen absoluten Abstände zu den lokalen Mittel nicht per Hand.
Dann können wir einmal alles einsetzen und erhalten unsere W Statistik.
\[ \begin{aligned} W &= \cfrac{14-2}{2-1}\cdot \cfrac{7 \cdot (1.57 - 1.93)^2 + 7 \cdot (2.28 - 1.93)^2} {10.39 + 11.43} \\ &= \cfrac{12}{1} \cdot \cfrac{1.76}{21.82} \\ &= \cfrac{21.12}{21.82} \approx 0.968 \end{aligned} \]
Wir würden jetzt die W Statistik zu einem kritischen Wert vergleichen um eine Entscheidung zu finden. Das überlassen wir dann aber R oder eben der Funktion leveneTest() aus dem R Paket {car}.
Hier dann einmal der mathematische Teil Schriit für Schritt in R. Hier kriegst du dann auch die Zahlen her für die ganzen Variablen aus der Formel des Levene Tests. Ich fülle dir dann am Ende auch nochmal die Formel mit den berechneten Zahlen hier aus. Das ist vermutlich einfacher nachzuvollziehen.
Datensatz
R Code [zeigen / verbergen]
animal_tbl <- tibble(dog = c(5.7, 8.9, 11.8, 8.2, 5.6, 9.1, 7.6),
cat = c(3.2, 2.2, 5.4, 4.1, 1.1, 7.9, 8.6))Absolute Abstände \(Z_{ij}\) zum Mittelwert
R Code [zeigen / verbergen]
z_tbl <- animal_tbl |>
mutate(dog_abs = abs(dog - mean(dog)),
cat_abs = abs(cat - mean(cat)))
z_tbl# A tibble: 7 × 4
dog cat dog_abs cat_abs
<dbl> <dbl> <dbl> <dbl>
1 5.7 3.2 2.43 1.44
2 8.9 2.2 0.771 2.44
3 11.8 5.4 3.67 0.757
4 8.2 4.1 0.0714 0.543
5 5.6 1.1 2.53 3.54
6 9.1 7.9 0.971 3.26
7 7.6 8.6 0.529 3.96 Lokale Mittelwerte \(Z_{i.}\) der Gruppen
R Code [zeigen / verbergen]
mean(z_tbl$dog_abs)[1] 1.567347R Code [zeigen / verbergen]
mean(z_tbl$cat_abs)[1] 2.277551Globaler Mittelwerte \(Z_{..}\)
R Code [zeigen / verbergen]
(mean(z_tbl$dog_abs) + mean(z_tbl$cat_abs))/2[1] 1.922449Summierte lokale Abweichungen der Gruppen \(Z_{ij}-\bar{Z}_{i.}\)
R Code [zeigen / verbergen]
sum((z_tbl$dog_abs - 1.57)^2)[1] 10.3983R Code [zeigen / verbergen]
sum((z_tbl$cat_abs - 2.28)^2)[1] 11.42651Einsetzen in die Formel
\[ \begin{aligned} W &= \frac{(N-k)}{(k-1)} \cdot \frac{\sum_{i=1}^k N_i (\bar{Z}_{i\cdot}-\bar{Z}_{\cdot\cdot})^2} {\sum_{i=1}^k \sum_{j=1}^{N_i} (Z_{ij}-\bar{Z}_{i\cdot})^2} \\ &=\cfrac{14-2}{2-1}\cdot \cfrac{7 \cdot (1.57 - 1.93)^2 + 7 \cdot (2.28 - 1.93)^2} {10.39 + 11.43} \\ &= \cfrac{12}{1} \cdot \cfrac{1.76}{21.82} \\ &= \cfrac{21.12}{21.82} \approx 0.968 \end{aligned} \]
Wir würden jetzt auch hier die W Statistik zu einem kritischen Wert vergleichen um eine Entscheidung zu finden. Das überlassen wir dann aber R oder eben der Funktion leveneTest() aus dem R Paket {car}.
Der Levene-Test ist eigentlich nichts anderes als eine einfaktorielle ANOVA auf den absoluten Abständen von den einzelnen Werten zu dem Mittelwert oder dem Median. Das können wir hier einmal nachvollziehen indem wir auf den absoluten Werten einmal eine einfaktorielle ANOVA in R rechnen. Wir erhalten die gleiche Teststatistik die dann eben einmal W und einemal F Statistik heißt. Häufig gibt es ähnliche Dinge in der Statistik, die dann unterschiedlich heißen.
R Code [zeigen / verbergen]
z_tbl |>
select(dog, cat) |>
gather(key = animal, value = jump_length) %$%
leveneTest(jump_length ~ animal, center = "mean")Levene's Test for Homogeneity of Variance (center = "mean")
Df F value Pr(>F)
group 1 0.9707 0.344
12 R Code [zeigen / verbergen]
z_tbl |>
select(dog_abs, cat_abs) |>
gather(key = animal, value = jump_length) %$%
lm(jump_length ~ animal) |>
anova()Analysis of Variance Table
Response: jump_length
Df Sum Sq Mean Sq F value Pr(>F)
animal 1 1.7654 1.7654 0.9707 0.344
Residuals 12 21.8247 1.8187 Es ist immer wieder spannend wie sich dann die einzelnen Methoden aufeinander reimen und was mit was zusammenhängt. Die Idee die absoluten Abstände zu nutzen um die Varianzhomogenität zu überprüfen ist dann auch eine recht pfiffige Idee.
Zum Testen der Varianzhomogenität in einem Modell können auch die Funktion check_homogeneity() aus dem Paket {performance} nutzen. Wir erhalten hier auch gleich eine Entscheidung in englischer Sprache ausgegeben. Die Funktion check_homogeneity() nutzt den Bartlett-Test um auf eine Abweichung von der Varianzhomogenität zu testen. Wir können in Funktion auch andere Methoden mit method = c("bartlett", "fligner", "levene", "auto") wählen. Wie du gleich noch in dem anderen Tab sehen wirst, unterscheidet sich die Implementierung des Bartlett-Tests in check_homogeneity() nicht von der Funktion bartlett.test(). Der riesige Vorteil ist hier, dass wir auch zweifaktorielle Modelle rechnen können. Die Entscheidung gegen die Varianzhomogenität wird aber zu einem Signifikanzniveau von 5% gefällt. Nicht immer hilft einem der Entscheidungtext einer Funktion.
Einfaktoriell
Beginnen wir wieder mit dem einfaktoriellen Modell. Wir stecken das Modell dann einfach in die Funktion check_homogeneity() und erhalten die Information über die Varianzhomogenität wiedergegeben.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
check_homogeneity()OK: There is not clear evidence for different variances across groups (Bartlett Test, p = 0.297).Wunderbar, wir haben keine Abweichung von der Varianzhomongenität. Wir können uns auch die Daten nochmal anschauen. Hier sehen wir aber schon, dass die Daten etwas heterogen aussehen der Test aber die Homogenität nicht ablehnt. Das ist immer schwierig bei kleinen Fallzahlen, wie wir schon wissen.
Zweifaktoriell
Jetzt können wir mal schauen, was passiert wenn wir die Anzahl an möglichen Faktorkombinationen erhöhen indem wir ein zweifaktorielles Modell nutzen. Hier haben wir dann ja sechs Faktorkombinationen oder Gruppen die dann alle homogen in den Varianzen sein müssen.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_homogeneity()OK: There is not clear evidence for different variances across groups (Bartlett Test, p = 0.651).R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_homogeneity()Warning: Variances differ between groups (Bartlett Test, p = 0.000).Wir haben auch hier Varianzhomogenität über alle Gruppen der Faktoren für die Sprungweiten vorliegen. Wenn du dir jetzt die Abbildung zu dem Test anschaust, dann siehst du auch hier, dass die Violinplots eben dann doch alle etwas anders aussehen. Wir haben aber hier auch das gleiche Problem wie bei dem einfaktoriellen Fall, wir haben eben dann doch recht wenig Fallzahl in unseren Daten.
Anders sieht es dann bei den Schlupfzeiten aus. Hier haben wir dann ganz klar Varianzheterogenität vorliegen. Die Violinplots passen hier auch, die sehen sehr verzerrt in eine Richtugn aus und vorallem nicht gleichmäßig. Die visuelle Überprüfung ist hier natürlich etwas schwerer, wo endet symmetrisch und wo beginnt eine symmetrische Verteilung? Deshalb hilft hier natürlich auch der Test bei der Entscheidung.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_homogeneity() |>
plot() +
scale_fill_okabeito()R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_homogeneity() |>
plot() +
scale_fill_okabeito()Neben der Möglichkeit unser Modell direkt zu testen und dann weiter in aov() oder emmeans() zu verwenden, können wir auch separat unsere Gruppen auf Varianzhomogenität testen. Wir nutzen dazu die Funktion leveneTest() aus dem R Paket {car}. Der Levene Test wird immer mit dem Median als Referenz gerechnet und damit eigentlich relativ robust gegen potenzielle Ausreißer. Eigentlich ist der Weg etwas umständlich, denn wir müssen auch hier ein Modell innerhalb der Funktion definieren. Das Modell können wir dann aber nicht weiter nutzen, so dass wir alles doppelt machen müssen. Das führt dann auch wieder zu neuen potenziellen Fehlern. Deshalb würde ich das R Paket {performance} empfehlen.
Einfaktoriell
Die einfaktorielle Analyse ist relativ einfach. Wir bauen uns das Modell direkt in der Funktion leveneTest() und erhalten dann einen p-Wert wieder. Den p-Wert können wir dann zu einem selbstgewähten Signifikanzniveau \(\alpha\) vergleichen. Da wir hier keinen Entscheidungstext wie bei check_homogeneity() haben, müssen wir selber entscheiden.
R Code [zeigen / verbergen]
leveneTest(jump_length ~ animal, data = fac1_tbl)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 2 0.7334 0.4941
18 Unabhängig welches Signifikanzniveau \(\alpha\) wir wählen, 5% oder eben 20%, würden wir hier die Varianzhomogenität nicht ablehnen. Wir haben also hier für die Sprungweite Varianzhomogenität vorliegen.
Zweifaktoriell
Für den zweifaktoriellen Fall müssen wir das Modell in der kompakten Form mit dem * angeben, ansonsten funktioniert die Funktion leveneTest() nicht. Meistens ist das auch die Formelschreibweise, die du dann weiter testen willst, aber das muss nicht immer der Fall sein. Daher hier auch einmal überlegen, ob du nicht besser dein Modell in {performance} testen willst.
Wie es zu erwarten war, können wir für die Sprungweite die Varianzhomogenität nicht ablehnen. Wir haben einen p-Wert der weit vom Signifikanzniveau entfernt ist. Bei der Schlupfzeit ist es dann spannender. Hier haben wir dann mit dem p-Wert von \(0.06\) gerade einen p-Wert wo wir mit einem Signifikanzniveau von 5% die Varianzhomogenität nicht ablehnen würden. Wenn wir mit einem Signifikanzniveau von 20% testen würden, dann hätten wir hier Varianzheterogenität vorliegen.
R Code [zeigen / verbergen]
leveneTest(jump_length ~ animal*sex, data = fac2_tbl)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 5 0.8015 0.5488
594 R Code [zeigen / verbergen]
leveneTest(hatch_time ~ animal*sex, data = fac2_tbl)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 5 2.1213 0.06131 .
594
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wir immer gibt es auch die Möglichkeit die Tests nur in der einfachen Variante in R zu nutzen. Ich stelle dann hier nochmal den Bartlett Test sowie den Fligner-Killeen Test vor.
Bartlett Test
Die Funktion bartlett.test() erlaubt es den Bartlett Test auf ein einfaktorielles Design anzuwenden. Auch hier ist es schnell doppelt, da wir zum einen ein Modell in der Funktion bartlett.test() spezifizieren und dann nochmal in den Folgefunktionen. Zweifaktoriell geht leider nicht in dieser Implementierung.
Einfaktoriell
R Code [zeigen / verbergen]
bartlett.test(jump_length ~ animal, data = fac1_tbl)
Bartlett test of homogeneity of variances
data: jump_length by animal
Bartlett's K-squared = 2.4266, df = 2, p-value = 0.2972Zweifaktoriell
Die zweifaktorielle Variante des Bartlett Test geht nicht in der Standardimplementierung in {stats}. Deshalb lohnt es sich hier dann die Funktionalität des R Pakets {performance} zu nutzen. Ich war jetzt auch zu faul hier nochmal tiefergreifend zu suchen, wir haben ja eine Lösung.
Fligner-Killeen Test
Es gibt noch den Fligner-Killeen Test mit der Funktion fligner.test() ist eine weitere Möglichkeit zu schauen, ob wir eine Abweichugn von der Varianzhomogenität haben. Der Test wird als nicht parametrische oder eben Rankalternative beschrieben.
Einfaktoriell
R Code [zeigen / verbergen]
fligner.test(jump_length ~ animal, data = fac1_tbl)
Fligner-Killeen test of homogeneity of variances
data: jump_length by animal
Fligner-Killeen:med chi-squared = 1.2823, df = 2, p-value = 0.5267Zweifaktoriell
Die zweifaktorielle Variante des Fligner-Killeen Test geht nicht in der Standardimplementierung in {stats}. Deshalb lohnt es sich hier dann die Funktionalität des R Pakets {performance} zu nutzen. Ich war jetzt auch zu faul hier nochmal tiefergreifend zu suchen, wir haben ja eine Lösung.
25.5.3 Varianzheterogenität
Nun könnte man meinen was diese Abschnitt hier nun noch soll. Es ist ist nunmal der Fall, dass es auch explizit Methoden gibt, die eben auf Varianzheterogenität testen sollen. Das stimmt dann wieder nur am Rande. Die Nullhypothese ist weiterhin, dass wir gleiche Varianzen in den Gruppen haben. Daher ist es hier etwas Augenwischerei, wenn wir auf Varianzheterogenität (eng. heteroscedasticity) testen wollen. Trotzdem gibt es die passenden Funktionen und wir finden auch immer wieder was dazu. Daher hier einmal die Methoden, die in dem Zusammenhang genannt und genutzt werden.
In der folgenden Abbidlung findest du wieder eine kleine Simulation um zu schauen, ob wir die Varianzheterogenitöt oder Varianzhomogenität in drei Gruppen wiederfinden. Ich habe hier 1000 Simulationen mit immer neuen Daten gerechnet und geschaut, ob die voreingestellte Vairanzheterogenität oder Varianzhomogenität von den statistischen Tests gefunden wird. Wie du schnell siehst, haben wir schwere Probleme bei keinen Fallzahlen die Varianzheterogenität in den Gruppen zu finden. Wenn wir das Signifikanzniveau auf 20% anheben, dann finden wir schon mehr. Bei der Varisnzhomogenitöt sieht es schon besser aus. Sollten wir uns aber für ein Signifikanzniveau von 20% entscheiden, dann haben wir auch hier Probleme.
Was nehmen wir aus den wilden Linien denn nun mit in unsere praktische Auswertung? Hier muss ich einmal einhaken, dass gerne geschrieben wird, dass die folgenden Tests alle irgendwie mit Breusch-Pagan-Test verwandt sind. Am Ende kriegen wir dann aber doch immer andere p-Werte raus. Daher muss es auch einen Unterschied im Algorithmus geben.
- Der Breusch-Pagan-Test (abk. Breusch-Pagan) ist eine etwas komplexere Angelegenheit was den Algorithmus angeht, aber hat Probleme, wenn wir keine Normalverteilung in den Residuen unserer Messwerte aus dem Modell vorliegen haben.
- Der White-Test (abk. White) ist nicht so problematisch, wenn wir keine Normalverteilung in dem Messwert vorliegen haben. Dafür brauchen wir hier deutlich mehr Fallzahl, damit der Test funktioniert und uns gute Ergebnisse liefert.
- Score Test for Non-Constant Error Variance (abk. NCV) soll eigentlich ähnlich wie der Breusch-Pagan-Test sein produziert hier dann aber als Test doch andere Ergebnisse in der Simulation. Das nehme ich dann mal so hin und wir lernen, nur weil etwas gleich sein soll, muss es nicht gleich sein.
In R haben wir dann wieder eine große Auswahl an möglichen Paketen und Algorithmen. Ich stelle wie immer alles einmal vor, würde mich aber auf die Funktion check_heteroscedasticity() aus dem R Paket {performance} mit dem Breusch-Pagan-Test festlegen, da wir hier eigentlich eine gute Abfolge haben und das Modell dann gleich testen können. Die anderen Pakete können es auch, aber hier musst du dann schauen, was besser passt.
Mit der Funktion check_heteroscedasticity() aus dem R Paket {performance} können wir den Breusch-Pagan Test auf unserem Modell rechnen um zu schauen, ob wir eine Varianzheterogenität in den Gruppen über den Messwert vorliegen haben. Wir kriegen hier auch einen Antworttext auf der Basis eines Signifikanzniveau von 5%. Der p-Wert wird aber auch angezeigt, so dass wir auch hier unsere Entscheidung anders treffen können.
Einfaktoriell
Beginnen wir wieder mit dem einfaktoriellen Modell. Wir stecken das Modell dann einfach in die Funktion check_heteroscedasticity() und erhalten die Information über die Varianzhomogenität wiedergegeben. Wunderbar, wir haben keine Abweichung von der Varianzhomongenität und der p-Wert ist auch recht groß, so dass wir hier nciht über ein angepasstes Signifkanzniveau nachdenken müssen.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
check_heteroscedasticity()OK: Error variance appears to be homoscedastic (p = 0.511).Zweifaktoriell
Jetzt können wir mal schauen, was passiert wenn wir die Anzahl an möglichen Faktorkombinationen erhöhen indem wir ein zweifaktorielles Modell nutzen. Hier haben wir dann ja sechs Faktorkombinationen oder Gruppen die dann alle homogen in den Varianzen sein müssen. Das ist danns chnon seltener der Fall. Dann hier auch die Anwendung einmal auf die Sprungweite sowie auf die Schlupfzeiten. Wie zu erwarten war, haben wir bei den Sprungweiten homogene Varianzen und bei den Schlupfzeiten heterogene Varianzen. Wenn wir zu 20% testen würden, wären beide Endpunkte heterogen. Hier könnte man anmerken, dass die Schlupfzeiten nicht normalverteilt sind und daher der Breusch-Pagan Test falsch liegen könnte.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_heteroscedasticity() OK: Error variance appears to be homoscedastic (p = 0.187).R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
check_heteroscedasticity() Warning: Heteroscedasticity (non-constant error variance) detected (p < .001).Als zweites R Paket möchte ich dann auch hier nochmal {oslrr} vorstellen. Das R Paket hat mit der Hilfeseite zur Heteroscedasticity nochmal mehr Informationen und Möglichkeiten. Ich zeige hier die zwei häufigsten Tests, nämlich einmal den Breusch Pagan Test sowie dien Score Test. Das gute an dem Paket ist, dass wir hier einmal eine saubere Nullhypothese geliefert kriegen und uns nicht fragen müssen, was testen wir hier den schon wieder? Das ist ja teilweise bei den anderen Paketen in den folgenden Tabs eher schwierig aus der Ausgabe abzulesen.
Breusch Pagan Test
Wenn wir nur den Breusch-Pagan Test rechnen wollen, dann können wir die Funktion ols_test_breusch_pagan() nutzen. Da wir hier dann das Modell in die Funktion stecken, können wir das Modell einmal zentral definieren und dann auch im Posthoc-Test weiternutzen, dass ist dann imemr sehr praktisch.
Einfaktoriell
Das einzige was etwas nervig an der Funktion ist, ist das wir den p-Wert über Prob > Chi2 angezeigt kriegen. Ja, das ist statistisch natürlich richtiger, aber für den Laien vermutlich schwer zu verstehen, wo den jetzt der p-Wert ist. Wir haben also einen p-Wert von 0.51 vorliegen und können die Nullhypothese nicht ablehnen. Wir haben also homogene Varianzen in den Sprungweiten der Flöhe.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
ols_test_breusch_pagan()
Breusch Pagan Test for Heteroskedasticity
-----------------------------------------
Ho: the variance is constant
Ha: the variance is not constant
Data
---------------------------------------
Response : jump_length
Variables: fitted values of jump_length
Test Summary
----------------------------
DF = 1
Chi2 = 0.4311253
Prob > Chi2 = 0.5114373 Zweifaktoriell
Im zweifaktoriellen Modell können wir dann die Varianzhomogenität in der Sprungweite zu einem Signifikanzniveau von 5% nicht ablehnen. Das können wir dann aber bei den Schlupfzeiten. Daher würden wir sagen, dass die Schlupfzeiten heterogene Varianzen haben. Der p_Wert versteckt sich hier wieder hinter Prob > Chi2 in der Ausgabe.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
ols_test_breusch_pagan()
Breusch Pagan Test for Heteroskedasticity
-----------------------------------------
Ho: the variance is constant
Ha: the variance is not constant
Data
---------------------------------------
Response : jump_length
Variables: fitted values of jump_length
Test Summary
----------------------------
DF = 1
Chi2 = 1.742438
Prob > Chi2 = 0.1868302 R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
ols_test_breusch_pagan()
Breusch Pagan Test for Heteroskedasticity
-----------------------------------------
Ho: the variance is constant
Ha: the variance is not constant
Data
--------------------------------------
Response : hatch_time
Variables: fitted values of hatch_time
Test Summary
------------------------------
DF = 1
Chi2 = 21.97986
Prob > Chi2 = 2.75526e-06 Score Test
Dann haben wir noch die Möglichkeit einen Score Test zu rechnen. Der Score Test ist nicht ganz so gut im Erkennen der Varianzheterogenität und daher würde ich den Score Test nicht so enmpfehlen. Wie du gleich siehst, sind die Ergebnisse in der Tendenz ähnlich zum Breusch-Pagan Test, aber wir würden doch zu anderen Entscheidungen kommen.
Einfaktoriell
Wir haben hier einen p-Wert von 0.48 vorliegen und können die Nullhypothese nicht ablehnen. Daher haben wir homogene Varianzen in den Sprungweiten der Flöhe. Das entspricht auch unseren Erwartungen.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
ols_test_score()
Score Test for Heteroskedasticity
---------------------------------
Ho: Variance is homogenous
Ha: Variance is not homogenous
Variables: fitted values of jump_length
Test Summary
----------------------------
DF = 1
Chi2 = 0.4875449
Prob > Chi2 = 0.4850245 Zweifaktoriell
Im zweifaktoriellen Modell können wir dann die Varianzhomogenität in der Sprungweite sowie der Schlupfzeit zu einem Signifikanzniveau von 5% nicht ablehnen. In beiden Fällen könnten wir das aber zu einem Signifikanzniveau von 20%. Der p_Wert versteckt sich hier wieder hinter Prob > Chi2 in der Ausgabe. Ja, am Ende ist es immer ärgerlich, wenn einige Funktionen super kleine p-Werte produzieren und dann andere Funktionen p-Werte direkt auf der Grenze.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
ols_test_score()
Score Test for Heteroskedasticity
---------------------------------
Ho: Variance is homogenous
Ha: Variance is not homogenous
Variables: fitted values of jump_length
Test Summary
----------------------------
DF = 1
Chi2 = 2.114086
Prob > Chi2 = 0.1459491 R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
ols_test_score()
Score Test for Heteroskedasticity
---------------------------------
Ho: Variance is homogenous
Ha: Variance is not homogenous
Variables: fitted values of hatch_time
Test Summary
-----------------------------
DF = 1
Chi2 = 3.150616
Prob > Chi2 = 0.07589833 Wenn wir nur den Breusch-Pagan Test rechnen wollen, dann können wir die Funktion bptest() aus dem R Paket {lmtest} nutzen. Hier gilt dann auch, dass wir es etwas doppelt machne, da wir zum einen ein Modell diefinieren müssen und dann dieses Modell neu für die folgenden Funktionen eines Posthoc-Test.
Einfaktoriell
Wir erhalten dann folgende Ausgabe des Breusch-Pagan Test. Wie wir sehen können, können wir die Nullhypothese der Varianzhomogenität nicht ablehnen. Wir würden also auch hier dann homogene Varianzen in den Gruppen der Flöhe annehmen.
R Code [zeigen / verbergen]
bptest(jump_length ~ animal, data = fac1_tbl)
studentized Breusch-Pagan test
data: jump_length ~ animal
BP = 2.4461, df = 2, p-value = 0.2943Zweifaktoriell
In dem zweifaktoriellen Fall schauen wir uns dann einmal die Sprungweite sowie die Schlupfzeiten an. Auch hier können wir in beiden Fällen die Varianzhomogenität nicht ablehnen. Das überrascht etwas bei den Schlupfzeiten, aber so ist es bei Tests manchmal.
R Code [zeigen / verbergen]
bptest(jump_length ~ animal + sex + animal:sex, data = fac2_tbl)
studentized Breusch-Pagan test
data: jump_length ~ animal + sex + animal:sex
BP = 4.036, df = 5, p-value = 0.5442R Code [zeigen / verbergen]
bptest(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl)
studentized Breusch-Pagan test
data: hatch_time ~ animal + sex + animal:sex
BP = 4.9837, df = 5, p-value = 0.4179Angeblich handelt es sich bei dem ncvTest() aus dem R Paket {car} ebenfalls um den Breusch-Pagan Test. Ich würde eher sagen, dass es sich um eine Variante davon handelt. Sonst könnte man den Test ja so nennen und müsste sich nicht einen anderen Namen ausdenken. Darüber hinaus unterscheiden sich die p-Werte und die Entscheidungen dann doch deutlich.
Einfaktoriell
Wir erhalten dann folgende Ausgabe des NCV-Test. Wie wir sehen können, können wir die Nullhypothese der Varianzhomogenität nicht ablehnen. Wir würden also auch hier dann homogene Varianzen in den Gruppen der Flöhe annehmen.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
ncvTest()Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 0.4311253, Df = 1, p = 0.51144Zweifaktoriell
In dem zweifaktoriellen Fall schauen wir uns dann einmal die Sprungweite sowie die Schlupfzeiten an. Auch hier können wir die Varianzhomogenität für die Sprungweite nicht ablehnen, wenn wir bei einem Signifikanzniveau von 5% bleiben. Die Schlupfzeiten sind definitiv nicht varianzhomogen. Wir würden hier von Varianzheterogenität ausgehen.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
ncvTest() Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 1.742438, Df = 1, p = 0.18683R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
ncvTest() Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 21.97986, Df = 1, p = 2.7553e-06Der White Test aus dem R Paket {skedastic} ist eien Spezeialfall des Breusch-Pagan Test, den ich hier nicht empfehlen kann. Im zweifaktoriellen Fall leifert der White Test keine plausibelen p-Werte. Daher würde ich hier von dem Test eher Abstand halten. Auch soll der Test schlechte Eigenschaften bei geringer Fallzahl haben. Ein Fall, den wir häufig in den Agrarwissenschaften vorliegen haben.
Einfaktoriell
Wir erhalten dann folgende Ausgabe des White Test. Wie wir sehen können, können wir die Nullhypothese der Varianzhomogenität nicht ablehnen. Wir würden also auch hier dann homogene Varianzen in den Gruppen der Flöhe annehmen.
R Code [zeigen / verbergen]
lm(jump_length ~ animal, data = fac1_tbl) |>
white()# A tibble: 1 × 5
statistic p.value parameter method alternative
<dbl> <dbl> <dbl> <chr> <chr>
1 2.45 0.654 4 White's Test greater Zweifaktoriell
In dem zweifaktoriellen Fall schauen wir uns dann einmal die Sprungweite sowie die Schlupfzeiten an. Wir wollen hier noch die Interaktion in unserem Modell mit beachten und geben dies mit der Option interactions an. Leider erhalten wir für beiden Modelle einen p-Wert von Eins, was jetzt nicht so plausibel wirkt. Da ich hier nicht tiefer in einzelne Funktionen und Algorithmen einsteige, lassen wir die Finger von dem White Test.
R Code [zeigen / verbergen]
lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl) |>
white(interactions = TRUE)# A tibble: 1 × 5
statistic p.value parameter method alternative
<dbl> <dbl> <dbl> <chr> <chr>
1 4.04 1.00 20 White's Test greater R Code [zeigen / verbergen]
lm(hatch_time ~ animal + sex + animal:sex, data = fac2_tbl) |>
white(interactions = TRUE)# A tibble: 1 × 5
statistic p.value parameter method alternative
<dbl> <dbl> <dbl> <chr> <chr>
1 4.98 1.00 20 White's Test greater “Hier stehe ich. Ich kann nicht anders.” — Martin Luther
Dann sind wir jetzt an dem Punkt angekommen, dass wir uns mit den Auswegen in den folgenden Abschnitten beschäftigen müssen. Insbesondere der vorherige Abschnitt zu der Varianzheterogenität zeigt nochmal schön, dass wir uns mit unterschiedlichsten Algorithmen die unterschiedlichsten Entscheidungen herbeitesten können. Am Ende haben wir immer nur eine Stichprobe vorliegen und müssen schauen, was wir mit den Daten der Stichprobe machen. Somit bleibt uns am Ende nichts anderes über als ein Modell zu wählen, die Daten zu analysieren und zu schauen, ob unsere Ergebnisse der statistischen Tests sich mit den Abbildungen der Daten in Einklang bringen lassen. Wenn das nicht der Fall ist, dann müssen wir nochmal ran und überlegen, was wir anders Modellieren können. Es ist eben immer ein hin und her.
25.6 Auswege
Nun gut, dann haben wir eben eine Abweichung von der Normalverteilung in unseren Daten gefunden. Oder aber wir haben eben dann keine Varianzhomogenität in unseren Gruppen vorliegen. Das ist erstmal nicht so schlimm. Wir können mit beiden Sachvwerhalten umgehen. Dabie ist die Abweichung von der Normalverteilung und der Varianzhomogenität nur in sofern ärgerlich, dass wir dann nicht den klasischen ANOVA Pfad mit der ANOVA und anschließendem TukeyHSD Test rechnen können. Das wäre noch vor Jahrzehnten ein echtes Problem gewesen, aber heutzutage haben wir im groben zwei Möglichkeiten mit Nicht normalverteilen Messwerten und varianzheterogenen Gruppen umzugehen. In der folgenden Flowschart zeige ich dir einmal die beiden Wege. Im Prinzip ist es einmal die Transformation des Messwertes y, so dass wir durch die Transformation wieder die Normalverteilung oder homogene Varianzen erreichen. Bei der Modellierung wollen wir dann den Zusammenhang \(y ~ x\) vom Messwert \(y\) und den Einflussvariablen \(x\) verändern oder eben modellieren.
flowchart LR
A("**Keine Normalverteilung**
oder
**Keine Varianzhomogenität**"):::factor --> C & B
B("**Modellierung**
*Zusammenhang*
*x ~ y wird verändert*"):::modell
C("**Transformation**
*Messwert wird verändert*"):::trans
classDef factor fill:#CC79A7,stroke:#333,stroke-width:0.75px
classDef modell fill:#E69F00,stroke:#333,stroke-width:0.75px
classDef trans fill:#56B4E9,stroke:#333,stroke-width:0.75px
Im den folgenden beiden Abschnitten gehe ich einmal auf die Transformtion von Daten sowie deren statistisches Modellieren ein. Du findest dann in den verlinkten Kapiteln noch eine tiefergreifende Übersicht. Doppelungen lassen sich manchmal nicht vermeiden, aber ich versuche die Doppelungen gering zu halten. Deshalb bitte nochmal in den anderen Kapiteln schauen, wenn du mehr oder tiefergreifende Informationen brauchst. Ich stelle hier die häufigsten und schnellsten Lösungen der Problematik der fehlenden Normalverteilung und Varianzhomogenität vor.
25.6.1 Transformation
Keine Transformation durchführen und danach rechnen, wenn du nicht vorher einmal in einem Densityplot geschaut hast, ob deine Verteilung wirklich mehr einer Normalverteilung ähnelt. Sonst machst du es vielleicht durch die Transformation schlimmer als ohne.
Die Transformation des Messwerts \(y\) ist recht alt. Die Idee ist auch super einleuchtend. Wenn der Messwert auf seiner ursprünglichen Zahlenform nicht normalverteilt ist, dann könnte es doch eine mathematische Funktion geben, die die Zahlen des Messwerts in eine normalverteilte Form bringt. Nun kann man ganz viele Funktionen ausprobieren und es gibt auch automatisierte Verfahren eine bestmögliche Transformation zu finden. Häufig sind diese Transformationen dann komplizierter und schwieriger zu berichten. Andere Wissenschaftler müssen ja auch verstehen, was du da gemacht hast. Deshalb konzentrieren wir uns hier auf die beiden häufigsten und verständlichsten Transformationen, der \(\log\)-Transformation und der Transformation mit Rängen. Mehr Transformationen kannst du dann im Kapitel zur Transformtion von Daten nachlesen.
“Wenn du deine Messwerte transformierst, dann verlierst du deine Einheit auf der du deine Messwerte erhoben hast. Damit verlierst du auch einen interpretierbaren Effektschätzer auf der Einheit deiner Messwerte. Es gibt dann eben keinen Mittelwertsunterschied mehr auf der Einheit deines Messwerts. Oder andersherum, mach nur eine Transformation, wenn du damit leben kannst, dass die Relevanz der signifikant gefundenen Unterschiede schwerer zu bestimmen ist.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.
Schauen wir uns im Folgenden also einmal die beiden häufigsten Transformationen an. Dabei ist wie immer zu beachten, bitte schaue dir die Abbildungen vor und nach der Transformations des Messwertes an. Wir wollen dann wirklich eine Noemalverteilung oder eine annährende Normalverteilung in dem Messwert sehen. Sonst brauchen wir auch nicht transformieren. Eine Transformation bewirkt nicht automatich eine Normalverteilung. Es kann auch sein, dass es eben nicht geklappt hat.
Transformation mit dem Logarithmus
Der Klassiker schlechthin. Wir nutzen einfach den Logarithmus mit der Funktion log() um unsere Daten zu transformieren. Danach sollten die Daten lognormal verteilt sein. Es gibt dafür sogr einen eigenen Namen, der eben auch an die Normalverteilung erinnert. Ich bin selber immer wieder überrascht, wie gut die log-Transformation dann doch funktioniert. Wir wollen hier einmal schauen, ob wir unsere schiefen Schlupfzeiten durch die log-Transformation etwas mehr in eine Normalverteilung schieben können.
R Code [zeigen / verbergen]
log_tbl <- fac2_tbl |>
mutate(log_hatch_time = log(hatch_time))Dann sollen wir uns einmal die Verteilung der Schlupfzeiten vor und nach der log-Transformation anschauen. Wir sehen hier gut, wie schief die Schlupfzeiten auf der orginalen Skala sind. Wenn wir jetzt eine log-Transformation durchführen, dann erhalten wir fast etwas, was wie eine Normalverteilung aussieht. Damit würde ich schon visuell leben können. Wenn du willst kannst du natürlich jetzt auch nochmal testen, ob die log-Transformation einer Normalverteilung genügt.
Transformation mit Rängen
Der Ausweg schlechthin bis in die 90ziger Jahre war vermutlich die nichtparametrische Statistik, wenn es um nicht normalverteilte Messwerte ging. Es wird dann eben ein nichtparametrischer Test, wie der Wilcoxon oder eben Mann-Whitney gerechnet. Und hier kommt dann die Rangtransformations ins Spiel. Eigentlich ist die gesamte Nichtparametrik nur eine Rangtransformation auf der wir dann auch genauso gut dann einen t-Test oder eine ANOVA rechnen könnten. Dazu dann aber mehr in den jeweiligen Kapiteln zu den einzelnen nichtparametrischen Tests. Was ist also die Transformation? Wir geben einfach den sortierten Rang des Messwertes über alle Gruppen. Dann können wir auf dem rangierten Messwert weiterrechnen. In den folgenden Tabellen siehst du dann einmal die orginalen Sprungweiten gemessen in [cm] sowie deren rangierten Gegenstücke.
Die orginalen Daten haben die Einheit in Zentimeter. Wir meinen zu sehen, dass die Katzenflöhe etwas kürzer springen.
| dog | cat | fox |
|---|---|---|
| 5.7 | 3.2 | 7.7 |
| 8.9 | 2.2 | 8.1 |
| 11.8 | 5.4 | 9.1 |
| 5.6 | 4.1 | 9.7 |
| 9.1 | 4.3 | 10.6 |
| 8.2 | 7.9 | 8.6 |
| 7.6 | 6.1 | 10.3 |
Auf den rangierten Daten verlieren wir die Einheit. Wir sehen aber, dass die Katzenflöhe tendenziell die kleinsten Ränge haben. Somit springen die Katzenflöhe am kürzesten.
| dog | cat | fox |
|---|---|---|
| 7 | 2 | 10 |
| 15 | 1 | 12 |
| 21 | 5 | 16 |
| 6 | 3 | 18 |
| 16 | 4 | 20 |
| 13 | 11 | 14 |
| 9 | 8 | 19 |
Traditionell würden wir jetzt in den Werkzeugkasten der nichtparametrischen Tests greifen. Hier nochmal die Verweise auf die entsprechenden Kapitel mit einer kurzen Beschreibung des nichtparametrischen Tests.
- Der Wilcoxon-Mann-Whitney-Test oder auch U-Test ist der t-Test auf den Rängen eines Messwertes. Wir vergleichen hier zwei Gruppen miteinander. Wenn wir mehr Gruppen haben, die wir vergleichen wollen, dann brauchen wir mehrere paarweise Wilcoxon Tests um die signifikanten Unterschiede zu bestimmen.
- Der Kruskal-Wallis-Test ist die einfaktorielle ANOVA auf den Rängen eines Messwertes. Wir vergleichen hier drei oder mehr Gruppen simultan miteinander. Wenn wir dann wissen wollen, welcher paarweise Vergleich signifikant ist, brauchen wir dann einen Posthoc-Test.
- Der Friedman Test ist keine zweifaktorielle ANOVA. Bitte einfach den Test sein lassen und vermeiden. Dann lieber eine zweifaktorielle ANOVA auf den Rängen des Messwerts rechnen als den Friedman Test zu verwenden. Mehr dazu dann im entsprechenden Kapitel zum Friedman Test.
Wenn es nach mir ginge würden wir die nichtparametrische Statistik ruhen lassen und uns auf die parametrische Modellierung konzentrieren. Die parametrische Modellierung lösst auch viele Probleme und nur wenige Fallbeispiele fallen unter die unbedingte Anwendung der Nichtparametrik. Aber wie immer, es mag genau bei dir der Fall sein, dass deine wissenschaftliche Fragestellung mit der Nichtparametrik gelöst werden kann.
25.6.2 Modellierung
Dank des statistisches Modellieren können wir viel machen, wenn unser Messwert nicht normalverteilt ist oder aber wir Varianzheterogenität in den Gruppen oder beides in den Gruppen vorliegen haben. Daher würde ich immer das Modellieren der Transformation vorziehen.
Keine Normalverteilung
Im Folgenden nochmal die Übersicht möglicher Verteilungen, die dein Messwert folgen könnte je nachdem was du gemessen hast. Dann musst du in den entsprechenden Kapiteln einmal reinschauen. Es muss also nicht immer die Normalverteilung sein, obwohl diese natürlich einiges an Vorzügen hat. Am Meisten vermutlich, dass jeder versteht was ein Mittelwert ist und somit die Effekte als Mittelwertsdifferenzen auch gut zu kommunizieren sind.
| Verteilung | Outcome \(\boldsymbol{y}\) | Beispiel |
|---|---|---|
| Gaussian / Normal | Kontinuierliche Kommazahlen | Größe; Gewicht; Höhe; Durchmesser |
| Poisson | Kontinuierliche Zähldaten | Anzahl Insekten; Anzahl Läsionen; Anzahl Früchte |
| Beta | Wahrscheinlichkeitswerte zwischen \([0,1]\) | Keimungsfähigkeit [%]; Jagderfolg [%]; Grünbedeckung [%] |
| Ordinal | Kategorielle Messwerte | Noten auf der Likert-Skala |
| Binomial | Kategorielle Messwerte \(0/1\) | Infiziert [ja/nein]; Beschädigt [ja/nein] |
Hier sei dann nur kurz erwähnt, dass du über die Funkion glm() viele dieser Modellierungen als simple oder multiple Regression abbilden kannst. Die Modelle lassen sich dann in {emmeans} für die Gruppeneffekte dann einfach testen. Nur in wenigen Ausnahmen ist keine ANOVA möglich und selbst in diesen selten Fällen gibt es auch nocht im Kapitel zur ANOVA Vorschläge von mir wie das R Paket {WRS2}. Mehr dazu dann aber im ANOVA Kapitel mit Beispielen und Anwendungen. Am Ende knnst du dir auch überlegen, ob du nicht eine nicht lineare Regression ausprobieren willst, um deine Zusammenhänge darzustellen. Wie du siehst, gibt es in der parametrischen Statistik eine Menge Lösungen für nicht normalverteilte Messwerte.
Varianzheterogenität
Wenn wir es mir der Varianzheterogenität zu tun haben, dann haben wir eine reichhalte Fülle an Möglichkeiten mit der Varianzheterogenität in den Gruppen umzugehen. Dafür können wir entweder das Modell über die Funktion gls() aus dem R Paket {nlme} direkt anpassen. Oder aber wir nutzen die Funktion model_parameters() um nach Fit das Modell für Varianzheterogenität zu adjustieren. Oder aber wir machen es dann eben in dem multiplen Vergleich direlt in der Funktion emmeans() aus dem R Paket {emmeans}. Bitte mach nur eins davon. Du brauchst nicht alles drei zu machen, davon wird nichts besser. Ich mache häufig erst die Adjustierung für die Vrainzheterogenität in {emmeans} aber das hat eher prozessuale Gründe als wirklich inhaltliche.
In dem R Paket {nlme} können wir die Funktion gls() nutzen um für jede Faktorkombination eine eigene Varianz zu schätzen. Damit können wir dann für die Varianzheterogenität in den Gruppen adjustieren.
R Code [zeigen / verbergen]
gls_fit <- gls(jump_length ~ animal + sex + animal:sex, data = fac2_tbl,
weights = varIdent(form = ~ 1 | animal*sex))Wir du siehst unterscheidet sich die Varianz als Fehler SE in den Koeffizienten der Regression innerhalb der Level der Faktoren. Mit diesem Modell können wir dann weiterechnen, wenn wir einen Posthoc-Tests durchführen wollten.
R Code [zeigen / verbergen]
gls_fit |>
model_parameters()# Fixed Effects
Parameter | Coefficient | SE | 95% CI | t(594) | p
-----------------------------------------------------------------------------------
(Intercept) | 15.38 | 0.19 | [15.01, 15.74] | 83.05 | < .001
animal [dog] | 2.73 | 0.27 | [ 2.21, 3.25] | 10.29 | < .001
animal [fox] | 5.33 | 0.27 | [ 4.80, 5.86] | 19.82 | < .001
sex [female] | 5.08 | 0.26 | [ 4.57, 5.58] | 19.78 | < .001
animal [dog] × sex [female] | -0.24 | 0.38 | [-0.99, 0.51] | -0.63 | 0.528
animal [fox] × sex [female] | -0.28 | 0.38 | [-1.03, 0.47] | -0.72 | 0.470
Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
using a Wald t-distribution approximation.Im PRinzip rechnest du hier eine klassiche Gaussian Regression nur ohne die Annahme der Varianzhomogenität. Jetzt könnte man fragen, warum man überhaupt mit der Annahme der Varianzhomogenität rechnt und nicht immer gls() nutzt, das hat aber mit der Geschichte der Entwicklung zu tun. Die Implementierung der Funktiongls() gibt es erst einen Bruchteil der Zeit wie es die normale Regression gibt.
Zuerst brauchen wir eine normale Modellanpassung in der wir dann eine Normalverteilung und homogene Varianzen annehmen. Erst danach werden wir dann für eine potenzielle Varianzheterogenität adustieren.
R Code [zeigen / verbergen]
performance_fit <- lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl)Wenn wir nach dem Fit des Modells für die Varianzheterogenität adjustieren wollen, dann nutzen wir die Funktion model_parameters() und setzen die Option vcov noch auf HC3 und können damit dann Fehler erhalten, die sich über die Koeffizienten in den Leveln der Faktoren entsprechend unterscheiden.
R Code [zeigen / verbergen]
performance_fit |>
model_parameters(vcov = "HC3")Parameter | Coefficient | SE | 95% CI | t(594) | p
-----------------------------------------------------------------------------------
(Intercept) | 15.38 | 0.19 | [15.01, 15.74] | 82.64 | < .001
animal [dog] | 2.73 | 0.27 | [ 2.21, 3.26] | 10.23 | < .001
animal [fox] | 5.33 | 0.27 | [ 4.80, 5.86] | 19.72 | < .001
sex [female] | 5.08 | 0.26 | [ 4.57, 5.58] | 19.69 | < .001
animal [dog] × sex [female] | -0.24 | 0.38 | [-0.99, 0.51] | -0.63 | 0.530
animal [fox] × sex [female] | -0.28 | 0.38 | [-1.03, 0.48] | -0.72 | 0.472
Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
using a Wald t-distribution approximation.Wenn du noch etwas weiter gehen möchtest, dann kannst du dir noch die Hilfeseite von dem R Paket {performance} Robust Estimation of Standard Errors, Confidence Intervals, and p-values anschauen. Die Idee ist hier, dass wir die Varianz/Kovarianz robuster daher mit der Berücksichtigung von Varianzheterogenität (eng. heteroskedasticity) schätzen.
Dann kommen wir noch zu {emmeans}. Hier bauen wir wieder unser Modell in dem wir dann eine Normalverteilung und homogene Varianzen annehmen.
R Code [zeigen / verbergen]
emmeans_fit <- lm(jump_length ~ animal + sex + animal:sex, data = fac2_tbl)Die eigentlich Anpassung erfolgt dann direkt in {emmeans}, wo wir dann über die Option vcov. eine entsprechende Anpassung auswählen können. Ich wähle hier meistens den Standard mit vcovHAC. Jede Faktorkombination hat jetzt seine eigene Varianz dargestellt und den Standardfehler SE in der Ausgabe von emmeans(). Ohne diese Adjustierung wäre der Standardfehler in allen Gruppen gleich.
R Code [zeigen / verbergen]
emmeans_fit |>
emmeans(~ animal * sex, vcov. = sandwich::vcovHAC) animal sex emmean SE df lower.CL upper.CL
cat male 15.4 0.188 594 15.0 15.7
dog male 18.1 0.176 594 17.8 18.5
fox male 20.7 0.197 594 20.3 21.1
cat female 20.5 0.181 594 20.1 20.8
dog female 22.9 0.189 594 22.6 23.3
fox female 25.5 0.211 594 25.1 25.9
Confidence level used: 0.95