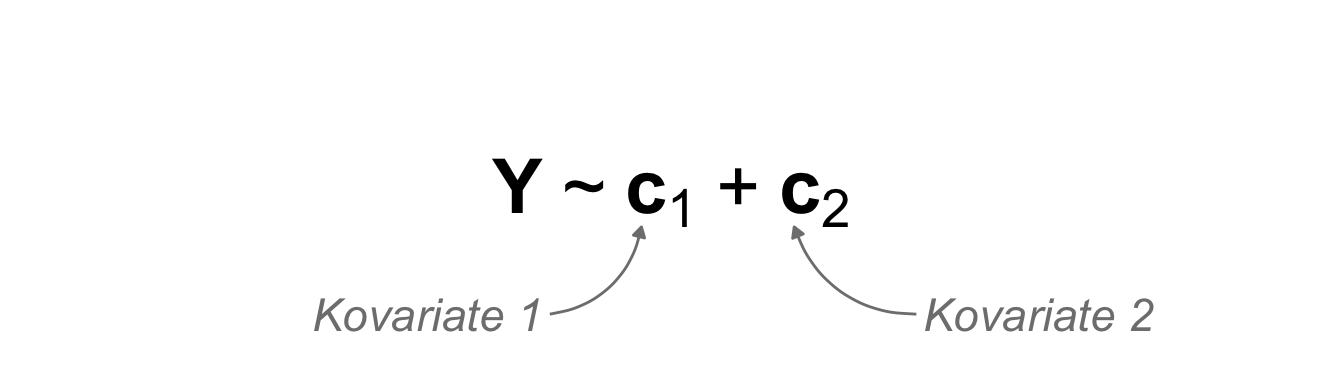21  Generierung von Daten

Letzte Änderung am 09. September 2025 um 07:36:12

“Je größer die Insel des Wissens, desto größer der Strand der Verzweiflung.” — unbekannt

Stand des Kapitels: Konstruktion

Dieses Kapitel wird in den nächsten Monaten geschrieben und ist damit eine zukünftige Großbaustelle. Ich plane zum Beginn des SoSe 2026 eine fertige Version des Kapitels erstellt zu haben. Während das Kapitel entsteht, funktioniert so manches dann nicht so wie es soll. Bitte daher hier dann abwarten.

In diesem Kapitel geht es um die Erstellung von zufälligen Daten. Oder anderherum, wir wollen uns künstliche Daten (eng. artificial data oder eng. synthetic data) generieren. Warum machen wir das? Eine Frage, die sich vermutlich kein Statistiker oder Date Scientist stellen würde, ist es doch Teil der wissenschaftlichen Arbeit simulierte Daten zu erstellen. Auf diesen simulierten Daten werden dann die neuen entwickelten Algorithmen getestet. Für Menschen außerhalb der Data Science mag es seltsam erscheinen, dass wir uns einfach Daten erschaffen können. Diese synthetischen Daten kommen dann aber den biologischen Daten manchmal recht Nahe. Daher kannst auch du dir deine Daten theoretisch einfach selber bauen, nachdem du dieses Kapitel gelesen hast.

Achtung, bitte beachten!

“With great power comes great responsibility.” — Uncle Ben to Peter Parker in Spiderman

Keine Daten für die Abschlussarbeit erschaffen. Auch wenn die Daten mal nicht so passen, wie du dir das aus einem Experiment erhofft hast, ist es nicht erlaubt sich einfach die Daten selber zu simulieren. Simulierte Daten haben keinen wissenschaftlichen Wert abseits der Validierung von neuen Algorithmen.

Was du aber machen kannst, ist deine experimentellen Daten schon mal im Design vorbauen um deine Analyse in R vorzurechnen. Wenn du dann aus deinem Experiment die echten Daten vorliegen hast, kannst du dann schneller die Analysen rechnen. Du hast dann ja schon alles einmal geübt und vorgearbeitet.

Daher nutzen wir diesen Kapitel auch anders. Wir erschaffen uns ja Daten um Algorithmen zu verstehen. Wenn wir wissen wie die Daten aufgebaut sind, dann können wir auch besser verstehen was uns ein Modell oder ein statistischer Test wiedergibt. Dafür brauchen wir dann die synthetischen Daten. Eine andere Möglichkeit ist, dass du einmal ausprobieren möchtest, wie eine potenzielle Analyse ablaufen würde. Dann macht es auch Sinn einmal über künstliche Daten nachzudenken. Ich komme dann immer mal wieder auf dieses Kapitel zurück, wenn ich in anderen Kapiteln mal künstliche Daten brauche. Wir schauen uns verschiedene Wege künstliche Daten zu erschaffen einmal an und es geht auch in Excel relativ einfach.

21.1 Allgemeiner Hintergrund

“We test our framework both on synthetic data, as the only source of ground truth on which we can objectively assess the performance of our algorithms, as well as on real data to demonstrate its real-world practicability.” — Jackson et al. (2009)

Wenn wir Daten generieren wollen, dann müssen wir auch wissen, was wir genieren wollen. Dafür müssen wir dann verstehen, wovon wir sprechen. Da wir es bei der Datengenerierung auch immer mit statistischen Modellen zu tun haben, müssen wir auch die Fachsprache der statistischen Modellierung nutzen. Dann wollen wir verstehen, was wir eigentlich simulieren. Klar, wir simulieren Daten, aber was brauchen wir dafür an statistischen Maßzahlen? Ich betrachte dann nochmal die Einschränkungen dieses Kapitels, denn wir können natürlich hier nicht alles simulieren, was möglich ist. Faktisch konzentrieren wir uns hier auf häufige Datenstrukturen in den Agrawissenschaften. Dann zeige stelle ich dir nochmal kurz die zwei R Pakete vor, die wir dann hier nutzen können.

Sprachlicher Hintergrund

“In statistics courses taught by statisticians we don’t use independent variable because we use independent on to mean stochastic independence. Instead we say predictor or covariate (either). And, similarly, we don’t say”dependent variable” either. We say response.” — User berf auf r/AskStatistics

Wenn wir uns mit dem statistischen Modellieren beschäftigen wollen, dann brauchen wir auch Worte um über das Thema reden zu können. Statistik wird in vielen Bereichen der Wissenschaft verwendet und in jedem Bereich nennen wir dann auch Dinge anders, die eigentlich gleich sind. Daher werde ich mir es hier herausnehmen und auch die Dinge so benennen, wie ich sie für didaktisch sinnvoll finde. Wir wollen hier was verstehen und lernen, somit brauchen wir auch eine klare Sprache.

“Jeder nennt in der Statistik sein Y und X wie er möchte. Da ich hier nicht nur von Y und X schreiben will, führe ich eben die Worte ein, die ich nutzen will. Damit sind die Worte dann auch richtig, da der Kontext definiert ist. Andere mögen es dann anders machen. Ich mache es eben dann so. Danke.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

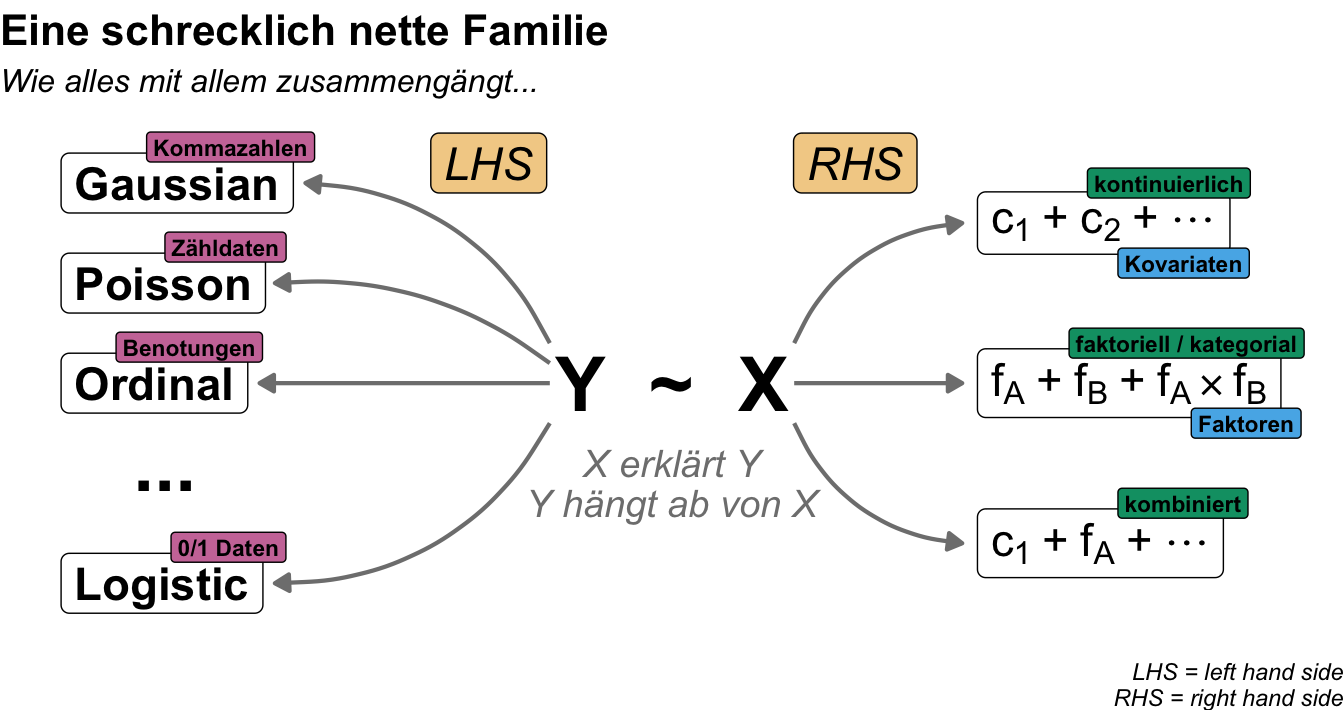
In dem folgenden Kasten erkläre ich nochmal den Gebrauch meiner Begriffe im statistischen Modellieren als Grundlage für die Generierung von Daten. Es ist wichtig, dass wir hier uns klar verstehen. Zum einen ist es angenehmer auch mal ein Wort für ein Symbol zu schreiben. Auf der anderen Seite möchte ich aber auch, dass du dann das Wort richtig einem Konzept im statistischen Modellieren zuordnen kannst. Deshalb einmal hier meine persönliche und didaktische Zusammenstellung meiner Wort im statistischen Modellieren. Du kannst dann immer zu dem Kasten zurückgehen, wenn wir mal ein Wort nicht mehr ganz klar ist. Die fetten Begriffe sind die üblichen in den folgenden Kapiteln. Die anderen Worte werden immer mal wieder in der Literatur genutzt.

Worte und Bedeutungen im statistischen Modellieren

“Die Grenzen meiner Sprache bedeuten die Grenzen meiner Welt.” — Ludwig Wittgenstein

Hier kommt einmal die Tabelle mit den wichtigsten Begriffen im statistischen Modellieren und wie ich die Worte benutzen werde. Damit wir uns verstehen und du was lernen kannst. In anderen Büchern und Quellen findest du teilweise die Worte in einem anderen Sinnzusammenhang. Das ist gut so dort. Bei mir ist es anders.

Tabelle 21.1— Zusammenfassende Tabelle des Sprachgebrauchs in meinem statistischen Modellieren. Die fett hervorgehobenen Bezeichnungen werden hier genutzt. (LHS = left hand side, RHS = right hand side)

	Symbol	Deutsch	Englisch
LHS	\(Y\) / \(y\)	Messwert / Endpunkt / Outcome / Abhängige Variable	response / outcome / endpoint / dependent variable
RHS	\(X\) / \(x\)	Einflussvariable / Erklärende Variable / Fester Effekt / Unabhängige Variable	risk factor / explanatory / fixed effect / independent variable
RHS	\(Z\) / \(z\)	Zufälliger Effekt	random effect
\(X\) ist kontinuierlich	\(c_1\)	Kovariate 1	covariate 1
\(X\) ist kategorial	\(f_A\)	Faktor \(A\) mit Level \(A.1\) bis \(A.j\)	factor \(A\) with levels \(A.1\) to \(A.j\)

Am Ende möchte ich nochmal darauf hinweisen, dass wirklich häufig von der abhängigen Variable (eng. dependent variable) als Messwert und unabhängigen Variablen (eng. independent variable) für die Einflussvariablen gesprochen wird. Aus meiner Erfahrung bringt die Begriffe jeder ununterbrochen durcheinander. Deshalb einfach nicht diese Worte nutzen.

Abbildung 21.1— Am Ende läuft es dann doch auf sowas raus…

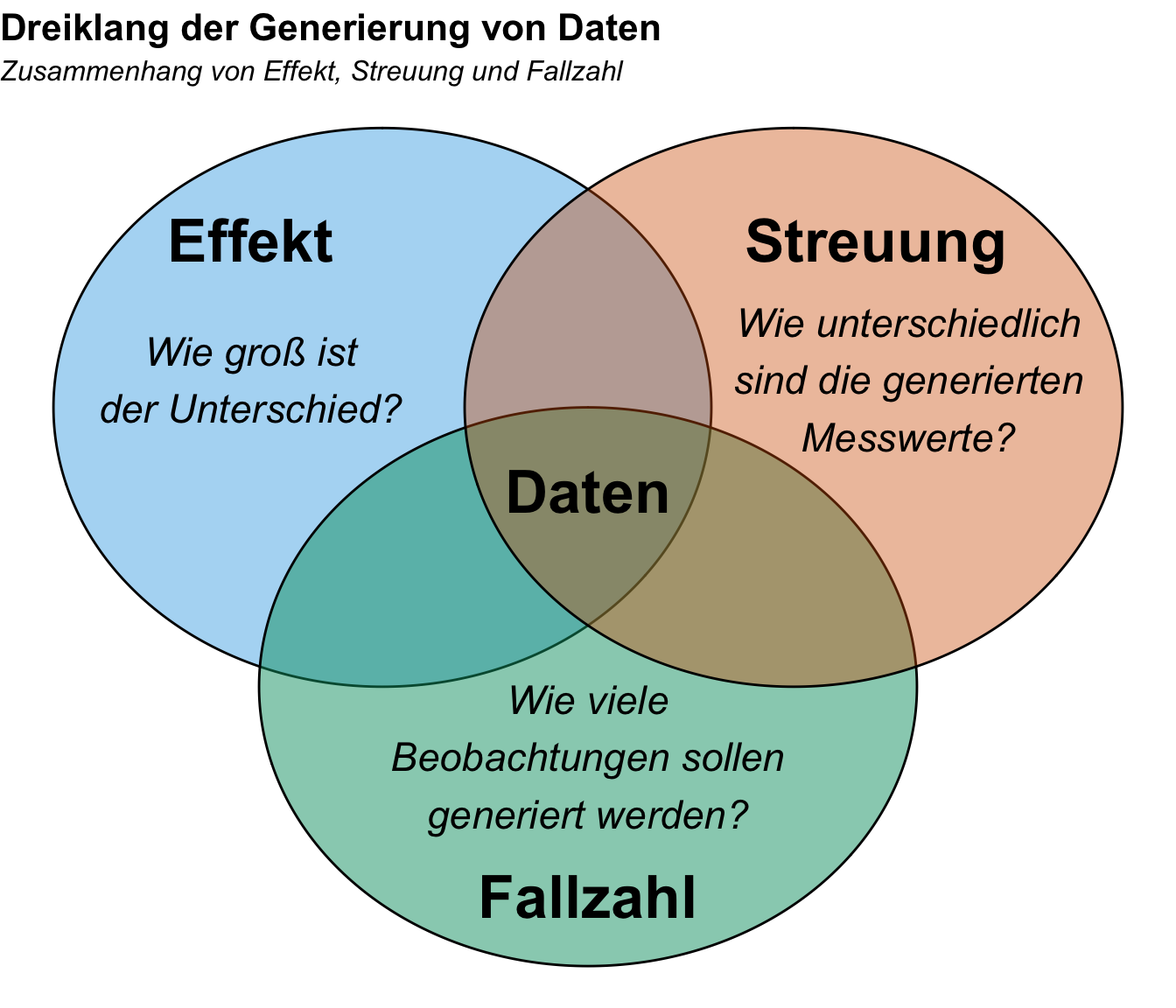
Effekt, Streuung und Fallzahl

Was brauchen wir um Daten zu generieren? Wir brauchen einen Effekt, eine Streuung der generierten Daten um den Mittelwert sowie die Fallzahl als Anzahl an Beobachtungen. Dann müssen wir noch entscheiden aus welcher Verteilung unsere Daten kommen sollen. In dem folgenden Venndiagramm habe ich dir nochmal den Dreiklang der drei statistischen Eigenschaften für die Generierung von Daten zusammengefasst. Wir müssen uns also klar werden, welchen Effekt wir simulieren wollen, welche Streuung in den Daten vorliegen soll und natürlich wie viele Beobachtungen wir in den generierten Daten vorfinden wollen.

Abbildung 21.2— Was wird benötigt um Daten zu generieren? Der Effekt beschreibt den Unterschied zwischen Gruppen oder spezieller den Mittelwert in einer Normalverteilung. Die Streuung beschreibt die Unsicherheit in den Daten oder eben die Standardabweichung. Über die Fallzahl wird definiert wie viele Beobachtungen erstellt werden sollen. [Zum Vergrößern anklicken]

Wir machen wir das jetzt praktisch in R. Dazu haben wir verschiedene Möglichkeiten, wir beginnen hier einmal mit der simpelsten Form. Mit der Funktion rnorm() können wir uns zufällige Daten aus einer theoretischen Normalverteilung ziehen. Es gibt natürlich noch viel mehr r*-Funktionen für die Generierung von Daten. Die Seite Probability Distributions in R zeigt nochmal einen großen Überblick. Im Kapitel zu den Verteilungen findest du dann auch nochmal mehr Informationen zu den einzelnen Funktionen.

Fangen wir aber einmal mit der einfachen Funktion für die Normalverteilung an. Hier genieren wir uns also einmal fünf Beobachtungen aus einer Normalverteilung. Wir brauchen dafür die Fallzahl (n), die wir generieren wollen. Dann den Mittelwert der theoretischen Verteilung (mean) sowie die Streuung (sd). Dann erhalten wir fünf Zahlen, die in der Gesamtheit den vorgestellten Zahlen entsprechen.

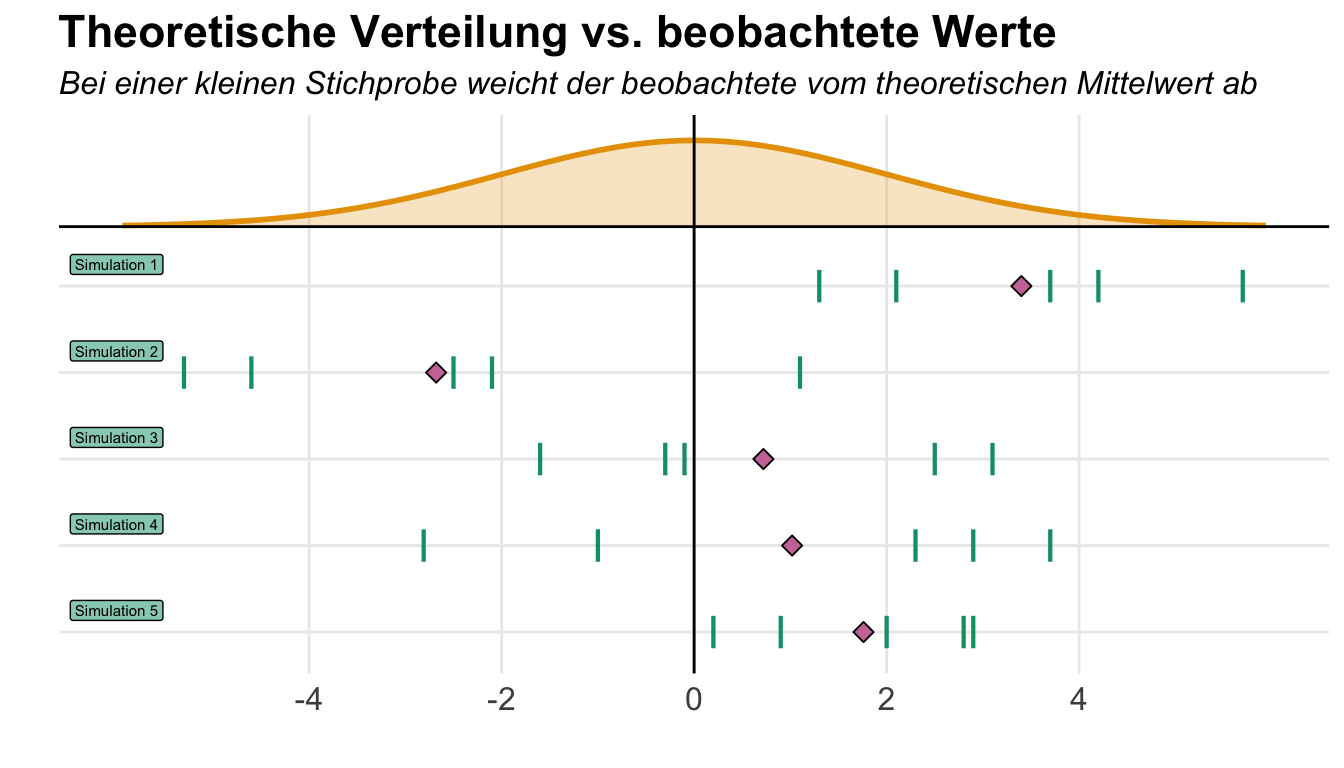
rnorm(n = 5, mean = 0, sd = 1) |> round(2)

[1]  0.75  0.02  0.77 -1.17  0.39

Wenn wir jetzt den Mittelwert der fünf Zahlen berechnen, dann erhalten wir aber gar nicht einen Mittelwert von \(0\) und auch nicht eine Standardabweichung von \(1\) wieder. Wie kann das sein? Häufig stolperst du hier ein wenig. Wieso Daten generieren, wenn die Daten dann nicht die Eigenschaften haben, die wir wollen? Hier kommt die Grundgesamtheit und die Stichprobe ins Spiel. In der Grundgesamtheit hast du einen Mittelwert von \(2\) und eine Standardabweichung von \(1\) vorliegen. Du ziehst aber nur eine kleine Stichprobe wie ich dir einmal in der folgenden Abbildung zeige. Zwar liegt der theoretische Mittelwert auf der Null, aber die Mittelwerte der einzelnen Simulationen können stark variieren.

Abbildung 21.3— Visualisierung der Abweichung des beobachteten Mittelwerts von dem theoretischen Mittelwert der Normalverteilung. Fünf Simulationen mit je fünf Beobachtungen wurden durchgeführt und jeweils der Mittelwert berechnet. Die Beobachtungen wurde aus einer Standardnormalverteilung mit \(\mathcal{N}(0, 1)\) gezogen. [Zum Vergrößern anklicken]

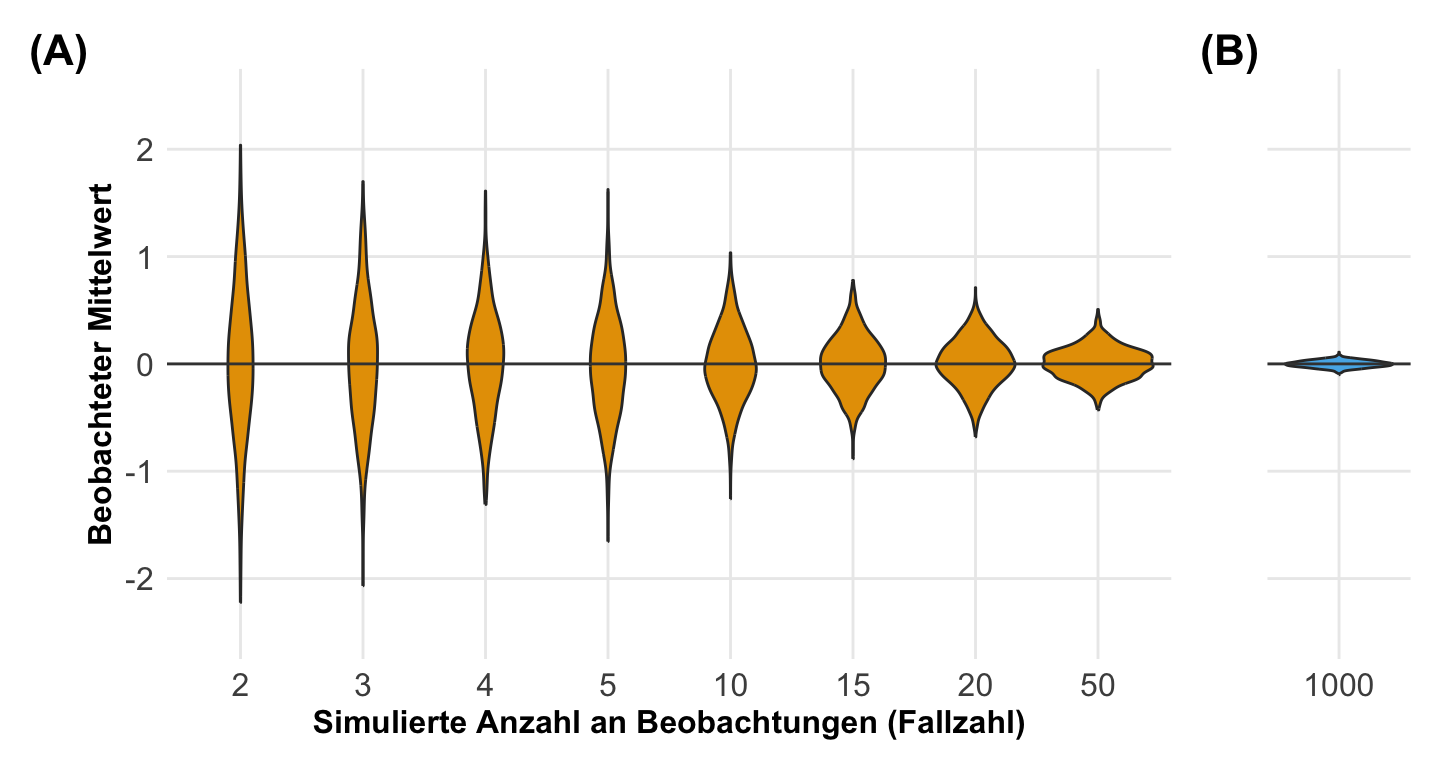
Der Zusammenhang wird dir vielleicht dann nochmal in der folgenden Abbildung klarer. Ich habe hier einmal eine kleine Simulation laufen lassen. Dabei habe ich immer Daten aus einer Standardnormalverteilung mit einem Mittelwert von \(0\) und einer Standardabweichung von \(1\) generiert. Was ich dabei geändert habe ist die Fallzahl. Wenn ich nur zwei Beobachtungen generiere, dann finde ich eine große Breite an beobachteten Mittelwerten. Wenn ich die Fallzahl erhöhe, dann komme ich immer näher an den erwarteten Mittelwert in meinen beobachteten Daten heran. Bei eintausend Beobachtungen habe ich faktisch kaum noch eine Abweichung vorliegen. Hier siehst du eben, es kommt auch stark auf die Fallzahl an. Wenn du dir zu wenig Beobachtungen anschaust, dann wirst du nicht immer den theoretischen Mittelwert oder Effekt in den generierten Daten wiederfinden.

Abbildung 21.4— Zusammenhang zwischen der simulierten Anzahl an Beobachtungen und dem beobachteten Mittelwert zu dem theoretischen Mittelwert der Verteilung aus der die Beobachtungen generiert wurden. Die Beobachtungen wurde aus einer Standardnormalverteilung mit \(\mathcal{N}(0, 1)\) gezogen. Es wurden 1000 Simulationen durchgeführt. [Zum Vergrößern anklicken]

Welche Möglichkeiten gibt es eigentlich?

Wenn wir Daten generieren wollen, dann haben wir im Prinzip zwei Möglichkeiten. Wir bauen uns die Daten selber per Hand in Excel oder aber nutzen die entsprechenden R Pakete. Ich stelle hier die zwei größeren R Pakete vor sowie die Lösungen per Hand in Excel. Wir haben natürlich auch die Möglichkeit die Daten in R ohne Pakete zu erstellen. Das macht in einem einfacheren Setting auch mehr Sinn.

• Das R Paket {simstudy} liefert eigentlich alles was wir brauchen, wenn die Daten komplizierter werden. Insbesondere wenn wir keinen normalverteilten Messwert vorliegen haben oder aber abhängige Einflussvariablen. Wenn ich größere Datensätze generiere, dann nutze ich gerne dieses Paket. Hier gibt es aber die Einschränkung, dass sich faktorielle Experimente nicht gut darstellen lassen. In diesem Fall ist die händische Erstellung manchmal einfacher.
• Das R Paket {simdata} hat den Vorteil große, komplexe Korrelationsstrukturen abzubilden. Wir können hier Netzwerkeffekte gut darstellen und dann auch in einen Datensatz übersetzen. Auch Transformationen von Daten lassen sich hier gut integrieren. Hier liegt aber nicht der Fokus auf einem faktoriellen Design mit Gruppeneffekten.
• Wir schauen uns natürlich auch Excel an. Hier haben wir natürlich gleich die Möglichkeit uns die Daten dort zu bauen, wo wir die erhobenen Messwerte dann später nach dem durchgeführten Experiment auch abspeichern. Deshalb zeige ich auch hier einmal wie wir dann die Daten händisch aufbauen.

Abschließend muss ich noch erwähnen, dass faktorielle Designs, die wir dann häufig in den Agrarwissenschaften finden, wir am besten dann händisch in R zusammenbauen. Wir nutzen dann die Funktionen, die es schon in R gibt und erstellen uns dann selber den Datensatz. Das ist im Prinzip so ähnlich wie in Excel nur das wir etwas besser nachvollziehbare Wege haben.

21.2 Theoretischer Hintergrund

Neben dem allgemeinen Hintergrund können wir natürlich auch etwas tiefer in die Materie einsteigen. Zum einen müssten wir überlegen, welche Effekte es eigentlich gibt. Wir wollen ja Daten generieren, die nicht gleich sind. Daher wollen wir etwas bauen, wo wir auch einen Effekt sehen. Zwar ist es auch interessant sich Daten zu generieren wo die Nullhypothese wahr ist und nichts passiert, aber das ist eher nicht der Fokus der praktischen Arbeit. Wenn wir ein Experiment machen, dann wollen wir eigentlich auch einen Effekt oder Unterschied in den Gruppen oder allgemeiner den Daten sehen.

Welche Effekte gibt es?

Wenn wir also Wissen, dass wir einen Effekt \(\Delta\), eine Streuung \(s\) und Fallzahl \(n\) definieren müssen um uns zufällige Daten zu generieren, was sind denn dann die Effekte? Die Streuung und die Fallzahl sind ja relativ einfach zu verstehen. Die Fallzahl legen wir fest und es ist eben die Anzahl an Beobachtungen, die wir generieren wollen. Im Prinzip also die Anzahl an Zeilen in unserem Datensatz. Die Streuung ist schon etwas schwerer zu fassen, ist aber am Ende nichts anderes als die Varianz in den Daten. Also zum Beispiel bei einer Normalverteilung, wie stark streuen meine Beobachtungen um den Mittelwert. Die Effekt sind schon etwas schwerer zu greifen, da wir hier erst mal definieren müssen, welche Effekte es gibt. Grob gesprochen gibt es im Rahmen der Generierung von Daten zwei Effekte von Bedeutung. Entweder sind wir an einer Mittelwertsdifferenz interessiert oder aber an einem Anteil.

Mittelwertsdifferenz

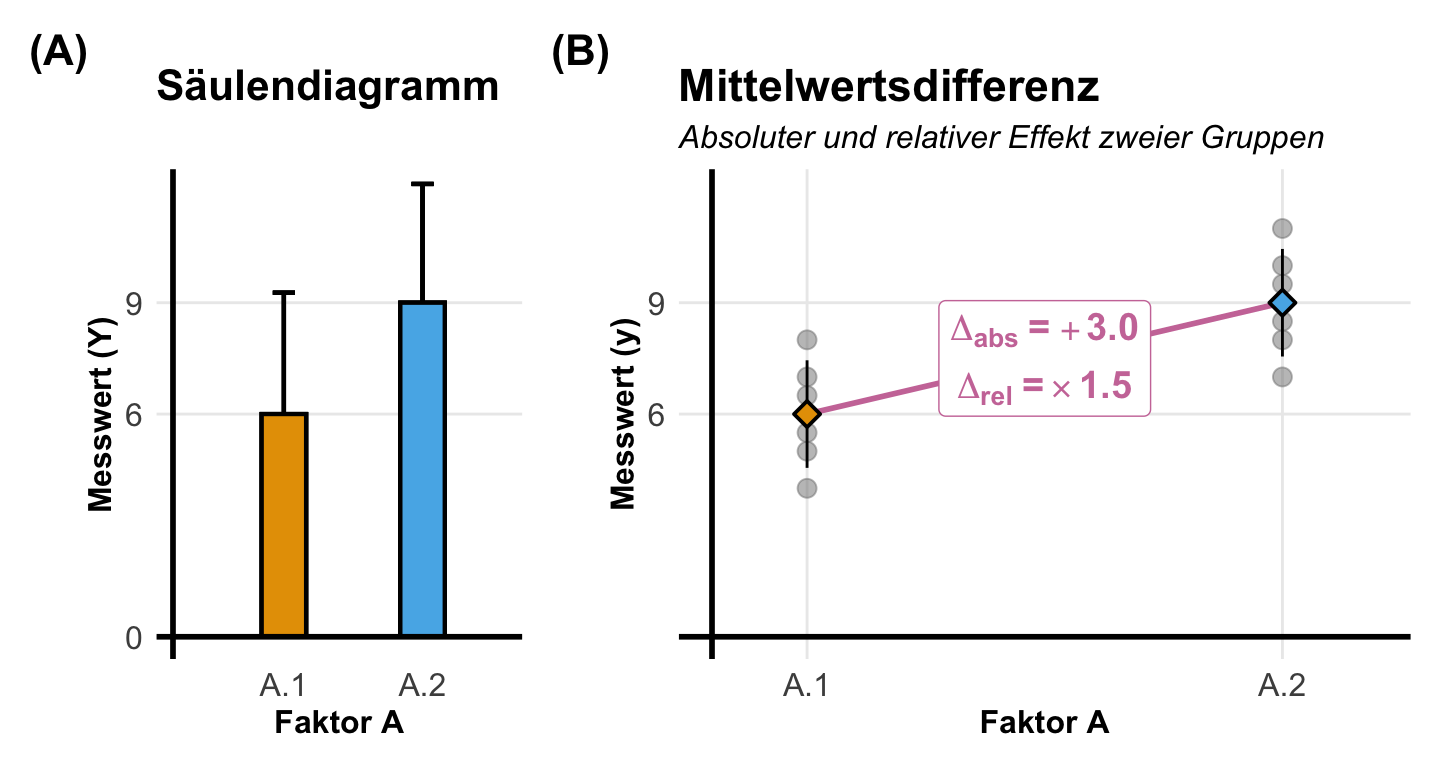
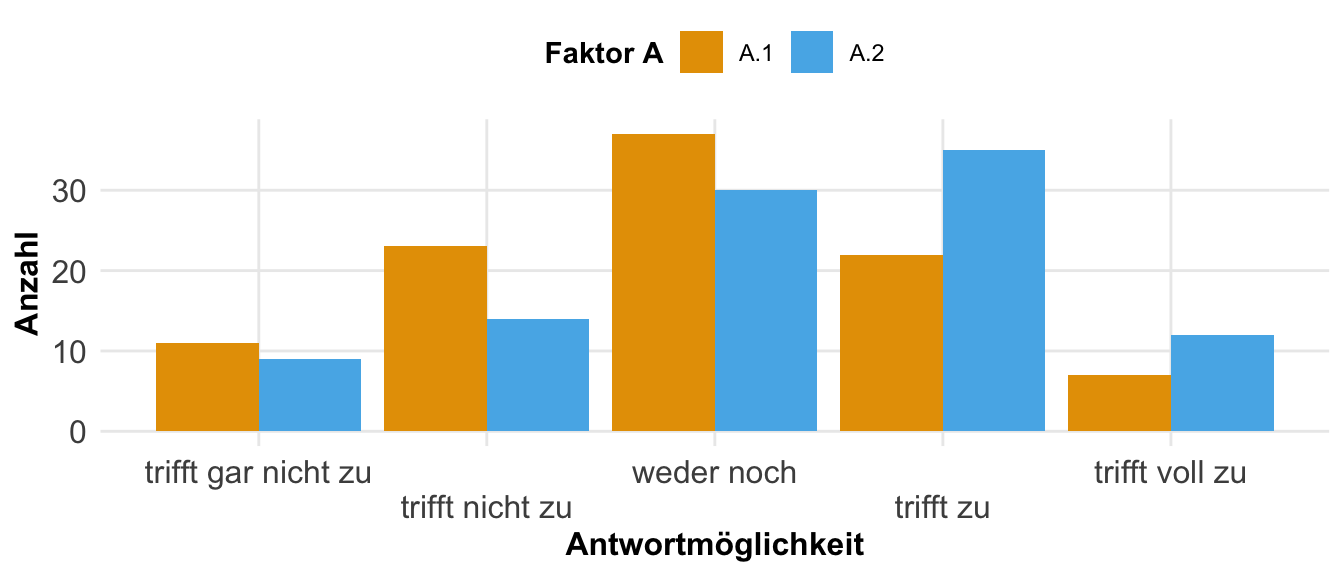
Die Mittelwertsdifferenz wird sehr häufig als Effektschätzer genutzt, wenn wir Daten erstellen wollen. Du kennst die Mittelwertsdifferenz schon aus der Darstellung der Mittelwerte von Gruppen anhand des Barplots. Hier können wir als Effekt entweder auf den absoluten Mittelwertsunterschied hinaus wollen oder aber die relative Veränderung angeben. Im Rahmen der Simulation nutzen wir die absolute Differenz sehr viel häufiger. In der folgenden Abbildung habe ich dir einmal für zwei Gruppen in einem Faktor einen Barplot sowie die Mittelwertsdifferenz mit Dotplots dargestellt.

Abbildung 21.5— Darstellung eines einfaktoriellen Datensatzes mit zwei Gruppen und unterschiedlichen Mittelwerten bei gleicher Varianz für einen normalverteilten Messwert. Der Effekt ist hier die Mittelwertsdifferenz. (A) Säulendiagramm (eng. barplot) (B) Dotplot mit absoluter und relativer Differenz zwischen den beiden Gruppen. [Zum Vergrößern anklicken]

Anteilsverhältnis

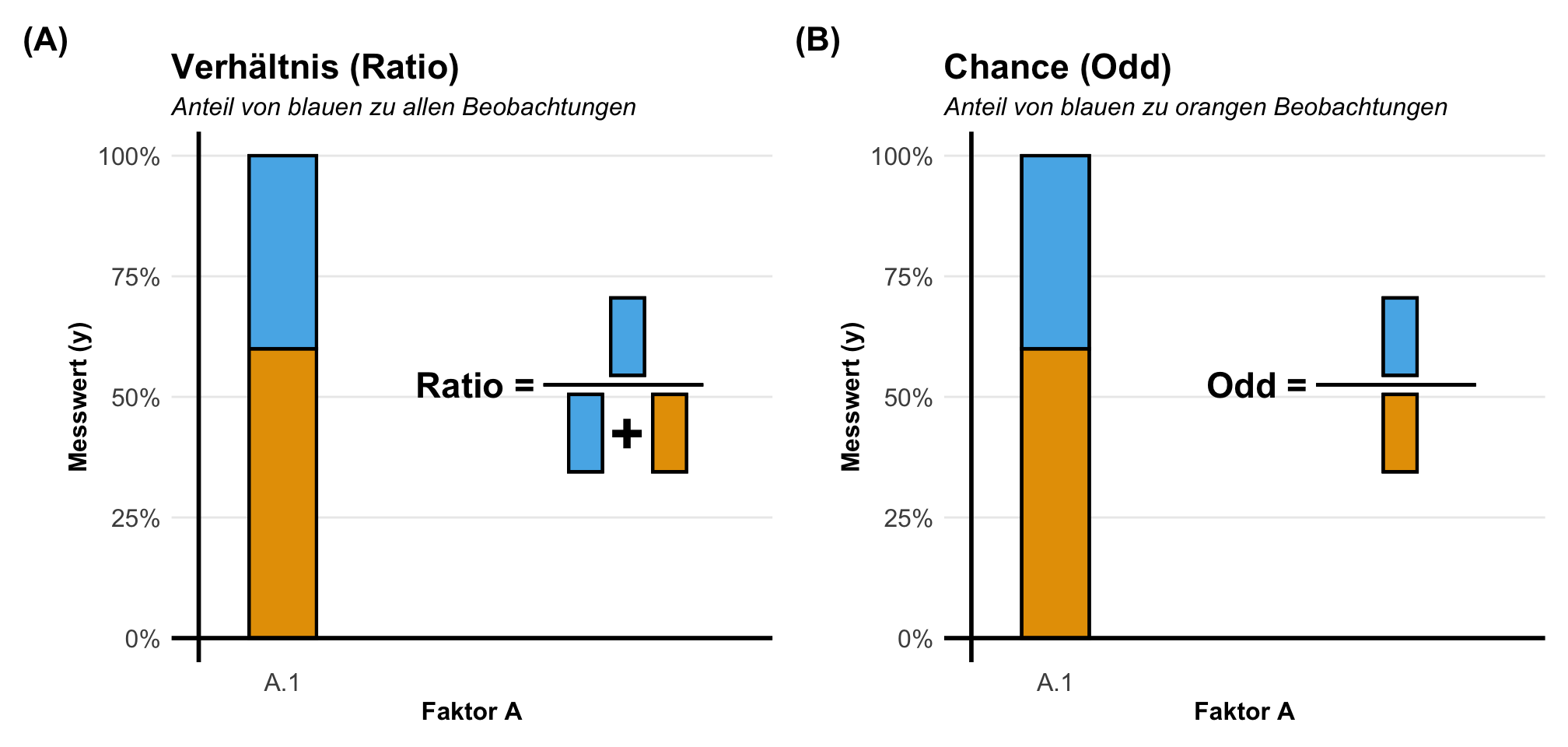
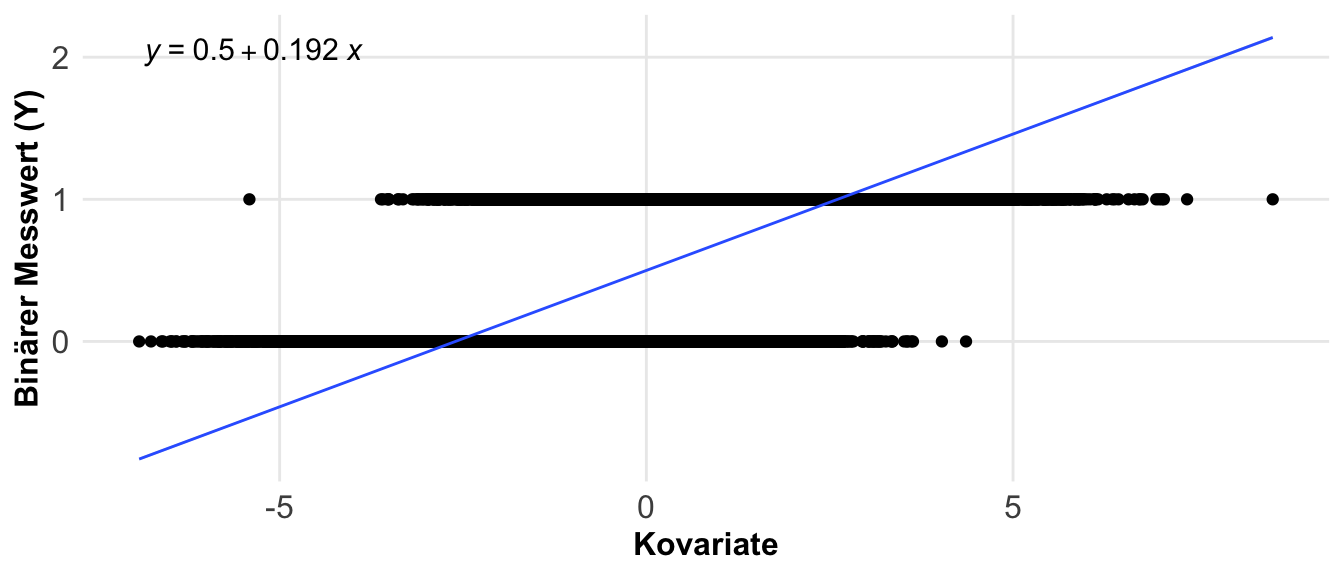
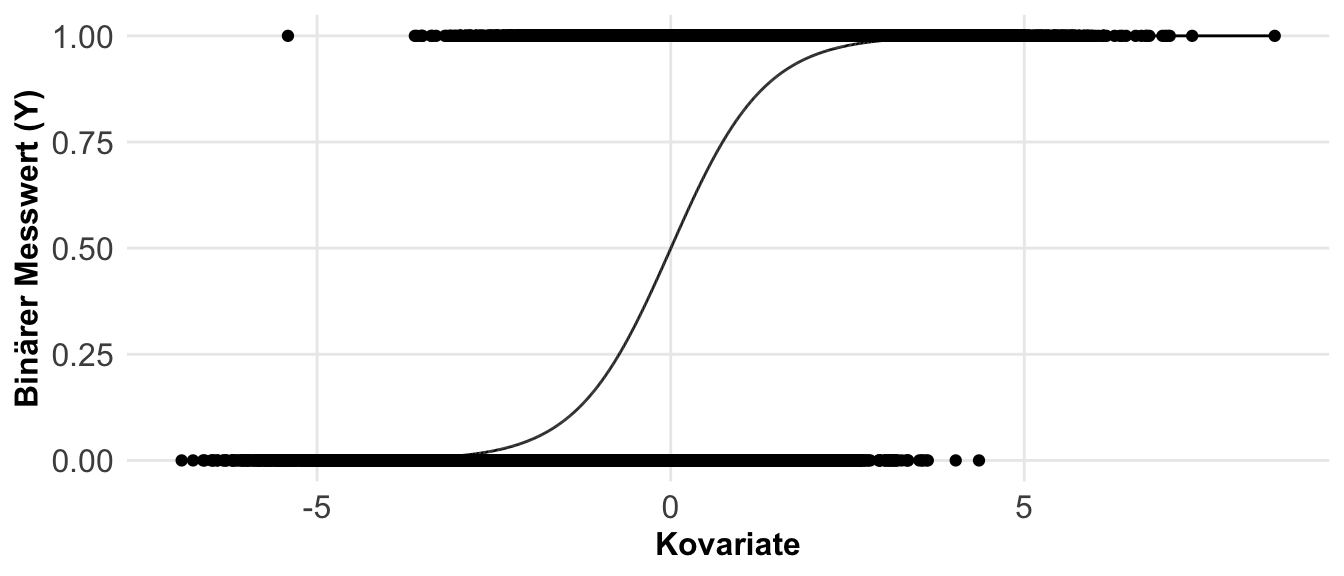
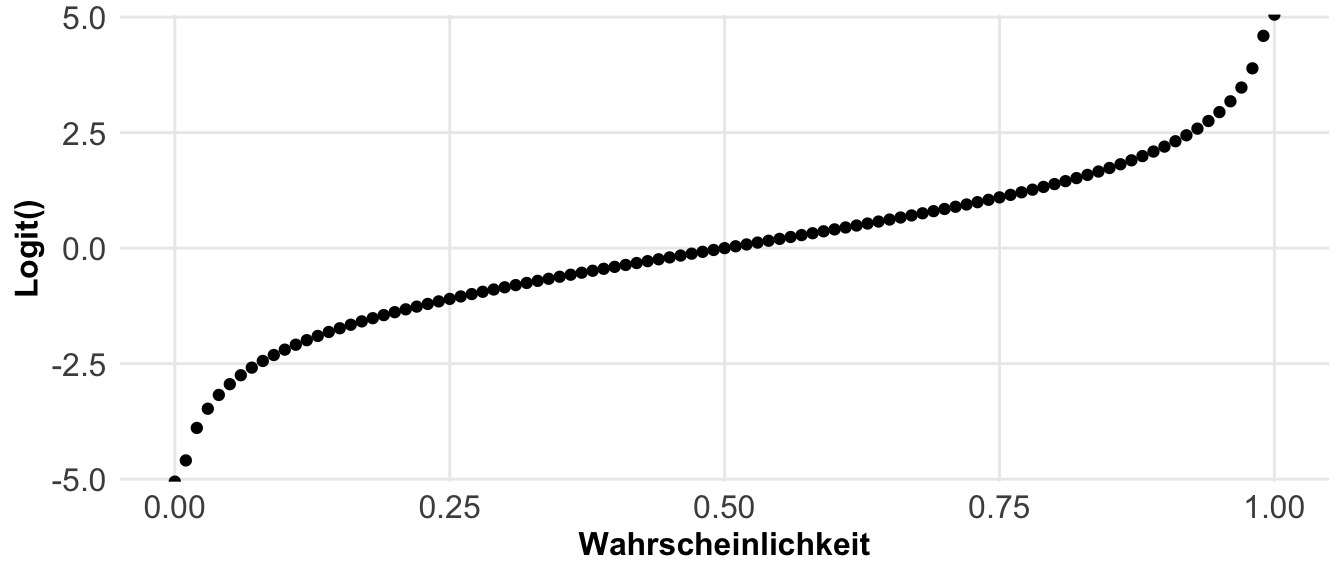
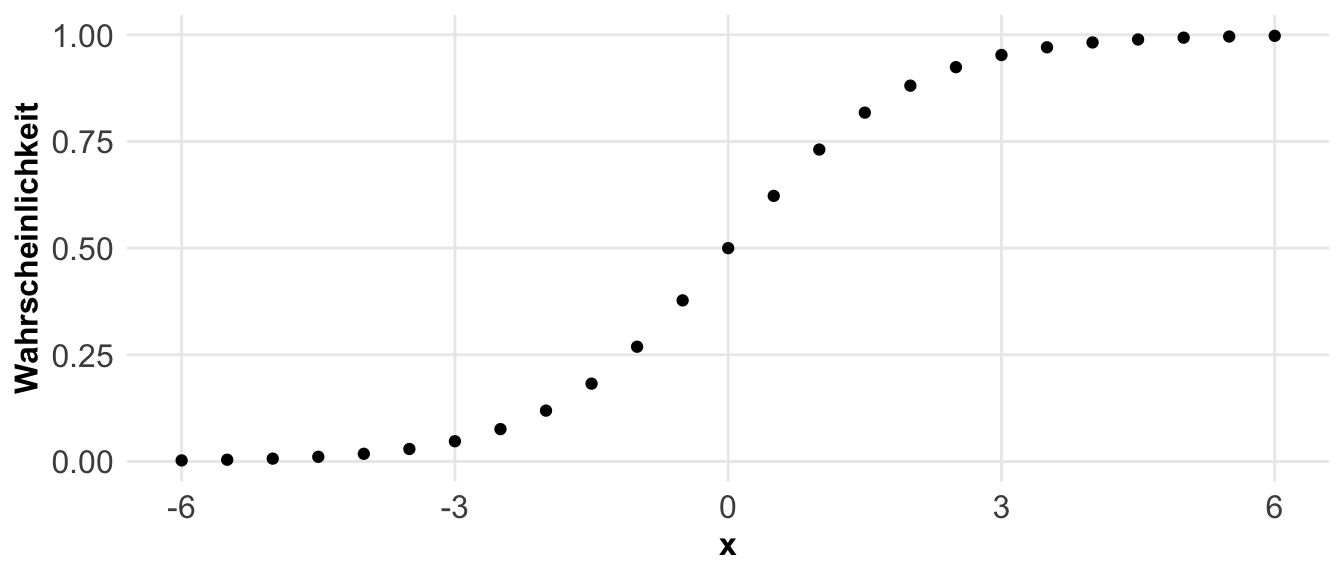
Eine andere Möglichkeit sind die Anteile. Hier fragen wir, wie häufig tritt ein Ereignis in der Population auf? Daher ist die Pflanze krank? Oder aber, liegen wir im Zielbereich? Wir sind hier an einem Anteilsverhältnis interessiert. Anteile werden in unserem Kontext eigentlich immer mit ja (1) oder nein (0) kodiert. Wenn wir also zwei Gruppen haben, die gesunden und die kranken Pflanzen, dann können wir die Anteile an gesunden und kranken Pflanzen auf zwei Arten berechnen. Entweder sind wir an dem Anteil von den kranken Pflanzen an allen Pflanzen interessiert, dann rechnen wir ein Verhältnis. Wenn wir aber den Anteil von kranken Pflanzen an gesunden Pflanzen wollen, dann berechnen wir die Chance. In der folgenden Abbildung habe ich dir den Zusammenhang nochmal dargestellt.

Abbildung 21.6— Visualisierung zweier Effektschätzer für Anteile an einem gestapelten Säulendiagramm (eng. stacked barplot) für einen Faktor mit einer Gruppe \(A.1\). (A) Das Verhältnis (eng. ratio) beschreibt den Anteil der blauen Beobachtungen an allen Beobachtungen. Daher ein Art mittleres Verhältnis. (B) Die Chance (eng. odd) beschreibt den Anteil von blauen zu orangen Beobachtungen. [Zum Vergrößern anklicken]

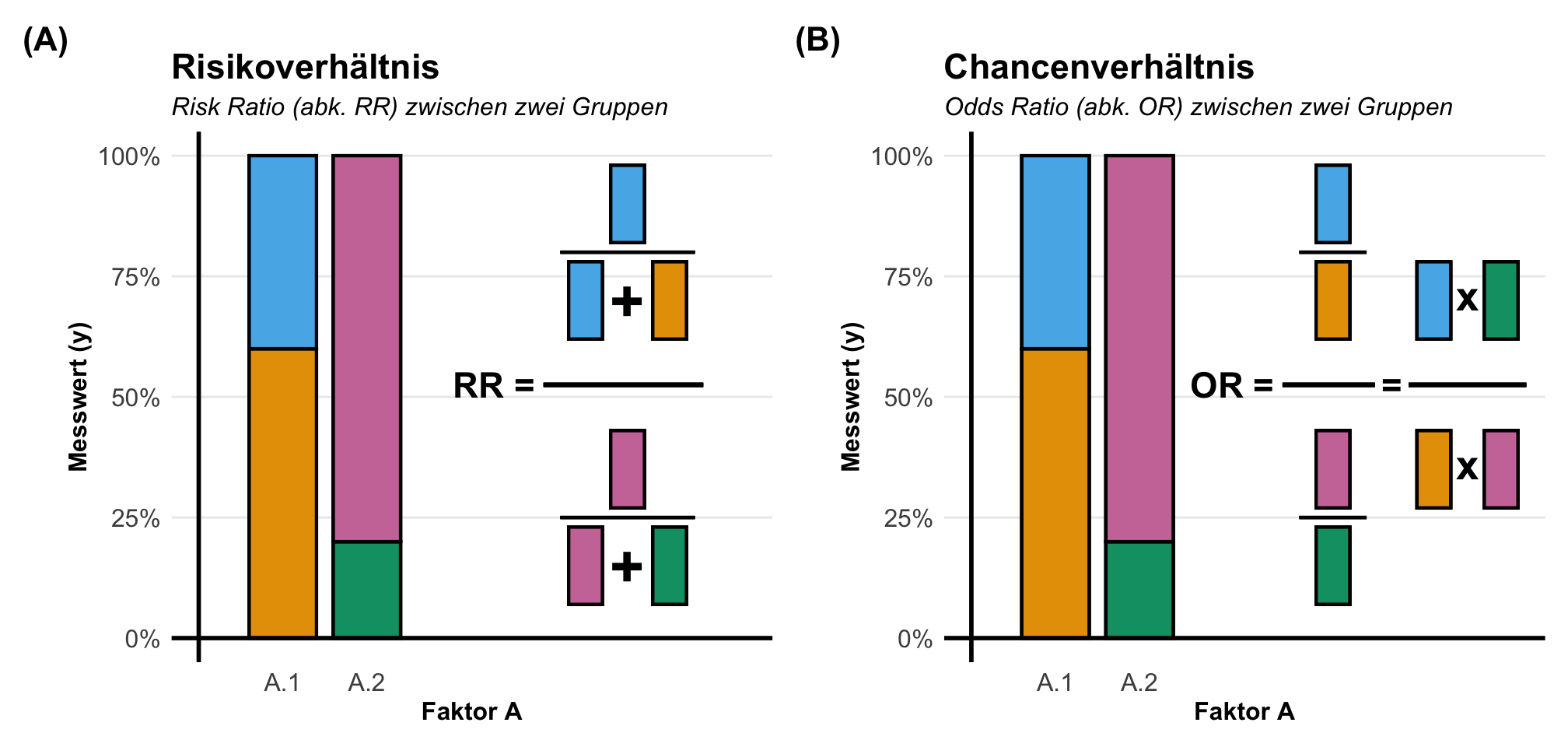
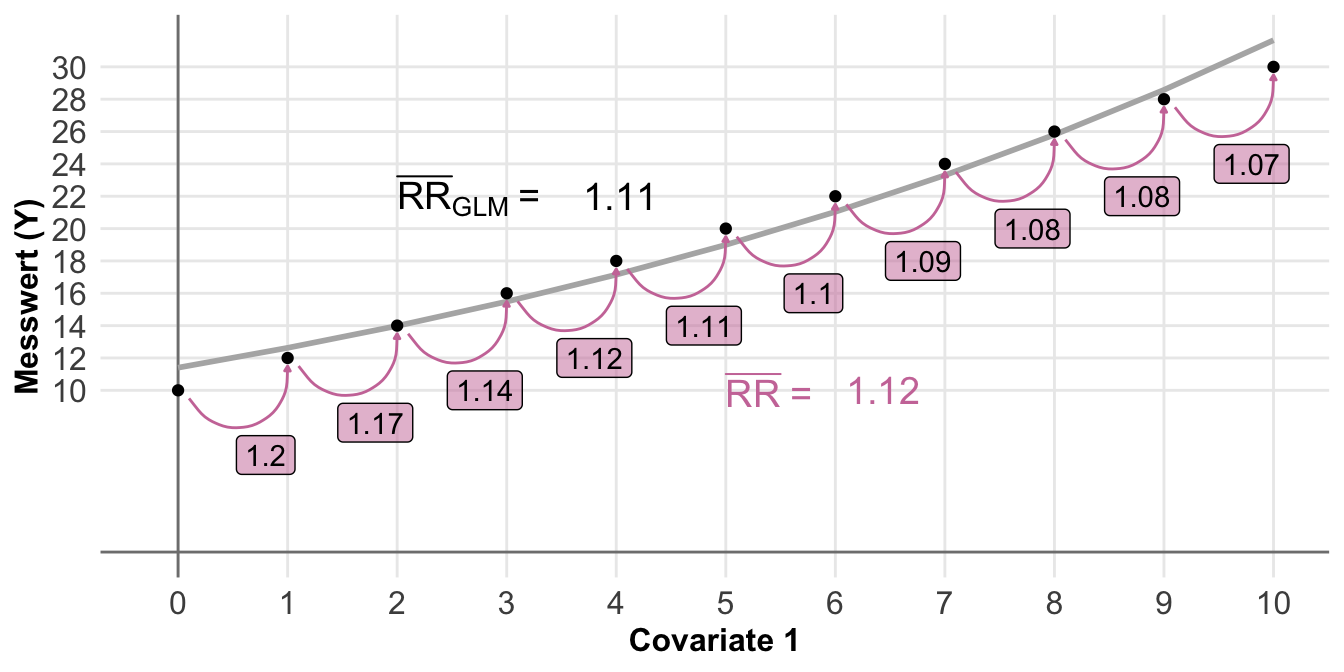
Etwas wilder wird es jetzt, wenn wir die Effekte zwischen zwei Gruppen mit Anteilen berechnen wollen. Hier nutzen wir dann nicht die Differenz sondern ebenfalls den Anteil. Daher haben wir es hier mit einem Anteil von einem Anteil zu tun. Daher berechnen wir hier dann das Risikoverhältnis (eng. risk ratio) oder aber das Chancenverhältnis (eng. odds ratio). Als reine Formel ist es dann meistens verwirrender, deshalb hier einmal als Abbildung visualisiert. In dem Kapitel zu den Effektschätzern kannst du noch mehr lesen und dein Wissen vertiefen.

Abbildung 21.7— Visualisierung zweier Effektschätzer für Anteilsverhältnisse an zwei gestapelten Säulendiagramm (eng. stacked barplot) für einem Faktor mit zwei Gruppen \(A.1\) und \(A.2\). (A) Das Risikoverhältnis (eng. risk ratio) beschreibt den Anteil der blauen Beobachtungen an allen Beobachtungen im Verhältnis der beiden Gruppen. (B) Das Chancenverhältnis (eng. odds ratio) beschreibt den Anteil von blauen zu orangen Beobachtungen im Verhältnis der beiden Gruppen. Der Doppelbruch kann dann entsprechend umgeformt werden. [Zum Vergrößern anklicken]

Was nehmen wir hier mit?

• Die Mittelwertsdifferenz ist zu gebrauchen, wenn wir von einem normalverteilten Messwert ausgehen. Oder aber, wenn wir mit den mittleren Effekt leben können. Wir wollen also die mittlere Anzahl an Blattläusen anstatt die Anzahl vergleichen. Oder aber die mittlere Infektionsrate anstatt den Anteil der kranken Pflanzen.
• Anteilsverhätnisse nutzen wir, wenn wir einen Messwert vorliegen haben, der nicht normalverteilt ist und wir über die Anteile von Gruppen in unserem Messwert sprechen wollen. Daher wir wollen über den Anteil in den Boniturnotenstufen reden oder aber den Anteil an kranken Pflanzen modellieren.

Häufig reicht erstmal eine Genierung mit dem Mittelwert und der Mittelwertsdifferenz. Wir können uns vielen Fragstellungen erst mal mit einem Mittel annäheren und dann später nochmal differenzierter Auswerten. Beachte immer, das es hier ja um die Erstellung von künstlichen Daten geht, die selten die Komplexizität echter Daten abbilden können. Daher habe ich hier auch den Fokus auf der Normalverteilung und der Generierung von mittleren Differenzen.

Effekt und Streuung

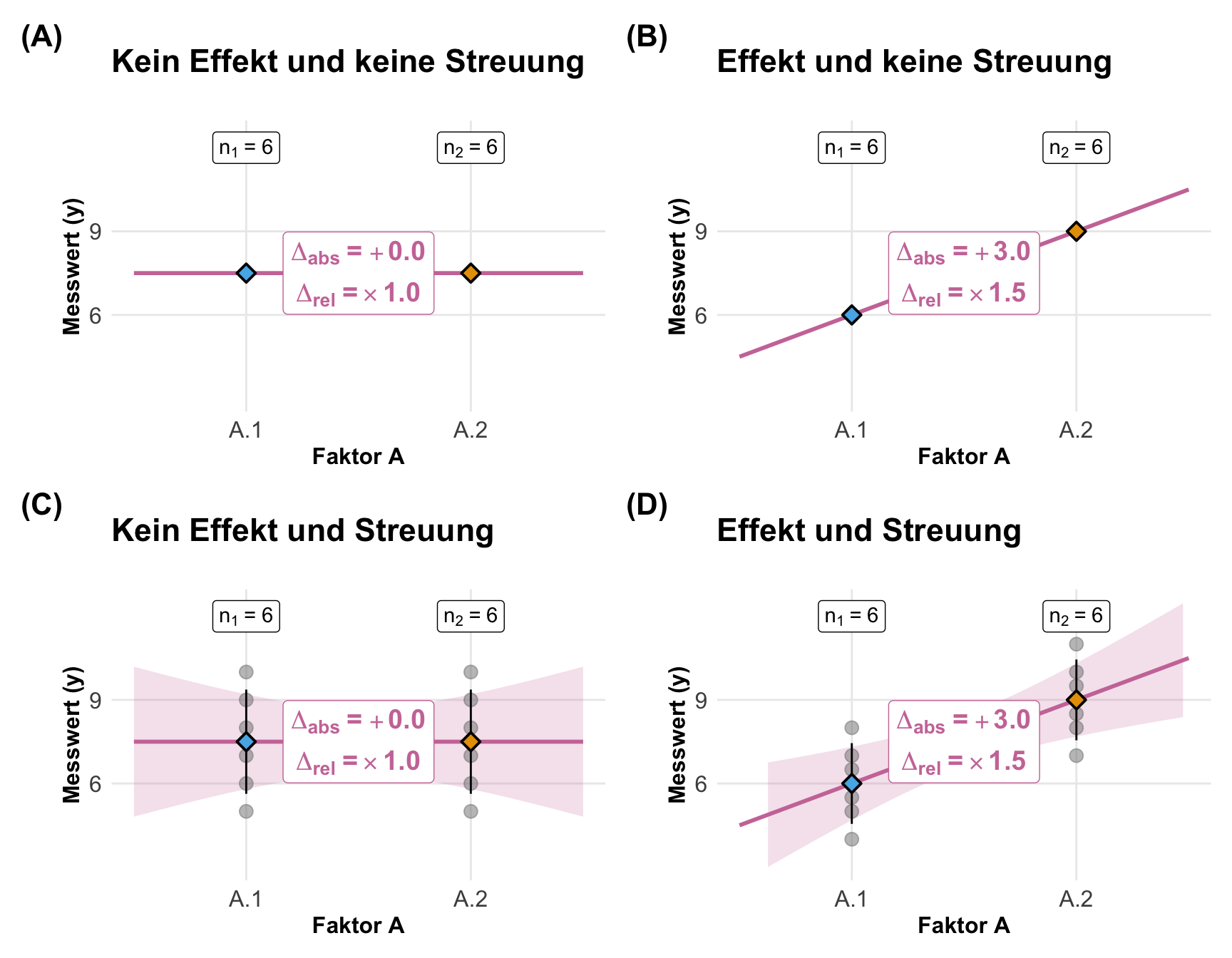
Jetzt müssen wir noch den Zusammenhang zwischen Effekt und Streuung verstehen. Je höher deine Fallzahl ist, desto eher wirst du in den genierten Daten deine voreingestellten Effekte wiederfinden. Es gibt aber noch die Variable der Streuung. Wenn du eine Streuung mit ins Spiel bringst, dann werden natürlich auch deine Effekte wiederum verzerrt. Bei einer Streuung erhälst du nicht deine voreingestellten Werte genau so wieder. Das ist manchmal etwas verwirrend, aber auch häufig der Grund warum wir nicht nur einen Datensatz simulieren sondern viele, die wir dann eben mitteln. Das hat aber keine Relevanz, wenn du deine Daten generierst um deine Analysepipeline zu testen. Wir schauen uns jetzt einmal den Fall eines faktoriellen und eines kovariaten Designs an.

Faktorielles Design

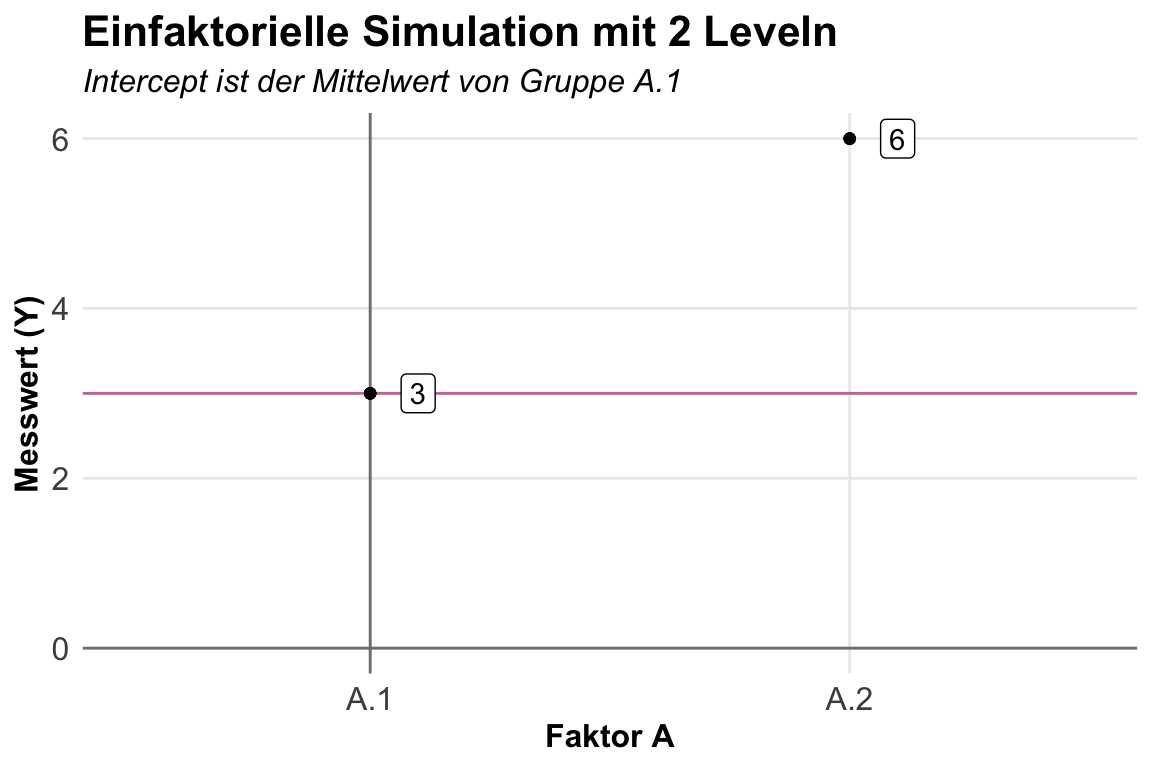
In dem folgenden Beispiel habe ich ein einfaktorielles Design mit nur zwei Leveln gewählt. Wir sehen recht gut, das wir bei keinem Effekt keinen Mittelwertsunterschied vorliegen haben. Ich habe hier eine Mittelwertsdifferenz von \(+3\) voreingestellt. Wenn wir dann auch keine Streuung vorliegen haben, dann liegen alle Beobachtungen auf dem Mittelwert als ein Punkt. Wenn wir dann Streuung vorliegen haben, dann spreizen die Punkte auf dem Faktorlevel. Durch die Streuung können wir dann auch nicht mehr exakt die voreingestellten Effekte wiederfinden. Je kleiner die Fallzahl, desto größer ist dann die Abweichung von den voreingestellten Effekten.

Abbildung 21.8— Darstellung eines absoluten und relativen Effekt in einem einfaktoriellen Design mit zwei Leveln \(A.1\) und \(A.2\) als Gruppen. Der Effekt ist die absolute oder relative Mittelwertsdifferenz. Pro Gruppe wurden sechs Beobachtungen erhoben. Ohne Streuung geht die Grade direkt durch die Mittelwerte der Gruppen. (A) Kein Effekt und keine Streuung. Die absolute Mittelwertsdifferenz ist 0 und die relative Mittelwertsdifferenz ist x1 als Faktor. (B) Effekt und keine Streuung. Die absolute Mittelwertsdifferenz ist +3 und die relative Mittelwertsdifferenz ist x1.5 als Faktor. (C) Kein Effekt und Streuung. Die absolute Mittelwertsdifferenz ist -0.5 und die relative Mittelwertsdifferenz ist x0.93 als Faktor.(D) Effekt und Streuung. Die absolute Mittelwertsdifferenz ist +2.7 und die relative Mittelwertsdifferenz ist x1.4 als Faktor. [Zum Vergrößern anklicken]

Kovariates Design

Haben wir ein kovariates Design vorliegen, dann wollen wir ja die Steigung in der Graden als Effekt einstellen. Ich habe hier eine Steigung von \(+1.5\) und einen Intercept von \(3\) voreingestellt. Wir brauchen immer etwas Streuung, sonst kann der Algorithmus keine Grade berechnen. Daher hier auch bei keiner Streuung ein winziger Wert, den wir dann eben auch in der Steigung wiederfinden. Ohne Streuung erhalten wir auch die voreingestellten Werte für die Steigung wieder. Haben wir keinen Effekt der Kovariaten auf den Messwert, dann haben wir auch keine Steigung. Sobald wir Streuung ins Spiel bringen, haben wir auch eine mehr oder minder starke Abweichung in den Daten. Insbesondere bei keinem Effekt und dann noch Streuung kann man schnell denken, dass wir doch was in den Daten hätten.

Abbildung 21.9— Darstellung eines Effekts als Steigung in einem kovariaten Design. Der Effekt der Steigung ist mit \(\beta_1\) gleich +1.5 und der Intercept ist mit \(\beta_0\) gleich 3 voreingestellt. Durch die Streuung mit der geringen Fallzahl von sechs Beobachtungen kann Steigung nicht immer erreicht werden. (A) Kein Effekt und keine Streuung. Die Steigung ist faktisch 0 und der Intercept 3. (B) Effekt und keine Streuung. Dei Steigung ist 1.5 und der Intercept ist 3. (C) Kein Effekt und moderate Streuung. Durch die Streuung entsteht eine leichte negative Steigung und eine Abweichung vom Intercept. (D) Effekt und moderate Streuung. Die Steigung und der Intercept werden durch die Streuung verzerrt. [Zum Vergrößern anklicken]

Einschränkungen bei der Generierung

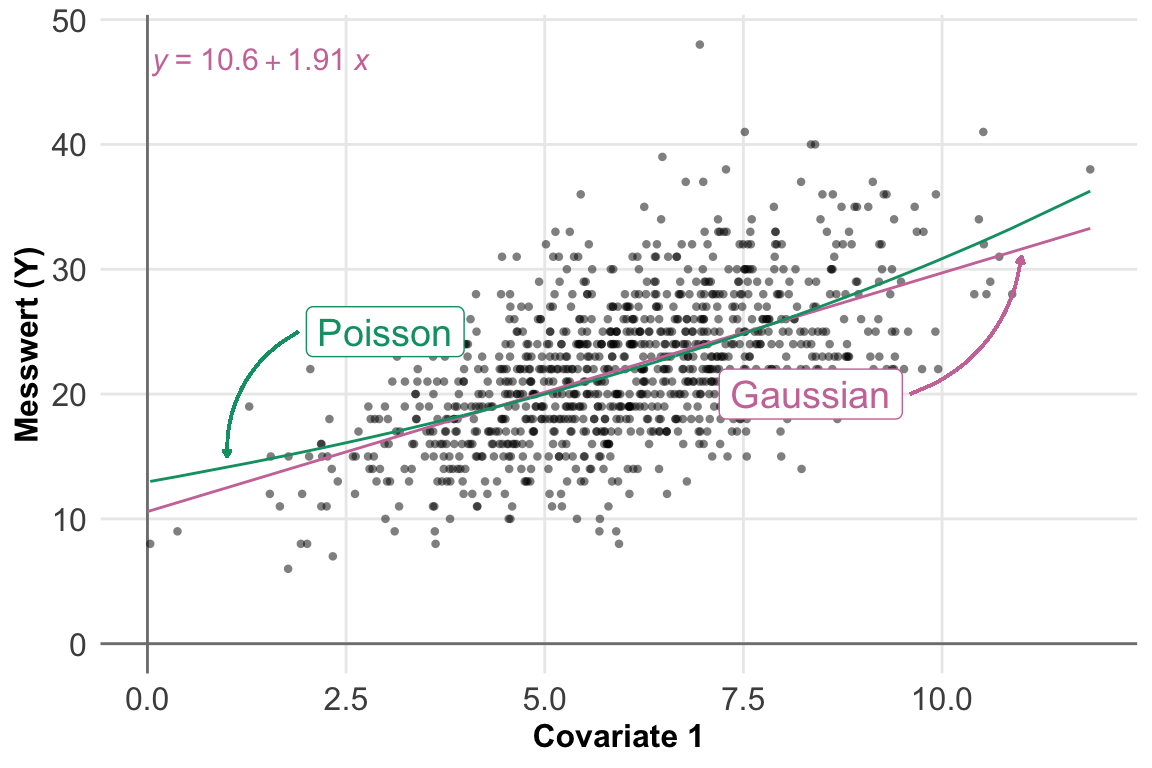
Wenn wir über die Simulation von Daten sprechen, dann kommen wir nicht darum herum einmal über die schrecklich nette Familie der Verteilungen zu sprechen. Wir haben ja nicht nur auf der rechten Seite der Tilde unsere Einflussvariablen, die entweder Faktoren oder Kovariaten sind, sondern auch die Messwerte, die wir simulieren wollen. Diese Messwerte gehören aber einer Verteilungsfamilie an. Zwar ist die Normalverteilung (eng. gaussian) sehr häufig aber können wir mit der Normalverteilung nicht alle Messwerte abbilden. Daher brauchen wir auch die anderen Verteilungen. Daher hier einmal die Übersicht für dich. Das R Paket {simstudy} hat eine Vielzahl an Verteilungen implementiert auf die wir hier nicht tiefer eingehen werden.

Abbildung 21.10— Erweiterte Darstellung der statistischen Modellierung. Die Messwerte \(Y\) folgen einer Verteilung. Die Einflussvariablen liegen kontinuierlich als Kovariaten oder aber kategorial als Faktoren vor. [Zum Vergrößern anklicken]

Wir konzentrieren uns hier nur auf einen kleinen Teil der möglichen Simulationen und Datengenerierungen. Das hat neben der vielen möglichen Verteilungen auch den Grund, dass wir usn hier ja nicht mit der algorithmischen Modellentwicklung in der Statistik beschäftigen wollen. Wir wollen ja nicht neue Algorithmen bauen und diese dann auf Daten evaluieren. Daher konzentrieren wir uns hier auf wenige Verteilungen, die dann aber das abbilden, was wir häufig brauchen. Wenn du mehr über Verteilungen wissen willst, dann ist die Shiny App The distribution zoo einen Besuch wert. Als Literatur kann ich dir nur Dormann (2013) empfehlen, der sehr detailliert für Einsteiger auf Verteilungen eingeht.

• Die Normalverteilung erlaubt uns das Frischegewicht, Trockengewicht oder aber Chlorophyllgehalt zu simulieren. Also im Prinzip die Messwerte, die wir hauptsächlich in einem agrawissenschaftlichen Umfeld erheben.
• Die Possionverteilung erlaubt uns alles was wir Zählen zu simulieren. Also im Prinzip alle Anzahlen von Schädlingen oder aber Blütenstände sowie Blättern. Wir zählen hier eben etwas.
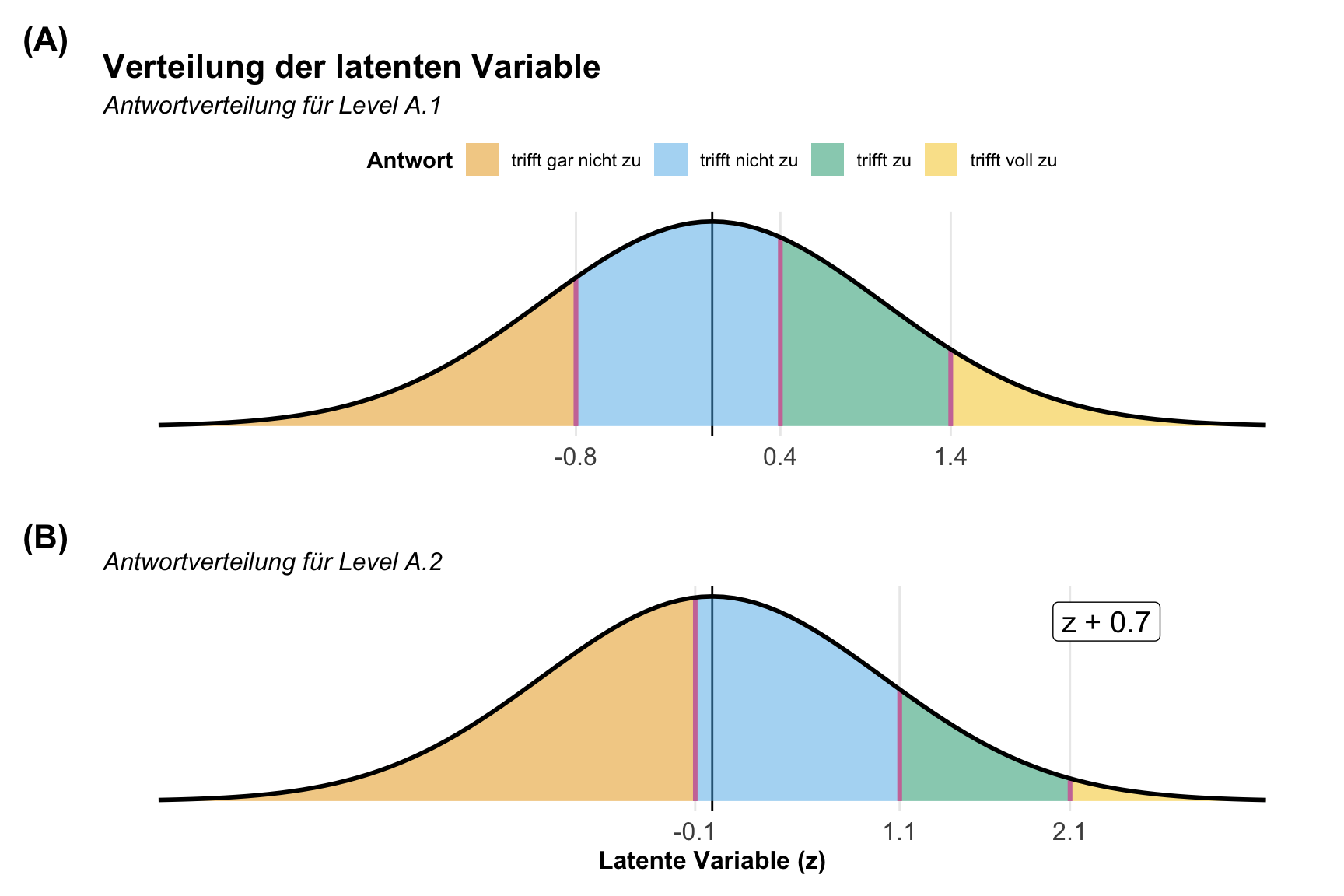
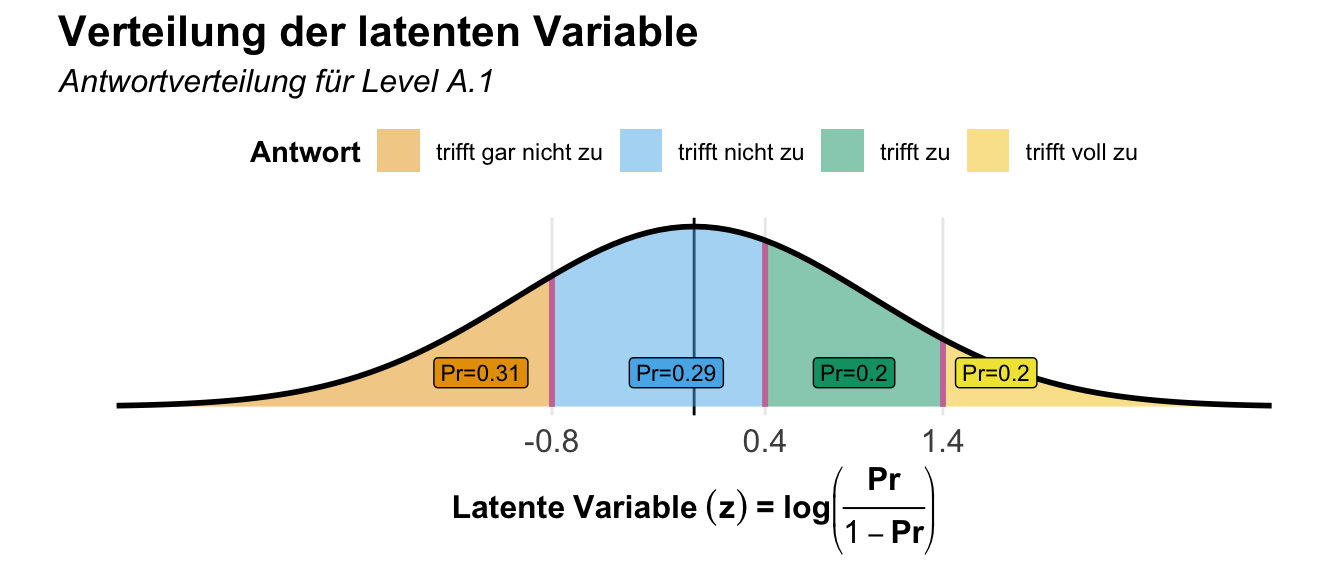
• Die Ordinalverteilung ist dafür gut, wenn wir Noten simulieren wollen. Daher brauchen wir die Ordinalverteilung um unsere Boniturnoten zu generieren. Prinzipiell aber auch die Antwortverteilungen in einem Fragebogen.
• Die Binomialverteilung ist die Verteilung, die wir nutzen, wenn wir nur zwei mögliche Messwerte haben. Also im prinzip gesunde Beobachtung oder kranke Beobachtung. Wir haben nur zwei Ausprägungen in dem Messwert vorliegen.

Neben den vorgestellten Verteilungen schauen wir uns dann noch die Simulation von pseudo Zeitreihen an. Wir haben hier dann verschiedene Messwerte über einen zeitlichen Verlauf vorliegen. Teilweise dann in einer etwas wirren Form, da wir eventuell keinen linearen Zusammenhang mehr vorliegen haben. Daher müssen wir dann hier etwas mehr schauen, dass wir die Daten gut simuliert kriegen.

Dann mache ich hier noch die Einschränkung, dass ich prinzipiell alles unter der Annahme der Varianzhomogenität generiere. Daher addiere ich über alle Faktorkombinationen oder Gruppen immer den gleichen Fehler auf. Im Prinzip kannst du natürlich auch für einzelne Faktorkombinationen dann einen anderen Fehler addieren und dir dafür einen Vektor mit unterschiedlichen Fehlertermen bauen, aber darauf gehe ich nur einmal kurz bei dem einfakoriellen Design ein. Und dann noch die Ergänzung, dass wir uns immer nur balancierte Designs erstellen. Das heißt wir haben keine fehlenden Werte in unseren Daten und die Gruppen in unseren Faktoren haben auch immer die gleiche Fallzahl.

Selbst gebaute Verteilungen

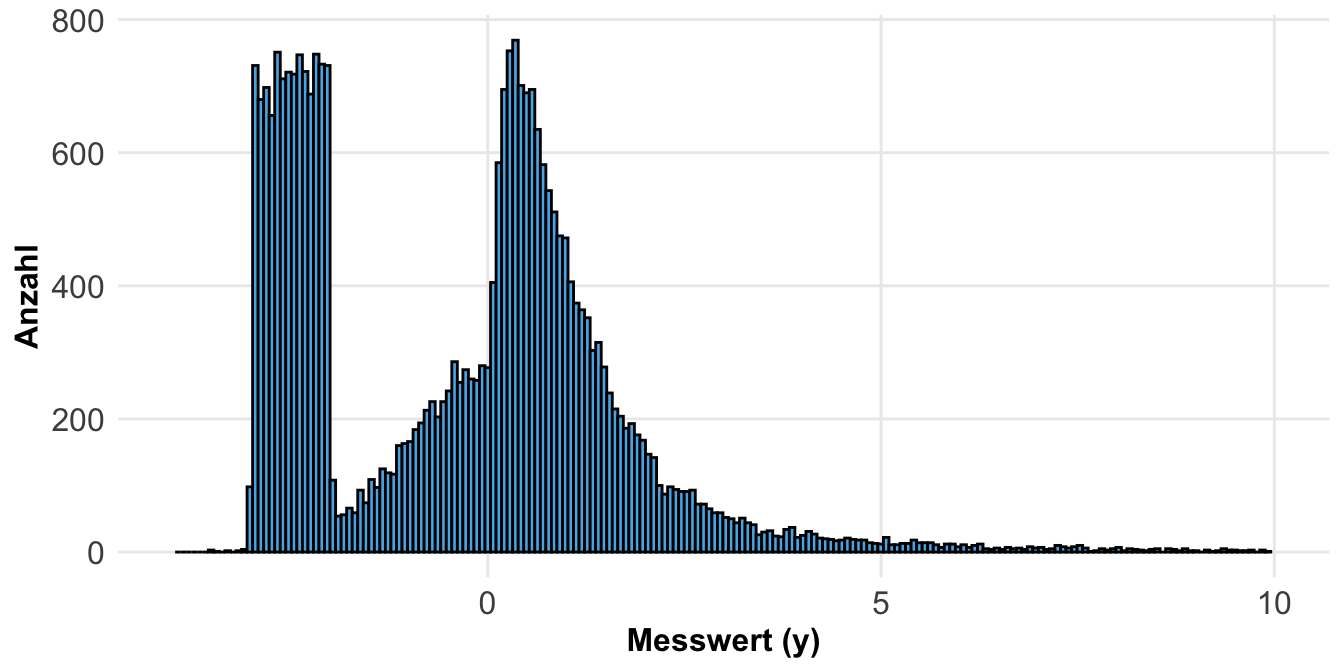
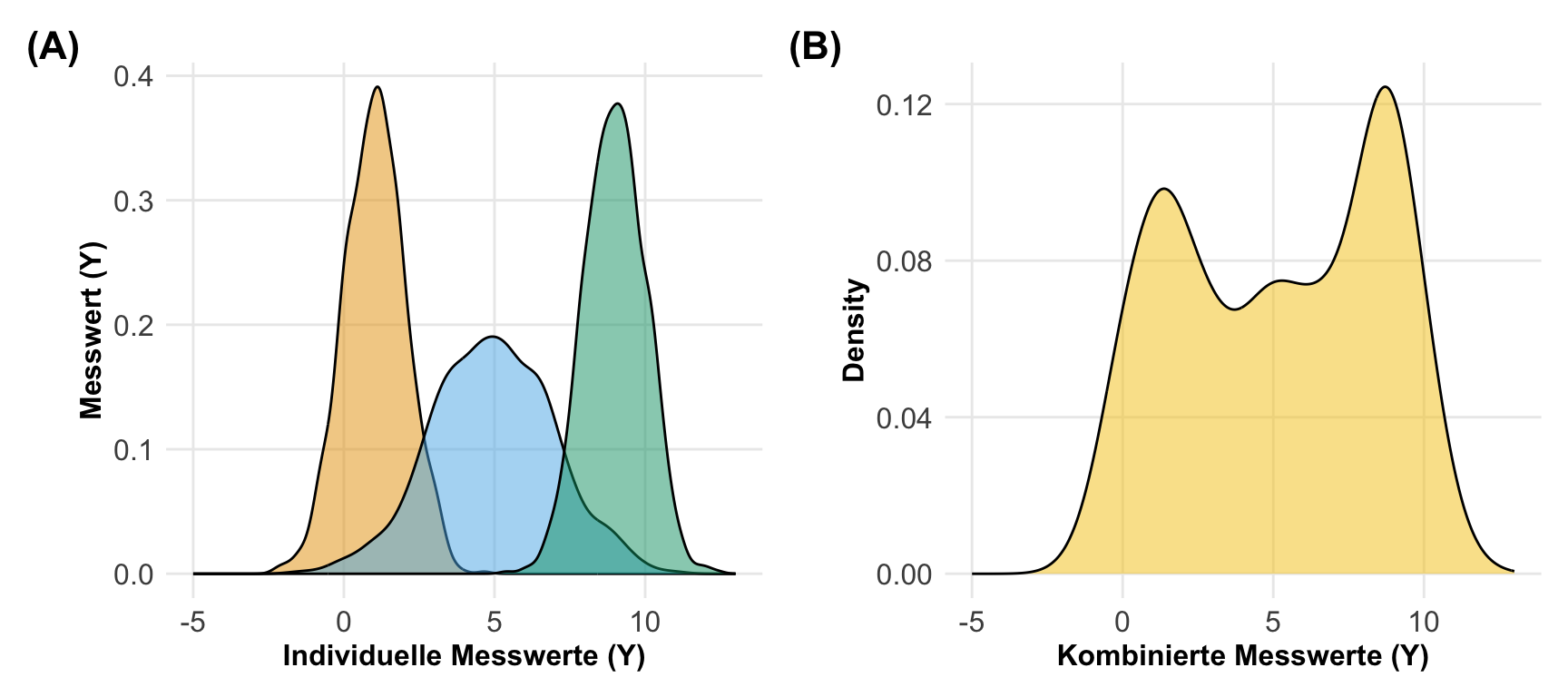
Am Ende möchte ich noch auf eine andere Art der Simulation von Daten eingehen. Wir können uns auch eine wilde Verteilung selber bauen und dann aus dieser wilden Verteilung dann unsere Beobachtungen ziehen. In dem Tutorium Wilcoxon is (almost) a one-sample t-test on signed ranks wird einmal gezeigt wie wir das machen könnten. Wir bauen uns dazu erst mal eine Verteilung, die aus drei Verteilungen besteht. Wir haben hier aber ein paar Einschränkungen. Zum einen ist unsere Verteilung um die Null angeordnet. Das macht es einfacher verschiedene Verteilungen miteinander zu verbinden.

null_dist_tbl <- tibble(y = c(rnorm(10000), 
                              exp(rnorm(10000)), 
                              runif(10000, min=-3, max=-2)),
                        type = "null")

Dann siehst du hier einmal die Verteilung dargestellt. Wenn wir nur aus dieser Verteilung Beobachtungen ziehen, dann haben wir natürlich einen Effekt zwischen potenziellen Gruppen.

Abbildung 21.11— Selbstgebaute Verteilung mit einem Plateu und einem steilen Peak. Die Messwerte sind auch negative, da alle ursprünglichen drei Verteilungen um die Null zentriert sind. [Zum Vergrößern anklicken]

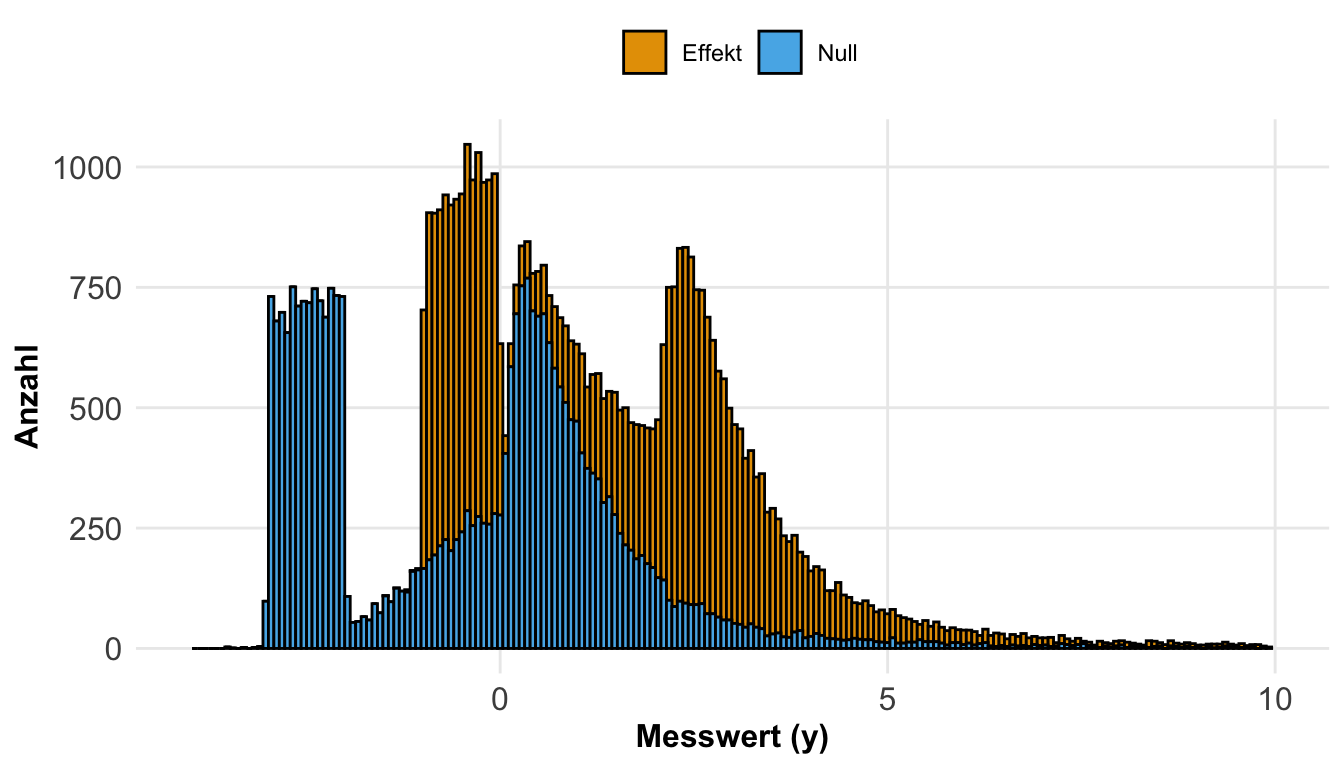
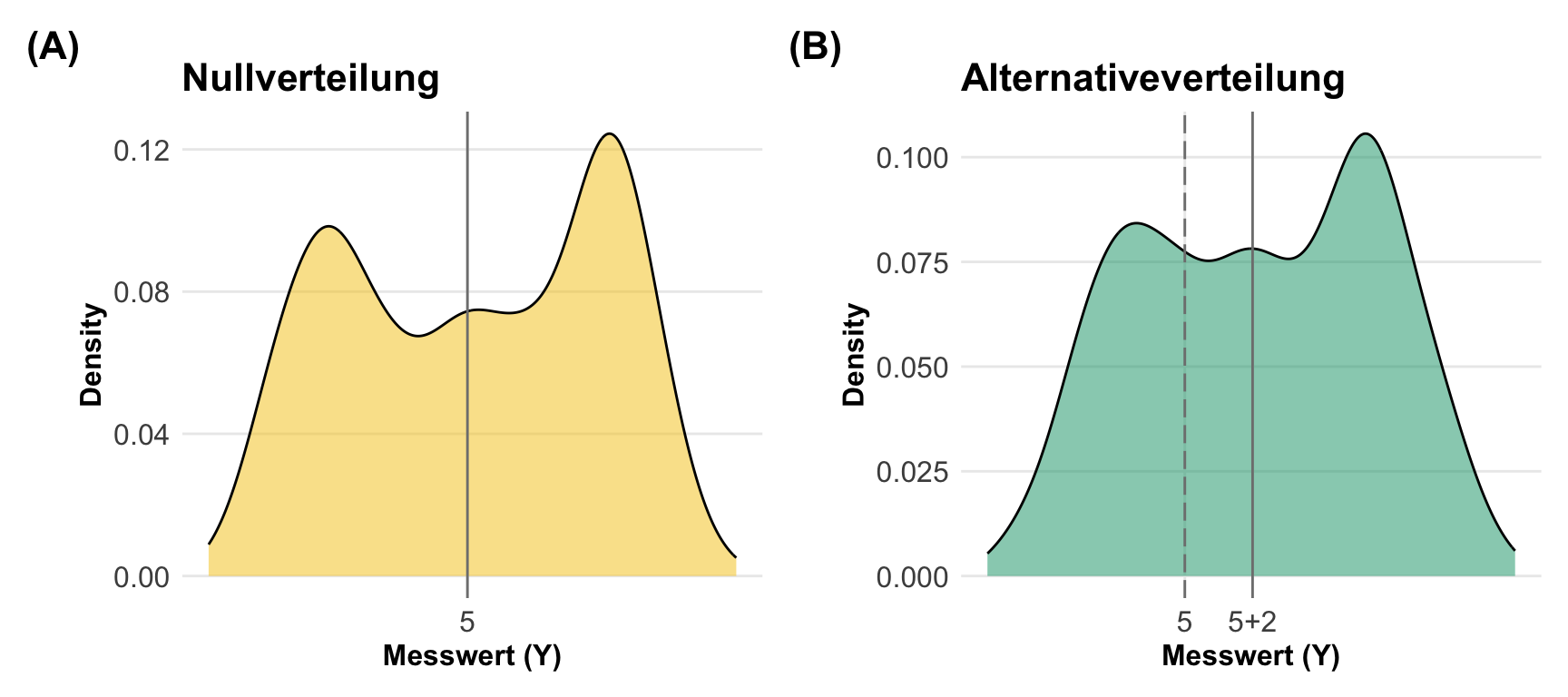
Wenn wir jetzt noch einen Effekt haben wollen, dann können wir natürlich die beiden Gruppen nicht aus der gleichen Verteilung ziehen. Daher können wir uns auch noch eine Alternative Verteilung bauen indem wir einfach die Messwerte um einen fixen Effekt erhöhen. Hier wähle einen Effekt von \(+2\). Du kannst natürlich auch die Nullverteilung erstmal aus dem negativen herausschieben und dann nochmal einen Effekt addieren.

eff_dist_tbl <- tibble(y = c(rnorm(10000), 
                             exp(rnorm(10000)), 
                             runif(10000, min=-3, max=-2)),
                       type = "alt") |> 
  mutate(y = y + 2) |> 
  bind_rows(null_dist_tbl)

In der folgenden Abbildung siehst du dann einmal wie sich die beiden Verteilungen mit den unterschiedlichen Effekten ergeben. Bitte beachte, dass die Alternative erst mal neu generiert wurde und nicht die verschobene Nullhypothese ist. Daher hat die Alternative natürlich auch eine andere Verteilung als die Nullhypothese.

Abbildung 21.12— Selbstgebaute Verteilung mit einem Plateu und einem steilen Peak für die Nullhypothese und die Alternativehypothese verschoben um den Effekt von \(+2\). [Zum Vergrößern anklicken]

Für die Generierung deiner Daten würdest du dann mit slice_sample() dir dann die gewünschten Anzahlen aus den beiden Verteilungen rausziehen. Hier hilft die tolle Funktion group_by(), die dir dann alles in einem Abwasch macht. Ich will hier pro Gruppe dann nur drei zufällig ausgewählte Beobachtungen haben.

eff_dist_tbl |> 
  group_by(type) |> 
  slice_sample(n = 3)

# A tibble: 6 × 2
# Groups:   type [2]
       y type 
   <dbl> <chr>
1 -0.794 alt  
2  2.86  alt  
3  2.83  alt  
4 -0.697 null 
5  6.27  null 
6 -1.13  null 

Bei den selbstgebauten Verteilungen ist die Effektzuweisung aber überhaupt nicht einfach und ab zwei Gruppen wird es wirklich nicht mehr schön. Daher zeige ich dir hier nur die Idee, in der Anwendung zeige ich dir etwas robustere Varianten, die einfacher zu bedienen sind. Wenn es aber wirklich mal was wirres sein soll, dann ist diese Art der Verteilungserstellung wirklich eine Möglichkeit um auf künstliche Daten zu kommen.

Weitere Tutorien für die Genierung von Daten

Wir immer geht natürlich mehr als ich hier Vorstellen kann. Du findest im Folgenden Tutorien, die mich hier in dem Kapitel inspiriert haben. Ich habe mich ja in diesem Kapitel auf die Durchführbarkeit in R und die allgemeine Verständlichkeit konzentriert.

• Einen guten Überblick liefert Brad Duthie in seinem Tutorium Creating simulated data sets in R. Hier kannst du dich dann nochmal in die Grundlagen einlesen.
• Auch Excel kann künstliche Daten generieren. Dafür schaue ich dann immer in die statistischen Funktionen (Referenz) Seite nach. Die Seite ist leider etwas schwer zu lesen.
• Getting started simulating data in R: some helpful functions and how to use them gibt nochmal einen guten Überblick über die Standardfunktionen in R um sich schnell Daten zu generieren.
• The distribution zoo sowie Probability Distributions in R oder aber auch Plotting Continuous Probability Distributions In R With ggplot2 gben nochmal einen Einblick in die Verteilungen. Dabei würde ich den Distribution Zoo als Shiny App erstmal vorziehen. Die anderen beiden Quelle liefern nochmal mehr mathematischen Hintergrund.

21.3 Genutzte R Pakete

Wir wollen folgende R Pakete in diesem Kapitel nutzen.

pacman::p_load(tidyverse, simstudy, simdata, modelr, 
               ggpmisc, janitor, emmeans, correlation,
               data.table, marginaleffects, conflicted)
set.seed(20250820)
conflicts_prefer(ggplot2::annotate)

An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.

21.4 R Paket {simstudy}

Der Fokus in diesem Kapitel liegt auf dem R Paket {simstudy} und deren Funktionen. Wir werden in dem Abschnitt zu der Normalverteilung nochmal auf die Standardfunktionen in R eingehen und die Daten etwas mehr händisch genierieren. Wennn die Verteilungen aber komplizierter werden, dann wird es auch mit dem Standard schwerer. So ist die Poissonverteilung, die Ordinalverteilung und auch die Binomialverteilung in einem mehrfaktoriellen Design schon nicht mehr schön selber zu bauen. Insbesondere wenn die Einflussvariablen noch untereinander miteinander in Beziehung stehen.

In der folgenden Tabelle siehst du einmal die drei Variablen für das Alter, das Geschlecht und die Sprungweite von Katzenflöhen. Wir sagen, dass der Effekt des Alters immer fix \(10\) ist. Das Geschlecht des Flohs hängt hier absurderweise vom Alter ab. Die Sprungweite ist dann eine Funktion des Alters und des Geschlechts. Dabei haben nicht alle Verteilungen eine Varianz wie die Normalverteilung. Deshalb haben wir hier auch Null in der Varianz bei den anderen Verteilungen stehen.

Tabelle 21.2— Beispielhafte Tabelle einer Datendefinition der Effekte der Variablen in {simstudy}. Jede Zeile beschreibt eine Variable in dem Datensatz und deren mathematischen Zusammenhang oder den Effekt untereinander. Dazu kommt noch die Varianz und die entsprechende Verteilung der Variable.

varname	formula	variance	dist	link
age	10	2	normal	identity
female	-2 + age * 0.1	0	binary	logit
jump_length	1.5 - 0.2 * age + 0.5 * female	0	poisson	log

Dann können wir die obige Tabelle auch einmal in {simstudy} nachbauen. Wir müssen dazu die Funktion defData() nutzen und dann immer erweitern. Dabei ist natürlich die Ordnung wichtig, da wir erst Variablen erschaffen müssen bevor wir mit den Variablen weiterrechnen können. Das verlangt etwas Übung und auch ein gewissen Gefühl für die Datenerstellung. Mir ist es am Anfang auch etwas schwerer gefallen, aber diese Art der Genierung hat echte Vorteile, wenn die Daten komplexer werden.

def <- 
  defData(varname = "age", dist = "normal", 
          formula = 10, variance = 2) |> 
  defData(varname = "female", dist = "binary",
          formula = "-2 + age * 0.1", link = "logit") |> 
  defData(varname = "jump_length", dist = "poisson",
          formula = "1.5 - 0.2 * age + 0.5 * female", link = "log")

Dann können wir schon die Funktion genData() nutzen um uns dann entsprechend viele Beobachtungen mit der entsprechenden Datendefinition zu erschaffen. Hier habe ich einmal fünf Beobachtungen gewäht, später nutze ich dann eher eintausend Beobachtungen.

dt <- genData(n = 5, def)
dt

Key: <id>
      id       age female jump_length
   <int>     <num>  <int>       <int>
1:     1 11.647845      0           0
2:     2 12.958943      0           1
3:     3  7.439934      0           1
4:     4 10.127518      1           0
5:     5  8.237693      0           0

Manchmal ist es so, dass wir einem bestehenden Datensatz mit Vairablen eine Definition hinzufügen wollen. Das ist insbesondere bei Faktorenrastern der Fall. Dort bauen wir uns ja erst alle Faktorkombinationen und wollen dann nochmal den Messwert berechnen. Dafür können wir dann die Funktion defDataAdd() nutzen, die auch Variablennamen akzeptiert, die nicht noch nicht definiert wurden. Hier bauen wir uns eine binäre Sprungweite zusammen.

def <- defDataAdd(varname = "jump_length_bin", formula = "-2 + 0.5*age + 0.5*female",
                  dist = "binary", link = "logit")

Da wir bis jetzt nur die Defintion haben, müssen wir noch die Daten mit der Datendefinition zusammenbringen. Die Funktion addColumn() verbindet einen bestehenden Datensatz mit einer neuen Definition und erschafft dann die neue Variable. Wir werden dieses Vorgehen dann häufiger bei den faktoriellen Daten nutzen.

addColumns(def, dt)

Key: <id>
      id       age female jump_length jump_length_bin
   <int>     <num>  <int>       <int>           <int>
1:     1 11.647845      0           0               1
2:     2 12.958943      0           1               1
3:     3  7.439934      0           1               0
4:     4 10.127518      1           0               1
5:     5  8.237693      0           0               1

Wenn dich die Datengenerierugn und das Drumrum interessiert, dann kannst du auch auf dem Blog ouR data generation – meditations on data generating processes, R, and statistics, welches die Themen rund um das R Paket {simstudy} aufgreift einmal weiterlesen. Leider muss man sich mühsam durch die Chronik klicken, da es keine Sortierung nach Schlagworten oder ein Inhaltsverzeichnis gibt. Dafür ist da die eine oder andere spannende Idee darunter. Wenn ich was gefunden habe, habe ich es weiter unten in den Abschnitten verlinkt.

21.5 Messwert

Im Folgenden wollen wir uns für die gängigen Verterilungsfamilien einmal die Generierung von Daten anschauen. Dabei bleibe ich länger bei der Normalverteilung und zeige dort einmal verschiedene Wege um auf künstliche Daten zu kommen. Dabei liegt auch hier der Fokus mehr auf dem faktoriellen Design, da wir es hier meistens mit etwas komplizierteren Generierungen zu tun bekommen. Nach der Normalverteilung gehe ich dann auf die Poissonverteilung und klassische Verteilung für Zähldaten ein. Dann kommt noch die ordinale und binomiale Verteilung dran. Dann haben wir die häufigsten Verteilungen besprochen. Mehr findet sich dann auch in der Vingette zu dem R Paket {simstudy}.

21.5.1 Normalverteilt

Beginnen wir mit der wichtigsten Art der Simulation von Messwerten. Wir fangen mit der Normalverteilung an. Das heißt, dass unser Messwert \(y\) normalverteilt ist und wir unsere Messwerte aus mehreren Normalverteilungen zusammenbauen. Jede der Faktoren oder Kovariaten ist normalverteilt und hat damit immer einen Mittelwert und eine Varianz als Streuung. Das macht es dann auch für uns einfacher einmal die Grundlagen zu verstehen. Am Ende kannst du dir auch mittlere Noten oder eine mittlere Anzahl generieren und dann eben etwas stärker Runden. Dazu mehr dann in den folgenden Verteilungen.

Faktorielles Design

Ein faktorielles Design heißt nichts anderes als das du einen Faktor mit Leveln vorliegen hast. Häufig ist dieser Faktor dann deine Behandlung und deine Level sind dann die Stufen der Behandlung. Wenn du nur zwei Behandlungen vorliegen hast, dann rechnest du dann später einen Zweigruppenvergleich wie eben den t-Test. Wenn du mehr als zwei Gruppen vorliegen hast, wirst du dann eine einfaktorielle ANOVA nutzen und den entsprechenden Post-hoc Test. Weil zwei Gruppen eben so schön einfach sind, fangen wir hier damit einmal an. An den zwei Gruppen kannst du dann immer schön die Grundlagen nachvollziehen.

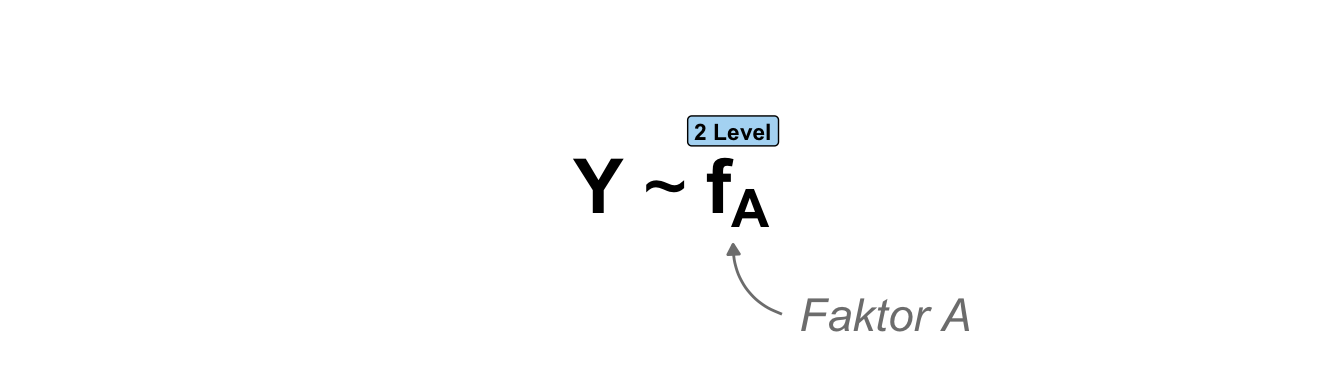
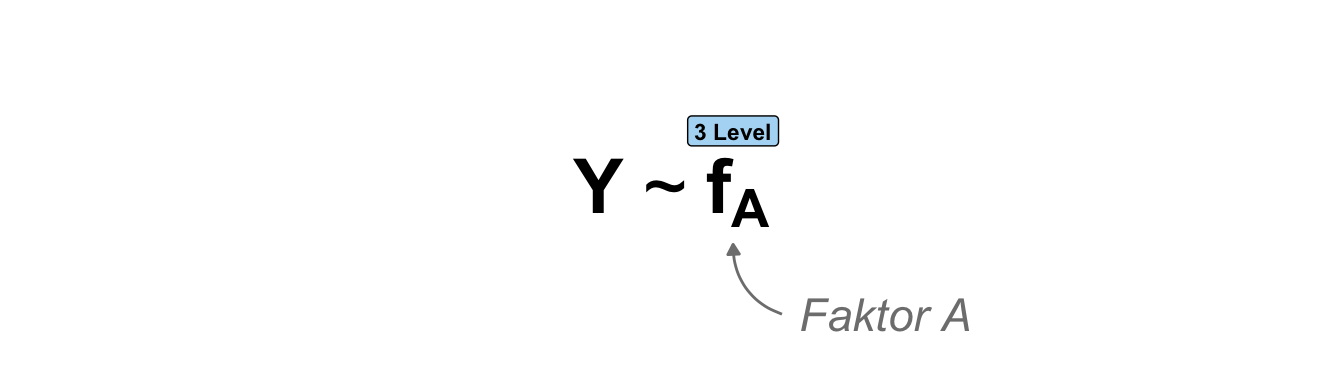
Einfaktoriell \(f_A\) mit 2 Leveln

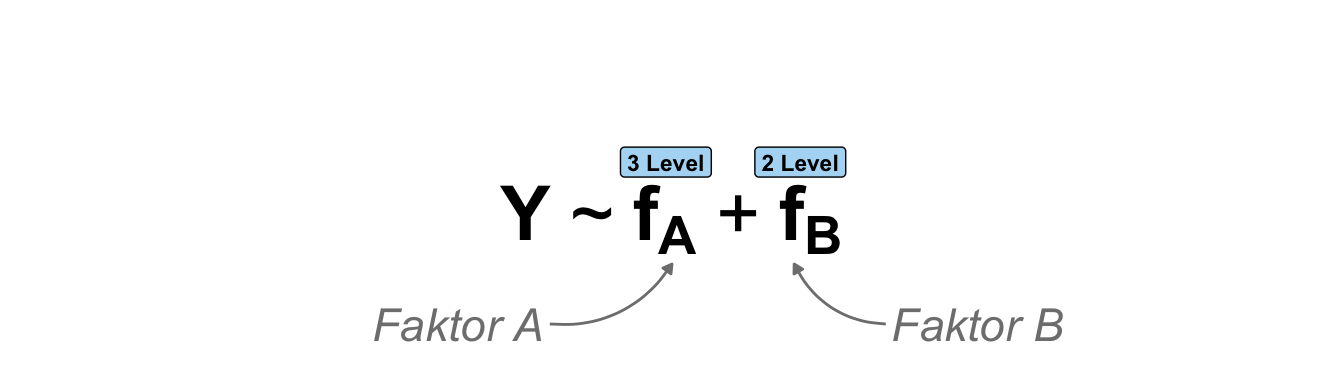
Beginnen wir also einmal mit dem einfaktoriellen Design mit nur zwei Gruppen. In der folgenden schematischen Darstellung ist einmal das Modell dargestellt. Wir haben einen Messwert und einen Faktor, der aus zwei Gruppen besteht. Das Modell ist sehr simple und soll uns nur helfen einmal die Simulation von Daten in R zu verstehen.

Abbildung 21.13— Schemantisches simples Modell mit einem Messwert \(Y\) und einer kategorialen Einflussvariablen als Faktor \(f_A\) mit zwei Leveln dargestellt. [Zum Vergrößern anklicken]

Wir haben jetzt unzählige Möglichkeiten die Daten zu generieren. Ich zeige hier einmal die zwei einfacheren Methoden. Einmal können wir die Daten getrennt in einem tibble() erstellen. Hierbei ist es wichtig, dass wir ein balanciertes Design vorliegen haben. Dann bauen wir uns das Long-Format über gather(). Wir schauen uns immer Gruppen mit gleicher Fallzahl an. Dann können wir auch die Spalten getrennt zusammenbauen und am Ende alles einmal aufaddieren. Wir haben hier einen Effekt von einer Mittelwertsdifferenz von \(+3\) vorliegen bei keiner Streuung.

Getrennt

Wenn wir wenig Gruppen haben, dann ist die getrennte Erstellung in einem tibble() sehr übersichtlich. Wir stellen ja den Effekt jeweils in den einzelnen Gruppen separat ein.

fac1_tbl <- tibble("1" = rnorm(n = 5, mean = 3, sd = 0.001),
                   "2" = rnorm(n = 5, mean = 6, sd = 0.001)) |> 
  gather(key = "f_a", value = "y")

Additiv

Im additiven Zusammenbauen nutzen wir viele Funktionen um uns die Spalten mit den Faktoren, Effekten und Fehler aufzubauen. Am Ende addieren wir die Spalten zum Messwert auf.

fac1_tbl <- tibble(f_a = gl(2, 5, labels = c("1", "2")),
                   eff_a = rep(c(3, 6), each = 5),
                   error = rnorm(length(f_a), 0, 0.001),
                   y = eff_a + error)

Das additive Zusammenbauen funktioniert hier nur in dieser Form so gut, da wir einen normalverteilten Messwert haben. In anderen Verteilungen können wir nicht einfach den Fehler addieren. Das hängt hier mit der Symmetrie der Normalverteilung um den Mittelwert zusammen.

Dann rechnen wir einfach einmal einen schnellen t-Test und schauen, ob wir die Differenz wieder erhalten. Wir sehen, dass wir die gleichen Mittelwerte wiedergeben bekommen und natürlich auch einen signifikanten Unterschied. Die Streuung ist ja super klein.

t.test(y ~ f_a, data = fac1_tbl)

    Welch Two Sample t-test

data:  y by f_a
t = -4231.5, df = 7.0551, p-value < 2.2e-16
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
 -3.001890 -2.998542
sample estimates:
mean in group 1 mean in group 2 
       2.999996        6.000212 

Wir können uns den Zusammenhang auch als eine simple lineare Regression darstellen lassen. Da ich die Streuung sehr gering eingestellt habe, können wir auch die Koeffizienten exakt so wieder erhalten. In der folgenden linearen Regression siehst du einmal wie die Mittelwertsdifferenz wieder der eingestellten Differenz entspricht.

lm(y ~ f_a, fac1_tbl) |> coef() |> round(2)

(Intercept)        f_a2 
          3           3 

In der folgenden Abbildung ist der Zusammenhang nochmal graphisch dargestellt. Wir haben den Mittelwert der ersten Gruppe als Intercept im Modell und die Steigung der Graden als Mittelwertsdifferenz. Wir sehen hier also nochmal den Zusammenhang zwischen der Datengenerierung und der linearen Regression.

Abbildung 21.14— Darstellung der einfaktoriellen Simulation mit zwei Gruppen. Der Intercept stellt den Mittelwert der ersten Gruppe dar. Die Mittelwertsdifferenz ist die Steigung der Graden. [Zum Vergrößern anklicken]

Manchmal wollen wir uns auch Daten erstellen, die nicht die gleiche Varianz in allen Gruppen haben. In diesem Fall hilft am meisten die getrennte Erstellung. Wir nehmen dann einfach in jeder Gruppe eine andere Varianz und lassen dann die Daten erstellen. In dem folgenden Kasten siehst du nochmal ein Beispiel für die Generierung von Daten mit Varianzheterogenität. Ob wir das brauchen hängt dann davon ab, was du mit den simulierten Daten ausprobieren möchtest.

Varianzheterogeniät zwischen den Gruppen

In der getrennten Erstellung von Daten können wir dann für jede Gruppe eine eigene Varianz festlegen. Hier habe ich in der einen Gruppe eine Standardabweichung von \(5\) und in der anderen Gruppe eine Standardabweichung von \(1\) angenommen. Ich brauche diese Art der Erstellung für den Welch t-Test oder aber in {emmeans} und dem multiplen Testen.

fac1_tbl <- tibble("1" = rnorm(n = 5, mean = 3, sd = 5),
                   "2" = rnorm(n = 5, mean = 6, sd = 1)) |> 
  gather(key = "f_a", value = "y")

Einfaktoriell \(f_A\) mit >2 Leveln

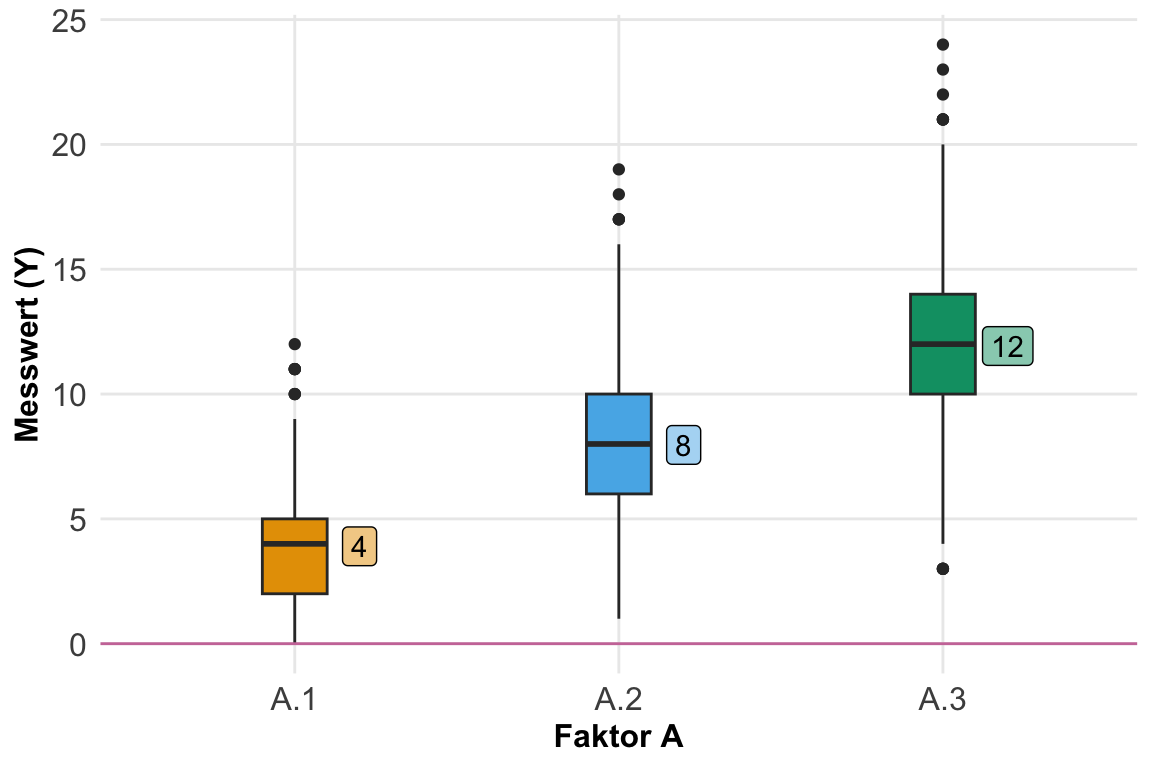
Kommen wir jetzt zu den etwas spannenderen Teil. Wir haben jetzt ein faktorielles Design mit einem Faktor und drei Leveln vorliegen. Ich habe dir einmal das Modell in der folgenden Abbildung einmal schematisch dargestellt. Wir würden hier also Daten bauen, die wir dann mit einer einfaktoriellen ANOVA oder aber dann mit einem Post-hoc Test wie {emmeans} auswerten würden. Der Messwert hier folgt daher einer Normalverteilung.

Abbildung 21.15— Schemantisches simples Modell mit einem Messwert \(Y\) und einer kategorialen Einflussvariablen als Faktor \(f_A\) mit drei Leveln dargestellt. [Zum Vergrößern anklicken]

Wir können die Daten einmal getrennt bauen und hätten dann auch einfach die Möglichkeit die Varianzen auch unterschiedlich zu machen. Beachte immer, dass ich hier extrem geringe Varianzen mit \(0.001\) eingestellt habe um dann bei der geringen Fallzahl auch auf die voreingestellten Effekte zu kommen. Du kannst dir das Modell auch additiv bauen, dann wird es aber etwas komplexer und der Fehler ist dann homogen, wenn du nicht den Fehlervektor nochmal aufbrechen willst. Dann zeige ich dir die Generation der Daten auch nochmal in Excel.

tibble()

Getrennt

Wenn wir wenig Gruppen haben, dann ist die getrennte Erstellung in einem tibble() sehr übersichtlich. Wir stellen ja den Effekt jeweils in den einzelnen Gruppen separat ein. Wir bauen hier alles um die Mittelwerte auf.

fac1_tbl <- tibble("1" = rnorm(5, 2, 0.001),
                   "2" = rnorm(5, 6, 0.001),
                   "3" = rnorm(5, 4, 0.001)) |> 
  gather(key = "f_a", value = "y")

Additiv

Im additiven Zusammenbauen nutzen wir viele Funktionen um uns die Spalten mit den Faktoren, Effekten und Fehler aufzubauen. Am Ende addieren wir die Spalten zum Messwert auf. Hier sind natürlich heterogene Varianzen schwerer darzustellen, da wir den Fehler für jedes Level einzeln generieren müssten. Auch hier wähle ich die Mittelwerte zuerst.

fac1_tbl <- tibble(f_a = gl(3, 5, labels = c("1", "2", "3")),
                   eff_a = rep(c(2, 6, 4), each = 5),
                   error = rnorm(length(f_a), 0, 0.001),
                   y = eff_a + error)

Effekt

Jetzt können wir aber das Ganze auch von der Effektseite aufziehen. Wir legen also fest, wie stark sich die Mittelwerte unterscheiden sollen anstatt die Mittelwerte selber. Daher eben der Effekt als Ausgangspunkt für unsere Datengenerierung. Als erstes bauen wir uns aber einmal den Datensatz nur für den Faktor. Die Spalte rep gibt an wie viele Wiederholungen wir pro Level haben.

fac1_tbl <- expand_grid(f_a = 1:3, rep = 1:5) |> 
  mutate(f_a = as_factor(f_a))

Dann nutzen wir den Faktor um eine Dummykodierung zuerstellen. Mit der Dummykodierung können wir dann den Leveln des Faktors die Effekte zuordnen.

fac1_mat <- fac1_tbl |> 
  model_matrix(~ f_a) |> 
  as.matrix()

Jetzt brauchen wir die Effekte. Wir haben hier den Mittelwert der ersten Gruppe in den Intercept und dann die Effekte danach. Daher hat das zweite Level einen um 4 höheren Mittelwert. Das dritte Level ist dann nur um 2 größer als der Intercept.

eff_vec <- c(intercept = 2, 
             f_a2 = 4, f_a3 = 2)

Dann kombinieren wir die Modellmatrix mit den Information wo der Effekt angewendet werden soll mit dem Vektor der Effekte. Wir erhalten dann unsere Messwerte in dem Vektor y_raw. Hier sind natürlich pro Faktor die Werte immer gleich. Wir haben ja noch keine Streuung hinzugefügt.

y_vec <- fac1_mat %*% eff_vec

Am Ende erhalten wir dann die echten generierten Messwerte indem wir zu unserem Messwert noch einen Fehler addieren. Ich nehme hier einen sehr kleinen Fehler, damit wir die Effekt auch gleich wiedersehen. Sonst müsste ich eine sehr hohe Fallzahl simulieren.

fac1_tbl <- fac1_tbl |> 
  mutate(y = y_vec + rnorm(length(y_vec), 0, 0.001))

Welche der drei Varianten du dann nutzt hängt davon ab, wozu du die generierten Datem brauchst. Jede Variante zeigt eben nochmal anders wie Daten entstehen.

Excel

Achtung, bitte beachten!

Die Erstellung von Daten in Excel ist nicht für die wissenschaftliche Bewertung von Algorithmen sinnvoll und angebracht. Wir nutzen hier Excel um recht einfach uns zufällig Daten zu erstellen. Wir nutzen dann die künstlichen Exceldaten um unsere Analyse für unsere echten experimentelle Daten zu üben. Auch ist die vereinfachte Erstellung von künstlichen Daten in Excel hilfreich um die zugrundeliegende Konzepte nochmal zu verstehen.

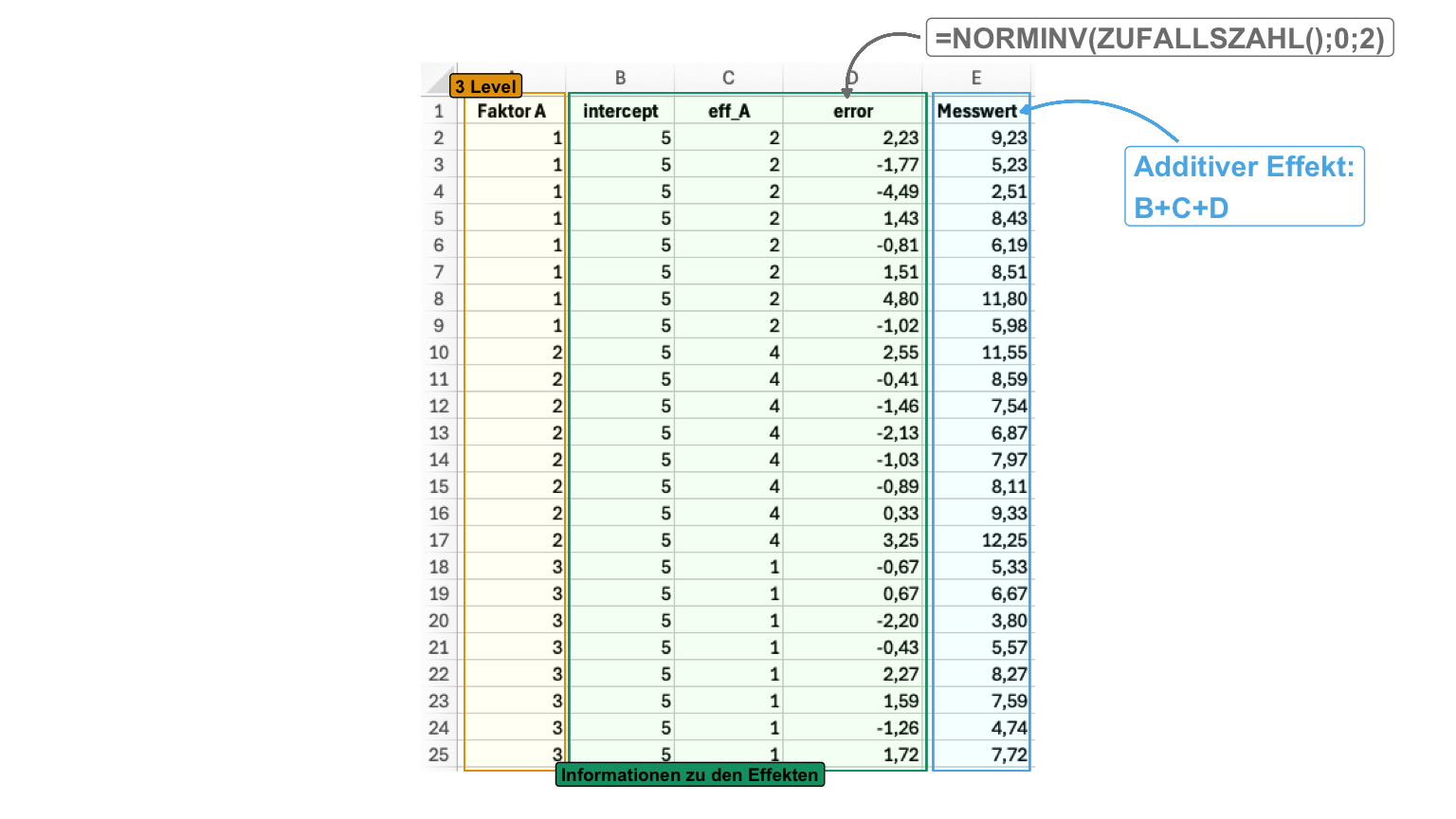
In der folgenden Datei findest du dann einmal die Generierung der einfaktoriellen Daten in Excel. Hier müssen wir dann das additive Zusammenbauen nutzen. Deshalb ist die Datei etwas größer. Am Ende brauchen wir die Spalte Faktor A und die Spalte Messwert.

excel_fac1_tbl <- read_excel("data/data_generation_excel.xlsx",
                             sheet = "einfaktoriell") |> 
  clean_names() |> 
  mutate(faktor_a = as_factor(faktor_a))

In der folgenden Abbildung habe ich dir einmal normalverteilte Messwerte in Excel aus einem einfaktoriellen Design generiert. Zuerst legen wir den allgemeinen Intercept fest, dann noch die Effekte der einzelnen Gruppen. Am Ende brauchen wir noch den Fehler oder die Streuung mit der Funktion NORMINV(). Hier habe ich eine Standardabweichung von \(2\) voreingestellt.

Abbildung 21.16— Annotierte Generierung von einfaktoriellen Daten mit drei Gruppen in Excel. Der Fehler wird durch die Funktion NORMINV() in Excel abgebildet. Der normalverteilte Messwert addiert sich aus den Spalten B:D auf. [Zum Vergrößern anklicken]

Dann schauen wir einmal, ob wir dann die Mittelwerte und die entsprechenden Differenzen auch in {emmeans} wiederfinden. Die Funktion pwpm() gibt uns auf der Diagonalen die Mittelwerte wieder und dann die Differenzen in der unteren Hälfte der Matrix. Damit haben wir dann auch alle Informationen auf einmal zusammen. Die Mittelwerte sind die voreingestellten und die Effekte sind ebenfalls richtig.

lm(y ~ f_a, fac1_tbl) |> 
  emmeans(~ f_a) |> 
  pwpm() 

         1        2        3
1 [1.9999]   <.0001   <.0001
2  -3.9997 [5.9996]   <.0001
3  -1.9995   2.0001 [3.9994]

Row and column labels: f_a
Upper triangle: P values   adjust = "tukey"
Diagonal: [Estimates] (emmean) 
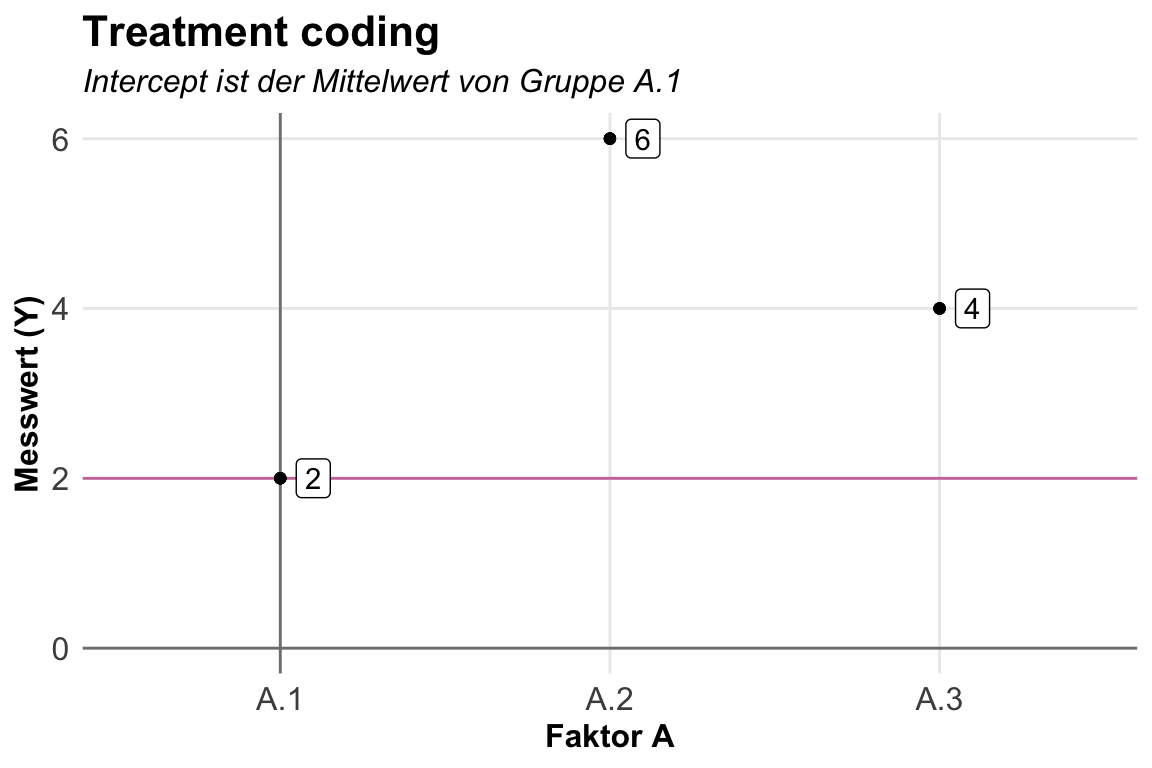
Lower triangle: Comparisons (estimate)   earlier vs. later

Wir können uns dann das Modell auch nochmal in dem linearen Kontext anschauen. Hier haben wir dann aber zwei Möglichkeiten die Referenz des Intercepts zu setzen. In der klassischen Kodierung setzen wir den Intercept auf den Mittelwert des ersten LEvels oder eben der ersten Gruppe. Wir nennen diese Kodierung dann Treatment coding. Dafür müssen wir nichts machen, dass ist die Standardeinstellung. Wir können aber auch das Effect coding wählen, dann liegt der Intercept auf dem globalen Mittelwert. Was ja eher der Interpretation der ANOVA entspricht. Es gibt natürlich noch weitere Kodierungen, wie du im Tutorial R Library Contrast Coding Systems for categorical variables nachlesen kannst.

Treatment coding (default)

Der Standard in der linearen Modellierung von Faktoren ist das Treatment coding mit contr.treatment in der Funktion lm(). Wir müssen da auch eigentlich nichts ändern, aber ich habe es hier einmal angeben damit du siehst, wo du die Kodierung ändern musst. Jeder Faktor muss einzeln geändert werden.

lm(y ~ f_a, fac1_tbl, contrasts = list(f_a = "contr.treatment")) |> 
  coef() |> round(2)

(Intercept)        f_a2        f_a3 
          2           4           2 

Wir erhalten dann aber die zu erwartenden Koeffizienten wieder. Der Mittelwert der ersten Gruppe ist der Intercept. Die Koeffizienten sind die Änderungen der anderen Level zum Intercept. Ich habe dir den Zusammenhang nochmal in der folgenden Abbildung dargestellt. Wir sehen hier sehr schön, dass eben das erste Level \(A.1\) den Intercept ausmacht. Die Änderungen als Mittelwertsdifferenzen zum Intercept sind die Koeffizienten in dem linearen Modell.

Abbildung 21.17— Darstellung des Treatment coding in einem linearen Modell. Der Intercept ist der Mittelwert des ersten Levels des Faktors. Die Koeffizienten des Modells beschreiben die Mittelwertsdifferenz zum Intercept in den anderen Leveln. [Zum Vergrößern anklicken]

Effect coding

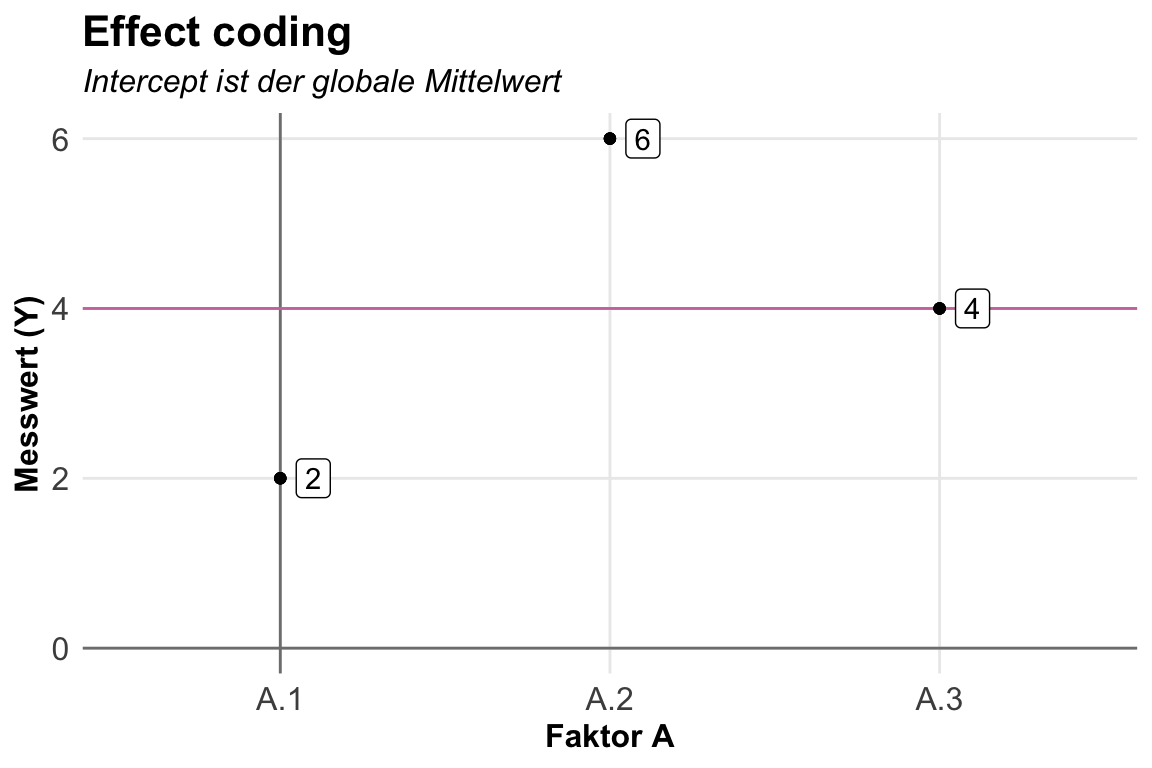
Das Effect coding können wir mit der Option contr.sum in der Funktion lm() nutzen. Wir müssen dies für jeden einzelnen Faktor einstellen. Ein Mischmasch würde ich stark vermeiden wollen. Wir haben dann als Intercept das globale Mittel des Messwerts über alle Gruppen. Die Koeffizienten sind dann die Mittelwertsdifferenzen zum globalen Mittel. Das letzte Level fehlt und lässt sich aus den vorherigen Leveln berechnen, da die Summe der Koeffizienten Null sein muss. In unserem Fall wäre die Mittelwertsdifferenz dann auch \(0\), da sich die beiden vorherigen Level schon auf Null aufaddieren.

lm(y ~ f_a, fac1_tbl, contrasts = list(f_a = "contr.sum")) |> 
  coef() |> round(2)

(Intercept)        f_a1        f_a2 
          4          -2           2 

Der Zusammenhang wird dann in der folgenden Darstellung nochmal klarer. Wir haben hier den globalen Mittelwert von \(4\) über alle Gruppen. Die Koeffizienten sind jetzt die Abweichung der lokalen Mittelwerte zu dem globalen Mittel. Eigentlich wie wir es auch aus einer einfaktoriellen ANOVA erwarten würden.

Abbildung 21.18— Darstellung des Effect coding in einem linearen Modell. Der Intercept ist der globale Mittelwert über alle Gruppen. Die Koeffizienten des Modells beschreiben die Mittelwertsdifferenz zum globalen Mittelwert in den anderen Leveln. Das letzte Level fehlt und lässt sich aus den vorherigen Leveln berechnen, da die Summe der Koeffizienten Null sein muss. [Zum Vergrößern anklicken]

Zweifaktoriell ohne Interaktion \(f_A + f_B\)

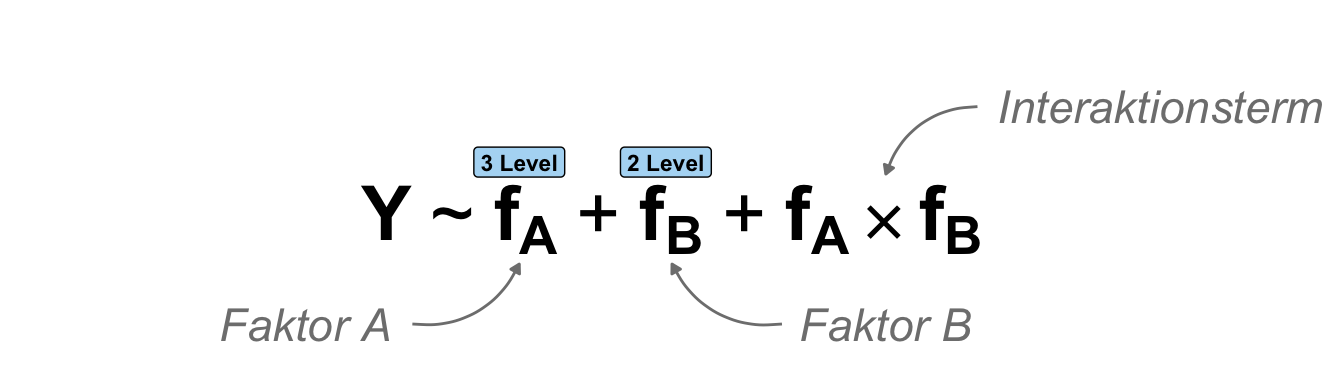
Sehr häufig haben wir aber mehrfaktorielle Designs vorliegen. Selten betrachten wir nur einen Faktor. Daher habe ich jetzt einmal ein zweifaktorielles Design in der folgenden schematischen Darstellung mitgebracht. Wir haben hier zwei Faktoren. Der Hauptfaktor \(f_A\) hat drei Level und der zweite Faktor \(f_B\) hat zwei Level. Der Messwert ist weiterhin normalverteilt. Jetzt müssen wir uns gleich etwas strecken um die Daten zusammenzubauen. Wir haben aber keine Interaktion zwischen den Faktoren vorliegen. Das schauen wir uns dann gleich nochmal getrennt an.

Abbildung 21.19— Schemantisches simples Modell mit einem Messwert \(Y\) und einer kategorialen Einflussvariablen als Faktor \(f_A\) mit drei Leveln sowie einer kategorialen Einflussvariablen als Faktor \(f_B\) mit zwei Leveln dargestellt. [Zum Vergrößern anklicken]

Da wir keine Interaktion vorliegen haben und auch Varianzhomogenität kann ich mir die Daten wie folgt bauen. Zuerst baue ich mir alle Faktorenkombinationen mit fünf Wiederholungen pro Kombination mit der Funktion expand_grid() dann kann ich mir den Messwert bauen indem ich immer den gleichen Effekt für jedes Level aufaddieren. Wir haben hier ja keine Interaktion vorliegen. Die Effekte steigen linear an. Darüber hinaus habe ich auch keine Streuung eingestellt, da mit wir bei der kleinen Fallzahl auch gleich unsere Effekte wiedersehen.

fac2_nointer_tbl <- expand_grid(f_a = 1:3,
                                f_b = 1:2,
                                rep = 1:5) |> 
  mutate(y = 2 +
             2 * f_a +
             3 * f_b +
             rnorm(15, 0, 0.001)) |> 
  mutate(f_a = as_factor(f_a),
         f_b = as_factor(f_b))

Dann schauen wir einmal, ob wir dann die Mittelwerte und die entsprechenden Differenzen auch in {emmeans} wiederfinden. Die Funktion pwpm() gibt uns auf der Diagonalen die Mittelwerte wieder und dann die Differenzen in der unteren Hälfte der Matrix. Damit haben wir dann auch alle Informationen auf einmal zusammen. Das wird dann doch recht groß und dann teilweise etwas unübersichtlich. Schaue gleich mal in der unteren Abbildung, da wird vermutlich alles etwas klarer.

lm(y ~ f_a + f_b, fac2_nointer_tbl) |> 
  emmeans(~ f_a * f_b)  |> 
  pwpm() 

          1 1       2 1       3 1       1 2       2 2       3 2
1 1 [ 7.0004]    <.0001    <.0001    <.0001    <.0001    <.0001
2 1  -1.99988 [ 9.0003]    <.0001    <.0001    <.0001    <.0001
3 1  -3.99969  -1.99981 [11.0001]    <.0001    <.0001    <.0001
1 2  -3.00000  -1.00012   0.99969 [10.0004]    <.0001    <.0001
2 2  -4.99988  -3.00000  -1.00019  -1.99988 [12.0003]    <.0001
3 2  -6.99969  -4.99981  -3.00000  -3.99969  -1.99981 [14.0001]

Row and column labels: f_a:f_b
Upper triangle: P values   adjust = "tukey"
Diagonal: [Estimates] (emmean) 
Lower triangle: Comparisons (estimate)   earlier vs. later

Da wir es hier auch wieder mit einem linearen Modell zu tun haben, können wir uns die Sachlage auch einmal mit den Koeffizienten des linearen Modells anschauen. Wir haben hier einen linearen Anstieg in unserem ersten Faktor und einen Unterschied von \(3\) in unserem zweiten Faktor. Der Intercept ist dabei die Faktorkombination \(A.1.B.1\) als niedrigste Levelkombination. Wir schauen uns hier nur das Treatment coding an.

lm(y ~ f_a + f_b, fac2_nointer_tbl) |> 
  coef() |> round(2)

(Intercept)        f_a2        f_a3        f_b2 
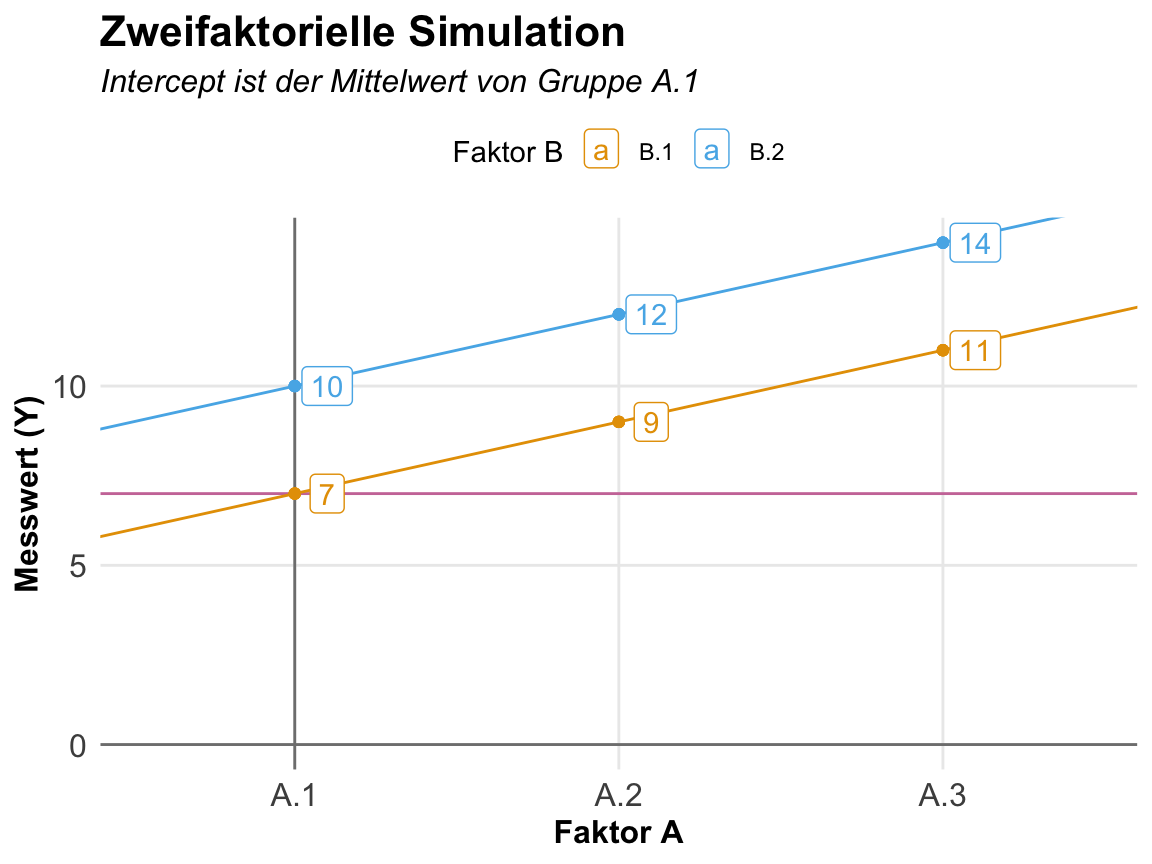
          7           2           4           3 

In der folgenden Abbildung siehst du dann einmal den Zusammenhang und die Koeffizienten visualisiert. Der Intercept liegt auf der Faktorkombination \(A.1.B.1\). Die Level von \(B.2\) sind parallel um den Koeffizienten von \(B.2\) verschoben. Der Anstieg ist aber immer noch \(+2\) da wir ja hier keine Interaktion vorliegen haben. Über den Faktor \(A\) verhält sich der Faktor \(B\) gleich. Hätten wir eine Interaktion vorliegen, dann würden wir keinen parallelen Verlauf sehen. In der Praxis beobachten wir solche Daten eher selten sondern sehen immer eine leichte Interaktion. Insbesondere da wir hier ja keine Streuung in den Daten vorliegen haben.

Abbildung 21.20— Darstellung des zweifaktoriellen Modells ohne Interaktion für die beiden Faktoren \(A\) und \(B\). Die Mittelwerte des Faktors \(B.2\) sind um den Koeffizienten des Levels verschoben. Die Graden verlaufen parallel, da keine Interaktion vorliegt. [Zum Vergrößern anklicken]

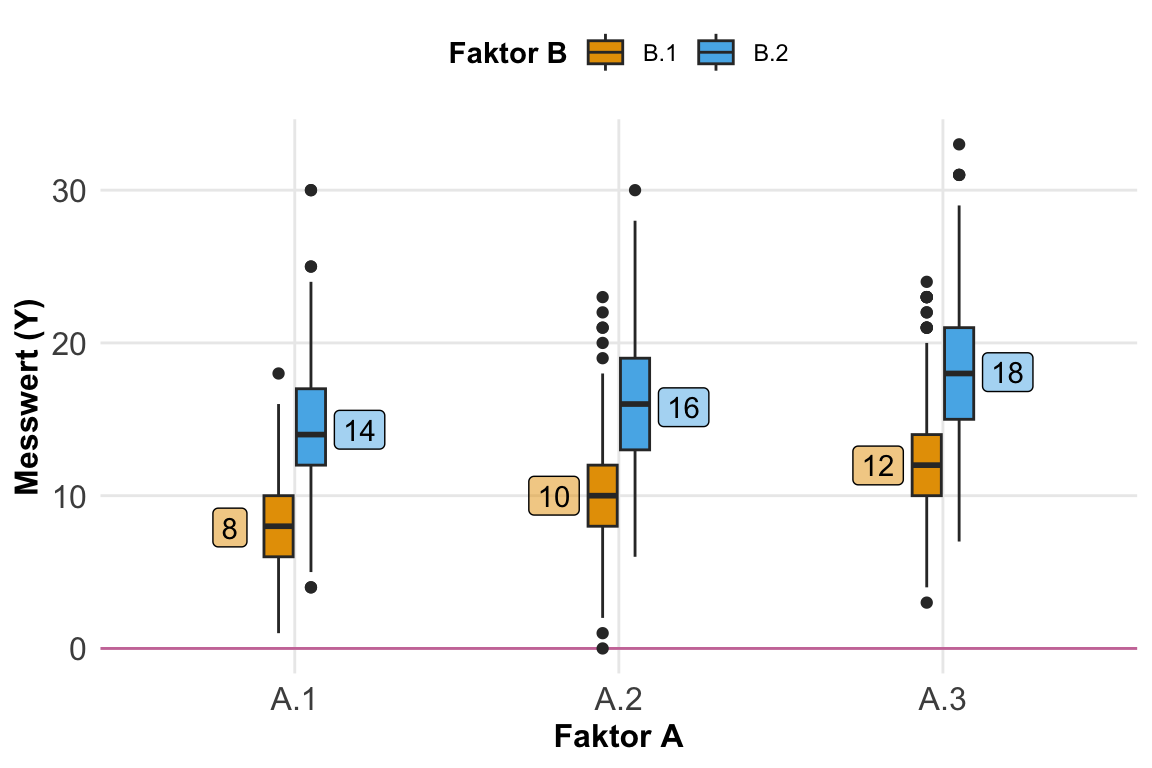
Zweifaktoriell mit Interaktion \(f_A + f_B + f_A \times f_B\)

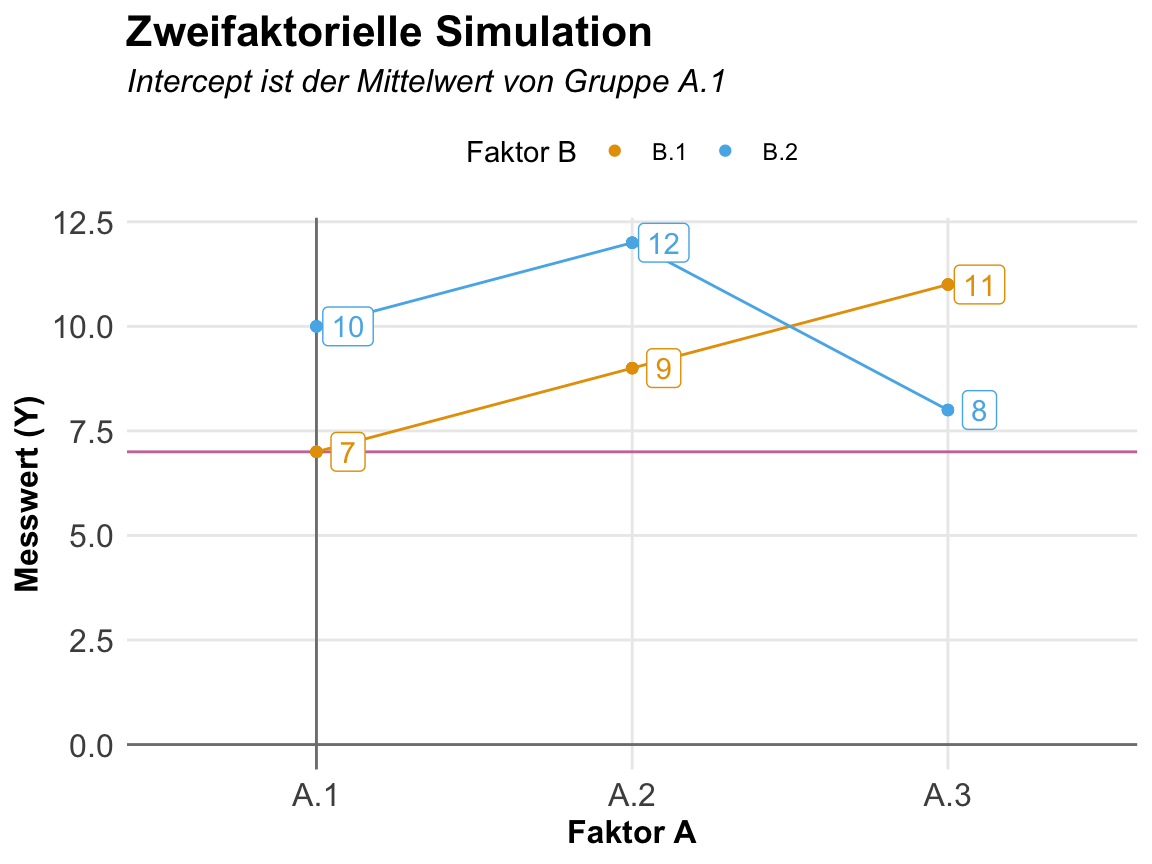
Selten betrachten wir nur einen Faktor sondern eben zwei Faktoren. Daher habe ich jetzt einmal ein zweifaktorielles Design in der folgenden schematischen Darstellung mitgebracht. Wir haben hier zwei Faktoren. Der Hauptfaktor \(f_A\) hat drei Level und der zweite Faktor \(f_B\) hat zwei Level. Der Messwert ist weiterhin normalverteilt. Jetzt müssen wir uns gleich etwas strecken um die Daten zusammenzubauen. Wir haben nun nämlich endlich eine Interaktion zwischen den beiden Faktoren vorliegen. Der Faktor \(f_B\) verhält sich nicht gleich in allen Leveln des Faktors \(f_A\). Die Graden laufen nicht parallel.

Abbildung 21.21— Schemantisches simples Modell mit einem Messwert \(Y\) und einer kategorialen Einflussvariablen als Faktor \(f_A\) mit drei Leveln sowie einer kategorialen Einflussvariablen als Faktor \(f_B\) mit zwei Leveln und deren Interaktion \(f_A \times f_B\) dargestellt. [Zum Vergrößern anklicken]

In den beiden folgenden Tabs zeige ich dir einmal wie du die Daten für ein zweifaktorielles Design mit Interaktion in einem tibble() sowie in Excel zusammenbaust. In Excel ist es etwas übersichtlicher, da du ja dort die einzelnen Spalten händisch anlegst. Zum Verstehen vielleicht etwas besser als in R. Dennoch ist die Erstellung in R stabiler und nicht so fehleranfällig. Für mal eben zum probieren reicht natürlich wie immer auch Excel super aus.

tibble()

Wenn wir mit Interaktionen einen Datensatz bauen, dann müssen wir den Datensatz über die Effekte aufbauen. Wir legen also fest, wie stark sich die Mitterlwerte unterscheiden sollen anstatt die Mittelwerte selber. Daher eben der Effekt als Ausgangspunkt für unsere Datengenerierung. Als erstes bauen wir uns aber einmal den Datensatz nur für die Faktoren. Die Spalte rep gibt an wie viele Wiederholungen wir pro Level haben.

fac2_tbl <- expand_grid(f_a = 1:3, f_b = 1:2, rep = 1:5) |> 
  mutate(f_a = as_factor(f_a),
         f_b = as_factor(f_b))

Dann nutzen wir die Faktoren um eine Dummykodierung zuerstellen. Mit der Dummykodierung können wir dann die Level der Faktor und der Interaktion die Effekte zuordnen. Das ist hier super wichtig, da wir sonst kaum die Interaktion modellieren können.

fac2_mat <- fac2_tbl |> 
  model_matrix(~ f_a * f_b) |> 
  as.matrix()

Jetzt brauchen wir die Effekte für die Faktoren und die Interaktion. Wir haben hier den Mittelwert der ersten Gruppe aus dem Faktor \(f_A\) und dem ersten Level im Faktor \(f_B\) in den Intercept. Danach kommen dann die Effekte der anderen Level plus die Interaktion. Ich schreibe hier die Effekte der Interaktion mit dem x zwischen den Namen.

eff_vec <- c(intercept = 7, 
             f_a2 = 2, f_a3 = 4, f_b2 = 3, 
             f_a2xf_b2 = 0, f_a3xf_b2 = -6)

Dann kombinieren wir die Modellmatrix mit den Information wo der Effekt angewendet werden soll mit dem Vektor der Effekte. Wir erhalten dann unsere Messwerte in dem Vektor y_raw. Hier sind natürlich pro Faktorkombination die Werte immer gleich. Wir haben ja noch keine Streuung hinzugefügt.

y_raw <- fac2_mat %*% eff_vec

Am Ende erhalten wir dann die echten generierten Messwerte indem wir zu unserem Messwert noch einen Fehler addieren. Ich nehme hier einen sehr kleinen Fehler, damit wir die Effekt auch gleich wiedersehen. Sonst müsste ich eine sehr hohe Fallzahl simulieren.

fac2_inter_tbl <- fac2_tbl |> 
  mutate(y = y_raw + rnorm(length(y_raw), 0, 0.001))

Wenn du jetzt noch Varianzheterogenität haben möchtest, dann müsstest du dir einen Vektor mit den verschiedenen Aufrufen der Funktion rnorm() für die jeweiligen Faktorkombinationen bauen. Hier wären es dann bei sechs Faktorkombinationen eben sechsmal rnorm() mit jeweils fünf Beobachtungen als Anzahl der Wiederholungen und dann eben einer eigenen Streuung.

Excel

Achtung, bitte beachten!

Die Erstellung von Daten in Excel ist nicht für die wissenschaftliche Bewertung von Algorithmen sinnvoll und angebracht. Wir nutzen hier Excel um recht einfach uns zufällig Daten zu erstellen. Wir nutzen dann die künstlichen Exceldaten um unsere Analyse für unsere echten experimentelle Daten zu üben. Auch ist die vereinfachte Erstellung von künstlichen Daten in Excel hilfreich um die zugrundeliegende Konzepte nochmal zu verstehen.

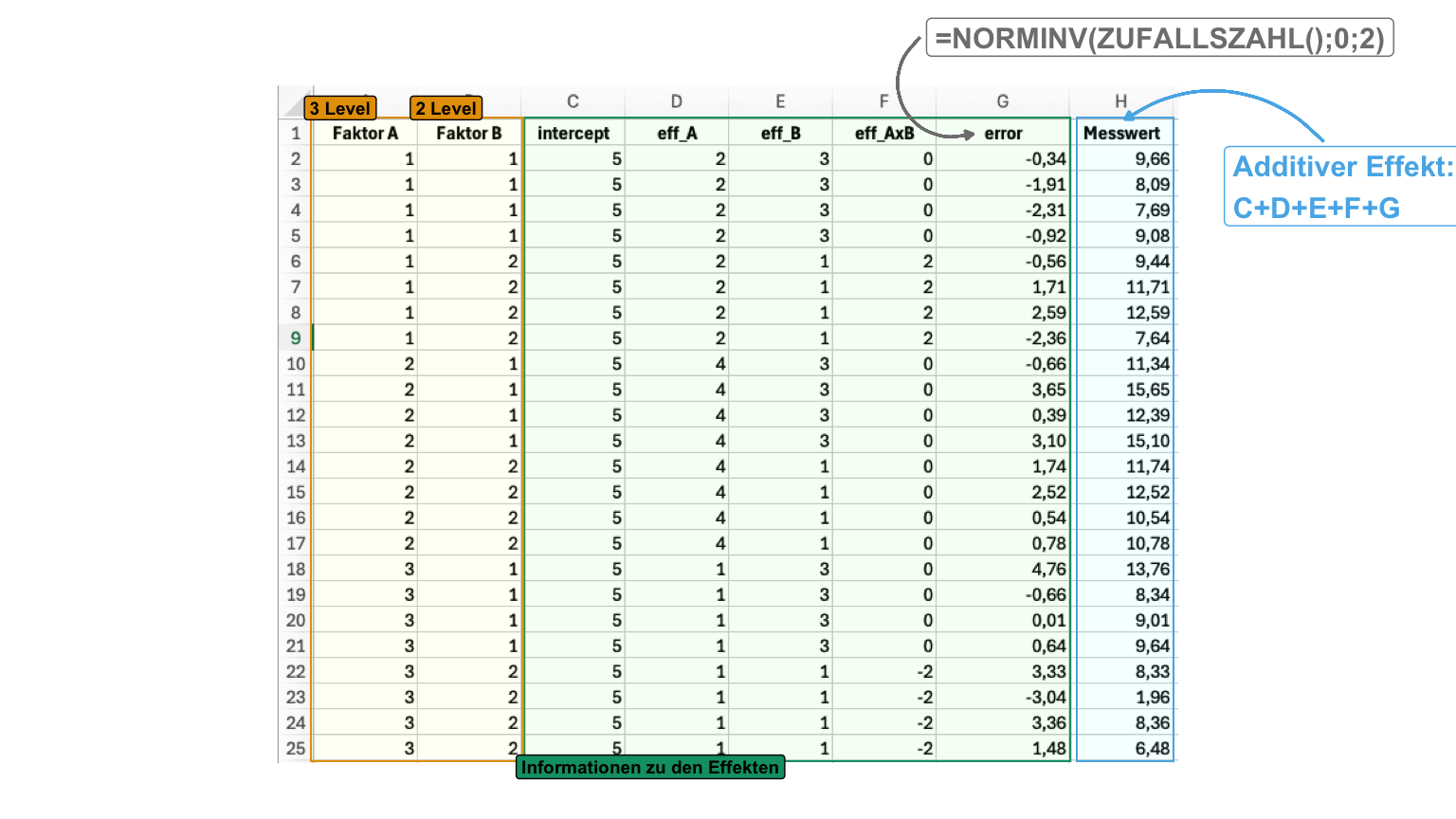
In der folgenden Datei findest du dann einmal die Generierung der zweifaktoriellen Daten mit Interaktion in Excel. Hier müssen wir dann das additive Zusammenbauen nutzen, da wir keine Matrizen in Excel muliplizieren wollen. Deshalb ist die Datei etwas größer. Am Ende brauchen wir die Spalte Faktor A und die Spalte Faktor B sowie die Spalte Messwert.

excel_fac2_tbl <- read_excel("data/data_generation_excel.xlsx",
                             sheet = "zweifaktoriell") |> 
  clean_names() |> 
  mutate(faktor_a = as_factor(faktor_a),
         faktor_b = as_factor(faktor_b))

In der folgenden Abbildung habe ich dir einmal normalverteilte Messwerte in Excel aus einem zweifaktoriellen Design mit Interaktion generiert. Zuerst legen wir den allgemeinen Intercept fest, dann noch die Effekte der einzelnen Gruppen sowie der Interaktion. Am Ende brauchen wir noch den Fehler oder die Streuung mit der Funktion NORMINV(). Hier habe ich eine Standardabweichung von \(2\) voreingestellt.

Abbildung 21.22— Annotierte Generierung von zweifaktoriellen Daten mit Interaktion in Excel. Der Fehler wird durch die Funktion NORMINV() in Excel abgebildet. Der normalverteilte Messwert addiert sich aus den Spalten C:G auf. [Zum Vergrößern anklicken]

Die Zahlen kommen jetzt nicht perfekt hin, da ich hier mit einer Standardabweichung von 2 eine recht hohe Streuung gewählt habe. Darüber hinaus habe ich dann auch sehr wenige Beobachtungen gebaut. Deshalb passt der Intercept nicht ganz, den der Intercept müsste eigentlich 10 sein und nicht 9. Daher stimmen dann auch die anderen Effekt nicht perfekt. Aber so ist das dann manchmal mit künstlichen Daten

lm(messwert ~ faktor_a * faktor_b, data = excel_fac2_tbl) |> 
  coef() |> round()

        (Intercept)           faktor_a2           faktor_a3           faktor_b2 
                  9                   5                   2                   2 
faktor_a2:faktor_b2 faktor_a3:faktor_b2 
                 -4                  -6 

Diese Generierung in Excel eigentlich sich sehr gut um dir selber Daten zu bauen, wenn du schonmal testen wilst wie die Analyse laufen würde bevor du eigentlich echte Daten aus deinem Experiment erhoben hast. Hier kommt es ja nicht auf die perfekten Effekte an. Hauptsache es sind Daten, die nicht alle gleich sind und du nichts siehst. Daher kann ich dir diesen Weg der Datengenerierung zum Testen deines R Codes nur empfehlen.

Fangen wir mit der Überprüfung an und schauen dafür erst mal in eine zweifaktorielle ANOVA mit Interaktion. Wir wollen hier natürlich, dass alle Faktoren signifikant sind und ebenfalls die Interaktion. So haben wir ja die Daten oben auch gebaut.

aov(y ~ f_a + f_b + f_a:f_b, fac2_inter_tbl) |> summary()

            Df Sum Sq Mean Sq  F value Pr(>F)    
f_a          2  20.00  10.001  9217080 <2e-16 ***
f_b          1   7.50   7.498  6910404 <2e-16 ***
f_a:f_b      2  60.01  30.004 27651951 <2e-16 ***
Residuals   24   0.00   0.000                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Das passt soweit, wir haben alles so wie wir es wollen. Leider sehen wir nicht die direkten Mittelwerte in einer ANOVA, daher hier nochmal emmeans() um uns die Mittelwerte wiedergeben zu lassen. Auch hier sehen wir, eine Menge Zahlen, aber soweit passen die Werte. Wir brauche in der Faktorkombination \(A.1.B.1\) einen Mittelwert von 7, da diese Gruppe ja unser Intercept ist. Das passt soweit. Die anderen Mittelwerte berechnen sich dann aus den obigen Effketen.

lm(y ~ f_a + f_b + f_a:f_b, fac2_inter_tbl) |> 
  emmeans(~ f_a * f_b) 

 f_a f_b  emmean       SE df lower.CL upper.CL
 1   1    7.0001 0.000466 24   6.9992   7.0011
 2   1    8.9999 0.000466 24   8.9990   9.0009
 3   1   11.0003 0.000466 24  10.9993  11.0012
 1   2    9.9998 0.000466 24   9.9989  10.0008
 2   2   12.0003 0.000466 24  11.9993  12.0013
 3   2    7.9999 0.000466 24   7.9989   8.0008

Confidence level used: 0.95 

Dann schauen wir nochmal die Koeffizienten eines linearen Modells an um dann nochmal die Effekte zu sehen. Das ist natürlich alles etwas doppelt, aber es ist auch eine Übung zu verstehen woher die Zahlen kommen. Hier also einmal die Effekte und die Interaktionen für unser zweifaktorielles Design. Bitte beachte, dass sich natürlich das niedrigste Level des Faktors \(f_A\) und des Faktors \(f_B\) im Intercept vereinen. Ja, das ist manchmal echt nicht so einfach.

lm(y ~ f_a + f_b + f_a:f_b, fac2_inter_tbl) |> 
    coef() |> round(2)

(Intercept)        f_a2        f_a3        f_b2   f_a2:f_b2   f_a3:f_b2 
          7           2           4           3           0          -6 

In der folgenden Abbildung siehst du einmal die Interaktion in der Faktorkombination \(A.3.B2\). Hier haben wir einen Effekt von -6 vorliegen. Durch die Interaktion fällt der Mittelwert weit nach unten. Weiter als er eigentlich sein sollte, wenn wir einen linearen Anstieg über den Faktor \(f_A\) erwarten würden. Wir haben eben nicht eine klassische Verschiebung der Graden durch den Faktor \(f_B\) sondern gegeben durch die Interaktion schneiden sich die Graden.

Abbildung 21.23— Darstellung des zweifaktoriellen Modells mit Interaktion für die beiden Faktoren \(A\) und \(B\). Die Mittelwerte des Faktors \(B.2\) sind um den Koeffizienten des Levels verschoben. Danach wird der Effek der Interaktion addiert. Die Graden verlaufen daher nicht parallel, da eine Interaktion vorliegt. [Zum Vergrößern anklicken]

Wir haben uns jetzt einmal durch das faktorielle Design durchgearbeitet. Das war jetzt auch bei einem normalverteilten Messwert relativ einfach. Wenn wir dann noch eine andere Verteilung im Messwert vorliegen haben, dann wird die Sache noch etwas komplizierter. In den folgenden Abschnitten gehe ich dann nicht für jede Verteilung auf alle Kombinationen ein, sondern nutze immer die wichtigsten faktoriellen Designs, wie eben die zweifaktoriellen mit und ohne Interaktion. Die einfaktoriellen Designs mit mehr als zwei Leveln dienen eher der Veranschaulichung und werden in der Praxis kaum genutzt.

Kovariates Design

Etwas seltener kommt der Fall vor, dass wir uns nur eine Kovariate anschauen wollen. In diesem Fall haben wir ja eine numerische, kontinuierliche Einflussvariable sowie einen normalverteilten Messwert vorliegen. Wir sind jetzt an der Steigung der Graden durch die Punktewolke interessiert. Daher stellen wir uns hier als Effekt eine Steigung ein und schauen, ob wir diese Steigung wiederfinden. Da wir natürlich auch einen Intercept für die Gradengleichung brauchen, müssen wir diesen auch definieren. Der Intercept ist aber meistens nicht von so großer praktischer Bedeutung.

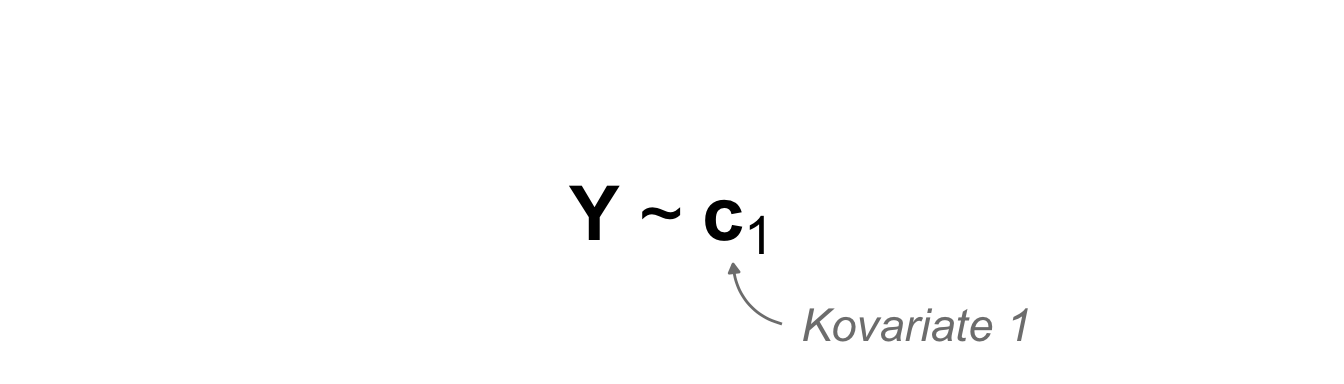
Einkovariat \(c_1\)

In der folgenden schematischen Darstellung ahbe ich dir einmal einkovariates Modell mitgebracht. Wir haben auf der linken Seite einen kontinuierlichen, normalverteilten Messwert und auf der rechten Seite der Tilde eine kontinuierliche Einflussvariable als Kovariate vorliegen. Wir wollen jetzt die Daten in diesem Kontext generieren.

Abbildung 21.24— Schemantisches simples Modell mit einem Messwert \(Y\) und einer kontinuierlichen Einflussvariable als Kovariate \(c_1\) dargestellt. [Zum Vergrößern anklicken]

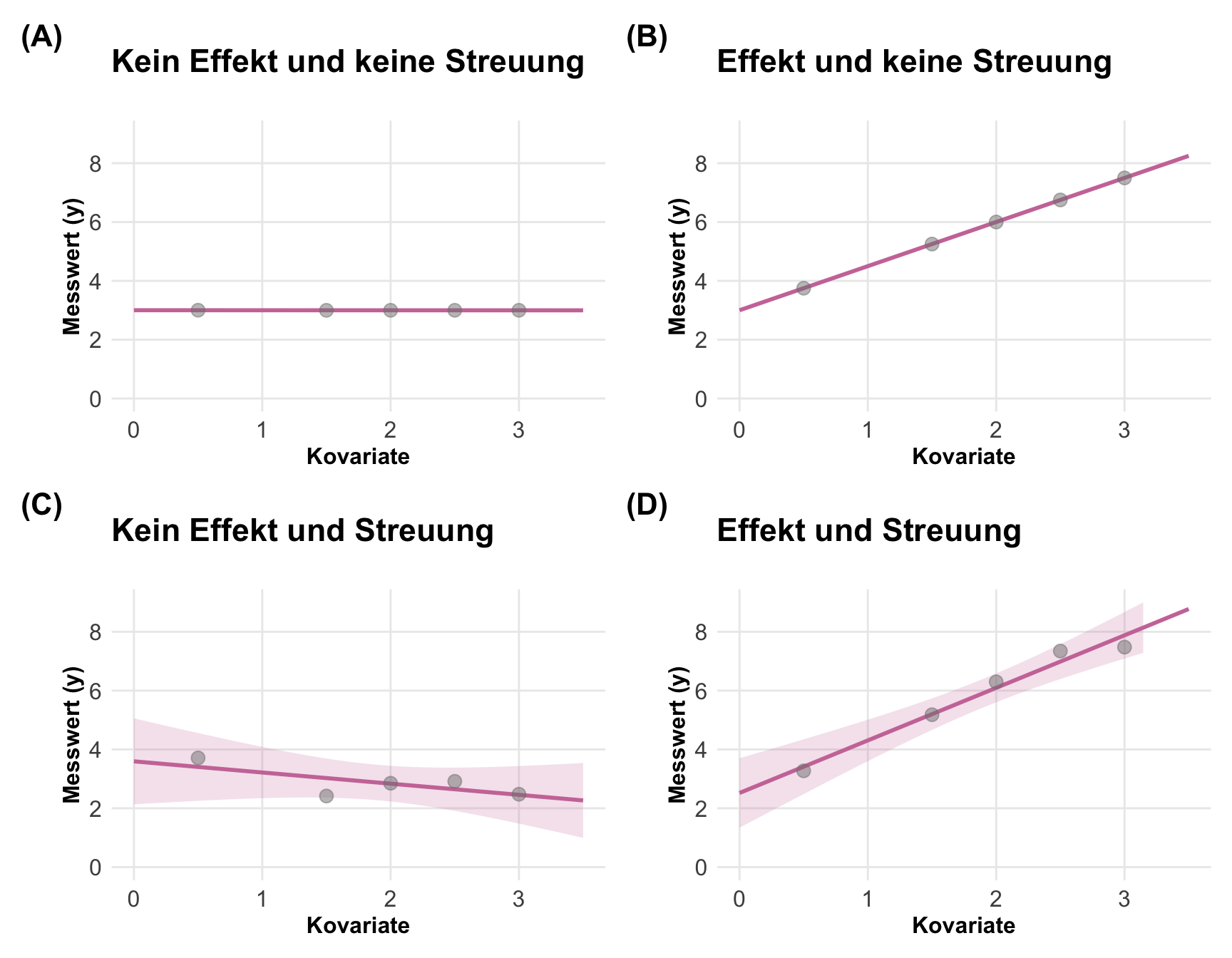
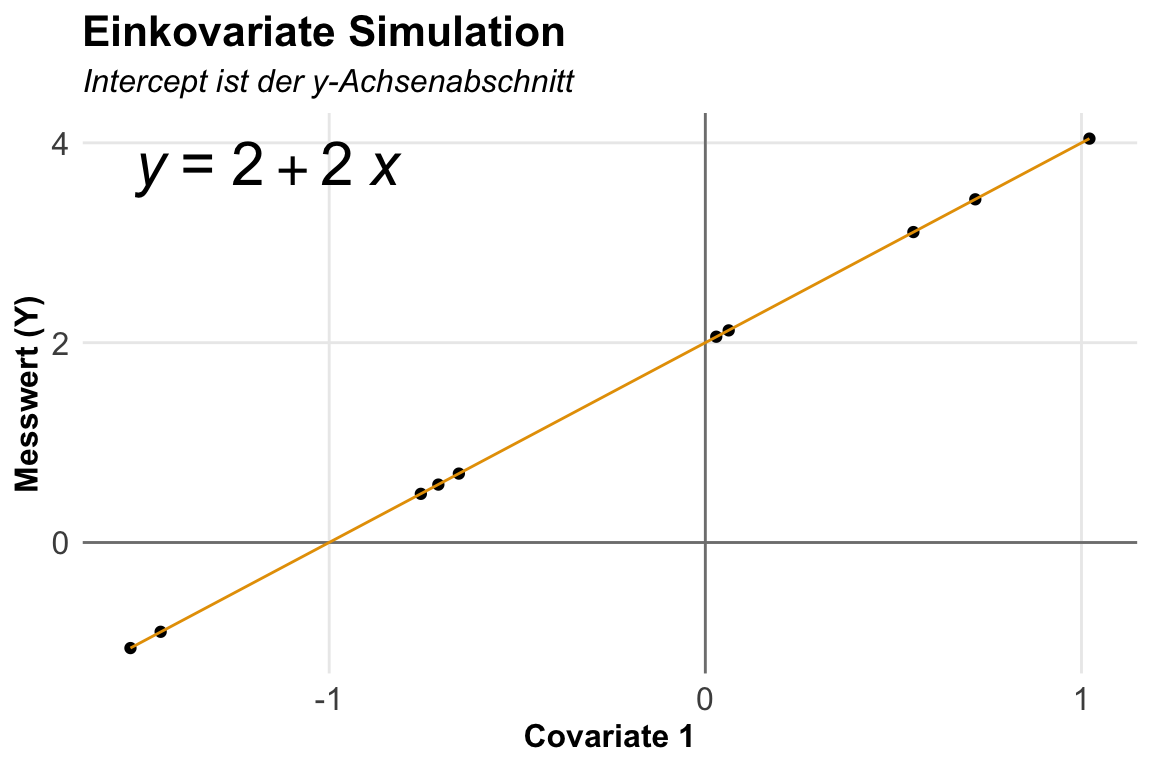
Wenn wir eine normalverteilte Kovariate haben, dann können wir erstmal die Kovariate erschaffen. Dafür nutzen wir dann die Funktion rnorm(). Dann müssen wir noch unseren Messwert mit der Gradengleichung festlegen. Ich zeige hier einmal die Variante mit dem linearen Zusammenhang und habe dann auch noch einen quadratischen mit der Helferfunktion I() ergänzt. Wie du dann möchtest, kannst du auch noch andere nicht lineare Zusammenhänge ergänzen.

cov1_tbl <- tibble(c_1 = rnorm(10, 0, 1),
                   y_lin = 2 + 2 * c_1 + rnorm(10, 0, 0.001),
                   y_square = 2 + 1.1 * c_1 + I(1.5*c_1^2) + rnorm(10, 0, 0.001)) |> 
  gather(key = "power", value = "y", y_lin:y_square)

In der folgenden Abbildung zeige ich dir einmal die Ergebnisse der Simulation. Da ich auch hier die Streuung faktisch ausgestellt habe, liegen die Punkte perfekt auf der Gradengleichung wie ich das will. Die lineare Gleichung hat noch einen Keoffizienten für den quadratischen Anteil, der ist hier ab faktisch Null. Wir können hier also sehr gut Zusammenhänge darstellen und dann schauen, ob wir die Koeffizienten dann in der linearen oder nicht-linearen Regression wiederfinden.

Abbildung 21.25— Darstellung einer linearen und einer quadratischen Simulation mit einer normalverteilten Kovariaten sowie einem normalverteilten Messwert. Der quadratische Term existeriert im linearen Modell nicht und der Koeffizient für \(x^2\) ist daher fast Null. [Zum Vergrößern anklicken]

Zweikovariat unabhängig \(c_1 + c_2\)

Wenn wir mehrere Kovariaten simulieren wollen, dann erweitern wir das Modell einfach um eine weitere Kovariate. Im simpelsten Fall sind die beiden Kovariaten voneinander unabhängig, daher kommen aus zwei verschiedenen Normalverteilungen und haben damit nichts miteinander zu tun. Daher sind die Werte der Kovariaten untereinander nicht korreliert oder sonst wie voneinander abhängig.

Abbildung 21.26— Schemantisches multiples Modell mit einem Messwert \(Y\) und zwei kontinuierlichen Einflussvariablen als Kovariate \(c_1\) und Kovariate \(c_2\) dargestellt. [Zum Vergrößern anklicken]

Hier bauen wir uns zwei voneinander unabhängige Kovariaten. Die beiden Kovariaten entstammen aus unterschiedlichen Normalverteilungen und sind somit untereinander nicht korreliert. Dann legen wir einmal den Intercept fest und ergänzen noch die Steigungen als Effekte für die Kovariaten. Am Ende ergänze ich dann noch einen winzigen Fehler damit das Modell auch gerechnet werden kann.

cov2_tbl <- tibble(c_1 = rnorm(10, 0, 1),
                   c_2 = rnorm(10, 2, 1),
                   y = 2 + 
                       1 * c_1 + 
                       2 * c_2 + 
                           rnorm(10, 0, 0.001))

Dann nutze ich die Funktion correlation() aus dem R Paket {correlation} um mir einmal die Korrelation zwischend den beiden Kovariaten wiedergeben zu lassen. Wir sehen hier, die beiden Kovariaten sind nicht miteinander korreliert. Der Korrelationskoeffizient liegt eher bei Null und ist nicht signifikant.

cov2_tbl |> 
  correlation(select = c("c_1", "c_2"))

# Correlation Matrix (pearson-method)

Parameter1 | Parameter2 |     r |        95% CI |  t(8) |     p
---------------------------------------------------------------
c_1        |        c_2 | -0.34 | [-0.80, 0.37] | -1.01 | 0.340

p-value adjustment method: Holm (1979)
Observations: 10

Dann schauen wir nochmal auf die Koeffizientend es Modells, ob wir auch unsere Effekte wiederfinden. Das sieht soweit gut aus. Wir haben die eingestellten Steigungen in den Koeffizienten wiedergefunden.

lm(y ~ c_1 + c_2, cov2_tbl) |> 
  coef() |> round(2)

(Intercept)         c_1         c_2 
          2           1           2 

Ich erstelle hier keine Abbildung in einem 3D Scatterplot, da mir das zu viel Aufwand ist und wir sehr wenig auf den 3D Scatterplots sinnvoll interpretieren können. Wir schauen uns auch selten zweikovariate Modelle in einer Abbildung an, sondern bewerten eben die Koeffizienten und andere statistsiche Maßzahlen für die Güte der Modellierung. Hier soll es dann reichen. Mehr dazu dann in den Kapiteln zu den Grundlagen des statistsichen Modellierens.

Multikovariat abhängig \(c_1 + c_2 + c_3\)

Jetzt kommen wir zu einem etwas nischigen Thema, nämlich der Tatsache, dass wir korrelierte Kovariaten vorliegen haben. Deshalb nehmen wir auch gleich drei Korvariaten. Das ist natürlich in der Statistik ein Problem, wie wir es auch im Kapitel zu der multiplen Regression nachlesen können. Mit Statistik meine ich, dass wir dann eben ein paar Probleme bei der Modellierung haben. Da gehe ich hier aber nicht tiefer drauf ein. Solche Daten zu generieren ist dann daher eher selten von Interesse in einem praktischen Kontext. Entweder liegen die Kovariaten korre,iert vor oder eben nicht. Wenn wir natürlich Algorithmen entwicklen wollen, dann ist das schon ein wichtiges Theme, wenn die Kovariaten nicht unabhängig voneinander sind.

Wir nutzen jetzt im Folgenden einmal das R Paket {simstudy} da die Genierung von korrelierten Daten mit einem Paket einfacher ist als alles per Hand zu machen. Es geht auch alles per Hand in einem tibble mit {mvtnorm} aber das machen wir hier jetzt nicht, da es viel zu kompliziert ist. Ich kann es nur empfehlen, wenn du dich mit dem Simulieren von Daten beschäftigen willst. Dann müsstest du dich auch nochmal mit dem Tutorium How would you explain the difference between correlation and covariance? beschäftigen, da wir in {mvtnorm} mit Kovarianzen beschäftigen.

Damit wären wir auch gleich beim großen Vorteil von {simstudy}. Wir können nämlich direkt eine Korrelationsmatrix einpflegen und müssen nicht über die Kovarianz als schwierigeres Konzept gehen. Die Kovarianz festlegen ist nämlich nicht ganz so einfach. Die Korrelation vorher festzulegen aber schon. Was wir dann auch in der Vingette Correlated Data nachlesen können. Im folgenden habe ich dir einmal eine Korrlationsmatrix für die drei Kovariaten \(c_1\) bis \(c_3\) mitgebracht. Die Korrelationsmatrix muss symmetrisch sein. Je höher die absolute Korrelation desto stärker ist der Zusammenhang.

cor_mat <- matrix(c(1, 0.7, 0.2, 
                    0.7, 1, 0.8, 
                    0.2, 0.8, 1), nrow = 3,
                  dimnames = list(c("c_1", "c_2", "c_3"), c("c_1", "c_2", "c_3")))
cor_mat

    c_1 c_2 c_3
c_1 1.0 0.7 0.2
c_2 0.7 1.0 0.8
c_3 0.2 0.8 1.0

Dann können wir die Funktion genCorData() nutzen um uns korreltierte Kovariaten zu erstellen. Ich habe hier einmal eintausend Beobachtungen gewählt. Dann müssen wir noch den Mittelwert in allen Kovariaten festlegen sowie die Streuung. Wir nehmen dann die Korrelationsmatrix mit in die Funktion und benennen noch die Kovariaten entsprechend. Wir erstellen uns dann den Messwert separat mit den gewollten Effekten.

cov2_dependent_dt <- genCorData(1000, mu = c(4, 12, 3), sigma = c(1, 2, 3), 
                                corMatrix = cor_mat,
                                cnames = c("c_1", "c_2", "c_3")) |> 
  mutate(y = 2 + 1.5 * c_1 + 2 * c_2 + 2.5 * c_3 + rnorm(1000, 0, 0.001))

Im Folgenden siehst du dann einmal die Datentabelle der eintausend Beobachtungen. Wir haben die ID Spalte und dann die drei Kovariaten gefolgt von dem Messwert.

cov2_dependent_dt

Key: <id>
         id      c_1       c_2       c_3        y
      <int>    <num>     <num>     <num>    <num>
   1:     1 6.396581 14.050618  3.067163 47.36484
   2:     2 4.139633 13.254738  6.046905 49.83687
   3:     3 3.428215  8.120047 -3.039935 15.78313
   4:     4 3.062534 11.051392  5.231867 41.77626
   5:     5 1.878001 10.890102  5.654227 40.73364
  ---                                            
 996:   996 4.459314 12.990747  4.349280 45.54327
 997:   997 4.217033 12.806682  3.063211 41.59494
 998:   998 3.619132 11.552059  3.209882 38.55683
 999:   999 3.964356 12.338354  2.840538 39.72552
1000:  1000 3.955933 12.639828  2.007950 38.23297

In den rohen Daten ist die Korrelation faktisch nicht zu sehen. Dafür müssen wir uns dann einmal die Korrelation berechnen lassen. Wie wir dann im Folgenden einmal sehen, passt es sehr gut. Wir erhalten die Korrelationen wieder, die wir auch eingestellt haben.

correlation(cov2_dependent_dt, select = c("c_1", "c_2", "c_3")) |> 
  summary(redundant = TRUE)

# Correlation Matrix (pearson-method)

Parameter |     c_1 |     c_2 |     c_3
---------------------------------------
c_1       |         | 0.72*** | 0.21***
c_2       | 0.72*** |         | 0.79***
c_3       | 0.21*** | 0.79*** |        

p-value adjustment method: Holm (1979)

Am Ende nochmal schauen, ob wir auch die Effekte wiederbekommen, die wir eingestellt haben. Auch hier sieht es sehr gut aus. Hier muss ich natürlich erwähnen, dass die Effekte groß sind die Fallzahl riesig und auch die Streuung in den Daten gering. Daher klappt hier auch alles so schön.

lm(y ~ c_1 + c_2 + c_3, data = cov2_dependent_dt)

Call:
lm(formula = y ~ c_1 + c_2 + c_3, data = cov2_dependent_dt)

Coefficients:
(Intercept)          c_1          c_2          c_3  
      1.999        1.500        2.000        2.500  

Dann haben wir auch unsere Effekte in dem Modell wiedergefunden. Es gibt verschiedene Korrelationsstrukturen, die wir auch in {simstudy} berücksichtigen können. Eine weitere Möglichkeit sind natürlich auch Zeitreihen in denen wir eine Abhängigkeit vorliegen haben. Aber auch hier reicht es meist, wenn der Trend einigermaßen stimmt. Dazu dann aber mehr in dem Abschnitt zu Zeitreihen.

“Brauchen wir eine Generierung von korrelierten Kovariaten? Ich würde mal sagen in der allgmeinen Anwendung und Auswertung reicht es, wenn wir die Daten einfach unkorreliert generieren und dann darauf die Algorithmen laufen lassen. Aber ich selber brauche es manchmal für Beispieldaten. Daher gibt es diesen Abschnitt wirklich.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

Mischung von Normalverteilungen

Wenn wir eine etwas komplexere Verteilung des Messwerts vorliegen haben wollen, dann lohnt sich auch einmal eine gemischte Normalverteilung zu bauen. Wir haben dann nicht eine Normalverteilung vorliegen sondern eine sehr bergige. Die bergige Normalverteilung besteht dann aber aus verschiedenen anderen Normalverteilungen, die wir dann übereinanderlegen. So können wir dann auch zweigipfelige oder wie in diesem Fall dreigipfelige Verteilungen bauen. Wir nutzen hier das R Paket {simstudy} und generieren uns erstmal drei Normalverteilungen.

mix_def <- defData(varname = "y_1", formula = 1, variance = 1)
mix_def <- defData(mix_def, varname = "y_2", formula = 5, variance = 4)
mix_def <- defData(mix_def, varname = "y_3", formula = 9, variance = 1)

Die drei Normalverteilungen, die wir gerade generiert haben \(y_1\) bis \(y_3\), mischen wir jetzt einmal nach festen Anteilen miteinander. Dafür nutzen wir die folgende Schreibweise in {simstudy}. Die Schreibweise ist erstmal etwas ungewohnt. Wir wollen 30% der Werte von \(y_1\) also schreiben wir y_1 | 0.3. Dann noch 40% der Werte von \(y_2\) mit y_2 | 0.4 sowie 30% der Werte von \(y_3\) mit y_3 | 0.3. Wir nennen dann die Spalte y_null. Wir haben hier dann die Nullverteilung erstellt.

mix_def <- defData(mix_def, varname = "y_null", 
                   formula = "y_1 | 0.3 + y_2 | 0.4 + y_3 | 0.3", 
                   dist = "mixture")

Ich generiere mir dann eintausend Beobachtungen, damit wir am Ende auch was sehen.

mix_null_dt <- genData(1000, mix_def)

Dann kannst du dir in der folgenden Abbildung einmal anschauen, wie die drei einzelnen Normalverteilungen aussehen und wie sich dann die Kombination durch die Addierung ergibt. Wir nennen diese Verteilung jetzt unsere Nullverteilung, da wir ja noch eine andere Verteilung benötigen um einen Effekt darzustellen.

Abbildung 21.27— Gemischte Normalverteilung in einem Densityplot. (A) Die drei einzelnen Normalverteilungen. (B) Die gemischte Normalverteilung. [Zum Vergrößern anklicken]

Jetzt möchte ich noch eine Alternative darstellen. Wir haben ja noch eine Gruppe mit Effekt. Daher adddiere ich einfach \(+2\) auf die Nullverteilung auf und generiere mir neue Werte. Achtung, ich verschiebe hier nicht einfach die Nullverteilung sondern generiere mir neue Zahlen mit einem um \(+2\) erhöhten kombinierten Mittelwert.

mixed_alt_def <- defDataAdd(varname = "y_alt", formula = "y_null + 2", variance = 1,
                            dist = "normal")

Dann müssen wir noch die beiden Verteilungen miteinander kombinieren.

mix_null_alt_dt <- addColumns(mixed_alt_def, mix_null_dt)

In der folgenden Abbildung siehst du nochmal die beiden Vereilungen der beiden Gruppen. Wir haben eine Gruppe, die der Nullverteilung folgt und einmal eine Verteilung für die Alternative. Wenn du noch mehr Gruppen haben wollen würdest, dann musst du entsprechend mehr Verteilungen verschieben.

Abbildung 21.28— Gemischte Normalverteilung in einem Densityplot. (A) Nullverteilung. (B) Alternativeverteilung mit einem Effekt. [Zum Vergrößern anklicken]

Dann wollen wir natürlich auch noch zufällige Zahlen genieren. Wir ziehen jetzt jeweils drei Beobachtungen aus den beiden Verteilungen. Wenn wir natürlich eine sehr komplexe Verteilung in der Grundgesamtheit haben, dann wird diese natürlich durch sehr kleine Stichproben kaum repräsentiert.

mix_null_alt_dt |> 
  select(y_null:y_alt) |> 
  pivot_longer(y_null:y_alt) |> 
  group_by(name) |> 
  slice_sample(n = 3)

# A tibble: 6 × 2
# Groups:   name [2]
  name   value
  <chr>  <dbl>
1 y_alt   4.23
2 y_alt   9.89
3 y_alt   9.20
4 y_null  8.51
5 y_null  9.30
6 y_null  6.51

Auch hier ist die Frage, wozu brauchen wir das? Vermutlich nicht im praktischen Alltag, aber in der Testung von Algorithmen mag eine mehrgipflige Verteilung schon von Interesse sein. Wir haben ja hier mehrere Normalverteilungen, die sich aufaddieren. Jede dieser Normalverteilungen könnte eine unentdeckte Subpopulation sein, die eben dann eine andere Verteilung des Frischegewichts hat. Ich vermute aber, dass die Anwendungsfälle eher selten sind.

21.5.2 Possionverteilt

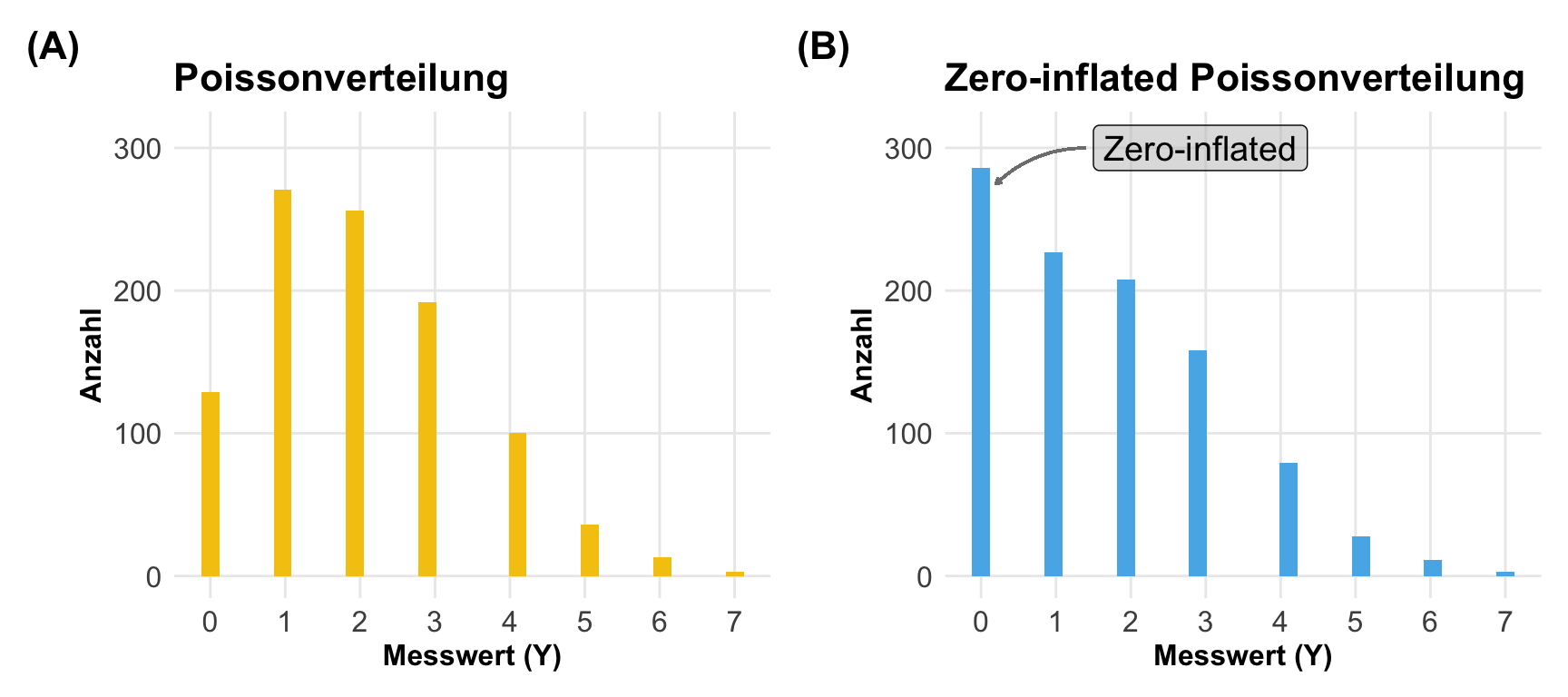
Nachdem wir vieles einmal mit einer Normalverteilung durchprobiert haben, kommen wir jetzt einmal zu einer anderen Verteilung. Wir fangen mit der Poissonverteilung an, da die Poissonverteilung der Normalverteilung gar nicht so unähnlich ist. Wir nutzen die Poissonverteilung wenn wir Zähldaten abbilden wollen. Daher ist die Poissonverteilung immer ganzzahlig oder diskret. Wenn wir was zählen, dann haben wir auch immer positive Werte einschließlich der Nullzählungen vorliegen. Mit dem Wissen können wir dann anfangen unsere Zähldaten in einer Poissonverteilung zu generieren. Wir generieren jetzt unsere Daten mit dem R Paket {simstudy}, da wir hier es dann sehr viel einfacher haben als händisch in R.

Normalverteilung und Runden

Gleich vorweg, es gibt auch eine einfachere Möglichkeit sich die Zähldaten zu genierieren. Du kannst auch eine Normalverteilung nehmen und dann einfach runden. Dann hast du zwar eine leichte Abweichung, aber für das Ausprobieren für Analysen macht es fast keinen Unterschied.

rnorm(n = 5, mean = 10, sd = 1) |> round()

[1] 11 11 10 11 11

Die Abweichungen sind tolerable wie Kruppa et al. (2016) gezeigt hat. Wenn du dann noch darauf achtest, dass du keine negativen Werte simulierst, dann ist alles soweit in Ordnung. Ich würde alle negativen Werte aus einer Normalverteilung dann auf Null setzen. Das simuliert eine Poissonverteilung am Besten.

Gegenüber der Normalverteilung müssen wir jetzt einige Anpassungen vornehmen. Im Folgenden müssen wir die Fallzahl erhöhen, da die Poissonverteilung keine eigenen Parameter für die Varianz hat. Die Streuung ist nämlich eien Funktion des Mittelwerts. Je größer der Mittelwert, desto größer die Varianz. Daher kann ich keine sehr kleine Streuung einstellen um auch bei kleinen Fallzahlen meine Effekte oder Mittelwerte wiederzuerhalten. Ich nutze daher hier immer um die eintausend Beobachtungen, damit wir hier auch stabile Effekte wiedergegeben bekommen.

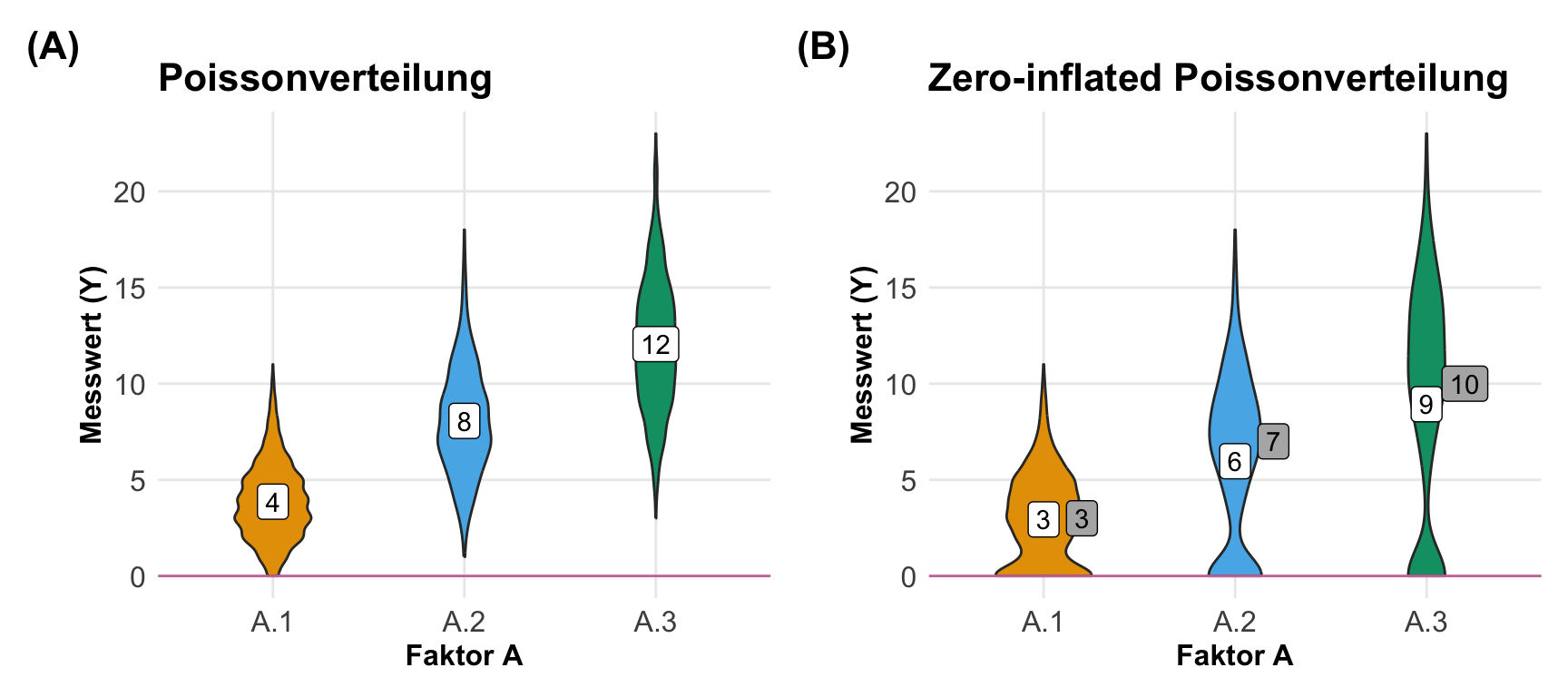
Faktorielles Design

Beginnen wir mit einem faktoriellen Design. Wir schauen uns jetzt einmal einen Faktor mit mehr als zwei Leveln an sowie zwei Faktoren mit einmal drei Leveln und einmal zwei Leveln. Dann nehmen wir noch die Interaktion mit hinzu. Wenn wir uns mit dem faktoriellen Design beschäftigen dann generieren wir zuerst das Faktorenraster und ergänzen dann den Messwert aus der Poissonverteilung. Das ist jetzt hier der etwas größere Unterschied zu den normalverteilten Messwerten. Wir brauchen hier immer unser Raster und dann ergänzen wir unseren Messwert mit dem R Paket {simstudy}. Prinzipiell geht es auch für das einfaktorielle Design einfacher über rpois(), aber wir üben ja hier auch für die komplexeren Modelle.

Achtung, bitte beachten!

Das R Paket {simstudy} nutzt als Speicherung der Daten nicht ein tibble sondern das R Paket {data.table}. Um unsere tibble dann umzuformen nutze ich die Funktion as.data.table(). Der Rest bleibt aber faktisch gleich.

Wir beginnne gleich mit einem einfaktoriellen Design mit mehr als 2 Leveln. Ich schaue hier mir mal einen Faktor mit drei Gruppen an. Der simple Fall mit nur zwei Gruppen ist eher selten und deshalb überspringe ich auch den Zweigruppenfall. Im Prinzip kannst du dir dann den Zweigruppenfall in rpois() schnell selber bauen.

Einfaktoriell \(f_A\) mit >2 Leveln

Wenn wir ein einfaktorielles Design vorliegen haben, dann brauchen wir einen Faktor mit drei Leveln sowie eine Anzahl an Beobachtungen pro Level. In den folgenden Tabs zeige ich dir dann einmal wie wir die Daten in {simstudy} generieren können. Das ist hier dann eher eine Fingerübung und etwas umständlich. Das geht natürlich für so einen einfachen Fall mit einem Faktor schneller mit der Funktion rpois() wo wir dann schneller die Daten erstellen können. Am Ende gehe ich nochmal auf Excel ein.

{simstudy}

Wir bauen uns hier erstmal das Datenraster für den Faktor auf, da wir dann das Raster mit dem R Paket {simstdy} erweitern und mit einem poissonverteilten Messwert ergänzen. Das heißt, wir nutzen die Funktion expand_grid() um uns für die drei Level jeweils eintausend Beobachtungen oder Wiederholungen zu erstellen. Da wir gleich mit {simstudy} weiterarbeiten brauche ich das Datenraster als ein data.table Objekt.

fac1_dt <- expand_grid(f_a = 1:3,
                       rep = 1:1000) |> 
  as.data.table()

Dann können wir uns auch schon einmal den Datensatz anschauen, wo wir eben nur das Datenraster für die Faktoren enthalten haben. Wir haben dreitausend Beobachtungen jeweils eintausend Beobachtungen pro Level des Faktors.

fac1_dt

        f_a   rep
      <int> <int>
   1:     1     1
   2:     1     2
   3:     1     3
   4:     1     4
   5:     1     5
  ---            
2996:     3   996
2997:     3   997
2998:     3   998
2999:     3   999
3000:     3  1000

Jetzt brauchen wir noch die Definition für unseren poissonverteilten Messwert in {simstudy}. Dafür benennen wir dann den Messwert mit y und geben noch die Formel an. Jedes Level hat einen Effekt von \(+4\). Dann noch die Verteilung angeben, damit wir hier auch aus der Possionverteilung ziehen.

y_pois_def <- defDataAdd(varname = "y", formula = "0 + 4*f_a",
                         dist = "poisson")

Jetzt bringen wir unser Datenraster mit unserer Datendefinition zusammen. Wir erhalten dann einen neuen Datensatz mit unserem poissonverteilten Messwert. Am Ende möchte ich dann noch die Spalte f_a als Faktor mutieren und die Level umbenennen. Dann sind wir auch schon fertig.

fac1_pois_dt <- addColumns(y_pois_def, fac1_dt) |>
  mutate(f_a = factor(f_a, labels = str_c("A.", 1:3))) 

In der folgenden Abbildung siehst du einmal die dreitausend generierten Beobachtungen pro Gruppe. Wir sehen hier einmal den Intercept bei Null sowie den Effekt von \(+4\) in jedem Level des Faktors. Die Varianz steigt mit dem Mittelwert an. Die Poissonverteilung ist eine schiefe Verteilung bei einem geringen Mittelwert. Je größer der Mittelwert wird, desto ähnlicher wird die Poissonverteilung einer Normalverteilung.

Abbildung 21.29— Boxplot der einfaktoriellen Poissondaten mit einem Intercept \(\beta_0\) von 0 sowie den Effekten von \(+4\) pro Faktorlevel. Die Gruppenmittelwerte sind mit dargestellt. Insgesamt wurden \(n = 1000\) Beobachtungen pro Gruppe generiert. Mit stiegendem Mittelwert steigt auch die Varianz in der Possionverteilung. [Zum Vergrößern anklicken]

rpois()

In dem einfaktoriellen Fall können wir uns auch die Daten einmal mit der Funktion rpois() erstellen. Wir brauchen hier einmal die Fallzahl sowie den Mittelwert als lambda. Wir können in einer Poissonverteilung keine Streuung angeben, da die Streuung eine Funktion des Mittelwerts ist. Je größer der Mittelwert desto größer die Streuung.

tibble("1" = rpois(n = 3, lambda = 2),
       "2" = rpois(n = 3, lambda = 8)) |> 
  gather(key = "f_a", value = "y")

# A tibble: 6 × 2
  f_a       y
  <chr> <int>
1 1         1
2 1         2
3 1         2
4 2         7
5 2         9
6 2        12

In diesem Fall ist eben sehr einfach sich die Daten zu bauen. Meiner Meinung nach reicht so eine simple Art auch vollkommen aus, wenn wir die Daten nur zum Ausprobieren brauchen und nicht unbedingt gerundete Normalverteilungsdaten wollen.

Excel

In Excel können wir uns keine Zuafallszahlen aus einer Poissonverteilung generieren lassen. Daher nutzen wir hier auch NORMINV() und runden dann die Ergebnisse ganzahlig. Wenn wir negative Werte haben sollten, dann müssen wir diese Werte dann auf Null setzen.

Zweifaktoriell ohne Interaktion \(f_A + f_B\)

Jetzt kommen wir zu den etwas interessanteren Design mit dem zweifakotriellen Experiment ohne Interaktion. Wir haben jetzt hier zwei Faktoren \(f_A\) und \(f_B\) mit jeweils drei oder zwei Leveln vorliegen. Die beiden Faktoren sind untereinander unabhängig, daher haben wir hier keine Interaktion vorliegen. Wir wollen jetzt einmal eintausend poissonverteilte Messwerte generieren. Dafür nutze ich wie immer einmal das R Paket {simstudy} sowie den Weg über die Funktion rpois(). In Excel können wir keine Poissondaten erschaffen. Hier müssen wir dann die Daten aus einer Normalverteilung entsprechend runden.

{simstudy}

Wir bauen uns hier erstmal das Datenraster für die beiden Faktoren auf, da wir dann das Raster mit dem R Paket {simstdy} erweitern und mit einem poissonverteilten Messwert ergänzen. Das heißt, wir nutzen die Funktion expand_grid() um uns für die drei Level in der Kombination der anderen zwei Level jeweils eintausend Beobachtungen oder Wiederholungen zu erstellen. Da wir gleich mit {simstudy} weiterarbeiten brauche ich das Datenraster als ein data.table Objekt.

fac2_dt <- expand_grid(f_a = 1:3,
                       f_b = 1:2,
                       rep = 1:1000) |> 
  as.data.table()

Dann können wir uns auch schon einmal den Datensatz anschauen, wo wir eben nur das Datenraster für die Faktoren enthalten haben. Wir haben sechstausend Beobachtungen jeweils eintausend Beobachtungen pro Faktorkombination der beiden Faktoren.

fac2_dt

        f_a   f_b   rep
      <int> <int> <int>
   1:     1     1     1
   2:     1     1     2
   3:     1     1     3
   4:     1     1     4
   5:     1     1     5
  ---                  
5996:     3     2   996
5997:     3     2   997
5998:     3     2   998
5999:     3     2   999
6000:     3     2  1000

Jetzt brauchen wir noch die Definition für unseren poissonverteilten Messwert in {simstudy}. Dafür benennen wir dann den Messwert mit y und geben noch die Formel an. Jedes Level des Faktors \(f_A\) hat einen Effekt von \(+2\) und jedes Level des Faktors \(f_B\) hat einen Effekt von \(+6\). Da wir hier nur zwei Level vorliegen haben, unterschieden sich die beiden Level \(B.1\) und \(B.2\) einfach um sechs Einheiten. Dann noch die Verteilung angeben, damit wir hier auch aus der Possionverteilung ziehen.

y_pois_def <- defDataAdd(varname = "y", formula = "0 + 2*f_a + 6*f_b",
                         dist = "poisson")

Jetzt bringen wir unser Datenraster mit unserer Datendefinition zusammen. Wir erhalten dann einen neuen Datensatz mit unserem poissonverteilten Messwert. Am Ende möchte ich dann noch die Spalte f_a und f_b als Faktoren mutieren und die Level umbenennen. Dann sind wir auch schon fertig.

fac2_pois_dt <- addColumns(y_pois_def, fac2_dt) |>
  mutate(f_a = factor(f_a, labels = str_c("A.", 1:3)),
         f_b = factor(f_b, labels = str_c("B.", 1:2)))

In der folgenden Abbildung siehst du einmal die sechstausend generierten Beobachtungen pro Gruppe. Wir sehen hier einmal den Intercept bei Null sowie den Effekt von \(+4\) in jedem Level des Faktors \(f_A\) sowie die Verschiebung in dem Faktor \(f_B\). Die Varianz steigt mit dem Mittelwert an. Die Poissonverteilung ist eine schiefe Verteilung bei einem geringen Mittelwert. Je größer der Mittelwert wird, desto ähnlicher wird die Poissonverteilung einer Normalverteilung.

Abbildung 21.30— Boxplot der zweifaktoriellen Poissondaten mit einem Intercept \(\beta_0\) von 0 sowie den Effekten von \(+2\) pro Faktorlevel von Faktor \(f_A\) sowie von \(+6\) pro Faktorlevel von Faktor \(f_B\). Da keine interaktion vorliegt, sind sind die Level \(B.2\) um den festen Wert des Effekts verschoben. Die Gruppenmittelwerte sind mit dargestellt. Insgesamt wurden \(n = 1000\) Beobachtungen pro Gruppe generiert. Mit stiegendem Mittelwert steigt auch die Varianz in der Possionverteilung. [Zum Vergrößern anklicken]

rpois()

In dem zweifaktoriellen Fall können wir uns auch die Daten auch einmal mit der Funktion rpois() erstellen. Wir brauchen hier einmal die Fallzahl sowie den Mittelwert als lambda. Wir können in einer Poissonverteilung keine Streuung angeben, da die Streuung eine Funktion des Mittelwerts ist. Je größer der Mittelwert desto größer die Streuung. Hier bauen wir uns aber erst den Vektor der Effekte und stecken dann diesen in die Funktion rpois(). Das ist etwas anders als bei der Normalverteilung. Wir haben ja hier keinen symmetrischen Fehlerterm, den wir aufaddieren.

fac2_nointer_tbl <- expand_grid(f_a = 1:3,
                                f_b = 1:2,
                                rep = 1:1000) |> 
  mutate(y_eff = 0 +
                 2 * f_a +
                 6 * f_b,
         y = rpois(length(y_eff), lambda = y_eff)) |> 
  mutate(f_a = as_factor(f_a),
         f_b = as_factor(f_b))

Dann schauen wir uns nochmal an, ob wir auch die Mittelwerte und Mediane wiedererhalten.

fac2_nointer_tbl |> 
  group_by(f_a, f_b) |> 
  summarise(round(mean(y)), median(y))

`summarise()` has grouped output by 'f_a'. You can override using the `.groups`
argument.

# A tibble: 6 × 4
# Groups:   f_a [3]
  f_a   f_b   `round(mean(y))` `median(y)`
  <fct> <fct>            <dbl>       <dbl>
1 1     1                    8           8
2 1     2                   14          14
3 2     1                   10          10
4 2     2                   16          16
5 3     1                   12          12
6 3     2                   18          18

In diesem Fall ist schon nicht mehr so einfach sich die Daten zu bauen. Meiner Meinung nach solltest du dann spätenstens hier einmal zu {simstudy} überwechseln. Die Funktionalität von dem R Paket ist da wirklich besser, als sich das selber in einem tibble zusammenzubauen.

Excel

In Excel können wir uns keine Zuafallszahlen aus einer Poissonverteilung generieren lassen. Daher nutzen wir hier auch NORMINV() und runden dann die Ergebnisse ganzahlig. Wenn wir negative Werte haben sollten, dann müssen wir diese Werte dann auf Null setzen. Bei zwei Faktoren hört hier schon etwas der Spaß auf, da wir ja alle Fakotrkombinationen dann einzeln anlegen müssen.

Zweifaktoriell mit Interaktion \(f_A + f_B + f_A \times f_B\)

Für den zweifaktoriellen Fall mit Interaktion haben wir jetzt hier zwei Faktoren \(f_A\) und \(f_B\) mit jeweils drei oder zwei Leveln vorliegen. Ich gehe diesmal nur nochauf auf das R Paket {simstdy} ein, da es händisch und in Excel jhier nicht mehr funktioniert. Wenn du es händisch machen möchtest, dann kannst du dir natürlich für alle Faktorkombinationen die Effekte zusammenbauen und dann rpois() für die Zufallszahlen nutzen. Ich empfinde daran aber keinen Gewinn mehr.

Wir bauen uns hier erstmal das Datenraster wie schon vorab für die beiden Faktoren auf, da wir dann das Raster mit dem R Paket {simstdy} erweitern und mit einem poissonverteilten Messwert ergänzen. Das heißt, wir nutzen die Funktion expand_grid() um uns für die drei Level in der Kombination der anderen zwei Level jeweils eintausend Beobachtungen oder Wiederholungen zu erstellen. Da wir gleich mit {simstudy} weiterarbeiten brauche ich das Datenraster als ein data.table Objekt. Soweit ist alles gleich. Wir bauen uns die Interalktion jetzt anders.

fac2_tbl <- expand_grid(f_a = 1:3, f_b = 1:2, rep = 1:1000) |> 
  mutate(f_a = as_factor(f_a),
         f_b = as_factor(f_b))

Jetzt gehen wir aber noch einen Schritt weiter und bauen das Datenraster als Dummykodierung. Somit steht jetzt jede Spalte dafür, ob ein Effekt dann entsprechend für die Beobachtung berücksichtigt wird. Hier können wir dann auch die Interaktion in den jeweiligen Faktorkombinationen \(A.2.B.2\) und \(A.3.B.2\) richtig modellieren. Es ist aber immer noch nicht einfach, das kann ich unterschreiben.

fac2_model_dt <- fac2_tbl |> 
  model_matrix(~ f_a * f_b) |> 
  clean_names() |> 
  as.data.table()

Dann können wir uns auch schon einmal die Modellmatrix für den Datensatz anschauen, wo wir eben die Faktoren und die Interaktion enthalten haben. Wir haben sechstausend Beobachtungen jeweils eintausend Beobachtungen pro Faktorkombination der beiden Faktoren. In den Faktorkombinationen sind dann auch die Interaktionen enthalten.

fac2_model_dt

      intercept  f_a2  f_a3  f_b2 f_a2_f_b2 f_a3_f_b2
          <num> <num> <num> <num>     <num>     <num>
   1:         1     0     0     0         0         0
   2:         1     0     0     0         0         0
   3:         1     0     0     0         0         0
   4:         1     0     0     0         0         0
   5:         1     0     0     0         0         0
  ---                                                
5996:         1     0     1     1         0         1
5997:         1     0     1     1         0         1
5998:         1     0     1     1         0         1
5999:         1     0     1     1         0         1
6000:         1     0     1     1         0         1

Jetzt müssen wir für jede Spalte den Effekt definieren. Daher haben wir dann sechs Effekte. Einmal einen für den Intercept und dann für die jeweiligen Faktorlevel. Hier müssen wir dann aber die Multiplikation mit selber einrechnen. Daher ist der Effekt des \(f_A\) zwar \(+2\), aber müssen wir dann schon bei \(A.3\) eben \(+2+2 = +4\) rechnen. Es ist wirklich etwas anstrengend. Dann kommen noch die beiden Terme für die Interaktion.

y_pois_def <- defDataAdd(varname = "y", 
                         formula = "5 * intercept + 2 * f_a2 + 4 * f_a3 + 
                         3 * f_b2 + 0 * f_a2_f_b2 + -6 * f_a3_f_b2",
                         dist = "poisson")

Jetzt bringen wir unser Datenraster mit unserer Datendefinition zusammen. Wir erhalten dann einen neuen Datensatz mit unserem poissonverteilten Messwert. Am Ende möchte ich dann noch die Spalte f_a und f_b auswählen sowie als Faktoren mutieren und die Level umbenennen. Dann sind wir auch schon fertig.

fac2_pois_dt <- addColumns(y_pois_def, fac2_model_dt) |>
  add_column(fac2_tbl) |> 
  select(f_a, f_b, y)  |>
  mutate(f_a = factor(f_a, labels = str_c("A.", 1:3)),
         f_b = factor(f_b, labels = str_c("B.", 1:2)))

Am Ende musst du dir das alles einmal in der Abbildung anschauen. Hier siehst du dann auch gut die Interaktion im letzten Level vom Faktor \(f_A\). Wir haben dort in der Faktorkombination \(A.3.A.2\) nicht einen Mittelwert von 12 sondern von 6 vorliegen. Hier dreht sich der immer positive Effekt des Faktors \(f_B\) einmal ins Negative um. Die Erstellung ist ohne einen Visualisierung wirklich schwer nachzuvollziehen und zu überprüfen. Am Ende musst du dann immer schauen, ob du dann die Effekte bei einer großen Fallzahl wiederfindest und dur dann einen kleineren Datensatz für dich bauen. Die Implementierung einer Interaktion ist eben nicht ganz so einfach, wenn es um die Generierung von faktoriellen Experimenten geht.

Abbildung 21.31— Boxplot der zweifaktoriellen Poissondaten mit einem Intercept \(\beta_0\) von 0 sowie den Effekten von \(+2\) pro Faktorlevel von Faktor \(f_A\) sowie von \(+3\) pro Faktorlevel von Faktor \(f_B\). Da eine interaktion vorliegt, sind sind die Level \(B.2\) um den festen Wert des Effekts verschoben. Es liegt eine Interaktion im Level \(A.3\) vor. Der Effekt in \(f_B\) ist gedreht. Die Gruppenmittelwerte sind mit dargestellt. Insgesamt wurden \(n = 1000\) Beobachtungen pro Gruppe generiert. Mit stiegendem Mittelwert steigt auch die Varianz in der Possionverteilung. [Zum Vergrößern anklicken]

“Brauchen wir eine Generierung von zweifaktoriellen Experimenten aus einer Poissonverteilung mit Interaktion wirklich? Diese Frage kann man sich auch hier stellen. Ich selber baue mir gerne die Interaktion dann händisch in Excel oder aber Runde mir eine Normalverteilung. Das reicht im Kontext der Lehre und zum Testen vollkommen aus. Ich hatte aber Spaß zu verstehen, wie die Interaktion entsteht und wie ich die Interaktion nachbauen kann. Dafür hat es sich gelohnt.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

Datenraster in {simstudy} für Faktoren

Nachdem ich hier schon sehr weit war mit der Funktion expand_grid() habe ich Abends dann noch per Zufall den Blogeintrag Testing multiple interventions in a single experiment gelesen. Wir können also auch ein faktorielles Design auch in {simstudy} bauen. Hätte mich dann auch etwas gewundert wenn es dann doch nicht ginge. Es ist immer eine Frage des Nestings oder der Schachtelung, also wie wollen wir die beiden Faktoren jeweils ineinander verschränkt wissen. Wir können die Funktion genMultiFac() nutzen um uns mehrere Faktoren zu erschaffen. Wir können dabei auch gleich die Spaltennamen setzen und sagen, wie oft eine Faktorkombination wiederholt werden soll.

fac2_dt <- genMultiFac(each = 5, nFactors = 2, levels = c(3, 2), 
                       colNames = c("f_a", "f_b")) 

Dann einmal die Daten anschauen. Ich zeige die hier als tibble damit nicht so viel ausgegeben wird. In der Standardimplementierung des data.table kriegen wir immer einen sehr langen Ausdruck.

fac2_dt |> as_tibble()

# A tibble: 30 × 3
      id   f_a   f_b
   <int> <int> <int>
 1     1     1     1
 2     2     1     1
 3     3     1     1
 4     4     1     1
 5     5     1     1
 6     6     2     1
 7     7     2     1
 8     8     2     1
 9     9     2     1
10    10     2     1
# ℹ 20 more rows

Jetzt brauchen wir noch die Definition für unseren poissonverteilten Messwert in {simstudy}. Das ist das Gleiche wie schon bevor. Hier muss ich definieren, wie die Effekte der beiden Faktoren sind. Auch hier gilt, das Ganze ist dann ohne Interaktion gebaut. Theoretisch könnest du noch einen globalen Interaktionseffekt mit 3 * f_a * _f_b hinzufügen, aber dann wäre der Effekt der Interaktion multiplikativ eben \(+3\) über die Level der Faktoren.

y_pois_def <- defDataAdd(varname = "y", 
                         formula = "-2 + 2*f_a + 6*f_b",
                         dist = "poisson")

Jetzt bringen wir unser Datenraster mit unserer Datendefinition zusammen. Wir erhalten dann einen neuen Datensatz mit unserem poissonverteilten Messwert. Am Ende möchte ich dann noch die Spalte f_a und f_b als Faktoren mutieren und die Level umbenennen. Dann sind wir auch schon fertig.

addColumns(y_pois_def, fac2_dt) |>
  mutate(f_a = factor(f_a, labels = str_c("A.", 1:3)),
         f_b = factor(f_b, labels = str_c("B.", 1:2))) |> 
  as_tibble()

# A tibble: 30 × 4
      id f_a   f_b       y
   <int> <fct> <fct> <int>
 1     1 A.1   B.1       6
 2     2 A.1   B.1       2
 3     3 A.1   B.1       7
 4     4 A.1   B.1       5
 5     5 A.1   B.1       8
 6     6 A.2   B.1       8
 7     7 A.2   B.1       7
 8     8 A.2   B.1       6
 9     9 A.2   B.1      11
10    10 A.2   B.1      11
# ℹ 20 more rows

Wir haben auch noch die Möglichkeit die Faktoren mit der Funktion genFactor() zu modifizieren, aber dann können wir wieder nicht mit den Leveln rechnen. Dann lohnt sich die Sache eigentlich nicht. Für mich hat die expand_grid() Variante mehr Charme. Die Variante ist einfach und schnell.

Zero-inflated Poisson

Wenn wir mit der Poissonverteilung arbeiten, dann haben wir manchmal den Fall vorliegen, dass wir eine zero-inflated Poissonverteilung (deu. Null-inflationiert, nicht gebräuchlich) vorliegen haben. Wir haben also noch mehr Nullen in dem Messwert als wir in einer normalen Poissonverteilung erwarten würden. Wir können eine solche Poissonverteilung dann ebenfalls mit {simstudy} bauen. Wir nutzen dazu das Tutorium Adding a “mixture” distribution to the {simstudy} package, welches und gut hilft einmal aus zwei Verteilungen eine Verteilung mit sehr vielen Nullen zu bauen.

Was heißt jetzt zwei Verteilungen? Wir bauen uns erstmal eine Poissonverteilung, die faktisch nur aus Nullen besteht. Die Poissonverteilung hat den Mittelwert von \(\lambda\) gleich \(0\). Wir nennen diese Verteilung dann y_0. Dann bauen wir uns noch eine klassische Poissonverteilung mit einem \(\lambda\) von \(2\) zusammen. Das können wir erstmal machen. Weiter unten zeige ich dir dann auch noch wie du dir einen Effekt mit einem einfaktoriellen Design als Beispiel baust.

zeroinf_def <- defData(varname = "y_0", formula = 0, dist = "nonrandom") |> 
  defData(varname = "y", formula = 2, dist = "poisson")

Jetzt kommt der Teil wo wir die beiden Verteilungen miteinander mischen. Wir nehmen \(20%\) der Werte der y_0 Verteilung und wir nehmen \(80%\) der Werte der y Verteilung. Das machen wir etwas umständlich über den Strich |. Wir sagen hier welche Anteile der beiden Verteilungen wir dann wollen. Am Ende benennen wir noch den Messwert neu.

zeroinf_def <- defData(zeroinf_def, varname = "y_zeroinf", formula = "y_0 | .2 + y | .8", 
                       dist = "mixture")

Dann können wir schon eintausend Beobachtungen erstellen.

zeroinf_dt <- genData(1000, zeroinf_def)

In der folgenden Abbidlung siesht du dann einmal die Histogramme der normalen Poissonverteilung sowie der zero-inflated Poissonverteilung. Wir haben hier als Unterschied eben den klaren Exzess an Nullen in der inflationierten Poissonverteilung. Das sieht man nicht unbedingt so gut, aber wir haben eben doch einiges mehr an Nullen als es nach der klassischen Verteilung sein sollte.

Abbildung 21.32— Histogramme von Zähldaten, die einer Poissonverteilung folgen. (A) Klassische Poissonverteilung. (B) Zero-inflated Poissonverteilung mit mehr Nullen. [Zum Vergrößern anklicken]

Wenn wir das ganze jetzt mit einem Behandlungsfaktor generieren wollen, dann müssen wir uns erstmal das Datenraster bauen. Wir nutzen dann das Raster um uns die Daten zu generieren und zu wissen wie viele Level mit Wiederholungen wir vorliegen haben.

fac1_dt <- expand_grid(f_a = 1:3,
                       rep = 1:1000) |> 
  as.data.table()

Zu unser Poissonverteilung mit den Mittelwert von Null kommt dann noch die klassische Poissonverteiung mit dem Effekt des Faktors. Hier hat jedes Faktorlevel einen Effekt von \(+4\) und wir nehmen einen Intercept von Null an. Dann mische ich noch die Verteilungen im Verhältnis von 1:3, daher 25% kommen aus der Poissonverteilung y_0 und 75% aus der Poissonverteilung mit Effekt. Damit haben wir dann die Datendefinition zusammen.

zeroinf_def <- defDataAdd(varname = "y_0", formula = 0, dist = "nonrandom")
zeroinf_def <- defDataAdd(zeroinf_def, varname = "y", 
                          formula = "0 + 4*f_a", dist = "poisson")
zeroinf_def <- defDataAdd(zeroinf_def, varname = "y_zeroinf", 
                          formula = "y_0 | .25 + y | .75", dist = "mixture")

Jetzt bringen wir unser Datenraster mit unserer Datendefinition zusammen. Wir erhalten dann einen neuen Datensatz mit unserem poissonverteilten Messwert. Das ist etwas anders als eben, aber hier müssen wir ja auch zwei Dinge zusammenbringen. Eben haben wir nur die Daten aus einer Datendefinition generiert. Am Ende möchte ich dann noch die Spalte f_a als Faktor mutieren und die Level umbenennen. Dann sind wir auch schon fertig.

fac1_zeroinf_dt <- addColumns(zeroinf_def, fac1_dt) |>
  mutate(f_a = factor(f_a, labels = str_c("A.", 1:3))) 

Dann schauen wir uns einmal die beiden Verteilungen im Vergleich in der folgenden Abbildung einmal an. Ich habe hier einmal den Violinplot gewählt, da kannst du dann besser den Fuß in der zero-inflated Poissonverteilung erkennen. Wir sehen dann aber auch, dass der Mittelwert nach unten gezogen wird. Auch der Median, als grau dargestellt, wird nach unten gezogen und entspricht dann nicht den vorgegeben Werten. Durch die Zeroinflation haben wir dann einen nicht mehr ganz sauberen Bezug zwischen den voreingestellten und den sich ergebenden Effekten.

Abbildung 21.33— Violinplot von einfaktoriellen Experimenten von Zähldaten, die einer Poissonverteilung folgen. Weiß sind die Mittelwerte und grau die Mediane dargestellt. (A) Klassische Poissonverteilung. (B) Zero-inflated Poissonverteilung mit mehr Nullen zu erkennen an den Füßen der Violinplots. [Zum Vergrößern anklicken]

Kovariates Design

Im Folgenden nutze ich das einkovariate und zweikovariate Design nochmal um etwas mit dem R Paket {simstudy} zu üben und die Funktionen zu zeigen. Am Ende nutzen wir eher selten ein kovariates Design in den Agrarwissenschaften, wenn es um ein poissonverteilten Messwert geht, aber zur Vollständigkeit gehört auch dieser Abschnitt mit dazu. Wir können hier verschiedene Modelle rechnen, ich nutze hier gleich die Gaussian Regression um auf meine Effekte zu kommen. Dann habe ich auch gleich die voreingestellten Mittelwerte wiedergegeben. Ein poissonverteilten Messwert analysieren wir ja eigentlich mit einer Poissonregression, aber dort erhalten wir dann als Effekte eben nicht die Steigung so direkt wieder sondern eben dann das Risk Ratio. Mehr dazu dann wie immer im entsprechenden Kapitel zu der Poissonregression, wenn dich mehr zum Thema interessiert.

Einkovariat \(c_1\)

Das Ziel der einkovariaten Datengenierung ist einfach. Wir haben eine normalverteilte Kovariate vorliegen und wollen einen Effekt für die Kovariate im poissonverteilten Messwert generieren. Bei einer Kovariate ist dann der Effekt auch gleichbedeutend mit der Steigung einer Graden durch die Punktewolke im Scatterplot. Ich nutze hier jetzt einmal sehr viel mehr Beobachtungen um dann auch auf die voreingestellten Effekte im Modell rauszukommen. Als erstes baue ich mir eine normalverteilte Kovariate mit einem Mittelwert von \(7\) und einer Streuung von \(3\) zusammen. Dann kann ich mir meinen Messwert in der folgenden Definition zusammenbauen. Hier habe ich dann einen Intercept von \(10\) und einen Effekt von \(2\) als Steigung vorliegen.

cov1_pois_def <- defData(varname = "c_1", dist = "normal", formula = "6",
                         variance = 3) |> 
  defData(varname = "y", dist = "poisson", formula = "10 + 2 * c_1")

Dann kann ich mir auch schon die eintausend Beobachtungen einmal generieren. Da ich hier keinn Faktoren vorliegen habe, brauche ich auch kein Datenraster für die Erstellung der Daten. Wir modellieren hier nicht in der gleichen Weise mit Effektschätzern unsere Daten wie wir dann in einer Poissonregression zurückkriegen würden. Das ist aber ein Preis, den wir aus Gründen der Einfachheit bezahlen wollen.

cov1_pois_tbl <- genData(1000, cov1_pois_def)

Dann können wir uns auch schon das Ergebnis der Datengenerierung in der folgenden Abbildung einmal anschauen. Hier wird dann auch sehr schön deutlich, dass wir durch den poissonverteilten Messwert Banden in dem Scatterplot sehen. Wir haben ja hier nur ganzzahlige Werte für die Messwert vorliegen. Bei einer so hohen Fallzahl an Beobachtungen erhalten wir dann auch unseren voreingestellten Effekte wieder. Hier müssen wir dann ein wenig aufpassen, wie wir denn die Daten analysieren wollen. Eine Poissonregression mit einem Risikoverhältnis als Effekt ist nicht das Gleiche wie eine Gaussianregression.

Abbildung 21.34— Darstellung einer linearen Simulation mit einer normalverteilten Kovariaten sowie einem poissonverteilten Messwert. Einmal ist die Regressiongleichung für den linearen Gaussian Zusammenhang sowie für die Poissonregression dargestellt. [Zum Vergrößern anklicken]

Wir können dann auch nochmal ein GLM rechnen und sehen, dass wir bei einer so hohen Fallzahl dann auch in einem GLM die passenden Effekte ungefähr herausbekommen. Ich nutze hier die Funktion parameters() aus dem gleichnamigen R Paket damit ich die Schätzer noch wieder zurücktransformieren kann. Auch hier findest du dann mehr in dem Kapitel zu der Poissonregression. Ich fitte hier erstmal die passende Poissonregression.

pois_c1_fit <- glm(y ~ c_1, data = cov1_pois_tbl, family = poisson)

Danns schauen wir uns einmal die Koeffizienten der Poissonregression an. Wir sind hier hauptsächlich am Inzidenzratenverhältnis (eng Incidence Rate Ratio, abk. IRR) interessiert.

pois_c1_fit |>
  parameters::model_parameters(exponentiate = TRUE)

Parameter   |   IRR |       SE |         95% CI |      z |      p
-----------------------------------------------------------------
(Intercept) | 12.96 |     0.33 | [12.34, 13.61] | 102.06 | < .001
c 1         |  1.09 | 4.21e-03 | [ 1.08,  1.10] |  22.46 | < .001

Was sehen wir hier als Effekte? Wir rechnen hier das Inzidenzratenverhältnis aus. Das Inzidenzratenverhältnis beschreibt die multiplikative Änderung der erwarteten Rate, wenn sich die Kovariate um eine Einheit ändert. Das heißt hier in unserem Fall, dass wenn wir die Kovariate \(c_1\) um eine Einheit erhöhen, dass unser Messwert um den Faktor \(1.09\) ansteigt. Leider siehst du auch, dass wir es hier nicht mit einer linearen Modellierung zu tun haben. Daher kann ich dir das Inzidenzratenverhältnis einmal zwischen zwei Punkten mit \(c_1 = 6\) und \(c_1 = 7\) berechnen. Das Problem ist hier wirklich, dass wir es mit einem Faktor zu tun haben. Mehr dazu nochmal weiter unten im Kasten zu den Effekten in der Poissonregression und die Vingette Targeted logistic model coefficients geht das Problem in {simstudy} nochmal an.

pois_c1_fit |> 
  predict(newdata = tibble(c_1 = c(6, 7)), type = "response")

       1        2 
21.80644 23.78146 

Jetzt können wir auch den Faktor zwischen den beiden Messwerten berechnen. Wie ändert sich also Multiplikativ der Messwert von \(c_1 = 6\) zu \(c_1 = 7\)? Dafür teilen wir dann die beiden Messwerte durcheinander und erhalten dann faktisch unser Inzidenzratenverhältnis aus dem obigen Modell.

23.86757 / 21.72900

[1] 1.09842

Jetzt können wir uns das Leben auch etwas einfacher machen und einmal die Marginal effect models mit dem R Paket {marginaleffects} nutzen um uns den Faktor zwischen den beiden Kovariatenwerten berechnen zu lassen. Das ist manchmal etwas schneller und auch einfacher durchzuführen. Darüber hinaus können wir eben dann nicht nur zwei Werte eingeben, sondern haben auch noch andere Möglichkeiten.

avg_comparisons(pois_c1_fit, comparison = "ratio",
                variables = list("c_1" = c(6, 7)))

 Estimate Std. Error   z Pr(>|z|)   S 2.5 % 97.5 %
     1.09    0.00421 259   <0.001 Inf  1.08    1.1

Term: c_1
Type: response
Comparison: mean(7) / mean(6)

Mehr zu den Möglichkeiten dann auch in der Vingette Change in numeric predictors auf der Hilfeseite dem R Paket {marginaleffects}. Bei denen heißt dann die numerische Einflussvaraiable dann numeric predictor. Je nachdem wo man dann weiterliest ändern sich dann leider auch immer wieder die Begrifflichkeiten.

Ein Wort zum Effekt in der Poissonregression

In der Poissonregression kriegen wir als Effektschätzer das Risk Ratio wiedergegeben. Das ist also nicht ein absoluter Wert, wie die Steigung, sondern ein Faktor um den sich die Messwerte unterschieden. Wenn wir die Einheit der Kovariate von 0 auf 1 erhöhen, dann würden wir vom Messwert von 10 auf 12 springen. Das würde einen Faktor von \(12/10 = 1.2\) ausmachen. Wenn wir jetzt aber unsere Kovariate von 1 auf 2 erhöhen, dann haben wir einen Messwert von 12 auf 14. Jetzt haben wir aber einen Faktor von \(14/12 = 1.17\) vorliegen. Der Faktor sinkt mit dem Anstieg der Kovariate. Da der absolute Anstieg immer weniger Anteil am Messwert ausmacht. Ich zeige dir den Zusammenhang einmal in der folgenden Abbildung. Mit jedem Sprung wird der Faktor kleiner. Am Ende ist dann das Risk Ratio aus einer Poissonregression mehr oder minder das Mittel über alle Sprünge. Wirklich linear ist dann der Zusammenhang nur auf der Linkskala. Hier hilft dann die Lektüre von Dormann (2013) oder aber das Kapitel zu der Poissonregression weiter. Die Vingette Targeted logistic model coefficients geht das Problem in {simstudy} nochmal an.

Abbildung 21.35— Darstellung des abnehmenden Risk Ratio über den Anstieg der Kovariate. Mit dem Anstieg der Kovariate nimmt der absolute Anstieg von \(+2\) immer weniger Anteil an dem Messwert. Der Faktor des Anstiegs wird von \(\times1.2\) zu \(\times1.07\) immer kleiner. Das Risk Ratio (abk. RR) aus einer Poissonregression ist mehr oder minder der mittlere Faktor. [Zum Vergrößern anklicken]

Zweikovariat unabhängig \(c_1 + c_2\)

Wir können natürlich auch mehrere Kovariaten vorliegen haben. Ich zeige hier dann einmal zwei Kovariaten, die einmal einer Normalverteilung und einmal einer Poissonverteilung entstammen. Wir müssen ja nicht nur normalverteilte Kovariaten vorliegen haben. Dann baue ich mir noch meinen poissonverteilten Messwert zusammen.

cov2_pois_def <- defData(varname = "c_1", dist = "normal", formula = "10",
                         variance = 2) |> 
  defData(varname = "c_2", dist = "poisson", formula = "5") |> 
  defData(varname = "y", dist = "poisson", formula = "8 + 2 * c_1 + 1 * c_2")

Dann generiere ich mir auch schon meine zehntausend Beobachtungen. Ich werde das Ergebnis der Generierung nicht visualiseren, daher können wir hier auch einmal mit mehr Beobachtungen arbeiten und haben dann auch etwas genauere Schätzer der Effekte in den Modellen.

cov2_pois_tbl <- genData(10000, cov2_pois_def)

Hier einmal das lineare Modell, dort sehen wir dann ob wir auch unsere eingestellten Effekte direkt wiedererhalten. Das ist natürlich jetzt nur so semi hilfreich, da wir ja auch schauen müssen wie denn die Werte in einem GLM aussehen würden.

lm(y ~ c_1 + c_2, data = cov2_pois_tbl) |> 
  coef() |> round(2)

(Intercept)         c_1         c_2 
       7.58        2.02        1.04 

Dafür passen wir einmal eine Poissonregression an und nutzen gleich einmal das Modell um uns die Inzidenzratenverhältnisse (eng Incidence Rate Ratio, abk. IRR) für die beiden Kovariaten berechnen zu lassen.

pois_c2_fit <- glm(y ~ c_1 + c_2, data = cov2_pois_tbl, family = poisson)

Wir können hier uns entweder die Koeffizienten einmal direkt über die Funktion model_parameters() wiedergeben lassen oder aber dann gleich einmal in der Funktionalität des R Pakets {marginaleffects}. Wir sehen hier, dass wir jeweils einen positiven Effekt haben. Mit steigenden Kovariaten erhöhen sich auch die Messwerte.

pois_c2_fit |> 
  parameters::model_parameters(exponentiate = TRUE)

Parameter   |   IRR |       SE |         95% CI |      z |      p
-----------------------------------------------------------------
(Intercept) | 15.24 |     0.20 | [14.85, 15.64] | 206.38 | < .001
c 1         |  1.06 | 1.31e-03 | [ 1.06,  1.07] |  49.55 | < .001
c 2         |  1.03 | 7.93e-04 | [ 1.03,  1.03] |  40.19 | < .001

Dam Ende dann nochmal die multiplikative Änderung als Inzidenzratenverhältnis für die beiden Kovariaten an zwei definierten Werten für die jeweiligen Kovariaten. Wir sehen dann auch hier das es dann eben auch auf die Werte ankommt, die wir uns anssehen wollen. Wir können eben nicht so einfach die Steigung wieder als Risk Ratio sehen. Aber das ist eben dann auch der Unterschied zwischen einem absoluten Effekt wie der Steigung und dem Risk Ratio also Faktor. Damit werden wir leben müssen. Die Vingette Targeted logistic model coefficients geht das Problem in {simstudy} nochmal an.

avg_comparisons(pois_c2_fit, comparison = "ratio",
                variables = list("c_1" = c(10, 11),
                                 "c_2" = c(5, 6)))

 Term            Contrast Estimate Std. Error    z Pr(>|z|)   S 2.5 % 97.5 %
  c_1 mean(11) / mean(10)     1.06   0.001310  811   <0.001 Inf  1.06   1.07
  c_2 mean(6) / mean(5)       1.03   0.000793 1301   <0.001 Inf  1.03   1.03

Type: response

Multikovariat abhängig \(c_1 + c_2 + c_3\)

Eine multivariate Poissonverteilung ist nicht einfach zu bauen. Jedenfalls um so viel schwerer, dass eine gerundete multivariate Normalverteilung mit Korrelationsstruktur viel einfacher zu erstellen ist. Die Funktionalität in {simstudy} erlaubt auch multivariate korrelierte Poissondaten zu erstellen. Die Vingette Correlated data: additional distributions hilft hierbei. Ich zeige hier einmal die Variante der Poissonverteilung mit drei Kovariaten und einer konstanten Korrelation zwischen den Kovariaten von 0.3 als compound symmetry (cs) Korrelationsmatrix.

cov2_dependent_dt <- genCorGen(1000, nvars = 3, params1 = c(8, 10, 12), dist = "poisson", 
                               rho = 0.3, corstr = "cs", wide = TRUE,
                               cnames = c("c_1", "c_2", "c_3")) 

Im Folgenden siehst du dann einmal die Datentabelle der eintausend Beobachtungen. Wir haben die ID Spalte und dann die drei Kovariaten gefolgt von dem Messwert. Die beobachtete Korrelation ist dann 0.3 zwischen den Kovariaten.

cov2_dependent_dt

Key: <id>
         id   c_1   c_2   c_3
      <int> <num> <num> <num>
   1:     1    15     8    20
   2:     2     7    17    13
   3:     3     9    13    16
   4:     4     8     9    16
   5:     5     8    12    17
  ---                        
 996:   996     6     8     3
 997:   997     4     8     6
 998:   998     7     6    13
 999:   999     6     8    11
1000:  1000    10     8    11

In den rohen Daten ist die Korrelation faktisch nicht zu sehen. Jedenfalls kann ich sowas nicht erkennen. Dafür müssen wir uns dann einmal die Korrelation berechnen lassen. Wie wir dann im Folgenden einmal sehen, passt es sehr gut. Wir erhalten die Korrelationen wieder, die wir auch eingestellt haben.

correlation(cov2_dependent_dt, select = c("c_1", "c_2", "c_3")) |> 
  summary(redundant = TRUE)

# Correlation Matrix (pearson-method)

Parameter |     c_1 |     c_2 |     c_3
---------------------------------------
c_1       |         | 0.30*** | 0.29***
c_2       | 0.30*** |         | 0.31***
c_3       | 0.29*** | 0.31*** |        

p-value adjustment method: Holm (1979)

Wir können jetzt mit den korrelierten Kovariaten uns nochmal neue Messwerte erstellen. Hierbei bitte bachten, dass multiple Modelle Probleme kriegen, wenn die Kovariaten zu stark miteinander korreliert sind. Dazu dann aber mehr in dem Kapitel zu der multiplen Regression.

“Brauchen wir das? Ein klares Jein. Ich finde korrelierte Daten eher sinnvoll in Zeitreihen und dann auch gerne mit einer auto-regressive Korrelationsstruktur. Ansonsten ist es sicherlich in der Theorie spannend, solche Daten zu erstellen.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

21.5.3 Ordinalverteilt

Was sind ordinalverteilte Messwerte? Wir können diese Art von Messwerten einmal als Antwortmöglichkeiten bei einem Fragebogen oder aber bei der Bonitur beobachten. Bei Fragebögen haben wir dann meistens drei bis fünf Antwortkategorien, die dann eben auch geordnet sind. Alle Kategorien haben dabei den gleichen Abstand. Bei der Bonitur haben wir häufig eine fünf- bis neunstufige Likertskala vorliegen, wobei die Neun immer die stärkste Ausprägung beschreibt. Wenn du nur zwei Antwortmöglichkeiten vorliegen hast, dann bist du im binären Fall, das machen wir dann weiter unten nochmal. Das R Paket {simstudy} hat mit der Vingette Ordinal Categorical Data eine Hilfeseite, die dir einmal beschreibt, wie wir ordinale Messwerte erstellen. Am Ende kannst du dir vorstellen, dass wir als Messwert wiederum einen Faktor vorliegen haben und eigentlich keinen numerischen Messwert. Wir wollen hier aber einmal verstehen, wie sich so ordinale Messwerte zusammensetzen. Das ist auch immer sehr hilfreich bei der Auswertung im Kapitel zur Multinomialen / Ordinalen Regression.

Achtung, bitte beachten!

Um jetzt irgendwas zu sehen, brauchen wir wirklich viele Fallzahlen. Wenn du später nur fünf Beobachtungen pro Gruppe hast, dann wird es sehr schwer die vorengestellten Gruppenwahrscheinlichkeiten wiederzufinden. Deshalb kann es sein, dass es beser ist, dir die Daten einfach per Hand selber in Excel zu bauen.

A refined brute force method to inform simulation of ordinal response data

Das Problem der vielen Ausprägungen von einer 9er Likert Skala und den Wahrscheinlichkeiten pro Ausprägung.

Faktorielles Design

Für die ordinalverteilten Daten nutzen wir jetzt hier hauptsächtlich das faktorielle Design. Wir nutzen hier dabei aber auch nur ein reduziertes Design zum Einstieg. Das hat den Grund, dass die Erstellung schon kompliziert genug ist und wir bei kleinen Fallzahlen später dann kaum noch was wieder erkennen. Daher wir stellen zwar Effekte ein, wollen aber nur so wenige Beobachtungen haben, dass wir die Effekte gar nicht wiedersehen. Dann können wir uns die Zahlen auch händisch in Excel zusammentippen. Gambarota & Altoè (2024) geht in seiner Arbeit Ordinal regression models made easy: A tutorial on parameter interpretation, data simulation and power analysis nochmal auf das faktorielle Design ein und zeigt auch, wie wir komplexere Modelle simulieren können.

Einfaktoriell \(f_A\) mit 2 Leveln

Wir beginnen mit dem einfaktoriellen Modell mit zwei Leveln. Wir nutzen wieder das simple Modell um einmal die Herausforderungen zu verstehen. Wir haben es nämlich bei einem ordinalen Messwert mit etwas komplizierteren Daten zu tun. Beginnen wir mit einem ordinalen Messwert mit fünf Kategorien. Wir haben hier also eine Frage vorliegen mit fünf Antwortmöglichkeiten. Die Antwortmöglichkeiten sind trifft gar nicht zu, trifft nicht zu, weder noch, trifft zu und trifft voll zu. Jetzt kommt der eigentlich Twist. Wir haben diese Antwortmöglichkeiten ja in unterschiedlichen Häufigkeiten vorliegen. Wir haben also 100 Personen befragt und diese 100 Personen haben jeweils eine der Antwortmöglichkeiten auf die Frage geantwortet. Damit erhalten wir dann folgende hypothetische Verteilung der Antworten.

null_prob <- c("trifft gar nicht zu" = 0.1, 
               "trifft nicht zu" = 0.2, 
               "weder noch" = 0.4, 
               "trifft zu" = 0.2, 
               "trifft voll zu" = 0.1)

Wir können hier nicht einfach einen Effekt aufaddieren um eien zweite Gruppe zu erschaffen. Wir können nicht die Wahrscheinlichkeiten einfach um \(+0.1\) erhöhen, dann hätten wir ja in der Summe \(5 \times 0.1 = +0.5\) erhöht. Wir brauchen aber eine Wahrschinlichkeit von Eins in Summe. Daher müssen wir von einigen Antwortmöglichkeiten etwas abziehen und bei anderen etwas aufaddieren. Die Änderungen müssen sich ja dann zu Null aufaddieren, wie du im folgenden Beispiel für eine alternative Gruppe siehst.

alt_prob <- c("trifft gar nicht zu" = 0.1 - 0.05, 
              "trifft nicht zu" = 0.2 - 0.1, 
              "weder noch" = 0.4 - 0.1, 
              "trifft zu" = 0.2 + 0.2, 
              "trifft voll zu" = 0.1 + 0.05)

Dann können wir einmal für die beiden Gruppen dann die fünf Antwortmöglichkeiten mit den jeweiligen Wahrscheinlichkeiten erschaffen. Beachte, dass wir die Namen der Wahrscheinlichkeitsvektoren nicht mitschleifen und dann in der Genierung verlieren. Daher müssen wir dann den Messwert nochmal wieder als Faktor mutieren. Für die Darstellung ist es dann aber mit einem numerischen Messwert einfacher.

ord_fac1_tbl <- tibble("A.1" = sample(1:5, 100, replace = TRUE, prob = null_prob),
                       "A.2" = sample(1:5, 100, replace = TRUE, prob = alt_prob))  |> 
  gather(key = "f_a", value = "y") |> 
  mutate(y_fct = factor(y, labels = c("trifft gar nicht zu", "trifft nicht zu", "weder noch",
                                      "trifft zu", "trifft voll zu")))
ord_fac1_tbl

# A tibble: 200 × 3
   f_a       y y_fct              
   <chr> <int> <fct>              
 1 A.1       3 weder noch         
 2 A.1       3 weder noch         
 3 A.1       1 trifft gar nicht zu
 4 A.1       4 trifft zu          
 5 A.1       3 weder noch         
 6 A.1       1 trifft gar nicht zu
 7 A.1       3 weder noch         
 8 A.1       3 weder noch         
 9 A.1       2 trifft nicht zu    
10 A.1       5 trifft voll zu     
# ℹ 190 more rows

Dann können wir uns einmal die Verteilungen der Antwortmöglichkeiten in den beiden Gruppen mit je einhundert Beobachtungen anschauen. Wie du siehst, sind die beiden Verteilungen ineinander verschoben. Dabei hat die zweite Gruppe mehr Antworten bei trifft zu und trifft voll zu. Daher muss die Anzahl der Antworten bei den negativen Antworten kleiner sein. Wie du dir vorstellen kannst, haben wir hier nicht so viel Raum um Veränderungen zu erreichen und dabei irgendiwe noch eine Verteilung zu sehen. Wenn sich alles auf einer Seite zusammenballt, dann haben wir auch schon fast keine Varianz mehr.

Abbildung 21.36— Histogramm der Verteilung der Antwortmöglichkeiten in einem einfaktoriellen Design mit zwei Gruppen. Die Häufigkeit der Antworten ist in den beiden Gruppen verschoben. Da die Summe der Antwortwahrscheinlichkeiten Eins sein muss und die Summe der Verschiebungen Null sein muss, ist die Verschiebung nicht trivial. [Zum Vergrößern anklicken]

Jetzt ist es natürlich super nervig einen Vektor zu bauen, der die Verschiebungen der Antwortwahrscheinlichkeiten beschreibt. Insbesondere wenn wir viele Antwortmöglichkeiten oder Notenausprägungen haben. Dann wird es sehr schwierig und sehr kleinteilig. Daher ist eine Idee eine latente Variable zu generieren, die wir verschieben können und uns über einen Umweg dann die Wahrscheinlichkeiten für die Antwortmöglichkeiten wiedergibt. Das ist die Lösung in {simstudy}.

In der folgenden Abbildung habe ich dir einmal das Prinzip visualisiert. Unsere Antwortwahrscheinlichkeiten sind die Flächen unter der Kurve. Damit wir hier alles etwas besser sehen, habe ich mich auf vier Antwortmöglichkeiten beschränkt. Wir können jetzt die z-Werte auf der x-Achse verschieben und damit ändern sich auch die Flächen zwischen den z-Werten. Da die Flächen die Antwortwahrscheinlichkeiten sind, können wir hier einen Wert ändern und erhalten neue Wahrscheinlicheiten wieder. Dabei ist zu beachten, das die Verschiebung für alle Antworten in die gleiche Richtung und um den gleichen Effekt erfolgt.

Abbildung 21.37— Darstellung der Idee der latenten Variable zur Generierung von ordnialen Daten. Die Fläche unter der Kurve stellt die Antwortwahrscheinlichkeit für vier Antworten dar. Wenn der z-Wert verschoben wird, dann ändert sich auch die Fläche und damit auch die Antwortwahrscheinlichkeiten. (A) Antwortverteilung für die Gruppe \(A.1\) (B) Verschobene Antwortverteilung um \(+0.7\) für die Gruppe \(A.2\). [Zum Vergrößern anklicken]

Natürlich ist das etwas zu schön um wahr zu sein. Wir haben hier eine ziemlich strenge Annahme getroffen. Durch die Verschiebung durch ein festes \(z\) gleich \(+0.7\) haben wir die Annahme an ein proportionales Wahrscheinlichkeitsmodell getroffen. Wir verschieben eben alle Antwortmöglichkeiten gleichmäßig um den gleichen Wert nach rechts. Die Richtung und auch die Effektstärke ist für alle Antwortmöglichkeiten gleich.

Proportionales Wahrscheinlichkeitsmodell

Was will und das Proportionales Wahrscheinlichkeitsmodell (eng. proportional odds model) sagen? Wenn wir die Wahrscheinlichkeiten der Antworten verschieben, dann verschieben wir in die gleiche Richtung und um den gleichen Wert. Alle Antwortwahrscheinlichkeiten verhalten sich gleich und dementsprechend proportional.

Wir können jetzt in {simstudy} beide Varianten durchführen. Wir können also einmal davon ausgehen, dass wir den gleichen Effekt in die gleiche Richtung für alle Antwortwahrscheinlichkeiten vorliegen haben. Wir rechnen dann mit der Proportional odds Annahme. Wir können aber auch den Fall vorliegen haben, dass wir die Antwortwahrscheinlichkeiten individuell verschieben. Dann haben wir die Annahme der Non-proportional odds getroffen. Ich zeige dir dann in beiden Tabs einmal die Durchführung in {simstudy} und wie wir dann die zufälligen ordinalen Werte erhalten.

Proportional odds

null_prob <- c(0.31, 0.29, 0.20, 0.20)

qlogis(cumsum(null_prob))[1:3]

[1] -0.8001193  0.4054651  1.3862944

ord_fac1_def <- defData(varname = "f_a", formula = "1;1", dist = "trtAssign") |> 
  defData(varname = "z", formula = "-0.7*f_a", dist = "nonrandom")

ord_fac1_pre_dt <- genData(25000, ord_fac1_def)

ord_fac1_dt <- genOrdCat(ord_fac1_pre_dt, adjVar = "z", null_prob, catVar = "r")

ord_fac1_dt |> 
  group_by(f_a) |> 
  sample_n(5)

# A tibble: 10 × 4
# Groups:   f_a [2]
      id   f_a     z r    
   <int> <int> <dbl> <fct>
 1 20108     0   0   3    
 2 20399     0   0   1    
 3 17044     0   0   2    
 4 16156     0   0   1    
 5 22539     0   0   1    
 6  6490     1  -0.7 2    
 7 17412     1  -0.7 1    
 8 19404     1  -0.7 3    
 9 12519     1  -0.7 1    
10  5976     1  -0.7 2    

simstudy update: ordinal data generation that violates proportionality

library(ordinal)
clmFit <- clm(r ~ f_a, data = ord_fac1_dt)
summary(clmFit)

formula: r ~ f_a
data:    ord_fac1_dt

 link  threshold nobs  logLik    AIC      niter max.grad cond.H 
 logit flexible  25000 -32428.82 64865.65 4(0)  1.89e-08 1.7e+01

Coefficients:
    Estimate Std. Error z value Pr(>|z|)    
f_a -0.68852    0.02335  -29.49   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Threshold coefficients:
    Estimate Std. Error z value
1|2 -0.78692    0.01785  -44.09
2|3  0.39761    0.01726   23.03
3|4  1.39756    0.02011   69.48

(logOdds.unexp <- qlogis(cumsum(ord_fac1_dt[f_a == 0, prop.table(table(r))]))[1:3])

         1          2          3 
-0.7855731  0.3968059  1.3963245 

Non-proportional odds

null_prob <- c(0.31, 0.29, 0.20, 0.20)

ord_fac1_def <- defData(varname = "f_a", formula = "1;1", dist = "trtAssign") |> 
  defData(varname = "z", formula = "-0.7*f_a", dist = "nonrandom")

ord_fac1_pre_dt <- genData(25000, ord_fac1_def)

shift_z <- c(-0.4, 0.0, -1.7, 0)

ord_fac1_dt <- genOrdCat(ord_fac1_pre_dt, baseprobs = null_prob, adjVar = "z",
                         catVar = "r", npVar = "f_a", npAdj = shift_z)

ord_fac1_dt |> 
  group_by(f_a) |> 
  sample_n(5)

# A tibble: 10 × 4
# Groups:   f_a [2]
      id   f_a     z r    
   <int> <int> <dbl> <fct>
 1 12592     0   0   4    
 2  8078     0   0   2    
 3 23404     0   0   1    
 4 12537     0   0   2    
 5  1302     0   0   4    
 6 17108     1  -0.7 3    
 7   319     1  -0.7 3    
 8  4848     1  -0.7 4    
 9 15104     1  -0.7 1    
10 22940     1  -0.7 1    

Einfaktoriell \(f_A\) mit 3 Leveln

null_prob <- c(0.31, 0.29, 0.20, 0.20)

ord_fac1_def <- defData(varname = "f_a", formula = "1;1;1", dist = "trtAssign") |> 
  defData(varname = "z", formula = "-0.7*f_a", dist = "nonrandom")

ord_fac1_pre_dt <- genData(25000, ord_fac1_def)

ord_fac1_dt <- genOrdCat(ord_fac1_pre_dt, adjVar = "z", null_prob, catVar = "r")

ord_fac1_dt |> 
  group_by(f_a) |> 
  sample_n(4)

# A tibble: 12 × 4
# Groups:   f_a [3]
      id   f_a     z r    
   <int> <int> <dbl> <fct>
 1  5079     1  -0.7 1    
 2 15518     1  -0.7 1    
 3 17197     1  -0.7 1    
 4  8497     1  -0.7 2    
 5 13987     2  -1.4 1    
 6 15224     2  -1.4 1    
 7  2640     2  -1.4 2    
 8 23962     2  -1.4 2    
 9 16870     3  -2.1 1    
10  7185     3  -2.1 1    
11 21142     3  -2.1 1    
12 11531     3  -2.1 1    

Multifaktoriell abhängig \(c_1 + c_2 + c_3\)

Correlated multivariate ordinal data

Kovariates Design

Machen wir es kurz, wir betrachten hier nicht ein kovariates Design mit einem ordinalen Messwert. Das ergibt für mich keinen wirklichen Sinn. Theoretisch könnten wir eine Kovariate messen und dann schauen, wie sich der ordinale Messwert ändert, aber das würde ich dann eher als Gaussian linear Regression modellieren. Wir nehmen also einfach die mittleren Noten. Das würde dann reichen. Hier jetzt noch für Kovariaten die ordinale Messwerte zu generieren ist zu wild.

21.5.4 Binomialverteilt

Generating binary data by specifying the relative risk, with simulations

fac1_dt <- expand_grid(f_a = 1:3,
                       rep = 1:1000) |> 
  as.data.table()

y_binom_def <- defDataAdd(varname = "y", formula = "0.5",
                          dist = "binomial", variance = 3, link = "identity")

addColumns(y_binom_def, fac1_dt) |> 
  tabyl(f_a, y)

 f_a   0   1   2   3
   1 138 381 337 144
   2 116 393 362 129
   3 137 361 390 112

fac1_dt <- expand_grid(f_a = 1:3,
                       rep = 1:10000) |> 
  as.data.table()

y_binary_def <- defDataAdd(varname = "y", formula = "0.2 + 0.2*f_a",
                          dist = "binary", link = "identity")

addColumns(y_binary_def, fac1_dt) |> 
  tabyl(f_a, y) |> adorn_percentages("row") |> adorn_pct_formatting(digits = 0)

 f_a   0   1
   1 60% 40%
   2 40% 60%
   3 20% 80%

logit() and logistic() functions in R

\[ \text{logit}(p) = \cfrac{p}{1-p} \]

qlogis(0.6) # logit

[1] 0.4054651

logit <- \(x) log(x / (1 - x))
logit(0.6)

[1] 0.4054651

\[ \text{logistic}(x) = \cfrac{1}{1 + exp(-x)} \]

plogis(0.4054651) # logistic

[1] 0.6

ggplot(tibble(x = seq(-6, 6, by = 0.5),
              y = plogis(x)),
       aes(x, y)) +
  geom_point()

Faktorielles Design

Kovariates Design

21.6 Komplexe Modelle

21.6.1 Multiple Modelle

21.6.2 Überlebenszeiten

21.6.3 Zeitreihen

Spline Data

Referenzen

Dormann, C. F. (2013). Parametrische Statistik. Springer.

Gambarota, F., & Altoè, G. (2024). Ordinal regression models made easy: A tutorial on parameter interpretation, data simulation and power analysis. International Journal of Psychology, 59(6), 1263–1292.

Jackson, C., Murphy, R. F., & Kovacevic, J. (2009). Intelligent acquisition and learning of fluorescence microscope data models. IEEE Transactions on Image Processing, 18(9), 2071–2084.

Kruppa, J., Kramer, F., Beißbarth, T., & Jung, K. (2016). A simulation framework for correlated count data of features subsets in high-throughput sequencing or proteomics experiments. Statistical applications in genetics and molecular biology, 15(5), 401–414.