60 Clusteranalysen

Letzte Änderung am 02. April 2024 um 09:52:43

“Cluster together like stars!” — Henry Miller

In diesem Kapitel wollen wir uns mit der Clusteranalyse beschäftigen. Zuerst was verstehen wir unter einem Cluster? Ein Cluster ist ein Zusammenschluss von ähnlichen Beobachtungen. Nun stellt sich zuerst die Frage, was heißt ähnlich? Wir brauchen also Maßzahlen für die Ähnlichkeit zwischen zwei und mehreren Beobachtungen. In unserem Datensatz haben wir ja nicht nur zwei Beobachtungen, also Zeilen, sondern sehr viel mehr. Im Weiteren haben wir in erster Linie kein Outcome $y$. Wir nehmen alle Spalten $x$ aus unseren Daten und versuchen anhand der Spalten Gruppen über die Beobachtungen in den Zeilen zu bilden. Manchmal wollen wir dann nachräglich die Cluster nach einer Spalte in unseren ursprünglichen Daten einfärben oder benennen. Dieses Benennen von bekannten Zuordnungen hat aber erstmal mit dem Clusteralgorithmus nichts zu tun. Wir schauen uns im Folgenden diese Schwerpunktthemen an.

Die hierarchisches Clustern über Dendrogramme in Kapitel 60.5.1
Das k-NN oder nächste Nachbarn Clustern in Kapitel 60.5.3
Die Heatmaps verbreitet in der genetischen Analysen in Kapitel 60.5.5
Einmal das hierarchisches Clustern und k-NN über das R Paket {tidyclust} in Kapitel 60.6

Wie immer können wir nicht alles erschlagen und deshalb machen wir hier auch nur ein Auswahl. Mehr geht immer und dafür ist dann der folgende Kasten mit weiteren Tutorien für die Clusteranalyse da.

Weitere Tutorien für die Clusteranalyse

Wie immer gibt es eine Vielzahl an tollen Tutorien, die eine Clusteranalyse gut erklären. Ich habe hier einmal eine Auswahl zusammengestellt und du kannst dich da ja mal vertiefend mit beschäftigen, wenn du willst. Teile der Tutorien findest du vermutlich hier im Kapitel wieder.

Das R Paket {dendextend} Introduction to dendextend um Dendrogramme wirklich schön zu zeichnen.
Das R Paket {pheatmap} Making a heatmap in R with the pheatmap package um Heatmaps mit allem was das Herz begehrt zu bauen. Dann haben wir noch das R Paket ComplexHeatmap, was sich vom R Paket {pheatmap} inspirieren lies. Das geht dann aber hier zu weit, schauen da, wenn du wirklich Heatmaps brauchst.
Das R Paket {cluster}, wenn auch ohne gute Hilfeseite ermöglicht die Paketbeschreibung eine gute Übersicht an möglichen Algorithmen.

Wir wollen uns die Clusteranalyse an zwei Spieldaten anschauen sowie einmal an den echten Daten zu den Gummibärchen. Eigentlich werden ja auch gerne Fragebögen mit der Clusteranalyse ausgewertet, aber hier muss ich nochmal warten bis ich ein gutes Beispiel in den Beratungen hatte.

60.1 Genutzte R Pakete

Wir wollen folgende R Pakete in diesem Kapitel nutzen.

set.seed(20230727)
pacman::p_load(tidyverse, magrittr, palmerpenguins, readxl,
               ggdendro, broom, cluster, factoextra, FactoMineR, 
               pheatmap, tidyclust, dlookr, janitor, corrplot,
               dendextend, see, conflicted)
conflicts_prefer(dplyr::filter)
conflicts_prefer(dlookr::transform)

An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.

60.2 Daten

Beginnen wir mit einem normierten Datensatz aus dem R Paket {cluster}. Der Datensatz animals wurde von mir noch mit ein paar Tieren ergänzt und schaut sich sechs Eigenschaften von 23 Tieren an. Wir wollen im Folgenden nun herausfinden, ob wir anhand der Eigenschaften in den Spalten die Tiere in den Zeilen in Gruppen einordnen können. Einige der Tiere sind ja näher miteinander verwandt als andere Tiere. Die ursprünglichen Daten liefen noch auf einem $1/2$-System, das ändern wir dann zu $0/1$ damit wir dann auch besser mit den Daten arbeiten können. Für die Algorithmen ist es egal, aber ich habe lieber $1$ gleich ja und $0$ gleich nein.

animals_tbl <- read_excel("data/cluster_animal.xlsx", sheet = 1) |> 
  clean_names() |> 
  mutate(across(where(is.numeric), \(x) x - 1))

Schauen wir uns einmal den Datensatz in der Tabelle 61.3 an. Wir sehen, dass wir noch einige fehlende Werte in den Daten vorliegen haben. Das ist manchmal ein Problem, deshalb werden wir im Laufe der Analyse die NA Werte mit na.omit() entfernen.

Tabelle 60.1— Übersicht über die 23 Tiere mit den sechs Eigenschaften in den Spalten. Eine 1 bedeutet, dass die Eigenschaft vorliegt; eine 0 das die Eigenschaft nicht vorliegt.

animal	warm_blooded	fly	vertebrate	threatened	live_in_groups	hair
ant	0	0	0	0	1	0
bee	0	1	0	0	1	1
cat	1	0	1	0	0	1
centipede	0	0	0	0	0	1
chimpanzee	1	0	1	1	1	1
cow	1	0	1	0	1	1
dolphin	1	0	1	1	1	0
duck	1	1	1	0	1	0
eagle	1	1	1	1	0	0
earthworm	0	0	0	0	0	0
elephant	1	0	1	1	1	0
fly	0	1	0	0	0	0
frog	0	0	1	1	NA	0
herring	0	0	1	0	1	0
horse	1	0	1	0	1	1
human	1	0	1	1	1	1
lion	1	0	1	NA	1	1
lizard	0	0	1	0	0	0
lobster	0	0	0	0	NA	0
rabbit	1	0	1	0	1	1
salmon	0	0	1	0	NA	0
spider	0	0	0	NA	0	1
whale	1	0	1	1	1	0

Der Tierdatensatz ist schön, da wir es hier nur mit 0/1 Werten zu tun haben. Wir werden später in dem preprocessing der Daten sehen, dass wir alle Spalten in der gleichen Spannweite der Werte wollen. Das klingt immer etwas kryptisch, aber der nächste Datensatz über verschiedene Kreaturen macht es deutlicher.

Eine andere Art die Daten zu Gruppieren kannst du im Tutorium Clustering Creatures nochmal nachvollziehen.

Im Folgenen einmal der Datensatz, den wir dann in der gleichen Exceldatei finden nur eben auf dem zweiten Tabellenblatt. Wir reinigen noch die Namen und setzen die creature-Spalte auf Klein geschrieben. Wie du siehst, haben wir dann nur 15 Kreaturen und drei Spalten mit dem Gewicht, der Herzrate und dem maximalen möglichen Alter.

creature_tbl <- read_excel("data/cluster_animal.xlsx", sheet = 2) |> 
  clean_names() |> 
  mutate(creature = tolower(creature))

In der Tabelle 61.4 sehen wir nochmal die Daten dargestellt und hier erkennst du auch gut, wo das Problem liegt. Die Masse der Tiere reicht von $6g$ beim Hamster bis $120000000g$ beim Wal. Diese Spannweiten in einer Spalte und zwischen den Spalten führt dann zu Problemen bei den Algorithmen. Deshalb müssen wir hier Daten nochmal normalisieren oder aber standardisieren. Je nachdem was da besser passt.

Tabelle 60.2— Übersicht über die 15 Kreaturen mit den drei Eigenschaften in den Spalten. Wir haben hier sehr große Unterschiede in den Datenwerten. Daher müssen wir vor dem Clustern nochmal normalisieren.

creature	mass_grams	heart_rate_bpm	longevity_years
human	9.0e+04	60	70
cat	2.0e+03	150	15
small dog	2.0e+03	100	10
medium dog	5.0e+03	90	15
large dog	8.0e+03	75	17
hamster	6.0e+01	450	3
chicken	1.5e+03	275	15
monkey	5.0e+03	190	15
horse	1.2e+06	44	40
cow	8.0e+05	65	22
pig	1.5e+05	70	25
rabbit	1.0e+03	205	9
elephant	5.0e+06	30	70
giraffe	9.0e+05	65	20
large whale	1.2e+08	20	80

Im Weiteren betrachten wir noch das Beispiel der Gummibärchendaten. Auch hier haben wir echte Daten vorliegen, so dass wir eventuell Ausreißer entdecken könnten. Da wir hier fehlende Werte in den Daten haben, entfernen wir alle fehlenden Werte mit der Funktion na.omit(). Damit löschen wir jede Zeile in den Daten, wo mindestens ein fehlender Wert auftritt. Da wir hier mittlerweile sehr viele Daten vorliegen haben, wollen wir das Problem auf die beiden Quellen FU Berlin und dem Girls and Boys Day eingrenzen.

gummi_tbl <- read_excel("data/gummibears.xlsx")  |>
  filter(module %in% c("FU Berlin", "Girls and Boys Day")) |> 
  select(gender, age, height, semester, most_liked) |> 
  mutate(gender = as_factor(gender),
         most_liked = as_factor(most_liked)) |> 
  na.omit()

Auch hier schauen wir uns in der Tabelle die ersten sieben Beobachtungen von den 192 Beobachtungen an. Wir sehen, dass wir hier mal ganz unterschiedliche Typen an Daten haben. Zum einen sehen wir dichotome Daten, wie das Geschlecht, sowie numerisch wie Alter und Größe, dann noch das Semester mit einer eher geordneten Struktur und nochmal ein Faktor mit sechs Stufen. Das schauen wir uns dann nochmal am Ende an, was wir dann machen können.

Tabelle 60.3— Auszuga us den Gummibärchendaten für die ersten sieben Beobachtungen.

gender	age	height	semester	most_liked
m	35	193	10	lightred
w	21	159	6	yellow
w	21	159	6	white
w	36	180	10	white
m	22	180	3	white
m	22	180	3	green
w	21	163	3	green

Bevor wir jetzt aber die Daten clustern können, müssen wir die Daten vorher nochmal aufbereiten, damit die Algorithmen mit den Daten arbeiten können. Dann müssen wir am Ende auch noch vom tibble() in den data.frame() wechseln, da wir die Zeilennamen häufig brauchen. Wenn du beim tibble() bleiben willst, dann gibt es am Ende noch eine mögliche Lösung für dich.

Weitere Datensätze fürs Clustern

Andere mögliche Datensätze für die Zukunft: chorSub, flower, plantTraits, pluton, ruspini und agriculture. Die Datensätze sind teilweise im R Paket {cluster} enthalten.

Im Weiteren noch die Palmer Penguins mit dem Datensatz penguins aus dem R Paket {palmerpenguins}.

60.3 Daten preprocessing

Wir können die Daten so wir wie sie vorliegen haben in einem Clusteralgorithmus verwenden. Wir führen also keine Transformation der Daten durch, wir nutzen die Daten untransformiert. Dieses untransfomierte Verwenden der Daten führt aber meist dazu, dass Variablen nicht im gleichen Maße berücksichtigt werden. Es macht eben einen Unterschied, ob wir wie bei dem Alter sehr viele verschiedene Werte haben als beim Geschlecht. Es macht auch einen Unterschied, ob das Alter numerische Werte von 20 bis 60 haben kann und das Semester nur numerische Werte von 1 bis 10.

In dem Kapitel 18 findest du die hier verwendeten Standardfunktionen in R aus dem Paket {dlookr} für die Normalisierung sowie Standardisierung mit der Funktion transform(). Wenn es komplexer wird, dann empfehle ich den Workflow, wie er im Kapitel 56 für die Klassifikation von Daten vorgestellt wird. Am Ende des Kapitels zeige ich dir auf den Gummibärechendaten, wie dann alles einmal zusammenkommt.

60.3.1 Normalisieren

Wenn wir Normalisieren dann Zwängen wir Variablen in ein Intervall von $[0;1]$. Es gehen natürlich auch andere Intervalle, aber das Intervall von 0 bis 1 ist wohl das häufigste Intervall was genutzt wird. Dazu nutzen wir die Funktion transform() aus dem R Paket {dlookr} und mit der Option minmax kriegen wir dann alle Werte einer Spalte zwischen 0 und 1. Dann machen wir das mal schnell mit den Daten aus dem Kreaturendatensatz.

norm_creature_tbl <- creature_tbl |> 
  mutate(mass_grams = transform(mass_grams, "minmax"),
         heart_rate_bpm = transform(heart_rate_bpm, "minmax"),
         longevity_years = transform(longevity_years, "minmax")) 
norm_creature_tbl

# A tibble: 15 x 4
   creature    mass_grams   heart_rate_bpm longevity_years
   <chr>       <transfrm>   <transfrm>     <transfrm>     
 1 human       7.495004e-04 0.09302326     0.87012987     
 2 cat         1.616667e-05 0.30232558     0.15584416     
 3 small dog   1.616667e-05 0.18604651     0.09090909     
 4 medium dog  4.116669e-05 0.16279070     0.15584416     
 5 large dog   6.616670e-05 0.12790698     0.18181818     
 6 hamster     0.000000e+00 1.00000000     0.00000000     
 7 chicken     1.200001e-05 0.59302326     0.15584416     
 8 monkey      4.116669e-05 0.39534884     0.15584416     
 9 horse       9.999505e-03 0.05581395     0.48051948     
10 cow         6.666170e-03 0.10465116     0.24675325     
11 pig         1.249501e-03 0.11627907     0.28571429     
12 rabbit      7.833337e-06 0.43023256     0.07792208     
13 elephant    4.166619e-02 0.02325581     0.87012987     
14 giraffe     7.499504e-03 0.10465116     0.22077922     
15 large whale 1.000000e+00 0.00000000     1.00000000

Wir sehen hier, dass in der Spalte mass_grams der Wal den maximalen Wert 1 kriegt und der Hamster den Wert 0. Alle anderen Kreaturen spannen sich numerisch zwischen diesen beiden Extremen auf. Das Gleiche erkenne wir dann auch bei der Herzrate und den Lebenspanne. Hier sind dann auch immer der Hamster und der Wal die extremsten numerischen Vertreter in den Spalten.

Hier helfen natürlich auch die Funktionen von dem R Paket {dplyr} und der Hilfsseite von across() um mehrere Spalten schneller in mutate zu transformieren. Aber wir üben hier nur begrenzt Programmierung und es ist dann an dir dieses Problem zu lösen.

60.3.2 Standardisieren

Die Standardisierung zwingt Variablen in eine $\mathcal{N(0,1)}$ Standardnormalverteilung. Das heißt, wir transformieren alle Variablen auf einen Mittelwert von $0$ und einer Standardabweichung von $1$. Das macht dann auch die Daten sehr schon gleichförmig. Wir wollen also für unseren Gummibärchendatensatz, dass das Alter einen Mittelwert von 0 und eien Standardabweichung von 1 kriegt. Hier nutzen wir auch die Funktion transform() aus dem R Paket {dlookr} mit der Option zscore. Es macht keinen Sinn Faktoren zu standardisieren, wir standardisieren nur numerische Spalte und das Semester zu transformieren ist schon so eine grenzwertige Sache.

scale_gummi_tbl <- gummi_tbl |> 
  mutate(gender = as_factor(gender),
         age = transform(age, "zscore"),
         height = transform(height, "zscore"),
         semester = transform(semester, "zscore"),
         most_liked = as_factor(most_liked))
scale_gummi_tbl

# A tibble: 210 x 5
   gender age        height     semester    most_liked
   <fct>  <transfrm> <transfrm> <transfrm>  <fct>     
 1 m       1.3171177  2.2399120  2.65128580 lightred  
 2 w      -0.4374478 -1.3833258  1.09714758 yellow    
 3 w      -0.4374478 -1.3833258  1.09714758 white     
 4 w       1.4424438  0.8545564  2.65128580 white     
 5 m      -0.3121217  0.8545564 -0.06845609 white     
 6 m      -0.3121217  0.8545564 -0.06845609 green     
 7 w      -0.4374478 -0.9570626 -0.06845609 green     
 8 m      -0.3121217 -0.2111018 -0.06845609 green     
 9 m      -0.1867956  0.4282931 -0.06845609 white     
10 m      -0.5627739  0.8545564 -0.06845609 lightred  
# i 200 more rows

Wie beim Normalisieren helfen hier natürlich auch die Funktionen von dem R Paket {dplyr} und der Hilfsseite von across() um mehrere Spalten schneller in mutate zu transformieren. Wie oben schon angemerkt, dass ist dann deine Fingerübung.

60.3.3 Das `data.frame()` Problem

Leider ist es so, dass fast alle Pakete im Kontext der Clusteranalyse mit den Zeilennamen bzw. row.names() eines data.frame() arbeiten. Das hat den Grund, dass wir gut das Label in den Zeilennamen parken können, ohne das uns eine Spalte in den Auswertungen stört. Meistens ist das Label ja ein character und soll gar nicht in den Clusteralgorithmus mit rein. Deshalb müssen wir hier einmal unsere tibble() in einen data.frame() umwandeln. Die tibble() haben aus gutem Grund keine Zeilennamen, die Zeilennamen sind ein Ärgernis und Quelle von Fehlern und aus gutem Grund nicht in einem tibble() drin. Hier brauchen wir die Zeilennamen aber.

Wir bauen uns also einmal einen data.frame() für unseren Tierdatensatz und setzen die Tiernamen als Zeilennamen bzw. row.names(). Wir entfernen dann auch noch schnell alle fehlenden Werte, denn wir wollen usn hier nicht noch mit der Imputation von fehlenden Werten beschäftigen.

animals_df <- animals_tbl |> 
  na.omit() |> 
  as.data.frame() |> 
  column_to_rownames("animal")

Das Ganze machen wir dann auch noch einmal für die normalisierten Kreaturendaten. Wir wollen dann ja nur auf den normalisierten Daten weitermachen.

norm_creature_df <- norm_creature_tbl |> 
  as.data.frame() |> 
  column_to_rownames("creature")

Wie eben gesagt, ist es teilweise echt nervig immer die row.names() mit zu nehmen und alles ein data.frame() zu nutzen. Insbesondere wenn die Daten sehr groß werden, kann kann es sehr ungünstig sein, alles in einem data.frame() zu lagern. Deshalb gibt es das Paket {tidyclust}, welches ich am Ende nochmal vorstelle.

60.4 Distanzmaße

Wie nah oder weit entfernt sind jetzt zwei Beobachtungen? Wenn wir die Distanz von zwei Beobachtungen zueinander haben, wie weit ist dann eine dritte Beobachtung entfernt? Aus den paarweisen Abständen aller Beobachtungen zueinander können wir dann Cluster bilden. Wir brauchen aber zuallerst die Distanzen der Beobachtungen zuaeinander. Wir betrachten dabei im Folgenden immer die Distanzen zwischen den Zeilen des Datensatzes. Das heißt, wir wollen immer die Distanzen zwischen den Beobachtungen berechnen. Wie nah oder fern sind sich zwei Beobachtungen gegeben den Spalten? Wir schauen uns einmal zwei sehr intuitive Distanzmaße mit der euklidischen sowie der manhattan Distanz an.

Euklidische Distanz: Die euklidische Distanz $d_E$ ist einfach die Wurzel des quadratischen Abstands zwischen zwei Punkten $p$ und $q$. \[ d_E(p,q) = \sqrt{(p-q)^2} \]
Manhattan Distanz: Die manhattan Distanz $d_M$ ist einfach der absolute Abstands zwischen zwei Punkten $p$ und $q$.\[ d_M(p,q) = \lvert p-q \rvert \]

Es gibt noch viel mehr Distanzen, die du berechnen kannst. Je nach R Paket sind unterschiedlich Distanzen dann auszuwählen. Hier eine generelle Empfehlung zu geben ist mir unmöglich. Da müssen wir dann zusammen mal schauen, was für deine Daten dann konkret passt.

Die Funktion dist() als die Standardfunktion: Die Funktion akzeptiert nur numerische Daten als Eingabe und das zu verwendende Abstandsmaß muss eines der Folgenden sein: euclidean, maximum, manhattan, canberra, binary oder minkowski. Die Hilfeseite ?dist() liefert mehr Informationen über die Distanzmaße.
Die Funktion get_dist() aus dem R Paket {factoextra}: Die Funktion akzeptiert nur numerische Daten als Eingabe. Im Vergleich zur Standardfunktion dist() unterstützt sie korrelationsbasierte Abstandsmaße einschließlich der Methoden pearson, kendall und spearman.
Die Funktion daisy() aus dem R Paket {cluster}: Die Funktion kann mit anderen Variablentypen umgehen als numerisch, also auch mit Kategorien und Faktoren. In diesem Fall wird automatisch der Gower-Koeffizient als Metrik verwendet. Der Gower-Koeffizient ist eines der beliebtesten Näherungsmaße für gemischte Datentypen. Weitere Einzelheiten findest du auf der Hilfeseite der Funktion ?daisy.
Die Funktion PCA() aus dem R Paket {FactoMineR}: Die Funktion erlaubt es dir eine Hauptkomponentenanalyse zu rechnen. Das ist aber dann ein eigens Thema für sich. In dem Kapitel 61 erkläre ich nochmal die Hauptkomponentenanalyse und zeige dort auch, wie du mit den Ergebnissen einer Hauptkomponentenanalyse clustern kannst.

Wenn du deine Daten transformierst, dann werden auch die Abstandmaße ähnlicher. Zum Beispiel werden durch die Standardisierung die folgenden Abstandsmaße kelinere Werte ergeben: Euklidisch, Manhattan und die Korrelation. Das ist aber nicht so schlimm, wenn du nicht untransformierte Daten mit transformierten Daten vergleichst.

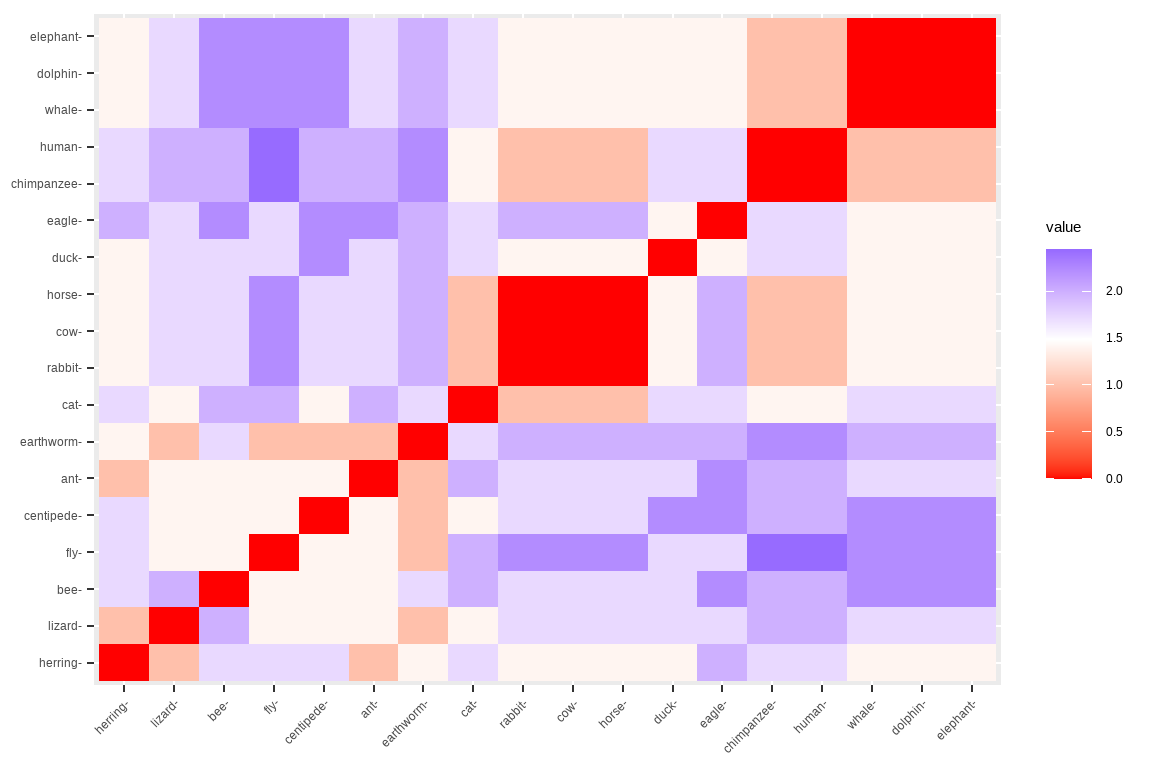
Die Funktion fviz_dist() aus dem R Paket {factorextra} ermöglicht dir die Distanzmatrix zu visualisieren. In der Abbildung 60.1 kannst du dir die Distanzmatrix der Funktion dist() als Heatmap anzuschauen. Wir nutzen die Distanzmatrix dann aber gleich um auf den Distanzen Cluster zu bilden.

animals_df  |> 
  dist(method = "euclidean") |> 
  fviz_dist()

Abbildung 60.1— Heatmap der euklidischen Distanzen des Tierdatensatzes. Die Matrix ist symmetrisch. Hohe, blaue Werte bedeuten eine große Distanz dagegen kleine,rote Werte eine geringe Distanz zwischen den Beobachtungen.

Wenn du also die Distanzen zwischen deinen Beobachtungen berechnet hast, kannst du mit der Distanzmatrix entweder hierarchisch Clustern oder über den $k$-NN Algorithmus Gruppen bilden.

60.5 Algorithmen fürs Clustern

Jetzt schauen wir uns die zwei wichtigsten Algorithmen für das Clustern von Daten einmal an. Zum einen ist es die Hierarchische Clusteranalyse, die einen Baum wachsen lässt und wir so eine Entscheidung über die Gruppenzugehörigkeit bekommen. Der andere Algorithmus ist der $k$ nächste Nachbarn (abk. k-NN) Methode, die sich immer die nächsten Beobachtungen anschaut und versucht ähnliche Beobachtungen zusammen zu führen.

Ein Clusteralgorithmus braucht zwingend eine Distanz(matrix)!

Du kannst nur auf Distanzen clustern. Das heißt, dass du deine Daten irgendwie in Distanzen zwischen den Beobachtungen umwandeln musst. Im vorherigen Abschnitt hast du ja schon die wichtigsten Distanzalgorithmen kennen gelernt.

Wie immer gibt es verschiedene Methoden und Optionen für die beiden Algorithmen. Am Ende musst du schauen, ob die Ergebnisse des Clustern einen Sinn innerhalb deiner Fragestellung ergeben. Es kann also sein, dass du recht viele Optionen und Varianten durchprobieren musst, bevor du dann was gefunden hast was dich zufrieden stellt.

60.5.1 Hierarchische Clusteranalyse

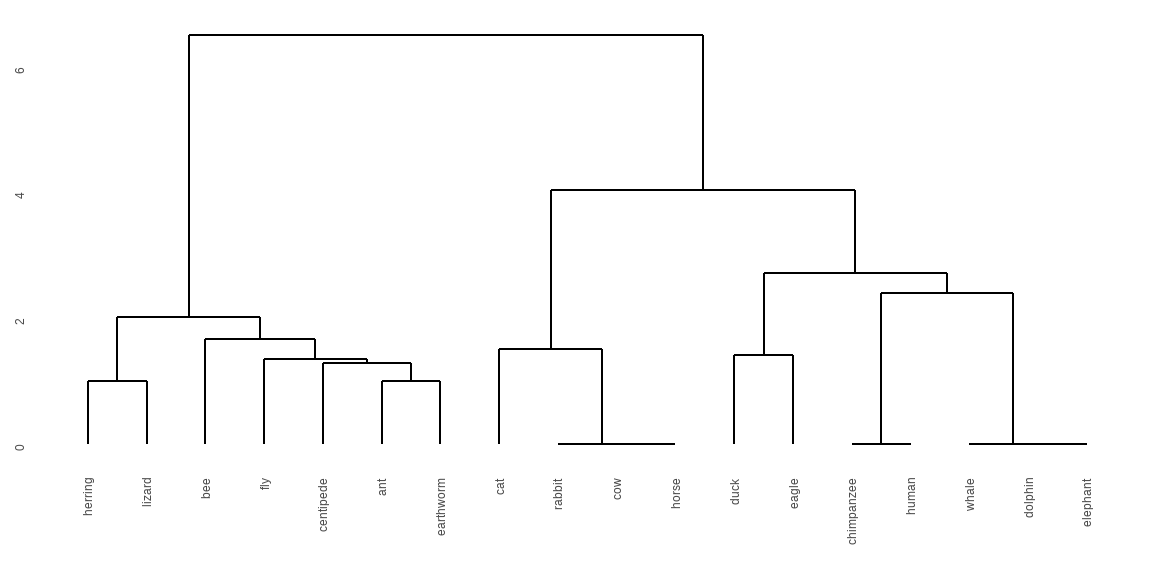
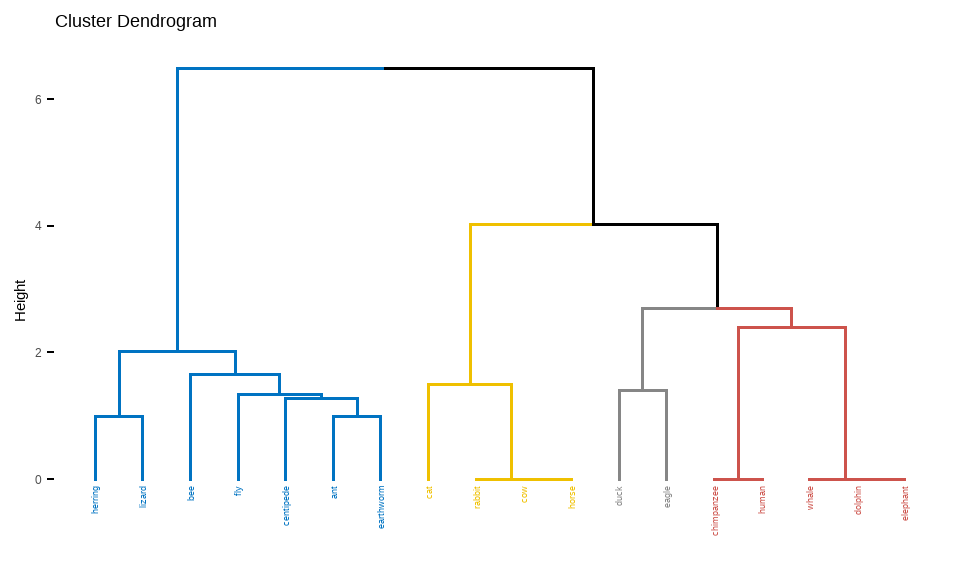
Gleich vorweg mal das Ergebnis einer hierarchischen Clusteranalyse der Tierdaten dargestellt als Dendrogramm in der Abbildung 60.2. Wir sehen, dass alle Beobachtungen anhand ihrer Distanz in einen Baum angeordnet werden. Das Tier ganz links ist maximal vom Tier ganz rechts entfernt. Damit ist also der Hering maximal weit vom Elefanten nach den Eigenschaften - also Spalten - in den Tierdaten entfernt.

Abbildung 60.2— Beispiel für das Ergebnis einer hierarchischen Clusteranalyse der Tierdaten dargestellt als Dendrogramm

Wie bauen wir uns so ein Dendrogramm? Wir nehmen als erstes eine Distanzmatrix und nutzen dann die Distanzmatrix um nach verschiedenen Regeln die hierarchische Clusteranalyse durchzuführen. Es gibt vier gängige Ansätze für die Cluster-Cluster-Distanzierung, auch Linkage genannt:

single linkage: Der Abstand zwischen zwei Clustern ist der Abstand zwischen den beiden nächstgelegenen Beobachtungen. In R nutzen wir dann single als Option.
average linkage: Der Abstand zwischen zwei Clustern ist der Durchschnitt aller Abstände zwischen den Beobachtungen in einem Cluster und den Beobachtungen im anderen Cluster. In R ist es dann die Option average.
complete linkage: Der Abstand zwischen zwei Clustern ist der Abstand zwischen den beiden am weitesten entfernten Beobachtungen. Auch hier passt es dann mit dem Optionnamen von complete.
centroid method: Der Abstand zwischen zwei Clustern ist der Abstand zwischen ihren geometrischen Mittel oder Medianen. Hier nutzen wir die Option median.
ward method: Der Abstand zwischen zwei Clustern ist proportional zur Zunahme der Fehlerquadratsumme, die sich aus der Verbindung der beiden Cluster ergeben würde. Die Fehlerquadratsumme wird als Summe der quadrierten Abstände zwischen den Beobachtungen in einem Cluster und dem Schwerpunkt des Clusters berechnet. In R haben wir hier die Wahl zwischen ward.D und ward.D2. Wenn, dann nutze bitte ward.D2 da es sich um die neuere Implementierung handelt, die weniger fehleranfällig ist.

Wir nehmen also die Daten und berechnen erst die Distanzmatrix und dann die hierarchische Clusteranalyse. Da wir zum einen aus verschiedenen Distanzalgorithmen plus verschiedenen Algorithmen für das hierarchische Clustern wählen können, musst du hier immer mal wieder rumprobieren, bis du das richtige für dich gefunden hast. Wir schauen uns später noch Kriterien an, aber am Ende musst du entscheiden, ob es inhaltlich mit den gefundenen Gruppen passt.

Die hierarchische Clusteranalyse führen wir in R mit dem Paket {hclust} durch. Die Distanz berechnen wir hier mit der Funktion dist(). Dann haben wir auch schon unser Clustern abgeschlossen. Der Baum ist gewachsen. Die Funktion hclust() ist nur eine mögliche Funktion für das hierarchische Clustern. Das R Paket {cluster} kennt noch eine mehr auch wenn ohne gute Hilfeseite. Du musst die Paketbeschreibung eine gute Übersicht an möglichen Algorithmen nehmen und unter den plot.* Funktionen schauen. Jeder Algorithmus hat eine eigene Funktion für einen Plot und so findest du schnell die Algorithmen. Hier jetzt aber weiter mit der Standardfunktion hclust().

h_clust_animal <- animals_df  |> 
  dist(method = "euclidean") |> 
  hclust(method = "ward.D")

Jetzt ist aber die Frage, wie kriegen wir die Gruppen? Bis jetzt ist ja jedes einzelne Tier für sich. Wir müssen also von den Enden des Baumes wieder noch oben gehen um unsere Tiere Gruppen zuzuordnen. Das macht die Funktion cutree(), die uns dann $k$ Gruppen bildet. Das können wir dann einfach einmal machen und uns die sortierten Gruppen wiedergeben lassen.

grp_animal <- cutree(h_clust_animal, k = 3)
grp_animal |> sort()

       ant        bee  centipede  earthworm        fly    herring     lizard 
         1          1          1          1          1          1          1 
       cat        cow      horse     rabbit chimpanzee    dolphin       duck 
         2          2          2          2          3          3          3 
     eagle   elephant      human      whale 
         3          3          3          3

Wie wir sehen haben wir drei Gruppen, die Zahl sagt die Gruppe aus und die Namen dann das Tier. Du kannst dir auch andere Gruppenzuordnungen ansehen und schauen, welche inhaltlich besser passen würde. Hier haben wir das Problem, das der Chimpanse zusammen mit dem Delphin und dem Adler eingeordnet wird. Irgendwie nicht so die richtige Aufteilung. Da würde eine oder zwei Gruppen mehr viellicht besser passen.

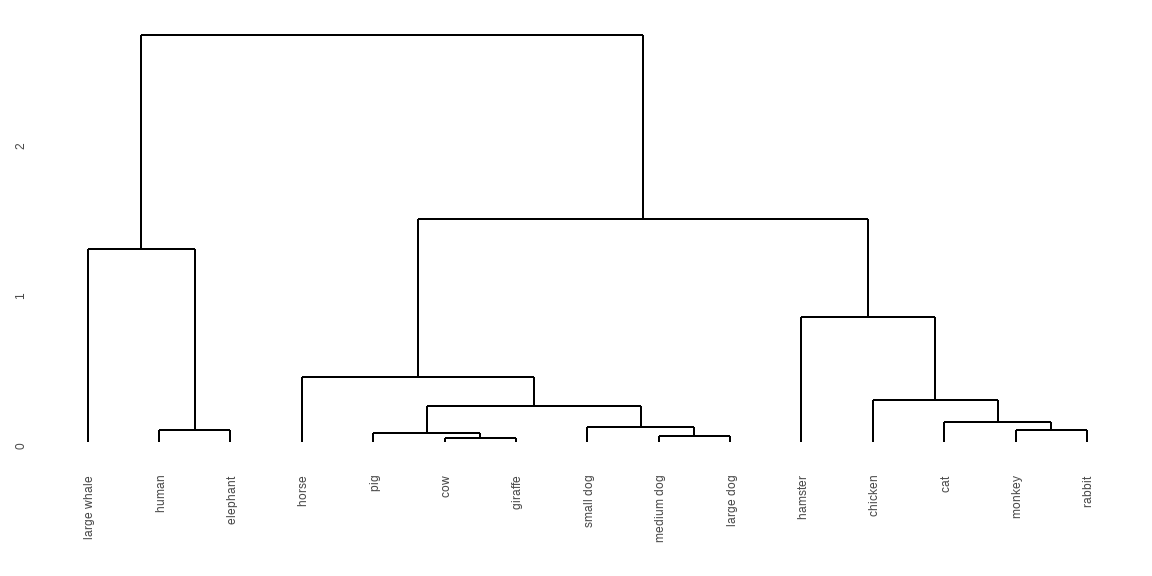
Wir nehmen jetzt mal die normalisierten Kreaturen und schauen was wir hier rauskriegen. Die Funktionen sind die gleichen wie eben schon bei den Tierdaten.

h_clust_creature <- norm_creature_df |> 
  dist(method = "euclidean") |> 
  hclust(method = "ward.D")

Auch hir schneiden wir die Bäume dann so zurecht, dass wir am Ende drei Gruppen erhalten. Auch hier kannst du dann immer wieder spielen, und schauen, ob du nicht mit mehr Gruppen ein besseres Ergebnis erhälst.

grp_creature <- cutree(h_clust_creature, k = 3)
grp_creature |> sort()

      human    elephant large whale         cat     hamster     chicken 
          1           1           1           2           2           2 
     monkey      rabbit   small dog  medium dog   large dog       horse 
          2           2           3           3           3           3 
        cow         pig     giraffe 
          3           3           3

Ja, jetzt haben wir den gleichen Fall, dass der Mensch zusammen mit dem Wal und dem Elefanten geclustert wurde. Irgendwie nicht so toll. Dann wollen wir uns mal im nächsten Schritt anschauen, wie wir ein Ergebnis einer hierarchischen Clusteranalyse visualisieren können.

60.5.2 Dendrogramm

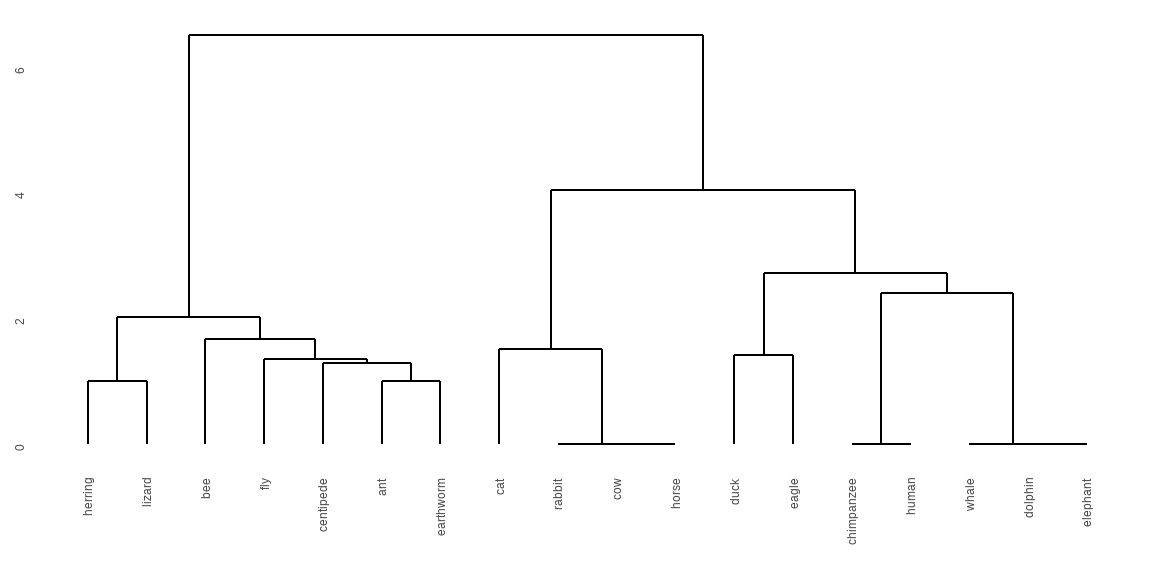
Nun können wir uns die Ergebnisse einer hierarchischen Clusteranalyse visualisieren. Dafür nutzen wir dann Dendrogramme. Dendrogramme sind nichts anders als Bäume. In der Abbildung 60.3 siehst du die Ergebnisse der hierarchischen Clusteranalyse als Dendrogramm. Wir nutzen hier die Funktion ggdendrogram(). Wie immer gibt es noch mehr uns noch schönere Dendrogramme, aber das übersteigt diesen Abschnitt. Schau dir das Paket {dendextend} und das Tutroium Introduction to dendextend einml genauer an. Dort findest du dann noch mehr zu Dendrogrammen.

Auch gibt es noch ein schönes Tutorium für die Analyse weiterer spannender Datensätzen unter Hierarchical cluster analysis on famous data sets - enhanced with the dendextend package

ggdendrogram(h_clust_animal)
ggdendrogram(h_clust_creature)

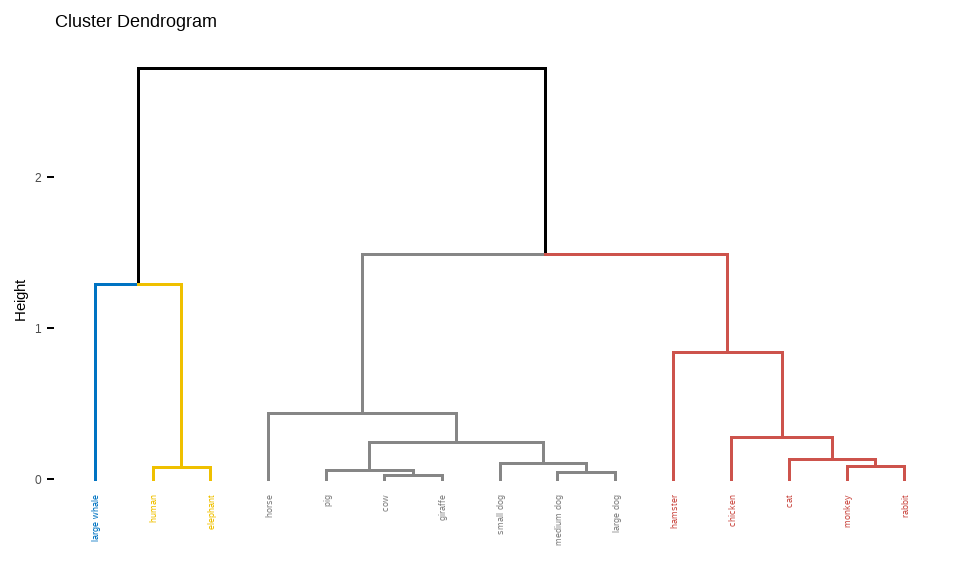
Hier sehen wir, was wir schon bei der Gruppenerstellung durch die Funktion cutree() gesehen haben. Irgendwie passt die Einteilung nicht so richtig. Wir sehen, dass bei den Tieren der Elefanten zusammen mit dem Wal und dem Delphin eingeordnet wird. Bei den Kreaturen haben wir den Mensch zusammen mit dem Elefanten. Also müssten wir hier nochmal zurück und entweder an den Distanzmaßen schrauben oder aber eine andere linkage in der hierarchischen Clusteranalyse nehmen.

Auch geht es noch schöner durch die Funktion fviz_dend() in der wir dann auch direkt die Gruppen farblich kennzeichnen können. Das macht die Überprüfung welches Tier wo eingeordnet wird leichter. Hier habe ich dann bei den Kreaturendaten mal vier Gruppen gewählt und dann ist wenigstens der Wal nicht mehr in der Gruppe der Menschen und Elefanten.

fviz_dend(h_clust_animal, cex = 0.5, k = 4, palette = "jco") 
fviz_dend(h_clust_creature, cex = 0.5, k = 4, palette = "jco")

Wie du schön siehst, ist eine hierarchische Clusteranalyse nur so gut wie das entsprechende Dendrogramm. Ohne eine visuelle Überpüfung ist es meistens schwer zu sehen ob es dann wirklich passt. Hast du hunderte von Beobachtungen, dann wird es natürlich schwerer, aber dennoch solltest du dir einmal die Dendrogramme ansehen. Aber da gibt es dann auch bei den Tutorien mehr Hilfe und noch andere Einblicke.

60.5.3 k-means Clusteranalyse

Kommen wir dann zum zweiten Algorithmus, der darauf basiert sich immer die $k$ nächsten Nachbarn anzuschauen und zu entscheiden zu welcher Gruppe die Beachtungen gehören sollen. Das ist sehr simple das Prinzip des Algorithmus. Wir gehen hier jetzt aber nicht weiter in die Tiefe, der $k$-NN Algorithmus clustert nicht in der Form eines Baumes sondern schaut sich die direkten Verwandtschaft zwischen von der Distanz nahe liegenden Beobachtungen an. Daher können wir den Algorithmus auch auf alle Distanzmatrizen anwenden. Auch hier verweise ich nochmal auf das R Paket {cluster} welches als eine mögliche Alternative für die Funktion kmeans() die robustere Funktion pam() kennt. Wir nutzen hier einmal die Standardfunktion für das Clustern mit $k$ nächsten Nachbarn, aber du solltest auch die anderen

Auch gibt es noch ein schönes Tutorium für die Analyse weiterer spannender Datensätzen unter K-means Cluster Analysis

Die kmeans() Funktion ist relativ simple. Wir definieren einfach wie viele Cluster oder Gruppen centers gebildet werden sollen. Der Algorithmus versucht jetzt die Beobachtungen um diese Zentren zu gruppieren. Dabei müssen wir vorab sagen wie viele Gruppen wir wollen. Wir sehen gleich nochmal ein Möglichkeit uns da iterativ zu nähern, das klappt aber nicht immer.

knn_animal <- animals_df |> 
  kmeans(centers = 4)
knn_creature <- norm_creature_df |> 
  kmeans(centers = 4)

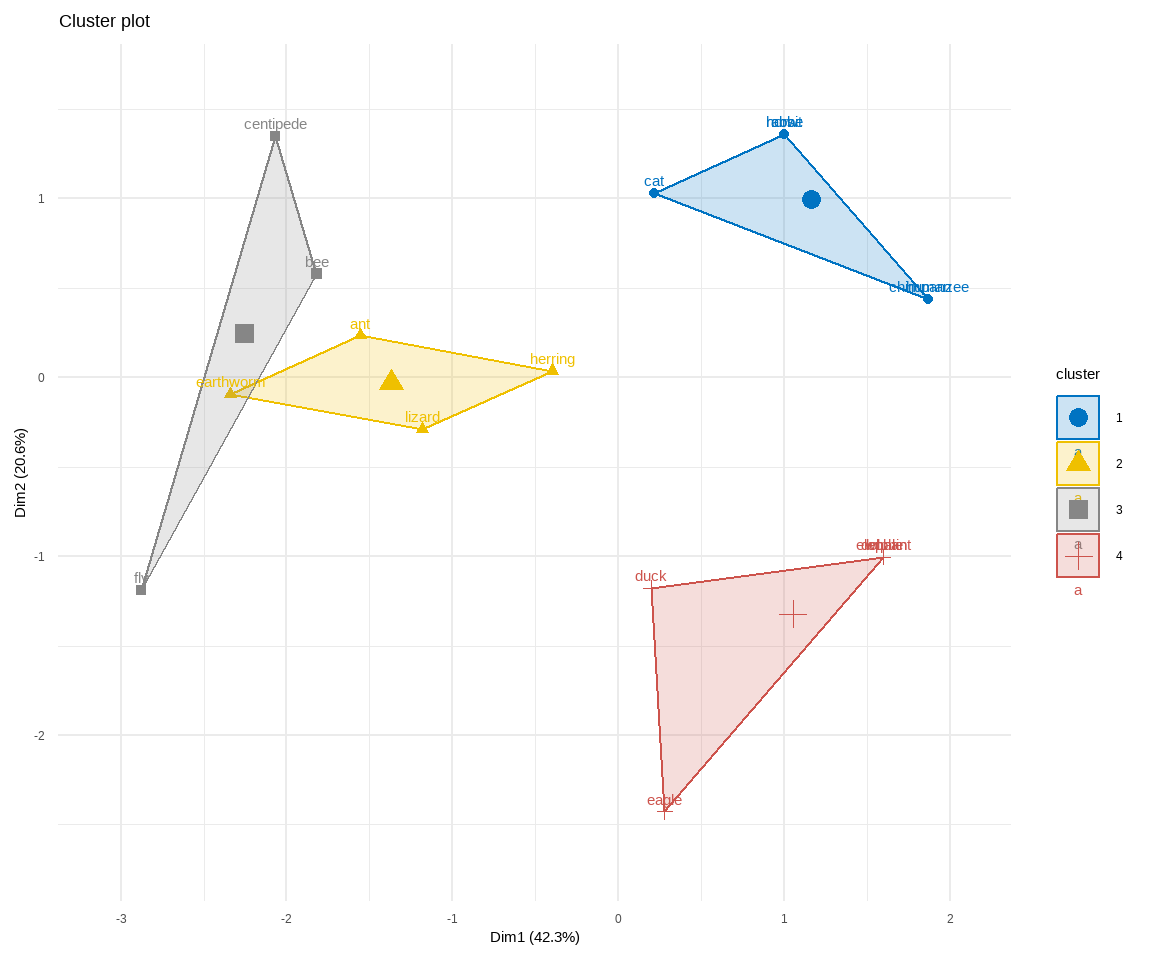
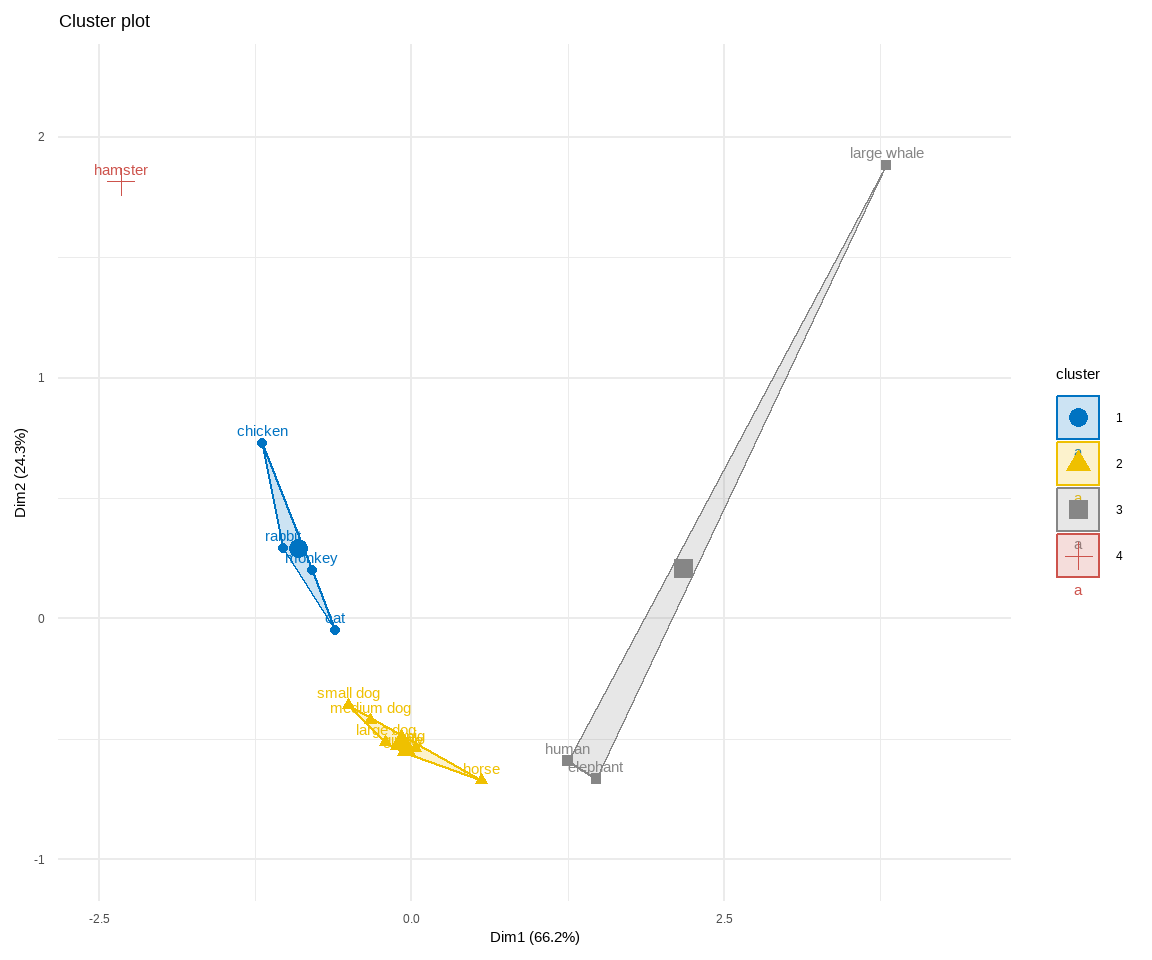
Wir schauen uns hetzt nicht die Ausgabe an, sondern wollen gleich mal in der Abbildung 60.5 die Ergebnisse des Clusterings. Da haben wir dann schon fast ein ähnlich gutes Bild drüber. Du kannst dir aber mit animals_df$cluster die Cluster angeben lassen. Wir müssen dann noch die Fläche links und rechts auf dem Plot etwas erweitern damit wir dann dort mehr drauf kriegen. Wir nutzen hier die Funktion fviz_cluster() welche dafür geeignet ist gut Cluster darzustellen.

fviz_cluster(knn_animal, data = animals_df, palette = "jco") +
  theme_minimal() +
  scale_x_continuous(expand = expansion(add = c(0.5, 0.5))) +
  scale_y_continuous(expand = expansion(add = c(0.5, 0.5))) 

fviz_cluster(knn_creature, data = norm_creature_df, palette = "jco") +
  theme_minimal() +
  scale_x_continuous(expand = expansion(add = c(0.5, 1))) +
  scale_y_continuous(expand = expansion(add = c(0.5, 0.5)))

Wie du siehst funktioniert es einigermaßen für die Tierdaten. Ich möchte nochmal den Fokus auf die Symbole in der Mitte der Clusterflächen lenken, dort siehst du dann den Mittelpunkt. Alle Beobachtungen, die nah an dem Wert sind, werden zu diesem Cluster gezählt. Teilweise funktioniert das etwas komplizierter, den der Regenwurm ist auf jeden Fall näher an dem Mittelpunkt des grauen Clusters als dem gelben Clusters. Es gibt also noch sekundäre Regeln, die versuchen einen Cluster möglichst symmetrisch zu erstellen. Bei den Kreaturdaten haben wir auch das Problem, dass wieder unser Wal mit dem Elefanten und dem Menschen zusammengepackt wird. Hier scheinen die Daten wirklich nicht gut zu sein.

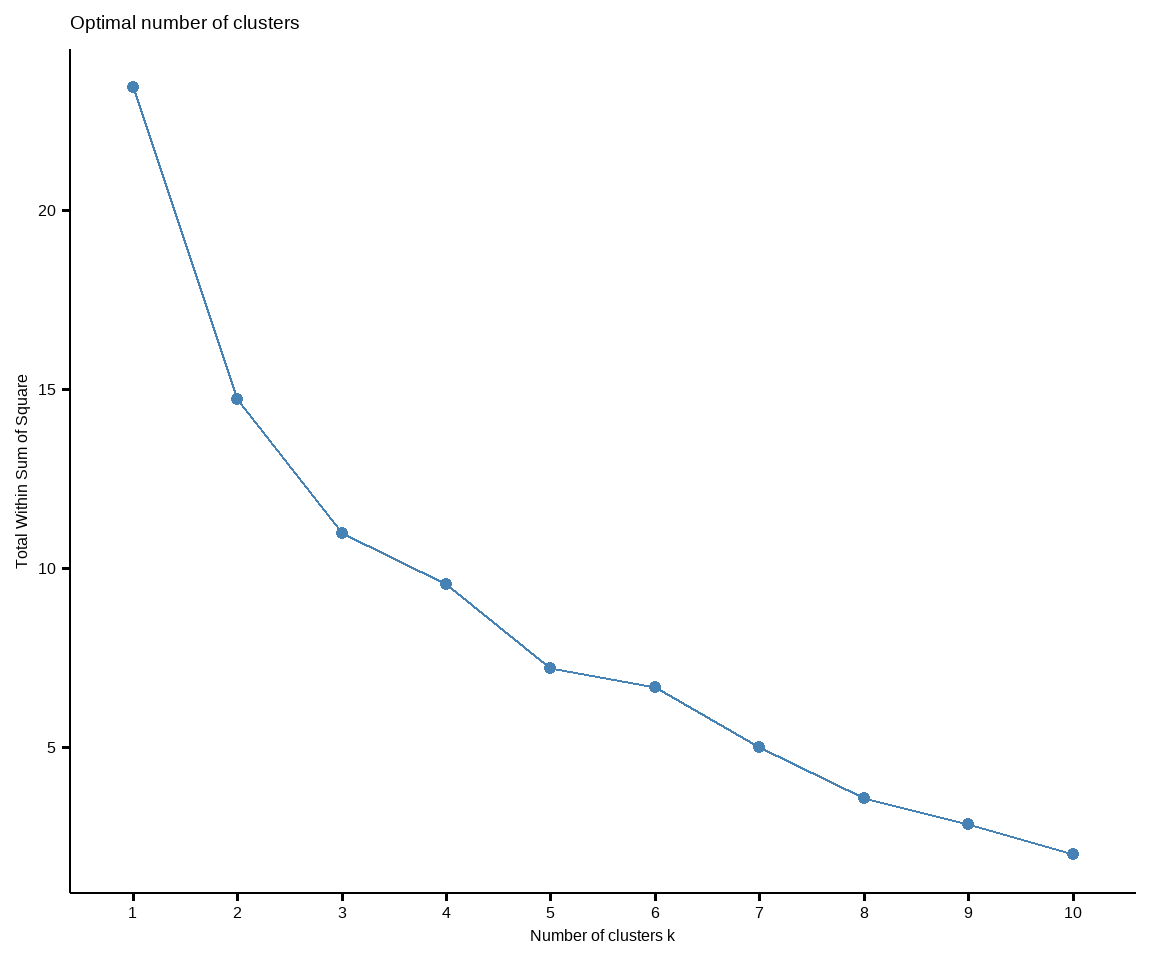
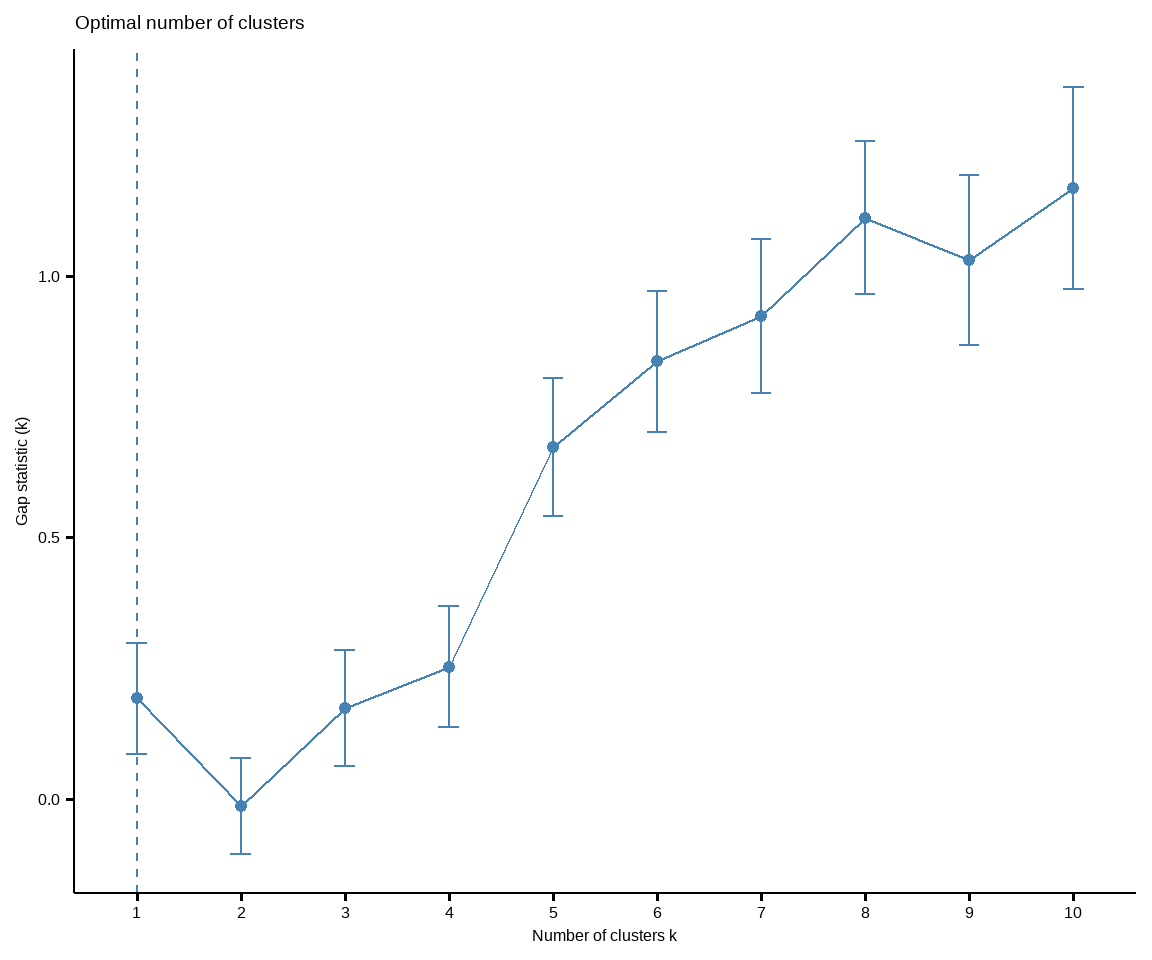
Was ist das optimale $k$ für die Anzahl an Gruppen, die wir in den Algorithmus stecken wollen? Dafür gibt es die Optimierungsfunktion fviz_nbclust(), die uns versucht die optimale Anzahl an Clustergruppen visuell abzuschätzen. Wir sehen die Kurven einmal in der Abbildung 60.6. Für die Tierdaten hat die Methode gap_stat nicht funktioniert, so dass wir da keine Entscheidung raus kriegen sondern selber schauen müssen.

animals_df |> 
  fviz_nbclust(kmeans, method = "wss")

norm_creature_df |> 
  fviz_nbclust(kmeans, method = "gap_stat")

Wie wir sehen gibt es bei den Tierdaten zwar einen größeren Sprung von einem auf zwei Cluster, aber das hilft uns nichts. Wir wollen ja nicht nur einen Cluster wählen, dann können wir uns das Clustern auch sparen. Die anderen Sprünge sind auch eher gleichmäßig, so dass wir hier gar keine optimale Anzahl an Clustern haben. Das heißt, dass wir vermutlich die Tierdaten gar nicht so gut clustern können. Auch liefert der Algorithmus gap_stat die Empfehlung für nur einen Cluster. Das hilft uns nun auch nichts besonders weiter. Hier scheinen die Daten wirklich etwas schwierig zum clustern zu sein.

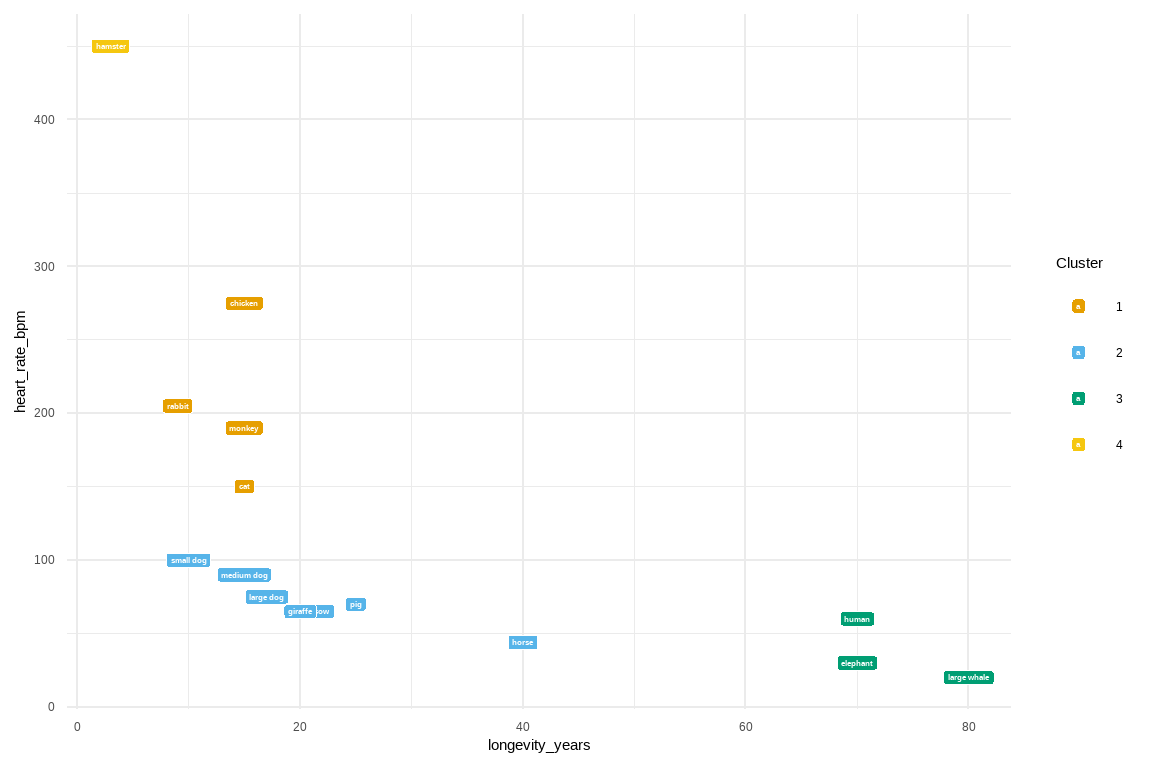
Wenn du kontienuierliche Spalten in deinen Daten hast, dann kannst du natürlichb auch zwei Spalten auswählen und dir die Aufteilung der Beobachtungen über diese beiden Spalten anschauen. In der Abbildung 60.7 habe ich das mal für zwei Spalten aus dem Kreaturendaten gemacht und dann die Individuen einmal nach den Clustern eingefärbt. Hier siehst du ganz gut, dass der Elefant und Mensch sowie Wal einfach alle drei lange Leben und eine geringe Herzrate haben. Das macht dann diese drei Wesen sehr ähnlich laut unseren Daten. Das heißt natürlich nicht, das der Mensch ein Wal ist. Es braucht einfach mehr Daten und damit Variablen um die Wesen voneinander zu trennen.

ggplot(creature_tbl, aes(longevity_years, heart_rate_bpm, label = creature)) + 
  theme_minimal() +
  geom_label(aes(fill = as_factor(knn_creature$cluster)), colour = "white", 
             fontface = "bold", size=2) +
  scale_fill_okabeito(name = "Cluster")

Das war es dann schon hier mit dem kurzen Ausflug zum Clustern mit dem kmeans Algorithmus. Du findest dann in dem Kapitel 61 zu der Hauptkomponentenanalyse nochmal die Anwendung auf einem anderem Gebiet. Hier ist aber vorerst einmal Schluß mit den Grundlagen.

60.5.4 Silhouettenplot

Jetzt haben wir Gruppen gefunden und wollen wissen, ob das jetzt auch gute Gurppen sind oder nicht. Wenn wir nicht so viele Beobachtungen haben, dann können wir uns ja die Daten direkt anschauen. Aber häufig wollen wir auch einen Wert haben, der uns eine Bewertung erleichtert. Um das Ergebnis der Clusteranalyse zu beurteilen, eignet sich ein Silhouettenplot. Ein Silhouettenplot zeigt für jede Beobachtung $i$ die Silhouettenbreite $s_i$, welche definiert ist als normierte Differenz der kleinsten Distanz zu den Beobachtungen außerhalb der eigenen Gruppe und dem Mittelwert der Distanzen innerhalb einer Gruppe. Die Silhouettenbreite $s_i$ kann jeden Wert im Intervall [-1, 1] annehmen und wird von dir folgendermaßen interpretiert.

$s_i = 1$ Die Beobachtung ist dem richtigen Cluster zugeordnet. Oder eher dem Cluster, der gut passt gegeben den Daten und der Anzahl an Clustern.
$s_i = 0$ Die Beobachtung hätte ebenso gut einer anderen Gruppe zugeordnet werden können. Und wurde also eher zufällig dem Cluster zugeordnet.
$s_i = -1$ Die Beobachtung ist schlecht zugeordnet. Und sollte damit eher einem anderen Cluster zugeordnet werden, den es vielleicht nicht gibt, da du zu wenige Clustergruppen vorab definiert hast.

Dann kannst du dir darüber hinaus die durchschnittliche Silhouettenbreite über alle Beobachtungen berechnen lassen, womit sich die Gruppenbildung als Ganzes beurteilen lässt. Die durchschnittliche Silhouettenbreite wird dann von dir analog interpretiert. Aber Achtung, nur weil du gute Werte der Qualität hier kriegst, heißt es nicht, dass du gute Cluster im Sinne deiner Fragestellung gefunden hast.

Das R Paket {tidyclust} hat auch die Funktion silhouette(), die dir auch ermöglicht die Silhouettenplots erstellen zu lassen.

Wir nutzen jetzt einmal die Funktion silhouette() aus dem R Paket {cluster} und berechnen uns aus dem Vektor der Gruppenzugehörigkeit, also den Clustern, und der Distanzmatrix aus der die Cluster bestimmt wurden dann die Silhouettenplots. Dafür müssen wir dann die Ausgabe der Funktion silhouette() noch auf ein tibble() umbauen damit wir die Ausgabe gut in {ggplot} abbilden können.

silhouette_animals_tbl <- cluster::silhouette(knn_animal$cluster, 
                                              dist(animals_df, "canberra")) |> 
  as_tibble() |> 
  mutate(animal = row.names(animals_df),
         cluster = as_factor(cluster))

Und das ganze dann nochmal für die Kreaturendaten.

silhouette_creature_tbl <- cluster::silhouette(knn_creature$cluster, 
                                               dist(norm_creature_df, "canberra")) |> 
  as_tibble() |> 
  mutate(creature = row.names(norm_creature_df),
         cluster = as_factor(cluster))

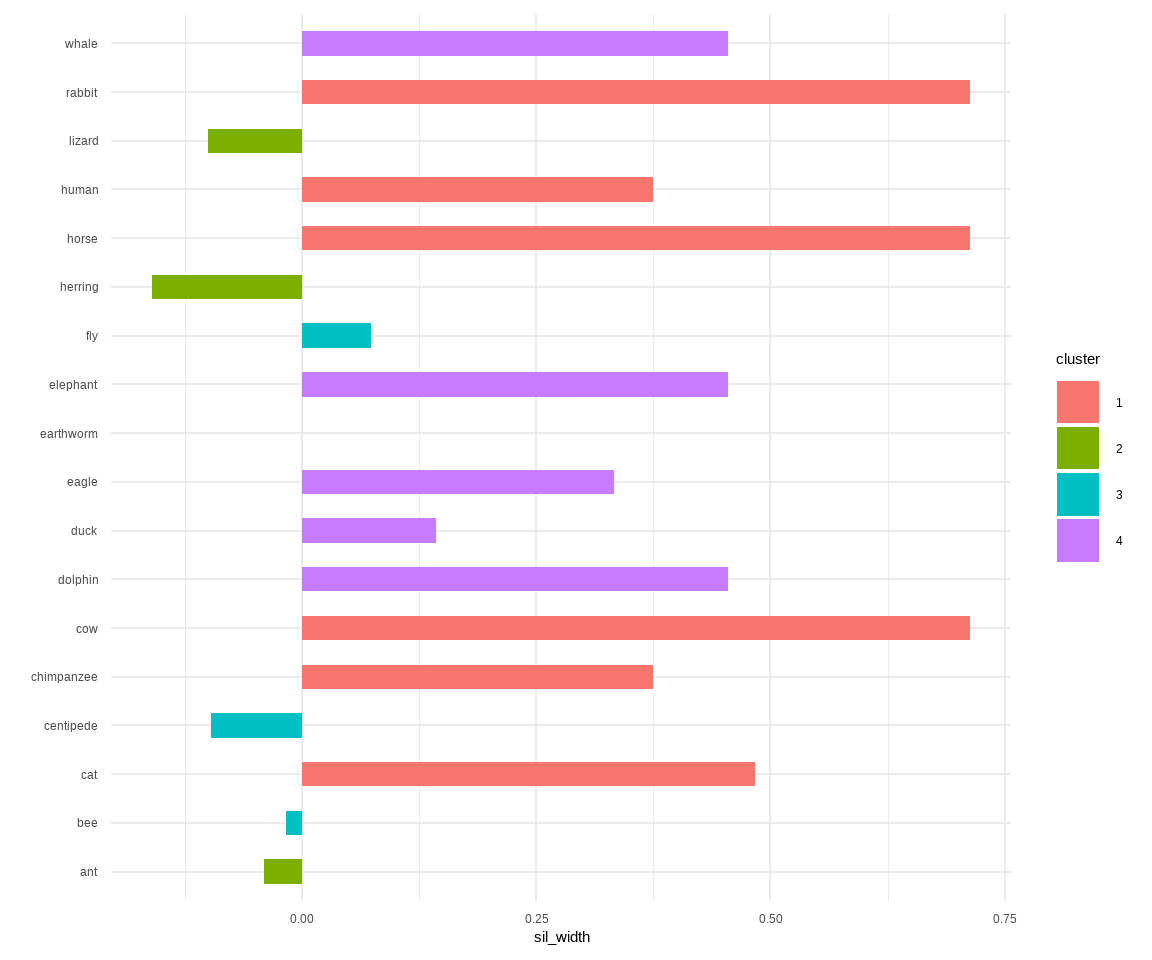
In der Abbildung 60.8 siehst du die Silhouettenplots für die beiden beispielhaften Datensätze. Die Regel ist, dass alles was nach links geht schlecht ist, was bei der Null liegt irrelevant und je weiter nach rechts, desto besser ist.

ggplot(silhouette_creature_tbl, aes(x = creature, y = sil_width, fill = cluster)) +
  theme_minimal() +
  geom_bar(stat = "identity", width = 0.5) + 
  coord_flip() + 
  labs(x = "")

ggplot(silhouette_animals_tbl, aes(x = animal, y = sil_width, fill = cluster)) +
  theme_minimal() +
  geom_bar(stat = "identity", width = 0.5) + 
  coord_flip() + 
  labs(x = "")

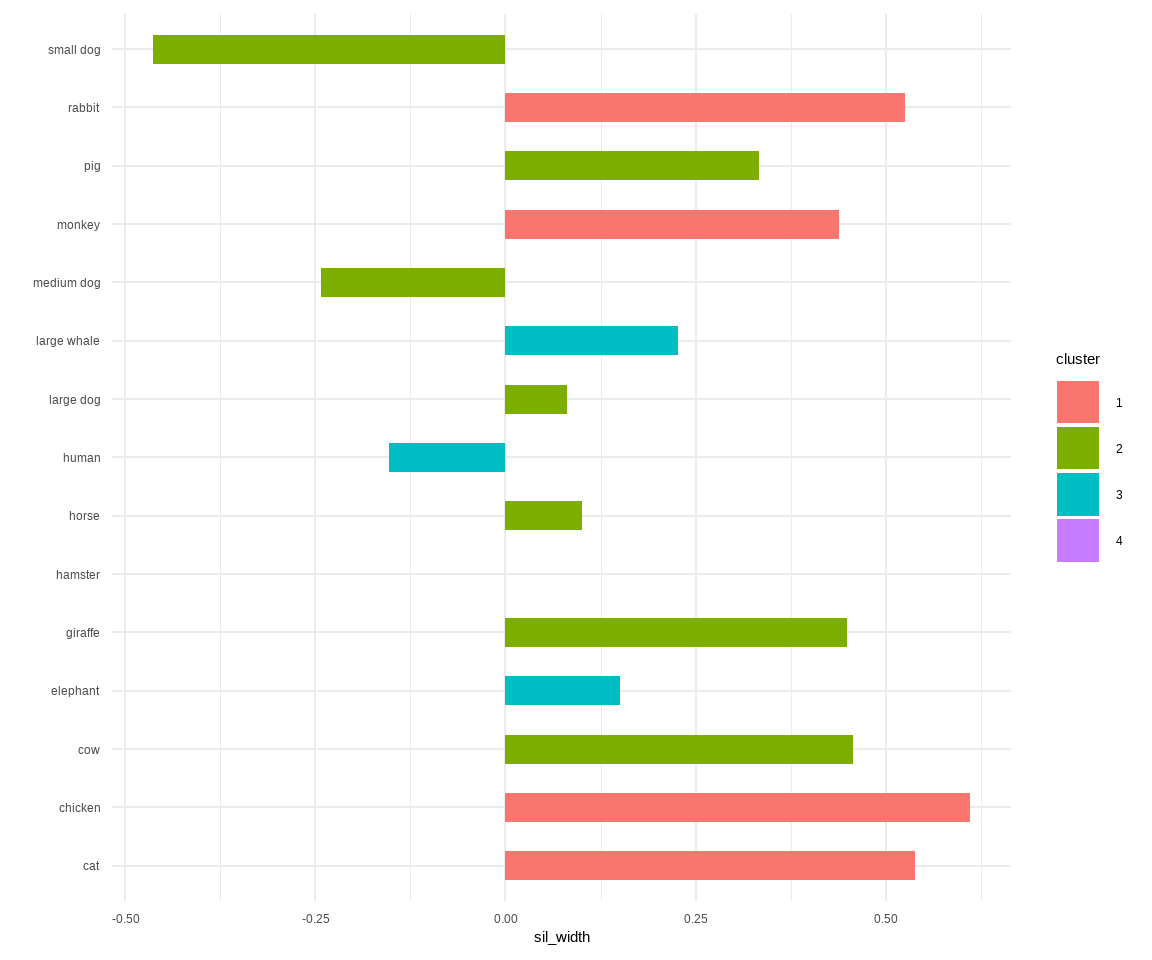
Bei den Tierdaten sehen wir, dass die Beobachtung des kleinen Hundes sowie des mittleren Hundes eigentlich schädlich für die Zuordnung der Cluster ist. Der Hamster ist dabei faktisch egal. Bei den Kreaturendaten ist es auch spannend, da wir hier den Hering und die Eidechse als problematisch sehen. Beachte, dass wir alles immer im Kontext der Distanzmatrix und dem Algorithmus sehen müssen. Daher kannst du dir für beliebige Kombinationen aus Distanzmatrix, Anzahl Clustern und dem Algorithmus dann jeweils die Silhouettenplots erstellen lassen und schauen, was ist das beste Clustering?

Wenn du dir die Silhouettenplots automatisiert ausgeben willst, dann kriegst du natürlich sehr viele Plots. Da ist es dann besser nach einem möglichst hohen Silhouettenwert zu schauen. Deshalb hier einmal der mittlere Silhouettenwert für die Tierdaten sowie deren Standardabweichung.

silhouette_animals_tbl |> 
  summarise(mean(sil_width),
            sd(sil_width))

# A tibble: 1 x 2
  `mean(sil_width)` `sd(sil_width)`
              <dbl>           <dbl>
1             0.271           0.300

Das Ganze dann auch einmal für die Kreaturendaten berechnet.

silhouette_creature_tbl |> 
  summarise(mean(sil_width),
            sd(sil_width))

# A tibble: 1 x 2
  `mean(sil_width)` `sd(sil_width)`
              <dbl>           <dbl>
1             0.204           0.318

Wir sehen, dass wir am Ende mit unserem Clustern bei den Kreaturendaten eine bessere Zuordnung zu den Clustern erhalten. Wenn wir den Algorithmus tunen wollen würden, dann würden wir für verschiedene Kombinationen aus Algorithmus und Distanzmatrixen dann jeweils die mittleren Silhouettenwerte berechnen. Dazu kommt dann noch, dass wir auch die Anzahl der Cluster tunen können. Du siehst, es wird sehr schnell sehr viel, was man hier machen kann. Ich schaue dann mal, ob ich dann was finde, was ich in den Beispielhaften Auswertungen zeige.

60.5.5 Heatmap

Heatmaps visualisieren die Distanzen zwischen Beobachtungen indem Heatmaps die numerischen Distanzwerte in einer Farbskala darstellen. Wenn es um Heatmaps in R geht, dann gibt es so viele Möglichkeiten eine Heatmap in R zu erstellen, so dass ich hier nur einen Ausschnitt aus den Sammlungen vorstellen kann. Ich selber mag gerne das R Paket {pheatmap} mit dem guten Tutorium Making a heatmap in R with the pheatmap package. Am Anfang des Kapitels wird dieses Paket auch als empfehlenswert genannt. Daneben schauen wir uns nochmal die Heatmaps in dem R Paket {gplots} mit der Funktion heatmap.2() an.

Weitere Tutorien für die Erstellung einer Heatmap

Wie immer gibt es eine Vielzahl an tollen Tutorien, die eine Heatmap gut erklären. Ich habe hier einmal eine Auswahl zusammengestellt und du kannst dich da ja mal vertiefend mit beschäftigen, wenn du willst. Teile der Tutorien findest du vermutlich hier im Kapitel wieder.

Eine Übersicht zu Heatmap in R: Static and Interactive Visualization
Das Tutorium Hierarchical cluster analysis on famous data sets.
Das R Paket {heatmaps} Tutorial heatmaps liefert nochmal Beispiele mit genetischen Datensätzen.
Das R Paket ComplexHeatmap, was sich vom R Paket {pheatmap} inspirieren lies. Das geht dann aber hier zu weit, schauen da, wenn du wirklich Heatmaps brauchst.

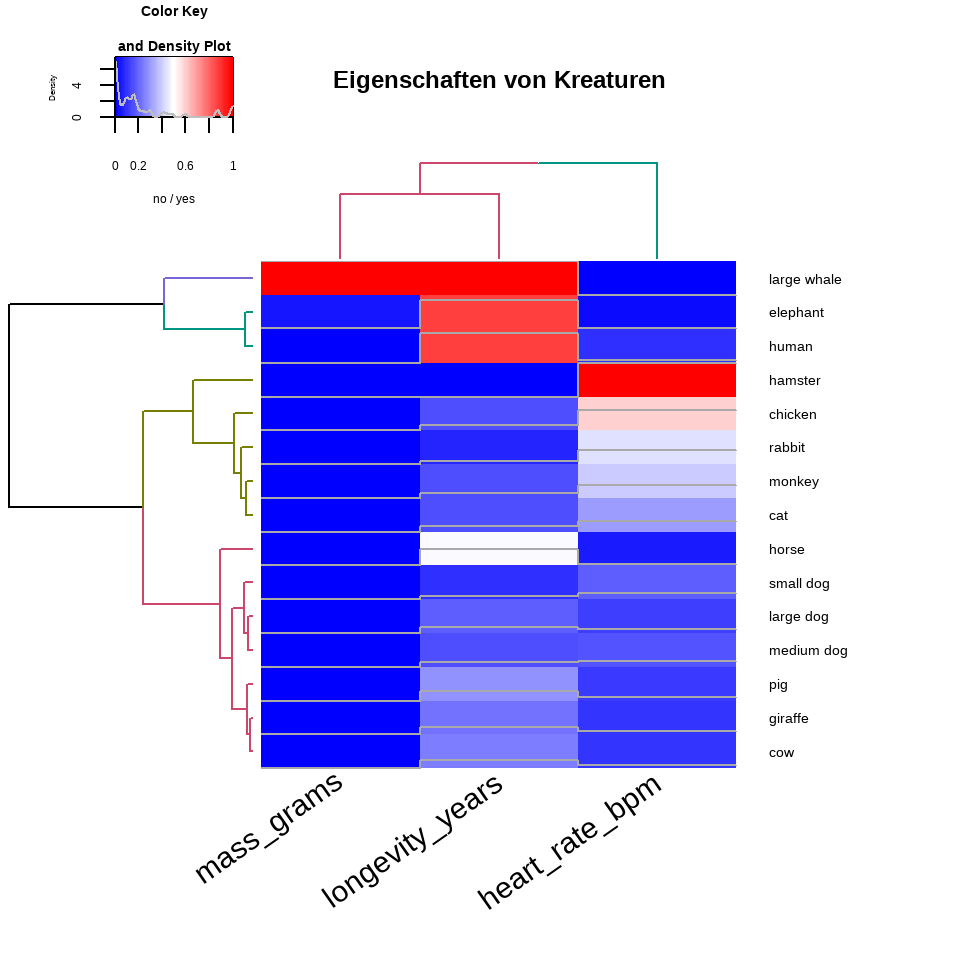
In der Abbildung 60.9 sehen wir einmal die Funktion pheatmap() und die sich daraus ergebenden Heatmaps. Die Ähnlichkeit wird einmal in der Legende angegeben. Je nach gewünschten Distanzmaß, kommt da eben was anderes bei raus. Du musst dir da einmal die Hilfeseite ?pheatmap zu anschauen ober aber das Tutorium. In unserem Fall wollte ich vier Gruppen für die Spalten des Dendrogramms bei den Tierdaten haben. Bei den Kreaturen habe ich nur zwei Gruppen gewählt. Du kannst auch über die Zeilen gruppieren, aber das sprengt hier alles. Probiere es einfach selber aus.

pheatmap(animals_df, cutree_cols = 4)
pheatmap(norm_creature_df, cutree_cols = 2)

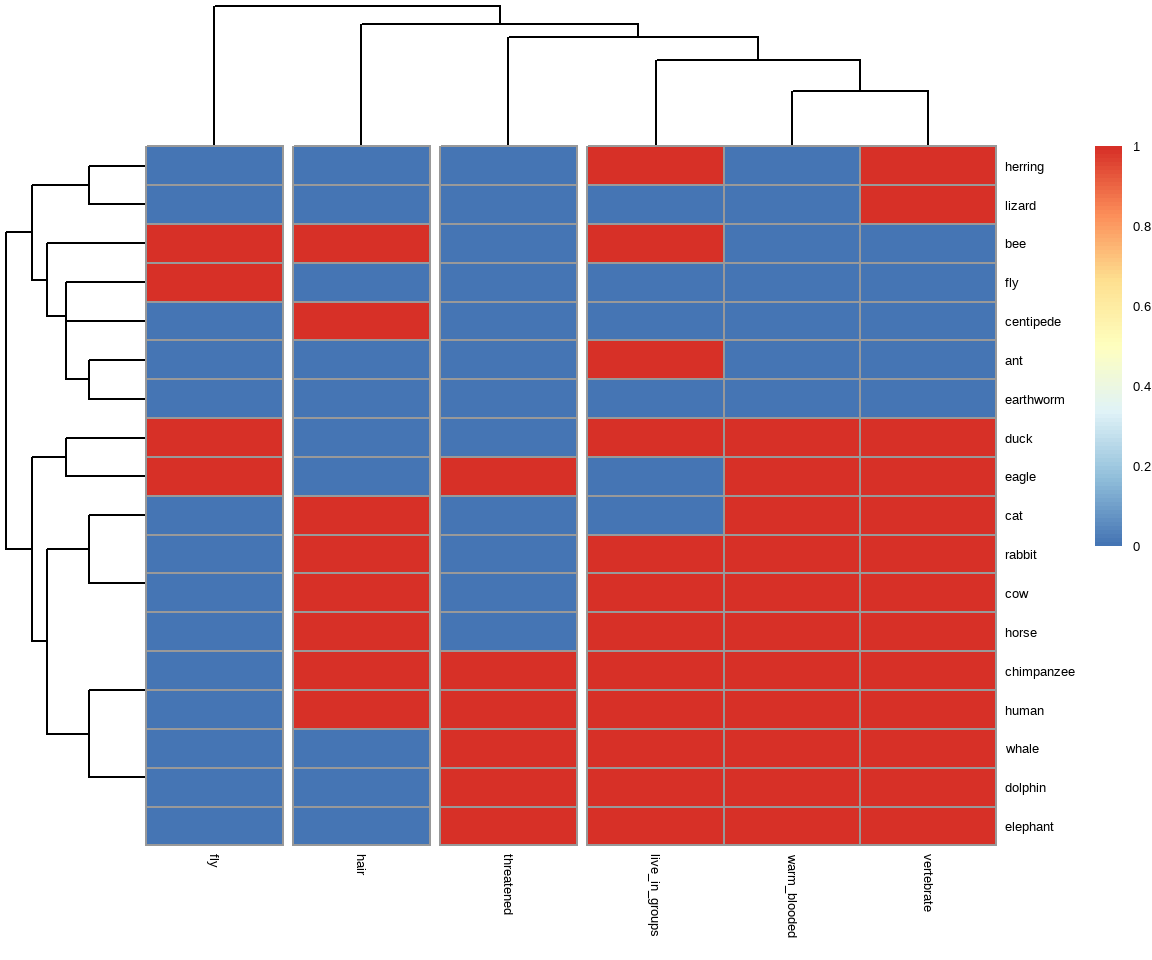
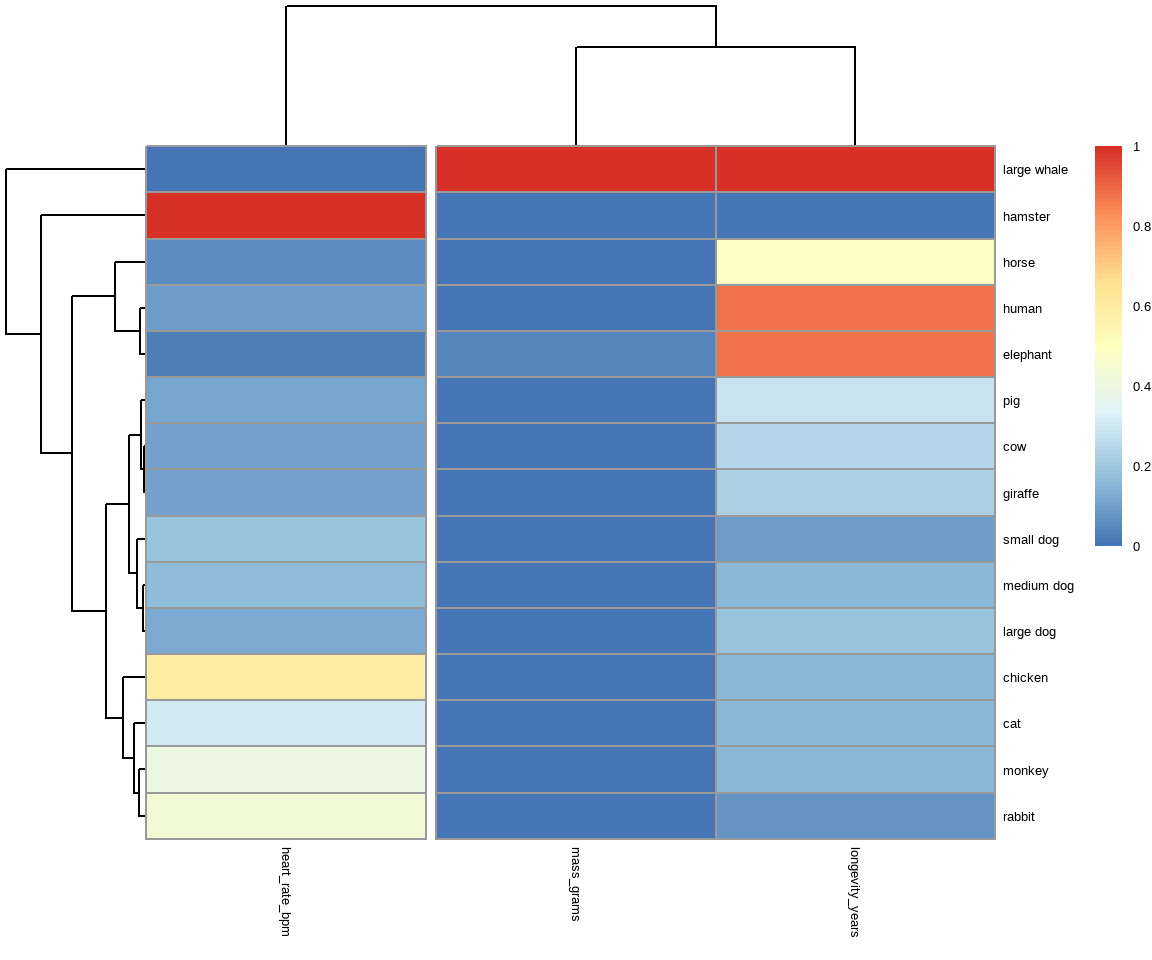
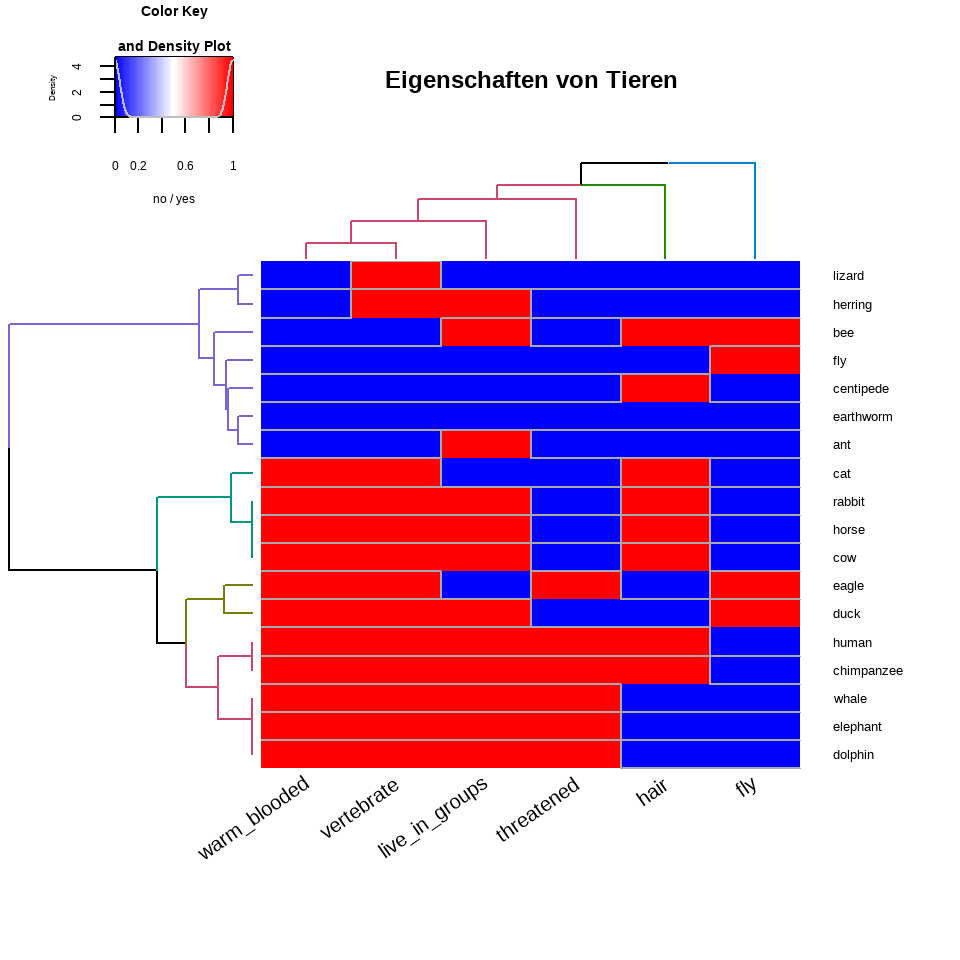
Die Funktion heatmap.2() liefert sehr viel mehr Optionen und erlaubt noch etwas feinere Abstimmungen. Du kannst ziemlich einfach noch Dendrogramme für die Zeilen und Spalten ergänzen. Damit die Erstellung der Dendrogramme nicht so fehleranfällig ist, packe ich mir den Code immer in eine Funktion und entscheide dann nach der Option dim, ob ich die Daten transponieren oder nicht-transponieren muss. Die Spalten rechne ich auf den untransponierten Daten und die Zeilen mache ich zu Spalten durch das Transponieren mit der Funktion t().

get_dendro_margin <- function(tbl, k, dim = "row"){
  if(dim == "row") {
    tmp_tbl <- tbl |> 
      dist(method = "man") |> 
      hclust(method = "ward.D") 
  } else {
    tmp_tbl <- t(tbl) |> 
      dist(method = "man") |> 
      hclust(method = "com") 
  }
  dendro_obj <- tmp_tbl |> 
    as.dendrogram() |> 
    ladderize() |>
    color_branches(k = k)
  return(dendro_obj)
}

Also einmal das Dendrogramm für vier Gruppen über die Zeilen gebaut. Wir nutzen $k = 4$ für die Anzahl an einzufärbenden Gruppen sowie die Option dim = "row" um über die untransponierten Zeilen zu Clustern. Das machen wir jetzt einmal für den Tierdatensatz und dann einmal für den Kreaturendatensatz.

dend_animal_r <- get_dendro_margin(animals_df, k = 4, dim = "row")
dend_creature_r <- get_dendro_margin(norm_creature_df, k = 4, dim = "row")

Das Ganze dann nochmal über die Spalten auf gleicher Weise nur dann eben mit der Option dim = "col". Hier haben wir aber nur drei Spalten in den Daten, da können wir dann keine drei Gruppen einfärben. Das wären ja dann die drei Spalten per se.

dend_animal_c <- get_dendro_margin(animals_df, k = 3, dim = "col")
dend_creature_c <- get_dendro_margin(norm_creature_df, k = 2, dim = "col")

In der Abbildung 60.10 kommt dann alles einmal zusammen gebaut. Wie du siehst, hat die Funktion heatmap.2() noch eine Menge zusätzliche Optionen. Ich habe hier einfach mal ein paar behalten mit denen du dann mal rumspielen kannst. Am Ende weiß ich dann auch immer nicht, was soll da denn so rein? Am besten die Dinge und Färbungen, die dann auch deine Fragestellung mit beantworten. Das ist dann aber an dir zu entscheiden.

gplots::heatmap.2(as.matrix(animals_df), 
          main = "Eigenschaften von Tieren",
          srtCol = 35,
          Rowv = dend_animal_r, Colv = dend_animal_c,
          trace="row", hline = NA, tracecol = "darkgrey",         
          margins =c(6, 5), key.xlab = "no / yes",
          denscol = "grey", density.info = "density",
          col = gplots::bluered(100))


gplots::heatmap.2(as.matrix(norm_creature_df), 
          main = "Eigenschaften von Kreaturen",
          srtCol = 35,
          Rowv = dend_creature_r, Colv = dend_creature_c,
          trace = "row", hline = NA, tracecol = "darkgrey",         
          margins = c(6, 7), key.xlab = "no / yes",
          denscol = "grey", density.info = "density",
          col = gplots::bluered(100))

Die Tierdaten sind nur $0/1$-codiert, deshalb sind natürlich die Farben der Heatmap nur rot und blau. Wie du an dem Kreaturendatensatz sehen kannst, werden Heatmaps eigentlich nicht auf so kleinen Datensätzen gerechnet. Wenn du mehr Spalten hast, dann werden auch die Spaltenunterschriften kleiner. Ich habe hier jetzt nicht die Muse nochmal in der Hilfe der Funktion ?heatmap.2 die Optionen zu suchen.

Wir sehen aber auch, dass wir über die Zeilen eine obere Gruppe haben, die Eidechse bis Ameise beinhaltet. Dann kommt eine größere Gruppe der Säugetiere, die sich dann nochmal kleiner aufspaltet. Ich finde die Spalten etwas schwerer zu deuten, deshalb lass ich das mal hier. Bei den Kreaturen finde ich es noch schwerer. Zwar sind der Wal und der Elefant zeilweise zusammen, aber der Rest ist schwer zu deuten. Da ist mir dann doch zu viel Heterogenität drin, dass ich da dem Clustern glauben würde. Vermutlich sind jetzt aber auch die Daten etwas zu klein für eine gute Darstellung in einer Heatmap.

60.6 Datenanalyse mit `tidyclust`

Wie du schon oben gesehen hast, ist es teilweise echt nervig immer die row.names() mit zu nehmen oder alles ein data.frame() zu nutzen. Insbesondere wenn die Daten sehr groß werden, kann kann es sehr ungünstig sein, alles in einem data.frame() zu lagern. Deshalb gibt es das Paket {tidyclust}, was ich hier nochmal vorstellen möchte. Die Visualisierungen von oben können alle genutzt werden. Der Vorteil ist eben, dass wir hier in der tidy-Welt sind und uns auch die recipes() aus dem Klassifikationskapiteln zu nutze machen können. Da ist dann das Normalisieren und andere Vorbereitungsschritte der Daten viel einfacher. Damit wir auch mal die Datenanalyse mit einem großen Datensatz sehen, nutze ich hier einmal den Datensatz der Gummibärchendaten. Im Folgenden analysieren wir also die Gummibärchendaten einmal mit dem R Paket {tidyclust}.

60.6.1 Hierarchical Clustering

Im Folgenden also einmal der Ablauf in tidyclust für die hierarchische Clusteranalyse. Auch hier müssen wir im ersten Schritt einmal festlegen welche Anzahl an Clustern num_clusters wir wollen. Dann müssen wir auch noch festlegen, welche linkage Methode wir wollen. Ich nehme hier einmal die average Methode. Damit haben wir aber noch nichts gerechnet, sondern nur ein Objekt erschaffen in dem steht, was wir machen wollen.

tidyclust Hilfeseite für das Hierarchical Clustering

hc_spec <- hier_clust(num_clusters = 3,
                      linkage_method = "average")

Jetzt können wir das Objekt hc_spec in die Funktion fit() pipen, die uns dann die hierarchische Clusteranalyse rechnet. Da wir in der Funktion fit() bestimmen können, welche Spalten mit in den Algorithmus sollen, müssen wir nicht umständlich mit einem vollem Datensatz arbeiten.

hc_fit <- hc_spec |>
  fit(~ gender + age + height + semester + most_liked,
      data = gummi_tbl)

Wenn es zu lang wird dann geht auch fit(~ .), dann ist es aber ehrlich gesagt besser, die Variante mit dem data.frame() zu nutzen. In diesem Fall nimmst du dann ja wieder alle Spalten mit rein. Mit dem hc_fit kannst du dann ganz normal weiterarbeiten. Die Funktion extract_fit_summary() erlaubt es dir dann die wichtigsten Informationen aus dem Fit rauszuziehen und über cluster_assignments kommst du dann an die Clusterzuordnungen ran.

hc_summary <- hc_fit |> 
  extract_fit_summary()

Im Folgenden einmal die ersten sieben Clusterzuordnungen.

hc_summary |> 
  pluck("cluster_assignments") |> 
  head(7)

[1] Cluster_1 Cluster_1 Cluster_1 Cluster_1 Cluster_1 Cluster_1 Cluster_1
Levels: Cluster_1 Cluster_2 Cluster_3

Die weitere Analyse ist dann wie auch oben. Du kannst dir dann einen Silhouettenplot erstellen lassen oder aber die Ergebnisse in einem Dendrogramm visualisieren. Das ist dann alles das Gleiche.

60.6.2 k-means Clustering

Auch gibt es für den kmeans Algorithmus eine bessere Variante für einen sauberen Workflow. Auch hier wird als erstes einmal der Algorithmus definiert. In unserem Fall heißt er dann k_means(). Wir wählen mit num_clusters die Anzahl an Gruppen, die am Ende raus kommen sollen.

tidyclust Hilfeseite für das k-means Clustering

kmeans_spec <- k_means(num_clusters = 3)

Danach können wir dann unsere Informationen über den Algorithmus in die Funktion fit() weiterleiten. In der fit() Funktion definieren wir dann die Spalten, die für das Clustern von Bedeutung sein sollen.

kmeans_fit <- kmeans_spec |>
  fit(~ age + height + semester,
      data = gummi_tbl)

Wir können auch hier über die Funktion extract_cluster_assignment() die Clusterzugehörigkeiten erhalten. Damit können wir dann prinzipiell auch schon aufhören und die Visualisierungen erstellen, die wir aus den vorherigen Abschnitten kennen.

kmeans_fit |>
  extract_cluster_assignment()

# A tibble: 210 x 1
   .cluster 
   <fct>    
 1 Cluster_1
 2 Cluster_2
 3 Cluster_2
 4 Cluster_3
 5 Cluster_1
 6 Cluster_1
 7 Cluster_2
 8 Cluster_2
 9 Cluster_1
10 Cluster_1
# i 200 more rows

Mit der Funktion extract_fit_summary() erhalten wir dann noch zusätzliche Informationen, da musst du dann aber mal auf der Hilfeseite schauen, was du konkret an Informationen brauchst. Da gibt es wieder eine Menge. Am Ende kannst du dir dann noch die Informationen zu dem durchschnittlichen Silhouettenwert wiedergeben lassen um Modelle untereinander vergleichen zu können. Der Vergleich geht hier natürlich schneller, da du einfacher Variablen aus dem Modell nehmen kannst als dir immer weider enue Datensätze zu bauen.

kmeans_fit |>
  tidyclust::silhouette_avg(select(gummi_tbl, age, height, semester))

# A tibble: 1 x 3
  .metric        .estimator .estimate
  <chr>          <chr>          <dbl>
1 silhouette_avg standard       0.425