pacman::p_load(tidyverse, magrittr, dlookr,
MASS, ranger, Boruta, broom,
scales, olsrr, gtsummary, parameters,
conflicted)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)42 Variablenselektion
Letzte Änderung am 25. March 2024 um 17:41:41
“Denn im Formulieren des Problems ist die Lösung schon enthalten!” — Käptn Peng & Die Tentakel von Delphi, Meister und Idiot
Die Selektion von Variablen in einem Modell. Ein schwieriges Thema. Entweder kenne ich mein Experiment und habe das Experiment so geplant, dass nur die bedeutenden Variablen mit in dem Experiment sind oder ich habe keine Ahnung. Gut, dass ist überspitzt und gemein formuliert. Wir wollen uns in diesem Kapitel den Fall anschauen, dass du sehr viele Variablen \(x\) erhoben hast und nun statistisch bestimmen willst, welche Variablen nun mit in das finale Modell sollen. Achtung, ich spreche hier nicht von einem Blockdesign oder aber einem Feldexperiment. Da hat die Variablenselektion nichts zu suchen. Daher tritt der Fall der Variablenselektion eher in dem Feld Verhaltensbiologie oder aber auch Ökologie auf. Ebenfalls kann die Anwendung in automatisch erfassten Daten einen Sinn machen. Wir nutzen dann die Variablenselektion (eng. feature selection) zu Dimensionsreduktion des Datensatzes. Der Datensatz soll damit einfacher sein… ob der Datensatz das damit auch wird, ist wieder eine andere Frage.
In diesem Kapitel prügeln wir aber einen statistischen Engel. Wir werden hier mal schauen müssen, was alles geht und was nicht. Variablen Selektion ist faktisch nicht ein Kapitel sondern ein Regal(kilo)meter voll mit Büchern.
Zu der Frage welches Verfahren denn nun das richtige Verfahren zur Selektion von Variablen ist, gibt es die Standardantwort in der Statistik: Es kommt auf die Fragestellung an…. Oder aber was ist wie gut implementiert, dass wir das Verfahren einigermaßen gut nutzen können. Wir gehen daher von einfach zu kompliziert und du musst dann schauen, was du nutzen willst und kannst. Wir müssen zum Beispiel unterscheiden, welcher Verteilung das Outcome \(y\) folgt. Wenn wir ein normalverteiltes \(y\) haben, dann haben wir andere Möglichkeiten, als wenn wir uns ein poissonverteiltes oder binominalverteiltes \(y\) anschauen.
Das R Paket {olsrr} erlaubt eine weitreichende Variablen Selektion, wenn ein normalverteiltes Outcome \(y\) vorliegt.
Im Folgenden will ich kurz die fünf Mythen der Variablenselektion von Heinze und Dunkler (2017) zusammenfassen. Wie immer ersetzt meine deutsche Zusammenfassung und Auswahl nicht das eigenständige Lesen der englischen Orgnialquelle, wenn du die Informationen in deiner Abschlussarbeit zitieren willst.
- Die Anzahl der Variablen in einem Modell sollte reduziert werden, bis es 10 Ereignisse pro Variable gibt. Simulationsstudien haben gezeigt, dass multivariable Modelle bei zu niedrigen Verhältnissen von Ereignissen bzw. Beobachtungen pro Variable (eng events per variable, abk. EPV) sehr instabil werden. Aktuelle Empfehlungen besagen, dass je nach Kontext mindestens 5-15 EPV verfügbar sein sollten. Wahrscheinlich sind sogar viel höhere Werte wie 50 EPV erforderlich, um annähernd stabile Ergebnisse zu erzielen.
- Nur Variablen mit nachgewiesener Signifikanz des univariaten Modells sollten in ein Modell aufgenommen werden. Die univariable Vorfilterung trägt nicht zur Stabilität des Auswahlprozesses bei, da sie auf stochastischen Quanten beruht und dazu führen kann, dass wichtige Anpassungsvariablen übersehen werden.
- Nicht signifikante Effekte sollten aus einem Modell entfernt werden. Regressionskoeffizienten hängen im Allgemeinen davon ab, welche anderen Variablen in einem Modell enthalten sind, und ändern folglich ihren Wert, wenn eine der anderen Variablen in einem Modell weggelassen wird.
- Der berichtete P-Wert quantifiziert den Typ-I-Fehler einer fälschlich ausgewählten Variablen. Ein P-Wert ist ein Ergebnis der Datenerhebung und -analyse und quantifiziert die Plausibilität der beobachteten Daten unter der Nullhypothese. Daher quantifiziert der P-Wert nicht den Fehler vom Typ I. Es besteht auch die Gefahr einer falschen Eliminierung von Variablen, deren Auswirkungen durch die bloße Angabe des endgültigen Modells eines Variablenauswahlverfahrens überhaupt nicht quantifiziert werden können.
- Variablenauswahl vereinfacht die Analyse. Für das jeweilige Problem muss eine geeignete Variablenauswahlmethode gewählt werden. Statistiker haben die Rückwärtselimination als die zuverlässigste unter den Methoden empfohlen, die sich mit Standardsoftware leicht durchführen lassen. Eine Auswahl ist eine “harte Entscheidung”, die aber oft auf vagen Größen beruht. Untersuchungen zur Modellstabilität sollten jede angewandte Variablenauswahl begleiten, um die Entscheidung für das schließlich berichtete Modell zu rechtfertigen oder zumindest die mit der Auswahl der Variablen verbundene Unsicherheit zu quantifizieren.
Im Weiteren sei auch noch auf Heinze u. a. (2018) und Talbot und Massamba (2019) verwiesen. Beide Veröffentlichungen liefern nochmal einen fundierten Block auf die Variablenselektion. Wiederum ist das natürlich nur ein winziger Ausschnitt aus der Literatur zur Variablenselektion. Im Zweifel einfach einmal bei Google Scholar nach Variablenselektion suchen und schauen was so in dem Feld der eigenen Forschung alles gemacht wird.
Sensitivitätsanalysen nach der Variablenselektion
“Variable selection should always be accompanied by sensitivity analyses to avoid wrong conclusions.” (Heinze und Dunkler 2017, p. 9)
Nachdem wir Variablen aus unseren Daten entfernt haben, ist es üblich noch eine Sensitivitätsanalysen durchzuführen. Wir Vergleich dann das selektierte Modell mit anderen Modellen. Oder wir wollen die Frage beantworten, was hat eigentlich meine Variablenselektion am Ergebnis geändert? Habe ich eine wichtige Variable rausgeschmissen? Das machen wir dann gesammelt in dem Kapitel 44 zu den Sensitivitätsanalysen.
42.1 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
42.2 Daten
Um die Variablenselektion einmal durchzuführen nurtzen wir zwei Datensätze. Zum einen den Datensatz zu den Kichererbsen in Brandenburg mit einem normalverteilten Outcome \(y\) mit dryweight. Wir laden wieder den Datensatz in R und schauen uns einmal die Daten in Tabelle 42.1 als Auszug aus dem Tabellenblatt an.
Wir du schon siehst, wir brauchen Fallzahl um hier überhaupt was zu machen. Bitte keine Variablenselektion im niedrigen zweistelligen Bereich an Beobachtungen.
chickpea_tbl <- read_excel("data/chickpeas.xlsx") Wir sehen, dass wir sehr viele Variablen vorleigen haben. Sind denn jetzt alle Variablen notwendig? Oder können auch ein paar Variablen raus aus dem Modell. So viele Beobachtungen haben wir mit \(n = 95\) ja nicht vorliegen. Daher wollen wir an diesem Datensatz die Variablenselektion unter der Annahme eines normalverteilten \(y\) durchgehen.
| temp | rained | location | no3 | fe | sand | forest | dryweight |
|---|---|---|---|---|---|---|---|
| 25.26 | high | north | 5.56 | 4.43 | 63 | >1000m | 253.42 |
| 21.4 | high | northeast | 9.15 | 2.58 | 51.17 | <1000m | 213.88 |
| 27.84 | high | northeast | 5.57 | 2.19 | 55.57 | >1000m | 230.71 |
| … | … | … | … | … | … | … | … |
| 29.04 | low | north | 5.64 | 2.87 | 53.27 | >1000m | 236.07 |
| 24.11 | high | northeast | 4.31 | 3.66 | 63 | <1000m | 259.82 |
| 28.88 | low | northeast | 7.92 | 2 | 65.75 | >1000m | 274.75 |
Was wir auch noch wissen, ist wie die Effekte in den Daten wirklich sind. Die Daten wurden ja künstlich erstellt, deshalb hier die Ordnung der Effektstärke für jede Variable. Im Prinzip müsste diese Reihenfolge auch bei der Variablenselektion rauskommen. Schauen wir mal, was wir erhalten.
\[ y \sim \beta_0 + 3 * sand + 2 * temp + 1.5 * rained - 1.2 * forest + 1.1 * no3 \]
Viele Beispiele laufen immer unter der Annahme der Normalverteilung. Deshalb als zweites Beispiel nochmal die Daten von den infizierten Ferkeln mit einem binomialverteilten Outcome \(y\) mit infected. Auch hier können wir uns den Auszug der Daten in Tabelle 42.2 anschauen.
pig_tbl <- read_excel("data/infected_pigs.xlsx") Das schöne an diesem Datensatz ist jetzt, dass wir mit \(n = 412\) Beobachtungen sehr viele Daten vorliegen haben. Daher können wir auch alle Methoden gut verwenden und haben nicht das Problem einer zu geringen Fallzahl.
| age | sex | location | activity | crp | frailty | bloodpressure | weight | creatinin | infected |
|---|---|---|---|---|---|---|---|---|---|
| 61 | male | northeast | 15.31 | 22.38 | robust | 62.24 | 19.05 | 4.44 | 1 |
| 53 | male | northwest | 13.01 | 18.64 | robust | 54.21 | 17.68 | 3.87 | 1 |
| 66 | female | northeast | 11.31 | 18.76 | robust | 57.94 | 16.76 | 3.01 | 0 |
| … | … | … | … | … | … | … | … | … | … |
| 61 | male | northwest | 15.26 | 23.1 | robust | 57.18 | 15.55 | 3.08 | 1 |
| 59 | female | north | 13.13 | 20.23 | robust | 56.64 | 18.6 | 3.41 | 0 |
| 63 | female | north | 10.01 | 19.89 | robust | 57.46 | 18.6 | 4.2 | 1 |
Auch in diesem Beispiel wurden die Daten von mir mit folgenden Effekten generiert. Schauen wir mal, was die Variablenselektion bei der hohen Fallzahl mit den Variablen macht bzw. welche Sortierung am Ende rauskommt.
\[ y \sim \beta_0 + 2 * crp + 0.5 * sex + 0.5 * frailty + 0.2 * bloodpressure + 0.05 * creatinin + 0.01 * weight \]
Damit haben wir unsere beiden Beispiel und jetzt gehen wir mal eine Auswahl an Methoden zur Variablenselektion durch. Besonders hier, haltet den statistsichen Engel nah bei euch. Es wird leider etwas ruppig für den statistischen Engel.
42.3 Methoden der Variablenselektion
In den folgenden Abschnitten wollen wir uns eine Reihe an Methoden anschauen um eine Variablenselektion durchzuführen. Dabei gehen wir von einfach nach komplex. Wobei das komplex eher die Methode und nicht die Anwendung meint. Wir nutzen R Pakete und gehen nicht sehr ins Detail wie der Algorithmus jetzt die Auswahl trifft. Für den Hintergrund sind dann die Verweise auf die anderen Kapitel.
42.3.1 Per Hand
Manchmal ist der Anfang auch das Ende. Wir müssen ja gar keinen Algorithmus auf unsere Daten loslassen um eine Variablenselektion durchzuführen. Deshalb möchte ich gleich den ersten Abschnitt mit einem Zitat von Heinze und Dunkler (2017) beginnen.
“Oft gibt es keinen wissenschaftlichen Grund, eine (algorithmische) Variablenauswahl durchzuführen. Insbesondere erfordern Methoden der (algorithmische) Variablenselektion einen viel größeren Stichprobenumfang als die Schätzung eines multiplen Modells mit einem festen Satz von Prädiktoren auf der Grundlage (klinischer) Erfahrung.” (Übersetzt und ergänzt nach Heinze und Dunkler 2017, p. 9)
Fazit dieses kurzen Abschnitts. Wir können auf alles Folgende einfach verzichten und uns überlegen welche Variablen sinnvollerweise mit ins Modell sollen und das mit unserem Expertenwissen begründen. Gut, und was ist, wenn ich kein Experte bin? Oder wir aber wirklich Neuland betreten? Dann können wir eine Reihe anderer Verfahren nutzen um uns algortimisch einer Wahrheit anzunähern.
42.3.2 Univariate Vorselektion
Und weiter geht es mit Zitaten aus Heinze und Dunkler (2017) zu der Variablenselektion. Dazu musst du wissen, dass die univariate Vorselektion sehr beliebt war und auch noch ist. Denn die univariate Vorselektion ist einfach durchzuführen und eben auch gut darzustellen.
“Obwohl die univariable Vorfilterung nachvollziehbar und mit Standardsoftware leicht durchführbar ist, sollte man sie besser ganz vergessen, da sie für die Erstellung multivariabler Modelle weder Voraussetzung noch von Nutzen ist.” (Übersetzt nach Heinze und Dunkler 2017, p. 8)
Ich sage immer, auch mit einem Hammer kann man Scheiben putzen. Halt nur einmal… Deshalb auch hier die univariate Variante der Vorselektion.
Wir sehen also, eigentlich ist die univariate Variablensleketion nicht so das gelbe vom Ei, aber vielleicht musst die Variablenselektion durchführen, so dass her die Lösung in R einmal dargestellt ist. Wir nutzen einmal die gaussian lineare Regression für den Kichererbsendatensatz. Es ist eine ganze Reihe an Code, das hat aber eher damit zu tun, dass wir die Modellausgabe noch filtern und anpassen wollen. Die eigentliche Idee ist simple. Wir nehmen unseren Datensatz und pipen den Datensatz in select und entfernen unser Outcome drymatter. Nun iterieren wir für jede Variable .x im Datensatz mit der Funktion map() und rechnen in jeder Iteration eine gaussian lineare Regression. Dann entferne wir noch den Intercept und sortieren nach den \(p\)-Werten.
chickpea_tbl |>
select(-dryweight) |>
map(~glm(dryweight ~ .x, data = chickpea_tbl, family = gaussian)) |>
map(tidy) |>
map(filter, term != "(Intercept)") |>
map(select, -term, -std.error, -statistic) |>
bind_rows(.id="term") |>
arrange(p.value) |>
mutate(p.value = pvalue(p.value),
estimate = round(estimate, 2))# A tibble: 8 × 3
term estimate p.value
<chr> <dbl> <chr>
1 sand 2.9 <0.001
2 temp 1.65 0.011
3 no3 2.51 0.037
4 fe 2.61 0.091
5 location -7.27 0.130
6 rained 4.95 0.165
7 forest -4.39 0.197
8 location -2.87 0.434 Würden wir nur nach dem Signifikanzniveau von 5% gehen, dann hätten wir die Variablen sand und location selektiert. Bei der selektion mit dem \(p\)-Wert wird aber eher eine Schwelle von 15.7% vorgeschlagen (Heinze und Dunkler 2017, p. 9). Daher würden wir auch noch no3 und temp mit Selektieren und in unser Modell nehmen.
Es gibt ja immer zwei Wege nach Rom. Deshalb hier auch nochmal die Funktion tbl_uvregression() aus dem R Paket {gtsummary}, die es erlaubt die univariaten Regressionen über alle Variablen laufen zu lassen. Wir kriegen dann auch eine schöne Tabelle 42.3 wieder.
Das R Paket {gtsummary} erlaubt es Ergebnisse der Regression in dem Tutorial: tbl_regression gut darzustellen.
chickpea_tbl |>
tbl_uvregression(
method = glm,
y = dryweight,
method.args = list(family = gaussian),
pvalue_fun = ~style_pvalue(.x, digits = 2)
) |>
add_global_p() |> # add global p-value
add_q() |> # adjusts global p-values for multiple testing
bold_p() |> # bold p-values under a given threshold (default 0.05)
bold_p(t = 0.10, q = TRUE) |> # now bold q-values under the threshold of 0.10
bold_labels()tbl_uvregression().
| Characteristic | N | Beta | 95% CI1 | p-value | q-value2 |
|---|---|---|---|---|---|
| temp | 95 | 1.6 | 0.41, 2.9 | 0.009 | 0.032 |
| rained | 95 | 0.16 | 0.23 | ||
| high | — | — | |||
| low | 4.9 | -2.0, 12 | |||
| location | 95 | 0.31 | 0.31 | ||
| north | — | — | |||
| northeast | -2.9 | -10, 4.3 | |||
| west | -7.3 | -17, 2.1 | |||
| no3 | 95 | 2.5 | 0.18, 4.8 | 0.035 | 0.081 |
| fe | 95 | 2.6 | -0.38, 5.6 | 0.087 | 0.15 |
| sand | 95 | 2.9 | 2.5, 3.3 | <0.001 | <0.001 |
| forest | 95 | 0.19 | 0.23 | ||
| <1000m | — | — | |||
| >1000m | -4.4 | -11, 2.2 | |||
| 1 CI = Confidence Interval | |||||
| 2 False discovery rate correction for multiple testing | |||||
Nun führen wir die univariate Regression erneut auf den Ferkeldaten aus. Hier ändern wir nur die family = binomial, da wir hier jetzt eine logistische lineare Regression rechnen müssen. Unser Outcome infected ist ja \(0/1\) codiert. Sonst ändert sich der Code nicht.
pig_tbl |>
select(-infected) |>
map(~glm(infected ~ .x, data = pig_tbl, family = binomial)) |>
map(tidy) |>
map(filter, term != "(Intercept)") |>
map(select, -term, -std.error, -statistic) |>
bind_rows(.id="term") |>
arrange(p.value) |>
mutate(p.value = pvalue(p.value),
estimate = round(estimate, 2))# A tibble: 12 × 3
term estimate p.value
<chr> <dbl> <chr>
1 crp 0.96 <0.001
2 bloodpressure 0.08 0.013
3 creatinin 0.11 0.133
4 location -0.4 0.141
5 sex -0.29 0.188
6 location -0.24 0.435
7 frailty 0.16 0.645
8 activity 0.02 0.698
9 frailty -0.12 0.699
10 location 0.12 0.712
11 weight -0.02 0.765
12 age 0 0.877 In diesem Fall reicht die Schwelle von 15.7% nur für zwei Variablen (Heinze und Dunkler 2017, p. 9). Wir erhalten die Variablen crp und bloodpressure für das Modell selektiert.
In der Tabelle 42.4 sehen wir dann nochmal die Anwendung der Funktion tbl_uvregression() auf den Ferkeldatensatz. Ich musste hier die Option pvalue_fun = ~style_pvalue(.x, digits = 2) entfernen, da sonst die Variable crp keinen \(p\)-Wert erhält. Leider sehe ich den \(p\)-Wert mit \(<0.001\) in meiner Ausgabe in R aber wie du siehst, wird die Tabelle auf der Webseite nicht korrekt angezeigt. Das Problem von automatischen Tabellen. Ein Fluch und Segen zugleich. Du musst immer wieder überprüfen, ob die Optionen dann auch für sich und deine Analyse passen.
pig_tbl |>
tbl_uvregression(
method = glm,
y = infected,
method.args = list(family = binomial),
exponentiate = TRUE
) |>
add_global_p() |> # add global p-value
add_nevent() |> # add number of events of the outcome
add_q() |> # adjusts global p-values for multiple testing
bold_p() |> # bold p-values under a given threshold (default 0.05)
bold_p(t = 0.10, q = TRUE) |> # now bold q-values under the threshold of 0.10
bold_labels()tbl_uvregression().
| Characteristic | N | Event N | OR1 | 95% CI1 | p-value | q-value2 |
|---|---|---|---|---|---|---|
| age | 412 | 276 | 1.00 | 0.95, 1.04 | 0.9 | 0.9 |
| sex | 412 | 276 | 0.2 | 0.4 | ||
| female | — | — | ||||
| male | 0.75 | 0.49, 1.15 | ||||
| location | 412 | 276 | 0.3 | 0.5 | ||
| north | — | — | ||||
| northeast | 1.12 | 0.61, 2.10 | ||||
| northwest | 0.67 | 0.39, 1.14 | ||||
| west | 0.79 | 0.43, 1.44 | ||||
| activity | 412 | 276 | 1.02 | 0.90, 1.16 | 0.7 | 0.9 |
| crp | 412 | 276 | 2.62 | 2.14, 3.27 | <0.001 | <0.001 |
| frailty | 412 | 276 | 0.5 | 0.7 | ||
| frail | — | — | ||||
| pre-frail | 1.17 | 0.59, 2.27 | ||||
| robust | 0.88 | 0.46, 1.64 | ||||
| bloodpressure | 412 | 276 | 1.08 | 1.02, 1.15 | 0.012 | 0.053 |
| weight | 412 | 276 | 0.98 | 0.86, 1.12 | 0.8 | 0.9 |
| creatinin | 412 | 276 | 1.12 | 0.97, 1.30 | 0.13 | 0.4 |
| 1 OR = Odds Ratio, CI = Confidence Interval | ||||||
| 2 False discovery rate correction for multiple testing | ||||||
Neben der Berechnung von univariaten logistischen Regressionen ist auch die Darstellung der Daten in einer Tabelle 42.5 bei Medizinern sehr beliebt. Deshalb an dieser Stelle auch die Tabelle 1 (eng. table 1) für die Zusammenfasung der Daten getrennt nach dem Infektionsstatus zusammen mit dem \(p\)-Wert. Ich nutze hier die Funktion tbl_summary() aus dem R Paket {gtsummary}.
pig_tbl |> tbl_summary(by = infected) |> add_p()| Characteristic | 0, N = 1361 | 1, N = 2761 | p-value2 |
|---|---|---|---|
| age | 59.5 (57.0, 63.0) | 60.0 (57.0, 63.0) | 0.9 |
| sex | 0.2 | ||
| female | 47 (35%) | 114 (41%) | |
| male | 89 (65%) | 162 (59%) | |
| location | 0.3 | ||
| north | 36 (26%) | 85 (31%) | |
| northeast | 23 (17%) | 61 (22%) | |
| northwest | 48 (35%) | 76 (28%) | |
| west | 29 (21%) | 54 (20%) | |
| activity | 13.40 (12.25, 14.34) | 13.24 (12.28, 14.54) | 0.8 |
| crp | 19.12 (18.13, 19.83) | 20.57 (19.77, 21.46) | <0.001 |
| frailty | 0.5 | ||
| frail | 18 (13%) | 37 (13%) | |
| pre-frail | 42 (31%) | 101 (37%) | |
| robust | 76 (56%) | 138 (50%) | |
| bloodpressure | 56.2 (54.3, 58.5) | 57.2 (55.1, 59.6) | 0.021 |
| weight | 18.61 (17.34, 19.41) | 18.32 (17.19, 19.60) | 0.8 |
| creatinin | 4.85 (3.67, 5.93) | 4.86 (4.06, 5.85) | 0.3 |
| 1 Median (IQR); n (%) | |||
| 2 Wilcoxon rank sum test; Pearson’s Chi-squared test | |||
Tja, auch hier ist dann die Frage, wie sortiere ich Variablen. Da es sich bei dem table 1-Stil um eine Übersichtstabelle handelt, ist die Tabelle nach den Variablen sortiert. Auch hier finden wir dann die Variablen crp und bloodpressure wieder. Das Problem hierbei ist natürlich, dass sich die \(p\)-Werte unterscheiden. Das muss ja auch so sein, denn eine logitische Regression ist nun mal kein Wilcoxon rank sum test oder ein Pearson’s Chi-squared test.
Fassen wir als Fazit dieses Abschnitts zusammen wie unsere Modelle nach der Variablenslektion aussehen würde. In unserem Beispiel für die Kichererbsen im sandigen Brandenburg würden wir dann folgendes Modell nehmen.
\[ y \sim \beta_0 + sand + location + no3 + temp \]
Unsere infizierten Ferkel würden dann folgendes selektiertes Modell erhalten.
\[ y \sim \beta_0 + crp + bloodpressure \]
Schauen wir mal, was die anderen Algorithmen noch so finden.
42.3.3 Sonderfall Gaussian linear Regression
Für die gaussian lineare Regression gibt es mit dem R Paket {oslrr} eine große Auswahl an Variable Selection Methods. Einfach mal die Möglichkeiten anschauen, die dort angeboten werden. Wir nutzen jetzt nicht alles was din oslrr möglich ist, sondern nur eien Auswahl. Zuerst müssen wir wieder unser Modell fitten. Wir nehmen alle Variablen mit rein und nutzen die Funktion lm() für ein lineares Modell mit einem normalverteilten Outcome \(y\) mit dryweight.
chickenpea_fit <- lm(dryweight ~ temp + rained + location + no3 + fe + sand + forest,
data = chickpea_tbl)Nun gibt es wirklich viele Lösungen in dem R Paket {oslrr}. Ich möchte einmal die Variante mit ols_step_all_possible präsentieren. In dem Fall rechnen wir alle Modelle die gehen. Und damit meine ich wirklich alle Modelle. Deshalb filtern wir noch nach dem \(R^2_{adj}\) um nicht von dem Angebot erschlagen zu werden. Darüber hinaus möchte ich nur Modelle sehen, die maximal vier Variablen mit in dem Modell haben. Das ist zufällig von mir gewählt… ich will ja ein kleineres Modell haben.
ols_step_all_possible(chickenpea_fit)$result |>
as_tibble() |>
arrange(desc(adjr)) |>
filter(n <= 4) |>
select(predictors, adjr, aic) # A tibble: 98 × 3
predictors adjr aic
<chr> <dbl> <dbl>
1 temp no3 sand forest 0.893 587.
2 temp rained no3 sand 0.886 592.
3 temp no3 fe sand 0.886 593.
4 temp no3 sand 0.884 593.
5 temp location no3 sand 0.882 596.
6 temp rained sand forest 0.881 597.
7 temp sand forest 0.877 599.
8 temp fe sand forest 0.876 600.
9 temp location sand forest 0.875 602.
10 temp rained fe sand 0.872 603.
# ℹ 88 more rowsEine Alternative ist die Funktion ols_step_backward_aic(), die es erlaubt die Selektion anhand dem \(AIC\)-Wert zu machen. Der \(AIC\)-Wert beschreibt die Güte eines Modells und je kleiner der \(AIC\)-Wert ist, desto besser ist das Modell im Vergleich zu anderen Modellen gleicher Art. Da der \(AIC\)-Wert von den Daten abhängt in denen der \(AIC\)-Wert geschätzt wurde, können verschiedene \(AIC\)-Werte nicht übergreifend vergleichen werden.
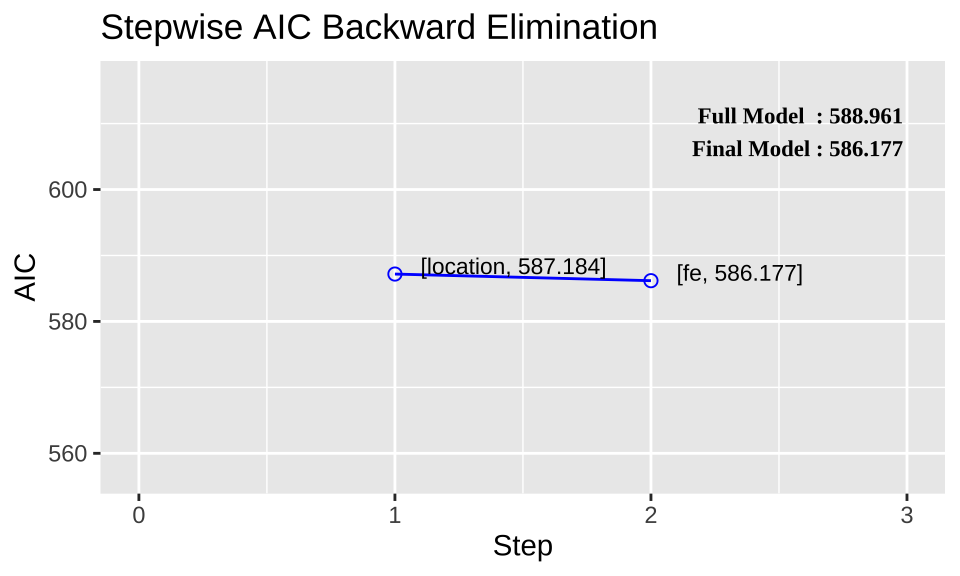
chick_step_aic <- ols_step_backward_aic(chickenpea_fit)In Abbildung 42.1 sehen wir einmal den Verlauf der \(AIC\)-Wert durch die Entfernung der jeweiligen Variable. Wenn du auf die y-Achse schaust, ist der Effekt numerisch nicht sehr groß. Davon darf man sich aber nicht beeindrucken lassen., Wir erhalten ein besseres Modell, wenn wir Variablen entfernen. Darüber hinaus sehen wir auch eine Sättigung.
plot(chick_step_aic) 
ols_step_backward_aic mit der Reduktion des AIC-Wertes.
Gut, und wie sieht nun unser finales Modell aus? Dafür müssen wir usn aus dem Objekt chick_step_aic das model raus ziehen. Dafür nutzen wir die Funktion pluck(). Dann noch die Ausgabe in die Funktion model_parameters() gepipt und schon haben wir das finale Modell nach \(AIC\)-Werten in einer gaussian linearen Regression.
pluck(chick_step_aic, "model") |>
model_parameters()Parameter | Coefficient | SE | 95% CI | t(89) | p
-----------------------------------------------------------------------
(Intercept) | -2.09 | 9.44 | [-20.85, 16.67] | -0.22 | 0.825
temp | 2.37 | 0.22 | [ 1.94, 2.81] | 10.88 | < .001
rained [low] | 1.79 | 1.18 | [ -0.56, 4.15] | 1.51 | 0.133
no3 | 1.42 | 0.40 | [ 0.62, 2.22] | 3.53 | < .001
sand | 3.03 | 0.12 | [ 2.80, 3.26] | 26.12 | < .001
forest [>1000m] | -3.17 | 1.11 | [ -5.38, -0.95] | -2.84 | 0.006 Spannenderweise ist location nicht mehr im finalen Modell plus die Variable location flog auch sehr früh raus. Das passt auch besser zu den Daten. Ich hatte die Daten so gebaut, dass der Ort eigentlich keinen Effekt haben sollte. Wir sehen, dass je nach Verfahren was anderes herauskommt. Aber Achtung, das schrittweise Verfahren ist der Auswahl nach \(p\)-Werten auf jeden Fall vorzuziehen!
42.3.4 Schrittweise mit stepAIC
Was das R Paket {oslrr} für die gaussian linear Regression kann, kann das R Paket {MASS} mit der Funktion stepAIC für den Rest der möglichen Verteilungen. Da wir mit dem Fekerldatensatz ein binominales Outcome \(y\) mit infected vorliegen haben nutzen wir un die Funktion stepAIC(). Wir hätten auch den Kichererbsendatensatz mit der Funktion bearbeiten können, aber im Falle der Normalverteilung stehen uns dann eben noch andere Algorithmen zu Verfügung. Wie immer müssen wir zuerst das volle Modell mit der Funktion glm() fitten. Wir geben noch die Verteilungsfamilie mit family = binomial noch mit an und definieren so eine logistische lineare Regression.
fit <- glm(infected ~ age + sex + location + activity + crp + frailty + bloodpressure + weight + creatinin,
data = pig_tbl, family = binomial)Nachdem wir das Modell gefittet haben, können wir das Modell direkt in die Funktion stepAIC stecken. Wir nutzen noch die Option direction = "backward" um eine Rückwärtsselektion durchzuführen.
fit_step <- stepAIC(fit, direction = "backward")Start: AIC=421.22
infected ~ age + sex + location + activity + crp + frailty +
bloodpressure + weight + creatinin
Df Deviance AIC
- location 3 398.49 418.49
- frailty 2 396.61 418.61
- weight 1 395.22 419.22
- age 1 395.24 419.24
- activity 1 395.47 419.47
- sex 1 395.93 419.93
- creatinin 1 396.74 420.74
<none> 395.22 421.22
- bloodpressure 1 399.67 423.67
- crp 1 504.90 528.90
Step: AIC=418.49
infected ~ age + sex + activity + crp + frailty + bloodpressure +
weight + creatinin
Df Deviance AIC
- frailty 2 399.68 415.68
- weight 1 398.50 416.50
- age 1 398.50 416.50
- activity 1 398.83 416.83
- sex 1 399.01 417.01
- creatinin 1 400.10 418.10
<none> 398.49 418.49
- bloodpressure 1 403.24 421.24
- crp 1 509.50 527.50
Step: AIC=415.68
infected ~ age + sex + activity + crp + bloodpressure + weight +
creatinin
Df Deviance AIC
- weight 1 399.69 413.69
- age 1 399.73 413.73
- activity 1 400.06 414.06
- sex 1 400.30 414.30
- creatinin 1 401.21 415.21
<none> 399.68 415.68
- bloodpressure 1 404.17 418.17
- crp 1 511.29 525.29
Step: AIC=413.69
infected ~ age + sex + activity + crp + bloodpressure + creatinin
Df Deviance AIC
- age 1 399.74 411.74
- activity 1 400.09 412.09
- sex 1 400.40 412.40
- creatinin 1 401.22 413.22
<none> 399.69 413.69
- bloodpressure 1 404.18 416.18
- crp 1 512.26 524.26
Step: AIC=411.74
infected ~ sex + activity + crp + bloodpressure + creatinin
Df Deviance AIC
- activity 1 400.11 410.11
- sex 1 400.45 410.45
- creatinin 1 401.40 411.40
<none> 399.74 411.74
- bloodpressure 1 404.20 414.20
- crp 1 512.28 522.28
Step: AIC=410.11
infected ~ sex + crp + bloodpressure + creatinin
Df Deviance AIC
- sex 1 400.47 408.47
- creatinin 1 401.86 409.86
<none> 400.11 410.11
- bloodpressure 1 404.72 412.72
- crp 1 513.77 521.77
Step: AIC=408.47
infected ~ crp + bloodpressure + creatinin
Df Deviance AIC
- creatinin 1 402.21 408.21
<none> 400.47 408.47
- bloodpressure 1 406.37 412.37
- crp 1 514.11 520.11
Step: AIC=408.21
infected ~ crp + bloodpressure
Df Deviance AIC
<none> 402.21 408.21
- bloodpressure 1 408.12 412.12
- crp 1 516.27 520.27Jetzt ist die Selektion durchgelaufen und wir sehen in jeden Schritt welche Variable jeweils entfernt wurde und wie sich dann der \(AIC\)-Wert ändert. Wir starten mit einem \(AIC = 425.65\) und enden bei einem \(AIC=415.01\). Schauen wir uns nochmal das finale Modell an.
fit_step |>
model_parameters()Parameter | Log-Odds | SE | 95% CI | z | p
-------------------------------------------------------------------
(Intercept) | -23.54 | 3.14 | [-29.96, -17.61] | -7.49 | < .001
crp | 0.97 | 0.11 | [ 0.76, 1.20] | 8.83 | < .001
bloodpressure | 0.09 | 0.04 | [ 0.02, 0.16] | 2.39 | 0.017 Hier erscheint jetzt noch die Variable sex mit in der Auswahl. Das hat natürlich auch weitreichende Auswirkungen! Es macht schon einen gewaltigen Unterschied, ob wir annehmen das, dass Geschelcht der Ferkel keinen Einfluss auf die Infektion hat oder eben doch. Wir sehen auch hier, dass wir Aufpassen müssen wenn wir eine Variablenselektion durchführen. Aber Achtung, das schrittweise Verfahren ist der Auswahl nach \(p\)-Werten auf jeden Fall vorzuziehen!
42.3.5 Feature Selektion mit ranger
In diesem Abschnitt wollen wir die Variablenselektion mit einem maschinellen Lernverfahren durchführen. Im Bereich des maschinellen Lernens heist die Variablenselektion dann aber Feature Selektion. Wir versuchen jetzt die Selektion auf den Orginaldaten durchzuführen. Eigentlich wird empfohlen die Daten vorher zu normalisieren und dann mit den maschinellen Lernverfahren zu nutzen.
Standardisieren oder Normalisieren von Daten
Eine Herausforderung für maschinelle Lernverfahren sind nicht normalisierte Daten. Das heist, dass wir Variablen haben, die kategorial oder kontinuierlich sein können oder aber sehr unterschiedlich von den Einheiten sind. Deshalb wird empfohlen die Daten vorher zu Standardisieren oder zu Normalisieren. In dem Kapitel 18 kannst du mehr über das Transformieren von Daten nachlesen.
Wir nutzen als erstes einen Random Forest Algorithmus wie er in Kapitel 70 beschrieben ist. Es bietet sich hier die Implementation im R Paket {ranger} an. Bevor wir aber einen Random Forest auf unsere Daten laufen lassen, Standardisieren wir unsere Daten nochmal. Überall wo wir einen numerischen Wert als Variableneintrag haben rechnen wir eine \(z\)-Transformation. Wir erhalten dann die standardisierten Daten zurück.
pig_norm_tbl <- pig_tbl |>
mutate(across(where(is.character), as_factor),
across(where(is.numeric), dlookr::transform, "zscore"))Warning: There was 1 warning in `mutate()`.
ℹ In argument: `across(where(is.numeric), dlookr::transform, "zscore")`.
Caused by warning:
! The `...` argument of `across()` is deprecated as of dplyr 1.1.0.
Supply arguments directly to `.fns` through an anonymous function instead.
# Previously
across(a:b, mean, na.rm = TRUE)
# Now
across(a:b, \(x) mean(x, na.rm = TRUE))pig_norm_tbl# A tibble: 412 × 10
age sex location activity crp frailty bloodpressure
<transfrm> <fct> <fct> <transfrm> <transfrm> <fct> <transfrm>
1 0.2156014 male northeast 1.23906607 1.6154076 robust 1.6152124
2 -1.5521155 male northwest -0.15495130 -0.9942285 robust -0.7895759
3 1.3204244 female northeast -1.18531196 -0.9104969 robust 0.3274677
4 -0.2263278 female north 0.03899895 -0.4848611 robust -0.2085934
5 0.6575306 male northwest 0.87540937 1.0502190 robust -0.4391895
6 -1.1101862 male northwest 1.54211333 0.9664873 robust 1.0312351
7 -2.4359739 male west 0.32386336 -0.7569889 pre-frail -0.6488224
8 -1.5521155 male northwest 0.13597407 -0.7569889 robust -0.4122367
9 -0.4472924 female west -0.87014282 1.2735034 robust 0.6838436
10 -0.6682570 male northwest 0.46326510 0.6245832 robust -0.3343731
# ℹ 402 more rows
# ℹ 3 more variables: weight <transfrm>, creatinin <transfrm>,
# infected <transfrm>Den Random Forest rechnen wir mit der Funktion ranger(). Dafür müssen wir wieder unser vollständiges Modell definieren und können dann die Funktion starten. Damit wir eine Variablenwichtigkeit (eng. variable importance) wiederbekommen, müssen wir noch die Option importance = "permutation" verwenden.
fit_raw <- ranger(infected ~ age + sex + location + activity + crp + frailty + bloodpressure + weight + creatinin,
data = pig_tbl, ntree = 1000, importance = "permutation")
pluck(fit_raw, "variable.importance") |>
sort(decreasing = TRUE) |>
round(3) crp creatinin bloodpressure location activity
0.095 0.006 0.003 0.002 0.000
frailty age sex weight
-0.001 -0.001 -0.001 -0.002 Wir sehen, dass wir als wichtigste Variable wiederum crp zurückbekommen. Danach wird es schon etwas schwieriger, da die Werte sehr schnell kleiner werden und auch ein Art Plateau bilden. Daher würde man hier nur annehmen, dass crp bedeutend für das Modell ist. Es kann aber auch sein, dass hier eine kontinuierliche Variable sehr vom Algorithmus bevorzugt wurde. Daher schauen wir uns die Sachlage einmal mit den standardisierten Daten an.
fit_norm <- ranger(infected ~ age + sex + location + activity + crp + frailty + bloodpressure + weight + creatinin,
data = pig_norm_tbl, ntree = 1000, importance = "permutation")
pluck(fit_norm , "variable.importance") |>
sort(decreasing = TRUE) |>
round(3) crp creatinin bloodpressure frailty location
0.415 0.024 0.013 0.001 -0.002
sex weight activity age
-0.003 -0.008 -0.010 -0.013 Auch hier erhalten wir ein ähnliches Bild. Audf jeden Fall ist crp bedeutend für den Infektionsstatus. Danach werden die Werte etwas zufällig. Wir können Werte für die variable importance nicht unter Datensätzen vergleichen. Jeder Datensatz hat seine eigene variable importance, die von den Werten in dem Datensatz abhängt.
Wir ziehen als Fazit, dass wir nur crp als bedeutenden Wert für die Klassifikation des Infektionsstatus ansehen würden. Hier stehen wir wirklich etwas wie das Schwein vor dem Uhrwerk, denn was nun richtiger ist, stepAIC oder ranger lässt sich so einfach nicht bewerten. Zum einen wollen wir ja eigentlich mit Random Forest eine Klassifikation durchführen und mit linearen Regressionsmodellen eher kausale Modelle schätzen. Am Ende musst du selber abschätzen, was in das finale Modell soll. Ich kann ja auch den Threshold für den Variablenausschluss selber wählen. Wähle ich einen Threshold von \(0.008\), dann hätte ich crp, weight, bloodpressure und sex mit in dem finalen Modell.
42.3.6 Feature Selektion mit boruta
Mit dem Boruta Algorithmus steht uns noch eine andere Implemnetierung des Random Forest Algorithmus zu verfügung um Feature Selektion zu betreiben. Wir nutzen wieder den Boruta Algorithmus in seine einfachen Form und gehen nicht tiefer auf alle Optionen ein. Wir nehmen wieder als Beispiel den Datensatz zu den infizierten Ferkeln und nutzen in diesem Fall auch nur die rohen Daten. Über eine Standardisierung könnte man wiederum nachdenken.
Ich empfehle noch das Tutorium Feature Selection in R with the Boruta R Package. Wir gehen hier nicht tiefer auf die Funktionalität von Boruta ein.
Standardisieren oder Normalisieren von Daten
Eine Herausforderung für maschinelle Lernverfahren sind nicht normalisierte Daten. Das heist, dass wir Variablen haben, die kategorial oder kontinuierlich sein können oder aber sehr unterschiedlich von den Einheiten sind. Deshalb wird empfohlen die Daten vorher zu Standardisieren oder zu Normalisieren. In dem Kapitel 18 kannst du mehr über das Transformieren von Daten nachlesen.
Um die Funktion Boruta() zu nutzen brauchen wir wieder das Modell und den Datensatz. Sonst ist erstmal nichts weiter anzugeben. Die Funktion läuft dann durch und gibt auch gleich den gewollten Informationshappen. Wichtig ist hierbei, dass wir natürlich noch andere Optionen mit angeben können. Wir können die Anzahl an Iterationen erhöhen und andere Tuning Parameter eingeben. Hier muss man immer schauen was am besten passt. Da würde ich auch immer rumprobieren und auf der Hilfeseite der Funktion ?Boruta einmal nachlesen.
set.seed(20221031)
boruta_output <- Boruta(infected ~ age + sex + location + activity + crp + frailty + bloodpressure + weight + creatinin,
data = pig_tbl)
boruta_outputBoruta performed 99 iterations in 4.861275 secs.
1 attributes confirmed important: crp;
6 attributes confirmed unimportant: activity, age, frailty, location,
sex and 1 more;
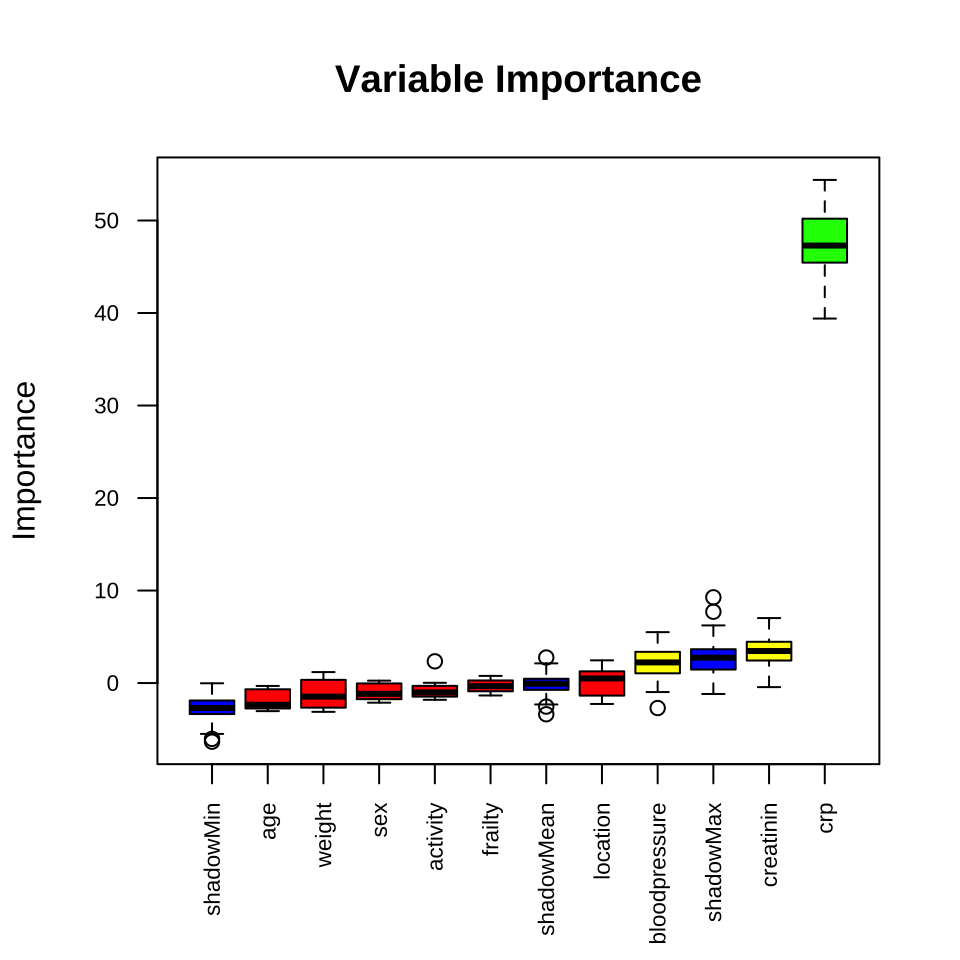
2 tentative attributes left: bloodpressure, creatinin;Manchmal ist es super praktisch, wenn eine Funktion einem die Antwort auf die Frage welche Variable bedeutend ist, gleich liefert. Wir erhalten die Information, dass die Variable crp als bedeutsam angesehen wird. Wir können uns den Zusammenhang auch in der Abbildung 42.2 auch einmal anschauen. Die grünen Variablen sind die bedeutenden Variablen.
plot(boruta_output, cex.axis=.7, las=2, xlab="", main="Variable Importance") 
Am Ende finden wir auch hier die Variable crp als einziges als bedeutend wieder. Wenn wir noch Variablen haben die verdächtig oder vorläufig bedeutend sind, angezeigt durch 2 tentative attributes left: bloodpressure, sex, dann können wir noch die Funktion TentativeRoughFix() nutzen. Die Funktion TentativeRoughFix() rechnet die Variablen nochmal nach und versucht alle Variablen in bedeutend oder nicht bedeutend zu klassifizieren. Wir haben ja zwei tentative Variablen in unseren Fall vorliegen, also nutzen wir noch kurz die Funktion um uns auch hier Klarheit zu schaffen.
TentativeRoughFix(boruta_output)Boruta performed 99 iterations in 4.861275 secs.
Tentatives roughfixed over the last 99 iterations.
2 attributes confirmed important: creatinin, crp;
7 attributes confirmed unimportant: activity, age, bloodpressure,
frailty, location and 2 more;Am Ende ist die klare Aussage einer Funktion auch immer ein zweischneidiges Schwert. Wir verlieren jetzt noch die beiden tentative Variablen. Wo wir bei ranger die Qual der Wahl haben, werden wir bei Boruta eher vor vollendete Tatsachen gestellt. Meistens neigt man nach einer Boruta-Analyse nicht dazu noch eine zusätzliche Variable mit ins Modell zu nehmen. Dafür ist dann die Ausgabe zu bestimmt, obwohl die Entscheidung am Ende auch genau so unsicher ist wie von ranger und den anderen Modellen.
Referenzen
Heinze G, Dunkler D. 2017. Five myths about variable selection. Transplant International 30: 6–10.
Heinze G, Wallisch C, Dunkler D. 2018. Variable selection–a review and recommendations for the practicing statistician. Biometrical journal 60: 431–449.
Talbot D, Massamba VK. 2019. A descriptive review of variable selection methods in four epidemiologic journals: there is still room for improvement. European journal of epidemiology 34: 725–730.