35  Der U-Test

Letzte Änderung am 08. June 2025 um 21:27:19

“Statisticians, like artists, have the bad habit of falling in love with their models.” — George Box

Der U-Test ist auch unter den Namen Wilcoxon-Mann-Whitney-Test, Mann-Whitney-U-Test oder Wilcoxon-Rangsummentest bekannt. Aus Gründen der Kürze werde ich hier immer von dem U-Test schreiben. Der U-Test wird häufig noch in den Grundlagenwissenschaften wie Zellforschung oder bei Mäusemodellen verwendet. Gerne auch bei genetischen Knockout-Experimenten mit einer kleinen Anzahl an Mäusen. In den Agrarwissenschaften treffen wir den U-Test nicht ganz so häufig, da wir meistens dann doch auf einem normalverteilten Messwert den ANOVA Pfad durchrechnen wollen. Dennoch treffen wir immer wieder auf die Nichtparametrik und dieses Kapitel liefert auch gleich eine tiefere Betrachtung gleich mit.

35.1 Allgemeiner Hintergrund

Wann nutzen wir den Wilcoxon-Mann-Whitney-Test? Wir nutzen den Wilcoxon-Mann-Whitney-Test wenn wir zwei Verteilungen miteinander vergleichen wollen. Das ist jetzt sehr abstrakt und auch eins der Probleme des U-Tests. Wir würden sagen, dass wenn wir zwei Gruppen haben und ein nicht normalverteiltes \(y\), dann nutzen wir einen U-Test. Das ist aber stark verkürzt, mittlerweile haben wir in unserer statistischen Toolbox auch über das statistische Modellieren eine Lösungen für eine Vielzahl von Verteilungen. Keine Normalverteilung heißt nicht automatisch jetzt aber Nichtparametrik. Das war vielleicht Anfang der 90ziger so. Wir haben heute mehr Möglichkeiten — im Prinzip meine ich damit, dass der U-Test seine Nische verdient hat, aber eigentlich etwas veraltet ist mit seinen Problemen. Haben wir ein normalverteiltes \(y\) rechnen wir meist einen t-Test. Wir könnten aber auch einen Wilcoxon-Mann-Whitney-Test auf einer Normalverteilung rechnen.

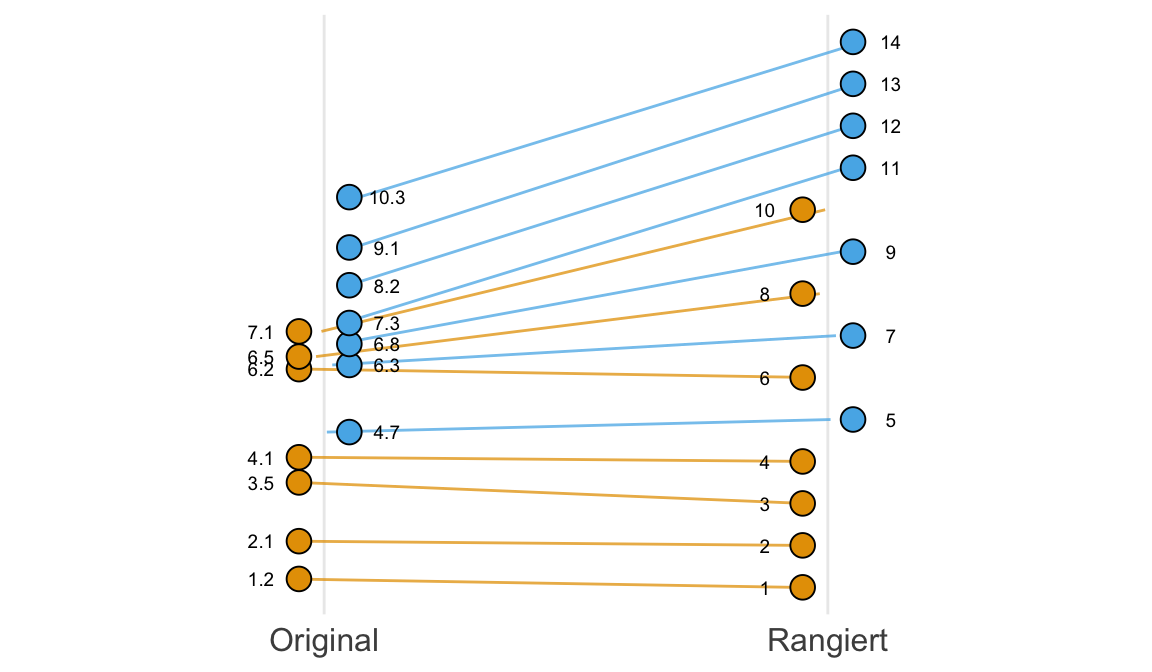
Was ist jetzt der Unterschied zwischen einem U-Test und einem t-Test? Der t-Test vergleicht die Mittelwerte zweier Normalverteilungen, also zum Beispiel die Verteilung der Sprungweiten der Hundeflöhe gegen die Verteilung der Sprungweiten der Katzenflöhe. Dazu nutzt der t-Test die Mittelwerte und die Standardabweichung. Beides sind Parameter einer Verteilung und somit ist der t-Test ein parametrischer Test. Der Wilcoxon-Mann-Whitney-Test ist die nichtparametrische Variante in dem wir die Zahlen in Ränge umwandeln, also sortieren, und mit den Rängen der Zahlen rechnen. Die deskriptiven Maßzahlen wären dann Median, Quantile und Quartile. Also im Prinzip eine Rangtransformation und dann anschließend ein statistischer Test der Ränge. In der folgenden Abbildung habe ich dir einmal den Zusammenhhang zwischen den originalen Messwerten und der Rangtransformation dargestellt.

Abbildung 35.1— Zusammenhang zwischen den originalen Messwerten und den rangierten Messwerten nach der Rangtransformation. Nach dem Rangieren haben alle Messwerte den gleichen Abstand.

Wenn wir von der Rangtransformation sprechen, dann treten auch häufiger Bindungen in den Messwerten auf. Bindungen sind kein Problem und können bei der Auswertung berücksichtigt werden. Je mehr Kommastellen ein kontinuierlicher Messwert hat, desto weniger Binden können natürlich auftreten. Bei ordinalen Daten wie Noten ist das natürlich nicht so einfach möglich.

Was sind Bindungen?

Bindungen treten bei der Rangtransformation auf, wenn wir gleiche originale Messwerte haben. Dann müssen wir zwei Messwerten den gleichen Rang geben. Wenn dieser Fall auftritt, dann sprechen wir von Bindungen in den Daten. Die nichtparametrischen Algorithmen haben dafür implementierte Lösungen.

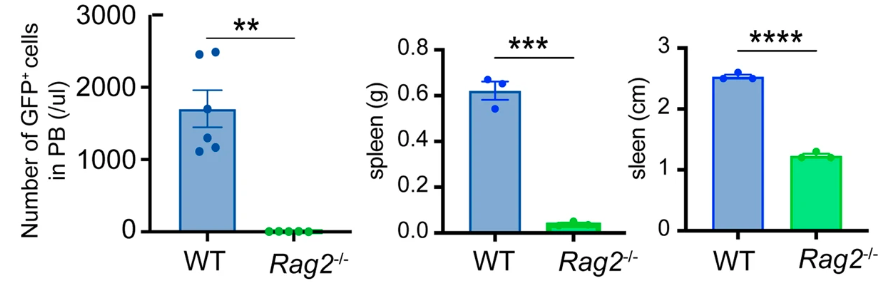
Steigen wir also einmal mit einem plakativen Beispiel aus der Studie von Sugimoto et al. (2023) in die Thematik des U-Test ein. Ich habe die folgende Abbildung einmal mitgebracht in der wir die Mittelwerte sowie die Standardabweichung von verschiedenen Messwerten für einen Wildtyp (WT) sowie einer genetischen Variante (Rag2) sehen. Die Sterne geben die Signifikanz des Vergleichs zwischen den Gruppen an.

Abbildung 35.2— Left: Number of GFP+ MLL-AF9 cells in peripheral blood of WT and Rag2−/− mice. PB was collected 11 days after transplantation. Data are shown as means ± s.e.m. [n = 6 (male: n = 3, female: n = 3) for each group]. **P < 0.01；two-tailed Mann–Whitney test. Middle/right: Weight and size of spleens collected from WT or Rag2−/− mice 11 days after transplantation. Data are shown as means ± s.e.m. (n = 3 for each group, male). ***P < 0.001, ****P < 0.0001; two-tailed Student’s t test. Quelle: Sugimoto et al. (2023)

Nachdem wir uns die Abbildung 36.1 einmal genauer angeschaut haben, stellt sich die Frage warum wird in der Abbildung ganz links ein Mann-Whitney oder U-Test gerechnet und in den beiden anderen Abbildungen ein Student t-Test? Warum nicht auf alles ein U-Test rechnen? Immerhin würde ja auf das Gewicht und die Größe der Milz (eng. spleen) auch ein U-Test als statistischer Test auch gehen. Wir haben hier unterschiedliche Fallzahlen in den Gruppen. In der linken Abbildung haben wir pro Gruppe sechs Mäuse und in der mittleren sowie rechten Abbidlung nur drei Mäuse pro Gruppe. Macht das einen Unterschied? Ja, für den U-Test macht das einen gewaltigen Unterschied, wie wir gleich einmal sehen werden.

35.2 Das Problem…

Es gibt ein paar Probleme, wenn wir uns mit dem U-Test im Allgemeinen beschäftigen wollen. Diese Probleme sind eigentlich nicht weitläufig bekannt. Mir waren die Probleme auch nicht bekannt bis ich angefangen habe dieses Kapitel zu schreiben. Deshalb gehen wir mal die Probleme durch und leider gibt es nicht so richtig eine Lösung dafür. Es sind Probleme, die aus dem Algorithmus und der Transformation in Ränge entstehen.

35.2.1 …der Gruppengröße

“Statistik fängt erst ab einer Gruppengröße von n gleich sieben überhaupt an.” — Ein anonymer Nichtparametriker

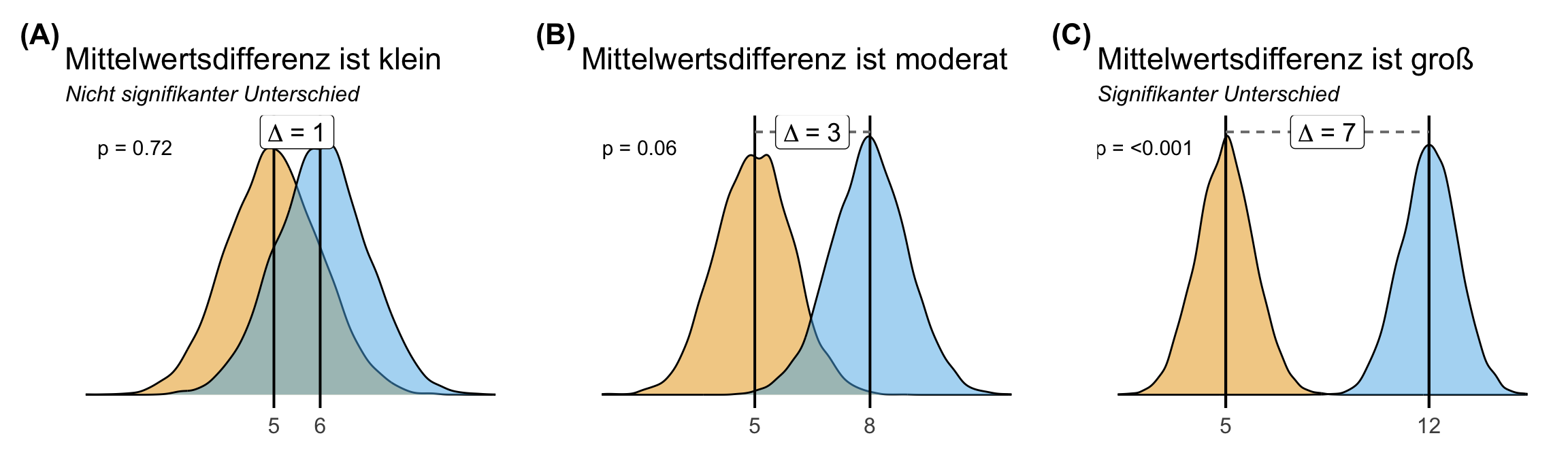
Um das Problem der geringen Gruppengröße zu verstehen, müssen wir erstmal den Zusammenhang zwischen einem signifikanten Ergebnis und der Mittelwertsdifferenz als ein statistsiches Maß für den Effekt verstehen. Je größer der Effekt, desto eher sollte ein Vergleich zwischen zwei Gruppen signifikant unterschiedlich sein. In der folgenden Abbildung habe ich dir einmal den Zusammenhang zwischen der Mittelwertsdifferenz \(\Delta\) und der Signifikanz dargestellt. Wie du siehst überlappen die Verteilungen der beiden Gruppen, wenn die Differenz der Mittelwerte klein ist. Je größer der Unterschied desto größer ist die Mittelwertsdifferenz. Soweit so klar. Damit sollten wir auch kleinere p-Werte erhalten, je größer die Mittelwertsdifferenz wird. Ich habe dir mal beispielhafte p-Werte in der Abbildung ergänzt.

Abbildung 35.3— Darstellung des Zusammenhangs zwischen der Mittelwertsdifferenz und der zu erwartenden Signifikanz aus einem statistischen Tests für einen Zweigruppenvergleich. Die p-Werte sind abgeschätzt. (A) Die Mittelwertsdifferenz ist klein, es ist kein signifikanter Unterschied zu erwarten. Der p-Wert ist groß. (B) Die Mittelwertsdifferenz ist moderat, es ist ein kleiner p-Wert zu erwarten. (C) Die Mittelwertsdifferenz ist groß, damit ist der p-Wert kleiner als \(0.001\) und hoch signifikant. [Zum Vergrößern anklicken]

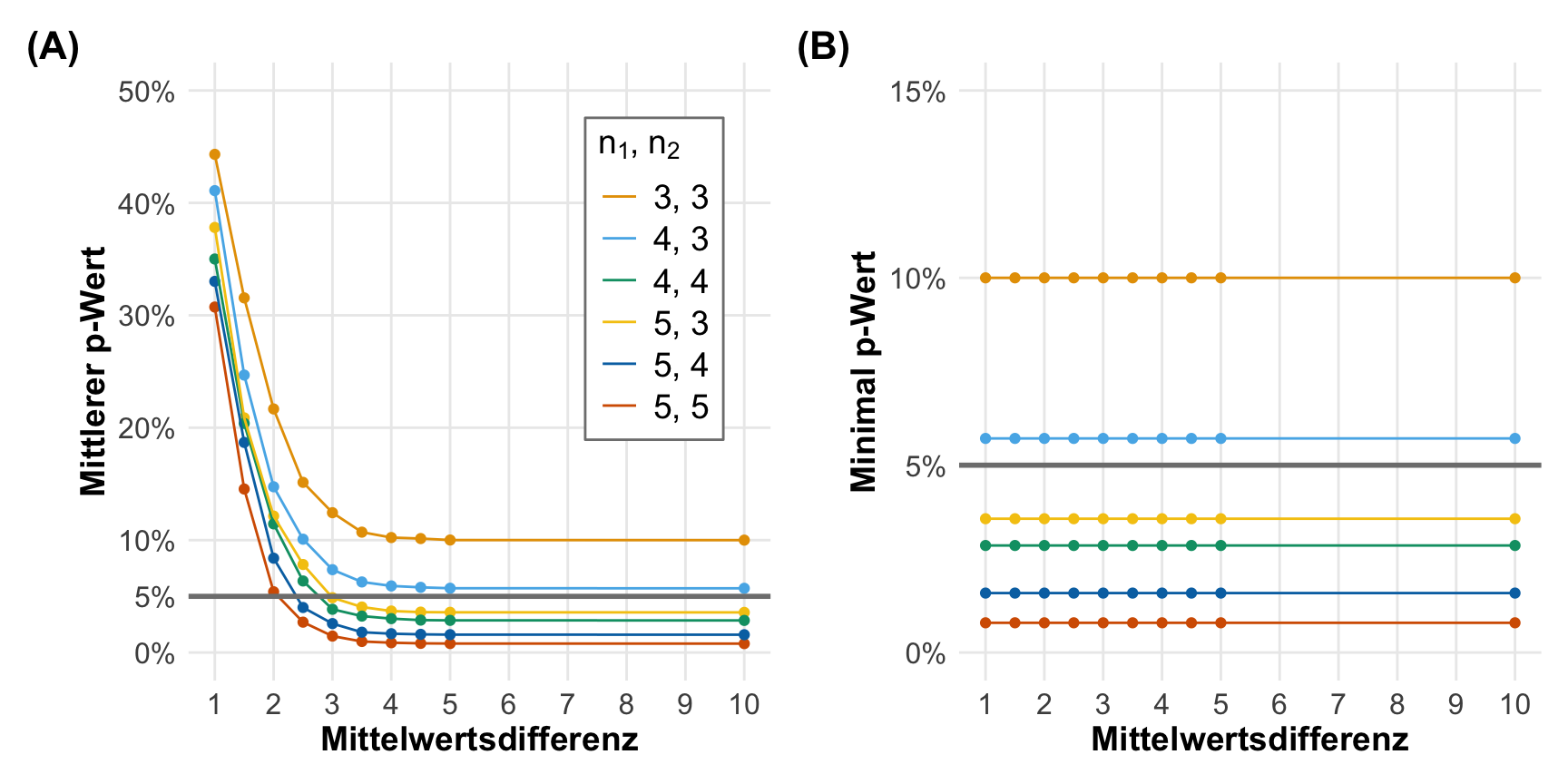
Wenn wir jetzt den Zusammenhang zwischen der Mittelwertsdifferenz und dem p-Wert verstanden haben, können wir jetzt zum Problem der geringen Fallzahl in den Gruppen kommen. Wenn die Mittelwertsdifferenz ansteigt, dann sollte der p-Wert fallen. Wie du in folgender Abbildung links auch siehst, ist das der Fall. Für alle Kombinationen der Fallzahlen in den beiden Gruppen \(n_1\) und \(n_2\) fallen die p-Werte mit steigendem Effekt. Nur haben die p-Werte ein Plateau unter das sie nicht fallen können. Und bei einer Gruppengröße von 3 und 3 oder 4 und 3 können die p-Werte nicht kleiner als 0.05 werden egal wie groß die Mittelwertsdifferenz wird. Daher können wir mit diesen beiden Fallzahlkombinationen keinen signifkanten Unterschied nachweisen. Das sehen wir auch nochmal in der anderen Abbildung rechts, hier siehst du die minimalen p-Werte. Die p-Werte können in einem U-Test nicht unter gewisse Schranken fallen, abhängig von der Gruppenfallzahl.

Abbildung 35.4— Zusammenhang zwischen der Mittelwertsdifferenz und dem mittleren p-Wert aus einer Simulationsstudie abhängig von der Fallzahl in zwei Gruppen \(n_1\) und \(n_2\). Die graue Linie zeigt das 5% Signifikanzniveau an. (A) Mit steigender Mittelwertsdifferenz fallen die mittleren p-Werte. Die p-Werte erreichen je nach Fallzahlkombination ein Plateau. (B) Kleinst möglicher p-Wert in den Simulationen für jede Fallzahlkombinationen. [Zum Vergrößern anklicken]

Jetzt verstehen wir auch warum Sugimoto et al. (2023) in der Abbildung 36.1 auf einen Student t-Test für die Gruppengröße \(n_1 = 3\) und \(n_2 = 3\) umgeschwenkt ist. Trotz des riesigen Effekts in den Barplots und damit dem Mittelwertsunterschied, wäre ein Mann-Whitney Test nie signifikant geworden. Der p-Werte wäre dann hier auf 10% begrenzt, egal wie groß der eigentliche Effekt ist. Diese harte Grenze kennt der t-Test nicht, deshalb wurde hier dann der t-Test als Ausweg gewählt.

35.2.2 …der Hypothesen

Das Problem mit den Mann-Whitney-U-Test und den Hypothesen hat mich etwas überraschend getroffen. Ich dachte lange immer, dass der U-Test eben die Mediane miteinander vergleicht. Das macht ja auch irgendwie Sinn, denn die Mediane müssen ja auch einen Test haben und basieren ja auch auf Rängen. Oder wie es so schön sinnig in der Veröffentlichung The Wilcoxon–Mann–Whitney Procedure Fails as a Test of Medians von Divine et al. (2018) geschrieben steht.

“A major impetus to reporting medians with Mann-Whitney-U-tests results is likely the major utility of reporting a summary statistic that reflects the same scale as the data being analyzed.” — Divine et al. (2018)

Gut, was testet den nun der U-Test? Kommt auf die Annahmen an die Daten und damit dem U-Test an. Oder konkreter an die beiden Verteilungsformen, die du miteinander vergleichst. Der U-Test kann nämlich unterschiedliche Nullhypothesen haben, je nachdem welche Annahmen du an deine Daten hast. Und hier kommt der schlechte Witz. Meistens hast du so wenig Beobachtungen, dass du selber keine Visualisierung der Verteilung erstellen kannst.

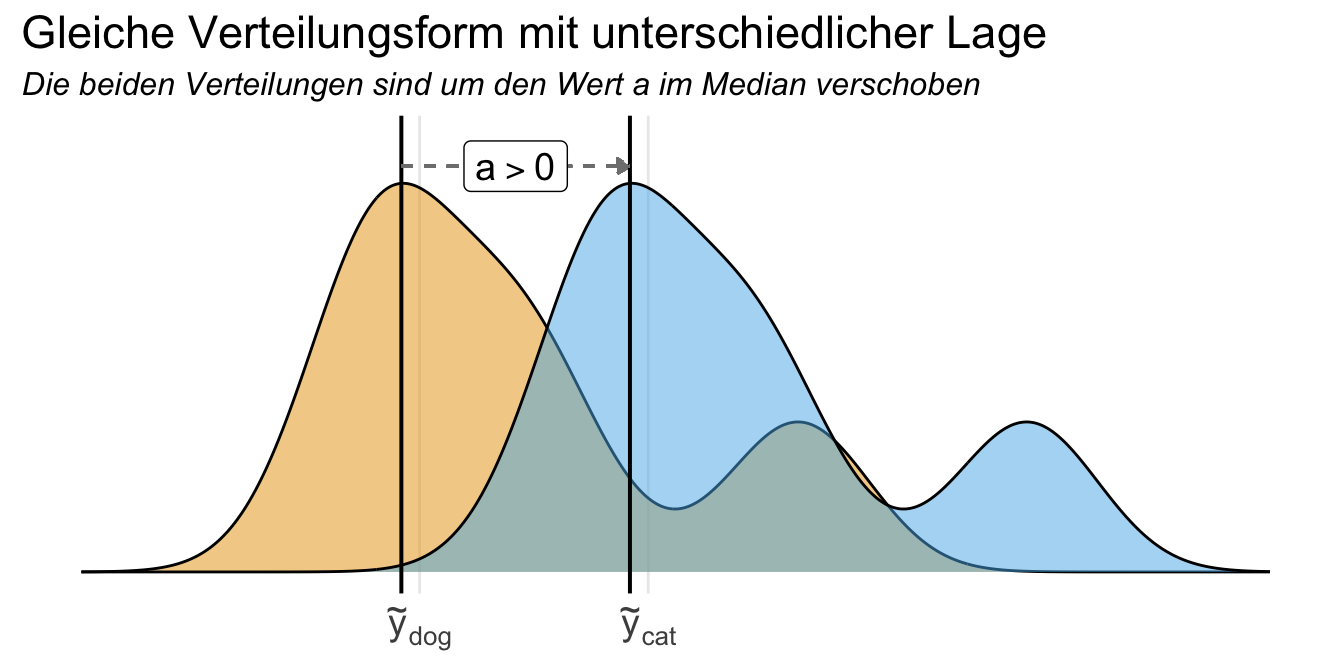
Gleiche Verteilungsform, unterschiedliche Lage

Weil die beiden Verteilungsfunktionen bis auf Verschiebung gleich sind, muss insbesondere Varianzhomogenität zwischen den beiden Gruppen gelten. Wenn wir also gleiche Verteilungen haben, die auch damit varianzhomogen sind, können wir folgende Hypothesen aufstellen. Ich habe dir den Fall einmal in der folgenden Abbildung dargestellt. Die Annahmen sind sehr restriktiv. Nach Conroy (2012) mit What Hypotheses do “Nonparametric” Two-Group Tests Actually Test? sollte daher der U-Test nicht für den Vergleich von Medianen genutzt werden.

Abbildung 35.5— Der U-Test kann unter der Annahme der gleichen Verteilungsform und damit angenommener Varianzhomogenität die Verschiebung a in den Medianen testen. Die Annahmen sind sehr restriktiv und treten nicht oft auf. [Zum Vergrößern anklicken]

Damit ergeben sich dann die folgenden Hypothesenpaare für den Vergleich der Mediane.

Prosa

\(H_0:\) Die Gleichheit der Mediane der zwei Gruppen liegt vor. Die Verschiebung der Mediane ist Null.

\(H_A:\) Die Mediane der zwei Gruppen unterscheiden sich. Die Verschiebung der Mediane ist ungleich Null.

Formel

\[ H_0: a = 0 \]

\[ H_A: a \neq 0 \]

Die Problematik ist recht umfangreich und der U-Test kann auch bei gleichen Medianen signifkante Ergebnisse liefern. Hart (2001) diskutiert in Mann-Whitney test is not just a test of medians: differences in spread can be important nochmal einige Sonderfälle. Also verbleibe ich dabei, der U-Test testet ursprünglich nicht die Unterschiede in den Median. Außer die Sterne stehen günstig, was aber keine Grundlage für sauberes wissenschaftliches Arbeiten ist.

Unterschiedliche Verteilungsform, unterschiedliche Lage

Nachdem wir uns nun davon verabschiedet haben, dass wir mit dem U-Test Mediane vergleichen, kommen wir nun zu den echten Hypothesen. Oder andersherum nur in sehr seltenen Fällen die Interpretation eines Vergleiches der Mediane erlaubt. Was ist also die Nullhypothese und die Alternativhypothese, die wir mit dem U-Test überprüfen wollen? Ich habe einmal ein schönes Zitat aus Guidelines von GraphPad mitgebracht sowie dann die Hypothesen auch einmal mathematisch aufgeschrieben.

Prosa

Der U-Test beantwortet folgende Frage an die Daten.

“If the groups are sampled from populations with identical distributions, what is the chance that random sampling would result in a sum of ranks as far apart (or more so) as observed in this experiment?” — The Mann-Whitney test doesn’t really compare medians

Damit haben wir dann in Prosa folgendes Hypothesenpaar vorliegen.

\(H_0:\) Es ist gleich wahrscheinlich, dass ein zufällig aus der einen Population ausgewählter Wert größer oder kleiner ist als ein zufällig ausgewählter Wert aus der anderen Population

\(H_A:\) Es ist nicht gleich wahrscheinlich, dass ein zufällig aus der einen Population ausgewählter Wert größer oder kleiner ist als ein zufällig ausgewählter Wert aus der anderen Population

Formel

In der Formel wird es schon etwas wilder und ich muss sagen, dass mir die Formel das Verständnis nicht leichter macht. Wir vergleichen hier zwei Populationen \(X\) und \(Y\) miteinander.

\[ H_0: Pr(X<Y) + \cfrac{1}{2} Pr(X = Y) = 0.5 \]

\[ H_A: Pr(X<Y) + \cfrac{1}{2} Pr(X = Y) \neq 0.5 \]

In dem R Paket {nparcomp} bezeichnen wir den Wert für \(Pr(X<Y) + \cfrac{1}{2} Pr(X = Y)\) auch als relativen Effekt.

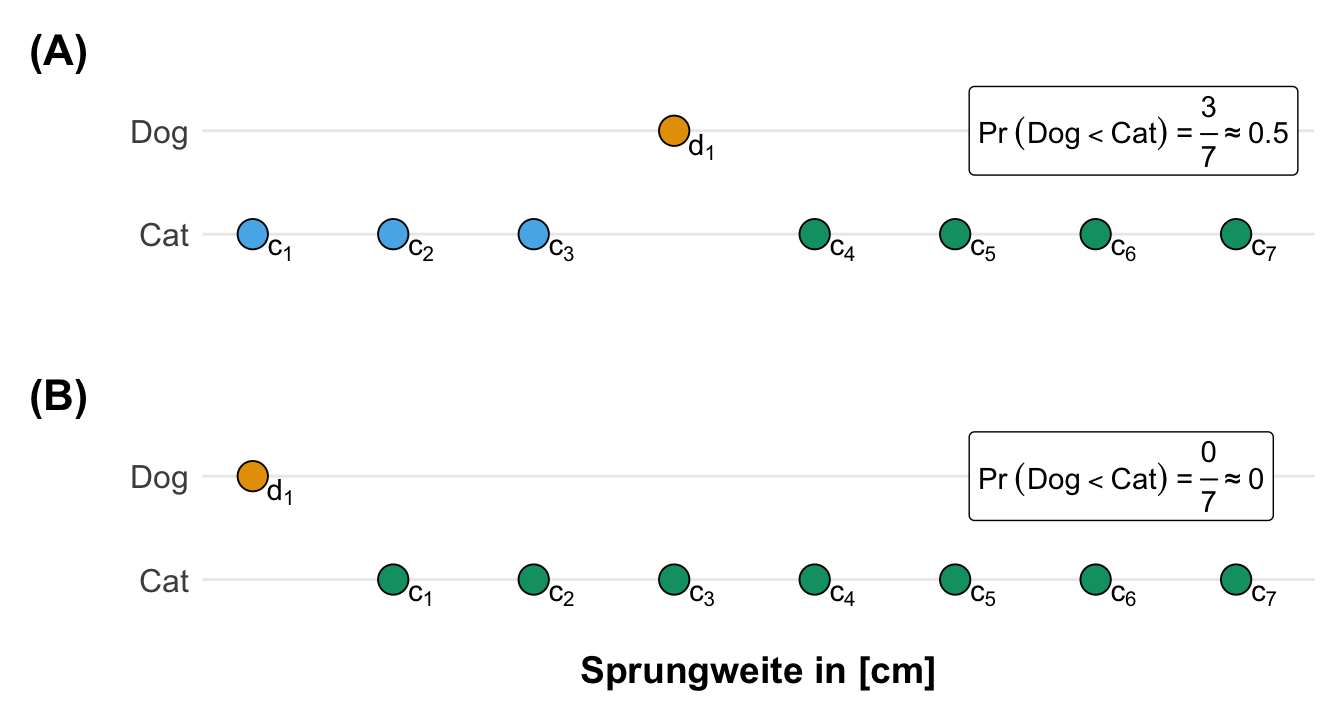
Da mir die Nullhypothese mit \(Pr(X<Y) + \cfrac{1}{2} Pr(X = Y) = 0.5\) nicht ganz einleuchtete habe ich einmal die Sachlage visualisiert und in R nachgerechnet. Ich verstehe den Zusammenhang sonst nicht. Die Nullhypothese besagt ja, dass es gleich wahrscheinlich ist, dass ein zufällig aus der einen Population ausgewählter Wert größer oder kleiner ist als ein zufällig ausgewählter Wert aus der anderen Population. Daher baue ich mit einfach mal zwei Vaktoren X und Y mit jeweils den gleichen Zahlen mit \(X = Y = {1, 2, 3, 4}\). Jetzt müsste ja auch der obigen Formel der Wert \(0.5\) rauskommen, denn die Nullhypothese ist ja wahr. Die Werte sind ja gleich.

Visualisierung

Was habe ich in der folgenden Abbildung einmal den Zusammenhang der Formel mit den Werten dargestellt. Wir haben insgesamt 16 Wertepaare für unsere 4 Zahlen pro Gruppe. Davon sind vier Wertepaar gleich, dargestellt in grün. Hier kriegen wir dann den Wert für \(\cfrac{1}{2} Pr(X = Y)\) mit \(0.125\) raus. Dann haben wir noch sechs Wertepaare wo X kleiner ist als Y. Daher haben wir hier die Werte für \(Pr(X<Y)\) mit \(0.375\) raus. Jetzt müssen wir noch die beiden Werte addieren und sehen, dass wir auf die \(0.5\) kommen. Das sieht doch gut aus. Was es jetzt uns sagt, ist nochmal eine andere Sache, aber immerhin haben wir mal verstanden, wie die Wahrscheinlichkeiten berechnet werden. Am Ende ist es dann doch nur ein Spiel der wilden Kombinatorik. Mehr zum Spielen im folgenden Tab.

Abbildung 35.6— Beispielhafte Berechnung der Wahrscheinlichkeit für die Nullhypothese in einem U-Test mit vier Werten für X und Y sowie den entsprechenden sechszehn Wertepaaren. Die Nullhypothese gilt, die Werte von X und Y sind gleich. Bindungen werden ignoriert, es handelt sich ja nicht um Ränge per se. Die grünen Linien zeigen Wertepaare die gleich sind. Die roten Linien Wertepaare wo X kleiner als Y ist. [Zum Vergrößern anklicken]

Du findest in dem Tutorium The Mann-Whitney U Test nochmal ein anschauliches Beispiel. Und auch in der Arbeit von Conroy (2012) wird versucht die Nullhypothese als Wertepaare über einen Kugelplot zu visualisieren.

{base}

Wir können uns auch einmal die Sachlage in R nachbauen. Wir haben dann die zwei Vektoren x und y mit beliebigen Werten. Ich nehme hier mal wieder die Werte 1, 2, 3, 4 für beide Vektoren.

x <- c(1, 2, 3, 4)
y <- c(1, 2, 3, 4)

Die Funktion crossing() gibt uns jetzt jedes paarweise Wertepaar der Kombinartion von x und y wieder. Dann können wir berechnen welche Wertepaare gleich sind, als x == y sowie die Wertepaare, wo x kleiner ist als y. Dann schauen wir uns einmal die Ausgabe an.

pair_tbl <- crossing(x, y) |> 
  mutate(p_x_equal_y = (x == y),
         p_x_less_y = (x < y)) 
pair_tbl

# A tibble: 16 × 4
       x     y p_x_equal_y p_x_less_y
   <dbl> <dbl> <lgl>       <lgl>     
 1     1     1 TRUE        FALSE     
 2     1     2 FALSE       TRUE      
 3     1     3 FALSE       TRUE      
 4     1     4 FALSE       TRUE      
 5     2     1 FALSE       FALSE     
 6     2     2 TRUE        FALSE     
 7     2     3 FALSE       TRUE      
 8     2     4 FALSE       TRUE      
 9     3     1 FALSE       FALSE     
10     3     2 FALSE       FALSE     
11     3     3 TRUE        FALSE     
12     3     4 FALSE       TRUE      
13     4     1 FALSE       FALSE     
14     4     2 FALSE       FALSE     
15     4     3 FALSE       FALSE     
16     4     4 TRUE        FALSE     

Jetzt können wir noch die Mittelwerte berechnen, was bei Wahrscheinlichkeiten nichts anders ist als die Wahrscheinlichkeit für TRUE zu erhalten. Wir sehen, dass wir auf die gleichen Wert kommen. Jetzt kannst du auch mit anderen Kombinationen der Vektoren spielen und sehen, wie sich die Werte und deren Summe ändern.

pair_tbl |> 
  summarise(mean(p_x_less_y),
            mean(p_x_equal_y)/2) 

# A tibble: 1 × 2
  `mean(p_x_less_y)` `mean(p_x_equal_y)/2`
               <dbl>                 <dbl>
1              0.375                 0.125

Beispiel

Dann können wir mal den Wert für \(Pr(X<Y) + \cfrac{1}{2} Pr(X = Y)\) einmal für unser Datenbeispiel zu den Sprungweiten berechnen. Du findest die Daten nochmal weiter unten zum selber laden. Wir nutzen dazu den R Code aus dem vorherigen Tab. Zuerst müssen wir einmal die Sprungweiten über die beiden Floharten rangieren. Dann wieder die beiden Floharten separieren damit wir dann mit den Spalten der Ränge weiterrechnen können.

fac1_ranks_tbl <- fac1_tbl |> 
  mutate(ranked_jump_length = rank(jump_length)) |>
  select(animal, ranked_jump_length) |> 
  pivot_wider(names_from = animal,
              values_from = ranked_jump_length) |> 
  unnest()
fac1_ranks_tbl

# A tibble: 7 × 2
    dog   cat
  <dbl> <dbl>
1     7     2
2    12     1
3    14     5
4     6     3
5    13     4
6    11    10
7     9     8

Jetzt setzen wir die Ränge der beiden Spalten einmal in die Funktion crossing() und rechnen einmal die Werte für \(Pr(X < Y)\) und \(\cfrac{1}{2} Pr(X = Y)\) aus. Wie wir sehen, ist eine der Wahrscheinlichkeiten null. Die Summierung der beiden Werte spare ich mir, dass geht ja auch so recht flott im Kopf.

crossing(dog = fac1_ranks_tbl$dog, 
         cat = fac1_ranks_tbl$cat) |> 
  mutate(p_x_equal_y = (dog == cat),
         p_x_less_y = (dog < cat)) |> 
  summarise(mean(p_x_less_y),
            mean(p_x_equal_y)/2) 

# A tibble: 1 × 2
  `mean(p_x_less_y)` `mean(p_x_equal_y)/2`
               <dbl>                 <dbl>
1              0.102                     0

Was wissen wir also? Wenn wir alle 49 Wertepaare jeder Sprungweite eines Katzenflohs mit jeder Sprungweite eines Hundeflohs vergleichen, dann springen in 10.2% der Wertepaare die Hundeflöhe kürzer (oder gleich) weit wie die Katzenflöhe. Oder andersherum springen in fast 90% der Wertepaare die Hundeflöhe weiter als die Katzenflöhe.

35.2.3 …des Effekts

Was ist der Effekt eines nichtparametrischen Tests? Oder andersherum, wenn wir eine Rangtransformation durchführen, dann verwandeln wir ja alle Zahlen mit einer Einheit in einen einheitslosen Rang. Damit rechnen wir also auf den Rängen des Messwertes. Wenn wir aber nun einheitslose Ränge haben, dann haben wir auch nur einheitslose Rangdifferenzen. Dazu kommt je mehr Beobachtungen desto mehr Ränge desto größer die Rangdifferenzen. Wir haben zwar dann die Möglichkeit wieder eine Art Cohen`s d oder eben r zu berechnen, aber hat dieser Wert wieder keien Einheit und ist auch schwer zu interpretieren. Es gibt wieder viele Arten dies zu tun und je nach Quelle haben wir dann ein anderes Adjektiv wie “kleiner”, “mittler” oder “starker” Effekt. Solche Worte können wir dann aber nicht mit Kosten/Nutzenrechnungen verbinden. Am Ende hat eben dann der nichtparametrische U-Test kein Effektmaß mit dem sich praktisch und relevant arbeiten lässt.

“Es gibt Gründe die Nichtparametrik als den Ausweg für die Nichtnormalverteilung zu sehen. In gewissen Anwendungsfeldern mag das auch so stimmen. Wenn du wirklich nicht an einem Effektmaß interessiert bist und nur einen p-Wert brauchst, dann ist die Nichtparametrik eine Lösung. Heutzutage wollen wir aber auch immer wissen, ist der Effekt relevant? Und die Frage ohne ein Effektmaß zu beantworten sehe ich als unmöglich an.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

35.3 Eine Lösung

“The rank transformation approach provides a vehicle for presenting both the parametric and nonparametric methods in a unified manner.” — Conover & Iman (1981)

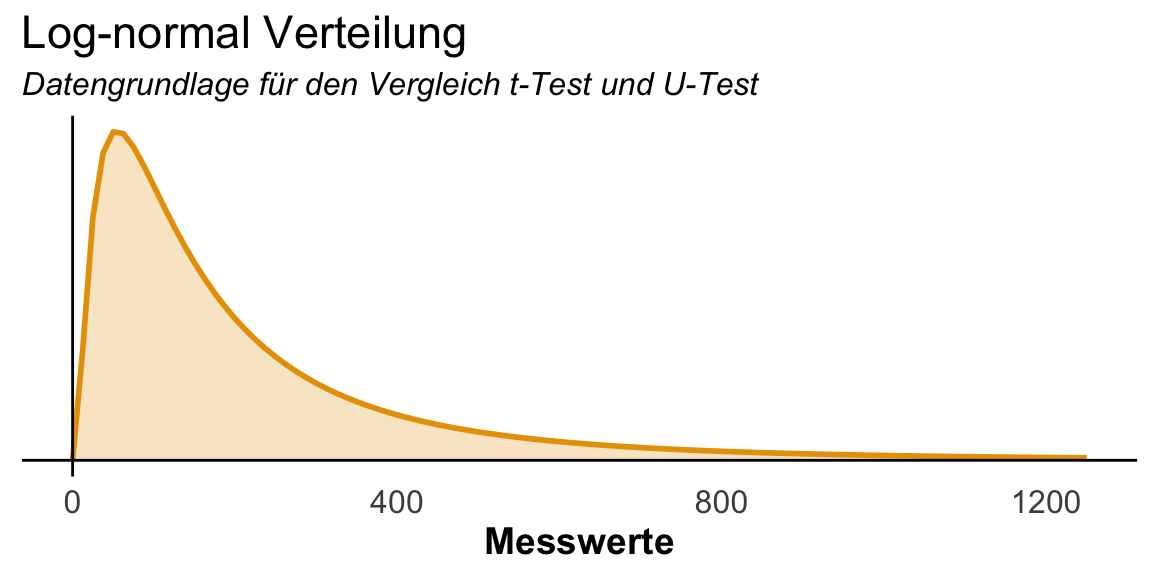
Jetzt fragst du dich sicherlich, ob es nicht noch eine einfache Lösung geben mag. Immerhin haben wir ja den Fall vorliegen, dass unsere Messwerte nicht normalverteilt sind. Ich bin dann auf einmal über folgende Seite zum Thema Nichtparametrik als Rangtransformation gestolpert. Wir rechnen einfach unsere parametrischen Tests, wie den t-Test oder die ANOVA, einfach auf den rangtransformierten Messwerten. Wir lassen also den ganzen U-Test weg, sondern nutzen die Funktion rank() um uns rangtransformierte Messwerte zu bauen. Das war es dann und wir haben dann einen p-Wert aus dem Welch t-Test. Die Idee ist nicht neu und auch schon Zimmerman & Zumbo (1993) haben sich in der Arbeit Relative Power of the Wilcoxon Test, the Friedman Test, and Repeated-Measures ANOVA on Ranks mit der Ähnlichkeit beschäftigt. Ich habe mich gefragt, wie ähnlich sind den nun die p-Werte aus einem Welche t-Test auf transformierten Messwerten gegenüber einem U-Test. Im folgenden siehst du einmal die Verteilung, die ich für die folgenden Simulationen genutzt habe. Ich baue mir eine log-normal Verteilung für zwei Gruppen und schaue unter der Nullhypothese wie die p-Werte aussehen.

Abbildung 35.7— Datengrundlage für die folgende Simulation und dem Vergleich des Welch t-Test auf rangierten Daten und dem U-Test ist die log-normal Verteilung. Die log-normal Verteilung ist nicht normalverteilt. [Zum Vergrößern anklicken]

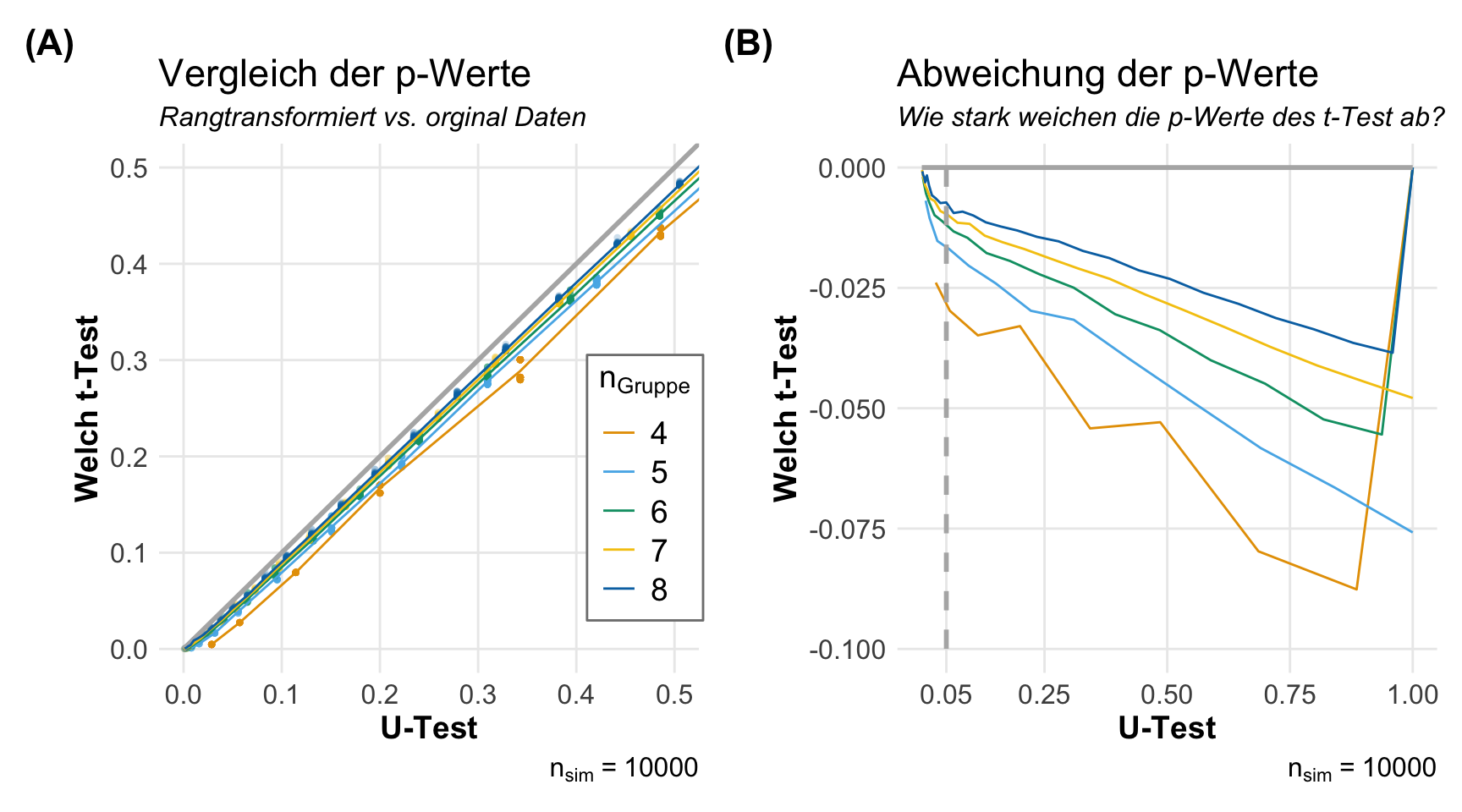
In der folgenden Abbildung siehst du die Ergebnisse meiner kleinen Simulationsstudie. Ich habe zwei Gruppen miteinander verglichen und das Ganze dann zehntausend Mal. Den Vergleich habe ich einmal mit einem Welch t-Test auf den rangtransformierten Daten gerechnet sowie auf den orifinalen Daten mit einem U-Test. Dann natürlich noch mit verschiedenen balancierten Gruppengrößen. Auf der linken Abbildung siehst du die Gegenüberstellung der p-Werte. Die p-Werte des t-Tests sind etwas kleiner als die p-Werte sein sollten, aber die Gleichheit ist schon überwältigend. Wenn wir jetzt noch in der rechten Abbildung die Abweichungen sehen, so sind diese Abweichungen gar nicht so dramatisch. Ja, die Abweichungen sind da, aber ich hätte mir die viel größer vorgestellt. Wenn du die Fallzahl noch weiter erhöhst, dann siehst du, dass die beiden Tests immer ähnlicher werden.

Abbildung 35.8— Gegenüberstellung des Welch t-Test auf rangtransformierten Daten und dem U-Test. Die Nullhypothese ist wahr, die zu vergleichenden Gruppen stammen aus der gleichen log-normal Verteilung. Es wurden 10000 Simulationen gerechnet. (A) Gegenüberstellung aller p-Werte für den Welch t-Test und dem U-Test. Die graue Linie stellt die Winkelhalbierende dar. (B) Abweichung der p-Werte des Welch t-Test zum U-Test. Die gestrichelte Linie stellt das Signifikanzniveau gleich 5% dar. Die graue Linie die Winkelhalbierende in der nebenstehenden Abbildung. [Zum Vergrößern anklicken]

Am Ende sind dann die Ergebnisse doch so ähnlich, dass sich eine Anwendung immer lohnt. Einfach mal die Messwerte rangtransformieren und schauen was der Welch t-Test, die ANOVA oder mixed ANOVA an p-Werten wiedergibt. Der Effektschätzer ist dann genauso wenig zu interpretieren wir im Falle des U-Tests und den relativen Effekt aus {nparcomp} kann ich mir auch händisch auf den Rängen selber berechnen.

Referenz zur Rangtransformation

Wenn du die Referenz brauchst, dann bitte Conover & Iman (1981) oder Zimmerman & Zumbo (1993) zitieren. Beide Arbeiten ziegen, dass du auf einem rangtransformierten Messwert dann einfach deinen ANOVA Pfad mit ANOVA und multiplen Vergleichen rechnen kannst.

35.4 Genutzte R Pakete

Wir wollen folgende R Pakete in diesem Kapitel nutzen.

pacman::p_load(tidyverse, magrittr, broom, tidyplots, rstatix,
               readxl, coin, ggpubr, nparcomp,
               conflicted)
conflicts_prefer(rstatix::wilcox_test)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)

An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.

35.5 Daten

In den folgenden Abschnitten brauchen wir dann zwei Datensätze. Der erste Datensatz beschreibt Hunde- und Katzenflöhe, die springen und deren Sprungweite dann gemessen wurde. Wir haben hier verschiedene Flöhe vorliegen, die nur einmal springen. Wir können aber auch den Fall haben, dass wir uns wiederholt einen Floh anschauen. Der zweite Datensatz betrachtet Hundeflöhe, die vor der Fütterung und nach der Fütterung gesprungen sind.

Unabhängige Messungen

Beginnen wir also mit unserem einfaktoriellen Datensatz mit zwei Gruppen. Wir haben hier die Sprungweite in [cm] von Hunde- und Katzenflöhen gemessen. Unser Faktor ist hierbei die Flohart. Entweder ein Hundefloh oder eben ein Katzenfloh. Wir wollen jetzt wissen, ob sich die beiden Floharten hinsichtlich ihrer Sprungweite unterscheiden.

fac1_tbl <- read_excel("data/flea_dog_cat.xlsx") |> 
  select(animal, jump_length) |> 
  mutate(animal = as_factor(animal))

In der folgenden Tabelle siehst du dann einmal einen Auszug aus den Daten der Sprungweiten für die beiden Floharten. Dabei ist dann die Spalte animal unser Faktor über den wir den Gruppenvergleich für die Sprungweiten als Messwert rechnen wollen.

Tabelle 35.1— Tabelle der Sprungweiten in [cm] als Messwert \(y\) von Hunde-, Katzen- und Fuchsflöhen. Der Datensatz ist einfaktoriell, da wir nur einen Faktor vorliegen haben.

animal	jump_length
dog	5.7
dog	8.9
dog	11.8
...	...
cat	4.3
cat	7.9
cat	6.1

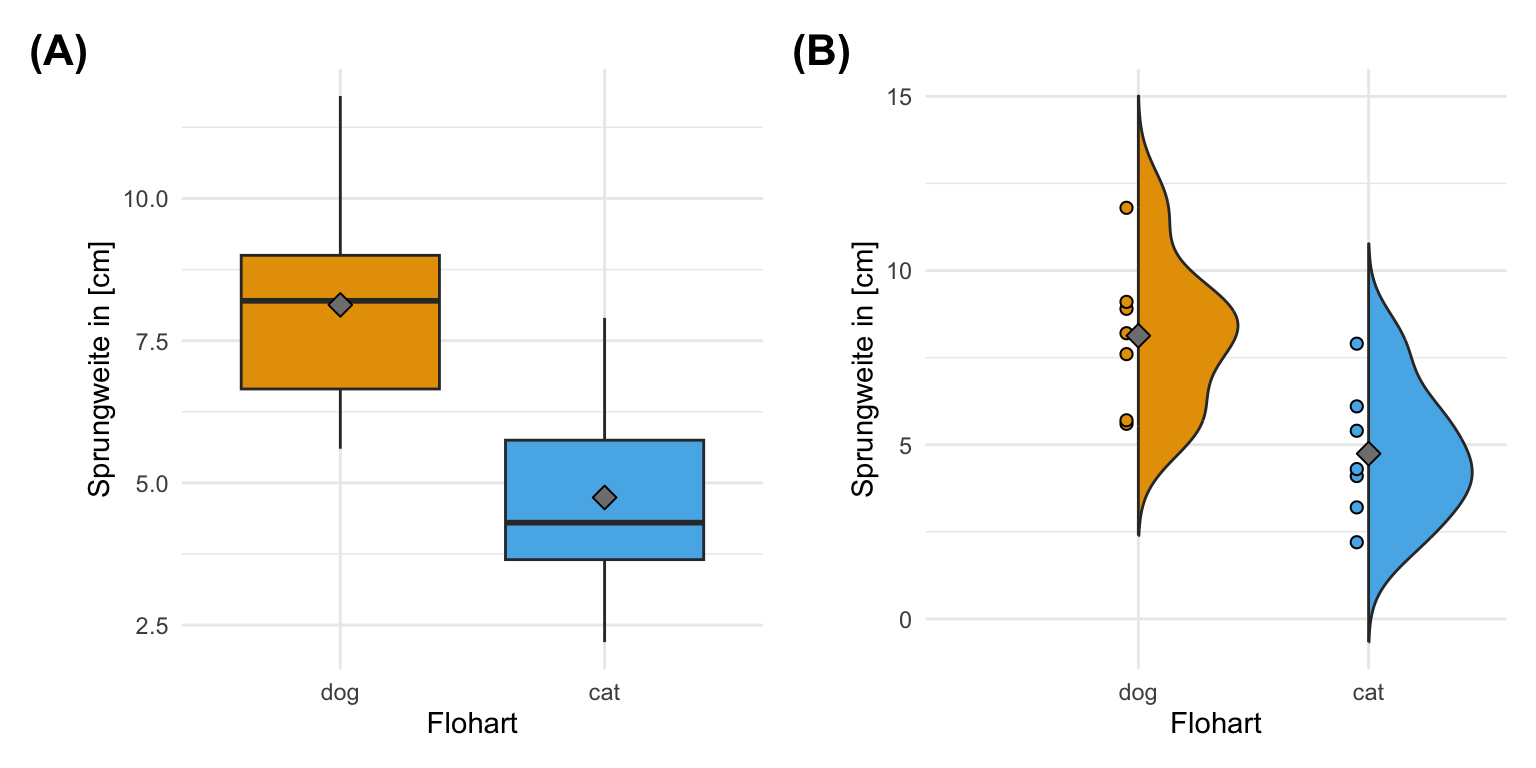
Dann wollen wir uns auch einmal die Daten visualisieren. Ich nutze dazu dann einmal den Boxplot sowie den Violinplot. Die Daten sehen einigermaßen normalverteilt aus, so dass wir hier auch einen t-Test rechnen könnten. Wie immer geht es hier auch um die Demonstration der Algorithmen, also nutzen wir hier auch diese Daten für den U-Test. Der U-Test funktioniert auch super auf normalverteilten Daten.

Abbildung 35.9— Darstellung der Sprungweiten in [cm] gruppiert nach Hunde- und Katzenflöhen. Die graue Raute stellt den entsprechnenden Mittelwert der Sprungweiten dar. (A) Einfaktorieller Boxplot. (B) Violinplot mit Dotplot. [Zum Vergrößern anklicken]

Abhängige Messungen

Der U-Test erlaubt auch abhängige Daten zu analysieren. Das heißt wir haben die gleichen sieben Hundeflöhe wiederholt gemessen. Einmal haben wir einen Hundefloh gemessen bevor er was gegessen hat, also hungrig ist, und einmal nachdem der gleiche Floh sich satt gegessen hat. Daher haben wir hier abhängige oder verbundene Bebachtungen. Im folgenden einmal der Datensatz eingelesen im Wide-Format.

paired_tbl <- read_excel("data/flea_dog_cat_repeated.xlsx") 

Wie du sehen kannst haben wir die sieben Flöhe wiederholt gemessen. Die Daten sind nicht im tidy-Format, da nicht jede Zeile nur eine Messunfg für eine Beobachtung beinhaltet. Das ändern wir dann einmal gleich in Long-Format.

Tabelle 35.2— Tabelle der Sprunglängen [cm] von fünf Hundeflöhen zu zwei Zeitpunkten. Einmal wurde die Sprungweite mit den hungrigen Flöhen und einmal mit den gleichen satten Flöhen bestimmt.

id	hungrig	satt
1	5.2	6.1
2	4.1	5.2
3	3.5	3.9
4	3.2	4.1
5	4.6	5.3

Dann hier nochmal die Long-Formatvariante mit der Funktion pivot_longer(). Wir brauchen das Long-Format für die Auswertung in den unteren Abschnitten für das R Paket {rstatix}.

paired_long_tbl <- paired_tbl |> 
  pivot_longer(cols = hungrig:satt,
               values_to = "jump_length",
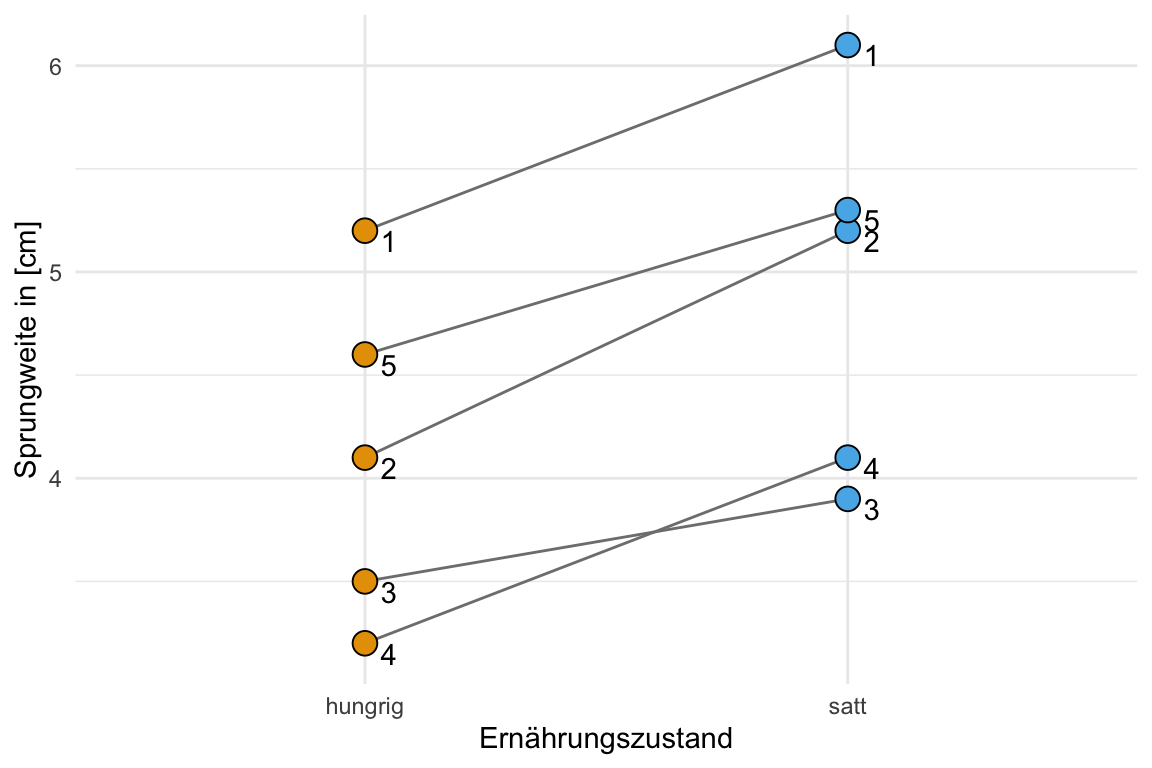
               names_to = "trt") 

Manchmal ist es schwer zu verstehen, was jetzt wiederholt oder gepaart heißen soll. Deshalb hier nochmal die Visualiserung der Daten für die beiden Sprünge vor und nach der Fütterung. Ich habe die Messungen, die zusammengehören mit einer Linie verbunden. Dazu dann auch noch die jeweiligen IDs der Flöhe ergänzt.

Abbildung 35.10— Dotplot der Sprungweiten [cm] für Hundeflöhe in zwei verschiedenen Ernährungszuständen gemessen an zwei Zeitpunkten. Die Linien verbinden die Messung an dem gleichen Floh.

35.6 Hypothesen

Achtung, bitte beachten!

Die Wahl der Nullhypothese durch die Annahmen an die Verteilungsfromen der beiden zu vergleichenden Gruppen hat natürlich einen gewaltigen Einfluss auf die Interpretation des p-Wertes. Also wenn man es statistisch genau nimmt. Deshalb hier auch einmal die simpelste Prosavariante für Einsteiger.

Bitte lesen nochmal oben den Abschnitt zu dem Problem der Nullhypothese im U-Test nach. Je nachdem wie tief du jetzt hier einsteigen willst, habe ich dir mal die drei Varianten angebenen. Am Ende findest du die simpelste Prosavariante gar nicht so selten in Tutorien. Die fortgeschrittene Variante trifft es schon sehr gut. Die mathematische Formel mag dann mehr Fragen als Antworten liefern. Die praktische Interpretation der Nullhypothese eines U-Test bleibt mir aktuell noch verschlossen.

Simpelste Prosa

Wenn wir nur den p-Wert betrachten, dann können wir auch folgende simple Aussage über den U-Test machen. Das ist jetzt genau so wahr wie falsch aber hilfreich.

\(H_0:\) Die beiden Gruppen sind gleich in ihrem Messwert.

\(H_A:\) Es liegt ein Unterschied im Messwert zwischen den Gruppen vor.

Damit hätten wir dann für unsere Sprungweiten folgende beiden Hypothesen.

\(H_0:\) Die beiden Floharten springen gleich weit.

\(H_A:\) Die beiden Floharten springen unterschiedlich weit.

Fortgeschrittene Prosa

Hier dann die richtige Interpretation der Nullhypothese. Obwohl ich mir sicher bin, dass die praktische Relevanz der Nullhypothese hier auch nicht sehr viel klarer wird.

\(H_0:\) Es ist gleich wahrscheinlich, dass ein zufällig aus der einen Population ausgewählter Wert größer oder kleiner ist als ein zufällig ausgewählter Wert aus der anderen Population

\(H_A:\) Es ist nicht gleich wahrscheinlich, dass ein zufällig aus der einen Population ausgewählter Wert größer oder kleiner ist als ein zufällig ausgewählter Wert aus der anderen Population

Für unser Anwendungsbeispiel mit den Sprungweiten der Hunde- und Katzenflöhen musst du nur die Populationen durch die Hunde und Katzen ersetzen.

Formel

Wir vergleichen hier zwei Populationen oder Gruppen \(X\) und \(Y\) miteinander. Die Formel repräsentiert die fortgeschrittene Prosa in dem vorherigen Tab. Bitte nochmal oben nachschauen, wenn du die Nullhypothese verstehen willst.

\[ H_0: Pr(X<Y) + \cfrac{1}{2} Pr(X = Y) = 0.5 \]

\[ H_A: Pr(X<Y) + \cfrac{1}{2} Pr(X = Y) \neq 0.5 \]

In dem R Paket {nparcomp} bezeichnen wir den Wert für \(Pr(X<Y) + \cfrac{1}{2} Pr(X = Y)\) auch als relativen Effekt. Faktisch ist es der Anteil an allen Wertepaaren, die kleiner oder gleich in der einen Gruppe \(X\) sind als in der anderen Gruppe \(Y\).

35.7 Der U-Test

Dann kommen wir zu der Implementierung des U-Tests in R. Wie immer gibt es reiche Auswahl an R Paketen, die für dich den U-Test auf unabhängigen wie auch abhängigen Daten rechnen. Wenn ich die Wahl habe, dann nehme ich die Funktionen aus dem R Paket {rstatix}. Das Paket hat eigentlich alles was man braucht um einen U-Test zu rechnen. Intern basiert das Paket auf dem Paket {coin} was von der Anwendung etwas veraltet ist. Ein neueres Paket ist die Implementierung in dem R Paket {nparcomp}. Hier wirst du mit viel Informationen versorgt aber dann inhaltlich etwas alleine gelassen, was die Interpretation angeht. Wir schauen aber auch hier einmal rein.

35.7.1 … mit unabhängigen Beobachtungen

Am häufigsten wirst du wohl den U-Test mit zwei Gruppen rechnen, die voneinander unabhängig sind. Das heißt, du misst deinen Messwert \(y\) in zwei Gruppen und jede Messung ist unabhängig von der anderen. Wir haben so einen Fall in unserem Datensatz zu den Sprungweiten der Hunde- und Katzenflöhe vorleigen. Wir haben sieben Hundeflöhe und sieben Katzenflöhe einmal gemessen und die Sprungweiten in dem Datensatz fac1_tbl gespeichert. Wir schauen uns für die unabhängigen Beobachtungen auch einmal die theoretische Berechung an, bevor wir uns dann in den anderen Tabs mit der Implementierung in R beschäftigen.

Theorie

Der Wilcoxon-Mann-Whitney-Test berechnet die U Teststatistik auf den Rängend der Daten. Es gibt genau soviele Ränge wie es Beobachtungen im Datensatz gibt. Wir haben vierzehn Beobachtungen in unseren Daten zu der Sprungweite in [cm] von den Hunde- und Katzenflöhen. Somit müssen wir auch vierzehn Ränge vergeben. Die Tabelle 35.3 zeigt das Vorgehen der Rangvergabe. Wir sortieren als erstes das \(y\) aufsteigend. In unserem Fall ist das \(y\) die Sprunglänge. Dann vergeben wir die Ränge jweiles zugehörig zu der Position der Sprunglänge und der Tierart. Abschließend addieren wir die Rangsummmen für cat und dog zu den Rangsummen \(R_{cat}\) und \(R_{dog}\).

Tabelle 35.3— Datentablle absteigend sortiert nach der Sprunglänge in [cm]. Die Level cat und dog haben jeweils die entsprechenden Ränge zugeordnet bekommen und die Rangsummen wurden berechnet

Rank	animal	jump_length	Ränge cat	Ränge dog
1	cat	2.2	1
2	cat	3.2	2
3	cat	4.1	3
4	cat	4.3	4
5	cat	5.4	5
6	dog	5.6		6
7	dog	5.7		7
8	cat	6.1	8
9	dog	7.6		9
10	cat	7.9	10
11	dog	8.2		11
12	dog	8.9		12
13	dog	9.1		13
14	dog	11.8		14
		Rangsummen	\(R_{cat} = 33\)	\(R_{dog} = 72\)
		Gruppengröße	7	7

Die Formel für die U Statistik sieht ein wenig wild aus, aber wir können eigentlich relativ einfach alle Zahlen einsetzen. Dann musst du dich etwas konzentrieren bei der Rechnung.

\[ U_{D} = n_1n_2 + \cfrac{n_1(n_1+1)}{2}-R_1 \]

mit

• \(R_1\) der größeren der beiden Rangsummen,
• \(n_1\) die Fallzahl der größeren der beiden Rangsummen
• \(n_2\) die Fallzahl der kleineren der beiden Rangsummen

Wir setzen nun die Zahlen ein. Da wir ein balanciertes Design vorliegen haben sind die Fallzahlen \(n_1 = n_2 = 7\) gleich. Wir müssen nur schauen, dass wir mit \(R_1\) die passende Rangsumme wählen. In unserem Fall ist \(R_1 = R_{dog} = 72\).

\[ U_{D} = 7 \cdot 7 + \cfrac{7(7+1)}{2}-72 = 5 \]

Der kritische Wert für die U Statistik ist \(U_{\alpha = 5\%} = 8\) für \(n_1 = 7\) und \(n_2 = 7\). Bei der Entscheidung mit der berechneten Teststatistik \(U_{D}\) gilt, wenn \(U_{D} \leq U_{\alpha = 5\%}\) wird die Nullhypothese (H\(_0\)) abgelehnt. Da in unserem Fall das \(U_{D}\) mit \(5\) kleiner ist als das \(U_{\alpha = 5\%} = 8\) können wir die Nullhypothese ablehnen. Wir haben ein signifkianten Unterschied in den Medianen zwischen den beiden Tierarten im Bezug auf die Sprungweite in [cm] von Flöhen.

Bei grosser Stichprobe, wenn \(n_1 + n_2 > 30\) ist, können wir die U Statistik auch standariseren und damit in den z-Wert transformieren.

\[ z_{D} = \cfrac{U_{D} - \bar{U}}{s_U} = \cfrac{U_{D} - \cfrac{n_1 \cdot n_2}{2}}{\sqrt{\cfrac{n_1 \cdot n_2 (n_1 + n_2 +1)}{12}}} \]

mit

• \(\bar{U}\) dem Mittelwert der U-Verteilung ohne Unterschied zwischen den Gruppen
• \(s_U\) Standardfehler des U-Wertes
• \(n_1\) Stichprobengrösse der Gruppe mit der grösseren Rangsumme
• \(n_2\) Stichprobengrösse der Gruppe mit der kleineren Rangsumme

Wir setzen dafür ebenfalls die berechnete U Statistik ein und müssen dann wieder konzentriert rechnen.

\[ z_{D} = \cfrac{5 - \cfrac{7 \cdot 7}{2}}{\sqrt{\cfrac{7 \cdot 7 (7 + 7 +1)}{12}}} = \cfrac{-19.5}{7.83} = |-2.46| \]

Der kritische Wert für die z-Statistik ist \(z_{\alpha = 5\%} = 1.96\). Bei der Entscheidung mit der berechneten Teststatistik \(z_{D}\) gilt, wenn \(z_{D} \geq z_{\alpha = 5\%}\) wird die Nullhypothese (H\(_0\)) abgelehnt. Wir haben eine berechnete z Statistik von \(z_{D} = 2.46\). Damit ist \(z_{D}\) größer als \(z_{\alpha = 5\%} = 1.96\) und wir können die Nullhypothese ablehnen. Wir haben einen signifkanten Unterschied zwischen den Medianen der beiden Floharten im Bezug auf die Sprunglänge in [cm].

{stats}

Die Standardimplementierung in R ist die Funktion wilxoc.test(). Leider kann der wilxoc.test() nicht mit Bindungen in den Daten umgehen. Daher würde ich die Funktion nicht empfehlen, da du im Zweifel dann nochmal die Funktion aus {coin} anwenden musst. Dann hast du doppelte Arbeit. Wir haben hier aber keien Bindungen in den Daten vorliegen.

wilcox.test(jump_length ~ animal, data = fac1_tbl, 
            conf.int = TRUE)

    Wilcoxon rank sum exact test

data:  jump_length by animal
W = 44, p-value = 0.01107
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
 1.0 5.9
sample estimates:
difference in location 
                   3.5 

Der U-Test liefert uns ein signifikantes Ergebnis, da der p-Wert kleiner ist als das Signifikanzniveau \(\alpha\) gleich 5%. Wir lehnen die Nullhypothese ab. Die Sprungweiten unterscheiden sich zwischen den Hunde- und Katzenflöhen.

{coin}

Ich muss jetzt gleich die Funktion wilcox_test() aus dem R Paket {coin} einmal explizit laden, da die Funktion in {rstatix} genauso heißt. Später musst du das natürlich nicht so machen. Wir können uns in der Funktion wilcox_test() auch die 95% Konfidenzintervalle wiedergeben lassen. Wir erhalten hier ein 95% Konfidenzintervall für die möglichen Verschiebung \(a\) in den Messwerten. Aber Achtung, dann interpretieren wir den U-Test als Mediantest, was spezielle Anforderungen an die Verteilungen der beiden Gruppen hat. Mehr dazu in dem obigen Abschnitt zu den Problemen der Hypothesen.

coin::wilcox_test(jump_length ~ animal, data = fac1_tbl, 
                  conf.int = TRUE) 

    Asymptotic Wilcoxon-Mann-Whitney Test

data:  jump_length by animal (dog, cat)
Z = 2.4916, p-value = 0.01272
alternative hypothesis: true mu is not equal to 0
95 percent confidence interval:
 1.2 5.7
sample estimates:
difference in location 
                   3.5 

Der U-Test liefert uns ein signifikantes Ergebnis, da der p-Wert kleiner ist als das Signifikanzniveau \(\alpha\) gleich 5%. Wir lehnen die Nullhypothese ab. Die Sprungweiten unterscheiden sich zwischen den Hunde- und Katzenflöhen.

{rstatix}

Wir können den Wilcoxon Test in R auch mit der Funktion wilcox_test() aus dem R Paket {rstatix} rechnen. Wir verlieren hier aber die Möglichkeit das 95% Konfidenzintervall berechnen zu können. Ansonsten ist die Funktion nichts anderes als der Aufruf der gleichnamigen Funktion in {coin}. Wir erhalten als Wiedergabe eine praktische Datentabelle und ich habe mal etwas vorgefiltert.

rstatix::wilcox_test(jump_length ~ animal, data = fac1_tbl) |> 
  select(group1, group2, p)

# A tibble: 1 × 3
  group1 group2      p
  <chr>  <chr>   <dbl>
1 dog    cat    0.0111

Der U-Test liefert uns ein signifikantes Ergebnis, da der p-Wert kleiner ist als das Signifikanzniveau \(\alpha\) gleich 5%. Wir lehnen die Nullhypothese ab. Die Sprungweiten unterscheiden sich zwischen den Hunde- und Katzenflöhen.

{nparcomp}

Als letztes möchte ich noch die neuste Implementierung der Nichtparametrik mit dem R Paket {nparcomp} vorstellen. Wir haben hier die Implementierung des U-Tests in der Funktion npar.t.test(). Interessanterweise steht hier schon der t-Test mit im Namen. Es handelt sich hier um die Implementierung des nichtparametrischen t-Tests. Oder sehr vereinfacht ausgedrückt, die Anwendung des t-Tests auf rangtransformierte Messwerte. Leider hat die Funktion die unangenehme Eigenschaften alles möglich wiederzugeben, auch wenn man nur den p-Wert braucht. Daher hier dann mehr Code, damit die Funktion ruhig ist.

npar_obj <- npar.t.test(jump_length ~ animal, data = fac1_tbl,
                        info = TRUE) 

 #------Nonparametric Test Procedures and Confidence Intervals for relative  effects-----# 
 
 - Alternative Hypothesis:  True relative effect p is less or equal than 1/2 
 - Confidence level: 95 % 
 - Method = Logit - Transformation 
 
 #---------------------------Interpretation----------------------------------# 
 p(a,b) > 1/2 : b tends to be larger than a 
 #---------------------------------------------------------------------------# 
 

npar_obj$Analysis

      Effect Estimator Lower Upper      T p.Value
1 p(dog,cat)     0.102 0.018 0.412 -2.345   0.019

Der U-Test liefert uns ein signifikantes Ergebnis, da der p-Wert kleiner ist als das Signifikanzniveau \(\alpha\) gleich 5%. Wir lehnen die Nullhypothese ab. Die Sprungweiten unterscheiden sich zwischen den Hunde- und Katzenflöhen.

Darüber hinaus erhalten wir auch als Effektschätzer die Wahrscheinlichkeit \(Pr(dog, cat)\) als p(dog, cat) wiedergeben. Wenn wir eine Wahrscheinlichkeit von \(0.5\) vorliegen haben, dann gilt die Nullhypothese. Hier haben wir einen Wert von \(0.102\) und damit springen die Hundeflöhe a weiter als die Katzenflöhe b. Die Sprungweiten sind bei den Hunden größer als bei den Katzen, da p(dog, cat) kleiner ist als 1/2. Was wir auch sagen können ist, dass nur in 10.2% der Wertepaare aller Sprungweiten der Hunde- und Katzenflöhe, die Hunde kürzer springen. Mit Wertepaaren meine ich, dass wir jeden Wert der Sprungweite der Hundeflöhe mit jedem Wert der Katzenflöhe vergleichen. Wir wissen aber nicht um wie viel kürzer in einer wie auch immer gearteten Einheit. Ohne handfeste biologisch definierte Relevanz auf der Sprungweite hat dann das 95% Konfidenzintervall auch keine direkte Bedeutung.

Wie du sehen kannst kommt bei allen Implementierungen des U-Tests im Prinzip das gleiche raus. Der U-Test liefert uns ein signifikantes Ergebnis, da der p-Wert kleiner ist als das Signifikanzniveau \(\alpha\) gleich 5%. Wir haben nur leichte Fluktuationen im p-Wert durch die Art des Algorithmus hinter dem U-Test des jeweiligen Pakets. Am Ende unterscheiden sich die Sprungweiten zwischen den Hunde- und Katzenflöhen. Jetzt bleibt noch die Frage, wie groß der Effekt ist.

Effektschätzer

Als Effektschätzer nutzen wir den rangbiserialer Korrelationskoeffizient \(r\). Mehr dazu auch in der Veröffentlichung von Tomczak & Tomczak (2014). Wir nutzen hier die Implementierung in {rstatix} mit der Funktion wilcox_effsize(). Praktischerweise erhalten wir dann auch gleich die Interpretation mit angegeben. Dann können wir die Abschätzung dann auch gleich mit übernehmen.

fac1_tbl |> 
  wilcox_effsize(jump_length ~ animal) |> 
  select(effsize, magnitude)

# A tibble: 1 × 2
  effsize magnitude
    <dbl> <ord>    
1   0.666 large    

Leider kannst du mit dem Wert von \(0.66\) nicht weiterrechnen. Der \(r\)-Wert ist einheitlos und kann nicht in eine Kosten/Nutzenrechnung überführt werden. Daher hast du nur die Information, dass der Effekt zwischen den Sprungweiten der Hunde- un Katzenflöhe groß ist.

Bitte nutze die Verschiebung der Mediane nur als Effektschätzer, wenn du dir sicher bist, dass die beiden Verteilungsformen der Gruppen gleich sind und Varianhomogenität zwischen deinen Gruppen vorliegt. Ansonsten ist die Medianverschiebung aus dem R Paket {coin} kein äquivalenter Effektschätzer.

Wir können natürlich auch als Effekctschätzer den relativen Effekt \(p(a,b)\) händisch berechnen, wenn wir nicht das R Paket {nparcomp} nutzen wollen. Aber auch hier stellt sich die Frage, was wir mit dem Wissen machen welcher prozentualer Anteil der Messwerte in der einen Gruppe kleiner oder gleich als in der anderen Gruppe ist. Wir wissen ja am Ende wiederum nicht um wieviel kleiner. Eine Transformation in Ränge hat eben dann auch Nachteile.

Parametrische Lösung: Der t-Test

Dann hier noch schnell die parametrische Lösung des Problems mit dem Welch t-Test. Wir wollen jetzt einfach nur unsere Messwerte einmal Rangtransformieren. Dafür nutze ich entweder die Funktion rank() oder aber die folgende Funktion signed_rank(), wenn ich negative Werte in meinen Messungen erwarte.

signed_rank <- function(x) sign(x) * rank(abs(x))

Konkret habe ich meine Sprungweiten der Hunde- und Katzenflöhe. Jetzt mutiere ich die Sprungweite über die Funktion signed_rank() in Ränge und nutze diese Spalte dann für den Welch t-Test. Ich nutze hier die Funktion t_test() aus dem R Paket {rstatix}, da ich dann einfacher pipen kann. Dann wähle ich noch die passenden Spalten und sehe, dass die Entscheidung die gleiche wäre wie bei den obigen Implementierungen des U-Tests. Wir können die Nullhypothese ablehnen, wir haben einen signifikanten Unterschied in den Sprungweiten.

fac1_tbl |> 
  mutate(ranked_jump_length = signed_rank(jump_length)) |> 
  t_test(ranked_jump_length ~ animal) |> 
  select(group1, group2, statistic, p)

# A tibble: 1 × 4
  group1 group2 statistic       p
  <chr>  <chr>      <dbl>   <dbl>
1 dog    cat         3.31 0.00624

Wie aus den obigen Simulationen zu erwarten, ist der p-Wert aus dem t-Test auf den Rängen der Sprungweite etwas kleiner als der aus den U-Tests. Am Ende wollen wir nach einer Rangtransformation eigentlich immer nur den p-Wert und p-Werte nahe an dem Signifikanzniveau von 5% sind nochmal eine ganz andere Geschichte.

35.7.2 … mit abhängigen Beobachtungen

Kommen wir jetzt zu dem Fall, dass wir Daten haben, wo die Beobachtungen und damit die Messwerte abhängig voneinander sind. Wir haben also jetzt unsere Hundeflöhe jeweils zweimal gemessen. Wir haben einmal hungrige und einmal satte Flöhe vorliegen. Dann haben wir die Sprungweiten notiert und wollen wissen, ob es einen Unterschied macht, ob wir die Hundeflöhe hungrig oder satt springen lassen. Ich nutze hier wieder die gänigen Pakete sowie die neuere Implementierung in {nparcomp}. Der Standard ist die Implementierung in {coin} mit der leichteren Zugänglichkeit durch das R Paket {rstatix}.

{stats}

Wir habne hier in den paarweisen Daten eine Bindung vorliegen. Das heißt wir haben hier zweimal die gleiche Sprungweite gemessen. Damit kann die Funktion wilxoc.test() nicht umgehen und wird dir eine Warnung wiedergeben. Wenn du die Warnung erhälst, dann nutze bitte die Funktion aus {coin} oder {rstatix}. Die Nutzung der Funktion ist maximal unangenehm, da wir nicht die Formelschreibweise implementiert haben. Die Interpretation der Medianverschiebung hängt davon ab, was deine Nullhypothese ist, dafür nochmal oben nachlesen. Ich würde den Teil lieber ignorieren und dich auf den p-Wert konzentrieren.

wilcox.test(paired_tbl$hungrig, paired_tbl$satt, paired = TRUE,
            conf.int = TRUE)

    Wilcoxon signed rank test with continuity correction

data:  paired_tbl$hungrig and paired_tbl$satt
V = 0, p-value = 0.05791
alternative hypothesis: true location shift is not equal to 0
90 percent confidence interval:
 -1.1 -0.4
sample estimates:
(pseudo)median 
    -0.8000017 

Der p-Wert liegt knapp über dem Signifikanzniveau von 5% und deshalb können wir hier die Nullhypothese nicht ablehnen. Da es eben dann doch sehr nah an der Grenze ist, müsstest du nochmal überlegen, ob es nicht doch ein starkes Indiz für eine Nachfolgestudie ist. Die Fallzahl ist mit fünf Flöhen hier auch sehr klein. Vielleicht hast du aber auch hier die Bindungen nicht richtig berücksichtigt und das ist der Grund für den p-Wert.

{coin}

Wir nutzen heir einmal den wilcoxsign_test() aus dem R Paket {coin}, was am Besten passen sollte. Der Vorzeichentest aus dem R Paket {coin} sollte hier sehr gut passen, jedenfalls sind es so die Empfehlungen. Hier haben wir leider wieder eine wirre Eingabe der Variablen in die Funktion, aber was will man machen. Dann ist es eben so.

wilcoxsign_test(paired_tbl$hungrig ~ paired_tbl$satt, 
                paired = TRUE) 

    Asymptotic Wilcoxon-Pratt Signed-Rank Test

data:  y by x (pos, neg) 
     stratified by block
Z = -2.0319, p-value = 0.04217
alternative hypothesis: true mu is not equal to 0

Der p-Wert liegt knapp unter dem Signifikanzniveau von 5%, da wir hier dann die Bindungen mit berücksichtigt haben und deshalb können wir hier die Nullhypothese ablehnen. Wir sehen hier sehr schön, dass es manchmal dann auf Kleinigkeiten ankommt. Am Ende ist der p-Wert aber nicht sehr klein. Die Fallzahl ist mit fünf Flöhen hier auch sehr klein.

{rstatix}

Dann nutzen wir noch den wilcox_test() aus dem R Paket {rstatix} woe du nochmal mehr im Tutroium unter Wilcoxon Test in R nachlesen kannst. Spannenderweise produziert die Funktion den gleichen p-Wert wie die Implementierung in {stats}, obwohl ich eigentlich dachte es wäre der Wrapper für die Funktion in {coin}. So ist das immer eine Sache mit den Paketen.

rstatix::wilcox_test(jump_length ~ trt, data = paired_long_tbl, 
                     paired = TRUE) |> 
  select(group1, group2, p)

# A tibble: 1 × 3
  group1  group2      p
  <chr>   <chr>   <dbl>
1 hungrig satt   0.0579

Der p-Wert liegt knapp über dem Signifikanzniveau von 5% und deshalb können wir hier die Nullhypothese nicht ablehnen. Da es eben dann doch sehr nah an der Grenze ist, müsstest du nochmal überlegen, ob es nicht doch ein starkes Indiz für eine Nachfolgestudie ist. Die Fallzahl ist mit fünf Flöhen hier auch sehr klein. Ob es an den Bindungen liegt weiß ich nicht. Aber ich würde hier dann doch {coin} wählen.

{nparcomp}

Kommen wir zum Schluß nochmal zur aktuellsten Implementierung mit der Funktion npar.t.test.paired() aus dem R Paket {nparcomp}. Der Vorteil hier ist, dass wir eben mit bindungen umgehen können, eine saubere Formelschreibwiese haben und am Ende auch sicher sind ein vertrauenswürdiges Ergebnis zu bekommen. Das Paket hat die Angewohnheit einem mehr Informationen wiederzugeben als man braucht, dehalb hier die Kurzvariante mit der Filterung der Analyseergebnisse.

npar_obj <- npar.t.test.paired(jump_length ~ trt, data = paired_long_tbl,
                               plot.simci = FALSE)

 #----------------Nonparametric Paired t Test-------------------------------------------# 
 
 - Sample Size:  5 
 - Factor Levels:  hungrig satt 
 - H0:  p=1/2 
 - Alternative Hypothesis:  True relative effect is less or greater than 1/2 
 - Confidence Level: 95 % 
 - Method: Brunner-Munzel (BM), Permutation (PERM) 
 
 #--------------------------------------------------------------------------------------# 
 

npar_obj$Analysis

     Lower p.hat Upper     T p.value
BM   0.656  0.76 0.864 6.949   0.002
PERM 0.500  0.76 1.020 6.949   0.000

Wir haben hier wieder die Qual der Wahl zwischen zwei Methoden. Am Ende haben wir aber erstmal Glück. Der p-Wert liegt unter dem Signifikanzniveau von 5% für beide Algorithmen BM und PERM und deshalb können wir hier die Nullhypothese ablehnen. Ich würde persönlich hier Brunner-Munzel (BM) einem Permutations p-Wert vorziehen, aber das ist eher Geschmackssache. Prinzipiell musst du dich vor der Anwendung entscheiden, damit du dir nicht einfach den kleineren p-Wert aussuchst, aber das ist eine andere Geschichte.

Dann sind wir auch schon mit den gepaarten U-Test durch. Ich stelle hier nochmal kurz die Variante des Vorzeichentests vor. Ich würde aber den Vorzeichentest nicht empfehlen. Der Vorzeichentest hat leider nicht so gute statistische Eigenschaften für kleinen Fallzahlen. Der p-Wert ist tendenziell größer als in den anderen U-Tests. Dann kannst du dir noch die Einbindung des gepaarten U-Test in das R Paket {tidyplots} anschauen. Dann hast du deine Barplots zusammen mit dem U-Test in einer Abbildung.

Ein Wort zum Sign-Test

Der Vorzeichentest (eng. Sign Test) kann weniger aussagekräftig sein als andere nichtparametrische Tests, insbesondere wenn die Stichprobengröße gering ist. Das ist ja dann häufiger der Fall. Darüber hinaus berücksichtigt der Sign Test keine Bindungen, was bei Zähldaten und Notendaten ein Problem darstellen kann. Am Ende will der Vorzeichentest, dass die Beobachtungen unabhängig sind, was nicht immer der Fall sein muss. Daher empfehle ich grundsätzlich nicht den Sign-Test.

Wir können den Sign-Test mit der Funktion sign_test() aus dem R Paket {rstatix} nutzen.

rstatix::sign_test(jump_length ~ trt, data = paired_long_tbl) |> 
  select(group1, group2, p)

# A tibble: 1 × 3
  group1  group2      p
  <chr>   <chr>   <dbl>
1 hungrig satt   0.0625

Am Ende rechne lieber den gepaarten U-Test von oben und ich lasse hier den Kasten als Referenz für dich zum Finden hier stehen.

Parametrische Lösung: Der paired t-Test

Dann hier noch schnell die parametrische Lösung des Problems mit dem Welch t-Test. Wir wollen jetzt einfach nur unsere Messwerte einmal Rangtransformieren. Dafür nutze ich entweder die Funktion rank() oder aber die folgende Funktion signed_rank(), wenn ich negative Werte in meinen Messungen erwarte.

signed_rank <- function(x) sign(x) * rank(abs(x))

Konkret habe ich meine Sprungweiten der widerholt gemessenen Hundeflöhe. Jetzt mutiere ich die Sprungweite über die Funktion signed_rank() in Ränge und nutze diese Spalte dann für den gepaarten t-Test. Ich nutze hier die Funktion t_test() aus dem R Paket {rstatix}, da ich dann einfacher pipen kann. Dann wähle ich noch die passenden Spalten und sehe, dass die Entscheidung die gleiche wäre wie bei den obigen Implementierungen des U-Tests. Wir können die Nullhypothese ablehnen, wir haben einen signifikanten Unterschied in den Sprungweiten.

paired_long_tbl |> 
  mutate(ranked_jump_length = signed_rank(jump_length)) |> 
  t_test(ranked_jump_length ~ trt, paired = TRUE) |> 
  select(group1, group2, statistic, p)

# A tibble: 1 × 4
  group1  group2 statistic       p
  <chr>   <chr>      <dbl>   <dbl>
1 hungrig satt       -6.04 0.00378

35.8 Ergebnisse mit {tidyplots}

Häufig wollen wir nicht nur den p-Wert aus einem U-Test berichten sondern natürlich auch gleich die richtige Abbildung dazu haben. Hier gibt es mit dem R Paket {tidyplots} eine gute Möglichkeit. Das R Paket verbindet dabei die Funktionalität von {ggplot} und {ggpubr}. Dabei bleibt es aber dann sehr einfahc zu bedienen. Insbesondere in dem Fall, dass du nur zwei Gruppen in einem U-Test miteinander vergleichen willst.

Alternativen zu {tidyplots}

Das R Paket {ggpubr} bietet auch noch andere Alternativen für die Darstellung von statistischen Vergleichen in deinen Daten unter ggpubr: ‘ggplot2’ Based Publication Ready Plots. Vielleicht findest du da auch noch eine bessere Abbildung als hier. Da wir hier sehr viel ähnliches haben, bleibe ich bei {tidyplots}.

Neben den p-Werten, die ich hier mit der Funktion add_test_pvalue() ergänze kannst du auch Sterne mit der Funktion add_test_asterisks() nutzen. Das liegt dann ganz bei dir. Es gibt auch die Möglichkeit nicht signifikante Ergebnisse auszublenden. Mehr dazu findest du dann auf der Hilfeseite zu den statistischen Vergleichen in {tidyplots}. Ich zeige hier dir nur die Standardanwendung. Wir rechnen hier immer den U-Test aus dem R Paket {rstatix}.

Barplot

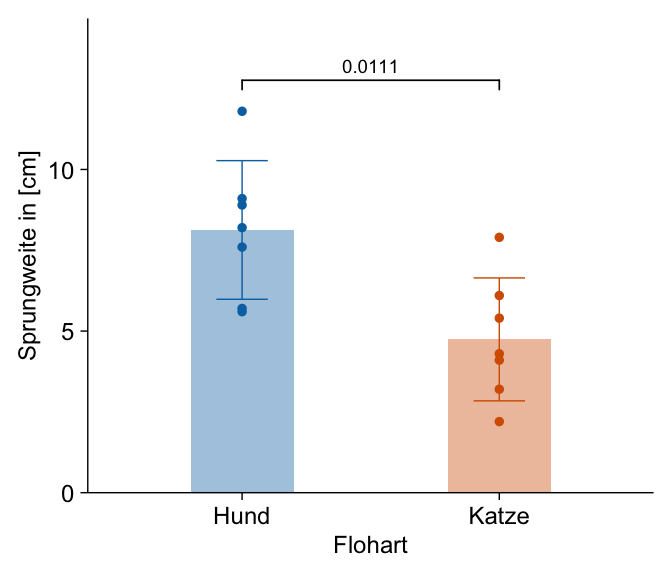
Die Standardabbildung ist sicherlich der Barplot zusammen mit der Standardabweichung als Fehlerbalken. Dann habe ich noch die einzelnen Beobachtungen ergänzt. Die Klammer über den beiden Säulen gibt den Vergleich an und die Zahl ist der p-Wert aus einem U-Test. Wir sehen hier, dass sich die beiden Floharten in den Sprungweiten signifikant unterscheiden. Der p-Wert ist kleiner als das Signifikanzniveau \(\alpha\) gleich 5%.

tidyplot(data = fac1_tbl, 
         x = animal, y = jump_length, color = animal) |> 
  add_data_points() |>
  add_mean_bar(alpha = 0.4, width = 0.4) |> 
  add_sd_errorbar(width = 0.2) |> 
  add_test_pvalue(method = "wilcox_test", hide_info = TRUE) |>
  remove_legend() |> 
  adjust_font(fontsize = 9) |>
  adjust_x_axis_title("Flohart") |>
  adjust_y_axis_title("Sprungweite in [cm]") |> 
  rename_x_axis_labels(new_names = c("dog" = "Hund", "cat" = "Katze")) |> 
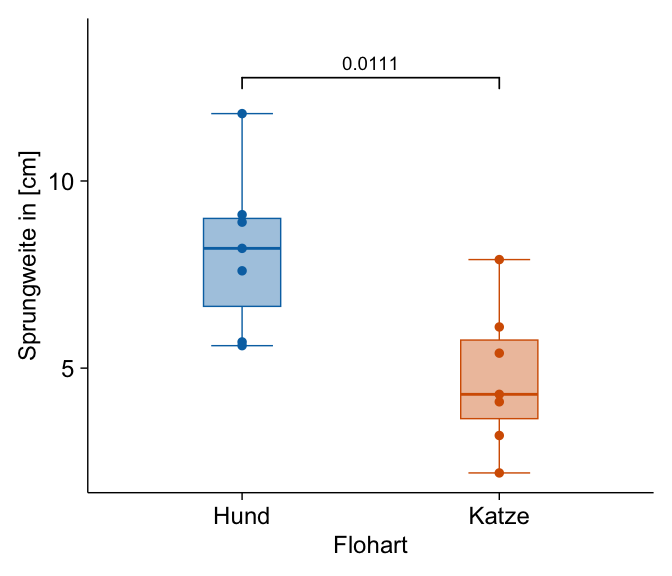
  adjust_size(width = NA, height = NA) 

Abbildung 35.11— Einfaktorieller Barplot für die Sprungweiten in [cm] gruppiert nach den Floharten mit mehr Optionen und angepassten Beschriftungen sowie den p-Wert aus einem U-Test.

Boxplot

Es gibt auch gute Gründe ienmal den Boxplot zu wählen, wenn wir etwas besser die Verteilung der Sprungweiten darstellen wollen. Ich habe dann noch die einzelnen Beobachtungen ergänzt. Die Klammer über den beiden Säulen gibt den Vergleich an und die Zahl ist der p-Wert aus einem U-Test. Wir sehen hier, dass sich die beiden Floharten in den Sprungweiten signifikant unterscheiden. Der p-Wert ist kleiner als das Signifikanzniveau \(\alpha\) gleich 5%.

tidyplot(data = fac1_tbl, 
         x = animal, y = jump_length, color = animal) |> 
  add_data_points() |>
  add_boxplot(alpha = 0.4, box_width = 0.3) |> 
  add_test_pvalue(method = "wilcox_test", hide_info = TRUE) |> 
  remove_legend() |> 
  adjust_font(fontsize = 9) |>
  adjust_x_axis_title("Flohart") |>
  adjust_y_axis_title("Sprungweite in [cm]") |> 
  rename_x_axis_labels(new_names = c("dog" = "Hund", "cat" = "Katze")) |> 
  adjust_size(width = NA, height = NA) 

Abbildung 35.12— Einfaktorieller Boxplot für die Sprungweiten in [cm] gruppiert nach den Floharten mit mehr Optionen und angepassten Beschriftungen sowie den p-Wert aus einem U-Test.

Gepaarter Dotplot

Am Ende wollen wir uns dann nochmal den gepaarten U-Test als Wilcoxon Test anschauen. Hier ist dann die Abbildung realtiv einfach. Wir können da die Daten paired_tbl aus dem gepaarten U-Test nutzen nachdem wir die Daten in das Long-Format überführt haben. Etwas schwieriger ist dann der p-Wert, den p-Wert müssen wir dann erst selber errechnen und dann ergänzen. Also fangen wir einmal an die Daten in das Long-Format zu überführen.

paired_long_tbl <- paired_tbl |> 
  pivot_longer(cols = satt:hungrig,
               values_to = "jump_length",
               names_to = "trt")

Jetzt können wir den gepaarten U-Test rechnen und zwar aus dem R Paket {rstatix}. Dann müssen wir noch alles so umbauen, dass wir die Informationen dann in {tidyplots} auch nutzen können.

stats_tbl <- paired_long_tbl |> 
  arrange(id) |> 
  wilcox_test(jump_length ~ trt, paired = TRUE) |> 
  add_significance() |> 
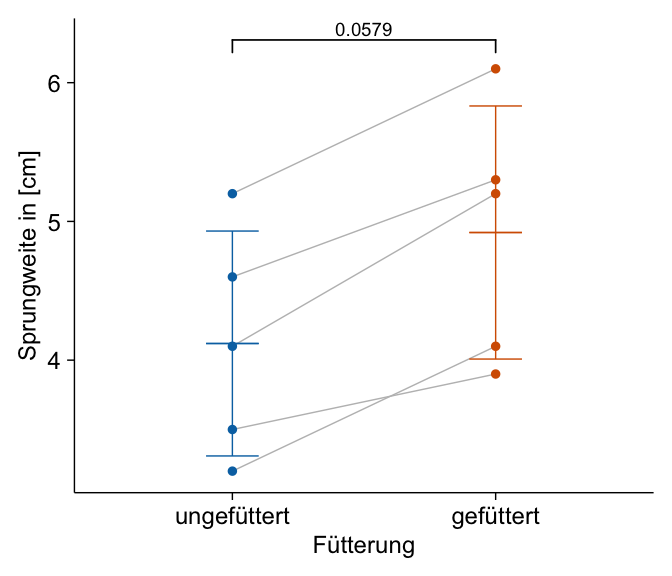
  add_xy_position()

Wir butzen hier die Funktion stat_pvalue_manual() um händisch die p-Werte zu den Dotplot mit den Mittelwert und Standardabweichung zu ergänzen. Die Verbindungen zwischen den Beobachtungen haben wir dann durch add_line() erzeugt. Ich gebe zu, dass ist etwas komplizierter. Wenn du dann die Sterne haben willst, dann musst due das Label auf "p.signif" setzen. Dann werden statt der p-Werte "p" dir die Sterne * angezeigt. Wir sehen hier, dass sich die beiden Fütterungslevel in den Sprungweiten signifikant unterscheiden. Der p-Wert ist kleiner als das Signifikanzniveau \(\alpha\) gleich 5%.

paired_long_tbl |> 
  tidyplot(x = trt, y = jump_length, color = trt, fill = NA) |> 
  add_line(group = id, color = "grey") |> 
  add_data_points() |>
  add_mean_dash(width = 0.2) |> 
  add_sd_errorbar(width = 0.2) |> 
  add(stat_pvalue_manual(stats_tbl, size = 7/.pt, label = "p",
                         bracket.nudge.y = 0.1)) |> 
  remove_legend() |> 
  adjust_font(fontsize = 9) |>
  adjust_x_axis_title("Fütterung") |>
  adjust_y_axis_title("Sprungweite in [cm]") |> 
  reorder_x_axis_labels("hungrig", "satt") |>  
  rename_x_axis_labels(new_names = c("satt" = "gefüttert", "hungrig" = "ungefüttert")) |>
  adjust_size(width = NA, height = NA) 

Abbildung 35.13— Dotplot mit Mittelwert und Standardabweichung für die Sprungweiten in [cm] gruppiert nach den Floharten mit mehr Optionen und angepassten Beschriftungen sowie den p-Wert aus einem gepaarten U-Test. Gleiche Messungen an gleichen Flöhen sind mit einer Linie verbunden.

Referenzen

Conover, W. J., & Iman, R. L. (1981). Rank transformations as a bridge between parametric and nonparametric statistics. The American Statistician, 35(3), 124–129.

Conroy, R. M. (2012). What hypotheses do „nonparametric“ two-group tests actually test? The Stata Journal, 12(2), 182–190.

Divine, G. W., Norton, H. J., Barón, A. E., & Juarez-Colunga, E. (2018). The Wilcoxon–Mann–Whitney procedure fails as a test of medians. The American Statistician, 72(3), 278–286.

Hart, A. (2001). Mann-Whitney test is not just a test of medians: differences in spread can be important. Bmj, 323(7309), 391–393.

Sugimoto, E., Li, J., Hayashi, Y., Iida, K., Asada, S., Fukushima, T., Tamura, M., Shikata, S., Zhang, W., Yamamoto, K., et al. (2023). Hyperactive Natural Killer cells in Rag2 knockout mice inhibit the development of acute myeloid leukemia. Communications Biology, 6(1), 1294.

Tomczak, M., & Tomczak, E. (2014). The need to report effect size estimates revisited. An overview of some recommended measures of effect size.

Zimmerman, D. W., & Zumbo, B. D. (1993). Relative power of the Wilcoxon test, the Friedman test, and repeated-measures ANOVA on ranks. The Journal of Experimental Education, 62(1), 75–86.