83 Baustelle

Letzte Änderung am 18. November 2025 um 19:34:21

Stand des Kapitels: Konstruktion (seit 07.2025)

Dieses Kapitel wird in den nächsten Wochen geschrieben. Ich plane zum Beginn des WiSe 2025/26 eine neue Version des Kapitels erstellt zu haben. Während das Kapitel entsteht, funktioniert so manches dann nicht so wie es soll.

Dieses Kapitel ist archiviert

Ich benötige die Thematik aktuell nicht in meiner Lehre oder der statistischen Beratung. Mir ist es als Nachschlagewerk aber immer noch wichtig zu behalten. Archivierte Kapitel werden nicht von mir weiter gepflegt oder ergänzt. Auftretende Fehler werden aber natürlich beseitigt, wenn die Fehler mir auffallen oder gemeldet werden.

83.1 Visualisierung von Verteilungen

rnorm(): Erzeugt Zufallszahlen aus einer Normalverteilung.
runif(): Erzeugt Zufallszahlen aus einer Gleichverteilung.
rbinom(): Generiert Zufallszahlen aus einer Binomialverteilung.
rpois(): Erzeugt Zufallszahlen aus einer Poisson-Verteilung.
rgamma(): Generiert Zufallszahlen aus einer Gamma-Verteilung.
rexp(): Erzeugt Zufallszahlen aus einer Exponentialverteilung.
rt(): Generiert Zufallszahlen aus einer Student’s t-Verteilung.
rchisq(): Erzeugt Zufallszahlen aus einer Chi-Quadrat-Verteilung.
rbeta(): Erzeugt Zufallszahlen aus einer Beta-Verteilung.
rf(): Erzeugt Zufallszahlen aus einer F-Verteilung.
rlogis(): Erzeugt Zufallszahlen aus einer logistischen Verteilung.
rweibull(): Erzeugt Zufallszahlen aus einer Weibull-Verteilung.

Abbildung 83.1— foo. *[Zum Vergrößern anklicken]*

Abbildung 83.2— foo. *[Zum Vergrößern anklicken]*

83.2 Daten generieren

R Code [zeigen / verbergen]

library(ggeffects)

Warning: package 'ggeffects' was built under R version 4.4.1

R Code [zeigen / verbergen]

set.seed(1234)
x <- rnorm(200, 5, 1)
z <- rnorm(200)
# quadratic relationship
# y <- 5 + 2 * x + x^2 + 4 * z + rnorm(200)
y <- 5 + 2 * (x-5) + (x-5)^2 + 4 * z + rnorm(200)
y <- x^2 - 8*x + 4*z +20 ## das war Gemini KI


d <- data.frame(x = x, y, z)
m <- lm(y ~ x + z, data = d)

pr <- predict_response(m, "x [all]")
p1 <- plot(pr, show_data = TRUE)

Data points may overlap. Use the `jitter` argument to add some amount of
  random variation to the location of data points and avoid overplotting.

R Code [zeigen / verbergen]

p2 <- plot(pr, show_residuals = TRUE, show_residuals_line = TRUE)

Data points may overlap. Use the `jitter` argument to add some amount of
  random variation to the location of data points and avoid overplotting.

R Code [zeigen / verbergen]

p1 + p2

`geom_smooth()` using formula = 'y ~ x'

R Code [zeigen / verbergen]

x <- seq(-3, 3, length.out = 200) + rnorm(200) + 5
z <- rnorm(200)
y <- 5 + 2 * x + x^2 + x^3 + 4 * z + rnorm(200)
y <- 5 + 2 * (x-5) - (x-5)^2 + (x-5)^3 + 4 * z + rnorm(200)
y <- x^3 - 16*x^2 + 87*x + 4*z - 155

d <- data.frame(x = x, y, z)
m <- lm(y ~ x + z, data = d)

pr <- predict_response(m, "x [all]")
p1 <- plot(pr, show_data = TRUE)

Data points may overlap. Use the `jitter` argument to add some amount of
  random variation to the location of data points and avoid overplotting.

R Code [zeigen / verbergen]

p2 <- plot(pr, show_residuals = TRUE, show_residuals_line = TRUE)

Data points may overlap. Use the `jitter` argument to add some amount of
  random variation to the location of data points and avoid overplotting.

R Code [zeigen / verbergen]

p1 + p2

`geom_smooth()` using formula = 'y ~ x'

Introduction: Adding Partial Residuals to Adjusted Predictions Plots

83.2.1 … mit `{modelbased}`

R Paket {modelbased}

83.3 Maximum Liklihood

83.4 Konfidenzintervall vs. Prädiktionsintervall

Ein Konfidenzintervall gibt den Wertebereich für einen gesuchten Parameter der Grundgesamtheit mit einer bestimmten Wahrscheinlichkeit an. Ein Prognoseintervall gibt den Wertebereich für einen individuellen, zukünftig zu beobachtenden Wert mit einer bestimmten Wahrscheinlichkeit an.

Konfidenzintervall: Ein Konfidenzintervall gibt den Wertebereich für einen gesuchten Parameter der Grundgesamtheit mit einer bestimmten Wahrscheinlichkeit an.
Prädiktionsintervall: Ein Prädiktionsintervall (auch Vorhersageintervall oder Prognoseintervall) gibt den Wertebereich für einen individuellen, zukünftig zu beobachtenden Wert mit einer bestimmten Wahrscheinlichkeit an.

Quantile Regression Forests for Prediction Intervals

The difference between prediction intervals and confidence intervals

P-values for prediction intervals machen keinen Sinn

83.5 Concordance Correlation Coefficient (CCC)

Kann auch in technische Gleichheit mit rein

R Code [zeigen / verbergen]

nirs_wide_tbl <- read_excel("data/nirs_qs_data.xlsx") |> 
  clean_names()

nirs_long_tbl <- nirs_wide_tbl |> 
  pivot_longer(cols = jd_ts:last_col(),
               values_to = "values",
               names_to = c("method", "type"),
               names_sep = "_") |> 
  mutate(gulleart = as_factor(gulleart),
         method = as_factor(method),
         type = as_factor(type))

Warning: Expected 2 pieces. Additional pieces discarded in 3 rows [3, 8, 13].

Technical note: Validation and comparison of 2 commercially available activity loggers

User’s guide to correlation coefficients

Concordance correlation coefficient calculation in R

How does Polychoric Correlation Work? (aka Ordinal-to-Ordinal correlation)

An Alternative to the Correlation Coefficient That Works For Numeric and Categorical Variables

83.6 Dummykodierung

R Library Contrast Coding Systems for categorical variables

Dummykodierung

fastDummies: Fast Creation of Dummy (Binary) Columns and Rows from Categorical Variables

83.7 Analyse von Zeitreihen mit `{gamm4}`

Hier nochmal {mgcv} und {gamm4}

Introduction to Generalized Additive Mixed Models

s() und Interaktion mit s(x_1, by = f_1)

83.8 Mediatoranalyse

Causal Inference in R

Simulating confounders, colliders and mediators

Statistical Control Requires Causal Justification

Causal influence and DAGs

Mediators, confounders, colliders – a crash course in causal inference

Collider Bias in Beobachtungsstudien: Konsequenzen für die medizinische Forschung

Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data

DAGitty — draw and analyze causal diagrams

In dem Begriff des Disturber (deu. Störenfried, abk. $D$) fassen wir die Begriffe des Confounder (deu. Störfaktor, abk. $D_{con}$), Collider (deu. Zusammenstoßen, abk. $D_{col}$) und Mediator (deu. Vermittlern, abk. $D_{med}$) zusammen.

Abbildung 83.3— foo **(A)** Confounder **(B)** Collider **(C)** Mediator. *[Zum Vergrößern anklicken]*

Structural Equation Modeling

Passt das hier rein? Müssen wir nochmal überlegen.

Van Lissa et al. (2023) tidySEM

Structural Equation Modeling

Introduction to structural equation modeling (sem) in r with lavaan

Intro to structural equation modeling

Schöne Diagramme Structural Equation Models

Bayes Ideen

https://paul-buerkner.github.io/brms/articles/index.html

https://paul-buerkner.github.io/brms/articles/brms_nonlinear.html

https://bookdown.org/content/4857/

https://bayesat.github.io/lund2018/slides/andrey_anikin_slides.pdf

http://mjskay.github.io/tidybayes/articles/tidybayes.html

Stan

R Paket rstanarm

R Paket tidyposterior

Half a dozen frequentist and Bayesian ways to measure the difference in means in two groups

https://bookdown.org/marklhc/notes_bookdown/group-comparisons.html

Van Lissa, C. J., Villarreal, M. G., & Anadria, D. (2023). Best Practices in Latent Class Analysis using the Open-Source R-Package tidySEM.

```{r echo = FALSE} #| message: false #| warning: false pacman::p_load(tidyverse, readxl, knitr, kableExtra, performance, parameters, latex2exp, see, patchwork, mfp, multcomp, emmeans, janitor, effectsize, broom, ggmosaic, tinytable, ggrepel, glue, ggtext, ggdag, conflicted) conflicts_prefer(dplyr::select) conflicts_prefer(dplyr::filter) cb_pal <- c("#000000", "#E69F00", "#56B4E9", "#009E73", "#F0E442", "#F5C710", "#0072B2", "#D55E00", "#CC79A7") cbbPalette <- cb_pal theme_marginal <- function() { theme_minimal() + theme(panel.grid.minor = element_blank(), plot.background = element_rect(fill = "white", color = NA), plot.title = element_text(size = 16, face = "bold"), plot.subtitle = element_text(size = 12, face = "italic"), plot.caption = element_text(face = "italic"), axis.title = element_text(face = "bold"), axis.text = element_text(size = 12), strip.text = element_text(face = "bold"), strip.background = element_rect(fill = "grey80", color = NA)) } ``` # Baustelle {#sec-construction} *Letzte Änderung am `r format(fs::file_info("construction-zone.qmd")$modification_time, '%d. %B %Y um %H:%M:%S')`* ![](images/caution.png){fig-align="center" width="100%"} ::: {.callout-caution appearance="simple"} ## Stand des Kapitels: Konstruktion (seit 07.2025) Dieses Kapitel wird in den nächsten Wochen geschrieben. Ich plane zum Beginn des WiSe 2025/26 eine neue Version des Kapitels erstellt zu haben. Während das Kapitel entsteht, funktioniert so manches dann nicht so wie es soll. ::: ::: {.callout-caution appearance="minimal"} ## Dieses Kapitel ist archiviert ![](images/archive.png){fig-align="center" width="100%"} Ich benötige die Thematik aktuell nicht in meiner Lehre oder der statistischen Beratung. Mir ist es als Nachschlagewerk aber immer noch wichtig zu behalten. Archivierte Kapitel werden nicht von mir weiter gepflegt oder ergänzt. Auftretende Fehler werden aber natürlich beseitigt, wenn die Fehler mir auffallen oder gemeldet werden. 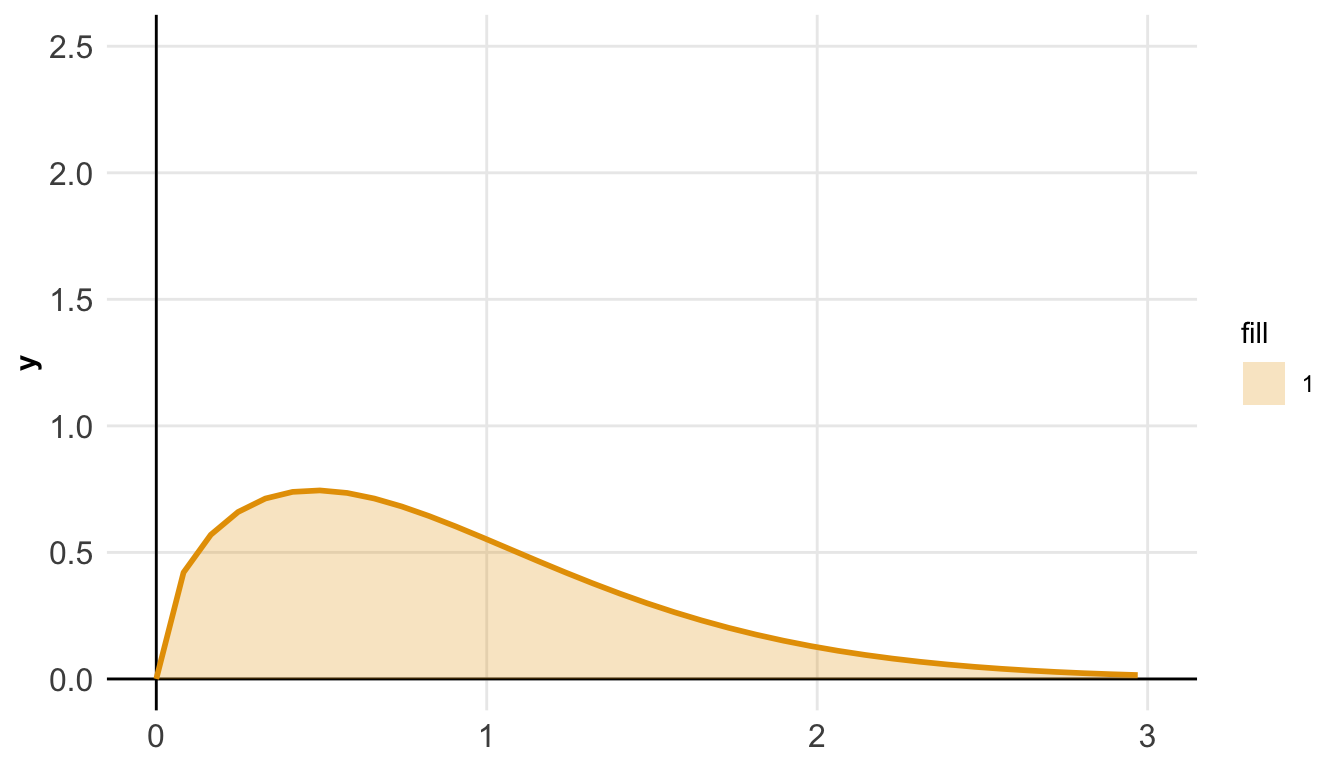::: ## Visualisierung von Verteilungen - `rnorm()`: Erzeugt Zufallszahlen aus einer [Normalverteilung](https://en.wikipedia.org/wiki/Normal_distribution). - `runif()`: Erzeugt Zufallszahlen aus einer [Gleichverteilung](https://en.wikipedia.org/wiki/Continuous_uniform_distribution). - `rbinom()`: Generiert Zufallszahlen aus einer [Binomialverteilung](https://en.wikipedia.org/wiki/Binomial_distribution). - `rpois()`: Erzeugt Zufallszahlen aus einer [Poisson-Verteilung](https://en.wikipedia.org/wiki/Poisson_distribution). - `rgamma()`: Generiert Zufallszahlen aus einer [Gamma-Verteilung](https://en.wikipedia.org/wiki/Gamma_distribution). - `rexp()`: Erzeugt Zufallszahlen aus einer [Exponentialverteilung](https://en.wikipedia.org/wiki/Exponential_distribution). - `rt()`: Generiert Zufallszahlen aus einer [Student's t-Verteilung](https://en.wikipedia.org/wiki/Student%27s_t-distribution). - `rchisq()`: Erzeugt Zufallszahlen aus einer [Chi-Quadrat-Verteilung](https://en.wikipedia.org/wiki/Chi-squared_distribution). 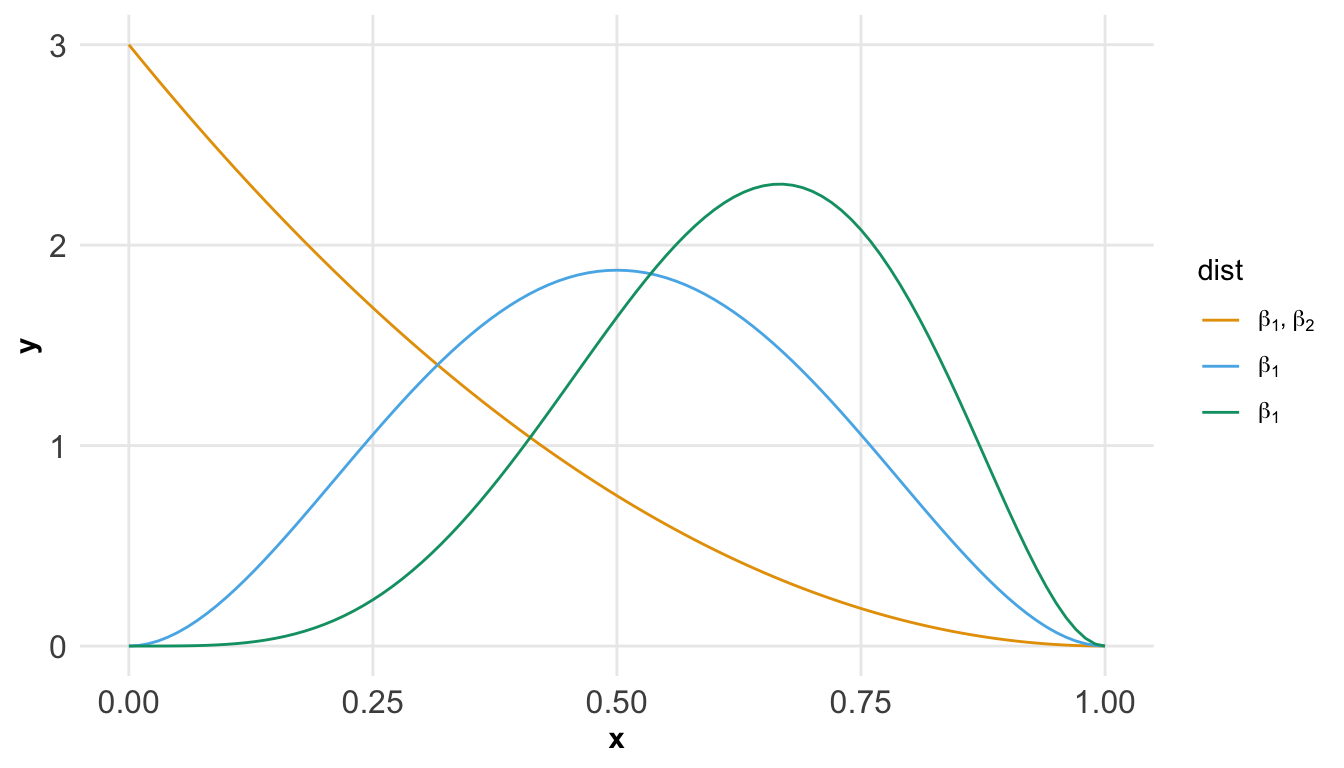- `rbeta()`: Erzeugt Zufallszahlen aus einer [Beta-Verteilung](https://en.wikipedia.org/wiki/Beta_distribution). - `rf()`: Erzeugt Zufallszahlen aus einer [F-Verteilung](https://en.wikipedia.org/wiki/F-distribution). - `rlogis()`: Erzeugt Zufallszahlen aus einer [logistischen Verteilung](https://en.wikipedia.org/wiki/Logistic_distribution). - `rweibull()`: Erzeugt Zufallszahlen aus einer [Weibull-Verteilung](https://en.wikipedia.org/wiki/Weibull_distribution). ```{r} #| message: false #| echo: false #| warning: false #| fig-align: center #| fig-height: 4 #| fig-width: 7 #| fig-cap: "foo. *[Zum Vergrößern anklicken]*" #| label: fig-gen-data-weibull ggplot() + theme_marginal() + geom_vline(xintercept = c(0)) + geom_hline(yintercept = c(0)) + stat_function(fun = dweibull, linewidth = 1, args = list(scale = 1, shape = 1.5), xlim = c(0, 8.25), aes(color = "1"), show.legend = FALSE) + stat_function(fun = dweibull, geom = "area", args = list(scale = 1, shape = 1.5), alpha = 0.25, xlim = c(0, 8.25), aes(fill = "1")) + ylim(0, 2.5) + xlim(0, 3) + scale_color_okabeito() + scale_fill_okabeito() ``` ```{r} #| message: false #| echo: false #| warning: false #| fig-align: center #| fig-height: 4 #| fig-width: 7 #| fig-cap: "foo. 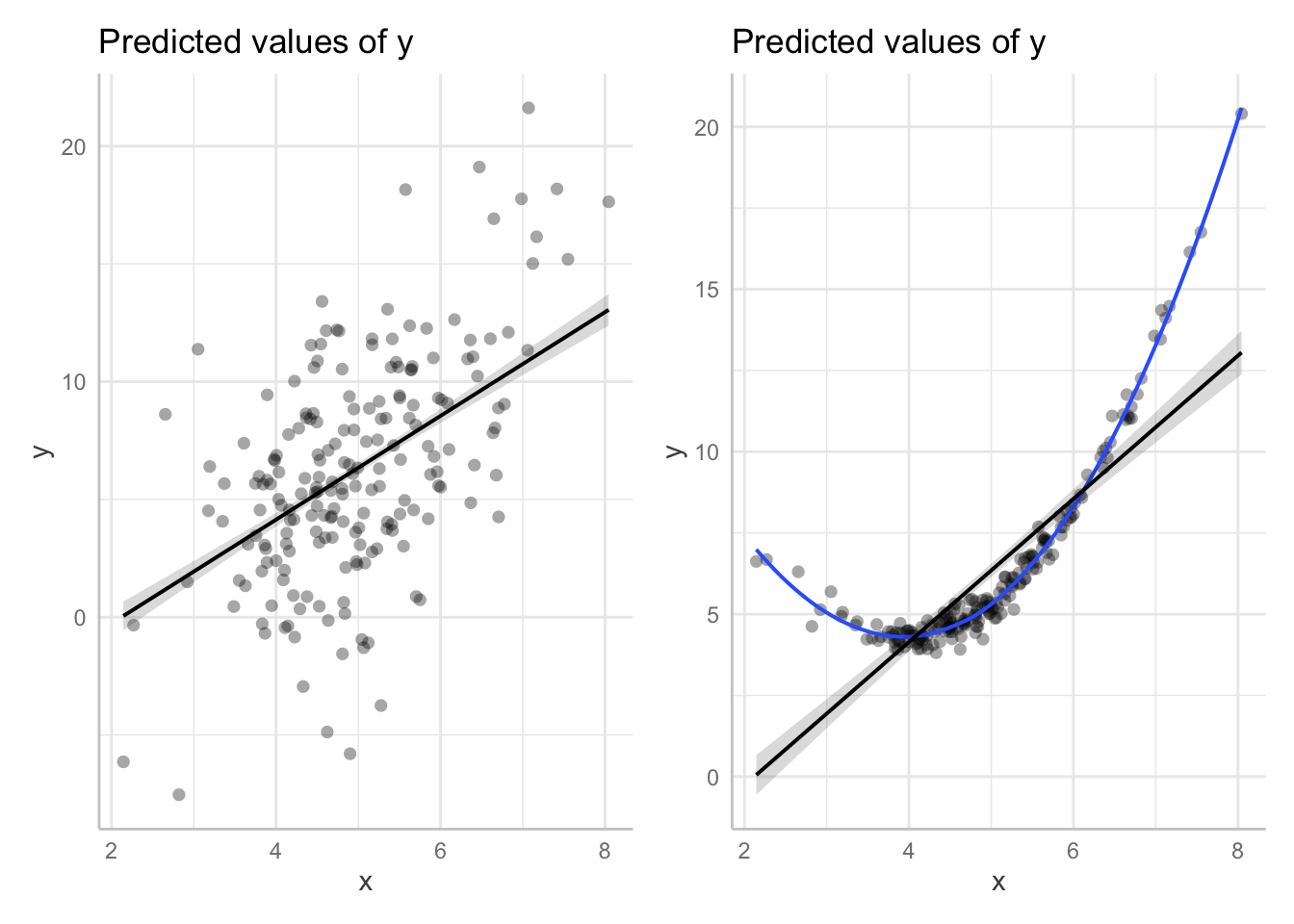*[Zum Vergrößern anklicken]*" #| label: fig-gen-data-beta df <- tibble(dist = c("a", "b", "c"), beta1 = c(1,3,5), beta2 = c(3,3,3)) df |> group_by(dist) |> reframe(x = seq(0, 1, 0.01), y = dbeta(x, beta1, beta2)) |> ggplot(aes(x, y, color = dist)) + theme_marginal() + geom_line() + scale_color_okabeito(labels = c(expression(beta[1]*","~beta[2]), expression(beta[1]),expression(beta[1]))) ``` ## Daten generieren ```{r} library(ggeffects) ``` ```{r} set.seed(1234) x <- rnorm(200, 5, 1) z <- rnorm(200) # quadratic relationship # y <- 5 + 2 * x + x^2 + 4 * z + rnorm(200) y <- 5 + 2 * (x-5) + (x-5)^2 + 4 * z + rnorm(200) y <- x^2 - 8*x + 4*z +20 ## das war Gemini KI d <- data.frame(x = x, y, z) m <- lm(y ~ x + z, data = d) pr <- predict_response(m, "x [all]") p1 <- plot(pr, show_data = TRUE) p2 <- plot(pr, show_residuals = TRUE, show_residuals_line = TRUE) p1 + p2 ``` ```{r} x <- seq(-3, 3, length.out = 200) + rnorm(200) + 5 z <- rnorm(200) y <- 5 + 2 * x + x^2 + x^3 + 4 * z + rnorm(200) y <- 5 + 2 * (x-5) - (x-5)^2 + (x-5)^3 + 4 * z + rnorm(200) y <- x^3 - 16*x^2 + 87*x + 4*z - 155 d <- data.frame(x = x, y, z) m <- lm(y ~ x + z, data = d) pr <- predict_response(m, "x [all]") p1 <- plot(pr, show_data = TRUE) p2 <- plot(pr, show_residuals = TRUE, show_residuals_line = TRUE) p1 + p2 ``` [Introduction: Adding Partial Residuals to Adjusted Predictions Plots](https://strengejacke.github.io/ggeffects/articles/introduction_partial_residuals.html) ### ... mit `{modelbased}` [R Paket `{modelbased}`](https://easystats.github.io/modelbased/) ## Maximum Liklihood - [In Statistics, Probability is not Likelihood.](https://www.youtube.com/watch?v=pYxNSUDSFH4) - [Maximum Likelihood, clearly explained!!!](https://www.youtube.com/watch?v=XepXtl9YKwc) - [Likelihood!](https://kevintshoemaker.github.io/NRES-746/LECTURE4.html) - [Maximum likelihood estimation from scratch](https://alemorales.info/post/mle-nonlinear/) ## Konfidenzintervall vs. Prädiktionsintervall Ein Konfidenzintervall gibt den Wertebereich für einen gesuchten Parameter der Grundgesamtheit mit einer bestimmten Wahrscheinlichkeit an. Ein Prognoseintervall gibt den Wertebereich für einen individuellen, zukünftig zu beobachtenden Wert mit einer bestimmten Wahrscheinlichkeit an. Konfidenzintervall : Ein Konfidenzintervall gibt den Wertebereich für einen gesuchten Parameter der Grundgesamtheit mit einer bestimmten Wahrscheinlichkeit an. Prädiktionsintervall : Ein Prädiktionsintervall (auch Vorhersageintervall oder Prognoseintervall) gibt den Wertebereich für einen individuellen, zukünftig zu beobachtenden Wert mit einer bestimmten Wahrscheinlichkeit an. [Quantile Regression Forests for Prediction Intervals](https://www.bryanshalloway.com/2021/04/21/quantile-regression-forests-for-prediction-intervals/) [The difference between prediction intervals and confidence intervals](https://robjhyndman.com/hyndsight/intervals/) [P-values for prediction intervals](https://robjhyndman.com/hyndsight/forecasting-pvalues.html) machen keinen Sinn ## Concordance Correlation Coefficient (CCC) *Kann auch in technische Gleichheit mit rein* ```{r} nirs_wide_tbl <- read_excel("data/nirs_qs_data.xlsx") |> clean_names() nirs_long_tbl <- nirs_wide_tbl |> pivot_longer(cols = jd_ts:last_col(), values_to = "values", names_to = c("method", "type"), names_sep = "_") |> mutate(gulleart = as_factor(gulleart), method = as_factor(method), type = as_factor(type)) ``` [Technical note: Validation and comparison of 2 commercially available activity loggers](https://www.sciencedirect.com/science/article/pii/S0022030218302418) [User's guide to correlation coefficients](https://pmc.ncbi.nlm.nih.gov/articles/PMC6107969/) [Concordance correlation coefficient calculation in R](https://medium.com/@amorimfranchi/concordance-correlation-coefficient-calculation-in-r-98d74ae5f0fc) [How does Polychoric Correlation Work? (aka Ordinal-to-Ordinal correlation)](https://www.r-bloggers.com/2021/02/how-does-polychoric-correlation-work-aka-ordinal-to-ordinal-correlation/) [An Alternative to the Correlation Coefficient That Works For Numeric and Categorical Variables](https://rviews.rstudio.com/2021/04/15/an-alternative-to-the-correlation-coefficient-that-works-for-numeric-and-categorical-variables/) ## Dummykodierung [R Library Contrast Coding Systems for categorical variables](https://stats.oarc.ucla.edu/r/library/r-library-contrast-coding-systems-for-categorical-variables/) [Dummykodierung](https://de.wikipedia.org/wiki/Dummy-Variable) [fastDummies: Fast Creation of Dummy (Binary) Columns and Rows from Categorical Variables](https://cran.r-project.org/web/packages/fastDummies/) ## Analyse von Zeitreihen mit `{gamm4}` Hier nochmal `{mgcv}` und `{gamm4}` [Introduction to Generalized Additive Mixed Models](https://r.qcbs.ca/workshop08/book-en/introduction-to-generalized-additive-mixed-models-gamms.html) `s()` und Interaktion mit `s(x_1, by = f_1)` ## Mediatoranalyse [Causal Inference in R](https://www.r-causal.org/) [Simulating confounders, colliders and mediators](https://freerangestats.info/blog/2023/06/04/causality-sims) [Statistical Control Requires Causal Justification](https://journals.sagepub.com/doi/10.1177/25152459221095823) [Causal influence and DAGs](https://dtkaplan.github.io/Lessons-in-statistical-thinking/L24-Causality-and-DAGS.html) [Mediators, confounders, colliders – a crash course in causal inference](https://theoreticalecology.wordpress.com/2019/04/14/mediators-confounders-colliders-a-crash-course-in-causal-inference/) [Collider Bias in Beobachtungsstudien: Konsequenzen für die medizinische Forschung](https://www.aerzteblatt.de/archiv/collider-bias-in-beobachtungsstudien-konsequenzen-fuer-die-medizinische-forschung-675e398b-1715-427e-b497-f210a57b605f) [Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data](https://osf.io/preprints/psyarxiv/t3qub_v1) [DAGitty — draw and analyze causal diagrams](https://www.dagitty.net/) 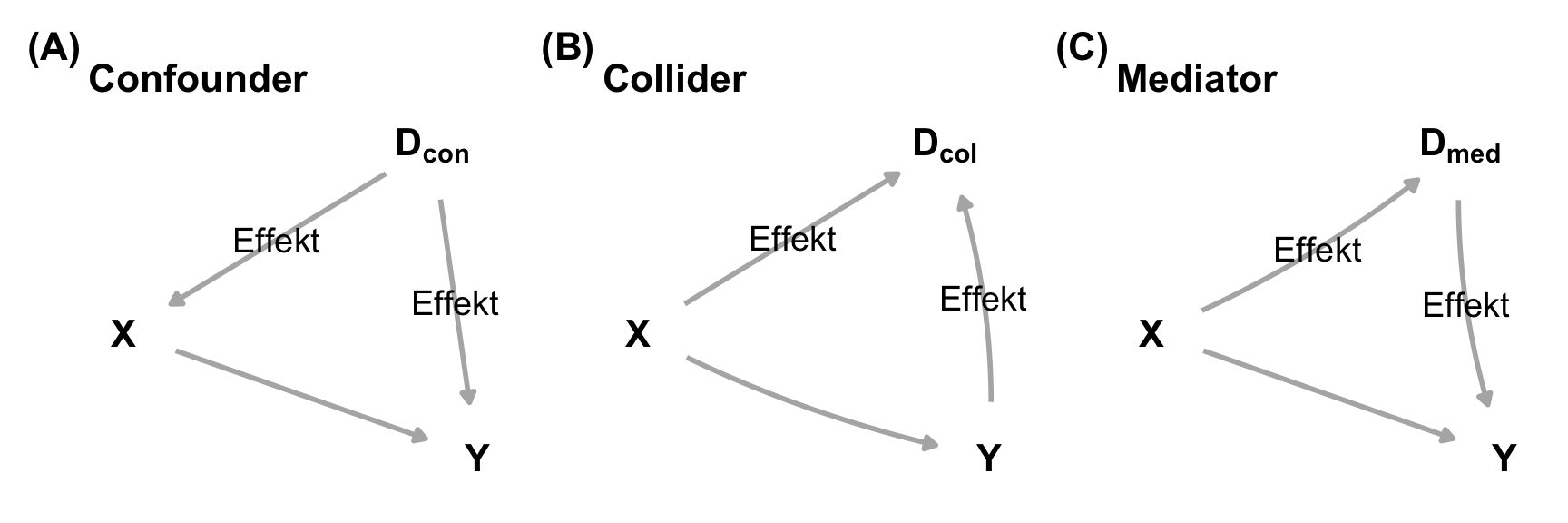In dem Begriff des Disturber (deu. *Störenfried*, abk. $D$) fassen wir die Begriffe des Confounder (deu. *Störfaktor*, abk. $D_{con}$), Collider (deu. *Zusammenstoßen*, abk. $D_{col}$) und Mediator (deu. *Vermittlern*, abk. $D_{med}$) zusammen. ```{r} #| message: false #| echo: false #| warning: false #| fig-align: center #| fig-height: 3 #| fig-width: 9 #| fig-cap: "foo **(A)** Confounder **(B)** Collider **(C)** Mediator. *[Zum Vergrößern anklicken]*" #| label: fig-model-m-dag arrow_col <- "grey70" set.seed(123) p1_dag <- dagify( Y ~ X + C, X ~ C ) %>% ggplot(aes(x = x, y = y, xend = xend, yend = yend)) + geom_dag_edges_fan(aes(label = c("Effekt", "Effekt", "", "")), edge_colour = arrow_col, label_size = 5, edge_width = 1, label_colour = "black") + geom_dag_text(colour = "black", size = 5.5, parse = TRUE, label = c(expression(bold(D[con])), expression(bold(X)), expression(bold(Y)))) + theme_dag() + labs(title = "Confounder") + theme(plot.title = element_text(size = 16, face = "bold"), plot.caption = element_text(face = "italic")) set.seed(123) p2_dag <- dagify( C ~ X + Y, Y ~ X ) %>% ggplot(aes(x = x, y = y, xend = xend, yend = yend)) + geom_dag_edges_fan(aes(label = c("", "Effekt", "", "Effekt")), edge_colour = arrow_col, label_size = 5, edge_width = 1, label_colour = "black") + geom_dag_text(colour = "black", size = 5.5, parse = TRUE, label = c(expression(bold(D[col])), expression(bold(X)), expression(bold(Y)))) + theme_dag() + labs(title = "Collider") + theme(plot.title = element_text(size = 16, face = "bold"), plot.caption = element_text(face = "italic")) set.seed(123) p3_dag <- dagify( C ~ X, Y ~ X + C ) %>% ggplot(aes(x = x, y = y, xend = xend, yend = yend)) + geom_dag_edges_fan(aes(label = c("Effekt", "Effekt", "", "")), edge_colour = arrow_col, label_size = 5, edge_width = 1, label_colour = "black") + geom_dag_text(colour = "black", size = 5.5, parse = TRUE, label = c(expression(bold(D[med])), expression(bold(X)), expression(bold(Y)))) + theme_dag() + labs(title = "Mediator") + theme(plot.title = element_text(size = 16, face = "bold"), plot.caption = element_text(face = "italic")) p1_dag + p2_dag + p3_dag + plot_layout(ncol = 3) + plot_annotation(tag_levels = 'A', tag_prefix = '(', tag_suffix = ')') & theme(plot.tag = element_text(size = 16, face = "bold")) ``` ### Structural Equation Modeling {.unnumbered} Passt das hier rein? Müssen wir nochmal überlegen. @van2023best [tidySEM](https://cjvanlissa.github.io/tidySEM/index.html) [Structural Equation Modeling](https://bookdown.org/bean_jerry/using_r_for_social_work_research/structural-equation-modeling.html) [Introduction to structural equation modeling (sem) in r with lavaan](https://stats.oarc.ucla.edu/r/seminars/rsem/) [Intro to structural equation modeling](https://rpubs.com/Agrele/SEM) Schöne Diagramme [Structural Equation Models](https://advstats.psychstat.org/book/sem/index.php) ## Bayes Ideen {.unnumbered} https://paul-buerkner.github.io/brms/articles/index.html https://paul-buerkner.github.io/brms/articles/brms_nonlinear.html https://bookdown.org/content/4857/ https://bayesat.github.io/lund2018/slides/andrey_anikin_slides.pdf http://mjskay.github.io/tidybayes/articles/tidybayes.html [Stan](https://mc-stan.org/) [R Paket rstanarm](https://mc-stan.org/rstanarm/articles/index.html) [R Paket tidyposterior](https://tidyposterior.tidymodels.org/) [Half a dozen frequentist and Bayesian ways to measure the difference in means in two groups](https://www.andrewheiss.com/blog/2019/01/29/diff-means-half-dozen-ways/#bayesian-regression) https://bookdown.org/marklhc/notes_bookdown/group-comparisons.html

83.1 Visualisierung von Verteilungen

83.2 Daten generieren

83.2.1 … mit {modelbased}

83.3 Maximum Liklihood

83.4 Konfidenzintervall vs. Prädiktionsintervall

83.5 Concordance Correlation Coefficient (CCC)

83.6 Dummykodierung

83.7 Analyse von Zeitreihen mit {gamm4}

83.8 Mediatoranalyse

Structural Equation Modeling

Bayes Ideen

83.2.1 … mit `{modelbased}`

83.7 Analyse von Zeitreihen mit `{gamm4}`