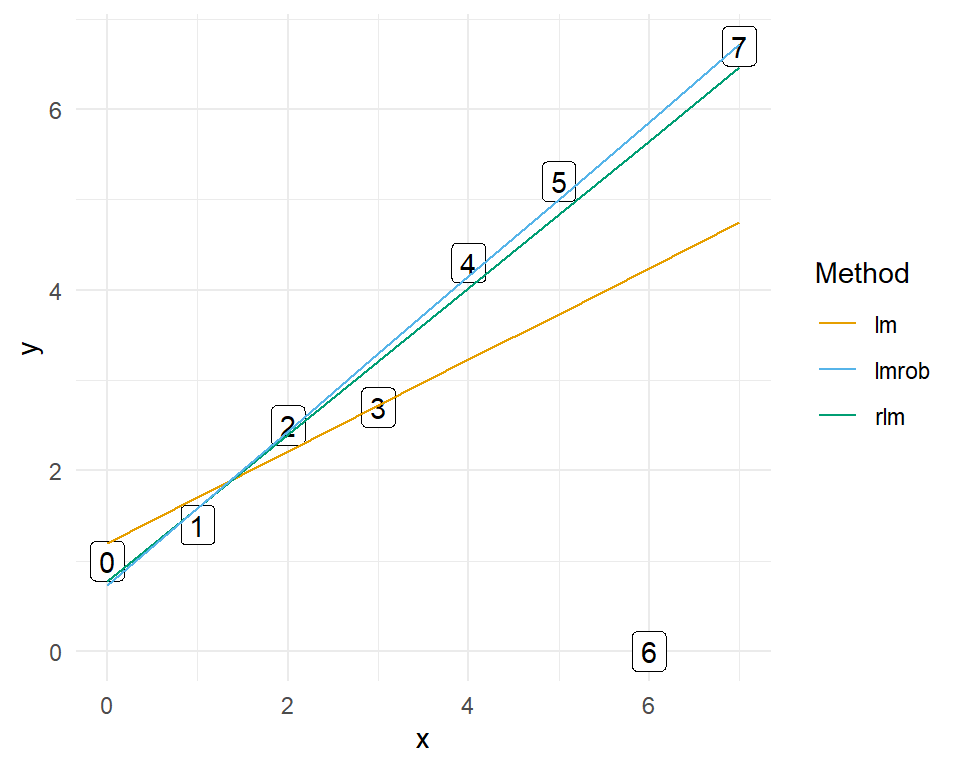```{r echo = FALSE}
#| echo: false
#| message: false
#| warning: false
pacman::p_load(tidyverse, magrittr, broom, nlme, quantreg,
see, performance, scales, parameters, knitr,
olsrr, readxl, car, gtsummary, emmeans,
multcomp, conflicted)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)
```
# Robuste und Quantilesregression {#sec-reg-quantile}
*Letzte Änderung am `r format(fs::file_info("stat-modeling-robust-quantile.qmd")$modification_time, '%d. %B %Y um %H:%M:%S')`*
> *"Methods for robust statistics, a state of the art in the early 2000s, notably for robust regression and robust multivariate analysis." --- [robust: Port of the S+ "Robust Library"](https://cran.r-project.org/web/packages/robust/index.html)*
In diesem Kapitel geht es um zwei Arten der Regression, die immer wieder genannt werden, aber dennoch eine Art Nischendasein fristen. Zum einen möchte ich hier die robuste Regression (eng. *robust regression*) und zum anderen die Quantilsregression (eng. *quantile regression*) vorstellen. Die robuste Regression ist faktisch statistisch tot. Das heißt, die Implementierungen werden kaum weiterentwickelt und auch findet methodische Forschung nur in der theoretischen Nische statt. Zwar wird die robuste Regression in ihrer ursprünglichen Form als Regression angewendet, aber das reicht meistens nicht. Selten wollen wir nur durch ein paar Punkte eine Gerade ziehen und uns über das gute Modell erfreuen. Wir haben mit dem Modell meist mehr vor. Wir wollen eine ANOVA rechnen und dann auch einen wie auch immer gearteten Mittelwertsvergleich. Wenn dies zwar theoretisch möglich ist, praktisch aber nicht implementiert, dann wollen und können wir die Methoden nur eingeschränkt verwenden. Bei der Quantilsregression sieht es etwas anders aus, hier können wir dann schon den ein oder anderen Mittelwertsvergleich rechnen. Was bei der Quantilsregression eher problematisch ist, ist das das Modell nicht immer konvergiert oder aber nicht algorithmisch eine Lösung für einen spezifischen Datensatz findet. In diesem Datensatz dann den einen Grund zu finden, ist dann meist so aufwendig, dass wir es auch gleich mit der Quantilsregression lassen können.
Der Charme der Quantilesregression ist ja am Ende, dass wir auch den Median als Quantile auswählen können. So haben wir dann die Möglichkeit eine Regression auf den Medianen zu rechnen. Wir vergleichen damit dann auch die Mediane und sind so nicht mehr auf die Normalverteilung unseres Outcomes wie in der gewöhnlichen Regression angewiesen. Also eigentlich eine tolle Sache, wenn wir nur an den Mittelwertsvergleichen interessiert sind. Eine klassische ANOVA geht leider nicht auf einer Medianregression. Eine klassische ANOVA wäre aber mit nicht parametrischen Methoden sowieso nicht möglich gewesen. Wir verlieren also nicht so viel, gewinnen aber etwas, wenn das Modell konvergiert und ein Ergebnis liefert.
In diesem Kapitel brechen wir etwas die bisherige Struktur der Regressionskapitel auf. Wir schauen uns hier zuerst die beiden Modelle an und entscheiden dann, ob wir die Modelle für die ANOVA oder den Gruppenvergleich *überhaupt* nutzen können. Am Ende vergleichen wir dann einmal alle Modell mit dem fantastische Paket `{modelsummary}` mit der gleichnamigen Funktion. Hier hilft dann wie immer die tolle [Hilfsseite von modelsummary](https://vincentarelbundock.github.io/modelsummary/articles/modelsummary.html) zu besuchen.
::: {.callout-note collapse="true"}
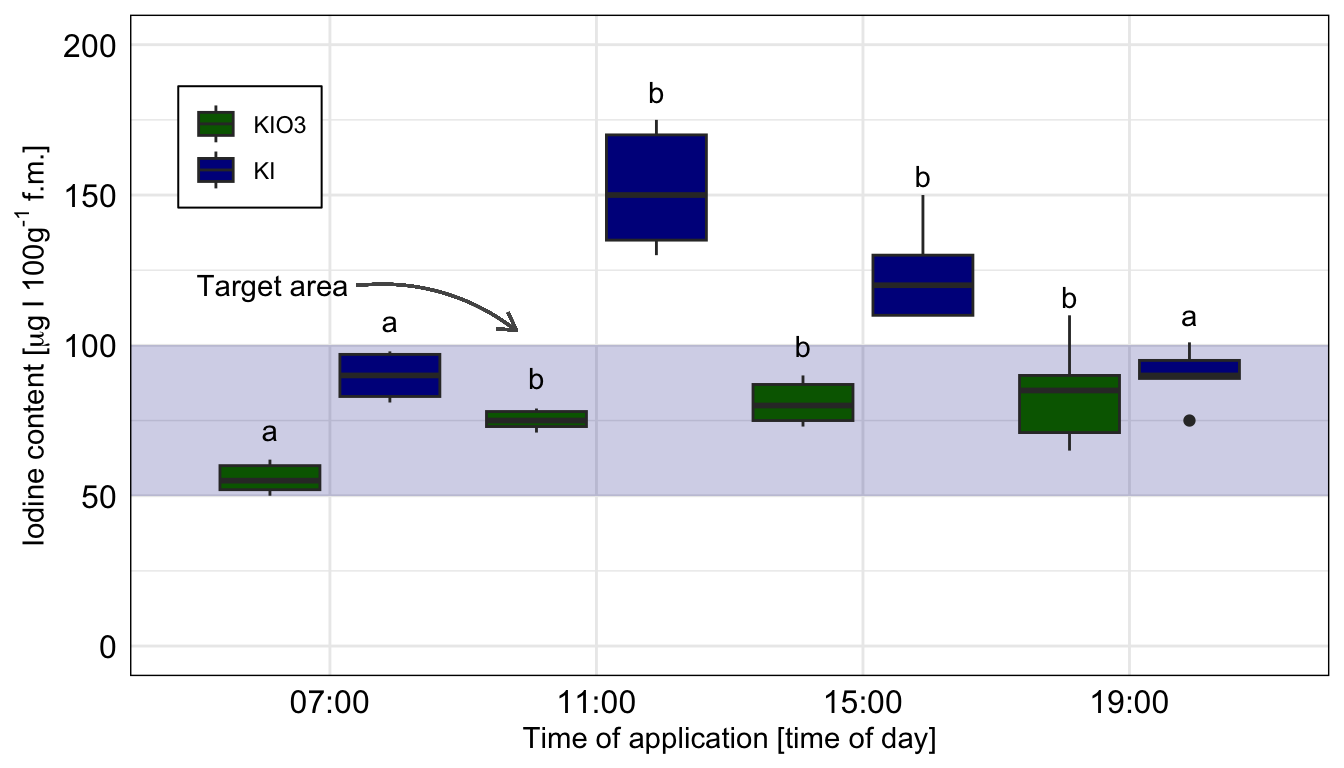
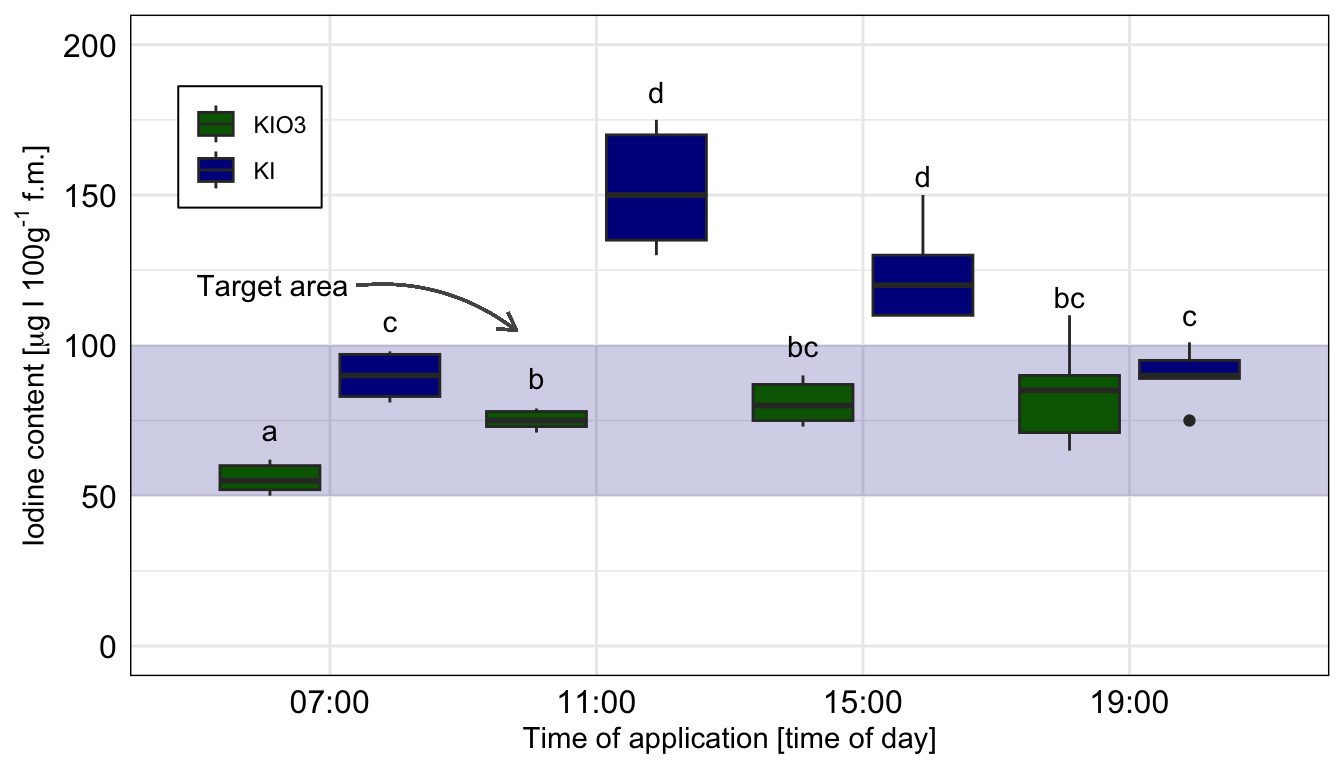
## Zerforschen: Zweifaktorieller Boxplot mit `rq()`
{{< include zerforschen/zerforschen-boxplot-2fac-target-emmeans.qmd >}}
:::
## Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
```{r echo = TRUE}
#| message: false
pacman::p_load(tidyverse, magrittr, conflicted, broom, quantreg,
see, performance, emmeans, multcomp, janitor,
parameters, effectsize, MASS, modelsummary,
robustbase, multcompView, conflicted)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)
#cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
# "#F0E442", "#0072B2", "#D55E00", "#CC79A7")
```
An der Seite des Kapitels findest du den Link *Quellcode anzeigen*, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
## Daten
Für unser erstes Beispiel nutzen wir die Daten aus einem Wachstumsversuch mit Basilikum mit vier Bodenbehandlungen und vier Blöcken, die Blöcke sind eigentlich Gewächshaustische. Wir wollen also einen klassischen Gruppenvergleich mit Berücksichtigung der Blockstruktur rechnen.
```{r}
basi_tbl <- read_excel("data/keimversuch_basilikum_block.xlsx") |>
clean_names() |>
mutate(versuchsgruppe = as_factor(versuchsgruppe)) |>
select(versuchsgruppe, block_1:block_4)
```
In @tbl-model-1 sehen wir einmal die Daten im Wide-Format. Wir haben also das Frischgewicht der Basilikumpflanzen gemessen und wollen wissen, ob die verschiedenen Bodenarten einen Einfluss auf das Wachstum haben.
```{r}
#| message: false
#| echo: false
#| tbl-cap: "Datensatz des Frischegewichts von Basilikumpflanzen auf vier Tischen bzw. Blöcken in vier Versuchsgruppen."
#| label: tbl-model-1
basi_raw_tbl <- basi_tbl |>
mutate(versuchsgruppe = as.character(versuchsgruppe))
rbind(head(basi_raw_tbl),
rep("...", times = ncol(basi_raw_tbl)),
tail(basi_raw_tbl)) |>
kable(align = "c", "pipe")
```
Da wir die Daten im Wide-Format vorliegen haben, müssen wir die Daten nochmal in Long-Format umwandeln. Wie immer nutzen wir dafür die Funktion `pivot_longer()`.
```{r}
#| message: false
#| warning: false
basi_block_tbl <- basi_tbl |>
pivot_longer(cols = block_1:block_4,
values_to = "weight",
names_to = "block") |>
mutate(block = as_factor(block))
```
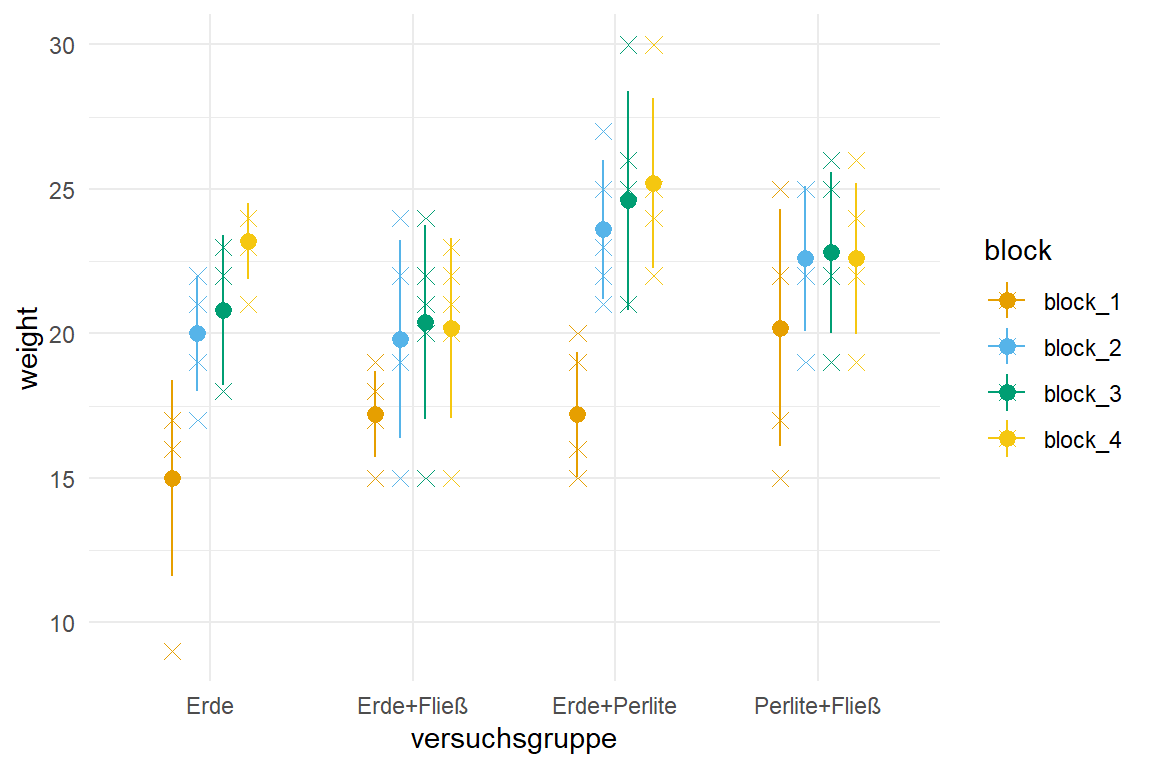
In der @fig-robust-basi-00 siehst du einmal die Daten als Dotplots mit Mittelwert und Standardabweichung. Wir machen hier mal einen etwas komplizierteren Plot, aber immer nur Barplot ist ja auch langweilig.
```{r}
#| echo: true
#| message: false
#| warning: false
#| label: fig-robust-basi-00
#| fig-align: center
#| fig-height: 4
#| fig-width: 6
#| fig-cap: "Dotplot des Frischegewichts von Basilikumpflanzen auf vier Tischen bzw. Blöcken in vier Versuchsgruppen mit Mittelwert und Standardabweichung."
ggplot(basi_block_tbl, aes(versuchsgruppe, weight, color = block)) +
theme_minimal() +
scale_color_okabeito() +
geom_point(position = position_dodge(0.5), shape = 4, size = 2.5) +
stat_summary(fun.data="mean_sdl", fun.args = list(mult = 1),
geom="pointrange", position = position_dodge(0.5)) +
stat_summary(fun = "mean", fun.min = "min", fun.max = "max", geom = "line",
position = position_dodge(0.5))
```
Unser zweiter Datensatz ist ein Anwendungsdatensatz aus dem Gemüsebau. Wir schauen uns das Wachstum von drei Gurkensorten über siebzehn Wochen an. Die Gurkensorten sind hier unsere Versuchsgruppen. Da wir es hier mit echten Daten zu tun haben, müssen wir uns etwas strecken damit die Daten dann auch passen. Wir wollen das Wachstum der drei Gurkensorten *über* die Zeit betrachten - also faktisch den Verlauf des Wachstums. Wir ignorieren hier einmal die abhängige Datenstruktur über die Zeitpunkte.
::: column-margin
Mit einer abhängigen Datenstruktur müssten wir eigentlich ein lineares gemischtes Modell rechnen. Aber wir nutzen hier die Daten einmal anders.
:::
Im Weiteren haben wir zwei Typen von Daten für das Gurkenwachstum. Einmal messen wir den Durchmesser für jede Sorte (`D` im Namen der Versuchsgruppe) oder aber die Länge (`L` im Namen der Versuchsgruppe). Wir betrachten hier nur das Längenwachstum und deshalb filtern wir erstmal nach allen Versuchsgruppen mit einem `L` im Namen. Am Ende schmeißen wir noch Spalten raus, die wir nicht weiter brauchen.
```{r}
#| message: false
#| warning: false
gurke_raw_tbl <- read_excel("data/wachstum_gurke.xlsx") |>
clean_names() |>
filter(str_detect(versuchsgruppe, "L$")) |>
select(-pfl, -erntegewicht) |>
mutate(versuchsgruppe = factor(versuchsgruppe,
labels = c("Katrina", "Proloog", "Quarto")))
```
In der @tbl-model-2 sehen wir einmal die rohen Daten dargestellt.
```{r}
#| message: false
#| echo: false
#| tbl-cap: "Datensatz zu dem Längen- und Dickenwachstum von Gurken."
#| label: tbl-model-2
gurke_raw_2_tbl <- gurke_raw_tbl |>
mutate(versuchsgruppe = as.character(versuchsgruppe))
rbind(head(gurke_raw_2_tbl),
rep("...", times = ncol(gurke_raw_2_tbl)),
tail(gurke_raw_2_tbl)) |>
kable(align = "c", "pipe")
```
Dann müssen wir die Daten noch in Long-Format bringen. Da wir dann auch noch auf zwei Arten die Daten über die Zeit darstellen wollen, brauchen wir einmal die Zeit als Faktor `time_fct` und einmal als numerisch `time_num`. Leider haben wir auch Gurken mit einer Länge von 0 cm, diese Gruken lassen wir jetzt mal drin, da wir ja eine robuste Regression noch rechnen wollen. Auch haben wir ab Woche 14 keine Messungen mehr in der Versuchsgruppe `Prolong`, also nehmen wir auch nur die Daten bis zur vierzehnten Woche.
```{r}
gurke_time_len_tbl <- gurke_raw_tbl |>
pivot_longer(cols = t1:t17,
values_to = "length",
names_to = "time") |>
mutate(time_fct = as_factor(time),
time_num = as.numeric(time_fct)) |>
filter(time_num <= 14)
```
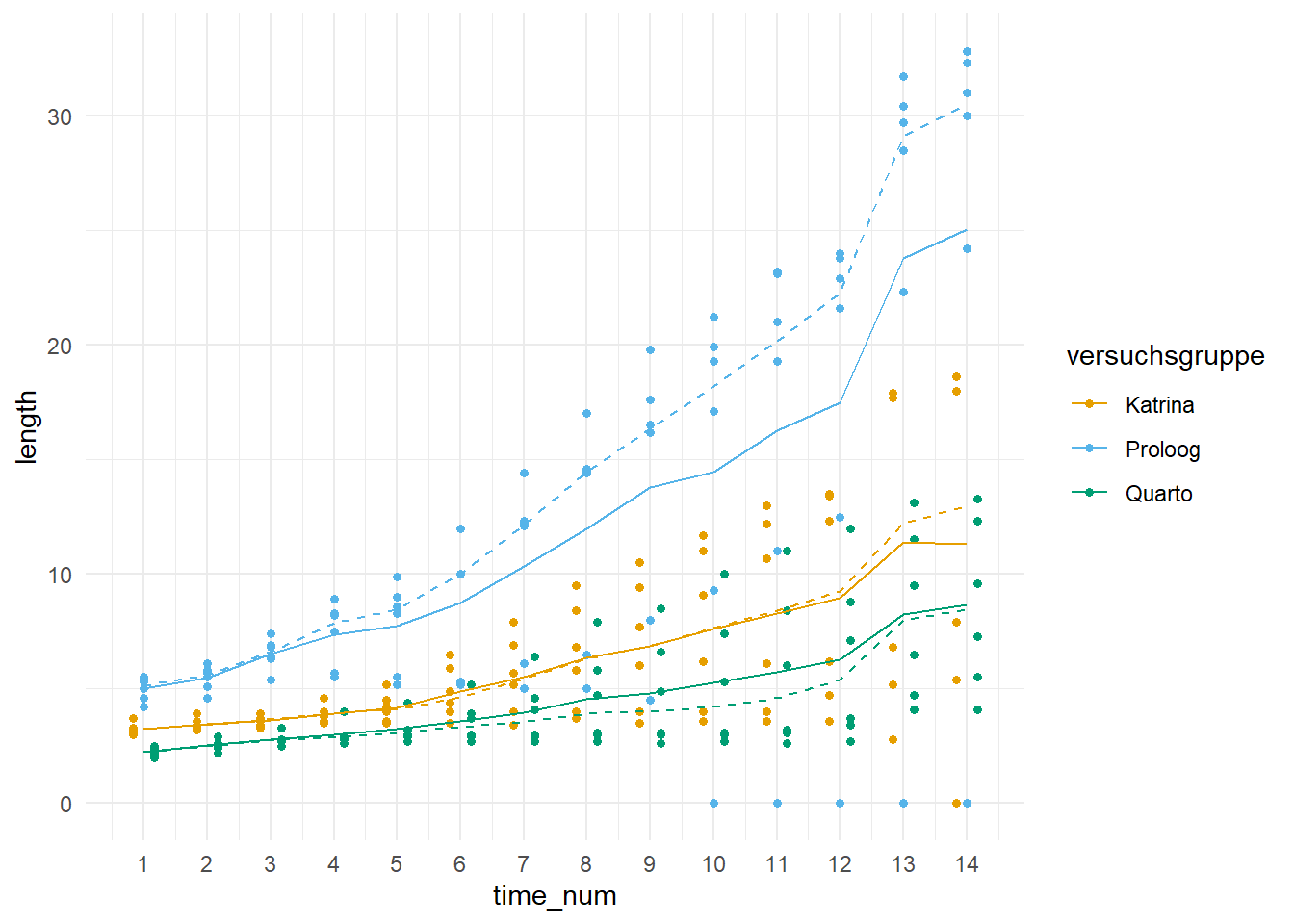
In der @fig-robust-gurke-00 sehen wir dann nochmal den Scatterplot für das Gurkenwachstum. Die gestrichtelten Linien stellen den Median und die durchgezogene Line den Mittelwert der Gruppen dar.
```{r}
#| echo: true
#| message: false
#| warning: false
#| label: fig-robust-gurke-00
#| fig-align: center
#| fig-height: 5
#| fig-width: 7
#| fig-cap: "Scatterplot des Längenwachstums der drei Gurkensorten über vierzehn Wochen. Die gestrichtelten Linien stellen den Median und die durchgezogene Line den Mittelwert der Gruppen dar."
ggplot(gurke_time_len_tbl, aes(time_num, length, color = versuchsgruppe)) +
theme_minimal() +
geom_point2(position = position_dodge(0.5)) +
stat_summary(fun = "mean", geom = "line") +
stat_summary(fun = "median", geom = "line", linetype = 2) +
scale_x_continuous(breaks = 1:14) +
scale_color_okabeito()
```
## Gewöhnliche lineare Regression
Damit wir einen Vergleich zu der robusten Regression und der Quantilsregression haben wollen wir hier zu Anfang nochmal schnell die gewöhnliche Regression (eng. *ordinary linear regression*), die du schon durch die Funktion `lm()` kennst. Wir fitten also einmal das Modell mit Interaktionsterm für den Basilikumdatensatz.
```{r}
#| message: false
#| warning: false
basi_lm_fit <- lm(weight ~ versuchsgruppe + block + versuchsgruppe:block, basi_block_tbl)
```
### ANOVA
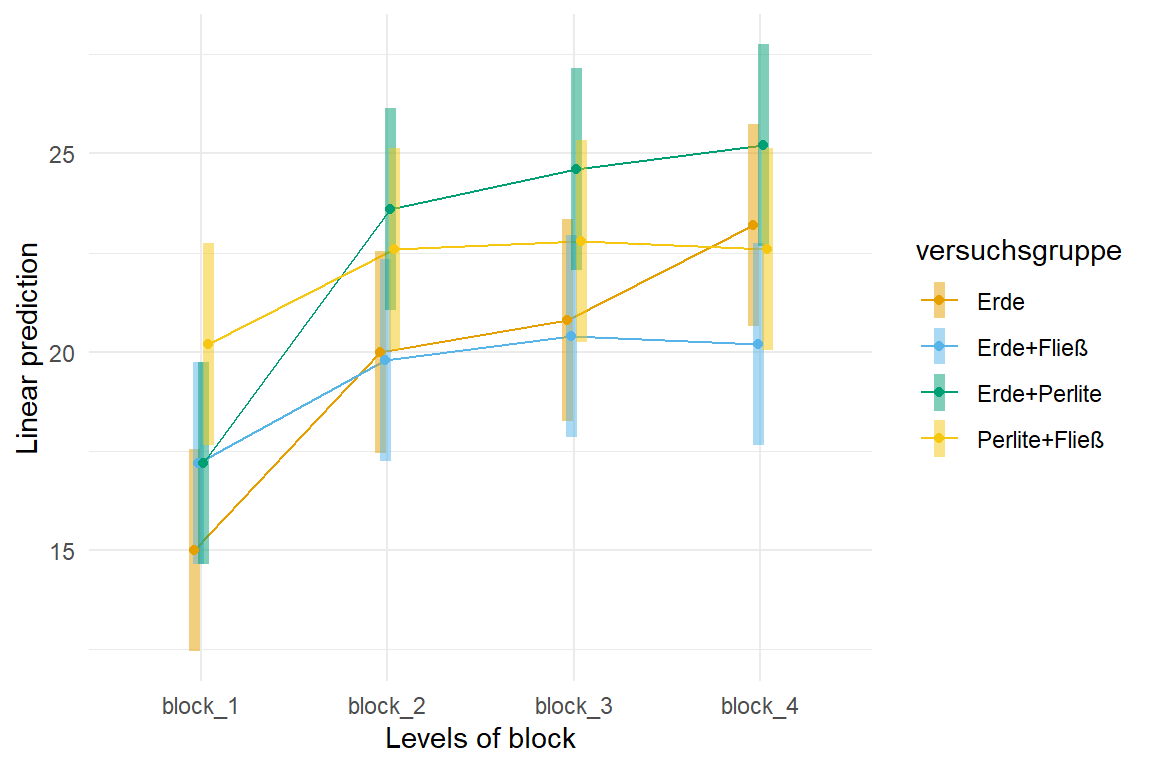
Dann schauen wir uns nochmal den Interaktionsplot in @fig-stat-robust mit der Funktion `emmip()` aus dem R Paket `{emmeans}` an. Wir sehen, das wir eventuell eine leichte Interaktion vorliegen haben könnten, da sich einige der Geraden überschneiden.
```{r}
#| message: false
#| echo: true
#| warning: false
#| fig-align: center
#| fig-height: 4
#| fig-width: 6
#| fig-cap: Interaktionsplot über die Versuchsgruppen und Blöcke.
#| label: fig-stat-robust
emmip(basi_lm_fit, versuchsgruppe ~ block, CIs = TRUE,
cov.reduce = FALSE) +
theme_minimal() +
scale_color_okabeito()
```
Schauen wir einmal in eine zweifaktorielle ANOVA, ob sich unser leichter Verdacht validieren lässt.
```{r}
#| message: false
#| warning: false
basi_lm_fit |>
anova() |>
model_parameters()
```
Wir sehen, dass wir mindestens einen paarweisen Unterschied zwischen den Versuchsgruppen und den Blöcken erwarten. Die Interaktion ist nicht signifikant. Betrachten wir noch kurz das $\eta^2$ um zu sehen, wie viel Varianz jeweils die Versuchsgruppe und Blöcke erklären.
```{r}
#| message: false
#| warning: false
basi_lm_fit |>
eta_squared()
```
Leider erklären hier die Blöcke sehr viel der Varianz, das ist nicht so schön, aber in diesem Kapitel lassen wir es dabei.
### Gruppenvergleich
Wir haben keine Interaktion vorliegen, alos mitteln wir einmal über alle Blöcke. Wenn du den Code `| block` zu dem Aufruf der `emmeans()` Funktion hinzufügst, dann hast du die Analyse für die Blöcke getrennt durchgeführt.
```{r}
#| message: false
#| warning: false
basi_lm_fit |>
emmeans(specs = ~ versuchsgruppe) |>
cld(Letters = letters, adjust = "none")
```
Wenn wir uns die unadjustierten $p$-Werte anschauen, dann sehen wir einen leichten Effekt zwischen den einzelnen Versuchsgruppen. Warum sage ich leichten Effekt? Die Mittelwerte der Gruppen in der spalte `emmean` unterscheiden sich kaum. Aber soviel zu der gewöhnlichen Regression, das war ja hier nur der Vergleich und die Erinnerung.
## Robuste Regression {#sec-robust-reg}
::: callout-note
## Nur Normalverteilung? Geht auch mehr?
Nein es geht auch mit allen anderen Modellen. So ist auch das `glm()` für die robuste Regression implementiert. Wir schauen uns aber nur die Grundlagen für die klassische robuste Regression unter der Annahme eines nromalverteilten Outcomes an.
:::
Bei einer robusten Regression werden jeder Beobachtung auf der Grundlage ihres Residuums unterschiedliche Gewichte (eng. *robustness weights*) von 0 bis 1 zugewiesen. Wir kennen ja ein Residuum als die Differenz zwischen den beobachteten und den vorhergesagten Werten der Daten. Die vorhergesagten Daten sind ja die Punkte auf der Geraden. Je kleiner also das Residuum ist, desto größer ist die Gewichtung und desto näher liegt eine Beobachtung an der geschätzten Geraden. Wir bestrafen also Punkte, die weit weg von unserer potenziellen Gerade liegen.
::: column-margin
Ein englisches Tutorium gibt es dann nochmal ausführlicher unter [R demo \| Robust Regression (don't depend on influential data!)](https://yuzar-blog.netlify.app/posts/2022-09-02-robustregression/)
Ebenso liefert auch das Tutorium [Robust regression \| R data analysis example](https://stats.oarc.ucla.edu/r/dae/robust-regression/) einen Überblick.
:::
Schauen wir uns das Problem an einem kleinen Spieldatensatz einmal an, den es so in vielen Geschmacksrichtungen gibt. Wir haben acht Beobachtungen mit jeweils einem $x$ und einem $y$ Wert in unserem Datensatz `reg_tbl`. Wie folgt einmal dargestellt.
```{r}
#| message: false
#| warning: false
reg_tbl <- tibble(x = c(0, 1, 2, 3, 4, 5, 6, 7),
y = c(1, 1.4, 2.5, 2.7, 4.3, 5.2, 0, 6.7))
```
Wir rechnen jetzt einmal eine gewöhnliche lineare Regression mit der Funktion `lm()` und eine robuste Regression mit dem Paket `{MASS}` und der Funtkion `rlm()`. Es gibt noch das R Paket `{robustbase}` und der Funktion `rq()` aber wir können die Ergebnisse dann nicht in `{emmeans}` weiter nutzen, was uns dann etwas den Weg mit versperrt. Wir können aber für die multiplen Mittelwertsvergleich mit `{robustbase}` das R Paket `{multcomp}` nutzen. Aber fangen wir hier erstmal mit dem Beispiel an und vergleichen die beiden Implementierungen der robusten Regression zu der gewöhnlichen Regression
```{r}
#| message: false
#| warning: false
reg_lm_fit <- lm(y ~ x, reg_tbl)
reg_rlm_fit <- rlm(y ~ x, reg_tbl)
reg_lmrob_fit <- lmrob(y ~ x, reg_tbl)
```
In der @fig-stat-robust-demo sehen wir einmal den Unterschied zwischen den beiden robusten Regressionen und der gewöhnlichen Regression.
```{r}
#| message: false
#| echo: true
#| warning: false
#| fig-align: center
#| fig-height: 4
#| fig-width: 5
#| fig-cap: "Scatterplot für den Unterschied zwischen einer robusten und gewöhnlichen Regression. Die gewöhnliche Regression ist gelb, die robuste Regression MASS::rlm() grün und die robuste Regression robustbase::lmrob() blau."
#| label: fig-stat-robust-demo
ggplot(reg_tbl, aes(x, y, label = x)) +
theme_minimal() +
geom_label() +
geom_line(aes(y = predict(reg_lm_fit), colour = "lm")) +
geom_line(aes(y = predict(reg_rlm_fit), colour = "rlm")) +
geom_line(aes(y = predict(reg_lmrob_fit), colour = "lmrob")) +
scale_colour_okabeito() +
labs(colour = "Method")
```
In unserem Beispiel ist die sechste Beobachtung der Ausreißer. Die `lm`-Regression wird durch den Wert 0 der sechsten Beobachtung nach unten gezogen. Die sechste Beobachtung erhält ein viel zu starkes Gewicht in der gewöhnlichen Regression im Bezug auf den Verlauf der Geraden. Die robusten Regressionen geben der sechsten Beobachtung hingegen ein viel geringeres Gewicht, so dass die Beobachtung keinen Einfluss auf den Verlauf der Geraden hat. In einer robusten Regression erhält eine Beobachtung mit einem großen Residuum sehr wenig Gewicht, in diesem konstruierten Beispiel fast 0. Daher können wir sagen, das unser Modell *robust* gegen Ausreißer ist.
Okay, soweit lernt es jeder und die Idee der robusten Regression ist auch ziemlich einleuchtend. Aber in der Wissenschaft zeichnen wir keine Gerade durch Punkte und freuen uns drüber, dass die eine gerade besser passt als die andere Gerade. Wir nutzen dann ja das Modell weiter in eine ANOVA oder aber eben in einem paarweisen Gruppenvergleich. Und hier fangen dann die Probleme der *Implementierung* an. Leider ist es so, dass nicht alle Funktionalitäten implementiert sind. Das heißt, die Funktion `anova()` oder `emmeans()` kann mit der Ausgabe der robusten Regressionen mit `MASS::rlm()` und `robustbase::lmrob()` nichts anfangen. Das ist problematisch und nicht anwenderfreundlich. Und wir sind hier nunmal Anwender...
Warum so unbeliebt? Das ist eine gute Frage. Zu der robusten Regression gibt es eine lange Geschichte mit vielen Wirrungen und Irrungen. Am Ende kannst du in Wikipedia noch etwas zur [History and unpopularity of robust regression](https://en.wikipedia.org/wiki/Robust_regression#History_and_unpopularity_of_robust_regression) nachlesen. Nach @stromberg2004write hat es auch etwas mit der schlechten und mangelhaften Implementierung in gängiger Statistiksoftware zu tun. Das merke ich hier auch gerade, als ich versuche die Funktionen zusammen zubauen und miteinander zu vernetzen. Sicherlich gibt es auch die biologische Diskussion. Gibt es in biologischen Daten eigentlich überhaupt Ausreißer? Oder müssten wir nicht Ausreißer besonders betrachten, weil die Ausreißer dann doch mehr über die Daten verraten? Macht es also Sinn die Ausreißer einfach platt zu bügeln und nicht mehr weiter zu beachten oder ist nicht die Beobachtung Nr.6 oben von Interesse? Denn vielleicht ist was mit dem Experiment schief gelaufen und diese Beobachtung ist gerade ein Anzeichen dafür. Dann müssten auch die anderen Messwerte kritisch hinterfragt werden.
Wie immer es auch sein. Wir fitten jetzt mal die beiden robusten Regression in der Standardausstattung mit der Funktion `MASS::rlm()` aus dem Paket `{MASS}` wie folgt.
```{r}
#| message: false
#| warning: false
basi_rlm_fit <- rlm(weight ~ versuchsgruppe + block + versuchsgruppe:block, basi_block_tbl)
```
Dann natürlich noch die Funktion `robustbase::lmrob()` aus dem Paket `{robustbase}`. Hinter dem Paket `{robusbase}` steht ein ganzen Buch von @maronna2019robust, aber leider keine gute Internetseite mit Beispielen und Anwendungen in R, wie es eigentlich heutzutage üblich ist. Aber dennoch, hier einmal das Modell.
```{r}
#| message: false
#| warning: false
basi_lmrob_fit <- lmrob(weight ~ versuchsgruppe + block + versuchsgruppe:block, basi_block_tbl)
```
### ANOVA
Dann wollen wir einmal eine zweifaktorielle ANOVA auf den Modell der robusten Regression mit der Funktion `MASS::rlm()` rechnen. Leider kann ich schon gleich sagen, dass wir hier ein Problem kriegen. Es ist nicht ganz klar unter Theoretikern welche Anzahl an Beobachtungen für die Residuen in der robusten Regression genutzt werden soll. Welche Beobachtungen werden den im Modell berücksichtigt und welche nicht? Daher ist dann der Wert für die Freiheitsgrade $df$ leer und wir erhalten keine $F$-Statistik und dann auch keine $p$-Werte. Für mich super unbefriedigend, so kann man dann auch keine Funktionen richtig nutzen. Die Funktion `robustbase::lmrob()` bietet die ANOVA nicht an.
```{r}
#| message: false
#| warning: false
basi_rlm_aov <- basi_rlm_fit |>
anova() |>
tidy()
basi_rlm_aov
```
Was als Freiheitsgrad für die Residuen nehmen? In unserem Datensatz haben wir `r nrow(basi_block_tbl)` Basilikumpflanzen und somit auch Beobachtungen vorliegen. Wir setzen jetzt einfach brutal die Freiheitsgrade `df` für die Residuen auf 80 und können dann die Mean Squares für die Residuen berechnen. Also einmal flott die `meansq` für die Residuen durch die Anzahl an Beobachtungen geteilt.
```{r}
ms_resid <- 527 / 80
```
Mit den Mean Square der Residuen können wir dann auch die $F$-Werte berechnen. Den rechnerischen Weg kennen wir ja schon aus der zweifaktoriellen ANOVA.
```{r}
f_calc <- basi_rlm_aov$meansq / ms_resid
```
Wie kriegen wir jetzt aus den ganzen berechneten $F$-Werten die entsprechenden $p$-Werte? Die $p$-Werte sind die Fläche rechts von den berechneten Werten. Wir können die Funktion `pf()` nutzen um diese Flächen zu berechnen. Wir machen das einmal beispielhaft für einen $F_{calc} = 3.41$ für 4 Gruppen mit $df_1 = 4 - 1 = 3$ und 12 Beobachtungen $df_2 = 12$. Die Berechnung von $df_2$ ist statistisch *falsch* aber für unseren MacGyver Hack hinreichend.
```{r}
pf(3.41, 3, 12, lower.tail = FALSE) |> round(3)
```
Und siehe da, wir erhalten einen $p$-Wert von $0.053$. Nun können wir das nicht nur für einzelnen $F$-Werte machen sondern auch für unseren ganzen Vektor `f_calc`. Als $df_2$ setzen wir die Anzahl an Basilikumpflanzen.
```{r}
p_vec <- pf(f_calc, c(3, 3, 9), c(80, 80, 80), lower.tail = FALSE) |>
scales::pvalue()
```
Die berechneten $F$-Werte und $p$-Werte können wir jetzt in die ANOVA Tabelle ergänzen.
```{r}
basi_rlm_aov |>
mutate(statistic = f_calc,
p.value = p_vec)
```
Das war jetzt ein ganz schöner Angang und den $p$-Werten ist nur approximativ zu trauen, aber wenn wir weit vom Signifikanzniveau $\alpha$ gleich 5% sind, dann macht eine numerische Ungenauigkeit auch nicht viel aus. Achtung deshalb bei $p$-Werten nahe des Signifikanzniveau $\alpha$, hier ist dann die Aussage mit Vorsicht zu treffen oder eher nicht möglich.
Glücklicherweise können wir aus den Sum of squares dann unsere $\eta^2$-Werte für die erklärte Varianz unserer ANOVA berechnen. Das ist dann doch schon mal was. Wir sehen, dass die Blöcke am meisten der Varianz erklären und die Versuchsgruppen sehr wenig. Das ist für das Modell dann nicht so schön, deckt sich aber mit den Ergebnissen gewöhnlichen Regression. Wir erhalten eine Konfidenzintervalle, woran du schon erkennen kannst, dass in der Ausgabe der ANOVA der robusten Regression was fehlt.
```{r}
#| message: false
#| warning: false
basi_rlm_fit |>
eta_squared()
```
Nochmal als Erinnerung, mit der Funktion `robustbase::lmrob()` ist die ANOVA nicht möglich. Die Funktionalität ist nicht implementiert.
### Gruppenvergleich
Dafür geht der Gruppenvergleich für die robuste Regression mit `MASS::rlm()` wie von alleine. Wir haben keine Interaktion vorliegen, daher müssen wir auch nicht den Block berücksichtigen. Das wir in Block 1 ein Problem haben, steht dann aber auf einem anderen Blatt. Da aber *alle* Basilikumpflanzen immer im Block 1 kleiner sind, passt es dann wieder im Sinne keiner Interaktion. Mit Interaktion hätten wir sonst `versuchsgruppe | block` statt nur `versuchsgruppe` hinter die Tilde geschrieben. Dann wollen wir noch das *compact letter disply* und alles ist wie es sein sollte.
```{r}
#| message: false
#| warning: false
basi_rlm_fit |>
emmeans(specs = ~ versuchsgruppe) |>
cld(Letters = letters, adjust = "none")
```
Wir sehen also, dass sich Erde+Fließ und Erde nicht unterscheiden. Die beiden aber dann von Perlite+Fließ sowie Erde+Perlite. Am Ende unterscheiden sich Perlite+Fließ und Erde+Perlite nicht.
Für die Funktion `robustbase::lmrob()` müssen wir dann auf das R Paket `{multcomp}` umswitchen. Hier kriegen wir dann ein Problem, wenn wir eine Interaktion vorliegen ahben, da ist `{multcomp}` nicht so schön anzuwenden, wie dann `{emmeans}`. Aber hier schauen wir uns dann mal die einfache Implementierung ohne Interaktion an. Bei einer Interaktion müssten wir dann händisch über die Funktion `filter()` die Analysen für die einzelnen Blöcke aufspalten.
Wir lassen jetzt aber erstmal auf dem Modell aus der Funktion `robustbase::lmrob()` den paarweisen Vergleich nach Tukey laufen.
```{r}
#| message: false
#| warning: false
mult_lmrob <- glht(basi_lmrob_fit, linfct = mcp(versuchsgruppe = "Tukey"))
```
Das erhaltende Objekt können wir dann mit `tidy()` aufräumen und uns dann die gewünschten Spalten wiedergeben lassen.
```{r}
#| message: false
#| warning: false
mult_lmrob_tbl <- mult_lmrob |>
tidy(conf.int = TRUE) |>
select(contrast, estimate, conf.low, conf.high, adj.p.value)
mult_lmrob_tbl
```
Wir sehen, dass wir mit der Adjustierung keinen signifikanten Unterschied zwischen den Bodensorten finden. Im Folgenden dann noch die Darstellung im *compact letter display*, wo wir etwas rumfrickeln müssen damit die Funktion `multcompLetters()` auch die Kontraste aus der Funktion `glht()` akzeptiert. Aber das haben wir dann alles zusammen.
```{r}
#| message: false
#| warning: false
mult_lmrob_tbl |>
mutate(contrast = str_replace_all(contrast, "\\s", "")) |>
pull(adj.p.value, contrast) |>
multcompLetters() |>
pluck("Letters")
```
Auch hier sehen wir keinen Unterschied im *compact letter display* für die adjustierten $p$-Werte. Für die unadjustierten rohen $p$-Werte nutzen wir dann den Umweg über die `summary()` Funktion. Die unadjustierten $p$-Werte können wir dann auch in das *compact letter display* umwandeln lassen.
```{r}
#| message: false
#| warning: false
summary(mult_lmrob, test = adjusted("none")) |>
tidy() |>
mutate(contrast = str_replace_all(contrast, "\\s", "")) |>
pull(p.value, contrast) |>
multcompLetters() |>
pluck("Letters")
```
Und wenn man eine andere Funktion nutzt, dann kommen auch leicht andere Ergebnisse raus. Bei den rohen $p$-Werten haben wir jetzt etwas andere Unterschiede. Aber das liegt auch an den sehr ähnlichen Mittelwerten. So groß sind die Unterschiede nicht, so dass wir hier natürlich durch unterschiedliche Algorithmen leicht andere Ergebnisse kriegen. Wieder ein Grund die $p$-Werte zu adjustieren um dann auch konsistente Ergebnisse zu haben.
## Quantilsregression {#sec-quantile-reg}
Jetzt wollen wir uns als Spezialfall der robusten Regression einmal die Quantilesregression anschauen. Wir der Name schon sagt, optimiert die Quantilregression nicht über den Mittelwert und die Standardabweichung als quadratische Abweichungen sondern über den Median und die absoluten Abweichungen. Wir haben es also hier mit einer Alternativen zu der gewöhnlichen Regression zu tun. Das schöne an der Quantilesregression ist, dass der Median nicht so anfällig gegenüber Ausreißern ist. Hier haben wir einen Vorteil. Wir können theoretisch auch andere Quantile als Referenzwert nehmen und die absoluten Abstände berechnen. Wenn wir aber später dann mit `emmeans` die Gruppenvergleiche rechnen wollen, geht das nur über den Median.
::: column-margin
Ein englisches Tutorium gibt es dann nochmal ausführlicher unter [Quantile Regression as an useful Alternative for Ordinary Linear Regression](https://yuzar-blog.netlify.app/posts/2022-12-01-quantileregression/)
:::
Um die Quantilesregression zu rechnen nutzen wir das R Paket `{quantreg}` und die Funktion `rq()`. Wichtig ist hier, dass wir das `tau` auf $0.5$ setzen und somit dann eine Median-Regression rechnen. Wir können theoretisch auch andere Quantile als Referenz wählen, aber dann passt es nicht mehr mit `emmeans()`. Wir nutzen hier auch nochmal die Gelegenheit zwei Modelle mit anzupassen. Wir rechnen einmal ein Modell mit einer linearen Komponente der Zeit `time_num` und einmal ein Modell mit der quadratischen Komponente der Zeit mit `poly(time_num, 2)` was nicht anderes als `time_num`$^2$ ist. Neben dieser Variante ist mit `nlrq()` auch eine Möglichkeit implementiert um noch komplexere nicht lineare Zusammenhänge zu modellieren. Hier dann einfach mal die Hilfeseite von `?nlrq` anschauen.
```{r}
#| message: false
#| warning: false
time_rq_lin_fit <- rq(length ~ versuchsgruppe + time_num + versuchsgruppe:time_num, tau = 0.5,
gurke_time_len_tbl)
time_rq_quad_fit <- rq(length ~ versuchsgruppe * poly(time_num, 2), tau = 0.5,
gurke_time_len_tbl)
```
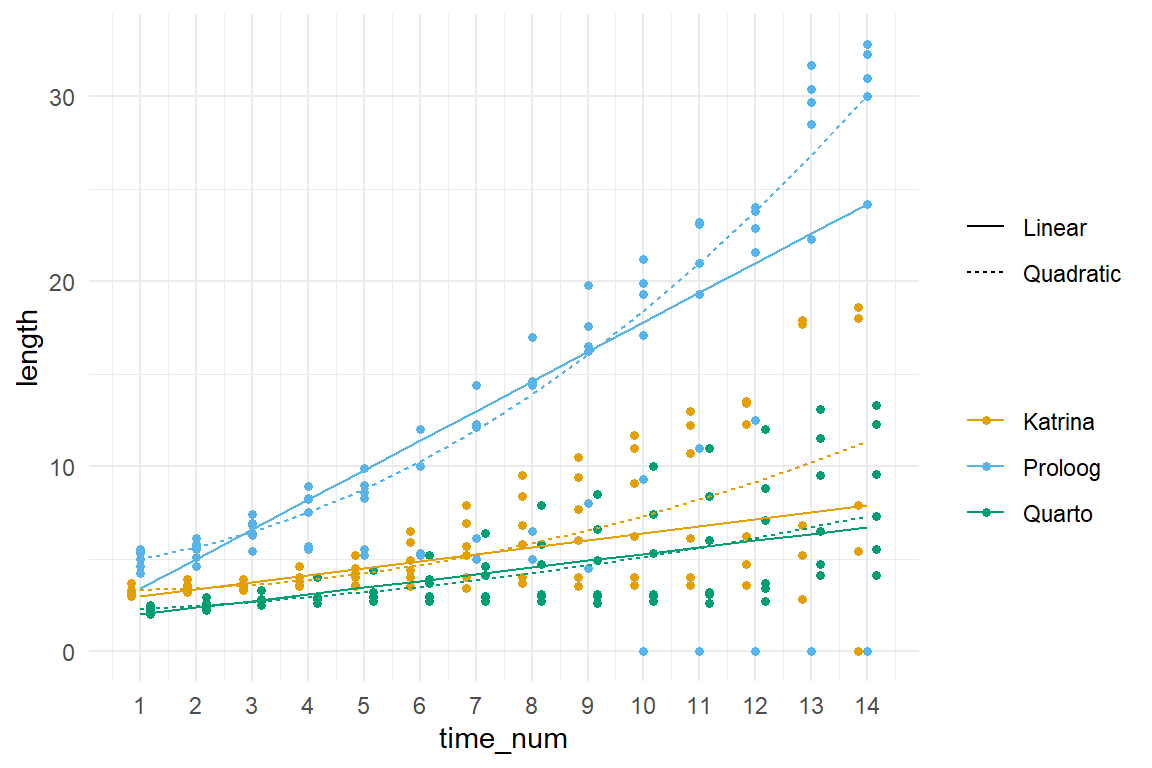
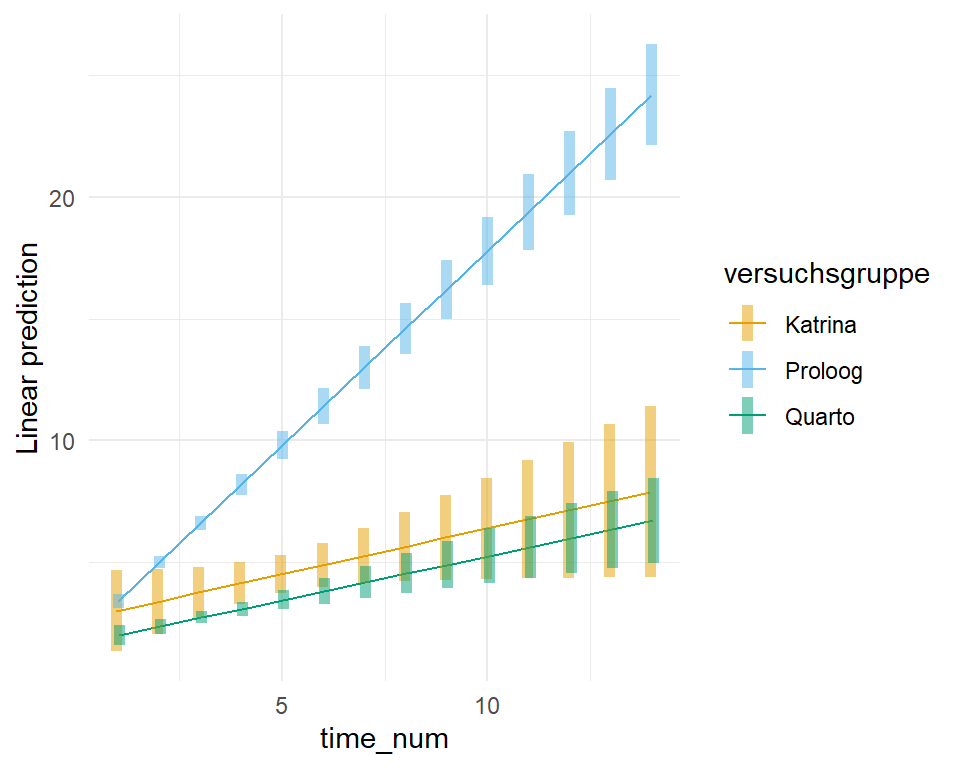
In der @fig-robust-gurke-01 plotten wir einmal die Modelle aus der linearen und der quadratischen Anpassung des zeitlichen Verlaufs in die Abbildung. Wir sehen, dass das Modell mit der quadratischen Anpassung besser zu den Daten passt. Daher nutzen wir jetzt im weiteren das Modell `time_rq_quad_fit`.
```{r}
#| echo: true
#| message: false
#| warning: false
#| label: fig-robust-gurke-01
#| fig-align: center
#| fig-height: 4
#| fig-width: 6
#| fig-cap: "Scatterplot des Längenwachstums der drei Gurkensorten über vierzehn Wochen. Die gestrichtelten Linien stellen den Median und die durchgezogene Line den Mittelwert der Gruppen dar."
ggplot(gurke_time_len_tbl, aes(time_num, length, color = versuchsgruppe)) +
theme_minimal() +
geom_point2(position = position_dodge(0.5)) +
scale_color_okabeito() +
geom_line(aes(y = predict(time_rq_quad_fit), linetype = "Quadratic")) +
geom_line(aes(y = predict(time_rq_lin_fit), linetype = "Linear")) +
scale_x_continuous(breaks = 1:14) +
labs(linetype = "", color = "")
```
### ANOVA
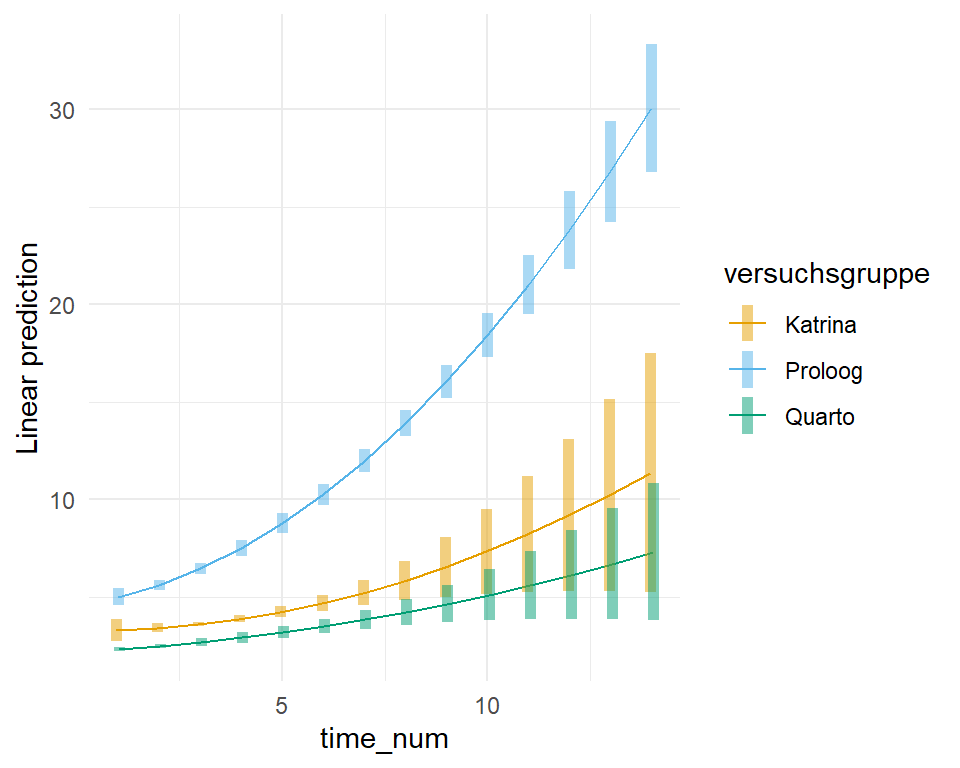
Machen wir es kurz. Die ANOVA ist für die Quantilsregression nicht implementiert und damit auch nicht anwendbar. Damit können wir aber leben, wenn wir die ANOVA nur als Vortest ansehen. Wir müssen dann eine mögliche Interaktion visuell überprüfen. Um die Interaktion visuell zu überprüfen nutzen wir die Funktion `emimp()` aus dem R Paket `{emmeans}`. Wir sehen in der @fig-rob-inter-time, dass sich die Gerade für die Versuchsgruppen über die Zeit nicht schneiden, was gegen eine starke Interaktion spricht. Die Steigung ist aber für alle drei Versuchsgruppen über die Zeit nicht gleich, wir haben zumindest eine mittlere Interaktion.
```{r}
#| message: false
#| echo: true
#| warning: false
#| fig-align: center
#| fig-height: 4
#| fig-width: 5
#| label: fig-rob-inter-time
#| fig-cap: "Interaktionsplot über den zeitlichen Verlauf für alle drei Sorten für die Quantilesregression."
#| fig-subcap:
#| - "Linear"
#| - "Quadratic"
#| layout-nrow: 1
emmip(time_rq_lin_fit, versuchsgruppe ~ time_num, CIs = TRUE,
cov.reduce = FALSE) +
theme_minimal() +
scale_color_okabeito()
emmip(time_rq_quad_fit, versuchsgruppe ~ time_num, CIs = TRUE,
cov.reduce = FALSE) +
theme_minimal() +
scale_color_okabeito()
```
Wir würden also in unseren Gruppenvergleich der Mediane auf jeden Fall die Interaktion mit rein nehmen und die `emmeans()` Funktion entsprechend mit dem `|` anpassen.
### Gruppenvergleich
Wenn wir den Gruppenvergleich in `emmeans()` rechnen wollen, dann geht es nur dem Spezialfall der Median-Regression. Wir müssen also zwangsweise in der Quantilesregression `rq()` das `tau = 0.5` setzen um dann eine Median-Regression zu rechnen. Sonst können wir nicht `emmeans` nutzen.
```{r}
#| message: false
#| warning: false
time_rq_quad_fit |>
emmeans(~ versuchsgruppe | time_num,
adjust = "none", at = list(time_num = c(1, 7, 14))) |>
cld(Letters = letters, adjust = "none")
```
Das sieht ja schon mal ganz gut aus. Interessant ist, dass wir an dann in der vierzehnten Woche dann keinen signifikanten Unterschied mehr vorliegen zwischen Quarto und Katrina vorliegen haben. Das liegt dann aber alleinig an dem hohen Standardfehler `SE` der Sorte Katrina mit $3.1$ gegenüber den anderen Sorten. Vermutlich sehe das Ergebnis leicht anders aus, wenn wir die unsinnigen Gurken mit einer Länge von 0 cm wirklich aus den Dten entfernen würden und nicht zu Demonstrationszwecken wie hier drin lassen würden.
Aber Achtung, die Spalte `emmean` beschriebt hier die Mediane. Wir haben also hier die Mediane des Längenwachstums für die Gurken vorliegen. Wenn wir die paarweisen Vergleich rechnen wollen würden dann können wir noch `pairwise ~ versuchsgruppe` statt `~ versuchsgruppe` schreiben. Auch liefert die Funktion `pwpm()` die Medianunterschiede wie wir im Folgenden einmal sehen. Ich habe hier mal das `at` entfernt und da die Zeit numrisch ist, haben wir dann auch nur noch eine Tabelle. Die `Diagonal: [Estimates] (emmean)` sind die Mediane des Längenwachstums.
```{r}
#| message: false
#| warning: false
time_rq_quad_fit |>
emmeans(~ versuchsgruppe | time_num, adjust = "none") |>
pwpm()
```
## Modellvergleich
Im Folgenden wollen wir einmal verschiedene Modelle miteinander vergleichen und schauen, welches Modell hier das beste ist. Das machen wir dann einmal für die Basilikumdaten sowie die Wachstumsdaten für die Gurken.
### Basilikumdaten
Für den Modellvergleich der gewöhnlichen, robusten und medianen Regression nutzen wir nochmal den Datensatz für das Basilikumwachstum. In einem ersten Schritt fitten wir wieder alle Modelle und achten darauf, dass wir bei der Quantilesregression angeben welches Quantile wir wollen. Wir wählen mit `tau = 0.5` dann den Median und rechnen so eine Medianregression.
```{r}
#| message: false
#| warning: false
basi_lm_fit <- lm(weight ~ versuchsgruppe + block + versuchsgruppe:block, basi_block_tbl)
basi_rlm_fit <- rlm(weight ~ versuchsgruppe + block + versuchsgruppe:block, basi_block_tbl)
basi_lmrob_fit <- lmrob(weight ~ versuchsgruppe + block + versuchsgruppe:block, basi_block_tbl)
basi_rq_fit <- rq(weight ~ versuchsgruppe + block + versuchsgruppe:block, basi_block_tbl,
tau = 0.5)
```
Im Folgenden nutzen wir dann das fantastische Paket `{modelsummary}` mit der gleichnamigen Funktion um uns einmal die Modelle im Vergleich anzuschauen. Hier hilft dann wie immer die tolle [Hilfsseite von `{modelsummary}`](https://vincentarelbundock.github.io/modelsummary/articles/modelsummary.html) zu besuchen. Ich möchte nur nicht den Intercept und die Schätzer für die Blöcke haben, deshalb fliegen die hier einmal raus.
```{r}
modelsummary(lst("Ordinary" = basi_lm_fit,
"MASS::rlm" = basi_rlm_fit,
"robustbase::lmrob" = basi_lmrob_fit,
"Quantile" = basi_rq_fit),
estimate = "{estimate}",
statistic = c("conf.int",
"s.e. = {std.error}",
"t = {statistic}",
"p = {p.value}"),
coef_omit = "Intercept|block")
```
Wie wir sehen sehen haben nicht alle Modelle die gleichen Informationen zurück gegeben. Insbesondere das fehlen des Bestimmtheitsmaßes $R^2$ bei der robusten Regression `MASS::rlm` ist schmerzlich, da wir hier dann nicht die Möglichkeit haben eine Aussage über die erklärte Varianz der robusten Regression zu treffen. Auch fehlt bei der Medianregression das adjustierte $R^2$, was die Nutzung bei Modellen mit mehr als einer Einflussvariable $x$ im Modell erschwert bis nutzlos macht. Da ist dann die Funktion aus dem Paket `{robustbase}` besser, hier haben wir dann ein $R^2$ vorliegen. Daher bleibt uns am Ende nur das AIC oder BIC, wobei wir dort den kleinsten Wert als besser erachten. Die AIC und BIC Werte sind somit am besten für die Quantilesregression. Für die Funktion `robustbase::lmrob` haben wir dann kein AIC. Dafür ist dann aber der Fehler RMSE bei der gewöhnlichen Regressionzusammen mit der Funktion `robustbase::lmrob` am niedrigsten. Und so stehe ich wieder davor und weiß nicht was das beste Modell ist. Hier müsste ich dann nochmal überlegen, ob ich lieber über Mittelwerte oder Mediane berichten möchte und das ist ohne die Forschungsfrage nicht hier zu lösen.
### Gurkendaten
Für den Modellvergleich der gewöhnlichen, robusten und medianen Regression nutzen wir nochmal den Datensatz für das Längenwachstum der Gurken. In einem ersten Schritt fitten wir wieder alle Modelle und achten darauf, dass wir bei der Quantilesregression angeben welches Quantile wir wollen. Wir wählen mit `tau = 0.5` dann den Median und rechnen so eine Median-Regression. Darüber hinaus schauen wir uns nochmal die quadratische Anpassung der Zeit in dem letzten Modell an. Mal schauen, ob das Modell dann auch bei den Kennzahlen das beste Modell ist. Visuell sah das quadratische Modell des zeitlichen Verlaufs schon mal sehr gut aus.
```{r}
#| message: false
#| warning: false
time_lm_fit <- lm(length ~ versuchsgruppe + time_num + versuchsgruppe:time_num, gurke_time_len_tbl)
time_rlm_fit <- rlm(length ~ versuchsgruppe + time_num + versuchsgruppe:time_num, gurke_time_len_tbl)
time_rq_lin_fit <- rq(length ~ versuchsgruppe + time_num + versuchsgruppe:time_num, tau = 0.5,
gurke_time_len_tbl)
time_rq_quad_fit <- rq(length ~ versuchsgruppe * poly(time_num, 2), tau = 0.5,
gurke_time_len_tbl)
```
Auch hier nutzen wir dann das fantastische Paket `{modelsummary}` mit der gleichnamigen Funktion um uns einmal die Modelle im Vergleich anzuschauen.
```{r}
modelsummary(lst("Ordinary" = time_lm_fit,
"Robust" = time_rlm_fit,
"Quantile linear" = time_rq_lin_fit,
"Quantile quadratic" = time_rq_quad_fit),
estimate = "{estimate}",
statistic = c("conf.int",
"s.e. = {std.error}",
"t = {statistic}",
"p = {p.value}"),
coef_omit = "Intercept|time_num")
```
Hier sieht es ähnlich aus wie bei den Modellvergleichen von den Basilikumdaten. Nur hier wissen wir, dass wir Ausreißer in der Form von Gurken mit einer Länge von 0 cm in den Daten haben. Daher sehen wir auch, dass die robuste Regression und die Median-Regression ein niedrigeres AIC und BIC haben. Für mich interessant ist, dass der Fehler RMSE wieder am kleinsten bei der gewöhnlichen Regression ist, das mag aber auch an der Berechnung liegen. Da wir Ausreißer haben, sind natürlich dann auch die robuste Regression und die Median-Regression vorzuziehen. Da die Median-Regression den kleineren AIC Wert hat, nehmen wir dann die Median-Regression als die beste Regression an. Der RMSE ist am kleinsten für die quadratische Anpassung des zeitlichen Verlaufs. Deshalb wäre dann das vierte Modell mit dem niedrigsten AIC und dem niedrigsten RMSE das Modell der Wahl.
Ich wiederhole mich hier wirklich, aber vermutlich wäre es schlauer zuerst die Daten zu bereinigen und die Gurken mit einem Wachstum von 0 cm zu entfernen. Auch die anderen Wachstumskurven von anderen Gurken sind etwas wirr. Da müsste man auch nochmal ran und schauen, ob nicht die Gurken lieber aus der Analyse raus müssen. Am Ende ist dann natürlich die Frage, ob man die Daten dann nicht doch lieber über ein gemischtes Modell auswertet, da natürlich die Zeitpunkte voneinander abhängig sind, wenn wir immer die glecihen Gurken messen und nicht ernten. Aber wie immer im Leben, alles geht nicht.
## Referenzen {.unnumbered}