55  Marginal effect models

Letzte Änderung am 18. October 2025 um 10:06:10

“Life is difficult.” — Morgan Scott Peck, The Road Less Traveled

VorsichtStand des Kapitels: Konstruktion (seit 07.2025)

Dieses Kapitel wird in den nächsten Wochen geschrieben und ist damit meine aktuelle Großbaustelle. Ich plane zum Beginn des SoSe 2026 eine fertige Version des Kapitels erstellt zu haben. Während das Kapitel entsteht, funktioniert so manches dann nicht so wie es soll. Bitte daher hier dann abwarten.

Lange habe ich gebraucht um mich dazu durchzuringen das Kapitel zu den Marginal effect models (deu. marginale Effektmodelle, ungebräuchlich) zu schreiben.¹ Ich werde hier bei dem englischen Begriff bleiben, den deutschen Begriff habe ich eher selten gehört und daher sind es für mich Marginal effect models. Insbesondere da der Begriff “marginal” auch sehr an gering oder minderwertig erinnert. Damit haben aber die Marginal effect models nicht im geringsten zu tun. Die Modelle sind sehr mächtig und können uns helfen wichtige Fragen an unsere Daten zu beantworten. Insbesondere die Dualität der beiden Pakete {emmeans} für experimentelle Daten und {marginaleffects} für beobachtete Daten ist spannend und möchte ich hier nochmal genauer betrachten. Neben diesen beiden Ecksteinen gibt es noch andere Pakete und ich werde auch hier einmal in die Pakete reinschauen.

Anfangen kann ich aber nicht ohne Heiss (2022) mit seinem Blogpost Marginalia: A guide to figuring out what the heck marginal effects, marginal slopes, average marginal effects, marginal effects at the mean, and all these other marginal things are zu erwähnen. Vieles entlehnt sich direkt oder indirekt an seine Ausführungen. Wie immer habe ich etwas angepasst, wenn ich der Meinung war, dass es noch besser zu verstehen ist. Teilweise entfalten die Marginal effect models ihre wahre Kraft erst bei den nicht linearen Zusammenhängen und der Interpretation von Generalized Additive Models und somit der nicht linearen Regression. Fangen wir also an Marginal effect models zu zerforschen und arbeiten uns dann voran.. Beginnen wollen wir aber mit einem allgemeinen Hintergrund bevor wir uns dann nochmal tiefer mit den Marginal effect models beschäftigen.

Sprachlicher Hintergrund

“In statistics courses taught by statisticians we don’t use independent variable because we use independent on to mean stochastic independence. Instead we say predictor or covariate (either). And, similarly, we don’t say”dependent variable” either. We say response.” — User berf auf r/AskStatistics

Wenn wir uns mit dem statistischen Modellieren beschäftigen wollen, dann brauchen wir auch Worte um über das Thema reden zu können. Statistik wird in vielen Bereichen der Wissenschaft verwendet und in jedem Bereich nennen wir dann auch Dinge anders, die eigentlich gleich sind. Daher werde ich mir es hier herausnehmen und auch die Dinge so benennen, wie ich sie für didaktisch sinnvoll finde. Wir wollen hier was verstehen und lernen, somit brauchen wir auch eine klare Sprache.

“Jeder nennt in der Statistik sein Y und X wie er möchte. Da ich hier nicht nur von Y und X schreiben will, führe ich eben die Worte ein, die ich nutzen will. Damit sind die Worte dann auch richtig, da der Kontext definiert ist. Andere mögen es dann anders machen. Ich mache es eben dann so. Danke.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

In dem folgenden Kasten erkläre ich nochmal den Gebrauch meiner Begriffe im statistischen Testen. Es ist wichtig, dass wir hier uns klar verstehen. Zum einen ist es angenehmer auch mal ein Wort für ein Symbol zu schreiben. Auf der anderen Seite möchte ich aber auch, dass du dann das Wort richtig einem Konzept im statistischen Modellieren zuordnen kannst. Deshalb einmal hier meine persönliche und didaktische Zusammenstellung meiner Wort im statistischen Modellieren. Du kannst dann immer zu dem Kasten zurückgehen, wenn wir mal ein Wort nicht mehr ganz klar ist. Die fetten Begriffe sind die üblichen in den folgenden Kapiteln. Die anderen Worte werden immer mal wieder in der Literatur genutzt.

WichtigWorte und Bedeutungen im statistischen Modellieren

“Die Grenzen meiner Sprache bedeuten die Grenzen meiner Welt.” — Ludwig Wittgenstein

Hier kommt einmal die Tabelle mit den wichtigsten Begriffen im statistischen Modellieren und wie ich die Worte benutzen werde. Damit wir uns verstehen und du was lernen kannst. In anderen Büchern und Quellen findest du teilweise die Worte in einem anderen Sinnzusammenhang. Das ist gut so dort. Bei mir ist es anders.

Tabelle 55.1— Zusammenfassende Tabelle des Sprachgebrauchs in meinem statistischen Modellieren. Die fett hervorgehobenen Bezeichnungen werden hier genutzt. (LHS = left hand side, RHS = right hand side)

	Symbol	Deutsch	Englisch
LHS	\(Y\) / \(y\)	Messwert / Endpunkt / Outcome / Abhängige Variable	response / outcome / endpoint / dependent variable
RHS	\(X\) / \(x\)	Einflussvariable / Erklärende Variable / Fester Effekt / Unabhängige Variable	risk factor / explanatory / fixed effect / independent variable
RHS	\(Z\) / \(z\)	Zufälliger Effekt	random effect
\(X\) ist kontinuierlich	\(c_1\)	Kovariate 1	covariate 1
\(X\) ist kategorial	\(f_A\)	Faktor \(A\) mit Level \(A.1\) bis \(A.j\)	factor \(A\) with levels \(A.1\) to \(A.j\)

Am Ende möchte ich nochmal darauf hinweisen, dass wirklich häufig von der abhängigen Variable (eng. dependent variable) als Messwert und unabhängigen Variablen (eng. independent variable) für die Einflussvariablen gesprochen wird. Aus meiner Erfahrung bringt die Begriffe jeder ununterbrochen durcheinander. Deshalb einfach nicht diese Worte nutzen.

Abbildung 55.1— Am Ende läuft es dann doch auf sowas raus…

55.1 Allgemeiner Hintergrund

“Statistics is all about lines, and lines have slopes, or derivatives. These slopes represent the marginal changes in an outcome. As you move an independent/explanatory variable, what happens to the dependent/outcome variable?” — Heiss (2022)

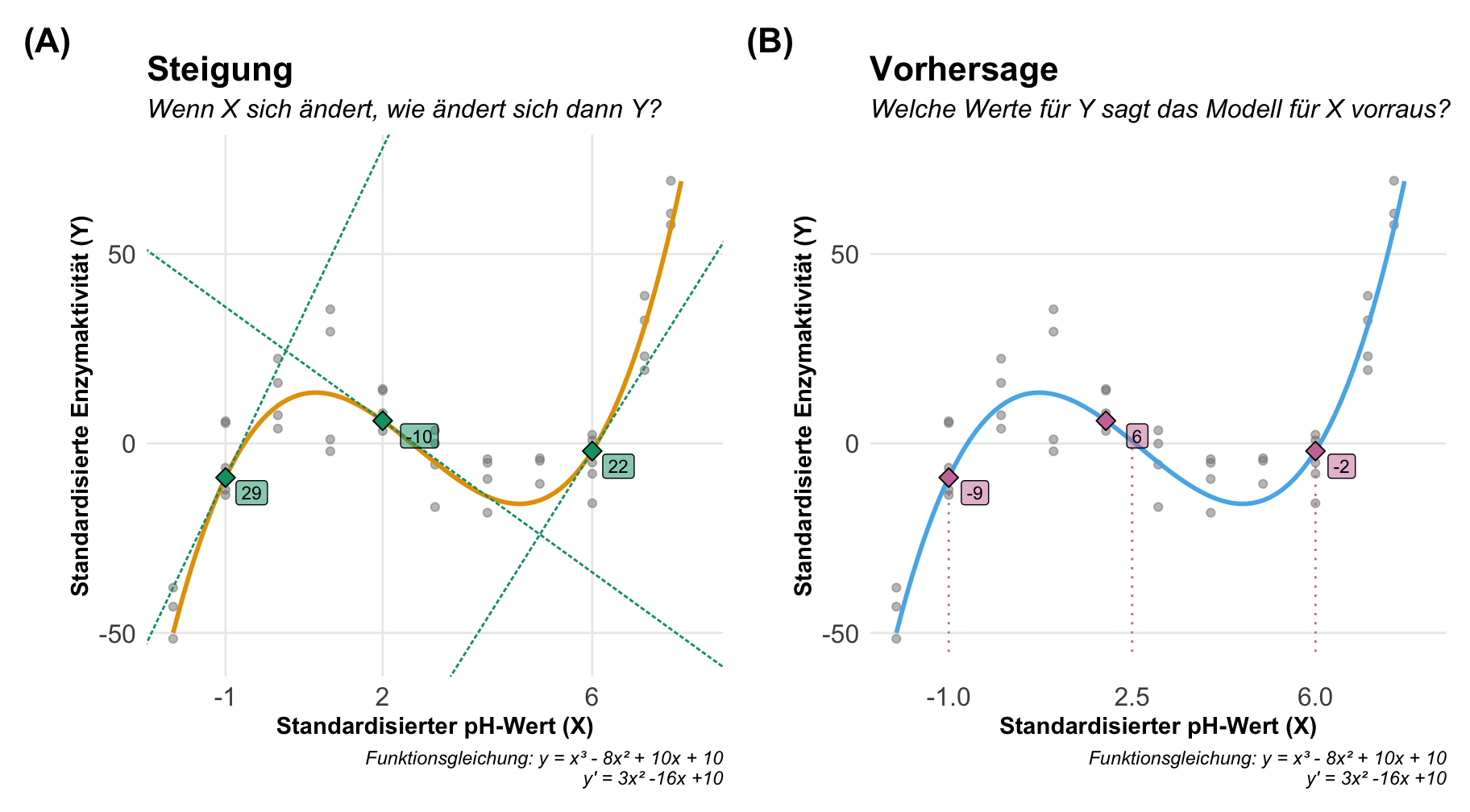
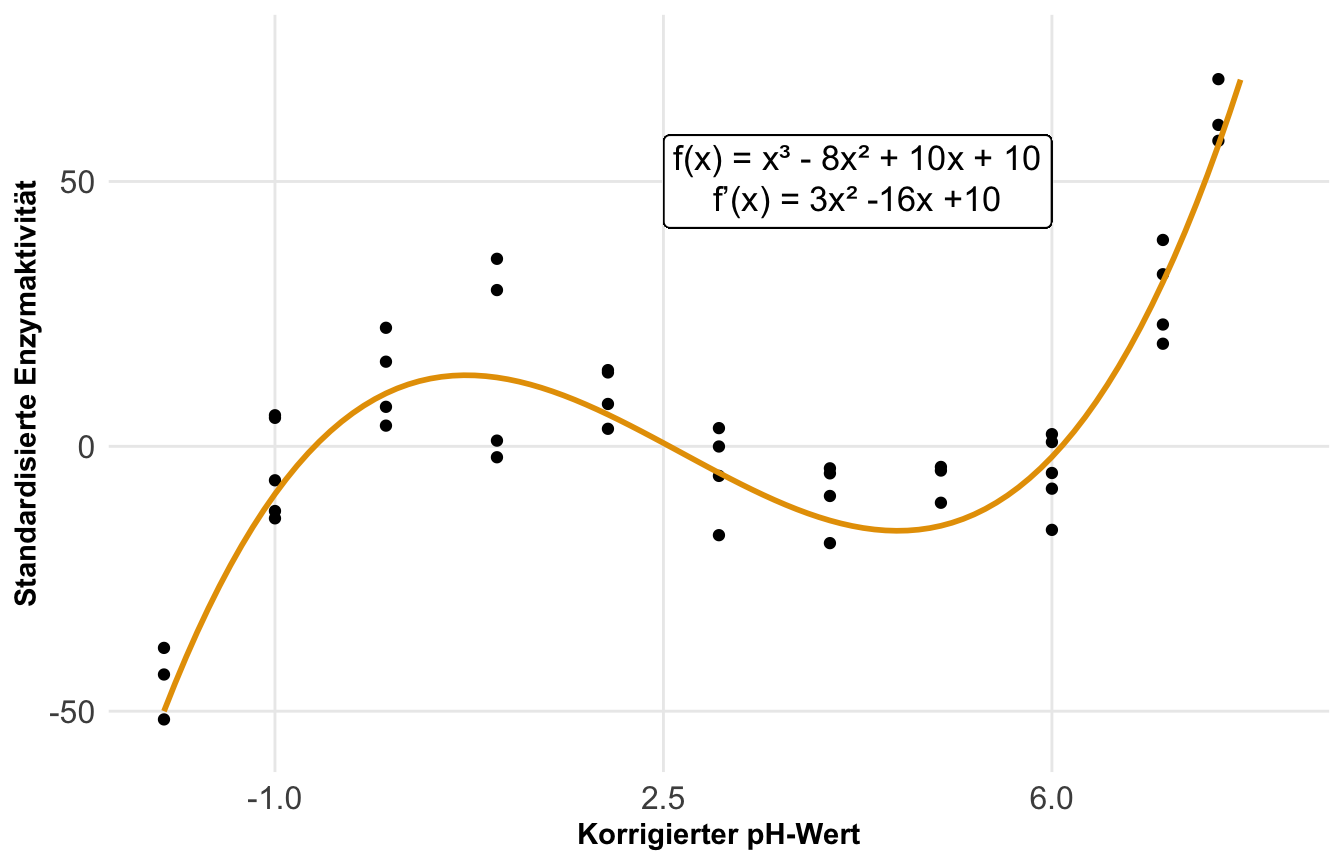
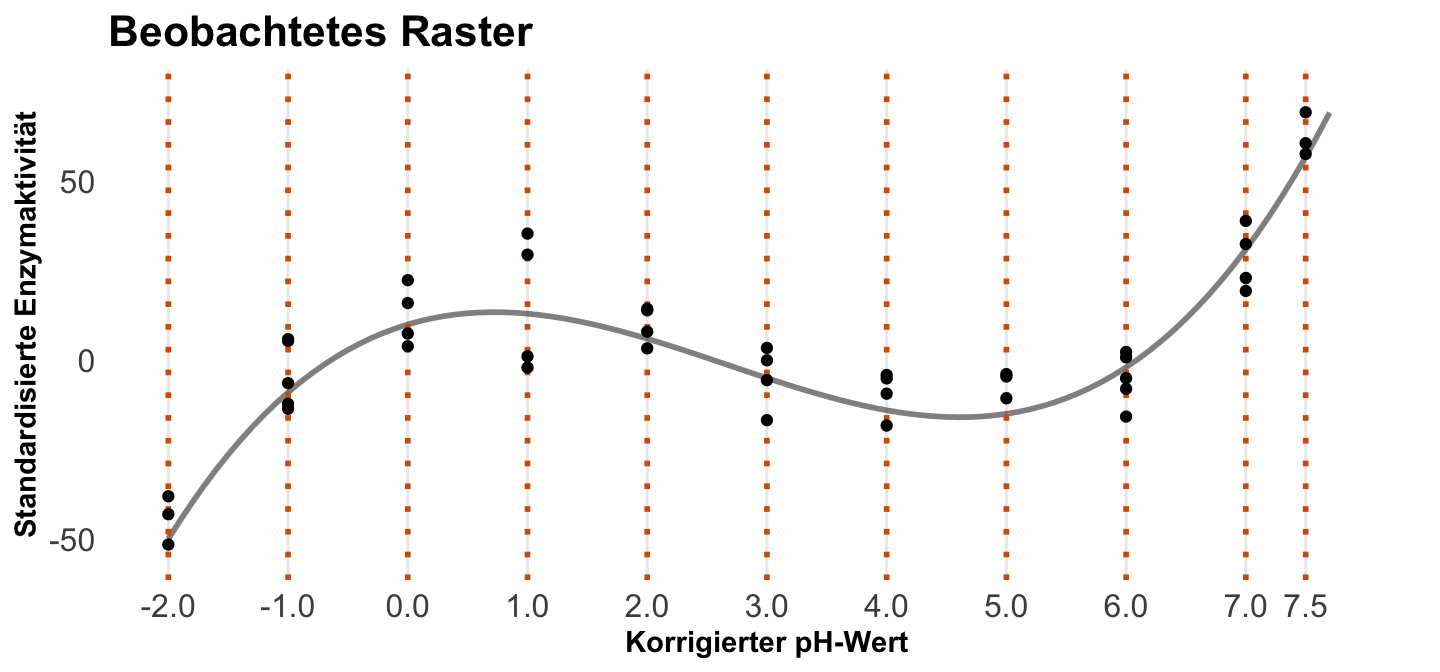
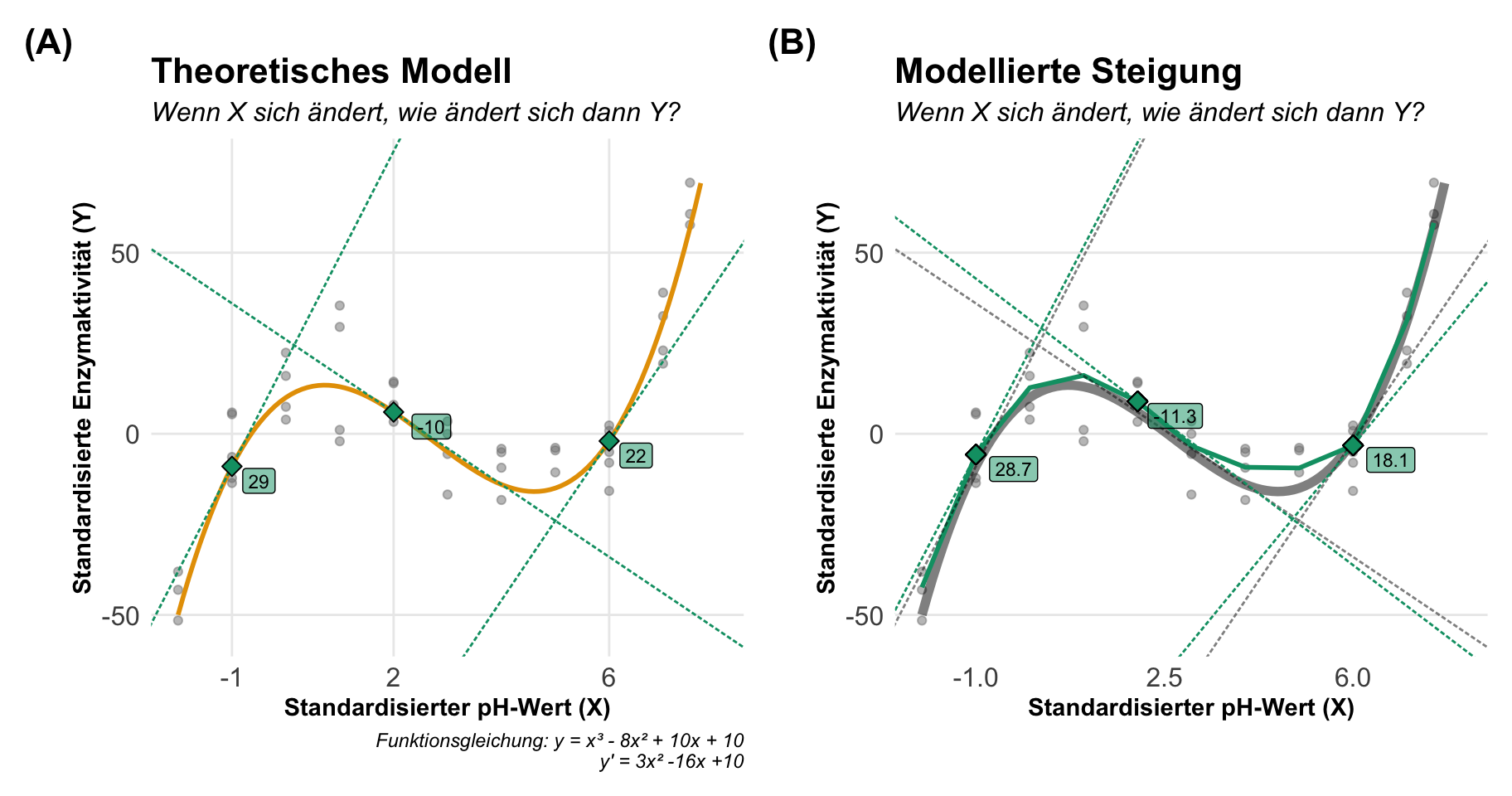
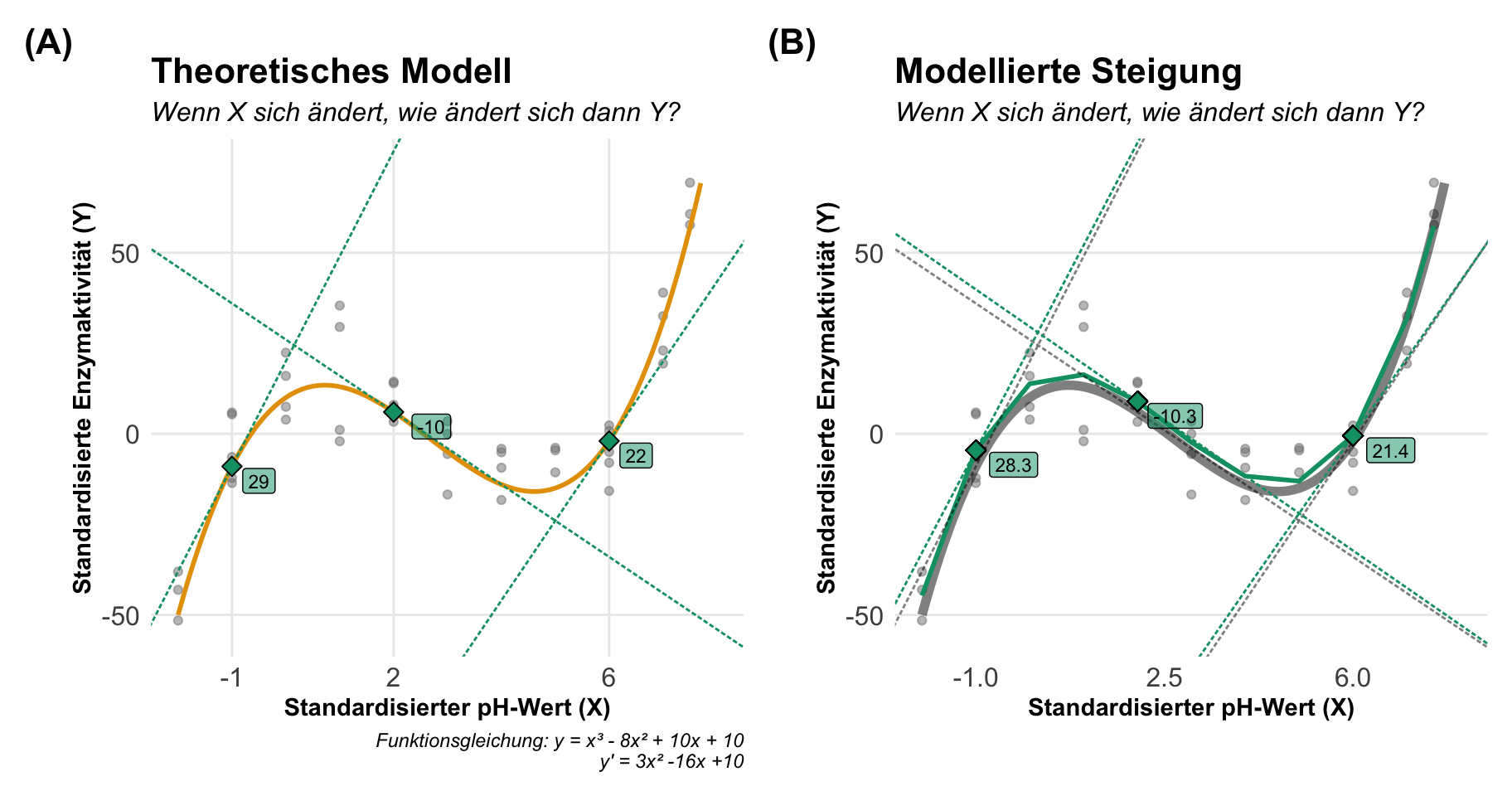
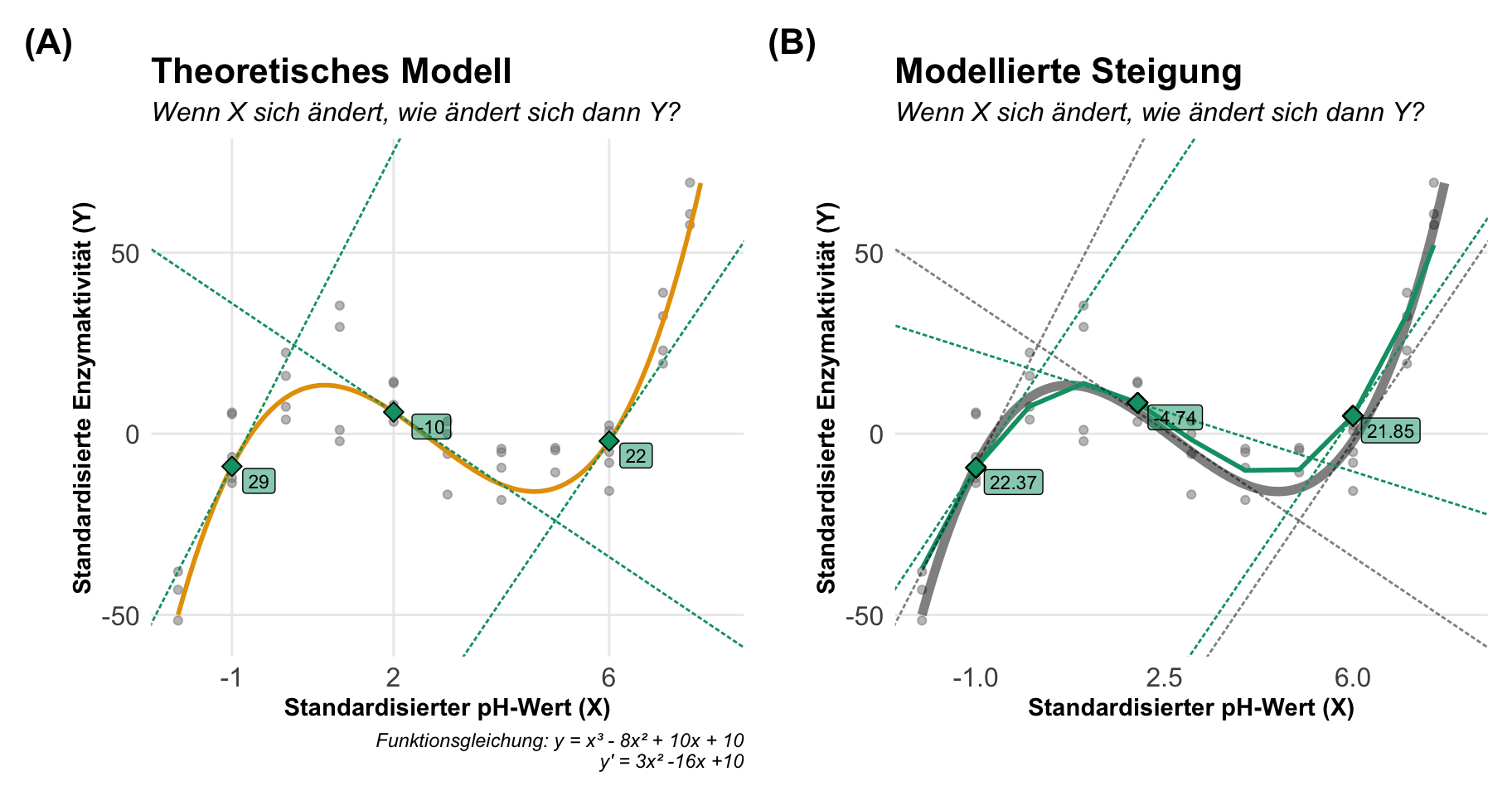
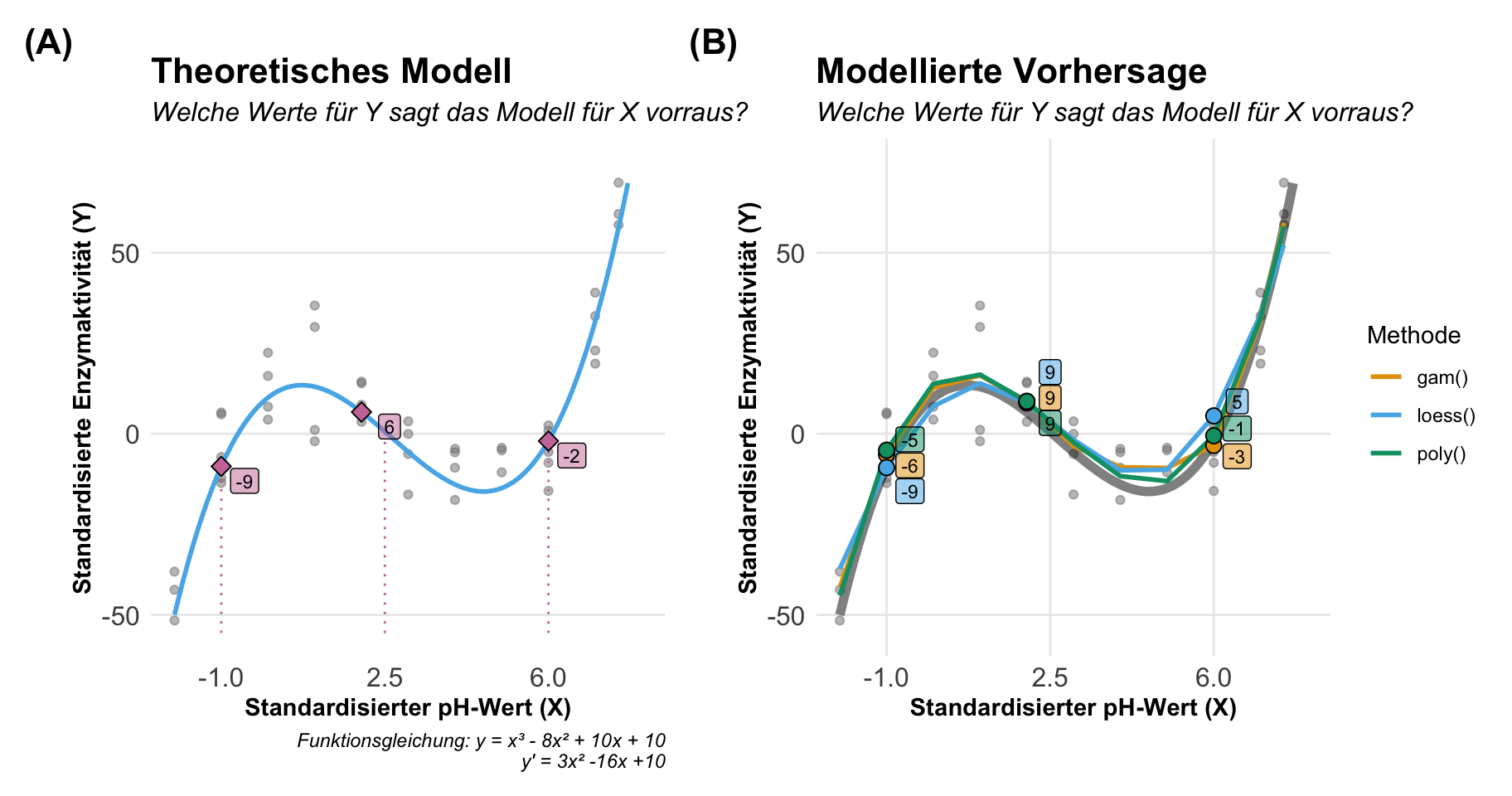
Wenn wir von Marginal effect models sprechen, dann können wir uns im Prinzip zwei Aspekte anschauen. Wir können über die Steigung einer Funktion einer Geraden sprechen oder aber über die vorhergesagten \(y\)-Werte auf der Geraden für beliebige \(x\)-Werte. Damit sind wir dann bei den beiden Aspekten Steigung und Vorhersage. Wenn wir uns in der Welt der linearen Modelle bewegen, dann ist die Steigung eigentlich kein Problem und die Vorhersage auch nicht so komplex. Spannender wird das Zusammenspiel eines nichtlinearen Modells und eben den Marginal effect models. Hier kommt dann die eigentliche Kraft der Marginal effect models zu trage. In den folgenden beiden Abbildungen habe ich dir einmal eine nichtlinere Funktion dargestellt. Wir schauen uns hier den Zusammenhang zwischen der standardisierten Enzymaktivität und dem standardisierten pH-Wert an. Wir haben die Enzymaktivität zu festen pH-Werten wiederholt gemessen. Auf der linken Seite betrachten wir die Steigung der Geraden an drei Punkten und auf der rechten Seite sehen wir einmal die Vorhersage für drei pH-Werte auf der Geraden. Die Gerade folgt der Funktion \(y = x^3 - 8x^2 + 10x + 10\) und ist mir somit für die Bestimmung der Steigung und der Vorhersage bekannt. Daher habe ich also die Möglichkeit die exakten Werte der Steigung und der Vorhersage zu bestimmen. Einen Luxus den wir selten mit echten Daten haben.

Abbildung 55.2— Modellierung des nichtlinearen Zusammenhangs zwischen der standardisierten Enzymaktivität und dem standardisierten pH-Wert. Der pH-Wert ist kontinuierlich. Die Funktionsgleichung ist bekannt. (A) Berechnung der Steigung (eng. slope) für ausgewählte pH Werte anhand der Modellierung. (B) Berechnete Vorhersagewerte (eng. prediction) der standardisierten Enzymaktivität für ausgewählte pH-Werte anhand der Modellierung. [Zum Vergrößern anklicken]

Betrachten wir also einmal die Antworten, die die Steigung und die Vorhersage liefert. Dabei haben wir hier in diesem Fall ein kontinuierliches \(X\) als Kovariate vorliegen und machen uns die Sachlage auch einfacher indem wir ein kontinuierliches \(Y\) mit der standardisierten Enzymektivität vorliegen haben.

Welche Antwort liefert die Steigung?

Wenn sich \(X\) ändert, wie ändert sich dann \(Y\) an dem Wert von \(X\)? Hierbei muss sich \(X\) nicht um eine Einheit verändern, wie wir es gerne im linearen Zusammenhang sagen, sondern wir wollen die Steigung direkt im Punkt von \((X;Y)\) haben.

Welche Antwort liefert die Vorhersage?

Welche Werte für \(Y\) sagt das Modell für \(X\) vorraus? Wir müssen hier die beobachteten Werte von \(Y\), die in unserem Beispiel für einen pH-Wert wiederholt vorkommen, von dem einen vorhergesagten \(Y\) Wert aus dem Modell für ein gegebenes \(X\) unterscheiden.

Dann können wir auch schon die Steigung und die Vorhersage einmal interpretieren. In dem linken Tab findest du einmal die Interpretation der Steigung sowie die Ausgabe der Funktion slopes() aus dem R Paket {marginaleffects}. In dem rechten Tab dann die Ergebnisse der Vorhersage und die Ausgabe der Funktion predictions(). Mehr zu den beiden Funktionen dann weiter unten in der Anwendung. Ich berechne hier die Steigung und bestimme die vorhergesagten Werte für drei ausgewählte pH-Werte.

Interpretation Steigung

Wir können einmal die Steigung \((dx/dy)\) aus der ersten Ableitung der quadratischen Geradenfunktion für unsere ausgewählten pH-Werte bestimmen und dann entsprechend interpretieren.

Tabelle 55.2— Interpretation der Steigung der Enzymaktivität an drei ausgewählten pH-Werten.

pH	Steigung	Interpretation
-1	29	Bei einem standardisierten pH-Wert von -1 steigt die Enzymaktivität um 29U an.
2	-10	Bei einem standardisierten pH-Wert von 2 sinkt die Enzymaktivität um 10U.
6	22	Bei einem standardisierten pH-Wert von 6 steigt die Enzymaktivität um 22U an.

Wir können uns dann die Steigung auch direkt mit der Funktion slopes() bestimmen lassen und erhalten dann die folgenden Informationen. Häufig haben wir ja nicht die Geradengleichung vorliegen. Hier haben wir dann auch die p-Werte sowie einen entsprechenden Fehler. Wir haben hier eine leichte Abweichung, da ich die obige Steigung durch die Ableitung der quadratischen Funktion erstellt habe und nicht aus einem Polynomialmodell entnommen habe.

 ph Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
 -1     28.3       2.44 11.57   <0.001 100.5  23.5  33.04
  2    -10.3       1.14 -9.08   <0.001  63.0 -12.6  -8.11
  6     21.4       1.63 13.16   <0.001 129.0  18.3  24.64

Term: ph
Type: response
Comparison: dY/dX

Interpretation Vorhersage

Auch hier können wir direkt durch das Einsetzen der pH-Werte in unsere quadratische Geradenfunktion die vorgesagten Enzymaktivitäten für die ausgewählten pH-Werte bestimmen.

Tabelle 55.3— Interpretation der Vorhersage der Enzymaktivität an drei ausgewählten pH-Werten.

pH	Vorhersage (y)	Interpretation
-1	-9	Für einen standardisierten pH-Wert von -1 sagt die Funktion eine Enzymaktivität von -9U vorher.
2	6	Für einen standardisierten pH-Wert von 2 sagt die Funktion eine Enzymaktivität von 6U vorher.
6	-2	Für einen standardisierten pH-Wert von 6 sagt die Funktion eine Enzymaktivität von -2U vorher.

Auch können wir die Steigung aus den Daten direkt mit der Funktion predictions() bestimmen. Häufig haben wir ja nicht die Geradengleichung vorliegen. Hier haben wir theoretisch noch eine riesige Auswahl an Funktionen in R, wir konzentrieren uns hier aber auf das R Paket {marginaleffects}. Wir haben auch hier eine leichte Abweichung, da ich die obigen Vorhersagen durch die quadratische Funktion bestimmt habe und nicht aus einem Polynomialmodell entnommen habe.

 ph Estimate Std. Error      z Pr(>|z|)    S 2.5 % 97.5 %
 -1   -4.545       2.48 -1.830   0.0673  3.9 -9.41  0.324
  2    8.951       2.23  4.013   <0.001 14.0  4.58 13.323
  6   -0.545       2.36 -0.231   0.8176  0.3 -5.18  4.089

Type: response

Wenn wir die Vorhersage betrachten dann können wir auch den Fall vorliegen haben, dass wir ein kategoriales \(X\) mit Gruppen gemessen haben. In R wäre es dann ein Faktor und daher dann auch der Begriff des faktoriellen Designs, wenn es um das experimentelle Design geht. Wir hatten bis jetzt ein kontinuierlichen pH-Wert vorliegen. Zwar hatten wir auch Messgruppen, aber wir konnten von einem konitnuierlichen pH-Wert im Sinne der Modellierung ausgehen. Jetzt wollen wir uns einmal den Fall anschauen, dass wir auf eben wirkliche pH-Wertgruppen mit niedrigen, mittleren und hohen pH-Wertgruppen für die Enzymaktivität vergleichen wollen. Ich schreibe hier schon gleiche von einem Vergleich, als erstes wollen wir aber die Mittelwerte pro Gruppe vorhersagen.

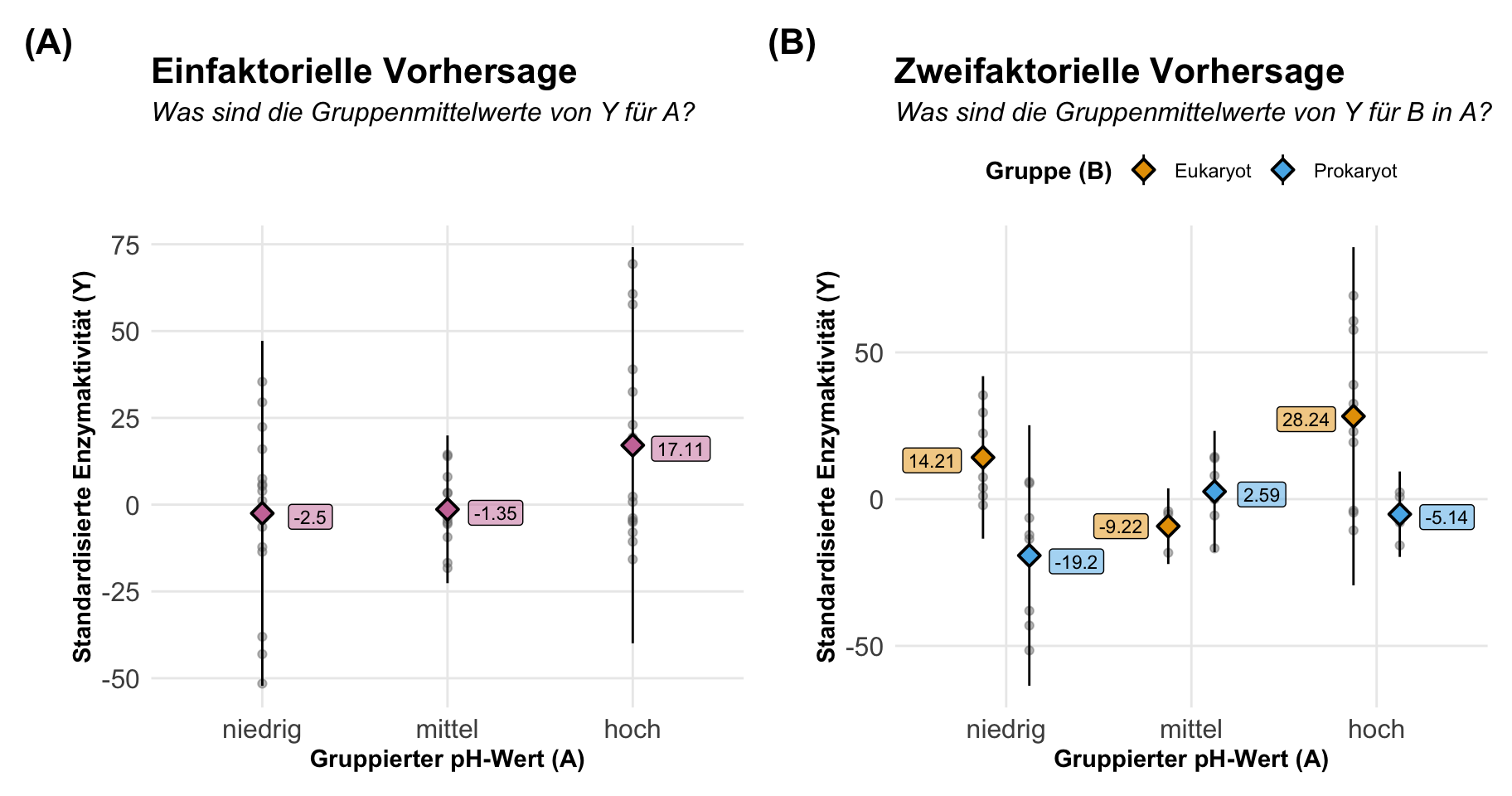
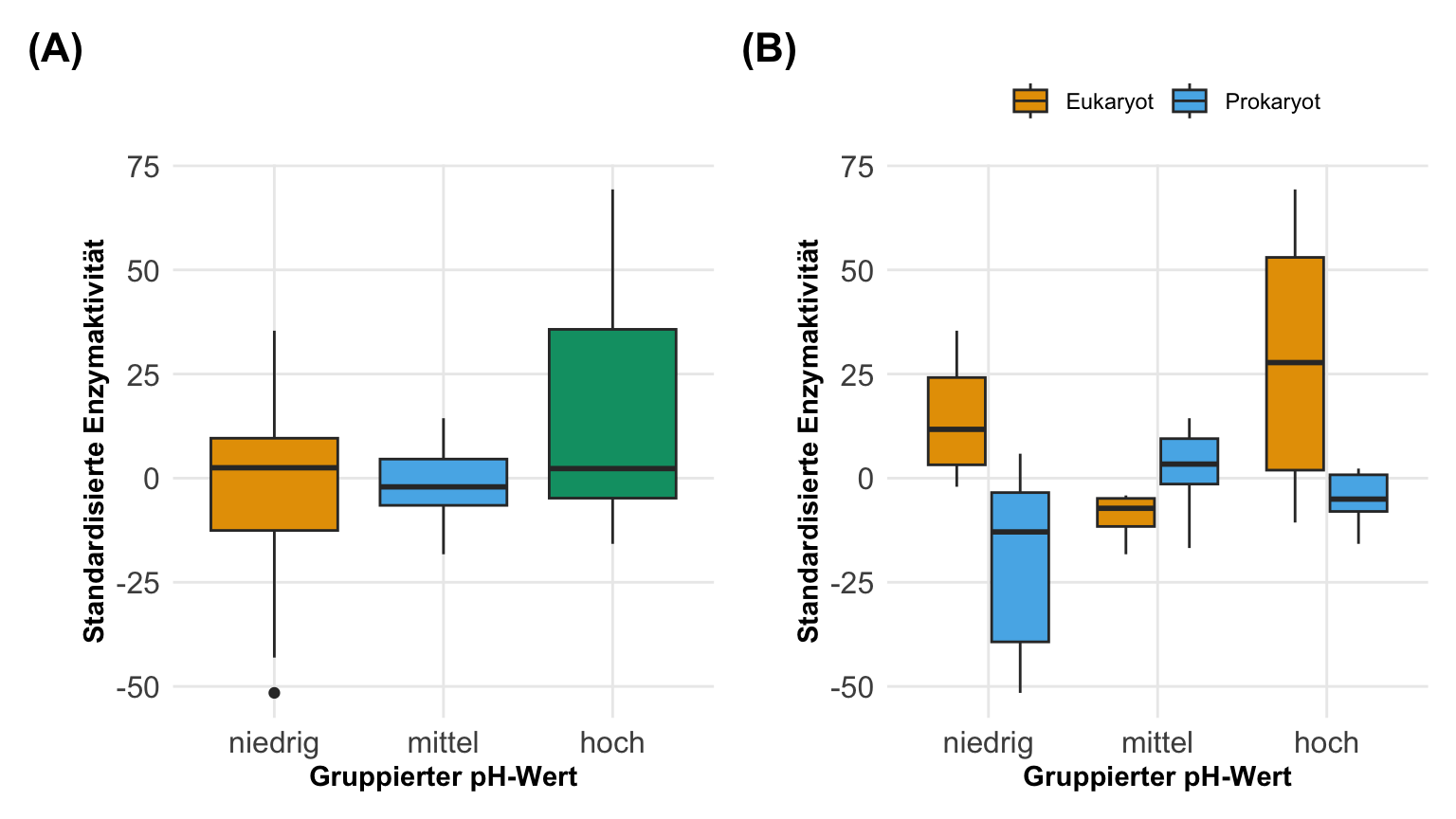
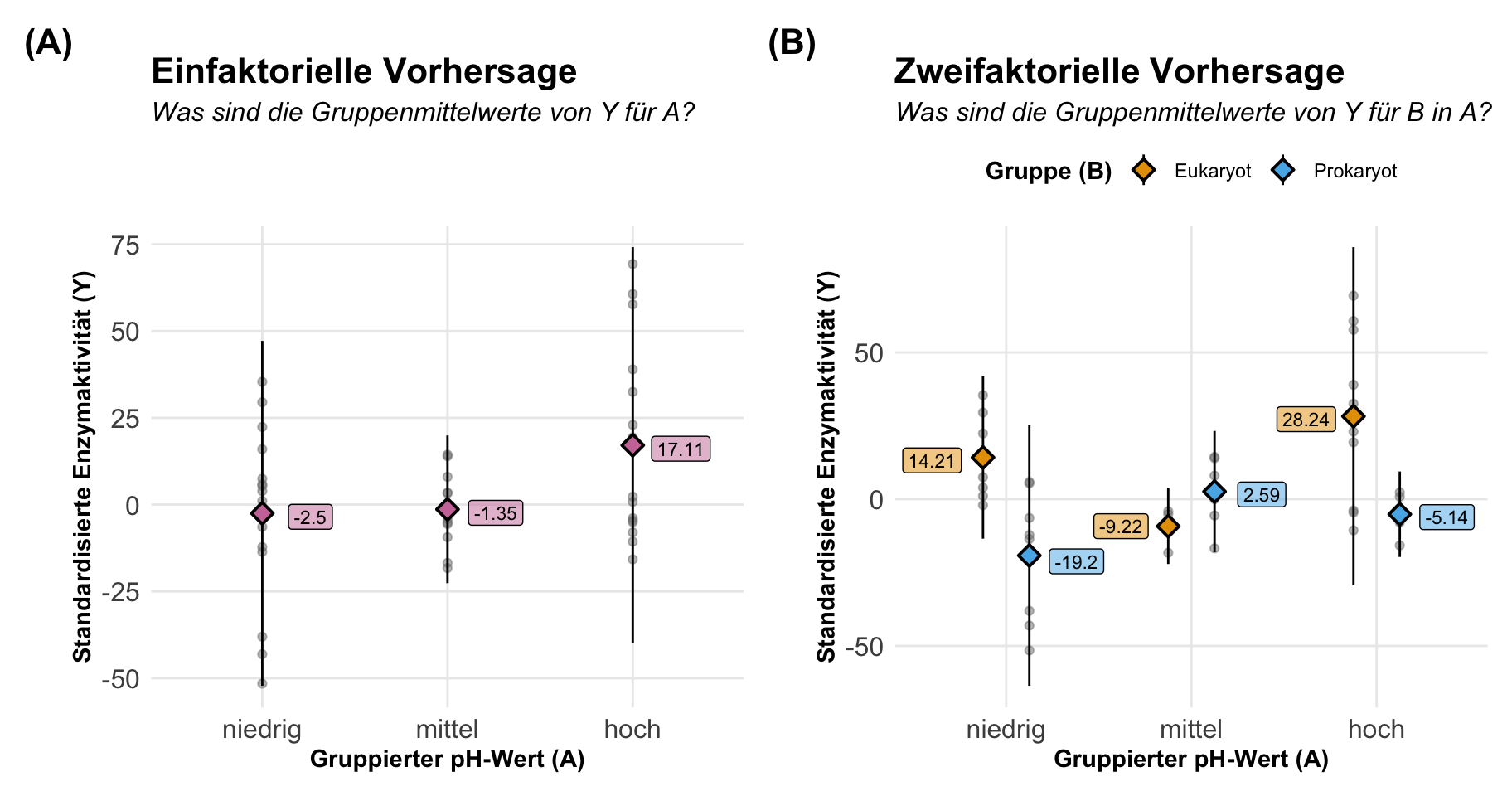
In der folgenden Abbildung siehst du auf der linken Seite einmal den einfaktoriellen Fall mit dem gruppierten pH-Wert als Gruppe. Auf der rechten Seite dann noch zusätzlich die beiden Gruppen der Prokaryoten sowie Eukaryoten. Wir sind jetzt an den Mittelwerten pro Gruppe interessiert und wir könnten diese Mittelwerte dann auch einfach berechnen. Dafür bräuchten wir dann erstmal kein Modell, wenn wir nur so ein simples Experiment vorliegen haben. Konkret bestimmen wir hier die marginal means aus einem Modell heraus.

Abbildung 55.3— Modellierung des Zusammenhangs zwischen der standardisierten Enzymaktivität und den gruppierten pH-Werten nach niedrigen, mittleren und hohen pH-Werten. Der pH-Wert ist kategorial. (A) Einfaktorielle Vorhersage der Gruppenmittelwerte der Enzymaktivität. (B) Zweifaktorielle Vorhersage der Gruppenmittelwerte der Enzymaktivität aufgetrennt nach der Gruppe der Eukaryoten und Prokaryoten. [Zum Vergrößern anklicken]

Wir wollen jetzt für alle Gruppen die Mittelwerte vorhersagen. Nichts anderes macht dann auch die Funktion predictions(). Hier muss ich auch schon gleich einmal eine leichte Warnung aussprechen. So gut {marginaleffects} in der Bestimmung der Steigung und der Vorhersagen ist, um so viel besser ist das R Paket {emmeans} wenn es um die Auswertung von einem faktoriellen Design geht. Hier ist dann einfach {emmeans} besser in der Anwendung. Das hat auch Gründe im Algorithmus der beiden Pakete, dazu dann aber später mehr. Hier erstmal die Interpretation der beiden Vorhersagen für kategoriale \(x\)-Werte oder eben auch Faktoren in R genannt.

Vorhersage 1-faktoriell

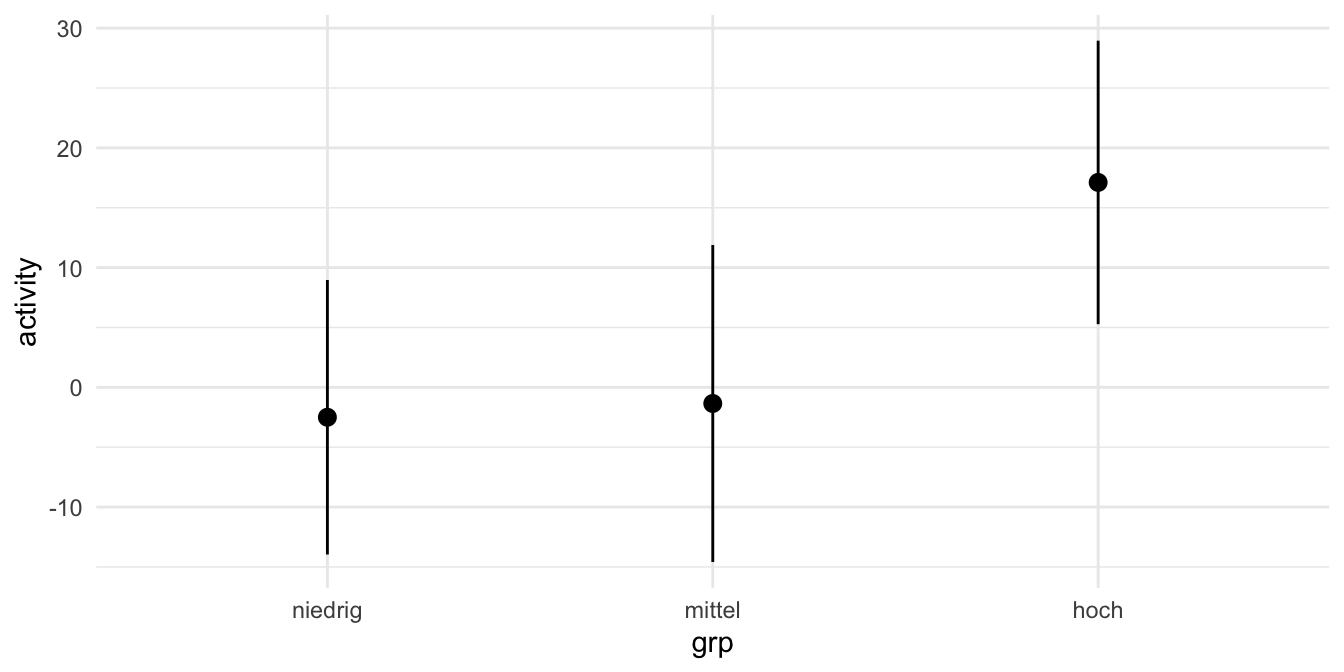
Wir haben hier also in unserem einfaktoriellen Modell einmal die gruppierten pH-Werte in den Gruppen niedrig, mittel und hoch vorliegen. Wir wollen dann den Mittelwert für jede der Gruppen bestimmen.

Tabelle 55.4— Interpretation der Vorhersage der Enzymaktivität an drei ausgewählten pH-Werten.

pH	Mittelwert	Interpretation
niedrig	3.2	Für die Gruppe der niedrigen pH-Werte haben wir im Mittel eine Enzymaktivität von 3.2U vorliegen.
mittel	2.59	Für die Gruppe der mittleren pH-Werte haben wir im Durchschnitt eine Enzymaktivität von 2.59U vorliegen.
hoch	-5.6	Für die Gruppe der hohen pH-Werte haben wir im Mittel eine Enzymaktivität von -5.9U vorliegen.

Jetzt können wir uns auch mit der Funktion predictions() aus dem R Paket {marginaleffects} die Mittelwerte für die Gruppen vorhersagen lassen. Wir erhalten dann auch die entsprechenden Standardfehler und andere statistische Maßzahlen. Hier kriegen wir noch keinen Vergleich, hier wird nur getestet, ob der Mittelwert sich von der Null unterscheidet.

     grp Estimate Std. Error      z Pr(>|z|)    S  2.5 % 97.5 %
 niedrig    -2.50       3.99 -0.626    0.531  0.9 -10.32  5.327
 mittel     -1.35       1.06 -1.276    0.202  2.3  -3.42  0.722
 hoch       17.11       4.91  3.483   <0.001 11.0   7.48 26.745

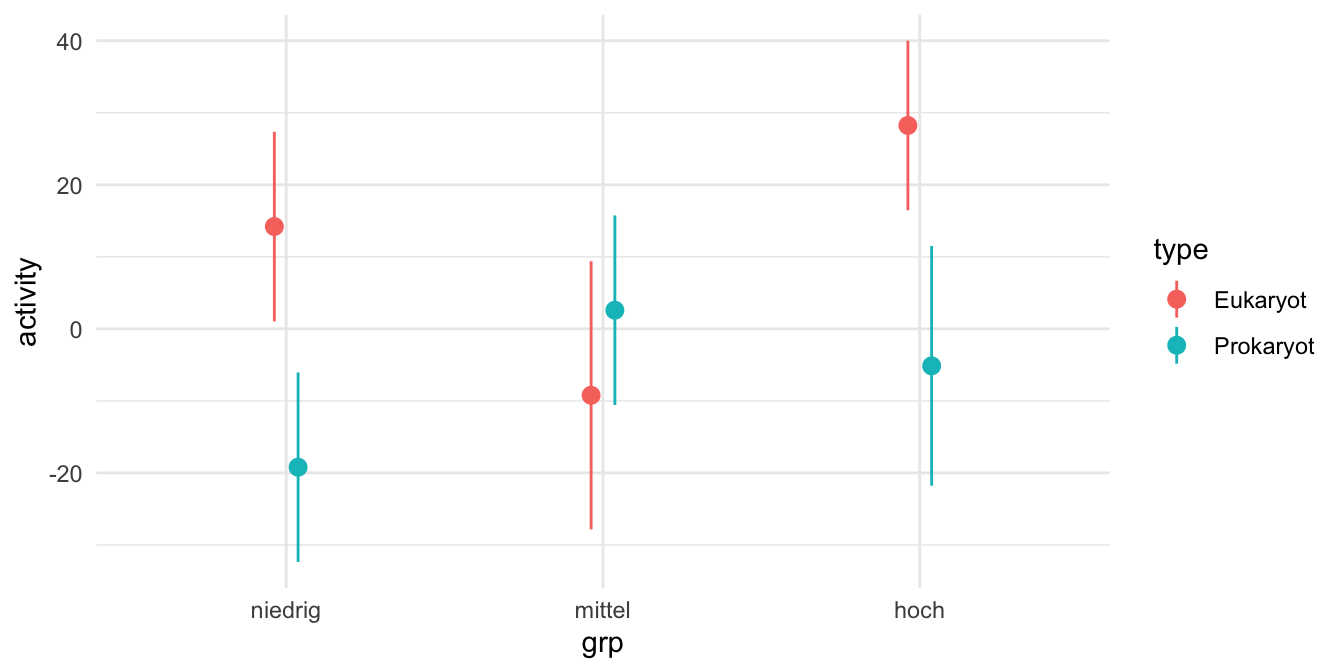
Type: response

Vorhersage 2-faktoriell

Kommen wir nun zu der Vorhersage der Mittelwerte oder Marginal means in den gruppierten pH-Werten aufgeteilt nach den beiden Gruppen der Prokaryoten sowie Eukaryonten. Daher haben wir hier ein zweifaktorielles Design vorliegen. Wir wollen eben die Mittelwerte für alle Faktorkombinationen wissen.

Tabelle 55.5— Interpretation der Vorhersage der Enzymaktivität an drei ausgewählten pH-Werten in den Prokaryoten und Eukaryonten

pH	Gruppe	Mittelwert	Interpretation
niedrig	Eukaryot	14.21	Für die Gruppe der niedrigen pH-Werte der Eukaryoten haben wir im Mittel eine Enzymaktivität von 14.21U vorliegen.
niedrig	Prokaryot	-19.2	Für die Gruppe der niedrigen pH-Werte der Prokaryoten haben wir im Mittel eine Enzymaktivität von -19.2U vorliegen.
mittel	Eukaryot	-9.22	Für die Gruppe der mittleren pH-Werte der Eukaryoten haben wir im Mittel eine Enzymaktivität von -9.22U vorliegen.
mittel	Prokaryot	2.59	Für die Gruppe der mittleren pH-Werte der Prokaryoten haben wir im Mittel eine Enzymaktivität von 2.59U vorliegen.
hoch	Eukaryot	26.24	Für die Gruppe der hohen pH-Werte der Eukaryoten haben wir im Mittel eine Enzymaktivität von 26.24U vorliegen.
hoch	Prokaryot	-5.14	Für die Gruppe der hohen pH-Werte der Prokaryoten haben wir im Mittel eine Enzymaktivität von -5.14U vorliegen.

Wenn wir dann die Funktion predictions() aus dem R Paket {marginaleffects} benutzen erhalten wir dann auch die Marginal means für alle Faktorkombinationen zurück. Hier sind die Werte die gleichen wir auch in der simplen Berechnung oben in der Abbildung, da unser Modell eben dann doch nur die beiden Faktoren enthält. Wir erhalten dann auch die Standardfehler und den p-Wert für den Test gegen einen Mittelwert von Null.

     grp      type Estimate Std. Error       z Pr(>|z|)     S   2.5 % 97.5 %
 niedrig Eukaryot     14.21     0.5498   25.84   <0.001 486.6  13.129  15.28
 niedrig Prokaryot   -19.20     4.1190   -4.66   <0.001  18.3 -27.277 -11.13
 mittel  Eukaryot     -9.22     0.0325 -283.79   <0.001   Inf  -9.286  -9.16
 mittel  Prokaryot     2.59     1.2580    2.06   0.0396   4.7   0.123   5.05
 hoch    Eukaryot     28.24    13.4263    2.10   0.0354   4.8   1.924  54.55
 hoch    Prokaryot    -5.14     0.5571   -9.22   <0.001  64.9  -6.228  -4.04

Type: response

Soviel dann einmal zu dem allgemeinen Hintergrund. Die Idee der Marginal effect models ist es also dir die Steigung einer Funktion oder die vorhergesagten Werte einer Funktion wiederzugeben. Hier kannst du dann Funktion auch mit Modell erstetzen. Für den linearen Fall auf einem normalverteilten Messwert ist die Anwendung und der Erkenntnisgewinn der Marginal effect models begrenzt. Da reichen dann auch die Ausgaben der Standardfunktionen. Aber auch dort werden wir dann noch in den entsprechenden Kapiteln sehen, dass wir hier noch was rausholen können. Die Marginal effect models entwicklen dann ihre Stärke für nicht normalverteilte Messwerte sowie eben nicht lineare Zusammenhänge.

TippWeitere Tutorien für die Marginal effects models

Wir oben schon erwähnt, kann dieses Kapitel nicht alle Themen der Marginal effects models abarbeiten. Daher präsentiere ich hier eine Liste von Literatur und Links, die mich für dieses Kapitel hier inspiriert haben. Nicht alles habe ich genutzt, aber vielleicht ist für dich was dabei.

• Ohne den Blogpost Marginalia: A guide to figuring out what the heck marginal effects, marginal slopes, average marginal effects, marginal effects at the mean, and all these other marginal things are von Heiss (2022) wäre dieses Kapitel nicht möglich gewesen.
• Wie alles im Leben ist nichts ohne Kritik. Is least squares means (lsmeans) statistical nonsense? ist dann auch eine gute Frage. Ich bin der Meinung nein und auch andere sind es, aber hier kannst du dann nochmal eine andere Meinung lesen.

55.2 Theoretischer Hintergrund

“What he says?” — Asterix, Sieg über Caesar

Soweit so gut. Wenn du verstanden hast, was die Marginal effect models können, dann kannst du auch bei den Daten und deren Auswertung weitermachen. Hier geht es dann etwas tiefer und ich gehe nochmal auf einzelne Aspekte etwas ausführlicher ein. So wollen wir nochmal verstehen, was eigentlich die Steigung nochmal war und wie wir die Steigung berechnen. Dann müssen wir nochmal über simple und multiple Modelle sprechen. Dann gehen wir nochmal auf die Vorhersage ein und ich gebe nochmal einen kurzen Überblick, was wir da eigentlich alles vorhersagen oder genauer was wie heißt. Dann besprechen wir nochmal die Unterschiede zwischen den Paketen {marginaleffects} und {emmeans}. Wie immer kann man den Teil hier auch überspringen, wenn es nur um die Anwendung geht.

Was ist die Steigung?

Wenn wir mit dem Verstehen und Zerforschen der Steigung vorankommen wollen, dann können wir Heiss (2022) und Arel-Bundock et al. (2024) mit der Veröffentlichung Model to meaning — How to Interpret Statistical Models With marginaleffects for R and Python nicht ignorieren. Ich nutze jetzt eine etwas allgemeinere Erklärung der Marginal effect models und konzentriere mich erstmal auf ein normalverteilte Kovariate \(c_1\) sowie ein normalverteiltes \(y\) in einem simplen Modell mit einem \(c_1\) und einem \(y\) in der folgenden Form.

\[ y \sim \beta_0 + \beta_1 c_1 \] mit

• \(\beta_0\), dem Koeffizienten des y-Achsenabschnitt oder Intercept der Geraden.
• \(\beta_1\), dem Koeffizienten der Steigung der Geraden

Daher haben wir hier in unserer Kovariate \(c_1\) keine Gruppen vorliegen sondern einen klassischen Scatterplot mit Punkten als Beobachtungen. Wir können die Marginal effect models auch auf beliebige Faktoren wie eben Behandlungsgruppen sowie jedes beliebige \(y\) anwenden, aber hier fangen wir einmal einfach an.

Welche Frage wollen wir mit Marginal effect models beantworten?

Wenn sich die Kovariate \(c_1\) um einen Wert oder eine Einheit erhöht, um wieviele Einheiten verändert sich dann der Wert von \(y\)?

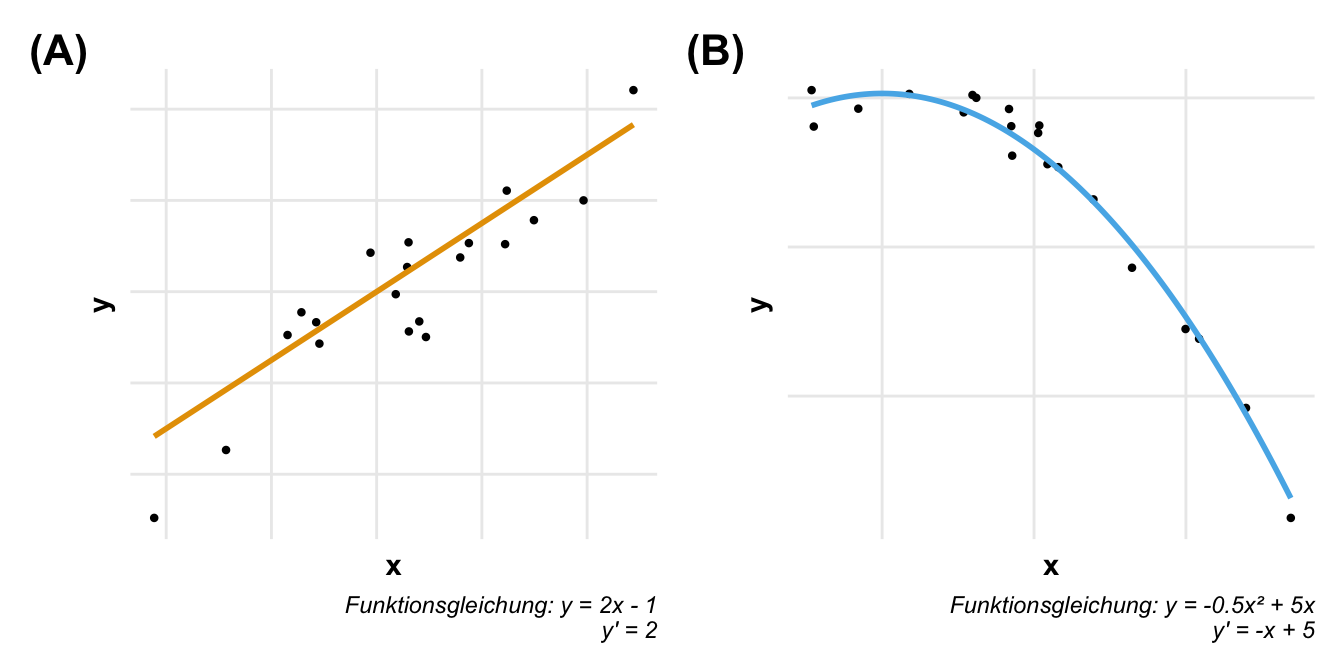
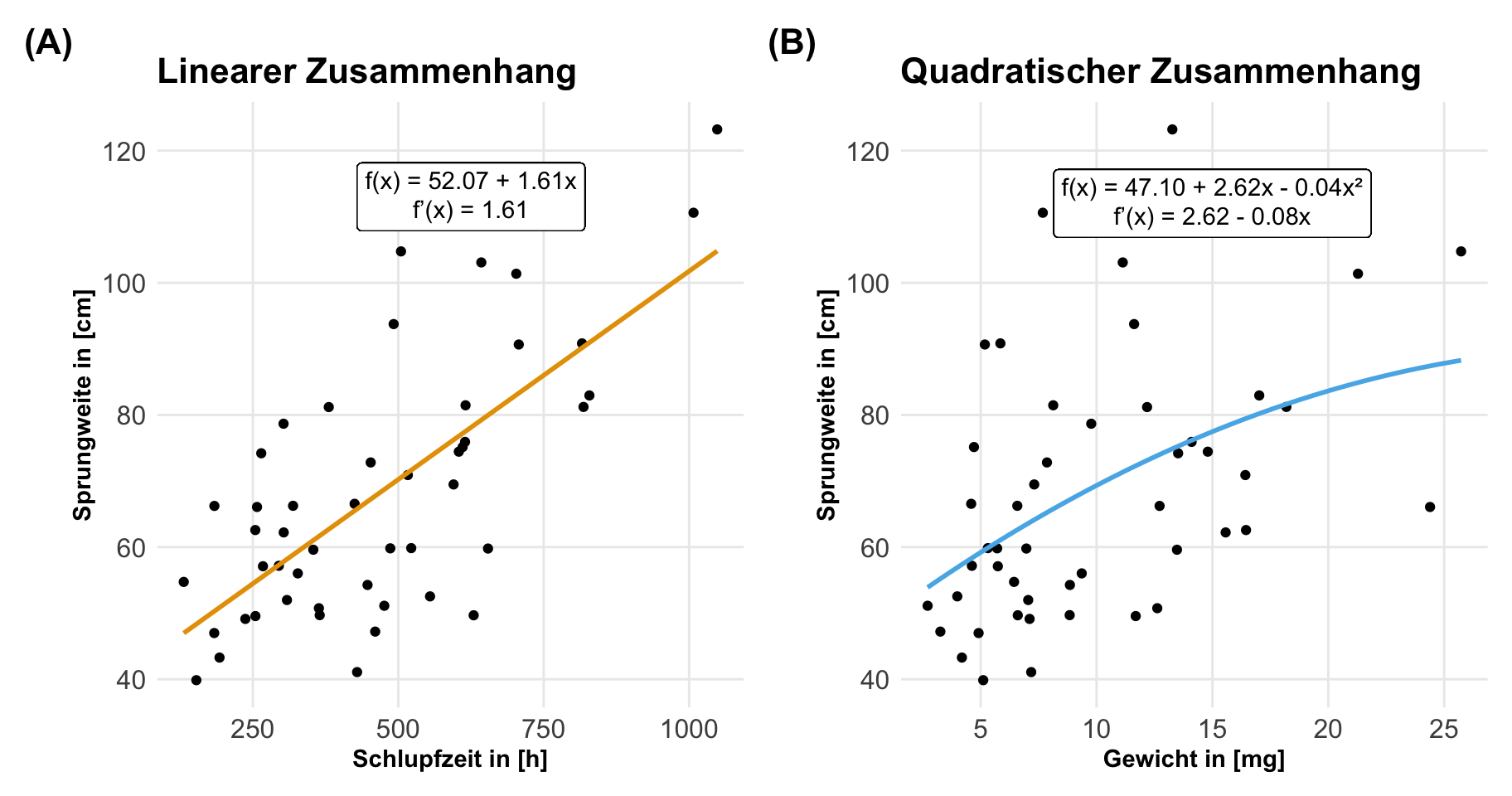
In der folgenden Abbildung siehst du einmal zwei Scatterplots. In dem linken Scatterplot haben wir einen linearen Zusammenhang zwischen unseren \(c_1\)-Werten der Kovariate und den \(y\)-Werten. Wir können sagen, dass wenn sich die Kovariate um einen Wert erhöht, dann erhöht sich auch \(y\) um einen konstanten Wert. Dieser konstante Wert um den sich die \(y\)-Werte mit ansteigenden \(c_1\) erhöhen, nennen wir auch die Steigung \(\beta_1\). In einem linearen Zusammenhang ist die Frage damit mit der Steigung der Geraden eigentlich beantwortet. Steigt die Kovariate um einen Wert, dann steigt \(y\) um den Wert der Steigung \(\beta_1\) der Geraden. Diesen konstanten Zusammenhang haben wir aber nicht bei einem quadratischen Zusammenhang wie in der rechten Abbildung. Wir können hier nicht sagen, dass wenn sich die Kovariate um einen Wert erhöht, sich auch \(y\) um einen konstanten Wert ändert. Hier hängt es von dem betrachteten \(c_1\)-Wert ab.

Abbildung 55.4— Scatterplot der kontinuierlichen Kovariate und kontinuierlichen Messwerten. In einem Modell wird die Abhängigkeit vom Messwert \(y\) und der Kovariate \(c_1\) modellieren. (A) Linearer Zusammenhang. (B) Quadratischer Zusammenhang. [Zum Vergrößern anklicken]

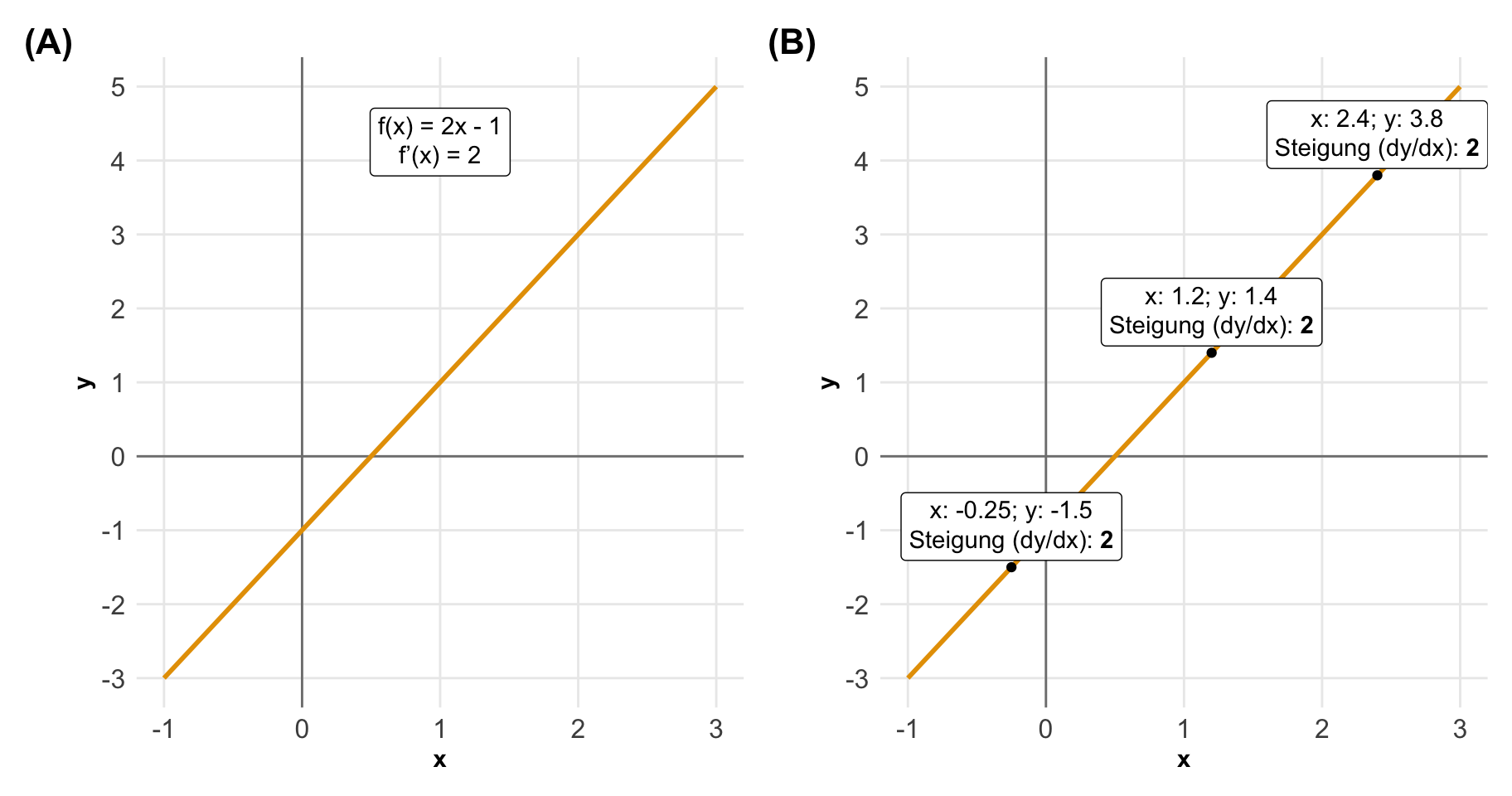
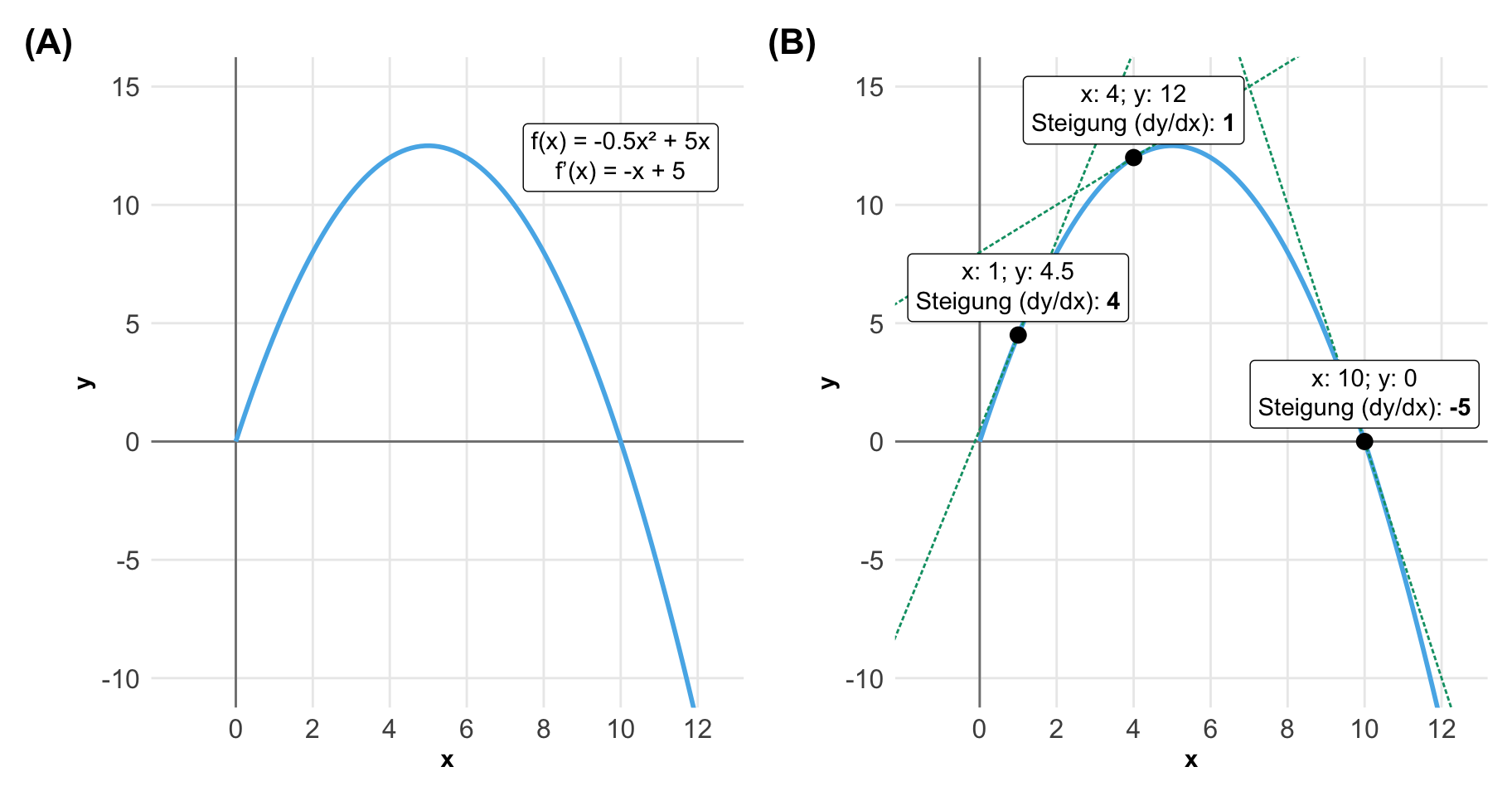
Schauen wir mal in ein Zahlenbeispiel und lassen die Beobachtungen weg. Beginnen wir einmal mit dem linearen Zusammenhang der Funktion \(f(x) = 2x-1\). Ich habe die Gerade einmal in der folgenden Abbildung eingezeichnet. Wenn uns jetzt die Steigung an jedem beliebigen Punkt von \(c_1\) interessiert, dann bilden wir die erste Abbleitung \(f'(x) = 2\). Erhöht sich also der Wert von der Kovariate um 1 dann steigt der Wert von \(y\) um 2 an. Wir sehen aber auch, dass für jedes beliebige Punktepaar wir eine Steigung von 2 vorliegen haben.

Abbildung 55.5— Gerade des Modells für einen linearen Zusammenhang. In einem Modell wird die Abhängigkeit vom Messwert und der Kovariate modellieren. (A) Lineares Modell mit Gleichung. (B) Steigung an der Geraden für ausgewählte Punktepaare. [Zum Vergrößern anklicken]

Spanndender wird die Sachlage in einem quadratischen Zusammenhang in der folgenden Abbildung. Oder allgemeiner gesprochen, wenn wir keinen linearen Zusammenhang vorliegen haben. Wir haben hier den Zusammenhgang \(f(x) = -0.5x^2+5x\) vorliegen. Damit haben wir dann eine erste Ableitung von \(f'(x) = x+5\). Wie du siehst, ändert sich auch die Steigung in Abhänigkeit von \(x\). Wenn wir die Werte der Kovariaten links betrachten, dann liegt hier eher eine positive Steigung vor. Wenn wir nach rechts laufen, dann sehen wir immer stärkere negative Steigungen. Und hier kommen dann die Marginal effect models ins Spiel. Wir können allgemein gesprochen uns mit den Marginal effect models für jeden Wert der Kovariate die Steigung wiedergeben lassen.

Abbildung 55.6— Gerade des Modells für einen quadratischen Zusammenhang. In einem Modell wird die Abhängigkeit vom Messwert und der Kovariate modellieren. (A) Quadratisches Modell mit Gleichung. (B) Steigung an der Geraden für ausgewählte Punktepaare. [Zum Vergrößern anklicken]

Aber Moment, denkst du jetzt, in dem linearen Zusammenhang ist es ja einfach mit der Steigung für jeden beliebigen Wert der Kovariate. Wir erhalten für jeden \(c_1\)-Wert genau die gleiche Steigung. Aber bei den nicht-linearen Zusammenhängen hat ja jeder Wert der Kovariate seine eigene Steigung. Wenn wir viele \(c_1\)-Werte gemessen haben, dann haben wir ja dutzende bis hunderte Steigungen durch ein Marginal effect model ermittelt. Das stimmt und damit kommen wir auch gleich zu dem nächsten Punkt, dem Aggregieren der Daten. Oder wie im folgenden Cartoon richtig dargestellt, müssen wir uns überlegen wie wir den den Durchschnitt der Steigungen berechnen.

Abbildung 55.7— “Should I cut the red wire or the blue one!?” “WAIT! We’re going to watch ALL the action movies from the ’80s and ’90s and then calculate the average!” Quelle: wumo.com

Wir haben uns in dem obigen Beispiel nur ein simples Modell mit einer Kovariate angeschaut. Jetzt kann es aber auch sein, dass deine \(x\)-Werte keine kontinuierlichen Messwerte wie das Gewicht oder die Zeit sind, sondern eben ein Gruppen sind. Also du hast verschiedene Düngestufen oder Behandlungsgruppen auf der \(x\)-Achse als Faktoren aufgetragen. Auch dann können wir eine lineare Regression rechnen, eine Linie durch die Punkte legen und anschließend ein Marginal effect model rechnen. Was ist also der Unterschied zwischen einer kontinuierlichen und einem kategoriellen Einflussvariablen? Oder wie uterscheiden sich nochmal Kovariaten von Faktoren?

Unterschied zwischen kontinuierlichen und kategoriale \(x\)-Werte

Wir kennen verschiedene Namen für das Gleiche. So nennen wir dann ein kontinuierliches \(x\) dann auch gerne eine stetige Variable oder intervalskaliert. Nichts destotrotz, wir haben ein \(x\) was in kleinen, marignalen Schritten anwachsen kann. Hier kannst du eben an das Gewicht der Flöhe oder aber Zeiteinheiten sowie das Einkommen denken. Wir verändert sich das \(y\), wenn wir die \(x\)-Werte erhöhen? Wir benennen daher auch die kontinuierliche Einflussvariablen als Kovariaten \(c\).

Auf der anderen Seite haben wir dann kategoriale oder kategorielle \(x\)-Werte. Diese bezeichnen wir dann auch gerne diskret. Wenn wir die Werte von \(x\) ändern, dann springen wir in eine neue Gruppe und es liegt hier eigentlich kein kleiner Schritt vor. Hier haben wir dann eben Düngestufen oder aber Behandlungsgruppen vorliegen. Hier fragen wir uns, wie ändert sich der Wert von \(y\), wenn wir eine Gruppe in \(x\) weiterspringen? Wir benennen dann kategoriale Einflussvariablen als Faktoren \(f\).

In der folgenden Abbildung von Heiss (2022) siehst du nochmal schön den Unterschied dargestellt. Wir haben bei der einer kategorialen Variable einen Schalter. Entweder ist der Schalter an oder eben aus. Im simpelsten Fall haben wir männliche oder eben weibliche Flöhe vorliegen. Das Geschlecht ist somit kategorial. Die Sprungweite oder das Gewicht von Flöhen ist eine kontinuierliche Variable. Wir haben einen Schieberegeler den wir ziemlich fein einstellen können. Mehr dazu im Kapitel zu der simplen linearen Regression.

Abbildung 55.8— Unterschied zwischen einer kategorialen Variable und einer kontinuierlichen Variable in einem statistischen Modell visualisiert als Schalter und Schieberegler. Übersetzt nach Heiss (2022)

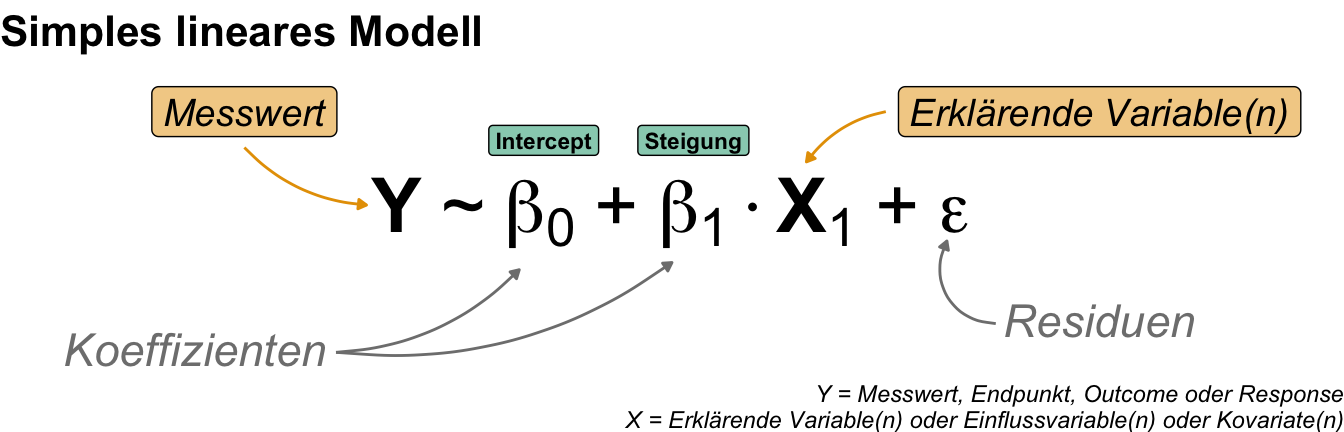
Wir können usn den Schieberegeler auch einmal mathematisch aufschreiben, Wir haben dann unseren Messwert auf der linken Seite und unsere erklärenden Variablen auf der rechten Seite. Unser \(X\) kann dann entweder eine Kovariate oder eben ein Faktor sein.

Abbildung 55.9— Formelschreibweise der simplen linearen Regression beinhaltend die Koeffizienten \(\beta_0\) für den y-Achsenabschnitt sowie \(\beta_1\) für die Steigung der Graden für eine Einflussvariable \(x_1\). Die Residuen werden durch \(\epsilon\) abgebildet. [Zum Vergrößern anklicken]

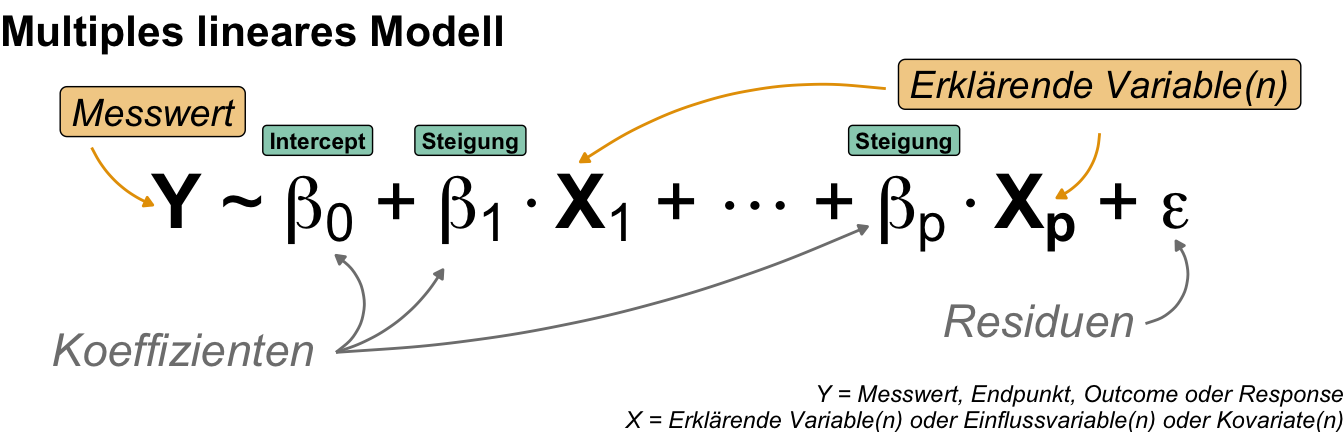
Als wäre das nicht kompliziert genug, schauen wir uns meistens dann nicht nur eine \(x\) Variable in einem Modell an, die wir dann ändern, sondern eben mehrere. Dann kombinieren wir noch gerne kontinuierliche und kategoriale \(x\)-Werte in einem Modell miteinander und erhalten ein Mischboard. Wir können einiges an Schiebereglern und Schaltern in einem Modell betätigen und erhalten entsprechende andere \(y\)-Werte. Hier helfen dann auch Marginal effect models um mehr Erkenntnisse aus einem Modell zu erhalten. Mehr dazu im Kapitel zu der multiplen linearen Regression.

Abbildung 55.10— Kombination verschiedener kategorialer Variablen und kontinuierlichen Variablen in einem statistischen Modell visualisiert als Mischboard. Übersetzt nach Heiss (2022)

Wenn wir uns dann eine multiple lineare Regression anschauen, dann haben wir immernoch einen Messwert vorliegen. Wir haben aber jetzt mehr erklärende Variablen, die eben nur Kovariaten oder Faktoren sein können oder eben auch eine Mischung aus beidem. Dann haben wir kombinierte Modelle aus Kovariaten und Faktoren vorliegen.

Abbildung 55.11— Formelschreibweise der multiplen linearen Regression beinhaltend die Koeffizienten \(\beta_0\) für den y-Achsenabschnitt sowie \(\beta_1\) bis \(\beta_p\) für die partielle Steigung der Graden für jede Einflussvariable \(x_1\) bis \(x_p\). Die Residuen werden durch \(\epsilon\) abgebildet. [Zum Vergrößern anklicken]

Somit kommen wir dann hier mal zu einer Definition, wie wir dann die beiden Arten der möglichen \(x\)-Werte als kontinuierliche und kategoriale Werte sprachlich unterscheiden. Wir immer, je nach wissenschaftlichen Hintergrund können sich dann die Namen ändern und anders sein. Das ist dann eben so in der Statistik.

Marginal effect (deu. marginaler Effekt)

Ein marginaler Effekt beschreibt den statistischen Effekt für kontinuierliche erklärende Variablen damit auch die partielle Ableitung einer Variablen in einem Regressionsmodell oder eben den Effekt eines einzelnen Schiebereglers.

Conditional effect (deu. bedingter Effekt) oder Gruppenkontrast (eng. group contrast)

Ein bedingter Effekt beschreibt den statistischen Effekt für kategoriale erklärende Variablen damit auch den Unterschied in den Mittelwerten, wenn eine Bedingung eingeschaltet ist und wenn sie ausgeschaltet ist. Der Effekt eines einzelnen Schalters.

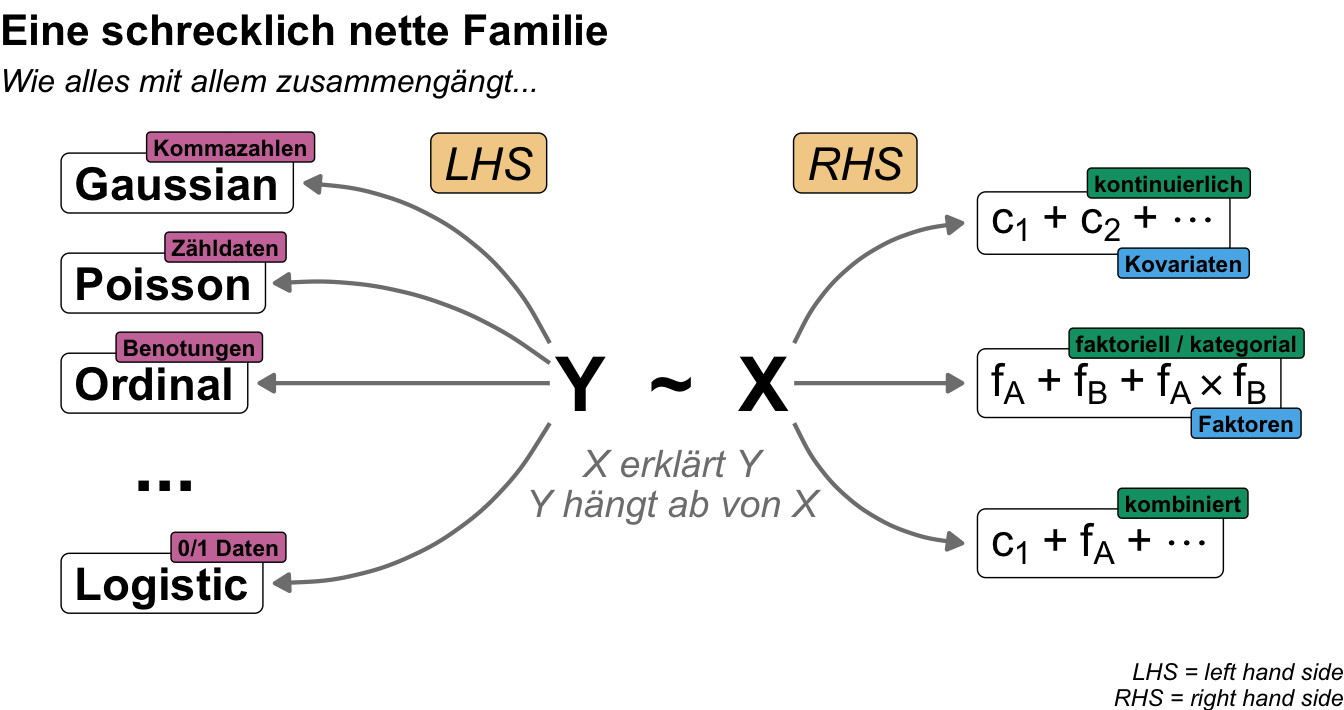
Als wäre das nicht schon kompliziert genug, variieren nicht nur die Einflussvariablen in der Anzahl und dem Typ. Wir haben auch je nach Messwert auch noch andere Eigenschaften unserer linken Seite. Je nach Messwert haben wir eine andere Verteilungsfamilie vorliegen und damit auch eine andere Interpretation unserer Einflussvariablen. In der folgenden Abbildung habe ich dir mal einen Auszuga aus der schreckliche netten Familie der Verteilungsfamilien mitgebracht. Wir sehen hier die Variationsmöglichkeiten in den Einflussvariablen wie auch in den Messwerten.

Abbildung 55.12— Erweiterte Darstellung der statistischen Modellierung. Die Messwerte \(Y\) folgen einer Verteilung. Die Einflussvariablen liegen kontinuierlich als Kovariaten oder aber kategorial als Faktoren vor. [Zum Vergrößern anklicken]

Unterschied {marginaleffects} und {emmeans}

Wenn wir Marginal effect models rechnen wollen, dann können wir im Prinzip auf zwei große Pakete zurückgreifen. Einmal das R Paket {marginaleffects} sowie das R Paket {emmeans}. Das R Paket {modelbased} setzt sich im Prinzip auf die beiden Pakete drauf und ist mehr oder minder ein Wrapper mit anderen Funktionsnamen. Das ist eigentlich eine gute Idee und ich zeige dann auch nochmal, wie sich das R Paket {modelbased} verhält. Kommen wir erstmal zu dem hauptsächlichen Unterschied zwischen unseren beiden Elefanten.

Wie unterscheiden sich {emmeans} und {marginaleffects}?

Das R Paket {emmeans} erstellt Durchschnittswerte der Daten und fügt diese Durchschnittswerte dann in Modelle ein. Das R Paket {marginaleffects} fügt alle Werte der Daten in ein Modell ein und erstellt dann Durchschnittswerte aus der Ausgabe des Modells. Am Ende ist es vermutlich dann auch wieder ein nur kleiner Unterschied, der was ausmachen kann. Aber da kommt es dann auf die wissenschaftliche Fragestellung an.

Dabei gibt es noch einen weiteren bedeutenden Unterschied zwischen den beiden Paketen, die sich dann direkt aus der Aggregierung der Daten ableitet. Die Frage ist ja, erst den Mittelwert bilden und dann Modellieren oder umgekehrt. Das R Paket {emmeans} hat als philosophischen Hintergrund experimentelle Daten als Basis. Das R Paket {marginaleffects} hingegen nimmt beobachtete Daten an. Hier möchte ich dann einmal die Vingette des R Pakets {emmeans} zitieren.

“To start off with, we should emphasize that the underpinnings of estimated marginal means – and much of what the {emmeans} package offers – relate more to experimental data than to observational data. In observational data, we sample from some population, and the goal of statistical analysis is to characterize that population in some way. In contrast, with experimental data, the experimenter controls the environment under which test runs are conducted, and in which responses are observed and recorded. Thus with experimentation, the population is an abstract entity consisting of potential outcomes of test runs made under conditions we enforce, rather than a physical entity that we observe without changing it.” — R Paket {emmeans}

Was will uns nun dieser Text sagen und was bedeutet der Unterschied zwischen experimentellen und beobachteten Daten?

• Wir nutzen {emmeans}, wenn wir Gruppenvergleiche aus einem experimentellen, faktoriellen Design rechnen wollen. Solche faktorielle Designs sind in den Agrarwissenschaften sehr häufig.
• Wir nutzen {marginaleffects}, wenn wir beobachtete Daten vorliegen haben. Dies ist sehr häufig bei zeitlichen Verläufen der Fall. Wenn wir also wissen wollen, wie ändert sich den Messwert über die Zeit?

Am Ende nutze ich dann in den Gruppebvergleichen immer noch {emmeans}, da das Paket einfach besser zu dem faktoriellen Design passt. Wenn wir uns aber mit Modellen beschäftigen, dann bevorzuge ich das R Paket {marginaleffects}. Oder um es etwas klarer zu sagen, sobald ich eine Kovariate in meinem Modell habe, dann wechsel ich das Paket und rechne alles in {marginaleffecst}. Damit haben wir alles zusammen, um uns jetzt einmal mit der Anwendung der Marginal effect models zu beschäftigen.

55.3 Genutzte R Pakete

Wir wollen folgende R Pakete in diesem Kapitel nutzen.

pacman::p_load(tidyverse, gtsummary, marginaleffects, emmeans, scales,
               janitor, ggpmisc, conflicted)
conflicts_prefer(dplyr::mutate)
conflicts_prefer(dplyr::summarize)
conflicts_prefer(dplyr::filter)
conflicts_prefer(ggplot2::annotate)
cb_pal <- c("#000000", "#E69F00", "#56B4E9", 
            "#009E73", "#F0E442", "#F5C710", 
            "#0072B2", "#D55E00", "#CC79A7")
## 
nice_number <- label_number(style_negative = "minus", accuracy = 0.01)
nice_p <- label_pvalue(prefix = c("p < ", "p = ", "p > "))
find_intercept <- function(x1, y1, slope) {
  intercept <- slope * (-x1) + y1
  return(intercept)
}

An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.

55.4 Daten

Wir brauchen auch hier nochmal Daten an denen wir uns die Prinzipien der Marginal effect models verstehen können. Ich nutze hier einmal einen simplen Datensatz zu der Enzymaktivität unter verschiedenen pH-Werten. Der Datensatz ist einfach und hat im Prinzip nur die Kovariate pH-Wert, die zwar auch als Faktor gesehen werden kann, aber wir machen es uns hier einfach. Anhand des Beispiels können wir gut die Grundlagen der Marginal effect models nachvollziehen. Als zweiten Datensatz habe ich nochmal die Modellierung von Flöhen mitgebracht. In dem Datensatz zu der Modellierung von Flöhen finden wir viele Kovariaten sowie Faktoren und verschiedene Messwerte, die von Interesse sind. Wir können uns also in dem Datensatz einiges anschauen.

Modellierung von Enzymen

Der Datensatz zu der Enzymaktivität ist ziemlich simple. Wir haben zu verschiedenen pH-Werten die Enzymaktivität gemessen. An jedem pH-Wert haben wir dann bis zu fünfmal wiederholt gemessen. Darüber hinaus haben wir noch drei pH-Wertgruppen gebildet und die Messungen in Prokaryoten sowie Eukaryonten durchgeführt. Die pH-Werte wurden abschließend nochmal standardisiert, so dass die Werte nicht nur im Intervall \({0,14}\) liegen. Mit dem Datensatz lassen sich nun die Steigung und die Vorhersage von der Enzymaktivität sehr gut in Marginal effect models veranschaulichen.

enzyme_tbl <- read_excel("data/enzyme_kinetic.xlsx") |> 
  mutate(grp = factor(grp, levels = c("niedrig", "mittel", "hoch")))  

In der folgenden Tabelle siehst du dann einmal die Daten mit den Messwiederholungen. Später werden wir dann die Enzymaktivität an den pH-Werten mitteln und die pH-Werte als eine Kovariate behandeln. Wenn wir einen Faktor betrachten wollen, dann nehmen wir die gruppierten pH-Werte. Wir werden für die Modellierung die Prokaryoten und Eukaryoten zusammen auswerten.

Tabelle 55.6— Daten für die Enzymaktivität in Prokaryoten und Eukaryoten unter standardisierten pH-Werten mit bis zu fünf Messwiederholungen sowie einer Einteilung der pH-Werte in drei Gruppen.

ph	activity	grp	type
-2	-38.05	niedrig	Prokaryot
-2	-43.07	niedrig	Prokaryot
-2	-51.55	niedrig	Prokaryot
…	…	…	…
7.5	57.68	hoch	Eukaryot
7.5	60.68	hoch	Eukaryot
7.5	69.32	hoch	Eukaryot

Dann sehen wir hier nochmal wie oft die Enzymaktivität dann jeweils wiederholt für einen standardisierten pH-Wert gemessen wurde. Wir haben hier keinen Unterschied zwischen den Prokaryoten und Eukaryoten gemacht. Für die Modellierung werden die Prokaryoten und Eukaryoten zusammen betrachtet. Das macht uns dann die Auswertung etwas einfacher.

Tabelle 55.7— Anzahl der Messweiderholungen der pH-Werte über die gesamten Daten. Für die Modellierung werden die Prokaryoten und Eukaryoten zusammen betrachtet.

ph	n	percent
-2.0	3	7.0%
-1.0	5	11.6%
0.0	4	9.3%
1.0	4	9.3%
2.0	4	9.3%
3.0	4	9.3%
4.0	4	9.3%
5.0	3	7.0%
6.0	5	11.6%
7.0	4	9.3%
7.5	3	7.0%

Da wir hier theoretische Daten vorliegen haben, kennen wir auch die Funktion der Datengenerierung im Hintergrund. Wir haben folgende mathematische Funktion als Grundlage vorliegen. Daraus ergibt sich dann auch die entsprechende erste Ableitung für die Steigung der Tangente entlang der Funktion der Enzymaktivität.

Funktion der Enzymaktivität \(f(x)\)

Mit der folgenden Funktion der Enzymaktivität wurden die Daten generiert. Damit ist dann auch die wahre Funktion bekannt.

\[ f(x) = x^3 - 8x^2 + 10x + 10 \]

Erste Ableitung der Enzymaktivität \(f'(x)\)

Mit der wahren Funktion der Enzymaktivität können wir dann auch einfach die erste Ableitung bilden und sind nicht auf eine Modellierung angewiesen.

\[ f'(x) = 3x^2 - 16x + 10 \]

Dann können wir uns auch schon einmal die Abbildungen unseres Datensatzes zu den Enzymaktivität anschauen. Dabei sehen wir sehr gut, wie die Grade durch die Punkte verläuft und dabei eine S-Kurve bildet. Wir haben hier klar keinen linearen Zusammenhang vorliegen und damit ist die Steigung entlang der Graden auch nicht konstant. Wir werden dann weiter unten einmal die Steigung entlang der Graden mit den Marginal effect models analysieren.

Abbildung 55.13— Scatterplot der Enzymaktivität in Abhängigkeit vom standardisierten pH-Wert kombiniert über die Prokaryoten und Eukaryoten. Die Grade stellt den wahre Zusammenhang aus der Funktionsgleichung dar. [Zum Vergrößern anklicken]

Neben der Steigung haben wir noch die Gruppen nach den Prokaryoten und Eukaryoten sowie den ph-Wertgruppen vorliegen. Auch hier können wir dann die Marginal effect models nutzen um mehr über die Unterschiede zwischen den Gruppen zu erfahren. Durch die S-Kurve sehen wir sehr schön, dass auch die Varianz in den pH-Wertgruppen unterschiedlich ist. Je nachdem wie viele ph-Werte zusammengefasst wurden, sind die Werte der Enzymaktivität stark unterschiedlich.

Abbildung 55.14— Darstellung der Enzymaktivität gruppiert nach den Gruppen des pH-Wertes. (A) Gruppierter pH-Wert über die Prokaryoten und Eukaryoten. (B) Gruppierter pH-Wert getrennt für die Prokaryoten und Eukaryoten. [Zum Vergrößern anklicken]

Modellierung von Flöhen

Kommen wir un zu unserem zweiten kpmlexeren Datensatz. Wir schauen usn hier die Sprungweiten von Katzenflöhen unter verschiedenen Fütterungebedingungen an. Dabei haben die Katzeflöhe einmal Zuckerwasser, Ketchup sowie Blut als Nahrung erhalten. Als zweiten Faktor betrachten wir dann noch juvenile udn adulte Flöhe. Neben diesen beiden Faktoren, haben wir dann noch die Kovariate des Egwichts der Flöhe erhoben. Als weitere Messwerte kommen dann die Schlupfzeiten, die Bonitur der Flöhe, die Anzahl der Haare an einem Flohbein sowie der Infektionsstatus mit Flohschnupfen in Betracht. Teilweise können wir dann die kontinuierlichen Messwerte auch als Kovariaten in unseren Modellen verwenden. Da sind wir ja nicht festgelegt. Wir laden dann die Daten einmal in R und müssen noch etwas die Faktoren anpassen.

flea_model_tbl <- read_excel("data/fleas_model_data.xlsx") |> 
  mutate(feeding = as_factor(feeding),
         stage = as_factor(stage),
         bonitur = as.numeric(bonitur),
         infected = factor(infected, labels = c("healthy", "infected"))) |> 
  select(feeding, stage, jump_length, weight, hatched, count_leg,  bonitur, infected) 

Wir haben jetzt hier das Problem, dass die Schlupfzeit in Stunden gemessen wurde, was extrem ungünstig ist, da die Einheiten so große Werte einnimmt. Daher haben wir dann später das Problem, dass eine Stunde Änderung einen sehr kleinen Effekt auf die Sprungweiten hat. Daher habe ich hier einmal die Schlupfzeit auf Wochen umgerechnet, dass macht dann die Effekte auf die Sprungweite größer und besser zu interpretieren.

flea_model_tbl <- flea_model_tbl |> 
  mutate(hatched = hatched/24/7)

Dann können wir uns auch schon mal einen Auszug aus der Datentabelle zu den Sprungweiten der Katzenflöhe anschauen.

Tabelle 55.8— Daten für die Modellierung verschiedener Messwerte für Katzenflöhe unter drei Ernährungsformen sowie zwei Entwicklungsstadien. Zusaätzlich wurde noch das Flohgewicht erhoben. Teilweise können die Messwerte auch als Einflussvariablen im Modell genutzt werden.

feeding	stage	jump_length	weight	count_leg	hatched	bonitur	infected
sugar_water	adult	77.2	16.42	63	516.41	4	infected
sugar_water	adult	56.25	12.62	55	363.5	1	healthy
sugar_water	adult	73.42	15.57	112	303.01	2	healthy
…	…	…	…	…	…	…	…
ketchup	juvenile	83.38	7.18	423	429.18	4	infected
ketchup	juvenile	104.48	6.6	548	629.58	5	infected
ketchup	juvenile	130.18	4.19	869	192.66	5	healthy

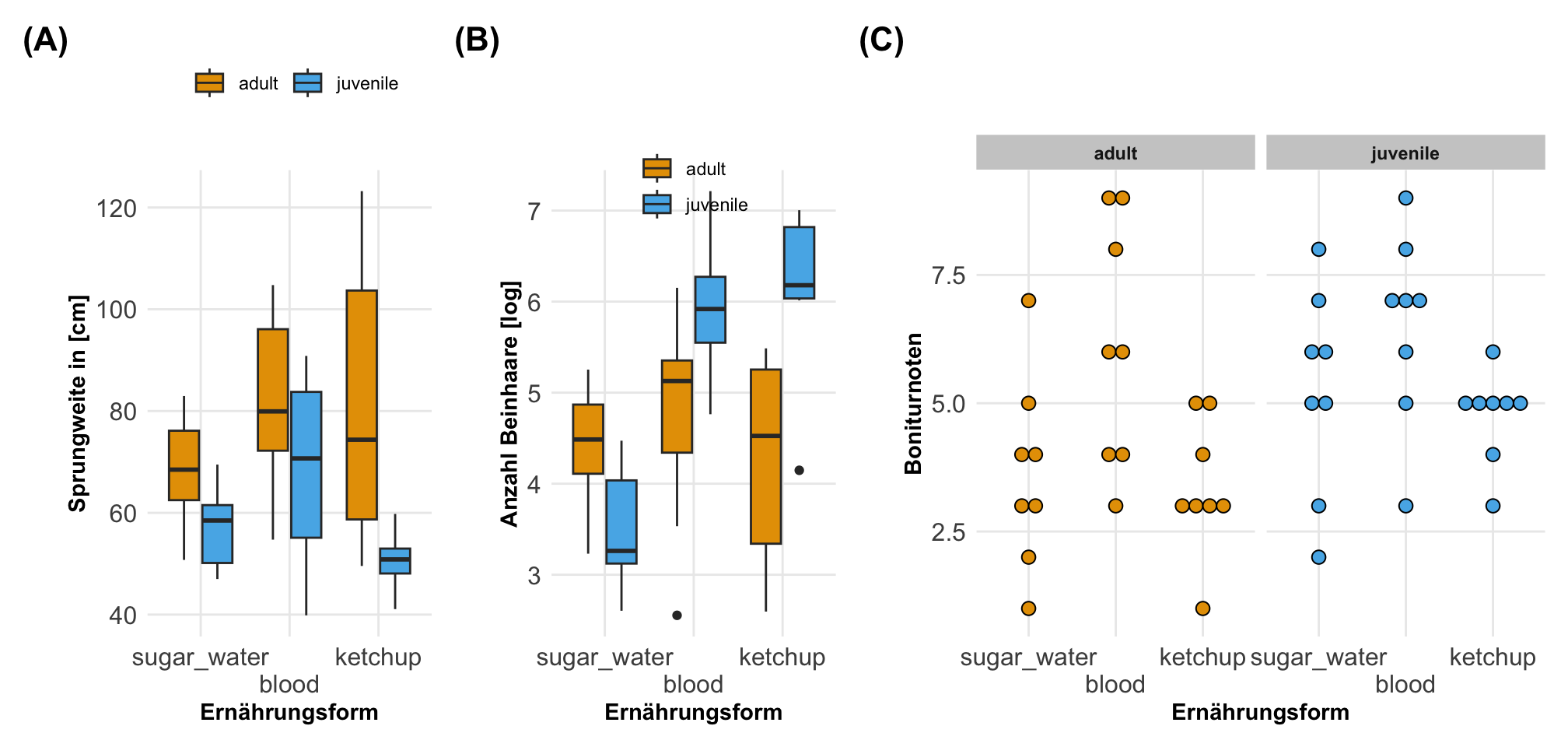
Dann können wir uns einmal ausgewählte Boxplots und Dotplots für die Flohdaten anschauen. Wir sehen hier sehr schön, dass sich die Sprungweiten über die Ernährungsformen und den Entwicklungsständen anscheinend unterschieden. Auch haben wir Effekte in der Anzahl an Beinhaaren. Die Boniturnoten sehen eher etwas gleichmäßiger aus. Die eigentlichen Effekte oder statistischen Tests wollen wir dann auszugsweise in den folgenden Abschnitten einmal rechnen.

Abbildung 55.15— Darstellung der Messwerte der Sprungweite, der Anzahl an Beinhaaren sowie der Boniturnoten der Katzenflöhe aufgeteilt nach den drei Ernährungsformen sowie dem Entwicklungsstand. (A) Boxplot der Sprungweiten nach Ernährungsform und Entwicklungssstand. (B) Boxplot der Anzahl an Beinhaaaren nach Ernährungsform und Entwicklungssstand. (C) Dotplot der Boniturnoten nach Ernährungsform und Entwicklungssstand. [Zum Vergrößern anklicken]

Da wir natürlich binäre Messwerte wie den Infektionsstatus mit Flohschnupfen schlecht als eine Abbildung über zwei Faktoren darstellen können, habe ich hier nochmal die klassische Tabelle gewählt. Wir sehen hier einmal wie sich die Anteile an gesunden und kranken Flöhen über die beiden Faktoren verteilen. In beiden Faktoren meint man einen Unterschied zwischen den Infektionen zu erkennen.

Tabelle 55.9— Deskriptive Statistik des Infektionsstatus der Katzenflöhe mit Flohschnupfen aufgeteilt nach der Ernährungsform und dem Entwicklungsstand.

Characteristic	healthy N = 211	infected N = 271
feeding
sugar_water	9 / 21 (43%)	7 / 27 (26%)
blood	3 / 21 (14%)	13 / 27 (48%)
ketchup	9 / 21 (43%)	7 / 27 (26%)
stage
adult	14 / 21 (67%)	10 / 27 (37%)
juvenile	7 / 21 (33%)	17 / 27 (63%)
1 n / N (%)

In den folgenden Abschnitten werden wir dann immer wieder Teile der Flohdaten nutzen um die Marginal effect models besser zu verstehen und anzuwenden. Ich werde nicht den ganzen Datensatz auswerten sondern immer wieder schauen, welcher Teilaspekte mehr von Interesse sind.

55.5 Visualisierung von Modellen

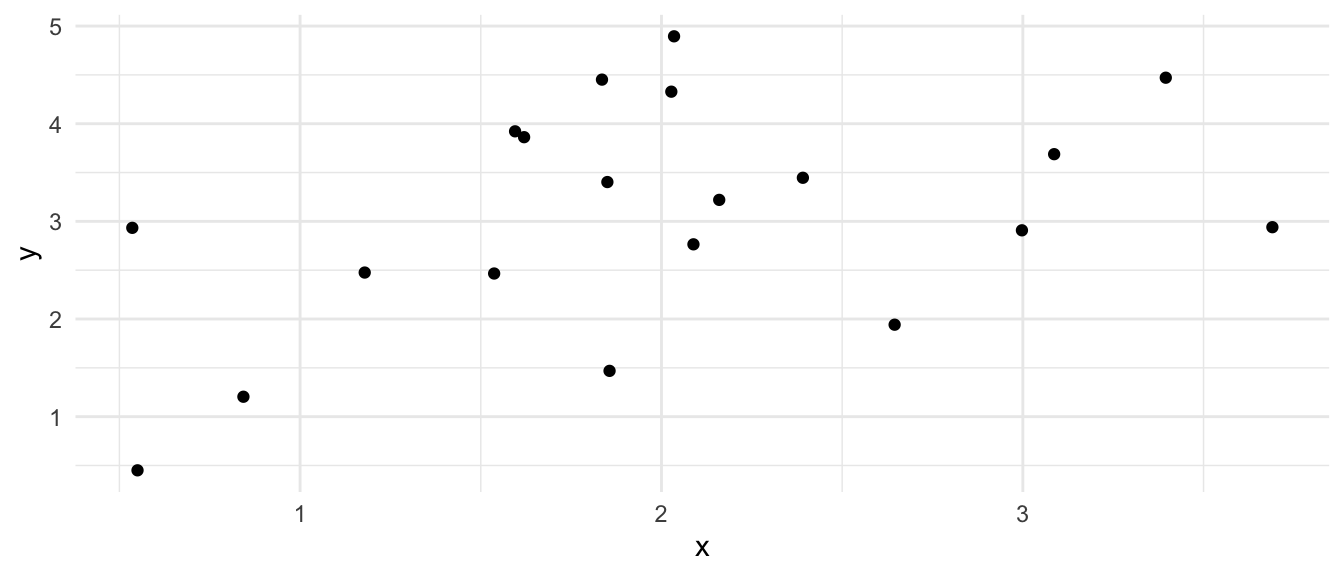
In dem folgenden Abschnitten wollen wir immer Modell in unsere Visualisierungen einzeichen. Nehmen wir einmal einen simplen Datensatz, den wir uns einfach selber bauen und dann wollen wir dort eine Linie durchzeichnen. Dafür nehmen wir einmal zwanzig x-Werte und bauen uns dann die y-Werte nach \(y = 1.5 + 0.75 \cdot x\) zusammen. Dann addieren wir noch einen Fehler aus einer Standardnormalverteilung hinzu. Wenn wir keinen Fehler hinzuaddieren würden, dann lägen die Punkte wie auf einer Perlenschnur aneinandergereit.

set.seed(20250703)
modell_line_tbl <- tibble(x = rnorm(20, 2, 1),
                          y = 1.5 + 0.75 * x + rnorm(length(x), 0, 1))

Jetzt können wir einmal das Modell anpassen und schauen, ob wir die Koeffizienten des Modells wiederfinden. Dann wollen wir natürlich auch sehen, ob unser Modell durch die Punkte läuft. Also erstmal das Modell mit lm() gebaut. Dann schauen wir uns noch die Koeffizienten einmal mit an. Bei nur so wenigen Beobachtungen werden die Koeffizienten aus dem Modell nicht mit den voreingestellten übereinstimmen.

model_fit <- lm(y ~ x, modell_line_tbl)
model_fit

Call:
lm(formula = y ~ x, data = modell_line_tbl)

Coefficients:
(Intercept)            x  
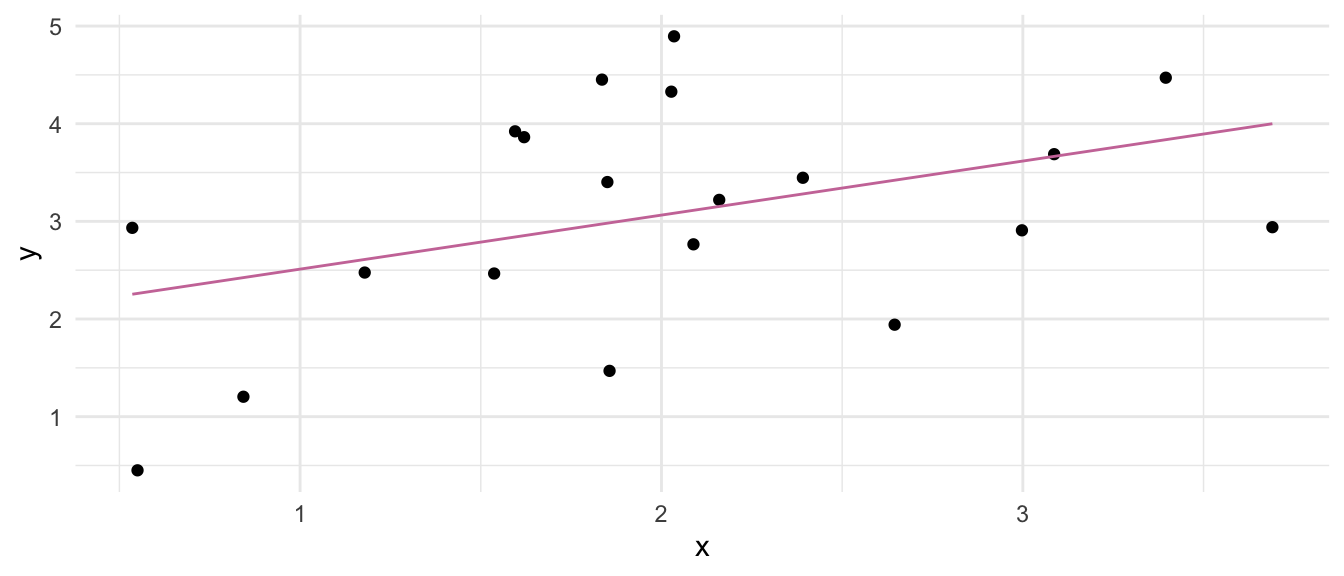
     1.9574       0.5534  

In der folgenden Abbildung siehst du dann einmal den Scatterplot von unseren x-Werten und y-Werten. Wir wollen jetzt die Gerade, die wir im Modell geschätzt haben einmal durch die Punkte legen um zu schauen, ob das Modell auch die Punkte beschreibt. Dabei soll die Gerade durch die Mitte der Punkte laufen und die Punkte sollten auf beiden Seiten der Geraden gleichmäßig verteilt sein.

Abbildung 55.16— Scatterplot der x-Werte und y-Werte. Durch die Punkte soll die Gerade aus dem Modell gelegt werden. [Zum Vergrößern anklicken]

Wir haben jetzt verschiedene Möglichkeiten die Koeffizienten und damit das Modell in den obigen Plot einzuzeichnen. Ich zeige dir hier einmal die häufigsten, die ich dann auch nutze. Erstmal die Anwendung direkt in {ggplot} und dann einmal noch in dem R Paket {ggpmisc}.

…mit {ggplot}

geom_function()

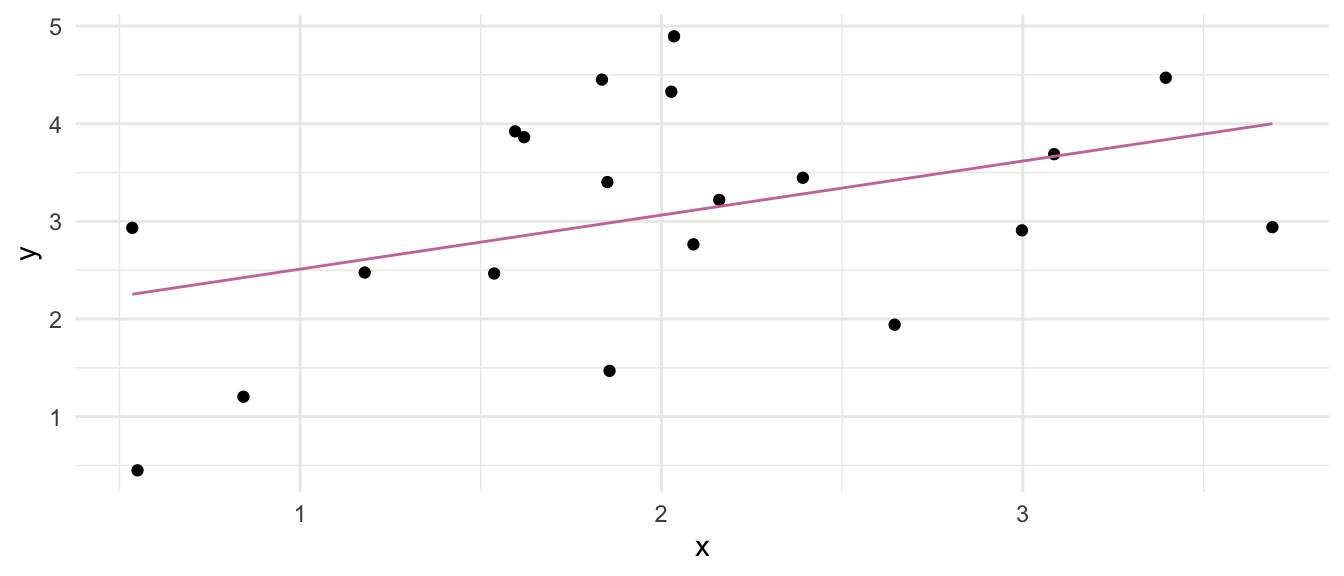
In der Funktion geom_function() müssen wir die Funktion angeben, die wir dann abbilden wollen. Wenn du verstehst, was die Koeffizienten in dem Modell bedeuten, dann kannst du natürlich die mathematische Funktion wie hier entsprechend ergänzen.

ggplot(modell_line_tbl, aes(x, y)) +
  theme_minimal() +
  geom_point() +
  geom_function(fun = \(x) 1.9574 + 0.5534 * x, 
                color = "#CC79A7")

Abbildung 55.17— Scatterplot der x-Werte und y-Werte. Durch die Punkte läuft die Gerade mit den Koeffizienten aus dem Modell. [Zum Vergrößern anklicken]

geom_line(aes(y = predict(model_fit)))

Manchmal ist das Modell zu komplex, dass wir die mathematische Funktion einfach aufschreiben könnten. In dem Fall hilft die Funktion geom_line() die wir dann die vorhergesagten y-Werte mit der Funktion predict() aus dem Modell übergeben. Das funktioniert auch sehr gut.

ggplot(modell_line_tbl, aes(x, y)) +
  theme_minimal() +
  geom_point() +
  geom_line(aes(y = predict(model_fit)), 
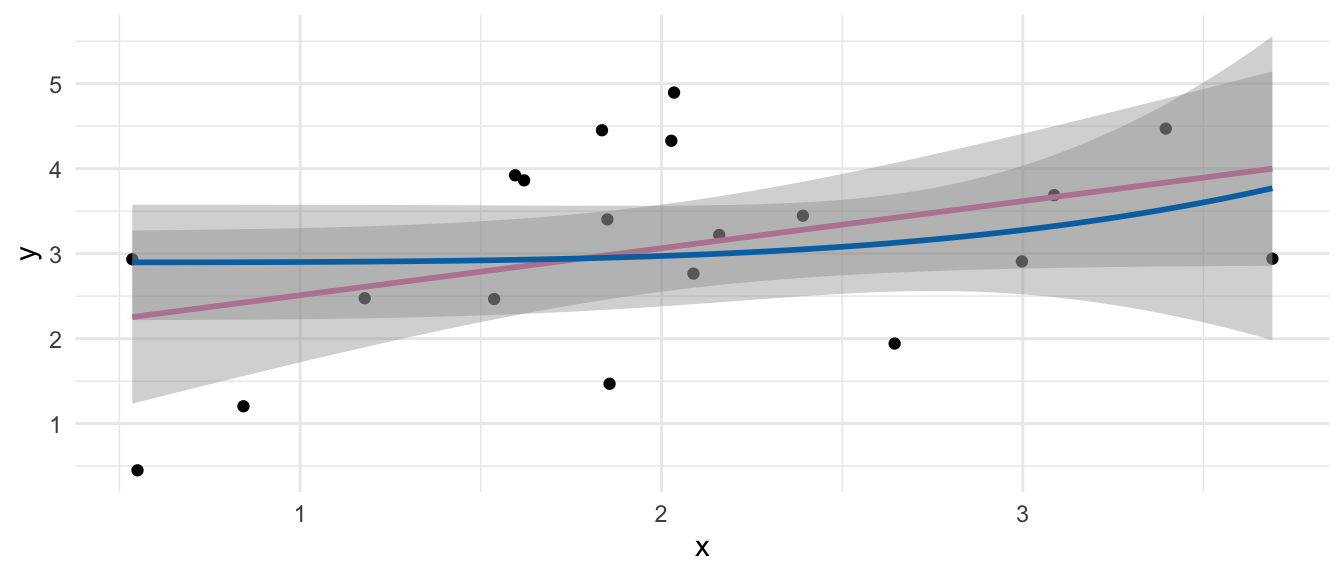
                color = "#CC79A7")

Abbildung 55.18— Scatterplot der x-Werte und y-Werte. Durch die Punkte läuft die Gerade mit den vorhergesagten Werten aus dem Modell. [Zum Vergrößern anklicken]

geom_smooth()

Abschließend können wir auch einfach so eine Gerade durch die Punkte legen indem wir die Funktion geom_smooth() als eine Art der Glättung nutzen. Aber hier muss ich sagen, dass uns dann die Geradengleichung fehlt. So mal zum gucken ist das wunderbar. Du kannst über die Option formula auch eine Funktion übergeben. Darüber hinaus erhalten wir dann noch einen Fehlerbalken des Standardfehlers, was in manchen Fällen nützlich ist. Wenn du die Geradengleichung brauchst, dann schaue einmal in dem Paket {ggpmisc} rein.

ggplot(modell_line_tbl, aes(x, y)) +
  theme_minimal() +
  geom_point() +
  geom_smooth(method = "lm", color = "#CC79A7") +
  geom_smooth(method = "lm", formula = y ~ I(x^4), 
              color = "#0072B2")

Abbildung 55.19— Scatterplot der x-Werte und y-Werte. Durch die Punkte läuft die Gerade aus einer Glättung. [Zum Vergrößern anklicken]

…mit {ggpmisc}

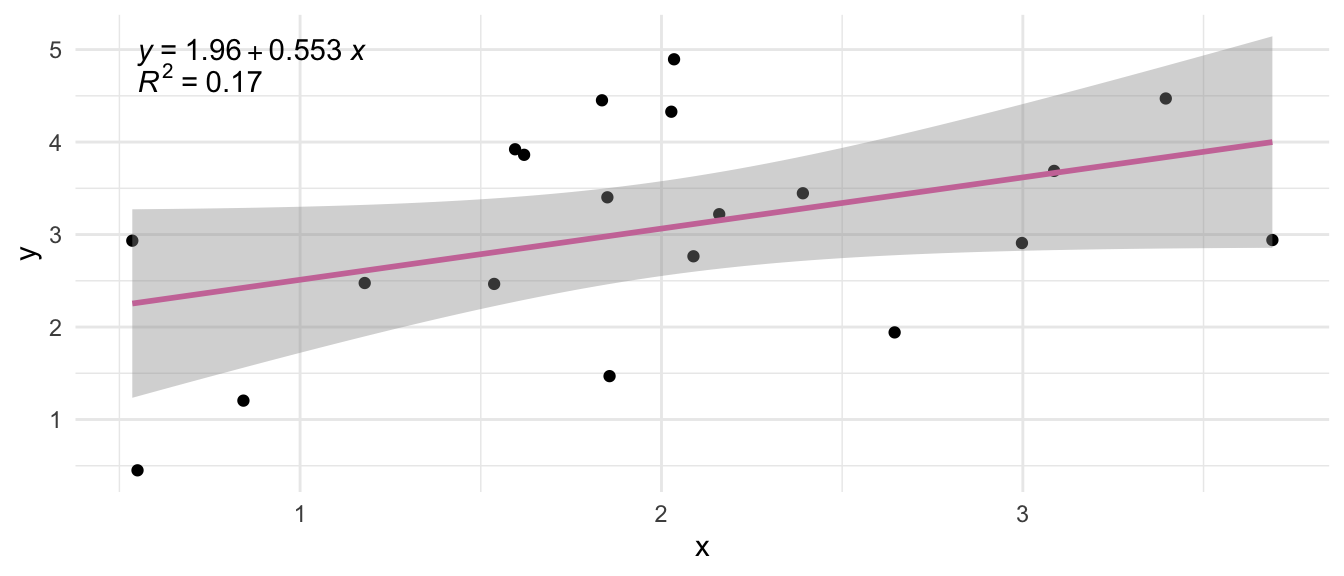
Ich möchte hier nich zu sehr in die Tiefe von {ggpmisc} gehen, aber das Paket verbindet im Prinzip die Funktion geom_smooth() mit der Wiedergabe der Informationen zu den Regressionsgleichungen. Du findest bei StackOverflow einmal eine schöne Übersicht in Add regression line equation and R^2 on graph. Wenn du mehr willst, dann schaue dir einmal die Hilfeseite von {ggpmisc} mit Fitted-Model-Based Annotations näher an. Es geht echt eine Menge, von dem ich hier nur einmal den Klassiker zeige. Wir wollen einmal die Regressionsgleichung plus das Bestimmtheitsmaß einzeichnen. Das geht über drei Funktionen zusammen mit der Regressionsgeraden.

ggplot(modell_line_tbl, aes(x, y)) +
  theme_minimal() +
  geom_point() +
  stat_poly_line(color = "#CC79A7") +
  stat_poly_eq(use_label("eq")) +
  stat_poly_eq(label.y = 0.9) 

Abbildung 55.20— Scatterplot der x-Werte und y-Werte. Durch die Punkte läuft die Gerade aus einer Glättung plus die Geradengleichung und das Bestimmtheitsmaß. [Zum Vergrößern anklicken]

55.6 Datenraster

Was ist ein Datenraster (eng. data grid) eigentlich? Wir brauchen die Idee des Datenrasters um überhaupt die Vorhersagen, die Steigung und die kontrafaktischen Vergleiche zu verstehen. Im Prinzip beinhaltet das Datenraster die Information zu welchen Beobachtungen wir eine Vorhersage machen oder die Steigung berechnen wollen. Wenn wir nochmal kurz zu dem Enyzmbeispiel kommen, zu welchen pH-Werten möchtest du dann eine Steigung oder aber eine Vorhersage der Enzymaktivität haben? Beginnen wir mit einem einfachen Beispiel um zu verstehen was die einzelnen Datenraster aussagen wollen. In Folgenden siehst du einmal einen kleinen Datensatz mit einer numerischen Variable, einer dichotomen Variable sowie einer Variable mit drei Kategorien. So ähnlich haben wir ja auch Datensätze in echt vorliegen.

set.seed(20250709)
grid_tbl <- tibble(numerisch = rnorm(n = 8),
                   dichotom = rbinom(n = 8, size = 1, prob = 0.5),
                   kategorial = sample(c("niedrig", "mittel", "hoch"), 
                                       size = 8, replace = TRUE))

Wir wollen uns nun einmal anhand des simplen Beispiels verschiedene Datenraster einmal anschauen und verstehen, was wir dann eigentlich damit machen. Im Prinzip kannst du dir ein Datenraster so vorstellen, dass wir fixe Werte für die Einflussvariablen definieren für die wir dann eine Aussage zu den Messwerten aus dem Modell haben wollen.

Beobachtetes Raster (eng. empirical grid)

Das beobachte Raster (eng. empirical grid) ist das einfachste Raster. Wir nehmen nämlich alle Beobachtungen, die wir im originalen Datensatz haben und berechnen dafür jeweils die Vorhersagen oder die Steigungen. Das heißt wir nutzen jede Einflussvariablenkombination, die wir dann in den Daten vorliegen haben. Im Sinne des Beispiels, ist es eben dann der Datensatz so wie er ist.

grid_tbl |> tt()

numerisch	dichotom	kategorial
0.32260788	1	niedrig
0.64136316	1	hoch
-0.81802243	1	mittel
-1.46551819	0	mittel
-0.01230531	1	mittel
-1.61493276	0	mittel
-0.82683177	0	mittel
0.76328096	1	hoch

In der folgenden Beobachtung siehst du das beobachtete Raster nochmal für die Daten der Enzymaktivität. Wir wollen für die pH-Werte in den Daten zum Beispiel jeweils die Enzymaktivität vorhersagen. Also welche Werte liegen auf der modellierten Grade? Hier wählen wir keine pH-Werte aus, sondern nehmen einfach alle. Ob das so Sinn macht ist eine andere Frage, wir müssten auf jeden Fall irgendwie unsere statistischen Maßzahlen zusammenfassen, sonst erhalten wir sehr viele Zahlen zurück.

Abbildung 55.21— Beobachtetes Raster für die Enzymaktivität abhängig von den pH-Werten. Alle pH-Werte in den Daten werden hier betrachtet. [Zum Vergrößern anklicken]

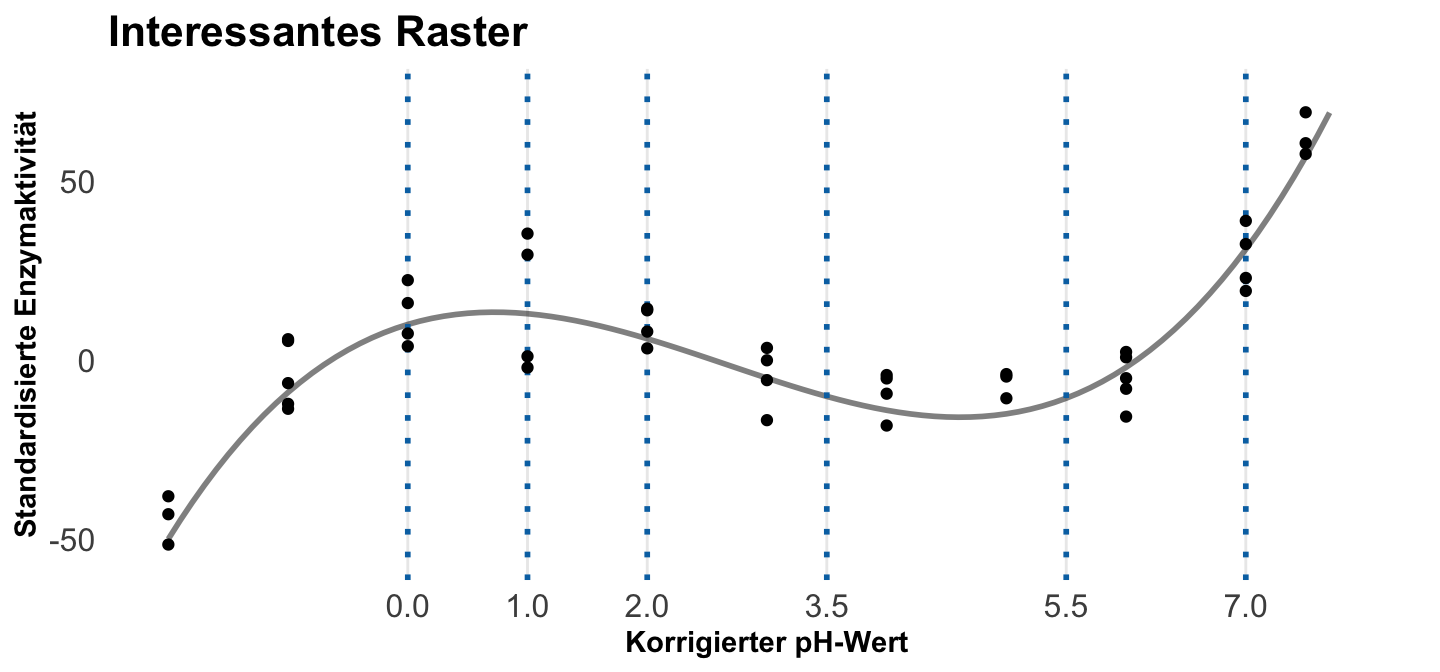
Interessantes Raster (eng. interesting grid)

Beim interessanten Raster (eng. interesting grid) nutzen wir nur die Werte einer oder mehrere Einflussvariablen, die uns dann wirklich interessieren. Dafür können wir dann das Datenraster so aufbauen, dass wir nur die für uns interessanten Werte mit ins Raster schreiben. Hier wollen wir die beiden Werte für die diochotome Variable einmal haben. Wenn wir nichts machen, dann erhalten wir dann die Mittelwerte für die numerische Variable und den Modus, also den häufigsten Wert, für die kategoriale Variable.

datagrid(dichotom = c(0, 1), newdata = grid_tbl) |> tt()

numerisch	kategorial	dichotom	rowid
-0.3762948	mittel	0	1
-0.3762948	mittel	1	2

Das ist natürlich etwas nervig, wenn wir nicht so genau wissen, was eigentlich mit den anderen Variablen passiert. Deshalb ist es hilfreich für die anderen Variablen auch mal anzugeben, was wir eigentlich wollen. Hier nochmal etwas wirrer der Mittelwert der dichotomen Variable und die Reichweite und die einzelnen Werte der kategorialen Variable in einem Raster. Der eigentlich Witz ist hier, dass eben die Funktion datagrid() auch andere Funktionen akzeptiert solange die Funktionen einen Vektor an Zahlen wiedergeben.

datagrid(numerisch = range, 
         dichotom = mean, 
         kategorial = unique, 
         newdata = grid_tbl) |> tt()

numerisch	dichotom	kategorial	rowid
-1.614933	0.625	niedrig	1
-1.614933	0.625	hoch	2
-1.614933	0.625	mittel	3
0.763281	0.625	niedrig	4
0.763281	0.625	hoch	5
0.763281	0.625	mittel	6

Das können wir uns in der folgenden Abbildung auch einmal beispielhaft für die Flohdaten anschauen. Wir wollen hier nur die Vorhersage oder die Steigung an bestimmten pH-Werten und nicht über alle pH-Werte hinweg.

Abbildung 55.22— Beobachtetes Raster für die Enzymaktivität abhängig von den pH-Werten. Nur ausgewählte pH-Werte werden in den folgenden Auswertungen betrachtet. [Zum Vergrößern anklicken]

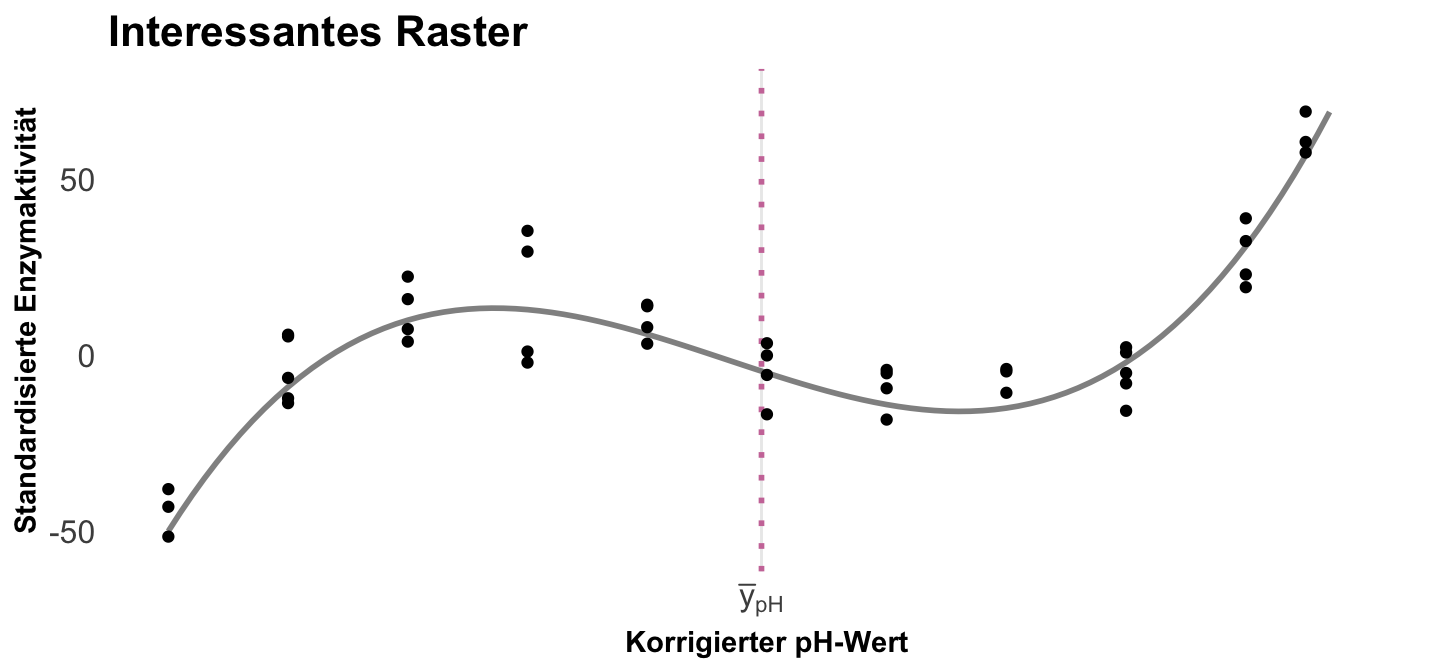
Repräsentatives Raster (eng. representative grid)

Das repräsentative Raster (eng. representative grid) dient eigentlich nur einer schnellen Übersicht. Wir erhalten hier eben die Werte an dem Median oder dem Mittelwert. Das ist von Interesse, wenn wir über komplexe Modelle mitteln wollen oder aber eben einen Wert haben wollen ohne ein Raster definieren zu müssen.

datagrid(grid_type = "mean_or_mode", newdata = grid_tbl) |> tt()

numerisch	dichotom	kategorial	rowid
-0.3762948	1	mittel	1

In der folgenden Abbildung siehst du einmal das repräsentative Raster mit dem Mittelwert der pH-Werte als einzigen Wert. Für diesen Wert würden wir dann die Steigung oder aber die Vorhersagen berechnen. Je nachdem wie unser Modell aussieht, ist dass eine mehr oder minder gut Idee.

Abbildung 55.23— Repräsentatives Raster für die Enzymaktivität abhängig von den pH-Werten. Wir betrachten als repräsentativen Wert hier den Mittelwert der pH-Werte. [Zum Vergrößern anklicken]

Balanciertes Raster (eng. balanced grid)

Manchmal brauchen wir auch ein balanciertes Raster in dem Sinne, dass wir jede Faktorkombination einmal vorhanden haben sowie die Mittelwerte der numerischen Einflussvariablen. Wie du im Folgenden siehst ist jede Kombination der dichotomen und kategorialen Variablen vorhanden und wir haben den Mittelwert der numerischen Variable.

datagrid(grid_type = "balanced", newdata = grid_tbl) |> tt()

numerisch	dichotom	kategorial	rowid
-0.3762948	0	hoch	1
-0.3762948	0	mittel	2
-0.3762948	0	niedrig	3
-0.3762948	1	hoch	4
-0.3762948	1	mittel	5
-0.3762948	1	niedrig	6

Wozu brauchen wir ein balanciertes Raster? Wir wollen manchmal eben eine Aussage über alle Faktorkombinationen treffen ohne den Modus der Kategorien zu verwenden. Dann macht eben ein balanciertes Raster schon Sinn. Ich habe es hier in den Beispielen nicht gebraucht, aber es ist gut zu wissen, dass wir sowas vorliegen haben.

Kontrafaktisches Raster (eng. counterfactual grid)

Das kontrafaktische Raster (eng. counterfactual grid) ist etwas schwerer zu verstehen. Wir fangen erstmal mit einem kleineren Datensatz an und nehmen uns die ersten fünf Zeilen unseres Spieldatensatzes. Wir sehen diese Daten dann einmal in dem folgenden linken Tab. In dem rechten Tab baue ich dann einmal das kontrafaktische Raster. Das kontrafaktische Raster baut für die Ausprägungen einer Variable alle Kombinationen in einem Raster nach. Wir wollen das hier einmal für unsere dichotome Variable machen.

Beobachtete Daten

Zuerst aber einmal unsere beobachteten Daten mit nur fünf Beobachtungen. Das ist hier einmal wichtig, da wir gleich unseren Datensatz durch das kontrafaktische Raster stark vergrößern werden.

cf_tbl <- grid_tbl[1:5,]

Wir haben hier also unsere fünf Beobachtungen vorliegen, die alle eine numerische Variable sowie eine kategoriale Variable vorliegen haben. Von Interesse ist gleich die dichotome Variable für die wir das kontrafaktische Raster bauen wollen.

cf_tbl |> tt()

numerisch	dichotom	kategorial
0.32260788	1	niedrig
0.64136316	1	hoch
-0.81802243	1	mittel
-1.46551819	0	mittel
-0.01230531	1	mittel

Kontrafaktisches Raster

Wir brauchen einmal die Option grid_type = "counterfactual" um uns ein kontrafaktische Raster zu bauen. Dazu kommt dann noch ein Datensatz und die Variable über die das kontrafaktische Raster gebaut werden soll. Wie wir gleich sehen, hat unser Raster doppelt so viele Beobachtungen wie unser ursprünglicher beobachteter Datensatz.

cf_grid <- datagrid(
  dichotom = c(0, 1),
  grid_type = "counterfactual",
  newdata = cf_tbl)
nrow(cf_grid )

[1] 10

Schauen wir uns einmal das kontrafaktische Raster genauer an. Wir sehen, dass wir für jede Ausprägung der dichotomen Variable alle Werte der restlichen Variablen einmal gesetzt haben. Wir bauen uns im Prinzip ein Raster bei dem wir so tun, als ob alle Beobachtungen einmal den Wert 0 bei der dichotomen Variable sowie den Wert 1 haben. Daher können wir berechnen, wie die Steigung oder die Vorhersagen sich ändern würden, wenn sich die dichotome Variable von Null auf Eins ändert.

cf_grid |> tt()

rowidcf	numerisch	kategorial	dichotom
1	0.32260788	niedrig	0
2	0.64136316	hoch	0
3	-0.81802243	mittel	0
4	-1.46551819	mittel	0
5	-0.01230531	mittel	0
1	0.32260788	niedrig	1
2	0.64136316	hoch	1
3	-0.81802243	mittel	1
4	-1.46551819	mittel	1
5	-0.01230531	mittel	1

Das kontrafaktische Raster ist schwerer zu verstehen, wenn wir es nicht in der Anwendung sehen. Dazu dann aber mehr in einem Abschnitt weiter unten. Dort gehe ich dann nochmal auf die direkte Anwendung ein. Hier soll es dann erstmal genug sein mit den Datenrastern. Stell dir einfach die Datenraster als einen zusärtzlichen Datensatz vor, der die Werte der Einflussvariablen beinhaltet, die dich im Bezug auf den Messwert interessieren.

55.7 Steigung (eng. slopes)

“Let us introduce another concept that is likely to get very popular in the near future within the world of regressions. Derivatives.” — {modelbased}

Beginnen wir einmal mit der Steigung. Das heißt, wir haben hier zumindest ein einkovariates Modell vorliegen. Wir haben auf der x-Achse die Kovariate und dann kann es noch sein, dass wir zusätzlich einen Faktor als gruppierende Variable vorliegen haben. Wenn du mehr als einen Faktor vorliegen hast, dann wird die Sache schon sehr kompliziert. Die Idee ist ja, wie sich die Werte des Messwerts in Abhängigkeit der Kovariate ändern. Darüber hinaus macht die Betrachtung der Steigung erst so richtig Sinn, wenn wir uns mit nicht lineare Modellen beschäftigen. Ansonsten ist die Steigung ja über den ganzen Zahlenraum der Kovariate konstant. Mag auch von Interesse sein, aber die Stärke der Marginal effect models liegt dann doch eher in der Beschreibung der Steigung von nicht linearen Modellen. Fangen wir aber einmal mit den Grundlagen in einem einkovariaten Modell an.

55.7.1 Einkovariates Modell

Im Folgenden schauen wir usn einmal die Modellierung der Flöhe an. Dort betrachten wir dann wie sich die Sprungweiten in Abhängigkeit von der Schlupfdauer verändert. Wir sidn hier wiedrum an der Steigung einer Tangente zu den Zeitpunkten der Schlupfzeiten interessiert. Hier sprechen wir dann auch von der Ableitung (eng. derivative). Die erste Ableitugn liefert uns ja die Steigung der Tangente an dem entsprechenden Punkt. Da wir hier nur ein einkovariates Modell vorliegen haben, müssen wir uns hier noch nicht mit komplexeren Abhängigkeiten rumschlagen.

Modellierung von Flöhen

In der folgenden Abbildung siehst du einmal die Zusammenhänge von der Schlupfzeit und der Sprungweite. In der linken Abbildung ist einmal der lineare Zusammenhang dargestellt. Da wir hier eine Grade zeichnen, haben wir natürlich nur eine Steigung. Die Steigung ist immer \(+10.5\) und damit nimmt die Sprungweite für jede Steigerung der Einheit in den Schlupfzeiten um \(+10.5cm\) zu. Das ist etwas langweilig und in einem linearen Modell benötigen wir auch prinzipiell keine Marginal effect models. Wir können trotzdem eines rechnen und dann von den statistischen Maßzahlen eines Marginal effect models profitieren, aber die Stärke liegt dann eben in dem nicht linearen Modell auf der rechten Seite. Wir haben hier eine S-Kurve und damit auch verschiedene Steigungen entlang der Graden. Das sehen wir dann auch an der ersten Ableitung, die wiederum noch die Kovariate enthält und somit ist die Steigung abhängig von dem Wert der Kovariate der Schlupfzeit.

Abbildung 55.24— Scatterplot der Sprungweiten und Schlupfzeiten von Flöhen. (A) Linearer Zusammenhang mit Gradengleichung und der ersten Ableitung (B) Quadratischer Zusammenhang mit S-Kurve sowie Gradengleichung und erster Ableitung. [Zum Vergrößern anklicken]

Schauen wir uns dann nochmal die Mathematik hinter den beiden Modellierungen an. Wir haben ja einmal den linearen Zusammenhang modelliert und eine Gradengleichung erhalten. Dann haben wir das Ganze auch einmal für den quadratischen Zusammenhang gemacht. Wir wollen jetzt einmal das Modell rechnen und dann noch die erste Ableitung bilden.

Linearer Zusammenhang (\(y \sim x\))

Beginnen wir mit dem linearen Zusammenhang. In der folgenden Modellierung rechnen wir einmal ein lineares Modell und erhalten dann den Intercept sowie die Steigung für die Schlupfzeiten. Wir haben hier eine Steigung von \(+10.5\) vorliegen. Für jede Woche mehr Schlupfzeit steigt die Sprungweite um \(10.5cm\) an.

model_ln <- lm(jump_length ~ hatched, data = flea_model_tbl)
tidy(model_ln)

# A tibble: 2 × 5
  term        estimate std.error statistic     p.value
  <chr>          <dbl>     <dbl>     <dbl>       <dbl>
1 (Intercept)     64.2     10.8       5.97 0.000000326
2 hatched         10.5      3.52      2.97 0.00468    

Wir können dann den Zusammenhang auch nochmal mathematisch aufschrieben. Wir wolle einmal die Ableitung für die Kovariate bilden. Die erste Ableitung bildet sich dann wie folgt.

\[ \begin{aligned} \operatorname{E}[y \mid x] &= \beta_0 + \beta_1 x \\[4pt] \frac{\partial \operatorname{E}[y \mid x]}{\partial x} &= \beta_1 \end{aligned} \]

Dann können wir das Ganze auch einmal durchführen. Wir haben ja die Zahlen für die Koeffizienten aus dem obigen Modell. Wir setzen also die Zahlen für den Intercept \(\beta_0\) und die Steigung \(\beta_1\) einmal ein und dann leiten wir nach der Schlupfzeit ab. Wir erhalten dann die Steigung von \(+10.5cm\) wieder.

\[ \begin{aligned} \operatorname{E}[\text{Sprungweite} \mid \text{Schlupfzeit}] &= 64.2 + 10.5 \times \text{Schlupfzeit} \\[6pt] \frac{\partial \operatorname{E}[\text{Sprungweite} \mid \text{Schlupfzeit}]}{\partial\ \text{Schlupfzeit}} &= 10.5 \end{aligned} \]

Das war jetzt kein großer Akt, aber wir sehen hier nochmal, wie die Idee ist. Wir hätten hier auch einfach die Koeffizienten aus dem Modell nehmen können, wie wir das auch ganz normal in der Interpretation eines linearen Modells machen. Spannender wird es in dem folgenden Tab, wenn wir eben keinen linearen Zuammenhang haben.

Quadratischer Zusammenhang (\(y \sim x + x^2 + x^3\))

Wenn wir eine quadratische Gleichung in R bauen, dann nutzen wir den Term I() um klar zu machen, dass wir jetzt einen quadratischen Term modellieren wollen. Prinzipiell könnten wir auch hier effizeinter die Funktion poly() nutzen, aber dann sehen wir nicht so gut die Koeffizienten und wir können auch nicht die Gradengleichung so einfach nachbauen. Mehr dazu dann im Kapitel zur nicht linearen Regression. Erstellen wir also einmal unser quadratisches Modell mit drei quadratischen Termen von \(x^1\) bis \(x^3\). Dann können wir die Koeffizienten einmal in unsere mathematische Formel einsetzen.

model_sq <- lm(jump_length ~ hatched + I(hatched^2) + I(hatched^3),
               data = flea_model_tbl)
tidy(model_sq)

# A tibble: 4 × 5
  term         estimate std.error statistic p.value
  <chr>           <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)    125.       44.7       2.80 0.00760
2 hatched        -53.8      49.0      -1.10 0.278  
3 I(hatched^2)    18.9      15.8       1.20 0.238  
4 I(hatched^3)    -1.61      1.51     -1.07 0.292  

Auch hier ist die mathematische Formel etwas länger und wir erhalten dann auch eine quadratische erste Ableitung für die Steigung an verschiedenen Werten der Schlupfzeiten.

\[ \begin{aligned} \operatorname{E}[y \mid x] &= \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3\\[4pt] \frac{\partial \operatorname{E}[y \mid x]}{\partial x} &= \beta_1 + 2 \beta_2 x + 3 \beta_3 x^2 \end{aligned} \]

Dann können wir die Koeffizienten aus dem Modell einmal in die Formel einsetzen und die erste Ableitung dann bilden. Hier sehen wir dann sehr schön, dass wir dann für verschiedende Schlupfzeiten immer andere Steigungen erhalten würden.

\[ \begin{aligned} \operatorname{E}[\text{Sprungweite} \mid \text{Schlupfzeit}] = 125 &+ (-53.8 \times \text{Schlupfzeit})\\ &+ (18.9 \times \text{Schlupfzeit}^2)\\ &+ (-1.6 \times \text{Schlupfzeit}^3) \end{aligned} \]

\[ \begin{aligned} \frac{\partial \operatorname{E}[\text{Sprungweite} \mid \text{Schlupfzeit}]}{\partial\ \text{Schlupfzeit}} = -53.8 &+ (2\times 18.9 \times \text{Schlupfzeit})\\ &+ (3 \times -1.6 \times \text{Schlupfzeit}^2) \end{aligned} \]

Wenn wir jetzt für jede Schlupfzeit dann immer die Steigung berechnen müssten, dann wäre das sehr aufwendig. Wir müssten ja erstmal das Modell rechnen, dann die mathematische Formel aufstellen. Danach könnten wir dann ja die erste Ableitung bilden. Je komplexer das Modell, desto aufwendiger wird es. Da kommen jetzt die Marginal effect models ins Spiel, die uns für sehr viele verschiedene Modelle die Steigungen wiedergeben können.

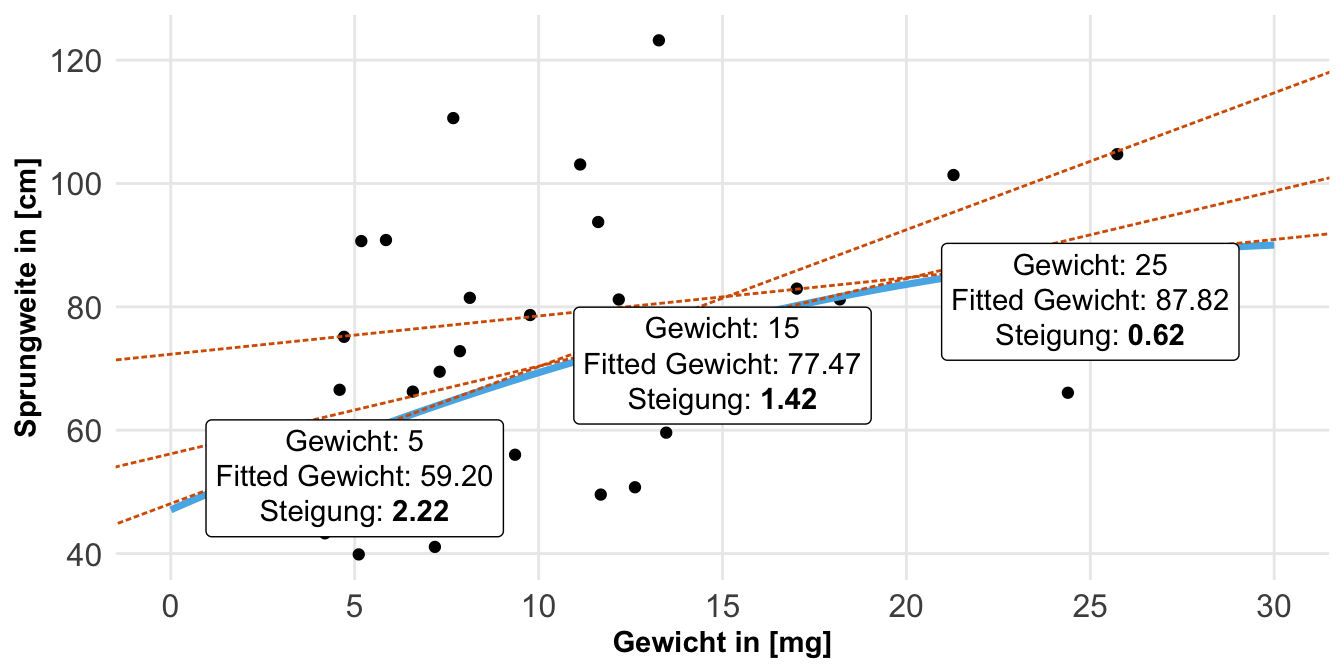
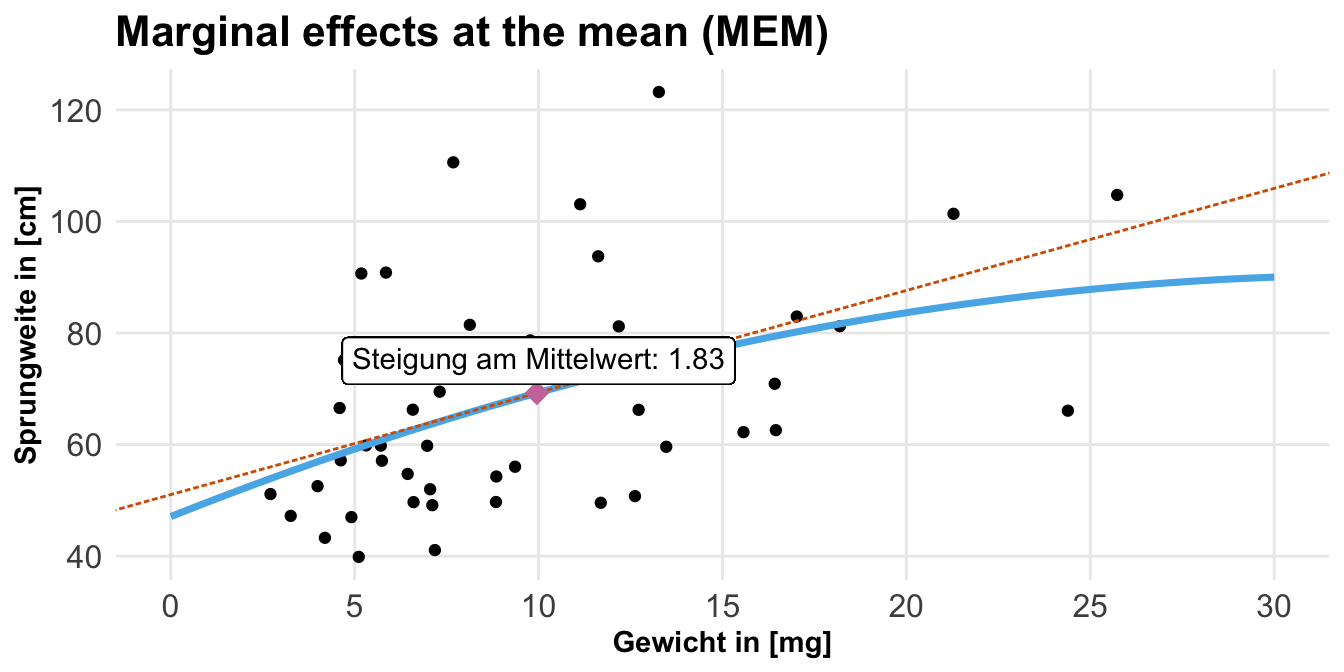
Betrachten wir nochmal die erste Ableitung der quadratischen Funktion für die Sprungweiten aus den Schlupfzeiten. Ich habe hier einmal die Funktion aufgeschrieben und dann einmal drei Werte für die Schlupfzeiten gewählt. Wir erhalten dann die Steigungen an den drei Schlupfzeiten durch die Funktion wiedergegeben. Für das erste ist es etwas ungewohnt, aber wir schauen uns die Steigung gleich einmal an.

jump_hatched_slope <- function(x) -53.8 + (2 * 18.9 * x) + (3 * -1.6 * x^2)
jump_hatched_slope(c(1.25, 3.5, 5.75))

[1] -14.05  19.70   4.85

In der folgenden Abbildung habe ich dir dan einmal für die drei Schlupfzeiten die Steigung mit der Tangente an den jeweiligen Punkten visualisiert. Wie du siehst haben die drei Punkte jeweils eine andere Steigung. Damit ist die Aussage auf die Sprungweite auch jeweils eine Andere, wenn wir uns verschiedene Schlupfzeiten anschauen. So haben wir zu geringen Schlupfzeiten eher einen Abfall der Sprungweiten und zu höhren Schlupzeiten eine Steigerung der Sprungweiten vorliegen.

Abbildung 55.25— Scatterplot der Sprungweite und der Schlupfzeiten. Die angepasste Grade läuft durch die Punkte. An drei Schlupfzeiten ist die Steigung der Tangente angegeben. Die Steigung unterscheidet sich durch die S-Kurve an allen drei Punkten. [Zum Vergrößern anklicken]

Jetzt ist es natürlich nicht immer möglich für jedes Modell die Gradengleichung zu erhalten. Auch wenn wir da mit WolframAlpha gute Möglichkeiten haben, Gleichungen abzuleiten oder aber zu bestimmen. Dennoch ist es für manche Modelle gar nicht so einfach möglich eien geschlossene ableitbare Gleichung zu erstellen. Oder es ist so komplex, dass es nicht erstrebenswert ist. Daher haben wir ja das R Paket {marginaleffects} welches uns für ein beliebiges Datenraster einmal die Steigung bestimmen lässt. Hier also einmal die Steigung für die drei Schlupzeiten.

model_sq |> 
  slopes(newdata = datagrid(hatched = c(1.25, 3.5, 5.75)),
         hypothesis = 0)

 hatched Estimate Std. Error      z Pr(>|z|)   S  2.5 % 97.5 %
    1.25    -14.2      17.52 -0.809    0.418 1.3 -48.50   20.2
    3.50     19.1       7.85  2.433    0.015 6.1   3.71   34.5
    5.75      3.4      20.83  0.163    0.870 0.2 -37.42   44.2

Term: hatched
Type: response
Comparison: dY/dX

Das Ganze geht super einfach und wir erhalten auch noch die jeweiligen Fehler sowie einen statistischen Test wiedergegeben, ob sich die Steigung von Null unterscheidet. Wir können hier auch die Option hypothesis = ändern und auf einen anderen Grenzwert testen. Das ist sehr praktisch dazu dann noch die 95% Konfidenzintervalle.

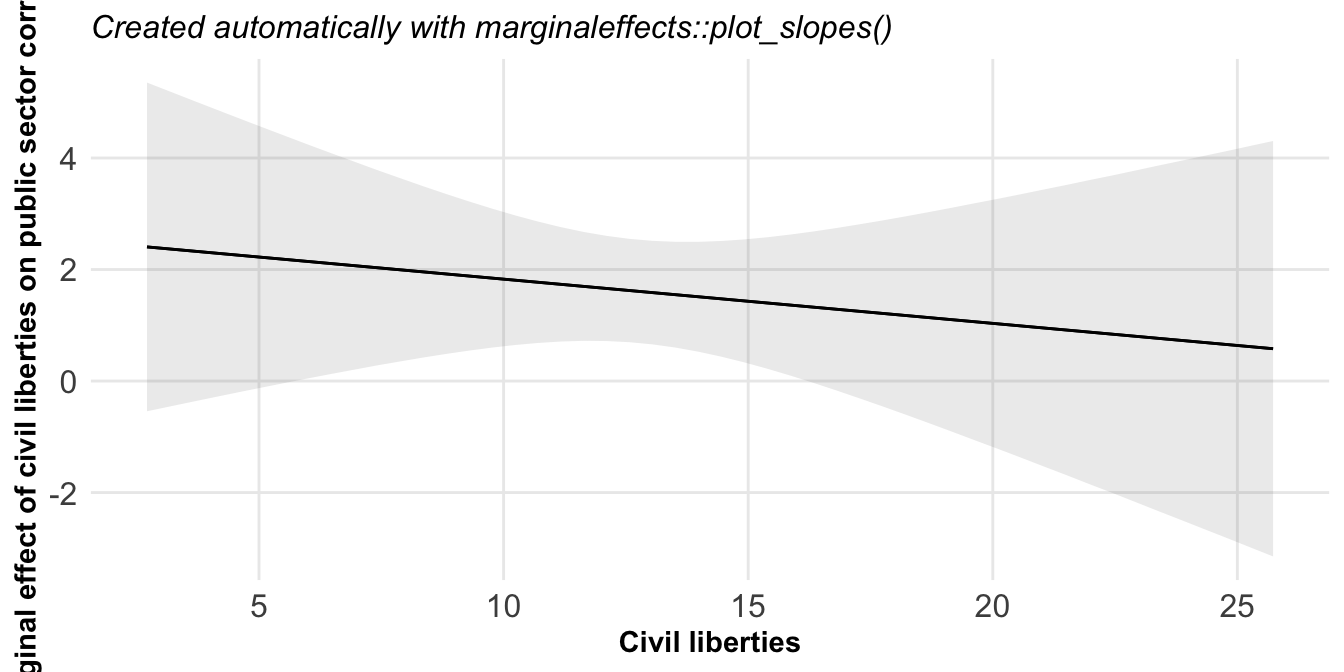
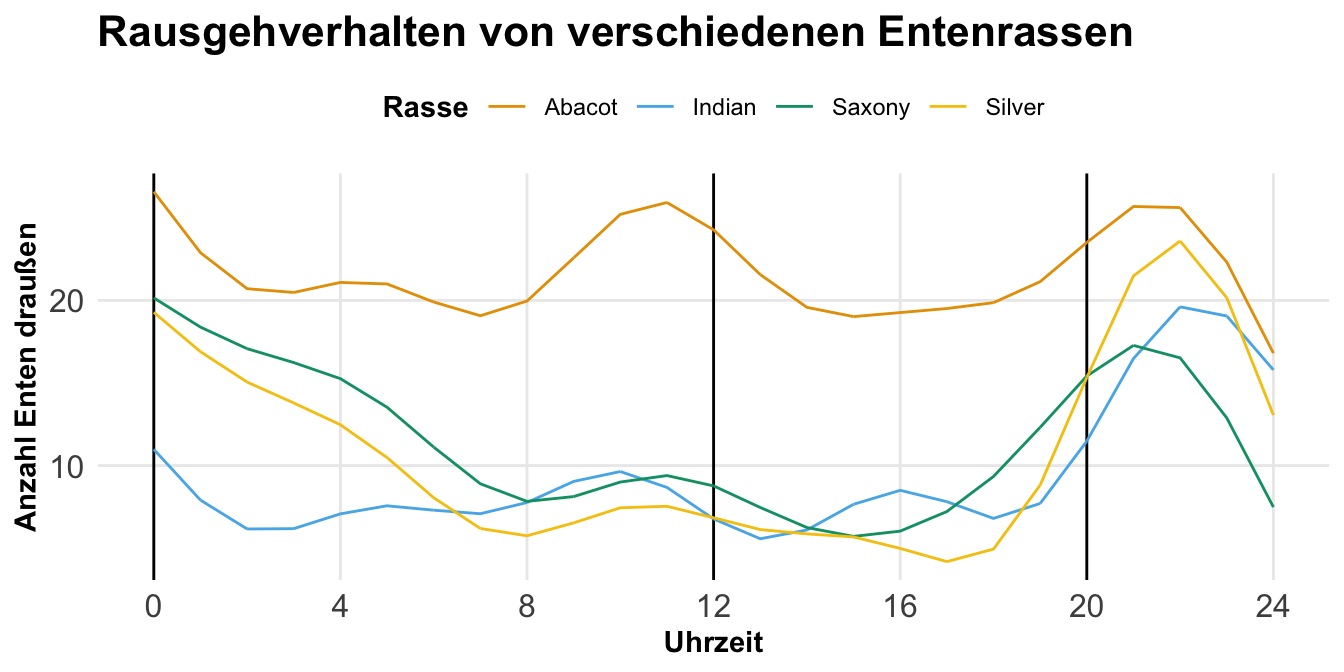
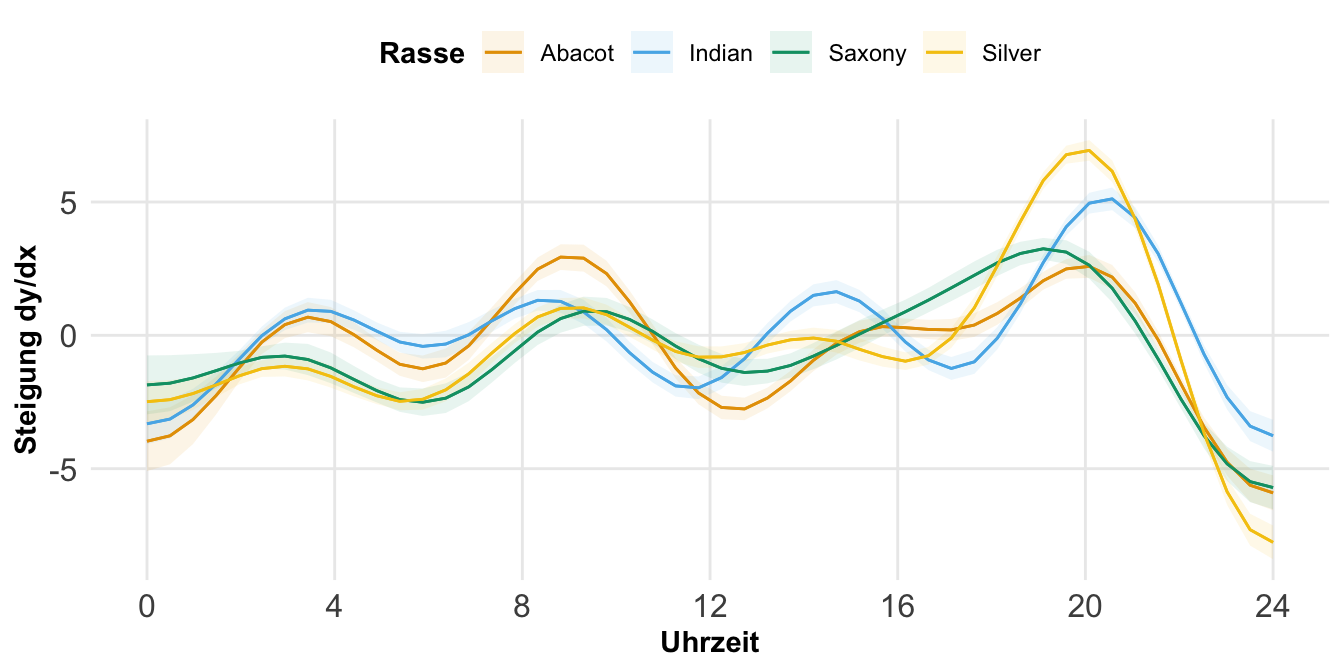
Abschließend mag es ganz interessant sein, wie sich die Steigung über die ganze Kovariate verhält. Also in unserem Fall wie ändert sich die Steigung über die Schlupfzeit? Dafür haben wir dann die Funktion plot_slopes(), die uns dann mit einem Fehlerterm einmal angibt, wie sich die Steigung ändert. Das ist natürlich sehr angenehm, wenn wir ein komplexes Modell haben, was wir uns nicht so einfach darstellen können.

Abbildung 55.26— Steigung der Tangente über die Schlupfzeiten zusammen mit dem 95% Konfidenzintervall. Kurze und lange Schlupfzeiten führen zu einer negativen Steigung im bezug zu der Sprungweite. [Zum Vergrößern anklicken]

Modellierung von Enzymen

Nachdem wir uns einmal konzeptionell mit der Steigung und damit der Ableitung beschäftigt haben, kommen wir einmal zu einem etwas komplexeren beispiel mit unseren Enzym. Wir haben ja hier eine klare S-Kurve in der Enzymaktivität vorliegen. Da wir ja das theoretische Modell kennen, können wir auch hier einfach die Ableitung bilden. In der Praxis kennen wir aber das theoretsiche Modell nicht sondern müssen eben die Grade mit einem Algorithmus anpassen. In den folgenden Tabs zeige ich dir dann einmal die Anpassung mit verschiedenen Algorithmen. Dazu habe ich dann auch immer mit dem R Paket {marginaleffects} an drei augewählten Werten des pH-Wertes die Steigung berechnet. Die Koeffizienten aller drei Modelle lassen sich nicht direkt einfach interpretieren. Die Steigung jedoch schon.

gam()

Die beste Möglichkeit eine Modellierung zu rechnen ist die Nutzung von Generalized additive model (abk. GAM), die sehr effizient komplexe Verläufe mit einer Graden versehen können. Der größte Nacvhteil ist, dass wir eigentlich mit der Ausgabe der Koeffizienten eines Generalized additive model wenig anfangen können. Jedenfalls was die direkte Interpretation angeht. Hier helfen dann die Steigungen an vordefinierten Punkten natürlich super weiter. oder aber wir berechnen die mittlere Steigung. Hier erstmal das Generalized additive model geschätzt. Wir müssen nur sagen, welche Variable mit s() nicht linear modelliert werden soll.

gam_fit <- gam(activity ~ s(ph), data = enzyme_tbl)

Dann können wir uns auch für drei standardisierte pH-Werte die Steigung wiedergeben lassen. Wir müssen hier also nicht schauen, wie das Modell aussieht oder aber was die Gradengleichung wäre. Alles macht dann die Funktion slope() für uns.

slopes(gam_fit, newdata = datagrid(ph = c(-1, 2, 6)))

 ph Estimate Std. Error     z Pr(>|z|)    S  2.5 % 97.5 %
 -1     28.7       3.95  7.27  < 0.001 41.4  20.99  36.47
  2    -11.4       4.12 -2.77  0.00552  7.5 -19.49  -3.35
  6     18.1       4.50  4.02  < 0.001 14.1   9.28  26.92

Term: ph
Type: response
Comparison: dY/dX

Manchmal wollen wir auch die durchschnittliche Steigung über alle Kovariatenwerte haben, dann können wir die Funktion avg_slopes() nutzen. Wenn wir eine sehr stark kurvige Grade haben, dann müssen wir überlegen, ob der Durchschnitt viel aussagt.

avg_slopes(gam_fit)

 Estimate Std. Error    z Pr(>|z|)     S 2.5 % 97.5 %
     15.3       1.17 13.1   <0.001 127.3    13   17.6

Term: ph
Type: response
Comparison: dY/dX

Am Ende können wir uns dann einmal die beiden Modelle mit den jeweiligen Steigungen anschauen. Auf der linken Seite findest du das theoretische Modell mit dem die Daten generiert wurden und damit auch die wahren Steigungen an den pH-Werten. In der rechten Abbildung siehst du dann die Abweichung durch das Generalized additive model. So weit liegen die Werte aber gar nicht auseinander.

Abbildung 55.27— Vergleich der theoretischen und Generalized additive model Modellierung für die Enzymaktivität. An drei pH-Werten wurde die Steigung der Tangenten der Graden bestimmt. (A) Theoretisches Modell mit den wahren Steigungen aus der Datengenierung. (B) Das angepasste Generalized additive model mit den entsprechenden Steigungen aus dem Modell. Die grauen Linien stellen die wahren Tangenten aus dem theoretischen Modell dar. [Zum Vergrößern anklicken]

poly()

Die polynomiale Regression bietet sich an, wenn wir eine effiziente Variante der I() Form haben wollen. Wir müssen ja sonst immer sehr lange Terme schreiben, da wir alle Hochzahlen in Form von I() ausformulieren müssen. Die Variante mit poly() erlaubt uns die Kovariate zu benennen die mit quadratischen Termen modelliert werden soll. Wir müssen nur angeben, wie viele Exponenten wir haben wollen. In diesem Fall wähle ich drei Exponenten aus und damit modellieren wir eben \(x^1 + x^2 + x^3\) in dem Modell. Darüber hinaus ist die Funktion poly() auch sehr effizient.

poly_fit <- lm(activity ~ poly(ph, 3), data = enzyme_tbl)

Dann können wir uns auch für drei standardisierte pH-Werte die Steigung wiedergeben lassen. Wir müssen hier also nicht schauen, wie das Modell aussieht oder aber was die Gradengleichung wäre. Alles macht dann die Funktion slope() für uns.

slopes(poly_fit, newdata = datagrid(ph = c(-1, 2, 6)))

 ph Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
 -1     28.3       2.44 11.57   <0.001 100.5  23.5  33.04
  2    -10.3       1.14 -9.08   <0.001  63.0 -12.6  -8.11
  6     21.4       1.63 13.16   <0.001 129.0  18.3  24.64

Term: ph
Type: response
Comparison: dY/dX

Manchmal wollen wir auch die durchschnittliche Steigung über alle Kovariatenwerte haben, dann können wir die Funktion avg_slopes() nutzen. Wenn wir eine sehr stark kurvige Grade haben, dann müssen wir überlegen, ob der Durchschnitt viel aussagt.

avg_slopes(poly_fit)

 Estimate Std. Error    z Pr(>|z|)     S 2.5 % 97.5 %
     15.9      0.973 16.4   <0.001 197.3    14   17.8

Term: ph
Type: response
Comparison: dY/dX

Am Ende können wir uns dann einmal die beiden Modelle mit den jeweiligen Steigungen anschauen. Auf der linken Seite findest du das theoretische Modell mit dem die Daten generiert wurden und damit auch die wahren Steigungen an den pH-Werten. In der rechten Abbildung siehst du dann die Abweichung durch polynomiale Regression. So weit liegen die Werte aber gar nicht auseinander.

Abbildung 55.28— Vergleich der theoretischen und der polynomialen Modellierung für die Enzymaktivität. An drei pH-Werten wurde die Steigung der Tangenten der Graden bestimmt. (A) Theoretisches Modell mit den wahren Steigungen aus der Datengenierung. (B) Das angepasste polynomiale Modell mit den entsprechenden Steigungen aus dem Modell. Die grauen Linien stellen die wahren Tangenten aus dem theoretischen Modell dar. [Zum Vergrößern anklicken]

loess()

Eine etwas ältere Alternative zu dem Generalized additive model ist die lokale lineare Kernregression (eng. locally estimated scatterplot smoothing, abk. loess) oder einfach Loessregression. Hier müssen wir gar nichts weiter angeben, sondern können einfach die Funktion aufrufen. Wir erhalten hier aber keine Informationen über die Streuung der Punkte um die Loessgrade, so dass wir gleich nicht alles mit {marginaleffects} machen können, was in den beiden anderen Modellierungen geht.

loess_fit <- loess(activity ~ ph, data = enzyme_tbl)

Dann können wir uns auch für drei standardisierte pH-Werte die Steigung wiedergeben lassen. Wir müssen hier also nicht schauen, wie das Modell aussieht oder aber was die Gradengleichung wäre. Alles macht dann die Funktion slope() für uns.

slopes(loess_fit, newdata = datagrid(ph = c(-1, 2, 6)))

 ph Estimate
 -1    22.37
  2    -4.74
  6    21.85

Term: ph
Type: response
Comparison: dY/dX

Manchmal wollen wir auch die durchschnittliche Steigung über alle Kovariatenwerte haben. Da wir hier ein Problem mit der Varianzmatrix haben, müssen wir uns den Durchschnitt einmal händisch berechnen. Das geht aber auch sehr fix und wir erhalten faktisch die gleichen Werte nur eben ohne Standardfehler und andere statistische Maßzahlen.

slopes(loess_fit) |> 
  summarise(avg_slope = mean(estimate))

  avg_slope
1   10.9319

Am Ende können wir uns dann einmal die beiden Modelle mit den jeweiligen Steigungen anschauen. Auf der linken Seite findest du das theoretische Modell mit dem die Daten generiert wurden und damit auch die wahren Steigungen an den pH-Werten. In der rechten Abbildung siehst du dann die Abweichung durch Loessregression. So weit liegen die Werte aber gar nicht auseinander. Ich würde hier aber nur die Loesregression nutzen, wenn es unbedingt sein muss. Die Generalized additive models sind mittlerweile einfach die bessere Alternative.

Abbildung 55.29— Vergleich der theoretischen und der Loess-Modellierung für die Enzymaktivität. An drei pH-Werten wurde die Steigung der Tangenten der Graden bestimmt. (A) Theoretisches Modell mit den wahren Steigungen aus der Datengenierung. (B) Das angepasste Loess-Modellierung mit den entsprechenden Steigungen aus dem Modell. Die grauen Linien stellen die wahren Tangenten aus dem theoretischen Modell dar. [Zum Vergrößern anklicken]

Damit haben wir den einfachen Fall mit einem einkovariaten Modell einmal bearbeitet. Häufig haben wir aber mehrere Kovariaten im Modell oder aber eine Kombination von einer Kovariate und einem grupppierenden Faktor. Dann können wir uns dennoch die Steigung berechnen lassen. Hier ist es vermutlich die Stärke von {marginaleffects}, dass wir hier dann einfach weiter machen können.

55.7.2 Mehrkovariates Modell

Wir können natürlich auch den Fall vorliegen haben, dass wir dann zwei oder mehr Kovariaten in einem Modell haben. Ich habe hier einmal das lineare Modell mit zwei Kovariaten der Schlupfzeit und dem Gewicht der Flöhe angepasst. Wir haben jetzt gleich verschiedene Möglichkeiten uns die Steigung einmal wiedergeben zu lassen.

model_ln <- lm(jump_length ~ hatched + weight, data = flea_model_tbl)
tidy(model_ln)

# A tibble: 3 × 5
  term        estimate std.error statistic    p.value
  <chr>          <dbl>     <dbl>     <dbl>      <dbl>
1 (Intercept)   65.4      13.1       5.01  0.00000903
2 hatched       10.5       3.59      2.94  0.00517   
3 weight        -0.141     0.850    -0.165 0.869     

Hier können wir uns auch die gemittelte Steigung an den für die Schlupfzeiten und die Flohgewichte wiedergeben lassen. Hier kommt es dann darauf an, was du wissen willst. Die lineare Regression liefert ja faktisch die Steigung und so erhalten wir hier auch die gleichen Werte wieder.

model_ln |> 
  avg_slopes()

    Term Estimate Std. Error      z Pr(>|z|)   S 2.5 % 97.5 %
 hatched   10.539       3.59  2.940  0.00329 8.2  3.51  17.57
 weight    -0.141       0.85 -0.165  0.86871 0.2 -1.81   1.53

Type: response
Comparison: dY/dX

Spannender wird es dann bei nicht linearen Modellen, wo wir dann natürlich nicht die gleiche Steigung an jeder Kombination vorliegen haben. Auch hier muss ich dich nochmal auf die Vingette zu den Steigungen (eng. slopes) des R Paketes {marginaleffects} für mehr verweisen. Meistens haben wir dann nicht ein mehrkovariates Modell vorliegen sondern wollen dann eine Kovariate nach einem Faktor gruppieren. Dazu kommen wir dann im nächsten Abschnitt.

55.7.3 Kombiniertes Modell

Jetzt wollen wir ein kombiniertes Modell rechnen. Wir haben hier eigentlich das klassische Design einer ANCOVA vorliegen. Wir kombinieren eine Kovariate mit einem Faktor. Bei der ANCOVA lesen wir das meist andersherum, aber hier geht es ja primär darum, wie sich die Kovariate ändert. Wenn wir dann noch einen gruppierenden Faktor mit ins Modell nehmen, dann geht es darum, wie sich die Kovariate in den Gruppen des Faktors ändert. Dann können wir natürlich noch Werte für die Kovariate festlegen, die uns dann besonders interessieren. Wenn wir das Modell bauen, dann ist die Anordnung der Einflussvariablen wichtig. Erst kommt die gruppierende Variable, dann der Rest. Hier haben wir also das Modell der Sprungweite und die beiden Einflussvariablen des Entwicklungsstandes sowie dem Gewicht. Dabei wollen wir das Gewicht dann quadratisch modellieren, was hier schon der große Unterschied zur ANCOVA ist. In der ANCOVA ist alles linear.

model_grp_sq <- lm(jump_length ~ stage * weight + I(weight^2),
                   data = flea_model_tbl)
tidy(model_grp_sq)

# A tibble: 5 × 5
  term                 estimate std.error statistic p.value
  <chr>                   <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)           130.       56.7       2.29   0.0267
2 stagejuvenile         -73.1      56.2      -1.30   0.200 
3 weight                 -6.17      7.50     -0.823  0.415 
4 I(weight^2)             0.213     0.231     0.920  0.363 
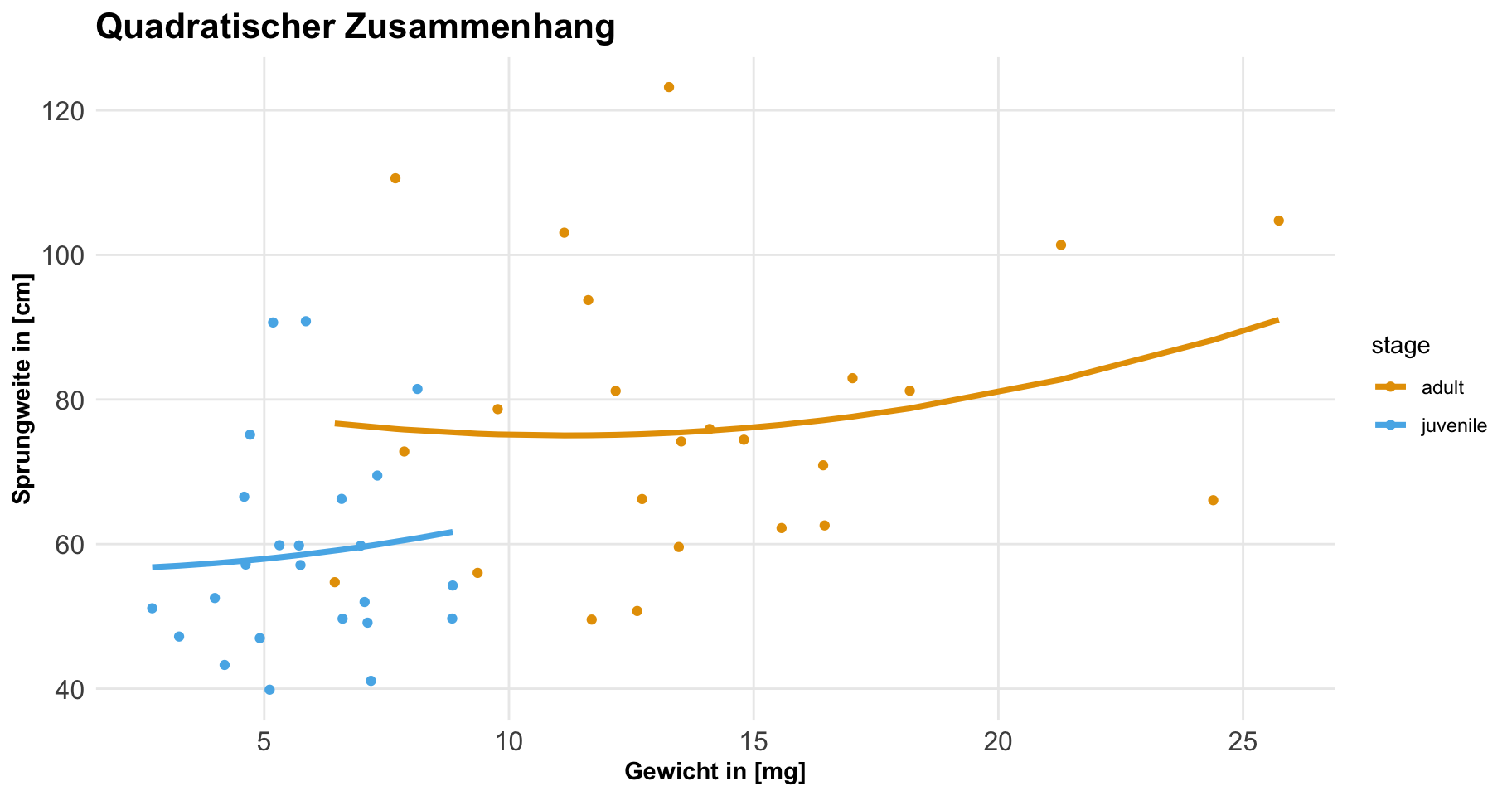
5 stagejuvenile:weight   11.5       6.45      1.78   0.0816

Wie immer ist komplexeres Modell schwierig an den Koeffizienten zu interpretieren. Deshalb schauen wir uns einmal in der folgenden Abbildung die Graden an. Wie wir sehen, ist der Zusammenhang zwischen dem Gewicht und der Sprungweite bei den juvenilen Flöhen eher linear, bei den adulten Flöhen dann eher quadratisch. Damit würden wir dann pro Gruppe auch eine andere Steigung über die Kovariate des Gewichts erwarten.

Abbildung 55.30— Scatterplot des Einflusses des Flohgewichts auf die Sprungweite aufgeteilt nach dem Entwicklungsstand in adult und juvenile Flöhe. Hier wurde ein quadratischer Zusammenhang modelliert, sodass die Steigung entlang der Grade über die Kovariate unterschiedlich ist. [Zum Vergrößern anklicken]

In den beiden folgenden Tabs zeige ich dir einmal wie du die Steigung in den beiden Gruppen für da Gewicht mit dem R Paket {marginaleffects} und slopes() berechnest. Dann habe ich das auch nochmal Schritt für Schritt gemacht, damit du nochmal nachvollziehen kannst, wie sich die Steigungen in den Gruppen ergeben.

slopes()

Wir können uns die Steigung für die Kovariate weight einmal berechnen lassen. Wir wollen die Steigung aber über den Faktor stage mitteln. Wir mitteln hier immer, da wir eben nicht für jeden Wert des Gewichts und der Gruppe einen Wert erhalten.

model_grp_sq |> 
  slopes(variables = "weight",
         by = "stage")

    stage Estimate Std. Error      z Pr(>|z|)   S  2.5 % 97.5 %
 adult      -0.192       1.68 -0.114    0.909 0.1 -3.486    3.1
 juvenile    7.826       4.27  1.832    0.067 3.9 -0.549   16.2

Term: weight
Type: response
Comparison: dY/dX

Wir wir sehen, ist die mittlere Steigung bei den juvenilen Flöhe sehr hoch, bei den adulten Flöhen eher niedrig. Hier müssen wir dann gleich nochmal in die Abbildung rein, da wir ja bei den adulten Flöhen eher einen quadratischen Zusammenhang vorliegen haben. Somit könnten sich auch Steigungen raus kürzen, wenn es erst runter und dann wieder rauf geht.

Schritt-für-Schritt

Wir können die Steigungen auch erst für die Variable weight berechnen und dann erhalten wir alle Werte wiedergeben.

mfx_grp_sq <- model_grp_sq |> 
  slopes(variables = "weight")
head(mfx_grp_sq)

 Estimate Std. Error       z Pr(>|z|)   S 2.5 % 97.5 %
    0.815       1.46  0.5574    0.577 0.8 -2.05   3.68
   -0.801       2.10 -0.3818    0.703 0.5 -4.91   3.31
    0.454       1.45  0.3123    0.755 0.4 -2.39   3.30
    4.205       4.17  1.0073    0.314 1.7 -3.98  12.39
    0.828       1.46  0.5653    0.572 0.8 -2.04   3.70
    0.126       1.53  0.0822    0.934 0.1 -2.88   3.13

Term: weight
Type: response
Comparison: dY/dX

Danach können wir dann die Steigungen nach dem Entwicklungsstand gruppieren und mitteln.

mfx_grp_sq |> 
  group_by(stage) |> 
  summarize(stage_ame = mean(estimate))

# A tibble: 2 × 2
  stage    stage_ame
  <fct>        <dbl>
1 adult       -0.192
2 juvenile     7.83 

Wir erhalten dann die gleichen Werte wie auch mit der Funktion slopes() aus dem vorherigen Tab nur eben ohne weitere statistische Maßzahlen.

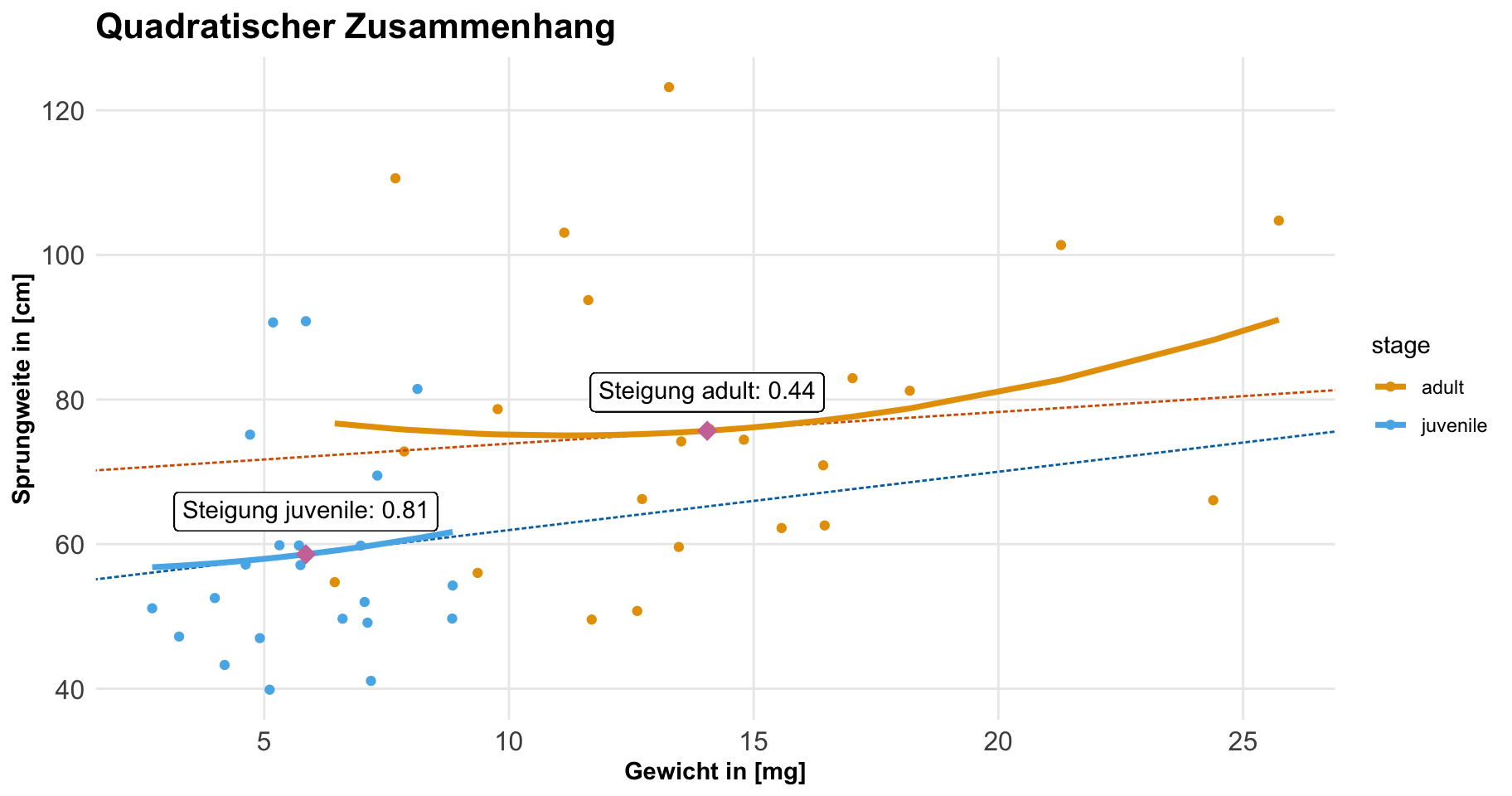
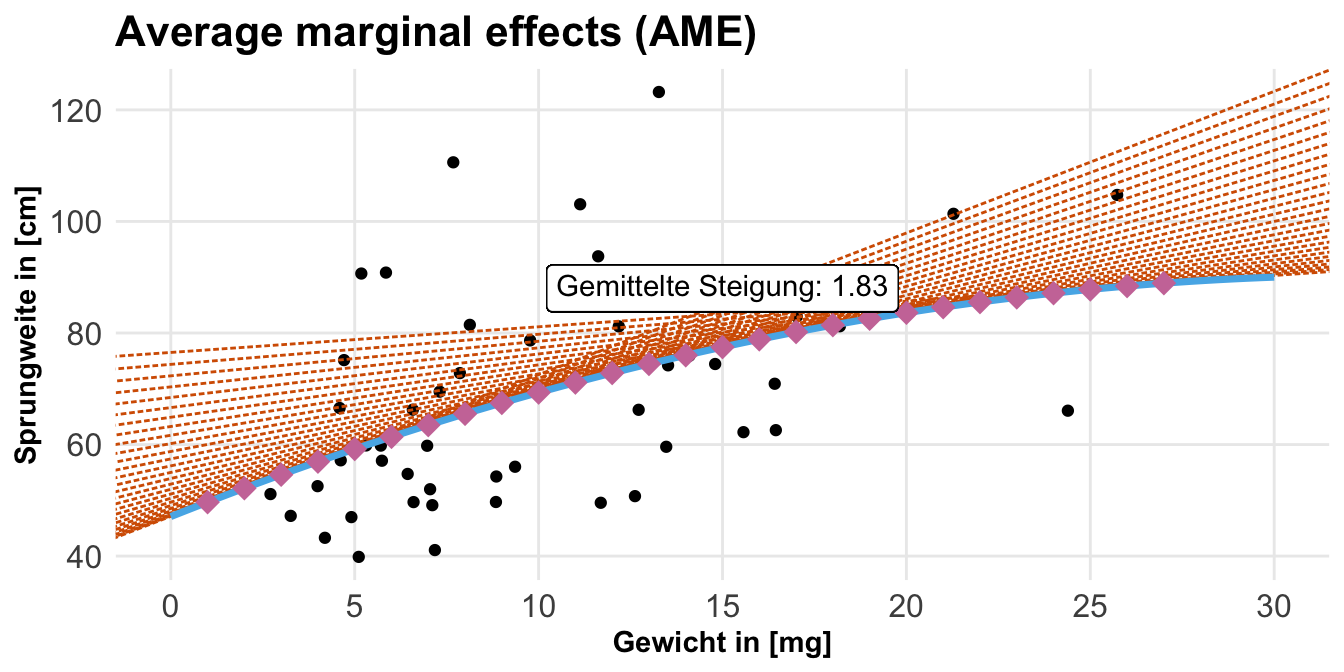
Dann ergänzen wir einmal die Steigungen in der folgenden Abbildung. Wir sehen hier sehr schön die Steigung bei den juvenilen Flöhen. Nehmen die juvenilen Flöhe zu, dann nimmt auch die Sprungweite sehr schnell an Wert zu. Anders sieht es bei den adulten Flöhen aus. Hier haben wir dann einen Abfall der Leistung mit einer Steigerung am Ende des Spektrums des Gewichts. Daher bietet sich hier insbesondere an, sich für repräsentative Werte einmal die Steigung wiedergeben zu lassen.

Abbildung 55.31— Scatterplot des Einflusses des Flohgewichts auf die Sprungweite aufgeteilt nach dem Entwicklungsstand in adult und juvenile Flöhe. Hier wurde ein quadratischer Zusammenhang modelliert, sodass die Steigung entlang der Grade über die Kovariate unterschiedlich ist. Die Tangenten mit den jeweiligen Steigungen an dem mittleren GEwicht wurden ergänzt. [Zum Vergrößern anklicken]

Wenn wir uns jetzt an verschiedenen Flohgewichten die Steigung anschauen wollen, dann müssen wir auch definieren, welchen Entwicklungsstand wir betrachten wollen. Da wir jetzt mal über beide Stadien uns die Steigung anschauen wollen, sage ich hier einmal, dass ich über jedes Level des Entwicklungsstadium haben will. Hier kann ich dann unique nutzen, damit ich nicht alle Level eintippen muss.

datagrid(model = model_grp_sq,
         weight = c(5, 10, 15, 20, 25),
         stage = unique)

   weight    stage rowid
1       5    adult     1
2       5 juvenile     2
3      10    adult     3
4      10 juvenile     4
5      15    adult     5
6      15 juvenile     6
7      20    adult     7
8      20 juvenile     8
9      25    adult     9
10     25 juvenile    10

Das Datenraster können wir dann einmal nutzen um uns dann an den jeweiligen Gewichten die Steigung für die beiden Entwicklungsstände wiedergeben zu lassen. Jetzt können wir noch entscheiden, ob wir dann einen statistischen Test rechnen wollen um die Steigungen zwischen den beiden Stadien zu vergleichen.

Ohne Gruppenvergleich

Ohne Gruppenvergleich ist die Anwendung sehr simple. Wir nehmen das Modell und rechnen dann in der Funktion slopes() die Variable weight und rechnen für die Flohgewichte die Steigung an den Werten des Gewichts im Datenraster. Hier habe ich dann mal fünf Werte für das Gewicht gewählt. Dann wähle ich noch aus, dass ich nach dem Entwicklungsstand sortieren will.

model_grp_sq |> 
  slopes(variables = "weight",
         newdata = datagrid(weight = c(5, 10, 15, 20, 25),
                            stage = unique)) |> 
  arrange(stage)

 weight    stage Estimate Std. Error      z Pr(>|z|)   S    2.5 % 97.5 %
      5 adult      -4.042       5.25 -0.770   0.4411 1.2 -14.3263   6.24
     10 adult      -1.916       3.09 -0.619   0.5356 0.9  -7.9768   4.15
     15 adult       0.211       1.50  0.140   0.8884 0.2  -2.7369   3.16
     20 adult       2.338       2.38  0.984   0.3253 1.6  -2.3204   7.00
     25 adult       4.464       4.44  1.005   0.3147 1.7  -4.2394  13.17
      5 juvenile    7.462       4.29  1.738   0.0822 3.6  -0.9541  15.88
     10 juvenile    9.589       4.67  2.055   0.0399 4.6   0.4416  18.74
     15 juvenile   11.716       5.99  1.957   0.0503 4.3  -0.0156  23.45
     20 juvenile   13.842       7.78  1.779   0.0752 3.7  -1.4071  29.09
     25 juvenile   15.969       9.80  1.630   0.1030 3.3  -3.2293  35.17

Term: weight
Type: response
Comparison: dY/dX

Wir hier sehr schön sehen, ist die Steigung der adulten Flöhe unterschiedlich. Wir haben hier eine andere Traktion je nachdem welches Gewicht wir uns anschauen. Adulte Flöhe springen bei geringen Gewicht schlechter als bei mittleren. Der Effekt steigt dann bei höherem Gewicht wieder an. Juvenile Flöhe haben einen konstanten Anstieg von ungefähr \(+2cm\) mehr Sprungweite pro Einheit mehr an Gewicht.

Mit Gruppenvergleich

Hier kommt der etwas nervigere Teil. Wir wollen jetzt auch die Steigungen innerhalb der beiden Entwicklungsstadien miteinander vergleichen. Je mehr Flohgewichte du jetzt mit in den Vergleich nimmst, desto schwieriger wird gleich das Lesen der Ausgabe. Deshalb würde ich dir empfehlen, die Vergleiche immer für ein Gewicht zu rechnen und dann die Vergleiche zu wiederholen. Dabei gehe ich davon aus, dass dich die Vergleich zwischen den Gewichten nicht interessieren. Das ist zwar etwas mühseliger, aber dann stabiler. Sonst weiß man immer nicht was genau der Koeffizient b jetzt sein soll. Hier also einmal der Vergleich der Steigungen in den beiden Entwicklungsstadien für zwei Gewichte. Dadurch haben wir jetzt vier Koeffizienten, die innerhalb von {marginaleffects} mit b1 bis b4 abkürzen. Ich habe das hier mal umständlicher rangeschrieben, damit du besser die Vergleiche verstehst.

model_grp_sq |> 
  slopes(variables = "weight",
         newdata = datagrid(weight = c(5, 10),
                            stage = unique)) |> 
  as_tibble() |> 
  add_column(coefficient = str_c("b", 1:4), .before = 1) |> 
  select(coefficient, weight, stage, estimate, p.value, conf.low, conf.high)

# A tibble: 4 × 7
  coefficient weight stage    estimate p.value conf.low conf.high
  <chr>        <dbl> <fct>       <dbl>   <dbl>    <dbl>     <dbl>
1 b1               5 adult       -4.04  0.441   -14.3        6.24
2 b2               5 juvenile     7.46  0.0822   -0.954     15.9 
3 b3              10 adult       -1.92  0.536    -7.98       4.15
4 b4              10 juvenile     9.59  0.0399    0.442     18.7 

Dann haben wir hier einmal alle Vergleiche für die jeweiligen Koeffizienten. Dabei steht dann b1 für die adulten Flöhe mit einem Gewicht von 5mg, b2 für die juvenilen Flöhe mit einem Gewicht von 5mg, b3 für die adulten sowie b4 für die juvenilen Flöhe mit jeweils einem Gewicht von 10mg. Dann können wir uns die folgenden Differenzen berechnen.

\[ \begin{aligned} (b2) - (b1) &= 7.46 - (-4.04) = 11.50\\ (b3) - (b1) &= -1.92 - (-4.04) = 2.12\\ (b4) - (b1) &= 9.59 - (-4.04) = 13.63\\ (b3) - (b2) &= -1.92 - 7.46 = -9.38\\ (b4) - (b2) &= 9.59 - 7.46 = 2.13\\ (b4) - (b3) &= 9.59 - (-1.92) = 11.50\\ \end{aligned} \]

In dieser Form kriegen wir dann auch die Vergleiche aus der Funktion slopes() wiedergeben. Nur das wir natürlich hier dann noch die Fehler sowie dann auch die p-Werte erhalten. Das anstrengende ist dann hier zu wissen, was hinter den Koeffizientenabkürzungen steht. Ich verstehe mittlerweile auch warum es so gemacht wird. Für mehrere Faktoren wird es dann wirklich sehr schwer allgemein über alle Modelle richtig die Koeffizienten zu bezeichnen. Auch können wir so recht einfach zwischen Differenzen diffence und Anteilen ratio wechseln. Aber so richtig befriedigend ist es nicht. Ich kann aber soweit damit leben.

model_grp_sq |> 
  slopes(variables = "weight",
         newdata = datagrid(weight = c(5, 10),
                            stage = unique),
         hypothesis = difference ~ pairwise)

  Hypothesis Estimate Std. Error      z Pr(>|z|)   S  2.5 % 97.5 %
 (b2) - (b1)    11.50       6.45  1.783   0.0745 3.7  -1.14 24.149
 (b3) - (b1)     2.13       2.31  0.921   0.3572 1.5  -2.40  6.653
 (b4) - (b1)    13.63       8.26  1.650   0.0990 3.3  -2.56 29.826
 (b3) - (b2)    -9.38       5.06 -1.852   0.0640 4.0 -19.30  0.547
 (b4) - (b2)     2.13       2.31  0.920   0.3574 1.5  -2.40  6.655
 (b4) - (b3)    11.50       6.45  1.783   0.0746 3.7  -1.14 24.150

Type: response

Sehen wir dann auch, wo die größten Unterschiede in den Steigungen sind. Signifikant sind dann am Ende keiner der Steigungen zwischen den beiden Gruppen. Wir sind zwar nah dran, aber es liegen alle p-Werte über den Signifikanzniveau von \(\alpha\) gleich 5%. Dabei sind alle p-Werte hier unadjustiert für multiple Vergleiche. Wenn du das wollen würdest, dann musst du den Code wie folgt anpassen und noch die Funktion hypotheses() nutzen.

model_grp_sq |> 
  slopes(variables = "weight",
         newdata = datagrid(weight = c(5, 10),
                            stage = unique)) |> 
  hypotheses(hypothesis = difference ~ pairwise,
             multcomp = "bonferroni")

  Hypothesis Estimate Std. Error      z Pr(>|z|)    S  2.5 % 97.5 %
 (b2) - (b1)    11.50       6.45  1.783    0.447  1.2  -3.04  26.05
 (b3) - (b1)     2.13       2.31  0.921    1.000 -0.0  -3.08   7.34
 (b4) - (b1)    13.63       8.26  1.650    0.594  0.8  -5.00  32.27
 (b3) - (b2)    -9.38       5.06 -1.852    0.384  1.4 -20.80   2.04
 (b4) - (b2)     2.13       2.31  0.920    1.000 -0.0  -3.08   7.34
 (b4) - (b3)    11.50       6.45  1.783    0.447  1.2  -3.05  26.06

Damit kommen wir hier auch zum Schluss. Wenn dich hier noch mehr interessiert, kannst du in den anderen Kapitel zum statistischen Modellieren noch Anwendungen finden. Auch ist in dem Kapitel zur nicht linearen Regression dann noch was enthalten. Am Ende ist der Gruppenvergleich von Steigungen dann aber doch irgendwie eine Nische.

“Nachdem ich mich hier schon eine Zeit durch die Vergleiche von Steigungen innerhalb von Gruppen gequält habe, muss ich sagen, dass es nicht ideal ist. Hier kommst du um ein gites Divide-and-conquer nicht herum. Einfach die Kovariate zerstückeln und für jeden Wert einzeln die Vergleiche rechen. Sonst wird es mit den Koeffizienten super unübersichtlich.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

Nachdem wir uns hier etwas durchgearbeitet haben, bin ich noch auf einen Teil gestoßen, der eigentlich gut beschreibt, wie sich die beiden R Pakete {marginaleffects} und {emmeans} unterscheiden. Es geht im Prinzip darum, wie die Mittelwerte der Steigungen gebildet werden. Es gibt nämlich zwei Wege. Entweder berechnen wir erst alle Koeffizienten oder statistischen Parameter und mitteln dann darüber oder aber wir mitteln erst unsere Daten und berechnen dann auf den gemittelten Daten die Koeffizienten. Am Ende kommt sehr häufig das Gleiche heraus. Wie immer aber in der Statistik, ist es nicht in allen Fällen so. Zu merken ist hierbei, dass {marginaleffects} die Koeffizienten mittelt und {emmeans} auf den gemittelten Daten die Koeffizienten berechnet. Möge es von Interesse sein, ich fand es nett mal aufzuarbeiten.

HinweisPhilosophien zur Mittelwertbildung

Die folgende Darstellung wurde stark von Heiss (2022) inspiriert. Ich habe hier dann aber mal mein Beispiel genommen und entsprechend angepasst. Die Idee ist eigentlich simple. Entweder rechnen wir die Steigungen an jeden Punkt des Kovariate und mitteln dann die Steigung. Dann berechnen wir die Average marginal effects (AME). Das ist mehr oder minder was das R Paket {marginaleffects} tut. Oder aber wir rechnen erst die mittleren Werte der Kovariaten aus und berechnen für diese Werte dann die Steigung. Damit haben wir dann die Marginal effects at the mean (MEM). Das ist dann die Lösung im R Paket {emmeans}. Das erste soll für beobachtete Daten besser sein, das letztere dann für experimentelle Daten. Versuchen wir mal den Unterschied zu verstehen.

Dann berechnen wir nochmal das quadratische Modell mit unseren drei Koeffizienten für die Schlupfzeiten. Wir nutzen jetzt gleich mal das Modell um uns die beiden unterschiedlichen Arten der gemittelten Steigung berechnen zu lassen.

model_sq <- lm(jump_length ~ hatched + I(hatched^2) + I(hatched^3),
               data = flea_model_tbl)
tidy(model_sq)

# A tibble: 4 × 5
  term         estimate std.error statistic p.value
  <chr>           <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)    125.       44.7       2.80 0.00760
2 hatched        -53.8      49.0      -1.10 0.278  
3 I(hatched^2)    18.9      15.8       1.20 0.238  
4 I(hatched^3)    -1.61      1.51     -1.07 0.292  

Wir interpretieren hier die Koeffizienten nicht weiter, da wir das Modell nur brauchen um die Steigungen entlang der Graden berechnen zu können.

Average marginal effects (AME)

Beginnen wir einmal mit den Average marginal effects (AME) wobei wir dann die Steigung an allen Punkten der Kovariaten berechnen. Wie du in der folgenden Abbildung siehst, sind die Steigungen sehr unterschiedlich, da wir ja eine S-Kurve vorliegen haben. So geht die Steigung erst nach unten um dann abzuflachen und wieder anzusteigen. Am Ende haben wir dann wieder fast keine Steigung vorliegen.

Abbildung 55.32— Scatterplot der Sprungweite und der Schlupfzeiten mit einer angepassten Graden. Für aufgewählte Werte der Schlupfzeit wurde die Steigung der Tangenten an der Graden berechnet. Die gemittelte Steigung über alle Steigungen wurde berechnet. [Zum Vergrößern anklicken]

Wir haben jetzt zwei Wege auf denen wir uns die gemittelte Steigung berechnen können. Entweder berechnen wir alle Steigungen und mitteln dann einmal über die Steigung. Oder wir nutzen dann die entsprechende Funktion. Im Folgenden habe ich einmal die Steigungen an allen Punkten der Kovariaten berechnet und zeige dir einmal über head() die ersten sechs Werte.

mfx_sq <- slopes(model_sq)
head(mfx_sq)

 Estimate Std. Error      z Pr(>|z|)   S  2.5 % 97.5 %
    16.56       7.26  2.281   0.0226 5.5   2.33   30.8
     5.25       5.81  0.903   0.3664 1.4  -6.14   16.6
    -1.44       8.82 -0.163   0.8703 0.2 -18.74   15.9
    -7.35      12.63 -0.582   0.5605 0.8 -32.10   17.4
    -7.76      12.90 -0.601   0.5477 0.9 -33.05   17.5
    19.43       7.85  2.476   0.0133 6.2   4.05   34.8

Term: hatched
Type: response
Comparison: dY/dX

Dann können wir einmal die Steigung mitteln. Wir nutzen dazu dann die Funktion summarise() und erhalten folgenden Wert.

mfx_sq |> 
  summarize(avg_slope = mean(estimate))

  avg_slope
1  5.711803

Das Ganze können wir dann auch schneller über die Funktion avg_slopes() berechnen, da wir hier die gemittelten Steigungen direkt erhalten. Das ist dann eben ein Schritt weniger und geht etwas schneller. Dafür sind dann die avg_* Funktionen in {marginaleffects} gedacht.

avg_slopes(model_sq)

 Estimate Std. Error   z Pr(>|z|)   S 2.5 % 97.5 %
     5.71       4.78 1.2    0.232 2.1 -3.66   15.1

Term: hatched
Type: response
Comparison: dY/dX

Wir müssen dann mit dem Wert leben, da es hier kein richtig oder falsch gibt. Wenn wir die Steigungen berechnen und dann mitteln erhalten wir eben eine mittlere Steigung von \(+5.71\) wieder.

Marginal effects at the mean (MEM)

Etwas anders sieht es aus, wenn wir die Steigung nach {emmeans} oder aber dem Marginal effects at the mean (MEM) berechnen wollen. In der folgenden Abbildung siehst du einmal die Vorgehensweise. Wir berechnen die Steigung jetzt direkt am Mittelwert der Kovariate also hier eben der mittleren Schlupfzeit. An der mittleren Schlupfzeit berechnen wir dann die Steigung.

Abbildung 55.33— Scatterplot der Sprungweite und der Schlupfzeiten mit einer angepassten Graden. Für die mittlere Schlupfzeit von \(2.77\) wurde die Steigung der Tangenten an der Graden berechnet. [Zum Vergrößern anklicken]

Technisch gesehen brauchen wir jetzt also einmal den Mittelwert der Kovariaten. Dafür berechnen wir also einmal den Mittelwert der Schlupfzeit.

avg_jump_hatched <- mean(flea_model_tbl$hatched)
avg_jump_hatched

[1] 2.772599

Dann sagen wir einmal den Wert für die Sprungweite an dem Mittelwert voraus sowie den Wert der Sprungweite an dem Mittelwert der Kovariaten plus ganz wenig. Das ganz wenig ist dann hier \(+0.001\) Wochen Schlupfzeit. Dann ahben wir die beiden Werte für die Sprungweiten. Da wir hier runden, sehen die Werte gleich aus.

jump_hatched_fitted <- model_sq |> 
  augment(newdata = tibble(hatched = c(avg_jump_hatched, avg_jump_hatched + 0.001)))
jump_hatched_fitted

# A tibble: 2 × 2
  hatched .fitted
    <dbl>   <dbl>
1    2.77    86.5
2    2.77    86.5

Dann wollen wir die Steigung mit \(dy/dx\) berechnen. Daher brauchen wir einmal unser Delta der Sprungweiten sowie das Delta der Kovariaten. Dabei müssen wir unser Delta der Sprungweiten nochmal ausrechnen.

delta_y <- (jump_hatched_fitted$.fitted[2] - jump_hatched_fitted$.fitted[1])
delta_x <- 0.001

Und dann können wir auch schon die Steigung berechnen. An der Stelle der mittleren Schlupfzeit ändert sich wie die Sprungweite?

delta_y / delta_x

[1] 13.71042

Wir haben aber auch die Möglichkeit, diesen Wert in {marginaleffects} zu berechnen indem wir die folgenden Option setzen. Wir rechnen hier eben die Steigung auf dem Mittelwert der Kovariaten.

model_sq |> 
  avg_slopes(newdata = "mean")

 Estimate Std. Error    z Pr(>|z|)   S 2.5 % 97.5 %
     13.7       6.34 2.16   0.0306 5.0  1.28   26.1

Term: hatched
Type: response
Comparison: dY/dX

Was besser ist kann ich nicht sagen. Es kommt drauf an. Wir erhalten natürlich andere Werte je nachdem was wir berechnen. Dazu dann bitte auch die Diskussion weiter oben zum Unterschied von {mariginaleffects} und {emmeans} beachten.

Kommen wir nochmal zu einer praktischen Anwendung aus meiner Beratung. Häufig haben wir ja den Fall vorliegen, dass wir nicht so genau wissen, wo wir den nun die Steigung über eine Grade wirklich gebrauchen könnten. Wenn wir aber die Zeit als Kovariate vorliegen haben, können wir wirklich sagen, dass pro Stunde sich der Messwert in die eine oder andere Richtung bewegt hat. Diese Bewegung oder Traktion ist dann die Steigung. Wir wollen uns also einmal das Verhalten von vier Entenrassen anschauen. Die Frage war hier, ob sich die Enten über den Tag unterschiedlich im Bezug auf das Reingehen und Draußenbleiben unterscheiden.

TippAnwendungsbeispiel: Zeitlicher Verlauf von Entenausflügen

In unserem Anwendungsbeispiel fragen wir uns, ob die vier Entenrassen Abbacot ranger, Indian runner, Saxony duck und Silver Bantam ein unterschiedliches Verhalten im Bezug auf das Reingehen und Draußenbleiben zeigen. Sind die vier Rassen also alle gleich gerne draußen oder drinnen? Dabei wollen wir uns aber auch die Veränderung über die Zeit anschauen. Dafür eignen sich dann die Marginal effect models besonders. Wir haben also dreißig Enten pro Rasse mit einer Videoanalyse aufgezeichnet und ausgewertet, wo jeweils wie viele der dreißig Enten waren. Dabei ging es hier gar nicht so sehr darum, wie viele Enten immer draußen oder drinnen waren, sondern wie eben die Änderung über die Zeit in den Rassen sich unterscheidet.

Abbildung 55.34— Comic der vier Entenrassen in unserem Reingehen oder Draußenbleiben Experiment mit dreißig Enten je Rasse. Die Frage ist hier, ob sich das Verhalten der vier Entenrassen über die Zeit unterscheidet.

Wir müssen jetzt einmal unsere Daten einlesen und dafür sorgen, dasss auch alle vier Tabellenblätter berücksichtigt werden. Jede Entenrasse hat eben ihr eigenes Tabellenblatt und daher müssen wir eben die Daten etwas komplizierter Einlesen.

path <- file.path("data/outside_ducks.xlsx")
duck_raw_tbl <- path |> 
  excel_sheets() |> 
  rlang::set_names() |> 
  map_dfr(read_excel, path = path)

Dann können wir Daten schon transformieren. Einen großen Teil verwenden wir darauf die Zeit in das entsprechende Format umzuwandeln. Wir wollen die Zeit in Blöcken von einer halben Stunde haben und nicht sekundengenau. Dann müssen wir noch die Zeit von einem Faktor in eine numerische Einflussvariable umwandeln. Am Ende sortieren und filtern wir dann noch etwas die Daten.

duck_tbl <- duck_raw_tbl |> 
  mutate(time = as.POSIXct(time, format = "%H:%M:%S"),
         time_block = floor_date(time, unit = "30 minutes"),
         time_hour = hour(time) + minute(time)/60,
         timeblock_fct = as.factor(time_block)) |> 
  select(breed, time_block, timeblock_fct, outside) |>
  group_by(timeblock_fct, breed) |> 
  mutate(timeblock_num = as.numeric(timeblock_fct) - 1,
         breed = as_factor(breed)) |> 
  filter(timeblock_num %in% 0:24)

Dann rechnen wir unser Generalized additive model (abk. GAM) mit der Funktion gam() und setzten unsere nicht lineare Einflussvariable mit einem s() fest. Dann müssen wir noch sagen, dass die Zeit und Enten draußen eben dann noch von der Rasse breed abhängen. Dann erhalten wir auch für jede Rasse eine eigene Grade.

model_full_sq <- gam(outside ~ breed + s(timeblock_num, by = breed),
                     data = duck_tbl)

In der folgenden Abbildung siehst du dann einmal den zeitlichen Verlauf der Enten. Wir sehen auf der y-Achse immer die Enten, die sich außerhalb vom Stall befinden. Je nach Rasse bewegen sich die Enten über die Zeit mehr oder minder stark in die Ställe oder eben wieder raus. Wir wollen dann gleich an drei Uhrzeiten einmal die Steigung bestimmen.

Abbildung 55.35— Zeitlicher Verlauf der Enten außerhalb der Ställe und deren Rückkehr in die Ställe für die vier Entenrassen. Die Daten wurden für Zeitblöcke je 30 Minuten gemittelt. Die Grade stellt das angepasste Generalized additive model dar. An drei Uhrzeiten (0:00, 12:00 und 20:00) wird die Steigung der Graden bestimmt. [Zum Vergrößern anklicken]

Zuerst interessiert mich aber die Steigung über alle Zeitpunkte für jede Rasse. Wir rechnen also die mittlere Steigung der vier Entenrassen aus. Was sagt uns jetzt die mittlere Steigung aus? Wir sehen, dass alle Steigungen negativ sind. Daher haben alle Enten einen Drang nach drinnen zu gehen. Die Anzahl an Enten draußen vermindert sich also über den gemessenen Tag.

model_full_sq |> 
  slopes(variables = "timeblock_num",
         by = "breed")

  breed Estimate Std. Error     z Pr(>|z|)     S  2.5 % 97.5 %
 Abacot   -0.921     0.0481 -19.1  < 0.001 268.8 -1.015 -0.827
 Indian   -0.140     0.0501  -2.8  0.00513   7.6 -0.238 -0.042
 Saxony   -0.806     0.0556 -14.5  < 0.001 156.2 -0.915 -0.698
 Silver   -0.569     0.0406 -14.0  < 0.001 145.4 -0.648 -0.489

Term: timeblock_num
Type: response
Comparison: dY/dX

Und wie siehst es nun an drei ausgewählten Uhrzeiten aus? Hier haben wir dann natürlich nochmal alles aufgeteilt nach den vier Rassen und es wird schnell unübersichtlich. Vermutlich ist es besser hier einzelne Uhrzeiten nacheinander durchzugehen.

model_full_sq |> 
  slopes(variables = "timeblock_num",
         newdata = datagrid(timeblock_num = c(0, 12, 20),
                            breed = unique))

 timeblock_num  breed Estimate Std. Error      z Pr(>|z|)     S 2.5 % 97.5 %
             0 Abacot   -3.971      0.572  -6.95   <0.001  38.0 -5.09 -2.851
             0 Indian   -3.317      0.390  -8.51   <0.001  55.6 -4.08 -2.553
             0 Silver   -2.488      0.392  -6.34   <0.001  32.1 -3.26 -1.719
             0 Saxony   -1.860      0.564  -3.30   <0.001  10.0 -2.96 -0.754
            12 Abacot   -2.489      0.222 -11.21   <0.001  94.4 -2.92 -2.054
            12 Indian   -1.825      0.219  -8.34   <0.001  53.5 -2.25 -1.396
            12 Silver   -0.837      0.205  -4.08   <0.001  14.4 -1.24 -0.434
            12 Saxony   -1.076      0.274  -3.93   <0.001  13.5 -1.61 -0.539
            20 Abacot    2.596      0.214  12.12   <0.001 109.9  2.18  3.016
            20 Indian    4.844      0.193  25.05   <0.001 457.5  4.46  5.223
            20 Silver    6.966      0.193  36.07   <0.001 943.9  6.59  7.344
            20 Saxony    2.737      0.253  10.80   <0.001  88.0  2.24  3.233

Term: timeblock_num
Type: response
Comparison: dY/dX

Daher jetzt hier einmal der Vergleich der Steigungen für die Mittagszeit um 12:00 Uhr. Hier ist es dann wieder wichtig zu verstehen, was die Koeffizienten b in den paarweisen Vergleichen heißen sollen. Daher müssen wir den Vergleich einmal aufbrechen. Erstmal berechnen wir die Steigungen und dann im Anschuss den paarweisen Vergleich.

clock_12_slopes_tbl <- model_full_sq |> 
  slopes(variables = "timeblock_num",
         newdata = datagrid(timeblock_num = c(12),
                            breed = unique))
clock_12_slopes_tbl

 timeblock_num  breed Estimate Std. Error      z Pr(>|z|)    S 2.5 % 97.5 %
            12 Abacot   -2.489      0.222 -11.21   <0.001 94.4 -2.92 -2.054
            12 Indian   -1.825      0.219  -8.34   <0.001 53.5 -2.25 -1.396
            12 Silver   -0.837      0.205  -4.08   <0.001 14.4 -1.24 -0.434
            12 Saxony   -1.076      0.274  -3.93   <0.001 13.5 -1.61 -0.539

Term: timeblock_num
Type: response
Comparison: dY/dX

Jetzt wissen wir das b1 für die Abacotenten steht, b2 für die Indianenten, b3 für die Silverenten sowie b4 für die Saxonyenten. Daher können wir dann auch die folgenden Vergleiche verstehen. Sonst wäre das schwer möglich. Leider gibt es keine charmante Version die b Koeffizienten durch den entsprechenden Namen zu ersetzen.

clock_12_slopes_tbl |> 
  hypotheses(hypothesis = difference~pairwise)

  Hypothesis Estimate Std. Error     z Pr(>|z|)    S   2.5 % 97.5 %
 (b2) - (b1)    0.664      0.312  2.13   0.0332  4.9  0.0527  1.275
 (b3) - (b1)    1.652      0.302  5.46   <0.001 24.4  1.0596  2.245
 (b4) - (b1)    1.413      0.353  4.01   <0.001 14.0  0.7215  2.104
 (b3) - (b2)    0.988      0.300  3.29   <0.001 10.0  0.4001  1.576
 (b4) - (b2)    0.749      0.351  2.14   0.0328  4.9  0.0614  1.436
 (b4) - (b3)   -0.240      0.342 -0.70   0.4841  1.0 -0.9104  0.431

Am Ende können wir uns den Verlauf der Steigungen über die Zeit anschauen. Hier sehen wir sehr schön die Traktion über den Tag. Gegen Ende des Tages wollen dann alle Enten eher in den Stall. Sonst haben wir eher einen zyklischen Verlauf.

Abbildung 55.36— Verlauf der Steigungen über die Zeit aufgeteilt nach den vier Entenrassen. [Zum Vergrößern anklicken]

In diesem Beispiel siehst du ganz schön, wie wir dann die Steigung verwenden können um eine Aussage über die zeit zu treffen. Wenn du viele Faktoren wie die Rasse in dem Modell hast, bitte es sich an, die Vergleiche dann aufzusplitten damit du besser interpretieren kannst, was du da an Koeffizienten eigentlich vergleichst.

Damit sind wir dann am Ende mit den Steigungen und kommen jetzt zu einem anderem Gebiet. Anstatt zu sagen, wie sich die Werte im Messwert an einer bestimmten Stelle der Einflussvariable verändern, können wir auch vorhersagen, wie der Wert des Messwertes für beliebige Einflussfaktoren nach dem Modell aussehen würde. Wir machen also eine klassische Vorhersage mit unserem statistischen Modell.

55.8 Vorhersagen (eng. predictions)

“A prediction is the outcome expected by a fitted model for a given combination of predictor values.” — Kapitel 5 zu Vorhersagen – {marginaleffects}

Vorhersagen sind der Ausgang aus der Nichtinterpretierbarkeit von Koeffizienten in komplexen Modellen. Das ist einfach geschrieben, wird aber hoffentlich dann hier noch klarer. Wir können über Vorhersagen uns die modellierten Messwerte wiedergeben lassen und damit dann leichter die Modelle interpretieren. Damit wir das aber können, müssen wir verstehen was ein Datenraster ist und wie wir das Datenraster einsetzen. Dafür bitte dann nochmal weiter oben nachlesen, wie wir Datenraster in {marginaleffects} definieren und nutzen können.

55.8.1 Kovariates Modell

Beginnen wir hier einmal wieder mit den kovariaten Modellen. Am Ende ist es egal wie viele Kovariaten du in deinem Modell hast. Auch ist es egal, ob du dann noch einen Faktor mit ins Modell nimmst und damit ein kombiniertes Modell baust. Da wir hier in der Folge eben nicht nicht Koeffizienten interpretieren sondern nur die vorhergesagten Werte, ist es fast egal wie komplex dein Modell ist. Wir brauchen hier eben dann immer als Haupteffekt eine Kovariate und ergänzen diese um weitere Einflussvariablen. Manchmal haben wir auch ein ganzes Set an interessanten Variablen. Beginnen wir aber einmal einfach und schauen uns die Modellierung der Enzyme mit einer Kovariate an.

Modellierung von Enzymen

Bei unseren Daten zu der Enzymaktivität können wir hier einmal ein Generalized additive model (abk. GAM) anpassen. Wir müssen nur einmal über das s() angeben, welche Einflussvariablen nicht linear sein sollen.

cov1_fit <- gam(activity ~ s(ph), data = enzyme_tbl)

Wir nutzen das Modell jetzt einmal gleich um uns die Vorhersagen für die Enzymaktivität für jeden pH-Wert wiedergeben zu lassen. Der Wert in der Spalte Estimate ist dabei die vorhergesagte Enzymaktivität. Wenn du jetzt stuzt, warum da dreimal der gleiche Werte kommt, hat es damit zu tun, dass wir jeden pH-Wert dreimal wiederholt gemessen haben. Daher erhalten wir für den gleichen pH-Wert auch die gleiche vorhergesagte Enzymaktivität. Das ist manchmal etwas verwirrend. Es gibt ja nur einen Wert auf der Graden.

predictions(cov1_fit)

 Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
   -42.39       5.04 -8.42   <0.001  54.5 -52.3 -32.52
   -42.39       5.04 -8.42   <0.001  54.5 -52.3 -32.52
   -42.39       5.04 -8.42   <0.001  54.5 -52.3 -32.52
    -5.73       3.57 -1.61    0.108   3.2 -12.7   1.27
    -5.73       3.57 -1.61    0.108   3.2 -12.7   1.27
--- 33 rows omitted. See ?print.marginaleffects ---
    31.32       3.27  9.56   <0.001  69.6  24.9  37.74
    31.32       3.27  9.56   <0.001  69.6  24.9  37.74
    58.21       4.55 12.80   <0.001 122.1  49.3  67.13
    58.21       4.55 12.80   <0.001 122.1  49.3  67.13
    58.21       4.55 12.80   <0.001 122.1  49.3  67.13
Type: response

Das Ganze wird etwas klarer, wenn wir für unsere pH-Werte einmal mitteln und alles mit der Option by zusammenfassen. Dann sehen wir auch besser, wie sich die Werte ergeben. Wir haben dann für jeden pH-Wert die vorhergesagte Enzymaktivität.

predictions(cov1_fit, by = "ph")

   ph Estimate Std. Error      z Pr(>|z|)     S  2.5 % 97.5 %
 -2.0   -42.39       5.04 -8.416   <0.001  54.5 -52.26 -32.52
 -1.0    -5.73       3.57 -1.605   0.1085   3.2 -12.73   1.27
  0.0    12.73       3.74  3.405   <0.001  10.6   5.40  20.05
  1.0    16.12       3.74  4.305   <0.001  15.9   8.78  23.45
  2.0     8.94       3.73  2.398   0.0165   5.9   1.63  16.24
  3.0    -3.34       3.71 -0.900   0.3681   1.4 -10.60   3.93
  4.0    -9.23       3.72 -2.483   0.0130   6.3 -16.52  -1.95
  5.0    -9.45       3.92 -2.407   0.0161   6.0 -17.14  -1.76
  6.0    -3.21       3.44 -0.935   0.3500   1.5  -9.95   3.53
  7.0    31.32       3.27  9.564   <0.001  69.6  24.90  37.74
  7.5    58.21       4.55 12.796   <0.001 122.1  49.30  67.13

Type: response

Wir können jetzt natürlich die ganze Vorhersage auch einmal für verschiedene Modelle durchführen. In dem folgenden Tabs findest du einmal die Vorhersage für drei ausgewählte pH-Werte für drei nicht lineare Regressionen. Im Anschluss schauen wir uns die Vorhersagen einmal in einer Abbildung an.

gam()

Fangen wir wieder mit der bekannten Modellierung in einem Generalized additive model an. Wir müssen nur einmal über das s() angeben, welche Einflussvariablen nicht linear sein sollen.

gam_fit <- gam(activity ~ s(ph), data = enzyme_tbl)

Dann können wir uns auch schon die Vorhersage für drei standardisierte pH-Werte wiedergeben lassen.

gam_pred <- predictions(gam_fit, newdata = datagrid(ph = c(-1, 2, 6)))
gam_pred

 ph Estimate Std. Error      z Pr(>|z|)   S  2.5 % 97.5 %
 -1    -5.73       3.57 -1.605   0.1085 3.2 -12.73   1.27
  2     8.94       3.73  2.398   0.0165 5.9   1.63  16.24
  6    -3.21       3.44 -0.935   0.3500 1.5  -9.95   3.53

Type: response

Wir kennen ja gleich das theoretische Modell nachdem die Enzymaktivität erstellt wurde und können dann die Modelle miteinander vergleichen.

poly()

Als zweite Methode nutzen wir die polynomiale Regression und geben hier an, dass wir bis zu drei quadratische Terme mit in unser Modell nehmen wollen.

poly_fit <- lm(activity ~ poly(ph, 3), data = enzyme_tbl)

Dann können wir uns auch schon die Vorhersage für drei standardisierte pH-Werte wiedergeben lassen.

poly_pred <- predictions(poly_fit, newdata = datagrid(ph = c(-1, 2, 6)))
poly_pred

 ph Estimate Std. Error      z Pr(>|z|)    S 2.5 % 97.5 %
 -1   -4.545       2.48 -1.830   0.0673  3.9 -9.41  0.324
  2    8.951       2.23  4.013   <0.001 14.0  4.58 13.323
  6   -0.545       2.36 -0.231   0.8176  0.3 -5.18  4.089

Type: response

Wir kennen ja gleich das theoretische Modell nachdem die Enzymaktivität erstellt wurde und können dann die Modelle miteinander vergleichen.

loess()

Die einfachste Variante und auch die älteste ist dann die Loessregression wo wir dann gleich leider auch nur die Vorhersagen aber keine statistsischen Maßzahlen mehr erhalten. Daher würde ich die Loessregression vermeiden.

loess_fit <- loess(activity ~ ph, data = enzyme_tbl)

Dann können wir uns auch schon die Vorhersage für drei standardisierte pH-Werte wiedergeben lassen.

loess_pred <- predictions(loess_fit, newdata = datagrid(ph = c(-1, 2, 6)))
loess_pred

 ph Estimate
 -1    -9.33
  2     8.54
  6     4.93

Type: response

Wir kennen ja gleich das theoretische Modell nachdem die Enzymaktivität erstellt wurde und können dann die Modelle miteinander vergleichen.

Am Ende können wir einmal das theoretische Modell mit den Vorhersagen aus den drei Algorithmen miteinander vergleichen. In dem theoretischen Modell kennen wir die Werte die als Enzymaktivität für die drei pH-Werte rauskommen müssen. In der modellierten Vorhersage sehen wir dann die Abweichungen. Am Ende sind aber alle drei Modelle relativ gut und sind dem theoretischen Werten sehr ähnlich. Hier sehen wir auch nochmal die Messwiederholungen für jeden pH-Wert als graue Punkte.

Abbildung 55.37— Vergleich des theoretischen Modells und der modellierten Vorhersage für drei pH-Werte. Jeder pH-Wert wurde mit drei Widerholungen gemessen. (A) Theoretisches Modell mit den wahren Werten der Enzymaktivität für die drei pH-Werte. (B) Modellierte Vorhersage mit der Enzymaktivität für die drei pH-Werte aus den drei Algorithmen. [Zum Vergrößern anklicken]

Modellierung von Flöhen

Jetzt wollen wir uns einmal ein etwas kompliziertes Beispiel mit den Flohdaten anschauen. Unsere Flohdaten haben insgesamt 48 Beobachtungen. Das brauchen wir gleich einmal damit auch immer sehen, wie die Daten zusammengefasst werden. Erstmal bauen wir uns wieder unser Generalized additive model für die Daten. Wir müssen nur einmal über das s() angeben, welche Einflussvariablen nicht linear sein sollen. In unserem Fall sind es die Schlupfzeiten, die Körpergewichte der Flöhe sowie die Anzahl an Haaren am rechten Bein. Alles zusammen bauen wir einmal in ein multiples Kovariatesmodell.

cov3_fit <- gam(jump_length ~ s(hatched) + s(weight) + s(count_leg), 
                data = flea_model_tbl)

Wir können uns jetzt über alle \(5 + 38 + 5\) Beobachtungen in den Daten einmal die Vorhersage wiedergeben lassen. Dabei sind die mittleren \(38\) Beobachtungen einmal in der Ausgabe weggelassen. Wir erhalten so für jede Beobachtung die entsprechende Sprungweite wiedergeben.

predictions(cov3_fit)

 Estimate Std. Error    z Pr(>|z|)     S 2.5 % 97.5 %
     76.8       4.43 17.3   <0.001 221.3  68.2   85.5
     74.7       3.41 21.9   <0.001 349.6  68.0   81.3
     71.3       4.19 17.0   <0.001 213.2  63.1   79.6
     96.5       7.02 13.7   <0.001 140.4  82.7  110.3
     73.1       4.82 15.2   <0.001 170.6  63.7   82.6
--- 38 rows omitted. See ?print.marginaleffects ---
    115.3       3.23 35.7   <0.001 924.0 109.0  121.6
     69.9       3.66 19.1   <0.001 267.6  62.7   77.1
    103.0       2.94 35.0   <0.001 888.4  97.2  108.7
    126.4       3.25 38.8   <0.001   Inf 120.0  132.8
    128.0       5.35 23.9   <0.001 418.2 117.5  138.5
Type: response

Mit den Vorhersagen können wir so nicht wirklich was anfangen. Wir haben jetzt für jeden Floh die vorhergesagte Sprungweite, aber eigentlich interessieren uns ja die Einflüsse der Kovariaten. Daher müssen wir uns mal ein interessantes Datenraster bauen, was unseren Ansprüchen genügt. Wir haben in {marginaleffects} ein paar Wrapper, die uns helfen die Kovariaten in ihren Werten besser zusammenzufassen.

• mit fivenum erhalten wir die Five-number summary mit dem Minimum, dem \(1^{st}\) Quartile, dem Median, dem \(3^{rd}\) Quartile sowie dem Maximum.
• mit mean erhalten wir den Mittelwert.
• mit median erhalten wir den Median.
• mit range erhalten wir die Minimum und Maximumwerte.

Dann können wir uns noch eigene Funktion schreiben, die aber immer einen Vektor an Zahlen wiedergeben müssen. Daher arbeite ich hier explizit mit c() damit ich sicher bin, dass wir auch einen Zahlenvektor wiederbekommen. Deshalb ist die Funktion nicht schön, aber wirksam. Wir berechnen hier den Mittelwert plusminus einer Standardabweichung. Das Runden ist nicht notwendig, macht aber alles etwas schöner.

mean_sd <- \(x){
  c(mean(x) - sd(x), mean(x), mean(x) + sd(x)) |> 
    round(2)
}

Jetzt können wir uns einmal das Datenraster anschauen, was wir dann nutzen wollen um für die Werte der Einflussvariablen im Datenraster die Vorhersagen der Sprungweiten zu bestimmen.

cov3_datagrid <- datagrid(model = cov3_fit, 
                          weight = fivenum, 
                          hatched = mean_sd, 
                          count_leg = median)
cov3_datagrid

   weight hatched count_leg rowid
1   2.710    1.47     138.5     1
2   2.710    2.77     138.5     2
3   2.710    4.07     138.5     3
4   5.725    1.47     138.5     4
5   5.725    2.77     138.5     5
6   5.725    4.07     138.5     6
7   7.995    1.47     138.5     7
8   7.995    2.77     138.5     8
9   7.995    4.07     138.5     9
10 13.370    1.47     138.5    10
11 13.370    2.77     138.5    11
12 13.370    4.07     138.5    12
13 25.730    1.47     138.5    13
14 25.730    2.77     138.5    14
15 25.730    4.07     138.5    15

Das Datenraster können wir dann in die Option newdata direkt in die Funktion predictions() einbauen. Dann erhalten wir die Sprungweiten der Flöhe für die jeweiligen Werte der Einflussvariablen in dem Datenraster. Damit haben wir jedenfalls in einem Kovariatenmodell eine bessere Vorstellung von dem Einfluss der Kovariaten auf den Messwert.

predictions(cov3_fit, 
            newdata = datagrid(weight = fivenum, 
                               hatched = mean_sd, 
                               count_leg = median))

 weight hatched count_leg Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
   2.71    1.47       138     55.7       6.55  8.51   <0.001  55.7  42.9   68.6
   2.71    2.77       138     66.5       6.28 10.59   <0.001  84.6  54.2   78.8
   2.71    4.07       138     81.2       6.68 12.14   <0.001 110.3  68.1   94.3
   5.72    1.47       138     64.6       3.32 19.46   <0.001 277.9  58.1   71.1
   5.72    2.77       138     75.4       3.08 24.48   <0.001 437.2  69.4   81.5
   5.72    4.07       138     90.0       3.58 25.16   <0.001 461.8  83.0   97.1
   8.00    1.47       138     69.2       3.69 18.77   <0.001 258.7  62.0   76.4
   8.00    2.77       138     80.0       3.34 23.95   <0.001 418.8  73.5   86.5
   8.00    4.07       138     94.6       3.84 24.66   <0.001 443.5  87.1  102.1
  13.37    1.47       138     76.0       3.75 20.30   <0.001 301.8  68.7   83.4
  13.37    2.77       138     86.8       3.58 24.24   <0.001 428.7  79.8   93.9
  13.37    4.07       138    101.5       3.98 25.52   <0.001 474.9  93.7  109.3
  25.73    1.47       138     97.4       8.90 10.94   <0.001  90.1  79.9  114.8
  25.73    2.77       138    108.2       8.74 12.38   <0.001 114.5  91.1  125.3
  25.73    4.07       138    122.8       9.04 13.59   <0.001 137.2 105.1  140.5

Type: response

Meistens wollen wir dann nicht nur Testen, ob die vorhergesagten Werte Null sind. Diese Nullhypothese macht bei Vorhersagen meistens nicht so einen Sinn. Deshalb können wir auch über die Funktion hypotheses() eine andere Nullhypothese definieren. Leider haben wir hier wieder die Koeffizientenschreibweise mit b*, die leider super schwer zu lesen ist. Deshalb einmal in den folgenden Tabs die normale Ausgabe von der Funktion hypotheses() und dann eben die Kombination mit dem Datenraster.

Mit hypotheses()

Wir wollen jetzt einmal statistisch Testen, ob sich die vorhergesagten Sprungweiten von \(75cm\) unterscheiden. Es ist immer sehr schwer sich zu merken, was denn jetzt die Koeffizienten für das Datenraster in der Ausgabe der Funktion hypotheses() sind. Wir erhalten hier ja nur die Kurzschreibweise der Koeffizienten mit b* wiedergeben. Das ist sehr schwer zu lesen. In dem nächsten Tab kombiniere ich dann einmal die Ausgabe hier mit dem Datenraster um dann besser zu verstehen, was die Koeffizienten b* aussagen sollen.

cov3_hypotheses <- predictions(cov3_fit, 
                               newdata = datagrid(weight = fivenum, 
                                                  hatched = mean_sd, 
                                                  count_leg = median)) |> 
  hypotheses(hypothesis = 75)
cov3_hypotheses

 Term Estimate Std. Error      z Pr(>|z|)    S 2.5 % 97.5 %
  b1      55.7       6.55 -2.940  0.00328  8.3  42.9   68.6
  b2      66.5       6.28 -1.348  0.17776  2.5  54.2   78.8
  b3      81.2       6.68  0.921  0.35697  1.5  68.1   94.3
  b4      64.6       3.32 -3.125  0.00178  9.1  58.1   71.1
  b5      75.4       3.08  0.135  0.89254  0.2  69.4   81.5
  b6      90.0       3.58  4.204  < 0.001 15.2  83.0   97.1
  b7      69.2       3.69 -1.570  0.11653  3.1  62.0   76.4
  b8      80.0       3.34  1.498  0.13419  2.9  73.5   86.5
  b9      94.6       3.84  5.114  < 0.001 21.6  87.1  102.1
  b10     76.0       3.75  0.279  0.78027  0.4  68.7   83.4
  b11     86.8       3.58  3.304  < 0.001 10.0  79.8   93.9
  b12    101.5       3.98  6.656  < 0.001 35.0  93.7  109.3
  b13     97.4       8.90  2.515  0.01192  6.4  79.9  114.8
  b14    108.2       8.74  3.797  < 0.001 12.7  91.1  125.3
  b15    122.8       9.04  5.289  < 0.001 23.0 105.1  140.5

Mit hypotheses() und datagrid()

Wir nehmen hier einmal unser Objekt cov3_datagrid was das Datenraster beinhaltet und kombinieren es mit dem Objekt cov3_hypotheses aus dem vorherigen Tab, welches unsere statistischen Tests beinhaltet. Dann müssen wir noch etwas selektieren und mutieren, damit alles wieder schön aussieht.

bind_cols(cov3_datagrid, cov3_hypotheses) |> 
  select(weight, hatched, count_leg, estimate, p.value) |> 
  mutate(estimate = round(estimate, 2),
         p.value = scales::pvalue(p.value))

   weight hatched count_leg estimate p.value
1   2.710    1.47     138.5    55.74   0.003
2   2.710    2.77     138.5    66.53   0.178
3   2.710    4.07     138.5    81.16   0.357
4   5.725    1.47     138.5    64.63   0.002
5   5.725    2.77     138.5    75.42   0.893
6   5.725    4.07     138.5    90.04  <0.001
7   7.995    1.47     138.5    69.21   0.117
8   7.995    2.77     138.5    80.00   0.134
9   7.995    4.07     138.5    94.63  <0.001
10 13.370    1.47     138.5    76.05   0.780
11 13.370    2.77     138.5    86.84  <0.001
12 13.370    4.07     138.5   101.46  <0.001
13 25.730    1.47     138.5    97.39   0.012
14 25.730    2.77     138.5   108.18  <0.001
15 25.730    4.07     138.5   122.81  <0.001

Jetzt können wir viel besser sehen welche Kombination der Werte der Kovariaten welchen Wert in der Sprungweite hat und ob dieser Wert in der Sprungweite sich signifikant von \(75cm\) unterscheidet. Das geht zwar nicht immer, aber wenn ich das Datenraster mit der Ausgabe der Funktion hypotheses() kombinieren kann, dann mache ich das gerne.

Soweit so gut zum reinen Kovariatenmodell. Wenn wir nur Kovariaten in unserem Modell haben, dann biette sich die Nutzung des Datenrasters sehr gut an um eben dann unsere Kovariaten irgendwie zu Gruppieren und so eine Aussage treffen zu können. Wir haben auch noch die Möglichkeit die Funktion avg_predictions() zu nutzen, aber das ist eine Funktion, die über alle Vorhersagen eben den Mittelwert bildet. Manchmal interessant, aber nicht wirklich, wenn wir mehrere Kovariaten haben und dann eine mittlere Sprungweite über alle Vorhersagen erhalten.

55.8.2 Kombiniertes Modell

Jetzt wird es komplizierter, da wir noch einen Faktor mit in unser Modell nehmen. Daher wollen wir unsere Vorhersagen nach einem gruppierenden Faktor auswerten. Das macht die Sache schon komplizierter. Der Fokus liegt aber je nach Perspektive eben auf den Kovariaten oder dem Faktor. Wir diskutieren hier jetzt aber gleich mal den Sachverhalt.

WarnungAchtung, bitte beachten!

Die Funktion avg_predictions(..., by = factor) und die Nutzung von predictions(..., by = factor) sind faktisch das Gleiche. Wir erhalten dann das gleiche Ergebnis und deshalb bleibe ich immer bei der Funktion predictions(). So haben wir eine Funktion weniger, die wir uns merken müssen. Die Funktion avg_predictions() nutzen wir nur, wenn wir wirklich mal die mittleren Vorhersagen haben wollen.

Dann schauen wir uns einmal das kombinierte Modell für unsere Flohdaten an. Wir wollen jetzt einmal modellieren welchen Einfluss die Schlupfzeit sowie das Gewicht der Flöhe auf die Sprungweite hat. Darüber hinaus nehmen wir dann noch den Entwicklungsstand mit in das Modell.

Modellierung von Flöhen

Jetzt wollen wir uns einmal ein etwas kompliziertes Beispiel mit den Flohdaten anschauen. Unsere Flohdaten haben insgesamt 48 Beobachtungen. Das brauchen wir gleich einmal damit auch immer sehen, wie die Daten zusammengefasst werden. Erstmal bauen wir uns wieder unser Generalized additive model für die Daten. Wir müssen nur einmal über das s() angeben, welche Einflussvariablen nicht linear sein sollen. In unserem Fall sind es die Schlupfzeiten, die Körpergewichte der Flöhe sowie als Faktor den Entwicklungsstand der Flöhe.

cov2_fac1_fit <- gam(jump_length ~ s(hatched) + s(weight) + stage, 
                     data = flea_model_tbl)

Wenn wir jetzt daran interessiert wären, wie sich die Sprungweite über das Gewicht und die Schlupfzeit verändert, dann können wir die Option by nutzen. Dadurch teilen wir dann die Vorhersagen für die beiden Entwicklungsstände einmal auf.

predictions(cov2_fac1_fit,
            by = "stage")

    stage Estimate Std. Error    z Pr(>|z|)     S 2.5 % 97.5 %
 adult        90.3       6.03 15.0   <0.001 165.7  78.5    102
 juvenile     96.1       6.03 15.9   <0.001 187.2  84.3    108

Type: response

Am Ende ist die Option by nichts anderes als ein group_by() kombiniert mit einer Zusammenfassung und dem Mittelwert über alle Vorhersagen. Daher auch die Ähnlichkeit zu der Funktion avg_predictions(), die ja auch nichts anderes macht, als den Mittelwert der Vorhersagen zu bilden.

predictions(cov2_fac1_fit) |> 
  group_by(stage) |> 
  summarize(mean(estimate))

# A tibble: 2 × 2
  stage    `mean(estimate)`
  <fct>               <dbl>
1 adult                90.3
2 juvenile             96.1

Das Ganze ist natürlich etwas unbefriedigend, da wir nur zwei Werte für unsere Vorhersagen erhalten und das Gewicht sowie die Schlupfzeiten vollkommen außer acht lassen. Hier hilft dann wieder das Datenraster, in dem wir uns dann die interessanten Werte der Kovariaten aussuchen können. Wir wollen dann alles für die Entwicklungstände einzelen haben und setzen daher einmal die Funktion unique. Dann müssen wir nicht die Namen der Level jetzt hier in das Datenraster schreiben.

cov2_fac1_datagrid <- datagrid(model = cov2_fac1_fit,
                               stage = unique,
                               weight = fivenum, 
                               hatched = mean)
cov2_fac1_datagrid

      stage weight  hatched rowid
1     adult  2.710 2.772599     1
2     adult  5.725 2.772599     2
3     adult  7.995 2.772599     3
4     adult 13.370 2.772599     4
5     adult 25.730 2.772599     5
6  juvenile  2.710 2.772599     6
7  juvenile  5.725 2.772599     7
8  juvenile  7.995 2.772599     8
9  juvenile 13.370 2.772599     9
10 juvenile 25.730 2.772599    10

Dann können wir auch schon die Vorhersage mit dem Datenraster kombinieren. Damit haben wir dann wirklich die Information der Kovariaten über die Vorhersage der Sprungweiten getrennt für die beiden Entwicklungsständer vorliegen. Das ist es ja was wir mit den Entwicklungsständen auch haben wollen nämlich eine Gruppierung unser Sprungweiten.

predictions(cov2_fac1_fit, 
            newdata = cov2_fac1_datagrid)

    stage weight hatched Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
 adult      2.71    2.77     51.6      24.36  2.12   0.0343   4.9  3.82   99.3
 adult      5.72    2.77     73.0      16.91  4.32   <0.001  15.9 39.83  106.1
 adult      8.00    2.77     83.3      13.12  6.35   <0.001  32.1 57.56  109.0
 adult     13.37    2.77     80.9       8.78  9.22   <0.001  64.8 63.68   98.1
 adult     25.73    2.77    108.0      21.46  5.03   <0.001  21.0 65.93  150.1
 juvenile   2.71    2.77     72.3      14.23  5.08   <0.001  21.3 44.41  100.2
 juvenile   5.72    2.77     93.7       7.18 13.05   <0.001 126.8 79.62  107.8
 juvenile   8.00    2.77    104.0       9.48 10.98   <0.001  90.7 85.45  122.6
 juvenile  13.37    2.77    101.6      17.53  5.80   <0.001  27.1 67.26  136.0
 juvenile  25.73    2.77    128.7      26.97  4.77   <0.001  19.1 75.88  181.6

Type: response

Was das statistische Testen angeht haben wir hier den gleichen Fall vorliegen wie auch schon in den kovariaten Modellen. Wir können auch hier dann die Funktion hypotheses() nutzen. Was etwas schwerer wird. Wir testen jetzt ja auch hier immer jede Zeile gegen einen Wert in der Nullhypothese. Was wir ja eventuell auch Testen wollen, ist der Unterschied zwischen den Gruppen global. Das würde ich aber dann wirklich über die anderen Kovariaten rechnen und nur die Option by setzen.

predictions(cov2_fac1_fit,
            by = "stage",
            hypothesis = ~ pairwise)

           Hypothesis Estimate Std. Error     z Pr(>|z|)   S 2.5 % 97.5 %
 (juvenile) - (adult)     5.82       8.53 0.682    0.495 1.0 -10.9   22.5

Type: response

Wir sehen hier, dass der paarweise Vergleich zwischen den beiden Entwicklungsständen im Bezug auf die mittlere vorhergesagte Sprungweite nicht signifikant ist. Wenn wir das noch für verschiedene Gewichte oder Schlupfweiten haben wollen würden, dann würde ich das alles schrittweise mit neuen Datenrastern testen. Aber hier breche ich mal ab, da es dann wirklich auf die wissenschaftliche Fragestellung ankommt.

55.8.3 Faktorielles Modell

Kommen wir nun zum reinen faktoriellen Design. Ich habe lange gebraucht um zu erkennen, dass die Vorhersage in einem faktoriellen Design eben dem klassischen Gruppenvergleich entspricht. Wir sagen ja für jede Faktorkombination die Mittelwerte des Messwerts voraus. Dann können wir ja auch diese vorhergesagten Mittelwerte miteinander vergleichen und rechnen dann eben einen paarweisen Gruppenvergleich. Wenn man es sich so überlegt ist es eben sehr naheliegend. Das Problem war für mich, dass es eben in {marginaleffects} noch die Funktion comparisons() gibt, die eben nicht Gruppenvergleiche rechnet. Wenn man sich das aber einmal auseinandergenommen hat, dann macht es auch mehr Sinn hier dann die Funktion predictions() zu verwenden. Davon mal ab, dass das R Paket {emmeans} für die Fragestellung des Gruppenvergleichs für mich einfach besser funktioniert. Aber das weiß man ja nie vorher.

WarnungAchtung, bitte beachten!

Ich persönlich finde die Implementierung des multiplen Testens in {emmeans} um Längen besser gelöst. Den Rest von {marginaleffects} dann eher nicht so. Daher würde ich dir hier davon abraten, deine Gruppenvergleiche mit predictions() zu rechnen. Es ist gut zu verstehen was die Funktion macht, aber {emmeans} hat den klaren Vorteil, dass wir das Compact letter display berechnen können. Darüber hinaus finde ich die zweifaktorielle Analyse durch die beiden Zeichen Stern * und Strich | besser gelöst. In {marginaleffects} haben wir dann die Problematik mit den Hypothesen und Gruppennamen innerhalb der Ausgabe der Funktion hypotheses(). Weiter unten zeige ich dir nochmal einen kurzen Vergleich der beiden Pakete. Bitte schaue dann nochmal in das Kapitel zu den Post-hoc Tests vorbei.

“Manchmal schaue ich mir sehr lange Funktionen oder Pakete wie hier {marginaleffects} an und muss dann feststellen, dass für eine spezielle Orichideenanwendung dann doch ein anderes Paket besser ist. Insbesondere wenn wir ein balanciertes Gruppendesign vorliegen haben und die gängige Nullhypothese testen wollen. Ist nicht schlimm, dann musst du dir nicht die Arbeit machen. Für das faktorielle Experiment würde ich dann immer {emmeans} nehmen.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

Dann wiederholen wir nochmal ganz kurz die Abbildung von der Einleitung damit wir die Abbildung auch nochmal hier vorliegen haben. Wir haben unseren gruppierten pH-Wert als Einflussvariable auf der x-Achse liegen und unsere standardisierte Enzymaktivität auf der y-Achse als Messwert vorliegen. Dann sagen wir die Gruppenmittelwerte mit unserem linearen Modell und der Funktion predictions() voraus. Dann können wir noch einen zweiten Faktor wie die Gruppe der Prokaryoten oder Eukaryoten vorliegen haben. Dann erweiterten sich unsere Faktorkombinationen natürlich entsprechend und wir sagen mehr Mittelwerte voraus. Für jede Faktorkombination dann jeweils einen Mittelwert. Der gedankliche Sprung ist hier, dass wir es mit Vorhersagen zu tun haben. Wir sagen eben die Mittelwerte in den Gruppen aus dem linearen Modell vorher.

Abbildung 55.38— Modellierung des Zusammenhangs zwischen der standardisierten Enzymaktivität und den gruppierten pH-Werten nach niedrigen, mittleren und hohen pH-Werten. Der pH-Wert ist kategorial. (A) Einfaktorielle Vorhersage der Gruppenmittelwerte der Enzymaktivität. (B) Zweifaktorielle Vorhersage der Gruppenmittelwerte der Enzymaktivität aufgetrennt nach der Gruppe der Eukaryoten und Prokaryoten. [Zum Vergrößern anklicken]

Was ist der große Vorteil von {marginaleffects} ist nun, dass wir die Funktion hypotheses() vorliegen haben und damit ziemlich viel machen können. Dazu mehr dann noch weiter unten im Abschnitt zu den Hypothesen- und Äquivalenztests. Die Frage ist eher, ob wir das alles wirklich brauchen, was die Funktion hypotheses() kann, aber das ist eine andere Frage. In den beiden folgenden Tabs zeige ich dir dann einmal wie wir die Vorhersagen und damit die Gruppenvergleiche in {marginaleffects} rechnen. Zuerst für den einfaktoriellen Fall und dann einmal für den zweifaktoriellen Fall.

Vorhersage 1-faktoriell

Für unseren einfaktoriellen Gruppenvergleich brauchen wir erstmal ein statistisches Modell. Ich nehme hier einmal das lineare Modell mit der Annahme der Normalverteilung an die Residuen, da ich durch die Standardisierung der Enzymaktivität eine approximative Normalverteilung im Messwert erreicht habe.

enzyme_1fac_fit <-  lm(activity ~ grp, data = enzyme_tbl)

Dann können wir uns schon die Gruppenmittelwerte für die drei pH-Wertgruppen berechnen lassen. Ich gehe hier gleich von Varianzheterogenität in den Gruppen aus und passen entsprechend den Varianzschätzer mit vcov = "HAC" an. Somit haben alle Gruppen ihre individuelle Varianz oder Std. Error in der folgenden Ausgabe.

predictions(enzyme_1fac_fit, by = "grp", vcov = "HAC")

     grp Estimate Std. Error      z Pr(>|z|)    S  2.5 % 97.5 %
 niedrig    -2.50       3.99 -0.626    0.531  0.9 -10.32  5.327
 mittel     -1.35       1.06 -1.276    0.202  2.3  -3.42  0.722
 hoch       17.11       4.91  3.483   <0.001 11.0   7.48 26.745

Type: response

Die Mittelwerte passen mit der obigen Abbildung überein. Dann können wir schon den paarweisen Vergleich rechnen. Zuerst einmal ohne die Adjustierung für multiple Vergleiche. Dann erhalten wir direkt die paarweisen Vergleiche für die Differenzen der Mittelwerte.

predictions(enzyme_1fac_fit, by = "grp", vcov = "HAC",
            hypothesis = difference ~ pairwise) 

           Hypothesis Estimate Std. Error     z Pr(>|z|)    S 2.5 % 97.5 %
 (mittel) - (niedrig)     1.15       4.67 0.246  0.80542  0.3 -8.00   10.3
 (hoch) - (niedrig)      19.61       7.07 2.774  0.00553  7.5  5.76   33.5
 (hoch) - (mittel)       18.46       5.59 3.304  < 0.001 10.0  7.51   29.4

Type: response

Wenn wir jetzt adjustieren wollen, dann müssen wir nochmal die Funktion hypotheses() nachschalten. Leider erhalten wir nur die Koeffizientenschreibweise mit b*, wenn wir die Option hypothesis nicht in die Funktion predictions() schreiben. Daher bitte dann so bauen, jedenfalls bis die Funktion predictions() auch die Option multcomp akzeptiert oder aber die Gruppennamen benutzt.

predictions(enzyme_1fac_fit, by = "grp", vcov = "HAC",
            hypothesis = difference ~ pairwise)  |> 
  hypotheses(multcomp = "bonferroni")

 Term           Hypothesis Estimate Std. Error     z Pr(>|z|)    S 2.5 % 97.5 %
   b1 (mittel) - (niedrig)     1.15       4.67 0.246  1.00000 -0.0 -9.69   12.0
   b2 (hoch) - (niedrig)      19.61       7.07 2.774  0.01659  5.9  3.20   36.0
   b3 (hoch) - (mittel)       18.46       5.59 3.304  0.00286  8.4  5.49   31.4

Wir haben dann mit der Funktion plot_predictions() auch eine schnelle Möglichkeit einmal uns die verschiedenen Mittelwerte der standardisierte Enzymaktivität nach den standardisierten pH-Wertgruppen einmal anzuschauen. Es ist am Ende ein einfacher Plot, der nochmal zeigt, ob wir dann auch alles richtig gemacht haben und die p-Werte aus den vergleichen dann auch zu den Daten passen.

plot_predictions(enzyme_1fac_fit, by = "grp") +
  theme_minimal() +
  labs(x = "Gruppierter pH-Wert", y = "Standardisierte Enzymaktivität")

Abbildung 55.39— Darstellung der Mittelwerte mit dem Standardfehler für die standardisierte Enzymaktivität nach den standardisierten pH-Wertgruppen. [Zum Vergrößern anklicken]

Vorhersage 2-faktoriell

Für unseren zweifaktoriellen Gruppenvergleich brauchen wir auch ein statistisches Modell. Ich nehme hier einmal das lineare Modell mit der Annahme der Normalverteilung an die Residuen, da ich durch die Standardisierung der Enzymaktivität eine approximative Normalverteilung im Messwert erreicht habe. Dann ergänze ich noch die Interaktion zwischen den pH-Wertgruppen und den Gruppen der Prokaryoten oder Eukaryoten.

enzyme_2fac_fit <- lm(activity ~ grp * type, data = enzyme_tbl)

Dann können wir uns schon die Gruppenmittelwerte für die drei pH-Wertgruppen und den Gruppen der Prokaryoten oder Eukaryoten berechnen lassen. Ich gehe hier gleich von Varianzheterogenität in den Gruppen aus und passen entsprechend den Varianzschätzer mit vcov = "HAC" an. Somit haben alle Gruppen ihre individuelle Varianz oder Std. Error in der folgenden Ausgabe. Das besondere hier ist dann die Schreibweise mit dem by, die uns erlaubt die Vorhersage über die Faktorkombinationen aufzuteilen.

predictions(enzyme_2fac_fit, by = c("grp", "type"), vcov = "HAC") 

     grp      type Estimate Std. Error       z Pr(>|z|)     S   2.5 % 97.5 %
 niedrig Eukaryot     14.21     0.5498   25.84   <0.001 486.6  13.129  15.28
 niedrig Prokaryot   -19.20     4.1190   -4.66   <0.001  18.3 -27.277 -11.13
 mittel  Eukaryot     -9.22     0.0325 -283.79   <0.001   Inf  -9.286  -9.16
 mittel  Prokaryot     2.59     1.2580    2.06   0.0396   4.7   0.123   5.05
 hoch    Eukaryot     28.24    13.4263    2.10   0.0354   4.8   1.924  54.55
 hoch    Prokaryot    -5.14     0.5571   -9.22   <0.001  64.9  -6.228  -4.04

Type: response

Die Mittelwerte passen mit der obigen Abbildung überein. Dann können wir schon den paarweisen Vergleich rechnen. Zuerst einmal ohne die Adjustierung für multiple Vergleiche. Dann erhalten wir direkt die paarweisen Vergleiche für die Differenzen der Mittelwerte. Hier müssen wir dann noch mit dem Strich | einmal die Vergleiche für den zweiten Faktor aufteilen. Am Ende noch angeben dass wir von einem balancierten Design ausgehen.

predictions(enzyme_2fac_fit, by = c("grp", "type"), vcov = "HAC",
            hypothesis = difference ~ pairwise | type, 
            newdata = "balanced") 

      type           Hypothesis Estimate Std. Error      z Pr(>|z|)    S  2.5 %
 Eukaryot  (mittel) - (niedrig)   -23.43      0.571 -41.00  < 0.001  Inf -24.55
 Eukaryot  (hoch) - (niedrig)      14.03     13.570   1.03  0.30109  1.7 -12.56
 Eukaryot  (hoch) - (mittel)       37.46     13.408   2.79  0.00521  7.6  11.18
 Prokaryot (mittel) - (niedrig)    21.79      3.460   6.30  < 0.001 31.6  15.01
 Prokaryot (hoch) - (niedrig)      14.07      4.257   3.30  < 0.001 10.0   5.72
 Prokaryot (hoch) - (mittel)       -7.72      1.647  -4.69  < 0.001 18.5 -10.95
 97.5 %
  -22.3
   40.6
   63.7
   28.6
   22.4
   -4.5

Type: response

Wenn wir jetzt adjustieren wollen, dann müssen wir nochmal die Funktion hypotheses() nachschalten. Leider erhalten wir nur die Koeffizientenschreibweise mit b* für einen Teil der Faktoren. Je nachdem wir du das dir baust, kriegst du dann eben einen Faktor nicht mit den Namen in die Ausgabe. In unserem Fall fehlt jetzt der Name des zweiten Faktors. Hier müssen wir jetzt wissen, dass erst die Eukaryoten kommen und dann die Prokayoten. Das ist die Sortierung der Level im Faktor type gewesen. Ich finde das super nervig, sich zu merken, wie die Ordnung der Level in den Faktoren ist.

predictions(enzyme_2fac_fit, by = c("grp", "type"), vcov = "HAC",
            hypothesis = difference ~ pairwise | type,
            newdata = "balanced") |> 
  hypotheses(multcomp = "bonferroni")

 Term           Hypothesis Estimate Std. Error      z Pr(>|z|)    S  2.5 %
   b1 (mittel) - (niedrig)   -23.43      0.571 -41.00  < 0.001  Inf -24.84
   b2 (hoch) - (niedrig)      14.03     13.570   1.03  1.00000 -0.0 -19.58
   b3 (hoch) - (mittel)       37.46     13.408   2.79  0.03124  5.0   4.25
   b4 (mittel) - (niedrig)    21.79      3.460   6.30  < 0.001 29.0  13.22
   b5 (hoch) - (niedrig)      14.07      4.257   3.30  0.00571  7.5   3.52
   b6 (hoch) - (mittel)       -7.72      1.647  -4.69  < 0.001 15.9 -11.80
 97.5 %
 -22.01
  47.64
  70.67
  30.36
  24.61
  -3.65

Am Ende ist es dann vermutlich eine Geschmacksfrage und die Anwendung die zählt. Wenn du sehr viele faktorielle Experimente auswertest, dann würde ich dir den Weg hier nicht empfehlen. Da ist dann {emmeans} besser für gebaut und auch optimaler zu Bedienen. Hier ist es eher der Versuch etwas nachzubauen, was woanders besser geht.

“Ich habe hier sehr lange gefrickelt um irgendwie beide Faktoren mit dem Namen der Level in die Ausgabe zu kriegen, bin aber dran gescheitert. Wenn du eine Lösung findest, dann freue ich mich sehr, wenn du mich anschreibst. Danke!” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

Wir haben dann mit der Funktion plot_predictions() auch eine schnelle Möglichkeit einmal uns die verschiedenen Mittelwerte der standardisierte Enzymaktivität nach den standardisierten pH-Wertgruppen und der Prokaryoten oder Eukaryoten einmal anzuschauen. Es ist am Ende ein einfacher Plot, der nochmal zeigt, ob wir dann auch alles richtig gemacht haben und die p-Werte aus den vergleichen dann auch zu den Daten passen.

plot_predictions(enzyme_2fac_fit, by = c("grp", "type")) +
  theme_minimal() +
  scale_color_okabeito() +
  labs(x = "Gruppierter pH-Wert", y = "Standardisierte Enzymaktivität",
       color = "Gruppe")

Abbildung 55.40— Darstellung der Mittelwerte mit dem Standardfehler für die standardisierte Enzymaktivität nach den standardisierten pH-Wertgruppen und der Prokaryoten oder Eukaryoten. [Zum Vergrößern anklicken]

Wir haben auf der Webseite zu den {marginaleffects} auch noch den Punkt zu der Alternativen Software – {emmeans}. Wie ich jetzt festgestellt habe, wurde nochmal der Vergleich dort geändert und bezieht sich jetzt auf die Funktion comparisons() und nicht mehr auf predictions(). Am Ende ist es aber wirklich ein an sich sinnloses Gequäle sich {emmeans} in {marginaleffects} nachzubauen. In dem folgenden Kasten ist dann nochmal der Vergleich enthalten, damit wir das hier auch nochmal haben.

HinweisVergleich {marginaleffects} und {emmeans}

Schauen wir uns für den Vergleich der Flöhe einmal das lineare Modell mit zwei Faktoren für die Ernährungsform und den Entwicklungsstand einmal an. Wir haben wieder die Interaktion mit in dem Modell und gehen von normalverteilten Sprungweiten aus. Dementsprechend ist es eine einfache lineare Modellierung.

feeding_fit <-  lm(jump_length ~ feeding * stage, data = flea_model_tbl)

Jetzt können wir auf zwei Arten die Gruppenvergleiche rechnen. Ich zeige also hier nochmal in beiden Tabs die Anwendung in {marginaleffects} mit der Funktion predictions() sowie die von mir präferierte Version in {emmeans}. Ich mache mir hier nicht mehr die Mühe nochmal alles mit der Funktion comparisons() nachzubauen. Mehr zu den multiplen Gruppenvergleichen findest du dann im Kapitel zu den Post-hoc Tests.

{marginaleffects}

Einmal die Mittelwerte aller Faktorkombinationen unter der Annahme der Varianzheterogenität mit der Funktion predictions() aus dem obigen linearen Modell.

predictions(feeding_fit, by = c("stage", "feeding"), vcov = "HAC")

    stage     feeding Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
 adult    sugar_water     79.0       4.13 19.11   <0.001 268.1  70.9   87.1
 adult    blood           99.7       9.80 10.17   <0.001  78.3  80.5  118.9
 adult    ketchup         92.1       9.44  9.76   <0.001  72.4  73.6  110.7
 juvenile sugar_water     61.0       2.97 20.53   <0.001 308.7  55.2   66.9
 juvenile blood          116.0      16.30  7.12   <0.001  39.7  84.1  148.0
 juvenile ketchup        111.2      13.06  8.52   <0.001  55.8  85.6  136.8

Type: response

Wenn wir jetzt einmal die paarweisen Vergleiche rechnen wollen, dann können wir die Option hypothesis nutzen. Wir können aber auf diese Weise nicht für multiple Vergleiche adjustieren.

predictions(feeding_fit, by = c("stage", "feeding"), vcov = "HAC",
            hypothesis = difference ~ pairwise | stage)

    stage                Hypothesis Estimate Std. Error      z Pr(>|z|)    S
 adult    (blood) - (sugar_water)      20.73       10.6  1.950   0.0512  4.3
 adult    (ketchup) - (sugar_water)    13.17       10.3  1.278   0.2012  2.3
 adult    (ketchup) - (blood)          -7.56       13.6 -0.556   0.5782  0.8
 juvenile (blood) - (sugar_water)      54.99       16.6  3.319   <0.001 10.1
 juvenile (ketchup) - (sugar_water)    50.21       13.4  3.749   <0.001 12.5
 juvenile (ketchup) - (blood)          -4.79       20.9 -0.229   0.8187  0.3
  2.5 % 97.5 %
  -0.11   41.6
  -7.03   33.4
 -34.23   19.1
  22.52   87.5
  23.96   76.5
 -45.74   36.2

Type: response

Um die Adjustierung durchzuführen müssen wir dann noch die Funktion hypotheses() nachschalten wobei wir dann die Namen der Level es zweiten Faktors verlieren. Das ist super nervig, da ich natürlich nicht immer die Sortierung im Kopf habe. Eine unnötige Fehlerquelle. In unserem Fall wäre es aber erst der Entwicklungsstand adult und dann juvenile.

predictions(feeding_fit, by = c("stage", "feeding"), vcov = "HAC",
            hypothesis = difference ~ pairwise | stage) |> 
  hypotheses(multcomp = "bonferroni")

 Term                Hypothesis Estimate Std. Error      z Pr(>|z|)    S  2.5 %
   b1 (blood) - (sugar_water)      20.73       10.6  1.950  0.30731  1.7  -6.73
   b2 (ketchup) - (sugar_water)    13.17       10.3  1.278  1.00000 -0.0 -13.44
   b3 (ketchup) - (blood)          -7.56       13.6 -0.556  1.00000 -0.0 -42.69
   b4 (blood) - (sugar_water)      54.99       16.6  3.319  0.00542  7.5  12.20
   b5 (ketchup) - (sugar_water)    50.21       13.4  3.749  0.00107  9.9  15.62
   b6 (ketchup) - (blood)          -4.79       20.9 -0.229  1.00000 -0.0 -58.74
 97.5 %
   48.2
   39.8
   27.6
   97.8
   84.8
   49.2

In dem folgenden Tab findest du dann einmal die Anwendung in {emmeans} für die multiplen Vergleiche, die ich jetzt nach diesem langen Weg in diesem Kapitel dann weiterhin nutzen werde. Am Ende beachte dann bitte noch das Kapitel zu den Post-hoc Tests in dem ich dann noch mehr zu den multiplen Vergleiche schreibe und erkläre.

{emmeans}

Wenn wir die Mittelwerte aufgeteilt nach den beiden Entwicklungsständen und den Ernährungsarten haben wollen, können wir die Funktion emmeans() nutzen und müssen noch angeben, dass wir für die Varianzheterogenität adjustieren wollen. Mehr zu den multiplen Gruppenvergleichen in {emmeans} findest du dann im Kapitel zu den Post-hoc Tests. Das hier dient nur der Veranschaulichung und dem Vergleich der Algorithmen.

feeding_fit |> 
  emmeans(~ feeding | stage, vcov = sandwich::vcovHAC)

stage = adult:
 feeding     emmean    SE df lower.CL upper.CL
 sugar_water   79.0  4.13 42     70.6     87.3
 blood         99.7  9.80 42     79.9    119.5
 ketchup       92.1  9.44 42     73.1    111.2

stage = juvenile:
 feeding     emmean    SE df lower.CL upper.CL
 sugar_water   61.0  2.97 42     55.0     67.0
 blood        116.0 16.30 42     83.1    148.9
 ketchup      111.2 13.10 42     84.9    137.6

Confidence level used: 0.95 

Die paarweisen Vergleiche können wir dann über die Funktion contrast() rechnen. In der Funktion geben wir dann auch an, ob wir für die multiplen Vergleiche adjustieren wollen. Die Namen der Level der Faktoren werden immer weitergegeben und erlauben eine direkte Interpretation.

feeding_fit |> 
  emmeans(~ feeding | stage, vcov = sandwich::vcovHAC) |> 
  contrast(method = "pairwise", adjust = "bonferroni")

stage = adult:
 contrast              estimate   SE df t.ratio p.value
 sugar_water - blood     -20.73 10.6 42  -1.950  0.1737
 sugar_water - ketchup   -13.17 10.3 42  -1.278  0.6247
 blood - ketchup           7.56 13.6 42   0.556  1.0000

stage = juvenile:
 contrast              estimate   SE df t.ratio p.value
 sugar_water - blood     -54.99 16.6 42  -3.319  0.0056
 sugar_water - ketchup   -50.21 13.4 42  -3.749  0.0016
 blood - ketchup           4.79 20.9 42   0.229  1.0000

P value adjustment: bonferroni method for 3 tests 

Die Stärke von {emmeans} liegt dann am Ende natürlich darin, dass wir in dem agrarwissenschaftlichen Kontext noch das Compact letter display mit der Funktion cld() berechnen können. Das geht dann eben in {marginaleffects} nicht so einfach. Ich habe mir hier dann auch nicht die Mühe gemacht.

55.9 Kontrafaktische Vergleiche (eng. counterfactual)

Kommen wir jetzt zu einem Abschnitt von dem wusste ich bis vor ein paar Monaten noch nicht, dass wir hier sowas überhaupt berechnen können. Die Rede ist von der Idee von den Counterfactual comparisons (deu. Kontrafaktische Vergleiche). Ich nutze hier dann gleich mal den deutschen Begriff, da ich kontrafaktische Vergleiche ist nicht so schlimm als Begriff finde. Die Idee ist eigentlich recht simpel und versteckt sich etwas hinter dem Begriff.

“A counterfactual comparison is a function of two or more model-based predictions, made with different predictor values.” — Counterfactual comparisons in {marginaleffects}

Hier müssen wir also einmal innehalten und überlegen, was diese kontrafaktische Vergleiche sein sollen. Zuerst geht es um die Vorhersagen eines Messwertes \(Y\). Wenn wir einen Messwert vorher sagen, dann schreiben wir auch gerne \(\hat{Y}\) für den vorgesagten Messwert aus unserem Modell. Damit können wir dann die vorgesagten Messwerte \(\hat{Y}\) aus unserem Modell von den beobachteten Messwerten \(Y\) unterscheiden. Wenn wir jetzt unseren Messwert für eine Einflussvariable \(X\) vorhersagen wollen, dann schreiben wir \(\hat{Y}_X\). Jetzt können wir uns verschiedene Fragen stellen, was mit dem vorgesagten Messwerte \(\hat{Y}\) passiert, wenn wir die Einflussvariable \(X\) ändern. Im Folgenden habe ich einmal ein paar Beispiel zusammengefasst, wenn wir uns auf die Differenz konzentrieren. Andere Varianten kommen dann gleich danach.

Erhöhung um eine Einheit

Wir erhöhen unsere Einflussvariable \(X\) um eine Einheit und berechnen die Differenz der vorhergesagten Messwerte mit \(\hat{Y}_{X=x+1} - \hat{Y}_{X=x}\). Du könntest jetzt meinen, dass wir es hier mit der klassischen Steigung zu tun haben, aber wir beziehen uns hier ja auf die vorhergesagten Messwerte nicht die Traktion entlang der Graden als Steigung.

Erhöhung um eine Standardabweichung

Wir erhöhen die Einflussvariable \(X\) um eine Standardabweichung und berechnen die Differenz der vorhergesagten Messwerte mit \(\hat{Y}_{X=x+\sigma_X} - \hat{Y}_{X=x}\).

Erhöhung vom Minimum zum Maximum

Wir berechnen die Differenz des minimalen Werts der Einflussvariable \(X\) zu dem maximalen Wert der Einflussvariable \(X\) mit \(\hat{Y}_{X=max(X)} - \hat{Y}_{X=min(X)}\).

Änderung zwischen den Werten \(a\) und \(b\)

Wir berechnen die Differenz zwischen zwei Werten der Einflussvariable \(X\) und berechnen die Differenz der vorhergesagten Messwerte mit \(\hat{Y}_{X=b} - \hat{Y}_{X=a}\). Der klassische Zweigruppenvergleich, wenn wir die vorhergesagten Mittelwerte der zwei Level \(A.1\) und \(A.2\) des Faktors \(A\) miteinander vergleichen.

Jetzt können wir natürlich neben den Differenzen zwischen zwei vorhergesagten Messwerten auch noch andere Effekte berechnen. Wir nennen hier mal die Differenz als Effekt. Neben der Differenz können wir auch das Verhältnis oder aber den Lift berechnen.

Differenz (eng. difference)

Mit \(\hat{Y}_{X=b} - \hat{Y}_{X=a}\) erhalten wir die Differenz zwischen zwei den beiden vorhergesagten Messwerten. Die am häufigsten genutzte statistische Maßzahl für die Bestimmung von Unterschieden zwischen zwei Gruppen. Bei Gleichheit oder keiner Änderung ist die Differenz Null.

Verhältnis (eng. ratio)

Mit \(\frac{\hat{Y}_{X=b}}{\hat{Y}_{X=a}}\) erhalten wir das Verhältnis der beiden vorhergesagten Messwerte für die Gruppen. Das Verhältnis wird nicht so häufig verwendet, da wir hier mit einem Anteil dann einen etwas schwerer zu interpretierenden Effektschätzer haben. Bei Gleichheit oder keiner Änderung ist das Verhältnis gleich Eins.

Lift

Mit \(\frac{\hat{Y}_{X=b} - \hat{Y}_{X=a}}{\hat{Y}_{X=a}}\) erhalten wir als Ergebnis die relative prozentuale Differenz der Gruppe \(b\) im Vergleich zur Gruppe \(a\). Häufig wird im Kontext des Lifts von der Behandlung in Gruppe \(b\) und der Kontrolle in Gruppe \(a\) gesprochen. Bei keinem Unterschied oder Gleichheit ist der Lift gleich Null. Der Lift wird eher selten im Bereich der Agrarwissenschaften genutzt.

In dem folgenden Kasten findest du dann nochmal die Effektschätzer zusammengefasst. Wir haben im Prinzip diese drei Effektschätzer mit denen wir zwei Gruppen und die Effekte zwischen den Gruppen vergleichen können. Oder aber die Änderung in der Einflussvariable führt allgemeiner gesprochen zu einer Änderung im Effektschätzer.

HinweisEffektschätzer

Die häufigsten Effektschätzer sind die Differenz, das Verhältnis sowie der Lift. Dabei ist der Lift eher nicht so gängig und eine Besonderheit im Bereich Marketing wie die folgende Seite Calculating lift in A/B tests: Measuring true business impact erklärt. Dabei hat dann der Lift hat auch verschiedene Definitionen, wenn wir über andere Bereiche sprechen.

\[ \begin{align*} \hat{Y}_{X=b} - \hat{Y}_{X=a} && \text{Difference}\\ \frac{\hat{Y}_{X=b}}{\hat{Y}_{X=a}} && \text{Ratio}\\ \frac{\hat{Y}_{X=b} - \hat{Y}_{X=a}}{\hat{Y}_{X=a}} && \text{Lift}\\ \end{align*} \]

Hier nochmal ein kurzes Beispiel auf den Anteilen. Wenn wir in der Behandlungsgruppe einen Anteil von 5% vorliegen haben und in unserer Kontrollgruppe einen Anteil von 3%, dann haben wir ja eine Differenz von 2%. Das stimmt aber nur bedingt, da wir ja fast den doppelten Anteil in der Behandlung vorliegen haben. Der Lift wäre dann wie folgt zu berechnen.

\[ \frac{5\% - 3\%}{3\%} = \frac{2\%}{3\%} = 66\%\; \text{Lift} \]

Wir haben also eine Steigerung von 66% Punkten von der Kontrolle zu der Behandlung. Es macht eben einen Unterschied, ob ich von 50% auf 53% erhöhe oder eben von 3% auf 5%. Daher hat der Lift schon seine Berechtigung.

Eine Sache fehlt dann noch. Wir können einen besonderen Fall vorliegen haben. In diesem Fall ist unser vorhergesagter Messwert \(\hat{Y}_X\) eine Wahrscheinlichkeit. Damit haben wir dann noch folgende Möglichkeiten mit der den Wahrscheinlichkeiten zu rechnen. Die ersten beiden sind dir bekannt, es sind die Differenz und das Verhältnis. Das Chancehnverhältnis ist hier dann noch die Ergänzung.

\[ \begin{align*} \hat{Y}_{X=b}-\hat{Y}_{X=a} && \text{Risikodifferenz (eng. risk difference)}\\ \hat{Y}_{X=b}/\hat{Y}_{X=a} && \text{Risikoverhältnis (eng. risk ratio)}\\ \frac{\hat{Y}_{X=b}}{1 - \hat{Y}_{X=b}} \bigg/ \frac{\hat{Y}_{X=a}}{1 - \hat{Y}_{X=a}} && \text{Chancenverhältnis (eng. odds ratio)} \end{align*} \]

Alles wäre relativ einfach, wenn wir nur zwei Gruppen hätten. Dann müssen wir nur die vorhergesagten Messwerte \(\hat{Y}_X\) für beide Gruppen oder Änderungen in der Einflussvariable berechnen und schon hätten wir ein Ergebnis. Häufig haben wir aber nicht nur eine Einflussvariable in unserem Modell. Nehmen wir einmal folgendes Modell in dem wir die Sprungweiten \(Y\) in Abhängigkeit von dem Eintwicklungsstand stage, der Ernährungsform feeding und dem Flohgewicht weight modellieren wollen. Wir modellieren hier auch das volle Modell mit allen Interaktionen sonst können wir uns nicht alle Effekte in den Subgruppen anschauen.

\[ jump\_length = stage * feeding * weight \]

WarnungAchtung, bitte beachten!

Ich bin hier auch erst reingefallen. Wenn du später bei der Nutzung der Funktion comparisons() für Faktorkombinationen oder andere Einflussvariablen immer den gleichen Wert als als Schätzer erhälst, dann liegt es daran, dass du nicht das entsprechende volle Modell angepasst hast. Spiel dann nochmal mit dem Modell herum und schaue, ob dann sich die Werte ändern.

Jetzt können wir uns folgende Frage stellen: “Wie ändert sich die Sprungweite von juvenilen zu adulten Flöhen, mit einem Gewicht von 12mg und einer Ketchupernährung?”. Das sehe dann wie folgt für die Differenz der beiden vorhergesagten Sprungweiten aus. Ich habe in den Index immer nochmal reingeschrieben woher die vorhergesagten Messwerte \(\hat{Y}_X\) stammen

\[ \hat{Y}_{stage=juvenile,feeding=ketchup,weight=12} - \hat{Y}_{stage=adult,feeding=ketchup,weight=12} \]

Wir könnten uns natürlich auch für das Verhältnis der Sprungweiten zwischen den juvenilen und adulten Flöhen interessieren. Dann würden wir die vorhergesagten Messwerte für die beiden Gruppen unter der Annahme eines Gewichts von 12mg und einer Ketchupernährung durcheinander teilen.

\[ \cfrac{\hat{Y}_{stage=juvenile,feeding=ketchup,weight=12}}{ \hat{Y}_{stage=adult,feeding=ketchup,weight=12}} \]

Da wir es hier mit einer abhängigen Berechnung der Änderung in dem Messwert zu tun haben, macht es nicht viel Sinn die Berechnungen nach den Einflussvariablen aufzuteilen. Die Idee ist ja gerade, dass wir uns spezielle Kombinationen an Einflussvariablen mit den entsprechenden Werten überlegen um dann über eine Variable eine Aussage treffen zu können. Wir können uns aber einmal verschiedene Einflussvariablen anschauen, die wir dann mit den kontrafaktischen Vergleichen analysieren wollen. Meistens ist es dann der Faktor, den wir betrachten wollen.

55.9.1 Kontinuierlicher Messwert

Beginnen wir einmal mit einem kontinuierlichen Messwert wie die Sprungweite und lassen uns dann verschiedene kontrafaktische Vergleiche berechnen. Dafür nehmen wir dann erstmal nur die Einflussvariablen mit in unseren Datensatz, die uns dann auch interessieren. Das macht dann die Bearbeitung später einfacher.

jump_tbl <- flea_model_tbl |> 
  select(feeding, stage, weight, jump_length)

Wir brauchen eigentlich immer das volle Modell. Wenn du weniger Interaktionen möchtest, dann kann es gleich sein, dass du für bestimmte Faktorkombinationen immer den gleichen Effekt erhälst. Wir interpretieren ja nicht die Ausgabe des Modells direkt sondern im Kontext der kontrafaktische Vergleiche. Also einmal das volle Modell geschätzt.

jump_fit <- lm(jump_length ~ stage * feeding * weight, 
               data = jump_tbl)

Dann können wir uns auch einmal alle Koeffizienten des Modell anschauen. Ich nutze hier die Funktion model_parameters(), da wir dann hier auch gleich alles zusammen haben. Das Modell ist riesig und schwer zu interpretieren. Dafür nutzen wir gleich einmal die kontrafaktische Vergleiche als ein Analysetool.

model_parameters(jump_fit)

Parameter                                       | Coefficient |     SE
----------------------------------------------------------------------
(Intercept)                                     |       43.22 |  59.35
stage [juvenile]                                |        0.25 |  72.36
feeding [blood]                                 |       29.67 |  66.18
feeding [ketchup]                               |       43.25 |  68.86
weight                                          |        2.11 |   3.44
stage [juvenile] × feeding [blood]              |       35.95 | 100.38
stage [juvenile] × feeding [ketchup]            |       26.50 |  92.05
stage [juvenile] × weight                       |        1.54 |   8.99
feeding [blood] × weight                        |       -0.03 |   4.03
feeding [ketchup] × weight                      |       -1.65 |   4.37
(stage [juvenile] × feeding [blood]) × weight   |       -2.48 |  13.81
(stage [juvenile] × feeding [ketchup]) × weight |       -2.30 |  11.41

Parameter                                       |            95% CI |     t(36) |     p
---------------------------------------------------------------------------------------
(Intercept)                                     | [ -77.15, 163.59] |      0.73 | 0.471
stage [juvenile]                                | [-146.51, 147.01] |  3.49e-03 | 0.997
feeding [blood]                                 | [-104.54, 163.89] |      0.45 | 0.657
feeding [ketchup]                               | [ -96.40, 182.89] |      0.63 | 0.534
weight                                          | [  -4.87,   9.10] |      0.61 | 0.544
stage [juvenile] × feeding [blood]              | [-167.63, 239.53] |      0.36 | 0.722
stage [juvenile] × feeding [ketchup]            | [-160.19, 213.18] |      0.29 | 0.775
stage [juvenile] × weight                       | [ -16.69,  19.78] |      0.17 | 0.865
feeding [blood] × weight                        | [  -8.21,   8.15] | -7.68e-03 | 0.994
feeding [ketchup] × weight                      | [ -10.50,   7.20] |     -0.38 | 0.707
(stage [juvenile] × feeding [blood]) × weight   | [ -30.49,  25.53] |     -0.18 | 0.858
(stage [juvenile] × feeding [ketchup]) × weight | [ -25.44,  20.84] |     -0.20 | 0.841

Grundsätzlich haben wir die Wahl bei den Vergleichen eine Menge Effekte auszuwählen. Wir können zwischen mehreren dutzend Arten wählen, wobei natürlich die Differenz difference, das Verhältnis ratio oder aber dem Lift lift. Du musst da einmal in der Hilfe zu der Funktion comparisons() nachschauen was alles geht und welche Effekte dir dann in deinem speziellen Fall zu Verfügung stehen. Wir sind jetzt auch an verschiedenen Haupteinflussvariablen oder Fokusvariable (eng focal variable) interessiert. Mehr dazu auch in der Vignette Change in focal variables in {marginaleffects}. Hier schauen wir uns einmal die häufigsten Haupteinflussvariablen an. Die Idee ist nämlich, dass wir meistens an einer Variable hauptsächlich interessiert sind. Der Rest der Einflussvariablen ist dann erklärendes Beiwerk.

Änderung Faktor (2 Level)

Wir können in der Änderung der Level in einem Faktor interessiert sein. Dabei hat der Faktor nur zwei Level. Wir könnten hier meinen, dass es sich um sowas simples wie einen t-Test handelt. Aber das ist nicht der Fall. Alle Effekte wurden auf dem vollen Modell bestimmt, so dass hier viel mehr erklärt wird als nur durch einen simplen t-Test. Wir wollen hier die Entwicklungsstände auf dem mittleren Gewicht für die Ernährungsform Ketchup vergleichen.

comparisons(jump_fit, comparison = "difference",
            variables = "stage", 
            newdata = datagrid(weight = mean, feeding = "ketchup"))

 weight feeding Estimate Std. Error     z Pr(>|z|)   S 2.5 % 97.5 %
   9.95 ketchup     19.2         27 0.712    0.476 1.1 -33.7   72.2

Term: stage
Type: response
Comparison: juvenile - adult

Damit erhalten wir die Information, dass sich juvenile und adulte Flöhe in der Sprungweite um 19.2cm in der Ernährungsform Ketchup bei einem mittleren Gewicht von 9.95mg unterschieden. Die juvenilen Flöhe springen weiter als die adulten Flöhe.

Änderung Faktor (>2 Level)

Jetzt schauen wir uns mal die Ernährungsformen an. Wir wollen auch hier das mittlere Gewicht nehmen und entscheiden uns einmal für die juvenilen Flöhe. Dabei berechnen wir auch hier die Differenz zwischen den den Ernährungsarten. Hier vergleichen wir einmal zur Referenze oder Kontrolle. Das ist immer das erste Level in unserem Faktor.

comparisons(jump_fit, comparison = "difference",
            variables = lst("feeding" = "reference"), 
            newdata = datagrid(weight = mean, stage = "juvenile"))

              Contrast weight    stage Estimate Std. Error     z Pr(>|z|)   S
 blood - sugar_water     9.95 juvenile     40.6       60.7 0.670    0.503 1.0
 ketchup - sugar_water   9.95 juvenile     30.4       50.2 0.606    0.545 0.9
 2.5 % 97.5 %
 -78.3    160
 -68.0    129

Term: feeding
Type: response

Dann können wir das Ganze auch einmal für die adulten Flöhe durchführen. Hier machen wir dann einmal einen paarweisen Vergleich.

comparisons(jump_fit, comparison = "difference",
            variables = lst("feeding" = "pairwise"), 
            newdata = datagrid(weight = mean, stage = "adult"))

              Contrast weight stage Estimate Std. Error      z Pr(>|z|)   S
 blood - sugar_water     9.95 adult    29.37       29.3  1.001    0.317 1.7
 ketchup - blood         9.95 adult    -2.55       18.0 -0.142    0.887 0.2
 ketchup - sugar_water   9.95 adult    26.81       29.4  0.912    0.362 1.5
 2.5 % 97.5 %
 -28.1   86.9
 -37.8   32.7
 -30.8   84.4

Term: feeding
Type: response

Das spannende ist eben hier, dass wir einstellen können auf welchen Subgruppen wir dann die Vergleiche rechnen wollen. Sonst rechnen wir sehr allgemein gesprochen immer über die Mittelwerte der Messwerte der entsprechenden Kovariaten oder Faktorkombinationen. Hier können wir dann auch andere statistische Maßzahlen nutzen.

Änderung Kovariate

Am Ende dann noch die Änderung in der Kovariaten. Hier müssen wir dann nochmal aufpassen, dass wir auch alle Interaktionen in dem Modell mit beachtet haben, sonst haben wir mal schnell das Problem, dass wir immer die gleichen Effekte in den Faktorkombinationen vorfinden.

WarnungAchtung, bitte beachten!

Wenn du in Faktorkombinationen immer den gleichen Schätzer Estimate für die Änderung in deiner Kovariate siehst, dann hat es damit zu tun, dass du nicht alle Interaktionen in deinem Modell spezifiziert hast. Daher musst du wirklich das volle Modell mit f_A * f_B * c_1 bauen und schauen ob es dann funktioniert. Mich hat es einiges an Zeit gekostet das rauszufinden.

Hier wollen wir einmal die Änderung der Sprungweite von dem minimalen min zu dem maximalen max Flohgewicht berechnen aufgeteilt nach den Faktorkombinationen für die Ernährungsform und dem Entwicklungsstand. Wir haben noch sehr viel andere Möglichkeiten die Änderung in der Kovariaten zu setzen. Mehr dazu dann in der Vignette unter Change in numeric predictors. Hier also einmal ein Beispiel für die Veränderung des Flohgewichts.

comparisons(jump_fit, comparison = "difference",
            variables = list("weight" = "minmax"), 
            newdata = datagrid(feeding = unique, stage = unique))

     feeding    stage Estimate Std. Error       z Pr(>|z|)   S 2.5 % 97.5 %
 sugar_water adult       48.61       79.3  0.6132    0.540 0.9  -107    204
 sugar_water juvenile    84.18      191.2  0.4403    0.660 0.6  -291    459
 blood       adult       47.90       48.4  0.9896    0.322 1.6   -47    143
 blood       juvenile    26.38      236.4  0.1116    0.911 0.1  -437    490
 ketchup     adult       10.60       61.8  0.1716    0.864 0.2  -110    132
 ketchup     juvenile    -6.78      149.4 -0.0454    0.964 0.1  -300    286

Term: weight
Type: response
Comparison: Max - Min

Was sehen wir hier, wenn wir von dem minimalen zu der maximalen Flohgewicht gehen, dann ändert sich die Sprungweite entsprechend der Effekte Estimate in den Faktorkombinationen. Wir könnten hier auch als Vergleich ein Verhältnis setzen, wenn wir uns dadurch mehr Informationen erhoffen.

Jetzt haben wir uns einmal ein Beispiel angeschaut wo wir die Änderung in einem normalverteilten Messwert wie die Sprungweite modellieren. Wir können aber auch andere Messwerte wie den Infektionsstatus mit den kontrafaktischen Vergleichen analysieren. Hier haben wir dann noch mehr Vorteile, da die Ausgaben eines generalisierten linearen Modells (abk. glm) meistens noch schwerer zu interpretieren sind.

55.9.2 Binärer Messwert

Wenn wir über einen binären Messwert oder dichotomen Messwert sprechen, dann sind wir in der logistischen Regression angekommen. Damit modellieren wir dann nicht mehr einen normalverteilten Messwert sondern eben einen Messwert, der nur noch aus Nullen und Einsen besteht. In dem Fall müssen wir dann auch unsere Ergebnisse der Modellierung anders interpretieren. Aber auch helfen die kontrafaktischen Vergleiche um mehr aus dem Modell rauszuholen. Wie immer bauen wir uns erstmal einen kleineren Datensatz mit dem Infektionsstatus als unseren binären Messwert.

infected_tbl <- flea_model_tbl |> 
  select(feeding, stage, weight, infected)

Bei der logistischen Regression nutzen wir einmal ein etwas simpleres Modell. Wir haben aber immer noch die Interaktion mit in dem Modell, damit wir auch die Kovariate entsprechend in den Faktorkombinationen modellieren können.

infected_fit <- glm(infected ~ stage * (feeding + weight), 
                    data = infected_tbl, family = binomial)

Wenn wir uns jetzt die Ergebnisse anschauen, dann können wir entweder die Koeffizienten auf dem Log-Link anschauen, was dann die Log-Odds sind, oder aber die leichter zu interpretierenden Odds Ratios als Chancenverhältnisse. Ich habe hier den beiden folgenden Tabs einmal beide Ausgaben der Funktion model_parameters() dargestellt.

Odds Ratio

Wenn wir die Ausgabe der logistischen Regression transformieren, dann haben wir die Odds Ratios vorliegen. Wir können die Odds Ratios in dem Sinne interpretieren, dass wir mit einem Odds Ratio von Eins keinen Unterschied vorliegen haben.

model_parameters(infected_fit, exponentiate = TRUE)

Parameter                            | Odds Ratio |       SE
------------------------------------------------------------
(Intercept)                          |       0.15 |     0.65
stage [juvenile]                     |       0.93 |     4.37
feeding [blood]                      |   1.17e+09 | 4.42e+12
feeding [ketchup]                    |   1.17e-08 | 4.44e-05
weight                               |       1.05 |     0.26
stage [juvenile] × feeding [blood]   |   4.37e-10 | 1.66e-06
stage [juvenile] × feeding [ketchup] |   1.67e+08 | 6.34e+11
stage [juvenile] × weight            |       1.62 |     0.75

Parameter                            |            95% CI |         z |     p
----------------------------------------------------------------------------
(Intercept)                          | [0.00,   2741.42] |     -0.44 | 0.660
stage [juvenile]                     | [0.00,  17566.57] |     -0.02 | 0.987
feeding [blood]                      | [0.00,          ] |  5.51e-03 | 0.996
feeding [ketchup]                    | [    , 1.07e+167] | -4.82e-03 | 0.996
weight                               | [0.57,      1.75] |      0.19 | 0.850
stage [juvenile] × feeding [blood]   | [    , 1.95e+110] | -5.69e-03 | 0.995
stage [juvenile] × feeding [ketchup] | [0.00,          ] |  4.99e-03 | 0.996
stage [juvenile] × weight            | [0.68,      4.53] |      1.03 | 0.302

Log-Odds

Wenn wir die Ausgabe der logistischen Regression nicht transformieren, dann haben wir die Log-Odds vorliegen. Wir können die Log-Odds nicht einfach interpretieren. Dafür müssen wir dann die Odds Ratios nutzen.

model_parameters(infected_fit, exponentiate = FALSE)

Parameter                            | Log-Odds |      SE |            95% CI
-----------------------------------------------------------------------------
(Intercept)                          |    -1.89 |    4.28 | [ -11.09,   7.92]
stage [juvenile]                     |    -0.08 |    4.72 | [ -10.53,   9.77]
feeding [blood]                      |    20.88 | 3790.35 | [-254.62,       ]
feeding [ketchup]                    |   -18.26 | 3793.00 | [       , 384.60]
weight                               |     0.05 |    0.24 | [  -0.56,   0.56]
stage [juvenile] × feeding [blood]   |   -21.55 | 3790.35 | [       , 253.95]
stage [juvenile] × feeding [ketchup] |    18.94 | 3793.00 | [-267.36,       ]
stage [juvenile] × weight            |     0.48 |    0.47 | [  -0.39,   1.51]

Parameter                            |         z |     p
--------------------------------------------------------
(Intercept)                          |     -0.44 | 0.660
stage [juvenile]                     |     -0.02 | 0.987
feeding [blood]                      |  5.51e-03 | 0.996
feeding [ketchup]                    | -4.82e-03 | 0.996
weight                               |      0.19 | 0.850
stage [juvenile] × feeding [blood]   | -5.69e-03 | 0.995
stage [juvenile] × feeding [ketchup] |  4.99e-03 | 0.996
stage [juvenile] × weight            |      1.03 | 0.302

Auch wenn wir die Odds Ratios bestimmt haben ist das Modell meistens sehr komplex und schwer zu interpretieren. Die kontrafaktischen Vergleiche helfen uns auch hier die entsprechenden Vergleiche und Subgruppen besser zu definieren, so dass wir hier dann auch unsere Effekte besser deuten können. In den folgenden Tabs zeige ich dir dann einmal die häufigsten Einflussvariablen und wie wir diese Einflussvariablen dann für die Effekte interpretieren. Mehr dazu auch in der Vignette Change in focal variables in {marginaleffects}. In der Vignette liegt der Fokus sehr viel mehr auf der logistischen Regression und damit kannst du dort auch noch mehr Beispiele finden.

Änderung Faktor (2 Level)

Hier wollen wir dann einmal die Änderung in den Entwicklungsständen für den Infektionsstatus bestimmen. Wir nehmen das mittlere Flohgewicht und setzen den Vergleich auf ein Verhältnis. Dann müssen wir noch die Nullhypothese auf Eins setzen, da wir es ja hier mit einem Verhältnis zu tun haben. Kein Unterschied in einem Verhältnis bedeutet, dass wir eine Eins wiedergegeben bekommen. Wir betrachten dann nur die Flöhe in der Kontrolle mit Zuckerwasser.

comparisons(infected_fit, comparison = "ratio", hypothesis = 1,
            variables = "stage", 
            newdata = datagrid(weight = mean, feeding = "sugar_water"))

 weight     feeding Estimate Std. Error     z Pr(>|z|)   S 2.5 % 97.5 %
   9.95 sugar_water     4.98       7.82 0.508    0.611 0.7 -10.4   20.3

Term: stage
Type: response
Comparison: juvenile / adult

Die juvenilen Flöhe haben eine 4.98-fache höhere Infektionsrate als die adulten Flöhe bei einem mittleren Gewicht sowie der Gabe von Zuckerwasser. Wegen dem hohen Fehler ist der Vergleich nicht signifikant.

Änderung Faktor (>2 Level)

Dann können wir uns die Sachlage auch nochmal für einen Faktor mit mehr als zwei Leveln anschauen. Wir betrachten dann einmal die Ernährungsformen. Wenn wir nur die Variable setzen, dann rechnen wir immer einen Vergleich zu der Referenz. In unserem Fall ist es das Zuckerwasser, da es das erste Level im Faktor feeding ist.

comparisons(infected_fit, comparison = "ratio", hypothesis = 1,
            variables = "feeding", 
            newdata = datagrid(weight = mean, stage = "juvenile"))

              Contrast weight    stage Estimate Std. Error      z Pr(>|z|)   S
 blood / sugar_water     9.95 juvenile    0.967     0.0651 -0.512    0.608 0.7
 ketchup / sugar_water   9.95 juvenile    1.018     0.0571  0.313    0.755 0.4
 2.5 % 97.5 %
 0.839   1.09
 0.906   1.13

Term: feeding
Type: response

Hier sehen wir nur sehr kleine Effekte. Faktisch sind die Infektionsraten in den beiden Gruppen gleich groß. Dann können wir auch nochmal einen paarweisen Vergleich für die adulten Flöhe bei einem mittleren Gewicht rechnen.

comparisons(infected_fit, comparison = "ratio", hypothesis = 1,
            variables = lst("feeding" = "pairwise"), 
            newdata = datagrid(weight = mean, stage = "adult"))

              Contrast weight stage Estimate Std. Error         z Pr(>|z|)   S
 blood / sugar_water     9.95 adult 5.16e+00   8.10e+00  5.14e-01    0.607 0.7
 ketchup / blood         9.95 adult 2.81e-09   1.07e-05 -9.39e+04   <0.001 Inf
 ketchup / sugar_water   9.95 adult 1.45e-08   5.50e-05 -1.82e+04   <0.001 Inf
     2.5 %   97.5 %
 -1.07e+01 2.10e+01
 -2.09e-05 2.09e-05
 -1.08e-04 1.08e-04

Term: feeding
Type: response

Hier müssen wir dann wieder auf die Einheiten oder die wissenschaftliche Schreibweise der Effekte achten. Wir sehen hier ja, dass wir bei dem Vergleich der Blut und Zuckerernährung schon eine 5.16-fache Erhöhung der Infektionen bei der Bluternährung vorliegen haben. In der Ketchupernährung haben wir fast keine Infektionen vorliegen, wenn wir uns diese Subgruppe anschauen.

Änderung Kovariate

Dann betrachten wir noch die Änderung in der Kovariaten. Wir wollen wissen, wie sich das Verhältnis der Infektionen von dem minimalen zu dem maximalen Gewicht verändert. Mit transform = "exp" erhalten wir hier den Faktor der Änderung. Wir betrachten dann hier alle Faktorkombinationen.

comparisons(infected_fit, transform = "exp",
            variables = list("weight" = "minmax"), 
            newdata = datagrid(feeding = unique, stage = unique))

     feeding    stage Estimate Pr(>|z|)   S 2.5 % 97.5 %
 sugar_water adult        1.20  0.83872 0.3 0.201   7.20
 sugar_water juvenile     1.88  0.01144 6.4 1.152   3.06
 blood       adult        1.00  0.99979 0.0 1.000   1.00
 blood       juvenile     2.16  0.00301 8.4 1.298   3.59
 ketchup     adult        1.00  0.99979 0.0 1.000   1.00
 ketchup     juvenile     1.59  0.24301 2.0 0.729   3.48

Term: weight
Type: response
Comparison: Max - Min

Ohne die Transformation erhalten wir dann die Änderung in der Wahrscheinlichkeit infiziert zu sein. Durch die wissenschaftliche Schreibweise ist es dann sehr schwer zu sehen, was die Zahlen genau aussagen. Hier musst du dann nochmal runden oder aber dir die Zahlen einmal extra rausziehen.

comparisons(infected_fit, 
            variables = list("weight" = "minmax"), 
            newdata = datagrid(feeding = unique, stage = unique)) 

     feeding    stage Estimate Std. Error        z Pr(>|z|)   S     2.5 %
 sugar_water adult    1.86e-01   9.12e-01 0.203526  0.83872 0.3 -1.60e+00
 sugar_water juvenile 6.30e-01   2.49e-01 2.528952  0.01144 6.4  1.42e-01
 blood       adult    3.27e-09   1.22e-05 0.000268  0.99979 0.0 -2.39e-05
 blood       juvenile 7.70e-01   2.59e-01 2.966311  0.00301 8.4  2.61e-01
 ketchup     adult    3.81e-09   1.45e-05 0.000264  0.99979 0.0 -2.83e-05
 ketchup     juvenile 4.66e-01   3.99e-01 1.167508  0.24301 2.0 -3.16e-01
   97.5 %
 1.97e+00
 1.12e+00
 2.39e-05
 1.28e+00
 2.83e-05
 1.25e+00

Term: weight
Type: response
Comparison: Max - Min

Bei unserer logistischen Regression bietet es sich auch an einmal die kontrafaktischen Vergleiche zu visualisieren. Die Vignette zur Visulation liefert hier nochmal mehr Inspirationen. Wir wollen uns in der folgenden Abbildung einmal die Auswirkung von der juvenilen zu adulten Entwicklung und der Flohinfektion anschauen. Hohe Werte auf der y-Achse zeigen an, dass die Änderung von juvenile zu adult einen starken Einfluss auf die vorhergesagte Wahrscheinlichkeit für Flohschnupfen hat. Jetzt können wir uns anschauen, wie der Effekt des Gewichts über alle Werte des Flohgewichts aussieht.

plot_comparisons(infected_fit,
                 variables = "stage",
                 condition = "weight") +
  labs(y = "Bedingte Risikodifferenz", x = "Flohgewicht") +
  theme_minimal()

Abbildung 55.41— Abbildung des kontrafaktischen Vergleiches für den Einfluss des Gewichts auf die Wahrscheinlichkeit Flohschnupfen zu bekommen, wenn der Entwicklungsstand von juvenile zu adult wechselt. [Zum Vergrößern anklicken]

Die ganze Abbildung können wir uns dann auch nochmal getrennt für die Ernährungsformen anschauen. Hier erhalten wir dann auch die gleiche Aussage wie schon bei der vorherigen Abbildung. Hohe Werte auf der y-Achse zeigen an, dass die Änderung von juvenile zu adult einen starken Einfluss auf die vorhergesagte Wahrscheinlichkeit für Flohschnupfen hat. Dabei hat Ketchup einen weit höheren Einfluss als die Ernährung mit Blut. Wir haben hier aber nur einen sehr kleinen Datensatz vorliegen, so dass die Aussagen hier mit Vorsicht zu genießen sind.

plot_comparisons(infected_fit, 
                 variables = "stage",
                 condition = c("weight", "feeding")) +
  labs(y = "Bedingte Risikodifferenz", x = "Flohgewicht", 
       fill = "Ernährung", color = "Ernährung") +
  theme_minimal() +
  scale_color_okabeito() +
  scale_fill_okabeito()

Abbildung 55.42— Abbildung des kontrafaktischen Vergleiches für den Einfluss des Gewichts aufgeteilt für die drei Ernährungsformen auf die Wahrscheinlichkeit Flohschnupfen zu bekommen, wenn der Entwicklungsstand von juvenile zu adult wechselt. [Zum Vergrößern anklicken]

Am Ende ist hier die Stärke der kontrafaktischen Vergleiche, dass wir uns für verschiedene Subgruppen die Änderungen in einer Kovariaten anschauen können. Ohne die kontrafaktischen Vergleiche ist die Interpretation einer Kovariate in einer logistischen Regression immer sehr mühsam.

Das soll es dann auch erstmal für die kontrafaktischen Vergleiche als Übersicht gewesen sein. Wir können die kontrafaktischen Vergleiche natürlich auch für andere Messwerte einsetzen und dann entsprechend die Differenzen oder Verhältnisse von Anzahlen oder Noten berechnen. Es kommt hier aber natürlich sehr auf die wissenschaftliche Fragestellung an. Die kontrafaktischen Vergleiche haben ja ihre Stärke darin, dass du die Subgruppen von Interesse festlegen musst. Ohne diese Festlegung im Datenraster können wir hier natürlich viel machen, aber das ist natürlich nicht der Sinn der kontrafaktischen Vergleiche und dieses Kapitels.

“Die kontrafaktischen Vergleiche sind auch für mich neu im Jahre 2025 und deshalb habe ich natürlich die kontrafaktischen Vergleiche noch nicht viel genutzt. Sobald ich dann aber mehr Beispiele aus der echten Anwendung habe, werde ich die Beispiele mal hier ergänzen. Solange bleiben die kontrafaktischen Vergleiche eben dann auch eine gute Idee, die noch ihrer Anwendung durch mich harrt.” — Jochen Kruppa-Scheetz, meiner bescheidener Meinung nach.

55.10 Hypothesen- und Äquivalenztests

Die Implementierung von Hypothesen- und Äquivalenztests in den Vignetten Hypothesis and equivalence tests und Hypothesis Tests ist herausragend für das Paket {marginaleffects}. Ich kann wirklich eine Menge einfach in einem Modell testen, was ich so nicht in den anderen Paketen kann. Hier gibt es natürlich die Einschränkung im faktoriellen Design und den multiplen Vergleichen, die dann etwas sperriger zu nutzen sind. Es geht auch, aber es ist nicht so einfach möglich wie in {emmeans}. Aber das Paket {emmeans} ist ja auch direkt für den reinen faktoriellen Vergleich gebaut worden. Wenn Faktoren und Kovariaten im Modell kombiniert werden, dann nutze ich lieber {marginaleffects}. Kurze Vorrede, in diesem Abschnitt soll es nochmal um die Möglichkeiten gehen Hypothesen in den Modellen von {marginaleffects} zu testen. Teilweise zeige ich die Anwendung schon weiter oben, aber hier dann nochmal mit dem Schwerpunkt auf Stärken und Schwächen.

Generelles Vorgehen

Es gibt zwei Haupteinstiegspunkte für Hypothesentests in {marginaleffects}. Wenn wir das einigermaßen unterschieden, dann wird auch vieles klarer.

1. Funktionen in {marginaleffects}: Wir verwenden die Option hypothesis in den entsprechenden Funktionen.
2. Andere R-Objekte und Modelle: Wir verwenden die Funktion hypotheses().

Die b-Schreibweise der Koeffizienten

Koeffizienten als b abkürzen

55.10.1 Hypothesentest

Das statistische Testen haben wir schon in einem eigenen Kapitel bearbeitet. Du kannst mehr über die Hintergründe im Kapitel zur Testentscheidung lesen. Wenn es um die Koeffizienten eines linearen Modells geht und deren statistische Tests und Interpretation hilft dir das Kapitel zur linearen Regression weiter. Wir wollen uns hier nochmal kurz auf die Prinzipien zurückerinnern und dann einmal zeigen was die Funktion hypotheses() so alles kann. Dann schauen wir auch nochmal auf die Anwendung in verschiedenen Beispielen.

\[ Z=\frac{h(\hat{\theta})-H_0}{\sqrt{\hat{V}[h(\hat{\theta})]}} \]

feeding_fit = lm(jump_length ~ 0 + feeding, data = flea_model_tbl)
coef(feeding_fit)

feedingsugar_water       feedingblood     feedingketchup 
          70.00562          107.87063          101.69437 

summary(feeding_fit) |> coef()

                    Estimate Std. Error   t value     Pr(>|t|)
feedingsugar_water  70.00562   7.516627  9.313436 4.598588e-12
feedingblood       107.87063   7.516627 14.350934 2.091381e-18
feedingketchup     101.69437   7.516627 13.529256 1.821420e-17

\[ Z = \cfrac{\hat{\beta_1}-H_0}{\sqrt{\widehat{V}[\beta_1]}} = \cfrac{70.00562 - 0}{7.516627} = 9.313435 \]

2*pt(9.313435, df = 45, lower.tail = FALSE)

[1] 4.598598e-12

hypotheses(feeding_fit, hypothesis = 0)

               Term Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
 feedingsugar_water       70       7.52  9.31   <0.001  66.1  55.3   84.7
 feedingblood            108       7.52 14.35   <0.001 152.7  93.1  122.6
 feedingketchup          102       7.52 13.53   <0.001 136.1  87.0  116.4

hypotheses(feeding_fit, hypothesis = difference ~ pairwise)

                              Hypothesis Estimate Std. Error      z Pr(>|z|)
 (feedingblood) - (feedingsugar_water)      37.87       10.6  3.562  < 0.001
 (feedingketchup) - (feedingsugar_water)    31.69       10.6  2.981  0.00287
 (feedingketchup) - (feedingblood)          -6.18       10.6 -0.581  0.56123
    S 2.5 % 97.5 %
 11.4  17.0   58.7
  8.4  10.9   52.5
  0.8 -27.0   14.7

hypotheses(feeding_fit, hypothesis = difference ~ pairwise,
           multcomp = "bonferroni")

                              Hypothesis Estimate Std. Error      z Pr(>|z|)
 (feedingblood) - (feedingsugar_water)      37.87       10.6  3.562  0.00110
 (feedingketchup) - (feedingsugar_water)    31.69       10.6  2.981  0.00862
 (feedingketchup) - (feedingblood)          -6.18       10.6 -0.581  1.00000
    S  2.5 % 97.5 %
  9.8  12.95   62.8
  6.9   6.77   56.6
 -0.0 -31.09   18.7

hypotheses(feeding_fit, hypothesis = difference ~ pairwise)

                              Hypothesis Estimate Std. Error      z Pr(>|z|)
 (feedingblood) - (feedingsugar_water)      37.87       10.6  3.562  < 0.001
 (feedingketchup) - (feedingsugar_water)    31.69       10.6  2.981  0.00287
 (feedingketchup) - (feedingblood)          -6.18       10.6 -0.581  0.56123
    S 2.5 % 97.5 %
 11.4  17.0   58.7
  8.4  10.9   52.5
  0.8 -27.0   14.7

TippEs geht so viel mehr…

In der Vignette zu dem Hypothesentesten in {marginaleffects} findest du noch weit mehr Beispiele wie du mit selbstdefinierten Funktionen oder eben auch komplexer deine Hypothesen testen kannst. Das hier aufzuarbeiten würde den Rahmen sprengen. Deshalb schau dir in der Vignette mal ein paar Beispiele an.

55.10.2 Äquivalenztest

stage_fit <- lm(jump_length ~ 0 + stage, data = flea_model_tbl)
coef(stage_fit)

   stageadult stagejuvenile 
     90.27958      96.10083 

hypotheses(stage_fit, hypothesis = "b2 - b1 = 0")

 Hypothesis Estimate Std. Error     z Pr(>|z|)   S 2.5 % 97.5 %
    b2-b1=0     5.82       9.84 0.591    0.554 0.9 -13.5   25.1

hypotheses(stage_fit, 
  hypothesis = "b2 - b1 = 0", 
  equivalence = c(-5, 5))

 Hypothesis Estimate Std. Error     z Pr(>|z|)   S 2.5 % 97.5 % p (NonInf)
    b2-b1=0     5.82       9.84 0.591    0.554 0.9 -13.5   25.1      0.136
 p (NonSup) p (Equiv)
      0.533     0.533

Referenzen

Arel-Bundock, V., Greifer, N., & Heiss, A. (2024). How to Interpret Statistical Models Using marginaleffects for R and Python. Journal of Statistical Software, 111(9), 1–32. https://doi.org/10.18637/jss.v111.i09

Heiss, A. (2022, Mai 20). Marginalia: A Guide to Figuring Out What the Heck Marginal Effects, Marginal Slopes, Average Marginal Effects, Marginal Effects at the Mean, and All These Other Marginal Things Are. https://doi.org/10.59350/40xaj-4e562

---

1. Und dann war ich auch endlich im Oktober 2025 mit dem Kapitel fertig. Es war wirklich eins der am kompliziertesten Kapitel zu erstellen. Ich habe auch lange gebraucht um konzeptionell hier durchzusteigen.