pacman::p_load(tidyverse, magrittr, conflicted, broom,
see, performance, ggResidpanel, ggdist)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
"#F0E442", "#0072B2", "#D55E00", "#CC79A7")40 Modelgüte
Letzte Änderung am 02. April 2024 um 09:52:43
“Uncontrolled variation is the enemy of quality.” — W. Edwards Deming
Wenn wir ein Modell in einer Regression gerechnet haben, dann müssen wir auch wissen, ob dieses Modell gut oder schlecht ist. Dafür brauchen wir dann statistische Gütekriterien für ein statistsiches Modell. Wir interpretieren keine der Gütekriterien und statistischen Maßzahlen alleine sondern in der Gesamtheit. Wir meinen mit Gütekriterien wie gut das statistische Modellieren funktioniert hat. Wir haben eine große Auswahl an Methoden und wir müssen das Ergebnis des Modellierens überprüfen. Es gibt daher eine Reihe von Maßzahlen für die Güte eines Modells, wir schauen uns hier einige an. Später werden wir uns noch andere Maßzahlen anschauen, wenn wir eine multiple lineare Regression rechnen. Das R Paket {performance} werden wir später auch nutzen um die notwendigen Gütekriterien zu erhalten. Wir wollen eine Gerade durch Punkte legen. Deshalb müssen wir folgende Fragen klären um zu wissen, ob das Ziehen der Gerade auch gut funktioniert hat:
- Läuft die Gerade durch die Mitte der Punkte? Hier hilft ein Residualplot für die Bewertung.
- Folgt unser Outcome \(y\) und damit auch die Residuen einer Normalverteilung? Hier kann der QQ-Plot helfen.
- Liegen die Punkte alle auf der Geraden? Hier hilft das Bestimmtheitsmaß \(R^2\).
Wir gehen jetzt mal alle Punkte durch und schauen, ob wir eine gute Gerade angepasst (eng. fit) haben. Wenn wir keine gute Gerade angepasst haben, dann müssen wir überlegen, ob wir nicht unser Modell der Regression ändern. Es ist also vollkommen okay, eine Regression zu rechnen und dann festzustellen, dass die Regression so nicht geklappt hat. Dann rechnen wir eine andere Regression. Wie du in den folgenden Kapiteln feststellen wirst, gibt es nämlich eine Menge Typen von Regression. Auch ist es eine Überlegung wert einmal das Outcome \(y\) zu transformieren. Mehr dazu kannst du dann im Kapitel zur Transformation von Variablen nachlesen.
Abschießend findest du in dem folgenden Kasten nochmal weitere Tutorien und Hilfen. Vielleicht kannst du dort nochmal mehr Lesen und die eine oder andere weitere Idee finden. Insbesondere die R Pakete liefern noch eine Vielzahl an weiteren Möglichkeiten und Visualisierungen von Modelgüten.
Weitere Tutorien für die Güte einer Regression
Wir immer geht natürlich mehr als ich hier Vorstellen kann. Du findest im Folgenden Tutorien, die mich hier in dem Kapitel inspiriert haben.
- Das R Paket
{olsrr}und die Webseite liefert nochmal sehr viel mehr Möglichkeiten sich die Qualität einer Gaussian linearen Regression anzuschauen. Wenn du einen normalverteiltes Outcome hast, dann ist das R Paket{olsrr}richtig gut geeignet eine Regression zu rechnen und zu bewerten. - Das R Paket
{ggfortify}und die Webseite sowie die Seite Concepts and Basics of{ggfortify}liefern noch andere Möglichkeiten sich automatisierte Abbildungenautoplot()über die Güte eines Modells zu erstellen. - Das R Paket
{ggResidpanel}und die Webseite liefert auch nochmal eine Möglichkeit sich sehr übersichtlich die Informationen zu Residuen anzuschauen. Ich finde die Abbildungen dann etwas schöner als von anderen Paketen. - Den QQ-Plot selber per Hand bauen und zu SPSS vergleichen kannst du dann auch nochmal in QQ-plots in R vs SPSS.
40.1 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
40.2 Daten
Nachdem wir uns im vorherigen Kapitel mit einem sehr kleinen Datensatz beschäftigt haben, nehmen wir einen großen Datensatz. Bleiben aber bei einem simplen Modell. Wir brauchen dafür den Datensatz flea_dog_cat_length_weight.xlsx. In einer simplen linearen Regression schauen wir uns den Zusammenhang zwischen einem \(y\) und einem \(x_1\) an. Daher wählen wir aus dem Datensatz die beiden Spalten jump_length und weight. Wir wollen nun feststellen, ob es einen Zusammenhang zwischen der Sprungweite in [cm] und dem Flohgewicht in [mg] gibt. In dem Datensatz finden wir 400 Flöhe von Hunden und Katzen.
model_tbl <- read_csv2("data/flea_dog_cat_length_weight.csv") |>
select(animal, jump_length, weight)In der Tabelle 56.1 ist der Datensatz model_tbl nochmal dargestellt.
jump_length und der normalverteilten Variable weight. Wir betrachten die ersten sieben Zeilen des Datensatzes.
| animal | jump_length | weight |
|---|---|---|
| cat | 15.79 | 6.02 |
| cat | 18.33 | 5.99 |
| cat | 17.58 | 8.05 |
| cat | 14.09 | 6.71 |
| cat | 18.22 | 6.19 |
| cat | 13.49 | 8.18 |
| cat | 16.28 | 7.46 |
Im Folgenden ignorieren wir, dass die Sprungweiten und die Gewichte der Flöhe auch noch von den Hunden oder Katzen sowie dem unterschiedlichen Geschlecht der Flöhe abhängen könnten. Wir schmeißen alles in einen Pott und schauen nur auf den Zusammenhang von Sprungweite und Gewicht.
40.3 Simples lineares Modell
Für dieses Kapitel nehmen wir nur ein simples lineares Modell mit nur einem Einflussfaktor weight auf die Sprunglänge jump_length. Später kannst du dann noch komplexere Modelle rechnen mit mehr Einflussfaktoren \(x\) oder aber einer anderen Verteilungsfamilie für \(y\). Wir erhalten dann das Objekt fit_1 aus einer simplen linearen Gaussianregression was wir dann im Weiteren nutzen werden.
fit_1 <- lm(jump_length ~ weight, data = model_tbl)Wir nutzen jetzt dieses simple lineare Modell für die weiteren Gütekritierien, da wir es uns hier erstmal etwas einfacher machen wollen. Dann erhalten wir folgende zusammenfassende Ausgabe von dem Modell, was wir uns jetzt im Bezug auf die Residuals und dem R-squared näher anschauen wollen. Alle anderen Werte haben wir ja schon in dem Kapitel zur simplen linearen Regression besprochen.
fit_1 |>
summary()
Call:
lm(formula = jump_length ~ weight, data = model_tbl)
Residuals:
Min 1Q Median 3Q Max
-9.3240 -2.2511 0.0488 2.3147 9.3958
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.79212 0.76901 12.73 <2e-16 ***
weight 1.34378 0.09491 14.16 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.268 on 598 degrees of freedom
Multiple R-squared: 0.2511, Adjusted R-squared: 0.2498
F-statistic: 200.5 on 1 and 598 DF, p-value: < 2.2e-1640.4 Residualplot
Die erste Frage ist natürlich, geht die Gerade aus dem lm()-Fit mittig durch die Punkte? Liegen also alle Punkte gleichmaäßig um die Gerade verteilt. Das ist ja die Idee der linearen Regression, wir legen eine Gerade durch eine Punktewolke und wollen das die Abstände von den Beobachtungen unterhalb und oberhalb der Gerade in etwa gleich sind. Die Abstände von den Beobachtungen nennen wir auch \(\epsilon\) als Fehler oder aber eben Residuen. Das R Paket {olsrr} mit der Hilfeseite Residual Diagnostics liefert noch mehr Möglichkeiten der Diagnose der Modellgüte über die Residuen als hier vorgestellt. Das R Paket {olsrr} funktioniert aber nur für einen normalverteiltes Outcome \(y\).
Wir wollen nun mit dem Residualplot die Frage beantworten, ob die Gerade mittig durch die Punktewolke läuft. Die Residuen \(\epsilon\) sollen normalverteilt sein mit einem Mittelwert von Null und einer Varianz von \(s^2_{\epsilon}\) und somit gilt \(\epsilon \sim \mathcal{N}(0, s^2_{\epsilon})\). In R wird in Modellausgaben die Standardabweichung der Residuen \(s_{\epsilon}\) häufig als sigma bezeichnet. Wir können auch hier die Funktion augment() aus dem R Paket {broom} nutzen um uns die Residuen wiedergeben zu lassen. Wir erhalten somit die Residuen resid und die angepassten Werte .fitted auf der Geraden über die Funktion augment(). Die Funktion augment() gibt noch mehr Informationen wieder, aber wir wollen uns jetzt erstmal auf die Residuen und deren Derivate konzentrieren.
resid_plot_tbl <- fit_1 |>
augment() |>
select(-.hat, -.cooksd)
resid_plot_tbl# A tibble: 600 x 6
jump_length weight .fitted .resid .sigma .std.resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 15.8 6.02 17.9 -2.09 3.27 -0.642
2 18.3 5.99 17.8 0.489 3.27 0.150
3 17.6 8.05 20.6 -3.03 3.27 -0.928
4 14.1 6.71 18.8 -4.72 3.27 -1.45
5 18.2 6.19 18.1 0.110 3.27 0.0337
6 13.5 8.18 20.8 -7.29 3.26 -2.23
7 16.3 7.46 19.8 -3.54 3.27 -1.08
8 14.5 5.58 17.3 -2.75 3.27 -0.844
9 16.4 6.19 18.1 -1.75 3.27 -0.537
10 15.1 7.53 19.9 -4.83 3.26 -1.48
# i 590 more rowsWir erhalten jetzt folgende Information über unser Modell aus der Ausgabe der Funktion augment() wiedergeben. Ich habe hier einmal sehr kurz die Informationen erklärt.
.fittedsind die vorhergesagten Werte auf der Geraden. Wir bezeichnen diese Werte auch die \(\hat{y}\) Werte..residsind die Residuen oder auch \(\epsilon\). Daher der Abstand zwischen den beobachteten \(y\)-Werten in der Spaltejump_lengthund den \(\hat{y}\) Werten auf der Geraden und somit der Spalte.fitted..sigmabeschreibt die geschätzte \(s^2_{\epsilon}\) , wenn die entsprechende Beobachtung aus dem Modell herausgenommen wird.std.residsind die standardisierten Residuen. Dabei werden die Residuen durch die Standardabweichung der Residuen \(s_{\epsilon}\) geteilt. Wir rechnen hier mehr oder minder den Quotienten der Spalten.resid/.sigma. Die standardisierten Residuen folgen dann einer Standardnormalverteilung. Dazu dann aber gleich noch mehr.
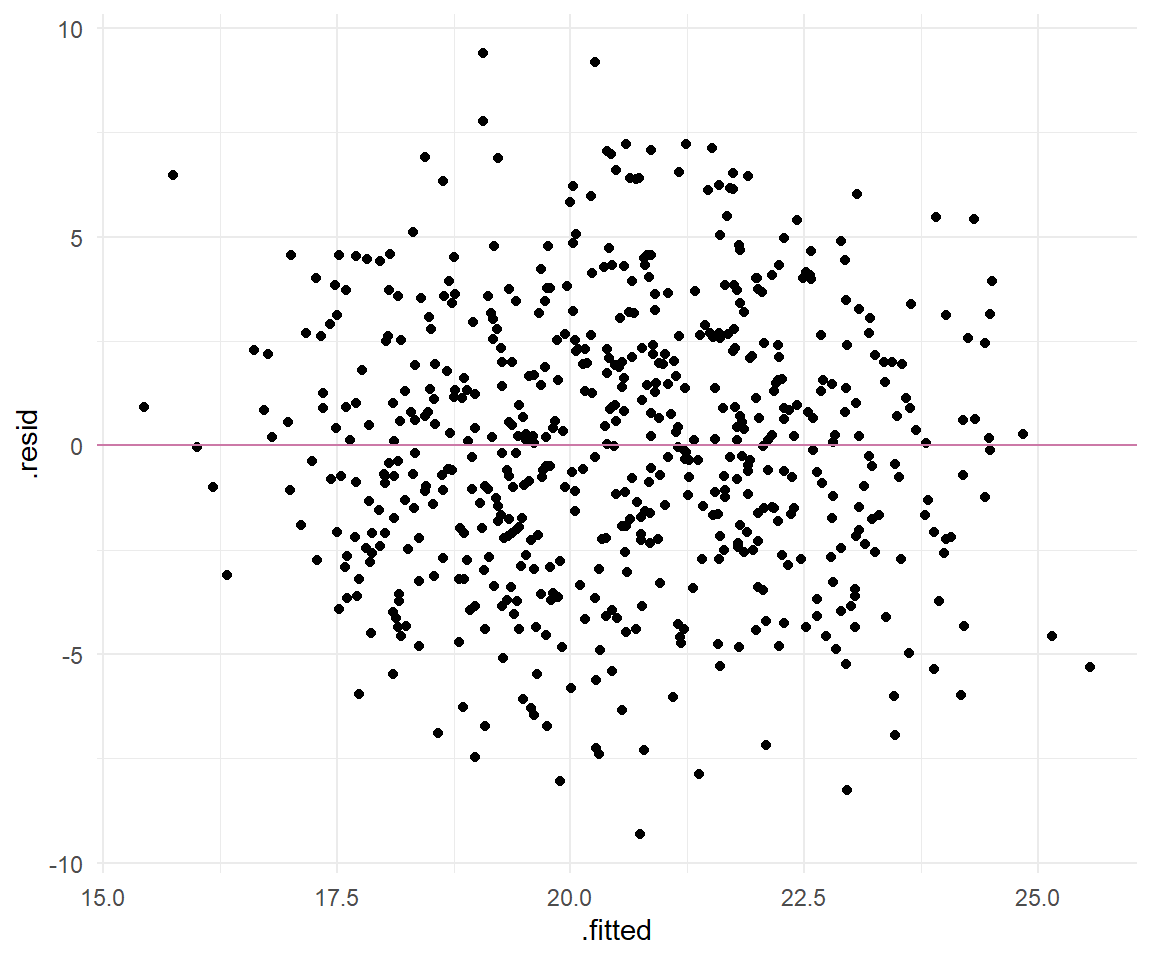
Die Daten selber interessieren uns nicht einer Tabelle. Stattdessen zeichnen wir einmal den Residualplot. Bei dem Residualplot tragen wir die Werte der Residuen .resid auf die \(y\)-Achse auf und die angepassten y-Werte auf der Geraden .fitted auf die \(x\)-Achse. Wir kippen im Prinzip die angepasste Gerade so, dass die Gerade parallel zu \(x\)-Achse läuft. Dann kommen wir auch schon zum berühmten Zitat, wie ein Residualplot aussehen soll.
“The residual plot should look like the sky at night, with no pattern of any sort.”
In Abbildung 40.1 sehen wir den Residualplot von unseren Beispieldaten. Wir sehen, dass wir keine Struktur in der Punktewolke erkennen. Auch sind die Punkte gleichmäßig um die Gerade verteilt. Wir haben zwar einen Punkt, der sehr weit von der Gerade weg ist, das können wir aber ignorieren. Später können wir uns noch in dem Kapitel zu den Ausreißern überlegen, ob wir einen Ausreißer (eng. outlier) vorliegen haben.
ggplot(resid_plot_tbl, aes(.fitted, .resid)) +
geom_point() +
geom_hline(yintercept = 0, color = "#CC79A7") +
theme_minimal()
fit_1. Die rote Linie stellt die geschätzte Gerade da. Die Punkte sollen gleichmäßig und ohne eine Struktur um die Gerade verteilt sein.
Es gibt viele Möglichkeiten sich die Residuen anzuschauen. Wir haben hier einmal den klassischen Residualplot nachgebaut. Wenn du dir andere Pakete anschaust, dann kriegts du immer eine Reihe von Abbildungen und nicht nur einen Scatterplot als Residualplot. Das R Paket {ggResidpanel} und die Webseite liefert eine Kombination von verschiedenen Abbildungen mit dem R Paket plotly, so dass wir hier mit der Funktion resid_interact() eine interaktive Abbildung vorliegen haben. Die statische Abbildung kannst du dir über die Funktion resid_panel() erstellen. Über den QQ-Plot erfährst du dann im nächsten Abschnitt mehr.
fit_1 |>
resid_interact()fit_1. Verschiedene Abbildungen geben Informationen über die Residuen und deren Eigenschaften wieder. Durch die Kombination mit dem R Paket {plotly} können wir direkt Informationen aus der Abbildung ablesen.
Verschiedene Arten von Residuen
Residuen beschreiben je den Anteil des Modells, den wir nicht erklären können. Neben den klassischen Residuen (eng. ordinary), die wir aus einer Regression erhalten, gibt es noch andere Varianten von Residuen. Hier sind die beiden bekanntesten Residuen mit standardisierte Residuen und den studentisierten Residuen. Beide Arten sind sehr nützlich, wenn wir verschiedene Modelle untereinander vergleichen wollen. Hier dann nochmal die Definition.
- Standardisierte Residuen (eng. standardized residuals)
-
… sind Residuen, die durch eine Schätzung ihrer Standardabweichung geteilt werden, mit dem Ergebnis, dass sie unabhängig von der Skala des Ergebnisses eine Standardabweichung sehr nahe bei 1 haben. Wir erhalten die standardisierte Residuen mit der R Funktion
rstandard(). - Studentisierte Residuen (eng. studentized residuals)
-
… sind den standardisierten Residuen ähnlich, außer dass für jeden Fall das Residuum durch die Standardabweichung geteilt wird, die aus der Regression ohne diese Beobachtung geschätzt wurde. Wir erhalten die studentisierte Residuen mit der R Funktion
rstudent().
Beide Arten von Residuen können wir mit der Standardnormalverteilung vergleichen. Ein standardisiertes Residuum von 2 entspricht zum Beispiel einem Punkt, der 2 Standardabweichungen über der Regressionslinie liegt. Damit haben wir dann eine Idee, wie weit weg einzelne Beobachtungen von der Geraden liegen. Beide Arten der Residuen haben ja keine Einheit mehr und so lässt sich hier recht einfach eine allgemeine Aussage machen. Beobachtungen, die ein Residuum von 2 oder mehr haben, liegen damit sehr weit von der Geraden entfernt. Im Folgenden nochmal der Vergleich aller drei Residuen Arten für unser Modell fit_1.
resid_tbl <- tibble(Ordinary = resid(fit_1),
Standard = rstandard(fit_1),
Student = rstudent(fit_1)) |>
gather()Dann können wir auch einmal die Mittelwerte und die Standardabweichung berechnen. Bei der relativ großen Fallzahl in unseren Daten sind die standardisierten und die studentisierten Residuen sehr ähnlich von den Werten.
resid_tbl |>
group_by(key) |>
summarise(mean(value), sd(value)) |>
mutate_if(is.numeric, round, 2)# A tibble: 3 x 3
key `mean(value)` `sd(value)`
<chr> <dbl> <dbl>
1 Ordinary 0 3.27
2 Standard 0 1
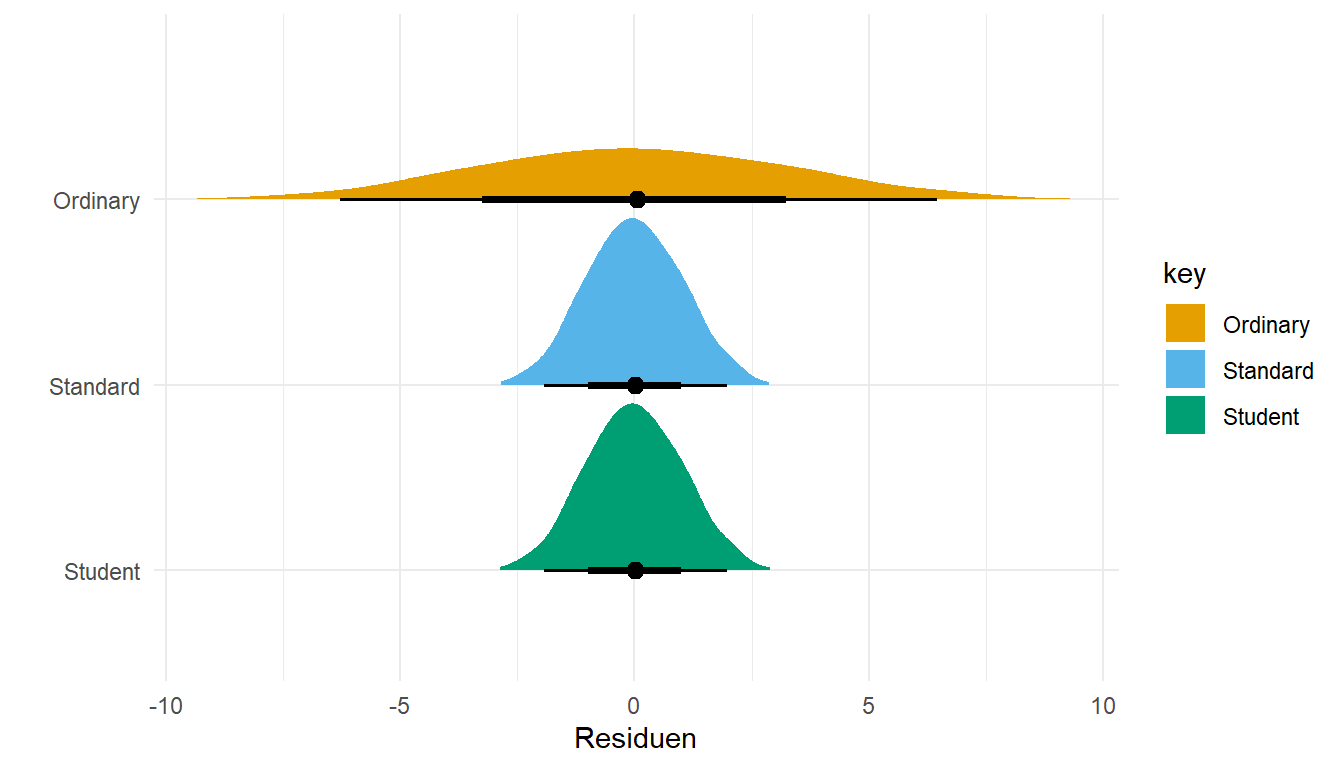
3 Student 0 1 Im Folgenden nutzen wir einmal das R Paket {ggdist} um uns in der Abbildung 40.3 die drei Arten der Residuen einmal zu visualisieren. Wo die klassischen Residuen noch eine sehr weite Verteilung haben sind die beiden einheitslosen Arten der Residuen sehr ähnlich und kompakt. Wir können daher sagen, das Beobachtungen mit einem Residuum größer als 2 schon sehr auffällige Werte haben und sehr weit von der angepassten Gerade liegen.
ggplot(resid_tbl, aes(value, fct_rev(key), fill = key)) +
theme_minimal() +
stat_halfeye() +
scale_fill_okabeito() +
labs(y = "", x = "Residuen")
40.5 QQ-Plot
Mit dem Quantile-Quantile Plot oder kurz QQ-Plot können wir überprüfen, ob unser \(y\) aus einer Normalverteilung stammt. Oder andersherum, ob unser \(y\) approximativ normalverteilt ist. Der QQ-Plot ist ein visuelles Tool. Daher musst du immer schauen, ob dir das Ergebnis passt oder die Abweichungen zu groß sind. Es hilft dann manchmal die Daten zum Beispiel einmal zu \(log\)-Transformieren und dann die beiden QQ-Plots miteinander zu vergleichen.
Wir brauchen für einen QQ-Plot eigentlich viele Beobachtungen. Das heißt, wir brauchen auf jeden Fall mehr als 20 Beobachtungen. Dann ist es auch häufig schwierig den QQ-Plot zu bewerten, wenn es viele Behandlungsgruppen oder Blöcke gibt. Am Ende haben wir dann zwar mehr als 20 Beobachtungen aber pro Kombination Behandlung und Block nur vier Wiederholungen. Und vier Wiederholungen sind zu wenig für eine sinnvolle Interpretation eines QQ-Plots.
Das klingt hier alles etwas wage… Ja, das stimmt. Aber wir wenden hier den QQ-Plot erstmal an und schauen uns dann im Anschluss nochmal genauer an, wie der QQ-Plot entsteht. Das kannst du dann einmal unten im Kasten nachlesen.
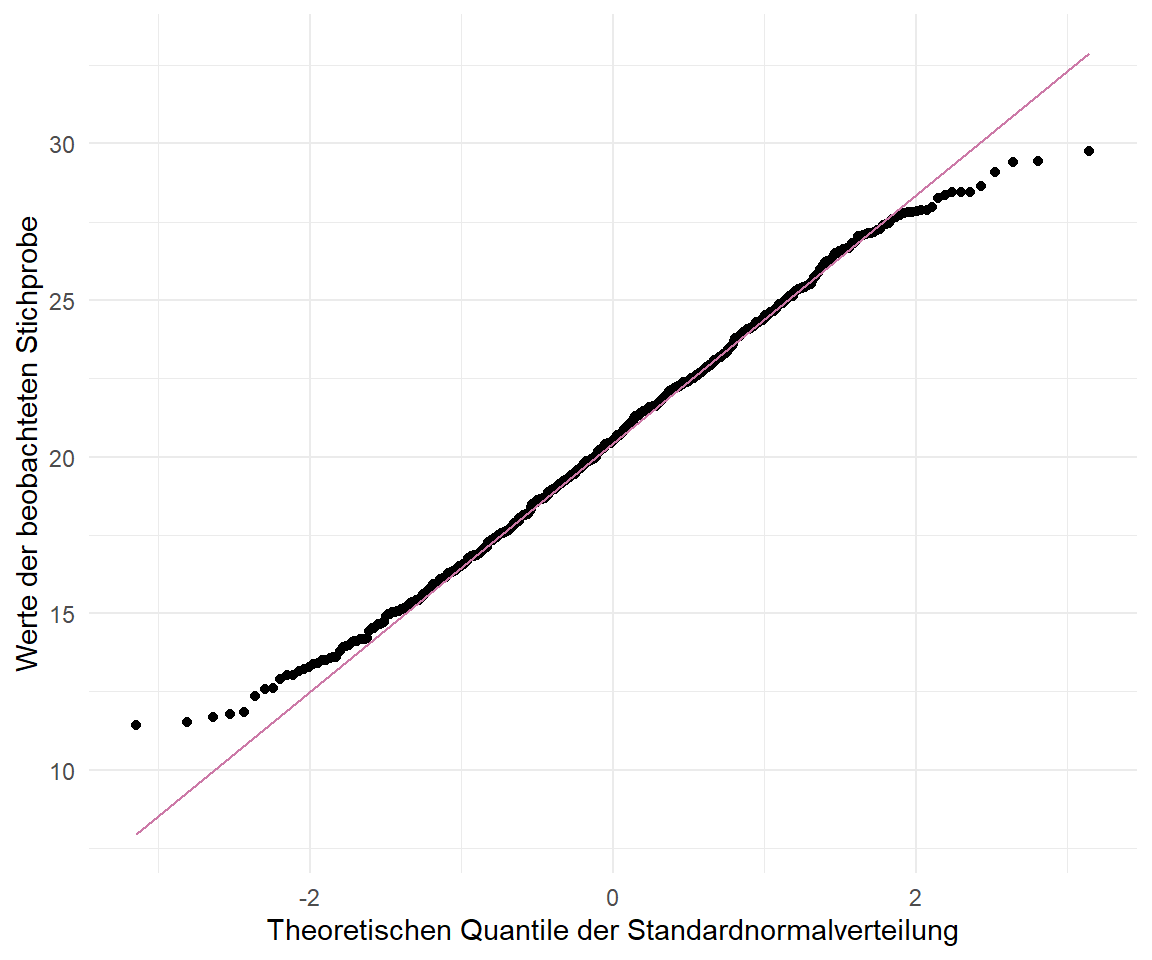
Grob gesprochen vergleicht der QQ Plot die Quantile der vorliegenden Beobachtungen, in unserem Fall der Variablen jump_length, mir den Quantilen einer theoretischen Normalverteilung, die sich aus den Daten mit dem Mittelwert und der Standardabweichung von jump_length ergeben würden. Wir können die Annahme der Normalverteilung recht einfach in ggplot überprüfen. Wir sehen in Abbildung 40.4 den QQ-Plot für die Variable jump_length. Die Punkte sollten alle auf einer Diagonalen liegen. Hier dargestellt durch die rote Linie. Häufig weichen die Punkte am Anfang und Ende der Spannweite der Beobachtungen etwas ab.
ggplot(model_tbl, aes(sample = jump_length)) +
stat_qq() +
stat_qq_line(color = "#CC79A7") +
labs(x = "Theoretischen Quantile der Standardnormalverteilung",
y = "Werte der beobachteten Stichprobe") +
theme_minimal()
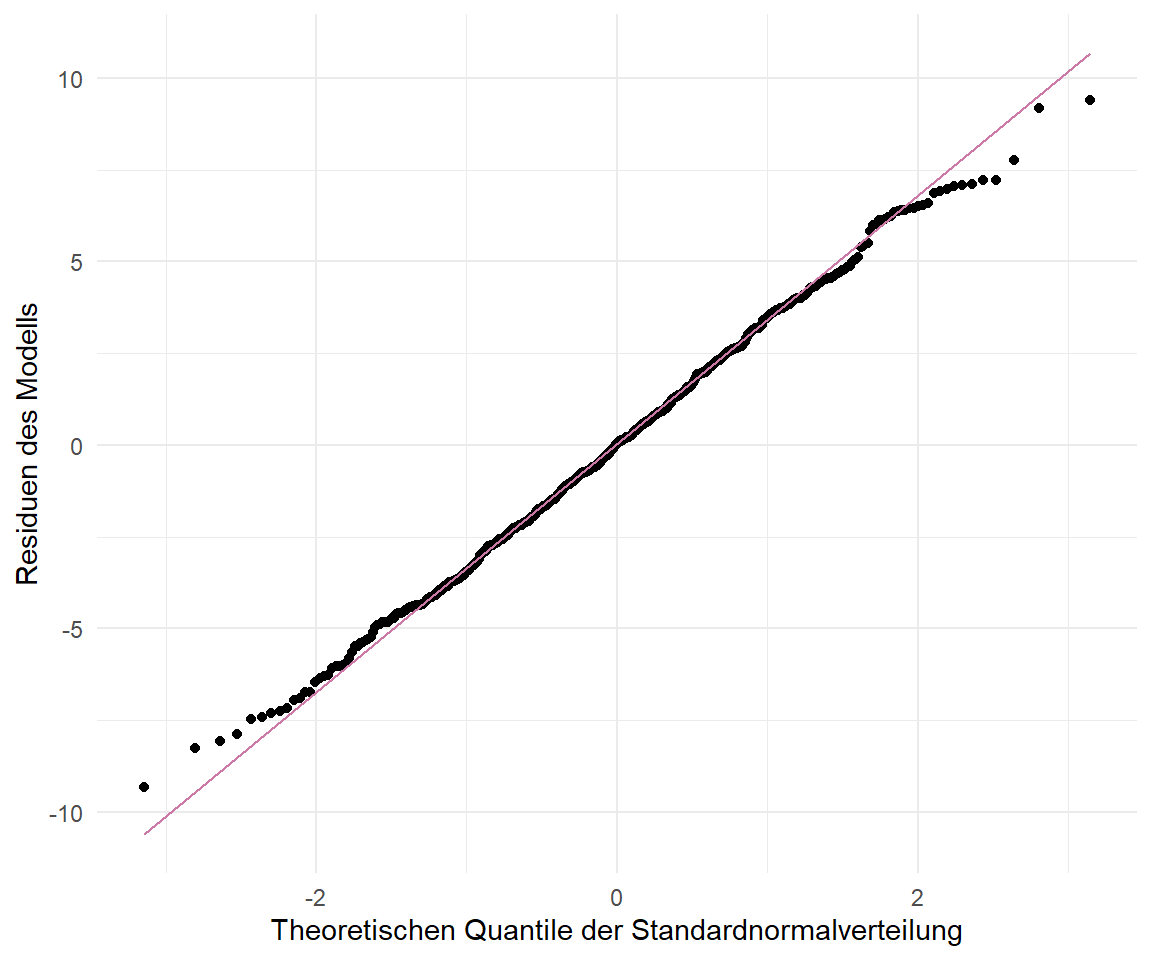
Wir werden uns später auch noch häufig die Residuen aus den Modellen anschauen. Die Residuen müssen nach dem Fit des Modells einer Normalverteilung folgen. Wir können diese Annahme an die Residuen mit einem QQ-Plot überprüfen. In Abbildung 40.5 sehen wir die Residuen aus dem Modell fit_1 in einem QQ-Plot. Wir würden sagen, dass die Residuen approximativ normalverteilt sind. Die Punkte liegen fast alle auf der roten Diagonalen.
ggplot(resid_plot_tbl, aes(sample = .resid)) +
stat_qq() +
stat_qq_line(color = "#CC79A7") +
theme_minimal() +
labs(x = "Theoretischen Quantile der Standardnormalverteilung",
y = "Residuen des Modells")
fit_1. Die Residuen müssen einer approximativen Normalverteilung folgen, sonst hat der Fit des Modelles nicht funktioniert.
Den QQ-Plot per Hand erstellen und verstehen
Gut das war jetzt die Anwendung und wie bauen wir uns jetzt einen QQ-Plot per Hand selber? Manchmal versteht man dann ja einen Algorithmus besser, wenn man ihn selber gebaut hat. Nehmen wir also einfach mal eine Reihe von Zahlen \(x\) und schauen, ob diese Zahlen einer Normalverteilung folgen. Wie oben schon gezeigt, sind die meist die Residuen einer linearen Regression. Wenn die Residuen einer Normalverteilung folgen, dann folgen auch unsere Daten einer Normalverteilung.
x <- c(7.19, 6.31, 5.89, 4.5, 3.77, 4.25, 5.19, 5.79, 6.79)Die Idee ist jetzt, dass wir eine Normalverteilung in \(n\) Blöcke aufteilen. Dabei ist \(n\) die Anzahl unserer Beobachtungen. In unserem Fall wäre \(n\) gleich 9. Wenn unsere Residuen normalverteilt wären, dann wären die \(x\)-Werte gleichmäßig um einen Mittelwert einer Normalverteilung verteilt. Jetzt ist natürlich die Frage, wie kriegen wir die Aufteilung hin?
n <- length(x)Dafür rangieren wir einmal unsere Daten mit der Funktion rank(). Das klappt in diesem Beispiel nur, da wir keine Bindungen in den Daten \(x\) vorliegen haben. Mit Bindungen sind gleiche Werte gemeint.
r <- rank(x)
r[1] 9 7 6 3 1 2 4 5 8Dann berechnen wir noch die Wahrscheinlichkeit des Auftreten des Ranges mit \(p=(r − 0.5)/n\). Die Formel fällt jetzt mal aus dem Himmel, ist aber nichts anderes als eine Transformation von einem Rang zu einer Wahrscheinlichkeit.
p <- (r - 0.5) / n
p |> round(2)[1] 0.94 0.72 0.61 0.28 0.06 0.17 0.39 0.50 0.83Jetzt können wir mit der Funktion qnorm() jeder Wahrscheinlichkeit p den entsprechenden \(z\)-Wert einer Normalverteilung zuordnen. Wir berechnen nichts anderes als die Werte auf der \(x\)-Achse einer Normalverteilung. Bei einer Normalverteilung heißen ja die \(x\)-Werte eben \(z\)-Werte.
z <- qnorm(p)
z[1] 1.5932188 0.5894558 0.2822161 -0.5894558 -1.5932188 -0.9674216 -0.2822161
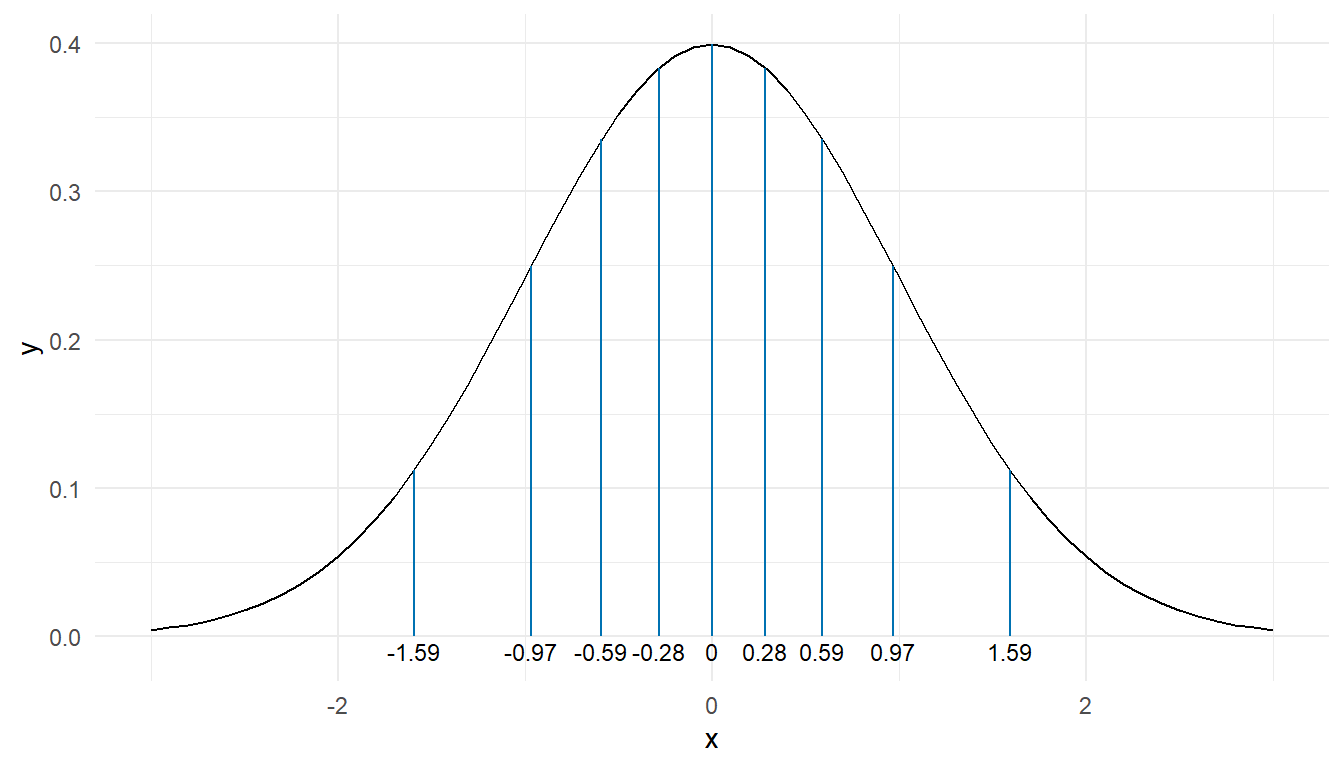
[8] 0.0000000 0.9674216In der Abbildung 40.6 habe ich dir einmal die neun \(z\)-Werte unserer entsprechenden \(x\)-Werte in einer Normalverteilung dargestellt. Die Fläche zwischen den \(z\)-Werten ist dabei immer gleich. Du siehst, dass die Werte entsprechend gleichmäßig über eine Normalverteilung verteilt sind.
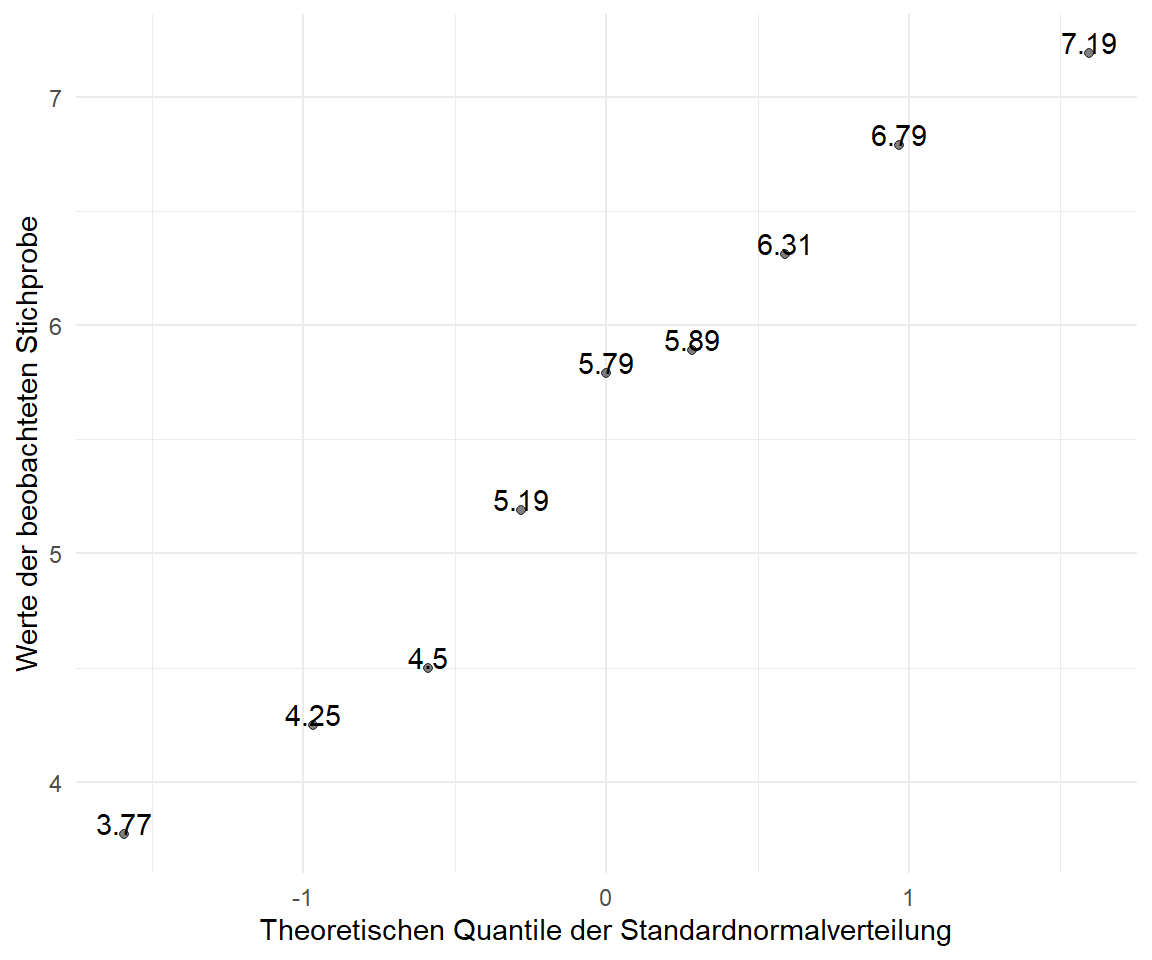
Dann können wir auch schon unseren QQ-Plot in der Abbildung 40.7 erstellen. Wir haben hier auf der \(x\)-Achse wieder die theoretischen Quantile der Standardnormalverteilung oder auch unsere \(z\)-Werte. Auf der \(y\)-Achse sind dann die Werte der beobachteten Stichprobe \(x\) aufgetragen. Wenn die Werte alle auf einer Geraden liegen, dann haben wir eine zumindestens approximative Normalverteilung vorliegen.
ggplot(tibble(x, z), aes(z, x)) +
theme_minimal() +
geom_point(alpha = 0.5) +
geom_text(aes(label = x), vjust = 0, hjust = 0.5) +
labs(x = "Theoretischen Quantile der Standardnormalverteilung",
y = "Werte der beobachteten Stichprobe")
Jetzt müssen wir nur noch die Gerade in dem QQ-Plot nachbauen. Hier nutzen wir das \(1^{st}\) und \(3^{rd}\) Quartile der beobachten Werte \(x\) sowie der theoretischen Normalverteilung. Dann können wir uns den unteren Punkt p1 sowie den oberen Punkt p2 berechnen und durch diese Punkte dann die Gerade zeichnen.
ref_prob <- c(.25, .75)
p1 <- qnorm(ref_prob)
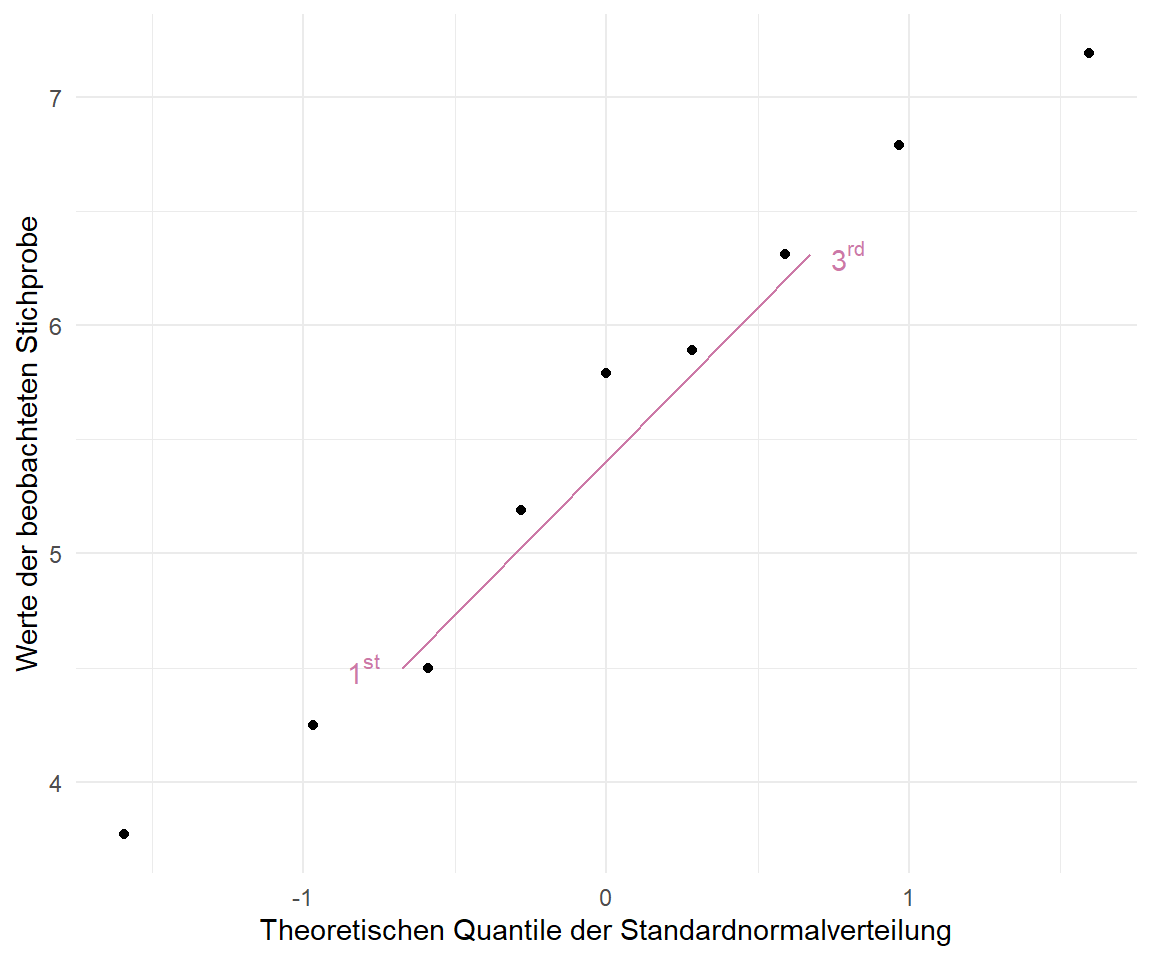
p2 <- quantile(x, ref_prob) In der Abbildung 40.8 siehst du dann einmal eine partielle QQ-Linie durch die Punkte des \(1^{st}\) und \(3^{rd}\) Quartiles. In der echten Anwendung wird die gerade dann noch weitergezeichnet, aber hier kann man dann gut sehen, wie die Gerade bestimmt wird. Hier also nur eine Demonstration der QQ-Linie.
ggplot(tibble(x, z), aes(z, x)) +
theme_minimal() +
geom_point() +
geom_segment(aes(p1[1], p2[1], xend = p1[2], yend = p2[2]), color = "#CC79A7") +
annotate("text", x = c(-0.8, 0.8), y = c(4.5, 6.31), color = "#CC79A7",
label = c(expression(1^{st}), expression(3^{rd}))) +
labs(x = "Theoretischen Quantile der Standardnormalverteilung",
y = "Werte der beobachteten Stichprobe")Warning in geom_segment(aes(p1[1], p2[1], xend = p1[2], yend = p2[2]), color = "#CC79A7"): All aesthetics have length 1, but the data has 9 rows.
i Did you mean to use `annotate()`?Warning in is.na(x): is.na() auf Nicht-(Liste oder Vektor) des Typs
'expression' angewendet
40.6 Bestimmtheitsmaß \(R^2\)
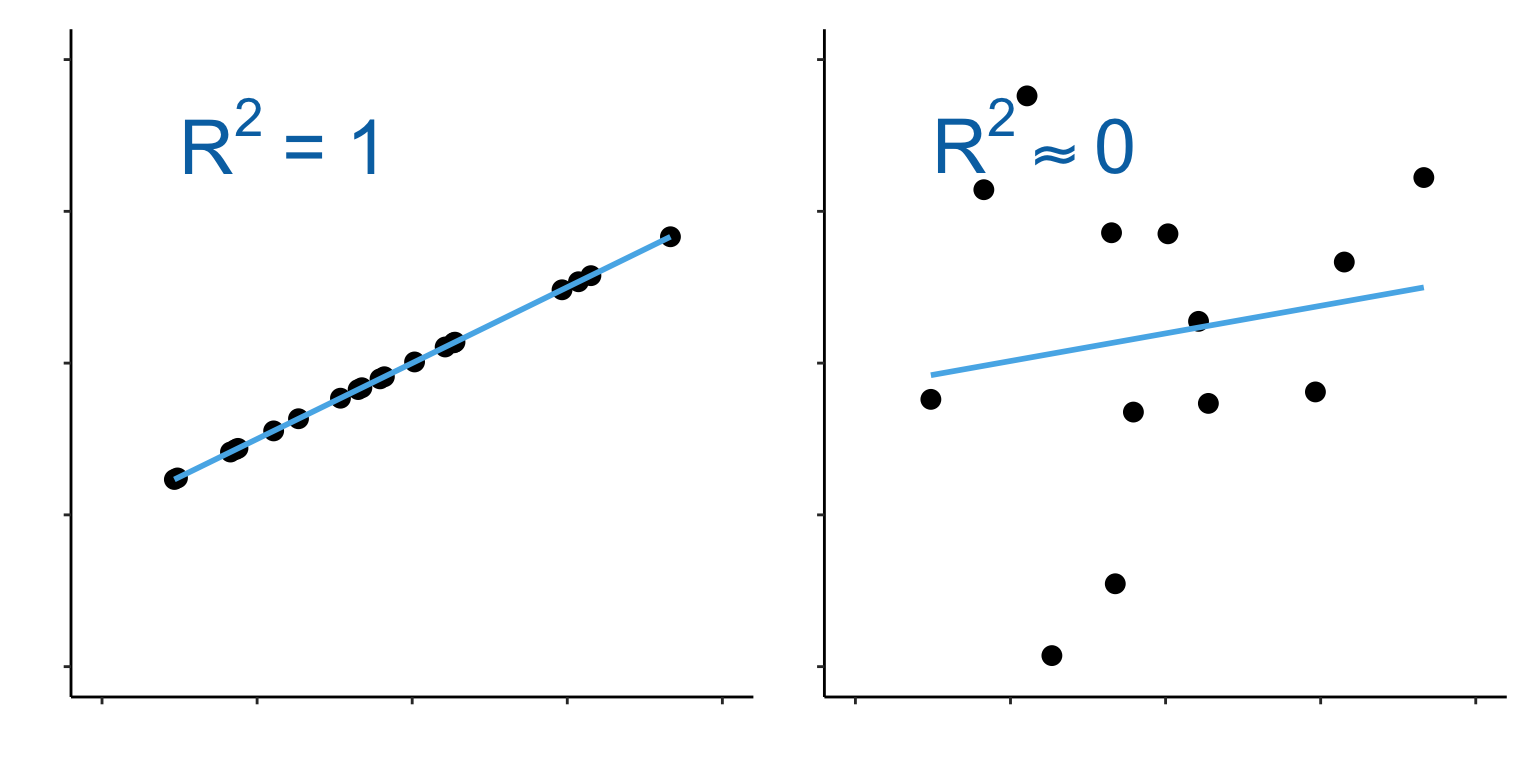
Nachdem wir nun wissen wie gut die Gerade durch die Punkte läuft, wollen wir noch bestimmen wie genau die Punkte auf der Geraden liegen. Das heißt wir wollen mit dem Bestimmtheitsmaß \(R^2\) ausdrücken wie stark die Punkte um die Gerade variieren. Wir können folgende Aussage über das Bestimmtheitsmaß \(R^2\) treffen. Die Abbildung 40.9 visualisiert nochmal den Zusammenhang.
- wenn alle Punkte auf der Geraden liegen, dann ist das Bestimmtheitsmaß \(R^2\) gleich 1.
- wenn alle Punkte sehr stark um die Gerade streuen, dann läuft das Bestimmtheitsmaß \(R^2\) gegen 0.
Da die Streuung um die Gerade auch gleichzeitig die Varianz widerspiegelt, können wir auch sagen, dass wenn alle Punkte auf der Geraden liegen, die Varianz gleich Null ist. Die Einflussvariable \(x_1\) erklärt die gesamte Varianz, die durch die Beobachtungen verursacht wurde. Damit beschreibt das Bestimmtheitsmaß \(R^2\) auch den Anteil der Varianz, der durch die lineare Regression, daher der Graden, erklärt wird. Wenn wir ein Bestimmtheitsmaß \(R^2\) von Eins haben, wird die gesamte Varianz von unserem Modell erklärt. Haben wir ein Bestimmtheitsmaß \(R^2\) von Null, wird gar keine Varianz von unserem Modell erklärt. Damit ist ein niedriges Bestimmtheitsmaß \(R^2\) schlecht.
Im Folgenden können wir uns noch einmal die Formel des Bestimmtheitsmaß \(R^2\) anschauen um etwas besser zu verstehen, wie die Zusammenhänge mathematisch sind.
\[ \mathit{R}^2 = \cfrac{\sum_{i=1}^N \left(\hat{y}_i- \bar{y}\right)^2}{\sum_{i=1}^N \left(y_i - \bar{y}\right)^2} \]
In der Abbildung 40.10 sehen wir den Zusammenhang nochmal visualisiert. Wenn die Abstände von dem Mittelwert zu den einzelnen Punkten mit \(y_i - \bar{y}\) gleich dem Abstand der Mittelwerte zu den Punkten auf der Geraden mit \(\hat{y}_i- \bar{y}\) ist, dann haben wir einen perfekten Zusammenhang.
Wir können die Funktion glance() nutzen um uns das r.squared und das adj.r.squared wiedergeben zu lassen.
fit_1 |>
glance() |>
select(r.squared, adj.r.squared)# A tibble: 1 x 2
r.squared adj.r.squared
<dbl> <dbl>
1 0.251 0.250Wir nutzen grundsätzlich das adjustierte \(R^2\)adj.r.squared in der Anwendung. Wir haben wir ein \(R^2\) von \(0.31\) vorliegen. Damit erklärt unser Modell bzw. die Gerade 31% der Varianz. Das ist jetzt nicht viel, aber wundert uns auch erstmal nicht. Wir haben ja die Faktoren animal und sex ignoriert. Beide Faktoren könnten ja auch einen Teil der Varianz erklären. Dafür müssten wir aber eine multiple lineare Regression mit mehren \(x\) rechnen.
Wenn wir eine multiple Regression rechnen, dann nutzen wir das adjustierte \(R^2\) in der Anwendung. Das hat den Grund, dass das \(R^2\) automatisch ansteigt je mehr Variablen wir in das Modell nehmen. Jede neue Variable wird immer etwas erklären. Um dieses Überanpassen (eng. overfitting) zu vermeiden nutzen wir das adjustierte \(R^2\). Im Falle des adjustierte \(R^2\) wird ein Strafterm eingeführt, der das adjustierte \(R^2\) kleiner macht je mehr Einflussvariablen in das Modell aufgenommen werdenn.
40.7 Das R Paket {performance}
Abschließend möchte ich hier nochmal das R Paket {performance} vorstellen. Wir können mit dem Paket auch die Normalverteilungsannahme der Residuen überprüfen. Das geht ganz einfach mit der Funktion check_normality() in die wir einfach das Objekt mit dem Fit des Modells übergeben.
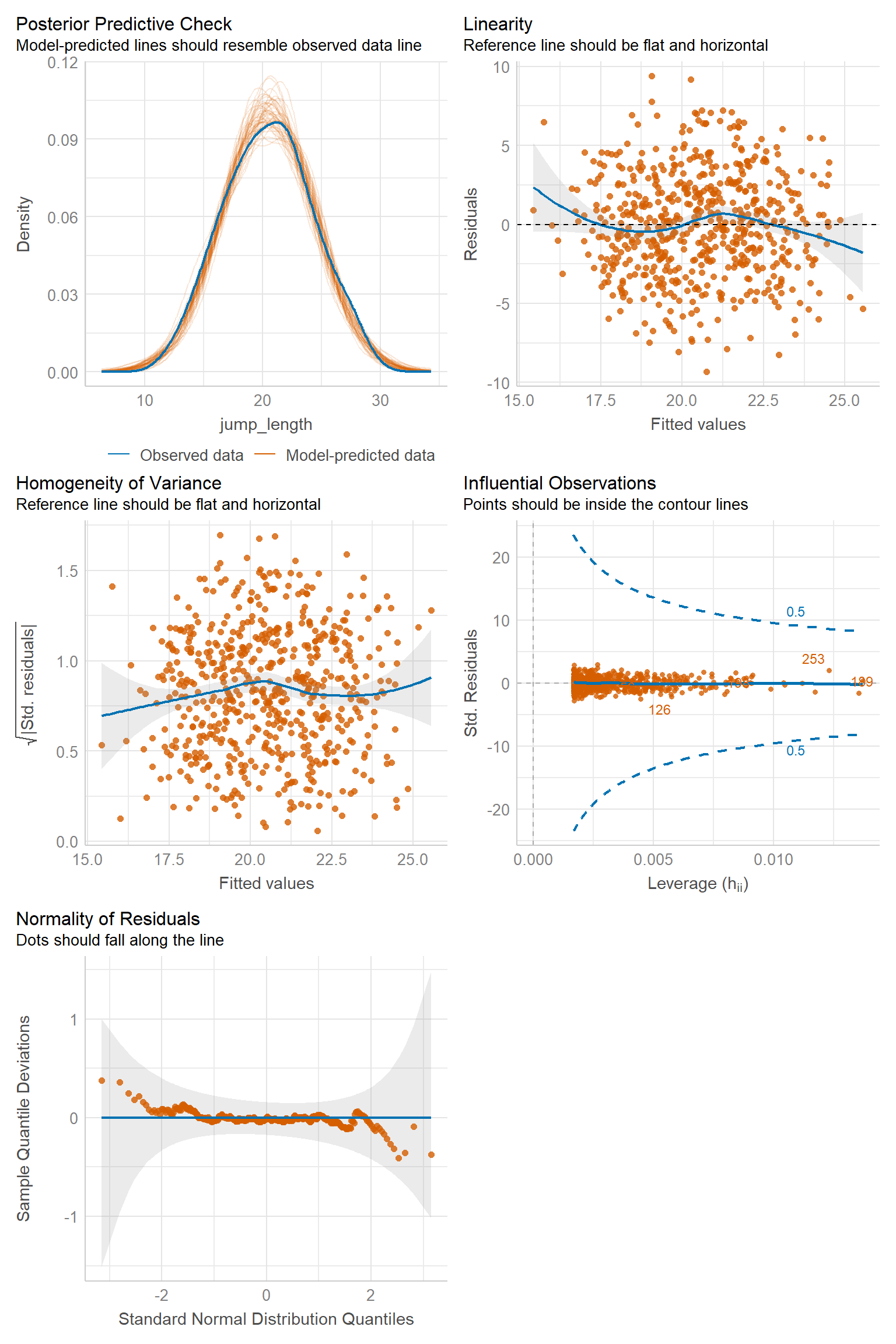
check_normality(fit_1)OK: residuals appear as normally distributed (p = 0.555).Wir haben auch die Möglichkeit uns einen Plot der Modellgüte anzeigen zu lassen. In Abbildung 40.11 sehen wir die Übersicht von bis zu sechs Abbildungen, die uns Informationen zu der Modellgüte liefern. Wir müssen nur den Fit unseres Modells an die Funktion check_model() übergeben. Das Schöne an der Funktion ist, dass jeder Subplot eine Beschreibung in Englisch hat, wie der Plot auszusehen hat, wenn alles gut mit dem Modellieren funktioniert hat. Wir kommen dann in der multiplen linearen Regression nochmal auf das Paket {performance} zurück. Für dieses Kapitel reicht dieser kurze Abriss.
check_model(fit_1, colors = cbbPalette[6:8])
check_model().