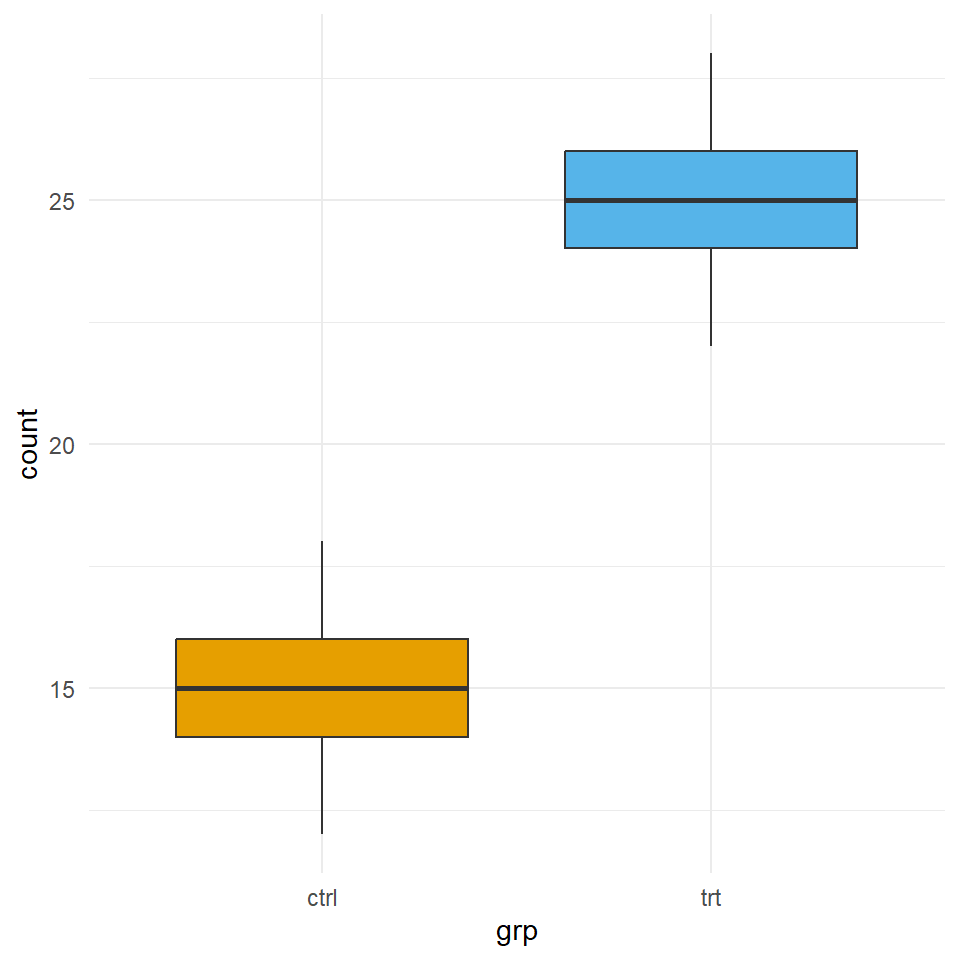56 Poisson Regression
Letzte Änderung am 09. April 2024 um 19:24:00
In diesem Kapitel wollen wir eine Poisson Regression rechnen. Wir müssen uns hier wieder überlegen, was ist eigentlich unser Outcome \(y\) und was sind unsere Einflussvariablen \(x\). Die Poisson Regression ist je nach Hintergrund des Anwenders eher selten. In der Ökologie, wo gerne mal gezaählt wird, wie oft etwas vorkommt, ist die Poisson Regression häufig vertreten. Sonst fristet die Poisson Regresson eher ein unbekanntes Dasein.
Ein häufig unterschätzter Vorteil der Poisson Regression ist, dass wir auch auch \(0/1\) Daten eine Poisson Regression rechnen können. Moment, wirst du jetzt vielleicht denken, das machen wir doch mit der logistischen Regression. Ja, das stimmt, aber wir können auf Zahlen viel rechnen. Wenn wir auf ein \(0/1\) Outcome eine Poisson Regression rechnen, dann kriegen wir nicht Odds Ratios \(OR\) als Effektschätzer sondern Risk Ratios \(RR\). Wir erhalten also keine Chancen sondern Wahrscheinlichkeiten. Unter der Annahme, dass das Modell auch konvergiert und wir sinnvolle Zahlen erhalten.
Ein weiteres Problem sind die zu vielen Nullen in dem Outcome \(y\). Daher wir zählen über die Maßen viel Nichts. Wir nennen diesen Fall zero inflation und beschreiben damit die zu vielen Nullen in den Daten. Hier muss dann noch speziell modelliert werden. Eine Poisson Regression hat schon so seine speziellen Tücken.
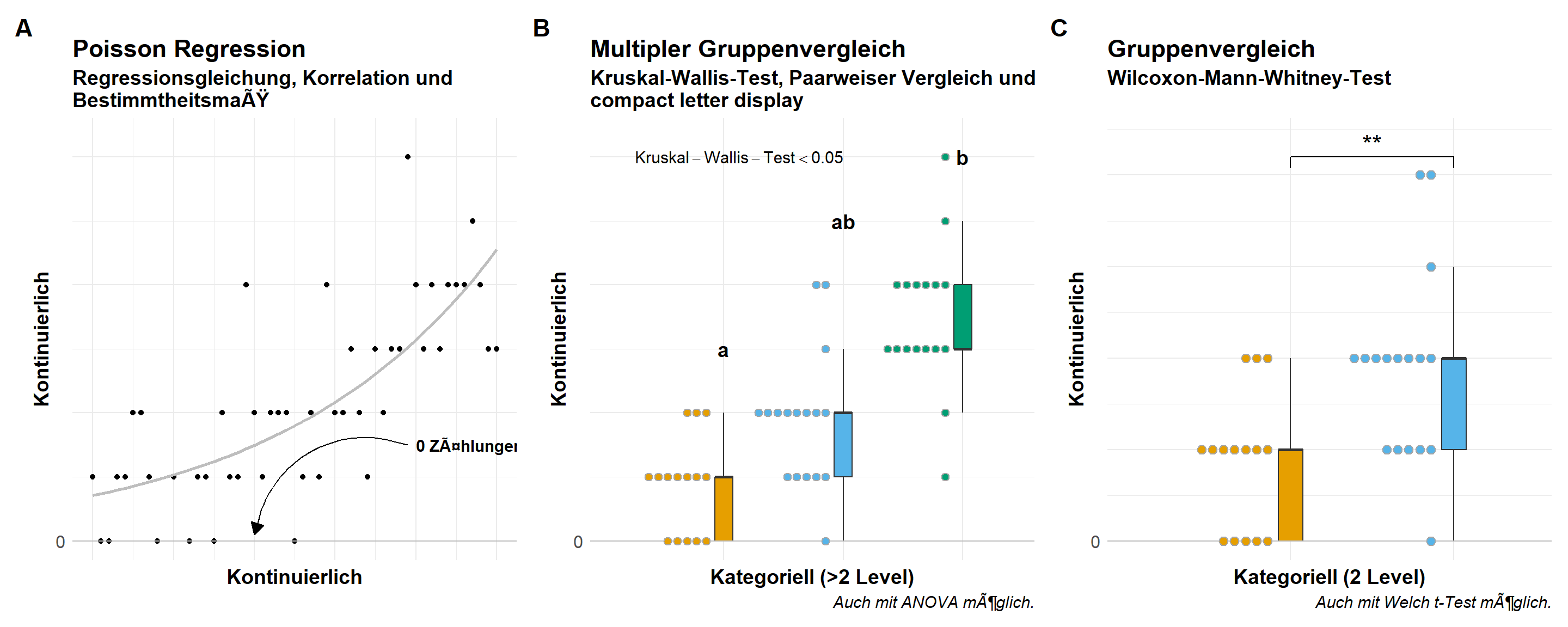
In der folgenden Abbildung 56.1 siehst du nochmal den Zusammenhang zwischen einem poissonverteilten Outcome, wie Anzahl oder Auftreten, im Bezug zu einem kontinuierlichen oder kategoriellen \(x\) als Einflussgröße. Wir sind dann eher im Bereich der Posthoc-Tests mit kategoriellen \(x\) als in wirklich einer Interpretation einer Poisson Regression mit einem kontinuierlichen \(x\). Dennoch müssen wir wissen, ob die Poisson Regression gut funktioniert hat. Die Überprüfung der Modellierung können wir dann in diesem Kapitel einmal durchgehen.
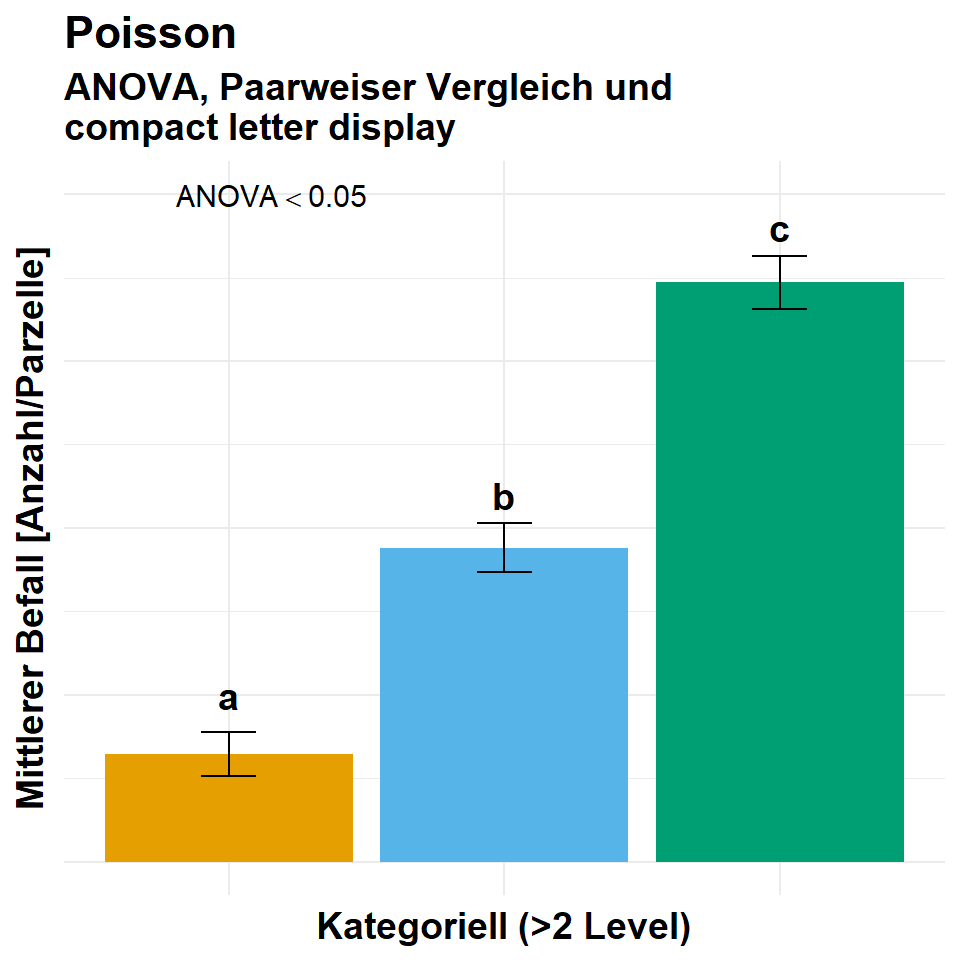
Häufig wollen wir dann die Ergebnisse aus einer Poisson Regression dann im Falle eines kategoriellen \(x\) dann als Barplots wie in der Abbildung 56.2 darstellen. Hier musst du dann einmal weiter unten in den Abschnitt zu den Gruppenvergleichen springen.
Im folgenden Kapitel zu der multiplen Poisson linearen Regression gehen wir davon aus, dass die Daten in der vorliegenden Form ideal sind. Das heißt wir haben weder fehlende Werte vorliegen, noch haben wir mögliche Ausreißer in den Daten. Auch wollen wir keine Variablen selektieren. Wir nehmen alles was wir haben mit ins Modell. Sollte eine oder mehre Bedingungen nicht zutreffen, dann schaue dir einfach die folgenden Kapitel an.
- Wenn du fehlende Werte in deinen Daten vorliegen hast, dann schaue bitte nochmal in das Kapitel 51 zu Imputation von fehlenden Werten.
- Wenn du denkst, dass du Ausreißer oder auffälige Werte in deinen Daten hast, dann schaue doch bitte nochmal in das Kapitel 49 zu Ausreißer in den Daten.
- Wenn du denkst, dass du zu viele Variablen in deinem Modell hast, dann hilft dir das Kapitel 50 bei der Variablenselektion.
Daher sieht unser Modell wie folgt aus. Wir haben ein \(y\) und \(p\)-mal \(x\). Wobei \(p\) für die Anzahl an Variablen auf der rechten Seite des Modells steht. Im Weiteren folgt unser \(y\) einer Poissonverteilung. Das ist hier sehr wichtig, denn wir wollen ja eine multiple Poisson lineare Regression rechnen.
\[ y \sim x_1 + x_2 + ... + x_p \]
Wir gehen jetzt einmal die lineare Regression mit einem normalverteilten Outcome \(y\) einmal durch. Wie schon oben erwähnt, können wir die Poisson Regression als vorangestelltes Modell für eine ANOVA oder dann eben einen Posthoc-Test in {emmeans} nutzen.
Wie immer gibt es auch für die Frage nach dem Tutorium für die Poisson Regression verschiedene Quellen. Ich kann noch folgende Informationen und Hilfen empfehlen.
56.1 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
pacman::p_load(tidyverse, magrittr, broom,
parameters, performance, MASS, pscl, see,
modelsummary, scales, emmeans, multcomp,
conflicted)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
"#F0E442", "#0072B2", "#D55E00", "#CC79A7")An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
56.2 Daten
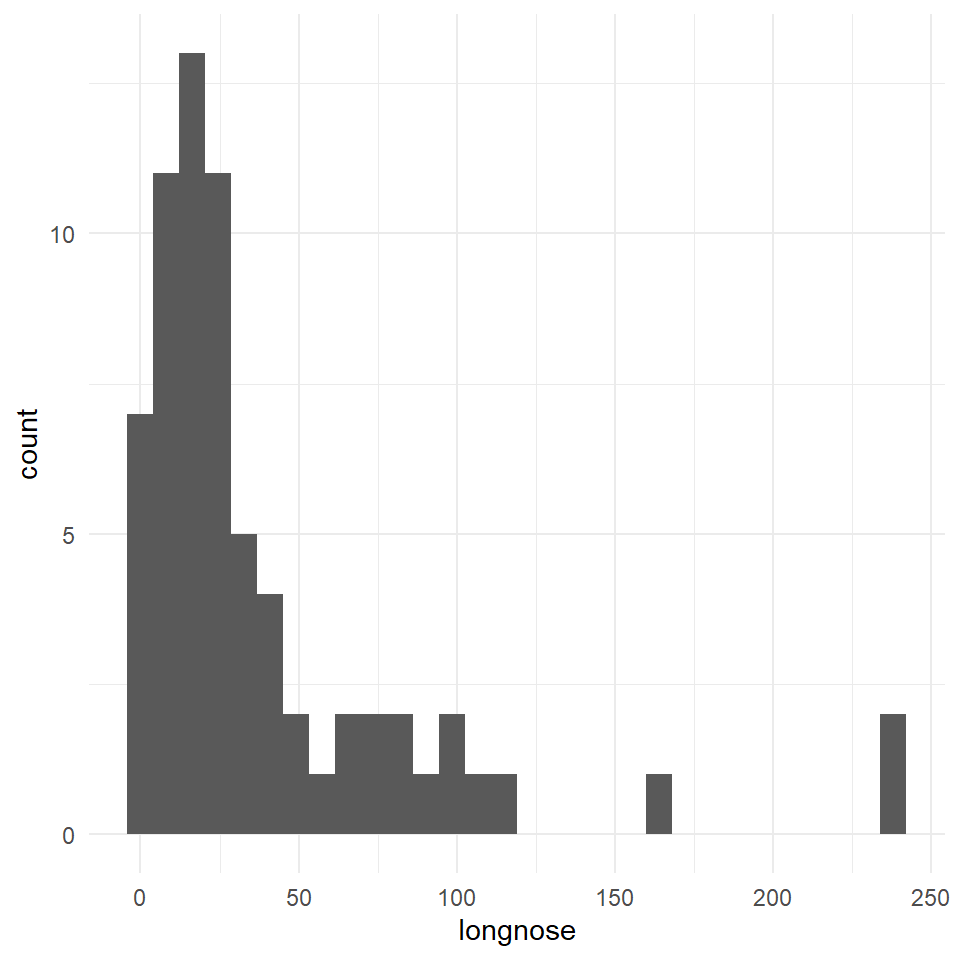
Im folgenden schauen wir uns ein Datenbeispiel mit Hechten an. Es handelt sich um langnasige Hechte in nordamerikanischen Flüssen. Wir haben uns insgesamt \(n = 68\) Flüsse einmal angesehen und dort die Anzahl an Hechten gezählt. Im Weiteren haben wir dann noch andere Flussparameter erhoben und fragen uns nun, welche dieser Parameter einen Einfluss auf die Anzahl an Hechten in den Flussarmen haben. In Kapitel 7.7 findest du nochmal mehr Informationen zu den Daten. Wir entfernen hier die Informationen zu den Flüssen, die brauchen wir in dieser Analyse nicht. Die Daten zu den langnasigen Hechten stammt von Salvatore S. Mangiafico - An R Companion for the Handbook of Biological Statistics. Besuche gerne mal seine Webseite, dort findest du auch andere tolle Beispiele zu statistischen Analysen.
R Code [zeigen / verbergen]
longnose_tbl <- read_csv2("data/longnose.csv") |>
select(-stream)| longnose | area | do2 | maxdepth | no3 | so4 | temp |
|---|---|---|---|---|---|---|
| 13 | 2528 | 9.6 | 80 | 2.28 | 16.75 | 15.3 |
| 12 | 3333 | 8.5 | 83 | 5.34 | 7.74 | 19.4 |
| 54 | 19611 | 8.3 | 96 | 0.99 | 10.92 | 19.5 |
| 19 | 3570 | 9.2 | 56 | 5.44 | 16.53 | 17 |
| … | … | … | … | … | … | … |
| 26 | 1450 | 7.9 | 60 | 2.96 | 8.84 | 18.6 |
| 20 | 4106 | 10 | 96 | 2.62 | 5.45 | 15.4 |
| 38 | 10274 | 9.3 | 90 | 5.45 | 24.76 | 15 |
| 19 | 510 | 6.7 | 82 | 5.25 | 14.19 | 26.5 |
Im Folgenden werden wir die Daten nur für das Fitten eines Modells verwenden. In den anderen oben genannten Kapiteln nutzen wir die Daten dann anders. In Abbildung 56.3 sehen wir nochmal die Verteilung der Anzahl der Hechte in den Flüssen.
56.3 Fit des Modells
In diesem Abschnitt wollen wir verschiedene Modelle für Zähldaten schätzen. Die Poissonverteilung hat keinen eignen Parameter für die Streung wie die Normalverteilung. Die Poissonverteilung ist mit \(\mathcal{Pois}(\lambda)\) definiert und hat somit die Eigenschaft das die Varianz eins zu eins mit dem Mittelwert \(\lambda\) der Poissonverteilung ansteigt. Es kann aber sein, dass wir in den Daten nicht diesen ein zu eins Zusammenhang von Mittelwert und Varianz vrliegen haben. Häufig ist die Varianz viel größer und steigt schneller an. Wenn die Varianz in Wirklichkeit sehr viel größer ist, dann würden wir die Varianz in unseren Modell unterschätzen.
- Ein klassisches Poissonmodell
glm(..., familiy = poisson)mit der Annahme keiner Overdisperison. - Ein Quasi-Poissonmodell
glm(..., family = quasipoisson)mit der Möglichkeit der Berücksichtigung einer Overdispersion. - Ein negative Binomialmodell
glm.nb(...)ebenfalls mit der Berücksichtigung einer Overdispersion.
Beginnen wollen wir aber mit einer klassischen Poissonregression ohne die Annahme von einer Overdispersion in den Daten. Wir nutzen dafür die Funktion glm() und spezifizieren die Verteilungsfamilie als poisson. Wir nehmen wieder alle Variablen in das Modell auf der rechten Seite des ~. Auf der linken Seite des ~ kommt dann unser Outcome longnose was die Anzahl an Hechten erhält.
Wir müssen für die Possionregression noch beachten, dass die Zähldaten von \(0\) bis \(+\infty\) laufen. Damit wir normalverteilte Residuen erhalten und einen lineren Zusammenhang, werden wir das Modell auf dem \(\log\)-scale fitten. Das heißt, wir werden den Zusammenhang von \(y\) und \(x\) logarithmieren. Wichtig ist hierbei der Zusammenhang. Wir transformieren nicht einfach \(y\) und lassen den Rest unberührt. Das führt dazu, dass wir am Ende die Koeffizienten der Poissonregression exponieren müssen. Das können die gängigen Funktionen, wir müssen das Exponieren aber aktiv durchführen. Deshalb hier schon mal erwähnt.
R Code [zeigen / verbergen]
poisson_fit <- glm(longnose ~ area + do2 + maxdepth + no3 + so4 + temp,
longnose_tbl, family = poisson)Wir schauen uns die Ausgabe des Modells einmal mit der summary() Funktion an, da wir hier einmal händisch schauen wollen, ob eine Overdispersion vorliegt. Sonst könnten wir auch die Funktion model_parameters() nehmen. Die nutzen wir später für die Interpretation des Modells, hier wollen wir erstmal sehen, ob alles geklappt hat.
R Code [zeigen / verbergen]
poisson_fit |> summary()
Call:
glm(formula = longnose ~ area + do2 + maxdepth + no3 + so4 +
temp, family = poisson, data = longnose_tbl)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.564e+00 2.818e-01 -5.551 2.83e-08 ***
area 3.843e-05 2.079e-06 18.480 < 2e-16 ***
do2 2.259e-01 2.126e-02 10.626 < 2e-16 ***
maxdepth 1.155e-02 6.688e-04 17.270 < 2e-16 ***
no3 1.813e-01 1.068e-02 16.974 < 2e-16 ***
so4 -6.810e-03 3.622e-03 -1.880 0.0601 .
temp 7.854e-02 6.530e-03 12.028 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2766.9 on 67 degrees of freedom
Residual deviance: 1590.0 on 61 degrees of freedom
AIC: 1936.9
Number of Fisher Scoring iterations: 5Wir schauen in die Summary-Ausgabe des Poissonmodells und sehen, dass dort steht, dass Dispersion parameter for poisson family taken to be 1. Wir modellieren also einen eins zu eins Zusammenhang von Mittelwert und Varianz. Wenn dieser Zusammenhang nicht in unseren Daten existiert, dann haben wir eine Overdispersion vorliegen.
Wir können die Overdispersion mit abschätzen indem wir die Residual deviance durch die Freiheitsgrade der Residual deviance teilen. Daher erhalten wir eine Overdispersion von \(\cfrac{1590.04}{61} \approx 26.1\). Damit haben wir eine eindeutige Overdispersion vorliegen. Damit steigt die Varianz in einem Verhältnis von ca. 1 zu 26. Wir können auch die Funktion check_overdispersion() aus dem R Paket {performance} nutzen um die Overdispersion zu berechnen. Die Funktion kann das schneller und ist auch in der Abfolge einer Analyse besser geeignet.
R Code [zeigen / verbergen]
poisson_fit |> check_overdispersion()# Overdispersion test
dispersion ratio = 29.403
Pearson's Chi-Squared = 1793.599
p-value = < 0.001Overdispersion detected.Wenn wir Overdispersion vorliegen haben und damit die Varianz zu niedrig schätzen, dann erhalten wir viel mehr signifikante Ergebnisse als es in den Daten zu erwarten wäre. Schauen wir uns nochmal die Parameter der Poissonverteilung und die \(p\)-Werte einmal an.
R Code [zeigen / verbergen]
poisson_fit |> model_parameters()Parameter | Log-Mean | SE | 95% CI | z | p
--------------------------------------------------------------------
(Intercept) | -1.56 | 0.28 | [-2.12, -1.01] | -5.55 | < .001
area | 3.84e-05 | 2.08e-06 | [ 0.00, 0.00] | 18.48 | < .001
do2 | 0.23 | 0.02 | [ 0.18, 0.27] | 10.63 | < .001
maxdepth | 0.01 | 6.69e-04 | [ 0.01, 0.01] | 17.27 | < .001
no3 | 0.18 | 0.01 | [ 0.16, 0.20] | 16.97 | < .001
so4 | -6.81e-03 | 3.62e-03 | [-0.01, 0.00] | -1.88 | 0.060
temp | 0.08 | 6.53e-03 | [ 0.07, 0.09] | 12.03 | < .001In der Spalte p finden wir die \(p\)-Werte für alle Variablen. Wir sehen, dass fast alle Variablen signifikant sind und das wir eine sehr niedrige Varianz in der Spalte SE sehen. Das heißt unser geschätzer Fehler ist sehr gering. Das ahnten wir ja schon, immerhin haben wir eine Overdisperson vorliegen. Das Modell ist somit falsch. Wir müssen uns ein neues Modell suchen, was Overdispersion berückscihtigen und modellieren kann.
Die Quasi-Poisson Verteilung hat einen zusätzlichen, unabhänigen Parameter um die Varianz der Verteilung zu schätzen. Daher können wir die Overdispersion mit einer Quasi-Poisson Verteilung berückscihtigen. Wir können eine Quasi-Poisson Verteilung auch mit der Funktion glm() schätzen nur müssen wir als Verteilungsfamilie quasipoisson angeben.
R Code [zeigen / verbergen]
quasipoisson_fit <- glm(longnose ~ area + do2 + maxdepth + no3 + so4 + temp,
data = longnose_tbl, family = quasipoisson)Nach dem Modellti können wir nochmal in der summary() Funktion schauen, ob wir die Overdispersion richtig berücksichtigt haben.
R Code [zeigen / verbergen]
quasipoisson_fit |> summary()
Call:
glm(formula = longnose ~ area + do2 + maxdepth + no3 + so4 +
temp, family = quasipoisson, data = longnose_tbl)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.564e+00 1.528e+00 -1.024 0.30999
area 3.843e-05 1.128e-05 3.408 0.00116 **
do2 2.259e-01 1.153e-01 1.960 0.05460 .
maxdepth 1.155e-02 3.626e-03 3.185 0.00228 **
no3 1.813e-01 5.792e-02 3.130 0.00268 **
so4 -6.810e-03 1.964e-02 -0.347 0.73001
temp 7.854e-02 3.541e-02 2.218 0.03027 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasipoisson family taken to be 29.40332)
Null deviance: 2766.9 on 67 degrees of freedom
Residual deviance: 1590.0 on 61 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 5An der Zeile Dispersion parameter for quasipoisson family taken to be 29.403319 in der Summary-Ausgabe sehen wir, dass das Modell der Quasi-Possion Verteilung die Overdispersion korrekt berücksichtigt hat. Wir können uns nun einmal die Modellparameter anschauen. Die Interpretation machen wir am Ende des Kapitels.
R Code [zeigen / verbergen]
quasipoisson_fit |> model_parameters()Parameter | Log-Mean | SE | 95% CI | t(61) | p
-------------------------------------------------------------------
(Intercept) | -1.56 | 1.53 | [-4.57, 1.41] | -1.02 | 0.306
area | 3.84e-05 | 1.13e-05 | [ 0.00, 0.00] | 3.41 | < .001
do2 | 0.23 | 0.12 | [ 0.00, 0.45] | 1.96 | 0.050
maxdepth | 0.01 | 3.63e-03 | [ 0.00, 0.02] | 3.18 | 0.001
no3 | 0.18 | 0.06 | [ 0.07, 0.29] | 3.13 | 0.002
so4 | -6.81e-03 | 0.02 | [-0.05, 0.03] | -0.35 | 0.729
temp | 0.08 | 0.04 | [ 0.01, 0.15] | 2.22 | 0.027 Jetzt sieht unser Modell und die \(p\)-Werte zusammen mit dem Standardfehler SE schon sehr viel besser aus. Wir können also diesem Modell erstmal von der Seite der Overdispersion vertrauen.
Am Ende wollen wir nochmal das Modell mit der negativen Binomialverteilung rechnen. Die negativen Binomialverteilung erlaubt auch eine Unabhängigkeit von dem Mittelwert zu der Varianz. Wir können hier auch für die Overdispersion adjustieren. Wir rechnen die negativen Binomialregression mit der Funktion glm.nb() aus dem R Paket {MASS}. Wir müssen keine Verteilungsfamilie angeben, die Funktion glm.nb() kann nur die negative Binomialverteilung modellieren.
R Code [zeigen / verbergen]
negativebinomial_fit <- glm.nb(longnose ~ area + do2 + maxdepth + no3 + so4 + temp,
data = longnose_tbl)Auch hier schauen wir mit der Funktion summary() einmal, ob die Overdisprsion richtig geschätzt wurde oder ob hier auch eine Unterschätzung des Zusammenhangs des Mittelwerts und der Varianz vorliegt.
R Code [zeigen / verbergen]
negativebinomial_fit |> summary()
Call:
glm.nb(formula = longnose ~ area + do2 + maxdepth + no3 + so4 +
temp, data = longnose_tbl, init.theta = 1.666933879, link = log)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.946e+00 1.305e+00 -2.256 0.024041 *
area 4.651e-05 1.300e-05 3.577 0.000347 ***
do2 3.419e-01 1.050e-01 3.256 0.001130 **
maxdepth 9.538e-03 3.465e-03 2.752 0.005919 **
no3 2.072e-01 5.627e-02 3.683 0.000230 ***
so4 -2.157e-03 1.517e-02 -0.142 0.886875
temp 9.460e-02 3.315e-02 2.854 0.004323 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for Negative Binomial(1.6669) family taken to be 1)
Null deviance: 127.670 on 67 degrees of freedom
Residual deviance: 73.648 on 61 degrees of freedom
AIC: 610.18
Number of Fisher Scoring iterations: 1
Theta: 1.667
Std. Err.: 0.289
2 x log-likelihood: -594.175 Auch hier sehen wir, dass die Overdispersion mit dem Parameter \(\theta\) berücksichtigt wird. Wir können die Zahl \(1.67\) nicht direkt mit der Overdispersion aus einer Poissonregression verglechen, aber wir sehen dass das Verhältnis von Residual deviance zu den Freiheitsgraden mit \(\cfrac{73.65}{61} \approx 1.20\) fast bei 1:1 liegt. Wir könnten also auch eine negative Binomialverteilung für das Modellieren nutzen.
R Code [zeigen / verbergen]
negativebinomial_fit |> model_parameters()Parameter | Log-Mean | SE | 95% CI | z | p
--------------------------------------------------------------------
(Intercept) | -2.95 | 1.31 | [-5.85, -0.10] | -2.26 | 0.024
area | 4.65e-05 | 1.30e-05 | [ 0.00, 0.00] | 3.58 | < .001
do2 | 0.34 | 0.11 | [ 0.11, 0.58] | 3.26 | 0.001
maxdepth | 9.54e-03 | 3.47e-03 | [ 0.00, 0.02] | 2.75 | 0.006
no3 | 0.21 | 0.06 | [ 0.10, 0.32] | 3.68 | < .001
so4 | -2.16e-03 | 0.02 | [-0.03, 0.03] | -0.14 | 0.887
temp | 0.09 | 0.03 | [ 0.03, 0.16] | 2.85 | 0.004 Wie immer gibt es reichlich Tipps & Tricks welches Modell du nun nehmen solltest. How to deal with overdispersion in Poisson regression: quasi-likelihood, negative binomial GLM, or subject-level random effect? und das Tutorial Modeling Count Data. Auch ich mus immer wieder schauen, was am besten konkret in der Anwendung passen könnte und würde.
Welches Modell nun das beste Modell ist, ist schwer zu sagen. Wenn du Overdisperion vorliegen hast, dann ist natürlich nur das Quasi-Poissonmodell oder das negative Binomialmodell möglich. Welche der beiden dann das bessere ist, hängt wieder von der Fragestellung ab. Allgemein gesprochen ist das Quasi-Poissonmodell besser wenn dich die Zusammenhänge von \(y\) zu \(x\) am meisten interessieren. Und das ist in unserem Fall hier die Sachlage. Daher gehen wir mit den Quasi-Poissonmdell dann weiter.
56.4 Performance des Modells
In diesem kurzen Abschnitt wollen wir uns einmal anschauen, ob das Modell neben der Overdispersion auch sonst aus statistischer Sicht in Ordnung ist. Wir wollen ja mit dem Modell aus dem Fit quasipoisson_fit weitermachen. Also schauen wir uns einmal das pseudo-\(R^2\) für die Poissonregression an. Da wir es mit einem GLM zu tun haben, ist das \(R^2\) mit Vorsicht zu genießen. In einer Gaussianregression können wir das \(R^2\) als Anteil der erklärten Varianz durch das Modell interpretieren. Im Falle von GLM’s müssen wir hier vorsichtiger sein. In GLM’s gibt es ja keine Varianz sondern eine Deviance.
R Code [zeigen / verbergen]
r2_efron(quasipoisson_fit)[1] 0.3257711Mit einem pseudo-\(R^2\) von \(0.33\) erklären wir ca. 33% der Varianz in der Anzahl der Hechte. Das ist zwar keine super gute Zahl, aber dafür, dass wir nur eine handvoll von Parametern erfasst haben, ist es dann auch wieder nicht so schlecht. Die Anzahl an Hechten wird sicherlich an ganz vielen Parametern hängen, wir konnten immerhin einige wichtige Stellschrauben vermutlich finden.
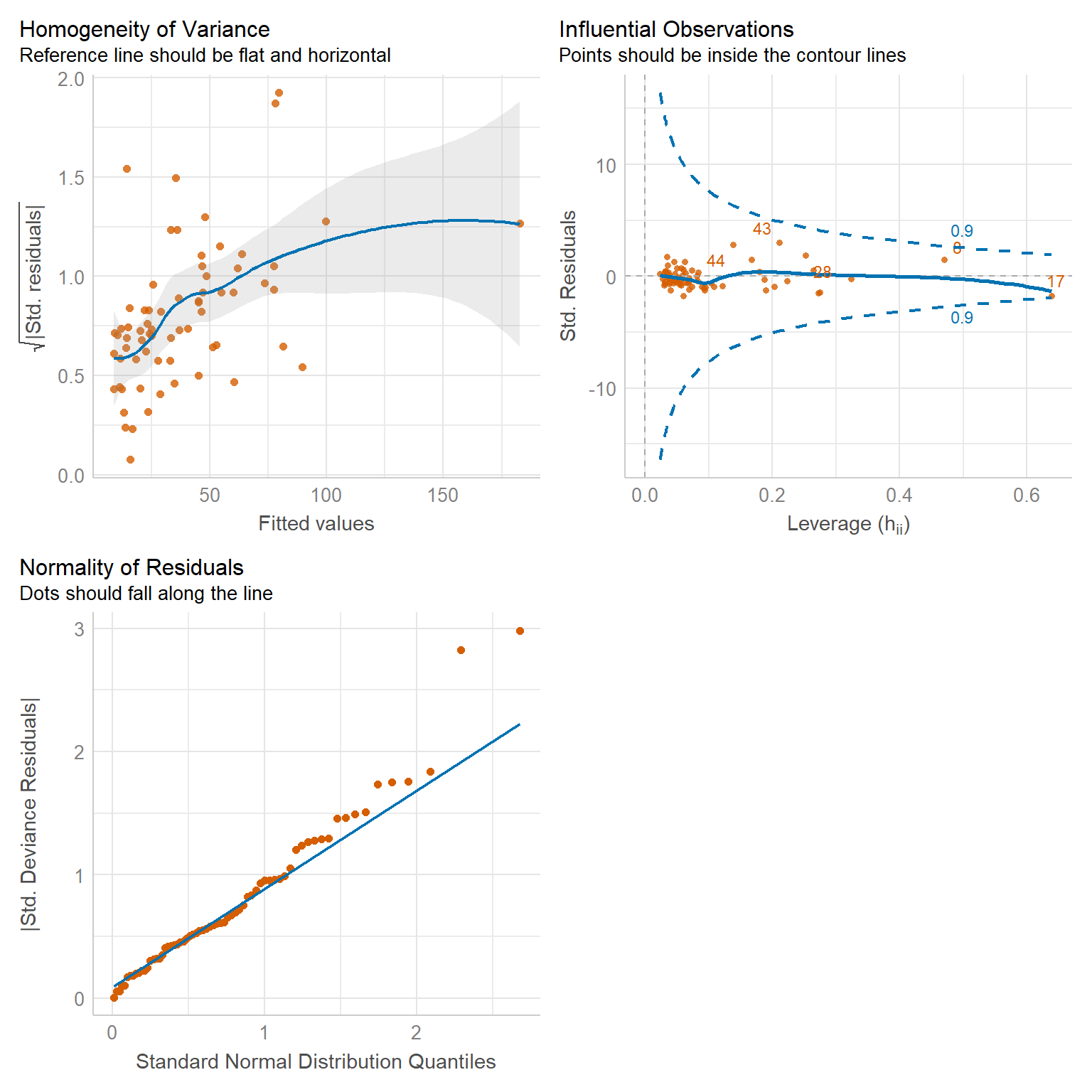
In Abbildung 56.4 schauen wir uns nochmal die Daten in den Modelgüteplots an. Wir sehen vorallem, dass wir vielelicht doch einen Ausreißer mit der Beobachtung 17 vorliegen haben. Auch ist der Fit nicht so super, wie wir an dem QQ-Plot sehen. Die Beobachtungen fallen in dem QQ-Plot nicht alle auf eine Linie. Auch sehen wir dieses Muster in dem Residualplot. Hiererwarten wir eine gerade blaue Linie und auch hier haben wir eventuell Ausreißer mit in den Daten.
56.5 Interpretation des Modells
Um die Effektschätzer einer Poissonregression oder aber einer Quasipoisson-Regression interpretieren zu können müssen wir uns einmal einen Beispieldatensatz mit bekannten Effekten zwischen den Gruppen bauen. Im Folgenden bauen wir uns einen Datensatz mit zwei Gruppen. Einmal einer Kontrollgruppe mit einer mittleren Anzahl an \(15\) und einer Behandlungsgruppe mit einer um \(\beta_1 = 10\) höheren Anzahl. Wir haben also in der Kontrolle im Mittel eine Anzahl von \(15\) und in der Behandlungsgruppe eine mittlere Anzahl von \(25\).
R Code [zeigen / verbergen]
sample_size <- 100
longnose_small_tbl <- tibble(grp = rep(c(0, 1), each = sample_size),
count = 15 + 10 * grp + rnorm(2 * sample_size, 0, 1)) |>
mutate(count = round(count),
grp = factor(grp, labels = c("ctrl", "trt")))In Tabelle 56.2 sehen wir nochmal die Daten als Ausschnitt dargestellt.
| grp | count |
|---|---|
| ctrl | 16 |
| ctrl | 16 |
| ctrl | 15 |
| ctrl | 14 |
| … | … |
| trt | 24 |
| trt | 25 |
| trt | 26 |
| trt | 26 |
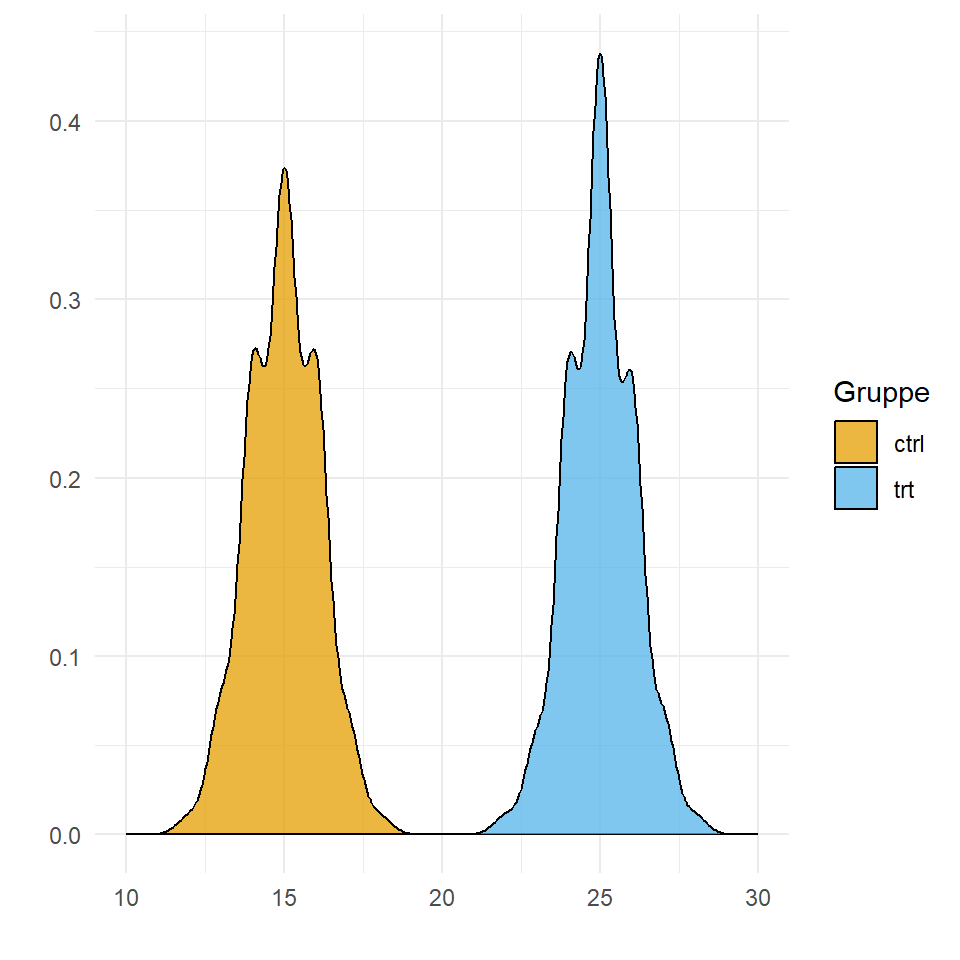
Da sich die Tabelle schlecht liest hier nochmal der Boxplot in Abbildung 56.5. Wir sehen den Grupenunterschied von \(10\) sowie die unterschiedlichen mittleren Anzahlen für die Kontrolle und die Behandlung.
R Code [zeigen / verbergen]
ggplot(longnose_small_tbl, aes(x = grp, y = count, fill = grp)) +
theme_minimal() +
geom_boxplot() +
theme(legend.position = "none") +
scale_fill_okabeito()
ggplot(data = longnose_small_tbl, aes(x = count, fill = grp)) +
theme_minimal() +
geom_density(alpha = 0.75) +
labs(x = "", y = "", fill = "Gruppe") +
scale_fill_okabeito() +
scale_x_continuous(breaks = seq(10, 30, by = 5), limits = c(10, 30)) Jetzt fitten wir einmal das simple Poissonmodell mit der Anzahl als Outcome und der Gruppe mit den zwei Leveln als \(x\). Wir pipen dann das Ergebnis des Fittes gleich in die Funktion model_parameters() weiter um die Ergebnisse des Modellierens zu erhalten.
R Code [zeigen / verbergen]
glm(count ~ grp, data = longnose_small_tbl, family = poisson) |>
model_parameters(exponentiate = TRUE)Parameter | IRR | SE | 95% CI | z | p
-------------------------------------------------------------
(Intercept) | 14.98 | 0.39 | [14.23, 15.75] | 104.76 | < .001
grp [trt] | 1.67 | 0.05 | [ 1.57, 1.78] | 15.69 | < .001Als erstes fällt auf, dass wir die Ausgabe des Modells exponieren müssen. Um einen linearen Zusamenhang hinzukriegen bedient sich die Poissonregression den Trick, das der Zusammenhang zwischen dem \(y\) und dem \(x\) transformiert wird. Wir rechnen unsere Regression nicht auf den echten Daten sondern auf dem \(\log\)-scale. Daher müssen wir die Koeffizienten der Poissonregression wieder zurücktransfomieren, wenn wir die Koeffizienten interpretieren wollen. Das können wir mit der Option exponentiate = TRUE durchführen.
Gut soweit, aber was heißen den jetzt die Zahlen? Wir haben einen Intercept von \(14.99\) das entspricht der mittleren Anzahl in der Kontrollgruppe. Und was sagt jetzt die \(1.67\) vom Level trt des Faktors grp? Wenn wir \(14.99 \cdot 1.67\) rechnen, dann erhalten wir als Ergebnis \(25.03\), also die mittlere Anzahl in der Behandlungsgruppe. Was sagt uns das jetzt aus? Wir erhalten aus der Poissonregression eine Wahrscheinlichkeit oder aber ein Risk Ratio. Wir können sagen, dass die Anzahl in der Behandlungsgruppe \(1.67\)-mal so groß ist wie in der Kontrollgruppe.
Schauen wir uns nochmal das volle Modell an und interpretieren die Effekte der einzelnen Variablen.
R Code [zeigen / verbergen]
quasipoisson_fit |>
model_parameters(exponentiate = TRUE) Parameter | IRR | SE | 95% CI | t(61) | p
-------------------------------------------------------------
(Intercept) | 0.21 | 0.32 | [0.01, 4.11] | -1.02 | 0.306
area | 1.00 | 1.13e-05 | [1.00, 1.00] | 3.41 | < .001
do2 | 1.25 | 0.14 | [1.00, 1.57] | 1.96 | 0.050
maxdepth | 1.01 | 3.67e-03 | [1.00, 1.02] | 3.18 | 0.001
no3 | 1.20 | 0.07 | [1.07, 1.34] | 3.13 | 0.002
so4 | 0.99 | 0.02 | [0.95, 1.03] | -0.35 | 0.729
temp | 1.08 | 0.04 | [1.01, 1.16] | 2.22 | 0.027 So schön auch die Funktion model_parameters() ist, so haben wir aber hier das Problem, dass wir den Effekt von area nicht mehr richtig sehen. Wir kriegen hier eine zu starke Rundung auf zwei Nachkommastellen. Wir nutzen jetzt mal die Funktion tidy() um hier Abhilfe zu leisten. Ich muss hier noch die Spalte estimate mit num(..., digits = 5) anpassen, damit du in der Ausgabe auf der Webseite auch die Nachkommastellen siehst.
R Code [zeigen / verbergen]
quasipoisson_fit |>
tidy(exponentiate = TRUE, digits = 5) |>
select(term, estimate, p.value) |>
mutate(p.value = pvalue(p.value),
estimate = num(estimate, digits = 5))# A tibble: 7 × 3
term estimate p.value
<chr> <num:.5!> <chr>
1 (Intercept) 0.20922 0.310
2 area 1.00004 0.001
3 do2 1.25342 0.055
4 maxdepth 1.01162 0.002
5 no3 1.19879 0.003
6 so4 0.99321 0.730
7 temp 1.08171 0.030 Schauen wir uns die Effekte der Poissonregression einmal an und versuchen die Ergebnisse zu interpretieren. Dabei ist wichtig sich zu erinnern, dass kein Effekt eine 1 bedeutet. Wir schauen hier auf einen Faktor. Wenn wir eine Anzahl mal Faktor 1 nehmen, dann ändert sich nichts an der Anzahl.
(Intercept)beschreibt den Intercept der Poissonregression. Wenn wir mehr als eine simple Regression vorliegen haben, wie in diesem Fall, dann ist der Intercept schwer zu interpretieren. Wir konzentrieren uns auf die Effekte der anderen Variablen.area, beschreibt den Effekt der Fläche. Steigt die Fläche um ein Quadratmeter an, so erhöht sich die Anzahl an Fischen um den \(1.00001\). Daher würde man hier eher sagen, erhöht sich die Fläche um jeweils 1000qm so erhöht sich die Anzahl an Fischen um den Faktor \(1.1\). Dann haben wir auch einen besser zu interpretierenden Effektschätzer. Die Signifikanz bleibt hier davon unbetroffen.do2, beschreibt den Partzialdruck des Sauerstoffs. Steigt dieser um eine Einheit an, so sehen wie eine Erhöhung der Anzahl an Fischen um den Faktor \(1.25\). Der Effekt ist gerade nicht signifikant.maxdepth, beschreibt die maximale Tiefe. Je tiefer ein Fluss, desto mehr Hechte werden wir beobachten. Der Effekt von \(1.01\) pro Meter Tiefe ist signifikant.no3, beschreibt den Anteil an Nitrat in den Flüssen. Je mehr Nitrat desto signifiant mehr Hechte werden wir beobachten. Hier steigt der Faktor auch um \(1.20\).so4, beschreibt den Schwefelgehalt und mit steigenden Schwefelgehalt nimmt die Anzahl an Fischen leicht ab. Der Effekt ist aber überhaupt nicht signifikant.temp, beschreibt die Temperatur der Flüsse. Mit steigender Temperatur erwarten wir mehr Hechte zu beobachten. Der Effekt von \(1.08\) Fischen pro Grad Erhöhung ist signifikant.
Was nehmen wir aus der Poissonregression zu den langnasigen Hechten mit? Zum einen haben die Fläche, die Tiefe und der Nitratgehalt einen signifikanten Einfluss auf die Anzahl an Hechten. Auch führt eine höhere Temperatur zu mehr gefundenen Hechten. Die erhöhte Temperatur steht etwas im Widerspuch zu dem Sauerstoffpartizaldruck. Denn je höher die Temperatur desto weniger Sauerstoff wird in dem Wasser gelöst sein. Auch scheint die Oberfläche mit der Tiefe korreliert. Allgemein scheinen Hechte große Flüsse zu mögen. Hier bietet sich also noch eine Variablenselektion oder eine Untersuchung auf Ausreißer an um solche Effekte nochmal gesondert zu betrachten.
56.6 Zeroinflation
So eine Poissonregression hat schon einiges an Eigenheiten. Neben dem Problem der Overdispersion gibt es aber noch eine weitere Sache, die wir beachten müssen. Wir können bei einer Poissonregression auch eine Zeroinflation vorliegen haben. Das heißt, wir beobachten viel mehr Nullen in den Daen, als wir aus der Poissonverteilung erwarten würden. Es gibt also einen biologischen oder künstlichn Prozess, der uns Nullen produziert. Häufig wissen wir nicht, ob wir den Prozess, der uns die Nullen in den Daten produziert, auch abbilden. Das heißt, es kann sein, dass wir einfach nichts Zählen, weil dort nichts ist oder aber es gibt dafür einen Grund. Diesen Grund müssten wir dann irgendwie in unseren Daten erfasst haben, aber meistens haben wir das nicht.
Schauen wir usn dafür einmal ein Datenbeispiel von Eidechsen in der Lüneburgerheide an. Wir haben Eidechsen lizard in zwei verschiedenen Habitaten grp gezählt. Einmal, ob die Eidechsen eher im offenen Gelände oder eher im bedeckten Gelände zu finden waren. Im Weiteren haben wir geschaut, ob der Boden keinen Regen erhalten hatte, trocken war oder gar feucht. Mit trocken ist hier eine gewisse Restfeuchte gemeint. Am Ende haben wir noch bestimmt, ob wir eher nah an einer Siedlung waren oder eher weiter entfernt. Du kannst dir den Daten satz in der Datei lizards.csv nochmal anschauen. In Tabelle 56.3 sind die Daten nochmal dargestellt.
| grp | rain | pop | lizard |
|---|---|---|---|
| open | no | near | 0 |
| open | no | near | 1 |
| open | no | near | 1 |
| open | no | near | 1 |
| open | no | near | 0 |
| open | no | far | 2 |
| open | no | far | 4 |
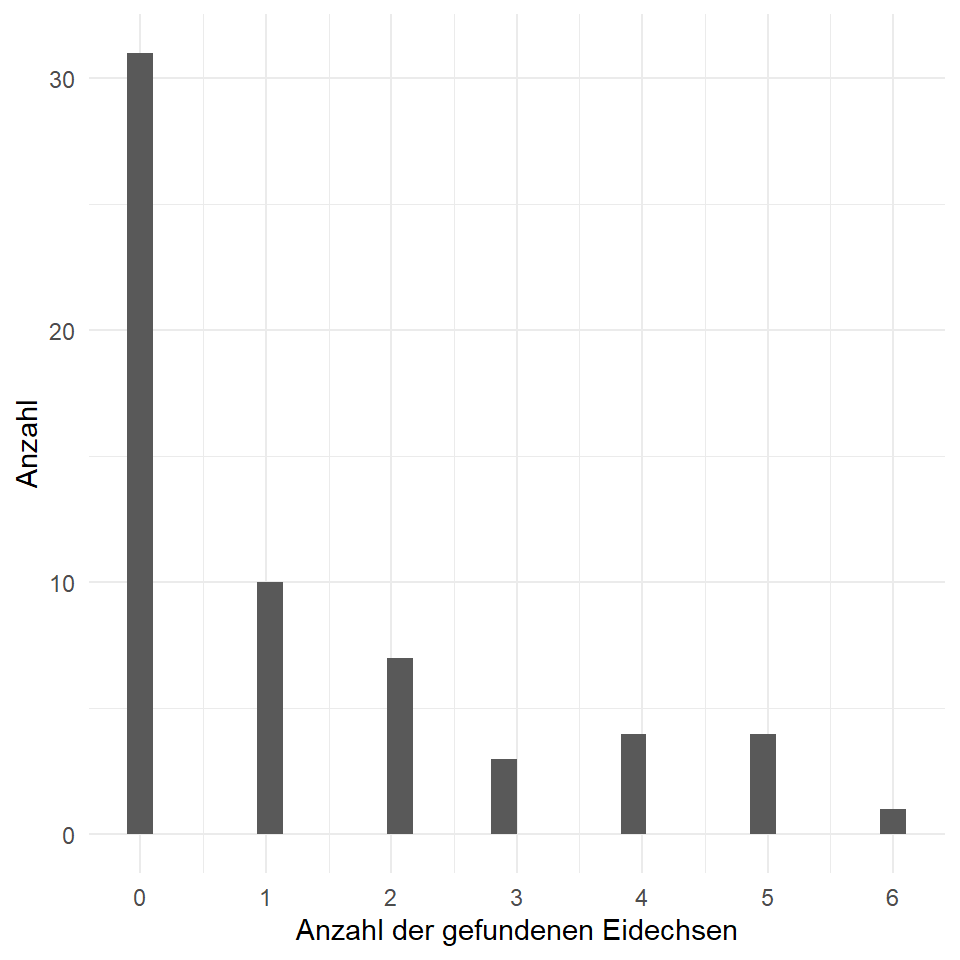
In Abbildung 56.6 sehen wir die Zähldaten der Eidechsen nochmal als Histogramm dargestellt. Wenn wir an einem Punkt keine Eidechsen gefunden haben, dann haben wir keine fehlenden Werte eingetragen, sondern eben, dass wir keine Eidechsen gezählt haben. Wir sehen das wir sehr viele Nullen in unseren Daten haben. Ein Indiz für eine Inflation an Nullen oder eben einer Zeroinflation.
R Code [zeigen / verbergen]
ggplot(lizard_zero_tbl, aes(lizard)) +
theme_minimal() +
geom_histogram() +
labs(x = "Anzahl der gefundenen Eidechsen", y = "Anzahl") +
scale_x_continuous(breaks = 0:7)Um zu überprüfen, ob wir eine Zeroinflation in den Daten vorliegen haben, werden wir erstmal eine ganz normale Poissonregression auf den Daten rechnen. Wir ignorieren auch eine potenzielle Overdispersion. Das schauen wir uns dann in den Daten später nochmal an.
R Code [zeigen / verbergen]
lizard_fit <- glm(lizard ~ grp + rain + pop, data = lizard_zero_tbl,
family = poisson)Wie immer nutzen wir die Funktion model_parameters() um uns die exponierten Koeffizienten aus dem Modell wiedergeben zu lassen. Das Modell dient uns jetzt nur als Ausgangsmodell und wir werden das Poissonmodell jetzt nicht weiter tiefer verwenden.
R Code [zeigen / verbergen]
lizard_fit |> model_parameters(exponentiate = TRUE)Parameter | IRR | SE | 95% CI | z | p
---------------------------------------------------------
(Intercept) | 1.06 | 0.29 | [0.60, 1.77] | 0.20 | 0.840
grp [cover] | 1.88 | 0.46 | [1.18, 3.07] | 2.61 | 0.009
rain [dry] | 0.31 | 0.09 | [0.17, 0.53] | -4.12 | < .001
rain [wet] | 0.13 | 0.05 | [0.06, 0.28] | -4.98 | < .001
pop [far] | 2.41 | 0.61 | [1.49, 4.04] | 3.47 | < .001Wir sehen, dass wir in der Variable rain eine starke Reduzierung der Anzahl an Eidechsen sehen. Vielleicht ist dies eine Variable, die zu viele Nullen produziert. Auch hat die Variable pop, die für die Nähe an einer Siedlung kodiert, einen starken positiven Effekt auf unsere Anzahl an Eidechsen. Hier wollen wir also einmal auf eine Zeroinflation überprüfen. Wir nutzen dazu die Funktion check_zeroinflation() aus dem R Paket {performance}. Die Funktion läuft nur auf einem Modellfit.
R Code [zeigen / verbergen]
check_zeroinflation(lizard_fit)# Check for zero-inflation
Observed zeros: 31
Predicted zeros: 27
Ratio: 0.87Die Funktion gibt uns wieder, dass wir vermutlich eine Zeroinflation vorliegen haben. Das können wir aber Modellieren. Um eine Zeroinflation ohne Overdispersion zu modellieren nutzen wir die Funktion zeroinfl() aus dem R Paket {pscl}. Der erste Teil der Funktion ist leicht erkläret. Wir bauen uns wieder unswer Model zusammen, was wir fitten wollen. Dann kommt aber ein | und mit diesem Symbol | definieren wir, ob wir wissen, woher die Nullen kommen oder aber ob wir die Nullen mit einem zufälligen Prozess modellieren wollen.
Wenn wir das Modell in der Form y ~ f1 + f2 | 1 schreiben, dann nehmen wir an, dass das Übermaß an Nullen in unseren Daten rein zufällig entstanden sind. Wir haben keine Spalte in de Daten, die uns eine Erklärung für die zusätzlichen Nullen liefern würde.
Wir können auch y ~ f1 + f2 | x3 schreiben. Dann haben wir eine Variable x3 in den Daten von der wir glauben ein Großteil der Nullen herrührt. Wir könnten also in unseren Daten annehmen, dass wir den Überschuss an Nullen durch den Regen erhalten haben und damit über die Spalte rain den Exzess an Nullen modellieren.
Man sollte immer mit dem einfachsten Modell anfangen, deshalb werden wir jetzt einmal ein Modell fitten, dass annimmt, dass die Nullen durch einen uns unbekannten Zufallsprozess entstanden sind.
R Code [zeigen / verbergen]
lizard_zero_infl_intercept_fit <- zeroinfl(lizard ~ grp + pop + rain | 1,
data = lizard_zero_tbl) Wir schauen uns das Modell dann wieder einmal an und sehen eine Zweiteilung der Ausgabe. In dem oberen Teil der Ausgabe wird unsere Anzahl an Eidechsen modelliert. In dem unteren Teil wird der Anteil der Nullen in den Daten modelliert. Daher können wir über Variablen in dem Zero-Inflation Block keine Aussagen über die Anzahl an Eidechsen treffen. Variablen tauchen nämlich nur in einem der beiden Blöcke auf.
R Code [zeigen / verbergen]
lizard_zero_infl_intercept_fit |>
model_parameters(exponentiate = TRUE)# Fixed Effects
Parameter | IRR | SE | 95% CI | z | p
---------------------------------------------------------
(Intercept) | 1.06 | 0.31 | [0.60, 1.87] | 0.22 | 0.830
grp [cover] | 2.03 | 0.51 | [1.25, 3.31] | 2.84 | 0.005
pop [far] | 2.59 | 0.67 | [1.56, 4.31] | 3.67 | < .001
rain [dry] | 0.31 | 0.10 | [0.17, 0.56] | -3.82 | < .001
rain [wet] | 0.14 | 0.06 | [0.06, 0.31] | -4.73 | < .001
# Zero-Inflation
Parameter | Odds Ratio | SE | 95% CI | z | p
--------------------------------------------------------------
(Intercept) | 0.11 | 0.11 | [0.02, 0.74] | -2.26 | 0.024Als erstes beobachten wir einen größeren Effekt der Variable grp. Das ist schon mal ein spannender Effekt. An der Signifikanz hat scih nicht viel geändert. Wir werden am Ende des Kapitels einmal alle Modell für die Modellierung der Zeroinflation vergleichen.
Nun könnte es auch sein, dass der Effekt der vielen Nullen in unserer Variable rain verborgen liegt. Wenn es also regnet, dann werden wir viel weniger Eidechsen beoabchten. Nehmen wir also rain als ursächliche Variable mit in das Modell für die Zeroinflation.
R Code [zeigen / verbergen]
lizard_zero_infl_rain_fit <- zeroinfl(lizard ~ grp + pop | rain,
data = lizard_zero_tbl)Wieder schauen wir uns einmal die Ausgabe des Modells einmal genauer an.
R Code [zeigen / verbergen]
lizard_zero_infl_rain_fit |> model_parameters(exponentiate = TRUE)# Fixed Effects
Parameter | IRR | SE | 95% CI | z | p
-------------------------------------------------------
(Intercept) | 1.13 | 0.34 | [0.63, 2.03] | 0.42 | 0.677
grp [cover] | 1.60 | 0.42 | [0.95, 2.67] | 1.77 | 0.077
pop [far] | 1.84 | 0.51 | [1.07, 3.18] | 2.20 | 0.028
# Zero-Inflation
Parameter | Odds Ratio | SE | 95% CI | z | p
-------------------------------------------------------------------
(Intercept) | 0.04 | 0.08 | [0.00, 2.09] | -1.60 | 0.109
rain [dry] | 27.93 | 59.03 | [0.44, 1758.19] | 1.58 | 0.115
rain [wet] | 83.69 | 178.35 | [1.28, 5452.98] | 2.08 | 0.038Es ändert sich einiges. Zum einen erfahren wir, dass der Regen anscheined doch viele Nullen in den Daten produziert. Wir haben ein extrem hohes \(OR\) für die Variable rain. Die Signifikanz ist jedoch eher gering. Wir haben nämlich auch eine sehr hohe Streuung mit den großen \(OR\) vorliegen. Au der anderen Seite verlieren wir jetzt auch die Signifikanz von unseren Habitaten und dem Standort der Population. Nur so mäßig super dieses Modell.
Wir können jetzt natürlich auch noch den Standort der Population mit in den Prozess für die Entstehung der Nullen hineinnehmen. Wir schauen uns dieses Modell aber nicht mehr im Detail an, sondern dann nur im Vergleich zu den anderen Modellen.
R Code [zeigen / verbergen]
lizard_zero_infl_rain_pop_fit <- zeroinfl(lizard ~ grp | rain + pop,
data = lizard_zero_tbl)Die Gefahr besteht immer, das man sich an die Wand modelliert und vor lauter Modellen die Übersicht verliert. Neben der Zeroinflation müssen wir ja auch schauen, ob wir eventuell eine Overdispersion in den Daten vorliegen haben. Wenn das der Fall ist, dann müsen wir nochmal überlegen, was wir dann machen. Wir testen nun auf Ovrdisprsion in unserem ursprünglichen Poissonmodell mit der Funktion check_overdispersion().
R Code [zeigen / verbergen]
check_overdispersion(lizard_fit)# Overdispersion test
dispersion ratio = 1.359
Pearson's Chi-Squared = 74.743
p-value = 0.039Tja, und so erfahren wir, dass wir auch noch Overdispersion in unseren Daten vorliegen haben. Wir müsen also beides Modellieren. Einmal modellieren wir die Zeroinflation und einmal die Overdispersion. Wir können beides in einem negativen binominalen Modell fitten. Auch hier hilft die Funktion zeroinfl() mit der Option dist = negbin. Mit der Option geben wir an, dass wir eine negative binominal Verteilungsfamilie wählen. Damit können wir dann auch die Ovrdispersion in unseren Daten modellieren.
R Code [zeigen / verbergen]
lizard_zero_nb_intercept_fit <- zeroinfl(lizard ~ grp + rain + pop | 1,
dist = "negbin", data = lizard_zero_tbl)Dann schauen wir usn einmal das Modell an. Zum einen sehen wir, dass der Effekt ähnlich groß ist, wie bei dem Intercept Modell der Funktion zeroinfl. Auch bleiben die Signifikanzen ähnlich.
R Code [zeigen / verbergen]
lizard_zero_nb_intercept_fit |> model_parameters(exponentiate = TRUE)# Fixed Effects
Parameter | IRR | SE | 95% CI | z | p
---------------------------------------------------------
(Intercept) | 1.06 | 0.31 | [0.60, 1.87] | 0.22 | 0.830
grp [cover] | 2.03 | 0.51 | [1.25, 3.31] | 2.84 | 0.005
rain [dry] | 0.31 | 0.10 | [0.17, 0.56] | -3.82 | < .001
rain [wet] | 0.14 | 0.06 | [0.06, 0.31] | -4.73 | < .001
pop [far] | 2.59 | 0.67 | [1.56, 4.31] | 3.67 | < .001
# Zero-Inflation
Parameter | Odds Ratio | SE | 95% CI | z | p
--------------------------------------------------------------
(Intercept) | 0.11 | 0.11 | [0.02, 0.74] | -2.26 | 0.024Nun haben wir vier Modelle geschätzt und wolen jetzt wissen, was ist das beste Modell. Dafür hilft usn dann eine Gegenüberstellung der Modelle mit der Funktion modelsummary(). Wir könnten die Modelle auch gegeneinander statistsich Testen, aber hier behalten wir uns einmal den beschreibenden Vergleich vor. In Tabelle 56.4 sehen wir einmal die vier Modelle nebeneinander gestellt. Für eine bessere Übrsicht, habe ich aus allen Modellen den Intercept entfernt.
R Code [zeigen / verbergen]
modelsummary(lst("ZeroInfl Intercept" = lizard_zero_infl_intercept_fit,
"ZeroInfl rain" = lizard_zero_infl_rain_fit,
"ZeroInfl rain+pop" = lizard_zero_infl_rain_pop_fit,
"NegBinom intercept" = lizard_zero_nb_intercept_fit),
statistic = c("conf.int",
"s.e. = {std.error}",
"t = {statistic}",
"p = {p.value}"),
coef_omit = "Intercept",
exponentiate = TRUE)| ZeroInfl Intercept | ZeroInfl rain | ZeroInfl rain+pop | NegBinom intercept | |
|---|---|---|---|---|
| count_grpcover | 2.031 | 1.595 | 1.611 | 2.031 |
| [1.245, 3.313] | [0.951, 2.675] | [0.912, 2.845000e+00] | [1.245, 3.313] | |
| s.e. = 0.507 | s.e. = 0.421 | s.e. = 0.468 | s.e. = 0.507 | |
| t = 2.839 | t = 1.771 | t = 1.642 | t = 2.839 | |
| p = 0.005 | p = 0.077 | p = 0.101 | p = 0.005 | |
| count_popfar | 2.591 | 1.844 | 2.591 | |
| [1.558, 4.310] | [1.069, 3.183] | [1.558, 4.311] | ||
| s.e. = 0.673 | s.e. = 0.513 | s.e. = 0.673 | ||
| t = 3.667 | t = 2.199 | t = 3.667 | ||
| p = <0.001 | p = 0.028 | p = <0.001 | ||
| count_raindry | 0.308 | 0.308 | ||
| [0.168, 0.564] | [0.168, 0.564] | |||
| s.e. = 0.095 | s.e. = 0.095 | |||
| t = -3.816 | t = -3.816 | |||
| p = <0.001 | p = <0.001 | |||
| count_rainwet | 0.135 | 0.135 | ||
| [0.059, 0.310] | [0.059, 0.310] | |||
| s.e. = 0.057 | s.e. = 0.057 | |||
| t = -4.726 | t = -4.726 | |||
| p = <0.001 | p = <0.001 | |||
| zero_raindry | 27.933 | 98.197 | ||
| [0.444, 1758.190] | [0.000, 7.612076e+07] | |||
| s.e. = 59.034 | s.e. = 679.419 | |||
| t = 1.576 | t = 0.663 | |||
| p = 0.115 | p = 0.507 | |||
| zero_rainwet | 83.692 | 402.413 | ||
| [1.285, 5452.976] | [0.000, 4.188183e+08] | |||
| s.e. = 178.352 | s.e. = 2844.758 | |||
| t = 2.077 | t = 0.848 | |||
| p = 0.038 | p = 0.396 | |||
| zero_popfar | 0.148 | |||
| [0.022, 1.000000e+00] | ||||
| s.e. = 0.144 | ||||
| t = -1.960 | ||||
| p = 0.050 | ||||
| Num.Obs. | 60 | 60 | 60 | 60 |
| R2 | 0.620 | 0.477 | 0.454 | 0.620 |
| R2 Adj. | 0.585 | 0.449 | 0.435 | 0.585 |
| AIC | 157.3 | 167.2 | 167.4 | 159.3 |
| BIC | 169.8 | 179.8 | 180.0 | 173.9 |
| RMSE | 1.27 | 1.27 | 1.32 | 1.27 |
Die beiden Intercept Modelle haben die kleinsten \(AIC\)-Werte der vier Modelle. Darüber hinaus haben dann beide Modelle auch die höchsten \(R^2_{adj}\) Werte. Beide Modelle erklären also im Verhältnis viel Varianz mit 58.5%. Auch ist der \(RMSE\) Wert als Fehler bei beiden Modellen am kleinsten. Damit haben wir die Qual der Wahl, welches Modell wir nehmen. Ich würde das negative binominal Modell nehmen. Wir haben ins unseren Daten vermutlich eine Zeroinflation sowie eine Overdispersion vorliegen. Daher bietest es sich an, beides in einer negativen binominalen Regression zu berücksichtigen. Zwar sind die beiden Intercept Modelle in diesem Beispielfall von den Koeffizienten fast numerisch gleich, aber das hat eher mit dem reduzierten Beispiel zu tun, als mit dem eigentlichen Modell. In unserem Fall ist die Overdispersion nicht so extrem.
Wie sehe den unser negative binominal Modell aus, wenn wir mit dem Modell einmal die zu erwartenden Eidechsen vorhersagen würden? Auch das kann helfen um abzuschätzen, ob das Modelle einigermaßen funktioniert hat. Wir haben ja hier den Vorteil, dass wir nur mit kategorialen Daten arbeiten. Wir haben keine kontiniuerlichen Variablen vorliegen und darüber hinaus auch nicht so viele Variablen insgesamt.
Daher bauen wir uns mit expand_grid() erstmal einen Datensatz, der nur aus den Faktorkombinationen besteht. Wir haben also nur eine Beobachtung je Faktorkombination. Danach nutzen wir die Daten einmal in der Funktion predict() um uns die vorhergesagten Eidechsen nach dem gefitten Modell wiedergeben zu lassen.
R Code [zeigen / verbergen]
newdata_tbl <- expand_grid(grp = factor(1:2, labels = c("open", "cover")),
rain = factor(1:3, labels = c("no", "dry", "wet")),
pop = factor(1:2, labels = c("near", "far")))
pred_lizards <- predict(lizard_zero_nb_intercept_fit, newdata = newdata_tbl)
newdata_tbl <- newdata_tbl |>
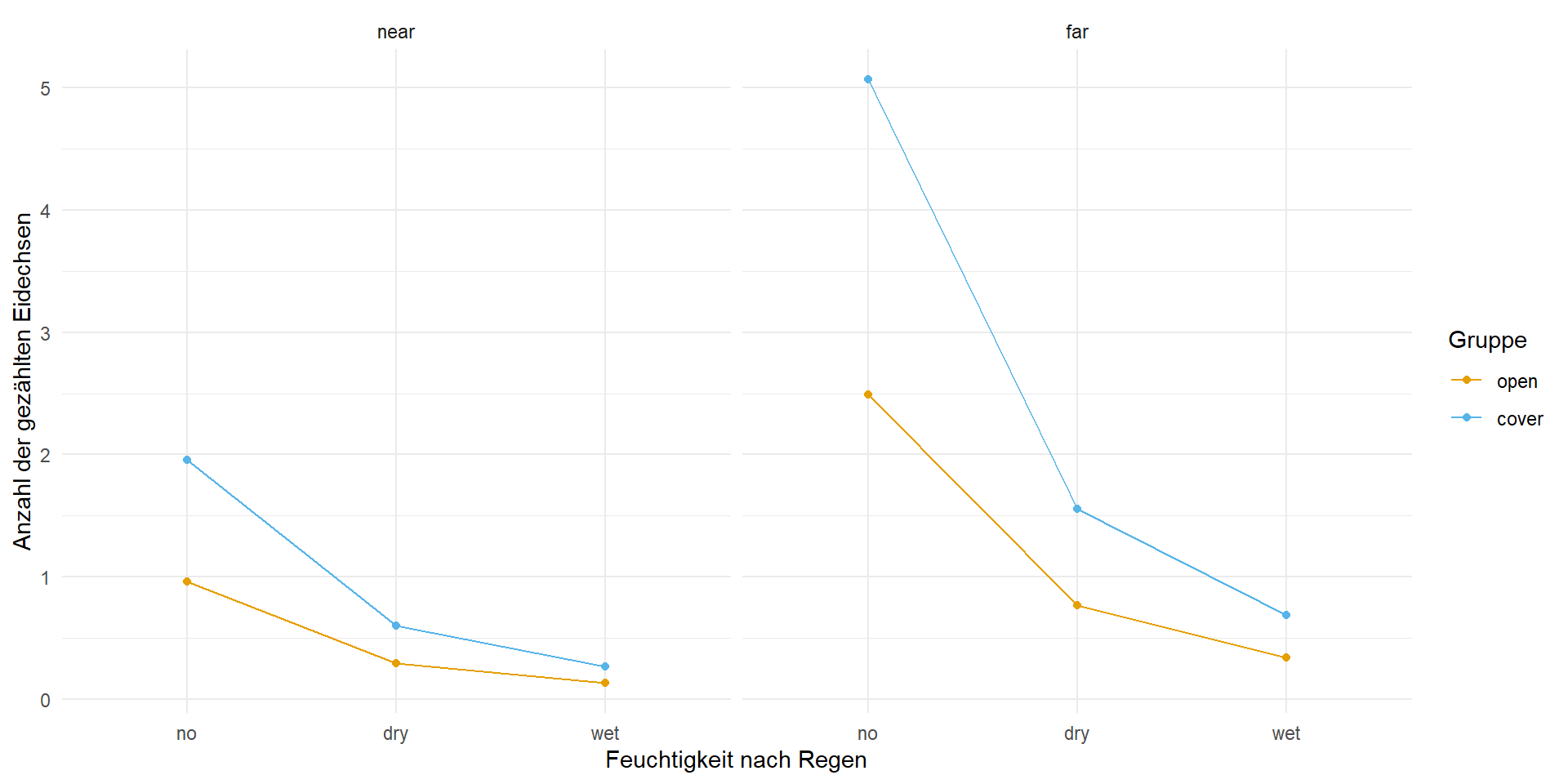
mutate(lizard = pred_lizards)Nachdem wir in dem Datensatz newdata_tbl nun die vorhergesagten Eidechsen haben, können wir uns jetzt in der Abbildung 56.7 die Zusammenhänge nochmal anschauen.
R Code [zeigen / verbergen]
ggplot(newdata_tbl, aes(x = rain, y = lizard, colour = grp, group = grp)) +
theme_minimal() +
geom_point() +
geom_line() +
facet_wrap(~ pop) +
labs(x = "Feuchtigkeit nach Regen", y = "Anzahl der gezählten Eidechsen",
color = "Gruppe") +
scale_color_okabeito()Wir erkennen, dass mit der Erhöhung der Feuchtigkeit die Anzahl an aufgefundenen Eidechsen sinkt. Der Effekt ist nicht mehr so stark, wenn es schon einmal geregnet hat. Ebenso macht es einen Unterschied, ob wir nahe einer Siedlung sind oder nicht. Grundsätzlich finden wir immer mehr Eidechsen in geschützten Habitaten als in offenen Habitaten.
56.7 Gruppenvergleich
Häufig ist es ja so, dass wir das Modell für die Poisson Regression nur schätzen um dann einen Gruppenvergleich zu rechnen. Das heißt, dass es uns interessiert, ob es einen Unterschied zwischen den Leveln eines Faktors gegeben dem Outcome \(y\) gibt. Da wir hier in unserem Beispiel zu den Flusshechten keine Gruppe drin haben, zeige ich dir das Prinzip einmal an einem ausgedachten Datensatz. Wir nehmen hier einen Datensatz zu Katzen-, Hunde- und Fuchsflöhen. Dabei erstellen wir uns einen Datensatz mit mittleren Anzahlen an Flöhen pro Tierart. Ich habe jetzt eine mittlere Flohanzahl von \(10\) Flöhen bei den Katzen, eine mittlere Anzahl von \(30\) Flöhen bei den Hunden und eine mittlere Anzahl von \(10\) Flöhen bei den Füchsen gewählt. Wir generieren uns jeweils \(20\) Beobachtungen je Tierart. Damit haben wir dann einen Datensatz zusammen, den wir nutzen können um einmal die Ergebnisse eines Gruppenvergleiches mit Zähldaten zu verstehen.
R Code [zeigen / verbergen]
set.seed(20231202)
n_rep <- 20
flea_count_tbl <- tibble(animal = gl(3, n_rep, labels = c("cat", "dog", "fox")),
count = round(c(rnorm(n_rep, 20, 1),
rnorm(n_rep, 30, 1),
rnorm(n_rep, 10, 1))))Wenn du gerade hierher gesprungen bist, nochmal das simple Modell für unseren Gruppenvergleich unter einer Poisson Regression. Wir haben hier nur einen Faktor animal mit in dem Modell. Am Ende des Abschnitts findest du dann noch ein Beispiel mit zwei Faktoren zu Thripsen auf Apfelbäumen. Wir modellieren hier eigentlich nicht die Zähldaten an sich, sondern die Raten. Du wirst das aber gleich bei der Ausgabe von emmeans() sehen.
R Code [zeigen / verbergen]
pois_fit <- glm(count ~ animal, data = flea_count_tbl, family = "poisson") Eigentlich ist es recht einfach, wie wir anfangen. Wir rechnen jetzt als erstes die ANOVA. Hier müssen wir dann einmal den Test angeben, der gerechnet werden soll um die p-Werte zu erhalten. Dann nutze ich noch die Funktion model_parameters() um eine schönere Ausgabe zu erhalten.
R Code [zeigen / verbergen]
pois_fit |>
anova(test = "Chisq") |>
model_parameters(drop = "NULL")Parameter | df | Deviance | df (error) | Deviance (error) | p
------------------------------------------------------------------
animal | 2 | 205.42 | 57 | 3.20 | < .001
Anova Table (Type 1 tests)Im Folgenden nutzen wir das R Paket {emmeans} wie folgt. Wenn wir die mittleren Anzahlen benötigen, dann müssen wir die Option type = "response" verwenden. Sonst würdest du Werte auf der Link-Skala wiederbekommen, die dir hier nicht helfen. Ich nutze später die emmeans Ausgabe um ein Säulendiagramm mit den mittleren Anzahlen zu erstellen. Wir du gleich sehen wirst, werden wir aber nicht die Anzahlen vergleichen sondern die Raten in den jeweiligen Gruppen.
R Code [zeigen / verbergen]
emm_obj <- pois_fit |>
emmeans(~ animal, type = "response")
emm_obj animal rate SE df asymp.LCL asymp.UCL
cat 20.1 1.000 Inf 18.23 22.2
dog 30.1 1.230 Inf 27.79 32.6
fox 10.2 0.714 Inf 8.89 11.7
Confidence level used: 0.95
Intervals are back-transformed from the log scale Jetzt steht hier zwar rate aber was ist das denn nun? Dafür berechnen wir mal die Mittelwerte der Anzahlen für die drei Tierarten über die Funktion summarise(). Dann vergleichen wir einmal die Ausgaben und schauen, was wir in emmeans() berechnet haben.
R Code [zeigen / verbergen]
flea_count_tbl |>
group_by(animal) |>
summarise(mean_count = mean(count))# A tibble: 3 × 2
animal mean_count
<fct> <dbl>
1 cat 20.1
2 dog 30.1
3 fox 10.2Wunderbar, es sind die Mittelwerte der Anzahlen, die in der Spalte rate in der Ausgabe von emmeans() stehen. Damit können wir dann arbeiten und die Ausgabe nutzen um ein Säulendigramm zu erstellen. Bitte schaue für die Umsetzung in das Beispiel am Ende des Abschnitts. Da zeige ich dir dann wie du ein Säulendigramm zu den Anzahlen von Thripsen auf Apfelbäumen erstellst.
Wenn du die mittleren Anzahlen pro Tierart jetzt für jede Tierart testen willst, dann erhälst du aber keinen Mittelwertsunterschied der Anzahlen, sondern eine Rate. Rechnen wir aber erstmal den paarweisen Vergleich und schauen uns dann an, was wir erhalten haben. Wir kriegen am Ende wiederum einen Vergleich von Wahrscheinlichkeiten, aber eben hier von Raten. Wie immer, es kommt darauf an, was du willst. Hier einmal die paarweisen Vergleiche, darunter dann gleich das compact letter display.
R Code [zeigen / verbergen]
emm_obj |>
pairs(adjust = "bonferroni") contrast ratio SE df null z.ratio p.value
cat / dog 0.668 0.043 Inf 1 -6.269 <.0001
cat / fox 1.971 0.169 Inf 1 7.891 <.0001
dog / fox 2.951 0.239 Inf 1 13.358 <.0001
P value adjustment: bonferroni method for 3 tests
Tests are performed on the log scale Okay, jetzt haben wir statt Raten also eine Ratio, also ein Verhältnis von Raten. Das schauen wir uns doch gleich mal in dem Beispiel an. Wir rechnen also einmal die mittlere Anzahl für jede Tierart durch die entsprechende andere mittlere Anzahl der anderen Tierart. Wir erhalten also folgende Ratios der mittleren Anzahlen.
\[ \cfrac{cat}{dog} = \cfrac{20.1}{30.1} = 0.67 \]
\[ \cfrac{cat}{fox} = \cfrac{20.1}{10.2} = 1.97 \]
\[ \cfrac{dog}{fox} = \cfrac{30.1}{10.2} = 2.95 \]
Wie interpretieren wir jetzt die Ratios? Eigentlich ist das intuitiver als man auf den ersten Blick denkt. Wir haben zum Beispiel fast doppelt so viele Flöhe bei Katzen wie bei Füchsen. Die Anzahl von Hundeflöhen ist fast dreimal so hoch wie die Anzahl an Fuchsflöhen. Wir haben fast nur halb so viele Flöhe auf Katzen gefunden als bei den Hunden. Damit können wir dann schon arbeiten und eine Aussage treffen.
Und fast am Ende können wir uns auch das compact letter display erstellen. Auch hier nutzen wir wieder die Funktion cld() aus dem R Paket {multcomp}. Hier erhälst du dann die Information über die mittlere Anzahl der jeweiligen Tierarten und ob sich die mittlere Anzahl unterscheidet. Ich nutze dann die Ausgabe von emmeans() um mir dann direkt das Säulendiagramm mit den Fehlerbalken und dem compact letter display zu erstellen. Mehr dazu dann im Kasten weiter unten zu dem Beispiel zu Thripsenanzahl auf Apfelbäumen.
R Code [zeigen / verbergen]
emm_obj |>
cld(Letters = letters, adjust = "none") animal rate SE df asymp.LCL asymp.UCL .group
fox 10.2 0.714 Inf 8.89 11.7 a
cat 20.1 1.000 Inf 18.23 22.2 b
dog 30.1 1.230 Inf 27.79 32.6 c
Confidence level used: 0.95
Intervals are back-transformed from the log scale
Tests are performed on the log scale
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Auch hier sehen wir, dass sich alle drei Gruppen signifikant unterschieden, keine der Tierarten teilt sich einen Buchstaben, so dass wir hier von einem Unterschied zwischen den mittleren Anzahlen an Flöhen auf den drei Tierarten ausgehen können.
Bei einem geplanten Experiment zählen wir meist in festgelegten Zeiteinheiten oder aber unser \(n\) ist vorgeben. Jetzt kann es aber sein, dass wir nicht mit festen Zeitintervallen oder aber einer Fallzahl zählen. Beispielsweise können wir die Anzahl der Baumarten in einem Wald zählen: Ereignisse (eng. event) wären Baumbeobachtungen, die Exposition (eng. exposure) wäre eine Flächeneinheit und die Rate wäre die Anzahl der Arten pro Flächeneinheit. Wir können die Sterberaten in geografischen Gebieten als die Anzahl der Todesfälle geteilt durch die Personenjahre modellieren. Allgemeiner ausgedrückt können Ereignisraten als Ereignisse pro Zeiteinheit berechnet werden, wobei das Beobachtungsfenster für jede Einheit variieren kann. In diesen Beispielen ist die Exposition jeweils eine Einheit Fläche, Personenjahre und Zeiteinheit. So sollten beispielsweise sechs Fälle innerhalb eines Jahres nicht den gleichen Wert haben wie sechs Fälle innerhalb von 10 Jahren. In der Poisson-Regression wird dies als Offset behandelt. Mehr dazu dann gerne im Wikipediartikel zu “Exposure” and offset oder aber die Antwort When to use an offset in a Poisson regression?.
In {emmeans} können wir Modelle mit Offset relativ einfach modellieren. Dazu nutzen wir die Funktion offset() in unserem glm() Modell. Aber zuerst einmal ein Spieldatensatz. Wir haben wir unseren Faktor Tierart und dann aber noch das Alter als Faktor mit zwei Stufen. Wir haben jetzt aber nicht immer die gleiche Anzahl an Hunden und Katzen sowie Füchsen ausgezählt. Unsere Anzahl an Flöhen basiert also auf einer anderen \(n\) Anzahl. Die Anzahl \(n\) modellieren wir dann als offset().
R Code [zeigen / verbergen]
toy_count_tbl <- tibble(n = c(500, 1200, 100, 400, 500, 300),
animal = factor(rep(1:3,2), labels = c("cat","dog","fox")),
age = gl(2, 3),
count = c(42, 37, 1, 101, 73, 14))Wir nehmen die Anzahl an ausgezählten Tieren dann als Offset mit Logarithmus in das Modell. Deshalb steht dann da auch log(n) im Offset.
R Code [zeigen / verbergen]
toy_count_fit <- glm(count ~ animal + age + offset(log(n)),
data = toy_count_tbl, family = "poisson")Dann können wir uns einmal das Modell anschauen, wie {emmeans} den Vergleich rechnen würde.
R Code [zeigen / verbergen]
ref_grid(toy_count_fit)'emmGrid' object with variables:
animal = cat, dog, fox
age = 1, 2
n = 500
Transformation: "log" Der Offset ist also grob \(log(500) \approx 5.97\). Das stimmt numerisch nicht hundertprozentig, hat aber noch mit einer internen Korrektur zu tun, die uns hier aber nicht weiter interessiert. Das Modell können wir dann wie gewohnt in emmeans() stecken und dann weiter rechnen. In dem Modell wird dann berücksichtigt, dass sich die Anzahlen für das Exposure, also dem Nenner der Raten, unterscheiden.
Damit sind wir einmal mit unserem Gruppenvergleich für die Poisson Regression auf Zähldaten durch. In dem Kapitel zu den Multiple Vergleichen oder Post-hoc Tests findest du dann noch mehr Inspirationen für die Nutzung von {emmeans}. Hier war es dann die Anwendung auf Zähldaten zusammen mit einem Faktor. Wenn du dir das Ganze nochmal an einem Beispiel für zwei Faktoren anschauen möchtest, dann findest du im folgenden Kasten ein Beispiel für die Auswertung von Thripsen auf Apfelbäumen nach Gabe verschiedener Dosen eines Insektizids und Zeitpunkten.
Im folgenden Beispiel schauen wir uns nochmal ein praktische Auswertung von einem agrarwissenschaftlichen Beispiel mit jungen Apfelbäumen an. Wir haben uns in diesem Experiment verschiedene Dosen trt von einem Insektizid aufgebracht sowie verschiedene Startanzahlen von Raubmilben als biologische Alternative untersucht. Dann haben wir noch fünf Zeitpunkte bestimmt, an denen wir die Anzahl an Thripsen auf den Blättern gezählt haben. Wir haben nicht die Blätter per se gezählt sondern Fallen waagerecht aufgestellt. Dann haben wir geschaut, wie viele Thripsen wir über above und unter below von den Fallen gefunden haben. In unserem Fall beschränken wir uns auf die obere Anzahl an Thripsen und schauen uns auch nur die Behandlung mit dem Insektizid an.
R Code [zeigen / verbergen]
insects_tbl <- read_excel("data/insects_count.xlsx") |>
mutate(timepoint = factor(timepoint, labels = c("1 Tag", "4 Tag", "7 Tag", "11 Tag", "14 Tag")),
rep = as_factor(rep),
trt = as_factor(trt)) |>
select(timepoint, trt, thripse = thripse_above) |>
filter(trt %in% c("10ml", "30ml", "60ml"))Dann können wir auch schon die Poisson Regression mit glm() rechnen. Auch hier wieder darauf achten, dass wir dann als Option family = poisson oder family = quasipoisson wählen. Es hängt jetzt davon ab, ob du in deinen Daten Overdispersion vorliegen hast oder nicht. In den beiden folgenden Tabs, rechne ich dann mal beide Modelle.
Als Erstes rechnen wir eine normale Poisson Regression und schauen einmal, ob wir Overdispersion vorliegen haben. Wenn wir Overdispersion vorliegen haben, dann können wir keine Poisson Regression rechnen, sondern müssen auf eine Quasipoisson Regression ausweichen. Das ist aber sehr einfach, wie du im anderen Tab sehen wirst.
R Code [zeigen / verbergen]
insects_poisson_fit <- glm(thripse ~ trt + timepoint + trt:timepoint,
data = insects_tbl,
family = poisson) Bevor wir uns das Modell mit summary() überhaupt anschauen, wollen wir erstmal überprüfen, ob wir überhaupt Overdispersion vorliegen haben. Wenn ja, dann können wir uns die summary() hier gleich sparen. Also einmal geguckt, was die Overdispersion macht.
R Code [zeigen / verbergen]
insects_poisson_fit |> check_overdispersion()# Overdispersion test
dispersion ratio = 23.498
Pearson's Chi-Squared = 3172.179
p-value = < 0.001Overdispersion detected.Wir haben sehr starke Overdispersion vorliegen und gehen daher rüber in den anderen Tab und rechnen eine Quasipoisson Regression. Nur wenn du keine Overdispersion vorliegen hast, dann kannst du eine eine Poisson Regression rechnen.
Entweder hast du in deinen Daten eine Overdispersion gefunden oder aber du meinst, es wäre besser gleich eine Quasipoisson zu rechnen. Beides ist vollkommen in Ordnung. Ich rechne meistens immer eine Quasipoisson und schaue dann nur, ob die Overdispersion sehr groß war. In den seltensten Fällen hast du eine Overdispersion vorliegen, die eher klein ist. Daher mache ich erst die Lösung und schaue, ob das Problem dann da war.
R Code [zeigen / verbergen]
insects_quasipoisson_fit <- glm(thripse ~ trt + timepoint + trt:timepoint,
data = insects_tbl,
family = quasipoisson) Du kannst in der summary() Ausgabe direkt sehen, ob du Overdispersion vorliegen hast. Du musst nur relativ weit unten schauen, was zu dem Dispersion parameter in den Klammern geschrieben ist. Wenn da eine Zahl größer als 1 drin steht, dann hast du Overdispersion.
R Code [zeigen / verbergen]
insects_quasipoisson_fit |>
summary()
Call:
glm(formula = thripse ~ trt + timepoint + trt:timepoint, family = quasipoisson,
data = insects_tbl)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.861686 0.211964 18.219 <2e-16 ***
trt30ml -0.565849 0.376336 -1.504 0.1350
trt60ml -1.058326 0.432830 -2.445 0.0158 *
timepoint4 Tag -0.448440 0.339528 -1.321 0.1888
timepoint7 Tag -0.001914 0.299907 -0.006 0.9949
timepoint11 Tag -0.121854 0.309323 -0.394 0.6942
timepoint14 Tag -0.177363 0.313970 -0.565 0.5731
trt30ml:timepoint4 Tag 0.476840 0.553141 0.862 0.3902
trt60ml:timepoint4 Tag -0.579968 0.809916 -0.716 0.4752
trt30ml:timepoint7 Tag 0.154299 0.519303 0.297 0.7668
trt60ml:timepoint7 Tag 0.252555 0.585830 0.431 0.6671
trt30ml:timepoint11 Tag 0.121854 0.537661 0.227 0.8210
trt60ml:timepoint11 Tag 0.091083 0.620448 0.147 0.8835
trt30ml:timepoint14 Tag -0.162407 0.575416 -0.282 0.7782
trt60ml:timepoint14 Tag -0.201195 0.670025 -0.300 0.7644
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for quasipoisson family taken to be 23.49807)
Null deviance: 4263.4 on 149 degrees of freedom
Residual deviance: 3345.0 on 135 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 5Wir haben hier auf jeden Fall Overdispersion vorliegen. Daher nutze ich dann auch das Modell hier mit der Annahme an eine Quasipoissonverteilung. Dann stimmt es auch mit unseren Varianzen und wir produzieren nicht zufällig zu viele signifikante Ergebnisse, die es dann gar nicht gibt.
Ich habe mich gerade in den obigen Tabs für eine Quasipoisson Regression entschieden, da wir Overdispersion vorliegen haben. Damit mache ich dann mit dem insects_quasipoisson_fit Modell weiter. In den beiden folgenden Tabs findest du dann einmal das Ergebnis für die ANOVA und einmal für den Gruppenvergleich mit dem R Paket {emmeans}. Bitte beachte, dass die ANOVA für ein glm()-Objekt nicht ganz gleich wie für ein lm()-Objekt ist. Du kannst aber die ANOVA erstmal ganz normal interpretieren, nur haben wir hier nicht die Möglichkeit ein \(\eta^2\) zu bestimmen. Dann nutzen wir {emmeans} für den Gruppenvergleich. Nochmal, weil wir Overdispersion festgestellt haben, nutzen wir das Objekt insects_quasipoisson_fit mit der Berücksichtigung der Overdispersion.
Wir rechnen hier einmal die ANOVA und nutzen den \(\mathcal{X}^2\)-Test für die Ermittelung der p-Werte. Wir müssen hier einen Test auswählen, da per Standardeinstellung kein Test gerechnet wird. Wir machen dann die Ausageb nochmal schöner und fertig sind wir.
R Code [zeigen / verbergen]
insects_quasipoisson_fit |>
anova(test = "Chisq") |>
model_parameters(drop = "NULL")Parameter | df | Deviance | df (error) | Deviance (error) | p
----------------------------------------------------------------------
trt | 2 | 730.20 | 147 | 3533.22 | < .001
timepoint | 4 | 112.27 | 143 | 3420.95 | 0.311
trt:timepoint | 8 | 75.93 | 135 | 3345.03 | 0.919
Anova Table (Type 1 tests)Wir sehen, dass der Effekt für die Behandlung signifikant ist, jedoch die Zeit und die Interaktion keinen signifikanten Einfluss haben. Wir haben aber also keine Interaktion vorliegen. Daher können wir dann die Analyse gemeinsam über alle Zeitpunkte rechnen.
Im Folgenden rechnen wir einmal über alle Faktorkombinationen von trt und timepoint einen Gruppenvergleich. Dafür nutzen wir die Opition trt * timepoint. Wenn du die Analyse getrennt für die Zeitpunkte durchführen willst, dann nutze die Option trt | timepoint. Wir wollen die Wahrscheinlichkeiten für das Auftreten einer Beschädigung von wiedergegeben bekommen, deshalb die Option regrid = "response. Dann adjustieren wir noch nach Bonferroni und sind fertig.
R Code [zeigen / verbergen]
emm_obj <- insects_quasipoisson_fit |>
emmeans(~ trt * timepoint, regrid = "response") |>
cld(Letters = letters, adjust = "bonferroni")
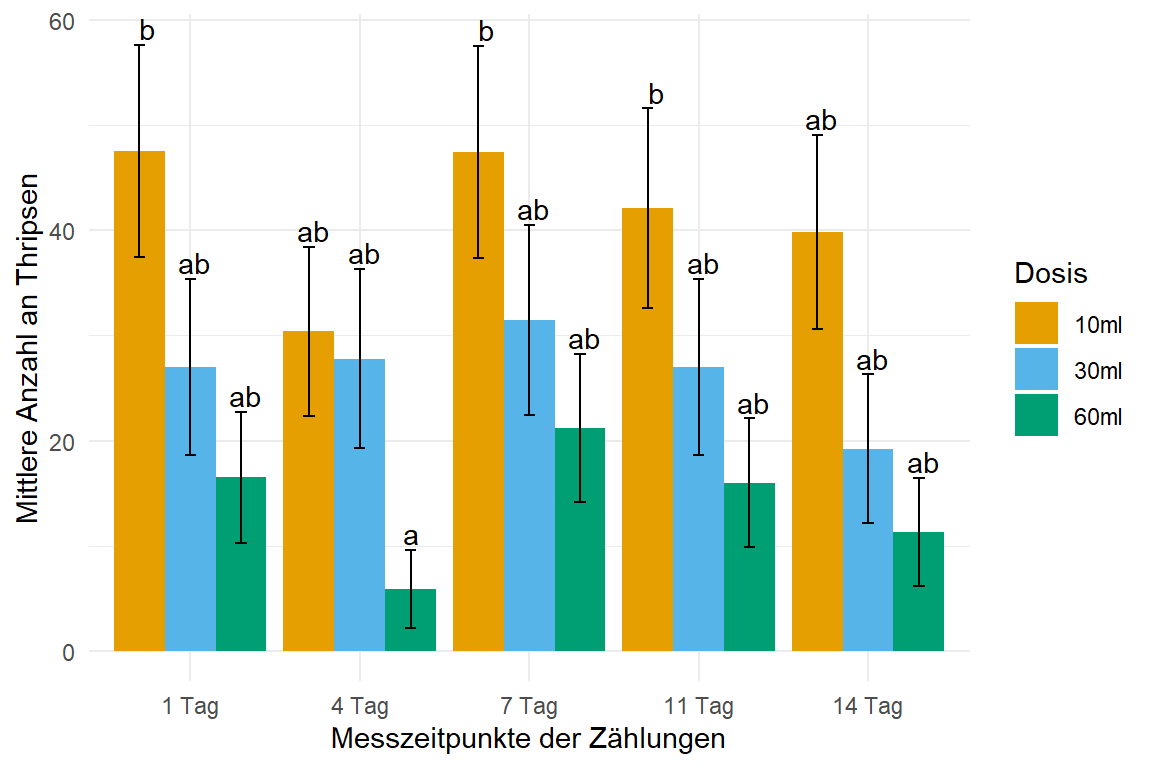
emm_obj trt timepoint rate SE df asymp.LCL asymp.UCL .group
60ml 4 Tag 5.9 3.72 Inf -5.029 16.8 a
60ml 14 Tag 11.3 5.15 Inf -3.825 26.4 ab
60ml 11 Tag 16.0 6.13 Inf -1.998 34.0 ab
60ml 1 Tag 16.5 6.23 Inf -1.777 34.8 ab
30ml 14 Tag 19.2 7.08 Inf -1.572 40.0 ab
60ml 7 Tag 21.2 7.06 Inf 0.483 41.9 ab
30ml 1 Tag 27.0 8.40 Inf 2.356 51.6 ab
30ml 11 Tag 27.0 8.40 Inf 2.356 51.6 ab
30ml 4 Tag 27.8 8.52 Inf 2.782 52.8 ab
10ml 4 Tag 30.4 8.05 Inf 6.725 54.0 ab
30ml 7 Tag 31.4 9.06 Inf 4.849 58.0 ab
10ml 14 Tag 39.8 9.22 Inf 12.748 66.9 ab
10ml 11 Tag 42.1 9.48 Inf 14.258 69.9 b
10ml 7 Tag 47.5 10.10 Inf 17.902 77.0 b
10ml 1 Tag 47.5 10.10 Inf 17.965 77.1 b
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 15 estimates
P value adjustment: bonferroni method for 105 tests
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same. Das emm_obj Objekt werden wir dann gleich einmal in {ggplot} visualisieren. Die rate stellt die mittlere Anzahl an Thripsen je Faktorkombination dar. Dann können wir auch das compact letter display anhand der Abbildung interpretieren.
In der Abbildung 61.20 siehst du das Ergebnis der Auswertung in einem Säulendiagramm. Hier unbedingt SE als den Standardfehler für die Fehlerbalken nutzen, da wir sonst Fehlerbalken größer und kleiner als \(0\) erhalten, wenn wir die Standardabweichung nutzen würden. Das ist in unserem Fall nicht so das Problem, aber wenn du eher kleine Anzahlen zählst, kann das schnell zu Werten kleiner Null führen. Wir sehen einen klaren Effekt der Behandlung 60ml. Die Zeit hat keinen Effekt, was ja schon aus der ANOVA klar war, die Säulen sehen für jeden Zeitpunkt vollkommen gleich aus. Gut etwas Unterschied ist ja immer.
R Code [zeigen / verbergen]
emm_obj |>
as_tibble() |>
ggplot(aes(x = timepoint, y = rate, fill = trt)) +
theme_minimal() +
labs(y = "Mittlere Anzahl an Thripsen", x = "Messzeitpunkte der Zählungen",
fill = "Dosis") +
geom_bar(stat = "identity",
position = position_dodge(width = 0.9, preserve = "single")) +
geom_text(aes(label = .group, y = rate + SE + 0.01),
position = position_dodge(width = 0.9), vjust = -0.25) +
geom_errorbar(aes(ymin = rate-SE, ymax = rate+SE),
width = 0.2,
position = position_dodge(width = 0.9, preserve = "single")) +
scale_fill_okabeito()