| Faktor A | Kovariate $C$ | Messwert $y$ |
|---|---|---|
| A.1 | 0.8 | 7 |
| A.1 | 1.6 | 8 |
| A.1 | 2.4 | 9 |
| A.2 | 3.2 | 2 |
| A.2 | 4.0 | 3 |
| A.2 | 4.8 | 4 |
| A.3 | 5.6 | 11 |
| A.3 | 6.4 | 12 |
| A.3 | 7.2 | 13 |
31 Die ANCOVA
Letzte Änderung am 17. February 2025 um 08:49:37
“It’s better to solve the right problem approximately than to solve the wrong problem exactly.” — John Tukey
Dieses Kapitel wird in den nächsten Wochen aktualisiert. Ich plane zum Ende des SoSe 2025 eine neue Version des Kapitels erstellt zu haben. Deshalb kann hier das ein oder andere kurzfristig nicht mehr funktionieren.
Eigentlich hat sich die Analysis of Covariance (ANCOVA) etwas überlebt. Wir können mit dem statistischen Modellieren eigentlich alles was die ANCOVA kann plus wir erhalten auch noch Effektschätzer für die Kovariaten und die Faktoren. Dennoch hat die ANCOVA ihren Platz in der Auswertung von Daten. Wenn du ein oder zwei Faktoren hast plus eine numerische Variable, wie das Startgewicht, für die du die Analyse adjustieren möchtest, dann ist die ANCOVA für dich gemacht.
31.1 Allgemeiner Hintergrund
Also kurz gesprochen adjustiert die Analysis of Covariance (ANCOVA) die Faktoren einer ANOVA um eine kontinuierliche Covariate. Eine Kovariate ist eine Variable, die mit berücksichtigt wird, um mögliche verzerrende Einflüsse auf die Analyseergebnisse (ungebräuchlich Konfundierung) abzuschätzen oder zu verringern. Adjustiert bedeutet in dem Fall, dass die Effekte des unterschiedlichen Startgewichts von Pflanzen durch das Einbringen der Kovariate mit in der statistischen Analyse berücksichtigt werden. Wir werden hier auch nur über die Nutzung in R sprechen und auf die theoretische Herleitung verzichten.
Wie immer gibt es auch passende Literatur um die ANCOVA herum. Karpen (2017) beschreibt in Misuses of Regression and ANCOVA in Educational Research nochmal Beispiele für die falsche oder widersprüchliche Nutzung der Regression und ANCOVA. Ich nutze die Quelle immer mal wieder in meinen vertiefenden Vorlesungen. Da wir hier ja nicht nur Agrawissenschaftler haben, hilft die Arbeit von Kim (2018) mit Statistical notes for clinical researchers: analysis of covariance (ANCOVA) auch nochmal weiter. Die Besonderheit bei der klinischen Forschung ist ja die “Beweglichkeit” der Beobachtungen. Menschen lassen sich eben nicht vollständig kontrollieren und daher ist die Thematik eine andere als bei Pflanzen und Tieren.
31.2 Theoretischer Hintergrund
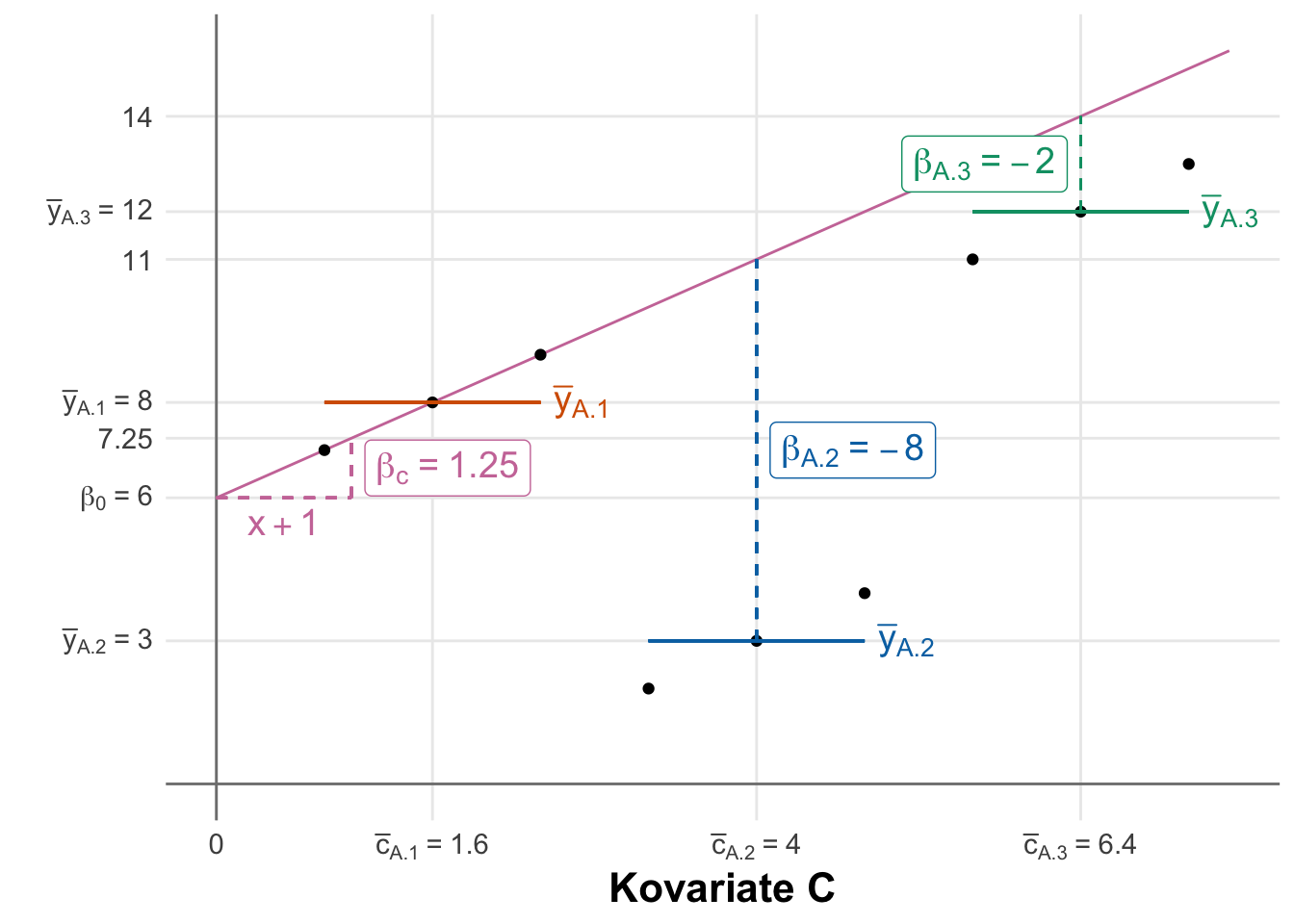
| Faktor A | Mittelwert Messwert | Mittelwert Kovariate |
|---|---|---|
| A.1 | 8 | 1.6 |
| A.2 | 3 | 4.0 |
| A.3 | 12 | 6.4 |
R Code [zeigen / verbergen]
lm(rsp ~ fa + cov, data = f1_ancova_theo_tbl) |>
coef() |> round(2)(Intercept) faA.2 faA.3 cov
6.00 -8.00 -2.00 1.25 Das Modell
Wenn wir neben einem bis mehreren Faktoren \(f\) noch eine numerische Kovariate \(c\) mit modellieren wollen, dann nutzen wir die ANCOVA (eng. Analysis of Covariance). Hier kommt dann immer als erstes die Frage, was heißt den Kovariate \(c\)? Hier kannst du dir eine numerische Variable vorstellen, die ebenfalls im Experiment gemessen wird. Es kann das Startgewicht oder aber die kummulierte Wassergabe sein. Wir haben eben hier keinen Faktor als Kategorie vorliegen, sondern eben etwas numerisch gemessen. Daher ist unsere Modellierung etwas anders.
\[ y \sim f_A + f_B + ... + f_P + f_A \times f_B + c_1 + ... + c_p \]
mit
- \(y\) gleich dem Messwert oder Outcome
- \(f_A + f_B + ... + f_P\) gleich experimenteller Faktoren
- \(f_A \times f_B\) gleich einem beispielhaften Interaktionsterm erster Ordnung
- \(c_1 + ... + c_p\) gleich einer oder mehrer numerischer Kovariaten
Hier muss ich gleich die Einschränkung machen, dass wir normalerweise maximal ein zweifaktorielles Modell mit einem Faktor \(A\) und einem Faktor \(B\) sowie einer Kovariate \(c\) betrachten. Sehr selten haben wir mehr Faktoren oder gar Kovariaten in dem Modell. Wenn das der Fall sein sollte, dann könnte eine andere Modellierung wie eine multiple Regression eine bessere Lösung sein.
Hypothesen
Wenn wir von der ANOVA sprechen, dann kommen wir natürlich nicht an den Hypothesen vorbei. Die ANOVA ist ja auch ein klassischer statistischer Test. Hier müssen wir unterscheiden, ob wir eine Behandlung mit zwei Gruppen, also einem Faktor \(A\) mit \(2\) Leveln vorliegen haben. Oder aber eine Behandlung mit drei oder mehr Gruppen vorliegen haben, also einem Faktor \(A\) mit \(\geq 3\) Leveln in den Daten haben. Da wir schnell in einer ANOVA mehrere Faktoren haben, haben wir auch schnell viele Hypothesen zu beachten. Jeweils ein Hypothesenpaar pro Faktor muss dann betrachtet werden. Das ist immer ganz wichtig, die Hypothesenpaare sind unter den Faktoren mehr oder minder unabhängig.
Bei einem Faktor \(A\) mit nur zwei Leveln \(A.1\) und \(A.2\) haben wir eine Nullhypothese, die du schon aus den Gruppenvergleichen wie dem t-Test kennst. Wir wollen zwei Mittelwerte vergleichen und in unserer Nullhypothese steht somit die Gleichheit. Da wir nur zwei Gruppen haben, sieht die Nullhypothese einfach aus.
\[ H_0: \; \bar{y}_{A.1} = \bar{y}_{A.2} \]
In der Alternativehypothese haben wir dann den Unterschied zwischen den beiden Mittelwerten. Wenn wir die Nullhypothese ablehnen können, dann wissen wir auch welche Mittelwertsunterschied signifikant ist. Wir haben ja auch nur einen Unterschied getestet.
\[ H_A: \; \bar{y}_{A.1} \neq \bar{y}_{A.2} \] Das Ganze wird dann etwas komplexer im Bezug auf die Alternativehypothese wenn wir mehr als zwei Gruppen haben. Hier kommt dann natürlich auch die Stärke der ANOVA zu tragen. Eben mehr als zwei Mittelwerte vergleichen zu können.
Die klassische Nullhypothese der ANOVA hat natürlich mehr als zwei Level. Hier einmal beispielhaft die Nullhypothese für den Vergleich von drei Gruppen des Faktors \(A\). Wir wollen als Nullhypothese testen, ob alle Mittelwerte der drei Gruppen gleich sind.
\[ H_0: \; \bar{y}_{A.1} = \bar{y}_{A.2} = \bar{y}_{A.3} \]
Wenn wir die Nullhypothese betrachten dann sehen wir auch gleich das Problem der Alternativehypothese. Wir haben eine Menge an paarweisen Vergleichen. Wenn wir jetzt die Nullhypothese ablehnen, dann wissen wir nicht welcher der drei paarweisen Mittelwertsvergleiche denn nun unterschiedlich ist. Praktisch können es auch alle drei oder eben zwei Vergleiche sein.
\[ \begin{aligned} H_A: &\; \bar{y}_{A.1} \ne \bar{y}_{A.2}\\ \phantom{H_A:} &\; \bar{y}_{A.1} \ne \bar{y}_{A.3}\\ \phantom{H_A:} &\; \bar{y}_{A.2} \ne \bar{y}_{A.3}\\ \phantom{H_A:} &\; \mbox{für mindestens einen Vergleich} \end{aligned} \]
Wenn wir die Nullhypothese abgelhent haben, dann müssen wir noch einen sogenannten Post-hoc Test anschließen um die paarweisen Unterschiede zu finden, die dann signifikant sind. Das ganze machen wir dann aber in einem eigenen Kapitel zum Post-hoc Test.
Wie immer gibt es auch für die Frage nach dem Tutorium für die ANCOVA verschiedene Quellen. Ich kann noch folgende Informationen und Hilfen empfehlen.
- How to perform ANCOVA in R liefert nochmal mehr Code und weitere Ideen zu der Analyse in R.
- ANCOVA in R beschreibt auch nochmal etwas anders die ANCOVA.
- Kovarianzanalyse ist eine deutsche Quelle, die nochmal vertiefend auf die Kovarianzanalyse eingeht.
31.3 Genutzte R Pakete
Wir wollen folgende R Pakete in diesem Kapitel nutzen.
R Code [zeigen / verbergen]
pacman::p_load(tidyverse, magrittr, broom, quantreg,
see, performance, emmeans, multcomp, janitor,
parameters, conflicted)
conflicts_prefer(dplyr::select)
conflicts_prefer(dplyr::filter)
cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73",
"#F0E442", "#0072B2", "#D55E00", "#CC79A7")An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
31.4 Daten
Für unser Beispiel nutzen wir die Daten der Sprungweite in [cm] von Flöhen auf Hunde-, Katzen- und Füchsen. Damit haben wir den ersten Faktor animal mit drei Leveln. Als Kovariate schauen wir uns das Gewicht als numerische Variable an. Schlussendlich brauchen wir noch das Outcome jump_length als \(y\). Für die zweifaktorielle ANCOVA nehmen wir noch den Faktor sex mit zwei Leveln hinzu.
R Code [zeigen / verbergen]
ancova_tbl <- read_csv2("data/flea_dog_cat_length_weight.csv") |>
select(animal, sex, jump_length, weight) |>
mutate(animal = as_factor(animal))In der Tabelle 59.1 ist der Datensatz ancova_tbl nochmal dargestellt.
| animal | sex | jump_length | weight |
|---|---|---|---|
| cat | male | 15.79 | 6.02 |
| cat | male | 18.33 | 5.99 |
| cat | male | 17.58 | 8.05 |
| cat | male | 14.09 | 6.71 |
| cat | male | 18.22 | 6.19 |
| cat | male | 13.49 | 8.18 |
| … | … | … | … |
| fox | female | 27.81 | 8.04 |
| fox | female | 24.02 | 9.03 |
| fox | female | 24.53 | 7.42 |
| fox | female | 24.35 | 9.26 |
| fox | female | 24.36 | 8.85 |
| fox | female | 22.13 | 7.89 |
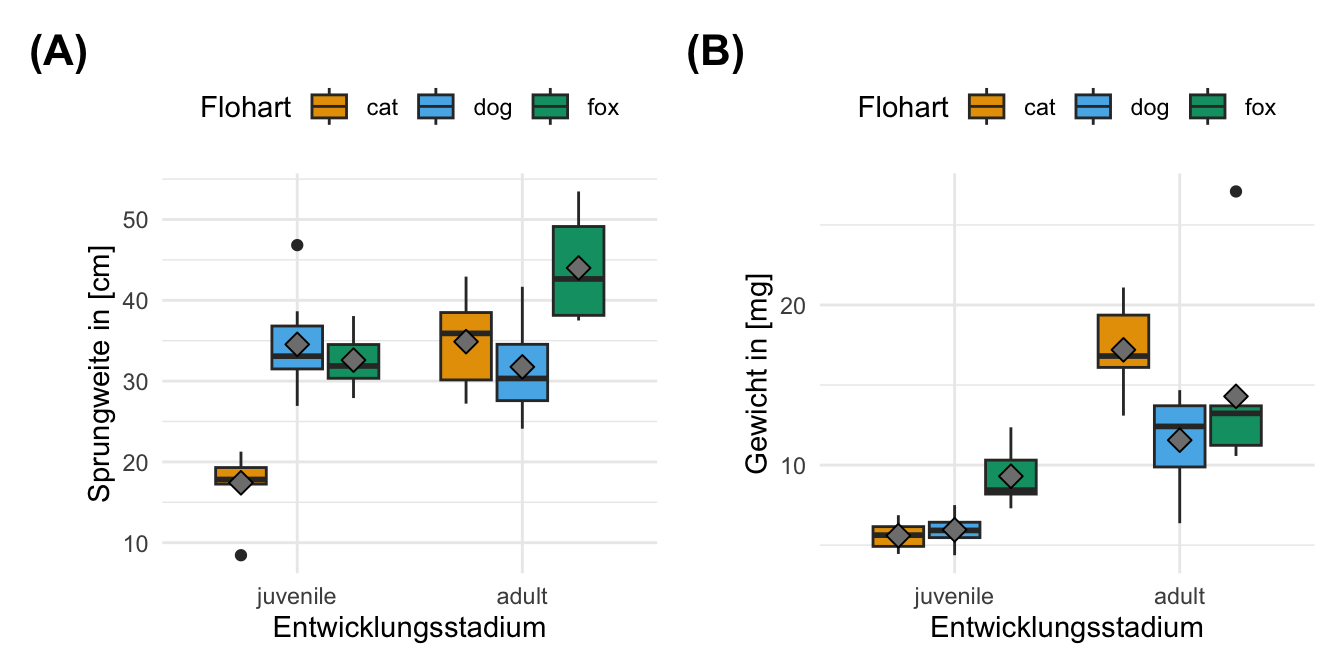
Zweifaktorieller Datensatz mit Kovariate
R Code [zeigen / verbergen]
fac2_cov_tbl <- read_excel("data/fleas_complex_data.xlsx", sheet = "covariate") |>
select(animal, stage, weight, jump_length) |>
mutate(animal = as_factor(animal),
stage = factor(stage, level = c("juvenile", "adult")),
weight = round(weight, 2),
jump_length = round(jump_length, 2))|>
rowid_to_column(".id")| animal | stage | weight | jump_length |
|---|---|---|---|
| cat | adult | 16.74 | 42.93 |
| cat | adult | 16.79 | 30.26 |
| cat | adult | 19.3 | 27.21 |
| … | … | … | … |
| fox | juvenile | 7.3 | 31.47 |
| fox | juvenile | 8.66 | 33.67 |
| fox | juvenile | 8.13 | 32.28 |
31.5 Einfaktorielle ANCOVA
Hier eine kurze Betrachtung. Mehr dazu in dem Kapitel zur ANCOVA
Wir können die ANCOVA ganz klassisch mit dem linaren Modell fitten. Wir nutzen die Funktion lm() um die Koeffizienten des linearen Modellls zu erhalten. Wir erinnern uns, wir haben haben einen Faktor \(f_1\) und eine Kovariate bezwiehungsweise ein numerisches \(c_1\). In unserem Beispiel sieht dann der Fit des Modells wie folgt aus.
R Code [zeigen / verbergen]
fit_1 <- lm(jump_length ~ animal + weight + animal:weight, data = ancova_tbl)Nachdem wir das Modell in dem Objekt fit_1 gespeichert haben können wir dann das Modell in die Funktion anova() pipen. Die Funktion erkennt, das wir eine ANCOVA rechnen wollen, da wir in unserem Modell einen Faktor und eine Kovariate mit enthalten haben.
R Code [zeigen / verbergen]
fit_1 |> anova ()Analysis of Variance Table
Response: jump_length
Df Sum Sq Mean Sq F value Pr(>F)
animal 2 2693.8 1346.88 204.2764 <2e-16 ***
weight 1 1918.0 1917.99 290.8961 <2e-16 ***
animal:weight 2 0.3 0.14 0.0214 0.9788
Residuals 594 3916.5 6.59
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1In der ANCOVA erkennne wir nun, dass der Faktor animal signifikant ist. Der \(p\)-Wert ist mit \(<0.001\) kleiner das das Signifikanzniveau \(\alpha\) von 5%. Ebenso ist die Kovariate weight signifikant. Der \(p\)-Wert ist ebenfalls mit \(<0.001\) kleiner das das Signifikanzniveau \(\alpha\) von 5%. Wir können also schlussfolgern, dass sich mindestens eine Gruppenvergleich der Level des Faktors animal voneinander unterscheidet. Wir wissen auch, dass mit der Zunahme des Gewichts, die Sprunglänge sich ändert. Die ANCOVA liefert keine Informationen zu der Größe oder der Richtung des Effekts der Kovariate.
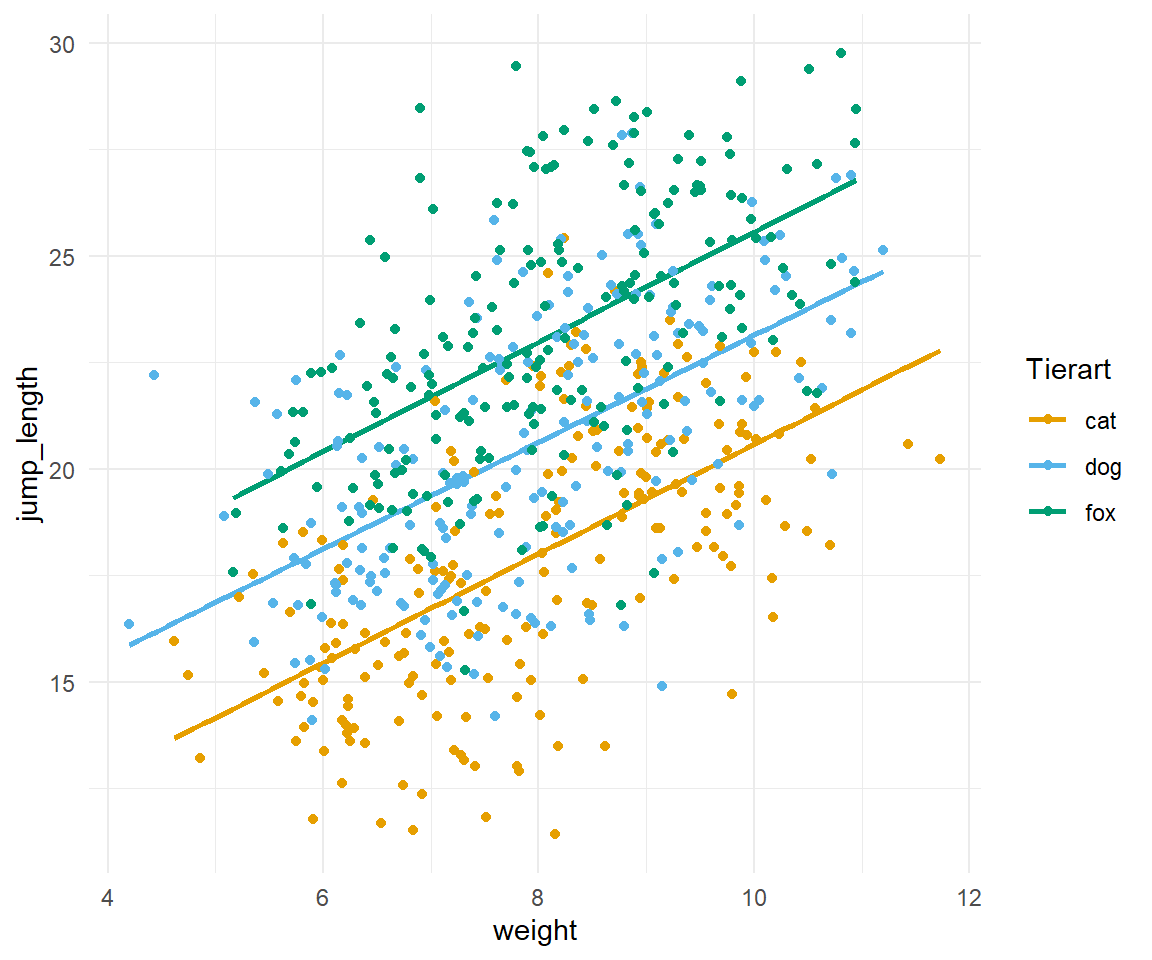
Was wir nicht wissen, ist die Richtung. Wir wissen nicht, ob mit ansteigenden Gewicht sich die Sprunglänge erhöht oder vermindert. Ebenso wenig wissen wir etwas über den Betrag des Effekts. Wieviel weiter springen denn nun Flöhe mit 1 mg Gewicht mehr? Wir haben aber die Möglichkeit, den Sachverhalt uns einmal in einer Abbildung zu visualisieren. In Abbildung 31.3 sehen wir die Daten einmal als Scatterplot dargestellt.
R Code [zeigen / verbergen]
ggplot(ancova_tbl, aes(weight, jump_length, color = animal)) +
geom_smooth(method = "lm", se = FALSE) +
scale_color_okabeito() +
theme_minimal() +
geom_point() +
labs(color = "Tierart", shape = "Geschlecht") Der Abbildung 31.3 können wir jetzt die positive Steigung entnehmen sowie die Reihenfolge der Tierarten nach Sprungweiten. Die ANCOVA sollte immer visualisiert werden, da sich hier die Stärke der Methode mit der Visualiserung verbindet.
31.6 Zweifaktorielle ANCOVA
Die zweifaktorielle ANCOVA erweitert die einfaktorielle ANCOVA um einen weiteren Faktor. Das ist manchmal etwas verwirrend, da wir auf einmal drei oder mehr Terme in einem Modell haben. Klassischerweise haben wir nun zwei Faktoren \(f_1\) und \(f_2\) in dem Modell. Weiterhin haben wir nur eine Kovariate \(c_1\). Damit sehe das Modell wie folgt aus.
\[ y \sim f_1 + f_2 + c_1 \]
Wir können das Modell dann in R übertragen und ergänzen noch den Interaktionsterm für die Faktoren animal und sex in dem Modell. Das Modell wird klassisch in der Funktion lm() gefittet.
R Code [zeigen / verbergen]
fit_2 <- lm(jump_length ~ animal + sex + weight + animal:sex, data = ancova_tbl)Nach dem Fit können wir das Modell in dem Obkjekt fit_2 in die Funktion anova() pipen. Die Funktion erkennt die Struktur des Modells und gibt uns eine ANCOVA Ausgabe wieder.
R Code [zeigen / verbergen]
fit_2 |> anova() Analysis of Variance Table
Response: jump_length
Df Sum Sq Mean Sq F value Pr(>F)
animal 2 2693.8 1346.9 359.0568 <2e-16 ***
sex 1 3608.1 3608.1 961.8568 <2e-16 ***
weight 1 0.0 0.0 0.0053 0.9422
animal:sex 2 2.2 1.1 0.2981 0.7424
Residuals 593 2224.4 3.8
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1In der ANCOVA erkennne wir nun, dass der Faktor animal signifikant ist. Der \(p\)-Wert ist mit \(<0.001\) kleiner das das Signifikanzniveau \(\alpha\) von 5%. Ebenso ist der Faktor sex signifikant. Der \(p\)-Wert ist mit \(<0.001\) kleiner das das Signifikanzniveau \(\alpha\) von 5%. Die Kovariate weight ist nicht mehr signifikant. Der \(p\)-Wert ist mit \(0.94\) größer das das Signifikanzniveau \(\alpha\) von 5%. Wir können also schlussfolgern, dass sich mindestens eine Gruppenvergleich der Level des Faktors animal voneinander unterscheidet. Ebenso wie können wir schlussfolgern, dass sich mindestens eine Gruppenvergleich der Level des Faktors site voneinander unterscheidet. Da wir nur zwei Level in dem Faktor sex haben, wissen wir nun, dass sich die beiden Geschlechter der Flöhe in der Sprungweite unterscheiden. Wir wissen auch, dass mit der Zunahme des Gewichts, sich die Sprunglänge nicht ändert.
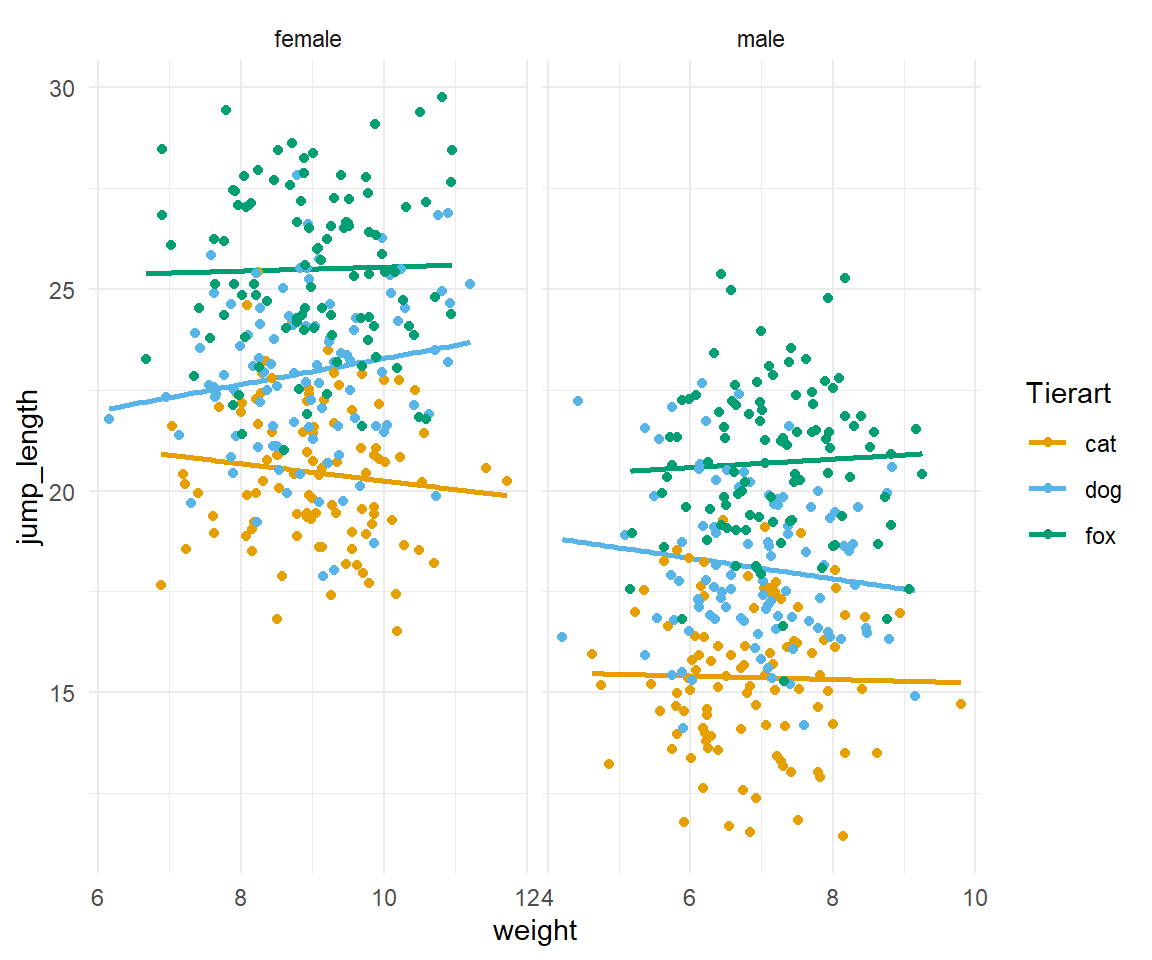
In Abbildung 31.4 sehen wir nochmal den Zusammenhang dargestellt. Wenn wir die Daten getrennt für den Faktor sex anschauen, dann sehen wir, dass das Gewicht keinen Einfluss mehr auf die Sprungweite hat.
R Code [zeigen / verbergen]
ggplot(ancova_tbl, aes(weight, jump_length, color = animal)) +
geom_smooth(method = "lm", se = FALSE) +
scale_color_okabeito() +
theme_minimal() +
geom_point() +
labs(color = "Tierart", shape = "Geschlecht") +
facet_wrap(~ sex, scales = "free_x")Nach einer berechneten ANCOVA können wir zwei Fälle vorliegen haben. Wenn du in deinem Experiment keine signifikanten Ergebnisse findest, ist das nicht schlimm. Du kannst deine Daten immer noch mit der explorativen Datenanalyse auswerten wie im Kapitel zur explorativen Datenanalyse gezeigt wird.
- Wir habe eine nicht signifikante ANCOVA berechnet. Wir können die Nullhypothese \(H_0\) nicht ablehnen und die Mittelwerte über den Faktor sind vermutlich alle gleich. Wir enden hier mit unserer statistischen Analyse.
- Wir haben eine signifikante ANCOVA berechnet. Wir können die Nullhypothese \(H_0\) ablehnen und mindestens ein Gruppenvergleich über mindestens einen Faktor ist vermutlich unterschiedlich. Wir können dann im Kapitel 41 eine Posthoc Analyse rechnen.