“Comparison is the thief of joy.” — Theodore Roosevelt
Stand des Kapitels: Aktualisierung (seit 01.2025)
Dieses Kapitel wird in den nächsten Wochen aktualisiert. Um zu gewährleisten, dass hier auch alles weiter so funktioniert, findet die Aktualisierung außerhalb dieses Kapitels statt. Ich plane zum SoSe 2025 eine neue Version des Kapitels erstellt zu haben.
In diesem Kapitel wollen wir uns mit den multiplen Vergleichen (eng. post hoc analysis) oder aber auch paarweise Gruppenvergleiche genannt beschäftigen. Wir kennen diese multiplen Tests auch unter dem Namen Posthoc Tests, da wir historisch diese Tests nach einer ANOVA durchgeführt haben. Das heißt, wir wollen statistisch Testen, ob sich verschiedene Gruppen einer Behandlung voneinander unterschieden. Technisch Testen wir dabei, ob sich die Level eines Faktors voneinander unterscheiden. Wir können dabei mehrere Faktoren bzw. Behandlungen berücksichtigen und gleichzeitig Testen. Wenn wir nur einen Faktor betrachten, dann sprechen wir von einem 1-faktoriellen Vergleich. Wenn wir zwei Behandlungen betrachten, dann entsprechend von einem 2-faktoriellen Vergleich. Sehr selten haben wir dann noch den Fall vorliegen, dass wir drei Faktoren betrachten wollen. In einer Abschlussarbeit haben wir faktisch keine Versuche wo wir mehr als drei Faktoren in einem Gruppenvergleich berücksichtigen.
Wo wollen wir also hin? Betrachten wir dazu einmal zwei wissenschaftliche Veröffentlichungen als Beispiele. In der Abbildung 40.1 sehen wir ein Säulendigramm aus der wissenschaftlichen Veröffentlichung von Salinas u. a. (2023) mit dem Titel “Plant Growth, Yield, and Fruit Size Improvements in ‘Alicia’ Papaya Multiplied by Grafting”. Wir haben hier also einen 2-faktoriellen Gruppenvergleich vorliegen. Der erste Faktor ist die TSS Behandlung mit seed, grafting und in virto. Der zweite Faktor sind dann die fünf Zeitpunkte zu denen jeweils die Behandlung auf die Papaya gegeben wurde. In diesem Kapitel wollen wir die Buchstaben aus einem paarweisen Gruppenvergleich über den Säulen erschaffen oder auch compact letter display genannt.
Abbildung 40.1— “Total soluble solids (TSS) in ‘Alicia’ papaya propagated by seed, grafting, and in vitro (n = 12 ± s.e.), evaluated from April 2020 to May 2021 at the maturation of 100% yellow skin color. The line marks the 10 °Brix value, commonly referred to as the minimum for papaya commercialization. Different letters on the same date indicate statistically significant differences between propagation procedures (Tukey’s test p < 0.05).” Quelle: Salinas u. a. (2023)
In der Abbildung 40.2 sehen wir ein Säulendigramm aus der wissenschaftlichen Veröffentlichung von Sánchez u. a. (2022) mit dem Titel “Hoverfly pollination enhances yield and fruit quality in mango under protected cultivation”. Auch hier haben wir ein 2-faktorielles Design vorliegen. Zum einen den Faktor treatment mit den Gruppen High density, medium density, Low density und Control. Der zweite Faktor ist dann das Jahr der Messung. Auch hier sehen wir wieder Buchstaben über den Säulen. Diese Buchstabenwollen wir dann als compact letter display hier in diesem Kapitel erstellen. Zu den Fehlerbalken liefert die Publikation Error bars in experimental biology von Cumming u. a. (2007) nochmal einen Überblick über Fehlerbalken und welche Fehlerbalken man den nun nutzen sollte.
Abbildung 40.2— “Panicles with commercial fruit (%) at 2019 and 2020 harvest. In the same year, different letters indicate significant differences among treatments (Tukey’s test p<0.05).” Quelle: Sánchez u. a. (2022)
Dann wissen wir jetzt wohin wir wollen. Jetzt stellt sich noch die Frage, welches statistisches Verfahren soll ich wählen um einen Gruppenvergleich zu rechnen? In der folgenden Box gebe ich dir da einmal einen Überblick. Abhängig von deinem Outcome oder deinen gemessenen Werten, musst du dich für ein anderes Verfahren entscheiden. Es kann also sein, dass du verschiedene statistische Tests in deiner Abschlussarbeit rechnest, da du verschiedene Outcomes statistisch analysierst. Wir schauen uns in diesem Kapitel zum größten Teil den Fall eines normalverteilten Outcomes an. An einem normalverteilten Outcome, wie Frische- oder Trockengewicht, lassen sich einfacher die Prinzipien des multiplen Testen erklären. Deshalb hier der Fokus auf der Normalverteilung – andere Möglichkeiten dann in der Box.
Welches statistisches Modell für welchen Gruppenvergleich?
Welches Verfahren soll ich für meinen Gruppenvergleich wählen? Ich habe in den jeweiligen Kapiteln zu den statistischen Modellen die jeweiligen Schritte für die Gruppenvergleiche hinterlegt und beschrieben. Daher kannst du in den Kapiteln einmal schauen, wie dein Outcome dort ausgewertet wird. Du findest dort auch immer ein Beispiel mit entsprechenden Daten.
Poissonverteiltes Outcome \(\boldsymbol{y}\) bzw. Zähldaten: Anzahl Insekten, gekeimte Pflanzen, Schädlinge…
Dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für Zähldaten an – dein Outcome besteht nämlich aus einer Zählung von einem Auftreten eines Ereignisses.
Ordinalverteiltes Outcome \(\boldsymbol{y}\): Bonitur von Rasen, Brokkolistängel, Wurzelwachstum…
Binomialverteiltes Outcome \(\boldsymbol{y}\) bzw. Anteile: Infektionsstatus, Zielgewicht erreicht…
Dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für Anteile an – dein Outcome ist \(0/1\) oder \(ja/nein\) kodiert. Ein Ereignis ist eingetreten oder eben nicht.
Betaverteiltes Outcome \(\boldsymbol{y}\) bzw. Wahrscheinlichkeiten: Anteil infizierte Pflanzen, Erfolg/Misserfolg…
Dann schaue dir den Abschnitt zu Multiple Gruppenvergleiche für Wahrscheinlichkeiten an – dein Outcome ist eine Wahrscheinlcihkeit für das Eintreten eines Ereignisses oder aber die Rate eines Erfolges an Misserfolgen.
Wenn wir multiple Mittelwertsvergleiche rechnen, dann tritt das Problem des multiplen Testens auf. Wir haben eine Inflation des \(\alpha\)-Fehlers vorliegen. Im Kapitel 21.3 kannst du mehr über die Problematik erfahren und wie wir mit der \(\alpha\) Inflation umgehen. Hier in diesem Kapitel gehe ich jetzt davon aus, dass dir die \(\alpha\) Adjustierung ein Begriff ist. Häufig sollen \(p\)-Werte nicht adjustiert werden, viele Verfahren in diesem Kapitel adjustieren aber automatisch die \(p\)-Werte. Deshalb musst du aktiv die Adjustierung der \(p\)-Werte abstellen. Du findest dann in Abschnitten zu den jeweiligen statistischen Verfahren die entsprechende Option. Der paarweise Mittelwertsvergleich wird auch gerne Tukey Test genannt. Das heißt, dass der Tukey Test alle Gruppen miteinander vergleicht. Der Tukey Test wird daher auch gerne all pair Vergleich genannt.
Schaue dir auch die folgenden Zerforschenbeispiele einmal an, wenn dich mehr zu dem Thema der Abbildung von multiplen Gruppenvergleichen interessiert. Du findest in den Kästen Beispiele für Posterabbildungen zur multiplen Gruppenvergleichen, die ich dann zerforscht habe.
Zerforschen: Einfaktorieller Barplot mit emmeans und compact letter display
In diesem Zerforschenbeispiel wollen wir uns einen einfaktoriellen Barplot oder Säulendiagramm anschauen. Daher fangen wir mit der folgenden Abbildung einmal an. Wir haben hier ein Säulendiagramm mit compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Behandlungen jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung. Die Standardabweichung addieren und subtrahieren wir dann jeweils von dem Mittelwert und schon haben wir die Fehlerbalken. Für eine detaillierte Betrachtung der Erstellung der Abbildung schauen einmal in das Kapitel zum Barplot oder Balkendiagramm oder Säulendiagramm.
Abbildung 40.3— Ursprüngliche Abbildung, die nachgebaut werden soll. Ein simples Säulendiagramm mit sehr für Farbblinde ungünstigen Farben. Es sind die Mittelwerte sowie die Standardabweichung durch die Fehlerbalken dargestellt.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_simple.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die vier Werte alle um den Mittelwert streuen lassen. Dabei habe ich darauf geachtet, dass die Streuung dann in der letzten Behandlung am größten ist.
Im Folgenden sparen wir uns den Aufruf mit group_by() den du aus dem Kapitel zum Barplot schon kennst. Wir machen das alles zusammen in der Funktion emmeans() aus dem gleichnamigen R Paket. Der Vorteil ist, dass wir dann auch gleich die Gruppenvergleiche und auch das compact letter display erhalten. Einzig die Standardabweichung \(s\) wird uns nicht wiedergegeben sondern der Standardfehler \(SE\). Da aber folgernder Zusammenhang vorliegt, können wir gleich den Standardfehler in die Standardabweichung umrechnen.
\[
SE = \cfrac{s}{\sqrt{n}}
\]
Wir rechnen also gleich einfach den Standardfehler \(SE\) mal der \(\sqrt{n}\) um dann die Standardabweichung zu erhalten. In unserem Fall ist \(n=4\) nämlich die Anzahl Beobachtungen je Gruppe. Wenn du mal etwas unterschiedliche Anzahlen hast, dann kannst du auch einfach den Mittelwert der Fallzahl der Gruppen nehmen. Da überfahren wir zwar einen statistischen Engel, aber der Genauigkeit ist genüge getan.
In den beiden Tabs siehst du jetzt einmal die Modellierung unter der Annahme der Varianzhomogenität mit der Funktion lm() und einmal die Modellierung unter der Annahme der Varianzheterogenität mit der Funktion gls() aus dem R Paket nlme. Wie immer lässt sich an Boxplots visuell überprüfen, ob wir Homogenität oder Heterogenität vorliegen haben. Oder aber du schaust nochmal in das Kapitel Der Pre-Test oder Vortest, wo du mehr erfährst.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim().
# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 5.08 12 109. 131. a 10.2
2 RQflex Nitra 130 5.08 12 119. 141. ab 10.2
3 Wasserdestilation 136. 5.08 12 125. 147. b 10.2
4 Laqua Nitrat 216. 5.08 12 205. 227. c 10.2
In dem Objekt emmeans_homogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. Wie dir vielleicht auffällt sind alle Standardfehler und damit alle Standardabweichungen für alle Gruppen gleich, das war ja auch unsere Annahme mit der Varianzhomogenität.
# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 7.07 3.00 97.5 143. a 14.1
2 RQflex Nitra 130 3.54 3.00 119. 141. a 7.07
3 Wasserdestilation 136. 3.15 3.00 126. 146. a 6.29
4 Laqua Nitrat 216. 5.54 3.00 199. 234. b 11.1
In dem Objekt emmeans_hetrogen_gls_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
# A tibble: 4 × 8
trt emmean SE df lower.CL upper.CL .group sd
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 Nitrachek 120 7.84 12 103. 137. a 15.7
2 RQflex Nitra 130 3.92 12 121. 139. a 7.84
3 Wasserdestilation 136. 2.06 12 132. 141. a 4.12
4 Laqua Nitrat 216. 4.94 12 205. 227. b 9.88
In dem Objekt emmeans_hetrogen_vcov_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
Und dann haben wir auch schon die Abbildungen hier erstellt. Ja vielleicht passen die Standardabweichungen nicht so richtig, da könnte man nochmal an den Daten spielen und die Werte solange ändern, bis es besser passt. Du hast aber jetzt eine Idee, wie der Aufbau funktioniert. Die beiden Tabs zeigen dir dann die Abbildungen für die beiden Annahmen der Varianzhomogenität oder Varianzheterogenität. Der Code ist der gleiche für die drei Abbildungen, die Daten emmeans_homogen_tbl oder emmeans_hetrogen_gls_tbl ober emmeans_hetrogen_vcov_tbl sind das Ausschlaggebende.
ggplot(data = emmeans_homogen_tbl, aes(x = trt, y = emmean, fill = trt)) +theme_minimal() +geom_bar(stat ="identity") +geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd), width =0.2) +labs(x ="", y ="Nitrat-Konzentration \n im Tannensaft [mg/L]") +ylim(0, 250) +theme(legend.position ="none") +scale_fill_okabeito() +geom_text(aes(label = .group, y = emmean + sd +10))
Abbildung 40.4— Die Abbildung des Säulendiagramms in ggplot nachgebaut mit den Informationen aus der Funktion emmeans(). Das compact letter display wird dann über das geom_text() gesetzt.
R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_gls_tbl, aes(x = trt, y = emmean, fill = trt)) +theme_minimal() +geom_bar(stat ="identity") +geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd), width =0.2) +labs(x ="", y ="Nitrat-Konzentration \n im Tannensaft [mg/L]") +ylim(0, 250) +theme(legend.position ="none") +scale_fill_okabeito() +geom_text(aes(label = .group, y = emmean + sd +10))
Abbildung 40.5— Die Abbildung des Säulendiagramms in ggplot nachgebaut mit den Informationen aus der Funktion emmeans(). Das compact letter display wird dann über das geom_text() gesetzt. Die Varianzheterogenität nach der Funktion gls() im obigen Modell berücksichtigt.
R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_vcov_tbl, aes(x = trt, y = emmean, fill = trt)) +theme_minimal() +geom_bar(stat ="identity") +geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd), width =0.2) +labs(x ="", y ="Nitrat-Konzentration \n im Tannensaft [mg/L]") +ylim(0, 250) +theme(legend.position ="none") +scale_fill_okabeito() +geom_text(aes(label = .group, y = emmean + sd +10))
Abbildung 40.6— Die Abbildung des Säulendiagramms in ggplot nachgebaut mit den Informationen aus der Funktion emmeans(). Das compact letter display wird dann über das geom_text() gesetzt. Die Varianzheterogenität nach der Funktion sandwich::vcovHAC im obigen Modell berücksichtigt.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
Zerforschen: Zweifaktorieller Barplot mit emmeans und compact letter display
In diesem Zerforschenbeispiel wollen wir uns einen zweifaktoriellen Barplot anschauen. Wir haben hier ein Säulendiagramm mit compact letter display vorliegen. Daher brauchen wir eigentlich gar nicht so viele Zahlen. Für jede der vier Zeitpunkte und der Kontrolle jeweils einmal einen Mittelwert für die Höhe der Säule sowie einmal die Standardabweichung. Da wir hier aber noch mit emmeans() eine Gruppenvergleich rechnen wollen, brauchen wir mehr Beobachtungen. Wir erschaffen uns also fünf Beobachtungen je Zeit/Jod-Kombination. Für eine detaillierte Betrachtung der Erstellung der Abbildung schauen einmal in das Kapitel zum Barplot oder Balkendiagramm oder Säulendiagramm.
Abbildung 40.7— Ursprüngliche Abbildung, die nachgebaut werden soll. Ein Barplot mit den zwei Faktoren Zeit und die Iodine Form.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_2fac_target_emmeans.xlsx selber ausgedacht. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die fünf Werte alle um den Mittelwert streuen lassen. Ich brauche hier eigentlich mehr als fünf Werte, sonst kriegen wir bei emmeans() und der Interaktion im gls()-Modell Probleme, aber da gibt es dann bei kleinen Fallzahlen noch ein Workaround. Bitte nicht mit weniger als fünf Beobachtungen versuchen, dann wird es schwierig mit der Konsistenz der Schätzer aus dem Modell.
Ach, und ganz wichtig. Wir entfernen die Kontrolle, da wir die Kontrolle nur mit einer Iodid-Stufe gemessen haben. Dann können wir weder die Interaktion rechnen, noch anständig eine Interpretation durchführen.
# A tibble: 40 × 3
time type iodine
<fct> <fct> <dbl>
1 07:00 KIO3 50
2 07:00 KIO3 55
3 07:00 KIO3 60
4 07:00 KIO3 52
5 07:00 KIO3 62
6 07:00 KI 97
7 07:00 KI 90
8 07:00 KI 83
9 07:00 KI 81
10 07:00 KI 98
# ℹ 30 more rows
Im Folgenden sparen wir uns den Aufruf mit group_by() den du aus dem Kapitel zum Barplot schon kennst. Wir machen das alles zusammen in der Funktion emmeans() aus dem gleichnamigen R Paket. Der Vorteil ist, dass wir dann auch gleich die Gruppenvergleiche und auch das compact letter display erhalten. Einzig die Standardabweichung \(s\) wird uns nicht wiedergegeben sondern der Standardfehler \(SE\). Da aber folgernder Zusammenhang vorliegt, können wir gleich den Standardfehler in die Standardabweichung umrechnen.
\[
SE = \cfrac{s}{\sqrt{n}}
\]
Wir rechnen also gleich einfach den Standardfehler \(SE\) mal der \(\sqrt{n}\) um dann die Standardabweichung zu erhalten. In unserem Fall ist \(n=5\) nämlich die Anzahl Beobachtungen je Gruppe. Wenn du mal etwas unterschiedliche Anzahlen hast, dann kannst du auch einfach den Mittelwert der Fallzahl der Gruppen nehmen. Da überfahren wir zwar einen statistischen Engel, aber der Genauigkeit ist genüge getan.
In den beiden Tabs siehst du jetzt einmal die Modellierung unter der Annahme der Varianzhomogenität mit der Funktion lm() und einmal die Modellierung unter der Annahme der Varianzheterogenität mit der Funktion gls() aus dem R Paket nlme. Wie immer lässt sich an Boxplots visuell überprüfen, ob wir Homogenität oder Heterogenität vorliegen haben. Oder aber du schaust nochmal in das Kapitel Der Pre-Test oder Vortest, wo du mehr erfährst.
Wenn du jeden Boxplot miteinander vergleichen willst, dann musst du in dem Code emmeans(~ time * type) setzen. Dann berechnet dir emmeans für jede Faktorkombination einen paarweisen Vergleich.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim(). Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen. Wenn du alles mit allem Vergleichen willst, dann setze bitte emmeans(~ time * type).
R Code [zeigen / verbergen]
emmeans_homogen_tbl <-lm(iodine ~ time + type + time:type, data = barplot_tbl) |>emmeans(~ time | type) |>cld(Letters = letters, adjust ="none") |>as_tibble() |>mutate(.group =str_trim(.group),sd = SE *sqrt(5)) emmeans_homogen_tbl
# A tibble: 8 × 9
time type emmean SE df lower.CL upper.CL .group sd
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 07:00 KIO3 55.8 5.58 32 44.4 67.2 a 12.5
2 11:00 KIO3 75.2 5.58 32 63.8 86.6 b 12.5
3 15:00 KIO3 81 5.58 32 69.6 92.4 b 12.5
4 19:00 KIO3 84.2 5.58 32 72.8 95.6 b 12.5
5 07:00 KI 89.8 5.58 32 78.4 101. a 12.5
6 19:00 KI 90 5.58 32 78.6 101. a 12.5
7 15:00 KI 124 5.58 32 113. 135. b 12.5
8 11:00 KI 152 5.58 32 141. 163. c 12.5
In dem Objekt emmeans_homogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. Wie dir vielleicht auffällt sind alle Standardfehler und damit alle Standardabweichungen für alle Gruppen gleich, das war ja auch unsere Annahme mit der Varianzhomogenität.
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim(). Da wir hier etwas Probleme mit der Fallzahl haben, nutzen wir die Option mode = "appx-satterthwaite" um dennoch ein vollwertiges, angepasstes Modell zu erhalten. Du kannst die Option auch erstmal entfernen und schauen, ob es mit deinen Daten auch so klappt. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen. Wenn du alles mit allem Vergleichen willst, dann setze bitte emmeans(~ time * type).
R Code [zeigen / verbergen]
emmeans_hetrogen_tbl <-gls(iodine ~ time + type + time:type, data = barplot_tbl, weights =varIdent(form =~1| time*type)) |>emmeans(~ time | type, mode ="appx-satterthwaite") |>cld(Letters = letters, adjust ="none") |>as_tibble() |>mutate(.group =str_trim(.group),sd = SE *sqrt(5)) emmeans_hetrogen_tbl
# A tibble: 8 × 9
time type emmean SE df lower.CL upper.CL .group sd
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 07:00 KIO3 55.8 2.29 3.96 49.4 62.2 a 5.12
2 11:00 KIO3 75.2 1.50 3.95 71.0 79.4 b 3.35
3 15:00 KIO3 81.0 3.30 3.97 71.8 90.2 b 7.38
4 19:00 KIO3 84.2 7.88 3.99 62.3 106. b 17.6
5 07:00 KI 89.8 3.48 3.96 80.1 99.5 a 7.79
6 19:00 KI 90.0 4.31 4.03 78.1 102. a 9.64
7 15:00 KI 124 7.48 4.02 103. 145. b 16.7
8 11:00 KI 152 9.03 4.00 127. 177. c 20.2
In dem Objekt emmeans_hetrogen_tbl ist jetzt alles enthalten für unsere Barplots mit dem compact letter display. In diesem Fall hier sind die Standardfehler und damit auch die Standardabweichungen nicht alle gleich, wir haben ja für jede Gruppe eine eigene Standardabweichung angenommen. Die Varianzen sollten ja auch heterogen sein.
Dann bauen wir usn auch schon die Abbildung. Wir müssen am Anfang einmal scale_x_discrete() setzen, damit wir gleich den Zielbereich ganz hinten zeichnen können. Sonst ist der blaue Bereich im Vordergrund. Dann färben wir auch mal die Balken anders ein. Muss ja auch mal sein. Auch nutzen wir die Funktion geom_text() um das compact letter display gut zu setzten. Die \(y\)-Position berechnet sich aus dem Mittelwert emmean plus Standardabweichung sd innerhalb des geom_text(). Da wir hier die Kontrollgruppe entfernen mussten, habe ich dann nochmal den Zielbereich verschoben und mit einem Pfeil ergänzt. Die beiden Tabs zeigen dir dann die Abbildungen für die beiden Annahmen der Varianzhomogenität oder Varianzheterogenität. Der Code ist der gleiche für beide Abbildungen, die Daten emmeans_homogen_tbl oder emmeans_hetrogen_tbl sind das Ausschlaggebende. Wie du sehen wirst, haben wir hier mal keinen Unterschied vorliegen.
ggplot(data = emmeans_homogen_tbl, aes(x = time, y = emmean, fill = type)) +theme_minimal() +scale_x_discrete() +annotate("rect", xmin =0.25, xmax =4.75, ymin =50, ymax =100, alpha =0.2, fill ="darkblue") +annotate("text", x =0.5, y =120, hjust ="left", label ="Target area", size =5) +geom_curve(aes(x =1.25, y =120, xend =1.7, yend =105), colour ="#555555", size =0.5, curvature =-0.2, arrow =arrow(length =unit(0.03, "npc"))) +geom_bar(stat ="identity", position =position_dodge(width =0.9, preserve ="single")) +geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),width =0.2, position =position_dodge(width =0.9, preserve ="single")) +scale_fill_manual(name ="Type", values =c("darkgreen", "darkblue")) +theme(legend.position =c(0.1, 0.8),legend.title =element_blank(), legend.spacing.y =unit(0, "mm"), panel.border =element_rect(colour ="black", fill=NA),axis.text =element_text(colour =1, size =12),legend.background =element_blank(),legend.box.background =element_rect(colour ="black")) +labs(x ="Time of application [time of day]",y =expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +scale_y_continuous(breaks =c(0, 50, 100, 150, 200),limits =c(0, 200)) +geom_text(aes(label = .group, y = emmean + sd +2), position =position_dodge(width =0.9), vjust =-0.25)
Abbildung 40.8— Die Abbildung des Säulendiagramms in ggplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen. Die Kontrolle wurde entfernt, sonst hätten wir hier nicht emmeans in der einfachen Form nutzen können. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen.
R Code [zeigen / verbergen]
ggplot(data = emmeans_hetrogen_tbl, aes(x = time, y = emmean, fill = type)) +theme_minimal() +scale_x_discrete() +annotate("rect", xmin =0.25, xmax =4.75, ymin =50, ymax =100, alpha =0.2, fill ="darkblue") +annotate("text", x =0.5, y =120, hjust ="left", label ="Target area", size =5) +geom_curve(aes(x =1.25, y =120, xend =1.7, yend =105), colour ="#555555", size =0.5, curvature =-0.2, arrow =arrow(length =unit(0.03, "npc"))) +geom_bar(stat ="identity", position =position_dodge(width =0.9, preserve ="single")) +geom_errorbar(aes(ymin = emmean-sd, ymax = emmean+sd),width =0.2, position =position_dodge(width =0.9, preserve ="single")) +scale_fill_manual(name ="Type", values =c("darkgreen", "darkblue")) +theme(legend.position =c(0.1, 0.8),legend.title =element_blank(), legend.spacing.y =unit(0, "mm"), panel.border =element_rect(colour ="black", fill=NA),axis.text =element_text(colour =1, size =12),legend.background =element_blank(),legend.box.background =element_rect(colour ="black")) +labs(x ="Time of application [time of day]",y =expression(Iodine~content~"["*mu*g~I~100*g^'-1'~f*.*m*.*"]")) +scale_y_continuous(breaks =c(0, 50, 100, 150, 200),limits =c(0, 200)) +geom_text(aes(label = .group, y = emmean + sd +2), position =position_dodge(width =0.9), vjust =-0.25)
Abbildung 40.9— Die Abbildung des Säulendiagramms in ggplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen. Die Kontrolle wurde entfernt, sonst hätten wir hier nicht emmeans in der einfachen Form nutzen können. Wir rechnen hier die Vergleiche getrennt für die beiden Jodformen.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
Zerforschen: Zweifaktorieller Boxplot mit emmeans und compact letter display
In diesem Zerforschenbeispiel wollen wir uns einen zweifaktoriellen Boxplot unter der Annahme nicht normalverteilter Daten anschauen. Dabei ist Iodanteil in den Pflanzen nicht normalverteilt, so dass wir hier eine Quantilesregression rechnen wollen. Die Daten siehst du wieder in der unteren Abbildung. Ich nehme für jede der vier Zeitpunkte jeweils fünf Beobachtungen an. Für die Kontrolle haben wir dann nur drei Beobachtungen in der Gruppe \(KIO_3\) vorliegen. Das ist wichtig, denn sonst können wir nicht mit emmeans rechnen. Wir haben einfach zu wenige Beobachtungen vorliegen.
Abbildung 40.10— Ursprüngliche Abbildung, die nachgebaut werden soll. Ein Barplot mit den zwei Faktoren Zeit und die Iodine Form. Hier soll es dann ein Boxplot werden.
Als erstes brauchen wir die Daten. Die Daten habe ich mir in dem Datensatz zerforschen_barplot_2fac_target_emmeans.xlsx selber ausgedacht. Ich nehme hier die gleichen Daten wie für den Barplot. Ich habe einfach die obige Abbildung genommen und den Mittelwert abgeschätzt. Dann habe ich die fünf Werte alle um den Mittelwert streuen lassen. Ich brauche hier eigentlich mehr als fünf Werte, sonst kriegen wir bei emmeans() und der Interaktion im gls()-Modell Probleme, aber da gibt es dann bei kleinen Fallzahlen noch ein Workaround. Bitte nicht mit weniger als fünf Beobachtungen versuchen, dann wird es schwierig mit der Konsistenz der Schätzer aus dem Modell.
Ach, und ganz wichtig. Wir entfernen die Kontrolle, da wir die Kontrolle nur mit einer Iodid-Stufe gemessen haben. Dann können wir weder die Interaktion rechnen, noch anständig eine Interpretation durchführen.
# A tibble: 40 × 3
time type iodine
<fct> <fct> <dbl>
1 07:00 KIO3 50
2 07:00 KIO3 55
3 07:00 KIO3 60
4 07:00 KIO3 52
5 07:00 KIO3 62
6 07:00 KI 97
7 07:00 KI 90
8 07:00 KI 83
9 07:00 KI 81
10 07:00 KI 98
# ℹ 30 more rows
Hier gehen wir nicht weiter auf die Funktionen ein, bitte schaue dann einmal in dem Abschnitt zu Gruppenvergleich mit dem emmeans Paket. Wir entfernen aber noch die Leerzeichen bei den Buchstaben mit der Funktion str_trim(). Wichtig ist hier, dass wir zur Modellierung die Funktion rq() aus dem R Paket quantreg nutzen. Wenn du den Aufbau mit den anderen Zerforschenbeispielen vergleichst, siehst du, dass hier viel ähnlich ist. Achtung, ganz wichtig! Du musst am Ende wieder die Ausgabe aus der cld()-Funktion nach der Zeit time und der Form type sortieren, sonst passt es gleich nicht mit den Beschriftungen der Boxplots.
Du musst dich nur noch entscheiden, ob du das compact letter display getrennt für die beiden Jodformen type berechnen willst oder aber zusammen. Wenn du das compact letter display für die beiden Jodformen zusammen berechnest, dann berechnest du für jede Faktorkombination einen paarweisen Vergleich.
Hier rechnen wir den Vergleich nur innerhalb der jeweiligen Jodform type. Daher vergleichen wir die Boxplots nicht untereinander sondern eben nur in den jeweiligen Leveln \(KIO_3\) und \(KI\).
R Code [zeigen / verbergen]
emmeans_quant_sep_tbl <-rq(iodine ~ time + type + time:type, data = boxplot_tbl, tau =0.5) |>emmeans(~ time | type) |>cld(Letters = letters, adjust ="none") |>as_tibble() |>mutate(.group =str_trim(.group)) |>arrange(time, type)emmeans_quant_sep_tbl
# A tibble: 8 × 8
time type emmean SE df lower.CL upper.CL .group
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
1 07:00 KIO3 55 3.15 32 48.6 61.4 a
2 07:00 KI 90 5.51 32 78.8 101. a
3 11:00 KIO3 75 1.97 32 71.0 79.0 b
4 11:00 KI 150 13.8 32 122. 178. b
5 15:00 KIO3 80 4.72 32 70.4 89.6 b
6 15:00 KI 120 7.87 32 104. 136. b
7 19:00 KIO3 85 7.48 32 69.8 100. b
8 19:00 KI 90 2.36 32 85.2 94.8 a
Dann einmal die Berechnung über alle Boxplots und damit allen Faktorkombinationen aus Zeit und Jodform. Wir können dann damit jeden Boxplot mit jedem anderen Boxplot vergleichen.
R Code [zeigen / verbergen]
emmeans_quant_comb_tbl <-rq(iodine ~ time + type + time:type, data = boxplot_tbl, tau =0.5) |>emmeans(~ time*type) |>cld(Letters = letters, adjust ="none") |>as_tibble() |>mutate(.group =str_trim(.group)) |>arrange(time, type)emmeans_quant_comb_tbl
# A tibble: 8 × 8
time type emmean SE df lower.CL upper.CL .group
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
1 07:00 KIO3 55 3.15 32 48.6 61.4 a
2 07:00 KI 90 5.51 32 78.8 101. c
3 11:00 KIO3 75 1.97 32 71.0 79.0 b
4 11:00 KI 150 13.8 32 122. 178. d
5 15:00 KIO3 80 4.72 32 70.4 89.6 bc
6 15:00 KI 120 7.87 32 104. 136. d
7 19:00 KIO3 85 7.48 32 69.8 100. bc
8 19:00 KI 90 2.36 32 85.2 94.8 c
Für die Boxplots brauchen wir dann noch ein Objekt mehr. Um das nach den Faktorkombinationen sortierte compacte letter dislay an die richtige Position zu setzen brauchen wir noch eine \(y\)-Position. Ich nehme hier dann das 95% Quantile. Das 95% Quantile sollte dann auf jeden Fall über die Schnurrhaare raus reichen. Wir nutzen dann den Datensatz letter_pos_tbl in dem geom_text() um die Buchstaben richtig zu setzen.
# A tibble: 8 × 3
# Groups: time [4]
time type quant_90
<fct> <fct> <dbl>
1 07:00 KIO3 61.6
2 07:00 KI 97.8
3 11:00 KIO3 78.8
4 11:00 KI 174
5 15:00 KIO3 89.4
6 15:00 KI 146
7 19:00 KIO3 106
8 19:00 KI 99.8
Das Problem sind natürlich die wenigen Beobachtungen, deshalb sehen die Boxplots teilweise etwas wild aus. Aber wir wollen hier eben die Mediane darstellen, die wir dann auch in der Quantilesregression berechnet haben. Wenn du mehr Beobachtungen erstellst, dann werden die Boxplots auch besser dargestellt.
Hier nehmen wir das compact letter display aus dem Objekt emmeans_quant_sep_tbl. Wichtig ist, dass die Sortierung gleich der Beschriftung der \(x\)-Achse ist. Deshalb nutzen wir weiter oben auch die Funktion arrange() zur Sortierung der Buchstaben. Beachte, dass wir hier jeweils die beiden Jodformen getrennt voneinander betrachten.
Abbildung 40.11— Die Abbildung des Säulendiagramms in ggplot als Boxplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen, dafür müssen wir uns aber nochmal ein Positionsdatensatz bauen. Hier ist das compact letter display getrennt für die beiden Jodformen berechnet.
Und hier nutzen wir das compact letter display aus dem Objekt emmeans_quant_comb_tbl. Wichtig ist, dass die Sortierung gleich der Beschriftung der \(x\)-Achse ist. Deshalb nutzen wir weiter oben auch die Funktion arrange() zur Sortierung der Buchstaben. Hier betrachten wir jeden Boxplot einzelne und du kannst auch jeden Boxplot mit jedem Boxplot vergleichen.
Abbildung 40.12— Die Abbildung des Säulendiagramms in ggplot als Boxplot nachgebaut. Wir nutzen das geom_text() um noch besser unser compact letter display zu setzen, dafür müssen wir uns aber nochmal ein Positionsdatensatz bauen. Hier ist das compact letter display für jede einzelne Faktorkombination berechnet.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
Zerforschen: Boxplots mit emmeans und compact letter display
Hier wollen wir einmal eine etwas größere Abbildung 40.13 mit einer Menge Boxplots zerforschen. Da ich den Datensatz dann nicht zu groß machen wollte und Boxplots zu zerforschen manchmal nicht so einfach ist, passen die Ausreißer dann manchmal dann doch nicht. Auch liefern die statistischen Tests dann nicht super genau die gleichen Ergebnisse. Aber das macht vermutlich nicht so viel, hier geht es ja dann eher um den Bau der Boxplots und dem rechnen des statistischen Tests in {emmeans}. Die Reihenfolge des compact letter displays habe ich dann auch nicht angepasst sondern die Buchstaben genommen, die ich dann erhalten habe. Die Sortierung kann man ja selber einfach ändern. Wir haben hier ein einfaktorielles Design mit einem Behandlungsfaktor mit drei Leveln vorliegen. Insgesamt schauen wir uns vier Endpunkte in veränderten Substrat- und Wasserbedingungen an.
Abbildung 40.13— Ursprüngliche Abbildung, die nachgebaut werden soll. Insgesamt vier Outcomes sollen für zwei Behandlungen ausgewertet werden. Das praktische ist hier, dass wir es nur mit einem einfaktoriellen Design zu tun haben.
Im Folgenden lade ich einmal den Datensatz, den ich dann per Auge zusammengesetzt habe. Das war jetzt etwas anstrengender als gedacht, da ich nicht weiß wie viele Beobachtungen einen Boxplot bilden. Je mehr Beobachtungen, desto feiner kann man den Boxplot abstimmen. Da ich hier nur mit sieben Beobachtungen ja Gruppe gearbeitet habe, habe ich es nicht geschafft die Ausreißer darzustellen. Das wäre mir dann zu viel Arbeit geworden. Nachdem ich jetzt die Daten geladen habe, muss ich noch über die Funktion pivot_longer() einen Datensatz passenden im Longformat bauen. Abschließend mutiere ich dann noch alle Faktoren richtig und vergebe bessere Namen als labels sonst versteht man ja nicht was die Spalten bedeuten.
Ich habe mir dann die beiden Behandlungen substrate und water in die neue Spalte type geschrieben. Die Spaltennamen der Outcomes wandern in die Spalte plant_measure und die entsprechenden Werte in die Spalte rsp. Dann werde ich hier mal alle Outcomes auf einmal auswerten und nutze dafür das R Paket {purrr} mit der Funktion nest() und map(). Ich packe mir als die Daten nach type und plant_measure einmal zusammen. Dann habe ich einen neuen genesteten Datensatz mit nur noch acht Zeilen. Auf jeder Zeile rechne ich dann jeweils mein Modell. Wie du dann siehst ist in der Spalte data dann jeweils ein Datensatz mit der Spalte trt und rsp für die entsprechenden 21 Beobachtungen.
# A tibble: 8 × 3
# Groups: type, plant_measure [8]
type plant_measure data
<fct> <fct> <list>
1 Substrate Fresh weight (g) <tibble [21 × 2]>
2 Substrate Dry weight (g) <tibble [21 × 2]>
3 Substrate Plant height (cm) <tibble [21 × 2]>
4 Substrate Flower number <tibble [21 × 2]>
5 Water Fresh weight (g) <tibble [21 × 2]>
6 Water Dry weight (g) <tibble [21 × 2]>
7 Water Plant height (cm) <tibble [21 × 2]>
8 Water Flower number <tibble [21 × 2]>
Zur Veranschaulichung rechne ich jetzt einmal mit mutate() und map() für jeden der Datensätze in der Spalte data einmal ein lineares Modell mit der Funktion lm(). Ich muss nur darauf achten, dass ich die Daten mit .x einmal an die richtige Stelle in der Funktion lm() übergebe. Dann habe ich alle Modell komprimiert in der Spalte model. Das geht natürlcih auch alles super in einem Rutsch.
# A tibble: 8 × 4
# Groups: type, plant_measure [8]
type plant_measure data model
<fct> <fct> <list> <list>
1 Substrate Fresh weight (g) <tibble [21 × 2]> <lm>
2 Substrate Dry weight (g) <tibble [21 × 2]> <lm>
3 Substrate Plant height (cm) <tibble [21 × 2]> <lm>
4 Substrate Flower number <tibble [21 × 2]> <lm>
5 Water Fresh weight (g) <tibble [21 × 2]> <lm>
6 Water Dry weight (g) <tibble [21 × 2]> <lm>
7 Water Plant height (cm) <tibble [21 × 2]> <lm>
8 Water Flower number <tibble [21 × 2]> <lm>
Jetzt können wir einmal eskalieren und insgesamt acht mal die ANOVA rechnen. Das sieht jetzt nach viel Code aus, aber am Ende ist es nur eine lange Pipe. Am Ende erhalten wir dann den \(p\)-Wert für die einfaktorielle ANOVA für die Behandlung trt wiedergegeben. Wir sehen, dass wir eigentlich nur einen signifikanten Unterschied in der Wassergruppe und der Pflanzenhöhe erwarten sollten. Da der \(p\)-Wert für die Wassergruppe und der Blütenanzahl auch sehr nah an dem Signifikanzniveau ist, könnte hier auch etwas sein, wenn wir die Gruppen nochmal getrennt testen.
# A tibble: 8 × 4
# Groups: type, plant_measure [8]
type plant_measure parameter p
<fct> <fct> <chr> <dbl>
1 Substrate Fresh weight (g) trt 0.813
2 Substrate Dry weight (g) trt 0.381
3 Substrate Plant height (cm) trt 0.959
4 Substrate Flower number trt 0.444
5 Water Fresh weight (g) trt 0.384
6 Water Dry weight (g) trt 0.843
7 Water Plant height (cm) trt 0.000138
8 Water Flower number trt 0.0600
Dann schauen wir uns nochmal das \(\eta^2\) an um zu sehen, wie viel Varianz unsere Behandlung in den Daten erklärt. Leider sieht es in unseren Daten sehr schlecht aus. Nur bei der Wassergruppe und der Pflanzenhöhe scheinen wir durch die Behandlung Varianz zu erklären.
# A tibble: 8 × 3
# Groups: type, plant_measure [8]
type plant_measure eta2
<fct> <fct> <dbl>
1 Substrate Fresh weight (g) 0.0228
2 Substrate Dry weight (g) 0.102
3 Substrate Plant height (cm) 0.00466
4 Substrate Flower number 0.0863
5 Water Fresh weight (g) 0.101
6 Water Dry weight (g) 0.0188
7 Water Plant height (cm) 0.628
8 Water Flower number 0.268
Dann können wir auch schon den Gruppenvergleich mit dem R Paket {emmeans} rechnen. Wir nutzen hier die Option vcov. = sandwich::vcovHAC um heterogene Varianzen zuzulassen. Im Weiteren adjustieren wir nicht für die Anzahl der Vergleiche und lassen uns am Ende das compact letter display wiedergeben.
# A tibble: 24 × 5
# Groups: type, plant_measure [8]
type plant_measure trt rsp group
<fct> <fct> <fct> <dbl> <chr>
1 Substrate Fresh weight (g) UWF 95.4 a
2 Substrate Fresh weight (g) TWF 101 a
3 Substrate Fresh weight (g) Peat 105 a
4 Substrate Dry weight (g) UWF 12.3 a
5 Substrate Dry weight (g) Peat 14.3 ab
6 Substrate Dry weight (g) TWF 15.1 b
7 Substrate Plant height (cm) TWF 37.9 a
8 Substrate Plant height (cm) Peat 38.0 a
9 Substrate Plant height (cm) UWF 39.1 a
10 Substrate Flower number UWF 14.6 a
# ℹ 14 more rows
Da die Ausgabe viel zu lang ist, wollen wir ja jetzt einmal unsere Abbildungen in {ggplot} nachbauen. Dazu nutze ich dann einmal zwei Wege. Einmal den etwas schnelleren mit facet_wrap() bei dem wir eigentlich alles automatisch machen lassen. Zum anderen zeige ich dir mit etwas Mehraufwand alle acht Abbildungen einzeln baust und dann über das R Paket {patchwork} wieder zusammenklebst. Der zweite Weg ist der Weg, wenn du mehr Kontrolle über die einzelnen Abbildungen haben willst.
Die Funktion facet_wrap() erlaubt es dir automatisch Subplots nach einem oder mehreren Faktoren zu erstellen. Dabei muss auch ich immer wieder probieren, wie ich die Faktoren anordne. In unserem Fall wollen wir zwei Zeilen und auch den Subplots erlauben eigene \(x\)-Achsen und \(y\)-Achsen zu haben. Wenn du die Option scale = "free" nicht wählst, dann haben alle Plots alle Einteilungen der \(x\)_Achse und die \(y\)-Achse läuft von dem kleinsten zu größten Wert in den gesamten Daten.
Abbildung 40.14— Nachbau der Abbildung mit der Funktion facte_wrap() mit Boxplots und dem Mittelwert. Neben dem Mittelwert finden sich das compact letter display. Auf eine Einfärbung nach der Behandlung wurde verzichtet um die Abbildung nicht noch mehr zu überladen.
Jetzt wird es etwas wilder. Wir bauen uns jetzt alle acht Plots einzeln und kleben diese dann mit dem R Paket {patchwork} zusammen. Das hat ein paar Vorteile. Wir können jetzt jeden einzelnen Plot bearbeiten und anpassen wie wir es wollen. Damit wir aber nicht zu viel Redundanz haben bauen wir uns erstmal ein Template für ggplot(). Dann können wir immer noch die Werte für scale_y_continuous() in den einzelnen Plots ändern. Hier also einmal das Template, was beinhaltet was für alle Abbildungen gelten soll.
Ja, jetzt geht es los. Wir bauen also jeden Plot einmal nach. Dafür müssen wir dann jeweils den Datensatz filtern, den wir auch brauchen. Dann ergänzen wir noch die korrekte \(y\)-Achsenbeschriftung. So können wir dann auch händisch das compact letter display über die Whisker einfach setzen. Im Weiteren habe ich dann auch einmal als Beispiel noch die \(y\)-Achseneinteilung mit scale_y_continuous() geändert. Ich habe das einmal für den Plot p1 gemacht, der Rest würde analog dazu funktionieren.
Dann kleben wir die Abbildungen einfach mit einem + zusammen und dann wählen wir noch aus, dass wir vier Spalten wollen. Dann können wir noch Buchstaben zu den Subplots hinzufügen und noch Titel und anderes wenn wir wollen würden. Dann haben wir auch den Plot schon nachgebaut. Ich verzichte hier händisch überall das compact letter display zu ergänzen. Das macht super viel Arbeit und endlos viel Code und hilft dir dann aber in deiner Abbildung auch nicht weiter. Du musst dann ja bei dir selber die Positionen für die Buchstaben finden.
R Code [zeigen / verbergen]
patch <- p1 + p2 + p3 + p4 + p5 + p6 + p7 + p8 +plot_layout(ncol =4)patch +plot_annotation(tag_levels ='A',title ='Ein Zerforschenbeispiel an Boxplots',subtitle ='Alle Plots wurden abgelesen und daher sagen Signifikanzen nichts.',caption ='Disclaimer: Die Abbildungen sagen nichts aus.')
Abbildung 40.15— Nachbau der Abbildung mit dem R Paket {patchwork} mit Boxplots und dem Mittelwert. Neben dem Mittelwert finden sich das compact letter display bei dem ersten Plot. Auf eine Einfärbung nach der Behanldung wurde verzichtet um die Abbildung nicht noch mehr zu überladen.
Am Ende kannst du dann folgenden Code noch hinter deinen ggplot Code ausführen um dann deine Abbildung als *.png-Datei zu speichern. Dann hast du die Abbildung super nachgebaut und sie sieht auch wirklich besser aus.
An der Seite des Kapitels findest du den Link Quellcode anzeigen, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.
40.2 Daten
Wir nutzen in diesem Kapitel den Datensatz aus dem Beispiel in Kapitel 5.3. Wir haben als Outcome die Sprunglänge in [cm] von Flöhen. Die Sprunglänge haben wir an Flöhen von Hunde, Katzen und Füchsen gemessen. Der Datensatz ist also recht übeerschaubar. Wir haben ein normalverteiltes \(y\) mit jump_length sowie einen multinomialverteiltes \(y\) mit grade und einen Faktor animal mit drei Leveln. Im Folgenden laden wir den Datensatz flea_dog_cat_fox.csv und selektieren mit der Funktion select() die benötigten Spalten. Abschließend müssen wir die Spalte animalnoch in einen Faktor umwandeln. Damit ist unsere Vorbereitung des Datensatzes abgeschlossen.
In der Tabelle 40.1 ist der Datensatz fac1_tbl nochmal dargestellt. Wir werden nun den Datensatz fac1_tbl in den folgenden Abschnitten immer wieder nutzen.
Für die vollständige Datentabelle bitte aufklappen
Tabelle 40.1— Selektierter Datensatz mit einer normalverteilten Variable jump_length sowie der multinominalverteilten Variable grade und einem Faktor animal mit drei Leveln.
animal
jump_length
grade
dog
5.7
8
dog
8.9
8
dog
11.8
6
dog
5.6
8
dog
9.1
7
dog
8.2
7
dog
7.6
9
cat
3.2
7
cat
2.2
5
cat
5.4
7
cat
4.1
6
cat
4.3
6
cat
7.9
6
cat
6.1
5
fox
7.7
5
fox
8.1
4
fox
9.1
4
fox
9.7
5
fox
10.6
4
fox
8.6
4
fox
10.3
3
40.3 Hypothesen für multiple Vergleiche
Als wir eine ANOVA gerechnet hatten, hatten wir nur eine Nullhypothese und eine Alternativehypothese. Wenn wir Nullhypothese abgelehnt hatten, wussten wir nur, dass sich mindestens ein paarweiser Vergleich unterschiedet. Multiple Vergleich lösen nun dieses Problem und führen ein Hypothesenpaar für jeden paarweisen Vergleich ein. Zum einen rechnen wir damit \(k\) Tests und haben damit auch \(k\) Hypothesenpaare (siehe auch Kapitel 21.3 zur Problematik des wiederholten Testens). Wenn wir zum Beispiel alle Level des Faktors animal miteinander Vergleichen wollen, dann rechnen wir \(k=3\) paarweise Vergleiche. Im Folgenden sind alle drei Hypothesenpaare dargestellt.
Wenn wir drei Vergleiche rechnen, dann haben wir eine \(\alpha\) Inflation vorliegen. Wir sagen, dass wir für das multiple Testen adjustieren müssen. In R gibt es eine Reihe von Adjustierungsverfahren. Wir nehmen meist Bonferroni oder das Verfahren, was in der jeweiligen Funktion als Standard (eng. default) gesetzt ist. Wir adjustieren grundsätzlich die \(p\)-Werte und erhalten adjustierte \(p\)-Werte aus den jeweiligen Funktionen in R. Die adjustierten p-Werte können wir dann mit dem Signifikanzniveau von \(\alpha\) gleich 5% vergleichen.
40.4 Simple Gruppenvergleiche
Wenn wir nur einen Faktor mit mehr als zwei Leveln vorliegen haben, dann können wir die Funktion pairwise.*.test() nutzen. Der Stern * steht entweder als Platzhalter für t für den t-Test oder aber für wilcox für den Wilcoxon Test. Die Funktion ist relativ einfach zu nutzen und liefert auch sofort die entsprechenden p-Werte. Die Funktion pairwise.*.test() ist in dem Sinne veraltet, da wir keine 95% Konfidenzintervalle generieren können. Da die Funktion aber immer mal wieder angefragt wird, ist die Funktion hier nochmal aufgeführt. Die Funktion pairwise.*.test() ist veraltet, wir nutzen das R Paket {emmeans} oder das R Paket {multcomp}.
40.4.1 Paarweiser t Test
Wir nutzen den paarweisen t-Test,
wenn wir ein normalverteiltes \(y\) vorliegen haben, wie jump_length.
wenn wir nur einen Faktor mit mehr als zwei Leveln vorliegen haben, wie animal.
wenn wir Varianzhomogenität über alle Level vorliegen haben, dann nutzen wir die Option pool.sd = TRUE. Wenn wir Varianzheterogenität über alle Level des Faktors vorliegen haben, dann nutzen wir pool.sd = FALSE.
Die Funktion pairwise.t.test kann nicht mit Datensätzen arbeiten sondern nur mit Vektoren. Daher können wir der Funktion auch keine formula übergeben sondern müssen die Vektoren aus dem Datensatz mit fac1_tbl$jump_length für das Outcome und mit fac1_tbl$animal für die Gruppierende Variable benennen. Das ist umständlich und daher auch fehleranfällig. Wir können auch den %$%-Operator aus dem R Paket {magrittr} nutzen um die Problematik zu umgehen. Weiter unten siehst du dann einmal beide Anwendungen.
Als Adjustierungsmethode für den \(\alpha\) Fehler wählen wir die Bonferroni-Methode mit p.adjust.method = "bonferroni" aus. Da wir eine etwas unübersichtliche Ausgabe in R erhalten nutzen wir die Funktion tidy()um die Ausgabe in ein sauberes tibble zu verwandeln. Abschließend runden wir noch alle numerischen Spalten mit der Funktion round auf drei Stellen hinter dem Komma.
# A tibble: 3 × 3
group1 group2 p.value
<chr> <chr> <dbl>
1 cat dog 0.007
2 fox dog 0.876
3 fox cat 0.001
Und das ganze nochmal mit dem %$%-Operator aus dem R Paket {magrittr}. In diesem Fall können wir uns das $ sparen und greifen direkt auf die Spalten des Datensatzes zu.
# A tibble: 3 × 3
group1 group2 p.value
<chr> <chr> <dbl>
1 cat dog 0.007
2 fox dog 0.876
3 fox cat 0.001
Wir erhalten in einem Tibble die adjustierten p-Werte nach Bonferroni. Wir können daher die adjustierten p-Werte ganz normal mit dem Signifikanzniveau \(\alpha\) von 5% vergleichen. Wenn du keine adjustierten p-Werte möchtest, dann nutze die Option p.adjust.method = "none". Wir sehen, dass der Gruppenvergleich cat - dog signifikant ist, der Gruppenvergleich fox - dog nicht signifikant ist und der Gruppenvergleich fox - cat wiederum signifikant ist. Leider können wir uns keine Konfidenzintervalle wiedergeben lassen, so dass die Funktion nicht dem Stand der Wissenschaft und deren Ansprüchen genügt.
Im Folgenden wollen wir uns nochmal die Visualisierung mit dem R Paket {ggpubr} anschauen. Die Hilfeseite des R Pakets {ggpubr} liefert noch eine Menge weitere Beispiele für den simplen Fall eines Modells \(y ~ x\), also von einem \(y\) und einem Faktor \(x\). Um die Abbildung 40.16 zu erstellen müssen wir als erstes die Funktion compare_mean() nutzen um mit der formula Syntax einen t-Test zu rechnen. wir adjustieren die p-Werte nach Bonferroni. Anschließend erstellen wir einen Boxplot mit der Funktion ggboxplot() und speichern die Ausgabe in dem Objekt p. Wie in ggplot üblich können wir jetzt auf das Layer p über das +-Zeichen noch weitere Layer ergänzen. Wir nutzen die Funktion stat_pvalue_manual() um die asjustierten p-Werte aus dem Objekt stat_test_obj zu ergänzen. Abschließend wollen wir noch den p-Wert einer einfaktoriellen ANOVA als globalen Test ergänzen.
Abbildung 40.16— Boxplot der Sprungweiten [cm] von Hunden und Katzen ergänzt um den paarweisen Vergleich mit dem t-Test und den Bonferroni adjustierten p-Werten.
40.4.2 Paarweiser Wilcoxon Test
Wir nutzen den paarweisen Wilxocon Test,
wenn wir ein nicht-normalverteiltes \(y\) vorliegen haben, wie grade.
wenn wir nur einen Faktor mit mehr als zwei Leveln vorliegen haben, wie animal.
Die Funktion pairwise.wilcox.test kann nicht mit Datensätzen arbeiten sondern nur mit Vektoren. Daher können wir der Funktion auch keine formula übergeben sondern müssen die Vektoren aus dem Datensatz mit fac1_tbl$jump_length für das Outcome und mit fac1_tbl$animal für die Gruppierende Variable benennen. Das ist umständlich und daher auch fehleranfällig.
Als Adjustierungsmethode für den \(\alpha\) Fehler wählen wir die Bonferroni-Methode mit p.adjust.method = "bonferroni" aus. Da wir eine etwas unübersichtliche Ausgabe in R erhalten nutzen wir die Funktion tidy()um die Ausgabe in ein sauberes tibble zu verwandeln. Abschließend runden wir noch alle numerischen Spalten mit der Funktion round auf drei Stellen hinter dem Komma.
# A tibble: 3 × 3
group1 group2 p.value
<chr> <chr> <dbl>
1 cat dog 0.045
2 fox dog 0.005
3 fox cat 0.011
Wir erhalten in einem Tibble die adujstierten p-Werte nach Bonferroni. Wir können daher die adjustierten p-Werte ganz normal mit dem Signifikanzniveau \(\alpha\) von 5% vergleichen. Wir sehen, dass der Gruppenvergleich cat - dog knapp signifikant ist, der Gruppenvergleich fox - dog ebenfalls signifikant ist und der Gruppenvergleich fox - cat auch signifikant ist. Leider können wir uns keine Konfidenzintervalle wiedergeben lassen, so dass die Funktion nicht dem Stand der Wissenschaft und deren Ansprüchen genügt.
Im Folgenden wollen wir uns nochmal die Visualisierung mit dem R Paket {ggpubr} anschauen. Die Hilfeseite des R Pakets {ggpubr} liefert noch eine Menge weitere Beispiele für den simplen Fall eines Modells \(y ~ x\), also von einem \(y\) und einem Faktor \(x\). Um die Abbildung 40.17 zu erstellen müssen wir als erstes die Funktion compare_mean() nutzen um mit der formula Syntax einen Wilcoxon Test zu rechnen. wir adjustieren die p-Werte nach Bonferroni. Anschließend erstellen wir einen Boxplot mit der Funktion ggboxplot() und speichern die Ausgabe in dem Objekt p. Wie in ggplot üblich können wir jetzt auf das Layer p über das +-Zeichen noch weitere Layer ergänzen. Wir nutzen die Funktion stat_pvalue_manual() um die asjustierten p-Werte aus dem Objekt stat_test_obj zu ergänzen. Abschließend wollen wir noch den p-Wert eines Kruskal Wallis als globalen Test ergänzen.
Abbildung 40.17— Boxplot der Sprungweiten [cm] von Hunden und Katzen ergänzt um den paarweisen Vergleich mit dem Wilcoxon Test und den Bonferroni adjustierten p-Werten.
40.5 Gruppenvergleich mit {emmeans}
Im Folgenden wollen wir uns mit einem anderen R Paket beschäftigen was auch multiple Vergleiche rechnen kann. In diesem Kapitel nutzen wir das R Paket {emmeans}. Im Prinzip kann {emmeans} das Gleiche wir das R Paket {multcomp}. Beide Pakete rechnen dir einen multiplen Vergleich. Das Paket {emmeans} kann noch mit nested comparisons umgehen. Deshalb hier nochmal die Vorstellung von {emmeans}. Du kannst aber für eine simple Auswertung mit nur einem Faktor beide Pakete verwenden.
Um den multiplen Vergleich in emmeans durchführen zu können brauchen wir zuerst ein lineares Modell, was uns die notwenidgen Parameter wie Mittelwerte und Standardabweichungen liefert. Wir nutzen in unserem simplen Beispiel ein lineares Modell mit einer Einflussvariable \(x\) und nehmen an, dass unser Outcome \(y\) normalverteilt ist. Achtung, hier muss natürlich das \(x\) ein Faktor sein. Dann können wir ganz einfach die Funktion lm() nutzen. Im Folgenden fitten wir das Modell fit_2 was wir dann auch weiter nutzen werden.
R Code [zeigen / verbergen]
fit_2 <-lm(jump_length ~ animal, data = fac1_tbl)
Der multiple Vergleich in emmeans ist mehrschrittig. Wir pipen unser Modell aus fit_2 in die Funktion emmeans(). Wir geben mit ~ animal an, dass wir über die Level des Faktors animal einen Vergleich rechnen wollen. Wir adjustieren die \(p\)-Werte nach Bonferroni. Danach pipen wir weiter in die Funktion contrast() wo der eigentliche Vergleich festgelegt wird. In unserem Fall wollen wir einen many-to-one Vergleich rechnen. Alle Gruppen zu der Gruppe fox. Du kannst mit ref = auch ein anderes Level deines Faktors wählen.
contrast estimate SE df t.ratio p.value
dog - fox -1.03 0.947 18 -1.086 0.5837
cat - fox -4.41 0.947 18 -4.660 0.0004
P value adjustment: bonferroni method for 2 tests
Wir können auch einen anderen Kontrast wählen. Wir überschreiben jetzt das Objekt comp_2_obj mit dem Kontrast all-pair, der alle möglichen Vergleiche rechnet. In emmeans heißt der all-pair Kontrast pairwise. Die Ausgabe von emmeans können über die Funktion tidy() aufgeräumt werden. Mehr dazu unter der Hilfeseite von tidy() zu emmeans.
contrast estimate SE df t.ratio p.value
dog - cat 3.39 0.947 18 3.574 0.0065
dog - fox -1.03 0.947 18 -1.086 0.8756
cat - fox -4.41 0.947 18 -4.660 0.0006
P value adjustment: bonferroni method for 3 tests
Wir können das Ergebnis auch noch mit der Funktion tidy() weiter aufräumen und dann die Spalten selektieren, die wir brauchen. Häufig benötigen wir nicht alle Spalten, die eine Funktion wiedergibt.
# A tibble: 3 × 5
contrast estimate adj.p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl>
1 dog - cat 3.39 0.0065 0.886 5.89
2 dog - fox -1.03 0.876 -3.53 1.47
3 cat - fox -4.41 0.0006 -6.91 -1.91
Abschließend wollen wir noch die 95% Konfidenzintervalle in Abbildung 40.18 abbilden. Hier ist es bei emmeans genauso wie bei multcomp. Wir können das Objekt res_2_obj direkt in ggplot() weiterverwenden und uns die 95% Konfidenzintervalle einmal plotten.
Abbildung 40.18— Die 95% Konfidenzintervalle für den allpair-Vergleich des simplen Datensatzes.
In Abbildung 40.19 sehen wir die Ergebnisse des multiplen Vergleiches nochmal anders als Pairwise P-value plot dargestellt. Wir haben auf der y-Achse zu Abwechselung mal die Gruppen dargestellt und auf der x-Achse die \(p\)-Werte. In den Kästchen sind die Effekte der Gruppen nochmal gezeigt. In unserem Fall die Mittelwerte der Sprungweiten für die drei Gruppen. Wir sehen jetzt immer den \(p\)-Wert für den jeweiligen Vergleich durch eine farbige Linie miteinander verbunden. So können wir nochmal eine andere Übersicht über das Ergebnis des multiplen Vergleich kriegen.
Abbildung 40.19— Visualisierung der Ergebnisse im Pairwise P-value plot.
Auch haben wir die Möglichkeit un die \(p\)-Werte mit der Funktion pwpm() als eine Matrix ausgeben zu lassen. Wir erhalten in dem oberen Triangel die \(p\)-Wert für den jeweiligen Vergleich. In dem unteren Triangel die geschätzten Mittelwertsunterschiede. Auf der Diagonalen dann die geschätzten Mittelwerte für die jeweilige Gruppe. So haben wir nochmal alles sehr kompakt zusammen dargestellt.
dog cat fox
dog [8.13] 0.0065 0.8756
cat 3.39 [4.74] 0.0006
fox -1.03 -4.41 [9.16]
Row and column labels: animal
Upper triangle: P values adjust = "bonferroni"
Diagonal: [Estimates] (emmean)
Lower triangle: Comparisons (estimate) earlier vs. later
Wir wollen uns noch einen etwas komplizierteren Fall anschauen, indem sich emmeans von multcomp in der Anwendung unterscheidet. Wir laden den Datensatz flea_dog_cat_fox_site.csv in dem wir zwei Faktoren haben. Damit können wir dann ein Modell mit einem Interaktionsterm bauen. Wir erinnern uns, dass wir in der zweifaktoriellen ANOAV eine signifikante Interaktion zwischen den beiden Faktoren animal und site festgestelt hatten.
Wir erhalten das Objekt fac2_tbl mit dem Datensatz in Tabelle 40.2 nochmal dargestellt.
Tabelle 40.2— Selektierter Datensatz mit einer normalverteilten Variable jump_length und einem Faktor animal mit drei Leveln sowie dem Faktor site mit vier Leveln.
animal
site
jump_length
cat
city
12.04
cat
city
11.98
cat
city
16.1
cat
city
13.42
cat
city
12.37
cat
city
16.36
…
…
…
fox
field
16.38
fox
field
14.59
fox
field
14.03
fox
field
13.63
fox
field
14.09
fox
field
15.52
In Abbildung 40.20 sehen wir nochmal die Daten visualisiert. Wichtig ist hier, dass wir zwei Faktoren vorliegen haben. Den Faktor animal und den Faktor site. Dabei ist der Faktor animal in dem Faktor site genested. Wir messen jedes Level des Faktors animal jeweils in jedem Level des Faktors site.
Abbildung 40.20— Boxplot der Sprungweiten [cm] von Hunden und Katzen gemessen an verschiedenen Orten.
Wir rechnen ein multiples lineares Modell mit einem Interaktionsterm. Daher packen wir beide Faktoren in das Modell sowie die Intraktion zwischen den beiden Faktoren. Wir erhalten nach dem fitten des Modells das Objekt fit_3.
R Code [zeigen / verbergen]
fit_3 <-lm(jump_length ~ animal + site + animal:site, data = fac2_tbl)
Der Unterschied zu unserem vorherigen multiplen Vergleich ist nun, dass wir auch einen multiplen Vergleich für animal nested in site rechnen können. Dafür müssen wir den Vergleich in der Form animal | site schreiben. Wir erhalten dann die Vergleiche der Level des faktors animalgetrennt für die Level es Faktors site.
site = city:
contrast estimate SE df t.ratio p.value
cat - dog -3.101 0.771 108 -4.022 0.0003
cat - fox -6.538 0.771 108 -8.479 <.0001
dog - fox -3.437 0.771 108 -4.457 0.0001
site = smalltown:
contrast estimate SE df t.ratio p.value
cat - dog -4.308 0.771 108 -5.587 <.0001
cat - fox -4.064 0.771 108 -5.271 <.0001
dog - fox 0.244 0.771 108 0.316 1.0000
site = village:
contrast estimate SE df t.ratio p.value
cat - dog -1.316 0.771 108 -1.707 0.2722
cat - fox -1.729 0.771 108 -2.242 0.0809
dog - fox -0.413 0.771 108 -0.536 1.0000
site = field:
contrast estimate SE df t.ratio p.value
cat - dog -0.982 0.771 108 -1.274 0.6167
cat - fox 1.366 0.771 108 1.772 0.2379
dog - fox 2.348 0.771 108 3.045 0.0088
P value adjustment: bonferroni method for 3 tests
Wir können uns das Ergebnis auch etwas schöner ausgeben lassen. Wir nutzen hier noch die Funktion format.pval() um die \(p\)-Werte besser zu formatieren. Die \(p\)-Wert, die kleiner sind als 0.001 werden als <0.001 ausgegeben und die anderen \(p\)-Werte auf zwei Nachstellen nach dem Komma gerundet.
# A tibble: 12 × 3
contrast site p.value
<fct> <fct> <chr>
1 cat - dog city <0.001
2 cat - fox city <0.001
3 dog - fox city <0.001
4 cat - dog smalltown <0.001
5 cat - fox smalltown <0.001
6 dog - fox smalltown 1.00
7 cat - dog village 0.27
8 cat - fox village 0.08
9 dog - fox village 1.00
10 cat - dog field 0.62
11 cat - fox field 0.24
12 dog - fox field 0.01
In der Ausgabe können wir erkennen, dass die Vergleich in der Stadt alle signifkant sind. Jedoch erkennen wir keine signifikanten Ergebnisse mehr in dem Dorf und im Feld ist nur der Vergleich dog - fox signifkant. Hier solltest du nochmal beachten, warum wir die Analyse getrennt machen. In der zweifaktoriellen ANOVA haben wir gesehen, dass ein signifkanter Interaktionsterm zwischen den beiden Faktoren animal und site vorliegt. Wir wollen uns noch über die Funktion confint() die 95% Konfidenzintervalle wiedergeben lassen.
# A tibble: 12 × 5
contrast site estimate conf.low conf.high
<fct> <fct> <dbl> <dbl> <dbl>
1 cat - dog city -3.10 -4.98 -1.23
2 cat - fox city -6.54 -8.41 -4.66
3 dog - fox city -3.44 -5.31 -1.56
4 cat - dog smalltown -4.31 -6.18 -2.43
5 cat - fox smalltown -4.06 -5.94 -2.19
6 dog - fox smalltown 0.244 -1.63 2.12
7 cat - dog village -1.32 -3.19 0.559
8 cat - fox village -1.73 -3.60 0.146
9 dog - fox village -0.413 -2.29 1.46
10 cat - dog field -0.982 -2.86 0.893
11 cat - fox field 1.37 -0.509 3.24
12 dog - fox field 2.35 0.473 4.22
Besonders mit den 95% Konfiendezintervallen sehen wir nochmal den Interaktionseffekt zwischen den beiden Faktoren animal und site. So dreht sich der Effekt von zum Beispiel dog - fox von \(-3.44\) in dem Level city zu \(+2.35\) in dem Level field. Wir haben eine Interaktion vorliegen und deshalb die Analyse getrennt für jeden Level des Faktors site durchgeführt. Abbildung 40.21 zeigt die entsprechenden 95% Konfidenzintervalle. Wir müssen hier etwas mit der position spielen, so dass die Punkte und der geom_errorbar richtig liegen.
Abbildung 40.21— Die 95% Konfidenzintervalle für den allpair-Vergleich des Models mit Interaktionseffekt.
40.6 Gruppenvergleich mit {multcomp}
Wir drehen hier einmal die Erklärung um. Wir machen erst die Anwendung in R und sollte dich dann noch mehr über die statistischen Hintergründe der Funktionen interessieren, folgt ein Abschnitt noch zur Theorie. Du wirst die Funktionen aus multcomp vermutlich in deiner Abschlussarbeit brauchen. Häufig werden multiple Gruppenvergleiche in Abschlussarbeiten gerechnet.
40.6.1 Gruppenvergleiche mit multcomp in R
Als erstes brauchen wir ein lineares Modell für die Verwendung von multcomp. Normalerweise verenden wir das gleiche Modell, was wir schon in der ANOVA verwendet haben. Wir nutzen hier ein simples lineares Modell mit nur einem Faktor. Im Prinzip kann das Modell auch größer sein, davon schauen wir uns dann später im Verlauf des Kapitels noch welche an.
R Code [zeigen / verbergen]
fit_1 <-lm(jump_length ~ animal, data = fac1_tbl)
Wir haben das Objekt fit_1 mit der Funktion lm() erstellt. Im Modell sind jetzt alle Mittelwerte und die entsprechenden Varianzen geschätzt worden. Mit summary(fit_1) kannst du dir gerne das Modell auch nochmal anschauen. Wenn wir keinen all-pair Vergleich rechnen wollen, dann können wir auch einen many-to-one Vergleich mit dem Dunnett Kontrast rechnen.
Im Anschluss nutzen wir die Funktion glht() um den multiplen Vergleich zu rechnen. Als erstes musst du wissen, dass wenn wir alle Vergleiche rechnen wollen, wir einen all-pair Vergleich rechnen. In der Statistik heißt dieser Typ von Vergleich Tukey. Wir wollen jetzt als für den Faktor animal einen multiplen Tukey-Vergleich rechnen. Nichts anders sagt mcp(animal = "Tukey") aus, dabei steht mcp für multiple comparison procedure. Mit dem hinteren Teil der Funktion weiß jetzt die Funktion glht() was gerechnet werden soll. Wir müssen jetzt der Funktion nur noch mitgeben auf was der multiple Vergleich gerechnet werden soll, mit dem Objekt fit_1. Wir speichern die Ausgabe der Funktion in comp_1_obj.
Mit dem Objekt comp_1_fit können wir noch nicht soviel anfangen. Der Inhalt ist etwas durcheinander und wir wollen noch die Konfidenzintervalle haben. Daher pipen wir comp_1_fit erstmal in die Funktion tidy() und lassen mit der Option conf.int = TRUE die simultanen 95% Konfidenzintervalle berechnen. Dann nutzen wir die Funktion select() um die wichtigen Spalten zu selektieren. Abschließend mutieren wir noch alle numerischen Spalten in dem wir auf die dritte Kommastelle runden. Wir speichern alles in das Objekt res_1_obj.
Wir lassen uns dann den Inhalt von dem Objekt res_1_obj ausgeben.
R Code [zeigen / verbergen]
res_1_obj
# A tibble: 3 × 5
contrast estimate adj.p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl>
1 cat - dog -3.39 0.006 -5.80 -0.967
2 fox - dog 1.03 0.535 -1.39 3.45
3 fox - cat 4.41 0.001 2.00 6.83
Wir erhalten ein tibble() mit fünf Spalten. Zum einen den contrast, der den Vergleich widerspiegelt. Wir vergleichen im ersten Kontrast die Katzen- mit den Hundeflöhen, wobei wir cat - dog rechnen. Also wirklich der Mittelwert der Sprungweite der Katzenflöhe minus den Mittelwert der Sprungweite der Hundeflöhe rechnen. In der Spalte estimate sehen wir den Mittelwertsunterschied. Der Mittelwertsunterschied ist in der Richtung nicht ohne den Kontrast zu interpretieren. Danach erhalten wir die adjustierten \(p\)-Wert sowie die simultanen 95% Konfidenzintervalle.
Wir können die Nullhypothese ablehnen für den Vergleichecat - dog mit einem p-Wert von \(0.006\) sowie für den Vergleich \(fox - cat\) mit einem p-Wert von \(0.001\). Beide p-Werte liegen unter dem Signifikanzniveau von \(\alpha\) gleich 5%.
Wenn es die unadjustierten \(p\)-Werte sein sollen, dann müssen wir nochmal das glht-Objekt in die Funktion summary() stecken und dann die Option test = adjusted("none") wählen. Dann können wir weiter machen wie gewohnt.
R Code [zeigen / verbergen]
summary(comp_1_obj, test =adjusted("none")) |>tidy()
# A tibble: 3 × 7
term contrast null.value estimate std.error statistic p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 animal cat - dog 0 -3.39 0.947 -3.57 0.00217
2 animal fox - dog 0 1.03 0.947 1.09 0.292
3 animal fox - cat 0 4.41 0.947 4.66 0.000195
In Abbildung 40.22 sind die simultanen und damit adjustierten 95% Konfidenzintervalle nochmal in einem ggplot visualisiert. Die Kontraste und die Position hängen von dem Faktorlevel ab. Mit der Funktion factor() kannst du die Sortierung der Level einem Faktor ändern und somit auch Position auf den Achsen.
Abbildung 40.22— Simultane 95% Konfidenzintervalle für den paarweisen Vergleich der Sprungweiten in [cm] der Hunde-, Katzen- und Fuchsflöhe.
Die Entscheidung gegen die Nullhypothese anhand der simultanen 95% Konfidenzintervalle ist inhaltlich gleich, wie die Entscheidung anhand der p-Werte. Wir entscheiden gegen die Nullhypothese, wenn die 0 nicht mit im Konfindenzintervall enthalten ist. Wir wählen hier die 0 zur Entscheidung gegen die Nullhypothese, weil wir einen Mittelwertsvergleich rechnen.
Für den Vergleich fox -dog ist die 0 im 95% Konfidenzintervall, wir können daher die Nullhypothese nicht ablehnen. Das 95% Konfidenzintervall ist nicht signifikant. Bei dem Vergleich fox - cat sowie dem Vergleich cat - dog ist jeweils die 0 nicht im 95% Konfidenzintervall enthalten. Beide 95% Konfidenzintervalle sind signifikant, wir können die Nullhypothese ablehnen.
40.7 Gruppenvergleich mit Varianzheterogenität
Bis jetzt sind wir von Varianzhomogenität über alle Gruppen in unserer Behandlung ausgegangen. Oder aber konkret auf unser Beispiel, die Tierarten haben alle die gleiche Varianz. Jetzt gibt es aber häufiger mal den Fall, da können oder wollen wir nicht an Varianzhomogenität über alle Gruppen glauben. Deshalb gibt es hier noch Alternativen, von denen ich ein paar Vorstellen werde.
40.7.1 Games-Howell-Test
Der Games-Howell-Test ist eine Alternative zu dem Paket {multcomp} und dem Paket {emmeans} für ein einfaktorielles Design. Wir nutzen den Games-Howell-Test, wenn die Annahme der Homogenität der Varianzen, der zum Vergleich aller möglichen Kombinationen von Gruppenunterschieden verwendet wird, verletzt ist. Dieser Post-Hoc-Test liefert Konfidenzintervalle für die Unterschiede zwischen den Gruppenmitteln und zeigt, ob die Unterschiede statistisch signifikant sind. Der Test basiert auf der Welch’schen Freiheitsgradkorrektur und adjustiert die \(p\)-Werte. Der Test vergleicht also die Differenz zwischen den einzelnen Mittelwertpaaren mit einer Adjustierung für den Mehrfachtest. Es besteht also keine Notwendigkeit, zusätzliche p-Wert-Korrekturen vorzunehmen. Mit dem Games-Howell-Test ist nur ein all-pair Vergleich möglich.
Für den Games-Howell-Test aus dem Paket {rstatix} müssen wir kein lineares Modell fitten. Wir schreiben einfach die wie in einem t-Test das Outcome und den Faktor mit den Gruppenleveln in die Funktion games_howell_test(). Wir erhalten dann direkt das Ergebnis des Games-Howell-Test. Wir nutzen in diesem Beispiel die Daten aus dem Objekt fac1_tbl zu sehen in Tabelle 40.1.
R Code [zeigen / verbergen]
fit_4 <-games_howell_test(jump_length ~ animal, data = fac1_tbl)
Wir wollen aber nicht mit der Ausgabe arbeiten sondern machen uns noch ein wenig Arbeit und passen die Ausgabe an. Zum einen brauchen wir noch die Kontraste und wir wollen die \(p\)-Werte auch ansprechend formatieren. Wir erhalten das Objekt res_4_obj und geben uns die Ausgabe wieder.
Wir erhalten ein tibble() mit fünf Spalten. Zum einen den contrast, der den Vergleich widerspiegelt, den haben wir uns selber mit der Funktion mutate() und str_c() aus den Spalten group1 und group2 gebaut. Wir vergleichen im ersten Kontrast die Katzen- mit den Hundeflöhen, wobei wir dog-cat rechnen. Also wirklich den Mittelwert der Sprungweite der Hundeflöhe minus den Mittelwert der Sprungweite der Katzenflöhe rechnen. In der Spalte estimate sehen wir den Mittelwertsunterschied. Der Mittelwertsunterschied ist in der Richtung nicht ohne den Kontrast zu interpretieren. Danach erhalten wir die adjustierten \(p\)-Wert sowie die simultanen 95% Konfidenzintervalle.
Wir können die Nullhypothese ablehnen für den Vergleiche dog - cat mit einem p-Wert von \(0.02\) sowie für den Vergleich \(cat - fox\) mit einem p-Wert von \(0.00\). Beide p-Werte liegen unter dem Signifikanzniveau von \(\alpha\) gleich 5%.
In Abbildung 40.23 sind die simultanen 95% Konfidenzintervalle nochmal in einem ggplot visualisiert. Die Kontraste und die Position hängen von dem Faktorlevel ab.
Abbildung 40.23— Die 95% Konfidenzintervalle für den allpair-Vergleich des Games-Howell-Test.
Die Entscheidungen nach den 95% Konfidenzintervallen sind die gleichen wie nach dem \(p\)-Wert. Da wir hier es mit einem Mittelwertsvergleich zu tun haben, ist die Entscheidung gegen die Nullhypothese zu treffen wenn die 0 im Konfidenzintervall ist.
40.7.2 Generalized Least Squares
Neben dem Games-Howell-Test gibt es auch die Möglichkeit Generalized Least Squares zu nutzen. Hier haben wir dann auch die Möglichkeit mehrfaktorielle Modelle zu schätzen und dann auch wieder emmeans zu nutzen. Das ist natürlich super, weil wir dann wieder in dem emmeans Framework sind und alle Funktionen von oben nutzen können. Deshalb hier auch nur die Modellanpassung, den Rest kopierst du dir dann von oben dazu.
Die Funktion gls() aus dem R Paket {nlme} passt ein lineares Modell unter Verwendung der verallgemeinerten kleinsten Quadrate an. Die Fehler dürfen dabei aber korreliert oder aber ungleiche Varianzen haben. Damit haben wir ein Modell, was wir nutzen können, wenn wir Varianzheterogenität vorliegen haben. Hier einmal das simple Beispiel für die Tierarten. Wir nehmen wieder die ganz normale Formelschreiweise. Wir können jetzt aber über die Option weights = angeben, wie wir die Varianz modellieren wollen. Die Schreibweise mag etwas ungewohnt sein, aber es gibt wirklich viele Arten die Varainz zu modellieren. Hier machen wir uns es einfach und nutzen die Helferfunktion varIdent und modellieren dann für jedes Tier eine eigene Gruppenvarianz.
Dann können wir die Modellanpasssung auch schon in emmeans() weiterleiten und schauen uns mal das Ergebnis gleich an. Wir achten jetzt auf die Spalte SE, die uns ja den Fehler der Mittelwerte für jede Gruppe wiedergibt.
Wir sehen, dass wir für jedes Tier eine eigene Varianz über den Standardfehler SE geschätzt haben. Das war es ja auch was wir wollten. Bis hierhin wäre es auch mit dem Games-Howell-Test gegangen. Was ist aber, wenn wir ein zweifaktorielles design mit Interaktion schätzen wollen? Das können wir analog wie eben machen. Wir erweitern einfach das Modell um die Terme site für den zweiten Faktor und den Interaktionsterm animal:site.
R Code [zeigen / verbergen]
gls_fac2_fit <-gls(jump_length ~ animal + site + animal:site, weights =varIdent(form =~1| animal), data = fac2_tbl)
Dann können wir uns wieder die multiplen Vergleiche getrennt für die Interaktionsterme wiedergeben lassen. Blöderweise haben jetzt alle Messorte site die gleiche Varianz für jede Tierart, aber auch da können wir noch ran.
R Code [zeigen / verbergen]
gls_fac2_fit |>emmeans(~ animal | site)
site = city:
animal emmean SE df lower.CL upper.CL
cat 13.6 0.603 36.0 12.4 14.8
dog 16.7 0.581 36.1 15.5 17.9
fox 20.1 0.437 36.0 19.2 21.0
site = smalltown:
animal emmean SE df lower.CL upper.CL
cat 13.7 0.603 36.0 12.5 15.0
dog 18.0 0.581 36.1 16.9 19.2
fox 17.8 0.437 36.0 16.9 18.7
site = village:
animal emmean SE df lower.CL upper.CL
cat 15.2 0.603 36.0 14.0 16.5
dog 16.6 0.581 36.1 15.4 17.7
fox 17.0 0.437 36.0 16.1 17.9
site = field:
animal emmean SE df lower.CL upper.CL
cat 16.2 0.603 36.0 15.0 17.4
dog 17.2 0.581 36.1 16.0 18.3
fox 14.8 0.437 36.0 13.9 15.7
Degrees-of-freedom method: satterthwaite
Confidence level used: 0.95
Die eigentliche Stärke von gls() kommt eigentlich erst zu tragen, wenn wir auch noch erlauben, dass wir die Varianz über alle Tierarten, Messsorte und Interaktionen variieren kann. Das machen wir, in dem wir einfach animal*site zu der varIdent() Funktion ergänzen.
R Code [zeigen / verbergen]
gls_fac2_fit <-gls(jump_length ~ animal + site + animal:site, weights =varIdent(form =~1| animal*site), data = fac2_tbl)
Dann noch schnell in emmeans() gesteckt und sich das Ergebnis angeschaut.
R Code [zeigen / verbergen]
gls_fac2_fit |>emmeans(~ animal | site)
site = city:
animal emmean SE df lower.CL upper.CL
cat 13.6 0.594 9.44 12.2 14.9
dog 16.7 0.713 9.03 15.1 18.3
fox 20.1 0.365 9.00 19.3 20.9
site = smalltown:
animal emmean SE df lower.CL upper.CL
cat 13.7 0.433 9.00 12.8 14.7
dog 18.0 0.614 10.19 16.7 19.4
fox 17.8 0.433 8.99 16.8 18.8
site = village:
animal emmean SE df lower.CL upper.CL
cat 15.2 0.743 9.00 13.6 16.9
dog 16.6 0.384 9.00 15.7 17.4
fox 17.0 0.548 8.87 15.7 18.2
site = field:
animal emmean SE df lower.CL upper.CL
cat 16.2 0.601 9.83 14.8 17.5
dog 17.2 0.563 9.64 15.9 18.4
fox 14.8 0.378 8.98 14.0 15.7
Degrees-of-freedom method: satterthwaite
Confidence level used: 0.95
Wie du jetzt siehst schätzen wir die Varianz für jede Tierart und jeden Messort separat. Wir haben also wirklich jede Varianz einzeln zugeordnet. Die Frage ist immer, ob das notwendig ist, denn wir brauchen auch eine gewisse Fallzahl, damit die Modelle funktionieren. Aber das kommt jetzt sehr auf deine Fragestellung an und müssten wir nochmal konkret besprechen.
Wir immer gibt es noch eine Möglichkeit die Varianzheterogenität zu behandeln. Wir nutzen jetzt hier einmal die Funktionen aus dem R Paket {sandwich}, die es uns ermöglichen Varianzheterogenität (eng. heteroskedasticity) zu modellieren. Es ist eigentlich super einfach, wir müssen als erstes wieder unser Modell anpassen. Hier einmal mit einer simplen linearen Regression.
R Code [zeigen / verbergen]
lm_fac1_fit <-lm(jump_length ~ animal, data = fac1_tbl)
Dann können wir auch schon für einen Gruppenvergleich direkt in der Funktion emmeans() für die Varianzheterogenität adjustieren. Es gibt verschiedene mögliche Sandwich-Schätzer, aber wir nehmen jetzt mal einen der häufigsten mit vcovHC. Wie immer gilt, es gibt ja nach Datenlage bessere und schlechtere Schätzer. Wir laden jetzt nicht das ganze Paket, sondern nur die Funktion mit sandwich::vcovHAC. Achtung, hinter der Option vcov. ist ein Punkt. Ohne den Aufruf vcov. = funktioniert die Funktion dann nicht.
Exkurs: Robuste Schätzung von Standardfehlern, Konfidenzintervallen und p-Werten
Wenn du noch etwas weiter gehen möchtest, dann kannst du dir noch die Hilfeseite von dem R Paket {performance}Robust Estimation of Standard Errors, Confidence Intervals, and p-values anschauen. Die Idee ist hier, dass wir die Varianz/Kovarianz robuster daher mit der Berücksichtigung von Varianzheterogenität (eng. heteroskedasticity) schätzen.
40.8 Compact letter display
In der Pflanzenernährung ist es nicht unüblich sehr viele Substrate miteinander zu vergleichen. Oder andersherum, wenn wir sehr viele Gruppen haben, dann kann die Darstellung in einem all-pair Vergleich sehr schnell sehr unübersichltich werden. Deshalb wure das compact letter display entwickelt. Das compact letter display zeigt an, bei welchen Vergleichen der Behandlungen die Nullhypothese gilt. Daher werden die nicht signifikanten Ergebnisse visualisiert. Gut zu lesen ist auch die Vignette Re-engineering CLDs der Hilfeseite zu {emmeans} sowie die Hilfeseite Compact Letter Display (CLD) - What is it?.
Schauen wir uns aber zuerst einmal ein größeres Beispiel mit neun Behandlungen mit jeweils zwanzig Beobachtungen an. Wir erstellen uns den Datensatz in der Form, dass sich die Mittelwerte für die Behandlungen teilweise unterscheiden.
In der Abbildung 40.24 ist der Datensatz data_tbl nochmal als Boxplot dargestellt.
Abbildung 40.24— Boxplot der Beispieldaten.
Wir sehen, dass sich die positive Kontrolle von dem Rest der Behandlungen unterscheidet. Danach haben wir ein Plateau mit der negativen Kontrolle und der Behanldung A und der Behandlung B. Nach diesem Plateau haben wir einen Sprung und sehen einen leicht linearen Anstieg der Mittelwerte der Behandlungen.
Schauen wir uns zuerst einmal an, wie ein compact letter display aussehen würde, wenn kein Effekt vorliegen würde. Daher die Nullhypothese ist wahr und die Mittelwerte der Gruppen unterscheiden sich nicht. Wir nutzen hier einmal ein kleineres Beispiel mit den Behandlungslevels ctrl, treat_A und treat_B. Alle drei Behandlungslevel haben einen Mittelwert von 10. Es gilt die Nullhypothese und wir erhalten folgendes compact letter display in Tabelle 40.3.
Tabelle 40.3— Das compact letter display für drei Behandlungen nach einem paarweisen Vergleich. Die Nullhypothese gilt, es gibt keinen Mittelwertsunterschied.
Behandlung
Mittelwert
\(\phantom{a}\)
ctrl
10
a
\(\phantom{a}\)
\(\phantom{a}\)
treat_A
10
a
treat_B
10
a
Das Gegenteil sehen wir in der Tabelle 40.4. Hier haben wir ein compact letter display wo sich alle drei Mittelwerte mit 10, 15 und 20 voneinander klar unterscheiden. Die Nullhypothese gilt für keinen der möglichen paarweisen Vergleiche.
Tabelle 40.4— Das compact letter display für drei Behandlungen nach einem paarweisen Vergleich. Die Nullhypothese gilt nicht, es gibt einen Mittelwertsunterschied.
Behandlung
Mittelwert
ctrl
10
a
\(\phantom{a}\)
\(\phantom{a}\)
treat_A
15
b
treat_B
20
\(\phantom{a}\)
c
Schauen wir uns nun die Implementierung des compact letter display für die verschiedenen Möglichkeiten der Multiplen Vergleiche einmal an.
40.8.1 … für pairwise.*.test()
Wenn wir für die Funktionen pairwise.*.test() das compact letter display berechnen wollen, dann müssen wir etwas ausholen. Denn wir müssen dafür die Funktion multcompLetters() nutzen. Diese Funktion braucht die \(p\)-Werte als Matrix und diese Matrix der \(p\)-Werte kriegen wir über die Funktion fullPTable(). Am Ende haben wir aber dann das was wir wollten. Ich habe hier nochmal das einfache Beispiel mit den Sprungweiten von oben genommen.
Als Ergebnis erhalten wir, dass Hund- und Fuchsflöhe gleich weit springen, beide teilen sich den gleichen Buchstaben. Katzenflöhe springen unterschiedlich zu Hunden- und Fuchsflöhen. Das Vorgehen ändert sich dann nicht, wenn wir eine andere Funktion wie pairwise.wilcox.test() nehmen.
40.8.2 … für das Paket {emmeans}
In dem Paket {emmeans} ist das compact letter display ebenfalls implementiert und wir müssen nicht die Funktion multcompLetters() nutzen. Durch die direkte Implementierung ist es etwas einfacher sich das compact letter display anzeigen zu lassen. Das Problem ist dann später sich die Buchstaben zu extrahieren um die Abbildung 40.25 zu ergänzen. Wir nutzen in {emmeans} die Funktion cld() um das compact letter display zu erstellen.
Wir erhalten dann die etwas besser sortierte Ausgabe für die Behandlungen wieder.
R Code [zeigen / verbergen]
emmeans_cld
trt emmean SE df lower.CL upper.CL .group
pos_ctrl 9.67 1.12 171 6.51 12.8 a
neg_ctrl 20.02 1.12 171 16.86 23.2 b
treat_A 20.97 1.12 171 17.81 24.1 b
treat_B 23.35 1.12 171 20.19 26.5 b
treat_C 34.96 1.12 171 31.80 38.1 c
treat_D 37.46 1.12 171 34.30 40.6 cd
treat_E 40.17 1.12 171 37.01 43.3 de
treat_F 43.23 1.12 171 40.07 46.4 e
treat_G 50.51 1.12 171 47.35 53.7 f
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 9 estimates
P value adjustment: bonferroni method for 36 tests
significance level used: alpha = 0.05
NOTE: If two or more means share the same grouping symbol,
then we cannot show them to be different.
But we also did not show them to be the same.
Wie die Ausgabe von cld() richtig anmerkt, können compact letter display irreführend sein weil sie eben Nicht-Unterschiede anstatt von signifikanten Unterschieden anzeigen. Zum Anderen sehen wir aber auch, dass wir 36 statistische Tests gerechnet haben und somit zu einem Signifikanzniveau von \(\cfrac{\alpha}{k} = \cfrac{0.05}{36} \approx 0.0014\) testen. Wir brauchen also schon sehr große Unterschiede oder aber eine sehr kleine Streuung um hier signifikante Effekte nachweisen zu können.
In Tabelle 40.5 sehen wir das Ergebnis des compact letter display nochmal mit den Mittelwerten der Behandlungslevel zusammen dargestellt. Wir sehen wieder, dass sich pos_crtl von allen anderen Behandlungen unterscheidet, deshalb hat nur die Behandlung pos_crtl den Buchstaben a. Die Mittelwerte vom neg_ctrl, treat_A und treat_B sind nahezu gleich, also damit nicht signifikant. Deshalb erhalten diese Behandlungslevel ein b. Wir gehen so alle Vergleiche einmal durch.
Tabelle 40.5— Kombination der Level der Behandlungen und deren Mittelwerte zur Generieung sowie dem compact letter display generiert aus den adjustierten \(p\)-Werten aus emmeans. Gleiche Buchstaben bedeuten kein signifikanter Unterschied.
Behandlung
Mittelwert
pos_crtl
10
a
neg_ctrl
20
b
treat_A
22
b
treat_B
24
b
treat_C
35
c
treat_D
37
c
d
treat_E
40
d
e
treat_F
43
e
treat_G
45
f
Abschließend können wir die Buchstaben aus dem compact letter display noch in die Abbildung 40.25 ergänzen. Hier müssen wir etwas mehr machen um die Buchstaben aus dem Objekt emmeans_cld zu bekommen. Du kannst dann noch die y-Position anpassen wenn du möchtest.
Abbildung 40.25— Boxplot der Beispieldaten zusammen mit den compact letter display.
Das compact letter display anders gebaut…
In dem kurzen Kapitel zu Re-engineering CLDs in der Vingette des R Pakets {emmeans} geht es darum, wie das compact letter display auch anders gebaut werden könnte. Nämlich einmal als wirkliches Anzeigen von Gleichheit über die Option delta oder aber über das Anzeigen von Signifikanz über die Option signif. Damit haben dann auch wirklich die Information, die wir dann wollen. Also eigentlich was Schönes. Wie machen wir das nun?
Wenn wir das compact letter display in dem Sinne der Gleichheit der Behandlungen interpretieren wollen, also das der gleiche Buchstabe bedeutet, dass sich die Behandlungen nicht unterscheiden, dann müssen wir ein delta setzen in deren Bandbreite oder Intervall die Behandlungen gleich sind. Ich habe hier mal ein delta von 20 gewählt und wir adjustieren bei einem Test auf Gleichheit nicht.
trt emmean SE df lower.CL upper.CL .equiv.set
pos_ctrl 9.67 1.12 171 7.45 11.9 a
neg_ctrl 20.02 1.12 171 17.80 22.2 ab
treat_A 20.97 1.12 171 18.75 23.2 abc
treat_B 23.35 1.12 171 21.13 25.6 abcd
treat_C 34.96 1.12 171 32.74 37.2 bcde
treat_D 37.46 1.12 171 35.24 39.7 cde
treat_E 40.17 1.12 171 37.94 42.4 de
treat_F 43.23 1.12 171 41.01 45.4 e
treat_G 50.51 1.12 171 48.29 52.7 e
Confidence level used: 0.95
Statistics are tests of equivalence with a threshold of 20
P values are left-tailed
significance level used: alpha = 0.05
Estimates sharing the same symbol test as equivalent
Wie wir jetzt sehen, bedeuten gleiche Buchstaben, dass die Behandlungen gleich sind. In dem Sinne gleich sind, dass die Behandlungen im Mittel nicht weiter als der Wert in delta auseinanderliegen. Wie du jetzt das delta bestimmst ist eine biologische und keine statistische Frage.
Können wir uns auch signifikante Unterschiede anzeigen lassen? Ja, können wir auch, aber das ist meiner Meinung nach die schlechtere der beiden Anpassungen. Wir haben ja im Kopf, dass das compact letter display eben mit gleichen Buchstaben das Gleiche anzeigt. Jetzt würden wir diese Eigenschaften zu Unterschied ändern. Schauen wir uns das einmal an einem kleineren Datensatz einmal an.
Dann können wir uns hier einmal das Problem mit den Buchstaben anschauen. Wir kriegen jetzt mit der Option signif = TRUE wiedergeben Estimates sharing the same symbol are significantly different und das ist irgendwie auch wirr, dass gleiche Buchstaben einen Unterschied darstellen. Das compact letter display wird eben als Gleichheit gelesen, so dass wir hier mehr verwirrt werden als es hilft.
trt emmean SE df lower.CL upper.CL .signif.set
pos_ctrl 9.67 1.08 76 6.9 12.4 ab
neg_ctrl 20.02 1.08 76 17.2 22.8 a
treat_A 20.97 1.08 76 18.2 23.7 b
treat_G 50.51 1.08 76 47.7 53.3 ab
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 4 estimates
P value adjustment: bonferroni method for 6 tests
significance level used: alpha = 0.05
Estimates sharing the same symbol are significantly different
Deshalb würde ich auf die Buchstaben verzichten und die Zahlen angeben, damit hier nicht noch mehr Verwirrung aufkommt. Wir nehmen also die Option für die Buchstaben einmal aus dem cld() Aufruf raus. Dann haben wir Zahlen als Gruppenzuweisung, was schon mal was anderes ist als die Buchstaben aus dem compact letter display.
trt emmean SE df lower.CL upper.CL .signif.set
pos_ctrl 9.67 1.08 76 6.9 12.4 12
neg_ctrl 20.02 1.08 76 17.2 22.8 1
treat_A 20.97 1.08 76 18.2 23.7 2
treat_G 50.51 1.08 76 47.7 53.3 12
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 4 estimates
P value adjustment: bonferroni method for 6 tests
significance level used: alpha = 0.05
Estimates sharing the same symbol are significantly different
Innerhalb des selben Konzepts dann zwei Arten von Interpretation des compact letter display zu haben, ist dann auch nicht zielführend. Den auch die gleichen Zahlen bedeuten jetzt einen Unterschied. Irgendwie mag ich persönlich nicht diese sehr verdrehte Interpretation nicht. Deshalb lieber ein delta einführen und auf echte Gleichheit testen.
40.8.3 … für das Paket {multcomp}
Wir schauen uns zuerst einmal die Implementierung des compact letter display in dem Paket {multcomp} an. Wir nutzen die Funktion multcompLetters() aus dem Paket {multcompView} um uns das compact letter display wiedergeben zu lassen. Davor müssen wir noch einige Schritte an Sortierung und Umbenennung durchführen. Das hat den Grund, dass die Funktion multcompLetters()nur einen benannten Vektor mit \(p\)-Werten akzeptiert. Das heist wir müssen aus der Funktion glht() die adjustierten \(p\)-Werte extrahieren und dann einen Vektor der Vergleiche bzw. Kontraste in der Form A-B bauen. Also ohne Leerzeichen und in der Beschreibung der Level der Behandlung trt. Die Funktion pull() erlaubt uns einen Spalte als Vektor aus einem tibble() zu ziehen und dann nach der Spalte contrast zu benennen.
Wir erhalten dann folgendes compact letter display für die paarweisen Vergleiche aus multcomp.
R Code [zeigen / verbergen]
multcomp_cld
neg_ctrl treat_A treat_B treat_C treat_D treat_E treat_F treat_G
"a" "a" "a" "b" "bc" "cd" "d" "e"
pos_ctrl
"f"
Leider sind diese Buchstaben in dieser Form schwer zu verstehen. Deshalb gibt es noch die Funktion plot() in dem Paket {multcompView} um uns die Buchstaben mit den Leveln der Behandlung einmal ausgeben zu lassen. Wir erhalten dann folgende Abbildung.
R Code [zeigen / verbergen]
multcomp_cld |>plot()
In dem compact letter display bedeuten gleiche Buchstaben, dass die Behandlungen gleich sind. Es gilt die Nullhypothese für diesen Vergleich. Was sehen wir also hier? Kombinieren wir einmal das compact letter display mit den Leveln der Behandlung und den Mittelwerten der Behandlungen in einer Tabelle 40.6. Wenn die Mittelwerte gleich sind, dann erhalten die Behandlungslevel den gleichen Buchstaben. Die Mittelwerte vom neg_ctrl, treat_A und treat_B sind nahezu gleich, also damit nicht signifikant. Deshalb erhalten diese Behandlungslevel ein a. Ebenso sind die MIttelwerte von treat_C und treat_D nahezu gleich, dehalb erhalten beide ein b. Das machen wir immer so weiter und konzentrieren uns also auf die nicht signifikanten Ergebnisse. Denn gleiche Buchstaben bedeuten, dass die Behandlungen gleich sind. Wir sehen hier also, bei welchen Vergleichen die Nullhypothese gilt.
Tabelle 40.6— Kombination der Level der Behandlungen und deren Mittelwerte zur Generieung sowie dem compact letter display generiert aus den adjustierten \(p\)-Werten aus multcomp. Gleiche Buchstaben bedeuten kein signifikanter Unterschied.
Behandlung
Mittelwert
neg_ctrl
20
a
treat_A
22
a
treat_B
24
a
treat_C
35
b
treat_D
37
b
c
treat_E
40
c
d
treat_F
43
d
treat_G
45
e
pos_crtl
10
f
Wir können dann die Buchstaben auch in den Boxplot ergaänzen. Die y-Position kann je nach Belieben dann noch angepasst werden. zum Beispiel könnten hier auch die Mittelwerte aus einer summarise() Funktion ergänzt werden und so die y-Position angepasst werden.
R Code [zeigen / verbergen]
letters_tbl <- multcomp_cld$Letters |>enframe("trt", "label") |>mutate(rsp =0)ggplot(data_tbl, aes(x = trt, y = rsp, fill = trt)) +theme_minimal() +geom_boxplot() +scale_fill_okabeito() +geom_jitter(width =0.15, alpha =0.5) +geom_text(data = letters_tbl, aes(x = trt , y = rsp, label = label)) +theme(legend.position ="none")
Abbildung 40.26— Boxplot der Beispieldaten zusammen mit den compact letter display.
40.8.4 … für den Games-Howell-Test
Abschließend wollen wir uns die Implementierung des compact letter display für den Games-Howell-Test einmal anschauen. Es gilt vieles von dem in diesem Abschnitt schon gesagtes. Wir nutzen die Funktion multcompLetters() aus dem Paket {multcompView} um uns das compact letter display aus dem Games-Howell-Test wiedergeben zu lassen. Davor müssen wir noch einige Schritte an Sortierung und Umbenennung durchführen. Das hat den Grund, dass die Funktion multcompLetters()nur einen benannten Vektor mit \(p\)-Werten akzeptiert. Die Funktion pull() erlaubt uns einen Spalte als Vektor aus einem tibble() zu ziehen und dann nach der Spalte contrast zu benennen.
Wir können uns dann auch das compact letter display als übersichtlicheren Plot wiedergeben lassen.
R Code [zeigen / verbergen]
ght_cld |>plot()
Um die Zusammenhänge besser zu verstehen ist in Tabelle 40.7 nochmal die Kombination der Level der Behandlungen und deren Mittelwerte zur Generieung sowie dem compact letter display dargestellt. Wir sehen wieder, dass sich pos_crtl von allen anderen Behandlungen unterscheidet, deshalb hat nur die Behandlung pos_crtl den Buchstaben a. Die Mittelwerte vom neg_ctrl, treat_A und treat_B sind nahezu gleich, also damit nicht signifikant. Deshalb erhalten diese Behandlungslevel ein b. In der Form können wir alle Vergleiche einmal durchgehen.
Tabelle 40.7— Kombination der Level der Behandlungen und deren Mittelwerte zur Generieung sowie dem compact letter display generiert aus den adjustierten \(p\)-Werten aus dem Games-Howell-Test. Gleiche Buchstaben bedeuten kein signifikanter Unterschied.
Behandlung
Mittelwert
pos_crtl
10
a
neg_ctrl
20
b
treat_A
22
b
treat_B
24
b
treat_C
35
c
treat_D
37
c
d
treat_E
40
d
treat_F
43
d
treat_G
45
e
Wir können dann auch in Abbildung 40.27 sehen, wie das compact letter display mit den Boxplots verbunden wird.
R Code [zeigen / verbergen]
letters_tbl <- ght_cld$Letters |>enframe("trt", "label") |>mutate(rsp =0)ggplot(data_tbl, aes(x = trt, y = rsp, fill = trt)) +theme_minimal() +geom_boxplot() +scale_fill_okabeito() +geom_jitter(width =0.15, alpha =0.5) +geom_text(data = letters_tbl, aes(x = trt , y = rsp, label = label)) +theme(legend.position ="none")
Abbildung 40.27— Boxplot der Beispieldaten zusammen mit den compact letter display.
Referenzen
Cumming G, Fidler F, Vaux DL. 2007. Error bars in experimental biology. The Journal of cell biology 177: 7–11.
Salinas I, Hueso JJ, Força Baroni D, Cuevas J. 2023. Plant Growth, Yield, and Fruit Size Improvements in ‘Alicia’Papaya Multiplied by Grafting. Plants 12: 1189.
Sánchez M, Velásquez Y, González M, Cuevas J. 2022. Hoverfly pollination enhances yield and fruit quality in mango under protected cultivation. Scientia Horticulturae 304: 111320.
```{r echo = FALSE}#| message: false#| warning: falsepacman::p_load(tidyverse, readxl, knitr, kableExtra, Hmisc, see, latex2exp, multcomp, emmeans, ggpubr, multcompView, nlme, quantreg, janitor, parameters, effectsize, patchwork, conflicted)conflicts_prefer(dplyr::select)conflicts_prefer(dplyr::filter)cbbPalette <- c("#000000", "#E69F00", "#56B4E9", "#009E73", "#F0E442", "#0072B2", "#D55E00", "#CC79A7")```# Der Post-hoc-Test {#sec-posthoc}*Letzte Änderung am `r format(fs::file_info("stat-tests-posthoc.qmd")$modification_time, '%d. %B %Y um %H:%M:%S')`*> *"Comparison is the thief of joy." --- Theodore Roosevelt*::: {.callout-caution appearance="simple"}## Stand des Kapitels: Aktualisierung (seit 01.2025)Dieses Kapitel wird in den nächsten Wochen aktualisiert. Um zu gewährleisten, dass hier auch alles weiter so funktioniert, findet die Aktualisierung *außerhalb* dieses Kapitels statt. Ich plane zum SoSe 2025 eine neue Version des Kapitels erstellt zu haben.:::In diesem Kapitel wollen wir uns mit den multiplen Vergleichen (eng. *post hoc analysis*) oder aber auch paarweise Gruppenvergleiche genannt beschäftigen. Wir kennen diese multiplen Tests auch unter dem Namen *Posthoc Tests*, da wir historisch diese Tests *nach* einer ANOVA durchgeführt haben. Das heißt, wir wollen statistisch Testen, ob sich verschiedene Gruppen einer Behandlung voneinander unterschieden. Technisch Testen wir dabei, ob sich die Level eines Faktors voneinander unterscheiden. Wir können dabei mehrere Faktoren bzw. Behandlungen berücksichtigen und gleichzeitig Testen. Wenn wir nur einen Faktor betrachten, dann sprechen wir von einem 1-faktoriellen Vergleich. Wenn wir zwei Behandlungen betrachten, dann entsprechend von einem 2-faktoriellen Vergleich. Sehr selten haben wir dann noch den Fall vorliegen, dass wir drei Faktoren betrachten wollen. In einer Abschlussarbeit haben wir faktisch keine Versuche wo wir mehr als drei Faktoren in einem Gruppenvergleich berücksichtigen.Wo wollen wir also hin? Betrachten wir dazu einmal zwei wissenschaftliche Veröffentlichungen als Beispiele. In der @fig-zerforschen-papaya sehen wir ein Säulendigramm aus der wissenschaftlichen Veröffentlichung von @salinas2023plant mit dem Titel ["Plant Growth, Yield, and Fruit Size Improvements in 'Alicia' Papaya Multiplied by Grafting"](https://www.mdpi.com/2223-7747/12/5/1189). Wir haben hier also einen 2-faktoriellen Gruppenvergleich vorliegen. Der erste Faktor ist die *TSS* Behandlung mit *seed*, *grafting* und *in virto*. Der zweite Faktor sind dann die fünf Zeitpunkte zu denen jeweils die Behandlung auf die Papaya gegeben wurde. In diesem Kapitel wollen wir die Buchstaben aus einem paarweisen Gruppenvergleich über den Säulen erschaffen oder auch *compact letter display* genannt.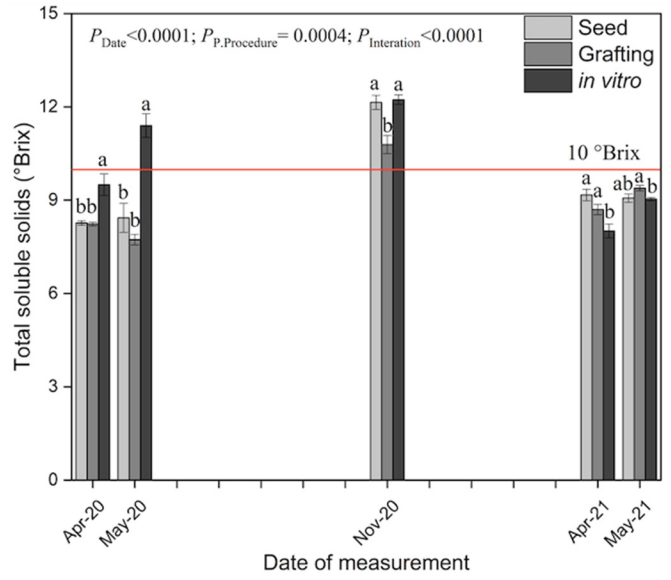{#fig-zerforschen-papaya fig-align="center" width="70%"}In der @fig-zerforschen-hoverfly sehen wir ein Säulendigramm aus der wissenschaftlichen Veröffentlichung von @sanchez2022hoverfly mit dem Titel ["Hoverfly pollination enhances yield and fruit quality in mango under protected cultivation"](https://www.sciencedirect.com/science/article/pii/S0304423822004411). Auch hier haben wir ein 2-faktorielles Design vorliegen. Zum einen den Faktor *treatment* mit den Gruppen *High density*, *medium density*, *Low density* und *Control*. Der zweite Faktor ist dann das Jahr der Messung. Auch hier sehen wir wieder Buchstaben über den Säulen. Diese Buchstabenwollen wir dann als *compact letter display* hier in diesem Kapitel erstellen. Zu den Fehlerbalken liefert die Publikation [Error bars in experimental biology](https://rupress.org/jcb/article/177/1/7/34602/Error-bars-in-experimental-biology) von @cumming2007error nochmal einen Überblick über Fehlerbalken und welche Fehlerbalken man den nun nutzen sollte.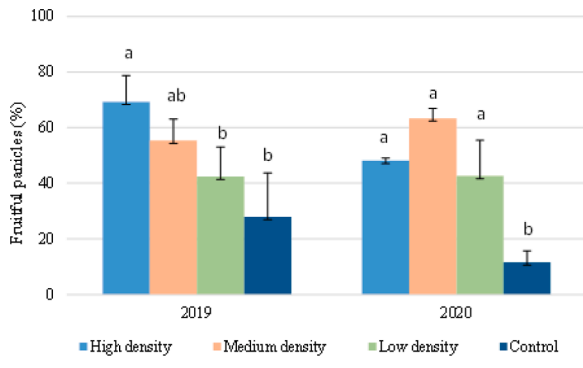{#fig-zerforschen-hoverfly fig-align="center" width="70%"}Dann wissen wir jetzt wohin wir wollen. Jetzt stellt sich noch die Frage, welches statistisches Verfahren soll ich wählen um einen Gruppenvergleich zu rechnen? In der folgenden Box gebe ich dir da einmal einen Überblick. Abhängig von deinem Outcome oder deinen gemessenen Werten, musst du dich für ein anderes Verfahren entscheiden. Es kann also sein, dass du verschiedene statistische Tests in deiner Abschlussarbeit rechnest, da du verschiedene Outcomes statistisch analysierst. Wir schauen uns in diesem Kapitel zum größten Teil den Fall eines normalverteilten Outcomes an. An einem normalverteilten Outcome, wie Frische- oder Trockengewicht, lassen sich einfacher die Prinzipien des multiplen Testen erklären. Deshalb hier der Fokus auf der Normalverteilung -- andere Möglichkeiten dann in der Box.::: callout-note## Welches statistisches Modell für welchen Gruppenvergleich?Welches Verfahren soll ich für meinen Gruppenvergleich wählen? Ich habe in den jeweiligen Kapiteln zu den statistischen Modellen die jeweiligen Schritte für die Gruppenvergleiche hinterlegt und beschrieben. Daher kannst du in den Kapiteln einmal schauen, wie dein Outcome dort ausgewertet wird. Du findest dort auch immer ein Beispiel mit entsprechenden Daten.Normalverteiltes Outcome $\boldsymbol{y}$: Frischgewicht, Trockengewicht, Chlorophyllgehalt...: Dann schaue dir den Abschnitt zu [Multiple Gruppenvergleiche für normalverteilte Daten](#sec-mult-comp-gaussian-reg) an. Das ist eigentlich *der* Standardfall und vieles in diesem Kapitel dreht sich um normalverteilte Daten.Poissonverteiltes Outcome $\boldsymbol{y}$ bzw. Zähldaten: Anzahl Insekten, gekeimte Pflanzen, Schädlinge...: Dann schaue dir den Abschnitt zu [Multiple Gruppenvergleiche für Zähldaten](#sec-mult-comp-pois-reg) an -- dein Outcome besteht nämlich aus einer Zählung von einem Auftreten eines Ereignisses.Ordinalverteiltes Outcome $\boldsymbol{y}$: Bonitur von Rasen, Brokkolistängel, Wurzelwachstum...: Dann schaue dir den Abschnitt zu [Multiple Gruppenvergleiche für Boniturdaten](#sec-mult-comp-ord-reg) an -- dein Outocme besteht aus Noten für ein Merkmal.Binomialverteiltes Outcome $\boldsymbol{y}$ bzw. Anteile: Infektionsstatus, Zielgewicht erreicht...: Dann schaue dir den Abschnitt zu [Multiple Gruppenvergleiche für Anteile](#sec-mult-comp-log-reg) an -- dein Outcome ist $0/1$ oder $ja/nein$ kodiert. Ein Ereignis ist eingetreten oder eben nicht.Betaverteiltes Outcome $\boldsymbol{y}$ bzw. Wahrscheinlichkeiten: Anteil infizierte Pflanzen, Erfolg/Misserfolg...: Dann schaue dir den Abschnitt zu [Multiple Gruppenvergleiche für Wahrscheinlichkeiten](#sec-mult-comp-beta-reg) an -- dein Outcome ist eine Wahrscheinlcihkeit für das Eintreten eines Ereignisses oder aber die Rate eines Erfolges an Misserfolgen.Auswertungen mit 3 oder mehr Faktoren:: Dann schaue dir den Abschnitt zu [Multiple Gruppenvergleiche für gemischte Modelle](#sec-mult-comp-lmer-reg) an -- dein Outcome wurde 3-faktoriell oder mit mehr Faktoren gemessen.:::Wenn wir multiple Mittelwertsvergleiche rechnen, dann tritt das Problem des multiplen Testens auf. Wir haben eine Inflation des $\alpha$-Fehlers vorliegen. Im @sec-statistisches-testen-alpha-adjust kannst du mehr über die Problematik erfahren und wie wir mit der $\alpha$ Inflation umgehen. Hier in diesem Kapitel gehe ich jetzt davon aus, dass dir die $\alpha$ Adjustierung ein Begriff ist. Häufig sollen $p$-Werte nicht adjustiert werden, viele Verfahren in diesem Kapitel adjustieren aber automatisch die $p$-Werte. Deshalb musst du aktiv die Adjustierung der $p$-Werte abstellen. Du findest dann in Abschnitten zu den jeweiligen statistischen Verfahren die entsprechende Option. Der paarweise Mittelwertsvergleich wird auch gerne Tukey Test genannt. Das heißt, dass der Tukey Test alle Gruppen miteinander vergleicht. Der Tukey Test wird daher auch gerne *all pair* Vergleich genannt.Schaue dir auch die folgenden Zerforschenbeispiele einmal an, wenn dich mehr zu dem Thema der Abbildung von multiplen Gruppenvergleichen interessiert. Du findest in den Kästen Beispiele für Posterabbildungen zur multiplen Gruppenvergleichen, die ich dann zerforscht habe.::: {.callout-note collapse="true"}## Zerforschen: Einfaktorieller Barplot mit `emmeans` und *compact letter display*{{< include zerforschen/zerforschen-simple-barplot-emmeans.qmd >}}:::::: {.callout-note collapse="true"}## Zerforschen: Zweifaktorieller Barplot mit `emmeans` und *compact letter display*{{< include zerforschen/zerforschen-barplot-2fac-target-emmeans.qmd >}}:::::: {.callout-note collapse="true"}## Zerforschen: Zweifaktorieller Boxplot mit `emmeans` und *compact letter display*{{< include zerforschen/zerforschen-boxplot-2fac-target-emmeans.qmd >}}:::::: {.callout-note collapse="true"}## Zerforschen: Boxplots mit `emmeans` und *compact letter display*{{< include zerforschen/zerforschen-boxplot-mult.qmd >}}:::## Genutzte R PaketeWir wollen folgende R Pakete in diesem Kapitel nutzen.```{r echo = TRUE}#| message: falsepacman::p_load(tidyverse, magrittr, broom, nlme, multcomp, emmeans, ggpubr, multcompView, rstatix, conflicted, see, rcompanion)```An der Seite des Kapitels findest du den Link *Quellcode anzeigen*, über den du Zugang zum gesamten R-Code dieses Kapitels erhältst.## DatenWir nutzen in diesem Kapitel den Datensatz aus dem Beispiel in @sec-example-3. Wir haben als Outcome die Sprunglänge in \[cm\] von Flöhen. Die Sprunglänge haben wir an Flöhen von Hunde, Katzen und Füchsen gemessen. Der Datensatz ist also recht übeerschaubar. Wir haben ein normalverteiltes $y$ mit `jump_length` sowie einen multinomialverteiltes $y$ mit `grade` und einen Faktor `animal` mit drei Leveln. Im Folgenden laden wir den Datensatz `flea_dog_cat_fox.csv` und selektieren mit der Funktion `select()` die benötigten Spalten. Abschließend müssen wir die Spalte `animal`noch in einen Faktor umwandeln. Damit ist unsere Vorbereitung des Datensatzes abgeschlossen.```{r}#| message: falsefac1_tbl <-read_csv2("data/flea_dog_cat_fox.csv") |>select(animal, jump_length, grade) |>mutate(animal =as_factor(animal))```In der @tbl-data-posthoc-1 ist der Datensatz `fac1_tbl` nochmal dargestellt. Wir werden nun den Datensatz `fac1_tbl` in den folgenden Abschnitten immer wieder nutzen.::: {.callout-tip collapse="true"}## Für die vollständige Datentabelle bitte aufklappen```{r}#| message: false#| echo: false#| tbl-cap: Selektierter Datensatz mit einer normalverteilten Variable `jump_length` sowie der multinominalverteilten Variable `grade` und einem Faktor `animal` mit drei Leveln.#| label: tbl-data-posthoc-1fac1_tbl |>kable(align ="c", "pipe")```:::## Hypothesen für multiple VergleicheAls wir eine ANOVA gerechnet hatten, hatten wir nur eine Nullhypothese und eine Alternativehypothese. Wenn wir Nullhypothese abgelehnt hatten, wussten wir nur, dass sich mindestens ein paarweiser Vergleich unterschiedet. Multiple Vergleich lösen nun dieses Problem und führen ein Hypothesen*paar* für jeden paarweisen Vergleich ein. Zum einen rechnen wir damit $k$ Tests und haben damit auch $k$ Hypothesenpaare (siehe auch @sec-statistisches-testen-alpha-adjust zur Problematik des wiederholten Testens). Wenn wir zum Beispiel alle Level des Faktors `animal` miteinander Vergleichen wollen, dann rechnen wir $k=3$ paarweise Vergleiche. Im Folgenden sind alle drei Hypothesenpaare dargestellt.$$\begin{aligned}H_{01}: &\; \bar{y}_{cat} = \bar{y}_{dog}\\H_{A1}: &\; \bar{y}_{cat} \ne \bar{y}_{dog}\\\end{aligned}$$$$\begin{aligned}H_{02}: &\; \bar{y}_{cat} = \bar{y}_{fox}\\H_{A2}: &\; \bar{y}_{cat} \ne \bar{y}_{fox}\\\end{aligned}$$$$\begin{aligned}H_{03}: &\; \bar{y}_{dog} = \bar{y}_{fox}\\H_{A3}: &\; \bar{y}_{dog} \ne \bar{y}_{fox}\\\end{aligned}$$Wenn wir drei Vergleiche rechnen, dann haben wir eine $\alpha$ Inflation vorliegen. Wir sagen, dass wir für das multiple Testen adjustieren müssen. In R gibt es eine Reihe von Adjustierungsverfahren. Wir nehmen meist Bonferroni oder das Verfahren, was in der jeweiligen Funktion als Standard (eng. *default*) gesetzt ist. Wir adjustieren grundsätzlich die $p$-Werte und erhalten adjustierte $p$-Werte aus den jeweiligen Funktionen in R. Die adjustierten p-Werte können wir dann mit dem Signifikanzniveau von $\alpha$ gleich 5% vergleichen.## Simple Gruppenvergleiche {#sec-posthoc-pairwise}Wenn wir nur einen Faktor mit mehr als zwei Leveln vorliegen haben, dann können wir die Funktion `pairwise.*.test()` nutzen. Der Stern `*` steht entweder als Platzhalter für `t` für den t-Test oder aber für `wilcox` für den Wilcoxon Test. Die Funktion ist relativ einfach zu nutzen und liefert auch sofort die entsprechenden p-Werte. Die Funktion `pairwise.*.test()` ist in dem Sinne *veraltet*, da wir keine 95% Konfidenzintervalle generieren können. Da die Funktion aber immer mal wieder angefragt wird, ist die Funktion hier nochmal aufgeführt. Die Funktion `pairwise.*.test()` ist *veraltet*, wir nutzen das R Paket `{emmeans}` oder das R Paket `{multcomp}`.### Paarweiser t TestWir nutzen den paarweisen t-Test,- wenn wir ein normalverteiltes $y$ vorliegen haben, wie `jump_length`.- wenn wir *nur* einen Faktor mit mehr als zwei Leveln vorliegen haben, wie `animal`.- wenn wir Varianzhomogenität über alle Level vorliegen haben, dann nutzen wir die Option `pool.sd = TRUE`. Wenn wir Varianzheterogenität über alle Level des Faktors vorliegen haben, dann nutzen wir `pool.sd = FALSE`.Die Funktion `pairwise.t.test` kann nicht mit Datensätzen arbeiten sondern nur mit Vektoren. Daher können wir der Funktion auch keine `formula` übergeben sondern müssen die Vektoren aus dem Datensatz mit `fac1_tbl$jump_length` für das Outcome und mit `fac1_tbl$animal` für die Gruppierende Variable benennen. Das ist umständlich und daher auch fehleranfällig. Wir können auch den `%$%`-Operator aus dem R Paket `{magrittr}` nutzen um die Problematik zu umgehen. Weiter unten siehst du dann einmal beide Anwendungen.Als Adjustierungsmethode für den $\alpha$ Fehler wählen wir die Bonferroni-Methode mit `p.adjust.method = "bonferroni"` aus. Da wir eine etwas unübersichtliche Ausgabe in R erhalten nutzen wir die Funktion `tidy()`um die Ausgabe in ein sauberes `tibble` zu verwandeln. Abschließend runden wir noch alle numerischen Spalten mit der Funktion `round` auf drei Stellen hinter dem Komma.```{r}pairwise.t.test(fac1_tbl$jump_length, fac1_tbl$animal,p.adjust.method ="bonferroni",pool.sd =TRUE) |>tidy() |>mutate_if(is.numeric, round, 3)```Und das ganze nochmal mit dem `%$%`-Operator aus dem R Paket `{magrittr}`. In diesem Fall können wir uns das `$` sparen und greifen direkt auf die Spalten des Datensatzes zu.```{r}fac1_tbl %$%pairwise.t.test(jump_length, animal,p.adjust.method ="bonferroni",pool.sd =TRUE) |>tidy() |>mutate_if(is.numeric, round, 3)```Wir erhalten in einem Tibble die adjustierten p-Werte nach Bonferroni. Wir können daher die adjustierten p-Werte ganz normal mit dem Signifikanzniveau $\alpha$ von 5% vergleichen. Wenn du keine adjustierten p-Werte möchtest, dann nutze die Option `p.adjust.method = "none"`. Wir sehen, dass der Gruppenvergleich `cat - dog` signifikant ist, der Gruppenvergleich `fox - dog` nicht signifikant ist und der Gruppenvergleich `fox - cat` wiederum signifikant ist. Leider können wir uns keine Konfidenzintervalle wiedergeben lassen, so dass die Funktion nicht dem Stand der Wissenschaft und deren Ansprüchen genügt.Im Folgenden wollen wir uns nochmal die Visualisierung mit dem R Paket `{ggpubr}` anschauen. Die [Hilfeseite des R Pakets `{ggpubr}`](https://rpkgs.datanovia.com/ggpubr/index.html) liefert noch eine Menge weitere Beispiele für den simplen Fall eines Modells $y ~ x$, also von einem $y$ und einem Faktor $x$. Um die @fig-ggpubr-1 zu erstellen müssen wir als erstes die Funktion `compare_mean()` nutzen um mit der `formula` Syntax einen t-Test zu rechnen. wir adjustieren die p-Werte nach Bonferroni. Anschließend erstellen wir einen Boxplot mit der Funktion `ggboxplot()` und speichern die Ausgabe in dem Objekt `p`. Wie in `ggplot` üblich können wir jetzt auf das Layer `p` über das `+`-Zeichen noch weitere Layer ergänzen. Wir nutzen die Funktion `stat_pvalue_manual()` um die asjustierten p-Werte aus dem Objekt `stat_test_obj` zu ergänzen. Abschließend wollen wir noch den p-Wert einer einfaktoriellen ANOVA als globalen Test ergänzen.```{r}#| message: false#| warning: false#| echo: true#| fig-align: center#| fig-height: 5#| fig-width: 6#| fig-cap: Boxplot der Sprungweiten [cm] von Hunden und Katzen ergänzt um den paarweisen Vergleich mit dem t-Test und den Bonferroni adjustierten p-Werten.#| label: fig-ggpubr-1stat_test_obj <-compare_means( jump_length ~ animal, data = fac1_tbl,method ="t.test",p.adjust.method ="bonferroni")p <-ggboxplot(data = fac1_tbl, x ="animal", y ="jump_length",color ="animal", palette =c("#00AFBB", "#E7B800", "#FC4E07"),add ="jitter", shape ="animal")p +stat_pvalue_manual(stat_test_obj, label ="p.adj", y.position =c(13, 16, 19)) +stat_compare_means(label.y =20, method ="anova") ```### Paarweiser Wilcoxon TestWir nutzen den paarweisen Wilxocon Test,- wenn wir ein *nicht*-normalverteiltes $y$ vorliegen haben, wie `grade`.- wenn wir *nur* einen Faktor mit mehr als zwei Leveln vorliegen haben, wie `animal`.Die Funktion `pairwise.wilcox.test` kann nicht mit Datensätzen arbeiten sondern nur mit Vektoren. Daher können wir der Funktion auch keine `formula` übergeben sondern müssen die Vektoren aus dem Datensatz mit `fac1_tbl$jump_length` für das Outcome und mit `fac1_tbl$animal` für die Gruppierende Variable benennen. Das ist umständlich und daher auch fehleranfällig.Als Adjustierungsmethode für den $\alpha$ Fehler wählen wir die Bonferroni-Methode mit `p.adjust.method = "bonferroni"` aus. Da wir eine etwas unübersichtliche Ausgabe in R erhalten nutzen wir die Funktion `tidy()`um die Ausgabe in ein sauberes `tibble` zu verwandeln. Abschließend runden wir noch alle numerischen Spalten mit der Funktion `round` auf drei Stellen hinter dem Komma.```{r}#| warning: falsepairwise.wilcox.test(fac1_tbl$grade, fac1_tbl$animal,p.adjust.method ="bonferroni") |>tidy() |>mutate_if(is.numeric, round, 3)```Wir erhalten in einem Tibble die adujstierten p-Werte nach Bonferroni. Wir können daher die adjustierten p-Werte ganz normal mit dem Signifikanzniveau $\alpha$ von 5% vergleichen. Wir sehen, dass der Gruppenvergleich `cat - dog` knapp signifikant ist, der Gruppenvergleich `fox - dog` ebenfalls signifikant ist und der Gruppenvergleich `fox - cat` auch signifikant ist. Leider können wir uns keine Konfidenzintervalle wiedergeben lassen, so dass die Funktion nicht dem Stand der Wissenschaft und deren Ansprüchen genügt.Im Folgenden wollen wir uns nochmal die Visualisierung mit dem R Paket `{ggpubr}` anschauen. Die [Hilfeseite des R Pakets `{ggpubr}`](https://rpkgs.datanovia.com/ggpubr/index.html) liefert noch eine Menge weitere Beispiele für den simplen Fall eines Modells $y ~ x$, also von einem $y$ und einem Faktor $x$. Um die @fig-ggpubr-2 zu erstellen müssen wir als erstes die Funktion `compare_mean()` nutzen um mit der `formula` Syntax einen Wilcoxon Test zu rechnen. wir adjustieren die p-Werte nach Bonferroni. Anschließend erstellen wir einen Boxplot mit der Funktion `ggboxplot()` und speichern die Ausgabe in dem Objekt `p`. Wie in `ggplot` üblich können wir jetzt auf das Layer `p` über das `+`-Zeichen noch weitere Layer ergänzen. Wir nutzen die Funktion `stat_pvalue_manual()` um die asjustierten p-Werte aus dem Objekt `stat_test_obj` zu ergänzen. Abschließend wollen wir noch den p-Wert eines Kruskal Wallis als globalen Test ergänzen.```{r}#| message: false#| warning: false#| echo: true#| fig-align: center#| fig-height: 5#| fig-width: 6#| fig-cap: Boxplot der Sprungweiten [cm] von Hunden und Katzen ergänzt um den paarweisen Vergleich mit dem Wilcoxon Test und den Bonferroni adjustierten p-Werten.#| label: fig-ggpubr-2stat_test_obj <-compare_means( grade ~ animal, data = fac1_tbl,method ="wilcox.test",p.adjust.method ="bonferroni")p <-ggboxplot(data = fac1_tbl, x ="animal", y ="grade",color ="animal", palette =c("#00AFBB", "#E7B800", "#FC4E07"),add ="jitter", shape ="animal")p +stat_pvalue_manual(stat_test_obj, label ="p.adj", y.position =c(10, 13, 16)) +stat_compare_means(label.y =20, method ="kruskal.test") ```## Gruppenvergleich mit `{emmeans}` {#sec-posthoc-emmeans}Im Folgenden wollen wir uns mit einem anderen R Paket beschäftigen was auch multiple Vergleiche rechnen kann. In diesem Kapitel nutzen wir das R Paket `{emmeans}`. Im Prinzip kann `{emmeans}` das Gleiche wir das R Paket `{multcomp}`. Beide Pakete rechnen dir einen multiplen Vergleich. Das Paket `{emmeans}` kann noch mit *nested comparisons* umgehen. Deshalb hier nochmal die Vorstellung von `{emmeans}`. Du kannst aber für eine simple Auswertung mit nur einem Faktor beide Pakete verwenden.Wir können hier nicht alles erklären und im Detail durchgehen. Hier gibt es noch ein aufwendiges Tutorium zu `emmeans`: [Getting started with emmeans](https://aosmith.rbind.io/2019/03/25/getting-started-with-emmeans/). Daneben gibt es auch noch die [Einführung mit Theorie auf der Seite des R Paktes](https://cran.r-project.org/web/packages/emmeans/vignettes/basics.html#contents) Es gibt hier auch ein weiteres englischsprachiges Tutorium [Don't Ignore Interactions - Unleash the Full Power of Models with {emmeans} R-package](https://yuzar-blog.netlify.app/posts/2022-12-29-emmeans2interactions/) oder [{emmeans} Game-Changing R-package Squeezes Hidden Knowledge out of Models!](https://yuzar-blog.netlify.app/posts/2022-11-29-emmeans/). **DISCLAIMER:** Der Text ist gut, die Bebilderung des entsprechenden Videos geht so leider mal gar nicht...### Gruppenvergleiche mit `emmeans` in RUm den multiplen Vergleich in `emmeans` durchführen zu können brauchen wir zuerst ein lineares Modell, was uns die notwenidgen Parameter wie Mittelwerte und Standardabweichungen liefert. Wir nutzen in unserem simplen Beispiel ein lineares Modell mit einer Einflussvariable $x$ und nehmen an, dass unser Outcome $y$ normalverteilt ist. Achtung, hier muss natürlich das $x$ ein Faktor sein. Dann können wir ganz einfach die Funktion `lm()` nutzen. Im Folgenden fitten wir das Modell `fit_2` was wir dann auch weiter nutzen werden.```{r}fit_2 <-lm(jump_length ~ animal, data = fac1_tbl)```Der multiple Vergleich in `emmeans` ist mehrschrittig. Wir pipen unser Modell aus `fit_2` in die Funktion `emmeans()`. Wir geben mit `~ animal` an, dass wir über die Level des Faktors `animal` einen Vergleich rechnen wollen. Wir adjustieren die $p$-Werte nach Bonferroni. Danach pipen wir weiter in die Funktion `contrast()` wo der eigentliche Vergleich festgelegt wird. In unserem Fall wollen wir einen *many-to-one* Vergleich rechnen. Alle Gruppen zu der Gruppe `fox`. Du kannst mit `ref =` auch ein anderes Level deines Faktors wählen.```{r}comp_2_obj <- fit_2 |>emmeans(~ animal) |>contrast(method ="trt.vs.ctrl", ref ="fox", adjust ="bonferroni") comp_2_obj```Wir können auch einen anderen Kontrast wählen. Wir überschreiben jetzt das Objekt `comp_2_obj` mit dem Kontrast *all-pair*, der alle möglichen Vergleiche rechnet. In `emmeans` heißt der *all-pair* Kontrast *pairwise*. Die Ausgabe von `emmeans` können über die Funktion `tidy()` aufgeräumt werden. Mehr dazu unter der [Hilfeseite von `tidy`() zu emmeans](https://broom.tidymodels.org/reference/tidy.emmGrid.html).```{r}comp_2_obj <- fit_2 |>emmeans(~ animal) |>contrast(method ="pairwise", adjust ="bonferroni") comp_2_obj```Wir können das Ergebnis auch noch mit der Funktion `tidy()` weiter aufräumen und dann die Spalten selektieren, die wir brauchen. Häufig benötigen wir nicht alle Spalten, die eine Funktion wiedergibt.```{r}#| message: false#| warning: falseres_2_obj <- comp_2_obj |>tidy(conf.int =TRUE) |>select(contrast, estimate, adj.p.value, conf.low, conf.high) |>mutate(across(where(is.numeric), round, 4))res_2_obj```Abschließend wollen wir noch die 95% Konfidenzintervalle in @fig-emmeans-1 abbilden. Hier ist es bei `emmeans` genauso wie bei `multcomp`. Wir können das Objekt `res_2_obj` direkt in `ggplot()` weiterverwenden und uns die 95% Konfidenzintervalle einmal plotten.```{r}#| message: false#| warning: false#| echo: true#| fig-align: center#| fig-height: 3#| fig-width: 5#| fig-cap: Die 95% Konfidenzintervalle für den *allpair*-Vergleich des simplen Datensatzes.#| label: fig-emmeans-1ggplot(res_2_obj, aes(contrast, y=estimate, ymin=conf.low, ymax=conf.high)) +geom_hline(yintercept=0, linetype="11", colour="grey60") +geom_errorbar(width=0.1) +geom_point() +coord_flip() +theme_classic()```In @fig-emmeans-3 sehen wir die Ergebnisse des multiplen Vergleiches nochmal anders als *Pairwise P-value plot* dargestellt. Wir haben auf der y-Achse zu Abwechselung mal die Gruppen dargestellt und auf der x-Achse die $p$-Werte. In den Kästchen sind die Effekte der Gruppen nochmal gezeigt. In unserem Fall die Mittelwerte der Sprungweiten für die drei Gruppen. Wir sehen jetzt immer den $p$-Wert für den jeweiligen Vergleich durch eine farbige Linie miteinander verbunden. So können wir nochmal eine andere Übersicht über das Ergebnis des multiplen Vergleich kriegen.```{r}#| message: false#| warning: false#| echo: true#| fig-align: center#| fig-height: 3#| fig-width: 5#| fig-cap: "Visualisierung der Ergebnisse im Pairwise P-value plot."#| label: fig-emmeans-3fit_2 |>emmeans(~ animal) |>pwpp(adjust ="bonferroni") +theme_minimal()```Auch haben wir die Möglichkeit un die $p$-Werte mit der Funktion `pwpm()` als eine Matrix ausgeben zu lassen. Wir erhalten in dem oberen Triangel die $p$-Wert für den jeweiligen Vergleich. In dem unteren Triangel die geschätzten Mittelwertsunterschiede. Auf der Diagonalen dann die geschätzten Mittelwerte für die jeweilige Gruppe. So haben wir nochmal alles sehr kompakt zusammen dargestellt.```{r}fit_2 |>emmeans(~ animal) |>pwpm(adjust ="bonferroni")```Wir wollen uns noch einen etwas komplizierteren Fall anschauen, indem sich `emmeans` von `multcomp` in der Anwendung unterscheidet. Wir laden den Datensatz `flea_dog_cat_fox_site.csv` in dem wir *zwei* Faktoren haben. Damit können wir dann ein Modell mit einem Interaktionsterm bauen. Wir erinnern uns, dass wir in der zweifaktoriellen ANOAV eine signifikante Interaktion zwischen den beiden Faktoren `animal` und `site` festgestelt hatten.```{r}#| message: falsefac2_tbl <-read_csv2("data/flea_dog_cat_fox_site.csv") |>select(animal, site, jump_length) |>mutate(animal =as_factor(animal),site =as_factor(site))```Wir erhalten das Objekt `fac2_tbl` mit dem Datensatz in @tbl-data-emmeans-1 nochmal dargestellt.```{r}#| message: false#| echo: false#| tbl-cap: Selektierter Datensatz mit einer normalverteilten Variable `jump_length` und einem Faktor `animal` mit drei Leveln sowie dem Faktor `site` mit vier Leveln.#| label: tbl-data-emmeans-1fac2_raw_tbl <- fac2_tbl |>mutate(animal =as.character(animal),site =as.character(site))rbind(head(fac2_raw_tbl),rep("...", times =ncol(fac2_raw_tbl)),tail(fac2_raw_tbl)) |>kable(align ="c", "pipe")```In @fig-boxplot-emmeans-1 sehen wir nochmal die Daten visualisiert. Wichtig ist hier, dass wir *zwei* Faktoren vorliegen haben. Den Faktor `animal` und den Faktor `site`. Dabei ist der Faktor `animal` in dem Faktor `site` genested. Wir messen jedes Level des Faktors `animal` jeweils in jedem Level des Faktors `site`.```{r}#| message: false#| echo: false#| fig-align: center#| fig-height: 5#| fig-width: 6#| fig-cap: Boxplot der Sprungweiten [cm] von Hunden und Katzen gemessen an verschiedenen Orten.#| label: fig-boxplot-emmeans-1ggplot(fac2_tbl, aes(x = animal, y = jump_length, fill = site)) +geom_boxplot() +scale_fill_okabeito() +labs(x ="Tierart", y ="Sprungweite [cm]") +theme_minimal() ```Wir rechnen ein multiples lineares Modell mit einem Interaktionsterm. Daher packen wir beide Faktoren in das Modell sowie die Intraktion zwischen den beiden Faktoren. Wir erhalten nach dem fitten des Modells das Objekt `fit_3`.```{r}fit_3 <-lm(jump_length ~ animal + site + animal:site, data = fac2_tbl)```Der Unterschied zu unserem vorherigen multiplen Vergleich ist nun, dass wir auch einen multiplen Vergleich für *animal nested in site* rechnen können. Dafür müssen wir den Vergleich in der Form `animal | site` schreiben. Wir erhalten dann die Vergleiche der Level des faktors `animal` *getrennt* für die Level es Faktors `site`.```{r}comp_3_obj <- fit_3 |>emmeans(~ animal | site) |>contrast(method ="pairwise", adjust ="bonferroni") comp_3_obj```Wir können uns das Ergebnis auch etwas schöner ausgeben lassen. Wir nutzen hier noch die Funktion `format.pval()` um die $p$-Werte besser zu formatieren. Die $p$-Wert, die kleiner sind als 0.001 werden als `<0.001` ausgegeben und die anderen $p$-Werte auf zwei Nachstellen nach dem Komma gerundet.```{r}comp_3_obj |>summary() |>as_tibble() |>select(contrast, site, p.value) |>mutate(p.value =format.pval(p.value, eps =0.001, digits =2))```In der Ausgabe können wir erkennen, dass die Vergleich in der Stadt alle signifkant sind. Jedoch erkennen wir keine signifikanten Ergebnisse mehr in dem Dorf und im Feld ist nur der Vergleich `dog - fox` signifkant. Hier solltest du nochmal beachten, warum wir die Analyse getrennt machen. In der zweifaktoriellen ANOVA haben wir gesehen, dass ein signifkanter Interaktionsterm zwischen den beiden Faktoren `animal` und `site` vorliegt. Wir wollen uns noch über die Funktion `confint()` die 95% Konfidenzintervalle wiedergeben lassen.```{r}res_3_obj <- comp_3_obj |>confint() |>as_tibble() |>select(contrast, site, estimate, conf.low = lower.CL, conf.high = upper.CL) res_3_obj```Besonders mit den 95% Konfiendezintervallen sehen wir nochmal den Interaktionseffekt zwischen den beiden Faktoren `animal` und `site`. So dreht sich der Effekt von zum Beispiel `dog - fox` von $-3.44$ in dem Level `city` zu $+2.35$ in dem Level `field`. Wir haben eine Interaktion vorliegen und deshalb die Analyse getrennt für jeden Level des Faktors `site` durchgeführt. @fig-emmeans-2 zeigt die entsprechenden 95% Konfidenzintervalle. Wir müssen hier etwas mit der `position` spielen, so dass die Punkte und der `geom_errorbar` richtig liegen.```{r}#| message: false#| warning: false#| echo: true#| fig-align: center#| fig-height: 3#| fig-width: 5#| fig-cap: Die 95% Konfidenzintervalle für den *allpair*-Vergleich des Models mit Interaktionseffekt.#| label: fig-emmeans-2ggplot(res_3_obj, aes(contrast, y=estimate, ymin=conf.low, ymax=conf.high,color = site, group = site)) +geom_hline(yintercept=0, linetype="11", colour="grey60") +geom_errorbar(width=0.1, position =position_dodge(0.5)) +geom_point(position =position_dodge(0.5)) +scale_color_okabeito() +coord_flip() +theme_classic()```## Gruppenvergleich mit `{multcomp}` {#sec-posthoc-multcomp}Wir drehen hier einmal die Erklärung um. Wir machen erst die Anwendung in R und sollte dich dann noch mehr über die statistischen Hintergründe der Funktionen interessieren, folgt ein Abschnitt noch zur Theorie. Du wirst die Funktionen aus `multcomp` vermutlich in deiner Abschlussarbeit brauchen. Häufig werden multiple Gruppenvergleiche in Abschlussarbeiten gerechnet.### Gruppenvergleiche mit `multcomp` in RAls erstes brauchen wir ein lineares Modell für die Verwendung von `multcomp`. Normalerweise verenden wir das gleiche Modell, was wir schon in der ANOVA verwendet haben. Wir nutzen hier ein simples lineares Modell mit nur einem Faktor. Im Prinzip kann das Modell auch größer sein, davon schauen wir uns dann später im Verlauf des Kapitels noch welche an.```{r}fit_1 <-lm(jump_length ~ animal, data = fac1_tbl)```Wir haben das Objekt `fit_1` mit der Funktion `lm()` erstellt. Im Modell sind jetzt alle Mittelwerte und die entsprechenden Varianzen geschätzt worden. Mit `summary(fit_1)` kannst du dir gerne das Modell auch nochmal anschauen. Wenn wir keinen *all-pair* Vergleich rechnen wollen, dann können wir auch einen *many-to-one* Vergleich mit dem `Dunnett` Kontrast rechnen.Im Anschluss nutzen wir die Funktion `glht()` um den multiplen Vergleich zu rechnen. Als erstes musst du wissen, dass wenn wir *alle* Vergleiche rechnen wollen, wir einen *all-pair* Vergleich rechnen. In der Statistik heißt dieser Typ von Vergleich `Tukey`. Wir wollen jetzt als für den Faktor `animal` einen multiplen `Tukey`-Vergleich rechnen. Nichts anders sagt `mcp(animal = "Tukey")` aus, dabei steht `mcp` für *multiple comparison procedure*. Mit dem hinteren Teil der Funktion weiß jetzt die Funktion `glht()` was gerechnet werden soll. Wir müssen jetzt der Funktion nur noch mitgeben auf was der multiple Vergleich gerechnet werden soll, mit dem Objekt `fit_1`. Wir speichern die Ausgabe der Funktion in `comp_1_obj`.```{r}comp_1_obj <-glht(fit_1, linfct =mcp(animal ="Tukey")) ```Mit dem Objekt `comp_1_fit` können wir noch nicht soviel anfangen. Der Inhalt ist etwas durcheinander und wir wollen noch die Konfidenzintervalle haben. Daher pipen wir `comp_1_fit` erstmal in die Funktion `tidy()` und lassen mit der Option `conf.int = TRUE` die simultanen 95% Konfidenzintervalle berechnen. Dann nutzen wir die Funktion `select()` um die wichtigen Spalten zu selektieren. Abschließend mutieren wir noch alle numerischen Spalten in dem wir auf die dritte Kommastelle runden. Wir speichern alles in das Objekt `res_1_obj`.```{r}#| message: falseres_1_obj <- comp_1_obj |>tidy(conf.int =TRUE) |>select(contrast, estimate, adj.p.value, conf.low, conf.high) |>mutate_if(is.numeric, round, 3)```Wir lassen uns dann den Inhalt von dem Objekt `res_1_obj` ausgeben.```{r}res_1_obj```Wir erhalten ein `tibble()` mit fünf Spalten. Zum einen den `contrast`, der den Vergleich widerspiegelt. Wir vergleichen im ersten Kontrast die Katzen- mit den Hundeflöhen, wobei wir `cat - dog` rechnen. Also wirklich der Mittelwert der Sprungweite der Katzenflöhe *minus* den Mittelwert der Sprungweite der Hundeflöhe rechnen. In der Spalte `estimate` sehen wir den Mittelwertsunterschied. Der Mittelwertsunterschied ist in der *Richtung* nicht ohne den Kontrast zu interpretieren. Danach erhalten wir die adjustierten $p$-Wert sowie die simultanen 95% Konfidenzintervalle.Wir können die Nullhypothese ablehnen für den Vergleiche`cat - dog` mit einem p-Wert von $0.006$ sowie für den Vergleich $fox - cat$ mit einem p-Wert von $0.001$. Beide p-Werte liegen unter dem Signifikanzniveau von $\alpha$ gleich 5%.Wenn es die unadjustierten $p$-Werte sein sollen, dann müssen wir nochmal das `glht`-Objekt in die Funktion `summary()` stecken und dann die Option `test = adjusted("none")` wählen. Dann können wir weiter machen wie gewohnt.```{r}#| message: false#| warning: falsesummary(comp_1_obj, test =adjusted("none")) |>tidy() ```In @fig-multcomp-1 sind die simultanen und damit adjustierten 95% Konfidenzintervalle nochmal in einem `ggplot` visualisiert. Die Kontraste und die Position hängen von dem Faktorlevel ab. Mit der Funktion `factor()` kannst du die Sortierung der Level einem Faktor ändern und somit auch Position auf den Achsen.```{r}#| message: false#| warning: false#| echo: true#| fig-align: center#| fig-height: 3#| fig-width: 5#| fig-cap: Simultane 95% Konfidenzintervalle für den paarweisen Vergleich der Sprungweiten in [cm] der Hunde-, Katzen- und Fuchsflöhe.#| label: fig-multcomp-1ggplot(res_1_obj, aes(contrast, y=estimate, ymin=conf.low, ymax=conf.high)) +geom_hline(yintercept=0, linetype="11", colour="grey60") +geom_errorbar(width=0.1) +geom_point() +coord_flip() +theme_classic()```Die Entscheidung gegen die Nullhypothese anhand der simultanen 95% Konfidenzintervalle ist inhaltlich gleich, wie die Entscheidung anhand der p-Werte. Wir entscheiden gegen die Nullhypothese, wenn die 0 nicht mit im Konfindenzintervall enthalten ist. Wir wählen hier die 0 zur Entscheidung gegen die Nullhypothese, weil wir einen Mittelwertsvergleich rechnen.Für den Vergleich `fox -dog` ist die 0 im 95% Konfidenzintervall, wir können daher die Nullhypothese nicht ablehnen. Das 95% Konfidenzintervall ist nicht signifikant. Bei dem Vergleich `fox - cat` sowie dem Vergleich `cat - dog` ist jeweils die 0 nicht im 95% Konfidenzintervall enthalten. Beide 95% Konfidenzintervalle sind signifikant, wir können die Nullhypothese ablehnen.## Gruppenvergleich mit Varianzheterogenität {#sec-posthoc-var-heterogen}Bis jetzt sind wir von Varianzhomogenität über alle Gruppen in unserer Behandlung ausgegangen. Oder aber konkret auf unser Beispiel, die Tierarten haben alle die gleiche Varianz. Jetzt gibt es aber häufiger mal den Fall, da können oder wollen wir nicht an Varianzhomogenität über alle Gruppen glauben. Deshalb gibt es hier noch Alternativen, von denen ich ein paar Vorstellen werde.### Games-Howell-Test {#sec-posthoc-ght}Der Games-Howell-Test ist eine Alternative zu dem Paket `{multcomp}` und dem Paket `{emmeans}` für ein einfaktorielles Design. Wir nutzen den Games-Howell-Test, wenn die Annahme der Homogenität der Varianzen, der zum Vergleich aller möglichen Kombinationen von Gruppenunterschieden verwendet wird, verletzt ist. Dieser Post-Hoc-Test liefert Konfidenzintervalle für die Unterschiede zwischen den Gruppenmitteln und zeigt, ob die Unterschiede statistisch signifikant sind. Der Test basiert auf der Welch'schen Freiheitsgradkorrektur und adjustiert die $p$-Werte. Der Test vergleicht also die Differenz zwischen den einzelnen Mittelwertpaaren mit einer Adjustierung für den Mehrfachtest. Es besteht also keine Notwendigkeit, zusätzliche p-Wert-Korrekturen vorzunehmen. Mit dem Games-Howell-Test ist nur ein *all-pair* Vergleich möglich.Für den Games-Howell-Test aus dem Paket `{rstatix}` müssen wir kein lineares Modell fitten. Wir schreiben einfach die wie in einem t-Test das Outcome und den Faktor mit den Gruppenleveln in die Funktion `games_howell_test()`. Wir erhalten dann direkt das Ergebnis des Games-Howell-Test. Wir nutzen in diesem Beispiel die Daten aus dem Objekt `fac1_tbl` zu sehen in @tbl-data-posthoc-1.```{r}fit_4 <-games_howell_test(jump_length ~ animal, data = fac1_tbl) ```Wir wollen aber nicht mit der Ausgabe arbeiten sondern machen uns noch ein wenig Arbeit und passen die Ausgabe an. Zum einen brauchen wir noch die Kontraste und wir wollen die $p$-Werte auch ansprechend formatieren. Wir erhalten das Objekt `res_4_obj` und geben uns die Ausgabe wieder.```{r}res_4_obj <- fit_4 |>as_tibble() |>mutate(contrast =str_c(group1, "-", group2)) |>select(contrast, estimate, p.adj, conf.low, conf.high) |>mutate(p.adj =format.pval(p.adj, eps =0.001, digits =2))res_4_obj```Wir erhalten ein `tibble()` mit fünf Spalten. Zum einen den `contrast`, der den Vergleich widerspiegelt, den haben wir uns selber mit der Funktion `mutate()` und `str_c()` aus den Spalten `group1` und `group2` gebaut. Wir vergleichen im ersten Kontrast die Katzen- mit den Hundeflöhen, wobei wir `dog-cat` rechnen. Also wirklich den Mittelwert der Sprungweite der Hundeflöhe *minus* den Mittelwert der Sprungweite der Katzenflöhe rechnen. In der Spalte `estimate` sehen wir den Mittelwertsunterschied. Der Mittelwertsunterschied ist in der *Richtung* nicht ohne den Kontrast zu interpretieren. Danach erhalten wir die adjustierten $p$-Wert sowie die simultanen 95% Konfidenzintervalle.Wir können die Nullhypothese ablehnen für den Vergleiche `dog - cat` mit einem p-Wert von $0.02$ sowie für den Vergleich $cat - fox$ mit einem p-Wert von $0.00$. Beide p-Werte liegen unter dem Signifikanzniveau von $\alpha$ gleich 5%.In @fig-ght-1 sind die simultanen 95% Konfidenzintervalle nochmal in einem `ggplot` visualisiert. Die Kontraste und die Position hängen von dem Faktorlevel ab.```{r}#| message: false#| warning: false#| echo: true#| fig-align: center#| fig-height: 3#| fig-width: 5#| fig-cap: Die 95% Konfidenzintervalle für den *allpair*-Vergleich des Games-Howell-Test.#| label: fig-ght-1ggplot(res_4_obj, aes(contrast, y=estimate, ymin=conf.low, ymax=conf.high)) +geom_hline(yintercept=0, linetype="11", colour="grey60") +geom_errorbar(width=0.1, position =position_dodge(0.5)) +geom_point(position =position_dodge(0.5)) +coord_flip() +theme_classic()```Die Entscheidungen nach den 95% Konfidenzintervallen sind die gleichen wie nach dem $p$-Wert. Da wir hier es mit einem Mittelwertsvergleich zu tun haben, ist die Entscheidung gegen die Nullhypothese zu treffen wenn die 0 im Konfidenzintervall ist.### Generalized Least SquaresNeben dem Games-Howell-Test gibt es auch die Möglichkeit *Generalized Least Squares* zu nutzen. Hier haben wir dann auch die Möglichkeit mehrfaktorielle Modelle zu schätzen und dann auch wieder `emmeans` zu nutzen. Das ist natürlich super, weil wir dann wieder in dem `emmeans` Framework sind und alle Funktionen von oben nutzen können. Deshalb hier auch nur die Modellanpassung, den Rest kopierst du dir dann von oben dazu.Die Funktion `gls()` aus dem R Paket `{nlme}` passt ein lineares Modell unter Verwendung der verallgemeinerten kleinsten Quadrate an. Die Fehler dürfen dabei aber korreliert oder aber ungleiche Varianzen haben. Damit haben wir ein Modell, was wir nutzen können, wenn wir Varianzheterogenität vorliegen haben. Hier einmal das simple Beispiel für die Tierarten. Wir nehmen wieder die ganz normale Formelschreiweise. Wir können jetzt aber über die Option `weights =` angeben, wie wir die Varianz modellieren wollen. Die Schreibweise mag etwas ungewohnt sein, aber es gibt wirklich viele Arten die Varainz zu modellieren. Hier machen wir uns es einfach und nutzen die Helferfunktion `varIdent` und modellieren dann für jedes Tier eine eigene Gruppenvarianz.```{r}gls_fac1_fit <-gls(jump_length ~ animal, weights =varIdent(form =~1| animal), data = fac1_tbl)```Dann können wir die Modellanpasssung auch schon in `emmeans()` weiterleiten und schauen uns mal das Ergebnis gleich an. Wir achten jetzt auf die Spalte `SE`, die uns ja den Fehler der Mittelwerte für jede Gruppe wiedergibt.```{r}gls_fac1_fit |>emmeans(~ animal)```Wir sehen, dass wir für jedes Tier eine eigene Varianz über den Standardfehler `SE` geschätzt haben. Das war es ja auch was wir wollten. Bis hierhin wäre es auch mit dem Games-Howell-Test gegangen. Was ist aber, wenn wir ein zweifaktorielles design mit Interaktion schätzen wollen? Das können wir analog wie eben machen. Wir erweitern einfach das Modell um die Terme `site` für den zweiten Faktor und den Interaktionsterm `animal:site`.```{r}gls_fac2_fit <-gls(jump_length ~ animal + site + animal:site, weights =varIdent(form =~1| animal), data = fac2_tbl)```Dann können wir uns wieder die multiplen Vergleiche getrennt für die Interaktionsterme wiedergeben lassen. Blöderweise haben jetzt alle Messorte `site` die gleiche Varianz für jede Tierart, aber auch da können wir noch ran.```{r}gls_fac2_fit |>emmeans(~ animal | site)```Die eigentliche Stärke von `gls()` kommt eigentlich erst zu tragen, wenn wir auch noch erlauben, dass wir die Varianz *über alle* Tierarten, Messsorte und Interaktionen variieren kann. Das machen wir, in dem wir einfach `animal*site` zu der `varIdent()` Funktion ergänzen.```{r}gls_fac2_fit <-gls(jump_length ~ animal + site + animal:site, weights =varIdent(form =~1| animal*site), data = fac2_tbl)```Dann noch schnell in `emmeans()` gesteckt und sich das Ergebnis angeschaut.```{r}gls_fac2_fit |>emmeans(~ animal | site)```Wie du jetzt siehst schätzen wir die Varianz für jede Tierart und jeden Messort separat. Wir haben also wirklich jede Varianz einzeln zugeordnet. Die Frage ist immer, ob das notwendig ist, denn wir brauchen auch eine gewisse Fallzahl, damit die Modelle funktionieren. Aber das kommt jetzt sehr auf deine Fragestellung an und müssten wir nochmal konkret besprechen.::: callout-tip## Weitere LiteraturAuf der Seite DSFAIR gibt es noch einen Artikel zu `emmeans` und der Frage [Why are the StdErr all the same?](https://schmidtpaul.github.io/dsfair_quarto/ch/summaryarticles/whyseequal.html) und dazu dann auch passend die Publikation [Analyzing designed experiments: Should we report standard deviations or standard errors of the mean or standard errors of the difference or what?](https://www.cambridge.org/core/services/aop-cambridge-core/content/view/92DB0AF151C157B9C6E2FA40F9C9B635/S0014479719000401a.pdf/analyzing-designed-experiments-should-we-report-standard-deviations-or-standard-errors-of-the-mean-or-standard-errors-of-the-difference-or-what.pdf):::### Robuste Schätzung von StandardfehlernWir immer gibt es noch eine Möglichkeit die Varianzheterogenität zu behandeln. Wir nutzen jetzt hier einmal die Funktionen aus dem R Paket `{sandwich}`, die es uns ermöglichen Varianzheterogenität (eng. *heteroskedasticity*) zu modellieren. Es ist eigentlich super einfach, wir müssen als erstes wieder unser Modell anpassen. Hier einmal mit einer simplen linearen Regression.```{r}lm_fac1_fit <-lm(jump_length ~ animal, data = fac1_tbl)```Dann können wir auch schon für einen Gruppenvergleich direkt in der Funktion `emmeans()` für die Varianzheterogenität adjustieren. Es gibt verschiedene mögliche Sandwich-Schätzer, aber wir nehmen jetzt mal einen der häufigsten mit `vcovHC`. Wie immer gilt, es gibt ja nach Datenlage bessere und schlechtere Schätzer. Wir laden jetzt nicht das ganze Paket, sondern nur die Funktion mit `sandwich::vcovHAC`. Achtung, hinter der Option `vcov.` ist ein *Punkt*. Ohne den Aufruf `vcov. =` funktioniert die Funktion dann nicht.```{r}em_obj <- lm_fac1_fit |>emmeans(~ animal, method ="pairwise", vcov. = sandwich::vcovHAC)em_obj```Wir du siehst, die Standardfehler sind jetzt nicht mehr über alle Gruppen gleich. Dann können wir uns auch die paarweisen Vergleiche ausgeben lassen.```{r}contr_obj <- em_obj |>contrast(method ="pairwise", adjust ="none")```Oder aber wir lassen uns das *compact letter display* wiedergeben.```{r}cld_obj <- em_obj |>cld(Letters = letters, adjust ="none")```::: {.callout-tip collapse="true"}## Exkurs: Robuste Schätzung von Standardfehlern, Konfidenzintervallen und p-WertenWenn du noch etwas weiter gehen möchtest, dann kannst du dir noch die Hilfeseite von dem R Paket `{performance}`[Robust Estimation of Standard Errors, Confidence Intervals, and p-values](https://easystats.github.io/parameters/articles/model_parameters_robust.html?q=Heteroskedasticity#robust-covariance-matrix-estimation-from-model-parameters) anschauen. Die Idee ist hier, dass wir die Varianz/Kovarianz robuster daher mit der Berücksichtigung von Varianzheterogenität (eng. *heteroskedasticity*) schätzen.:::## Compact letter display {#sec-compact-letter}In der Pflanzenernährung ist es nicht unüblich sehr viele Substrate miteinander zu vergleichen. Oder andersherum, wenn wir sehr viele Gruppen haben, dann kann die Darstellung in einem *all-pair* Vergleich sehr schnell sehr unübersichltich werden. Deshalb wure das *compact letter display* entwickelt. Das *compact letter display* zeigt an, bei welchen Vergleichen der Behandlungen die Nullhypothese gilt. Daher werden die *nicht* signifikanten Ergebnisse visualisiert. Gut zu lesen ist auch die Vignette [Re-engineering CLDs](https://cran.r-project.org/web/packages/emmeans/vignettes/re-engineering-clds.html) der Hilfeseite zu `{emmeans}` sowie die Hilfeseite [Compact Letter Display (CLD) - What is it?](https://schmidtpaul.github.io/DSFAIR/compactletterdisplay.html).Schauen wir uns aber zuerst einmal ein größeres Beispiel mit neun Behandlungen mit jeweils zwanzig Beobachtungen an. Wir erstellen uns den Datensatz in der Form, dass sich die Mittelwerte für die Behandlungen teilweise unterscheiden.```{r}set.seed(20220914)data_tbl <-tibble(trt =gl(n =9, k =20, labels =c("pos_ctrl", "neg_ctrl", "treat_A", "treat_B", "treat_C", "treat_D", "treat_E", "treat_F", "treat_G")),rsp =c(rnorm(20, 10, 5), rnorm(20, 20, 5), rnorm(20, 22, 5), rnorm(20, 24, 5),rnorm(20, 35, 5), rnorm(20, 37, 5), rnorm(20, 40, 5), rnorm(20, 43, 5),rnorm(20, 50, 5)))```In der @fig-boxplot-cld-1 ist der Datensatz `data_tbl` nochmal als Boxplot dargestellt.```{r}#| message: false#| echo: false#| fig-align: center#| fig-height: 5#| fig-width: 6#| fig-cap: Boxplot der Beispieldaten.#| label: fig-boxplot-cld-1ggplot(data_tbl, aes(x = trt, y = rsp, fill = trt)) +theme_minimal() +geom_boxplot() +scale_fill_okabeito() +geom_jitter(width =0.15, alpha =0.5) +theme(legend.position ="none")```Wir sehen, dass sich die positive Kontrolle von dem Rest der Behandlungen unterscheidet. Danach haben wir ein Plateau mit der negativen Kontrolle und der Behanldung A und der Behandlung B. Nach diesem Plateau haben wir einen Sprung und sehen einen leicht linearen Anstieg der Mittelwerte der Behandlungen.Schauen wir uns zuerst einmal an, wie ein *compact letter display* aussehen würde, wenn kein Effekt vorliegen würde. Daher die Nullhypothese ist wahr und die Mittelwerte der Gruppen unterscheiden sich nicht. Wir nutzen hier einmal ein kleineres Beispiel mit den Behandlungslevels `ctrl`, `treat_A` und `treat_B`. Alle drei Behandlungslevel haben einen Mittelwert von 10. Es gilt die Nullhypothese und wir erhalten folgendes *compact letter display* in @tbl-no-effect-cld.| Behandlung | Mittelwert | $\phantom{a}$ | | ||:----------:|:----------:|:-------------:|:-------------:|:-------------:|| ctrl | 10 | a | $\phantom{a}$ | $\phantom{a}$ || treat_A | 10 | a | | || treat_B | 10 | a | | |: Das *compact letter display* für drei Behandlungen nach einem paarweisen Vergleich. Die Nullhypothese gilt, es gibt keinen Mittelwertsunterschied. {#tbl-no-effect-cld}Das Gegenteil sehen wir in der @tbl-effect-cld. Hier haben wir ein *compact letter display* wo sich alle drei Mittelwerte mit 10, 15 und 20 voneinander klar unterscheiden. Die Nullhypothese gilt für keinen der möglichen paarweisen Vergleiche.| Behandlung | Mittelwert | | | ||:----------:|:----------:|:-------------:|:-------------:|:-------------:|| ctrl | 10 | a | $\phantom{a}$ | $\phantom{a}$ || treat_A | 15 | | b | || treat_B | 20 | $\phantom{a}$ | | c |: Das *compact letter display* für drei Behandlungen nach einem paarweisen Vergleich. Die Nullhypothese gilt nicht, es gibt einen Mittelwertsunterschied. {#tbl-effect-cld}Schauen wir uns nun die Implementierung des *compact letter display* für die verschiedenen Möglichkeiten der Multiplen Vergleiche einmal an.### ... für `pairwise.*.test()`Wenn wir für die Funktionen `pairwise.*.test()` das *compact letter display* berechnen wollen, dann müssen wir etwas ausholen. Denn wir müssen dafür die Funktion `multcompLetters()` nutzen. Diese Funktion braucht die $p$-Werte als Matrix und diese Matrix der $p$-Werte kriegen wir über die Funktion `fullPTable()`. Am Ende haben wir aber dann das was wir wollten. Ich habe hier nochmal das einfache Beispiel mit den Sprungweiten von oben genommen.```{r}pairwise.t.test(fac1_tbl$jump_length, fac1_tbl$animal,p.adjust.method ="bonferroni") |>extract2("p.value") |>fullPTable() |>multcompLetters()```Als Ergebnis erhalten wir, dass Hund- und Fuchsflöhe gleich weit springen, beide teilen sich den gleichen Buchstaben. Katzenflöhe springen unterschiedlich zu Hunden- und Fuchsflöhen. Das Vorgehen ändert sich dann nicht, wenn wir eine andere Funktion wie `pairwise.wilcox.test()` nehmen.### ... für das Paket `{emmeans}`In dem Paket `{emmeans}` ist das *compact letter display* ebenfalls implementiert und wir müssen nicht die Funktion `multcompLetters()` nutzen. Durch die direkte Implementierung ist es etwas einfacher sich das *compact letter display* anzeigen zu lassen. Das Problem ist dann später sich die Buchstaben zu extrahieren um die @fig-boxplot-cld-3 zu ergänzen. Wir nutzen in `{emmeans}` die Funktion `cld()` um das *compact letter display* zu erstellen.```{r}emmeans_cld <-lm(rsp ~ trt, data = data_tbl) |>emmeans(~ trt) |>cld(Letters = letters, adjust ="bonferroni")```Wir erhalten dann die etwas besser sortierte Ausgabe für die Behandlungen wieder.```{r}emmeans_cld ```Wie die Ausgabe von `cld()` richtig anmerkt, können *compact letter display* irreführend sein weil sie eben **Nicht**-Unterschiede anstatt von signifikanten Unterschieden anzeigen. Zum Anderen sehen wir aber auch, dass wir 36 statistische Tests gerechnet haben und somit zu einem Signifikanzniveau von $\cfrac{\alpha}{k} = \cfrac{0.05}{36} \approx 0.0014$ testen. Wir brauchen also schon sehr große Unterschiede oder aber eine sehr kleine Streuung um hier signifikante Effekte nachweisen zu können.In @tbl-mean-to-letter-emmeans sehen wir das Ergebnis des *compact letter display* nochmal mit den Mittelwerten der Behandlungslevel zusammen dargestellt. Wir sehen wieder, dass sich `pos_crtl` von allen anderen Behandlungen unterscheidet, deshalb hat nur die Behandlung `pos_crtl` den Buchstaben `a`. Die Mittelwerte vom `neg_ctrl`, `treat_A` und `treat_B` sind nahezu gleich, also damit nicht signifikant. Deshalb erhalten diese Behandlungslevel ein `b`. Wir gehen so alle Vergleiche einmal durch.| Behandlung | Mittelwert | | | | | | ||:----------:|:----------:|:---:|:---:|:---:|:---:|:---:|:---:|| pos_crtl | 10 | a | | | | | || neg_ctrl | 20 | | b | | | | || treat_A | 22 | | b | | | | || treat_B | 24 | | b | | | | || treat_C | 35 | | | c | | | || treat_D | 37 | | | c | d | | || treat_E | 40 | | | | d | e | || treat_F | 43 | | | | | e | || treat_G | 45 | | | | | | f |: Kombination der Level der Behandlungen und deren Mittelwerte zur Generieung sowie dem *compact letter display* generiert aus den adjustierten $p$-Werten aus `emmeans`. Gleiche Buchstaben bedeuten *kein* signifikanter Unterschied. {#tbl-mean-to-letter-emmeans}Abschließend können wir die Buchstaben aus dem *compact letter display* noch in die @fig-boxplot-cld-3 ergänzen. Hier müssen wir etwas mehr machen um die Buchstaben aus dem Objekt `emmeans_cld` zu bekommen. Du kannst dann noch die y-Position anpassen wenn du möchtest.```{r}#| message: false#| echo: true#| fig-align: center#| fig-height: 5#| fig-width: 6#| fig-cap: Boxplot der Beispieldaten zusammen mit den *compact letter display*.#| label: fig-boxplot-cld-3letters_tbl <- emmeans_cld |>tidy() |>select(trt, label = .group) |>mutate(rsp =0)ggplot(data_tbl, aes(x = trt, y = rsp, fill = trt)) +theme_minimal() +geom_boxplot() +scale_fill_okabeito() +geom_jitter(width =0.15, alpha =0.5) +geom_text(data = letters_tbl, aes(x = trt , y = rsp, label = label)) +theme(legend.position ="none")```::: callout-note## Das *compact letter display* anders gebaut...In dem kurzen Kapitel zu [Re-engineering CLDs](https://cran.r-project.org/web/packages/emmeans/vignettes/re-engineering-clds.html) in der Vingette des R Pakets `{emmeans}` geht es darum, wie das *compact letter display* auch anders gebaut werden könnte. Nämlich einmal als wirkliches Anzeigen von Gleichheit über die Option `delta` oder aber über das Anzeigen von Signifikanz über die Option `signif`. Damit haben dann auch wirklich die Information, die wir dann wollen. Also eigentlich was Schönes. Wie machen wir das nun?Wenn wir das *compact letter display* in dem Sinne der Gleichheit der Behandlungen interpretieren wollen, also das der gleiche Buchstabe bedeutet, dass sich die Behandlungen nicht unterscheiden, dann müssen wir ein `delta` setzen in deren Bandbreite oder Intervall die Behandlungen gleich sind. Ich habe hier mal ein `delta` von 20 gewählt und wir adjustieren bei einem Test auf Gleichheit nicht.```{r}emmeans_cld <-lm(rsp ~ trt, data = data_tbl) |>emmeans(~ trt) |>cld(Letters = letters, adjust ="none", delta =20)emmeans_cld ```Wie wir jetzt sehen, bedeuten gleiche Buchstaben, dass die Behandlungen gleich sind. In dem Sinne gleich sind, dass die Behandlungen im Mittel nicht weiter als der Wert in `delta` auseinanderliegen. Wie du jetzt das `delta` bestimmst ist eine biologische und keine statistische Frage.Können wir uns auch signifikante Unterschiede anzeigen lassen? Ja, können wir auch, aber das ist meiner Meinung nach die schlechtere der beiden Anpassungen. Wir haben ja im Kopf, dass das *compact letter display* eben mit gleichen Buchstaben das Gleiche anzeigt. Jetzt würden wir diese Eigenschaften zu Unterschied ändern. Schauen wir uns das einmal an einem kleineren Datensatz einmal an.```{r}small_fit <- data_tbl |>filter(trt %in%c("pos_ctrl", "neg_ctrl", "treat_A", "treat_G")) |>lm(rsp ~ trt, data = _) ```Dann können wir uns hier einmal das Problem mit den Buchstaben anschauen. Wir kriegen jetzt mit der Option `signif = TRUE` wiedergeben `Estimates sharing the same symbol are significantly different` und das ist irgendwie auch wirr, dass *gleiche* Buchstaben einen Unterschied darstellen. Das *compact letter display* wird eben als Gleichheit gelesen, so dass wir hier mehr verwirrt werden als es hilft.```{r}small_fit |>emmeans(~ trt) |>cld(Letters = letters, adjust ="bonferroni", signif =TRUE)```Deshalb würde ich auf die Buchstaben verzichten und die Zahlen angeben, damit hier nicht noch mehr Verwirrung aufkommt. Wir nehmen also die Option für die Buchstaben einmal aus dem `cld()` Aufruf raus. Dann haben wir Zahlen als Gruppenzuweisung, was schon mal was anderes ist als die Buchstaben aus dem *compact letter display*.```{r}small_fit |>emmeans(~ trt) |>cld(adjust ="bonferroni", signif =TRUE)```Innerhalb des selben Konzepts dann zwei Arten von Interpretation des *compact letter display* zu haben, ist dann auch nicht zielführend. Den auch die *gleichen* Zahlen bedeuten jetzt einen Unterschied. Irgendwie mag ich persönlich nicht diese sehr verdrehte Interpretation nicht. Deshalb lieber ein `delta` einführen und auf echte Gleichheit testen.:::### ... für das Paket `{multcomp}`Wir schauen uns zuerst einmal die Implementierung des *compact letter display* in dem Paket `{multcomp}` an. Wir nutzen die Funktion `multcompLetters()` aus dem Paket `{multcompView}` um uns das *compact letter display* wiedergeben zu lassen. Davor müssen wir noch einige Schritte an Sortierung und Umbenennung durchführen. Das hat den Grund, dass die Funktion `multcompLetters()` *nur* einen benannten Vektor mit $p$-Werten akzeptiert. Das heist wir müssen aus der Funktion `glht()` die adjustierten $p$-Werte extrahieren und dann einen Vektor der Vergleiche bzw. Kontraste in der Form `A-B` bauen. Also ohne Leerzeichen und in der Beschreibung der Level der Behandlung `trt`. Die Funktion `pull()` erlaubt uns einen Spalte als Vektor aus einem `tibble()` zu ziehen und dann nach der Spalte `contrast` zu benennen.```{r}#| warning: falsemultcomp_cld <-lm(rsp ~ trt, data = data_tbl) |>glht(linfct =mcp(trt ="Tukey")) |>tidy() |>mutate(contrast =str_replace_all(contrast, "\\s", "")) |>pull(adj.p.value, contrast) |>multcompLetters() ```Wir erhalten dann folgendes *compact letter display* für die paarweisen Vergleiche aus `multcomp`.```{r}multcomp_cld ```Leider sind diese Buchstaben in dieser Form schwer zu verstehen. Deshalb gibt es noch die Funktion `plot()` in dem Paket `{multcompView}` um uns die Buchstaben mit den Leveln der Behandlung einmal ausgeben zu lassen. Wir erhalten dann folgende Abbildung.```{r}#| warning: false#| message: false#| results: hidemultcomp_cld |>plot()```In dem *compact letter display* bedeuten gleiche Buchstaben, dass die Behandlungen gleich sind. Es gilt die Nullhypothese für diesen Vergleich. Was sehen wir also hier? Kombinieren wir einmal das *compact letter display* mit den Leveln der Behandlung und den Mittelwerten der Behandlungen in einer @tbl-mean-to-letter-multcomp. Wenn die Mittelwerte *gleich* sind, dann erhalten die Behandlungslevel den gleichen Buchstaben. Die Mittelwerte vom `neg_ctrl`, `treat_A` und `treat_B` sind nahezu gleich, also damit nicht signifikant. Deshalb erhalten diese Behandlungslevel ein `a`. Ebenso sind die MIttelwerte von `treat_C` und `treat_D` nahezu gleich, dehalb erhalten beide ein `b`. Das machen wir immer so weiter und konzentrieren uns also auf die *nicht* signifikanten Ergebnisse. Denn gleiche Buchstaben bedeuten, dass die Behandlungen gleich sind. Wir sehen hier also, bei welchen Vergleichen die Nullhypothese gilt.| Behandlung | Mittelwert | | | | | | ||:----------:|:----------:|:---:|:---:|:---:|:---:|:---:|:---:|| neg_ctrl | 20 | a | | | | | || treat_A | 22 | a | | | | | || treat_B | 24 | a | | | | | || treat_C | 35 | | b | | | | || treat_D | 37 | | b | c | | | || treat_E | 40 | | | c | d | | || treat_F | 43 | | | | d | | || treat_G | 45 | | | | | e | || pos_crtl | 10 | | | | | | f |: Kombination der Level der Behandlungen und deren Mittelwerte zur Generieung sowie dem *compact letter display* generiert aus den adjustierten $p$-Werten aus `multcomp`. Gleiche Buchstaben bedeuten *kein* signifikanter Unterschied. {#tbl-mean-to-letter-multcomp}Wir können dann die Buchstaben auch in den Boxplot ergaänzen. Die y-Position kann je nach Belieben dann noch angepasst werden. zum Beispiel könnten hier auch die Mittelwerte aus einer `summarise()` Funktion ergänzt werden und so die y-Position angepasst werden.```{r}#| message: false#| echo: true#| fig-align: center#| fig-height: 5#| fig-width: 6#| fig-cap: Boxplot der Beispieldaten zusammen mit den *compact letter display*.#| label: fig-boxplot-cld-2letters_tbl <- multcomp_cld$Letters |>enframe("trt", "label") |>mutate(rsp =0)ggplot(data_tbl, aes(x = trt, y = rsp, fill = trt)) +theme_minimal() +geom_boxplot() +scale_fill_okabeito() +geom_jitter(width =0.15, alpha =0.5) +geom_text(data = letters_tbl, aes(x = trt , y = rsp, label = label)) +theme(legend.position ="none")```### ... für den Games-Howell-TestAbschließend wollen wir uns die Implementierung des *compact letter display* für den Games-Howell-Test einmal anschauen. Es gilt vieles von dem in diesem Abschnitt schon gesagtes. Wir nutzen die Funktion `multcompLetters()` aus dem Paket `{multcompView}` um uns das *compact letter display* aus dem Games-Howell-Test wiedergeben zu lassen. Davor müssen wir noch einige Schritte an Sortierung und Umbenennung durchführen. Das hat den Grund, dass die Funktion `multcompLetters()` *nur* einen benannten Vektor mit $p$-Werten akzeptiert. Die Funktion `pull()` erlaubt uns einen Spalte als Vektor aus einem `tibble()` zu ziehen und dann nach der Spalte `contrast` zu benennen.```{r}ght_cld <-games_howell_test(rsp ~ trt, data = data_tbl) |>mutate(contrast =str_c(group1, "-", group2)) |>pull(p.adj, contrast) |>multcompLetters() ```Das *compact letter display* kennen wir schon aus der obigen Beschreibung.```{r}ght_cld```Wir können uns dann auch das *compact letter display* als übersichtlicheren Plot wiedergeben lassen.```{r}#| warning: false#| message: false#| results: hideght_cld |>plot()```Um die Zusammenhänge besser zu verstehen ist in @tbl-mean-to-letter-ght nochmal die Kombination der Level der Behandlungen und deren Mittelwerte zur Generieung sowie dem *compact letter display* dargestellt. Wir sehen wieder, dass sich `pos_crtl` von allen anderen Behandlungen unterscheidet, deshalb hat nur die Behandlung `pos_crtl` den Buchstaben `a`. Die Mittelwerte vom `neg_ctrl`, `treat_A` und `treat_B` sind nahezu gleich, also damit nicht signifikant. Deshalb erhalten diese Behandlungslevel ein `b`. In der Form können wir alle Vergleiche einmal durchgehen.| Behandlung | Mittelwert | | | | | ||:----------:|:----------:|:---:|:---:|:---:|:---:|:---:|| pos_crtl | 10 | a | | | | || neg_ctrl | 20 | | b | | | || treat_A | 22 | | b | | | || treat_B | 24 | | b | | | || treat_C | 35 | | | c | | || treat_D | 37 | | | c | d | || treat_E | 40 | | | | d | || treat_F | 43 | | | | d | || treat_G | 45 | | | | | e |: Kombination der Level der Behandlungen und deren Mittelwerte zur Generieung sowie dem *compact letter display* generiert aus den adjustierten $p$-Werten aus dem Games-Howell-Test. Gleiche Buchstaben bedeuten *kein* signifikanter Unterschied. {#tbl-mean-to-letter-ght}Wir können dann auch in @fig-boxplot-cld-4 sehen, wie das *compact letter display* mit den Boxplots verbunden wird.```{r}#| message: false#| echo: true#| fig-align: center#| fig-height: 5#| fig-width: 6#| fig-cap: Boxplot der Beispieldaten zusammen mit den *compact letter display*.#| label: fig-boxplot-cld-4letters_tbl <- ght_cld$Letters |>enframe("trt", "label") |>mutate(rsp =0)ggplot(data_tbl, aes(x = trt, y = rsp, fill = trt)) +theme_minimal() +geom_boxplot() +scale_fill_okabeito() +geom_jitter(width =0.15, alpha =0.5) +geom_text(data = letters_tbl, aes(x = trt , y = rsp, label = label)) +theme(legend.position ="none")```## Referenzen {.unnumbered}