```{r echo = FALSE, warning = FALSE, message=FALSE}
source("init.R")
```
# Correlation and $R^2$ {#sec-temp}
*Last modified on `r format(fs::file_info("chapter-42-r2-r.qmd")$modification_time, '%d. %B %Y at %H:%M:%S')`*
> *"A quote." --- Dan Meyer*
## General background
```{r}
#| message: false
#| warning: false
r2_good_tbl <- tibble(weight = abs(rnorm(5, 3, 4)),
jumplength = 10 + 1.2 * weight + rnorm(5, 0, 3))
r2_good_fit <- lm(jumplength ~ weight, data = r2_good_tbl)
mean_good_cat_jump <- mean(r2_good_tbl$jumplength)
r2_good_plot_tbl <- r2_good_tbl |>
mutate(sy = jumplength - mean(jumplength),
e = residuals(r2_good_fit))
sum_good_sy <- (r2_good_plot_tbl$sy)^2 |> abs() |> sum() |> round(2)
sum_good_e <- (r2_good_plot_tbl$e)^2 |> abs() |> sum() |> round(2)
r2_good <- 1-(sum_good_e/sum_good_sy)
r2_bad_tbl <- tibble(weight = r2_good_tbl$weight,
jumplength = 9 + 0.5 * weight + rnorm(5, 0, 4))
r2_bad_fit <- lm(jumplength ~ weight, data = r2_bad_tbl)
mean_bad_cat_jump <- mean(r2_bad_tbl$jumplength)
r2_bad_plot_tbl <- r2_bad_tbl |>
mutate(sy = jumplength - mean(jumplength),
e = residuals(r2_bad_fit),
e2 = e^2)
sum_bad_sy <- (r2_bad_plot_tbl$sy)^2 |> abs() |> sum() |> round(2)
sum_bad_e <- (r2_bad_plot_tbl$e)^2 |> abs() |> sum() |> round(2)
r2_bad <- 1-(sum_bad_e/sum_bad_sy)
```
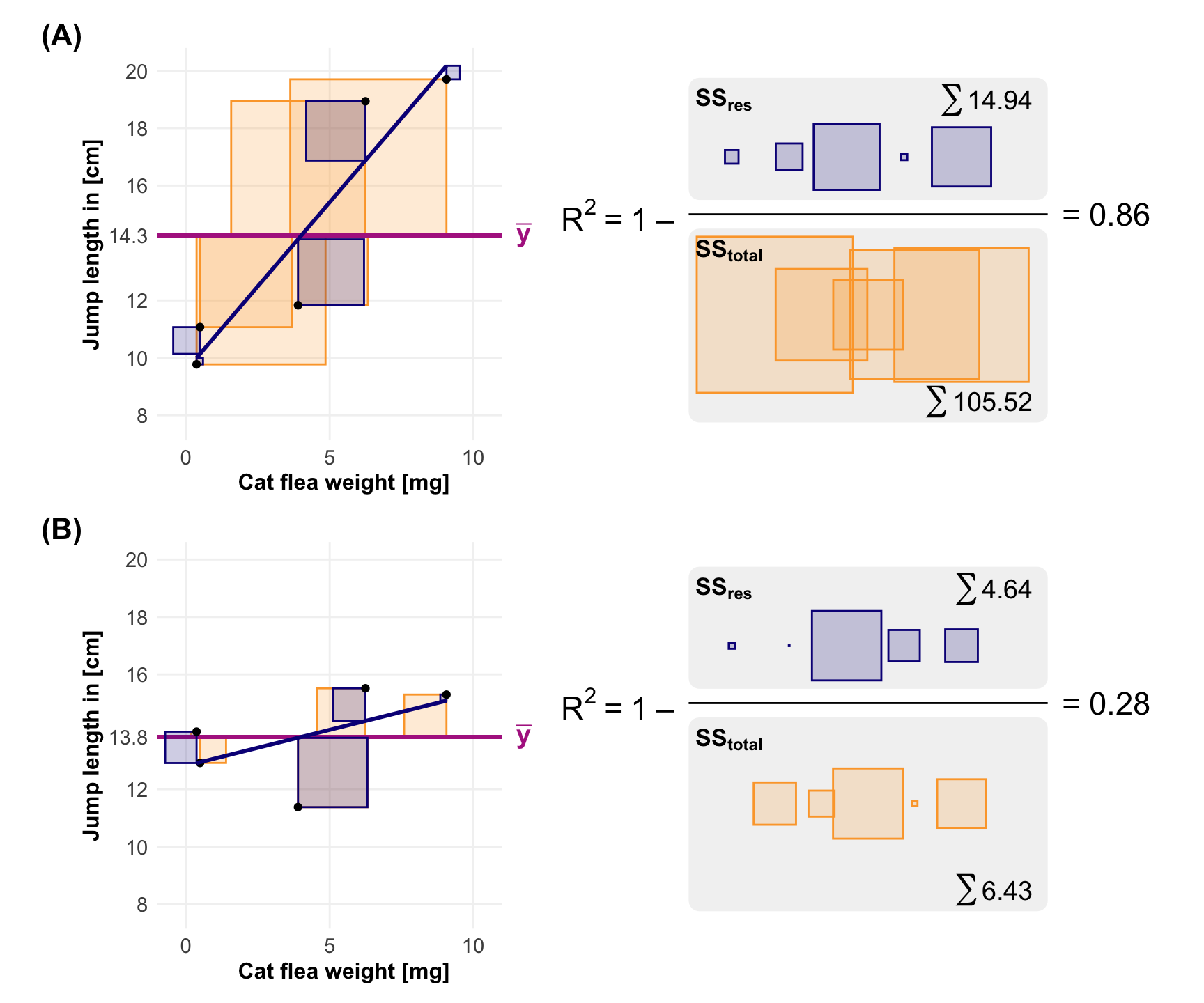
$$
R^2 = 1 - \cfrac{SS_{res}}{SS_{total}}
$$
```{r}
#| message: false
#| echo: false
#| warning: false
#| fig-align: center
#| fig-height: 7.5
#| fig-width: 9
#| fig-cap: "foo"
#| label: fig-r2-example
p_r2_good <- r2_good_plot_tbl |>
ggplot(aes(x = weight, y = jumplength)) +
theme_book() +
coord_equal() +
annotate("segment", x = rep(-1, 7), xend = rep(11, 7),
y = c(8, 10, 12, mean_good_cat_jump, 16, 18, 20),
yend = c(8, 10, 12, mean_good_cat_jump, 16, 18, 20),
color = "gray95") +
geom_vline(xintercept = c(0,5,10), color = "gray95") +
geom_tile(aes(x = weight - sy/2,
y = jumplength - sy/2,
width = sy, height = sy), fill = "#FCA63680",
alpha = 0.2, color = "#FCA636FF", linewidth = 0.5) +
geom_segment(x = -1, xend = 11,
y = mean_good_cat_jump, yend = mean_good_cat_jump, color = "#B12A90FF", size = 1) +
annotate("text", x = 11.5, y = mean_good_cat_jump, hjust = "left", label = expression(bold(bar(y))),
size = 5, color = "#B12A90FF") +
geom_tile(aes(x = weight - e/2,
y = jumplength - e/2,
width = e, height = e), fill = "#0D088780",
alpha = 0.2, color = "#0D0887FF", linewidth = 0.5) +
geom_point() +
geom_line(aes(y = predict(r2_good_fit)), color = "#0D0887FF", size = 1) +
annotate("text", x = 17, y = 15, hjust = "right", label = expression(R^2~"="~1~"\u2013"),
size = 6) +
geom_shape(data = tibble(x = c(17.5, 30, 30, 17.5),
y = c(15.5, 15.5, 19.75, 19.75)),
aes(x, y), radius = unit(0.2, 'cm'), fill = "gray95") +
geom_shape(data = tibble(x = c(17.5, 30, 30, 17.5),
y = c(14.5, 14.5, 7.75, 7.75)),
aes(x, y), radius = unit(0.2, 'cm'), fill = "gray95") +
annotate("text", x = 29.5, y = 19, label = expression(sum()*14.94), size = 5,
hjust = "right") +
geom_tile(aes(x = c(19, 21, 23, 25, 27),
y = c(17, 17, 17, 17, 17),
width = e, height = e), fill = "#0D088780",
alpha = 0.2, color = "#0D0887FF", linewidth = 0.5) +
annotate("segment", x = 17.5, xend = 30, y = 15, yend = 15) +
geom_tile(aes(x = seq(20.5, 27, length.out =5),
y = c(11.5, 11.5, 11.5, 11.5, 11.5),
width = sy, height = sy), fill = "#FCA63680",
alpha = 0.2, color = "#FCA636FF", linewidth = 0.5) +
annotate("text", x = 29.5, y = 8.5, label = expression(sum()*105.52), size = 5,
hjust = "right") +
annotate("text", x = 30.5, y = 15, hjust = "left", label = expression("= 0.86"),
size = 6) +
scale_x_continuous(breaks = c(0,5,10), limits = c(NA, 34),
expand = expand_scale(mult = 0)) +
scale_y_continuous(breaks = c(8, 10, 12, mean_good_cat_jump, 16, 18, 20),
labels = c("8", "10", "12", round(mean_good_cat_jump, 1), "16", "18", "20"),
limits = c(NA, NA)) +
labs(x = str_pad("Cat flea weight [mg]", 122.5, "right"), y = "Jump length in [cm]") +
scale_color_viridis(discrete = TRUE, option = "plasma", end = 0.9) +
annotate("text", x = 17.75, y = 19, label = expression(bold(SS[res])), size = 4.5,
hjust = "left") +
annotate("text", x = 17.75, y = 13.75, label = expression(bold(SS[total])), size = 4.5,
hjust = "left") +
theme(panel.grid = element_blank())
p_r2_bad <- r2_bad_plot_tbl |>
ggplot(aes(x = weight, y = jumplength)) +
theme_book() +
coord_equal() +
annotate("segment", x = rep(-1, 7), xend = rep(11, 7),
y = c(8, 10, 12, mean_bad_cat_jump, 16, 18, 20),
yend = c(8, 10, 12, mean_bad_cat_jump, 16, 18, 20),
color = "gray95") +
geom_vline(xintercept = c(0,5,10), color = "gray95") +
geom_tile(aes(x = weight - sy/2,
y = jumplength - sy/2,
width = sy, height = sy), fill = "#FCA63680",
alpha = 0.2, color = "#FCA636FF", linewidth = 0.5) +
geom_segment(x = -1, xend = 11,
y = mean_bad_cat_jump, yend = mean_bad_cat_jump, color = "#B12A90FF", size = 1) +
annotate("text", x = 11.5, y = mean_bad_cat_jump, hjust = "left", label = expression(bold(bar(y))),
size = 5, color = "#B12A90FF") +
geom_tile(aes(x = weight - e/2,
y = jumplength - e/2,
width = e, height = e), fill = "#0D088780",
alpha = 0.2, color = "#0D0887FF", linewidth = 0.5) +
geom_point() +
geom_line(aes(y = predict(r2_bad_fit)), color = "#0D0887FF", size = 1) +
annotate("text", x = 17, y = 15, hjust = "right", label = expression(R^2~"="~1~"\u2013"),
size = 6) +
geom_shape(data = tibble(x = c(17.5, 30, 30, 17.5),
y = c(15.5, 15.5, 19.75, 19.75)),
aes(x, y), radius = unit(0.2, 'cm'), fill = "gray95") +
geom_shape(data = tibble(x = c(17.5, 30, 30, 17.5),
y = c(14.5, 14.5, 7.75, 7.75)),
aes(x, y), radius = unit(0.2, 'cm'), fill = "gray95") +
annotate("text", x = 29.5, y = 19, label = expression(sum()*4.64), size = 5,
hjust = "right") +
geom_tile(aes(x = c(19, 21, 23, 25, 27),
y = c(17, 17, 17, 17, 17),
width = e, height = e), fill = "#0D088780",
alpha = 0.2, color = "#0D0887FF", linewidth = 0.5) +
annotate("segment", x = 17.5, xend = 30, y = 15, yend = 15) +
geom_tile(aes(x = seq(20.5, 27, length.out =5),
y = c(11.5, 11.5, 11.5, 11.5, 11.5),
width = sy, height = sy), fill = "#FCA63680",
alpha = 0.2, color = "#FCA636FF", linewidth = 0.5) +
annotate("text", x = 29.5, y = 8.5, label = expression(sum()*6.43), size = 5,
hjust = "right") +
annotate("text", x = 30.5, y = 15, hjust = "left", label = expression("= 0.28"),
size = 6) +
scale_x_continuous(breaks = c(0,5,10), limits = c(NA, 34),
expand = expand_scale(mult = 0)) +
scale_y_continuous(breaks = c(8, 10, 12, mean_bad_cat_jump, 16, 18, 20),
labels = c("8", "10", "12", round(mean_bad_cat_jump, 1), "16", "18", "20"),
limits = c(NA, NA)) +
labs(x = str_pad("Cat flea weight [mg]", 122.5, "right"), y = "Jump length in [cm]") +
scale_color_viridis(discrete = TRUE, option = "plasma", end = 0.9) +
annotate("text", x = 17.75, y = 19, label = expression(bold(SS[res])), size = 4.5,
hjust = "left") +
annotate("text", x = 17.75, y = 13.75, label = expression(bold(SS[total])), size = 4.5,
hjust = "left") +
theme(panel.grid = element_blank())
p_r2_good + p_r2_bad +
plot_layout(ncol = 1) +
plot_annotation(tag_levels = 'A', tag_prefix = '(', tag_suffix = ')') &
theme(plot.tag = element_text(size = 16, face = "bold"))
```
```{r}
set.seed(20251226) #20251226
cor_high_tbl <- tibble(weight = abs(rnorm(5, 3, 4)),
jumplength = 10 + 1 * weight + rnorm(5, 0, 4)) |>
mutate(sweight = weight - mean(weight),
sjump = jumplength - mean(jumplength),
ss_xy = sweight * sjump,
ss_x = sweight^2,
ss_y = sjump^2,
sign_xy = ifelse(sign(ss_xy) == -1, "\U2012", "+"))
set.seed(202511)
sum(cor_high_tbl$ss_x)
sum(cor_high_tbl$ss_x) |> sqrt()
sum(cor_high_tbl$ss_y)
sum(cor_high_tbl$ss_y) |> sqrt()
sum(cor_high_tbl$ss_xy)
cor(cor_high_tbl$weight, cor_high_tbl$jumplength)
```
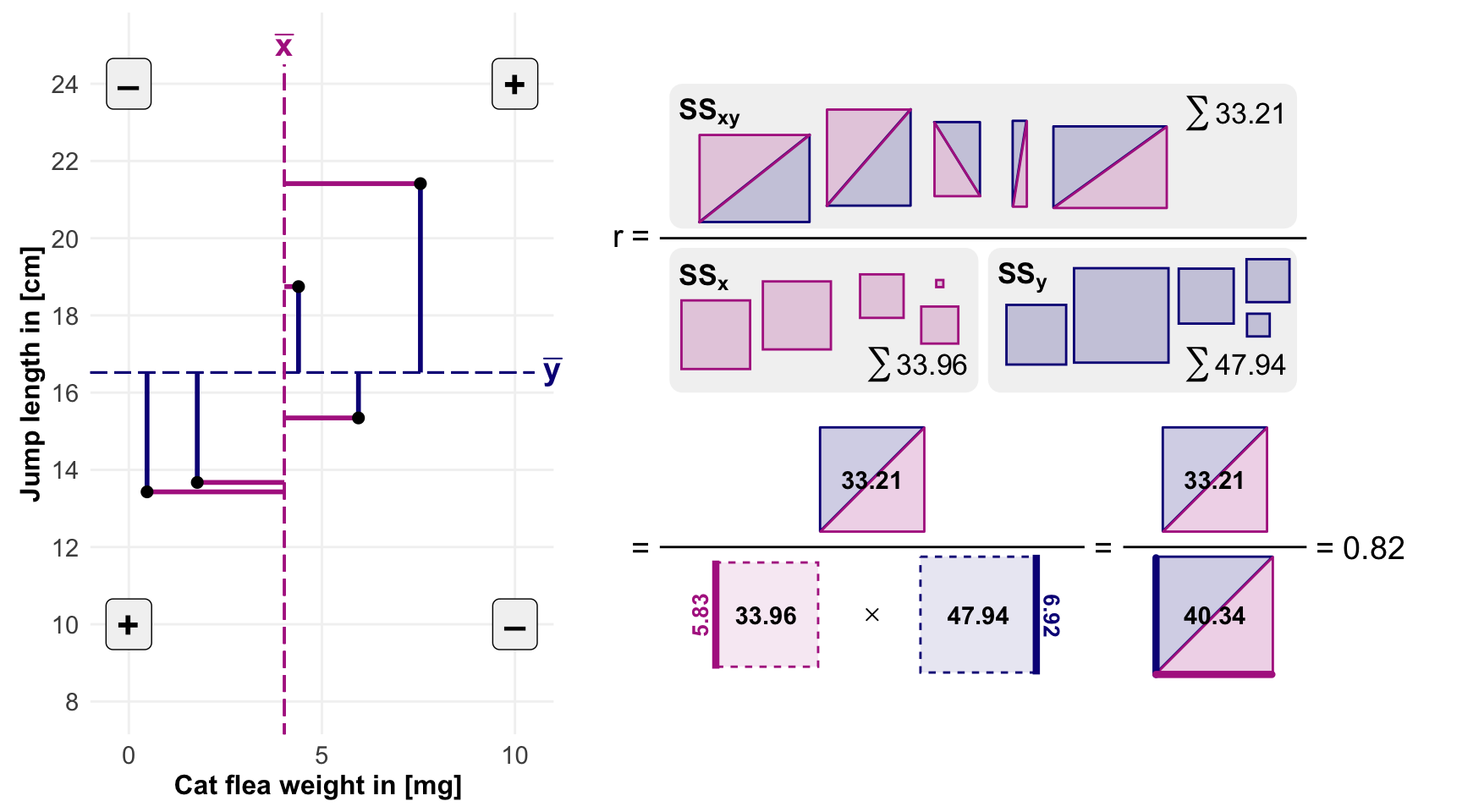
$$
r = \cfrac{SS_{xy}}{\sqrt{SS_x}\cdot\sqrt{SS_y}}
$$
```{r}
#| message: false
#| echo: false
#| warning: false
#| fig-align: center
#| fig-height: 5
#| fig-width: 9
#| fig-cap: "foo"
#| label: fig-corr-theo-example
geom_spit_tile <- function(x, y, a, b, weight, color, fill) {
a <- a*weight
b <- b*weight
x <- x - a/2
y <- y - b/2
list(
geom_shape(data = tibble(x = c(x, x+b-0.01, x),
y = c(y+0.01, y+a, y+a)),
aes(x, y), color = color[1], fill = fill[1], alpha = 0.2),
geom_shape(data = tibble(x = c(x+0.01, x+b, x+b),
y = c(y, y, y+a-0.01)),
aes(x, y), color = color[2], fill = fill[2], alpha = 0.2)
)
}
cor_high_tbl |>
ggplot(aes(x = weight, y = jumplength)) +
theme_book() +
coord_equal() +
annotate("segment", x = rep(-1, 9), xend = rep(11, 9),
y = c(8, 10, 12, 14, 16, 18, 20, 22, 24),
yend = c(8, 10, 12, 14, 16, 18, 20, 22, 24),
color = "gray95") +
geom_vline(xintercept = c(0,5,10), color = "gray95") +
geom_segment(x = -1, xend = 10.5,
y = mean(cor_high_tbl$jumplength),
yend = mean(cor_high_tbl$jumplength), color = "#0D0887FF", linetype = 11) +
annotate("text", x = 10.75, y = mean(cor_high_tbl$jumplength),
hjust = "left", label = expression(bold(bar(y))),
size = 5, color = "#0D0887FF") +
geom_segment(aes(x = mean(cor_high_tbl$weight), xend = weight,
y = jumplength, yend = jumplength), color = "#B12A90FF", size = 1) +
geom_segment(x = mean(cor_high_tbl$weight),
xend = mean(cor_high_tbl$weight),
y = 7, yend = 24.5, color = "#B12A90FF", linetype = 11) +
annotate("text", x = mean(cor_high_tbl$weight), y = 25,
hjust = "center", label = expression(bold(bar(x))),
size = 5, color = "#B12A90FF") +
geom_segment(aes(y = mean(cor_high_tbl$jumplength), yend = jumplength,
x = weight, yend = weight), color = "#0D0887FF", size = 1) +
geom_point(size = 2) +
scale_x_continuous(breaks = c(0,5,10), limits = c(NA, 34),
expand = expand_scale(mult = 0)) +
scale_y_continuous(breaks = c(8, 10, 12, 14, 16, 18, 20, 22, 24),
labels = c("8", "10", "12", "14", "16", "18", "20", "22", "24"),
limits = c(NA, NA)) +
labs(x = str_pad("Cat flea weight in [mg]", 142.5, "right"), y = "Jump length in [cm]") +
scale_color_viridis(discrete = TRUE, option = "plasma", end = 0.9) +
## upper right
annotate("text", x = 13.5, y = 20, hjust = "right", label = expression(r~"="),
size = 5) +
geom_shape(data = tibble(x = c(14, 30.25, 30.25, 14),
y = c(20.25, 20.25, 24, 24)),
aes(x, y), radius = unit(0.2, 'cm'), fill = "gray95") +
annotate("segment", x = 13.75, xend = 30.5, y = 20, yend = 20) +
geom_shape(data = tibble(x = c(14, 22, 22, 14),
y = c(19.75, 19.75, 16, 16)),
aes(x, y), radius = unit(0.2, 'cm'), fill = "gray95") +
geom_shape(data = tibble(x = c(22.25, 30.25, 30.25, 22.25),
y = c(19.75, 19.75, 16, 16)),
aes(x, y), radius = unit(0.2, 'cm'), fill = "gray95") +
geom_spit_tile(x = c(19), y = c(22.25),
a = cor_high_tbl$sweight[1], b = cor_high_tbl$sjump[1], weight = 0.7,
color = c("#0D0887FF", "#B12A90FF"), fill = c("#0D088780", "#B12A9080")) +
geom_spit_tile(x = c(16.5), y = c(21.25),
a = cor_high_tbl$sweight[2], b = cor_high_tbl$sjump[2], weight = 1,
color = c("#0D0887FF", "#B12A90FF"), fill = c("#0D088780", "#B12A9080")) +
geom_spit_tile(x = c(23), y = c(20.5),
a = cor_high_tbl$sweight[3], b = cor_high_tbl$sjump[3], weight = 1,
color = c("#0D0887FF", "#B12A90FF"), fill = c("#0D088780", "#B12A9080")) +
geom_spit_tile(x = c(24), y = c(21),
b = cor_high_tbl$sweight[4], a = cor_high_tbl$sjump[4], weight = 1,
color = c("#0D0887FF", "#B12A90FF"), fill = c("#0D088780", "#B12A9080")) +
geom_spit_tile(x = c(25), y = c(22.25),
a = cor_high_tbl$sweight[5], b = cor_high_tbl$sjump[5], weight = 0.6,
color = c("#0D0887FF", "#B12A90FF"), fill = c("#0D088780", "#B12A9080")) +
annotate("text", x = 30, y = 23.25, label = expression(sum()*33.21), size = 4.5,
hjust = "right") +
annotate("text", x = 14.25, y = 23.25, label = expression(bold(SS[xy])), size = 4.5,
hjust = "left") +
annotate("label", x = c(0, 0, 10, 10), y = c(10, 24, 10, 24),
label = c("+", "\U2012", "\U2012", "+"), size = 6, fontface = 2,
fill = "gray95") +
##
geom_tile(aes(x = c(23.5, 27.9, 29.25, 29.5, 25.7),
y = c(17.5, 18.5, 17.75, 18.9, 18),
width = sjump/2, height = sjump/2), fill = "#0D088780",
alpha = 0.2, color = "#0D0887FF", linewidth = 0.5) +
annotate("text", x = 30, y = 16.75, label = expression(sum()*47.94), size = 4.5,
hjust = "right") +
annotate("text", x = 14.25, y = 19, label = expression(bold(SS[x])), size = 4.5,
hjust = "left") +
##
geom_tile(aes(x = c(15.2, 19.5, 21, 21, 17.3),
y = c(17.5, 18.5, 17.75, 18.825, 18),
width = sweight/2, height = sweight/2), fill = "#B12A9080",
alpha = 0.2, color = "#B12A90FF", linewidth = 0.5) +
annotate("text", x = 21.75, y = 16.75, label = expression(sum()*33.96), size = 4.5,
hjust = "right") +
annotate("text", x = 22.5, y = 19, label = expression(bold(SS[y])), size = 4.5,
hjust = "left") +
## lower right left
annotate("text", x = 13.5, y = 12, hjust = "right", label = expression("="),
size = 5) +
annotate("segment", x = 13.75, xend = 24.75, y = 12, yend = 12) +
geom_spit_tile(x = 19.25, y = 12.25+3/2, a = 3, b = 3, weight = 0.9,
color = c("#0D0887FF", "#B12A90FF"), fill = c("#0D088780", "#B12A9080")) +
annotate("text", x = 19.25, y = 12.25+3/2, label = "33.21", fontface = 2) +
##
annotate("tile", x = 22, y = 11.75-3+3/2,
width = 3, height = 3, fill = "#0D088780",
alpha = 0.1, color = "#0D0887FF", linewidth = 0.5, linetype = "33") +
annotate("text", x = 22, y = 11.75-3+3/2, label = "47.94", fontface = 2) +
annotate("segment", x = 23.5, xend = 23.5,
y = 8.7, yend = 11.8, size = 1.5, color = "#0D0887FF") +
annotate("text", x = 23.9, y = 10.2375, hjust = "center", label = "6.92", color = "#0D0887FF",
fontface = 2, angle = -90, size = 3.5) +
##
annotate("tile", x = 16.5, y = 11.75-3+3/2,
width = 3*0.9, height = 3*0.9, fill = "#B12A9080",
alpha = 0.1, color = "#B12A90FF", linewidth = 0.5, linetype = "33") +
annotate("text", x = 16.5, y = 11.75-3+3/2, label = "33.96", fontface = 2) +
annotate("segment", x = 15.2, xend = 15.2,
y = 8.85, yend = 11.65, size = 1.5, color = "#B12A90FF") +
annotate("text", x = 14.8, y = 10.25, hjust = "center", label = "5.83", color = "#B12A90FF",
fontface = 2, angle = 90, size = 3.5) +
annotate("point", x = 19.25, y = 10.25, size = 2, shape = 4) +
## lower right right
annotate("text", x = 25.5, y = 12, hjust = "right", label = expression("="),
size = 5) +
annotate("segment", x = 25.75, xend = 30.5, y = 12, yend = 12) +
annotate("text", x = 30.75, y = 12, hjust = "left", label = expression("="~0.82),
size = 5) +
geom_spit_tile(x = 28.125, y = 12.25+3/2, a = 3, b = 3, weight = 0.9,
color = c("#0D0887FF", "#B12A90FF"), fill = c("#0D088780", "#B12A9080")) +
annotate("text", x = 28.125, y = 12.25+3/2, label = "33.21", fontface = 2) +
geom_spit_tile(x = 28.125, y = 11.75-3+3/2, a = 3, b = 3, weight = 1,
color = c("#0D0887FF", "#B12A90FF"), fill = c("#0D088780", "#B12A9080")) +
annotate("text", x = 28.125, y = 11.75-3+3/2, label = "40.34", fontface = 2) +
annotate("segment", x = 26.6, xend = 26.6, lineend = "round",
y = 8.7, yend = 11.72, size = 1.5, color = "#0D0887FF") +
annotate("segment", x = 26.6, xend = 29.6, lineend = "round",
y = 8.7, yend = 8.7, size = 1.5, color = "#B12A90FF") +
theme(panel.grid = element_blank())
```
```{r}
#| message: false
#| echo: false
#| warning: false
#| eval: false
#| fig-align: center
#| fig-height: 4.5
#| fig-width: 7.5
#| fig-cap: "foo"
#| label: fig-var-2-example
p1_corr <- cor_high_tbl |>
ggplot(aes(x = weight, y = jumplength)) +
theme_book() +
coord_equal() +
geom_point() +
labs(x = "Cat flea weight [mg]", y = "Jump length in [cm]") +
geom_tile(aes(x = weight - sx/2,
y = jumplength - sx/2,
width = sx, height = sx), fill = "#FCA63680",
alpha = 0.2, color = "#FCA636FF", linewidth = 0.5)
p2_corr <- cor_high_tbl |>
ggplot(aes(x = weight, y = jumplength)) +
theme_book() +
coord_equal() +
geom_point() +
labs(x = "Cat flea weight [mg]", y = "Jump length in [cm]") +
geom_tile(aes(x = weight - sy/2,
y = jumplength - sy/2,
width = sy, height = sy), fill = "#B12A9080",
alpha = 0.2, color = "#B12A90FF", linewidth = 0.5)
p1_corr + p2_corr +
plot_layout(ncol = 2) +
plot_annotation(tag_levels = 'A', tag_prefix = '(', tag_suffix = ')') &
theme(plot.tag = element_text(size = 16, face = "bold"))
jump_weight_plot_tbl |>
ggplot(aes(x = weight, y = jumplength)) +
theme_book() +
coord_equal() +
geom_point() +
labs(x = "Cat flea weight [mg]", y = "Jump length in [cm]") +
geom_tile(aes(x = weight - sx/2,
y = jumplength - sy/2,
width = sx, height = sy), fill = "#B12A9080",
alpha = 0.2, color = "#B12A90FF", linewidth = 0.5)
```
## Theoretical background
## R packages used
## Data
## Alternatives
Further tutorials and R packages on XXX
## Glossary
term
: what does it mean.
## The meaning of "Models of Reality" in this chapter.
- itemize with max. 5-6 words
## Summary
## References {.unnumbered}