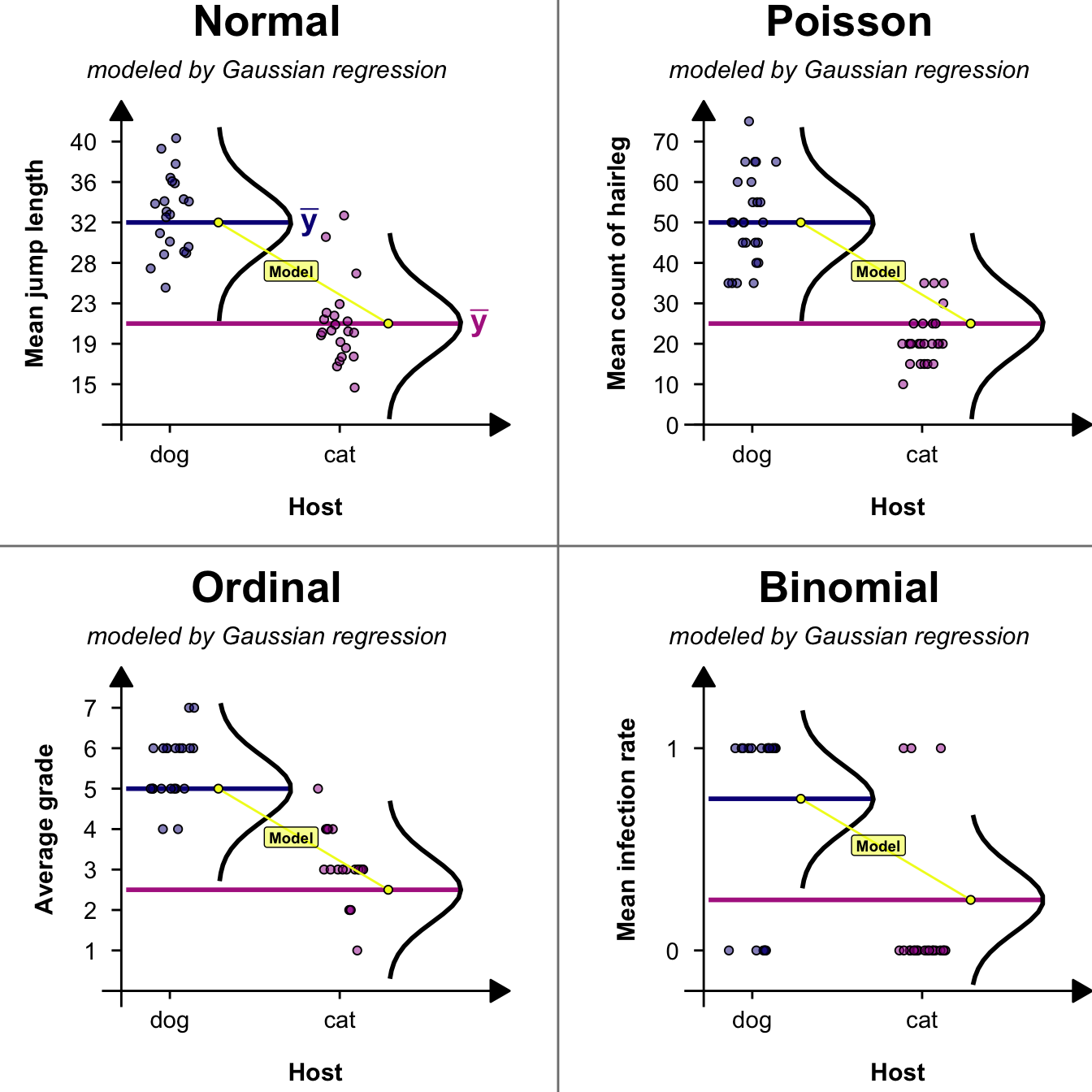
```{r echo = FALSE, warning = FALSE, message=FALSE}
source("init.R")
```
# Visualisation of data
*Last modified on `r format(fs::file_info("chapter-40-preface.qmd")$modification_time, '%d. %B %Y at %H:%M:%S')`*
> *"What problem have you solved, ever, that was worth solving where you knew all the given information in advance? No problem worth solving is like that. In the real world, you have a surplus of information and you have to filter it, or you don't have sufficient information and you have to go find some." --- [Dan Meyer in Math class needs a makeover](https://www.ted.com/talks/dan_meyer_math_class_needs_a_makeover?language=en&subtitle=en&trigger=5s)*
Here comes the preface text
```{r}
#| message: false
#| echo: false
#| warning: false
#| fig-align: center
#| fig-height: 7
#| fig-width: 7
#| fig-cap: "foo"
#| label: fig-reg-cross
geom_coord_cross <- function(x, y, yticks = "numeric", xticks = "numeric", zero = FALSE) {
list(
annotate("segment", x = x-0.2, xend = x+4, y = y, yend = y,
arrow = arrow(length = unit(0.02, "npc"), type = "closed")),
annotate("segment", x = x, xend = x, y = y-0.2, yend = y+4,
arrow = arrow(length = unit(0.02, "npc"), type = "closed")),
if(yticks == "numeric") {
if(zero){
list(
annotate("segment", x = x-0.1, xend = x, y = y + seq(0, 3.5, 0.5), yend = y+ seq(0, 3.5, 0.5)),
annotate("text", x = x -0.25, y = y + seq(0, 3.5, 0.5), label = seq(0, 70, 10),
hjust = "right"),
annotate("text", x = x - 0.9, y = y + 2, label = c("Mean count of hairleg"), fontface = 2,
size = 4, angle = 90)
)
} else {
list(
annotate("segment", x = x-0.1, xend = x, y = y + seq(0, 3.5, 0.5), yend = y+ seq(0, 3.5, 0.5)),
annotate("text", x = x -0.25, y = y + seq(0.5, 3.5, 0.5),
label = round(seq(15, 40, length.out = 7)), hjust = "right") ,
annotate("text", x = x - 0.9, y = y +2, label = c("Mean jump length"), fontface = 2, size = 4,
angle = 90)
)
}
},
if(yticks == "3lvl") {
list(
annotate("segment", x = x-0.1, xend = x, y = y + (1:7)/2, yend = y + (1:7)/2),
annotate("text", x = x -0.25, y = y + (1:7)/2, label = c("1", "2", "3", "4", "5", "6", "7"),
hjust = "right") ,
annotate("text", x = x - 0.8, y = y +2, label = c("Average grade"), fontface = 2, size = 4,
angle = 90)
)
},
if(yticks == "2lvl") {
list(
annotate("segment", x = x-0.1, xend = x, y = y + c(0.5, 3), yend = y+ c(0.5, 3)),
annotate("text", x = x -0.25, y = y + c(0.5, 3), label = c("0", "1"), hjust = "right") ,
annotate("text", x = x - 0.8, y = y +2, label = c("Mean infection rate"), fontface = 2, size = 4,
angle = 90)
)
},
if(xticks == "2lvl") {
list(
annotate("segment", x = x+ c(0.5, 2.25), xend = x+ c(0.5, 2.25), y = y -0.1 , yend = y),
annotate("text", x = x + c(0.5, 2.25), y = y -0.35, label = c("dog", "cat")),
annotate("text", x = x + 2, y = y -1, label = c("Host"), fontface = 2, size = 4)
)
}
)
}
ggplot() +
theme_void() +
##theme_minimal() +
coord_cartesian(xlim = c(2.25, 13.5), ylim = c(0.25, 13.75)) +
annotate("segment", x = c(8), xend = c(8),
y = c(0), yend = 14, color = "gray50") +
annotate("segment", x = c(0.25), xend = c(14),
y = c(7), yend = c(7), color = "gray50") +
scale_x_continuous(breaks = 0:14, expand = expansion(mult = 0)) +
scale_y_continuous(breaks = 0:14, expand = expansion(mult = 0)) +
## outer text
annotate("text", x = 11, y = 26.5, label = "Characteristic of the influencer (X)",
size = 8, fontface = 2) +
annotate("text", x = c(5, 14), y = 25.25,
label = c("Covariate", "Factor"), size = 7, fontface = 2) +
annotate("text", x = c(5, 11, 17), y = 24.5,
label = c("X is numeric", "X has 3 or more levels", "X has 2 levels"),
size = 6, fontface = 3) +
## coords
geom_coord_cross(x = 3.5, y = 8.5, yticks = "numeric", xticks = "2lvl") +
geom_coord_cross(x = 9.5, y = 8.5, yticks = "numeric", xticks = "2lvl", zero = TRUE) +
geom_coord_cross(x = 3.5, y = 1.5, yticks = "3lvl", xticks = "2lvl") +
geom_coord_cross(x = 9.5, y = 1.5, yticks = "2lvl", xticks = "2lvl") +
annotate("text", x = c(11, 5, 11, 5), y = c(6.5, 6.5, 13.5, 13.5),
label = c("Binomial", "Ordinal", "Poisson", "Normal"),
size = 7, fontface = 2) +
annotate("text", x = c(11, 5, 11, 5), y = c(5.9, 5.9, 12.9, 12.9),
label = c("modeled by Gaussian regression", "modeled by Gaussian regression",
"modeled by Gaussian regression", "modeled by Gaussian regression"), size = 4,
fontface = 3) +
# annotate("label", x = c(5, 6.5, 5, 6.5, 11, 12.5, 11, 12.5),
# y = c(12.5, 12.5, 5.5, 5.5, 12.5, 12.5, 5.5, 5.5)-0.25,
# label = rep("Model", 8), fill = "#F0F92180", size = 2.5, fontface = 2) +
### normal
annotate("segment", x = 3.55, xend = 5.25, y = 11, yend = 11, color = "#0D0887FF", size = 1) +
annotate("text", x = 5.35, y = 11, hjust = "left", label = expression(bold(bar(y))),
size = 5, color = "#0D0887FF") +
geom_path(data = tibble(x_raw = seq(11-11/9,
11+11/9, 0.1),
y_raw = dnorm(x_raw, mean = 11, sd = 0.4)),
aes(y = x_raw, x = y_raw*0.75+4.5),
linewidth = 1, color = "black", angle = 90) +
geom_jitter(data = tibble(x = 4, y = rnorm(21, 11, 0.6)), aes(x, y),
shape = 21, width = 0.2, fill = "#0D088780") +
annotate("segment", x = 3.55, xend = 7, y = 9.75, yend = 9.75, color = "#B12A90FF", size = 1) +
annotate("text", x = 7.1, y = 9.75, hjust = "left", label = expression(bold(bar(y))),
size = 5, color = "#B12A90FF") +
geom_path(data = tibble(x_raw = seq(9.75-9.75/8.25,
9.75+9.75/8.25, 0.1),
y_raw = dnorm(x_raw, mean = 9.75, sd = 0.4)),
aes(y = x_raw, x = y_raw*0.75+6.25),
linewidth = 1, color = "black", angle = 90) +
geom_jitter(data = tibble(x = 5.75, y = rnorm(21, 9.75, 0.4)), aes(x, y),
shape = 21, width = 0.2, fill = "#A21D9A80") +
annotate("segment", x = 4.5, xend = 6.25, y = 11, yend = 9.75, linetype = 1, color = "#F0F921FF") +
annotate("point", x = c(4.5, 6.25), y = c(11, 9.75), shape = 21, fill = "#F0F921FF") +
## Poisson
annotate("segment", x = 9.55, xend = 11.25, y = 11, yend = 11, color = "#0D0887FF", size = 1) +
geom_path(data = tibble(x_raw = seq(11-11/9,
11+11/9, 0.1),
y_raw = dnorm(x_raw, mean = 11, sd = 0.4)),
aes(y = x_raw, x = y_raw*0.75+10.5),
linewidth = 1, color = "black", angle = 90) +
geom_jitter(data = tibble(x = 10, y = (rpois(25, 3))/4+10.25), aes(x, y),
shape = 21, width = 0.25, height = 0, fill = "#0D088780") +
annotate("segment", x = 9.55, xend = 13, y = 9.75, yend = 9.75, color = "#B12A90FF", size = 1) +
geom_path(data = tibble(x_raw = seq(9.75-9.75/8.25,
9.75+9.75/8.25, 0.1),
y_raw = dnorm(x_raw, mean = 9.75, sd = 0.4)),
aes(y = x_raw, x = y_raw*0.75+12.25),
linewidth = 1, color = "black", angle = 90) +
geom_jitter(data = tibble(x = 11.75, y = (rpois(25, 3))/4+9), aes(x, y),
shape = 21, width = 0.25, height = 0, fill = "#A21D9A80") +
annotate("segment", x = 10.5, xend = 12.25, y = 11, yend = 9.75, linetype = 1, color = "#F0F921FF") +
annotate("point", x = c(10.5, 12.25), y = c(11, 9.75), shape = 21, fill = "#F0F921FF") +
## ordinal
annotate("segment", x = 3.55, xend = 5.25, y = 4, yend = 4, color = "#0D0887FF", size = 1) +
geom_path(data = tibble(x_raw = seq(4-4/3.5,
4+4/3.5, 0.1),
y_raw = dnorm(x_raw, mean = 4, sd = 0.4)),
aes(y = x_raw, x = y_raw*0.75+4.5),
linewidth = 1, color = "black", angle = 90) +
geom_jitter(data = tibble(x = 4, y = ceiling(rnorm(21, 4, 0.4)/0.5)*0.5), aes(x, y),
shape = 21, width = 0.25, height = 0, fill = "#0D088780") +
annotate("segment", x = 3.55, xend = 7, y = 2.75, yend = 2.75, color = "#B12A90FF", size = 1) +
geom_path(data = tibble(x_raw = seq(2.75-2.75/2.5,
2.75+2.75/2.5, 0.1),
y_raw = dnorm(x_raw, mean = 2.75, sd = 0.4)),
aes(y = x_raw, x = y_raw*0.75+6.25),
linewidth = 1, color = "black", angle = 90) +
geom_jitter(data = tibble(x = 5.75, y = ceiling(rnorm(21, 2.75, 0.4)/0.5)*0.5), aes(x, y),
shape = 21, width = 0.25, height = 0, fill = "#A21D9A80") +
annotate("segment", x = 4.5, xend = 6.25, y = 4, yend = 2.75, linetype = 1, color = "#F0F921FF") +
annotate("point", x = c(4.5, 6.25), y = c(4, 2.75), shape = 21, fill = "#F0F921FF") +
## binomial
annotate("segment", x = 9.55, xend = 11.25, y = 3.875, yend = 3.875, color = "#0D0887FF", size = 1) +
geom_path(data = tibble(x_raw = seq(3.875-3.875/3.5,
3.875+3.875/3.5, 0.1),
y_raw = dnorm(x_raw, mean = 2+(2.5*0.75), sd = 0.4)),
aes(y = x_raw, x = y_raw*0.75+10.5),
linewidth = 1, color = "black", angle = 90) +
geom_jitter(data = tibble(x = 10, y = (rbinom(21, 1, 0.75)*2.5)+2), aes(x, y),
shape = 21, width = 0.25, height = 0, fill = "#0D088780") +
annotate("segment", x = 9.55, xend = 13, y = 2.625, yend = 2.625, color = "#B12A90FF", size = 1) +
geom_path(data = tibble(x_raw = seq(2.625-2.625/2.5,
2.625+2.625/2.5, 0.1),
y_raw = dnorm(x_raw, mean = 2+(2.5*0.25), sd = 0.4)),
aes(y = x_raw, x = y_raw*0.75+12.25),
linewidth = 1, color = "black", angle = 90) +
geom_jitter(data = tibble(x = 11.75, y = (rbinom(21, 1, 0.25)*2.5)+2), aes(x, y),
shape = 21, width = 0.25, height = 0, fill = "#A21D9A80") +
annotate("segment", x = 10.5, xend = 12.25, y = 3.875, yend = 2.625,
linetype = 1, color = "#F0F921FF") +
annotate("point", x = c(10.5, 12.25), y = c(3.875, 2.625), shape = 21, fill = "#F0F921FF") +
annotate("label", x = c(5.25, 5.25, 11.3, 11.3),
y = c(10.4, 3.4, 10.4, 3.3),
label = rep("Model", 4), fill = "#F0F92180", size = 2.5, fontface = 2)
```
```{r}
pacman::p_load(emmeans, parameters, nlme, broom)
foo <- tibble(A = rnorm(10000, 5, 4),
B = rnorm(10000, 8, 2)) |>
gather()
foo |>
group_by(key) |>
summarise(mean(value), var(value), sd(value))
```
```{r}
sqrt((16.77840 + 3.94372)/2)
```
```{r}
fit <- lm(value ~ 0+key, foo)
fit |> parameters()
```
```{r}
fit |> glance()
```
```{r}
0.02012848 * sqrt(10000)
```
```{r}
sqrt(diag(vcov(fit)))
```
```{r}
model_parameters(fit, vcov = "HC3")
```
```{r}
gls(value ~ 0 + key, weights = varIdent(form = ~ 1 | key), foo) |>
parameters()
```
```{r}
emm <- emmeans(fit, "key", vcov = sandwich::vcovHAC)
summary_emm <- summary(emm)
# Calculate SD from SE and sample size (n)
summary_emm$SE * sqrt(summary_emm$df/2)
```